Class 10th Sanskrit Anand Chapter 2 व्यसने मित्रपरीक्षा Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Anand Chapter 2 व्यसने मित्रपरीक्षा Notes, Textbook Exercise Important Questions and Answers.
Std 10 Sanskrit Chapter 2 Question Answer
Sanskrit Anand Std 10 Digest Chapter 2 व्यसने मित्रपरीक्षा Textbook Questions and Answers
अवबोधनम् :
1. पूर्णवाक्येन उत्तरं लिखत ।
प्रश्न अ.
अरण्ये कौ निवसतः स्म ?
उत्तरम् :
अरण्ये मृग: काक:च निवसतः स्म।
प्रश्न आ.
काकः किम् उपादिशत् ?
उत्तरम् :
काक: उपादिशत्, “अकस्मादागन्तुना सह मित्रता न युक्ता।”

प्रश्न इ.
मृगः प्रत्यहं क्षेत्रं गत्वा किम् अकरोत् ?
उत्तरम् :
मृगः प्रत्यहं क्षेत्रं गत्वा सस्यम् अखादत् ।
प्रश्न ई.
क्षुद्रबुद्धिः कुत्र निभृतं स्थितः ?
उत्तरम् :
क्षुद्रबुद्धिः समीपमेव वक्षस्य पृष्ठतः निभृतं स्थितः।
प्रश्न उ.
शृगालः केन हतः ?
उत्तरम् :
क्षेत्रपतिना क्षिप्तेन लगुडेन शृगालः हतः।
2. कः कं वदति ?
प्रश्न अ.
‘वनेऽस्मिन् एकं सस्यपूर्ण क्षेत्रमस्ति ।’
उत्तरम् :
जम्बूक; मृगं वदति।

प्रश्न आ.
‘मित्र, छिन्धि तावन्मम बन्धनम् ।’
उत्तरम् :
मृग: जम्बूकं वदति।
प्रश्न इ.
‘स वञ्चक: क्वास्ते ?’
उत्तरम् :
काकः मृगं वदति।
3. उत्तरपदं लिखत ।
प्रश्न 1.
अ. काकोऽवदत् = काकः + …………… ।
आ. मृगेणोक्तम् = मृगेण + …………… ।
इ. जम्बूकोऽयम् = जम्बूकः + ………….. ।
उत्तरम् :
अ. काकोऽवदत् – काकः + अवदत्।
आ. मृगेणोक्तम् – मृगेण + उक्तम्।
इ. जम्बूकोऽयम् – जम्बूकः + अयम्।

4. पूर्वपदं लिखत ।
प्रश्न 1.
अ. मृगोऽब्रवीत् = …………….. + अब्रवीत्
आ. वातेनोदरम् = …………… + उदरम्
इ. मृतोऽसि = ………………. + असि
उत्तरम् :
अ. मृगोऽब्रवीत् – मृगः + अब्रवीत्।
आ. वातेनोदरम् – वातेन + उदरम्।
इ. मृतोऽसि – मृत: + असि।
5. माध्यमभाषया उत्तरत ।
प्रश्न अ.
‘स नरः शत्रुनन्दनः’ इति वचनं कथायाः आधारेण स्पष्टीकुरुत ।
उत्तरम् :
व्यसने मित्रपरीक्षा या कथेच्या संदर्भात ‘स: नरः शत्रुनन्दनः ही उक्ती आलेली दिसून येते. हितोपदेश या पुस्तकात मित्रलाभ (1.3) या प्रकरणात ही कथा आढळते.
धूर्त कोल्हा हरिणाला त्याच्या शब्दांमध्ये फसवितो व त्याच्याशी मैत्री करतो. कोल्हा हरिणाला धान्यांनी भरलेले एक शेत दाखवितो. साहजिकच हरिणाच्या मनात धान्याबद्दल हाव निर्माण होते. पण नंतर, शेताच्या मालकाने टाकलेल्या जाळ्यात हरिण अडकते. हरिणाने कोल्ह्याकडे मदत मागताच धूर्त कोल्हा जाळे घट्ट असल्याचे सांगतो, त्यामुळे तो तोडण्यास समर्थ नाही असे दर्शवितो.
हरिणाला कोल्ह्याचा धूर्तपणा हळूहळू लक्षात येतो. कावळ्याने न ऐकल्याचा त्याला पश्चात्ताप होतो. जेव्हा कावळा हरिणाला शोधत शोधत हरिणाजवळ पोहोचतो, तेव्हा तो सुद्धा सः नरः शत्रुनन्दनः’ हा श्लोक उद्धृत करतो. या श्लोकाचा अर्थ असा, की, “जो आपल्या मित्रांचा, हितचिंतकांचा सल्ला ऐकत नाही, तो संकटात सापडतो व त्याच्या शजूंना आनंदित करतो, त्यांचे शत्रुत्व ओढून घेतो.
हरिणाने अनोळखी प्राण्यांशी (कोल्ह्याशी) मैत्री न करण्याचा कावळ्याचा सल्ला ऐकला नाही व कोल्ह्याशी मैत्री केल्याने अखेर त्याला जाळ्यात अडकावे लागले, म्हणजे तो संकटात सापडला व हरिणाला शत्रुनन्दन हे विशेषण लागू पडले.
‘सः नरः शत्रुनन्दनः’ occurs in the context of the story व्यसने मित्रपरीक्षा. It is found in the chapter 1.3 of मित्रलाभ, in हितोपदेश.
The crooked jackal trapped the deer in its words. It intentionally showed the deer a field full of grains. Due to greed towards the grains, the deer got caught in the net set by the owner of the field. When the deer asked the jackal for his help, it cleverly answered, the net is tendon, so it can’t break it.
The deer understood the jackal’s plan. It repented for not listening to the crow’s advice. When crow came searching for him, It uttereded the verse सुहदा ….. स: नरः शत्रुनन्दनः which means, “The one who does not listen to the words of well-wishing friends, calamity becomes his neighbour and he pleases enemies.”
The deer disregarded crow’s advice of not making friendship with strangers. It had friendship with a deceitful jackal and was finally trapped in the net. Seeing him caught in the net, the jackal became happy.
In this way, the deer proved himself as शत्रुनन्दन, the one who pleases enemies as the deer also pleased the mind of a crooked jackal.

प्रश्न आ.
काकेन क: उपाय: उक्तः ?
उत्तरम् :
व्यसने मित्रपरीक्षा या कथेच्या संदर्भात ‘सः नरः शत्रुनन्दनः’ ही उक्ती आलेली दिसून येते. हितोपदेश या पुस्तकात मित्रलाभ (1.3) या प्रकरणात ही कथा आढळते.
शेताच्या मालकाने हरिणाला जाळ्यात अडकविले. कावळा हरिणाला शोधत तेथे आला. कावळ्याने विचारले असता हरिणाने सर्व हकीकत त्याला सांगितली. कोल्याच्या धूर्तपणामुळे हरिण जाळ्यात अडकले होते. कावळ्याने हरिणाला मेल्यासारखे दर्शविण्यास सांगितले. तसेच कावळ्याने हरिणाला पोट फुगवायला व पायही स्तब्ध ठेवण्यास सांगितले.
कावळ्याच्या म्हणण्यानुसार वागल्यामुळे शेताच्या मालकाला हरिण मृत असल्याचा भास झाला. शेताचा मालक हरिणाजवळ आला व जाळे काढले. ठरल्याप्रमाणे कावळ्याने काव-काव असा आवाज केला, आवाज ऐकताच हरिण उठले व पटकन पळून गेले. कावळ्याने शोधलेल्या या उपायामुळे व त्याच्या चातुर्यामुळे हरिणाचे प्राण वाचले.
‘स: नरः शत्रुनन्दनः’ occurs in the context of the story व्यसने मित्रपरीक्षा. It is found in the chapter ङ्के13 of मालाभ, in हितोपदेशा The deer was trapped in the net set by the owner of the field. The crow came in search of the deer. The crow saw the trapped deer. The deer narrated the account of a deceitful jackal.
The crow told the deer to pretend to be dead by blowing up its belly with air and told to keep legs stiff. The crow gave the deer an idea of running away. The deer followed likewise. The owner of the field thought the deer is certainly dead.
So, he released the deer. At the same time, the crow made sound and the deer ran away quickly. The crow’s wisdom and true friendship with the deer saved the deer’s life.

6. विरुद्धार्थकशब्द लिखत ।
दृढः, मैत्री, बद्धः, प्रभूतम् ।
प्रश्न 1.
विरुद्धार्थकशब्द लिखत ।
दृढः, मैत्री, बद्धः, प्रभूतम् ।
उत्तरम् :
- दृढः × शिथिलः।
- मैत्री × शत्रुत्वम्, वैरम्।
- बद्धः × मुक्तः।
- प्रभूतम् × अल्पम्, स्तोकम्, स्वल्पम्, न्यूनम्।
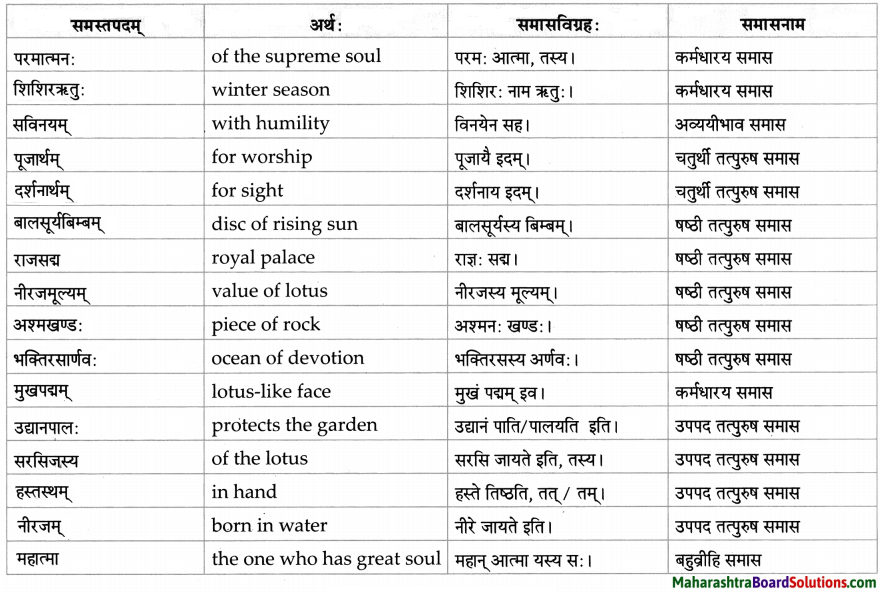
7. अमरकोषात् योग्यं समानार्थक शब्द योजयित्वा वाक्यं पुनर्लिखत ।
प्रश्न अ.
अरण्ये मृगः काकः च स्नेहेन निवसतः ।
उत्तरम् :
अरण्ये कुरङ्गः/वातायु:/हरिण:/अजिनयोनिः काकः च नेहेन निवसतः ।

प्रश्न आ.
जम्बूकः तेन सह मृगस्य निवासस्थानं गतः ।
उत्तरम् :
शृगाल:/वज्ञक:/क्रोष्टा/फेरु:/फेरवः तेन सह मृगस्य निवासस्थानं गतः।
प्रश्न इ.
मृगमन्विष्यन् काकः तत्र उपस्थितः ।
उत्तरम् :
मृगमन्विष्यन् करट:/अरिष्ट:/बलिपुष्ट:/सकृत्प्रजः तत्र उपस्थितः।
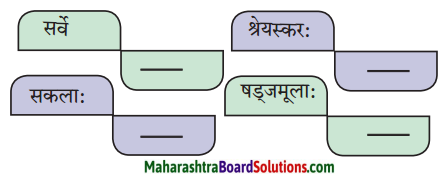
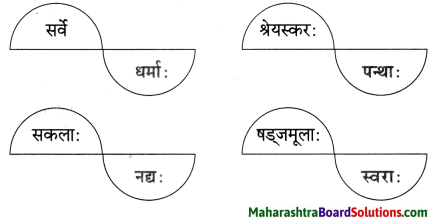
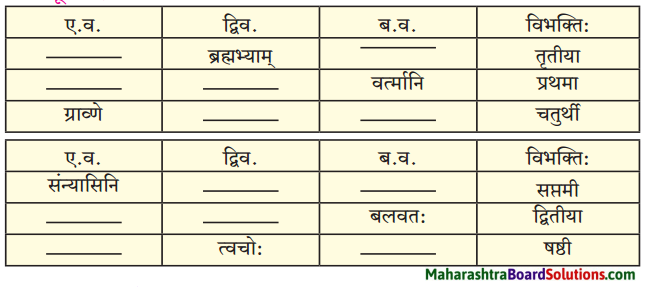
8. स्तम्भमेलनं कुरुत।
प्रश्न 1.
स्तम्भमेलनं कुरुत।
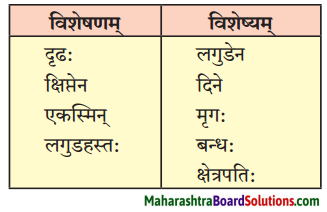
उत्तरम् :
| विशेषणम् |
विशेष्यम् |
| 1. दृढः |
बन्धः |
| 2. क्षिप्तेन |
लगुडेन |
| 3. एकस्मिन् |
दिने |
| 4. लगुडहस्तः |
क्षेत्रपतिः |

9. तालिकां पूरयत ।
प्रश्न अ.
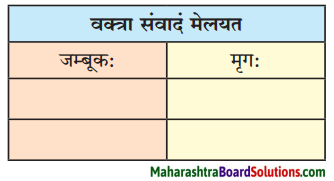
(मञ्जूषा – त्रायस्व माम्, दर्शयामि त्वाम्, दृढोऽयं बन्धः, छिन्धि मम बन्धनम्)
उत्तरम् :
| जम्बूकः |
मृगः |
| दर्शयामि त्वाम्। |
त्रायस्व माम्। |
| दृढोऽयं बन्धः |
छिन्धि मम बन्धनम् |
प्रश्न आ.
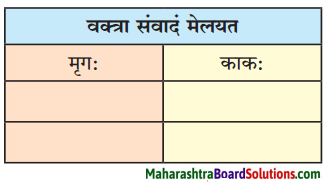
(मञ्जूषा – अलं विवादेन, कोऽयं द्वितीयः?, एवमस्तु, अस्मत्सख्यम् इच्छति ।)
उत्तरम् :
| मृगः |
काकः |
| अलं विवादेन। |
कोऽयं द्वितीयः? |
| अस्मत्सख्यम् इच्छति। |
एवमस्तु। |

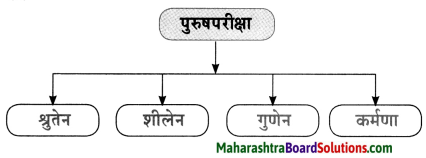
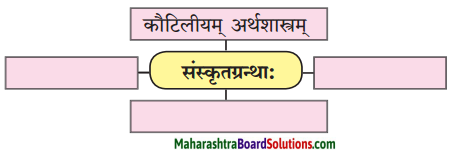
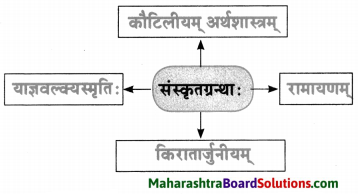
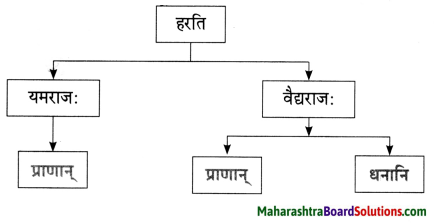
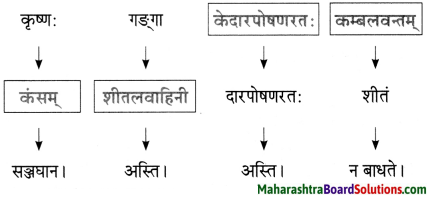
10. जालरेखाचित्रं पूरयत ।
प्रश्न 1.
जालरेखाचित्रं पूरयत ।
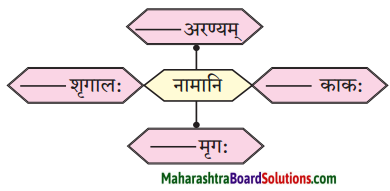
उत्तरम् :

Sanskrit Anand Class 10 Textbook Solutions Chapter 2 व्यसने मित्रपरीक्षा Additional Important Questions and Answers
अवबोधनम्।
(क) उचितं कारणं चित्वा वाक्यं पुनर्लिखत।
प्रश्न 1.
शृगालः मृगेण सह सख्यम् इच्छति यतः
(अ) शृगाल: मृगमांसं खादितुम् इच्छति।
(ब) शृगालः मृगे स्निह्यति।
उत्तरम् :
(अ) शृगाल: मृगमांसं खादितुम् इच्छति।

(ख) उचितं पर्यायं चित्वा वाक्यं लिखत।
प्रश्न 1.
शृगालः स्वार्थहतुना ………… सह मैत्रम् ऐच्छत्। (मृगेण / काकेन)
उत्तरम् :
शृगालः स्वार्थहतुना मगेण सह मैत्रम् ऐच्छत्।
(ग) पूर्णवाक्येन उत्तरत।
प्रश्न 1.
क: चित्राङ्गम् अपश्यत्?
उत्तरम् :
गाल: चित्राङ्गम् अपश्यत्।
प्रश्न 2.
शृगालस्य नाम किम् आसीत्?
उत्तरम् :
शृगालस्य नाम क्षुद्रबुद्धिः आसीत्।
प्रश्न 3.
शृगालः किमर्थं मृगेण सह मित्रताम् ऐच्छत्?
उत्तरम् :
शृगालः स्वार्थहेतुं पूरयितुं मृगेण सह मित्रताम् ऐच्छत्।

प्रश्न 4.
कदा क्षुद्रबुद्धिः निवासस्थानं गतः?
उत्तरम् :
अस्तङ्गते सवितरि क्षुद्रबुद्धिः निवासस्थानं गतः।
प्रश्न 5.
जम्बूकः किम् इच्छति?
उत्तरम् :
जम्बूक: मृगशृगालयोः सख्यम् इच्छति।
(घ) वाक्यं पुनर्लिखित्वा सत्यम्/असत्यम् इति लिखत।
प्रश्न 1.
- अरण्ये एकाक्ष: नाम मृगः चित्राङ्ग नाम काक: निवसतः स्म।
- शुदबुद्धिः उदिते सवितरि (सूर्योदये) निवासस्थानं गतः।
- अकस्मात् आगन्तुना सह मैत्री युक्ता।
उत्तरम् :
- असत्यम्।
- असत्यम्।
- असत्यम्।
(च) कः कं वदति।
प्रश्न 1.
“सखे चित्राङ्ग, कोऽयं द्वितीयः?”
उत्तरम् :
काक: मृगं वदति।

प्रश्न 2.
“जम्बूकोऽयम्। अस्मत्सख्यम् इच्छति।”
उत्तरम् :
मृगः काकं वदति।
प्रश्न 3.
“अकस्मादागन्तुना सह मित्रता न युक्ता।”
उत्तरम् :
काक: मृगं वदति।
प्रश्न 4.
मृगस्य प्रथमदर्शने भवानपि अपरिचितः एव आसीत्।
उत्तरम् :
शृगालः काकं वदति।
प्रश्न 5.
यथायं मृगः मम बन्धुः तथा भवानपि।
उत्तरम् :
शृगालः काकं वदति।

प्रश्न 6.
अलं विवादेन।
उत्तरम् :
मृग: काकशृगालौ वदति।
प्रश्न 7.
वयं सर्वे आनन्देन एकत्र निवसामः ।
उत्तरम् :
मृगः काकशृगाली वदति।
प्रश्न 8.
एवमस्तु।
उत्तरम् :
काकः मृगशृगाली वदति।

शब्दज्ञानम्।
(क) सन्धिविग्रहं कुरूत।
- चित्राङ्गो नाम – चित्राङ्गः + नाम ।
- एकाक्षो नाम – एकाक्ष: + नाम।
- काकश्च – काकः + च।
- केनापि – केन+अपि।
- कोऽयम् – क + अयम्।
- अकस्मादागन्तुना – अकस्मात् + आगन्तुना।
- तदाकर्ण्य – तत् + आकर्य।
- भवानपि – भवान् + अपि।
- यथायम् – यथा + अयम्।
- काकेनोक्तम् – काकेन + उक्तम्।
- एवमस्तु – एवम् + अस्तु।
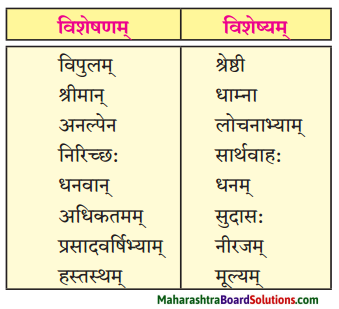
(ख) विशेषण – विशेष्य – सम्बन्धः।
| विशेषणम् |
विशेष्यम् |
| 1. भ्रमन् |
चित्राङ्गः |
| 2. अस्त गते |
सवितर |
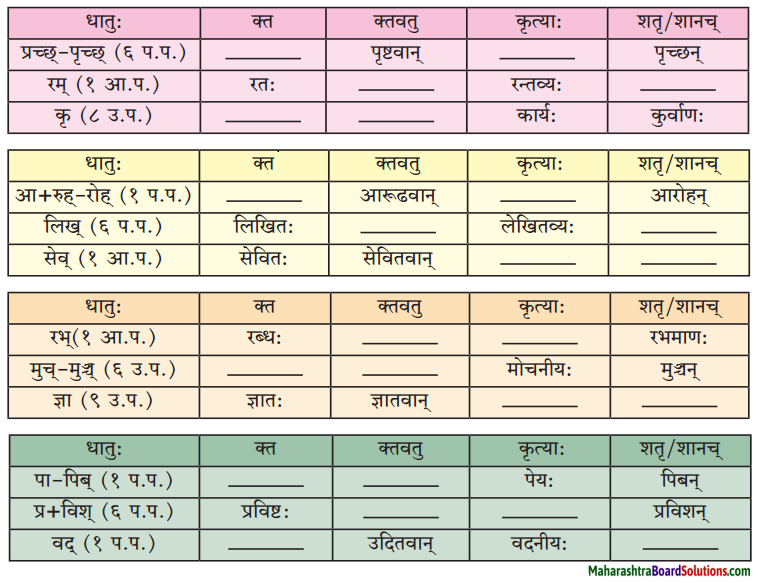
(ग) त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि।
| त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा / अयित्वा |
ल्यबन्त अव्यय – उपसर्ग + धातु + य / त्य |
| आकर्य |
दृष्ट्वा |

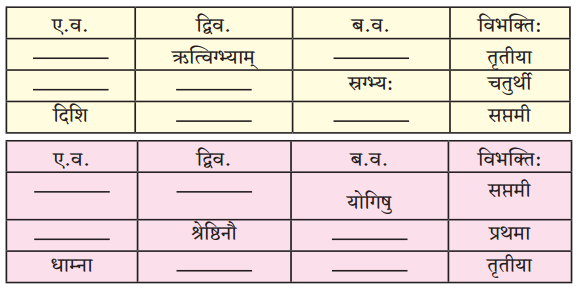
(घ) विभक्त्यन्तरूपाणि।
- प्रथमा – मृगः, काकः, भ्रमन्, सः, अयम्, जम्बूकः, भवान्, बन्धुः, वयम्, सर्वे।
- द्वितीया – सख्यम्, मित्रताम्।
- तृतीया – स्नेहेन, केन, शृगालेन, हेतुना, मृगेण, आगन्तुना, विवादेन, आनन्देन, काकेन।
- पञ्चमी – अस्मत्।
- सप्तमी – वने, सवितरि, दर्शन।
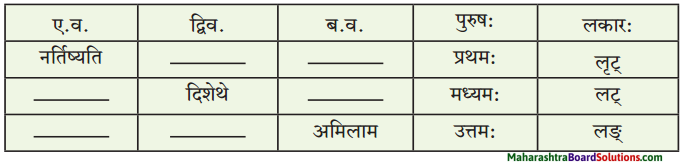
(च) लकारं लिखत।
प्रश्न 1.
1. शृगालः मृगेण सह मित्रताम् ऐच्छत्।
2. जम्बूक: सकोपम् आह।
उत्तरम् :
1. लङ्लकारः
2. लङ्लकार:

क्रमेण योजयत।
प्रश्न 1.
- मृगकाकयोः नेहेन निवासः।
- काकस्य उपदेशः।
- मृगकाकशृगालानाम् एकत्र निवासः।
- शुगालस्य मृगेण सह मित्रता।
उत्तरम् :
- मृगकाकयोः स्नेहेन निवासः।
- शृगालस्य मृगेण सह मित्रता।
- काकस्य उपदेशः।
- मृगकाकशृगालानाम् एका निवासः।
भाषाभ्यासः
(क) समानार्थकशब्दाः
- अरण्यम् – काननम्, वनम्, विपिनम्, अटवी।
- मृगः – हरिणः, कुरङ्गः, वातायुः, अजिनयोनिः ।
- काकः – वायसः, करटः, ध्वाक्षः, अरिष्टः, बलिपुष्टः, सकृत्प्रजः।
- शृगालः – जम्बूकः, वाकः, क्रोष्टा, फेरुः, फेरवः।

(क) उचितं कारणं चित्त्वा वाक्यं पुनर्लिखत।
प्रश्न 1.
जम्बूक: मनसि आनन्दितः यतः
(अ) मृगः पाशे बद्धः।
(ब) जम्बूकस्य अन्येन सह मित्रता अभवत्।
उत्तरम् :
(अ) मृग: पाशे बद्धः।
(ख) उचितं पर्यायं चित्त्वा वाक्यं लिखत।
प्रश्न 1.
- फलितं मे ……………..। (प्रयोजनम् / मनोरथम्)
- ………………. मम शरणम्। (शत्रवः / सुहद:)
- बने …………. क्षेत्रम् अस्ति। (सस्यविहीनं / सस्ययुक्त)
उत्तरम् :
- मनोरथम्
- सुहृदः
- सस्ययुक्तं
(ग) पूर्णवाक्येन लिखत।
प्रश्न 1.
केन मृगस्य कृते पाशः योजितः?
उत्तरम् :
क्षेत्रपतिना मृगस्य कृते पाश: योजितः।

प्रश्न 2.
मृगं पाशैर्बद्धं दृष्ट्वा क: मनसि आनन्दितः?
उत्तरम् :
मृगं पाशैर्वद्धं दृष्ट्वा जम्बूक: मनसि आनन्दितः।
प्रश्न 3.
जम्बूक: मनसि किम् अचिन्तयत्?
उत्तरम् :
जम्बूक: मनसि अचिन्तयत्, ‘यत् फलितं मे मनोरथम्। इदानीं प्रभूतं भोजनं प्राप्स्यामि ।’
प्रश्न 4.
मृग: जम्बूकं दृष्ट्वा किम् अब्रवीत्?
उत्तरम् :
मृगः जम्बूकं दृष्ट्वा अब्रवीत्, “मित्र, छिन्धि तावन्मम बन्धनम्। त्रायस्व माम्।” इति ।
(घ) कः कं वदति।
प्रश्न 1.
दर्शयामि त्वाम्।
उत्तरम् :
जम्बूक: मृगं वदति।

प्रश्न 2.
दृढोऽयं बन्धः।
उत्तरम् :
जम्बूक: मृगं वदति।
प्रश्न 3.
स्नायुनिर्मितान् पाशानेतान् कथं वा व्रतदिवसे स्मृशामि।
उत्तरम् :
जम्बूकः मृगं वदति।
(च) वाक्यं पुनलिखित्वा सत्यम् / असत्यम् इति लिखत।
प्रश्न 1.
- मृगः शृगालं सस्यपूर्ण क्षेत्रम् अदर्शयत्।
- मृगः प्रतिदिन क्षेत्रे सस्यम् अखादत्।
- जम्बूकः पाशैर्बद्धः।
- जम्बूक: मनसि खिन्नः जातः।
- जम्बूक: मृगं साहाय्यम् अकरोत्।
- जम्बूक: निभृतं स्थितः।
उत्तरम् :
- असत्यम्।
- सत्यम्।
- असत्यम्।
- असत्यम्।
- असत्यम्।
- सत्यम्।

शब्दज्ञानम् ।
(क) सन्धिविग्रहः।
- किञ्चित्कालानन्तरम् – किञ्चित् + कालानन्तरम् ।
- वनेऽस्मिन् – बने + अस्मिन्।
- क्षेत्रमस्ति – क्षेत्रम् + अस्ति ।
- तत्रागतः – तत्र + आगतः।
- पाशैर्बद्धः – पाशैः + बद्धः।
- मित्राण्येव – मित्राणि + एव।
- सोऽचिन्तयत् – स: + अचिन्तयत्।
- मृगस्तम् – मृगः + तम्।
- तावन्मम – तावत् + मम।
- जम्बूको दूरादेवावदत् – जम्बूक: + दुरात् + एव + अवदत्।
- दृढोऽयम् – दृढ : + अयम्।
- पाशानेतान् – पाशान् + एतान्।
- इत्युक्त्वा . इति + उक्त्वा ।
- समीपमेव – समीपम् + एव।
(ख) विशेषाण – विशेष्य – सम्बन्धः।
| विशेषणम् |
विशेष्यम् |
| 1. सस्यपूर्णम् |
क्षेत्रम् |
| 2. मगः |
बद्धः |
| 3. प्रभूतम |
भोजनम् |
| 4. स्नायुनिर्मितान् |
पाशान् |
(ग) त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि।
| त्वान्त अव्यय धातु + त्वा/ध्वा/ट्वा/वा/इत्वा/अयित्वा |
| दृष्ट्वा, उक्त्वा |

(घ) विभक्त्यन्तरूपाणि।
- प्रथमा – शृगालः, पाशः, सः, जम्बूकः, अयम्, बन्धः, मिवाणि।
- द्वितीया – मृगम्, क्षेत्रम्, एकम, त्वाम्, भोजनम्, तम्, माम, पाशान, एतान्।
- तृतीया – क्षेत्रपतिना, पाशैः।
- पशमी – दूरात्। षष्ठी – वृक्षस्य, मम।
- सप्तमी – एकस्मिन्, दिने, मनसि, व्रतदिवसे।
- सम्बोधन – मित्र।
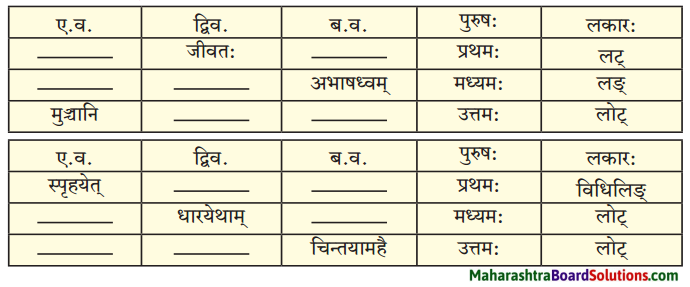
(च) लकारं लिखत।
प्रश्न 1.
1. प्रभूतं भोजनं प्राप्स्यामि।
2. त्रायस्व माम्।
उत्तरम् :
1. लृट्लकार:
2. लोट्लकार:

क्रमेण योजयत।
(क)
प्रश्न 1.
- क्षेत्रपतिना पाशयोजनम्।
- शृगालेन मृगाय सस्यपूर्णक्षेत्रस्य दर्शनम्।
- मृगस्य पाशबन्धनम्।
- मृगस्य प्रत्यहं क्षेत्रं गमनम्।
उत्तरम् :
- शृगालेन मृगाय सस्यपूर्णक्षेत्रस्य दर्शनम्।
- मृगस्य प्रत्यहं क्षेत्रं गमनम्।
- क्षेत्रपतिना पाशयोजनम्।
- मृगस्य पाशबन्धनम्।
(ख)
प्रश्न 1.
- मृगः पाशैर्बद्धः।
- मृगः सस्यम् अखादत्।
- जम्बूक; मनसि आनन्दितः।
- क्षेत्रपतिना पाश: योजितः।
उत्तरम् :
- मृगः सस्यम् अखादत्।
- क्षेत्रपतिना पाश: योजितः।
- मृगः पाशैर्बद्धः।
- जम्बूक: मनसि आनन्दितः ।
भाषाभ्यासः
(क) समानार्थकशब्दाः
- कालः – समयम, वेला।
- प्रत्यहम् – प्रतिदिनम्।
- सस्यम् – धान्यम्।
- गत्वा उपगम्य।
- क्षेत्रपतिः – सस्यपालः।
- इदानीम् – सम्पति, साम्प्रतम्।
- मनसि – चित्ते, चेतसि, अन्त:करणे।
- आनन्दितः – प्रमुदितः, हर्षितः, प्रहृष्टः।
- मनोरथम् – मनोकामना, मनीषा, ईहा।
- प्रभूतम् – भूरि, विपुलम्, पुष्कलम्, प्रचुरम्।
(ख) विरुद्धार्थकशब्दाः
1. अनन्तरम् × पूर्वम्, प्राक्।

अवबोधनम् ।
(क) उचितं कारणं चित्वा वाक्यं पुनर्लिखत।
प्रश्न 1.
मृगः क्षेत्रपतिना बद्धः यतः ……….
(अ) मृगः क्षेत्रपतेः शत्रुः आसीत्।
(ब) मृगः सुहद्वाक्यस्य अनादरम् अकरोत्।
उत्तरम् :
(ब) मृगः सुहृद्वाक्यस्य अनादरम् अकरोत्।
प्रश्न 2.
शृगालः हत: यत:
(अ) क्षेत्रपतिना लगुडं क्षिप्तम्।
(ब) काकः शृगालम् अमारयत्।
उत्तरम् :
(अ) क्षेत्रपतिना लगुडं क्षिप्तम्।
प्रश्न 3.
क्षेत्रपतिः मृगं बन्धनात् व्यमुशत् यतः
(अ) सः ‘मृगः मृतः’ इति चिन्तितवान् ।
(ब) पाशबद्धं मृगं दृष्ट्वा तस्य हृदयं करुणया अद्रवत्।
उत्तरम् :
(अ) सः ‘मृगः मृतः’ इति चिन्तितवान्।

(ख) पूर्णवाक्येन उत्तरत।
प्रश्न 1.
क्षेत्रपतिः कदा हस्ते लगुडं धृत्वा आगच्छत् ?
उत्तरम् :
क्षेत्रपतिः प्रभाते हस्ते लगुडं धृत्वा आगच्छत्।
प्रश्न 2.
केन क्षेत्रपति: अवलोकित:?
उत्तरम् :
काकेन क्षेत्रपति: अवलोकितः।
प्रश्न 3.
क्षेत्रपतिना मृगं विलोक्य किम् उक्तम्?
उत्तरम् :
क्षेत्रपतिना मृगं विलोक्य उक्तं, “आ ! स्वयं मृतोऽसि।”
प्रश्न 4.
मृगः कदा पलायित:?
उत्तरम् :
काकशब्द श्रुत्वा मृग: पलायितः।

(ग) वाक्यं पुनलिखित्वा सत्यम् / असत्यम् इति लिखत।
प्रश्न 1.
- काकः सायङ्काले मृगमन्विष्यन् आगतः।
- मृगः मृतः आसीत्।
- मृगः मृतवत् संदर्शयत्।
- मृगः शनैः शनै: पलायितः।
- क्षेत्रपतिना क्षिप्तेन लगुडेन जम्बूक: हतः।
- क्षेत्रपति: मृगं बन्धनात् व्यमुञ्चत्।
उत्तरम् :
- सत्यम्।
- असत्यम्।
- सत्यम्।
- असत्यम्।
- सत्यम्।
- सत्यम्।
(घ) कः कं वदति?
प्रश्न 1.
“सखे ! किमेतत् ?”
उत्तरम् :
काक: मृगं वदति।

प्रश्न 2.
सुहद्वाक्यस्य अनादरात् बद्धोऽहम्।
उत्तरम् :
मृग: काकं वदति।
प्रश्न 3.
मन्मांसार्थी तिष्ठति अत्रैव ।
उत्तरम् :
मृग: काकं वदति।
प्रश्न 4.
उपायस्तावत् चिन्तनीयः।
उत्तरम् :
काकः मृगं वदति।
प्रश्न 5.
त्वमात्मानं मृतवत्संदर्शय।
उत्तरम् :
काकः मृगं वदति।

शब्दज्ञानम्
(क) सन्धिविग्रहः।
- मृगमन्विष्यन् – मृगम् + अन्विष्यन् ।
- काकस्तत्रोपस्थितः – काक: + तत्र + उपस्थितः।
- किमेतत् – किम् + एतत्।
- बद्धोऽहम् – बद्धः + अहम्।
- स्वास्ते – क्व + आस्ते।
- तिष्ठत्यत्रैव – तिष्ठति + अत्र + एव।
- उपायस्तावत् उपाय: + तावत्।
- क्षेत्रपतिलगुडहस्तः – क्षेत्रपतिः + लगुडहस्तः।
- काकेनावलोकितः – काकेन + अवलोकितः।
- तमालोक्य – तम् + आलोक्य।
- काकेनोक्तम् – काकेन + उक्तम्।
- त्वमात्मानम् – त्वम् + आत्मानम्।
- मृतवत्संदर्शय – मृतवत् + संदर्शय।
- पादास्तब्धीकृत्य – पादान् + स्तब्धीकृत्य ।
- यदाहम् – यदा + अहम्।
- त्वमुत्थाय – त्वम् + उत्थाय।
- मृगस्तथैव – मृग: + तथा + एव।
- उक्तञ्च – उक्त म् + च।
- तमुद्दिश्य – तम् + उहिश्य।
- शृगालस्तावद् हतः – शृगालः + तावत् + हतः।
(ग) त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि ।
| त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा / अयित्वा |
ल्यबन्त अव्यय उपसर्ग + धातु + या / त्य |
| दृष्ट्वा, पूरयित्वा, श्रुत्वा |
आलोक्य, स्तब्धीकृत्य, उद्दिश्य, उत्थाय |

(घ) विभक्त्यन्तरूपाणि ।
- प्रथमा – काकः, सः,अहम, यः, नरः, वञ्चकः, क्षेत्रपतिः, आगच्छन्, त्वम्, मृगः, शृगालः।
- द्वितीया – मृगम्, किम्, एतत्, तम्, आत्मानम्, उदरम्, पादान्, शब्दम्।
- तृतीया – मृगेण, काकेन, वातेन, क्षेत्रपतिना, लगुडेन।
- पञ्चमी – अनादरात्, बन्धनात्।
- षष्ठी – वाक्यस्य, सुहृदाम, हितकामानाम, तस्य।
- सप्तमी – प्रदोषकाले, प्रभाते।
- सम्बोधन – सखे, मृग।
(च) लकारं लिखत।
प्रश्न 1.
- मृगं तथाविधं दृष्ट्वा स उवाच।
- स वशक: क्व आस्ते?
- त्वमात्मानं मृतवत्संदर्शय।
- सत्वरं पलायिष्यसे।
- सः मृगं बन्धनात् व्यमुञ्चत्।
उत्तरम् :
- लिट्लकारः
- लट्लकारः
- लोट्लकार:
- लट्लकारः
- लङ्लकार:

क्रमेण योजयत।
(क)
प्रश्न 1.
- मृगः मृतवत् स्थितः ।
- शृगाल: लगुडेन हतः।
- काकेन क्षेत्रपति: अवलोकितः।
- काकेन शब्दः कृतः।
उत्तरम् :
- काकेन क्षेत्रपति: अवलोकितः।
- मृगः मृतवत् स्थितः।
- काकेन शब्दः कृतः।
- शृगाल: लगुडेन हतः।
भाषाभ्यासः
(क) समानार्थकशब्दाः
- प्रदोषकालः – सन्ध्याकालः।
- सुहृद् – सखा, मित्रम्।
- विपत् – आपत्तिः, सङ्कटम्।
- आलोक्य – अवलोक्य, विलोक्य, वीक्ष्य।
- वातेन – पवनेन, वायुना।
- सत्वरम् – शीघ्रम्, तूर्णम्, झटिति, आशु।

(ख) विरुद्धार्थकशब्दाः
- सुहद् × शत्रुः, अरिः, वैरी।
- अनादरात् × आदरात्।
- मृतः × जीवितः।
- सत्वरम् × शनैः शनैः।
लेखनकौशलम्
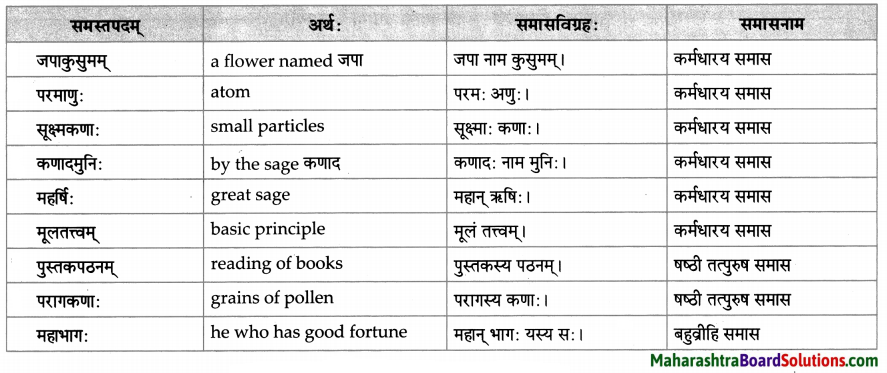
समासाः
| समस्तपदम् |
अर्थ |
समासविग्रहः |
समासनाम |
| मृगशृगालो |
deer and jackal |
मृगः च शृगाल: च। |
इतरेतर द्वन्द्व समास |
| प्रत्यहम् |
every day |
अहनि अहनि। |
अव्ययीभाव समास |
| सकोपम् |
with anger |
कोपेन सह। |
अव्ययीभाव समास |
| अपरिचितः |
not known |
न परिचितः। |
नञ्तत्पुरुष समास |
| क्षेत्रपतिः |
owner of the field(s) |
क्षेत्रस्य / क्षेत्राणां पतिः। |
षष्ठी तत्पुरुष समास |
| क्षुदबुद्धिः |
he who has mean intellect |
क्षुद्रा बुद्धिः यस्य सः। |
बहुव्रीहि समास |
| लगुडहस्तः |
he who hasastick in the hand |
लगुडं हस्ते यस्य सः। |
बहुव्रीहि समास |

व्यसने मित्रपरीक्षा Summary in Marathi and English
प्रस्तावना :
हितोपदेश हे प्राणी व मानवी पात्रांनी युक्त कथांचे भारतीय पुस्तक आहे. यात नीतिसूत्रे, उपदेशात्मक वचने, तसेच राजकीय संबंधावर आधारित मूल्ये यांचे सहज व रोचक पद्धतीने स्पष्टीकरण केलेले आहे.
नारायण पंडित हा या ग्रंथाचा कर्ता मानला जातो. योग्य आचरण शिकवणे हा त्याचा यामागील हेतू आहे. पक्षी, प्राणी व मानव यांच्या परस्पर संभाषणातून हे त्याने व्यक्त केले आहे.
हितोपदेशाचे चार भाग आहेत. 1) मित्रलाभ, 2) सुहृद्भेद, 3) विग्रह 4) सन्धि ‘व्यसने मित्रपरीक्षा’ या पाठाचा कथाभाग ‘मित्रलाभ’ या भागातील 2.3 या प्रकरणात सापडतो. अनोळखी व्यक्तीवर विश्वास ठेवल्याचे दुष्परिणाम हरिण, कोल्हा व कावळ्याच्या गोष्टीद्वारे उत्तमरीत्या कथन केले आहेत.
हितोपदेश is an ancient Indian text in Sanskrit language consisting of fables of animals and human characters. It incorporates maxims, wordly wisdom and morals on political affairs in a simple and an entertaining manner.
नारायण पंडित is considered to be the author of this book. His purpose behind composing Faludy is to give the knowledge to be wise. This is done through moral stories in which birds, beasts and humans interact. हितोपदेश has four sections – मित्रलाभ, सुहृद्भेद, विग्रह, सन्धि The story of the lesson व्यसने मित्रपरीक्षा is found in the chapter 1.3 of ‘मित्रलाभ’. The repercussion of Trusting strangers is well brought out through the story of deer, jackal and correct.

परिच्छेदः 1.
अस्ति कश्चित् …………… एवमस्तु।
अनुवादः
चंपक नावाचे एक जंगल होते. जंगलात चित्रांग नावाचे हरिण व एकाक्ष नावाचा कावळा प्रेमाने (एकत्र) राहत होते. एकदा चित्रांग वनात भटकत असताना कोण्या एका कोल्ह्याने पाहिले. क्षुदबुद्धी नावाच्या त्या कोल्ह्याची स्वार्थापोटी हरिणाबरोबर मैत्री करण्याची इच्छा होती. सूर्यास्त झाल्यावर, क्षुद्रबुद्धी हरिणाबरोबर हरिणाच्या घरी गेला. हरिण व कोल्ह्याला पाहून कावळा म्हणाला, “अरे मित्रा चित्रांग! हा दुसरा कोण आहे?” हरिण म्हणाले, “हा कोल्हा आहे. त्याला आपल्याबरोबर मैत्री करण्याची इच्छा आहे.”
(त्यावर) कावळा म्हणाला “अचानक आलेल्या अपरिचितासोबत मैत्री योग्य नव्हे.” ते ऐकून कोल्हा रागाने म्हणाला, हरिणाच्या प्रथमदर्शनी तू सुद्धा अनोळखी होतास. ज्याप्रमाणे हे हरिण माझ्या मित्रासमान आहे, त्याप्रमाणे तू आहेस. हरिण म्हणाले, “(हा) वाद पुरे! आपण सर्व आनंदाने एकत्र राहूया.” कावळा म्हणला, “असेच होवो.”
There was a certain forest named चंपक. A deer named feiland a crow named Te used to live in the forest affectionately. Once, a certain jackal saw feai who was wandering in the forest. That jackal named क्षुद्रबुद्धी wished to befriend the deer with a selfish purpose.
At the time of sunset, क्षुदबुद्धी went to deer’s place with the deer, The crow said having seen the deer and the jackal, “O friend चित्रांग ! Who is this second (another) one?” The deer said, “This is a jackal.
He wishes our friendship.” (He wishes to be friend us.) The crow advised, “Friendship with a stranger, suddenly is not appropriate.’ Having heard it, the jackal angrily said, “At first sight you were a stranger as well. Just as this deer is my friend so too are you.” The deer said, “Enough of this argument. All of us will live together happily.” The crow said, “May it be so.”

परिच्छेद: 2
किञ्चित्कालानन्तरं ……………….. स्थितः।
अनुवादः
थोड्या वेळानंतर, कोल्हा हरिणाला म्हणाला, ‘या जंगलात धान्याने भरलेले एक शेत आहे. मी तुला दाखवतो.’ तसे केल्यावर, दररोज हरिण तेथे जाऊन धान्य खात असे.
ते पाहून, एके दिवशी शेतमालकाने जाळे टाकले. तेथे आलेले हरिण जाळ्यामध्ये अडकले. त्याने विचार केला, “आता फक्त मित्रच माझा आसरा आहेत.” दूरवरून ते पाहणारा कोल्हा मनातून खूष झाला.
त्याने विचार केला, “माझे ईप्सित फळास आले. आता मला पुष्कळ खाद्य मिळेल.” त्याला पाहून हरिण म्हणाले, “अरे मित्रा, माझे हे बंध तोडून टाक, मला वाचव.” कोल्हा लांबूनच म्हणाला, “अरे मित्रा, हे बंध (फार) घट्ट आहेत. मी स्नायूंनी बनविलेल्या जाळ्याला उपवासाच्या दिवशी कसे तोंड लावू? असे म्हणून तो जवळ असलेल्या झाडाच्या मागे स्थिर उभा राहिला.
After some time, the jackal said to the deer, there is a field, full of grains in this forest. I(will) show (it) to you.’ Having done so, the deer ate the grain, going there everyday. Having seen this, one day a trap was set by the owner of the field.
The deer, who had come (arrived) there, was trapped in the net. He thought, “Now, my friends only are my resort.” The jackal, who was seeing it from far was delighted in the mind. He thought, “My desire is fulfilled. Now I shall get plenty of food.” Having seen it, the deer said, “O friend, cut through my bonds.
Please save me.” The jackal replied from afar, “O friend, this bond is strong. How can I touch the net made of sinews on my fasting day?” Having said this, he stood steady behind the tree – that was nearby.
परिच्छेदः 3.
प्रदोषकाले …………………हतः।
अनुवादः
तिन्हीसांजेच्या वेळी (सायंकाळी), हरिणाला शोधत कावळा तेथे हजर झाला. हरिणाला तशा प्रकारे पाहून तो म्हणाला, “अरे मित्रा ! हे काय?” हरिण म्हणाले, “मित्राच्या शब्दांची अवहेलना केल्यामुळे (शब्दांकडे दुर्लक्ष केल्यामुळे) मी अडकलो.
मराठी आणि म्हटलेले आहे – जो हितचिंतक मित्रांचे शब्द (सल्ला) ऐकत नाही, त्याच्याजवळ विपत्ती (निवास करते), अशी व्यक्ती शजूंना आनंदित करते.” (शत्रुत्व ओढवून घेते) कावळा म्हणाला, “तो (कपटी) फसविणारा कोठे आहे?” हरिण म्हणाले, “माझ्या मांसाच्या हावेने इथेच थांबला आहे.”
कावळा म्हणाला, ‘तर मग (यावर) उपाय शोधला पाहिजे.’ नंतर सकाळी, हातामध्ये काठी घेऊन येणाऱ्या शेतमालकाला कावळ्याने पाहिले. त्याला पाहून कावळा म्हणाला, “मित्रा हरिणा, तू स्वत:ला मेल्यासारखा दाखव.” (तुझे) पोट हवेने फुगवून पाय स्थिर ठेव.
जेव्हा मी आवाज करेन / ओरडेन, तेव्हा तू उठून पटकन पळ.” हरिण तसेच थांबले. शेतमालकाने हरिणाला पाहिले व म्हणाला, “बापरे ! तू तर मेलेला आहेस.” त्याने हरिणाला जाळ्यातून मुक्त केले. नंतर, कावळ्याचे ओरडणे ऐकल्यावर हरिण पटकन पळून गेले. शेताच्या मालकाने त्याला (हरिणाला) रोखून फेकलेल्या काठीने कोल्हा मारला गेला.
English At nightfall, the crow arrived there looking for the deer. Seeing the deer so (trapped) he said, “O friend! What is this?” The deer said, “I was caught (trapped) due to disregarding a friend’s words (advice).
and it is said The one who does not listen to words/advice of friends well-wishing, the calamity is placed close to him. That person is the delight of enemies. The crow said, “where is the deceiver ?” The deer said, “(He) is waiting here itself longing for my flesh.” The crow said, ‘We must think of a solution.’ Then in the morning, the crow saw the owner of the field coming with a stick in the hand.
Seeing him, the crow said, “O friend deer, pretend as if you are dead. Blow your belly with air, stiffen your legs and lie still. When I shall make a sound then, having stood up, you run away quickly The deer stayed accordingly. The owner of the field saw the deer and said, “Oh! You are dead on your own.” He released the deer from the bonds.
Then, listening to the sound of the crow, the deer ran away quickly. Meanwhile, the stick which was thrown towards the deer by the owner of the field, killed the jackal.

शब्दार्थाः
- कक्षित् – certain – कोणी एक
- मृगः – deer – हरिण
- काकः – crow – कावळा
- स्नेहेन – affectionately – प्रेमाने
- निवसतः स्म – both used to live – दोघे राहत होते
- भ्रमन् – wandering – भटकत असताना
- शृगालेन – by jackal – कोल्याने
- अवलोकित: – was seen – पाहिले
- स्वार्थहतुना – with selfish purpose – स्वार्थापोटी
- अस्तबते – at the time of – सूर्यास्त
- सवितरि – sunset – झाल्यावर
- जम्बूकः – jackal – कोल्हा
- सख्यम् – friendship – मैत्री
- अकस्मात् – at once – अचानक
- आगन्तुना सह – with a stranger – अनोळखी माणसासह
- युक्ता proper – योग्य
- आक having heard – ऐकून
- सकोपम् angrily – रागाने
- प्रथमदर्शन at the first sight – प्रथमदर्शनी
- अपरिचितः stranger – अनोळखी
- अब्रूत/अब्रवीत्/उक्तम्। – said – म्हणाला
- आह – says – म्हणतो
- आकर्ण्य – having heard – ऐकून
- अकस्मात् – at once – अचानक
- सकोपम् – angrily – रागाने
- आगन्तुना सह – with a stranger – अनोळखी माणसासह
- दृढः – strong – घट्ट
- बन्धः – bond – बंध
- पाश: – noose – जाळे
- योजितः – arranged – व्यवस्था केली
- बद्धः – got stuck/caught – अडकले
- सस्यपूर्णम् – full of grains – धान्ययुक्त
- क्षेत्रम् – field – शेत
- शरणम् – resort – आश्रयस्थान, आसरा
- फलितम् – fulfilled – फळास आले
- मनोरथम् – desire – ईप्सित/इच्छा
- स्नायुनिर्मितान् – made of sinews – स्नायूंनी बनलेले
- क्षेत्रपतिना – by the field-owner – शेतमालकाने
- व्रतदिवसे – on the day of fast – उपवासादिवशी
- दर्शयामि – I show – मी दाखवतो
- प्रापयामि – I shall get – मला मिळेल
- छिन्धि – you break – तू तोड
- जायस्व – you save – तू वाचव
- प्रत्यहम् – every day – दररोज
- इदानीम् – now – आता
- प्रभूतम् – plenty of – भरपूर
- निभृतम् – still – निश्चल
- तथा कृते – having done so – तसे केल्यावर
- उपस्थितः – arrived – हजर झाला
- वञ्चक: – crooked / deceitful – फसविणारा
- लगुडहस्त: – stick in the hand – काठी हातात घेतलेला
- हतः – killed – मेलेला
- अन्विष्यन् – searching – शोधत
- विपत् – calamity – संकट
- सन्निहिता – placed close by – जवळ
- मृतवत् – like dead – मेल्यासारखा
- सुङद्वाक्यम् – friend’s speech – मित्राचे बोलणे
- वातेन – with air – हवेने
- क्षिप्तेन – thrown – फेकलेल्या
- अनादरात् – due to disrespecting – अवहेलना केल्यामुळे
- हितकामानाम् – of well-wishers – हितचिंतकांचे
- प्रदोषकाले – at the nightfall – तिन्हीसांजेला
- शृणोति – listens – ऐकतो
- पलायिष्यसे – you will run – पळशील
- व्यमुञ्चत् – released – मुक्त केले
- अब्रूत – said – म्हणाला
- संदर्शय – appear – दाखव
- उद्दिश्य – pointing – रोखून
- उत्थाय – having got up – उठून
- आलोक्य – seeing – पाहून
- स्तब्धीकृत्य – keeping still – स्थिर / स्तब्ध राहून
- क्व – where – कोठे
- उदरं पूरयित्वा – blowing the belly – पोट भरून
- मन्मांसार्थी – longing for my flesh – माझ्या मांसाच्या हावेने

10th Standard Sanskrit Anand Digest Pdf
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()