Class 10

Class 10 English Chapter 4.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 4.3 O Captain! My Captain! Notes, Textbook Exercise Important Questions and Answers.

O Captain! My Captain! Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 4.3 O Captain! My Captain! Textbook Questions and Answers

Warming Up:
Chit-chat

1. Discuss the following with your classmates:

Question (a)
What are the important games played in your school?
Answer:
We play cricket, baseball, kabaddi, foot-ball, langadi, etc. in our school.

Question(b)
Who are the captains of the various team games? Name them:
Answer:

Games	Captain
1. Cricket	Roshan More
2. Baseball	Karan Shirke
3. Kabaddi	Akshay Dalvi
4. Football	John D’Mello
5. Langadi	Kshitija Bhosale

Question (c)
What is the role played by a team-game captain? What are his/her responsibilities?
Answer:
A team-game captain plays a pivotal role for the team. He/She is the backbone of the team. He inspires and motivates the team. He creates team spirit among his players. He also plays ; crucial role to maintain good relations among all the teammates. He/She keeps the bonding with the team. He keeps the team united. He takes the responsibility of drawbacks and defeats of the team.

Question (d)
What is the role of a captain of a ship? What are the responsibilities of a captain of a ship?
Answer:
A captain of a ship plays an important role. He is solely responsible for keeping the ship safe and sound. He guides and takes the ship safely to its destination. He navigates safely to reach wherever he wants to take the ship and the people on the ship. He is responsible for the safety of the ship and his crew. Sometimes he has to risk his life to overcome difficulties he faces on his way.

1. In pairs find as many meaningful words as you can from the following grid within five minutes. You can find words horizontal and vertically. (Hint – The words are related to battles or battleships. For example, soldier.

Question 1.
In pairs find as many meaningful words as you can from the following grid within five minutes. You can find words horizontal and vertically. (Hint – The words are related to battles or battleships. For example, soldier. (Answers are directly given.)

Answer:

English workshop:

1. Pick out from the poem all words related to ‘ship’. Make a list of them in a word register:

Question 1.
Pick out from the poem all words related to ‘ship’. Make a list of them in a word register:
(a) Port
(b) …………..
(c) …………..
(d) …………..
(e) …………..
(f) …………..
(g) anchored
(h) …………..
Answer:
(a) port
(b) keel
(c) vessel
(d) captain
(e) deck
(f) flag
(g) ship anchored voyage.
(h) shores

2. Read the poem again and complete the following sentences.

Question 1.
Read the poem again and complete the following sentences.
(a) The Captain lies on the deck ……………………….
(b) The Captain doesn’t answer as ……………………
(c) Captain does not feel anything ……………………
(d) The bugle and flag are ……………………………….
Answer:
(a) The Captain lies cold and dead on the deck.
(b) The Captain doesn’t answer as he is dead.
(c) The captain does not feel anything beneath the poet’s arm because he has no pulse nor will.
(d) The bugle is trilled and the flag is flung.

3. The poem has a direct reference to the assassination of President Abraham Lincoln on 15th April, 1865, after the Civil War was won. Match the symbols/images in Column A with what they refer to, in Column B.

Question 1.
The poem has a direct reference to the assassination of President Abraham Lincoln on 15th April, 1865, after the Civil War was won. Match the symbols/images in Column A with what they refer to, in Column B.

Column ‘A’	Column ‘B’
1. the ship	(a) victory (in the war)
2. the fearful (trip/ voyage)	(b) the President of USA
3. the port	(c) United States of America
4. the bells (ringing)	(d) lifeless/dead
5. Captain	(e) the deadly Civil War
6. anchored safe	(f) celebrating victory
7. no pulse, nor will	(g) peace after winning the war

Answer:

1. the ship – United States of America
2. the fearful (trip/voyage) – the deadly Civil War
3. the port – peace after wining the war
4. the bells (ringing) – celebrating victory
5. Captain – the President of USA
6. anchored safe – victory (in the war)
7. no pulse, nor will – lifeless/dead

4. The figures of speech ‘Apostrophe’ exists throughout the poem. Pick out lines where the poet directly addresses:

Question (a)
the dead captain:
Answer:
1. O Captain! My Captain!
2. rise up and hear the bells.

Question (b)
The grief in his heart:
Answer:
1. But O heart! heart! heart!
2. O the bleeding drops of red.

Question (c)
The sea shore:
Answer:
1. Exult, O shores and ring,
2. O bells!

B. Find from the poem, one example of each of the following.

Question (B)
Find from the poem, one example of each of the following.
Answer:
(a) Personification – O Captain! My Captain! Our fearful trip is done.
(b) Alliteration – The ship is anchor’d safe and sound, its voyage closed and done.
(c) Tautology – Where on the deck my Captain lies, fallen cold and dead.
(d) Exclamation – But O heart! heart! heart!
(e) Antithesis – While follow eyes the steady keel, the vessel grim and daring.

5. Find and answer in your own words:

Question (a)
What are the signs that the captain has passed away?
Answer:
Everyone’s eyes follow the steady keel of the ship, the vessel that seems so serious and bold. Where on the deck my Captain lies, fallen cold and dead. These lines shows that the captain has passed away.

Question (b)
Why was the crowd on the shore eagerly waiting to felicitate their captain?
Answer:
As the people saw the ship very close to the port, they felt that their captain is back. So they started shouting and enjoying to welcome their king. They wanted to felicitate their king for his great victory in the Civil War.

Question (c)
What are the signs that show the people are celebrating victory ?
Answer:
The bells are ringing when the victorious ship is near. The flag is flung. The bugle is playing loudly. People are crowding along the shores. They are rejoicing. They have come with bouquets and ribboned garlands to welcome their victorious Captain. These signs show that the people are celebrating victory.

Question (d)
……. dear father! This arm beneath your head…” Why do you think the speaker in the poem puts his arm under the Captain’s head?
Answer:
The speaker in the poem puts his arms under the Captain’s head because he wants to help him to hear the bells of happiness, he wants to show him the flag of victory and the happiness of the people who were there with bouquets and wreaths.

Question (e)
Describe the grief that the speaker in the poem feels at the death of his Captain.
Answer:
When the speaker in the poem saw steady keel of the ship that seems serious and bold; his heart is suddenly filled with very strong emotion. He urged his captain to rise up and hear the bells. He told him to rise up because the flag is flung for him. For him the bugle sounds. For him people have brought bouquets and wreaths. People are crowding along the shore to welcome him. He felt very sad and lamented after seeing captain’s dead body on the deck.

6. Glance through the poem again to find who the speaker addresses in the first two stanzas and the last stanza.

Question 1.
Glance through the poem again to find who the speaker addresses in the first two stanzas and the last stanza.
Answer:
In the first two stanzas the speaker addresses the Captain of the ship. In the last stanza, the speaker addresses the crowd gathered at the shore to welcome the Captain.

7. Fill the qualities in the diagram given below: (Answers is directly given.)

Question 1.
Fill the qualities in the diagram given below: (Answers is directly given.)

1. courage
2. naval expert
3. integrity
4. visionary
5. confidence
6. humane
7. self-disciplined
8. sympathetic
9. leadership
10. foresight
11. knowledge of weather signs
12. positive attitude
13. role – model
14. selfless service
15. good administrator

Answer:

8. Complete the following sentences choosing from the alternatives:

Question 1.
Complete the following sentences choosing from the alternatives:
(Answers are directly given and underlined.)
Answer:
(a) The rhyme scheme of the poem is aabbcded. (aabbccdd/abcdede/aabbcded)
(b) The line repeated in every stanza fallen cold and dead. (O Captain! My Captain!/Fallen cold and dead)
(c) The steady rhythm in the poem consists of a pattern of three beats (three/four/five)
(d) In the third stanza the speaker does not address the Captain, (first/second/third)
(e) The type of poem is elegy because it is composed in memory of a passed away personality. (sonnet, lyric, elegy)

9. The feeling of grief and pain of the speaker in this poem are comparable to those of a great Maratha leader, inspite of winning the battle at a fort in Maharashtra. Guess who the great Maratha leader was and the Captain who was killed in the battle. Write down other basic historical facts of the above.

Question 1.
The feeling of grief and pain of the speaker in this poem are comparable to those of a great Maratha leader, inspite of winning the battle at a fort in Maharashtra. Guess who the great Maratha leader was and the Captain who was killed in the battle. Write down other basic historical facts of the above.
Answer:
Chhatrapati Shivaji Maharaj, the king of Marathas, wished to capture the strong and unconquerable Kondana fort, which was under the Mughal Emperor, Aurangazeb. Keeper of the Kondana was Udaybhan Rathor, a great warrior of the Mughals. Tanaji Malusare, the brave lion-hearted general of Shivaji Maharaj took the responsibility to fulfil his king’s wish.

Tanaji, with a few mavalas climbed up the fort at night with the help of ropes. He fought gallantly against the Mughals and conquered Kondana. Unfortunately Tanaji was killed in the battle. When Maharaj heard that heart-breaking news of the great warrior’s death, he expressed his grief and pain with the words – ‘I have won the fort but I have lost my lion.’ Since then the Kondana fort was called as ‘Sinhagadh.’

10. The poem has described the sad demise of the Captain. How would you console the son of | the Captain? Write a short paragraph using the points given below:

Question 1.
The poem has described the sad demise of the Captain. How would you console the son of | the Captain? Write a short paragraph using the points given below:
(a) Expressing grief on the death,
(b) An act of God.
(c) Words/sentences giving strength and courage to face the situation.
(d) Add your own points.
Answer:
Consoling the son of the Captain

I am at a total loss for words to express my feelings. I don’t understand how to console you for ! the loss of your father. Your father was a great man, full of integrity and character. Losing your dad can | be extremely difficult for you because you have lost your source of strength, stability and consistency in your life. I am extremely sorry for your loss.

He was a real hero for the nation and a real patriot giving inspiration to all. Your dad was a brave man. He had great courage and valour. He will be missed greatly and always remembered during the time of crisis. I extend my heartfelt sympathy to you and your family. May the soul of your father be at peace with our Heavenly father.

11. Read the poem. Write an appreciation of the poem in about 12 to 15 sentences.

Question 1.
Read the poem. Write an appreciation of the poem in about 12 to 15 sentences.
Answer:

1. Title: O Captain! My Captain!
2. Poet: Walt Whitman.
3. Rhyme Scheme: The rhyme scheme for the stanzas 1, 3, and 5 is ‘aabb’. For stanzas 2, 4, and 6, it is ‘abcb’.
4. Figure of Speech (Any 1): Repetition, Tautology, Personification.
5. Theme/Central Idea: The Central Idea of the poem is the lamentation (an expression of great sadness) for the death of the Captain.

Here, America, which had undergone the Civil War, is compared to a ship that had weathered a rough voyage; Abraham Lincoln, who steered the state through the Civil War is compared to the Captain. Five days after the war ended Abraham Lincoln was shot dead. The poet laments the death of this great leader.

My English Coursebook 10th Digest Chapter 4.3 O Captain! My Captain! Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
State whether the following statements are True or False:
Answer:

1. The speaker expresses his relief that the ship has reached its home port. – True
2. Captain’s dead body is lying on the land. – False
3. According to the speaker, his captain’s death feels like a horrible dream. – True
4. The people are cheering because the voyage of the ship is successful. – True

Question 2.
Fill in the blanks and complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. The Captain lies cold and dead on the deck.
2. When the ship reached its home port he heard the people rejoicing and celebrating.
3. The poet tells the Captain to rise up and hear the bell.
4. The speaker is filled with grief because his captain is fallen cold and dead.
5. The location of the battleship is near the port.
6. While waiting to welcome the captain of the ship the people are rejoicing and celebrating.

Question 3.
State whether you agree or disagree with the following statements:
Answer:

1. Stanza II portrays how people celebrate the triumph of the ship and their leader. – Agree
2. The poet refers to the fallen Captain as “Father”- the father of nation. – Agree
3. Stanza III expresses the poet’s profound sorrow for President Lincoln’s death. – Agree
4. The poet is celebrating victory with the people of his country with joy. – Disagree

Question 4.
Fill in the blanks:
(Answers are directly given and underlined.)
Answer:

1. The poet steps slowly and sadly on the deck.
2. It is like a dream the Captain is fallen on the deck cold and dead.
3. The poet tells his Captain to rise up and hear the bells.

Complex Factual Activities:

Find out the line/lines from the extract as ‘a proof’ for the following:

Question 1.
The civil war has ended.
Answer:
our fearful trip is done.

Question 2.
America has braved the tough storm of Civil War.
Answer:
The ship has weather’d every rack.

Question 3.
The speaker calls out to the Captain to rise up and join in the celebration of the end of the war.
Answer:
O Captain! My Captain! rise up and hear the bells.

Question 4.
The Captain is felicitated for the victory in the war.
Answer:
for you the flag is flung-for you the bulge trills.

Complete the following:

Question 1.
Complete the following:
(Answers are directly given and underlined.)
Answer:
(a) Captain does not feel anything because he has no pulse nor will as he is cold and dead.
(b) The ship is anchored safe and sound.

Activities based on Poetic Devices:

Question 1.
Find from the extract one example each of the following:
Answer:

1. Exclamation – Exult O shores, and ring, O bells!
2. Tautology – My Captain does not answer, his lips are pale and still.
3. Personification – From fearful trip, the victor ship, comes in with object won.

Question 2.
Pick out rhyming pairs from the extract.
Answer:
1. Stanza 1: done-one; exulting-daring; red-dead
2. Stanza 2: bells-trills; a crowding-turning head-dead.

My English Coursebook 10th Class Solutions Pdf Unit 4

• The World is Mine Class 10 English Solutions
• Bholi Class 10 English Solutions
• O Captain! My Captain! Class 10 English Solutions
• Unbeatable Super Mom – Mary Kom Class 10 English Solutions
• Joan of Arc Class 10 English Solutions
• A Brave Heart Dedicated to Science and Humanity Class 10 English Solutions

Class 10 English Chapter 2.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 2.4 An Epitome of Courage Notes, Textbook Exercise Important Questions and Answers.

An Epitome of Courage Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 2.4 An Epitome of Courage Textbook Questions and Answers

Warming up!

Chit-chat:

A Strange Truth – ‘Handicapped are those who refuse to take up challenges, even with all their senses and physiology in perfect condition.’

Question 1.
Understand and discuss the above truth.
Answer:
(वरील सत्याविषयी समजून घ्या व चर्चा करा.)

Question 2.
How can you encourage such people to change and become confident? Discuss at least 4 to 5 ways you can do the above.
Answer:
1. The discussion should be related to the people who are not really disabled mentally or physically. This truth is about the people who are mentally and physically perfect but avoid, hesitate or neglect doing something challenging. By some reasons, they are not ready to change their attitude or fixed ideas. They don’t wish to change their mindset and stick to their passive and inactive attitude.

2. Think and try to understand the reasons behind their lethargy, inactiveness or indifference and try to encourage them and give them confidence.

3. Ways to encourage them and give confidence :

• Know his mindset, know his/her handicaps and obstacles he faced.
• Talk to him/her in friendly manner about his good qualities.
• Give examples of successful persons who have faced the challenges.
• Advice him/her to be brave, courageous and active.
• Help him/her in the fields where he/she lacks (confidence, courage, boldness, openness, etc.)

1. There are pleasant and polite ways of referring to people with physical and mental disabilities. Fill in the table below:

Question 1.
There are pleasant and polite ways of referring to people with physical and mental disabilities. Fill in the table below:

Answer:

Previously used Term	New Polite Terms
1. Blind	(a) Visually challenged
2. Deaf	(b) Hearing impaired
3. Dumb	(c) Speech impaired
4. mad	(d) mentally ill
5. lame	(e) physically handicapped

2. Read the beginning and complete the story in your own words:
Sumit, the son oç a shoe maker, was a highly intelligent student in a municipal school. His Maths teacher Called him 1Einstein’, for he was brilliant in Maths.
He loved Maths. umit wanted to study further after C, however he suffered
from Polio and …..
Now, continue the story with a favourable/positive ending.
………………………………………………………………………………………………………
………………………………………………………………………………………………………
………………………………………………………………………………………………………

English Workshop:

1. Match the following. 

Question 1.
Match the following.

Answer:

Group ‘A’	Group ‘B’
1. Galileo	(d) The greatest scientist 300 years before Hawking.
2. Dr. Stephen Hawking	(c) The greatest scientist of this century.
3. Black Holes	(a) The concept which helped Stephen to get his Ph.D.
4. Stephen’s favourite subjects	(b) Music andMathematics

2. Complete the following web-chart containing the qualities of Dr. Stephen Hawking.

Question 1.
Complete the following web-chart containing the qualities of Dr. Stephen Hawking.

Answer:

3. Arrange the following statements according to the occurance in the life history of Dr Stephen Hawking.

Question 1.
Arrange the following statements according to the occurance in the life history of Dr Stephen Hawking.
(a) At the age of 17, Stephen noticed that he fell down a couple of times for no reason.
(b) He became a fellow of the Royal Society and a member of the US National Academy of Science.
(c) He believes that in the next millenium, science will discover the core secrets of the universe.
(d) Stephen was born on 8th January, 1942 and then grew up like an average child and a normal teenager.
(e) The disease worked its way into Stephen’s body and left him disabled.
(f) Stephen decided to continue his doctoral research work with renewed vigor.
(g) Stephen was diagnosed with a rare disease – ALS or LOU.
(h) Though confined to a wheelchair he worked on computer and expressed his thoughts.
Answer:
(a) Stephen was born on 8th January, 1942 and then grew up like an average child and a normal teenager.
(b) At the age of 17, Stephen noticed that he fell down a couple of times for no reason.
(c) Stephen was diagnosed with a rare disease- ALS or LOU.
(d) Stephen decided to continue his doctoral research work with renewed vigour.
(e) The disease worked its way into Stephen’s body and left him disabled.
(f) Though confined to a wheelchair he worked on computer and expressed his thoughts.
(g) He became a fellow of the Royal Society and a member of the US National Academy of Science.
(h) He believes that in the next millennium, science will discover the core secrets of the universe.

4. Homographs – Pairs of words that are spelled and pronounced the same, but have different meanings, in different contexts.
For example

• watch – observe
• watch – device that shows time

Question 1.
Use the following words in two different contexts.
Answer:
(a) couple – couple
1. The bowler managed to take a couple of wickets.
2. The elderly couple was taking a walk in the park.

(b) mind – mind
1. There were many thoughts in his mind, before he left his house.
2. Do you mind, if I put on the fan?

(c) space – space
1. We shall make some space for our new table.
2. Man is thinking of building a space station on the moon.

(d) sound – sound
1. The loud sound at midnight startled everyone.
2. His idea of celebrating birthday in a different way sounds quite interesting.

(e) left – left
1. Go straight and then turn left to reach the station.
2. As soon as he completed his Ph.D., he left for USA.

5. Use the following words/phrases in your own sentences.

Question 1.
Use the following words/phrases in your own sentences.
(a) quirk of fate
(b) confined to
(c) exaggeration
(d) an epitome of
(e) millennium.
Answer:
(a) By the quirk of fate, all the members of the happy family died in an accident.
(b) My neighbour is confined to bed for a long time with paralysis.
(c) He told me the strange news without any . exaggeration.
(d) The champion cricketer is an epitome of modesty
(e) I believe that man will go to stay on other planets before the next millennium.

6. Expand the given themes. Make use of this support/hints:

Question 1.

Expand the given themes.	Make use of this support/hints:
(a) If you fall ill during your final exam.	First step/what to do support/help
(b) If you meet a disabled person who needs help.	Act/behave Contact whom?
(c) If your friend is in trouble.	Gestures/Body language Patience/Tolerance
(d) If you meet a great person like Dr. Stephen Hawking.	Plan/organise Face /Handle/Overcome Succeed/Accomplish

Answer:
Question a.
Falling ill during the Final Exam.
Answer:
If I fall ill during my final exam, I’ll feel worried in the beginning. But soon I’ll collect myself and will face the problem boldly. Determinedly I’ll continue to appear for the remaining exam papers because there will be no reason getting into a panic about the final exam. I already have completed my study and revised it well before the exam.
My parents, I am sure, will be there to nurse me well and look after my health, medicines and my fast recovery. My friends also will help me in my

studies. They will comfort me and give me confidence. If I feel a little better, I myself will continue my studies for the final exam. So everything will fall into place.

Question b.
Helping a Disabled Person.
Answer:
If I meet a disabled person who needs help, I’ll treat him kindly. I shall sympathetically enquire about his difficulties and his requirements. I shall, with the help of my friends, try to provide him with the things he needs. If his needs are beyond our reach, we shall contact the persons or the organizations who could support him and fulfill his needs and requirements. We shall continue our efforts till he meets all his essential needs and equipment.

Question c.
Helping a Friend in Trouble.
Answer:
If any of my friends is in trouble, I will immediately visit him and find out the nature of his trouble. I shall try to pacify him if he is really very much affected. I shall console him if his trouble is because of emotional or financial problems. My friends and I will promise him to share his problem if he speaks it up clearly and freely. A trouble shared is a trouble halved. We shall advise him to be patient and tolerate the situation bravely and courageously. We shall try to help and support our friend in every possible way.

Question d.
Meeting a Great Person like Dr. Stephen Hawking.
Answer:
Before meeting such a great person like Dr. Stephen Hawking, I will have to preplan my visit and get permission for the visit from him. I must be ready with the information about his life history, his characteristics, his education, his achievements and his display of exemplary courage in the face of overwhelming odds.

It is difficult to face and get to talk to such an awe-inspiring person. But I know how to handle myself in this situation. I will talk to him boldly and respectfully. I will overcome my fear of meeting such a great man. I will tell him how I am impressed and inspired by his work and achievements. I will get the greatest joy of my life in meeting such a great personality.

7. You happen to meet a successful person who is a disabled. Write an imaginary dialogue between you and him/her. You can take support of the hints provided.

Question 1.
You happen to meet a successful person who is a disabled. Write an imaginary dialogue between you and him/her. You can take support of the hints provided.
(a) introductionlwelcome/greetings
(b) congratulating/honouring
(c) cause/reason for the disability
(d) decisionlplan/organisationlimplementation
(e) idols in life
(f) parents/friends – support if any
(g) success stories/accomplishments
(h) conclusion/final message if any
Answer:
Answer:
An Imaginary Dialogue between Sumit, a disabled and you:

• Myself: Hello, Sir, nice to meet you. I have read that you have received ‘The Sangeet Samrat’ Award of our city. Congratulations!
• Sumit: Yes, you are right, and thank you for your good wishes.
• Myself: You are confined to the wheelchair and both your legs are amputated. What made you disabled?
• Sumit: At the age of five I was crippled by Polio, The disease worked its way into my legs and they had to be amputated. I was confined to this wheelchair since then.
• Myself: I wonder how you could achieve such a great feat. Didn’t you feel depressed?
• Sumit: That is a long story. Music was in my blood. My father was a great classical singer. I used to listen to him since my childhood. He was my first Guru.
• Myself: With all your sufferings and this disability, what made you live a normal life and who inspired you?

Sumit: God is great! And courage is a wonderful thing! I was optimistic, so I faced the calamity without losing heart. Fortunately one of our teachers in our special school inspired me. He told me the story of Wilma Rudolf whose legs were crippled by Polio. Even then she wanted to become the fastest runner in the world and she did it! She practised with determination.

She failed in many races got up started again. The day came when she reached Rome for participating in the 1960 Olympics. In women’s running races (events), she won gold medals in 100 metres running, 200 metres running and 400 metres relay race, defeating all the participants. She became the fastest runner in the then world. The story inspired me and I started my riyaz undauntedly for hours together and here I am today.

• Myself: Were there any obstacles?
• Sumit: Yes, there were. I faced them boldly and moved ahead. People began to admire my songs and music. Now people respect me as rich and famous, but a humble music director.
• Myself: Could you please tell me about the most memorable day in your career as a music composer?
• Sumit: Yes, It is unforgettable that I received my ‘Sangeet Samrat Award’ from Godlike Guru Pandit Hridaynath Mangeshkar.
• Myself: What are your plans for future?
• Sumit: I will continue my service to music and please my fans.
• Myself: What is your advice to the younger generation?
• Sumit: Come what may. Work hard determinently. Win over your physical or mental calamities courageously. Don’t give up and try your best to get success in life.
• Myself: Thank you for giving your precious time and talk.
• Sumit: It’s my pleasure!

Language Study:

1. Complete the following Word Chain of adjectives.

Question 1.
Complete the following Word Chain of adjectives
(a) cruel →____→ ____ → ____ → ____.
(b) medicine →____ → ____ → ____ → ____.
(c) grow →____ →____ → ____ → ____.
(d) physics →______ → ______→ ______ → ______.
Answer:
(a) cruel → lazy → yearlong → genuine → enthusiastic.
(b) medicine → energy → yardstick → keyboard → diary.
(c) grow → withstand → develop → practice → entertain.
(d) physics → secretary → yawn → nature → eligible

2. (A) Convert the following to Exclamatory sentences of the same meaning.

Question 1.
Convert the following to Exclamatory sentences of the same meaning.
(a) Dr Hawking is a very humble man.
(b) He was very clumsy.
(c) He was very simple and intelligent.
(d) Courage is a truly wonderful thing.

Answer:
(a) How humble a man Dr. Hawking is!
(b) How clumsy was he!
(c) How simple and intelligent was he!
(d) How truly wonderful a thing courage is!

(B) Convert the following to Interrogative (Question) form.

Question 1.
Convert the following to Interrogative (Question) form.

1. The prognosis was bad.
2. Stephen decided to continue his research.
3. There are many people who display exemplary courage.
4. His mind would soar up into space like light.

Answer:

1. Wasn’t the prognosis bad?
2. Didn’t Stephen decide to continue his research?
3. Aren’t there many people who display exemplary courage?
4. Wouldn’t his mind soar up into space, like light?

My English Coursebook 10th Digest Chapter 2.4 An Epitome of Courage Additional Important Questions and Answers

Read the following passage and do the activities:

Simple Factual Activities:

Question 1.
Complete the following sentences with the help of the information from the passage:
(Answers are directly given and underlined.)
Answer:

1. Dr. Stephen Hawking was born on the eighth day of January 1942 in Oxford.
2. Courage is the quality which makes people not to lose heart when faced with a great calamity.
3. Dr. Stephen Hawking was a living legend of Cosmology.
4. He wanted to study mathematics but the Oxford University did not have mathematics course then, so he opted to study physics instead.
5. Stephen Hawking’s parents failed to know ! about Stephen that one day their little boy ; will be acclaimed as one of the greatest scientist of this century.
6. Stephen Hawkings was sent to the University of Oxford to study Mathematics.

Question 2.
State whether the following sentences are True or False:
Answer:

1. Dr. Stephen Hawking was born on the eighth day of February 1942. – False
2. Dr. Stephen Hawking was a living legend of Biology. – False
3. Courage makes people not lose heart when faced with a great calamity. – True
4. Dr. Stephen Hawking was born before the death of Galileo. – False

Question 3.
Say whether the following statements are True or False:
Answer:

1. At the age of 17 Dr. Stephen Hawking was suffering from an extremely rare disease. – True
2. Stephen’s teachers liked his handwriting very much. – False
3. He got his Ph.D. studying the concept of ‘Black Holes’. – True
4. At the dismal stage Dr. Hawking enjoyed his life the most. – True

Question 4.
Complete the following sentences with the help of the information given in the passage:
(Answers are directly given and underlined.)
Answer:

1. Dr. Hawking is a very humble man, though he is considered Einstein’s equal in intelligence.
2. Dr. Hawking expressed his thoughts with the help of his finger and with a computer.
3. He was bestowed with numerous honorary doctorates and awards.
4. Dr. Hawking’s ‘A Brief History of Time’ is one of the best selling books of our time.

Complex Factual Activities

Question 1.
What do you know about Dr Stephen Hawking from this passage?
Answer:
Dr Stephen Hawking was born in Oxford on the 8th of January 1942. Nobody could imagine that the little boy would be one of the greatest scientists of this century. He faced a great calamity with great courage and became living legend of Cosmology. His body was bound to a wheelchair but his mind was working and that made him one of the greatest scientists of this century.

As a child he had a lot of love for music and mathematics. His father wanted him to study medicine but he was bent on studying mathematics. The Oxford University did not have a course in mathematics, so he opted to study physics.

Question 2.
Complete the web:
(Answers are directly given and underlined.)
Answer:

Question 3.
Complete the following web showing the effects of the disease ALS or LOU on Dr Hawking:
(Answers are directly given and underlined.)
Answer:

Question 4.
What did Dr. Stephen achieve even after the disease disabled him?
Answer:
Even after the disease disabled Stephen he continued his doctoral research work with renewed vigour. He studied the concept of “Black Holes” and got his Ph.D. in the subject. The study sparked his imagination with bright ideas. He made many epoch-making statements that shook established theories. To explain the concept of ‘Big Bang’ better, Stephen invented what is known as “Lie Algebra”.

Question 5.
What does the writer say about the books authored by Dr. Hawking?
Answer:
The writer says about Dr. Hawking’s books that he wrote many books dealing with his terrific ideas keeping a common man in mind. His writing is full of wit and humour. His style is so lucid that non-scientists can also understand his writing. His book ‘A Brief History of Time’ is one of the best selling books of our time.

Question 6.
Which of Dr. Hawking’s achievements are mentioned in this passage?
Answer:
Dr. Hawking is an authority on profound subjects of science. Numerous honorary doctorates and awards have been bestowed upon him. He is a Fellow of the Royal Society and a member of the US National Academy of Sciences. He has authored many books dealing with his awesome ideas. His book ‘A Brief History of Time’ is one of best selling books of our times.

Activities based on Vocabulary:

Question 1.
Classify the following words into verbs, adjectives and nouns:
whole, know, little, predict, calamity, legend, mind, physics, great, imagine, wonderful, cruel, courage, faced, grew, heart, fate, course.
Answer:

1. Verbs – know, predict, imagine, faced, grew
   
2. Adjectives – little, wonderful, cruel, whole, great
3. Nouns – calamity, legend, mind, physics, courage, heart, fate, course

Question 2.
Find the similar meaning word/phrase for the following from the passage
Answer:

1. a period of hundred years – century
2. a very fine example of something – epitome
3. acclaimed – hailed
4. unexpected change of destiny – quirk of fate

Question 3.
Match the words in Column ‘A’ with their meanings in Column ‘B’:

Column ‘A’	Column ‘B’
1. confined	(a) determined despite difficulties
2. undaunted	(b) awkward
3. perplexed	(c) restricted
4. clumsy	(d) worried because of difficulty

Answer:

Column ‘A’	Column ‘B’
1. confined	(c) restricted
2. undaunted	(a) determined despite difficulties
3. perplexed	(d) worried because of difficulty
4. clumsy	(b) awkward

Question 4.
Write the adjectives for the following nouns from the passage:

1. ideas
2. style
3. courage
4. secrets.

Answer:

1. awesome ideas
2. lucid style
3. exemplary courage
4. core secrets

Question 5.
Match the words in Column ‘A’ with their meanings in Column ‘B’:

Column ‘A’	Column ‘B’
1. profound	(a) a person without any special skill
2. awesome	(b) a perfect example
3. layman	(c) showing very (knowledge) great
4. quintessence	(d) very impressive

Answer:

Column ‘A’	Column ‘B’
1. profound	(c) showing very (knowledge)
2. awesome	(d) very impressive
3. layman	(a) a person without any special skill
4. quintessence	(b) a perfect example

Activities based on Contextual Grammar:

Question 1.
Make the following sentences exclamatory:

i. Courage is truly a wonderful thing.
Answer:
What a wonderful thing courage is!

ii. He was very clumsy.
Answer:
How clumsy he was!

Question 2.
Change the following sentence into positive and comparative degree:
Dr Hawking is one of the greatest scientists of this century.
Answer:
i. Positive degree: Very few (Not many) scientists of this century are as great as Dr. Hawking.
ii. Comparative degree: Dr. Hawking is greater than most other scientists of this century.

Question 3.
He is one of the greatest scientists of this century. (Choose the correct question tag from the given alternatives.)
(a) aren’t he?
(b) is he?
(c) wasn’t he?
(d) isn’t he?
Answer:
He is one of the greatest scientists of this century; isn’t he?

Question 4.
He made many epoch-making statements. (Rewrite the sentence using Present Continuous Tense.)
Answer:
He is making many epoch-making statements.

Question 5.
This disease came as a bolt from the blue. (Rewrite the sentence using Past Perfect Tense.)
Answer:
This disease had come as a bolt from the blue.

Personal Responses:

Question 1.
Do you think, that courage is a wonderful thing? Why do you think so?
Answer:
Yes, I do think that courage is a wonderful I think because it can work miracles in one’s life. A person with great courage stimulates an ordinary or even a disabled person to achieve the impossible, I know a small boy who rescued his younger sister from a tiger’s fierce attack. A courageous person is brave enough to do whatever he/she feels to be right and good in his or her opinion.

Question 2.
What, do you think, are the miseries of a person who is confined to wheelchair?
Answer:
I think, the person who is confined to a wheelchair has to face many restrictions, difficulties and inconveniences. He is mentally and physically depressed all the time. He is deprived of living comfortable happy life. He neither has control over his limbs nor on his mind.

Question 3.
How do you know that Dr. Hawking is a perfect example of optimism and hope?
Answer:
He fully believed in his courage, his intelligence and his authority on profound subjects of science. He did not lose his hopes, even when he was suffering from the dreaded ALS disease. He believed that his life was not different from other people. He tried his best and lived a normal life like other people. He did not think about his sufferings or regret the things that prevented him from doing the things he hoped. His optimism helped him to fulfill his hopes and goals.

Do as directed:

Question 1.
His writing is full of wit and humour.
(Rewrite the sentence using Past Perfect Tense.)
Answer:
His writing had been full of wit and humour.

Question 2.
He is a fellow of the Royal society and a member of the US National Academy of Science.
(Use not only – but also)
Answer:
He is not only a fellow of the Royal society but also a member.

Activities based on Language Study

Do as directed:

Question 1.
Complete the words by using the correct letter:

1. d e _ t h
2. s t _ g e
3. b o o _ s
4. b _ a v e

Answer:

1. d e a t h
2. s t a g e
3. b o o k s
4. b r a v e

Question 2.
Put the following words in alphabetical order:

1. profound, prognosis, planet, possible
2. undaunted, confined, awesome, explain

Answer:

1. planet, possible, profound, prognosis
2. awesome, confined, explain, undaunted

Question 3.
Punctuate the following sentences:

1. he said to her we must have to come out of this calamity
2. shall we reach meeras house on time i asked.

Answer:

1. He said to her, “We must have to come out of this calamity.”
2. “Shall we reach Meera’s house on time?” I asked.

Question 4.
Make four words (minimum 3 letters each) using the letters in the word meanwhile:
Answer:
mean, while, meal, mile

Question 5.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Do as directed:

1. Attempt anyone:

b. Add a clause to the following sentence to expand it meaningfully.
Nobody thought that
Answer:
Nobody thought that he would become such a great sportsman.

2. Attempt anyone:

a. Add a prefix or suffix to make new words:
1. known
2. lucky
Answer:
1. unknown
2. unlucky

OR

b. Make a meaningful sentence using any one of the following words:
1. known
2. lucky
Answer:
1. Satyendra Nath Bose was one of the known scientists of India.
2. Our school team was lucky to win the Kabaddi match at the last moment.

My English Coursebook 10th Digest Pdf Unit 2

• You Start Dying Slowly … Class 10 English Solutions
• The Boy who Broke The Bank Class 10 English Solutions
• The Twins Class 10 English Solutions
• An Epitome of Courage Class 10 English Solutions
• Book Review – Swami and Friends Class 10 English Solutions
• World Heritage Class 10 English Solutions

Class 10th Sanskrit Aamod Chapter 11 जटायुशौर्यम् Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Amod Chapter 11 जटायुशौर्यम् Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 11 Question Answer

Sanskrit Amod Std 10 Digest Chapter 11 जटायुशौर्यम् Textbook Questions and Answers

भाषाभ्यास:

1. लिट्पाणि चित्वा लिखत ।

प्रश्न 1.

2. नाम-तालिकां पूरयत ।

3. सन्धिविग्रहं कुरुत ।

प्रश्न अ.
ततस्सा
उत्तरम् :
ततऽस्य – ततः + अस्य। महातेजा

प्रश्न आ.
ददर्शायतलोचना
उत्तरम् :
ददर्शायतलोचना – ददर्श + आयतलोचना।

प्रश्न इ.
वृद्धोऽहम्
उत्तरम् :
वृद्धोऽहम् – वृद्धः + अहम्।

प्रश्न ई.
तथाप्यादाय
उत्तरम् :
तथाप्यादाय – तथा + अपि + आदाय।

4. माध्यमभाषया उत्तरं लिखत ।
जटायुरावणयोः सङ्घर्षस्य वर्णनं कुरुत ।

प्रश्न 1.
जटायुरावणयोः सङ्घर्षस्य वर्णनं कुरुत।
उत्तरम् :
‘जटायुशौर्यम्’ या पाठात जटायू नामक गिधाडाने सीतेला रावणाच्या तावडीतून सोडवण्यासाठी स्वत:च्या प्राणांची आहुती कशी दिली, याचे वर्णन केले आहे. सीतेचे अपहरण करण्यासाठी रावण साधूच्या वेशात सीतेच्या पर्णकुटीपाशी पोहोचला. त्याला भिक्षा देण्यासाठी सीता कुटीबाहेर आली असता त्याने कपटाने तिचे अपहरण केले व तिला आपल्या सोबत लंकेस घेऊन जाऊ लागला. ती दुःखाने रामाचा धावा करत असताना तिच्या दृष्टीस जटायू पडला. तिने बचावासाठी मारलेली आर्त हाक जटायूने ऐकली व तिला मदत करण्यासाठी तो पुढे सरसावला.

प्रथम जटायूने नम शब्दात रावणाला विनंती केली की, “परस्त्रीचा अपमान करु नकोस, हे नीच कृत्य थांबव. कारण दुसऱ्यांना त्रास होईल असे वर्तन वीरपुरुषाने करू नये, मी वृद्ध आहे, पण तू तरुण, धनुष्यबाणधारी, रथारूढ, चिलखत घातलेले आहेस. तरीही मी तुला सहजासहजी सीतेला नेऊ देणार नाही.”

असे बोलून त्याने आपल्या तीक्ष्ण नखांनी रावणावर हल्ला चढवला. आपल्या पायांनी रावणाचे मोतीजडीत धनुष्यबाण मोडून टाकले. जटायू पूर्ण शक्तीने रावणावर तुटून पडला. त्यामुळे संतप्त होऊन रावणाने त्याला चिरडून टाकले. तलवारीने त्याचे पंख, व पाय छाटून टाकले. रावणाच्या या क्रूर कर्मामुळे जटायू गतप्राण होऊन जमिनीवर पडला.

आजच्या काळात एक माणूस दुसऱ्या माणसाला मदत करताना संकोच करतो. अशा समाजाच्या डोळ्यांत अंजन घालण्याचे काम या पाठाद्वारे होते.

The chapter ‘teryxid describes how a vulture sacrificed it’s life for helping file to get released from the custody of रावण. रावण reached the hermitage of सीता disguised as a monk. As she came out of the hermitage to give him alms, he abducted her deceitfully and took her along him to Lanka. She saw as she was lamenting in grief and pleaded TH to come for her rescue. Hearing her lamenting with grief Fery came forward to help her.

At first Hery humbly requested to that “You should not disrespect other’s wife. Stop this inferior deed as a brave man should not behave in such a way that it troubles others. I am old. You are young, armed with bow and arrows, seated on a chariot and wearing an armour.

Yet I can easily stop you from abducting सीता. Saying thus, it attacked 17 with sharp nails. He broke as bow, that was adorned with pearls, with his feet. It fought with strength. But 74 crushed it with anger. He cut his wings and feet with a sword, 24 got dead and fell on the ground due to cruel behavior of रावण. This story is an eye-opener in today’s world where people hesitate to help others in their time of need.

5. समानार्थकशब्दान् लिखत ।
सीता, रावणः, शृङ्गम्, तुण्डम्, पतगः

प्रश्न 1.
समानार्थकशब्दान् लिखत ।
सीता, रावणः, शृङ्गम्, तुण्डम्, पतगः
उत्तरम् :

• सीता – वैदेही, जानकी, मैथिली।
• रावणः – दशाननः, दशग्रीवः, लङ्काधीशः, लकेशः।
• शृङ्गम् – शिखरम्।
• तुण्डम् – मुखम्, आननम्, वदनम्, वक्त्रम्।
• पतगः – पक्षी, द्विजः, खगः।

6. धातु-तालिकां पूरयत ।

7. सर्वनाम-तालिकां पूरयत ।

8. विशेषणानि अन्विष्य लिखत ।

प्रश्न अ.

उत्तरम् :

प्रश्न आ.

उत्तरम् :

प्रश्न इ.

उत्तरम् :

9. सूचनानुसारं कृती: कुरुत।

प्रश्न अ.
सीता वनस्पतिगतं गृधं ददर्श (लङ्-लकारे परिवर्तयत ।)
उत्तरम् :
सीता वनस्पतिगतं गृधम् अपश्यत् ।

प्रश्न आ.
जटायुः रावणस्य गात्रे व्रणान् चकार (लङ्-लकारे परिवर्तयत ।)
उत्तरम् :
जटायुः रावणस्य गात्रे व्रणान् अकरोत्।

प्रश्न इ.
रावणः खड्गमुद्धृत्य पक्षौ अच्छिनत् ।(पूर्वकालवाचकम् अव्ययं निष्कासयत ।)
उत्तरम् :
रावणः खड्गम् उदधरत् पक्षौ अच्छिनत् च ।

Sanskrit Amod Class 10 Textbook Solutions Chapter 11 जटायुशौर्यम् Additional Important Questions and Answers

सन्धिविग्रहं :

1. गृहीताऽतिचुक्रोश – गृहीता + अतिचुक्रोश।
2. रामेति – राम + इति।
3. करुणा वाचो विलपन्ती – करुणा: + वाचः + विलपन्ती।
4. मामार्य – माम् + आर्य।
5. ह्रियमाणामनाथवत् – ह्रियमाणाम् + अनाथवत्।
6. राक्षसेन्द्रेणाकरुणम् – राक्षसेन्द्रेण + अकरुणम्।
7. शब्दमवसुप्तस्तु – शब्दम् + अवसुप्त: +तु।
8. जटायुरथ – जटायु: + अथ।
9. निरैक्षद् वैदेहीम् – निक्षत् + वैदेहीम्।
10. पर्वतशृङ्गाभस्तीक्ष्णतुण्डः – पर्वतशृङ्गाभः + तीक्ष्णातुण्डः।
11. श्रीमान्व्याजहार – श्रीमान् + व्याजहार।
12. तत्समाचरेद्धीरो परो यदि – तत् + समाचरेत् + धीरः + पर: + यत् + हि।

अवबोधनम्

(क) पूर्णवाक्येन उत्तरं लिखत।

प्रश्न 1.
सीता किम् अतिचुक्रोश?
उत्तरम् :
सीता रामेति अतिचुक्रोश।

प्रश्न 2.
सीतायाः कानि विशेषणानि?
उत्तरम् :
गृहीता, यशस्विनी, दुःखार्ता इति सीतायाः विशेषणानि।

प्रश्न 3.
सीता कं ददर्श?
उत्तरम् :
सीता वनस्पतिगतं गृधं ददर्श।

प्रश्न 4.
सीता केन ह्रियमाणा?
उत्तरम् :
सीता राक्षसेन्द्रेण ह्रियमाणा।

प्रश्न 5.
राक्षसेन्द्रः कीदृशः?
उत्तरम् :
राक्षसेन्द्रः पापकर्मा।

प्रश्न 6.
जटायुः कं कं अपश्यत्?
उत्तरम् :
जटायुः रावणं वैदेहीं च अपश्यत्।

प्रश्न 7.
क: शब्दं शुश्रुवे?
उत्तरम् :
जटायु: शब्दं शुश्रुवे।

प्रश्न 8.
कः अवसुप्तः?
उत्तरम् :
जटायुः अवसुप्तः।

प्रश्न 9.
जटायुः कीदृशः आसीत्?
उत्तरम् :
जटायुः पर्वतशृङ्गाभः, तीक्ष्णतुण्डः, खगोत्तमः, वनस्पतिगतः, श्रीमान आसीत।

प्रश्न 10.
धीर: किं न समाचरेत्?
उत्तरम् :
यत् पर: विगर्हयेत् तत् धीर: न समाचरेत्।

प्रश्न 11.
जटायुः कीदृशः आसीत् ?
उत्तरम् :
जटायुः वद्धः आसीत्।।

प्रश्न 12.
रावणः कीदृशः आसीत्?
उत्तरम् :
रावणः युवा, बन्ची, सरधः, कवची, शरी च आसीत्।

प्रश्न 13.
जटायुः कीदृशः आसीत्?
उत्तरम् :
जटायुः महाबलः, पतगसत्तमः च आसीत्।

प्रश्न 14.
जटायुः कथं व्रणान् चकार?
उत्तरम् :
जटायुः तस्य तीक्ष्णनखाभ्यां चरणाभ्यां च व्रणान् चकार ।

प्रश्न 15.
जटायुः कीदृशः आसीत्?
उत्तरम् :
जटायु:महातेजाः, पतगोत्तमः च आसीत्।

प्रश्न 16.
रावणस्य चापः कीदृशः आसीत्?
उत्तरम् :
रावणस्य चाप:मुक्तामणिविभूषितः च आसीत्।

प्रश्न 17.
जटायुः चापं कथं बभञ्ज?
उत्तरम् :
जटायुः चापंचरणाभ्यां बभञ्ज ।

प्रश्न 18.
दशग्रीवः क्रोधात् किमकरोत् ?
उत्तरम् :
दशग्रीवः क्रोधात् गृध्रराजम् अपोथयत्।

प्रश्न 19.
दशग्रीवः खड्गमुद्धृत्य किमकरोत् ?
उत्तरम् :
दशग्रीवः खड्गमुद्धृत्य गृध्रराजस्य पक्षी, पाश्वी,पादौ च अच्छिनत्।

प्रश्न 20.
केन रौद्रकर्मणा गृधः हत:?
उत्तरम् :
रक्षसा रौद्रकर्मणा गृध्रः हतः।

प्रश्न 21.
क; धरण्याम् निपपात?
उत्तरम् :
गृध: धरण्याम् निपपात।

प्रश्न 22.
गृधः कीदृशः आसीत्?
उत्तरम् :
गृधः छिन्नपक्षः, अल्पजीवित:, च आसीत्।

प्रश्न 23.
रावणेन गृहीता सीता।
उत्तरम् :
रावण : गृहीतवान् सीताम्।

(ख) विशेषण – विशेष्य – सम्बन्धः।

विशेषणम्	विशेष्यम्
गृहीता / यशस्विनी / दुःखार्ता	सीता
विलपन्ती, सुदुःखिता, आयतलोचना	सीता
आर्य	जटायो
पापकर्मणा	राक्षसेन्द्रेण
अवसुप्तः	जटायुः
पर्वतशृङ्गाभः, तीक्ष्णतुण्डः, खगोत्तमः, वनस्पतिगतः, श्रीमान्	जटायुः
शुभाम्	गिरम
वृध्दः	जटायुः
युवा, धन्वी, सरथः, कवची, शरी	रावणः
महाबलः, पतगसत्तमः	जटायुः
महातेजाः, पतगोत्तमः	जटायु:
सशरम्, मुक्तामणिविभूषितम्	चापम्
हतः, छिन्नपक्षः, अल्पजीवितः	गृध्रः

(ग) त्वं’ स्थाने ‘भवान्’ योजयत।

प्रश्न 1.
त्वं कुशली न गमिष्यसि।
उत्तरम् :
भवान् कुशली न गमिष्यति।

प्रश्न 2.
त्वं युवा असि।
उत्तरम् :
भवान् युवा अस्ति।

(घ) लकारं परिवर्तयत ।

प्रश्न 1.
त्वं कुशली न गमिष्यसि । (विधिलिङ्लकारे परिवर्तयत।)
उत्तरम् :
त्वं कुशली न गच्छे ।

प्रश्न 2.
गृधः धरण्यां निपपात। (लङ्लकारे परिवर्तयत।)
उत्तरम् :
गृधः धरण्यां न्यपतत् ।

समासाः

समस्तपदम्	अर्थ	समासविग्रहः	समासनाम
खगोत्तमः	the excellent bird	उत्तमः खगः।	कर्मधारय समास
आयतलोचना	the one with wide eyes	आयते लोचने यस्याः सा।	बहुव्रीहि समास
वनस्पतिगतः	in the plant/woods	वनस्पतिं गतः।	द्वितीया तत्पुरुष समास
गृध्रराज:	king of vultures	गृधाणां राजा।	षष्ठी तत्पुरुष समास
महाबलः	the one with great strength	महत् बलं यस्य सः।	बहुव्रीहि समास
राक्षसेन्द्रः	king of demons	राक्षसाणाम् इन्द्रः।	षष्ठी तत्पुरुष समास
तीक्ष्णतुण्ड:	the one with sharp beak	तीक्ष्णं तुण्डं यस्य सः।	बहुव्रीहि समास

भाषाभ्यास:

समानार्थकशब्दान् लिखत।

• लोचने – नेत्रे, नयने ।
• शब्दः – नादः, रवः ।
• गिर् – वाक्, वाणी, भाषा।

जटायुशौर्यम् Summary in Marathi and English

प्रस्तावना :

रामायण व महाभारताचा भारतातील ‘आर्ष महाकाव्ये’ असा गौरव केला जातो. यापैकी रामायण ही महर्षी वाल्मीकींनी लिहिलेली जगभरातील सर्वात प्रथम रचलेली काव्यकृती आहे. त्यात 7 कांडे असून 24,000 श्लोक आहेत. वनवासादरम्यान, रावण साधूच्या वेशात सीतेच्या पर्णकुटीपाशी गेला आणि कपटाने तिचे अपहरण केले.

परंतु हे पापकर्म करण्यापासून रोखण्याचा जटायू नामक गिधाडाने जीवापाड प्रयत्न केला. ‘जटायुशौर्यम्’ या पाठात जटायू नामक गिधाडाने सौतेला रावणाच्या तावडीतून सोडवण्यासाठी स्वत:च्या प्राणांची आहुती कशी दिली याचे वर्णन केले आहे.

आजच्या काळात एक माणूस दुसऱ्या माणसाला अडचणीतून सोडवताना संकोच करतो, अशा समाजाच्या डोळ्यांत अंजन घालण्याचे कार्य हा पाठ करतो. रामायणात अशा अनेक प्राणिमात्रांनी स्वत:च्या जीवाची पर्वा न करता रामाला सहकार्य केले होते.

रामायणम् and महाभारतम् are honoured as the epic poetries of India. Out of these, रामायणम् is the first ever poetry composed in the world, by the great sage वाल्मीकि. It contains seven cantos comprising 24,000 verses.

During the exile, Tu reached the hermitage of to having disguised as a monk and abducted her deceitfully. जटायू a vulture tried to stop रावण from doing this sinful deed. The chapter ‘जटायुशौर्यम्’ describes how a vulture sacrificed it’s life for helping it to get released from the custody of 144.

This story is an eyeopener in today’s world where people hesitate to help others in their time of need. In रामायणम्, many animals help राम without caring for their lives.

श्लोकः 1

सा गृहीताऽतिचुक्रोश रावणेन वशस्विनी।
रामेति सीता दुःखार्ता रामे दूरगते वने ।।१।।

अनुवादः

राम वनात दूरवर गेला असता, रावणाने धरलेली तेजस्वी सीता दु:खाने व्याकूळ होऊन ‘राम’ असा आक्रोश करू लागली.

The illustrious lady, सीता, held by रावण, lamented aloud as राम being sunk in grief, when राम had gone far in the forest.

श्लोक: 2

सा तदा करुणा वाचो विलपन्ती सुदुःखिता।
वनस्पतिगतं गृधं ददर्शायतलोचना ।।2।।

अनुवादः

तेव्हा मोठ्या डोळ्यांच्या, अत्यंत दु:खीकष्टी झालेल्या सीतेने करुण आवाजात विलाप करत असताना झाडावर गिधाड पाहिले.

The wide-eyed in who was extremely grieved, was lamenting in pitiable voice, saw a vulture seated on a tree.

श्लोक: 3

जटायो पश्य मामार्य ह्रियमाणामनाथवत्।
अनेन राक्षसेन्द्रेणाकरुणं पापकर्मणा ।।3।।

अनुवादः

“हे आर्य जटायू, पहा या पापी राक्षसेंद्राकरवी एखाद्या अनाथाप्रमाणे निर्दयीपणे माझे अपहरण केले जात आहे.”

“Oh noble जटायू, see me being abducted like an orphan without mercy by this sinful lord of the demons रावण.”

श्लोकः 4

तं शब्दमवसुप्तस्तु जटायुरथ शश्रुवे।
निरक्षद् रावणं क्षिप्रं वैदेहीं च ददर्श सः ।।4।।

अनुवादः

निद्रिस्त असलेल्या त्या जटायूने ते शब्द ऐकले, वेगाने जाणाऱ्या रावणाला व सीतेला पाहिले.

जटायू, who was asleep, heard those words, saw रावण and He going hurriedly.

श्लोक: 5

तत: पर्वतशृङ्गाभस्तीक्ष्णतुण्डः खगोत्तमः।
वनस्पतिगतः श्रीमान्व्याजहार शुभां गिरम् ।।5।।

अनुवादः

तेव्हा पर्वतशिखराप्रमाणे रंग असलेला, तीक्ष्ण चोच असलेला, श्रेष्ठ खग, झाडावर बसलेला आदरणीय (जटायू) नम्र आवाजात म्हणाला.

Then the excellent bird whose colour was like the peak of the mountain, one with a sharp beak, the respected one, seated on a tree spoke in humble speech.

श्लोक: 6

निवर्तय मति नीचां परदाराभिमर्शनात् ।
न तत्समाचरेद्धीरो परो यद्धि विगर्हयेत् ।।६।।

अनुवादः

“(हे रावणा) परक्या स्त्रीचा मान राखण्यासाठी तुझा नीच विचार थांबव. कारण दुसऱ्याने निंदा करावी असे शूरवीर वागत नाहीत.”
“(Oh रावण) changeyour ill-mind as other’s wife should be respected. Because indeed a brave man does not – behave in such a way that is condemned by others.

श्लोकः 7

बद्धोऽहं त्वं युवा धन्वी सरथः कवची शरी।
तथाप्यादाय वैदेहीं कुशली न गमिष्यसि ।।7।।

अनुवादः

मी जरी वृद्ध असलो आणि तू तरुण, धनुष्यबाणासहित, रथारूढ, चिलखत घालून असलास, तरी तू वैदेहीला सहजपणे नेऊ शकत नाहीस.” Although I am old and you are young, armed with bows and arrows, seated on a chariot, wearing an armour, yet you will not go taking & easily.

श्लोक: 8

तस्य तीक्ष्णनखाभ्यां तु चरणाभ्यां महाबलः।
चकार बहुधा गात्रे व्रणान्यतगसत्तमः ।।8।।

अनुवादः

बलाढ्य असलेल्या (जटायू) ने तीक्ष्ण नखांनी व पायांनी (रावणाच्या) शरीरावर बऱ्याच जखमा केल्या.
The extremely strong and the best bird did many wounds on his (रावण’s) body with sharp nails and feet.

श्लोकः 9

ततोऽस्य सशरं चापं मुक्तामणिविभूषितम्।
चरणाभ्यां महातेजा बभञ्ज पतगोत्तमः।।९।।

अनुवाद:

तेव्हा अत्यंत पराक्रमी, श्रेष्ठ खग असलेल्या (जटायू) ने त्याचे मोती जडवलेले व बाण लावलेले धनुष्य पायांनी मोडून टाकले.

Then the extremely brave, great bird (er) broke his bow, that was adorned with pearls and attached with an arrow with his feet.

श्लोकः 10

ततः क्रोधादशग्रीवो गृध्रराजमपोथयत् ।
पक्षौ पाश्वा च पादौ च खड्गमुद्धृत्य सोऽच्छिनत्।।10।।

अनुवादः

तेव्हा त्या दशग्रीव (रावणा) ने रागाने त्या गिधाडाला चिरडून टाकले. तलवार उपसून त्याचे पंख आणि पाय छाटून टाकले.

दशग्रीव (रावण) crushed the great vulture angrily. Raising his sword, cut his wings, and feet.

श्लोक: 11

स छिन्नपक्षः सहसा रक्षसा रौद्रकर्मणा।
निपपात हतो गृधो धरण्यामल्पजीवितः ।।11।।

अनुवादः

राक्षसाच्या रौद्र कृत्यामुळे लगेच मारले गेलेले, पंख छाटलेले ते अल्पायुषी गिधाड जमिनीवर पडले.

That short-lived vulture, whose wings were cut, got killed immediately due to the terrible deeds of the demon and fell on the ground.

शब्दार्था:

1. गृह्यता – held – धरले होते
2. यशस्विनी – illustrious – तेजस्वी
3. अतिचुक्रोश – lamented aloud – मोठ्याने आक्रोश करत ह्येतो
4. दुःखार्ता – sunk in grief – दुःखात बुडालेली
5. पापकर्मणा – by the sinful one – पापी माणसाकडून
6. अकरुणम् – without mercy – निर्दयीपणे
7. अनाथवत् – like an orphan – अनाथ असल्याप्रमाणे
8. ह्रियमाणाम् – being abducted – अपहरण केले जात असपाऱ्या
9. अवसुप्तः – asleep – झोपलेला
10. क्षिप्रम् – speedily – वेगाने
11. निरक्षत् – observed – पाहिले
12. शुश्रुवे – had heard – ऐकले होते+
13. पर्वतशृङ्गाभः – colour like the peak of the mountain – पर्वतशिखराप्रमाणे रंग असलेला
14. तीक्ष्णतुण्डः – having sharp beak – तीक्ष्ण चोच असलेला
15. व्याजहार – spoke – बोलला
16. शुभां – in humble speech – गिरम्
17. सरथः – seated on a chariot – रथी / रथारूढ़
18. धन्वी – armed with a bow – धनुष्यधारी
19. कवची – wearing armour – चिलखत घातलेला
20. शरी – having arrows – बाण जवळ असलेला
21. कुशली – (here) easily – (इथे) सहजपणे
22. महाबलः – extremely strong – बलाढ्य
23. पतगसत्तमः – the best bird – सर्वोत्तम पक्षी
24. वणान् – wounds – जखमा
25. गात्रे – on the body – शरीरावर
26. चकार – did / made – केले
27. महातेजाः – extremely lustrous / extremely brave – अत्यंत तेजस्वी / अत्यंत शूर
28. पतगोत्तमः – great bird – श्रेष्ठ खग
29. मुक्तामणिविभूषितम् – adorned with pearls – मोती जडवलेले
30. बभज – broke – तोडले
31. दशग्रीवः – Ravan – रावण
32. खड्गम् – sword – तलवार
33. अपोथयत् – crushed – चिरडून टाकले
34. अच्छिनत् – cut – कापले
35. छिनपक्ष: – whose wings are cut – पंख छाटलेला
36. सहसा – at once – लगेच
37. रौद्रकर्मणा – due to terrible deeds – रौद्र कृत्यामुळे
38. निपपात – fell – पडला
39. अल्पजीवितः – short-lived – अल्पायुषी

Aamod Sanskrit Book 10th Class Solutions

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• अमूल्यं कमलम् Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्ययुग्मम् Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• धेनोर्व्याघ्रः पलायते Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• जटायुशौर्यम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• प्रतिपदं संस्कृतम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Anand Chapter 1 आद्यकृषक: पृथुवैन्यः Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Anand Chapter 1 आद्यकृषक: पृथुवैन्यः Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 1 Question Answer

Sanskrit Anand Std 10 Digest Chapter 1 आद्यकृषक: पृथुवैन्यः Textbook Questions and Answers

भाषाभ्यास:

1. पूर्णवाक्येन उत्तरं लिखत ।

प्रश्न अ.
चारणाः किमर्थम् उत्सुका: ?
उत्तरम् :
चारणाः पृथुनृपस्य स्तुतिं गातुम् उत्सुकाः ।

प्रश्न आ.
भ्रमणसमये पृथुराजेन किं दृष्टम् ?
उत्तरम् :
भ्रमणसमये पृथुराजेन दृष्टं यत् प्रजा: अतीव कृशाः अशक्ता: च। ताः पशुवत् जीवन्ति । निकृष्टान्नं खादन्ति।

प्रश्न इ.
वसुन्धरायाः उदरे किं वर्तते ?
उत्तरम् :
वसुन्धराया: उदरे धनधान्यादि सर्व वस्तुजातं वर्तते।

प्रश्न ई.
स्त्रीरूपं धृत्वा पृथुनृपस्य पुरतः का प्रकटिता अभवत् ?
उत्तरम् :
स्त्रीरूपं धृत्वा पृथुनूपस्य पुरतः भूमि: प्रकटिता अभवत्।

प्रश्न उ.
पृथुवैन्यः कृषिकार्यार्थं जलस्य व्यवस्थापनं कथम् अकरोत् ?
उत्तरम् :
पृथुवैन्यः वृष्टिजलसञ्चयं कृत्वा जलव्यवस्थापनम् अकरोत्।

2. जालरेखाचित्रं पूरयत ।

प्रश्न अ.

उत्तरम् :

प्रश्न आ.

उत्तरम् :

प्रश्न इ.

उत्तरम् :

3. पाठ्यांशं पठित्वा प्रवाहिजालं पूरयत ।

प्रश्न 1.
पाठ्यांशं पठित्वा प्रवाहिजालं पूरयत ।

उत्तरम् :

4. माध्यमभाषया उत्तरत ।

प्रश्न अ.
भूमाता पृथुवैन्यं किम् उपादिशत् ?
उत्तरम् :
आद्यकृषक: पृथुवैन्यः हा पाठ म्हणजे पृथुवैन्य राजाच्या कृषिविषयक कार्याचा प्रारंभ व त्याचा विकास याचा इतिहास स्पष्ट करणारी आख्यायिका आहे. एकदा पृथुवैन्य राजा त्याच्या राज्यात फिरत असताना त्याने प्रजेला दयनीय अवस्थेत पाहिले. त्याच्या राज्यातील लोक हलक्या प्रतीच्या अन्नामुळे क्षीण, अशक्त झाले होते. हे पाहून राजाचे मन द्रवले व तो चिंताग्रस्त झाला.

पुरोहितांच्या सांगण्यानुसार त्याने पृथ्वीमधून धन-धान्य बाहेर काढण्याकरिता धनुष्य सज्ज केले. तेव्हा पृथ्वीने स्त्रीरूप धारण केले व राजाला कृषिकार्य करण्याचा आदेश दिला.

भूमातेने नांगर, कुदळ, फावडे, कोयता या उपकरणांच्या साहाय्याने राजाला कृषिकार्य करण्यास सांगितले. भूमातेने राजाला त्याच्या अन्यायी वडिलांचा संदर्भ दिला तसेच त्यावेळी राजाच्या सदाचरणाचे कौतुक केले आणि राजाच्या कृषिकार्यावर तिची कृपा होईल, असे आश्वासन दिले.

आद्यकृषक: पृथुवेन्य: is the legend that reveals the history of Pruthuvainya’s initiation of agricultural work and civilization. Once, the king पृथुवैन्यं was wandering in his kingdom; He saw the pitiable condition of his subjects. His subjects were thin and weak due to low-quality food. The king’s heart melted with compassion and his mind was filled with worry.

On the advice of a priest, he set the bow; when he was about to take out wealth and grains from the earth, the earth disguised as a woman and advised him to do agricultural work.

The earth advised the king to work with the help of hoe, plough, spade, sickles along with his subjects. She reminded the king of his father who was the corrupt king. She praised the king’s righteous behaviour and assured him with her favor in agricultural work.

प्रश्न आ.
धरित्र्याः उपदेशं मनसि निधाय पृथुवैन्यः किं किम् अकरोत् ?
उत्तरम् :
आद्यकृषक: पृथुवैन्यः हा पाठ म्हणजे पृथुवैन्य राजाच्या कृषिविषयक कार्याचा प्रारंभ व त्याचा विकास याचा इतिहास स्पष्ट करणारी आख्यायिका आहे. राजाने नदीचा मार्ग अडविला व ते पाणी कृषिकार्यासाठी उपयोगात आणले. पावसाच्या पाण्याचा संचय करून पाण्याचे व्यवस्थापन केले.

जमिनीला सुपीक करण्यासाठी राजाने विशेष प्रयत्न केले, नंतर लोकांनी धान्याच्या बिया पेरल्या. राजाने सुद्धा विविध प्रकारची बी-बियाणे गोळा करून, त्याचे संस्करण केले व प्रयत्नपूर्वक त्याची पेरणी केली. पाऊस झाल्यानंतर धान्यांत अंकुर फुटला. राजाच्या परिश्रमामुळे धान्यलाभ झाला व सगळी प्रजा अतिशय आनंदित झाली.

आद्यकृषक: पृथुवैन्य: is the legend that reveals the history of Pruthuvaiya’s initiation of agricultural work and civilization The king obstructed the river’s path for agricultural work. He stored the rain water and did the water-management. He took special efforts to make the land fertile.

Afterwards, people sowed the seeds of grains. The king gathered varied seeds, refined it and sowed with efforts. After the rains, the sprouts were germinated and all subjects became happy by the gain of grains.

5. अमरकोषात् योग्यं समानार्थक शब्दं योजयित्वा वाक्यं पुनर्लिखत ।

प्रश्न अ.
राजा चिन्ताकुलः जातः ।
उत्तरम् :
राजायाः दैन्यावस्थां दृष्ट्वा राजा चिन्ताकुलः जातः।

प्रश्न आ.
भूमिः स्त्रीरूपं धृत्वा प्रकटिता ।
उत्तरम् :
गोत्रा / कुः / पृथिवी / पृथ्वी / क्ष्मा / अवनिः । मेदिनी / मही स्त्रीरूपं धृत्वा प्रकटिता।

6. मेलनं कुरुत।

प्रश्न 1.
मेलनं कुरुत

उत्तरम् :

विशेषणम्	विशेष्यम्
कृशाः	प्रजाः
उर्वरा	भूमिः
आनन्दिताः	प्रजाजना:
दःशासकः	वेनः
प्रजाहितदक्षः	पृथुः

7. समानार्थकशब्द लिखत ।
वृक्षः, भूमिः, राजा, धनुः, नदी ।

प्रश्न 1.
समानार्थकशब्द लिखत ।
वृक्षः, भूमिः, राजा, धनुः, नदी ।
उत्तरम् :

• वृक्षः – तरुः, महीरुहः, पादयः, द्रुमः ।
• भूमिः – पृथिवी, पृथ्वी, धरा, वसुन्धरा, अवनी, मही, मेदिनी, क्षमा, गोत्रा, कुः।
• राजा – महीपतिः, महीपालः, नरेशः, नृपः, भूपः, नरपतिः, भूपाल: ।
• धनुः – त्रिणता, चापः, शरासन:, कोदण्डः ।
• नदी – तटिनी, निम्नगा, आपगा, सरित्।

8. विरुद्धार्थकशब्दं लिखत ।
स्तुतिः, सद्गुणाः, प्रसन्नाः, अशक्ताः, पुरतः, कृशाः ।

प्रश्न 1.
विरुद्धार्थकशब्दं लिखत ।
स्तुतिः , सद्गुणाः, प्रसन्नाः, अशक्ताः, पुरतः, कृशाः ।
उत्तरम् :

• स्तुतिः × निन्दा।
• सद्गुणाः × दुर्गुणाः।
• प्रसन्नाः × खिन्नाः, दुःखिताः, विषण्णाः।
• अशक्ताः × सशक्ताः।
• पुरतः × पश्चात्, पृष्ठतः।
• कृशाः × पीवराः।

9. कः कं वदति ?

प्रश्न अ.
तिष्ठन्तु चारणाः ।
उत्तरम् :
लोट्लकारः।

प्रश्न आ.
तत्प्राप्तुं यतस्व ।
उत्तरम् :
पुरोहितः पृथुवैन्यं वदति।

प्रश्न इ.
तव पिता दुःशासकः ।
उत्तरम् :
भूमिः पृथुवैन्यं वदति।

प्रश्न ई.
अत: धनुः त्यज ।
उत्तरम् :
भूमिः पृथुवैन्यं वदति।

10. सन्धिविग्रहं कुरुत ।

प्रश्न अ.
उदर एव
उत्तरम् :
उदर एव – उदरे + एव।

प्रश्न आ.
पशुवजीवन्ति
उत्तरम् :
पशुवजीवन्ति – पशुवत् + जीवन्ति ।

प्रश्न इ.
अशक्ताश्च
उत्तरम् :
अशक्ताश्च – अशक्ताः + च।

प्रश्न ई.
पुरोहितोऽवदत् ।
उत्तरम् :
पुरोहितोऽवदत् – पुरोहितः + अवदत्।

Sanskrit Anand Class 10 Textbook Solutions Chapter 1 आद्यकृषक: पृथुवैन्यः Additional Important Questions and Answers

अवबोधनम्‌ :

उचितं‌ ‌कारणं‌ ‌चित्वा‌ ‌वाक्यं‌ ‌पुनर्लिखत।‌ ‌

प्रश्न 1.
स्तुतिगायकाः‌ ‌प्रसन्नाः‌ ‌अभवन्‌ ‌यतः‌ ‌
(अ)‌ ‌पाठकाः‌ ‌राज्ञः‌ ‌प्रशंसाम्‌ ‌अकुर्वन्‌ ‌।‌‌
(ब)‌ ‌स्तुतिपाठकाः‌ ‌राज्ञः‌ ‌निःस्पृहताम्‌ ‌अजानन्।‌
‌उत्तरम्‌ ‌
(ब)‌ ‌स्तुतिपाठका:‌ ‌राज्ञः‌ ‌नि:स्पृहताम्‌ ‌अजानन्।‌

प्रश्न 2.‌
‌प्रजाः‌ ‌अतीव‌ ‌कृशाः‌ ‌अशक्ता:‌ ‌च‌ ‌यतः‌‌
(अ)‌ ‌ताः‌ ‌पशुवज्जीवन्ति‌ ‌निकृष्टानं‌ ‌खादन्ति‌ ‌च।‌‌
(ब)‌ ‌ता:‌ ‌मिष्टान्नं‌ ‌खादन्ति।‌
‌उत्तरम्‌
‌(अ)‌ ‌ता:‌ ‌पशुवज्जीवन्ति‌ ‌निकष्टानं‌ ‌खादन्ति‌ ‌च।‌ ‌

प्रश्न 3.
पृथुवैन्यः‌ ‌स्वप्रजाः‌ ‌दृष्ट्वा‌ ‌चिन्ताकुल:‌ ‌जात:‌ ‌यतः‌‌
(अ)‌ ‌तस्य‌ ‌प्रजाजनाः‌ ‌परस्परं‌ ‌वादविवादं‌ ‌कुर्वन्ति।‌‌
(ब)‌ ‌तस्य‌ ‌प्रजाजना:‌ ‌पशुवत्‌ ‌जीवन्ति।‌ ‌
उत्तरम्‌
‌(ब)‌ ‌तस्य‌ ‌प्रजाजनाः‌ ‌पशुवत्‌ ‌जीवन्ति‌ ‌।‌‌

प्रश्न 4.
भूम्या धनधान्यपुष्पफलानि स्व-उदरे निहितानि यत: ……..
(अ) वेनभूप: दुःशासक: आसीत्।
(ब) भूमिः स्वभावेन कृपणा आसीत्।
उत्तरम् :
(अ) वेनभूप: दुःशासकः आसीत्।

प्रश्न 5.
पृथुभूपेन स्वधनुः सज्जीकृतं यतः ………
(अ) सः शचुं हन्तुम् इच्छति स्म।
(ब) सः धनधान्यादि सर्व वस्तुजातं वसुन्धरायाः प्राप्तुम् इच्छति स्म।
उत्तरम् :
(ब) सः धनधान्यादि सर्वं वस्तुजातं वसुन्धरायाः प्राप्तुम् इच्छति स्म।

प्रश्न 6.
पृथुभूपस्य प्रजाजनाः सन्तुष्टा: अभवन् यतः …………..
(अ) ते प्रभूतं धान्यम् अलभन्त।
(ब) ते प्रभूतं सुवर्णम् अलभन्त।
उत्तरम् :
(अ) ते प्रभूतं धान्यम् अलभन्त।

उचितं‌ ‌पर्यायं‌ ‌चित्वा‌ ‌वाक्यं‌ ‌पुनर्लिखत।‌ ‌

प्रश्न 1.

1. प्रजा:‌ ‌अतीव‌ ‌……………. आसन्।‌ ‌(कृशाः‌ ‌/‌ ‌सुदृवाः)‌ ‌
2. सर्व‌ ‌वस्तुजातं‌ ‌………….‌ ‌उदरे‌ ‌एव‌ ‌वर्तते।‌ ‌(धरायाः‌ ‌/‌ ‌सूर्यस्य‌)
3. पृथुभूपेन ……. सज्जीकृतम्। (धनुः/लवित्रम्)
4. दु:शासकः नृपः …………..। (वेनराज:/पृथुवैन्यः)
5. ………… बीजेभ्यः अङकुराः उद्भूताः। (पर्जन्यानन्तरं/ शीतकालानन्तरं)
6. ………….. प्रजाजनाः सन्तुष्टा : अभवन्। (धनलाभेन/धान्यलाभेन)

उत्तरम्‌ :

1. कशाः‌
2. धराया:‌
3. धनुः
4. वेनराजः
5. पर्जन्यानन्तरं।
6. धान्यलाभेन।

कः‌ ‌कं‌ ‌वदति‌ ‌।‌

‌प्रश्न 1.
स्तवनं‌ ‌तु‌ ‌ईश्वरस्यैव‌ ‌भवेत्।‌
उत्तरम्‌ :
पृथुवैन्यः‌ ‌चारणा‌‌ बदति।‌

‌प्रश्न 2.
त्वं तु प्रजाहितदक्षः नृपः।
उत्तरम् :
भूमिः पृथुवैन्यं वदति।

‌प्रश्न 3.
प्रजाजनैः सह कृषिकार्यं कुरु ।
उत्तरम् :
भूमिः पृथुवैन्यं वदति।

पूर्णवाक्येन‌ ‌उत्तरत।‌

प्रश्न 1.
‌कः‌ ‌धरायां‌ ‌प्रथम:‌ ‌अभिषिक्तः‌ ‌सम्राट्?‌
‌उत्तरम्‌
‌भूपालः‌ ‌पृथुवैन्य:‌ ‌धरायां‌ ‌प्रथम:‌ ‌अभिषिक्तः‌ ‌सम्राट्।‌‌

प्रश्न 2.‌
‌पृथुनृपस्य‌ ‌राजधानी‌ ‌कुत्र‌ ‌आसीत्?‌ ‌
उत्तरम्‌ :
पृथुनृपस्य‌ ‌राजधानी‌ ‌प्रयागक्षेत्रे‌ ‌आसीत्।‌

प्रश्न 3.
के‌ ‌पृथुनृपस्य‌ ‌स्तुति‌ ‌गातुमुत्सुकाः?‌ ‌
उत्तरम्‌ ‌:
चारणाः‌ ‌पृथुनृपस्य‌ ‌स्तुतिं‌ ‌गातुमुत्सुकाः।‌

प्रश्न 4. ‌
‌स्तुतिगायकाः‌ ‌किं‌ ‌ज्ञात्वा‌ ‌प्रसन्नाः‌ ‌अभवन्?‌ ‌/‌ ‌स्तुतिगायका:‌‌ किमर्थ‌ ‌प्रसन्नाः‌ ‌अभवन्?‌ ‌
उत्तरम्‌ ‌
स्तुतिगायका:‌ ‌पृथुनृपस्य‌ ‌नि:स्पृहतां‌ ‌ज्ञात्वा‌ ‌प्रसन्नाः‌ ‌अभवन्।‌

प्रश्न 5.
पृथुः‌ ‌चारणान्‌ ‌किम्‌ ‌आज्ञापयत्?‌
‌उत्तरम्‌ ‌
पृथुः‌ ‌चारणान्‌ ‌स्थातुम्‌ ‌आज्ञापयत्‌ ‌अकथयत्‌ ‌च‌ ‌यावत्‌ ‌पृथो:‌‌ सद्गुणा:‌ ‌न‌ ‌प्रकटीभवन्ति‌ ‌तावत्‌ ‌सः‌ ‌न‌ ‌स्तोतव्यः‌ ।‌ ‌
स्तवनं‌‌ तु‌ ‌ईश्वरस्य‌ ‌एव‌ ‌भवेत्।‌ ‌

प्रश्न 6.
‌चिन्ताकुलं‌ ‌राजानं‌ ‌पुरोहितः‌ ‌किम्‌ ‌अवदत्‌ ‌?‌
‌उत्तरम्‌
‌चिन्ताकुलं‌ ‌राजानं‌ ‌पुरोहितः‌ ‌अवदत,‌ ‌”हे‌ ‌राजन्,‌ ‌धनधान्यादि‌‌ सर्व‌ ‌वस्तुजातं‌ ‌वस्तुत:‌ ‌वसुन्धराया:‌ ‌उदरे‌ ‌एवं‌ ‌वर्तते‌ ‌।‌ ‌तत्प्राप्तुं‌‌

प्रश्न 7.
‌‌एषः‌ ‌गद्यांश:‌ ‌कस्मात्‌ ‌पाठात्‌ ‌उद्धृतः?‌
उत्तरम्‌
‌एषः‌ ‌गद्यांश:‌ ‌आद्यकृषक:‌ ‌पृथुवैन्यः‌ ‌पाठात्‌ ‌उद्धृतः।‌

प्रश्न 8.
केन धनुः सज्जीकृतम्?
उत्तरम् :
पृथुभूपेन धनुः सज्जीकृतम्।

प्रश्न 9.
कया धनधान्यपुष्पफलानि उदरे निहितानि ?
उत्तरम् :
भूम्या धनधान्यपुष्पफलानि उदरे निहितानि।

प्रश्न 10.
कः दुःशासक:?
उत्तरम् :
पृथराजस्य पिता बेनराजः दुःशासकः।

प्रश्न 11.
भूमि: राजानं कृषिकार्यस्य कानि साधनानि उक्तवती?
उत्तरम् :
भूमि: राजानं खनित्राणि, हला:, कुद्दालकाः, लवित्राणि च एतानि साधनानि उक्तवती।

प्रश्न 12.
जनाः कुत्र धान्यबीजानि अवपन्?
उत्तरम् :
जनाः क्षेत्रे धान्यबीजानि अवपन्।

प्रश्न 13.
कदा बीजेभ्यः अङ्कुराः उद्भूता?
उत्तरम् :
पर्जन्यानन्तरं बीजेभ्य: अङ्कुराः उद्भूता।

प्रश्न 14.
प्रजाजना: केन/कश्यं सन्तुष्टाः अभवन्?
उत्तरम् :
धान्यलाभेन सर्वे प्रजाजनाः सन्तुष्टा: अभवन्।

वाक्यं‌ ‌पुनर्लिखित्वा‌ ‌सत्यम्‌ ‌/‌ ‌असत्यम्‌ ‌इति‌ ‌लिखत।‌‌

प्रश्न 1.

1. पृथुवैन्यः‌ ‌नाम‌ ‌धरायाम्‌ ‌आदिम:‌ ‌सम्राट्।‌ ‌
2. ‌स्तवनं‌ ‌तु‌ ‌मानवस्यैव‌ ‌भवेत्।‌ ‌
3. स्तुतिगायकाः‌ ‌पृथुनृपस्य‌ ‌नि:स्पृहतां‌ ‌ज्ञात्वा‌ ‌विषण्णा:‌ ‌अभवन्।‌‌
4. पृथुराजेन‌ ‌दृष्टं‌ ‌यत्‌ ‌प्रजाः‌ ‌अतीव‌ ‌सशक्ताः‌ ‌।‌‌
5. प्रजा:‌ ‌पशुवत्‌ ‌जीवन्ति।‌
6. धनधान्यादि‌ ‌वस्तुजातं‌ ‌वसुन्धराया:‌ ‌जठरे‌ ‌एव‌ ‌वर्तते।‌ ‌

उत्तरम्‌ ‌:

1. सत्यम्।‌ ‌
2. ‌असत्यम्।‌
3. ‌असत्यम्।‌
4. ‌असत्यम्।‌‌
5. ‌सत्यम्।‌ ‌
6. ‌सत्यम्।‌‌

प्रश्न 2.

1. भूमि: नररूपम् अधारयत्।
2. वेनराजः दुःशासकः आसीत्।
3. वेनराजः राजधर्मस्य उल्लङ्घनम् अकरोत्।
4. पृथुः प्रजाहितदक्षः नृपः।

उत्तरम् :

1. असत्यम्।
2. सत्यम्।
3. सत्यम्।
4. सत्यम्।

प्रश्न 3.

1. पृथुवैन्यः भूमिम् अनुर्वराम् अकरोत्।
2. पृथुवैन्य: उद्यमेन बीजानां सङ्कलनम् अकरोत्।
3. पर्जन्यानन्तरम् अकुरेभ्य: बीजानि उद्भूतानि ।
4. प्रजाजनाः विषण्णा: अभवन्।

उत्तरम् :

1. असत्यम्।
2. सत्यम्।
3. असत्यम्।
4. असत्यम्।

शब्दज्ञानम्‌ ‌

सन्धिविग्रहः।‌

1. ‌गातुमुत्सुकाः‌ ‌-‌ ‌गातुम्‌ ‌+‌ ‌उत्सुकाः‌ ‌।‌
2. ‌तावदहम्‌ ‌-‌ ‌तावत्‌ ‌+‌ ‌अहम्।‌
3. ‌ईश्वरस्यैव‌ ‌.‌ ‌ईश्वरस्य‌ ‌+‌ ‌एव‌ ‌।‌
4. ‌तत्प्राप्तुम्‌ ‌-‌ ‌तत्‌ ‌+‌ ‌प्राप्तुम्।‌
5. नाकरोत् – न + अकरोत् ।
6. स नैकेभ्यः – स: + नैकेभ्यः ।

विशेषण‌ ‌-‌ ‌विशेष्य‌ ‌-‌ ‌सम्बन्धः।‌‌

विशेषणम्‌	विशेष्यम्‌
1.‌ प्रथमः‌‌	सम्राट‌
2. ‌अभिषिक्तः‌	समाट्‌
3. प्रसन्नाः‌‌	स्तुतिगायकाः‌‌
4. राजा‌‌	चिन्ताकुल:‌
5. नैकेभ्यः	वृक्षेभ्यः
6. विविधप्रकारकाणाम्	बीजानाम्
7. कल्याणकारी	नृपः
8. अग्रणी:	नृपः
9. जनसेवाव्रती	नृपः

चान्त-ल्यबन्त-तुमन्त-अव्ययानि।‌

त्वान्त‌ ‌अव्यय‌‌ धातु‌ ‌+‌ ‌त्वा / ध्या / टवा / ‌ढवा ‌/ इत्वा / अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्त‌ ‌अव्यय‌ ‌‌‌धातु‌ ‌+‌ ‌तुम् / धुम् / टुम् / ढुम् / ‌‌इतुम् / अयितुम्‌‌
दृष्ट्वा,‌ ‌ज्ञात्वा, धृत्वा, गृहीत्वा, कृत्वा	निधाय, अवरुध्य	गातुम,‌ ‌प्राप्तुम्‌, कर्तुम्

विभक्त्यन्तरूपाणि।‌

• ‌प्रथमा‌ ‌-‌ ‌भूपालः,‌ ‌सम्राट्,‌ ‌राजधानी,‌ ‌चारणाः,‌ ‌अहम्,‌‌ ‌गायकाः,‌ ‌प्रजाः,‌ ‌ताः,‌ ‌राजा,‌ ‌पुरोहितः, भूमिः, पिता, नृपः, अहम्।
• ‌द्वितीया‌ ‌-‌ ‌अन्नम्,‌ ‌सर्वम्, धनुः, फलानि, खनित्राणि, हलान, कुद्दालकान, लवित्राणि।
• तृतीया‌ ‌-‌ ‌तेन, भूपेन, मया, प्रयत्लेन, प्रजाजनैः, परिश्रमेण, धान्यलाभेन ।
• पञ्चमी – भयात्, बीजेभ्यः, वृक्षेभ्यः ।
• षष्ठी‌ ‌-‌ ‌नृपस्य,‌ ‌मम,‌ ‌ईश्वरस्य,‌ ‌वसुन्धरायाः, तस्य, राजधर्मस्य, भूमातुः, नदीनाम, जलस्य, बीजानाम्।
• सप्तमी‌ ‌-‌ ‌धरायाम,‌ ‌क्षेत्रे,‌ ‌राज्याभिषेकसमये,‌ ‌स्वराज्ये, हस्ते, मनसि, तस्मिन्, क्षेत्रे, प्रशासने, पृथिव्याम्।
• ‌सम्बोधन‌ ‌-‌ ‌हे‌ ‌राजन्।‌‌

लकारं‌ ‌लिखत।‌

प्रश्न 1.

1. पृथुराजः‌ ‌स्वराज्ये‌ ‌भ्रमणम्‌ ‌अकरोत्।‌ ‌
2. ‌ता:‌ ‌मजा:‌ ‌पशुवत्‌ ‌जीवन्ति‌ ‌।‌
3. तत्‌ ‌प्राप्तुं‌ ‌यतस्व।‌

उत्तरम्‌ ‌:

1. ‌लङ्लकारः‌
2. ‌लट्लकारः‌
3. लोट्लकार:‌‌

प्रश्न 2.

1. भूमि: तस्य पुरत: प्रकटिता अभवत्।
2. त्वं प्रयत्नेन कृषिकार्य करोषि।
3. अहं प्रसन्ना भविष्यामि।
4. प्रजाजनैः सह कृषिकार्य कुरु।
5. जनाः धान्यबीजानि अवपन्।
6. पृथुवैन्य; भूमिम् उर्वरतमां कर्तुं प्रायतत।

उत्तरम् :

1. लङ्लकारः।
2. लट्लकारः।
3. लृट्लकारः।
4. लोट्लकारः।
5. लङ्लकार:।
6. लङ्लकारः।

‘भूमातुः’ इति स्थाने ‘भूमि’ शब्दस्य योग्य रूपं लिखत।

प्रश्न 1.
भूमातुः उपदेशं मनसि निधाय पृथुवैन्यः कृषिकार्यम् अकरोत्।
उत्तरम् :
भूम्या: भूमेः उपदेशं मनसि निधाय पृथुवैन्यः कृषिकार्यम् अकरोत्।

भाषाभ्यास:

समानार्थकशब्दाः ।

1. नाम – अभिधानम्, नामधेयम्, आख्या।
2. सम्राट – अधिराजः, राजेन्द्रः, सार्वभौमः ।
3. चारणाः – स्तुतिपाठकाः, स्तुतिगायकाः ।
4. स्तवनम् – स्तुतिः, प्रशंसा।
5. ईश्वरः – देवः, भगवान्, सुरः।
6. ज्ञात्वा – अवगम्य।
7. प्रसन्नाः – सन्तुष्टाः, आनन्दिताः।
8. भ्रमणम् – अटनम्।
9. कृशः – क्षीणः ।
10. अशक्तः – दुर्बलः।
11. दृष्ट्वा – अवलोक्य, विलोक्य, वीक्ष्य।
12. चिन्ताकुलः – चिन्ताग्रस्तः, चिन्तितः, चिन्ताक्रान्तः।
13. पुरोहितः – उपाध्यायः।
14. वसुन्धरा – धरिणी, धरा, धरित्री, पृथिवी।
15. उदरम् – जठरम्, कोष्ठम्।
16. प्राप्तुम् – लब्धम्।
17. स्त्री – नारी, वनिता, महिला, योषित्।
18. पिता – जनकः, तात;, जन्मदाता।
19. चोरः – चौर:, स्तेनः, तस्करः, पाटच्चरः, लुण्ठकः ।
20. धनम् – वित्तम, द्रव्यम्, सम्पत्तिः ।
21. धान्यम् – सस्यम्।
22. पुष्पम् – प्रसूनम, सुमनः, सुमम, कुसुमम्।
23. मनसि – अन्त:करणे, चेतसि, चित्ते, मानसे।
24. निधाय – हित्वा।
25. मार्गः – पन्थाः , सरणिः।
26. जलम् – तोयम्, नौरम्, अम्बु, उदकम्, वारि।
27. सञ्चयम् – सङ्कलनम्।
28. बीजानि – सस्यानि।
29. कल्याणकारी – हितकारी।

विरुद्धार्थकशब्दाः‌

• ‌उत्सुकाः‌ ×‌ ‌अनुत्सुकाः।‌
• उपयोग: × निरुपयोगः।
• उर्वरा × अनुर्वरा/वन्ध्या ।
• लाभः × हानिः।

योग्यं क्रियापदं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.

1. त्वं तत्प्राप्तुं …………….। (यतस्व/यतन्ताम्)
2. त्वं प्रयत्लेन कृषिकार्य ……..। (करोति/करोषि)
3. त्वं धनुः …….। (त्यज/त्यजतु)
4. त्वं प्रजाननै: सह कृषिकार्य ……… । (कुरु/करोतु)

उत्तरम् :

1. त्वं तत्प्राप्तुं यतस्व।
2. करोधि ।
3. त्यज।
4. कुरु

योग्य वाच्यपर्याय चिनुत ।

प्रश्न 1.
ता: प्रजाः पशुवज्जीवन्ति। (कर्तृवाच्यम्/कर्मवाच्यम्)
उत्तरम् :
कर्तृवाच्यम्।

प्रश्न 2.
पृथुभूपेन धनुः सज्जीकृतम्। (कर्तृवाच्यम्/कर्मवाच्यम्)
उत्तरम् :
कर्मवाच्यम्।

प्रश्न 3.
मया धनधान्यपुष्पफलानि उदरे निहितानि । (कर्तृवाच्यम्/कर्मवाच्यम्)
उत्तरम् :
कर्मवाच्यम्।

प्रश्न 4.
त्वं धनुः त्यज। (कर्तृवाच्यम्/कर्मवाच्यम्)
उत्तरम् :
कर्तृवाच्यम्।

प्रश्न 5.
जनाः धान्यबीजानि अवपन्। (कर्तृवाच्यम्/कर्मवाच्यम्)
उत्तरम् :
कर्तृवाच्यम्।

योग्यं विशेषणं चिनुत।

प्रश्न 1.
पर्जन्यानन्तरं बीजेभ्यः अङकुराः ….। (उद्भूतः/उद्भूताः)
उत्तरम् :
उद्भूताः।

अमरकोषात् शब्दं योजयित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
भूपाल: पृथुवैन्य: नाम धराया: प्रथम: अभिषिक्त: सम्राट्।
उत्तरम् :
राट् / पार्थिवः / क्ष्माभूत् / नृपः / भूपः / महीक्षित् पृथुवैन्य: नाम धरायाः प्रथम: अभिषिक्तः सम्राट्।

समासाः

समस्तपदम्	अर्थ:	समासविग्रहः	समासनाम
प्रयागक्षेत्रम्	place named प्रयाग	प्रयागं नाम / इति क्षेत्रम्।	कर्मधारयः समासः।
विविधबीजानि	various seeds	विविधानि बीजानि।	कर्मधारयः समासः।
धनधान्यपृष्यफलानि	wealth, grains, flowers and fruits	धनानि च धान्यानि च पुष्पाणि च फलानि च।	इतरेतर-द्वन्द्वः समासः ।
चिन्ताकुलः	perturbed with worry	चिन्तया आकुलः।	तृतीया-तत्पुरुषः समासः।
चोरलण्ठकभयम्	fear from thieves and robbers	चोरलण्ठकेभ्य: भयम्।	पञ्चमी-तत्पुरुषः समासः।
जलव्यवस्थापनम्	management of water	जलस्य व्यवस्थापनम्।	षष्ठी-तत्पुरुषः समासः।
प्रजाहितदक्षः	alert in the subjects’ welfare	प्रजाहिते दक्षः।	सप्तमी-तत्पुरुषः समासः।
कल्याणकारी	does welfare	कल्याणं करोति इति।	उपपद-तत्पुरुषः समास:।

आद्यकृषक: पृथुवैन्यः Summary in Marathi and English

प्रस्तावना :

भारत हा कृषिप्रधान देश आहे. देशाच्या सामाजिक व आर्थिक उभारणीमध्ये कृषी (शेती) महत्त्वाची भूमिका बजावते. वेन राजाचा पुत्र, पृथुवैन्य/ पृथु राजाने शेतीविषयक कार्याचे संशोधन केले त्याचा प्रारंभ करून विकसित केले.

पृथु राजाला पृथ्वीवरील सर्वप्रथम अभिषिक्त राजा मानले जाते. पृथु राजाच्या कार्यस्मरणार्थ वसुंधरेस पृथ्वी असे संबोधले जाते. प्रस्तुत भाग म्हणजे पृथु राजाने केलेल्या कृषिविषयक कार्याचा प्रारंभ तसेच कृषी संस्कृती याचे विवरण करणारी आख्यायिका आहे.

India is an agriculture-based country. Agriculture plays a significant role in the socio-economic fabric of the country. Agricultural work was invented, initialised and developed by the king Pruthuvainya who was the son of Vena.

Pruthu (पृथु) is considered to be the first coronated king of the earth. The earth is known as Prithvi, in the memory of Pruthu’s work. The given extract is the legend that reveals the history of Pruthu’s initiation of agricultural work and civilization.

परिच्छेदः 1

भूपाल: ……………… यतस्व।

अनुवादः

राजा पृथुवैन्य म्हणजे पृथ्वीवरील सर्वप्रथम अभिषिक्त सम्राट (होय.) प्रयागक्षेत्रात पृथु राजाची राजधानी होती, राज्याभिषेकासमयी, भाट (स्तुतिपाठक) पृथु राजाची स्तुती गाण्यास उत्सुक होते. नंतर, पृथु राजाने आदेश दिला, “कृपया भाटांनी थांबावे! जोपर्यंत माझ्यातील सद्गुणांचे दर्शन होत नाही, तोपर्यंत माझी स्तुती केली जाऊ नये.

ईश्वराचेच स्तबन व्हावे.” पृथु राजाची अशी निःस्पृह (निःस्वार्थी) वृत्ती जाणून स्तुतिपाठक संतुष्ट झाले. एकदा पृथु राजा त्याच्या राज्यात भ्रमण करत होता. त्याने फिरताना पाहिले की, त्याची प्रजा क्षीण (बारीक) व अशक्त झाली आहे.

ते प्रजाजन प्राण्यांप्रमाणे आयुष्य जगत होते. (ते) हलक्या दर्जाचे/कमी प्रतीचे अन्न खात होते. ते पाहून राजा चिंताग्रस्त झाला. तेव्हा पुरोहित (उपाध्याय) म्हणाले, “हे राजा, खरेतर धन (समृद्धी), धान्य इत्यादी सर्व वस्तू धरणीच्या पोटातच असतात. (वास करतात.)
(कृपया) त्या प्राप्त करण्यासाठी तू प्रयत्न कर.”

The king named पृथुवैन्य was the first coronated (enthroned) emperor on the earth. The king पृथु’s capital was in the region of प्रयाग. The bards were eager to praise king पृथु at the time of coronation.

Then, पृथु ordered, “May the bards stop (praising me)! As long as, my virtues are not manifested (don’t appear) till then I am not worthy of praise (appreciation).

The Almighty is praiseworthy alone.” Having realized such desirelessness of king पृथु, the bards got pleased. Once, king पृथु was wandering in his kingdom. While wandering, he saw that his subjects are very thin and weak.

Those people were living life like an animal. They were eating low-quality food. Seeing that, The king got perturbed (disturbed). Then the priest said, “O King, in fact all the things like wealth and grains are in the belly of the earth itself (generated from the earth). Please strive to obtain it.”

परिच्छेदः 2

तदा ………….. पृथुभूपेन

अनुवादः

त्यानंतर, त्याकरिता पृथुराजाने धनुष्य तयार ठेवले, मग पृथ्वी स्त्रीचे रूप धारण करून त्याच्यासमोर प्रकट झाली व म्हणाली, “हे राजा ! जुलमी असणाऱ्या तुझ्या वडिलांनी, वेन राजाने राजधर्माचे पालन केले नाही.

त्यानंतर, चोर-लुटारूंच्या भयामुळे मी, धन-धान्य-फुले-फळे माझ्या पोटात ठेवले. तू निश्चितच प्रजेच्या हितामध्ये सतर्क असणारा राजा आहेस, जर तू प्रयत्नपूर्वक कृषिकार्य केलेस, तर मी प्रसन्न होईन, म्हणूनच धनुष्य सोडून दे. तुझ्या प्रजाजनांसमवेत फावडे, नांगर, कुदळ, विळे (हे सर्व) हातात घेऊन कृषिकार्य कर.”

Then king Ty set the bow for that. Then, having taken the form of a woman, the earth appeared in front of him and said, “O King! your father, the bad ruler , did not follow royal duty. Then, I placed wealth, grains, flowers, fruits in my belly, due to fear of thieves, robbers.

But, you are engaged in welfare of the subjects. If you strive in farming, I will be pleased. Hence, give up a bow. Start farming with the subjects by taking spades, ploughs, hoes, sickles in hand”.

परिच्छेदः 3

भूमातु: ………………………………….. अभवत्।

अनुवादः

धरणीमातेचा उपदेश लक्षात येऊन, पृथुवैन्य राजाने नद्यांचा मार्ग थांबवून पाण्याचा उपयोग शेतीकामासाठी केला. (राजाने) पावसाच्या पाण्याचा साठा करून पाण्याचे व्यवस्थापन केले. (त्याने) जमीन अधिक सुपीक होण्यासाठी प्रयत्न केले. नंतर, लोकांनी त्या ठिकाणी (शेतात) धान्यबीजे पेरली.

त्याने अनेक वृक्षांपासून विविध प्रकारच्या बीजांचे परिश्रमपूर्वक संचय व निवड केली. (व) नंतर बीजांचे संस्करण करून पेरणी केली. पावसानंतर बीजांतून अंकुर फुटले. धान्याच्या प्राप्तीमुळे सर्व प्रजा आनंदित झाली. हा कल्याणकारी राजा पृथ्वीवर, प्रशासनात अग्रेसर व जनसेवाव्रती ठरला.

Keeping in mind the advice of the mother earth, पृथुवैन्य used water for agricultural work by obstructing the way of rivers. Having stored the rain-water, he did water-management. He strived to make the land most fertile.

After that, people sowed the seeds of grains in that field (farm). He collected and selected the various seeds from many trees with so much of effort. After that, having refined (polished) the seeds, he sowed. After the rain, sprouts germinated from the seeds.

After obtaining grains, all subjects were pleased (satisfied). This welfare-oriented king became the foremost in the administration on the earth and was committed to the service of public.

शब्दार्थाः

1. भूपाल: – king – राजा
2. धरायाम् – on the earth – पृथ्वीवर
3. अभिषिक्तः – coronated – अभिषेक झालेला
4. चारणा: – bards – भाट (स्तुतिपाठक)
5. आज्ञापयत् – ordered – आज्ञा केली
6. तिष्ठन्तु – please wait – थांबावे
7. यावत्-तावत् – as long as-till then – जोपर्यंत-तोपर्यंत
8. प्रकटीभवन्ति – manifested – प्रकट होतात
9. स्तोतव्यः – worthy to be praised – स्तुती करण्यायोग्य
10. एतादृशीम् – such – अशी
11. निःस्पृहताम् – detachment – निःस्पृहा, निरिच्छा
12. भ्रमणम् – wandering – फिरणे
13. कृशाः – lean – बारीक
14. अशक्ताः – weak – अशक्त
15. पशुवत् – like animals – पशुप्रमाणे/प्राण्याप्रमाणे
16. निकृष्टान्नम् – low quality food – हलक्या दर्जाचे अन्न
17. दृष्ट्वा – having seen – पाहून
18. चिन्ताकुल: – worried – चिंताग्रस्त
19. पुरोहितः – priest – उपाध्याय
20. वस्तुजातम् – things – सर्व वस्तू
21. वस्तुतः – in fact – मुळ्यात, खरे पाहता
22. उदरे – in the belly – पोटात
23. प्राप्तुम् – to obtain – मिळविण्यासाठी
24. यतस्व – you strive – प्रयत्न कर
25. तदर्थम् – for that – त्यासाठी
26. सज्जीकृतम् – set – तयार केले
27. भूमिः – earth – पृथ्वी
28. धृत्वा – taking/bearing – घेऊन/धारण करून
29. पुरतः – in front of – च्या पुढे
30. प्रकटिता अभवत् – appeared – प्रकट झाली
31. दुःशासकः – bad ruler – जुलमी राजा
32. चोरलुण्ठक – due to fear from – चोर, लुटारुच्या
33. भयात् – thief and robber – भीतीने
34. निहितानि – placed/laid – ठेवलेले
35. प्रजाहितदक्षः – prompt towards subject’s welfare – प्रजाहितासाठी तयार / सतर्क
36. त्यज – leave – सोड
37. खनित्राणि – spades – फावडे
38. हलान् – ploughs – नांगर
39. कालकान – hoes – कुदळ
40. लवित्राणि – sickles – विळे
41. गृहीत्वा – having taken – घेऊन
42. धनुः – bow – धनुष्य
43. उपदेशम् – advice – सल्ला
44. मनसि निधाय – having taken into consideration – लक्षात घेऊन
45. अवरुध्य – obstructing – अडवून
46. जलसञ्चयम् – accumulation of water – पाण्याचा साठा
47. जल – व्यवस्थापनम् – management of water – पाण्याचे व्यवस्थापन
48. उर्वरतमाम् – most fertile – अधिक सुपीकता
49. धान्यबीजानि – seeds of grains – धान्याच्या बिया
50. अवपन् – sowed – पेरली
51. सङ्कलनम् – collection – साठा
52. चयनम् – selection – निवड
53. संस्करणम् – having polished / refined – शुद्धीकरण करून
54. अडकुराः – were sprouted – अंकुर फुटले
55. उद्भूताः – germinated
56. सन्तुष्टाः – satisfied – समाधानी
57. कल्याणकारी – welfare-oriented – कल्याण करणारा
58. अग्रणी: – foremost – अग्रेसर
59. जनसेवाव्रती – committed to the service of public – जनसेवेचे व्रत घेतलेला

10th Standard Sanskrit Anand Digest Pdf  

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्यस्तबकः Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Anand Chapter 3 सूक्तिसुधा Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Anand Chapter 3 सूक्तिसुधा Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 3 Question Answer

Sanskrit Anand Std 10 Digest Chapter 3 सूक्तिसुधा Textbook Questions and Answers

भाषाभ्यासः

श्लोकः 1

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
का गुरूणां गुरुः ?
उत्तरम्‌ :‌
विद्या गुरूणां गुरुः।

प्रश्न आ.
किं राजसु न पूज्यते ?
उत्तरम्‌ :‌
धनं राजसु न पूज्यते।

प्रश्न इ.
कः पशुः एव ?
उत्तरम्‌ :‌
विद्याविहीन : पशुः एव।

2. माध्यमभाषया उत्तरत ।

प्रश्न अ.
‘विद्या नाम नरस्य’ …….. इति श्लोकाधारण विद्यायाः महत्त्वं लिखत ।
उत्तरम्‌ :‌
सूक्ति म्हणजे चांगल्या उक्ती. सूक्तिसुधा अशा नीतिपर उक्तींचा संग्रह आहे. ‘विद्याविहीनः पशुः’ ही सूक्ति ज्ञानाचे महत्त्व विशद करते. विद्या नाना भोग (समाधान) प्राप्त करून देणारी आहे. तसेच ती यश व आनंदही प्राप्त करून देणारी आहे. विद्या हे संरक्षिलेले गुप्त धन आहे. परदेशातही विद्या बंधुसम असते. राजसभेतही विद्यावान व्यक्तीचा सन्मान केला जातो. विद्येमुळे माणसाला ज्ञानाचे तेज प्राप्त होते व त्याचे सौंदर्य वाढते.

ज्ञानामुळे सर्व उद्दिष्टे साध्य होऊ शकतात, ‘किं किं न साधयति कल्पकतेव विद्या’ या उक्तीप्रमाणे विद्या कल्पकतेप्रमाणे सर्व इच्छांची पूर्ती करते. म्हणूनच ज्ञानहीन मनुष्यास पशूच मानले जाते.

सूक्तिs are good sayings. सूक्तिसुधा is a collection of all such value-based quotations. The सूक्ति ‘विद्याविहीनः पशुः’ ellobarates the importance of knowledge.

Knowledge alone gives enjoyment, happiness and fame to a person. It is the preceptor of all preceptors. Hence, knowledge is precious wealth. It is well-guarded and concealed wealth.

It enhances the beauty of a person. Knowledge is considered to be relative while travelling in foreign country. It is said to be supreme deity. Even royal courts admire knowledgeable people.

A man who is devoid of knowledge / learning, is said to be an animal; as knowledge helps achieving all ends. It is rightly said, “किं किं न साधयति कल्पलतेब विद्या’ – what does not knowledge achieve like wish yielding-creeper.

3. जालरेखाचित्रं पूरयत ।

प्रश्न 1.
जालरेखाचित्रं पूरयत

उत्तरम्‌ :‌

श्लोक: 2.

1. मञ्जूषात: उचितं शब्दं चित्वा तालिकां पूरयत ।

प्रश्न 1.
मञ्जूषात: उचितं शब्दं चित्वा तालिकां पूरयत ।

(निन्दन्तु, गच्छतु, युगान्तरे, मरणम्, लक्ष्मी:, स्तुवन्तु ।)
उत्तरम्‌ :‌

नीतिनिपुणाः	निन्दन्तु	स्तुवन्तु	वा
लक्ष्मीः	समाविशतु	गच्छतु	वा
मरणम्	अद्यैव	युगान्तरे	वा

2. सन्धिविग्रहं कुरुत।

प्रश्न अ.
मरणमस्तु ।
उत्तरम्‌ :‌
मरणमस्तु – मरणम् + अस्तु।

प्रश्न आ.
अद्यैव ।
उत्तरम्‌ :‌
अद्यैव – अद्य + एव।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
“न्याय्यात्पथः प्रविचलन्ति पदं न धीराः । इति सूक्तिं स्पष्टीकुरुत।
उत्तरम्‌ :‌
सूक्ति म्हणजे चांगल्या उक्ती. सूक्तिसुधा अशा नीतिपर उक्तींचा संग्रह आहे. विद्याविटेन: पशुः हो सूक्ति ज्ञानाचे महत्व विशद करते. धैर्यवान लोकांमध्ये दृढनिश्चय ही स्थायी व विशेष गुण आहे. असे लोक स्थिर बुद्धीचे असतात. व ते स्वत:ला ध्येयापासून टू देत नाहीत ते त्याच मार्गाचा अवलंब करतात, व हवे ते परिणाम प्राप्त करून घेतात. ‘न्याय्यात्पथः प्रविचलन्ति पदं न धीराः’ ही सूक्ति हे विशद करते.

नीतिमध्ये कुशल लोक निंदानालस्ती करो वा प्रशंसा करोत, लक्ष्मी तिच्या इच्छेप्रमाणे येवो अथवा जावो, आजच मरण येवो वा युगान्त झाल्यावर (दुसऱ्या युगात / भरपूर काळ लोटल्यावर) येवो, (तरीही) धैर्यवान लोक न्याय्यमार्गावरून आपले पाऊल ढळू देत नाहीत (ते न्याय्यमार्ग सोडत नाहीत).

सूक्तिs are good sayings. सूक्तिसुधा is a collection of all such value-based.quotations. Resolute people have distinct quality of firmness. They are of stable intelellect and do not deviate their minds from their aim. They follow the path of justice, till they achieve fruitful results.

The सूक्ति ‘न्याय्यात्पथः प्रविचलन्ति पदं न धीराः’ says that experts/skilled people may praise or criticise courageous people; may goddess Laxmi assist them by pleasing on them or not; may they have to face death instantly or after long time; passing through all circumstances, resolute ones follow the justice path, achieve fruitful results and enlighten other’s lives too.

श्लोक: 3.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
शुकसारिका: केन बध्यन्ते ?
उत्तरम्‌ :‌
आत्मन: मुखदोषेण शुकसारिकाः बध्यन्ते।

प्रश्न आ.
के न बध्यन्ते ?
उत्तरम्‌ :‌
बका: न बध्यन्ते।

2. सन्धिविग्रहं कुरुत ।

प्रश्न अ.
बकास्तत्र
उत्तरम्‌ :‌
बकास्तत्र – बकाः + तत्र।

प्रश्न आ.
आत्मनो मुखदोषेण
उत्तरम्‌ :‌
आत्मनो मुखदोषेण – आत्मनः + मुखदोषेण।

श्लोकः 4.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
का कार्यसाधिका भवति ?
उत्तरम्‌ :‌
अल्पानां वस्तूनां संहतिः कार्यसाधिका भवति।

प्रश्न आ.
कै: मत्तदन्तिन: बध्यन्ते ?
उत्तरम्‌ :‌
आपन्न : तृणैः मत्तदन्तिन: बध्यन्ते।

2. सन्धिविग्रहं कुरुत।

प्रश्न अ.
अल्पानामपि
उत्तरम्‌ :‌
अल्पानामपि – अल्पानाम् + अपि।

प्रश्न आ.
तृणैर्गुणत्वमापनर्बध्यन्ते
उत्तरम्‌ :‌
तृणैर्गुणत्वमापनैर्बध्यन्ते – तृणैः + गुणत्वम् + आपनैः + बध्यन्ते।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
‘संहतिः कार्यसाधिका’ इति सूक्तिं स्पष्टीकुरुत ।
उत्तरम्‌ :‌
संहतिः – एकता, ऐक्यम्।

श्लोक: 5.

1. एकवाक्येन उत्तरत।

प्रश्न अ.
नरः किं छिन्द्यात् ?
उत्तरम्‌ :‌
नरः पटं छिन्द्यात्।

प्रश्न आ.
मनुजः किं भिन्द्यात् ?
उत्तरम्‌ :‌
मनुजः घटं भिन्द्यात्।

2. श्लोकात् लिङ्लकारस्य रूपाणि चित्वा लिखत ।

प्रश्न 1.
श्लोकात् लिङ्लकारस्य रूपाणि चित्वा लिखत ।
उत्तरम्‌ :‌
भिन्द्यात्, छिन्द्यात्, कुर्यात्, भवेत्।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
‘येन केन प्रकारेण’ इति उक्तिं स्पष्टीकुरुत ।
उत्तरम्‌ :‌
सूक्ति म्हणजे चांगल्या उक्ती. सूक्तिसुधा अशा नीतिपर उक्तींचा संग्रह आहे. येन केन प्रकारेण’ ही सूक्ति उपहासाने माणसाच्या प्रवृत्तीचे वर्णन करते.

या जगात मनुष्याने कोणत्याही मार्गाने प्रसिद्ध व्हावे. इतरांचे लक्ष वेधून घेण्यासाठी घडे फोडावेत, कपडे फाडावेत, गाढवावर बसावे, या कृती खरेतर हास्यास्पद आहेत, तरीसुद्धा प्रसिद्ध होण्यासाठी व्यक्तीने हे सर्व करावे.

सूक्तिs are good sayings. सूक्तिसुधा is a collection of all such value-based quotations. The सूक्ति ‘येन केन प्रकारेण describes human nature satirically.

In this world, a man should try to be famous by some way or the other. He should grab the attention of people by breaking pots, tearing clothes, riding a donkey such acts which are unusual and ridiculous. Yet, one should do it for the sake of popularity.

प्रश्न 2.
समानार्थकशब्दान् लिखत ।
विद्या, पशुः, धनम्, लक्ष्मी:, शुकः, संहतिः, दन्ती, पटम्, रासभः ।
उत्तरम्‌ :‌

• विद्या – ज्ञानम्, बोधः ।
• पशुः – प्राणी, तिर्यङ्, मृगः ।
• धनम् – द्रव्यम, वित्तम्, स्थापतेयम्, रिक्थम्, ऋक्यम्, वसुः।
• लक्ष्मीः – पद्मा, कमला, श्रीः, हरिप्रिया, पद्मालया।
• शुकः – किङ्किरातः, कौरः।
• संहतिः – संघ
• दन्ती – हस्ती, करी, गजः, कुञ्जरः, वारणः ।
• पटम् – वस्त्रम्, वसनम् ।
• रासभः – गर्दभः, खरः, धूमकर्णः ।

प्रश्न 3.
विरुद्धार्थकशब्दान् लिखत ।
विदेशः, प्रच्छन्नम्, निन्दन्तु, रोहणम् ।
उत्तरम्‌ :‌

• विदेशः × स्वदेशः।
• प्रच्छन्नम् × प्रकाशितम्, प्रकटीकृतम्।
• निन्दन्तु × स्तुवन्तु।
• रोहणम् × अवतरणम्, अवरोहणम्।

Sanskrit Anand Class 10 Textbook Solutions Chapter 3 सूक्तिसुधा Additional Important Questions and Answers

अवबोधनम्।

(क) पूर्णवाक्येन उत्तरत।

प्रश्न 1.
विद्या कीदृशं धनम् अस्ति?
उत्तरम् :
विद्या प्रच्छन्नगुप्तं धनम् अस्ति।

प्रश्न 2.
विद्या केषां गुरुः?
उत्तरम् :
विद्या गुरूणां गुरुः।

प्रश्न 3.
विदेशगमने कृते विद्या कीदृशं भाति ?
उत्तरम् :
विदेशगमने कृते विद्या बन्धुजन : इव भाति।

प्रश्न 4.
किं परं दैवतम्?
उत्तरम् :
विद्या परं दैवतम्।

प्रश्न 5.
धीराः कस्मात् न प्रविचलन्ति?
उत्तरम् :
धीरा: न्याय्यात् पथ: न प्रविचलन्ति।

प्रश्न 6.
न्याय्यात्पथ: के न विचलन्ति ?
उत्तरम् :
न्याय्यात्पथ: धीराः न विचलन्ति।

प्रश्न 7.
के निन्दन्तु स्तुवन्तु वा?
उत्तरम् :
नीतिनिपुणा: निन्दन्तु स्तुवन्तु वा।

प्रश्न 8.
लक्ष्मी: कथं समाविशतु गच्छतु वा?
उत्तरम् :
लक्ष्मी: यथेष्टं समाविशतु गच्छतु वा।

प्रश्न 9.
किं सर्वार्थसाधनम्?
उत्तरम् :
मौनं सर्वार्थसाधनम्।

प्रश्न 10.
रविः प्रतिदिनं कुत्र याति?
उत्तरम् :
रविः प्रतिदिनं अपारस्य नभसः अन्तं याति।

प्रश्न 11.
महर्ता क्रियासिद्धिः कस्मिन् भवति?
उत्तरम् :
महतां क्रियासिद्धिः सत्त्वे भवति।

प्रश्न 12.
के तृणैर्गुणत्वमापनैः बध्यन्ते ?
उत्तरम् :
मतदन्तिन: तृणैर्गुणत्वमापन: बध्यन्ते।

प्रश्न 13.
पुरुषः कथं प्रसिद्धः भवेत्?
उत्तरम् :
येन केन प्रकारेण पुरुष: प्रसिद्धः भवेत्।

शब्दज्ञानम्

(क) विशेषण – विशेष्य – सम्बन्धः ।

विशेषणम्	विशेष्यम्
1. प्रच्छन्नगुप्तम्	धनम्
2. भोगकरी	विद्या
3. यशःसुखकरी	विद्या
4. परम्	दैवतम्
5. सर्वार्थसाधनम्	मौनम्
6. भुजगयमिता:	तुरगा:
7. अपारस्य	नभसः
8. अल्पानाम्	वस्तूनाम्
9. संहतिः	कार्यसाधिका
10. अल्पम्	तोयम्
11. कृतम्	उपकारम्
12. प्रसिद्धः	पुरुषः

(ख) विभक्त्यन्तपदानि।

• प्रथमा – विद्या, गुरुः, यशः, बन्धुजनः, पशुः ।
• षष्ठी – नरस्य, गुरूणाम्।
• सप्तमी – विदेशगमने, राजसु।
• तृतीया – दोषेण।
• षष्ठी – आत्मनः
• प्रथमा – संहतिः, कार्यसाधिका, दन्तिनः।
• तृतीया – तृणैः, आपनैः।
• षष्ठी – अल्पानाम्, वस्तूनाम्।

पृथक्करणम्

पद्यांशं पठित्वा जालरेखाचित्रं पूरयत।

1.

2.

3.

भाषाभ्यासः

(क) समानार्थकशब्दाः

• नरः – मनुष्यः, मानवः, मानुषः, मर्त्यः, मनुजः।
• यशः – ख्यातिः, कीर्तिः, प्रसिद्धिः।
• गुरुः – आचार्यः, अध्यापकः, उपाध्यायः।
• बन्धुजनः – बान्धवः।
• राजसु – पार्थिवेषु, नृपेषु, भूपेषु।
• निपुणः – कुशलः, प्रवीणः, पारङ्गतः।
• स्तुवन्तु – प्रशंसन्तु।
• यथेष्टम् – यथेच्छम्।
• मरणम् – मृत्युः ।
• पन्थाः – वर्त्म, सरणिः, मार्गः।
• धीरः – धैर्यवान्, धैर्यशीलः।
• आत्मनः – स्वस्य।
• मुखम् – तुण्डम, वदनम्, आननम्।
• दोषः – प्रमादः।
• बकः – मरुवकः, सर्पभुक्।
• अल्पम् – स्वल्पम्।
• तृणम् – घासः, यवसम्, कुशः, शष्पम्, अर्जुनम्।

(ख) विरुद्धार्थकशब्दाः

1. गुप्तम् × अनावृतम्।
2. विद्याविहीन: × ज्ञानयुक्तम्।
3. गच्छतु × आगच्छतु।
4. मरणम् × जनिः, जन्म, जनुः।
5. दोषः × गुणः।
6. बध्यन्ते × मुच्यन्ते।
7. मौनम् × भाषितम्।
8. संहतिः × भिन्नता, भेदः ।

(क) विभक्त्यन्तरूपाणि।

• प्रश्थमा – निपुणाः, लक्ष्मीः, धीराः।
• द्वितीया – मरणम्, पदम्।
• पन्चमी – न्याय्यात्, पथः।
• सप्तमी – युगान्तरे।

समासाः

समस्तपदम्	अर्थ:	समासविग्रहः	समासनाम
विद्याविहीनः	devoid of knowledge	विद्यया विहीनः।	तृतीया तत्पुरुष समास
नीतिनिपुणाः	experts in ethics	नीत्यां/नीतिषु निपुणाः।	सप्तमी तत्पुरुष समास
यथेष्टम्	as per/according to wish	इष्टम् अनुसृत्य /अनतिक्रम्य।	अव्ययीभाव समास
शुकसारिकाः	parrots and mynas	शुकाः च सारिका: च।	इतरेतर द्वन्द्व समास
सर्वार्थसाधनम्	mean/medium of achieving all ends	सर्वार्थानां साधनम्।	षष्ठी तत्पुरुष समास
रासभरोहणम्	ascending the donkey	रासभं रोहणम्।	द्वितीया तत्पुरुष समास
भुजगयमिताः	controlled by a snake	भुजगेन यमिताः।	तृतीया तत्पुरुष समास
चरणविकल:	lame with legs	चरणेन / चरणाभ्यां विकलः।	तृतीया तत्पुरुष समास
क्रियासिद्धिः	accomplishment of the task	क्रियायाः सिद्धिः।	षष्ठी तत्पुरुष समास

सूक्तिसुधा Summary in Marathi and English

प्रस्तावना :

“सूक्तयः नाम सुवचनानि।” सूक्ती म्हणजे चांगली उक्ती (बोलणे). संस्कृत भाषा अशा अनेक सुवचनांनी समृद्ध आहे. सुभाषितांचा संदर्भ लक्षात घेऊन सूक्तींचा अर्थ जाणून घेतल्यास नैतिकदृष्ट्या श्रेष्ठ व्यक्तिमत्त्व विकसित केले जाऊ शकते.

पुष्कळदा, अनेक संस्कृत सूक्ती इतर भारतीय भाषांमध्ये सुध्दा वापरलेल्या दिसून येतात. प्रत्यक्षात, अशा सूक्तींचे स्मरण केल्याने व्यक्तीची शब्दसंपदा वाढते व इतर भाषांवर प्रभुत्व निर्माण होते.

“सूक्तिः नाम शोभना उक्तिः ” means a good saying. Sanskrit language is enriched with such good sayings. One can cultivate a strong and morally superior character by understanding the meaning of a good saying with reference to the given सुभाषित.

Several Sanskrit sayings are often used in other Indian languages. In fact, remembering such sayings definitely enhances one’s ocabulary and command over languages.

श्लोकः 1

विद्या नाम नरस्य रूपमधिकं प्रच्छन्नगुप्तं धनम्
विद्या भोगकरी यश:सुखकरी विद्या गुरूणां गुरुः।
विद्या बन्धुजनो विदेशगमने विद्या परं दैवतम्
विद्या राजमु पूज्यते न तु धनं विद्याविहीन: पशुः ।।1।। (वृत्तम् – शार्दूलविक्रीडितम्, स्रोत: – नीतिशतकम्)

सन्थिविग्रहः

1. रूपमधिकम् – रूपम् + अधिकम्।
2. बन्धुजनो विदेशगमने – बन्धुजन: + विदेशगमने।

अन्वय:- विद्या नाम नरस्य अधिकं रूपम्, प्रच्छन्नगुप्तं धनम्, विद्या भोगकरी यश:सुखकरी (च)। विद्या गुरूणां गुरुः । विदेशगमने विद्या बन्धुजनः ।
विद्या पर दैवतम्। विद्या राजसु पूज्यते न तु धनम्। विद्याविहीनः पशुः (एव)।

अनुवादः

मराठी विद्येमुळे मानवाचे सौंदर्य वाढते. विद्या हे संरक्षिलेले गुप्त धन आहे. विद्या नाना भोग (समाधान) प्राप्त करून देणारी आहे. (ती) यश व आनंद मिळवून देणारी आहे. विद्या गुरुंची गुरु आहे. परदेशी गेले असता विद्या ही बांधव असते. (बांधवाप्रमाणे उपयोगी पडते/सहाय्यभूत होते) विद्या सर्वश्रेष्ठ दैवत आहे. विद्या राजांमध्ये (राजसभांमध्ये) पूजनीय आहे; धन नाही. ज्याच्याजवळ विद्या नाही तो पशू(च) (समजावा).

English Knowledge enhances the beauty of man. It is secretly hidden treasure. Knowledge brings pleasure. It brings glory and comforts. Knowledge is the teacher of all teachers. Knowledge is kith and kin when going to a foreign land. Knowledge is a superior deity itself. Knowledge is worshipped amongst kings, not money. One without knowledge is a beast.

श्लोकः 2

निन्दन्तु नीतिनिपुणा यदि वा स्तुवन्तु
लक्ष्मीः समाविशतु गच्छतु वा यथेष्टम्।
अद्यैव वा मरणमस्तु युगान्तरे वा
न्याय्यात्पथः प्रविचलन्ति पदं न धीराः।।2।। (वृत्तम् – वसन्ततिलका, स्रोत: – नीतिशतकम्)

सन्धिविग्रहः

1. नीतिनिपुणा यदि – नीतिनिपुणाः + यदि।
2. न्याय्यात्पथः – न्याय्यात् + पथ: ।

अन्वय:- यदि (अपि) नीतिनिपुणा: निन्दन्तु स्तुवन्तु वा, लक्ष्मी समाविशतु यथेष्ट गच्छतु वा, मरणम् अद्य एव अस्तु युगान्तरे वा, (तथापि) धीराः न्याय्यात् पथः पदं न प्रविचलन्ति।

अनुवादः

नीतिमध्ये कुशल लोक निंदानालस्ती करोत वा प्रशंसा करोत, लक्ष्मी तिच्या इच्छेप्रमाणे येवो अथवा जावो, आजच मरण येवो वा युगान्त झाल्यावर दुसऱ्या युगात / भरपूर काळ लोटल्यावर) येवो, (तरीही) धैर्यवान लोक न्याय्यमार्गावरून आपले पाऊल ढळू देत नाहीत (ते न्याय्यमार्ग सोडत नाहीत).

English Experts in ethics may insult or praise, wealth may come or go by itself, may there be death today or after many years; courageous ones never divert (take a step back) from the path of justice.

श्लोकः 3

आत्मनो मुखदोषेण बध्यन्ते शुकसारिकाः।
बकास्तत्र न बध्यन्ते मौनं सर्वार्थसाधनम् ।।3।। (वृत्तम् – अनुष्टुप, स्रोत: – पञ्चतन्त्रम्)

अनुवादः

मराठी पोपट, साळुक्या (मैना) त्यांच्या स्वत:च्या तोंडाच्या दोषाने (बडबडीमुळे) अडकले जातात. (पण) बगळे (मात्र) अडकत नाहीत. (अशा प्रकारे) मौन पाळणे हे सर्व हेतू (गोष्टी) प्राप्त करण्याचे (मिळविण्याचे) साधन आहे.

English Parrots and mynas get trapped by fault of their own mouths (voices/sounds). Cranes do not get trapped. Silence is an instrument for obtaining all objects.

श्लोक: 4

रथस्यैकं चक्रं भुजगयमिताः सप्त तुरगाः
निरालम्बो मार्गश्चरणविकल: सारथिरपि।
रविर्यात्येवान्तं प्रतिदिनमपारस्य नभसः
क्रियासिद्धिः सत्त्वे भवति महतां नोपकरणे।।4।। (वृत्तम् – शिखरिणी, स्रोतः – भोजप्रबन्धः)

सन्धिविग्रहः

1. मार्गश्चरणविकलः – मार्गः + चरणविकलः।
2. रवियत्येवान्तम् – रविः + याति + एव + अन्तम्।
3. प्रतिदिनमपारस्य – प्रतिदिनम् + अपारस्य।
4. नोपकरणे – न + उपकरणे।

अन्वयः- रथस्य एकं चक्रं, सप्त भुजगयमिता: तुरगाः, निरालम्ब: मार्गः, सारथिः अपि चरणविकलः, (तथापि) रविः प्रतिदिनम् अपारस्य नभसः अन्तं याति एव। महतां क्रियासिद्धिः सत्त्वे भवति, उपकरणे न (भवति)।

अनुवादः

सूर्य दररोज, सापांनी नियंत्रित सात घोडे जोडलेल्या, एकच चाक असलेल्या रथातून, निराधार मार्गावरून, पायाने विकलांग अशा सारथीबरोबर अनंत अशा आकाशाच्या शेवटापर्यंत जातो. (जसे) महान लोकांच्या कार्याचे यश त्यांच्यातील सत्त्वाने (सामध्यनि) होते. साधनांनी नाही.

Even with a single wheel to the chariot of seven horses controlled by the bridle of snake, a supportless (difficult) path and a lame charioteer, the sun surely reaches the end of the unending sky everyday. The success of great people is in their spirit (valour) and does not depend on the means.

श्लोकः 5

अल्पानामपि वस्तूनां संहतिः कार्यसाधिका।
तृणैर्गुणत्वमापनष्यन्ते मत्तदन्तिनः।।4।। (वृत्तम् – अनुष्टुप, स्रोत: – हितोपदेशः।)

अनुवादः

लहानसहान वस्तूंचा संघ कार्य यशस्वी करतो (पूर्णत्वास नेतो). गवतापासून बनविलेल्या दोरखंडाने मत्त हत्ती (सुद्धा) नियंत्रित केले जातात.

Union of even small things accomplishes (big) tasks. Just as the intoxicated elephants are tied by a rope made of hay-sticks.

श्लोकः 6

प्रथमवयसि पीतं तोयमल्पं स्मरन्तः
शिरसि निहितभारा नारिकेला नराणाम्।
ददति जलमनल्पास्वादमाजीवितान्त।
न हि कृतमुपकारं साधवो विस्मरन्ति ।।6।। (वृत्तम् – मालिनी, स्रोत: – विक्रमचरितम्।)

सन्धिविग्रहः

1. तोयमल्पम् – तोयम् + अल्पम्।
2. कृतमुपकारम् – कृतम् + उपकारम्।
3. साधवो विस्मरन्ति – साधवः + विस्मरन्ति।
4. जलमनल्पास्वादमाजीवितान्तम् – जलम् + अनल्पास्वादम् + आजीवितान्तम्।
5. निहितभारा नारिकेला नराणाम् – निहितभारा: + नारिकेला: + नराणाम्।

अन्वय:- प्रथमवयसि पीतम् अल्पं तोयं स्मरन्तः शिरसि निहितभारा: आजीवितान्तं नराणां (नरेभ्यः) अनल्पास्वाद जलं ददति। साधवः कृतम् उपकारं नहि विस्मरन्ति।

अनुवादः

नारळाचे झाड लहानपणी मिळालेले थोडे पाणी लक्षात ठेवून, नारळांचे ओझे डोक्यावर बाळगून माणसांना आजन्म भरपूर गोड पाणी देते. (जसे) दुसऱ्याने केलेले उपकार सज्जन लोक कधीही विसरत नाहीत. (त्याची अनेक पटीने परतफेड करतात.)

In memory of the little water consumed in early age (as a seedling), a coconut tree, bearing weight on its head throughout its life, gives sweet water abundantly to humans. The noble people never forget benevolence (help offered by others).

श्लोक: 7

घटं भिन्द्यात् पटं छिन्द्यात् कुर्याद्रासभरोहणम्।
येन केन प्रकारेण प्रसिद्धः पुरुषो भवेत् ।।7।। (वृत्तम – अनुष्टुप, प्रकार: – हास्योक्तिः )

सन्धिविग्रहः

1. कुर्याद्रासभरोहणम् – कुर्यात् + रासभरोहणम्।
2. पुरुषो भवेत् . पुरुष: + भवेत्।

अन्वय:- पुरुषः घटं भिन्द्यात्, पटं छिन्द्यात, रासभरोहणं (अपि) कुर्यात्। येन केन प्रकारेण (स:) प्रसिद्धः भवेत्।

अनुवादः

घडा (भांडी) फोडावा, कपडे फाडावेत, गाढवावर (देखील) बसावे, पण काही तरी करून मनुष्याने प्रसिद्ध व्हावे.
One should break a pot, tear clothes and ride a donkey. By some way or the other (hook or crook), one should become popular.

शब्दार्थाः

1. रूपमधिकम् – more than beauty – रूपाहून अधिक
2. प्रच्छन्नगुप्तम् – secretly hidden – गुप्त/लपविलेले
3. भोगकरी – brings pleasure – आनंद / समाधान प्राप्त करून देणारे
4. सुखकरी – gives happiness – सुख देणारे
5. गुरूणाम् – of preceptors – गुरूंचे
6. बन्धुजनः – relative – नातेवाईक
7. विदेशगमने – when travelled in foreign land परदेशी प्रवास केला असता
8. परं दैवतम् – supreme deity – सर्वश्रेष्ठ दैवत
9. राजसु – among kings – राजांमध्ये
10. विद्याविहीन: – devoid of knowledge – विद्याहीन, ज्ञानहीन
11. निन्दन्तु – may censure – निंदानालस्ती करो
12. नीतिनिपुणाः – expert in ethics – नीतिमध्ये कुशल
13. स्तुवन्तु – may praise – स्तुती करो
14. समाविशतु – may come – येवो
15. यथेष्टम् – as per will – स्वेच्छेने
16. अद्यैव – today itself – आजच
17. युगान्तरे – in another era – युगानंतर (दुसऱ्या युगात)
18. न्याय्यात्पथ: – from the path of justice – न्याय्यमार्गावरून
19. प्रविचलन्ति – deviate – ढळतात
20. धीराः – courageous – धैर्यवान
21. भुजगयमिता: – controlled by serpants – सापांनी नियंत्रित
22. निरालम्बः – unsupported – निराधार
23. चरणविकल: – lame by a leg – पायाने पंगु
24. सारथिः – charioteer – सारथी
25. अन्तं याति – goes to the end – शेवटपर्यंत जातो
26. अपारस्य नभसः – of the endless sky – अनंत आकाशाच्या
27. क्रियासिद्धिः – accomplishment of the task – कार्याची पूर्तता
28. उपकरणे – on the means – साधनांवर
29. प्रथमवयसि – in early age – लहानपणी
30. तोयम् – water – पाणी
31. निहितभाराः – bearing weight – वजन घेऊन
32. आजीवितान्तम् – throughout life – संपूर्ण आयुष्यभर
33. अनल्पास्वादम् abundant of sweet water – भरपूर प्रमाणात गोड पाणी
34. उपकारम् – favour/benevolence – उपकार
35. अल्पनाम – of small (insignificant) things – लहानसहान गोष्टींचा
36. संहतिः – unity / union – संघ
37. कार्यसाधिका – that which accomplishes the task – कार्य साधणारी
38. गुणत्वम् – collection of a rope – दोरखंड
39. तृणैः – by grasses – गवतापासून बनविलेले
40. बध्यन्ते – can control – बांधले जातात/नियंत्रित केले जातात
41. घटम् – a pot – घडा
42. भिन्द्यात् – should break – फोडावा
43. पटम् – a cloth – वस्त्र
44. छिन्द्यात् – should tear – फाडावे
45. रासभरोहणम् – should ride – गाढवावर बसावे
46. कुर्यात् – adonkey
47. येन केन प्रकारेप – by hook or crook – काहीतरी करून
48. प्रसिद्धः भवेत् – should become famous – प्रसिद्ध व्हावे
49. आत्मनः – own – स्वत:च्या
50. मुखदोषेण’ – due to fault of mouths – तोंडाच्या दोषाने (आवाजामुळे)
51. बध्यन्ते – caged/trapped – अडकले जातात
52. शुकसारिकाः – parrots and mynas – पोपट व साळुक्या/मैना
53. बकाः – cranes – बगळे
54. मौनम् – silence – मौन
55. सर्वार्थसाधनम् – instrument of achieving all purposes – सर्व हेतू प्राप्त करण्याचे साधन

10th Standard Sanskrit Anand Digest Pdf  

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्यस्तबकः Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Aamod Chapter 9 धेनोाघः पलायते Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Amod Chapter 9 धेनोाघः पलायते Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 9 Question Answer

Sanskrit Amod Std 10 Digest Chapter 9 धेनोाघः पलायते Textbook Questions and Answers

भाषाभ्यास:

1. पूर्णवाक्येन उत्तरं लिखत ।

प्रश्न अ.
चिमणराव: कस्यां मग्नः?
उत्तरम् :
चिमणराव: पत्रक्रीडायां मग्नः।

प्रश्न आ.
क्रीडायां को व्याघ्रं भल्लूकं च नाटयत:?
उत्तरम् :
क्रीडायां द्वौ बहुरूपधारिणौ नरौ व्यानं भल्लूकं च नाटयतः।

प्रश्न इ.
महिला केन मूर्च्छिता?
उत्तरम् :
महिला व्याघ्रस्य मनुष्यबाण्या भाषणेन मूर्छिता।

प्रश्न ई.
चिमणरावेण किं निश्चितम् ?
उत्तरम् :
सर्कसस्वामिन : साहाय्य करणीयम् इति चिमणरावेण निश्चितम्।

प्रश्न उ.
सर्कसक्रीडायाः प्रारम्भः कदा जात: ?
उत्तरम् :
सर्कसक्रीडाया: प्रारम्भः रात्रौ दशवादने जातः ।

प्रश्न ऊ.
चिमणराव: किमर्थं प्रयत्तवान् ?
उत्तरम् :
चिमणराव यावत् शक्यं जनान् रञ्जयितुं प्रयत्तवान्।

प्रश्न ए.
कैः आनन्देन तालिकावादनम् आरब्धम् ?
उत्तरम् :
उत्तेजितैः प्रेक्षकै: आनन्देन तालिकावादनम् आरब्धम्।

प्रश्न ऐ.
धेन्वा किं लक्षितम् ?
उत्तरम् :
धेनुना इमौ न परिचिती व्याघ्रभल्लूको इति लक्षितम्।

प्रश्न ओ.
भल्लूकः कुत्र आरूढवान् ?
उत्तरम् :
भल्लूक: पटमण्डपस्तम्भम् आरूढवान्।

प्रश्न औ.
प्रेक्षकाः कदा कोलाहलं कृतवन्त: ?

2. माध्यमभाषया उत्तरं लिखत ।

प्रश्न अ.
सर्कसस्वामी किमर्थं चिमणरावं प्रति आगतः ?
उत्तरम् :
‘धेनोर्व्याघ्रः पलायते।’ या कथेत चिमणरावांच्या स्वभाव वैशिष्ट्यांमुळे जी विनोदनिर्मिती होते त्यामुळे वाचकांच्या चेहऱ्यावर स्मितहास्य उमटते. त्याचप्रमाणे ही कथा म्हणजे एका प्रादेशिक भाषेतून प्राचीन भाषेतील अनुवादाचा उत्कृष्ट नमुना आहे.

या कथेचा नायक चिमणराव हा साधाभोळा, प्रामाणिक आणि देशभक्त आहे. त्यांनी ‘स्काऊट’ सारखाच शूरवीर मुलांचा संघ स्थापन केला, ज्याद्वारे लहान मुलांच्या मनात परोपकार, शौर्य, सहकार्य, समाजसेवेचे संस्कार रुजवण्याचा त्याचा मानस आहे.

सुट्टीमध्ये त्याने बनेश्वर नावाच्या गावात या मुलांच्या चमूला शिबिरासाठी नेले. शिबिराच्या पहिल्याच दिवशी दुपारचे जेवण आटपून चिमणराव मुलांसोबत पत्ते खेळण्यात मग्न असताना, नुकताच परिचय झालेले प्रोफेसर सर्कसवाले त्यांना शोधत आले. सर्कशीच्या मालकांना प्रयोगासाठी चिमणरावांचे सहकार्य अपेक्षित होते.

प्रयोगात अस्वल आणि वाघाचे सोंग घेणाऱ्या व्यक्ती भांडणादरम्यान जखमी झाल्या होत्या. त्यामुळे सर्कसच्या मालकांनी चिमणरावांना विनंती केली, की मुलांच्या संघातील दोघांना त्या दिवशीच्या प्रयोगात अस्वल व वाघाचे सोंग घेण्याची परवानगी द्यावी, जेणेकरुन प्रयोग न फसता यशस्वीपणे पूर्ण होईल.

The story ‘धेनोर्व्याघ्रः पलायते।’ brings smile on the faces of the readers due to the humor caused by innocent nature of चिमणराव. It is also an excellent example of translation skills from a regional language to the ancient language of India.

चिमणराव, the hero of this story isa sincere, innocent and patriotic person, made a troop of brave children like ‘scout’. The purpose behind it, was to inculcate values like benevolence, bravery, co-operation, social service etc. in the minds of the children.

During vacations, he took this troop of children to a village called ‘बनेश्वर for a camp. On the first day of the camp itself, when चिमणराव was busy playing cards with the children in the afternoon, प्रोफेसर सर्कसवाले, an owner of a circus came to meet him.

He was seeking help from चिमणराव in his circus show. The men enacting a bear and a tiger in his show were wounded. So the owner of the circus requested चिमणराव to allow any two soldiers from the troop to enact the animals and save the show from being a flop.

प्रश्न आ.
सर्कसक्रीडायाः आरम्भात् पूर्वं किं किम् अभवत् ?
उत्तरम् :
धेनोर्व्याघ्रः पलायते।’ या कथेत चिमणरावांच्या स्वभाव वैशिष्ट्यांमुळे जी विनोदनिर्मिती होते त्यामुळे वाचकांच्या चेहऱ्यावर स्मितहास्य उमटते. त्याचप्रमाणे ही कथा म्हणजे एका प्रादेशिक भाषेतून प्राचीन भाषेतील अनुवादाचा उत्कृष्ट नमुना आहे.

सर्कशीच्या मालकांनी प्रयोगासाठी सहकार्य करण्याच्या विनंतीचा चिमणरावांनी स्वीकार केला. त्यांनी आपल्या चमूतील बालवीरांपैकी अब्दुलची निवड अस्वलाच्या सोंगासाठी केली आणि ते स्वतः वाघाच्या वेशात तयार झाले. प्रयोग सुरु होण्यापूर्वी ते दोघे आपापले सोंग घेऊन नेमलेल्या पिंजऱ्यांत शिरले. वाघाचे सोंग घेतलेल्या चिमणरावांच्या पिंजऱ्यासमोर तोबा गर्दी जमली होती, त्यांनी प्रेक्षकांचे मनोरंजन करण्याचा प्रयत्न केला मात्र प्रेक्षक, ‘अरे, हा काय वाघ आहे? किती कृश आहे,’ अशी त्यांची खिल्ली उडवू लागले.

चिमणरावांनी वाघासारखी डरकाळी फोडल्यामुळे आईसोबत वाघ बघायला आलेला एक मुलगा घाबरला. तेव्हा त्याच्या आईन रागात वाघाला दगड फेकून मारला. परंतु त्यामुळे वाघाच्या वेशातील चिमणराव जखमी झाले. क्षणभर हे सगळे नाटक विसरून ते वेदनेने ओरडले, ‘पिंजऱ्यातल्या वाघाला बघून बायका दगड मारतात.’ त्यांचे हे वाक्य पूर्ण होण्याआधीच मनुष्यवाणीत बोलणाऱ्या वाघाला बघून ती बाई चक्रावली.

‘भूत आहे भूत’, असे किंचाळत ती चक्कर येऊन जमिनीवर पडली. त्यानंतर चिमणरावांचा मुलगा राषु पिंजऱ्याजवळ येऊन मधेच त्यांना म्हणाला, ‘आप्पा, तुम्हांला चहा प्यायचा आहे का?’ अशाप्रकारे वाघाला वडील म्हणून संबोधणारा मुलगा पाहून प्रेक्षक अधिकच संभ्रमात पडले. अशाप्रकारे, सर्कशीचा प्रयोग सुरु होण्यापूर्वीच तंबूत गडबड-गोंधळाचे वातावरण निर्माण झाले.

The story ‘धेनोक्नः पलायते।’ brings smile on the faces of the readers due to the humor caused by innocent nature of चिमणराव. It is also an excellent example of translation skills from a regional language to the ancient language of India. चिमणराव accepted the request of the circus owner to help him in his show.

He appointed अब्दुल, one of the cadets of his troop, as the bear and he himself got ready to enact the tiger in the show. Before the show would begin, both of them entered their allotted cages in the disguise of the bear and the tiger. A huge crowd. gathered around चिमणराव’s cage, who was disguised as the tiger.

He tried to entertain the crowd but the people mockingly said, “Is this a tiger? How weak is this!” A boy, who came to see the tiger along with his mother, got afraid due to the roaring of the tiger. So his mother threw a stone at him with anger. But behind the tiger’s disguise got wounded. For a second, he forgot about all the drama and screamed with pain, “Seeing the caged tigers, ladies throw stones.”

Before he could end his sentence, that lady got surprised seeing a tiger speaking in human voice. She fell on the ground being unconscious, screaming, “Ghost, it’s ghost!” Further चिमणराव’s son राघु came near the cage and asked him, “Father, would you like to have some tea?” With this the audience got even more confused. Thus, even before the circus show began, there was situation of chaos and confusion in the tent of circus.

प्रश्न इ.
पशूनां सहभोजनसमये क: हास्यपूर्णः अनवस्थाप्रसङ्गः समुत्पन्नः?
उत्तरम् :
‘धेनोव्याघ्रः पलायते।’ या कथेत चिमणरावांच्या स्वभाव वैशिष्ट्यांमुळे जी विनोदनिर्मिती होते त्यामुळे वाचकांच्या चेहऱ्यावर स्मितहास्य उमटते. त्याचप्रमाणे ही कथा म्हणजे एका प्रादेशिक भाषेतून प्राचीन भाषेतील अनुवादाचा उत्कृष्ट नमुना आहे. सर्कशीच्या मालकांच्या विनंतीचा स्वीकार करून चिमणराव व अब्दुलने अनुक्रमे वाघ व अस्वलाचे सोंग घेतले. प्रयोग रात्री 10 ला सुरू झाला. प्राण्यांच्या सहभोजनाचा लोकप्रिय कार्यक्रम 12 वाजता सुरू झाला.

प्रेक्षकांची उत्सुकता शिगेला पोहोचली. मंचावर तीन खुर्त्या आणि मधोमध एक गोलाकार टेबल ठेवण्यात आले. चिमणराव व अब्दुल आपापल्या खुर्चीत जाऊन बसले. त्या कार्यक्रमातील तिसरा प्राणी म्हणजे गाय सुद्धा मंचावर आली. चिमणराव आणि अब्दुल प्राण्यांचे सोंग घेऊन बसले होते, ती गाय मात्र खरीखुरी होते.

प्राण्यांसमोर खाद्य वाढले जात असता प्रेक्षकांनी आनंद आणि उत्सुकतेने टाळ्यांचा कडकडाट केला. त्या गायीला पूर्वी जे प्राण्यांचे सोंग घ्यायचे त्यांच्यासोबत कार्यक्रम करण्याचा सराव होता. परंतु थोड्याच वेळात गायीच्या लक्षात आले की, हे वाघ आणि अस्वल नेहमीचे नाहीत, ती संशय आणि गोंधळाने दोघांकडे पाहू लागली. आपली शिंगं उगारून ती दोघांवर गुरकावू लागली. चिमणरावांनी डरकाळी फोडून व आपले तीक्ष्ण दात दाखवून तिला घाबरवण्याचा प्रयत्न केला, परंतु ती त्याला बधली नाही. अब्दुलने हाताने तिला चापट मारली. तेव्हा चिडून ती दोघांवर धावून गेली.

प्रेक्षकांनी पाहिले की अस्वल घावरून तंबूच्या खांबावर चढले. हा त्यांना प्रयोगातील पूर्वनियोजित भाग आहे असे वाटले. परंतु अस्वल हातातून निसटल्यामुळे चिडून ती गाय आता चिमणराव म्हणजेच वाघावर धावून गेली. अशा संकटसमयी पूर्वी ठरवलेला सगळा बनाव आणि घेतलेले वाघाचे सोंग विसरून भितीने किंचाळत चिमणराव पळू लागले, ‘वाचवा, प्रोफेसरसाहेब, वाचवा!’ गायीला घाबरुन पळणारा वाघ पाहून प्रेक्षक गोंधळात पडले.पुढे त्यांना या नाटकाची कल्पना आली.

त्यांनी वाघाचे सोंग उतरवून चिमणरावांना बेदम मारले. इतके, की ते वेदनेने बेशुद्ध होऊन पडले. अशा प्रकारे चिमणराव प्रोफेसर सर्कसवाले यांना सर्कशीच्या प्रयोगासाठी सहकार्य करण्याचा प्रयत्न करत असताना प्रयोगाचा मात्र फज्जा उडाला.

The story ‘धेनोर्व्याघ्रः पलायते।’ brings smile on the faces of the readers due to the humor caused due to innocent nature of चिमणराव. It is also an excellent example of translation skills from a regional language to the ancient language of India.

Accepting the request of the circus owner, चिमणराव and अब्दुल were disguised as the tiger and the bear respectively. The circus began at 10 at night. The popular event of animal’s meal together began at 12. Audiences’ enthusiasm raised up. Three chairs and a circular stool in the middle were arranged on the stage. चिमणराव and अब्दुल took their seats. The cow, the third animal of the show, too came on the stage.

While चिमणराव and अब्दुल were disguised as the animals, the cow was a real one. As food was being arranged in front of the animals, the audience started clapping with joy and excitement. The cow was trained to perform in the show along with the earlier disguised men. But in a short while, she realised that these tiger and bear were not the usual ones.

She looked at both of them with confusion and doubt. Raising her horns she attacked them, चिमणराव tried to frighten her by roaring and displaying his sharp teeth, but she didn’t bother. अब्दुल beather with his hand. With this she got angry and ran over him. The audience saw that the bear climbed on the pole of the tent and they thought it was a part of the show. But the cow, being angry as the bear escaped, now attacked चिमणराव-the tiger.

Here चिमणराव forgot the planned drama and the tiger’s disguise due to fear and ran away screaming, “Help, professor, help!”. Seeing the tiger being afraid of a cow and running away, the audience got confused and then realised the drama. They removed the tiger’s disguise off चिमणराव’s body and beat him harshly, so much so that he fell unconscious with pain. Thus, चिमणराव tried to help प्रोफेसर सर्कसवाले in his show, but it turned out to be a fiasco.

3. समानार्थकशब्दान् लिखत ।
मनः, गौः, व्याघ्रः, सैनिकः, क्रीडा, वेदना, भाषणम्, उत्कण्ठा, मनुष्यः, शृङ्गे, दन्ताः, उत्तमानम्

प्रश्न 1.
समानार्थकशब्दान् लिखत ।
मनः, गौः, व्याघ्रः, सैनिकः, क्रीडा, वेदना, भाषणम्, उत्कण्ठा, मनुष्यः, शृङ्गे, दन्ताः, उत्तमाङ्गम्
उत्तरम् :

• मग्नः – रतः, लीनः ।
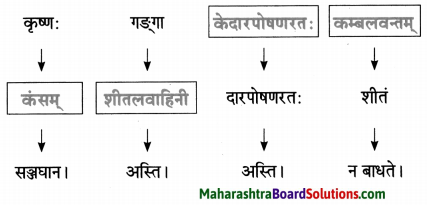
• गौः – धेनुः, माहेयी, सौरभेयी, उस्रा, माता, शृङ्गिणी।
• व्याघ्रः – शार्दूल:, द्विपी ।
• सैनिकः – भटः, योध्दा, सेनारक्षः, योधः ।
• क्रीडा – खेलः।
• वेदना – संवेदः, निर्वेशः, उपलम्भः।
• उत्कण्ठा – उत्सुकता।
• भाषणम् – व्याहारः, भाषितम्।
• मनुष्यः – नरः, मानुषः, मर्त्यः, मनुजः, मानवः ।
• शृङ्गे – ककुदे, विषाणे।
• दन्ताः – रदनाः, दशना:।
• उत्तमाङ्गम् – मस्तकम्, शिरः, शीर्षम्, मूर्धा।

4. विरुद्धार्थकशब्दान् लिखत ।
समाप्य, प्राक्, विस्मृत्य, कृशः

प्रश्न 1.
विरुद्धार्थकशब्दान् लिखत ।
समाप्य, प्राक्, विस्मृत्य, कृशः
उत्तरम् :

• समाप्य × आरभ्य ।
• प्राक् × अनन्तरम्।
• विस्मृत्य × स्मृत्वा ।
• कृशः × बलवान, बलिष्ठः।

5. प्रश्ननिर्माणं कुरुत।।

प्रश्न अ.
अहं बालैः सह पत्रक्रीडायां मनः आसम् ।
उत्तरम् :
अहं कै: सह पत्रक्रीडायां मग्न: आसम्?

प्रश्न आ.
धेनुः वास्तविकी एव ।
उत्तरम् :
माहेयी / सौरभेयी / गौः / उस्रा / माता / शृङ्गिणी तु वास्तविकी एव।

प्रश्न इ.
सर्कसस्वामिनः विवशता मया अवगता ।
उत्तरम् :
कस्य विवशता मया अवगता?

प्रश्न ई.
भल्लूकवेशे अब्दुलः शोभेत ।
उत्तरम् :
भल्लूकवेषे कः शोभेत?

प्रश्न उ.
महिला मयि पाषाणखण्डान् अक्षिपत् ।
उत्तरम् :
महिला मयि कान् अक्षिपत्?

प्रश्न ऊ.
गौः मञ्चं समागता ।
उत्तरम् :
का मञ्चं समागता?

6. क: कं वदति ?

प्रश्न अ.
‘विज्ञापनं कृत्वा प्रवेशपत्राणि अपि विक्रीतानि ।’
उत्तरम् :
सर्कसक्रीडास्वामी लेखकं चिमणरावं वदति।

प्रश्न आ.
किं धेनुरपि …?’
उत्तरम् :
लेखक : चिमणराव : सर्कसक्रीडास्वामिनं वदति।

प्रश्न इ.
‘चायं पातुम् इच्छति किम्?’
उत्तरम् :
राघु: चिमणरावं/ लेखकं वदति।

7. विशेषण-विशेष्याणां मेलनं कुरुत ।

प्रश्न 1.
विशेषण-विशेष्याणां मेलनं कुरुत ।

विशेषणम्	विशेष्यम्
लोकप्रियः	आकर्षणम्
सर्वोच्चम्	शुल्कम्
बहुरूपधारिणी	व्याघ्रान्
अधिकम्	प्रेक्षकाः
अधिक:	प्रेक्षकेषु
भीत:	सहभोजनकार्यक्रमः
पञ्जरस्थितान्	नरौ
सम्भ्रान्ताः	सम्पर्दः
त्रीणि	व्याघ्रभल्लूको
निमग्रेषु	बाल:
परिचितौ	आसनानि

उत्तरम् :

विशेषणम्	विशेष्यम्
लोकप्रियः	सहभोजनकार्यक्रमः
सर्वोच्चम्	आकर्षणम्
बहुरूपधारिणी	नरौ
अधिकम्	शुल्कम्
अधिक:	सम्पर्दः
भीत:	बाल:
पञ्जरस्थितान्	व्याघ्रान्
सम्भ्रान्ताः	प्रेक्षकाः
त्रीणि	आसनानि
निमग्रेषु	प्रेक्षकेषु
परिचितौ	व्याघ्रभल्लूको

8. अमरकोषात् शब्दं प्रयुज्य वाक्यं पुनर्लिखत ।

प्रश्न अ.
धेनुः तु वास्तविकी एव ।
उत्तरम् :
धेनुः कीदृशी?

प्रश्न आ.
मम उत्तमाङ्गम् उपचारपट्टिकाभिः विभूषितम् ।
उत्तरम् :
मममस्तकम् / शिरः/ शीर्षम् / मूर्धा / मस्तक: उपचारपट्टिकाभिः विभूषितम्।

9. सूचनानुसारं कृती: कुरुत ।

प्रश्न अ.
पत्रक्रीडायां मनः आसम् अहम् । (बहुवचने लिखत।)
उत्तरम् :
पत्रक्रीडायां मग्नाः आस्म वयम्।

प्रश्न आ.
जनाः न सन्तुष्टाः । (एकवचने लिखत)
उत्तरम् :
जन: न सन्तुष्टः।

प्रश्न इ.
प्रेक्षकाः मां निघृणं ताडितवन्तः । (वाच्यपरिवर्तनं कुरुत ।)
उत्तरम् :
प्रेक्षकैः अहं निघृणं ताडितः।

Sanskrit Amod Class 10 Textbook Solutions Chapter 9 धेनोाघः पलायते Additional Important Questions and Answers

अवबोधनम्

(क) उचितं कारण चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
सर्कस-क्रीडारङ्गस्य स्वामी लेखकम् अन्विष्यन् शिबिरं समागत: यतः ………….
(अ) सः लेखकस्य साहय्यम् इच्छति।
(ब) सः लेखक सर्कसक्रीडां द्रष्टुं निमन्वितवान्।
उत्तरम् :
(अ) लेखकस्य साहाय्यम् इच्छति।

प्रश्न 2.
सर्कसक्रीडायां व्याघ्रभल्लूको द्विपादौ एव यतः ……………
(अ) वास्तविको व्याघ्रभल्लूको पालयितुं तेषां सामर्थ्य नासीत्।
(ब) स: वास्तविक-व्याघ्रभल्लूकाभ्यां भीतः।
उत्तरम् :
(अ) वास्तविको व्याघ्रभल्लूको पालयितु तेषां सामथ्र्य नासीत्।

प्रश्न 3.
अब्दुल: भल्लूकपात्रे नियोजित: यतः ……….
(अ) लेखक: भल्लूकपात्रम् अभिनेतुं नैच्छत्।
(ब) अब्दुल: भल्लूकवेषे शोभेत इति लेखक: अमन्यत।
उत्तरम् :
(अ) अब्दुल: भल्लूकवेधे शोभेत इति लेखक: अमन्यत ।

प्रश्न 4.
माता व्याघ्र पाषाणखण्डान् क्षिपति यतः
(अ) तस्याः पुत्रः व्याघ्रगर्जनां श्रुत्वा भीतः।
(ब) माता व्याघ्र पीडयितुम् इच्छति स्म।
उत्तरम् :
(अ) तस्याः पुत्र : व्याघ्रगर्जनां श्रुत्वा भीतः।

प्रश्न 5.
माता मूच्छिता यतः ………
(अ) माता ज्वरपीडिता।
(ब) तस्याः पुरत: व्याघ्रः मनुष्यवाण्या अवदत्।
उत्तरम् :
(ब) तस्याः पुरत: व्याघ्रः मनुष्यवाण्या अवदत्।

प्रश्न 6.
कार्यक्रमस्य अन्ते प्रेक्षका: व्याघ्रवेषधारिणं मनुष्यं ताडितवन्तः यतः
(अ) व्याघ्रवेषधारिणा मनुष्येण चौर्यकार्य कृतम्।
(ब) तेन मनुष्येण व्याघ्रवेषं धृत्वा प्रेक्षकाणां वञ्चना कृता।
उत्तरम् :
(ब) तेन मनुष्येण व्याघ्रवेषं धृत्वा प्रेक्षकाणां वनना कता।

(ख) उचितं पर्यायं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
1. तथा विज्ञापनं कृत्वा …………….. विक्रीतानि। (प्रवेशपत्राणि/पिहितपत्राणि)
2. अस्माकं सर्कसक्रीडायां …………….., भल्लूक: च द्विपादौ एव। (गौः/ व्याघ्रः)
उत्तरम् :
1. प्रवेशपत्राणि
2. व्याघः

प्रश्न 2.

1. ……….. भल्लूकवेषे नियोजितः । (लेखक:/अब्दुल:)
2. व्याघ्रस्य अभिनयाथै ……. सिद्धः । (लेखक:/अब्दुल:)
3. ……….. पारस्य पुरत: सम्मदः जातः । (व्याघ्रस्य/ भल्लूकस्य)
4. महिला पुत्रेण सह ……….. द्रष्टुम् आगता। (व्याघ्र/भल्लूकं)

उत्तरम् :

1. अब्दुल:
2. लेखक
3. व्याघ्रस्य
4. व्याधं

प्रश्न 3.
1. ……… मनुष्यवाण्या भाषणेन सा महिला मूर्छिता। (भल्लूकस्य / व्यावस्य)
2. ……. क्रीडाया: चरमबिन्दुः समायातः। (द्वादशवादने / दशवादने)
उत्तरम् :
1. व्याघ्रस्य
2. द्वादशवादने

प्रश्न 4.

1. सम्भ्रमेण संशयेन च ……… दृष्टवती। (आवां / वयम्)
2. अब्दुल: तां ………… ताडितवान्। (हस्तेन / हस्तात)
3. प्रेक्षका: मम व्याघ्रवेषं निष्कास्य मां ………. ताडितवन्तः। (निपुणं / सस्नेह)

उत्तरम् :

1. आवां
2. हस्तेन
3. निघणं

(ग) कः कं वदति।

प्रश्न 1.
किं प्राणिनो: कलहः?
उत्तरम् :
लेखक: चिमणराव: सर्कसक्रीडास्वामिनं वदति।

प्रश्न 2.
नहि, नहि, धेनुस्तु वास्तविकी एव।
उत्तरम् :
सर्कसक्रीडास्वामी लेखक चिमणरावं वदति।

प्रश्न 3.
कृपया साहाय्यं करोतु।
उत्तरम् :
सर्कसक्रीडास्वामी लेखकं चिमणरावं वदति।

(घ) पूर्णवाक्येन उत्तरं लिखत।

प्रश्न 1.
एषः गद्यांश: कस्मात् पाठात् उद्धृतः?
उत्तरम् :
एषः गद्यांश: ‘धेनोर्व्याघ्र : पलायते’ इति पाठात् उद्धृतः ।

प्रश्न 2.
भल्लूकपात्रे क: नियोजितः?
उत्तरम् :
भल्लूकपात्रे अब्दुल : नियोजितः।

प्रश्न 3.
कुत्र सम्मः जातः?
उत्तरम् :
व्याघ्रपञ्जरस्य पुरत: सम्मर्द जातः ।

प्रश्न 4.
का पाषाणखण्डान् अक्षिपत्?
उत्तरम् :
व्याघ्र द्रष्टुं स्वपुत्रेण सह आगता माता पाषाणखण्डान् अक्षिपत्।

प्रश्न 5.
कः धेनुं हस्तेन ताडितवान्?
उत्तरम् :
अब्दुल: धेनुं हस्तेन ताडितवान्।

प्रश्न 6.
कदा प्रेक्षागारे मझन् कोलाहल: उत्पन्नः?
उत्तरम् :
धेनो: भीतं, पलायमानं व्याघ्रं दृष्ट्वा पेक्षागारे महान् कोलाहल: उत्पनः ।

(च) वाक्यं पुनलिखित्वा सत्यम् / असत्यम् इति लिखत।

प्रश्न 1.
1. सर्कसक्रीडायां लोकप्रियः सङ्गीतकार्यक्रमः प्रचलति।
2. बहुरूपधारिणौ नरौ गोव्याघ्रौ नाटयतः।
उत्तरम् :
1. असत्यम्।
2. असत्यम्।

प्रश्न 2.

1. व्यानवेषे अब्दुलः समुपस्थितः।
2. व्याघ्रवेषे लेखक: समुपस्थितः।
3. महिला भल्लूकं द्रष्टुम् आगता।
4. व्याघ्रस्य गर्जनया बाल: आनन्दितः।

उत्तरम् :

1. असत्यम्।
2. सत्यम्।
3. असत्यम्।
4. असत्यम्।

प्रश्न 3.

1. रात्रौ दशवादने सर्कसक्रीडायाः प्रारम्भः जातः ।
2. श्रोतृवृन्दः लेखने मग्नः।
3. पूर्व व्याघ्रभल्लूको वास्तविकौ आस्ताम्।

उत्तरम् :

1. सत्यम्।
2. असत्यम्।
3. असत्यम्।

प्रश्न 4.
1. धेनु: व्याघ्रात् भीता।
2. प्रेक्षका; भल्लूकवेषधारिणम् अब्दुलं ताडितवन्तः।
उत्तरम् :
1. असत्यम्।
2. असत्यम्।

शब्दज्ञानम् ।

(क) सन्धिविग्रहः।

1. धेनोर्व्याघः – धेनोः + व्याघ्रः।
2. मामेव – माम् + एव।
3. व्याघ्रश्च – व्याघ्रः + च।
4. इत्येतेषाम् – इति + एतेषाम्।
5. द्वावपि . द्वौ + अपि।
6. नास्ति – न + अस्ति ।
7. धेनुरपि – धेनु: + अपि।
8. धेनुस्तु – धेनुः + तु।
9. करणीयमिति – करणीयम् + इति।
10. प्रागेव – प्राक् + एव।
11. यावच्छक्यम् – यावत् + शक्यम्।
12. किमयम् – किम् + अयम्।
13. कृशोऽयम् – कृशः + अयम्।
14. पूर्वमेव – पूर्वम् + एव।
15. भूतोऽयम् – भूतः + अयम्।
16. पूर्वमपि – पूर्वम् + अपि।
17. तथापि – तथा + अपि ।
18. अचिरादेव – अचिरात् + एव।
19. अहमपि – अहम् + अपि।
20. किञ्चिदपि – किञ्चित् + अपि ।
21. मूलस्वरूपमाश्रितवान् – मूलस्वरूपम् + आश्रितवान्।

(ख) त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि ।

1.

त्वान्त अव्यय धातु + त्वा / ध्या / ट्वा / ड्वा / इत्वा / अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्न अव्यय धातु + तुम् / धुम् / टुम् / दम् / इतुम् / अयितुम्
कृत्वा, धृत्वा	समाप्य	पालयितुम्
यितुम् मत्वा, धृत्वा, दृष्ट्वा	विस्मृत्य	रञ्जयितुम्, द्रष्टुम्

2.

ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्त अव्यय धातु + तुम् / धुम् / टुम् / दुम् / इतुम् / अयितुम्
आगत्य	पातुम, कर्तुम्

(ख) त्वान्त – ल्यबन्त – अव्ययानि।

तुमन्त अव्यय धातु + त्वा / ध्वा / ट्वा /  दवा / इत्वा / अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य
कृत्वा, दृष्ट्वा	उन्नम्य, विचिन्त्य, विस्मृत्य, निष्कास्य

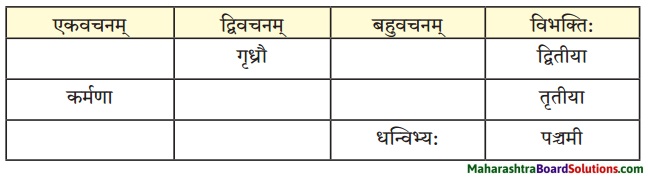
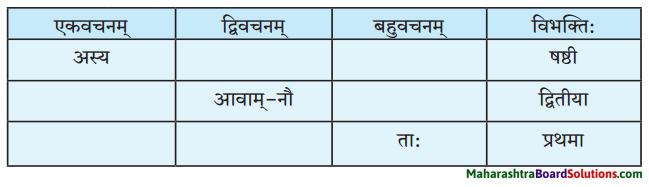
(ग) विभक्त्यन्तरूपाणि।

द्वितीया – भोजनादिकम्, माम, विज्ञापनम, व्याघ्रम्, भल्लूकम्, साहाय्यम्, व्याघ्रभल्लूकवेषौ, जनान, व्याघम्, पाषाणखण्डान्, पञ्जरस्थितान्, व्याघान्, त्रीणि, आसनानि, वर्तुलाकारम्, पीठम्, मञ्चम्, आवाम्, शृङ्गे, नौ, तीक्ष्णदन्तान, ताम, तम्, पटमण्डपस्तम्भम, व्याघ्रम, माम, लक्ष्यम्, व्याघ्रत्वम्, द्विपादम, मूलस्वरूपम्, भीतम्, पलायमानम्, पुण्यपत्तनदिशम्।

तृतीया – बालैः, प्राध्यापकमहाशयेन, मया, मया, यदृच्छया, उपहासेन, स्वपुत्रेण, गर्जनया, वेदनया, मनुष्यवाण्या, भाषणेन, उच्चैः, उत्तेजितैः, प्रेक्षकैः, आनन्देन, ताभ्याम्, धेनुना, सम्भमेण, संशयेन, हस्तेन, तेन, चापल्येन, भीत्या, वेदनाभिः, उपचारपट्टिकाभिः।
पञ्चमी – कतिपयेभ्यः, मासेभ्यः, कलहकारणात्, अचिरात्, तस्याः, धेनोः।

षष्ठी – शिबिरस्य, अस्माकम्, एतेषाम, पशूनाम्, प्रयोगस्य, भल्लूकयोः, प्राणिनोः, भवतः, प्रेक्षकाणाम्, सर्कसस्वामिनः, तस्य, परोपकारस्य, व्याघ्रस्य, मम, पारस्य, मम, वाक्यसमाप्तेः, व्याघ्रस्य, सर्कसक्रीडाया:, प्रेक्षकाणाम्, उत्कण्ठायाः, अस्माकम्, खाद्यस्य, सहभोजनस्य, भल्लूकवेषे, भल्लूकपात्रे, स्वपञ्जरयोः, मयि, भूमौ, रात्रौ, दशवादने, द्वादशवादने, मझे, मध्यभागे, एकस्मिन्, आसने, प्रारम्भे, जाते।

सप्तमी – प्रथमदिने, मध्याहे, पत्रक्रीडायाम, सर्कसक्रीडायाम्।

सम्बोधनम् – कॅप्टनसाहेब, महाशय।

(घ) विशेषण – विशेष्य – सम्बन्धः।

विशेषणम्	विशेष्यम्
1. कतिपयेभ्यः	मासेभ्यः
2. द्विपादौ	भल्लूको
3. वास्तविकी	धेनुः
4. महान्	उपकार:
5. मनुष्यवाण्या	भाषणेन
6. मूर्छिता	महिला
7. वर्तुलाकारम्	पीठम्
8. भल्लूकवेषधारी	अब्दुल:
9. उत्तेजितैः	प्रेक्षकैः
10. अभ्यस्ता	धेनुः
11. सन्तुष्टाः	जनाः
12. कृशः	व्याघ्रः
13. पूर्वनियोजिता	क्रीडा
14. प्रमुदिताः	प्रेक्षका:
15. क्रुद्धा	धेनुः
16. चतुष्पादविशिष्टम्	व्याघ्रत्वम्
17. द्विपादम्	मूलस्वरूपम्
18. भीतम्, पलायमानम्	व्याघ्रम्
19. महान्	कोलाहल:
20. अनुत्तमानि	अङ्गानि

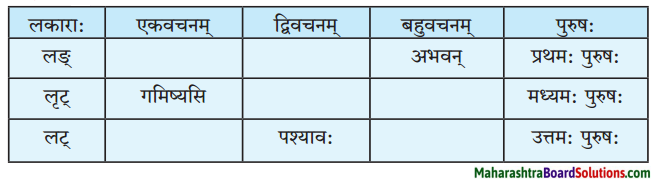
(च) लकारं लिखत।

प्रश्न 1.

1. पत्रक्रीडायां मग्न: आसम् अहम्।
2. शृणोतु कॅप्टनसाहेब।
3. बहुरूपधारिणौ नरौ व्याघ्रभल्लूको नाटयतः।
4. अहं प्रार्थये।
5. महान् उपकार: स्यात्।
6. कृपया साहाय्यं करोतु।

उत्तरम् :

1. लङ्लकार :
2. लोट्लकार :
3. लट्लकार:
4. लट्लकार:
5. विधिलिङ्लकार:
6. लोट्लकार:

प्रश्न 2.

1. भल्लूकवेषे अब्दुल: शोभेत।
2. जनाः उपहासेन अवदन्।
3. महिला: क्षिपन्ति पाषाणखण्डान्।

उत्तरम् :

1. विधिलिङ्लकार:
2. लङ्लकार:
3. लट्लकार:

प्रश्न 3.
1. सा शृङ्गे उन्नम्य नौ आक्रामत्।
2. प्राध्यापकमहाशय, परित्रायताम्।
उत्तरम् :
1. लङ्लकारः
2. लोट्लकार:

(छ) प्रश्ननिर्माणं कुरुत।

प्रश्न 1.
प्राध्यापकमहाशयेन रहस्यभेद: कृतः।
उत्तरम् :
केन रहस्यभेदः कृतः? ।

प्रश्न 2.
बहुरूपधारिणौ नरौ व्याघ्रभल्लूको नाटयतः।
उत्तरम् :
को व्याघ्रभल्लूको नाटयतः?

प्रश्न 3.
व्याघ्रस्य मनुष्यवाण्या भाषणेन सा महिला मूर्छिता।
उत्तरम् :
केन कारणेन सा महिला मूर्छिता?

प्रश्न 4.
रात्रौ दशवादने सर्कसक्रीडायाः प्रारम्भः जातः ।
उत्तरम् :
कस्मिन् समये / कदा सर्कसक्रीडाया: प्रारम्भः जातः?

प्रश्न 5.
क्रुद्धा धेनु: व्याघ्र लक्ष्यं कृतवती।
उत्तरम् :
क्रुद्धा धेनुः कं लक्ष्यं कृतवती?

प्रश्न 6.
प्रेक्षागारे महान् कोलाहल: उत्पन्नः ।
उत्तरम् :
कुत्र महान् कोलाहल: उत्पन्नः?

पृथक्करणम्

क्रमेण योजयत।

प्रश्न 1.

1. शिबिरस्य प्रथमं दिनम्।
2. सर्कसस्वामिनः साहाय्ययाचना।
3. सहभोजनस्य रहस्यभेदः।
4. सर्कसस्वामिनः आगमनम्।

उत्तरम् :

1. शिबिरस्य प्रथमं दिनम्।
2. सर्कसस्वामिनः आगमनम्।
3. सहभोजनस्य रहस्यभेदः।
4. सर्कसस्वामिनः साहाय्ययाचना।

प्रश्न 2.

1. माता व्याघ्र पाषाणखण्डान् अक्षिपत्।
2. व्याघ्रस्य पुरत: सम्मर्दः जातः।
3. व्याघ्रस्य मनुष्यवाण्या भाषणेन महिला मूर्छिता।
4. व्याघ्रस्य गर्जनया बाल: भीतः।

उत्तरम् :

1. व्याघ्रस्य पुरतः सम्मदः जातः।
2. व्याघ्रस्य गर्जनया बाल: भीतः।
3. माता व्याघ्र पाषाणखण्डान् अक्षिपत्।
4. व्याघ्रस्य मनुष्यवाण्या भाषणेन महिला मूर्च्छिता।

प्रश्न 3.

1. भल्लूकवेषधारिण: अब्दुलस्य आगमनम्।
2. सर्कसक्रीडाया: प्रारम्भः ।
3. उत्तेजितैः प्रेक्षकैः तालिकावादनम्।
4. पशूनां खाद्यस्य योजना।

उत्तरम् :

1. सर्कसक्रीडायाः प्रारम्भः ।
2. भल्लूकवेषधारिणः अब्दुलस्य आगमनम्।
3. पशूनां खाद्यस्य योजना।
4. उत्तेजितै: प्रेक्षकै; तालिकावादनम्।

प्रश्न 4.

1. भल्लूकस्य पटमण्डपस्तम्भम् आरोहणम्।
2. धेनोः सम्भ्रमः आक्रमणं च।
3. चिमणरावस्य व्याघ्रत्वं विस्मृत्य द्विपादरूपाश्रयः ।
4. सहभोजनस्य प्रारम्भः।

उत्तरम् :

1. सहभोजनस्य प्रारम्भः।
2. धेनोः सम्भ्रम: आक्रमणं च।
3. भल्लूकस्य पटमण्डपस्तम्भम् आरोहणम्।
4. चिमणरावस्य व्याघ्रत्वं विस्मृत्य द्विपादरूपाश्रयः ।

भाषाभ्यास:

योग्य रूपं लिखित्वा रिक्तस्थानपूर्ति कुरुत।

प्रश्न 1.

1. क्रीडायां ……….. नरौव्याघ्रभल्लूकौनाटयतः (द्वि-सङ्ख्यावाचक)
2. ………… सैनिकौ प्रेक्षकाणां मनोरञ्जनं कुर्याताम्। (द्वि-सजावाचक)
3. ………… महिला स्वपुत्रेण सह व्यानं द्रष्टुम् आगता। (एक – सङ्ख्यावाचक)
4. राघुः पञ्जरसमीपम् आगत्य पृष्टवान्। (एक-आवृत्तिवाचक)
5. सेवक: मझे “आसनानि स्थापितवान्। (त्रि-सङ्ख्यावाचक)
6. अहम् “आसने उपवेशितः। (एक – सङ्ख्यावाचक)

उत्तरम् :

1. द्वौ
2. द्वौ
3. एका
4. एकवारं
5. त्रीणि
6. एकस्मिन्

सूचनानुसारं कृती: कुरुत।

(क) वाच्यपरिवर्तनं कुरुत।

प्रश्न 1.
अहं विरोधं दर्शितवान्।
उत्तरम् :
मया विरोध: दर्शितः।

प्रश्न 2.
सेवक: त्रीणि आसनानि स्थापितवान्।
उत्तरम् :
सेवकेन त्रीणि आसनानि स्थापितानि।

प्रश्न 3.
अब्दुल: तां हस्तेन ताडितवान्।
उत्तरम् :
अब्दुलेन सा हस्तेन ताडिता।

(ख) त्वान्त / ल्यबन्त अव्ययं निष्कासयत।

प्रश्न 1.
अहं व्याघ्रः न वदति इति विस्मृत्य अवदम्।
उत्तरम् :
अहं व्याघ्रः न वदति इति व्यस्मरम् अवदम् च ।

प्रश्न 2.
अहं गर्जनां कृत्वा तीक्ष्णदन्तान् दर्शितवान्।
उत्तरम् :
अहं गर्जनां कृतवान् तीक्ष्णदन्तान् दर्शितवान् च ।

(ग) स्म निष्कासयत।

प्रश्न 1.
जनाः वन्यपशून् द्रष्टुम् आगच्छन्ति स्म।
उत्तरम् :
जना: वन्यपशून् द्रष्टुम् आगच्छन् ।

(घ) भवान् स्थाने त्वं योजयत।

प्रश्न 1.
भवान् सहाय्यं करोतु ।
उत्तरम् :
त्वं साहाय्यं कुरु।

प्रश्न 2.
भवान् चायं पातुम् इच्छति किम्?
उत्तरम् :
त्वं चायं पातुम् इच्छसि किम्?

प्रश्न 3.
भवान् परित्रायताम्।
उत्तरम् :
त्वं परित्राबस्व।

(च) वचनं परिवर्तयत।

प्रश्न 1.
पत्रक्रीडायां मग्नः आसम् अहम्। (बहुवचने परिवर्तयत।)
उत्तरम् :
पत्रक्रीडायां मग्नाः आस्म वयम्।

प्रश्न 3.
एका महिला आगता। (द्विवचने परिवर्तयत।)
उत्तरम् :
द्वे महिले आगते।

(छ) लकारं परिवर्तयत।

प्रश्न 1.
पत्रक्रीडायां मग्नः आसम् अहम्। (विधिलिङ्लकारे परिवर्तयत।)
उत्तरम् :
पत्रक्रीडायां मग्नः स्याम् अहम्।

प्रश्न 2.
महान् उपकारः स्यात्। (लङ्लकारे परिवर्तयत।)
उत्तरम् :
महान् उपकारः आसीत्।

प्रश्न 3.
भल्लूकवेषे अब्दुल: शोभेत। (लङ्लकारे परिवर्तयत।)
उत्तरम् :
भल्लूकवेषे अब्दुलः अशोभत।

प्रश्न 4.
धेनुः नौ आक्रामत्। (विधिलिङ्लकारे परिवर्तयत।)
उत्तरम् :
धेनु: नौ आक्रामेत्।

(ज) वाक्यं शुद्धं कुरुत।

प्रश्न 1.
द्वौ नरौ व्याघ्रभल्लूको नाटयन्ति।
उत्तरम् :
द्वौ नरौ व्याघ्रभल्लूको नाटयतः।

प्रश्न 2.
मम पञ्जरात् पुरत: सम्मदः जातः ।
उत्तरम् :
मम पञ्जरस्य पुरतः सम्मर्दः जातः ।

प्रश्न 3.
धेनुः तयोः सह कार्यक्रमः कर्तुम् अभ्यस्ता आसीत्।
उत्तरम् :
धेनुः ताभ्यां सह कार्यक्रमः कर्तुम् अभ्यस्ता आसीत्।

प्रश्न 4.
कृद्धाः धेनु: मां लक्ष्यं कृतवती।
उत्तरम् :
कद्धा धेनु: मां लक्ष्यं कृतवती।

समासाः

समस्तपदम्	अर्थ:	समासविग्रहः	समासनाम
व्याघ्रभल्लूको	tiger and bear	व्याघ्रः च भल्लूक: च।	इतरेतर द्वन्द्व समास
चरमबिन्दुः	peak point	चरम: बिन्दुः।	कर्मधारय समास
तीक्ष्णदन्ताः	sharp teeth	तीक्ष्णा: दन्ताः।	कर्मधारय समास
उत्तमाङ्गम्	topmost organ	उत्तमम् अङ्गम्।	कर्मधारय समास
अभिनयार्थम्	for enacting	अभिनयाय इदम्।	चतुर्थी तत्पुरुष समास
बालवीरचमः	a troop of brave children	बालवीराणां चमूः।	षष्ठी तत्पुरुष समास
पाषाणखण्डा:	pieces of stone	पाषाणस्य खण्डाः।	षष्ठी तत्पुरुष समास
लोकप्रियः	dear amongst people	लोकेषु प्रियः।	सप्तमी तत्पुरुष समास
भल्लूकवेषधारी	a man disguised as a bear	भल्लूकवेषं धारयति इति।	उपपद तत्पुरुष समास
अनुत्तमानि	not excellent	न उत्तमानि।	नञ्तत्पुरुष समास

धेनोाघः पलायते Summary in Marathi and English

प्रस्तावना :

‘धेनोव्याघ्रः पलायते।’ हे शीर्षक संस्कृत साहित्यातील भोजराजाच्या कथेतील एका प्रसिद्ध समस्येवर आधारीत आहे. ती म्हणजे ‘मृगात् सिंहः पलायते।’ या दोन्ही वाक्यांमध्ये लेखकांनी सृष्टीनियमांविरुद्ध अशा परिस्थितीचे चित्रण केले आहे. परंतु त्यातूनच निर्माण होणारा विनोद वाचकांच्या चेहऱ्यावर स्मितहास्य आणतो.

ही कथा मराठी साहित्यातील अजरामर कलाकृती असलेल्या ‘चिमणरावांचे चव्हाट’ या कथा संग्रहातील ‘कॅप्टन चिमणराव – स्काउटमास्तर’ या कथेचा अनुवाद असून संस्कृत वार्षिक अंक ‘समर्पणम्’ मधून प्रसिद्ध झाली होती. या कथेचा नायक व मराठी साहित्यातील प्रसिद्ध पात्र असलेला चिमणराव स्काऊटच्या धर्तीवर बालवीरांचा गट निर्माण करु इच्छितो.

परोपकार, शूरता, समाजसेवा इ. मूल्यांचे महत्त्व त्या लहान मुलांच्या मनावर बिंबवणे हा त्यामागचा शुद्ध हेतू. या बालचमूला सुट्टीत शिबिरासाठी घेऊन गेला असताना त्यांना परोपकाराचे धडे देण्याची संधी त्याला मिळते.

मात्र त्यातून जो अनावस्था प्रसंग उद्भवतो आणि त्यात चिमणराव स्वत:च कसा अडकतो, याचे वर्णन चिमणराव स्वत: करतो. ‘धेनोयाघ्रः पलायते।’ या कथेत चिमणरावांच्या स्वभाववैशिष्ट्यांमुळे जी विनोदनिर्मिती होते त्यामुळे वाचकांच्या चेहऱ्यावर स्मितहास्य उमटते. त्याचप्रमाणे ही कथा म्हणजे एका प्रादेशिक भाषेतून प्राचीन भाषेतील अनुवादाचा उत्कृष्ट नमुना आहे.

The title ‘धेनोर्व्याघ्रः पलायते।’ is based on a famous समस्या in Sanskrit literature, ‘मृगात् सिंहः पलायते।’ which comes from the stories of king 11. In both the quotes, the author has imagined a situation exactly opposite to the nature’s law. These situations surely bring smile on the reader’s face.

This story is a translated version of a Marathi story ‘कॅप्टन चिमणराव – स्काउटमास्तर’ from a renowned story book ‘चिमणरावांचे चव्हाट’ and tuns published in annual संस्कृत magazine named ‘समर्पणम्’. चिमणराव, the hero of this story and an immortal character of Marathi literature, wished to train a troop of brave youngsters/teenagers, similar to the scouts.

His aim behind this training uns to inculcate qualities like benevolence, bravery, social service etc. in the minds of the young children. But as he took them for a camp during mcations and got an opportunity to teach them a lesson of benevolence, he himself got stuck in a difficult situation.

The story ‘धेनोर्व्याघ्रः पलायते।’ brings smile on the faces of the readers due to the humor caused due to innocent nature of चिमणराव. It is also an excellent example of translation skills from a regional language to the ancient language of India.

परिच्छेदः 1

शिबिरस्य प्रथमदिबसे ……… साहाय्यं करोतु।

अनुवादः

शिबिराच्या पहिल्या दिवशीच दुपारी जेवण वगैरे आवरून मी मुलांसोबत पत्ते खेळण्यात मग्न होतो. तेव्हा नुकतीच ओळख झालेले प्राध्यापक सर्कसवाले (सर्कशीचे मालक) मलाच शोधत तेथे पोहचले. “कॅप्टनसाहेब, ऐका कॅप्टनसाहेब! आमच्या सर्कशीत कित्येक महिन्यांपासून लोकप्रिय असा सहभोजनाचा कार्यक्रम चालतो.

गाय, अस्वल आणि वाघ इ. प्राण्यांचा हा कार्यक्रम प्रयोगाचे सर्वोच्च आकर्षण आहे. तसेच जाहिरात करुन तिकिटे सुद्धा विकली आहेत. परंतु वाघ आणि अस्वलामध्ये झालेल्या भांडणामुळे दोघेही जखमी झाले आहेत.”

“काय? प्राण्यांचे भांडण?” “साहेब, आमच्या सर्कशीच्या खेळात वाघ आणि अस्वल दोन पायांचे (मनुष्य) आहेत.” अशाप्रकारे प्राध्यापकमहोदयांनी रहस्यभेद केला. “अस्वल किंवा वाघ पाळण्याची आमची क्षमता नाही. दोन बहुरूपी पुरुषच प्रयोगात वाघ आणि अस्वलाचा अभिनय करतात.”

“गाय सुद्धा……?”
“नाही, नाही, गाय खरी आहे.”
“हं….. मग मी इथे काय करू सांगा?”
“मी विनंती करतो, की आपल्या बालवीरांच्या चमूतील कोणत्याही दोन सैनिकांनी जर आजच्या प्रयोगात वाघ-अस्वलाचा वेश घेऊन प्रेक्षकांचे मनोरंजन केले, तर खूप उपकार होतील. कृपया मदत करा.”

On the first day of the camp itself, I was engrossed in playing the game of cards with children, after completing lunch etc. in the afternoon At that time, professor सर्कसवाले (owner of a circus) who was newly introduced, reached there looking for me only.

“Respected captain, listen (to me). Our circus has a popular programme of a joint meal since many months. This programme of the cow, the bear and the tiger etc. animals is the biggest attraction of our show. Tickets are also sold with the advertisement. but due to a fight between the bear and the tiger, both are wounded.” “What? Fight between animals?” “Sir, the tiger and the bear in our circus are human indeed.”

Thus, the respected professor revealed the secret. “We are not able to pet a bear or a tiger. Two disguised men only enact the tiger and the bear in the show.” “Is the cow too….?” “No, No, the cow is real.” “Hmm…. tell me then what should I do here?” “I request that, if any two cadets from your troop of brave boys entertain the audience, disguised as the tiger and the bear in today’s show, it would be a great favour. Please help me.”

परिच्छेदः 2

सर्कसस्वामिनः विवशता ………….. क्षिपन्ति पाषाणखण्डान्।

अनुवादः

सर्कशीच्या मालकाची विवशता/अगतिकता माझ्या लक्षात आली. ही परोपकाराची संधी योगायोगाने मिळाली आहे, असा विचार करून त्याची मदत करावी असे मी ठरवले. अस्वलाच्या वेशात अब्दुल शोभेल अशा विचाराने त्याला अस्वलाचे पात्र दिले. वाघाचा अभिनय करण्यासाठी मी स्वत:च तयार झालो. अशाप्रकारे पात्रयोजना झाली.

कार्यक्रमापूर्वीच मी तसेच अब्दुल, वाघ आणि अस्वलाचा वेश घेऊन आपापल्या पिंजऱ्यात थांबलो. माझ्या पिंजऱ्यासमोरच जास्त गर्दी झाली होती. मी शक्यतोवर लोकांचे मनोरंजन करण्याचा प्रयत्न केला. परंतु लोक संतुष्ट नव्हते. “हा काय वाघ आहे ? (किती) दुबळा आहे,” असे थट्टेने म्हणत होते.

तेव्हाच एक बाई वाघ पाहण्यासाठी स्वत:च्या मुलासोबत आली. माझ्या गर्जनेमुळे मुलगा घाबरला, म्हणून ती आई माझ्यावर दगड फेकू लागली. तेव्हा वेदनेने व्याकुळ झालेला मी, वाघ बोलत नाही हे क्षणभर विसरून म्हणालो, “पिंजऱ्यातल्या वाघाला बघून महिला दगड फेकतात/ मारतात.”

I understood the helplessness of the owner of the circus. Thinking that, I have obtained an opportunity to help him by chance I decided to help him. I assigned the character of the bear to Abdul, thinking that he would be apt/suitable for the role. I myself got ready to enact the tiger.

Thus, the characters/roles were decided/fixed. Me and Abdul stayed in our own cages disguised as the tiger and the bear before the show itself. There was more crowd gathered in front of my cage. I tried to entertain people as much as possible but crowd was not satisfied. “Is this a tiger? How weak he is!” They said mockingly.

Then, a woman, along with her son came to see the tiger. The boy got afraid due to my roaring. Hence, that mother threw pieces of stones at me. At that time, for a moment I forgot that the tiger doesn’t speak; I said, “Seeing the caged tigers, women throw pieces of stones.”

परिच्छेदः 3

मम वाक्यसमाप्तेः ……… अभ्यस्ता आसीत्।

अनुवादः

माझं वाक्य संपण्यापूर्वीच, वाघाच्या माणसाच्या भाषेत बोलण्यामुळे मूर्च्छित झालेली ती महिला, ‘हे भूत आहे भूत….’ असे मोठ्याने किंचाळत जमिनीवर पडली. माझा मुलगा राघूसुद्धा एकदा पिंजऱ्याजवळ येऊन, “अप्पा, चहा प्यायचा आहे का?” असे विचारू लागला तेव्हा प्रेक्षक गोंधळात पडले. रात्री दहा वाजता सर्कशीचा खेळ सुरु झाला. बारा वाजता खेळाचा सर्वोच्च बिंदू आला – सहभोजन. प्रेक्षकांची उत्सुकता शिगेला पोहोचली.

गड्याने रंगमंचावर तीन खुा ठेवल्या व मधोमध गोलाकार टेबल ठेवला. एका खुर्चीत मला बसवले होते. नंतर अस्वलाच्या वेशातील अब्दुल तेथे आला. गाय सुद्धा मंचावर आली. त्यानंतर आमच्यासमोर खाद्यपदार्थ ठेवले गेले. सहभोजन सुरु होताच उत्तेजित झालेल्या प्रेक्षकांनी आनंदाने टाळ्या वाजवण्यास सुरुवात केली. पूर्वीसुद्धा वाघ आणि अस्वल ही माणसेच होती. परंतु ती गाय त्यांच्यासोबत कार्यक्रम करण्यासाठी सरावलेली होती.

Even before my sentence would end, that woman screaming aloud, “ghost, it’s a ghost”, fell on the ground being unconscious due to the tiger speaking human language. Even when my son coming near the cage asked, “Father, would you like to have some tea?”, the audience got confused. The circus show began at 100clock in the night. The peak point of the show came at 120dock- joint meal. The excitement of the audience reached the height.

A servant placed three chairs on the stage and a circular stool in the middle. I was made to sit in one chair. Then , disguised as a bear came there. Even the cow arrived on the stage. Then, food was arranged in front of us. As the meal started, the audience that was excited started clapping happily. Even earlier, the tiger and the bear were human. But the cow was trained/used to perform with them.

परिच्छेद: 4

अचिरादेव न इमौ ……… विभूषितानि आसन्।

अनुवादः

थोड्याच वेळात गायीच्या लक्षात आले की, हे वाघ आणि अस्वल | ओळखीचे नाहीत, ती गोंधळाने व संशयाने आम्हाला एकेक करून पाहू लागली.
परिस्थितीची जाणीव होताच तिने शिंग उगारून आमच्यावर हल्ला केला. मी सुद्धा गर्जना करुन माझे तीक्ष्ण दात दाखवले. पण ती जराही घाबरली नाही.

अब्दुलने हाताने तिला मारले. त्यामुळे चिडून ती त्याच्यामागे धावू लागली. अस्वल लगेच तंबूच्या खांबावर चढले. हा सगळा खेळ पूर्वनियोजित आहे असा विचार करुन प्रेक्षकसुद्धा खूश झाले. अस्वल निसटले म्हणून चिडलेली ती गाय आता माझ्याकडे – वाघाकडे वळली. भीतीमुळे चार पायाच्या वाघाचे रूप विसरून मी मूळच्या द्विपाद स्वरूपात आलो.

“प्राध्यापक महोदय, वाचवा, वाचवा”, असा करुण विलाप करत धावत सुटलो. तेव्हा, गाईला घाबरुन पळणाऱ्या वाघाला पाहून प्रेक्षकवर्गात प्रचंड गोंधळ उडाला. प्रेक्षकांनी माझा वाघाचा वेश काढून मला निर्दयीपणे मारले. वेदनेमुळे मी मूच्छित झालो आणि जेव्हा जाग आली तेव्हा आमची गाडी पुन्हा पुण्याच्या दिशेने निघाली होती. माझे मस्तक व इतर अवयव मलमपट्टीमुळे सुशोभित झालेले होते.

In a short while, the cow realized that these tiger and bear are not familiar. She looked at us turn by turn with confusion and doubt. When she realized the fact, she attacked us having raised her horns. I too having roared displayed sharp teeth. But she wasn’t even a little afraid.

अब्दुल beat her with hand. Being angry due to this, she ran after him. The bear quickly climbed the pole of the tent. The audience too got happy thinking that all this show is pre-planned. The cow being angry as the bear escaped, now targeted me, the tiger.

Forgetting the disguise of four-legged tiger due to fear, I resorted to my original bipedal form (stood up). I started running, lamenting “Respected professor, help, help.” At that time, seeing the tiger running, being afraid of the cow, huge chaos took place in the audience.

The audience beat me cruelly removing my tiger’s disguise. I fainted due to pain and when I woke up, our vehicle was already on the way back to Pune. My head and other organs were decorated with bandages.

शब्दार्थाः

1. रहस्यभेदः – revelation of a secret – रहस्याचा उलगडा
2. व्रणिती – (both) got wounded – (दोघे) जखमी झाले
3. द्विपादौ – having two legs – दोन पायांचे प्राणी (दोन माणसे)
4. बहुरूपधारिणौ – taking many forms – बहुरूपी
5. पत्रक्रीडा – game of cards – पत्त्यांचा खेळ
6. विज्ञापनम् – advertisement जाहिरात
7. कलहकारणात् – due to quarrel/fight – भांडणामुळे
8. मध्याहे – in the afternoon – दुपारी
9. अन्विष्य – looking for/searching – शोधत शोधत
10. पालयितुम् – to nurture – पाळण्यासाठी
11. सम्मर्दः – crowd – गर्दी
12. अवसर: – opportunity – संधी
13. कृशः – weak/lean – दुबळा/क्षीण
14. नियोजितः – appointed – नियुक्त केलेले
15. बाधितः – affected – व्याकुळ झाला
16. सिद्धः – got ready – तयार झाला
17. विवशता – helplessness – अगतिकता
18. अवगता – understood – समजली
19. उपहासेन – mockingly – थट्टेने
20. गर्जनया – due to roaring – गर्जनेमुळे
21. स्वपञ्जरयो: – in own cages – स्वत:च्या पिंजऱ्यात
22. अक्षिपत् – threw – फेकला
23. रञ्जयितुम् – to entertain – मनोरंजन करण्यासाठी
24. यदृच्छया – by chance – योगायोगाने
25. पात्रयोजना – characters – पात्रयोजना
26. निर्धारिता – were decided – निश्चित झाली
27. चरमबिन्दुः – peak point – सर्वोच्च बिंदू
28. उत्कण्ठा – excitement – उत्सुकता
29. मूर्छिता – fainted – चक्कर/भोवळ आली
30. आक्रोशन्ती – crying/shouting – ओरडत/किंचाळत
31. तालिकावादनम् – clapping – टाळ्या वाजवणे
32. मनुष्यवाण्या – in human speech – माणसाच्या भाषेत
33. मझे – on stage – रंगमंचावर
34. अभ्यस्ता आसीत् – was trained – प्रशिक्षित होती
35. पराकाष्ठा जाता – reached height – शिखर गाठले
36. कोलाहल: – chaos – गाँधळ
37. शकटः – cart – गाडी/वाहन
38. ताडितवान् – beat – मारले
39. आरूद्धवान् – climbed – चढला
40. विलपन् – lamenting – विलाप करीत
41. क्षुब्धा/कुद्धा – angry – संतप्त
42. उत्तमाङ्गम् – head – मस्तक
43. प्रमुदिताः – delighted / happy – आनंदी
44. अनुत्तमानि – lower – वाईट
45. पटमण्डप स्तम्भम् – pole of the tent – तंबूचा खांब
46. सम्भ्रमेण – due to confusion – गोंधळामुळे
47. उपचारपट्टिकाभिः – with bandages – औषधाच्या पट्टीमुळे
48. शृङ्गे – horns – शिंगे
49. परित्रायताम् – help/save – वाचवा
50. उन्नम्य – having raised – उगारून
51. निष्कास्य – removing – काढून
52. निघृणम् without mercy – दयामाया न दाखवता

Aamod Sanskrit Book 10th Class Solutions

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• अमूल्यं कमलम् Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्ययुग्मम् Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• धेनोर्व्याघ्रः पलायते Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• जटायुशौर्यम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• प्रतिपदं संस्कृतम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Aamod Chapter 3 सूक्तिसुधा Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Amod Chapter 3 सूक्तिसुधा Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 3 Question Answer

Sanskrit Amod Std 10 Digest Chapter 3 सूक्तिसुधा Textbook Questions and Answers

भाषाभ्यासः

श्लोकः 1

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
का गुरूणां गुरुः ?
उत्तरम्‌ :‌
विद्या गुरूणां गुरुः।

प्रश्न आ.
किं राजसु न पूज्यते ?
उत्तरम्‌ :‌
धनं राजसु न पूज्यते।

प्रश्न इ.
कः पशुः एव ?
उत्तरम्‌ :‌
विद्याविहीन : पशुः एव।

2. माध्यमभाषया उत्तरत ।

प्रश्न अ.
‘विद्या नाम नरस्य’ . . . इति श्लोकाधारण विद्यायाः महत्त्वं लिखत ।
उत्तरम्‌ :‌
सूक्ति म्हणजे चांगल्या उक्ती. सूक्तिसुधा अशा नीतिपर उक्तींचा संग्रह आहे. ‘विद्याविहीनः पशुः’ ही सूक्ति ज्ञानाचे महत्त्व विशद करते. विद्या नाना भोग (समाधान) प्राप्त करून देणारी आहे. तसेच ती यश व आनंदही प्राप्त करून देणारी आहे. विद्या हे संरक्षिलेले गुप्त धन आहे. परदेशातही विद्या बंधुसम असते. राजसभेतही विद्यावान व्यक्तीचा सन्मान केला जातो. विद्येमुळे माणसाला ज्ञानाचे तेज प्राप्त होते व त्याचे सौंदर्य वाढते.

ज्ञानामुळे सर्व उद्दिष्टे साध्य होऊ शकतात, ‘किं किं न साधयति कल्पकतेव विद्या’ या उक्तीप्रमाणे विद्या कल्पकतेप्रमाणे सर्व इच्छांची पूर्ती करते. म्हणूनच ज्ञानहीन मनुष्यास पशूच मानले जाते.

सूक्तिs are good sayings. सूक्तिसुधा is a collection of all such value-based quotations. The सूक्ति ‘विद्याविहीनः पशुः’ ellobarates the importance of knowledge.

Knowledge alone gives enjoyment, happiness and fame to a person. It is the preceptor of all preceptors. Hence, knowledge is precious wealth. It is well-guarded and concealed wealth.

It enhances the beauty of a person. Knowledge is considered to be relative while travelling in foreign country. It is said to be supreme deity. Even royal courts admire knowledgeable people.

A man who is devoid of knowledge / learning, is said to be an animal; as knowledge helps achieving all ends. It is rightly said, “किं किं न साधयति कल्पलतेब विद्या’ – what does not knowledge achieve like wish yielding-creeper.

3. जालरेखाचित्रं पूरयत ।

प्रश्न 1.
जालरेखाचित्रं पूरयत

उत्तरम्‌ :‌

श्लोक: 2.

1. मञ्जूषात: उचितं शब्दं चित्वा तालिकां पूरयत ।

प्रश्न 1.
मञ्जूषात: उचितं शब्दं चित्वा तालिकां पूरयत ।

(निन्दन्तु, गच्छतु, युगान्तरे, मरणम्, लक्ष्मी:, स्तुवन्तु ।)
उत्तरम्‌ :‌

नीतिनिपुणाः	निन्दन्तु	स्तुवन्तु	वा
लक्ष्मीः	समाविशतु	गच्छतु	वा
मरणम्	अद्यैव	युगान्तरे	वा

2. सन्धिविग्रहं कुरुत।

प्रश्न अ.
मरणमस्तु ।
उत्तरम्‌ :‌
मरणमस्तु – मरणम् + अस्तु।

प्रश्न आ.
अद्यैव ।
उत्तरम्‌ :‌
अद्यैव – अद्य + एव।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
“न्याय्यात्पथः प्रविचलन्ति पदं न धीराः । इति सूक्तिं स्पष्टीकुरुत।
उत्तरम्‌ :‌
सूक्ति म्हणजे चांगल्या उक्ती. सूक्तिसुधा अशा नीतिपर उक्तींचा संग्रह आहे. विद्याविटेन: पशुः हो सूक्ति ज्ञानाचे महत्व विशद करते. धैर्यवान लोकांमध्ये दृढनिश्चय ही स्थायी व विशेष गुण आहे. असे लोक स्थिर बुद्धीचे असतात. व ते स्वत:ला ध्येयापासून टू देत नाहीत ते त्याच मार्गाचा अवलंब करतात, व हवे ते परिणाम प्राप्त करून घेतात. ‘न्याय्यात्पथः प्रविचलन्ति पदं न धीराः’ ही सूक्ति हे विशद करते.

नीतिमध्ये कुशल लोक निंदानालस्ती करो वा प्रशंसा करोत, लक्ष्मी तिच्या इच्छेप्रमाणे येवो अथवा जावो, आजच मरण येवो वा युगान्त झाल्यावर (दुसऱ्या युगात / भरपूर काळ लोटल्यावर) येवो, (तरीही) धैर्यवान लोक न्याय्यमार्गावरून आपले पाऊल ढळू देत नाहीत (ते न्याय्यमार्ग सोडत नाहीत).

सूक्तिs are good sayings. सूक्तिसुधा is a collection of all such value-based.quotations. Resolute people have distinct quality of firmness. They are of stable intelellect and do not deviate their minds from their aim. They follow the path of justice, till they achieve fruitful results.

The सूक्ति ‘न्याय्यात्पथः प्रविचलन्ति पदं न धीराः’ says that experts/skilled people may praise or criticise courageous people; may goddess Laxmi assist them by pleasing on them or not; may they have to face death instantly or after long time; passing through all circumstances, resolute ones follow the justice path, achieve fruitful results and enlighten other’s lives too.

4. माध्यमभाषया उत्तरत ।

प्रश्न 1.
‘क्रियासिद्धिः सत्त्वे भवति’ इति सूर्यस्य उदाहरणेन स्पष्टीकुरुत ।
उत्तरम्‌ :‌
सुभाषितांचा संदर्भ लक्षात घेऊन सूक्तींचा अर्थ जाणून घेतल्यास नैतिकदृष्ट्या श्रेष्ठ व्यक्तिमत्त्व विकसित केले जाऊ शकते. ‘क्रियासिद्धिः सत्त्वे भवति,’ हे सुभाषित सूर्याच्या उदाहरणाने महान लोकांचे आंतरिक सामर्थ्य दर्शविते. सूर्य दररोज, सापांनी नियंत्रित सात घोडे जोडलेल्या, एकच चाक असलेल्या रथातून, निराधार मार्गावरुन पायाने विकलांग अशा सारधीबरोबर अनंत अशा आकाशाच्या शेवटापर्यंत जातो.

(जसे) महान लोकांच्या कार्याची पूर्तता त्यांच्यातील सत्त्वाने (सामर्थ्याने) होते. इतर साधनांनी) नाही. सूर्य सर्व बाजूंनी प्रतिकूल गोष्टींनी वेढला असला तरी आकाशाच्या अंतापर्यंत पोहोचतो. महान लोकही सर्वतोपरी प्रतिकूल गोष्टींचा सामना करत कार्य पूर्णत्वास नेतात.

One can cultivate a strong and morally superior character by understanding the meaning of a good saying with reference to the given सुभाषित. “क्रियासिद्धिः सत्त्वे भवति,’ is a सुभाषित that explains the power of great people with the example of the sun Even with a single wheel to the chariot of seven horses controlled by the bridle of a snake, a supportless (difficult) path and a lame charioteer, the Sun surely reaches the end of the unending sky everyday.

The success of great people is in their spirit (valour) and does not depend on the means. The sun though surrounded by all unfavourable conditions succeeds in reaching last end of the sky. In the same way, great people though suffer due to unfavourable condition, accomplish the task.

श्लोक: 3.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
शुकसारिका: केन बध्यन्ते ?
उत्तरम्‌ :‌
आत्मन: मुखदोषेण शुकसारिकाः बध्यन्ते।

प्रश्न आ.
के न बध्यन्ते ?
उत्तरम्‌ :‌
बका: न बध्यन्ते।

2. सन्धिविग्रहं कुरुत ।

प्रश्न अ.
बकास्तत्र
उत्तरम्‌ :‌
बकास्तत्र – बकाः + तत्र।

प्रश्न आ.
आत्मनो मुखदोषेण
उत्तरम्‌ :‌
आत्मनो मुखदोषेण – आत्मनः + मुखदोषेण।

श्लोकः 4.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
रवे: रथस्य कति तुरगा: सन्ति ?
उत्तरम्‌ :‌
रवे: रथस्य सप्त तुरगाः सन्ति।

प्रश्न आ.
रवे: सारथिः कीदृशः अस्ति ?
उत्तरम्‌ :‌
रवे: सारथिः चरणविकलः अस्ति।

2. सन्धिविग्रहं कुरुत।

प्रश्न अ.
रथस्यैकम् ।
उत्तरम्‌ :‌
रथस्यैकम् – रथस्य + एकम्।

प्रश्न आ.
सारथिरपि ।
उत्तरम्‌ :‌
सारथिरपि – सारथिः + अपि।

3. मञ्जूषात: शब्द चित्वा तालिकां पूरयत ।

प्रश्न 1.

(मार्गः, सारथिः, एकम्, सप्त ।)
उत्तरम्‌ :‌

निरालम्ब:	मार्ग:
सप्त	तुरगा:
चरणविकल:	सारथि:
एकम्	चक्रम्

4. जालरेखाचित्रं पूरयत ।

प्रश्न 1.

उत्तरम्‌ :‌

श्लोक: 5.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
का कार्यसाधिका भवति ?
उत्तरम्‌ :‌
अल्पानां वस्तूनां संहतिः कार्यसाधिका भवति।

प्रश्न आ.
कै: मत्तदन्तिन: बध्यन्ते ?
उत्तरम्‌ :‌
आपन्न : तृणैः मत्तदन्तिन: बध्यन्ते।

2. सन्धिविग्रहं कुरुत।

प्रश्न अ.
अल्पानामपि
उत्तरम्‌ :‌
अल्पानामपि – अल्पानाम् + अपि।

प्रश्न आ.
तृणैर्गुणत्वमापनर्बध्यन्ते
उत्तरम्‌ :‌
तृणैर्गुणत्वमापनैर्बध्यन्ते – तृणैः + गुणत्वम् + आपनैः + बध्यन्ते।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
‘संहतिः कार्यसाधिका’ इति सूक्तिं स्पष्टीकुरुत ।
उत्तरम्‌ :‌
संहतिः – एकता, ऐक्यम्।

श्लोक: 6.

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
साधवः किं न विस्मरन्ति ?
उत्तरम्‌ :‌
साधवः कृतम् उपकारं न विस्मरन्ति।

प्रश्न आ.
नारिकेलाः किं स्मरन्ति ?
उत्तरम्‌ :‌
नारिकेलाः प्रथमवयसि पीतम् अल्पं तोयं स्मरन्ति।

प्रश्न इ.
नारिकेलाः भारं कुत्र वहन्ति ?
उत्तरम्‌ :‌
नारिकेला: भारं शिरसि वहन्ति।

2. माध्यमभाषया उत्तरत ।

प्रश्न 1.
नारिकेला: नराणाम् उपकारं कथं स्मरन्ति ?
उत्तरम्‌ :‌
सुभाषितांचा संदर्भ लक्षात घेऊन सूक्तींचा अर्थ जाणून घेतल्यास नैतिकदृष्ट्या श्रेष्ठ व्यक्तिमत्त्व विकसित केले जाऊ शकते. येथे कवीने सज्जन माणसांचा स्वभाव नारळाच्या झाडाच्या उदाहरणाने स्पष्ट केला आहे.

नारळाच्या झाडाला अधिक पाणी लागत नाही. लहानपणी दिलेले थोडेसे पाणी देखील झाड मोठे होण्यास/वाढण्यास मदत करते. झाडाचा वृक्ष झाल्यावर ते मोठमोठ्या नारळांचे ओझेही सांभाळते. त्या बदल्यात आजन्म माणसांना भरपूर गोड पाणी देते. यावरून सज्जनांच्या कृतज्ञतेच्या गुणावर प्रकाश टाकला आहे. सज्जन लोक कधीही दुसऱ्याने केलेले उपकार विसरत नाहीत व त्यांना शक्य असेल त्या सर्व मार्गांनी उपकाराची परतफेड करतात.

One can cultivate a strong and morally superior character by understanding the meaning of a good saying with reference to the given सुभाषित. Here, poet illustrates the nature of noble people through the example of a coconut tree.

Coconut tree does not need much water to grow. Even the little water given in the starting helps it to grow further. Once the plant turns into a big tree, it carries the burden of coconuts and gives abundant of sweet water for lifetime.

This highlights the nature of good people as they too never forget the help rendered by others and become helpful to others in all possible ways.

श्लोक: 7.

1. एकवाक्येन उत्तरत।

प्रश्न अ.
नरः किं छिन्द्यात् ?
उत्तरम्‌ :‌
नरः पटं छिन्द्यात्।

प्रश्न आ.
मनुजः किं भिन्द्यात् ?
उत्तरम्‌ :‌
मनुजः घटं भिन्द्यात्।

2. श्लोकात् लिङ्लकारस्य रूपाणि चित्वा लिखत ।

प्रश्न 1.
श्लोकात् लिङ्लकारस्य रूपाणि चित्वा लिखत ।
उत्तरम्‌ :‌
भिन्द्यात्, छिन्द्यात्, कुर्यात्, भवेत्।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
‘येन केन प्रकारेण’ इति उक्तिं स्पष्टीकुरुत ।
उत्तरम्‌ :‌
सूक्ति म्हणजे चांगल्या उक्ती. सूक्तिसुधा अशा नीतिपर उक्तींचा संग्रह आहे. येन केन प्रकारेण’ ही सूक्ति उपहासाने माणसाच्या प्रवृत्तीचे वर्णन करते.

या जगात मनुष्याने कोणत्याही मार्गाने प्रसिद्ध व्हावे. इतरांचे लक्ष वेधून घेण्यासाठी घडे फोडावेत, कपडे फाडावेत, गाढवावर बसावे, या कृती खरेतर हास्यास्पद आहेत, तरीसुद्धा प्रसिद्ध होण्यासाठी व्यक्तीने हे सर्व करावे.

सूक्तिs are good sayings. सूक्तिसुधा is a collection of all such value-based quotations. The सूक्ति ‘येन केन प्रकारेण describes human nature satirically.

In this world, a man should try to be famous by some way or the other. He should grab the attention of people by breaking pots, tearing clothes, riding a donkey such acts which are unusual and ridiculous. Yet, one should do it for the sake of popularity.

प्रश्न 2.
समानार्थकशब्दान् लिखत ।
विद्या, पशुः, धनम्, लक्ष्मी:, शुकः, तुरगः, नभः, रविः, संहतिः, दन्ती, तोयम्, शिरः, साधवः, पटम्, रासभः ।
उत्तरम्‌ :‌

• विद्या – ज्ञानम्, बोधः ।
• पशुः – प्राणी, तिर्यङ्, मृगः ।
• धनम् – द्रव्यम, वित्तम्, स्थापतेयम्, रिक्थम्, ऋक्यम्, वसुः।
• लक्ष्मीः . पद्मा, कमला, श्रीः, हरिप्रिया, पद्मालया।
• शुकः – किङ्किरातः, कौरः।
• तुरगः – अश्वः, घोटकः।
• नभः – अन्तरिक्षम्, गगनम्, अनन्तम्, सुरवर्त्म, खम्।
• रविः – भानुः, हंसः, सहस्रांशुः, तपनः, सविता।
• दन्ती – हस्ती, करी, गजः, कुञ्जरः, वारणः ।
• संहतिः – संघ
• तोयम् – जलम्, नीरम्।
• शिरः – मस्तकम्, मूर्धा।
• साधवः – सज्जनाः।
• पटम् – वस्त्रम्, वसनम् ।
• रासभः – गर्दभः, खरः, धूमकर्णः ।

प्रश्न 3.
विरुद्धार्थकशब्दान् लिखत ।
विदेशः, प्रच्छन्नम्, निन्दन्तु, अल्पम्, उपकारः, साधवः, रोहणम् ।
उत्तरम्‌ :‌

• विदेशः × स्वदेशः।
• प्रच्छन्नम् × प्रकाशितम्, प्रकटीकृतम्।
• निन्दन्तु × स्तुवन्तु।
• अल्पम् × बहु, भूरि, विपुलम्।
• उपकार: × अपकारः।
• साधवः × दुर्जनाः, दुष्टाः, खलाः।
• रोहणम् × अवतरणम्, अवरोहणम्।

Sanskrit Amod Class 10 Textbook Solutions Chapter 3 सूक्तिसुधा Additional Important Questions and Answers

अवबोधनम्।

(क) पूर्णवाक्येन उत्तरत।

प्रश्न 1.
विद्या कीदृशं धनम् अस्ति?
उत्तरम् :
विद्या प्रच्छन्नगुप्तं धनम् अस्ति।

प्रश्न 2.
विद्या केषां गुरुः?
उत्तरम् :
विद्या गुरूणां गुरुः।

प्रश्न 3.
विदेशगमने कृते विद्या कीदृशं भाति ?
उत्तरम् :
विदेशगमने कृते विद्या बन्धुजन : इव भाति।

प्रश्न 4.
किं परं दैवतम्?
उत्तरम् :
विद्या परं दैवतम्।

प्रश्न 5.
धीराः कस्मात् न प्रविचलन्ति?
उत्तरम् :
धीरा: न्याय्यात् पथ: न प्रविचलन्ति।

प्रश्न 6.
न्याय्यात्पथ: के न विचलन्ति ?
उत्तरम् :
न्याय्यात्पथ: धीराः न विचलन्ति।

प्रश्न 7.
के निन्दन्तु स्तुवन्तु वा?
उत्तरम् :
नीतिनिपुणा: निन्दन्तु स्तुवन्तु वा।

प्रश्न 8.
लक्ष्मी: कथं समाविशतु गच्छतु वा?
उत्तरम् :
लक्ष्मी: यथेष्टं समाविशतु गच्छतु वा।

प्रश्न 9.
किं सर्वार्थसाधनम्?
उत्तरम् :
मौनं सर्वार्थसाधनम्।

प्रश्न 10.
रविः प्रतिदिनं कुत्र याति?
उत्तरम् :
रविः प्रतिदिनं अपारस्य नभसः अन्तं याति।

प्रश्न 11.
महर्ता क्रियासिद्धिः कस्मिन् भवति?
उत्तरम् :
महतां क्रियासिद्धिः सत्त्वे भवति।

प्रश्न 12.
के तृणैर्गुणत्वमापनैः बध्यन्ते ?
उत्तरम् :
मतदन्तिन: तृणैर्गुणत्वमापन: बध्यन्ते।

प्रश्न 13.
पुरुषः कथं प्रसिद्धः भवेत्?
उत्तरम् :
येन केन प्रकारेण पुरुष: प्रसिद्धः भवेत्।

शब्दज्ञानम्

(क) विशेषण – विशेष्य – सम्बन्धः ।

विशेषणम्	विशेष्यम्
1. प्रच्छन्नगुप्तम्	धनम्
2. भोगकरी	विद्या
3. यशःसुखकरी	विद्या
4. परम्	दैवतम्
5. सर्वार्थसाधनम्	मौनम्
6. भुजगयमिता:	तुरगा:
7. अपारस्य	नभसः
8. अल्पानाम्	वस्तूनाम्
9. संहतिः	कार्यसाधिका
10. अल्पम्	तोयम्
11. कृतम्	उपकारम्
12. प्रसिद्धः	पुरुषः

(ख) विभक्त्यन्तपदानि।

• प्रथमा – विद्या, गुरुः, यशः, बन्धुजनः, पशुः ।
• षष्ठी – नरस्य, गुरूणाम्।
• सप्तमी – विदेशगमने, राजसु।
• तृतीया – दोषेण।
• षष्ठी – आत्मनः
• प्रथमा – संहतिः, कार्यसाधिका, दन्तिनः।
• तृतीया – तृणैः, आपनैः।
• षष्ठी – अल्पानाम्, वस्तूनाम्।

पृथक्करणम्

पद्यांशं पठित्वा जालरेखाचित्रं पूरयत।

1.

2.

3.

भाषाभ्यासः

(क) समानार्थकशब्दाः

• नरः – मनुष्यः, मानवः, मानुषः, मर्त्यः, मनुजः।
• यशः – ख्यातिः, कीर्तिः, प्रसिद्धिः।
• गुरुः – आचार्यः, अध्यापकः, उपाध्यायः।
• बन्धुजनः – बान्धवः।
• राजसु – पार्थिवेषु, नृपेषु, भूपेषु।
• निपुणः – कुशलः, प्रवीणः, पारङ्गतः।
• स्तुवन्तु – प्रशंसन्तु।
• यथेष्टम् – यथेच्छम्।
• मरणम् – मृत्युः ।
• पन्थाः – वर्त्म, सरणिः, मार्गः।
• धीरः – धैर्यवान्, धैर्यशीलः।
• आत्मनः – स्वस्य।
• मुखम् – तुण्डम, वदनम्, आननम्।
• दोषः – प्रमादः।
• बकः – मरुवकः, सर्पभुक्।
• अल्पम् – स्वल्पम्।
• तृणम् – घासः, यवसम्, कुशः, शष्पम्, अर्जुनम्।

(ख) विरुद्धार्थकशब्दाः

1. गुप्तम् × अनावृतम्।
2. विद्याविहीन: × ज्ञानयुक्तम्।
3. गच्छतु × आगच्छतु।
4. मरणम् × जनिः, जन्म, जनुः।
5. दोषः × गुणः।
6. बध्यन्ते × मुच्यन्ते।
7. मौनम् × भाषितम्।
8. संहतिः × भिन्नता, भेदः ।

(क) विभक्त्यन्तरूपाणि।

• प्रश्थमा – निपुणाः, लक्ष्मीः, धीराः।
• द्वितीया – मरणम्, पदम्।
• पन्चमी – न्याय्यात्, पथः।
• सप्तमी – युगान्तरे।

समासाः

समस्तपदम्	अर्थ:	समासविग्रहः	समासनाम
विद्याविहीनः	devoid of knowledge	विद्यया विहीनः।	तृतीया तत्पुरुष समास
नीतिनिपुणाः	experts in ethics	नीत्यां/नीतिषु निपुणाः।	सप्तमी तत्पुरुष समास
यथेष्टम्	as per/according to wish	इष्टम् अनुसृत्य /अनतिक्रम्य।	अव्ययीभाव समास
शुकसारिकाः	parrots and mynas	शुकाः च सारिका: च।	इतरेतर द्वन्द्व समास
सर्वार्थसाधनम्	mean/medium of achieving all ends	सर्वार्थानां साधनम्।	षष्ठी तत्पुरुष समास
रासभरोहणम्	ascending the donkey	रासभं रोहणम्।	द्वितीया तत्पुरुष समास
भुजगयमिताः	controlled by a snake	भुजगेन यमिताः।	तृतीया तत्पुरुष समास
चरणविकल:	lame with legs	चरणेन / चरणाभ्यां विकलः।	तृतीया तत्पुरुष समास
क्रियासिद्धिः	accomplishment of the task	क्रियायाः सिद्धिः।	षष्ठी तत्पुरुष समास

सूक्तिसुधा Summary in Marathi and English

प्रस्तावना :

“सूक्तयः नाम सुवचनानि।” सूक्ती म्हणजे चांगली उक्ती (बोलणे). संस्कृत भाषा अशा अनेक सुवचनांनी समृद्ध आहे. सुभाषितांचा संदर्भ लक्षात घेऊन सूक्तींचा अर्थ जाणून घेतल्यास नैतिकदृष्ट्या श्रेष्ठ व्यक्तिमत्त्व विकसित केले जाऊ शकते.

पुष्कळदा, अनेक संस्कृत सूक्ती इतर भारतीय भाषांमध्ये सुध्दा वापरलेल्या दिसून येतात. प्रत्यक्षात, अशा सूक्तींचे स्मरण केल्याने व्यक्तीची शब्दसंपदा वाढते व इतर भाषांवर प्रभुत्व निर्माण होते.

“सूक्तिः नाम शोभना उक्तिः ” means a good saying. Sanskrit language is enriched with such good sayings. One can cultivate a strong and morally superior character by understanding the meaning of a good saying with reference to the given सुभाषित.

Several Sanskrit sayings are often used in other Indian languages. In fact, remembering such sayings definitely enhances one’s ocabulary and command over languages.

श्लोकः 1

विद्या नाम नरस्य रूपमधिकं प्रच्छन्नगुप्तं धनम्
विद्या भोगकरी यश:सुखकरी विद्या गुरूणां गुरुः।
विद्या बन्धुजनो विदेशगमने विद्या परं दैवतम्
विद्या राजमु पूज्यते न तु धनं विद्याविहीन: पशुः ।।1।। (वृत्तम् – शार्दूलविक्रीडितम्, स्रोत: – नीतिशतकम्)

सन्थिविग्रहः

1. रूपमधिकम् – रूपम् + अधिकम्।
2. बन्धुजनो विदेशगमने – बन्धुजन: + विदेशगमने।

अन्वय:- विद्या नाम नरस्य अधिकं रूपम्, प्रच्छन्नगुप्तं धनम्, विद्या भोगकरी यश:सुखकरी (च)। विद्या गुरूणां गुरुः । विदेशगमने विद्या बन्धुजनः ।
विद्या पर दैवतम्। विद्या राजसु पूज्यते न तु धनम्। विद्याविहीनः पशुः (एव)।

अनुवादः

मराठी विद्येमुळे मानवाचे सौंदर्य वाढते. विद्या हे संरक्षिलेले गुप्त धन आहे. विद्या नाना भोग (समाधान) प्राप्त करून देणारी आहे. (ती) यश व आनंद मिळवून देणारी आहे. विद्या गुरुंची गुरु आहे. परदेशी गेले असता विद्या ही बांधव असते. (बांधवाप्रमाणे उपयोगी पडते/सहाय्यभूत होते) विद्या सर्वश्रेष्ठ दैवत आहे. विद्या राजांमध्ये (राजसभांमध्ये) पूजनीय आहे; धन नाही. ज्याच्याजवळ विद्या नाही तो पशू(च) (समजावा).

English Knowledge enhances the beauty of man. It is secretly hidden treasure. Knowledge brings pleasure. It brings glory and comforts. Knowledge is the teacher of all teachers. Knowledge is kith and kin when going to a foreign land. Knowledge is a superior deity itself. Knowledge is worshipped amongst kings, not money. One without knowledge is a beast.

श्लोकः 2

निन्दन्तु नीतिनिपुणा यदि वा स्तुवन्तु
लक्ष्मीः समाविशतु गच्छतु वा यथेष्टम्।
अद्यैव वा मरणमस्तु युगान्तरे वा
न्याय्यात्पथः प्रविचलन्ति पदं न धीराः।।2।। (वृत्तम् – वसन्ततिलका, स्रोत: – नीतिशतकम्)

सन्धिविग्रहः

1. नीतिनिपुणा यदि – नीतिनिपुणाः + यदि।
2. न्याय्यात्पथः – न्याय्यात् + पथ: ।

अन्वय:- यदि (अपि) नीतिनिपुणा: निन्दन्तु स्तुवन्तु वा, लक्ष्मी समाविशतु यथेष्ट गच्छतु वा, मरणम् अद्य एव अस्तु युगान्तरे वा, (तथापि) धीराः न्याय्यात् पथः पदं न प्रविचलन्ति।

अनुवादः

नीतिमध्ये कुशल लोक निंदानालस्ती करोत वा प्रशंसा करोत, लक्ष्मी तिच्या इच्छेप्रमाणे येवो अथवा जावो, आजच मरण येवो वा युगान्त झाल्यावर दुसऱ्या युगात / भरपूर काळ लोटल्यावर) येवो, (तरीही) धैर्यवान लोक न्याय्यमार्गावरून आपले पाऊल ढळू देत नाहीत (ते न्याय्यमार्ग सोडत नाहीत).

English Experts in ethics may insult or praise, wealth may come or go by itself, may there be death today or after many years; courageous ones never divert (take a step back) from the path of justice.

श्लोकः 3

आत्मनो मुखदोषेण बध्यन्ते शुकसारिकाः।
बकास्तत्र न बध्यन्ते मौनं सर्वार्थसाधनम् ।।3।। (वृत्तम् – अनुष्टुप, स्रोत: – पञ्चतन्त्रम्)

अनुवादः

मराठी पोपट, साळुक्या (मैना) त्यांच्या स्वत:च्या तोंडाच्या दोषाने (बडबडीमुळे) अडकले जातात. (पण) बगळे (मात्र) अडकत नाहीत. (अशा प्रकारे) मौन पाळणे हे सर्व हेतू (गोष्टी) प्राप्त करण्याचे (मिळविण्याचे) साधन आहे.

English Parrots and mynas get trapped by fault of their own mouths (voices/sounds). Cranes do not get trapped. Silence is an instrument for obtaining all objects.

श्लोक: 4

रथस्यैकं चक्रं भुजगयमिताः सप्त तुरगाः
निरालम्बो मार्गश्चरणविकल: सारथिरपि।
रविर्यात्येवान्तं प्रतिदिनमपारस्य नभसः
क्रियासिद्धिः सत्त्वे भवति महतां नोपकरणे।।4।। (वृत्तम् – शिखरिणी, स्रोतः – भोजप्रबन्धः)

सन्धिविग्रहः

1. मार्गश्चरणविकलः – मार्गः + चरणविकलः।
2. रवियत्येवान्तम् – रविः + याति + एव + अन्तम्।
3. प्रतिदिनमपारस्य – प्रतिदिनम् + अपारस्य।
4. नोपकरणे – न + उपकरणे।

अन्वयः- रथस्य एकं चक्रं, सप्त भुजगयमिता: तुरगाः, निरालम्ब: मार्गः, सारथिः अपि चरणविकलः, (तथापि) रविः प्रतिदिनम् अपारस्य नभसः अन्तं याति एव। महतां क्रियासिद्धिः सत्त्वे भवति, उपकरणे न (भवति)।

अनुवादः

सूर्य दररोज, सापांनी नियंत्रित सात घोडे जोडलेल्या, एकच चाक असलेल्या रथातून, निराधार मार्गावरून, पायाने विकलांग अशा सारथीबरोबर अनंत अशा आकाशाच्या शेवटापर्यंत जातो. (जसे) महान लोकांच्या कार्याचे यश त्यांच्यातील सत्त्वाने (सामध्यनि) होते. साधनांनी नाही.

Even with a single wheel to the chariot of seven horses controlled by the bridle of snake, a supportless (difficult) path and a lame charioteer, the sun surely reaches the end of the unending sky everyday. The success of great people is in their spirit (valour) and does not depend on the means.

श्लोकः 5

अल्पानामपि वस्तूनां संहतिः कार्यसाधिका।
तृणैर्गुणत्वमापनष्यन्ते मत्तदन्तिनः।।4।। (वृत्तम् – अनुष्टुप, स्रोत: – हितोपदेशः।)

अनुवादः

लहानसहान वस्तूंचा संघ कार्य यशस्वी करतो (पूर्णत्वास नेतो). गवतापासून बनविलेल्या दोरखंडाने मत्त हत्ती (सुद्धा) नियंत्रित केले जातात.

Union of even small things accomplishes (big) tasks. Just as the intoxicated elephants are tied by a rope made of hay-sticks.

श्लोकः 6

प्रथमवयसि पीतं तोयमल्पं स्मरन्तः
शिरसि निहितभारा नारिकेला नराणाम्।
ददति जलमनल्पास्वादमाजीवितान्त।
न हि कृतमुपकारं साधवो विस्मरन्ति ।।6।। (वृत्तम् – मालिनी, स्रोत: – विक्रमचरितम्।)

सन्धिविग्रहः

1. तोयमल्पम् – तोयम् + अल्पम्।
2. कृतमुपकारम् – कृतम् + उपकारम्।
3. साधवो विस्मरन्ति – साधवः + विस्मरन्ति।
4. जलमनल्पास्वादमाजीवितान्तम् – जलम् + अनल्पास्वादम् + आजीवितान्तम्।
5. निहितभारा नारिकेला नराणाम् – निहितभारा: + नारिकेला: + नराणाम्।

अन्वय:- प्रथमवयसि पीतम् अल्पं तोयं स्मरन्तः शिरसि निहितभारा: आजीवितान्तं नराणां (नरेभ्यः) अनल्पास्वाद जलं ददति। साधवः कृतम् उपकारं नहि विस्मरन्ति।

अनुवादः

नारळाचे झाड लहानपणी मिळालेले थोडे पाणी लक्षात ठेवून, नारळांचे ओझे डोक्यावर बाळगून माणसांना आजन्म भरपूर गोड पाणी देते. (जसे) दुसऱ्याने केलेले उपकार सज्जन लोक कधीही विसरत नाहीत. (त्याची अनेक पटीने परतफेड करतात.)

In memory of the little water consumed in early age (as a seedling), a coconut tree, bearing weight on its head throughout its life, gives sweet water abundantly to humans. The noble people never forget benevolence (help offered by others).

श्लोक: 7

घटं भिन्द्यात् पटं छिन्द्यात् कुर्याद्रासभरोहणम्।
येन केन प्रकारेण प्रसिद्धः पुरुषो भवेत् ।।7।। (वृत्तम – अनुष्टुप, प्रकार: – हास्योक्तिः )

सन्धिविग्रहः

1. कुर्याद्रासभरोहणम् – कुर्यात् + रासभरोहणम्।
2. पुरुषो भवेत् . पुरुष: + भवेत्।

अन्वय:- पुरुषः घटं भिन्द्यात्, पटं छिन्द्यात, रासभरोहणं (अपि) कुर्यात्। येन केन प्रकारेण (स:) प्रसिद्धः भवेत्।

अनुवादः

घडा (भांडी) फोडावा, कपडे फाडावेत, गाढवावर (देखील) बसावे, पण काही तरी करून मनुष्याने प्रसिद्ध व्हावे.
One should break a pot, tear clothes and ride a donkey. By some way or the other (hook or crook), one should become popular.

शब्दार्थाः

1. रूपमधिकम् – more than beauty – रूपाहून अधिक
2. प्रच्छन्नगुप्तम् – secretly hidden – गुप्त/लपविलेले
3. भोगकरी – brings pleasure – आनंद / समाधान प्राप्त करून देणारे
4. सुखकरी – gives happiness – सुख देणारे
5. गुरूणाम् – of preceptors – गुरूंचे
6. बन्धुजनः – relative – नातेवाईक
7. विदेशगमने – when travelled in foreign land परदेशी प्रवास केला असता
8. परं दैवतम् – supreme deity – सर्वश्रेष्ठ दैवत
9. राजसु – among kings – राजांमध्ये
10. विद्याविहीन: – devoid of knowledge – विद्याहीन, ज्ञानहीन
11. निन्दन्तु – may censure – निंदानालस्ती करो
12. नीतिनिपुणाः – expert in ethics – नीतिमध्ये कुशल
13. स्तुवन्तु – may praise – स्तुती करो
14. समाविशतु – may come – येवो
15. यथेष्टम् – as per will – स्वेच्छेने
16. अद्यैव – today itself – आजच
17. युगान्तरे – in another era – युगानंतर (दुसऱ्या युगात)
18. न्याय्यात्पथ: – from the path of justice – न्याय्यमार्गावरून
19. प्रविचलन्ति – deviate – ढळतात
20. धीराः – courageous – धैर्यवान
21. भुजगयमिता: – controlled by serpants – सापांनी नियंत्रित
22. निरालम्बः – unsupported – निराधार
23. चरणविकल: – lame by a leg – पायाने पंगु
24. सारथिः – charioteer – सारथी
25. अन्तं याति – goes to the end – शेवटपर्यंत जातो
26. अपारस्य नभसः – of the endless sky – अनंत आकाशाच्या
27. क्रियासिद्धिः – accomplishment of the task – कार्याची पूर्तता
28. उपकरणे – on the means – साधनांवर
29. प्रथमवयसि – in early age – लहानपणी
30. तोयम् – water – पाणी
31. निहितभाराः – bearing weight – वजन घेऊन
32. आजीवितान्तम् – throughout life – संपूर्ण आयुष्यभर
33. अनल्पास्वादम् abundant of sweet water – भरपूर प्रमाणात गोड पाणी
34. उपकारम् – favour/benevolence – उपकार
35. अल्पनाम – of small (insignificant) things – लहानसहान गोष्टींचा
36. संहतिः – unity / union – संघ
37. कार्यसाधिका – that which accomplishes the task – कार्य साधणारी
38. गुणत्वम् – collection of a rope – दोरखंड
39. तृणैः – by grasses – गवतापासून बनविलेले
40. बध्यन्ते – can control – बांधले जातात/नियंत्रित केले जातात
41. घटम् – a pot – घडा
42. भिन्द्यात् – should break – फोडावा
43. पटम् – a cloth – वस्त्र
44. छिन्द्यात् – should tear – फाडावे
45. रासभरोहणम् – should ride – गाढवावर बसावे
46. कुर्यात् – adonkey
47. येन केन प्रकारेप – by hook or crook – काहीतरी करून
48. प्रसिद्धः भवेत् – should become famous – प्रसिद्ध व्हावे
49. आत्मनः – own – स्वत:च्या
50. मुखदोषेण’ – due to fault of mouths – तोंडाच्या दोषाने (आवाजामुळे)
51. बध्यन्ते – caged/trapped – अडकले जातात
52. शुकसारिकाः – parrots and mynas – पोपट व साळुक्या/मैना
53. बकाः – cranes – बगळे
54. मौनम् – silence – मौन
55. सर्वार्थसाधनम् – instrument of achieving all purposes – सर्व हेतू प्राप्त करण्याचे साधन

Aamod Sanskrit Book 10th Class Solutions

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• अमूल्यं कमलम् Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्ययुग्मम् Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• धेनोर्व्याघ्रः पलायते Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• जटायुशौर्यम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• प्रतिपदं संस्कृतम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Anand Chapter 6 संस्कृतनाट्यस्तबकः Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Anand Chapter 6 संस्कृतनाट्यस्तबकः Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 6 Question Answer

Sanskrit Anand Std 10 Digest Chapter 6 संस्कृतनाट्यस्तबकः Textbook Questions and Answers

भाषाभ्यास:

प्रथमं पुष्यम्।

1. माध्यमभाषया उत्तरत । दुष्यन्तस्य कानि स्वभाववैशिष्ट्यानि ज्ञायन्ते?

प्रश्न 1.
दुष्यन्तस्य कानि स्वभाववैशिष्ट्यानि ज्ञायन्ते?
उत्तरम् :
अभिज्ञानशाकुंतल ही कालिदासाची प्रसिद्ध व रंजक अशी कलाकृती आहे. त्याच्या कलाकृतींमध्ये मानवी स्वभाव उत्कृष्टरित्या रंगविले आहेत. अभिज्ञानशाकुंतल या नाटकाचा नायक, दुष्यंत ही गाजलेली व्यक्तिरेखा आहे.

जेव्हा दुष्यंत राजा हरिणाची शिकार करावयास येतो, तेव्हा तपस्वी त्या आश्रमातील हरिणासाठी राजाकडे अभय मागतात. राजा तपस्वींच्या शब्दासरशी बाण मागे घेतो. येथे, एक राजा असूनही तपस्वींच्या शब्दांना मान देऊन तो त्याची ‘नम्रता’ सिद्ध करतो.

राजा हेतुपुरस्सर साध्या वेषात तपोवनात प्रवेश करतो. यातून त्याचा साधेपणा दिसतो, सालसता दिसते. राजा तपोवनाकडे आकृष्ट झालेला असून तो मिळणाऱ्या पाहुणचाराबद्दल उत्सुक आहे.

राजा दुष्यंताने साध्या वेषात तपोवनात प्रवेश करण्याकरिता सर्व आभूषणे ठेवून दिली असली तरी राजाची कर्तव्ये त्याच्या मनात जागृत आहेत. जोपर्यंत तो तपोवनातून परत येईल, तोपर्यंत राजा सारथ्यास घोड्यांस स्वच्छ करण्यास सांगतो. एकंदरीतच, दुष्यंत हा सदाचरणी, सद्गुणांनी युक्त आदर्श राजा दाखविला आहे.

अभिज्ञानशाकुन्तलम् is a famous and amusing work of कालिदास, Human characters are beautifully potrayed with their characteristics in his works. दुष्यन्त, the hero of this drama, is one of the well-known characters.

The king you tries to capture a deer, when a hermit seeks protection of a hermitdeer. The king honours the words of the hermit, hence, withdraws his arrow. Here, being a king, he obeys the words of the hermit and proves his modesty.

The king cautiously enters the hermitage with simple attire. This shows his simplicity. He is attracted towards the hermitage and is curious to receive hospitality from the noble people of hermitage The king, although, takes off royal ornaments and gives away the bow, yet he carries the kingship in his mind.

He is alert about his duties. So he orders the charioteer to water the horses meanwhile. Thus, solis portrayed as an ideal king with all good virtues.

द्वितीयं पुष्यम्।

1. माध्यमभाषया उत्तरत । शक्रस्य कपटं विशदीकुरुत।

प्रश्न 1.
शक्रस्य कपटं विशदीकुरुत।
उत्तरम् :
‘कर्णभारम्’ ही आद्य नाटककार भासाने लिहिलेली, महाभारतावर आधारित एकांकी शोकांतिका आहे. भासाने रंगविलेल्या शक्र व कर्णाचा संवाद, कांच्या उदारतेला सर्वोच्च दर्जा प्राप्त करुन देतो.

इंद्रदेव, शक्राच्या रूपात, एक याचक बनून कर्णाकडे सर्वाधिक भिक्षेची याचना करतो, कर्णाने दिलेली, हजार गायी, असीमित सोने, जिंकलेली पृथ्वी, कर्णाचे शिर ही सर्व दाने इंद्र नाकारतो. अखेर, कर्णाच्या प्राणांचे संरक्षक, कवचकुंडलांच्या दानाबद्दल बोलताच, शक्र लगेच ते मान्य करतो.

शक्राला कवच आणि कुंडलांचीच इच्छा असते. कारण या कवचकुंडलांच्या कृपेने कर्ण अमर होता. शिवाय त्यामुळे कर्णाकडून युध्दात अर्जुन मारला गेला असता. शक्राला इंद्राचा उदार स्वभाव माहीत होता. म्हणून जोवर कपनि कवचकुंडलांचे दान देण्याचे सांगितले नाही, तोवर शक्र सर्व दाने नाकारून सर्वोत्तम दानाची विनवणी करत राहिला. श्रीकृष्णाने आखलेल्या या योजनेत शक्राने दानशूर कर्णाला कपटाने शब्दबध्द केले व अखेर कर्णान देवी कवचकुंडलांचा त्याग केता.

‘कर्णभारम्’, written by the preliminary Sanskrit dramatist HR is a tragedy filled ore act play, based on HENRT story. The dialogue between शक्र (इन्द्र) and कर्ण portrayed by भास, takes कर्ण’s magnanimity to its peak.

Lord i disguised himself as a seeker .asks for superior alms to कर्ण. इन्द्र rejects the alms in the form of thousand cows, unlimited gold, even the conquered earth, कर्ण’s head. At the end, when auf talks about giving away the guards of his life, his कवचकुण्डल, शक्र immediately accepts it.

शक्र wanted कवचकुण्डल itself. Because, due to its effect, it could have been immortal and could have killed अर्जुन. शक्र knew the generous nature of of. Hence, he persuaded कर्ण’s words till he was ready togiveकवचकुण्डल. Thus, Ich cunningly takes away the divine कवचकुण्डल as plotted by श्रीकृष्ण.

संस्कृतनाट्यस्तबकः Summary in Marathi and English

प्रथमं पुष्यम्।

प्रस्तावना :

कालिदास हा संस्कृत-साहित्यातील अद्वितीय कवी व नाटककार म्हणून ओळखला जातो. त्याची नाटके, काव्य हे वेद, महाभारत व पुराणे यांवर आधारित आहे. मूल्याधिष्ठित भारतीय संस्कृतीचे प्रतिबिंब कालिदासाच्या रचनांमधून दिसून येते. केवळ भारतातच नव्हे, तर भारताबाहेरही कालिदासाच्या रचना प्रसिद्ध व रंजक मानल्या जातात.

खालील परिच्छेद हा कालिदासाच्या ‘अभिज्ञानशाकुन्तलम्’ या प्रसिद्ध नाटकातील पहिल्या अंकाचा भाग आहे. येथे नाटकाचा नायक दुष्यंत हरिणाची शिकार करायला निघालेला असतो. तेव्हा तपस्वी वैखानस आश्रमातील प्राण्यांना अभय देण्यासाठी त्याला विनंती करतात, राजा तपस्वींच्या शब्दांना मान देतो व बाण मागे घेतो.

कालिदास is regarded as an extraordinary poet and dramatist in Sanskrit literature. His plays, poetry are primarily based on the Vedas, Mahabharata and Puranas. Value-based Indian culture is reflected through his creations…

His creations/writings are popular and Amusing across India and the world. The following extract is from the 1st chapter (अंक) of कालिदास’s famous drama, अभिज्ञानशाकुन्तलम्, where the hero of drama king दुष्यंत tries to capture a deer when a hermit all intervenes and requests him for the protection of an animal in that hermitage. The king honors the words of the hermit and withdraws his arrow and puts it back into the quiver.

अनुवादः

(त्यानंतर वैखानस व इतर तपस्वी प्रवेश करतात.)

• वैखानस – (राजाला थांबवून) हे राजा! हे आश्रमातील (निष्पाप) हरिण आहे. (याचा वध केला जाऊ नये) याला मारु नये.
  बाण त्वरित मागे घ्यावा. राजांचे शस्त्र हे त्रासलेल्या लोकांच्या संरक्षणासाठी आहे, निष्यापांवर प्रहार करण्यासाठी नव्हे. (निरागसांना मारण्यासाठी नव्हे.)
• दुष्यंत – हा बाण मागे घेतला आहे. (सांगितल्याप्रमाणे करतो.)
• वैखानस – हे राजा! आम्ही यज्ञाकरिता समिधा गोळा करण्यासाठी निघालो आहोत. हा कुलपती कण्वांचा मालिनी तीरावरील आश्रम दिसतो आहे. येथे प्रवेश करून अतिथियोग्य सत्काराचा लाभ घ्या.
• दुष्यन्त – आपण तपस्व्यांना त्रास देणे योग्य नाही (त्यांचे वातावरण भंग करणे योग्य नाही) इथेच रच थांबव, तोवर मी उतरतो.
• सारथी – लगाम धरले आहेत. औक्षवंत राजाने उतरावे.
• दुष्यन्त – (उतरून) आश्रमात प्रवेश करताना वेष साधा असावा. तेव्हा तू हे घे. (सारथ्याला अलंकार व धनुष्य देऊन.) हे सारथी जोवर मी तपस्वीजनांचे आलोकन करून परततो, तोवर घोड्यांच्या पाठीला पाणी लाव. (त्यांना स्वच्छ कर.)
• सारथी – बरे. (असे म्हणून जातो.)

(Then entersdans and other hermits.)

वैखानस – (obstructing/stopping the king)o king, This is the deer from the hermitage. It must not be slayed. Please take back the arrow quickly. King’s weapon is for the protection of the distressed, not to attack the innocent.
दुष्यन्त – This arrow is withdrawn. (follows what is said).
वैखानस – o king! We are set off for collecting wood for the solemn sacrifice. On the banks of मालिनी, the hermitage of noble preceptor 90 is seen. Having entered (here), please accept the hospitality (receive a welcome.)
दुष्यन्त – We must not disturb the hermits. Stop the chariot here itself while I alight (get down).
Charioteer – The bridles are held. May the long-living majesty alight.
दुष्यन्त – (Having alighted)
O Charioteer, one must enter in penance groves with humble attire. So, you take this. (giving the jewels and the bow to the charioteer.) O Charioteer, while I return meeting (seeing) those hermits, have the back of horses be cleaned with water.
Charioteer – Alright. (Thus exits.)

द्वितीयं पुष्यम्।

प्रस्तावना :

भारतीय आद्य नाटककार ‘भास’ विरचित कर्णभारम् हे एकांकी संस्कृत नाटक आहे. कर्णभारम् हे मुख्यत्वे भारतीय महाकाव्य महाभारतातील, एका भागाचे वेगळ्या दृष्टिकोनातून केलेले पुनर्कथन आहे. कर्णभारम् ही संभाव्य शोकांतिका आहे. खालील परिच्छेदात, इंद्र हा याचकाच्या रूपात कर्णासमोर येतो व अखेर दानशूर कर्णाकडून जन्मजात असलेली कवचकुंडले घेण्यात यशस्वी ठरतो.

कर्णभारम् is a Sanskrit one act play written by preliminary Indian dramatist भास. कर्णभारम् is essentially a retelling of an episode of Indian epic HENC presented in a different perspective. कर्णभारम् is the potential tragedy. In the following passage, who is disguised as a seeker finally succeeds in taking away embodied her from – the most magnanimous कर्ण.

अनुवादः

(नंतर याचक रूपात शक्र प्रवेश करतो.)

• शक्र : (कर्णाजवळ जाऊन) अरे कर्णा, मला मोठी भिक्षा हवी आहे.
• कर्ण : अझे स्वामी ! मला खूप आनंद झाला आहे. मी तुम्हांला नमस्कार करतो.
• शक्र: (स्वत:ला) आता मी काय बोलावे? जर मी ‘दीर्घायु हो’ असे बोललो तर हा दीर्घायु होईल, जर मी (काहीच) नाही बोललो तर हा मला मूर्ख समजेल. तेव्हा, हे दोन्ही सोडून काय बरे बोलावे? असो. लक्षात आले. (मोठ्याने) कर्णा, सूर्याप्रमाणे, चंद्राप्रमाणे, हिमालयाप्रमाणे व समुद्राप्रमाणे तुझे यश (चिरंतन) राहो.
• कर्ण : स्वामी! तुम्ही दीर्घायू हो, असे का नाही म्हणालात? अन्यथा असो, जे बोलला आहात (जो आशीर्वाद दिला आहे) तेच योग्य असेल, कारण, मर्त्य शरीरामध्ये (केवळ) सद्गुणच शेवटपर्यंत राहतात. स्वामी, तुम्हांला काय हवे आहे? (तुम्ही कशाची इच्छा करत आहात?) मी आपल्याला काय देऊ?
• शक्र: मला मोठी भिक्षा हवी आहे.
• कर्ण : मी तुम्हाला सर्वात मोठी भिक्षा (महत्तम दान) देतो. मी आपणाला हजार गायी देतो.
• शक्र : हजार गायी? (पण) मी दूध क्वचित पितो. मला त्यांची इच्छा नाही.
• कर्ण: आपणास (त्यांची) इच्छा नाही. (तर मग) आपणांस पुष्कळ सोने देईन.
• शक्र: ते तर (केवळ) घेऊन जाता येईल. कर्णा, मला त्याची (सोन्याची) इच्छा नाही.
• कर्ण: मग तुम्हाला पृथ्वी जिंकून ती देईन.
• शक्र: पृथ्वी (घेऊन) मी काय करु? मला (तिची) इच्छा नाही.
• कर्ण: किंवा माझे मस्तकच तुम्हाला देईन.
• शक्र: असे बोलू नकोस.
• कर्ण: घाबरु नका. घाबरु नका. हे पण ऐका, जन्मजात असलेले हे कवच कुंडलांसकट मी देईन.
• शक्र: (आनंदी होऊन) कृपया दे.

(Then enters शक्र disguised as a seeker.)

• शक्र: (Approaching कर्ण) कर्ण, I ask for the great alms.
• कर्ण : O lord! I am very pleased. Here, I salute you.
• शक्र: (To himself) What shall I say now? If I will say, ‘Live long’ then he would live longIf I would not say, he would consider me as ignorant. Therefore, leaving these two (except these two) indeed what shall I say? Let it be, I got it. (Loudly)0 कर्ण may your fame remain like the sun, moon, Himalaya and like ocean.
• कर्ण : O Lord ! Why you did not say, live long or else what is said that is alright. Because, virtues remain (forever) in the mortal bodies. O lord, what do you wish? what shall I give you?
• शक्र: I ask for the great alms.
• कर्ण : I give the great alms to the respected one. I shall give you thousand cows. Thousand cows? I rarely drink its milk. O कर्ण, Ido not wish it.
• कर्ण: O, doesn’t the respected one wish it? (Then) I will give you lots of gold.
• शक्र: I will just go taking it. O कर्ण, I do not wish it.
• कर्ण: Then I will conquer the earth and give (it) to you.
• शक्रः What shall I do with the earth? I do not wish it.
• कर्ण: Or else, I will give you my head.
• शक्रः Don’t say so! Please don’t say so.
• कर्ण: Don’t be scared. Listen to this also. I will give the shield (कवच) along with the earrings that are born with my body.
• कर्ण: (Happily) Please give it.

शब्दार्थाः

1. 1. मृगः – deer – हरिण
   2. न हन्तव्यः – should not be killed – मारले जाऊ नये
   3. सायक: – arrow – बाण
   4. तापसौ – hermits – तपस्वी
   5. धृताः प्रग्राः – bridles are held – लगाम धरले आहेत
   6. वाजिनः – horses – घोडे
   7. आभरणानि – ornaments – अलंकार
   8. विनीतवेषेण – with humble attire – साध्या वेषात
   9. समिदाहरणाय – to collect wood for sacrifice – यज्ञासाठी समिधा गोळा करण्यासाठी
   10. आर्तत्राणाय – for protecting the oppressed/afflicted- हतबलांच्या रक्षणासाठी
   11. अपावर्ते – I return – मी परततो
   12. प्रतिगृह्यताम् – may it be accepted – स्वीकार केला जावा
   13. अवरुध्य – stopping – अडवून
   14. आशु – quickly – झटकन
   15. अनागसि- for the destruction – निरागसांना
   16. प्रहर्तुम् – of the innocent – मारण्यासाठी
   17. तपोवन – no trouble for – तपोवनात राहणाऱ्यांना
   18. निवासिनाम् उपरोध: मा भूत् – the hermits – व्यत्यय होऊ नये
   19. यावत् अवतरामि – till I get down – तोपर्यंत/तोवर मी उतरतो
   20. आर्द्रपृष्ठाः क्रियन्ताम् – let (it) be watered – पाण्याने स्वच्छ केले जावेत
   21. वत्स – child – बाळ
   22. प्रतिवेशिक – neighbour – शेजारी
   23. दारक: – child – मूल/ बाळ
   24. अनलकृत – body without – अलंकारहीन शरीर
   25. शरीरः – ornaments
   26. सौवर्ण शकटिकाम् – golden cart – सोन्याची गाडी
   27. अनुकृतं रूपम् – followed the form – रूप अनुसरले आहे
   28. शकटिकया – with a cart – गाडीबरोबर
   29. ऋढ्या – with richness – श्रीमंतीने
   30. विनोदयामि – amuse, entertain – खेळविते
   31. घटय – you make तू घडव.
   32. सकरुणम् – crying pitiably – रडत रडत
   33. सनिर्वेदम् – wearily – त्रासून / वेदनेने
   34. समीपम् उपसर्पिष्यामि – shall approach – जवळ नेते
   35. मच्छिरः – my head – माझे मस्तक/शिर
   36. क्षीरम् – milk – दूध –
   37. गोसहस्रम् – thousand cows – हजार गायी
   38. मुहूर्तकम् – rarely – क्वचित
   39. महत्तराम् – most big – सर्वात मोठी
   40. न भेतव्यम् – don’t be scared – घाबरु नका
   41. धरन्ते – remain – राहतात
   42. प्रदास्ये – I will give – मी देईन
   43. उपगम्य – approaching – जवळ जाऊन
   44. परिहत्य – leaving – सोडून
   45. उभयम् – both – दोन्ही
   46. अविहा – don’t say so – असे बोलू नको
   47. दृढं प्रीत: – I am very happy – खूप आनंदित
   48. अस्मि – झालो आहे

10th Standard Sanskrit Anand Digest Pdf  

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्यस्तबकः Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Anand Chapter 9 आदिशङ्कराचार्यः Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Anand Chapter 9 आदिशङ्कराचार्यः Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 9 Question Answer

Sanskrit Anand Std 10 Digest Chapter 9 आदिशङ्कराचार्यः Textbook Questions and Answers

भाषाभ्यास:

1. पूर्णवाक्येन उत्तरं लिखत ।

प्रश्न अ.
गुरुमुपगम्य शङ्करः किम् अधीतवान् ?
उत्तरम् :
गुरुमुपगम्य शङ्करः वेद-वेदाङ्गानि, विविधशास्त्राणि च अधीतवान्।

प्रश्न आ.
शङ्करः किमर्थम् आक्रोशत् ?
उत्तरम् :
यदा शकर स्नाने मग्नः आसीत् तदा एक: ननतस्य पादम् अगृह्णात् अत: भीत्या शङ्करः उच्चैः आक्रोशत्।

प्रश्न इ.
शङ्करः मात्रे किं प्रतिश्रुत्य गृहाद् निरगच्छत् ?
उत्तरम् :
‘मात: यदा त्वं स्मरिष्यसि तदा एवं त्वत्समीपमागमिष्यामि’ इति मात्रे प्रतिश्रुत्य शङ्करः गृहद् निरगच्छत्।

प्रश्न ई.
शङ्करः कस्य शिष्यः अभवत् ?
उत्तरम् :
शङ्कर: गोविन्दभगवत्पादानां शिष्यः अभवत्।

प्रश्न उ.
शङ्करः संन्यासदीक्षां गृहीत्वा किम् अकरोत्?
उत्तरम् :
शङ्कर: संन्यासदीक्षां गृहीत्वा वैदिकधर्मस्य प्रचारार्थ प्रस्थानम् अकरोत्।

2. माध्यमभाषया उत्तरत।

प्रश्न अ.
शङ्करेण संन्यासार्थ कथम् अनुमतिः लब्धा ?
उत्तरम् :
‘आदिशङ्कराचार्य:’ या पाठामध्ये शंकराचार्यांच्या जीवनातील दोन प्रसंग उद्धृत करण्यात आले आहेत. पहिल्या प्रसंगात, एका अटळ परिस्थितीत सापडले असताना, संन्यासी बनू इच्छिणाऱ्या शंकराचार्यांना त्यांची माता कशी अनुमती देते, याचे वर्णन आले आहे.

एकदा शंकर स्नानासाठी पूर्णा नदीवर गेले होते. स्नान करत असताना अनपेक्षितपणे एका मगरीने त्यांचा पाय पकडला. वेदना असहा झाल्याने शंकर जोरात ओरडू लागले. तेव्हा त्यांची आई आर्याबा तिथे पोहोचली. अशा दयनीय अवस्थेत शंकराला रडताना पाहून त्याची आई सुद्धा गांगरून गेली.

हा अनावस्था प्रसंग म्हणजे आयुष्याचा शेवट अशी शंकराची समजूत झाली व त्याने संन्यासी होण्याची अतृप्त इच्छा आईकडे बोलून दाखविली. हतबल झालेल्या आबिने मनात नसतानाही ही शंकराची शेवटची इच्छा मानून, संन्यास घेण्यासाठी अनुमती दिली.

In the lesson, आदिशङ्कराचार्यः, two incidents of शंकराचार्य’s life are given. The first incident explains how आदिशङ्कराचार्य, who was keen to become a monk was granted permission by his mother for practising monkship due to an inescapable situation.

Once, it went to पूर्ण river for bathing, a crocodile caught his leg. शंकर screamed loudly with pain. His mother अर्याम्बा came there. Seeing शंकर crying in miserable condition, even his mother got perturbed.

शंकर finding / thinking this situation as the end of his life, expressed his unfulfilled wish to become a monk to his mother and requested her to permit for the same. Unwillingly, helpless अर्याम्बा granted शंकर for monkship, considering this as his last wish.

3. सन्धिविग्रहं कुरुत।

प्रश्न अ.
चास्ताम्
उत्तरम् :
चास्ताम् – च + आस्ताम्।

प्रश्न आ.
त्वत्समीपमागमिष्यामि
उत्तरम् :
त्वत्समीपमागमिष्यामि – त्वत् + समीपम् + आगमिष्यामि।

प्रश्न इ.
गुरुमुपागच्छत्
उत्तरम् :
गुरुमुपागच्छत् – गुरुम् + उपागच्छत्।

प्रश्न ई
मुनिरभ्यगात्
उत्तरम् :
मुनिरभ्यगात् – मुनिः + अभ्यगात्।

प्रश्न उ.
मातैव
उत्तरम् :
मातैव – तस्मात् + माता + एव।

4. मेलनं कुरुत ।

प्रश्न 1.
विशेष्यम् – शिवगुरुः, आर्याम्बा, शङ्करः, जगत्, मनुष्यः ।
विशेषणम् – मलिनकायः, प्रसन्नः, विशालम्, दिवङ्गतः, विरक्तः, चिन्तामना ।
उत्तरम् :

विशेषणम्	विशेष्यम्
1. मलिनकायः	मनुष्यः
2. विशालम्	जगत्
3. दिवङ्गतः	शिवगुरुः
4. विरक्तः	शङ्करः
5. चिन्तामग्ना	आर्याम्बा

5. समानार्थकशब्दं लिखत ।

प्रश्न 1.
समानार्थकशब्दं लिखत
दिवङ्गतः, शीघ्रम्, मग्नः, नक्र:, पादः, पुत्रः, शिष्यः।
उत्तरम् :

• दिवङ्गतः – परिंगतः, परलोकगतः, मृतः।
• शीघ्रम् – झटिति, सत्वरम्, तूर्णम्, त्वरितम्।
• मग्नः – लीनः, रत: व्यग्रः।
• नक्रः – मकरः, गुम्भीरः, कुटिचर:, मायादः ।
• पादः – चरण:, पदम्।
• पुत्रः . – तनयः, आत्मजः, सुतः, सूनुः ।
• शिष्यः – विद्यार्थी, छात्रः, अन्तेवासी।

6. स्थानाधारण शब्दपेटिकां पूरयत ।

प्रश्न 1.
स्थानाधारण शब्दपेटिकां पूरयत

(कालडीग्रामः, केरलप्रदेशः, भारतदेशः, आलुवानगरम्,)
उत्तरम् :

7. प्रवाहि जालचित्रं पूरयत ।

प्रश्न 1.
प्रवाहि जालचित्रं पूरयत ।

(गृहं प्रत्यागमनम्, गुरुमुपगमनम्, मातृसेवा, वेद-वेदाङ्गानाम् अध्ययनम्)
उत्तरम् :

8. जालरेखाचित्रं पूरयत ।

प्रश्न अ.

उत्तरम् :

प्रश्न आ.

उत्तरम् :

Sanskrit Anand Class 10 Textbook Solutions Chapter 9 आदिशङ्कराचार्यः Additional Important Questions and Answers

अवबोधनम् :

उचितं कारणं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
शङ्करस्य मातैव पुत्रस्य पालनम् अकरोत् यतः …………………
(अ) शङ्कराय केवलं माता अरोचत।
(ब) बाल्ये एव तस्य पिता शिवगुरुः दिवङ्गतः।
उत्तरम् :
(ब) बाल्ये एव तस्य पिता शिवगुरुः दिवङ्गतः।

प्रश्न 2.
आर्याम्बा चिन्तामग्ना जाता यतः ……………….
(अ) शङ्कर: ऐहिकविषयेषु अरुचिं प्रादर्शयत्।
(ब) शङ्करः ऐहिकविषयेषु रुचिं प्रादर्शयत्।
उत्तरम् :
(अ) शङ्करः ऐहिकविषयेषु अरुचिं प्रदर्शयत् ।

प्रश्न 3.
शङ्कर: उच्चैः आक्रोशत् यतः ………………
(अ) सः नदीजले अमज्जत्।
(ब) नक्र: तस्य पादम् अगृह्णात्।
उत्तरम् :
(ब) नक्र: तस्य पादम् अगृणात्।

प्रश्न 4.
आर्याम्बा रोदनम् आरभत यतः ………………………
(अ) शङ्करं नक्रेण गृहीतं दृष्ट्वा सा भीता जाता।
(ब) नक्र: तस्याः पादम् अगृह्णात्।
उत्तरम् :
(अ) शकरं नक्रेण गृहीतं दृष्ट्वा सा भीता जाता।

प्रश्न 5.
शङ्कर: मलिनकायं मनुष्य प्रणनाम यतः ………………………
(अ) मलिनकाय: मनुष्यः शङ्करं सङ्कटात् अरक्षत्।
(ब) स: मलिनकाय; मनुष्य: वेदान्तस्य सारं जानाति स्म।
उत्तरम् :
(ब) स: मलिनकाय; मनुष्य : वेदान्तस्य सारं जानाति स्म।

उचितं पर्यायं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.

1. शङ्करस्य ……………… शिवगुरुः आसीत्। (पिता/माता)
2. ……………. एव शङ्करस्य पालनम् अकरोत्। (पिता / माता)
3. पठनादिकं समाप्य शङ्करः …………. प्रत्यागतवान्। (गृह/नदी)
4. ……. वयसि उपनीतः सः पठनार्थ गुरुम् उपागच्छत्। (पञ्चमे/दशमे)

उत्तरम् :

1. पिता
2. माता
3. गृहं
4. पञ्चमे

प्रश्न 2.

1. आर्याम्बा पुत्रं ……. गृहीतम् अपश्यत्। (नक्रेण, मत्स्येन)
2. शङ्करः …………… आर्ततया प्रार्थयत। (गुरुम्, मातरम्)
3. शङ्कर: मातरं …………. महत्त्वम् अवाबोधयत्। (संन्यासस्य, संसारस्य)
4. शङ्कराचार्य: …………… शिष्यः अभवत्। (गोविन्दहरदासानां गोविन्दभगवात्पादानां)

उत्तरम् :

1. चक्रेण
2. मातरम्
3. संन्यासस्य
4. गोविन्दभगवात्पादाना

प्रश्न 3.

1. आचार्य: शिष्यगणेन सह …………. अगच्छत्। (गङ्गास्नानार्थम्/समुद्रस्नानार्थम्)
2. यस्मात् ज्ञानं लभते सः ………….. (ज्येष्ठः / गुरु:)
3. शिष्या: मलिनकायं मनुष्यं …………. इति अवदन्। (अपसर/आगच्छ)
4. सर्वेषां …………….. पञ्चमहाभूतात्मकानि। (स्तोत्राणि / शरीराणि)
5. स: ……… सिद्धान्तस्य प्रचारम् अकरोत्। (अद्वैत / परमाणु)

उत्तरम् :

1. गङ्गास्नानार्थम्
2. गुरु:
3. अपसर
4. शरीराणि
5. अद्वैत

(ग) पूर्णवाक्येन उत्तरत।

प्रश्न 1.
शङ्कराचार्यस्य जन्म कदा अभवत्?
उत्तरम् :
शङ्कराचार्यस्य जन्म ख्रिस्ताब्दे अष्टमे शतके अभवत्।

प्रश्न 2.
शङ्कर: गृहं प्राप्य किम् अकरोत् ?
उत्तरम् :
शङ्करः गृहं प्राप्य मातृसेवाम् आरभत।

प्रश्न 3.
किमर्थम् आर्याम्बा चिन्तामग्ना जाता?
उत्तरम् :
शङ्करस्य ऐहिकविषयेषु अरुचि दृष्ट्वा आर्याम्बा चिन्तामग्ना जाता।

प्रश्न 4.
शङ्कर: मातरं किं प्रार्थयत?
उत्तरम् :
शङ्कर: मातरम् प्रार्थयत यत् सः जीवितुं न शक्नोति। अत: मरणात् पूर्वं स: संन्यासी भवितुम् इच्छति।

प्रश्न 5.
शङ्कराचार्यानुसारेण कः गुरुः?
उत्तरम् :
शङ्कराचार्यानुसारेण यस्माद् ज्ञानं लभते स: गुरुः ।

वाक्यं पुनलिखित्वा सत्यम् असत्यम् इति लिखत।

प्रश्न 1.
1. शङ्कराचार्यस्य जन्म एकोनविंशतितमे शतके अभवत्।
2. शङ्कर: अतीव प्रज्ञावान् बालकः ।
उत्तरम् :
1. असत्यम्।
2. सत्यम्।

शब्दज्ञानम्

सन्धिविग्रहः।

1. बालकोऽयम् – बालकः + अयम्।
2. सदैव – सदा + एव।
3. गृहीतमपश्यत् – गृहीतम् + अपश्यत्।
4. तथैव – तथा + एव।
5. इदानीमेव – इदानीम् + एव।
6. नक्राद् मुक्तः – नक्रात् + मुक्तः ।
7. जगद् एव – जगत् + एव।
8. शिष्यो भूत्वा – शिष्यः + भूत्वा।
9. यस्माद् ज्ञानम् – यस्मात् + ज्ञानम्।
10. स गुरुः – सः + गुरुः।
11. कोऽपि – कः + अपि।
12. शरीराद् भिन्नम् – शरीरात् + भिन्नम्।
13. त्वद् भिन्नः – त्वत् + भिन्नः ।
14. कस्मादपि – कस्मात् + अपि।
15. गुरुरेव – गुरु: + एव।
16. तत्रैव – तत्र + एव।

त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि ।

त्वान्त अव्यय धातु + त्वा / ध्या / ट्वा / वा / इत्वा/अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्त अव्यय धातु + तुम् / धुम् / ट्म् / ट्म् / इतुम् अयित्वा
दृष्ट्वा, श्रुत्वा, भूत्वा	समाप्य, प्राप्य, आगत्य	भवितुम्

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.
माता आर्याम्बा पुत्रस्य विवाहविषये सदैव चिन्तयति स्म।
उत्तरम् :
माता आर्याम्बा कस्य विवाहविषये सदैव चिन्तयति स्म?

प्रश्न 2.
कालडी ग्राम : पूर्णानदीतीरे वर्तते।
उत्तरम् :
कालडी ग्रामः कुत्र वर्तते?

प्रश्न 3.
माता शङ्करस्य पालनम् अकरोत्।
उत्तरम् :
का पुत्रशङ्करस्य पालनम् अकरोत्?

प्रश्न 4.
शङ्करः गृहं प्राप्य मातृसेवाम् आरभत।
उत्तरम् :
शङ्करः गृहं प्राप्य किम् आरभत?

प्रश्न 5.
आर्याम्बा पुत्रं नक्रेण गृहीतम् अपश्यत्।
उत्तरम् :
आर्याम्बा कं नक्रेण गृहीतम् अपश्यत्?

प्रश्न 6.
शङ्कर: मातरं आर्ततया प्रार्थयत।
उत्तरम् :
शङ्कर: मातरं पूर्व कथं प्रार्थयत?

प्रश्न 7.
शङ्कर: मरणात् पूर्व संन्यासी भवितुम् इच्छति।
उत्तरम् :
शङ्कर: मरणात् पूर्व कः भवितुम् इच्छति?

प्रश्न 8.
विवशा माता शङ्कराय संन्यासार्थम् अनुमतिम् अयच्छत्।
उत्तरम् :
कीदृशी माता शङ्कराय संन्यासार्थम् अनुमतिम् अयच्छत्।

प्रश्न 9.
शङ्कर: मातरं संन्यासस्य महत्वम् अवाबोधयत्।
उत्तरम् :
शङ्कर: का संन्यासस्य महत्त्वम् अवाबोधयत्?

प्रश्न 10.
विशालं जगद् संन्यासिनः गृहम्।
उत्तरम् :
विशालं जगद् कस्य गृहम्?

प्रश्न 11.
वैदिकधर्मस्य स्थापनार्थ शङ्कर: प्रस्थानम् अकरोत्।
उत्तरम् :
किमर्थं शङ्करः प्रस्थानम् अकरोत् ?

प्रश्न 12.
दरिद्रः मनुष्य: मार्गे आचार्यस्य पुरतः आगच्छत्।
उत्तरम् :
कीदृशः मनुष्यः मार्गे आचार्यस्य पुरतः आगच्छत्?

प्रश्न 13.
आत्मा परमेश्वरस्य अंशः।
उत्तरम् :
कः परमेश्वरस्य अंश:?

प्रश्न 14.
आचार्यः षोडशे भाष्यं कृतवान्।
उत्तरम् :
आचार्यः कदा भाष्यं कृतवान् ?

विभक्त्यन्तरूपाणि।

• प्रथमा – सः, नक्र:, सा, अहम्, संन्यासी, त्वम्, सः, गुरुः, कः, जीर्णवस्त्रधारी, शिष्याः, आत्मा, अहम्, सः, सः, जन्म, पिता, माता, अयम्।
• द्वितीया – पादम्, मातरम्, अनुमतिम्, संन्यासम्, चरणौ, जगत, दीक्षाम्, सर्वाणि, दर्शनानि, ज्ञानम्, तम्, कम्, शरीरम, आत्मानम्, शरीराणि, गुरुम्, शास्त्राणि, सेवाम्।
• तृतीया – नक्रेण, आर्ततया, चेतसा। चतुर्थी – तुभ्यम्, मात्रे, गणेन, मनसा, वचसा, कर्मणा।
• पञमी – नक्रात्, वशात, तेभ्यः, गृहात्, शरीरात्, त्वत्, मुखात, कस्मात, यस्मात्।
• षष्ठी – मातुः, एकस्याः, धर्मस्य, तस्यतस्य, परमेश्वरस्य, सर्वेषाम्, तत्त्वस्य, नगरस्य, गुरोः, तस्य, पुत्रस्य, आचार्यस्य, शङ्करस्य।
• सप्तमी – एकस्मिन्, दिने, स्नाने, एकस्मिन्, दिने, मार्गे, द्वादशे, षोडशे, दिशि, प्रदेशे, तीरे, शतके, बाल्ये, पञ्चमे, वयसि।
• सम्बोधन – अम्ब, वत्स, मातः।

विशेषण – विशेष्य – सम्बन्धः।

विशेषणम्	विशेष्यम्
1. जगद्गुरोः	शङ्कराचार्यस्य
2. अष्टमे	शतके
3. दिवङ्गतः	शिवगुरुः
4. पञमे	वयसि
5. विरक्तः	शङ्करः
6. चिन्तामग्ना	आर्याम्बा
7. एकस्मिन्	दिने
8. एक:	नक्र:
9. भयाकुला	सा
10. विवशा	माता
11. विशालम्	जगत्
12. सर्वाणि	दर्शनानि
13. दरिद्र	मनुष्यः
14. मलिनकायः	मनुष्यः
15. जीर्णवस्त्रधारी	मनुष्यः
16. पञ्चमहाभूतात्मकानि	शरीराणि

लकारं लिखत।

प्रश्न 1.
शङ्करस्य पिता शिवगुरु: माता आर्याम्बा च आस्ताम्।
उत्तरम् :
लङ्लकारः

प्रश्न 2.

1. यदा त्वं स्मरिष्यसि तदा एव त्वसमीपमागमिष्यामि।
2. शङ्कर; उच्चैः आक्रोशत्।
3. नक्रात् त्रायस्व।
4. देहि अनुमतिम्।
5. यथा तुभ्यं रोचते तथैव भवतु।
6. इदानीमेव संन्यासं स्वीकुरु।
7. शङ्कर: मातरं संन्यासस्य महत्वम् अवाबोधयत्।

उत्तरम् :

1. लृट्लकारः
2. लङ्लकारः
3. लोट्लकारः
4. लोट्लकारः
5. लट्लकारः
6. लोट्लकार:
7. लङ्लकार:

प्रश्न 3.

1. आचार्य: तं प्रणनाम।
2. शिष्या: अपसर इति अवदन्।
3. शिष्या: अपसर इति अवदन्।

उत्तरम् :

1. लिट्लकार :
2. लोट्लकार:
3. लल्लकार:

पृथक्करणम्

1. क्रमेण योजयत।

1. शङ्करस्य पठनार्थं गुरुं प्रति गमनम्।
2. शिवगुरु: दिवङ्गतः।
3. शङ्कराचार्यस्य जन्म।
4. मात्रा शङ्करस्य पालनम्।
5. गोविन्दभगवत्पादानां शिष्यत्वम्।
6. मात्रै प्रतिश्रुत्य गृहात् निर्गमनम्।
7. वैदिकधर्मस्य स्थापनार्थ प्रस्थानम्।
8. मातरं संन्यासस्य महत्वबोधनम्।
9. संन्यासार्थम् अनुमतियाचना।
10. नक्रेण पादग्रहणम्।
11. मात्रा अनुमतिप्रदानम्।
12. शङ्करस्य आक्रोशः।

उत्तरम् :

1. शङ्कराचार्यस्य जन्म।
2. शिवगुरु: दिवङ्गतः।
3. मात्रा शङ्करस्य पालनम्।
4. शङ्करस्य पठनार्थं गुरुं प्रति गमनम्।
5. मातरं संन्यासस्य महत्त्वबोधनम्।।
6. मात्रे प्रतिश्रुत्य गृहात् निर्गमनम्।
7. गोविन्दभगवत्पादानां शिष्यत्वम्।
8. वैदिकधर्मस्य स्थापनार्थं प्रस्थानम्।
9. नक्रेण पादग्रहणम्।
10. शङ्करस्य आक्रोशः।
11. संन्यासार्थम् अनुमतियाचना।
12. मात्रा अनुमतिप्रदानम्।

कः कं वदति।

प्रश्न 1.
नक्रात् त्रायस्व!
उत्तरम् :
शङ्कर: मातरं वदति।

प्रश्न 2.
इतः परम् अहं न जीवामि।
उत्तरम् :
शङ्कर : मातरं वदति।

प्रश्न 3.
यथा तुभ्यं रोचते तथैव भवतु।
उत्तरम् :
माता शङ्करं वदति।

प्रश्न 4.
मम अनुमतिः अस्ति।
उत्तरम् :
माता शङ्करं वदति।

प्रश्न 5.
‘अपसर, अपसर!’
उत्तरम् :
शिष्या: मलि कायं / दरिद्रं / जीर्णवस्त्रधारिणं मनुष्यं वदन्ति।

प्रश्न 6.
आत्मा तु परमेश्वरस्य अंशः एव।
उत्तरम् :
दरिद्रः/मलिनकाय:/जीर्णवस्वधारी मनुष्य : शिष्यान् वदति।

प्रश्न 7.
कथं तव शरीरं मम शरीराद् भिन्नम्?
उत्तरम् :
दरिद्रः/मलिनकाय:/जीर्णवस्त्रधारी मनुष्य : शिष्यान् वदति।

वाक्यं पुनलिखित्वा सत्यम् असत्यम् इति लिखत।

प्रश्न 1.

1. सर्वेषां शरीराणि सप्तमहाभूतात्मकानि ।
2. आचार्यः तत्रैव कनकधारास्तोत्रं रचितवान्।
3. आत्मा तु ईश्वरस्य / भगवतः अंशः।
4. आचार्य: दरिद्राय अकुप्यत्।

उत्तरम् :

1. असत्यम्।
2. असत्यम्।
3. सत्यम्।
4. असत्यम्।

प्रश्न 2.
एष: गद्यांश: कस्मात् पाठात् उद्धृतः?
उत्तरम् :
एषः गद्यांश: ‘आदिशङ्कराचार्यः’ इति पाठात् उद्धृतः ।

पृथक्करणम्

क्रमेण योजयत।

प्रश्न 1.
1. मार्गे मलिनकायपुरुषस्य आगमनम्।
2. शिष्यगणेन सह गङ्गास्नानार्थ गमनम्।
3. ‘मनीषापञ्चकम्’ इति स्तोत्रस्य रचना।
4. मलिनकायपुरुषस्य मुखात् वेदान्ततत्त्वसारस्य श्रवणम्।
उत्तरम् :
2. शिष्यगणेन सह गङ्गास्नानार्थं गमनम्।
1. मार्गे मलिनकायपुरुषस्य आगमनम्।
4. मलिनकायपुरुषस्य मुखात् वेदान्ततत्त्वसारस्य श्रवणम्।
3. ‘मनीषापञ्चकम्’ इति स्तोत्रस्य रचना।

भाषाभ्यासः

समानार्थकशब्दाः

1. अनुमतिः – अनुज्ञा।
2. पिता – तातः, जनकः ।
3. माता – अम्बा, जननी, जनयित्री।
4. बाल्ये – शैशवे।
5. श्रुत्वा – निशम्य, आकर्ण्य।
6. दृष्ट्वा – अवलोक्य, विलोक्य, वीक्ष्य।
7. चेतसा – मनसा ।
8. दरिद्रः – निर्धनः, दीनः।
9. शरीरम् – वपुः, देहम् ।
10. गुरुः – उपाध्यायः, अध्यापकः, निषेकादिकृत्।

विरुद्धार्थकशब्दाः

1. अनुमतिः × नकारः, अपतापः ।
2. असाधारण: × साधारणः।
3. समाप्य × आरभ्य ।
4. झटिति × शनैः शनैः, मृदुः मुदुः ।
5. रोदनम् × हास्यम्।
6. अधुना × अनन्तरम्।
7. मुक्तः × बद्धः।
8. समीपम् × दूरम्।
9. दरिद्रः × धनवान्।
10. भिन्नः × समानः ।

पूर्वकालवाचकं निष्कासयत।

प्रश्न 1.
शङ्कर: गृहं प्राप्य मातृसेवाम् आरभत।
उत्तरम् :
शङ्कर: गृहं प्राप्नोत् मातृसेवाम् आरभत च।

प्रश्न 2.
प्रश्नं श्रुत्वा सर्वे आश्चर्यचकिताः अभवन्।
उत्तरम् :
प्रश्नं अश्रुण्वन् सर्वे आश्चर्यचकिता: अभवन् च।

वचनं परिवर्तयत।

प्रश्न 1.
सः गृहात् निरगच्छत्। (बहुवचनं कुरुत।)
उत्तरम् :
ते गृहात् निरगच्छन्।

प्रश्न 2.
सः मनुष्यः अपृच्छत्। (बहुवचनं कुरुत।)
उत्तरम् :
ते मनुष्या: अपृच्छन्।

लकारं परिवर्तयत।

प्रश्न 1.
मम अनुमतिः अस्ति । (लङ्लकारे परिवर्तयत।)
उत्तरम् :
मम अनुमतिः आसीत्।

समासा:

समस्तपदम्	अर्थ	समासविग्रहः	समासनाम
भयाकुला	perplexed with fear	भयेन आकुला।	तृतीया तत्पुरुष समास
अरुचिः	no interest	न रुचिः ।	नञ्तत्पुरुष समास
अनिच्छन्ती	not desiring	न इच्छन्ती।	नञ्तत्पुरुष समास
मलिनकायः	one who has unclean body	मलिनः कायः यस्य सः।	बहुव्रीहि समास
जीर्णवस्त्रधारी	wearing torn clothes	जीर्णवस्वं धारयति इति।	उपपद तत्पुरुष समास
सर्वशास्वस्ववित्	knows all scriptures	सर्वशास्त्राणि वेत्ति इति।	उपपद तत्पुरुष समास
पूर्णानदी	river named पूर्णा	पूर्णा नाम नदी।	कर्मधारय समास
चिन्तामग्ना	engrossed in worry	चिन्तायां मग्ना।	सप्तमी तत्पुरुष समास
मातृसेवा	service to mother	मातुः सेवा।	षष्ठी तत्पुरुष समास

आदिशङ्कराचार्यः Summary in Marathi and English

प्रस्तावना :

शंकराचार्य हे आठव्या शतकातील अद्वैत वेदांताचे उद्गाते व भारतीय तत्त्वज्ञ मानले जातात. शंकराचार्यांनी द्वारका, जगन्नाथपुरी, शृंगेरी व ज्योतिर्मठ येथे चार पीठे स्थापून त्यांच्या चार मुख्य शिष्यांना पीठासीन आचार्य नेमून आचार्य परंपरा घालून दिली व लोकांना मार्गदर्शन करणे सुरू ठेवले. त्यांनी प्रस्थानत्रयींवर (वेद, उपनिषदे, गीता) विपुल भाष्य लिहिले. तसेच त्यांनी आज प्रचलित असणाऱ्या अनेक काव्यात्मक स्तोत्रांची रचना केली.

‘आदिशङ्कराचार्यः’ या पाठामध्ये त्यांच्या जीवनातील दोन प्रसंग उद्धृत करण्यात आले आहेत. पहिल्या प्रसंगात, एका अटळ परिस्थितीत सापडले असताना, संन्यासी बनू इच्छिणाऱ्या शंकराचार्यांना त्यांची माता कशी अनुमती देते, याचे वर्णन आले आहे. दुसऱ्या प्रसंगातून शंकराचार्यांच्या शिकवणीचा उलगडा होतो. ती शिकवण अशी – जो (कोणी) ज्ञान देतो, तो गुरु मानावा.

शङ्कराचार्य runs an early eigth century Indian philosopher and theologian who consolidated the doctrine of अद्वैत वेदान्त. शङ्कराचार्य is reputed to have founded four mathas (monasteries) at द्वारका, जगन्नाथपुरी, शृंगेरी and ज्योतिर्मठ. He placed his primary four disciples to head it and guide people.

He wrote copious commentaries on the vedic canon (ब्रह्मसूत्र). principal उपनिषद् and भगवद्गीता. Also, he composed poetic words in the form of 45, which are prevalant even today. In the lesson, आदिशङ्कराचार्य:, two incidents of his life are given.

The first incident explains how आदिशङ्कराचार्य, who was keen to become a monk was granted by his mother for practising monkship, due to an inescapable situation. The second event unfolds आदिशङ्कराचार्य’s preaching – whosoever imparts knowledge is the preceptor.

परिच्छेदः 1

भारतस्य दक्षिणदिशि ……………… चिन्तामग्ना जाता।

अनुवादः

पहिला प्रसंग :

संन्यासाकरिता अनुमती मिळाली.
भारताच्या दक्षिणदिशेस, केरळ प्रदेशात आलुवा नगराच्या जवळ कालडी नावाचे गाव आहे. ते गाव पूर्णा नदीजवळ आहे. तेथे आठव्या शतकात जगद्गुरु शंकराचार्यांचा जन्म झाला.

शिवगुरु हे त्यांचे वडील आणि आर्यांबा त्यांची आई होती. लहानपणीच त्यांचे वडील शिवगुरु यांचे निधन झाले. त्यामुळे केवळ आईनेच मुलाचे पालनपोषण केले. जेव्हा ते पाच वर्षांचे झाले, तेव्हा मुंज झाल्यावर शिकण्यासाठी ते गुरुंजवळ गेले. तिथे या बालकाने वेद-वेदांगे व विविधशास्त्रे असामान्य वेगाने आत्मसात केली.

अभ्यास संपल्यावर शंकर घरी परतला. घरी परतल्यावर त्यांनी मातृसेवा सुरू केली. आर्यांबा सतत त्याच्या विवाहाचा विचार करत असे. पण मनाने, वाणीने व कर्माने (सांसारिक सुखापासून) विरक्त असलेल्या शंकरने आईकडे संन्यास घेण्याकरिता परवानगी मागितली. शंकराची ऐहिक विषयांतील नावड (अलिप्तता) पाहून आर्यांबा चिंतातुर झाल्या.

First incident :

Received permission for renunciation
In the southern direction of India, there is a village named कालडी near आलुवा city in केरळ region. That village is near पृर्णा river. There, the world’s preceptor 1844 was born in eight century CE. His father was शिवगुरु and mother was आर्यांम्बा.

In his childhood itself, his father शिवगुरु passed away. Therefore, the mother alone reared her son. He who was initiated at the age of five approached the preceptor for studying. There, this child acquired knowledge of वेद-वेदाङ्ग and many scriptures with exceptional speed. After completing studies, शङ्कर returned home.

After coming home, he started serving his mother. Mother आर्यांबा always used to think about his marriage. But, शङ्कर who was detached (from worldly objects) by mind (mentally), speech and by his deeds, asked for permission (from his mother) for renunciation. आर्यांबा was distressed seeing the disinterest of शङ्कर in worldly pleasures.

परिच्छेदः 2

एकस्मिन् दिने ……………….. मुनिरभ्यगात्।

अनुवादः

एके दिवशी शंकर पूर्णानदीवर स्नानासाठी गेला. जेव्हा तो स्नान करण्यात मग्न होता, तेव्हा एक मगर तेथे आली.

मगरीने पटकन त्याचा पाय पकडला. तेव्हा शंकर जोरात ओरडला. “आई! मला वाचव! या मगरीपासून मला वाचव!” तो आक्रोश ऐकून, नदीवर पोहोचल्या आर्यांबेने मुलाला मगरीने धरलेले पाहिले.

भीतीने गांगरलेल्या तिनेही रडणे सुरू केले. शंकराने, आईला आर्ततेने विनवणी केली. “हे आई, यापुढे मी जगू शकणार नाही. मरण्यापूर्वी मला संन्यासी होण्याची इच्छा आहे. तेव्हा आता तरी मला अनुमती दे.” मनात नसताना सुद्धा हतबल आई (त्याला) म्हणाली – “बाळा, जशी तुझी इच्छा आहे, तसेच होऊ दे.

आताच संन्यास स्वीकार. माझी अनुमती आहे.” त्याच क्षणी आश्चर्य घडले. देवकृपेने मगरीने शंकराला मुक्त केले. नदीकाठी येऊन त्याने आईच्या चरणांना नमस्कार केला.

नंतर शंकराने आईला संन्यासाचे महत्व समजावून दिले. संन्यासी फक्त एकीचा पुत्र नाही.

हे विशाल जगच, त्याचे घर आहे. ‘हे माते, तू जेव्हा माझी आठवण काढशील, तेव्हा मी तुझ्याकडे येईन’ असे आईला वचन देऊन तो घरातून निघून गेला.

त्यानंतर, गोविन्दभगवात्पादांचे शिष्य होऊन सर्व दर्शनांचे अध्ययन केले. त्यांच्याकडून संन्यासदीक्षा घेऊन वैदिक धर्म स्थापनेसाठी प्रस्थान केले.

मुनींनी (शंकराचार्यांनी) वयाच्या आठव्या वर्षी चार वेद जाणले. बाराव्या वर्षी सर्वशास्त्रांचे जाणकार झाले. सोळाव्या वर्षी भाष्यांची रचना केली. (आणि) बत्तीसाव्या वर्षी ते स्वगृही (पंचत्वात विलीन) निघून गेले.

One day शंकर went to the river पूर्ण for a bath. When he was busy in taking a bath, a crocodile came there. A crocodile caught his leg swiftly. At that time, ist screamed loudly. “O mother! Please save me. Save me from (this) crocodile.”

Listening to the loud cry, अर्याम्बा who had reached the river-bank, saw her son seized by the crocodile. Perplexed with fear, even she started crying. शंकर requested mother intensely.

“O mother! Henceforth, I shall not live. I wish to become a monk, before I die. Now please give me permission.” Unwillingly helpless mother said- “o child, whatever you wish, let it happen. Now itself you accept renunciation. I grant you permission.” At that very moment, a wonder happened.

By god’s grace, शंकर it was realased by the crocodile. Coming to the river-bank, he bowed down to mother’s feet. Later imade mother realise the importance of renunciation. A monk is not a son of a lady alone.

This big world itself is his home. He went from his house after assuring the mother ‘O mother, whenever you will remember me, I will come to you.” Then, he learnt all दर्शन by becoming a desciple of गोविन्दभगवत्पाद.

He proceeded further to establish वैदिक धर्म, after receiving an initiation from (गोविन्दभगवत्पाद) to become a monk. He (शङ्कराचार्य) grasped the four वेदs at the age of eight, he mastered all the scriptures at the age of twelve. He composed (magnificent) भाष्य (commentary) at the age of sixteen. He reached the heavenly abode at the age of thirty-two.

शब्दार्थाः

1. 1. दिवङ्गतः – passed away – वारले
   2. विरक्तः – detached – विरक्त
   3. अधीतवान् – studied – अभ्यास केला
   4. अनुमतिः – permission – परवानगी
   5. चिन्तामग्ना जाता – was distressed – चिंतातुर झाली
   6. वचसा – by speech – वाणीने
   7. जगद्गुरोः – of the world’s preceptor – जगद्गुरुंचा
   8. ऐहिकविषयेषु – in worldly pleasures – सांसारिक सुखामध्ये
   9. संन्यासार्थम् – for renunciation – संन्यास घेण्यासाठी
   10. मग्न: – engaged – मग्न होते
   11. नक्र: – crocodile – मगर
   12. संन्यास – renunciation – ऐहिक जगाचा त्याग
   13. भयाकुला – perplexed with fear – भीतीने गांगरलेली
   14. विवशा – helpless – हतबल
   15. अनिच्छन्ती – not desiring – इच्छा नसताना
   16. आर्ततया – intensely – आर्ततेने
   17. अगृह्णात् – caught – पकडले
   18. आक्रोशत् – screamed – ओरडला
   19. अवाबोधयत् – made realise – समजावून दिले
   20. त्रायस्व – please save – वाचव
   21. प्रतिश्रुत्य – having promised – वचन देऊन
   22. झटिति – quickly /swiftly – झटकन/पटकन
   23. इत:परम् – henceforth – यापुढे
   24. प्रस्थानम् अकरोत् – set off – प्रस्थान केले
   25. जीर्णवस्वधारी – one who was wearing tom clothes – फाटके-तुटके कपडे घातलेला
   26. आत्मा – soul – आत्मा
   27. सर्वशास्त्रवित् – knower of all scriptures – सर्व शास्त्रे जाणणारा
   28. पर्यटन् – wandering – हिंडून
   29. सारम् – essence (real meaning) – सार (मूलतत्त्व)
   30. ग्रहाम् – should be comprehended – ग्रहण करण्यायोग्य
   31. पञ्चमहाभूता – consisting of five – पंचमहाभूतांनी युक्त
   32. त्मकानि – eternal elments
   33. आसेतुहिमाचलम् – from Himalyas to सेतू (whole India) – हिमालयापासून सेतू (संपूर्ण भारत)
   34. अपसर – get aside/go back – बाजूला हो/मागे हो
   35. प्रणनाम – saluted – नमस्कार केला
   36. प्रचारम् अकरोत् – propogated – प्रचार केला

10th Standard Sanskrit Anand Digest Pdf  

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्यस्तबकः Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Aamod Chapter 13 चित्रकाव्यम् Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Amod Chapter 13 चित्रकाव्यम् Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 13 Question Answer

Sanskrit Amod Std 10 Digest Chapter 13 चित्रकाव्यम् Textbook Questions and Answers

भाषाभ्यास:

श्लोकः 1

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
कृष्णः कं जघान?
उत्तरम् :
कृष्ण: कंसं जघान।

प्रश्न आ.
दारपोषणे के रताः?
उत्तरम् :
केदारपोषणरता: दारपोषणे रताः।

प्रश्न इ.
कं शीतं न बाधते?
उत्तरम् :
कम्बलवन्तं शीतं न बाधते।

2. समानार्थकं शब्द लिखत ।

प्रश्न 1.
समानार्थकं शब्द लिखत ।
कृष्णः, गङ्गा, रतः, बलवान् ।
उत्तरम् :

• कृष्णः – माधवः, केशवः, मुरारिः, दामोदरः।
• गङ्गा – विष्णुपदी, जहुतनया, सुरनिम्नगा, जाह्नवी, भागीरथी।
• रतः – लीनः, मग्नः ।
• बलवान् – शक्तिशाली।

3. ‘गङ्गा’ इति पदस्य विशेषणम् अन्विष्यत लिखत च ।

प्रश्न 1.
‘गङ्गा’ इति पदस्य विशेषणम् अन्विष्यत लिखत च ।
उत्तरम् :

विशेषणम्	विशेष्यम्
शीतलवाहिनी	गङ्गा

4. ‘कं संजघान’ इति श्लोकं माध्यमभाषया स्पष्टीकुरुत ।

प्रश्न 1.
‘कं संजघान’ इति श्लोकं माध्यमभाषया स्पष्टीकुरुत ।
उत्तरम् :
चित्रकाव्यम् हे काल्पनिक काव्य आहे. असे काव्य कवीची अफाट बुद्धिमत्ता तर दर्शवितात, त्याच बरोबर मनोरंजन व आनंदही निर्माण करतात. ‘के संजघान’ हे त्याचे उत्तम उदाहरण आहे. हे अन्तरालापाचे उदाहरण आहे.

येथे श्लोकात विचारलेल्या चार प्रश्नांची उत्तरेही तिथेच दडली आहेत. शब्दालंकारावर आधारित असा हा श्लोक आहे. काही अक्षरे जोडल्यास अथवा विभाजित केल्यास विचारलेल्या प्रश्नांची उत्तरे मिळू शकतात.

ज्याप्रमाणे (1) कं संजघान कृष्ण म्हणजे, कृष्णाने कोणाला ठार मारले? येथे, प्रथम चरणातील पहिली दोन अक्षरे जोडल्यास कंस असे योग्य उत्तर मिळते. (2) का शीतलवाहिनी गंगा? शीतल वाहणारी गंगा नदी कोणती? दुसऱ्या चरणातील पहिली दोन अक्षरे जोडल्यास काशी म्हणजे काशीक्षेत्र असे उत्तर मिळते. याचा अर्थ, काशीक्षेत्रात वाहणारी गङ्गा.

(3) कुटुंबाचे पोषण करण्यात कोण मग्न असतात? तिसऱ्या चरणातील पहिली दोन अक्षरे जोडल्यास केदारपोषणरताः (शेतकरी) असे उत्तर मिळते. (4) कोणत्या बलवानास थंडी बाधत नाही? येथेही, चौथ्या चरणातील तीन अक्षरे जोडल्यास कंबलवन्तं असा शब्द म्हणजेच उत्तर मिळते, त्याचा अर्थ, कांबळे धारण करणाऱ्या बलवानास थंडी वाजत नाही.

चित्रकाव्यम् is image poetry. Such poems show the prodigious intellect of the poets as well as arouse amusement and pleasure.

This श्लोक is the example of अन्तरालाप, Here are four different questions along with their answers within. It is based on शब्दालङ्कार. One can obtain the answer of given question either by joining or dividing letters. Just as, (1) कं संजधान कृष्णः means, whom did कृष्ण kill? The answer the can be obtained by joining first two letters together.

(2) का शीतलवाहिनी गङ्गा? Which is cool river गङ्गा? Answer (काशी) तलवाहिनी is obtained by joining the first two letters. (3)Who is engrossed in looking after wife? के दारपोषणरता: The answer केदारपोषणरताः (They who are engaged in taking care of fields – farmers), can be found by joining first three letters.

(4) कं बलवन्तं न बाधते शीतम्? which strong man is not affected by the cold? the one who has alc, means blanket. This is obtained by joining first three letters.

श्लोक: 2.

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
गगने के सन्ति?
उत्तरम् :
गगने बहवः अम्भोदा: सन्ति।

प्रश्न आ.
कविः कं ‘मित्र’ इति सम्बोधयति?
उत्तरम् :
कविः चातकं “मित्र’ इति सम्बोधयति।

प्रश्न इ.
जलदाः काम् आर्द्रयन्ति?
उत्तरम् :
जलदा: वसुधाम् आर्द्रयन्ति।

2. मेलनं कुरुत।

प्रश्न 1.
मेलनं कुरुत।

उत्तरम् :

विशेषणम्	विशेष्यम्
बहवः	अम्भोदाः
दीनम्	वचः

3. सूचनानुसारं कृती: कुरुत ।

प्रश्न अ.
अम्भोदा: वसुधाम् आर्द्रयन्ति । (कर्तृपदम् एकवचने परिवर्तयत ।)
उत्तरम् :
अम्भोदः वसुधाम् आर्द्रयति।

प्रश्न आ.
त्वं दीनं वचः मा ब्रूहि । (‘त्वं’ स्थाने भवान् योजयत ।)
उत्तरम् :
भवान् दीनं वच: मा ब्रवीतु।

4. ‘रेरे चातक’ इति श्लोकं माध्यमभाषया स्पष्टीकुरुत ।

प्रश्न 1.
‘रेरे चातक’ इति श्लोकं माध्यमभाषया स्पष्टीकुरुत ।
उत्तरम् :
चित्रकाव्यम् हे काल्पनिक काव्य आहे. असे काव्य कवीची अफाट बुद्धिमत्ता तर दर्शवितात, त्याच बरोबर मनोरंजन व आनंदही निर्माण करतात. ‘रेरे चातक’ हे अन्योक्ती या काव्यप्रकारचे उदाहरण आहे. येथे, चातक पक्षी वर्षाकाळाचा अग्रदूत (सूचक) मानला आहे व तो पावसाचे पाणी पिऊन तहान भागवतो असे समजतात. तेव्हा चातक पक्षी, पाणी देणारा एकमेव स्रोत म्हणून केवळ ढगावरच अवलंबून राहतो.

येथे दोन प्रकाराच्या ढगांच्या गुणवैशिष्ट्यांना दर्शवत कवीने त्यांच्यातील फरक सष्ट केला आहे. काही ढग केवळ गर्जना करतात, तर काही खरोखरच पाणी देतात. कवी चातकास केवळ गर्जना करणात्या ढगांकडे पाणी न मागण्याचा सल्ला देतो.

प्रत्यक्षात कवीला पाणी मागणाऱ्या चातकाचा संदर्भ घेऊन, दीनजनांना उद्देशून सांगायचे आहे की सर्वच धनी माणसे उदार नसतात. म्हणून दीनजनांनी विचारपूर्वक, धनी माणसांकडे याचना करावी. चातकाला उद्देशून दीन लोकांना सल्ला देणारी ही अन्योक्ती आहे.

चित्रकाव्यम् is an image poetry. Such poems show the prodigious intellect of the poets as well as arouse amusement and pleasure.

‘रे रे चातक’ is the example of poetic form named अन्योक्ती. Here the चातक bird is harbinger of monsoon and he is assumed to drink water directly from rain. So, चातक bird, considering cloud as the only resort depends on the cloud itself for water.

Some clouds are best givers of water, but some merely roar. So, a poet suggests चातक not to ask for water to roaring clouds. In a way, a poet wants poor people not to beg to all. All people are not generous.

In brief, a poet points out to the चातक bird but it is intended for poor people. Thus, अन्योक्ती is beautifully created here.

श्लोक: 3.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
कवि: कं नमति?
उत्तरम् :
कविः वैद्यराजं नमति।

प्रश्न आ.
को प्राणान् हरतः?
उत्तरम् :
वैद्यराज तथा यमराज: प्राणान् हरतः।

प्रश्न इ.
वैद्यः किं किं हरति?
उत्तरम् :
वैद्यः प्राणान् धनानि च हरति।

2. श्लोकात् सम्बोधनान्तपदद्वयम् अन्विष्य लिखत ।

प्रश्न 1.
श्लोकात् सम्बोधनान्तपदद्वयम् अन्विष्य लिखत ।
उत्तरम् :
1. वैद्यराज
2. यमराजसहोदर

3. समानार्थकशब्द लिखत ।

प्रश्न 1.
समानार्थकशब्द लिखत
यमः, वैद्यः, सहोदरः, धनम्
उत्तरम् :

• यमः – त्रिदशेश्वरः, अन्तकः, दण्डी।
• वैद्यः – भिषक्, चिकित्सकः।
• सहोदरः – भ्राता, बन्धुः।
• धनम् – द्रव्यम्, वित्तम्, स्थापतेयम्, रिक्यम्, ऋक्यम्, वसुः।

4. सूचनानुसारं कृती: कुरुत ।

प्रश्न अ.
नमः । (‘वैद्यराज’ शब्दस्य योग्यं रूपं लिखत)
उत्तरम् :
वैद्यराजाय नमः।

प्रश्न आ.
वैद्यः प्राणान् हरति । (वाक्यं लङ्-लकारे परिवर्तयत ।)
उत्तरम् :
वैद्य: प्राणान् अहरत्।

5. ‘वैद्यराज नमस्तुभ्यम्’ अस्य श्लोकस्य स्पष्टीकरण माध्यमभाषया लिखत।

प्रश्न 1.
‘वैद्यराज नमस्तुभ्यम्’ अस्य श्लोकस्य स्पष्टीकरण माध्यमभाषया लिखत।
उत्तरम् :
चित्रकाव्यम् हे काल्पनिक काव्य आहे. असे काव्य कवीची अफाट बुद्धिमत्ता तर दर्शवितात, त्याच बरोबर मनोरंजन व आनंदही निर्माण करतात. ‘वैद्यराज नमस्तुभ्यम्’ हा उपहास त्याचे उत्तम उदाहरण आहे. या श्लोकात कवी वैद्यराजास उपरोधात्मक वृत्तीने नमस्कार सांगतो.

खरे तर वैद्यराज म्हणजे जो वैद्यकशास्त्राचा अवलंब करून आजारी लोकांना बरे करतो व त्याबदल्यात धन घेतो. पण येथे कवी वैद्यराजास मानवातील प्राणतत्व घेऊन जाणाऱ्या यमराजाचा भाऊ म्हणतो.

कवीच्या मते, जे कार्य यम करतो, ते वैद्यही करतो. वैद्य तर पैसे घेतोच त्याच बरोबर यमासारखे माणसांचे प्राणही हरण करतो. मुख्यत: अपरिपक्व अशा वैद्यांना उद्देशून हा श्लोक कवीने लिहिला आहे.

चित्रकाव्यम् is an image poetry. Such poems show the prodigious intellect of the poets as well as arouse amusement and pleasure.

वैद्यराज नमस्तुभ्यम् – This satire is the appropriate example of it. Here, a poet sarcastically offers his salutations to वैद्यराज, that means a person who practises medicine, treats sick pepole and charges fee in return of money.

However, the poet terms वैद्यराज, as a real brother of यम, who is the god assigned to the job of taking life force out of person.

The poet further explains वैद्यराज too does the same that यम does, वैद्यराज along with the money takes even life of a person. This is intended for an incompetent doctor, who just takes money from people, without curing them.

6. जालरेखाचित्रं पूरयत ।

प्रश्न 1.
जालरेखाचित्रं पूरयत ।

उत्तरम् :

श्लोक: 4.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
जनकस्य सुतां हृत्वा क: ययौ?
उत्तरम् :
जनकस्य सुतां हत्वा रावण: ययौ।

प्रश्न आ.
अत्र कर्तृपदं किम् ?
उत्तरम् :
अत्र कर्तृपदं राक्षसेभ्यः इति अस्ति।

2. समानार्थकं पदं लिखत ।

प्रश्न  1.
समानार्थकं पदं लिखत ।
सुता, पुरी, ययौ, पण्डितः ।
उत्तरम् :

• सुता – तनया, आत्मजा, कन्या।
• पुरी – नगरी।
• ययौ – जगाम।
• पण्डितः – विद्वान्, प्राज्ञः, बुधः ।

3. सूचनानुसारं कृती: कुरुत ।

प्रश्न अ.
राक्षसेभ्यः जनकस्य सुतां हत्वा पुरीं ययौ । (लङ्लकारे परिवर्तयत ।)
उत्तरम् :
राक्षसेभ्यः जनकस्य सुतां हत्वा पुरीम् अयात्।

प्रश्न आ.
यो जानाति स पण्डितः । (बहुवचने परिवर्तयत।)
उत्तरम् :
ये जानन्ति ते पण्डिताः।

4. प्रथमान्तं द्वितीयान्तं च पदं चित्वा लिखत ।

प्रश्न 1.
प्रथमान्तं द्वितीयान्तं च पदं चित्वा लिखत ।
उत्तरम् :

• प्रथमान्तम् – यः / सः / पण्डित: / राक्षसेभ्यः
• द्वितीयान्तम् – सुताम् / पुरीम्

श्लोकः 5.

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
कः धनं याचते?
उत्तरम् :
याचक: / निर्धनः / लोकयानवाहक: धनं याचते।

प्रश्न आ.
‘अयं न भक्तो’ इति प्रहेलिकाया: उत्तरं किम्?
उत्तरम् :
‘अयं न भक्तो’ इति प्रहेलिकाया: उत्तरं “लोकयानवाहकः ।

2. सन्धिविग्रहं कुरुत।

प्रश्न अ.
याचतेऽयम् = याचते + ……..
उत्तरम् :
याचतेऽयम् – याचते + अयम्।

प्रश्न आ.
याचको वा = ………. + वा।
उत्तरम् :
याचको वा – याचकः + वा।

3. जालरेखाचित्रं पूस्यत ।

प्रश्न 1.
जालरेखाचित्रं पूस्यत ।

उत्तरम् :

श्लोक: 6.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
कः शब्दं करोति?
उत्तरम् :
हेमघट: शब्दं करोति।

प्रश्न आ.
कस्याः हस्तात् सुवर्णघटः पतितः?
उत्तरम् :
युवत्याः हस्तात् सुवर्णघटः पतितः।

2. समानार्थकशब्दं लिखत ।

प्रश्न 1.
समानार्थकशब्दं लिखत ।
हेम, जलम्, शब्दः ।
उत्तरम् :

• हेम .- कनकम, स्वर्णम्, सुवर्णम्, हिरण्यम्, हाटकम्।
• जलम् – पयः, कौलालम्, अमृतम्, जीवनम, भुवनम्।
• शब्दः – पदम्।

3. ‘रामाभिषेके’ अस्य श्लोकस्य स्पष्टीकरण माध्यमभाषया लिखत ।

प्रश्न 1.
‘रामाभिषेके’ अस्य श्लोकस्य स्पष्टीकरण माध्यमभाषया लिखत ।
उत्तरम् :
चित्रकाव्यम् हे काल्पनिक काव्य आहे. असे काव्य कवीची अफाट बुद्धिमत्ता तर दर्शवितात, त्याच बरोबर मनोरंजन व आनंदही निर्माण करतात. ‘रामाभिषेके’ ही समस्यापूर्ती याचे उत्तम उदाहरण आहे.

समस्यापूर्ति या काव्यप्रकारात शेवटचा चरण दिलेला असतो. हा चरण बहुदा विचित्र असतो. उरलेल्या तीन चरणांसहित अर्थपूर्ण श्लोक/ काव्य तयार करणे हे कवीचे आव्हान असते.

या श्लोकात, ‘ठंठं ठठं ठं ठठ ठं ठठं ठ’, हा चरण दिलेला होता व कवीने चातुर्याने उरलेले तीन चरण त्यास जोडून अर्थपूर्ण श्लोक तयार करणे अपेक्षित होते. कवीने हे चातुर्य पुढीलप्रमाणे दाखविले. रामाच्या राज्याभिषेकासमयी एक युवती पाणी आणण्याकारिता सोन्याचा घडा घेऊन जात असताना, तो घडा तिच्या हातातून निसटतो व जिन्यावरून आवाज करत जातो. तो आवाज म्हणजेच ठंठं ठठं ठं ठठ ठं ठठंठ।

चित्रकाव्यम् is an image poetry, such poems show the prodigious intellect of the poets as well as arouse amusement and pleasure. ‘रामाभिषेके’ is the best example of समस्यापूर्ती. In समस्यापूर्ती, last चरण is stated but it is often absurd. The poet’s challenge is to create a meaningful poetry /etc.

In this श्लोक, चरण ‘ठठं ठठं ठं ठठ ठ ठठं ठः’ is already given. The poet wisely composes remaining three us to make meaningful श्लोक. The poet composes it as – at the time of राम’s coronation, certain young lady having gold pot in her hand, went to bring water.

While going, the gold pot was fallen from her hands. At that time, the sound that was generated is ठंठं ठठं ठं ठठ ठं ठठं ठः। Thus, he completes the समस्या.

श्लोक: 7.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
श्लोके कयोः सम्भाषणं वर्तते?
उत्तरम् :
श्लोके गिरिजासमुद्रसुतयोः सम्भाषणं वर्तते।

प्रश्न आ.
श्लोके निर्दिष्टानि सम्बोधनपदानि लिखत ।
उत्तरम् :
मुग्धे, सखि, आर्ये, कमले एतानि सम्बोधनपदानि श्लोके निर्दिष्टानि।

प्रश्न इ.
विष्णुः भिक्षुरूपेण कुत्र गच्छति ?
उत्तरम् :
विष्णु: भिक्षुरूपेण बले: मखे अस्ति/भवति।

प्रश्न ई.
विष्णुः कुत्र शेते ?
उत्तरम् :
विष्णुः पन्नगे शेते।

2. समानार्थकं पदं लिखत ।

प्रश्न 1.
समानार्थकं पदं लिखत ।
भिक्षुः, मखः, पशुपतिः, कमला, गिरिजा
उत्तरम् :

• भिक्षुः – याचकः।
• मखः – क्रतुः, यज्ञः।
• पशुपतिः – शङ्करः, शिवः, शम्भुः, ईशः, शूली, महेश्वरः ।
• कमला – लक्ष्मीः , पद्मालया, पद्मा, श्री: हरिप्रिया।
• गिरिजा . अपर्णा, पार्वती, दुर्गा, मृडानी, चण्डिका, अम्बिका।

3. श्लोके कानि क्रियापदानि ?

प्रश्न 1.
श्लोके कानि क्रियापदानि
उत्तरम् :
श्लोके अस्ति, शेते, मुञ्च, पातु एतानि क्रियापदानि सन्ति।

उपक्रम:

1. ‘समस्यापूर्ति’-श्लोकानां सङ्ग्रहं कुरुत । 

प्रश्न अ.
मृगात् सिंहः पलायते ।

प्रश्न आ.
शतचन्द्रं नभस्तलम् ।

2. अन्योक्तिश्लोकानां सङ्ग्रहं कुरुत ।

3. कामपि अन्याम् एका प्रहेलिकां लिखत ।

Sanskrit Amod Class 10 Textbook Solutions Chapter 13 चित्रकाव्यम् Additional Important Questions and Answers

अवबोधनम्

(क) पूर्णवाक्येन उत्तरत।

प्रश्न 1.
शीतलवाहिनी का?
उत्तरम् :
गङ्गा शीतलवाहिनी।

प्रश्न 2.
जलदा: काभि: वसुधाम् आर्द्रयन्ति?
उत्तरम् :
जलदाः वृष्टिभि: वसुधाम् आर्द्रयन्ति।

प्रश्न 3.
कः यमराजसहोदरः?
उत्तरम् :
वैद्यराज: यमराजसहोदरः।

(ग) विभक्त्यन्तरूपाणि।

प्रश्न 1.
श्लोकात् प्रथमान्तपदानि चित्वा लिखत।
उत्तरम् :
कृष्णः, शीतलवाहिनी, गङ्गा, दारपोषणरताः,शीतम्।

प्रश्न 2.
श्लोकात् द्वितीयान्तपदे चित्वा लिखत।
उत्तरम् :
कं, बलवन्तम्।

प्रश्न 3.
श्लोकात् तृतीयाविभक्त्यन्तपदे चित्वा लिखत।
उत्तरम् :
सावधानमनसा, वृष्टिभिः।।

प्रश्न 4.
श्लोकात् सम्बोधनविभक्त्यन्तपदे चित्वा लिखत।
उत्तरम् :
चातक, मित्र।

प्रश्न 5.
लोकयानवाहक: किं नादयते?
उत्तरम् :
लोकयानवाहक: घण्टां नादयते।

सन्थिविग्रहः

1. बहवोऽपि – बहवः + अपि।
2. सर्वेऽपि – सर्वे + अपि।
3. केचिद् वृष्टिभिरार्द्रयन्ति – केचित् + वृष्टिभिः + आर्द्रयन्ति।
4. केचिद् वृथा – केचित् + ‘वृथा।
5. पुरतो मा – पुरतः + मा।
6. नमस्तुभ्यम् – नमः + तुभ्यम्।
7. यमस्तु – यमः + तु।
8. यो जानाति – यः + जानाति।
9. स पण्डितः – सः + पण्डितः।
10. भक्तो न – भक्तः + न।
11. पूजको वा – पूजक:+ वा।
12. तथापि – तथा + अपि।
13. निर्धनो वा – निर्धनः + वा।
14. जलमाहरन्त्या – जलम् + आहरन्त्या।
15. सृतो हेमघटो युवत्याः – सूतः + हेमघट: + युवत्याः ।
16. क्वास्ति – क्व + अस्ति।
17. बलेर्मखे – बले: + मखे।
18. नास्त्यसौ – न + अस्ति + असौ।
19. तस्योपरि – तस्य + उपरि।
20. विषादमाशु – विषादम् + आशु।
21. नाहम् – न+ अहम्।
22. चेत्थम् – च + इत्थम्।

अमरकोषात् योग्यं समानार्थक शब्दं योजयित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
गङ्गा शीतलवाहिनी अस्ति।
उत्तरम् :
विष्णुपदी / जहुतनया / सुरनिम्नगा शीतलवाहिनी अस्ति।

भाषाभ्यास:

(क) समानार्थकशब्दाः

1. मित्र – वयस्यः, सखा।
2. अम्भोदः – मेषः, धाराधरः, जलधरः, तडित्वान्, वारिदः, अम्बुभृत, जलदः, वारिवाहः।
3. बहवः – भूरयः, विपुलाः ।
4. गगनम् – व्योम, आकाशम् ।
5. वृष्टिः – पर्जन्यः।
6. वसुधा – पृथ्वी, धरा, वसुन्धरा।
7. पुरतः – पुरस्तात्।
8. गुप्तम् – प्रच्छन्नम् ।
9. किल – ननु, खलु।
10. निर्धनः – धनहीनः ।
11. आशु – सत्वरम्, त्वरितम्।

(ख) विरुद्धार्थकशब्दाः

1. शीतम् × उष्णम्।
2. पुरतः × पृष्ठतः।
3. बहवः × अल्पाः।
4. आशु × शनैः शनैः।
5. पण्डित: × मूढः, मूर्खः ।
6. निर्धनः × धनिकः ।
7. चला × स्थिरा।

पृथक्करणम्

(ख) जालरेखाचित्रं पूरयत।

1.

2.

3.

(ग) त्वं स्थाने भवान् / भवती अथवा भवान् / भवती स्थाने त्वं योजयत।

प्रश्न 1.
त्वं प्राणान् धनानि च हरसि।
उत्तरम् :
भवान् प्राणान् धनानि च हरति।

प्रश्न 2.
त्वं आशु विषादं मुञ्च।
उत्तरम् :
भवान्/भवती आशु विषादं मुञ्चतु।

वचनं परिवर्तयत ।

प्रश्न 1.
भिक्षुः क्व अस्ति? (बहुवचने परिवर्तयत।)
उत्तरम् :
भिक्षवः क्व सन्ति?

समासा:

समस्तपदम्	अर्थ	समासविग्रहः	समासनाम
1. गिरिजासमुद्रसुतयोः	of गिरिजा and समुद्रसुता	गिरिजा च समुद्रसुता च, तयोः।	इतरेतर-द्वन्द्वः समासः।
2. दारपोषणरता:	engaged in looking after wife	दारपोषणे रताः।	सप्तमी-तत्पुरुषः समासः।
3. यमराजसहोदरः	brother of यम	यमराजस्य सहोदरः।	षष्ठी-तत्पुरुषः समासः।
4. रामाभिषेक:	coronation of राम	रामस्य अभिषेकः।	षष्ठी-तत्पुरुषः समासः।
5. हेमघट:	pot of gold	हेम्न: घटः।	षष्ठी-तत्पुरुषः समासः।
6. पशुपतिः	lord of animals	पशूनां पतिः।	षष्ठी-तत्पुरुषः समासः।
7. समुद्रसुता	daughter of an ocean	समुद्रस्य सुता।	षष्ठी-तत्पुरुषः समासः।
8. पन्नगभूषण:	one whose ornament is a snake	पन्नगः भूषणं यस्य सः ।	बहुव्रीहिः समासः।
9. अम्भोदा:	water giving	अम्भः ददति इति।	उपपद-तत्पुरुषः समासः।
10. सावधानमनः	attentive mind	सावधानं मनः।	कर्मधारयः समासः।

चित्रकाव्यम् Summary in Marathi and English

प्रस्तावना :

संस्कृत भाषा विविध वैशिष्ट्यपूर्ण सुभाषितांनी अलंकृत झाली आहे. “चित्रकाव्यम्’ हे यातीलच एक. ‘बुद्धिविकासकानि सुभाषितानि नाम चित्रकाव्यानि’ याचा अर्थ बुद्धीचा विकास करणारी सुभाषिते म्हणजे चित्रकाव्ये. काही विशिष्ट वृत्तांच्या बांधणीने व नावीन्यपूर्ण काव्यात्मक रचनेद्वारा चमत्कृतीकाव्य तयार करणे हा चित्रकाव्यांचा हेतू आहे. यातून मनोरंजन व आनंदही प्राप्त होतो.

चित्रकाव्यम् हे ‘काल्पनिक काव्य’ आहे. असे काव्य कवीची अफाट बुद्धिमत्ता व त्यांचे भाषेवरील प्रभुत्व दर्शविते. प्रस्तुत ‘चित्रकाव्यम्’ काव्यामध्ये, अन्तरालाप, अन्योक्ति, हास्योक्ति, कर्तृगुप्ता प्रहेलिका, समस्यापूर्ति, वाकोवाक्यम् इ. काव्याच्या विविध प्रकारांचा अंतर्भाव झाला आहे.

Sanskrit language is adorned with curious peculiar सुभाषितs. चित्रकाव्य is one of them. ‘बुद्धिविकासकानि सुभाषितानि नाम चित्रकाव्यानि’ that means, सुभाषितs developing/ provoking the intelligence is चित्रकाव्य, Aim of चित्रकाव्य is to generate a sense of wonder by resorting to unusual management of certain meters and innovative poetic structures. It also arouses amusement and pleasure.

चित्रकाव्य is an image poetry. Such poems show the prodigious intellect of the poets and their command over language. The given foc poetry consists of varied types of poetry such as अन्तरालाप, अन्योक्ति, हास्योक्ति, कर्तृगुप्ता प्रहेलिका, समस्यापूर्ति, वाकोवाक्यम् etc.

श्लोकः 1

के संजघान कृष्ण का शीतलवाहिनी गङ्गा।
के दारपोषणरता: कं बलवन्तं न बाधते शीतम्।।1।। (अन्तरालाप:)

अनुवादः

कृष्णाने कोणाला मारले? (कंस), शीतल वाहणारी गंगा कोणती आहे? (काशीक्षेत्रात वाहणारी). बायकोचे पोषण करण्यात कोण मग्न असतात? (केदारपोषणरत) कोणत्या बलवानाला थंडी बाधत नाही ? (कंबलवंत-कांबळे धारण करणाऱ्याला) स्पष्टीकरण – हे अन्तरालापाचे उदाहरण आहे.

येथे श्लोकात विचारलेल्या चार प्रश्नांची उत्तरेही तिथेच दडली आहेत. शब्दालंकारावर आधारित असा हा श्लोक आहे. काही अक्षरांना जोडल्यास अथवा विभाजित केल्यास विचारलेल्या प्रश्नांची उत्तरे मिळू शकतात, ज्याप्रमाणे

1. के संजघान’ कृष्ण म्हणजे, कृष्णाने कोणाला ठार मारले? येथे, प्रथम चरणातील पहिली दोन अक्षरे जोडल्यास ‘कंस’ असे योग्य उत्तर मिळते. 2. ‘का शीतलवाहिनी गंगा?’ शीतल वाहणारी गंगा नदी कोणती? दुसऱ्या चरणातील पहिली दोन अक्षरे जोडल्यास काशी म्हणजे काशीक्षेत्र असे उत्तर मिळते. याचा अर्थ, काशी क्षेत्रात वाहणारी गंगा शीतल आहे.

3. बायकोचे पोषण करण्यात कोण मग्न असतात? तिसऱ्या चरणातील पहिली दोन अक्षरे जोडल्यास केदार (शेत) असे उत्तर मिळते. येथे केदारपोषणरत याचा अर्थ शेतकरी असा होतो. 4. कोणत्या बलवानास थंडी बाधत नाही? येथेही, चौथ्या चरणातील तीन अक्षरे जोडल्यास कम्बलवन्त असा शब्द म्हणजेच उत्तर मिळते, त्याचा अर्थ, कांबळे धारण करणाऱ्या बलवानास थंडी वाजत नाही.

Whom did कृष्ण kill? (कंस). Which is cool flowing river गङ्गा? (in काशी). Who is engrossed in looking after the wife?

(केदारपोषणरत – the one who is engrossed in taking care of the field) Which strong man is not affected by the cold? (chade the one who has a means blanket) Explanation – This श्लोक is the example of अन्तरालाप. Here are four different questions along with their answers within. It is based on शब्दालङ्कार.

One can obtain the answer of a given question either by joining or dividing letters. Just as, (1) कसजधानकृष्णmeans, who did कृष्ण kill? The answer ‘कंसं’ is obtained by joining the first two letters. (2) का शीतलवाहिनी गङ्गा? Which is cool river गङ्गा? The answer is flowing in काशी. (3) Who is engrossed in looking after a wife? The answer is केदारपोषणरता.

which means the ones who are engrossed in taking care of the field (4) कंबलवन्तं न बाधते शीतम्? Which strong man is not affected by the cold? The answer is कंबलवन्तं This is obtained by joining the first three letters.

श्लोक: 2

रे रे चातक सावधानमनसा मित्र क्षणं श्रूयताम्
अम्भोदा बहवोऽपि सन्ति गगने सर्वेऽपि नैतादृशाः।
केचिद् वृष्टिभिरार्द्रयन्ति वसुधां गर्जन्ति केचिद् वृथा .
यं यं पश्यसि तस्य तस्य पुरतो मा ब्रूहि दीनं वचः।।2।। (अन्योक्तिः ) (वृत्तम् – शार्दूलविक्रीडितम्)

अनुवादः

रे रे चातक मित्रा, क्षणभर लक्ष देऊन (सावधानपूर्वक) ऐक, आकाशात असंख्य (पुष्कळ) ढग असतात (परंतु) सगळेच सारखे नसतात. काही ढग पावसाच्या वर्षावांनी पृथ्वी जलमय करतात, तर काही व्यर्थ (विना कारण) गर्जना करतात. (म्हणून) तुला जो जो ढग दिसेल त्याच्यापुढे दीनवाणीने बोलू नकोस.

स्पष्टीकरण – हे ‘अन्योक्ती’ – ‘दुसऱ्याला उद्देशून बोलणे’ या काव्यप्रकारचे उदाहरण आहे. येथे, चातक पक्षी वर्षाकाळाचा अग्रदूत (सूचक) मानला आहे व तो पावसाचे पाणी पिऊन तहान भागवतो असे समजतात. येथे दोन प्रकाराच्या ढगांच्या गुणवैशिष्ट्यांना दर्शवत कवीने त्यांच्यातील फरक स्पष्ट केला आहे. काही ढग केवळ गर्जना करतात, तर काही खरोखरच पाणी देतात.

कवी चातकास केवळ गर्जना करणाऱ्या ढगांकडे पाणी न मागण्याचा सल्ला देतो. कवीला दीनजनांना उद्देशून सांगायचे आहे की सर्वच धनी माणसे उदार नसतात. चातकाला उद्देशून दीन लोकांना सल्ला देणारी ही अन्योक्ती आहे.

O चातक, my friend, please listen carefully for a moment. There are innumerable clouds in the sky but all are not alike. Few humidify the earth by showering rain. (However) Few just roars in vain, (therefore) Do not speak pitiable words in front of whichever cloud you see.

Explanation – This is the example of a poetic form named अन्योक्ति- ‘speech directed to other’. Here, the Ellah bird is a harbinger of monsoon and it is assumed to drink water directly from the cloud.

Some clouds are best givers of water but some mere roar. So, the poet suggests चातक not to ask for water to the roaring clouds. In a way, the poet wants to indicate poor people, not to beg to all people are not generous.

श्लोक: 3

वैद्यराज नमस्तुभ्यं यमराजसहोदर।
यमस्तु हरति प्राणान् त्वं तु प्राणान् धनानि च ।।3।। (हास्योक्तिः ) (वृत्तम् – अनुष्टुप्)

अनुवादः

हे वैद्यराजा, यमराजाच्या सख्ख्या भावा, तुला नमस्कार असो! यम (केवळ) प्राणच हरतो, पण तू प्राण व धनही दोन्ही हरतोस. स्पष्टीकरण – हा श्लोक हास्योक्तीचे उदाहरण असून, येथे अपरिपक्व आणि लोभी वैद्याची निंदा विनोदी पद्धतीने केली आहे.

O great doctor, salutation to you as a real brother of यमराज while यमराज takes away only the life (of people) but you fetch both life as well as wealth. Explanation – This is an example of a satire about an incompetent and a greedy doctor, in a humorous way.

श्लोकः 4

राक्षसेभ्य: सुतां हत्वा जनकस्य पुरीं ययौ।
अत्र कर्तृपदं गुप्तं यो जानाति स पण्डितः।।4।। (कर्तृगुप्ता प्रहेलिका) (वृत्तम् – अनुष्टुप)

अनुवादः

(कोणी एक जण) राक्षसांकडून कन्येचे हरण करून जनकाच्या नगरीस गेला किंवा (कोणी एक जण ) जनकाच्या मुलीचे हरण करून नगरीस गेला. येथे कर्ता गुप्त आहे. जो जाणतो तो खरा विद्वान.

स्पष्टीकरण – वरील श्लोक हा चित्रकाव्याचा वेगळा प्रकार आहे. ही कर्तृगुप्त- प्रहेलिका आहे. येथे ‘राक्षसेभ्यः’ या शब्दात कर्ता गुप्त आहे. या शब्दाचे दोन भाग केले असता, राक्षस व इभ्यः असे दोन शब्द मिळतात.

‘इभ्यः’ चा अर्थ राजा असा होतो. याचाच अर्थ राक्षसांचा राजा. राक्षसानाम् इभ्यः म्हणजे रावण. या रीतीने, एक अर्थपूर्ण वाक्य तयार होते. राक्षसांचा राजा रावण जनकाच्या कन्येचे हरण करून नगरीस गेला.

(Someone) had gone to He’s city abducting the daughter from the demons or (Someone) had gone to the city abducting जनक’s daughter. The subject (कर्तृपदम्) is hidden here. The one who knows is the scholar.

Explanation – The above ce is a different kind of चित्रकाव्य. It is कर्तृगुप्त-प्रहेलिका, The subject is hidden in the word राक्षसेभ्यः, If we split the word, we get two words राक्षस and इभ्यः. इभ्यः means ‘aking’. It means राक्षसानाम् इभ्य: a king of demons that is रावण. Thus, we get a meaningful sentence, ‘A king of demons’, रावण abducting जनक’s daughter (सीता), had gone to the city.

श्लोक: 5

अयं न भक्तो न च पूजको वा
घण्टां स्वयं नादयते तथापि।
धनं जनेभ्यः किल याचतेऽयं
न याचको वा न च निर्धनो वा।।5।। (प्रहेलिका) (वृत्तम् – उपजाति:)

अनुवादः

हा भक्त नाही व पूजकहीं नाही तरीही स्वत:हून घंटा वाजवितो. खरोखर याचक व धनहीन नसतानाही. हा लोकांकडून पैसे घेतो. (तर मग सांगा कोण बरे आहे हा?)

स्पष्टीकरण – श्री सदाशिव त्र्यंबक रहातेकर लिखित हा श्लोक काव्यप्रवाह या काव्यसंग्रहातून घेण्यात आला आहे. हे अपहनुति अलंकाराचे उदाहरण आहे. या श्लोकाचे उत्तर ‘क:हवानयाकलो’ असे आहे. उलट दिशेने वाचले असता आपल्याला योग्य उत्तर मिळते ते असे, लोकयानवाहक:- याचा अर्थ बस-कंडक्टर अथवा बस-वाहक,

This is neither the devotee nor a worshipper. Yet rings the bell on its own. Indeed this one asks for money from people, but is not beggar or poor. (Then who is this?) Explanation – This श्लोक is taken from काव्यप्रवाह, composed by श्री सदाशिव त्र्यंबक रहातेकर, It is the example ofअपहनुति अलङ्कार.

The answer to this श्लोक is’क:हवानयाकलो,’ reading it in the inverse order, one gets the correct answer that is, लोकयानवाहकः means a bus-conductor because we hear a bell-sound in a bus, though it is not necessarily done by any devotee or a worshipper.)

श्लोकः 6

रामाभिषेके जलमाहरन्त्या हस्तात् मृतो हेमघटो युवत्याः।
सोपानमार्गेण करोति शब्दं ठंठं ठठं ठं ठठठं ठठं ठः।।6।। (समस्यापूर्तिः) (वृत्तम् – इन्द्रवज्रा)

अनुवादः

रामाच्या राज्याभिषेकासमयी युवतीच्या हतातून पाण्याने भरलेला सोन्याचा घडा निसटला, तो जिन्यावरुन आवाज करत गेला. ठंठ ठठं ठं ठठठं ठठं ठः.

At the time of राम’s coronation, the golden pot filled with water was skipped from the hands of a young lady. It made the voice from the stairs ठंठं ठठं ठंठठठं ठठंठ:.

श्लोक : 7

भिक्षुः क्वास्ति बलेर्मखे पशुपति: किं नास्त्यसौ गोकुले
मुग्धे पन्नगभूषण: सखि सदा शेते च तस्योपरि।
आर्ये मुज्ञ विषादमाशु कमले नाहं प्रकृत्या चला
चेत्यं वै गिरिजासमुद्रसुतयोः सम्भाषणं पातु वः।।7।। (वाकोवाक्यम्) (वृत्तम् – शार्दूलविक्रीडितम्)

अनुवादः

(लक्ष्मी विचारते) तो भिक्षुक कोठे आहे ? (पार्वती उत्तर देते) बळीच्या यज्ञात. पशूपती कोठे आहेत? ते गोकुळात नाहीत का? प्रिये, ज्याचा अलंकारच साप आहे तो कोठे आहे? सखि, तो त्यावरच नेहमी निद्रासुख घेतो.

आर्ये, दु:ख (विष खाणाऱ्याला) सोडून दे. अगं लक्ष्मी, मी तुझ्यासारखी चंचल नाही. अशा रितीने पार्वती (पर्वताची कन्या) व लक्ष्मी (समुद्राची कन्या) यातील हे संभाषण आपले रक्षण करो.

(वरील संवादात, लक्ष्मी पार्वतीला विचित्र विशेषणांचा प्रयोग करून शंकराबद्दल विचारते. याला चोख प्रत्युतर देण्याच्या हेतूने, पार्वती देखील तीच विशेषणे विष्णूकरिता वापरून तिचे चातुर्य दर्शविते.)

Where is the mendicant? He is in the sacrifice performed by बलि. Where is the lord of animals? Is he not in Gokul? O dear one where is the one whose ornament is a snake? O friend, he sleeps on the same always.

O noble one, leave disappointment (the one who consumes poison) at once! O Laxmi I am not fickle minded like you. In this way, this conversation between पार्वती (daughter of mountain) and लक्ष्मी (daughter of an ocean) may protect us.

(In the above dialogue, लक्ष्मी asks about lord शंकर by using strange adjectives. Witty पार्वती reverts to लक्ष्मी using the same adjectives intended for लक्ष्मी’s husband i.e. Lord विष्णु.)

शब्दार्थाः

1. संजधान – had killed – मारले
2. कंसं जघान – had killed – कंसाला मारले
3. शीतलवाहिनी – cool flowing – थंड वाहणारी
4. दारपोषणरताः – engrossed in – बायकोचे पोषण
5. nurturing wife – करण्यात मग्न
6. केदार – field – शेत
7. कं बलवन्तम् – to which strong man – कोणत्या बलवान माणसाला
8. न बाधते – does not affect – बाधत नाही
9. कंबलवन्तम् – one who has a blanket – ज्याच्याकडे कांबळे आहे त्याला
10. चातक – a bird named चातक – चातक पक्षी
11. सावधानमनसा – with attentive mind – सावधानपूर्वक
12. श्रूयताम् – may listen – कृपया ऐकावे
13. अम्भोदा: – clouds – ढग
14. वृष्टिभिः – by rain shower – पावसाच्या वर्षावाने
15. आर्द्रयन्ति – humidify – जलमय करतात
16. वृथा गन्ति – roar in vain – व्यर्थ गर्जना करतात
17. तस्य पुरतः – in front of him – त्याच्या समोर
18. मा ब्रूहि – do not speak – बोलू नकोस
19. दीनं वचः – pitiable words – दीनवाणी
20. यमराजसहोदर – Othe real brother of यमराज – यमराजाच्या हे सख्ख्या भावा
21. वैद्यराज – O great doctor – वैद्यराज
22. सुता – daughter – कन्या
23. पूरी – city – नगरी
24. ययो – had gone – गेला
25. स्वयं नादयते – makes sound on its own – स्वतःहून वाजवते
26. किल – indeed – खरोखर
27. याचकः – beggar – याचक
28. निर्धनः – poor – धनहीन
29. रामाभिषेके – at the time of – रामाच्या
30. राम’s coronation – राज्याभिषेकासमयी
31. आहरन्त्या – taking – घेऊन जाणाऱ्या
32. सूतः – escaped/skipped – निसटलेला
33. हेमघट: – golden pot – सोन्याचा घडा
34. युवत्याः – from a young lady – तरुणीकडून
35. सोपानमार्गेण – from stairs – जिन्यावरून
36. क्व – where – कुठे
37. बलेमखे – in the sacrifice of बली – बळीच्या यज्ञात
38. पशुपतिः – lord of animals – शंकर
39. पनगभूषण: – whose ornament – ज्याचा अलंकार
40. is a snake – सर्प आहे तो
41. शेते – sleeps – झोपलेला आहे
42. मुञ्च विषादम् – leave the disappointment – दु:ख सोडून दे
43. कमले – o goddess Laxmi – लक्ष्मी
44. गिरिजा – Goddess Parvati – पार्वती
45. समुद्रसुता – daughter of an ocean – समुद्राची कन्या
46. पातु वः – may protect us – आपले संरक्षण करो

Aamod Sanskrit Book 10th Class Solutions

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• अमूल्यं कमलम् Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्ययुग्मम् Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• धेनोर्व्याघ्रः पलायते Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• जटायुशौर्यम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• प्रतिपदं संस्कृतम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer