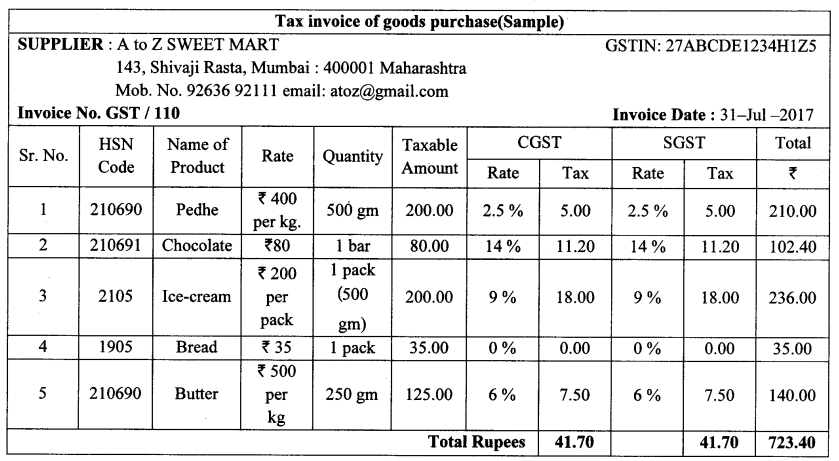
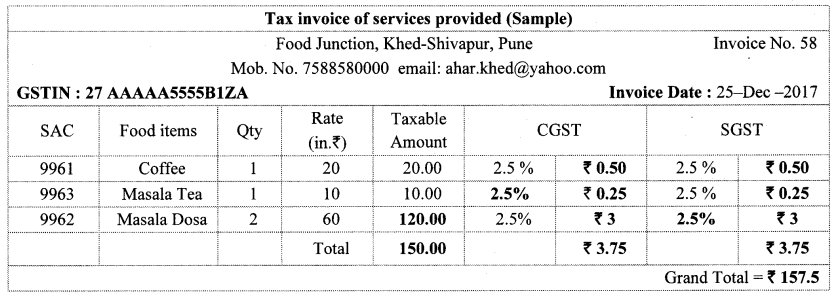
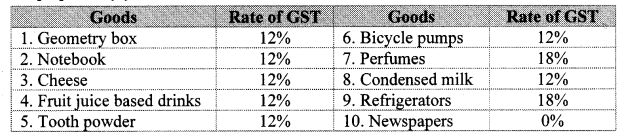
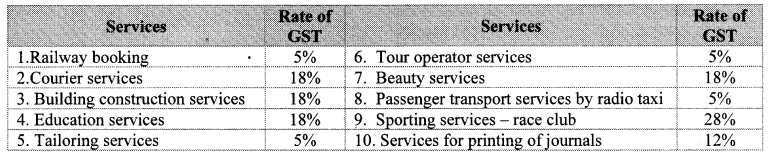
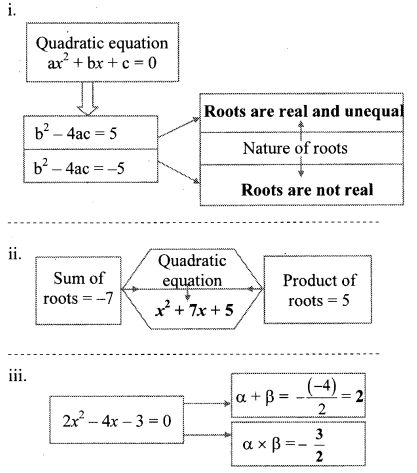
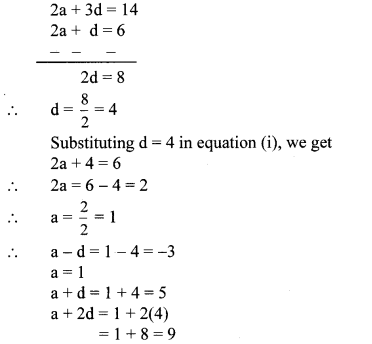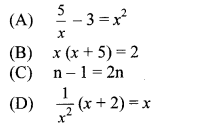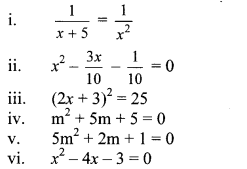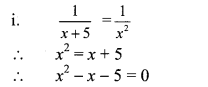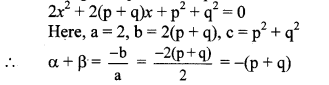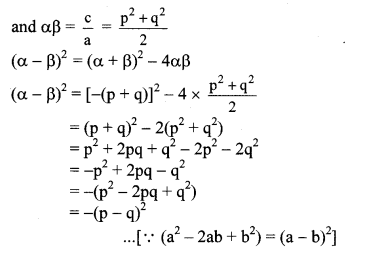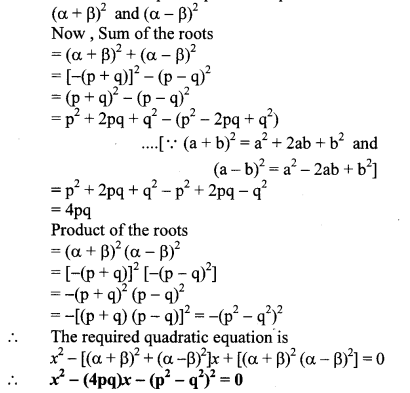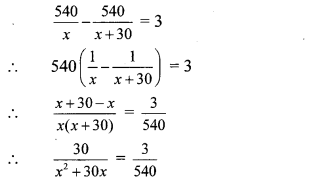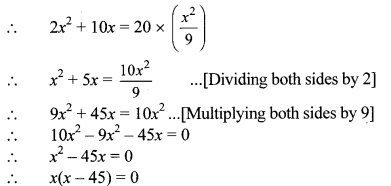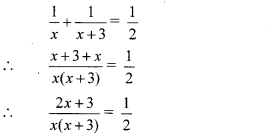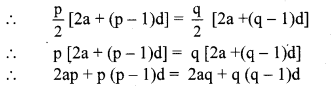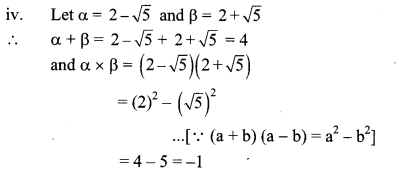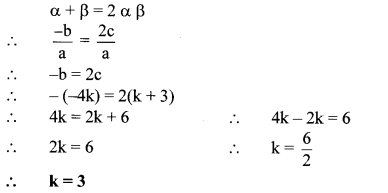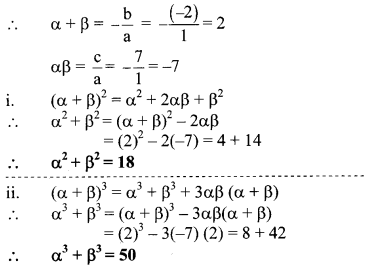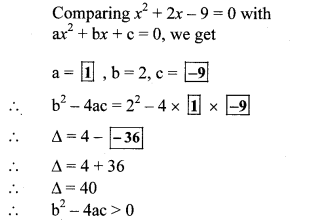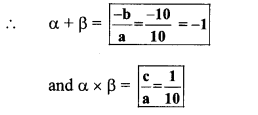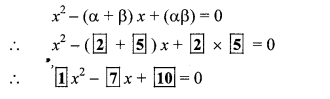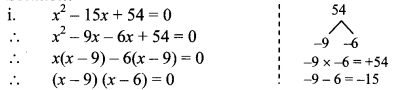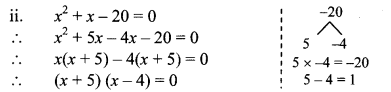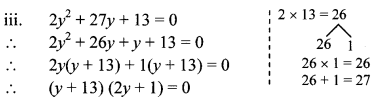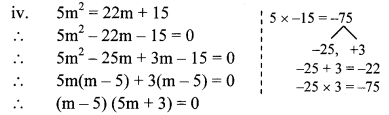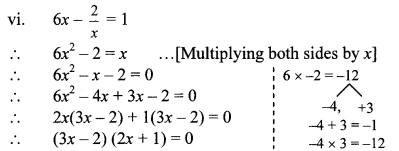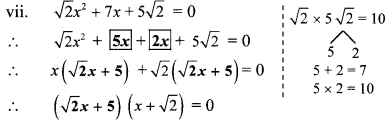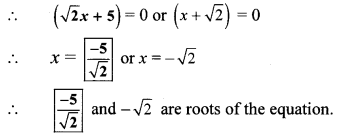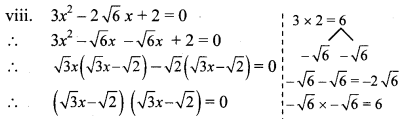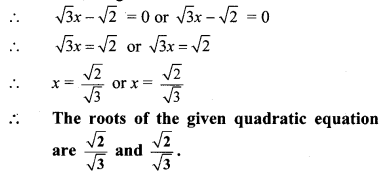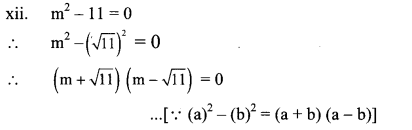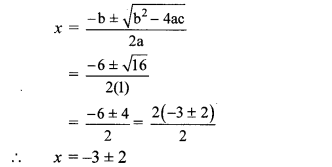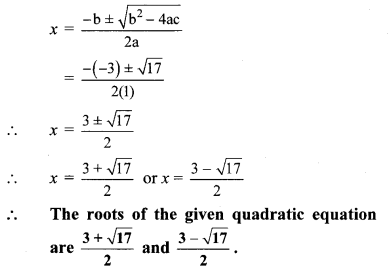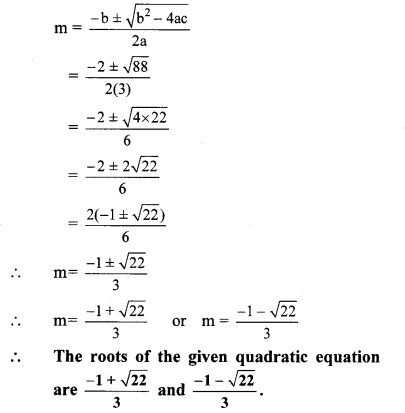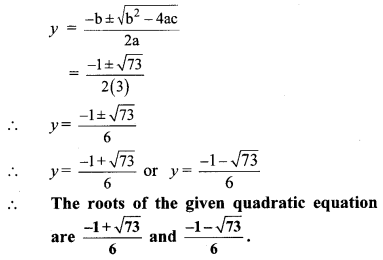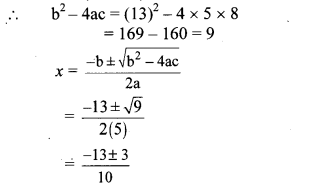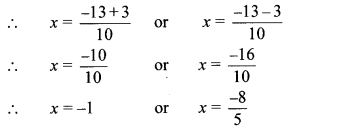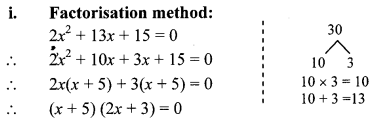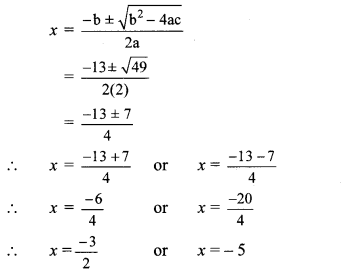Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.
10th Standard Maths 1 Problem Set 2 Chapter 2 Quadratic Equations Textbook Answers Maharashtra Board
Class 10 Maths Part 1 Problem Set 2 Chapter 2 Quadratic Equations Questions With Answers Maharashtra Board
Question 1.
Choose the correct answers for the following questions.
i. Which one is the quadratic equation?
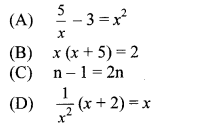
Answer:
(B)
ii. Out of the following equations which one is not a quadratic equation?
(A) x2 + 4x = 11 + x2
(B) x = 4x
(C) 5x2 = 90
(D) 2x – x2 = x2 + 5
Answer:
(A)
iii. The roots of x2 + kx + k = 0 are real and equal, find k.
(A) 0
(B) 4
(C) 0 or 4
(D) 2
Answer:
(C)
iv. For √2 x2 – 5x + √2 = 0, find the value of the discriminant.
(A) -5
(B) 17
(C) √2
(D) 2 √2 – 5
Answer:
(B)
v. Which of the following quadratic equations has roots 3,5?
(A) x2 – 15x + 8 = 0
(B) x2 – 8x + 15 = 0
(C) x2 + 3x + 5 = 0
(D) x2 + 8x – 15 = 0
Answer:
(B)
vi. Out of the following equations, find the equation having the sum of its roots -5.
(A) 3x2 – 15x + 3 = 0
(B) x2 – 5x + 3 = 0
(C) x2 + 3x – 5 = 0
(D) 3x2 + 15x + 3 = 0
Answer:
(D)
vii. √5m2 – √5 m + √5 =0 which of the following statement is true for this given equation?
(A) Real and unequal roots
(B) Real and equal roots
(C) Roots are not real
(D) Three roots
Answer:
(C)
viii. One of the roots of equation x2 + mx – 5 = 0 is 2; find m.
(A) -2
(B) – \(\frac { 1 }{ 2 } \)
(C) \(\frac { 1 }{ 2 } \)
(D) 2
Answer:
(C)
Question 2.
Which of the following equations is quadratic
i. x2 + 2x + 11 = 0
ii. x2 – 2x + 5 = x2
iii. (x + 2)2 = 2x2
Solution:
i. The given equation is
x2 + 2x + 11 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = 2, c = 11 are real numbers and
a ≠ 0.
The given equation is a quadratic equation.
ii. The given equation is
x2 – 2x + 5 = x2
∴ x2 – x2 + 2x – 5 = 0
∴ 2x – 5 = 0
Here, x is the only variable and maximum index of the variable is not 2.
∴ The given equation is not a quadratic equation.
iii. The given equation is
(x + 2)2 = 2x2
∴ x2 + 4x + 4 = 2x2
∴ 2x2 – x2 – 4x – 4 = 0
∴ x2 – 4x – 4 = 0
Here, x is the only variable and maximum index of the variable is 2.
a = 1, b = -4, c = —4 are real numbers and
a ≠ 0.
∴ The given equation is a quadratic equation.
Question 3.
Find the value of discriminant for each of the following equations.
i. 2y2 – y + 2 = 0
ii. 5m2 – m = 0
iii. √5 x2 – x – √5 = 0
Solution:
i. 2y2 – y + 2 = 0
Comparing the above equation with
ay2 + by + c = 0, we get
a = 2, b = -1, c = 2
∴ b2 – 4ac = (-1)2 – 4 × 2 × 2
= 1 – 16
∴ b2 – 4ac = -15
ii. 5m2 – m = 0
∴ 5m2 – m + 0 = 0
Comparing the above equation with
am2 + bm + c = 0, we get
a = 5, b = -1, c = 0
∴ b2 – 4ac = (-1)2 – 4 × 5 × 0
= 1 – 0
∴ b2 – 4ac = 1
iii. √5x2 – x – √5 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = √5, b = -1, c = -√5
∴ b2 – 4ac = (-1)2 – 4 × √5 × √5
= 1 + 20
∴ b2 – 4ac = 21
Question 4.
One of the roots of quadratic equation 2x2 + kx – 2 = 0 is – 2, find k.
Solution:
-2 is one of the roots of the equation
2x2 + kx – 2 = 0.
∴ Putting x = – 2 in the given equation, we get
2(-2)2 + k(-2) -2 = 0
∴ 8 – 2k – 2 = 0
∴ 6 – 2k = 0
∴ 2k = 6
∴ k = \(\frac { 6 }{ 2 } \)
∴ k = 3
Question 5.
Two roots of quadratic equations are given; frame the equation.
i. 10 and -10
ii. 1 – 3√5 and 1 + 3√5
iii. 0 and 7
Solution:
i. Let α = 10 and β = -10
∴ α + β = 10 – 10 = 0
and α × p = 10 × -10 = -100
∴ The required quadratic equation is
x2 – (α + β)x + αβ = 0
∴ x2 – 0x + (-100) = 0
∴ x2 – 100 = 0
ii. Let α = 1 – 3 √5 and β = 1 + 3 √5
α + β = 1 – 3 √5 + 1 + 3 √5 = 2
and α × β = (1 – 3√5) (1 + 3 √5)
= (1)2 – (3√5)2
= 1 – 45
= -44
∴ The required quadratic equation is
x2 – (α + β)x + αβ = 0
∴ x2 – 2x – 44 = 0
iii. Let α = 0 and β = 7
∴ α + β = 0 + 7 = 7
and α × β = 0 × 7 = 0
∴ The required quadratic equation is
x2 – (α + β)x + αβ = 0
∴ x2 – 7x + 0 = 0
∴ x2 – 7x = 0
Question 6.
Determine the nature of roots for each of the quadratic equation.
i. 3x2 – 5x + 7 = 0
ii. √3 x2 + √2 x – 2 √3 = 0
iii. m2 – 2m + 1 = 0
Solution:
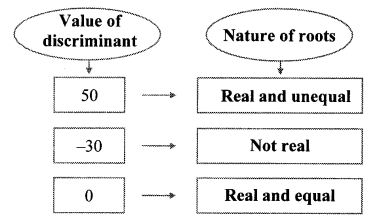
i. 3x2 – 5x + 7 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 3, b = -5, c = 7
∴ ∆ = b2 – 4ac
= (-5)2 -4 × 3 × 7
= 25 – 84
∴ ∆ = -59
∴ ∆ < 0
∴ Roots of the given quadratic equation are not real.
ii. √3 x2 + √2 x – 2 √3 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = √3 , b = √2, c = -2√3
∴ ∆ = b2 – 4ac
= (√2)2 – 4 × √3 × (-2√3)
= 2 + 24
∴ ∆ = 26
∴ ∆ > 0
∴ Roots of the given quadratic equation are real and unequal.
iii. m2 – 2m + 1 = 0
Comparing the above equation with
am2 + bm + c = 0, we get
a = 1, b = -2, c = 1
∴ ∆ = b2 – 4ac
= (-2)2 – 4 × 1 × 1
= 4 – 4
∴ ∆ = 0
∴ Roots of the given quadratic equation are real and equal
Question 7.
Solve the following quadratic equations.
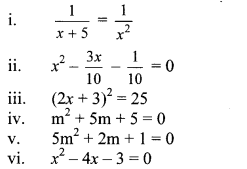
Solution:
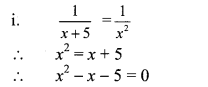

ii. x2 – \(\frac { 3x }{ 10 } \) – \(\frac { 1 }{ 10 } \) = 0
∴ 10x2 – 3x – 1 = 0
…[Multiplying both sides by 10]
∴ 10x2 – 5x + 2x – 1 = 0
∴ 5x(2x – 1) + 1(2x – 1) = 0
∴ (2x – 1)(5x + 1) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴2x – 1 = 0 or 5x + 1 = 0
∴2x = 1 or 5x = -1
∴ x = –\(\frac { 1 }{ 2 } \) or x = \(\frac { -1 }{ 5 } \)
∴ The roots of the given quadratic equation are \(\frac { 1 }{ 2 } \) and \(\frac { -1 }{ 5 } \)
iii. (2x + 3)2 = 25
∴ (2x + 3)2 – 25 = 0
∴ (2x + 3)2 – (5)2 = 0
∴ (2x + 3 – 5) (2x + 3 + 5) = 0 ….. [∵ a2 – b2 = (a – b) (a + b)]
∴ (2x – 2) (2x + 8) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ 2x – 2 = 0 or 2x + 8 = 0
∴ 2x = 2 or 2x = -8
∴ x = \(\frac { 2 }{ 2 } \) or x = \(\frac { -8 }{ 2 } \)
∴ x = 1 or x = -4
∴ The roots of the given quadratic equation are 1 and -4.
iv. m2 + 5m + 5 = 0
Comparing the above equation with
am2 + bm + c = 0, we get
a = 1, b = 5, c = 5
∴ b2 – 4ac = (5)2 – 4 × 1 × 5
= 25 – 20 = 5

v. 5m2 + 2m+1 = 0
Comparing the above equation with
am2 + bm + c = 0, we get
a = 5, b = 2, c = 1
∴ b2 – 4ac = (2)2 -4 × 5 × 1
= 4 – 20
= -16
∴ b2 – 4ac < 0
∴ Roots of the given quadratic equation are not real.
vi. x2 – 4x – 3 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 1, b = -4, c = -3
∴ b2 – 4ac = (-4)2 – 4 × 1 × -3
= 16 + 12
= 28

Question 8.
Find m, if (m – 12) x2 + 2(m – 12) x + 2 = 0 has real and equal roots.
Solution:
(m – 12) x2 + 2(m – 12)x + 2 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = m – 12, b = 2(m – 12), c = 2
∴ ∆ = b2 – 4ac
= [2(m -12)]2 – 4 × (m – 12) × 2
= 4(m – 12)2 – 8(m – 12)
= 4(m – 12) (m – 12 – 2)
∴ ∆ = 4(m – 12) (m – 14)
Since, the roots are real and equal.
∴ ∆ = 0
∴ 4(m – 12) (m – 14) = 0 (m – 12) (m – 14) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m – 12 = 0 or m – 14 = 0
∴ m = 12 or m = 14
But ,if m = 12, then quadratic coefficient becomes zero.
∴ m ≠ 12
∴m = 14
Question 9.
The sum of two roots of a quadratic equation is 5 and sum of their cubes is 35, find the equation.
Solution:
Let α and β be the roots of the quadratic equation.
According to the given conditions,
α + β = 5 and α3 + β3 = 35
Now, (α + β)3 = α3 + 3α2β + 3αβ2 + β3
∴ (α + β)3 = α3 + β3 + 3αβ (α + β)
∴ (5)3 = 35 + 3αβ(5)
∴ 125 = 35 + 15αβ
∴ 125 – 35 = 15αβ
∴ 15αβ = 90
∴ αβ = \(\frac { 90 }{ 15 } \)
∴ αβ = 6
∴ The required quadratic equation is
x2 – (α + β)x + αβ = 0
∴ x2 – 5x + 6 = 0
Question 10.
Find quadratic equation such that its roots are square of sum of the roots and square of difference of the roots of equation
2x2 + 2(p + q)x + p2 + q2 = 0.
Solution:
The given quadratic equation is
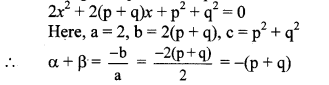
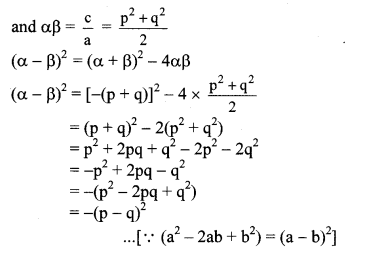
According to the given condition,
Roots of the required quadratic equation are
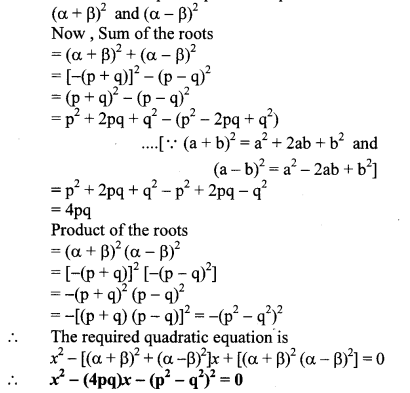
Question 11.
Mukund possesses ₹ 50 more than what Sagar possesses. The product of the amount they have is 15,000. Find the amount each one has.
Solution:
Let the amount Sagar possesses be ₹ x.
∴ the amount Mukund possesses = ₹ (x + 50)
According to the given condition,
x(x +50)= 15000
∴ x2 + 50x – 15000 = 0
∴ x2 + 150x- 100x- 15000 = 0
∴ x(x + 150) – 100(x + 150) = 0
∴ (x + 150)(x – 100) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 150 = 0 or x – 100 = 0
∴ x = -150 or x = 100
But, amount cannot be negative.
∴ x= 100 and x + 50 = 100 + 50 = 150
∴ The amount possessed by Sagar and Mukund are ₹ 100 and ₹150 respectively.
Question 12.
The difference between squares of two numbers is 120. The square of smaller number is twice the greater number. Find the numbers.
Solution:
Let the numbers be x and y (x > y).
According to the given condition,
x2 – y2 = 120 …(i)
y2 = 2x …(ii)
Substituting y2 = 2x in equation (i), we get
x2 – 2x = 120
∴ x2 – 2x – 120 = 0
∴ x2 – 12x + 10x – 120 = 0
∴ x(x – 12) + 10(x – 12) = 0
∴ (x – 12)(x + 10) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 12 = 0 or x + 10 = 0
∴ x = 12 or x = -10
But x ≠ -10
as, y2 = 2x = 2(-10) = -20 …[Since, the square of number cannot be negative]
∴ x = 12
Smaller number = y2 =2x
∴ y2 = 2 × 12
∴ y2 = 24
∴ y = ± √24 …[Taking square root of both sides]
∴ The smaller number is √24 and greater number is 12 or the smaller number is – √24 and greater number is 12.
Question 13.
Ranjana wants to distribute 540 oranges among some students. If 30 students were more each would get 3 oranges less. Find the number of students.
Solution:
Let the number of students be x.
Total number of oranges = 540
∴ the number of oranges each student gets = \(\frac { 540 }{ x } \)
If there were 30 more students, the total number of students = (x + 30) and the total number of oranges each student gets
= (\(\frac { 540 }{ x+30 } \)
According to the given condition,
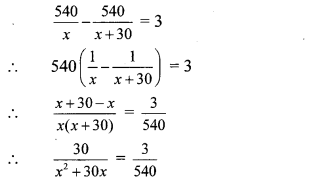
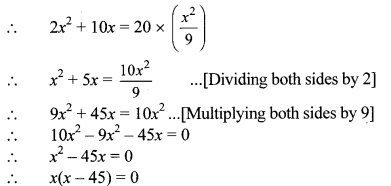
∴ 30 × 540 = 3x2 + 90 x
∴ 3x2 + 90x= 16200
∴ x2 + 30x – 5400 = 0
…[Dividing both sides by 3]
∴ x2 + 90x – 60x – 5400 = 0
∴ x(x + 90) – 60(x + 90) = 0
∴ (x + 90) (x – 60) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 90 = 0 or x – 60 = 0
∴ x = – 90 or x = 60
But, number of students cannot be negative,
x = 60
∴ The total number of students is 60.
Question 14.
Mr. Dinesh owns an rectangular agricultural farm at village Talvel. The length of the farm is 10 metre more than twice the breadth. In order to harvest rain water, he dug a square shaped pond inside the farm. The side of pond is \(\frac { 1 }{ 3 } \) of the breadth of the farm. The
area of the farm is 20 times the area of the pond. Find the length and breadth of the farm and side of the pond.
Solution:
Let the breadth of the rectangular farm be x m.
∴ Length of rectangular farm = (2x + 10) m
Area of rectangular farm = Length × Breadth
= (2x + 10) × x
= (2x2+ 10x) sq. m
Now ,side of square shaped pond = \(\frac { x }{ 3 } \) m
∴ Area of square shaped pond = (side)2
= (\(\frac { x }{ 3 } \))2 m
= \(\frac { { x }^{ 2 } }{ 9 } \) m
According to the given condition,
Area of rectangular farm = 20 × Area of pond
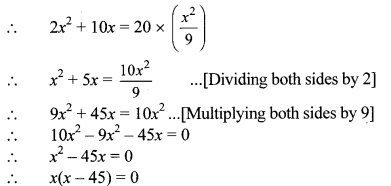
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x = 0 or x – 45 = 0
x = 0 or x = 45
But, breadth of the rectangular farm cannot be zero,
∴ x = 45
Length of rectangular farm
= 2x + 10 = 2(45) + 10 = 100 m
Side of the pond = \(\frac { x }{ 3 } \) = \(\frac { 45 }{ 3 } \) = 15 m
∴ Length and breadth of the farm and the side of the pond are 100 m, 45 m and 15 m respectively.
Question 15.
A tank fills completely in 2 hours if both the taps are open. If only one of the taps is open at the given time, the smaller tap takes 3 hours more than the larger one to fill the tank. How much time does each tap take to fill the tank completely?
Solution:
Let the larger tap take x hours to fill the tank completely.
∴ Part of tank filled by the larger tap in 1 hour = \(\frac { 1 }{ x } \)
Also, the smaller tap takes (x + 3) hours to fill the tank completely.
∴ Part of tank filled by the smaller tap in 1 hour = \(\frac { 1 }{ x+3 } \)
∴Part of tank filled by both the taps in 1 hour
= (\(\frac { 1 }{ x } \) + \(\frac { 1 }{ x+3 } \))
But, the tank gets filled in 2 hours by both the taps.
∴ Part of tank filled by both the taps in 1 hour = \(\frac { 1 }{ 2 } \)
According to the given condition,
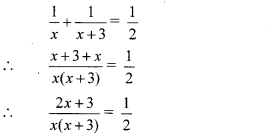
∴ 2(2x + 3) = x(x + 3)
∴ 4x + 6 = x2 + 3x
∴ x2 + 3x – 4x – 6 = 0
∴ x2 – x – 6 = 0
∴ x2 – 3x + 2x – 6 = 0
∴ x(x – 3) + 2(x – 3) = 0
∴ (x – 3)(x + 2) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 3 = 0 or x + 2 = 0
∴ x = 3 or x = -2
But, time cannot be negative.
∴ x = 3 and x + 3 = 3 + 3 = 6
∴ The larger tap takes 3 hours and the smaller tap takes 6 hours to fill the tank completely.
Class 10 Maths Digest