Class 10

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 20.1 व्युत्पत्ती कोश Notes, Textbook Exercise Important Questions, and Answers.

Class 10th Marathi Kumarbharti Chapter 20.1 व्युत्पत्ती कोश Question Answer Maharashtra Board

Std 10 Marathi Chapter 20.1 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 20.1 व्युत्पत्ती कोश Textbook Questions and Answers

प्रश्न 1.
टिपा लिहा.
(अ) व्युत्पत्ती कोशाचे कार्य
उत्तर:
व्युत्पत्ती कोशाचे कार्य: व्युत्पत्ती म्हणजे एखादया शब्दाच्या किंवा अर्थाच्या मुळाचे ज्ञान होय. व्युत्पत्ती सांगणे म्हणजे एखादया शब्दाच्या मुळाविषयी माहिती देणे होय, अशा अनेक शब्दांच्या व्युत्पत्तींचा संग्रह म्हणजे व्युत्पत्ती कोश !

व्युत्पत्ती कोशाचे कार्य पुढीलप्रमाणे चार प्रकारे चालते:

• मराठी भाषेतील – प्रमाण व बोली – शब्दांचे मूळ रूप दाखवणे,
• विशिष्ट प्रदेशात व भौगोलिक परिसरात एकाच शब्दातील उच्चारात बदल होत असतो. हा शब्दाच्या उच्चारातील बदल व फरक दाखवणे.
• भाषेमध्ये इतिहासाच्या दृष्टीने फरक होत असतात. भिन्न भिन्न काळात जे शब्दांत बदल होतात, त्या बदलांचे कारण स्पष्ट करणे.
• भिन्न भिन्न समाजांत वेगवेगळ्या कारणांनी शब्दाच्या अर्थाच्या अंगानेही बदल संभवतात. हे अर्थातील बदल स्पष्ट करणे.

(आ) शब्द तयार होण्याचे विविध प्रकार

प्रश्न 2.
खालील मुद्द्यांच्या आधारे एक परिच्छेद तयार करा. (७ ते ८ वाक्यांत)

उत्तर:
व्युत्पत्ती कोश: एखादया शब्दाबद्दलचे कुतूहल शमवण्यासाठी आपण व्युत्पत्ती कोशाची मदत घेतो, व्युत्पत्ती कोशात आपल्याला मूळ शब्द कसा, केव्हा, कुठे निर्माण झाला हे तर कळतेच परंतु अन्य भाषांत तो शब्द कसा आला आहे व कोणत्या रूपात आहे, हेही कळते. असा हा शब्दांचा किमयागार कसा अस्तित्वात आला हे समजून घेणे उद्बोधक ठरेल.

१९३८ साली मुंबई येथे अखिल भारतीय मराठी साहित्य संमेलन भरले होते. स्वातंत्र्यवीर सावरकर हे संमेलनाचे अध्यक्ष होते. त्यांच्या अध्यक्षतेखाली ‘व्युत्पत्ती कोश रचनेचे कार्य हाती घ्यावे’ असा ठराव या संमेलनात मंजूर करण्यात आला. कृ. पां. कुलकर्णी यांच्यावर संपादनाची जबाबदारी सोपवण्यात आली. बॅ. मुकुंदराव जयकर यांनी अर्थसाहाय्य केले व श्री. दाजीसाहेब तुळजापूरकर यांनी पुरस्कृत केल्यामुळे निर्मितीस भरीव मदत केली. अखेर १९४६ साली मराठी व्युत्पत्ती कोशाचे पहिले प्रकाशन झाले.

प्रश्न 3.
पाठाबाहेरची उदाहरणे शोधून खालील कृती करा.

उत्तर:

Marathi Kumarbharti Std 10 Guide Pdf भाग-४

• आकाशी झेप घे रे Question Answer (कविता)
• सोनाली Question Answer
• निर्णय Question Answer
• तू झालास मूक समाजाचा नायक Question Answer (कविता)
• सर्व विश्वचि व्हावे सुखी Question Answer
• व्युत्पत्ती कोश Question Answer (स्थूलवाचन)

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 20 सर्व विश्वचि व्हावे सुखी Notes, Textbook Exercise Important Questions, and Answers.

Class 10th Marathi Kumarbharti Chapter 20 सर्व विश्वचि व्हावे सुखी Question Answer Maharashtra Board

Std 10 Marathi Chapter 20 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 20 सर्व विश्वचि व्हावे सुखी Textbook Questions and Answers

कृति

कृतिपत्रिकेतील प्रश्न १ (अ) आणि (आ) यांसाठी…

प्रश्न 1.
खालील चौकटी पूर्ण करा.
(अ) संत ज्ञानेश्वर यांनी मानवाच्या कल्याणासाठी केलेली विश्वप्रार्थना – [ ]
(आ) मानवी सुखदुःखाशी सहृदयतेने समरस होणे – [ ]
(इ) ‘सर्वांभूती भगवद्भावो’ अशी प्रार्थना करणारे संत – [ ]
(ई) सामाजिक प्रबोधनावर भर देणारे संत – [ ]
(उ) संत तुकारामांचे जीवनसूत्र – [ ]
उत्तर:
(अ) संत ज्ञानेश्वर यांनी मानवाच्या कल्याणासाठी केलेली विश्वप्रार्थना – [पसायदान]
(आ) मानवी सुखदु:खाशी सहृदयतेने समरस होणे – [मैत्री]
(इ) ‘सर्वांभूती भगवद्भावो’ अशी प्रार्थना करणारे संत – [संत एकनाथ]
(ई) सामाजिक प्रबोधनावर भर देणारे संत – [संत गाडगे महाराज]
(उ) संत तुकारामांचे जीवनसूत्र – [परस्पर सहकार्य]

प्रश्न 2.
आकृत्या पूर्ण करा.


उत्तर:

प्रश्न 3.
फरक संग

उत्तर:

प्रश्न 4.
खालील काव्यपंक्तींचा अर्थ लिहा.
(अ) जे खळांची व्यंकटी सांडो – [ ]
(आ) दुरिताचे तिमिर जावो – [ ]
उत्तर:
(i) जे खळांची व्यंकटी सांडो – [माणसांच्या मनातील दुष्ट भाव नष्ट होऊ दे.]
(ii) दुरितांचे तिमिर जावो – [(दुरित म्हणजे दुष्कर्म.) सर्व दुष्कर्माचा अंधार नष्ट होऊ दे.]

प्रश्न 5.
खालील तक्ता पूर्ण करा. त्यासाठी कंसातील शब्दांचा उपयोग करा.
(नम्रता, मैत्रभाव, विश्वकल्याण, स्वप्रयत्न, सहकार्य)

उत्तर:

प्रश्न 6.
स्वमत.
(अ) सर्व संतांच्या प्रार्थनमधील सामाईक सूत्र तुमच्या शब्दांत थोडक्यात लिहा.
उत्तर:
संत स्वत:पलीकडे जाऊन संपूर्ण जगाकडे पाहतात. त्यांना सर्व प्राणिमात्रांबद्दलच कळवळा वाटतो. त्यांच्या मनात आपपरभाव नसतो, त्यांना सर्व माणसे समान वाटतात; सारखीच प्रिय वाटतात. म्हणून संतमहात्मे सर्व मानवजातीचे कल्याण इच्छितात. म्हणूनच ‘जो जे वांछील तो ते लाहो’ असे ज्ञानदेव म्हणतात, नामदेवांना वाटते की, सर्वांच्या मनातला अहंकार नष्ट व्हावा. म्हणजे सगळेजण एकमेकाला स्वत:च्या हृदयात सामावून घेतील. संत एकनाथांना सर्वांच्याच ठिकाणी भगवद्भाव आढळतो. संत तुकाराम महाराज सर्वांनी एकमेकाला साहाय्य करीत परमेश्वर चरणांपर्यंत जाण्याचा मार्ग दाखवतात. सर्वच संत स्वतःसाठी काहीही मागत नाहीत, ते समस्त मानवजातीसाठी, समस्त प्राणिमात्रांसाठी परमेश्वराकडे हात जोडून प्रार्थना करतात.

(आ) ‘भूतां परस्परें पडो । मैत्र जीवाचें ।’ या ओळीचा तुम्हांला समजलेला अर्थ लिहा.
उत्तर:
या ओळीतील भूत, मैत्र आणि जीव’ हे तीन शब्द खूप महत्त्वाचे आहेत. देह धारण करणारा प्रत्येकजण ‘भूत’ होय. म्हणून जगातली सगळी माणसे भूत होत. पण फक्त माणसेच नव्हेत, तर सूक्ष्मजीवांपासून ते हत्ती-गेंडे यांसारखे सर्व प्राणिमात्र भूत होत. तसेच. वृक्षवेली यासुद्घा सजीवच आहेत. त्यासुद्घा भूत होत. या सर्वांच्या मनात एकमेकांबद्दल निर्मळ, पवित्र अशी प्रेमभावना निर्माण झाली पाहिजे, ही इच्छा ज्ञानदेव देवाजवळ व्यक्त करतात. जात, धर्म, भाषा, प्रांत वगैरे गोष्टींवरून आपण अनेकांना शत्रू समजतो. या भावना बाह्य गुणांवर अवलंबून आहेत. ज्ञानदेव या गोष्टींच्या पलीकडे जायला सांगतात. प्रत्येक जण सुखीच असेल. नेमकी हीच मागणी ज्ञानदेव विश्वात्मक देवाकडे करीत आहेत.

(इ) या पाठातून तुम्ही काय शिकलात, ते तुमच्या शब्दांत लिहा.
उत्तर:
सर्व संतांनी घ्यापक दृष्टिकोन बाळगून लोकांना उपदेश केला आहे. सर्व लोकांनी एकमेकांशी प्रेमाने वागावे. एकमेकांना, अडीअडचणीत असलेल्या सर्वांना मदत करावी. सर्वांमध्ये सहकार्याची भावना हवी. या त-हेने सर्वजण वागू लागले, तर समाजात शांती नांदेल. माणसे सुखासमाधानाने जगू लागतील. या अशा वातावरणातच माणसे प्रगती करु शकतात. अशा वातावरणात चोऱ्यामाऱ्या होणार नाहीत. दंगेधोपे होणार नाहीत. कोणाची पिळवणूक होणार नाही. कोणाची फसवणूक होणार नाही. कोणावर अन्याय होणार नाही. एकंदरीत, सर्व व्यवस्था ही न्यायावर आधारलेली राहील. म्हणून सर्वांनी एकोप्याने राहावे, असे सर्व संत सांगतात. इतरेजनांशी सहृदयतेने समरस झाले पाहिजे. सर्वांनी शिक्षण घेतले पाहिजे. वैज्ञानिक दृष्टिकोन बाळगला पाहिजे. हा पाठ वाचून मला हाच संदेश मिळाला.

भाषाभ्यास

खालील ओळींतील वृत्त ओळखा.

(i) म्हणे वासरा । घात झाला असा रे
तुझ्या माऊलीचेच हे खेळ सारे
वृथा धाडिला राम माझा वनासी
न देखो शके त्या जगज्जीवनासी

(ii) अविरत पथि चाले, पांथ नेमस्त मानी
कधि न मुळि न थांबे, कोणत्या कारणांनी
वचनि मननि त्याच्या, ध्येय हे एक ठावे
स्वपर जनसमूहा सौख्य कारी बनावे

(iii) मातीत ते पसरले अति रम्य पंख।
केले वरी उदर पांडुर निष्कलंक।।
चंचू तशीच उघडी पद लांबवीले।
निष्प्राण देह पडला श्रमही निमाले।।
उत्तर:

वृत्त: हे भुजंगप्रयात अक्षरगणवृत्त आहे.]

वृत्त: हे मालिनी अक्षरगणवृत्त आहे.

वृत्त: हे वसंततिलका अक्षरगणवृत्त आहे.

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 20 सर्व विश्वचि व्हावे सुखी Additional Important Questions and Answers

प्रश्न. पुढील उतारा वाचा आणि दिलेल्या सूचनांनुसार कृती करा:
कृती १: (आकलन)

प्रश्न 1.
चौकटी पूर्ण करा:
(ii) संतांची भूमी – [ ]
(iii) संत म्हणजे – [ ]
(iv) सर्व संतांच्या प्रार्थनांमधून व्यक्त झालेली भावना – [ ]
उत्तर:
(i) संतांची भूमी – [महाराष्ट्र]
(ii) संत म्हणजे – [सत्पुरुष]
(iii) सर्व संतांच्या प्रार्थनांमधून व्यक्त झालेली भावना – [मानवता]

कृती २: (आकलन)

प्रश्न 1.
आकृत्या सोडवा:

उत्तर:

प्रश्न 2.
सर्वांनी गुण्यागोविंदाने राहावे, हे सांगताना दिलेला दाखला सांगा.
उत्तर:
पाने, फुले, फळे, झाडे, झरे, नदया, समुद्र, आकाशातील सर्व ग्रहगोल हे सारे एकोप्याने राहतात. त्यांच्यात कधीही कलह होत नाही, त्यांच्याप्रमाणेच सर्वांनी एकोप्याने राहावे, असा दाखला ज्ञानदेवांनी दिला आहे.

प्रश्न 3.
विधान पूर्ण करा:
पसायदान म्हणजे …………………..
उत्तर:
पसायदान म्हणजे मानवाच्या कल्याणासाठी विश्वात्मक देवाला हात जोडून केलेली प्रार्थना होय.

कृती ३: (व्याकरण)

प्रश्न 1.
पुढे दिलेली वाक्ये वाचा आणि योग्य त्या नामासाठी योग्य ते सर्वनाम वापरा:
(i) ही संतांची खरी भूमिका आहे.
(ii) संतांच्या साहित्याचा आत्मा भक्ती हा आहे.
(iii) संत परमेश्वराकडे स्वतःसाठी काहीही मागत नाहीत.
उत्तर:
(i) ही संतांची खरी भूमिका आहे.
(ii) त्यांच्या साहित्याचा आत्मा भक्ती हा आहे.
(iii) ते परमेश्वराकडे स्वत:साठी काहीही मागत नाहीत.

प्रश्न 2.
‘विश्वकल्याण = विश्वाचे कल्याण’ यासारखे आणखी दोन शब्द विग्रहासह लिहा.
उत्तर:
(i) शांतिनिकेतन = शांतीचे निकेतन.
(ii) रजनीनाथ = रजनीचा नाथ.

प्रश्न 3.
अधोरेखित शब्दांचे अनेकवचन योजून वाक्य पुन्हा लिहा:
माणसाच्या मनातील माणुसकीचा झरा जिवंत ठेवला पाहिजे.
उत्तर:
माणसांच्या मनांतील माणुसकीचे झरे जिवंत ठेवले पाहिजेत.

उतारा क्र. २
प्रश्न. पुढील उतारा वाचा आणि दिलेल्या सूचनांनुसार कृती करा:

कृती १: (आकलन)

प्रश्न 1.
विधाने पूर्ण करा:
(i) आयुष्यात मोठे व्हायचे असेल, तर अंगी नम्रता हवी; म्हणजे अंगी नम्रता असेल, तर ……………………….
(ii) थोरांच्या चरित्रांतून आपल्याला शिकवण मिळते की, ……………………….
उत्तर:
(i) आयुष्यात मोठे व्हायचे असेल, तर अंगी नम्रता हवी; म्हणजे अंगी नम्रता असेल, तर आयुष्यात मोठे होता येईल.
(ii) थोरांच्या चरित्रांतून आपल्याला शिकवण मिळते की, विनम्रता ही केव्हाही जगाला आपलेसे करते.

प्रश्न 2.
स्पष्ट करा:
(i) सर्वांभूती भगवद्भावो.
(ii) संतसंग देई सदा.
उत्तर:
(i) सर्वांभूती भगवद्भावो म्हणजे प्राणिमात्रांशी मैत्री केली पाहिजे. येथे मैत्री म्हणजे काय? मैत्री म्हणजे माणसांच्या सुखदुःखांशी समरस होणे आणि असे समरस होताना आपपरभाव न बाळगणे.
(ii) संतांचा सदोदित सहवास लाभावा. त्यामुळे संतांचे गुण, त्यांची वृत्ती, त्यांचा दृष्टिकोन अंगी भिनतो. मग सगळेच जण परस्पर सहकार्यासाठी उभे ठाकतात. या परस्पर सहकार्यातून मानवी जीवनाचे कल्याण साधले जाते. म्हणून मला सदोदित संतांचा सहवास दें.

प्रश्न 3.
रामदासांनी दिलेला संदेश लिहा.
उत्तर:
संत रामदासांचा संदेश: हे परमेश्वरा, जनहित तेच बघ. सर्वांचे कल्याण कर.

प्रश्न 4.
गाडगेबाबांचा संदेश लिहा.
उत्तर:
संत गाडगे महाराजांचा संदेश: धर्मकार्यासाठी वाटेल तसा पैसा उधळण्यापेक्षा तोच पैसा शिक्षण मिळवण्यासाठी खर्च करावा. स्वत:च स्वत:च्या उद्धारासाठी सिद्ध झाले पाहिजे. त्यातच माणसाचे कल्याण आहे.

कृती ३: (व्याकरण)

प्रश्न 1.
विरुद्ध अर्थाचे शब्द लिहा:
(i) कल्याण
(ii) वैयक्तिक
(iii) माणुसकी
(iv) समारोप.
उत्तर:
(i) कल्याण × अकल्याण
(ii) वैयक्तिक × सामूहिक
(iii) माणुसकी × माणुसकीहीनता
(iv) समारोप × सुरुवात

प्रश्न 2.
कंसात दिलेला प्रत्यय जोडून शब्दांचे पूर्ण रूप लिहा:
(i) भूमिका (ला)
(ii) झरा (चे)
(iii) ग्रंथ (ला)
(iv) नदी (ना).
उत्तर:
(i) भूमिकेला
(ii) झऱ्याचे
(ii) ग्रंथाला
(iv) नदयांना.

प्रश्न 3.
समानार्थी शब्द लिहा:
(i) कळवळा
(i) कल्याण
(iii) प्रार्थना
(iv) सहृदयता.
उत्तर:
(i) कळवळा = करुणा
(ii) कल्याण = उत्कर्ष
(iii) प्रार्थना = विनंती
(iv) सहृदयता = सहानुभूती.

उतारा क्र.३
प्रश्न. पुढील उतारा वाचा आणि दिलेल्या सूचनांनुसार कृती करा:

कृती १: (आकलन)

प्रश्न 1.
चौकटी पूर्ण करा:
(i) संपूर्ण गावाची भगवद्गीता – [ ]
(ii) गावाचे मंदिर – [ ]
(iii) मंदिरातील मूर्ती – [ ]
उत्तर:
(i) संपूर्ण गावाची भगवद्गीता – [गावस्वच्छता]
(ii) गावाचे मंदिर – [संपूर्ण गाव]
(iii) मंदिरातील मूर्ती – [माणूस]

प्रश्न 2.
आकृत्या पूर्ण करा:

उत्तर:

(३) चौकटी पूर्ण करा:

उत्तर:

कृती २: (आकलन)

प्रश्न 1.
‘माणूस हा सामाजिक प्राणी आहे,’ या विधानाची सत्यता पटवून देणारी वाक्ये लिहा.
उत्तर:
(i) माणूस हा कधीही एकाकी राहू शकत नाही.
(ii) त्याला संवादाची नितांत गरज असते.
(iii) माणसाने कुणालाही दुखावता कामा नये.
(iv) शक्यतो दुसऱ्याच्या उपयोगी पडले पाहिजे.

प्रश्न 2.
‘हे विश्वचि माझे घर’ या ज्ञानदेवांच्या उद्गारामागील भावनेचा:
(i) आज पूर्ण होताना दिसून येणारा भाग:
(ii) आज आपण गमावलेला भाग:
उत्तर:
(i) आज पूर्ण होताना दिसून येणारा भाग: विज्ञान-तंत्रज्ञानामुळे जग खूप जवळ आले आहे; लहान झाले आहे. आज माणसे सहजगत्या कुठेही जाऊ शकतात, राहू शकतात. जग जणू एक घरच बनले आहे.
(ii) आज आपण गमावलेला भाग: घरातल्या माणसांच्या मनात घरातल्या इतरांबद्दल जिव्हाळा, आपुलकी असते. थोडक्यात, आपापसांतील नात्यांत भावनेचा ओलावा असतो. आज आपण हा ओलावा गमावून बसलो आहोत. माणसामाणसांना जोडणारा जिव्हाळा आज हरवला आहे.

प्रश्न 3.
झाड व पर्वत यांतील साम्य लिहा.
उत्तर:
झाड व पर्वत यांच्यात एक साम्य आहे. झाड स्वत: उन्हाचा ताप सहन करते आणि थंड सावली इतरांना देते. त्याप्रमाणेच पर्वतही वागताना दिसतो. पर्वताच्या कुशीत नदी उगम पावते. पण नदी तिथे थांबत नाही. ती पर्वतापासून दूर जाते. पर्वत तिचा हा वियोग सहन करतो आणि नदीला सर्व जगाची तहान भागवू देतो.

प्रश्न 4.

उत्तर:

कृती ३: (व्याकरण)

प्रश्न 1.
पुढील शब्दांतील प्रत्यय ओळखा आणि त्या प्रत्ययासह आणखी दोन शब्द लिहा:
(i) साधर्म्य
(ii) सहृदयता.
उत्तर:
(i) साधर्म्य – य:
सुंदर + य = सौंदर्य,
गद + य = गय.

(ii) सहृदयता – ता:
कोमल + ता = कोमलता,
विविध + ता = विविधता.

प्रश्न 2.
कंसांतील सूचनांनुसार उत्तर: लिहा:
(i) या संकल्पना संतसाहित्यातून प्रकट झाल्या आहेत. (भूतकाळ करा.)
(ii) हा ग्रंथ पूर्ण करण्याच्या तयारीत ते होते. (भविष्यकाळ करा.)
(iii) यातून प्रार्थना निर्माण झाली. (वर्तमानकाळ करा.)
उत्तर:
(i) या संकल्पना संतसाहित्यातून प्रकट झाल्या होत्या.
(ii) हा ग्रंथ पूर्ण करण्याच्या तयारीत ते असतील.
(iii) यातून प्रार्थना निर्माण होते.

प्रश्न 3.
कंसांतील सूचनेनुसार बदल करून वाक्ये पुन्हा लिहा:
(i) संत ज्ञानेश्वरांनी सांगितलेली ही प्रार्थना मराठी मनाच्या स्मरणात कायम आहे. (मिश्र वाध्य करा.)
(ii) वैयक्तिक इच्छा पूर्ण व्हावी म्हणून आपण नेहमीच प्रार्थना करतो. (केवल वाक्य करा.)
उत्तर:
(i) संत ज्ञानेश्वरांनी जी प्रार्थना सांगितली, ती मराठी मनाच्या स्मरणात कायम आहे.
(ii) वैयक्तिक इच्छा पूर्ण होण्यासाठी आपण नेहमीच प्रार्थना करतो.

प्रश्न 4.
पुढील वाक्यातील अधोरेखित शब्दांबद्दल पुढील माहिती लिहून तक्ता पूर्ण करा.
विज्ञानातील चांगले प्रकल्प समृद्धी आणतात, पण सुंदर मने ही राष्ट्राची श्रीमंती वाढवतात.

उत्तर:

कृती ४: (स्वमत/अभिव्यक्ती)

प्रश्न 1.
समाजातील जिव्हाळा हरवल्याबद्दलची व्यक्त केलेली खंत व त्याचा परिणाम तुमच्या शब्दांत लिहा.
उत्तर:
सध्या जवळजवळ सर्वांच्या मनात इतरांबद्दल जिव्हाळा राहिलेला नाही. साध्या साध्या प्रसंगात माणसे हमरातुमरीवर येतात. साधे बसमध्ये चढताना लोक धक्काबुक्की करतात. त्यामुळे मुले, म्हातारी माणसे, आजारी माणसे व अपंग यांचे खूप हाल होतात. काही दुष्ट दुधात भेसळ करतात, अन्नपदार्थात भेसळ करतात. त्यामुळे कित्येकांना विषबाधा होते. काहीजणांना प्राण गमवावे लागतात. वाईट बांधकामामुळे रस्त्यांवर भीषण अपघात घडतात. घरे कोसळतात. पूल कोसळतात. त्यांत अनेकांचे अतोनात नुकसान होते. या माणसांवर कोणती संकटे कोसळतात, कोणत्या दु:खांना तोंड द्यावे लागते. याबद्दल भ्रष्टाचाऱ्यांना ना खेद वाटतो, ना खंत वाटते. इतरांबद्दल जिव्हाळाच वाटत नसल्याने अशी कृत्ये माणसांकडून घडून जातात.

व्याकरण व भाषाभ्यास

कृतिपत्रिकेतील प्रश्न ४ (अ) आणि (आ) यांसाठी…
व्याकरण घटकांवर आधारित कृती:

१. समास:
पुढील सामासिक शब्दांचा विग्रह करून समास ओळखा:

उत्तर:

२. अलंकार:
रूपक अलंकाराची लक्षणे सांगून उदाहरण दया:
उत्तर:
लक्षणे: उपमेय व उपमान यांत एकरूपता असते व ती भिन्न नाहीत असे वर्णन जेथे असते तिथे रूपक अलंकार होतो.
उदाहरण: काय बाई सांगो। स्वामीची ती दृष्टी।
अमृताची वृष्टी । मज होय ।।

४. शब्दसिद्धी:
* पुढील चौकटीत दिलेल्या शब्दांचे वर्गीकरण करून तक्ता पूर्ण करा:

उत्तर:

५. सामान्यरूप:
तक्ता पूर्ण करा:

६. वाक्प्रचार:
(१) वाक्प्रचार व अर्थ यांच्या जोड्या लावा:

(२) तक्ता पूर्ण करा: (सराव कृतिपत्रिका-१)

भाषिक घटकांवर आधारित कृती:

१. शब्दसंपत्ती:

(१) विरुद्धार्थी शब्द लिहा:
(i) आधुनिक × ……………………….
(ii) मर्यादित × ……………………….
(iii) स्मरण × ……………………….
(iv) तिमिर × ……………………….
(v) दुष्कर्म × ……………………….
(vi) स्वार्थ × ……………………….
(vii) व्यर्ध × ……………………….
(viii) वैयक्तिक × ……………………….
उत्तर:
(i) आधुनिक × प्राचीन
(iii) स्मरण × विस्मरण
(v) दुष्कर्म × सत्कर्म
(vii) व्यर्थ × सार्थ
(ii) मर्यादित × अमर्यादित
(iv) तिमिर × प्रकाश
(vi) स्वार्थ × निःस्वार्थ
(viii) वैयक्तिक × सार्वजनिक,

(२) समानार्थी शब्द लिहा: (प्रत्येकी दोन)
(i) [ ………. ] = [वृक्ष] = [ ………. ]
(ii) [ ………. ] = [समुद्र] = [ ………. ]
(iii) [ ………. ] = [सूर्य] = [ ………. ]
(iv) [ ………. ] = [चंद्र] = [ ………. ]
उत्तर:
(i) [ झाड ] = [वृक्ष] = [ तारू ]
(ii) [ सागर ] = [समुद्र] = [ सिंधू ]
(iii) [ रवी ] = [सूर्य] = [ भास्कर ]
(iv) [ शशी ] = [चंद्र] = [ रजनीनाथ ]

(३) पुढील शब्दांतील समानार्थी व विरुद्धार्थी शब्दाच्या चार जोड्या तयार करा: (सराव कृतिपत्रिका-१)

उत्तर:

(४) पुढील शब्दांतील अक्षरांपासून चार अर्थपूर्ण शब्द तयार करा:
(i) तुकाराम → [ ] [ ] [ ] [ ]
(ii) महाराज → [ ] [ ] [ ] [ ]
(iii) गगनभरारी → [ ] [ ] [ ] [ ] (सराव कृतिपत्रिका-१)
उत्तर:
(i) तुकाराम → [राम] [कारा] [मका] [मरा]
(ii) महाराज → [महा] [राज] [जरा] [राम]
(iii) गगनभरारी → [नभ] [भरा] [राग] [रान]

(५) गटात न बसणारा शब्द लिहा:
(i) तम, तिमिर, समर, काळोख, अंधार.
(ii) उजेड, तेज, प्रकाश, आकाश, आभा.
(iii) खोदाई, लढाई, शिष्टाई, मुंबई. (सराव कृतिपत्रिका-२)
(iv) हरिहर, हररोज, हरघडी, हरसाल. (सराव कृतिपत्रिका-२)
उत्तर:
(i) समर
(ii) आकाश
(ii) मुंबई –
(iv) हरिहर लेखननियम:

(१) अचूक शब्द निवडा:
उत्तर:
(i) सहायक / साहय्यक / सहय्यक / सहाय्यक. – [सहायक]
(ii) उतरार्ध / उत्तरार्ध / उतर्राध/ उत्तर्राध. – [उत्तरार्ध]
(iii) अतिशयोक्ती / अतीशयोक्ती/ अतिशयोक्ति / अतीशयोक्ति. – [अतिशयोक्ती]
(iv) कल्पवृक्ष /कप्लवृक्ष / कल्पव्रक्ष / कल्पवृक्ष. – [कल्पवृक्ष] (सराव कृतिपत्रिका-१)
(v) उप्तन्न/उत्पन/ उत्पन्न/ऊत्पन्न. – [उत्पन्न]
(vi) सुचना / सूचना / सुचणा / सूचाना. – [सूचना]
(vii) स्मृतीदीन /स्मृतिदिन / स्मृतिदीन /स्मृतीदिन. – [स्मृतिदिन]
(viii) परंपरिक / पारंपारिक / परंपारिक / पारंपरिक. – [पारंपरिक]
(ix) तिर्थरूप/तीर्थरूप/तीर्थरुप / तिथरूंप – [तीर्थरुप]
(x) आशिर्वाद/आशीर्वाद/आर्शीवाद/आशिरवाद – [आशीर्वाद] (मार्च १९)

(२) पुढील वाक्ये लेखननियमांनुसार लिहा:
(i) शिक्षणामुळे माणुस सूसंस्क्रुत व्हावा.
(ii) आपल्या पूरवजांनी अर्जीठा वेरूळ बनवलाय. (सराव कृतिपत्रिका-१)
उत्तर:
(i) शिक्षणामुळे माणूस सुसंस्कृत होतो.
(ii) आपल्या पूर्वजांनी अजिंठा वेरूळ बनवलाय.

३. विरामचिन्हे:
(१) पुढील वाक्यांतील विरामचिन्हे ओळखा:
संत ज्ञानेश्वरांच्या ‘ज्ञानेश्वरी’ या ग्रंथात पसायदान आहे.
उत्तर:
[ ‘ ‘ ] → एकेरी अवतरणचिन्ह
[ . ] → पूर्णविराम.

(२) पुढील वाक्यात योग्य ती विरामचिन्हे भरून वाक्य पुन्हा लिहा:
निसर्गातील फुले फळे वृक्ष नदया समुद्र सूर्य चंद्र तारे एकोप्याने राहतात
उत्तर:
निसर्गातील फुले, फळे, वृक्ष, नया, समुद्र, सूर्य, चंद्र, तारे एकोप्याने राहतात.

(३) प्रस्तुत वाक्यातील चुकीची विरामचिन्हे ओळखा व दुरुस्त करून लिहा: (सराव कृतिपत्रिका-१)
मी तिला म्हटले. कर्त्यांच्या पुतळ्यापाशी बसून रडायला तुला काहीच कसे वाटत नाही!
उत्तर:
मी तिला म्हटले, “कव्यांच्या पुतळ्यापाशी बसून रडायला तुला काहीच कसे वाटत नाही?”

(४) पुढे विरामचिन्हाचा उपयोग दिला आहे त्यानुसार त्या आशयाचे विरामचिन्ह चौकटीत भरा: (सराव कृतिपत्रिका-१)
(i) बोलणाऱ्याच्या तोंडचे शब्द दाखवण्यासाठी → [ ” ” ]
(ii) दोन शब्द जोडण्यासाठी किंवा जोडशब्दातील पदे सुटी करून दाखवण्यासाठी → [ – ]

४. पारिभाषिक शब्द: *पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द लिहा:
उत्तर:
(i) Children’s Theatre – बालरंगभूमी
(ii) Daily Wages – दैनिक वेतन / रोजंदारी
(iii) Joint Meeting – संयुक्त सभा
(iv) Junior Clerk – कनिष्ठ लिपिक
(v) Letter-Head – नाममुद्रित प्रत
(vi) Up-to-date – अदययावत
(vii) Open Letter – अनावृत पत्र
(viii) Press Note – प्रसिद्धिपत्रक
(ix) Registered Letter – नोंदणीकृत पत्र
(x) Revaluation – पुनर्मूल्यांकन
(xi) Survey – सर्वेक्षण / पाहणी
(xii) Secretary – सचिव / कार्यवाह

५. अकारविल्हे / भाषिक खेळ:
(१) पुढील शब्द अकारविल्हेनुसार लिहा:
(i) संत → महंत → साधू → महापुरुष.
(ii) संस्कृत → मराठी → हिंदी → इंग्रजी.
उत्तर:
(i) महंत → महापुरुष → संत → साधू.
(ii) इंग्रजी → मराठी → संस्कृत → हिंदी.

(२) आकृती पूर्ण करा:

उत्तर:

सर्व विश्वचि व्हावे सुखी शब्दार्थ

• साधर्म्य – समान गोष्ट.
• चिरंजीव – चिरकाल टिकणारी गोष्ट.

सर्व विश्वचि व्हावे सुखी वाक्प्रचार व त्यांचे अर्थ

• साकडे घालणे : विनवणी करणे.
• आपलेसे करणे : आपुलकी निर्माण करणे,
• समरस होणे : एकरूप होणे.

Marathi Kumarbharti Std 10 Guide Pdf भाग-४

• आकाशी झेप घे रे Question Answer (कविता)
• सोनाली Question Answer
• निर्णय Question Answer
• तू झालास मूक समाजाचा नायक Question Answer (कविता)
• सर्व विश्वचि व्हावे सुखी Question Answer
• व्युत्पत्ती कोश Question Answer (स्थूलवाचन)

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 19 तू झालास मूक समाजाचा नायक (कविता) Notes, Textbook Exercise Important Questions, and Answers.

Class 10th Marathi Kumarbharti Chapter 19 तू झालास मूक समाजाचा नायक (कविता) Question Answer Maharashtra Board

Std 10 Marathi Chapter 19 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 19 तू झालास मूक समाजाचा नायक Textbook Questions and Answers

कृति

कृतिपत्रिकेतील प्रश्न २ (अ) साठी…

प्रश्न 1.
खालील आकृत्या पूर्ण करा.
(अ) (१) डॉ. बाबासाहेब आंबेडकरांनी नाकारलेली गोष्ट
उत्तर:
डॉ. बाबासाहेब आंबेडकरांनी नाकारलेली गोष्ट – [मळवाट]

(२) डॉ. बाबासाहेब आंबेडकरांचे स्वागत करणारे
उत्तर:
डॉ. बाबासाहेब आंबेडकरांचे स्वागत करणारे – [खाचखळगे]

(आ)

उत्तर:

प्रश्न 2.
कवितेतील संदर्भ आणि स्पष्टीकरणे यांच्या जोड्या लावा.
कवितेतील संदर्भ – स्पष्टीकरण
(१) मळवाट – (अ) अन्यायाविरुद्ध आवाज उठवू न शकणारा समाज
(२) खाचखळगे – (आ) पारंपरिक वाट
(३) मूक समाज – (इ) अडचणी, कठीण परिस्थिती
उत्तर:
(१) मळवाट – पारंपरिक वाट
(२) खाचखळगे – अडचणी, कठीण परिस्थिती
(३) मूक समाज – अन्यायाविरुद्ध आवाज उठवू न शकणारा समाज

प्रश्न 3.
चवदार तळ्याच्या घटनेनंतरच्या पन्नास वर्षांत वातावरणात झालेल्या बदलाचे वर्णन करणाऱ्या ओळी लिहा.
उत्तर:
(i) सूर्यफुले ध्यास घेत आहेत.
(ii) बिगूल प्रतीक्षा करीत आहे.
(iii) चवदार तळ्याचे पाणी थंड झाले आहे.

प्रश्न 4.
चवदार तळ्याच्या घटनेसंदर्भाने तुलना करा.
पन्नास वर्षांपूर्वीची परिस्थिती – पन्नास वर्षांनंतरची परिस्थिती
………………… – …………………
………………… – …………………
………………… – …………………
उत्तर:
पन्नास वर्षांपूर्वीची परिस्थिती पन्नास वर्षानंतरची परिस्थिती
(i) सूर्यफुलांनी पाठ फिरवली सूर्यफुले ध्यास घेत आहेत. होती.
(ii) रणशिंग फुकले होते. आता बिगूल वाट पाहत आहे.
(iii) चवदार तळ्याचे पाणी आता चवदार तळ्याचे पाणी पेटले होते थंड आहे.

प्रश्न 5.
काव्यसौंदर्य.
(अ) ‘तुझे शब्द जसे की
महाकाव्ये तुझ्या पायाजवळ गळून पडावीत
तुझा संघर्ष असा की
काठ्यांच्या संगिनी व्हाव्यात.’, या ओळींचे रसग्रहण करा.
उत्तर:
आशयसौंदर्य: डॉ. बाबासाहेब आंबेडकरांनी प्रस्थापित वर्णव्यवस्थेविरुद्ध महाड येथे चवदार तळ्याचा जो संग्राम केला व शोषितांवरील अन्यायाविरुद्ध लढा उभारला, त्याच्या पन्नास वर्षे पूर्तीनंतर कवी ज. वि. पवार यांनी ‘तू झालास मूक समाजाचा नायक’ या कवितेमध्ये आपले मनोगत व्यक्त केले आहे. मूक समाजाच्या या महानायकाला अभिवादन करताना त्यांच्या कार्याचा यथोचित गौरव केला आहे.

काव्यसौंदर्य: उपरोक्त ओळींमध्ये डॉ. बाबासाहेब आंबेडकर यांच्या शब्दांची किमया आणि संघर्षाचा परिणाम यांची महती कथन केली आहे. चवदार तळ्यावर सर्वांसाठी पाणी खुले करताना महामानवाने जी घोषणा केली त्या शब्दांपुढे सर्व महाकाव्ये नतमस्तक व्हावीत अशी होती. तसेच जो संघर्ष केला त्याचा प्रभाव असा पडला की शोषितांच्या हातातल्या काठ्या जणू जहाल बंदुका झाल्या. डॉ. बाबासाहेबांचा शब्द व संघर्षाचे सामर्थ्य यातून व्यक्त होते.

भाषिक वैशिष्ट्ये: मुक्तछंदात (मुक्तशैली) लिहिलेली ही कविता, त्यातील ओजस्वी शब्दकळेमुळे कार्यकर्त्यांच्या काळजाला थेट भिडते. काव्यात्म पण थेट विधानांमुळे त्यातील विचार परिणामकारक झाले आहेत. ‘महाकाव्याची नम्रता’ व ‘काठ्यांच्या बंदुका’ या प्रत्येकी शांतरस व अद्भुतरस यांची निर्मिती करतात.

(आ) डॉ. बाबासाहेब आंबेडकरांचे कवितेतून जाणवलेले कर्तृत्व तुमच्या शब्दांत लिहा.
उत्तर:
पारंपरिक वर्णव्यवस्थेने नाकारलेल्या व दैन्य, दारिद्रयाच्या अंधारात खितपत पडणाऱ्या मूक समाजाला डॉ. बाबासाहेब आंबेडकरांनी नवविचारांचा प्रकाश दाखवला. .अन्यायाविरुद्ध न बोलणाऱ्या समाजात जागृती निर्माण केली. सर्व सुखांनी पाठ फिरवलेली असताना व अडचणींचा मार्ग असताना पारंपरिक वाटेने जायचे नाकारून, कठीण परिस्थितीवर मात करून डॉ. बाबासाहेबांनी नवा इतिहास घडवला. बहिष्कृत भारताला आत्मविश्वास दिला. अगाध ज्ञानाच्या बळावर लढा पुकारून शोषित जनतेच्या पायातल्या बेड्या मुक्त केल्या. चवदार तळ्याचा संग्राम यशस्वी केला. अशा प्रकारे पीडित व शोषित समाजाला सन्मानाने जगायला शिकवले.

(ई) अगाध ज्ञानाच्या बळावर डॉ. बाबासाहेब आंबेडकर यांनी केलेले कार्य, तुमच्या शब्दांत थोडक्यात लिहा.
उत्तर:
अतिशय कठीण परिस्थितीमध्ये डॉ. बाबासाहेब आंबेडकरांनी आपले शिक्षण पूर्ण केले. त्यांनी बॅरिस्टर ही पदवी संपादन केली. ते उच्च विद्याविभूषित होते. त्यांनी आपल्या अगाध ज्ञानाच्या बळावर इथल्या बहिष्कृत समाजाला अन्यायापासून मुक्त करण्याचे अतिशय महत्त्वाचे कार्य अंगिकारले. शोषित, पीडित व वर्णव्यवस्थेतून नाकारलेल्या, समृद्धीपासून वंचित असलेल्या जनतेला संघटित केले. त्यांनी ‘शिका, संघटित व्हा व संघर्ष करा’ हा मूलमंत्र देऊन शोषित समाजाला आत्मविश्वास दिला. अन्यायाविरुद्ध लढा देण्यास प्रवृत्त केले. चवदार तळ्याचा संग्राम यशस्वी केला. समाजाला बोधितत्त्वाची शिकवण देऊन बौद्ध धर्म स्वीकारला. स्वतंत्र भारताचे संविधान लिहून भारतीय राज्यघटनेचे ते शिल्पकार ठरले. डॉ. बाबासाहेब आंबेडकरांना, त्यांच्या अगाध कर्तृत्वाला मानवंदना देण्यासाठी ‘भारतरत्न’ हा सर्वोच्च बहुमान सन्मानाने बहाल करण्यात आला.

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 19 तू झालास मूक समाजाचा नायक Additional Important Questions and Answers

प्रश्न. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:
कृती १: (आकलन)

प्रश्न 1.
चौकटी पूर्ण करा:
(i) मूक समाजाचे नायक
(ii) पाठ फिरवणारी
(iii) संपूर्ण जागृत केलेला
(iv) अगाध ज्ञानाच्या बळावर कुंकलेले –
(v) डॉ. आंबेडकरांच्या पायाजवळ गळून पडणारी
(vi) डॉ. बाबासाहेबांच्या डरकाळीने डळमळलेले
(vii) अजूनही प्रतीक्षा करणारा –
(vii) प्रस्तुत कविता या काव्यसंग्रहातून घेतली आहे
उत्तर:
(i) मूक समाजाचे नायक – डॉ. बाबासाहेब आंबेडकर
(ii) पाठ फिरवणारी – सूर्यफुले
(iii) संपूर्ण जागृत केलेला – बहिष्कृत भारत
(iv) अगाध ज्ञानाच्या बळावर फुकलेले – रणशिंग
(v) डॉ. आंबेडकरांच्या पायाजवळ गळून पडणारी – महाकाव्ये
(vi) डॉ. बाबासाहेबांच्या डरकाळीने डळमळलेले – आकाश व पृथ्वी
(vii) अजूनही प्रतीक्षा करणारा – बिगूल
(viii) प्रस्तुत कविता या काव्यसंग्रहातून घेतली आहे. – नाकेबंदी

कृतिपत्रिकेतील प्रश्न २ (आ) साठी…

प्रश्न.
पुढील कवितेसंबंधीत्याखाली दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा: कविता-तू झालास मूक समाजाचा नायक.
उत्तर:
(१) प्रस्तुत कवितेचे कवी: ज. वि. पवार.
(२) कवितेचा रचनाप्रकार: मुक्तछंद.
(३) कवितेचा काव्यसंग्रह: नाकेबंदी.
(४) कवितेचा विषय: डॉ. बाबासाहेब आंबेडकरांचे माहात्म्य,

(५) कवितेतून व्यक्त होणारा (स्थायी) भाव: सर्वहारा समाजात अशक्यप्राय वाटणारी जागृती करून त्याला स्वबळावर उभे केल्याबद्दलचा कृतज्ञता भाव,

(६) कवितेच्या कवींची लेखनवैशिष्ट्ये: कविता मुक्तछंदात आहे. ‘तू परिस्थितीवर स्वार झालास’, ‘इतिहास घडवलास’, ‘रणशिंग फुकलेस’, ‘गुलामांच्या पायातल्या बेड्या तोडल्यास’, ‘आकाश हादरलं’, ‘पृथ्वी डचमळली’, ‘चवदार तळ्याला आग लागली’ यांसारख्या लढवय्या शब्दप्रयोगांनी कविता ओजस्वी बनली आहे. पूर्वी दलित समाज बाबासाहेबांच्या नेतृत्वाखाली खवळून उठला होता. तथाकथित उच्चवर्णीयांमध्ये खळबळ माजली होती. हे ‘चवदार तळ्याला आग लागली’ या शब्दांतून प्रखरपणे व्यक्त होते. ‘आता दलित समाज शांत झाला आहे, ही बाब ‘चवदार तळ्याचे पाणी थंड झालंय’ या शब्दांतून व्यक्त होते.

(७) कवितेंची मध्यवर्ती कल्पना: डॉ. बाबासाहेब आंबेडकर यांनी केलेल्या महान कार्याबद्दल त्यांचे माहात्म्य कथन करण्यासाठी ही कविता लिहिली आहे. बाबासाहेबांनी सर्वार्थानी गांजलेल्या, पिचलेल्या समाजात जागृती निर्माण केली. त्यांना आत्मसन्मान मिळवून दिला. दलित समाजाला नवा जन्म दिला. पूर्ण खचलेल्या मनांमध्ये आत्मविश्वास ओतला. ही बाबासाहेबांची कर्तबगारी या कवितेचा आशय आहे.

(८) कवितेतून व्यक्त होणारा विचार: पारंपरिक वर्णव्यवस्थेने नाकारलेल्या व दैन्य, दारिद्र्याच्या चिखलात खितपत पडलेल्या समाजाला डॉ. बाबासाहेब आंबेडकरांनी बाहेर काढले. त्याला आत्मविश्वास दिला. स्वत:च्या पायावर उभे केले. संपूर्ण दलित समाज त्या वेळी बाबासाहेबांच्या पाठीशी उभा राहिला, चवदार तळ्याच्या सत्याग्रहाला, दलित चळवळीला तेज प्राप्त करून दिले. पण आता मात्र तोच दलित समाज थंड झाला आहे. त्याचे बाबासाहेबांनी मिळवून दिलेले तेज आता विरून गेले आहे. याविषयीची खंत कवींनी या कवितेत व्यक्त केली आहे.

(९) कवितेतील आवडलेली ओळ: आज पन्नास वर्षांनी अनुभवतोय सूर्यफुले तुझा ध्यास घेतायत बिगूल प्रतीक्षा करतोय चवदार तळ्याचं पाणी, तेही आता थंड झालंय.

(१०) कविता आवडण्याची वा न आवडण्याची कारणे: ही कविता अतिशय चांगली आहे. ओजस्वी शब्दांनी ओतप्रोत भरलेली आहे. कविता वाचत वाचत जाता बाबासाहेबांची महानता स्पष्ट होत जाते. त्यांनी दलित समाजाला दिलेल्या तेजाचा प्रत्यय येतो. शेवटच्या कडव्यात मात्र कलाटणी आहे. शेवटच्या कडव्याच्या आधीच्या कडव्यात प्रखर तेजाचा प्रत्यय येत राहतो. मात्र आता तोच दलित समाज शांत, थंड झाल्याची दु:खद जाणीव व्यक्त होते. ही दुःखद जाणीव शेवटच्या केवळ चार ओळींमध्ये व्यक्त झाली असतानाही आधीच्या जाज्वल्य भक्तीच्या पार्श्वभूमीवर मनाला व्याकूळ करते. हा दु:खभाव हाच या कवितेचा आत्मा आहे.

(११) कवितेतून मिळणारा संदेश: अज्ञान, दारिद्रय, जातीयता यांच्या चिखलात रुतून पडलेल्या समाजाला बाबासाहेबांनी बाहेर काढले. त्याला पृथ्वीच्या पाठीवर सन्मान मिळवून दिला. प्रखर आत्मविश्वास दिला. या लढ्याच्या काळात दलितांनी बाबासाहेबांना पूर्ण साथ दिली. पण आता मात्र दलित समाजामध्ये तेज मावळले आहे. तो थंड झाला आहे. तेव्हा या दलित समाजाने पुन्हा पूर्वीप्रमाणे सर्व ताकदीनिशी उठावे आणि पुन्हा एकदा विषमतेविरुद्ध लढ्याला सिद्ध व्हावे, अशी इच्छा कवी व्यक्त करतात. हाच या कवितेचा संदेश आहे.

रसग्रहण
कृतिपत्रिकेतील प्रश्न २ (इ) साठी…
प्रश्न. पुढील पंक्तींचे रसग्रहण तुमच्या शब्दांत लिहा:

प्रश्न 1.
‘आज पन्नास वर्षांनी अनुभवतोय सूर्यफुले तुझा ध्यास घेतायत बिगूल प्रतीक्षा करतोय चवदार तळ्याचं पाणी, तेही आता थंड झालंय.’ (सराव कृतिपत्रिका-२)
उत्तर:
आशयसौंदर्य: दलितांवरील अन्यायाविरुद्ध डॉ. बाबासाहेब आंबेडकरांनी पुकारलेला लढा हा ‘चवदार तळ्याचा संग्राम’ म्हणून प्रसिद्ध आहे. या लढ्याला पन्नास वर्षे उलटून गेल्यावर ज. वि. पवार यांनी ‘तू झालास मूक समाजाचा नायक’ या कवितेमध्ये या महामानवाला अभिवादन केले आहे. उपरोक्त ओळीत आताच्या परिस्थितीचे विदारक वर्णन केले आहे.

काव्यसौंदर्य: पन्नास वर्षे झाल्यानंतर चवदार तळ्याच्या संग्रामाचा ऊहापोह करताना व लढा थंड झाल्याची खंत व्यक्त करताना कवी म्हणतात-सुख-समृद्धीचे प्रतीक असणाऱ्या सूर्यफुलांनी भूतकाळात पाठ फिरवली होती, ती सूर्यफुले अजून तुझा ध्यास घेतायत. परिस्थितीत बदल न झाल्यामुळे संघर्षाला प्रवृत्त करणारा बिगूल तुझी वाट बघत आहे. चवदार तळ्याचे पाणी आता थंड पडले आहे. संघर्ष मावळला असला, तरी पुन्हा पेटण्यासाठी पाणी आसुसलेले आहे.

भाषिक वैशिष्ट्ये: ही कविता मुक्तच्छंदात (मुक्तशैली) आहे. त्यामळे भावनांचे व विचारांचे थेट प्रसारण योग्य शब्दांत झाले आहे. सूर्यफुले व बिगूल या प्रतीकांमुळे आशयघनता वाढली आहे. ‘चवदार तळ्याचं पाणी थंड पडणं’ या वाक्यखंडातून आताच्या विदारक परिस्थितीवर मार्मिकपणे बोट ठेवले आहे.

प्रश्न 2.
‘तू झालास परिस्थितीवर स्वार आणि घडविलास नवा इतिहास तू झालास मूक समाजाचा नायक आणि जागा केलास उभा बहिष्कृत भारत.’
उत्तर:
आशयसौंदर्य: डॉ. बाबासाहेब आंबेडकरांनी शोषित व पीडित जनतेवर होणाऱ्या अन्यायाविरुद्ध लढा उभारला. मूकसमाजाच्या या महानायकाला अभिवादन करताना ज. वि. पवार यांनी ‘तू झालास मूक समाजाचा नायक’ या कवितेमध्ये त्यांच्या महत्कार्याचा गौरव करताना उपरोक्त ओळी लिहिल्या आहेत.

काव्यसौंदर्य: चवदार तळ्याच्या संग्रामाला पन्नास वर्षे पूर्ण झाल्याच्या पार्श्वभूमीवर डॉ. बाबासाहेब आंबेडकरांच्या कर्तृत्वाची थोरवी गाताना कवी म्हणतात-प्रतिकूल परिस्थितीवर मात करून तुम्ही या वर्णव्यवस्थेने ग्रासलेल्या समाजाला जागृत केलेत. त्यांना नवविचारांची प्रेरणा देऊन नवीन इतिहास घडविला. अन्याय सहन करणाऱ्या जनतेचे तुम्ही महानायक झालात. बहिष्कृत असलेल्या पीडित समाजात नवचैतन्य निर्माण केलेत. त्यांच्यातील आत्मविश्वास जागवलात.

भाषिक वैशिष्ट्ये: मुक्तशैलीमध्ये लिहिलेली ही कविता त्यातील समर्पक शब्दांमुळे अर्थवाहक झाली आहे. ‘मूक समाज’ ‘बहिष्कृत भारत’ या संकल्पनांचा यथोचित वापर केल्यामुळे कविता परिणामकारक झाली आहे. सुयोग्य व ठाशीव शब्दकळा हे या कवितेचे बलस्थान आहे. थेट शब्दकळेमुळे ओज हा गुण दिसून येतो. आशयाला समर्पक अभिव्यक्तीची जोड मिळाल्यामुळे ओळी रसिकांच्या काळजाला भिडतात.

व्याकरण व भाषाभ्यास

(कृतिपत्रिकेतील प्रश्न ४ (अ) आणि (आ) यांसाठी…
व्याकरण घटकांवर आधारित कृतीः

१. समास:
पुढील समासांचे प्रत्येकी एकेक उदाहरण लिहा:
(i) अव्ययीभाव
(ii) विभक्ती तत्पुरुष
(iii) इतरेतर द्वंद्व
(iv) वैकल्पिक द्वंद्व
(v) समाहार वंद्व
(vi) द्विगू
(vii) कर्मधारय.
उत्तर:
(i) बेशक
(ii) भयमुक्त
(iii) आईबाबा
(iv) बरेवाईट
(v) हळदकुंकू
(vi) चौकोन
(vii) नीलपुष्प.

२. अलंकार:
‘व्यतिरेक’ या अलंकाराचे लक्षण सांगून उदाहरण लिहा:
उत्तर:
लक्षणे: उपमेय हे उपमानापेक्षा श्रेष्ठ असते, असे वर्णन केले असेल तर ‘व्यतिरेक’ हा अलंकार होतो.

उदाहरण:
‘तू माउलीहून मयाळ । चंद्राहुनि शीतळ ।
पाणियाहूनि पातळ । कल्लोळ प्रेमाचा ।।

३. वृत्त:
पुढील ओळींचे गण पाहून वृत्त ओळखा:
तुझ्या आसवांचा नभी पावसाळा
जशी सांज होता फुलांनी रडावे
उत्तर:

वृत्त – हे भुजंगप्रयात अक्षरगणवृत्त आहे.

४. शब्दसिद्धी:

प्रश्न 1.
‘गैर’ हा उपसर्ग असलेले चार शब्द लिहा:
[ ] [ ] [ ] [ ]
उत्तर:
[गैरहजर] [गैरसमज] [गैरसोय] [गैरशिस्त]

प्रश्न 2.
‘णारा’ हा प्रत्यय असलेले चार शब्द तयार करा:
उत्तर:
[ ] [ ] [ ] [ ]
[बोलणारा] [चालणारा] [लिहिणारा] [हसणारा]

प्रश्न 3.
‘शेजारीपाजारी’ यासारखे चार अभ्यस्त शब्द तयार करा:
उत्तर:
[बारीकसारीक] [उरलासुरला] [अघळपघळ] [आडवातिडवा]

५. सामान्यरूप:

पुढील शब्दांतील सामान्यरूप ओळखा:
(i) सूर्यफुलांनी
(ii) परिस्थितीवर
(iii) युद्धात
(iv) डरकाळीने
(v) वर्षांनी
(vi) ज्ञानाच्या.
उत्तर:
(i) सूर्यफुलांनी – सूर्यफुलां
(ii) परिस्थितीवर – परिस्थिती
(iii) युद्धात – युद्धा
(iv) डरकाळीने – डरकाळी
(v) वर्षांनी – वर्षां
(vi) ज्ञानाच्या – ज्ञाना.

६. वाक्प्रचार:

पुढील अर्थ असलेले वाक्प्रचार निवडा:
(i) वाट पाहणे –
(अ) प्रतीक्षा करणे
(आ) सहन करणे.
उत्तर:
वाट पाहणे – प्रतीक्षा करणे.

(ii) मदत न करणे – …………………………
(अ) अंग धरणे
(आ) पाठ फिरवणे.
उत्तर:
मदत न करणे – पाठ फिरवणे.

(iii) बाहेर ठेवणे – …………………………
(अ) उपकृत करणे
(आ) बहिष्कृत करणे.
उत्तर:
बाहेर ठेवणे – बहिष्कृत करणे.

भाषिक घटकांवर आधारित कृती:

१. शब्दसंपत्ती:

प्रश्न 1.
समानार्थी शब्द लिहा:
(i) खळगा= …………………………
(ii) जवान = …………………………
(ii) संघर्ष= …………………………
(iv) फूल = …………………………
उत्तर:
(i) खळगा = खड्डा
(ii) जवान = सैनिक, तरुण
(iii) संघर्ष = लढा
(iv) फूल = पुष्प.

प्रश्न 2.
विरुद्धार्थी शब्द लिहा:
(i) काळोख x …………………………
(ii) चवदार x …………………………
(iii) मूक x …………………………
(iv) थंड x …………………………
उत्तर:
(i) काळोख x उजेड
(ii) चवदार x बेचव
(iii) मूक x बोलका
(iv) थंड x उष्ण, गरम.

प्रश्न 3.
पुढील शब्दांतील अक्षरांपासून चार अर्थपूर्ण शब्द बनवा:
(i) मळवाटेने →
(ii) चवदार →
उत्तर:
(i) मळवाटेने → मळ – वाम – मवाळ – वाटेने
(ii) चवदार → चव – दार – वर – रख

प्रश्न 4.
गटात न बसणारा शब्द लिहा:
(i) पृथ्वी, अवनी, जमीन, वसुंधरा, रसा.
(ii) पाणी, जलद, तोय, उदक, नीर.
उत्तर:
(i) जमीन
(ii) जलद.

२. लेखननियम:
अचूक शब्द लिहा:
(i) ऐतिहासिक/ ऐतिहासीक / एतिहासिक /ऐतीहासिक.
(ii) वैश्विक / वेश्विक / वैश्वीक/वैस्विक.
(iii) माहीती /माहिती/माहिति /माहीति.
(iv) भवतिक / भौतीक / भौतिक / भौवतिक.
(v) वीपरीत / विपरीत / विपरित / वीपरित.
उत्तर:
(i) ऐतिहासिक
(ii) वैश्विक
(iii) माहिती
(iv) भौतिक
(v) विपरीत.

३. विरामचिन्हे:
विरामचिन्हांसमोर नावे लिहा:
[ : ] [ ]
[ ! ] [ ]
[ ; ] [ ]
[ ? ] [ ]
उत्तर:
(i) [ : ] [अपूर्णविराम]
(ii) [ ! ] [उद्गारचिन्ह]
(iii) [ ; ] [अर्धविराम]
(iv) [ ? ] [प्रश्नचिन्ह]

४. पारिभाषिक शब्द:

योग्य पर्याय निवडा:
(i) Correspondence – …………………………
(१) व्यवहार
(२) पत्रवाटप
(३) पत्रव्यवहार
(४) कर्जवाटप
उत्तर:
(३) पत्र्यव्यवहार

(ii) Humanism – …………………………
(१) व्यक्तिवाद
(२) भूतदया
(३) मानवतावाद
(४) सामाजिक
उत्तर:
(३) मानवतावाद

(iii) Journalism – …………………………
(१) वृत्तपत्र
(२) मुखपत्र
(३) पत्रकारिता
(४) प्रसिद्धी माध्यम
उत्तर:
(३) पत्रकारिता

(iv) Lecturer – …………………………
(१) शिक्षक
(२) प्राचार्य
(३) अधिव्याख्याता
(४) व्याख्याता
उत्तर:
(३) अधिव्याख्याता

(v) Pocket Money – …………………………
(१) जमाखर्च
(२) पैसाअडका
(३) हातखर्च
(४) पावती
उत्तर:
(३) हातखर्च

(vi) Qualitative – …………………………
(१) गुणपत्रक
(२) गुणात्मक
(३) प्रसिद्धी
(४) गणसंख्या
उत्तर:
(२) गुणात्मक

५. अकारविल्हे /भाषिक खेळ:
(१) पुढील शब्द अकारविल्हेनुसार लिहा:
(i) रणशिंग → बिगूल → तुतारी → नगारा.
(ii) सूर्यफूल → मोगरा → गुलाब → चाफा.
उत्तर:
(i) तुतारी → नगारा → बिगूल → रणशिंग.
(ii) चाफा → गुलाब → मोगरा → सूर्यफूल.

(२) शब्द बनवा:

उत्तर:

तू झालास मूक समाजाचा नायक Summary in Marathi

तू झालास मूक समाजाचा नायक कवितेचा भावार्थ

वर्णव्यवस्थेला क्रूर दुष्ट चक्रात खितपत पडलेल्या शोषित व पीडित जनतेमध्ये जागृती आणण्यासाठी व त्यांच्यामध्ये आत्मविश्वास जागवण्यासाठी डॉ. बाबासाहेब आंबेडकर यांनी महाड येथे चवदार तळ्याचा संग्राम केला. या घटनेला पन्नास वर्षे पूर्ण झाल्याच्या निमित्ताने या महानायकाला कवींनी कवितेतून अभिवादन केले आहे. कवी म्हणतात –

हे महानायका, तू या शोषित वर्गासाठी लढा उभारायला निघालास तेव्हा काळोखाचे साम्राज्य होते. दु:ख, दैन्य, दारिद्रय व सामाजिक असमता यांच्या अंधाराने शोषित वर्ग ग्रासलेला होता. सतेज किरणांनी न्हायलेल्या उमेदीच्या सुखाच्या सूर्यफुलांनी साथ दिली नाही. तू एकाकी होतास, तरी डगमगला नाहीस. तू बुरसटलेल्या विचारांच्या पारंपरिक वाटेने जायचे नाकारलेस. नवविचारांचा, जागृतीचा मार्ग खाचखळग्यांनी भरलेला अतिशय खडतर होता. खड्ड्यांनी म्हणजे अनेक अडचणींनी तुझे स्वागत केले.

अशा या प्रतिकूल परिस्थितीची तू तमा बाळगली नाहीस. त्यावरही तू मात केलीस आणि नवविचारांच्या प्रेरणांचा नवीन इतिहास तू घडवलास, आतापर्यंत वर्णव्यवस्थेने नाकारलेल्या, अन्याय सहन करणाऱ्या सर्वहारा जनतेचा तू नायक झालास आणि दुर्लक्षित असलेल्या, बहिष्कृत असलेल्या भारतीय समाजात तू जागृती आणलीस. नवचैतन्य आणलेस, त्यांच्यात आत्मविश्वास जागा केलास.

तुझ्या अपरिमित, प्रचंड ज्ञानाच्या सामर्थ्याने तू संग्रामाचे रणशिंग फुकलेस, अन्यायाविरुद्ध बंड करण्यास सज्ज झालास. आतापर्यंत गुलामगिरीत खितपत पडणाऱ्या बांधवांच्या पायातल्या दास्याच्या साखळ्या तू तोडून टाकल्यास आणि एखादया युद्धात सैनिकांना सज्ज करावे, तसे चवदार तळ्याच्या संग्रामासाठी सर्व दलित बांधवांना तळ्याच्या काठी उभे केलेस.

सर्व महाकाव्यांनी तुझ्या चरणाशी नतमस्तक व्हावे, असे तुझे संघर्षमय शब्द होते. हातातील सर्व काठ्या बंदुका होऊन बरसाव्यात, असा तुझा अनोखा संघर्ष होता. तुझ्या बुलंद घोषणेमुळे आकाश हादरून गेले नि पृथ्वी डळमळू लागली आणि बघता बघता चवदार तळ्याच्या पाण्याला आग लागली म्हणजेच संघर्ष पेटला.

या चवदार तळ्याच्या संग्रामाला आता पन्नास वर्षे उलटून गेली. कवी म्हणतात – पन्नास वर्षांनी तो संघर्ष पुन्हा मी अनुभवू पाहतो. अजूनही ज्या सूर्यफुलांनी भूतकाळात पाठ फिरवली होती, ती सूर्यफुले अजून तुझा ध्यास घेत आहेत. पुन्हा संघर्ष करण्यासाठी संघर्षाला प्रवृत्त करणारे बिगूल तुझी वाट बघत आहे. चवदार तळ्याचे पाणी आता थंड पडले आहे. संघर्ष मावळला आहे. (पण चवदार तळ्याचे पाणी आजही पुन्हा पेटण्यासाठी आसुसलेले आहे. शोषितांची परिस्थिती फारशी चांगली नाही.)

तू झालास मूक समाजाचा नायक शब्दार्थ

• मूक – अबोल,
• नायक – नेते, कप्तान, अग्रणी, प्रणेता.
• खाचखळगे – खड्डे.
• स्वार – आरूढ.
• बहिष्कृत – बाहेर टाकलेला, परित्यक्त.
• अगाध – प्रचंड.
• बळ – शक्ती, सामर्थ्य.
• बेड्या – साखळ्या.
• जवान – सैनिक.
• संघर्ष – लढा, झुंज.
• संगिनी – बंदुका,
• डरकाळी – वाघाची आरोळी.
• हादरणे – थरथरणे.
• डचमळली – डळमळीत झाली.
• प्रतीक्षा – वाट पाहणे.

तू झालास मूक समाजाचा नायक वाक्प्रचार व त्यांचे अर्थ

• पाठ फिरवणे : मदत न करणे, वंचित ठेवणे.
• स्वागत करणे : मानाने, आदराने एखादया व्यक्तीला या म्हणणे.
• परिस्थितीवर स्वार होणे : परिस्थितीवर मात करणे,
• बहिष्कृत करणे : बाहेर ठेवणे, वंचित करणे.
• रणशिंग फुकणे : युद्ध सुरू होण्याचा इशारा देणे.
• बेड्या तोडणे : स्वतंत्र होणे,
• गळून पडणे : निखळून पडणे.
• ध्यास घेणे : एखाद्या गोष्टीची ओढ वाटणे.
• प्रतीक्षा करणे : वाट पाहणे.

Marathi Kumarbharti Std 10 Guide Pdf भाग-४

• आकाशी झेप घे रे Question Answer (कविता)
• सोनाली Question Answer
• निर्णय Question Answer
• तू झालास मूक समाजाचा नायक Question Answer (कविता)
• सर्व विश्वचि व्हावे सुखी Question Answer
• व्युत्पत्ती कोश Question Answer (स्थूलवाचन)

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 13 कर्ते सुधारक कर्वे Notes, Textbook Exercise Important Questions and Answers.

Class 10th Marathi Kumarbharti Chapter 13 कर्ते सुधारक कर्वे Question Answer Maharashtra Board

Std 10 Marathi Chapter 13 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 13 कर्ते सुधारक कर्वे Textbook Questions and Answers

प्रश्न 1.
खालील आकृत्या पूर्ण करा.

उत्तर:

प्रश्न 2.
महर्षी कर्वे यांच्या कार्यकुशलतेचा ओघतक्ता तयार करा.

उत्तर:

प्रश्न 3
हे केव्हा घडेल ते लिहा.
(अ) का सुधारकाने सुरू केलेले कार्य पूर्णत्वास जाईल – ……………………………………..
(आ) स्त्री पुरुषांशी स्पर्धा करू शकेल – ……………………………………..
उत्तर :
(अ) का सुधारकाने सुरू केलेले कार्य पूर्णत्वास जाईल, जेव्हा पुरुषांचेही ‘शिक्षण’ होईल.
(आ) स्त्री पुरुषांशी स्पर्धा करू शकेल, जेव्हा ती उच्चविद्याविभूषित होईल.

प्रश्न 4.
चौकटी पूर्ण करा.
(अ) लेखकांच्या मते दुसऱ्याच्या दुःखात दुःखी व सुखात सुखी होणारा – [ ]
(आ) कर्वे यांना लोकमानसाने दिलेली पदवी – [ ]
उत्तर :
(अ) लेखकांच्या मते, दुसऱ्याच्या दुःखात – स्थितप्रज्ञ दुःखी व सुखात सुखी होणारा
(आ) कर्वे यांना लोकमानसाने दिलेली पदवी – महर्षी

प्रश्न 5.
पाठाच्या आधारे वाक्यांचा उर्वरित भाग लिहून वाक्ये पूर्ण करा.
(अ) स्त्रीने स्वातंत्र्य कमवावे असे वाटणे म्हणजे
(आ) समाजाविरूद्ध विद्रोह केला तर
(इ) लोकांनी कर्वे यांची ससेहोलपट चालवली तरी
उत्तर:
(i) स्त्रीने स्वातंत्र्य कमवावे असे वाटणे म्हणजे खडकावर डोके आपटण्यासारखे आहे.
(ii) समाजाविरुद्ध विद्रोह केला तर विद्रोह करणाऱ्याला समाज गिळून टाकायला येईल.
(iii) लोकांनी कर्वे यांची ससेहोलपट चालवली तरी कव्यांनी त्यांना शिव्याशाप दिले नाहीत किंवा आपल्या कार्यापासून कर्वे विचलित झाले नाहीत.

प्रश्न 6.
‘कार्य’ या शब्दासाठी पाठात आलेली विशेषणे शोधा.
उत्तर:
कार्य या नामाची विशेषणे : मोठे, अतोनात, कठीण, ऐतिहासिक, जटिल, अटीतटीचे, महाकठीण, अलौकिक, महान इत्यादी.

प्रश्न 7.
खालील वाक्यांतील वाक्प्रचार शोधा.
(अ) शिक्षकांनी सांगितलेली हृदय आठवण आमच्या मनात घर करून राहिली.
(आ) वक्त्याचे विचार अनेकांच्या पचनी पडले नाहीत.
उत्तर:
(अ) मनात घर करून राहणे.
(आ) पचनी न पडणे.

प्रश्न 8.
खालील वाक्यांतील उभयान्वयी अव्यये शोधून लिहा.
(अ) त्याने लाडू व करंज्या खाल्ल्या.
(आ) पाऊस आला आणि गारा पडल्या.
(इ) तो येणार, कारण त्याला पैशांची गरज आहे.
(ई) आजी म्हणाली, की मी उद्या गावाला जाणार आहे.
उत्तर:
(i) व
(ii) आणि
(iii) कारण
(iv) की.

प्रश्न 9.
केवलप्रयोगी अव्ययांचा वापर करून वाक्ये पुन्हा लिहा.
(अ) …………..! काय सुंदर देखावा आहे हा!
(आ) ………….! असा प्रसंग वैऱ्यावर देखील येऊ नये,
(इ) …………..! तुझी कल्पनाच मुळी मला पसंत नाही.
(ई) …………..! आज तू खूप चांगला खेळलास.
उत्तर:
(i) ओहो! काय सुंदर देखावा आहे हा!
(ii) अरेरे! असा प्रसंग वैऱ्यावर देखील येऊ नये.
(iii) छे! तुझी कल्पनाच मुळी मला पसंत नाही.
(iv) वाहव्वा! आज तू फार चांगला खेळलास.

प्रश्न 10.
स्वमत.
(अ) ‘स्त्रियांनी शिकणे अत्यंत गरजेचे आहे’, या विधानामागील अण्णांचा दृष्टिकोन स्पष्ट करा.
उत्तर :
समाजात स्त्रियांची संख्या पुरुषांइतकीच असते. थोडी कमी-जास्त भरेल. पण साधारणपणे स्त्रिया म्हणजे समाजाचा अर्धा भाग होय. दुर्दैवाने आपल्या समाजाने स्त्रियांना मागासलेले ठेवले. त्यामुळे अर्धा समाज मागासलेला राहिला. त्याचे अनंत तोटे समाजाला आजसुद्धा भोगावे लागत आहेत. बहुतेक वेळा हे नुकसान मोजता येत नाही. मोजता न आल्यामुळे आपले किती नुकसान झालेले आहे, हे कळतही नाही. स्त्रियांना मागासलेले ठेवल्यामुळे समाजाची अर्धी बुद्धिमत्ता निरुपयोगी राहते. त्या बुद्धीचा समाजाला उपयोग झाला असता, पण ती वाया जाते. पुरुष बहुतांश वेळा स्वार्थी व आत्मकेंद्री असतो, स्त्री अधिक सामाजिक असते. यामुळे कुटुंबातला पुरुष शिकला तर कुटुंबातील एका व्यक्तीचा विकास होतो. मात्र स्त्री शिकली तर त्याचा परिणाम संपूर्ण कुटुंबावर होतो. अखंड कुटुंब शिक्षित होते. आपण हे ओळखले पाहिजे. स्त्रीला पुरुषांच्या बरोबरीचे स्थान दिले पाहिजे.

(आ) ‘जया अंगी मोठेपण, तया यातना कठीण’ हे वचन महर्षी कर्वे यांच्या जीवनाला कसे लागू पडते, ते स्पष्ट करा.
उत्तर :
अण्णासाहेबांनी फार मोठे स्वप्न पाहिले होते. ते फार मोठी ! झेप घेऊ पाहत होते. त्यांच्या स्वप्नाला संपूर्ण समाजाची साथ मिळाली नाही. समाजाने अण्णासाहेबांना ओळखलेच नाही. समाजाने साथ दिली नाहीच; उलट पराकोटीचा विरोध केला. त्यांचा सतत अपमान केला. त्यांना धक्काबुक्की केली. त्यांचे कपडे फाडले. हे रोज घडत होते. त्यामुळे स्वत:चे कपडे रोज रोज शिवण्याची पाळी त्यांच्यावर येई. स्त्री-शिक्षणासाठी देणग्या गोळा केल्या तर भ्रष्टाचाराचा सतत धाक दाखवला जाई. त्यांच्या चळवळीमुळे कुटुंबीयांनाही त्रास सहन करावा लागे. त्यांच्यावर बहिष्कार टाकण्यातही आला होता. हे सर्व यातनामय होते. लोककल्याणासाठी अण्णासाहेबांनी या यातना सहन केल्या. आज आपण अण्णासाहेबांची स्मारके उभारतो. परंतु प्रत्यक्ष जीवनात त्यांना दुःख, कष्ट आणि यातनाच सहन कराव्या लागल्या. ‘जया अंगी मोठेपण, तया यातना कठीण’ हे तुकाराम महाराजांचे वचन अण्णासाहेबांना तंतोतंत लागू पडते.

(इ) ‘कर्ते सुधारक कर्वे’ या पाठातून महर्षी अण्णा कर्वे यांचे तुम्हाला जाणवलेले वेगळेपण, तुमच्या शब्दांत सांगा.
उत्तर :
अण्णासाहेब कर्वे यांचे फार मोठे वेगळेपण या पाठातून वाचकांसमोर येते, बऱ्याच वेळा सामाजिक कार्य करणाऱ्या लोकांना स्वतःच्या सामाजिक कार्याचा गर्व असतो. ती माणसे या गर्वामुळे आक्रमक बनतात, अण्णासाहेबांची प्रकृती याबाबतीत नेमकी उलटी होती. त्यांना प्रचंड आत्मविश्वास होता. पण गर्व नव्हता. ते कधीच आक्रमक बनले नाहीत, उलट ते शांतपणे, कोणावरही न रागावता, आक्रस्ताळेपणा न करता आपले काम करीत. त्यांचे अपमान झाले. अडवणूक झाली. त्यांच्यावर हल्ले झाले. जाता-येता त्यांचे कपडे फाडले गेले. पण ते विचलित झाले नाहीत. घाबरले नाहीत किंवा दुःखी-कष्टीही झाले नाहीत. ते स्थितप्रज्ञाप्रमाणे शांत राहिले. नव्हे ते स्थितप्रज्ञच होते. हा त्यांचा गुण, त्यांचा वेगळेपणा मला खूप भावला आहे. खूप आवडला आहे.

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 13 कर्ते सुधारक कर्वे Additional Important Questions and Answers

कृति

कृतिपत्रिकेतील प्रश्न १ (अ) आणि (आ) यांसाठी…

उतारा क्र.१
प्रश्न. पुढील उतारा वाचा आणि दिलेल्या सूचनांनुसार कृती करा :

कृती १ : (आकलन)

प्रश्न 1.
कारणे लिहा :
(i) नातेवाईक नसलेले महर्षी कर्वे हे निवर्तल्यानंतर लेखकांच्या आजोबांच्या डोळ्यांत अश्रू आले; कारण –
(ii) अण्णासाहेब कर्वे यांच्या मते, केवळ राष्ट्रीय स्वातंत्र्य मिळणे उपयोगाचे नव्हते; कारण –
(iii) भारतीय स्त्री स्वत:च आपल्या गुलामीला दागिना मानीत होती; कारण –
उत्तर:
(i) नातेवाईक नसलेले महर्षी कर्वे हे निवर्तल्यानंतर लेखकांच्या आजोबांच्या डोळ्यांत अश्रू आले; कारण महान कार्य केलेले महर्षी कर्वे आपल्यातून गेले याची दुःखद जाणीव आजोबांना झाली.
(ii) अण्णासाहेब कर्वे यांच्या मते, केवळ राष्ट्रीय स्वातंत्र्य मिळणे उपयोगाचे नव्हते; कारण स्त्रियांना स्वातंत्र्य मिळाले नाही, तर राष्ट्रीय स्वातंत्र्याला काहीही अर्थ राहत नाही.
(iii) भारतीय स्त्री स्वत:च आपल्या गुलामीला दागिना मानीत होती; कारण तसे मानण्याचे संस्कारच तिच्यावर झाले होते.

प्रश्न 2.
विसंगती लिहा :
(i) अण्णासाहेब कर्वे समाजासाठी कार्य करीत होते, पण समाज ………………………………
(ii) आपल्या समाजात स्त्रीला देवीचे स्थान आहे, असे दाखवले जाते, पण प्रत्यक्षात मात्र ………………………………
(iii) भारतीय स्त्री गुलामीत जगत होती, पण ती ………………………………
उत्तर:
(i) अण्णासाहेब कर्वे समाजासाठी कार्य करीत होते, पण समाज त्यांना समाजविरोधक समजत होता.
(ii) आपल्या समाजात स्त्रीला देवीचे स्थान आहे, असे दाखवले जाते, पण प्रत्यक्षात मात्र तिला शूद्रातिशूद्र समजून तिचा प्रच्छन्न छळच केला जाई.
(iii) भारतीय स्त्री गुलामीत जगत होती, पण ती आपल्या गुलामीलाच दागिना समजत होती.

प्रश्न 3.
माहिती लिहा :
(i) अण्णासाहेब कर्वे यांनी घालून दिलेला वस्तुपाठ
(ii) प्रा. अण्णासाहेब कर्वे यांचा कॉलेजात शिकवण्याचा विषय
(iii) त्या वेळच्या अज्ञ समाजाने मानलेले स्वत:चे ‘ऐतिहासिक कार्य
(iv) अण्णासाहेबांनी सुरुवातीला स्थापन केलेली संस्था
(v) अनाथ बालिकाश्रमाचे रूपांतर झालेली संस्था
(vi) निधी उभारणीसाठी अण्णासाहेबांनी निर्माण केलेल्या यंत्रणा
उत्तर:
(i) अण्णासाहेब कर्वे यांनी घालून दिलेला वस्तुपाठ – पहिल्या पत्नीच्या मृत्यूनंतर त्यांनी स्वतः विधवेशी विवाह केला.
(ii) प्रा. अण्णासाहेब कर्वे यांचा कॉलेजात शिकवण्याचा विषय – गणित.
(iii) त्या वेळच्या अज्ञ समाजाने मानलेले स्वत:चे ‘ऐतिहासिक कार्य’ – सत्पुरुषांचा छळ करावा.
(iv) अण्णासाहेबांनी सुरुवातीला स्थापन केलेली संस्था – अनाथ बालिकाश्रम.
(v) अनाथ बालिकाश्रमाचे रूपांतर झालेली संस्था – हिंगणे स्त्री-शिक्षण संस्था.
(vi) निधी उभारणीसाठी अण्णा साहेबांनी निर्माण केलेल्या यंत्रणा – ‘पै पै चा निधी’ आणि ‘मुरूड निधी.’

कृती ३ : (व्याकरण)

प्रश्न 1.
कंसांतील सूचनांनुसार उत्तर: लिहा :
(i) सुरुवात त्यांनी स्वत:पासून केली. (अधोरेखित शब्दाच्या जागी ‘करतात’ हा शब्द वापरून वाक्य पुन्हा लिहा.)
(ii) त्याच अनपढ राहिल्या तर? (अधोरेखित शब्दाच्या जागी ‘तीच’ हा शब्द वापरून वाक्य पुन्हा लिहा.)
(iii) कव्यांच्या पुतळ्याच्या मागे एक मुलगी रडत बसली होती. (‘मुलगा’ हा शब्द अधोरेखित शब्दाच्या जागी योजा आणि वाक्य पुन्हा लिहा.)
उत्तर:
(i) सुरुवात ते स्वत:पासून करतात.
(ii) तीच अनपढ़ राहिली तर?
(iii) कर्त्यांच्या पुतळ्याच्या मागे एक मुलगा रडत बसला होता.

प्रश्न 2.
अनेकवचन लिहा :
(i) रात्र
(ii) डोळा
(iii) कार्य
(iv) स्त्री
(v) पोथी
(vi) मेढ.
उत्तर:
(i) रात्र – रात्री
(ii) डोळा – डोळे
(iii) कार्य – कायें
(iv) स्त्री – स्त्रिया
(v) पोथी – पोथ्या
(vi) मेढ – मेढी.

उतारा क्र. २

प्रश्न. पुढील उतारा वाचा आणि दिलेल्या सूचनांनुसार कृती करा :
कृती १: (आकलन)

प्रश्न 1.
आकृती पूर्ण करा :

उत्तर :

प्रश्न 3.
चौकटी पूर्ण करा :
(i) कर्वे यांना राजमानसाने दिलेली पदवी
उत्तर :
(i) कर्वे यांना राजमानसाने दिलेली पदवी – भारतरत्न।

कृती २ : (आकलन)

प्रश्न 1.
आकृत्या पूर्ण करा :

उत्तर:

कृती ३ : (व्याकरण)

प्रश्न 1.
पुढील वाक्यातील नामे ओळखा आणि ती मूळ रूपांत लिहा :
महर्षी कर्वे यांनी ‘अनाथ बालिकाश्रमा’ची मुहूर्तमेढ रोवली.
उत्तर:
नामे : महर्षी, बालिकाश्रम, मुहूर्तमेढ.

प्रश्न 2.
पुढील वाक्यातील उभयान्वयी अव्यये लिहा :
तिला स्वतंत्र व्हायचे असेल तर तिला भान यावयास हवे, की आपण गुलाम आहोत आणि हे भान शिक्षणाशिवाय येऊ शकत नाही.
उत्तर:
उभयान्वयी अव्यये : तर, की, आणि.

प्रश्न 3.
अधोरेखित शब्दातील प्रत्यय ओळखा आणि तो प्रत्यय जोडलेले अन्य दोन शब्द लिहा :
स्त्रीने शिक्षित झालेच पाहिजे.
उत्तर:
प्रत्यय : इत. अन्य शब्द : प्रमाणित, प्रभावित.

प्रश्न 4.
पुढील शब्दांतून शब्दयोगी अव्यय जोडलेले शब्द ओळखून लिहा :
शिक्षणाशिवाय, विरोधाभास, ऋणातही, व्यक्तीसारखा, अर्धागवायू, दुसरीकडे, पृथ्वीबाहेर, जगप्रवास, पुरुषप्रधान, स्त्रियांवरील, जन्मलेला.
उत्तर:
शिक्षणाशिवाय, ऋणातही, व्यक्तीसारखा, दुसरीकडे, पृथ्वीबाहेर, स्त्रियांवरील.

व्याकरण व भाषाभ्यास

कृतिपत्रिकेतील प्रश्न ४ (अ) आणि (आ) यांसाठी…

व्याकरण घटकांवर आधारित कृती :

१. समास :
(१) पुढील विग्रहांवरून सामासिक शब्द तयार करा :
(i) खाणे, पिणे वगैरे
(ii) चार कोनांचा समूह
(iii) पास किंवा नापास
(iv) प्रत्येक रस्त्यावर
(v) बाप आणि लेक
(vi) वसतीसाठी गृह.
उत्तर:
विग्रह – सामासिक शब्द
(i) खाणे, पिणे वगैरे – खाणेपिणे
(ii) चार कोनांचा समूह – चौकोन
(iii) पास. किंवा नापास – पासनापास
(iv) प्रत्येक रस्त्यावर – रस्तोरस्ती
(v) बाप आणि लेक – बापलेक
(vi) वसतीसाठी गृह – वसतिगृह

(२) पुढील तक्ता पूर्ण करा : (सराव कृतिपत्रिका-३)
समासाचे नाव – उदाहरण – समास विग्रह
(i) समाहार वंद्व समास – केरकचरा – ……………………….
(ii) ………………………. – प्रतिक्षण – प्रत्येक क्षणाला
(iii) द्विगू समास – ………………………. – पाच आरत्यांचा समूह
(iv) विभक्ती तत्पुरुष समास – ………………………. – राजाचा वाडा
उत्तर:
समासाचे नाव – उदाहरण – समास विग्रह
(i) समाहार द्वंद्व समास – केरकचरा केर, कचरा वगैरे
(ii) अव्ययीभाव समास – प्रतिक्षण प्रत्येक क्षणाला
(iii) द्विगू समास – पंचारती पाच आरत्यांचा समूह
(iv) विभक्ती तत्पुरुष समास – राजवाडा राजाचा वाडा

२. अलंकार :
पुढील आकृती पाहून अलंकार ओळखा व एक उदाहरण दया :

उत्तर :
अलंकार – [दृष्टान्त]
उदाहरण : लहानपण दे गा देवा। मुंगी साखरेचा रवा।
ऐरावत रत्न थोर। त्यासी अंकुशाचा मार।।

३. वृत्त:

(१) पुढील ओळीचा लगक्रम लिहा :
प्रभाते मनी राम चिंतीत जावा
उत्तर :

(२) पुढील काव्यपंक्तीतील वृत्त ओळखा : (सराव कृतिपत्रिका-१)
द्रव्यास हे गमन मार्ग यथावकाश
उत्तर:

वृत्त : हे वसंततिलका वृत्त आहे.

४. शब्दसिद्धी :
(१) पुढील शब्दांना ‘इक’ हा प्रत्यय लावून शब्द बनवा :
जसे → नगर + इक → नागरिक
(i) समाज → [ ]
(ii) शरीर → [ ]
उत्तर:
(i) [सामाजिक]
(ii) [शारीरिक]

(२) परि’ हा उपसर्ग लावून दोन शब्द तयार करा :
जसे → परि + पूर्ण → परिपूर्ण
(i) क्रमा → [ ]
(ii) श्रम → [ ]
उत्तर:
(i) [परिक्रमा]
(ii) [परिश्रम]

(३) ‘अडीअडचणी’ सारखे पाठातील चार अभ्यस्त शब्द लिहा :
उत्तर:
(i) धक्काबुक्की
(ii) हालअपेष्टा
(iii) अटीतटी
(iv) कुरबूर

५. सामान्यरूप :
पुढील तक्ता पूर्ण करा :
शब्द – विभक्ती प्रत्यय – सामान्यरूप
(i) दु:खात – …………………… – ……………………
(ii) कव्यांनी – …………………… – ……………………
(iii) कन्येशी – …………………… – ……………………
(iv) स्वातंत्र्याचा – …………………… – ……………………
उत्तर:
शब्द – विभक्ती प्रत्यय – सामान्यरूप
(i) दु:खात – त – दु:ख
(ii) कव्यांनी – नी – कव्यां
(iii) कन्येशी – शी – कन्ये
(iv) स्वातंत्र्याचा – चा – स्वातंत्र्य

६. वाक्प्रचार :
(१) कंसातील वाक्प्रचारांचा त्या खालील वाक्यांत योग्य ठिकाणी वापर करून वाक्ये पुन्हा लिहा : (खूणगाठ बांधणे, वस्तुपाठ घालून देणे, मुहूर्तमेढ रोवणे, ससेहोलपट होणे)
(i) रात्रीच्या वेळी रानातला रस्ता शोधता शोधता प्रवाशांना खूप त्रास झाला.
(ii) गाडगेमहाराजांनी स्वच्छता मोहिमेचा पाया घातला,
(iii) अजयने दररोज नियमित व्यायाम करण्याचा मनाशी दृढ निश्चय केला.
(iv) जनसेवा कशी करावी, याचा महात्मा गांधीजींनी आदर्श घालून दिला.
उत्तर:
(i) रात्रीच्या वेळी रानातला रस्ता शोधता शोधता प्रवाशांची ससेहोलपट झाली.
(ii) गाडगेमहाराजांनी स्वच्छता मोहिमेची मुहूर्तमेढ रोवली.
(iii) अजयने दररोज नियमित व्यायाम करण्याची मनाशी खूणगाठ बांधली.
(iv) जनसेवा कशी करावी, याचा महात्मा गांधीजींनी वस्तुपाठ घालून दिला.

*(२) पुढील वाक्यांतील वाक्प्रचार शोधा :
(i) शिक्षकांनी सांगितलेली हृदय आठवण आमच्या मनात घर करून राहिली.
(ii) वक्त्याचे विचार अनेकांच्या पचनी पडले नाहीत.

आभाषिक घटकांवर आधारित कृती :

१. शब्दसंपत्ती :
(१) पुढील शब्दसमूहांसाठी एक शब्द लिहा :
(i) लिहिता-वाचता न येणारा – ………………………
(ii) चांगल्या प्रकारे शिक्षित असलेला – ………………………
(iii) लिहिता-वाचता येणारा – ………………………
(iv) जिचे सौभाग्य हरपले आहे अशी स्त्री – ………………………
(v) केलेले उपकार जाणणारा – ……………………… (मार्च १९)
(vi) कोणाचाही आधार नसलेला – ……………………… (मार्च १९)
उत्तर:
(i) निरक्षर
(ii) सुशिक्षित
(iii) साक्षर
(iv) विधवा
(v) कृतज्ञ
(iv) निराधार.

(४) विरुद्धार्थी शब्द लिहा :
(i) सहिष्णू x ……………………
(ii) स्वातंत्र्य x ……………………
(iii) सुरुवात x ……………………
(iv) जन्म x ……………………
(v) जमा x ……………………
(vi) सोय x ……………………
(vii) उधळपट्टी x ……………………
(viii) अनाथ x ……………………
उत्तर:
(i) सहिष्णू x असहिष्णू
(i) स्वातंत्र्य x पारतंत्र्य
(iii) सुरुवात x शेवट
(iv) जन्म र मृत्यू
(v) जमा x खर्च
(vi) सोय x गैरसोय
(vii) उधळपट्टी x कंजुषी
(viii) अनाथ x सनाथ.

(५) गटात न बसणारा शब्द लिहा :
(i) आई, वडील, बहीण, बायको, कन्या – ……………………
(ii) मन, तन, चित्त, जिव्हार, अंत:करण – ……………………
उत्तर:
(i) वडील
(ii) तन,

(६) दिलेल्या शब्दांतून दोन अर्थपूर्ण शब्द तयार करा :
(सराव कृतिपत्रिका-३) (नगर व पालिका हे दोन शब्द सोडून)
नगरपालिका → [ ] [ ]
उत्तर :
नगरपालिका – [नग] [नर]

२. लेखननियम :
(१) अचूक शब्द निवडा :
(i) विभूषित/वीभूषित/विभुशित/विभुषीत.
(ii) पुर्नविवाह/पुनर्विवाह/पूर्नवीवाह/पुनर्वीवाह.
(iii) शैक्षणीक शैक्षणिक/शैक्षाणिक/शैक्शणिक.
(iv) सावर्जनिक/सर्वजनिक/सार्वजनीक/सार्वजनिक.
उत्तर:
(i) विभूषित
(ii) पुनर्विवाह
(iii) शैक्षणिक
(iv) सार्वजनिक.

(२) पुढील वाक्ये लेखननियमांनुसार लिहा :
(i) सरस्वतिला आपन वाङमयाची जननि मानतो.
(ii) एकदा वीदयापिठातल्या कर्त्यांच्या पूतळ्यामागे एक मूलगी रडत बसलि होती.
उत्तर:
(i) सरस्वतीला आपण वाङ्मयाची जननी मानतो.
(ii) एकदा विदयापीठातल्या कर्त्यांच्या पुतळ्यामागे एक मुलगी रडत बसली होती.

३. विरामचिन्हे :
पुढील वाक्यांत योग्य विरामचिन्हे घालून वाक्ये पुन्हा लिहा :
(i) तिला म्हटले कर्त्यांच्या पुतळ्यापाशी बसून रडायला तुला काहीच कसे वाटत नाही
(ii) आपण आपल्या आईशी बहिणीशी बायकोशी कन्येशी पुष्कळदा चुकीचे वागतो
उत्तर:
(i) तिला म्हटले, “कर्त्यांच्या पुतळ्यापाशी बसून रडायला तुला काहीच कसे वाटत नाही?”
(ii) आपण आपल्या आईशी, बहिणीशी, बायकोशी, कन्येशी पुष्कळदा चुकीचे वागतो.

४. पारिभाषिक शब्द :

पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द लिहा :
(i) Book Stall – ……………………………..
(ii) Book Post – ……………………………..
(iii) Casual Leave – ……………………………..
(iv) No Objection Certificate – ……………………………..
(v) Highway – …………………………….. (सराव कृतिपत्रिका-३)
(vi) Interview – …………………………….. (सराव कृतिपत्रिका-३)
उत्तर:
(i) Book Stall – पुस्तक विक्री केंद्र
(ii) Book Post – पुस्त-प्रेष
(iii) Casual Leave – नैमित्तिक रजा
(iv) No Objection Certificate – ना हरकत प्रमाणपत्र
(v) Highway – महामार्ग
(vi) Interview – मुलाखत.

५. अकारविल्हे/भाषिक खेळ :
(१) पुढील शब्द अकारविल्हेनुसार लिहा :
(i) चार → तीन → दोन → एक.
(ii) राग → क्रोध → संताप → चीड.
उत्तर:
(i) एक → चार → तीन → दोन,
(ii) क्रोध → चीड → राग → संताप.

(२) आकृती पूर्ण करा:

उत्तर:

उत्तर:

कर्ते सुधारक कर्वे शब्दार्थ

• प्रच्छन्न – गूढ, गुप्त, लपलेला, झाकलेला.
• असिधाराव्रत – तलवारीच्या धारेवरून चालण्याइतके कठीण व्रत.
• पै – पूर्वीचे एक लहान नाणे.
• मैलोन्गणती – अनेक मैल, खूप अंतर.
• मिसाल – प्रतीक.
• राजमानसाने – सरकारने.
• टिचणे – फुटणे, तडकणे.

कर्ते सुधारक कर्वे टिपा

(१) भारतरत्न : भारतातील हा सर्वोच्च नागरी पुरस्कार आहे. देशासाठी सर्वोच्च प्रतीचे आणि जगभरात देशाचे नाव कीर्तिवंत करणारे कार्य ज्यांच्या हातून घडते, अशा व्यक्तीला हा सर्वोच्च पुरस्कार बहाल केला जातो. त्या व्यक्तीने त्या कार्यासाठी आपले संपूर्ण आयुष्य खर्ची घातलेले असते. सेवा, कला, साहित्य, विज्ञान, विश्वशांती, मानवविकास, कारखानदारी, क्रीडा अशा मूलभूत क्षेत्रांमध्ये अतुलनीय कामगिरी करणाऱ्या व्यक्तीला हा सर्वश्रेष्ठ पुरस्कार देऊन सन्मानित करण्याचा निर्णय १९५४ साली तत्कालीन सरकारने घेतला.

(२) महामेरू : पुराणात पृथ्वीचे वर्णन करताना सात द्वीपे सांगितली आहेत. त्यांपैकी जंबुद्वीपामध्ये केंद्रस्थानी मेरू हा पर्वत आहे. हा पर्वत सोन्याचा असून त्यावर नेहमी देव राहतात, असे पुराणात सांगितले आहे. या मेरू पर्वतापेक्षाही महर्षी कर्वे मोठे असे आलंकारिक वर्णन येथे केले आहे.

Marathi Kumarbharti Class 10th Digest भाग-३

• गोष्ट अरुणिमाची Question Answer
• भरतवाक्य Question Answer (कविता)
• कर्ते सुधारक कर्वे Question Answer
• काळे केस Question Answer
• खोद आणखी थोडेसे Question Answer (कविता)
• वीरांगना Question Answer (स्थूलवाचन)

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 10.1 मनक्या पेरेन लागा (स्थूलवाचन) Notes, Textbook Exercise Important Questions and Answers.

Class 10th Marathi Kumarbharti Chapter 10.1 मनक्या पेरेन लागा (स्थूलवाचन) Question Answer Maharashtra Board

Std 10 Marathi Chapter 10.1 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 10.1 मनक्या पेरेन लागा Textbook Questions and Answers

कृति

कृतिपत्रिकेतील प्रश्न ३ साठी…

प्रश्न 1.
खालील संकल्पनांमधील सहसंबंध स्पष्ट करा.

उत्तर:

प्रश्न 2.
‘माणसं पेरायला लागू’ या शीर्षकातून कवीला अभिप्रेत असलेला भावार्थ उलगडून दाखवा.
उत्तर:
कवी वीरा राठोड यांनी ‘मनक्या पेरेन लागा’ या कवितेत ‘बीज’ व ‘माती’ यांचा जिव्हाळ्याचा स्नेहभाव व्यक्त करताना माणसे पेरण्याचा बहुमोल सल्ला दिला आहे.

त्यांनी माती व बीज यांच्या प्रतीकांतून एक सुंदर विचार मांडला आहे. एका चिमुकल्या बीजातून झाड होईपर्यंतचा प्रवास माती ममतेने जोपासते, बीजाचे झाड करण्यात तिच्या जन्माचे सार्थक आहे. त्याप्रमाणे या समाजाच्या मातीत माणसे रुजवली व त्यांच्यावर चांगले संस्कार केले तर त्यातून चिरंतन माणुसकी निर्माण होईल, हा आशय या कवितेतून अभिव्यक्त होतो. म्हणून ‘माणसं पेरायला लागू’ हे शीर्षक अतिशय समर्पक ठरते.

प्रश्न 3.
‘माणसे पेरा । माणुसकी उगवेल’ या विधानाचा तुम्हांला समजलेला अर्थ लिहा.
उत्तर:
मातीत बीज पेरलं की, मातीच्या कष्टमय मायेतून त्याचे झाड होते. माती त्या बीजाला सगळ्या नैसर्गिक आपत्तींपासून वाचवते. दुष्काळाशी लढते. बीजाची मायेने निगराणी करते. या सर्व प्रक्रियेतून बीजाचा वृक्ष होतो. त्याप्रमाणेच आजच्या मूल्यहीन समाजामध्ये चांगल्या संस्काराच्या मातीत जर माणसांना पेरले, तर त्यातून मानवतेचा निकोप वृक्ष उभा राहील, अशी आशादायक भावना या विधानातून व्यक्त झाली आहे. नवविचारांच्या नवसमाजात माणुसकीला बहर येईल व मानवजात सुखी होईल, असा सर्जनशील आशय ‘माणूस पेरा! माणुसकी उगवेल!’ या विधानातून व्यक्त होतो.

प्रश्न 4.
‘माणुसकी पेरणे काळाची गरज’ या विधानाचा तुम्हाला कळलेला अर्थ लिहा.
उत्तर:
मातीमध्ये बी पेरले की, मातीच्या मायेच्या संस्कारांमधून वृक्ष जन्माला येतो. माती ऊन-वारा-पाऊस-वादळाची झळ सोसून बीजाची जोपासना करते. बीजाला दुष्काळाची झळ सोसावी लागू नये; म्हणून ती दुष्काळाशी सामना करते. या प्रतीकांतून कवीनं सामाजिक आशय मांडला आहे. आज भ्रष्टाचार, दैन्य, अंधश्रद्धा व इतर धर्माध घटक यांमुळे समाज पोखरलेला आहे व त्यात माणुसकी लयाला जात आहे. अशा या आधुनिक काळात माणसांवर चांगले संस्कार होऊन माणुसकी निर्माण होणे आवश्यक आहे. म्हणून माणुसकी पेरणे म्हणजेच विवेकी माणूस निर्माण करण्याची आजच्या काळाची गरज अधोरेखित होते.

उपक्रम:
वरील कविता तुमच्या परिसरात बोलल्या जाणाऱ्या भाषेत/बोलीभाषेत (उदा., पावरी, गोंडी, कोरकू, वारली, व-हाडी, अहिराणी, मालवणी इत्यादी.) रूपांतरित करा व तिचा आस्वाद घ्या.

वाचा
विचारांचं संतुलन हवं! माणसाचं मन एक अजब यंत्रणा आहे. अनेक परस्परविरोधी भावना आणि विचारप्रवाह तिथे वास करत असतात, पण बहुतेक वेळा आपण नकारात्मक भावना आणि छळवादी विचारांच्या अमलाखाली वावरतो. त्यामुळे आपण निष्क्रिय तरी होतो किंवा हातून चांगलं काम घडत असलं तरी त्यातून आनंद, आत्मविश्वास आणि समाधान मिळत नाही. अशा नकारात्मक भावना व विचार मनातून नष्ट व्हावेत. अशी इच्छा बाळगून वावरतो. ते शक्य असतं का?

प्रत्येक नाण्याला दोन बाजू असतात. त्यामुळे होकारात्मक आणि सृजनात्मक विचार झाले तरी त्यांना विरुद्ध बाजूही असतेच. त्याचप्रमाणे नकारात्मक विचार व भावना यांचादेखील काही उपयोग होतच असतो. तो उपयोग करून घेणं हे आपलं कौशल्य आणि हुशारी, हे लक्षात ठेवायला हवं, म्हणून तर अशा परस्परविरोधी भावना व विचार मनात वावरतात. त्या नकारात्मक गोष्टींनी गांगरून जाण्याचं जरासुद्धा कारण नाही. त्यांचं संतुलन राखणं महत्त्वाचं

ज्याप्रमाणे चार चाकी गाडीत ब्रेक व अॅक्सिलेटर म्हणजे वेगनियंत्रक व प्रवर्तक असतात. त्याप्रमाणे मनाला वेगानं पुढे नेणारे होकारात्मक विचार आणि प्रगतीला रोखणारे नकारात्मक विचार असतात. गाडीच्या सुरक्षिततेसाठी ब्रेकची आवश्यकता भासते म्हणून ते असतात. त्यांना भिण्याचं काहीच कारण नाही. त्याप्रमाणे मनात नकारात्मक विचार येतात. त्यांच्या मदतीने सावधगिरी कशी व कुठे बाळगायची याचं स्पष्ट भान निर्माण होतं आणि चुकीच्या निर्णयांनादेखील आळा बसतो. अर्थात नुसताच ब्रेक दाबला तर गाडी सुरूही होणार नाही आणि वेगदेखील घेणार नाही. म्हणूनच सतत आपल्या विचारांचं संतुलन असणं आवश्यक आहे.

– (गंमत शब्दांची- डॉ. द. दि. पुंडे)

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 10.1 मनक्या पेरेन लागा Additional Important Questions and Answers

कृती: (स्वमत / अभिव्यक्ती)

प्रश्न 1.
पुढील ओळींतील भावसौंदर्य विशद करा:

(i) ‘माती त्याला लावते जीव’ (धुड वोनं लगाडछ जीव)
उत्तर:
‘मनक्या पेरेन लागा’ या कवितेत वीरा राठोड यांनी बीजाला माती कशी जपते याविषयी हृदय शब्दांत सांगितले आहे.
कवी म्हणतात, एक बीज मातीत पडते. तेव्हा माती त्या बीजाला आईच्या मायेने जोपासते. मातीचे व त्याचे घट्ट नाते तयार होते. माती त्याच्यावर माया ओतते. त्याचे पालन-पोषण करते. त्याला सांभाळते. त्याची निगराणी करते. माती बीजाला जीव लावते. ऊन-वारा-पाऊसवादळ यांपासून त्याचे संरक्षण करते. जणू ते तिचे बाळ असते. त्याचा वृक्षापर्यंतचा प्रवास ती ममतेने घडवते. माती व बीजाचे मानवीकरण करून कवीने ही हृदयस्पर्शी ओळ लिहिली आहे.

(ii) ‘एक दिवस त्याला झाड करूनच सोडते’ (एक दन वोनं झाड करूनच छोडचं)
उत्तर:
कवी वीरा राठोड यांनी मनक्या पेरेन लागा’ या कवितेमध्ये मातीची महती सांगितली आहे. कवी म्हणतात, एक चिमुकले बीज मातीत पडते. माती त्याला आईच्या ममतेने जोपासते. मातीशी त्याचे दृढ नाते जडते. माती त्याला जीव लावते. एखादया लहान बाळासारखे त्याचे पालन-पोषण करते.

ऊन-वारा-पाऊस-वादळ यांची त्याला झळ लागू देत नाही. दुष्काळाशी माती लढते. कारण तिला बीजाचा वृक्ष करण्याचा आंतरिक ध्यास लागलेला असतो. बघता बघता तिचे स्वप्न साकार होते. एक दिवस त्या बीजाचे पूर्ण झाड होते, तेव्हा मातीला धन्यता वाटते.

या ओळीतून मातीचे कष्ट व जिद्द यांचा प्रत्यय येतो.

Marathi Kumarbharti Class 10 Textbook Solutions भाग-२

• वस्तू Question Answer (कविता)
• गवताचे पाते Question Answer
• वाट पाहताना Question Answer
• आश्वासक चित्र Question Answer (कविता)
• आप्पांचे पत्र Question Answer
• मनक्या पेरेन लागा Question Answer (स्थूलवाचन)

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 15 खोद आणखी थोडेसे (कविता) Notes, Textbook Exercise Important Questions and Answers.

Class 10th Marathi Kumarbharti Chapter 15 खोद आणखी थोडेसे (कविता) Question Answer Maharashtra Board

Std 10 Marathi Chapter 15 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 15 खोद आणखी थोडेसे Textbook Questions and Answers

कृति – स्वाध्याय व उत्तरे

कृतिपत्रिकेतील प्रश्न २ (अ) साठी…

प्रश्न 1.
योग्य पर्याय शोधून वाक्य पूर्ण करा.
(अ) ‘खोदणे’ या शब्दाचा कवितेतील अर्थ म्हणजे…… – (आ) गाणे असते मनी म्हणजे ……
(१) विहीर आणखी खोदणे. – (१) मन आनंदी असते.
(२) जिद्दीने आणखी प्रयत्न करणे. – (२) गाणे गाण्याची इच्छा असते.
(३) घरबांधणीसाठी खोदणे. – (३) मनात नवनिर्मिती क्षमता असते.
(४) वृक्षलागवडीसाठी खोदणे. – (४) गाणे लिहिण्याची इच्छा असते.

प्रश्न 2.
आकृती पूर्ण करा.

उत्तर:
(i) उघडून ओंजळीत
(ii) जन्माचे आर्त
(iii) स्वत:चे ओठ
(iv) लाहो.

प्रश्न 3.
कवितेतील खालील संकल्पना आणि त्यांचे अर्थ यांच्या जोड्या लावा.
कवितेतील संकल्पना – संकल्पनेचा अर्थ
(१) सारी खोटी नसतात नाणी – (अ) मनातील विचार व्यक्त करावेत.
(२) घट्ट मिटू नका ओठ – (आ) मनातील सामर्थ्य व्यापक बनवावे.
(३) मूठ मिटून कशाला म्हणायचे भरलेली – (इ) सगळे लोक फसवे नसतात.
(४) उघडून ओंजळीत घ्यावी मनातली तळी – (ई) भ्रामक खोट्या समजुती बाळगू नयेत.

प्रश्न 4.
कवितेच्या आधारे खालील विधाने योग्य की अयोग्य ते लिहा.
(१) संयमाने वागा
(२) सकारात्मक राहा
(३) उतावळे व्हा
(४) चांगुलपणावर विश्वास ठेवा
(५) नकारात्मक विचार करा
(६) खूप हुरळून जा
(७) संवेदनशीलता जपा
(८) जिद, चिकाटी, आत्मविश्वास कायम ठेवा
(९) जुन्याच निर्मितीवर विश्वास ठेवा
(१०) नवनिर्मितीवर विश्वास ठेवा
(११) धीर सोडू नका
(१२) यशाचा विजयोत्सव करा
उत्तर:
(i) संयमाने वागा – [योग्य]
(ii) सकारात्मक राहा – [योग्य]
(iii) उतावळे व्हा – [अयोग्य]
(iv) चांगुलपणावर विश्वास ठेवा – [योग्य]
(v) नकारात्मक विचार करा – [अयोग्य]
(vi) खूप हुरळून जा – [अयोग्य]
(vii) संवेदनशीलता जपा – [योग्य]
(viii) जिद्द, चिकाटी, आत्मविश्वास कायम ठेवा – [योग्य]
(ix) जुन्याच निर्मितीवर विश्वास ठेवा – [अयोग्य]
(x) नवनिर्मितीवर विश्वास ठेवा – [योग्य]
(xi) धीर सोडू नका – [योग्य]
(xii) यशाचा विजयोत्सव करा – [अयोग्य]

प्रश्न 5.
काव्यसौंदर्य.

(अ) खालील ओळींचे रसग्रहण करा.
‘झरा लागेलच तिथे, खोद आणखी जरासे’
उत्तर:
आशयसौंदर्य: ‘खोद आणखी थोडेसे’ या कवितेमधून कवयित्रींनी संयम, जिद्द, आत्मविश्वास व चिकाटी या गुणांच्या मदतीने जीवनध्येय साध्य करण्याची उमेद माणसाला दिली आहे. माणसाने सकारात्मक आयुष्य कसे जगावे, हे समजावून सांगताना वरील ओळीमध्ये प्रयत्नांती परमेश्वर’ या उक्तीचा प्रत्यय दिला आहे. अविरत प्रयत्न करून आदर्श जीवन जगण्याचा संदेश ही कविता देते.

काव्यसौंदर्य: कोणतेही कार्य करताना धीर सोडू नये. खोल खोल मातीखाली निर्मळ झरा असतो, तो प्राप्त करण्यासाठी सतत प्रयत्न करून आणखी थोडेसे खोदावे लागते. हतबल न होता, हिंमत न हारता प्रयत्नरत असावे. दुःखाच्या मातीच्या जाड थराखाली सुखाचा, आनंदाचा अक्षय झरा असतोच. म्हणून निराश न होता ओठ घट्ट मिटून खोदण्याचे म्हणजेच सुख धुंडाळण्याचे कार्य मध्येच थांबवू नये. अंतिमतः प्रयत्नपूर्वक दुःखावर मात करताच येते.

भाषिक वैशिष्ट्ये: साध्या, सोप्या अष्टाक्षरी छंदात कवितेची रचना केल्यामुळे व यमकप्रधानतेमुळे कवितेला गेय लय प्राप्त झाली आहे. नादानुकूल शब्दकळा व ओघवती भाषा यामुळे कवितेला सौंदर्य प्राप्त झाले आहे. ‘झरा’ या संकल्पनेमधून प्रयत्नवाद रसिकांच्या मनावर पूर्णतः ठसवला आहे.

(आ) ‘आर्त जन्मांचे असते, रित्या गळणाऱ्या पानी’, या ओळींमधील अर्थ तुमच्या भाषेत स्पष्ट करा.
उत्तर:
फवयित्री sal काकडे यांनी ‘खोद आणखी थोडेसे’ या कवितेमध्ये माणसाने प्रयत्नवादी होऊन जगण्याची उमेद धरावी, असा उपदेश केला आहे. कवयित्री म्हणतात – घट्ट ओठ मिटून दुःख सोसत बसू नये. आपल्या मनात खोलवर एक गाणे लपलेले असते, ते शोधून काढायला हवे, हे समजावताना त्यांनी ‘गळणाऱ्या पानाचे’ प्रतीक वापरले आहे. शिशिर ऋतूमध्ये पानगळ होते. झाड निष्पर्ण होते. परंतु जे पान सुकून, रिते होऊन झाडापासून विलग होते, त्या पानात झाडावर असताना सोसलेल्या वेदना असतात. हे जन्माचे आर्त, आयुष्यात सोसलेल्या वेदना, त्या सुरकुतलेल्या गळणाऱ्या पानात सामावलेल्या असतात म्हणून पुन्हा वसंतात पालवी फुटण्याची उमेद ते बाळगून असते.

गळणाऱ्या पानामघून जीवन जगण्याची उमेद पुन्हा जागृत होते, हा आशावाद या ओळींतून व्यक्त झाला आहे.

(इ) ‘गाणे असते गं मनी’, या ओळीतील तुम्हाला समजलेला नवनिर्मिती क्षमतेचा संदेश स्पष्ट करा.
उत्तर:
आसावरी काकडे यांनी ‘खोद आणखी थोडेसे’ या कवितेमधून सकारात्मक जीवन जगण्याची शिकवण देताना प्रत्येकाच्या मनात असलेल्या निर्मितिक्षमतेला आवाहन केले आहे.

कवयित्रींच्या मते – मातीखाली लपलेला झरा शोधेपर्यंत माणसाने अथक प्रयत्न करायला हवेत, धीर एकवटून आयुष्याचा सकारात्मक शोध घ्यायला हवा. घट्ट ओठ मिटून दुःख सोसत राहू नये. प्रत्येकाचे मन हे निर्मितिक्षम असते. त्या अंतर्मनातील गाभ्याशी ज्याचे त्याचे गाणे दडलेले असते, मनाच्या तळाशी असलेले हे गाणे मर्मबंधाची ठेव असते. आपल्यात मग्न होऊन ते गाणे अनुभवणे हे जीवनाचे सार्थक ठरते. आपल्यातल्या निर्मितिक्षमतेचा शोध आपणच घ्यायला हवा.

मनात असलेली निर्मितिक्षमता जागी करायला हवी म्हणजे मग ‘आनंदाचे डोही। आनंद तरंग।’ ही अवस्था अनुभवता येईल.

अशा प्रकारे कवयित्रींनी ‘गाणे असते गं मनी’ या ओळीतून माणसाला नवनिर्मिती क्षमतेचा संदेश दिला आहे.

(ई) ‘परिश्रमाशिवाय फळ मिळत नाही’, याबाबतीत तुम्ही घेतलेला अनुभव लिहा.
उत्तर:
आमचे ‘बाभूळगाव’ हे गरीब शेतकऱ्यांचे गाव होय! डोंगरझाडी व बिकट मार्ग त्यामुळे ते तालुक्याच्या गावापासून लांब व सोयींच्या बाबतीत अडचणीचे आहे. आमच्या गावात जेमतेम चौथीपर्यंतच शाळा, तीही एकशिक्षकी एका पडक्या घरात भरायची. पाचवीनंतरच्या विदयार्थ्यांना जंगलातून वाट काढत दहा किलोमीटर लांबवर तालुक्याच्या गावच्या शाळेत जावे लागायचे. आमचे रोकडे मास्तर फार मेहनती होते. त्यांनी तालुक्याच्या शिक्षणाधिकाऱ्याला एक अर्ज लिहिला व आम्हां मुलांना प्रत्येक पालकाची त्यावर सही आणायला सांगितले. प्रत्येक विदयार्थ्याने आपापल्या पालकांची सही व अंगठा आणला, पंचक्रोशीतही आम्ही जाऊन मोठमोठ्या माणसांना भेटलो. त्यांच्या शिफारशी गोळा केल्या. गेल्या १५ ऑगस्टला आम्ही शिक्षणाधिकाऱ्यांना प्रमुख पाहुणे म्हणून बोलावले व गुरुजींनी त्यांना पुढच्या शिक्षणव्यवस्थेचा अर्ज दिला. काही निवडक मुलांनी भाषणे करून पुढील शिक्षणाची व्यवस्था गावात होण्यासाठी विनवले. अखेर अथक व निष्ठेने केलेल्या प्रयत्नांमुळे आमच्या गावात जि.प. ची शाळा मंजूर झाली. आम्हांला ‘परिश्रमाचे फळ ‘ मिळाले! किंवा

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 15 खोद आणखी थोडेसे Additional Important Questions and Answers

प्रश्न. पुढील कवितेच्या आधारे दिलेल्या
सूचनांनुसार कृती करा:

कृती १: (आकलन)

प्रश्न 1.
योग्य पर्याय निवडून विधाने पूर्ण करा:
(i) सारी खोटी नसतात …………………………..
(१) गाणी
(२) म्हणी
(३) नाणी
(४) वाणी.
उत्तर:

(ii) उघडून ओंजळीत घ्यावी मनातली …………………………..
(१) जाळी
(२) तळी
(३) ओळी
(४) झोळी.
उत्तर:

(iii) उमेदीने जगण्याला ………………………….. लागते थोडेसे!
(१) बळ
(२) कळ
(३) वळ
(४) झळ.
उत्तर:

कृती ३: (काव्यसौंदर्य)

प्रश्न 1.
उमेदीने जगण्याला बळ लागतेच थोडेसे’ या काव्यपंक्तीतील विचारसौंदर्य स्पष्ट करा. (सराव कृतिपत्रिका-१)
उत्तर:
‘खोद आणखी थोडेसे’ या कवितेमध्ये कवयित्रींनी माणसाने प्रयत्नवादी होऊन उमेदीने जीवन जगावे, हा सकारात्मक विचार मांडला आहे.

जगत असताना माणसाने कधीही निराश होऊ नये. स्वतःवर विश्वास ठेवून अथक प्रयत्न करावेत. प्रयत्नानंतर यश हमखास मिळेलच ! ओठ दाबून दुःख सहन करू नये. दुःख सरेल हा आशावाद बाळगावा. मनात सकारात्मक तळी असतात. ती खोदावीत. अखेर निर्मळ झरा लागतोच ही उमेद मनात हवी. जिद्दीने परिस्थितीवर मात करता येते, त्यासाठी आत्मबळ हवे. समृद्ध जगण्यासाठी सतत प्रयत्नवादी राहायला हवे.

अशा प्रकारे या ओळींमधून कवयित्रीने जीवनातील सकारात्मक आशावाद मांडला आहे.

कृतिपत्रिकेतील प्रश्न २ (आ) साठी…
प्रश्न. पुढील कवितेसंबंधी त्याखाली दिलेल्या मुद्द्यांच्या आधारे कृती सोडता:

कविता-खोद आणखी थोडेसे.
उत्तर:
(१) प्रस्तुत कवितेच्या कवयित्री: आसावरी काकडे.
(२) कवितेचा रचनाप्रकार: अष्टाक्षरी ओवी.
(३) कवितेचा काव्यसंग्रह: लाहो.
(४) कवितेचा विषय: प्रयत्न व सकारात्मकता यांचे महत्त्व,

(५) कवितेतून व्यक्त होणारा (स्थायी) भाव: चिकाटी, जिद्द, आशावाद यांमुळे मनाला उमेद लाभते.

(६) कवितेच्या कवयित्रींची लेखनवैशिष्ट्ये: प्रत्येक चरणात आठ अक्षरे, दुसऱ्या व चौथ्या चरणांत यमक आणि प्रत्येक कडव्यात चार चरण अशी या ओवीची रचना असते. कवितेला आपोआपच गेयता लाभली आहे. नादानुकूल शब्दकळा व ओघवती भाषा यांमुळे कवितेला सौंदर्य प्राप्त झाले आहे. ‘सारी खोटी नसतात नाणी’ या शब्दांतून आशावाद व्यक्त होतो. संपूर्ण कविताच आशावादाने भारलेली आहे. ‘मरणाचे कष्ट घ्या’, ‘प्राण गेले तरी चालेल’ अशा शब्दांतून प्रयत्न करायला सांगितले तर दडपण येते. ‘जरासा प्रयत्न कर, थोडेसे कष्ट घे’, असे सांगितले की माणूस कष्ट करायला सिद्ध होतो. या कवितेतील प्रत्येक कडव्यातील शेवटच्या दोन ओळी मनात अशी उमेद निर्माण करतात.

(७) कवितेची मध्यवर्ती कल्पना: संयम, जिद्द, आत्मविश्वास व चिकाटी यांच्या योगे ध्येय साध्य करण्यास सिद्घ व्हावे, हा विचार या कवितेच्या केंद्रस्थानी आहे. जीवनात अपयश येण्याच्या, निराशा येण्याच्या घटना खूप घडतात. माणसे त्यामुळे कोलमडून जातात. असे कोलमडून न जाता आपल्याला यश मिळेलच, याची मनोमन खात्री बाळगावी, असा आशावाद ही कविता जागवत राहते.

(८) कवितेतून व्यक्त होणारा विचार: जीवनात खूप कष्ट. उपसावे लागतात, तरीही अनेकदा यश हुलकावणी देते. कधीही प्रयत्न केल्याबरोबर वा कष्ट घेतल्याबरोबर लागलीच यश मिळत नसते. माणसे त्यामुळे नाउमेद होतात. असे माणसाने कधीच नाउमेद होऊ नये. सतत प्रयत्न करीत राहावे. आपल्याला यश मिळेलच अशी आशा बाळगावी, असा विचार या कवितेतून व्यक्त केला आहे.

(९) कवितेतील आवडलेली ओळ:
झरा लागेलच तिथे खोद आणखी जरासे उमेदीने जगण्याला बळ लागते थोडेसे !

(१०) कविता आवडण्याची वा न आवडण्याची कारणे: ही कविता मला खूप खूप आवडली आहे. ही कविता वाचता वाचता मनातील निराशेचे मळभ दूर होते. प्रयत्न करीत राहण्यातच यशाचा मार्ग आहे, हे मनोमन पटते. थोड्याशा प्रयत्नाने, थोड्याशा बळानेही उमेद निर्माण होते. या शब्दांनी मनाला उभारी येते. ही कविता माणसाला चांगले जीवन जगण्याची प्रेरणा देते.

(११) कवितेतून मिळणारा संदेश: आपल्या आयुष्यातला प्रत्येक क्षण सुखाने व यशाने भरलेला नसतो. खरे तर सदोदित अडचणीच असतात. या अडचणींना घाबरून आपण खचून जाता कामा नये, थोड्याशा प्रयत्नानेही यश मिळेल, असा सकारात्मक दृष्टिकोन बाळगला पाहिजे. जग अगदीच वाईट नाही; किंवा सगळीकडे वाईटपणा वा खोटेपणाच भरलेला आहे, असे मानू नये. प्रयत्न करीत राहिले पाहिजे, असा संदेश या कवितेतून मिळतो.

व्याकरण व भाषाभ्यास

कृतिपत्रिकेतील प्रश्न ४ (अ) आणि (आ) यांसाठी…
व्याकरण घटकांवर आधारित कृती:

१. समास:
पुढील सामासिक शब्दांवरून समास ओळखा:
(i) दहाबारा
(ii) राजवाडा
(iii) चिल्लीपिल्ली
(iv) दशदिशा
(v) विटीदांडू
(vi) गैरहजर.
उत्तर:
(i) दहाबारा – वैकल्पिक द्वंद्व
(ii) राजवाडा – विभक्ती तत्पुरुष
(iii) चिल्लीपिल्ली – समाहार वंद्व
(iv) दशदिशा – द्विगू
(v) विटीदांडू – इतरेतर द्वंद्व
(vi) गैरहजर – अव्ययीभाव.

२. अलंकार:
पुढील ओळींतील अलंकार ओळखून स्पष्टीकरण लिहा:
पावसाळी ढग आलं डोंगराच्या मागं
झाडं झाली वेडीपिशी खुळी लगबगं
उत्तर:
अलंकार: हा चेतनगुणोक्ती अलंकार आहे.

स्पष्टीकरण: पावसाची चाहूल लागताच शेतकऱ्यांची कामे करण्याची लगबग सुरू होते. तशी काळे ढग पाहून झाडांची खुळी लगबग सुरू झाली आहे. झाडांवर मानवी भावनांचे आरोपण केल्यामुळे हा चेतनगुणोक्ती अलंकार आहे.

३. वृत्त:
‘वसंततिलका’ या वृत्ताची लक्षणे सांगून उदाहरण दया.
उत्तर:
लक्षण: हे एक अक्षरगणवृत्त आहे.
चार चरण, प्रत्येक चरणात १४ अक्षरे
गण – त भ ज ज ग ग
यति – ८ व्या अक्षरावर.
उदाहरण: आरक्त होय फुलुनी प्रणयी पलाश
फेकी रसाल तरुही मधुगंधपाश
ऐकू न ये तुज पिकस्वर मंजुळे का?
वृत्ती वसंततिलका न तुझी खुले का?

४. शब्दसिद्धी:
(i) ‘अभि’ हा उपसर्ग असलेले चार शब्द लिहा:
[ ] [ ] [ ] [ ]

(ii) ‘आई’ हा प्रत्यय लागलेले चार शब्द तयार करा:
जसे: खोद + आई → खोदाई
उत्तर:
(i) [अभिनंदन] [अभिरुची] [अभिमान] [अभिनय]
(ii) [शिलाई] [घुलाई] [चराई] [उजळाई]

५. सामान्यरूप:
• पुढील शब्दांचे सामान्यरूप लिहा:
(i) जन्मांचे
(ii) ओंजळीत
(iii) उमेदीने
(iv) जगण्याला.
उत्तर:
(i) जन्मांचे – जन्मां
(ii) ओंजळीत – ओंजळी
(ii) उमेदीने – उमेदी
(iv) जगण्याला – जगण्या.

६. वाक्प्रचार:
योग्य अर्थ निवडा:

उत्तर:
उमेदीने जगणे → जिद्दीने जगणे

भाषिक घटकांवर आधारित
कृती: १. शब्दसंपत्ती:

(१) विरुद्धार्थी शब्द लिहा:
(i) थोडेसे x ……………………..
(ii) खोटी x ……………………..
(iii) घट्ट x ……………………..
(iv) रिते x ……………………..
उत्तर:
(i) थोडेसे x जास्त
(ii) खोटीx खरी
(iii) घट्ट x सैल
(iv) रिते x भरलेले.

(२) पुढील शब्दांतील अक्षरांपासून चार अर्थपूर्ण शब्द बनवा:
(i) मनातली → [ ] [ ] [ ] [ ]
(ii) नसतात → [ ] [ ] [ ] [ ]
उत्तर:
(i) मनातील → [मत] [तम] [मनात] [नात]
(i) नसतात → [नस] [तान] [तन] [ताता]

(३) समानार्थी शब्द लिहा:
(i) झरा = ……………………….
(ii) उमेद = ……………………….
(iii) पान = ……………………….
(iv) गाणे = ……………………….
उत्तर:
(i) झरा = निर्झर
(iii) पान = पर्ण
(ii) उमेद = जिद्द, आशा
(iv) गाणे = गीत.

(४) पुढील शब्दांचे भिन्न अर्थ लिहा:
(i) [ ] ← तळी → [ ]
(ii) [ ] ← अंबर → [ ] (मार्च १९)
उत्तर:
(i) [तळाला] ← तळी → [तलाव]
(ii) [गगन] ← अंबर → [वस्त्र] (मार्च १९)

२. लेखननियम:
अचूक शब्द निवडून लिहा:
(i) जिवनध्येय/जीवनधेय/जीवनध्येय/जीवनधेय्य.
(ii) विश्लेषण/विश्लेशण/वीश्लेषण/विश्लेषन.
उत्तर:
(i) जीवनध्येय
(ii) विश्लेषण.

३. विरामचिन्हे:
पुढील ओळीतील विरामचिन्हे ओळखा:
धीर सोडू नको, सारी खोटी नसतात नाणी.
उत्तर:
(i) [ , ] स्वल्पविराम
(ii) [ . ] पूर्णविराम.

४. पारिभाषिक शब्द:
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द लिहा:
उत्तर:
(i) Zero Hour – शून्य तास
(ii) Unauthorized – अनधिकृत
(iii) Souvenir – स्मरणिका
(iv) Lesson Note – पाठ टिपणी

५. अकारविल्हे / भाषिक खेळ:
पुढील शब्द अकारविल्हेनुसार लावा:
(i) झरा → खोद → उमेद → आणखी.
(ii) बळ → गाणे → घट्ट → पाणी.
उत्तर:
(i) आणखी → उमेद → खोद → झरा.
(ii) गाणे → घट्ट → पाणी → बळ.

खोद आणखी थोडेसे Summary in Marathi

खोद आणखी थोडेसे कवितेचा भावार्थ

सकारात्मक (पॉझिटिव्ह) जीवन कसे जगावे व प्रयत्नवादी कसे असावे, हा मोलाचा संदेश देताना कवयित्री म्हणतात –

निराश होऊ नकोस. जमीन खणत राहा. आणखी थोडेसे खोद. जमिनीखाली नक्कीच तुला पाणी मिळेल. जिद्दीने प्रयत्न कर. जीवन जगताना हिंमत सोडू नको. सर्व माणसे स्वार्थी नसतात. काही प्रामाणिक माणसेही (खरी नाणी) जगात असतात, हा विश्वास मनात असू दे.

ओठ घट्ट दाबून आतल्या आत दुःख सहन करू नकोस. अबोलपणे वेदना सहन करू नकोस. आत खोल मनात प्रत्येकाचे एक आनंदी गाणे दडलेले असते. ते शोध. (शिशिरात) झाडावरून मूकपणे गळणाऱ्या पानातही जन्मभराची वेदना साठलेली असते. (ते गळताना दुःख करीत नाही. पुन्हा पालवी फुटेल या आशेवर ते गळून पडते.)

मुठीत काहीच नसताना उगाच ती भरलेलीच आहे, असे म्हणू नये, म्हणजे स्वत:कडे काही सत्ता, संपत्ती, वैभव नसताना ते असल्याचा बडेजाव मिरवू नये. जे नाही त्याची हाव धरू नये. उलट उघड्या ओंजळीत मनात असलेली तळी व त्यातील गारवा धारण करावा, मनात जो ओलावा आहे, त्याच्यामध्ये आनंद घ्यावा. तीच आपली समृद्धी समजावी.

खोलवर आणखी थोडे मातीत खण म्हणजे तुला तिथे निर्मळ झरा लागेल, तीच तुझी जिद्द आहे. उमेदीने जगण्यासाठी मनाची शक्ती आवश्यक आहे. म्हणून समृद्ध जगण्यासाठी आत्मबळ गरजेचे आहे. प्रयत्नवादी राहणे आवश्यक आहे.

खोद आणखी थोडेसे शब्दार्थ

• खोदणे – उकरणे, खणणे, खड्डा करणे.
• सारी – सर्व.
• नाणी – शिक्के, पैसे.
• आर्त – वेदना.
• रित्या – रिकाम्या, ओसाड,
• पानी – पानावर.
• तळी – तलाव,
• उमेद – जिद्द.
• बळ – शक्ती.

खोद आणखी थोडेसे वाक्प्रचार व त्यांचे अर्थ

• धीर न सुटणे : हिंमत न हारणे.
• उमेदीने जगणे : जिद्दीने जीवन कंठणे.
• मूठ भरलेली असणे : जीवनात वैभव, सुख असणे.

Marathi Kumarbharti Class 10th Digest भाग-३

• गोष्ट अरुणिमाची Question Answer
• भरतवाक्य Question Answer (कविता)
• कर्ते सुधारक कर्वे Question Answer
• काळे केस Question Answer
• खोद आणखी थोडेसे Question Answer (कविता)
• वीरांगना Question Answer (स्थूलवाचन)

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 2 बोलतो मराठी… Notes, Textbook Exercise Important Questions and Answers.

Class 10th Marathi Kumarbharti Chapter 2 बोलतो मराठी Question Answer Maharashtra Board

Std 10 Marathi Chapter 2 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 2 बोलतो मराठी… Textbook Questions and Answers

प्रश्न, पुढील उताश वाचा आणि दिलेल्या सूचनांनुसार ती करा:

कृती १: (आकलन)

प्रश्न 1.
आकृत्या पूर्ण करा :
(i)

उत्तर :

(ii)

उत्तर :

(iii)

उत्तर :

प्रश्न 2.
विनोद करणाऱ्या नव्याने पुढील वाक्याचा लावलेला अर्थ लिय :
तुम्हांला मी उत्तप्या बनवू का?
उत्तर :
मी तुमचे उत्तायामप्ये गपांतर वर का?

प्रश्न 3.
क्यों वो वाक्यातून विपरीत अर्य व्यक्त होतो. त्यामागील कारण तिहा.
उत्तर :
मराठी शब्दाचा व अर्थ बाजूला साशन त्या शब्दाला असलेला परभाषेतला अर्थ घेऊन वाक्ये तयार केली जातात, त्यामुळे विपरीत अर्थ व्यसा होतो.

उतारा क्र.१ : (पाठापुस्तक पृष्ठ क्र. २)

परवा वर्तमानपत्रात एक विनोद आता सेना.
बायको : “तुम्हांला, मी उत्तप्पा बनयू का?”
नवा : “नको. मी माणूसब टीक आहे. आली मोठी जादूगार !”

आता इथे विनोद निमांग झाला आहे. कारण ‘बनवणे हे क्रियापद निशे शोभणारे नाही. ते हल्ली हिंदी भाषेतून आपल्या स्वयंपाकपरा नको शार्क पुसतं आहे. मराठीत पोळया लारपे, भानी कोहगीत टाकणे, कडी करपे, पान संपणे, कुकर लायगे अशा वेगवेगळ्या क्रियांसाठी वेगवेगळे शब्दप्रयोग आहेत; पण हल्ती सगळे पदार्थ करत ‘बनवते’ जातात. मादीन ‘बनये’ म्हणजे ‘फायगे’ असा अर्थ खरं तर स्व आहे, त्यामुळे माणसायं माझ्ट आणि पुन्हा माकडाचा माणूस बनवणारा जादूगार, विनोद करणाऱ्या नवऱ्याला आठवला, तर आश्चर्य नाही.

मराठी रंगाचे शब्दप्रयोग ही आपल्या भाषेची श्रीमंती आहे. माठीत मारणे हे एक क्रियापद घेतले, ता ते किती वेगवेगळ्या प्रकारे वापरले जाते. हे लक्षात घेण्याजोगी आहे. जसे, गप्पा मारणे, उड्या मारगे, पापा मारणे, दिनकी मारणे, शिट्टी मारणे, पाकीट मारणे, वेवणावर ताव मारणे, (पोहताना) हातपाय मारणे. माझ्या मारपे इत्यादी, ‘मारणे’ भणजे मार देणे’ हा अचं यात कोठेही आलेला नाही. हीच तर भाषेची गंमत असते.

सन्दप्रयोगाप्रमाणे भावना हीदेखील भाषेनी खास शैली असते. ‘यस्ता खाणे ‘मचे वास्ता हा साक्षापदार्थ नाही. हे माहीत आहे ना? तसेच कंतम्नान घालणे’ समाचार युदाणाविषयीच्या यातायामप्ये असतो. कंठस्नान पाणगे महावे गयाखातून ‘अंघोळ थालगे’, असा शब्दशः अ. नाही, ‘घांदयाला यांदा सावणे’ (सहकार्य करणे) आणि ‘खांदा देणे’ (प्रेताला खांदा देणे) यांतला फरकही लक्षात घ्यायला कदा, एकाऐवजी दुसरे क्रियापद वापरले, तर अर्थाचा अर्थ होईल. अशी अनेक उदाहरणे देता येतील. त्यासाठी शब्दकोश वापरम्पाची सकप कापला की, ‘अक्कलवान’ म्हणजे शार; पण ‘अकलेचा कांदा’ म्हणजे ‘अतिशहाणा’ हे माहीत नसेल, तर कोण आपले खो कौतुक करतोय की फिरकी घेतोय, हेच आपल्याला कळणार नाही.

क्रियापद बापाताना त्यापूर्वी नामाला कोमता प्रत्यप लावायचा असतो, हे नीट माहीत नाले तरीदेखील अर्थाचा गोंधळ होतो. उदा., अंगाला लावणे आणि अंगावर घेणे, शिला हसगे (तिची नेष्टा करणे या अर्थी) आणि तिच्याशी हसणे (सहजपणे हमाणे) गांन प्रत्यय महत्त्वाचा आहे. हल्ली सार्वजनिक समारंभांमध्ये आगि वाहिन्यांवर प्रत्ययांची जागा अनेकदा कुकलेली असते. उदा., “तुझी मदत करणे’ याऐवजी ‘तुला मदत करणे’ हवे. “न्यांचे पन्यवाद’ पाऐवजी त्यांना पन्यवाद” असे म्हणायला हवे.

पायेमध्ये अनेक शब्द सतत पेत असतात, कारण तो नदीसारखी प्रणाली असते. आपणही संगणकासंबंधी अनेक नवे इंग्रजी शब्द मातत्याने आत्मसात केले आहेत. मराठीने आजवर संस्कृत, फारसी, अरबी, कन्नड़, इंग्रजी अशा अनेक भाषांमपले शब्द आपले मानले आहेत. ‘टेबल’ हा शब्द आता आपल्याला पाका वाटत नाही; पण गरज असताना इतर भाषांमपले शब्द आणि नेही जैं केली’ म्हणण्यातून काय नवीन अर्थ करतो? लाऐवजी ‘मी अभ्यास केला’ मम चोय नाही का?

नोंद : प्रस्तुत पुस्तकातील स पहिष्णा कृति-स्वाध्याय आहे. लामुळे या पाठातील स्वाध्यायात संपूर्ण वारा दिलेला आहे. यापुढे | मात्र प्रत्येक पाठातील स्वाध्यापांत संपूर्ण मारा न देता सान्याचे सुरवातीचे काही शब्द व शेवटचे काही शब्द दिलेले आहेत. विद्याभ्यांनी पाठयपुस्तकातून पूर्ण उतारा वाचावा.

मीक्षेत १३० ते १५० शब्दांचा उतारा दिला जाईल. इये विवाथ्यांच्या सोयीसाठी थोडा मोठा सारा दिलेला आहे. कारण त्यामुळे अधिक कृती देता येणे शक्य झाले आहे.

कृती २ : (आवलन)

प्रश्न 1.
उताऱ्याच्या आधाने पुढील चोवटी पूर्ण करा :

उत्तर :

प्रश्न 2.
हल्ली आढळून पेणाऱ्या आपल्या लोकांच्या दोन चुकीच्या भाषिक सक्यो सांगा.
उत्तर :

• वेगवेगळ्या कृतांसाठी वेगवेगळे शब्द वापरात असताना, स्या कोंसाठी केवळ एकच शब्द बोलला जातो.
• गरज नसताना अन्य भाषांतील शब्दांचा वापर केला जातो.

कृती ३ : (व्याकरण)

प्रश्न 1.
वेगवेगळ्या अर्थछटा व्यक्त करण्यासाठी चापाले नागारे तुम्हांला माहीत असलेले क्रियापद सोदाहरण लिहा. (फमा ४ अर्थछटा)
उत्तर :

• महापालिकेने एकान दिवसात तीनशे बेकायदेशीर यांपकामे पाडलि.
• छपरावर वाळत घातलेले पापड कानळ्यांनी खालि पाडले.
• चक्कीवरून दळण आणताना गोपू पीच पाहत पाहतच घरी आला.
• विरोधी पक्षाच्या उमेदवाराने मंत्र्याला प्रचंड बहुमानाने पाडले.

प्रश्न 2.
‘वाटणे’ हे क्रियापद नापल नेगवेगळ्या अर्थाची दोन वाक्ये तपार कता.
उत्तर :

• मी केलेल्या त्या नुकीनी मला साल वाटली. (बाटणे : भावना जापत्य)
• पास झाल्याबद्दल रश्मीचे पेढे वारले. (वाटणे : देण्याची कृती)

कृती ४ : (स्वयत/ अभिव्यक्ती)

प्रश्न 1.
भाषा सतत बदलत असले, याची कारणमीमांसा दया.
उत्तर :
एखाच्या परिस्तात राहणाव्या लोगांचा एक समाज बनतो. त्यांची पापा एकच असते. विख्यातले शब्द, वाश्य पढवण्याचे नियम हे ती भाषा बोलणाऱ्या सगळयांना ठाऊक असतात. मात्र, प्रत्येक पिढीमध्ये त्या त्या ठिकागाच्या भाषेमध्ये यूक्ष्मपणे बदला सेन जसजसा लोकांचा विकास होतो, तसतशी त्यांची भाषामुपा विकसित होत जाते. आधुनिक काळात अनेक गमार एकमेकांच्या अबळ नांदतात. एकमेकांत मिसळतात. या मेगवेगळ्या समाजांचा प्रभाव एकमेकांच्या भाषेवर पडतो. प्रांक भाषा अशी बदलत राहते. म्हणून कोणतीही भाषा कपीही स्थिर नलो. तीन सातवाने बदल होत राहतो. काळ बदलतो, तशी लोकांची जगण्याची रीन बदलते.

त्यामुळे भाषेतले शब्द बदलतात. जुने शब्द लोप पावतात, जवान शब्दांची भर पडते. अन्य भाषांमपीत शब्द-संकल्पना स्थानिक भाषेत सामावले जातात, स्थानिक भाषेतील शब्द-संकल्पना अन्य भाषांमध्ये शिरतात. अशा प्रकारे प्रत्येक भाषा प्रत्येक क्षणी बदलत असते.

प्रश्न 2.
स्वत:च्या भाषेवर प्रभुत्व मिळवणे म्हणजे स्वा:च्या भाषेचा सन्मान करणे होय’, हे विधान समजावून सांगा.
उत्तर :
स्वत:च्या भाषेवा सन्मान आपण कसा करणार? सर्वात प्रथम म्हणजे मी माझी स्वाःची भाषा उत्तम रितीने आत्यपान कौन. माझे सन विचार, भावना माझ्या भाषेत कसोशीने व्यक्त करम्पाना प्रयत्न कनीन, माझी भाषा उत्तम येण्यासाठी मी माझ्या भाषेतील वर्तमानपत्रे, नियतकालिके पांचे नियमित वाचन करीन. माझ्या पायेतीत अनमोलन साहित्याचा आस्वाद घेत रडीन, भाषा चांगल्या रितीने आत्मपान करण्यासाठी शब्दकोश, व्युत्पत्ती कोश यांसारख्या पोशांचा वेळोवेळी मनापासून उपयोग करीत. यामुळे माझे माझ्या भाषेवरील प्रमुख वाडेल. अशा प्रकारे स्वत:च्या भाषेवरीत प्रभुत्व बाहरणे म्हणजे त्या भाषेचा सन्मान करणे होय.

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 2 बोलतो मराठी… Additional Important Questions and Answers

प्रश्न. पुढील उतारा वाचा आणि दिलेल्या मूचनांनुसार कृती करा :

कृती १ : (आकलन)

प्रश्न 1.
आकृत्या पूर्ण करा:

उत्तर :

प्रश्न 2.

उत्तर :

प्रश्न 3.
पाठाच्या आधारे पुढील चौकी पूर्ण करा :

उत्तर :

कृती २ : (आकलन)

प्रश्न 1.
कंसातील योग्य शब्द योजून रिकाम्या चौकटी भरा :
(कलेवर, सूतकताई, पुण्यात, मोरांबा)

उत्तर :

प्रश्न 2.
लेखिकांच्या मते, भाषेवरील प्रेमासाठी पुढील कृती केल्या पाहिजेत :
(i) …….. (ii) ……… (iii) ………. (iv) ……….
उत्तर :
(i) भाषेतली शक्तिस्थळे जाणून घेतली पाहिजेत.
(ii) भाषेचा योग्य सन्मान राखायला हवा.
(iii) भाषेशी जिव्हाळ्याचे नाते राखायला हवे.
(iv) भाषेचे ज्ञानही मिळवायला हवे.

कृती ३ : (व्याकरण)

प्रश्न 1.
‘सम + आरंभ = समारंभ’ या प्रकारातील संधीची आणखी दोन उदाहरणे लिहा.
उत्तर :
(i) अन् + आदर = अनादर
(ii) सत् + आचार = सदाचार

प्रश्न 2.
‘शब्दरूपे’ या प्रकारच्या समासाची दोन उदाहरणे विग्रहासह लिहा.
उत्तर :
(i) शालागृह : शाळेचे गृह, षष्ठी तत्पुरुष.
(ii) विद्यार्थिदशा : विदयार्थ्याची दशा, षष्ठी तत्पुरुष.

कृती ४ : (स्वमत / अभिव्यक्ती)

प्रश्न 1.
लेखिकांनी मराठी भाषेचा केलेला सन्मान तुमच्या शब्दांत लिहा.
उत्तर :
लेखिकांनी मराठी भाषेला श्रीमंत म्हटले आहे. होय, माझी मराठी श्रीमंत आहे. मला या गोष्टीचा प्रचंड अभिमान वाटतो.

माझ्या भाषेकडे बारकाईने पाहा. विविध ढंगांचे शब्दप्रयोग ही माझ्या भाषेची खासियत आहे. अनेकदा एकच शब्द अनेकानेक अर्थछटा प्रकट करतो. ‘चालणे’ हे साधे क्रियापद बघा. प्रत्यक्ष पायांनी चालणे या अर्थाशिवाय आणखी अनेक अर्थछटा ‘चालणे’ या क्रियापदादवारे व्यक्त करता येतात. उदाहरणार्थ, लुट्लट्र चालणे, लबाडी चालणे, नोटा-नाणी चालणे, एखादे तत्त्व चालणे, एखादया रितीनुसार चालणे, घड्याळ चालणे वगैरे वगैरे. अशी किती वाक्ये सांगू? वाक्प्रचार हा माझ्या भाषेचा खास गोडवा आहे. माझ्या भाषेने अनेक भाषांमधील शब्द स्वत:च्या हृदयात सामावून घेतले आहेत. म्हणून माझी भाषा अधिकाधिक श्रीमंत होत चालली आहे.

प्रश्न 2.
मराठी भाषेबद्दलच्या तुमच्या भावना स्पष्ट करा.
उत्तर :
आपण सर्वजण सतत एकमेकांना काहीतरी सांगण्याचा प्रयत्न करतो. म्हणजे आपले मनच आपण इतरांसमोर प्रकट करीत असतो. याचा अर्थ, कोणतीही भाषा म्हणजे ती बोलणाऱ्या माणसांचे मन असते.

आपले समृद्ध जीवन आपल्या भाषेत व्यक्त होते तेव्हा ती भाषा समृद्ध होते. पण हे असे केव्हा होईल? तर जेव्हा माझे मन मी पूर्णांशाने, अगदी बारीक-सारीक तपशिलांसह माझ्या भाषेत व्यक्त करू शकेन तेव्हाच. अशा प्रकारे मन व्यक्त करण्याचे सामर्थ्य माझ्या भाषेत नक्कीच आहे. माझ्या भाषेत खास मराठी वळणाचे शब्दप्रयोग आहेत. वाक्प्रचार ही तर माझ्या मराठीची खासियत आहे. अनेकदा एकच शब्द अनेक अर्थछटा सहज प्रकट करू शकतो. माझ्या भाषेत अनेक भाषांमधील शब्द सामावले गेले आहेत. त्यामुळे मी माझे सर्व भाव खुलवून मांडू शकतो. सूक्ष्मपणे मांडू शकतो. इतकी श्रीमंत भाषा ही माझी भाषा आहे, हे माझे भाग्यच आहे.

प्रश्न 3.
‘तुम्ही शहाणे आहात,’ या वाक्यातील ‘शहाणे’ या शब्दाच्या अर्थछटा लिहा.
उत्तर :
‘तुम्ही शहाणे आहात,’ असे अनेकदा म्हटले जाते. त्या वेळी ऐकणाऱ्याच्या समजूतदारपणावर, त्याच्या विवेकावर बोलणाऱ्याचा विश्वास असतो. आई आपल्या मुलांना हे उद्गार ऐकवते, तेव्हा तिच्या मनात आपल्या मुलांबद्दल अशीच खात्री असते.

मात्र प्रत्येक वेळेला ‘तुम्ही शहाणे आहात,’ या वाक्याचा असा सरळ, प्रांजळ व निष्कपट अर्थ असतोच, असे नाही. काही व्यक्ती मुळातच लबाड असतात. चूक लपवण्यासाठी बुद्धीचा दुरुपयोग करतात. कधी कधी तर काही माणसांना खरोखरच साधी, सोपी गोष्टही कळत नाही. कितीही समजावून सांगितले, तरी त्यांना ते समजतच नाही. मग त्यांना ‘तुम्ही शहाणे आहात,’ असे ऐकवावे लागते. येथे ‘शहाणे’ हा शब्द वापरलेला असला तरी आपण मनातल्या मनात ‘तुम्ही मूर्ख आहात,’ असेच म्हणत असतो.

प्रश्न 4.
गरज नसताना इतर भाषांमधील शब्द वापरून बोलू नये,’ या लेखिकेच्या मताबाबत तुमचे मत सोदाहरण लिहा.
उत्तर :
परभाषेतून आपल्या भाषेत अनेक नवीन शब्द आले आहेत, ते केव्हाच मराठी झाले आहेत. ते मराठी शब्द नाहीत, अशी कोणाला शंकाही येणार नाही.

मात्र काही वेळा परभाषेतील शब्द अकारण वापरले जातात. आणि तेसुद्धा आपल्या भाषेत त्यासाठी अत्यंत सार्थ, समर्पक शब्द असताना! अलीकडे “ती पिवळीवाली दया,” “तो पांढरावाला पट्टा दाखवा’ अशी वाक्ये सर्रास ऐकू येतात. वास्तविक पाहता ‘पिवळी बॅग’ आणि ‘पिवळीवाली बॅग’ यांत कोणता फरक आहे? ‘पिवळी बॅग’ या शब्दप्रयोगातून आधीपासूनच योग्य अर्थ व्यक्त होत असताना ‘पिवळीवाली’ हा नवीन शब्दप्रयोग का करावा? मराठीत आपण असे बोलतच नाही. मराठीत ‘वाला’ हा प्रत्यय फक्त नामाला जोडला जातो. “पिवळी’ हे विशेषण आहे. मराठीत विशेषणाला किंवा सर्वनामाला ‘वाला’ हा प्रत्यय जोडण्याची प्रथाच नाही. शिवाय त्या नवीन शब्दप्रयोगाने अर्थामध्ये कोणतीही भर पडत नाही. म्हणून गरज नसताना परभाषेतील शब्द वापरून बोलू नये, हे लेखिकांचे मत योग्यच आहे.

व्याकरण व भाषाभ्यास

कृतिपत्रिकेतील प्रश्न ४ (अ) आणि (आ) यांसाठी…

अ. व्याकरण घटकांवर आधारित कृती:

समास

समासात कमीत कमी दोन शब्द असतात. हे दोन शब्द एकत्र करून जो जोडशब्द तयार होतो, त्यास सामासिक शब्द म्हणतात. या सामासिक शब्दाची फोड करून दाखवणाऱ्या पद्धतीला विग्रह म्हणतात.
उदा., शब्द + शब्द = सामासिक शब्द – विग्रह
(१) प्रति + दिन = प्रतिदिन – प्रत्येक दिवशी
(२) विदया + आलय = विदयालय – विदयेचे आलय (घर) .
(३) राम + लक्ष्मण = रामलक्ष्मण – राम आणि लक्ष्मण
(४) नील + कंठ = नीलकंठ – निळा आहे ज्याचा कंठ तो (शंकर)

समासाचे प्रकार :
1. समासातील शब्दांना ‘पद’ म्हणतात.
पहिला शब्द → पहिले पद.
दुसरा शब्द → दुसरे पद. समासातील कोणते पद महत्त्वाचे किंवा प्रधान आणि कमी महत्त्वाचे किंवा गौण आहे, यावरून समासाचे चार प्रकार पडतात. [प्रधान पद +/गौण पद -]

समासाचे चार मुख्य प्रकार होतात :

[या इयत्तेत आपल्याला अव्ययीभाव, तत्पुरुष (विभक्ती व द्विगू) आणि द्वंद्व हे समास शिकायचे आहेत.]

(१) अव्ययीभाव समास :

• ज्या समासातील पहिले पद प्रधान असते व सामासिक – शब्द क्रियाविशेषण अव्ययाचे कार्य करतो, त्यास अव्ययीभाव समास म्हणतात.

उदा., आजन्म, दररोज, बिनचूक, यथाशक्ती, बेशिस्त, दारोदार, प्रतिदिन इत्यादी.

(२) तत्पुरुष समास :
(१) विभक्ती तत्पुरुष :
ज्या समासातील दुसरे पद प्रधान असून, ज्या सामासिक शब्दांमधील विभक्ती प्रत्यय गाळलेले असतात, त्यास विभक्ती तत्पुरुष समास म्हणतात.
उदा., तोंडपाठ (तोंडाने पाठ), क्रीडांगण (क्रीडेसाठी अंगण), विदयालय (विदयेचे आलय), घरकाम (घरातील काम) इत्यादी.

(२) द्विगू समास :
ज्या समासातील दुसरे पद प्रधान असून, पहिले पद संख्याविशेषण असते, त्यास द्विगू समास म्हणतात. उदा., त्रिभुवन, चौकोन, पंचपाळे, दशदिशा, नवरात्र इत्यादी.

(३) वंद्व समास :
ज्या समासातील दोन्ही पदे प्रधान असतात, त्यास द्वंद्व समास म्हणतात.
उदा., आईवडील, खरेखोटे, केरकचरा इत्यादी.
द्वंद्व समासाचे प्रकार :
(१) इतरेतर द्वंद्व : ज्या सामासिक शब्दाचा विग्रह करताना ‘आणि’, ‘व’ या उभयान्वयी अव्ययांचा उपयोग करतात, त्यास इतरेतर द्वंद्व समास म्हणतात. उदा., आईवडील (आई आणि वडील); रामलक्ष्मण (राम आणि लक्ष्मण)

(२) वैकल्पिक वंद्व : ज्या सामासिक शब्दाचा विग्रह करताना ‘किंवा’, ‘अथवा’ या उभयान्वयी अव्ययांचा वापर केला जातो, त्यास वैकल्पिक वंद्व समास म्हणतात. (यात बहुधा परस्परविरोधी पदे असतात.) उदा., खरेखोटे (खरे किंवा खोटे), सुखदुःख (सुख किंवा दुःख) इत्यादी.

(३) समाहार वंद्व : ज्या सामासिक शब्दात अनेक गोष्टींचा समावेश असतो व ज्याचा विग्रह करताना ‘वगैरे, इतर’ या शब्दांचा वापर केला जातो, त्यास समाहार दवंदव समास म्हणतात. उदा., गप्पागोष्टी (गप्पा, गोष्टी वगैरे), मीठभाकर (मीठ, भाकर व इतर पदार्थ) इत्यादी.

१. समास :
पुढील सामासिक शब्दांचा विग्रह करा :
प्रश्न 1.
आजन्म
उत्तर:
आजन्म – जन्मापासून

प्रश्न 2.
मोरपीस
उत्तर :
मोरपीस – मोराचे पीस

प्रश्न 3.
त्रिभुवन
उत्तर :
त्रिभुवन – तीन भुवनांचा समूह

प्रश्न 4.
खरेखोटे
उत्तर :
खरेखोटे – खरे किंवा खोटे

प्रश्न 5.
विटीदांडू .
उत्तर :
विटीदांडू – विटी आणि दांडू

प्रश्न 6.
गुरेवासरे.
उत्तर :
गुरेवासरे – गुरे, वासरे वगैरे.

२. शब्दसिद्धी :

प्रश्न 1.
‘अति’ हा उपसर्ग लागलेले चार उपसर्गघटित शब्द लिहा.
उत्तर :

• अतिशहाणा
• अतिसुंदर
• अतिआनंद (अत्यानंद)
• अतिआवश्यक (अत्यावश्यक).

प्रश्न 2.
‘वान’ हा प्रत्यय लागलेले चार प्रत्ययघटित शब्द लिहा.
उत्तर :

• गुणवान
• धनवान
• गाडीवान
• अक्कलवान.

प्रश्न 3.
सामान्यरूप :
पुढील शब्दांतील सामान्यरूपे ओळखा :
(i) भाषेची
उत्तर :
भाषे

(ii) घरात (मार्च ‘१९)
उत्तर :
घरा

(iii) विनोदाने
उत्तर :
विनोदा

(iv) महोत्सवाला
उत्तर :
महोत्सवा

(v) जिभेला (मार्च ‘१९).
उत्तर :
जिभे.

प्रश्न 4.
वाक्प्रचार :
वाक्प्रचार व अर्थ यांच्या जोड्या लावा :

उत्तर :
(i) खांदयाला खांदा लावणे – सहकार्य करणे.
(ii) कंठस्नान घालणे – ठार मारणे.
(iii) माश्या मारणे – निरुदयोगी असणे.
(iv) खस्ता खाणे – खूप कष्ट उपसणे.

आ. भाषिक घटकांवर आधारित कृती

१. शब्दसंपत्ती :

प्रश्न 1.
समानार्थी शब्द लिहा :
(i) कंठ
उत्तर :
कंठ = गळा

(ii) मयूर
उत्तर :
मयूर = मोर

(iii) नदी
उत्तर :
नदी = सरिता

(iv) पाऊस.
उत्तर :
पाऊस = पर्जन्य.

प्रश्न 2.

उत्तर :

प्रश्न 3.
पुढे दिलेल्या अनेकवचनी नामांचे एकवचनी रूप लिहून त्यांचा वापर करून प्रत्येकी एक वाक्य तयार करा :
(i) रस्ते
उत्तर :
रस्ते – रस्ता.
वाक्य : डोंगरावरचा रस्ता वळणदार आहे.

(ii) वेळा
उत्तर :
वेळा – वेळ.
वाक्य : परीक्षेची वेळ जवळ आली.

(iii) भिंती
उत्तर :
भिंती – भिंत.
वाक्य : रंग लावलेली भिंत छान दिसते.

(iv) विहिरी
उत्तर :
विहिरी – विहीर.
वाक्य : आमची विहीर खूप खोल आहे.

(v) घड्याळे
उत्तर :
घड्याळे – घड्याळ.
वाक्य : बाबांनी मला नवीन घड्याळ आणले.

(vi) माणसे.
उत्तर :
माणसे – माणूस.
वाक्य : पावसात एकही माणूस घराबाहेर पडला नाही.

प्रश्न 4.
गटात न बसणारा शब्द ओळखून चौकट पूर्ण करा :
(i) ऐट, डौल, रूबाब, चैन.
उत्तर :
चैन

(ii) कपाळ, हस्त, ललाट, भाल.
उत्तर :
हस्त

(iii) विनोद, नवल, आश्चर्य, विस्मय.
उत्तर :
विनोद

(iv) संपत्ती, संपदा, कांता, दौलत.
उत्तर :
कांता

(v) प्रख्यात, प्रज्ञा, नामांकित, प्रसिद्ध.
उत्तर :
प्रज्ञा

प्रश्न 5.
पुढील शब्दसमूहाबद्दल एक शब्द लिहा :
(i) पसरवलेली खोटी बातमी
उत्तर :
अफवा

(ii) ज्याला मरण नाही असा
उत्तर :
अमर

(iii) समाजाची सेवा करणारा
उत्तर :
समाजसेवक

(iv) संपादन करणारा
उत्तर :
संपादक

प्रश्न 6.
पुढील शब्दांतील अक्षरांपासून चार अर्थपूर्ण शब्द लिहा :

उत्तर :

प्रश्न 7.
लेखननियम :
अचूक शब्द ओळखा :
(i) भाशातज्ञ/भाषातज्ञ/भाषातज्ज्ञ/भाशातज्ज्ञ.
उत्तर :
भाषातज्ज्ञ

(ii) साहित्यिक/साहीत्यिक/साहित्यीक/साहीत्यीक. उत्तरे :
उत्तर :
साहित्यिक.

प्रश्न 8.
विरामचिन्हे :
पुढील विरामचिन्हे ओळखा :

उत्तर :

प्रश्न 9.
पारिभाषिक शब्द :
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द लिहा :
(i) Event
उत्तर :
घटना

(ii) Drama
उत्तर :
नाटक

(iii) Yard
उत्तर :
आवार

(iv) Mobile
उत्तर :
भ्रमणध्वनी

प्रश्न 10.
अकारविल्हे/भाषिक खेळ :
पुढील शब्द अकारविल्हेनुसार लिहा :
(i) भाषा → मराठी → क्रियापद → भाव.
उत्तर :
क्रियापद → भाव → भाषा → मराठी.

(ii) गणित → भूगोल → भाषा → इतिहास (मार्च ‘१९).
उत्तर :
इतिहास → गणित → भाषा → भूगोल.

बोलतो मराठी… शब्दार्थ

• व्युत्पत्ती – शब्दाचे मूळ शोधण्याचे शास्त्र.

बोलतो मराठी… वाक्प्रचार व त्यांचे अर्थ

• पाकीट मारणे : पैशाचे पाकीट शिताफीने चोरणे.
• ताव मारणे : भरपूर खाणे.
• माश्या मारणे : रिकामटेकडेपणाने वेळ घालवणे.
• खस्ता खाणे : खूप कष्ट करणे.
• कंठस्नान घालणे : गळा कापून ठार मारणे.
• खांदयाला खांदा लावणे : सहकार्य करणे.
• खांदा देणे : प्रेत वाहून नेण्यात सहभागी होणे.
• अकलेचा कांदा असणे : अतिशहाणा असणे.
• एखाद्याला हसणे : एखादयाची थट्टा करण्याच्या हेतूने हसणे.

Marathi Kumarbharti Std 10 Digest Pdf भाग-१

• जय जय हे भारत देशा (गीत) Question Answer
• बोलतो मराठी… Question Answer
• आजी : कुटुंबाचं आगळ Question Answer
• उत्तमलक्षण (संतकाव्य) Question Answer
• वसंतहृदय चैत्र Question Answer
• बालसाहित्यिका : गिरिजा कीर Question Answer (स्थूलवाचन)

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 6 वस्तू (कविता) Notes, Textbook Exercise Important Questions and Answers.

Class 10th Marathi Kumarbharti Chapter 6 वस्तू (कविता) Question Answer Maharashtra Board

Std 10 Marathi Chapter 6 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 6 वस्तू Textbook Questions and Answers

कृतिपत्रिकेतील प्रश्न २ (अ) साठी…

प्रश्न 1.
आकृत्या पूर्ण करा.

उत्तर:

प्रश्न 2.
कारणे लिहा.
(अ) वस्तूंना जपावे आणि त्यांचे लाडही करावेत, कारण ……………………………..
(आ) वस्तूंना हक्काच्या घरात राहू दिले जात नाही, कारण ……………………………..
उत्तर:
(अ) वस्तूंना जपावे आणि त्यांचे लाडही करावेत; कारण नंतरच्या काळातही त्या आपला स्नेह जिवंत ठेवणार आहेत.
(आ) वस्तूंना हक्काच्या घरात राहू दिले जात नाही; कारण त्यांचे आयुष्य संपते.

प्रश्न 3.
काव्यसौंदर्य.
(अ) कवितेतील खालील ओळींचे रसग्रहण तुमच्या शब्दांत करा. वस्तूंना मनही नसेल कदाचित, पण ते असल्यासारखे वागलो तर वस्तू प्रचंड सुखावतात.

(आ) ‘वस्तूंनाही असते आवड स्वच्छ राहण्याची’ याबाबतचा तुमचा दृष्टिकोन सांगा.
उत्तर:
द. भा. धामणस्कर यांनी ‘वस्तू’ या कवितेमध्ये वस्तूंना कसे हाताळावे व जोपासावे याचा वस्तुपाठ देताना वस्तूंचे मानवीकरण केले आहे.

बरीच माणसे वस्तूंना सजीव समजत नाहीत. त्यांनाही भावना असू शकतात, हे लक्षात घेत नाहीत. कवी म्हणतात की, त्यांनाही जीव आहे, मन आहे, असे आपण समजून त्यांच्याशी वागलो, तर वस्तूंना परमानंद होतो. वस्तूंना कसेही हाताळू नये. त्यांना एखादया लहान मुलांसारखे लाडावून मायेने हाताळावे. हाताळताना आपले अस्वच्छ हात लावू नयेत. कारण वस्तूंनाही स्वच्छतेची आवड असते. महात्मा गांधींचे वचन आहे की ‘स्वच्छता हा परमेश्वर आहे’, म्हणून केवळ माणसाने स्वच्छ राहावे असे नाही. आपण ज्या वस्तू वापरतो, त्यांनाही स्वच्छ राखता आले पाहिजे, ‘वस्तूंना असते आवड स्वच्छ राहण्याची’ या ओळीतून माणसाला वस्तू हाताळण्याचा निकोप दृष्टिकोन दिलेला आहे.

(इ) एखादी वस्तू बिघडल्यामुळे तुमची फजिती कशी झाली, याचे वर्णन करा.
उत्तर:
माझे दप्तर खूप छान आहे. मला ते खूप आवडते. पाठीवर त्याला घेऊन शाळेत मिरवत मिरवत जाण्यात एक वेगळा आनंद आहे. मी माझ्या दप्तराचे खूप लाड करतो. त्याला दर रविवारी घुतो, स्वच्छ करतो. पण एकदा काय झाले! गृहपाठ खूप असल्यामुळे माझ्या दप्तरात मी सर्व पुस्तके, वया कोंबल्या. त्यात खाऊचा डबा व पाण्याची बाटली ठेवली; त्यामुळे दप्तर जड झाले व फुगले होते. तसेच ते मी पाठीवर मारून रस्त्याने ऐटीत चालू लागलो. थोड्या वेळाने कोपऱ्यात ते फाटले व त्यातून बऱ्याच वस्तू हळूहळू टपटपत खाली पडल्या दहा-बारा पावले पुढे गेल्यावर मला कळले. मी परत फिरलो नि पुस्तके-वह्या गोळा करीत मागे आलो. रस्त्यावरची मंडळी मला हसत होती. माझी फजिती झाली. पण त्यातून मी धडा शिकलो की दप्तर असले म्हणून काय झाले? त्यालाही जीव आहे. किती पेलणार ते ओझे! मी दप्तराची क्षमा मागितली व पुन्हा असे होणार नाही, याची दक्षता घेतली. दप्तरावरचे माझे प्रेम खूप वाढले.

(ई) तुमचा वर्गमित्र वर्गखोली/शालेय परिसरातील वस्तूचे नुकसान करत आहे. या प्रसंगी तुम्ही काय कराल ते सांगा.
उत्तर:
आमच्या शाळेच्या गेटपासून शाळेच्या मुख्य इमारतीपर्यंत रस्त्याच्या दुतर्फा फुलझाडांच्या कुंड्या रांगेने लावलेल्या आहेत. माझा मित्र रमेश खूप खोडसाळ आहे. एकदा शाळेत शिरताना त्याने मुद्दाम एका कुंडीला लाथ मारून खाली पाडली. आतील फुलरोपासहित माती विखुरली गेली. मी सोबतच होतो. मी त्याला या कृत्याबद्दल विचारले तेव्हा ते चुकून झाले असे सांगितले. पण मला माहीत होते, त्याने ते मुद्दामहून केले आहे. मी त्याला समजावले ‘ठीक आहे. तू चुकून लाथ लागली म्हणतोस ना! मग आता आपण ती नीट उचलून ठेव!’ तो मानेना. तो पुढे जाऊ लागला तेव्हा मी त्याला या कुंड्या शाळेने फक्त शोभेसाठी लावलेल्या नाहीत. विदयार्थ्यांना शाळेत येताना प्रसन्न वाटावे, हाही त्यामध्ये चांगला हेतू आहे. तसेच शास्त्रात आपण शिकलो की दिवसा झाडे प्राणवायू सोडतात व कार्बन डायऑक्साइड घेतात. हा प्राणवायू आपल्याला मिळतो. शिवाय फुलांचे विविध रंग आपल्या डोळ्यांना सुखावतात – असे समजावून सांगितले. तो मला ‘सॉरी’ म्हणाला व निमूटपणे आम्ही दोघांनी कुंडी जशी होती तशी करून ठेवली.

उपक्रम:

(१) तुमच्या घरातील आजी, आजोबा, पणजोबा यांच्या काळात असणाऱ्या वस्तूंची माहिती मिळवा.
(२) वस्तूंची नीट काळजी घेणाऱ्या आपल्या कुटुंबातील सदस्याची मुलाखत घेऊन संवादलेखन करा.
(३) तुमच्या घरातील अडगळीत टाकलेली वस्तू/विकायला काढलेली वस्तू जर तुमच्याशी बोलू लागली, तर ती काय बोलेल याची कल्पना करून लिहा.

कंदील व विजेरी (बॅटरी) यांच्यातील संवादाची कल्पना करून संवादलेखन करा,

कंदील : …………………………………………………………………..
विजेरी : …………………………………………………………………..
कंदील : …………………………………………………………………..
विजेरी : …………………………………………………………………..
कंदील : …………………………………………………………………..
विजेरी : …………………………………………………………………..
कंदील : …………………………………………………………………..
विजेरी : …………………………………………………………………..
कंदील : …………………………………………………………………..
विजेरी : …………………………………………………………………..
कंदील : …………………………………………………………………..
विजेरी : …………………………………………………………………..
उत्तर : …………………………………………………………………..
कंदील: फार दिवसांनी भेट झाली आपली! कशी आहेस तू?
विजेरी: मी बरी आहे. पण तू इथे काय करतोस? तुझी आता गरज उरली नाही.
कंदील: असे का म्हणतेस? तुझे नि माझे एकच तर कार्य आहे. स्वतः जळून दुसऱ्यांना प्रकाश देणे.
विजेरी: ते ठीक आहे. पण तू अगदी जुनापुराणा झालास. तुला पेटवताना किती कष्ट पडतात. मी पाहा, एक बटन दाबले की लांबवर झोत पडतो.
कंदील: हो. पण तुझा प्रकाश डोळ्यांना त्रास देतो. मी अगदी मंद तेवतो!
विजेरी: तू तर उगाचच मिणमिणतोस. माझ्या प्रकाशाचा झगमगाट तर बघ, कशी लखलखते मी!
कंदील: अग, तुला सेल लागतात पेटवायला. ते गेले की तुझा खेळ’। समाप्त! मी तर अखंड तेवत राहतो.
विजेरी: तुलाही तेल लागतंच की! तेल घाला, वात ठेवा. ती भिजवा. तेव्हा कुठे तू पेटतोस!
कंदील: माझ्याकडे तेल आहे. खरंच! तेलाला स्नेह म्हणतात. फार प्राचीन काळापासून माझा व माणसांचा स्नेहबंध आहे.
विजेरी: हो. पण काळ बदलला. आता तुझी गरज नाही.
कंदील: असे म्हणू नकोस! प्रकाश देणे आपले व्रत आहे. आपल्या दोघांचेही कार्य एकच आहे. आपल्या कार्याचा विसर पडू देता कामा नये!

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 6 वस्तू Additional Important Questions and Answers

प्रश्न. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती १: (आकलन)

प्रश्न 1.
चौकटी पूर्ण करा:
(i) नंतरच्या काळात वस्तूंना जिवंत ठेवणारा –
(ii) शाबूत ठेवावा असा वस्तूंचा हक्क –
उत्तर:
(i) नंतरच्या काळात वस्तूंना जिवंत ठेवणारा – आपला स्नेह
(ii) शाबूत ठेवावा असा वस्तूंचा हक्क – कृतग्नतापूर्ण निरोपाचा

प्रश्न 3.
एका वाक्यात लिहा:
(i) वस्तू केव्हा सुखावतात?
(ii) वस्तूंना कोणती हमी दयावी?
उत्तर:
(i) वस्तूंना जीव व मन असल्यासारखे वागवले की वस्तू प्रचंड सुखावतात.
(ii) आपल्या मानलेल्या जागेवरून त्यांना हटवणार नाही, याची वस्तूंना हमी दयावी.

वस्तूंना जीव नसेलही कदाचित, पण
जीव नसल्यासारखे वागवू नये त्यांना.
वस्तूंना मनही नसेल कदाचित, पण ते
असल्यासारखे वागलो तर वस्तू
प्रचंड सुखावतात.
वस्तू निखालस सेवकच असतात आपल्या,
तरीही बरोबरीचाच मान दयावा त्यांना.
वस्तूंना वेगळी, स्वतंत्र खोली नको असते,
त्यांना फक्त ‘आपल्या मानलेल्या’ जागेवरून
निष्कासित न होण्याची हमी दया.
वस्तूंनाही असते आवड स्वच्छ राहण्याची,
हे हातांना लक्षात ठेवायला सांगा.
वस्तूंना जपावे, लाडावूनही ठेवावे त्यापुढे जाऊन,
त्याच जिवंत ठेवणार आहेत आपला स्नेह
नंतरच्या काळातही.
आयुष्य संपले की वस्तूंनाही आजवरच्या
हक्काच्या घरात राहू देत नाहीत, तेव्हा
कृतज्ञतापूर्ण निरोपाचा त्यांचा हक्क
शाबूत ठेवावा,

कृती २: (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 3.
योग्य पर्याय निवडून विधाने पूर्ण करा:
(i) वस्तूंना वेगळी, ………………………………. खोली नको असते. (कुठलीही/स्वतंत्र/आपलीशी/माणसांची)
(ii) वस्तूंना ………………………………. न होण्याची हमी दया. (विकसित/आधारित/निष्कासित/पुलकित)
उत्तर:
(i) वस्तूंना वेगळी, स्वतंत्र खोली नको असते.
(ii) वस्तूंना निष्कासित न होण्याची हमी दया.

कृतिपत्रिकेतील प्रश्न २ (आ) साठी…

प्रश्न. पुढील कवितेसंबंधी त्याखाली दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:
नोंद: – प्रश्नामधील कृतींची पुनरावृत्ती टाळण्यासाठी यापुढे सर्व पक्ष्यपाठांमध्ये प्रश्नाखाली केवळ कवितेचे नाव आणि त्यापुढे मुद्द्यांसमोर उत्तरे देण्यात आली आहेत.
कविता-वस्तू. (मार्च ‘१९)
उत्तर:
(१) प्रस्तुत कवितेचे कवी: द. भा. धामणस्कर.
(२) कवितेचा रचनाप्रकार: मुक्तछंद.
(३) कवितेचा काव्यसंग्रह: भरून आलेले आकाश.
(४) कवितेचा विषय: निर्जीव वस्तूंचा सजीवपणा.
(५) कवितेतून व्यक्त होणारा (स्थायी) भाव: निर्जीव वस्तूंमधून खरे तर मानवी जीवनच व्यक्त होत असते.
(६) कवितेच्या कवींची लेखनवैशिष्ट्ये: या कवितेची रचना मुक्तछंदातील आहे. मुक्तछंदामुळे लेखनशैली मुक्त राहते. शब्द निवडण्यावर कोणतीही बंधने येत नाहीत. त्यामुळे दैनंदिन व्यवहारातील भाषा सहजगत्या वापरता येते. या कवितेत तसेच घडले आहे. दैनंदिन व्यवहारातील भाषेमुळे या कवितेचा वाचकांशी सहजसंवाद घडतो. साध्या पण आवाहक शब्दांतून मोठे तत्त्व येथे व्यक्त होते. अत्यंत हळुवार, संवेदनशील भावना कवी नेहमीच्याच साध्या शब्दांतून व्यक्त करतात.

(७) कवितेची मध्यवर्ती कल्पना: निर्जीव वस्तूंनाही भावना असते, त्यांनाही मन असते, असा महत्त्वाचा विचार कवी या कवितेत मांडतात. माणसे वस्तूंचा वापर करतात. त्यांना हाताळतात. त्यांच्या वस्तूंशी वागण्याच्या पद्घतीतून वस्तूंचे स्वरूप घडत जाते. म्हणून कोणतीही वस्तू नजरेला पडताच, त्या वस्तूच्या स्वरूपावरून संबंधित व्यक्तीचे व्यक्तिमत्त्व कळते. यावरूनच वस्तू सजीव असतात, असे कवींना वाटते. वस्तू आणि माणसे यांच्यातील नाते या कवितेतून उलगडून दाखवले आहे.

(८) कवितेतून व्यक्त होणारा विचार: निर्जीव वस्तूंना आपण मन नसते असे म्हणतो. कवींच्या मते, त्यांना मन असते, भावना असते. त्या संवेदनशीलही असतात. त्यांच्या दर्शनाने त्या वापरणाऱ्याचे व्यक्तिमत्त्व लक्षात येते. म्हणून माणसाने वस्तूंशी प्रेमाने, आत्मीयतेने वागले पाहिजे. आपण माणसांशी वागतो, तसेच वस्तूंशी वागले पाहिजे, असा महत्त्वाचा विचार या कवितेतून मांडला आहे.

(९) कवितेतील आवडलेली ओळ:
वस्तूंना जपावे, लाडावूनही ठेवावे त्यापुढे जाऊन. त्याच जिवंत ठेवणार आहेत आपला स्नेह नंतरच्या काळातही.

(१०) कविता आवडण्याची वा न आवडण्याची कारणे: ही कविता सुंदर आहे. आधुनिक जगात वावरणाऱ्या कोणालाही ही कविता आवडेल अशी आहे. एक वेगळाच चाकोरीबाहेरचा विचार कवींनी या कवितेतून मांडला आहे. सहसा आपण वस्तू आणि ती वापरणारा माणूस यांना वेगळे वेगळे मानतो. वापरकर्त्या व्यक्तीच्या मनाप्रमाणे वस्तूचे स्वरूप घडते. म्हणजे वस्तूवरून वापरकर्त्यांचे मन कळते. आपण वस्तूशी प्रेमाने वागतो. म्हणजे स्वतःशीच प्रेमाने वागत असतो, असा वेगळा नावीन्यपूर्ण भाव या कवितेतून व्यक्त होतो. म्हणून ही कविता मला आवडते.

(११) कवितेतून मिळणारा संदेश: वस्तूंशी माणसाने प्रेमानेच वागले पाहिजे. आपण वापरलेल्या वस्तूंच्या रूपाने आपले अस्तित्व मागे शिल्लक राहते. वस्तूंचा उपयोग संपला की वस्तूंना टाकून देऊ नये. त्यांना टाकून देणे म्हणजे आपले अस्तित्व आपण स्वतः संपवून टाकणे. हे टाळण्यासाठी आपण वस्तूंशी स्नेहाने, संवेदनशीलतेने वागले पाहिजे.

रसग्रहण
कृतिपत्रिकेतील प्रश्न २ (इ) साठी…

प्रश्न.
पुढील ओळींचे रसग्रहण तुमच्या शब्दांत लिहा: ‘वस्तूंना मनही नसेल कदाचित, पण ते असल्यासारखे वागलो तर वस्तू प्रचंड सुखावतात.’
उत्तर:
आशयसौंदर्य: ‘वस्तू’ या कवितेत कवी द. भा. धामणस्कर यांनी निर्जीव वस्तूंनाही सजीव प्राणिमात्रांसारख्या भावना असतात, त्या संवेदनशील असतात, हे बिंबवले आहे. तसेच वस्तूंना सहानुभूतीने समजून घ्यायला हवे व त्यांना प्रेमाने वागवायला हवे, असे प्रतिपादन केले आहे.

काव्यसौंदर्य: बहुतेक माणसे वस्तूंना निर्जीव समजतात व त्यांच्याशी निर्दयतेने वागतात. त्यांना कसेही हाताळतात. माणसांच्या या कठोर कृत्यावर भाष्य करताना वरील ओळींत कवी म्हणतात की कदाचित वस्तूंना जीव नसेलही आणि मनही नसेल, म्हणून त्यांना आपण कठोरपणे वागवावे का? वस्तूंना मन आहे, असे समजून जर त्यांच्याशी आपण चांगले वर्तन केले तर वस्तूंना खूप आनंद होतो. त्या सुखावतात. आपल्या कुटुंबातील त्या घटक आहेत, अशी आपुलकी आपण दाखवली तर वस्तूही आपल्याला प्रेम व माया देतील.

भाषिक सौंदर्य: मुक्तशैलीतल्या या रचनेमुळे कवींनी या ओळींतून रसिकांशी थेट संवाद साधला आहे. अगदी साध्या पण आवाहक शब्दांत मोठे तत्त्व बिंबवले आहे. वस्तू व माणूस यांतील स्नेहबंध आत्मीयतेने जपायला हवा, हा संदेश अगदी हळूवार पद्धतीने कवींनी दिला आहे.

व्याकरण व भाषाभ्यास

कृतिपत्रिकेतील प्रश्न ४ (अ) आणि (आ) यांसाठी…
व्याकरण घटकांवर आधारित कृती:

१. समास:

सामासिक शब्द व विग्रह यांच्या जोड्या लावा:
सामासिक शब्द – विग्रह
(i) प्रतिमास – (अ) मागे किंवा पुढे
(ii) ईश्वरनिर्मित – (आ) सात स्वर्गाचा समूह
(iii) सप्तस्वर्ग – (इ) धावणे, पळणे वगैरे
(iv) ऊनपाऊस – (ई) ईश्वराने निर्मित
(v) मागेपुढे – (उ) प्रत्येक महिन्याला
(vi) धावपळ – (ऊ) ऊन आणि पाऊस
उत्तर:
(i) प्रतिमास – प्रत्येक महिन्याला
(ii) ईश्वरनिर्मित – ईश्वराने निर्मित
(iii) सप्तस्वर्ग – सात स्वर्गांचा समूह
(iv) ऊनपाऊस – ऊन आणि पाऊस
(v) मागेपुढे – मागे किंवा पुढे
(vi) धावपळ – धावणे, पळणे वगैरे

२. अलंकार:

पुढील उदाहरण वाचून तक्ता पूर्ण करा:
(i) उदा., संगे असता नाथा आपण, प्रासादाहुन प्रसन्न कानन उपमेय → [ ] उपमान → [ ] अलंकाराचे नाव → [ ]
(ii) लहानपण देगा देवा। मुंगी साखरेचा रवा।। अलंकाराचे नाव → [ ] अलंकाराचे स्पष्टीकरण → [ ]
उत्तर:
(i) उपमेय → जंगल उपमान → प्रासाद (राजवाडा) अलंकाराचे नाव → व्यतिरेक अलंकार
(ii) अलंकाराचे नाव → दृष्टान्त अलंकार अलंकाराचे स्पष्टीकरण → या चरणात मुंगी लहान होऊन साखरेचा कण खाते.. तशी नम्रता मला दयावी अशी देवाकडे विनवणी केली आहे. नम्रता गुण अंगिकारावा हे सांगताना मुंगीचा दृष्टान्त दिला आहे. म्हणून हा दृष्टान्त अलंकार आहे.

३. वृत्त:

पुढील काव्यपंक्तींचे गण पाडून वृत्त ओळखा:
स्वये सर्वथा नम्र वाचे वदावे।
मना सर्व लोकांसि रे नीववावे।।
उत्तर:

वृत्त: हे भुजंगप्रयात वृत्त आहे.

४. शब्दसिद्धी:
(i) निः + कासित = निष्कासित, याप्रमाणे निः हा उपसर्ग लावून पुढील शब्द लिहा:
(१) फळ – ………………………
(२) काम – ………………………
(३) कर्ष – ………………………
(४) कांचन – ………………………
उत्तर:
(१) निष्फळ
(२) निष्काम
(३) निष्कर्ष
(४) निष्कांचन.

(ii) ‘क’ हा प्रत्यय असलेले चार शब्द लिहा.
उत्तर:
(१) सेवक
(२) लेखक
(३) वाचक
(४) साधक.

५. सामान्यरूप:

पुढील तक्ता पूर्ण करा:
शब्द – सामान्यरूप
(i) वस्तूंना …………………..
(ii) जागेवरून …………………..
(iii) हक्काच्या …………………..
(iv) हाताला …………………..
उत्तर:
शब्द – सामान्यरूप
(i) वस्तूंना – वस्तूं
(ii) जागेवरून – जागे
(iii) हक्काच्या – हक्का
(iv) हाताला – हाता

६. वाकप्रचार:

योग्य अर्थ निवडा:


उत्तर:
(i) शिल्लक ठेवणे
(ii) आश्वासन देणे

भाषिक घटकांवर आधारित कृती:

१. शब्दसंपत्ती:

प्रश्न 1.
पुढील शब्दांचे दोन अर्थ लिहा:

उत्तर:

प्रश्न 2.
पुढील शब्दाच्या अक्षरांतून चार अर्थपूर्ण शब्द तयार करा:

उत्तर:

प्रश्न 3.
समानार्थी शब्द लिहा:
(i) जीव – …………………………
(ii) मन = …………………………
(iii) आयुष्य = …………………………
(iv) घर = …………………………
उत्तर:
(i) जीव = प्राण
(ii) मन = चित्त
(iii) आयुष्य = जीवन
(iv) घर = गृह.

प्रश्न 4.
विरुद्धार्थी शब्द लिहा:
(i) सुखावतात x …………………………
(ii) सेवक x …………………………
(iii) मान x …………………………
(iv) स्वतंत्र x …………………………
(v) आवड x …………………………
(vi) स्वच्छ x …………………………
(vii) जिवंत x …………………………
(viii) नंतर x …………………………
(ix) कृतज्ञता x …………………………
(x) सजीव x …………………………
उत्तर:
(i) सुखावतात x दुखावतात
(ii) सेवक x मालक
(iii) मान x अपमान
(iv) स्वतंत्र x परतंत्र
(v) आवड x नावड
(vi) स्वच्छ x अस्वच्छ
(vii) जिवंत x मृत
(viii) नंतर x आधी
(ix) कृतज्ञता x कृतघ्नता
(x) सजीव x निर्जीव,

२. लेखननियम:

अचूक शब्द ओळखा:
(i) नीर्जीव/निर्जिव/निर्जीव/नीर्जिव.
(ii) अतर्मुख/अंतर्मुख/अंर्तमुख/अंतर्मूख.
(iii) सामुहिक/सामुहीक/सामूहिक/सामूहीक.
(iv) अंतकरण/अतःकरण/अंतःकरन/अंतःकरण,
उत्तर:
(i) निर्जीव
(ii) अंतर्मुख
(iii) सामूहिक
(iv) अंतःकरण,

३. विरामचिन्हे:

पुढील वाक्यातील विरामचिन्हे ओळखून लिहा: त्यांना फक्त ‘आपल्या मानलेल्या’ जागेवरून निष्कासित न होण्याची हमी दया.
उत्तर:
(i) [ ‘ ‘ ] → एकेरी अवतरण चिन्ह
(ii) [ . ] → पूर्ण विराम.

४. पारिभाषिक शब्द:

पुढील इंग्रजी पारिभाषिक शब्दांसाठी अचूक मराठी प्रतिशब्द कोणता?

उत्तर:
(i) परिवहन
(ii) आदयाक्षरे
(iii) गणसंख्या
(iv) पर्यवेक्षक.

५. भाषिक खेळ:
जसे –

जसे –

उत्तर:

वस्तू Summary in Marathi

कवितेचा भावार्थवस्तू कशा हाताळाव्यात व कशा जपाव्यात, हे सांगताना कवी म्हणतात – कदाचित वस्तूंना प्राण नसेल, पण म्हणून त्यांना निर्जीव समजून जीव नसल्यासारखे वागवू नये. (वस्तूंनाही माणसासारखा जीव असतो.) कदाचित वस्तूंना मनही नसेल, परंतु त्यांना मन असल्यासारखे जर आपण वागवले तर त्या वस्तूंनाही प्रचंड आनंद होतो. (वस्तू माणसासारख्या संवेदनशील असतात.)

खरे म्हणजे वस्तू आपल्या सेवेत रमतात. त्या आपल्या चाकर असतात, पण तरीही त्यांना समान दर्जा दयावा, बरोबरीच्या स्नेहभावाने सन्मान दयावा. वस्तूंना वेगळी आणि स्वतंत्र खोली नको असते. (त्यांना तुमच्याबरोबरच राहायचे असते. त्या स्वतःला वेगळे मानत नाहीत.) फक्त त्यांना नेमलेल्या व मानलेल्या जागेवरून न हटवण्याचे आश्वासन दया. (त्या ज्या जागेवर असतात, त्या जागेवर त्यांचे प्रेम जडलेले असते.)

वस्तू हाताळताना आपले घाणेरडे हात त्यांना लावू नका. वस्तूंनाही स्वच्छतेची प्रचंड आवड असते, हे हातांनीही चांगले लक्षात ठेवायला हवे. वस्तूंना जिवापाड जपावे, काळजी घ्यावी, क्वचित त्यांचे खूप लाड करावेत. (एखादया लहान गोजिरवाण्या बालकासारखी त्यांची काळजी घ्यावी व लाडावून ठेवावे.) कारण भविष्यकाळात याच वस्तू आपली माया, जिव्हाळा, स्नेह निरंतर जिवंत ठेवणार आहेत.

माणसांसारखेच वस्तूंचेही आयुष्य संपते. मरणानंतर माणूस हक्काच्या घरात राहत नाही. त्याला भावपूर्ण निरोप दिला जातो. त्याचप्रमाणे वस्तूंचे आयुष्य संपले की आपण त्यांना हक्काच्या जागेवरून हलवतो. तेव्हा माणसाने हे लक्षात ठेवावे की त्यांनाही कृतज्ञतापूर्वक निरोप यायचा असतो. हा निरोपाचा त्यांचा हक्क माणसाने कायम ठेवावा.

वस्तू शब्दार्थ

• प्रचंड सुखावतात – खूप आनंदित होतात.
• निखालस – अगदी खरे.
• सेवक – चाकर, सेवा करणारे.
• बरोबरीचा मान – समान दर्जा.
• निष्कासित – पदच्युत, जागेवरून हलवणे.
• स्नेह – प्रेम, जिव्हाळा, माया.
• हक्क – स्व-अधिकार,
• कृतज्ञता – भावनिक ऋण, आदरयुक्त भावना.

वस्तू वाक्प्रचार व त्यांचे अर्थ

• जीव नसणे : प्राण नसणे, अचेतन असणे.
• मान देणे : आदर करणे, सन्मान देणे,
• हमी देणे : आश्वासन देणे.
• लाडावून ठेवणे : सतत कौतुक करणे,
• आयुष्य संपणे : मरण येणे.
• निरोप देणे : सोडणे.
• शाबूत ठेवणे : जपून शिल्लक ठेवणे.

Marathi Kumarbharti Class 10 Textbook Solutions भाग-२

• वस्तू Question Answer (कविता)
• गवताचे पाते Question Answer
• वाट पाहताना Question Answer
• आश्वासक चित्र Question Answer (कविता)
• आप्पांचे पत्र Question Answer
• मनक्या पेरेन लागा Question Answer (स्थूलवाचन)

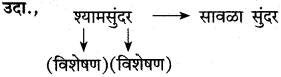
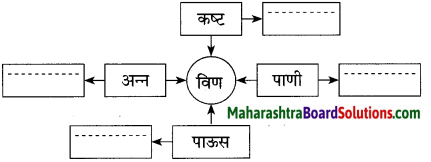
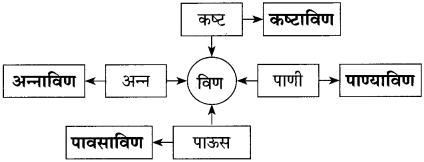
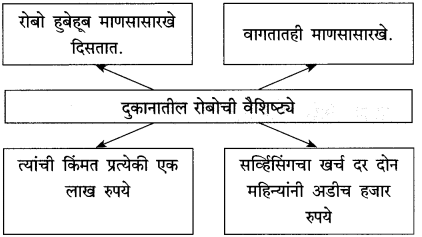
Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 3 आजी : कुटुंबाचं आगळ Notes, Textbook Exercise Important Questions and Answers.

Class 10th Marathi Kumarbharti Chapter 3 आजी : कुटुंबाचं आगळ Question Answer Maharashtra Board

Std 10 Marathi Chapter 3 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 3 आजी : कुटुंबाचं आगळ Textbook Questions and Answers

प्रश्न. पुढील उतारा वाचा आणि दिलेल्या सूचनांनुसार कृती करा :

कृती १ : (आकलन)

प्रश्न 1.
विधाने पूर्ण करा :
(i) स्वत:च्या कपाळावरचे गोंदण दिसू नये, म्हणून आजी —————
उत्तर :
स्वत:च्या कपाळावरचे गोंदण दिसू नये, म्हणून आजी कपाळावर बुक्का लावत असे.

(ii) वर्ष-दीड वर्षाने जन्मणाऱ्या वासरांमध्ये एकाआड एक खोंड नक्की असे, म्हणून —————–
उत्तर :
वर्ष-दीड वर्षाने जन्मणाऱ्या वासरांमध्ये एकाआड एक खोंड नक्की असे, म्हणून दावणीला कायम कपिलीचे बैल असत.

(iii) सुनांनी चहा करून पिऊ नये, म्हणून —————-
उत्तर :
सुनांनी चहा करून पिऊ नये, म्हणून ढाळजेतून सोप्यात येऊन आजी सक्त पहारा करायची.

प्रश्न 2.
पुढील मुद्द्यांच्या आधारे आजीचे शब्दचित्र रेखाटा :

(i) आजीचे दिसणे : ——————–
उत्तर :
आजीचे दिसणे : आजीला साडेपाच फूट उंची लाभली होती. तिचा वर्ण गोरा होता. उन्हापावसामुळे तिची त्वचा काळपटली होती. आजीच्या वयाची माणसे कमरेत वाकतात. त्यामुळे चालताना काठी घ्यावी लागते. पण आजी अजूनही ताठ कण्याने चालत होती. अजूनही तिचे सगळे दात शाबूत होते. डोक्यावरचे सगळे केस पिकले होते.

(ii) आजीची शिस्त : ——————–
उत्तर :
आजीची शिस्त : आजीची शिस्त कडक होती. सगळ्यांना सगळी कामे करता आली पाहिजेत, असा तिचा कटाक्ष होता. तिने कामांची वाटणी केली होती. ती कामे आजी सर्व सुनांना आलटूनपालटून करायला लावी. दुपारच्या कामांचेही तिने नियोजन केलेले असे. सुनांनी मुलांच्या बाबतीत आपपरभाव करू नये म्हणून मुलांना खाऊपिऊ घालताना आजीचा सक्त पहारा असे. गल्लीतल्या बायका दुपारी गप्पागोष्टींना येत असत. त्या वेळी ती बायकांनी सांगितलेल्या गोष्टींची शहानिशा करीत असे.

(iii) आजीचे सौंदर्य : —————-
उत्तर :
आजीचे सौंदर्य : आजीचे वय आता सत्तर वर्षांचे होते. उन्हापावसामुळे आजीची त्वचा रापली होती. पण तिचा मूळ गोरा वर्ण लपत नव्हता. तिचे दात मोत्यांसारखे चमकत होते. विशाल कान व धारदार नाक यांनी आजीच्या सौंदर्यात भर पडत होती. चेहऱ्यावर सुरकुत्या पडल्या तरी तिच्या सौंदर्यात उणेपणा आला नव्हता.

(iv) आजीचे राहणीमान : ————-
उत्तर :
आजीचे राहणीमान : त्या काळात इरकली लुगडे उच्च राहणीमानाचे लक्षण होते. हिरव्या व लाल रंगांची नऊवारी इरकली लुगडी व अंगात चोळी हा तिचा पेहराव असे. कपाळावरचं गोंदण दिसू नये म्हणून त्यावर ती बुक्का लावी. ती नेहमी नाली ठोकलेल्या जुन्या वळणाच्या वहाणा वापरत असे.

प्रश्न 3.
चूक की बरोबर सांगा :
(i) राहिलेली अर्धी चरवी घरात आली, की म्हातारी ढाळजंतनं सोप्यात. अवतरायची.
उत्तर :
बरोबर

(ii) आजीच्या डोक्यावरील सर्व केस पांढरे होते……………….
उत्तर :
बरोबर

(iii) सुनांच्या कामाबाबत आजी फारशी काटेकोर नसायची.
उत्तर :
चूक.

कृती २ : (आकलन)

प्रश्न 1.
विधाने पूर्ण करा :
(i) मुलांनी भरपूर खावे-प्यावे व त्यांची आबाळ होऊ नये, म्हणून —————-
उत्तर :
मुलांनी भरपूर खावे-प्यावे व त्यांची आबाळ होऊ नये, म्हणून आजी त्यांना धपाटे घालून घालून खायला घाली.

(ii) प्रत्येक सुनेला प्रत्येक काम आलेच पाहिजे, असा आजीचा आग्रह होता, म्हणून ती ——–
उत्तर :
प्रत्येक सुनेला प्रत्येक काम आलेच पाहिजे, असा आजीचा, आग्रह होता, म्हणून ती रोटेशनप्रमाणे काम बदलत जाई.

(iii) मुलांना दूध प्यायला देण्याबाबत सुना आपपरभाव करतील, अशी भीती आजीला वाटे, म्हणून ————–
उत्तर :
मुलांना दूध प्यायला देण्याबाबतं सुना आपपरभाव करतील, अशी भीती आजीला वाटे, म्हणून ती मुलांना गोठ्यातच दूध प्यायला लावी.

प्रश्न 2.
पुढीलपैकी चुकीची वाक्ये दुरुस्त करून बरोबर वाक्ये व दुरुस्त केलेली वाक्ये पुन्हा लिहा :
(i) दुपारची कामे आटोपून आजी ढाळजेत यायची.
उत्तर :
दुपारच्या कामांचे नियोजन करून आजी ढाळजेत यायची.

(ii) गाईने पान्हा सोडला की वासराला सोडायचे.
उत्तर :
गाईने पान्हा सोडला की वासराला धरून ठेवायचे.

(iii) आजीच्या घरी एक गावरान गाय होती.
उत्तर :
आमच्या घरी एक गावरान गाय होती.

कृती ३ : (व्याकरण)

प्रश्न 1.
पुढील वाक्यांतील वाक्प्रचार शोधून अधोरेखित करा :
(i) आजीच्या छत्रछायेखाली आमचे सर्व कुटुंब गुण्यागोविंदाने नांदत होते.
उत्तर :
आजीच्या छत्रछायेखाली आमचे सर्व कुटुंब गुण्यागोविंदाने नांदत होते.

(ii) सत्तरीनंतरही आजीच्या हातात काठी आली नव्हती.
उत्तर :
सत्तरीनंतरही आजीच्या हातात काठी आली नव्हती.

प्रश्न 2.
पुढील अधोरेखित शब्दांच्या जाती ओळखा आणि त्यांचे उपप्रकार लिहा :
(i) चार घरच्या चार सुना नांदायला आल्या.
उत्तर :
चार : विशेषण. संख्यावाचक विशेषण.
सुना : नाम. सामान्य नाम.
आल्या : क्रियापद. अकर्मक क्रियापद.

(ii) प्रत्येकीला काम आलंच पाहिजे.
उत्तर :
काम : नाम. भाववाचक नाम.

(iii) आजीला एकाही सुनेचा भरवसा नव्हता.
उत्तर :
ही : शब्दयोगी अव्यय.
भरवसा : नाम. भाववाचक नाम.

(iv) आमच्या घरी एक गावरान गाय होती.
उत्तर :
एक : विशेषण. संख्यावाचक विशेषण.
गावरान : विशेषण. गुणवाचक विशेषण.
गाय : नाम. सामान्य नाम.

कृती ४ : (स्वमत / अभिव्यक्ती)

प्रश्न 1.
तुम्हांला आठवत असलेला किंवा तुमच्या आईबाबांनी सांगितलेला तुमच्या लहानपणचा एखादा प्रसंग लिहा.
उत्तर :
मी लहान होतो तेव्हा सकाळी उठलो की, दात घासून, तोंड धुऊन मी तडक रानातल्या आमच्या वाड्याकडे धावत सुटायचो. कोकणात गुरांच्या गोठ्याला वाडा म्हणतात. तेथे माझे आजोबा माझी वाटच बघत असत. दरदिवशी ते माझ्यासाठी एक तांब्याएवढे मडके भरून दूध गरम करून ठेवत. मी गेलो की, घटाघटा ते दूध पीत असे. त्यानंतर त्या मडक्याला चिकटलेली साय खरवडून खाणे हा माझा मोठा आनंदाचा भाग असे. माझ्या या अखंडित दिनक्रमामुळे कोणत्या गाई-म्हशीचे दूध कोणत्या चवीचे आहे, हे मी सहज ओळखू शकतो. दुधाला एक स्वत:चे माधुर्य असते. दूध पिताना लोक दुधात साखर का घालतात, हे मला अजून कळलेले नाही.

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 3 आजी : कुटुंबाचं आगळ Additional Important Questions and Answers

प्रश्न. पुढील उतारा वाचा आणि दिलेल्या सूचनांनुसार कृती करा :

कृती १ : (आकलन)

प्रश्न 1.
एका शब्दात उत्तर लिहा : (मार्च १९)

उत्तर :

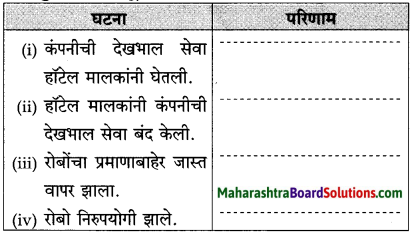
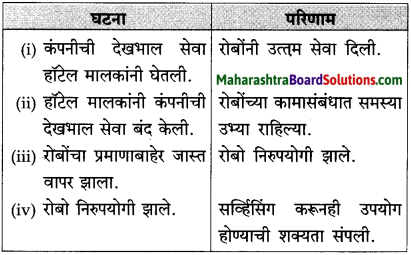
प्रश्न 2.
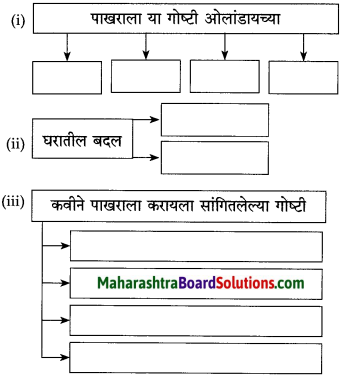
आकृती पूर्ण करा :
(i)

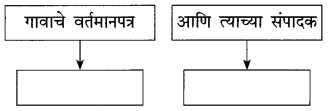
उत्तर :

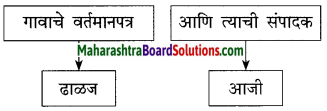
(ii)

उत्तर :

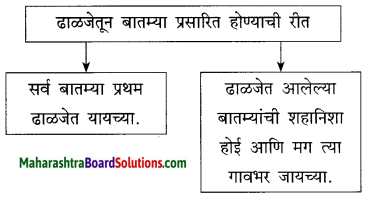
(iii)

उत्तर :

(iv)

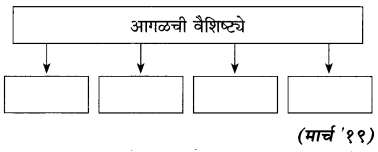
उत्तर :

कृती २ : (आकलन)

प्रश्न 1.
दुपारच्या वेळी रूढ खेळांखेरीज मुले ज्या गमतीजमती करीत, त्या लिहा.
उत्तर :

• वडाच्या पारंब्यांना लटकत, लोंबत राहायचे आणि पारंब्यांच्या टोकाला फुटलेली पिवळी पालवी खात बसायचे.
• देवळातली घंटा वाजवाजवून झोपलेल्यांची झोपमोड करायची.
• विहिरीत मनसोक्त पोहायचे.
• शिवणापानी खेळायचे.
• हातपाय पोटाशी आवळून घेऊन शरीराचे मुटके करून विहिरीत धडादिशी उड्या घ्यायची.
• ओल्या अंगाने मातीत लोळायचे आणि पुन्हा पाण्यात इंबायचे आणि शेवटी थकून भागून घरी जायचे.

[टीप : परीक्षेत कोणतीही दोन किंवा चार नावे लिहायला सांगितली जाऊ शकतात.]

प्रश्न 2.
बालपणी लाभलेल्या रानमेव्यांची नावे सांगा. (कोणतीही चार नावे लिहा.)
उत्तर :

• गाभोळ्या चिंचा, मिठाचे खडे व कच्च्या कैऱ्या, बोरे, चिंचेची कोवळी पाने.
• उंबर, ढाळे, भाजलेली कणसे, हुरडा.
• कच्ची वांगी, गवार, टोमॅटो, शहाळे.
• कलिंगड, शिंगाडे (चिबूड), करडीची भाजी, ज्वारीचे कणीस.
• कवठ, तुरी-मटकीच्या शेंगा, उकडलेल्या शेंगा, कुळथाचे पिठले.

प्रश्न 3.
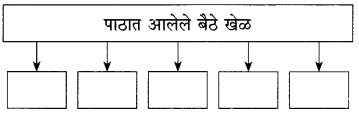
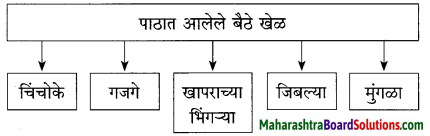
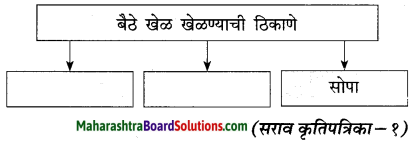
आकृत्या पूर्ण करा :
(i)

उत्तर :

(ii)

उत्तर :

(iii)

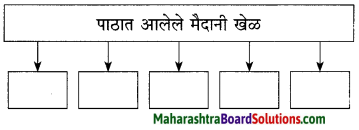
उत्तर :

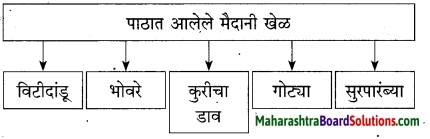
प्रश्न 4.
पुढील घटना उताऱ्याच्या आधारे क्रमाने लिहा : (मार्च ‘१९)
(i) म्हातारीची ढाळज सुटायची
(ii) वाडा शांत व्हायचा
(iii) कडुसं पडायच्या आधी मैफिल मोडायची
(iv) माणसं ढाळजंत बसायची
उत्तर :
(iii) कडुसं पडायच्या आधी मैफिल मोडायची
(i) म्हातारीची ढाळज सुटायची
(iv) माणसं ढाळजंत बसायची
(ii) वाडा शांत व्हायचा

कृती ३ : (व्याकरण)

प्रश्न 1.
सहसंबंध लक्षात घेऊन उत्तरे लिहा :

उत्तर :

प्रश्न 2.
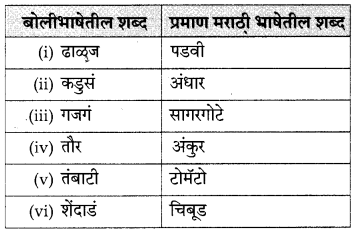
पुढील बोलीभाषेतील शब्दांना प्रचलित प्रमाण मराठी भाषेतील शब्द शोधून लिहा :

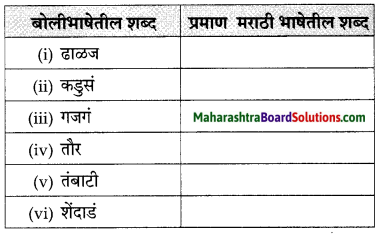
उत्तर :

प्रश्न 3.
तक्ता पूर्ण करा :

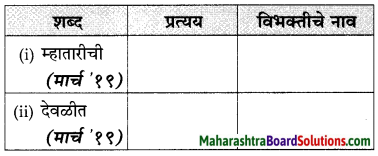
उत्तर :

प्रश्न 4.
पुढील वाक्यांतील अधोरेखित शब्दाचे लिंग बदलून वाक्य पुन्हा लिहा :
आजी त्याची संपादक होती. (सराव कृतिपत्रिका-१)
उत्तर :
आजोबा त्याचे संपादक होते.

कृती ४ : (स्वमत / अभिव्यक्ती)

प्रश्न 1.
‘आमची ढाळज म्हणजे गावाचं वर्तमानपत्र होतं,’ या वाक्याचा तुम्हांला कळलेला अर्थ लिहा.
उत्तर :
‘आगळ’ या कादंबरीच्या नायकाची आजी ही त्याच्या घराची सत्ताधीश होती. घरात तिचा वचक होता. घराबाहेरही तिच्या शब्दाला मान होता. दुपारपर्यंतच्या सर्व कामांचे नियोजन करून आजी ढाळजेत यायची. गल्लीतल्या बायकाही जमा व्हायच्या. निवडटिपण करता करता गप्पाटप्पा व्हायच्या. अनेक बातम्या, गुपिते उघड व्हायची. सगळ्याजणी बातम्यांवर चर्चा करीत. त्यातून बातम्यांची शहानिशा व्हायची.

वर्तमानपत्राचे वार्ताहर गावांतून बातम्या आणतात. संपादक या बातम्यांची शहानिशा करतात. मगच त्या बातम्या वर्तमानपत्रात छापल्या जातात. आजीच्या घराची ढाळज वर्तमानपत्रासारखीच होती. तिथे आलेल्या बातम्यांची शहानिशा झाल्यावरच बायका त्या बातम्या गावभर सांगायला मोकळ्या होत.

प्रश्न 2.
तुलना करा / साम्य लिहा :
आगळ : वाड्याचे संरक्षक कवच
आजी : कुटुंबाचे संरक्षक कवच किंवा
‘आजी म्हणजे घराचा आधार’ हे विधान सोदाहरण पटवून दया. (मार्च ‘१९)
उत्तर :
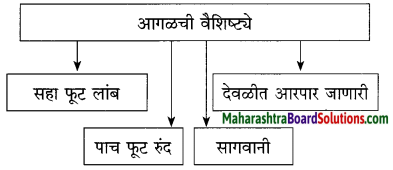
आगळ म्हणजे उंची-रुंदीला नऊ इंच आणि लांबीला सहा फूट असा भक्कम सागवानी वासा. एकदा आगळ लावली की चोऱ्यामाऱ्या होणे किंवा दरोडा पडणे शक्यच नसे. त्यामुळेच ही आगळ म्हणजे वाड्याला संरक्षणाचे एक भरभक्कम कवच लाभले होते.

प्रस्तुत उताऱ्यात आजीची भूमिकाही अगदी याच प्रकारची आहे. आजीमुळे कुटुंबात सुव्यवस्था नांदत होती. सुना आपापसात हेवेदावे करू शकत नव्हत्या. आपली कामे दुसरीवर ढकलू शकत नव्हत्या. सर्व कामे प्रत्येकीला करावी लागत. या वातावरणामुळे कोणावर अन्याय होत नव्हता. कोणालाही तक्रार करायला वावच राहत नसे. आजीमुळे प्रत्येकीला किंवा प्रत्येकाला भरभक्कम संरक्षण मिळाले होते. हे संरक्षण आगळेइतकेच भक्कम होते.

प्रश्न 3.
आगळ लावण्याची/टाकण्याची पद्धत समजावून सांगा.
उत्तर :
आगळ म्हणजे एक सागवानी अवजड वासा होता. त्याच्या एका टोकाला वाघाचा मुखवटा बसवला होता. वाघाच्या जबड्यात एक भक्कम कडी बसवलेली होती. त्या कडीला धरून आगळ ओढायची किंवा ढकलायची असते. दरवाज्याच्या दोन बाजूंना आगळ अडकवण्यासाठी भिंतींत दोन कोनाडे केलेले असतात. त्यांपैकी एक कोनाडा आगळ पूर्ण सामावली जाईल इतका खोल असतो. कडीला धरून आगळ कोनाड्यात पूर्ण ढकलली की दरवाजा उघडता येतो.

रात्रीच्या वेळी, दरवाजा बंद करून कोनाड्यात ढकलून ठेवलेली आगळ कडीला धरून ओढून बाहेर काढली जाते आणि ते टोक दुसऱ्या भिंतीच्या कोनाड्यात अडकवले जाते. अशा त-हेने आगळ बसवली की दरवाजा कोणीही उघडू शकत नाही.

प्रश्न 4.
दुपारच्या वेळी मुलांकडून केल्या जाणाऱ्या कल्पक कृती सांगा.
उत्तर :
कधी कधी बैठ्या खेळांऐवजी मुले वेगवेगळ्या कल्पक कृती करीत असत. एखादया वेळी सरपणातली लाकडे काढून विटीदांडू किंवा भोवरे तयार करीत बसत. भिंगऱ्या तयार करण्यासाठी घेतलेला लाकडाचा तुकडा दगडावर घासून घासून त्याला गोल आकार देण्याचा मुले प्रयत्न करीत. हे मोठे कष्टाचे काम असे. चुलीची काजळी लागून लागून काळ्या कुळकुळीत बनलेल्या खापऱ्या पाटीवर घासून घासून पाठीला काळा कुळकुळीत रंग आणण्याचा प्रयत्न करीत बसत.

बैलगाड्या बनवण्यासाठी ज्वारीची ताटे वापरीत. लाल माती आणून बैल बनवत बसत. गोल आकाराचे गोटे जमवून ते सर्व बाजूंनी दगडावर घासून घासून त्याने छान गोल आकार दयायचा प्रयत्न करीत बसत. अशा अनेक कल्पक कृती करण्यात मुले दंग होत.

प्रश्न 5.
पाठात चित्रित झालेल्या एकत्र कुटुंबपद्धतीबाबतचे तुमचे विचार स्पष्ट करा.
उत्तर :
या पाठात ग्रामीण भागातील मागील पिढीचे चित्रण आले आहे. त्या काळातील हे एक एकत्र कुटुंब होते. आजी ही कुटुंबप्रमुख होती. कुटुंबाच्या सर्व बाबींवर, सर्व व्यक्तींवर आजीचीच सत्ता चालत असे. कोणी कोणकोणती कामे कधी व कशी करावीत, हे आजी ठरवत असे.

या पद्धतीमुळे कुटुंबातील सर्व व्यवहारांना एकसूत्रीपणा येतो आणि कामे सुरळीतपणे पार पडतात; याचा कुटुंबालाच फायदा होतो, हे खरे आहे. पण या पद्धतीमध्ये कोणालाही स्वातंत्र्य राहत नाही. सुनांना साधा चहासुद्धा करून पिण्याची मोकळीक नव्हती. म्हणजे कोणालाही जरासुद्धा हौसमौज करण्याची परवानगी नव्हती. याचाच अर्थ कुटुंबातल्या सदस्यांना जीवनातील लहानसहान आनंदसुद्धा घेता येत नव्हते. त्यातही स्त्रियांना तर पूर्ण पारतंत्र्यातच राहावे लागे. ही चांगली स्थिती अजिबात नाही. आधुनिक काळात म्हणूनच एकत्र कुटुंबपद्धत टिकली नाही.

प्रश्न 6.
पाठाच्या शीर्षकाची समर्पकता थोडक्यात स्पष्ट करा.
उत्तर :
ग्रामीण भागात पूर्वी घराभोवती एक भलीमोठी, मजबूत भिंत बांधली जाई. भिंतीत एक मजबूत दार असे. त्याला कड्याकोयंडे असतच; शिवाय एक भलीभक्कम आगळ बसवलेली असे. एकदा ही आगळ लावली की घर पूर्णपणे बंद होत असे. घरातील कोणीही बाहेर जाऊ शकत नसे किंवा कोणीही बाहेरून आत येऊ शकत नसे. घरावर कोणाचाही हल्ला होणे शक्य नसे. यामुळे घर पूर्णपणे सुरक्षित होई. म्हणून ग्रामीण जीवनात या आगळीला एक महत्त्वपूर्ण स्थान लाभले होते.

पाठाच्या शीर्षकावरून असे दिसते की, त्या कुटुंबातील आजी ही त्या कुटुंबाची एक प्रकारे आगळच होती. तिच्या दराऱ्यामुळे कुटुंबाचे सर्व व्यवहार सुरळीत चालत असत. कुटुंबाला आपोआपच पूर्ण संरक्षण लाभायचे. घराची आगळ लावल्यावर आपल्या माणसांना बाहेर जाता येत नसे. म्हणजेच त्यांच्यावर बंधने येत. त्याचप्रमाणे आजीच्या नियंत्रणामुळे कुटुंबातील व्यक्तींवर बंधने येत. या बंधनांचा एक चांगला फायदा होई. कुटुंबातील कोणीही गैरवर्तन करू शकत नसे. त्यामुळे कुटुंबाचे व्यवहार कोलमडून पडत नसत. कुटुंबाला अंतर्गत व बाह्य असे दोन्ही अंगांनी संरक्षण मिळे. म्हणून ‘आजी : कुटुंबाचं आगळ’ हे शीर्षक अत्यंत समर्पक आहे.

प्रश्न 7.
आजच्या काळात एकत्र कुटुंब पद्धतीची आवश्यकता वाटते का? तुमचे मत सोदाहरण लिहा. (सराव कृतिपत्रिका-१)
उत्तर :
एकत्र कुटुंब पद्धतीचे काही फायदे आहेत; तसे काही तोटेही आहेत. तोटे काढून टाकले, तर एकत्र कुटुंब पद्धत आजच्या काळात खूप उपयोगी होऊ शकते. एकत्र कुटुंब पद्धतीत व्यक्तीला स्वत:चा वैयक्तिक विकास करून घेण्याची संधी खूप कमी प्रमाणात मिळते. व्यक्ती कुटुंबाशी बांधली जाते. कुटुंबाच्या अडीअडचणी, कुटुंबाची कामे, जबाबदाऱ्या यांच्यात ती गुरफटली जाते. कुटुंब एका व्यक्तीच्या नियंत्रणात राहते.

एकत्र कुटुंब पद्धतीमुळे कुटुंबात सर्व वयोगटातील माणसे असतात. वयस्क माणसांची कार्यक्षमता खुप कमी झालेली असते. त्यांना स्वत:च्या गरज भागवणे जिकिरीचे बनते. त्या वयात त्यांना इतरांच्या मदतीची खूप गरज असते. त्यांना एकत्र कुटुंब पद्धतीमध्ये आधार मिळतो. त्याचप्रमाणे लहान मुलांनाही एकत्र कुटुंब पद्धतीत खूप आधार मिळतो. आजच्या काळात आई-बाबा दोघेही नोकरी करतात. त्यामुळे घरी मुलांची काळजी घेणारे कोणीही नसते. मुलांची आबाळ होते. त्यांचे खाणेपिणे, त्यांचा अभ्यास वगैरे बाबींकडे लक्ष देणारे कोणी नसते. अशा स्थितीत घरी आजी-आजोबा असतील, तर ते मुलांकडे लक्ष देऊ शकतात. आजीआजोबांना समाधानही मिळते. पगारी माणसे घरातल्या माणसांप्रमाणे काळजी घेऊ शकत नाहीत. म्हणून आजच्या काळात एकत्र कुटुंब पद्धतीचा फायदा होऊ शकतो.

व्याकरण व भाषाभ्यास

कृतिपत्रिकेतील प्रश्न ४ (अ) आणि (आ) यांसाठी…

अ. व्याकरण घटकांवर आधारित कृती : .

१. समास :

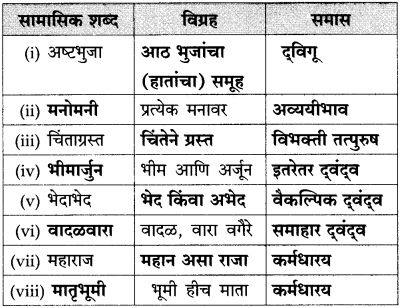
प्रश्न 1.
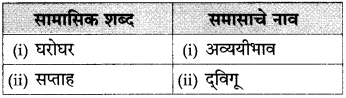
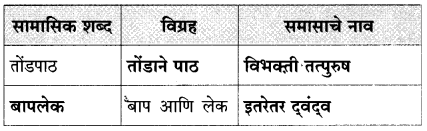
पुढील विग्रहांवरून सामासिक शब्द ओळखा :

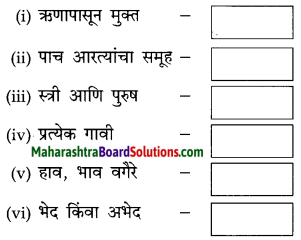
उत्तर :

प्रश्न 2.
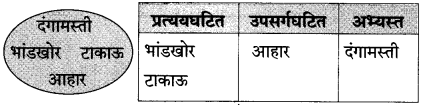
तक्ता पूर्ण करा : (मार्च ‘१९)

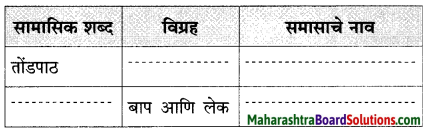
उत्तर :

२. अलंकार :

प्रश्न 1.
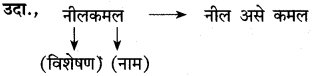
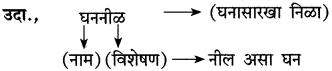
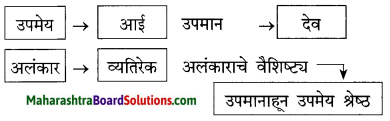
पुढील उदाहरण वाचून तक्ता पूर्ण करा :
देवाहुनही महान आहे माझी आई

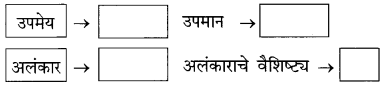
उत्तर :

३. शब्दसिद्धी :

प्रश्न 1.
‘बे’ हा उपसर्ग लागून तयार होणारे चार शब्द लिहा.
उत्तर :

• बेबंद
• बेजबाबदार
• बेहिशेब
• बेबनाव.

प्रश्न 2.
पुढील शब्दांना ‘अनीय’ हा प्रत्यय लावून शब्द तयार करा :
(i) श्रवण – ……………
उत्तर :
श्रवणीय

(ii) वाचन – ………….
उत्तर :
वाचनीय.

प्रश्न 4.
दोन अभ्यस्त शब्द लिहा.
उत्तर :

• लालेलाल
• गारेगार.

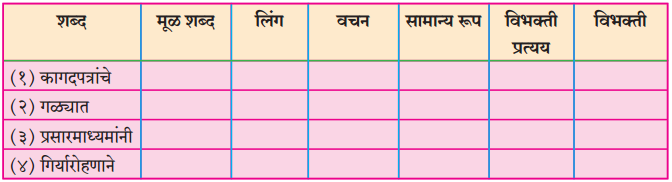
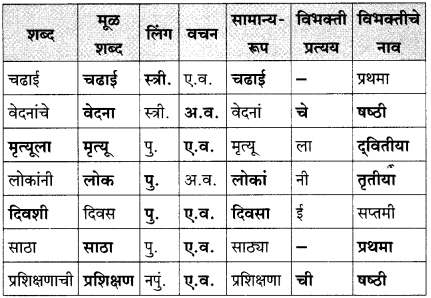
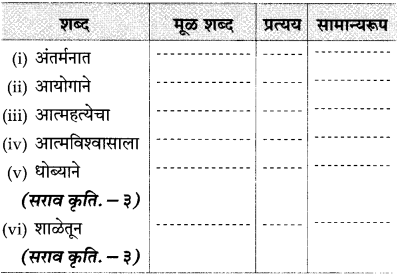
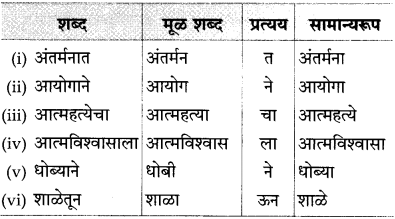
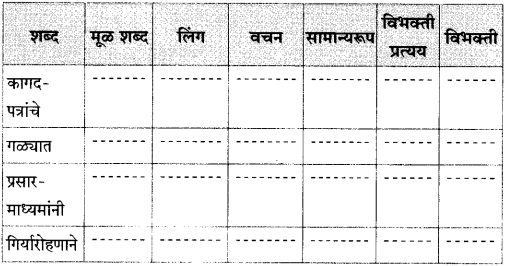
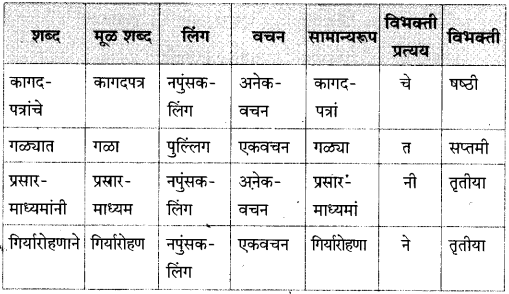
४. सामान्यरूप :

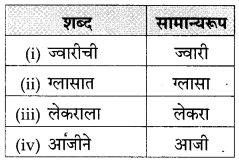
प्रश्न 1.
पुढील तक्ता पूर्ण करा :

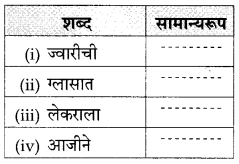
उत्तर :

५. वाक्प्रचार :

(१) कंसातील वाक्प्रचारांचा त्या खालील वाक्यांत योग्य ठिकाणी वापर करून वाक्ये पुन्हा लिहा :
(शाबूत असणे, कानोसा घेणे, कडुसं पडणे, शहानिशा होणे, गुण्यागोविंदाने नांदणे)
प्रश्न 1.
शाळेतून घरी आलो की बाबा नेहमी अभ्यासाची चौकशी करायचे.
उत्तर :
शाळेतून घरी आलो की बाबा नेहमी अभ्यासाची शहानिशा करायचे.

प्रश्न 2.
मावळतीला सूर्य गेला नि अंधार पडला.
उत्तर :
मावळतीला सूर्य गेला नि कडुसं पडले.

प्रश्न 3.
घरातील दोन्ही जावा अगदी खेळीमेळीने राहत.
उत्तर :
घरातील दोन्ही जावा अगदी गुण्यागोविंदाने नांदत होत्या.

प्रश्न 4.
पाऊस पडणार आहे की नाही, याचा आमचा मोती कान टवकारून अंदाज घेतो.
उत्तर :
पाऊस पडणार आहे की नाही, याचा आमचा मोती कान टवकारून कानोसा घेतो.

(२) पुढील वाक्यांतील वाक्प्रचार शोधून अधोरेखित करा :

प्रश्न 1.
सहलीच्या वेळी शिस्तभंग होऊ नये याकडे शिक्षकांचा कटाक्ष असतो.
उत्तर :
सहलीच्या वेळी शिस्तभंग होऊ नये याकडे शिक्षकांचा कटाक्ष असतो.

प्रश्न 2.
दोन व्यक्तींतील संवादाचा तिसऱ्या व्यक्तीने कानोसा घेणे अयोग्यच.
उत्तर :
दोन व्यक्तींतील संवादाचा तिसऱ्या व्यक्तीने कानोसा घेणे अयोग्यच.

प्रश्न 3.
कारण नसताना हुकमत गाजवणाऱ्या व्यक्ती इतरांच्या नजरेतून उतरतात.
उत्तर :
कारण नसताना हुकमत गाजवणाऱ्या व्यक्ती इतरांच्या नजरेतून उतरतात.

आ. (भाषिक घटकांवर आधारित कृतीः

१. शब्दसंपत्ती :

प्रश्न 1.
विरुद्धार्थी शब्दांच्या योग्य जोड्या जुळवा :

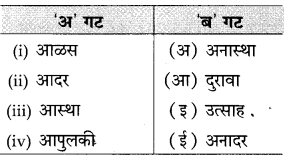
उत्तरे :
(i) आळस × उत्साह
(ii) आदर × अनादर
(iii) आस्था × अनास्था
(iv) आपुलकी × दुरावा

आजी : कुटुंबाचं आगळ Summary in Marathi

पाठाचा आशय या कथानकातील आजी खमकी आहे. तिच्या देहाची ठेवण, तिचे दिसणे, तिचा पेहराव इत्यादी बाबींमध्ये तिचा खमकेपणा दिसून येतो.

‘आगळ ‘मधील नायकाच्या घरी एक गाय होती. ती वरवर्षी व्यायची. त्यामुळे घरामध्ये दुधाची खूप रेलचेल होती. मुलांना भरपूर दुध प्यायला मिळे. आजीला चार सुना होत्या. आजीचा दरारा असल्यामुळे मुलांना खायलाप्यायला देताना सुना आपपरभाव करू शकत नव्हत्या. कामचुकारपणा करू शकत नव्हत्या. आपली कामे दुसरीवर टाकू शकत नव्हत्या. सर्व कामे प्रत्येकीला करावी लागत. या वातावरणामुळे कोणावर अन्याय होत नव्हता. कोणालाही तक्रार करायला वावच नसे. आजीमुळे प्रत्येकीला किंवा प्रत्येकाला भरभक्कम संरक्षण मिळाले होते. हे संरक्षण आगळइतकेच भक्कम होते.

दुपारच्या वेळी मुलांचे बैठे खेळ किंवा क्वचितप्रसंगी मैदानी खेळ खेळले जात. अशा प्रकारे मुलांचे बालपण तर निसर्गामध्ये सहजगत्या घडत होते. या सगळ्याला आजीच्या मायेच्या सावलीचा आधार होता.

दुपारपर्यंतची कामे आटोपल्यावर थोडीशी विश्रांती घेऊन आजी ढाळजेत येऊन बसायची. गल्लीतल्या बायका जमायच्या. निवडटिपण असली कामे करता करता गप्पा होत. गावभरच्या बातम्या कळत. आजीच्या समोरच बातम्यांची शहानिशा होई. ही ढाळज म्हणजे एक प्रकारे गावाचे वर्तमानपत्रच होती. रात्री आठ वाजता वाड्याचा दरवाजा बंद होई आणि आगळ बसवली जाई. आगळ बसवली की संरक्षणाची हमी मिळे.

आजी : कुटुंबाचं आगळ शब्दार्थ

• रापणे – त्वचेवर काळपटलेली छटा येणे.
• गोंदण – विशिष्ट प्रकारच्या सुईने त्वचेवर टोचून टोचून नक्षी काढणे.
• गावरान – गावठी. वेत – वासराला जन्म देणे.
• धार काढणे – गाई-म्हशीचे दूध काढणे.
• चरवी – दूध काढण्याचे भांडे.
• धारोष्ण – उष्णपणा निवला नाही असे ताजे दूध.
• सरपण – इंधन (विशेषतः लाकडांचे).
• ढाळज – मोठा वाडा वगैरेंसारख्या घराच्या मुख्य दरवाजाजवळची आतल्या बाजूची
• जागा, पडवी, वाकळ – गोधडी.
• शहानिशा – खातरजमा,
• कडुसं – काळोख होण्याची वेळ,
• आगळ – अडसर (येथे अर्थ-भक्कम आधार.).
• देवळी – भिंतीतला कोनाडा.
• चिंचोके – चिंचेच्या बिया.
• गजगे – सागरगोटे,
• जिबल्या – अर्धा कापलेला जोड्यांचा तळ.
• मुटके – हातपाय पोटाशी आवळून घेऊन आजूबाजूला खूप पाणी उडेल अशा रितीने पाण्यात मारलेली उडी.

आजी : कुटुंबाचं आगळ वाक्प्रचार व त्यांचे अर्थ

• हुकूमत गाजवणे : अधिकार गाजवणे.
• हातात काठी येणे : म्हातारपण येणे; तोल सांभाळता न येणे.
• गुण्यागोविंदाने नांदणे : समंजसपणे व आनंदाने राहणे.
• धार काढणे : गायी-म्हशीचे दूध काढणे.
• कटाक्ष असणे : खास लक्ष देणे.
• धान्य निवडणे : धान्यातले गोटे इत्यादी वेचून बाहेर काढणे.
• हुक्की येणे : लहर येणे.

Marathi Kumarbharti Std 10 Digest Pdf भाग-१

• जय जय हे भारत देशा (गीत) Question Answer
• बोलतो मराठी… Question Answer
• आजी : कुटुंबाचं आगळ Question Answer
• उत्तमलक्षण (संतकाव्य) Question Answer
• वसंतहृदय चैत्र Question Answer
• बालसाहित्यिका : गिरिजा कीर Question Answer (स्थूलवाचन)

Balbharti Maharashtra State Board Class 10 Marathi Solutions Kumarbharti Chapter 16 आकाशी झेप घे रे (कविता) Notes, Textbook Exercise Important Questions and Answers.

Class 10th Marathi Kumarbharti Chapter 16 आकाशी झेप घे रे (कविता) Question Answer Maharashtra Board

Std 10 Marathi Chapter 16 Question Answer

Marathi Kumarbharti Std 10 Digest Chapter 16 आकाशी झेप घे रे Textbook Questions and Answers

प्रश्न 1.
योग्य पर्याय ओळखा.
(अ) सुखलोलुप झाली काया म्हणजे …………………………………
(१) सुखाचा तिरस्कार वाटतो.
(२) सुखाबद्दल प्रेम वाटते.
(३) सुखाचे आकर्षण वाटते.
(४) सुख उपभोगण्याची सवय लागते.
उत्तर:
सुखलोलुप झाली काया म्हणजे – सुख उपभोगण्याची सवय लागते.

(आ) पिंजरा सोडून झेप घेतल्याने …………………………………
(१) काया सुखलोलुप होते.
(२) पाखराला आनंद होतो.
(३) आपल्याला स्वसामर्थ्याची जाणीव होते.
(४) आकाशाची प्राप्ती होते.
उत्तर:
पिंजरा सोडून झेप घेतल्याने – आपल्याला स्व-सामर्थ्याची जाणीव होते.

प्रश्न 2.
तुलना करा.
पिंजऱ्यातील पोपट – पिंजऱ्याबाहेरील पोपट पिंजरा
उत्तर:
पिंजऱ्यातील पोपट – पिंजऱ्याबाहेरील पोपट
(i) पारतंत्र्यात राहतो – स्वातंत्र्य उपभोगतो
(ii) लौकिक सुखात रमतो – स्वबळाने संचार करतो
(iii) कष्टाविण राहतो – कष्टात आनंद घेतो
(iv) जीव कावराबावरा होतो – सुंदर जीवन जगतो।
(v) मनात खंत करतो – मन प्रफुल्लित होते

प्रश्न 3.
पाखराला स्वसामर्थ्याची ओळख करून देणाऱ्या कवितेतील ओळी शोधून लिहा.
उत्तर:
तुज पंख दिले देवाने कर विहार सामर्थ्याने

प्रश्न 4.
कवीने यशप्राप्तीच्या संदर्भात सांगितलेली सुवचने लिहा.
उत्तर:
(i) तुला देवाने पंख दिले आहेत. सामर्थ्याने विहार कर.
(ii) कष्टाविण फळ मिळत नाही.

प्रश्न 5.
काव्यसौंदर्य.
(अ) खालील ओळींचे रसग्रहण करा.
‘घामातुन मोती फुलले
श्रमदेव घरी अवतरले’

(आ) ‘आकाशी झेप घे रे पाखरा सोडी सोन्याचा पिंजरा’, या ओळीतील मथितार्थ स्पष्ट करा.
उत्तर:
‘आकाशी झेप घे रे’ या कवितेमध्ये कवी जगदीश खेबुडकर यांनी पारतंत्र्यात खितपत पडलेल्या पाखराला म्हणजेच माणसांच्या परावलंबी मनाला मोलाचा उपदेश केला आहे व स्वातंत्र्याचे मोल समजावून सांगितले आहे.

प्रस्तुत ओळीतील मथितार्थ असा की यामध्ये पाखराला आकाशात भरारी घेण्याचे आवाहन केले आहे. वैभव, सत्ता, संपत्ती हा लौकिकातील सोन्याचा पिंजरा आहे. त्यात अडकलेल्या जिवाची गती खुंटते. त्याच्या जीवनाची प्रगती होत नाही. सुखसोईमुळे कर्तृत्व थांबते, म्हणून हा सोन्याचा पिंजरा सोडून ध्येयाच्या मोकळ्या व उंच आकाशात तू झेप घे. अशा प्रकारची आत्मिक शिकवण या ओळींतून प्रत्ययाला येते.

(इ) ‘स्वसामर्थ्याची जाणीव’ हा उत्तम व्यक्तिमत्त्व विकासाचा पाया आहे. हे विधान स्पष्ट करा.
उत्तर:
जीवन जगत असताना माणसाला अनेक अडचणींना तोंड दयावे लागते. समस्यांचा सामना करता करता कधी माणूस हतबल होऊन जातो. मग तो देवावर हवाला ठेवू लागतो. नशिबाला दोष देतो. पण हे असे वागणे अगदी नकारात्मक आहे. परिस्थिती बदलण्याचा माणसाने निकराने प्रयत्न करायला हवा. ‘प्रयत्ने वाळूचे कण रगडिता तेलही गळे।’ अशी समर्थ रामदासांची उक्ती आहे. त्याप्रमाणे आत्मबळ एकवटणे महत्त्वाचे ठरते. स्वत:च्या सामर्थ्यावर भरवसा ठेवता आला पाहिजे. कर्मवीर भाऊराव पाटील यांनी स्वत:च्या पोटाला चिमटा घेऊन गोरगरिबांच्या शिक्षणाची सोय केली. ‘रयत शिक्षण संस्था’ निर्माण केली. आज त्याचा महावृक्ष झाला आहे. यावरून असे स्पष्ट होते की ‘स्वसामर्थ्याची जाणीव’ हा उत्तम व्यक्तिमत्त्व विकासाचा पाया आहे.

(ई) ‘घर प्रसन्नतेने नटले’, याची प्रचिती देणारा तुमचा अनुभव लिहा.
उत्तर:
कवी जगदीश खेबुडकर यांनी ‘आकाशी झेप घे रे’ या कवितेमध्ये माणसाला उपदेश करताना घर प्रसन्नतेने नटायचे असेल तर श्रमदेवाची पूजा करावी लागेल व घामातून मोती फुलवावे लागतील हे समजावून सांगितले आहे. कोणतीही गोष्ट घरबसल्या मिळत नाही. ‘दे रे हरी। खाटल्यावरी।’ असा चमत्कार होणे शक्य नसते. घर प्रसन्नतेने कसे नटते याची प्रचिती देणारा माझा स्वत:चा अनुभव सांगतो – ‘मला माझ्या आईसाठी थंडीमध्ये स्वेटर विणायचे होते. मी अभ्यासाची व शाळेची वेळ सांभाळून फावल्या थोड्या वेळात दररोज एक तास काढून कष्टाने स्वेटर विणले. ते आईला देताना तिच्या डोळ्यांत जे आनंदाश्रू चमकले, तेच माझ्या कष्टाचे फळ होते. आईचा तो आनंद पाहून मला ‘घर प्रसन्नतेने नटल्याचा व घामातुन मोती फुलले’ या विधानाचा अर्थ कळला.

Marathi Kumarbharti Class 10 Textbook Solutions Chapter 16 आकाशी झेप घे रे Additional Important Questions and Answers

कृति

कृतिपत्रिकेतील प्रश्न २ (अ) साठी…
प्रश्न. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती १: (आकलन)

प्रश्न 1.
(i) देवाने पंख दिल्यामुळे – …………………………..
(१) हृदयात व्यथा जळते.
(२) जीव बिचारा होतो.
(३) सोन्याचा पिंजरा मिळतो.
(४) शक्तीने संचार करता येतो.
उत्तर:
देवाने पंख दिल्यामुळे – शक्तीने संचार करता येतो.

प्रश्न 2.
पुढील क्रियापदांपुढे कोठे, कोण, काय ते लिहा:
(i) झेप घे – …………………………..
(ii) सोडून दे – …………………………..
(iii) जळते – …………………………..
(iv) अवतरले – …………………………..
(v) नटले – …………………………..
(vi) खायला मिळते – …………………………..
उत्तर:
(i) झेप घे – आकाशात
(ii) सोडून दे – सोन्याचा पिंजरा
(iii) जळते – हृदयात व्यथा
(iv) अवतरले – श्रमदेव घरात
(v) नटले – प्रसन्नतेने घर
(vi) खायला मिळते – रसाळ फळ.

प्रश्न 3.
(i) एका किंवा दोन शब्दांत उत्तर लिहा: (सराव कृतिपत्रिका-३)
(अ) पोपटाचे राहण्याचे ठिकाण – …………………………..
(आ) पोपटाचे खादय – …………………………..
उत्तर:
(i) (अ) पोपटाचे राहण्याचे ठिकाण – पिंजरा (सोन्याचा)
(आ) पोपटाचे खादय – फळे

(ii) पुढील शब्दसमूहाचा अर्थ स्पष्ट करा: (सराव कृतिपत्रिका-३)
‘तुज कळते परि ना वळते’
आकाशी झेप घे रे पाखरा
सोडी सोन्याचा पिंजरा
तुजभवती वैभव, माया
फळ रसाळ मिळते खाया
सुखलोलुप झाली काया
हा कुठवर वेड्या घेसी आसरा
तुज पंख दिले देवाने
कर विहार सामर्थ्याने
दरि-डोंगर, हिरवी राने
जा ओलांडुनी या सरिता-सागरा
कष्टाविण फळ ना मिळते
तुज कळते परि ना वळते
हृदयात व्यथा ही जळते
का जीव बिचारा होई बावरा
घामातुन मोती फुलले
श्रमदेव घरी अवतरले
घर प्रसन्नतेने नटले
हा योग जीवनी आला साजिरा
उत्तर:
‘तुज कळते परि ना वळते’ – एखादी गोष्ट कशी करायची हे समजते परंतु कृती करता येत नाही.

कृती २: (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा: (सराव कृतिपत्रिका-३)

उत्तर:

प्रश्न 2.
पुढील गोष्टींचे परिणाम लिहा:
(i) काया होते – …………………………..
(ii) कष्ट केल्यावर – …………………………..
(iii) जीवनात येतो – …………………………..
(iv) कळते पण – …………………………..
(v) बिचारा जीव होतो – …………………………..
उत्तर:
(i) काया होते. – सुखलोलुप
(ii) कष्ट केल्यावर – फळ मिळते
(iii) जीवनात येतो – सुंदर योग
(iv) कळते पण – वळत नाही
(v) बिचारा जीव होतो – बावरा

कृती ३: (काव्यसौंदर्य)

प्रश्न 3.
“सुखलोलुप झाली काया हा कुठवर वेड्या घेसी आसरा” या काव्यपंक्तीतील विचारसौंदर्य स्पष्ट करा. (सराव कृतिपत्रिका-३)
उत्तर:
कवी जगदीश खेबुडकर यांनी ‘आकाशी झेप घे रे’ या कवितेमध्ये लौकिक गोष्टींमध्ये व नाशिवंत गोष्टींमध्ये रस घेणाऱ्या सुखलोलुप माणसांना मोलाचा उपदेश केला आहे. कवी म्हणतात-मोह माया, पैसा, संपत्ती यांच्या लोभात माणूस गुरफटला की त्याची फसगत होते. प्रगती खुंटते. तात्पुरते हे फळ रसाळ वाटते, पण ते सुख नाशिवंत आहे. हे सुख फार काळ टिकणारे नाही. या सुखाला शरीर चटावते म्हणून यातून जागृत हो. या लौकिक सुखाचा आश्रय घेऊ नको. हा सोन्याचा पिंजरा सोडून भरारी घे, अशा प्रकारे या ओळीतून कवींनी सुखाला लालचावलेल्या माणसांना मौलिक संदेश दिला आहे.

कृतिपत्रिकेतील प्रश्न २ (आ) साठी…

प्रश्न.
पुढील कवितेसंबंधी त्याखाली दिलेल्या मुद्दयांच्या आधारे कृती सोडवा: कविता-आकाशी झेप घे रे.
उत्तर:
(१) प्रस्तुत कवितेचे कवी: जगदीश खेबुडकर.
(२) कवितेचा रचनाप्रकार: गीतरचना.
(३) कवितेचा काव्यसंग्रह: (एक चित्रपटगीत).
(४) कवितेचा विषय: स्वसामर्थ्य व स्वातंत्र्य मोलाचे असते.

(५) कवितेतून व्यक्त होणारा (स्थायी) भाव: स्वसामर्थ्यावर विश्वास ठेवून स्वातंत्र्याचे मोल जाणत जगण्याची प्रेरणा देणारा भाव.

(६) कवितेच्या कवींची लेखनवैशिष्ट्ये: ध्रुपद व कडवी अशी या गीताची सुटसुटीत रचना आहे. रसाळ शब्दकळा व नेमके मर्म सांगणारी भाषा हे या कवितेचे प्रमुख वैशिष्ट्य आहे. पिंजरा हे पारतंत्र्याचे प्रतीक, तर पंख हे मुक्तपणे आकाशात विहार करण्याचे प्रतीक, दऱ्या-डोंगर, सरिता-सागर ही सर्व अडचणींची प्रतीके. सर्वसामान्य लोकांना सहज कळतील, आशय थेट मनाला भिडेल, अशी ही सोपी, साधी प्रतीके कवींनी वापरली आहेत. ‘फळ रसाळ मिळते’ याप्रमाणे अनुप्रासांचा सुंदर उपयोग केलेला आहे. एकूण, ही कविता रसाळ, प्रासादिक बनली आहे.

(७) कवितेची मध्यवर्ती कल्पना: स्वत:च्या क्षमतेवर, स्वत:च्या सामर्थ्यावर अढळ विश्वास ठेवावा आणि त्या बळावर यशाच्या दिशेने दमदार पावले टाकीत पुढे जावे. ध्येयाकडे आपण पोहोचणारच याची मनोमन खात्री बाळगावी. तात्कालिक मोहाच्या गोष्टींमध्ये गुंतून पडू नये. स्वत:च्या मनाला मुक्त, स्वतंत्र ठेवावे. सुखलोलुपतेमध्ये मनाला अडकू देऊ नये. स्वातंत्र्याचे महत्त्व ओळखले पाहिजे, अशी या कवितेची मध्यवर्ती कल्पना आहे.

(८) कवितेतून व्यक्त होणारा विचार: माणसे अनेकदा दैवाच्या आहारी जातात. नशिबावर भरवसा ठेवतात. नशिबात असेल, तेच मिळेल; अधिक काहीही मिळणे शक्य नाही, अशी त्यांची ठाम समजूत असते. कवी जगदीश खेबुडकर ही समजूत दूर करायला सांगतात. त्यांच्या मते, माणसाने स्वत:चे सामर्थ्य ओळखले पाहिजे आणि कठोर परिश्रमांना सिद्ध झाले पाहिजे. कठोर परिश्रम केले, तर यश नक्कीच मिळते. प्रयत्नवाद हाच खरा विचार आहे.

(९) कवितेतील आवडलेली ओळ:
कष्टाविण फळ ना मिळते तुज कळते परि ना वळते हृदयात व्यथा ही जळते का जीव बिचारा होई बावरा

(१०) कविता आवडण्याची वा न आवडण्याची कारणे: ही कविता म्हणजे एक गाजलेले चित्रपट गीत आहे. त्याची चाल, संगीत चांगले आहे. गीत ऐकत राहावे असे वाटते. गीत दमदारपणे गायलेले आहे. ते लक्षातही राहते. मात्र एका ठिकाणी मन अडकते. अवतीभवती मोहाचा पसारा आहे; मन त्यात सहजपणे अडकते. हे सांगताना कवी म्हणतात, “तुजभवती वैभव माया/फळ रसाळ मिळते खाया.” पुढे, कष्ट केल्याशिवाय, खस्ता खाल्ल्याशिवाय फळ मिळत नाही. हे सांगताना कवी म्हणतात, “कष्टाविण फळ ना मिळते,” असे म्हटले आहे. यात काहीसा विरोध जाणवतो. हे थोडेसे खटकते.

(११) कवितेतून मिळणारा संदेश: माणसाने कष्टावर, प्रयत्नावर विश्वास ठेवला पाहिजे, ‘असेल हरी, तर देईल खाटल्यावरी’ असे मानू नये. नशिबाने काहीही मिळत नाही. प्रयत्नाने आपण आपले नशीब घडवत असतो. तसेच, केवळ देहाला तृप्त करणारी सुखे महत्त्वाची नसतात, ती तात्कालिक असतात. ती चिरकाल टिकत नाहीत. आपल्या प्रयत्नाने गगनात भरारी मारली पाहिजे. त्यातच खरे सुख असते; असा संदेश ही कविता देते.

रसग्रहण
कृतिपत्रिकेतील प्रश्न २ (इ) साठी…

प्रश्न.
पुढील ओळींचे रसग्रहण तुमच्या शब्दांत लिहा: ‘घामातुन मोती फुलले श्रमदेव घरी अवतरले.’
उत्तर:
आशयसौंदर्य: सुप्रसिद्ध मराठी गीतकार जगदीश खेबुडकर यांची ‘आकाशी झेप घे रे’ ही मराठी चित्रपटातील एक गीतरचना आहे. स्वसामर्थ्यावर अदम्य विश्वास ठेवून कर्तृत्वाचे मोकळे आकाश ओळखावे आणि ध्येयाकडे उंच भरारी घ्यावी, परावलंबित्व सोडून स्वावलंबी व्हावे, ही या कवितेची मध्यवर्ती कल्पना आहे. स्वकर्तृत्वाने यशाचे शिखर गाठावे व उच्च ध्येयाकडे झेप घ्यावी. पारतंत्र्याचा त्याग करून स्वातंत्र्याचे मोल जाणावे, हा अमूल्य संदेश ही कविता देते.

काव्यसौंदर्य: वरील ओळींमध्ये कवींनी श्रमाचे महत्त्व सांगितले आहे. कष्ट केल्याशिवाय फळ मिळत नाही, अविरत प्रयत्न व काबाडकष्ट करून जेव्हा शेतकरी शेतामध्ये खपतो, तेव्हा त्याला मोत्यांसारखे पीक मिळते. त्याच्या घामातून मोती फुलतात. ते धनधान्य त्याच्या घरी येते, तेव्हा त्याच्या श्रमाचे सार्थक होते. जणू श्रमदेव त्याच्या घरी अवतरतात.

भाषिक वैशिष्ट्ये: ध्रुपद व कडवी अशी या गीताची सुटसुटीत रचना आहे. रसाळ शब्दकळा व नेमके मर्म सांगणारी भाषा हे या कवितेचे प्रमुख वैशिष्ट्य आहे. ‘पिंजरा’ हे सुखलोलुपतेचे प्रतीक वापरले आहे व त्यात कैद झालेल्या मानवी मनाला ‘पक्षी’ म्हटले आहे. साध्या शब्दांत गहन आशय मांडला आहे. यमकप्रधान गेय रूपामुळे कविता मनात ठसते.

व्याकरण व भाषाभ्यास

कृतिपत्रिकेतील प्रश्न ४ (अ) आणि (आ) यांसाठी…
व्याकरण घटकांवर आधारित कृती:

कर्मधारय समास

• कर्मधारय समास हा तत्पुरुष समासाचा एक प्रकार आहे.
• कर्मधारय समासाची वैशिष्ट्ये:

(i) कधी पहिले पद विशेषण असते.

(ii) कधी दूसरी पद विशेषण असते.

(iii) कधी दोन्ही पदे विशेषण असतात.

(iv) कधी पहिले पद उपमान असते.
उदा., कमलनयन → कमलासारखे डोळे

(v) कधी दुसरे पद उपमान असते.
उदा., बरसिंह → सिंहासारखा नर

(vi) कधी दोन्ही पदे एकरूप असतात.
उदा., विदयाधन → विदया हेच धन

१. समास:
(पाठ्यपुस्तक पृष्ठ क्र. ६२)

प्रश्न 1.
पुढील वाक्ये वाचून त्यांतील सामासिक शब्द ओळखा व त्यांचा विग्रह करा:
उदा., तलावातील नीलकमल किती शोभून दिसते आहे.
नीलकमल → नील असे कमल
(i) महाराष्ट्र राज्य समृद्ध आहे.
(ii) या पुस्तकाचे भाषांतर चांगले झाले आहे. –
(iii) आकाशात पांढराशुभ्र ढग तरंगत आहे.
उत्तर:
(i) महाराष्ट्र → महान असे राष्ट्र
(ii) भाषांतर → अन्य अशी भाषा (अंतर = अन्य)
(iii) पांढराशुभ्र → शुभ्र असा पांढरा
(पाठ्यपुस्तक पृष्ठ क्र. ६३)

प्रश्न 2.
पुढील सामासिक शब्दांचा विग्रह करा:
(i) रक्तचंदन → ………………………….
(ii) घनश्याम → ………………………….
(iii) काव्यामृत → ………………………….
(iv) पुरुषोत्तम → ………………………….
उत्तर:
(i) रक्तचंदन → रक्तासारखे चंदन
(ii) घनश्याम → घनासारखा श्यामल
(ii) काव्यामृत → काव्य हेच अमृत
(iv) पुरुषोत्तम → उत्तम असा पुरुष
(पाठ्यपुस्तक पृष्ठ क्र. ६३)

प्रश्न 3.
पुढील वाक्ये वाचून त्यातील सामासिक शब्द ओळखा
व विग्रह करा: उदा., नेत्रांच्या पंचारतीनी सैनिकांना ओवाळले.
पंचारती → पाच आरत्यांचा समूह.
(i) असा माणूस त्रिभुवन शोधले तरी सापडायचा नाही.
(ii) नवरात्रात ठिकठिकाणी गरबा नृत्य चालते.
(iii) शाळेत आता हिंदी सप्ताह चालू आहे.
उत्तर:
(i) त्रिभुवन → तीन भुवनांचा समूह.
(ii) नवरात्र → नऊ रात्रींचा समूह.
(iii) सप्ताह → सात दिवसांचा समूह (आह = दिवस).
(पाठ्यपुस्तक पृष्ठ क्र. ६३)

प्रश्न 4.
पुढील सामासिक शब्दांचा विग्रह करा:
(i) अष्टाध्यायी → ………………………….
(ii) पंचपाळे → ………………………….
(iii) द्विदल → ………………………….
(iv) बारभाई → ………………………….
(v) त्रैलोक्य → ………………………….
उत्तर:
(i) अष्टाध्यायी → आठ अध्यायांचा समूह.
(ii) पंचपाळे → पाच पाळ्यांचा समूह.
(iii) द्विदल → दोन दलांचा समूह. (दल = पान)
(iv) बारभाई → बारा भाईंचा समूह.
(v) त्रैलोक्य → तीन लोकांचा समूह.

२. अलंकार:

कृती करा: शिवप्रभू म्हणजे साक्षात तळपती तलवार होय.
उपमेय → [ ] उपमान → [ ]
अलंकार → [ ] अलंकाराचे वैशिष्ट्य → [ ]
उत्तर:
उपमेय → [शिवप्रभू]
उपमान → [तळपती तलवार]
अलंकार → [रूपक]
अलंकाराचे वैशिष्ट्य → [उपमेय व उपमान यांत अभेद आहे]

३. वृत्त:

‘मालिनी’ या वृत्ताची लक्षणे सांगून उदाहरण दया.
उत्तर:
लक्षणे – हे एक अक्षरगण वृत्त आहे. चार चरण, प्रत्येक चरणात १५ अक्षरे. गण – न न म य य यति -८व्या अक्षरावर उदाहरण: तदितर खग भेणे वेगळाले पळाले
उपवन जल केली जे कराया मिळाले स्वजन गवसला तो त्याजपाशी नसे तो कठिण समय येता कोण कामास येतो.

४. शब्दसिद्धी:

प्रश्न 1.
पुढील शब्दांना आळ’ हा प्रत्यय लावून शब्द तयार करा:
(i) रस – ………………………….
(ii) मध – ………………………….
उत्तर:
(i) रस – रसाळ
(ii) मध – मधाळ.

प्रश्न 2.
‘प्रति’ हा उपसर्ग असलेले चार शब्द लिहा:
(i) ……………………………….
(ii) ……………………………….
(ii) ……………………………….
(iv) ……………………………….
उत्तर:
(i) प्रतिबिंब
(ii) प्रतिदिन
(iii) प्रतिध्वनी
(iv) प्रतिकूल.

५. सामान्यरूप:

तक्ता पूर्ण करा:
शब्द – सामान्यरूप
(i) सामर्थ्याने – …………………….
(ii) कष्टाविण – …………………….
(iii) हृदयात – …………………….
(iv) प्रसन्नतेने – …………………….
उत्तर:
शब्द – सामान्यरूप
(i) सामथ्याने – सामर्थ्या
(ii) कष्टाविण – कष्टा
(iii) हृदयात – हृदया
(iv) प्रसन्नतेने – प्रसन्नते

६. वाक्प्रचार:
योग्य अर्थाची निवड करा:
(i) फळ मिळणे –
(अ) कार्य यशस्वी होणे
(आ) खायला मिळणे.

(ii) विहार करणे –
(अ) संचार करणे
(आ) फिरून येणे.
उत्तर:
(i) फळ मिळणे – कार्य यशस्वी होणे.
(ii) विहार करणे – संचार करणे,

आ (भाषिक घटकांवर आधारित कृती:
१. शब्दसंपत्ती:
(१) प्रत्येकी दोन समानार्थी शब्द लिहा:
(i) काया =
(ii) आकाश =
(iii) कष्ट =
(iv) देव =
उत्तर:
(i) काया = शरीर – देह
(ii) आकाश = आभाळ – गगन
(iii) कष्ट = श्रम – मेहनत
(iv) देव = ईश्वर – ईश

(२) पुढील शब्दांच्या अक्षरांपासून चार अर्थपूर्ण शब्द बनवा:
(i) तुजभवती –
(ii) जीवनात –
उत्तर:
(i) तुजभवती → तुज – भवती – भव – भज
(ii) जीवनात → जीव – जीना – जीत – वनात

(३) गटात न बसणारा शब्द लिहा:
(i) डोंगर, गिरी, अचल, टेकडी, पर्वत.
(ii) सागर, घागर, समुद्र, सिंधू, रत्नाकर.
(iii) रान, जंगल, झाडे, कानन, विपीन,
(iv) घर, गृह, सहवास, निवास, आलय.
उत्तर:
(i) टेकडी
(ii) घागर
(iii) झाडे
(iv) सहवास.

(४) पुढील शब्दांचे भिन्न अर्थ लिहा:
[ ] ← परी → [ ]
[ ] ← माया → [ ]
उत्तर:
परंतु ← परी → पंख असलेली देवता
पैसा ← माया → जिव्हाळा

२. लेखननियम:
अचूक शब्द निवडा:
(i) सर्वोच्च/सर्वोच/सरवोच्च/सर्वोच्य,
(ii) स्फूर्ती/स्फूर्ति/स्फुर्ती/स्फुर्ति.
(iii) सयूक्तिक/सयुक्तीक/सयुक्तिक/संयुक्तीक.
(iv) पश्चाताप/पश्चात्ताप/प्रश्याताप/पश्चत्ताप.
उत्तर:
(i) सर्वोच्च
(ii) स्फूर्ती
(iii) सयुक्तिक
(iv) पश्चात्ताप:

३. विरामचिन्हे:
पुढील ओळीतील विरामचिन्हे ओळखा:
दरि-डोंगर, हिरवी राने
उत्तर:
[ – ] संयोगचिन्ह
[ , ] स्वल्पविराम

४. पारिभाषिक शब्द:
पुढील इंग्रजी पारिभाषिक शब्दांसाठी योग्य पर्याय निवडा:

(i) Category – ……………………………………
(१) अवर्ग
(२) प्रवर्ग
(३) निवडक
(४) सूचक.

(ii) Documentary – ……………………………………
(१) बोलपट
(२) चित्रपट
(३) माहितीपट
(४) रंगपट.

(iii) Honourable – …………………………………… (मार्च ‘१९)
(१) वंदनीय
(२) पूजनीय
(३) श्रवणीय
(४) माननीय.

(iv) Verbal – ……………………………………
(१) आर्थिक
(२) शाब्दिक
(३) आंतरिक
(४) सामाजिक.
उत्तर:
(i) प्रवर्ग
(ii) माहितीपट
(iii) माननीय
(iv) शाब्दिक.

५. अकारविल्हे / भाषिक खेळ:

प्रश्न 1.
पुढील शब्द अकारविल्हेनुसार लिहा:
पिंजरा → पक्षी → जायबंदी → सुटका.
उत्तर:
जायबंदी → पक्षी → पिंजरा → सुटका.

प्रश्न 2.
कृती करा:

उत्तर:

आकाशी झेप घे रे Summary in Marathi

आकाशी झेप घे रे कवितेचा भावार्थ

लौकिक विनाशी गोष्टीत गुंतलेल्या मनाला मोलाचा उपदेश करताना कवी म्हणतात –

हे पाखरा (हे माणसाच्या चंचल मना), तू ध्येयपूर्तीसाठी आकाशात उंच भरारी मार, सत्ता, संपत्ती याने वेढलेल्या सोन्याच्या या पिंजऱ्याचा मोह तू सोडून दे. हा सोन्याचा पिंजरा तुझ्या इच्छांच्या सफलतेला घातक आहे. या पिंजऱ्याचा त्याग करून तू यशाच्या शिखराकडे झेप घे. पारतंत्र्याचा त्याग करून स्वातंत्र्याचा आनंद घे.

आता तू मोहमाया, पैसा, संपत्ती यांच्या गराड्यात घेरलेला आहेस. तुला सुखाचे फळ खायला मिळते आहे. तुझे शरीर या लौकिक सुखाला लालचावलेले आहे. या सुखात तू लोळतो आहेस. पण हे सुख किती काळ टिकेल? या सुखाचा आश्रय लवकरच संपेल. हे वेड्या मना, तू जागृत हो आणि लौकिक तात्पुरत्या सुखाचा त्याग कर.

हे पाखरा (मनपाखरा), ईश्वराने तुला उडण्यासाठी पंख दिले आहेत. पंखांतील बळाने तू आकाशात मुक्तपणे संचार कर. जमिनीलगत असणारे डोंगर–दऱ्या, हिरवी राने, नया व समुद्र सारे (अडथळे) ओलांडून दिशांच्या पार जा.

कष्ट केल्याशिवाय फळ मिळत नाही. आयते कोणतेही सुख मिळत नाही. त्यासाठी अपार मेहनत करावी लागते; हे तुला समजते पण कृतीमध्ये, आचरणात, वागणुकीत येत नाही. त्यामुळे तुझे मनातले दुःख मनातल्या मनात जळत राहते, धुमसत राहते, स्वातंत्र्याची ओढ तर आहे; पण त्याची पूर्तता होत नाही. त्यामुळे तुझा बिचारा जीव कावराबावरा होतो, कासावीस होतो.

घाम गाळला की शेतात मोती पिकतात. पिके बहरतात. हा श्रमरुपी ईश्वराचा चमत्कार आहे. कष्ट करून घरात येणारे धान्य म्हणजेच श्रमदेवाचे घरात होणारे आगमन होय, त्या वेळी घरात समृद्धी व प्रसन्नता होते. कष्ट केल्याने असा सुखाचा गोड, सुंदर प्रसंग आयुष्यात येतो, हे जाणून घे व स्वातंत्र्याचे मोल जाण.

आकाशी झेप घे रे शब्दार्थ

• तुजभवती – तुझ्या भोवताली, आजूबाजूला.
• वैभव – समृद्धी.
• माया – पैसा, संपत्ती.
• रसाळ – रसपूर्ण, मधुर, गोड.
• सुखलोलुप – सुखाची आसक्ती, सुखाने घेरलेली.
• काया – शरीर.
• आसरा – आश्रय, निवारा.
• विहार – संचार,
• सामर्थ्याने – शक्तीने, बळाने.
• सरिता – नदी.
• सागर – समुद्र.
• कष्टाविण – मेहनतीशिवाय,
• परि – पण, परंतु.
• व्यथा – दुःख, वेदना.
• बिचारा – गरीब.
• बावरा – गोंधळलेला, बावरलेला.
• श्रमदेव – कष्टाचा ईश्वर.
• अवतरले – प्रकटले, आले.
• प्रसन्नता – टवटवीतपणा, उल्हसित.
• नटले – शोभले.
• योग – घटना, प्रसंग.
• साजिरा – सुंदर, सुरेख.

आकाशी झेप घे रे वाक्प्रचार व त्यांचे अर्थ

• आकाशी झेप घेणे : मन ध्येयाकडे उंच झेपावणे.
• विहार करणे : विहरणे, संचार करणे.
• फळ मिळणे : कार्य यशस्वी होणे.
• जीव बिचारा होणे : गोंधळून जाणे, गडबडून जाणे.
• घामातून मोती फुलणे : कष्टातून फळ (यश) मिळणे.
• जीवनात योग येणे : आयुष्यात सुखकारी घटना घडणे.

आकाशी झेप घे रे म्हण व तिचा अर्थ

कळते पण वळत नाही – एखादी गोष्ट किंवा तत्त्व समजते, परंतु त्याप्रमाणे आचरण होत नाही, कृती होत नाही.

Marathi Kumarbharti Std 10 Guide Pdf भाग-४

• आकाशी झेप घे रे Question Answer (कविता)
• सोनाली Question Answer
• निर्णय Question Answer
• तू झालास मूक समाजाचा नायक Question Answer (कविता)
• सर्व विश्वचि व्हावे सुखी Question Answer
• व्युत्पत्ती कोश Question Answer (स्थूलवाचन)