Prasanna

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 2 Parallel Lines.

9th Standard Maths 2 Practice Set 2 Chapter 2 Parallel Lines Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 2 Chapter 2 Parallel Lines Questions With Answers Maharashtra Board

Question 1.
Select the correct alternative and fill in the blanks in the following statements.

i. If a transversal intersects two parallel lines then the sum of interior angles on the same side of the transversal is ____.
(A) 0°
(B) 90°
(C) 180°
(D) 360°
Answer:
(C) 180°

ii. The number of angles formed by a transversal of two lines is _____.
(A) 2
(B) 4
(C) 8
(D) 16
Answer:
(C) 8

iii. A transversal intersects two parallel lines. If the measure of one of the angles is 40°, then the measure of its corresponding angle is ______.
(A) 40°
(B) 140°
(C) 50°
(D) 180°
Answer:
(A) 40°

iv. In ∆ABC, ∠A = 76°, ∠B = 48°, then ∠C = _____.
(A) 66°
(B) 56°
(C) 124°
(D) 28°
Answer:
In ∆ABC, ∠A + ∠B + ∠C = 180°
∴ ∠C = 180° – 76° – 48° = 56°
(B) 56°

v. Two parallel lines are intersected by a transversal. If measure of one of the alternate interior angles is 75° then the measure of the other angle is _____.
(A) 105°
(B) 15°
(C) 75°
(D) 45°
Answer:
(C) 75°

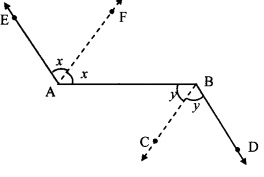
Question 2.
Ray PQ and ray PR are perpendicular to each other. Points B and A are in the interior and exterior of ∠QPR respectively. Ray PB and ray PA are perpendicular to each other.
Draw a figure showing all these rays and write –
i. A pair of complementary angles
ii. A pair of supplementary angles
iii. A pair of congruent angles.
Solution:

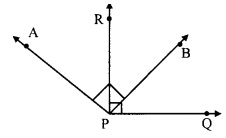
i. Complementary angles:
∠RPQ = 90° [Ray PQ ⊥ ray PR]
∴ ∠RPB + ∠BPQ = 90° [Angle addition property]
∠RPB and ∠BPQ are pair of complementary angles
∠APB = 90° [Ray PA ⊥ ray PB]
∴ ∠APR + ∠RPB = 90°
∠APR and ∠RPB are pair of complementary angles.

ii. Supplementary angles:
∠APB + ∠RPQ = 90° + 90° = 180°
∴ ∠APB and ∠RPQ are a pair of supplementary angles.

iii. Congruent angles:
a. ∠APB = ∠RPQ [Each is of 90°]
b. ∠APB = ∠RPQ
∴ ∠APR + ∠RPB = ∠RPB + ∠BPQ [Angle addition property]
∴ ∠APR = ∠BPQ
∴ ∠APR ≅ ∠BPQ

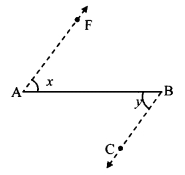
Question 3.
Prove that, if a line is perpendicular to one of the two parallel lines, then it is perpendicular to the other line also.

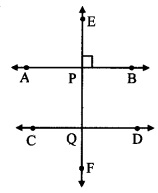
Given: line AB || line CD and line EF intersects them at P and Q respectively.
line EF ⊥ line AB
To prove: line EF ⊥ line CD
Solution:
Proof:
line EF ⊥ line AB [Given]
∴ ∠APR = 90° ….(i)
line AB || line CD and line EF is their transversal.
∴ ∠EPB ≅ ∠PQD …..(ii) [Corresponding angles]
∴ ∠PQD = 90° [From (i) and (ii)]
∴ line EF ⊥ line CD

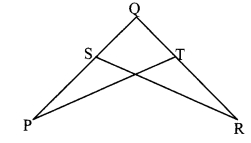
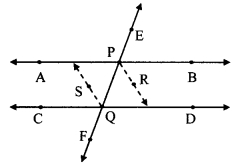
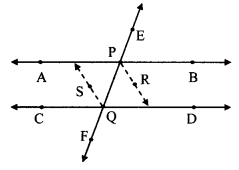
Question 4.
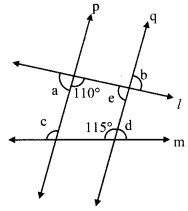
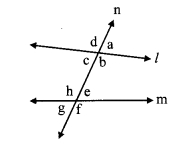
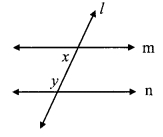
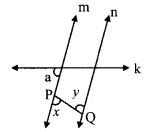
In the given figure, measures of some angles are shown. Using the measures find the measures of ∠x and ∠y and hence show that line l || line m.

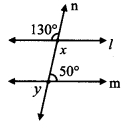
Solution:
Proof:
∠x = 130°
∠y = 50° [Vertically opposite angles]
Here, m∠PQT + m∠QTS = 130° + 50° = 180°
But, ∠ PQT and ∠ QTS are a pair of interior angles on lines l and m when line n is the transversal,

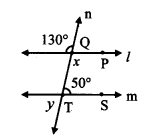
∴ line l || line m [Interior angles test]

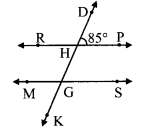
Question 5.
In the given figure, Line AB || line CD || line EF and line QP is their transversal. If y : z = 3 : 7 then find the measure of ∠x.

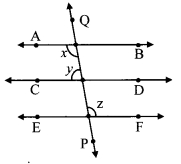
Solution:
y : z = 3 : 7 [Given]
Let the common multiple be m
∴ ∠j = 3m and ∠z = 7m ….(i)
line AB || line EF and line PQ is their transversal [Given]
∠x = ∠z
∴ ∠x = 7m …..(ii) [From (i)]
line AB || line CD and line PQ is their transversal [Given]
∠x + ∠y = 180°
∴ 7m + 3m = 180°
∴ 10m = 180°
∴ m = 18°
∴ ∠x = 7m = 7(18°) [From (ii)]
∴ ∠x = 126°

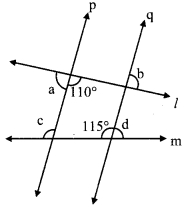
Question 6.
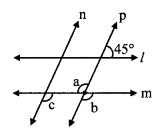
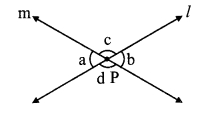
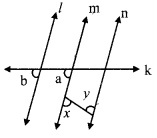
In the given figure, if line q || line r, line p is their transversal and if a = 80°, find the values of f and g.

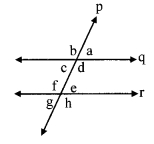
Solution:
i. ∠a = 80° [Given]
∠g = ∠a [Alternate exterior angles]
∴ ∠g = 80° …..(i)

ii. Now, line q || line r and line p is their transversal.
∴ ∠f + ∠g = 180°
∴ ∠f + 80° = 180° [Interior angles]
∴ ∠f = 180° – 80° [From (i)]
∴ ∠f=100°

Question 7.
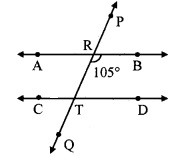
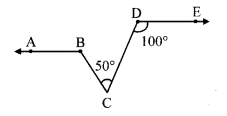
In the given figure, if line AB || line CF and line BC || line ED then prove that ∠ABC = ∠FDE.

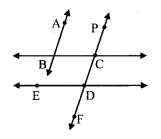
Given: line AB || line CF and line BC || line ED
To prove: ∠ABC = ∠FDE
Solution:
Proof:
line AB || line PF and line BC is their transversal.
∴ ∠ABC = ∠BCD ….(i) [Alternate angles]
line BC || line ED and line CD is their transversal.
∴ ∠BCD = ∠FDE ….(ii) [Corresponding angles]
∴ ∠ABC = ∠FDE [From (i) and (ii)]

Question 8.
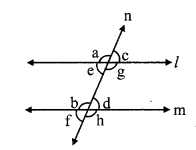
In the given figure, line PS is a transversal of parallel line AB and line CD. If Ray QX, ray QY, ray RX, ray RY are angle bisectors, then prove that □ QXRY is a rectangle.

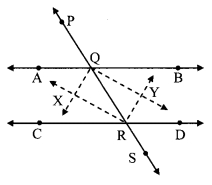
Given: line AB || line CD
Rays QX, RX, QY, RY are the bisectors of ∠AQR, ∠QRC, ∠BQR and ∠QRD respectively.
To prove: □QXRY is a rectangle.
Proof:
∠XQA = ∠XQR = x° ……(i) [Ray QX bisects ∠AQR]
∠YQR = ∠YQB =y° …….(ii) [Ray QY bisects ∠BQR]
∠XRQ = ∠XRC = u° …….. (iii) [Ray RX bisects ∠CRQ]
∠YRQ = ∠YRD = v° ……(iv) [Ray RY bisects ∠DRQ]
line AB || line CD and line PS is their transversal.

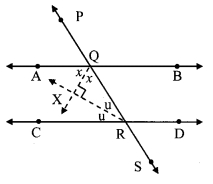
∠AQR+ ∠CRQ= 180° [Interior angles]
(∠XQA + ∠XQR) + (∠XRQ + ∠XRC) = 180° [Angle addition property]
∴ (x + x) + (u + u) = 180° [From (i) and (ii)]
∴ 2x + 2u = 180°
∴ 2(x + u) = 180°
∴ x + u = 90° ……..(v)
In ∆XQR
∠XQR + ∠XRQ + ∠QXR = 180° [Sum of the measures of the angles of triangle is 180°]
∴ x + u + ∠QXR = 180° [From (i) and (iii)]
∴ 90 + ∠QXR = 180° [From (v)]
∴ ∠QXR = 180°- 90°
∴ ∠QXR = 90° …..(vi)
Similarily we can prove that,

∴ y + v = 90°
Hence ∠QYR = 90° ……(vii)
Now, ∠AQR + ∠BQR = 180° [Angles is linear pair]
(∠XQA + ∠XQR) + (∠YQR + ∠YQB) = 180° [Angle addition property]
∴ (x + x) + (y + y) = 180° [From (i) and (ii)]
∴ 2x + 2y = 180°
∴ 2(x+y) = 180°
∴ x +y = 90°
i.e. ∠XQR + ∠YQR = 90° [From (i) and (ii)]
∴ ∠XQY = 90° ….(viii) [Angle addition property]
Similarly we can prove that,
∠XRY = 90° …(ix)
In □QXRY
∠QXR = ∠QYR = ∠XQY = ∠XRY = 90° [From (vi), (vii), (viii) and (ix)]
∴□ QXRY is a rectangle.

Maharashtra Board Class 9 Maths Chapter 2 Parallel Lines Problem Set 2 Intext Questions and Activities

Question 1.
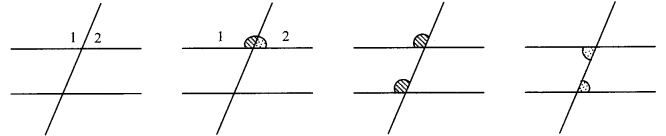
To verify the properties of angles formed by a transversal of two parallel lines. (Textbook pg. no. 14)
Take a piece of thick coloured paper. Draw a pair of parallel lines and a transversal on it. Paste straight sticks on the lines. Eight angles will be formed. Cut pieces of coloured paper, as shown in the figure, which will just fit at the comers of ∠1 and ∠2. Place the pieces near different pairs of corresponding angles, alternate angles and interior angles and verify their properties.

Class 9 Maths Digest

• Practice Set 1.1 Class 9 Answers
• Practice Set 1.2 Class 9 Answers
• Practice Set 1.3 Class 9 Answers
• Problem Set 1 Class 9 Answers
• Practice Set 2.1 Class 9 Answers
• Practice Set 2.2 Class 9 Answers
• Problem Set 2 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 3 Triangles.

9th Standard Maths 2 Practice Set 3.2 Chapter 3 Triangles Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 3.2 Chapter 3 Triangles Questions With Answers Maharashtra Board

Question 1.
In each of the examples given below, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same signs. Observe the figures and state the test by which the triangles in each pair are congruent.

By SSS test
∆ABC ≅ ∆PQR

By SAS test
∆ XYZ ≅ ∆LMN

By ASA test
∆PRQ ≅ ∆STU

By hypotenuse side test
∆LMN ≅ ∆PTR

Question 2.
Observe the information shown in pairs of triangles given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
Solution:

From the information shown in the figure,
In ∆ABC and ∆PQR,
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ∆ABC ≅ ∆PQR [ASA test]
∴ ∠BAC ≅ ∠QPR [Corresponding angles of congruent triangles]
seg AB ≅ segPQ and segAC ≅ seg PR [Corresponding sides of congruent triangles]

From the information shown in the figure,
In ∆PTQ and ∆STR,
seg PT ≅ seg ST
∠PTQ ≅ ∠STR [Vertically opposite angles]
seg TQ ≅ seg TR
∴ ∆PTQ ≅ ∆STR [SAS test]
∴ ∠TPQ ≅ ∠TSR and ∠TQP ≅ ∠TRS [Corresponding angles of congruent triangles]
seg PQ ≅ seg SR [Corresponding sides of congruent triangles]

Question 3.
From the information shown in the figure, state the test assuring the congruence of ∆ABC and ∆PQR. Write the remaining congruent parts of the triangles.

Solution:
In ∆BAC and ∆PQR,
seg BA ≅ seg PQ
seg BC ≅ seg PR
∠BAC ≅ ∠PQR = 90° [Given]
∴ ∆BAC ≅ ∆PQR [Hypotenuse side test]
∴ seg AC ≅ seg QR [c.s.c.t.]
∠ABC ≅ ∠QPR and ∠ACB ≅ ∠QRP [c.a.c.t.]

Question 4.
As shown in the adjoining figure, in ∆LMN and ∆PNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.

Solution:
In ∆LMN and ∆PNM,
seg LM ≅ seg PN
seg LN ≅ seg PM [Given]
seg MN ≅ seg NM [Common side]
∴ ∆LMN ≅ ∆PNM [SSS test]
∴ ∠LMN ≅ ∠PNM,
∴ ∠MLN ≅ ∠NPM, and ∠LNM ≅ ∠PMN [c.a.c.t.]

Question 5.
In the adjoining figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ∆ABD ≅ ∆CBD.

Solution:
proof:
In ∆ABD and ∆CBD,
seg AB ≅ seg CB
seg AD ≅ seg CD [Given]
seg BD ≅ seg BD [Common side]
∴ ∆ABD ≅ ∆CBD [SSS test]

Question 6.
In the adjoining figure, ZP ≅ ZR, seg PQ ≅ seg RQ. Prove that APQT ≅ ARQS.

Proof:
In ∆PQT and ∆RQS,
∠P ≅ ∠R
seg PQ ≅ seg RQ [Given]
∠Q ≅ ∠Q [Common angle]
∴ ∆PQT ≅ ∆RQS [ASA test]

Class 9 Maths Digest

• Practice Set 3.1 Class 9 Answers
• Practice Set 3.2 Class 9 Answers
• Practice Set 3.3 Class 9 Answers
• Practice Set 3.4 Class 9 Answers
• Practice Set 3.5 Class 9 Answers
• Problem Set 3 Class 9 Answers
• Practice Set 4.1 Class 9 Answers
• Practice Set 4.2 Class 9 Answers
• Practice Set 4.3 Class 9 Answers
• Problem Set 4 Class 9 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 12.1 8th Std Maths Answers Solutions Chapter 12 Equations in One Variable.

Equations in One Variable Class 8 Maths Chapter 12 Practice Set 12.1 Solutions Maharashtra Board

Std 8 Maths Practice Set 12.1 Chapter 12 Solutions Answers

Equation in One Variable Practice Set 12.1 Question 1. Each equation is followed by the values of the variable. Decide whether these values are the solutions of that equation.
i. x – 4 = 3, x = – 1, 7, – 7
ii. 9m = 81, m = 3, 9, -3
iii. 2a + 4 = 0, a = 2, – 2, 1
iv. 3 – y = 4, y = – 1, 1, 2
Solution:
i. x – 4 = 3 ….(i)
Substituting x = – 1 in L.H.S. of equation (i),
L.H.S. = (-1) – 4
= – 5
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 1 is not the solution of the given equation.

Substituting x = 7 in L.H.S. of equation (i),
L.H.S. = (7) – 4
= 3
R.H.S. = 3
∴ L.H.S. = R.H.S.
∴ x = 7 is the solution of the given equation.

Substituting x = – 7 in L.H.S. of equation (i),
L.H.S. = (- 7) – 4
= -11
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 7 is not the solution of the given equation.

ii. 9m = 81 …(i)
Substituting m = 3 in L.H.S. of equation (i),
L.H.S. = 9 × (3)
= 27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = 3 is not the solution of the given equation.

Substituting m = 9 in L.H.S. of equation (i),
L.H.S. = 9 × (9)
= 81
R.H.S. = 81
∴L.H.S. = R.H.S.
∴m = 9 is the solution of the given equation.

Substituting m = – 3 in L.H.S. of equation (i),
L.H.S. = 9 × (- 3)
= -27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = – 3 is not the solution of the given equation.

iii. 2a + 4 = 0 …..(i)
Substituting a = 2 in L.H.S. of equation (i),
L.H.S. = 2 (2) + 4
= 4 + 4
= 8
R.H.S. = 0
∴L.H.S. ≠ R.H.S.
∴a = 2 is not the solution of the given equation.

Substituting a = – 2 in L.H.S. of equation (i),
L.H.S. = 2 (-2)+ 4
= -4 + 4
= 0
R.H.S. = 0
∴L.H.S. = R.H.S.
∴a = – 2 is the solution of the given equation.

Substituting a = 1 in L.H.S. of equation (i),
L.H.S. = 2(1)+ 4
= 2 + 4
= 6
R.H.S. = 0
∴ L.H.S. ≠ R.H.S.
∴a = 1 is not the solution of the given equation.

iv. 3 – y = 4 …(i)
Substituting y = -1 in L.H.S. of equation (i),
L.H.S. = 3 – (- 1)
= 3 + 1
= 4
R.H.S. = 4
∴L.H.S. = R.H.S.
∴y = – 1 is the solution of the given equation.

Substituting y = 1 in L.H.S. of equation (i),
L.H.S. = 3-(1)
= 2
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 1 is not the solution of the given equation.

Substituting y = 2 in L.H.S. of equation (i),
L.H.S. = 3-(2)
= 1
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 2 is not the solution of the given equation.

Practice Set 12.1 Question 2.
Solve the following equations:
i. 17p – 2 = 49
ii. 2m + 7 = 9
iii. 3x + 12 = 2x – 4
iv. 5 (x – 3) = 3 (x + 2)
v. \(\frac { 9x }{ 8 }+1=10\)
vi. \(\frac{y}{7}+\frac{y-4}{3}=2\)
vii. 13x – 5 = \(\frac { 3 }{ 2 }\)
viii. 3 (y + 8) = 10 (y – 4) + 8
ix. \(\frac{x-9}{x-5}=\frac{5}{7}\)
x. \(\frac{y-4}{3}+3 y=4\)
xi. \(\frac{b+(b+1)+(b+2)}{4}=21\)
Solution:
i. 17p – 2 = 49
∴ 17p – 2 + 2 = 49 + 2
…[Adding 2 on both the sides]
∴ 17p = 51
∴ \(\frac{17 p}{17}=\frac{51}{17}\) …[Dividing both the sides by 17]
p = 3

ii. 2m + 7 = 9
∴ 2m + 7 – 7 = 9 – 7
…[Subtracting 7 from both the sides]
∴ 2m = 2
∴ \(\frac{2 m}{2}=\frac{2}{2}\) [Dividing both the sides by 2]
∴ m = 1

iii. 3x + 12 = 2x – 4
∴ 3x + 12 – 12 = 2x – 4 – 12
…[Subtracting 12 from both the sides]
∴ 3x = 2x – 16
∴ 3x – 2x = 2x – 16 – 2x
…[Subtracting 2x from both the sides]
∴ x = – 16

iv. 5 (x – 3) = 3 (x + 2)
∴ 5x – 15 = 3x + 6
∴ 5x – 15 + 15 = 3x + 6 + 15
…[Adding 15 on both the sides]
∴ 5x = 3x + 21
∴ 5x – 3x = 3x + 21 – 3x
…[Subtracting 3x from both the sides]
∴ 2x = 21
∴ \(\frac{2 x}{2}=\frac{21}{2}\) …[Dividing both the sides by 2]
∴ \(x=\frac{21}{2}\)

v. \(\frac { 9x }{ 8 }+1=10\)

vi. \(\frac{y}{7}+\frac{y-4}{3}=2\)

vii. 13x – 5 = \(\frac { 3 }{ 2 }\)

viii. 3 (y + 8) = 10 (y – 4) + 8
∴ 3y + 24 = 10y – 40 + 8
∴ 3y + 24 = 10y – 32
∴ 3y + 24 – 24 = 10y – 32 – 24
…[Subtracting 24 from both the sides]
∴ 3y = 10y – 56
∴ 3y – 10y = 10y – 56
…[Subtracting 10y from both the sides]
∴ – 7y = – 56
∴ \(\frac{-7 y}{-7}=\frac{-56}{-7}\)…[Dividing both the sides by – 7]
∴ y = 8

ix. \(\frac{x-9}{x-5}=\frac{5}{7}\)
∴\(\frac{x-9}{x-5} \times 7(x-5)=\frac{5}{7} \times 7(x-5)\)
…[Multiplying both the sides by 7 (x – 5)]
∴7 (x – 9) = 5 (x – 5)
∴7x – 63 = 5x – 25
∴7x – 63 + 63 = 5x – 25 + 63
…[Adding 63 on both the sides]
∴7x = 5x + 38
∴7x – 5x = 5x + 38 – 5x
…[Subtracting 5x from both the sides]
∴ 2x = 38
∴\(\frac{2 x}{2}=\frac{38}{2}\) …[Dividing both the sides by 2]
∴x = 19

x. \(\frac{y-4}{3}+3 y=4\)
∴\(\frac{y-4}{3} \times 3+3 y \times 3=4 \times 3\)
…[Multiplying both the sides by 3]
∴y – 4 + 9y = 12
∴10y – 4 = 12
∴10y – 4 + 4=12 + 4
…[Adding 4 on both the sides]
∴10y = 16
∴\(\frac{10 y}{10}=\frac{16}{10}\)…[Dividing both the sides by 10]
∴y = \(\frac { 8 }{ 5 }\)

xi. \(\frac{b+(b+1)+(b+2)}{4}=21\)
∴\(\frac{b+(b+1)+(b+2)}{4} \times 4=21 \times 4\)
…[Multiplying both the sides by 4]
∴b + b + 1 + b + 2 = 84
∴3b + 3 = 84
∴3b + 3 – 3 = 84 – 3
…[ Subtracting 3 from both the sides]
∴3b = 81
∴\(\frac{3 b}{3}=\frac{81}{3}[/latex …[Dividing both the sides by 3]
∴b = 27

Maharashtra Board Class 8 Maths Chapter 12 Equations in One Variable Practice Set 12.1 Intext Questions and Activities

Std 8 Maths Practice Set 12.1 Question 1.
Fill in the boxes to solve the following equations. (Textbook pg. no. 75)
i. x + 4 = 9
∴x + 4 – __ = 9 – __
… [Subtracting 4 from both the sides]
∴ x = __

ii. x – 2 = 7
∴x – 2 + __ = 7 + __
… [Adding 2 on both the sides]
∴x = __

iii. [latex]\frac { x }{ 3 }=4\)
∴\(\frac { x }{ 3 }\) × __ = 4 ×__
∴x = __

iv. 4x = 24
∴ __ = __
∴x = __
Solution:
i. x + 4 = 9
∴x + 4 – 4 = 9 – 4
… [Subtracting 4 from both the sides]
∴ x = 5

ii. x – 2 = 7
∴x – 2 + 2 = 7 + 2
… [Adding 2 on both the sides]
∴x = 9

iii. \(\frac { x }{ 3 }=4\)
∴\(\frac { x }{ 3 }\) × 3 = 4 × 3
… [Multiplying both the sides by 3]
∴x = 12

iv. 4x = 24
∴ \(\frac{4 x}{[4]}=\frac{24}{[4]}\)
… [Dividing both the sides by 4]
∴x = 6

Std 8 Maths Digest

• Practice Set 11.1 Class 8 Answers
• Practice Set 11.2 Class 8 Answers
• Practice Set 11.3 Class 8 Answers
• Practice Set 12.1 Class 8 Answers
• Practice Set 12.2 Class 8 Answers
• Practice Set 13.1 Class 8 Answers
• Practice Set 13.2 Class 8 Answers
• Practice Set 14.1 Class 8 Answers
• Practice Set 14.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 2 Parallel Lines.

9th Standard Maths 2 Practice Set 2.1 Chapter 2 Parallel Lines Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 2.1 Chapter 2 Parallel Lines Questions With Answers Maharashtra Board

Question :
In the given figure, line RP || line MS and line DK is their transversal. ∠DHP = 85°. Find the measures of following angles.

i. ∠RHD
ii. ∠PHG
iii. ∠HGS
iv. ∠MGK
Solution:
i. ∠DHP = 85° …..(i)
∠DHP + ∠RHD = 180° [Angles in a linear pair]
85° + ∠RHD = 180°
∴ ∠RHD = 180°- 85°
∴ ∠RHD = 95° …..(ii)

ii. ∠PHG = ∠RHD [Vertically opposite angles]
∴ ∠PHG = 95° [From (ii)]

iii. line RP || line MS and line DK is their transversal. [Corresponding angles]
∴ ∠HGS = ∠DHP …..(iii) [From (i)]

iv. ∠HGS = 85° [Vertically opposite angles]
∴ ∠MGK = ∠HGS ∠MGK = 85° [From (iii)]

Question 2.
In the given figure line p line q and line l and line m are tranversals.
Measures of some angles are shown. Hence find the measures of ∠a, ∠b, ∠c, ∠d.

Solution:

i. 110 + ∠a = 180° [Angles in a linear pair]
∴ ∠a = 180° – 110°
∴ ∠a = 70°

ii. consider ∠e as shown in the figure line p || line q, and line lis their transversal.
∠e + 110° = 180° [Interior angles]
∴ ∠e = 180° – 110°
∴ ∠e = 70°
But, ∠b = ∠e [Vertically opposite angles]
∴ ∠b = 70°

iii. line p || line q, and line m is their transversal.
∴ ∠c = 115° [Corresponding angles]

iv. 115° + ∠d = 180° [Angles in a linear pair]
∴ ∠d = 180° – 115°
∴ ∠d = 65°

Question 3.
In the given figure, line 11| line m and line n || line p. Find ∠a, ∠b, ∠c from the given measure of an angle.

Solution:

i. consider ∠d as shown in the figure
line l || line m, and line p is their transversal.
∴ ∠d = 45° [Corresponding angles]
Now, ∠d + ∠b = 180° [Angles in a linear pair]
∴ 45° +∠b = 180°
∴ ∠b = 180° – 45°
∴ ∠b = 135° …..(i)

ii. ∠a = ∠b [Vertically opposite angles]
∴ ∠a = 135° [From (i)]

iii. line n || line p, and line m is their transversal.
∴ ∠c = ∠b [Corresponding angles]
∴ ∠c = 135° [From (i)]

Question 4.
In the given figure, sides of ∠PQR and ∠XYZ are parallel to each other. Prove that, ∠PQR ≅ ∠XYZ.

Given: Ray YZ || ray QRandray YX || ray QP
To prove: ∠PQR ≅ ∠XYZ
Construction: Extend ray YZ in the opposite direction. It intersects ray QP at point S.
Solution:
Proof:
Ray YX || ray QP [Given]
Ray YX || ray SP and seg SY is their transversal [P-S-Q]
∴ ∠XYZ ≅ ∠PSY ……(i) [Corresponding angles]
ray YZ || ray QR [Given]
ray SZ || ray QR and seg PQ is their transversal. [S-Y-Z]
∴ ∠PSY ≅ ∠SQR [Corresponding angles]
∴ ∠PSY ≅ ∠PQR …….. (ii) [P-S-Q]
∴ ∠PQR ≅ ∠XYZ [From (i) and (ii)]

Question 5.
In the given figure, line AB || line CD and line PQ is transversal. Measure of one of the angles is given. Hence find the measures of the following angles.

i. ∠ART
ii. ∠CTQ
iii. ∠DTQ
iv. ∠PRB
Solution:
i. ∠BRT = 105° ….(i)
∠ART + ∠BRT = 180° [Angles in a linear pair]
∴ ∠ART + 105° = 180°
∴ ∠ART = 180° – 105°
∴ ∠ART = 75° …(ii)

ii. line AB || line CD and line PQ is their transversal.
∴ ∠CTQ = ∠ART [Corresponding angles]
∴ ∠CTQ = 75° [From (ii)]

iii. line AB || line CD and line PQ is their transversal.
∴ ∠DTQ = ∠BRT [Corresponding angles]
∴ ∠DTQ = 105° [From (i)]

iv. ∠PRB = ∠ART [Vertically opposite angles]
∴ ∠PRB = 75° [From (ii)]

Maharashtra Board Class 9 Maths Chapter 2 Parallel Lines Practice Set 2.1 Intext Questions and Activities

Question 1.
Angles formed by two lines and their transversal. (Textbook pg, no. 13)
When a transversal (line n) intersects two lines (line l and m) in two distinct points, 8 angles are formed as shown in the figure. Pairs of angles formed out of these angles are as follows:

Pairs of corresponding angles
i. ∠d, ∠h
ii. ∠a, ∠e
iii. ∠c, ∠g
iv. ∠b, ∠f

Pairs of alternate interior angles
i. ∠c, ∠e
ii. ∠b, ∠h

Pairs of alternate exterior angles
i. ∠d, ∠f
ii. ∠a, ∠g

Pairs of interior angles on the same side of the transversal
i. ∠c, ∠h
ii. ∠b, ∠e

Some important properties:
1. When two lines intersect, the pairs of vertically opposite angles formed are congruent.
Example:
In the given diagram,
line l and m intersect at point P.
The pairs of vertically opposite angles that are congruent are:
i. ∠a ≅ ∠b
ii. ∠c ≅ ∠d

2. The angles in a linear pair are supplementary.
Example:
For the given diagram,
∠a and ∠c are in linear pair
∴ ∠a + ∠c = 180°
Also, ∠d and ∠b are in linear pair
∴ ∠d + ∠b = 180°

3. When one pair of corresponding angles is congruent, then all the remaining pairs of corresponding angles are congruent.
Example:
In the given diagram,
If ∠a ≅ ∠b
then ∠e ≅ ∠f, ∠c ≅ ∠d and ∠g ≅ ∠h

4. When one pair of alternate angles is congruent, then all the remaining pairs of alternate angles are congruent.
Example:
For the given diagram,
If ∠e ≅ ∠d, then ∠g ≅ ∠b
Also, ∠a ≅ ∠h and ∠c ≅ ∠f

5. When one pair of interior angles on one side of the transversal is supplementary, then the other pair of interior angles is also supplementary.
Example:
For the given diagram,
If ∠e + ∠b = 180°, then ∠g + ∠d = 180°.

Class 9 Maths Digest

• Practice Set 1.1 Class 9 Answers
• Practice Set 1.2 Class 9 Answers
• Practice Set 1.3 Class 9 Answers
• Problem Set 1 Class 9 Answers
• Practice Set 2.1 Class 9 Answers
• Practice Set 2.2 Class 9 Answers
• Problem Set 2 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 1 Basic Concepts in Geometry.

9th Standard Maths 2 Problem Set 1 Chapter 1 Basic Concepts in Geometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Problem Set 1 Chapter 1 Basic Concepts in Geometry Questions With Answers Maharashtra Board

Question 1.
Select the correct alternative answer for the questions given below.

i. How many midpoints does a segment have ?
(A) only one
(B) two
(C) three
(D) many
Answer:
(A) only one

ii. How many points are there in the intersection of two distinct lines ?
(A) infinite
(B) two
(C) one
(D) not a single
Answer:
(C) one

iii. How many lines are determined by three distinct points?
(A) two
(B) three
(C) one or three
(D) six
Answer:
(C) one or three

iv. Find d(A, B), if co-ordinates of A and B are – 2 and 5 respectively.
(A) -2
(B) 5
(C) 7
(D) 3
Answer:
Since, 5 > -2
∴ d(A, B) = 5 – (-2) = 5+2 = 7
(C) 7

v. If P – Q – R and d(P, Q) = 2, d(P, R) = 10, then find d(Q, R).
(A) 12
(B) 8
(C) √96
(D) 20
Answer:
d(P, R) = d(P, Q) + d(Q, R)
∴ 10 = 2 + d(Q, R)
∴ d(Q, R) = 8
(B) 8

Question 2.
On a number line, co-ordinates of P, Q, R are 3,-5 and 6 respectively. State with reason whether the following statements are true or false.
i. d(p, Q) + d(Q, R) = d(P, R)
ii. d(P, R) + d(R, Q) = d(P, Q)
iii. d(R, P) + d(P, Q) = d(R, Q)
iv. d(P, Q) – d(P, R) = d(Q, R)
Solution:

Co-ordinate of the point P is 3.
Co-ordinate of the point Q is -5.
Since, 3 > -5
d(P, Q) = 3 – (-5) = 3 + 5
∴ d(P,Q) = 8
Co-ordinate of the point Q is -5.
Co-ordinate of the point R is 6.
Since, 6 > -5
d(Q, R) = 6 – (-5) = 6 + 5
∴ d(Q, R) = 11
Co-ordinate of the point P is 3.
Co-ordinate of the point R is 6.
Since, 6 > 3
d(P, R) = 6 – 3
∴ d(P, R) = 3

i. d(P, Q) + d(Q, R) = 8 + 11
= 19 …(i)
d(P, R) = 3 …(ii)
∴ d(P, Q) + d(Q, R) ≠ d(P, R) … [From (i) and (ii)]
∴ The given statement is false.

ii. d(P, R) + d(R, Q) = 3 + 11
d(P,Q) = 8 …(ii)
∴ d(P, R) + d(R, Q) + d(P, Q) …[From (i) and (ii)]
∴ The given statement is false.

iii. d(R, P) + d(P, Q) = 3 + 8
= 11 …(i)
d(R, Q) =11 . -(ii)
∴ d(R,P) + d(P,Q) = d(R,Q) ….[From (i) and (ii)]
∴ The given statement is true.

iv. d(P, Q) – d(P, R) = 8 – 3
= 5 …(i)
d(Q,R) = 11 ..(h)
∴ d(P, Q) – d(P, R) ≠ d(Q, R) …[From (i) and (ii)]
∴ The given statement is false.

Question 3.
Co-ordinates of some pairs of points are given below. Hence find the distance between each pair.
i. 3,6
ii. -9, -1
iii. A, 5
iv. 0,-2
v. x + 3, x – 3
vi. -25, -47
vii. 80, -85
Solution:
i. Co-ordinate of first point is 3.
Co-ordinate of second point is 6.
Since, 6 > 3
∴ Distance between the points = 6 – 3 = 3

ii. Co-ordinate of first point is -9.
Co-ordinate of second point is -1.
Since, -1 > -9
∴ Distance between the points = -1 – (-9) = -1+9 = 8

iii. Co-ordinate of first point is -4.
Co-ordinate of second point is 5.
Since, 5 > -4
∴ Distance between the points = 5 – (-4)
= 5 + 4 = 9

iv. Co-ordinate of first point is 0.
Co-ordinate of second point is -2. Since,
0 > – 2
∴ Distance between the points = 0 – (-2)
= 0 + 2
= 2

v. Co-ordinate of first point is x + 3.
Co-ordinate of second point is x – 3.
Since, x + 3 > x – 3
∴ Distance between the points = x + 3 – (x – 3)
= x + 3 – x + 3 = 3 + 3
= 6

vi. Co-ordinate of first point is -25.
Co-ordinate of second point is -47.
Since, -25 > -47
∴ Distance between the points = -25 – (-47)
= -25 + 47
= 22

vii. Co-ordinate of first point is 80.
Co-ordinate of second point is -85.
Since, 80 > -85
∴ Distance between the points = 80 – (-85)
= 80 + 85
= 165

Question 4.
Co-ordinate of point P on a number line is – 7. Find the co-ordinates of points on the number line which are at a distance of 8 units from point P.
Solution:
Let point Q be at a distance of 8 units from P and on left side of P
Let point R be at a distance of 8 units from P and on right side of P.

i. Let the co-ordinate of point Q be x.
Co-ordinate of point P is -7.
Since, point Q is to the left of point P.
∴ -7 > x
∴ d(P, Q) = -7 -x
∴8 = -7 – x
∴ x = – 7 – 8
∴x = -15

ii. Let the co-ordinate of point R be y.
Co-ordinate of point P is -7.
Since, point R is to the right of point P.
∴ y > -7
∴ d(P, R) = 7- (-7)
∴ 8 = y + 7
∴ 8 – 7 = 7
∴ y = 1
∴ The co-ordinates of the points at a distance of 8 units from P are -15 and 1.

Question 5.
Answer the following questions.
i. If A – B – C and d(A, C) = 17, d(B, C) = 6.5, then d (A, B) = ?
ii. If P – Q – R and d(P, Q) = 3.4, d(Q, R) = 5.7, then d(P, R) = ?
Solution:
i. Given, (A, C) = 17, d(B, C) = 6.5
d(A, C) = d(A, B) + d(B, C) …[A – B – C]
∴ 17 = d(A, B) + 6.5
∴ d(A,B)= 17 – 6.5
∴ d(A, B) = 10.5

ii. Given, d(P, Q) = 3.4, d(Q, R) = 5.7
d(P,R) = d(P,Q) + d(Q,R) …[P – Q – R]
= 34 + 5.7
∴ d(P, R) = 9.1

Question 6.
Co-ordinate of point A on a number line is 1. What are the co-ordinates of points on the number line which are at a distance of 7 units from A ?
Solution:
Let point C be at a distance of 7 units from A and on left side of A
Let point B be at a distance of 7 units from A and on right side of A.

i. Let the co-ordinate of point C be x.
Co-ordinate of point A is 1.
Since, point C is to the left of point A.
∴ 1 > x
∴ d(A, C) = 1 – x
∴ 7 = 1 -x
∴x = 1 – 7
∴ x = – 6

ii. Let the co-ordinate of point B be y.
Co-ordinate of point A is 1.
Since, point B is to the right of point A.
∴y > 1
∴ d(A, B) = 7 – 1
∴ 7 = y – 1
∴ 7 + 1 = 7
∴ 7 = 8
∴ The co-ordinates of the points at a distance of 7 units from A are -6 and 8.

Question 7.
Write the following statements in conditional form.
i. Every rhombus is a square.
ii. Annies in a linear pair are supplementary.
iii. A triangle is a figure formed by three segments
iv. A number having only two divisors is called a prime number.
Solution:
i If a quadrilateral is a rhombus, then it is a square.
ii. If iwo angles are in a linear pair, then they are supplementary.
iii. If a figure is a triangle, then it is formed by three segments.
iv. If a number has only two divisors, then it is a prime number.

Question 8.
Write the converse of each of the following statements.
i. If the sum of measures of angles in a figure is 180°, then the figure is a triangle.
ii If the sum of measures of two angles is 90°, thfcn they are eomplement of each other.
iii. If the corresponding angles formed by a transversal of two lines are congruent, then the two lines are parallel.
iv. If the sum of the digits of a number is divisible by 3, then the number is divisible by 3.
Answer:
i. If a figure is a triangle, then the sum of the measures of its angles is 180°.
ii. if two angles are eomplement of each other, then sum of their measures is 90°,
iii. If two lines are parallel, then the corresponding angles formed by a transversal of two lines are congruent.
iv. If a number is divisible by 3, then the sum of its digits is also divisible by 3.

Question 9.
Write the antecedent (given part) and the consequent (part to be proved) in the following statements.
i. If all sides of a triangle are congruent, then its all angles are congruent.
ii. The diagonals of a parallelogram bisect each other.
Answer:
i. If all sides of a triangle are congruent, then its all angles are congruent.
Antecedent (Given): All the sides of the triangle are congruent.
Consequent (To prove): All the angles are congruent.

ii. The diagonals of a parallelogram bisect each other.
Conditional statement: “If a quadrilateral is a parallelogram then its diagonals bisect each other.
Antecedent (Given): Quadrilateral is a parallelogram.
Consequent (To prove): Its diagonals bisect each other.

Question 10.
Draw a labelled figure showing information in each of the following statements and write the antecedent and the consequent.
i. Two equilateral triangles are similar.
ii. If angles in a linear pair are congruent, then each of them is a right angle.
iii. If the altitudes drawn on two sides of a triangle are congruent, then these two sides are congruent.
Answer:
i. Two equilateral triangles are similar.
Conditional statement: “If two triangles are equilateral, then they are similar.
Antecedent (Given): Two triangles are equailateral.
i.e. ∆ABC and ∆PQR are equilatral triangle.
Consequent (To prove): Triangles are similar
i.e. ∆ABC ∼ ∆PQR

ii. If angles in a linear pair are congruent, then each of them is a right angle.
Antecedent (Given): Angles in a linear pair are congrunent.
∠ABC and ∠ABD are angles in a linear pair i.e. ∠ABC = ∠ABD
Consequent (To prove): Each angle is a right angle.
i.e. ∠ABC – ∠ABD = 90°

iii. If the altitudes drawn on two sides of a triangle are congruent, then these two sides are congruent.
Antecedent (Given): Altitude drawn on two sides of triangle are congrunent.
In ∆ABC, AD ⊥ BC . and BE ⊥ AC. seg AD ≅ seg BE

Consequent (To prove): Two sides are congruent.
side BC ≅ side AC A

Maharashtra Board Class 9 Maths Chapter 1 Basic Concepts in Geometry Problem Set 1 Intext Questions and Activities

Question 1.
Points A, B, C are given below. Check, with a stretched thread, whether the three points are collinear or not. If they are collinear, write which one of them is between the other two. (Textbook pg. no. 4)

Answer:
Point B is between the points A and C.

Question 2.
Given below are four points P, Q, R, and S. Check which three of them are collinear and which three are non collinear. In the case of three collinear points, state which of them is between the other two. (Textbook pg. no. 4)

Answer:
Points P, R and S are collinear.
Point R is between the points P and S.

Question 3.
Students are asked to stand in a line for mass drill. How will you check whether the students standing are in a line or not ? (Textbook pg. no. 4)
Answer:
If one stands in front of the line and observes only the first student standing in the line, then all the students standing in that line are collinear i.e., standing in the same line. We can use this property of collinearity to check whether the students are standing in the same line or not.

Question 4.
How had you verified that light rays travel in a straight line? Recall an experiment in science which you have done in a previous standard. (Textbook pg. no. 4)
Answer:

The flame of the candle can be seen only when the pin holes in all cardboards are in the same straight line. We can use the set up shown in the figure above to verify that light rays travels in a straight line.

Class 9 Maths Digest

• Practice Set 1.1 Class 9 Answers
• Practice Set 1.2 Class 9 Answers
• Practice Set 1.3 Class 9 Answers
• Problem Set 1 Class 9 Answers
• Practice Set 2.1 Class 9 Answers
• Practice Set 2.2 Class 9 Answers
• Problem Set 2 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 2 Parallel Lines.

9th Standard Maths 2 Practice Set 2.2 Chapter 2 Parallel Lines Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 2.2 Chapter 2 Parallel Lines Questions With Answers Maharashtra Board

Question 1.
In the given figure, y = 108° and x = 71°. Are the lines m and n parallel? Justify?

Solution:
y = 108°, x = 71° …[Given]
x + y = 71° + 108°
= 179°
∴ x + y = 180°
∴ The angles x andy are not supplementary.
∴ The angles do not satisfy the interior angles test for parallel lines
∴ line m and line n are not parallel lines.

Question 2.
In the given figure, if ∠a = ∠b then prove that line l || line m.

Given: ∠a ≅ ∠b
To prove: line l| line m
Solution:
Proof:

consider ∠c as shown in the figure ∠a ≅ ∠c …….. (i) [Vertically opposite angles]
But, ∠a ≅ ∠b I (ii) [Given]
∴ ∠b ≅ ∠c [From (i) and (ii)]
But, ∠b and ∠c are corresponding angles on lines l and m when line n is the transversal.
∴ line l || line m. [Corresponding angles test]

Question 3.
In the given figure, if ∠a ≅ ∠b and ∠x ≅ ∠y, then prove that line l | line n.

Given: ∠a ≅ ∠b and ∠x ≅ ∠y
To prove: line l | line n
Solution:
Proof:

∠a = ∠b [Given]
But, ∠a and ∠b are corresponding angles on lines l and m when line k is the transversal.
∴ line l || line m ….(i) [Corresponding angles test]
∠x ≅ ∠y [Given]
But, ∠x and ∠y are alternate angles on lines m and n when seg PQ is the transversal,

∴ line m || line n ……(ii) [Alternate angles test]
∴ From (i) and (ii),
line l || line m || line n
i.e., line l || line n

Question 4.
In the given figure, if ray BA || ray DE, ∠C = 50° and ∠D = 100°. Find the measure of ∠ABC.
(Hint: Draw a line passing through point C and parallel to line AB.)

Solution:
Draw a line FG passing through point
C and parallel to line AB
line FG || ray BA …….(i) [Construction]
Ray BA || ray DE ….(ii) [Given]
line FG || ray BA || ray DE …(iii) [From (i) and (ii)]
line FG||rayDE [From (iii)]
and seg DC is their transvensal
∴ ∠ DCF = ∠ EDC [Alternate angles]
∴ ∠ DCF = 100° [∵ ∠D = 100°]
Now, ∠ DCF = ∠ BCF + ∠ BCD [Angle addition property]
∴ 100° = ∠BCF + 50°
∴ 100° – 50° = ∠BCF
∴ ∠BCF = 50° ….(iv)
Now, line FG || ray BA and seg BC is their transversal.

∴ ∠ABC + ∠BCF = 180° [Interior angles]
∴ ∠ABC + 50° = 180° [From (iv)]
∴ ∠ABC = 180°- 50°
∴ ∠ABC = 130°

Question 5.
In the given figure, ray AE || ray BD, ray AF is the bisector of ∠EAB and ray BC is the bisector of ∠ABD. Prove that line AF || line BC.

Given: Ray AE || ray BD, and
ray AF and ray BC are the bisectors of ∠EAB and ∠ABD respectively.
To prove: line AF || line BC
Solution:
Proof:
Ray AE || ray BD and seg AB is their transversal.
∴ ∠EAB = ∠ABD ….(i) [Alternate angles]
∠FAB = \(\frac { 1 }{ 2 }\)∠EAB [Ray AF bisects ∠EAB]
∴ 2∠FAB = ∠EAB …..(ii)
∠CBA = \(\frac { 1 }{ 2 }\)∠ABD [Ray BC bisects ∠ABD]
∴ 2∠CBA = ∠ABD …(iii)
∴ 2∠FAB = 2∠CBA [From (i), (ii) and (iii)]
∴ ∠FAB = ∠CBA
But, ∠FAB and ∠ABC are alternate angles on lines AF and BC when seg AB is the transversal.

∴ line AF || line BC [Alternate angles test]

Question 6.
A transversal EF of line AB and line CD intersects the lines at points P and Q respectively. Ray PR and ray QS are parallel and bisectors of ∠BPQ and ∠PQC respectively. Prove that line AB || line CD.

Given: Ray PR || ray QS
Ray PR and ray QS are the bisectors of ∠BPQ and ∠PQC respectively.
To prove: line AB || line CD
Solution:

Proof:
Ray PR || ray QS and seg PQ is their transversal.
∠RPQ = ∠SQP ….(i) [Alternate angles]
∠RPQ = \(\frac { 1 }{ 2 }\)∠BPQ …. (ii) [Ray PR bisects ∠BPQ]
∠SQP = \(\frac { 1 }{ 2 }\)∠PQC [Ray QS bisects ∠PQC]
∴ \(\frac { 1 }{ 2 }\)∠BPQ = \(\frac { 1 }{ 2 }\)∠PQC
∴ ∠BPQ = ∠PQC
But, ∠BPQ and ∠PQC are alternate angles on lines AB and CD when line EF is the transversal.
∴ line AB || line CD [Alternate angles test]

Maharashtra Board Class 9 Maths Chapter 2 Parallel Lines Practice Set 2.2 Intext Questions and Activities

Question 1.
In the given figure, how will you decide whether line ¡ and line m are parallel or not? (Textbook pg. no. 19)

Answer:
In the figure, we observe that line I and line m are coplanar and do not intersect each other.
∴ Line l and line m are parallel lines.

Class 9 Maths Digest

• Practice Set 1.1 Class 9 Answers
• Practice Set 1.2 Class 9 Answers
• ProblemSet 1.3 Class 9 Answers
• Practice Set 1 Class 9 Answers
• Practice Set 2.1 Class 9 Answers
• Practice Set 2.2 Class 9 Answers
• Problem Set 2 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 1.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 1 Basic Concepts in Geometry.

9th Standard Maths 2 Practice Set 1.3 Chapter 1 Basic Concepts in Geometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 1.3 Chapter 1 Basic Concepts in Geometry Questions With Answers Maharashtra Board

Question 1.
Write the following statements in ‘if-then’ form.
i. The opposite angles of a parallelogram are congruent.
ii. The diagonals of a rectangle are congruent.
iii. In an isosceles triangle, the segment joining the vertex and the midpoint of the base is perpendicular to the base.
Answer:
i. If a quadrilateral is a parallelogram, then its opposite angles are congruent.
ii. If a quadrilateral is a rectangle, then its diagonals are congruent.
iii. If a triangle is isosceles triangle, then segment joining the vertex of a triangle and midpoint of the base is perpendicular to the base.

Question 2.
Write converses of the following statements.
i. The alternate angles formed by two parallel lines and their transversal are congruent.
ii. If a pair of the interior angles made by a transversal of two lines are supplementary, then the lines are parallel.
iii. The diagonals of a rectangle are congruent.
Answer:
i. If the alternate angles made by two lines and their transversal are congruent, then the two lines are parallel.
ii. If two parallel lines are intersected by a transversal, then the interior angles formed bv the transversal are supplementary.
iii. If the diagonals of a quadrilateral are congruent, then that quadrilateral is a rectangle.

Class 9 Maths Digest

• Practice Set 1.1 Class 9 Answers
• Practice Set 1.2 Class 9 Answers
• Practice Set 1.3 Class 9 Answers
• Problem Set 1 Class 9 Answers
• Practice Set 2.1 Class 9 Answers
• Practice Set 2.2 Class 9 Answers
• Problem Set 2 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 1.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 1 Basic Concepts in Geometry.

9th Standard Maths 2 Practice Set 1.2 Chapter 1 Basic Concepts in Geometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 1.2 Chapter 1 Basic Concepts in Geometry Questions With Answers Maharashtra Board

Question 1.
The following table shows points on a number line and their co-ordinates. Decide whether the pair of segments given below the table are congruent or not.

i. seg DE and seg AB
ii. seg BC and seg AD
iii. seg BE and seg AD
Solution:
i. Co-ordinate of the point E is 9.
Co-ordinate of the point D is -7.
Since, 9 > -7
∴ d(D, E) = 9 – (-7) = 9 + 7 = 16
∴ l(DE) = 16 …(i)
Co-ordinate of the point A is -3.
Co-ordinate of the point B is 5.
Since, 5 > -3
∴ d(A, B) = 5 – (-3) = 5 + 3 = 8
∴ l(AB) = 8 …(ii)
∴ l(DE) ≠ l(AB) …[From (i) and (ii)]
∴ seg DE and seg AB are not congruent.

ii. Co-ordinate of the point B is 5.
Co-ordinate of the point C is 2.
Since, 5 > 2
∴ d(B, C) = 5 – 2 = 3
∴ l(BC) = 3 …(i)
Co-ordinate of the point A is -3.
Co-ordinate of the point D is -7.
Since, -3 > -7
∴ d(A, D) = -3 – (-7) = -3 + 7 = 4
∴ l(AD) = 4 . ..(ii)
∴ l(BC) ≠ l(AD) … [From (i) and (ii)]
∴ seg BC and seg AD are not congruent.

iii. Co-ordinate of the point E is 9.
Co-ordinate of the point B is 5.
Since, 9 > 5
∴ d(B, E) = 9 – 5 = 4
∴ l(BE) = 4 …(i)
Co-ordinate of the point A is -3.
Co-ordinate of the point D is -7.
Since, -3 > -7
∴ d(A, D) = -3 – (-7) = 4
∴ l(AD) = 4 …(ii)
∴ l(BE) =l(AD) …[From (i) and (ii)]
∴ seg BE and seg AD are congruent.
i.e, seg BE ≅ seg AD

Question 2.
Point M is the midpoint of seg AB. If AB = 8, then find the length of AM.
Solution:
Point M is the midpoint of seg AB and l(AB) = 8. …[Given]

Question 3.
Point P is the midpoint of seg CD. If CP = 2.5, find l(CD).
Solution:
Point P is the midpoint of seg CD and l(CP) = 2.5 …[Given]

∴ l(CD) = 2.5 x 2
∴ l(CD) = 5

Question 4.
If AB = 5 cm, BP = 2 cm and AP = 3.4 cm, compare the segments.
Solution:
Given, l(AB) = 5 cm, l(BP) = 2 cm,
l(AP) = 3.4 cm … [Given]
r Since, 2 < 3.4 < 5
∴ l(BP) < l(AP) < l(AB)
i.e., seg BP < seg AP < seg AB

Question 5.
Write the answers to the following questions with reference to the figure given below:

i. Write the name of the opposite ray of ray RP
ii. Write the intersection set of ray PQ and ray RP.
iii. Write the union set of ray PQ and ray QR.
iv. State the rays of which seg QR is a subset.
v. Write the pair of opposite rays with common end point R.
vi. Write any two rays with common end point S.
vii. Write the intersection set of ray SP and ray ST.
Answer:
i. Ray RS or ray RT
ii. Ray PQ
iii. Line QR
iv. Ray QR, ray QS, ray QT, ray RQ, ray SQ, ray TQ
v. Ray RP and ray RS, ray RQ and ray RT vi. Ray ST, ray SR
vii. Point S

Question 6.
Answer the questions with the help of figure given below.

i. State the points which are equidistant from point B.
ii. Write a pair of points equidistant from point iii. Find d(U,V), d(P,C), d(V,B), d(U, L).
Answer:
i. Points equidistant from point B are a. A and C, because d(B, A) = d(B, C) = 2 b. D and P, because d(B, D) = d(B, P) = 4
ii. Points equidistant from point Q are a. L and U, because d(Q, L) = d(Q, U) = 1 b. P and R, because d(P, Q) = d(Q, R) = 2
iii. a. Co-ordinate of the point U is -5. Co-ordinate of the point V is 5. Since, 5 > -5
∴ d(U, V) = 5 – (-5)
= 5 + 5
∴ d(U, V) = 10

b. Co-ordinate of the point P is -2.
Co-ordinate of the point C is 4.
Since, 4 > -2
∴ d(P, C) = 4 – (-2)
= 4 + 2
∴ d(P, C) = 6

c. Co-ordinate of the point V is 5.
Co-ordinate of the point B is 2.
Since, 5 > 2
∴ d(V, B) = 5 – 2
∴ d(V, B) = 3

d. Co-ordinate of the point U is -5.
Co-ordinate of the point L is -3.
Since, -3 > -5
∴ d(U, L) = -3 – (-5)
= -3 + 5
∴ d(U, L) = 2

Class 9 Maths Digest

• Practice Set 1.1 Class 9 Answers
• Practice Set 1.2 Class 9 Answers
• Practice Set 1.3 Class 9 Answers
• Problem Set 1 Class 9 Answers
• Practice Set 2.1 Class 9 Answers
• Practice Set 2.2 Class 9 Answers
• Problem Set 2 Class 9 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 10.2 8th Std Maths Answers Solutions Chapter 10 Division of Polynomials.

Division of Polynomials Class 8 Maths Chapter 10 Practice Set 10.2 Solutions Maharashtra Board

Std 8 Maths Practice Set 10.2 Chapter 10 Solutions Answers

Division of Polynomials Class 8 Practice Set 10.2 Question 1. Divide and write the quotient and the remainder.
i. (y² + 10y + 24) ÷ (y + 4)
ii. (p² + 7p – 5) ÷ (p + 3)
iii. (3x + 2x² + 4x³) ÷ (x – 4)
iv. (2m³ + m² + m + 9) ÷ (2m – 1)
v. (3x – 3x² – 12 + x⁴ + x³) ÷ (2 + x²)
vi. (a⁴ – a³ + a² – a + 1) ÷ (a³ – 2)
vii. (4x⁴ – 5x³ – 7x + 1) ÷ (4x – 1)
Solution:
i. (y² + 10y + 24) ÷ (y + 4)

∴ Quotient = y + 6
Remainder = 0

ii. (p² + 7p – 5) ÷ (p + 3)

∴ Quotient = p + 4
Remainder = -17

iii. (3x + 2x² + 4x³) ÷ (x – 4)
Write the dividend in descending order of their indices.
3x + 2x² + 4x³ = 4x³ + 2x² + 3x

∴ Quotient = 4x² + 18x + 75
Remainder = 300

iv. (2m³ + m² + m + 9) ÷ (2m – 1)

∴ Quotient = m² + m + 1
Remainder = 10

v. (3x – 3x² – 12 + x⁴ + x³) ÷ (2 + x²)
Write the dividend in descending order of their indices.
(x⁴ + x³ – 3x² + 3x – 12) ÷ (x² + 2)

∴ Quotient = x² + x – 5
Remainder = x – 2

vi. (a⁴ – a³ + a² – a + 1) ÷ (a³ – 2)

∴ Quotient = a – 1
Remainder = a² + a – 1

vii. (4x⁴ – 5x³ – 7x + 1) ÷ (4x – 1)
Write the dividend in descending order of their indices.
(4x⁴ – 5x³ – 7x + 1) = (4x⁴ – 5x³ + 0x² – 7x + 1)

∴ Quotient = \(x^{3}-x^{2}-\frac{x}{4}-\frac{29}{16}\)
Remainder = \(\frac { -13 }{ 16 }\)

Std 8 Maths Digest

• Practice Set 8.1 Class 8 Answers
• Practice Set 8.2 Class 8 Answers
• Practice Set 8.3 Class 8 Answers
• Practice Set 9.1 Class 8 Answers
• Practice Set 9.2 Class 8 Answers
• Practice Set 10.1 Class 8 Answers
• Practice Set 10.2 Class 8 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 11.3 8th Std Maths Answers Solutions Chapter 11 Statistics.

Statistics Class 8 Maths Chapter 11 Practice Set 11.3 Solutions Maharashtra Board

Std 8 Maths Practice Set 11.3 Chapter 11 Solutions Answers

Exercise 11.3 Class 8 Question 1.
Show the following information by a percentage bar graph.

Division of standard 8	A	B	C	D
Number of students securing grade A	45	33	10	15
Total number of students	60	55	40	75

Solution:

Division of standard 8	A	B	C	D
Number of students securing grade A	45	33	10	15
Total number of students	60	55	40	75
Percentage of students securing grade A	75%	60%	25%	20%
Percentage of students not securing grade A	25%	40%	75%	80%

Statistics for Class 8 Question 2.
Observe the following graph and answer the questions.

1. State the type of the bar graph.
2. How much percent is the Tur production to total production in Ajita’s farm?
3. Compare the production of Gram in the farms of Yash and Ravi and state whose percentage of production is more and by how much?
4. Whose percentage production of Tur is the least?
5. State production percentages of Tur and Gram in Sudha’s farm.

Solution:

1. The given graph is a percentage bar graph.
2. Percent of tur production to the total production in Ajita’s farm is 60%.
3. Production of Gram in the farm of Yash = 50%
   Production of Gram in the farm of Ravi = 30%
   ∴ Difference in the production = 50% – 30% =20%
   ∴ Yash’s production of Gram is more and by 20%.
4. Sudha’s percentage production of Tur is the least.
5. Production percentages of Tur and Gram in Sudha’s farm are 40% and 60% respectively.

8th Standard Statistics Question 3.
The following data is collected in a survey of some students of 10th standard from some schools. Draw the percentage bar graph of the data.

School	1st	2nd	3rd	4th
Inclination towards science stream	90	60	25	16
Inclination towards commerce stream	60	20	25	24

Solution:

School	1st	2nd	3rd	4th
Inclination towards science stream	90	60	25	16
Inclination towards commerce stream	60	20	25	24
Total number of students	150	80	50	40
Percentage of students having inclination towards science stream	60%	75%	50%	40%
Percentage of students having inclination towards commerce stream	40%	25%	50%	60%

Maharashtra Board Class 8 Maths Chapter 11 Statistics Practice Set 11.3 Intext Questions and Activities

Statistics 8th Class Question 1.
Compare and discuss a percentage bar diagram and a subdivided bar diagram. Use it to learn the graphs in the subjects like Science, Geography. (Textbook pg, no. 74)
Solution:
[Students should attempt the above activity on their own.].

Std 8 Maths Digest

• Practice Set 11.1 Class 8 Answers
• Practice Set 11.2 Class 8 Answers
• Practice Set 11.3 Class 8 Answers
• Practice Set 12.1 Class 8 Answers
• Practice Set 12.2 Class 8 Answers
• Practice Set 13.1 Class 8 Answers
• Practice Set 13.2 Class 8 Answers
• Practice Set 14.1 Class 8 Answers
• Practice Set 14.2 Class 8 Answers