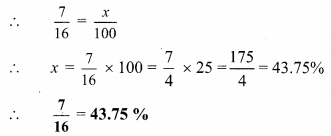Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 3 Polynomials.
9th Standard Maths 1 Problem Set 3 Chapter 3 Polynomials Textbook Answers Maharashtra Board
Class 9 Maths Part 1 Problem Set 3 Chapter 3 Polynomials Questions With Answers Maharashtra Board
Question 1.
Write the correct alternative answer for each of the following questions.
i. Which of the following is a polynomial?

Answer:
(D) √2x² + \(\frac { 1 }{ 2 }\)
ii. What is the degree of the polynomial √7 ?
(A) \(\frac { 1 }{ 2 }\)
(B) 5
(C) 2
(D) 0
Answer:
(D) 0
iii. What is the degree of the polynomial ?
(A) 0
(B) 1
(C) undefined
(D) any real number
Answer:
(C) undefined
iv. What is the degree of the polynomial 2x2 + 5xsup>3 + 7?
(A) 3
(B) 2
(C) 5
(D) 7
Answer:
(A) 3
v. What is the coefficient form of x3 – 1 ?
(A) (1, -1)
(B) (3, -1)
(C) (1, 0, 0, -1)
(D) (1, 3, -1)
Answer:
(C) (1, 0, 0, -1)
vi. p(x) = x2 – x + 3, then p (7√7) = ?
(A) 3
(B) 7√7
(C) 42√7+3
(D) 49√7
Answer:
(D) 49√7
vii. When x = – 1, what is the value of the polynomial 2x3 + 2x ?
(A) 4
(B) 2
(C) -2
(D) -4
Answer:
(A) 4
viii. If x – 1 is a factor of the polynomial 3x2 + mx, then find the value of m.
(A) 2
(B) -2
(C) -3
(D) 3
Answer:
(C) -3
ix. Multiply (x2 – 3) (2x – 7x3 + 4) and write the degree of the product.
(A) 5
(B) 3
(C) 2
(D) 0
Answer:
(A) 5
x. Which is the following is a linear polynomials?
(A) x + 5
(B) x2 + 5
(C) x3 + 5
(D) x4 + 5
Answer:
(A) x + 5
Hints:
v. x3 – 1 = x3 + 0x2 + 0x – 1
vi. p(7√ 7) = (7√ 7)2 (7√ 7) (7√ 7) + 3
= 3
vii. p(-1) = 2(-1)3 + 2(-1)
= -2 – 2 = -4
vii. p(1) = 0
∴ 3(1)2 + m(1) = 0
∴ 3 + m =0
∴ m = -3
ix. Here, degree of first polynomial = 2 and
degree of second polynomial 3
∴ Degree of polynomial obtained by multiplication = 2 + 3 = 5
Question 2.
Write the degree of the polynomial for each of the following.
i. 5 + 3x4
ii. 7
iii. ax7 + bx9 (a, b are constants)
Answer:
i. 5 + 3x4
Here, the highest power of x is 4.
∴Degree of the polynomial = 4
ii. 7 = 7x°
∴ Degree of the polynomial = 0
iii. ax7 + bx9
Here, the highest power ofx is 9.
∴Degree of the polynomial = 9
Question 3.
Write the following polynomials in standard form. [1 Mark each]
i. 4x2 + 7x4 – x3 – x + 9
ii. p + 2p3 + 10p2 + 5p4 – 8
Answer:
i. 7x4 – x3 + 4x2 – x + 9
ii. 5p4 + 2p3 + 10p2 + p – 8
Question 4.
Write the following polynomial in coefficient form.
i. x4 + 16
ii. m5 + 2m2 + 3m+15
Answer:
i. x4 + 16
Index form = x4 + 0x3 + 0x2 + 0x + 16
∴ Coefficient form of the polynomial = (1,0,0,0,16)
ii. m5 + 2m2 + 3m + 15
Index form = m5 + 0m4 + 0m3 + 2m2 + 3m + 15
∴ Coefficient form of the polynomial = (1, 0, 0, 2, 3, 15)
Question 5.
Write the index form of the polynomial using variable x from its coefficient form.
i. (3, -2, 0, 7, 18)
ii. (6, 1, 0, 7)
iii. (4, 5, -3, 0)
Answer:
i. Number of coefficients = 5
∴ Degree = 5 – 1 = 4
∴Index form = 3x4 – 2x3 + 0x2 + 7x + 18
ii. Number of coefficients = 4
∴Degree = 4 – 1 = 3
∴ Index form = 6x3 + x2 + 0x + 7
iii. Number of coefficients = 4
∴ Degree = 4 – 1 = 3
∴ Index form = 4x3 + 5x2 – 3x + 0
Question 6.
Add the following polynomials.
i. 7x4 – 2x3 + x + 10;
3x4 + 15x3 + 9x2 – 8x + 2
ii. 3p3q + 2p2q + 7;
2p2q + 4pq – 2p3q
Solution:
i. (7x4 – 2x3 + x + 10) + (3x4 + 15x3 + 9x2 – 8x + 2)
= 7x4 – 2x3 + x + 10 + 3x4 + 15x3 + 9x2 – 8x + 2
= 7x4 + 3x4 – 2x3 + 1 5x3 + 9x2 + x – 8x + 10 + 2
= 10x4 + 13x3 + 9x2 – 7x + 12
ii. (3p3q + 2p2q + 7) + (2p2q + 4pq – 2p3q)
= 3p3q + 2p2q + 7 + 2p2q + 4pq – 2p3q
= 3p3q – 2p3q + 2p2q + 2p2q + 4pq + 7
= p3q + 4p2q + 4pq + 7
Question 7.
Subtract the second polynomial from the first.
i. 5x2 – 2y + 9 ; 3x2 + 5y – 7
ii. 2x2 + 3x + 5 ; x2 – 2x + 3
Solution:
i. (5x2 – 2y + 9) – (3x2 + 5y – 7)
= 5x2 – 2y+ 9 – 3x2 – 5y + 1
= 5x2 – 3x2 – 2y – 5y + 9 + 7
= 2x2 – 1y + 16
ii. (2x2+ 3x + 5) – (x2 – 2x + 3)
= 2x2 + 3x + 5 – x2 + 2x – 3
= 2x2 – x2 + 3x + 2x + 5 – 3
= x2 + 5x + 2
Question 8.
Multiply the following polynomials.
i. (m3 – 2m + 3) (m4 – 2m2 + 3m + 2)
ii. (5m3 – 2) (m2 – m + 3)
Solution:
i. (m3 – 2m + 3) (m4 – 2m2 + 3m + 2)
= m3(m4 – 2m2 + 3m + 2) – 2m(m4 – 2m2 + 3m + 2) + 3(m4 – 2m2 + 3m + 2)
= m7 – 2m5 + 3m4 + 2m3 – 2m5 + 4m3 – 6m2 – 4m + 3m4 – 6m2 + 9m + 6
= m7 – 2m5 – 2m5 + 3m4 + 3m4 + 2m3 + 4m3 – 6m2 – 6m2 – 4m + 9m + 6
= m7 – 4m5 + 6m4 + 6m3 – 12m2 + 5m + 6
ii. (5m3 – 2) (m2 – m + 3)
= 5m3(m2 – m + 3) – 2(m2 – m + 3)
= 5m5 – 5m4 + 15m3 – 2m2 + 2m – 6
Question 9.
Divide polynomial 3x3 – 8x2 + x + 7 by x – 3 using synthetic method and write the quotient and remainder.
Solution:
Dividend = 3x3 – 8x2 + x + 7
∴ Coefficient form of dividend = (3, – 8, 1,7)
Divisor = x – 3
∴ Opposite of – 3 is 3
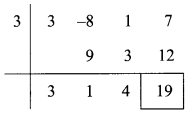
Coefficient form of quotient = (3, 1,4)
∴ Quotient = 3x2 + x + 4 and
Remainder =19
Question 10.
For which value of m, x + 3 is the factor of the polynomial x3 – 2mx + 21?
Solution:
Here, p(x) = x3 – 2mx + 21
(x + 3) is a factor of x3 – 2mx + 21.
∴ By factor theorem,
Remainder = 0
∴ P(- 3) = 0
p(x) = x3 – 2mx + 21
∴ p(-3) = (-3)3 – 2(m)(-3) + 21
∴ 0 = – 27 + 6m + 21
∴ 6 + 6m = 0
∴ 6m = 6
∴ m = 1
∴ x + 3 is the factor of x3 – 2mx + 21 for m = 1.
Question 11.
At the end of the year 2016, the population of villages Kovad, Varud, Chikhali is 5x2 – 3y2, 7y2 + 2xy and 9x2 + 4xy respectively. At the beginning of the year 2017, x2 + xy – y2, 5xy and 3x2 + xy persons from each of the three villages respectively went to another village for education, then what is the remaining total population of these three villages ?
Solution:
Total population of villages at the end of 2016 = (5x2 – 3y2) + (7y2 + 2xy) + (9x2 + 4xy)
= 5x2 + 9x2 – 3y2 + 7y2 + 2xy + 4xy
= 14x2 + 4y2 + 6xy …….(i)
Total number of persons who went to other village at the beginning of 2017 = (x2 + xy – y2) + (5xy) + (3x2 + xy)
= x2 + 3x2 – y2 + xy + 5xy + xy
= 4x2 – y2 + 7xy … (ii)
Remaining total population of villages = Total population at the end of 2016 – total number of persons who went to other village at the beginning of 2017
= 14x2 + 4y2 + 6xy – (4x2 – y2 + 7xy) … [From (i) and (ii)]
= 14x2 + 4y2 + 6xy – 4x2 + y2 – 7xy
= 14x2 – 4x2 + 4y2 + y2 + 6xy – 7xy = 1
= 10x2 + 5y2 – xy
∴ The remaining total population of the three villages is 10x2 + 5y2 – xy.
Question 12.
Polynomials bx2 + x + 5 and bx3 – 2x + 5 are divided by polynomial x – 3 and the remainders are m and n respectively. If m – n = 0, then find the value of b.
Solution:
When polynomial bx2 + x + 5 is divided by (x – 3), the remainder is m.
∴ By remainder theorem,
Remainder = p(3) = m
p(x) = bx2 + x + 5
∴ p(3) = b(3)2 + 3 + 5
∴m = b(9) + 8
m = 9b + 8 …(i)
When polynomial bx3 – 2x + 5 is divided by x – 3 the remainder is n
∴ remainder = p(3) = n
p(x) = bx3 – 2x + 5
∴ P(3)= b(3)3 – 2(3) + 5
∴ n = b(27) – 6 + 5
∴ n = 27b – 1 …(ii)
Now, m – n = 0 …[Given]
∴ m = n
∴ 9b + 8 = 27b – 1 …[From (i) and (ii)]
∴ 8 + 1 = 27b – 9b
∴ 9 = 18b
∴ b = \(\frac { 1 }{ 2 }\)
Question 13.
Simplify.
(8m2 + 3m – 6) – (9m – 7) + (3m2 – 2m + 4)
Solution:
(8m2 + 3m – 6) – (9m – 7) + (3m2 – 2m + 4)
= 8m2 + 3m – 6 – 9m + 7 + 3m2 – 2m + 4
= 8m2 + 3m2 + 3m – 9m – 2m – 6 + 7 + 4
= 11m2 – 8m + 5
Question 14.
Which polynomial is to be subtracted from x2 + 13x + 7 to get the polynomial 3x2 + 5x – 4?
Solution:
Let the required polynomial be A.
∴ (x2 + 13x + 7) – A = 3x2 + 5x – 4
∴ A = (x2 + 13x + 7) – (3x2 + 5x – 4)
= x2 + 13x + 7 – 3x2 – 5x + 4
= x2 – 3x2 + 13x – 5x + 7+4
= -2x2 + 8x + 11
∴ – 2x2 + 8x + 11 must be subtracted from x2 + 13x + 7 to get 3x2 + 5x – 4.
Question 15.
Which polynomial is to be added to 4m + 2n + 3 to get the polynomial 6m + 3n + 10?
Solution:
Let the required polynomial be A.
∴ (4m + 2n + 3) + A = 6m + 3n + 10
∴ A = 6m + 3n + 10 – (4m + 2n + 3)
= 6m + 3n + 10 – 4m – 2n – 3
= 6m – 4m + 3n – 2n + 10 – 3
= 2m + n + 7
∴ 2m + n + 7 must be added to 4m + 2n + 3 to get 6m + 3n + 10.
Question 1.
Read the following passage, write the appropriate amount in the boxes and discuss.
Govind, who is a dry land farmer from Shiralas has a 5 acre field. His family includes his wife, two children and his old mother. He borrowed one lakh twenty five thousand rupees from the bank for one year as agricultural loan at 10 p.c.p.a. He cultivated soyabean in x acres and cotton and tur in y acres. The expenditure he incurred was as follows :
He spent ₹10,000 on seeds. The expenses for fertilizers and pesticides for the soyabean crop was ₹ 2000x and ₹ 4000x2 were spent on wages and cultivation of land. He spent ₹ 8000y on fertilizers and pesticides and ₹ 9000y2 for wages and cultivation of land for the cotton and tur crops.
Let us write the total expenditure on all the crops by using variables x and y.
₹ 10000 + 2000x + 4000×2 + 8000y + 9000y2
He harvested 5x2 quintals soyabean and sold it at ₹ 2800 per quintal. The cotton crop yield was \(\frac { 5 }{ 3 }\) y2 quintals which fetched ₹ 5000 per quintal.
The tur crop yield was 4y quintals and was sold at ₹ 4000 per quintal. Write the total income in rupees that was obtained by selling the entire farm produce, with the help of an expression using variables x and y. (Textbook pg. no. 44)
Answer:
Total income = income on soyabean crop + income on cotton crop + income on tur crop
= ₹ (5x2 x 2800) + ₹(\(\frac { 5 }{ 3 }\) y2 x 5000) + ₹ (4y x 4000)
= ₹ ( 14000x2 + \(\frac { 25000 }{ 3 }\)y2 + 16000y)
Question 2.
We have seen the example of expenditure and income (in terms of polynomials) of Govind who is a dry land farmer. He has borrowed rupees one lakh twenty-five thousand from the bank as an agriculture loan and repaid the said loan at 10 p.c.p.a. He had spent ₹ 10,000 on seeds. The expenses on soyabean crop was ₹ 2000x for fertilizers and pesticides and ₹ 4000x2 was spent on wages and cultivation. He spent ₹ 8000y on fertilizers and pesticides and ₹9000y2 on cultivation and wages for cotton and tur crop.
His total income was
₹ (14000x2 + \(\frac { 25000 }{ 3 }\)y2 + 16000y)
By taking x = 2, y = 3 write the income expenditure account of Govind’s farming. (Textbook pg. no. 52)
Solution:
– Credit (Income)
₹ 1,25,000 Bank loan
₹ 56000 Income from soyabean
₹ 75000 Income from cotton
₹ 48000 Income from tur
₹ 304000 Total income
– Debit (Expenses)
₹ 1,37,000 loan paid with interest for seeds
₹ 10000 For seeds
₹ 4000 Fertilizers and pesticides for soyabean
₹ 16000 Wages and cultivation charges for soyabean
₹ 24000 Fertilizers and pesticides for cotton & tur
₹ 81000 Wages and cultivation charges for cotton & tur
₹ 272000 Total expenditure
Class 9 Maths Digest