Practice Set 2.3 Algebra 9th Standard Maths Part 1 Chapter 2 Real Numbers Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.

9th Standard Maths 1 Practice Set 2.3 Chapter 2 Real Numbers Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 2.3 Chapter 2 Real Numbers Questions With Answers Maharashtra Board

Question 1.
State the order of the surds given below.

Answer:
i. 3, ii. 2, iii. 4, iv. 2, v. 3

Question 2.
State which of the following are surds Justify. [2 Marks each]

Answer:
i. \(\sqrt [ 3 ]{ 51 }\) is a surd because 51 is a positive rational number, 3 is a positive integer greater than 1 and \(\sqrt [ 3 ]{ 51 }\) is irrational.

ii. \(\sqrt [ 4 ]{ 16 }\) is not a surd because

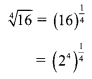
= 2, which is not an irrational number.

iii. \(\sqrt [ 5 ]{ 81 }\) is a surd because 81 is a positive rational number, 5 is a positive integer greater than 1 and \(\sqrt [ 5 ]{ 81 }\) is irrational.

iv. \(\sqrt { 256 }\) is not a surd because

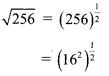
= 16, which is not an irrational number.

v. \(\sqrt [ 3 ]{ 64 }\) is not a surd because

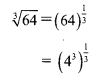
= 4, which is not an irrational number.

vi. \(\sqrt { \frac { 22 }{ 7 } }\) is a surd because \(\frac { 22 }{ 7 }\) is a positive rational number, 2 is a positive integer greater than 1 and \(\sqrt { \frac { 22 }{ 7 } }\) is irrational.

Question 3.
Classify the given pair of surds into like surds and unlike surds. [2 Marks each]

Solution:
If the order of the surds and the radicands are same, then the surds are like surds.

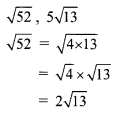
Here, the order of 2\(\sqrt { 13 }\) and 5\(\sqrt { 13 }\) is same and their radicands are also same.
∴ \(\sqrt { 52 }\) and 5\(\sqrt { 13 }\) are like surds.

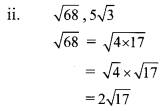
Here, the order of 2\(\sqrt { 17 }\) and 5\(\sqrt { 3 }\) is same but their radicands are not.
∴ \(\sqrt { 68 }\) and 5\(\sqrt { 3 }\) are unlike surds.

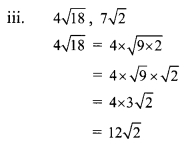
Here, the order of 12\(\sqrt { 2 }\) and 7\(\sqrt { 2 }\) is same and their radicands are also same.
∴ 4\(\sqrt { 18 }\) and 7\(\sqrt { 2 }\) are like surds.

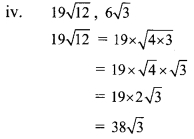
Here, the order of 38\(\sqrt { 3 }\) and 6\(\sqrt { 3 }\) is same and their radicands are also same.
∴ 19\(\sqrt { 12 }\) and 6\(\sqrt { 3 }\) are like surds.

v. 5\(\sqrt { 22 }\), 7\(\sqrt { 33 }\)
Here, the order of 5\(\sqrt { 22 }\) and 7\(\sqrt { 33 }\) is same but their radicands are not.
∴ 5\(\sqrt { 22 }\) and 7\(\sqrt { 33 }\) are unlike surds.

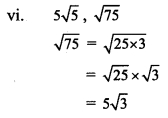
Here, the order of 5√5 and 5√3 is same but their radicands are not.
∴ 5√5 and √75 are unlike surds.

Question 4.
Simplify the following surds.

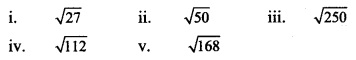
Solution:

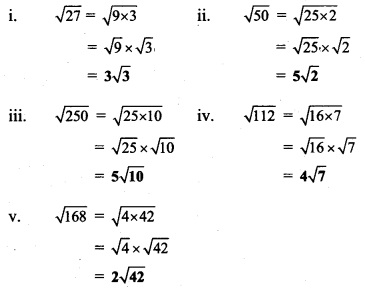
Question 5.
Compare the following pair of surds.


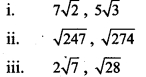
Solution:

Question 6.
Simplify.

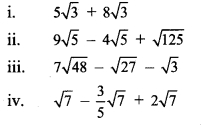
Solution:

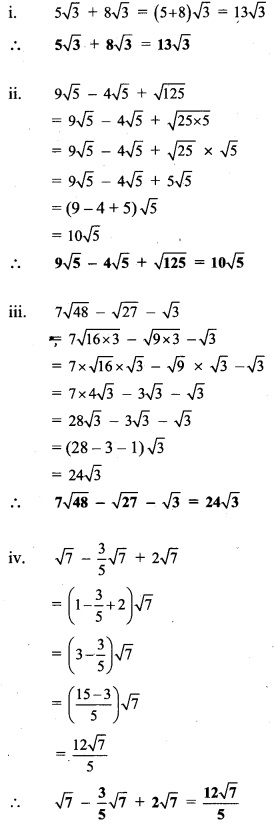
Question 7.
Multiply and write the answer in the simplest form.

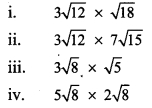
Solution:

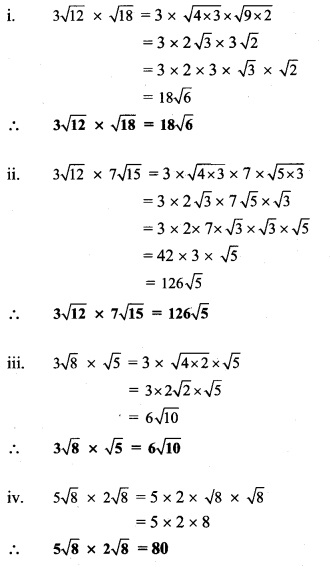
Question 8.
Divide and write form.

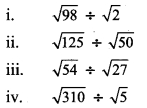
Solution:

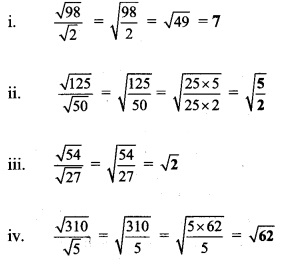
Question 9.
Rationalize the denominator.

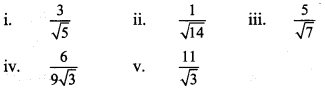
Solution:

Question 1.
\(\sqrt { 9+16 }\) ? + \(\sqrt { 9 }\) + \(\sqrt { 16 }\) (Texbookpg. no. 28)
Solution:

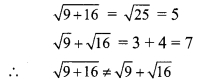
Question 2.
\(\sqrt { 100+36 }\) ? \(\sqrt { 100 }\) + \(\sqrt { 36 }\) (Textbook pg. no. 28)
Solution:

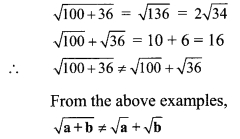
Question 3.
Follow the arrows and complete the chart by doing the operations given. (Textbook pg. no. 34)

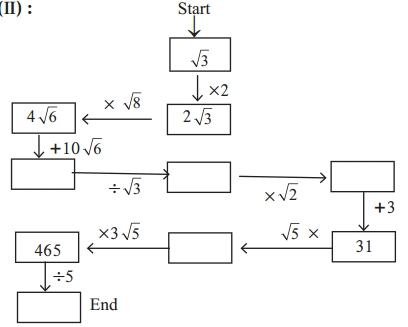
Solution:

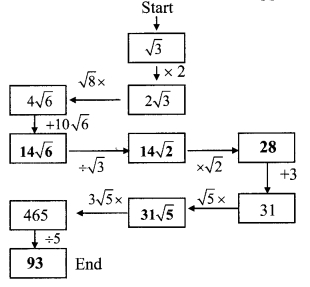
Question 4.
There are some real numbers written on a card sheet. Use these numbers and construct two examples each of addition, subtraction, multiplication and division. Solve these examples. (Textbook pg. no. 34)

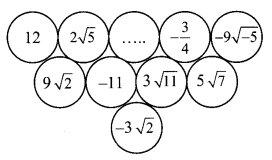
Solution:

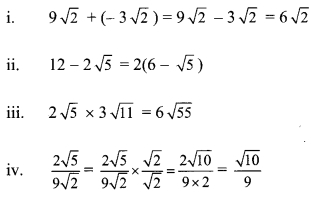
Class 9 Maths Digest

• Practice Set 1.1 Class 9 Answers
• Practice Set 1.2 Class 9 Answers
• Practice Set 1.3 Class 9 Answers
• Practice Set 1.4 Class 9 Answers
• Problem Set 1 Class 9 Answers
• Practice Set 2.1 Class 9 Answers
• Practice Set 2.2 Class 9 Answers
• Practice Set 2.3 Class 9 Answers
• Practice Set 2.4 Class 9 Answers
• Practice Set 2.5 Class 9 Answers
• Problem Set 2 Class 9 Answers