Balbharti Maharashtra State Board Class 10 English Solutions Unit 3.2 The Night I Met Einstein Notes, Textbook Exercise Important Questions and Answers.
Class 10 English Chapter 3.2 Question Answer Maharashtra Board
The Night I Met Einstein Poem 10th Std Question Answer
The Night I Met Einstein Questions And Answers Question 1.
With your bench-mate prepare a profile of Albert Einstein.
ALBERT EINSTEIN
- Profession : ………………………………….
- Field of Science : ………………………………….
- World-famous theory proposed : ………………………………….
- Awards : ………………………………….
- Disability in childhood : ………………………………….
- Books wrote: ………………………………….
Answer:
ALBERT EINSTEIN
- Profession : Scientist
- Field of Science : Theoretical Physics
- World famous theory proposed : Theory of Relativity
- Awards : Nobel Prize in Physics (1921), Copley j Medal by the Royal Society (1925), Gold Medal of the Royal Astronomical Society (1926), Max Planck medal of the German Physical Society (1929), Prix Jules Janssen (1931)
- Disability in childhood : Dyslexia (Asperger’s Syndrome, Autism)
- Books written :
- The World as I see it
- Relativity : The Special and the General Theory
- The Evolution of Physics
- The Meaning of Relativity
- Einstein’s Essays in Science
- Einstein on Peace
- Why War?
- Essays in Humanism
![]()
The Night I Met Einstein English Workshop Question 2.
Look at the picures of musical instruments and write their names; what the player of the instrument is called and a famous player of the instrument.

Answer:
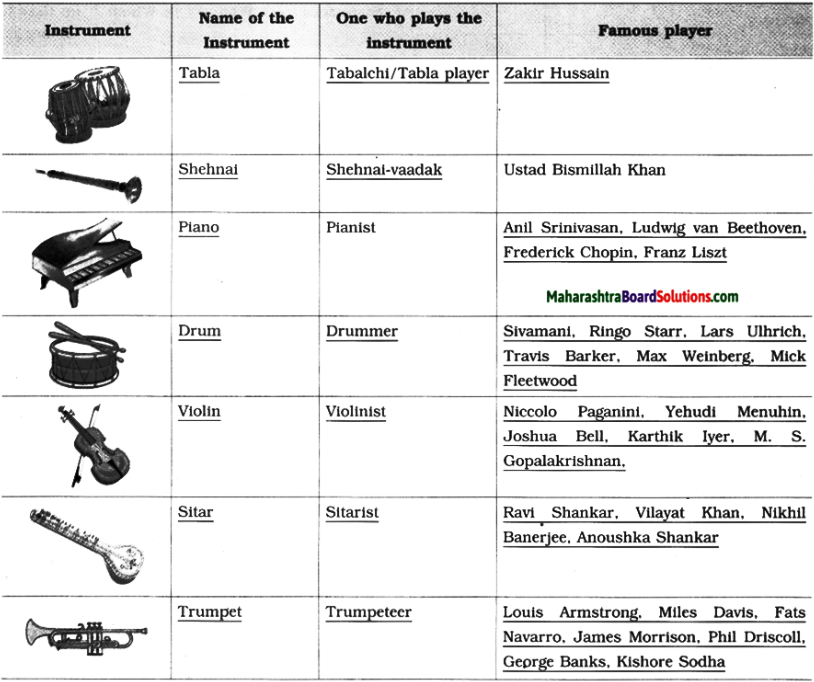
![]()
The Night I Met Einstein Pdf Questions And Answers Question 3.
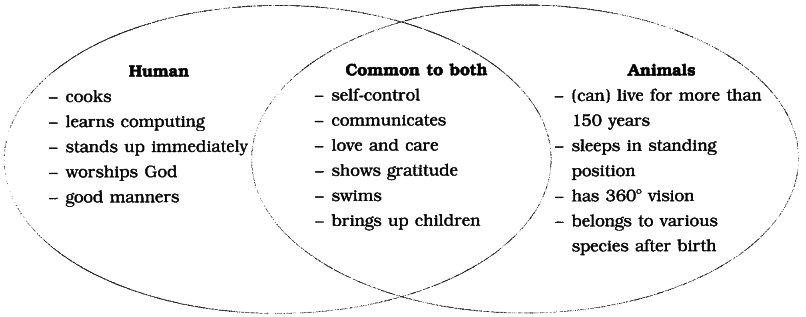
Separate the words in the columns they belong to.
(chorus, ballet, melody, swar, kathak, raga, salsa, symphony, mudra, serenade, choreography, tune, audience, tango, allegro, duet, odissi, choir, concert, performance, hip-hop)
| Music | Common to both arts | Dance |
Answer:
| Music | Common to both arts | Dance |
| chorus | salsa | ballet |
| melody | audience | kathak |
| swar | concert | mudra |
| raga | performance | tango |
| symphony | odissi | |
| serenade | hip-hop | |
| tune | choreography | |
| allegro | ||
| duet | ||
| choir |
The Night I Met Einstein Class 10 English Workshop Questions and Answers Maharashtra Board
The Night I Met Einstein Question 1.
Complete the following sentences.
(a) The narrator was not happy about the concert because …………………………………….. .
(b) When the narrator turned to look at his neighbour, he …………………………………….. .
(c) Einstein was surprised to hear that …………………………………….. .
(d) The narrator’s memory has an image of Einstein as …………………………………….. .
(e) The greatest act towards human beings is …………………………………….. .
Answer:
(a) he did not understand classical music.
(b) he saw a very famous face with a shock of white hair and a pipe.
(c) the narrator had never heard any of Bach’s music and did not know anything about him.
Question 2.
Who said to whom?
| Statement | Who | To whom | Effect on the listener |
| “We are going to listen to a very good pianist.” | |||
| “I do not know anything about Bach.” | |||
| “You are not tone-deaf.” | |||
| “Just allow yourself to listen that’s all there is to it” |
Answer:
| Statement | Who | To Whom | Effect on the listener |
| “We are going to listen to a very good pianist.” | The hostess | The narrator | not very happy |
| “You’re fond of Bach?” | A guest at the party (Albert Einstein) | The narrator | wanted to say something ordinary to get out of the situation |
| “You are not tone deaf.” | Albert Einstein | The narrator/writer | The listener tried to justify himself |
| “Just allow yourself to listen. That’s all there is to it.” | Einstein | the narrator |
The listener was able to appreciate the concert and clap sincerçy. |
Question 3.
List all the words from the story related to ‘Music’.
……………………………………………………………………………………………….
……………………………………………………………………………………………….
Answer:
concert, pianist. classical music, tone-deaf, piece, Bach, gramophone, song, tune, Bing Crosby, John McCormack. The Trumpeter.
Question 4.
Rewrite the following sentences inserting the appropriate phrases in their proper form.
(to get out of, to come up, to turn on, to give in, to get into, to come down, to work out, to turn off, to give off, to give out, to work in)
(a) He ………………………….. bed and ………………………….. the living room, to see if the door was closed.
(b) To enjoy the music and relax, he ………………………….. the music and ………………………….. the lights.
(c) Smita ………………………….. to her desire and ………………………….. her favourite toys to the poor.
(d) You should ………………………….. Mathematics so that you can ………………………….. problem.
Answer:
(a) got out of, came down
(b) turned on, turned off
(c) gave In, gave off
(d) get into, work out
Question 5.
(A) Give two points of difference between :
| Instrumental Music | Vocal Music |
| (1) | |
| (2) |
Answer:
| Instrumental Music | Vocal Music |
| (1) Instruments are used. | The voice (vocal cords) are used. |
| (2) Some part of the body is used as a medium to produce the sound, but the final sound is produced by the instrument. | Some parts of the body aid the production of sound (e.g., lungs, vocal tract, etc.), but the final sound emerges through the mouth. |
| (3) The output of the instrument is more or less of the same type, although the way the musician plays can give it an individualistic flavour. | Individual voices vary from the very low bass to the very high tenor. Hence the output varies and is very individualistic. |
| (4) An instrument can hardly be expected to sound like a voice (although some musicians try). | The voice can be used to imithte the sound of an instrument. |
(B)
| Light music | Classical music | Folk music |
Answer:
| Light music | Classical music | Folk music |
| (1) Pleasant to hear (2) Does not demand any great attention or effort from the listener (3) Could be from any genre. |
(1) Based on discipline (2) Strict rules of rhythm and patterns |
(1) Comes from the heart (2) Voices popular emotion s (3) No strict rules |
Question 6.
Prepare a word list of occupations in alphabetical order from the letters A upto T. (You may skip ‘K’ and ‘Q’)

Answer:
Actor – Banker – Carpenter
Driver – Engineer – Farmer
Gardener – Hairdresser – Inspector
Jockey – Keyboardist – Labourer
Musician – Neurosurgeon – Optician
Painter – Quarryworker – Radiologist
Singer – Tailor – Upholsterer
Vendor – Walter – Zoologist
Question 7.
Rewrite the following in indirect narration.
(a) ‘‘You are not tone-deaf’’, he said to me.
(b) ‘‘Could you have done it?’’, said Einstein.
(c) ‘‘Sing that back’’, he ordered me.
(d) He said, ‘‘What kind of music do you like?’’
(e) ‘‘I’m so sorry, Dr. Einstein’’, she said.
Answer:
(a) He told me that I was not tone-deaf.
(b) Einstein asked whether (if) I could have done it.
(c) He ordered me to sing that back.
(d) He asked what kind of music I (the narrator) liked.
(e) She told Dr Einstein that she was very sorry.
Question 8.
(A) Degrees of Comparison (Positive / Comparative / Superlative) Insert the appropriate expressions, choosing from those given after each sentences, for the positive degree.
(1) I am not ……………………………. my friend.
(taller than/ more taller/just as tall as)
(2) They are ……………………………. their neighbours.
(as helpful as/most helpful/more helpful)
![]()
(3) No other desert in Africa is ……………………………. the Sahara Desert.
(biggest of all/nearly so big as/bigger as)
(4) Very few animals in the wild are ……………………………. an elephant.
(exactly huger than/exactly as huge as/hugest than)
(5) Some snacks are ……………………………. a pizza.
(at least as tasty as/tastier as/most tasty as)
Answer:
(1) as tall as
(2) as helpful as
(3) nearly as big as
(4) exactly as huge as
(5) at least as tasty as
(B) Change the Degree of Comparision, as directed and rewrite without changing the meaning.
(1) No one in the class is as brilliant as Tanvi. (Superlative)
……………………………………………………………………………………………………………………….
Answer:
Tanvi is the most brilliant one in class.
(2) A diamond is one of the most precious of all stones. (Comparative)
……………………………………………………………………………………………………………………….
Answer:
A diamond is more precious than most other stones.
(3) Her handwriting is better than that of her sister. (Positive)
……………………………………………………………………………………………………………………….
Answer:
Her sister’s handwriting is not as good as hers.
(4) Jupiter is the largest of all planets. (Comparative)
……………………………………………………………………………………………………………………….
Answer:
Jupiter is larger than any other planet.
(5) He is not the greatest of all leaders. (Positive)
……………………………………………………………………………………………………………………….
Answer:
He is not as great as some of the other leaders.
(6) This painting is better than any other painting in the palace. (Superlative)
……………………………………………………………………………………………………………………….
Answer:
This is the best painting in the palace.
Question 9.
Prepare a word chain.
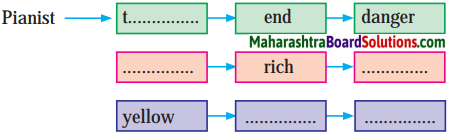
Answer:
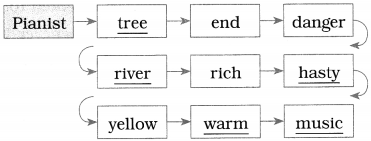
![]()
Question 10.
Pick out words that refer to the following:
(1) A musical performance in public …………………………….
(2) A lady who invites and looks after guests …………………………….
(3) A device used to play recorded music …………………………….
(4) One who is poor at deciphering musical notes …………………………….
(5) Boundaries or limits of a field …………………………….
Answer:
(1) concert
(2) hostess
(3) gramophone
(4) tone-deaf
(5) frontiers
Question 11.
‘Music is the medicine of the mind’. Narrate an experience that leads to the above conclusion. Write it in your own words, in
your notebook.
Answer:
Music is the medicine of the mind Music is good therapy. It is particularly effective because it registers on multiple sites of the brain. This means that even if the brain is very badly affected by a stroke or illness, there are s^till parts of the brain that recognise music.
I remember how upset all of us were when Grandfather suffered a stroke. The left side of his body and almost all of his face were affected. The once great and active Grandpa now lay still on the bed and had to be fed through a tube going down his nostrils. Little Rani could not stop weeping.
Grandfather had once presented me with a mobile phone. He knew my love for music and had told me I could download my favourite songs and create a playlist and listen to them whenever I wanted to.
I would sit by Grandfather’s bed whenever I was at home and had finished my studies and play the songs and listen to them.
One evening, to my surprise, I saw a shadow of a smile beginning to appear on Grandpa’s face. At first I couldn’t believe it. Then it became more definite and prominent. Grandpa was actually smiling!
I called Mom and Dad and Rani and everyone to see. Yes, Grandpa was indeed smiling. The music had reached out to him and had drawn out a response from him.
That was one of the happiest moments during his illness.
Question 12.
You will come across many famous personalities in the story. Go to library or search on internet the following names and write a few lines about the personalities given below.
(a) Albert Einstein
(b) Johann S. Bach
(c) Bing Crosby
(d) John McCormack
Answer:
(a) The last line tells us that Einstein believes in making others understand the joy there is in knowing the beauty that is all around us.
(b) Einstein then made him hear a little more advanced song by John.
(c) Two singers mentioned in the passage are : Bing Crosby
(d) The singer whose song was more advanced was : John McCormack
![]()
Question 13.
Imagine you are the monitor of the class. You are asked to conduct an interview of a famous scientist who is in your city/village. Frame 8 to 10 interview questions with the help of the following points.
(1) Early life and education
(2) Interest for this particular field
(3) Any inspirational incident that occurred in his/her life
(4) Guru or mentor
(5) Inventions and awards
(6) Future plans
(7) Advice/Message to youngsters
Answer:
Interview questions to be asked to the scientist :
(1) Good morning, Sir. I ani prMleged to interview an eminent scientist like you. Sir, could you tell me about your early life and education?
(2) Apart from science were there any other subjects that Interested you in school or college?
(3) Is there any specific incident you can mention that Inspired you to go ahead and achieve greatness?
(4) Who would you say was your Guru or mentor?
(5) Sir, could you give us a brief idea about your Inventions?
(6) WhIch awards have you received?
(7) Sir, what are your future plans?
(8) What advice do you have for the youngsters of today?
Question 14.
Project :
Divide the class into four groups. Collect pictures or draw images of various musical instruments, of the following categories.
(a) Stringed Instruments (Guitar)
(b) Wind Instruments (Flute)
(c) Percussion Instruments (Tabla)
(d) Solid Metal Instruments (Cymbals)
Paste and decorate pictures on separate sheets of paper. Give proper headings and names. Compile into a file with a cover and suitable file-title.
Question 15.
Complete the following sentences :
(a) The entertainment arranged-for by the hostess was a concert where everyone ……………………..
Answer:
(a) would listen to a very good pianist.
Question 16.
What was the writer’s reaction to classical music?
Answer:
The writer did not understand classical music.
Question 17.
Rewrite the following sentences using the phrases given in the brackets : (to pay attention to, to be fond of, to get out of shock of hair)
(a) Sachin ………………….. of playing cricket.
(b) The teacher asked her students ………………….. their studies.
(c) The rabbit trapped in the snare was trying to ……………….. it.
(d) He moved and I saw a ………………….. gleaming in the sun.
Answer:
(a) was fond
(b) to pay attention to
(c) get out of
(d) shock of hair
![]()
Question 18.
Write one word for :
(a) a man who helps the poor by giving them money
(b) one who plays the piano
Answer:
(a) philanthropist
(b) pIanist
Question 19.
Chairs were being arranged. (Change to the active voice.)
Answer:
They were arranging chairs.
Question 20.
I heard a gentle, but firm, voice saying, “You’re fond of Bach?” (Rewrite using the indirect form of narration.)
Answer:
I heard a gentie, but firm voice asking if (whether) I was fond of Bach.
Question 21.
I heard everyone clapping, so I realised that the piece was over. (Rewrite using ‘when/because’.)
Answer:
I realized that the piece was over when/because I heard everyone clapping.
Question 22.
Have you ever attended a concert? Write a few lines about it.
Answer:
Yes, I have’ attended a concert of Justin Bieber. It was so exciting to see my favourite popstar live on stage and to hear him singing my favouritesongs. It was quite ecstatic to be part of a crowd that were equally enthusiastic fans.
Question 23.
Write True or False for the statements :
(a) The narrator had heard of Bach.
(b) The narrator’s answer displeased Einstein.
(c) The upper room had a gramophone.
(d) The narrator liked the kind of music where he could follow the words.
Answer:
(a) False
(b) True
(c) True
(d) False
Question 24.
Complete the following sentences : (The answers are given directly and underlined.)
(a) The narrator could not understand music because …………………..
Answer:
(a) he was tone-deaf.
Question 25.
How were Einstein and the writer different in the way they listened to music?
Answer:
Einstein was used to listening to classical music, whereas the writer preferred songs that had words and the kind of music where he could follow the tune. Einstein had a keen ear for music, but the writer was tone-deaf and so could not understand music.
![]()
Question 26.
I’m not able to. (Rewrite using a modal auxiliary.)
Answer:
I cannot.
Question 27.
State what the underlined modal auxiliaries indicate :
(a) I must tell this man the truth.
(b) You can give me an example, perhaps?
Answer:
(a) compulsion – obligation
(b) formal request.
Question 28.
What do you learn from Einstein’s treatment of the young man?
Answer:
From Einstein’s treatment of the young man, we learn that Einstein expected others to be truthful. He questioned the young man and managed to persuade him into trying to understand another point of view. This shows Einstein as a man who gave importance to the perceptions of others, but at the same time, was quite persistent about his own viewpoint. Being a man of science, he liked to use the question-answer method to put across his point of view.
Question 29.
Complete the following :
(a) The writer thought that the simplest answerwas ……………………
Answer:
(a) to sing the lines back to him.
Question 30.
How did Einstein help the narrator appreciate music?
Answer:
Einstein made the narrator first hear Bing Crosby, who sang popular songs. The narrator was able to sing the lines back to Einstein. This was because he had heard it hundreds of times before. Not stopping at this, Einstein then made him hear a little more advanced song by John McCormack. Thus they went from lower level to higher level. In this way, Einstein helped the narrator to appreciate higher forms of music.
Question 31
Rewrite the sentences inserting the appropriate phrases in their proper form : (in order to, to get into, to work out)
(a) You should ……………………. Mathematics so that you can ………………. problems.
(b) He read the passage two or three times in ……………. understand it.
Answer:
(a) get Into, work out
(b) order to
Question 32.
The simplest answer seemed to be to sing the lines. So I sang it back to him.
Answer:
The simplest answer seemed to be to sing the lines. So I sang it back to him.
![]()
Question 33.
Add question tags:
(a) It proves everything.
(b) It’s like learning maths.
(c) Sing that back.
Answer:
(a) It proves everything, doesn’t it?
(b) It’s like learning maths, isn’t it?
(c) Sing that back, will you?
Question 34.
(1) What do you learn from Einstein’s treatment of the young man?
Answer:
From Einstein’s treatment of the young man we learn how patient and polite Einstein was. We come to know that he was a very good teacher, moving step by step in attempting to teach the young man to appreciate classical music. Also by using a comparison from maths and the question and answer method, Einstein comes across as a true scientist.
Question 35.
Do you think the comparison between music and arithmetic was a good one? In what way?
Answer:
Yes, I think that the comparison between music and arithmetic was a good one because music too involves timing, rhythm and beats that require some mathematical knowledge. Also Einstein showed how when we are taught arithmetic, we begin with the simple and then move on to the complicated. It is the same thing with music. From music with words – which is within the grasp of the average listener, Einstein progressed to music without words – which is what classical music is all about.
Question 36.
Choose the correct alternatives and fill in the blanks:
(1) Whenever the narrator hears the piece of Bach, he remembers ………………… (Einstein/the hostess)
(2) The hostess was …………. with the narrator. (happy/angry)
(3) Finally, the narrator …………….. the concert. (enjoyed/did not enjoy)
(4) Einstein was …………… with the narrator. (pleased/displeased)
Answer:
(1) Einstein
(2) angry
(3) enjoyed
(4) pleased
Question 37.
Complete the following:
(a) The narrator’s memory has an image of Einstein as …………………………
(b) The greatest act towards human beings is ……………………..
Answer:
(a) a small man with a shock of untidy hair and a pipe in his mouth.
(b) opening up the frontiers of beauty.
![]()
Question 38.
What does the last line tell you about Einstein?
Answer:
The last line tells us that Einstein believes in making others understand the joy there is in knowing the beauty that is all around us.
Question 39.
(1) Choose the correct meaning in the context of the passage:
(i) down:
(a) southwards
(b) downstairs
(c) soft feathers
Answer:
(b) down – downstairs
(ii) piece:
(a) a thing
(b) an example of artistic workmanship
(c) musical composition
Answer:
(c) piece – musical composition.
Question 40.
Rewrite the sentences inserting the appropriate phrases in their proper form: (to open up, to turn on, to turn off)
(a) His new discovery is …………………. new areas of research in digital technology.
Answer:
(a) opening-up
Question 41.
Write from the passage words that sound the same as:
(a) grate
(b) knew
(c) their
(d) peace
(e) sew
(f) two.
Answer:
(a) great
(b) new
(c) there
(d) piece
(e) so
(f) to.
![]()
Question 42.
Pick out from the passage words that refer to:
(a) an unfriendly expression on the face: ………………..
Answer:
(a) a cold look
Question 43.
I was the most important person in the world. (Rewrite in the comparative and positive degree.)
Answer:
(a) I was more important than any other person in the world. (Comparative)
(b) No other person in the world was as important as I was. (Positive)
Question 44.
Why, do you think, did the lady look ‘puzzled’?
Answer:
The lady believed that listening to classical music was the highest form of human activity. Einstein did not stay to listen. Instead he took the narrator to the next room and played songs on the gramophone. Through his efforts he was able to make the narrator really appreciate classical music. For Einstein, opening the minds of others to the appreciation of beauty was the highest form of human activity. This viewpoint ‘puzzled’ the lady.
Question 45.
(1) Write two compound words from the lesson.
(2) Identify the type of sentence: Please come with me.
(3) Punctuate the sentence: can you give me an example perhaps he said
(4) Write the hidden words in the given words: understand
(5) Frame a sentence using given the phrase: in order to
(6) Pick out the gerund and use it in your own sentence: It’s like learning maths.
(7) Spot the error and correct the sentence: I was hear everyone is clapping.
(8) Write the present and past participles of the given verbs: clap, rot.
Answer:
(1) anything, everything
(2) Imperative sentence
(3) “ Can you give me an example, perhaps?” he said.
(4) under, stand, sand, rest
(5) In order to succeed, one must work hard.
(6) gerund: learning Sentence: She is interested in learning French.
(7) I heard everyone clapping.
(8) clapping, clapped; rotting, rotted.
![]()
Question 46.
(1) The word ‘kind’ has two different meanings. Write sentences to bring out the two meanings.
(2) Rewrite the following sentence using the underlined verb in the present perfect continuous tense : Can you tell me what you just heard?
(3) I must tell this man the truth. (Rewrite beginning ‘This man…’)
Answer:
(1) (a) This was a different kind of music that he had never heard before, (a group of things having the same characteristics)
(b) The old lady was kind to the little children in the neighbourhood, (generous or considerate)
(2) Can you tell me what you have just been hearing?
(3) This man must be told the truth. (by me)
Question 47.
(1) Change to the positive degree of comparison. He was one of the kindest persons I ever met.
(2) Use the word ‘face’ as a noun as well as a verb in sentences.
Answer:
(1) Not many people I had ever met were as kind as he was.
(2) (a) He has an aristocratic face. (noun)
(b) Let us face the danger together.
Read More: