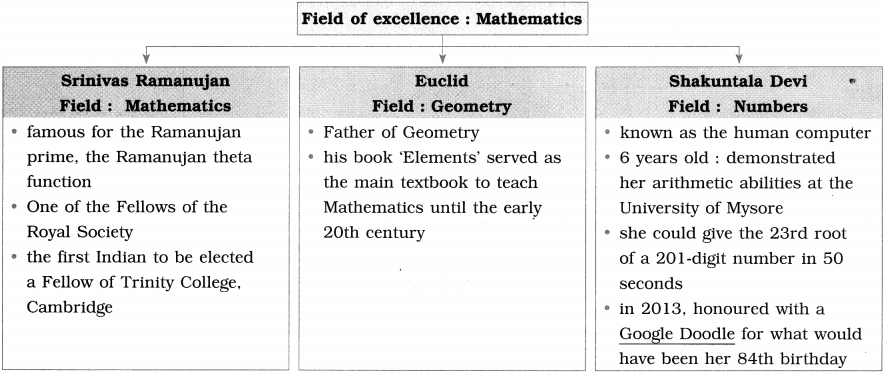
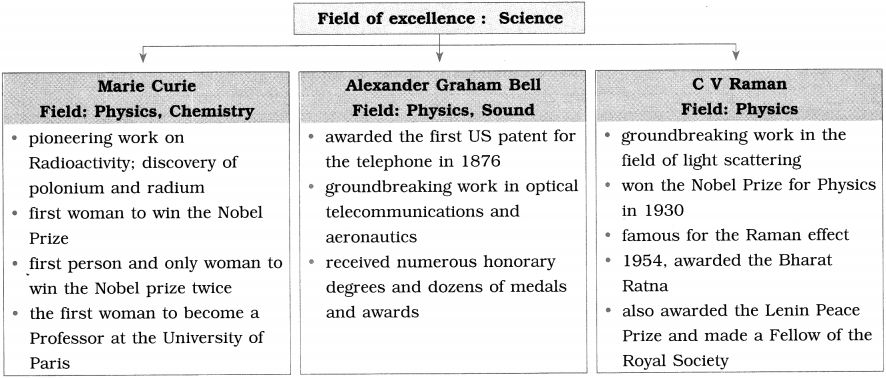
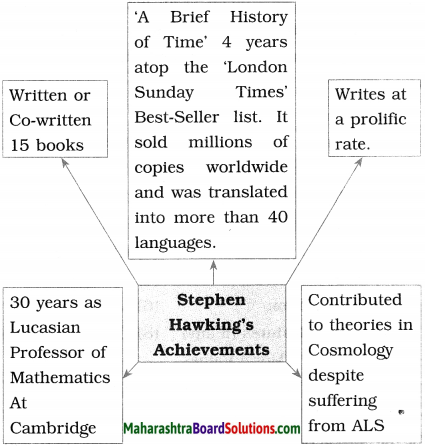
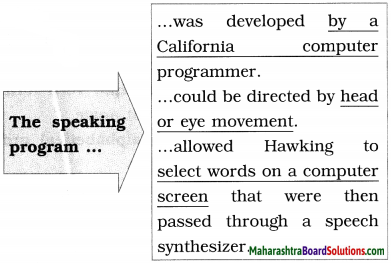
Balbharti Maharashtra State Board Class 10 English Solutions Unit 2.3 Connecting the Dots Notes, Textbook Exercise Important Questions and Answers.
Class 10 English Chapter 2.3 Question Answer Maharashtra Board
Connecting Fear Poem 10th Std Question Answer
Question 1.
(A) Connect the dots to get what means a lot to you.

The word is ……………………………… .
Answer:
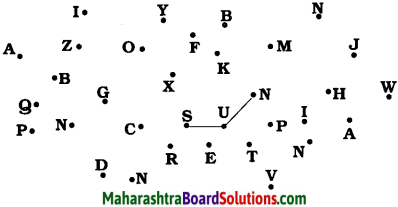
The word is SUN
![]()
(B) With your benchmark, use the letters given above to make a word register of ‘computers’. Set a time -limit of 5 minutes and compare your list with that of other classmates.
Answer:
AI, adobe, android, arithmetic, binary, browser, byte, bit, download, document, data, database, disk, format, http, hardware, homepage, java, keyboard, key, Microsoft, malware, memory, network, netscape, program, reboot, spam, spreadsheet, software, virus, web, windows, update, zip.
Question 2.
You are quite familiar with computers, especially the personal computer. Form pairs and make a list of famous computer manufacturing companies. One is given to you.
(a) Apple
(b) ……………………….
(c) ……………………….
(d) ……………………….
(e) ……………………….
(f) ……………………….
Answer:
(a) Apple
(b) Samsung
(c) IBM
(d) Lenovo
(e) Foxconn
(f) HP Inc.
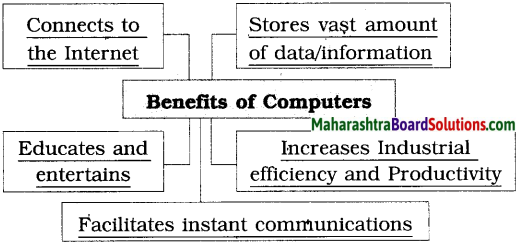
Question 3.
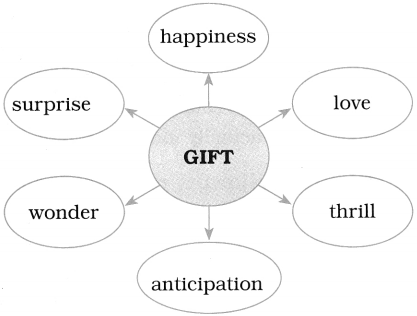
Complete the web by filling the various benefits of computers.

Answer:
Question 4.
(A) Expand the following into their full forms.
(a) that’s
(b) didn’t
(c) here’s
(d) can’t
(e) I’ve
Answer:
(a) that’s – that is
(b) didn’t – did not
(c) here’s – here is
(d) can’t – cannot
(e) I’ve – I have
(B) Write the shortened forms of the following.
(a) You have ……………………….
(b) I would ……………………….
(c) It is ……………………….
(d) You are ……………………….
(e) He will ……………………….
(f) I had ……………………….
(g) will not ……………………….
(h) shall not ……………………….
(i) are not ……………………….
(j) need not ……………………….
(k) must not ……………………….
(l) ought not ……………………….
Answer:
(a) you have – you’ve
(b) I would – I’d
(c) it is – it’s
(d) you are – you’re
(e) he will – he’ll
(f) I had – rd
(g) will not – won’t
(h) shall not – shan’t
(i) arc not – aren’t
(j) need not – needn’t
(k) must not – mustn’t
(l) ought not – oughtn’t
![]()
Connecting the Dots Class 10 English Workshop Questions and Answers Maharashtra Board
Question 1.
(A) Rearrange the incidents in the life of Steve Jobs in chronological order.
(a) Steve Jobs started Next.
(b) Jobs underwent a surgery.
(c) Jobs learned about serif and sans serif type faces.
(d) Jobs returned to Apple Inc.
(e) Jobs married Laurene.
(f) Jobs was diagnosed with cancer.
(g) Jobs dropped out of Reed College.
Answer:
(a) Jobs started Next.
(b) Jobs underwent surgery.
(c) Jobs learned about serif and san serif typefaces.
(d) Jobs returned to Apple Inc.
(e) Jobs married Laurene.
(f) Jobs was diagnosed with cancer.
(g) Jobs dropped out of Reed College.
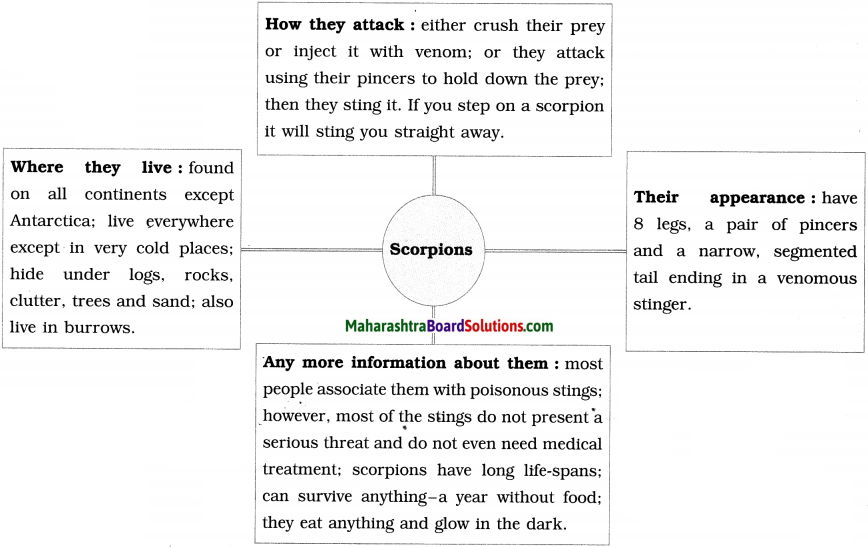
(B) Read the third story again. Complete the flow-chart given below.
Answer:
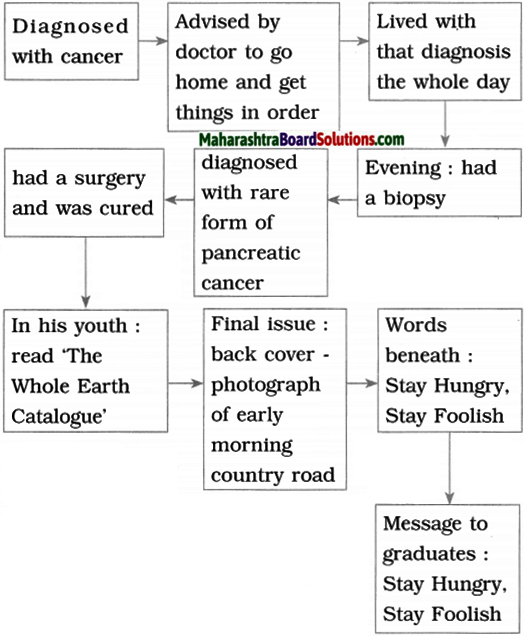
![]()
Question 2.
Read the lesson. Refer to a dictionary and match the words in column ‘A’ with their meanings in column ‘B’.
| No | ‘A’ | ‘B’ | |
| (a) | diagnosis | (i) | the power believed to control events |
| (b) | devastating | (ii) | complete list of items especially in a special order and description. |
| (c) | intuition | (iii) | act of identifying the nature of a problem or illness. |
| (d) | calligraphy | (iv) | power of understanding situations or people’s feelings before hand. |
| (e) | destiny | (v) | causing great destruction |
| (f) | catalogue | (vi) | beautiful handwriting done with a special pen or brush. |
Answer:
| No | ‘A’ | ‘B’ | |
| (a) | diagnosis | (iii) | act of identifying the nature of a problem or illness. |
| (b) | devastating | (v) | causing great destruction |
| (c) | intuition | (iv) | power of understanding situations or people’s feelings before hand. |
| (d) | calligraphy | (vi) | beautiful handwriting done with a special pen or brush. |
| (e) | destiny | (a) | the power believed to control events |
| (f) | catalogue | (ii) | complete list of items especially in a special order and description. |
Question 3.
Go through all the three stories. Identify some qualities of Steve Jobs and complete the web chart.
Answer:
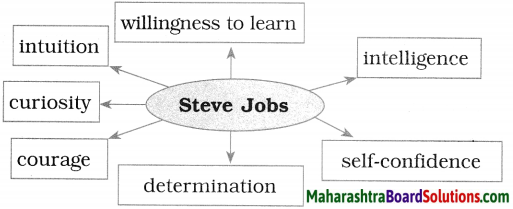
![]()
Question 4.
Complete the following table.
‘The Three Stories in the Life of Steve Jobs’
| About | Setbacks | Reactions | Achievements and benefits | |
| First story | ||||
| Second story | ||||
| Third story |
Answer:
| About | Setbacks | Reactions | Achievements and benefits | |
| First story | College days | no boarding and lodging | managed with friends and at a temple | learnt calligraphy |
| Second story | starting ’Apple’ | fired from the company | started a new company ‘Next’ | most creative period; renaissance’ of ‘Apple’ |
| Third story | death | diagnosed with cancer | surgery, cure | learnt not to waste time living someone else’s life |
Question 5.
Say HOW?
→ the calligraphy classes helped Steve Jobs after 10 years.
Answer:
10 years later when Steve Jobs was designing the first Macintosh computer, he recalled what he had learned in the calligraphy classes about serif and san serif typefaces as well as other elements that go into great typography. He designed all this into the Macintosh computer.
→ You can connect dots.
Answer:
We can’t connect dots by looking forward; we can only connect them looking backwards. We have to trust that the dots will somehow connect in our destiny.
→ Jobs reacted later on, after the shock of being fired from Apple.
Answer:
After he overcame the shock of being fired from Apple, Jobs felt the lightness of being a beginner again. He felt free to enter one of the most creative periods of his life. He started two companies – Next and Pixar.
![]()
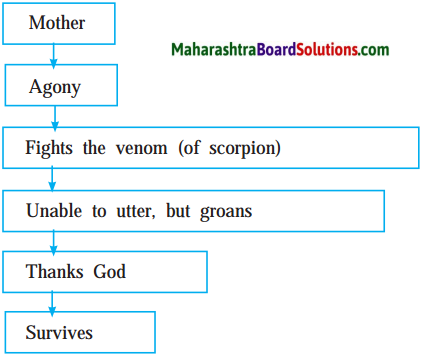
→ Jobs was cured of a rare cancer.
Answer:
Jobs was diagnosed with a very rare form of pancreatic cancer. It was curable by surgery. Jobs had the surgery and he was cured.
→ Jobs acquired the famous words ‘Stay Hungry. Stay Foolish’
Answer:
When Jobs was young, he used to read an amazing publication called The Whole Earth Catalogue’. In the final issue was a photograph of an early morning country road beneath which were the words ‘Stay Hungry, Stay Foolish’. Steve acquired these words from the magazine.
Question 6.
Besides those given at the end of the talk by Steve Jobs, pick out other pieces of advice that Jobs gives in his speech.
Answer:
(a) Learn to connect the dots.
(b) Learn whatever you can whenever you can.
(c) We can learn even from negative experiences.
(d) Have trust that somehow the dots will connect in your future.
(e) Have trust in your gut. destiny, life, karma, whatever …
(f) Love what you do.
(g) Keep looking for what you love and don’t ever settle for less.
(h) Even under the most devastating circumstances, you can start all over again.
(i) Don’t lose faith.
(j) Your time is limited, so don’t waste it lining someone else’s life.
Question 7.
(A) Use the following idioms/phrases in sentences of your own.
(a) drop in …………………..
(b) drop out …………………..
(c) stumble on …………………..
(d) look backwards …………………..
(e) look forward …………………..
(f) let (someone) down …………………..
(g) sign off …………………..
(h) begin anew …………………..
Answer:
(a) Though I am not a member of the club, I often play tennis there as a drop in.
(b) I decided to drop out of karate classes as it was taking too much of my time.
(c) While surfing the net, he stumbled into a portal that showed only horror movies.
(d) After his terrible experience in his native place, he went to the city and never looked backwards.
(e) He tried to forget his terrible experience in his native place and looked forward.
(f) He placed great trust in his secretary, and she never let him down.
(g) I would like to sign off by telling you a short story with a beautiful message.
(h) It is never too late to forget past mistakes and begin anew.
![]()
(B) Fill in the gaps in choosing the appropriate idioms.
(drown out, hits in the head with a brick, get one’s affairs in order, connect the dots, begin to dawn, stay hungry)
(a) The wealthy landlord made a will before he could die.
(b) Those who aspire for success should always to learn more.
(c) If you you will realise that crime ultimately leads to poverty.
(d) The siren of the ambulance all other traffic noise.
(e) When the father learned about his son’s misdeeds, it
(f) On reading exactly same essays in both answer sheets, it the examiner, that the students had cheated during exams.
Answer:
(a) Getting his affairs in order
(b) Stay hungry
(c) Connect the dots
(d) Drowned out
(e) It hit him on the head with a brick.
(f) Began to dawn on
Question 8.
(A) Name the Tense of the Verbs underlined to include Time (Past/Present/Future) and Aspect (Simple/Continuous/Perfect/Perfect Continuous)
(1) I slept on the floor
(2) We were designing the first Macintosh computer
(3) It had made all the difference
(4) I am fine, now
(5) I have been facing death
(6) I shall be telling you three stories
Answer:
(1) Time – Past; Aspect – Simple.
(2) Time – Past Tense; Aspect – Progressive (continuous).
(3) Time – Past tense Aspect – Perfect
(4) Time – Present; Aspect – Simple.
(5) Time – Present; Aspect – Perfect.
(6) Time – Future; Aspect – Progressive (continuous).
(B) Change the Tense as instructed.
(1) I got fired. (Future Perfect)
(2) Life hits you in the head. (Present Perfect Continuous)
(3) The dots will somehow connect. (Past Perfect)
(4) I started a company. (Present Continuous)
(5) My doctor advised me. (Past Perfect Continuous)
Answer:
(1) Jobs got fired.
(2) Life hits you in the head.
(3) The dots had somehow connected.
(4) I started a company.
(5) My doctor had been advising me.
![]()
Question 9.
Read the News item and write an application for a suitable job in the same company. Attach a seperate CV/Resume.
May 19, 2016
Apple Opens Development Office in Hyderabad
(A) The new office in Hyderabad will focus on development of maps, Apple products, like iPhone, iPad, Mac. etc. This will create upto 4000 jobs
Answer:
Answer:
Ratan Shah
11 Salsa Apts.
Hafeczpeth
Hyderabad
Telangana – 500 049.
27th May, 2020
The HR Manager
Apple Development Office
18-23, Rd Number 2
Financial District
Nanakram Guda
Hydcrabad
Telangana — 500 032.
Subject : Application for post of Systems Analyst ‘
Sir,
I read the news item in the Times of India’ dated May 20, which stated that Apple has opened a Development office in Hyderabad, which is likely to create up to 4000 jobs. I am interested in applying for the post of Systems Analyst.
I have a bachelor’s degree In Computer Information Systems (CIS) and 6 months experience in Cornputronic& Ltd. as Systems Analyst. I am well-versed in analyzing, designing and implementing Information Systems. I wish to further my prospects and hence am applying to your company.
I do hope that you will give me the opportunity to prove my mettle.
Yours truly,
Ratan Shah
![]()
Attachments: CV, photocopies of Academic and Professional Certificates
Resume:
Name: Ratan Shah
Age: 24 years
Educational Qualification: B.Com (1st class); B.Computer Science (CIS)
Experience: 6 months experience in Computronics Ltd. as Systems Analyst
Marital Status: Single
Special Interests: Chess, Football, Cycling
Contact information: Address as above
Mobile no.: 097
(B) Imagine you are already working as an Engineer in Apple Development Office, Hyderabad. Write an application for 2 weeks leave to the HR Manager as you have to undergo an urgent surgery.
Answer:
Ms. Sara Kanchwala
11 Salsa Apts.
Hafeezpeth
Hyderabad
Telangana 500 049.
3 September, 2020
The HR Manager,
Apple Development Office
18-23, Rd. Number 2
Financial District
Nanakram Guda
Hyderabad
Telangana – 500 032.
Subject : ApplicatIon’ for leave of absence due to Imminent surgery (4th September to 17th September)
Dear Sir,
I had a bad fall a couple of days back and tore a ligament ‘In my knee. The pain is Intense and my doctor has advised me that immediate surgery is necessary.
Please grant me 2 weeks medical leave as the doctor has advised a fortnight’s complete bed rest post-op. Thanking you in advance,
I remain,
Yours truly,
Sara Kanchwala
Question 10.
Prepare a speech on the title “The Will to Win” to be delivered before the class during a competition.
Hints –
- Title
- Introduction
- Objective and Illustrations
- Specific examples
- Purpose of the title.
- Sources/Resourses for implementation.
- Usefulness/Benefits
- Conclusion.
Answer:
The Will to Win
Friends,
The topic before us today is The Will to Win’. This title brings to my mind the story of the hare and the tortoise. When the hare challenged the tortoise to a race, the tortoise knew very well that its speed was in no way comparable to that of the hare. Yet this little animal agreed to the race. And why, may I ask you? Only because it had the will to win. Come what may, the tortoise had to prove to the hare that it could win if it wanted to. And finally it won!
This, in fact, is the driving force behind all great ventures and achievements. The Will to Win!
I remember the time when I went to Std. V. My father had been transferred from Agra to Bhusaval. A subject that I had trouble mastering was the language Marathi. Needless to say in the first term I flunked very badly. But I was a student who usually scored high marks in all subjects. This failure was devastating.
However, I did not let it faze me. I took great interest in class lessons. Read my Marathi textbook over and over. Made friends who spoke fluently in Marathi and ventured speaking to them. At first they poked fun at me. But within a month I had picked up the basic structure of the language and began writing answers to questions on my own. Believe it or not, at the end of the term I topped the class in Marathi. ; Today I can speak in the language as if it is my mother tongue.
Friends, my message to you today is that you can do anything. All you require is the will. If you have the will, the skill will follow. So set your goals, define your objectives and I wish all of you the very best in ; whatever you decide to do in life.
Be sure of one thing: If you have the will, You Will Win!
Thank you.
![]()
Question 11.
Project :
Collect more information about Steve Jobs with the help of Internet. Complete it with images into a file.
Question 12.
Do you remember doing some activities in your childhood that you didn’t like it. Form pairs and make a list of all those activities. Do you think, any one of these activities have helped you in solving your problems? Share your experience with the class.
- chopping vegetables:
- cleaning the home; sweeping and dusting
- hanging out clothes to dry
- looking after my little brother
- helping dad to repair the bicycle
Answer:
Once while driving home from school, the chain of my bicycle got dislodged and I almost fell off. There was no bicycle repair shop nearby and no passers-by were able to help me. Since I had experience helping dad to repair his bicycle, somehow I managed to get the chain fixed and wobbled back home. My hands were black and dirty with grease and oil, but at least I didn’t have to walk back home, pushing my bicycle along.
Question 13.
Write True or False for these statements: (The answers are given directly and underlined.)
Answer:
(1) Steve Jobs slept in his dorm room. False
(2) Steve took his required courses as a registered student of Reed College. False
(3) During Steve’s College days, one had to pay 5 cents deposit for a Coke bdttle. True
(4) Steve ha’d comfortable college experiences. False
Question 14.
What basic course in Reed College helped while designing the Mac?
Answer:
The basic course of calligraphy in Reed College helped while designing the Mac.
Question 15.
Arrange the following incidents in Steve Jobs’ life in proper sequence based on this passage:
(a) Jobs stayed as a drop-in for 18 months.
(b) Jobs used to sleep on the floor in his friend’s house.
Answer:
(a) Jobs stayed as a drop-in for 18 months.
(b) Jobs used to sleep on the floor in his friend’s house.
Question 16.
Complete the following: (The answers are given directly and underlined.)
(1) Steve’s first story is about connecting the dots.
(2) Steve got one good meal every Sunday night at the Hare Krishna temple.
Answer:
Connecting the dots.
Hare Krishna temple.
Question 17.
What did Steve Jobs do for two years after he joined Reed College?
Answer:
After joining Reed College, for two years Steve would stop taking the required classes that didn’t interest him. Instead he began dropping in on the ones that looked interesting.
Question 18.
List the hardships that Steve faced.
Answer:
- Steve didn’t have a dorm room and so had to sleep on the floor in friends’ rooms.
- Steve returned Coke bottles for the 5 cent deposits to buy food with.
- Steve would walk seven miles across town every Sunday night to get one good meal a week at the Hare Krishna temple.
![]()
Question 19.
Write from the passage a phrase that means ‘Apart from this, I have nothing more to tell.’
Answer:
That’s it.
Question 20.
Choose the correct contextual meaning of the phrase: connecting the dots.
(a) making a pattern with the help of dots
(b) associating one previous idea with other ideas that follow
(c) joining dots in a puzzle to get the correct picture
(d) understanding a procedure
Answer:
(b) associating one previous idea with other ideas that follow
Question 21.
Match the words in column A with their meanings in column B:
| A | B | ||
| (i) | intuition | (a) | a set of characters like letters, symbols, etc. in one design |
| (ii) | calligraphy | (b) | the style and appearance of printed matter |
| (iii) | typography | (c) | power of understanding the feelings of people |
| (iv) | typeface | (d) | beautiful handwriting done with a special pen or brush |
Answer:
| (i) | intuition | (c) | power of understanding the feelings of people |
| (ii) | calligraphy | (d) | beautiful handwriting done with a special pen or brush |
| (iii) | ypography | (b) | the style and appearance of printed matter |
| (iv) | typeface | (a) | a set of characters like letters, symbols, etc. in one design |
Question 22.
It was one of the best decisions I ever made. (Rewrite using ‘better than’.)
Answer:
It was better than most other decisions I ever made.
Question 23.
Personal Response: What impression of Steve Jobs do you get from this passage?
Answer:
In this passage, it appears that Steve Jobs is a student who goes by his impulses. He has a thirst for knowledge, but prefers subjects that he finds interesting and avoids those that he finds uninteresting, even though he has enrolled for them. He is ready to face all kinds of hardships in order to study what he wants to. Steve Jobs had a natural curiosity and intuition. He also had an instinct about what makes something really great and the habit of storing it away in his mind for future use.
Question 24.
Fill in the blanks: (The answers are given directly and underlined.)
(1) Steve designed the Macintosh computer.
(2) Windows copied the Macintosh computer.
(3) It was impossible to connect the dots looking forward when Steve was in college.
(4) You can only connect the dots looking backward.
Answer:
(1) Macintosh
(2) Windows
(3) forward
(4) backward
![]()
Question 25.
Complete the following: (The answers are given directly and underlined.)
(1) The Mac ‘computer which he designed would not have had multiple typefaces or proportionally spaced fonts.
(2) Since Windows just copied Mac, it was likely no personal computer would have had them.
Answer:
(1) not have had multiple typefaces or proportionally spaced fonts.
(2) no personal computer would have had them.
Question 26.
Complete the following: (The answers are given directly and underlined.)
Words connected with typography from the passage are: typeface and font.
Answer:
typeface and font.
Question 27.
Match the words /phrases in column A with their meanings in column B:
| (A) | (B) | ||
| (i) | gut | (a) | Macintosh computer. |
| (ii) | destiny | (b) | having several parts. |
| (iii) | Mac | (c) | the power believed to control events. |
| (iv) | multiple | (d) | courage and determination. |
Answer:
| A | B | ||
| (i) | gut | (d) | courage and determination |
| (ii) | destiny | (c) | the power believed to control events |
| (iii) | Mac | (a) | Macintosh computer |
| (iv) | multiple | (b) | having several parts |
Question 28.
It was impossible to connect the dots looking forward. (Pick out the verbs and say if they are finite or non-finite.)
Answer:
was – finite; to connect, looking – non-finites
Question 29.
It was very clear. (Rewrite as an exclamatory sentence.)
Answer:
How clear it was!
Question 30.
Mac would never have had multiple typefaces. (Rewrite as an interrogative sentence.)
Answer:
Would Mac ever have had multiple typefaces?
![]()
Question 31.
Personal Response: Write about something which you learned in the past and which has helped you in the present.
Answer:
When I was in Std. V, mother enrol led me for dancing classes, I had to stop when I reached Std. IX. However, now whenever I need a break or I am feeling stressed, I put on some music and dance. That gives me relief from stress.
Question 32.
Name the following: (The answers are given directly and underlined.)
Answer:
(1) The world’s most successful animation studio. Pixar
(2) The company that Steve Jobs took five years to establish. Next
(3) The company that bought Next. Apple
(4) Steve Jobs’ wife. Laurene
Question 33.
What setback did Jobs suffer when he was thirty?
Answer:
When Jobs was thirty, he was fired from the company which he himself had started. This was devastating and a major setback in his life.
Question 34.
Match the words/phrases in column A with their meanings in column B:
| A | B | ||
| (i) | renaissance | (a) | causing great destruction |
| (ii) | to start over | (b) | lost one’s job |
| (iii) | fired | (c) | revival |
| (iv) | devastating | (d) | to begin again |
Answer:
| A | B | ||
| (i) | renaissance | (c) | revival |
| (ii) | to start over | (d) | to begin again |
| (iii) | fired | (b) | lost one’s job |
| (iv) | devastating | (a) | causing great destruction |
Question 35.
Fill in the blanks choosing the appropriate idioms: (at the heart of, hit him on the head with brick, begin to dawn, lose faith)
(1) Even if you don’t succeed at first, don’t lose faith in yourself.
(2) It is corruption in high places that lies at the heart of the non-development of this locality.
Answer:
(1) Lose faith
(2) At the heart of
![]()
Question 36.
Personal Response: What does this second story of Jobs convey to you?
Answer:
The second story of Jobs – about love and loss – conveys to us that even if our efforts result in complete disaster, we should continue believing in ourselves. It tells us that we should love our work. If we haven’t yet found it, we should keep on searching. We should never accept less than what we aim for in life.
Question 37.
Which quality of Steve Jobs impresses you the most? How would you apply it in your life?
Answer:
I admire Steve’s quality of not giving up even after facing a terribly shocking loss. It inspires me never to be disheartened by failure, but to always keep trying. Even if one loses everything, one has to have the courage to start all over again.
Question 38.
Arrange the following incidents in Steve Jobs’ life in proper sequence based on this passage:
(a) Jobs was advised to get his affairs in order.
(b) Jobs was cured of a rare form of cancer.
Answer:
(a) Jobs was advised to get his affairs in order.
(b) Jobs was cured of a rare form of cancer.
Question 39.
Fill in the blanks: (The answers are given directly and underlined.)
(1) Steve’s third story is about death.
(2) The doctor describes the last stage of cancer as the ‘prepare to die’ stage.
(3) Steve ‘says that you should follow your heart and intuition.
(4) We should not waste time.
Answer:
(1) death
(2) ‘prepare to die’
(3) heart and intuition.
(4) time.
Question 40.
What does Jobs warn you about life and dogma?
Answer:
Jobs warns us not be trapped by dogma. Dogma is living with the results of other people’s thinking. The overpowering influence of other’s opinions should not drown out our own inner voice.
Question 41.
How does Jobs close his address to the graduate students?
Answer:
Steve Jobs closes his address to the graduate students by telling them about an amazing publication called The Whole Earth Catalogue’. In the final issue on the back cover there was a photograph of an early morning country road. Beneath it were the words ‘Stay Hungry, Stay Foolish’. Jobs wishes the students the same words as his farewell message to them.
Question 42.
Write from the passage four medical words / phrases / terms.
Answer:
pancreatic cancer, diagnosis, biopsy, surgery
![]()
Question 43.
Match the words in column ‘A’ with their meanings in column ‘B’:
| A | B | ||
| (a) | diagnosis | (1) | a set of beliefs held by an organisation which others are expected to accept without argument. |
| (b) | catalogue | (2) | act of identifying the nature of a problem or illness. |
| (c) | dogma | (3) | in a new or different way. |
| (d) | anew | (4) | complete list of items especially in a special order and description. |
Answer:
| A | B | ||
| (a) | diagnosis | (2) | act of identifying the nature of a problem or illness. |
| (b) | catalogue | (4) | complete list, of items especially in a special order and description. |
| (c) | dogma | (1) | a set of beliefs held by an organisation which others are expected to accept without argument |
| (d) | anew | (3) | in a new or different way. |
Question 44.
Choose correct question tags for the sentences and rewrite: wasn’t it? isn’t it? aren’t I? will you?
(a) Don’t be trapped by dogma.
(b) It was their farewell message.
(c) Your time is limited.
(d) I’m fine now.
Answer:
(a) Don’t be trapped by dogma, will you?
(b) It was their farewell message, wasn’t it?
(c) Your time is limited, isn’t it?
(d) I’m fine now, aren’t I?
Question 45.
Don’t waste it. (Rewrite without ‘don’t’.)
Answer:
Avoid wasting it.
Question 46.
Personal Response: “Your time is limited. So don’t waste it living someone else’s life.” What are your views about these statements?
Answer:
These are the conclusions that Steve Jobs came to when he discovered that he was suffering from pancreatic cancer. Coming face to face with death, he realized how very little time we have on earth to realize our true potential. Most of our lives are spent following the dictates of others. By this statement, Steve Jobs means that we should spend every moment of our lives trying to discover our own potential and determine our own purpose and path in life.
Question 47.
(1) Pick out the compound words from the given words: dropping, calligraphy, backwards, graduate, photograph
(2) Pick out the gerund and use it in your own sentence: I could begin dropping in on the ones that looked interesting.
(3) Punctuate the sentence: heres one ekample reed college offered perhaps the best calligraphy instruction in the country
(4) Spot the error and rewrite the correct sentence: At the calligraphy class, I learn about what make great typography great.
(5) Identify the type of sentence: Don’t settle.
(6) Find out two hidden words of at least 4 letters each from the word ‘devastating’.
(7) Form present participles in which the last letter is doubled: drop, quit
(8) Arrange these words in alphabetical order: friend, follow, found, freed.
Answer:
(1) backwards = back + wards; photograph = photo + graph
(2) Gerund: dropping Sentence: Stop dropping in here without any warning.
(3) Here’s one example: Reed College offered perhaps the best calligraphy instruction in the country.
(4) At the calligraphy class, I learned about what makes great typography great.
(5) Imperative Sentence in the Negative.
(6) devastating-vast, taste (gate, stain.)
(7) dropping, quitting
(8) follow, found, freed, friend
![]()
Question 48.
(1) Write the homophone for the word ‘story’ and frame a sentence.
(2) Rewrite the sentence using the past perfect continuous tense: We were designing the first Macintosh computer.
(3) Rewrite beginning with underlined part: The heaviness of being successful was replaced by the lightness of being a beginner again.
(4) Write a word register for the word: ‘doctor’ (4 words).
Answer:
(1) Homophones: story – storey Sentence: I live in a seven-storys building.
(2) We had been designing the first Macintosh computer.
(3) The lightness of being a beginner again replaced the heaviness of being successful.
(4) physician, surgeon, medico, healer, practitioner. (MD, medic, scientist, specialist)
Question 49.
(1) Use the word,‘trust’ in sentences as a noun as well as a verb.
(2) Underline the modal auxiliary and state its function: I had to take a calligraphy class.
Answer:
(1) (a) I have great trust in my teacher, (noun)
(b) Trust in God. (verb)
(2) I had to take a calligraphy class, (necessity/ obligation/compulsion)
Read More: