Std 12 Geography Chapter 7 Question Answer Region and Regional Development Maharashtra Board
Balbharti Maharashtra State Board Class 12 Geography Solutions Chapter 7 Region and Regional Development Textbook Exercise Questions and Answers.
Class 12 Geography Chapter 7 Region and Regional Development Question Answer Maharashtra Board
Geography Class 12 Chapter 7 Question Answer Maharashtra Board
1. Identify the correct group.
Question 1.
| A | B | C | D |
| Satpuda | Yavatmal | Thar | Marathwada |
| Deccan | Amravati | Sahara | Khandesh |
| Alps | Solapur | Himalaya | Vidarbha |
| Rockies | Greater Mumbai | Gobi | Konkan |
Answer:
D
![]()
Question 2.
| A | B | C | D |
| Plain | Pressure | Tropical forest | Fishing |
| Lake | Rivers | Thorny forest | Lumbering |
| Mountain | Temperature | Mangrove forest | Agriculture |
| Plateau | Humidity | Deciduous forest | Bakery |
Answer:
C
2. Differentiate between.
Question 1.
Functional region and Formal region
Answer:
| Functional region | Formal region |
| (i) Specific to one area. | (i) Often physical in nature. |
| (ii) Areas organised around a node or focus one point like university, airport, etc. | (ii) Has specific boundaries that set them apart. |
| (iii) This region has no common characteristics but functions are more important, functions bind regions together. | (iii) This region has some common characteristics such as common economic activity or common language. |
| (iv) Often a metropolitan area that consists of major city and lot of smaller towns. | (iv) Homogeneous areas or habitats inhabited by social groups, societies or nation. |
| (v) The region is tied to a central point by transportation system or economic or functional associations. | (v) Organised and represented by small systems or part systems. |
| (vi) It functions and works together to form a part of an economic and social system. | (vi) Has clear-cut political boundaries. |
| (vii) Defined by a set of activities. | (vii) Defined by common political units where all people are subject to same law and government. |
![]()
Question 2.
Physical and Political region
Answer:
| Physical region | Political region |
| (i) Physical region is an area of land divided by natural borders. | (i) Political region tends to be based on political units such as sovereign states like administrative region, province, states, township, etc. |
| (ii) For example, interior plains of USA with borders of Appalachian Mountains in the east and Rocky Mountains in the west. | (ii) For example, USA, State of Maharashtra, etc. |
| (iii) Physical regions are natural regions. | (iii) Political regions are man-made regions. |
| (iv) Physical regions are almost unchanged regions. | (iv) Political regions are not permanent regions. |
3. Write short notes on.
Question 1.
Factors affecting regional development.
Answer:
The physical factors like relief, climate, location, population and land use of the region affects the regional development.
Regional development occurs near areas with favourable location, plain relief, sufficient rainfall, developed agriculture, transportation, industries and trade. For example, Asian countries have developed agriculture and trade of agricultural goods. USA has developed industries and trade.
There is poor development of economic activities in areas with unfavourable relief like mountains or hills and extreme climate. For example, in the northern part of Russia, economic development is poor due to extreme cold climate.
Location of the region is an important factor. If there is a long and broken coastline, then there is development of ports and thus development of trade and economy. For example, Japan has economically developed in spite of limited natural resources, due to development of trade.
On the other hand, landlocked countries remain isolated. They cannot develop trade due to absence of coastline. Such countries have poor economic development. For example, Afghanistan, Nepal.
The economic development in any region depends upon the quantity and quality of its people.
Where more suitable land is available, different economic activities are developed. For example, cities use land for various purposes such as industries, education, entertainment, transport, commerce, etc. Therefore, cities have economic development.
Hence, physical factors are said to affect the economic development of the region.
Question 2.
Measures to reduce regional imbalance.
Answer:
- The following measures along with numerous policies are considered by the government to reduce regional imbalance.
- The underdeveloped regions are identified and its economic, physical and social reasons for the non-development are studied.
- Regions which require monetary support in a particular sector or field are funded through sector-wise investments to improve the conditions.
- Subsidies are given to certain sectors. Investment is made for improvements of roads, schools, agriculture, irrigation, industries, housing, medical and health facilities, etc.
- Special attention is given to areas facing problems such as frequent droughts, deserts or hilly and tribal-dominated areas.
- The very important strategy to reduce regional imbalances is decentralisation of industries.
![]()
4. Give geographical reasons.
Question 1.
Regional development is dependent on physical setting.
Answer:
- The physical factors like relief, climate and location of the region affect the regional development.
- Regional development occurs where agriculture, agro-based industries and trade is developed in areas where there is plain relief and sufficient rainfall. For example, Asian countries have developed agriculture and trade of agricultural goods.
- Plain relief and sufficient rainfall encourage development of transportation and industries.
- There is poor development of economic activities in areas with unfavourable relief like mountains or hills and extreme climate. For example, in the northern part of Russia, economic development is poor due to extreme cold climate.
- Location of the country is an important factor. If there is a long and broken coastline, then there is development of trade and economy. For example, Japan has economically developed in spite of limited natural resources, due to the development of trade.
- On the other hand, landlocked countries remain isolated. They cannot develop trade due to absence of coastline. Such countries have poor economic development. For example, Afghanistan, Nepal.
- Thus, there is relationship between regional development and physical factors and therefore, we can say the regional development depends on physical factors.
Question 2.
Factors like literacy, poverty affect the regional development.
Answer:
- Literacy and poverty are the important factors affecting the regional development.
- High literacy rate determines the quality of human population. This increases the availability of employment opportunities and development of resources, which contributes to the economic growth and regional development.
- Due to high literacy rate, the population growth is controlled and resources are shared among less people in the country.
- However, poverty decreases the purchasing powers resulting in a decline in the demand for goods, which reduces the production and drops the economic development and GDP of a country.
- Hence, poverty and literacy affect regional development.
Question 3.
Development is not seen in the Himalayan region.
Answer:
- Relief and climate are the most important factors affecting the development of any region.
- The Himalayan region has high mountains with a steep slope. The climate is cold and the mountains are covered with snow. There is heavy soil erosion and hardly plain land, so agriculture is not developed.
- In this mountainous region, it is difficult and expensive to develop transportation facilities. Hence, there is poor development of industries.
- Since all above factors are neither suitable for agricultural, industrial or trade development is not seen in the Himalayan region.
5. Answer the following questions in detail.
Question 1.
What is a region?
Answer:
- A region is an area of a country or any part of the world having common features. Thus, there is a difference between two regions on the basis of its features.
- The common features may be physical (relief, climate, soil, natural vegetation, etc.), socio¬cultural factors (language, religion, etc.), man-made like political features (administrative or political boundaries).
- Regions may be small or large. The large regions include sub-regions. For example, the plateau region of India has various sub-regions such as Chota Nagpur plateau, Malwa plateau, Marwar plateau, Deccan plateau, etc.
The main characteristics of regions are :
- Regions have its geographical location mentioned in latitudes and longitude.
- Every region has a specific boundary, the area of another region starts beyond that boundary.
- The extent of a region depends upon the homogeneity of a region.
- There are sub-regions in one region and therefore regions can be arranged into different orders on the basis of same features.
There are two types of regions – formal and functional regions.
1. A formal region is also known as uniform region or homogeneous region. It is an area in which everyone shares in common one or more distinctive characteristics. It can be common physical characteristic such as relief or climate of the region. It can be socio-cultural or economic activity such as common language. For example, rice producing regions.
2. In some formal regions, there are boundaries. Thus, district, state or country may be formal region. For example, USA and Canada are the examples of formal regions.
3. In functional regions characteristics are not important but functions are more important.
4. In one functional region, there may be many political or physical regions but due to one common function it is said to be functional. For example, Mumbai metropolitan or Pune metropolitan regions.
5. Functional regions act as a focal point that connects surrounding areas by transportation and communication. For example, Mumbai metropolitan city is well connected with its surrounding areas through transportation.
![]()
Question 2.
On what factors are the regions differentiated? Give examples.
Answer:
A region is an area of a country or any part of the world with same common features. Thus, regions are differentiated on the basis of physical or man-made or socio-cultural factors.
For example, Chota Nagpur plateau region has plateau relief. Himalayan mountain region has mountainous relief. The desert region of Rajasthan has shortage of rainfall and very high temperature. Northern plain region has plain relief, fertile soil and moderate climate.
The region may be differentiated on the basis of man-made factors like political factors such as administrative boundaries or political boundaries. For example, Uttar Pradesh and Punjab are two different regions because they have different political boundaries and government bodies.
The region may be differentiated on the basis of socio-cultural factors such as language, religion or ethnicity. For example, in Mumbai there is an area, where people speaking Gujarati language live in one region. The Middle East countries form one region where people of Muslim religion stay together.
Thus, regions are differentiated on the basis of various factors.
Question 3.
Per capita income is not the real indicator of regional development. Explain.
Answer:
- The per capita income is the income of per person in the country or region. It is the ratio between the country’s national income and total population.
- Per capital income is an index of development because more the per capita income, higher the standard of living of people. But it is not always true.
- The per capita income gives an idea about the average income of people in the country but it does not explain how income is distributed among the people. Some people may be rich and some may be below the poverty line.
- The per capita income is related to only economic aspect of the country but it does not take into account literacy rate, health, sex ratio, age structure, life expectancy etc.
- Sometimes rise in per capita income is due to increase in prices of commodities.
- If the population is low the per capita income will be high, but the regional development will be slow, because such regions have shortage of skilled labour supply for further development. Therefore, we can say that the per capita income is not the real indication of regional development.
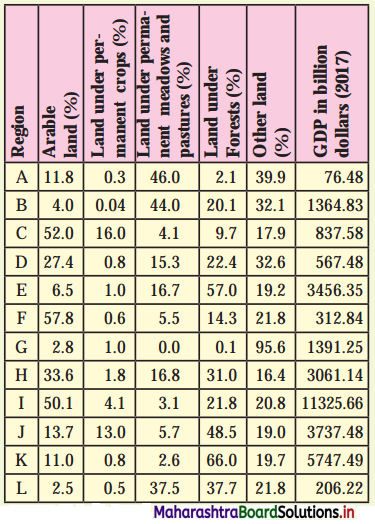
6. Find the correlation between land under permanent crops and GDP given in the table 7.5 using Spearman’s Rank Correlation. Write the conclusion in your own words.
Answer:
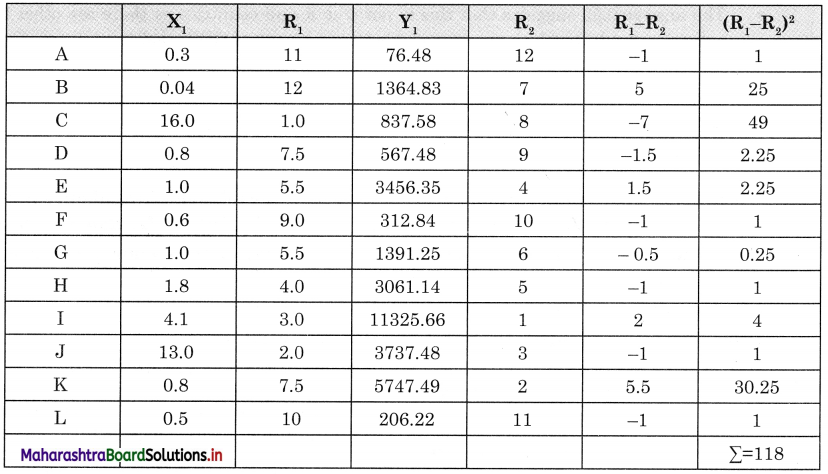
X<sub>1</sub> = Land under permanent crops
Y<sub>1</sub> = GDP
R<sub>1</sub> = Rank – 1, R<sub>2</sub> = Rank – 2, n = 12 (No. of pairs)
Rank correlation R = 1 – \(\frac {6Σ(R_1-R_2)^2}{n(n^2-1)}\)
= 1 – \(\frac {6×118}{12(144-1)}\)
= 1 – \(\frac {708}{1716}\)
= 1 – 0.412
= 0.588
= 0.59

The answer of correction between (1) Land under permanent crops (2) GDP is 0.59 or +0.59 which means there is a positive correlation between these two variables.
It is not perfect positive correlation (+1.0). It is slightly less than this i.e. (+0.59).
It means when the amount of land under permanent crops is more, GDP is also more and when the amount of land under permanent crops is less, GDP is also less.
This is because the production of crops contributes to the growth of GDP.
The answer 0.59 suggests that this is not true for all countries as there are other factors, activities, products which are responsible for the growth of GDP other than the production of crops.
![]()
Class 12 Geography Chapter 7 Region and Regional Development Intext Questions and Answers
Try this
Question 1.
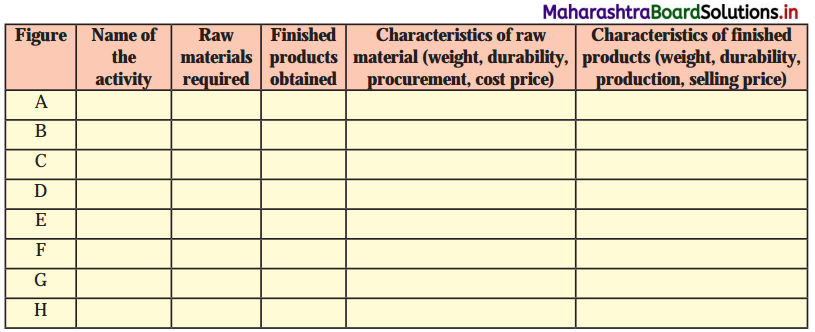
Given below are some geographical areas. Complete the table thinking about similarities between them and their types. Answer the questions that follow: (Textbook Page No. 66)
(i) While completing the above table how did you decide the common factor between these areas?
(ii) How did you differentiate one area from another?
(iii) Is the common factor the only basis of differentiation?
(iv) Make a list of characteristics which can be the basis of different area.
Answer:
| Common factors / characteristics | Types (political / physical) | |
| Ganga river basin, Amazon river basin, Mississippi river basin, Nile river basin | River | Physical |
| The Himalayan region, The Alps, The Western Ghats, The Rockies, The Caucasus | Mountain | Physical |
| Marathwada, Vidarbha, Khandesh, Konkan, Western Maharashtra | Administrative | Political |
| The Thar Desert, The Arabian Desert, The Gobi Desert, The Sahar Desert | Desert | Physical |
| Rajasthan, Madhya Pradesh, West Bengal, Kerala, Manipur | Administrative States | Political |
| Pune, Bhopal, New York, Manchester, Munich, Shanghai | Cities | Political |
| Parbhani, Nagpur, Palghar, Kolhapur, Solapur | Administrative Districts | Political |
| Hindi-speaking belt, Bengali-speaking belt, Marathi-speaking belt, Kannada-speaking belt, Urdu-speaking belt | Language | Political (Linguistic) |
| Delhi University, Punjab University, Mumbai University, Banasthali University Campus | Education | Social |
(i) We decide on the basis of the function of each geographical area.
(ii) We differentiate one area from another on the basis of the type of physical, socio- cultural and political nature of the geographical areas.
(iii) Yes, the common factor is the only basis of differentiation.
(iv) Common basis is physical characteristics like river, desert, mountains, climate, soil, natural vegetation etc., and political characteristics like states, districts and cities and cultural characteristics like language, education, etc.
![]()
Question 2.
Here is the list of regions. Classify them into formal and functional regions. (Textbook Page No. 68)
Ujani Dam catchment area, area served by Pune Municipal Transport (PMT), area served by Citi Cable Service, Uttar Pradesh, District Kolhapur, Taluka Haveli, rice producing region of Konkan, Black cotton soil region of India, areas served by local trains of Mumbai, area served by a Primary Health Centre
Answer:
| Formal Regions | Functional Regions |
| (i) Uttar Pradesh | Ujani Dam catchment area |
| (ii) District Kolhapur | Area served by Pune Municipal Transport (PMT) |
| (iii) Taluka Haveli | Area served by Citi Cable Service |
| (iv) Rice producing region of Konkan | Area served by local trains of Mumbai |
| (v) Black cotton soil region of India | Area served by a Primary Health Centre |
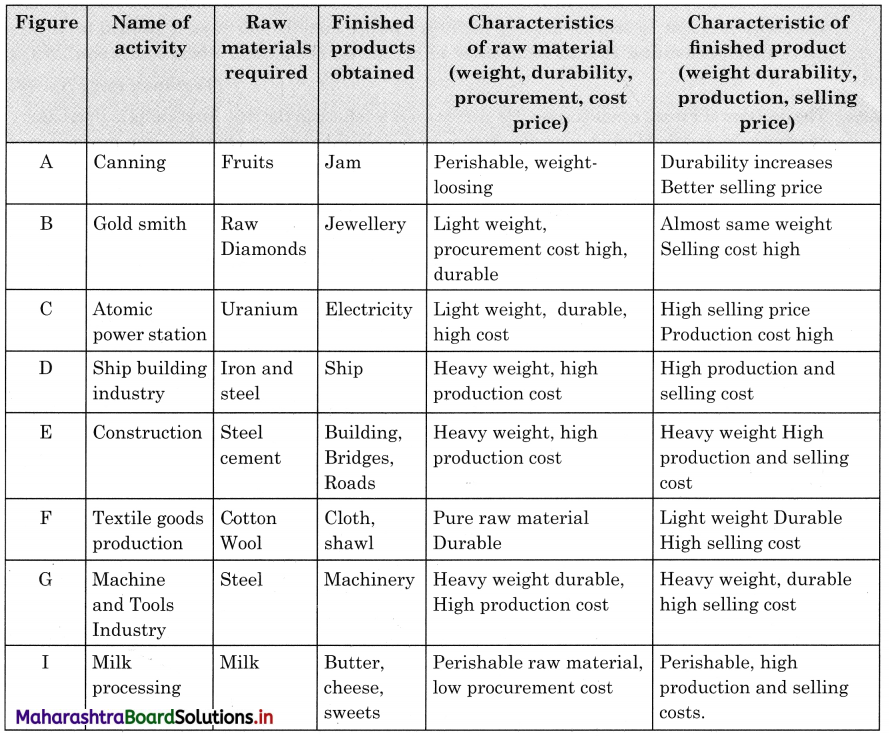
Question 3.
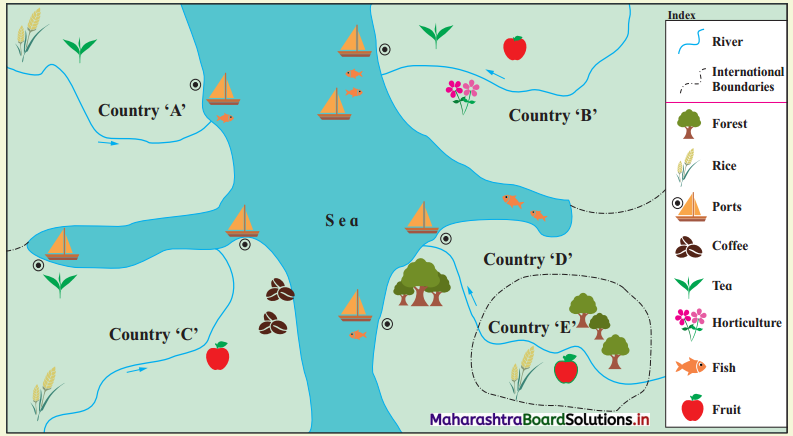
In the following table, regions are given. At the same time, some geographical factors and effects are also given. Complete the table 7.3 accordingly, with the help of solved examples. (Textbook Page No. 69 & 70)
Answer:
| Region | Geographical factors | Effects on the region |
| Nile River basin | Deep and fertile soil, Sufficient water supply by river, Gently sloping land | Agricultural Development, Development of Industries, Hydro-electricity project, Irrigation etc. |
| Canada, Norway, Sweden, Finland and Northern part of Russia | Coniferous forest areas. | Lumbering, Paper and pulp Industry, Furniture manufacturing industry, Saw mills, Deforestation, Landslides Flooding |
| Japan | Island location, Low mineral resources, Narrow geographical extent | Fishing, Development of trade, Industrial development, Hydel power projects |
| Indonesia | Malaysia Fertile volcanic soil, Beautiful scenery | Agricultural development, Trade, Tourism |
Question 4.
Look at the land use of the following regions in Table 7.5 and answer the questions that follow: (Textbook Page No. 72)
(i) What does the table show?
(ii) Which region has the highest land use under agriculture?
(iii) Which region has the highest GDP?
(iv) Which country (region) has more land use under forest?
(v) Which region has the highest land use under category ‘other land’? What’s its GDP?
(vi) Write your conclusion in few sentences.
Answer:
(i) The table shows land use in different regions.
(ii) The region C has the highest land use under agriculture.
(iii) The region I has the highest GDP.
(iv) The country (region) K has more land use under forest.
(iv) The region G has the highest land use under category ‘other land’. Its GDP is 1391.5 billion dollars.
(v) The region I is having highest GDP in which there is 50% arable land, it means agriculture must be major activity.
The region A is having lowest GDP where land under permanent meadows and pastures is highest. It means there is limited development of agricultural activities.
It is surprising, region F where arable land is highest in percentage even then GDP is comparatively low, because the land under permanent crop is very less.
In region K, GDP is 5747.49 and land under forest is 66%. It must be because the development of lumbering activities and forest-based industries is greater.
The region G has the highest area under other land use (95.6%) and GDP 1391.25. This region must have developed activities other than agriculture and forestry.
![]()
Use your brain power!
Question 1.
Can you tell what the identifying characteristic in the following regions?
(i) Pune Metropolitan Region
(ii) Nagpur hub
(iii) Dal Lake in Srinagar
(iv) Alleppey tourism centre
Answer:
(i) Pune Metropolitan Region – Functional region – Administration
(ii) Nagpur hub – Functional region – Industrial complex
(iii) Dal Lake in Srinagar – Functional region – Tourism
(iv) Alleppey tourism centre – Functional region – Tourism
Question 2.
(i) Identify your formal region.
(ii) Can you identify and demarcate your own functional region?
(iii) Which one is larger? (Textbook Page No. 68)
Answer:
(i) Maharashtra State
(ii) Yes, I can identify my functional region as government milk centre or D-mart departmental store.
(iii) Area served by D-mart departmental store is larger than the government milk centre.
Can you tell?
Question 1.
Read the table and answer the questions that follow. (Textbook Page No. 69)
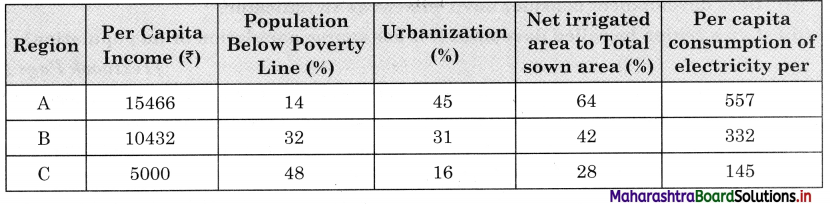
(i) In which region do you think there are more resources available?
(ii) In which region do you think people are richer?
(iii) In which region do you think people may be happier? Why?
(iv) Do you think the given indicators or factors are enough to decide the standard of living of the people in the region?
(v) In which region would you like to stay? Why?
Answer:
(i) I think in region A more resources are available.
(ii) I think in region A people are richer.
(iii) People may be happier in region A because of higher per capita income, less population below poverty line, more urbanisation, more net sown area under irrigation.
(iv) I do not think the given indicator or factors are enough to decide the standard of living because other important factors like literacy rate, enrolment ratio / dropout ratio, sex ratio, crime rate etc., are not taken into consideration
(v) I will like to stay in region A because in this region per capita income is high, population below poverty line is low, percentage of urbanisation is highest, net sown and irrigated area is highest.
![]()
Question 2.
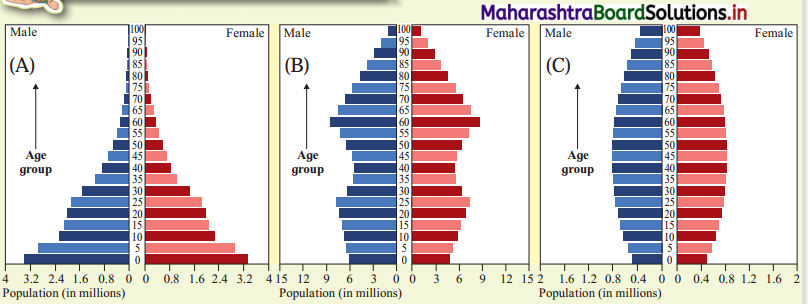
(i) Looking at the five stages of demographic transition theory, countries in which stage do you think, will be called developed?
(ii) Having looked at the various shapes of pyramids, which pyramid will represent a developed country? (Fig 2.1, Textbook Page No. 12)
(iii) After having answered both the questions above, what can you comment upon the role of population in regional development? (Textbook Page No. 70)
Answer:
(i) Countries in stage 4 and 5 will be called developed for e.g., USA, Sweden, Finland.
(ii) The pyramid (C) will represent a developed country.
(iii) The role of population in the regional development of any country is very important as man is a human resource. Quality of human resources is very important, which depends upon birth rate, death rate, expectancy of life, literacy ratio, male female ratio, mortality rate, etc.
A country having to qualitatively better population will help in the regional development of that country. For example, qualitatively population of the USA is better than population of India and hence, in USA there is better regional development than India.
Think about it
Question 1.
(i) Does development mean maximum utilisation of resources?
(ii) Does development consider environment as an indicator?
(iii) Can a region be called developed if it has sparse population or no population? (Textbook Page No. 69)
Answer:
(i) Development does not mean maximum utilisation of resources. Development of a region is the function of its resources and its population. There are many factors which affect the development of a region. For the holistic development of regions, skilled human resources and optimum utilisation of natural resources is necessary.
(ii) We must consider the environment as an indicator of development. Development at the cost of the environment is not real development. Since we ignore the environment while developing economy in the past 50 years, we are now suffering by many environment problems like global warming, etc.
(iii) Population is one of the most important factors in development. If there is sparse population or no population, then there will be shortage of man-power and resources will remain unutilized and therefore, quantity and quality of human resources is very important in the process of development.
Give it try
Question 1.
Draw a conclusion on the basis of the data given in table 7.4. Use Spearman’s Rank Correlation, find the correlation between the two variables. What can you comment about the development in this region? (Textbook Page No. 71)
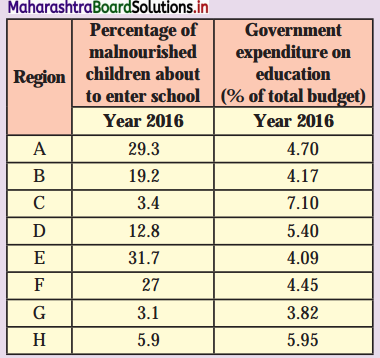
Answer:
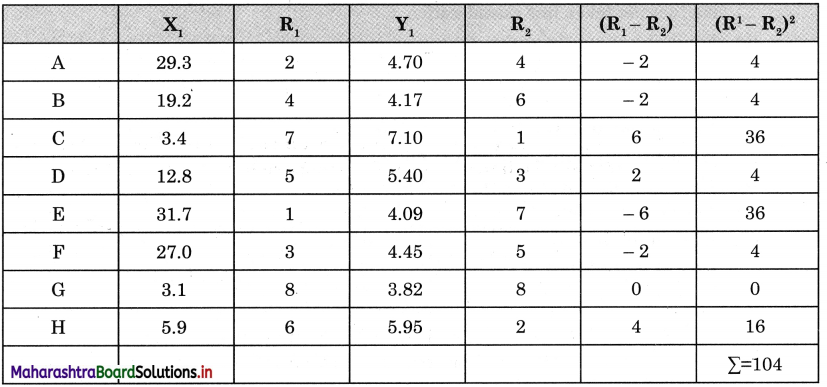
X<sub>1</sub> Percentage of malnourished children about to enter school.
Y<sub>1</sub> Government expenditure on education (% of total budget)
R<sub>1</sub> = Rank – 1, R<sub>2</sub> = Rank – 2, n = 8
Rank correlation R = 1 – \(\frac {6Σ(R_1-R_2)^2}{n(n^2-1)}\)
= 1 – \(\frac {6×104}{8(64-1)}\)
= 1 – \(\frac {624}{8(63)}\)
= 1 – \(\frac {624}{504}\)
= 1 – 1.24
= -0.24
The correlation between the percentage of malnourished children about to enter school and government expenditure on education is -0.24.
This value is very near to zero, which means no correlation. Hence, it is very slightly a negative correlation.

It means where the percentage of malnourished children about to enter school is more, the government expenditure on education is less e.g., in E region percentage of children is 31.7% but the expenditure is 4.09% and in C region percentage of children is only 3.4% but the expenditure is 7.10% (highest).
Considering the fact, we cannot consider this as well developed. There is no logical sequence in distribution of government expenditure on education. It is necessary that government authorities should take into consideration actual status of the region, need of the region before releasing grant to that region. This will surely help in proper allocation of the funds and overall development of the region.
![]()
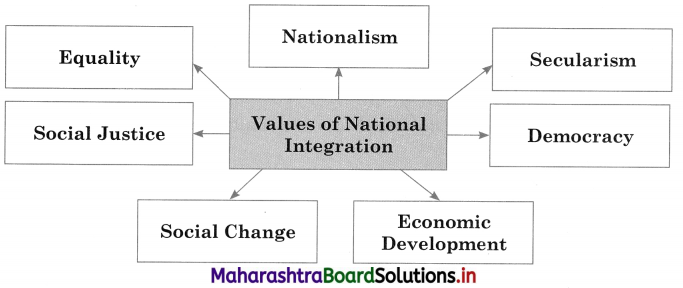
Question 2.
Go through the fig. 7.2 and write two sentences on each factor. Tell how they will help in reducing regional imbalance. Also add some more to the list, if necessary. (Textbook Page No. 73)
Answer:
No country, in the world is having uniform regional development and thus, there is regional imbalance in development. Hence, a country must have a regional imbalance reduction strategy. Regional imbalance can be reverted through provision of public/services to backward areas by providing drinking water, education facilities and electricity to all.
It can also be reverted by making provision of infrastructure stimulus by allotment of special funds, development of special skills, good governance, support to infrastructural project and policy review and reform.
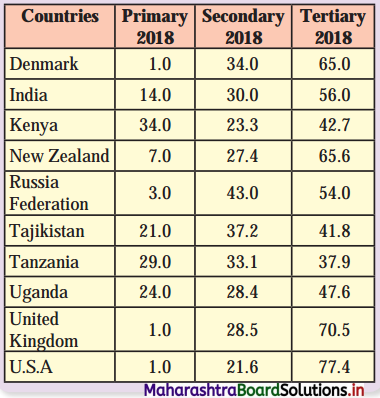
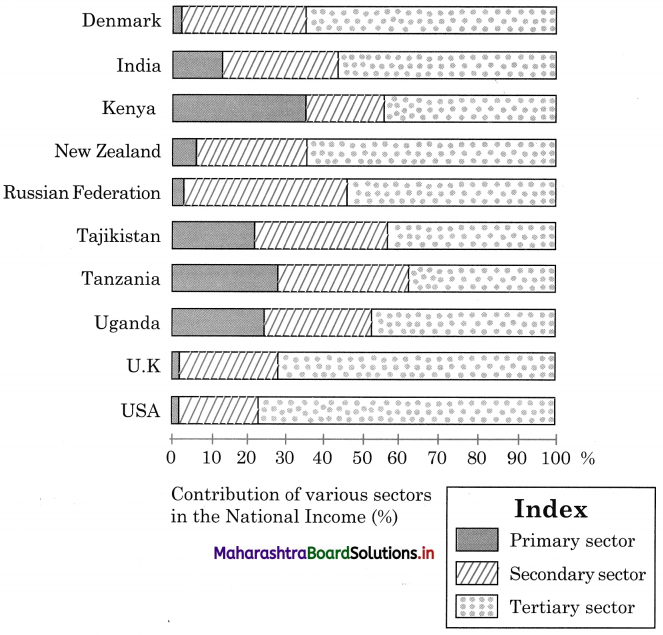
Question 1.
Look at the following data and answer the questions that follow: (Textbook Page No. 72)
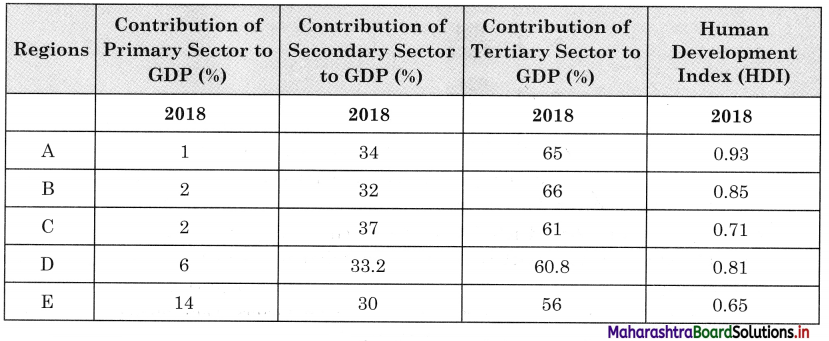
(i) In which region is contribution of primary activities the least?
(ii) In which region is the contribution of primary activities the most?
(iii) In which region the contribution of tertiary activities is the most?
(iv) Which region has the highest HDI?
(v) Can you draw a conclusion on basis of the answers from Q (i) to Q (iv)?
Answer:
(i) In region A, the contribution of primary activities is the least.
(ii) In region E, the contribution of primary activities is the most.
(iii) In region B, the contribution of tertiary activities is the most.
(iv) In region A, there is highest HDI.
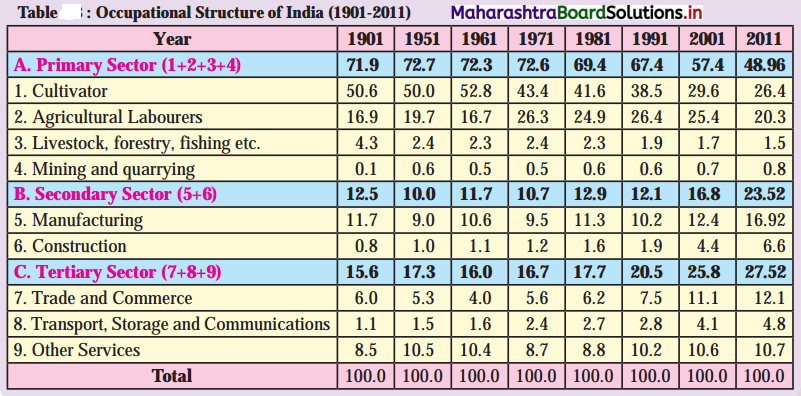
(v) We can conclude by saying that Human Development Index is high in countries where contribution of secondary and tertiary sector to GDP is high compared to the contribution of primary sector to GDP.
Region A, B, C and D have more than 30% contribution of secondary sector to GDP and more than 60% contribution of tertiary sector to GDP, it means these regions are developed regions.
The contribution of primary sector to GDP in region E is more but the contribution from secondary and tertiary sector is less compared to other regions, so region E is in the developing stage.
Class 12 Geography Solutions Digest
- Population Part 1 Geography Class 12 Question Answer
- Population Part 2 Geography Class 12 Question Answer
- Human Settlements and Land Use Geography Class 12 Question Answer
- Primary Economic Activities Geography Class 12 Question Answer
- Secondary Economic Activities Geography Class 12 Question Answer
- Tertiary Economic Activities Geography Class 12 Question Answer
- Region and Regional Development Geography Class 12 Question Answer
- Geography: Nature and Scope Geography Class 12 Question Answer