Class 7 Hindi Chapter 6 Chanda Mama Ki Jay Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 6 चंदा मामा की जय Notes, Textbook Exercise Important Questions and Answers.
Std 7 Hindi Chapter 6 Chanda Mama Ki Jay Question Answer Maharashtra Board
Hindi Sulabhbharti Class 7 Solutions Chapter 6 चंदा मामा की जय Textbook Questions and Answers
जरा सोचो….. चर्चा करो
‘यदि तुम्हारा घर मंगल ग्रह पर होता तो…’ विषय पर अपने विचार लिखिए। (कल्पनात्मकलेखन)
Answer:
यदि हमारा घर मंगल ग्रह पर होता, तो हम सब मंगलवासी कहे जाते। पृथ्वी सबसे अधिक मंगल के करीब है अत: वहाँ से पृथ्वी का नजारा देखा करते । मंगल को ‘लाल ग्रह’ कहा जाता है। हम वहाँ के इस सौंदर्य का आनंद लेते। सूर्य से दूर होने की वजह से मंगल ग्रह पर मौसम की लम्बाई पृथ्वी से दोगुनी होगी। ऐसे में मंगल का एक साल पृथ्वी के दो साल के बराबर हो जाएगा। इस प्रकार पृथ्वी की एक साल की पढ़ाई वहाँ दो साल करनी पड़ेगी।
मंगल ग्रह को अपने अक्ष पर घुमने में २५घंटे और सूर्य की परिक्रमा करने में ६८७ दिन लगते हैं। समय के हिसाब से मंगल ग्रह धीमी गति का है। दो वर्ष पर एक बार जन्मदिन मनाने मिलेगा। सभी ऋतुएँ चार-चार महीने की होने लगेगी। इस प्रकार मंगल ग्रह पर एक नया अनुभव होगा। यदि वहाँ से धरती पर वापस आएँगे, तो पता चलेगा कि मेरे सभी दोस्त मुझसे पढ़ाई में काफ़ी आगे निकल चुके हैं। फिर भी एक नए ग्रह पर घर होना और घुमने की कल्पना ही मन में उत्साह और रोमांचक एहसास भर देती है।

वाचन जगत से
भारतीय मूल की किसी महिला अंतरिक्ष यात्री संबंधी जानकारी पढ़ो तथा अंतरिक्ष यात्रियों के नाम बताओ।
स्वयं अध्ययन
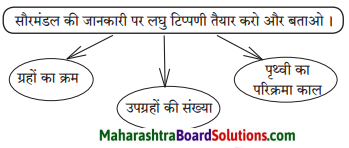
Answer:
ग्रहों का क्रम – क्रमशः इस प्रकार है: शनि, गुरु, मंगल, रवि, शुक्र, बुध, अरुण, वरुण और पृथ्वी।
उपग्रहों की संख्या – सौरमंडल में पहचाने गए उपग्रहों की संख्या १७८ है। प्राकृतिक उपग्रह एकमात्र चंद्रमा है। पृथ्वी अपने अक्ष पर घूमते हुए ३६५ दिन ५ घंटा ४८ मिनट ४५ सेंकेड में सूर्य की एक परिक्रमा लगाती है।
किसने, किससे कहा?
Question 1.
यह अपनी माँ का कहना नहीं मानता।
Answer:
नौंदपरी ने रातरानी से कहा।
Question 2.
अच्छे बच्चे बड़ों को जवाब नहीं देते।
उत्तरः
सुनील ने रातरानी से कहा।
Question 3.
हम तुम्हें कड़ी से कड़ी सजा देंगे।
Answer:
रातरानी ने सुनील से कहा।
Question 4.
सुनील भैया को कड़ी सजा मत दो।
Answer:
अनिल ने रातरानी से कहा।
Question 5.
मैं अब कभी कोई शैतानी नहीं करूंगा।
Answer:
सुनील ने रातरानी से कहा।
Question 6.
सबको क्षमा किया जाता है।
Answer:
रातरानी ने सभी बच्चों से कहा।

निम्नलिखित प्रश्नों के उत्तर लिखिए।
Question 1.
इस एकांकी का सारांश अपने शब्दों में लिखो।
Answer:
प्रस्तुत एकांकी ‘चंदा मामा की जय’ में लेखक ने शांति प्रियता, बड़ों का आदर, छोटों से प्यार और बुरी आदतों को त्यागने के लिए प्रोत्साहित किया है। इसमें प्रकृति का मानवीकरण किया गया है। जिसमें एक लड़की जज की भूमिका में है और बाकी पाँच बच्चे जिनकी शिकायत नींद परी करती है। बाद में चंदा मामा उन बच्चों के गुणों को याद कराते हैं और बच्चों से बुरी आदतें छोड़ने की प्रतिज्ञा कराते हैं। अंत में सभी बच्चों को क्षमा किया जाता है।
Question 2.
‘चंदा मामा की जय’ एकांकी के पसंदीदा पात्र का वर्णन कीजिए।
उत्तरः
‘चंदा मामा की जय’ एकांकी का सबसे पसंदीदा पात्र चंदामामा है। बच्चे चंदा मामा को अपना मामा मानते हैं। उनके आते ही वे सब खड़े हो जाते हैं और ताली बजाकर अपनी खुशी प्रकट करते हैं। चंदामामा भी बच्चों का पक्ष लेते हुए उनके गुणों का वर्णन करते हैं। वे बच्चों को माफी दिलवाते हैं और बच्चे चंदामामा की जय-जयकार करने लगते हैं।
Question 3.
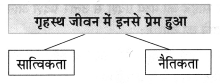
नैतिक मूल्यों की सूची बनाइए और उन पर अमल कीजिए।
Answer:
दैनिक जीवन में उपयोगी कुछ नैतिक मूल्य निम्नलिखित हैं:
- छोटे बच्चों से स्नेह एवं प्यार करना।
- बड़ों की बात मानना।
- बड़ों का आदर करना।
- भोजन करते समय प्रसन्न रहना एवं समय पर खाना।
- खेलने के समय पर ही खेलना।
- पढ़ाई के समय मन लगाकर पढ़ना।
- सभी काम समय पर करना।
- सभी से मिलकर रहना।
- घर की वस्तुओं को संभालकर रखना।
- छोटी-बड़ी सभी बुरी आदतों से दूर रहना।

Question 4.
आप अपनी माँ की कौन-कौन सी बातें मानते हैं? उनकी सूची बनाइए।
Answer:
हम अपनी माँ की निम्नलिखित बातें मानते हैं:
- सुबह जल्दी उठना।
- नित्य क्रिया के बाद पढ़ने बैठना।
- मन लगाकर पढ़ाई करना।
- विद्यालय में सबसे प्रेमपूर्वक रहना।
- समय पर गृहकार्य करना।
- घर के छोटे-छोटे कार्यों में हाथ बटाना।
- कभी-कभी दुकान से समान लाना।
- छोटे भाई और बहन को पढ़ाई में मदद करना।
- सत्य बोलना और बड़ों का आदर करना।
- घर में स्वच्छता रखना।
Question 5.
आपको कौन-सा काम करना अच्छा लगता है और क्यों?
Answer:
मुझे घर में साफ-सफाई करना और दुकान से सामान लाना अच्छा लगता है क्योंकि इस काम के बाद मुझे कुछ पुरस्कार भी पारितोषिक रूप में प्राप्त होता है।
खोजबीन
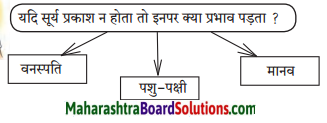
इस वर्ष का सूर्यग्रहण कब है? उस समय पशु-पक्षी के वर्तन-परिवर्तन का निरीक्षण करो और बताओ।
मेरी कलम से
किसी दुकानदार और ग्राहक के बीच होने वाला संवाद लिखिए और सुनाइए। (संवाद-लेखन)
जैसे – माँ और सब्जीवाली
Answer:
माँ – भिंडी क्या भाव है? बहन!
सब्जीवाली – ५० रु. किलो
माँ – और टमाटर?
सब्जीवाली – ८०रु.
माँ – क्या? ८० रु. किलो?कल ही तो५०रु. का एक किलो लिया था मैने।
सब्जीवाली – कल की बात कल थी। आज तो ८० रु. का भाव है।
माँ – तुम लोग इस तरह एक ही रात में इतना भाव बढ़ाओगे, तो गरीब आदमी क्या खाएगा?
सब्जीवाली – देखो बहन जी! हमारे घर की खेती तो है नहीं। हम बाजार से जो भाव लेते हैं। उसी भाव में हमें बेचना पड़ता है।
माँ – चलो ठीक है। आज आधा किलो ही टमाटर दे दो। महँगाई की मार बहुत बुरा दिन दिखाने लगी है।
सब्जीवाली – हाँ, वो तो हैं। अभी देती हूँ।

विचार मंथन
‘बिन माँगे मोती मिले’ विषय पर आधारित एक अनुच्छेद लिखिए। (अनुच्छेद-लेखन)
Answer:
एक प्राचीन कहावत है ‘बिन मांगे मोती मिले, माँगे मिले न भीख।’ कहने का आशय यह है कि हम छोटी-छोटी बात पर लोगों से माँगने लगते हैं। कुछ तो भगवान के मंदिर में भी जाते हैं, तो भगवान से न जाने क्या-क्या माँग करते रहते हैं। वे यह भूल जाते हैं कि माँगने से हमें कुछ प्राप्त नहीं होता। हम जिससे मांगते हैं उसकी नजरों में स्वयं को छोटा बना देते हैं।
रही बात भगवान की तो मेरा यह काम हो गया तो मैं आपके लिए उपवास रखूगा। नारियल और प्रसाद चढ़ाऊँगा। वे यह भूल जाते हैं कि हमारा काम हमारे परिश्रम से ही सफल हो सकता है। उसके लिए किसी के सामने हाथ फैलाने की आवश्यकता नहीं है। यदि हम परिश्रमपूर्वक मन लगाकर कोई भी कार्य करेंगे, तो अवश्य सफल होंगे और बिन मांगे हमें सब कुछ मिल जाएगा। यदि हम सिर्फ माँगने पर ही निर्भर रहेंगे, तो भीख भी नहीं मिलेगी।
सदैव ध्यान में रखो
निवेदन सदैव विनम्र शब्दों में ही करना चाहिए।

भाषा की ओर
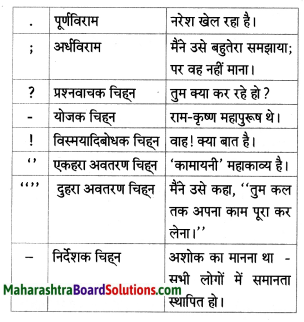
निम्नलिखित वाक्य पढ़ो और मोटे और में छपे शब्दों पर ध्यान दो :
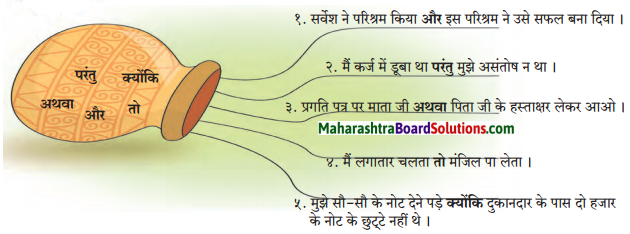
“उपर्युक्त वाक्यों में और, परंतु, अथवा, तो, क्योंकि शब्द अलग-अलग स्वतंत्र वाक्यों या शब्दों को जोड़ते हैं । ये शब्द समुच्चयबोधक अव्यय हैं।
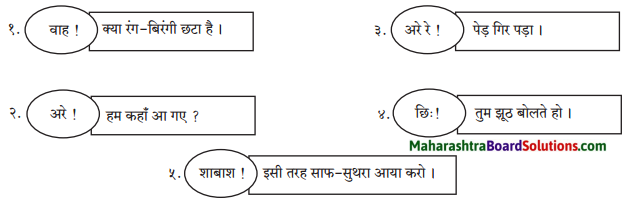
उपर्युक्त वाक्यों में वाह, अरे, अरे रे, छि:, शाबाश, ये शब्द क्रमशः खुशी, आश्चर्य, दुख, घृणा, प्रशंसा के भाव दिखाते हैं। – ये शब्द विस्मयादिबोधक अव्यय हैं ।
Hindi Sulabhbharti Class 7 Solutions Chapter 6 चंदा मामा की जय Additional Important Questions and Answers
निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए।
Question 1.
अनिल कैसा बच्चा है?
Answer:
रोनेवाला
Question 2.
चाय की कप-प्लेट किसने तोड़ी थी?
Answer:
सुनील
Question 3.
सभी बच्चे चाँद को क्या कहते हैं?
Answer:
मामा
Question 4.
बच्चों पर अन्याय कौन कर रहा था?
Answer:
रातरानी

निम्नलिखित वाक्य सही है या गलत लिखिए।
Question 1.
अनिल ५ वर्ष का बालक है।
Answer:
सही
Question 2.
सुनील उसका छोटा भाई है।
Answer:
गलत
Question 3.
सुनील अनिल को मार-पीटकर सोया था।
Answer:
गलत
Question 4.
अनिल सुनील को सजा दिलाना चाहता था।
Answer:
गलत
Question 5.
सुनील अपने से छोटे बच्चों को कभी नहीं पीटता था।
Answer:
सही
Question 6.
ये बच्चे अपने से बड़ों का कहना मानते हैं।
Answer:
सही
Question 7.
अंत में सबको क्षमा दी जाती है।
Answer:
सही

निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।
Question 1.
रातरानी किसी तरह बच्चों को चुप कराना क्यों चाहती है?
Answer:
कार्यवाही चालू करने के लिए रातरानी किसी तरह बच्चों को चुप कराना चाहती है।
Question 2.
रातरानी गुस्से से क्यों काँपने लगती है?
Answer:
रातरानी गुस्से से काँपने लगती है क्योंकि सभी बच्चे गला फाड़कर रोने लगते हैं।
Question 3.
सब बच्चे किसे देखकर खड़े हो जाते हैं?
Answer:
सब बच्चे चंदामामा को देखकर खड़े हो जाते हैं।

व्याकरण और भाषाभ्यास
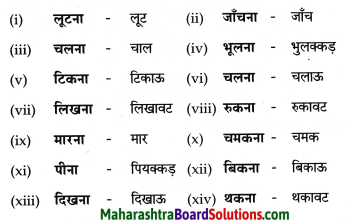
निम्नलिखित वाक्यों से समुच्चयबोधक अव्यय चुनकर लिखिए।
Question 1.
इन्हें किसी तरह चुप कराओ; ताकि कार्यवाही चालू की जाए।
Answer:
ताकि
Question 2.
अच्छे बच्चे बड़ों को जवाब नहीं देते इसलिए मैं जवाब नहीं दूंगा।
Answer:
इसलिए
Question 3.
यह चाय की कप-प्लेट तोड़कर और अपनी माँ से पिटकर सोया था।
Answer:
और
Question 4.
रोने से हमको बताशे मिलते हैं। इसलिए हम रोते हैं।
Answer:
इसलिए
Question 5.
हम कभी नहीं रोएँगे, परंतु सुनील भैया को सजा न दी जाए।
Answer:
परंतु
Question 6.
एक व्यक्ति में अगर गुण अधिक हों और बुरी आदतें कम तो उसे क्षमा कर दिया जाता है।
Answer:
और

कोष्ठक में दिए गए विस्मयादिबोधक अव्यय से रिक्त स्थानों की पूर्ति कीजिए।
(जी!, छि-छि!, अरे!, खबरदार!, वाह!, बाप रे!, काश!, उफ़!)
Question 1.
……….. चुप हो जाओ!
Answer:
अरे!
Question 2.
………….. चारों ओर कितनी गंदगी है।
Answer:
छि-छि!
Question 3.
………………. पीछे गाड़ी आ रही है।
Answer:
खबरदार
Question 4.
………………… तुमने तो कमाल कर दिया।
Answer:
वाह!
Question 5.
……………………. सिर में बहुत दर्द हो रहा है।
Answer:
उफ!
Question 6.
……………………….. मैं भी अच्छा गा सकता।
Answer:
काश!
Question 7.
……………………….. सब्जियाँ कितनी महंगी हो गई हैं।
Answer:
बाप रे!
Question 8.
…………….. आपने ठीक का।
Answer:
जी!

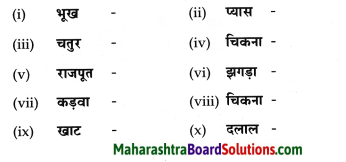
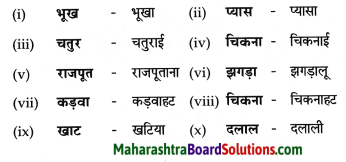
निम्नलिखित शब्दों के विलोम शब्द लिखिए।
- सजा
- आदर
- अपराध
- अन्याय
- गुण
- प्यार
- जय
- शांति
Answer:
- माफ
- निरादार
- निरपराध
- न्याय
- अवगुण
- घृणा
- पराजय
- अशांति

निम्नलिखित रिक्त स्थानों की पूर्ति उचित किया विशेषण शब्द से कीजिए।
जोर-जोर, अचानक, पिटकर, चौंककर, गला फाड़कर, अचानक
Question 1.
यह अपनी माँ से …………..”सोया था।
Answer:
पिटकर
Question 2.
सब बच्चे . …………” उधर देखते हैं।
Answer:
चौंककर
Question 3.
सभी ………………” रो पड़ते हैं।
Answer:
गला फाड़कर
Question 4.
तब मैं और ……………. से रोऊँगा।
Answer:
जोर-जोर
Question 5.
मैं ………. देख चुकी हूँ।
Answer:
अभी-अभी
Question 6.
चंदामामा …… आ गए।
Answer:
अचानक

निम्नलिखित क्रियाओं का वाक्य में प्रयोग कीजिए।
Question 1.
अकड़ना
Answer:
हमें बड़ों के सामने अकड़ना नहीं चाहिए।
Question 2.
डाँटना
Answer:
छोटे बच्चों को हमेशा डाँटना नहीं चाहिए।
Question 3.
चौंकना
Answer:
सभी बच्चे चौंकना नहीं जानते हैं।
Question 4.
शरमाना
Answer:
शरमाना मनुष्य का स्वाभाविक गुण है।

निम्नलिखित बाक्यों में से कारक चिहन चुनकर लिखिए।
कारक – “संज्ञा या सर्वनाम के जिस रूप से उसका संबंध वाक्य में क्रिया के साथ जाना जाए, उसे कारक कहते हैं।”
कारक के मुख्य आठ भेद होते हैं
- कर्ता कारक
- कर्म कारक
- करण कारक
- संप्रदान कारक
- अपादान कारक
- संबंध कारक
- अधिकरण कारक
- संबोधन कारक

Question 1.
यह अपनी माँ का कहना नहीं मानता।
Answer:
का
Question 2.
खाने के समय खाना नहीं खाता।
Answer:
के
Question 3.
कोई काम समय पर नहीं करता।
Answer:
पर
Question 4.
अच्छे बच्चे बड़ों को जवाब नहीं देते।
Answer:
को

Question 5.
ये बच्चे अपने से बड़ों का कहना मानते हैं।
Answer:
से, का
Question 6.
सुनील अपने से छोटे बच्चों को कभी नहीं पीटता।
Answer:
से, को
Hindi Sulabhbharati 7th Standard Digest Guide दूसरी इकाई

![]()

![]()
![]()
![]()
![]()