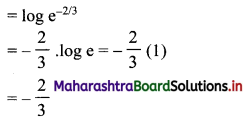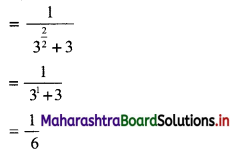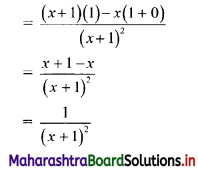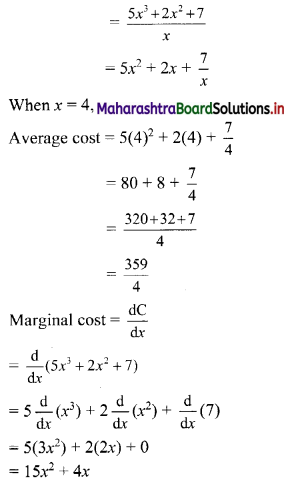Sequences and Series Class 11 Commerce Maths 1 Chapter 4 Exercise 4.1 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.1 Questions and Answers.
Std 11 Maths 1 Exercise 4.1 Solutions Commerce Maths
Question 1.
Verify whether the following sequences are G.P. If so, write tn.
(i) 2, 6, 18, 54, ……
(ii) 1, -5, 25, -125, …….
(iii) \(\sqrt{5}, \frac{1}{\sqrt{5}}, \frac{1}{5 \sqrt{5}}, \frac{1}{25 \sqrt{5}}, \ldots\)
(iv) 3, 4, 5, 6, ……
(v) 7, 14, 21, 28, …..
Solution:
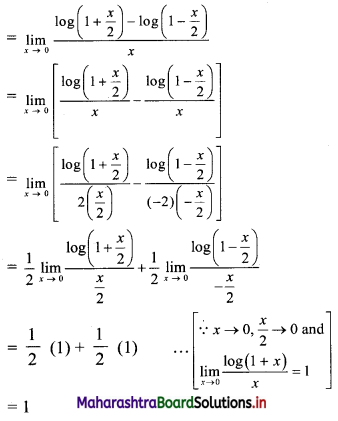
(i) 2, 6, 18, 54, …….
t1 = 2, t2 = 6, t3 = 18, t4 = 54, …..
Here, \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}=\frac{t_{4}}{t_{3}}=3\)
Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.
Here, a = 2, r = 3
tn= arn-1
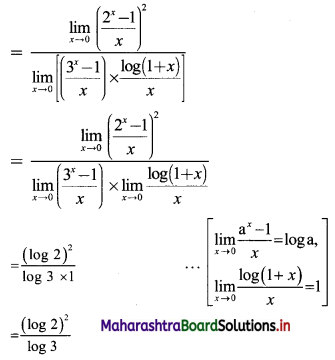
∴ tn = 2(3n-1)
![]()
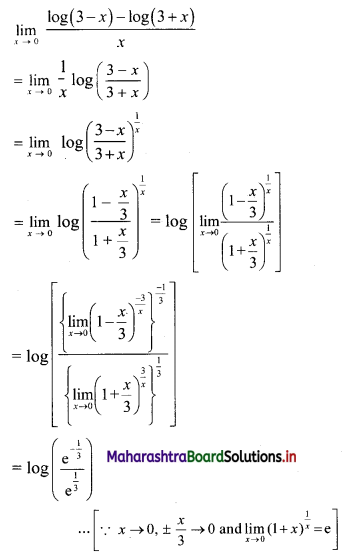
(ii) 1, -5, 25, -125, ……
t1 = 1, t2 = -5, t3 = 25, t4 = -125, …..
Here, \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}=\frac{t_{4}}{t_{3}}=-5\)
Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.
Here, a = 1, r = -5
tn = arn-1
∴ tn = (-5)n-1
(iii) \(\sqrt{5}, \frac{1}{\sqrt{5}}, \frac{1}{5 \sqrt{5}}, \frac{1}{25 \sqrt{5}}, \ldots\)
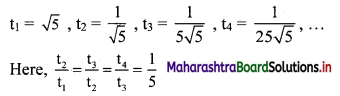
Since, the ratio of any two consecutive terms is a constant, the given sequence is a geometric progression.
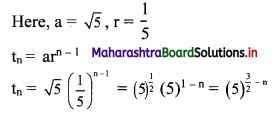
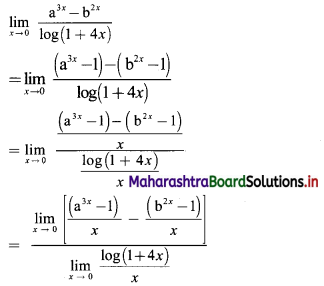
(iv) 3, 4, 5, 6,……
t1 = 3, t2 = 4, t3 = 5, t4 = 6, …..
Here, \(\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}}=\frac{4}{3}, \frac{\mathrm{t}_{3}}{\mathrm{t}_{2}}=\frac{5}{4}, \frac{\mathrm{t}_{4}}{\mathrm{t}_{3}}=\frac{6}{5}\)
Since, \(\frac{t_{2}}{t_{1}} \neq \frac{t_{3}}{t_{2}} \neq \frac{t_{4}}{t_{3}}\)
∴ the given sequence is not a geometric progression.
(v) 7, 14, 21, 28, …..
t1 = 7, t2 = 14, t3 = 21, t4 = 28, …..
Here, \(\frac{t_{2}}{t_{1}}=2, \frac{t_{3}}{t_{2}}=\frac{3}{2}, \frac{t_{4}}{t_{3}}=\frac{4}{3}\)
Since, \(\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}} \neq \frac{\mathrm{t}_{3}}{\mathrm{t}_{2}} \neq \frac{\mathrm{t}_{4}}{\mathrm{t}_{3}}\)
∴ the given sequence is not a geometric progression.
![]()
Question 2.
For the G.P.,
(i) if r = \(\frac{1}{3}\), a = 9, find t7.
(ii) if a = \(\frac{7}{243}\), r = \(\frac{1}{3}\), find t3.
(iii) if a = 7, r = -3, find t6.
(iv) if a = \(\frac{2}{3}\), t6 = 162, find r.
Solution:


Question 3.
Which term of the G. P. 5, 25, 125, 625, ….. is 510?
Solution:

Question 4.
For what values of x, \(\frac{4}{3}\), x, \(\frac{4}{27}\) are in G. P.?
Solution:

Question 5.
If for a sequence, \(t_{n}=\frac{5^{n-3}}{2^{n-3}}\), show that the sequence is a G. P. Find its first term and the common ratio.
Solution:
The sequence (tn) is a G.P., if \(\frac{t_{n}}{t_{n-1}}\) = constant, for all n ∈ N

∴ the sequence is a G. P. with common ratio \(\frac{5}{2}\)
First term, t1 = \(\frac{5^{\mathrm{l}-3}}{2^{1-3}}=\frac{2^{2}}{5^{2}}=\frac{4}{25}\)
![]()
Question 6.
Find three numbers in G. P. such that their sum is 21 and sum of their squares is 189.
Solution:
Let the three numbers in G. P. be \(\frac{a}{\mathrm{r}}\), a, ar.
According to the first condition,



∴ the three numbers are 12, 6, 3 or 3, 6, 12.
Check:
First condition:
12, 6, 3 are in G.P. with r = \(\frac{1}{2}\)
12 + 6 + 3 = 21
Second condition:
122 + 62 + 32 = 144 + 36 + 9 = 189
Thus, both the conditions are satisfied.
Question 7.
Find four numbers in G. P. such that sum of the middle two numbers is \(\frac{10}{3}\) and their product is 1.
Solution:
Let the four numbers in G.P. be \(\frac{a}{r^{3}}, \frac{a}{r}, a r, a r^{3}\).
According to the second condition,
\(\frac{\mathrm{a}}{\mathrm{r}^{3}}\left(\frac{\mathrm{a}}{\mathrm{r}}\right)(\mathrm{ar})\left(\mathrm{ar}^{3}\right)=1\)
∴ a4 = 1
∴ a = 1
According to the first condition,

Question 8.
Find five numbers in G. P. such that their product is 1024 and the fifth term is square of the third term.
Solution:
Let the five numbers in G. P. be
\(\frac{a}{r^{2}}, \frac{a}{r}, a, a r, a r^{2}\)
According to the given conditions,

When a = 4, r = -2
\(\frac{a}{r^{2}}\) = 1, \(\frac{a}{r}\) = -2, a = 4, ar = -8, ar2 = 16
∴ the five numbers in G.P. are 1, 2, 4, 8, 16 or 1, -2, 4, -8, 16.
![]()
Question 9.
The fifth term of a G. P. is x, eighth term of the G. P. is y and eleventh term of the G. P. is z. Verify whether y2 = xz.
Solution:

Question 10.
If p, q, r, s are in G. P., show that p + q, q + r, r + s are also in G.P.
Solution:
p, q, r, s are in G.P.

∴ p + q, q + r, r + s are in G.P.
11th Commerce Maths Digest Pdf