Bhagya

Class 10 English Chapter 2.1 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 2.1 You Start Dying Slowly Notes, Textbook Exercise Important Questions and Answers.

You Start Dying Slowly Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 2.1 You Start Dying Slowly Textbook Questions and Answers

Warming up!

Chit-chat:

1. Assuming A, B, C, D, as speakers, ask the assigned questions in your group and discuss.

Question 1.
Assuming A, B, C, D, as speakers, ask the assigned questions in your group and discuss.

Answer:

A	Responses
If you do not study well what will happen?	I will not get good marks in examination. I may fail in the examination. I will be blamed for neglecting studies. Parents will be angry for my negligence.
If you do not participate in school activities/games.	My teacher and friends will treat me as idle and inactive student. I will not be called a sociable student. I will feel solitary and dull. I will not be able to show my skills in games and other co-curricular activities. I will lose my opportunity to gain importance.
B	Responses
If you wake up late on a working day.	I will miss cool, peaceful mornings. Morning chores will get delayed. I will feel dull and lazy. I will lose best hours of work.
If you ignore a friend in need.	Other friends will lose their faith in me. They will leave/avoid me for ignoring my duties towards friend. Many will blame me for my betrayal. I shall face big emotional loss.
C	Responses
If you do not do exercise regularly what will happen?	I will not stay healthy and fit physically and mentally. I will suffer from obesity. I will be easily affected by infections and diseases. I will not feel energetic and active.
D	Responses
If you eat too much junk food what will happen?	I will suffer from obesity. I may lose my immunity. I will not be able to live active life. I will have to spend a lot on my health problems.

2. Things I can do in my life

Question 1.
Things I can do in my life

Answer:

3. Complete the following with and write a paragraph.

Question 1.
Complete the following with and write a paragraph.

Answer:

Space Travel-My Wish According to the novelist H. G. Wells, one of the things to come in future was space travel. It was a fantastic dream then. It has turned into reality now. The invention of rockets, satellites and spaceships (spacecraft) have opened the gates of space travels.

Since I read about the accomplishments of the astronauts of different countries, I had my secret wish of space travelling. I don’t know when and how it will realize but I do wish to travel to space. How shall I enjoy the travel to space!

First I wish to go into the orbit round the earth. Then I shall emerge from the capsule and, still tied to my space vehicle, I shall walk in space. I shall move about in space with the help of space-gun. Then I wish to land on different planets. My first visit will be the moon, of course.

Then waiting and taking rest on a space station built by scientists and engineers, I shall travel to nearby planets. I shall visit Mars, Venus, Jupiter, etc. For that I shall travel by shuttle rocket service between the earth and the space station and from the space station to any other planet of my wish. I shall enjoy different weather, land, food and aliens if at all they exist there. What a marvellous travel it will be!

English Workshop:

1. Read the different messages in the poem given below. Choose the one that suits this poem, best.

Question 1.
Read the different messages in the poem given below. Choose the one that suits this poem, best.
(a) Face life whatever it may give you.
(b) Fulfil all your dreams and unfulfilled desires.
(c) Be yourself and do what your heart tells you.
(d) Accept all possible changes or risks that you have taken.
(e) Keeping your self-esteem intact, just try to relax in life.
Answer:
(c) Be yourself and do what your heart tells you.

2. State the following:

Question a.
Theme/central idea of the poem.
Answer:
Refer to point no (5) of the appreciation of this poem.

Question b.
Line that provides evidence of the theme.
Answer:
If you do not change your life, you start I dying slowly.

Question c.
Three characteristics, from the poem, that makes one dull and uninteresting.
Answer:
The three characteristics from the poem that makes one dull and uninteresting are:

1. becoming a slave of your habits.
2. not going with fresh emotions.
3. not facing exciting, risky challenges.

3. Pick out four Adjectives from the poem and write them down with the nouns they describe.

Question 1.
Pick out four Adjectives from the poem and write them down with the nouns they describe.

1. ………………………
2. ……………………..
3. ……………………..
4. ……………………….

Answer:

1. same paths
2. different colours
3. turbulent emotions
4. sensible advice.

4. Compare the structure of the poem, ‘You start dying slowly to the poems in Unit One (1.1 and 1.3) To which poem does the structure match? ……………….
What differences do you notice in the other ones. Note them down.
1. ……………………..
2. …………………….
3. …………………….
4. …………………….

Question 1.
Compare the structure of the poem, ‘You start dying slowly to the poems in Unit One (1.1 and 1.3) To which poem does the structure match? ……………….
Answer:
1. The structure of the poem 1.3 ‘Basketful of Moonlight’ matches with this poem.
2. What differences do you notice in the other ones. Note them down.

‘A Teenager’s Prayer’	‘You start dying slowly…’
1. Metric, Rhythmic Rhymes, Rhyme Scheme	Free Verse, No rhymes or rhyming scheme.
2. Narrative-Teenager’s prayer to God.	Didactic poem (imparting advice)
3. Quatrain (a group of four lines in each stanza)	Different number of lines in each stanza.
4. Different figures of speech.	Mainly Repetition in the beginning of each line.

5. What expression is repeated in the poem? How many times? Why, do you think, the poet emphasizes it? 

Question 1.
What expression is repeated in the poem? How many times? Why, do you think, the poet emphasizes it?
Answer:
The expression ‘If you do not-‘ is repeated in the poem. It has been repeated 12 times in the beginning of lines in the poem. The poet emphasizes it because he wants to urge strongly to read the poem and stress the things that we should not do. He reminds us every time what we should avoid to do for living good life.

6. Write the opposite of the following in the form of advice using different words and phrases: 

Question 1.
Write the opposite of the following in the form of advice using different words and phrases:
(a) You do not travel × you should travel, as much as you can.
(b) You do not appreciate yourself × …………………..
(c) You kill your self-esteem × you should keep up your self- esteem.
(d) You become a slave of habits ×………………….
(e) You refuse to speak to strangers ×……………………
(f) You do not change your life ×…………………….
(g) You refuse to take a risk × ………………….
Answer:
(a) You do not travel × you should travel, as much as you can.
(b) You do not appreciate yourself × You should appreciate yourself.
(c) You kill your self-esteem × You should keep up your self-esteem.
(d) You become a slave of habits × Don’t become a slave of habits.
(e) You refuse to speak to strangers × You should speak to strangers.
(f) You do not change your life × You should change your life.
(g) You refuse to take a risk × You should always be ready to take a risk.

7. Go through the following steps and discuss in pairs about the facts mentioned in it. Write a paragraph using the points. Give another interesting title.

Question 1.
Go through the following steps and discuss in pairs about the facts mentioned in it. Write a paragraph using the points. Give another interesting title.

Answer:
Mould your living for Brighter Life
Everyone in the world craves for happy life. Everyone has his own concept of happy life. What, in general, can we do for living better life? Living wise and virtuous life is living happy life. Here are some facts and ways of living better life.

You should give up all your bad habits. Bad habits can spoil your whole life and your happiness. Resolve to get rid of one bad habit at a time and finish them off determinently. Never allow negative thoughts to enter your mind. Be always positive. Positive attitude will lead you to happiness and negative thoughts affect your life as well as others around you. Be confident and trust yourself and love whatever you do for good life.

You must be a good learner. Learn from any small things beneath the sun. Enrich your mind and soul by becoming a lifelong learner. Every moment of learning will give you a new experience of life. That also keeps you updated and gives you knowledge of vivid visions of glory.

Sharing and caring are two very important aspects of happy life. Share your sorrows and happiness with others. Take care of those who are around you. You will get love and respect from them. It is our moral abligation and that gives us satisfaction. Be humble to everyone who meets you on the way of your life. Respect and welcome everyone with smile. That gives you joy of your life. If you follow all these rules and values, you will surely live better life.

8. Complete the following table with the things in your life which help you to change your habits and routine.

Question 1.
Complete the following table with the things in your life which help you to change your habits and routine.

Answer:

If I do this	I shall….
If I travel	I shall widen my worldly knowledge and experience.
If I read	I shall be wise and knowledgeable.
If I change my bad habits	I shall lead a gentle and civilized life.
If I play continuously on a mobile phone	I shall miss the pleasures of playing on a playground.
If I don’t make friends	I shall live dull, tedious, solitary and secluded life.

9. Everyone needs inspiration to move ahead or make progress in our life. There are some things which inspire us to live better. What are those things?

Question 1.
Everyone needs inspiration to move ahead or make progress in our life. There are some things which inspire us to live better. What are those things?
(a) Stories
(b) ………….
(c) ………….
(d) ………….
(e) ………….
(f) …………..
Answer:
(a) stories
(b) parent’s support
(c) dreams
(d) role model
(e) faith in your own diligence
(f) motivation.

10. Complete the web diagrams with words that go with their topics.

Question 1.
Complete the web diagrams with words that go with their topics.

Answer:

11. Write about a day when you felt very happy. Use the following questions to help you. Think/Recollect a day.
Note down the points.

1. Do you remember the exact day and date?
2. Was it a special occasion or celebration?
3. What happened on that day?
4. How did you react to the things that happened on that day?
5. How did other people react when they saw you were so happy?
6. What did you do next?
7. What happened in the end?
8. Describe any other emotions you felt that day.

Now, with the help of the guidelines write a short paragraph of at least loo words about that happy day. Give a suitable title for your narrative/write-up.

Question 1.
Write about a day when you felt very happy. Use the following questions to help you. Think/Recollect a day.
Answer:

My Happiest Day
It was Wednesday, the 20th March, 2019. It was my birthday and also was the ‘Sparrows Day’. I had recently read an article about the ‘disappearing sparrows in Mumbai’. I felt very sorry about their miserable condition. From that day I was thinking of doing something for the poor sparrows. Then I decided to celebrate my birthday differently.

I had collected the material I required for making the sparrows happy. I started to set up an open bird- cote near the window of my house. I made a box of light wooden planks. Then I nailed two steel bowls of water on both sides of the cote. I put some grains and seeds on the cote. I filled the bowls with water. I also put some sparrow food inside the box. The box was big enough for the sparrows to move in and out.

Then I waited for the sparrows to come. In the beginning they did come near the cote but did not enter in the cote. They were afraid. But soon, after some hesitation, they began to alight on the cote one after another. They ate grains and drank water.

They chirped and twittered. The whole atmosphere was filled with joy at the sight of the twittering tiny sparrows. My parents and neighbours were very happy and thanked me for the gift I gave them on my birthday. The sparrows were assured that they were safe and no harm was done to them.

It was the biggest and the happiest day of my life. Everyone spoke high of me and praised me for my kind act. My joy knew no bounds. I was feeling proud that I could do something nice for the sparrows in my own small way.

12. Use Internet or any hook to write four inspirational or motivational quotes, related to the message/s in the poem.

Question 1.
Use Internet or any hook to write four inspirational or motivational quotes, related to the message/s in the poem.
Answer:
1. The path from dreams to success does exist, may you have the vision to find it, the courage to get on to it and perseverance to follow it.
2. Variety is the spice of life.
(Students should try to find more such quotes from internet/books.)

My English Coursebook 10th Digest Chapter 2.1 You Start Dying Slowly Additional Important Questions and Answers

Read the extract and do the activities:

Simple Factual Activity:

Question 1.
Say whether the following pieces of advice by the poet are Right or Wrong:
Answer:

1. Appreciate your own good qualities. – Right
2. You should kill your self-esteem. – Wrong
3. Be a slave of your bad habits. – Wrong
4. Don’t bother to change the routine. – Right
5. Avoid strong feelings and their unsteady emotions. – Wrong
6. When you are not satisfied even then don’t change your life. – Wrong
7. Go after your dream. – Right
8. Show the courage to risk something. – Right

Complex Factual Activities:

Question 1.
Complete the Web:
(Answer is directly given.)
Answer:

Question 2.
What things can lead to slow death?
Answer:
Following things can lead one to a slow death. If one ignores travelling, reading, listening to the sounds of life, knowing one’s own qualities, keeping your self-respect, telling others to help you, then one can lead to slow death. Also, if one becomes a slave of one’s habits, does the same things every day without changing the routine, wears the same colours, avoids speaking to strangers, one can lose his/her happy future.

Question 3.
What is it that makes life worth living? Give four points:
Answer:

1. Be passionate.
2. If we are not satisfied with our job or love, change our ways of Life.
3. Be ready to take any risk courageously.
4. Go after our dreams with perseverance.

Question 4.
Complete the following lines with the help of the extract:
(Answers are directly given and underlined.)
Answer:
1. Passions and their emotions shine your eyes and beat your heart fast.
2. If you are not satisfied with your job or love, change your life.

Activity-based on Poetic Devices:

Question 1.
Give your own rhyming words for
1. read and
2. change.
Answer:
1. read – feed
2. change – range

Question 2.
Find out a pair of rhyming words from the extract.
Answer:
Passion – emotion.

Question 3.
Give your own rhyming words for:
1. job
2. fast
Answer:
1. job – rob
2. fast – last.

Appreciation of the Poem

1. Title: The title of the poem is-“You start dying slowly…”
2. Name of the poet: This poem was written by the poet Pablo Neruda.
3. Rhyme scheme: There is no rhyme scheme in the poem. It is written in ‘free verse’ style.
4. Figure of speech (Any one): Apostrophe, Repetition, Antithesis.
5. Theme/Central Idea: (in 2 or 3 lines) The theme of the poem in short is like this: Life must flow and renew itself at every moment of its being. We live fully only when we enrich ourselves with new knowledge, wide experience, fresh emotions, daring encounters and exciting challenges. If we settle for a life that is stagnant, repetitive or conventional, we start dying slowly instead of living the life fully.

English Workshop
(Based on Whole Poem)

Question 1.
The poet has left the last stanza incomplete. What line will you add to complete it?
Answer:
Added line will be – you will lose your hope of happy future.

My English Coursebook 10th Digest Pdf Unit 2

• You Start Dying Slowly … Class 10 English Solutions
• The Boy who Broke The Bank Class 10 English Solutions
• The Twins Class 10 English Solutions
• An Epitome of Courage Class 10 English Solutions
• Book Review – Swami and Friends Class 10 English Solutions
• World Heritage Class 10 English Solutions

Class 10 English Chapter 3.1 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 3.1 If … Notes, Textbook Exercise Important Questions and Answers.

If … Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.1 If … Textbook Questions and Answers

Warming up:
Chit-chat:

Form groups and chat.

Question 1.
How do you react when your parents scold you?
Answer:
My parents do not scold me without any rhyme or reason. If they scold me, it should be my mistake. Whenever they get angry and scold me, I try to keep mum so that they cool down. I also accept my mistake frankly if that is the only reason of their scolding.

Question 2.
How do you feel when someone insults you?
Answer:
When someone insults me, I try to find out the reason why he/she behaves like that. If there is a mistake from my side I try to avoid the same mistake again. I never get angry even if someone insults me for my petty mistake.

Question 3.
How would you react when you are cheated by your friend?
Answer:
I am quite sure that any of my friend wouldn’t dare to cheat me. But if it happens I would try to make him/her realize whatever he/she has done is very wrong. And whatever he/she has done is not good for him/her too.

Question 4.
Why is it wrong to make a difference among friends who belong to a different class, colour or community?
Answer:
We are friendly with those who are good at soul and mind. When our behaviour and mind match with each other, we become friends. I personally feel that friendship is not built on the basis of caste, colour or community. It develops on the basis of how we understand one another.

1. Complete the table by providing suitable responses to the given actions:

Question 1.
Complete the table by providing suitable responses to the given actions:
(Answers are directly given.)

Answer:

Action	Response
1. You are punished by the teacher without any reason.	I shall not lose my temper but I shall talk to the teacher afterwards to clear the doubt.
2. Your friends spread rumour about you.	I shall try to keep myself cool and confident and try to find out the reason.
3. Someone doubts you.	I shall try to clear his/her doubts about me personally.
4. Your relative blames you for something.	I shall try to find out the reason and I shall convince him/her not to blame me un­necessarily.
5. Someone hurts you.	I shall try to keep away from such people but I shall definitely introspect.

2. Complete the sentences meaningfully and share them with the class:

Question 2.
Complete the sentences meaningfully and share them with the class:
(Answers are directly given and underlined.)

1. If you read books, you will gain knowledge.
2. If you do exercise daily, ………………………… .
3. If ……………………… , you will pass the exam.
4. If ……………………….., …………………………….. .
5. ……………………………, If …………………………… .

Answer:

1. If you read books, you will gain knowledge.
2. If you do exercise daily, you will become healthy.
3. If you work hard, you will pass the exam.
4. If you respect others, others will respect you.
5. We should accept the truth, if we know it very well.

3. Classify the following into weaknesses and strengths:

Question 1.
Classify the following into weaknesses and strengths:
fear, confidence, clarity, confusion, worry, courage, cowardice, compassion, bravery, hesitation, punctuality, laziness, anger, faith, patience, ambition, generous, impatient, cheerful, tolerant, arrogant, aggressive.

Answer:

Weaknesses	Strengths
fear, confusion, worry, cowardice, hesitation, laziness, anger, impatience, arrogant, aggressive	confidence, clarity, courage, compassion, bravery, punctuality, faith, patience, generous, cheerful, tolerant, ambition

English Workshop:

1. Read the following bits of advice and state whether you Agree or Disagree with them:

Question 1.
Read the following bits of advice and state whether you Agree or Disagree with them:

Answer:

Advice	Answer
1. Get angry when others commit mistakes.	Disagree
2. Run away from troubles.	Disagree
3. Get angry when others blame us	Disagree
4. Reconstruct something we have built with care even if it has been broken by others.	Agree

2. Pick out and enlist the positive and negative qualities in respective columns from the extract:

Question 2.
Pick out and enlist the positive and negative qualities in respective columns from the extract:
(Answers are directly given)

Answer:

Positive qualities	Negative qualities
keep your head	lose your head
1. trust yourself	1. doubt others.
2. be truthful	2. deal in lies.
3. be smart	3. give way to hating.

3. Why do the lines in the poem begin with, ‘If you can …?’ What effect does this have?

Question 1.
Why do the lines in the poem begin with, ‘If you can …?’ What effect does this have?
Answer:
The lines in the poem begin with ‘If you can… ’ because the poet insistently wants to emphasise the importance of his good advice and attract his son’s attention to every piece of advice given by him. The repetition of the lines has a musical effect.

4. Look at the use of opposite reactions in the Poem.

Question 1.
Look at the use of opposite reactions in the Poem.
For example, “If you can keep your head when all about you are losing theirs”. Find four other such opposite reactions from the extract.
Answer:

1. or being lied about, don’t deal in lies.
2. or being hated, don’t give way to hating.
3. you can think and not make thoughts your aim.
4. you can trust yourself when all men doubt you.

5. Complete the following:
(Answers are directly given and underlined.)

Question (a)
Say WHAT …………….
are the two imposters ? …………………….. .
can the unforgiving minute be made up of? …………………….. .
Answer:
Say WHAT …………….
are the two imposters ? Triumph and Disaster.
can the unforgiving minute be made up of? sixty seconds, worth of distance run.

Question (b)
Say WHO …………….
should you trust, when doubted? …………………….. .
can you talk with and walk with? ……………………… .
Answer:
Say WHO …………….
should you trust, when doubted? oneself.
can you talk with and walk with? crowd and kings.

Question (c)
Say WHEN ……………..
can the Earth become yours? …………………….. .
should you start re-building with old tools? …………………….. .
Answer:
Say WHEN ……………..
can the Earth become yours? when we can make good use of every single minute.
should you start re-building with old tools? when we watch things created by us being broken up.

Question (d)
Say WHY ………….
do knaves twist the truth? …………………….. .
should you consider all men equally important? …………………….. .
Answer:
Say WHY ………….
do knaves twist the truth? to make trap for fools.
should you consider all men equally important? because neither foe nor friend can hurt us.

6. What should be our attitude towards the people of different strata and classes?

Question 1.
What should be our attitude towards the people of different strata and classes?
Answer:
Our attitude towards the people of different strata and classes should be positive and fair. We should treat all of them equally. We should not discriminate them on the ground of race, gender, class or religion. We may keep company with the rich but at the same time you should connect with the common man and the poor. Whatever their place in the society intermingle with them wholeheartedly. We should make efforts to integrate with all of them.

7. What, according to Rudyard Kipling, is the highest quality that makes a man a true human being?

Question 1.
What, according to Rudyard Kipling, is the highest quality that makes a man a true human being?
Answer:
According to Rudyard Kipling, treating all people equally without any discrimination makes a man a true human being.

8. Identify the figures of speech used in the following lines : (Choose from the brackets.)

Question 1.
Identify the figures of speech used in the following lines : (Choose from the brackets.)
(Simile/Repetition/Antithesis/Personification/ Metaphor/Alliteration/Apostrophe)
Answer:

1. “If you can keep your head when all about you are losing theirs” – Antithesis
2. “If you can meet with Triumph and Disaster and treat those two imposters just the same” – personification
3. “And yet don’t look too good, nor talk too wise” – Repitition
4. With worn-out tools – Alliteration

9. Write a letter to your parents, thanking them for advising you; when you were in a confused state of mind. Cover up the following points in the body of the letter:

Question 1.
Write a letter to your parents, thanking them for advising you; when you were in a confused state of mind. Cover up the following points in the body of the letter:

• Your problem and confusion.
• The advice of your parents.
• How you followed their advice.
• How the problem got solved.
• Your deep gratitude to them.

Answer:
Prathamesh Purandare,
10, K.B.P. Boy’s Hostel,
Satara – 415 001.
23rd Nov., 2020.
Dear Aai and Baba,

I am extremely happy to write this letter and thank both of you for your good advice. Actually when I joined the hostel, I was not willing to stay here any longer. I couldn’t adjust to the environment and even with the boys here. But in Diwali vacation you both convinced me and told me, how to mingle with the boys here and even how to get accustomed to the conditions here, so now I am quite sure that I would live here happily. Whatever advice you have given, is definitely good for me.

When I came back here, the whole scenario of the hostel and my preconceptions about the hostel life got totally changed. Why I don’t know, but now I am very much happy to live here and intermingle with my hostel mates. If you had not advised me on this issue, I would have left the hostel long before. And my whole academic year would have gone wasted. Thank you very much for making me realize the importance of education and adjustment in the life. Thank you once again for whatever you have done for me. Convey my regards to Grandma and love to little Preksha. Waiting for your next letter as early as possible.

Your loving son,
Prathamesh

10. Draft a speech to be given during the farewell for Standard X on the topic Changes, I would like in the School Education of our State.

Question 1.
Draft a speech to be given during the farewell for Standard X on the topic Changes, I would like in the School Education of our State.

• Greeting and salutation
• Self introduction and introduction of the topic
• A catchy thought/episode/news etc. to start with
• 2 to 3 changes that you suggest with their reason
• Conclusion
• Thank you/greeting

Answer:
“Changes, I would like in School Education of our State ”

Honourable Chairperson, respected Headmaster and teachers.

I, Nikita Desai from Std. X-A wishing you a very pleasant morning. I am here to express my views on behalf of all my classmates and to bid farewell to our school, teachers and all of you.

After spending almost 10-12 years in this school, we are now capable to keep our steps out in a very different world. And I am sure being the students of this school; we would never fall short anywhere and in any field. I know the Chief Guest of today’s programme is the Education Minister of our state. So I take this opportunity to suggest some changes in the school education of our state.

The first and very important thing I would recommend is about the option. There should be internal option to each and every subject. The child should be free to opt whatever he or she likes. Teaching and learning process should not be monotonous. It should be interesting. Every child should take part in this process. Teacher should not be an authoritarian.

One more thing, I would suggest about the examination. Examination should not be mandatory. Even upgradation of a child should be based on his / her internal performance. Written examination should not be given the whole credit. There should not be a burden of homework. It should be done at school.

I know, it is quite difficult to implement everything all of a sudden. But if you go step-by-step, it is quite a feasible suggestion. I know education in Maharashtra is better than other states. But if we make these changes, teaching and learning will be more enjoyable. I hope you will try to understand the views of every child.

Wishing my friends all the best for their examination and for their bright future life. Thank you for listening to me carefully and attentively.

Jai Hind.

Project:

Question 1.
Rudyard Kipling’s work is known to all of us. Write at least five poems of Kipling in your ; notebook and submit it to your teacher. You f can take help of your school library or search for these poems on the internet.

Question 2.
Rudyard Kipling’s book, entitled ‘The Jungle Book’ is famous world wide. Its theme and setting of the story attracts the readers from the beginning. Write a book review of Kipling’s book ‘The Jungle Book’ in 100 to 150words.

Language Study:

1. Look at the following sentences:

Question 1.
Look at the following sentences:
1. If I practise hard, I shall win the game.
2. If you buy a new car, it will cost you a lot of money.
Each of those sentences has two clauses – main clause and subordinate clause.

Here, the subordinate clause indicates ‘possibility’ or ‘likelihood’. The tense of a subordinate clause depends on the main clause.

Complete the following sentences:

Question 1.
Complete the following sentences:
(Answers are directly given and underline.)
a. If I like it, ………………………….. .
b. If it rains, ………………………….. .
c. If ………………………….., you would catch the train.
d. If she had obeyed her parents, ………………………….. .
Answer:
a. If I like it, I will buy it at any cost.
b. If it rains, I will remain at home.
c. If you came on time, you would catch the train.
d. If she had obeyed her parents, she would have saved her life.

2. Pick out lines that contain the following figures of speech.

Question (a)
Antithesis (Opposite ideas): ………………………………………… .
……………………………………………………………………………….. .
Answer:
Antithesis (Opposite ideas): If you can trust yourself when all men doubt you.

Question (b)
Personification: …………………………………………………………. .
……………………………………………………………………………….. .
Answer:
Personification: If you can meet with Triumph and Disaster….

Question (c)
Repetition: ………………………………………………………………. .
……………………………………………………………………………….. .
Answer:
Repetition: If you can dream and not make dreams your master.

Question (d)
Metaphor: ………………………………………………………………… .
……………………………………………………………………………….. .
Answer:
Metaphor: And stoop and rebuilt them up with worn-out tools.

My English Coursebook 10th Digest Chapter 3.1 If … Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. When the people around us doubt us, we should trust ourselves.
2. We can dream but we should not be slave to our dreams.
3. We can bear to hear the truth spoken by dishonest people.
4. When all people around us are unable to act in sensible way, we should keep our head cool.

Question 2.
Read the following bits of advice and state whether you Agree or Disagree with them:
Answer:

Advice	Answer
1. Keep friendship with all classes of people.	Agree
2. Hate the rich people and help the poor.	Disagree
3. We should treat everyone equally.	Agree
4. If we use every minute for the sake of good, we will be a real ‘human being’.	Agree

Question 3.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. We should not lose the common touch even while walking with the kings.
2. If we treat everyone equally, neither foes nor loving friends can hurt us.
3. The speaker in this poem is ‘the father’.
4. The poem is addressed to ‘the son’.

Complex Factual Activities:

Find the line/lines from the extract as a proof for the following explanations:

Question 1.
If you watch the things created by you are being broken, you can build them up by using worn out tools.
Answer:
or watch the things you gave your life to broken, And stoop and build’em up with worn-out tools :

Question 2.
You should treat both Triumph and Disaster in the same way as they treat you.
Answer:
If you can meet with Triumph and Disaster. And treat those two imposters just the same;

Question 3.
How should you react when someone lies about you and hates you?
Answer:
If someone lies about me, I will not tell such lies to others about him/her. And if someone hates me I will not allow myself to be controlled by his / her hatred and I would not appear to be perfect or show off my knowledge.

Question 4.
What does the poet call people who twist the truth to suit them?
Answer:
The poet calls “knaves” to the people who twist the truth to suit them.

Question 5.
Match the following idiomatic expressions in column ‘A’ with meaning in column ’B’:

Column ‘A’	Column ‘B’
1. lose the common touch	(a) keep one’s goodness or morals under any condition
2. unforgiving minute	(b) refuse to interact with common people
3. keep one’s virtue	(c) to be a good, perfect human being
4. to be a man	(d) time that does not wait for anyone

Answer:

1. lose the common touch – refuse to interact with common people
2. unforgiving minute – time that does not wait for anyone
3. keep one’s virtue – keep one’s goodness or morals under any condition
4. to be a man – to be a good, perfect human being

Question 6.
Pick out and enlist the positive and negative qualities in respective columns from the extract: (Answers are directly given.)
Answer:

Positive qualities	Negative qualities
1. walk with the kings	lose the connect with common man
2. treat all people equally	differentiate people unfairly

Activities based on Poetic Devices:

Question 1.
Write down all musical pairs from the extract and add your own rhyming word for each of them.
Answer:

Musical pairs	Added rhyming word
you  – too	two
waiting – hating	rating
lies – wise	prize
master – disaster	monster
aim – same	claim
spoken – broken	grown
fools – tools	wools

Question 2.
Name the figures of speech:
Answer:
1. If neither foes nor loving friends can hurt you. – Antithesis
2. Yours is the Earth and everything that’s in it. – Tautology

Question 3.
Find and write the rhyming pairs from the extract and add your own rhyming word for each of them
Answer:

Rhyming pairs	Added rhyming word
1. virtue – you	too
2. touch – much	such
3. minute- it	wit
4. run – son	fun

Appreciation of Poem:

1. Title: The title of the poem is ‘If’.
2. Poet: The poet of this poem is Rudyard Kipling.
3. Rhyme scheme: The rhyme scheme for the ; first stanza is ‘aaaa’. All the other five stanzas have the rhyme scheme ‘abab’.
4. Figure of speech (Any 1): Antithesis, Tautology, Personification anaphora.
5. Theme / Central Idea: The central idea of the poem is certain valuable pieces of advice ; imparted by a father to his son.

Several of the lines in the poem begin with the conjunction ‘if’. ; (The very title of the poem is ‘If’.) The theme j running through the poem is that ‘if the son ; fulfils certain conditions, he can be rest assured of certain favourable results’. Both the conditions and the results have a direct bearing upon the lives of all young people.

My English Coursebook Standard Ten Digest Answers Pdf Unit 3

• If … Class 10 English Solutions
• A Lesson in Life from a Beggar Class 10 English Solutions
• Stopping by Woods on a Snowy Evening Class 10 English Solutions
• Let us March! Class 10 English Solutions
• The Alchemy of Nature Class 10 English Solutions

Class 10 English Chapter 3.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 3.3 Stopping by Woods on a Snowy Evening Notes, Textbook Exercise Important Questions and Answers.

Stopping by Woods on a Snowy Evening Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.3 Stopping by Woods on a Snowy Evening Textbook Questions and Answers

Warming up:
Chit-chat

Share this chat with your classmate:

Question 1.
Where did you go for a picnic recently?
Answer:
Recently I went to Mahabaleshwar.

Question 2.
Who all accompanied you?
Answer:
My family members accompanied me.

Question 3.
Why did you select that picnic spot?
Answer:
It is very close to Mumbai. We could enjoy the scenic beauty, invigorating and refreshing climate so we selected that picnic spot.

Question 4.
What games/food/sights did you enjoy there?
Answer:
We enjoyed Antakshari on the way. We also enjoyed veg, non-veg food. We visited different points, Venna lake, Panchgani and Pratapgarh.

Question 5.
What did you feel when it was time to return home?
Answer:
The memories of our pleasant picnic were unforgettable. The picnic was a nice change in our dull routine life. We returned home happily with refreshed minds.
(Note: Students may share their own experience with classmates based on the above guidelines.)

1. Look at the picture given on textbook page 101 and frame questions:

Question 1.
Look at the picture given on textbook page 101 and frame questions:

(a) Where are the trekkers trekking?
(b) …………………………………………… .
(c) …………………………………………… .
(d) …………………………………………… .
(e) …………………………………………… .
Answer:
(a) Where are the trekkers trekking?
(b) Which season is it?
(c) What equipment do you think they are carrying?
(d) In which region of India do you find such trekkers?
(e) What is the role of mountaineers in such trekking?

2. Form group of 4 to 6 students. Every student should close his/her eyes. As the group leader reads aloud the following lines, the students try to create a picture in his/her mind. Later, each one gives a heading for each description.

Question (a)
Bright blue sky – soft white clouds sweeping by tiny specks of birds flying high – sun playing hide and seek behind the clouds.
Heading: ………………………….. .
Answer:
Heading: The Enchanting Beauty of the Sky.

Question (b)
Miles of smooth barren land – sparkling sand stretched till the horizon, in wave – like forms – thorny, cacti propping here and there – an occasional cluster of palms provide a shady spot – a carvan of camels moving in a line in the distance.
Heading: ………………………….. .
Answer:
Heading: Life in the Desert

Such a figurative description that creates mental pictures, in the mind of the reader/listener is called Imagery. It is a poetic device that enhances the poem.

Compose in your group, a four to six-line poem, which contains imagery.

(1) A host of golden daffodils,
Beside the lake, beneath the trees,
Fluttering and dancing in the breeze,
Continuous as the stars that shine
And twinkle on the milky way.

(2) The night was black as ever,
but bright stars lit up the sky in beautiful and
varied constellation which were sprinkled
across the astronomical landscape.

English Workshop:

1. Put (✓) mark in front of True statement or (✗) mark in front of False statement:

Question 1.
Put (✓) mark in front of True statement or (✗) mark in front of False statement:
(Answers are directly given.)
Answer:

1. The speaker stops to watch rain falling among the trees. (✗)
2. The owner of the woods is known to the speaker. (✓)
3. The horse is worried about the cold and wants to keep going. (✗)
4. The speaker doesn’t emphasize upon the beauty of woods he is passing through. (✗)

2. Find outline/lines from the poem as a proof for the following explanation:

Question (a)
There is no one to catch the speaker trespassing.
Answer:
He will not see me stopping here
To watch his woods fill up with snow.

Question (b)
The little horse draws his master’s attention.
Answer:
He gives his harness bells a shake
To ask if there is some mistake.

Question (c)
His horse seems anxious to keep going.
Answer:
My little horse must think it queer
To stop without a farmhouse near.

Question (d)
The speaker prefers to stay but is forced to move onwards.
Answer:
But I have promises to keep And miles to go before I sleep ….

Question (e)
The poem is set in bygone era.
Answer:
He gives his harness bells a shake. Shows that the poem is set in the bygone era.

3. The poem is believed to have a reference to the poet’s life itself. What could the following signify? Choose from the brackets below:

Question 1.
The poem is believed to have a reference to the poet’s life itself. What could the following signify? Choose from the brackets below: (duties and responsibilities/old age/life/death/ everlasting peace)
Answer:

1. The speaker’s journey – life
2. Snowy Evening – old age
3. Lovely, deep, dark woods – everlasting peace
4. Promises – duties and responsibilities
5. Sleep – death

4. Tell whether the rhyming scheme of the following stanzas is right or wrong. Give the correct rhyme scheme for the wrong one:

Question 1.
Tell whether the rhyming scheme of the following stanzas is right or wrong. Give the correct rhyme scheme for the wrong one:
Answer:

1. stanza 1 – aaba : right
2. stanza 2 – bbcb : wrong – it is ‘aaba’
3. stanza 3 – ccdc : wrong – it is ‘aaba’
4. stanza 4 – dded : wrong – it is aaaa’

5. Give your own rhyming words for the following: (Answers are directly given.)

Question 1.
Give your own rhyming words for the following: (Answers are directly given.)
Answer:

1. house – spouse
2. woods – goods
3. easy – busy
4. wind – skinned
5. dark – bark
6. watch – botch

6. Match the lines of the poem with their figures of speech:

Question 1.
Match the lines of the poem with their figures of speech:

Answer:

1. Whose woods these are I think I know – Inversion
2. The woods are lovely, dark and deep – Alliteration
3. And miles to go before I sleep
   And miles to go before I sleep. – Repititon
4. My little horse must think it queer – personification

7. Match the words given in Group A with their meanings in Group B:

Question 1.
Match the words given in Group A with their meanings in Group B:

Answer:

1. mistake – error
2. downy flakes – soft snow falling
3. woods – jungle
4. queer – strange

8. Complete the following web-diagrams by adding suitable describing words in the boxes.

Question 1.
Complete the following web-diagrams by adding suitable describing words in the boxes. (Answers are directly given.)

Answer:

9. Pick out lines from the poem that contain imagery. Write them in your notebook.

Question 1.
Pick out lines from the poem that contain imagery. Write them in your notebook.

10. Prepare a set of questions to interview:

Question (a)
a person who has just returned from a trek in the woods:
Answer:

1. Welcome back, how did you feel when you visited the woods?
2. What was the purpose of your visit?
3. Did you take any precautions while roaming in the woods?
4. Which strange or rare things did you find in the woods?
5. Did you come across any wild animals ? What was your feeling then?
6. How did you manage to get your food, water and other essential things ?
7. What difference did you find in the woods and the place where you live?
8. Were you able to fulfil your expectations from this visit?
9. What should be your role to conserve the woods?
10. Would you like to suggest the youngsters to undertake such expeditions? Why?

Question (b)
a person who has recently scaled Mt. Everest:
Answer:

1. Welcome back, What preparations did you make before the climb?
2. What did you do to stay fit when you were at the base?
3. What did you do to make your climb interesting?
4. What food did you take along with you while climbing?
5. What was the purpose of your adventure?
6. How did you face difficulties on the way to the top?
7. What is the memorable moment of your ascent?
8. What was the hardest adjustment you had to make during the ascent?
9. What were your feelings when you scaled the peak?
10. What message would you give to the youngsters?

My English Coursebook 10th Digest Chapter 3.3 Stopping by Woods on a Snowy Evening Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. The speaker stops in the woods.
2. Winter season of the year is described in the poem.
3. The day described in the poem is evening.
4. The speaker is riding on his little horse.

Question 2.
Fill in the blanks:
(Answers are directly given.)
Answer:

1. The person who owns the woods lives in the village.
2. The speaker stopped his horse at a place between the frozen lake and the woods.
3. The speaker was really captivated by the lovely, dark and deep woods.
4. The little horse gives a shake to its harness bells attached to its neck.

Question 3.
List the sounds mentioned in the poem.
Answer:
harness bells, sound of wind, sound of soft feathers like snow flakes falling.

Question 4.
On what date every year is the darkest evening?
Answer:
On 21st December.

Complex Factual Activities:

Question 1.
Why does the traveller have to leave the lovely woods?
Answer:
The traveller is really captivated by the lovely woods. He is supposed to discharge his duties on time. He promises himself to keep his word. So he has to leave the lovely woods to keep his word.

Language Study:

Question 1.
Write your own lines using the words given below: (Answers are directly given.)
Answer:
(a) village: Life in my village, I long to live.
(b) wind: Wind was twisting the heads of trees.
(c) frozen: With frozen heart I stared at the remains of my dear friend.
(d) promise: Let every day of yours dawn, with the promises of new light.

Appreciation of the poem:

1. Title : The title of the poem ‘Stopping by Woods on a Snowy Evening’.
2. Poet: The poet of this poem is Robert (Lee) Frost.
3. Rhyme scheme: The rhyme scheme of the first three stanzas is ‘aaba’. The final stanza has a uniform rhyme of ‘aaaa’.
4. Figure of speech (any 1): Inversion, alliteration
5. Theme / Central Idea: The theme of the poem is that a traveller on horseback stops by a little forest on a winter evening.

The little forest in the speaker’s own words, is lovely, dark and deep. Though he is greatly fascinated by the scene, the call of duty urges him to move on. He reminds himself that he must discharge his duties before it is too late.

My English Coursebook Standard Ten Digest Answers Pdf Unit 3

• If … Class 10 English Solutions
• A Lesson in Life from a Beggar Class 10 English Solutions
• Stopping by Woods on a Snowy Evening Class 10 English Solutions
• Let us March! Class 10 English Solutions
• The Alchemy of Nature Class 10 English Solutions

Class 10 English Chapter 4.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 4.4 Unbeatable Super Mom – Mary Kom Notes, Textbook Exercise Important Questions and Answers.

Unbeatable Super Mom – Mary Kom Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 4.4 Unbeatable Super Mom – Mary Kom Textbook Questions and Answers

Warming Up:
Chit-Chat

1. Discuss in your class.

Question 1.
Indian women who have made it to International Levels in sports and games. Discuss the following points about each of them.
Answer:
(a) Name of the sportsperson. – Lauta Shivaji Babar
(b) Sport or Game-Long distance running.
(c) Level reached-World championship, Olympic Games.
(d) Outstanding achievem ents-Sportsperson of the Year Award 2015.
(e) Awards/Prizes/Titles-Arjuna Award by Government of India.
Indian Sports Award by FICCI and Ministry of Youth Affairs and Sports.

1. Fill in the Table:

Question 1.
Fill in the Table: (Answers are directly given.)

Answer:

Name of Sport/Game	Place where played	Individual or Team Event	Sports Equipment
1. Boxing	Ring	Individual	Boxing gloves
2. Shooting	Shooting range	Individual	Rifle, shooting stand
3. Hockey	Ground	Team	Hockey stick and ball
4. Football	Ground	Team	Football, Net
5. Badminton	Court	Individual/Pair	Racket and Shuttlecock
6. Kabaddi	Ground	Team

Question 2.
Complete the interview with an imaginary captain of Ladies Cricket Team of your Town/City/State. Conclude with a farewell message.
Answer:

Interview

Interviewer – J. Prasad (J. P.)
Captain – Vijetha Bhide (V. B.)

• J.P.: Good Morning. We are simply privileged and delighted to have the presence of the Captain j of our State Women’s Cricket Team, which won the final of the Inter State series in Mumbai, last week. Hello Vijetha, welcome to our show.
• V.B.: Thank you for inviting me. I am really grateful to the Government of Maharastra for recognizing my services to state women’s cricket team.
• J.P.: That’s great. You have shown your talent and performance in this Inter State series in Mumbai.
• V.B.: That’s right. The girls gave commendable performances, so the credit goes to the whole team.
• J.P.: Your individual performance was also great. It was a great feat for you.
• V.B.: Thank you. 48 runs in 40 balls is quite good and helping score for the team. Anjali co-ordinated well with me and so it was easy to reach the score.
• J.P.: Do you think regular practice is needed at the domestic level?
• V.B.: Yes, of course! More importantly there is huge need for more tournaments at the domestic level so that the girls can intermingle with the different talents in cricket.
• J.P.: Absolutely right. It gives confidence to girls. Do you think, the coach plays important role in your success? What is your opinion?
• V.B.: You are right. Without a coach how can we develop our game? He guides us at every stage and so we have reached up to this level.
• J.P.: What will be your next move and dream?
• V.B.: Now we will practise for the National level tournaments. And I think the girls have that calibre to pull off some trophies at the National level.
• J.P.: That’s really great. Wish you all the best for your future cricketing career.
• V.B.: Thanks a lot!

English Workshop:

1. Choose the correct alternatives:

Question (a)
What kind of text is it?
(i) story
(ii) speech
(iii) interview
(iv) essay
Answer:
(iii) interview

Question (b)
Which State does Mary Kom belong to?
(i) Maharashtra
(ii) Tamil Nadu
(iii) Kerala
(iv) Manipur
Answer:
(iv) Manipur

Question (c)
Who inspired Mary Kom and other youngsters in Manipur to choose boxing as a career?
(i) Dingko Singh
(ii) Charles Atkinson
(iii) Mangte Tanpa Kom
(iv) Adams
Answer:
(i) Dingko Singh

Question (d)
When did Mary Kom start her career?
(i) 2012
(ii) 2000
(iii) 2001
Answer:
(ii) 2000

2. Go through the text again and find out the name of cities and their importance in Mary Kom’s life. One is given for you. 

Question 1.
Go through the text again and find out the name of cities and their importance in Mary Kom’s life. One is given for you. (Answers are directly given.)
Answer:
(a) Kangthei – Mary Korn’s birth place.
(b) West-Bengal – Regional championship
(c) Pune – Preparation for the Olympics with male boxers.
(d) Manipur – State women’s boxing championship.

3. Write down the full forms of-

Question 1.
Write down the full forms of-
Answer:
(a) OGQ – Olympic Gold Quest
(b) IBN – Indian Broadcasting Network
(c) MTV – Music Television
(d) YPA – Yearly Plan of Action
(e) AIBA – The Amateur International Boxing Association.
(f) CNN – Cable News Network

4. Write the Factfile of Mary Kom, in your notebook.

Question 1.
Write the Factfile of Mary Kom, in your notebook.
Answer:
(a) Full Name – Mary Mangte Kom
(b) Native of – Kangthei village, Moirang Lamkhai in Churachandpur district of rural Manipur in eastern India.

(c) Early life and interests – Grown in humble surroundings of tenant farmers and helping her parents in farm related chores. She was interested in athletics initially and later turned to boxing.

(d) Special sports taken up – Boxing was her main sport.

(e) Inspired by – Dingko Singh who returned from Bangkok Asian games with a gold medal.

(f) Coach – Charles Atkinson.

(g) Early achievements:
1. Victory in the Manipur State Women’s Boxing Championship and the Regional Championship in West Bengal.
2. International debut at the first AIBA Women’s World Boxing Championship in United States.

(h) International achievement:
1. Five times World Boxing Champion and the only boxer to win a medal in every one of the six World Championships.
2. In 2012 Olympics she won a Bronze medal.

(i) Her passion – To make boxing popular among all Indians, especially women and girls.

(j) Future plan – To coach Indian women in boxing in future.

5. Glance through the text and find the special qualities of Mary Kom. Complete the web by putting different qualities of Mary Kom in the boxes: (Answers are directly given.)

Question 1.
Glance through the text and find the special qualities of Mary Kom. Complete the web by putting different qualities of Mary Kom in the boxes: (Answers are directly given.)

Answer:

6. ‘Super mom’ refers to an excellent mother. Give three reasons why ‘super’ has been added to the word ‘mom’ as in the title?

Question 1.
‘Super mom’ refers to an excellent mother. Give three reasons why ‘super’ has been added to the word ‘mom’ as in the title?
1. …………………………………………..
……………………………………………..
2. …………………………………………..
……………………………………………..
3. …………………………………………..
……………………………………………..
Answer:
1. It is quite difficult to balance home and profession and she has managed it like an outstanding woman.
2. Even though she is a successful sportswoman she gives more importance to her family so she has that super understanding.
3. Though a mother, she is an exceptional woman in Indian society to go out and make boxing a career. So she is a super mother.

7. Answer in your own words.

Question (a)
What makes the writer call Mary Kom ‘a legend’?
Answer:
A legend is a famous person, icon or superstar in a particular field. Mary Kom is a famous woman as an Indian boxer. The field is male dominated, but with her efforts and determination she earned name and fame, so in real sense she is a legend not only to the writer but also to all Indians and a real ‘torch-bearer’ for Indian women.

Question (b)
What prime quality did Mary Kom display during her first attempt in Olympic Games? What was her bad luck?
Answer:
Mary practised for Olympics with the male boxers. Her coach was not allowed to accompany her but she went on with confidence, because she had done her homework and was well prepared with her coach. She could play with good tactical knowledge. In semi-finals she was fighting against Adams, a clever counter puncher but Mary was scoring well, but the judges were not pressing the buttons and favouring her rival. So it was her bad luck that she lost in the semi-finals.

Question (c)
What does Mary Kom suggest, for India to win more Olympic Gold Medals?

8. Fill in the flow chart after rearranging the facts below in their proper order, as per the text:

Question 1.
Fill in the flow chart after rearranging the facts below in their proper order, as per the text:
(a) Mary Kom made her first appearance at international level.
(b) She sparred with male boxers in Pune.
(c) Mary Kom won the Manipur State Women’s Boxing Championship.
(d) She won a bronze medal in the 2012 Olympics.
(e) Mary Kom decided to take up boxing.

Answer:

9. Make sentences of your own using the following words:

Question (a)
debut:
Answer:
Sonu Nigam made his singing debut at a very early age.

Question (b)
elation:
Answer:
My father is a man who seldom gives away to elation of mind.

Question (c)
sponsor:
Answer:
The sports events of the club were sponsored by Seth Narayandas Zaveri.

Question (d)
reinforced:
Answer:
The pockets on my jeans are reinforced with double stitching.

Question (e)
humble surroundings:
Answer:
Many people in India live in humble surroundings.

10. Find antonyms of the following words from the text:

Question 1.
Find antonyms of the following words from the text:
(Answers are directly given and underlined.)
Answer:

1. arrogant × humble
2. disqualify × qualify
3. finally × initially

11. Imagine that you are the Captain of your team. A famous cricketer is going to visit your school. You are assigned the task to conduct an interview of that famous cricketer. Frame a set of 10 questions that you will ask the cricketer. Take help of the points given below:

Question 1.
Imagine that you are the Captain of your team. A famous cricketer is going to visit your school. You are assigned the task to conduct an interview of that famous cricketer. Frame a set of 10 questions that you will ask the cricketer. Take help of the points given below:
(a) Early Life
(b) Interest in this field
(c) Inspiration
(d) Coaching and guidance
(e) Achievement/Records
(f) Future plans
(g) Advice to youngsters
Answer:
Interview Questions to be asked to the cricketer:

1. Was it your passion to become a cricketer from your childhood?
2. Who inspired you to become a cricketer?
3. Did your parents help you in your decision? What was their role?
4. What are some of your superstitions before going in to bat?
5. Who is your idol in other games other than cricket?
6. In whose bowling did you score the most runs?
7. If you were not a cricketer what would you be then?
8. What are your future plans?
9. What message would you like to give to the young generation?
10. What is your best achievement till today?

12. Imagine that you are Captain of your team. A famous cricketer is going to visit your school. You are assigned the task to conduct an interview of that famous cricketer. Frame a set of 10 questions that you will ask the cricketer. Take help of the points given below.

Question 1.
Imagine that you are Captain of your team. A famous cricketer is going to visit your school. You are assigned the task to conduct an interview of that famous cricketer. Frame a set of 10 questions that you will ask the cricketer. Take help of the points given below.
(a) Early Life
(b) Training
(c) Achievement
(d) Future plans
Answer:
Mary Kom is a sportswoman who has made India proud with her glorious achievements as a boxer. Basically from Manipur, India, she was the eldest of four siblings and had to work hard from young age to support her family. She took care of her younger siblings and worked in the field with her parents to help them. She is the only Indian woman boxer to have qualified for the 2012 summer Olympics where she won a Bronze Medal.

She is also the first Indian woman boxer to get a Gold medal in Asian games and Commonwealth Games. She was trained by Charles Atkinson. Mary set a new standard in amateur boxing without ever competing in professional boxing. The AIBA awarded Mary Kom with the first AIBA Legends Award for promising boxing career. She is also the recipient of Padma Bhushan, Padma Shri and Arjuna Award for her tremendous achievement in Boxing. She is a legend for Indian women.

13. ‘What Men can do, Women can do better’. Divide your class in 2 groups. Let one group offer points ‘For the topic’ and the other, ‘against the topic’ given above. Note down the points in your notebooks, expand the points in two separate paragraphs of about 15 to 20 lines each. Suggest suitable titles for each:

Question 1.
‘What Men can do, Women can do better’. Divide your class in 2 groups. Let one group offer points ‘For the topic’ and the other, ‘against the topic’ given above. Note down the points in your notebooks, expand the points in two separate paragraphs of about 15 to 20 lines each. Suggest suitable titles for each:
Answer:
Two beautiful Creations of God-Men and Women

For the topic

Men cannot look after their family well compared : to women. It is still believed that men are supposed to be the bread winners and be able to support their wives and children. But now a days many women do this work very easily. Women have proved that they can do anything if given a chance. Now they have started working in Army with men.

In politics, they have proved that they can work better than men. Games like cricket, football, wrestling were the monopoly of men but now by entering in these fields they are proving they can do anything better than men. In astronomy, medicines, teaching they are in the forefront. It is important to remember that differences between men and women do not mean that one gender is less important than the other.

Against the topic

Being raised in a socially conscious environment, we believe men and women are generally equal and should be treated as such. But there are certain fields in which women can’t work as they do not possess the physical strength to work in adverse conditions like protecting our borders. They are rarely found as coal miners. Women cannot climb electricity poles and work on power transformers. They cannot fight in wars or battles. They are not found in off-shore oil drilling platforms.

My English Coursebook 10th Digest Chapter 4.4 Unbeatable Super Mom – Mary Kom Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
Name the following:

1. The warrior mentioned in the passage –
2. Native place of Mary Kom –
3. Mary Korn’s parents –
4. The sportsperson who won gold medal in Asian games –

Answer:

1. Mary Mangte Kom
2. Kangthei village, Moirang Lamkhai in Churachandpur district of rural Manipur in eastern India.
3. Mangte Tonpa Kom and Mangte Akham Kom.
4. Dingko Singh.

Complete the sentences:

Question 1.
Complete the sentences:

1. Kom grew up in
2. She came from a
3. She had an eager interest in
4. Mary Korn’s career started in

Answer:

1. Kom grew up in humble surroundings.
2. She came from a poor family.
3. She had an eager interest in athletics.
4. Mary Korn’s career started in 2000.

Question 2.
Answer in one-two words:
Answer:

1. Coach -Charles Atkinson
2. Interviewer – Sportskeeda correspondent Taru- kal Srivastava
3. Place of Training – Pune
4. Total medals won in 2012 Olympics by India – 6

Question 3.
State whether you Agree or Disagree with the following statements:
Answer:

1. Mary Korn’s coach was allowed to accompany her during her preparation for Olympics – Disagree
2. Mary practised with male boxers in Pune – Agree
3. Mary is the first Indian female boxer to win an Olympics medal for India – Agree
4. Dodgy judging was not at all the part of the reason for her loss in the semi-finals. – Disagree

Question 4.
Complete the following web chart. (Answers are directly given.)
Answer:

Choose the correct alternatives:

Question 1.
What did Mary Kom prefer being called?
(i) Super mom
(ii) Super woman
(iii) Super being
(iv) Super Boxer
Answer:
(i) Super mom

Question 2.
What would be a key factor in your conditioning for the Olympics?
(i) saturated fats
(ii) diet and nutrition
(iii) trophies and medals
Answer:
(ii) Diet and nutrition

Question 3.
Which traditional feminine activity is mentioned in the extract?
(i) washing
(ii) dusting
(iii) cooking
Answer:
(iii) cooking

Question 4.
Which award did Mary receive in 2009?
(i) Sahara Sports Award
(ii) Rajiv Gandhi Khel Ratna Award
(iii) Arjuna Award
Answer:
(ii) Rajiv Gandhi Khel Ratna Award

Complex Factual Activities:

Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
1. Mary Korn’s exceptional achievement is she is famed as a five times world Boxing Champion and the only boxer to win a medal in every one of the six world championships.
2. Mary Korn’s parents made their living by working as tenant farmers in jhum fields.

Question 2.
What has added to Mary Kom’s greatness as a boxing champion?
Answer:
Mary Kom made her debut at the first AIBA Women’s World Boxing Championship in United States and won silver medal in the 48 kg weight category. Her greatness is strengthened by the way she apologized to the whole nation for not being able to win the Gold Medal. It has added to Mary Kom’s greatness as a boxing champion.

Question 3.
How did Mary spend her childhood?
Answer:
Mary grew up in humble surroundings. She used to help her parents with farm related chores. She used to learn athletics initially and later boxing simultaneously. She had an eager interest in athletics since childhood.

Question 4.
Complete the following web:
(Answer is directly given and underlined.)
Answer:

Question 5.
What failed to pressurize Mary Kom during the Olympics?
Answer:
She was the only female representative from India and her coach Charles Atkinson was not allowed to accompany her to the Olympics failed to pressurize Mary Kom during the Olympics.

Question 6.
What can help Indian sportsmen to win more Olympic medals?
Answer:
More corporates should come in and sponsor players, so that the players don’t have to face financial pressure and can just focus on their game. More and more people should take up sports as a full-time career if we want to win more gold medals. This can help Indian sportsmen to win more Olympic medals.

Question 7.
What did OGQ do for Mary Kom?
Answer:
OGQ played a big role in shaping the boxing scene in India. OGQ really played an important part in Mary’s success. They helped her out whenever she needed something. They took care of everything Which helped her focus on her boxing and kept her stress-free.

Question 8.
What is Mary’s opinion about future of Indian boxing?
Answer:
According to Mary Kom the future of Indian boxing is bright. She is also sure that many boxers would win medals for India.

Question 9.
How did Mary Kom increase her weight?
Answer:
According to Mary diet and nutrition must be the key factor in conditioning body, but that is a neglected area in Indian sports. She had to focus on what to eat. When she started diet and nutritions, she put on her weight by 3 kg. And she could compete in 51 kg event instead of usual 48 kg.

Activities based on Vocabulary:

Question 1.
Give one word for the following explanation:
Answer:

1. The first public appearance – debut
2. One who makes history – legend
3. Farming, shifting cultivation – Jhum
4. Successful ending of a struggle or contest – victory

Question 2.
Find the full form of:
(Answers are directly given and underlined.)
Answer:
U.S. – United States

Use the following words in your own sentences:

Question 1.
legend:
Answer:
Lata is a legend in her own lifetime.

Find out antonyms of the following words from the text:

Question 1.
Find out antonyms of the following words from the text:
(Answers are directly given and underlined.)
Answer:

1. failure × success
2. rich × poor
3. died × born
4. urban × rural
5. defeat × victory

Question 2.
Pick out from the passage the verb forms of:
Answer:
1. birth – born
2. qualification – qualify

Question 3.
Pick out from the passage the noun forms of:
1. succeed
2. prepare
Answer:
1. succeed – success
2. prepare – preparation

Question 4.
Pick out from the passage the adjective forms of:
1. dodge
2. tactic
Answer:
1. dodge – dodgy
2. tactic – tactical

Find out opposite words for the following from the passage.

Question 1.
Find out opposite words for the following from the passage.
Answer:

1. hated × adored/admired
2. fair × unfair
3. inclusive × exclusive
4. losing × winning

Pick out from the passage the verb forms of the following:

Question 1.
Pick out from the passage the verb forms of the following:
Answer:

1. company – accompany
2. practice – practise
3. decision – decide
4. requirement – require

Pick out the noun forms of the following:

Question 1.
Pick out the noun forms of the following:
Answer:

1. add – addition
2. achieve – achievement
3. represent – representative
4. change – change

Pick out the adjective form of the following:

Question 1.
Pick out the adjective form of the following:
Answer:

1. finance – financial
2. confidence – confident
3. favour – favourite
4. proportion. – proportionate

Question 2.
Write down the full forms of –
Answer:

1. OGQ – Olympic Gold Quest
2. CNN – Cable News Network
3. IBN – Indian Broadcasting Network
4. MTV – Music Television
5. YPA – Yearly Plan of Action

Question 3.
Pick out from the passage the adjective forms of.
Answer:

1. nutrition – nutritional
2. female – feminine
3. tradition – traditional
4. saturate – saturated
5. addition – additional

Question 4.
Pick out from the passage the verb forms of. (Answers are directly given and underlined)
Answer:

1. competition – compete
2. negligence – neglect
3. cooking – cook
4. preference – prefer

Question 5.
Pick out from the passage the noun forms of.
(Answers are directly given and underlined.)
Answer:
1. aware – awareness
2. require – requirement

Question 6.
Pick out from the passage the adjective forms of.
Answer:

1. nutrition – nutritional
2. female – feminine
3. tradition – traditional
4. saturate – saturated
5. addition – additional

Question 7.
Pick out from the passage the verb forms of. (Answers are directly given and underlined)
Answer:

1. competition – compete
2. negligence – neglect
3. cooking – cook
4. preference – prefer

Question 8.
Pick out from the passage the noun forms of.
(Answers are directly given and underlined.)
Answer:

1. aware – awareness
2. require – requirement

Activities based on Contextual Grammar:

Question 1.
Choose the tail tags given in the brackets and complete the following sentences:
(isn’t she?, hadn’t he?, wasn’t he?, weren’t they?) (Answers are directly given and underlined.)
Answer:

1. Her father was a keen wrestler in his younger age; wasn’t he?
2. Dingko Singh had inspired many youngsters in Manipur, hadn’t he?
3. Her parents were tenant farmers in jhum fields, weren’t they?
4. She is famed as a five times World Boxing Champion, isn’t she?

Question 2.
Underline the subordinate clause in the given sentence and state its kind.
Enough has been said about this great warrior, who conquered the world.
Answer:
Enough has been said about this great warrior who conquered the world – Adjective clause.

Question 3.
Identify the tense:

1. Sometimes it becomes really difficult to keep them under control.
2. They took care of everything.
3. In a few years boxing will be very popular among everyone in India.
4. You have broken several stereotypes about the women in India.

Answer:

1. Simple Present Tense
2. Simple Past Tense
3. Simple Future Tense
4. Present Perfect Tense.

Pick out the subordinate clause and state its kind:

Question 1.
Do you think nutrition is a neglected area in Indian sports?
Answer:
Subordinate clause – (that) nutrition is a neglected area in Indian sports?
Kind-Noun clause.

Question 2.
Identify the tense:

1. Sometimes it becomes really difficult to keep them under control.
2. They took care of everything.
3. In a few years boxing will be very popular among everyone in India.
4. You have several stereotypes about the women in India.

Answer:

1. Simple Present Tense
2. Simple Past Tense
3. Simple Future Tense
4. Present Perfect Tense.

Pick out the subordinate clause and state its kind:

Question 1.
Do you think nutrition is a neglected area in Indian sports?
Answer:
Subordinate clause – (that) nutrition is a neglected area in Indian sports?
Kind-Noun clause.

Question 2.
That’s the best thing, that has happened to me
Answer:
Subordinate clause – that has happened to me.
Kind-Adjective clause.

Do as directed:

Question 1.
She came from a poor family.
(Rewrite as a negative sentence without changing its meaning.)
Answer:
She didn’t come from a rich family.

Question 2.
Her father was a keen wrestler.
(Rewrite the sentence in simple present tense.)
Answer:
Her father is a keen wrestler.

Question 3.
Charles Atkinson was not allowed to accompany Mary to the Olympics.
Answer:
Charles Atkinson was prevented from accompanying Mary to the Olympics.

Question 4.
Mary was the only female representative from India in boxing. (Make it negative.)
Answer:
No other female representative except Mary represented India in boxing.

Question 5.
Some of the decisions were unfortunate. (Make it negative.)
Answer:
Some of the decisions were not fortunate.

Question 6.
Some of the decisions did not work to my benefit. (Make it Affirmative.)
Answer:
Some of the decisions hardly worked to my benefit.

Underline the subordinate clause and state its kind: (Subordinate clauses are directly underlined.)

Question 1.
Underline the subordinate clause and state its kind:
(Subordinate clauses are directly underlined.)
Answer:
1. The male boxers were kind enough to practise with me, whenever I required them.
Kind: Adverb clause of time
2. I think more and more people should take up sports as a full-time career.
Kind: Noun clause.
3. India managed just 6 medals in the 2012 Olympics, even though we are a nation of 1.3 billion people.
Kind: Adverb clause of contrast/condition.

Question 2.
Complete the words by using correct letters:
Answer:

1. b o _ e r – boxer
2. t r _ i n – train
3. sp_rts – sports
4. f i _ h t – fight

Question 3.
Put the words in alphabetical order:
1. boxing, elation, success, change
2. awareness, award, already, achievement
Answer:
1. boxing, change, elation, success
2. achievement, already, award, awareness

Question 4.
Punctuate the following sentences:
1. mary said trained hard in pune and the male boxers were kind enough to practise with me whenever required them
2. interviewer asked mary kom what do you prefer being called super mom or super boxer
Answer:
1. Mary said, “I trained hard in Pune and the male boxers were kind enough to practise with me whenever I required them.”
2. Interviewer asked Mary Kom, “What do you prefer being called-Super Mom or Super Boxer?”

Question 5.
Make four words (minimum 3 letters each) using the letters in the word: ‘representative’
Answer:

1. present
2. native
3. rent
4. rate

Question 6.
Write related words as shown in the example: (Answer is directly given and underlined.)
Answer:

Question 7.
Complete the word-chain of verbs. Add four words, each beginning with the last letter of the previous word.
start, → t…………., …………., …………., ………….
Answer:
start, → treat, take, enter, redress.

1. Attempt anyone:

Question (a)
Make a meaningful sentence by using the phrase ‘to be successful.’ :
Ans.
Hardwork and perseverance are the key ; components to be successful in life.

OR

Question (b)
Add a clause to the sentence to expand it meaningfully:
This is our world
Ans.
This is our world where we can get strange experiences.

2. Attempt anyone:

Question (a)
Add prefix or suffix to make new words:
1. amaze
2. educate
Answer:
1. amaze – amazing
2. educate – educated, education

OR

Question (b)
Make a meaningful sentence using any one of the following words:
1. amaze
2. educate
Answer:
1. I was amazed at her general knowledge.
2. It is the duty of our government to educate every child of our country.

Personal Response:

Question 1.
Describe your favourite sportswoman.
Answer:
Saina Nehwal is my favorite sports woman. She is the ace badminton player representing India. She started playing badminton at a tender age of eight. She was trained by Nani Prasad and was under strict fitness regime prepared by her trainer. She proved her mettle in 2006 when she became under-19 National Champion in badminton. She is one of the athletes supported by ‘Olympic Gold Quest’-a foundation that supports athletes, who have potential to win Olympic gold.

Question 2.
Do you like games? Why?
Answer:
Yes. I like games because it makes me active and energetic. It builds my mental and physical power. It develops my concentration. Overall, it develops my personality so I play different games.

Question 3.
Do you think financial support is very necessary for the sportsmen? Why?
Answer:
The sportsmen whose financial condition is not good cannot afford proper diet due to lack of money. They can neither buy sports material necessary for them nor participate in some important events due to shortage of money. If they get good financial support, they can get training from a good coach to improve their game. So it is very necessary for them to get financial support.

Question 4.
Name some sportswomen you know:
Answer:

1. Saina Nehwal
2. P.V. Sindhu
3. Mithali Raj
4. Geeta Phogat
5. Sania Mirza
6. Anjali Bhagwat

Question 5.
What is Mary Kom more proud of being a boxer or a mother?
Answer:
It is well said, ‘The hand that rocks the cradle rules the world.’ She is more proud of being a mother because she knows with her hands she can make lives of her kids. Mother is next to God-in fact a visible God, so even on the ground she thinks about her children. Children are the first priority in her life, because she has to nurture her children and bring them up with love and care.

My English Coursebook 10th Class Solutions Pdf Unit 4

• The World is Mine Class 10 English Solutions
• Bholi Class 10 English Solutions
• O Captain! My Captain! Class 10 English Solutions
• Unbeatable Super Mom – Mary Kom Class 10 English Solutions
• Joan of Arc Class 10 English Solutions
• A Brave Heart Dedicated to Science and Humanity Class 10 English Solutions

Class 10 English Chapter 4.6 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 4.6 A Brave Heart Dedicated to Science and Humanity Notes, Textbook Exercise Important Questions and Answers.

A Brave Heart Dedicated to Science and Humanity Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 4.6 A Brave Heart Dedicated to Science and Humanity Textbook Questions and Answers

Warming up:
Chit-chat

Question 1.
Have you ever participated in or visited a science exhibition?
Answer:
Yes, last year I along with my friends participated in ward level science exhibition and selected for district level exhibition.

Question 2.
Did you observe/learn any new things there ? What are those ?
Answer:
Yes, we observed and learnt a lot there.

1. Everyone was busy in his/her experiment.
2. Everyone was trying to prove something. We learnt that if we work consistently we can achieve anything in our life.
3. The pairs or groups of students were working hard together to make the exhibit successful.

Question 3.
“Scientists have to work very hard and make many sacrifices for years to achieve success in their experiments”. Why?
Answer:
Hard work is the key to success. While working on any project they forget everything around them and concentrate on the experiment while doing so they sacrifice their health, hunger, family, likes, hobbies and then only they are able to carry out the undertaken experiment and get the results of it.

Question 4.
What is the difference between a discovery and an invention?
Answer:
Discovery is the process of finding information, a place or an object, especially for the first time. It is an act of finding something which is in existence but not known before. Invention is something that has never been made or processed before. It is something newly designed or created.

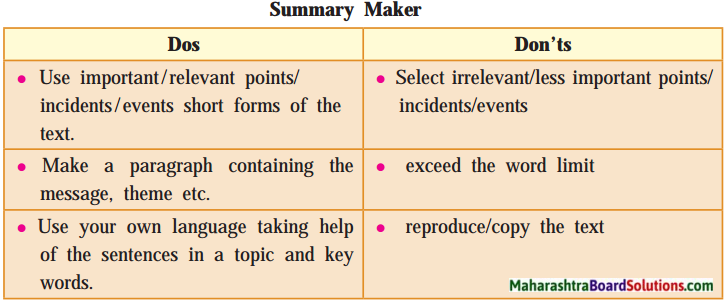
1. Discuss in pairs/groups about the precautions one has to take while working in a science laboratory. Write them in the form of Dos and Dont’s:

Question 1.
Discuss in pairs/groups about the precautions one has to take while working in a science laboratory. Write them in the form of Dos and Dont’s:

Answer:

Dos	Don’ts
1. Handle test tubes and glass apparatus with care.	1. Don’t touch chemicals with bare hands.
2. Inform the lab attendant if there is a problem.	2. Don’t eat, drink, chew gum or apply cosmetics in the lab.
3. Wash your hands before you leave the lab for the day.	3. Do not work with chemical until you are sure of their safe handling.
4. Wear appropriate safety attire when in the laboratory-safety goggles, lab aprons, etc.	4. Do not use the phone or computer with gloves on your hands.

2. Study the underlined Predicate in each of the sentences below and note the difference:

Question 1.
Study the underlined Predicate in each of the sentences below and note the difference:
Answer:
1. I met Debbie, [(verb (met) + noun (Debbie)]
We study Grammar, [verb (study) + noun (Grammar)]
(The object answers WHAT? or WHO? when asked to the verb.)

2. He become tired, [(verb (become) + complement (tired)]
They are hungry, [(verb (are) + complement (hungry)]
The verbs (became/are) incomplete without the words that follow (tired/hungry.) So ‘tired’ and ‘hungry’ are Complements of the verbs ‘became’ and ‘are’.)

3. She spoke softly.
They live here.
He turned early.
(The verbs in the Predicates are followed by Adverbials since they indicate
How?/Where/When the action in the verb takes place.)
Now Say whether the Predicate in the following sentence contain Object or Complement or Adverbial after the verb:
Answer:
(a) He looked upwards. Complement
(b) My brother is injured. Complement
(c) We scored a goal. Object
(d) We beat the opponents. Object
(e) She answered perfectly. Adverbial
(f) The guests arrived early. Adverbial
(g) I shall be happy. Complement
(h) You wrote the address. Object

English Workshop:

1. Write one sentence each, why the following years were landmarks in the lives of Pierre and Marie Curie:

Question 1.
Write one sentence each, why the following years were landmarks in the lives of Pierre and Marie Curie: (Answers are directly given.)
Answer:

1. 1895 – Marie and Pierre got married.
2. 1902 – Radium was discovered.
3. 1903 – The Curies along with Henry Becquerel were awarded the Nobel Prize in Physics for the discovery of Radium and Polonium.
4. 1906 – Pierre was knocked down and killed by a horse-drawn wagon.
5. 1911 – Marie was awarded the Nobel Prize for the second time for Chemistry.

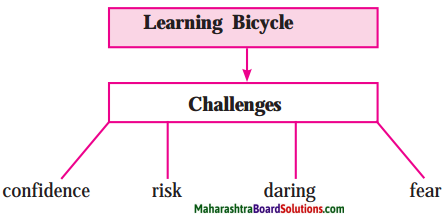
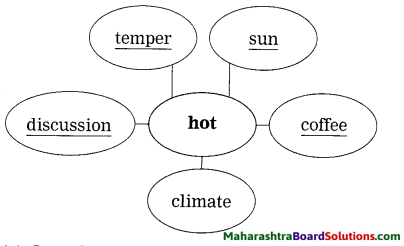
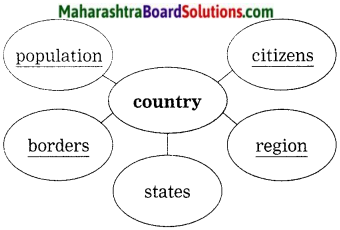
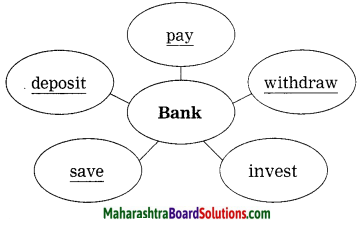
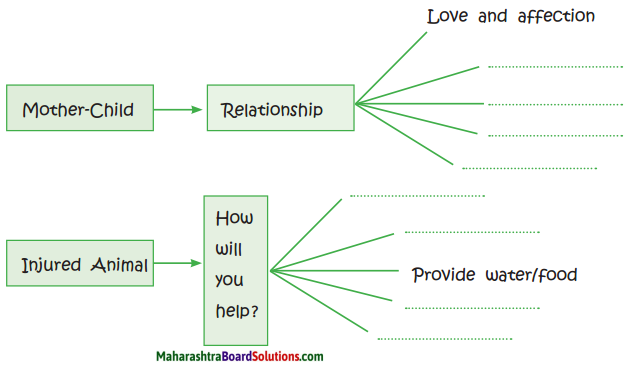
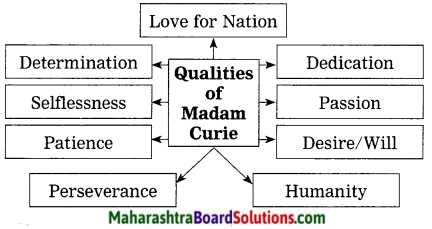
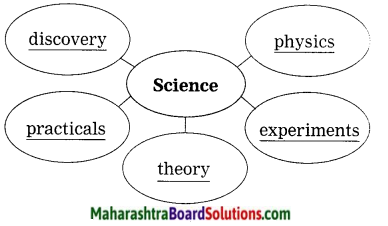
2. Complete the web diagram with the qualities of Madame Curie:

Question 1.
Complete the web diagram with the qualities of Madame Curie:

Answer:

3. Name the following:

Question (a)
Two discoverers of New lands.
1. ……………………..
2. …………………….
Answer:
1. Columbus
2. Vasco da Gama

Question (b)
Two conquerers of the peak of Mt. Everest.
1. …………………..
2. ………………….
Answer:
1. Hillary
2. Tenzing

Question (c)
Original name of Madame Curie.
…………………………………………….
Answer:
Marja Sklowdaska

Question (d)
Her place of birth.
………………………………………………
Answer:
Warsaw, in Poland

Question (e)
Subjects Marie majored in, at the University of Paris.
………………………………………………
Answer:
Physics and Mathematics.

Question (f)
Nationality of her husband Pierre:
………………………………………………
Answer:
French.

Question (g)
Scientist who discovered the properties of uranium-
Answer:
Henri Becquerel

Question (h)
Two radioactive elements discovered by Curies-
Answer:
Polonium and Radium.

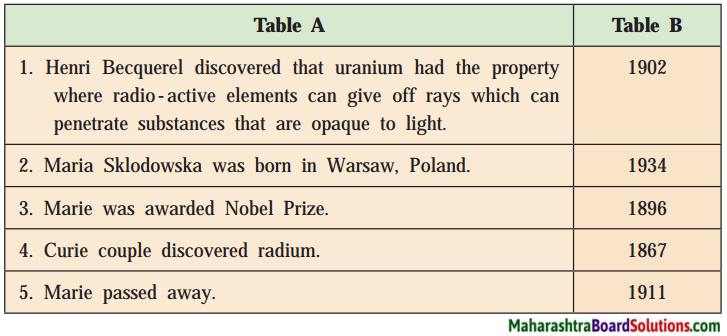
4. Read the text carefully and match the incidents occured in Madam Curie’s life given in table A with the years in table B.

5. Think and answer in your own words.

Question (a)
What common characteristics did Marie and Pierre share, as a student?
Answer:
When Marie went to Sorbonne the University of Paris she spent her days in poverty. Her friend Pierre was brilliant but a poor scientist. Due to lack of money they began to work in a shabby laboratory. Being students they were brilliant scholars but poverty was an obstacle in their way.

Question (b)
Which of the two scientists was greater than the other? Say why.
Answer:
I think Madame Curie was greater than Pierre Curie because she wanted to study in Paris but the poverty at home did not allow her to continue. But with her own efforts and confidence she could fulfil her childhood dream. Even in that condition she got married to a person who was poor. And even after his death, she did not deter and continued her work and was awarded the Nobel Prize. It shows that she was really a great human being and a scientist.

Question (c)
Why was the gift of a ton of pitchblende, a great stroke of luck to the Curies?
Answer:
Being very expensive the Curies couldn’t buy pitchblende on a large scale but when their admirer, the emperor of Austria gifted them the most precious gift of a ton of pitchblende they could do their experiment on a large scale and find out what they wanted to achieve. So it was a great stroke of luck to the Curies.

Question (d)
Besides the uses of Radium and Polonium mentioned in the text, in what other way do you think, it is used in the field of medicine?
Answer:
Radium is used to produce radon gas which in turn, is used to treat cancer. Radiation given off by radium is sometimes used also to study the composition of metals, plastics and other material.

The alpha rays emitted by Polonium can be used to eliminate static electricity. Polonium is also used in anti-static brushes to eliminate dust on photographic film.

Question (e)
What proves that Marie Curie was a true lover of humanity and not of wealth?
Answer:
Marie Curie could have patented her discovery and earned a lot of money. But she believed in working for Science and whatever she discovered belonged to the people and not to her so in real sense she thought about humanity not money. She was a true lover of humanity and not of wealth.

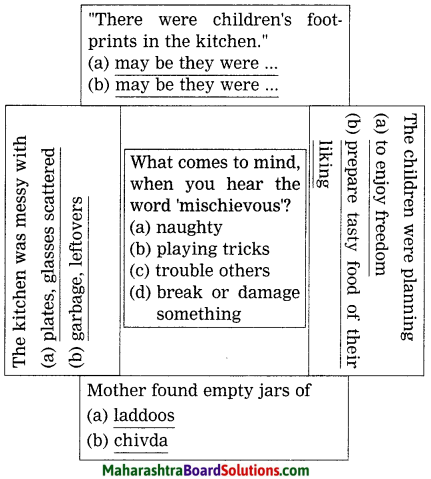
6. Find words/phrases from the text that are synonyms of the word ‘brave’:

Question 1.
Find words/phrases from the text that are synonyms of the word ‘brave’:
Answer:
courageous indomitable powerful

7. Read and understand the following words. Find out/search for proverbs/thoughts/quotes/ slogans that are related to each of them:

Question 1.
Read and understand the following words. Find out/search for proverbs/thoughts/quotes/ slogans that are related to each of them:
Answer:
(a) Courage: Courage is the complement of fear. One with courage to laugh is master of the world. Courage is a kingdom without a crown.
(b) Strength of character: Knowledge will give you power, but weakness of attitude becomes weakness of character.
(c) Determination: A dream doesn’t become reality through magic, it takes sweat, determination and hardwork. The difference between the impossible and the possible lies in a man’s determination.
(d) Hard-work: Success is the result of perfection, hardwork, learning from failure, loyalty and persistence. There is simply no substitute for hardwork when it comes to achieving success.

8. Match the branches of Science with what fields they study:

Question 1.
Match the branches of Science with what fields they study:

’A’	B’
(a) Ecology	(i) Study of Atmosphere
(b) Geology	(ii) Study of Plant-life
(c) Meteorology	(iii) Study of the Universe
(d) Anatomy	(iv) Study of living organisms and environment
(e) Botany	(v) Study of human mind and emotions
(f) Psychology	(vi) Study of structure and functions of the body
(g) Cosmology	(vii) Study of solid earth and rocks

Answer:
(a) Ecology – Study of living organisms and environment
(b) Geology – Study of solid earth and rocks
(c) Meteorology – Study of Atmosphere
(d) Anatomy – Study of structure and functions of the body
(e) Botany – Study of Plant-life
(f) Psychology – Study of human mind and emotions
(g) Cosmology – Study of the Universe

9. Imagine that your school needs some Scientific equipment, apparatus and formulae charts for the laboratory. Being the in-charge of Science Committee, write a letter to the Headmaster of your school suggesting him some Scientific equipment and apparatus required for Standard X Science practicals. Take help of the information given below to complete your letter.

Question 1.
Imagine that your school needs some Scientific equipment, apparatus and formulae charts for the laboratory. Being the in-charge of Science Committee, write a letter to the Headmaster of your school suggesting him some Scientific equipment and apparatus required for Standard X Science practicals. Take help of the information given below to complete your letter.

Answer:
Sanjay Sharma,
In-charge of Science Committee,
New English High School,
Akola-444 001.
1 January, 2020.

To,
The Headmaster,
New English High School,
Akola.
Subject: Requirement of scientific equipment, apparatus and formulae charts for the laboratory.

Respected sir,

With regard to learning Science content, processes and views of the nature of Science experiments play significant role in Science. As per the new syllabus, new subjects and some experiments are included in revised Science coursebooks. Experiments give immense pleasure of self-learning and observations.

The equipment and apparatus that we have been using in our Science laboratory are outdated and rarely of any use. If we bring some new, definitely it will arose interest in learning Science and doing some experiments on our own. Being in-charge of Science Committee, I request you on behalf of all students and teachers to bring following equipment and apparatus in our Science laboratory.

1. 2 compound microscope
2. 2 Hand lens
3. 6 Beakers
4. 3 Beakers Tongs
5. 3 Test Tube holder
6. Thermometer
7. Safety goggles-6
8. 6 funnels
9. 1 microwave oven
10. 2 pipette
11. Graduated Cylinder
12. Vernier Calliper
13. Meters
14. Compass
15. Stop clock

You are well aware that due to lack of equipment our Science teachers can’t conduct some experiments in the lab.

Hope you will understand our difficulty and buy the listed equipment and apparatus as early as possible so that the subject of Science can be well understood by doing various experiments in the laboratory.
Anticipating your valuable help in this respect.

Thanking you,

Yours obediently,
Sanjay Sharma
In-charge of Science Committee.

10. ‘There is no short-cut to success’. Expand this maxim with a suitable introduction, body, examples and conclusion. Write it in your notebook in about 20 lines.

Question 1.
‘There is no short-cut to success’. Expand this maxim with a suitable introduction, body, examples and conclusion. Write it in your notebook in about 20 lines.
Answer:
‘There is no Short-cut to Success.’
It is often said that success requires hardwork and great diligence as well as commitment. This makes success a long-term achievement. Everybody thinks that there are some easier ways to live life, no need to work hard for livelihood but the truth is that easier ways are always the toughest ways. Most of us forget that for reaching success, the road is not strewn with roses. Success is an achievement by constant diligence and most of us lack the essential quality, diligence. The magic of hardwork and perseverance cannot be underestimated.

Most of the time it happens that we start our efforts but soon lose heart half-way and give up our efforts and thus fail to reach the pinnacle of success. If we have the confidence in our efforts, there is nothing that can deter us from achieving. Sitting in front of Television and watching the shopping network channel, fascinating over the new-miracle making abs machine which promises you the six- pack abs only in 5 minutes of daily exercises, you think that product is heaven sent, so you grab your phone book the order and start dreaming about your perfect body. Two months later, that wonder abs machine is at the back of your master closet gathering dust. As you can see, you will have to do the work when reaching a goal and the success that comes with it.

You have to understand that you might have to make sacrifices during your journey and you need to put in the hours required in order to get where you want to reach. Those who sit pretty and just complain about the success of others are the ones who do not do much in life. Those who make continuous efforts for a long time in the right direction rarely lose in the struggle of life. So one important password for all of us to follow is that there is no short cut to success.

Project:

The life and work and inventions of Marie Curie are given in detail in the text. Go to your library or search on internet at least five famous scientists who have given great inventions to the world and write about them or prepare a chart showing the information about them.

Language Study:

1. Pick out the Prefixes and Suffixes from the following words and find the root word:

Question 1.
Pick out the Prefixes and Suffixes from the following words and find the root word:

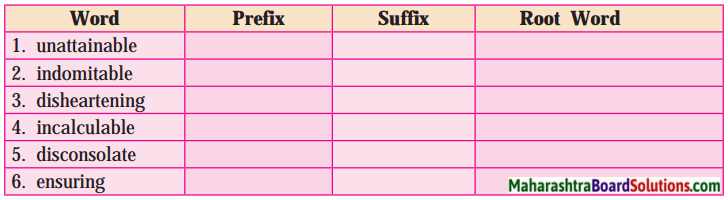
Answer:

Word	Prefix	Suffix	Root Word
1. unattainable	un	able	attain
2. indomitable	in	able	–
3. disheartening	dis	ing	hearten
4. incalculable	in	able	calculate
5. disconsolate	dis	ate	console
6. ensuring	en	ing	sure

2. Say whether the Predicates in the sentences below contain Objects/Complements/Adverbials:

Question (A)
Say whether the Predicates in the sentences below contain Objects/Complements/Adverbials: (Answers are directly given.)
Answer:
(a) Madame Curie discovered radium. – Object
(b) Pierre was knocked down. – Complement
(c) Pitchblende was expensive. – Complement
(d) The couple took a flat. – Object
(e) They moved cautiously, success came finally. – Adverbial

Question (B)
Pick out the Conjunctions in the following sentences and say whether they are Subordinators or Coordinators.
Answer:
(a) There are women who show extreme courage. – who – subordinator
(b) Pitchblende was an extremely expensive substance, so they could not afford to buy. – so-subordinator
(c) After her daily household work, Marie settled down to studv. – After-subordinator
(d) Marie wanted to study in Paris but her father could not afford it. – but-coordinator
(e) History is full of chapters that tell of extraordinary people! – that-subordinator

Live English!

Question (a)
What is Blogging?
Answer:
The term blog is short for web log. It is an online public diary which lists each diary entry in reverse order so that new diary entries are placed on the top of the page, and older entries are placed below. Each entry is called a post.

Question (b)
Who Blogs?
Answer:
Anyone can create a blog, if they have a basic understanding of the way the software works. There are privately owned blogs on individual webpages, which require a little knowledge about creating webpages, but there are also blog creation services which allow you to quickly and easily set up your own blog. You can add posts as often as you like, and can say almost anything that you want. Blogs are created for a lot of different reasons, and by many different people.

Question (c)
What Are Blogs About?
Answer:
There are many topics that a blog may contain, depending on who is updating it and why. Many blogs provide news or comment in response to a particular subject, like local news, politics or even hobbies. Food blogs are popular for people who want to share recipes, and many political activists and writers have blogs which are used to respond to current political topics. Many blogs also function as personal online diaries.

Question (d)
Blog Classification
Answer:
A blog is usually textual, based on news and commentary, although there are other types of blogs which are gaining popularity. Artlogs are blogs which focus on art, Photoblogs focus on photography, Sketch- blogs focus on sketching, and so on. There are also a few specialised types of blogs, including Vblogging or video blogging, and Podcasting or audio blogging.

Question (e)
Creating a Blog on the Internet
Answer:
If you have a good understanding of webpage design and development, you may be able to create your own blog on a personal website. Otherwise, your best option is to choose a website that does the setting up for you, so that all you have to do is join, customise a little and begin to write. There are many blog websites like www.livejournal.com, www.wordpress.com, www.blogger.com or www.blogs.myspace.com which will allow you to quickly and easily create your own blog. They also give you the option to set controls so that you can choose to allow only friends or only yourself to read them.

Question (f)
Blog Popularity
Answer:
Blogs are becoming more and more popular for many reasons. This is because they offer a wealth of information on a lot of different topics. They also drive traffic to websites by attracting new visitors with interesting blog column commentary. Blogs are a great tool because they allow anyone to express themselves on the Internet. If you are looking for a way to express yourself online, or to share information regarding a favourite subject of yours, beginning your own blog may be the best option for you because everyone has an opinion on the Internet, and soon everyone will have their own personal weblog too.

Now with the help of your teacher create your own Blog on one of the following given topics.

1. Your experiences and recently celebrated birthday party.
2. Your expectations from the school.
3. Describe the surroundings of your residence.
4. Describe a cultural programme/campaign/project conducted at your school.

My English Coursebook 10th Digest Chapter 4.6 A Brave Heart Dedicated to Science and Humanity Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
Write the importance of the years. (Answers are directly given.)
Answer:
1. 1867-Marie Curie was born.
2. 1895-Marie and Pierre got married.

Question 2.
State whether the following statements are True or False:
Answer:

1. Pitchblende is a black, very hard and cheap substance – False
2. Men could see many substances through the powerful rays of Uranium. – True
3. The emperor of Austria gifted a ton of pitchblende to the Curies – True
4. The Curies sacrificed all their luxuries of life to save money to buy pitchblende. – True

Name the following:

Question 1.
An admirer of the Curies.
Answer:
The emperor of Austria.

Question 2.
A black, very hard and expensive substance-
Answer:
Pitchblende.

Complex Factual Activities:

Question 1.
What qualities do great achievers possess?
Answer:
Great achievers possess qualities like commitment, courage, dedication and singleness of
purpose in their effort.

Question 2.
What information do you get about Marie’s early life?
Answer:
Marie was born in a poor family. Her childhood dream was to study Science in Paris but her father could not afford the expenses for this. So she worked as a governess and saved a little money and went to Sorbonne, the University of Paris to study science. Thus she worked hard in her childhood to fulfil her dream.

Question 3.
What are the signs of poverty suffered by the young couple? ( wt WT oTFlcft?)
Answer:
The young couple was very poor indeed. They started their journey from a shabby laboratory. They took a flat in Paris which contained hardly any furniture. Marie used to work and settle down to study in laboratory in a wooden shed near their flat. It had a leaky skylight and an earthen floor. All these things are the signs of poverty suffered by the young couple.

Question 4.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. Madame Curie dedicated her life to the cause of Science and to the welfare of humanity.
2. The qualities that great achievers possess are extraordinary courage, determination and singleness of purpose.
3. Marie Curie could not study Science in Paris and fulfil her childhood dream because her father could not afford the expenses of her studies.
4. Marie and Pierre set up a laboratory in a wooden shed near their flat.

Question 5.
What proves Marie’s strong will power?
Answer:
When the couple could not buy pitchblende which was an expensive substance they sacrificed all the luxuries of life to save money. They lived in extreme poverty. They could not buy costly food and warm clothes for extremely cold Parisian winter. They could not sleep due to lack of warmth. Marie refused to take rest whenever her husband begged her to give up the struggle. All the above incidents prove that Marie had a strong will power to achieve the aim of her life.

Question 6.
Why were the two new substances named Polonium and Radium?
Answer:
When Pierre and Marie found two new substances in their new discovery, she called one Polonium in honour of her country Poland and being the most powerful of the radioactive elements another was called “Radium”.

Question 7.
Which gift did she receive from the emperor of Austria? Why was it the most precious for them?
Answer:
Pitchblende is a very expensive substance which Pierre and Marie could not afford to buy in large quantity for their experiments. The emperor of Austria was an admirer of the Curies. So he gifted them a ton of pitchblende so that the Curies could carry out their experiments easily.

Question 8.
How is radium used in the medical field?
Answer:
The benefits of radium in the world of medicine are incalculable. It has been used with great effect in treatment of cancer. The bacteria of such diseases as typhus, cholera and anthrax can also be killed by radium so it was a great gift in the medical field.

Question 9.
How did Pierre meet with an early death?
Answer:
In 1906 Pierre was knocked down and killed by a horse – drawn wagon and thus met with an early death leaving Marie disconsolate.

Question 10.
What makes Marie Curie an exceptional scientist?
Answer:
When Marie and Perrie discovered Radium and Polonium they could have patented their discovery and become rich but Marie refused to do so and gave it free to the world and the world of medicine. She also believed that Radium belongs to the people not to her. She worked selflessly without expecting money. Her humanity and selflessness make Marie Curie an exceptional scientist.

Question 11.
Describe how Curies first sighted Radium. What was its colour?
Answer:
After continuing their work for more than four years on a September night, the Curies after a day’s tiresome work, went to the laboratory to have another look at the hundreds of small bowls into which they had poured filtered pitchblende. While moving forward in the dark laboratory they found rays of soft, bluish purple light coming from the small glass-covered bowls. Thus they sighted the Radium for the first time. Its colour was bluish purple.

Activity-based on Vocabulary:

Question 1.
Find out the words from the passage which mean:

1. unbeatable
2. discouraging
3. hardly
4. illiteracy

Answer:

1. indomitable
2. disheartening
3. scarcely
4. ignorance

Question 2.
Find out antonyms for the following from the passage: (Answers are directly given.)
Answer:

1. economical × expensive
2. poverty × luxury
3. chill × warmth
4. worthless × precious

Question 3.
Write down the describing words used for the following nouns:

1. work
2. pitchblende
3. colour
4. desire.

Answer:

1. tiresome work
2. filtered pitchblende
3. beautiful colour
4. compulsive desire

Activities based on Contextual Grammar:

Question 1.
Her father could not afford the expenses of her education in Paris. (Make it affirmative.)
Answer:
Her father was unable to afford the expenses of her education in Paris.

Question 2.
Her life in the University was a disheartening experience in poverty and hunger. (Make it negative.)
Answer:
Her life in the University was not an encouraging/heartening experience in poverty and hunger.

Question 3.
Marie took a job as a governess and saved a little money. (Rewrite using ‘by’ + ing.)
Answer:
Marie saved a little money by taking a job as a governess.

Question 4.
Marie Curie’s childhood dream was to study science in Paris, but her father could not afford the j expense for this. (Rewrite using’Though’.)
Answer:
Though Marie Curie’s childhood dream was to study science in Paris, her father could not afford ; the expense for this.

Change the degree:

Question 1.
Pitchblende was the most precious gift the Curies had received.
Answer:
(a) Positive – No other gift the Curies had, received was as precious as pitchblende.
(b) Comparative – Pitchblende was more precious gift than any other gifts the Curies had received.

Question 2.
Pitchblende is one of the most expensive substances.
Answer:
(a) Positive – Very few substances are as expensive as pitchblende.
(b) Comparative – Pitchblende is more expensive substance than most other substances.

Change the voice:

Question 1.
In 1906, Pierre was knocked down by a horse – drawn wagon. (Begin the sentence with ‘A horse-drawn wagon’.)
Answer:
A horse-drawn wagon knocked down Pierre in 1906.

Question 2.
In 1911, Marie was awarded the Nobel Prize. (Begin the sentence with ‘They’)
Answer:
They awarded Marie the Nobel Prize in 1911.

Personal Response:

Question 1.
Describe your favourite scientist.
Answer:
C.V. Raman who won the Nobel Prize for Physics in 1930 is my favourite scientist. He was the first Asian and first non-white to receive any Nobel Prize in Science. He was the first to investigate the harmonic nature of the sound of the Indian drums such as the tabla and the Mrudangam. He discovered that, when light traverses a transparent material, some of the deflected light changes in wavelength.

Question 2.
What qualities, do you think, are important to get success in our life?
Answer:
There are some key components of success without which we cannot succeed in our life. First our mindset-without a positive mindset the rest of these components won’t have as much power as they should. Staying focused on goal is also important. Besides it, dedication, discipline and determination are important factors to get success in our life.

Question 3.
Why are awards and prizes given to the people in different fields?
Answer:
An award or a prize is something given to a person, in recognition of his or her excellence in a certain field. It may also simply be a public acknowledgement of excellence. It boosts the j recipient’s confidence. It also encourages and inspires him/her to do better in his/her life. It also inspires other people in different fields to achieve something great.

Language Study:

1. Coordinators: Coordinators are words that join grammatically, equal units together. E.g., and, but, or, nor are the main Coordinators.

2. Subordinators: Words whose function is to establish an unequal grammatical relationship are called subordinators. that, for, who, whether, if, because, so. Dependent clauses Principal clause that, for, who, whether, if, because, so subordinate conjunctions (subordinators)

Do as directed:

Question 1.
Complete the words by using correct letters:
Answer:

1. bre _ d – bread
2. b i _ t h – birth
3. la _ ge – large
4. p r i _ e – prize

Question 2.
Put these words in alphabetical order:
1. lifeless, hostile, endurance, progress
2. commitment, characterise, courage, costly
Answer:
1. endurance, hostile, lifeless, progress
2. characterise, commitment, costly, courage

Question 3.
Punctuate the following sentences:
1. do you remember the day when you told me that you wanted radium to have a beautiful colour marie said to her husband
2. she replied i am working for science radium belongs to the people not to me
Answer:
1. “Do you remember the day when you told me that you wanted radium to have a beautiful colour?” Marie said to her husband.
2. She replied, “I am working for science. Radium belongs to the people, not to me.”

Question 4.
Make four words (minimum 3 letters each) using the letters in the given word: ‘ incalculable’
Answer:

1. ill
2. call
3. able
4. cube

Question 5.
Write related words as shown in the example:
(Answer is directly given and underlined.)
Answer:

Question 6.
Complete the word-chain of verbs. Add four words, each beginning with the last letter of the previous word!
eat → t……….., ……………, ………….., …………….
Answer:
eat → take , extend , develop , paddle.

1. Attempt any one:

Question (a)
Make a meaningful sentence of your own using the phrase: ‘to fight against ’
Answer:
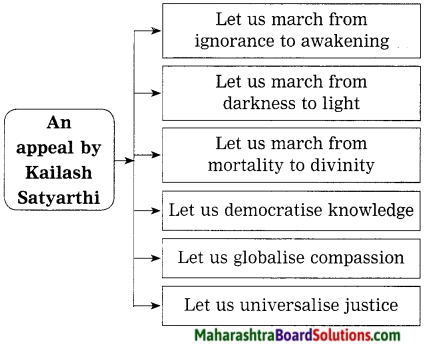
Kailash Satyarthi has been fighting against child labour for the last several years.

OR

Question (b)
Add a clause to the following sentence to expand it meaningfully:
The history is the subject ………………. .
Answer:
The history is the subject which gives the narration of episodes happened in the past.

2. Attempt any one:

Question (a)
Add prefix or suffix to make new words :
1. ignore
2. dedicate
Answer:
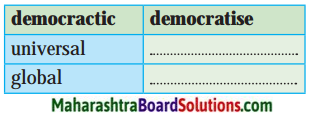
1. ignorance
2. dedication

OR

Question (b)
Make a meaningful sentence using any one of the following words :
1. ignore
2. dedicate
Answer:
1. Don’t ignore your parent’s advice.
2. Dedicate your life for poor; the father told his son.

Live English:

Blogging:

1. Terms – (Blogging)
2. Blog – Web log which is an online public diary.
3. Purpose – Anybody can create blog for any reason.
4. About – Function as personal online diaries
5. Types – Artlogs – Focus on art
6. Photologs – Focus on photography
7. Sketch – Focus on sketching
   blogging – Video blogging
8. Podcasting – Audio blogging
9. Creating – You can create your own blog on a personal website or any other websites like www.livejournal.com, www.wordpress.com, www.blogger. corn, www.blogs.rny-space.com
10. Popularity – Blogs allow anyone to express themselves on the Internet and it becomes popular if people like it.

Steps of creating blogs:

Starting a blog is the best way to share your Ideas and expertise online.
Follow the given steps to create your blog.

• Choose your blogging platform. (word press)
• Choose a Domain name. (www.yourblog.com)
• Sign up with Web Host and install Word Press (www.bluehost.com is good hosting provider)
• Sign up with a web hosting.
• Choose the hosting plan.
• Choose the domain name you want.
• Complete your registration.
• Install wordpress with one-click installation.
• Log into your new blog.
• Customizing and choosing a blog theme.
• Adding Post and Pages.
• Get Traffic and monetize your blog.

My English Coursebook 10th Class Solutions Pdf Unit 4

• The World is Mine Class 10 English Solutions
• Bholi Class 10 English Solutions
• O Captain! My Captain! Class 10 English Solutions
• Unbeatable Super Mom – Mary Kom Class 10 English Solutions
• Joan of Arc Class 10 English Solutions
• A Brave Heart Dedicated to Science and Humanity Class 10 English Solutions

Class 10 English Chapter 2.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 2.3 The Twins Notes, Textbook Exercise Important Questions and Answers.

The Twins Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 2.3 The Twins Textbook Questions and Answers

Warming up!

Chit-chat:

1. Two babies born at the same time are called twins. Guess and share who are :

• triplets
• quadraplets
• quintiplets

Question 1.
Two babies born at the same time are called twins. Guess and share who are :
Answer:

1. Three babies born at the same time to the same mother are called triplets.
2. Four babies born at the same time to the same mother are called quadruplets.
3. Five babies born at the same time to the same mother are called quintuplets.

2. Imagine you liad an identical twin (brother or sisiter). Imagine and share with your classmates what pranks you two would play on your friends, elders in the family and even in school.

Question 1.
Imagine you liad an identical twin (brother or sisiter). Imagine and share with your classmates what pranks you two would play on your friends, elders in the family and even in school.
Answer:
Points: At home : Blame your twin brother for the wrongs/breakage/damage done by you – eat his sweets/sweetmeats and demand it again as the other one – if one did some thing special good, the other pretends as it is done by him – In school: One makes mischief in the class and points his finger at the other, he is guilty of doing something wrong throws blame on the other.

1. Study the following pairs or groups of words. Cup and saucer/needle and thread/birds and beasts/take a risk/sip tea or coffee/hide and seek etc.
These are sets of words that more than often go together and occur together. We call such sets Collocation.
Insert the proper words from the bracket to form collocations.
(a) afford (b) time (c) defeat (d) clothes (e) owners (f) necessary (g) role (h) interview (i) morning (j) cold
(a) absolutely ……………
(b) cannot ………………
(c) formal ……………..
(d) job ……………….
(e) pass ………………
(f) accept …………….
(g) early ………………
(h) catch a …………….
(i) leading ……………..
(j) joint ………………..

Question 1.
Insert the proper words from the bracket to form collocations.
[(a) afford, (b) time, (c) defeat, (d) clothes, (e) owners, (f) necessary, (g) role, (h) interview, (i) morning, (j) cold.]
Answer:
(a) absolutely necessary
(b) cannot afford
(c) formal clothes
(d) job interview
(e) pass time
(f) accept defeat
(g) early morning
(h) catch a cold
(î) leading role
(j) joint owners

2. Exaggeration or overstatement often causes humour. For example, She is thin as a pin.

• He has a pea-sized brain
• My shoes are killthg me.

When such exaggerated lines occur in poetry, they are examples of the Figure of Speech: Hyperbole.
Complete the following examples of Hyperbole using words from the bracket below.
(a) She wept …………………… of tears.
(b) The hungry man ate a …………………… of food.
(c) He runs faster than a ……………………
(d) Brrrr..! I am freezing to ……………………
(e) I shall come over in just a ……………………
(horse/lion/death/an ocean/ton/second/help)

Question 1.
Complete the following examples of Hyperbole using words from the bracket below.
(a) She wept …………………… of tears.
(b) The hungry man ate a …………………… of food.
(c) He runs faster than a ……………………
(d) Brrrr..! I am freezing to ……………………
(e) I shall come over in just a ……………………
(horse/lion/death/an ocean/ton/second/help)
Answer:
(a) She wept an ocean of tears.
(b) The hungry man ate a ton of food.
(c) He runs faster than a horse.
(d) Brrrr..! I am freezing to death.
(e) I shall come over in just a second.

English Workshop:

1. Rewrite putting the mistakes in the speaker’s life, in their proper order.
(a) The speaker got beaten-up, often, at school.
(b) The speaker’s bride became his brother’s wife.
(c) The speaker desparately asked for guidance.
(d) No one in the family could distinguish between the twin – babies.
(e) At the naming ceremony wrong names were given to the two twin brothers.
(f) Even in death, the twins were not spared during burial.

Question 1.
Rewrite putting the mistakes in the speaker’s life, in their proper order.
(a) The speaker got beaten-up, often, at school.
(b) The speaker’s bride became his brother’s wife.
(c) The speaker desparately asked for guidance.
(d) No one in the family could distinguish between the twin – babies.
(e) At the naming ceremony wrong names were given to the two twin brothers.
(f) Even in death, the twins were not spared during burial.
Answer:
(a) No one in the family could distinguish between the twin-babies.
(b) At the naming ceremony wrong names were given to the twin brothers.
(c) He (the narrator) got beaten-up, often, at school.
(d) The speaker desperately asked for guidance.
(e) The speaker’s bride became his brother’s wife.
(f) Even in death, the twins were not spared during burial.

2. Pick out four situations in the lives of the twins, which are too absurd and senseless to believe.
1. ………………..
2. ………………..
3. ………………..
4. ………………..

Question 1.
Pick out four situations in the lives of the twins, which are too absurd and senseless to believe.
Answer:

1. The people began mistaking one for the other.
2. The speaker’s brother got the name John, intended for the speaker.
3. The speaker’s intended bride became his brother’s wife.
4. When the speaker died, the neighbours came and buried his brother John.

3. (A) Complete the web diagram.

(B) Write any two lines from the poem, that you find most humorous.

Question a.
Complete the web diagram.

Answer:

Question b.
Write any two lines from the poem, that you find most humorous.
Answer:
1. For somehow, my intended bride Became my brother’s wife.
2. When I died, the neighbours came And buried brother John.

4. Pick out lines that contain :
Alliteration
(a) ………………………………
(b) ………………………………
(c) ………………………………

Pun
(a) ………………………………
(b) ………………………………

Hyperbole
(a) ………………………………
(b) ………………………………

Question 1.
Pick out lines that contain
Answer:
Alliteration:
(a) In form and feature, face and limb.
(b) It puzzled all our kith and kin.
(c) One day, to make the matter worse.

Pun:
(a) I grew so like my brother.
(b) That folks got taking me for him.

Hyperbole:
(a) It reached a fearful pitch.
(b) We got completely mixed.

5. Pick out from the poem sets of words that generally go together.

Question 1.
Pick out from the poem sets of words that generally go together.
For example, kith and kin.
(a) ………………………………
(b) ……………………………….
(c) ……………………………….
(d) ……………………………….
Answer:
(a) form and feature
(b) face and limb
(c) turned the tide
(d) fearful pitch
(e) domestic life
(f) fate’s decree

6. Write in your notebook, the summary of this poem in about 15 to 20 lines in your own words. You can suggest another humourous title.

Question 1.
Write in your notebook, the summary of this poem in about 15 to 20 lines in your own words. You can suggest another humourous title.
Answer:
(Student should write the summary with the help of the paraphrase of the poem given in this book.)
Another humorous title: Twists in the lives of Twins.

7. Write an Appreciation of the poem with reference to all the points mentioned on Page 5.

Question 1.
Write an Appreciation of the poem with reference to all the points mentioned on Page 5.
Answer:
Appreciation of the Poem

1. Title: The title of the poem is ‘The Twins’.
2. Name of the poet: The name of the poet is Henry S. Leigh.
3. Rhyme scheme: The rhyme scheme of the poem is “abab”.
4. Figure of speech (Any one): Alliteration, hyperbole.
5. Theme / Central Idea: The central idea of the poem is the problems faced by one of the identical twins.
6. All the problems are so exaggerated that they create humorous effect. Still, the poet achieves a balance by making the reader believe, at least for a short time, the way of thinking of his argument.

My English Coursebook 10th Digest Chapter 2.3 The Twins Additional Important Questions and Answers

Read the extract and do the activities:

Simple Factual Activity:

Question 1.
Complete the following with the information given in the extract:
(Answers are directly given and underlined.)
Answer:

1. The twins were similar to each other in form and feature and face and limb.
2. The people mistook the twins, one for the another.
3. No one knew who was a twin.
4. Kith and Kin were puzzled by the brother’s similarity.

Question 2.
Complete the following sentences using the information from the extract:
(Answers are directly given and underlined.)
Answer:

1. The narrator should have been christened John.
2. The narrator’s brother was named as John.
3. The twins got mixed up when they were being washed by nurse.
4. The twins were mixed up before their names were fixed.

Question 3.
Complete the following sentences using the information from the extract:
(Answers are directly given and underlined.)
Answer:

1. The narrator got flogged when John turned out a fool.
2. The narrator got punishment with a flogging.
3. His likeness with his brother dogged poet’s footsteps at school.
4. The narrator asked the question fruitlessly.

Question 4.
Who became the wife of narrator’s brother ?
Answer:
The narrator’s intended wife became his brother’s wife.

Question 5.
What turned the tide of the narrator’s domestic life?
Answer:
The close resemblance between the twins turned the tide of the narrator’s domestic life.

Question 6.
What continued year after year?
Answer:
The same absurd mistakes continued year after year.

Question 7.
Who according to the poet died?
Answer:
According to the poet (narrator) he himself died.

Complex Factual Activities:

Question 1.
What was the puzzling thing about the twins?
Answer:
Both twins were so much alike in every way that no one could distinguish one from the other.

Question 2.
Pick out from the extract words/phrases that tell that the narrator was like his brother John.
Answer:
‘In form and feature, face and limb, I grew so like my brother,’ ‘That folks got taking me for him and each for one another’, and ‘not a soul knew which’

Question 3.
What is the mix-up mentioned in this extract?
Answer:
The narrator got christened his brother and the brother got christened John. The name, John, was actually intended for the narrator.

Question 4.
Write any two lines from the extract that you find humorous.
Answer:
1. As we were being washed by nurse, we got completely mixed.
2. My brother John got christened me, And I get christened him.

Question 5.
Pick out from the extract the question that narrator asks everyone. Can you answer the question?
Answer:
The narrator asked everyone what he would do if he were he (the narrator) to prove that he was actually himself. The only advice that can be given in such a case is to keep some different outward signs like mode of dress, hairstyle, mannerisms, etc. to identify oneself.

Question 6.
How did the narrator suffer at school?
OR
Who was put to disadvantage at school due to the similarity? How?
Answer:
As a result of the similarity between the narrator and his brother, he (the narrator) was always getting beaten for the mistakes committed at school by his brother.

Question 7.
Complete the web:
(Answers are directly given.)
Answer:

Activities based on Poetic Device:

Question 1.
Write the rhyming pairs from the extract:
Answer:

1. limb – him
2. brother – another
3. kin – twin
4. pitch – which.

Question 2.
Name the figures of speech:

Question a.
In form and feature, face and limb.
Answer:
Alliteration.

Question b.
For one of us was born a twin, Yet not a soul knew which.
Answer:
Hyperbole.

Question 3.
List the rhyming pairs from the extract:
Answer:

1. worse – nurse
2. fixed – mixed
3. decree – me
4. whim – him.

Question 4.
Name and explain the figure of speech:

Question a.
As we were being washed by nurse.
Answer:
Alliteration: The letter ‘w’ is pleasingly repeated.

Question b.
My brother John got christened me, And I got christened him.
Answer:
Hyperbole: The statement is exaggerated for humour.

Question 5.
Write the rhyming words for the following from the extract:

1. dogged
2. school
3. knew
4. fruitlessly

Answer:

1. dogged – flogged
2. school – fool
3. knew – you
4. fruitlessly – me.

Question 6.
Write lines from the extract that show the figure of speech:
– hyperbole
Answer:
And I was always getting flogged, For John turned out a fool.
The lines are exaggerated for creating humour.

Question 7.
Write the rhyming pairs from the extract:
Answer:

1. tide – bride
2. life – wife
3. same – came
4. on – John.

Question 8.
Write an example of the figure of speech – Hyperbole:
Answer:
And when I died, the neighbours came And buried brother John.
The statement or fact has been exaggerated to create humour.

Vocabulary Focus:

Question 1.
Find from the poem the words that generally go together:
Answer:

1. orm and features
2. face and limb
3. kith and kin
4. fearful pitch
5. fate’s decree
6. got christened
7. close resemblance
8. turn the tide
9. domestic life
10. intended bride
11. absurd mistake
12. put (this) question
13. get flogged

Question 2.
Write as many words as you can using-ful as suffix.
Answer:
basketful-bucketful-handful-spoonful- colourful-sackful-bagful-potful

My English Coursebook 10th Digest Pdf Unit 2

• You Start Dying Slowly … Class 10 English Solutions
• The Boy who Broke The Bank Class 10 English Solutions
• The Twins Class 10 English Solutions
• An Epitome of Courage Class 10 English Solutions
• Book Review – Swami and Friends Class 10 English Solutions
• World Heritage Class 10 English Solutions

Class 10 English Chapter 3.2 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 3.2 A Lesson in Life from a Beggar Notes, Textbook Exercise Important Questions and Answers.

A Lesson in Life from a Beggar Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.2 A Lesson in Life from a Beggar Textbook Questions and Answers

Warming up:
Chit-chat

Make small groups and share:

Question 1.
A piece of advice that stopped a bad habit in you.
Answer:
“Bad habits interrupt your life and prevent you from accomplishing your goal.” The advice given by my uncle stopped a bad habit in me.

Question 2.
A quote proverb that you love to use often.
Answer:
I often love to use the quote, ‘Let’s move ahead.’

Question 3.
An experience that taught you a lifelong lesson.
Answer:
Getting up early morning is quite a difficult job for me. Once we were called at 6 o’clock in the morning to go for picnic. My mother was trying to wake me up from 5 o’clock but I got up at 5.30 and reached school by 6.30. By then our picnic bus had already left the school. I realised that I had missed the fun. It gave me a lifelong lesson to be punctual.

Question 4.
A story / news / episode / movie / play that has impressed and changed you.
Answer:
I miserably failed in Standard IX. I lost all my hopes. I had decided to discontinue my studies forever. Meanwhile I happened to read a story of King Bruce, the King of Scotland. He fought many battles to free his country from English rule. Lost many battles. Once while hiding in a cave, he saw a spider trying to make his web on the wall of the cave. He slipped and fell again and again. But perseveringly tried again and finally succeeded and made his web.

King Bruce learnt a lesson, got together his army, defeated the English and freed his country. The story impressed me. I was moved by the story and decided to study hard and make an effort to appear for the exam again. The story changed my life.

1. Many slang expressions terms are used for people having positive or negative traits.

Question 1.
Match the expressions in Column A with type of persons in Column B:

Answer:

1. Couch Potato – lazy/good for nothing
2. Worry Wart – always nervous/worried
3. Fuddy-duddy – old-fashioned / refuses change.
4. Wet blanket – spoils other people’s fun/mood
5. Whiz – brilliant / genius
6. Black sheep – shameful person
7. Live wire – very energetic/active

Question 2.
Discuss with your group and write the difference in reactions of an Optimist and a Pessimist:

Answer:

Answer	Optimist	Pessimist
Failure in exams /tests	I will try my level best in next exam.	Leave it. It is not my cup of tea.
Lose a good amount of cash	bad luck streak!	What a bad luck!
Unexpected rainfall/bad weather.	Let’s enjoy the rain.	Shit! this rain again.
Illness	I want to get well as early as possible.	I will die.
Extra classes in school	Teacher is going to teach something new.	What will it serve? It’s a waste of time.

English Workshop:

1. Complete the following table:

Question 1.
Complete the following table:

Answer:

Utterance	Who said	To whom
1. “Shwetha is a very beautiful girl, isn’t she?”	The writer	Meena
2. “When a pony is young, he looks handsome.”	Meena	The writer
3. “It’s a beautiful day.”	The writer	Meena
4. “No, the sun is too hot.”	Meena	The writer
5. “I’m all excited, it’s nice to meet old friends.”	Meena	The writer

2. State whether the following statements are (✓) or (✗). Correct the wrong ones:

Question 1.
State whether the following statements are (✓) or (✗). Correct the wrong ones:
Answer:
(a) The author and Meena were Wrong great enemies.
Corrected sentence: They were good friends.
(b) Meena was a very cheerful Wrong person initially.
Corrected sentence: Meena was forever unhappy.
(c) Meena stayed alone in an Wrong apartment in Delhi.
Corrected sentence: She stayed alone in an apartment in Mumbai.
(d) Meena was the second child of Wrong her parents.
Corrected sentence: She was the only child of her parents.
(e) The author spotted Meena at Bombay’s Flora Fountain. [✓]
(f) The beggar and the young girl were playing on the road because there was a lot of traffic. [✗]
Corrected Sentence: The beggar and the young girl were playing on the road because there was no traffic.
(g) The scene of the beggar and the girl made Meena peep into her own life. [✓]
(h) The beggar became Meena’s role model. [✓]
(i) It took Meena almost two years to put the change into effect. [✓]
(j) Meena was able to give Gurudakshina directly to her Guru, the beggar. [✗]
Corrected Sentence: Meena gave Gurudakshina indirectly by sponsoring his granddaughter to a boarding school.

3. Choose the correct alternative and rewrite the sentences:
(Answers are directly given and underlined.)

Question (a)
Meena who is an LIC officer, is ………………… .

1. a pessimistic person
2. an optimistic person
3. a disabled person.

Answer:
Meena who is an LIC officer, is a pessimistic person.

1. a pessimistic person
2. an optimistic person
3. a disabled person.

Question (b)
The writer was standing near Akbarallys, a popular department store because …………………. .

1. she was waiting for her friend Meena.
2. she was waiting for the rain to stop.
3. she wanted to buy something in Akbarallys.

Answer:
The writer was standing near Akbarallys, a popular department store because she was waiting for the rain to stop.

1. she was waiting for her friend Meena.
2. she was waiting for the rain to stop.
3. she wanted to buy something in Akbarallys.

Question (c)
The only thought in the writer’s mind till they reached the Grand Hotel was ……………………. .

1. why the rain was not stopping.
2. what had brought about such a change in Meena.
3. how the beggar had changed the entire life of Meena.

Answer:
The only thought in the writer’s mind till they reached the Grand Hotel was what had brought about such a change in Meena.

1. why the rain was not stopping.
2. what had brought about such a change in Meena.
3. how the beggar had changed the entire life of Meena.

Question (d)
Meena sponsored the granddaughter of the beggar because ……………………………… .

1. she was alone in her life after his death.
2. it was a token of respect to the beggar.
3. she was rich and so she wanted to help.

Answer:
Meena sponsored the granddaughter of the beggar because it was a token of respect to the beggar.

1. she was alone in her life after his death.
2. it was a token of respect to the beggar.
3. she was rich and so she wanted to help.

4. How did the beggar change Meena’s attitude? Discuss with your partner Complete the following web.

Question 1.
How did the beggar change Meena’s attitude? Complete the following web with the help of the information from this passage:

(Answer is directly given.)
Answer:

5. Write in your own words:

Question (A)
How did Meena show her gratitude to her guru?

Question (B)
Why would Meena be sad initially? Give reasons. Pick out sentences from the passage which prove that Meena was a pessimist.

1. She was forever unhappy.
2. ………………………………………….. .
3. ………………………………………….. .
4. ………………………………………….. .
5. ………………………………………….. .
6. ………………………………………….. .

Answer:

1. She was forever unhappy.
2. Whenever author met her, she would start to feel depressed.
3. Her gloom and cynicism had a way of spreading to others.
4. She never had anything positive to say about anything.
5. She always had negative responses to everyone and everything.
6. She would be pessimist all the time.

6. Find antonyms of the following words from the story.

Question (A)
Find antonyms of the following words from the story.

1. optimistic × ………………
2. drizzle × ………………
3. lie × ………………
4. new × ………………
5. ugly × ………………
6. frowned × ………………
7. hell × ………………
8. unhappy × ………………
9. disrespect × ………………
10. unimportant × ………………

Answer:

1. optimistic × pessimistic
2. drizzle × pouring
3. lie × truth
4. new × old
5. ugly × beautiful
6. frowned × laughed
7. hell × paradise
8. unhappy × happy
9. disrespect × respect
10. unimportant × important

Question (B)
Go through the points below showing Meena’s encounter with the beggar that transformed her completely. The sequence of events are jumbled up below. Arrange the events according to the occurrence. Fill in the number as per sequence.

Answer:

7. How did the beggar change Meena’s attitude towards life? Write it down in 5 to 6 lines.

Question 1.
How did the beggar change Meena’s attitude towards life? Write it down in 5 to 6 lines.

1. The incident made Meena to look at her own life.
2. ……………………………………………………………………… .
3. ……………………………………………………………………… .
4. ……………………………………………………………………… .
5. ……………………………………………………………………… .
6. ……………………………………………………………………… .

Answer:

1. The incident made Meena to look at her own life.
2. She realized that she had many comforts of which they had none.
3. But they knew how to be happy with life as it was.
4. She found that she had more to be grateful for than most people could imagine.
5. She felt ashamed of herself.
6. She decided to change her attitude towards her life.

8. Summarise the story with the help of the points given below.

Question 1.
Summarise the story with the help of the points given below.
(a) Meena’s initial attitude
(b) Meena’s meeting with Sudha Murthy in Mumbai.
(c) Beggar’s incident
(d) Change in attitude.

Answer:
Meena and Sudha were very good friends. Meena was an LIC officer and earning a good salary. But she was always unhappy and never had anything I positive to say on any subject or about any person. So whenever Sudha met her, she would start to feel depressed. Meena stayed alone in an apartment and had the habit of complaining about anything and everything; she wasn’t a very pleasant company and nobody wanted to visit her.

After some days Meena was transferred to Bombay and soon Sudha forgot about her. Many years later, Sudha was caught in the rain at Bombay’s Flora Fountain. She didn’t have an umbrella. She was standing near Akbarallys and waiting for the rain to stop. Suddenly she saw Meena. But her first reaction was to run. She was anxious to avoid being seen by her. But she couldn’t escape.

Meena saw her and caught hold of her hands ; warmly. She was very cheerful and excited to meet Sudha. She was also ready to get wet and walk in the rain. But Sudha was so surprised that she couldn’t believe she is meeting her pessimistic friend Meena. So she enthusiastically asked her, “Was there a Prince Charming who had managed to change her so?”

Meena told her there wasn’t anybody like that but a beggar changed her life who used to stay in front of her house with his five-years-old granddaughter. She used to give her leftover to that beggar everyday. One monsoon day she was surprised to see the beggar. As it was raining heavily, she couldn’t give anything to that beggar. She didn’t want to get wet in that pouring rain she was just looking out of her bedroom window when she saw the beggar and the young girl were playing on the road because there was no traffic.

They were enjoying the rain and laughing, clapping and screaming joyously as if they were in paradise. Hunger and rain did not matter. They were totally drenched but totally happy. That scene forced Meena to look at her own life. Even though she had so many comforts, none of which they had. But they had the most important of all assets one which she lacked.

They knew how to be happy with life as it was. So she decided to change her attitude towards life using the beggar as her role model. It took her almost two years to put the change into effect but now she finds happiness in every small thing, in every situation and in every person.

Sudha was surprised to listen to the changed story of her friend and asked Meena enthusiastically, whether she had given any gurudakshina to her guru or not. But Meena told her that the beggar was dead and she had sponsored his granddaughter to a boarding school as a mark of respect to him. Sudha was stunned but happy to hear the changed story and attitude of her friend.

9. Write the above summary making Meena the narrator. Begin with I worked in Bangalore in LIC. Sudha was my school friend …………..

Question 1.
Write the above summary making Meena the narrator. Begin with I worked in Bangalore in LIC. Sudha was my school friend …………..
Answer:

Lesson in a Life from A Beggar

I worked in Bangalore in LIC. Sudha was my good friend, living in the same city. Being pessimistic and having the habit of complaining about anything and everything, nobody was friendly with me. One day I was transferred to Mumbai and no one was in contact with me.
[Note: Students should try to complete the remaining part of summary of the story as told by Meena, in their notebook.]

Project:

Question 1.
Divide the class in four groups. Collect four different stories written by Sudha Murthy. Select a story for every group and write it in the form of a play. Enact it in front of the class.

Language Study:

1. Punctuate the following sentences:

Question 1.
(a) did you give any gurudakshina to your guru i asked.
(b) no there isnt anyone like that she said.
Answer:
(a) “Did you give any gurudakshina to your guru?” I asked.

2. Add a suffix to the following words and make nouns.

Question (a)
Add a suffix to the following words and make nouns.

1. kind
2. happy
3. ignore
4. assure
5. imagine
6. depute
7. manage
8. assess

Answer:
1. Always be kind to poor, needy and disabled people in the society.
2. Why don’t you look happy today?
[Note : Students may frame sentences based on the remaining words on their own.]

Question (b)
Make four words (minimum 3 letters each). Using letters from the word ‘Pessimistic’.

1. ………………….
2. ………………….
3. ………………….
4. ………………….

Answer:

1. Pessimist,
2. mist,
3. pest,
4. pet

3. Change into indirect speech:

Question (a)
“Meena, it’s a beautiful day.” I said.
Answer:
I told Meena that it was a beautiful day.

Question (b)
“Hey! I am really excited. It’s nice to meet old friends. What are you doing here?” Meena said to the writer.
Answer:
Meena exclaimed with excitement (joy) that it was nice to meet old friends. She further asked the writer what she was doing there.

Question (c)
“We won’t get a taxi in this rain,” I grumbled,
Answer:
I grumbled that we would not get a taxi in that rain.

Question (d)
“So what? We’ll buy an umbrella and then go to the Grand Hotel,” she said.
Answer:
Meena insistently asked her (the writer) what difference could it make and further told her that they would buy an umbrella and then go to the Grand Hotel.

Question (e)
“Did you give any gurudakshina to your Guru?” I asked.
Answer:
I asked her if she had given any gurudakshina to her guru.

My English Coursebook 10th Digest Chapter 3.2 A Lesson in Life from a Beggar Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
1. Meena was a good friend of the writer.
2. The writer was caught in the rain at Bombay’s Flora Fountain.

Question 2.
What is meant by ‘She never had anything positive to say’?
Answer:
It meant that her thoughts and actions had always been negative.

Question 3.
Who said to whom?
Answer:

Sentence	Who said	To whom
1. “Let’s chat.”	Meena	To the writer
2. “We won’t get a taxi in this rain.”	The writer	Meena
3. “Then, what’s the secret of your energy?”	The writer	Meena
4. “A beggar changed my life.”	Meena	The writer

Question 4.
State whether the following statements are Right or Wrong. Correct the wrong ones:
Answer:

1. This wasn’t the same Meena that the writer had known. – Right
2. The writer bought an umbrella and went to the Grand Hotel with Meena.
   Corrected sentence: Instead of buying an umbrella they walked to the Hotel in rain. – Wrong
3. There was a Prince Charming in Meena’s life who managed to change her.
   Corrected sentence: A beggar had changed Meenas life. – Wrong
4. There was no change in Meena’s behaviour.
   Corrected sentence: Meena’s behaviour was completely changed. – Wrong

Question 5.
State whether the following statements are Right or Wrong. Correct the wrong ones :
Answer:

1. Rakesh’s father is a school teacher. [✓]
2. The writer was transferred to Bombay.
   Corrected sentence: The writer was in Bombay on an official work. [✗]
3. Meena is always pessimistic. [✓]
4. Meena had the habit of complaining about anything and everything. [✓]

Question 6.
Read the passage and fill in the blanks:
(Answers are directly given and underlined.)
Answer:

1. Meena was a chronic pessimist.
2. A begger changed Meena’s life.
3. The begger lived with his five-year old grand daughter.
4. The beggars were playing on the road because there was no traffic.

Complex Factual Activities:

Question 1.
What was Meena’s nature like?
Answer:
There was always something strange about Meena. She was always unhappy. Any person who came in contact with her would feel depressed. Her thoughts were negative about everything and about every person.

Question 2.
Arrange the following sentences in proper sequence according to their occurrence in the passage:

1. Many years later the writer saw Meena at Bombay’s Flora Fountain in pouring rain.
2. Unfortunately Meena saw the writer and caught hold of her hands warmly.
3. Meena was really excited to meet her old friend.
4. The writer wanted to avoid her for her never ending complaints.

Answer:

1. Many years later the writer saw Meena at Bombay’s Flora Fountain in pouring rain.
2. The writer wanted to avoid her for her never ending complaints.
3. Unfortunately Meena saw the writer and caught hold of her hands warmly.
4. Meena was really excited to meet her old friend.

Question 3.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. Old wine, old friends and memories are precious and rare.
2. A few strands of grey in her hair had reminded the writer that years had passed.
3. Meena was ready to make any number of adjustments.
4. The only thought in the writer’s mind was to find out who or what had brought about such a change in the pessimistic Meena.

Choose the correct alternative and complete the following sentences: (Answers are directly given and underlined.)

1. The only thought in the writer’s mind till they reached the Grand Hotel was what had brought about such a change in Meena.

1. why the rain was not stopping.
2. what had brought about such a change in Meena.
3. how the beggar had changed the entire life of Meena.

2. The writer wanted to attend a dinner.

1. a marriage party.
2. a dinner.
3. a birthday party.

3. When the writer met Meena in a pouring rain, she was ready to make any number of adjustments.

1. make any number of adjustments.
2. get wet in the rain.
3. buy an umbrella for them.

4. A beggar had managed to change Meena.

1. a Prince Charming,
2. The writer.
3. A beggar.

Question 4.
What surprised the writer?
Answer:
The writer was greatly surprised by the difference in Meena’s attitude of bygone days. She looked happy and was smiling. That was not the same Meena the writer had known. She seemed ready to make any number of adjustments.

Question 5.
Choose the correct alternative and rewrite the sentences:
(Answers are directly given and underlined.)
Answer:
1. The writer took almost two years to put the change into effect.

1. three years
2. two years
3. five years

2. The beggar and his granddaughter were enjoying the rain as if they were in paradise.

1. in paradise
2. in a palace
3. in front of the writer’s house

3. Attitude towards life was the most important of all assets, that the beggar and his granddaughter had but the writer was lacking.

1. Attitude towards life
2. So many comforts
3. Hunger

Question 6.
Complete the web:
(Answer is directly given.)
Answer:

Question 7.
What lesson did Meena learn from her Guru-the beggar?
Answer:
From her Guru-the beggar, Meena learnt how to be happy with life as it was. She also learnt to find happiness in every small thing, in every situation and in every person.

Question 8.
What did Meena do to show gratitude to her Guru?
Answer:
Meena changed her attitude towards life using the beggar as her role model. Unfortunately, by the time she understood things, he was dead. So she sponsored his granddaughter to a boarding school as a mark of respect to him.

Activities based on Vocabulary:

1. Find antonyms of the following words from the passage:

Question 1.

1. bad
2. never
3. negative
4. cold.

Answer:

1. bad × good
2. never × always
3. negative × positive
4. cold × hot

Question 2.
Match the following:

Group ‘A’	Group ‘B’
1. gloom	(a) to abate
2. cynicism	(b) expecting the worst
3. subside	(c) feeling of sadness
4. pessimistic	(d) a distrustful attitude

Answer:

1. gloom – feeling of sadness
2. cynicism – a distrustful attitude
3. subside – to abate
4. pessimistic – expecting the worst

Question 3.
Add suffix to the following words and make nouns:
(a) good
(b) happy
(c) assure
(d) feel
(e) achieve
(f) strange
(g) popular
(h) excite.
Answer:
(a) goodness
(b) happiness
(c) assurance
(d) feeling
(e) achievement
(f) stranger
(g) popularity
(h) excitement

Question 4.
Find out synonyms for the following from the passage :

1. inquisitive
2. displeased
3. attractive
4. valued.

Answer:

1. inquisitive – curious
2. displeased – disappointed
3. attractive – charming
4. valued – precious

Question 5.
Find the antonyms of the following from the passage:

1. dry
2. common
3. wrong.

Answer:

1. dry × drenched
2. common × rare
3. wrong × right

Question 6.
Write four words that have ‘ness’ as suffix :
Example – happiness
Answer:

1. kindness
2. boldness
3. greediness
4. greatness

Question 7.
Write two words that have ‘re’ as prefix :
Example – reassure
Answer:

1. rekindle
2. reappear
3. reinforce
4. repay

Question 8.
Find synonyms for the following words from the passage:
(a) heaven
(b) happily
(c) rainy
(d) very surprised
Answer:
(a) Paradise
(b) Joyously
(c) Monsoon
(d) Dumbfounded.

Activities based on Contextual Grammar:

Make the following sentences negative:

Question 1.
She was forever unhappy.
Answer:
She was never happy.

Question 2.
Meena was a pessimistic girl.
Answer:
Meena was not an optimistic girl.

Choose the correct alternative of afffirmative sentence.

Question 1.
She wasn’t a very pleasant company.
(a) She was a very unpleasant company.
(b) She wasn’t a very unpleasant company.
(c) She was a very pleasant company.
(d) She was a very beautiful company.
Answer:
She was a very unpleasant company.

Question 2.
Make it exclamatory:
She was very cheerful.
Answer:
How cheerful she was!

Question 3.
Shwetha is a very beautiful girl.
(Choose correct alternative of exclamatory sentence.)
(a) How beautiful girl Shwetha is!
(b) What a beautiful girl Shwetha is!
(c) What a beautiful girl Shwetha was!
(d) What a beautiful girl is Shwetha!
Answer:
What a beautiful girl Shwetha is!

Question 4.
Complete the following table:
(Answers are directly given and underlined.)
Answer:

Present Tense	Past Tense	Past Participle
1. see	saw	seen
2. pour	poured	poured
3. bring	brought	brought
4. know	knew	known

Make the following sentences affirmative:

Question 1.
I couldn’t believe it.
Answer:
I was unable to believe it.
OR
I could hardly believed it.

Question 2.
I can’t stay with you tonight.
Answer:
I am unable to stay with you tonight.

Choose the correct tail tag for the following sentences from the brackets:
(wasn’t she?, will we?, were here?, weren’t there?,will you?, won’t you?)

Question 1.
We wont get a taxi in this rain;
Answer:
will we?

Question 2.
There were a few wrinkles in her face;
Answer:
weren’t there?

Question 3.
Give me your card,
Answer:
will you?

Question 4.
Meena was surprised by my question,
Answer:
wasn’t she?

Personal Response:

Question 1.
Would you avoid your friend, if you are meeting himher after a long time?
Answer:
Welcoming or avoiding our old friend totally depends upon how close you are with that person. If you are really close to some friend by heart and soul you will never avoid himher even if you are meeting himher after a long time. Whereas we always wait for such occasions to meet our old buddies.

Question 2.
What is meant by ‘ Meena never had anything positive to say ’?
Answer:
Meena was always pessimistic in her life. Whoever said or asked anything, her answer was always negative. She never thought positively. It was her habit to take everything negatively. So the writer said “Meena never had anything positive to say.”

Question 3.
What, according to you, is the difference between an optimistic person and a pessimistic person?
Answer:
According to me, an optimist enjoys every moment. Optimists are confident and hopeful in themselves and believe they can overcome whatever life throws at them and continue on their way. Pessimists always have negative thoughts. They always feel defeated. They are never hopeful and lose confidence. Pessimists are unhappy and gloomy.

Question 4.
Change is the law of life-Explain.
Answer:
Change is the law of life. And those who look only at the past or present are certain to miss the future. Change is inevitable. We can’t ignore it. Changing means doing something new and challenging. That gives you a great joy of life. If we do not change ourselves, we cannot enjoy our life to the fullest.

Question 5.
Is it possible to bring change in our life like Meena?
Answer:
Yes, it is definitely possible to bring change like Meena in our life also. We can learn a lot from the examples and attitudes of other less-gifted people. If we have clear (good) conscience and we are determined to act according to it, we can surely | change our behaviour, attitude towards our life like Meena.

Question 6.
Describe an experience, where somebody has changed your way of looking at life.
Answer:
Once while travelling by a bus, I came across one of my friends with whom I had a quarrel on a petty thing. I ignored him and asked the conductor to give a ticket by giving a 100-rupee note.

The conductor had no change so he told me to get down and come by another bus. I was about to get down when my friend came forward and paid for my ticket. I felt ashamed and asked him to pardon me. The incident changed my attitude about him and now we are friends forever.

Question 7.
According to you, how can we help beggars?
Answer:
We should convince beggars that begging is not good. We should tell them the importance of ‘Self respect.’ If possible we will provide them opportunities to earn money and insist them to give up begging.

Do as directed:

Question 1.
They were laughing and screaming.
(Choose the correct option of ‘Not only-but also’)
(a) They were not only but also laughing and screaming.
(b) They were not only laughing but also screaming.
(c) They were laughing not only but also screaming.
(d) They were not only laughing and but also screaming.
Answer:
(b) They were not only laughing but also screaming.

Question 2.
He used to stay in front of my house.
(Rewrite the sentence by using ‘would’)
Answer:
He would stay in front of my house.

Change the voice:

Question 1.
That scene forced me to look at my own life.
(Begin the sentence with “I )
Answer:
I was forced to look at my own life by that scene.

Question 2.
I find happiness in every small thing in every situation and in every person.
(Begin the sentence with “Happiness ….)
Answer:
Happiness is found in every small thing, in every situation and in every person by me.

1. Attempt anyone:

Question (a)
Make a meaningful sentence by using given phrase: ‘in the pursuit of’
Answer:
In the age of technology everyone is in the pursuit of money.

OR

Question (b)
Add a clause to expand the following sentence meaningfully.
My friend is an LIC Officer ……………
Answer:
My friend is an LIC Officer who stays at Nagpur.

2. Attempt any one:

Question (a)
Add a prefix or suffix make new words :
Note: Two words will be given in the activity sheet.
(a) kind
(b) happy
(c) ignore
(d) assure
(e) imagine
(f) depute
(g) manage
(h) assess
Answer:
(a) kindness, unkind.
(b) unhappy, happiness
(c) ignorance
(d) assurance
(e) imagine
(f) deputation
(g) management, mismanage
(h) assessment,

Activities based on Language Study:

Question 1.
Complete the words by using correct letters:
Answer:

1. g _ oo _ – gloom
2. y o_n g – young
3. p r o_f – proof
4. t o_c h – touch

Question 2.
Put the words in alphabetical order:
1. chronic, squeezing, assets, zest.
2. pleasant, parents, paradise, pause.
Answer:
1. assets, chronic, squeezing, zest.
2. paradise, parents, pause, pleasant.

Question 3.
Punctuate the following sentences:
then whats the secret of your energy i asked
Answer:
“Then, what’s the secret of your energy?” I asked.

Question 4.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Question 5.
Complete the word-chain of ‘nouns’. Add four words, each beginning with the last letter of the previous word:
friend, → d …………, …………., …………, ………….,
Answer:
friend → dream , minute , elephant , thief.

Projects Task:

Question 1.
Find out more about Sudha Murthy and her writing from the internet.

My English Coursebook Standard Ten Digest Answers Pdf Unit 3

• If … Class 10 English Solutions
• A Lesson in Life from a Beggar Class 10 English Solutions
• Stopping by Woods on a Snowy Evening Class 10 English Solutions
• Let us March! Class 10 English Solutions
• The Alchemy of Nature Class 10 English Solutions

Class 10 English Chapter 1.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 1.5 His First Flight Notes, Textbook Exercise Important Questions and Answers.

His First Flight Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 1.5 His First Flight Textbook Questions and Answers

Warming up!

Chit-chat:

1. Form Groups of 5. Remember your past days and share with your friends about memories of your first day at school or your first attempt at cooking. What role did your parents, siblings play to help you to overcome your fear?

1. Discuss and answer.

Question 1.
Discuss and answer.

Answer:

1. Are there any situations when you get afraid?	– I Yes, I am afraid of sleeping in the dark at night, cold weather, street dogs, ghost stories and quarrels.
2. How would you react if you had to travel alone?	– I would be greatly disturbed and depressed if I had to travel alone. It annoys me and I feel uncomfortable.
3.  How would you react if you have to stay alone at home?	– It would be afraid of staying alone at home and become uneasy and endlessly think that something untoward will happen when I am alone at home.
4. What would you do if you were lost in a new city?	would cause confusion in my mind. I would lose my nerve and run helter- skelter to find any lead to my home or I shall collect myself and reach the police to get help from them.

2. Complete the following table.

Question 1.
Complete the following table.

Answer:

Idioms	Meanings	Your own sentences
1. bird’s-eye view	view from somewhere high	We enjoyed the bird’s-eye view from the top of the mountain.
2. as free as a bird	If he/she is care-free	After finishing her exam, she will be as free as a bird.
3. eagle’s eye	His ability to observe something closely	The detective was watching every move of the thief with his eagle eyes.
4. spread one’s wings	to try to work on things independently	After getting his training in papermaking, Kumar spread his wings to start his own paper mill.

Find more such idioms using the following keywords.

Question 1.
Find more such idioms using the following keywords.

Answer:

• Fly – with flying colours, fly high, fly the nest, fly the coop, fly at somebody, fly into rage/temper, get off to flying start.
• Animals – the lion’s share, let sleeping dog lie, a dog in the manger, a snake in the grass, rain cats and dogs, to lead a cat and dog life, let the cat out of the bag, to smell a rat.
• Colours – loose colours, with flying colours on black and white, catch red-handed, to become red and blue, a bolt from blue, once in a blue moon, look at the black side of things, stick to one’s colour.
  (Note: Students may collect more such idioms and their meanings from good dictionary.)

English Workshop:

1. State whether the following statements are true or false.

Question 1.
State whether the following statements are true or false.
(a) The young seagull was not confident about the ability of his wings.
(b) The young seagull’s parents guided and improved his siblings in the art of flying.
(c) When the young seagull pretended to be falling asleep, his parents noticed him.
(d) Flying across the young seagull, the mother dropped a piece of fish into his beak.
Answer:
(a) The young seagull was not confident about the ability of his wings. – True
(b) The young seagull’s parents guided and improved his siblings in the art of flying. – True
(c) When the young seagull pretended to be falling asleep, his parents took notice of him. – False
(d) Flying across the young seagull, the mother dropped into his beak a piece of fish. – False

2. Complete the following statements.

Question 1.
Complete the following statements.
(a) The seagull was afraid to fly because …………………………………………………………….
……………………………………………………………………………………………………………………………………..
(b) Young birds are afraid to make their first flight because …………………………..
………………………………………………………………………………………………………………………………………
(c) Human beings find it difficult to face great challenges because ……………….
………………………………………………………………………………………………………………………………………
Answer:
(a) the seagull is afraid to fly because he thought that his small, short wings would never support him to fly and he would fall and drown in the sea.
(b) Young birds are afraid to make their first flight because they are not confident at their first flight.
(c) Human beings find it difficult to face great challenges because I think, human being also finds it a challenge to take its first steps. It is their natural instinct. When they try to stand and then to take further steps, they are afraid of falling and getting injured, so they are cautious and alert but do not give up.

3. Read the following words carefully and make meaningful sentences of your own, and write in your notebook.

Question 1.
Read the following words carefully and make meaningful sentences of your own, and write in your notebook.

4. Read the following words carefully and fill in the blanks by choosing appropriate word given in brackets.

Question 1.
Read the following words carefully and fill in the blanks by choosing appropriate word given in brackets.
(afraid, plunged, appeared, shrilly, skimmed, devoured, cowardice)
(a) Arun is full of ……….. .
(b) The violin played very ……….. .
(c) Ravi said, “Are you really ……….. of the dark?”
(d) The whole village ……….. into darkness.
(e) The lions ……….. their prey, hungrily.
(f) He ……….. through the report.
(g) One by one, the stars ……….. in the sky.
Answer:
(a) Arun is full of cowardice.
(b) The violin played very shrilly and merrily.
(c) Ravi said, “Are you really afraid of the dark?”
(d) The whole village plunged into darkness.
(e) The lions devoured their prey, hungrily.
(f) He skimmed through the report.
(g) One by one, the stars appeared in the sky.

5. Read about the space mission of Sunita Williams. Imagine you are going to interview her. Frame 10 to 12 interview relevant questions regarding –

1. her early life, training
2. education
3. her actual flight into space
4. future plans
5. her message to viewers.

Question 1.
Read about the space mission of Sunita Williams. Imagine you are going to interview her. Frame 10 to 12 interview relevant questions regarding –
Answer:
Interview Questions to Sunita Williams :
Hello Madam! Congratulations on your great achievements in the Space Mission! May I ask you a few questions about your career and mission?

1. 1. Could you please tell me about your birthplace, family and early education?
   2. What motivated you to do M.Sc. in engineering Management? Where did you do it?
   3. What was your experience as a Naval Aviator in 1989?
   4. When and where did you begin your Astronaut Candidate Training?
   5. When were you selected by NASA for Astronaut Program?
   6. Will you please tell me about your experience at NASA?
   7. How did you feel when you were aboard the space shuttle Discovery to join the Expedition 14?
   8. How many days did you stay in the space during the Expedition 14?
   9. You have eclipsed the record in space by a woman. What was that record?
   10. What can you tell me about your second Expedition 32/33. What was your part in it?
   11. You took to the ISS a copy of Bhagavat Gita and a figurine of the God Ganesh and samosas. What was the thought behind it?
   12. How did the Government of India honour you? Why?
   13. What is your message to the young Indian generation?

6. Describe in your notebook the challenges you faced while learning to ride a bicycle, swimming or any skilL Take hints from the web to complete your write-up.

Question 1.
Describe in your notebook the challenges you faced while learning to ride a bicycle, swimming or any skilL Take hints from the web to complete your write-up.
Answer:
Riding a Bicycle:
Though some people think that riding a bicycle is a very simple easy thing, but it is not true. It is a challenging job. When you begin to learn cycle you must have to drive away and win over the fear of falling. While riding a cycle you are bound to fall once or twice or more and may get injured. So you must be bold and forget your fear of falling.

Secondly as a beginner don’t fully depend on a trainer or a supporter, otherwise you will never learn cycling. You should ride on your own with determination. You must be steady, stable and patient. You will have to look straight ahead of you and not to the handle or pedal or anywhere else. Sit properly on the seat and hold the handle firmly. Balancing is the next task/challenge. Be alert and ride the cycle carefully.

Pay attention to the vehicles coming in your way and you should be able to avoid them or there will be a possibility of an accident. Your concentration must be only on riding. Remember the traffic rules and follow them. After practising a lot you will be able to ride a bicycle confidently.

7. Project :

Question a.
Collect the career options related to flying. Find out the institutes where training of your options is given.
Find out the detailed information about the fees, duration of training and future prospects of it.
Answer:
(Students should collect the information asked for and present them in their class.)

Question b.
Collect or draw different pictures of birds from your surroundings and write about them. Make a chart with some information about each.
Answer:
(Make a chart with some information about the birds.)

Language Study:

1. There are words that have the same pronunciation but differ in spellings. They are called Homophones. For example, (a) fair – fare (b) know – no Sometimes the words have the same spellings and pronunciation but can have different meanings in different situations.
They are called Homographs.
For example:
(a) watch – observe watch – portable timepiece
(b) fair – not very good, not very bad
fair – an exhibition and sale of items
fair – of complexion, skin tone
Note: Homophones and Homographs are together known as Homonyms.
Give the Homophones of the following.
(a) blue …. (b) bear …… (c) beet……… (d) to……… (e) son …………

Question 1
Give the Homophones of the following.
Answer:
(a) blue – blew
(b) bear – bare
(c) beet – beat
(d) to – two
(e) son – sun

2. Find from the lesson the Homophones of the following.

Question a.
Pick the Homophones from the text.

1. see –
2. wood –
3. there –
4. scene –
5. won –
6. eye –
7. peace –
8. threw –
9. hence –
10. knot –

Answer:

1. see – sea
2. wood – would
3. there – their
4. scene – seen
5. won – one
6. I – eye
7. peace – piece
8. threw – through
9. hence – hens
10. knot – not

Question b.
Explain how the underlined Homographs differ in meaning.
1. (a) He saw his two brothers. ……………………….
(b) The woodcutter cut the weakened branch with his sharp saw ……………………….
2. (a) The bird injured his wings. ………………………..
(b) He lives in the ‘c’ wing of the building. ……………………….
3. (a) The aeroplane will land at 9.00 pm. sharp. ……………………….
(b) He owns 10 acres of land ………………………..
4. (a) The head of the institution was on leave. ……………………….
(b) He bent his head down with chin. ………………………….
Answer:
1. (a) He saw his two brothers.
(b) The woodcutter cut the weakened branch with his sharp saw.
Answer:
In the sentence:
(a) the Homograph ‘saw’ is the past tense of the word ‘see’.

In the sentence:
(b) the Homograph ‘saw’ means a tool of a carpenter used for cutting wood.

2. (a) The bird injured his wing.
(b) He lives in the ‘C’ wing of the building.
Answer:
In the sentence:
(a) the Homograph ‘wing’ means the part of the body of a bird used for flying.

In the sentence:
(b) the Homograph ‘wing’ is one of the parts of a large building.

3. (a) The aeroplane will land at 9.00 pm. sharp.
(b) He owns 10 acres of land.
Answer:
In the sentence
(a) the Homograph ‘land’ means to come down through the air onto the ground.

In the sentence
(b) land means an area of ground used for some purpose.

4. (a) The head of the institution was on leave.
(b) He bend his head down with respect.
Answer:
In sentence
(a) head means the person in charge of an institution/organization.

In sentence
(b) head means the part of the body on top of the neck.

3. Read the following sentences carefully, underline the verbs and find out the tenses in the sentences.

Question 1.
(a) The sun was now ascending the sky.
(b) Still they took no notice of him.
(c) She is standing on a little high hump on the plateau.
(d) He leaned out eagerly.
(e) He just felt dizzy.
Answer:
(a) The sun was now ascending the sky. – Past Continuous Tense
(b) Still they took no notice of him. – Simple Past Tense
(c) She is standing on a little high hump on the plateau. – Present Continuous Tense
(d) He leaned out eagerly. – Simple Past Tense
(e) He just felt dizzy. – Simple Past Tense

Live English :

Form Filling:

Form filling is a skill. It is a functional skill and a life skill. Today, a big amount of data is collected offline and online through forms. From a tedious task to an interesting task, the online tools have made form filling a unique experience. We will see how offline and online forms are filled and what steps are followed and what care is taken while filling the forms.

Preparing for the form filling process:

• Gather all the essential information. (personal, professional, educational etc.)
• Verify names, addresses, references, contact details to be entered.
• Know the information not to be provided.
• Get a template and create a model form.

Question 1.


Answer:

My English Coursebook 10th Digest Chapter 1.5 His First Flight Additional Important Questions and Answers

Read the following passage and do the activities :

Simple Factual Activity :

Question 1.
State whether the following statements are True or False :
Answer:

1. The wings of the young seagull were not as short as his own. – False
2. The whole family of seagulls commended him for his cowardice. – False
3. The young seagull was fed a piece of fish by his mother. – False
4. The young seagull’s father was preening the feathers on his white back. –True

Question 2.
Complete the following sentences using information in the passage:
(Answers are directly given and underlined.)
Answer:

1. The young seagull commended himself to dive and soar and curve.
2. He completely forgot that he had not always been able to fly.
3. He flapped his wings once and he soared upwards.
4. He turned his beak sideways and cawed amusedly.

Complex Factual Activities :

Question 1.
How did the seagull parents perfect the young seagull’s brothers and sister in the art Of flight?
Answer:
The parents of the seagull flew about with his brothers and sister, perfecting them in the art of flying. They trained them how to skim the waves and how to dive for fish. When they succeeded in the art, the parents circled about them raising a proud cackle to encourage them.

Question 2.
Complete the web describing the young seagull’s feelings while trying to fly:
(Answers are directly given.)
Answer:

Question 3.
What were the young seagull’s parents doing?
Answer:
The young seagull’s father was cleaning his white back feathers smooth with his beak. His mother was looking at the young seagull. She stood on a little high hump on the plateau. Her white breast was thrust forward. Now and again, she tore at a piece of fish that lay at her feet and then scrapped each side of her beak on the rock. She was trying to attract the young one’s attention towards the piece of fish.

Question 4.
Complete the web :
(Answers are directly given and underlined.)
Answer:

Question 5.
How did the young seagull learn his first flight?
Answer:
When the young seagull was calling his mother plaintively, his mother had picked up a piece of fish and was flying across to him with it. He leaned out eagerly trying to get nearer to her as she flew across. But when the piece of fish in her beak was almost within his reach, his mother halted, her wings motionless. Maddened by hunger, the young one dived at the fish.

While doing so he fell outwards and downwards into space. He was frightened but the next moment he felt his wings spread outwards. The wind rushed against his breast, then under his stomach and against his wings. His wings cut through the air. He was not falling headlong now. He was soaring gradually downwards and outwards. This is how he learnt his first lesson of flight.

Question 6.
Complete the web :
(The answers are directly given and underlined.)
Answer:

Question 7.
What did the young seagull forget? What did he do then?
Answer:
The young seagull completely forgot that he had not always been able to fly. He commended himself for his diving and soaring and curveting shrieking shrilly.

Question 8.
When did the young seagull get his prized scraps of dog-fish?
Answer:
The young seagull was completely exhausted after his first flight. He drooped his legs to stand on the green sea. His legs sank in it. He screamed with fright and tried to rise again flapping his wings. But he was tired and weak with hunger and he could not rise. His feet sank into the green sea and then his belly touched it and he could sink no farther. He was floating on it. His family admired his feat (achievement) and offered him scraps of dog-fish which he deserved.

Activities based on Vocabulary:

Question 1.
Guess the meanings of:
Answer:

1. muster up courage – to gather courage
2. cliff – a high steep face of a rock
3. upbraiding – scolding
4. brink – the edge of a steep place

Question 2.
Match the words in Column ‘A’ with their meanings in Column ‘B’ :

‘A’	‘B’
1. ascending	(a) grabbed
2. maddened	(b) flying upward into the air
3. soaring	(c) made one very angry
4. seized	(d) rising up

Answer:

‘A’	‘B’
1. ascending	(d) rising up
2. maddened	(c) made one very angry
3. soaring	(b) flying upward into the air
4. seized	(a) grabbed

Question 3.
Find the present participles from the passage :
Answer:
ascending, standing, falling, lying, dozing, preening, looking, scrapping, begging, calling, flying, tapping, trying, wondering, cutting, soaring.

Question 4.
Match adjectives given in Column ‘A’ with the nouns given in Column ‘B’ :

‘A’	‘B’
1. high	(a) scream
2. joyful	(b) nightfall
3. monstrous	(c) hump
4. previous	(d) terror

Answer:

‘A’	‘B’
1. high	(c) hump
2. joyful	(a) scream
3. monstrous	(d) terror
4. previous	(b) nightfall

Question 5.
Read the following words carefully and make meaningful sentences of your own by using them :

1. plaintively
2. monstrous
3. whet
4. soar.

Answer:

1. The young widow plaintively mourned when she saw her husband’s dead body in a coffin covered by tricolour.
2. A monstrous wave swallowed the boat with some fishermen in it.
3. He whetted his knife to cut the unwanted plants in the garden.
4. The rocket soared up into the air.

Question 6.
Read the following words and fill in the blanks by using appropriate words given in the brackets :
(Answers are directly given and underlined.)
(commended, attempted, exhausted, soared)
Answer:

1. The rocket soared up into space.
2. Our achievements in Science Exhibition was highly commended by our Principal.
3. He was totally exhausted after the day’s tedious work.
4. The thief attempted to give the slip, but was caught by the police.

Question 7.
Match the words in Column ‘A’ with their meanings in Column ‘B’ :

Column ‘A’	Column ‘B’
1. ridge	(a) wear out
2. exhaust	(b) small and thin pieces
3. shriek	(c) a chain of hills
4. scraps	(d) make a loud cry

Answer:

Column ‘A’	Column ‘B’
1. ridge	(c) a chain of hills
2. exhaust	(a) wear out
3. shriek	(d) make a loud cry
4. scraps	(b) small and thin pieces

Question 8.
Read the following words and make meaningful sentences of your own by using them :

1. beckon
2. curveting
3. exhausted
4. amusedly

Answer:

1. They were all beckoning him to join their team, but he did not respond.
2. The eagle was curveting to land onto the ground to catch his prey.
3. The old man was completely exhausted after the day’s long work.
4. The children played in the rain merrily and amusedly.

Activity-based on Contextual Grammar :

Question 1.
Read the following sentences carefully, underline the verbs and then find out the tenses in the sentences : (Verbs are directly underlined.)
Answer:

1. His two brothers and his sister had already flown away. – Past Perfect Tense
2. But for the life of him he could not move. – simple Past Tense
3. He became afraid. – simple Past Tense
4. Since then nobody had come near him. – Past Perfect Tense

Question 2.
Identify the tense and then change it to Present Perfect Continuous tense:
The sun is ascending the sky.
Answer:
The sun has been ascending the sky.

Personal Response:

Question 1.
Are you afraid of playing any outdoor game? Explain why?
Answer:
Yes, I am afraid of playing Kabbadi. It appears to me that it is a very rough and tough game. I am very much afraid of the injuries caused in it. I cannot endure the thought of injury. I believe that it is a game for only strong and hefty people.

Question 2.
You are a teacher directing a play for your school/Annual Gathering. A boy is not acting according to your instructions. How will you make him act well?
Answer:
At first I shall tell the boy about the scene and the emotions in dialogues by giving him demonstration. If he goes wrong, I myself will show him how to do the piece. If he repeatedly makes mistakes, I will scold him and even threaten him of the consequences. But anyhow finally I will make him act well, acting the scene myself repeatedly.

Question 3.
How does your family help you to achieve your goal?
Answer:
My family is always there to help me in my work. Each one of them, especially my parents, help me in deciding my goal. If I neglect any day, they remind me of my goal all the while. They all are ready to guide me, in their own way, to achieve whatever I desire. They always encourage, admire and praise me even for my smallest achievement.

Activity-based on Contextual Grammar:

Do as directed:

Question 1.
He was near the sea now. (Frame a Wh-question to get the underlined as an answer.)
Answer:
Where was he now?

Question 2.
He could not rise. (Add a question tag.)
Answer:
He could not rise, could he?

Question 3.
But he was tired and weak with hunger.
(Use ‘not only – but also’.)
Answer:
But he was not only tired but also weak with hunger.

Activities based on Language Study

Do as directed :

Question 1.
Complete the words by using correct

1. s t _ n d
2. y o _ n g
3. c l _ f f
4. d i z _ y

Answer:

1. s t a n d
2. y o u n g
3. c 1 i f f
4. d i z z y

Question 2.
Put the following words in alphabetical order :

1. motionless, scrapped, leaned, opposite
2. feathers, felt, flapped, father

Answer:

1. leaned, motionless, opposite, scrapped.
2. father, feathers, felt, flapped

Question 3.
Punctuate the following sentences :

1. ga ga ga he cried begging her to bring him some food
2. the young seagulls father was curveting banking and soaring

Answer:

1. “Ga, ga, ga”, he cried begging her, to bring him some food.
2. The young seagull’s father was curveting, banking and soaring.

Question 4.
Make four words each (minimum 3 letters each) using the letters in the given word brother:
Answer:
both, bother, rot, other

Question 5.
Write related words as shown in the example :
(Answer is directly given and underlined.)
Answer:

Question 6.
Complete the following word chain of nouns. Add four words each beginning with the last letter of the previous word :
ledge → ……………… → ……………… → ……………… → ………………
Answer:
ledge → egg → goal → land → doll

Do as directed :

1. Attempt anyone :

a. Make a meaningful sentence using the given phrase:
to muster up courage
Answer:
The young man could not muster up courage to pick up the mysterious box on the road.

OR

b. Add a clause to the following sentence to expand it meaningfully :
The bird dared not fly
Answer:
The bird dared not fly because he was afraid of falling in the sea.

2. Attempt anyone :

a. Add a prefix or suffix to make new words :
1. manage
2. arrange
Answer:
1. management
2. rearrange

OR

b. Make a meaningful sentence using any one of the following words :
1. manage
2. arrange
Answer:
1. He could manage to collect enough money to pay his school fees.
2. She arranged the flowers in a vase.

My English Coursebook Standard Ten Guide Unit 1

• A Teenager’s Prayer Class 10 English Solutions
• An Encounter of a Special Kind Class 10 English Solutions
• Basketful of Moonlight Class 10 English Solutions
• Be SMART…! Class 10 English Solutions
• His First Flight Class 10 English Solutions

Class 10 English Chapter 3.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Solutions Chapter 3.4 Let us March! Notes, Textbook Exercise Important Questions and Answers.

Let us March! Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.4 Let us March! Textbook Questions and Answers

Warming up:
Chit-chat

Discuss in your group:

Question 1.
What difference do you notice in the two images?
Answer:
The boy in the first picture is working and the boy in the second picture is going to school on his bicycle.

Question 2.
Which of the two situations should change?
Answer:
The situation in the first picture should change.

Question 3.
How and when can the situation be changed?
Answer:
The boy in the first picture should be sent to school. Somebody should convince his parents that it is not his right age to work. He should go to school at this age. Then the situation can change.

Question 4.
How can you, as a student, contribute and help make a difference to the needy children?
Answer:
As a student I will help the needy children to go to school and take education. If possible I will try to give them monetary help to take education. I will also convince their parents
to understand the importance of education.

1. A good well-organized speech contains the following characteristics and steps.

Question (A)
A good well-organized speech contains the following characteristics and steps.
Answer:

1. A speech should be well-planned.
2. The language used should be suitable to the audience.
3. It should have the right duration.
4. It should be supported with good examples, episodes or visual aids, where possible.

Question (B)
Refer to Page 26 for a reference to the steps to be followed in the speech and do the activity given below. Read the expressions given below on Coursebook and insert them in the proper boxes:
(a) Imagine what will happen after ten years.
(b) I would like to share with you an example from my own experience.
(c) Hon. chief guest, eminent dignitaries, respected management and staff, student – friends
(d) The research report says that ……………
(e) I don’t understand why we are so negative about this issue.
(f) Think again and again and then move forward.
(g) Today, I would like to put forth my views on ………………
(h) The renowned personality xyz says “……………..”
(i) Good Morning, one and all present today.
(j) I would like to express my gratitude towards the organisers of this function for giving me opportunity ……………
(k) If we think about the situation around us, we notice that ………………
(l) Let me explain this to you ……………..

Answer:

Greeting / Salutation	Introduction	Body of the speech	Conclusion
1. Good morning, one and all present today.	1. If we think about the situation around us we notice that	1. The renowned personality xyz says “……………………….	1. Think again and again and then move forward.
2. Hon. Chief guest, eminent dignitaries respected management and staff, student- friends.	2. Let me explain this to you	2. The research report says that …………………..	2. I would like to express my gratitude towards the organizers of this function for giving me the opportunity ………
	3. Today, I would like to put forth my views on	3. I don’t understand why we are so negative about this issue.
	4. Imagine what will happen after ten years.	4. I would like to share with you an example from my own experience.

English Workshop:

1. Name the following:

Question (a)
The persons to whom Kailash Satyarthi gives the highest credit of his honour:
Answer:
Kaalu Kumar, Dhoom Das and Adarsh Kishore from India and Iqbal Masih from Pakistan.

Question (b)
The greatest personalities from the great land-India.
Answer:
Lord Buddha, Guru Nanak and Mahatma Gandhi.

Question (c)
The daughters of Kailash Satyarthi mentioned in this speech:
Answer:
Malala, Kayanat and Shazia

Question (d)
The foreign activists of equal rights mentioned in this speech:
Answer:
Nelson Mandela and Martin Luther King.

2. Mention the social issues highlighted by Kailash Satyarthi in his speech. One social issue is given for you.

Question 1.
Mention the social issues highlighted by Kailash Satyarthi in his speech. One social issue is given for you.
(a) Child labour
(b) …………………
(c) …………………
(d) …………………
(e) …………………

3. Complete the following diagram/chart:

Question 1.
Complete the following diagram/chart:

Answer:

4. Complete the following web-chart:

Question 1.
Complete the following web-chart:

Answer:

5. Find out the describing words used for the following nouns and make your own sentences by using any three combinations.

Question 1.
Find out the describing words used for the following nouns and make your own sentences by using any three combinations.
(a) …………… sacrifice
(b) …………… faces
(c) …………… militia
(d) …………… challenge
(e) …………… globalise
(f) …………… agencies
Answer:
(a) supreme sacrifice
(b) beautiful faces
(c) extremist-militia
(d)great challenge
(e) globalise – globe, globalization
(f) intergovernmental agencies

6. Choose the correct option and write in front of the given word:

Question (a)
divinity: ……………
Answer
divinity: godliness
1. goodness
2. godliness
3. god fearing

Question (b)
extremist: militant
1. militant
2. robber
3. spy

Question (c)
culminate: rise to a peak
1. destroy
2. succeed
3. rise to a peak

7. What will you do in the following situations?

Question (a)
If you see a child working in a restaurant.
Answer:
I will lodge a complaint against the owner under the Child Labour Act, 1986.

Question (b)
If you find a child working on a construction site.
Answer:
I will lodge a complaint in the police station nearby and convince them to send him to a nearby school.

Question (c)
If you find a child working on a brickwork site.
Answer:
I will tell his parents not to do so, instead to send him to a school nearby.

Question (d)
If you come across a beggar child.
Answer:
I will tell the child, it is not good to beg. I will also tell him the importance of schooling and help him to go to school.

(B) Write any 2 efforts that you can make to enrol deprived children/ out of school children into a school. One is given for you.
(a) I will persuade parents of such children to send them to school.
(b) …………………………………………………………………………………….. .
(c) …………………………………………………………………………………….. .
(d) …………………………………………………………………………………….. .
(e) …………………………………………………………………………………….. .

8. Today, it is time for every child to have a right to –

education, ……………….., ……………….. .
……………….., ……………….., ……………….. .
……………….., ……………….., ……………….. .

9. Make a list of Indian Nobel laureates.

Question 1.
Make a list of Indian Nobel laureates.
Answer:

Name	Field	Year
1. Rabindranath Tagore	Literature	1913
2. C. V. Raman	Physics	1930
3. Mother Teresa	Peace	1979
4. Subrahmanyan Chandrasekhar	Physics	1983
5. Amartya Sen	Economics	1998
6. Kailash Satyarthi	Peace	2014

10. Make a list of prestigious awards in India:

Question 1.
Make a list of prestigious awards in India:

Answer:

Civilian Awards	Highest gallantry awards
Bharat Ratna	Param Vir Chakra
Padma Vibhushan	Maha Vir Chakra
Padma Bhushan	Vir Chakra
Padma Shri	Ashok Chakra

11. Make a meaningful sentence by using the phrases:

Question 1.
Make a meaningful sentences by using the phrases: (Note: One phrase will be asked in the activity sheet.)
(a) in the pursuit of
(b) to be afraid of
(c) to give up
Answer:
(a) Most of the people spend a lot of time in the pursuit of money.
(b) Don’t be afraid of saying what you sincerely think.
(c) His wife finally persuaded him to give up smoking.

12. Write minimum 5 hidden words of more than 4 letters from- ‘intergovernmental’.

Question 1.
Write minimum 5 hidden words of more than 4 letters from- ‘intergovernmental’
Answer:

1. internal
2. government
3. torment
4. term
5. governmental

13. Imagine your school invites Malala to preside over celebration of ‘Children’s Day’. Draft a welcome speech for this noble young girl. Gather her bio-data from the internet.

Question 1.
Imagine your school invites Malala to preside over celebration of ‘Children’s Day’. Draft a welcome speech for this noble young girl. Gather her bio-data from the internet.
Answer:
Honourable Chairperson, respected Principal, teachers, our today’s guest Malala Didi and all my dear friends.

We have gathered here to celebrate Children’s Day. On this auspicious occasion I would like to limit my few words on the Children’s Day. Children are the integral part of the society and home as well as the future of the country. We cannot ignore their involvement and contribution in the life of parents teachers and other related people all through the life.

Children are blessed by God and they conquer our hearts with their beautiful eyes, innocent activities and smiles. Life becomes very boring andupset without them. This day is celebrated every year to pay tribute to all the children all over the world. In India it is celebrated on 14th November on the birth anniversary of the legendary freedom fighter and the first Prime Minister of the independent India; Pandit Jawaharlal Nehru.

The celebration of this day reminds us to renew our commitment towards children’s welfare including their health, care and education. It is an occasion to appreciate the qualities of childhood. Children are considered as the building blocks of the strong nation. They have capabilities to change the nation positively. They are the responsible citizens of tomorrow. The development of the country lies in their hand. Children’s Day celebration also reminds us about their rights.

Children are leaders of tomorrow so they need to get respect, special care and protection from their parents, teachers and from the society. Do they really get it? They are being abused in many ways in our nation by their family members, relatives, neighbours or other people. Government should work on it to help them to live life happily. Malala Didi is a Pakistani activist who works for girls’ females’ education. She works for the human rights, especially the right to education of women and children.

We are really proud of her. On this auspicious day if we take inspiration from her, no child will be abused, no girl will be molested. She is a great source of inspiration and so she is here with us. We are eager to hear her valuable thoughts and voice, so I think I would better stop here. Wish you all happy Children’s Day and all the best for your future endeavour. Thanks a lot for listening to me patiently and attentively.

Jai Hind!

14. Use the following words as a noun and a verb and make meaningful sentences:

Question 1.
Use the following words as a noun and a verb and make meaningful sentences:

1. march
2. honour
3. credit
4. stitch

Answer:

1. march – The workers began their march to protest against their factory owners, (noun)
   The physical education teacher marched the children to the playground, (verb)
2. honour – A dinner was arranged in his honour, (noun)
   The actor was honoured with the Padmashri.(verb)
3. credit – The bank refused to extend their credit.(Noun)
   She has been wrongly credited as the author. (Verb)
4. stitch – The wound needed eight stitches, (noun)
   The tailor was asked to stitch the clothes quickly, (verb)

Language Study:

Question (a)
Match the sentences given in part ‘A’ with the sentences given in part ‘B’. Note the differences in structure.
Answer:

Question (b)
Observe the following underlined phrases. Here ‘have/has’ are followed by the past participle form of the verb. This construction indicates the perfect present tense. Find more such sentences from the speech.
Answer:

1. We have made progress in the last couple of decades.
2. We have prevented millions of child deaths.
3. It has happened.
4. We have reduced the number of out-of-school children by half.
5. We have reduced the child labourers by a third.

Question (c)
In the following sentences the underlined words are called infinitives. Find such examples from the speech and underline the infinitives.
Answer:

1. Every child is free to grow.
2. I refuse to accept that all the laws and constitutions, police and judges are unable to protect our children.
3. that all the temples and mosques and churches and prayer houses have no place for the dreams of our children.
4. just one week of global military expenditure can bring all the children to classrooms.
5. The shackles of slavery can be stronger than the quest for freedom.

Question (d)
Pick out from the lesson, the Antonyms of
Answer:

1. ignorance × knowledge
2. deny × admit
3. immortality × mortality
4. violence × non-violence
5. well-known × known
6. slavery × freedom

(e) Do as directed.

Question (i)
Make nouns of the following.

Answer:

Words	Nouns
1. deliberate	deliberation
2. organize	organization/organiser
3. violent	violence
4. tolerant	tolerance
5. extreme	extremism/extremist
6. educate	education/educator
7. globalize	globalization
8. distant	distance
9. prescribe	prescription/prescriber

Question (ii)
Make verbs of the following.

Answer:

1. universal – universalize
2. global – globalize

Question (f)
Complete the following sentences with the help of the sentence given below:
(Answers are directly given and underlined.)
(a) The biggest challenge knocking on the doors of human kind is fear and intolerance.

(i) No other challenge knocking …………………………………………………… .
as big as …………………………………………………………………………………… .
(ii) Fear and intolerance are bigger ……………………………………………….. .
………………………………………………………………………………………………… .

(b) The Nobel Prize is one of the greatest honours in the world.

(i) Very few honours …………………………………………………………… .
(ii) The Nobel Prize is greater than …………………………………………. .
………………………………………………………………………………………………… .
Answer:
(a) The biggest challenge knocking on the doors of humankind is fear and intolerance.
1. No other challenge knocking on the doors of humankind is as big as fear and intolerance.
2. Fear and intolerance are bigger than any other challenge knocking on the doors of humankind.

(b) The Nobel Prize is one of the greatest honour in the world.
1. Very few honours in the world are as great as the Nobel Prize.
2. The Nobel Prize is greater than most other honours in the world.

My English Coursebook 10th Digest Chapter 3.4 Let us March! Additional Important Questions and Answers

Simple Factual Activities:

1. Name the following:

Question 1.
The American politician, attorney and author mentioned in the speech –
Answer:
Tom Harkin.

Question 2.
Answer in one word:
Answer:

1. The motherland of Kailash Satyarthi – India
2. The country which Iqbal Masih represents – Pakistan
3. The place where Nobel Prize distribution programme was held – Norway
4. The ancient texts of wisdom – Vedas

Question 3.
State whether you agree or disagree with the following statements:
Answer:

1. The Holy Quran s ays the kingdom of God belongs to the children.
2. Jesus says not to kill your children because of poverty. – Disagree
3. Denying the dreams of our children is greater violence. – Agree
4. The writer has never given up against any threat or attack. – Agree

Question 4.
Match the following:
Answer:

1. A small, skinny child labourer – to care for our children
2. A Sudanese child-soldier – children’s frightened and exhausted eyes
3. Satyarthi had looked into – was forced to kill his friends and family.
4. The great religions teach us – The world forced me to take a gun or a tool

Question 5.
State whether the following statements are True or False:
Answer:

1. The biggest challenge of humankind is fear and intolerance. – True
2. Education gives the meaning and objective of life. – True
3. An unprecedented violence will not be suicidal for humankind. – False
4. Rights, security, hope can only be restored through education. – True

Question 6.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. Even though we have made progress in the last couple of decades, we are facing great challenges.
2. An education gives a sense of global citizenship among the youth.
3. Small groups, local organisations and individuals are confronting with the problem every day.

Question 7.
Answer in few words:

1. he age in which we live –
2. The serious disconnect of the world –
3. We can unite the world through –
4. Children are questioning and watching our –

Answer:

1. rapid globalization
2. lack of compassion
3. the compassion for our children
4. inactions and actions

Question 8.
Complete the sentences:
(Answers are directly given and underlined.)
Answer:

1. A tiny bird was rushing towards the fire.
2. A heavy fire had broken out in the forest.
3. The speaker is appealing to compassion.
4. The tiny bird was going to extinguish the fire.

Question 9.
Make a list of the problems that we are facing and creating violence against children –
Answer:

1. slavery
2. trafficking
3. child marriage
4. child labour
5. sexual abuse
6. illiteracy

Question 10.
Complete the following web:
(Answers are directly given and underlined.)
Answer:

Question 11.
State whether the following statements are Right or Wrong:
Answer:

1. We should have vision for today not tomorrow. – Right
2. If we close our eyes and feel the child inside us, we can listen to that child. – Right
3. Mahatma Gandhi, Nelson Mandela and Martin Luther King are calling on us. – Right
4. Mahatma Gandhi, Nelson Mandela and Martin Luther King are calling on us. – Right
5. Satyarthi’s vision of tomorrow is to see that cobbler’s boy sitting with him in his classroom. – Right

Complex Factual Activities:

Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. We can create knowledge for all that benefits all by learning from the experiences of our ancestors.
2. The mantras that carries a prayer has the potential to liberate humanity from all man-made crises.
3. The writer humbly accepts this award on behalf of all martyrs, his fellow activists across the world and his countrymen.
4. The journey of the writer, that is India to Norway is a connect between two centres of global peace and brotherhood, ancient and modern.
5. The speaker feels honoured to recite a mantra from the ancient text of wisdom.

Question 2.
Complete the following web:
Answer:

Question 3.
What are the children’s issues highlighted by Kailash Satyarthi in this passage?
Answer:
The children’s issues highlighted by Kailash Satyarthi in this passage are-

1. The burning problem in India-child labour
2. The Right of children to free and compulsory education
3. Mortality and malnutrition,
4. Child labour as a human rights issue as well as a welfare matter and charitable cause.

Question 4.
Complete the following web stating the sign of progress mentioned by Satyarthi:
Answer:

Question 5.
What social role are the ‘three daughters’ laying?
Answer:
These three daughters are rising up and choosing peace over violence, tolerance over extremism and courage over fear.

Question 6.
Complete the following web:
Answer:

Question 7.
What problems do the poor children face?
Answer:
The poor children face the following problems –

1. They harvest cocoa yet they have never tasted chocolate.
2. They are dying of Ebola.
3. They are kidnapped and held hostage.
4. They stitch football, yet they never play with it.

Question 8.
What did millions of individuals demand eighteen years ago?
Answer:
Eighteen years ago, millions of individuals demanded a new international law for the abolition of worst form of child labour.

Question 9.
Why does the eight-year-old girl’s question shake Mr Satyarthi? (r^T srrc qqMi HyfMi srt SKcfTT Wt?)
Answer:
The eight-year-old girl’s question ‘Why did you not come earlier?’ itself implies that the girl was really suffering a lot. Even though we are grown ups, we have failed to rescue number of small girls from forced labour. So her question shakes not only Satyarthi, but also the whole world.

Question 10.
What matters according to Satyarthi?
Answer:
Every single minute, every single child and every single childhood matters according to Satyarthi.

Question 11.
Complete the following web:
(Answer is directly given and underlined.)
Answer:

Question 12.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
1. Government should make child-friendly policies and invest in education and young people.
2. Faith leaders, institutions and all of us must stand with our children.

Question 13.
Complete the following web:
(Answer is directly given.)
Answer:

Question 14.
What was the response of the boy’s father? What was Satyarthi’s reaction to it?
Answer:
The response of the boy’s father was that he had never thought about it and they were born to work. His answer made Satyarthi angry and it still makes him angry.

Question 15.
Complete the following:
(Answers are directly given and underlined.)
Answer:
1. Satyarthi requests the listeners to put their hands close to their heart, close their eyes and feel the child inside them.
2. The writer calls all the listeners for a march,

1. from → exploitation to → education
2. from → exploitation to → education
3. from → poverty to → shared prosperity
4. from → slavery to → liberty
5. from → violence to → peace
6. from → ignorance to → awakening
7. from → darkness to → light
8. from → mortality to → divinity

Question 16.
Complete the following web-chart:
(Answers are directly given)
Answer:

Activities based on Vocabulary:

Question 1.
Find out the describing words used for the following nouns and make your own sentences using any two combinations:
(a) peace
(b) chair
Answer:
(a) global peace
(b) empty chair

Sentences:
1. UNO was founded (established) for global peace.
2. We should never forget the supreme sacrifice of our martyrs.

Question 2.
Match the words with their meanings:

Group ‘A’	Group ‘B’
1. aspiration 2. potential 3. dignity 4. liberate	(a) inherent capacity (b) set free (c) ambition (d) self-respect

Answer:

1. aspiration – ambition
2. potential – inherent capacity
3. dignity – self-respect
4. liberate – set free

Question 3.
1. eyes
Answer:
1. exhausted-eyes.
Sentence: Extremist militia is an active force found in Sudan.

Question 4.
Choose the correct option and write in front of the given word:
(Answers are directly given.)
Answer:
courageous: brave

1. cowards
2. brave
3. friendly

Question 5.
Make a word register related with “God” from the passage.
Answer:
Jesus, Holy Quran, temples, mosques, churches, prayer houses, religions, the kingdom of God.

Question 6.
Find out antonyms for the following from the passage:

1. reject
2. ignore
3. timid

Answer:

1. reject × accept
2. ignore × notice
3. timid × fearless

Question 7.
Choose the correct option and write infront of the given word:
(Answers are directly given and underlined.)
Answer:
crisis: unstable situation

1. unstable situation
2. problems
3. difficulty

Question 8.
Find out the describing words used forthe following nouns and make your own sentences by using any three combinations:

1. organizations
2. citizenship
3. groups

Answer:

1. local organizations
2. global citizenship
3. small groups

Sentences:

1. Global citizenship nurtures personal respect and respect for others.
2. The role of local organizations are often overlooked by the government.
3. We can understand any difficult thing very well in small groups.

Question 9.
Classify the following words in Nouns and Verbs in the form of a table:
labour, prevent, knock, start, include, peace, world, problem.
Answer:

Nouns	Verbs
labour peace world problem	prevent knock start include

Question 10.
Find out the describing words used for the following nouns and make your own sentence by using any one combination:
1. globalization
2. compassion
Answer:
1. rapid globalization
2. global compassion
Sentence: Due to rapid globalization we have been facing number of problems.

Question 11.
Choose the correct meaning from the option and write in front of the given word:
Answer:
1. adamant: stubborn
(a) stubborn
(b) flexible
(c) kind

2. abolition: termination
(a) fixation
(b) termination
(c) prevention

3. neutrality: indifference
(a) interesting
(b) sadness
(c) indifference

4. compassion: kindness
(a) kindness
(b) passion
(c) wish

Question 12.
Find out the describing words from the passage for the following words:
(Answers are directly given and underlined.)
Answer:

1. rapid globalization
2. tiny bird
3. high-speed internet
4. serious disconnect.

Question 13.
Write the antonyms of:
(Answers are directly given and underlined.)
Answer:
1. recognized × unrecognized
2. known × unknown

Question 14.
Write the infinitive forms of the following and use any two of them in your own sentences:
Answer:

1. dancing – to dance
2. playing – to play
3. growing – to grow
4. happening – to happen

Sentences:
1. Anish wanted to dance in the procession but his father did not allow him.
2. It is our duty to grow more and more trees to save the planet Earth.

Question 15.
Choose the correct option and write in front of the given word:
(Answers are directly given and underlined.) J
Answer:
mortality: death rate

1. birth rate
2. life rate
3. death rate

Question 16.
Find out the describing words used for the following noun and make your own sentences by using any combination:
…………………… partnership
Answer:
innovative partnership

Sentence: In a developing country like India, intergovernmental agencies play important role in / the process of development.

Question 17.
Pick out any four “infinitives” from the passage:
Answer:
to put, to innovate, to accelerate, to work

Activities based on Contextual Grammar:

Question 1.
Indirect speech:
1. I asked my teachers, “Why is he working outside? Why is he not with us in the school?”
2. The boy’s father said to the writer, “I have never thought about it. We are born to work.”
Answer:
1. I asked my teacher why he was working outside and why he was not with them in the school.
2. The boy’s father told the writer that he had ; never thought about it. He further told him that ; they were born to work.

2. Make the sentences affirmative:

Question 1.
My teacher had no answer,
Answer:
My teacher was speechless.

Question 2.
I have never thought about it.
Answer:
I have always ignored it.

Activity-based on Contextual Grammar:

Question 1.
Name the tense:

1. The Nobel committee has generously invited me to present a “Lecture.”
2. I am representing the millions of children.
3. I humbly accept this award on behalf of all my fellow activists across the world.
4. I have kept an empty chair here as a reminder.

Answer:

1. Present Perfect Tense
2. Present Continuous Tense
3. Simple Present Tense
4. Present Perfect Tense

Question 2.
Make adjectives of:

1. honour
2. create
3. silence
4. peace

Answer:

1. honour – honourable
2. create – creative
3. silence – silent
4. peace – peaceful.

1. Change the voice:

Question 1.
He was kidnapped by an extremist militia. (Begin the sentence with “An extremist militia….)
Answer:
An extremist militia kidnapped him.

Question 2.
He was forced to kill his friends and family.
(Begin the sentence with “They….”)
Answer:
They forced him to kill his friends and family.

Question 3.
All the great religions teach us to care for our children. (Begin the sentence with “We are….)
Answer:
We are taught to care for our children by all the great religions.

Question 4.
I have held their injured bodies. (Begin the sentence with “Their injured bodies…)
Answer:
Their injured bodies have been held by me.

Rewrite the following into indirect speech:

Question 1.
Rewrite the following into indirect speech:
Answer:
A skinny child labourer asked Satyarthi, “Is the world so poor that it cannot give me a toy and a book, instead of forcing me to take a gun or a tool?” Ans. A skinny child labourer asked Satyarthi if the world was so poor that it could not give him a toy and a book, instead of forcing him to take a gun or a tool.

Question 1.
Change these sentences into indirect speech:

1. The lion asked the bird, “What are you doing?”
2. The bird said to the lion, “I am going to extinguish the fire.”
3. The lion said, “How can you do it keeping just one drop of water in your beak?”
4. The bird said, “I am doing my bit.”

Answer:

1. The lion asked the bird what it was doing.
2. The bird told the lion that it was going to extinguish the fire.
3. The lion asked how it could do it keeping just one drop of water in its beak.
4. The bird said that it was doing its bit.

Question 2.
Add a question tag:

1. We are connected through high-speed internet.
2. We exchange our goods and services in one single global market.
3. Let us globalize compassion.
4. All the animals were running away.

Answer:

1. We are connected through high-speed internet, aren’t we?
2. We exchange our goods and services in one single global market, don’t we?
3. Let us globalize compassion, shall we?
4. All the animals were running away, weren’t they?

Question 3.
He asked the bird “What are you doing?” (Make it indirect)
Answer:
He asked the bird what he was doing.

Question 4.
Make nouns of the following:
1. play
2. grow
Answer:
1. play – play, player
2. grow – growth

Question 5.
Make verbs of the following:
1. knowledge
2. exploitation
Answer:
1. knowledge – know
2. exploitation – exploit

Personal Response:

Question 1.
What type of text is this? How do you decide it?
Answer:
This text is a speech. I have decided it on the basis of the beginning of the text. In the beginning the speaker has addressed the dignitaries and the audience assembled in the hall /auditorium. This shows that the text is a speech/lecture.

Question 2.
What do you know about Kailash Satyarthi?
Answer:
Kailash Satyarthi is an activist who fought for the Indian children’s rights. He is a Nobel Peace Prize recipient and the Founder of Bachpan Bachao Andolan. He and his team at the Bachpan Bachao Andolan have liberated more than 86,000 children in India from child labour slavery and trafficking. He is basically from Vidisha in Madhya Pradesh.

Question 3.
What efforts will you take to enrol the out-of-school children?
Answer:
If I see any children out of school, I will tell them the importance of education in their life. I will also tell them about the Right of Children to Free and Compulsory Education. By convincing them I will help them to take admission in schools nearby so that they can stand and face the life independently and get success in their life. Also, I shall try to convince their parents to send their children to school.

Question 4.
What is the role of education in nation-building?
Answer:
Education plays a very critical and crucial role in deciding the growth of a nation. Educated citizens of the country bring fame, wealth and prosperity to the country which helps in development of a country. People who are educated think and work to achieve the dream of any country. Education helps in dream building so education is a big invaluable asset in nation-building.

Question 5.
What lesson does the story of the lion and the tiny bird teach us?
Answer:
I think the story of the lion and the tiny bird teaches us not to belittle other individuals who atleast do something and make an effort. No matter how small it is in their eyes but it might be big in result. Small things shouldn’t be valued too little sometimes. Big things always start from something small.

Question 6.
What will you do for our country?
Answer:
First I will try to take higher education. As for as possible I will try to use that knowledge for the developement of our country, I will also help the people to take education so that they will also help our country to prosper and become a developed country.

Question 7.
What is your vision of tomorrow?
Answer:
My vision for tomorrow is to empower the people with a vision to have the confidence and ability to achieve their dream. If I help them to gain their confidence, they will work hard to achieve their goal. Ultimately they will help the nation to prosper.

Question 8.
Do you think, our parents are the most beautiful gift of our life?
Answer:
Our life is a journey full of joy, sorrow fantasy, expectations, hellos, goodbyes and farewells. Our parents are always with us in all ups and downs; so we can live our life happily. They are always with us to solve our problems and to sort out any situation. So they are the most beautiful gift of our life.

Question 9.
What do you mean by “Every child has a right to life”?
Answer:
The right to life is a moral principle based on the belief that a human being has the right to live. Every child has some inherent right to life which is protected by laws. No one shall be arbitrarily deprived of his life. So it is our duty to protect every child and help him/her to live a happy and healthy life.

Question 10.
Why should the government invest in education and young people?
Answer:
Education is the systematic process of gaining knowledge and skills. It has positive impact on our life. It also promotes national interest. It is the backbone of developing countries. If the government invests in education and young people, they help the nation to develop as they are called real nation-builders and future of the country so the government should invest in education and young people.

Question 11.
Why should we stop “Child labour”?
Answer:
“Child labour” is a stigma on our society. It is sure to interfere with his/her right to education. It is also harmful to their physical, mental, spiritual, moral and social development. It is harmful to the development of any country, as “the child” is the future citizen of every country. So we should stop child labour and child exploitation.

Do as directed:

Question 1.
Complete the words/spellings by using correct letters:
Answer:

1. m a _ c h – m a r c h
2. p l _ n t – p l a n t
3. w o _ l d – w o r l d
4. N _ b e l – N o b e l

Question 2.
Put the words in alphabetical order:
1. create, activist, world, freedom
2. exhausted, experience, extinguish, equality
Answer:
1. activist, create, freedom, world.
2. equality, exhausted, experience, extinguish.

Question 3.
Punctuate the following sentences:
1. the lion laughed and said how can you do it keeping just one drop of water in your beak
2. lets walk together.
Answer:
1. The lion laughed and said, “How can you do it keeping just one drop of water, in your beak?”
2. Let’s walk together.

Question 4.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Question 5.
Complete the word-chain of ‘adjective’. Add four words each beginning with last letter of the previous letter :
Supreme, → e ……………, …………., …………., ……………..
Answer:
Supreme, → easy, young , grateful, less.

1. Attempt anyone:

Question (a)
Add a clause to expand the following sentence meaningfully.
The bird ………………
Answer:
The bird which was in a cage was at last freed by his owner.

2. Attempt any one:

Question (a)
Add preffix or suffix to make new words:
1. inspire
2. expend
Answer:
1. inspiration
2. expenditure

OR

Question (b)
Make a meaningful sentence by using one of the following words:
1. inspire
2. expand
Answer:
1. Our parents always inspire us to do something good.
2. Reading always expands our knowledge.

Writing Skill

Malala’S Bio-Data

Name: Malala Yousafzai
Father’s Name: Ziauddin Yousafzai
Mother’s Name: Tar Pekal Yousafzai
Date of birth: 12 July, 1997
Religion: Sunni Islam
Occupation: Activist for rights to female education.
Awards:

• Nobel Peace Prize
• Simone de Beauvour Prize
• National Youth Peace Prize
• Honorary Canadian
• Citizenship

My English Coursebook Standard Ten Digest Answers Pdf Unit 3

• If … Class 10 English Solutions
• A Lesson in Life from a Beggar Class 10 English Solutions
• Stopping by Woods on a Snowy Evening Class 10 English Solutions
• Let us March! Class 10 English Solutions
• The Alchemy of Nature Class 10 English Solutions

Class 10 English Chapter 1.3 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 1.3 Basketful of Moonlight Notes, Textbook Exercise Important Questions and Answers.

Basketful of Moonlight Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 1.3 Basketful of Moonlight Textbook Questions and Answers

warming up!

Chit-chat:

Question 1.
Did you like to hear bedtime stories when you were a child?
Answer:
Points: Yes, very much-crazy for hearing-got into the habit.

Question 2.
Who usually told you the stories?
Answer:
Points: Mostly grandmother or grandfather-mother, father, old servant.

Question 3.
Why did you like them?
Answer:
Points: Because of simple, interesting, amusing narration-teaching lessons of life-sometimes very funny.

Question 4.
Do you still like to hear those stories again?
Answer:
Points: Yes, sure-everlasting excitement- attraction-inspire reading more stories.

1. Discuss in groups about the procedure of planting a tree. Write the steps in bullet points and present them before the class.

Question 1.
Discuss in groups about the procedure of planting a tree. Write the steps in bullet points and present them before the class.
Answer:

• Choosing good seeds of plants.
• Digging in the ground/garden
• Putting seeds in the loose soil
• Add manure
• Fill in the pit/hole
• Water it.

2. Discuss in pairs and write what your father and mother do for your family.

Question 1.
Discuss in pairs and write what your father and mother do for your family.
Answer:

Father	Mother
Works hard to earn money	Cooks food and feeds the family.
Performs duties as the head of the family	Takes utmost care of the children and family.
Guides in children’s problems.	Keeps the house clean and tidy.
Role model of the all family members.	Brings up children with love and compassion.
Decides the ways of children’s life/careers.	Looks after children’s education/career.
Takes most of the decisions for the well-being of the family.	Sometimes takes a job to meet the expenses.

English Workshop:

1. Complete the following sentences with the help of the poem.

Question 1.
Complete the following sentences with the help of the poem.
(a) The child wants to sow small moons of light from ………….. .
(b) According to the child the route of his village is tough and full of ………….. .
(c) The child wants a basketful of moonlight on ………….. .
(d) The child wants to light the dark route so that his ………….. .
Answer:
(a) The child wants to sow moons of light from the city to his village on the sides of the path.
(b) According to the child, the route of his village is tough and full of snakes and scorpions.
(c) Thechild wants a basketful of moonlight on loan.
(d) The child wants to light the dark route so that his father returns early.

2. Write down the describing words used for the following nouns.

Question 1.
Write down the describing words used for the following nouns.

1. ………… moons
2. ………… route
3. ………… village
4. ………… morning

Answer:

1. small moons
2. tough route
3. my/whole village
4. early morning

3. The child in the poem wants to solve the problems of his vifiage. How can the child solve them with the following wishes? Answer in your notebook.

Question a.
Give me moonlight, basketful or two baskets full, with seeds of moonlight.
Answer:
He can seek help of local people and urge the government or local bodies to provide lights on the roads from the city to his village.

Question b.
I want to light the dark route so that my father returns early.
Answer:
He can, with the help of villagers/government, build good roads and make the roads safe so that his father and other villagers can return safe and early to their village.

4. Pick out and write the lines from the poem that prove the following.
(a) Father reaches home late, after dark. …………………..
(b) Eager to hear fairy tales from his father. ………………….
(c) Remove darkness and bring light among the darker paths. …………

Question a.
Father reaches home late, after dark.
Answer:
When my father returns home, I am asleep.

Question b.
Eager to hear fairy tales from his father.
Answer:
I too want to hear fairy tales and stories from him.

Question c.
Remove darkness and bring light among the darker paths.
Answer:
I want to light the dark route so that my father returns early.

5. Write as many words as you can, using – ‘ful’ as suffix.

For example basketful, ……………………… bucketful, ……………………… ……………………… ………………………
……………………… ……………………… ……………………… ………………………

Question 1.
Write as many words as you can, using – ‘ful’ as suffix.
For example basketful, ……………………… bucketful, ……………………… ……………………… ………………………
……………………… ……………………… ……………………… ………………………
Answer:
basketful – bucketful – handful – spoonful – colourful – sackful – bagful – potful

6. Pick out the examples of Alliteration and Repeiltion from the poem.

Question 1.
Pick out the examples of Alliteration and Repeiltion from the poem.
Answer:
1. Alliteration:

• O moon, give me a basketful of moonlight on loan.
• I want to sow seeds of moon on the sides of the path.

2. Repetition: No repetition in these stanzas.

7. Write an appreciation of the poem. (Refer to Page 5.)

Question 1.
Write an appreciation of the poem. (Refer to Page 5.)
Answer:

1. Title: The title of the poem is “Basketful of Moonlight.”
2. The name of the Poet: The name of the poet is Sunil Sharma.
3. Rhyme scheme: There is no rhyme scheme in this poem. This a poem is in ‘free verse.’
4. Figure of Speech: Repetition, alliteration, apostrophy.
5. Theme/Central Idea: The central idea of the poem is the loneliness of a child in a remote village untouched by modern amenities.
6. The child is too far from the modern urban life that even his remedy for the plight of his villagers seems quite innocent and plain.

8. Write an imaginary letter to the moon, to convey your feelings about it. Discuss about it with your partner and draft the letter using the poem as a basis for the letter.
Supporting points:
(a) Sign of beauty
(b) Symbol of joy
(c) Infinite pleasure
(d) Urge to compose poems/songs/music

Question 1.
Write an imaginary letter to the moon, to convey your feelings about it. Discuss about it with your partner and draft the letter using the poem as a basis for the letter.
Supporting points:
(a) Sign of beauty
(b) Symbol of joy
(c) Infinite pleasure
(d) Urge to compose poems/songs/music
Answer:

A Letter to the Moon

Atul More,
Gavali Pada,
Chandrapur,
17th August, 2020.
Dear Chandamama,
How we love you!
Dear, you are the symbol of love and beauty not only for children like us but also for the grown¬ups. You are the one who looks after all the living ‘ things on the earth and gives joy to all of them. Looking at you gives us a great heavenly joy. Your cool light gives us comfort and soothes our body and soul.

Your cool light guides the travellers at night and gives infinite pleasure of walking in the serenely: beautiful light. Mothers sing your songs to make children sleep. Your beauty inspires poets and musicians to compose songs.

Without your presence, who will write lullabies for us, your dear children? Who will write romantic poems without your presence? Chandamama, be with us all the time to fill our hearts with your beauty, love and pleasant appearance.
With Basketful of Love,
Your loving nephew,
Atul More

9. Discuss with your friend/brother/sister/your classmate and write your list of wishes to make your village town city people happy.
You can use the following words.

Question 1.
Discuss with your friend/brother/sister/your classmate and write your list of wishes to make your village town city people happy.
You can use the following words.
Answer:

1. To provide all modern facilities like electricity, good roads, water supply, etc. to villagers living in remote areas.
2. To improve the conditions of poor farmers with aids, funds and full support during drought.
3. To eradicate poverty, ignorance and illiteracy.
4. To keep their surroundings clean and healthy.
5. To fight against injustice, corruption and terrorism.
6. To maintain peace and order in the society.
7. To remove their beliefs in superstitions.
8. To make them aware of their sense of duty.

10. Let’s compose imaginary poetic lines.

Question 1.
Let’s compose imaginary poetic lines.
Answer:

My English Coursebook 10th Digest Chapter 1.3 Basketful of Moonlight Additional Important Questions and Answers

Read the extract and do the activities:

Simple Factual Activity:

Question 1.
Complete the following lines with the help of the poem:
(Answers are directly given and underlined.)
Answer:

1. The poet wants to sow many small moons of light.
2. The whole village goes to the city daily to work.
3. It becomes dark on its way back as his village is quite far.
4. When the poet’s father returns home he is asleep.

Complex Factual Activities:

Question 1.
What does the poet wish to get from the moon and why?
Answer:
The poet wishes to get basketful or two baskets of moon-light from the moon so that he can sow the seeds of moonlight to light the dark path from the city to his village.

Question 2.
Why is the road from the city to the village dangerous?
Answer:
The road from the city to the village is dangerous because it is dark, tough and full of snakes and scorpions.

Question 3.
Choose from the options, appropriate message in the poem:
(a) Bring light to the villages.
(b) Help his father to reach home early.
(c) Listen fairy tales from his father.
(d) Remove darkness and bring light along the darker paths.
Answer:
(a) Bring light to the villages.

Question 4.
Pick out and write the lines from the poem that prove the following:

b. The path from city to village is having many difficulties.
Answer:
The route is tough and full of snakes and scorpions.

Question 5.
What does deliberate repetition of lines ‘O moon, give me moonlight, basketful of moonlight’ signify?
Answer:
The repetition of lines emphasises the intense desire of the child to light the dark route from city to his village with a lot of moonlight. The lines tell us that the child is repeatedly requesting the moon to give him basketful of moonlight because he is in a state of agitation and anxiety. The lines show the child’s intensity and eagerness to free his villagers from their sufferings of dark paths.

Question 6.
Tell what is implied in the following lines:
I want to light the dark route so that my father returns early.
OR
Complete the web:
(Answer is directly given and underlined.)
Answer:

Activities based on Poetic Device:

Question 1.
Pick out the examples of alliteration and repetition:
Answer:
1. Alliteration: O moon, give me moonlight, basketful or two baskets full’,
2. Repetition: ‘I want to sow many, small small moons of light,’

Question 2.
Write rhyming words for the following from the extract:

1. Pack
2. deeds
3. any
4. pity

Answer:

1. Pack-back
2. deeds-seeds
3. any-many
4. pity-city

Question 3.
Give your own rhyming words for the following:
1. dark
2. sow
Answer:
1. dark – park
2. sow – bow.

Vocabulary Focus:

Question 1.
Write down from the extract the describing words used for the following nouns:

1. …………… baskets
2. ……………. route
3. …………….. tales

Answer:

1. two baskets
2. dark route
3. fairy tales

My English Coursebook Standard Ten Guide Unit 1

• A Teenager’s Prayer Class 10 English Solutions
• An Encounter of a Special Kind Class 10 English Solutions
• Basketful of Moonlight Class 10 English Solutions
• Be SMART…! Class 10 English Solutions
• His First Flight Class 10 English Solutions