Class 10 English Chapter 3.4 Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Solutions Chapter 3.4 Let us March! Notes, Textbook Exercise Important Questions and Answers.
Let us March! Poem 10th Std Question Answer
My English Coursebook Standard Ten Guide Chapter 3.4 Let us March! Textbook Questions and Answers
Warming up:
Chit-chat
Discuss in your group:
Question 1.
What difference do you notice in the two images?
Answer:
The boy in the first picture is working and the boy in the second picture is going to school on his bicycle.
![]()
Question 2.
Which of the two situations should change?
Answer:
The situation in the first picture should change.
Question 3.
How and when can the situation be changed?
Answer:
The boy in the first picture should be sent to school. Somebody should convince his parents that it is not his right age to work. He should go to school at this age. Then the situation can change.
Question 4.
How can you, as a student, contribute and help make a difference to the needy children?
Answer:
As a student I will help the needy children to go to school and take education. If possible I will try to give them monetary help to take education. I will also convince their parents
to understand the importance of education.
1. A good well-organized speech contains the following characteristics and steps.
Question (A)
A good well-organized speech contains the following characteristics and steps.
Answer:
- A speech should be well-planned.
- The language used should be suitable to the audience.
- It should have the right duration.
- It should be supported with good examples, episodes or visual aids, where possible.
![]()
Question (B)
Refer to Page 26 for a reference to the steps to be followed in the speech and do the activity given below. Read the expressions given below on Coursebook and insert them in the proper boxes:
(a) Imagine what will happen after ten years.
(b) I would like to share with you an example from my own experience.
(c) Hon. chief guest, eminent dignitaries, respected management and staff, student – friends
(d) The research report says that ……………
(e) I don’t understand why we are so negative about this issue.
(f) Think again and again and then move forward.
(g) Today, I would like to put forth my views on ………………
(h) The renowned personality xyz says “……………..”
(i) Good Morning, one and all present today.
(j) I would like to express my gratitude towards the organisers of this function for giving me opportunity ……………
(k) If we think about the situation around us, we notice that ………………
(l) Let me explain this to you ……………..

Answer:
| Greeting / Salutation | Introduction | Body of the speech | Conclusion |
| 1. Good morning, one and all present today. | 1. If we think about the situation around us we notice that | 1. The renowned personality xyz says “………………………. | 1. Think again and again and then move forward. |
| 2. Hon. Chief guest, eminent dignitaries respected management and staff, student- friends. | 2. Let me explain this to you | 2. The research report says that ………………….. | 2. I would like to express my gratitude towards the organizers of this function for giving me the opportunity ……… |
| 3. Today, I would like to put forth my views on | 3. I don’t understand why we are so negative about this issue. | ||
| 4. Imagine what will happen after ten years. | 4. I would like to share with you an example from my own experience. |
English Workshop:
1. Name the following:
Question (a)
The persons to whom Kailash Satyarthi gives the highest credit of his honour:
Answer:
Kaalu Kumar, Dhoom Das and Adarsh Kishore from India and Iqbal Masih from Pakistan.
![]()
Question (b)
The greatest personalities from the great land-India.
Answer:
Lord Buddha, Guru Nanak and Mahatma Gandhi.
Question (c)
The daughters of Kailash Satyarthi mentioned in this speech:
Answer:
Malala, Kayanat and Shazia
Question (d)
The foreign activists of equal rights mentioned in this speech:
Answer:
Nelson Mandela and Martin Luther King.
2. Mention the social issues highlighted by Kailash Satyarthi in his speech. One social issue is given for you.
Question 1.
Mention the social issues highlighted by Kailash Satyarthi in his speech. One social issue is given for you.
(a) Child labour
(b) …………………
(c) …………………
(d) …………………
(e) …………………
![]()
3. Complete the following diagram/chart:
Question 1.
Complete the following diagram/chart:
Answer:

4. Complete the following web-chart:
Question 1.
Complete the following web-chart:

Answer:
5. Find out the describing words used for the following nouns and make your own sentences by using any three combinations.
Question 1.
Find out the describing words used for the following nouns and make your own sentences by using any three combinations.
(a) …………… sacrifice
(b) …………… faces
(c) …………… militia
(d) …………… challenge
(e) …………… globalise
(f) …………… agencies
Answer:
(a) supreme sacrifice
(b) beautiful faces
(c) extremist-militia
(d)great challenge
(e) globalise – globe, globalization
(f) intergovernmental agencies
![]()
6. Choose the correct option and write in front of the given word:
Question (a)
divinity: ……………
Answer
divinity: godliness
1. goodness
2. godliness
3. god fearing
Question (b)
extremist: militant
1. militant
2. robber
3. spy
Question (c)
culminate: rise to a peak
1. destroy
2. succeed
3. rise to a peak
7. What will you do in the following situations?
Question (a)
If you see a child working in a restaurant.
Answer:
I will lodge a complaint against the owner under the Child Labour Act, 1986.
Question (b)
If you find a child working on a construction site.
Answer:
I will lodge a complaint in the police station nearby and convince them to send him to a nearby school.
![]()
Question (c)
If you find a child working on a brickwork site.
Answer:
I will tell his parents not to do so, instead to send him to a school nearby.
Question (d)
If you come across a beggar child.
Answer:
I will tell the child, it is not good to beg. I will also tell him the importance of schooling and help him to go to school.
(B) Write any 2 efforts that you can make to enrol deprived children/ out of school children into a school. One is given for you.
(a) I will persuade parents of such children to send them to school.
(b) …………………………………………………………………………………….. .
(c) …………………………………………………………………………………….. .
(d) …………………………………………………………………………………….. .
(e) …………………………………………………………………………………….. .
8. Today, it is time for every child to have a right to –
education, ……………….., ……………….. .
……………….., ……………….., ……………….. .
……………….., ……………….., ……………….. .
9. Make a list of Indian Nobel laureates.
Question 1.
Make a list of Indian Nobel laureates.
Answer:
| Name | Field | Year |
| 1. Rabindranath Tagore | Literature | 1913 |
| 2. C. V. Raman | Physics | 1930 |
| 3. Mother Teresa | Peace | 1979 |
| 4. Subrahmanyan Chandrasekhar | Physics | 1983 |
| 5. Amartya Sen | Economics | 1998 |
| 6. Kailash Satyarthi | Peace | 2014 |
![]()
10. Make a list of prestigious awards in India:
Question 1.
Make a list of prestigious awards in India:

Answer:
| Civilian Awards | Highest gallantry awards |
| Bharat Ratna | Param Vir Chakra |
| Padma Vibhushan | Maha Vir Chakra |
| Padma Bhushan | Vir Chakra |
| Padma Shri | Ashok Chakra |
11. Make a meaningful sentence by using the phrases:
Question 1.
Make a meaningful sentences by using the phrases: (Note: One phrase will be asked in the activity sheet.)
(a) in the pursuit of
(b) to be afraid of
(c) to give up
Answer:
(a) Most of the people spend a lot of time in the pursuit of money.
(b) Don’t be afraid of saying what you sincerely think.
(c) His wife finally persuaded him to give up smoking.
12. Write minimum 5 hidden words of more than 4 letters from- ‘intergovernmental’.
Question 1.
Write minimum 5 hidden words of more than 4 letters from- ‘intergovernmental’
Answer:
- internal
- government
- torment
- term
- governmental
![]()
13. Imagine your school invites Malala to preside over celebration of ‘Children’s Day’. Draft a welcome speech for this noble young girl. Gather her bio-data from the internet.
Question 1.
Imagine your school invites Malala to preside over celebration of ‘Children’s Day’. Draft a welcome speech for this noble young girl. Gather her bio-data from the internet.
Answer:
Honourable Chairperson, respected Principal, teachers, our today’s guest Malala Didi and all my dear friends.
We have gathered here to celebrate Children’s Day. On this auspicious occasion I would like to limit my few words on the Children’s Day. Children are the integral part of the society and home as well as the future of the country. We cannot ignore their involvement and contribution in the life of parents teachers and other related people all through the life.
Children are blessed by God and they conquer our hearts with their beautiful eyes, innocent activities and smiles. Life becomes very boring andupset without them. This day is celebrated every year to pay tribute to all the children all over the world. In India it is celebrated on 14th November on the birth anniversary of the legendary freedom fighter and the first Prime Minister of the independent India; Pandit Jawaharlal Nehru.
The celebration of this day reminds us to renew our commitment towards children’s welfare including their health, care and education. It is an occasion to appreciate the qualities of childhood. Children are considered as the building blocks of the strong nation. They have capabilities to change the nation positively. They are the responsible citizens of tomorrow. The development of the country lies in their hand. Children’s Day celebration also reminds us about their rights.
Children are leaders of tomorrow so they need to get respect, special care and protection from their parents, teachers and from the society. Do they really get it? They are being abused in many ways in our nation by their family members, relatives, neighbours or other people. Government should work on it to help them to live life happily. Malala Didi is a Pakistani activist who works for girls’ females’ education. She works for the human rights, especially the right to education of women and children.
We are really proud of her. On this auspicious day if we take inspiration from her, no child will be abused, no girl will be molested. She is a great source of inspiration and so she is here with us. We are eager to hear her valuable thoughts and voice, so I think I would better stop here. Wish you all happy Children’s Day and all the best for your future endeavour. Thanks a lot for listening to me patiently and attentively.
Jai Hind!
14. Use the following words as a noun and a verb and make meaningful sentences:
Question 1.
Use the following words as a noun and a verb and make meaningful sentences:
- march
- honour
- credit
- stitch
Answer:
- march – The workers began their march to protest against their factory owners, (noun)
The physical education teacher marched the children to the playground, (verb) - honour – A dinner was arranged in his honour, (noun)
The actor was honoured with the Padmashri.(verb) - credit – The bank refused to extend their credit.(Noun)
She has been wrongly credited as the author. (Verb) - stitch – The wound needed eight stitches, (noun)
The tailor was asked to stitch the clothes quickly, (verb)
![]()
Language Study:
Question (a)
Match the sentences given in part ‘A’ with the sentences given in part ‘B’. Note the differences in structure.
Answer:

Question (b)
Observe the following underlined phrases. Here ‘have/has’ are followed by the past participle form of the verb. This construction indicates the perfect present tense. Find more such sentences from the speech.
Answer:
- We have made progress in the last couple of decades.
- We have prevented millions of child deaths.
- It has happened.
- We have reduced the number of out-of-school children by half.
- We have reduced the child labourers by a third.
Question (c)
In the following sentences the underlined words are called infinitives. Find such examples from the speech and underline the infinitives.
Answer:
- Every child is free to grow.
- I refuse to accept that all the laws and constitutions, police and judges are unable to protect our children.
- that all the temples and mosques and churches and prayer houses have no place for the dreams of our children.
- just one week of global military expenditure can bring all the children to classrooms.
- The shackles of slavery can be stronger than the quest for freedom.
Question (d)
Pick out from the lesson, the Antonyms of
Answer:
- ignorance × knowledge
- deny × admit
- immortality × mortality
- violence × non-violence
- well-known × known
- slavery × freedom
![]()
(e) Do as directed.
Question (i)
Make nouns of the following.

Answer:
| Words | Nouns |
| 1. deliberate | deliberation |
| 2. organize | organization/organiser |
| 3. violent | violence |
| 4. tolerant | tolerance |
| 5. extreme | extremism/extremist |
| 6. educate | education/educator |
| 7. globalize | globalization |
| 8. distant | distance |
| 9. prescribe | prescription/prescriber |
Question (ii)
Make verbs of the following.
Answer:
- universal – universalize
- global – globalize
Question (f)
Complete the following sentences with the help of the sentence given below:
(Answers are directly given and underlined.)
(a) The biggest challenge knocking on the doors of human kind is fear and intolerance.
(i) No other challenge knocking …………………………………………………… .
as big as …………………………………………………………………………………… .
(ii) Fear and intolerance are bigger ……………………………………………….. .
………………………………………………………………………………………………… .
(b) The Nobel Prize is one of the greatest honours in the world.
(i) Very few honours …………………………………………………………… .
(ii) The Nobel Prize is greater than …………………………………………. .
………………………………………………………………………………………………… .
Answer:
(a) The biggest challenge knocking on the doors of humankind is fear and intolerance.
1. No other challenge knocking on the doors of humankind is as big as fear and intolerance.
2. Fear and intolerance are bigger than any other challenge knocking on the doors of humankind.
(b) The Nobel Prize is one of the greatest honour in the world.
1. Very few honours in the world are as great as the Nobel Prize.
2. The Nobel Prize is greater than most other honours in the world.
My English Coursebook 10th Digest Chapter 3.4 Let us March! Additional Important Questions and Answers
Simple Factual Activities:
1. Name the following:
Question 1.
The American politician, attorney and author mentioned in the speech –
Answer:
Tom Harkin.
![]()
Question 2.
Answer in one word:
Answer:
- The motherland of Kailash Satyarthi – India
- The country which Iqbal Masih represents – Pakistan
- The place where Nobel Prize distribution programme was held – Norway
- The ancient texts of wisdom – Vedas
Question 3.
State whether you agree or disagree with the following statements:
Answer:
- The Holy Quran s ays the kingdom of God belongs to the children.
- Jesus says not to kill your children because of poverty. – Disagree
- Denying the dreams of our children is greater violence. – Agree
- The writer has never given up against any threat or attack. – Agree
Question 4.
Match the following:
Answer:
- A small, skinny child labourer – to care for our children
- A Sudanese child-soldier – children’s frightened and exhausted eyes
- Satyarthi had looked into – was forced to kill his friends and family.
- The great religions teach us – The world forced me to take a gun or a tool
Question 5.
State whether the following statements are True or False:
Answer:
- The biggest challenge of humankind is fear and intolerance. – True
- Education gives the meaning and objective of life. – True
- An unprecedented violence will not be suicidal for humankind. – False
- Rights, security, hope can only be restored through education. – True
![]()
Question 6.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
- Even though we have made progress in the last couple of decades, we are facing great challenges.
- An education gives a sense of global citizenship among the youth.
- Small groups, local organisations and individuals are confronting with the problem every day.
Question 7.
Answer in few words:
- he age in which we live –
- The serious disconnect of the world –
- We can unite the world through –
- Children are questioning and watching our –
Answer:
- rapid globalization
- lack of compassion
- the compassion for our children
- inactions and actions
Question 8.
Complete the sentences:
(Answers are directly given and underlined.)
Answer:
- A tiny bird was rushing towards the fire.
- A heavy fire had broken out in the forest.
- The speaker is appealing to compassion.
- The tiny bird was going to extinguish the fire.
![]()
Question 9.
Make a list of the problems that we are facing and creating violence against children –
Answer:
- slavery
- trafficking
- child marriage
- child labour
- sexual abuse
- illiteracy
Question 10.
Complete the following web:
(Answers are directly given and underlined.)
Answer:
Question 11.
State whether the following statements are Right or Wrong:
Answer:
- We should have vision for today not tomorrow. – Right
- If we close our eyes and feel the child inside us, we can listen to that child. – Right
- Mahatma Gandhi, Nelson Mandela and Martin Luther King are calling on us. – Right
- Mahatma Gandhi, Nelson Mandela and Martin Luther King are calling on us. – Right
- Satyarthi’s vision of tomorrow is to see that cobbler’s boy sitting with him in his classroom. – Right
Complex Factual Activities:
Question 1.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
- We can create knowledge for all that benefits all by learning from the experiences of our ancestors.
- The mantras that carries a prayer has the potential to liberate humanity from all man-made crises.
- The writer humbly accepts this award on behalf of all martyrs, his fellow activists across the world and his countrymen.
- The journey of the writer, that is India to Norway is a connect between two centres of global peace and brotherhood, ancient and modern.
- The speaker feels honoured to recite a mantra from the ancient text of wisdom.
![]()
Question 2.
Complete the following web:
Answer:

Question 3.
What are the children’s issues highlighted by Kailash Satyarthi in this passage?
Answer:
The children’s issues highlighted by Kailash Satyarthi in this passage are-
- The burning problem in India-child labour
- The Right of children to free and compulsory education
- Mortality and malnutrition,
- Child labour as a human rights issue as well as a welfare matter and charitable cause.
Question 4.
Complete the following web stating the sign of progress mentioned by Satyarthi:
Answer:

Question 5.
What social role are the ‘three daughters’ laying?
Answer:
These three daughters are rising up and choosing peace over violence, tolerance over extremism and courage over fear.
![]()
Question 6.
Complete the following web:
Answer:
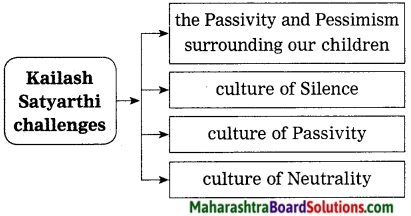
Question 7.
What problems do the poor children face?
Answer:
The poor children face the following problems –
- They harvest cocoa yet they have never tasted chocolate.
- They are dying of Ebola.
- They are kidnapped and held hostage.
- They stitch football, yet they never play with it.
Question 8.
What did millions of individuals demand eighteen years ago?
Answer:
Eighteen years ago, millions of individuals demanded a new international law for the abolition of worst form of child labour.
Question 9.
Why does the eight-year-old girl’s question shake Mr Satyarthi? (r^T srrc qqMi HyfMi srt SKcfTT Wt?)
Answer:
The eight-year-old girl’s question ‘Why did you not come earlier?’ itself implies that the girl was really suffering a lot. Even though we are grown ups, we have failed to rescue number of small girls from forced labour. So her question shakes not only Satyarthi, but also the whole world.
![]()
Question 10.
What matters according to Satyarthi?
Answer:
Every single minute, every single child and every single childhood matters according to Satyarthi.
Question 11.
Complete the following web:
(Answer is directly given and underlined.)
Answer:

Question 12.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
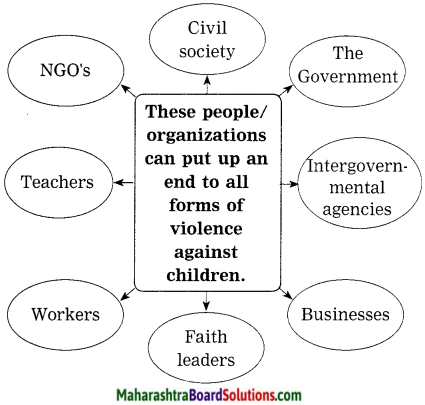
1. Government should make child-friendly policies and invest in education and young people.
2. Faith leaders, institutions and all of us must stand with our children.
Question 13.
Complete the following web:
(Answer is directly given.)
Answer:
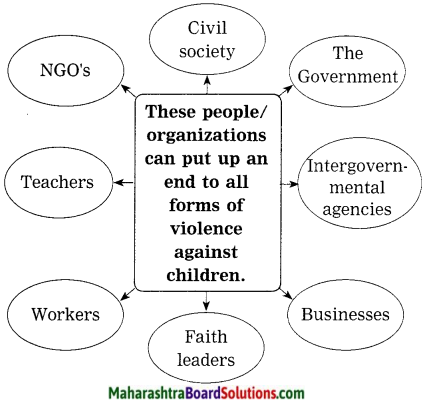
Question 14.
What was the response of the boy’s father? What was Satyarthi’s reaction to it?
Answer:
The response of the boy’s father was that he had never thought about it and they were born to work. His answer made Satyarthi angry and it still makes him angry.
![]()
Question 15.
Complete the following:
(Answers are directly given and underlined.)
Answer:
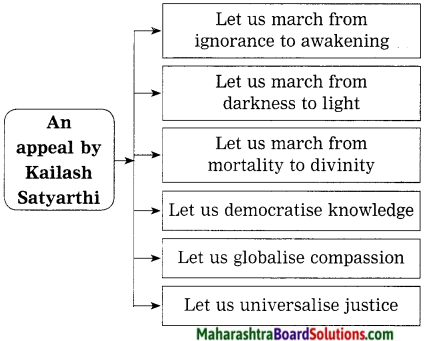
1. Satyarthi requests the listeners to put their hands close to their heart, close their eyes and feel the child inside them.
2. The writer calls all the listeners for a march,
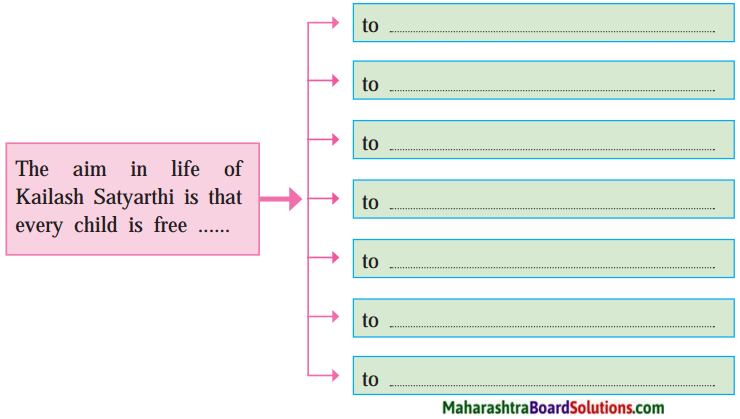
- from → exploitation to → education
- from → exploitation to → education
- from → poverty to → shared prosperity
- from → slavery to → liberty
- from → violence to → peace
- from → ignorance to → awakening
- from → darkness to → light
- from → mortality to → divinity
Question 16.
Complete the following web-chart:
(Answers are directly given)
Answer:
Activities based on Vocabulary:
Question 1.
Find out the describing words used for the following nouns and make your own sentences using any two combinations:
(a) peace
(b) chair
Answer:
(a) global peace
(b) empty chair
Sentences:
1. UNO was founded (established) for global peace.
2. We should never forget the supreme sacrifice of our martyrs.
![]()
Question 2.
Match the words with their meanings:
| Group ‘A’ | Group ‘B’ |
| 1. aspiration 2. potential 3. dignity 4. liberate |
(a) inherent capacity (b) set free (c) ambition (d) self-respect |
Answer:
- aspiration – ambition
- potential – inherent capacity
- dignity – self-respect
- liberate – set free
Question 3.
1. eyes
Answer:
1. exhausted-eyes.
Sentence: Extremist militia is an active force found in Sudan.
Question 4.
Choose the correct option and write in front of the given word:
(Answers are directly given.)
Answer:
courageous: brave
- cowards
- brave
- friendly
Question 5.
Make a word register related with “God” from the passage.
Answer:
Jesus, Holy Quran, temples, mosques, churches, prayer houses, religions, the kingdom of God.
![]()
Question 6.
Find out antonyms for the following from the passage:
- reject
- ignore
- timid
Answer:
- reject × accept
- ignore × notice
- timid × fearless
Question 7.
Choose the correct option and write infront of the given word:
(Answers are directly given and underlined.)
Answer:
crisis: unstable situation
- unstable situation
- problems
- difficulty
Question 8.
Find out the describing words used forthe following nouns and make your own sentences by using any three combinations:
- organizations
- citizenship
- groups
Answer:
- local organizations
- global citizenship
- small groups
Sentences:
- Global citizenship nurtures personal respect and respect for others.
- The role of local organizations are often overlooked by the government.
- We can understand any difficult thing very well in small groups.
![]()
Question 9.
Classify the following words in Nouns and Verbs in the form of a table:
labour, prevent, knock, start, include, peace, world, problem.
Answer:
| Nouns | Verbs |
| labour peace world problem |
prevent knock start include |
Question 10.
Find out the describing words used for the following nouns and make your own sentence by using any one combination:
1. globalization
2. compassion
Answer:
1. rapid globalization
2. global compassion
Sentence: Due to rapid globalization we have been facing number of problems.
Question 11.
Choose the correct meaning from the option and write in front of the given word:
Answer:
1. adamant: stubborn
(a) stubborn
(b) flexible
(c) kind
2. abolition: termination
(a) fixation
(b) termination
(c) prevention
3. neutrality: indifference
(a) interesting
(b) sadness
(c) indifference
4. compassion: kindness
(a) kindness
(b) passion
(c) wish
Question 12.
Find out the describing words from the passage for the following words:
(Answers are directly given and underlined.)
Answer:
- rapid globalization
- tiny bird
- high-speed internet
- serious disconnect.
![]()
Question 13.
Write the antonyms of:
(Answers are directly given and underlined.)
Answer:
1. recognized × unrecognized
2. known × unknown
Question 14.
Write the infinitive forms of the following and use any two of them in your own sentences:
Answer:
- dancing – to dance
- playing – to play
- growing – to grow
- happening – to happen
Sentences:
1. Anish wanted to dance in the procession but his father did not allow him.
2. It is our duty to grow more and more trees to save the planet Earth.
Question 15.
Choose the correct option and write in front of the given word:
(Answers are directly given and underlined.) J
Answer:
mortality: death rate
- birth rate
- life rate
- death rate
Question 16.
Find out the describing words used for the following noun and make your own sentences by using any combination:
…………………… partnership
Answer:
innovative partnership
Sentence: In a developing country like India, intergovernmental agencies play important role in / the process of development.
Question 17.
Pick out any four “infinitives” from the passage:
Answer:
to put, to innovate, to accelerate, to work
Activities based on Contextual Grammar:
Question 1.
Indirect speech:
1. I asked my teachers, “Why is he working outside? Why is he not with us in the school?”
2. The boy’s father said to the writer, “I have never thought about it. We are born to work.”
Answer:
1. I asked my teacher why he was working outside and why he was not with them in the school.
2. The boy’s father told the writer that he had ; never thought about it. He further told him that ; they were born to work.
2. Make the sentences affirmative:
Question 1.
My teacher had no answer,
Answer:
My teacher was speechless.
![]()
Question 2.
I have never thought about it.
Answer:
I have always ignored it.
Activity-based on Contextual Grammar:
Question 1.
Name the tense:
- The Nobel committee has generously invited me to present a “Lecture.”
- I am representing the millions of children.
- I humbly accept this award on behalf of all my fellow activists across the world.
- I have kept an empty chair here as a reminder.
Answer:
- Present Perfect Tense
- Present Continuous Tense
- Simple Present Tense
- Present Perfect Tense
Question 2.
Make adjectives of:
- honour
- create
- silence
- peace
Answer:
- honour – honourable
- create – creative
- silence – silent
- peace – peaceful.
1. Change the voice:
Question 1.
He was kidnapped by an extremist militia. (Begin the sentence with “An extremist militia….)
Answer:
An extremist militia kidnapped him.
Question 2.
He was forced to kill his friends and family.
(Begin the sentence with “They….”)
Answer:
They forced him to kill his friends and family.
![]()
Question 3.
All the great religions teach us to care for our children. (Begin the sentence with “We are….)
Answer:
We are taught to care for our children by all the great religions.
Question 4.
I have held their injured bodies. (Begin the sentence with “Their injured bodies…)
Answer:
Their injured bodies have been held by me.
Rewrite the following into indirect speech:
Question 1.
Rewrite the following into indirect speech:
Answer:
A skinny child labourer asked Satyarthi, “Is the world so poor that it cannot give me a toy and a book, instead of forcing me to take a gun or a tool?” Ans. A skinny child labourer asked Satyarthi if the world was so poor that it could not give him a toy and a book, instead of forcing him to take a gun or a tool.
Question 1.
Change these sentences into indirect speech:
- The lion asked the bird, “What are you doing?”
- The bird said to the lion, “I am going to extinguish the fire.”
- The lion said, “How can you do it keeping just one drop of water in your beak?”
- The bird said, “I am doing my bit.”
Answer:
- The lion asked the bird what it was doing.
- The bird told the lion that it was going to extinguish the fire.
- The lion asked how it could do it keeping just one drop of water in its beak.
- The bird said that it was doing its bit.
![]()
Question 2.
Add a question tag:
- We are connected through high-speed internet.
- We exchange our goods and services in one single global market.
- Let us globalize compassion.
- All the animals were running away.
Answer:
- We are connected through high-speed internet, aren’t we?
- We exchange our goods and services in one single global market, don’t we?
- Let us globalize compassion, shall we?
- All the animals were running away, weren’t they?
Question 3.
He asked the bird “What are you doing?” (Make it indirect)
Answer:
He asked the bird what he was doing.
Question 4.
Make nouns of the following:
1. play
2. grow
Answer:
1. play – play, player
2. grow – growth
Question 5.
Make verbs of the following:
1. knowledge
2. exploitation
Answer:
1. knowledge – know
2. exploitation – exploit
Personal Response:
Question 1.
What type of text is this? How do you decide it?
Answer:
This text is a speech. I have decided it on the basis of the beginning of the text. In the beginning the speaker has addressed the dignitaries and the audience assembled in the hall /auditorium. This shows that the text is a speech/lecture.
Question 2.
What do you know about Kailash Satyarthi?
Answer:
Kailash Satyarthi is an activist who fought for the Indian children’s rights. He is a Nobel Peace Prize recipient and the Founder of Bachpan Bachao Andolan. He and his team at the Bachpan Bachao Andolan have liberated more than 86,000 children in India from child labour slavery and trafficking. He is basically from Vidisha in Madhya Pradesh.
![]()
Question 3.
What efforts will you take to enrol the out-of-school children?
Answer:
If I see any children out of school, I will tell them the importance of education in their life. I will also tell them about the Right of Children to Free and Compulsory Education. By convincing them I will help them to take admission in schools nearby so that they can stand and face the life independently and get success in their life. Also, I shall try to convince their parents to send their children to school.
Question 4.
What is the role of education in nation-building?
Answer:
Education plays a very critical and crucial role in deciding the growth of a nation. Educated citizens of the country bring fame, wealth and prosperity to the country which helps in development of a country. People who are educated think and work to achieve the dream of any country. Education helps in dream building so education is a big invaluable asset in nation-building.
Question 5.
What lesson does the story of the lion and the tiny bird teach us?
Answer:
I think the story of the lion and the tiny bird teaches us not to belittle other individuals who atleast do something and make an effort. No matter how small it is in their eyes but it might be big in result. Small things shouldn’t be valued too little sometimes. Big things always start from something small.
Question 6.
What will you do for our country?
Answer:
First I will try to take higher education. As for as possible I will try to use that knowledge for the developement of our country, I will also help the people to take education so that they will also help our country to prosper and become a developed country.
Question 7.
What is your vision of tomorrow?
Answer:
My vision for tomorrow is to empower the people with a vision to have the confidence and ability to achieve their dream. If I help them to gain their confidence, they will work hard to achieve their goal. Ultimately they will help the nation to prosper.
Question 8.
Do you think, our parents are the most beautiful gift of our life?
Answer:
Our life is a journey full of joy, sorrow fantasy, expectations, hellos, goodbyes and farewells. Our parents are always with us in all ups and downs; so we can live our life happily. They are always with us to solve our problems and to sort out any situation. So they are the most beautiful gift of our life.
![]()
Question 9.
What do you mean by “Every child has a right to life”?
Answer:
The right to life is a moral principle based on the belief that a human being has the right to live. Every child has some inherent right to life which is protected by laws. No one shall be arbitrarily deprived of his life. So it is our duty to protect every child and help him/her to live a happy and healthy life.
Question 10.
Why should the government invest in education and young people?
Answer:
Education is the systematic process of gaining knowledge and skills. It has positive impact on our life. It also promotes national interest. It is the backbone of developing countries. If the government invests in education and young people, they help the nation to develop as they are called real nation-builders and future of the country so the government should invest in education and young people.
Question 11.
Why should we stop “Child labour”?
Answer:
“Child labour” is a stigma on our society. It is sure to interfere with his/her right to education. It is also harmful to their physical, mental, spiritual, moral and social development. It is harmful to the development of any country, as “the child” is the future citizen of every country. So we should stop child labour and child exploitation.
Do as directed:
Question 1.
Complete the words/spellings by using correct letters:
Answer:
- m a _ c h – m a r c h
- p l _ n t – p l a n t
- w o _ l d – w o r l d
- N _ b e l – N o b e l
Question 2.
Put the words in alphabetical order:
1. create, activist, world, freedom
2. exhausted, experience, extinguish, equality
Answer:
1. activist, create, freedom, world.
2. equality, exhausted, experience, extinguish.
![]()
Question 3.
Punctuate the following sentences:
1. the lion laughed and said how can you do it keeping just one drop of water in your beak
2. lets walk together.
Answer:
1. The lion laughed and said, “How can you do it keeping just one drop of water, in your beak?”
2. Let’s walk together.
Question 4.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:
Question 5.
Complete the word-chain of ‘adjective’. Add four words each beginning with last letter of the previous letter :
Supreme, → e ……………, …………., …………., ……………..
Answer:
Supreme, → easy, young , grateful, less.
1. Attempt anyone:
Question (a)
Add a clause to expand the following sentence meaningfully.
The bird ………………
Answer:
The bird which was in a cage was at last freed by his owner.
2. Attempt any one:
Question (a)
Add preffix or suffix to make new words:
1. inspire
2. expend
Answer:
1. inspiration
2. expenditure
OR
Question (b)
Make a meaningful sentence by using one of the following words:
1. inspire
2. expand
Answer:
1. Our parents always inspire us to do something good.
2. Reading always expands our knowledge.
![]()
Writing Skill
Malala’S Bio-Data
Name: Malala Yousafzai
Father’s Name: Ziauddin Yousafzai
Mother’s Name: Tar Pekal Yousafzai
Date of birth: 12 July, 1997
Religion: Sunni Islam
Occupation: Activist for rights to female education.
Awards:
- Nobel Peace Prize
- Simone de Beauvour Prize
- National Youth Peace Prize
- Honorary Canadian
- Citizenship
My English Coursebook Standard Ten Digest Answers Pdf Unit 3