Bhagya

Correspondence with Members 12th Secretarial Practice Chapter 6 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 6 Correspondence with Members Textbook Exercise Questions and Answers.

Class 12 Secretarial Practice Chapter 6 Exercise Solutions

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
Directors are the ____________
(a) paid employee of the company
(b) representatives of the shareholders
(c) creditors of the company
Answer:
(b) representatives of the shareholders

Question 2.
The dividend is to be paid to the shareholders within ____________ days from the date of declaration.
(a) 30
(b) 40
(c) 20
Answer:
(a) 30

Question 3.
Registered shareholders receive dividend through ____________ warrant.
(a) share
(b) debenture
(c) dividend
Answer:
(c) dividend

Question 4.
Shares issued free of cost to the shareholders are known as ____________ shares.
(a) preference
(b) equity
(c) bonus
Answer:
(b) equity

Question 5.
Share Certificate should be ready for delivery by the company within ____________ months after the allotment of shares.
(a) 3
(b) 5
(c) 2
Answer:
(c) 2

Question 6.
Secretarial correspondence with members should be ____________
(a) lengthy
(b) shortcut
(c) prompt and precise
Answer:
(c) prompt and precise

Question 7.
Dividend is recommended by ____________
(a) Board of Directors
(b) shareholders
(c) Depositors
Answer:
(a) Board of Directors

Question 8.
Dividend is paid out of ____________ of the company.
(a) Capital
(b) Building Fund
(c) Profit
Answer:
(c) Profit

Question 9.
____________ is issued by the company to its registered shareholders after the declaration of dividend at the Annual General Meeting of the company.
(a) Dividend Warrant
(b) Interest Warrant
(c) Share Warrant
Answer:
(a) Dividend Warrant

1B. Match the pairs.

Question 1.

Answer:

Group ‘A’	Group ‘B’
(a) Dividend Warrant	(9) Instrument for Payment of Dividend
(b) Return on Shares	(6) Dividend
(c) Bonus Shares	(4) Capitalisation of Reserve Fund
(d) ECS	(3) Electronic Clearing Service
(e) NEFT	(5) National Electronic Fund Transfer

1C. Write a word or term or a phrase which can substitute each of the following statements.

Question 1.
Shares given free of cost to the existing equity shareholders.
Answer:
Bonus shares

Question 2.
Instrument for payment of dividend.
Answer:
Dividend Warrant

Question 3.
The shareholders to whom the bonus shares are issued.
Answer:
Equity shareholders

Question 4.
The authority which recommends the rate of dividend.
Answer:
Board of Directors

Question 5.
An officer who comes into contact with all the members of the company through correspondence.
Answer:
Secretary

Question 6.
A special kind of cheque issued by a company on its banker to pay certain sum of money as dividend to its members.
Answer:
Dividend warrant

1D. State whether the following statement are True or False.

Question 1.
Bonus shares are issued to existing equity shareholders.
Answer:
True

Question 2.
Building fund is used for issue of bonus shares.
Answer:
False

Question 3.
Bonus shares means capitalisation of reserve fund.
Answer:
True

Question 4.
Registered shareholder gets dividend through dividend coupons.
Answer:
True

Question 5.
Dividend is the portion of the profits of the company which is allotted to the holders of the debentures of the company.
Answer:
True

Question 6.
Every company must issue or dispatch a share certificate to the allottee within three months after allotment of shares.
Answer:
False

Question 7.
A complaint letter should not be replied promptly.
Answer:
True

1E. Find the odd one.

Question 1.
Secrecy, Dividend, Interest
Answer:
Secrecy

Question 2.
Bonus Letter, Dividend Letter, Board of Directors
Answer:
Board of directors

Question 3.
Dividend Warrant, Interest Warrant, Demat
Answer:
Demat

Question 4.
Secretary, Board of Directors, Dividend, Lucid Language
Answer:
Lucid Language

1F. Complete the sentences.

Question 1.
Dividend is recommended by ____________
Answer:
Board of Directors

Question 2.
A company capitalises its Reserve Fund for issue of ____________ shares.
Answer:
Bonus

Question 3.
Payment of dividend must be made within ____________ days of its declaration.
Answer:
30

Question 4.
Dividend is approved by the ____________ in the Annual General Meeting.
Answer:
Shareholders

Question 5.
The ____________ has to communicate the decisions of the management to the members by conducting correspondence.
Answer:
Secretary

1G. Select the correct option from the bracket.

Question 1.

(Written communication, Bonus shares, Dividend, ECS)
Answer:

Group ‘A’	Group ‘B’
(a) Return on shares	(1) Dividend
(b) Capitalisation of Reserve Fund	(2) Bonus shares
(c) Correspondence	(3) Written communication
(d) ECS	(4) Payment of Dividend Electronically

1H. Answer in one sentence.

Question 1.
What is dividend warrant?
Answer:
Dividend warrant is written order given by the company to its banker to pay amount mentioned in it to the shareholder whose name is specified therein.

Question 2.
What is capitalization of reserve?
Answer:
Capitalization of reserves is the use of corporate reserves to pay a bonus to the shareholders in the form of additional shares.

Question 3.
What is Dividend?
Answer:
Dividend is the portion of profits of the company which is distributed to the shareholders of the company.

Question 4.
Who recommends the rate of dividend?
Answer:
The Board of Directors of the company recommends the rate of dividend.

Question 5.
Which type of shareholders enjoys the benefit of Bonus Shares?
Answer:
Equity share holders enjoy the benefit of bonus shares.

Question 6.
What is meant by payment of dividend electronically?
Answer:
Payment of dividend electronically means transfer of dividend amount through ECS (Electronic Clearing Service) NEFT(National Electronic Fund Transfer) etc.

1I. Correct the underlined word and rewrite the following sentences.

Question 1.
Dividend is recommended by shareholders.
Answer:
Dividend is recommended by shareholder.

Question 2.
The person who purchases shares of the company is called Depositor.
Answer:
The person who purchases shares of the company is called shareholder.

Question 3.
Bonus shares are issued as a free gift to the preference shareholders.
Answer:
Bonus shares are issued as a free gift to the equity shareholders.

Question 4.
Payment of dividend must be made within 21 days of its declaration.
Answer:
Payment of dividend must be made within 30 days of its declaration.

Question 5.
A company must issue the Share Certificate within three months of allotment of shares.
Answer:
A company must issue the Share Certificate within two months of allotment of shares.

1J. Arrange in proper order.

Question 1.
(a) Allotment of shares
(b) Application for shares
(c) Share certificate
Answer:
(a) Application for shares
(b) Allotment of shares
(c) Share certificate

Question 2.
(a) Member
(b) Applicant
(c) Bonus shares
Answer:
(a) Applicant
(b) Member
(c) Bonus shares

2. Explain the following terms/concepts.

Question 1.
Capitalisation of Reserve
Answer:
Capitalisation of reserves is the use of corporate reserves to pay a bonus to the shareholders in the form of additional shares. It is distributed to equity shareholders in pre-determined ratio.

Question 2.
Bonus Shares
Answer:
Bonus shares are fully paid up shares given by a company as a gift out of its accumulated profits or reserves to the existing equity share holders in proportion of shares held by them. It is given free of cost and also known as capitalization of reserves.

Question 3.
Dividend Warrant
Answer:
Dividend warrant is written order given by the company to its banker to pay amount mentioned in it to the shareholder whose name is specified therein. Dividend can be paid through Dividend warrant or by means of electronic mode ECS or NEFT etc. to those shareholders who are registered members i.e their names appear in the Register of members.

3. Answer in brief.

Question 1.
Which precautions are to be taken by the Secretary while corresponding with members?
Answer:
The Secretary has to communicate the decisions of the Management and other information to the members through correspondence. The Secretary should be very cautious and careful while corresponding with members of the company. Writing letters to the members is a challenging task and it requires skills, knowledge and techniques.
Following are the precautions that are needed to be taken by the secretary while writing different letters on different occasions:
(i) Correct Information:
The Secretary should always provide correct, up- to date and factual information to the members. Due care should be taken while giving facts and figures.

(ii) Lucid Language:
The Secretary must use simple words and sentences and adopt convincing style while writing letters to the members. The use of simple language makes it easy to understand. Technical words, long sentences should be avoided in the letter.

(iii) Prompt Response:
The Secretary must be prompt in sending replies to the letters received from the members. Any questions or queries raised by the members must be replied promptly by the Secretary. Complaint letters should be attended to without any delay.

(iv) Secrecy:
The Secretary should not disclose any confidential information of the company to the members. The Secretary should tactfully answer letters without giving any secret information of the company.

(v) Politeness (Courtesy):
A courteous letter shows sympathy, respect mutual understanding and consideration for the receiver. Use of courteous language means using polite words. A complaint letter should be replied politely. Rude language should be strictly avoided as it spoils image of the company.

(vi) Legal matters:
The Secretary should compulsorily follow provisions of the Companies Act, 2013 with latest amendments and other relevant laws. If necessary, secretary should consult with legal advisor on certain matters before drafting.

(vii) Consideration:
The Secretary should give importance and consideration to the reader and write the contents keeping in mind the problems of the member. While sending negative replies, he should draft these letters more carefully, so that members should not be hurt. Secretary should make the member feel that the management honestly regrets refusal.

(viii) Image of the Company:
The Secretary should try to project good image of the company in every situation. While drafting the letters, Secretary has to try his best to remove their doubts, queries and difficulties in a polite and courteous manner.

Question 2.
What are the circumstances under which Secretary undertakes correspondence with members?
Answer:
The following are the various occasions when the Secretary writes the letters to the members of the company:

• Allotment Letter when shares are issued to an applicant.
• Letter of Regret when shares are not issued to an applicant for any reason.
• Letter for issue of Share Certificate to the allotted members.
• Letter for Payment of Dividend through Dividend Warrant or Electronic Payment of Dividend.
• Letter for issue of Bonus Shares or rights issue.
• Reply letter to the query of the member on low rate of dividend.
• Approval of Transfer of Shares after serving lodgement notice to the transferor as well as the transferee.
• Refusal of Transfer of Shares, if call money is unpaid or any lien.
• Notice and Agenda of General Meeting.
• Reply to certain queries raised by the members.
• Letters to legal representatives regarding Transmission of Shares.
• Notice of loss of Share Certificate.

4. Justify the following statements.

Question 1.
The Company Secretary should take certain precautions while corresponding with members.
Answer:

• The Secretary has to communicate the decisions of the management and other information to the members through correspondence and hence, should be very cautious and careful while corresponding with members of the company. The Secretary should take precautionary measures while writing the letter by giving due respect to the members, and also provide complete and correct information techniques.
• The Secretary should always provide correct, up- to date and factual information to the members.
• The language used should be simple and convincing.
• The Secretary must be prompt in sending replies to the letters received from the members.
• He should compulsorily follow provisions of the Companies Act, 2013 with latest amendments and other relevant laws.
• The Secretary should try to project good image of the company in every situation.
• Thus, it is rightly said that, the Company Secretary should take certain precautions while corresponding with members.

Question 2.
There are certain circumstances when a Secretary has to correspond with members.
Answer:

• Secretary correspond with members on behalf of the company.
• Secretary acts as a link between the company and its members.
• When the shares are allotted to the members they are been informed through the allotment letter. Similarly, if the application of shares has been rejected then members are been informed by the regret letter.
• Secretary also informs members through letters on various occasions like issue of share certificate, payment of dividend, issue of bonus share, reply to the query raised by the member, etc.
• Thus, it is rightly said that, there are certain circumstances when a Secretary has to correspond with members.

5. Attempt the following.

Question 1.
Write a letter to the shareholder regarding issue of Bonus Shares.
Answer:

YASH INDUSTRIES LIMITED
Registered Office: 102, New MIDC, Usha Tower, Shahu Chowk, Mumbai – 400 031.
CIN : L40407 MH 2005 PLC710007

Tel. No.: 022-23252323
Fax No.: 022-23600445
Ref. No.: Y/MR-B/5/19-20

Website: www.yashindustrieslimited.com
Email: yash30@gmail.com
Date: 16th October, 2019

Ms. Yukta Shroff
715, Narayan Peth,
Laxmi Road,
Pune – 411 038.

Sub.: Issue of Bonus Shares

Dear Madam,

I am directed by the Board of Directors to inform you that in accordance with the resolution passed in the Extra-ordinary General Meeting of the company held on 14th October, 2019, shareholders have unanimously approved the recommendation of Board of Directors to issue Bonus Shares. Bonus Shares are issued in the ratio of 1:1, i.e. one additional equity share for every equity share held as on 13th October, 2019.

The Details of issue of Bonus Shares are as follows:

1	2	3	4	5
No. of Shares held on record date	No. of Bonus Shares Issued/Allotted	D.P. ID No. Credited to Demat Account No.	Client ID No. Credited to Demat Account No.	Date of Credit to Demat A/c
25	25	IN 300100	10116061	31-10-2019

The Company has complied with the provisions for the issue of Bonus Shares.
The Bonus Shares issued will rank pari passu /equal with the existing equity shares.

Thanking you,

Yours faithfully,
For Yash Industries Limited

Sign
(Mr. S. R. Naik)
Company Secretary

Question 2.
Write a letter to the member for the issue of Share Certificate.
Ans.

COMFORT MOTORS LTD.
Registered Office : A/30, Aurora Towers, M. G. Road, Camp, Pune 411 012.
CIN : U12111 MH 2000 PCL300477

Tel. No.: 020-80032844
Fax No.: 020-50063015
Ref. No.: C/MR-SC/30/19-20

Website: www.comfortmotorsltd.com
Email: comfort31@gmail.com
Date: 12th November, 2019

Mr. Jayant Modi
Abhiman Apartment
30, L. B. Road,
Pune-411 001.

Sub.: Issue of Share Certificate

Dear Sir,
As per your Request Application No. 50, I am, hereby, authorized by the Board to issue you a Share Certificate. The said Share Certificate will be delivered to you within 15 days from the date of this letter by registered post to your registered address as mentioned in the Register of Members.

1	2	3		4
Folio No.	Share Certificate Numbers	Distinctive Numbers		Total No. of Shares
		From	To
1006	9630	301	400	100

It shall always be our endeavor/attempt to provide best of our services to you.
Thanking you,

Yours faithfully,
For Comfort Motors Ltd.

Sign
Mr. Anand Swami
Company Secretary

Question 3.
Write a letter to the member for the payment of dividend through Dividend Warrant.
Answer:

ANMOL STEEL INDUSTRIES LIMITED
Registered Office : 30, Anmol Niwas, J. M. Road, Nariman Point, Mumbai – 400 020.
CIN : L30408 MH 2003 PLC110845

Tel. No.: 022-97675877
Fax No.: 022-30010331
Ref. No.: A/MR-D/7/19-20

Website: www.anmolindustrieslimited.com
Email: anmol5@gmail.com
Date: 7th May, 2019

Mrs. Jyoti Surti 12, Laxmi Niwas,
Amrapali Marg, Bandra,
Mumbai – 400 050.

Sub.: Payment of Dividend on Equity Shares
(Equity Shares of ₹ 10 each at par)

Dear Madam,
As per the instructions issued by the Board of Directors it is being conveyed to you that in the, Final Dividend @ ₹ 2.5 per equity share of ₹ 10/- each has been approved by the members for the year ending 31st March, 2019 in the 31st Annual General Meeting held on 20th April, 2019.

Your company has complied with all the statutory provisions (Sec. 123 of the Companies Act. 2013) relating to declaration of dividend. Details of dividend payable to you are as follows:

1	2	3		4	5	6	7
Register Folio No.	No. of Shares held	Distinctive Numbers		Dividend Warrant No.	Gross Dividend	Income Tax Deducted (TDS)	Net Dividend
		From	To
A-30	100	301	400	B-9931	Rs.250/-	NIL	250/-

The ‘Dividend Warrant’ is attached herewith. Please detach the ‘Dividend Warrant’ along the perforated line.
Thanking you,

Yours faithfully,
For Anmol Steel Industries Limited.

Sign
Secretary

Encl.: Dividend Warrant

Question 4.
Write a letter to the member for the payment of Interim dividend electronically.
Answer:

GURUSAI AUTO LIMITED
Registered Office: 31, Tulsi Complex, Lodhi Road, Camp, Pune – 411 001.
CIN : L40103 MH 1999 PLC300477

Tel. No.: 020-24032844
Fax No.: 020-24356101
Ref. No.: S/MR-D/12/19-20

Website: www.gurusailimited.com
Email: sai31@gmail.com
Date: 3rd June, 2019

Mr. Jay ant Modi
15, Sagar Apartment,
Van Vihar Road,
Pune-411 030.

Sub.: Payment of Interim Dividend through Electronic Clearing Service (ECS), Direct Credit/NEFT

Dear Sir,

We are pleased to inform you that the Board of Directors of Gurusai Auto Limited in its meeting held on Thursday, 28th May 2019 has declared Interim Dividend @ ₹ 1/- (i.e. 10%) per equity share of face value of ₹ 10/- each.

As per the instructions given by you (either in person or through Depository Participant), we have remitted the amount of the Interim Dividend to your Banker for crediting your Bank Account, for electronic transfer. Your company has complied with all the provisions relating to declaration and payment of dividend.

Details of Dividend payable to you are given below:

1	2	3	4	5	6
No. of Equity Shares held on Record Date (May 31st, 2019)	Dividend Per Share (₹)	Dividend Amount (₹)	DPID and Client ID No.	Date of Remittance	Bank A/c. (Bank of Baroda)
500	1	500	12033 200074 79005	6th June, 2019	5656000 22105 (Bank of Baroda)

Please verify the credit of amount in your Pass Book/Statement of accounts.
As per the provisions of the Income Tax Act, 1961 no tax is required to be deducted at source in respect of Dividend payment, but dividend Distribution Tax has been paid by the Company.
Thanking you,

Yours faithfully,
For Gurusai Auto Limited.

Sign
(Mr. Jitesh M. Gandhi)
Company Secretary

Question 5.
Draft a reply letter resolving the query of the member on the low rate of dividend.
Answer:

SHREE CEMENT INDUSTRIES LIMITED
Registered Office: 31, Tulsi Tower, Bandra (East), Mumbai – 400 050
CIN : L50307 MH 2000 PLC160699

Tel. No.: 022-24245025
Fax No.: 022-45456035
Ref. No.: S/MR-D/25/19-20

Website: www.shreecementindustriesltd.com
Email: shree3@gmail.com
Date: 20th April, 2019

Ms. Kishor Malpani
15/21, Lotus Apt.,
Borivali (W),
Mumbai – 400 103.

Sub.: Resolving Query on Low Rate of Dividend made by the Company.

Dear Sir,
This is to inform you that as per your letter dated 15th April, 20191 am, hereby, authorized to resolve your query regarding the low rate of dividend paid by the company to their faithful members. The reasons for the low rate of dividends are mentioned below:

1. During the last year, due to the floods, the company’s factory situated at Mahim (E) was not in a condition | to operate in a full-fledged manner.
2. Due to such unavoidable circumstances of natural disaster company faced huge financial losses.
3. Hence, the Board of Directors has decided to transfer 12.5 crores to General Reserves which is 50%; more than the amount transferred to Reserves last year.

Hope you will be satisfied by the above information as provided by the company. We assure you that the company will easily come over from such unavoidable circumstances and will deliver/pay/declare much better! dividend in the coming years.

Thanking you,

Yours faithfully,
For Shree Cement Industries

Sign
(Mr. Suhas Bajaj)

Company Secretary

Maharashtra State Board 12th Std Secretarial Practice Textbook Solutions

• Introduction to Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Sources of Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Issue of Shares Class 12 Secretarial Practice Textbook Solutions
• Issue of Debentures Class 12 Secretarial Practice Textbook Solutions
• Deposits Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Members Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Debentureholders Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Depositors Class 12 Secretarial Practice Textbook Solutions
• Depository System Class 12 Secretarial Practice Textbook Solutions
• Dividend and Interest Class 12 Secretarial Practice Textbook Solutions
• Financial Market Class 12 Secretarial Practice Textbook Solutions
• Stock Exchange Class 12 Secretarial Practice Textbook Solutions

Deposits 12th Secretarial Practice Chapter 5 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 5 Deposits Textbook Exercise Questions and Answers.

Class 12 Secretarial Practice Chapter 5 Exercise Solutions

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
Deposit is a type of ____________
(a) Owned capital
(b) Short term loan
(c) Long term loan
Answer:
(b) Short term loan

Question 2.
Eligible Public Company and Government Company can collect deposits from ____________
(a) It’s employees
(b) Public
(c) RBI
Answer:
(b) Public

Question 3.
A private company can accept deposits from its Member of Directors up to not more than ____________ % of its aggregate of paid-up share capital and free reserves.
(a) 100
(b) 35
(c) 25
Answer:
(a) 100

Question 4.
A ____________ Company can accept deposits from the public not exceeding 35% of its paid-up share capital and free reserves.
(a) Government
(b) Private
(c) Eligible Public
Answer:
(a) Government

Question 5.
Deposits can be accepted for a minimum of 6 months and maximum for ____________ months.
(a) 36
(b) 3
(c) 30
Answer:
(a) 36

Question 6.
Company issues ____________ to invite its members to subscribe for its deposit scheme.
(a) Advertisement
(b) Circular
(c) Newspaper
Answer:
(b) Circular

Question 7.
The company can issue a circular or advertisement for inviting deposits after ____________ days of filing it with the Registrar of Companies.
(a) 30
(b) 21
(c) 7
Answer:
(a) 30

Question 8.
Company has to appoint ____________ to protect the interest of depositors.
(a) Debenture Trustees
(b) Deposit Trustees
(c) Credit Rating Agency
Answer:
(a) Deposit Trustees

Question 9.
Charge on assets is to be created when a company issues ____________
(a) Unsecured deposit
(b) Unsecured Debenture
(c) Secured deposit
Answer:
(c) Secured deposit

Question 10.
Deposit Receipt is issued within ____________ days of receipt of deposit.
(a) 7
(b) 30
(c) 21
Answer:
(c) 21

Question 11.
For premature repayment of deposit, company deducts ____________ % of interest.
(a) 1
(b) 18
(c) 20
Answer:
(a) 1

Question 12.
Return of deposit must be filed every year on or before ____________
(a) 30 June
(b) 31 March
(c) 30 April
Answer:
(a) 30 June

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(a) Private Company	(1) 10% of the aggregate of paid-up share capital + free reserves
(b) Deposit Trust Deed	(2) Signed at least 7 days before issuing advertisement
(c) Secured Deposit	(3) Maximum 30 months
(d) Tenure of deposit	(4) Charge on tangible assets
(e) Return of Deposit	(5) 100% aggregate of paid-up share capital + free reserves
	(6) File on or before 31 March every year
	(7) Signed 21 days after issuing advertisement
	(8) Maximum 36 months
	(9) Charge on intangible assets
	(10) File on or before 30 June every year

Answer:

Group ‘A’	Group ‘B’
(a) Private Company	(5) 100% aggregate of paid-up share capital + free reserves
(b) Deposit Trust Deed	(2) Signed at least 7 days before issuing advertisement
(c) Secured Deposit	(4) Charge on tangible assets
(d) Tenure of deposit	(8) Maximum 36 months
(e) Return of Deposit	(10) File on or before 30 June every year

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
A company that can accept deposits from its members, directors, or their relatives not exceeding 100% of the aggregate of paid-up share capital and free reserves.
Answer:
Private Company

Question 2.
The company can accept deposits from the public up to 35% of its paid-up share capital and free reserves.
Answer:
Government Company

Question 3.
Minimum tenure of a deposit.
Answer:
6 months

Question 4.
The maximum tenure of the deposit.
Answer:
36 months

Question 5.
Period within which a company has to create a charge on its tangible assets.
Answer:
30 days of Acceptance

Question 6.
Document issued by a company to invite its members to subscribe for its Deposits.
Answer:
Circular

Question 7.
Agreement between the company and Deposit Trustee.
Answer:
Deposit Trust Deed

Question 8.
The account can be used only for repaying deposits.
Answer:
Deposit Repayment Reserve Account

Question 9.
Time within which company has to issue deposit Receipt.
Answer:
21 days

Question 10.
Book which contains details of deposits accepted or renewed.
Answer:
Register of Deposits

1D. State whether the following statements are true or false.

Question 1.
Return of deposit must be filed every year on or before 31 March.
Answer:
False

Question 2.
An eligible public company can collect deposits from its members.
Answer:
True

Question 3.
A government company can collect deposits from its members.
Answer:
False

Question 4.
A private company can collect deposits from the public.
Answer:
False

Question 5.
The deposit can be accepted for a maximum of 36 months.
Answer:
True

Question 6.
An eligible public company can collect deposits from the public not exceeding 35% of its paid-up share capital and free reserves.
Answer:
False

Question 7.
For secured deposits, the company has to create a charge on its tangible assets.
Answer:
True

Question 8.
Deposit Receipt is issued within 21 days of receipt of deposits.
Answer:
True

Question 9.
Company appoints Credit Rating Agency to protect the interest of depositors.
Answer:
False

Question 10.
Deposit Trust Deed is an agreement between the company and Deposit Trustee.
Answer:
True

1E. Find the odd one.

Question 1.
Private Company, Eligible Public Company, Government Company.
Answer:
Private company

Question 2.
Deposit Trustee, Deposit Trust Deed, Special Resolution.+
Answer:
Special Resolution

Question 3.
Appointment of Deposit Trustee, Appointment of Registrar of companies, Appointment of Credit Rating Agency.
Answer:
Appointment of Registrar of companies

1F. Complete the sentences.

Question 1.
Deposit is a type of ____________ term loan.
Answer:
Short term loan

Question 2.
Eligible Public company and Government Company can accept deposits from ____________
Answer:
Public

Question 3.
To collect deposits from the public, Eligible public company must have a net worth of not less than ₹ ____________
Answer:
₹ 100 Crores

Question 4.
A Government company can accept deposits from public not exceeding ____________
Answer:
35% of the paid-up share capital and free reserves of the company

Question 5.
Deposits can be accepted or renewed for a period not less 6 months and not more than ____________
Answer:
36 months

Question 6.
Company cannot accept or renew deposits repayable on ____________
Answer:
Demand

Question 7.
Premature repayment of deposits can be done by a company but not before ____________
Answer:
3 months

Question 8.
To invite the public to subscribe for its deposits, a company issues ____________
Answer:
Advertisement

Question 9.
Agency which gives ratings of the deposits of a company is called ____________
Answer:
Credit rating agency

Question 10.
Account which is used only for repaying deposits is called ____________
Answer:
Deposit Repayment Reserve Account

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group B’
(a) Government Company	(1) ………………….
(b) …………………….	(2) Deposits from members
(c) 36 months	(3) …………………….
(d) …………………….	(4) Charge on tangible assets
(e) Return of deposit	(5) ……………………

(File on or before 30 June, Private Company, Secured deposits, Deposits from public, Maximum tenure of deposits)
Answer:

Group ‘A’	Group B’
(a) Government Company	(1) Deposits from public
(b) Private Company	(2) Deposits from members
(c) 36 months	(3) Maximum tenure of deposits
(d) Secured deposits	(4) Charge on tangible assets
(e) Return of deposit	(5) File on or before 30 June

1H. Answer in one sentence.

Question 1.
Which companies can accept deposits from the public?
Answer:
Government Companies and Eligible Public companies can accept deposits from the public.

Question 2.
What is the maximum deposit the Government company can collect?
Answer:
Government companies can accept deposits from the public not exceeding 35% of the paid-up share capital and free reserves of the company.

Question 3.
What is the tenure of a deposit?
Answer:
A company can accept deposits for a minimum of 6 months and a maximum of 36 months.

Question 4.
Who are Deposit Trustees?
Answer:
Eligible companies and public companies have to appoint one or more Deposit Trustees to protect the interest of the depositor, in case a company defaults in repaying the depositors.

Question 5.
What is Deposit Trust Deed?
Answer:
Company signs a contract with the Deposit Trustees called as Trust Deed which contains the terms and conditions of the contract.

Question 6.
When does a company create a charge on its tangible assets?
Answer:
A Company accepting secured deposits from the public has to create a charge on its tangible assets.

Question 7.
Within what period should a company issue a Deposit Receipt?
Answer:
The company has to issue a Deposit Receipt to the depositors within twenty-one (21) days from the date of receipt of money or realization of cheque.

Question 8.
When should a company file Return of Deposit?
Answer:
A company has to file a Return of Deposit on or before 30 June every year with the Registrar of Companies.

Question 9.
What is Deposit Repayment Reserve Account?
Answer:
Every company accepting deposits has to open a Deposit Repayment Reserve Account in a scheduled Bank which can be used only for repaying deposits.

Question 10.
What is the Register of Deposit?
Answer:
A company has to maintain a separate Register for deposits accepted or renewed at its registered office which is called as Register of Deposits.

1I. Correct the underlined word/s and rewrite the following sentences.

Question 1.
Government companies can accept deposits from members.
Answer:
Government companies can accept deposits from the public.

Question 2.
Company issues advertisement to invite its members for subscribing to its deposits.
Answer:
Company issues are circular to invite its members for subscribing to its deposits.

Question 3.
Company appoints Credit Rating Agency to protect the interest of Depositors.
Answer:
Company appoints Deposit Trustees to protect the interest of Depositors.

Question 4.
Deposit Receipt is issued within 7 days from the date of receipt of deposits.
Answer:
Deposit Receipt is issued within 21 days from the date of receipt of deposits.

Question 5.
Register of deposits is to be filed with the Registrar of companies on or before 30th June every year.
Answer:
Return of deposits is to be filed with the Registrar of companies on or before 30th June every year.

Question 6.
Charge on assets is created when a company issues unsecured deposits.
Answer:
Charge on assets is created when the company issues secured deposits.

Question 7.
The minimum tenure of the deposit is 36 months.
Answer:
The minimum tenure of the deposit is 6 months.

1J. Arrange in proper order.

Question 1.
Appoint Deposit Trustee, Hold General Meeting, Create charge on assets.
Answer:
Hold General Meeting, Appoint Deposit Trustee, Create charge on assets.

Question 2.
File Return of deposit, Issue Deposit Receipt, Issue advertisement.
Answer:
Issue advertisement, Issue Deposit Receipt, File Return of deposit.

Question 3.
Obtain Credit Rating, Entries in Register of Deposits, Issue Deposit Receipt.
Answer:
Obtain Credit Rating, Issue Deposit Receipt, Entries in Register of Deposits.

2. Explain the following terms/concepts:

Question 1.
Eligible Public Company
Answer:
These companies can accept deposits from their members and also from the public.
Eligible public company means a company having:

• A net worth, not less than ₹ 100 crores or
• Turnover not less than ₹ 500 crores and which has obtained prior approval of its shareholders through special resolution for accepting public deposits.

Question 2.
Tenure of Deposit
Answer:

• Tenure of the deposit is the term or period of deposit.
• A company can accept deposits for a period of six months or more than thirty-six months.
• In certain circumstances, a company may accept deposits repayable earlier than six months to meet its short-term needs.
  Premature repayment is made after 3 months.

Question 3.
Secured Deposit
Answer:

• Secured deposits are those deposits against which a charge is created within 30 days of the issue.
• A company can accept secured or unsecured deposits which should be clearly mentioned in the circular or advertisement inviting deposits.

Question 4.
Deposit Trustee
Answer:

• Deposit Trustee acts as a link between the company and deposit holder.
• Eligible companies and public companies issuing secured deposits appoint one or more Deposit Trustees.
• The Trustees protect the interest of the depositor in case a company defaults in repaying the depositors.

Question 5.
Charge on tangible assets
Answer:

• A Company accepting a secured deposit from the public, within thirty days of acceptance, has to create a charge on its tangible assets for an amount not less than the amount of deposit accepted.
• It means keeping tangible assets as security for the secured deposit hold.

Question 6.
Deposit Insurance
Answer:

• Deposit Insurance is a protection cover for deposit holders.
• It is to be taken at least 30 days before the issue of circular or advertisement.
• If the amount of deposit plus interest on it is up to ₹ 20,000, insurance is to be taken.

Question 7.
Deposit Repayment Reserve Account
Answer:

• DRRA is an account opened in a scheduled bank for repaying the deposit amount.
• Every company has to open DRRA that accepts deposits.
• Every year, on or before 30 April, the company has to deposit an amount not less than 15% of the number of deposits maturing during the current year and following financial year.

Question 8.
Credit Rating
Answer:

• Credit rating is an estimate of the ability of the organization to fulfill its financial commitments.
• Every company has to get a credit rating of its deposits through a Credit Rating Agency.
• The Credit Rating Agency considers the net worth of the company, liquidity position, ability to repay deposits on time, etc., and accordingly gives a rating.
• The rating shall be obtained every year during the tenure of the deposits.

Question 9.
Deposit Receipt
Answer:

• A deposit Receipt is issued by the company to depositors.
• Deposit Receipt is issued within twenty-one (21) days from the date of receipt of money or realization of cheque.
• The receipt has to be signed by the officer duly authorized by the Board of Directors.
• The Receipt contains the name and address of the depositor, amount of deposit, rate of interest payable, and date on which it is repayable.

Question 10.
Return of Deposit
Answer:

• A company has to file a Return of Deposit, on or before 30 June every year, with the Registrar of Companies.
• The Return gives details of deposit with the company as of 31 March of that year.

3. Study the following case/situation and express your opinion.

1. Apple Company Ltd. plans to raise funds through Public Deposits. Its net worth is ₹ 10 Crores.

Question (a).
Can they accept deposits from the public?
Answer:
No, the company cannot accept deposits from the public as its net worth is less than ₹ 100 crores.

Question (b).
Can they accept deposits that mature after 4 years?
Answer:
No, the deposit can be accepted or renewed which mature after four years.

Question (c).
Within what period should the company issue deposit Receipts to its depositors?
Answer:
The company has to issue a Deposit Receipt to the depositors within twenty-one (21) days from the date of receipt of money or realization of the cheque.

2. ABC Company Ltd. is an Eligible Public Company as per the Companies Act, 2013 with reference to accepting Public Deposits.

Question (a).
Can the company accept deposits in joint names?
Answer:
Yes, the company can accept deposits in joint names of depositors. But there should not be more than 3 names.

Question (b).
Can the company accept deposits from it’s members?
Answer:
Yes, the company can accept fresh deposits only if the amount of such deposits together with the previous deposits does not exceed 10% of the aggregate of paid-up share capital and free reserves.

Question (c).
Can the company issue secure deposits?
Answer:
Yes, the company can issue a secured deposit only if it is clear which should be clearly mentioned in the circular or advertisement inviting deposits.

3. Apple Company Ltd. is an Eligible Public Company. It plans to raise secured deposits from the public. Please advise its Board on the following.

Question (a).
Does the company need to get shareholders’ approval for accepting deposits?
Answer:
Yes, the company has to seek the shareholder’s approval for accepting deposits by passing a special resolution.

Question (b).
Does the company have to appoint a Deposit Trustee?
Answer:
Yes, the company has to appoint a Deposit Trustee as it is issuing secured deposits.

Question (c).
Within what period should the company create a charge on it’s assets?
Answer:
A Company can create a charge on its tangible assets within 30 days of acceptance.

4. SUN Pvt. Ltd. company wants to raise funds through deposits.

Question (a).
Can the company accept deposits from the public?
Answer:
No, it cannot accept deposits from the public because it is a private company.

Question (b).
Which document should the company issue to invite deposits?
Answer:
A Private Ltd. Company can issue circulars to invite deposits.

Question (c).
What is the maximum period for which they can accept deposits?
Answer:
The maximum period for accepting deposits is 36 months.

4. Answer in brief.

Question 1.
State the number of deposits that different types of companies can collect by way of deposits.
Answer:
Deposits are a source of short-term funds for the company. Deposits can be accepted by the company by the public, directors, or its members. It is a loan taken by the company and there are various terms and conditions that a company needs to follow to accept them.

The amount of deposits that different types of companies can collect by way of deposits is as follows:
Amount of Deposit:
a) Private Company: A Private Company can accept deposits from its members or Directors or Relatives of Directors not more than 100 percent of its aggregate of paid-up share capital and free reserves.

However, a certain class of Private Companies as specified by the Companies Act can accept deposits of more than 100 percent of its aggregate of paid-up share capital and free reserves.

b) Public Company (other than Eligible Company): These Companies cannot accept fresh deposits from members if the amount of such deposits together with the previous deposits exceeds 25% of the aggregate of the paid-up share capital and free reserves of the company.

c) Eligible Public Company:
An ‘Eligible Company’, i.e. company eligible to accept deposits from the public under section 76(1) of Companies Act, 2013, can accept deposits up to 25% of paid-up capital, free reserves, and securities premium account from the ic.

In addition, it can accept deposits up to 10% of the gate of paid-up share capital, free reserves, and securities premium account from members Rule 3(4) of Companies (Acceptance of Deposits) Rules, 2014.

(d) Government Company:
A Government company is eligible to accept deposits under section 76 of the Companies Act, 2013.
It can accept deposits up to 35% of paid-up capital, free reserves, and securities premium account From the ic.

Question 2.
State the contents of Circular or Advertisement for Deposit.
Answer:
Circular or Advertisement:

• If a company invites deposits from its members, it issues a circular.
• If a company invites deposits from the public, it issues an advertisement.

Contents of circular or advertisement:

• Statement about the financial position of the company.
• The portion of secured and unsecured deposit of fresh issue.
• Credit rating obtained from a Credit Rating Agency (only for eligible public companies).
• Details of the scheme.
• Name of Deposit Trustees.
• Amount due towards deposits of any previous deposits accepted by the company.

Question 3.
State the provisions regarding the appointment of Deposit Trustee.
Answer:
Appointment of Deposit Trustee:

• Eligible companies and public companies appoint one or more Deposit Trustees while issuing secured deposits.
• They protect the interest of the depositor, in case a company defaults in repaying the deposit amount and interest.
• Company signs a contract with the Deposit Trustees called as Trust Deed.
• It contains the terms and conditions of the contract.
• The deed has to be signed at least 7 days before issuing the circular or advertisement.
• The Deposit Trustee on his own or on the request of one-tenth of depositors can call a meeting of all depositors when a company defaults in repaying deposits.

Question 4.
State any four terms and conditions regarding the acceptance of the Deposit.
Answer:
(i) Period/Tenure of Deposit:

• The tenure of deposit should be more than six months but less than thirty-six months.
• Under certain circumstances only, the company can accept deposits for 3 months.
• The company can make premature repayment of deposits after a minimum of 3 months.

(ii) No demand deposit:
The company cannot accept or renew deposits repayable on demand.

(iii) Secured or Unsecured Deposit:

• A company can accept secured or unsecured deposit if it is mentioned in the circular or advertisement.
• A company offering secured deposits has the right to create a charge on its tangible assets within 30 days of acceptance of deposits.

(iv) Application Form:

• A prescribed application form is to be filled by the applicant.
• This application form is given by the company.
• It includes a declaration made by the applicant that the deposit he is making is not borrowed from any person.

(v) Joint names:
The company can accept deposits in joint names of depositors. But there should not be more than three names.

5. Justify the following statements.

Question 1.
All companies cannot accept deposits from the public.
Answer:

• Accepting deposits from the public is an important source of raising funds for a company.
• The company needs to follow certain terms and conditions while collecting deposits from the public.
• Similarly, on the other side, provisions issued by the Central Government, Companies Rules 2014, and directives issued by the Reserve Bank of India do not allow companies to accept deposits.
• Banking companies, Non-Banking Finance Companies, Housing Finance companies are not allowed to accept deposits.
  Thus, it is rightly said, that all companies cannot accept deposits from the public.

Question 2.
There is a limit or restriction on the amount that a company can collect as Deposits.
Answer:

• There are different types of companies that can accept deposits from the public as well as members.
• A private company can accept deposits from the public of more than 100% of their aggregate of paid-up share capital and free reserves.
• Eligible Public Company and Public Company cannot accept deposits from the public exceeding 25% of the aggregate paid-up share capital and free reserves of the company.
• Government company can accept deposits up to 35% of the paid-up share capital and free reserves. Thus, we can conclude that there is a limit or restriction on the amount that a company can collect as Deposits and the statement stands justified.

Question 3.
The company has to fulfill certain provisions related to the issue of circular or advertisement.
Answer:

• The company has to file a copy of the circular or advertisement with the Registrar of Companies before inviting the public.
• Circular or advertisement should be issued to the public after 30 days of filing.
• It should be signed by all directors of the company.
• Circular is sent to the members by the speed post, registered post, or email.
• Thus, it is rightly said that a company has to fulfill certain provisions related to the issue of circular or advertisement.

Question 4.
While issuing secured deposits, the company has to appoint a Deposit Trustee.
Answer:

• When issuing secured deposits, eligible companies and public companies have to appoint one or more Deposit Trustees.
• The Trustees protect the interest of the depositor in case a company defaults in repaying the depositors.
• Company signs a contract with the Deposit Trustees called as Trust Deed.
• It contains the terms and conditions of the contract.
• The deed has to be signed at least 7 days before issuing the circular or advertisement.
• The Deposit Trustee on its own or on the request of one-tenth of depositors can call a meeting of all depositors when a company defaults in repaying deposits.
• Thus, the statement, while issuing secured deposits, the company has to appoint a Deposit Trustee is fully justified.

Question 5.
Companies have to create a charge on their tangible assets while issuing secured deposits.
Answer:

• A Company accepting a secured deposit from the public, within thirty days of acceptance, has to create a charge on its tangible assets for an amount not less than the amount of deposit accepted.
• The chargeable asset amount should not be less than the amount of deposit accepted.
• The minimum amount of security should be equal to the amount not covered by Deposit Insurance.
• The Security is created in favour of the Deposit trustees.
• Creating a charge on the assets ensures safety to the deposits of deposit holders.
• In case a company fails to repay the number of deposits, the deposit holders can sell the assets and recover the amount invested.
• Thus, it is rightly justified that the companies have to create a charge on their tangible assets while issuing secured deposits.

Question 6.
The company issuing deposit must open Deposit Repayment Reserve Account.
Answer:

• Every company accepting deposits has to open a Deposit Repayment Reserve Account in a Scheduled Bank.
• These banks satisfy certain criteria laid by RBI and enjoy certain facilities of RBI.
• Every year, on or before 30 April, the company has to deposit an amount not less than 15% of the number of deposits maturing during the current year and following financial year.
• This account can be used only for repaying deposits.
• Thus, it is rightly justified that, a company issuing deposit must open Deposit Repayment Reserve Account.

6. Answer the following questions.

Question 1.
Explain the type of companies that can raise deposits along with the maximum amount they can raise as deposits.
Answer:
The company can accept deposits from both public and private companies. This acceptance of deposits by companies are further classified into:

(i) Private Company:

• A private company can accept deposits from
  • Member or Directors or Relatives of Directors.
  • The certain class specified by Companies Act.
• They can accept deposits up to 100% of its aggregate of paid-up Share Capital.

(ii) Public Company (other than an eligible company):

• Public companies (other than eligible companies) accept deposits from members.
• They cannot accept fresh deposits if the previous deposits combined exceed 25% of the aggregate of the paid-up Share Capital and Free Reserves of the company.

(iii) Eligible Public Company:

• Eligible Public Company can accept deposits from Members and Public
• Eligible Public Company can accept fresh deposits only if the previous deposits combined do not exceed 10% of the aggregate of paid-up share capital and free reserves.
• Eligible Public Company can accept fresh deposits only if the previous deposits combined do not exceed 25% of the aggregate of paid-up share capital and free reserves.

(iv) Government Company:

• Government companies can accept deposits from the public.
• These deposits can be accepted not exceeding 35% of the paid-up share capital and free reserves.

Question 2.
Explain the provisions related to circular or advertisement for inviting deposits.
Answer:
A circular is issued when the company invites deposits from its members. An advertisement is issued when the company invites deposits from the public.
(a) Contents of Circular or Advertisement:

• Statement showing the financial position of the company
• The portion of secured and unsecured deposit of fresh issue
• Credit rating obtained from a Credit Rating Agency (only for eligible public companies)
• Details of the scheme
• Name of Deposit Trustees
• Amount due towards deposits of any previous deposits accepted by the company.

(b) Filing of Circular or Advertisement with Registrar of Companies:
A company has to file a copy of a circular or advertisement signed by all directors with the Registrar of Companies.

(c) Issue of Circular or Advertisement:

• The company must file a copy of the circular or advertisement with the Registrar of the Company.
• The filing of circular or advertisement must be done within 30 days.
• Only after filing the circular or advertisement, the company can issue it to the public.
• The advertisement must be published in an English newspaper and in the regional language newspaper where the company’s registered office is located.
• The company can send the circular to the members through registered post, speed post, or email.

(d) Validity of Circular or Advertisement:
The validity of circular or advertisement is valid for 6 months from the end of the financial year in which it was issued or the date on which the Annual General Meeting was held, whichever is earlier.

Maharashtra State Board 12th Std Secretarial Practice Textbook Solutions

• Introduction to Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Sources of Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Issue of Shares Class 12 Secretarial Practice Textbook Solutions
• Issue of Debentures Class 12 Secretarial Practice Textbook Solutions
• Deposits Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Members Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Debentureholders Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Depositors Class 12 Secretarial Practice Textbook Solutions
• Depository System Class 12 Secretarial Practice Textbook Solutions
• Dividend and Interest Class 12 Secretarial Practice Textbook Solutions
• Financial Market Class 12 Secretarial Practice Textbook Solutions
• Stock Exchange Class 12 Secretarial Practice Textbook Solutions

Issue of Debentures 12th Secretarial Practice Chapter 4 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 4 Issue of Debentures Textbook Exercise Questions and Answers.

Class 12 Secretarial Practice Chapter 4 Exercise Solutions

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
A company cannot issue ___________ with voting rights.
(a) Equity shares
(b) Debentures
(c) Securities
Answer:
(a) Equity shares

Question 2.
A company can issue ___________ convertible debentures.
(a) Only Partly
(b) Only fully
(c) Partly or fully
Answer:
(c) Partly or fully

Question 3.
Money from ___________ Account is used for redemption of debentures.
(a) Capital
(b) Debenture Redemption Reserve
(c) Profit or Loss
Answer:
(b) Debenture Redemption Reserve

Question 4.
___________ protects the interest of debenture holders.
(a) Debenture Trustees
(b) Debenture holders
(c) Redemption Reserve
Answer:
(a) Debenture Trustee

Question 5.
Secured debentures must be redeemed within ___________ from the date of its issue.
(a) 10 days
(b) 10 years
(c) 15 years
Answer:
(b) 10 years

Question 6.
A company issuing ___________ debenture must create a charge on the assets of the company.
(a) Secured
(b) Unsecured
(c) Redeemable
Answer:
(a) secured

Question 7.
Debenture certificate must be issued within ___________ of allotment of debentures.
(a) 3 months
(b) 6 months
(c) 60 days
Answer:
(b) 6 months

Question 8.
The details of allotment of Debentures must be entered in ___________
(a) Register of debenture
(b) Register of members
(c) Register of creditors
Answer:
(a) register of debenture

Question 9.
A company that issues a prospectus or invites more than 500 persons to buy its debenture has to appoint ___________
(a) Register of companies
(b) Debenture holders
(c) Debenture trustees
Answer:
(c) Debenture Trustees

Question 10.
The contract between the company and Debenture trustees of companies is called as ___________
(a) Debenture trust deed
(b) Letter of offer
(c) Prospectus
Answer:
(a) Debenture Trusts Deed

Question 11.
Procedure for allotment of Debenture should be completed within ___________ from the date of receipt of applications.
(a) 6 months
(b) 3 months
(c) 60 days
Answer:
(c) 60 days

1B. Match the pairs.

Question 1.

Answer:

Group ‘A’	Group ‘B’
a) Debenture Trustees	7) Protects interest of debenture holders
b) Debenture holders	5) No voting rights
c) Charge on assets	3) Secured debentures
d) Board of Directors	1) Power to issue debentures
e) Debenture certificate	10) Issued within 6 months of allotment of debentures

1C. Write a word or term or a phrase that can substitute each of the following statements.

Question 1.
Type of resolution needed to issue convertible debentures.
Answer:
Special Resolution

Question 2.
Account to be created for the redemption of debentures.
Answer:
Debenture Redemption Reserve Account

Question 3.
Institution appointed by the company to protect the interest of debenture holders.
Answer:
Debenture Trustee

Question 4.
Period within which secured debenture should be redeemed.
Answer:
10 years

Question 5.
Type of debentures on which the company has to create a charge on its assets.
Answer:
Secured Debenture

Question 6.
The document contains terms and conditions agreed upon by the company and the Debenture trustees.
Answer:
Debenture Trust Deed

Question 7.
The time period within which the procedure for allotment of debenture is to be completed from the date of receipt of applications.
Answer:
60 days

Question 8.
Period within which debenture certificate must be issued by a company.
Answer:
6 months

Question 9.
An institution that redresses grievances of debenture holders.
Answer:
Debenture Trustee/NCLT

Question 10.
The authority has the power to issue debentures.
Answer:
Board of Directors

1D. State whether the following statements are True or False.

Question 1.
Debenture holders have no voting rights.
Answer:
True

Question 2.
The company cannot issue non-convertible debentures.
Answer:
False

Question 3.
Special Resolution is needed to issue convertible debentures.
Answer:
True

Question 4.
Debentures holders are paid interest.
Answer:
True

Question 5.
Debenture Trustees cannot approach NCLT to redress grievances of debenture holders.
Answer:
False

Question 6.
All secured debentures should be redeemed within 20 years from the date of their issue.
Answer:
False

Question 7.
The company has to create a charge on its assets when it issues secured debentures.
Answer:
True

Question 8.
Debenture Trustees are appointed to protect shareholders.
Answer:
False

Question 9.
Debentures certificate should issue within 6 months of allotment of debentures.
Answer:
True

Question 10.
After allotment of Debentures names of Debenture holders is entered in the Register of Members.
Answer:
True

1E. Find the odd one.

Question 1.
Debenture holders, Interest, Dividend
Answer:
Dividend

Question 2.
Debenture Trustee, Court, NCLT
Answer:
Court

Question 3.
Secured debenture, convertible debenture, Irredeemable debenture
Answer:
Irredeemable

Question 4.
Debenture Trustee, Trust deed, Shareholder.
Answer:
Shareholder

1F. Complete the sentences.

Question 1.
A legal instrument conveying the assets of a company to the Debenture trustees is called ___________
Answer:
Debenture Trust Deed

Question 2.
To protect the interest of Debenture holders a company appoints ___________
Answer:
Debenture Trustee

Question 3.
On receipt of application and money, the procedure for allotment of debentures should be completed within ___________
Answer:
60 days

Question 4.
Authority to create charge on company’s assets is with the ___________
Answer:
Debenture Trustee

Question 5.
Secured debentures should be redeemed within ___________
Answer:
10 years

Question 6.
To stop a company from incurring further liabilities, the Debenture trustee can approach ___________
Answer:
NCLT

Question 7.
A company which issues prospectus or invites more than 500 persons to subscribe for its debentures, has to appoint ___________
Answer:
Debenture Trustee

Question 8.
Return on investment on debenture is called ___________
Answer:
Interest

Question 9.
For public issue of debentures of ₹ 100 crores, minimum subscription should be ___________
Answer:
75%

Question 10.
For public issue or rights issue of convertible debentures, as per SEBI, a company must obtain ___________
Answer:
Consent of shareholder

1G. Select the correct option from the bracket.

Question 1.

(Issued within 6 months of allotment, Names of debenture holders, Secured debentures, Trust Deed, Debenture holders)
Answer:

Group ‘A’	Group ‘B’
(1) Debenture Trustees	(a) Trust deed
(2) Secured debenture	(b) Charge on assets
(3) Register of Debenture	(c) Name of debenture holders
(4) Issued within 6 months of allotment	(d) Debenture certificate
(5) No voting rights	(e) Debenture holder

1H. Answer in one sentence.

Question 1.
Who are the debenture holders?
Answer:
Debenture holders are the applicants who purchase the debentures of the company. They are the creditors of the company.

Question 2.
What do debenture holders receive as a return on Investment?
Answer:
Debenture holders receive interest on investment.

Question 3.
Whom does the company appoint to protect the interest of debenture holders?
Answer:
Debenture Trustees are appointed to protect the interest of debenture holders.

Question 4.
Within what period should secured debenture be redeemed?
Answer:
Within 10 years, secured debenture should be redeemed.

Question 5.
Name of the document which acts as an agreement between company and trustee.
Answer:
The debenture Trust deed is a document that acts as an agreement between the company and the Trustee.

Question 6.
Who has the authority to create charges on assets of a company?
Answer:
Debenture Trustees have the authority to create charges on the assets of a company.

Question 7.
Name of the meeting in which approval for increasing the borrowing powers of the Board is passed.
Answer:
An Extra-Ordinary General Meeting, a resolution regarding the increase in borrowing powers of Board is passed.

Question 8.
Within what period should the debenture certificate be issued?
Answer:
A period of 6 months is required to issue a debenture certificate.

Question 9.
What is the minimum subscription that a company must collect for an issue of debentures of ₹ 100 crores?
Answer:
The minimum subscription that a company must collect for an issue of debentures of Rs.100 crores is 75% of the base issue size.

Question 10.
When should the company appoint a credit rating agency?
Answer:
In order to credit rating of securities, the company can appoint a Credit Rating Agency.

1I. Correct the underlined word and rewrite the following sentences.

Question 1.
The details of debenture holders are entered in the Register of Members.
Answer:
The details of debenture holders are entered in the Register of the debenture.

Question 2.
Secured debentures must be redeemed within 15 years from the date of its issue.
Answer:
Secured debentures must be redeemed within 10 years from the date of its issue.

Question 3.
A company issuing irredeemable debentures must create a charge on the assets of the company.
Answer:
A company issuing Secured Debentures must create a charge on assets of the company.

Question 4.
Return on investment on debentures is the dividend.
Answer:
Return on investment on debentures is Interest.

Question 5.
Debenture Trustees redress the grievances of shareholders.
Answer:
Debenture Trustees redress the grievances of Debenture holders.

Question 6.
Debenture certificates are issued within 3 months of allotment of debentures.
Answer:
Debenture certificates are issued within 6 months of allotment of debentures.

Question 7.
The procedure for allotment of debentures should be completed within 90 days from the date of receipt of applications.
Answer:
The procedure for allotment of debentures should be completed within 60 days from the date of receipt of applications.

Question 8.
To rate its debentures a company appoints underwrites.
Answer:
To rate its debentures a company appoints a Credit Rating Agency.

1J. Arrange in proper order.

Question 1.
(a) Obtain Credit Rating
(b) Entry in register of debenture
(c) Receive application with money
Answer:
(a) Obtain Credit Rating
(b) Receive application with money
(c) Entry in register of debenture

Question 2.
(a) Issue debenture certificate
(b) Issue prospectus
(c) Open Bank Account
Answer:
(a) Issue prospectus
(b) Open Bank Account
(c) Issue debenture certificate

Question 3.
(a) Hold Board Meeting for allotment
(b) Issue debenture certificate
(c) Receive application with money
Answer:
(a) Hold Board Meeting for allotment
(b) Receive application with money
(c) Issue debenture certificate

2. Explain the following terms/concepts.

Question 1.
Debenture Certificate
Answer:
A debenture Certificate is an acknowledgment issued by a company with its common seal and signature against debenture issued. It includes all the information of debenture issued, its face value, rate of interest details of debenture holder, etc. A debenture certificate should be issued by the company within 6 months -from the debenture’s allotment.

Question 2.
Debenture Trustee
Answer:
Debenture Trustees are institutions that are responsible to protect the interest of debenture holders. If the company invites more than 500 persons to buy debentures, then it has to appoint one more debenture trustee. The company issuing secured debentures also must appoint a debenture trustee. The company enters into a contract with debenture trustee

Question 3.
Charge on Assets
Answer:
Charge on assets means the right of the lender to be paid from a borrower’s asset if the debt is not paid on time. Every year the company must report its total debts secured by a charge on assets. The value of the charge should be adequate to cover the entire debenture issued.

Question 4.
Debenture Trust Deed
Answer:
Debenture Trust Deed is an agreement between the company and debenture trustees. It is a legal instrument stating a relationship between the company and the trustee. It covers all terms of conditions to be followed by the debenture trustee.

3. Study the following case/situation and express your opinion:

1. Rose limited company proposes to issue debenture to the public to raise funds. After discussion, the Board of directors has decided to issue secured, Redeemable non-convertible debentures with a tenure of ten years. Please advise the board on the following matters:

Question (a).
Should the company appoint a Debenture trustee?
Answer:
The company should appoint debenture trustees as they are responsible to protect the interests of debenture holders and they are the link between the company and Debenture holders.

Question (b).
Should the company create a charge on its assets?
Answer:
The company should create a charge on its assets because if the company failed to repay the amount to debenture holders, assets can be realized and the claim can be settled.

Question (c).
Can the tenure of debentures be less than ten years?
Answer:
The maximum tenure of redemption of secured debenture is 10 years. It can be less than 10 years. It shows the strong liquidity position of a company.

2. Violet Ltd. Company plans to raise ₹ 10 crores by issuing debentures. The Board of Directors has some queries. Please advise them on the following:

Question (a).
Can the company issue unsecured debentures?
Answer:
In India, as per the guidelines of SEBI, the issue of unsecured debenture is prohibited. So, the company can’t issue unsecured debenture.

Question (b).
Can they issue irredeemable debentures?
Answer:
The company can issue irredeemable debenture if it is permitted by the Ministry or department of central government or by RBI. It can be issued for a maximum period of 30 years.

Question (c).
As the company is offering debenture to its members, can such debentures have normal voting rights?
Answer:
As the company is offering debentures to its members, such debentures have no normal voting rights. It can enjoy the voting rights on the matters associated with them.

3. DDS financial plans to raise ₹ 10 crores by issuing secured, Non-convertible debentures. However, as per the Articles of Association, the board of directors has authority only to raise up to 5 crores. They are also considering whether to go for a private placement or make a public offer. Please advise them on the following:

Question (A).
What can be the maximum tenure of the debentures to be issued?
Answer:
All the secured debentures should be redeemed for 10 years. Only those companies permitted by RBI/ Dept. Of corporate affairs can issue debentures of more than 10 years but less than 30 years.

Question (b).
Is the proposed issue within the borrowing powers of the board?
Answer:
The proposed issue is not within the borrowing powers of the Board of Directors. If they want to increase their borrowing powers, they have to get the approval of shareholders.

Question (c).
Within what period should the company issue a Debenture certificate?
Answer:
A debenture certificate should be issued within 6 months from the date of allotment of debentures.

4. Answer in brief.

Question 1.
State any four provisions of the Companies act 2013 for the issue of debenture?
Answer:
The company can issue debentures to the public. But to issue debentures, companies need to follow provisions.
Following are the provisions of the Companies Act, 2013:
1. No Voting Rights:
A Company cannot issue debentures with voting rights. Debentures are the creditors of the company and hence, they do not have any voting rights. However, they can enjoy voting rights on the matters associated with them.

2. Payment of interest and redemption:
A debenture holder is responsible to get fixed interest on their investment from the company. The rate of interest is decided at the time of the issue of the debenture. A Company shall redeem the debentures after a specific period of time. It is a temporary capital of a company.

3. Debenture Certificate:
The company issues debenture certificates to the debenture holders. It should be issued by the company within six months from the date of allotment of debentures.

4. Create Debenture Redemption Reserve:
The company has to create a Debenture Redemption Reserve Account out of the profits of the company. Debenture Redemption Reserve is created for the payment of dividends and redemption of debentures only As per the Companies Amendment Act, 2019 no Listed companies, NBFC’s and Housing Finance Companies require Debenture Redemption Reserve.

Question 2.
What is Debenture Trust Deed?
OR
Write a note on Debenture Trust Deed.
Answer:

• A debenture is a loan document that helps the company to raise long-term loans from the Market.
• A person who purchases debenture of a company is called a debenture holder.
• A debenture holder is a creditor of the company and cannot participate in the management of the company.
• The company appoints debenture trustees to protect the interest of debenture holders.
• The company enters into the contract with debenture trustees, which is called as ‘Debenture Trust Deed’.
• The company can enter into a contract with one or more debenture trustees.
• The Terms and Conditions of debenture trustees are written into the debenture trust deed.
• It is a legal instrument conveying the assets of the company to the trustees.
• Debenture Trust Deed is a right of debenture holder and duty of debenture trustees.
• A company has to execute a trust deed within 3 months of the closure of the issue.
• Member and debenture holder can inspect the copy of the deed and also get the copy by paying a certain fee.

Question 3.
Who are debentures trustees?
Answer:

1. Debentures Trustee is a person or institution which protects the interest of the debenture holders. The Trustees become the custodian of the assets on which charge has been created.
2. A company that issues a prospectus or invites more than 500 persons to buy its debentures has to appoint one or more Debentures Trustees. Companies issuing secured debentures also must appoint Debentures Trustee.
3. Debentures Trustee is appointed before prospectus or letter of offer/offer letter is issued or within 60 days after the allotment of the debenture. The Trustees must give written consent to act as Debenture Trustees.
4. According to SEBI Rules, 1993 “debentures trustee” means a trustee of a trust deed for securing any issue of debentures of a body corporate (section 2 (bb)). (Applicable to public companies only).
5. The trustee can appoint a nominee to the board of directors of the company. Before the trustee appoints the nominee, the following conditions must be satisfied:
   • Two consecutive defaults made by the company in payment of interest to the debenture holders; or
   • Default in the creation of security for debentures or default in the redemption of debentures.

5. Justify the following statements.

Question 1.
A company has to create a charge on its asset for issuing secured debenture.
Answer:

• A debenture is a debt instrument, which helps the company to raise long-term loans.
• A secured debenture is a debenture against which a charge has been created.
• In case, if the company has failed to make redemption of debenture or interest, in that case by the order of NCLT, the charged asset can be realized by the company and dues can be settled.
• Thus, it is rightly said that a company has to create a charge on its asset for issuing secured debenture.

Question 2.
Debenture trustees are appointed by a company issuing debentures.
Answer:

• Debenture trustees are appointed when the company issues a prospectus or invites more than 500 people.
• They are appointed to protect the interest and redress the grievances of debenture holders.
• Debenture trustees act as custodians of assets and create a charge on assets of the company on behalf of debenture holders.
• In case, the company failed to redemption of a debenture or its interest, then debenture trustees by the order of NCLT can realize the assets and settle the dues.
• Thus, it is rightly said that debenture trustees are appointed by the company for issuing debenture.

Question 3.
A company can issue only certain types of debentures.
Answer:

• The debenture holders are the creditors of the company. They offered borrowed capital to the company but cannot participate in the management of the company.
• Therefore, in order to protect the interest of debenture holders, SEBI, through its guidelines allowing companies to issue certain types of debentures in India.
• Therefore, the companies operating in India can issue secured debentures, convertible debentures, redeemable debentures to the applicant.
• It protects the interest of creditors in the company.
• Thus, it is rightly said that a company can issue only certain types of debentures.

6. Answer the following questions.

Question 1.
Briefly explain the provisions of the Companies Act, 2013 for the issue of debentures.
OR
State the statutory provisions related to the issue of debentures.
Answer:
The company can issue debentures to the public. But to issue debentures companies need to follow provisions.
Following are the provisions of the Companies Act, 2013:
1. No Voting Rights:
A Company cannot issue debentures with voting rights. Debentures are the creditors of the company and hence, they do not have any voting rights. However, they can enjoy voting rights on the matters associated with them.

2. Types of Debentures:
There are various types of debentures like secured and unsecured debentures, convertible and non-convertible debentures, redeemable and irredeemable debentures, registered and bearer debentures, etc. All the debentures are redeemable in nature. A special resolution is to be passed in the general meeting for issuing convertible debentures.

3. Payment of interest and redemption:
A debenture holder is responsible to get fixed interest on his investment from the company. The rate of interest is decided at the time of the issue of the debenture. A Company shall redeem the debentures after a specific period of time. It is a temporary capital of a company.

4. Debenture Certificate:
The company issues debenture certificates to the debenture holders. It should be issued by the company within six months from the date of allotment of debentures.

5. Create Debenture Redemption Reserve:
The company has to create a Debenture Redemption Reserve Account out of the profits of the company. Debenture Redemption Reserve is created for the payment of dividends and redemption of debentures only. As per the Companies Amendment Act, 2019 no Listed companies, NBFC’s and Housing Finance Companies require Debenture Redemption Reserve.

6. Appointment of Debenture Trustees:
The company issuing debentures for more than 500 people or issuing prospectus has to appoint one or more Debenture Trustees. They are responsible to protect the interest of the debenture holders. Trustees are appointed by entering into the contract with the company which is called Debenture Trust Deed.

7. Debenture Trustees can approach NCLT:
Debenture Trustees have to redress the problem of debenture holders. Debenture Trustees can approach National Company Law Tribunal (NCLT) if the company fails to repay the principal amount on maturity or paying interest. NCLT can direct a defaulting company to repay the principal amount of interest.

8. Impose Restrictions:
Debenture Trustees can also approach NCLT when the company is not able to pay the principal amount of debentures, even after selling the company assets. In such a case, NCLT can order a company to restrict incurring further liabilities so as to protect the interest of the debenture holders.

9. Punishment for not complying with the provisions of the Companies Act:
If the company or any of its officers fails to comply with any of the provisions, then the company or the responsible officer who is in default will be liable to pay a fine or imprisonment or both as prescribed in the Act.

Question 2.
Explain briefly the procedure for the issue of debentures.
Answer:
A Company’s Secretary is mainly responsible to supervise the process of issue of the debenture. As the employee of the company, the secretary has to look into the matter that company complies with all the provisions.
Procedure for Issue of Debentures:

• Board Meeting and Resolution
• EOGM and Shareholder’s Approval
• Filing with Registrar of Companies
• Approval and Permission
• Credit Rating
• Underwriting Contract
• Trust Deed
• Issue of prospectus
• Open Bank Account with Scheduled Bank
• Receiving Applications and Allotment
• Board Meeting
• Issue Debenture Certificate
• Entries in register of member

1. Board Meeting and Resolution:

• Board Meetings should be conducted before issuing debentures. A resolution is passed before issuing debentures to the public. The resolution should specify the following points:
• Amount and type of debentures to be issued with terms and conditions
• Approve Prospectus/Offer Letter/Letter of Offer
• Appointment of Debenture Trustees with their consent
• Call Extra Ordinary General Meeting
• Opening of Separate Bank Account to receive money from applicants

2. EOGM and Shareholder’s Approval:
If the issue of debenture exceeds the limit of paid-up capital and free reserve, then the company needs to conduct extraordinary general meetings. An extraordinary General Meeting is held for passing a special resolution and getting the shareholder’s approval related to the increase in the issue of debentures.

3. Filing with Registrar of Companies:
Secretary has to file the special resolution and copy of the prospectus with the Registrar of Companies. It has to be filed within 30 days of the board meeting.

4. Approval and Permission:
Permission of SEBI is compulsory, in case the issue of debenture exceeds ₹ 1 crore or more. Simultaneously, approval of the stock exchange is required to be taken before a prospectus is issued to the public. It is mandatory to list the debentures on the recognized stock exchange before issuing them to the public.

5. Credit Rating:
As per SEBI guidelines, the company has to get its debenture rated by two recognized credit rating agencies such as CRISIL, CARE, ICRA, etc.

6. Underwriting contract:
The company may enter into an underwriting agreement with underwriters for its public issue of debentures. The appointment of underwriters must be mentioned in the prospectus.

7. Trust Deed:
The Trust Deed has to be executed between the company and trustees. Trustees give a guarantee of protection of debenture holder’s interest.

8. Issue of Prospectus/Letter of Offer/Offer Letter:
Company issues prospectus, if it is inviting the general public. An offer letter is issued if the company makes a private placement. Letter of Offer is issued for Right Issue (Offer to exist shareholders).

9. Appointment of Banker:
Issuing Company must appoint a ‘Scheduled Bank’ as a banker of the company. The company must open a separate account in the name of the company. This account is opened to receive the money from the applicants.

10. Receiving and Allotment of debenture:
A board meeting is held to decide and approve the allotment of debentures. Board also approves the creation of charges on the company assets. The company must make the arrangement to receive the application with application money. After Board Meeting, the company allows debentures to the applicants.

11. Issue of Debenture Certificate:
The allotment procedure has to be completed within 60 days from the receipt of application money. Debenture certificates are prepared by the secretary and issued to the debenture holders within 180 days from the date of allotment.

12. Entries in Register of Debenture:
If the debentures are issued in DEMAT form, the company does not maintain the Register of Debenture holders. After allotment, all details of debenture holders are entered in the register of the debenture. In case of debenture holders exceed 50, the company should maintain the ‘Index of Debenture holders.

Maharashtra State Board 12th Std Secretarial Practice Textbook Solutions

• Introduction to Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Sources of Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Issue of Shares Class 12 Secretarial Practice Textbook Solutions
• Issue of Debentures Class 12 Secretarial Practice Textbook Solutions
• Deposits Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Members Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Debentureholders Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Depositors Class 12 Secretarial Practice Textbook Solutions
• Depository System Class 12 Secretarial Practice Textbook Solutions
• Dividend and Interest Class 12 Secretarial Practice Textbook Solutions
• Financial Market Class 12 Secretarial Practice Textbook Solutions
• Stock Exchange Class 12 Secretarial Practice Textbook Solutions

Issue of Shares 12th Secretarial Practice Chapter 3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 3 Issue of Shares Textbook Exercise Questions and Answers.

Class 12 Secretarial Practice Chapter 3 Exercise Solutions

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
___________ refers to capital made up of Equity and preference shares.
(a) Share capital
(b) Debt capital
(c) Reserve fund
Answer:
(a) Share capital

Question 2.
___________ capital refers to maximum capital a company can raise by issuing shares.
(a) Issued
(b) Authorised
(c) Paid up
Answer:
(b) Authorised

Question 3.
___________ means shares are offered to the public.
(a) Rights Issue
(b) Private Placement
(c) Public Issue
Answer:
(c) Public Issue

Question 4.
Under ___________ method, issue price of shares is based on bidding.
(a) Book Building
(b) Fixed Price
(c) Bonus Issue
Answer:
(a) Book Building

Question 5.
In ___________, shares of a company are offered to the public for the first time.
(a) Further Public Offer
(b) Initial Public Offer
(c) Public Offer
Answer:
(b) Initial Public Offer

Question 6.
___________ is offered to existing equity shareholders.
(a) IPO
(b) ESOS
(c) Rights Issue
Answer:
(c) Rights Issue

Question 7.
Bonus shares are issued free of cost to ___________
(a) existing Equity shareholders
(b) existing employees
(c) Directors
Answer:
(a) existing Equity shareholders

Question 8.
___________ are offered to permanent employees Directors and Officers of a company.
(a) Bonus Shares
(b) Rights Issue
(c) ESOS
Answer:
(c) ESOS

Question 9.
Under ___________, a company offers its securities to a select group of persons not exceeding 200.
(a) Private Placement
(b) IPO
(c) Public Offer
Answer:
(a) Private Placement

Question 10.
The ___________ have the power to allot shares.
(a) Director
(b) Board of Directors
(c) Company Secretary
Answer:
(b) Board of Directors

Question 11.
Letter of ___________ is sent to applicants who have been given shares by the company.
(a) Regret
(b) Renunciation
(c) Allotment
Answer:
(c) Allotment

Question 12.
___________ is a proof of title to Shares.
(a) Share Certificate
(b) Register of Member
(c) Letter of Allotment
Answer:
(a) Share Certificate

Question 13.
The gap between two calls should not be less than ___________
(a) 14 days
(b) One month
(c) 21 days
Answer:
(b) One month

Question 14.
Company can ___________ shares on non-payment of calls.
(a) forfeit
(b) surrender
(c) allot
Answer:
(a) forfeit

Question 15.
Voluntarily giving away one’s share to another person is called as ___________ of shares.
(a) Transfer
(b) Transmission
(c) Surrender
Answer:
(a) Transfer

Question 16.
___________ of shares takes place due to operation of law.
(a) Forfeiture
(b) Allotment
(c) Transmission
Answer:
(c) Transmission

1B. Match the Pairs.

Question (I).

Answer:

Group ‘A’	Group ‘B’
(a) Death of member	(5) Transmission of shares
(b) Voluntary return of shares to company by member	(4) Surrender of shares
(c) Price of shares mentioned in prospectus	(7) Offered to existing Equity Shareholders
(d) ESPS	(3) Offered to existing employees
(e) Regret Letter	(6) Non-allotment of shares

Question (II).

Answer:

Group ‘A’	Group ‘B’
(a) Issued capital	(4) Capital offered to public to subscribe
(b) FPO	(8) Maximum capital a company can raise
(c) Bonus shares	(7) Free shares issued to existing equity shareholder
(d) Issued within two months of allotment of shares	(5) Share Certificate
(e) Forfeiture of shares	(1) Non-payment of calls

1C. Write a word or a term or a phrase which can substitute each of the following statements.

Question 1.
Capital collected by way of issue of Equity and Preference shares.
Answer:
Share Capital

Question 2.
Part of issued capital subscribed by investors.
Answer:
Subscribed capital

Question 3.
Capital that will be collected only at the time of winding up of a company.
Answer:
Reserve capital

Question 4.
Highest bid price in Book Building method.
Answer:
Cap price

Question 5.
Offering of shares by a company to the public for the first time.
Answer:
IPO

Question 6.
Subsequent issue of shares after an IPO.
Answer:
FPO

Question 7.
Pre-emptive right given to existing Equity shareholders to subscribe to new issue of shares by company.
Answer:
Rights issue/shares

Question 8.
It is also called as ‘Capitalization of Profits’.
Answer:
Bonus shares

Question 9.
Appropriation of shares to an applicant.
Answer:
Allotment of shares

Question 10.
Committee set up to decide the formula for allotment of shares in case of over-subscription.
Answer:
Allotment committee

Question 11.
Minimum amount to be collected from subscribers within thirty days of issue of prospectus.
Answer:
Minimum subscription

Question 12.
Document which is a prima facie evidence of ownership of certain shares of a company.
Answer:
Share certificate

Question 13.
Penal action taken by company on non-payment of calls.
Answer:
Forfeiture of shares

Question 14.
Person to whom transferor is transferring the shares.
Answer:
Transferee

Question 15.
Transfer of shares due to operation of law.
Answer:
Transmission of shares

1D. State whether the following statements are true or false.

Question 1.
Only fully paid-up shares can be forfeited.
Answer:
False

Question 2.
The member transferring shares is called a transferor.
Answer:
True

Question 3.
A share certificate is issued for partly or fully paid up shares.
Answer:
True

Question 4.
Allotment of shares must be done within one month of receipt of application money.
Answer:
False

Question 5.
Sweat Equity shares are offered to Directors or employees of a company.
Answer:
True

Question 6.
Bonus Shares are issued at a discounted price to the Equity Shareholder.
Answer:
False

Question 7.
The floor price is the highest bid price under the Book Building method.
Answer:
False

Question 8.
Calls not paid by shareholders are called calls in arrears.
Answer:
True

Question 9.
Shares not offered to the public for subscription are called subscribed capital.
Answer:
False

Question 10.
Authorized capital is mentioned in the capital clause of the Memorandum of Association.
Answer:
True

1E. Find the odd one.

Question 1.
Authorized capital, Equity share capital, Issued capital, Paid-up Capital.
Answer:
Equity share capital

Question 2.
ESOS, ESPS, Rights Shares, Sweat Equity.
Answer:
Rights Shares

Question 3.
Floor Price, Cap Price, Cut-off price, Face Value.
Answer:
Face Value

Question 4.
Bonus Shares, Rights Shares, ESOS.
Answer:
ESOS

Question 5.
Allotment of Shares, Forfeiture of shares, Surrender of shares.
Answer:
Allotment of shares

1F. Complete the sentences.

Question 1.
Share Capital refers to capital made up of Equity shares and ___________
Answer:
Preference Share

Question 2.
Reserve capital is part of ___________
Answer:
Uncalled Capital

Question 3.
Transfer of shares due to death, insolvency, or insanity of the member is called ___________
Answer:
Transmission Shares

Question 4.
The two parties involved in transfer of shares are transferor and ___________
Answer:
transferee

Question 5.
Voluntarily giving up of shares by a member due to inability to pay calls is called as ___________
Answer:
surrender of shares

Question 6.
Company can forfeit only ___________ paid shares.
Answer:
partly

Question 7.
In case the original Share Certificate is torn or mutilated, company can issue ___________
Answer:
Duplicate Share Certificate

Question 8.
In case of transfer of shares, the company has to issue to the transferee a new share certificate within ___________
Answer:
one month

Question 9.
Letter sent to applicants for informing them shares are allotted is called as ___________
Answer:
Letter of Allotment

Question 10.
When applications received is more than the number of shares offered, it is called as ___________
Answer:
Over Subscription

Question 11.
In Book Building Method, the final price at which shares are offered to investors is called as ___________
Answer:
Cut-off price

Question 12.
Shares issued free of cost to existing Equity shareholders is called as ___________
Answer:
Bonus Shares

1G. Select the correct option from the bracket.

Question 1.

(The first-time offer of shares, Shares offered to the public, Shares offered to exist, Equity shareholders, Shares offered to exist, employees, Transmission of shares)
Answer:

Group ‘A’	Group ‘B’
(a) Public offer of shares	(1) Shares offered to Public
(b) First time offer of shares	(2) Initial public offer
(c) Rights Issue	(3) Shares offered to existing equity share holders
(d) Shares offered to existing employees	(4) ESOS
(e) Operation of law	(5) Transmission of Shares

1H. Answer in one sentence.

Question 1.
When does the transmission of shares take place?
Answer:
Transmission of Shares takes place on death, insolvency, or insanity of the members.

Question 2.
Name the two parties involved in the transfer of shares.
Answer:
The transferor and Transferee are the two parties involved in the transfer of shares.

Question 3.
What is the time limit to issue a share certificate on allotment of shares?
Answer:
Secretary should issue share certificate within two months of allotment of shares.

Question 4.
What is the time limit for Filing a Return of Allotment with the Registrar on the allotment of shares?
Answer:
Secretary has to file a ‘Return of Allotment’ with the Registrar of Companies within 30 days of allotment of shares.

Question 5.
When can a company forfeit shares?
Answer:
If a shareholder fails to pay calls on shares within a certain period company can forfeit shares.

Question 6.
What is a share certificate?
Answer:
Share Certificate is a registered document issued by a company that is evidence of ownership of a specified number of shares of the company.

Question 7.
What is the minimum application money to be collected by Company as per the Companies Act?
Answer:
As per the companies act, the company should collect a minimum of 25% of the nominal value of shares.

Question 8.
To whom should the prospectus be filed before issuing it to the public?
Answer:
The prospectus should be filed with the Registrar of Companies before issuing it to the public.

Question 9.
What is meant by private placement?
Answer:
When a company offers its securities to a select group of persons not exceeding 200, it is called Private Placement.

Question 10.
To whom is Sweat Equity shares offered by a company?
Answer:
Sweat equity shares are issued to directors or employees of the company.

Question 11.
To whom can a company issue Bonus Shares?
Answer:
The company can issue Bonus Shares to its existing equity shares.

Question 12.
What is the subsequent issue after IPO called as?
Answer:
The subsequent issue after IPO is called FPO.

Question 13.
Name the method under which the issue price of shares is fixed through a bidding process.
Answer:
Under the Book Building method, the issue price of shares is fixed through a bidding process.

Question 14.
What is Public Issue?
Answer:
Public issue or offer means offering the shares to the public. The company invites the public to subscribe to its shares by issuing a prospectus.

Question 15.
Name the capital which is mentioned in the capital clause of the Memorandum of Association.
Answer:
Authorized Capital is mentioned in the capital clause of the Memorandum of Association.

1I. Correct the underlined words/and rewrite the following sentences.

Question 1.
Issued capital is the maximum capital that a company can raise by issuing shares.
Answer:
Authorized capital is the maximum capital that a company can raise by issuing shares.

Question 2.
Under the Fixed-Price issue method, the price of shares is fixed through a bidding process.
Answer:
Under Book Building Method the price of shares is fixed through a bidding process.

Question 3.
FPO refers to offering shares to the public for the first time.
Answer:
IPO refers to the offering of shares to the public for the first time.

Question 4.
Only Fully paid up shares can be forfeited.
Answer:
Only Partly paid-up shares can be forfeited.

Question 5.
Bonus shares are offered to existing employees of a company.
Answer:
Bonus shares are offered to existing shareholders of a company.

Question 6.
The company enters into an underwriting agreement with the shareholders.
Answer:
The company enters into an underwriting agreement with the underwriters.

Question 7.
Letter of Allotment is sent to applicants when no shares are allotted to them.
Answer:
Letter of Regret is sent to applicants when no shares are allotted to them.

Question 7.
IPO refers to the offering of shares to the public for the second time.
Answer:
FPO refers to offering shares to the public for the second time.

Question 8.
A duplicate share certificate must be issued within one month from the date of application.
Answer:
A duplicate share certificate must be issued within three months from the date of application.

Question 9.
Call money can not exceed 5% of the nominal value of shares.
Answer:
Call money can not exceed 25% of the nominal value of shares.

1J. Arrange in proper order.

Question 1.
(a) Forfeiture of shares
(b) Calls on shares
(c) Allotment of shares
Answer:
(a) Allotment of shares
(b) Calls on shares
(c) forfeiture of shares

Question 2.
(a) Share certificate
(b) Allotment letter
(c) Application from
Answer:
(a) Application form
(b) Allotment letter
(c) share certificate

Question 3.
(a) Return of allotment
(b) Application form
(c) Minimum Subscription
Answer:
(a) Minimum subscription
(b) Application form
(c) Return of allocation

2. Explain the following terms/concepts.

Question 1.
Transmission of shares.
Answer:

• Transmission of shares means the transfer of the title of shares by the operation of law.
• When the shares of a member are automatically transferred to another person on the death, insolvency, or insanity of a member it is called Transmission of shares.
• Transmission of shares is an involuntary action.
• There is only one party i.e., a legal heir who indicates the process of transmission.
• The legal heir or official receiver need not pay any consideration for the shares.
• There is no need to submit an Instrument of Transfer of pay stamp duty.

Question 2.
Bonus shares
Answer:

• Bonus Shares are shares distributed by a company to its current shareholders as fully paid shares free of charge.
• The Bonus Shares are given to the existing equity shareholders according to their existing proportion of equity shareholdings.

Question 3.
Allotment of Shares
Answer:

• Allotment means the distribution of shares among the applicants. It means giving shares to share applicants of to specific persons with whom the company has entered into the contract.
• Allotment of shares is a procedure in which shares are distributed to those applicants who have submitted a written application along with the application money.

Question 4.
Employees Stock Option Scheme
Answer:
An employee stock option plan is an employee benefits scheme under which the company encourages its employees to acquire ownership in the form of shares. Under this scheme, permanent employees, Directors or Officers of the Company or its holding company or subsidiary company are offered the benefit or right to purchase the equity shares of the company at a future date at a predetermined price.

Question 5.
Surrender of Shares
Answer:

• This means the voluntary return of shares by the member to the company for cancellation.
• Surrender of shares is allowed only if there is no other option but to forfeit the shares.
• Only partly paid-up shares can be surrendered.
• Surrendered shares can be surrendered when a company provides for such surrender of shares.

Question 6.
Sweat equity shares
Answer:
These are shares issued by a company to its directors or employees at a discount or for consideration other than cash. It is one of the modes of making share-based payments to employees. It is issued in recognition of their valuable contribution to the prosperity of the company.

Question 7.
Share Certificate
Answer:
A Share certificate refers to documents that are issued by a company evidencing that a person named in such certificate is the owner of the shares of the company stated in the share certificate. Share certificate has to be issued under the common seal of the company. It should be issued within 2 months from the date of allotment against the allotment letter.

Question 8.
Authorized Capital
Answer:

• The Authorized capital is the maximum amount of capital that a company can raise through the issue of shares to the shareholders.
• The Authorized capital of a company is also called Registered Capital or Nominal Capital.
• Authorized capital is the maximum capital that is authorized by the company’s memorandum of Association.

Question 9.
Forfeiture of shares
Answer:
If a shareholder, who is called upon to pay any call fails to pay the amount, even after sending many reminders the company may forfeit its shares. Thus forfeiture of shares means cancellation of shares.

Question 10.
Paid-up capital
Answer:

• Paid-up capital is the amount of money a company has received from shareholders in exchange for shares.
• It is the total amount of money paid up by the shareholders when the company has called up or demanded them to pay.
• The paid-up capital can be equal to or less than the authorized capital.

Question 11.
Calls on Shares
Answer:

• Whenever a company issue shares, the company may ask shareholders to pay the value of shares in installment which is known as calls on shares.
• The company can demand part or full amount of the balance amount of unpaid shares.

Question 12.
Subscribed Capital.
Answer:

• Subscribed share capital is that part of issued share capital for which a company has positively received a subscription from the investor.
• It is a part of Issued Capital that has been subscribed by investors or purchased by the general public.

Question 13.
Minimum Subscription
Answer:
Minimum subscription means a minimum amount decided by the ROC which should be build-up by the company by issuing securities to the general public. If the company failed in minimum subscription then it has to return the entire amount back to the applicants.

Question 14.
Transfer of shares
Answer:

• Transfer of shares means the transfer of ownership of the shares from one person to another against consideration.
• Transfer of shares is effected by removing the name of the existing shareholders (transferor) from the register of members and inserting the name of the new member (transferee).
• Transfer of shares is a voluntary process of transferring shares by a member of a company.

Question 15.
Initial Public Offer (IPO)
Answer:
The initial public offering is the sale of equity shares to the public first time in order to raise capital. This is the most popular and common method used by companies. The company invites the public to subscribe to its shares by issuing prospects.

Question 16.
Blank Transfer
Answer:

• The Blank transfer means the sale or transfer of securities in which the name of the buyer or transferee is not recorded.
• When a member signs the Instrument of transfer without filling in the name of the transferee and hands it over to the transferee with the share certificate it is called ‘Blank Transfer.’
• The blank transfer enables easy to purchase and sale of shares as the blank transfer form can be sold any number of times.
• The intermediate buyers need not pay stamp duty.

Question 17.
Further Public Offer (FPO)
Answer:
It is also called a follow-on public offer. When the company issue shares to the public after IPO, it is called a further public offer. Thus every issue of shares by a listed company after its IPO is called an FPO. FPO leads to an increase in the subscribed capital of the company.

Question 18.
Forged Transfer
Answer:

• An instrument on which if the signature of the transferor is forged is called forged transfer.
• It is a null transfer and does not counter any title.
• As the signature of the transferor is forged, the company should not register such transfer of shares.

Question 19.
Rights issue
Answer:
A rights issue is an invitation to existing shareholders to purchase additional new shares in the company. A rights issue is a way by which a listed company can raise additional capital.

Question 20.
Private Placement
Answer:
When a company offers its securities to a selected group of persons not exceeding 200, it is called private placement. Here securities are not offered to the general public.

5. Study the following cases and express your opinion.

1. Eva Ltd. Company’s capital structure is made up of 1,00,000 equity shares having a face value of ₹ 10/- each. The company has offered to the public 40,000 equity shares and out of this, the public has subscribed for 30,000 equity shares. State the following in rupees-

Question (a).
Authorized capital
Answer:
The authorized capital is ₹ 10,00,000 (1,00,000 equity shares × ₹ 10/- each)

Question (b).
Subscribed capital
Ans. The subscribed capital is ₹ 3,00,000 (30,000 equity shares × ₹ 10/- each)

Question (c).
Issued capital
Answer:
The issued capital is ₹ 4,00,000 (40,000 equity shares × ₹ 10/- each)

2. TRI. Ltd company is a newly incorporated public company and wants to raise share capital by issuing equity shares in the market. The board of directors is considering various options for this. Advise the board on the following matters:

Question (a).
What should the company offer – IPO or FPO?
Answer:
The Company should offer IPO.

Question (b).
Can the company offer Bonus shares to raise its capital?
Answer:
The company cannot offer Bonus Shares. Bonus Shares are given out of only accumulated capital or reserves only.

Question (c).
Can the company enter into an underwriting Agreement?
Answer:
Yes. The company can enter into an Underwriting Agreement. The underwriters assure the company to take up the unsold shares so that company can be able to raise the minimum subscription.

3. Silver ltd. The company has recently come out with its public offer through FPO. Their issue was over-subscribed. The board of directors now wants to start the allotment process.

Question (a).
Should the company set up an allotment committee?
Answer:
Yes. The company should set up an allotment committee as the issue is over-subscribed so the Board has to set up an allotment committee.

Question (b).
How should the company information to whom the company is allotting shares?
Answer:
The company should inform the applicants through a letter of allotment for allotting shares.

Question (c).
Within what period should the company issue a share certificate?
Answer:
The company should issue share certificates within two months from the date of allotment.

4. Red Tubes Ltd. has made a demand on its shareholders to pay the balance unpaid amount of ₹ 20/- per share (having a face value of ₹ 100) held by them. The company has sent letters asking the shareholders to pay the money to its Bankers within the specified time.

Question (a).
Are the shareholders liable to pay ₹ 20/- for the shares held by them?
Answer:
Yes. The shareholders are liable to pay ₹ 20 for the shares held by them. When a company demands the shareholder to pay a part or full amount of the balance amount unpaid on shares it is called ‘calls on shares’.

Question (b).
Name the letter sent by the company to its shareholders asking them to pay ₹ 20/-
Answer:
The company will send a ‘Call Letter’ to its shareholders for asking them to pay ₹ 20.

Question (c).
What happens if the shareholders fail to pay the money within a specific time?
Answer:
If a shareholder fails to pay call money within the specified time, the company can forfeit the shares.

5. X owns 100 shares and Y owns 500 shares of RED tubes. The company has asked all its shareholders to pay the balance unpaid amount of rupees 20. X pays full money demanded by the company and Y failed to pay the money due to poor financial condition.

Question (a).
Can the company forfeit the shares of Y?
Answer:
Yes. The company can forfeit the shares of ‘Y’ as he failed to pay calls on shares within a certain period.

Question (b).
Can the company forfeit the shares of X?
Answer:
The company cannot forfeit the shares of ‘X’ as he paid the full amount of shares. Only partly paid-up shares can be forfeited.

Question (c).
Can X transfer his shares?
Answer:
Yes. X can transfer his shares by filling Instrument of transfer.

4. Distinguish between the following.

Question 1.
Initial Public Offer and Further Public Offer
Answer:

Points	Initial Public offer	Further Public offer
1. Meaning	IPO refers to an offer of Securities by an unlisted public company to the public for the first time.	FPO means an offer of securities by a listed public company to the public to raise subsequent capital.
2. Raising Money	Raising Money for the first time from the public.	Before FPO Company has already raised money through an IPO.
3. When Issued	It is usually issued by an existing company that wants to raise capital from the public for the first time.	It is usually issued by a listed public company when it wants to raise further capital from the public.
4. Order of Issue	IPO precedes FPO. IPO is the first time sale of shares to the public.	FPO is always done after IPO. FPO is the second or subsequent sale of shares to the public.
5. Listing	The company has to get itself listed for the first time before issuing IPO.	A company making an FPO is already a listed company.
6. Risk	It is very risky for the investor as he cannot predict the company’s performance.	It is less risky for the investor as he has an idea of the company’s past performance and can judge its future performance.

Question 2.
Fixed Price Issue Method and Book Building Method
Answer:

Points	Fixed Price Issue Method	Book Building Method
1. Meaning	Under this method, the issue price of shares is mentioned in the prospectus and investors have to buy shares at that price only.	Under this method, the issue price is determined by a bidding process.
2. Price of Shares	The exact price of shares is known in advance and it is mentioned in the prospectus.	The price of shares is not known in advance only the minimum price and maximum price at which the company is willing to sell the shares is known in advance.
3. Prospectus	The company has to issue a prospectus and it contains the details of the price at which shares are offered and the total number of shares offered by the company.	The company issues a Red Herring Prospectus. It contains only the price band and the total size of the issue.
4. Determination of Demand	The company comes to know the public demand for its shares only after the closure of the issue.	The company comes to know the public demand for its shares every day. The bids are registered in the book .everyday till the closure of the issue.
5. Payment of Application Money	Application money or entire money has to be paid by the investor at the time of submitting the application for shares.	Only application money has to be paid at the time of bidding. Money will be collected only after the issue price has been fixed.
6. When Used	It can be used for any issue i.e., Public issues, Rights Issues, FSOS, etc.	It is usually used in public issues i.e., IPO and FPO

Question 3.
Right shares and Bonus shares
Answer:

Points	Rights Shares	Bonus Shares
1. Meaning	In the rights issues, shares are offered to the existing equity shareholders.	Bonus shares are issued to the existing equity shareholders free of cost.
2. Payment	Subscribers have to pay for the Right Shares.	Bonus Shares are issued free of cost to the shareholders.
3. Partly/Fully paid-up shares	Shareholders have to pay for these shares as Application Money, Allotment, Call money, etc.	Bonus Shares are fully paid up shares so no money has to be paid by shareholders to the company.
4. Minimum Subscription	The company has to obtain a minimum subscription for Rights shares.	There is no minimum Subscription to be collected for Bonus shares.
5. Right to Renounce	The shareholders can renounce their shares.	Shareholders cannot renounce their bonus share.
6. Purpose of Issue	The main purpose to issue rights shares is to raise fresh funds and along with it to give a chance to their existing members to increase their shareholding.	The main purpose of issuing bonus shares, is to give rewards to its existing equity shareholders out of its accumulated huge profits or Reserves.

Question 4.
Transfer of shares and Transmission of shares
Answer:

Points	Transfer of shares	Transmission of shares
1. Meaning	Transfer of shares means the transfer of ownership of shares from one person to another by entering into a contract.	It means the transfer of ownership of a member’s shares to his legal representative due to the operation of law. It takes place on the death of insolvency or insanity of the members.
2. When Done	It is done when the member wants to sell his shares or give his shares as a gift.	It is done when the member dies or becomes insolvent or suffering from insanity.
3. Nature of Action	It is a voluntary action taken by the member.	It is an involuntary action. It is performed by operation of law.
4. Parties Involved	In the transfer of shares, there are two parties involved – the member who is called as transferor and the buyer who is called as transferee.	There is only one party e.g., the nominee of the members in case of death of the member or the legal representative.
5. Instrument of transfer	Transfer requires an Instrument of transfer.	No instrument of transfer is needed.
6. Initiated by	The transferor initiates the transfer process.	Legal representative or official receiver initiates the process of transmission.
7. Consideration	Transfer of shares is done often by the member to receiving some consideration e.g., money.	In the transmission of shares, no consideration is involved.
8. Liability	The liability of the transferor ends after the shares are transferred.	Original liability of the member continues in case of transmission of shares.
9. Stamp duty	Stamp duty as per the market value of shares has to be paid.	No stamp duty is to be paid.

5. Answer in brief.

Question 1.
What is Book Building Method?
Answer:

• The method of offering shares by providing a price range is called the book building method.
• In the book, building method shares will be sold by the bidding process.
• The company issues a Red Herring Prospectus which contains a price range or price band and as the investor to bid on it.
• In this method, the company doesn’t fix up a particular price for the share but gives a price range e.g., ₹ 80 to ₹ 100.
• When bidding for the shares, investors have to decide at which price they would like to bid for the shares e.g. ₹ 80, ₹ 90, ₹ 100.
• The lower price band (₹ 80) is known as the floor price and the highest price band (₹ 100) is known as the cap price. The final price at which shares are offered to investors is called the cut-off price.
• Board on the demand and supply of the shares, decides the final price is to be fixed.
• Investors can bid on any number of shares that they are willing to buy at a given price band. Such Bidding is kept open for 5 days.
• The bids with application money are to be submitted to the Lead Merchant Bankers called ‘Book Runners’ who enter the bids in a book.
• After bidding, the company fixes a cut-off price at which shares on offer can be sold.
• The company issues a prospectus that contains the final price.
• Book Building method is used for public issues i.e., IPO and FPO.

Question 2.
State the provisions for the Rights issue.
Answer:

• When a company wants to issue further capital it can issue shares to its existing equity shareholders which are called Rights Issue.
• According to the Companies Act, 2013 company has to fulfill certain provisions for making a Rights Issue.
• the provisions are
  • Rights shares are sold to the existing shareholders at a price that is lesser than its market price.
  • A company has to send a ‘Letter of offer’ to the existing shareholders at the time of issuing Rights Shares.
  • The letter of offer shall mention
  • The number of shares offered.
  • The period of offer i.e., offer is valid for a period not less than fifteen days and not exceeding thirty days from the date of offer.
  • The letter of offer can be sent by registered post, speed post, courier, or through electronic mode.
  • If a shareholder does not respond to the Rights Issue offer within a given time, it is implied that he is not interested in the offer and the company can offer the unsold shares to new Investors.

Question 3.
State the provisions related to Bonus Shares.
Answer:

• Bonus Shares are fully paid shares issued free of cost to the existing equity shareholders.
• According to Companies Act 2013, every company has to follow certain provisions to issue Bonus Shares.

Following are the provisions related to Bonus Issue-

• A company can issue Bonus Shares only out of
  • Free reserves or
  • Securities Premium Account
  • Capital Redemption Reserve Account
• A company cannot issue Bonus Shares only out of Reserves credited by the Revaluation of Assets.
• It also cannot issue Bonus Shares instead of paying dividend.
• Once the announcement for Bonus Shares is made by the Board of Directors, it cannot be then withdrawn.
• Bonus shares are fully paid up shares.
• Shareholders cannot renounce i.e give away their Bonus Shares to another person.
• There is no minimum subscription to be collected.

Question 4.
State the general principles/rules for allotment of shares.
Answer:
Every company issuing shares has to follow rules or general principles given by the Companies Act 2013 as follows:

• Proper Authority: The Board of Directors or the allotment committee set up by the Board has the authority to allot shares.
• Allotment must be against application only: A Company can allot shares only if it has received a written application for shares from the applicant. Allotment of shares cannot take place on the basis of an oral request.
• Reasonable time: As per the Act, allotment shall be done within 60 days of receipt of application money. Allotment can be made from the fifth day from the date of issue of prospectus.
• Absolute and Unconditional allotment: Shares should be allotted on the same terms as stated in the prospectus and application form. No change in terms of allotment or new conditions can be added at the time of allotment.
• Communication: Company has to inform the applicant that shares have been allotted, to him by sending a letter of allotment or allotment advice. The letter gives details of a number of shares allotted amount of Allotment money to be paid etc.
• Allotment should not be in Contravention (Violation) of any other laws: A company cannot allot shares by violating or contradicting any other existing laws e.g., shares cannot be allotted to a minor, of a country where a company operates its business.

Question 5.
State the contents of the Share Certificate.
Answer:
A Share certificate refers to a document which is issued by a company evidencing that a person named in such certificate is the owner of the shares of the company stated in the share certificate.
Share certificate has to be issued under the common seal of the company. It should be issued within 2 months from the date of allotment against the allotment letter.

Contents of Share Certificate:
Share Certificate should be in Form SH – 1 as prescribed under Companies (Share Capital and Debenture) Rules 2014.

• Name of the company with Registered office address
• Folio Number
• Share Certificate Number
• Name of Member
• Nature of share number of shares and a distinctive number of shares.
• Amount paid on shares
• Common seal, if any, and signature of two directors and company secretary.

Question 6.
What are the effects of forfeiture of shares?
Answer:
If a shareholder, who is called upon to pay any call fails to pay the amount, even after sending many reminders the company may forfeit his shares. Thus forfeiture of shares means cancellation of shares.

Effects of Forfeiture

• Cessation of Membership: On forfeiture, a member ceases to be a member of a company and loses all membership rights. The member’s name is removed from the Register of Members.
• Liability of Member: A member is liable for unpaid calls even after forfeiture of shares. The liability ceases only when the company reissues the forfeited shares.
• Liquidation of Company: If a company goes in for liquidation within one year of forfeiture of shares, the member whose shares have been forfeited is liable to pay the calls as a past member.

Question 7.
When can the Board of Directors refuse the transfer of shares?
Answer:

• Board of Directors can refuse transfer of shares as they have authority to refuse registration of transfer of shares.
• A notice of refusal of transfer is to be sent by the board to a member within 30 days from the date on which the instrument of transfer is received by the company.
• The board may refuse to register the transfer under following conditions.
  • When the provisions for transfer of shares as given in the Articles of Association are not fulfilled by the member.
  • When the instrument of transfer is not as per the rules prescribed under the Companies Act.
  • When the instrument is not accompanied by the share certificate.
  • When the company has a lien on the shares to be transferred.

Question 8.
Explain Employee Stock Option Scheme.
Answer:
An employee stock option plan is an employee benefits scheme under which the company encourages its employees to acquire ownership in the form of shares. Under this scheme, permanent employees, Directors or Officers of the Company or its holding company or subsidiary company are offered the benefit or right to purchase the equity shares of the company at a future date at a predetermined price. Generally these shares are issued at discount. The shares are offered at a price lesser than their market price.

Following are the provisions related to ESOS:

• A company may offer the shares directly to the employees or through an Employee Welfare Trust.
• The shares are offered at a price lesser than their market price.
• There is a minimum vesting period of one year.
• Company specifies the lock-in period. It is a minimum of one year between grant of option and vesting.
• Shares issued under this scheme enjoys dividend or voting rights only after buying by employees.
• Company has to get the approval of shareholders through a special resolution to issue ESOS.
• Employee neither transfer his option to any other person nor pledge/mortgage the shares issued under ESOS.
• Company has to set up a compensation committee to administer ESOS.
• The company has to fulfil the provision of SEBI (Share Based Employee Benefits) Regulations, 2014.

Question 9.
What are Calls on shares?
Answer:

• Whenever a company issues shares, the company may ask its shareholder to pay value of shares in installment which is known as calls on shares.
• Company can demand part or full amount of balance amount of unpaid shares.
• Beside the application money and allotment money if a company demands the balance unpaid amount on shares it is called as calls on shares.
• The unpaid amount on partly paid-up shares is a liability of the shareholders.
• Calls on shares can be made by the Board of Directors in the interest of the company.
• To make a call on shares, company has to send a call letter or notice to the shareholders. This notice is drafted by a secretary and issued in the name of the board of directors. The company gives them a minimum of 14 days notice to pay calls money to the Company’s Banker.
• No call can be made for more than 25% of the nominal value of shares.

Question 10.
Explain private placement method for the issue of shares.
Answer:

• When a company offers its securities to a select group of persons not exceeding 200, it is called a private placement.
• In private placement, the company offers its securities only to identified person and not to the general public.
• Statement in lieu of prospectus should be filed by the company with ROC before making a private placement.
• The Board of directors selects or identify the persons to be included in the select group. They can be mutual funds, Institutional Investors etc.
• Company has to issue private placement offer letter along with the application.
• The shares offered can be fully or partly paid up and the consideration should be paid by cheque, Demand Draft, etc. but not by cash.
• Right to renunciation is not given to applicants under private placement. The company has to get approval of shareholders through a special resolution.
• A company can make private placement through a rights issue and preferential allotment.

6. Justify the following statements.

Question 1.
Company has to fulfill certain provisions while making Right Issue.
Answer:

• When a company wants to issue further capital it can issue shares to its existing equity shareholders which is called Rights Issue.
• According to the Companies Act 2013 company has to fulfil certain provisions for a making Rights Issue.
• The provisions are
  • Rights shares are sold to the existing shareholders at a price that is lesser than its market price.
  • A company has to send ‘Letter of offer’ to the existing shareholders at the time of issuing Right Shares.
  • The letter of offer shall mention
    • The number of shares offered.
    • The Period of offer i.e., offer is valid for a period not less than fifteen days and not exceeding thirty days from the date of offer.
  • The letter of offer can be sent by registered post, speed post, courier or through electronic mode.
  • If a shareholder does not respond to the Rights Issue offer within a given time, it is implied that he is not interested in the offer and company can offer the unsold shares to new Investors.

Question 2.
To issue Bonus shares a company has to fulfil certain provisions.
Answer:

• Bonus shares are fully paid shares issued free of cost to the existing equity shareholders.
• According to Companies Act 2013, every company has to follow certain provisions to issue Bonus Shares.

Following are the provisions related to Bonus Issue-

• A company can issue Bonus shares only out of
  • Free reserves or
  • Securities Premium Account
  • Capital Redemption Reserve Account
• A company cannot issue Bonus Shares only out of Reserves credited by the Revaluation of Assets.
• It also cannot issue Bonus Shares instead of paying dividends.
• Once the announcement for Bonus Shares is made by the Board of Directors, it cannot be then withdrawn.
• Bonus shares are fully paid up shares.
• Shareholders cannot renounce i.e., give away their Bonus Shares to another person.
• There is no minimum subscription to be collected.

Question 3.
ESOS is offered by a company to its permanent employees, Directors, and officers.
Answer:

• A company can raise funds by offering shares to its existing permanent employees by ESOS Scheme.
• Under this scheme permanent employees Directors or officers of the company are offered the benefit or right to purchase the equity shares of the company at a future date with a pre-determined price.
• ESOS is followed by the company to encourage its employees and to give certain benefits to them.
• Through ESOS, the company can retain its good and talented employees.
• A company may offer the shares directly to the employees or through an Employee Welfare Trust.
• It is helpful to the company to generate goodwill in the market also.

Question 4.
The company has to fulfill general principles/rules for allotment of shares.
Answer:
Every company issuing shares has to follow rules or general principles given by the Companies Act, 2013 as follows:

• Proper Authority: The Board of Directors or the allotment committee set up by the Board has the authority to allot shares.
• Allotment must be against application only: A Company can allot shares only if it has received a written application for shares from the applicant. Allotment of shares cannot take place on the basis of an oral request.
• Reasonable time: As per the Act, allotment shall be done within 60 days of receipt of application money. Allotment can be made from the fifth day from the date of issue of prospectus.
• Absolute and Unconditional allotment: Shares should be allotted on the same terms as stated in the prospectus and application form. No change in terms of allotment or new conditions can be added at the time of allotment.
• Communication: Company has to inform the applicant that shares have been allotted to him by sending a letter of allotment or allotment advice. The letter gives details of a number of shares allotted, amount of Allotment Money to be paid etc.
• Allotment should not be in Contravention (Violation) of any other laws: A company cannot allot shares by violating or contradicting any other existing laws e.g., shares cannot be allotted to a minor, of a country where a company operates its business.

Question 5.
A Company can issue a duplicate share certificate.
Answer:
A Company can issue a duplicate share certificate in the following circumstances:

• If original share certificate has been defaced, mutilated or tom and is surrendered to the company.
• If it has been proved by the holder that the original share certificate is lost or destroyed.
• In case of loss of share certificate, the company puts up a notice in the newspaper to announce the loss of the share certificate.
• If the company does not get any response from the public within the specified time, then the company issues a duplicate share certificate.
• Duplicate share certificate should be issued within three months from the date of application.
• Duplicate share certificate should be issued within 3 months from the date of application with bold ‘duplicate share certificate’ marked on it.

Question 6.
Board of directors has the authority to forfeit shares.
Answer:

• Forfeiture of shares is a process where the company forfeits the shares of a member or shareholder who fails to pay a call on shares. The forfeiture of a share is a forceful activity performed by a company due to non-payment of calls by shareholders.
• Only the Board of directors can forfeit the shares if the process of forfeiture is authorised by the Articles of Association.
• Board of directors can forfeit shares only in the interest of the company.
• A 14 days of notice should be sent to a concerned member.
• Thus Board of directors can make forfeiture of shares.

Question 7.
A member of a public company can transfer shares.
Answer:

• Transfer of shares means voluntary transfer of shares by a member of a company to another person against consideration.
• In the case of public companies, shares are freely transferable subject to provisions of the Articles of Association.
• A member has to apply to the company for the transfer of shares by filling the ‘Instrument of Transfer’.
• Member who is transferring the shares is called as Transferor and to whom shares are transferred is called Transferee.
• Transfer is said to be completed only when the transfer is registered in the Register of Members.

Question 8.
The Board of Directors can refuse the transfer of shares.
Answer:

• Board of Directors can refuse transfer of shares as they have authority to refuse registration of transfer of shares.
• A notice of refusal of transfer is to be sent by the board to a member within 30 days from the date on which the instrument of transfer is received by the company.
• The board may refuse to register the transfer under the following conditions.
  • When the provisions for transfer of shares as given in the Articles of Association is not fulfilled by the member.
  • When the instrument of transfer is not as per the rules prescribed under the Companies Act.
  • When the instrument is not accompanied by the share certificate.
  • When the company has a lien on the shares to be transferred.

7. Answer the following questions.

Question 1.
Explain the classification of Share Capital.
OR
Explain types of Share Capital.
Answer:
Share capital is the capital that is built up by the company by issuing shares in the market. Share capital consist of capital that is made up of Equity shares and Preference shares.
Share capital can be classified as-

(i) Authorised or Nominal or Registered Capital

• The Authorized capital is the maximum amount of capital that a company can raise through the issue of shares to the shareholders.
• The Authorized capital of a company is also called as the Registered capital or Nominal Capital.
• Authorized capital is the maximum capital that is authorized by the company’s Memorandum of Association.
• The Authorized capital is mentioned in the Memorandum of Association of the company under the heading ‘capital clause’ and the company pays stamp duty on this amount at the time of incorporation.
• Authorized capital is also called as ‘Nominal Capital’ as usually a company never issues the entire Authorized Capital.
• A company can increase its Authorized Capital by altering its Memorandum of Association.
• The maximum limit of authorized capital is registered with the registrar of the companies.
• Example of Authorized Capital: XYZ Ltd. Company has an authorized capital of ₹ 10,00,000, then it can issue shares worth up to ₹ 10,00,000 to its shareholders and cannot issue anything beyond it.

(ii) Issued and Unissued capital:

• Issued capital is that portion of authorized shares capital that had been raised by issuing shares to the general public.
• These are the shares that the company offers to prospective investors for a subscription.
• The issued capital of a company may be equal to or less than the Authorized Capital of incorporation.
• The balance part of Authorized Capital which is not offered to the public for subscription is called ‘unissued capital’.
• Unissued capital is that capital which a Company is authorized to issue but has not issued as shares.
• Unissued capital is the balance part of Authorised capital which is not offered to the public.
• Example of Issued and Unissued Capital: XYZ Ltd Company can have issued Capital of ₹ 4,00,000 divided into 40,000
• Equity Shares at Face Value of ₹ 10/- each and the Unissued Capital 6,00,000 divided into 60,000 equity shares of ₹ 10/- each.

(iii) Subscribed and Unsubscribed Capital:

• Subscribed share capital is that part of issued share capital for which a company has positively received a subscription from the investor.
• It is a part of Issued Capital that has been subscribed by investors or purchased by the general public.
• The subscribed capital may be equal to or less than the issued capital.
• The part of the Issued Capital which is not subscribed by the investors is called as ‘Unsubscribed Capital’.
• Example of Issued and Unissued capital: If XYZ Ltd company has issued capital ₹ 4,00,000 i.e., it has issued 40,000 equity shares of ₹ 10 each and company has received subscription for 30,000 shares i.e., for 30,000 equity shares of ₹ 10/- each then its subscribed capital is ₹ 3,00,000 and unsubscribed capital will be ₹ 1,00,000 divided into 10,000 Equity shares of ₹ 10/- each.

(iv) Called up and Uncalled capital and Reserve capital:

• Called up share capital is that part of share capital that has been called by the company for payment from shareholders.
• The company collects the full value of shares in installments and each installment is called a ‘call’.
• Uncalled Capital is that part of subscribed capital that is not demanded from the shareholders.
• A company can decide to keep aside a part of its uncalled capital to be called up only at the time of winding up of a company to meet its financial requirements. Which is called a Reserve Capital.

Example of call up, uncalled and Reserve Capital.
If XYZ Ltd company is to subscribed capital is ₹ 3,00,000 i.e., 30,000 equity shares of face value of ₹ 10/- each. Out of which company made first call of ₹ 5/- per share, so company called up capital will be ₹ 1,50,000 (30,000 Equity shares × ₹ 5/- each = ₹ 1,50,000)

If the company decides to keep ₹ 1/- per share as capital to be collected at the time of the winding-up, the Reserve Capital will be 30,000 (30,000 equity shares of ₹ 10 each.)
Uncalled Capital will be ₹ 1,20,000 (30,000 equity shares were 4 per share which will be called up in the future.)

(v) Paid-up capital and calls in Arrears:

• Paid-up capital is the amount of money a company has received from shareholders in exchange for shares.
• It is the total amount of money paid up by the shareholders when the company has called up or demanded them to pay.
• The paid-up capital can be equal to or less than the authorized capital.
• Unpaid capital means any uncalled or unpaid share capital. The amount not paid to shareholders is also called as calls in Arrears.
• Every shareholder has to pay calls as and when the company demands, failure to pay the calls may lead to future forfeiture of shares (cancellation of shares).

Example of paid up capital and calls in Arrears.
‘XYZ’ Ltd Company has made a call of ₹ 5/- per share on 30,000 equity shares, so if all the shareholder have paid the calls, then paid-up capital will be ₹ 1,50,000 (30,000 equity shares of ₹ 5/- per share). But if 10,000 Equity Shareholders have not paid calls then the paid-up capital will be ₹ 1,00,000 (20,000 Equity Shares × ₹ 5/- per share) and calls in Arrears will be ₹ 50,000 (10,000 Equity Shares × ₹ 5/- per share).

Question 2.
What are the methods of issue of shares to the public through public offer?
Answer:
Issue of shares is the process in which companies offer new shares to shareholders. The company follows different methods prescribed by the Companies Act 2013 while issuing the shares. There are two methods of issue of shares to the public through public offer, they are – Public issue or Public offer of shares.

A public offering is the sale of equity shares to the public in order to raise capital. This is the most popular and common method used by companies. The company invites the public to subscribe to its shares by issuing prospects. A company can use two pricing methods to offer shares to the public.

(i) Fixed Price Issue method:

• In an initial public offering (IPO), if the shares are offered at a fixed price such issue is known as Fixed Price issue.
• In this method, company mentions the Quantity and the price at which shares are offered.
• Investors can pay a certain portion of face value of shares or the entire issue price along with the application.
• Company issues shares at par. E.g., shares having a face value of ₹ 100 and is issued as ₹ 100, at premium e.g., a share having a face value of 100 and is issued at ₹ 150, or at discount e.g., face value is ₹ 100 and the insured price is ₹ 80/-.
• Fixed price method is used for all types of issues i.e. Public issue, Right issue, Esos etc.

(ii) Book Building Method:

• The method of offering shares by providing a price range is called the book building method.
• In the book building method shares will be sold by the bidding process.
• The company issues a Red Herring Prospectus which contains a price range or price band and asks the investor to bid on it.
• In this method the company doesn’t fix up a particular price for the share but gives a price range e.g., ₹ 80 to 100.
• When bidding for the shares, investors have to decide at which price they would like to bid for the shares e.g., ₹ 80, ₹ 90, ₹ 100.
• The lower price band (₹ 80) is known as the floor price and the highest price band (₹ 100) is known as cap price. The final price at which shares are offered to investors is called cut off price.
• Based on the demand and supply of the shares, the final price is fixed.
• Investors can bid on any number of shares that they are willing to buy at given price band. Such bidding is kept open for 5 days.
• The bids with application money is to be submitted to the Lead Merchant Bankers called ‘Book Runners’ who enter the bids in a book.
• After bidding, the company fixes cut off the price at which shares on offer can be sold.
• Company issues a prospectus which contains the final price.
• Book Building method is used for public issues i.e. IPO and FPO.

Further public offer:
It is also called a follow on public offer. When the company issue shares to the public after IPO, it is called a a further public offer. Thus every issue of shares by a listed company after its IPO is called as FPO. FPO leads to an increase in the subscribed capital of the company.

Question 3.
Explain briefly the different types of shares offered by a company to its existing equity shareholders.
Answer:
The company issues equity shares in the market. The equity shareholders are the real owner of the company.
A company can raise funds by offering shares to its existing equity shareholders as follows.

(i) Right Issue:
A right issue is an invitation to existing shareholders to purchase additional new shares in the company. A right issue is a way by which a listed company can raise additional capital. Instead of going for the public issue of shares, the company gives its existing shareholders, the right to subscribe to newly issued shares in proportion to their existing equity shareholding.

Whenever a company makes the further issue of shares the existing equity shareholders have preemptive rights means the first option to buy shares.

Company making rights issue has to fulfil the following provision:

• Rights shares are sold to the existing shareholders at a price that is lesser than its market price.
• A company has to send a ‘Letter of offer’ to the existing shareholders at the time of issuing Rights Shares.
• The letter of offer shall mention
• The number of shares offered.
• The period of offer i.e., offer is valid for a period not less than fifteen days and not exceeding thirty days from the date of the offer.
• The letter of offer can be sent by registered post, speed post, courier or through electronic mode.
• If a shareholder does not respond to the Rights Issue offer within a given time, it is implied that he is not interested in the offer and company can offer the unsold shares to new Investors.

(ii) Bonus Issue/Bonus Shares:
Bonus Shares are shares distributed by a company to its current shareholders as fully paid shares free of charge. The Bonus shares are given to the existing equity shareholders according to their existing proportion of equity shareholdings.

Like for example, a company declaring one for two bonus share proportion means that an existing shareholder would get one bonus share of the company for every two shares held. Financially sound companies issue Bonus shares out of their accumulated distributable profits or reserves. Hence as the profits or reserves are capitalized, it is called “Capitalisation of Profits or Reserves.”

Following are the provisions related to Bonus Issue-

• A company can issue Bonus shares only out of
• Free reserves or
• Securities Premium Account
• Capital Redemption Reserve Account
• A company cannot issue bonus shares only out of Reserves Credited by the Revaluation of Assets.
• It also cannot issue Bonus Shares instead of paying dividends.
• Once the announcement for Bonus shares is made by the Board of Directors, it cannot be then withdrawn.
• Bonus shares are fully paid up shares.
• Shareholders cannot renounce i.e, give away their Bonus Shares to another person.
• There is no minimum subscription to be collected.

Question 4.
Explain the statutory provisions for the allotment of shares.
Answer:

• The allotment of shares is the issuing of new shares to an applicant based on the application submitted or to the existing shareholders.
• Every company has to fulfill the provisions of the Companies Act for making allotment of shares.
• The provisions which are laid down by the Companies Act, 2013 are called statutory provisions.

(i) Registration of Prospectus:

• A copy of the prospectus must be filed with the Registrar of Companies for registration on or before the date of its publication.
• In the case of the newly formed company, a prospectus must be signed by every proposed director or director or his duly authorized advocate. The copy of the prospectus is drafted by the secretary of the company with the permission of the board of directors.

(ii) Application Money:

• The applicant has to pay a minimum of 5% of nominal amount of the shares along with the application form.
• For public limited companies SEBI has specified that application money should be minimum of 25% of the nominal amount of shares.
• The application money is to be paid in the Bank specified by the company.

(iii) Minimum Subscription:

• Minimum Subscription is the amount which is mentioned in the prospectus. It is the minimum amount of shares which should be bought by the subscribers.
• According to SEBI minimum subscription should be 90% of the issue.
• In case the minimum subscription is not collected within the specified time, the company has to return the entire amount of application money to the subscribers.

(iv) Closing of Subscription list:

• According to SEBI a company has to keep open its subscription list for at least three working days and not more than ten working days.
• Applicants can apply for shares only when the subscription list is open.

(v) Basic of allotment:

• Allotment of shares will be decided on the basis of each category of subscribers.
• Allotment of shares will be as per the minimum application size which is fixed by the company.

(vi) Over Subscription:

• Oversubscription refers to a situation in which a company receives more application of shares than the number of shares offered.
• SEBI does not allow any allotment which is in excess of the offer given by the company through a document or prospectus.
• SEBI may permit to allot the shares not more than 10% of the net offer.

(vii) Permission to deal on Stock Exchanges:

• Every company, before making a public offer shall apply to one or more recognized Stock Exchanges to take permission for listing its shares with them
• The prospectus must mention the name of the stock exchange in which the company is listed.
• The prospectus should also state the fact that an application for permission to list in that stock exchange has been made by the company.

(viii) Appointment of Managers to the issue and various other agencies.

• The company has to appoint one or more Merchant Bankers to act as managers to the public issue.
• The company has to appoint Registrar to the issue (institutions that keeps the records of the issue), collecting bankers and underwriters to the issue as well as brokers to the issue.
• The company has to also appoint self-certified syndicate banks (banks certified by SEBI which offers ASBA facility to investors), which are certified by SEBI, advertising agents, etc.

Question 5.
Explain briefly the procedure for allotment of shares.
Answer:
Allotment of Shares:

• Allotment means distribution of shares among the applicants. It means giving shares to share applicants or to specific persons with whom the company has entered into contract.
• Allotment of shares is a procedure in which shares are distributed to those applicants who have submitted a written application along with the application money. If company allots shares alter fulfilling all statutory and general provisions of Companies Act, 2013 such allotment is called as “Regular Allotment”.

Procedure for Allotment of Shares
(i) Appointment of Allotment Committee

• When the subscription list is closed the secretary informs the Board of Directors to make preparations for allotment of shares.
• If the issue is par subscribed or under subscribed, the Board can do the allotment of shares.
• In case of over subscription the board has to appoint and Allotment Committee to undertake the work of Allotment.
• The Allotment Committees decides the basis of allotment and submits a report to the Board.

(ii) Hold Board Meeting to Decide Basis of Allotment

• Board meeting is held to approve the allotment formula suggested by the Allotment Committee.
• A representative of SEBI should be present when the allotment committee prepares the allotment formula.
• After approval of the allotment formula, an allotment list is made.
• If the shares are listed, then the company should take the permission of the concerned stock exchange.
• The allotment list contains the names of allotters. Which should be signed by the chairman and secretary.

(iii) Pass Board Resolution for allotment:

• A resolution is passed to allot shares in board meeting.
• Secretary sends ‘Letter of Allotment’ to allotters those applicant whom shares are allotted.
• Secretary has to send a ‘Letter of Regret’ to those applicants to whom no shares have been issued.
• Along with the letter of Regret the application money is also refunded.
• The company that issues shares in electronic form informs respective Depository (NSDL or CDSL) about allotment of shares.
• It also provides details of applicants whom shares are allotted, number of shares allotted, etc.

(iv) Collection of Allotment Money:

• The letter of allotment states the money to be paid by the applicant on the allotment of shares.
• The money has to be paid in the Bank specified by the company within the stipulated time.
• For all public issues and rights issues ASBA is compulsory since January 2016.

(v) Arrangement Relating to Letters of Renunciation:

• An applicant who has been allotted shares can renounce the shares in favor of another person.
• The applicant has to fill up a form for renunciation to the company with the original copy of the letter of allotment.
• After the permission of the board, the secretary enters the detail of the new person in the application and allotment list.

(vi) Arrangement Relating to Splitting of Allotment letters:

• An applicant who has been allotted shares can request for the splitting of allotment shares.
• After getting the approval of the Board for the splitting. Secretary enters the details of the split in the list of split allotment for which secretary has to ensure spilled letter.

(vii) File Return of Allotment:

• Secretary has to file a “Return of Allotment’ with the Registrar of Companies within 30 days of allotment of shares.
• The return of allotment contains details of allotment of shares which includes the names and addresses of allotters, the value of shares allotted amount paid or payable on each share, etc.

(viii) Prepare Register of Members and Issue of Share Certificate

• Secretary has to enter the names of all those applicants who have paid the allotment money in the Register of Members.
• Secretary also has to prepare the share certificates and distributes them to all the members within two months from the date of allotment of shares.

Maharashtra State Board 12th Std Secretarial Practice Textbook Solutions

• Introduction to Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Sources of Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Issue of Shares Class 12 Secretarial Practice Textbook Solutions
• Issue of Debentures Class 12 Secretarial Practice Textbook Solutions
• Deposits Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Members Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Debentureholders Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Depositors Class 12 Secretarial Practice Textbook Solutions
• Depository System Class 12 Secretarial Practice Textbook Solutions
• Dividend and Interest Class 12 Secretarial Practice Textbook Solutions
• Financial Market Class 12 Secretarial Practice Textbook Solutions
• Stock Exchange Class 12 Secretarial Practice Textbook Solutions

Sources of Corporate Finance 12th Secretarial Practice Chapter 2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 2 Sources of Corporate Finance Textbook Exercise Questions and Answers.

Class 12 Secretarial Practice Chapter 2 Exercise Solutions

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
___________ is the smallest unit in the total share capital of the company.
(a) Debenture
(b) Bonds
(c) Share
Answer:
(c) Share

Question 2.
The benefit of Depository Receipt is ability to raise capital in ___________ market.
(a) national
(b) local
(c) international
Answer:
(c) international

Question 3.
___________ are residual claimants against the income or assets of the company.
(a) Bondholders
(b) Equity shareholders
(c) Debenture holders
Answer:
(b) Equity shareholders

Question 4.
___________ participate in the management of their company.
(a) Preference shareholders
(b) Depositors
(c) Equity shareholders.
Answer:
(c) Equity shareholders

Question 5.
___________ shares are issued free of cost to existing equity shareholders.
(a) Bonus
(b) Right
(c) Equity
Answer:
(a) Bonus

Question 6.
The holder of preference share has the right to receive ___________ rate of dividend.
(a) fixed
(b) fluctuating
(c) lower
Answer:
(a) Fixed

Question 7.
Accumulated dividend is paid to ___________ preference shares.
(a) redeemable
(b) cumulative
(c) convertible
Answer:
(b) Cumulative

Question 8.
The holder of ___________ preference shares has the right to convert their shares into equity shares.
(a) cumulative
(b) convertible
(c) redeemable
Answer:
(b) Convertible

Question 9.
Debenture holders are ___________ of the company.
(a) creditors
(b) owners
(c) suppliers
Answer:
(a) creditors

Question 10.
___________ is paid on borrowed capital.
(a) Interest
(b) Discount
(c) Dividend
Answer:
(a) Interest

Question 11.
Debenture holders get fixed rate of ___________ return on their investment.
(a) interest
(b) dividend
(c) discount
Answer:
(a) interest

Question 12.
Convertible debentures are converted into ___________ after a specific period.
(a) equity shares
(b) deposits
(c) bonds
Answer:
(a) equity shares

Question 13.
Retained earnings are ___________ source of financing.
(a) internal
(b) external
(c) additional
Answer:
(a) internal

Question 14.
The holder of bond is ___________ of the company.
(a) secretary
(b) owner
(c) creditor
Answer:
(c) creditor

Question 15.
Company can accept deposits from public, minimum for ___________ months.
(a) six
(b) nine
(c) twelve
Answer:
(a) six

Question 16.
Company can accept deposits from public maximum for ___________ months.
(a) 12
(b) 24
(c) 36
Answer:
(c) 36

Question 17.
A depository receipt traded in ___________ is called American Depository Receipt.
(a) London
(b) Japan
(c) USA
Answer:
(c) the USA

1B. Match the pairs.

Question 1.

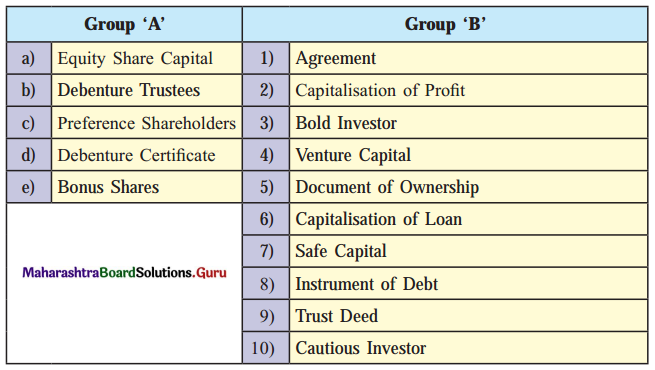
Answer:

Group ‘A’	Group ‘B’
(a) Equity share capital	(1) Venture capital
(b) Debenture Trustees	(2) Trust Deed
(c) Preference shareholders	(3) Cautious investor
(d) Debenture Certificate	(4) Instrument of Debt
(e) Bonus shares	(5) Capitalisation of profit

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
The real masters of the company.
Answer:
Equity shareholders

Question 2.
A document of ownership of shares.
Answer:
Share certificate

Question 3.
The holders of these shares are entitled to participate in surplus profits.
Answer:
Participating preference shares

Question 4.
A party through whom the company deals with debenture holders.
Answer:
Debenture trustees

Question 5.
Name the shareholder who participates in the management.
Answer:
Equity shareholders

Question 6.
The value of a share is written on the share certificate.
Answer:
Face value

Question 7.
The value of a share is determined by demand and supply forces in the share market.
Answer:
Market value

Question 8.
The policy of using undistributed profit for the business.
Answer:
Retained earnings/ploughing back of profit

Question 9.
It is an acknowledgment of a loan issued by the company to the depositor.
Answer:
Deposit receipt

Question 10.
A dollar-denominated instrument trader in the USA.
Answer:
American Depository Receipt

Question 11.
The Depository Receipt is traded in a country other than the USA.
Answer:
Global depository receipt

Question 12.
Money raised by the company from the public for a minimum of 6 months to a maximum of 39 months.
Answer:
Public Deposits

Question 13.
Credit extended by the suppliers with an intention to increase their sales.
Answer:
Trade Credit

Question 14.
The credit facility is provided to a company having a current account with the bank.
Answer:
Overdraft

1D. State Whether the following statements are True or False.

Question 1.
Equity share capital is known as venture capital.
Answer:
True

Question 2.
Equity shareholders enjoy a fixed rate of dividends.
Answer:
False

Question 3.
Debenture holders have the right to vote at a general meeting of the company.
Answer:
False

Question 4.
Equity shareholders are described as ‘shock absorbers’ when a company has a financial crisis.
Answer:
True

Question 5.
Bondholders are owners of the company.
Answer:
True

Question 6.
Cash credit is given against hypothecation of goods and security.
Answer:
True

Question 7.
Trade credit is a major source of long-term finance.
Answer:
False

Question 8.
Depository bank stores the shares on behalf of the GDR holder.
Answer:
True

Question 9.
Financial institutions underwrite the issue of securities.
Answer:
True

1E. Find the odd one.

Question 1.
Debenture, Public Deposit, Retained Earnings
Answer:
Retained earnings

Question 2.
Face value, Market value, Redemption value
Answer:
Redemption value

Question 3.
Share certificate, Debenture certificate, ADR
Answer:
ADR

Question 4.
Trade credit, Overdraft, Cash credit
Answer:
Trade credit

1F. Complete the sentences.

Question 1.
The finance needed by business organisation is termed as ___________
Answer:
Capital

Question 2.
The convertible preference shareholders have a right to convert their shares into ___________
Answer:
Equity shares

Question 3.
Equity shareholders elect their representative Called ___________
Answer:
Directors

Question 4.
Bonus shares are issued as gift to ___________
Answer:
Equity share holders

Question 5.
The bondholders are ___________of the company.
Answer:
Creditors

Question 6.
Depository receipt traded in a country other than USA is called ___________
Answer:
Global Depository Receipt

Question 7.
First Industrial policy was declared in the year ___________
Answer:
1948

Question 8.
When goods are delivered by the supplier to the customer on the basis of deferred payment is called as ___________
Answer:
Trade credit

1G. Select the correct option from the bracket.

Question 1.

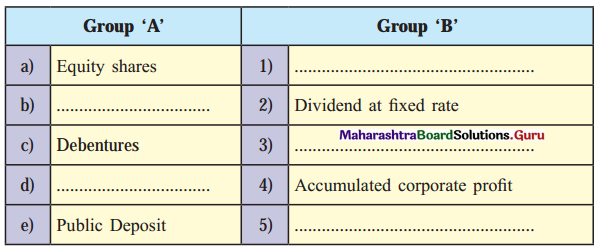
(Fluctuating rate of dividend, Preference shares, Interest at fixed rate, Retained earnings, short term loan)
Answer:

Group ‘A’	Group ‘B’
(a) Equity shares	(1) Fluctuating rate of dividend
(b) Preference shares	(2) Dividend at a fixed rate
(c) Debentures	(3) Interest at a fixed rate
(d) Retained earnings	(4) Accumulated corporate profit
(e) Public Deposit	(5) short term loan

1H. Answer in one sentence.

Question 1.
What is a share?
Answer:
A share is the smallest unit of the share capital of a company.

Question 2.
What are equity shares?
Answer:
Equity shares are shares that do not preference shares and do not carry priority in receiving dividends nor repayment of capital.

Question 3.
What are preference shares?
Answer:
Preference shares are shares that have preferential rights with regard to receiving dividends and repayment of capital.

Question 4.
What are retained earnings?
Answer:
A part of the net profit which is not distributed to shareholders as dividend but retained by the company as reserve fund is retained earnings.

Question 5.
What is a debenture?
Answer:
It is a document/instrument issued in the form of a debenture certificate under the common seal of the company acknowledging/evidencing the debt.

Question 6.
What is a bond?
Answer:
A bond is a debt security and a formal contract to repay borrowed money with interest.

Question 7.
In which country can ADR be issued?
Answer:
ADR (American Depository Receipt) is a depository Receipt that is issued in the USA.

Question 8.
In which country can GDR be issued?
Answer:
GDR (Global depository receipt) can be issued in countries other than the USA.

Question 9.
What are convertible debentures?
Answer:
Convertible debentures are debentures that are converted into equity shares after a specific period as specified at the time of issue.

Question 10.
What are cumulative preference shares?
Answer:
Cumulative preference shares are shares where dividend, if not paid in a year accumulates till it is paid.

1I. Correct the underlined words and rewrite the following sentences.

Question 1.
Owned capital is temporary capital.
Answer:
Owned capital is permanent capital.

Question 2.
Equity shares get dividends at a fixed rate.
Answer:
Equity shares get dividends at fluctuating rates.

Question 3.
Preference shares get dividends at fluctuating rates.
Answer:
Preference shares get dividends at a fixed rate.

Question 4.
Retained earnings are an external source of finance.
Answer:
Retained earnings are an internal source of finance.

Question 5.
The debenture holder is the owner of the company.
Answer:
The debenture holder is a creditor of the company.

Question 6.
Bond is a source of short-term finance.
Answer:
Bond is a source of long-term finance.

Question 7.
Depository receipt traded in the USA is called Global Depository Receipt.
Answer:
Depository receipt traded in the USA is called American Depository Receipt.

2. Explain the following terms/Concepts.

Question 1.
Borrowed capital
Answer:

• It consists of capital that is raised through borrowings.
• It can be raised by issuing debentures, deposits, loans from banks or financial institutions.

Question 2.
Owned capital
Answer:

• Owned capital is the capital raised by the company with the help of owners (shareholders).
• It can be raised by issuing equity and preference shares.

Question 3.
Ploughing back of profit
Answer:

• Ploughing back of profit or retained earnings is a management policy under which all profits are not distributed amongst shareholders.
• It is an internal source of financing or self-financing as when the need arises, such reserves are ploughed back, brought into the business to meet the financial needs.

Question 4.
Overdraft
Answer:

• It is a credit agreement made with a bank that allows an account holder to withdraw more money than what a company has in its account up to a specific/prescribed limit.
• This facility is available to current account holders.

Question 5.
Trade Credit
Answer:

• Trade credit is credit extended by one trader to another when goods and services are bought/sold on credit.
• It facilitates the purchase of supplies without making an immediate payment.
• It is used by business organisations as a source of short-term financing and granted to those having reasonable standing and goodwill.

3. Study the following case/situation and express your opinion.

1. The Balance sheet of a Donald Company for the year 2018-19 reveals equity share capital of Rs. 25,00,000 and retained earnings of Rs. 50,00,000.

Question (a).
Is the company financially sound?
Answer:
The company is financially sound as it has double the amount as reserves or retained earnings or kept aside profits.

Question (b).
Can the retained earnings be converted into capital?
Answer:
Yes, the retained earnings can be converted into capital by means of capitalisation of reserves.

Question (c).
What type of source retained earning is?
Answer:
Retained earning is self-financing or an internal source of finance.

2. Mr. Satish is a speculator. He desires to take advantage of the growing market for the company’s products and earn handsomely.

Question (a).
According to you, which type of share Mr. Satish will choose to invest in.
Answer:
As Mr. Satish is a speculator, he will choose equity shares to invest in because if there are good earnings/profits, so will be the rate of dividend.

Question (b).
What does he receive as a return on investment?
Answer:
He receives a fluctuating rate of dividends.

Question (C).
State anyone, right he will enjoy as a shareholder.
Answer:
The right to attend the meeting and vote on resolutions can be the right Mr. Satish can exercise as a member.

3. Mr. Rohit, an individual investor, invests his own funds in the securities. He depends on investment income and does not want to take any risk. He is interested in the definite rate of income and safety of the principal.

Question (a).
Name the type of security that Mr. Rohit will opt for.
Answer:
As Mr. Rohit does not want to take risks, he will opt for preference shares which will assure him of steady income and safety of his investment.

Question (b).
What does he receive as a return on his investment?
Answer:
Mr. Rohit will receive dividends in return.

Question (c).
The return on investment which he receives is fixed or fluctuating.
Answer:
The return on his investment will be fixed and not fluctuating.

4. Distinguish between the following.

Question 1.
Equity Shares and Preference Shares
Answer:

Points	Equity Shares	Preference Shares
1. Meaning	Shares that are not preference shares are called equity shares i.e. these shares do not have the preferential rights for payment of dividends and repayment of capital.	Preferences shares are shares that carry preferential rights as to payment of: Dividend and Repayment of capital.
2. Rate of Dividend	Equity shares are given dividends at a fluctuating rate depending upon the profits of the company.	Preference shareholders get dividends at a fixed rate.
3. Voting Right	Equity shareholders enjoy normal voting rights. They participate in the management of their company.	Preference shareholders do not enjoy normal voting right. They can vote only on matters affecting their interest.
4. Return of Capital	Equity capital can not be returned during the lifetime of the company, (except in case of buyback).	A company can issue redeemable preference shares, which can be repaid during the lifetime of the company.
5. Nature of capital	Equity capital is known as ‘Risk Capital’.	Preference capital is ‘Safe Capital’ with a stable return.
6. Nature of investor	The investors who are ready to take risks to invest in equity shares.	Investors who are cautious about the safety of their investment invest in preference shares.
7. Face Value	The face value of equity shares is generally ₹ 1/- or ₹ 10/- it is relatively low.	The face value of preference shares is relatively higher i.e. ₹ 100/- and so on.
8. Right and bonus issue	Equity shareholder is entitled to get bonus and right issue.	Preference shareholders are not eligible for bonuses and right issues.
9. Capital appreciation	The market value of equity shares increases with the prosperity of the company. It leads to an increase in the value of shares.	The market value of preference shares does not fluctuate, so there is no possibility/cheques of capital appreciation.
10. Risk	Equity shares are subject to higher risk.	Preference shares are subject to less risk.
11. Types	Equity shares are classified into: Equity shares with normal voting rights. Equity shares with differential voting rights.	Preference shares are classified as: Cumulative Preference Shares Non-Cumulative Preference Shares Convertible Preference Shares Non-Convertible Preference Shares Redeemable Preference Shares Irredeemable Preference Shares Participating Preference Shares Non-Participating Preference Shares

Question 2.
Shares and Debentures
Answer:

Points	Shares	Debentures
1. Meaning	Share is the smallest unit in the total share capital of the company. It is known as ownership securities.	A debenture is an instrument evidencing debt under the seal of the Company. They are also known as creditor ship securities.
2. Status	A holder of shares is the owner of the company. Hence, share capital is owned capital.	A holder of debenture is the creditor of the company. Hence, Debenture capital is loan capital or borrowed capital.
3. Nature	It is permanent capital. It is not repaid during the lifetime of the company.	It is temporary capital. Generally, it is repaid after a specific period.
4. Voting/Right	Shareholders being owners enjoy normal voting rights in general meetings and can participate in the management of the company.	Debenture holders being creditors, do not have any voting right and can not participate in the management of the company.
5. Return on Investment	Return on shares is called a dividend. Equity shareholders receive dividends at a fluctuating rate whereas preference shareholders receive dividends at a fixed rate.	Return on debenture is called interest. It is fixed at the time of issue. Interest is paid even when a company has no profit.
6. Security	Share capital is unsecured capital. No security is offered to the shareholder.	Debenture capital being loan capital is secured by creating a charge on Company’s property.
7. Time of Issue	Shares are issued in the initial stages of the company formation.	Debentures are issued at a later stage when the company has properties to offer as security.
8. Suitability	Shares are suitable for long-term finance.	Debentures are suitable for medium-term finance.
9. Types	Shares are classified into: Equity shares Preference	A debenture is classified as: Registered Debentures Bearer Debentures Secured Debentures Unsecured Debentures Redeemable Debentures Irredeemable Debentures Convertible Debentures Non-Convertible Debentures
10. Position on liquidation	On liquidation of a company, shareholders rank last in the list of claimants.	Debenture holders being creditors, rank prior to shareholders for repayment on liquidation of the company.

Question 3.
Owned Capital and Borrowed Capital
Answer:

Points	Owned Capital	Borrowed Capital
1. Meaning	It is that capital that is contributed by shareholders.	It is that capital that is borrowed from creditors. It is also known as debt capital.
2. Sources	This capital is collected by the issue of equity shares and preference shares, ploughing back of profits (ownership securities).	It is collected by way of the issue of debentures, fixed deposits, loans from banks/financial institutions, etc. (loan, borrowings).
3. Return on Investment	The shareholders get dividends as income on their investment. The rate of dividend is fluctuating, in the case of equity shares but is fixed in the case of preference shares.	The debt capital holders get interested as income on their investment. Interest is paid at a fixed rate.
4. Status	The shareholders are owners of the company.	The debt holders are creditors of the company.
5. Voting right	The equity shareholders enjoy normal voting right at the general meetings.	The creditors do not enjoy voting rights at the general meeting.
6. Repayment of Capital Redemption	The shareholders do not enjoy priority over creditors. They are eligible for repayment of Capital only after making payment to creditors at the time of windings up of the company.	The creditors get priority over the shareholders in case of return of principal amount at the time of winding up of the company.
7. Charge on assets	The shareholders do not have any charge on the assets of the company.	The secured debenture holders have a change on the assets of the company.

5. Answer in brief:

Question 1.
What is a public deposit?
Answer:

• Public deposit is an important source of financing short-term requirements of the company.
• Companies generally receive public deposits for a period ranging from 6 months to 36 months.
• Interest is paid by the companies on such deposits.
• The company issues a’ Deposit Receipt’ to the depositor.
• The receipt is an acknowledgment of debt/loan by the company.
• Deposits are either secured or unsecured loans offered by a company.
• It is considered a risky investment but investors can earn high returns on public deposits.

Advantages of deposits to the company

• It is an easier method of mobilizing funds during periods of credit squeeze.
• The rate of interest payable by the company on public deposits is lower than the interest from banks and financial institutions.
• It helps the company to borrow funds from a larger segment and thus, reduces dependence on financial institutions.

Question 2.
What are Global Depository Receipt and American Depository Receipt?
Answer:

• The shares that are issued by public limited companies are traded in various share markets.
• In India, shares are traded in the Bombay Stock Exchange (BSE) National Stock Exchange (NSE), etc.
• Similarly, Shares are traded in foreign stock exchanges like NYSE (New York Stock Exchange) or NASDAQ (National Association of Securities Dealers Automated Quotation).
• Companies that cannot list directly on foreign stock exchange get listed indirectly using GDR & ADR.
• GDR and ADR are Dollar/Euro denominated instruments traded on stock exchanges of foreign countries and are depository receipts containing a fixed number of shares.
• The Depository Receipts which are traded in the USA are called ADRs and Depository Receipts which are traded in all foreign countries other than the USA are called GDR.
• Indian Companies raise equity capital in the international market through GDR and ADR.
• Companies issue shares to an intermediary called ‘depository’.
• Bank of New York, Citigroup, etc act as Foreign Depository Bank.
• The Depository Banks issue GDRs or ADRs to investors against Indian Company’s shares.
• These ‘Depository Receipts’ are then, sold to foreign investors who wish to invest their savings in Indian Cost.
• The Depository Receipts are listed on the stock exchanges like regular shares.
• It is a depository bank that stores the shares on behalf of the receipt holder.
• NRI and foreign investors buy Depository Receipt Using their regular equity trading account.
• The company pays dividends in the home currency to the depository and the depository converts them into the currency of investor and pays dividends.
• Indian Companies like HDFC, ICICI, Infosys Technologies, MTNL, WIPRO have ADR and GDR.
  • Tata Motors and VSNL have ADRs.
  • Bajaj Auto Limited ITC, L&T, Hindalco, Ranbaxy Laboratories, and SBI have GDRs.
  • ADR allows the sale of securities only in the American market whereas GDR allows the sale of securities globally.

Question 3.
What is Trade Credit?
Answer:

• Every business requires trade credit and is common to all business types.
• Credit sales or granting of credit is inevitable in the present competitive business world.
• It is short-term financing to businesses.
• The small retailers, to a large extent, rely on obtaining trade credit from their suppliers.
• The cheapest method of financing; it is an easy kind of credit that can be obtained without signing any debt instrument.
• This is not a cash loan. It results from a sale of goods services which have to be paid sometime after the sale takes place.
• It is given by one trader to another trader to delay payment for goods and services involved in the transaction.
• Suppliers sell goods and willingly allow 30 days or more credit period for the bill to be paid.
• They offer discounts if bills are cleared within a short period such as 10 or 15 days.
• Such credit is given/granted to those having reasonable standing and goodwill.

Advantages of Trade Credit:

• Trade Credit is the cheapest and easiest method for raising short-term finance.
• It can be obtained without making any formal and written agreement or signing the same.
• It is readily available whenever goods and services are purchased on credit in bulk.
• It is free of cost source of financing.
• The terms of trade are lenient and not rigid.

Question 4.
What are the schemes for disbursement of credit by banks?
Answer:
Meaning: Banks play an important role in terms of providing finance to the companies.
They provide short-term finance for working capital, in the form of bank and trade credits.

The innovative schemes by banks for disbursement of credit are as follows:
(i) Overdraft:

• A company having a current account with the bank is allowed an overdraft facility.
• The borrower can withdraw funds/overdraw on his current account up to the credit limit sanctioned by the bank.
• Any number of drawings up to the sanctioned limit is allowed for a stipulated term period.
• Interest is determined/calculated on the basis of the actual amount overdrawn.
• Repayments can be made during the time period.

(ii) Cash Credit:

• The borrower can withdraw the amount from his cash credit up to a stipulated/granted limit based on security margin.
• Cash credit is given against pledge or hypothecation of goods or by providing alternate securities.
• Interest is charged on the outstanding amount borrowed and not on the credit limit sanctioned.

(iii) Cash Loans:

• In this, the total amount of the loan is credited by the bank to the borrower’s account.
• Interest is payable on the actual outstanding balance.

(iv) Discounting bills of exchange:

• In the bill of exchange, the drawer of the bill (seller) receives money from the drawee (buyer) on the date or after the due date (the term mentioned in the bill).
• But due to discounting facility the drawer can receive money before the due date by discounting the bill with the bank (by giving the bill as security to the bank).
• The bank gives money to the drawer less than the face value of the bill (amount mentioned in the bill) after deducting a certain amount known as discounting charges.
• The bills are usually traded bills i.e. outcome of trade transactions.
• The bills are accepted by the banks and cash is advanced against them.

Question 5.
State the features of bonds.
Answer:
Definition:
According to Webster Dictionary, “a bond is an interest bearing certificate issued by a Government or business firm promising to pay the holder a specific sum at a specified date”.
A bond is thus-

• A formal contract to repay borrowed money with interest.
• Interest is payable at a fixed internal or on the maturity of the bond.
• A bond is a loan.
• The holder is a lender to the company.
• He gets a fixed rate of interest.

Features:
(i) Nature of finance:

• It is debt or loan finance.
• It provides long-term finance of 5 years, 10 years, 25 years, 50 years.

(ii) Status of investor:

• The bondholders are creditors.
• They are non-owners and hence, not entitled to participate in the general meetings.
• The bondholder has no right to vote.

(iii) Return on bonds:

• The bondholders get a fixed rate of interest.
• It is payable on maturity or at a regular interval.
• Interest is paid to the bondholder at a fixed rate.

(iv) Repayment:

• A bond is a formal contract to repay borrowed money.
• Bonds have a specific maturity date, on which the principal amount is repaid.

6. Justify the following statements:

Question 1.
Equity shareholders are real owners and controllers of the company.
Answer:

• They do not have special preferential rights as to dividends or returns of capital in the event of the winding-up of the company.
• They are joint owners and thus, have ownership rights.
• They have the right to participate in the management of the company and to vote on every resolution in the meetings thus, having exclusive voting rights.
• They use the right to vote to appoint directors, amend Memorandum of Association, Articles of Association, can remove directors appoint bankers, etc.
• Their shares bear ultimate risks associated with ownership.
• Thus, it is rightly said, that the equity shareholders are real owners and controllers of the company.

Question 2.
Preference Shares do not carry normal voting rights.
Answer:

• Preference shares enjoy priority or preference over equity shareholders as regards payment of dividends and repayment of capital.
• They carry a fixed rate of dividend.
• They do not take much risk as they are cautious investors.
• They attend class meetings if they have any problem affecting their interests or dividend is not paid to them for two or more consecutive years.
• As they do not take risks, they do not attend general meetings or take part in the management nor vote at the meetings.
• Thus, it is rightly said, that the preference shares do not carry voting rights.

Question 3.
The debenture is secured by a charge on assets of the company.
Answer:

• A debenture is a document that grants lenders a charge over a company’s assets giving them a means of collecting debt if a default occurs.
• The charges may be floating or fixed.
• A specific property is pledged as security.
• In case the debenture is not redeemed or exercised, the lenders can recover the cost by selling the fixed assets.
• Thus, it is rightly said, that the debenture is secured by a charge on assets of the company.

Question 4.
Retained earnings are the simple and cheapest method of raising finance.
Answer:

• Retained earnings is an internal source of financing used by established companies.
• Retained earnings is a kept aside profit by the company instead of distributing all the dividends to the shareholders.
• The accumulated profits are re-invested by the companies by issuing bonus shares.
• It does not create a charge on assets, nor dilute the shareholdings.
• Thus, it is rightly said, that the retained earnings also known as ploughing back of profit/capitalization of reserves/self-financing are the simple and cheapest methods of raising finance.

Question 5.
Public deposit is a good source of short-term financing.
Answer:

• Deposits can be accepted by the general public by public limited companies and not private limited companies.
• Deposits are accepted from the general public for a short term i.e. minimum 6 months and a maximum of 36 months or a 3-year term.
• The amount so raised is used for short-term financial requirements.
• The time of deposit is predetermined in advance and paid after the expiry of such period as per terms and conditions agreed.
• The depositors form the general public not necessarily equity shareholders.
• The administrative cost of deposits of the company is lower than that involved in the issue of shares and debentures.
• The rate of interest payable is lower than other loans. Thus, it is rightly said, that the public deposit is a good source for meeting short-term requirements.

Question 6.
The bondholder is a creditor of the company.
Answer:

• A bond is a debt security which the company borrows for long-term finance and issues certificates under its seal as acknowledgment.
• The owners get interested as a return on their investment which is decided and fixed at the time of issue.
• The interest payable to bondholders is a fixed charge and a direct expenditure.
• It has to be paid whether the company makes a profit or not.
• As the bondholders are creditors they do not have the right to attend meetings or participate in management.
• Thus, it is rightly said, that the bondholder is a creditor of the company.

Question 7.
Trade credit is not a cash loan.
Answer:

• Trade credit is a business-to-business agreement wherein there is an arrangement to purchase goods and services on credit and pays at a later date and not immediately.
• The credit period extends up to a month.
• Discount is given if the same is paid earlier.
• It is an interest-free loan given by one businessman to another.
• It does not involve loan formalities but only a trade transaction. Hence, not a cash loan.
• Thus, it is rightly said, that the trade credit is not a cash loan.

Question 8.
Different investors have different preferences.
Answer:

• Investors make different decisions and have different risk preferences when getting gains and losses.
• Educated ones may opt for capital markets as compared to others who may invest in gold or silver.
• Cautious investors are ready to have steady income rather than fluctuations.
• Risk-takers are ready to face the ups and downs of their invested money and on their returns.
• Active investors try to beat the market while passive track the market index.
• Thus, it is rightly said, that the different investors have different choices and preferences.

Question 9.
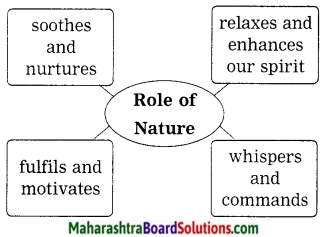
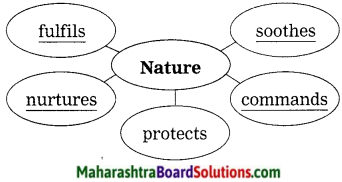
Equity Capital is risk capital.
Answer:

• Equity shareholders have a claim over residual proceeds of the company.
• In the event of winding up, they are the last to be paid off after setting the claims of creditors and external liabilities.
• They have fluctuating returns and risk of fluctuating market value.
• Equity capital is permanent capital and not refunded during the lifetime of the company.
• Not having any assurance as regards dividend, repayment of capital Equity Capital becomes risk capital.
• Thus, it is rightly said, that equity capital is risk capital.

7. Answer the following questions.

Question 1.
What are a share and state its features?
Answer:

• The term share is defined by section 2(84) of the Companies Act 2013 ‘Share means a share in the share capital of a company and includes stock.’ The capital of a company is divided into a large number of shares.
• It facilitates the public to subscribe to the company’s capital in smaller amounts.
• The share is thus, an indivisible unit of share capital.
• It is a unit by which the share capital is divided.
• The total capital is divided into small parts and each such part is called a share.
• The value of each part/unit is known as face value.
• A person can purchase any number of shares as and when he or she desires.
• A person who purchases shares of the company is known as a shareholder of the company.
• Generally, companies issue equity shares and preference shares in the market.

Features of shares:
(i) Meaning:

• Share is the smallest unit in the total share capital of a company.
• The total share capital of a company is divided into small parts and each part is called a share.

(ii) Ownership:

• A share shows the ownership of the shareholder.
• The owner of the share is called a shareholder.

(iii) Distinctive number:

• Unless dematerialized, each share has a distinct number, which is noted in the share certificate.
• A share has a distinct number for identification.

(iv) Evidence of title:

• The company issues a share certificate under its common seal.
• It is a document of title of ownership of the share.
• A share is not a visible thing.
• It is shown by share certificate or in the form of ‘Demat share’

(v) Value of a share:

• Each share has a value expressed in terms of money.
• Face value: This value is written on the share certificate and mentioned in the Memorandum of Association.
• Issue Value: It is the price at which a company sells its shares. At par – equal to face value; At premium – more than the face value; At discount – Less than the face value.

(vi) Rights:

• A share confers/gives certain rights to the shareholders.
• Rights such as the right to receive dividends, right to inspect statutory books, right to attend shareholders’ meetings, right to vote in meetings, etc. (group rights), and right to receive notice, circulars, dividends, bonus shares, rights issue, etc. (individual rights).

(vii) Income:

• A shareholder is entitled to get a share in the net profit of the company.
• It is called a dividend.

(viii) Transferability:

• The shares of the public Ltd. company are freely transferable as per the rules laid down in the Articles of Association.
• Shares of a private company cannot be transferred.

(ix) Property of shareholder:

• A share is a movable property of a member.
• It can be transferred (gifted, sold) or transmitted (passed on to the legal heir after/due to death, insolvency or insanity of a member).

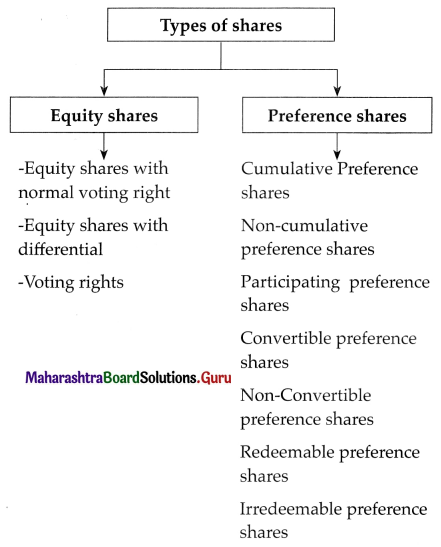
(x) Kinds of shares:

• A company issues two types of shares depending upon the right to control, income and risk.
• Equity shares – which do not carry preferential right to receive dividend or repayment of capital when the company winds up its activities.
• Preference shares – which carry preferential rights as regards dividend and repayment of capital in the event of winding up of the company.

Question 2.
What is an equity share? Explain its features.
Answer:

• Equity shares are the fundamental and basic source of financing activities of the business.
• Equity shares are also known as ordinary shares.
• Indian Companies Act 1956 defines equity shares as those shares which do not preference shares.
• The equity shares do not enjoy a preference in getting dividends.

Features of equity shares:
(i) Permanent Capital:

• Equity shares are irredeemable shares. It is permanent capital.
• The amount received from equity shares is not refunded by the company during its lifetime.
• Equity shares become redeemable/refundable only in the event of the winding-up of the company or the company decides to buy back shares.
• Equity shareholders provide long-term and permanent capital to the company.

(ii) Fluctuating dividend:

• Equity shares do not have a fixed rate of dividend.
• The rate of dividend depends upon the amount of profit earned by the company.
• If a company earns more profit, the dividend is paid at a higher rate.
• If there is insufficient profit, the Board of Directors may postpone the payment of dividends.
• The shareholders cannot compel them to declare and pay the dividend.
• The dividend is thus, always uncertain and fluctuating.
• The income of equity shares is uncertain and irregular.

(iii) Rights:

• Equity shareholders enjoy certain rights.
• Right to share in profit when distributed as dividend.
• Right to vote by which they elect Directors, amend Memorandum, Articles, etc.
• Right to inspect books of account of their company.
• Right to transfer shares.
• Participation in management.
• Enjoy Right Issue and Bonus Issue.

(iv) No preferential right:

• Equity shareholders do not enjoy preferential rights in respect to the payment of dividends.
• They are paid dividends only after the dividend is paid to preference shareholders.
• At the time of winding up, they are the last claimants. They are paid last after all the other claims are settled.

(v) Controlling power:

• The control of a company vests in the hands of equity shareholders.
• They are often described as real masters of the company as they enjoy exclusive voting rights.
• Equity shareholders may exercise their voting right by proxies, without attending the meeting in person.
• The Act provides the right to cast vote in proportion to the number of shareholdings.
• They participate in the management of the company.
• They elect their representatives called the Board of Directors for management of the company.

(vi) Risk:

• Equity shareholders bear maximum risk in the company.
• They are described as ‘shock absorbers when the company is in a financial crisis.
• The rate of dividend falls if the income of the company falls.
• The market value of shares goes down resulting in capital loss.

(vii) Residual claimants:

• A residual claim means the last claim on the earnings of the company.
• Equity shareholders are owners and they are residual claimants to all earnings after expenses, taxes, dividends, interests are paid.
• Even though equity shareholders are the last claimants, they have the advantage of receiving the entire earnings that are leftover.

(viii) No charge on assets:

• The equity share does not create any charge over the assets of the company.
• There is no security/guarantee of capital invested being returned.

(ix) Bonus issue:

• Bonus shares are issued as gifts to equity shareholders.
• They are issued ‘free of cost’.
• These shares are issued out of accumulated profits.
• These shares are issued to existing equity shareholders in a certain ratio or proportion of their existing shareholdings.
• Capital investment of equity shareholders grows on its own.
• This facility is available only to equity shareholders.

(x) Rights issue:

• Equity shareholders get the benefit of rights issues.
• When a company raises further capital by issue of shares, the existing shareholders are given priority to get newly offered shares, known as a rights issue.

(xi) Face value:

• The face value of equity share is very less.
• It can be ₹ 10 per share or even ₹ 1/- per share

(xii) Market value:

• Market value fluctuates, according to the demand and supply of shares.
• The demand and supply of equity shares depend on profits earned and dividends declared.
• When a company earns huge profits, the market value of shares increases.
• When it incurs a loss, the market value of shares decreases.
• There are frequent fluctuations in the market value of shares in comparison to other securities.
• Equity shares are more appealing to speculators.

(xiii) Capital Appreciation:

• Share capital appreciation takes place when the market value of share increases in the share market.
• The profitability and prosperity of a company enhance the reputation of the company in the share market and thus, facilitates appreciation of the market value of equity shares.

Question 3.
Define preference shares/What are preference shares? What are the different types of preference shares?
Answer:

• These shares have certain privileges and preferential rights such as to payment of dividends, return of capital, etc.
• Preference Share has which fixed rate of dividend is prescribed at the time of issue.
• The preference shareholders are co-owners but not controllers.
• They are cautious investors as they are interested in the safety of the investment.

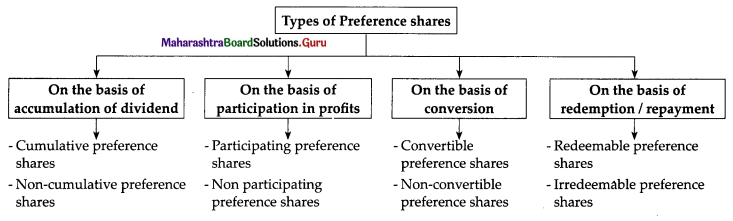
(i) Cumulative Preference Shares:

• Cumulative preference shares are those shares on which dividend accumulates until it is fully paid.
• That is if the dividend is not paid in one or more years due to inadequate profit, then such unpaid dividend gets accumulated and is carried forward till next year.
• The accumulated dividend is paid when the company performs well.
• The arrears of dividends are paid before making payment to equity shareholders.
• The preference shares are always cumulative unless otherwise stated in Articles of Association.

(ii) Non-Cumulative Preference Shares:

• The dividend on these shares does not accumulate.
• That is the dividend on shares can be paid only out of profits of that particular year.
• The right to claim dividends will lapse if the company does not make a profit in that particular year.
• If the dividend is not paid in a year, it is lost.

(iii) Participating Preference Shares:

• The holders of these shares are entitled to participate in surplus profit besides preferential dividends. They participate in the high-profit condition of the company.
• Surplus profit here means excess profit that remains after making payment of dividends to equity shareholders.
• Such surplus profit up to a certain limit is distributed to preference shareholders.

(iv) Non-Participating Preference Shares:

• The preference shares are deemed to be non-participating if there is no clear provision in Articles of Association regarding participation in surplus profit.
• Such shareholders are entitled to receive a fixed rate of a dividend prescribed in the issue.

(v) Convertible Preference Shares:

• These shares have a right to convert their preference shares into equity shares.
• The conversion takes place within a certain agreed fixed period.

(vi) Non-Convertible Preference Shares:

• These shares are not converted into equity shares.
• They will remain as preference shares forever till paid back.

(vii) Redeemable Preference Shares:

• Shares that can be redeemed after a certain fixed period are called redeemable preference shares.
• A company limited by shares if authorized by Articles of Association issues redeemable preference shares.
• Such shares must be fully paid.
• The shares are redeemed out of divisible profit or out of the fresh issue of shares made for this purpose.

(viii) Irredeemable Preference Shares:

• Shares which are not redeemable are payable only on winding up of the company and are called irredeemable preference shares.
• As per section 55(1) of the Companies Act 2013, the company cannot issue irredeemable preference shares in India.
• Thus, are the types of preference shares.

Question 4.
What are preference shares? State its features.
Answer:

• The shares which carry preferential rights are termed preference shares.
• These shares have certain privileges and preferential rights such as payment of dividend, return of capital, etc.
• The preference shareholders are co-owners but not controllers.
• They are cautious investors as they are interested in the safety of the investment.
• They prefer a steady rate of returns on investment.

Features of preference shares:
(i) Preference for dividend:

• They have the first charge on the distributable amount of annual profits.
• The dividend is payable to preference shareholders before anything else is paid to equity shares, but after the settlement of dues of debentures, bonds and loans.

(ii) Prior repayment of capital:

• Preference shareholders have a preference over equity shareholders in respect of return of capital when the company is liquidated.
• It saves preference shareholders from capital losses.

(iii) Fixed return:

• These shares carry dividends at a fixed rate.
• The rate of dividend is predetermined at the time of issue.
• It may be in the form of a fixed sum or may be calculated at a fixed rate.
• The preference shareholders are entitled to dividends which can be paid only out of profit.
• Though the rate of dividend is fixed, the director in the financial crisis of the company may decide that no dividend be paid if there are no profits, the preference shareholders would have no claims for the dividend.

(iv) Nature of capital:

• Preference share capital is safe capital as the rate of dividend and market value do not fluctuate.
• Preference shares do not provide permanent share capital.
• They are redeemed after a certain period of time.
• It is generally issued at a later stage when a company gets established business.
• They are used to satisfy the need for additional capital of the company.

(v) Market value:

• The market value of preference shares does not change as the rate of dividend payable to them is fixed.
• The capital appreciation is considered to be low as compared with equity shares.

(vi) Voting right:

• The preference shares do not have normal voting rights.
• They have voting rights in matters that affect their interests – change of rights in terms of repayment of capital, or dividend payable to them are in arrears for two or more years.

(vii) Risk:

• Cautious investors generally purchase preference shares.
• Safety of capital and fixed return on investment are advantages attached with preference shares.
• These shares are a boon for shareholders during the depression when the interest rate is continuously falling.

(viii) Face value:

• The face value of preference shares is relatively higher than equity shares.
• They are normally issued at a face value of ₹ 100/-

(ix) Right or Bonus issue:

• Preference shareholders are not entitled to bonus or rights issues.
• It can be issued to the equity shares only.

(x) Nature of investor:

• Preference shares attract a moderate type of investors.
• Investors who are conservative, cautious, interested in the safety of capital, expect a steady rate of returns on investment purchase preference shares.

Question 5.
What is Debenture/Define Debenture. Discuss the different types of Debentures.
Answer:

• Debentures are one of the main sources of raising debt capital for meeting long-term and medium-term financial needs.
• Debentures represent borrowed capital.
• A person who purchased debenture is called a debenture holder.
• The holders get a fixed rate of interest as a return on their investment.
• The Board of Directors has the power to issue debentures.

Definitions:
Topham defines: “A debenture is a document given by a company as evidence of debt to the holder, usually arising out of the loan and most commonly secured by the charge.”

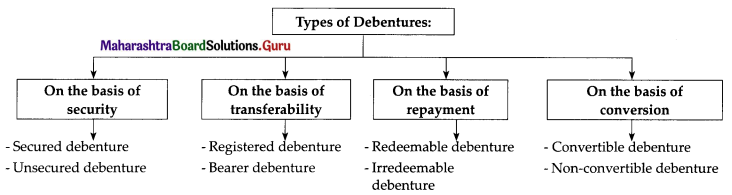
They are as follows:
(i) Secured Debentures:

• The debentures can be secured.
• The property of a company is charged as security for the loan.
• The security may be for some particular asset (fixed charge) or it may be the asset in general (floating charge).
• The debentures are secured through ‘Trust Deed’.

(ii) Unsecured Debentures:

• These debentures do not have security.
• The issue of unsecured debentures is prohibited by the Companies Act, 2013.

(iii) Registered Debentures:

• They are the ones whose details are mentioned in the Register of debenture maintained by the company.
• The details include the name, address, particulars of
• The transfer of such debentures requires the execution of regular transfer deeds.
• Interest is paid through Dividend warrants.

(iv) Bearer Debentures:

• The details of the debentures are not recorded in the register of the debenture.
• Their names do not appear in the Register of Debenture Holders.
• Such debentures are transferred by mere delivery.
• Payment of interest is made by means of coupons attached to the debentures certificate.

(v) Redeemable Debentures:

• Debentures are mostly redeemable i.e. payable at the end of some fixed period, mentioned on the Debentures Certificate.
• Repayment may be made at a fixed date, at the end of a specific period, or six installments during the lifetime of the company.
• The provision of repayment is normally made in Trust Deed.

(vi) Irredeemable Debentures:

• These debentures are not repayable during the lifetime of the company.
• They are repayable only on liquidation of the company or when there is a breach of any condition or in contingencies.

(vii) Convertible Debentures:

• These debentures give the right to the holder to convert the debentures into equity shares after a specific period.
  the period of conversion is mentioned in the debenture certificate.
• The issue must be approved by a special resolution in the general meeting before they are issued to the public.
• A Convertible debentures holder is hence entitled to equity shares at a rate lower than the market value after which he can participate in the profits and meetings of the company.

(viii) Non-Convertible Debentures:

• These are not convertible into equity shares on maturity.
• They are normally redeemed on the maturity date.
• There is no appreciation in their value which acts as a disadvantage.

Question 6.
Define Debenture/What is a debenture? Explain the features of debenture?
Answer:

• A debenture is one of the main sources of raising debt capital for meeting long-term and medium-term financial needs.
• Debentures represent borrowed capital.
• A person who purchases debenture is called a debenture holder.
• The holders get a fixed rate of interest as a return on their investment.
• The Board of Directors has the power to issue debentures.

Definitions:
Topham defines: “A debenture is a document given by a company as evidence of debt to the holder, usually arising out of the loan and most commonly secured by the charge.”
A debenture is evidence of indebtedness.

Features of Debenture:
(i) Written Promise:

• A debenture is a written promise by a company that it owes a specified sum of money to the holder of the debenture.

(ii) Face Value:

• The face value of debenture normally carries a high denomination.
• It is ₹ 100 or multiples of ₹ 100.

(iii) Time of payment:

• A debenture is issued with the due date stated in the Debenture Certificate.
• It provides for repayment of the principal amount on the maturity date.

(iv) Priority of Payment:

• Debenture holders have a priority in repayment of their capital over other claimants of the company.
• The amounts of debentures are settled before shareholders.

(v) Assurance of repayment:

• Debenture constitutes a long-term debt.
• They carry an assurance of repayment on the due date.

(vi) Terms of issue and redemption of Debenture:

• Debenture can be issued at par, premium, and even at discount.
• Its redemption takes place only at par and premium.

(vii) Authority to issue:
Board of Directors has the authority/power to issue debenture as per Companies Act 2013 Section 179(3).

(viii) Interest:

• A fixed-rate of interest is agreed upon and is paid periodically.
• The rate of interest that a company pays/offers depends upon the market conditions and nature of the business.
• Payment of interest is a liability of the company. It has to be paid whether the company makes a profit or not.

(ix) Parties to Debenture:

• Company: This is an entity that borrows money.
• Trustees: The company has to appoint Debenture Trust if it is offering debenture to more than 500 people.
• Trust is a party through whom the company deals with debenture holders and enters into an agreement known as Trust Deed.
• Trust Deed contains obligations of the company rights of debenture holders, power of trustees, etc.
• Debenture holders: They are the parties who provide loans to the company and receive a ‘Debenture Certificate’ as evidence.

(x) Status of debenture holder:

• The debenture holder is a creditor of the company.
• Debenture being loan taken by the company interest is payable on it at a fixed interval and fixed-rate till redeemed/paid.
• They cannot participate in the management of the company.

(xi) No Voting Right:

• According to sec. 71 (2) of Companies Act 2013, no company shall issue debenture carrying voting rights.
• Debenture holders do not have the right to vote in the general meetings of the company.

(xii) Security:

• Debenture can be secured with some property of the company by fixed or floating charge.
• Debenture holders can sell of charged property of the company and recover their money if the company is not in a position to make payment of interest or repayment of capital.

(xiii) Issuers:

• Debenture can be issued by both, private as well as public limited companies.

(xiv) Listing:

• A debenture must be listed with at least one recognized stock exchange.

(xv) Transferability:

• Debentures can be easily transferred through instruments of transfer.

Maharashtra State Board 12th Std Secretarial Practice Textbook Solutions

• Introduction to Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Sources of Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Issue of Shares Class 12 Secretarial Practice Textbook Solutions
• Issue of Debentures Class 12 Secretarial Practice Textbook Solutions
• Deposits Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Members Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Debentureholders Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Depositors Class 12 Secretarial Practice Textbook Solutions
• Depository System Class 12 Secretarial Practice Textbook Solutions
• Dividend and Interest Class 12 Secretarial Practice Textbook Solutions
• Financial Market Class 12 Secretarial Practice Textbook Solutions
• Stock Exchange Class 12 Secretarial Practice Textbook Solutions

Introduction to Corporate Finance 12th Secretarial Practice Chapter 1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 1 Introduction to Corporate Finance Textbook Exercise Questions and Answers.

Class 12 Secretarial Practice Chapter 1 Exercise Solutions

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
_____________ is related to money and money management.
(a) Production
(b) Marketing
(c) Finance
Answer:
(c) Finance

Question 2.
Finance is the management of _____________ affairs of the company.
(a) monetary
(b) marketing
(c) production
Answer:
(a) monetary

Question 3.
Corporation finance deals with the acquisition and use of _____________ by business corporation.
(a) goods
(b) capital
(c) land
Answer:
(b) capital

Question 4.
Company has to pay _____________ to government.
(a) taxes
(b) dividend
(c) interest
Answer:
(a) taxes

Question 5.
_____________ refers to any kind of fixed assets.
(a) Authorised capital
(b) Issued capital
(c) Fixed capital
Answer:
(c) Fixed capital

Question 6.
_____________ refers to the excess of current assets over current liabilities.
(a) Working capital
(b) Paid-up capital
(c) Subscribed capital
Answer:
(a) Working capital

Question 7.
Manufacturing industries have to invest _____________ amount of funds to acquire fixed assets.
(a) huge
(b) less
(c) minimal
Answer:
(a) huge

Question 8.
When the population is increasing at a high rate, certain manufacturers find this as an opportunity to _____________ business.
(a) close
(b) expand
(c) contract
Answer:
(b) expand

Question 9.
The sum of all _____________ is gross working capital.
(a) expenses
(b) current assets
(c) current liabilities
Answer:
(b) current assets

Question 10.
_____________ means mix up of various sources of funds in desired proportion.
(a) Capital budgeting
(b) Capital structure
(c) Capital goods
Answer:
(b) Capital structure

1B. Match the pairs:

Question 1.

Answer:

Group ‘A’	Group ‘B’
(a) Capital budgeting	(6) Investment decision
(b) Fixed capital	(5) Fixed assets
(c) Working capital	(1) Sum of current assets
(d) Capital structure	(9) Mix up various sources of funds
(e) Corporate finance	(2) Deals with acquisition and use of capital

1C. Write a word or term or a phrase that can substitute each of the following statements:

Question 1.
A key determinant of the success of any business function.
Answer:
Finance

Question 2.
The decision of the finance manager ensures that the firm is well-capitalized.
Answer:
Financing decision

Question 3.
The decision of the finance manager to deploy the funds in a systematic manner.
Answer:
Investment decision

Question 4.
Capital is needed to acquire fixed assets that are used for a longer period of time.
Answer:
Fixed capital

Question 5.
The sum of current assets.
Answer:
Gross working capital

Question 6.
The excess of current assets over current liabilities.
Answer:
Networking capital

Question 7.
The process of converting raw material into finished goods.
Answer:
Production cycle

Question 8.
The boom and recession cycle in the economy.
Answer:
Economic Trend

Question 9.
The ratio of different sources of funds in the total capital.
Answer:
Capital Structure

Question 10.
The internal source of financing.
Answer:
Retained earnings

1D. State whether the following statements are True or False:

Question 1.
Finance is related to money and money management.
Answer:
True

Question 2.
The business firm gives a green signal to the project only when it is profitable.
Answer:
True

Question 3.
Corporate finance brings coordination between various business activities.
Answer:
True

Question 4.
Fixed capital is also referred as circulating capital.
Answer:
False

Question 5.
Working capital stays in the business almost permanently.
Answer:
False

Question 6.
The business will require huge funds if assets are acquired on a lease basis.
Answer:
False

Question 7.
The business dealing in luxurious products will require a huge amount of working capital.
Answer:
True

Question 8.
A firm with large-scale operations will require more working capital.
Answer:
True

Question 9.
Liberal credit policy creates a problem of bad debt.
Answer:
True

Question 10.
Financial institutions and banks cater to the working capital requirement of the business.
Answer:
True

1E. Find the odd one.

Question 1.
Land and Building, Plant and Machinery, Cash.
Answer:
Cash

Question 2.
Debenture Capital, Equity Share Capital, Preference Share Capital.
Answer:
Debenture Capital

Question 3.
Fixed Capital, Capital Structure, Working Capital.
Answer:
Capital Structure

1F. Complete the sentences.

Question 1.
Initial planning of capital requirement is made by _____________
Answer:
entrepreneur

Question 2.
When there is boom in economy, sales will _____________
Answer:
increase

Question 3.
The process of converting raw material into finished goods is called _____________
Answer:
production cycle

Question 4.
During recession period sales will _____________
Answer:
decrease

1G. Select the correct option from the bracket.

Question 1.

(To have the right amount of capital, deploy funds in a systematic manner, fixed capital, working capital, capital structure, carry dividend at a fixed rate)
Answer:

Group ‘A’	Group ‘B’
(a) Financing decision	(1) To have the right amount of capital
(b) Fixed capital	(2) Longer period of time
(c) Investment decision	(3) Deploy funds in a systematic manner
(d) Working capital	(4) Circulating capital
(e) Combination of various sources of funds	(5) capital structure

1H. Answer in one sentence.

Question 1.
Define corporate finance.
Answer:
Corporate finance deals with the raising and using of finance by a corporation.

Question 2.
What is fixed capital?
Answer:
Fixed capital is the capital that is used for buying fixed assets that are used for a longer period of time in the business eg. Capital for plant and machinery etc.

Question 3.
What is working capital?/Define working capital.
Answer:
Working capital is the capital that is used to carry out day-to-day business activities and takes into consideration all current assets of the company.
Eg: for building up inventories.

Question 4.
What is the production cycle?
Answer:
The process of converting raw material into finished goods is called the production cycle.

Question 5.
Define capital structure.
Answer:
Capital structure means to mix up various sources of funds in the desired proportion. To decide capital structure means to decide upon the ratio of different types of capital.

1I. Correct the underlined word and rewrite the following sentences.

Question 1.
Finance is needed to pay dividends to debenture holders.
Answer:
Finance is needed to pay interest to debenture holders.

Question 2.
When there is a recession in the economy sales will increase.
Answer:
When there is a boom in the economy sales will increase.

Question 3.
Share is an acknowledgment of a loan raised by the company.
Answer:
A debenture is an acknowledgment of a loan raised by a company.

Question 4.
Equity shares carry dividends at a fixed rate.
Answer:
Preference shares carry dividends at a fixed rate.

2. Explain the following terms/concepts.

Question 1.
Financing decision
Answer:
A financing decision is a right decision that is made by a finance manager of any corporation ensuring that the firm is well capitalized with the right combination of debt and equity, having access to multiple choices of sources of financing.

Question 2.
Investment decision
Answer:
Investment decisions mean capital budgeting i.e. finding investments and deploying them successfully in the business for greater profits.

Question 3.
Fixed capital
Answer:
Fixed capital is the capital that is used for buying fixed assets that are used for a longer period of time in the business. These assets are not meant for. resale. Examples of fixed capital are capital used for purchasing land and building, furniture, plant, and machinery, etc.

Question 4.
Working Capital
Answer:
Working capital is the capital that is used to carry out day-to-day business activities. It takes into consideration all current assets, of the company. It also refers to ‘Gross Working Capital’.
Examples of working capital are

• for building up inventories.
• for financing receivables.
• for covering day-to-day operating expenses.

3. Study the following case/situation and express your opinion.

1. The management of ‘Maharashtra State Road Transport Corporation’ wants to determine the size of working capital.

Question (a).
Being a public utility service provider will it need less working capital or more?
Answer:
MSRTC being a public utility service provider will need less working capital because of a continuous flow of cash from there, customers thus liabilities are taken care of.

Question (b).
Being a public utility service provider, will it need more fixed capital?
Answer:
Being a public utility service provider MSRTC will need a huge amount of funds to acquire fixed assets thus it will need more fixed capital.

Question (c).
Give one example of a public utility service that you come across on a day-to-day basis.
Answer:
The Indian Railways.

2. A company is planning to enhance its production capacity and is evaluating the possibility of purchasing new machinery whose cost is ₹ 2 crore or has alternative of machinery available on a lease basis.

Question (a).
What type of asset is machinery?
Answer:
Machinery is a Fixed Asset.
A fixed asset may be held for 5, 10 or 20 years and more. But if assets are acquired on a lease or rental basis, then less amount of funds for fixed assets will be needed for business.

Question (b).
Capital used for the purchase of machinery is fixed capital or working capital.
Answer:
Capital used for the purchase of machinery is fixed capital.

Question (c).
Does the size of a business determine the fixed capital requirement?
Answer:
Yes. Where a business firm is set up to carry on large-scale operations, its fixed capital requirements are likely to be high.

4. Distinguish between the following.

Question 1.
Fixed Capital and Working Capital
Answer:

Points	Fixed Capital	Working Capital
1. Meaning	Fixed capital refers to any kind of physical asset, a portion of total capital that is invested in fixed assets.	Working capital refers to the sum of current assets or gross working capital.
2. Nature	It stays in the business almost permanently.	Working capital is circulatory capital. It keeps changing.
3. Purpose	It is invested in fixed assets such as land, building, equipment, etc.	Working capital is invested in short-term assets such as cash, account receivable, inventory, etc.
4. Sources	Fixed capital funding can come from selling shares, debentures, bonds, long-term loans, etc.	Working capital can be funded with short-term loans, deposits, trade credit, etc.
5. Objectives of investors	Investors invest money in fixed capital hoping to make a future profit.	Investors invest money in working capital for getting immediate returns.
6. Risk	Investment in fixed capital implies more risk.	Investment in working capital is less risky. Eg. Land, building, plant and machinery
7. Decisions	Decisions relating to fixed capital investment are generally made by top-level management. Eg. Cash, bills receivable, inventories, cash at the bank	Decisions relating to working capital needs are generally made by middle-level or lower-level management.

5. Answer in brief:

Question 1.
Define capital structure and state its components.
Answer:
Definition: R.H. Wessel “The long term sources of funds employed in a business enterprise.”
John H. Hampton “A firm’s capital structure is the relation between the debt and equity securities that make up the firm’s financing of its assets.” Thus, the term capital structure means security mix. It refers to the proportion of different securities raised by a firm for long-term finance.

Components/Parts of Capital Structure:
There are four basic components of capital structure. They are as follows:
(i) Equity Share Capital:

• It is the basic source of financing activities of the business. Equity share capital is provided by equity shareholders.
• They buy equity shares and help a business firm to raise necessary funds. They bear the ultimate risk associated with ownership.
• Equity shares carry dividends at a fluctuating rate depending upon profit.

(ii) Preference Share Capital:

• Preference shares carry preferential rights as to payment of dividends and have priority over equity shares for return of capital when the company is liquidated.
• These shares carry dividends at a fixed rate.
• They enjoy limited voting rights.

(iii) Retained earnings:

• It is an internal source of financing.
• It is nothing but ploughing back of profit.

(iv) Borrowed capital: It comprises of the following:

• Debentures: A debenture is an acknowledgment of a loan raised by the company. The company has to pay interest at an agreed rate.
• Term Loan: Term loans are provided by the bank and other financial institutions. They carry fixed rate of interest.

Question 2.
State any four factors affecting fixed capital requirements?
Answer:
(i) Nature of business:

• The nature of business certainly plays a role in determining fixed capital requirements. They need to invest a huge amount of money in fixed assets.
• e.g. Rail, road, and other public utility services have large fixed investments.
• Their working capital requirements are nominal because they supply services and not the product.
• They deal in cash sales only.

(ii) Size of business:
The size of a business also affects fixed capital needs. A general rule applies that the bigger the business, the higher the need for fixed capital. The size of the firm, either in terms of its assets or sales, affects the need for fixed capital.

(iii) Scope of business:
Some business firms that manufacture the entire range of their production would require a huge investment in fixed capital. However, those companies that are labour intensive and who do not use the latest technology may require less fixed capital and vice versa.

(iv) Extent of lease or rent:
Companies who take their assets on a lease basis or on a rental basis will require less amount of funds for fixed assets. On the other side, firms that purchase assets will naturally require more fixed capital in the initial stages.

Question 3.
What are Corporate Finance and State’s two decisions which are basic of corporate finance?
OR
Write short note on Corporate Finance
Answer:
Corporate finance deals with the raising and using of finance by a corporation. It includes various financial activities like capital structuring and making investment decisions, financial planning, capital formation, and foreign capital, etc. Even financial organisations and banks play a vital role in corporate financing.

Henry Hoagland expresses, “Corporate Finance deals primarily with the acquisition and use of capital by the business corporation”.

Following two decisions are the basis of corporate finances:
(i) Financing decision:
Every business firm must carefully estimate its capital needs i.e. working capital and fixed capital. The firm needs to mobilize funds from the right sources also maintaining the right combination of debt capital and equity capital. For this balance, a company may go for or raise equity capital or even opt for borrowed funds by way of debentures, public deposits term loans, etc. to raise funds.

(ii) Investment decision:
Once the capital needs are accessed, the finance manager needs to take correct decisions regarding the use of the funds in a systematic manner, productively, using effective cost control measures to generate high profits. Finding investments through proper decisions and using them successfully in business is called ‘capital budgeting

6. Justify the following statements.

Question 1.
The firm has multiple choices of sources of financing.
Answer:

• Business firms require finance in terms of working capital and fixed capital.
• Funds are required at different stages of business.
• The company can raise funds from various sources i.e. from internal and external sources.
• Internal sources could be cash inflows on sales turnover, income from investments, and retained earnings.
• External sources can be obtained for short-term requirements through cash credit, overdraft trade credit, discounting bills of Exchange issues of commercial paper, etc.
• For long-term needs, a firm can meet its financing needs through the issue of shares, debentures, bonds, public deposits, etc. Thus, it is rightly said that the firm has multiple choices of sources of financing.

Question 2.
There are various factors affecting the requirements of fixed capital.
Answer:

• Fixed capital being long-term capital is required for the development and expansion of the company.
• The nature and size of a business have a great impact on fixed capital. Manufacturing businesses require huge fixed capital whereas trading organizations like retailers require less fixed capital.
• Methods of acquiring assets on rentals or on a lease/installment basis will require less amount of fixed assets.
• If fixed assets are available at low prices and concessional rates then it would reduce the need for investment in fixed assets.
• International conditions and economic trends like a boom period will require high investment in fixed assets and a recession will lead to less requirement.
• Similarly, consumer preferences, competition, and highly demanded goods and services will require a large amount of fixed capital. E.g. Mobile phones. Thus, it is rightly said that there are various factors affecting the requirements of fixed capital.

Question 3.
Fixed capital stays in the business almost permanently.
Answer:
Factors determining fixed capital requirements are:

• Fixed capital refers to capital invested for acquiring fixed assets.
• These assets are not meant for resale.
• Fixed capital is capital used for purchasing land and building, furniture, plant, and machinery, etc.
• Such cap al is usually required at the time of the establishment of a new company.
• Existing companies may also need such capital for their expansion and development, replacement of equipment, etc.
• Modern industrial processes require the increased use of heavy automated machinery. Thus, it is rightly said that fixed capital stays in the business almost permanently.

Question 4.
Capital structure is composed of owned funds and borrowed funds.
Answer:

• Capital structure means to mix up of various sources of funds in desired proportions.
• To decide capital structures means to decide upon the ratio of different types of capital.
• A firm’s capital structure is the relation between the debt and equity securities that make up the firm’s financing of its assets.
• The capital structure is composed of own funds which include share capital, free serves, and surplus, and borrowed funds which represent debentures, bank loans, and long-term loans provided by financial institutions.
• Thus capital structure = Equity share capital + preference share capital + reserves + debentures.
• Thus, it is rightly said that capital structure is composed of owned funds and borrowed funds.

Question 5.
There are various factors affecting the requirement of working capital.
Answer:

• The nature and size of a business affect the requirement of working capital. Trading or merchandising firms and big retail enterprises need a large amount of capital compared to small firms which need a small amount of working capital.
• If the period of the production cycle is longer then the firm needs more amount of working capital. If the manufacturing cycle is short, it requires less working capital.
• During the boom period sales will increase leading to increased investment in stocks, thus requiring additional working capital and during the recession, it is vice versa.
• Along with the expansion and growth of the firm or company in terms of sales and fixed assets, the requirement of working capital increases.
• If there is proper coordination, communication, and co-operation between production and sales departments then the requirement of working capital is less.
• A liberal credit policy increases the possibility of bad debts and in such cases, the requirement of working capital is high, whereas a firm making cash sales requires less working capital.

7. Answer the following questions.

Question 1.
Discuss the importance of Corporate Finance?
Answer:
Corporate finance deals with the raising and utilizing of finance by a corporation. It also deals with capital structuring and making investment decisions, financial planning of capital, and the money market. The finance manager should ensure that:
The firm has adequate finance and it’s being utilized effectively;
Generate minimum return for its owners.

The importance of Corporate Finance are as follows:
(i) Helps in decision making:
Most important decisions of business enterprises are made on the basis of availability of funds, as without finance any function of business enterprise is difficult to be performed independently. Obtaining the funds from the right sources at a lower cost and productive utilization of funds would lead to higher profits. Thus corporate finance plays a significant role in the decision-making process.

(ii) Helps in raising capital for a project:
A new business venture needs to raise capital. Business firms can raise funds by issuing shares, debentures, bonds or even by taking loans from the banks.

(iii) Helps in Research and Development
Research and Development need to be undertaken by firms for growth and expansion of business and to enjoy a competitive advantage. Research and development mostly involve lengthy and detailed technical work for the execution of projects. Through surveys and market analysis etc. companies may have to upgrade old products or develop new products to face competition and attract consumers. Thus the availability of adequate finance helps to generate high efficiency.

(iv) Helps in the smooth running of the business firm:
A smooth flow of corporate finance is important to pay the salaries of employees on time, pay loans, and purchase the required raw materials. At the same time finance is needed for sales promotion of existing products and more so for the launch of new products effectively.

(v) Brings co-ordination between various activities:
Corporate finance plays a significant role in the coordination and control of all activities in an organization. Production activity requires adequate finance for the purchase of raw materials and meeting other day-to-day financial requirements for the smooth running of the production unit. If the production increases, sales will also increase by contributing the income of the concern and profit to increase.

(vi) Promotes expansion and diversification:
Corporate finance provides money for the purchase of modern machines and sophisticated technology. Modern machines and technology help to improve the performance of the firm in terms of profits. It also helps the firm to expand and diversify the business.

(vii) Managing risk:
Companies have to manage several risks such as sudden fall in sales, loss due to natural calamity, loss due to workers strikes, change in government policies, etc. Financial aids help in such situations to manage such risks.

(viii) Replace old assets:
Assets like plants and machinery have become old and outdated over the years. Finance is required to purchase new assets or replace the old assets with new assets having new technology and features.

(ix) Payment of dividend and interest:
Finance is needed to pay the dividend to shareholders, interest to creditors, bank, etc.

(x) Payment of taxes/fees:
The company has to pay taxes to the government such as Income tax, Goods and Service Tax (GST), and fees to the Registrar of Companies on various occasions. Finance is needed for paying these taxes and fees.

Question 2.
Discuss the factors determining working capital requirements?
Answer:
Working Capital = Current Assets – Current Liabilities.
In other words, it is also called ‘Circulating Capital’. Also, refer to ‘GROSS WORKING CAPITAL.’ Management needs to determine the size of working capital with reference to the economic environment and other aspects within the business firm.

Factors determining/influencing working capital requirements are as follows:
(i) Nature of Business:
The working capital requirements are highly influenced by the nature of the business. Trading/ merchandising forms concerned with the distribution of goods require a huge amount of working capital to maintain a large stock of the variety of goods to meet customers’ demands are extend credit facilities to attract them. Whereas public utility concerns have to maintain small working capital because of a continuous flow of cash from their customers.

(ii) Size of business:
The size of a business also affects the requirements of working capital. Size of the firm refers to the scale of operation i.e. a firm with large scale operations will require more working capital and vice versa.

(iii) Volume of Sales:
The volume of sales and the size of the working capital have a direct relationship with each other. If the volume of sales increases there is an increase in the amount of working capital.

(iv) Production cycle:
The process of converting raw material into finished goods is called the ‘production cycle’. If the production cycle period is longer, the firm needs more amount of working capital. If the manufacturing cycle is short, it requires less working capital.

(v) Business cycle:
When there is a boom in the economy, sales will increase resulting in to increase in investment in stock. This will require additional working capital. During a recession period, sales will decline and consequently, the need for working capital will also decrease.

(vi) Terms of purchases and sales:
If credit terms of purchase are favourable and terms of sales are less liberal, then the requirement of cash will be less. Thus, the working capital requirement will be reduced.
A firm that enjoys more credit facilities needs less working capital. On the other hand, if a firm does not get proper credit for purchases and adopts a liberal credit policy for sales if requires more working capital.

(vii) Credit Control:
Credit control includes the factors such as volume of credit sales, the terms of credit sales, the collection policy etc. A firm with a good credit control policy will have more cash flow reducing the working capital requirement. Whereas if the firm’s credit policy is liberal there would be more requirements of the working capital.

(viii) Growth and Expansion:
Those firms which are growing and expanding at a rapid pace need more working capital compared to those firms which are stable in their growth.

(ix) Management ability:
The requirement of working capital is reduced if there is proper coordination in the production and distribution of goods. A firm stocking on heavy inventory calls for a higher level of working capital.

(x) External factors:
If the financial institutions and banks provide funds to the firm as and when required, the need for working capital is reduced.

Maharashtra State Board 12th Std Secretarial Practice Textbook Solutions

• Introduction to Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Sources of Corporate Finance Class 12 Secretarial Practice Textbook Solutions
• Issue of Shares Class 12 Secretarial Practice Textbook Solutions
• Issue of Debentures Class 12 Secretarial Practice Textbook Solutions
• Deposits Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Members Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Debentureholders Class 12 Secretarial Practice Textbook Solutions
• Correspondence with Depositors Class 12 Secretarial Practice Textbook Solutions
• Depository System Class 12 Secretarial Practice Textbook Solutions
• Dividend and Interest Class 12 Secretarial Practice Textbook Solutions
• Financial Market Class 12 Secretarial Practice Textbook Solutions
• Stock Exchange Class 12 Secretarial Practice Textbook Solutions

Class 10 English Chapter 3.5 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 3.5 The Alchemy of Nature Notes, Textbook Exercise Important Questions and Answers.

The Alchemy of Nature Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 3.5 The Alchemy of Nature Textbook Questions and Answers

Warming up:
Chit-chat:

1. Divide the class into five groups. Discuss in the group the following topics. (One question for each group.)

Question (a)
Seeds regenerate from another seed.
Answer:
Regeneration is the renewal of germplasm accessions by sowing seeds which will possess the same characteristics as the original population.

Question (b)
Plants and flowers wilt and become one with the other.
Answer:
Wilting is the loss of rigidity of non- woody parts of plants if they do not get water to thrive and soil is too dry.

Question (c)
Cacti (-Pidgd ) thrive in the desert region.
Answer:
Cacti (plural of cactus) lack leaves, instead they have spines which help preventing the loss of water and mineral content in the desert plants.

Question (d)
Bare nature turns green in spring.
Answer:
As temperatures warm and days get longer, forest ecosystem begins the transition from winter to spring.

Question (e)
Caterpillar turns into butterfly.
Answer:
It is truly a fantastic mechanism developed by nature. For a caterpillar to turn into a butterfly, it digests itself using enzymes triggered by hormones.
(Each group will present their discussion in front of the class.)

2. Role of Nature:

Question 1.
Role of Nature:
Discuss in pairs, the role played by nature and complete the web-diagram.

Answer:

3. Look at the following things. Discuss with your friend, what you learn from them.

Question 1.
Look at the following things. Discuss with your friend, what you learn from them.
(a) A bee …………………..
(b) An eagle ……………….
(c) A creeper ……………..
(d) The river ………………
(e) Rainfall ………………..
(f) Sun ………………………
Answer:
(a) A bee – teamwork and hard work
(b) An eagle – a strong vision/far-sightedness
(c) A creeper – perseverance
(d) The river – go with the flow/to face calamities
(e) Rainfall – dedication
(f) Sunlight up the lives of others/to give light and energy to others.

English Workshop:

1. Go through the text again and complete the web that highlights the various features of flower of ‘hibiscus’ plant. One is done for you.

Question 1.
Go through the text again and complete the web that highlights the various features of flower of ‘hibiscus’ plant. One is done for you.

Answer:

2. The writer explains the contrast features of ‘water’ and ‘rock’ in the text. Write all the features of both water and rock in the given table:

Question 1.
The writer explains the contrast features of ‘water’ and ‘rock’ in the text. Write all the features of both water and rock in the given table:

Answer:

Water	Rock
gentle	hard
command	gives in (humble)
flows over stone (perseverance)	takes the shape that water commands (obedient)

3. Impossible itself says ‘I M possible’. Do you agree? Justify your answer by citing some examples from the text and some that you have experienced or heard from someone.

Question 1.
Impossible itself says ‘I M possible’. Do you agree? Justify your answer by citing some examples from the text and some that you have experienced or heard from someone.
Answer:
Yes I agree, it is possible to do the most difficult of things, provided we have the will and conviction to do so. We can clearly know this from the passage. The bits of grass, the tree in the winter and the tiny ants, etc. are the examples from the passage.

The example that comes to my mind as justification is that of Sudha Chandran, the dancer. Though her leg was amputated below the knee, with great grit and determination, she restarted dancing and went on to become a famous dancer and actress. This shows that one can do things which seem to be impossible.

4. Find synonyms from the text for the following words/phrases.

Question 1.
Find synonyms from the text for the following words/phrases.
Answer:

1. a strong feeling of fear or respect – awe
2. to direct authoritatively – command
3. to peer through – peep
4. large and impressively beautiful – majestic
5. easily broken or damaged – delicate

5. How can you prove this maxim to be incorrect-’Too many cooks spoil the broth.’ Write a counterview on the given topic. (clue-teamwork)

Question 1.
How can you prove this maxim to be incorrect-’Too many cooks spoil the broth.’ Write a counterview on the given topic. (clue-teamwork)
Answer:
The maxim says when there are too many people involved in trying to do the same thing, the final result will not be good. But I believe that the teamwork is always good. We all know that unity is strength and it is of great value in every walk of life. If we come together and work, definitely our strength gets increased.

When there are a lot of people working on a project, then that project may not be completed to such a high standard because an individual can work better than many. It is the common perception of the people. But I think if a lot of people are working on a project, every one will use his talent, calibre, strength to take that project to higher level. So it will be completed on time with good standard.

Even when many cooks come together and try to make a single dish with their experience in different fields, it will become fantabulous. One dish will be prepared in variety of taste, colour and with varieties of combination. So it never gets spoiled. So I think the maxim too many cooks spoil the broth, is totally wrong in fact it adds flavour to that dish.

6. Make a list of all the words related to the word Ocean:

Question 1.
Make a list of all the words related to the word Ocean:
Answer:
Fishers, fish, salty, saline water, species, different water, high tide, low tide, pacific, gulf, bay, ships, pirates, piracy, warships, cruisers, oceanic currents.

7. The author has very positively described the different things in nature. Add the special features of each one of them:

Question 1.
The author has very positively described the different things in nature. Add the special features of each one of them. Add on the list.

Answer:

Part of Nature	Special feature	Value learnt
1. Water	It gently flows every day and for years.	Keep on working gently for the well-being of the people.
2. Rainbow	Beauty	Add colours to the surroundings, make all happy.
3. Caterpillar	Sacrifice for creating new life.	Changing (turning) for better results.
4. Hibiscus	one day life.	We should live our life to its fullest.
5. Rocks	Though hard, it does not dominate or offer resistance.	Be humble and stay still and endure unpleasant things without complaining.
6. Grass	Evergreen	There is always an opening even when the things seem to be impossible.
7. Tree	Stands firmly in cold winter.	Wait resolutely in difficult times.
8. Ants	Organized	Teamwork and perseverance are always rewarded.
9. The wind	Flow	Make people happy with your activities and passion.
10. Spider webs	Delicate	Be strong in every situation and difficulty.

8. Your friend has his board exam. He studies for 14 hours a day, sitting at one place. Write a letter to him giving him tips to relax and be stress-free.

Question 1.
Your friend has his board exam. He studies for 14 hours a day, sitting at one place. Write a letter to him giving him tips to relax and be stress free.
Answer:
Vikas Shinde
16, Malhar Sankul,
Hadapsar,
Pune,
12th Jan., 2021.

Dear Mahesh,

I received a call from aunty telling about your preparations for forthcoming board examinations. I am shocked to hear that you study for 14 to 15 hours a day sitting at one place. I don’t understand how do you bear it?

You might have heard about “All work and no play makes Jack a dull boy.” It means without time off from work a person becomes both bored and dull. I know the board’s exams are around the corner, but if you work as usual with your tension, anxiety and pressure, it is going to be harmful to your health. Our body is not a machine. It needs some rest. It’s my advice to you to take some rest after certain l intervals. Watch T.V. for sometime, listen to music to refresh your mind, chat with your family members and friends, play with your friends. It will refresh your mind.

Take a break after 2-3 hours and give essential time to your mind and body. It will be good for you. I know you are a scholar and always get good marks in exam. But it doesn’t mean that you should ignore your health. Health is wealth. So concentrate on it, too. Hope you will try to understand what I mean to say and follow my tips rigorously.

Convey my regards to uncle and aunt and love to little Riya. Be in touch on mobile.

Your loving friend,
Vikas

9. You have an Environment Protection Week to be celebrated in your school. You have invited an environmentalist. You have to interview him/her about how to save environment. Frame about 10-12 questions for the interview.

Question 1.
You have an Environment Protection Week to be celebrated in your school. You have invited an environmentalist. You have to interview him/her about how to save environment. Frame about 10-12 questions for the interview.
Answer:
Good morning Sir/Madam. Happy to see you here in our school. I welcome you on behalf of our school.

1. Will you please tell us about your work in this field?
2. Were you really interested in this field from the beginning?
3. As an environmentalist, when did you start your work? What exactly do you do?
4. What do you think about diminishing percentage of trees and forest?
5. What is your ‘end of the world prediction’, If we don’t keep global temperature below 1.5°C?
6. What do you think the Government should do?
7. What will you tell the people who do not believe in widely discussed climate change?
8. Being a citizen of our country, what do you expect from every citizen about this intense problem?
9. If there’s one thing that everyone could do today to help protect the environment, what would that be?
10. What advice would you give to young generation at this moment?

10. Write a news report on ‘Environment Day’ celebrated in your school.

Question 1.
Write a news report on ‘Environment Day’ celebrated in your school.
Answer:
Environment Day Celebrations

Nagpur, June 7: ‘World Environment Day’ was celebrated in New Era School with great funfare on June 5. The main purpose of the celebration was to spread awareness among people and students about the need to protect the environment and the ways to do it.

The day was flagged off by a tree plantation drive in the locality. 300 quick-growing trees, which do not need much water on a daily basis, were planted near the school compound wall and in the surrounding area. An eminent environmentalist, Mr. A. T. Ali, spoke on the ways to protect the environment. He also judged the ‘Posters and Photographs’ exhibition organized by the school students and gave away prizes for the best entries.

Environment-friendly articles, like disposable plates and cups made from bamboo and banana stem, bags made from leaf wastes, etc. were on sale. Students gave continuous power-point presentations on the threats to the environment. Last but not the least, was the spirited debate on the topic. ‘Man: The worst enemy of the Environment’.

All in all, the day was a great success, and has certainly made a difference to the way people view our environment.

11. Develop a story with the given ending. Give a suitable title and moral.

Question 1.
Develop a story with the given ending. Give a suitable title and moral.
……………….. and so, Aditi decided to plant more trees.
Answer:
Save trees, save earth

It was the world earth day celebration in Aditi’s school. Aditi was attending it with a least interest as she was not interested in listening to such a boring subject from anybody. She was sitting forcefully for the guest’s lecture with her friends.

The chief guest, who was a renowned environmentalist started with a good slogan based on the earth and emphasised that the earth is the only known planet in this universe where we get all the necessary requisites of life, but the healthy survival is possible for years and years only when we take care and love our earth. Aditi suddenly became curious and started listening with apt attention.

He continued saying “because of the advancement in the life style, industrialization and deforestation; the condition of the earth is deteriorating day by day. It is being full of pollution, global warming and greenhouse gases. There is an urgent need to save our earth because it is the planet where we live. We need to do nothing more in order to maintain the greenery of the earth.

We just need to plant more trees, grow them well, to reduce the pollution level, to maintain the temperature level and to save our mother planet. We should understand our responsibility towards our mother earth and the future of the next generations. As they would not survive on this earth if there will not be a clean and natural climate.”

Aditi realised it and thought a lot and decided to take a positive step very seriously to save the earth. She thought seriously over the solution and that was planting more and more trees. She decided to create awareness among the people as well. She told everyone…

Save earth; save life
No earth… No life
No earth, No birth
Plant trees, Save mother earth

She understood that there will be no human beings on this earth if there will be no trees. If we have to save our lives, we have to plant more and more trees. So, Aditi decided to plant many trees after listening to that effective lecture of the chief, guest.

12. Just for laughs!

Question 1.
Divide the class into two groups : On 12 to 15 slips of paper, Group A writes 12 to 15 conditional clauses beginning with ‘if’.
(For example: If I work hard, I shall have a pizza. (Group B write 12 to 15 main clauses)
Now one student from Group ‘A’ reads the first conditional clause (possibility) and one student from Group ‘B’ reads the first main clause. It forms crazy sentences, just for laughter and fun. Enjoy.
Answer:

Group ‘A’	Group ‘B’
1. If I read a book,	my mother will shout at me.
2. If I do not study hard,	I will become the chief minister.
3. If you do not come to school,	teacher will come to your home.
4. If she gets a new mobile	she will run away from her home.
5. If the boys get freedom in the class,	they will keep silence in the class.

Language Study

Question 1.
Match the pairs of antonyms:

Answer:

1. gentle × hard
2. impossible × possible
3. colossal × small
4. short × long
5. difficult × easy
6. delicate × strong

Question 2.
Complete the table:

Answer:

Noun	Verb	Adjectives	Adverb
strongness, strength	strengthen	strong	strongly
passion	×	passionate	passionately
change	change	changeable	×
organization	organize	organizational	organizationally

Live English

Be a Netizen

Question (a)
Read the extract and underline the words which suggest that emails are fast, cheap and an easy communication tool.
Answer:
Email stands for electronic mail. Slowly and gradually email has replaced the old postal mails or snail mails. Having an email address is like having a postal address in a global village of internet. If you do not have one, you do not exist in today’s virtual world.

The reasons for popularity of emails are many. Emails can be achieved, saved, retrieved. Email is eco-friendly as people rarely take printouts of the mails. The main reason is its ease of access as anybody can access it on phone at the cost of cheap internet, anytime, anywhere.

Email writing is easy but it’s different from writing text messages. Text message is informal and rapid sharing of thoughts between two acquaintances. Emails are written and read by professionals, however, both arrive in inbox.

Like a citizen has his own home address, let’s sign up for the email and be a netizen. There are many free email service providers like Google, Yahoo, Outlook, Rediff, icloud, etc.

Question (b)
Follow these five simple steps to write an effective email. Click Compose to start writing email.
Answer:
Steps for Writing a Formal E-Mail:
1. Begin with a greeting.
Example: ‘Dear Sunil”, “Dear Sir/Madam”
2. Thank the recipient.
If you are replying, say Thank you for contacting”, If you got a reply, say Thank you for your prompt reply”
3. State your purpose.
For new email, begin by saying “I am writing in reference to..”
4. Add your closing remarks.
Example: Thank You for…”, I look forward to hearing from you.”
5. End with a closing.
Example: “Best Regards, Sincerely, Thanks and Regards etc.,”

Steps for sending an email:

Question 1.
Steps for sending an email:
1. Write proper mail ID in ‘To’
2. Use a short and accurate ‘subject’ line.
3. Click ‘Send’ button to send the email.
Answer:
1. Log in to your gmail account so that you are on the dashboard (main page) of your mail account.
2. Click ‘Compose’.
3. A new blank email window will open up in the
‘To’ box, type in the email address of the recipient.
4. Write the ‘Subject’.
5. Type your message in the main body field of your email.
6. Click the ‘Send’ button at the bottom of the composed window.
7. You will receive a message i.e. ‘Sent mail’.

Question (c)
Read the following sample email formats and prepare your own.
Sample Email formats
Answer:

My English Coursebook 10th Digest Chapter 3.5 The Alchemy of Nature Additional Important Questions and Answers

Simple Factual Activities:

Question 1.
Complete the following web: (Answers are directly given.)
Answer:

Question 2.
State whether the following are True or False:
Answer:

1. On the rocky beach the writer found rocks curved and sculpted by the water – True
2. When we listen to the Nature, it leaves us in complete awe. – True
3. We should not live our life to its fullest. – False
4. The water was shaped by the rocks. – False

Question 3.
Choose the correct alternatives and complete the following sentences :
(Answers are directly given and underlined.)
Answer:
1. In the cold winter month, the tree was bare of all leaves.
(a) full
(b) withdrew
(c) bare
(d) short

2. We find innumerable stars in the infinite sky.
(a) clouds
(b) crowds
(c) stars
(d) moons.

3. There is always an opening even in impossible things.
(a) opening
(b) closing
(c) enjoying
(d) singing

4. Water without hint of ego, changes its form according to the dictates of the sun and the wind.
(a) the earth
(b) the sun
(c) the moon
(d) the horizon.

Question 4.
State who/what:
Answer:

1. Colours the entire sky. – Rainbow
2. Takes new shapes with every passing moment, – Clouds
3. Makes trees dance. – The wind
4. Changes its form according to the dictates of the sun and the wind. – Water

Question 5.
State whether you Agree or Disagree with the following statements:
Answer:

1. ‘There is always an opening even in impossible things’-we learn it from small bits of grass. – Agree
2. Our difficult time never changes. – Disagree
3. The team work and perseverance of the ants were impressive. – Agree
4. Clouds take new shapes with every passing moment. – Agree

Complex Factual Activities:

Question 1.
Complete the following sentences: (Answer is directly given.)
Answer:

1. Hibiscus flower smiles with the sun and dances with the wind.
2. ‘However short our life is, we should live to its fullest’ is the lesson we learn from the hibiscus plant.
3. The rock on the beach was curved, sculpted and shaped.
4. The poet William Blake tells us to hold infinity in the palm of our hand and eternity in an hour.

Question 2.
Complete the following web: (Answers are directly given.)
Answer:

Question 3.
Who teaches us that hard times do not 1 last forever? How?
Answer:
Bits of grass peeping through small cracks in concrete pavement and the green leaves on a tree in spring teach us that hard times do not last forever.

The grass is destroyed by the concrete but comes to life again. The tree is bare all through the cold winter months, but when the spring sets in, it is full of leaves, regaining its green majesty.

Question 4.
What are the alchemies of nature mentioned in the extract?
Answer:
The alchemies of nature mentioned in the extract are-

1. Grass peeps through small cracks of a concrete pavement.
2. A rainbow colours the entire sky.
3. Oysters take in a grain of sand they open up with a pearl.
4. Innumerable stars shine across the infinite sky.
5. The wind makes trees dance with unhindered passion.
6. A caterpillar turns into a butterfly.

Activities based on Vocabulary:

Question 1.
Match the pairs of antonyms.
Answer:
1. remember × forget
2. persist × quit

Question 2.
Find out synonyms from the text for the following words/phrases:
Answer:
1. mysterious power – alchemy
2. drag with great efforts – lugging

Question 3.
Frame meaningful sentences by using the given words:
1. impressive
2. passion
Answer:
1.The show put up by the street children was really impressive.
2. One could see the passion and emotion in the artist’s work.

Question 4.
Find from the passage the antonyms of:
Answer:

1. weak × strong
2. easy × difficult
3. hot × cold
4. unimpressive × impressive

Activities based on Contextual Grammar:

1. Frame Wh-questions to get the underlined parts as answers:

Question 1.
The flower comes to life only for a day.
Answer:
How long does the flower come to life?

Question 2.
We saw the spread of the majestic ocean.
Answer:
What did we see of the majestic ocean?

Use ‘not only……….but also’.

Question 1.
Outdoor activities enhance and relax our well-being.
Answer:
Outdoor activities not only enhance but also relax our well-being.

Question 2.
Nature whispers and commands.
Answer:
Nature not only whispers but also commands.

Personal Response:

Question 1.
Explain the line ‘Nature whispers and commands.
Answer:
Nature is continually enticing us to spend time in her embrace; through the calling of birds, the babbling of brooks and streams, the fragrance of flowers and the whispers of trees as the wind blows through their branches. It commands us not to go against it otherwise it will curse us.

Question 2.
The rock is hard but is it dominating? Give reason for your answer.
Answer:
Even though the rock is hard, it is not dominating. I think water is stronger than rocks. It wears down the hard rock by its gentle patience, persistence and perseverance. Rock takes the shape that water commands. It shows that it is not dominating like water whereas it is ready to accept any change.

Question 3.
How can learning from nature help human beings?
Answer:

1. Limitless sky with trillions of galaxies reminds us how insignificant we humans are in this vast universe.
2. Water always flows from high to low in the same way knowledge should be transferred from the learned to ignorant.
3. Trees provide shade selflessly to everyone, we should be selfless in our life too.
4. Nature does not hurry; yet everything is accomplished.
5. Trees stand deeply rooted in the ground even though seasons change. We should face any difficulty in our life with patience.

Question 4.
‘Nature is our best teacher’ – Explain.
OR
According to the writer we learn many things from the nature. Do you agree with this sentence? Support your answer.
Answer:
Nature is a great teacher. No wonder our ancestors used to look up to nature to understand about life itself. The things like the sun, moon, trees, rivers, etc. all were treated as divine beings. We learn a lot from them and they teach us a lot about how to live happy life. Divinity exists in all aspects of life. When we are aware of ourselves, we become aware of God in everything big or small. We then learn to live life well and become complete. So Nature is always treated as our best teacher.

Do as directed:

Question 1.
Complete the words by using correct letters:

1. d a _ c e
2. s h _ p e
3. f r u _ t
4. b i _ d s

Answer:

1. d a n c e
2. s h a p e
3. f r u i t
4. b i r d s

Question 2.
Put the words in alphabetical order:
1. splendour, colossal, alchemy, frail
2. consistent, caterpillar, command, complete.
Answer:
1. alchemy, colossal, frail, splendour.
2. caterpillar, command, complete, consistent

Question 3.
Punctuate the following sentences :
1. I asked my teachers why is he working outside
2. he asked me is the world so poor that it cannot give me a toy and a book, instead of forcing me to take a gun or a tool
Answer:
1. I asked my teachers, “Why is he working outside?”
2. He asked me, “Is the world so poor that it cannot give me a toy and a book, instead of forcing me to take a gun or a tool?”

Question 4.
Make four words each (minimum 3 letters) using the letters in the given word: “perseverance”
Answer:

1. reserve
2. presence
3. peer
4. seven

Question 5.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Question 6.
Complete the word-chain of ‘Nouns’. Add four words, each beginning with the last letter of ‘ the previous word:
Pavement, → t……….., ……….., ……….., ………..
Answer:
Pavement, → treasure, editor, roughness, sheep.

1. Attempt anyone:

Question (a)
Make a meaningful sentence by using the phrase: ‘in full splendour’
Answer:
The morning sun appeared in the sky, in its full splendour.

OR

Question (b)
Add a clause to expand the following sentence meaningfully: we saw a small tree …………….
Answer:
We saw a small tree which was full of flowers and fruits.

2. Attempt anyone:

Question (a)
Add prefix or suffix to make new words.
1. continue
2. pleasant
Answer:
1. discontinue, continuous
2. unpleasant, pleasantly

OR

Question (b)
Make a meaningful sentence using any one of the following words:
1. continue
2. pleasant
Answer:
1. This exhibition will continue till the end of this month.
2. The pleasant atmosphere in the morning attracts many birds.

Question 3.
Do as directed:
We saw an army of ants. (Choose the correct sentence of passive voice.)
(a) An army of ants was seen by us.
(b) An army of ants were seen by us
(c) An army of ants is seen by us.
(d) An army of ants are seen by us.
Answer:
(a) An army of ants was seen by us.

Question 4.
We touch it. (Rewrite the sentence in ‘Past Perfect Tense.)
Answer:
We had touched it.

Question 5.
Identify the tenses:
Answer:

1. We saw an army of ants – Simple Past Tense
2. We experience the alchemy of nature – Simple Present Tense
3. It will not remain so for ever – Simple Future Tense
4. Ants were lugging a fly. – Past Continuous Tense

My English Coursebook Standard Ten Digest Answers Pdf Unit 3

• If … Class 10 English Solutions
• A Lesson in Life from a Beggar Class 10 English Solutions
• Stopping by Woods on a Snowy Evening Class 10 English Solutions
• Let us March! Class 10 English Solutions
• The Alchemy of Nature Class 10 English Solutions

Class 10 English Chapter 1.4 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 1.4 Be SMART Notes, Textbook Exercise Important Questions and Answers.

Be SMART Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 1.4 Be SMART Textbook Questions and Answers

Warming up!

Chit-chat:

1. Planning your career is not an easy task. But we can reduce the distress by making a proper choice. If we do, what we love to do, the journey becomes smooth and leads to success.
The following diagram shows important factors to be considered while choosing a career. Discuss in your group, which factors you regard as important ones.

2. An Acroslic is a form of writing where the first letters in each of the lines form another word.
For example FRIEND

Prepare on your own such acrostics for-

• Your dearest family member
• Name of your best friend
• A quality or feeling
• Any profession

Question 1.
Prepare your own such acrostics for:
Your favourite family member.
Name of your best friend.
A quality or feeling.
Any profession.
Answer:
1. Best friend: TEJAL
True
Efficient
Jolly
Ambitious
Loving

2. Quality: Smart
Sober
Mannerly
Active
Radiant
Talented

3. Say whether the underlined words in the following sentences are used as a Noun or Verb or Adjective.

Question 1.
(a) I walk to school everyday. (………….)
(b) I go for a walk everyday. (………….)
(c) They gave me a gift everyday. (………….)
(d) You can gift her a story book. (………….)
(e) It was sold as a gift pack. (………….)
(f) They bought a new house on 10th street. (………….)
(g) The water – tanks leak a lot. (………….)
(h) The old-age home houses loo aging and homeless people. (………….)
Answer:
(a) I walk to school everyday. – Verb
(b) I go for a walk everyday – Noun
(e) They gave me a gift everyday – Noun
(d) You can gift her a story book – Verb
(e) It was sold as a gift pack – Adjective
(f) They bought a new house on 10th street – Noun
(g) The water-tanks leak a lot – Verb
(h) The old-age home houses 100 aging and homeless people. – Verb

English Workshop:

1. Complete the following web with the words associated with the passage and the given title :

Question 1.
Complete the following web with the words associated with the passage and the given title

Answer:

2. (A) Pick out examples from the text that support each of the following facts :

Question a.
Goals should be achievable.
Answer:
Example: We can’t become a President, a Prime Minister, but we can hope to hold the office of an important social worker and deliver results.

Question b.
A time-limit should be set to achieve goals.
Answer:
Example: To reduce weight we know how to go about it. But without consistent time-bound action, it never becomes a reality. It may be exercise, diet and stress-free thoughts. All these have to be practised and implemented within a deadline.

Question c.
A specific field/area has to be fixed to achieve goals.
Answer:
Example: If it is building a house, what exactly is the capacity required and how long can it stretch?

Question d.
Good results depend upon the quality and quantity of work put in.
Answer:
Example: Life is like a trumpet. If we don’t put anything in, we can’t get anything out.

Question e.
A benchmark is needed to track progress.
Answer:
Example: While playing football, a player’s exact role and position has to be clearly defined.

3. Complete the following sentences.

Question 1.
Complete the following sentences
(a) SMART goals are …………….
(b) Two valuable assets of setting goals are …………
Answer:
(a) SMART goals are a methodology of thinking I that helps people reach success.
(b) Two valuable assets of setting goals are-a ! sense of originality and a stepping stone to illuminate the path.

4. Read this quote.
‘If we don’t put anything in, we can’t get anything out.’ Guess the meaning. Discuss in pairs and find similar quotes that bring in the same meaning.
Question 1.
‘If we don’t put anything in, we can’t get anything out.’ Guess the meaning. Discuss in pairs and find similar quotes that bring in the same meaning.
(a) You reap as you sow
(b) Input is equal to output
(c) …………………………….
(d) …………………………….
(e) …………………………….
Answer:
(a) As you sow, so shall you reap.
(b) Input is equal to output.
(c) No pains, no gains.
(d) Nothing ventures, nothing have.
(e) The longer you work, the more you get.
(f) Well begun is half done.

5. Drafting a Speech. Discuss in groups each block and make notes about it.

Question 1.
Drafting a Speech. Discuss in groups each block and make notes about it.

Answer:
Do it yourself.

6. Speech development
(A) Content
(a) Greeting and introduction of the topic
(b) Exposition of main theme/clarity of message/organised thoughts and ideas.
(c) Moral and practical application with examples.
(d) Conclusion

(B) Speaking Presentation
(a) Verbal clarity – pronunciation of words, voice modulation and projection.
(b) Presentation/Speaking style – mannerism, audience eye contact, ability to keep the audience engaged.
(c) Confidence – gestures and expressions, stage courage

(C) Useful phrases and vocabulary
(a) It’s pleasure to see you all/I am happy to see you today/It’s good to see you all here.
(b) Today’s topic is ………../My talk is about………….. My topic is …………….
(c) The purpose/aim of this speech. …………
(d) I will focus on one/two/three major issues.
(e) If you have any question, feel free to ask me.
Answer:
Do it yourself.

7. Dos and Don’ts for delivering a speech. Add some more points.

Answer:

Dos	Don’ts
Talk slowly	Don’t mumble
Emphasize keywords	Don’t look up /down
Be confident	Don’t use too many hand gestures
Maintain a good posture	Don’t keep your speech too lengthy
Make eye contact with the entire audience	Don’t repeat the same words multiple times

8. You are going to participate in interschool elocution competition. The subject given to you is “How to achieve success in life.” Draft a speech to present it, in a competition.

Question 1.
You are going to participate in interschool elocution competition. The subject given to you is “How to achieve success in life.” Draft a speech to present it, in a competition.

Answer:
How to achieve success in life?
Honourable chairperson, respected headmaster, teachers and my dear friends. Today I am going to give my speech on “How to achieve success in life.” I request you to listen to me carefully. So my friends, success is very important in everyone’s life.

Everyone has a dream of becoming a successful human being in life. There is a good saying that, “Success is a journey and not a destination.” How true it is! If we look at the life of all successful people, we realize the truthfulness of the statement. The definition of success is different for every person. For a child, success is to solve a puzzle, for a S.S.C. student, success is to get good marks, for a businessman, success is to get a contract and for grandparents, success is to see the whole family live happily together.

Everyone wants to become rich and successful in life. To achieve ambition, there are many steps which are to be followed. First of all, we have to set our goal, means we have to decide what we are and what we want to be. So proper plan and execution of the plan are very important. The tragedy of life does not lie in not reaching the goal, the tragedy lies in having no goal to reach.

For a great success we need a lot of confidence, patience, knowledge, perseverance and hard work. We should not waste our time because time is money. Don’t compare yourself with any other person in the world. If you do so you are demeaning yourself. The main thing is that we should always think positively and never give up hope. Many of our failures are the people who did not realize how close they were to success when they gave up.

Always remember that the word “Impossible” means, I’m possible and if destiny is accompanied with the three D’s : determination, dedication and devotion, then everything becomes possible. We should learn from our own mistakes. We should always follow in the footsteps of great, successful people. Let’s take an example of Dhirubhai Ambani.

He was born in a poor family, but struggled a lot to achieve his ambition and never gave up hope because he knew that there is always a room at the top. He kept the hope alive in his heart and tried his level best and as you know he became one of the richest industrialists in the world. After all, no gains, without pains.

There is a great saying that successful people do not do different things, they do the things differently. So work hard, continuously. God’s blessings are always there with you. Thank you for listening to me carefully.
Jai Hind.

9. Project Work :
Your goal, this year, is to successfully pass out from secondary school. So let us be SMART and note down the following.
(a) Specific Area :
(Subjects) and number of units/lessons
1. English 4 units
2. ………………..
3. ………………..
4. ………………..
5. ………………..
6. ………………..

(b) Measurable :
Comparison of scores in previous examinations and in recent one.

(c) Achievable goal :
(Target scores/performance in SSC Exams.)
1. Good %
2. ……………
3. ……………
4. ……………
5. ……………
6. ……………

(d) Realisitc approach :
Plan of action that matches with your expertise/resources.
For example :
1. Make a study time table and follow it regularly.
2. ……………………………………………………..
3. ……………………………………………………..
4. ……………………………………………………..
5. ……………………………………………………..

(e) Time-bound Action :
Days required for revision

Answer:
Do it yourself.

Language Study:

Gerund:
When the – ‘ing’ form of a verb is used as a noun, it is known as a gerund a verbal noun. For example, The fighting went on. Here, we see that the – ‘ing’ form of the verb ‘fight’ is used as a subject in ‘The fighting went on’. It does a work of a noun.
Read the following examples of gerunds:

• Gardening is an art.
• Cooking is a science.
• I enjoy reading poems.
• I like reading more than writing.

Rewrite the above sentences using other appropriate gerunds in place of the given here.

Question 1.
Rewrite the above sentences using other appropriate gerunds in place of the given here.
Answer:

1. Painting is an art.
2. Banking is a science.
3. I enjoy acting.
4. I like riding more than swimming.

Infinitives:
Sometimes the form of a verb in a sentence names the action but does not change according to tense, number or person. Such a form is known as a non-finite form or an infinitive. An infinitive is used with or without ‘to’.
Examples: How did people first begin to drink tea? Can you name the beverage?
Underline the infinitive in the following sentences.
It was funny to read words that stood still.
Can I read the book?
To be or not to be – that is the question.

Question 1.
Underline the infinitive in the following sentences :
(The answers are directly given and underlined.)
Answer:

1. It was funny to read words that stood still.
2. Can I read the book?
3. To be or not to be – that is the question.

Finite:

Underline the verbs and choose the correct option from the brackets.

Thus, we see that verb forms show tense, number, etc. Here, the verb form changes according to the subject. A verb form which is decided by and changes according to the subject of the sentence is known as a Iuikite verb.
Example: ‘You are very kind.’ If the subject ‘you’ is changed to ‘she’, the sentence will be ‘She is very kind.’

Now change the verb form according to the change in the subject.

• I don’t know: Change ‘I’ to ‘She’ ……….
• My father knows: Change ‘My father’ to ‘We’ ……….
• I am following in your footsteps: Change ‘I’ to ‘He’ ……….

Underline the gerund/present participles/infinitive.
(a) Setting goal may appear easy, but it is quite challenging.
(b) Quantifying goals provide specific ways to track progress.
(c) It is important to create goals that are within a current skill set or area of expertise.
(d) We need to bring down life images down to earth and plan to execute our strategies.
(e) Finding the right footing, precisely mastering the skills and getting to the next place, all depend on how we approach and tackle the problem.

Classify the following words in their respective columns.
tackle, trumpet, directly, execute, aggressive, natural, absence, exactly, achieve, clearly, imagination, precisely, create, important, expert, specific. of, if, and, oh, from, we, but, it.

Changing word class:

Sometimes, the word class of a word changes without adding any prefix or suffix. For example, ‘run’ is used as a verb. So, ‘verb’ is its word class in ‘I can run faster than him.’ But when ‘run’ is used as a noun, its word class changes. For example, India has to score ten more runs to win the match.’ This is called a change of word class. Look at the following examples. Change of word class from verb to noun :
‘I doubt if I can write as fast as you can’ (verb). I have a doubt about this topic (noun). Similarly : laugh, walk, catch, throw, turn
Change of word class from noun to verb :
‘Remove the potato peels (noun). Peel the potato (verb).
‘She works as a nurse (noun). You have to nurse a patient till he/she recovers (verb).

Change the verb form according to the change in the subject.

• I don’t know: Change ‘I’ to ‘She’ ……….
• My father knows: Change ‘My father’ to ‘We’ ……….
• I am following in your footsteps: Change ‘I’ to ‘He’ ……….

Question 1.
I don’t know. (Change T to ‘She’.)
Answer:
She doesn’t know.

Question 2.
My father knows it. (Change ‘My father’ to ’We)
Answer:
We know it.

Question 3.
I am following in your footsteps.
(Change T to ‘He’)
Answer:
He is following in your footsteps.

Underline the gerund/present participles/infinitive.
(a) Setting goal may appear easy, but it is quite challenging.
(b) Quantifying goals provide specific ways to track progress.
(c) It is important to create goals that are within a current skill set or area of expertise.
(d) We need to bring down life images down to earth and plan to execute our strategies.
(e) Finding the right footing, precisely mastering the skills and getting to the next place, all depend on how we approach and tackle the problem.

Question 1.
Underline the gerund/present participles/infinitive.
(Answers are directly given.)
(a) Setting goal may appear easy, but it is quite challenging.
(b) Quantifying goals provide specific ways to track progress.
(c) It is important to create goals that are within a current skill set or area of expertise.
(d) We need to bring down life images down to earth and plan to execute our strategies.
(e) Finding the right footing, precisely mastering the skills and getting to the next place, all depend on how we approach and tackle the problem.

Classify the following words in their respective columns.

Question 1.
Classify the following words in their respective columns.
(Answers are directly given.)
vision, professional, natural, achieve, originality, 1 simply, failure, absence, expert, specific, easily, thrive, appear, five
Answer:

Nouns	Adjectives	Adverbs	Verbs
vision	natural	simply	achieve
professional	expert	easily	thrive
originality	specific		appear
failure	five
absence

Question 2.
Classify the following words in their respective columns.
(Answers are directly given.)
improvement, exactly, achievement, exact, clearly, important, create, aggressive, skill, help, hope, ability, defensive.
Answer:

Nouns	Adjectives	Adverbs	Verbs
improvement	exact	exactly	create
achievement	important	clearly	help
skill	aggressive		hope
help	defensive
hope
ability

Question 3.
Classify the following words in their respective columns.
(Answers are directly given.)
increase, consistent, imagination, execute, directly, tackle, reach, successful, expertise, unrealistic, reduce, precisely, hesitation, problem, valuable
Answer:

Nouns	Adjectives	Adverbs	Verbs
imagination	consistent	directly	increase
expertise	successful	precisely	execute
hesitation	unrealistic		tackle
problem	valuable		reach
			reduce

Question 4.
Classify the following words in their respective columns.
(Answers are directly given.)
ah, of, if, and, oh, from, we, but, it, hurrah
Answer:

Pronoun	Preposition	Conjunction	Interj­ection
we	of	if	oh
it	from	and	ah
		but	hurrah

My English Coursebook 10th Digest Chapter 1.4 Be SMART Additional Important Questions and Answers

Read the following passage and do the activities :

Simple Factual Activity :

Question 1.
Write whether the following statements are True or False :
Answer:

1. We won’t achieve our goals unless we take action to achieve them. – True
2. We all don’t have natural talents. – False
3. The skill must be stronger than will. – False
4. Goals help to steer a course of life. – True

Question 2.
Write whether the following sentences are True or False : (Board’s Model Activity Sheet)
Answer:

1. Quantifying goals provides specific ways to track progress against goals. – True
2. Setting goals that can’t be completed in the designated period of time. – False
3. It is important to create goals that are within one’s current skill set or area of expertise. – True
4. Being realistic will make it difficult to be successful at attaining goals. – False

Question 3.
Complete the following sentences with the help of the passage :
(Answers are directly given and underlined.)
Answer:

1. Specific goals make it easier to set parameters and work towards the goal.
2. Achievable goals may act like stepping stones to help meeting broader goals.
3. Expecting to become an expert in a short amount of time is unrealistic.

Question 4.
Complete the sentences with the help of the information in the passage :
(Answers are directly given and underlined.)
Answer:

1. For reducing weight, exercise, diet and stress- I free thoughts should be practised and implemented without hesitation.
2. Vision, wishes, intentions and dreams spark off imagination and encourage us to define where we want to reach.
3. The quality and quantity of energy we put forth, directly impact the results.
4. Success is a walk in the dark.

Complex Factual Activities:

Question 1.
Complete the web :
(Answer is directly given.)
Answer:

Question 2.
Complete the sentences using the information from the passage :
(Answers are directly given and underlined.)
Answer:

1. If we use our talent to set our goal in life, we can easily get success in life.
2. One has to decide what one wants to achieve in the end.
3. Setting goals sometimes appear easy but for some it is quite challenging.
4. We shall not achieve our goals if we do not take action to achieve them.

Question 3.
How does quantifying goals help us?
Answer:
Quantifying goals help us to provide detailed and exact ways to track progress against goals. This makes it easy to benchmark performance throughout the goal period, including areas to improve. In the game of football, the player’s exact role and position has to be clearly defined.

Question 4.
What factor is unreal, while setting goals?
Answer:
Expecting to become an expert in a short amount of time is an unreal factor, while setting goals. Building expertise always takes time.

Activities based on Vocabulary:

Question 1.
Find from the passage adjectives for :

1. nature
2. value
3. success
4. ease

Answer:

1. nature – natural
2. value – valuable
3. success – successful
4. ease – easy

Question 2.
Find from the passage adjectives for the following :

1. area
2. period
3. role
4. stones
5. picture

Answer:

1. specific – area
2. goal – period
3. exact – role
4. stepping – stones
5. clear – picture

Question 3.
Cross the odd man out:
(Answers are directly given.)
Answer:

Question 4.
Write from the passage noun forms of the following :
(Answers are directly given.)
Answer:

1. accountable – accountability
2. real – reality
3. imagine – imagination
4. hesitate – hesitation

Question 5.
Write from the passage words related to qualities required for success :
Answer:
accountability, consistent, vision, wish, intention, dream, imagination, execute, energy, skills, approach, strategy.

Activities based on Contextual Grammar :

Question 1.
Underline the gerund /present participles/ infinitives:
(Answers are directly given and underlined.)
Answer:

1. After all, one has to decide what one wants to achieve in the end.
2. If we use that talent to set in our Life, we call easily get success in Life.
3. They help to steer a course of our Life.

Question 2.
Underline the Present Participles/ Infinitives :
(Answers are directly given and underlined.)
Answer:

1. It makes it easier to set parameters.
2. These goals may act like stepping stones to help broader goals.
3. So expecting to become an expert in a short time is unrealistic.
4. Being realistic will make it easy to be successful at attaining goals.
5. You must have the ability to adhere to that picture.

Do as directed:

Question 1.
We all have natural talents,
(Add a question tag.)
Answer:
We all have natural talents, haven’t we?

Question 2.
The will must be stronger than the skill.
(Begin with-The skill must not be and change into positive degree.)
Answer:
The skill must not be as strong as the will.

Question 3.
It is important to create goals.
(Pick out the infinitive)
Answer:
to create.

Question 4.
These goals may act like stepping stones.
(Pick out the present participle)
Answer:
stepping.

Question 5.
Life is like a trumpet. (Frame a Wh-question to get the underlined word as answer.)
Answer:
What is life like?

Question 6.
Establish time parameters around each goal. (Rewrite the sentence beginning with ‘Let’and change the sentence into passive voice.)
Answer:
Let time parameters around each goal be established.

Question 7.
If we don’t put anything in, we can’t get anything out. (Rewrite the sentence using ‘unless’ in the beginning.)
Answer:
Unless we put anything in, we can’t get anything out.

Question 8.
It will help increase focus and accountability.
(Identify the Tense of the sentence.)
Answer:
Simple Future Tense

Question 9.
Complete the words by using correct

1. d r_a m
2. g o_l s
3. s m_r t
4. r i_h t

Answer:

1. dream
2. goals
3. smart
4. right

Question 10.
Put the following words in alphabetical order :
1. situation, some, specific, skill
2. stretch, involve, goal, rubric
Answer:
1. situation, skill, some, specific
2. goal, involve, rubric, stretch

Question 11.
Punctuate the following sentences :
1. Where are you going at this time said raja to smeeta
(2) The servant said what a kind nobleman he is
Answer:
1. “Where are you going at this time?” said Raja to Smeeta.
2. The servant said, “What a kind nobleman he is!”

Question 12.
Make four smaller words each (minimum 3 letters each) using the letters in the word : measurable
Answer:
meal, able, sure, marble

Question 13.
Write related words as shown in the example :
(Answer is directly given and underlined.)
Answer:

Question 14.
Complete the following word-chain based on nouns. Add four words, each beginning with the last letter of the previous word :
Tree → …………. → …………. → …………. → ………….
Answer:
Tree → egg → goat → team → mat.

1. Attempt any one :

a. Make your own meaningful sentence using the phrase ‘down to earth’ :
Answer:
He has achieved many awards but he remains down to earth all the time.
OR
b. Add a clause to the following sentence to expand it meaningfully :
I asked him
Answer:
I asked him if he was ready to come with me.

2. Attempt any one :
a. Add a prefix or suffix to make new words.
1. correct
2. fear
Answer:
1. incorrect
2. fearful/fearless
OR
b. Make meaningful sentence using any one of the following words :
1. correct
2. fear
Answer:
1. Whatever he said was correct.
2. The girl was shaking with fear.

Personal Response :

Question 1.
Do you have a goal in your life? What efforts will you make to achieve it?
Answer:
Yes, I do have decided my goal in my life. I aspire to be a top musician. To achieve my goal I will ‘ keep on trying and going ahead despite difficulties with the help of talent and hard work. I am sure that my faith in God, my perseverance, courage and , positive thinking will lead me to success.

Question 2.
Why do think that your goal should be achievable?
Answer:
I think, I must be very careful about choosing my goal. My goal must be achievable. That should be completed within the set deadline.
I should consider my talent and ability and then go for such a goal which will not remain incomplete and unsuccessful.

Question 3.
Why is it necessary to set our goals realistic?
Answer:
It is important to create goals that are within j your current skills limit. You must be expert in the area you have undertaken. Your approach towards your goal must be realistic and positive. You must have to work hard and know how and when you can | attain the goal.

Question 4.
Do you think, your attitude will change sifter your great success? Explain.
Answer:
No, I don’t think my great success will change my attitude towards the world. I shall be as humble as before. I shall not allow my success to go to my head. I shall be always down to earth. I will never trumpet my achievement and will express my views about my success without sounding boastful. Nothing will change in my life.

Question 5.
‘If we don’t put anything in, we can’t get anything out.’ Explain,
Answer:
When we wish to achieve something we must have to give time and put forth every quality and quantity of our energy. You have to prepare plan and execute it meticulously, concentrating on your goal. We will have to put everything at stake to get fruitful results. Efforts we put in the process wholeheartedly can only give us the output (success) we desire. The more you work in the direction of success, the more benefits you get.

Writing Skill:

Drafting a Speech :

Points: Understand the given topic for the speech – Collect all information from all sources – put your thoughts, ideas clearly, systematically in correct sequence – use good but – simple and impressive language – use slogans, quotes, maxims, proverbs, etc. – give examples to justify your points of view – emphasize your good points – conclude with thanks.

Delivering the Speech : Begin with greetings – introduce the topic – modulate your voice – be bold, straightforward and confident – look straight at the audience – speak slowly but loudly and clearly – avoid odd mannerisms or gestures – impress the audience – end the speech with thanks to audience.

Activities:

Question 1.
Your goal, this year, is to successfully pass from Secondary School to Higher Secondary School. So let us be SMART and note down the following :
(Note : Students should try to fill in their own ideas/information in the tables given on the coursebook pages 27 and 28.)
Points :
(a) Specific area : Note down the subjects and units.
(b) Measurable : Compare the scores of previous tests.
(c) Achievable goal: Set goals/target to be achieved.
(d) Realistic approach : Make action plans to get good marks.
(e) Time-bound Action : Study, Revision-required days

Language Study:

Question 1.
Change of word class from noun to verb :
Answer:
1. Remove the potato peels (noun). Peel the potato (verb).
2. She works as a nurse (noun). You have to nurse a patient till he/she recovers (verb).

My English Coursebook Standard Ten Guide Unit 1

• A Teenager’s Prayer Class 10 English Solutions
• An Encounter of a Special Kind Class 10 English Solutions
• Basketful of Moonlight Class 10 English Solutions
• Be SMART…! Class 10 English Solutions
• His First Flight Class 10 English Solutions

Class 10 English Chapter 2.6 Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 English Solutions My English Coursebook Chapter 2.6 World Heritage Notes, Textbook Exercise Important Questions and Answers.

World Heritage Poem 10th Std Question Answer

My English Coursebook Standard Ten Guide Chapter 2.6 World Heritage Textbook Questions and Answers

Warming up!

Chit-chat:

1. I can talk about the world:
Form groups of 6 to 8 students. Each group should select any one Continent and share the following information about each.
1. Important cities
2. Sight-seeing places of tourist interest
3. Food speciality-cuisine
4. Wild life
5. Different types of region and vegetation.
6. Human life.
Now each group representative from the previously formed groups, should narrate the information to the class, using proper attractive sentences.

Question 1.
I can talk about the world:
Form groups of 6 to 8 students. Each group should select any one Continent and share the following information about each.

1. Important cities
2. Sight-seeing places of tourist interest
3. Food specialty-cuisine
4. Wild life
5. Different types of region and vegetation.
6. Human life.

Now each group representative from the previously formed groups, should narrate the information to the class, using proper attractive sentences.
Answer:
1. Important cities:
Mumbai, Tokyo, Hong Kong, Singapore, Dubai

2. Sight-seeing places of tourist interest:
Taj Mahal, Great Wall of China, Mount Fuji, Burj Khalifa etc.

3. Food speciality-cuisine:
Indian, Chinese, Middle-eastern

4. Wild life:
Tigers are naturally found in India. Panda’s are native to China.

5. Different types of region and vegetation:
Asia is blessed with a variety of regions including mountains, desserts, meadows, oceans etc. Some of the main crops grown in Asia are rice, grains, pulses, spices etc.

6. Human life:
Being the biggest continent in the world, Asia has diverse culture and each region within the continent have their own languages, festivals, religions etc.

2. Prepare a Travel Brochure or leaflet of your native place or any town/historical place/hill station to attract tourist using the points below.

Answer:
Tourist Place: Koihapur
How to reach there?

• Nearest Railway Station: Chhatrapati Shahumaharaj Terminus (Koihapur)
• Nearest Air Port: Chhatrapati Rajaram Maharaj Airport, Kothapur Domestic Airport.
• Nearest Bus Stand: S.T. stand, Koihapur. Local transport is available.

Top five spots to visit: Mahalaxmi Temple, Panhala Fort, Rankala Lake, Maharaja Palace, Chhatrapati Shahumaharaj Museum, Gandharva Resort and Amusement Park.

Special features of these spots:

• Mahalaxmi Temple: Holy seat of Amba Mata.
• Rankala Lake: Famous for its beauty.
• Maharaj Palace: Magnificent structure of Chhatrapati Shahumaharaj’s palace, Indo-British architecture.
• Maharaj Museum: Great collections of historical period.
• Gandharva Resort and Amusement Park: Pleasant and attractive, beautiful site with amusing games.

Mouth-watering /special cuisines: Delightful tasty non-veg food, Pandhara Rassa, Tambda Rassa, Kothapur Misal/Bhel, Mohak lassi,
Davangiri Dosa, etc.

Other nearby sight-seeing spots: Panhala Fort, Kanheri Math, Radhanagari, Wildlife sanctuary.
For Further details contact
Vikas Tours & Travels
Mob.: 98xxxxxx34
email: vikastt@rmail.com

English Workshop:

1. Write the importance of the years given below, with reference to World Heritage Sites.

Question 1.
Write the importance of the years given below, with reference to World Heritage Sites.

Answer:

Year	Importance
1959	UNESCO launched an International campaign to protect temples and artifacts.
1965	White House Conference in United States called for a ‘World Heritage Trust’.
1968	The International Union for Conservation of Nature similar goals and presented them at the United Nations Conference on Human Environment.
1972	The Convention Concerning the Protection of World Cultural and Natural Heritage was adopted by UNESCO’s General Conference.
2009	890 World Heritage Sites were located in 148 countries.

2. Name the following.

Question 1.
(a) The country where Mount Huangshan is situated ……………………
(b) The famous dam in Egypt on River Nile …………………..
(c) The place where the conference based on Human Environment was held …………………..
(d) The country in which the highest number of World Heritage Sites are ……………………
(e) The body which can exclude a site from World Heritage list ……………………
Answer:
(a) The country where Mount Huangshan is situated in – China
(b) The famous dam in Egypt on River Nile – Anwan High Dam
(c) The place where the conference based on Human Environment was held – Stockholm, Sweden.
(d) The country in which the highest number of World Heritage Sites are – Italy
(e) The body which can exclude a site from World Heritage list – World Heritage Committee.

3. Complete the following sentences.

Question 1.
Complete the following sentences.
(a) The World Heritage Sites include ……………….. .
(b) There are around ……………. World Heritage Sites in the world.
(c) The Role of World Heritage Committee is ………………. .
(d) The tenure of World Heritage Committee is ……………… .
(e) We can get more information about World Heritage Sites from its …………………. .
Answer:
(a) The World Heritage Sites include cultural and natural areas.
(b) There are around 890 World Heritage Sites in the world.
(c) The Role of World Heritage Committee is to be responsible for establishing which sites will be listed as a UNESCO World heritage site.
(d) The tenure of World Heritage Committee is six years.
(e) We can get more information about World Heritage Sites from its website at whc.unesco.org.

4. Complete the following Web by giving reasons why World Heritage Sites are in danger.

Question 1.
Complete the following Web by giving reasons why World Heritage Sites are in danger.

Answer:

5. Answer in your own words:

Question a.
What are our duties towards preservation of any historical site?
Answer:
Historical sites like forts, monuments, palaces, etc. are our national heritage. They have stood all the vagaries of time and weather and are on the verge of losing their splendour. It is our duty to preserve them carefully. When you visit these places don’t spoil their beauty and grandeur by scratching, writing and carving names and making them look ugly and dirty. We must renovate them with the help of the residence in the area or NGOs. We should persuade and insist the government to take complete responsibility of preserving them as their foremost duty.

Question b.
Why should we preserve the World Heritage Sites?
Answer:
Our ancestors all over the world have bestowed upon us the spectacular, wonderful monuments, structures and sculptures, etc. They are the wonders of arts and architectures. The whole world feels proud of these ancestral treasures. They remind us of the past glory, art, culture and great, glorious memorials. They will continue to inspire us and give knowledge of patient and prolonged human endeavours such as the Taj Mahal, Ajanta Caves, Pyramids, China’s Great Wall and many other majestic structures. So, we must preserve them with utmost care.

Question c.
What is the role of World Heritage Sites in promoting tourism in any country?
Answer:
The ‘World Heritage Sites’ plays a very important role in promoting tourism in countries like India. The organisation is responsible, with the country’s contribution, for preserving the site and if required restore it, providing funds. If the site retains its original grandeur, splendour and beauty, flocks of passionate tourists from all over the world are sure to visit the site. Naturally, tourism of the site will flourish and it also will provide employment.

6. Read the following duties towards preservation of any historical site and make sentences about each of our duties.

• Obey rules and regulations – Visitors must obey the rules and regulations, displayed at the Entrance.
• Maintain discipline and order
• Maintain cleanliness
• Use dustbins and garbage bags
• Observe silence
• Maintain environmental safety
• Protect our country’s history/heritage.

Question 1.
Read the following duties towards preservation of any historical site and make sentences about each of our duties.

• Obey rules and regulations – Visitors must obey the rules and regulations, displayed at the Entrance.
• Maintain discipline and order
• Maintain cleanliness
• Use dustbins and garbage bags
• Observe silence
• Maintain environmental safety
• Protect our country’s history/heritage.

Answer:

• Obey rules and regulations – Visitors must obey the rules and regulations, displayed at the Entrance.
• Maintain discipline and order – All visitors must maintain discipline and order in the place.
• Maintain cleanliness – They should maintain cleanliness in the area.
• Use dustbins and garbage bags – They must use dustbins and garbage bags for throwing leftovers.
• Observe silence – Visitors must observe complete silence at the site.
• Maintain environmental safety – They should maintain environment safety for their own safety.
• Protect our country’s history/heritage – It is our duty to protect our countries historical heritage.

7. Complete the following flow – chart by choosing from the options given below to show how any site of any country can become a World Heritage Site.

Question 1.
Complete the following flow – chart by choosing from the options given below to show how any site of any country can become a World Heritage Site.

1. Inclusion of the name of a site from the tentative list to the nomination file.
2. Name of the site is inscribed on the World Heritage list after meeting the criteria.
3. Inclusion of the name of site for the nomination in a tentative list after an inventory in the country or the state.
4. Decision of the World Heritage Committee after review of the nominated file.
5. A review of the file included by the advisory bodies.

Answer:

8. Match the pairs to defme different roles of the World Heritage Sites.

Question 1.
Match the pairs to defme different roles of the World Heritage Sites.

Answer:

Column ‘A’	Column ‘B’
1. Identify cultural and natural sites	(b) of outstanding universal value across countries.
2. Identify sites of	(h) special importance for everyone.
3. Identify sites that represent	(g) best examples of world’s cultural and/or natural heritage.
4. UNESCO seeks to	(c) preserve outstanding sites and natural resources.
5. World Heritage Sites should have	(i) relevant development plan policies.
6. World Heritage Site should	(f) protect these sites.
7. World Heritage Site serve as	(e) an asset for economic development and investment.
8. World Heritage Site should ensure	(a) green, local based, stable and decent jobs.
9. It should at large develop	(d) tourism.

9. Do you know the difference between
Refer to a dictionary/encyclopedia/reference books/website/google search to get the detailed meaning.

Question 1.
Do you know the difference between:

• World heritage.
• Cultural heritage.

Refer to a dictionary/encyclopedia/reference books/website/google search to get the detailed meaning.
Answer:
World Heritage: As per UNESCO, World Heritage is the designation for places on Earth that are of outstanding universal value to humanity and as such, have been inscribed on the World Heritage List to be protected for future generations to appreciate and enjoy.

Cultural Heritage: Cultural Heritage means elements of great human value and creation. These could be tangible or intangible cultural heritage. Tangible Cultural Heritage include paintings, coins, sculptures, monuments, shipwrecks ruins, archaeological sites etc. Intangible Cultural Heritage can include traditions, performance arts, rituals etc.

10. Following are the ways to preserve ‘World Heritage Sites.’ Transfer these points into a small paragraph. Suggest a suitable title.

• Practical conservation of posterity
• Humanlanimal trespassing
• Unmonitored/uncontrolled/unrestricted access
• Threat of local administrative negligence

Question 1.
Following are the ways to preserve ‘World Heritage Sites.’ Transfer these points into a small paragraph. Suggest a suitable title.

• Practical conservation of posterity
• Humanlanimal trespassing
• Unmonitored/uncontrolled/unrestricted access
• Threat of local administrative negligence

Answer:
Preserving ‘World Heritage Sites’ for Future Generations Let us be sensible and practical to preserve our World Heritage Sites for future generations. It depends on well-organized and well-managed plan, The plan should be skillfully monitored and implemented to the details. It is the responsibility of the country where it is situated. So it is our national duty to protect or restore the Heritage Sites.

To maintain the original, natural characteristics of the site we must take utmost care and prevent them from being lost, damaged or destroyed. We must use funds and resources allocated by our state and the World Heritage Fund for mending and repairing work. Many a times, human and animal trespassing damage, deface and make them ugly and insecure.

Their activities and disturbances should be controlled and restricted to retain their natural beauty and grandeur. Buildings, structures, historical monuments and natural beauty should be taken care of.

In many cases, the local administrators are lethargic and they are responsible for the damages. The administrative apathy and negligence are the threats to our Heritage sites. Strict actions should be taken against them for their neglect to protect the sites.
Everyone of us, who visit the sites, should have a sense of national pride in preserving our World Heritage sites for the sake of our future generations.

11. Find from the text minimum 8 words related to cultural heritage and make a word register. Arrange them in an alphabetical order: 

Question 1.
Find from the text minimum 8 words related to cultural heritage and make a word register. Arrange them in an alphabetical order:
Answer:
Words related to cultural heritage:

1. temples
2. culture
3. literature
4. artefacts
5. sites
6. territory
7. monuments
8. art

Alphabetical order: art, artefacts, culture, literature, monuments, sites, temples, territory.

13. Rewrite the following sentences using ‘not only but also’ and ‘as well as’ in 2 seperate sentences.

Question i.
UNESCO and the International Council on monuments initiated a draft convention to create an international organisation responsible for protecting cultural heritage.
Answer
1. Not only UNESCO but also the international council on monuments initiated a draft convention to create an international organisation responsible for protecting cultural heritage.
2. UNESCO as well as the International council on monuments initiated a draft convention to create an international organisation responsible for protecting cultural heritage.

Question ii.
The state parties are responsible for identifying and nominating new sites.
Answer
1. The State Parties are responsible not only for identifying but also for nominating new sites.
2. The State Parties are responsible for identifying as well as nominating new sites.

Question iii.
Opera House in Australia and the Historic Center of Vienna in Austria are cultural sites of World Heritage.
Answer
1. Not only Opera House in Australia but also the Historic Center of Vienna in Austria are cultural sites of the World Heritage.
2. Opera House in Australia as well as the Historic Center of Vienna in Austria are cultural sites of the World Heritage.

Question iv.
World Heritage Sites can be a combination of both cultural and natural areas.
Answer
1. World Heritage Sites can be a combination of not only cultural but also natural areas.
2. World Heritage Sites can be a combination of cultural as well as natural areas.

Question v.
To protect the temples and artifacts. UNESCO launched an international campaign.
Answer
1. To protect not only the temples but also artifacts, UNESCO launched an international campaign.
2. To protect the temples as well as artifacts, UNESCO launched an international campaign.

14. Rewrite the following sentences replacing ‘as soon as’ by ‘No sooner than.’
(Note: The phrase, ‘No sooner’ must always be followed by an auxiliary
(helping verb).
For example : As soon as he came, they all gave an applause.
No sooner did he come, than all gave an applause.
(a) As soon as the Bill is passed, it will become an Act.
(b) As soon as the thief escaped, the family informed the police.
(c) As soon as you have finished, you can submit your answer – papers.
(d) As soon as they can manage, they should change their house.
(e) As soon as the bell will ring, the School Assembly will start.

Question 1.
Rewrite the following sentences replacing ‘as soon as’ by ‘No sooner… than…’
(a) As soon as the Bill is passed, it will become an Act.
(b) As soon as the thief escaped, the family informed the police.
(c) As soon as you have finished, you can submit your answer-papers.
(d) As soon as they can manage, they should change their house.
(e) As soon as the bell will ring, the School Assembly will start.
Answer:
(a) No sooner is the Bill passed than it will become an Act.
(b) No sooner did the thief escape than the family informed the police.
(c) No sooner have you finished than you can submit your answer papers.
(d) No sooner can they manage than they should change their house.
(e) No sooner will the bell ring than the School Assembly will start.

15. Prepare a ‘tourism leaflet’ on any one of the following. (You may refer to the points given in Warming Up.)
(A) Your Home Town
(B) A Historical Place
(C) A Place of Natural Beauty
(D) A Place of Pilgrimage

Question 1.
Prepare a ‘tourism leaflet’ on any one of the following. (You may refer to the points given in Warming Up.)
(A) Your Home Town
(B) A Historical Place
(C) A Place of Natural Beauty
(D) A Place of Pilgrimage
Answer:
(उत्तराकरिता Warming Up! मधील Kolhapur विषयी दिलेले पर्यटन माहितीपत्रक पाहा.)

16.Project :

Question a.
Make a list of sites from our State that are included in the World Heritage Sites. Try to visit one of them. Write the importance of that World Heritage Site. Also write your impression of it in your notebook.

Live English:

Question a.
Making PowerPoint Presentation:
Answer:

Question b.
Rearrange the following steps of creating a PowerPoint slide in proper sequence:
(Answers is directly given.)
Answer:

1. Open Microsoft PowerPoint.
2. Click ‘New’ to create Blank Presentation.
3. Add New Slide from Home menu.
4. Click to add Text and Title in the slide.
5. Add Pictures by clicking ‘Insert’ button.
6. Resize your pictures or graphics.
7. Add effects from “Transition” menu.
8. Add New slide from Home menu.
9. Save your slide and start slide show from the beginning.

Question c.
Follow the slide Handout on ‘Types of Sentences’ given on coursebook page No. 85. Create similar slide Handout on any one of given topics:

1. pollution
2. Modes of Transport
3. Our Solar System
4. The United Nations

Question d.
Tips for writing an effective Slide Handout
Answer:

1. Begin with writing a Title and name of presenter on the Slide 1.
2. Write points you want to explain in main bullet points in the Slide 2.
3. Give meanings, definitions and exanples in bullet points.
4. Use aphoristic style of language, give only main points.
5. Give your contact number and email ID for feedback towards the en)

Question e.
Tips for making an effective Power point Presentation
Answer:

1. While speaking, show your passion and use positive body gestures.
2. Start strongly try to connect with your audience using propertone.
3. Keep it simple: concentrate on your core message.
4. Smile and make eye contact with your audience.
5. Conclude on positive note.

Question f.
The 10/20/30 rule of Power Point
Answer:
( If you are notfamiliarwith the 10/20/30 Ruleof PowerPoint created way back in 2005 by Guy Kawasaki, here’s how it goes:
“The most effective Power Poin t presentations should
containno more than lOslides,
Iastno longer than 20 minutes,
and feature fontno smaller than 30 points.”

My English Coursebook 10th Digest Chapter 2.6 World Heritage Additional Important Questions and Answers

Read the following passage and do the activities:

Simple Factual Activities:

Question 1.
Name the following:
(Answers are directly given and underlined.)
Answer:
i. The International World Heritage Programme is administered by – The UNESCO WORLD Heritage Committee
ii. The Nile valley contains many ancient – Egyptian artifacts.

Question 2.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:
A draft convention was started for creating an international organization responsible for protecting cultural heritage.

Question 3.
Name the following:
(Answers are directly given and underlined.)
Answer:
State parties are elected by the World Heritage Centre’s General Assembly.

Question 4.
Complete the following sentences:
(Answers are directly given and underlined)
Answer:

1. The role of World Heritage Committee is to list the sites as – a UNESCO World Heritage Site.
2. The tenure of World Heritage Committee is – six years.
3. The World Heritage Committee consists of representatives from – 21 State Parties.

Question 5.
Complete the following sentences:
(Answers are directly given and underlined.)
Answer:

1. The inventory of the State Party is called the Tentative List.
2. Tentative List is included on the Nomination File.
3. Two advisory bodies make recommendations to the World Heritage Committee.
4. When the site is chosen it also becomes considered within the international community.
5. 25 of the World Heritage Sites are considered mixed.

Complex Factual Activities:

Question 1.
Complete the web:
(Answer is directly given and underlined.)
Answer:

Question 2.
Why did UNESCO launch an international campaign in 1959?
Answer:
Egypt started plans to build the Aswan High Dam to collect and control water from the Nile River. The dam’s construction would have flooded the Nile valley containing the Abu Simbel Temples and many of ancient Egyptian artefacts. To protect the temples and the artefacts UNESCO launched an international campaign in 1959.

Question 3.
Complete the web:
(Answer is directly given.)
answer:

Question 4.
Why did a White House Conference in the United States call for a ‘World Heritage Trust’?
Answer:
A White House Conference in the United States called for a ‘World Heritage Trust’ to protect historic cultural sites and also for protecting the world’s significant natural and scenic sites.

Question 5.
What measures are taken about the World Heritage Sites that are in danger?
Answer:
The World Heritage Committee first prepares a separate list of sites that are in danger. The World Heritage Committee allocates resources from the World Heritage Fund to that site to restore it. In addition, different plans are put into place to protect and/or restore the site. However, if a site loses its characteristics which allowed it to be originally included on the World Heritage List, the World Heritage Committee can delete the site from the list.

Activities based on Vocabulary:

Question 1.
Look at the words and their meanings. Underline the correct alternatives:
(Answers are directly underlined.)
Answer:
(i) determine:
(a) think over
(b) decide
(c) ask for
(d) look over

(ii) monument:
(a) statue
(b) pillar
(c) memorial building
(d) fort

(iii) significant:
(a) clever
(b) effective
(c) systematic
(d) important

(iv) disaster:
(a) problem
(b) incident
(c) calamity
(d) accident

Question 2.
Find from the passage adjective forms for the following:

1. culture
2. history
3. nature
4. significance

Answer:

1. cultural
2. historical
3. natural
4. significant

Question 3.
Write the long form of ‘UNESCO’.
Answer:
United Nations Educational Scientific and Cultural Organisation.

Question 4.
Write from the passage nouns for the following:

1. present
2. protect
3. conserve
4. include

Answer:

1. presentation
2. protection
3. conservation
4. inclusion

Question 5.
Write the list of adjectives from the passage.
Answer:
historic, cultural, significant, natural, scenic, international, similar, general, main, responsible, six.

Question 6.
Match the words in Column ‘A’ with their meanings in Column ‘B’:

Column ‘A’	Column ‘B’
1. inventory	(a) fixed basis to judge
2. territory	(b) suggestions
3. criteria	(c) region
4. recommendations	(d) a written list of material

Answer:

Column ‘A’	Column ‘B’
1. inventory	(d) a written list of material
2. territory	(c) region
3. criteria	(a) fixed basis to judge
4. recommendations	(b) suggestions

Question 7.
Find from the passage the antonyms for the following:

1. exclude
2. artificial
3. insignificant
4. final

Answer:

1. exclude × include
2. artificial × natural
3. insignificant × significant
4. final × tentative

Question 8.
Find out opposites from the passage for the following:
Answer:

1. artificial × natural
2. lowest × highest
3. exclude × include
4. safe × danger

Question 9.
Find from the passage the nouns of the following :

1. locate
2. urbanize
3. pollute
4. add

Answer:

1. locate – location
2. urbanize – urbanization
3. pollute – pollution
4. add – addition

Personal Response:

Question 1.
Why do you like to visit tourist spots?
Answer:
I like to visit some tourist spots not only for comfort and relaxation but for expanding my knowledge and for knowing our culture, history and glory of the past. They enhance our knowledge, vision of life and enlighten your intelligence. These visits give us true education of life and soothe our minds.

Activity-based on Contextual Grammar:

Rewrite the sentences using ‘not only….but also’ and ‘as well as’ in two separate sentences:

Question 1.
A White House Conference called for a ‘World Heritage Trust’ to protect historic cultural sites and the world’s significant natural and scenic sites.
Answer:
i. A White House Conference called for a ‘World Heritage Trust’ to protect not only historic cultural sites but also the world’s significant natural and scenic sites.
ii. A White House Conference called for a ‘World Heritage Trust’ to protect historical cultural sites as well as the world’s significant natural and scenic sites.

Question 2.
Write the following sentence using ‘as soon as’ and ‘no sooner …… in two separate sentences.
Immediately after the World Heritage Sites are in danger, they are inscribed on a separate list.
Answer:
(i) As soon as the World Heritage Sites are in danger, they are inscribed on a separate list.
(ii) No sooner are the World Heritage Sites in danger than they are inscribed on a separate list.

English Workshop:
(based on whole lesson).

Question 1.
What is the difference between the words ‘World Heritage’ and ‘Cultural Heritage’?
Answer:
The word ‘World Heritage’ is related with the natural or man-made places that are recognized as having international importance, cultural values of the world and humanity in general. Whereas ‘Cultural Heritage’ is related with a particular society or groups, its ideas, customs, beliefs, art and literature, etc. that have existed and inherited from past generations, maintained in the present and preserved for the benefits of future generation.

Activities based on Language Study

(A) Do as directed:

Question 1.
Complete the words by using correct letters:

1. w o _ l d
2. l a k _ s
3. s i _ e s
4. s _ a t e

Answer:

1. w o r l d
2. l a k e s
3. s i t e s
4. s t a t e

Question 2.
Put the following words in alphabetical order:
1. world, becoming, property, territory
2. step, site, selection, significant
Answer:
1. becoming, property, territory, world
2. selection, significant, site, step

Question 3.
Punctuate the following sentences:
1. Then what’s the secret of your energy I asked
2. No there isn’t anyone like Raghu veer
Answer:
1. “Then what’s the secret of your energy?” I asked.
2. “No, there isn’t anyone like Raghuveer.”

Question 4.
Make four words (minimum 3 letters each) using letters in the word ‘ mountain ’
Answer:
mount, out, main, tin

Question 5.
Write related words as shown in the example:
(Answers are directly given and underlined.)
Answer:

Question 6.
Complete the following word-chain of the adjectives. Add four words each beginning with the last letter of the previous word: ;
dear → …………… → …………… → …………… → …………… .
Answer:
dear → real → large → eager → red.

(B) Do as directed:

1. Attempt anyone:

Question a.
Make your own meaningful sentence using the phrase ‘to fall prey’:
Answer:
Young people fall prey to attractive, tasty food.

OR

Question b.
Add a clause to the following sentence to expand it meaningfully:
This is how I …………….
Answer: This is how the poor man got shelter in the Old age Home.

2. Attempt anyone:

Question a.
Add a prefix or suffix to make new words:
1. agree
2. satisfy
Answer:
1. disagree/agreement
2. satisfaction/dissatisfy

OR

Question b.
Make a meaningful sentence using any one of the following words:
1. agree
2. satisfy
Answer:
1. Do you agree with my opinion?
2. The food he got did not satisfy his hunger.

My English Coursebook 10th Digest Pdf Unit 2

• You Start Dying Slowly … Class 10 English Solutions
• The Boy who Broke The Bank Class 10 English Solutions
• The Twins Class 10 English Solutions
• An Epitome of Courage Class 10 English Solutions
• Book Review – Swami and Friends Class 10 English Solutions
• World Heritage Class 10 English Solutions