Bhagya

Balbharti Maharashtra State Board Class 12 History Important Questions Chapter 5 India: Social and Religious Reforms Important Questions and Answers.

Maharashtra State Board 12th History Important Questions Chapter 5 India: Social and Religious Reforms

1A. Choose the correct alternative and rewrite the statement.

Question 1.
The practice of Sati was abolished by a law passed in the year __________
(a) 1829
(b) 1830
(c) 1831
(d) 1832
Answer:
(a) 1829

Question 2.
Raja Ram Mohan Roy started a philosophical discussion circle named ‘ __________’.
(a) Prarthana Samaj
(b) Arya Samaj
(c) Satyashodhak Samaj
(d) Atmiya Sabha
Answer:
(d) Atmiya Sabha

Question 3.
The Brahmo Samaj was founded in the year __________
(a) 1826
(b) 1827
(c) 1828
(d) 1829
Answer:
(c) 1828

Question 4.
The Mughal emperor of India conferred the title of ‘____________’ on Ram Mohan Roy.
(a) Pandit
(b) Raja
(c) Alamgir
(d) Badshah
Answer:
(b) Raja

Question 5.
__________ has its origins in Paramhamsa Sabha.
(a) Prarthana Samaj
(b) Arya Samaj
(c) Brahmo Samaj
(d) Satyashodhak Samaj
Answer:
(a) Prarthana Samaj

Question 6.
__________ established ‘Scientific Society’ for Muslims.
(a) Mahatma Phule
(b) Sir Sayyad Ahmad
(c) Swami Dayanand
(d) Tarabai Shinde
Answer:
(b) Sir Sayyad Ahmad

Question 7.
__________ participated in the Vykom Satyagraha in Travancore against untouchability.
(a) Ramaswamy Naikar
(b) Kamaladevi Chattopadhyay
(c) Dr. Ambedkar
(d) Swami Vivekananda
Answer:
(a) Ramaswamy Naikar

Question 8.
Rajarshi Shahu Maharaj was strongly opposed to __________
(a) Bajubandi
(b) Setubandi
(c) Rajbandi
(d) Rotibandi
Answer:
(d) Rotibandi

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Group ‘A’	Group ‘B’
(a) Sati Act	1829
(b) Restriction of Press	1830
(c) Arya Samaj	1875
(d) Ramkrishna Mission	1897

Answer:
Restriction of Press – 1824

2A. Write the names of historical places/persons/events.

Question 1.
Governor-General who abolished Sati in 1829 –
Answer:
Lord William Bentinck

Question 2.
The company that put restrictions on the freedom of the press –
Answer:
The British East India Company

Question 3.
The social reformer who severely criticized untouchability in his book ‘Vital Vidhwamsan’ –
Answer:
Gopalbaba Walangkar

Question 4.
Editor of ‘Ain-i-Akbari’ written by Abul Fazl –
Answer:
Sir Sayyad Ahmad Khan

Question 5.
The movement led by Dr. Babasaheb Ambedkar at Mahad –
Answer:
Satyagraha of Chavadar Tank

Question 6.
Founder of ‘Independent Labour Party –
Answer:
Dr. Babasaheb Ambedkar

Question 7.
The ruler who organised‘Sahabhoj for all castes –
Answer:
Maharaja Sayajirao Gaikwad

Question 8.
The ruler who opposed ‘Vyavasaybandi’ –
Answer:
Rajarshi Shahu Maharaj

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
The progress of Indian society was stunted because of __________
(a) superstitions
(b) the orthodox way of life
(c) caste discriminations
(d) all of the above
Answer:
(d) all of the above

Question 2.
Sati was abolished in 1829 because __________
(a) a law was passed by Lord William Bentinck abolishing this inhuman practice
(b) the people of India wanted this custom to be abolished
(c) the Brahmin class wanted Sati to be abolished
(d) women wanted to put an end to this custom
Answer:
(a) a law was passed by Lord William Bentinck abolishing this inhuman practice

Question 3.
The Mughal emperor conferred the title of‘Raja’ on Ram Mohan Roy because __________
(a) Ram Mohan Roy was the emperor’s favourite
(b) Ram Mohan Roy had gone to England to plead the case of the Mughal emperor
(c) Ram Mohan Roy was an efficient lawyer
(d) Ram Mohan Roy visited England
Answer:
(b) Ram Mohan Roy had gone to England to plead the case of the Mughal emperor

Question 4.
Swami Vivekanand established the Ramkrishna Mission because __________
(a) he was asked by his Guru to do so
(b) he wanted to compete with other organisations
(c) he wanted to serve the needy people
(d) so that many people join his Mission
Answer:
(c) he wanted to serve the needy people

3. Complete the following concept map.

Question 1.

Answer:

Question 2.

Social Reformers	Participated in Movements
1. Maharshi V.R.Shinde	………………………………..
2. …………………………………	Kala Ram Temple, Nasik
3. Ramaswamy Naikar	………………………………..
4. Kamaladevi Chattopadhyay	………………………………..
5. ………………………………..	Non-Brahmanical Movement, Kolhapur

Answer:

Social Reformers	Participated in Movements
1. Maharshi V. R. Shinde	Parvati Temple, Pune
2. Dr. B. R. Ambedkar	Kala Ram Temple, Nasik
3. Ramaswamy Naikar	Vykom Satyagraha, Travancore
4. Kamaladevi Chattopadhyay	Quit India Movement
5. Rajarshi Shahu Maharaj	Non-Brahminical Movement, Kolhapur

4A. Write short notes.

Question 1.
Arya Samaj.
Answer:
Arya Samaj:

• Founded by Swami Dayanand Saraswati in 1875.
• Regarded Vedas as holy.
• Rejected discrimination based on caste differences.
• Encouraged education of women, widow remarriage, and inter-caste marriage.

Question 2.
Tarabai Shinde.
Answer:
Tarabai Shinde:

• Born in 1839.
• She demanded gender equality.
• She was the first woman to challenge the patriarchal system.
• She was of the opinion that religious systems suppress women because religions are created by men.

4B. Explain the following statements with reasons.

Question 1.
The British wanted to bring progress to Indian society.
Answer:
The progress of Indian society was stunted because of superstitions, an orthodox way of life, caste discriminations, false social notions, lack of curiosity, and rationality that prevailed on a large scale. The British felt the need to create a new society that was based on the values of ‘Freedom, Equality, Fraternity, and Humanism’.

Question 2.
Raja Ram Mohan Roy was the first Indian to oppose the custom of Sati.
Answer:
Raja Ram Mohan Roy witnessed his brother’s wife commit Sati and this disturbed him deeply. He pointed out that none of the religious texts mentioned the practice of Sati as a prescribed religious obligation. It is because of his efforts that a law was passed by Governor-General Lord William Bentinck abolishing the practice of Sati in 1829.

Question 3.
Dr. Babasaheb Ambedkar used print media to create public awareness.
Answer:
Dr. B. R. Ambedkar knew the importance of print media. For him, it was the best instrument to create awareness and to build the movement for social equality. Therefore, he began to publish his own newspapers namely ‘Mooknayak’, ‘Bahishkrut Bharat’, ‘Janata’ and ‘Samata’.

5. State your opinion.

Question 1.
Tarabai Shinde was the first Indian woman to challenge the patriarchal system.
Answer:
Tarabai Shinde was of the opinion that religious systems suppress women because religious systems are created by men. Therefore, she took a brave step in expressing her thoughts in a brave manner in her essay on women’s rights. In this essay, she not only discussed reforms like widow remarriage, women’s education, abolition of Sati but demanded greater gender equality.

Question 2.
Arya Samaj was founded by Swami Dayanand Saraswati in 1875.
Answer:
Arya Samaj:

• Founded by Swami Dayanand Saraswati in 1875.
• Regarded Vedas as holy.
• Rejected discrimination based on caste differences.
• Encouraged education of women, widow remarriage, and inter-caste marriage.

6. Answer the following question with the help of the given points.

Question 1.
Discuss the role played by Religious Reform Organisations in the field of religious awakening.
(a) Prarthana Samaj
(b) Satyashodhak Samaj
(c) Arya Samaj
(d) Ramkrishna Mission
Answer:
(a) Prarthana Samaj:

• Had its origins in Paramhamsa Sabha.
• Founded by Dadoba Pandurang Tarkhadkar.
• Founding members like Dr. Atmaram Pandurang, Justice M. G. Ranade, Dr. R. G. Bhandarkar opposed idol worship and emphasized monotheism.
• Opened schools for girls, orphanages, and night schools for workers.
• Focussed on gender equality, wiping outcaste discriminations, and appreciating the values of mundane life.

(b) Satyashodhak Samaj:

• Founded in 1873 by Mahatma Jotirao Phule in Pune.
• Cracked a whip on the social customs and practices which pushed the Indian masses into a miserable state.
• Showed a new path to artisans, workers, and other downtrodden people.
• Characteristics of Satyashodhak Samaj included monotheism, rejection of the authority of Vedas and Puranas, acceptance of rationality, opposition to the dominance of priests and idol worship, etc.
• Mahatma Phule and his wife Savitribai Phule started a school for girls.
• His work was continued by Gopalbaba Walangkar who criticized untouchability in his book ‘Vital Vidhwamsan’.
• Shivram Janba drew attention to the problems of deprived women like Murali, Jagatini, and Devdasi.

(c) Arya Samaj:

• Founded by Swami Dayanand Saraswati in 1875.
• Regarded Vedas as holy.
• Rejected discrimination based on caste differences.
• Encouraged education of women, widow remarriage, and inter-caste marriage.

(d) Ramkrishna Mission:

• Swami Vivekananda founded the Ramkrishna Mission in 1897.
• Focussed on serving needy people, working for people affected by famine, health care for the sick people, education for women, etc.
• It also gave a message to the Indian youth to get up to awaken and keep moving until the goal is achieved.

Question 2.
What role did the following social reformers play in bringing about social change?
(a) Sir Sayyad Ahmad Khan
(b) Tarabai Shinde
(c) Maharshi Vitthal Ramji Shinde
(d) Kamaladevi Chattopadhyay.
(e) Ramaswamy Naikar
Answer:
(a) Sir Sayyad Ahmad Khan:

• Was born in 1817 in Delhi.
• Fluent in Urdu, Persian, Arabic, and English.
• Established ‘Scientific Society’ for Muslims.
• After returning from England he founded the Mohammadan Anglo-Oriental College in 1875 which later developed into ‘Aligarh Muslim University.
• Started a periodical entitled ‘Mohammadan Social Reformer’.
• Worked for the propagation of modern education, science, and technology.

(b) Tarabai Shinde:

• Born in 1839.
• She demanded gender equality.
• She was the first woman to challenge the patriarchal system.
• She was of the opinion that religious systems suppress women because religions are created by men.

(c) Maharshi Vitthal Ramji Shinde:

• Opened Marathi schools and schools for technical training in Parel, Deonar in Mumbai under the umbrella of ‘Depressed Classes Mission’ that was established by him.
• Worked to create public awareness about the issues affecting the depressed classes like entry into temples (for example, protestations for the right of entry in Parvati temple in Pune), agricultural conference, and joint electorate system of depressed classes.

(d) Kamaladevi Chattopadhyay:

• Was an active volunteer of Congress.
• She convinced Mahatma Gandhi to let women participate in salt satyagraha, and she participated in the satyagraha.
• She worked for women’s rights.
• Organized demonstrations to draw attention to the problems of workers and farmers.
• Emphasized justice to female agricultural labourers.
• Insisted that women working in factories should have the necessary facilities.
• Followed up the issue of maternity leave to women.
• Imprisoned by the British for one year for participating in the Quit India Movement.

(e) Ramaswamy Naikar:

• Born in ‘Erode’ in Tamil Nadu in 1879.
• He became a follower of Mahatma Gandhi’s philosophy and worked for propagating the use of ‘Swadeshi’.
• He participated in the Vykom Satyagraha in Travancore against untouchability.
• Started the ‘Swabhiman Andolan’ in Tamil Nadu.
• Fought against the varna system and child marriage.
• He was addressed as ‘Periyar’ or Great Soul because of his magnanimous work.
• Was a great speaker and author.
• Took a radical position on issues like women’s rights and family planning.

Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 3A Demand Analysis Important Questions and Answers.

Maharashtra State Board 12th Economics Important Questions Chapter 3A Demand Analysis

1. A. Choose the correct option:

Question 1.
The demand curve slopes downward.
(a) Inverse relationship between price quantity demanded
(b) from left to right
(c) from right to left
(d) Direct relationship quantity demanded
Options :
(1) a,b and c
(2) a, b, c and d
(3) a and b
(4) a and d
Answer:
(3) a and b

Question 2.
Demand for a commodity from an individual consumer.
(a) Direct demand
(b) Market demand
(c) Individual demand
(d) Increase in demand
Options:
(1) a
(2) b
(3) c
(4) d
Answer:
(3) c

Question 3.
Demand for a commodity from different consumer at different prices.
(a) Decrease in demand
(b) Contraction in demand
(c) Individual demand
(d) Market demand
Options:
(1) c
(2) b
(3) a
(4) d
Answer:
(4) d

Question 4.
Direct demand.
(a) Vegetable
(b) Milk
(c) Land
(d) Cloth
Options :
(1) a,b and c
(2) a, b and d
(3) b, c and d
(4) c
Answer:
(2) a, b and d

Question 5.
Indirect demand.
(a) Machinery
(b) Sugar
(c) Labour
(d) Capital
Options :
(1) a, b, c and d
(2) a, b and c
(3) a, b and d
(4) a, c and d
Answer:
(4) a, c and d

Question 6.
Joint demand for i tea.
(a) Sugar
(b) Milk
(c) Tea powder
(d) Rice
Options :
(1) a,b and c
(2) b and d
(3) a,b and d
(4) b, c and d
Answer:
(1) a,b and c

Question 7.
Determinant of Demand.
(a) Price
(b) Population
(c) Income
(d) Advertisement
Options :
(1) a and d
(2) a, c and d
(3) a, b, c and d
(4) c and d
Answer:
(3) a, b, c and d

Question 8.
Composite demand.
(a) Electricity
(b) Water
(c) Steel
(d) Xerox machine
Answer:
(1) a, b and d
(2) a, b and c
(3) a, b and d
(4) a and d
Answer:
(2) a, b and c

Question 9.
Competitive demand.
(a) Thums-up
(b) Pepsi
(c) Buttermilk
(d) Coco-cola
Options:
(1) a, b and c
(2) a, c and d
(3) a, b and d
(4) c and d
Answer:
(3) a, b and d

Question 10.
The law of demand was introduced by neo-classical economist.
(a) Alfred Marshall
(b) Adam Smith
(c) Ragnar Frisch
(d) Samuelson
Options:
(1) e
(2) b
(3) d
(4) a
Answer:
(4) a

Question 11.
Assumptions for the law of Demand.
(a) Constant Income
(b) No change in taxation policy
(c) Change in tradition
(d) Stable population
Options :
(1) a, b and d
(2) a, b and c
(3) a and d
(4) only d
Answer:
(1) a, b and d

Question 12.
Exceptions to the law of Demand.
(a) Inferior goods
(b) Jewellery
(c) Habitual goods
(d) Price of substitute goods
Options :
(1) a, b and d
(2) a, b and c
(3) only d
(4) a, c and d
Answer:
(2) a, b and c

Question 13.
Variation in Demand.
(a) Change in Price
(b) Change in quantity demanded
(c) Change in other factors
(d) No change in other factors
Options :
(1) a, b and c
(2) a, b and d
(3) c and d
(4) only a and b
Answer:
(2) a, b and d

Question 14.
Expansion of Demand.
(a) Fall in price
(b) Rise in quantity demanded
(c) No change in income
(d) Change in population
Options :
(1) only c
(2) a, b and c
(3) a, b and d
(4) b, c, and d
Answer:
(2) a, b and c

Question 15.
Change in Demand.
(a) Constant price
(b) Change in demand
(c) Changes in other factors
(d) Increase and Decrease in demand
Options :
(1) a and b
(2) c and d
(3) a, b, c and d
(4) None of these
Answer:
(3) a, b, c and d

Question 16.
Individual demand.
(a) Micro economics
(b) Slicing method
(c) Lumping method
(d) Study of individual unit
Options :
(1) a, b and d
(2) b and c
(3) b, c and d
(4) only a
Answer:
(1) a, b and d

Question 17.
Market demand.
(a) Aggregate demand
(b) Macro economics
(c) Micro economics
(d) Lumping method
Options :
(1) a, b and d
(2) b, c and d
(3) b and c
(4) only c
Answer:
(1) a, b and d

Question 18.
Decrease in demand.
(a) Favourable changes in other factors
(b) Unfavourable changes in other factors
(c) Decrease in quantity demanded
(d) Changes in income of the consumer
Options :
(1) b, c and d
(2) a, b and c
(3) a and b
(4) a, c and d
Answer:
(1) b, c and d

(B) Complete the Correlation.

(1) Individual consumer ……………… :: Total of all the individual: Market demand
(2) Labour : Indirect demand:: Clothes : ………………
(3) Joint demand : Pencil and Paper :: ……………… Electricity
(4) Complementary demand : Car and Petrol:: ………………: Pepsi and Coke
(5) Constant level of Income : Assumption : : Prestige goods : ………………
(6) Expansion in demand : Downward movement on the demand curve :: ………………: Upward movement on the demand curve
(7) Change in demand : Increase in Demand :: ………………: Extension in demand
(8) Increase in demand : Favourable changes in other factors :: Decrease in demand : ………………
(9) Fall in Price : ……………… :: Rise in Price : Quantity demanded falls
(10) ……………… : Tea :: Composite demand : Milk
Answer:
(1) Individual demand
(2) Direct demand
(3) Composite demand
(4) Competitive demand
(5) Exception
(6) Contraction in demand
(7) Variation in demand
(8) Unfavourable changes in other factors
(9) Quantity demanded rises
(10) Joint demand

(C) Give economic terms.

(6) Desire + willingness to purchase + Ability to pay.
(7) The demand by a single consumer in a market.
(8) The demand by all consumer in a market.
(9) Other factors remaining constant, a fall in demand due to a rise in price.
(10) Other factors remaining constant, a rise in demand due to a fall in price.
(11) To satisfying a want of sewing, needle and thread is required.
(12) A rise in demand due to changes in other factors, price remaining constant.
(13) Fall in demand due to changes in other factors, price remaining constant.
(14) Goods of low quality are considered as inferior goods.
(15) The demand for commodities to satisfy the human wants directly.
(16) The demand for factors of production like land, labour, etc.
(17) Two or more goods are demanded at a time to satisfy one want.
Answer:
(6) Demand
(7) Individual Demand
(8) Market Demand
(9) Contraction in Demand
(10) Expansion in Demand
(11) Complementary or Joint Demand
(12) Increase in Demand
(13) Decrease in Demand
(14) Giffen’s Goods
(15) Direct Demand
(16) Indirect Demand
(17) Joint or Complementary Demand

(D) Find the o’dd word out.

(1) Desire, Ability to pay, Uselessness, \ Willingness to purchase
(2) Pepsi, Limca, Coffee, Coke
(3) Cloth, Sugar, Fertilizer, Milk
(4) Land, Capital, Raw material, Flowers
(5) Tea and Sugar, Pen and Pencil, Car and Petrol, Mobile phones and Sim cards
(6) Indirect demand, Individual demand, Composite demand, Competitive demand
(7) Consumer demand, Complementary demand, Composite demand, Competitive demand
(8) Tea – Coffee, Car – Fuel, Thums-up – Pepsi, Rice – Wheat
(9) Coffee powder, Chilli powder, Milk, Sug >r
(10) Gold, Diamond, Platinum, Aluminium
(11) Sony, Samsung, Onida, Karbonn
Answer:
(1) Uselessness
(2) Coffee
(3) Fertilizer
(4) Flowers
(5) Pen and Pencil
(6) Individual demand
(7) Consumer demand
(8) Car – Fuel
(9) Chilli powder
(10) Aluminium
(11) Karbonn

(E) Complete the following statements.

(1) The willingness to have something is called …………….
(2) Desire, willingness to purchase and ability to pay are the three necessary conditions for …………….
(3) The total quantities of a commodity demanded by a particular buyer is ……………..
(4) The sum of the total quantities of a commodity demanded by all buyers in a market is ……………..
(5) Commodities and services satisfying the human wants directly is known as ……………..
(6) The purchasing power of the consumer depends on ……………..
(7) One commodity can be put to several uses, it is known as ……………..
(8) Marshall’s law of demand describes the functional relationship between ……………..
(9) Inferior goods like cheap bread, vegetable ghee, etc., is known as ……………..
(10) Expensive goods such as diamonds, luxury cars are known as ……………..
(11) When demand changes due to changes in price, it is known as ………………
(12) A rise in demand caused by favourable changes in other factors at same price is called ………………
Answer:
(1) desire
(2) demand
(3) individual demand
(4) market demand
(5) direct demand
(6) ability to pay
(7) composite demand
(8) Demand and Price
(9) Giffen goods
(10) Prestige goods
(11) variation in demand
(12) increase in demand

(F) Choose the wrong pair :

I.

Group ‘A’	Group ‘B’
(1) Individual demand	Particular consumer
(2) Complementary demand	Pen – Ink
(3) Competitive demand	Milk – Sugar
(4) Indirect demand	Labour

Answer:
Wrong pair : Competitive demand – Milk- 5 Sugar

II.

Group ‘A’	Group ‘B’
(1) Expansion of demand	Other factors remaining constant
(2) Law of demand	Slopes downwards from left to right
(3) Market demand	Demand of all consumers
(4) Direct demand	Factors of production

Answer:
Wrong pair : Direct demand – Factors production

III.

Group ‘A’	Group ‘B’
(i) Inferior goods	Giffen goods
(2) Prestige goods	Luxury goods
(3) Expanasion of demand	Fall in price
(4) Increase in demand	Unfavourable changes in other factors

Answer:
Wrong pair : Increase in demand Unfavourable changes in other factors

IV.

Group ‘A’	Group ‘B’
(1) Sir Robert Giffen	England
(2) Increase in real income	Decrease in demand
(3) Inferior goods	Bread
(4) Superior goods	Meat

Answer:
Wrong pair : Increase in real income Decrease in demand

V.

Group ‘A’	Group ‘B’
(1) Individual demand	Individual consumer
(2) Joint demand	Tea-coffee
(3) Variation in demand	Other factors remaining constant
(4) Decrease in demand	Price remains constant

Answer:
(2) Joint demand Tea-coffee

(G) Assertion and Reasoning

Question 1.
Assertion (A) – Individual demand refers to the quantity of a commodity demanded by particular consumer.
Reasoning (R) – Market demand refers to the total demand for commodity from all the consumers.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true. .
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) is true but (R) is not the correct explanation of (A).
Answer:
(iv) Both (A) and (R) is true but (R) is not the correct explanation of (A).

Question 2.
Assertion (A) – Marginal utility goes on diminishing with an increase in the stock of ) a commodity. I
Reasoning (R) – Purchasing power of a consumer increases when the price of a commodity increases. 5-
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) is true and (R) is the correct l explanation of (A).
(iv) Both (A) and (R) is true but (R) is not the ( correct explanation of (A).
Answer:
(i) (A) is true but (R) is false.

Question 3.
Assertion (A) – Indirect demand refers to the demand for goods and services which are needed for further production.
Reasoning (R) – All factors of production have indirect or derived demand.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) is true but (R) is not the correct explanation of (A).
Answer:
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).

Question 4.
Assertion (A) – When the population size is larger, demand for commodity will be less.
Reasoning (R) – Change in the price of one commodity would also affect the demand of substitute goods.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) is true but (R) is not the correct explanation of (A).
Answer:
(ii) (A) is false but (R) is true.

Question 5.
Assertion (A) – Demand curve slopes downwards from left to right.
Reasoning (R) – The price of a commodity falls, quantity demanded rises and when S price of commodity rises, quantity demanded falls.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) is True but (R) is not the correct explanation of (A).
Answer:
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).

Question 6.
Assertion (A) – If consumer can anticipate the future price of a commodity then it will affect the present demand of a commodity.
Reasoning (R) – Ram buy’s less mangoes in anticipation of getting it at cheaper rate in further date.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) is true but (R) is not the correct explanation of (A).
Answer:
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).

Question 7.
Assertion (A) – Variations in demand refers to change in quantity demanded due to change in price alone and other factors remain constant.
Reasoning (R) – Increase in demand and decrease in demand are the types of variations in demand.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) is true but (R) is not the correct explanation of (A).
Answer:
(i) (A) is true but (R) is false.

Question 8.
Assertion (A) – Increase in demand refers rise in quantity demanded due to favourable changes in other factors and price remains constant.
Reasoning (R) – Decrease in demand refers to fall in quantity demand due to unfavourable changes in other factors and price remains constant.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) is True but (R) is not the ) correct explanation of (A).
Answer:
(iii) Both (A) and (R) is true and (R) is the correct explanation of (A).

(H) Choose the correct pair :

I.

Group ‘A’	Group ‘B’
(1) Joint Demand	(a) Luxury car
(2) Demand and price	(b) Exception to the law of demand
(3) Giffen’s goods	(c) Inverse relationship
(4) Prestige goods	(d) Several commodities
	(e) Vegetables

Answer:
(1)-(d), (2)-(c), (3)-(b), (4)-(a).

II.

Group ‘A’	Group ‘B’
(1) Factors of production	(a) Change in price alone
(2) Inferior goods	(b) Change in other factors
(3) Pen and Pencil	(c) Substitute goods
(4) Change in Demand	(d) Giffen’s goods
	(e) Indirect demand

Answer:
(1) – (e), (2) – (d), (3) – (c), (4) – (b).

III.

Group ‘A’	Group ‘B’
(1) Contraction in demand	(a) Less is demanded at a same price
(2) Decrease in demand	(b) Complementary goods
(3) Demand curve	(c) Substitute goods
(4) Tea and Coffee	(d) Less is demanded at a higher price
	(e) Slopes downwards from left to right

Answer:
(1)-(d), (2)-(a), (3)-(e), (4) – (c).

IV.

Group ‘A’	Group ‘B’
(1) Demand	(a) A new demand curve
(2) Variation in Demand	(b) Same demand curve
(3) Extension of demand	(c) Ability and willingness to pay
(4) Increase in demand	(d) Change in price alone
	(e) Distribution of income

Answer:
(1)-(c), (2)-(d), (3)-(b), (4)-(a).

V.

Group ‘A’	Group ‘B’
(1) Demand	(a) Exceptional demand
(2) Prestige goods	(b) Prof. Marshall
(3) Joint demand	(c) Demand curve shift to right
(4) Demand increases	(d) Complementary demand
	(e) A higher price

Answer:
(1)-(b), (2)-(a), (3)-(d), (4)-(c).

2.[A] Identify and explain the concept from given illustrations.

Question 1.
Ramesh has bought 1kg of Tea powder instead of expensive coffee powder.
Answer:
Concept: Competitive Demand
Explanation : Competitive Demand refers to demand for those goods which substitute for each other.
Change in the price of one commodity can affect the demand for substitute goods. Ramesh has found price of coffee at very high level, thus he bought tea powder.

Question 2.
Since Manoj’s salary has increased he has bought 5 kgs of rice instead of 3 kgs rice which he buys normally.
Answer:
Concept: Increase in demand
Explanation : Increase in demand refers to change in quantity demanded due to favourable changes in other factors like tastes, income, etc., and price remains constant.
Manoj has got increment this month and hence he has bought more quantity of rice at same price.

Question 3.
Due to increase in population of Mumbai, demand for electricity is rising day by day.
Answer:
Concept: Composite demand
Explanation : Composite demand refers to the demand for a commodity which can be put to several uses.
Demand for electricity is rising due to more industries, increase in household consumption etc.
Due to urbanization and industrialization many people are getting migrated to Mumbai and thus the consumption of electricity in increasing day by day.

Question 4.
Pari has bought most desirable Apple iphone 11 pro.
Answer:
Concept: Demand
Explanation : In economics demand means a desire which is backed by willingness and ability to pay.
It was Part’s most favourite phone, thus she spend whatever price for it was and bought the phone.

Question 5.
Whenever there is decrease in price of gold, demand for gold rises.
Answer:
Concept : Expansion or Extension of Demand
Explanation : Expansion of Demand refers to rise in quantity demanded due to fall in price alone while other factors like tastes, income, etc., remain unchanged.
There is general tendency of consumer to buy more whenever price falls.
Gold is most preferred investment of general public thus it is most demanded with fall in price.

(B) Distinguish between.

Question 1.
Individual Demand and Market Demand.
Answer:
Individual Demand:

1. Individual demand refers to total quantities of a commodity demanded by an individual or household at a given price during a period of time.
2. It is basically micro or narrow concept and not very useful in framing business, production and price policies.
3. Individual demand depend on the price of goods, disposable income credit facilities, taste, preference, etc.
4. It can be presented with the help of individual demand schedule and individual demand curve.

Market Demand :

1. Market demand refers to the total quantities of a commodity demanded by all the individuals in the market at a given price, during a given period of time.
2. It is a macro or broader concept and is very useful in framing, business, production and price policies. Even the law of demand is based on market demand.
3. Market demand depends on size of population, social customs, distribution of income, etc.
4. It can be presented with the help of market demand schedule and market demand curve.

Question 4.
Inferior Goods or Giffen’s Goods and Normal Goods.
Answer:
Inferior Goods or Giffen’s Goods:

1. Giffen’s goods refers to inferior goods like cheap quality rice, vegetable ghee, bread, etc. purchased by poor people.
2. The demand for inferior goods falls when prices falls.
3. The demand curve for Giffen’s goods is upward sloping from left to right as shown below.
   
4. Giffen’s goods are exceptions to the law of demand. As price and demand are directly related.

Normal Goods:

1. Normal goods are those goods which are better in quality and purchased by higher income group like rice, sugar, clothes.
2. The demand for normal goods falls when price rises.
3. The demand curve for normal goods is downwards sloping from left to right as shown below.
   
4. Normal goods represent the law of demand.
   As price and demand are inversely related.

Question 5.
Normal Demand Curve and Exceptional Demand Curve.
Answer:
Normal Demand Curve:

1. Normal demand curve represents the law of demand, which states that demand is inversely related to price.
2. The normal demand curve slopes downwards from left to right.
3. Normal goods like rice, wheat, clothes have normal demand curve.
   

Exceptional Demand Curve:

1. Exceptional demand curve goes against the law of demand. It represents a direct relationship between price and demand.
2. Exceptional demand curve slopes upwards from left to right.
3. Giffen’s goods, prestige goods, branded goods, habituated goods, like cigarette have exceptional demand curve.
   

Question 6.
Direct Demand and Derived Demand / Indirect Demand
Answer:
Direct Demand:

1. Demand for consumer goods is direct because it satisfies our wants directly.
2. Demand for consumers goods are directly for consumption.
3. Direct demand comes from consumers or household sector.
4. Direct demand depends on price, income, taste, habits, etc. of consumers.
5. E.g. all consumer goods like books, furniture, T.V., tea, etc. have direct demand.

Derived Demand / Indirect Demand:

1. Demand for factors of production like land, labour, capital is derived as they satisfy our wants indirectly
2. Demand for factors of production are for further production.
3. Derived demand comes from producers or firms.
4. Derived demand depends on demand for final goods and services.
5. E.g. when demand for cotton shirt will increase, demand for raw cotton increases.

Question 7.
Extension I Expansion of Demand and Increase in Demand.
Answer:
Extension / Expansion of Demand:

1. Extension of demand refers to a rise in demand due to fall in price. Other factors remaining constant.
2. It is a case of variation in demand.
3. Extension in demand takes place due to a fall in price, other things remaining constant.
4. When there is extension in demand the demand curve moves downward on the same demand curve.
   

Increase in Demand:

1. Increase in demand takes place when more quantity is demanded at the same price.
2. It is a case of changes in demand.
3. Increase in demand takes place due to change in other factors, price remaining constant such as change in income, taste, habits, population, etc.
4. When there is a increase in demand the demand curve shifts to the right of the otiginal demand curve.
   

Question 8.
Contraction of Demand and Decrease in Demand
Answer:
Contraction of Demand

1. Contraction of demand means fall in demand due to a rise in price alone, other factors remaining constant.
2. Contraction of demand is a case of variation of demand.
3. Contraction in demand takes place due to rise in price alone.
4. It is shown by an upward movement along the same demand curve.
   

Decrease in Demand

1. Decrease in demand means when less is demanded at the same price or same quantity demanded at a lower price.
2. Decrease in demand is a case of changes in demand.
3. Decrease in demand is due to –
   (a) decrease in income
   (b) decrease in price of substitute
   (c) increase in price of complementary goods
   (d) decrease in population, etc.
4. A decrease in demand is shown by a shift in demand curve to the left of the original demand curve.
   

Question 9.
Variation in Demand and Chañges in Di
Answer:
Variation in Demand :

1. Variation in demand refers to changes in quantity demanded due to changes in price, other things remaining constant.
2. There are two types of variation in demand –
   (a) Expansion or Extension in demand.
   (b) Contraction in demand.
3. When price rises, quantity demanded falls, it is known as contraction and when price falls quantity demanded rises, it is known as expansion.
4. Variation in demand are shown by a movement along the same demand curve. Upward movement indicates contraction and downward movement indicates expansion.
   

Changes in Demand:

1. Changes in demand refers to changes in quantity demanded due to changes in factor other than price like change in income of consumer, size of population, change in fashion, change in price of substitute, etc.
2. There are two types of changes in demand –
   (a) Increase in demand
   (b) Decrease in demand
3. Increase in demand means when more quantity is demanded at the same price and decrease in demand means when less quantity is demanded at a same price.
4. Changes in demand are shown by shift in demand curve. Increase in demand is shown by a shift in demand curve to right side and decrease in demand is shown by a shift to the left side.
   

Question 10.
Joint Demand and Composite Demand.
Answer:
Joint Demand:

1. When two or more goods are demanded jointly to satisfy a single want, it is called joint or complementary demand.
2. E.g. of joint demand are car and petrol, ink cartridge and printers, mobile and sim card.
3. A rise in demand for one product will lead to a rise in the demand for other and vice versa.
4. In case of joint demand an increase in price of one good will reduce the demand for its joint product i.e. a rise in price of petrol will reduce the demand for car.
5. The demand for joint products is inelastic.

Composite Demand:

1. When goods are demanded for several uses, it is the case of composite demand.
2. E.g. of composite demand are for electricity, coal, steel, sugar, etc.
3. A change in demand for one use will affect the supply in other use.
4. In case of composite demand, an increase in the price of product will reduce its demand for different uses. Electricity / coal will be put to only important uses when its price rises.
5. The demand for composite commodities is elastic.

Question 11.
Complementary Demand or Joint Demand and Competitive Demand.
Answer:
Complementary Demand or Joint Demand:

1. When two or more goods are demanded jointly to satisfy one want, it is called complementary or joint demand.
2. E.g. bread and butter, car and petrol, mobile and sim card.
3. A rise in demand for one product will lead to a rise in the demand for the other and vice versa.
4. The cross elasticity of demand is negative.
5. When price of one commodity rises the demand for the other commodity i.e. its joint product falls. When price of car falls the demand for petrol rises.
6. The demand curve has a negative slope.
   

Competitive Demand Demand:

1. When two goods are close substitutes i.e. the demand for one competes with that of the other it is a case of competitive demand.
2. E.g. tea or coffee, pepsi or coke, petrol or diesel, Lux or Dove.
3. Rise in demand for one product will lead to a fall in the demand for other and vice versa.
4. The cross elasticity of demand is positive.
5. When the price of one commodity rises, the demand for the substitute commodity rises. When price of tea rise, the demand for coffee increases.
6. The demand curve has a positive slope.
   

Question 12.
Demand and Aggregate Demand.
Answer:
Demand:

1. Demand is a micro concept.
2. It refers to that quantity of a commodity which a person is ready to buy at a particular price and during a specific period of time.

Aggregate Demand:

1. Aggregate demand is a macro concept.
2. It refers to the total amount of sales proceeds which an entrepreneur actually expects from the sale of output produced at a given level of employment during the year.

3. Answer the following questions.

Question 1.
Write short notes on types of demand.
Answer:
Types of Demand:

1. Direct Demand : When a commodity satisfies the want of a consumer directly, it is said to have direct demand. Demand for consumer goods like food, clothes, sugar, vegetables, milk, etc.
2. Indirect Demand : It refers to demand for goods which are required for further production. It is also called as derived demand. Demand for factors of production like land, labour, capital, etc.
3. Joint or Complementary Demand : When two or more goods are demanded at a same time to satisfy single want, it is known as Joint or Complementary Demand. E.g. car and fuel, pen and ink, mobile phone and sim card, etc.
4. Composite Demand : When one commodity can be utilize for several needs or multiple uses, it is known as composite demand. E.g. electricity, steel, coal, etc.
5. Competitive Demand : It is demand for those goods which are substitute for each other. E.g. tea or coffee, sugar or jaggery, pepsi or Thumsup, etc.

Question 2.
Explain Market Demand schedule with a suitable diagram.
Answer:
It refers to total demand for a commodity from all the consumers. It is total quantity of commodity demanded by different consumers at different prices during a given period of time.
Market Demand Schedule is a tabular representation of various quantities of a commodity demanded by different consumers at different prices during a given period of time.
This can be explained with the help of following schedule-

The above market demand schedule shows an inverse relationship between price and market demanded of commodity ‘X’. At a high price of ₹10 per kg of commodity ‘X’, the market demand is only 30 kg and at a lower price of market demand rises to 90 kg of commodity ‘X’.

Market Demand Curve.
It is a graphical representation of market demand schedule X-axis represents quantity demanded (Market Demand) and Y-axis represents the price of the commodity. When the above market demand schedule is plotted on the graph, we derive the market demand curve ‘DD’, which slopes downward from left to right indicating inverse relationship between price and quantity demanded.

Question 3.
Explain the concept of change in j demand.
Answer:
Change in demand refers to change in s quantity demanded due to change in other factors of demand and price remains constant.
There are two types of changes in demand. They are : (1) Increase in demand (2) Decrease in demand.

(1) Increase in demand : It refers to rise in quantity demanded due to favourable changes in other factors like tastes, income, etc. and price remains constant.
Demand curve shifts to the right hand side of the original demand curve.

In the above diagram, DD is the demand curve which is showing downward movement on the same demand curve from point ‘b’ to point ‘c’ which indicates an expansion of demand.

(2) Decrease in demand : It refers to fall in quantity demanded due to unfavourable changes in other factors like tastes, income, etc. and price remains constant. Demand curve shift to the left hand side of the original demand curve.

In the above diagram DD is the original demand curve. D₂ D₂ demand curve indicates, decrease in demand by shifting towards the left hand side of original demand curve from point ‘b’ to point ‘a’.

Question 4.
Explain the assumptions to the Law of Demand.
Answer:
Assumptions to the Law of Demand:

• Prices of Substitute goods remain constant : The price of substitute goods should remain unchanged, as change in the price will affect the demand for the commodity.
• Prices of Complementary goods remains constant : A change in the price of one good will affect the demand for other, thus the prices of complementary goods should remain unchanged.
• No Expectation about future changes in prices : The consumers do not expect any significance rise or fall in the future prices.
• No change in size of Population : The size of population, gender ratio and age composition are assumed to remain constant. As such changes are sure to affect demand.
• No change in Taxation Policy : The level of direct and indirect tax imposed by the government on the income and goods should remain constant.
• Constant Level of Income : Consumer’s income must remain unchanged because if income increases, consumer may buy more even at a higher price not following the law of demand.
• No Change in Tastes, Habits,
  Preference, Fashions, etc. : If the taste changes then the consumers preference will also change which will affect the demand. When commodities are out of fashion, then demand will be low even at a lower price.

Question 5.
What is meant by extension and contraction of demand?
Answer:
Variations in demand refers to change in quantity demanded for a commodity due to change in price alone and other factors remaining constant.
There are two types of variations in demand.
They are (1) Expansion or Extension of demand (2) Contraction of Demand.

(1) Expansion or Extension of demand : It refers to rise in quantity demanded due to fall in price alone and other factors like tastes, income, etc. remaining unchanged. It is shown by a downward movement on the same demand curve.

In the above diagram, DD is the demand curve which is showing downward movement on the same demand curve from point ‘b’ to point ‘c’ which indicates an expansion of demand.

(2) Contraction of demand : It refers to fall in quantity demanded due to rise in price alone and other factors like tastes, income, population, etc. remaining unchanged. It is shown by a upward movement on the same demand curve.

In the above diagram, DD is the demand curve which is showing upward movement on the same demand curve from point ‘e’ to point ‘b’ and indicates contraction of demand.

Question 6.
Explain the concept of Giffen Paradox
Answer:
Giffen Paradox:

1. Giffen good are low quality or inferior goods like jowar, palm oil, etc.
2. Demand for low quality goods and inferior goods decrease even if there prices falls.
3. This behaviour of consumer was observed by Sit Robert Giffen in england.
4. Sir Robert Giffen observed that when price of bread (inferior good)declined, people did not buy more of it, because with increased real income they preferred to buy superior goods like meat.
5. In this case, demand curve slopes upward from left to right, showing exception to the law of demand.
   

4. State with reasons whether you agree or disagree with the following statements:

Question 1.
There are no exceptions to the Law of Demand.
Answer:
No, I do not agree with this statement.
There are some important cases in which the demand for the commodity is greater when price rises and smaller when price falls. Such cases are called exceptions to the law of Demand. In such case, demand curve slopes upwards from left to right and it has a positive slope.

• Prestige Goods : Rich people buy more expensive goods like gold, diamonds, etc., even when there prices are high to maintain their status.
• Giffen Paradox : Demand for low quality goods and inferior goods decrease even if there prices falls.
  According to Sir Robert Giffen when price of bread declined, people did not buy more because of increase in their real income and they prefer to buy superior goods like meat.
• Speculation : People are tend to buy more commodities if they expect prices to rise further. E.g. prices of oil, sugar. etc., are expected to rise before Diwali, so people buy more of these commodities even at higher price.
• Habitual goods : Due to habit of consumption, certain goods like tea is purchased in required quantities even at higher price.
• Ignorance : Sometimes people completely ignore the price of commodity and buy more of that commodity ignoring higher price.
• Price Illusion : Consumer feels that good at higher price are of better quality, therefore demand for such goods are higher even at rise in their prices.
  

Question 2.
Various factors influence the demand for a commodity.
Answer:
Yes, I agree with this statement.

Meaning of Demand : Demand refers to a desire or want for goods. Desire is the willingness to have some commodity which is backed by willingness and ability to pay.
Definition : According to Benham, “The demand for anything at a given price is the amount of it, which will be bought per unit of time at that price.

Features of Demand :

1. Demand is a relative concept.
2. Demand is essentially expressed with reference to time and price. ?

Determinants of Demand :

1. Price of Complementary Goods : Demand changes with changes in price of complementary goods like car and petrol, etc.
2. Advertisement : Effective advertisement and sales promotion will lead to greater demand of product. E.g. cosmetics, toothbrush, etc.
3. Price : Demand for a commodity is mainly influenced by its price. Normally at a higher price the demand is less and at a lower price it is more. Thus, demand varies inversely with price of a commodity.
4. Taste, Habits and Fashions : Habits influence market demand. If people habituated to the consumption of certain goods they will not give up such habits easily. E.g. demand for liquor, cigarettes, etc. Sometimes fashion change attitude and preference of people which in turn changes market demand.
5. Income: Income determines the purchasing power. Rise in income will lead to a rise in demand of a commodity and fall in income will lead to a fall in demand of a commodity.
6. Other Factors : (a) Climatic condition, (b) Changes in technology, (c) Government policy, (d) Customs and traditions, etc.
7. Nature of Product: Under necessary and unavailable circumstances the demand of a commodity will continue to be same irrespective of the corresponding price. E.g. medicine to control blood-pressure.
8. Level of Taxation : There would be increase in price of goods and services due to high rates of taxes which results in a decrease in demand and vice-versa.
9. Expectation about the Future Prices : If the consumer expect a rise in price in the near future they will demand more at present price. Similarly, when they expect price to fall, then they will buy less at present prices.
10. Price of Substitute Goods : Demand for cheaper substitute goods will rise when there is fall in price of such goods. E.g. when sugar price rises, then the demand for jaggery will rise.
11. Size of Population: Demand for commodity depends upon size and composition of population like age structure, gender ratio which influence demand for certain goods. E.g. larger the child population, more will be the demand for toys, chocolates, etc.

Question 3.
The demand curve slopes upwards from left to right.
Answer:
No, I do not agree with this statement.
OR
Demand curve slopes downward from left to right.
Answer:
Yes, I agree with this statement.
Reasons justifying downwards sloping demand curve are as follows:

• The law ofDiminishing Marginal Utility: Marginal utility goes on diminishing when there is increase in the stock of commodity and consumer tends to buy more when price falls and vice-versa.
• Income Effects : Whenever there is a fall in price of a commodity, purchasing power of a consumer gets increased, which enables him to buy more of that commodity.
• Substitution Effect : When price of commodity rises consumer tends to buy more of cheaper substitute goods and less of the commodity whose price has increased.
• Multi-purpose Uses : When a commodity can be used for satisfying multiple needs, its demand will rise with a fall in its price and vice-versa.
• New Consumers : When there is fall in price of a commodity, a new consumer class buy the commodity as they can afford it.
  Thus total demand for commodity increases with fall in price.

Question 4.
The law of Demand is based on assumptions.
Answer:
Yes, I agree with this statement.

Assumptions to the Law of Demand:

• Prices of Substitute goods remain constant : The price of substitute goods should remain unchanged, as change in the price will affect the demand for the commodity.
• Prices of Complementary goods remains constant : A change in the price of one good will affect the demand for other, thus the prices of complementary goods should remain unchanged.
• No Expectation about future changes in prices : The consumers do not expect any significance rise or fall in the future prices.
• No change in size of Population : The size of population, gender ratio and age composition are assumed to remain constant. As such changes are sure to affect demand.
• No change in Taxation Policy : The level of direct and indirect tax imposed by the government on the income and goods should remain constant.
• Constant Level of Income : Consumer’s income must remain unchanged because if income increases, consumer may buy more even at a higher price not following the law of demand.
• No Change in Tastes, Habits,
  Preference, Fashions, etc. : If the taste changes then the consumers preference will also change which will affect the demand. When commodities are out of fashion, then demand will be low even at a lower price.

Question 5.
Price is the only determinant of demand.
OR
Price is the only factor that affects demand for a commodity.
Answer:
No, I do not agree with this statement.
There are many other determinants of demand beside price, like –

1. Income: Income determines the purchasing power. Rise in income will lead to a rise in demand of a commodity and fall in income will lead to a fall in demand of a commodity.
2. Price of Substitute Goods : Demand for cheaper substitute goods will rise when there is fall in price of such goods. E.g. when sugar price rises, then the demand for jaggery will rise.
3. Price : Demand for a commodity is mainly influenced by its price. Normally at a higher price the demand is less and at a lower price it is more. Thus, demand varies inversely with price of a commodity.
4. Nature of Product: Under necessary and unavailable circumstances the demand of a commodity will continue to be same irrespective of the corresponding price. E.g. medicine to control blood-pressure.
5. Size of Population: Demand for commodity depends upon size and composition of population like age structure, gender ratio which influence demand for certain goods. E.g. larger the child population, more will be the demand for toys, chocolates, etc.

Question 6.
All desires are not demand.
Answer:
Yes, I agree with this statement.

• Desire means an individual’s wish to acquire a commodity.
• In economics, demand means desire which is backed by willingness and ability to pay.
• Symbolically, Demand = Desire + Ability to pay + Willingness to pay
• All desires may not be backed by ability to pay and willingness to pay.
• Therefore, all desires are not demand.

Question 7.
Population is the only determinant or factors of demand. (Mar. ‘15)
Answer:
No, I do not agree with this statement.

Determinants of Demand :

1. Price of Complementary Goods : Demand changes with changes in price of complementary goods like car and petrol, etc.
2. Advertisement : Effective advertisement and sales promotion will lead to greater demand of product. E.g. cosmetics, toothbrush, etc.
3. Price : Demand for a commodity is mainly influenced by its price. Normally at a higher price the demand is less and at a lower price it is more. Thus, demand varies inversely with price of a commodity.
4. Taste, Habits and Fashions : Habits influence market demand. If people habituated to the consumption of certain goods they will not give up such habits easily. E.g. demand for liquor, cigarettes, etc. Sometimes fashion change attitude and preference of people which in turn changes market demand.
5. Income: Income determines the purchasing power. Rise in income will lead to a rise in demand of a commodity and fall in income will lead to a fall in demand of a commodity.
6. Other Factors : (a) Climatic condition, (b) Changes in technology, (c) Government policy, (d) Customs and traditions, etc.

Question 8.
There are many types of demand.
Answer:
Yes, I agree with this statement.

1. Direct Demand : When a commodity satisfies the want of a consumer directly, it is said to have direct demand. Demand for consumer goods like food, clothes, sugar, vegetables, milk, etc.
2. Indirect Demand : It refers to demand for goods which are required for further production. It is also called as derived demand. Demand for factors of production like land, labour, capital, etc.
3. Joint or Complementary Demand : When two or more goods are demanded at a same time to satisfy single want, it is known as Joint or Complementary Demand. E.g. car and fuel, pen and ink, mobile phone and sim card, etc.
4. Composite Demand : When one commodity can be utilize for several needs or multiple uses, it is known as composite demand. E.g. electricity, steel, coal, etc.
5. Competitive Demand : It is demand for those goods which are substitute for each other. E.g. tea or coffee, sugar or jaggery, pepsi or Thumsup, etc.

5. Answer in detail:

Question 1.
State and explain the law of Demand with assumptions.
Answer:
(A) Introduction : The law of demand is one of the important law of consumption which explain the functional relationship between price and quantity demanded of a commodity. Prof. Alfred Marshall in his book ‘Principle of Economics’ which was published in 1890, has explained the consumer’s behaviour as follows:

(B) Statement of the Law : According to Prof. Alfred Marshall, “Other things being equal, higher the price of a commodity, smaller is the quantity demanded and lower the price of a commodity, larger is the quantity demanded.
In other words, other things remaining constant, demand varies inversely with price. Marshall’s law of demand describes the functional relationship between demand and price. It can be presented as:
D_x = f(P_x)
where D = Demand for Commodity
x = Commodity
f = function
P_x = Price of a commodity
(C) Assumption :

• Prices of Substitute goods remain constant : The price of substitute goods should remain unchanged, as change in the price will affect the demand for the commodity.
• Prices of Complementary goods s remains constant : A change in the price j of one good will affect the demand for other,  thus the prices of complementary goods  should remain unchanged.
• No Expectation about future changes jj in prices: The consumers do not expect any \ significance rise or fall in the future prices.
• No change in Taxation Policy : The level of direct and indirect tax imposed by the government on the income and goods should remain constant.
• Constant Level of Income : Consumer’s income must remain unchanged because if income increases, consumer may buy more even at a higher price not following the law of demand.
• No Change in Tastes, Habits, Preference, Fashions, etc. : If the taste changes then the consumers preference will also change which will affect the demand. When commodities are out of fashion, then demand will be low even at a lower price.

(D) Explanation of the law of Demand :
The law of demand is explained with the help of the following demand schedule and diagram:
Demand Schedule

Price of Commodity ‘X’ (in Rs.)	Quantity Demanded of Commodity ‘X’ (in kgs)
50	1
40	2
30	3
20	4
10	5

From the above demand schedule we observe that at higher price of ₹ 50 per kg, quantity demanded is 1 kg. When price fall from ₹ 50 to ₹ 40, quantity demanded rises from 1 kg to 2 kg. Similarly, at price ₹ 30 quantity demanded is 3kg and when price falls from ₹ 20 to ₹ 10 quantity demanded rises from 4 kg to 5 kg. This shows an inverse relationship between price and demand.

In the above diagram X-axis represent quantity demanded and Y-axis represent the price of the commodity. The demand curve DD slopes downwards from left to right ] showing an inverse relationship between price and demand. It has a negative slope.

Balbharti Maharashtra State Board Class 12 Sociology Important Questions Chapter 3 Diversity and Unity in Indian Society Important Questions and Answers.

Maharashtra State Board 12th Sociology Important Questions Chapter 3 Diversity and Unity in Indian Society

1A. Complete the following statements by choosing the correct alternative given in the brackets and rewrite it.

Question 1.
India is a ___________ country. (homogenous, secular, non-religious)
Answer:
secular

Question 2.
Dr. B.S. Guha classifies the population of India into ___________ main racial groups. (four, five, six)
Answer:
six

Question 3.
___________ tends to bring together people of the faith to celebrate commonly cherished festivals and
events. (Race, Religion, Caste)
Answer:
Religion

Question 4.
In ___________ Indian States were organized on a linguistic basis. (1947, 1971, 1956)
Answer:
1956

Question 5.
The Constitution of India has approved ___________ Official languages. (20, 27, 22)
Answer:
22

Question 6.
21st February 2017 was declared as an International ___________ Language Day by the United Nation. (Mother, Father, Spiritual)
Answer:
Mother

Question 7.
___________ refers to territorial entities found within the country. (Religion, Language, Region)
Answer:
Region

Question 8.
Sharing of natural resources gives the people a sense of ___________ unity. (religious, cultural, geographical)
Answer:
geographical

Question 9.
___________ examines the role of religion in social integration as a binding force among individuals and groups. (M. N. Srinivas, Iravati Karve, G. S. Ghurye)
Answer:
M. N. Srinivas

Question 10.
___________ refers mainly to loyalty to one’s own religion before the nation. (Casteism, Communalism, Regionalism)
Answer:
Communalism

Question 11.
Indian States have been divided on a ___________ basis. (religious, caste, linguistic)
Answer:
linguistic

Question 12.
___________ is built into the fabric of society and passed down from one generation to the next. (Equality, Inequality, democracy)
Answer:
inequality

Question 13.
The spirit of tolerance promotes ___________ (economic growth, national integration, diversity)
Answer:
national integration

Question 14.
Economic disparity means ___________ distribution of wealth. (normal, uneven, even)
Answer:
uneven

Question 15.
India is federal Union comprising of ___________ states with seven union territories. (29, 30, 28)
Answer:
29

Question 16.
Language plays an important role of ___________ in an organisation. (interest, communication, transport)
Answer:
communication

Question 17.
Caste an example of ___________ (equality, inequality, none)
Answer:
inequality

Question 18.
___________ refers to loyalty to one’s own religion before nation. (Casteism, Communalism, Linguism)
Answer:
Communalism

Question 19.
Unity implies a sense of oneness meaning ___________ (uniformity, integration, identity)
Answer:
integration

Question 20.
After independence India has adopted ___________ system. (presidential, federal, dictatorship)
Answer:
federal

Question 21.
In the constitution of India there are ___________ fundamental rights. (six, seven, eight)
Answer:
six

Question 22.
State were formed on the linguistic basis in the year ___________ (1956, 1951, 1947)
Answer:
1956

Question 23.
___________ is a multi-religious Country. (India, Bangladesh, China)
Answer:
India

Question 24.
India has always ___________ different cultures. (assimilated, diversified, obstructed)
Answer:
assimilated

Question 25.
Thrissurpuram is the festival held which state ___________ (Tamil Nadu, Kerala, Karnataka)
Answer:
Kerala

Question 26.
A large section of the tribal population of India live in ___________ State. (North eastern, southern, western)
Answer:
Noth eastern

Question 27.
Gender expression is linked to gender ___________ (culture, biology, socialisation)
Answer:
socialisation

Question 28.
___________ implies respect and tolerance for people of all faiths. (communalism, secularism, casteism)
Answer:
secularism

Question 29.
The Constitution of India, allows affirmative action through ___________ in education and employment. (discrimination, reservation, tolerance)
Answer:
reservation

B. Correct the incorrect pair and rewrite it.

Question 1.
(a) Kerala – Onam
(b) Tamil Nadu – Pongal
(c) Punjab – Baisakhi
(d) Assam – Makar Sankranti
Answer:
(d) Assam – Bihu

Question 2.
(a) North – Badrainarayan
(b) South – Rameshwaram
(c) East – Golden Temple
(d) West – Dwarka
Answer:
(c) East – Puri

Question 3.
(a) Hindus – Diwali
(b) Muslims – Muharram
(c) Christians – Christmas
(d) Parsi – Easter
Answer:
(d) Parsi – Pateti

Question 4.
(a) Secularism – Sarvadharmasamabhav
(b) Linguism – Language patriotism
(c) Communalism – Religious patriotism
(d) Religionism – Excessive attachment of one’s own caste
Answer:
(d) Religionism – Excessive attachment of one’s own state

Question 5.
(a) Kaveri water dispute – Linguism
(b) Babari – Masjid demolition – Communalism
(c) Unequal distribution of wealth – Economic inequalities
(d) Caste-based vote banks – Casteism
Answer:
(a) Kaveri water dispute – Regionalism

Question 6.
(a) Sanskrit, Kashmiri, Hindi, Bengali – Indo-Aryan
(b) Telugu, Kurukh, Oraon, Maler – Dravidian
(c) Himalayan and Bhutia Languages – Austro-Asiatic
(d) Aka – Jeru, Ongan and Sentinelese – Andamanese
Answer:
(c) Himalayan and Bhutia Languages – Sino-Tibetan

Question 7.
(a) The Three Language Formula – Religious unity
(b) The rule of law – Political unity
(c) Celebration of festivals – Cultural unity
(d) Sharing of natural resources – Geographical unity
Answer:
(a) The Three Language Formula – Linguistic unity

Question 8.
(a) ‘Below Poverty Line’ – Private property
(b) Private school differences – Educational differences
(c) The mall culture – Social environment
(d) Capacities and capabilities – Individual differences
Answer:
(a) ‘Below Poverty Line’ – Family influence

1C. Identify the appropriate term from the given options in the box and rewrite it against the given statement.

Unity, Language, Race, Regionalism, Class, Gender fluidity, North East, Jajmani, Sexuality, Culture, Egalitarian society, Secularism, Kannada, Northeast, Ethnocentrism, Totalitarianism.

Question 1.
The state of togetherness and oneness.
Answer:
Unity

Question 2.
A classical language of India.
Answer:
Kannada

Question 3.
A group of people with set distinctive physical features.
Answer:
Race

Question 4.
The region comprises seven sisters.
Answer:
East North

Question 5.
Relating to another person physically, emotionally and/or sexually.
Answer:
Sexuality

Question 6.
Those who do not limit themselves within the binary.
Answer:
Gender fluidity

Question 7.
The exchange of goods and services between various jatis.
Answer:
Jajmani

Question 8.
People belonging to different religious feel that their religion is superior.
Answer:
Ethnocentrism

Question 9.
Respect and tolerance for people of all faith.
Answer:
Secularism

Question 10.
Loyalty to one’s own state or region before one’s nation.
Answer:
Regionalism

Question 11.
It is based on the principle of cultural integration.
Answer:
National Anthem

Question 12.
It is caused by Religious fundamentalism.
Answer:
Terrorism

Question 13.
Malnutrition deaths of infants.
Answer:
Below Poverty Line

1D. Correct underlined words and complete the statement.

Question 1.
In Kolkata, the festival of lights (Diwali) is celebrated along with the Parsis Festival of Lights (Hannukah).
Answer:
In Kolkata, the festival of lights (Diwali) is celebrated along with the Jewish Festival of Lights (Hannukah).

Question 2.
700 jatis are classified under the Scheduled Caste communities.
Answer:
750 jatis are classified under the Scheduled Caste communities.

Question 3.
Religion has become a means for competing for access to resources and power in modern India.
Answer:
Caste has become a means for competing for access to resources and power in modern India.

Question 4.
Communalism leads to Inter-State rivalries.
Answer:
Regionalism leads to Inter-State rivalries.

Question 5.
In all societies, we see economic equality.
Answer:
In all societies, we see economic inequality.

Question 6.
When people are identified on the basis of wealth, education and job is caste.
Answer:
When people are identified on the basis of wealth, education and job is class.

Question 7.
In traditional Indian society, importance was given to achieved status.
Answer:
In traditional Indian society, importance was given to ascribed status.

Question 8.
Due to racial discrimination, women are denied many rights privileges and opportunities that they deserve.
Answer:
Due to gender discrimination, women are denied many rights privileges, and opportunities that they deserve.

Question 9.
Class diversity is observed in various fields like costumes tradition, food, habits, norms, values, festivals, and lifestyle.
Answer:
Cultural diversity is observed in various fields like costumes tradition, food, habits, norms, values, festivals, and lifestyle.

Question 10.
Indians have faith in dictatorships.
Answer:
Indians have faith in democracy.

Question 11.
Regional fundamentalism can lead to acts of terrorism.
Answer:
Religious fundamentalism can lead to acts of terrorism.

Question 12.
Disputes created among the racists are the distribution of river water, constructions, dams, demand separate states, etc.
Answer:
Disputes created among the regions/states are the distribution of river water, constructions, dams, demand for separate state etc.

Question 13.
Many regions of south India disapprove of the acceptance of English as an official language.
Answer:
Many regions of south India disapprove of the acceptance of Hindi as an official language.

Question 14.
Religion participation is required to conserve language diversity.
Answer:
Community participation is required to conserve language diversity.

Question 15.
The role and significance of Chhatrapati Shivaji Maharaj are well-established in Gujarat.
Answer:
The role and significance of Chhatrapati Shivaji Maharaj are well-established in Maharashtra.

2. Write short notes.

Question 1.
Secularism
Answer:
Given the nature of our religious plurality, the concept of secularism in India fosters a modern outlook showing religious tolerance. In India, secularism implies respect and tolerance for people of all faiths, beautifully encapsulated in the term, ‘Sarva dharma samabhav’.

India has been and continues to be a land with multiple faith systems. This necessarily includes acceptance of people who do not subscribe to any religious identity, custom or practice, but who may express their loyalty and commitment to secular values such as scientific endeavor, humanitarianism, humanism, and so forth.

The term secularism implies respect and tolerance for people of all faith. The concept of secularism dates back to 2300 years ago by emperor Ashoka the term ‘Sarva Dharma Samabhav’ is one of the most cherished Indian values it is one of the biggest achievements of a democratic country. Secularism is a simple word that refers to an ideology that provides people with the right to follow any religion. It means separate religion from political, economic, social, and cultural aspects of life.

The constitution of India gives the right of freedom to all religions, protects the belief patterns and values of their religion. It permits the state with the responsibility to maintain neutrality in matters of religion. Secularism states that no one shall be subject to discrimination by any state or any social institution on grounds of religion or belief patterns.

Living in a secular state brings faith and acceptance of people from different religious backgrounds. In this way, secularism fosters a modern outlook showing religious tolerance, humanity and promotes the integration of all people in society.

Question 2.
Linguistic Unity
Answer:
Linguistic Unity means that every language in the country whether regional or national language must be treated equally. The Indian State recognizes linguistic diversities and makes special provisions to protect and support some of the languages and dialects that are on the verge of extinction.

People speaking different languages have been living harmoniously without any conflicts. The three-language formula followed by all State Education Boards enables the inculcation of Hindi and English as languages to connect with the Union, English to connect with the outside world, and the regional/local language for communication within the State.

As per the policy the three languages recommended were:

• 1st language: Regional Language or Mother Tongue.
• 2nd language: English or Modern Indian Language (in Hindi speaking States) Hindi or English (in non-Hindi speaking States)
• 3rd language: English or Modern Indian Language (in Hindi speaking States)

Classical languages and languages of linguistic minorities have also found a place in the educational curriculum

Many educational bodies offer learners the option of answering their examinations in a range of mediums (e.g. Marathi, Hindi, Urdu, Gujarati, Kannada, English). Doordarshan and Akashwani have programmes in multiple Indian languages that reach out to millions of persons. These are measures that promote a sense of linguistic unity among multi-lingual people of the land.

Question 3.
Process of Unity in India
Answer:
At the root of all the co-existing diversities, there exists an underlying unity. This has created a composite culture decisively pan-Indian in nature. In India, secularism implies respect and tolerance for people of all faiths. India has been and continues to be a land with multiple faith systems

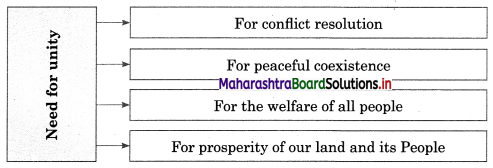
Following are the unifying factors in India:
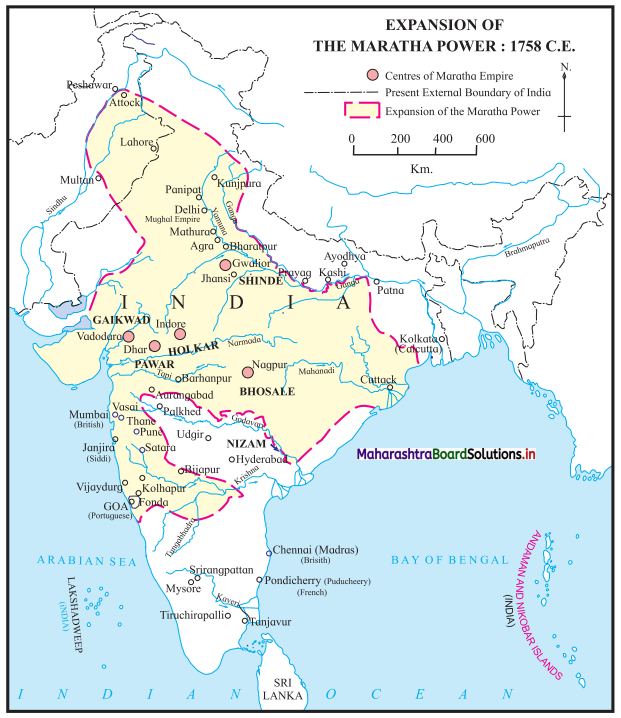
Geographical unity: one would find unity in the agrarian cycles such as the sowing season and the harvest season. Sharing of natural resources gives people a sense of oneness. Festivals such as Onam in Kerala, Makar Sankrant in Western and South India, Pongal in Tamil Nadu, Baisakhi in Punjab, and Bihu in Assam revolve around the harvest season.

Religious Unity: Although various religious groups in India present external differences, there are some commonly shared elements. India is a land of diverse religious faiths. Religious unity in India finds its expression through places of worship scattered all over the country.

Political Unity: National unity and integrity have been maintained even though sharp economic and social inequalities have obstructed the emergence of an egalitarian society. The Five-Year Plans and several developmental schemes were geared towards uplifting the poor and weaker sections of society. The Constitution of India has established the “rule of law” throughout the country. All citizens are equal and subject to the same authority.

Linguistic diversity: The Indian State recognizes linguistic diversities and makes special provisions to protect and support some of the languages and dialects that are on the verge of extinction. The three-language formula followed by all State Education Boards enables the inculcation of Hindi and English as languages to connect with the Union, English to connect with the outside world, and the regional/local language for communication within the States.

3. Write differences.

Question 1.
Religious diversity and Caste diversity
Answer:

Religious diversity	Caste diversity
(i) Meaning: Religious diversity means people practicing different religions living together Religions like Hinduism, Jainism, Buddhism, Christianity, Islam, Zoroastrianism, and Sikhism have flourished in India.	(i) Meaning: There is caste diversity in India with four varnas or caste groups Caste diversity means people belonging to different castes living together.
(ii) Sub Division: Each major religion is subdivided along the lines of religious doctrines, sects, and cults.	(ii) Sub Division: There are thousands of castes and subcastes in India.
(iii) Features: Each religion has its own philosophy, ideology, and rituals.	(iii) Features: Each caste has its own lifestyle, rituals, festivals, and deities.
(iv) Impact: This diversity leads to communalism i.e. loyalty to one’s own religion leads.	(iv) Impact: This diversity creates a negative and conservative attitudes and leads to casteism i.e. extreme loyalty to one’s own caste.
(v) Result: It creates a feeling of insecurity and gives rise to communal tensions.	(v) Result: It breaks up the solidarity and creates disunity.
(vi) Function: Religion tends to bring together people of the faith to celebrate commonly cherished festivals and events.	(vi) Function: The different castes functioned in an interdependent barter relationship which was the basis of the agrarian economy.

Question 2.
Gender Binary and Gender Diversity
Answer:

Gender Binary	Gender Diversity
(i) Meaning: Gender binary is the classification of gender into two distinct, opposite forms of masculine and feminine, due to the social system.	(i) Meaning: Gender diversity go beyond gender binaries of female-male, masculine and feminine, etc
(ii) Socialization: It results in Gender stereotypes determining people’s beliefs about the characteristics of males and females.	(ii) Socialization: It results in gender plurality which seeks to identify all gender identities or expressions in addition to the binary.
(iii) Approach: It excludes non-conformists, and supports patriarchal values.	(iii) Approach: It has an inclusive approach and promotes Constitutional gender equality.
(iv) Effect: It results in the dominance of heteronormativity in society and in all its institutions.	(iv) Effect: It results in acceptance of gender fluidity.

4. Explain the following concepts with examples.

Question 1.
Regionalism
Answer:
Regionalism refers to loyalty to one’s own State or region before one’s nation. This interferes with national integration to a great extent. The history of a particular region is glorified and often it is misused to stress divisive forces, thus ignoring the common cultural legacy and heritage.

Regionalism emerges due to the desire of people speaking one language to have one State. There is also a strong urge to give priority to the economic development of one’s own region. This leads to Inter-State rivalries. So long as this Inter-State rivalry is economic and social (e.g. for funds and welfare schemes), it is healthy.

But when this rivalry takes political overtones, it becomes very dangerous. Political parties give more importance and weightage to local and regional matters and problems rather than the nation. Regionalism thus strengthens sectarian biases by political parties. Inter-regional tensions escalate over economic, political, and such issues. This has led to regional movements for State rights and militant movements for separatism.

Example: The Jammu and Kashmir issue, the Punjab problem, Assam issue, etc. All this, if unchecked, can strike at the very root of democracy.

Question 2.
Linguistic Unity
Answer:
Linguistic unity means that every language in the country, whether regional or national language, must be treated equally. The Indian State recognizes linguistic diversities and also makes special provisions to protect and support some of the languages and dialects that are on the verge of extinction.

Classical languages and languages of linguistic minorities have also found a place in educational curricula. Many educational bodies offer learners the option of answering their examinations in a range of mediums (e.g., Marathi, Hindi, Urdu, Gujarati, Kannada, and English). Doordarshan and Akashwani have programmes in multiple Indian languages that reach out to millions of persons who tune in to them. These are measures that promote a sense of linguistic unity among multi-lingual people of the land.

Example: The three-language formula followed by all State Education Boards enables the inculcation of Hindi and English as languages to connect with the Union, English to connect with the outside world, and the regional/local language for communication within the State.

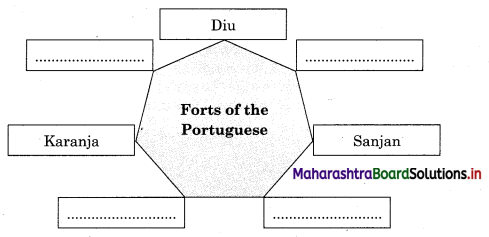
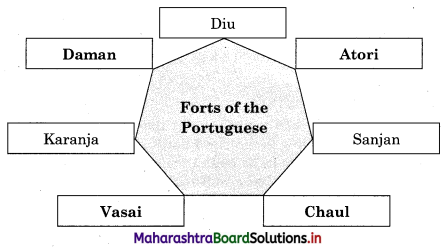
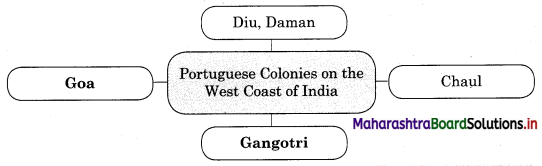
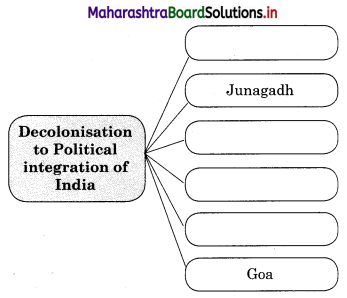
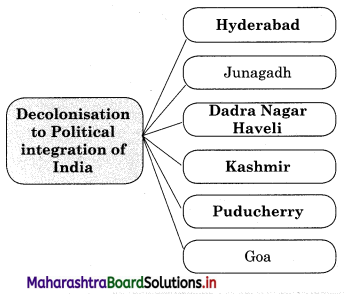
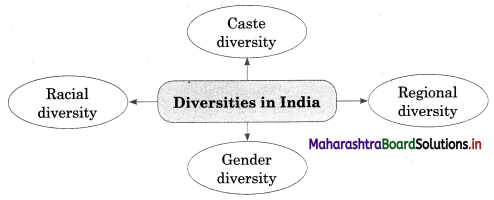
5A. Complete the concept map.

Question 1.

Answer:

Question 2.

Answer:

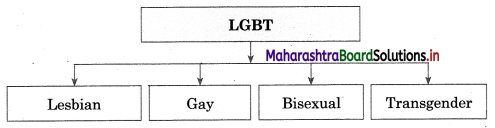
Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

Question 7.

Answer:

5B. State whether the following statements are True or False with reasons.

Question 1.
Discrimination based on caste is a major hurdle for national integration.
Answer:
This statement is True.

Casteism refers to loyalty to one’s own caste before loyalty to the nation. Caste ties are so strong that people are inclined to think in terms of caste before the nation. This may lead to caste members protecting their own caste group through social service, education, medical, and other welfare schemes. Caste members take with them their biases and prejudices into politics. They then begin to express their sectarian interests in various ways. People are influenced by them and vote for their own caste members. Those castes having numerical strength rise up through politics. Those who win the elections then favour their caste groups in various ways. In view of all this, the problem of national integration becomes very serious.

Despite laws, urbanization, industrialization, and education, the caste system continues in the mindsets of many people. Caste has become a means for competing for access to resources and power in modern India. Discrimination based on caste is a major hurdle for national integration. People engaged in weakening the unity of the country tried desperately to create divisions and rifts in the name of caste, creed, and culture. The feeling of social neglect among scheduled castes due to suppression by upper castes has disturbed the sense of ‘we feeling’ and unity which has resulted in caste atrocities and caste prejudices. Excessive caste-based loyalty is particularly evident at the time of elections, with political parties wooing members of their own caste for the sake of votes.

Question 2.
India is a diversified country
Answer:
This statement is True.

India is a land of variety, there is so much diversity along the lines of regions, language, religion, caste, etc. Here, we see various places of religious worship, a celebration of festivals, values of equality, secularism, humanity, etc., are nourished.

Some of the diversifying factors are:
(i) Religious diversity: Religion is one of the key facts of diversity in Indian society. Although India is a multi-religious and multi-cultural country, the Constitution of India ensures that the secular fabric of society is maintained. The Right to Freedom of Religion is also declared as a Fundamental Right by the Indian Constitution. Religion tends to bring together people of the faith to celebrate commonly cherished festivals and events.

(ii) Linguistic diversity: India is a land of many languages. The Constitution of India has approved 22 official languages. Among these, three languages have been recognized as classical languages viz. Sanskrit, Tamil, and Kannada. The Language Policy of India guarantees protection to linguistic minorities. A unique feature of India is the concept of protecting the interest of children to get basic education in their mother tongues (i.e., home language).

(iii) Caste diversity: Caste is a major source of diversity in Indian society. That there are about 3500 jatis found in India, out of which 751 are classified under the Scheduled Caste communities. The caste system provided the basis of social structure. The practice of the caste system is not confined to Hindus. Caste-like divisions are seen among Muslims, Christians, and Sikhs as well.

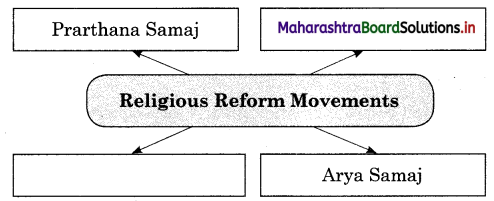
Balbharti Maharashtra State Board Class 12 History Important Questions Chapter 4 Colonialism and the Marathas Important Questions and Answers.

Maharashtra State Board 12th History Important Questions Chapter 4 Colonialism and the Marathas

1A. Choose the correct alternative and rewrite the statement.

Question 1.
In __________ Chhatrapati Shivaji Maharaj attacked the region of Bardesh.
(a) 1667
(b) 1668
(c) 1669
(d) 1670
Answer:
(a) 1667

Question 2.
In 1668, the __________ established their factory at Rajapur.
(a) British
(b) Dutch
(c) French
(d) Portuguese
Answer:
(c) French

Question 3.
The __________ fort was under siege laid by Adilshah’s army.
(a) Panhala
(b) Raigad
(c) Raj gad
(d) Simhagad
Answer:
(a) Panhala

Question 4.
__________ was offered asylum by the British.
(a) Madhavrao Peshwa
(b) Narayanrao Peshwa
(c) Raghunathrao
(d) Vishwasrao
Answer:
(c) Raghunathrao

Question 5.
The third Anglo-Maratha War was fought in __________
(a) 1815
(b) 1816
(c) 1817
(d) 1818
Answer:
(c) 1817

Question 6.
The __________ arrived from Abyssinia.
(a) British
(b) French
(c) Dutch
(d) Siddis
Answer:
(d) Siddis

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Group ‘A’	Group ‘B’
(a) Ibrahim Khan Gardi	Mercenary
(b) Fazal Khan	Brother of Afzal Khan
(c) Abdul Karim	Subhedar of Rajapur
(d) Henry Oxenden	British agent

Answer:
Fazal Khan – son of Afzal Khan

2A. Write the names of historical places/persons/events.

Question 1.
A book was written by Cosme da Guarda-
Answer:
Vide de Celehro Sevagy (Life of the Celebrated Shivaji)

Question 2.
The Portuguese emissary who met Chhatrapati Shivaji Maharaj-
Answer:
Gonsalo Martez

Question 3.
A type of revenue collected by the Maratha rulers-
Answer:
Chauthai

Question 4.
The younger brother of Peshwa Bajirao I-
Answer:
Chimajiappa

Question 5.
Treaty signed by the British and Peshwa Bajirao II-
Answer:
Treaty of Vasai

Question 6.
The battle fought between the Marathas and Ahmadshah Abdali in 1761-
Answer:
The Third Battle of Panipat

Question 7.
The northern region of Goa was known as-
Answer:
Bardish

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
The Portuguese were alarmed because __________
(a) Chhatrapati Shivaji Maharaj built a strong navy
(b) Chhatrapati Shivaji Maharaj had a strong army
(c) Chhatrapati Shivaji Maharaj had the support of other European powers
(d) Chhatrapati Shivaji Maharaj had a good network of spies
Answer:
(a) Chhatrapati Shivaji Maharaj built a strong navy

Question 2.
Chhatrapati Shivaji Maharaj was determined to humble the Portuguese __________
(a) The Portuguese opposing the construction work by the Marathas in Chaul
(b) Forcing their subjects in Goa for religious conversion
(c) Pillaging of the trading ships
(d) All of the above
Answer:
(d) All of the above

3A. Observe the map on textbook page 29 and answer the questions based on it.

Question 1.
Who was in charge of Indore?
Answer:
The Holkars were in charge of Indore.

Question 2.
Where was the seat of the Mughal empire?
Answer:
The seat of the Mughal empire was in Delhi.

Question 3.
Where were the centers of the Maratha empire?
Answer:
Dhar, Indore, Gwalior, Nagpur, and Vadodara were centers of the Maratha empire.

Question 4.
Under whose command was Goa?
Answer:
Goa was under the command of Portuguese.

Question 5.
Name the places that were under British rule.
Answer:
Mumbai (Bombay) and Chennai (Madras) were under the rule of the British.

Question 6.
What is the old name of Kolkata?
Answer:
The old name of Kolkata is Calcutta.

Question 7.
Who captured Janjira?
Answer:
The Siddis captured Janjira.

3B. Complete the following concept map.

Question 1.

Answer:

4A. Write short notes.

Question 1.
Vide de Celebre Sevagy
Answer:
A book written by Cosme da Guarda, a Portuguese historian, is a very important source of the history of Maharashtra. This book is entitled Vide de Celebre Sevagy (Life of the Celebrated Shivaji). He was the first European author to write a biography of Chhatrapati Shivaji Maharaj.

Question 2.
Dutch and the Maratha Empire
Answer:
The Dutch established a factory at Vengurla in 1649. Their trade flourished there. However, their trade was severely affected when Chhatrapati Shivaji Maharaj attacked Kudal. In 1665, the Mughal subedar of Surat asked for help for destroying the Maratha naval force. However, the Dutch offered no help. Chhatrapati Shivaji Maharaj had allowed them to build a factory at Dabhol. The political relations between the Dutch and the Marathas kept changing to suit the need of the time.

The Marathas did not harm the Dutch factory at Surat. Also, during the Karnataka campaign, the Marathas ensured the safety of the Dutch factory and also issued them trading permits. For these favours the Dutch paid tributes to Chhatrapati Shivaji Maharaj. The Dutch factories at Porto Novo/Parangipettai and Tegnapattam/ Devanapattinam were unharmed by Chhatrapati Shivaji Maharaj.

4B. Explain the following statements with reasons.

Question 1.
Chhatrapati Shivaji Maharaj adopted a strong policy against the European colonisers.
Answer:
Chhatrapati Shivaji Maharaj had foreseen the ulterior motives of the foreigners and their ways of infiltration. He built strategies to arrest their advances in India. He took immediate measures by creating a strong naval force. He levied octroi on British trade salt as a measure to protect the local salt trade. Thus, Chhatrapati Shivaji Maharaj adopted a strong policy against the European colonisers.

Question 2.
Another Anglo-Maratha War took place in 1803.
Answer:
The relations between Holkar and Peshwa Bajirao II turned bitter. As a result, Yashwantrao Holkar attacked Pune. Bajirao Peshwa II panicked and sought asylum from the British. A treaty was signed by the British and the Peshwa is known as the ‘Treaty of Vasai’. However, this treaty was not acceptable to Shinde and Holkar. Hence, there was another Anglo-Maratha War in 1803.

5. State your opinion.

Question 1.
Ibrahim Khan Gardi was hired by the Marathas.
Answer:
Ibrahim Khan Gardi was a mercenary who had trained under the French. He was hired by Sadashivraobhau Peshwa as the chief of artillery. In the Third Battle of Panipat, Mahadji Shinde had observed Ibrahim Khan’s skills. Inspired by it, he built a trained army with the help of de Boigne, a French military trainer, and also established well-equipped artillery.

Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 6 Index Numbers Important Questions and Answers.

Maharashtra State Board 12th Economics Important Questions Chapter 6 Index Numbers

1. A. Choose the correct option:

Question 1.
Index Numbers are used –
(a) to determine production
(b) to determine the level of employment
(c) to revise dearness allowance
(d) to revise cost of living
Options :
(1) a, b and c
(2) b, c and d
(3) c and d
(4) only d
Answer:
(3) c and d

Question 2.
Statements related to features of Index Numbers.
These are specialised form of averages. These help to determine price index.
These are not the barometers of economic activity.
Base year is taken as 100.
Options :
(1) a, b and d
(2) b, c and d
(3) b and c
(4) All of these
Answer:
(1) a, b and d

Question 3.
How does purchasing power changes with the increase in price level?
(a) Remains unchanged
(b) Increases
(c) Decreases
(d) None of these
Options :
(1) a, b and c
(2) b, c and d
(3) only c
(4) only b
Answer:
(3) only c

Question 4.
What do Index numbers measure?
(a) Value of money
(b) Relative prices
(c) Relative change in prices
(d) All of these
Options :
(1) b, c and d
(2) only b
(3) only c
(2) a, b and c
Answer:
(3) only c

(B) Complete the Correlation.

1. Base year quantity : …………….. :: Current year quantity : 125
2. Present period : Current period :: Past period : ……………..
3. All commodities with equal importance : …………….. :: All commodities with different importance :: Weighted Index
4. Dearness Allowance : Consumer Price Index :: Standard of Living : ……………..
5. P₀₁ = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100 : Laspeyre’s Index ::
   P₀₁ = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) x 100 = ……………..

Answers:

1. 100
2. Base period
3. Simple Index
4. Cost of Living Index
5. Paasche’s Index

(C) Give economic terms.

(1) Index number calculated from a single variate.
(2) Index number calculated from a group of variable.
(3) The year for which Index number is being prepared.
(4) The year from which the changes are measured.
(5) Barometer of economic activity.
(6) Index which measures price level of goods traded in whole sale market.
(7) Average of quantity of commodities produced in different sectors of the economy.
(8) Index which measures price level of goods in retail market.
(9) Base year index number.
(10) Purchasing power of money is measured by.
(11) Quantity Index number is also called.
(12) Index which helps in determining the depreciation cost of durable goods.
(13) Base year is also known as.
(14) Laspeyre uses period quantity as weights.
(15) Paasche uses period quantity as weights.
Answer:
(1) Unvariate index
(2) Composite index
(3) Current year
(4) Base year
(5) Index numbers
(6) Wholesale Price index
(7) Quantity Index number
(8) Retail Price Index number
(9) 100
(10) Cost of Living Index
(11) Volume Index number
(12) Price Index
(13) Reference year
(14) Base
(15) Current

(D) Complete the following sentences.

(1) Index numbers are ………….. averages.
(2) Index number is an ………….. barometer.
(3) A base year should be a………….. year.
(4) The ratio of current year price to the base year price multiplied by 100 is called ………….. index number.
(5) ………….. index number is the average of all quantity of commodities produced in different sectors.
(6) ………….. index number is a simple average of the index numbers of individual goods.
(7) ………….. Index number gives equal importance to all items.
(8) Purchasing power of money can be measured by………….. index number.
(9) To know the changes in production………….. index number is more useful.
(10) Index number for the base year is …………..
(11) ………….. refer to the relative importance of different items in the construction of Index Number.
Answers:

1. specialised
2. economic
3. recent
4. Price
5. Quantity
6. Simple
7. Simple
8. cost of living
9. quantity
10. 100
11. Weights

(E) Choose the correct pair :

I.

Answer:
Options :
(1) (1) – d, (2) – c, (3) – a, (4) – b
(2) (1) – d, (2) – a, (3) – b, (4) – c
(3) (1) – b, (2) – c, (3) – d, (4) – a
(4) (1) – c, (2) – d, (3) – a, (4) – b
Answer:
(2) (1) – d, (2) – a, (3) – b, (4) – c

II.

Group ‘A’	Group ‘B’
(1) Index Number	(a) Cost of living
(2) Dearness Allowance	(b) Economic Barometer
(3) Base year	(c) Wholesale Price Index
(4) Whole sale market goods	(d) 100

Options :
(1) (1) – b, (2) – a, (3) – d, (4) – c
(2) (1)- c, (2) – d, (3)- a, (4) – b
(3) (1)- d, (2) c, (3)- b, (4) – a
(4) (1)- a, (2) b, (3) c, (4) – d
Answer:
(1) (1) – b, (2) – a, (3) – d, (4) – c

2. Answer the following :

Question 1.
What are the different methods of constructing Index numbers?
Answer:
Following chart helps to know different methods of constructing Index Numbers:

(A) Simple Index Number : A Simple Index Number is constructed when all the items like food, clothing, transport, housing, etc. are given equal importance. There are three methods of constructing it.

1. Price Index Number : It is calculated using the following formula:
P₀₁ = \(\frac{\Sigma p_{1}}{\Sigma p_{0}}\) x 100
where – P₀₁ = Price Index Number
Σp₁ = Total of the current year price of various commodities.
Σp₀ = Total of base year prices of various commodities.

2. Quantity Index Number : It is calculated by using the following formula :
Quality Index Number Q₀₁ = \(\frac{\Sigma q_{1}}{\Sigma q_{0}}\) x 100
where, Σq₁ = Sum total of current year quantities of all commodities
Σq₀ = Sum total of base year quantities of all commodities

3. Value Index Number : It is calculated by using the following formula:
Value Index Number V₀₁ = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{0}}\) x 100
where, Σp₁q₁ = Sum total of the product of the prices and quantities of the current year
Σp₀q₀ = Sum total of the product of the prices and quantities of the base year.

(B) Weighted Index Number : Under this method, physical quantities are used as weights, therefore prices themselves are weighted by quantities. We can take either the base year quantities or current year quantities as weights or the average of the two.
These index numbers are the simple aggregative type with the fundamental difference that weights are assigned to the various items included in the index.
There are two methods of constructing it.
(1) Laspeyre’s Method
(2) Paasche’s Method

(1) Laspeyre’s Method : This method was devised by Laspeyre’s, a German economist in 1871. In this method the weights are determined by quantities in the base year.
P₀₁ = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100
where, P₀₁ = Price Index Number.
p₀ = Prices of the base year.
q₀ = Quantities of the base year,
p₁ = Prices of the current year.
Σ p₁q₀ = Sum of all the products of p, and q₀.
Σ p₀q₀ = Sum of all the products of p0 and q₀.

(2) Paasche’s Method : This method was devised by a German economist known as Hermann Paasche in 1874. The weights of current year are used as base year in constructing the Index Number.

P₀₁ = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) x 100
where, P₀₁ = Price Index Number.
p₁ = Prices of the current year.
q₁ = Quantities of the current year.
p₀ = Prices of the base year.
Σp₁q₁ = Sum of all the products of p₁ and q₁,
Σp₀q₁ = Sum of all the products of p₀ and q₁

Question 2.
Explain the features of Index Numbers. ?
Answer:
Features of Index Numbers :

• Index numbers are a specialised form of averages.
• They are expressed in percentage form without using a percentage sign.
• The year for which index number is being prepared is the current year.
• The year from which index number is being prepared is called the base year which is always taken as 100.
• They are used in measuring the changes in magnitudes which cannot be measured directly.
• The formula used for Price Index Number = \(\frac { Total price of the current year }{ Total price of the base year }\) x 100
• They are considered as barometer of economic activity.
• Index number which is calculated from a single variable is called “univariate • index” and which is constructed from a group of variables is called a “composite index”.

Question 3.
Explain the steps involved in the construction of index numbers.
Answer:
Steps involved in the construction of index numbers are as follows :

• Purpose of an Index Number : Before constructing an index number, one must know the purpose for which the index number is constructed. E.g. for the whole c sale price or retail price or for agricultural output, etc.
• Selection of a Base Year : It is important to select a base year against which comparisons are made. So base year or reference year should be a recent year and not a distant past. it should be normal and free from natural calamities, war, etc.
• Selection of Commodities: When the cost c of living index number of the middle class families is to be constructed, the items that are used by middle class families in everyday life should be included and items like big cars, AC’s, etc. should not be included.
• Selection of Prices : Prices differ from city ‘I to city and even from shop to shop in the same city. Hence, we should take a few standard shops from where middle class families buy goods and take the average of the prices of goods sold by them. Otherwise index number constructed may be misleading.
• Selection of suitable Average : An ; index number is a special kind of average, Generally arithmetic mean is commonly ? used for construction of index number as it is simple to calculate.
• Selection of Formula : Number of formulae can be used for construction, of index numbers. Economists have to decide which formula to use for the construction of a particular index number.
• Assigning proper Weights : Weights refer to the relative importance of different items in the construction of an index number. Weights may either be quantity weights (q) or value weights (p). All weights may not be equally important. Therefore, by s assigning specific weights better result can be obtained.

3. State with reasons whether you agree or disagree with the following statements:

Question 1.
Index Numbers can be constructed without the base year.
Answer:
No, I do not agree with this statement.
Index numbers can be constructed without the base year because :

• Index Numbers are the tools for measuring the changes in the magnitude of a variable or a group of variables over time with respect to a chosen year.
• Prices of some goods may increase and of other may decrease during the two periods. Index numbers solves this problem by taking the average change.
• For example, to know cost of living of people in general in India, Government chooses a base year 2010 which is taken as 100. Then cost of living is calculated in 2019 which may be 140.
• This difference of 40(140-100) shows that cost of living in India has increased by 40% since 2010.
  Hence, Index Numbers cannot be constructed – without the base year.

Question 2.
Any year can be taken as a base year for index number.
Answer:
No, I do not agree with this statement.

• In preparing index number the first step is c to select a year which serves as a reference)period.
• The prices in any other year are compared to the prices in the base year.
• The base year should be a recent year.
• If the base year is in the distant past, the result will not be meaningful. E.g. if the index number of the cost of living is calculated for the current year and compared with adistant past of 1970 as a base year it will not be meaningful.
• Base year should also be a year when the prices are regarded as normal prices.
  Hence, any year cannot be taken as a base year for index number.

Question 3.
Index numbers are very useful in economics and business.
OR
Index numbers are economic barometer.
Answer:
Yes, I do agree with this statement. Index numbers are very useful in economics and business and are used as powerful tools to measure the changes in various phenomena over a period of time like; measuring changes in the cost of living, wholesale prices, industrial production, exports, etc.
Uses of Index Numbers are :

• They help in the study of trends.
• They act as an economic barometer.
• They measure the purchasing power of money.
• They help to adjust national income.
• They provide guidelines for formulating policies and arriving at decisions.
  Hence, Index numbers are very useful in economics and business.

4. Answer in detail

Question 1.
Define index number. What are its main features?
Answer:
(A) Definition:
Different economists define index numbers in different ways.

• According to Spiegel, index number is, “a statistical measure to show changes in variable or a group of related variables with reference to time, geographical location and other characteristics such as income, profession, etc.”
• Croxton and Cowden defines index numbers as, “a device for measuring difference in the magnitude of a group of related variables.”
• According to Bewley, “Index Numbers are used to measure the changes in some quantity which cannot be observed directly. ”

(B) Meaning:
An index number is a specialised average which measures percentage changes in a variable (or a group of variables) over a specified time. When we say that the index of the whole sale price for the year 2018 is 125, taking the base year as 2015, it means that there is an increase of the wholesale price by 25%. Hence, index numbers are used to measure general changes in price, cost of living, wages, production, stock market, etc. Therefore, they are called “economic barometer”.

(C) Features of Index Numbers :

• Index numbers are a specialised form of averages.
• They are expressed in percentage form without using a percentage sign.
• The year for which index number is being prepared is the current year.
• The year from which index number is being prepared is called the base year which is always taken as 100.
• They are used in measuring the changes in magnitudes which cannot be measured directly.
• The formula used for Price Index Number = \(\frac { Total price of the current year }{ Total price of the base year }\) x 100
• They are considered as barometer of economic activity.
• Index number which is calculated from a single variable is called “univariate • index” and which is constructed from a group of variables is called a “composite index”.

Question 2.
What are the different types of Index Numbers?
Answer:
Index numbers may be of following types.
(A) Price Index Number It may be further classified into:

• Retail Price Index Number
• Wholesale Price Index Number
• Cost of Living Index Number

(B) Quantity Index Number
(C) Special Purpose Index Number
(D) Value Index Number

(A) Price Index Number : A price index number measures the changes in the prices of an entire group of related commodities over a period of time. It may be of following three types.

(i) Retail Price Index Number : These are ; complied to measure the changes in the retail price of various commodities eg. index number of consumer prices, bonds, etc.

(ii) Wholesale Price Index Number : This measures price level of goods traded in the wholesale market. They indicate general changes in the purchasing power of money.

(iii) Cost of Living Index Number: It is special type of retail price index which shows the price variations in a group of commodities consumed by different classes of people over a period of time. This index number aims ‘ to measure the changes in cost of living of different classes of people over a period of time e.g. cost of living index number of middle class people, rich class people, etc.

(B) Quantity Index Number: It is the average of the quantity of commodities produced in different sectors of the economy. It helps us to know whether the level of production in the country is rising or falling as compared to the production in previous years. It is also called volume index number.

(C) Special Purpose Index Number : Special purpose index numbers are constructed to know the index of productivity of labour, exports and imports, shares on stock market, etc.

(D) Value Index Number : It measures the relative changes in the total value of items like retail sales, profit, etc. as compared to their level in the base year. It is obtained by multiplying the price of an item with its quantity (P x Q).

Question 3.
Explain the significance / uses of index numbers in economics?
Answer:
Index numbers are significant tools of economic analysis in the following ways:
(1) Help in formulating Policies : Index numbers help the government and business organisations in framing their suitable economic policies for agriculture and industrial sector, wage and dearness allowance policies, etc.

(2) Help in the study of Trends and Tendencies : Index numbers study the relative changes in the level of phenomenon of different periods of time, so they can be used to predict future events. The economists can study the general trends of changes in price levels, agricultural and industrial production, export, imports, etc.

(3) Economic Barometer : Just as barometer is used to measure atmospheric pressure, index numbers measure the level of economic and business behaviour. They are very important for an economist, businessman, planners, policy makers, etc.

(4) Helps in Measurement of Inflation :
It helps the government to take measures against inflation by giving additional D.A. to the employees on the basis of Dearness Index.

(5) Help to adjust National Income : By comparing current year’s national product prices with the base year’s prices, the Domestic Product (GDP) produced. Hence, this shows changes in real national income.

(6) To present Financial Data in Real Income : Index numbers are used to adjust price change, wage change, etc. Thus deflating helps to present the financial data at constant prices.
(Note: Deflating means to make adj ustments / in the original data)

(7) Helps in determining Depreciation Cost: The price index helps in determining the depreciation cost of durable goods. At the time of inflation, it is useful to know the ) original cost of the commodities.

Question 4.
What are the limitation of Index Numbers?
Answer:
Although index numbers are very useful to business and industry, they suffer from the ) following limitations: ;

(1) Bias in the Data : Index numbers are constructed on the basis of various types of data. If the data is not collected properly, we may not get proper index numbers.

(2) Misuse of Index Numbers: Index numbers can be misused. We compare the index numbers with the base year. Hence a person may choose a base year which is suitable forhis purpose. A businessman may use a base year in which profits are high and show that his profits are falling now.

(3) Based on Samples : Index numbers are based on samples so it cannot include all the items in the consideration of index numbers. Hence index numbers are not free from sampling errors.

(4) Defects in the Formulae : There are number of formulae, but every formula suffers from some defects. Index number is an average , so index number may have the same limitations which an average may have.

(5) Changes in the Economy : In the long run, habits, tastes and expectations of people change, so it is difficult to incorporate all these changes in index numbers. For a good index number items should remain the same price wise over a period of time. But this is practically not possible.

(6) Neglecting Qualitative Change : The index number of price (or) production (or) quantity may ignore the change in quality of the commodities which may be significant at any point of time. A better quality commodity will cost more than an inferior commodity. So a rise in the price index may be due to an improvement in the quality and not due to a rise in prices.

(7) Arbitrary Weights : The weights (relative importance) assigned to different commodities may be random.

(8) Limited Scope : An index number is useful for the purpose for which it is designed. So its use is limited only to that phenomenon and not for another purpose.

5. Solved Examples Construction of Index Numbers

Question 1.
Calculate the price index number based for the following data.

Solution:
Calculate the price index number

where, P₀₁ = Price Index
Σp₁ = Sum total of current year prices of all commodities
Σp₀ = Sum total of base year prices of all commodities
p₀₁ = \(\frac{\Sigma p_{1}}{\Sigma p_{0}}\) x 100
= \(=\frac{400}{310}\) x 100
= 129.03 g
Hence, P₀₁ = 129.03 g

Question 2.
Calculate a Quantity Index number of g the given data.

Solution :

where, Σq₀ = Sum total of all the commodities of the base year
Σq₁ Sum total of all the commodities of the current year
Quantity Index Number Q₀₁ = \(\frac{\Sigma q_{1}}{\Sigma q_{0}}\) x 100
= \(\frac{300}{200}\) x 100
= 150
Hence, Q₀₁ = 150

Question 3.
Calculate Value Index number using a simple method of the following data:

Solution:


Steps : Σp₀q₀ = Sum total of product of the p₀ and q₀ of base year
Σp₁q₁ = Sum total of product of the p₁ and q₁ of current year
Value Index Number V₀₁ = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{4,200}{290}\) x 100
= 1,448
Hence, V₀₁ = 1,448

Question 4.
Given below are the price quantity data with price quoted in Rs. per kg and production in quintals. Construct index number by Laspeyre’s method.

Solution:

Steps: Σp₁q₀ = Sum total of product p₁ and q₀
Σp₀q₀ = Sum total of product p₀ and q₀
P₀₁ = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{34,370}{28,020}\) x 100
= 122.66
Hence P₀₁ = 122.66

Question 5.
Construct the index number by Paasche’s method.

Solution :

Steps : Σp₁q₁ = Sum total of product of the P₁ and q₁
Σp₁q₁= Sum total of product P₀ and q₁
p₀₁ = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) x 100
= \(\frac{38,720}{31,520}\) x 100
= 122.84
Hence P₀₁ = 122.84

Question 6.
Calculate Laspeyre’s and Paasche’s Index from the given data.

Answer:
(A) Calculation of Laspeyre’s Index Number:

Laspeyre’s Index P₀₁ = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{1,200}{660}\) x 100
= 181.81

(B) Paasche’s Index Number :

Paasche’s Index Number
P₀₁ = \(\) x 100
= \(\) x 100
= 172.22
Laspeyre’s Index = 181.81
Paasche’s Index = 172.22

Question 7.
Construct Price Index Number from the given data.

Answer:

Price Index P₀₁ = \(\) x 100
= \(\frac{42}{40}\) x 100
= 105
Hence, P₀₁ = 105

Question 8.
Construct Value Index Number of the following data.

Answer:

V₀₁ = \(\) x 100
= \(\) x 100
= 138.18
Hence V₀₁ = 138.18

Question 9.
Calculate Laspeyre’s and Paasche’s Price Index numbers from the given data.

Answer:
Construction of Laspeyre’s and Paasche’s Price index Numbers.

(A) Laspeyre’s Price Index Number:
P₀₁ = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{200}{110}\) x 100
= 181.81

(B) Paasche’s Price Index Number:
P₀₁ = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) x 100
= \(\frac{187}{97}\) x 100
= 192.78
(A) Laspeyre’s P₀₁ = 181.81
(B) Paasche’s P₀₁ = 192.78

Balbharti Maharashtra State Board Class 12 History Important Questions Chapter 8 World Wars and India Important Questions and Answers.

Maharashtra State Board 12th History Important Questions Chapter 8 World Wars and India

1A. Choose the correct alternative and rewrite the statement.

Question 1.
The Austrian prince __________ and his wife assassinated in Serbia.
(a) King George II
(b) Kaiser William II
(c) Prince William
(d) Archduke Franz Ferdinand
Answer:
(d) Archduke Franz Ferdinand

Question 2.
Austria and Hungary were trying to suppress __________
(a) England
(b) America
(c) Germany
(d) Serbia
Answer:
(d) Serbia

Question 3.
During the First World War __________ stood up with Belgium and called a war against Germany.
(a) Bulgaria
(b) England
(c) Serbia
(d) Austria
Answer:
(b) England

Question 4.
After the end of the First World War, the treaty of __________ was signed.
(a) Brazil
(b) Tokyo
(c) Versailles
(d) Holland
Answer:
(c) Versailles

Question 5.
An organisation known as __________ was established after World War I to maintain peace in the
world.
(a) World Health Organisation
(b) League of Nations
(c) United Nation Organisation
(d) North Atlantic Treaty Organisation
Answer:
(b) League of Nations

Question 6.
After the end of the First World War, the Nazis under the leadership of __________ grabbed the power
in Germany.
(a) Woodrow Wilson
(b) Hitler
(c) Benito Mussolini
(d) Linlithgow
Answer:
(b) Hitler

Question 7.
In 1938, Hitler won __________ province in Czechoslovakia.
(a) Sudeten
(b) Prague
(c) Bratislava
(d) Bohemia
Answer:
(a) Sudeten

Question 8.
During the Second World War, Prime Minister of England __________ resigned from the post.
(a) Ramsay MacDonald
(b) Woodrow Wilson
(c) David Lloyd George
(d) Neville Chamberlain
Answer:
(d) Neville Chamberlain

Question 9.
__________ was the leader of Azad Hind Sena.
(a) Pandit Nehru
(b) Lokmanya Tilak
(c) Netaji Subhash Chandra Bose
(d) Mahatma Gandhi
Answer:
(c) Netaji Subhash Chandra Bose

Question 10.
__________ was appointed as the first Field Marshall of independent India.
(a) Sam Manekshaw
(b) Lord Mountbatten
(c) Pandit Nehru
(d) Dr. Dwarkanath Kotnis
Answer:
(a) Sam Manekshaw

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Group ‘A’	Group ‘B’
(a) Russia	Communism
(b) Italy	Fascism
(c) Germany	Socialism
(d) England	Imperialism

Answer:
Germany – Nazism

2A. Write the names of historical places/persons/events.

Question 1.
Germany’s attack on this country directly provoked Britain to go to war –
Answer:
Belgium

Question 2.
Governor-General of India during First World War –
Answer:
Lord Chelmsford

Question 3.
Secretary of State of India in 1917 –
Answer:
Edwin Samuel Montagu

Question 4.
The leader of Indian migrants on Kamagata Maru steamship –
Answer:
Baba Gurudit Singh

Question 5.
The port where 30 passengers of Kamagata Maru steamship died due to firing of British officers –
Answer:
Bajbaj

Question 6.
A place where a naval war was fought between Germany and England and England defeated the German navy –
Answer:
Jutland in the North Sea

Question 7.
The American President who took a lead for the establishment of the League of Nations –
Answer:
Woodrow Wilson

Question 8.
Prime Minister of England after the resignation of Neville Chamberlain during World War II –
Answer:
Winston Churchill

Question 9.
The Viceroy of India who announced India’s participation in World War II –
Answer:
Lord Linlithgow

Question 10.
Dictator of Russia during World War II –
Answer:
Stalin

Question 11.
Daughter of Pandit Jawaharlal Nehru –
Answer:
Indira Gandhi

Question 12.
An international organization formed after World War II to maintain peace in the world –
Answer:
United Nations

Question 13.
The leader of the Soviet Russian army who defeated Germany during Second World War –
Answer:
Marshal Georgy Zhukov

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
The main responsibility of the United Nations __________
(a) to avoid war
(b) independence of colonies
(c) improving the economies of different countries
(d) disarmament
Answer:
(a) to avoid war

Question 2.
America declared war against Japan in 1941 because __________
(a) Japan attacked Pearl Harbour and destroyed the American naval base
(b) Japan conquered the Maldives
(c) Japan violated the treaty of Brest-Litovsk
(d) Japan entered into the North Sea
Answer:
(a) Japan attacked Pearl Harbour and destroyed the American naval base

Question 3.
Japan surrendered on 15th August 1945 because __________
(a) Japan was against the war
(b) they lacked financial help
(c) Germany convinced Japan to surrender
(d) America launched aerial attacks on Hiroshima and Nagasaki with atom bombs
Answer:
(d) America launched aerial attacks on Hiroshima and Nagasaki with atom bombs

Question 4.
Imperialistic European nations began to search for newer lands __________
(a) for more raw material and more markets to sell their surplus products
(b) to help other nations financially
(c) to maintain peace in the world
(d) to enhance the industrial production of these nations
Answer:
(a) for more raw material and more markets to sell their surplus products

3. Complete the following concept map.

Question 1.

Answer:

Question 2.

Points	First World War	Second World War
1. Period	…………………………	1939 – 1945
2. Involved nations	Allied Nations: Britain, France, Russia, Italy, America Central Powers: ……………….	Allied Nations: ……………… Axis powers: Germany, Japan, Italy

Answer:

Points	First World War	Second World War
1. Period	1914 – 1918	1939 – 1945
2. Involved nations	Allied Nations: Britain, France, Russia, Italy, America Central Powers: Germany, Austria-Hungary, Turkey, Bulgaria	Allied Nations: Britain, France, Soviet Union, America Axis powers: Germany, Japan, Italy

4A. Write short notes.

Question 1.
Fascism
Answer:

• Fascism is derived from the Latin word ‘Fasces’ which suggests ‘strength through unity.
• An Italian leader and former Prime Minister of Italy Benito Mussolini built this movement.
• The major characteristics of Fascism are as follows:
  • Opposition to democratic institutions-It is a political ideology that does not believe in democracy, liberalism, individual freedom, and equality.
  • In Fascism, the greater focus is on the action, absolute political authority, centralization of political power, justification of war, and violence.
  • Aggressive nationalism, Militarism, and Anti-Communism.

Question 2.
Nazism
Answer:

• Nazism is a set of political beliefs associated with the Nazi party of Germany.
• Nazism is in a way slightly diverse form of fascism. Nazism gave more importance to racism.
• It was an extremely aggressive and corrupt manifestation of fascism.
• The genocide (the murder of all the people of a particular race, religion, etc.) of European Jews in Germany by Hitler had its roots in racism.

Question 3.
The ‘Kamagata Maru’ incidence.
Answer:

• During the time of the Second World War Indian people began to migrate to Canada and America.
• The government of Canada was heavily under the influence of the British government.
• It rejected the entry of Indian migrants. It did not allow ‘Kamagata Maru’ a steamship with Indian migrants aboard under the leadership of Baba Gurudit Singh, to anchor in the Canadian port of Vancouver.
• People on this ship returned to India. On their return journey, Kamagata Maru reached the port of ‘Bajbaj’ near Kolkata. There the British officers ordered Indian passengers to return immediately to their own towns and villages.
• But the Indians did not follow the orders so the British officers began to shoot and 30 Indian passengers died in it.
• This incidence of cruelty on the part of British officers created public outcry throughout India.

Question 4.
Azad Hind Sena
Answer:

• Netaji Subhash Chandra Bose was a great freedom fighter. He officially took charge of the Azad Hind Sena also known as Indian National Army in 1943.
• During the Second World War when the Japanese army reached the eastern border of India several volunteers joined this army. They were the patriotic members of Azad Hind Sena.
• Netaji’s policy was to take advantage of the situation to move the Indians for the intense opposition to the British, while the Britishers were engaged in war.
• He felt that even the enemy of the British may be approached for help if the need be.
• Azad Hind Sena fought fiercely for attaining its goal of independence of India and contributed to India’s freedom struggle.

Question 5.
Congress and Defence Policy
Answer:
Indian National Congress had formed a number of policies related to the defense issues of the country. It included:

• There should be a defense academy in India.
• The British Government should share part of the defense expenditure meant for India’s protection from its treasury.
• The official expenditure on defense should be curbed.
• Indian citizens should be provided facilities of education and training to make themselves capable of self-defense and defense of the nation.
• Indian men should be recruited in the regional units of the army.
• Home Guards and a group of volunteers should be established.
• By the ‘Queen’s Proclamation’, Indian people should be appointed on the posts of higher grades.

Question 6.
First World War and TISCO.
Answer:

• There is a very close relationship between First World War and Tata Iron and Steel Company.
• During First World War England required good railway tracks in Europe and military logistics in the province of Iraq.
• The company took great efforts and manufactured 1500 miles long tracks.
• In 1919, after the end of the First World War, Viceroy Lord Chelmsford visited the TISCO factory. In his speech, he attributed their victory to the railway track supplied by India.

Question 7.
Field Marshall Sam Manekshaw.
Answer:

• During World War II Sam Manekshaw was sent under the 17th Infantry Division to prevent Japanese attacks in Burma.
• He was appointed as the acting Commander. The army attacked the Sittang Bridge under his leadership. The enemy attacked him.
• He was hit by nine bullets fired from the Japanese machine guns. Maj. Gen. David Cowan, a senior commanding officer witnessed Manekshaw’s unmatched valour and pinned his own Military Cross ribbon on Manekshaw.
• A Military Cross could be awarded only to a soldier who is alive. He was appointed as the first Field Marshall of independent India.

Question 8.
Second World War and India.
Answer:

• In the period of war, England required manpower and money. So, they enforced the recruitment of army personnel from India.
• Extra taxes levied on Indians and taxes on trade and industries increased to raise funds needed for war.
• Due to inflation, prices of essential items increased and Indians have also been affected by an increase in unemployment.
• England exploited India and its resources to achieve victory in this war. India was a British colony and they took it in their right to use it as a source of supplying industrial products, cloth, and other commodities of daily use to their allied nations.
• Due to exploitation by the Britishers, a large number of Indians, from various societies, workers, and farmers joined the national movement against the British.
• India was pulled forcibly into this war by the British Government. India did not gain anything from this war.

4B. Explain the following statements with reasons.

Question 1.
Japan surrendered in August 1945 and Second World War came to an end.
Answer:

• The Second World War was fought between Allied powers and Axis powers.
• Japan entered this war in support of Germany. In 1941, Japan attacked Pearl Harbour and destroyed an American naval base. This resulted in America declared war against Japan.
• Later Japan went on capturing the regions of the Philippines, Myanmar, Malaya, Singapore and even marched up to Assam, Arakan, and Imphal.
• This drove the British to act against Japan’s aggression. America launched aerial attacks on two Japanese cities with atom bombs, first on Hiroshima and then on Nagasaki. So, finally, Japan surrendered on 15 August 1945. This put an end to the Second World War.

5. State your opinion.

Question 1.
World War II witnessed the rise of nationalism throughout the world but there is a difference between Indian nationalism and German nationalism.
Answer:
Nationalism means love, loyalty, and devotion to a nation. The differences between German nationalism and Indian nationalism were as follows:

• Germany is a country which, nourished nationalism. India was also greatly influenced by nationalism. But there is a difference between Indian nationalism and German nationalism.
• Germans were out to conquer other countries in order to make their country the most powerful and biggest in the world whereas the nationalism of the Indians was making them fight for regaining their independence.
• Indian nationalism was based on a broader perspective of the spread of Democracy all over the world including India.
• Germany was strongly influenced by racism. Hitler killed many European Jews. However, in India people of varied religions, races and castes were staying together for ages. These are the characteristics of Indian nationalism, which confirms its magnanimity.

6. Answer the following questions in detail.

Question 1.
Explain the impact of World War II on India.
Answer:
Lord Linlithgow’s announcement of India joining the war:

• The Second World War was started in September 1939. In the Second World War England and France fought against Italy and Germany.
• England declared war against Germany. At the same time, Viceroy of India Lord Linlithgow declared that India would also join the war in support of England.

Protest of Indian National Congress:

• Indian National Congress was against the aggressive dictatorship of Germany and Italy. Congress did not support colonialism so they protested against the viceroy’s announcement.
• England claimed that it was fighting for the protection of democracy in Europe. Indian National Congress now demanded the freedom of India from British domination.

The decision of the Indian National Congress:

• Indian National Congress gave assurance to England that India as an independent nation would support England in World War II. They also announced that Indians will not help the British if the British continued with their imperialist administration in India.
• Lord Linlithgow announced that British Government will not look upon any issues related to India till the end of the war, reacting to this Indian National Congress decided not to participate in the war.

Contribution of Azad Hind Sena:

• When the Japanese army reached the eastern border of India several volunteers of Azad Hind Sena joined this army under the leadership of Netaji Subash Chandra Bose against the British.
• Netaji thought that even the enemy of the British may be approached for help if needed. Azad Hind Sena fought bravely to attain its goal of freedom of India and in this way contributed a lot to India’s Freedom Struggle.

Question 2.
Explain the impact of the First World War on India.
Answer:
(i) The British Government of India compelled India, one of their colonies, to participate in the World War.

(ii) India became the source of procuring help in the form of money, food, clothing, and other war supplies. During 1919-20, the British Government in India provided help to England worth Rs.19 billion. India also contributed one hundred and fifty crores of rupees to the war expenses.

(iii) Seventeen of the Indian soldiers were honoured and decorated with ‘Victoria Cross’, a medal, given for gallantry.

(iv) War left a significant impact on various fields including production of war supplies, civil industries, trade, economic policies, farming and agricultural production, etc. This war boosted India’s industrial growth, especially in the Iron and steel industry. Considerable growth was also seen in motor transportation and motor vehicles.

(v) During the wartime and post-war period there was a decrease in export. The prices of agricultural products reduced but the prices of industrial products increased. Indian food grains were exported to allied nations. It caused a shortage of food and increasing prices of food grains for the Indians.

(vi) Due to war experience Indians realized that India could be considered backward in the matters of aircraft, mechanized war instruments, medical facilities. In 1917, Montagu- Chelmsford administrative reforms were introduced in India. India became extremely poor due to war.

7. Answer the following question with the help of the given points.

Question 1.
Explain the causes of the First World War.
(i) Increase in production
(ii) Imperialism
(iii) Division of Europe into two hostile groups
(iv) Immediate cause
Answer:
The First World War was fought between allied nations and central powers. The First World War
began in 1914 C.E. The causes of the war were:
(i) Increase in production: Due to the industrial revolution machines came into use for the various production processes. It also led to increasing in production because of mechanization.

(ii) Imperialism: The European countries needed more raw material to match the quantitative increase in production and more markets to sell their surplus products. Imperialistic European nations began to search for newer lands to meet these needs.

(iii) Growing Militarisation: The search for newer lands and colonies would often create warlike situations among them. Keeping this in view more powerful nations in Europe felt the need to continuously increase their military power and armory.

(iv) Division of Europe into two hostile groups: Germany, England, Russia, France, Austria, Hungary where the nations of primary importance. Among them, rival groups were formed. Because of the rivalry, every nation began to enhance its military and naval strength, There was a competition to produce more and more destructive weapons.

(v) Immediate cause: The Austrian Prince Archduke Franz Ferdinand and his wife were assassinated by a Serbian maniac. In Austria, people believed that this whole act was maneuvered by the Serbian Kingdom. Hence, Austria called a war against Serbia. Russia came to help Serbia. Two distinct groups were formed, one group supporting Austria (Germany, Turkey, Bulgaria) known as central powers and another supporting Serbia (England, France, Russia) known as allied nations.

Question 3.
Explain the impacts of the World Wars on India.
(i) Awareness against the exploitative rule of the British and participation of masses in the Indian freedom struggle
(ii) Protest of Indian National Congress
(iii) Contribution of Azad Hind Sena
(iv) India got independence
Answer:
India was forced into both the World Wars started by the British Imperial rule. The impacts of wars on India were as follows:
(i) Awareness against the exploitative rule of the British and participation of masses in the Indian freedom struggle: During wartime, the British Government started recruiting army personnel from India. Extra taxes were levied on Indians for raising funds. The prices of essential commodities went up. Indians suffered from the problems of inflation, unemployment. Indians from all strata of society, workers, farmers, middle class, and women joined in the Indian national movement against British rule.

(ii) Protest of Indian National Congress: The Indian National Congress protested against the Viceroy’s announcement of India’s participation in the war. The Congress demanded India’s freedom in return to India’s help to England in war. However, Lord Linlithgow turned the demand of the Congress so Congress decided not to participate in World War II.

(iii) Contribution of Azad Hind Sena: Azad Hind Sena under the leadership of Netaji Subhash Chandra Bose joined Japanese forces against the British and fought fiercely for attaining independence of India.

(iv) India got independence: After the end of the Second World War British realized that India was not going to be the perennial source of profit for them as it used to be. They decided to return home and India got Independence.

Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 10 Foreign Trade of India Important Questions and Answers.

Maharashtra State Board 12th Economics Important Questions Chapter 10 Foreign Trade of India

1. A. Choose the correct option:

Question 1.
Before independence, India was exporting raw materials to –
(a) USA (b) Japan
(c) England (Britain)
(d) None of these
Options :
(1) a and b
(2) c and a
(3) d
(4) only c
Answer:
(4) only c

Question 2.
Internal trade also known as –
(a) Domestic trade
(b) Home trade
(c) External trade
(d) all of these
Options :
(1) a, b and c
(2) b and c
(3) a and b
(4) only d
Answer:
(3) a and b

Question 3.
International or External trade takes place between –
(a) two or more districts
(b) two or more states
(c) two or more countries
(d) none of these
Options :
(1) a and b
(2) a and c
(3) a, b and c
(4) only c
Answer:
(4) only c

Question 4.
Most important commodity in India’s import is –
(a) Petroleum, oil and lubricants
(b) Food grains .
(c) Engineering goods
(d) Readymade garments
Options :
(1) a and b
(2) b and c
(3) only a
(4) c and d
Answer:
(3) only a

Question 5.
According to Walter Krause definition of Balance of Payment, value of exchange of goods and services is considered among –
(a) the citizens and businessmen
(b) the firms
(c) the government
(d) none of these
Options :
(1) a, b and c
(2) b and c
(3) c and d
(4) only a
Answer:
(1) a, b and c

Question 6.
Trade surplus means –
(a) Export value > Import value
(b) Export value < Import value
(c) Export value = Import value
(d) All of these
Options :
(1) only a
(2) b and c
(3) only b
(4) only d
Answer:
(1) only a

Question 7.
Balance of trade includes –
(a) the value of imports of visible and invisible goods
(b) the value of imports of only visible goods
(c) the value of imports and exports of visible and invisible goods
(d) the value of exports of visible and invisible goods.
Options :
(1) a and d
(2) only b
(3) only c
(4) All of these
Answer:
(3) only c

Question 8.
International trade is important because –
(a) it helps in optimal utilisation of resources
(b) it brings stability in price level
(c) it helps to earn foreign exchange
(d) it encourages investment
Options :
(1) a and b
(2) b and c
(3) a and c
(4) all of these
Answer:
(4) all of these

Question 9.
The share of India’s foreign trade in Gross National Income during 2016-17 was –
(a) 25%
(b) 17.55
(c) 48.8 %
(d) None of these
Options :
(1) only a
(2) only b
(3) only c
(4) only d
Answer:
(3) only c

Question 9.
In recent years India’s leading trading partners are –
(a) USA, Germany, Japan, UK
(b) Britain
(c) Nepal, Sri Lanka, UK
(d) None of these
Options :
(1) only a
(2) b and c
(3) a and c
(4) only d
Answer:
(1) only a

Question 10.
Which of the following is not a benefit of international trade –
(a) provides multiple choices of imported goods
(b) leads to division of labour
(c) high wage levels for all domestic workers
(d) can earn reputation and goodwill in the international market
Options :
(1) a and d
(2) only c
(3) a, c and d
(4) a, b and d
Answer:
(2) only c

Question 11.
There is a change in the composition of India’s exports from –
(a) primary products to manufactured products
(b) manufactured products to primary products
(c) manufactured products to software
(d) All of these Options:
(1) a and b
(2) only a
(3) a, b and e
(4) only d
Answer:
(2) only a

(B) Complete the Correlation

(1) Internal trade : Home trade :: …………. : Foreign trade
Answer:
International trade

(2) Trade surplus: …………. :: Trade deficit: Export > Import
Answer:
Export > Import

(3) …………. : jute, cotton :: Manufactured goods: readymade garments
Answer:
Primary goods

(4) OECD : Organisation for Economic Co-operation and Development :: …………. : Organisation of Petroleum Exporting Countries
Answer:
OPEC

(5) Import goods : …………. :: Export goods : Engineering goods
Answer:
Gold

(6) Trade within the country : Internal trade :: Trade between two or more countries : …………..
Answer:
External trade

(7) Highest share in export: Engineering goods :: Highest share in import: ………….
Answer:
Petroleum

(8) Old ports : Mumbai, Kolkata and Chennai:: …………. : Kandla, Cochin, Vishakhapatnam
Answer:
New ports

(9) International trade : External trade :: Domestic trade : …………. :
Answer:
Internal trade

(10) Foreign trade before independence : …………. :: Foreign trade after independence : USA
Answer:
Britain / England

(11) Machinery : Capital goods :: Motor vehicles : ………….
Answer:
Consumer goods

(C) Give economic terms.

(1) To purchase goods and services by one country from another country.
Answer:
Import trade

(2) To sale goods and services by one country to another country.
Answer:
Export trade

(3) To purchase goods and services from one country and then selling them to another country after processing.
Answer:
Entrepot trade

(4) Exchange of goods and services.
Answer:
Trade

(5) Export value is greater than the import value.
Answer:
Trade surplus

(6) Import value is greater than the export value.
Answer:
Trade deficit

(7) The trade is by sea.
Answer:
Oceanic trade

(8) This leads division of labour and specialization.
Answer:
Foreign trade

(9) We can see or touch these goods.
Answer:
Visible / tangible goods

(10) We can’t see or touch these goods.
Answer:
Invisible / intangible goods

(D) Find the odd word out.

(1) Internal trade, Domestic trade, Foreign trade, Home trade.
Answer:
Foreign trade

(2) International trade, Internal trade, External trade, Foreign trade.
Answer:
Internal trade

(3) Types of foreign trade :
Import trade, Export trade, National trade, Entrepot trade.
Answer:
National trade

(4) Need of Foreign trade :
To earn foreign exchange, To earn rupees, To encourage investment,To stabilize price ; level
Answer:
To earn rupees

(5) Important features of India’s foreign trade :
Change in the composition of exports, ; Change in composition of imports, Change in composition of internal trade
Answer:
Change in composition of internal trade

(6) Trade relation with neighbouring countries :
Nepal, Afghanistan, Myanmar, Sri Lanka, England
Answer:
England

(7) New ports for foreign trade :
Mumbai, Kandla, Cochin, Vishakhapatnam ;
Answer:
Mumbai

(8) Major imported goods :
Gold, Fertilizers, Gems and Jewellery, Petroleum
Answer:
Gems and jewellery

(9) Major exported goods :
Iron and Steel, ‘ Engineering goods, Chemicals, Textiles and readymade garments
Answer:
Iron and steel

(10) Useful concept in foreign trade :
Balance of payment, Balance of trade, Balance budget
Answer:
Balance budget

(11) Organisation related to foreign trade : OECD, OPEC, EGEPC, NABARD
Answer:
NABARD

(12) Manufactured products :
Gems and jewellery, Electronic goods, s Computer hardware and software, Food grains
Answer:
Food grains

(13) Primary products :
Jute and cotton, Readymade garments, Oil seeds, Mineral products
Answer:
Readymade garments

(14) Visible goods :
Gold, Petroleum, Fertilizers, Communication
Answer:
Communication

(15) Invisible goods (service):
Banking, Communication, Engineering goods, Transport
Answer:
Engineering goods

(16) Cloth, Machinery, Technology, Fertilizers
Answer:
Cloth

(E) Complete the sentences.

(1) During the British rule …………………. industries suffered set back.
Answer:
handicraft

(2) In the post World War II, …………………. trade is considered as an investment.
Answer:
Foreign trade

(3) Buying and selling of goods and services within the boundaries of a nation are known as ………………….
Answer:
Internal trade

(4) Internal trade is also known as ………………….
Answer:
Domestic / Home trade

(5) The trade between Maharashtra, Uttar Pradesh, Tamil Nadu, etc, is known as ………………….
Answer:
Internal trade

(6) International trade is also known as ………………….
Answer:
Foreign / External trade

(7) Trade which consists of transaction between residents of different countries is called ………………….
Answer:
International trade

(8) …………………. is a remarkable factor in expanding the market and encouraging the production of goods.
Answer:
Foreign trade

(9) …………………. helps to earn goodwill and reputation in the international market.
Answer:
Export trade

(10) After independence, there was change in the composition of imports from consumer goods to ………………….
Answer:
capital goods

(11) Share of …………………. trade-in-India is around 68%.
Answer:
Oceanic trade

(12) Goods such as cloth, motor vehicles, electrical goods, etc, are known as ………………….
Answer:
consumer goods

(13) Goods and services that are made in one country but purchased and consumed in another country is called ………………….
Answer:
export

(F) Choose the wrong pair ; (1 mark each)

I.

Group‘A	Group ‘B’
1. Internal trade	Between two or more countries
2. Oceanic trade	Trade by sea
3. Export trade	Sale of goods by one country to another country

Answer:
Wrong pair : Internal trade – Between two or more countries

II.

Group ‘A’	Group ‘B’
1. Primary goods	Jute, cotton, tea
2. Invisible goods	Cloth, medicine, car
3. Capital goods	Machinery, technology, steel

Answer:
Wrong pair : Invisible goods – Cloth, medicine, car

III.

Group ‘A’	Group ‘B’
1. Encourage investment	Foreign trade
2. To earn foreign exchange	Internal trade
3. International trade	Multiple choices of imported goods

Answer:Wrong pair : To earn foreign exchange Internal trade

(G) Assertion and Reasoning:

Question 1.
Assertion (A): Trade is an engine of growth of an economy.
Reasoning (R) : It plays an important role for economic development.
(1) Both (A) and (R) are true and (R) is the correct reason for (A).
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).
(iii) (A) is true but (R) is false.
(iv) (A) and (R) both are false.
Answer:
(i) Both (A) and (R) are true and (R) is the correct reason for (A).

Question 2.
Assertion (A) : International trade consists of transaction between residents of different countries.
Reasoning (R): This is given by Wasserman and Hultman
(i) Both (A) and (R) are true and (R) is the correct reason for (A).
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).
(iii) (A) is true but (R) is false.
(iv) (A) and (R) both are false.
Answer:
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).

Question 3.
Assertion (A) : During the British rule foreign trade did not permit industrialisation in India.
Reasoning (R) : India was a supplier of raw material to the England and importer of manufactured goods.
(i) Both (A) and (R) are true and (R) is the correct reason for (A).
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).
(iii) (A) is true but (R) is false.
(iv) (A) and (R) both are false.
Answer:
(i) Both (A) and (R) are true and (R) is the correct reason for (A).

Question 4.
Assertion (A): Buying and selling of goods and services across the boundaries of a nation are known as internal trade. Reasoning (R) : Goods produced in
Maharashtra are sold to West Bengal then it is known as international trade.
(i) Both (A) and (R) are true and (R) is the correct reason for (A).
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).
(iii) (A) is true but (R) is false.
(iv) (A) and (R) both are false.
(iv) (A) and (R) both are false.

Question 5.
Assertion (A) : Due to specialization resources are channelized for the production of only those goods which would give highest ( return.
Reasoning (R): There is rational allocation and specialization.
(i) Both (A) and (R) are true and (R) is the correct reason for (A).
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).
(iii)(A) is true but (R) is false.
(iv)(A) and (R) both are false.
Answer:
(i) Both (A) and (R) are true and (R) is the correct reason for (A).

Question 6.
Assertion (A) : An increase in total investment leads to development of an economy. .
Reasoning (R) : Foreign trade creates an opportunity for the producers to reach beyond the domestic markets.
(i) Both (A) and (R) are true and (R) is the correct reason for (A).
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).
(iii) (A) is true but (R) is false.
(iv) (A) and (R) both are false.
Answer:
(i) Both (A) and (R) are true and (R) is the correct reason for (A).

Question 7.
Assertion (A) : Balance of payments is a summary statement of all the transaction between the residents of one country and the rest of the world.
Reasoning (R): This is given by Samuelson.
(i)Both (A) and (R) are true and (R) is the
correct reason for (A).
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).
(iii) (A) is true but (R) is false.
(iv)(A) and (R) both are false.
Answer:
(iii) (A) is true but (R) is false.

Question 8.
Assertion (A) : Balance of trade is the difference between the value of countries export and import for a given period. Reasoning (R) : Balance of trade is also referred to as international trade balance.
(i)Both (A) and (R) are true and (R) is the correct reason for (A).
(ii) Both (A) and (R) are true but (R) is not the correct reason for (A).
(iii)(A) is true but (R) is false.
(iv)(A) and (R) both are false.
Answer:
(iii) (A) is true but (R) is false.

(H) Choose the right group of pairs :

I.

Group ‘A’	Group ‘B’
1. Balance of Trade	(a)International trade balance
2. OPEC	(b) Oil and Petrol Export Commission
3. Trade	(c) Buying and selling of goods and services
4. Invisible goods	(d) Banking, insurance
5. WTO	(e) World Trade Organisation

II.

Group ‘A’	Group ‘B’
1. OPEC	(a) Organisation of Petroleum Exporting Countries
2. Trade deficit	(b) Value of export < Value of import
3. Internal trade	(c) Trade within the country
4. India’s imported goods	(d) Petroleum, Gold, fertilizer
5. Entrepot Trade	(e) Re-export

Answer:
II group is correct.

2.[A] Identify and explain the concept from given illustrations.

Question 1.
Antwerp city of Belgium imports raw diamonds and exports finished diamonds to other countries.
Answer:
Concept: Entrepot Trade
Explanation : It means purchase of goods and services from one country and selling them to another country after processing.

Question 2.
The country ‘A’ value of import was $200 billion and value of export was $150 billion.
Answer:
Concept: Trade deficit
Explanation : When value of import is greater than value of export it is called as trade deficit.

Question 3.
The country ‘X’ value of export was $500 billion and value of import was $200 billion.
Answer:
Concept: Trade Surplus
Explanation : When value of export is greater than value of import it is called as trade surplus.

Question 4.
Kashmir sold its apples to the other parts of country.
Answer:
Concept: Internal trade
Explanation : This trade is also known as home or domestic trade. It means buying and selling of goods and services within the country.

Question 5.
India is selling its spices to USA, China, Vietnam, etc.
Answer:
Concept: Export Trade
Explanation : It means selling of goods and services by one country to another country. It helps to earn foreign exchange.

Question 6.
India based Tata Consultancy Services (TCS) is selling their software and services to the USA.
Answer:
Concept: Export trade
Explanation : It means selling of goods and services by one country to another country. It helps to earn foreign exchange.

(B) Distinguish between

Question 1.
Import trade and Export trade.
Answer:
Import trade:

1. It means to purchase of goods and services by one country from another country.
2. E.g. India imports petroleum from Iraq, Kuwait
3. It is inflow of goods and services.

Export trade:

1. It means to the sale goods and services by one country to another country.
2. E.g. India exports tea, rice, jute to China, Hong Kong, etc.
3. It is outflow of goods and services.

Question 2.
Export trade and Entrepot trade.
Answer:
Export trade:

1. Export trade means sale of goods by one country to another country.
2. E.g. India selling its spices to USA, China, etc.

Entrepot trade:

1. Entrepot trade means purchase of goods and services from one country and selling them to another country.
2. E.g. Antwerp city of Belgium importing raw diamonds and exporting finished diamonds to other countries.

Question 3.
Trade surplus and Trade deficit.
Answer:
Trade surplus:

1. When country’s exports are more than its imports, it is called as trade surplus.
2. Generally, it is considered as a positive development.

Trade deficit:

1. When country’s import are more than its exports, it is called as trade deficit.
2. Generally, it is considered as a negative development.

3. Answer the following:

Question 1.
Explain the concepts of Balance of Trade.
Answer:
Balance of trade is the important concept of foreign trade. Balance of trade is the difference between the values of country’s exports and imports for a given period.
Balance of trade can be positive or negative.

(i) Trade surplus : When country’s value of export is more than its value of import, it is called trade surplus. It is also known as positive balance of trade.

(ii) Trade Deficit : When country’s value of import is more than its value of export, it is called as trade deficit. It is also known as negative balance of trade.

The formula for calculating balance of trade is as follows :
BOT = Total value of Exports – Total value of Imports.

4. State with reasons whether you agree or disagree with the following statements :

Question 1.
During British rule, indigenous handicraft suffered a severe blow.
Answer:
Yes, I do agree with this statement.

1. During the British rule India was exporting raw materials to England and was importing final goods from England.
2. Indian handicraft was unable to face competition with imported goods from England.
3. An imported goods were cheaper as compared to handicraft goods.
4. The demand for machine made cheap commodity had raised in Indian market.
5. That’s why Indian handicraft industries suffered during the British rule.

Question 2.
Trade is an engine of growth for an economy.
Answer:
Yes, I agree with this statement.

• Trade permits a more efficient allocation of national resources.
• Foreign trade provide foreign exchange which can be used to import modern machinery and technology from advanced countries.
• Foreign trade encourages producers to produce more goods for export.
• It leads to an increase in total investment in an economy.
• Thus, we can say, trade is an engine to growth for an economy.

Question 3.
Foreign trade leads to division of labour and specialisation at world level.
Answer:
Yes, I agree with this statement.

• Some countries have abundant natural resources.
• These countries should export raw material and import finished goods from countries which are advanced in skilled man power,
• Under specialisation specific work is given to the workers within a production process.
• Specialisation can increase the productivity of a firm or economy.
• Eg. Incase of car manufacturing company, some workers will design the cars, some workers will work on different section of assembly line, some workers will work on testing cars, some workers will work on marketing of cars.

Question 4.
Foreign trade is not playing an important role for economic development.
Answer:
No, I do not agree with this statement.

• It helps to earn foreign exchange which can be used for productive purpose.
• It leads to an increase in a total investment in an economy.
• It helps to control the changes in the price level.
• It helps to maximum allocation and utlisation of resources at international level.
• Due to availability of imported goods, it helps to improve standard of living of the people in the country.
• During the natural calamities, foreign trade enables a country to import food grains and medicines from other countries to help the affected people.
• It promotes world peace by bringing countries closer.

Question 5.
During the pre and post independence period, India’s composition of import and export is the same.
Answer:
No, I do not agree with this statement.

• Prior to independence, India used to export primary products like Jute, Cotton, Tea, Oil-Seeds etc.
• In the recent time India is exporting manufactured product like readymade garments, gems and jewellery, computer hardware and software, etc.
• Prior to independence India used to import consumer goods like medicines, cloth, motor vehicles, electrical goods, etc.
• In the recent time, India is importing capital goods like advanced technology and machinery, chemicals, fertilizers, steel, etc.

Question 6.
India is importing only petroleum from other countries.
Answer:
No, I do not agree with this statement. India is importing many commodities like :

• Electronic goods : In the total import of country, share of electronic goods in 10.9% in the year 2016-17.
• Pearls and Gems : In the total import, share of peals and gems was 6.2% in the year 2016-17.
• Edible oils : India also imports edible oil from Malaysia and Indonesia and its share is 2.8% in the year 2016-17.
• Gold : There was growing demand for gold in the Indian market. In the year 2018-19, the value of gold imported was upto $32.8 billion.
• Fertilizers : India is importing fertilizers from China, US, Iraq, Russia. In the year 2016-17, the share of fertilizers was 1.3% in the total import of country.

Question 7.
India is exporting many commodities goods.
Answer:
Yes, I do agree with this statement. India exports many commodities like :

• Engineering goods : It has the large share in the export of India. The share of engineering goods was 25% in the total exports in 2017-18.
• Petroleum products : India turned as a net exporter of petroleum refinery products.
  India’s export of petroleum product was 20.1% in 2013-14.
• Chemicals and chemical product :
  India is exporting chemicals and chemical products to many countries from last few years. In the year 2014-15 the share of chemicals was 10.4% in total exports of the country.
• Gems and Jewellery : It is one of the major contributor which helps to earn foreign exchange. According to DGCI Kolkata, the value of Gems and Jewellery export was $38.96 billion in 2018-19.

5. Study the following table, chart, graph, passage and answer the questions.

1. India’s Merchandise Trade (US $ Billion)

Question 1.
In the above bar diagram during which year export was maximum and how much was it?
The export was maximum in the year 2018¬19. It was $331billion.

Question 2.
In which year import was maximum and how much was it?
In the year 2018-19 import was maximum and it was $507.4 billion.

Question 3.
In which year import was least and how much was it?
In the year 2015-16 import was least and it was $381 billion.

Question 4.
Find out the trade deficit in the year 2017-18?
Trade deficit = Export – Import = 303.5 – 465.6
= $162.1 billion.

Question 5.
How much is the export increase in the year 2018-19 as compared to 2014-15?
Answer:
In the year 2018-19 export has increased by $20.7 billion as compared to 2014-15.

Question 6.
How much is the import increase in the year 2018-19 as compared to 2017-18?
Answer:
In the year 2018-19 imports has increased by $41.8 billion as compared to 2017-18.

Question 7.
Express your views on India’s merchandise trade.
Answer:
In the above bar diagram, India’s import is always greater then its export. India should take measures to reduce the imports. The Government of India should encourage the industries those are exporting goods by providing them various facilities such as availability of raw materials at cheaper rate, credit at low interest, etc.

(2) Share of top Five Commodities in India’s Export 2018-19

Question 1.
Name the second largest exported commodity in the year 2018-19.
Petroleum products are second largest exported commodity in the year 2018-19.

Question 2.
How much is the share of drug formulations, biologicals (chemical products) in total export of India.
Answer:
The share of chemical products is 4.37% in the total export of India.

Question 3.
Which commodity has least share in the total export of India and how much was it?
Answer:
Iron and Steel has least share and it is 2.96%.

Question 4.
Give your opinion on India’s export.
Answer:
India should focus on above five commodities to increase their export. The government of India should provide credit at low rate of interest, easy availability of raw materials required by above industries, as it will help to produce more goods.

3. Table A : Trade data for period 2009 – 10 to 2017 – 18

Question 1.
In which year export growth was least and how much?
Answer:
In the year 2015-16, export growth was least and it was -9.49%.

Question 2.
In which year import growth was maximum and how much?
Answer:
In the year 2011-12, import growth was maximum and it was 39.32%.

Question 3.
During which year trade balance was minimum?
Answer:
In the year 2009-10 trade balance was minimum.

Question 4.
Which concept of Balance of Trade is applicable here?
Answer:
The concept of trade deficit is applicable here, because in the above data every year India’s imports are more than its exports.

Question 5.
How much was India’s export value in the year 2017-18?
Answer:
In the year 2017-18 India’s export value was ? 19,56,515 crores.

Question 6.
Give your opinion on India’s foreign trade.
Answer:
Above data shows that every year India’s trade balance is deficit. It means imports are more than exports. The Government should formulate such policies that increases our export and reduces our imports.

Balbharti Maharashtra State Board Class 12 History Important Questions Chapter 3 India and European Colonialism Important Questions and Answers.

Maharashtra State Board 12th History Important Questions Chapter 3 India and European Colonialism

1A. Choose the correct alternative and rewrite the statement.

Question 1.
The ____________ established the East India Company in December 1600.
(a) British
(b) French
(c) Dutch
(d) Portuguese
Answer:
(a) British

Question 2.
The Cartaz was a ____________ which the Indian rulers had to get from the Portuguese.
(a) passbook
(b) license
(c) diary
(d) notebook
Answer:
(b) license

Question 3.
The main building of the British factory carried the ____________
(a) Union Jack
(b) American flag
(c) Indian flag
(d) Dutch flag
Answer:
(a) Union Jack

Question 4.
The fort named at Chennai was ‘Fort ____________’.
(a) St. Peter
(b) St. George
(c) St. Francis
(d) St. Xavier
Answer:
(b) St. George

Question 5.
____________was appointed as the Governor of Bombay.
(a) Abraham Shipman
(b) George Oxenden
(c) Jean Baptiste Colbert
(d) Charles II
Answer:
(a) Abraham Shipman

Question 6.
The Dutch established their first colony at ____________
(a) Surat
(b) Machilipatnam
(c) Bombay
(d) Chandranagar
Answer:
(b) Machilipatnam

Question 7.
The wars fought between the British and the French are known as ‘___________’.
(a) Bombay wars
(b) Madras wars
(c) Carnatic wars
(d) Calcutta wars
Answer:
(c) Carnatic Wars

Question 8.
The Dutch established their first factory at ____________
(a) Pondicherry
(b) Pulicat
(c) Port Nova
(d) Petapuli
Answer:
(d) Petapuli

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Group ‘A’	Group ‘B’
(a) Vasco da Gama	Seafarer
(b) Abraham Shipman	Governor of Bombay
(c) George Oxenden	Governor of Surat
(d) Jean Baptiste Colbert	Italian finance minister

Answer:
Jean Baptiste Colbert – French finance minister

2A. Write the names of historical places/persons/events.

Question 1.
License which the Indian rulers had to get from the Portuguese-
Answer:
Cartaz

Question 2.
Indian king who built his own navy-
Answer:
Chhatrapati Shivaji Maharaj

Question 3.
The company was established by the British in 1600-
Answer:
The East India company

Question 4.
The staff of factories was called-
Answer:
Factors

Question 5.
Flag of the British-
Answer:
Union Jack

Question 6.
Commander-in-chief of Mumbai-
Answer:
George Oxenden

Question 7.
The company formed by several Dutch companies-
Answer:
United East India

Question 8.
Port city mentioned in ‘Periplus’ of Erythrean sea-
Answer:
Machilipatnam (Mosalia)

Question 9.
Mughal emperor who granted permission to the French to open a factory in Surat-
Answer:
Aurangzeb

Question 10.
The main center of French operations-
Answer:
Pondicherry (Puducherry)

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
The Indian rulers had to get Cartaz (license) from the Portuguese ____________
(a) for sailing on the Indian Ocean
(b) for carrying on a trade
(c) for enjoyment
(d) for conducting naval exercises
Answer:
(a) for sailing on the Indian Ocean

Question 2.
The British built factories in India because ____________
(a) they wanted to store machines
(b) they wanted to store goods bought at low prices
(c) they wanted to employ Indians in these factories
(d) they wanted to accommodate the staff at these factories
Answer:
(b) they wanted to store goods bought at low prices

Question 3.
Charles II leased Mumbai to the East India Company because ____________
(a) the East India company wanted Mumbai
(b) Mumbai was too far away to administer
(c) the expenditure for its maintenance exceeded the income earned from it
(d) the East India Company was a rich company
Answer:
(c) the expenditure for its maintenance exceeded the income earned from it

Question 4.
A British mint was established in Mumbai because ____________
(a) Mumbai was an ideal place for setting up a mint
(b) the British could keep an eye on the mint
(c) the British had competition from other European powers
(d) this encouraged merchants and artisans to come and settle down in Mumbai
Answer:
(d) this encouraged merchants and artisans to come and settle down in Mumbai

3. Complete the following concept map.

Question 1.

Office Holders	Office Holders
Vice-rei and Capitaon-i-Jaral	…………………………
……………………………	Archbishop
Chancellor	…………………………
……………………………	Captain

Answer:

Office Holders	Office Holders
Vice-rei and Capitaon-i-Jaral	Viceroy and General of the army
Arcebispo	Archbishop
Chancellor	Judge
Capitaon	Captain

Question 2.

Answer:

4A. Write short notes.

Question 1.
Cartaz
Answer:
The Cartaz was a license issued by the Portuguese to the Indian rulers for sailing on the Indian Ocean when they established firm control on the Indian Ocean. It usually carried details like the name of the vessel (ship), the name of the captain of the ship, port of departure and arrival, the list of weaponry on the ship loaded for the purpose of self-defense, etc.

Question 2.
Portuguese Trade
Answer:
The king of Calicut wrote to the King of Portugal in a letter sent with Vasco da Gama “Our state is rich in spices like cloves, ginger, black pepper, and precious stones. We expect you to pay us in gold, silver, corals in exchange for our spices and precious stones”. Vasco da Gama sold the commodities in Portugal, which he carried from India. He could earn a huge amount of money in that trade which was sixty times more than the money he spent for his return journey to Portugal.

Question 3.
Factory
Answer:
The British established factories in India. For this, they used to acquire large plots of land. These plots were used to build warehouses, residential quarters, and offices. The main building of the factory carried the ‘Union Jack’. The staff of these factories was called ‘Factors’. The meals provided to the staff included bread, meat, rice, Khichadi of pulses and rice, pickles, etc. The company had created beautiful gardens for the benefit of the staff at Surat, Karwar, Machilipatnam, Petapuli, Chennai, and Mumbai.

Question 4.
Machilipatnam
Answer:
The Dutch established their first colony at Machilipatnam. This port city came into existence in the 3rd century B.C.E. It is also mentioned in ‘Periplus’ of the Erythrean Sea as ‘Mosalia’.

4B. Explain the following statements with reasons.

Question 1.
The British built ‘Factories’ in India.
Answer:
The British used to acquire large plots of land for their factories. These plots were used to build warehouses, residential quarters, and offices. The British needed a permanent place to store the goods at low prices. It was required of them to stay in India for a period of 9 to 13 months to carry out trading transactions. Hence they decided to build ‘Factories’ or ‘emporiums’ in India. The staff of these factories was called ‘factors’.

Question 2.
The ‘Carnatic Wars’ were fought between the British and the French.
Answer:
Pondicherry which was the main center of French operations was ruled by the Nawab of Karnataka. The members of the Nawab family were fighting amongst themselves for the throne. The British and the French started intervening in the matter which resulted in three battles between the British and the French from 1744 to 1763 C.E. known as the ‘Carnatic Wars’.

5. State your opinion.

Question 1.
Charles II leased Mumbai to the East India Company.
Answer:
Charles II had received the islands of Mumbai as a gift from the King of Portugal on his engagement to Princess Braganza of Portugal. He found it difficult to maintain the islands as the expenditure incurred on its maintenance exceeded the income earned from it. So, he leased it to the East India Company.

Question 2.
In 1602, several Dutch companies got together to form ‘United East India’.
Answer:
The Dutch government issued a license to the company to conduct trading with the eastern countries. The same license permitted them to appoint staff, establish factories, build forts, engage in battles against the eastern countries, and also sign treaties with them. Accordingly, the company appointed a Governor-General to take care of Indian affairs.

6. Answer the following questions in detail.

Question 1.
What rights were ‘the French East India Company’ given by the French King Louis XIV?
Answer:
The French East India Company was established in 1664 by Jean Baptiste Colbert. The company was given the authority to trade with eastern countries to maintain army and navy and also exemption from taxes. The company was also given the authority to enter war or treaty with the eastern rulers. In 1666, the company sent a contingent to the court of Mughal Emperor Aurangzeb and obtained permission to establish a factory in Surat.

Balbharti Maharashtra State Board Class 12 History Important Questions Chapter 7 Decolonisation to Political Integration of India Important Questions and Answers.

Maharashtra State Board 12th History Important Questions Chapter 7 Decolonisation to Political Integration of India

1A. Choose the correct alternative and rewrite the statement.

Question 1.
Decolonisation is the process of ending the colonial rule and handing over __________ to local people by colonialists.
(a) The political and administrative power
(b) The political and social power
(c) The social and cultural power
(d) The social and economical power
Answer:
(a) The political and administrative power

Question 2.
__________ handled the situation with great skill and tact.
(a) Sardar Vallabhbhai Patel
(b) Maulana Abdul Kalam Azad
(c) Pandit Jawaharlal Nehru
(d) Dr. T.B. Kunha
Answer:
(a) Sardar Vallabhbhai Patel

Question 3.
In February 1948, __________ merged in India.
(a) Junagadh
(b) Dadra and Nagar Haveli
(c) Hyderabad
(d) Kashmir
Answer:
(a) Junagadh

Question 4.
In __________ people wanted to merge in India and the Nawab wanted to merge in Pakistan.
(a) Saurashtra
(b) Kashmir
(c) Hyderabad
(d) Rajasthan
Answer:
(a) Saurashtra

Question 5.
The __________ passed a resolution in favour of Hyderabad’s merger in India.
(a) Hyderabad State Congress
(b) Marathwada Parishad
(c) Karnataka Parishad
(d) Andhra Parishad
Answer:
(a) Hyderabad State Congress

Question 6.
17th September 1948 the day of Hyderabad’s freedom is celebrated as the __________
(a) Marathwada Liberation Day
(b) Hyderabad Liberation Day
(c) Marathwada Labour Day
(d) Hyderabad Day
Answer:
(a) Marathwada Liberation Day

Question 7.
__________ was started by the Indian Army in Goa to free from the Portuguese.
(a) Operation Vijay
(b) Operation Thunder
(c) Operation Blue Star
(d) Operation Anti-Portuguese
Answer:
(a) Operation Vijay

Question 8.
According to __________ Jammu and Kashmir got special status.
(a) Article 370
(b) Article 470
(c) Article 315
(d) Article 365
Answer:
(a) Article 370

Question 9.
In 1939, posters with __________ slogans were posted all over Goa.
(a) Quit Goa
(b) Quit Portuguese
(c) Quit India
(d) Non-Cooperation Movement
Answer:
(a) Quit Goa

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Group ‘A’	Group ‘B’
(a) Hyderabad’s Organisation	Hyderabad State Congress
(b) Goa’s Organisation	Goa Congress Committee
(c) Puducherry Leader	Dr. T.B. Kunha
(d) Kashmir’s King	King Hari Singh

Answer:
Puducherry Leader – Subbayya

Question 2.

Group ‘A’	Group ‘B’
(a) Junagadh merged in India	February 1948
(b) Hyderabad merged in India	September 1948
(c) Dadra and Nagar Haveli merged in India	August 1955
(d) Goa became part of India	December 1961

Answer:
Dadra and Nagar Haveli merged in India – August 1954

Question 3.

Group ‘A’	Group ‘B’
(a) Sardar Patel	1st Prime Minister
(b) Swami Ramanand Tirth	Hyderabad Freedom Struggle
(c) Francis Mascarenhas	United Goan Front
(d) Keshavrao Jedhe	Goa Vimochan Sahayak Samiti

Answer:
Sardar Patel – Deputy Prime Minister

Question 4.

Group ‘A’	Group ‘B’
(a) Junagadh	February 1948 merged in India
(b) Hyderabad	September 1948 merged in India
(c) Dadra and Nagar Haveli	In 1961 Union Territory
(d) Jammu and Kashmir	Article 470

Answer:
Jammu and Kashmir – Article 370

2A. Write the names of historical places/persons/events.

Question 1.
Languages were spoken in Hyderabad –
Answer:
Telugu, Kannada, and Marathi

Question 2.
Various organisations in Hyderabad –
Answer:
Andhra Parishad, Maharashtra Parishad, and Karnataka Parishad

Question 3.
Head of the Razakar Organisation –
Answer:
Kasim Razvi

Question 4.
Name of the mission planned by the Indian Army in Goa –
Answer:
Operation Vijay

Question 5.
People of Puducherry got united under the leadership of –
Answer:
Subbayya

Question 6.
Name of the regions controlled by the French –
Answer:
Puducherry, Karaikal, Maho, Yanam, and Chandranagar

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
Junagadh merged in India because __________
(a) Nawab wanted to merge in Pakistan
(b) People of Junagadh wanted to merge in India
(c) People of Junagadh opposed Nawab’s decision
(d) All of above
Answer:
(d) All of above

Question 2.
Nizam had opposed the resolution passed by Hyderabad State Congress because __________
(a) He was willing to join Pakistan
(b) Fear of losing his hold over Hyderabad
(c) people were in favour of India
(d) All of above
Answer:
(d) All of above

Question 3.
Pakistan attacked on Kashmir because __________
(a) Pakistan wanted to capture Kashmir
(b) King Hari Singh wanted to join India
(c) People of Kashmir wanted to join India
(d) King Hari Singh neither wanted to join Pakistan nor India
Answer:
(a) Pakistan wanted to capture Kashmir

3A. Observe the map on textbook page 61 and answer the questions based on it.

Question 1.
Name the countries located at the northeast border of India.
Answer:
China, Nepal, Bhutan, and East Pakistan.

Question 2.
What is the theme of the map?
Answer:
Independent India, 15th August 1947.

Question 3.
Name of the island located nearby India.
Answer:
Andaman and Nicobar island.

Question 4.
Name of the regions located on the western coast of India.
Answer:
Diu, Daman, Mumbai, Goa, and Mahe.

Question 5.
Name of the regions located on the eastern coast of India.
Answer:
Kolkata, Yanam, Chennai, Puducherry, and Karaikal.

3B. Complete the following concept map.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

4A. Write short notes.

Question 1.
Junagadh
Answer:

• Junagadh was located in Gujarat.
• Nawab of Junagadh was planning to merge the state into Pakistan, but the people of Junagadh were in favour of India.
• After getting the people against him, he flew to Pakistan, in February 1948 Junagadh became part of Independent India.

Question 2.
Kashmir merged in India
Answer:

• After declaring British Policy regarding princely states, King Hari Sigh of Kashmir neither wanted to join Pakistan nor India.
• But Pakistan wanted to capture Kashmir.
• Soon Pakistan attacked Kashmir, King Hari Singh sought help from Pandit Jawaharlal Nehru.
• Indian army had already started recapturing parts of the land which had been captured by the Pakistani army.
• Meanwhile, UNO intervened in this matter and Pakistan and India had to stop the war. But by this decision, some parts of Kashmir remained occupied by Pakistan.
• Later on, King Hari Singh was ready to merge in India. Special provisions were passed and through this Kashmir got special status under Article 370.

Question 3.
Dadra and Nagar Haveli
Answer:

• Dadra and Nagar Haveli is located in Gujarat, near the Damanganga river, it was under the control of the Portuguese.
• Like other regions of India, the people of Dadra and Nagar Haveli also got freedom from the Portuguese.
• Many organisations like the United Front of Goans and Azad Gomantak Dal came together to fight against the Portuguese reign.
• These organisations and their branches started capturing the area under it. Many police stations and administration offices were attacked.
• The Portuguese army was called to control people. At the same time, the Government of India appointed Governor and signed the agreement.
• According to this treaty, Dadra and Nagar Haveli merged in India on 2nd August 1954 and in 1961, got status of ‘Union Territories.’

Question 4.
Puducherry
Answer:

• Similar to Dadra and Nagar Haveli, Puducherry was under French rule.
• Most of the east coast of India regions like Puducherry, Karaikal, Mahe, Yanam, and Chandrangar in West Bengal were under French rule as well.
• People and many political parties under the leadership of V. Subbayya came together to get rid of the French.
• It was a serious matter for the Government of India; hence they demanded that French Government return the Indian regions. In 1948, an agreement was signed by both governments for Puducherry
• In 1949, Chandranagar was merged in India.
• In 1954, the French government passed the draft, according to it all French ruling regions will merge in India. And in 1963 Puducherry was declared a ‘Union Territory’.

Question 5.
Goa
Answer:

• Goa was under Portuguese control. In 1928 ‘Goa Congress Committee was formed and it became the branch of the Indian National Congress.
• ‘Quit Goa’ slogans were posted all over Goa.
• Dr. Kunha played an important role in Goa. Dr. Lohia got arrested in Civil Disobedience Movement.
• Dr. Kunha was also arrested. After his release from jail, he started a newspaper namely ‘Azad Goa’ and ‘Swatantra Goa’.
• One of the groups of activists unfurled the Indian flag at the fort of Panaji.
• Many eminent people participated in Goa Liberation Movement. Mohan Ranade systematically began anti-Portuguese propaganda in Goa. He was arrested and kept in jail till 1972.
• ‘Maratha’, a newspaper, was trying to get support from Maharashtra for Goa. Soon Pandit Jawaharlal Nehru sent the Indian army to Goa for the mission called “Operation Vijay”.
• Within 48 hours Portuguese surrendered and Goa became a part of the Indian Republic. And 450 years rule of foreign power came to an end.

4B. Explain the following statements with reasons.

Question 1.
Kashmir got special Status under Article 370.
Answer:

• From the beginning, Kashmir received special attention from all.
• After British policy for the princely states, Kashmir King Hari Singh decided not to be a part of Pakistan and also not to be a part of India.
• However, when Pakistan Pakistan attacked Kashmir, King Hari Singh asked India to help and he consented to merge Kashmir in India and officially submitted an agreement.
• Indian Army was sent to save Kashmir.
• Later on, the constitution of Jammu and Kashmir was drafted and it became part of India and got special status under ‘Article 370.’

Question 2.
‘Operation Vijay’ was planned in Goa.
Answer:

• Goa was under Portuguese control. In 1928 ‘Goa Congress Committee was formed and it became the branch of the Indian National Congress.
• ‘Quit Goa’ slogans were posted all over Goa.
• Dr. Kunha played an important role in Goa. Dr. Lohia got arrested in Civil Disobedience Movement.
• Dr. Kunha was also arrested. After his release from jail, he started a newspaper namely ‘Azad Goa’ and ‘Swatantra Goa’.
• One of the groups of activists unfurled the Indian flag at the fort of Panaji.
• Many eminent people participated in Goa Liberation Movement. Mohan Ranade systematically began anti-Portuguese propaganda in Goa. He was arrested and kept in jail till 1972.
• ‘Maratha’, a newspaper, was trying to get support from Maharashtra for Goa. Soon Pandit Jawaharlal Nehru sent the Indian army to Goa for the mission called “Operation Vijay”.
• Within 48 hours Portuguese surrendered and Goa became a part of the Indian Republic. And 450 years rule of foreign power came to an end.

Question 3.
Dadra and Nagar Haveli were declared Union territories.
Answer:

• Dadra and Nagar Haveli is located in Gujarat, near the Damanganga river, it was under the control of the Portuguese.
• Like other regions of India, the people of Dadra and Nagar Haveli also got freedom from the Portuguese.
• Many organisations like the United Front of Goans and Azad Gomantak Dal came together to fight against the Portuguese reign.
• These organisations and their branches started capturing the area under it. Many police stations and administration offices were attacked.
• The Portuguese army was called to control people. At the same time, the Government of India appointed Governor and signed the agreement.
• According to this treaty, Dadra and Nagar Haveli merged in India on 2nd August 1954 and in 1961, got status of ‘Union Territories.’

5. State your opinion.

Question 1.
‘Operation Polo’ was started in Hyderabad.
Answer:

• Swami Ramanand Tirth with loyal workers was leading a political organization to free Hyderabad from the Nizam.
• Hyderabad State Congress passed a resolution that Hyderabad will merge in India and this was not liked by Nizam, he was willing to join Pakistan.
• People of Hyderabad however, wanted to merge with India. Kasim Razvi formed the ‘Razakar’ organisation against people who were fighting for democracy.
• In the end Indian Government launched a police campaign against Nizam, called ‘Operation Polo’.

Question 2.
The Indian Army was sent for Kashmir’s Protection.
Answer:

• Kashmir King Hari Singh decided not to be a part of Pakistan and also not to be a part of India.
• However, when Pakistan attacked Kashmir, King Hari Singh asked India to help and he consented to merge Kashmir in India and officially submitted an agreement.
• Indian Army was sent to save Kashmir.

Question 3.
Dadra and Nagar Haveli got status of Union Territory.
Answer:

• Dadra and Nagar Haveli is located in Gujarat, near the Damanganga river, it was under the control of the Portuguese.
• Like other regions of India, the people of Dadra and Nagar Haveli also got freedom from the Portuguese.
• Many organisations like the United Front of Goans and Azad Gomantak Dal came together to fight against the Portuguese reign.
• These organisations and their branches started capturing the area under it. Many police stations and administration offices were attacked.
• The Portuguese army was called to control people. At the same time, the Government of India appointed Governor and signed the agreement.
• According to this treaty, Dadra and Nagar Haveli merged in India on 2nd August 1954 and in 1961, got status of ‘Union Territories.’

Question 4.
Contribution of Dr. Lohia and Dr. T.B. Kunha in Goa’s Freedom Struggle.
Answer:

• Dr. Ram Manohar Lohia started a movement called Civil Disobedience.
• Dr. Lohia and Dr. T.B. Kunha were arrested and sent to jail.
• Dr. Kunha was sent to Portugal for 8 years imprisonment.
• After returning to India he started the newspapers, ‘Azad Goa’ and ‘Swatantra Goa’.
• Both these leaders have contributed a lot to the freedom of Goa.

6. Answer the following questions in detail.

Question 1.
(a) Hyderabad Freedom Struggle
(b) The Kashmir Issue
(c) Dadra and Nagar Haveli
(d) Goa
(e) Puducherry
Answer:
(a) Hyderabad Freedom Struggle:
Hyderabad was under Nizam rule, it was one of the largest amongst princely states along with Telugu, Kannada, and Marathi regional sections. Various organisations were formed to fight against Nizam’s policy for their people.

• Nizam’s decision: Nizam was ruler and wanted to merge Hyderabad into Pakistan. The people of Hyderabad wanted democracy. It was not about one regional section. He put restrictions on the Civil and Political rights of his subjects to a great extent.
• Organisations: To fight against the suppressive policy of Nizam people of the state started various organisations namely Andhra Parishad in Telangana, Maharashtra Parishad in Marathwada, and Karnataka Parishad in Karnataka. Swami Ramananda Tirth formed an organisation with loyal workers called Hyderabad State Congress and gave direction for freedom.
• Operation Polo: People of Hyderabad wanted to merge in India. Kasim Razvi formed a ‘Razakar’ organisation against people. In the end, the Indian Government launched a police campaign against Nizam, called ‘Operation Polo’. In 1948 Nizam surrendered and Hyderabad merged in India.

(b) The Kashmir Issue:
From the beginning, Kashmir is special attention for all. After British policy for the princely states, Kashmir king Hari Singh decided not to be a part of Pakistan and also not be a part of India.

But Pakistan attacked Kashmir and King Hari Singh asked India to help and he consented to merge Kashmir in India and officially submitted an agreement. Indian Army was sent to save Kashmir. Later on, the constitution of Jammu and Kashmir was drafted and it became part of India and got special status under article 370.’

The intervention of UNO: In 1948, Pandit Jawaharlal Nehru took this matter to UNO. It became an international issue. Even UNO could not persuade Pakistan to withdraw their troops from the territory of Kashmir occupied by them. However, then the National Conference Party decided on a plebiscite to solve the issue and to accede Kashmir to India.

(c) Dadra and Nagar Haveli:

• Dadra and Nagar Haveli is located in Gujarat, near the Damanganga river, it was under the control of the Portuguese.
• Like other regions of India, the people of Dadra and Nagar Haveli also got freedom from the Portuguese.
• Many organisations like the United Front of Goans and Azad Gomantak Dal came together to fight against the Portuguese reign.
• These organisations and their branches started capturing the area under it. Many police stations and administration offices were attacked.
• The Portuguese army was called to control people. At the same time, the Government of India appointed Governor and signed the agreement.
• According to this treaty, Dadra and Nagar Haveli merged in India on 2nd August 1954 and in 1961, got status of ‘Union Territories.’

(d) Goa:

• Goa was under Portuguese control. In 1928 ‘Goa Congress Committee was formed and it became the branch of the Indian National Congress.
• ‘Quit Goa’ slogans were posted all over Goa.
• Dr. Kunha played an important role in Goa. Dr. Lohia got arrested in Civil Disobedience Movement.
• Dr. Kunha was also arrested. After his release from jail, he started a newspaper namely ‘Azad Goa’ and ‘Swatantra Goa’.
• One of the groups of activists unfurled the Indian flag at the fort of Panaji.
• Many eminent people participated in Goa Liberation Movement. Mohan Ranade systematically began anti-Portuguese propaganda in Goa. He was arrested and kept in jail till 1972.
• ‘Maratha’, a newspaper, was trying to get support from Maharashtra for Goa. Soon Pandit Jawaharlal Nehru sent the Indian army to Goa for the mission called “Operation Vijay”.
• Within 48 hours Portuguese surrendered and Goa became a part of the Indian Republic. And 450 years rule of foreign power came to an end.

(e) Puducherry:

• Similar to Dadra and Nagar Haveli, Puducherry was under French rule.
• Most of the east coast of India regions like Puducherry, Karaikal, Mahe, Yanam, and Chandrangar in West Bengal were under French rule as well.
• People and many political parties under the leadership of V. Subbayya came together to get rid of the French.
• It was a serious matter for the Government of India; hence they demanded that French Government return the Indian regions. In 1948, an agreement was signed by both governments for Puducherry
• In 1949, Chandranagar was merged in India.
• In 1954, the French government passed the draft, according to it all French ruling regions will merge in India. And in 1963 Puducherry was declared a ‘Union Territory’.

Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 3B Elasticity of Demand Important Questions and Answers.

Maharashtra State Board 12th Economics Important Questions Chapter 3B Elasticity of Demand

1.[A] Choose the correct option.

Question 1.
When the percentage change in quantity demanded is less than the percentage change in price, the demand curve is ……………..
(a) flatter
(b) steeper
(c) rectangular
(d) vertical
Answer:
(b) steeper

Question 2.
When changes in price does not affect demand at all, it is called as ……………..
(a) unitary elastic
(b) perfectly inelastic
(c) relatively elastic
(d) perfectly elastic
Answer:
(b) perfectly inelastic

Question 3.
When slight change in price brings infinite change in demand, then ……………..
(a) Ed = 0
(b) Ed = ∞
(c) Ed <1 (d) Ed > 1
Answer:
(b) Ed = ∞

Question 4.
When percentage change in quantity demanded is equal to changes in price, the demand curve is …………
(a) steeper
(b) flatter
(c) rectangular hyperbola
(d) vertical
Answer:
(c) rectangular hyperbola

Question 5.
Demand for salt is …………….
(a) elastic
(b) inelastic
(c) perfectly elastic
(d) perfectly inelastic
Answer:
(d) perfectly inelastic

Question 6.
Demand for Medicine is ……………
(a) elastic
(b) inelastic
(c) relatively elastic
(d) relatively inelastic
Answer:
(d) relatively inelastic

Question 7.
Demand for cosmetics is ……………..
(a) relatively elastic
(b) relatively inelastic
(c) perfectly elastic
(d) perfectly inelastic
Answer:
(a) relatively elastic

Question 8.
Demand for air conditions is ………….
(a) elastic
(b) inelastic
(c) vertical
(d) horizontal
Answer:
(a) elastic

Question 9.
Demand for essential commodities in life is …………..
(a) elastic demand
(b) relatively inelastic
(c) perfectly elastic
(d) perfectly inelastic
Answer:
(b) relatively inelastic

Question 10.
Demand for school uniform is……………..
(a) relatively elastic
(b) relatively inelastic
(c) perfectly elastic
(d) none of the above
Answer:
(b) relatively inelastic

Question 11.
Demand for not habituated goods is ………….. demand.
(a) relatively inelastic
(b) perfectly inelastic
(c) perfectly elastic
(d) relatively inelastic
Answer:
(c) perfectly elastic

Question 12.
Specific uses of a commodity demand is …………………..
(a) relatively elastic
(b) relatively inelastic
(c) perfectly elastic
(d) none of the above
Answer:
(b) relatively inelastic

Question 13.
In case of inferior goods the income elasticity of demand is ………………..
(a) positive
(b) negative
(c) infinite
(d) zero
Answer:
(b) negative

Question 14.
In case of necessary goods the income elasticity of demand is ………………..
(a) positive
(b) negative
(c) infinite
(d) zero
Answer:
(d) zero

Question 15.
In case of substitute goods the cross elasticity of demand is ………………..
(a) negative
(b) positive
(c) zero
(d) infinite
Answer:
(b) positive

(B) Complete the Correlation . (1 mark each)

(1) Demand for pins : Inelastic :: Demand for perfume : ……………….
(2) Demand for specialised labour : ………………. :: Demand for luxury goods : Relatively Elastic
(3) The demand for durable goods : ………………. :: Demand for perishable goods : inelastic
(4) Normal goods the income elasticity of demand is : Positive :: Complementary goods the cross elasticity of demand is : ……………….
(5) After devaluation exports become : ………………. :: Devaluation succeeds when exports have elastic demand
(6) Demand for luxury goods : Elastic :: Demand for food grain : ……………….
(7) Rectangular hyperbola curve : Ed = 1 :: Steeper demand curve : ……………….
(8) Total outlay remains same : Ed = 1 :: Total outlay increases : ……………….
(9) Total outlay decreases : Ed < 1:: Total outlay remains same : ……………….
Answer:

1. Elastic
2. Inelastic
3. Relatively elastic
4. Negative
5. Cheaper
6. inelastic
7. Ed < 1
8. Ed > 1
9. Ed = 1

(C) Give economic terms.

1. Elasticity resulting from changes in price does not affect demand at all.
2. Product of price and quantity demanded.
3. Elasticity resulting from changes in demand is more than change in price.
4. Elasticity of demand is measured with the following formula:
   \(\frac { Lower segment of demand curve below a given point }{ Upper segment of demand curve above a given point }\)
5. A fall in the price of mobile handsets may lead to rise in the demand for sim cards.

Answer:

1. Perfectly inelastic
2. Total Expenditure
3. Relatively elastic
4. Point I Geometric method
5. Complementary goods

[D] Find the odd word out.

1. Types of price elasticity of demand:
   Perfectly elastic demand, Perfectly inelastic demand, Relatively inelastic demand, Cross elasticity of demand.
2. Types of elasticity of demand:
   Total outlay, Cross elasticity, Income elasticity, Price elasticity.
3. Methods of measuring price elasticity of demand:
   Ratio method, Geometric method, Total outlay method, Unitary elastic demand.
4. Types of Income Elasticity of demand:
   Positive, Negative, Cross, Zero
5. Examples of Substitute Goods:
   Coca-cola, Pepsi, Thumsup, Fanta
6. Examples of Complementary Goods:
   Tea – Sugar, Car – Petrol, Tea – Coffee

Answers:

1. Cross elasticity of demand
2. Total outlay
3. Unitary elastic demand
4. Cross
5. Fanta
6. Tea – Coffee

(E) Complete the following statements.

(1) Price multiplied by quantity = …………………
(2) Demand for luxuries is ………………… demand.
(3) The life saving medicines have ………………… demand.
(4) A unitary elastic demand curve is a …………………
(5) The demand for necessaries is …………………
(6) The demand for durable goods tends to be …………………
(7) Degree of responsiveness of a change in quantity demanded to a change in the income is called as …………………
(8) Normal goods for which demand increases with increases in income …………………
(9) Inferior goods for which demand decreases with increase in income of consumer …………………
(10) Necessary goods for which demand remain constant with increase in income of the consumer …………………
(11) explained the concept of elasticity ………………… of demand.
(12) Demand for perishable goods is …………………
Answers:

1. Total outlay
2. elastic
3. inelastic
4. rectangular hyperbola
5. inelastic
6. elastic
7. income elasticity
8. positive income elasticity
9. negative income elasticity
10. zero income elasticity
11. Prof. Alfred Marshall
12. inelastic

(F) Choose the wrong pair

Group ‘A’	Group ‘B’
1. Car and petrol	Complementary goods
2. Point method	Geometric method
3. Necessaries	Inelastic demand
4. Unitary elastic	Steeper curve

Answer:
Wrong pair : Unitary elastic – Steeper curve

II.

Group ‘A’	Group ‘B’
1. Inelastic demand	Steep slope of demand curve
2. BMW Car	Inelastic demand
3. Income elasticity	Responsiveness of quantity demanded of a commodity to change in income
4. Elastic demand	Flatter slope of demand curve

Answer:
Wrong pair: BMW Car – Inelastic demand

(G) Assertion and Reasoning

Question 1.
Assertion (A) Degree of Price Elasticity is less than one in case of relatively inelastic demand.
Reasoning (R) – Change in demand is less than the change in price.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(i) (A) is true but (R) is false.

Question 2.
Assertion (A) – Substitute goods have positive elasticity.
Reasoning (R) – Increase in price of tea leads to increase in demand of coffee.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).

Question 3.
Assertion (A) – Cross elasticity of non – related goods is more than one.
Reasoning (R) – Tea and books are the examples of non-related goods.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(ii) (A) is false but (R) is true.

Question 4.
Assertion (A) – Perfectly Elastic demand is infinite.
Reasoning (R) – 10 % fall in price leads to 200% increase in demand.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).

Question 5.
Assertion (A) – Unitary elastic demand has rectangular hyberbola curve.
Reasoning (R) – 50% decrease in price, brings 50% increase in demand of a commodity.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A)’.

(H) Choose the correct pair

I.

Group ‘A’	Group ‘B’
1. Salt	(a) Demand  curve parallel to ‘X’ axis
2. Income elasticity	(b) Flatter in shape
3. Perfectly elastic demand	(c) Related goods
4. Relatively elastic demand	(d) Inelastic demand
5. Cross elasticity	(e) Change in demand due to change in income

Answer:
(1) – (d), (2) – (e), (3) – (a), (4) – (b), (5)-(c).

II.

Group ‘A’	Group ‘B’
1. Essential commodities	(a) flatter in shape
2. Unitary elastic demand	(b) change in income
3. Elasticity of demand	(c) Ed = 1
4. Relatively elastic demand	(d) Prof. Alfred Marshall
5. Income Elasticity	(e) Inelastic demand

Answer:
(1) – (e), (2) – (c), (3) – (d), (4) – (a), (5)-(b).

2. (B) Distinguish between :

Question 1.
Income Elasticity and Cross Elasticity.
Answer:
Income Elasticity:

1. Income elasticity of demand is the proportionate change in quantity demanded of a commodity to a given change in the consumer’s income.
2. Income Elasticity of demand are of three types –
   • Positive Income Elasticity is found in case of Normal Goods.
   • Negative Income Elasticity for inferior goods cheap bread, rice, etc.
   • Zero Income Elasticity.

Cross Elasticity:

1. Cross Elasticity of demand is the proportionate change in the quantity demanded of a commodity to a given change in the price of substitute or complementary goods.
2. Cross Elasticity of demand are of three types –
   • Positive Cross Elasticity is found in case of substitute goods like tea and coffee.
   • Negative Cross Elasticity is seen in case of Complementary Goods.
   • Zero Cross Elasticity in case of unrelated goods like cup and book.

Question 2.
Positive Income Elasticity and Negative Income Elasticity.
Answer:
Positive Income Elasticity

1. When a change in income brings about change in demand in the same direction the Income Elasticity of demand is positive.
2. When income rises demand also rises and fall in income brings a fall in demand.
3. In case of normal goods, the Income Elasticity is positive.
4. The slope of  Income Curve is positive. It slopes upward indicating that as income rises the demand also rises
   

Negative Income Elasticity:

1. When a change in income of the consumer brings about a change in demand of the commodity in the opposite direction then Income Elasticity is negative.
2. When income increases the demand decreases and when income decreases demand increases.
3. In case of inferior goods, the Income Elasticity is negative.
4. The slope of the Income Curve is negative. It slopes downward indicating that as income increases, demand decreases.
   

Question 3.
Perfectly Inelastic Demand and Perfectly Elastic Demand.
Answer:
Perfectly Inelastic Demand:

1. When a change in price brings no change in quantity demanded, then demand is said to be Perfectly Inelastic demand.
2. The numerical co-efficient is zero (e = 0).
3. The demand curve is vertical straight line parallel to Y-axis.
   

Perfectly Elastic Demand:

1. When a small change in price brings infinite change in the quantity demanded, then demand is said to be Perfectly Elastic demand.
2. The numerical co-efficient is infinity (e = ∞).
3. The demand curve is a horizontal straight line parallel to X-axis.
   

Question 6.
Price Elasticity and Income Elasticity.
Answer:
Price Elasticity:

1. Price Elasticity of demand refers to the degree of responsiveness of quantity demanded of a commodity to given change in price.
2. Symbolically:
   
3. There is inverse relation between price and demand.
4. Price Elasticity of demand are of five type :
   1. Relatively elastic demand
   2. Relatively inelastic demand
   3. Unitary elastic demand
   4. Perfectly elastic demand
   5. erfectly inelastic demand

Income Elasticity:

1. Income elasticity of demand refers, to the degree of responsiveness of quantity demanded of the commodity to a given change in income.
2. Symbolically :
   
3. There is direct relation between Income and demand.
4. Income elasticity of demand are of three types:
   • Positive Income elasticity
   • Negative Income elasticity
   • Zero Income elasticity

Question 7.
Perfectly Inelastic Demand and Relatively Inelastic Demand.
Answer:
Perfectly Inelastic Demand:

1. When a change in price brings no change in quantity demanded then, demand is said to be Perfectly Inelastic demand.
2. The numerical co-efficient is zero (e = 0).
3. The slope of the demand curve is straight line parallel to Y-axis.
   
4. Example : life saving drugs, salt, etc

Relatively Inelastic Demand:

1. When percentage change in quantity demanded is less than percentage change in price then, demand is said to be Relatively Inelastic demand.
2. The numerical co-efficient is less than one (e < 1).
3. The slope of the demand curve is steeper.
   
4. Example: food grains

Question 8.
Perfectly Elastic Demand and Relatively Elastic Demand.
Answer:
Perfectly Elastic Demand:

1. When with a small change in price brings infinite change in the quantity then it is said to be Perfectly Elastic demand.
2. The numerical co-efficient is infinity (e = ∞).
3. The demand curve is a horizontal straight line parallel to X-axis.
   

Relatively Elastic Demand :

1. When percentage change in quantity demanded is greater than the percentage change in price demand then it is said to be Relatively Elastic demand.
2. The numerical co-efficient is greater than one (e > 1)
3. The demand curve slope is flatter.
   

Question 9.
Percentage Method and Total Outlay Method.
Answer:
Percentage Method:

1. According to this method elasticity of demand is equal to the ratio of percentage change in the quantity demanded to percentage change in the price.
2. (1) If the result in one, the Elasticity is unitary.
   (2) If the result is > 1 the demand is relatively elastic and
   (3) If the result is < 1 then demand is relatively Inelastic.

Total Outlay Method:

1. Under this method Elasticity is measured by observing the changes in outlay in response to change in price.
2. Elasticity of demand is measured by the kind of changes in total expenditure.
   • When with increase or decrease in price, the outlay remain constant the elasticity is equal to one.
   • If outlay and price are inversely related then demand is relatively elastic.
   • If outlay and price are directly related then demand is relatively Inelastic.

3. Answer the following questions:

Question 1.
Explain the concept of Elasticity of Demand?
Answer:
The concept of Price Elasticity was developed by great neo-classical economist Dr. Alfred Marshall in the year 1890.

According to Dr. Alfred Marshall, “The elasticity or responsiveness of demand in a market is great or small, according to the amount demanded which increases much or little for a given fall in price, and diminishes much or little for a given rise in price. ”
Elasticity of demand in fact refers to the degree of responsiveness of the quantity demanded of a commodity to change in the variable on which demand depends.

Question 2.
Which are the types of Elasticity of Demand.
Answer:
Types of Elasticity of Demand :

1. Price Elasticity of Demand
2. Income Elasticity of Demand
3. Cross Elasticity of Demand

1. Price Elasticity of Demand : It is a ratio of proportionate change in the quantity demanded of a commodity to a given proportionate change in its price.
ed = \(\frac { Percentage change in Quantity Demanded }{ Percentage change in Price }\)
There are 5 types of Price Elasticity of demand i.e.

1. Perfectly Elastic demand (Ed = ∞)
2. Perfectly Inelastic demand (Ed = 0)
3. Unitary Elastic demand (Ed = 1)
4. Relatively Elastic demand (Ed > 1)
5. Relatively Inelastic demand (Ed < 1)

2. Income Elasticity of demand : It refers to the degree of responsiveness of a change in the quantity demanded to a change in the income only, other factors including price remaining unchanged.
\(\frac { Percentage change in Quantity Demanded }{ Percentage change in Income }\)
There are 3 types of Income elasticity i.e.:

1. Positive Income elasticity
2. Negative Income elasticity
3. Zero Income elasticity

3. Cross Elasticity of Demand :
It refers to a change in quantity demanded of one commodity due to a change in the price of other commodity i.e. complementary goods or substitute goods.
\(\frac { of commodity ‘X’ }{ Percentage change in Price of commodity ‘Y’ }\)

Cross elasticity of demand are of 3 types i.e.

1. Positive Cross elasticity
2. Negative Cross elasticity
3. Zero Cross elasticity

Question 3.
Explain any two types of price elasticity of demand.
Answer:
Types of price elasticity of demand :
(a) Perfectly Elastic Demand (Ed = ∞) :

When a change in price leads to infinite change in quantity demanded of a commodity it is called as perfectly elastic demand. It is an extreme case, which is very rare. It is a theoretical concept not found in real life.

In the diagram demand curve ‘DD’ is horizontal straight line parallel to X-axis,

(b) Perfectly Inelastic Demand (Ed = 0) : When a change in price has no effect on the quantity demanded of that commodity then it is called Perfectly Inelastic Demand. The demand does not respond to the change in price at all. For instance, if price changes by 10% and the demand does not change at all then e = 0.

In this case the numerical coefficient value is zero. It is also extreme case which rarely exists. Salt and life saving medicine are a ) few example of Perfectly Inelastic Demand as they are absolute necessity. The demand ) curve ‘DD’ is a vertical straight line parallel to Y-axis.

Question 4.
Explain the types of Income Elasticity.
Answer:
(a) Positive Income Elasticity (Normal goods)
(b) Negative Income Elasticity (Inferior goods
(c) Zero Income Elasticity

(a) Positive Income Elasticity : In case of normal goods the income elasticity of demand is positive. When a change in income brings about a change in demand in same direction then income elasticity is positive. There is a direct relationship between income and quantity demanded. Normal goods which include necessities, comforts and luxuries have positive Income Elasticity.

(b) Negative Income Elasticity : Inferior goods have a negative income elasticity. As income increases the demand for inferior goods fall. There is an inverse relation between income and quantity demanded of inferior commodity. Inferior goods are substituted by superior goods.

(c) Zero Income Elasticity : When change in income does not have any effect on the demand for a commodity then the income elasticity is Zero – for E.g. goods like salt, pins etc.

Question 5.
Explain the types of Cross Elasticity of Demand.
Answer:
(a) Positive Cross Elasticity (Substitutes)
(b) Negative Cross Elasticity (Complementary)
(c) Zero Cross Elasticity (Unrelated goods)

(a) Positive Cross Elasticity : Positive cross elasticity of demand takes place in the case of substitute such as tea and coffee, pepsi and coke. If the price of coffee rises it will lead to an increase in the demand for tea. Similarly a fall in price of coffee will cause a decrease in demand for tea. Thus price and demand move in the same direction in case of substitute.

(b) Negative Cross Elasticity : Negative cross elasticity takes place in the case of complementary goods. It takes place when a change in the price of (petrol) one complementary good brings about a change in demand for (car) another commodity in the opposite direction. For e.g. a rise in petrol prices may lead to fall in demand for car and vice-versa.

(c) Zero Cross Elasticity: Zero cross elasticity of demand takes place in case of unrelated goods. For instance a rise or fall in price of car may not affect the demand for books.

Question 6.
Explain the importance of the concept of Elasticity of Demand.
Or
Give the significance of Price elasticity of demand.
Answer:
Importance of Concept of Elasticity of Demand:
1. To a Producer : It helps the producer to decide the price for his product. If the demand for his product is relatively inelastic, he will fix higher price and vice versa.

2. To Government : In order to raise additional revenue by means of new taxes like excise duties on commodities Govt, has to keep in mind the elasticity of demand for a commodity. So a high tax can be imposed on commodities like petrol or cigarettes, the demand for which is relatively inelastic.

3. In International Trade : If the foreign demand for exportable products of a country is relatively elastic, its export will rise much after a slight reduction in their prices. But if foreign demand is relatively inelastic, the exporters can raise their prices without much fall in exports.

4. Trade Union : Knowledge of elasticity of demand can help the trade union in wage bargaining. They can ask the employees { to pay higher wages to the workers by changing the price policy of their product. If the demand for the product produced by them is inelastic then the trade unionist may suggest the employer to raise the price, so as to earn higher profit. Which then can be used to pay higher wages.

5. Public Utility Services : It is the Government who takes the decision to distribute certain essential goods and services, which have inelastic demand. For eg. Indian Railways, bank service, water supply, etc. If such services are left to private sector they will exploit the consumers by charging high prices.

6. Devaluation : Devaluation measure is adopted by the government to promote exports and correct deficit in the balance of payment. Devaluation makes our goods cheaper in the foreign market. However, devaluation is successful only if exports have elastic demand.

7. Factor Pricing: It is helpful in determining the prices of various factors of production like rent for land, wages or salary for labour, interest for capital, etc.

4. State with reasons whether you agtae or disagree with the following statements;

Question 1.
Various factors influence elasticity of demand.
Answer:
Yes, I agree with this statement.

• Nature of Commodity : By nature, commodities are classified as necessaries, comforts and luxuries. Normally demand for necessaries like food grains are relatively inelastic and for comforts and luxuries like diamond, perfumes, etc is relatively elastic.
• Availability of Substitutes : The larger the number of substitutes available for a commodity, the greater would be the elasticity. Demand for products like soap, soft drinks, detergents, tooth paste, etc. have many substitute so demand is elastic, ‘However, salt, garlic, onions have no substitute so demand is inelastic.
• Durability of the Commodity : The demand for durable goods like T.V., car, fridge, etc is relatively inelastic in the short run and elastic in the long run. Whereas the demand for perishable goods is relatively inelastic.
• Uses of Commodity : Single use commodities have less elastic demand and multi-use goods like coal, electricity, sugar, etc. have relatively elastic demand.
• Range of Price : The demand for commodities which are highly priced and will have a inelastic demand like AC, car, etc. Even very low priced goods have inelastic demand.
• Consumer’s Income : Generally if income is very high, the demand for over allcommodities tends to be relatively inelastic. The demand pattern of the rich people is rarely affected even when there is significant price change.

Question 2.
The price elasticity of demand depends only on the nature of commodity.
Answer:

• Nature of Commodity : By nature, commodities are classified as necessaries, comforts and luxuries. Normally demand for necessaries like food grains are relatively inelastic and for comforts and luxuries like diamond, perfumes, etc is relatively elastic.
• Availability of Substitutes : The larger the number of substitutes available for a commodity, the greater would be the elasticity. Demand for products like soap, soft drinks, detergents, tooth paste, etc. have many substitute so demand is elastic, ‘However, salt, garlic, onions have no substitute so demand is inelastic.
• Durability of the Commodity : The demand for durable goods like T.V., car, fridge, etc is relatively inelastic in the short run and elastic in the long run. Whereas the demand for perishable goods is relatively inelastic.
• Uses of Commodity : Single use commodities have less elastic demand and multi-use goods like coal, electricity, sugar, etc. have relatively elastic demand.
• Range of Price : The demand for commodities which are highly priced and will have a inelastic demand like AC, car, etc. Even very low priced goods have inelastic demand.
• Consumer’s Income : Generally if income is very high, the demand for over allcommodities tends to be relatively inelastic. The demand pattern of the rich people is rarely affected even when there is significant price change.

Question 3.
The Income Elasticity of Demand is only positive.
Answer:
No, I do not agree with this statement, s Income Elasticity of demand is not only positive but can also be negative or zero.

• Negative Income Elasticity : Inferior goods have a negative income elasticity. As income increases the demand for inferior goods fall. There is an inverse relation s between income and quantity demanded of inferior commodity. Inferior goods are substituted by superior goods.
• Zero Income Elasticity : When change in income does not have any effect on the demand for a commodity then the income elasticity is Zero – for E.g. goods like salt, pins etc.

Question 4.
Elasticity of Demand cannot be measured.
Answer:
No, I do not agree with this statement,
Elasticity of demand can be measured in 3 methods i.e. Percentage method, Point method or Total Outlay method.

(i) Percentage Method : This method is also known as Arithmetic Method. In this method we compare the percentage of change in demand with percentage of change in price. When we divide the percentage of change in demand by the percentage of change in price, we get Elasticity of demand.

By applying the above formula we can calculate and find the type of elasticity. If the result is one, then elasticity is unitary, if it is more than one, then it is relatively elastic and if it is less than one, it is relatively inelastic.
Ed = \(\frac { Percentage change in Quantity demanded }{ Percentage change in Price }\)

(ii) Point Method : In this method we can find elasticity of demand at a point on a given demand curve by using the following formula –
Ed = \(\frac { Lower segment of the demand curve }{ Upper segment of the demand curve }\)

(iii) Total Outlay Method : According to this method, elasticity of demand is measured on the basis of expenditure incurred by consumer when the price of a commodity changes.
Total outlay can be calculated by multiplying the price with the quantity demanded i.e. Total Outlay = Price x Quantity Demanded

5. Answer in detail:

Question 1.
What is Elasticity of demand? Explain the types of Elasticity of Demand.
Answer:

The concept of Price Elasticity was developed by great neo-classical economist Dr. Alfred Marshall in the year 1890.

According to Dr. Alfred Marshall, “The elasticity or responsiveness of demand in a market is great or small, according to the amount demanded which increases much or little for a given fall in price, and diminishes much or little for a given rise in price. ”
Elasticity of demand in fact refers to the degree of responsiveness of the quantity demanded of a commodity to change in the variable on which demand depends.

Types of Elasticity of Demand :

1. Price Elasticity of Demand
2. Income Elasticity of Demand
3. Cross Elasticity of Demand

1. Price Elasticity of Demand : It is a ratio of proportionate change in the quantity demanded of a commodity to a given proportionate change in its price.
ed = \(\frac { Percentage change in Quantity Demanded }{ Percentage change in Price }\)
There are 5 types of Price Elasticity of demand i.e.

1. Perfectly Elastic demand (Ed = ∞)
2. Perfectly Inelastic demand (Ed = 0)
3. Unitary Elastic demand (Ed = 1)
4. Relatively Elastic demand (Ed > 1)
5. Relatively Inelastic demand (Ed < 1)

2. Income Elasticity of demand : It refers to the degree of responsiveness of a change in the quantity demanded to a change in the income only, other factors including price remaining unchanged.
\(\frac { Percentage change in Quantity Demanded }{ Percentage change in Income }\)
There are 3 types of Income elasticity i.e.:

1. Positive Income elasticity
2. Negative Income elasticity
3. Zero Income elasticity

3. Cross Elasticity of Demand :
It refers to a change in quantity demanded of one commodity due to a change in the price of other commodity i.e. complementary goods or substitute goods.
Percentage change in Quantity demanded
\(\frac { of commodity ‘X’ }{ Percentage change in Price of commodity ‘Y’ }\)

Cross elasticity of demand are of 3 types i.e.

1. Positive Cross elasticity
2. Negative Cross elasticity
3. Zero Cross elasticity

Question 2.
What is Price Elasticity of Demand? Explain the types of Price Elasticity of Demand?
Answer:
(A) Price Elasticity of Demand :
Price Elasticity of demand refers to the degree of responsiveness of quantity demanded of a commodity to the change in its price, other factors remaining constant. According to Marshall Price Elasticity of Demand (Ed) is the ratio of proportionate change in quantity demanded of a commodity to a \ given proportionate change in its price.

∆ (delta) = Stands for change
∆Q = Change in Quantity demanded (New Qty. – Old Qty. demanded)
AP = Change in Price (New price – Old price)
P & Q = Original Price and Original Quantity Demanded

Using this formula price Elasticity of demand can be calculated for any set of data of demand and price. The value obtained may range from zero to infinity. Since quantity demanded has a negative relationship with price, the elasticity of demand so obtained will have negative sign, we ignore the negative sign altogether.

(B) Types of price elasticity of demand :
Answer:
Types of price elasticity of demand :
(a) Perfectly Elastic Demand (Ed = ∞) :
When a change in price leads to infinite change in quantity demanded of a commodity it is called as perfectly elastic demand. It is an extreme case, which is very rare. It is a theoretical concept not found in real life.

In the diagram demand curve ‘DD’ is horizontal straight line parallel to X-axis,

(b) Perfectly Inelastic Demand (Ed = 0) : When a change in price has no effect on the quantity demanded of that commodity then it is called Perfectly Inelastic Demand. The demand does not respond to the change in price at all. For instance, if price changes by 10% and the demand does not change at all then e = 0.

In this case the numerical coefficient value is zero. It is also extreme case which rarely exists. Salt and life saving medicine are a ) few example of Perfectly Inelastic Demand as they are absolute necessity. The demand ) curve ‘DD’ is a vertical straight line parallel to Y-axis.

(c) Relatively Elastic Demand (Ed > 1):
When the proportionate or percentage change in the quantity demanded of a commodity is greater than proportionate or percentage change in its price then, demand is said to the relatively elastic.
Here the amount demanded of a commodity rises much after a slight fall in its price. For instance a 5% fall in price will bring a 10% rise in demand for that commodity.

The numerical coefficient value is greater than one and lies between 1 and ∞.

Example : Luxury goods BMW Car, air – conditioners, LED TV etc. will have relatively elastic demand. In the diagram the demand curve DD has a flatter slope. It slopes gradually.

(d) Relatively Inelastic Demand (Ed < 1):
When the proportionate or percentage change in quantity demanded of a commodity is less than proportionate or percentage change in its price then demand is said to be relatively inelastic. Here the degree of responsiveness of demand is very little to a given change in its price. For instance, if price falls by 10% then quantity demanded may rise by say 5%.

The numerical coefficient value is less than one and lies between 0 and 1.
Example : The demand for necessary goods like wheat, rice, sugar etc. is said to be relatively inelastic as the demand is less responsive to a given change in price. In the diagram the demand curve DD has a rapid and steep slope.

(e) Unitary Elastic Demand (Ed = 1) :
When proportionate or percentage change in quantity demanded is exactly equal to proportionate or percentage change in price, then demand is said to be unitary elastic. For instance a 10% fall in price of a commodity leads to 10% rise in demand of that commodity.

In this case the demand curve slopes downwards uniformly. This demand curve is called a rectangular hyperbola as shown in the figure. The unity elasticity of demand is a dividing line to distinguish between relatively elastic demand and relatively inelastic demand.

Question 3.
Explain the different method of measuring Price Elasticity of Demand.
Answer:
(A) Percentage Method or Ratio Method : This method is also known as Arithmetic Method. In this method} we compare the percentage of change in demand with percentage of change in price. When we divide the percentage of change in demand by the percentage of change in price, we get Elasticity of demand.

ΔQ = Change in demand (Original – new ( quantity)
ΔP = Change in price (Original – new price)
Q = Original quantity
P = Original price
By applying the above formula we can ( calculate and find the type of elasticity. If the ) result is one, then elasticity is unitary. If it

[ ΔQ (Change in Qty) = (10 -14) = -4, Original Qty = 10, ΔP (Change in price) = (6 – 8) = -2, Original price = 8 ]
= \(\frac{-4}{-2} \times \frac{8}{10}=\frac{8}{5}\)
= 1.6 (e > 1)
So the commodity has Relatively Elastic Demand e > 1.
If the Answer was < 1 then it would have been relatively inelastic.

(B) Total Outlay Method : This method was introduced by Dr. Alfred Marshall. The limitation of this method is that in this method unlike ratio method, the exact numerical value of the elasticity of demand cannot be determined. According, to this method, the elasticity of demand is measured on the basis of expenditure incurred by consumer when the price of a commodity changes.

Total outlay or total expenditure can be calculated by multiplying the price with the quantity demanded (Price x Quantity demand = Total Expenditure). Depending upon the kind of change in total outlay, whether it increases, or decreases, or remain constant with the change in price we will be able to decide the type of elasticity. This can be explained with the following example:-

(1) If the total outlay remains the same with a rise or fall in price then the demand is said to be unitary (e = 1) elastic.
(2) If the total outlay decreases with a rise in price and increases with a fall in price, the elasticity of demand is greater than one or Relatively Elastic e > 1.
(3) If the total outlay increases with a rise in price and decreases with a fall in price, then elasticity is less than one or relatively inelastic, e < 1.

(C) Point Method : In this method given by Prof. Marshall we will be able to find out elasticity at a point on a given demand curve.
To find out elasticity at any given point ‘P on a linear demand curve DD (Straight Line) extend the demand curve towards Y axis and X axis to meet at point A and B respectively as shown in the diagram. Then measure the distance of segment PA and segment PB. Then divide the distance of lower segment PB by upper segment PA.
Point Elasticity of demand = \(\frac { Lower segment of the demand curve }{ Upper segment of the demand curve }\)

Suppose the distance of lower segment PB is 6 cm and upper segment PA is 4 cm.
\(\frac{6}{4}=\frac{\mathrm{PB}}{\mathrm{PA}}\) = 1.5
Then Elasticity at point “P” is 1.5 which is e > 1. So demand is Relatively Elastic. On a given linear demand curve elasticity of demand at different point is different as shown in the diagram.
Now to find elasticity of demand on a non-linear demand curve on a given point “P” as shown in the diagram. First draw a tangent line AB to meet Y and X axis at Point A and B. Then divide the
PB
lower Seg PB by the upper Seg PA i.e. \(\frac{\mathrm{PB}}{\mathrm{PA}}\)

Suppose distance PA’is 8 cm and PB is 4 cm, then ED = \(\frac{4}{8}\) = 0.5 i.e. e < 1. It is a case of Relatively Inelastic demand.

Question 4.
Explain Ratio method and Geometric method of measuring price elasticity of demand.
Answer:
(A) Percentage Method or Ratio Method : This method is also known as Arithmetic Method. In this method} we compare the percentage of change in demand with percentage of change in price. When we divide the percentage of change in demand by the percentage of change in price, we get Elasticity of demand.

ΔQ = Change in demand (Original – new ( quantity)
ΔP = Change in price (Original – new price)
Q = Original quantity
P = Original price
By applying the above formula we can ( calculate and find the type of elasticity. If the ) result is one, then elasticity is unitary. If it

[ ΔQ (Change in Qty) = (10 -14) = -4, Original Qty = 10, ΔP (Change in price) = (6 – 8) = -2, Original price = 8 ]
= \(\frac{-4}{-2} \times \frac{8}{10}=\frac{8}{5}\)
= 1.6 (e > 1)
So the commodity has Relatively Elastic Demand e > 1.
If the Answer was < 1 then it would have been relatively inelastic.

(C) Point Method : In this method given by Prof. Marshall we will be able to find out elasticity at a point on a given demand curve.
To find out elasticity at any given point ‘P on a linear demand curve DD (Straight Line) extend the demand curve towards Y axis and X axis to meet at point A and B respectively as shown in the diagram. Then measure the distance of segment PA and segment PB. Then divide the distance of lower segment PB by upper segment PA.
Point Elasticity of demand = \(\frac { Lower segment of the demand curve }{ Upper segment of the demand curve }\)

Suppose the distance of lower segment PB is 6 cm and upper segment PA is 4 cm.
\(\frac{6}{4}=\frac{\mathrm{PB}}{\mathrm{PA}}\) = 1.5
Then Elasticity at point “P” is 1.5 which is e > 1. So demand is Relatively Elastic. On a given linear demand curve elasticity of demand at different point is different as shown in the diagram.
Now to find elasticity of demand on a non-linear demand curve on a given point “P” as shown in the diagram. First draw a tangent line AB to meet Y and X axis at Point A and B. Then divide the
PB
lower Seg PB by the upper Seg PA i.e. \(\frac{\mathrm{PB}}{\mathrm{PA}}\)

Suppose distance PA’is 8 cm and PB is 4 cm, then ED = \(\frac{4}{8}\) = 0.5 i.e. e < 1. It is a case of Relatively Inelastic demand.