Bhagya

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 9 Depository System Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 9 Depository System

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
Dematerialization removes the problem of _____________ handling of securities.
(a) Physical
(b) Public
(c) Social
Answer:
(a) Physical

Question 2.
The National Securities Depository Limited (NSDL) was established in the year _____________
(a) 1995
(b) 1996
(c) 1997
Answer:
(b) 1996

Question 3.
The process of converting shares from the electronic form into physical form is called _____________
(a) Rematerialization
(b) Dematerialization
(c) Depository
Answer:
(a) Rematerialisation

Question 4.
An agent of the depository is _____________
(a) Depository Participant (DP)
(b) Depository Officer (DO)
(c) Beneficial Owner (BO)
Answer:
(a) Depository Participant (DP)

Question 5.
An intermediary between the investors and depository is _____________
(a) Depository Participant
(b) SEBI
(c) Chief Executive Officer (CEO)
Answer:
(a) Depository Participant (DP)

Question 6.
An investor has to open _____________ with the Depository Participant for handling shares in electronic form.
(a) Demat A/c
(b) Securities
(c) Depository A/c
Answer:
(a) Demat A/c

Question 7.
Depository Participant is an agent of _____________
(a) Investor
(b) Securities and Exchange Board of India
(c) Depository
Answer:
(a) Investor

Question 8.
_____________ is a process by which share certificates of investors are converted into an electronic form.
(a) Dematerialization
(b) Rematerialization
(c) Depository
Answer:
(a) Dematerialization

Question 9.
Dematerialization is a process in which share in physical form is converted into _____________
(a) Electronic form
(b) Paper form
(c) Computer form
Answer:
(a) Electronic form

Question 10.
The provisions regarding dematerialization of securities are made in _____________
(a) Law
(b) Memorandum of Articles
(c) Articles of Association
Answer:
(c) Articles of Association

Question 11.
Demat account holder can _____________ any person of his choice.
(a) Elect
(b) Nominate
(c) Choose
Answer:
(b) Nominate

Question 12.
All depository participants are to be registered with _____________
(a) Registrar of companies
(b) Securities and Exchange Board of India (SEBI)
(c) Depository
Answer:
(b) Securities and Exchange Board of India (SEBI)

Question 13.
An institution which records share certificate in the electronic form is known as _____________
(a) Stock exchange
(b) Depository
(c) Depository Participant
Answer:
(b) Depository

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Dematerialization	(a) State of being interchangeable
(2) Rematerialisation	(b) Register with Depository
(3) Fungibility	(c) Demat Request Form
(4) Issuer	(d) Transferor informs DP
(5) Sale of Shares	(e) Transferee intimates the DP
(6) Purchase of Shares	(f) Remat Request Form
	(g) Broker

Answer:

Group ‘A’	Group ‘B’
(1) Dematerialization	(c) Demat Request Form
(2) Rematerialisation	(f) Remat Request Form
(3) Fungibility	(a) State of being interchangeable
(4) Issuer	(b) Register with Depository
(5) Sale of Shares	(d) Transferor informs DP
(6) Purchase of Shares	(e) Transferee intimates the DP

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
The year in which the Depository act was passed.
Answer:
1996

Question 2.
The largest institution in India which gives Depository services.
Answer:
NSDL (National Security Depository limited)

Question 3.
The year in which National Security Depository Limited (NSDL) Started functioning.
Answer:
1996

Question 4.
Investor in whose name Demat account is opened.
Answer:
Beneficial owner (ISIN)

Question 5.
An account to be opened by an investor for handling shares in electronic form.
Answer:
Demat A/c

1D. State whether the following statements are true or false.

Question 1.
CDSL is the oldest Depository in India.
Answer:
False

Question 2.
An investor can keep his Securities with his savings bank account.
Answer:
False

Question 3.
ISIN number is given to the Depository Participant.
Answer:
False

Question 4.
Dealing in Demated Securities is a time-consuming process.
Answer:
True

Question 5.
Settlement of cash is easy in case of rematerialized Securities.
Answer:
False

Question 6.
For Dematerialized Securities Company has to be registered with the Depository.
Answer:
True

1E. Find the odd one.

Question 1.
Physical, Electronic, Capital
Answer:
Capital

Question 2.
Off Market Trade, Market Trade, Clearing blouse.
Answer:
Clearing House

1F. Complete the sentences.

Question 1.
An agent of Depository is called as _____________
Answer:
Depository Participant

Question 2.
An investor who opens an account with the Depository participant is known as _____________
Answer:
Beneficial Owner

Question 3.
An account through which the Securities are held in electronic form is called as _____________
Answer:
Demat A/c

Question 4.
For converting physical Securities into electronic Securities an investor has to submit _____________
Answer:
Demat Request Form (DRF)

Question 5.
For converting electronic Securities into physical certificates an investor has to submit _____________
Answer:
Remat Request Form (RRF)

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group ‘B’
(a) Depository Participant	(1) ……………………….
(b) ……………………	(2) Holds securities electronically
(c) Issuer	(3) ………………………
(d) …………………….	(4) Investor

(Beneficial owner, Depository, Links investor and depository, Company issuing securities)
Answer:

Group ‘A’	Group ‘B’
(a) Depository Participant	(1) Links investor and depository
(b) Depository	(2) Holds securities electronically
(c) Issuer	(3) Company issuing securities
(d) Beneficial owner	(4) Investor

1H. Answer in one sentence.

Question 1.
Who is the Beneficial Owner?
Answer:
The investor in whose name Securities are credited to his Demat A/c is the ‘Beneficial Owner’.

Question 2.
What are the two modes of holding securities?
Answer:
The two modes of holding securities are:

• Physical
• Electronic

Question 3.
When and where was the world’s first depository system set up?
Answer:
The world’s first depository system was set up in Germany in 1947.

Question 4.
What is Corporate Action?
Answer:
When the investor accounts get automatically credited/debited for securities in case of change initiated by the company is called Corporate Action.

Question 5.
Who is the Issuer?
Answer:
The issuer is the company that issues securities in the dematerialized form.

Question 6.
What is the full form of IPO?
Answer:
IPO means Initial Public Offer.

2. Explain the following terms/concepts.

Question 1.
Depository
Answer:

• It is an organization like the Central Bank where securities are held in electronic form at the investor’s request.
• It also provides different services related to different transactions in such securities.
• It is responsible for the safe-keeping of the investor’s securities.
• There is no direct access of investors with the Depository.
• It works as a link between the company and investors.

Question 2.
Depository Participant (DP)
Answer:

• Depository Participant is an agent of Depository who is registered under the SEBI Act.
• He acts as a link between the Depository and the investor.

Question 3.
Beneficial Owner (BO)
Answer:

• The BO is the investor of securities who have accepted the services of a Depository Participant.
• The BO can also be called Client of Depository and DP. BO is given a unique account number in which securities are held.

Question 4.
Off Market Trade
Answer:

• Trade settled between two parties i.e. transferor or transferee on certain agreed terms without the involvement of the third party i.e. clearing corporation, share broker, or stock exchange is called, ‘Off Market Trade’.
• For e.g. Legacy transfers, gifts, shifting of securities between a client and a sub-broker, etc.

Question 5.
Market Trade
Answer:
Trade settled between two parties i.e. transferor or transferee with the help of the third party i.e. clearing corporation, share broker, or stock exchange is called, ‘Market Trade’.

3. Study the following case/situation and express your opinion.

1. KPCL Bank is a well-established banking institution. Now, it got registered as a Depository Participant.

Question (a).
Under which act did KPCL Bank got registered as a DP?
Answer:
Under SEBI Act, KPCL Bank got registered as a DP.

Question (b).
KPCL Bank as an intermediary will be a link between whom?
Answer:
KPCL Bank as an intermediary will be a link between the Depository and the investor.

Question (c).
Name the two depositories in India, of whom KPCL Bank can be a DP (Agent).
Answer:
NSDL and CDSL.

2. Mr.K wants to rematerialize his 50 shares of PQR Ltd.

Question (a).
Which form he is required to fill as a written request to the DP?
Answer:
He is required to fill Remat Request Form (RRF).

Question (b).
Does he have to fill instrument of transfer if he wishes to transfer the same after remit?
Answer:
Yes. He needs to fill instrument of transfer if he wishes to transfer the same after remit.

Question (c).
Does he have to quote certificate no. and distinctive no. if he wishes to transfer his shares after it is in remat form?
Answer:
Yes, he has to quote certificate no. and distinctive no. if he wishes to transfer his shares after it is in Remat form.

3. Mariam is a broker working with Abacus Co.

Question (a).
Who is the depositor?
Answer:
Abacus Co is the depositor.

Question (b).
Who is the depository participant?
Answer:
Mariam is a depositor participant.

Question (c).
Mariam should be registered with whom?
Answer:
Mariam being the broker must be registered with SEBI and comply with SEBI norms.

4. Distinguish between the following.

Question 1.
Depository and Depository Participant.
Answer:

Points	Depository	Depository Participant
1. Meaning	A depository is an entity that helps the investor to buy or sell securities online.	A depository participant is a link between companies and investors.
2. Types	There are two depositories functional in India. They are NSDL and CDSL.	Various depository participants are linked to NSDL and CDSL.
3. Who can be?	A Depository may be organizations, banks, or institutions.	A Depository Participant can be a bank, financial institution, a broker.
4. Registered	Depositories must be registered as a company under the Companies Act and obtain a Certificate of Commencement of business from SEBI.	Depository Participants should be registered under the SEBI Act.

Question 2.
NSDL and CDSL
Answer:

Points	NSDL	CDSL
1. Full Form	NSDL means National Securities Depository Ltd.	CDSL means Central Depository Services India Ltd.
2. Formed	NSDL was formed in 1996	CDSL was formed in 1999
3. Works for	NSDL mainly works for National Stock Exchange (NSE)	CDSL mainly works for the Bombay Stock Exchange(BSE)
4. Registered	Depositories must be registered as a company under the Companies Act and obtain a Certificate of Commencement of business from SEBI.	Depository Participants should be registered under the SEBI Act.

5. Answer the brief.

Question 1.
What are the two ways of holding securities?
Answer:
There are two ways of holding the securities:
(i) Physical mode:
Securities are held in physical form i.e. paper form. Holding securities in physical form is riskier as it can be torn, misplaced, stolen, damaged, etc. It also consumes a lot of time in storing and handling certificates and documents. Transfer and Transmission of shares is a time-consuming process.

(ii) Electronic/Dematerialized:
In this system, securities are held in electronic or dematerialized form. Holding securities in electronic form is a safe and secure way. It saves a lot of time in storing and handling certificates and documents. Transfer and Transmission of shares is a time-saving process. The electronic system is a much faster and easier system of holding securities.

Question 2.
Explain Depository System. State its importance.
Answer:
A depository system is a system, where securities are held in electronic form. The transfer and settlement of securities are done electronically. On behalf of shareholders, the Depository System maintains accounts of the shareholder, enables transfer, collects dividends, bonus shares, etc.

It is also known as, ‘Scripless trading system’. The Depository Act was passed in the year 1996 under which the depository system was introduced. NSDL and CDSL are the two depositories operating in India.

Importance of Depository System:

• Depository plays a very important role in the smooth functioning of the capital market.
• Reduced paperwork: The aim of the depository system is to reduce the paperwork. It is scriptless system.
• Use of Technology: Paperless trading is possible as it uses the technology. It facilitates electronic transfer.
• Elimination of Storage and handing: As it is a scriptless system storing and handing of certificates work gets eliminated.
• Reduces cost and efforts: Depository system the cost and efforts involved in storage and handling of physical certificates.

Question 3.
Explain the various concepts/terms related to Depository System:
Answer:
(i) Dematerialization:
It is the process in which share certificates are converted into electronic form. The client has to open a DEMAT account with the help of DP.

(ii) Fungibility:
Fungibility means interchangeable. Financial assets may or may not be fungible. The shares in depositories are fungible. They don’t have distinctive numbers for identification.

(iii) Rematerialization:
Rematerialization is the process in which shares are reconverted into physical form.

(iv) International Securities Identification Number:
ISIN is an identification number given to a security of an issuer company at the time of issuing such security for the first time in the depository system. ISIN consists of a 12 (Twelve) digit alpha-numeric code which is divided into 3 (Three) parts. For Govt, securities allotment of ISIN is done by the RBI & for others by NSDL. It is accepted globally.

Question 4.
How many depositories are established in India, under the Depository Act of 1996?
Answer:
There are two depositories established in India under the Depository Act of 1996:
(i) NSDL (National Security Depository Limited):

• NSDL is the first and the largest depository in India established in November 1996.
• It is established by IDBI (Industrial Development Bank of India), Unit Trust of India (UTI), and National Stock Exchange (NSE).
• NSDL has its headquarters in Mumbai.
• It is registered under the Companies Act as a Public Limited Company.
• Investors, Stock Exchanges, Banks, Clearing Members, etc. receive a variety of services from NSDL.
• Services provided by NSDL include account maintenance, dematerialization, rematerialization, settlement of trades through market transfers and off-market transfer, nomination, transmission, distribution of noncash corporate actions, dividend distributions, facility of freezing, or locking of investors’ accounts, Investor grievances, etc.

(ii) CDSL (Central Depository Services Limited:

• CDSL began its operations in February 1999.
• It was promoted by the Bombay Stock Exchange jointly with several banks.
• The headquarters of CDSL is in Mumbai.
• CDSL also offers Demat services like NSDL across the country and has a wide DP network.
• NSDL and CDSL have played a great role in the success of the Depository System in India.

6. Justify the following statements.

Question 1.
The depository system has some advantages to the Investor.
Answer:

• The depository system holds certificates of the Investor in an electronic form.
• Safety is ensured as the entire system functions under the Depository Act and is monitored by SEBI.
• The investor even can freeze his account to avoid fraud.
• Investors can easily transfer the securities in electronic form.
• The investor receives a statement of account periodically which keeps him updated.
• Investors can raise easy loans against the Dematerialized securities.
• A nomination facility is also available for investors.
• Dividend, Bonus Shares, Right Issue, Redemption amount gets automatically credited to Investors account.
• Thus, it is rightly justified that Depository systems have some advantages to the investor.

Question 2.
An investor can raise loan against dematerialized securities.
Answer:

• Investors can take a loan against securities (shares, debentures, bonds, mutual fund units) that are held in their Demat accounts.
• The time required for the documentation process to take loans is less.
• In order to raise a loan against dematerialized securities, both the borrower and lender should have Demat accounts with the same depository
• The Demat accounts can be held with the same or different depository participant (DP).
• Thus, it is rightly said that investors can raise loans against dematerialized securities.

Question 3.
Better and quicker services of the Depository system attract investment from abroad.
Answer:

• Paperless trading is a boon for company management.
• Automatic and transparent screen-based trading in securities, shorter settlement periods have improved liquidity in investment in securities.
• The transfer process under the depository system is prompt and free from defects.
• The company is able to know the particulars of beneficial owners and their holdings periodically.
• Thus, it is rightly said that Better and quicker services of the Depository system attract investment from abroad.

Question 4.
It is necessary for the Beneficial Owner to open a DEMAT account with the DP.
Answer:

• The beneficial Owner is the investor of the company.
• For holding the securities in electronic form, it is necessary to open a DEMAT account.
• DEMAT account can be opened with the help of DP.
• The BO can also be called a client of Depository and DP.
• BO has to pay charges to the DP for availing the services of DP.
• BO is entitled to all rights, benefits and is subject to all liabilities with respect to securities.
• BO is given a unique account number in which securities are held.
• Thus, it is rightly said that it is necessary for the Beneficial Owner to open a DEMAT account with the DP.

7. Answer the following questions.

Question 1.
What is the procedure for the Transfer of Securities under the Depository System in case of the sale of shares?
Answer:
When shares are sold the Transferor (Investor) has to inform his DP by issuing Delivery Instruction Slip (DIS) duly filled and signed with the details of the security sold. At the end of the transaction, the said securities are debited from his Demat Account.

Transfer of shares can be done in two ways:
(i) Off Market Trade:
Trade settled between two parties i.e. transferor or transferee on certain agreed terms without the involvement of the third party i.e. clearing corporation, share broker, or stock exchange is called, ‘Off Market Trade’. For e.g. Legacy transfers, gifts, shifting of securities between a client and a sub-broker, etc.

Procedure:

• Seller i.e. the transferor gives instructions to the DP to transfer securities from the seller’s account to the buyer’s account.
• The buyer i.e. transferee will get securities credited to his account through his DP. DP will transfer the securities only after receiving confirmation from the depository.
• The transferee will directly pay the money to the transferor.

Diagrammatic presentation:

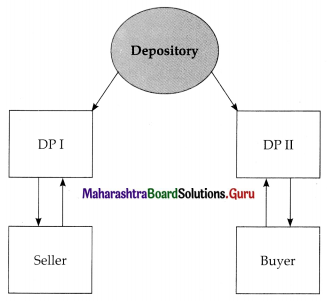
(ii) Market Trade:
Trade settled between two parties i.e. transferor or transferee with the help of the third party i.e. clearing corporation, share broker, or stock exchange is called, ‘Market Trade’.

Procedure:

• The Seller i.e. the transferor gives instruction to his DP. The securities are then transferred from Transferor’s account to the Transferor’s Broker account.
• From the Transferor’s Brokers account securities are transferred to the clearinghouse of the Stock Exchange.
• On the pay-out day, securities move from the clearinghouse to the account of the broker of the transferee.
• After instructions and confirmation from Depository, securities are transferred to the buyer’s account.

8. Attempt the following.

Question 1.
Explain the process of Dematerialisation?
Answer:
Dematerialization is the process of converting physical certificates into electronic form/mode. When an investor opts for a depository system, he has to approach a Depository participant, who is the authorized agent of the depository. The investor needs to surrender his share certificate to the company through a depository participants. On confirmation from the company and Depository DP arranges to credit investors account with an equivalent number of shares.

Following steps are involved in the process of Dematerialisation:

• Submission of DRF by Investor: The investor has to submit the DRF (Demat Request Form) in triplicate and original certificates to DP.
• Entry in the system and forwarding request to Depository: DP enters the details of Demat request in the system and sends it to the Depository.
• Forwarding Copy to the Issuer: DP sends the physical certificates and copy of DRF to the Issuer i.e. Company
• Verification by the Issuer: The Issuer (Company) verifies and confirms to Depository about dematerializing of the securities.
• Updating records by the Depository: Depository records the request in the system and forwards it to the Issuer Company.
• Intimation to the DP: Depositor credits the dematerialized securities to the beneficiary/investors Demat A/c and informs the DP.
• Intimation to the investor: A statement of account is issued to the Investor periodically. It contains all the details of the investor.

Question 2.
Explain the functioning of the depository under the IPO scheme.
Answer:
IPO is the first sale of shares by a privately owned company to the general public. A public company can raise capital by making an appeal to the general public to purchase shares of the company by issuing a prospectus.

The process of IPO is as follows:

• Submission of Application: The investor (applicant/BO) has to submit an application for securities to the issuer company.
• Verification with Depository: The details of the investor are verified by the company with Depository.
• Report by Depository: After verification depository submits the investors report to the issuer company
• Details of Allotment: The issuer company submits the details of allotment to the depository for updating their records.
• Crediting the account: The depository credits the account of the beneficial owner with a specific number of securities.
• Intimation to the DP: Depository then informs the Depository Participant (DP) about the details of the beneficial owner account.
• Intimation to the BO: Depository Participant informs the beneficial owner (investor) about his investment through Statement of Accounts.

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 8 Correspondence with Depositors Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 8 Correspondence with Depositors

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
_____________ capital is raised by accepting deposits.
(a) owned
(b) fixed
(c) borrowed
Answer:
(c) borrowed

Question 2.
Deposits are accepted to fulfil _____________ capital need of the company.
(a) working
(b) fixed
(c) owned
Answer:
(a) working

Question 3.
A company can accept deposit for minimum _____________ months.
(a) 12
(b) 36
(c) 6
Answer:
(c) 6

Question 4.
Person investing in company’s deposit is called _____________
(a) depositor
(b) debenture holder
(c) shareholder
Answer:
(a) depositor

Question 5.
Company makes payment of interest on deposits after deducting _____________
(a) ACS
(b) CGS
(c) TDS
Answer:
(c) TDS

Question 6.
Company can also make electronic payment of interest through _____________
(a) DGFT
(b) NEFT
(c) IEPF
Answer:
(b) NEFT

Question 7.
A government Company can accept maximum _____________ percent deposit.
(a) 25
(b) 35
(c) 30
Answer:
(b) 35

Question 8.
A private company can accept deposits from _____________
(a) directors
(b) government
(c) public
Answer:
(c) public

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
1. Deposit maturity	(a) Letter of renewal
2. Accuracy	(b) Investment up to ₹ 25000
3. Deposit receipt	(c) 21 days
4. Small depositors	(d) Precaution
5. Renewal of deposit	(e) 36 months
	(f) Creditors

Answer:

Group ‘A’	Group ‘B’
1. Deposit maturity	(e) 36 months
2. Accuracy	(d) Precaution
3. Deposit receipt	(c) 21 days
4. Small depositors	(b) Investment up to ₹ 25000
5. Renewal of deposit	(a) Letter of renewal

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
A person who invests in a company’s deposits.
Answer:
Depositor

Question 2.
The status of the deposit holder in the company.
Answer:
Creditor

Question 3.
Amount deducted from gross interest exceeding ₹ 10,000.
Answer:
TDS

Question 4.
Avoiding rude and harsh words while writing letters to the depositor’s means.
Answer:
Courtesy

Question 5.
The way of writing letters from depositors’ point of view.
Answer:
You attitude

1D. State whether the following statements are true or false.

Question 1.
The deposit represents owned capital of the company.
Answer:
False

Question 2.
Fixed deposit is a long-term source of finance.
Answer:
False

Question 3.
Company Secretary has to follow legal provisions while corresponding with depositors.
Answer:
True

Question 4.
Correspondence with depositors helps to maintain the goodwill of the company.
Answer:
True

Question 5.
The deposit receipt should be issued within 21 days from the date of acceptance of the deposit.
Answer:
True

Question 6.
Government companies can raise deposits up to 35 percent.
Answer:
True

1E. Find the odd one.

Question 1.
Repayment of Deposit, Convertible Debentures, Renewal of Deposit
Answer:
Convertible Debentures

Question 2.
Depositor, Creditor, Evidence of Ownership
Answer:
Evidence of Ownership

Question 3.
6 months, 25 months, 36 months
Answer:
25 months

1F. Complete the sentences.

Question 1.
Company cannot accept deposits for a period more than _____________ months.
Answer:
36 months

Question 2.
The company is liable to pay regular _____________ on the deposits at a fixed rate.
Answer:
Interest

Question 3.
Company cannot accept deposits for period less than _____________ months.
Answer:
6 months

Question 4.
Unnecessary and irrelevant information in the letter should be _____________
Answer:
Avoided

Question 5.
Secretary conducts correspondence with the depositors as per the instructions of the _____________
Answer:
Board of Directors

1G. Answer in one sentence.

Question 1.
Who gives instructions to the company secretary for corresponding with the depositors?
Answer:
The Board of Directors gives instructions to the company secretary for corresponding with the depositors.

Question 2.
Who’s consent is necessary for the renewal of the deposit?
Answer:
Depositors’ consent is necessary for the renewal of the deposit.

Question 3.
What is the time limit for sending deposit receipts to the depositor from the date of acceptance?
Answer:
A deposit receipt is sent to the depositor within 21 days from the date of acceptance of a deposit.

1H. Correct the underlined words and rewrite the following sentences.

Question 1.
Deposits can be accepted for a minimum period of 12 months.
Answer:
Deposits can be accepted for a minimum period of 6 months.

Question 2.
Deposit receipt can be issued within a period of 15 days of acceptance.
Answer:
Deposit receipt can be issued within a period of 21 days of acceptance.

1I. Arrange in proper order.

Question 1.
Legal provision, Board Resolution, Acceptance of deposits
Answer:
Legal provision, Board Resolution, Acceptance of deposits

Question 2.
Appoint banker, Credit rating, Deposit insurance
Answer:
Appoint banker, Credit rating, Deposit insurance

Question 3.
Return with depositors, Entries in register of deposit, Issue of the deposit receipt
Answer:
Issue of deposit receipt, Entries in the register of deposit, Return with depositors

2. Justify the following statements.

Question 1.
Public deposits can be renewed after the maturity period.
Answer:

• Deposits are unsecured loans offered to the company.
• Deposits can be accepted for a minimum period of 6 months and a maximum period of 36 months.
• If the Depositor agrees, deposits can be renewed for a further period.
• Renewal may take place with the same terms and conditions or maybe with different terms and conditions.
• For renewal, the depositor has to submit the old deposit receipt with the renewal request.
• The company will cancel the old deposit receipt and issue the new deposit receipt.
• The depositor enjoys a fixed rate of interest till further maturity.
• Thus, it is rightly said that Public deposits can be renewed after the maturity period.

Question 2.
Deposits are repaid on maturity.
Answer:

• Deposit is a short-term source of finance of the company and it is used in order to satisfy the short-term working capital needs of the company.
• The company cannot accept deposits for a period less than 6 months or more than 36 months,
• The company is liable to pay regular interest on the deposits at a fixed rate along with the principal amount on maturity.
• On maturity of tenure of deposits, it is binding on the company to repay the deposit.
• Default in repayment of deposit results in levy of penalty.
• The letter for repayment of the deposit is to be sent to the depositor when the deposit is to be redeemed.
• Thus, it is rightly justified that deposits are repaid on maturity.

Question 3.
Correspondence with the depositors enhances the goodwill of the company.
Answer:

• The depositors of the company are the creditors of the company.
• They provide borrowed capital to the company to meet its working capital needs.
• proper correspondence with the depositors is helpful to convey proper information about their investments.
• It generates a bridge of good relations between company and depositors which ultimately helps to generate goodwill in the Corporate market.

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 7 Correspondence with Debentureholders Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 7 Correspondence with Debentureholders

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
Debenture holders receive ______________ as a proof of their investment in the company.
(a) Share Certificate
(b) Debenture Certificate
(c) Share Warrant
Answer:
(b) Debenture Certificate

Question 2.
______________ have no right to attend company’s meetings.
(a) Shareholders
(b) Directors
(c) Debenture holders
Answer:
(c) Debentureholders

Question 3.
______________ have priority in the repayment of the capital at the time of winding up of the company.
(a) Debenture holders
(b) Shareholders
(c) Secretary
Answer:
(a) Debenture holders

Question 4.
Debentures are secured through charge on the ______________ of the company.
(a) Liability
(b) Profits
(c) Assets
Answer:
(c) Assets

Question 5.
The fund created for the redemption of debentures is known as ______________
(a) DRRF
(b) DHFL
(c) IEPF
Answer:
(a) DRRF

Question 6.
Debentures are repaid on maturity by using debenture ______________ reserve.
(a) Redemption
(b) Depreciation
(c) General
Answer:
(a) Redemption

Question 7.
Debenture holder has the right to inspect ______________
(a) Partnership Deed
(b) Memorandum of Association
(c) Trust Deed
Answer:
(c) Trust Deed

Question 8.
From the date of request, trust deed should be provided by the company with in ______________
(a) 14 days
(b) 7 days
(c) 21 days
Answer:
(b) 7 days

Question 9.
Communication in writing means ______________
(a) Correspondence
(b) Motion
(c) Voting
Answer:
(a) Correspondence

Question 10.
Debentures are issued after passing resolution at ______________
(a) Board Meeting
(b) General Meeting
(c) Committee Meeting
Answer:
(a) Board Meeting

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Courtesy	(a) Wrong Publicity
(2) Prompt Response	(b) True and Real Facts
(3) Transparency	(c) Politeness
(4) Conciseness	(d) Up to date information
(5) Precise Information	(e) Reply without delay
(6) Secretary	(f) Irrelevant Information
(7) Goodwill	(g) Hide Information
	(h) Confidential Officer
	(i) False and incorrect Information
	(j) Rude and harsh wording
	(k) Brief and to the point
	(l) Delay in replying
	(m) Good image of the company
	(n) Disclose Secrets

Answer:

Group ‘A’	Group ‘B’
(1) Courtesy	(c) Politeness
(2) Prompt Response	(e) Reply without delay
(3) Transparency	(b) True and Real Facts
(4) Conciseness	(k) Brief and to the point
(5) Precise Information	(d) Up to date information
(6) Secretary	(h) Confidential Officer
(7) Goodwill	(m) Good image of the company

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
Capital raised by the company by issuing debentures.
Answer:
Debenture Capital

Question 2.
Rate of interest on debentures.
Answer:
Fixed

Question 3.
Debentures are secured by a charge of the assets of the company.
Answer:
Secured Debentures

Question 4.
Debentures are redeemable after a certain period of time.
Answer:
Redeemable Debentures

Question 5.
The Debenture holder has a right to inspect and obtain copies of this deed.
Answer:
Trust Deed

Question 6.
Debenture holder who gets interested through interest coupons.
Answer:
Bearer Debenture holder

Question 7.
The Debentures are issued to the public by issuing this document.
Answer:
Prospectus

Question 8.
The type of Debentures which can be converted into equity shares.
Answer:
Convertible Debentures

1D. State whether the following statements are true or false.

Question 1.
Debenture holders are the creditors of the company.
Answer:
True

Question 2.
Debenture holders enjoy normal voting rights.
Answer:
False

Question 3.
Debentures can be issued to more than 500 people without appointing Debenture Trustee.
Answer:
False

Question 4.
Debenture Certificate is issued within 6 months from the date of allotment of debentures.
Answer:
True

Question 5.
Secretary is the confidential officer of the company.
Answer:
True

1E. Find the odd one.

Question 1.
Courtesy, Transparency, Enclosure
Answer:
Enclosure

Question 2.
Conciseness, Accuracy, Inside address
Answer:
Inside address

Question 3.
Convertible Debentures, Secured Debentures, Cumulative Preference Shares.
Answer:
Cumulative Preference Share

1F. Complete the sentences.

Question 1.
Convertible Debentures are converted into ______________ on the maturity.
Answer:
Equity shares

Question 2.
Redeemable Debentures are ______________ on the date of maturity.
Answer:
Repaid

Question 3.
Registered Debenture holders get interest through ______________
Answer:
Interest Warrant

Question 4.
Bearer Debenture holders get interest through ______________
Answer:
Interest Coupons

Question 5.
Secured Debentures are secured by ______________ on the assets of the company.
Answer:
Charge

Question 6.
Being the creditors, due ______________ should be given to the Debenture holders while corresponding.
Answer:
Respect

Question 7.
The secretary should follow the ______________ of the Companies Act, 2013 .
Answer:
Statutory Provisions

Question 8.
As a Confidential Officer of the company, the secretary should not disclose any important and ______________ information related to the company while corresponding.
Answer:
Secret

Question 9.
The information provided by the secretary must be factual and ______________
Answer:
True

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group ‘B’
(a) Interest Warrant	(1) …………………..
(b) ………………………..	(2) Interest Coupons
(c) …………………………	(3) Secured Debenture

(Bearer Debentures, Registered Debentures, Charge on the assets)
Answer:

Group ‘A’	Group ‘B’
(a) Interest Warrant	(1) Registered Debentures
(b) Bearer Debentures	(2) Interest Coupons
(c) Charge on the assets	(3) Secured Debenture

1H. Answer in one sentence.

Question 1.
Who is appointed when the issue of debentures exceeds more than 500 people?
Answer:
Debenture trustees are appointed when the issue of debentures exceeds more than 500 people.

Question 2.
Debenture Certificate should be issued within how many months from the date of allotment of Debentures?
Answer:
Debenture Certificate should be issued within 6 months from the date of allotment of Debentures.

Question 3.
Which debentures are converted into equity shares?
Answer:
Convertible Debentures are converted into equity shares.

Question 4.
Who has to communicate the decisions of the management and other information to the Debenture holders?
Answer:
The secretary has to communicate the decisions of the management and other information to the debenture holders.

Question 5.
Which fund is created for Redemption of Debentures?
Answer:
A Debenture Redemption Reserve Fund is created for Redemption of Debentures.

1I. Correct the underlined word/s and rewrite the following sentences.

Question 1.
Debentures carry a fluctuating rate of interest as a return on investment in debentures.
Answer:
Debentures carry a fixed rate of interest as a return on investment in debentures.

Question 2.
Debenture Capital is the owned capital of a company.
Answer:
Debenture Capital is the borrowed capital of a company.

1J. Arrange in proper order.

Question 1.
Redemption of Debentures, Debenture Redemption Reserve Fund, Debenture Redemption Form.
Answer:
Debenture Redemption Reserve Fund, Debenture Redemption Form, Redemption of Debentures

2. Study the case/situation and express your opinion.

1. As a secretary of Velon Industries Limited.

Question (a).
Give any three circumstances where the company will have to correspond with the debenture holders.
Answer:
Secretary will correspond with the debenture holder under the following circumstances:

• Allotment Letter to debenture holders.
• Payment of Interest.
• Redemption of debentures.

Question (b).
What precautions should be taken while drafting the letters?
Answer:
As a secretary, one should be polite, transparency should be maintained and the image of the company should be kept in mind while drafting the letters.

Question (c).
Board Resolution is necessary for the payment of interest?
Answer:
Yes, Board Resolution is necessary for the payment of interest.

2. Disha Industries Ltd. Allots debentures to Mr. Vijay Mittal.

Question (A).
Which letter will be sent to Mr. Vijay Mittal?
Answer:
Letter of Allotment of Debentures will be sent to Mr. Vijay Mittal.

Question (b).
Why does Vijay Mittal preserve the Allotment Letter?
Answer:
Mr. Vijay Mittal preserves the allotment letter because he will receive a Debenture Certificate in exchange for the allotment letter.

Question (c).
What details does the letter contain?
Answer:
The letter contains the details of the issue of debentures i.e number of debentures applied, numbers of debentures allotted, distinctive numbers of debentures, amount received, types of debentures, rate of interest, maturity date, etc.

3. Rolta India Limited wants to pay interest to the debenture holders.

Question (a).
Which resolution is required for the payment of interest to debenture holders?
Answer:
Board Resolution is required for the payment of interest to the debenture holders.

Question (b).
Can the company pay interest in the next year as in the current year company has incurred a loss?
Answer:
No, the company has to pay the interest as it does not depend upon the profits of the company.

Question (c).
How can the company pay interest to the debenture holders?
Answer:
The company can pay interest to debenture holders by the way of interest warrant and electronic mode i.e. ECS and NEFT.

3. Answer in brief.

Question 1.
What is a debenture? Explain Debenture Capital.
Answer:
Debentures is an instrument in writing, acknowledging a debt under a common seal of a company.

• Debenture represents the borrowed capital of a company.
• The debenture is an acknowledgment of debt.
• The debenture holder is a creditor of the company.
• Compared to equity shares, debenture capital is considered safe and secured capital.
• Debentures are repaid on the expiry of a fixed period at the winding up of the company before equity shares are repaid.
• A debenture may be secured, unsecured, redeemable, convertible, non-convertible, etc
• Secured debentures have a charge on the assets of the company.
• Redeemable debentures are repaid on the expiry of a fixed period.
• Convertible debentures are converted into equity shares on the expiry of a fixed period.
• Non-convertible debentures cannot be converted into equity shares but are repaid on the expiry of the fixed period.

Question 2.
State any four precautions to be taken while drafting letters to the debenture holders.
Answer:
The following precautions are to be kept in mind by the secretary while corresponding with the debentures.
(i) Transparency:

• Transparency with debenture holders has to be maintained.
• It is necessary to disclose correct and accurate information of the company, favourable as well as the adverse credit rating of the company, etc. in correspondence.

(ii) Politeness (Courtesy):

• As debenture holders are the creditors of the company, proper respect should be given to them in correspondence.
• The use of words in the letter should be proper which depicts respect to the debenture holders.
• Rude and harsh words should be strictly avoided.

(iii) Conciseness:

• Letters to the debenture holders should be brief and to the point.
• Unnecessary information should be avoided.

(iv) Accuracy/Precise information:

• The secretary should provide precise and up-to-date information to debenture holders.
• The information must be true and correct.

Question 3.
When does a secretary enter into correspondence with debenture holders?
Answer:

1. Debenture holders are creditors of the company.
2. Therefore, they do not participate in the management of the company.
3. They do not enjoy voting rights.
4. Whatever decisions are taken by the management, are communicated to them by the secretary.
5. A secretary has to enter into correspondence with the debenture holders under the following circumstances:
   • Informing the applicant about allotment of debentures.
   • Informing about payment of interest through
     • Interest warrant
     • Electronic payment of Interest
   • Letter of conversion of debentures into equity shares.
   • Letter for the redemption of debentures.

4. Justify the following statements.

Question 1.
Debenture holders are the creditors of the company.
Answer:

• Debenture represents borrowed capital of the company.
• It is an acknowledgment of debt issued by the company under its common seal.
• The person buying the debenture is known as the ‘Debenture holder’.
• Debenture holders are the creditors of the company.
• They provide loans to the company and hence, enjoy fixed-rate interest as a return on their investment.
• Debentures are secured and redeemable. They are repaid after a certain period of time, i.e. on the maturity date.
• Thus, it is rightly justified that, debenture holders are the creditors of the company.

Question 2.
The company secretary should follow legal provisions while corresponding with Debenture holders.
Answer:

• Debenture holders are the creditors of the company and hence, the secretary has to correspond with Debenture holders on different occasions.
• The secretary should follow the statutory provisions of the Companies Act, 2013 and other relevant laws while corresponding with Debenture holders.
• Secretary should be cautious and careful while corresponding with debenture holders on legal matters. He should be aware of legal consequences.
• Non-compliance with legal provisions can result in legal consequences, creating problems for the company.
• Thus, it is rightly justified that, the company secretary should follow legal provisions while corresponding with debenture holders.

Question 3.
Interest is a debt.
Answer:

• Debenture capital is the borrowed capital of the company.
• Debenture holders are the creditors of the company receiving the fixed rate of interest.
• The company pays the interest through interest warrant and electronic mode i.e. Electronic Clearing System (ECS) or National Electronic Fund Transfer (NEFT).
• Interest is to be paid compulsorily even if the company makes a loss. It does not depend upon the profits of the company.
• Thus, it is rightly justified that, interest is debt.

5. Attempt the following.

Question 1.
Explain the different types of letters written to the debenture holders.
Answer:
Secretary has to communicate with the management and the debenture holders for various reasons. This communication is done by drafting letters to the debenture holders. A secretary should be very cautious and careful while corresponding with debenture holders of the company. Following are the circumstances when the secretary corresponds with the debenture holders.

(i) Debenture Allotment Letter.

• An allotment Letter is sent to the debenture holders when the company allows debentures to the applicant.
• Allotment Letter is preserved by the debenture holder till he receives Debenture Certificate in exchange for this letter.
• Allotment Letter contains details of the issue of debentures, i.e. name of debenture holder, debentures issued, face value, types of debentures, rate of interest, etc.

(ii) Payment of Interest Letter.

• Interest is paid to the debenture holders through:
  • Interest Warrant
  • Electronically
• Payment of Interest Letter contains details such as a number of debentures, distinctive numbers, the gross amount of interest payable, TDS deducted, the net amount of interest payable, etc.
• Board Resolution is required for the payment of interest on debentures.

(iii) Conversion of Debentures Letter.

• Debentures are converted into equity shares.
• Conversion of Debenture Letter is issued only when the company receives Letter of Option.
• After conversion, a share certificate is issued.
• Approval of shareholders is necessary by passing a special resolution at Extra-Ordinary General Meeting.
• Only after receiving the shareholders’ approval, letter of conversion of debentures is sent to debenture holders.

(iv) Redemption of Debentures Letter.

• Debentures are redeemed after a specific period.
• Debenture Redemption Reserve Fund (DRRF) is created for the redemption of debentures.
• Debenture Redemption Form (DRF) is sent along with the letter.
• This letter informs that their debentures have become due for redemption.

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 6 Correspondence with Members Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 6 Correspondence with Members

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
Shareholders are ____________ of the company.
(a) Owners
(b) creditors
(c) loan givers
Answer:
Owners

Question 2.
Important decisions need approval of ____________ at the meeting.
(a) auditors
(b) shareholders
(c) directors
Answer:
shareholders

Question 3.
Secretary writes letter to members as ____________
(a) auditor
(b) Public Relations Officer
(c) Director
Answer:
Public Relations Officer

Question 4.
____________ shares are issued to existing equity shareholders.
(a) deferred
(b) preference
(c) bonus
Answer:
bonus

Question 5.
Polite and prompt correspondence by secretary creates ____________ of the company.
(a) goodwill
(b) prestige
(c) image
Answer:
goodwill

Question 6.
Secretary is a ____________ of confidential matter.
(a) caretaker
(b) custodian
(c) auditor
Answer:
custodian

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Secretary	(a) Registered Document
(2) Electronic Mode	(b) Fluctuating rate of dividend
(3) Share Certificate	(c) Correspondence with members
(4) Reply Letter	(d) Dividend Warrant
(5) Bon as Share	(e) Payment of Dividend
	(f) Existing Equity Shareholder
	(g) Bearer Document
	(h) Low rate of dividend
	(i) Fluctuations in the market
	(j) Correspondence with Bank

Answer:

Group ‘A’	Group ‘B’
(1) Secretary	(c) Correspondence with members
(2) Electronic Mode	(e) Payment of Dividend
(3) Share Certificate	(a) Registered Document
(4) Reply Letter	(h) Low rate of dividend
(5) Bon as Share	(f) Existing Equity Shareholder

1C. Write a word or term or a phrase that can substitute each of the following statements.

Question 1.
Return of investment in shares.
Answer:
Dividend

Question 2.
Warrant attached with notice of dividend.
Answer:
Dividend warrant

Question 3.
Title to the shares issued by the company.
Answer:
Share Certificate

Question 4.
A portion of profits is distributed to the shareholders of the company.
Answer:
Dividend

Question 5.
The letter containing reasons for the low rate of dividends.
Answer:
Reply Letter

1D. State whether the following statements are True or False.

Question 1.
Secretary should always provide correct, updated, and tactful information to the members.
Answer:
True

Question 2.
Secretary should disclose confidential information to the members.
Answer:
False

Question 3.
Share certificates must be duly stamped and signed under the common seal of the company.
Answer:
True

Question 4.
The dividend is declared and approved in General Meeting.
Answer:
False

Question 5.
A dividend warrant is a written order given by the company to its banker to pay the amount mentioned in it to the shareholder whose name is specified therein.
Answer:
True

Question 6.
The dividend is to be paid to shareholders within 30 days from the date of declaration.
Answer:
False

1E. Find the odd one.

Question 1.
Allotment letter, Allotment slip, Refund order
Answer:
Refund order

Question 2.
Dividend Coupon, Dividend warrant, Transfer receipt
Answer:
Transfer receipt

1F. Complete the sentences.

Question 1.
Shareholders are the ____________ of the company.
Answer:
owners

Question 2.
The role of secretary while writing to members is of ____________
Answer:
Public Relations Officer

Question 3.
Share Certificate must be signed by at least ____________ directors.
Answer:
2

Question 4.
Dividend is the portion of ____________
Answer:
Profits

Question 10.
Bonus Shares issued are credited to Shareholders ____________ Account.
Answer:
Demat

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group ‘B’
(1) …………………..	(a) Directors and Members
(2) ………………….	(b) Registered Post
(3) Correspondence	(c) …………………….
(4) ………………….	(d) Payment of Dividend Electronically

(Written communication, Share Certificate, Secretary, ECS)
Answer:

Group ‘A’	Group ‘B’
(1) Secretary	(a) Directors and Members
(2) Share Certificate	(b) Registered Post
(3) Correspondence	(c) Written communication
(4) ECS	(d) Payment of Dividend Electronically

1H. Answer in one sentence.

Question 1.
What is politeness?
Answer:
Politeness means the use of courteous language. A courteous letter shows sympathy, respect, and mutual understanding.

Question 2.
What is the time period to dispatch the share certificate by the company?
Answer:
The company must dispatch a share certificate to the allottee within two months after the allotment of shares.

Question 3.
What is the time limit to pay the dividend?
Answer:
The dividend is to be paid to the shareholders within 30 days from the date of declaration.

1I. Correct the underlined word and rewrite the following sentences.

Question 1.
Secretary should follow relevant provisions of the Companies Act, 1986.
Answer:
Secretary should follow relevant provisions of the Board of Directors.

Question 2.
Share Certificate must be countersigned by the shareholder.
Answer:
Share Certificate must be countersigned by the Board of Directors.

Question 3.
The interim dividend is declared by shareholders.
Answer:
The interim dividend is declared by Equity.

Question 4.
Interim Dividend is paid through cash.
Answer:
Interim Dividend is paid through electronic mode.

Question 5.
Rights shares are the shares given to existing shareholders free of cost.
Answer:
Bonus shares are the shares given to existing shareholders free of cost.

1J. Arrange in proper order.

Question 1.
(a) Reply Letter
(b) Issue of Share Certificate
(c) Payment of Dividend
Answer:
(a) Issue of Share Certificate
(b) Payment of Dividend
(c) Reply Letter

2. Explain the following terms/concepts.

Question 1.
Correspondence with Members
Answer:
Correspondence with members means communicating the decisions and information of the management to the members through letters. The letter not only includes casual informing but also sending replies to the letters.

Question 2.
Share Certificate
Answer:
Share Certificate is a registered document. It is a title of shares issued by the company under the common seal of the company. It should be duly stamped and signed by two directors and countersigned by the secretary of the company.

3. Answer in brief.

Question 1.
Explain Secretary acts as a link between the Directors and the Members.
Answer:

• A secretary is an employee in the organization. The secretary is responsible for all the compliances with statutory and regulatory requirements.
• The Secretary communicates the decisions and information taken by the management to the members through correspondence.
• The secretary also deals with government agencies and private institutions.
• The secretary replies to the queries raised by the members. Complaint letters should be promptly attended without any delay by the secretary.
• The secretary should provide correct and updated information to the members as and when demanded.

Question 2.
Write a note on Payment of dividend.
Answer:

• The dividend is the portion of the company’s profits that is distributed among the shareholders of the company.
• The dividend is paid through the Dividend Warrants or through Electronic Mode i.e. ECS, NEFT, etc. to the registered shareholders.
• The rate of dividend is recommended by the Board of Directors.
• It is declared and approved by shareholders in the Annual General Meeting.
• The dividend is to be paid to the shareholders within 30 days from the date of declaration.
• The letter related to the payment of the dividend is sent to the concerned shareholders. The letter contains detailed information regarding the payment of dividends.

4. Justify the following statements.

Question 1.
Share Certificate is a registered document.
Answer:

• Share Certificate is the title to the shares issued by the company.
• It is duly stamped and signed by two directors and countersigned by the directors under the common seal of the company.
• It contains all the details regarding the issue of shares, shareholders’ names, number of shares issued, share certificate number, etc.
• It is issued or dispatched to the allottee within two months after allotment of shares.
• Thus, it is rightly said that a share certificate is a registered document.

Question 2.
Registered shareholders get dividends through dividend warrants or electronically.
Answer:

• The dividend is the portion of profits of the company which is distributed to the shareholders of the company.
• Dividend can be paid through dividend warrant or by means of electronic mode i.e. ECS or NEFT, etc only to the registered shareholders.
• The dividend is paid through dividend coupons to share warrant holders. Share warrant is a bearer document of title to shares.
• The letter contains a number of equity shares held, dividend warrant number, gross dividend, TDS if any, the net amount of dividend, etc.
• Thus, it is rightly said that the registered shareholders get dividends through dividend warrants or electronically.

Question 3.
Reply letter contains or specifies the reasons for the low rate of dividend.
Answer:

• Reply letter is the answer given to the query raised by the member.
• The letter is sent to the concerned member who is not satisfied with the payment of dividend made by the company.
• The letter contains reasons for the lowering down of the rate of dividend.
• The secretary has to convince the shareholders that the dividend is lowered due to void reasons and assure that company will overcome the situation.
• Thus, it is rightly said that a reply letter contains or specifies the reasons for the low rate of dividend.

5. Study the case/situation and express your opinion.

1. As a Secretary of Networks limited.

Question (a).
Give any 3 occasions where he will have to correspond with members.
Answer:
Secretary will correspond with members on the following occasions:

• Issue of Share Certificate;
• Payment of Dividend;
• Reply to query letter

Question (b).
3 points of precautions he will take while drafting a letter.
Answer:
Correct Information, Lucid language, and the image of the company have to be borne in mind.

Question (c).
Whether he should take Director’s approval before drafting any letter.
Answer:
Yes, Director’s approval is a must for major matters.

2. Comfort Motors Ltd. has allotted shares to Mr. Jayant Modi.

Question (a).
Will Comfort Motors Ltd. send a letter to Mr. Jayant Modi when demanded?
Answer:
Yes, when Mr. Jayant Modi demands, the company will send the letter for the issue of the share certificate.

Question (b).
How will the company send the share certificate?
Answer:
The company will send the share certificate through registered post.

Question (c).
What information should the letter of issue of share certificate contain?
Answer:
The letter will contain information such as folio no., share certificate no., no. of shares, etc.

3. Mr. Ashish Rai has applied for 100 shares of ₹ 10 each payable as ₹ 2 per share on application, ₹ 4 on the allotment, and ₹ 4 on 1st and final call.

Question (a).
Is there any compulsion that he get the number of shares he has applied for?
Answer:
No, there is no such compulsion to get the shares. he has applied for. In case of oversubscription he may or may not be allotted shares.

Question (b).
What is the amount he will have to pay at the time of application?
Answer:
Mr. Ashish will have to pay ₹ 200/- (₹ 2/- x 100 shares applied for) at the time of application.

Question (c).
What is the maximum amount he will have to pay for the above shares?
Answer:
₹ 1000/- (₹ 10 * 100 shares) is the maximum amount that Mr. Ashish will have to pay as a total amount for the shares.

4. Anmol Steel Industries Ltd. wants to pay dividends to the registered shareholders.

Question (a).
Who recommends and approves the rate of dividend?
Answer:
The Directors recommends and shareholders approve the rate of dividend.

Question (b).
How will the dividend be paid to the shareholders?
Answer:
The dividend can be paid through a dividend warrant or through electronic mode i.e. ECS, NEFT.

Question (c).
Is the letter sent to the registered shareholders before the payment of the dividend?
Answer:
Yes, the companies send the letter of payment of dividend.

5. Mr. Raj She seeks information about interim dividends as heard from one of his fellow shareholders.

Question (a).
What does the Secretary refer to?
Answer:
The Secretary will refer to the date of dividend notice sent to the members

Question (b).
Does he need to give the details of the interim dividend?
Answer:
Yes, he can give the date and details sent.

Question (c).
After getting the details does Mr. Raj have any document that he can refer to as proof?
Answer:
Mr. Rajat can verify with the Passbook/ statement as regards the amount credited.

6. Yash Industries Ltd. is issuing bonus shares.

Question (a).
Can the company issues bonus shares to all the shareholders?
Answer:
No, the company can issue bonus shares to only existing shareholders of the company.

Question (b).
Is it necessary for the shareholders to pay a certain amount for bonus shares?
Answer:
No, bonus shares are fully paid up shares given by the company as a gift.

Question (c).
How are the shareholders informed regarding the issue of bonus shares?
Answer:
Bonus Shares are credited to shareholders Demat Account or share certificate is issued if shares are held in physical form.

7. Mr.Anand Khot has complained of a low rate of dividends. As a Secretary,

Question (a).
Is it necessary to reply to the complaint letter?
Answer:
Yes, it is a must for the Secretary to send a reply letter.

Question (b).
Is it necessary to give reasons for the low rate of dividends?
Answer:
Yes, reasons, as discussed in the AGM, can be written in the letter in order to convince about the low rate of dividend.

Question (c).
Which points he has to keep in mind while drafting the above letter?
Answer:
Prompt response, correct information, politeness, and image of the company are some of the major points to be considered while drafting the letter.

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 5 Deposits Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 5 Deposits

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
No Deposits can be repaid before ___________ months.
(a) One
(b) Six
(c) Nine
Answer:
(b) Six

Question 2.
Premature deposits can be repaid after ___________ months.
(a) Two
(b) Three
(c) Four
Answer:
(b) Three

Question 3.
___________ company cannot collect deposits from the public.
(a) Private
(b) Public
(c) Government
Answer:
(a) Private

Question 4.
A copy of return of deposits must be sent to ___________
(a) Registrar of companies
(b) Govt of India
(c) State bank of India
Answer:
(a) Registrar of companies

Question 5.
On acceptance of deposits, companies required to keep register of deposits at ___________
(a) Office of the registrar
(b) Sebi office
(c) Registered office of the company
Answer:
(c) Registered office of the company

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Return of deposits	(a) Cognisable criminal offense
(2) Deposits in contravention of the law	(b) 25% of paid-up capital
(3) Deposit Repayment Reserve Account	(c) Delivered to the registrar of companies
(4) Registrar of Companies	(d) Approved by the SEBI
(5) Eligible public company	(e) Filing of circular or advertisement
	(f) On or before 30th June every year
	(g) Not less than 15%
	(h) Net worth 100 crores
	(i) Net worth 10 crores
	(j) No punishment

Answer:

Group ‘A’	Group ‘B’
(1) Return of deposits	(f) On or before 30th June every year
(2) Deposits in contravention of the law	(a) Cognisable criminal offense
(3) Deposit Repayment Reserve Account	(g) Not less than 15%
(4) Registrar of Companies	(e) Filing of circular or advertisement
(5) Eligible public company	(h) Net worth 100 crores

Question 2.

Group ‘A’	Group ‘B’
(1) Private company	(a) Approval of secretary
(2) Period of deposit	(b) Can accept deposits from the public
(3) Validity of advertisement	(c) Can accept deposits from its members or relatives of directors or directors
(4) Board of directors	(d) Six months to three years
(5) Public company	(e) Approval of depositors
	(f) Right to accept deposits
	(g) Six months to forty-two months
	(h) Refund of deposit before maturity
	(i) Ten months after the expiry of the financial year
	(j) Six months after the expiry of the financial year

Answer:

Group ‘A’	Group ‘B’
(1) Private company	(c) Can accept deposits from its members or relatives of directors or directors
(2) Period of deposit	(d) Six months to three years
(3) Validity of advertisement	(j) Six months after the expiry of the financial year
(4) Board of directors	(f) Right to accept deposits
(5) Public company	(b) Can accept deposits from the public

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
An acknowledgment of deposit accepted by the company.
Answer:
Deposit Receipt

Question 2.
Type of company that can accept deposits from members as well as the public.
Answer:
Eligible Public Company

Question 3.
A record of details of public deposits maintained by the company.
Answer:
Deposit register

Question 4.
The authority which has the power to accept deposits.
Answer:
Board of Directors

Question 5.
Return on investments as deposits in the company.
Answer:
Interest

Question 6.
Time within which company has to issue deposit receipt.
Answer:
30 Days

1D. State whether the following statements are true or false.

Question 1.
A company can accept deposits payable on demand.
Answer:
False

Question 2.
A company can accept deposits to any extent.
Answer:
False

Question 3.
Acceptance of deposits is the same as a renewal.
Answer:
False

Question 4.
Deposits may be secured or unsecured.
Answer:
True

1E. Find the odd one.

Question 1.
Record of deposits registered office of the companies, Registrar of companies.
Answer:
Registrar of companies

Question 2.
Six months, thirty-six months, forty-two months.
Answer:
Forty-two months

Question 3.
Advertisements, Circular, Board meeting.
Answer:
Board meetings

Question 4.
English newspaper, application for, a regional newspaper.
Answer:
Application forms

Question 5.
Return of deposits, stock exchange, registrar of companies.
Answer:
Stock Exchange

1F. Answer in one sentence.

Question 1.
Are loans and deposits the same?
Answer:
Loans mean any sum borrowed by a company. It has to be repaid instantly or when demanded by the lender whereas deposits are sums borrowed by the company but repaid only on a fixed maturity date.

2. Explain the following terms/concepts.

Question 1.
Register of Deposit
Answer:

• Register for Deposits records all the deposits accepted or renewed by the company at its registered office.
• The details of the deposit along with the details of the depositors should be entered in the Register of Deposits within seven days from the date of issue of the Deposit Receipt.

Question 2.
Interest on Deposit
Answer:

• The return received on the deposit amount is called Interest on Deposit.
• The rate of interest on deposits is decided by the Reserve Bank of India from time to time.
• In case of premature repayment of deposits, the company can deduct 1% interest from the rate of interest stated at the time of acceptance of the deposit.

3. Answer in brief.

Question 1.
Explain the provisions related to the period/tenure of deposits.
Answer:
The provisions related to the period/tenure of deposits are as follows:

• No deposit can be accepted or renewed which is to be repaid within a period of six months or more than thirty-six months.
• In certain circumstances, a company may accept deposits repayable earlier than six months to meet its short-term needs.
• Such deposits must have a tenure of a minimum of three months and the number of such deposits cannot be more than 10% of the aggregate of the paid-up share capital and free reserves of the company.
• Under certain circumstances, at the request of the depositor, the company makes premature repayment of deposits.
• The company may also renew its deposits with the same terms of issue and it will be considered as fresh deposits.

4. Answer the following questions.

Question 1.
Explain terms and conditions for acceptance of deposits.
Answer:
The company raises funds by accepting deposits from the public and its own members. In other words, it is a short-term loan taken by the company. The company can collect deposits on certain terms and conditions laid down by the Companies Act 2013. They are as follows:
(i) Amount of Deposit:
Different types of companies have different terms and conditions for accepting deposits.
The following table shows the percentage of acceptance of deposits.

Companies	Acceptance of Deposits (%)
(i) Private Company	Up to 100% of the aggregate of paid-up share capital and free reserves
(ii) Public Company	Should not exceed 25% of the aggregate of paid-up capital and free resources
(iii) Eligible Public Company	Should not exceed 25% of the aggregate paid-up capital and free reserves in case of the public. Should not exceed 10% of the aggregate paid-up capital and free reserves in case of members.
(iv) Government Company	Should not exceed 35% of the paid-up share capital and free reserves.

(ii) Period/Tenure of Deposit:

• The tenure of deposit should be more than six months but less than thirty-six months.
• Under certain circumstances only, the company can accept deposits for 3 months.
• The company can make premature repayment of deposits after a minimum of 3 months.

(iii) No demand deposit:
The company cannot accept or renew deposits repayable on demand.

(iv) Secured or Unsecured Deposit:

• A company can accept secured or unsecured deposit if it is mentioned in the circular or advertisement.
• A company offering secured deposits has the right to create a charge on its tangible assets within 30 days of acceptance of deposits.

(v) Application Form:

• A prescribed application form is to be filled by the applicant.
• This application form is given by the company.
• It includes a declaration made by the applicant that the deposit he is making is not borrowed from any person.

(vi) Joint names:
The company can accept deposits in joint names of depositors. But there should not be more than three names.

(vii) Nomination:

• Every depositor has to nominate at least one person.
• Nominee enjoys all the benefits in the event of death of the depositor.

(viii) Circular or Advertisement:

• If a company invites deposits from its members, it issues a circular. But if it invites deposits from the public, the company has to issue an advertisement.
• A copy of the circular or advertisement signed by all directors must be filed with the Registrar of Companies.
• Issue of Circular or Advertisement:
• The company has to publish the advertisement in one English newspaper and one vernacular/regional newspaper.

(ix) Appointment of Deposit Trustee:

• Deposit Trustee is appointed by the public companies and eligible public companies.
• One of the more deposit trustees is appointed if secured deposits are issued.
• A contract ‘Trust Deed’ is signed between the company and deposit trustee.

(x) Create charge on assets:
The company secured deposits create a charge on its tangible assets within 30 days of acceptance.

(xi) Deposit Insurance:

• A company needs to take Deposit Insurance at least 30 days before the issue of circular or advertisement.
• Deposit insurance is necessary only when the deposit amount plus interest is up to ₹ 20,000.

(xii) To obtain a credit rating:

• The company obtains credit ratings for deposits on the basis of the net worth of the company, liquidating position, ability to repay deposits on time, etc.
• Credit rating for deposits is given by credit rating agencies.
• The rating is done every year during the tenure of deposits.

(xiii) Open Deposit Repayment Reserve Account:

• A Deposit Repayment Reserve Account is opened in a scheduled bank for accepting deposits.
• The company has to deposit an amount up to 15% of the number of deposits maturing during the current year and following the financial year on or before 30th April.
• This account is used only for repaying deposits only.

(xiv) Deposit Receipt:

• Deposit Receipt is to be issued to the depositors within 21 days from the date of receipt of money or realization of cheque.
• The receipt has to be signed by the officer duly authorized by the Board of Directors.
• The Receipt contains the name and address of the depositor, amount of deposit, rate of interest payable, and date on which it is repayable.

(xv) Register of Deposit:

• Register of Deposit is to be maintained by the company at its registered office.
• The details of the deposit accepted and renewal of the deposits are recorded and depositors are recorded in the Register of Deposits.
• Deposit Receipt should be issued within 7 days from the date of issue.

(xvi) Return of Deposit:

• A Return of Deposit should be recorded with the company on or before 30th June every year.
• The return includes details of deposit with the company as of 31st March of that year.

(xvii) Interest:

• Reserve Bank of India decides the rate of interest on deposits.
• The rate of interest changes from time to time.
• In case of premature repayment of deposits, the company can deduct 1% interest from the rate of interest.
• If the deposits matured and are claimed but remain unpaid by the company, the company will be liable to pay a penal rate of interest at the rate of 18%.

(xviii) Right to alter the Terms and Conditions:
A company cannot directly or indirectly alter the terms and conditions of the Deposit, Deposit Trust Deed, and Deposit Insurance, once the circular or advertisement is issued and deposits are accepted.

(xix) Disclosure in financial statements:
Deposit money received by the company from the Directors or the relatives of the Directors (in the case of a private company) should be disclosed in the company financial statement.

(xx) Punishment:

• As per the Companies Act, an officer of the company will be liable for punishment if found guilty / not fulfilling the provisions of the Act.
• The Maharashtra Protection of Interest of Depositors (in Financial establishments) Act, 1999 has the right to take action against companies and also punish if found guilty.
• Companies in Maharashtra will be punished for contravening the provisions of this Act also.

Question 2.
Explain the procedure for accepting deposits from the public.
Answer:
Only Eligible Public Companies can accept deposits from the public.
Following is the procedure to be followed for accepting deposits from the public:
(i) Hold Board Meeting:

• A resolution is passed in the Board Meeting for accepting the deposits from the public.
• The details of the amount of deposit, terms and conditions of issue, etc. are decided in this meeting.

(ii) Hold a General Meeting:

• A General Meeting is held by the company for seeking shareholders’ approval for accepting deposits.
• A Special resolution is passed and filed with the Registrar of Companies and if needed with RBI also.

(iii) Hold Board Meeting:

• The board meeting is held to verify and approve the draft of the advertisement.
• The draft should be signed by the majority of the Directors of the company.

(iv) Appoint Banker:
The company has to appoint a banker so that the applicants can submit their application form along with the deposit money.

(v) Obtain Credit Rating:

• The company has to obtain a Credit rating from a recognized Credit Rating Agency.
• This helps in the goodwill of the company.
• This credit rating should be mentioned in the advertisement.

(vi) Appoint Deposit Trustee:

• The company appoints Deposit Trustees when secured deposits are issued.
• It is a contract between the company and Trustee i.e. Deposit Trustee Deed.
• The Deposit Trust deed contains the terms and conditions.
• The deed has to be signed at least 7 days before issuing the advertisement.

(vii) Take Deposit Insurance:

• The company enters into an agreement with the Insurance Company 30 days before issuing the advertisement.
• Deposit Insurance is necessary only when the deposit amount plus interest exceeds ₹ 20,000.

(viii) File a copy of the advertisement with the Registrar of Companies:

• A copy of the advertisement has to be filed with the Registrar of Companies.
• The company can publish the advertisement after 30 days of filing.

(ix) Advertisement to the Public:

• Advertisement is published for the public after 30 days of filing with the Registrar of Companies.
• The advertisement has to be published in one English newspaper and one regional newspaper having wide circulation in the state where the company’s registered office is located.

(x) Upload the advertisement on the company’s website:
After releasing the advertisement to the public, it is also necessary to upload it on the company’s website.

(xi) Collect application form and money:
The banker collects the application forms along with the deposit money on behalf of the company.

(xii) Issue Deposit Receipt:
The company has to issue a Deposit Receipt within 21 days from the date of receipt of money or realization of cheque.

(xiii) Create charge on assets:

• The company issuing secured deposits can create charges on its assets.
• This charge of assets should be created within 30 days of acceptance of the deposit.

(xiv) Make entries in Register of Deposits:
Secretary has to record the details of deposits in the Register of Deposits within the 7 days after issuing the Deposit Receipt.
The entries have to be verified by an authorized officer.

(xv) File Return of Deposits with Registrar of Companies:

• The company has to file a Return of Deposit before 30th June every year.
• The return has details of Deposits with the company as of 31st March

Question 3.
Explain the procedure for accepting deposits from members.
Answer:
The following is the procedure to accept deposits from members:
(i) Hold Board Meeting:

• Secretary arranges for a Board Meeting.
• In the Board Meeting, decisions regarding the amount of deposit, terms of issue of deposit, etc. are decided.

(ii) Hold a General Meeting:

• To seek approval from shareholders for accepting deposits, the company holds a general meeting.
• A special resolution is passed in a general meeting and filed with the Registrar of Companies.

(iii) Hold Board Meeting:

• After getting shareholder’s approval, a Board meeting is held to approve the draft of the circular for inviting applications for deposits from members.
• The draft should be signed by a majority of the Directors of the company.

(iv) Appoint Banker:
A Banker is appointed for collecting the application forms and the Deposit money on behalf of the company.

(v) Obtain Credit Rating:

• Credit rating agencies rate the company’s deposit.
• The rating given by the Credit Rating Agency must be mentioned in the circular.

(vi) Appoint Deposit Trustee:

• Company appoints Deposit Trustees.
• The Trust deed is signed at least 7 days before issuing the circular.

(vii) Take Deposit Insurance:
The company takes Deposit Insurance at least 30 days before issuing the circular.

(viii) File a copy with Registrar of Companies:
A copy of the circular is filed with the Registrar of Companies and can be issued to the members-only after 30 days of filing.

(ix) Issue circular to members:

• The company sends the circulars to members after 30 days of filing them with the Registrar.
• It is sent by registered post, speed post, or email. The company may even publish the circular in newspapers.

(x) Upload circular on company’s website:

• An eligible public company has to upload the circular on the company’s website.
• Whereas, it is optional for a private company and other public companies.

(xi) Collect application form and money:
The company informs the bank to collect the application form along with the deposit money.

(xii) Issue of Deposit Receipt:

• A deposit Receipt is issued by the company.
• It should be issued within 21 days from the date of receipt of the money or realization of the cheque.

(xiii) Create charge on assets:
If a company accepts secured deposits, it has to create a charge on its assets within 30 days of acceptance of deposits.

(xiv) Make entries in Register of Deposits:

• Secretary has to enter the details of deposits in the Register of Depositors within 7 days from the date of issue of Deposit Receipt.
• It has to be signed by an authorized officer.

(xv) File Return of Deposits:

• The company has to file a return of deposit before 30th June every year.
• The return has details of deposits with the company as of 31st March.

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 2 Functions of Management Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 2 Functions of Management

Select the correct options and rewrite the sentences

Question 1.
Planning is …………… function.
(a) advanced
(b) basic
(c) end
Answer:
(b) basic

Question 2.
Division of work is involved in ……………… function.
(a) Planning
(b) Organising
(c) Directing
Answer:
(b) Organising

Question 3.
Directing is initiated at ……………….. level.
(a) Top
(b) Middle
(c) Lower
Answer:
(a) Top

Question 4.
Staffing function is a ……………… activity.
(a) basic
(b) continuous
(c) neutral
Answer:
(b) continuous

Question 5.
A process to establish harmony among different activities to achieve desired results is called ………………..
(a) Controlling
(b) Co-ordinating
(c) Co-operation
Answer:
(b) Co-ordinating

Question 6.
Unification, integration and synchronization of the efforts of group members so as to achieve common goals is a ……………… function.
(a) Planning
(b) Organising
(c) Co-ordinating
Answer:
(c) Co-ordinating

Question 7.
Staffing is concerned with ……………….
(a) physical factor
(b) financial factor
(c) human factor
Answer:
(c) human factor

Question 8.
Controlling measures the ……………… of actual performance from the standard performance.
(a) action
(b) deviation
(c) objective
Answer:
(b) deviation

Question 9.
Directing is a responsibility of ……………… at all levels.
(a) Manager
(b) Worker
(c) People
Answer:
(a) Manager

Question 10.
Physical, financial and human resources to develop productive relationship is a ………………. function.
(a) Organising
(b) Directing
(c) Staffing
Answer:
(a) Organising

Match the pairs

Question 1.

Group A	Group B
(A) Planning	(1) Individual Taste
(B) Organising	(2) Goodwill
(C) Staffing	(3) Bridges the gap between where we are now and where we want to go
(D) Co-ordinating	(4) All the people are employed
(E) Controlling	(5) Not directly related to Human Beings
	(6) Identify and Grouping the work to be performed
	(7) Corrective Action taking
	(8) Right People at Right Jobs
	(9) Taking action against employees
	(10) Aims only at Organisational Goals

Answer:

Group A	Group B
(A) Planning	(3) Bridges the gap between where we are now and where we want to go
(B) Organising	(6) Identify and Grouping the work to be performed
(C) Staffing	(8) Right People at Right Jobs
(D) Co-ordinating	(2) Goodwill
(E) Controlling	(7) Corrective Action taking

Question 2.

Group A	Group B
(A) Planning	(1) Unimportant management function
(B) Organising	(2) Increases productivity
(C) Staffing	(3) Goal-oriented /Basic function
(D) Co-ordinating	(4) Manager
(E) Controlling	(5) Departmentalisation
	(6) Following orders
	(7) Human Resource Development
	(8) Worker
	(9) Chain of action
	(10) Deviations in performance

Answer:

Group A	Group B
(A) Planning	(3) Goal-oriented /Basic function
(B) Organising	(5) Departmentalisation
(C) Staffing	(7) Human Resource Development
(D) Co-ordinating	(9) Chain of action
(E) Controlling	(10) Deviations in performance

Give one word/phrase/term for the following statements

Question 1.
One of the functions of management is considered as a base for all functions.
Answer:
Planning function

Question 2.
The function of management, which identifies and divides the work of the organisation.
Answer:
Organising function

Question 3.
A process where standards are set, actual performance is measured and corrective action is taken.
Answer:
Controlling function

Question 4.
An end function where the performance is evaluated in accordance with plan.
Answer:
Controlling function

Question 5.
An orderly arrangement of group efforts to provide unity of action to achieve common goals.
Answer:
Co-ordinating function

Question 6.
A process of taking steps to bring actual results and desired results closer together.
Answer:
Controlling function

Question 7.
A function which provides instructions from top level management to the lower level.
Answer:
Directing function.

Complete the sentences

Question 1.
A few philosophers called ………………. as ‘Life spark of an Enterprise’.
Answer:
Directing

Question 2.
……………….. is an integral part of direction function.
Answer:
Supervision

Question 3.
……………….. is a hidden force that binds all other functions of management.
Answer:
Co-ordination.

Explain the following terms/concepts

Question 1.
Co-ordination
Answer:
Co-ordination is the integration and synchronisation of the efforts of a group of employees so as to provide unity of action for organisational goals. It is a hidden force which binds all other functions of management. Different activities of different departments are integrated and harmonised in achieving desired goal of an organisation. Thus, co-ordination between different functions and all levels of employee is the heart of success of an organisation.

Question 2.
Controlling
Answer:
Controlling is the process of bringing about conformity of performance with actual planned action. It helps is taking timely corrective measures to bring the actual and desired results close to each other. Controlling helps in formatting future plan also. It is required in all types of organisation and at all levels of management.

Distinguish between

Question 1.
Planning and Staffing
Answer:

	Planning	Staffing
1. Meaning	Planning refers to a process of deciding in advance what to do, where to do, how to do, when to do and who is to do it.	Staffing is a process of recruitment through which competent employees are selected, properly trained, effectively developed, suitably rewarded.
2. Objective	The objective of planning is to set the goals and choose the means to achieve those goals.	The objective of the staffing is to obtain the most competent and efficient staff to improve the overall performance.
3. Area of function	Planning involves setting objectives, identifying alternative courses of actions and selecting best plain for the organisation.	Staffing involves selection, recruitment, training, development, promotion, transfer, etc. of employees
4. Factors	In planning function, internal as well as external factors are considered to set the targets.	In staffing function, only internal factors such as human factor, finance, workload, etc. are considered.
5. Resources	Planning is related to those resources which are required for achieving the targets.	Staffing is related to human resources only.
6. Levels of management	Usually, overall planning for the entire organization is done by the top-level management.	Usually, the function of staffing is undertaken by the middle-level management.

 

Balbharti Maharashtra State Board 12th OCM Important Questions Chapter 1 Principles of Management Important Questions and Answers.

Maharashtra State Board 12th Commerce OCM Important Questions Chapter 1 Principles of Management

Select the correct options and rewrite the sentences

Question 1.
The technique of study of ………………. concentrates on the body movements of the worker.
(a) Motion
(b) Time
(c) Organization
Answer:
(a) Motion

Question 2.
14 principles of management are developed by ………………
(a) F. W. Taylor
(b) Henry Fayol
(c) Peter Drucker
Answer:
(b) Henry Fayol

Question 3.
Management principles influence ……………..
(a) human behaviour
(b) organization
(c) government
Answer:
(a) human behaviour

Question 4.
Management principles are …………….. in nature.
(a) constant
(b) universal
(c) limited
Answer:
(b) universal

Question 5.
Management principles establish ……………….. relationship.
(a) social
(b) legal
(c) cause and effect
Answer:
(c) cause and effect

Question 6.
‘One-plan-one head’ is stated in ……………….
(a) Principle of Direction
(b) Principle of Unity of Command
(c) Scalar Chain
Answer:
(a) Principle of Direction

Question 7.
Principle that focuses on complete change in the attitude of the employees is known as the Principles of …………………
(a) Attitude Change
(b) Scientific Management
(c) Mental Revolution
Answer:
(c) Mental Revolution

Match the pairs

Question 1.

Group A	Group B
(A) Division of work	(1) Direct communication
(B) Authority	(2) Adhering to rules
(C) Fair  remuneration	(3) Specialisation
(D) Discipline	(4) Long chain of communication
(E) Gang Plank	(5) Right wages to the employees
	(6) Responsibility
	(7) No confidence in management policies
	(8) Allotting work to any employee
	(9) Exploitation of workers
	(10) Misuse of power

Answer:

Group A	Group B
(A) Division of work	(3) Specialisation
(B) Authority	(6) Responsibility
(C) Fair  remuneration	(5) Right wages to the employees
(D) Discipline	(2) Adhering to rules
(E) Gang Plank	(1) Direct communication

Give one word/phrase/term for the following statements

Question 1.
Father of Scientific Management.
Answer:
Fredrick Winslow Taylor

Question 2.
The principle of management which says unity is strength.
Answer:
Principle of Esprit de corps

Question 3.
The principle of management explaining about fair payment to workers.
Answer:
Principle of Remuneration

Question 4.
The statements which disclose fundamental truth of management.
Answer:
Principle of Management

Question 5.
Principle of management which states that there should be balance between the authority and responsibility.
Answer:
Principle of Authority and Responsibility

Question 6.
Principle of management which states that every employee should receive orders and instructions from one boss only.
Answer:
Principle of Unity of Command.

State whether the following statements are True or False

Question 1.
Management principles are applicable to all types of organisation.
Answer:
True

Question 2.
Employees can be motivated by following the principle of fair remuneration.
Answer:
True

Question 3.
The goal of organisation must not be sacrificed for individual goal.
Answer:
True

Question 4.
F. W. Taylor recommended total six foremen to control the various aspects of production.
Answer:
False.

Find the odd one

Question 1.
Principle of Unity of Direction, Principle of Centralisation, Principle of Order, Time Study.
Answer:
Time Study

Question 2.
Standardisation of tools and equipment, Science – not rule of thumb, Mental Revolution, Division of Responsibility.
Answer:
Standardisation of tools and equipment

Question 3.
Scientific task setting, Scientific selection and training. Principle of Stability of Tenure, Differential Piece – Rate Wage Plan.
Answer:
Principle of stability of tenure

Justify the following statements

Question 1.
Principles of management improve the efficiency of employees.
Answer:
(1) Principles of management if used and applied by the organisation in right direction, they help to improve understanding and the overall efficiency of the employees. Principles of management advocate planned activities and : systematic organisation of men, materials, methods, machinery, etc. which in turn help to improve and increase the efficiency of employees.

(2) Principles of management guide the managers about handling the human resource, reducing the wastage, co-ordinating the activities of different departments, etc. This helps to improve the productivity in the organisation and consequently efficiency of employees. Principles of management also help to develop the objective approach.

(3) Application and use of principles of management leads to specialisation, increased productivity and efficiency. It boosts the morale of employees. These principles help to co-ordinate and control various activities of the organisation and also motivate the employees to perform more efficiently and effectively.

(4) Principle of fair remuneration indicates the management to pay adequate wages and other incentives to the employees. This goes a long way to increase the morale of employees who in turn would put their best efforts to perform their duties more efficiently. Principles of management also help to understand social responsibilities and to carry out research and development activities to improve the efficiency of employees.

Question 2.
Principles of management are applicable to all types of organisations.
Answer:
(1) Principles of management are the statements of fundamental truth which act as guidelines for managerial decision-making and actions. They establish cause and effect relationship. They are evolved through observation, analysis and experiments.

(2) However, managers can suitably modify the principles of management keeping in mind the requirements of the organisation.

(3) Principles of management are also helpful in achieving and attaining social and cultural goals. They are also directed to maximising profit without ignoring social values.

(4) Thus, Principles of management are universal in nature. They are applicable to all types of organisations irrespective of the type, size or nature of the organisations.

Attempt the following

Question 1.
Explain the significance of management principles.
Answer:
The significance of management principles is explained as follows:
(1) Provides useful insight to manager : The study of management principles helps the manager to understand the organisation, its situations and problems. They act as guidelines to find out the ‘ solutions to the problems and handle the situation accordingly. The use and application of these principles help the manager to know the manner in which they should act in different situations, Timely guidance provided by the management principles reduces the wastage of resources and help to achieve goals in exact manner.

(2) Helpful in efficient utilisation of resources : The two resources used in the organisations Eire classified as physiCEd resources such as materials, machine, money, etc. and human resources i.e. manpower. The main function of management is to mEiintain proper balance between these resources by putting them to optimum use and control the wastage of resources. It uses different techniques Emd management principles and maintains discipline and healthy working environment. This helps to establish cordial relation between management and employees. This in turn increases the efficiency level of employees.

(3) Scientific decisions : Scientific decisions in relation to business organisation implies systematic and balanced decision. Management principles train and help the manager to tackle the situation tactfully instead of using trial and error method. Managers get an idea to analyse the situation systematically, to search alternative options and their results with the use of management principles.

(4) Understanding social responsibility: A business is a part of society. It makes use of the resources of the society and therefore, it has to perform some social responsibilities. Management principles guide the managers to understand and perform social responsibilities so that management can focus on providing quality products at reasonable prices, avoiding unfair trade practices and artificial monopolistic situations in the market, fair remuneration to employees, a healthy working environment, standard tools, and equipment, etc.

(5) Encourage Research and Development: Principles of management are evolutionary in nature and have evolved with the passage of time. They have undergone certain changes on account of changes in the business world. They are modified and developed over the years to suit the current trends. They stress scientific study, research, and development in the organization. Research and Development always work to find out new techniques in the field of production, marketing, finance, human resources, etc.

(6) Helps to coordinate and control: Principles of management serve as guidelines for better coordination and control. These principles help the managers in this challenge to coordinate the activities of different departments. Managers can easily exercise control over the performance of their employees. The proper use of these principles helps to achieve the given target easily.

(7) Develops objective approach: By using various principles of management, the manager can develop an objective approach. The manager can find out and identify opportunities, root causes of the problems and can provide appropriate solutions on it in the right direction. This approach also helps to build confidence in the minds of the managers.

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 4 Issue of Debentures Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 4 Issue of Debentures

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
A company raises debt capital through the issue of ___________
(a) equity shares
(b) preference shares
(c) debentures
Answer:
(c) debenture

Question 2.
Debenture holder is ___________ of the company.
(a) Owner
(b) debtor
(c) creditor
Answer:
(c) creditor

Question 3.
Debenture holders get income in the form of ___________
(a) Dividend
(b) Interest
(c) Bonus
Answer:
(b) Interest

Question 4.
Power to issue debentures rests with ___________
(a) Chairman
(b) Secretary
(c) Board of Directors
Answer:
(c) Board of Directors

Question 5.
The word ‘Debenture’ is derived from the Latin word ___________
(a) Debere
(b) Debenture
(c) Debire
Answer:
(a) Debere

Question 6.
Debenture cannot be redeemed ___________
(a) at par
(b) at premium
(c) at discount
Answer:
(c) at discount

Question 7.
The company has to obtain the consent of ___________ if the issue of debentures exceeds ₹ 1.
(a) SEBI
(b) Registrar
(c) National Stock Exchange
Answer:
(a) SEBI

Question 8.
Debenture certificate must be issued within ___________ months of allotment.
(a) 3
(b) 6
(c) 9
Answer:
(b) 6 months

Question 9.
The ___________ is an advertisement for the issue of debentures.
(a) memorandum of association
(b) articles of association
(c) prospectus
Answer:
(c) prospectus

Question 10.
Debenture holders is entitled to receive ___________ certificate from the company.
(a) Share
(b) Debenture
(c) Dividend
Answer:
(b) Debenture

Question 11.
Fully convertible debentures are converted into ___________ shares on maturity.
(a) equity
(b) deferred
(c) bonus
Answer:
(a) Equity

Question 12.
A return of allotment is filed with the Registrar within ___________ days of allotment.
(a) 30
(b) 60
(c) 90
Answer:
(a) 30

Question 13.
The ___________ can direct the company to repay the principal amount of debenture with interest.
(a) Company Law Board
(b) Registrar
(c) Shareholders
Answer:
(a) Company Law Board

Question 14.
In order to redeem old debentures the company issues ___________
(a) assets
(b) public deposits
(c) fresh debenture
Answer:
(c) fresh debenture

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Debenture Trustees	(a) No voting rights
(2) Debenture	(b) ICRA
(3) Convertible debenture	(c) Security about Repayment
(4) Secured debenture	(d) CARE
(5) Debenture holder	(e) Equity Shares
	(f) Borrowed capital
	(g) Protect Debenture holders

Answer:

Group ‘A’	Group ‘B’
(1) Debenture Trustees	(g) Protect Debenture holders
(2) Debenture	(f) Borrowed capital
(3) Convertible debenture	(e) Equity Shares
(4) Secured debenture	(c) Security about Repayment
(5) Debenture holder	(a) No voting rights

Question 2.

Group ‘A’	Group ‘B’
(1) Charge on Asset	(a) Credit Rating
(2) Redeemable debenture	(b) Secured debenture
(3) Board of Directors	(c) 90 days
(4) CRISIL	(d) Power to issue debenture
(5) Debenture Certificate	(e) Unsecured Debenture
	(f) Repaid on maturity
	(g) 6 months

Answer:

Group ‘A’	Group ‘B’
(1) Charge on Asset	(b) Secured debenture
(2) Redeemable debenture	(f) Repaid on maturity
(3) Board of Directors	(d) Power to issue debenture
(4) CRISIL	(a) Credit Rating
(5) Debenture Certificate	(g) 6 months

Question 3.

Group ‘A’	Group ‘B’
(1) Board of Directors	(a) Within 6 months after allotment
(2) Debentures	(b) No voting right
(3) Debenture holder	(c) Application of debentures
(4) CARE	(d) Interest
(5) Debenture Certificate	(e) Voting right
	(f) Within 120 days after allotment
	(g) Credit rating agency
	(h) Dividend
	(i) SEBI
	(j) Creditors

Answer:

Group ‘A’	Group ‘B’
(1) Board of Directors	(c) Application of debentures
(2) Debentures	(d) Interest
(3) Debenture holder	(b) No voting right
(4) CARE	(g) Credit rating agency
(5) Debenture Certificate	(a) Within 6 months after allotment

Question 4.

Group ‘A’	Group ‘B’
(1) Trust Deed	(a) Owner
(2) Debenture Certificate	(b) Deed for debenture holders
(3) Secured Debenture	(c) Charge on company’s assets
(4) Redemption by annual installment	(d) Creditors of the company
(5) Debenture holders	(e) Signature of two directors
	(f) Two coupons
	(g) Deed for depositors
	(h) No charge on the company’s assets
	(i) CARE
	(j) Credit rating

Answer:

Group ‘A’	Group ‘B’
(1) Trust Deed	(b) Deed for debenture holders
(2) Debenture Certificate	(e) Signature of two directors
(3) Secured Debenture	(c) Charge on company’s assets
(4) Redemption by annual installment	(f) Two coupons
(5) Debenture holders	(d) Creditors of the company

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
The provision dealing with the issue of debenture.
Answer:
Section 71 of the companies Act 2013

Question 2.
Name of the capital controller in India.
Answer:
SEBI

Question 3.
Debenture converted in equity shares.
Answer:
Convertible Debenture

Question 4.
Redemption time of secured debenture.
Answer:
10 years

Question 5.
The authority which listing the debentures.
Answer:
Stock Exchange

Question 6.
Application received more than the issue.
Answer:
Over Subscription

Question 7.
Authority consulted by Debenture Trustee.
Answer:
NCLT

Question 8.
The agency provides a credit rating of the security.
Answer:
Credit Rating Agency

Question 9.
Register of Entries of the debenture.
Answer:
Register of debenture

Question 10.
Meeting conducted in an emergency.
Answer:
Extraordinary General Meeting.

1D. State whether the following statements are true or false.

Question 1.
Debenture holders are the creditors of the company.
Answer:
True

Question 2.
Board has no power to issue debenture.
Answer:
False

Question 3.
Debenture helps to raise borrowed capital.
Answer:
True

Question 4.
Debenture holders enjoy normal voting rights.
Answer:
False

Question 5.
The debenture is permanent capital.
Answer:
False

Question 6.
A debenture trustee is a link between the company and Debenture holders.
Answer:
True

Question 7.
Appointment of the underwriter is compulsory.
Answer:
False

Question 8.
Listing of debenture is compulsory.
Answer:
True

Question 9.
SEBI has contracted over the security market.
Answer:
True

Question 10.
The allotment procedure should be completed within 60 days.
Answer:
True

Question 11.
A debenture Trust deed is a legal Agreement.
Answer:
True

1E. Find the odd one.

Question 1.
SEBI, NCLT, SBI
Answer:
SBI

Question 2.
25%, 15%, 10%
Answer:
10%

Question 3.
CARE, CRISIL, SEBI
Answer:
SEBI

Question 4.
Credit Rating Agency Stock Exchange, SBI
Answer:
SBI

Question 5.
SEBI, NCLT, CRISIL
Answer:
CRISIL

Question 6.
Debenture Certificate Trust Deed, share certificate
Answer:
Share Certificate

1F. Complete the sentences.

Question 1.
Debenture holder has no ___________ rights.
Answer:
Voting

Question 2.
CRISIL is responsible to ___________ of securities.
Answer:
Credit Rating

Question 3.
Company enters into ___________ with underwriter.
Answer:
Underwriting Agreement

Question 4.
___________ is needed to increase borrowing power.
Answer:
Special Resolution

Question 5.
If borrowing power of board is to be increased ___________ must be held.
Answer:
Extra Ordinary General Meeting

1G. Select the correct option from the bracket.

Question 1.

Group ’A’	Group ’B’
(1) Board of Directors	(a) …………………….
(2) …………………….	(b) Interest
(3) Debenture holders	(c) ……………………..
(4) ……………………..	(d) Credit Rating Agency
(5) Debenture certificate	(e) ………………………..

(Debenture, Application of debenture, No Voting Rights, 6 months, CARE)
Answer:

Group ’A’	Group ’B’
(1) Board of Directors	(a) Application of debenture
(2) Debenture	(b) Interest
(3) Debenture holders	(c) No Voting Rights
(4) CARE	(d) Credit Rating Agency
(5) Debenture certificate	(e) 6 months

1H. Answer in one sentence.

Question 1.
Who creates a charge over assets?
Answer:
Debenture Trustee can create a charge over asset.

Question 2.
When is the permission of SEBI required?
Answer:
When borrowing capital exceeds 1 crore, consent of SEBI is required.

1I. Correct the underlined word and rewrite the following sentences.

Question 1.
Debenture holders get fluctuating interest.
Answer:
Debenture holders get Fixed interest.

Question 2.
Convertible debenture holders can be converted into preference shares.
Answer:
Convertible debenture holders can be converted into Equity Shares.

Question 3.
Shareholders have the power to issue debenture.
Answer:
The Board of directors has the power to issue debenture.

Question 4.
A debenture Trust deed is an illegal document.
Answer:
A debenture Trust deed is a legal document.

Question 5.
Debenture certificate issued by the company within 3 months.
Answer:
Debenture certificate issued by the company within 6 months.

Question 6.
Debenture holders are the owners of the company.
Answer:
Debenture holders are the creditor of the company.

Question 7.
Debentures generate owned capital for the company.
Answer:
Debentures generate borrowed capital for the company.

1J. Arrange in proper order.

Question 1.
(a) Offer letter
(b) Debenture Trust Deed
(c) Written Consent
Answer:
(a) Offer letter
(b) Written Consent
(c) Debenture Trust Deed

Question 2.
(a) Allotments of debenture
(b) Return with ROC
(c) Debenture Certificate
Answer:
(a) Allotments of debenture
(b) Debenture Certificate
(c) Return with ROC

Question 3.
(a) Issue of prospectus
(b) Return with ROC
(c) Underwriting Agreement
Answer:
(a) Issue of prospectus
(b) Underwriting Agreement
(c) Return with ROC

Question 4.
(a) Board meeting
(b) Open Separate Bank Account
(c) Extra-Ordinary General Meeting
Answer:
(a) Board meeting
(b) Extra-Ordinary General Meeting
(c) Open Separate Bank Account

Question 5.
(a) Receiving Application Money
(b) Allotment of debenture
(c) Open Bank Account
Answer:
(a) Receiving Application Money
(b) Open Bank Account
(c) Allotment of debenture

Question 6.
(a) Preparation and consent to the prospectus
(b) Filing with ROC
(c) Special Resolution Passed
Answer:
(a) Special Resolution Passed
(b) Preparation and consent to the prospectus
(c) Filing with ROC

Question 7.
(a) Debenture Certificate
(b) Entries in Register
(c) Underwriting contract
Answer:
(a) Underwriting contract
(b) Debenture Certificate
(c) Entries in Register

2. Explain the following terms/concepts.

Question 1.
Debenture
Answer:
The company raises capital by borrowing money from the public or its members. It is a proof of loan taken by the company. A person who purchases debenture is called a debenture holder. Interest is paid to the debenture holders.

Question 2.
Debenture Redemption Reserve
Answer:
Debenture Redemption Reserve is useful for the redemption of the debenture. It is created out of the profit of the company which has maintained a 25% minimum of the value of outstanding debenture in DRR.

Question 3.
Minimum Subscription
Answer:
Minimum subscription is a term that is used to represent the amount of the issue which has to be subscribed or else the shares can’t be issued if it is not being subscribed.

Question 4.
Underwriting
Answer:
An underwriting contract is a contract between an underwriter and the issuer of securities. It is helpful to issuer companies when securities are not being subscribed by the public. Here, underwriters guarantee the sale of issued stock at the agreed price.

Question 5.
Credit Rating
Answer:
It is an estimation of the ability of a person or organization to fulfill their financial requirement, commitments, based on previous dealings. Credit Rating Agencies are responsible for credit rating.

Question 6.
Secured debenture
Answer:
Secured debentures are bonds that are issued with collateral. Here, a charge is created against the assets of the company. If a company is in default, assets can be realized to recover the dues.

3. Study the following case/situation and express your opinion.

1. ABC Limited is going to redeem its 1000 debentures of ₹ 100 each. Please advise them on the following:

Question (a).
Which fund should be created by the company to redeem debentures?
Answer:
The company should create a Debenture Redemption Reserve to redeem debentures.

Question (b).
Can debenture trustees consult NCLT if the company is at default?
Answer:
If the company is at default regarding repayment of debentures, then Debenture trustees can consult the NCLT.

Question (c).
What will be the change in the register of debenture holders?
Answer:
If debentures are redeemed, their entries will be cancelled from requisite.

2. Zeal Co. Ltd. is going to issue 2000 debentures. Please advise them on the following:

Question (a).
Does the company have to list the debentures on the stock exchange?
Answer:
Yes, the company has to list the debentures on the stock exchange.

Question (b).
Should the company get a credit rating for issuing debentures?
Answer:
Yes, the company should get a credit rating for issuing debenture and from SEBI.

Question (c).
Can the company show a credit rating in the prospectus?
Answer:
Yes, the credit rating should be mentioned in the prospectus/offer letter/letter of offer.

4. Answer in brief.

Question 1.
Define Debenture and State its meaning.
Answer:
Definitions of Debenture:

• According to Section 82 of Companies Act, “Debenture to any member of the company is a movable property, transferable in the manner provided by the Articles of Association:
• According to the Oxford dictionary “Debenture is a certificate issued by a company act now leading that it has borrowed money on which interest is being paid”.

Meaning:

• The word ‘Debenture’ is derived from the Latin word ‘Debere’- which means to owe something to someone.
• It is a proof of loan taken by the company on certain terms and conditions.
• It can be issued by public or private companies to raise borrowed capital.
• A person who purchases it is called a debenture holder and he is a creditor of a company.
• It can be issued at par, premium, and discount.
• The Board of Directors has the power to issue debentures.
• Debenture holders get a fixed rate of interest on their investments.

Question 2.
State the provisions as per Companies (Share Capital and Debenture) Rules, 2014 (i.e. Rule 18).
Answer:
If a company issued secured debenture, then it has to follow Rule 18 of Companies Rules, 2014. The provisions are as follows:
(i) Tenure of secured debenture:
All secured debentures should be redeemed within 10 years from the date of its issue. Infrastructure companies, Companies permitted by the Ministry of Corporate Affairs, Central Government, or RBI can issue debentures beyond the period of 10 years but not exceeding 30 years.

(ii) Create charge on assets:
Secured debentures create charges on assets. The value of the charge should be adequate to cover the entire value of debentures issued and the interest to be paid on it.

(iii) Debenture Trustee:
Before issuing a prospectus, the company has to appoint a Debenture Trustee. The company should execute the trust deed within 60 days from allotment of a debenture or before issuing the prospectus/offer letter. The Rules and Regulations of Trust Deed decide the role of debenture trustees.

(iv) Debenture Redemption Reserve:
The company has to create a Debenture Redemption Reserve to redeem debentures. The company should maintain at least 25% of the value of outstanding debentures in the DRR account. Money from this account is used for the redemption of the debenture. Every year on or before 31st March, the company has to invest or deposit a sum of not less than 15% in the DRR account for the maturing debentures in the next year.

Question 3.
What are/Explain the requirement of SEBI for the issue of debentures?
Answer:
Following are the requirements as per SEBI for the issue of debentures in the market:
(i) Condition of minimum subscription: Regulation 12 of SEBI Regulation Act 2008 is responsible to regulate the minimum subscription collected by the company. As per SEBI, the minimum subscription for public issues is 75% of the issue price. If the minimum subscription is not received, then it should be refunded within 12 days from the date of closure of the issue.

(ii) Over Subscription:
Oversubscription means a situation where a company has more buyers than the shares to fulfill the client’s order. The company can retain oversubscription on up to a maximum of 100% of the issue price or any lower unit as specified by the prospectus.

(iii) Underwriting:
A company may enter into an underwriting agreement with underwriters for its public issue of debentures. The appointment of underwriters must be mentioned in the prospectus/offer letter/letter of offer.

(iv) Credit Rating:
As per SEBI, the company making public issue, or right issue of convertible debenture must obtain a credit rating from one or more credit rating agencies. The rating must be mentioned in the offer letter/prospectus. In India, ICRA, CRISIS, CARE are famous or recognized credit rating agencies for the corporate sector.

Question 4.
Who are Debenture Trustees?
OR
Explain the role of Debenture Trustees.
OR
Write a note on Debenture Trustees.
Answer:

• Debenture holders are the creditors of the company and they cannot participate in the routine affairs of the management of the company. So, in order to protect the interest of debentures, the company appointed debenture trustees.
• Debenture trustees are the institutions that protect the interest of debenture holders.
• Debenture Trustees create a charge on assets of the company on behalf of debenture holders. They are the custodian of assets on which charge has been created.
• In order to appoint debenture trustees, the company has to execute the debenture trust deed within 3 months, and the offer letter should be issued within 60 days after the allotment.
• The prospectus or offer letter must mention the names of debenture trustees.

5. Justify the following statements.

Question 1.
The company can list its debentures on Stock Exchange.
Answer:

• A company can issue secured as well as unsecured debentures.
• Debentures are issued to the general public.
• The company can issue debentures to its members through public offers or offer through private placement.
• The company gets its debentures rate from one or more credit rating agencies which attract the general public or members of the company.
• Thus, it is rightly said that a company can list its debentures on Stock Exchange.

Question 2.
Debenture holders do not enjoy any voting rights.
Answer:

• The company borrows a large amount of money by issuing debentures.
• Debentures are considered to be the long-term loan that is repaid after a long period.
• Debenture holders are the creditors of the company.
• The company has to pay interest to the debenture holders even if the company makes a loss in the current year.
• Thus, it is rightly said that debenture holders do not enjoy any voting rights.

Question 3.
Debenture Redemption Reserve Account is used for the redemption of debentures.
Answer:

• Debenture Redemption Reserve is created from the profits earned by the company.
• The company has to maintain at least 25% of the value for the outstanding debentures in the DRR account.
• Similarly, every year on or before 31st March, the company has to invest or deposit a sum of not less than 15% in the DRR account for the maturing debentures in the next year.
• Thus, it is rightly said that Debenture Redemption Reserve Account is used for the redemption of debentures.

Question 4.
Members, as well as debenture holders, can inspect the debenture trust deed.
Answer:

• The company enters into the contract with the debenture trustees which is called as ‘Debenture Trust Deed”.
• It is a legal instrument conveying the assets of a company of the trustees.
• The deed includes the rights of debenture holders and the duties and powers of debenture trustees.
• It contains terms and conditions agreed between the company and debenture trustee.
• Thus, it is rightly said that members, as well as debenture holders, can inspect the debenture trust deed.

6. Attempt the following.

Question 1.
Explain the regulations governing the issue of different types of debentures.
Answer:
A company has to comply with the provisions while issuing different types of debentures. Depending upon the type of debenture, the company has to fulfill the following provisions/regulations:
(i) Companies Act, 2013: Sec. 71 of Companies Act, 2013 contains provisions for the issue of debentures.

(ii) Company Rules 2014 (Share Capital and Debentures), Rule 18: Rule 18 of Companies (Share Capital and Debentures) Rules, 2014 contains provisions for the issue of the secured debenture.

(iii) SEBI Regulations, 2008: SEBI Regulations, 2008 covers the provisions related to the issue and listing of debentures that are not convertible, either wholly or partly into equity shares. It is applicable to only those debentures which are issued through public offer, private placement. Disclosure requirements are to be followed the same as the public issue of equity shares.

(iv) SEBI Regulations, 2009: SEBI Regulations, 2009 (Issue of Capital and Disclosure Requirement) covers provisions for issue of debentures and listing of debentures that are convertible, rather partially, fully, or optionally into listed or unlisted equity shares. It also has to follow the same disclosure norms as applicable to equity shares.

(v) SEBI Regulations, 2015: SEBI Regulations, 2015 (Listing Obligations and Disclosure Requirements) covers provisions for the listed company issuing non-convertible debentures, perpetual debt instruments, etc. It includes various listing conditions which a company has to comply with.

(vi) RBI Guidelines: RBI Guidelines are formed for the banks which raise capital by issuing non-equity instruments.

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 3 Issue of Shares Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 3 Issue of Shares

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
____________ of company must have provision regarding issue of bonus shares.
(a) Memorandum of Association
(b) Articles of Association
(c) Prospectus
Answer:
(b) Articles of Association

Question 2.
If a share of ₹ 100 is issued at ₹ 100, it is said to be issued at ____________
(a) Par
(b) Premium
(c) Discount
Answer:
(a) Par

Question 3.
If a share ₹ 100 is issued at ₹ 90, it is said to be issued at ____________
(a) Par
(b) Discount
(c) Premium
Answer:
(b) discount

Question 4.
____________ means placing the shares privately without inviting the public for subscription.
(a) Private placement
(b) Public placement
(c) Transfer
Answer:
(a) Private placement

Question 5.
A share certificate must be signed by at least ____________ directors.
(a) two
(b) three
(c) four
Answer:
(a) two

Question 6.
Letter of regret is accompanied by ____________
(a) refund order
(b) Call Letter
(c) Dividend warrant
Answer:
(a) refund order

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Share certificate	(a) Capitalization of profit
(2) Bonus shares	(b) Transfer of shares due to operation of law
(3) Under subscription	(c) Bearer document
(4) Transfer of shares	(d) More applications than expected
(5) Private placement	(e) Sale or gift of shares to another person
	(f) Private company collecting capital privately
	(g) Right Issue
	(h) Registered document
	(i) Public company collecting capital privately
	(j) Fewer applications than expected

Answer:

Group ‘A’	Group ‘B’
(1) Share certificate	(h) Registered document
(2) Bonus shares	(a) Capitalization of profit
(3) Under subscription	(j) Fewer applications than expected
(4) Transfer of shares	(e) Sale or gift of shares to another person
(5) Private placement	(i) Public company collecting capital privately

Question 2.

Group ‘A’	Group ‘B’
(1) Right issue	(a) Shares allotted to the Board of Directors
(2) IPO	(b) Negotiable instrument
(3) Share Warrant	(c) Secondary market
(4) Bonus issue	(d) Application letter
(5) Regret Letter	(e) Partial issue
	(f) Shares allotted to existing shareholders
	(g) Non-negotiable instrument
	(h) Shares issued at free of cost
	(i) Refund order
	(j) Primary market

Answer:

Group ‘A’	Group ‘B’
(1) Right issue	(f) Shares allotted to existing shareholders
(2) IPO	(j) Primary market
(3) Share Warrant	(b) Negotiable instrument
(4) Bonus issue	(h) Shares issued at free of cost
(5) Regret Letter	(i) Refund order

Question 3.

Group ‘A’	Group ‘B’
(1) Employees Stock Option	(a) Board of Directors
(2) Oversubscription	(b) Conversion of shares to stock
(3) Allotment of shares	(c) Control over stock exchanges
(4) Transmission of shares	(d) Shares issued at more than face value
(5) Issue at par	(e) More capital
	(f) Transmission of ownership shares due to the operation of law
	(g) Less capital
	(h) Shares issued at face value
	(i) Employees participation in business
	(j) Refund of money

Answer:

Group ‘A’	Group ‘B’
(1) Employees Stock Option	(i) Employees participation in business
(2) Oversubscription	(e) More capital
(3) Allotment of shares	(a) Board of Directors
(4) Transmission of shares	(f) Transmission of ownership shares due to the operation of law
(5) Issue at par	(h) Shares issued at face value

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
A letter that informs the applicant that shares are allotted to him.
Answer:
Letter of Allotment

Question 2.
A letter that informs the applicant that shares are not allotted to him.
Answer:
Letter of Regret

Question 3.
Passing ownership of shares from Shareholders to another person voluntarily.
Answer:
Transfer of shares

Question 4.
A document that is an invitation to the general public to subscribe for shares of the company.
Answer:
Prospectus

Question 5.
Money paid along with the application of shares.
Answer:
Application money

Question 6.
The authority has the right to make calls on shares.
Answer:
Board of Directors

Question 7.
Giving shares to share applicant or specific person with whom the company has entered into the contract.
Answer:
Allotment of shares

1D. Find the odd one.

Question 1.
IPO, FPO, ESES.
Answer:
ESES

Question 2.
ESOS, ESPS, Bonus Shares, Sweat Equity.
Answer:
Bonus Shares

1E. Correct the underlined word/s and rewrite the following sentences.

Question 1.
Rights shares are offered to existing employees of a company.
Answer:
Rights shares are offered to existing shareholders of a company.

Question 2.
Letter of Regret should be sent to applicants whom shares are allocated.
Answer:
Letter of Allotment should be sent to applicants whom shares are allocated.

Question 3.
Transfer of Shares is done by operation of law.
Answer:
Transmission of shares is done by operation of law.

2. Explain the following terms/concepts.

Question 1.
Fixed Price Method
Answer:

• In an initial public offering (IPO), if the shares are offered at a fixed price such issue is known as the Fixed Price issue.
• In this method, the company mentions the quantity and the price at which shares are offered.

Question 2.
SARS
Answer:

• It is a method for companies to offer their employees a bonus compensation if the company performs well financially.
• The company allows a specified number of ‘Stock Appreciation Righf Units that are linked to the value of the Company’s shares on the date of allotment.

3. Answer in brief.

Question 1.
What is Transfer of Shares?
Answer:

• Transfer of shares means the transfer of ownership of the shares from one person to another against consideration.
• Transfer of shares is effected by removing the name of the existing shareholders (transferor) from the register of members and inserting the name of the new member (transferee).
• Transfer of shares is a voluntary process of transferring shares by a member of a company.
• A member may transfer the shares for consideration or give them away as a gift.
• In the case of public companies, shares are freely transferable subject to the provisions of the Articles of Association.
• In the case of private companies, there are restrictions on the free transfer of shares.
• A member has to apply to the company for the transfer of shares by filling the ‘Instrument of Transfer’ and submit the share certificate along with the required transfer fees.
• A member who is transferring the shares is called a Transferor and to whom the shares are to be transferred is called Transferor.

4. Answer the following questions.

Question 1.
Explain briefly the different offering shares to Existing Employees.
Answer:
A company can raise funds by offering shares to its existing employees as follows:

• Employees Stock Option Scheme (ESOS)
• Employee Stock Purchase Scheme (ESPS)
• Stock Appreciation Rights Scheme (EARS)
• Sweat Equity Shares

(i) Employees Stock Option Scheme (ESOS):
An employee stock option plan is an employee benefits scheme under which the company encourages its employees to acquire ownership in the form of shares. Under this scheme, permanent employees, Directors or Officers of the Company or its holding company or subsidiary company- are offered the benefit or right to purchase the equity shares of the company at a future date at a predetermined price. Generally, these shares are issued at discount. The shares are offered at a price lesser than their market price.

Following are the provisions related to ESOS:

• A company may offer the shares directly to the employees or through an Employee Welfare Trust.
• The shares are offered at a price lesser than their market price.
• There is a minimum vesting period of one year.
• The company specifies the lock-in period. It is a minimum of one year between the grant of option and vesting.
• Shares issued under this scheme enjoy dividends or voting rights only after buying by employees.
• The company has to get the approval of shareholders through a special resolution to issue ESOS.
• An employee can neither transfer his option to any other person nor pledge/mortgage the shares issued under ESOS.
• The company has to set up a compensation committee to administer ESOS
• The company has to fulfill the provision of SEBI (Share Based Employee Benefits) Regulations, 2014.

(ii) Employee Stock Purchase Scheme:
An employee stock purchase scheme is a company-run programme in which participating employees can purchase companies equity shares at a discounted price which they can buy at a future date. The company deducts a certain amount from the salary of the employee towards the payment for the shares.

Provisions:

• A different number of shares can be offered to different categories of employees.
• Shares issued through ESPS – should be listed on a recognized stock exchange.
• If ESPS is not a part of a public issue then it will have a one-year lock-in period from the date of allotment.
• The company has to fulfill the provisions of SEBI.
• The company has to get the approval of the shareholders by passing a special resolution to offer ESPS.

(iii) Stock Appreciation Rights Scheme:

• It is a method for companies to offer their employees a bonus compensation if the company performs well financially.
• The company allows a specified number of ‘Stock Appreciation Right’ Units that are linked to the value of the Company’s shares on the date of allotment. On the future date, the employee is paid the appreciation value in cash or through Equity Shares.
• There is no lock-in period for SARS. To issue SARS company has to get the approval of shareholders by a special resolution.

(iv) Sweat Equity Shares:
These are shares issued by a company to its directors or employees at a discount or for consideration other than cash. It is one of the modes of making share-based payments to employees. It is issued in recognition of their valuable contribution in the prosperity of the company.

Sweat Equity Shares rank “Pari Passu” (equal footing) with other equity shares. These shares have a lock-in period of three years. The company has to get the approval of shareholders by passing a special resolution to issue Sweat Equity Shares.

Balbharti Maharashtra State Board Class 12 Secretarial Practice Important Questions Chapter 2 Sources of Corporate Finance Important Questions and Answers.

Maharashtra State Board 12th Secretarial Practice Important Questions Chapter 2 Sources of Corporate Finance

1A. Select the correct answer from the options given below and rewrite the statements.

Question 1.
____________ is considered as Supreme controlling factor in business.
(a) Finance
(b) Material
(c) Machinery
Answer:
(a) Finance

Question 2.
A Company with share capital must issue ____________ shares.
(a) preference
(b) equity
(c) right
Answer:
(b) Equity

Question 3.
A person who purchases shares of a company is known as ____________
(a) Bondholder
(b) Shareholder
(c) creditor
Answer:
(b) Shareholder

Question 4.
A ____________ is indivisible unit of share capital.
(a) Debenture
(b) Share
(c) Bond
Answer:
(b) Share

Question 5.
A shareholder is entitled to receive ____________ as return on investment.
(a) Dividend
(b) Interest
(c) Discount
Answer:
(a) Dividend

Question 6.
____________ shares bear ultimate risk associated with ownership
(a) equity
(b) preference
(c) deferred
Answer:
(a) Equity

Question 7.
The control of the company is vested in ____________ shareholders.
(a) preference
(b) equity
(c) deferred
Answer:
(b) Equity

Question 8.
Bonus shares are issued as free gift to ____________ shareholder.
(a) equity
(b) deferred
(c) preference
Answer:
(a) Equity

Question 9.
Debentures are issued to raise ____________ capital.
(a) owned
(b) borrowed
(c) internal
Answer:
(b) Borrowed

Question 10.
Debentures are secured through ____________
(a) agreement
(b) trust deed
(c) contract
Answer:
(b) Trust Deed

Question 11.
Overdraft facility is allowed to ____________ account holder.
(a) savings
(b) current
(c) fixed
Answer:
(b) Current

Question 12.
Small retailers rely on ____________ credit from their suppliers.
(a) cash
(b) trade
(c) bank
Answer:
(b) Trade

Question 13.
____________ is the Depository receipt traded in countries other than USA.
(a) GDR
(b) ADR
(c) Fixed Deposit
Answer:
(a) GDR

1B. Match the pairs.

Question 1.

Group ‘A’	Group ‘B’
(1) Debenture holder	(a) Owners of the company
(2) Retained profit	(b) Capitalisation of profit
(3) Public deposit	(c) Savings account holder
(4) Overdraft facility	(d) Creditor of the company
(5) Equity shares	(e) Maximum 3 years
	(f) Maximum 5 years
	(g) Current account holder
	(h) Ploughing back of profit
	(i) Permanent capital
	(j) Temporary capital

Answer:

Group ‘A’	Group ‘B’
(1) Debenture holder	(d) Creditor of the company
(2) Retained profit	(h) Ploughing back of profit
(3) Public deposit	(e) Maximum 3 years
(4) Overdraft facility	(g) Current account holder
(5) Equity shares	(i) Permanent capital

1C. Write a word or a term or a phrase that can substitute each of the following statements.

Question 1.
The type of shareholders who can participate in the management of the company.
Answer:
Equity shareholders

Question 2.
Name the shareholder who attends a particular meeting when his interest is affected.
Answer:
Preference shareholder

Question 3.
Shareholders who are residual claimants against assets and income.
Answer:
Equity share

Question 4.
The type of shares which can be redeemed after a certain period of time.
Answer:
Redeemable preference shares

Question 5.
Debentures that can be redeemed after a particular date.
Answer:
Redeemable debentures

Question 6.
Debentures can be converted into equity shares after a specific period.
Answer:
Convertible debentures

Question 7.
A definite promise in writing from the buyer for paying a certain amount on a specific date.
Answer:
Bill of exchange

1D. State whether the following statements are true or false.

Question 1.
Preference shareholders do not enjoy normal voting rights.
Answer:
True

Question 2.
Equity shareholders are real owners and controllers of the company.
Answer:
True

Question 3.
Retained earnings is a difficult and costly method of raising capital.
Answer:
False

Question 4.
Debenture holders get a fixed rate of dividend.
Answer:
False

Question 5.
Debentures are secured with some property of the company.
Answer:
True

Question 6.
Public deposits are a good source of long-term financing.
Answer:
True

Question 7.
A private company can collect deposits from the general public.
Answer:
False

Question 8.
Providing loans to businesses is the primary function of banks.
Answer:
True

Question 9.
Financial institutions play an important role in financing industrial firms.
Answer:
True

1E. Find the odd one.

Question 1.
An equity share, Preference share, Bond
Answer:
Bond

Question 2.
Debenture, Bond, Preference share
Answer:
Preference share

Question 3.
Public deposits, Debentures, Retained earning
Answer:
Retained earnings

Question 4.
ADR, GDR, Fixed Deposit
Answer:
Fixed Deposit

Question 5.
6, 24, 36
Answer:
24

Question 6.
Bonds, Debentures, Shares
Answer:
Shares

1F. Complete the sentences.

Question 1.
The value of share which is determined by demand and supply forces in the share market is ____________
Answer:
Market value

Question 2.
The shares which have a preferential right over equity shares in respect of dividend and return of capital are ____________
Answer:
Preference shares

Question 3.
____________ preference shares which are redeemed after a certain period of time.
Answer:
Redeemable Preference Shares

Question 4.
____________ is the value of share which is written on the share certificate and mentioned in the Memorandum of Association.
Answer:
Face value

1G. Select the correct option from the bracket.

Question 1.

Group ‘A’	Group ‘B’
(1) Debentures	(a) …………………….
(2) ……………………	(b) Public deposit
(3) Bondholder	(c) ……………………..
(4) …………………..	(d) Equity share capital
(5) Depository Receipt traded in the USA	(e) ……………………..

(Maximum 36 months, Trust Deed, ADR, Creditor, Permanent Capital)
Answer:

Group ‘A’	Group ‘B’
(1) Debentures	(a) Trust Deed
(2) Maximum 36 months	(b) Public deposit
(3) Bondholder	(c) Creditor
(4) Permanent capital	(d) Equity share capital
(5) Depository Receipt traded in the USA	(e) ADR

1H. Answer in one sentence.

Question 1.
Who can accept the deposit?
Answer:
A public company having a net worth of not less than 100 crore rupees or a turnover of not less than 500 crore rupees; has obtained the prior consent of shareholders and resolution filed with Registrar before inviting deposits can accept deposits.

Question 2.
What are the minimum and maximum periods of deposits that can be accepted by the general public?
Answer:
Minimum 6 months and maximum 36 months is the period for accepting deposits from the general public.

Question 3.
Who is given overdraft facility?
Answer:
A current account holder of a bank is given an overdraft facility.

1I. Correct the underlined word/s and rewrite the following sentences.

Question 1.
Bondholders are owners of the company.
Answer:
Bondholders are creditors of the company.

Question 2.
Private companies can collect deposits from the public.
Answer:
Private companies cannot collect deposits from the public.

1J. Arrange in proper order.

Question 1.
Equity Shares, Preference Share, Debenture.
Answer:
Debentures, Preference shares, Equity Shares

Question 2.
Forecasting, Board Meeting, Issue of Securities
Answer:
Forecasting, Board Meeting, Issue of Securities

Question 3.
Call loans, debentures, short term loans
Answer:
Call Loans, Short term loans, Debentures

2 Explain the following terms/concepts.

Question 1.
Public Deposits
Answer:

• Public deposits are unsecured deposits invited by public limited company’s to finance working capital needs.
• Prior consent from shareholders must be with the passing of the special resolution and a copy of the same to be filed with the Registrar.

Question 2.
Bonds
Answer:

• A bond is a debt security and a formal contract to repay borrowed money with interest.
• A bondholder is a lender to the institution hence, the creditor.

Question 3.
Discounting of the bill of exchange
Answer:

• Discounting of a bill of exchange is a facility in which the holder of the bill can convert the bill to cash by discounting (giving as security) the bill with the bank before the date of maturity.
• The bank charges its commission (discounting charges) and pays the balance to the holder.
• It is an advance/short-term loan given to the holder of the bill.

3. Study the following case/situation and express your opinion.

1. There are 2 companies namely company A and company B with the same financial positions and in the same line (producing the same type of products) willing to issue debentures to more than 500 people. Company A is issuing 12% redeemable debentures to be redeemed after 5 years and Company B is issuing 12% convertible debentures which will be converted after 5 years. As an investor.

Question (a).
Which company would one like to invest in?
Answer:
As an investor one would like to invest in Company B.

Question (b).
Is it worth investing or going for convertible or redeemable? Why?
Answer:
‘It is wise and worth investing in 12% Convertible debentures as for 5 years both companies are going to give same returns but after 5 years Company B gives conversion facility due to which creditor becomes a member and can enjoy all rights of membership.

Question (c).
Is there any party to be appointed to look into the safety of debenture holders?
Answer:
As the number of persons to whom the debentures are to be issued is more than 500, there has to be a party known as Debenture Trustee to be appointed who will look into the safety of Debenture holders.

2. A public limited company wants to invite depositor from the public at large as it neither wants to dilute its shareholdings nor at present want to use its reserves.

Question (a).
Does it require prior approval from shareholders?
Answer:
Yes, prior approval from shareholders is a must.

Question (b).
What type of resolution does the company need to pass?
Answer:
The company needs to pass a special resolution for allowing to invite and accept deposits.

Question (c).
Is it necessary to file the resolution with the Registrar?
Answer:
Yes, a copy of the special resolution passed in the general meeting has to be filed before inviting the deposits.

3. A Company has an export order which is to be completed by June 15. It feels it may fall short of funds (₹ 5,00,000) as all its investments are likely to mature after July 15.

Question (a).
Does it cancel the export order?
Answer:
No, it need not cancel the order as it can approach a bank in which it has its current account for providing the funds.

Question (b).
What financial arrangements are to be made if it has to complete the order?
Answer:
It can enter into or avail overdraft facility for the required term period so that in case it falls short of funds, it can overdraw the required amount.

Question (c).
What is the amount of interest it has to pay?
Answer:
It will have to pay interest on excess amount overdrawn and for the term, it has used this extra amount.

4. A trader has drawn a bill of exchange for ₹ 50,000 on the sales made to a trader. The bill is drawn on the 1st of March 2020 for a period of 4 months. It is already a month from the date of the drawing.

Question (a).
Is there any source of finance available to him?
Answer:
Yes, a bill of exchange can act as a security and on the basis of the security, finance can be available to the trader.

Question (b).
Can he in present situation avail any facilities?
Answer:
Yes even though a month has been completed, discounting facility with the bank is available.

Question (c).
How will the charges be calculated?
Answer:
Discounting charges will be calculated on the bill amount for 3 months at the prevailing rate decided by the bank.

4. Answer in brief.

Question 1.
What are the different sources of finance?
Answer:
(i) A business organisation requires finance

• for various purposes
• at different stages
• for different term/period

(ii) The nature and size of the business determine the actual requirement of funds.

(iii) The company collects huge funds through different sources depending on the time period the funds are needed.

The various sources of finance available to the business may be as follows.
(a) External Sources: When capital is raised from outsiders/ outside the firm.

• Used for collecting initial capital

The important external sources are:

• Issue of shares
• Issue of debentures/bonds
• Public deposits
• A loan from financial institutions
• Bank Credit

(b) Internal Sources:

• The capital is made available from within the organisation.
• This is developed after a few years of profitable working of the firm.
• The important internal source of finance is retained profit also known as ‘ploughing back of profit.’
• The undistributed profit of the firm is re-invested in the business.

The external sources and internal sources can be further classified depending upon the financial requirements as:
(a) Long-term source: A business requires long-term finance for meeting fixed capital needs i.e. for a long duration.

The main sources of long term finance may be:

• Owned capital
• Debt capital

(b) Short-term source: The short-term funds are required for meeting short-term requirements i.e. working capital requirement. The short term funds are arranged by means of

• Public deposits
• Bank credit
• Trade credit
• Loans from Directors
• Advance from customers
• Native money lenders
• Government assistance

Question 2.
Describe different types of equity shares.
Answer:
The equity shares can be of two types:
(i) Equity share (with normal) with voting rights

• The voting right of such equity holders is in proportion to his shareholdings.

(ii) Equity shares with differential voting right

• Such equity shareholders shall have varying rights regarding dividend voting or otherwise in accordance with Rule 4 of Companies Act (Share Capital and Debenture) Rules 2014.
• A company can thus, issue shares with limited voting rights or no voting rights.
• They may be entitled to an extra rate of dividend.

Question 3.
What are retained earnings? What are the determinants of retained earnings?
Answer:

• A part of the profit is retained by the company in the form of the reserve fund.
• It is sum total of those profits, accumulated over the years and are reinvested in the business rather than distributed as dividends.
• The process of accumulating corporate profits and their utilization in business is called ‘self-financing or ploughing back of profit.
• It is the simple and cheapest method of raising finance by established companies.

Determinants of retained profits.
(i) Total earning of the company:

• The company can save and retain some part of the profit, if there is ample profit ‘Larger the earnings, larger the savings.’
• It is subject to the attitude of top management to determine the part of retained earnings.

(ii) Taxation policy:

• The taxation policy of the government is an important determinant of corporate savings.
• If the taxes rates charged/levied are high, a company cannot save much in the form of reserves.

(iii) Dividend policy:

• The policy of the Board of Directors as regards to the distribution of profit is another determinant.
• A conservative dividend policy helps to have a good accumulation of profit.
• The conservative policy affects the shareholders as they get dividends at a low rate.

(iv) Government Control:

• A Government is a regulatory body of the economic system of the country.
• Its policies, rules, and regulations compel the companies to work in that direction.
• A Company has to formulate its dividend policy in accordance with the rules and regulations formed by the government.

(v) Expenditure policy of the company:

• The expenditure of the company is classified as capital expenditure and revenue expenditure.
• More and more expenditure of the company towards various projects and needs will be responsible to lesser saving and lesser retain earning.

Question 4.
List out the Financial Institutions in India.
Answer:

• The Government has established special financial institutions for providing industrial finance.
• These institutions provide medium and long-term finance.
• They provide assistance to new companies as well as ongoing companies in the form of term loans, subscribing for shares and debentures, underwriting securities, and guaranteeing loans raised by cost.

(i) Development Banks:
They provide risk capital for economic development projects on a non-commercial basis. They play a crucial role in providing credit in the form of high-risk loans, equity positions, and risk guarantee instruments.
They include:

• Industrial Development Bank of India (IDBI)
• Industrial Finance Corporation of India Ltd. (IFCI)
• Industrial Credit and Investment Corporation of India Ltd. (ICICI)
• Small Industries Development Bank of India (SIDBI)
• Industrial Reconstruction Bank of India (IRBI)

(ii) Financial Institutions:
They are institutions engaged in business dealing with financial and monetary transactions such as deposits, loans, investments, and currency exchange.
They include:

• Risk Capital and Technology Finance Company Ltd. (RCTC)
• Technology Development and Information Company of India Limited (TDICI)
• Tourism Finance Corporation of India Limited (TFCI)

(iii) Investment Institutions:
Institutional investors are organisations that pool together on behalf of others and invest those funds in a variety of different financial instruments and asset classes.

They may be investment funds like Mutual funds, ETFs, (Exchange Traded Funds) Insurance Funds, Pension plans as well as investment banks and hedge Funds (alternative investment designed to protect investment portfolios from market uncertainty) They include:

• Life Insurance Corporation of India (LIC)
• Unit Trust of India (UTI)
• General Insurance Corporation of India (GIC)

(iv) State Level Institutions:

• They are financial agencies at the state level for the development of medium and small-scale industries. They include:
• State Financial Corporations (SFC)
• State Industrial Development Corporation (SIDC)

Question 5.
Explain the need/Importance/Significance of Institutional Financing.
Answer:
Financial Institutions provide debt capital to business enterprises and their need and importance may be as follows:
(i) To develop a sound capital market:

• Financial Institutions help in developing a sound financial capital market.
• They help in promoting and financing business enterprises either by underwriting issues or by subscribing to shares.

(ii) To mobilize financial resources:

• Financial, institutions mobilize the scattered savings, merge them and provide the same to industries.
• Capital is reluctantly provided to new ventures.
• Financial Corporations have become important for the economic development of economically backward countries that fail to mobilize financial resources for development.

(iii) Capital Formation:

• The rate of capital formation is very low in developing countries due to low per capita income and a lack of sufficient savings.
• The gap between saving and investment is filled by financial institutions.

(iv) Planned Economy:

• Financial institutions play an important role in the planned economic development of the country.
• The projects of national importance are taken up by them.
• Scarce finance resources are utilized at the optimum level.
• Certain basic industries like iron and steel, cement, etc. are developed by the government through these institutions.

(v) Financing Small Business:

• Special Corporations like SIDBI have been established for financing small-scale industries.
• The problems related to small business are of different nature which is tackled by such setup corporations.

(vi) Foreign Exchange Need:

• Foreign exchange requirement is also one of the needs of such institutions.
• They provide long-term loans in foreign curries.

(vii) Government taxation policy:

• Business enterprises depend more on debt capital as investment/amount paid against debt is tax-deductible expenditure.
• Financial institutions provide such debts to business organisations.

(viii) Rate of Interest:

• The corporations charge a uniform rate of interest, irrespective of the amount of loan in relation to the total cost.
• This also has become the reason for heavy borrowing from such institutions.

5. Justify the following statements.

Question 1.
Public Companies can accept deposits from the public.
Answer:

• Public companies having a net worth of not less than ₹ 100 crores or a turnover of fewer than ₹ 500 crores can accept deposits from the general public.
• A meeting has to be convened to get the approval of shareholders.
• After consent, a special resolution has to pass and the same has to be filed with the Registrar.
• Advertisements in newspapers have to be given to let people know regarding the acceptance of deposits.
• Deposits thus can be accepted for a minimum period of 6 months and a maximum period of 36 months or 3 years.
• Thus, it is rightly said, that public companies can accept deposits from the public.

6. Attempt the following questions.

Question 1.
Explain any five features of equity shares?
Answer:
Features of equity shares:
(i) Permanent Capital:

• Equity shares are irredeemable shares. It is permanent capital.
• The amount received from equity shares is not refunded by the company during its lifetime.
• Equity shares become redeemable/refundable only in the event of the winding-up of the company or the company decides to buy back shares.
• Equity shareholders provide long-term and permanent capital to the company.

(ii) Fluctuating dividend:

• Equity shares do not have a fixed rate of dividend.
• The rate of dividend depends upon the amount of profit earned by the company.
• If a company earns more profit, the dividend is paid at a higher rate.
• If there is insufficient profit, the Board of Directors may postpone the payment of dividends.
• The shareholders cannot compel them to declare and pay the dividend.
• The dividend is thus, always uncertain and fluctuating.
• The income of equity shares is uncertain and irregular.

(iii) Controlling power:

• The control of a company vests in the hands of equity shareholders.
• They are often described as real masters of the company as they enjoy exclusive voting rights.
• Equity shareholders may exercise their voting right by proxies, without attending the meeting in person.
• The Act provides the right to cast vote in proportion to the number of shareholdings.
• They participate in the management of the company.
• They elect their representatives called the Board of Directors for management of the company.

(iv) Market value:

• Market value fluctuates according to the demand and supply of shares.
• The demand and supply of equity shares depend on profits earned and dividends declared.
• When a company earns huge profits, the market value of shares increases.
• When it incurs loss the market value of shares decreases.
• There are frequent fluctuations in the market value of shares in comparison to other securities.
• Equity shares are more appealing to speculators.

(v) Capital Appreciation:

• Share capital appreciation takes place when the market value of a sharp increase in the share market.
• The profitability and prosperity of the company enhance the reputation of the company in the share market and thus, facilitates appreciation of the market value of equity shares.

Question 2.
Explain any four types of preference shares?
Answer:
(i) Cumulative Preference Shares:

• Cumulative preference shares are those shares on which dividend accumulates until it is fully paid.
• That is, if the dividend is not paid in one or more years due to inadequate profit, then such unpaid dividend gets accumulated and is carried forward till next year.
• The accumulated dividend is paid when the company performs well.
• The arrears of dividends are paid before making payment to equity shareholders.
• The preference shares are always cumulative unless otherwise stated in Articles of Association.

(ii) Participating Preference Shares:

• The holders of these shares are entitled to participate in surplus profit besides preferential dividends.
• They participate in the high-profit condition of the company.
• Surplus profit here means excess profit that remains after making payment of dividends to equity shareholders.
• Such surplus profit up to a certain limit is distributed to preference shareholders.

(iii) Non-Convertible Preference Shares:

• These shares are not converted into equity shares.
• They will remain as preference shares forever till paid back.

(iv) Irredeemable Preference Shares:

• Shares which are not redeemable are payable only on winding up of the company and are called irredeemable preference shares.
• As per section 55(1) of the Companies Act 2013, the company cannot issue irredeemable preference shares in India.

Question 3.
Explain features of debentures.
Answer:
Features of Debenture:
(i) Written Promise:
A debenture is a written promise by a company that it owes a specified sum of money to the holder of the debenture.

(ii) Priority of Payment:
Debenture holders have a priority in repayment of their capital over other claimants of the company. The amounts of debentures are settled before shareholders.

(iii) Assurance of repayment:

• Debenture constitutes a long-term debt.
• They carry an assurance of repayment on the due date.

(iv) Terms of issue and redemption of Debenture:

• Debenture can be issued at par, premium, and even at discount.
• Its redemption takes place only at par and premium.

(v) Interest:

• A fixed-rate of interest is agreed upon and is paid periodically.
• The rate of interest that a company pays/offers, depends upon the market conditions and nature of the business.
• Payment of interest is a liability of a company. It has to be paid whether the company makes a profit or not.

(vi) Status of Debenture holder:

• The debenture holder is a creditor of the company.
• Debenture being loan taken by the company interest is payable on it at fixed internal and fixed-rate till redeemed/paid.
• They cannot participate in the management of the company.

(vii) No Voting Right:

• According to sec. 71(2) of Companies Act 2013, no company shall issue debenture carrying voting rights.
• Debenture holders do not have the right to vote in the general meetings of the company.

(viii) Security:

• Debenture can be secured with some property of the company by fixed or floating charge.
• Debenture holders can sell of charged property of the company and recover their money if the company is not in a position to make payment of interest or repayment of capital.

Question 4.
Explain the features of bonds.
Answer:
(i) Nature of finance:

• It is debt or loan finance.
• It provides long-term finance 5 years, 10 years, 25 years, 50 years.

(ii) Status of investor:

• The bondholders are creditors.
• They are non-owners and hence, not entitled to participate in the general meetings.
• The bondholder has no right to vote.

(iii) Return on bonds:

• The bondholders get a fixed rate of interest.
• It is payable on maturity or at a regular interval.
• Interest is paid to the bondholder at a fixed rate.

(iv) Repayment:

• A bond is a formal contract to repay borrowed money.
• Bonds have a specific maturity date, on which the principal amount is repaid.