Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.
Practice Set 4.3 Geometry 9th Std Maths Part 2 Answers Chapter 4 Constructions of Triangles
Question 1.
Construct ∆PQR, in which ∠Q = 70°, ∠R = 80° and PQ + QR + PR = 9.5 cm.
Solution:
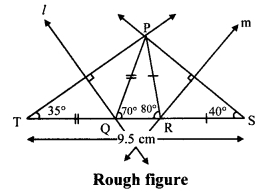
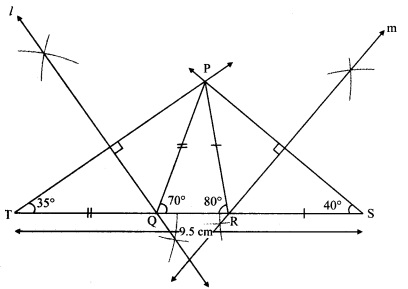
i. As shown in the figure, take point T and S on line QR, such that
QT = PQ and RS = PR ….(i)
QT + QR + RS = TS [T-Q-R, Q-R-S]
∴ PQ + QR + PR = TS …..(ii) [From (i)]
Also,
PQ + QR + PR = 9.5 cm ….(iii) [Given]
∴ TS = 9.5 cm
ii. In ∆PQT
PQ = QT [From (i)]
∴ ∠QPT = ∠QTP = x° ….(iv) [Isosceles triangle theorem]
In ∆PQT, ∠PQR is the exterior angle.
∴ ∠QPT + ∠QTP = ∠PQR [Remote interior angles theorem]
∴ x + x = 70° [From (iv)]
∴ 2x = 70° x = 35°
∴ ∠PTQ = 35°
∴ ∠T = 35°
Similarly, ∠S = 40°
iii. Now, in ∆PTS
∠T = 35°, ∠S = 40° and TS = 9.5 cm Hence, ∆PTS can be drawn.
iv. Since, PQ = TQ,
∴ Point Q lies on perpendicular bisector of seg PT.
Also, RP = RS
∴ Point R lies on perpendicular bisector of seg PS.
Points Q and R can be located by drawing the perpendicular bisector of PT and PS respectively.
∴ ∆PQR can be drawn.
Steps of construction:
i. Draw seg TS of length 9.5 cm.
ii. From point T draw ray making angle of 35°.
iii. From point S draw ray making angle of 40°.
iv. Name the point of intersection of two rays as P.
v. Draw the perpendicular bisector of seg PT and seg PS intersecting seg TS in Q and R respectively.
vi. Join PQ and PR.
Hence, ∆PQR is the required triangle.
Question 2.
Construct ∆XYZ, in which ∠Y = 58°, ∠X = 46° and perimeter of triangle is 10.5 cm.
Solution:
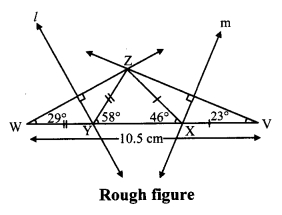
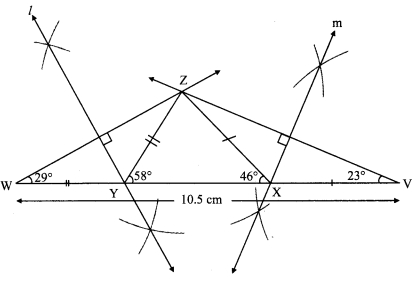
i. As shown in the figure, take point W and V on line YX, such that
YW = ZY and XV = ZX ……(i)
YW + YX + XV = WV [W-Y-X, Y-X-V]
∠Y + YX + ∠X = WV ……(ii) [From (i)]
Also,
∠Y + YX + ∠X = 10.5 cm …..(iii) [Given]
∴ WV = 10.5 cm [From (ii) and (iii)]
ii. In ∆ZWY
∠Y = YM [From (i)]
∴ ∠YZW = ∠YWZ = x° …..(iv) [Isosceles triangle theorem]
In ∆ZYW, ∠ZYX is the exterior angle.
∴ ∠YZW + ∠YWZ = ∠ZYX [Remote interior angles theorem]
∴ x + x = 58° [From (iv)]
∴ 2x = 58°
∴ x = 29°
∴ ∠ZWY = 29°
∴ ∠W = 29°
∴ Similarly, ∠V = 23°
iii. Now, in ∆ZWV
∠W = 29°, ∠V = 23° and
WV= 10.5 cm
Hence, ∆ZWV can be drawn.
iv. Since, ZY = YW
∴ Point Y lies on perpendicular bisector of seg ZW.
Also, ZX = XV
∴ Point X lies on perpendicular bisector of seg ZV.
∴ Points Y and X can be located by drawing the perpendicular bisector of ZW and ZV respectively.
∴ ∆XYZ can be drawn.
Steps of construction:
i. Draw seg WV of length 10.5 cm.
ii. From point W draw ray making angle of 29°.
iii. From point V draw ray making angle of 23°.
iv. Name the point of intersection of two rays as Z.
v. Draw the perpendicular bisector of seg WZ and seg VZ intersecting seg WV in Y and X respectively.
vi. Join XY and XX.
Hence, ∆XYX is the required triangle
Question 3.
Construct ∆LMN, in which ∠M = 60°, ∠N = 80° and LM + MN + NL = 11 cm.
Solution:
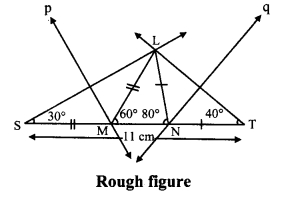
i. As shown in the figure, take point S and T on line MN, such that
MS = LM and NT = LN …..(i)
MS + MN + NT = ST [S-M-N, M-N-T]
∴ LM + MN + LN = ST …..(ii)
Also,
LM + MN + LN = 11 cm ….(iii)
∴ ST = 11 cm [From (ii) and (iii)]
ii. In ∆LSM
LM = MS
∴ ∠MLS = ∠MSL = x° …..(iv) [isosceles triangle theorem]
In ∆LMS, ∠LMN is the exterior angle.
∴ ∠MLS + ∠MSL = ∠LMN [Remote interior angles theorem]
∴ x + x = 60° [From (iv)]
∴ 2x = 60°
∴ x = 30°
∴ ∠LSM = 30°
∴ ∠S = 30°
Similarly, ∠T = 40°
iii. Now, in ∆LST
∠S = 30°, ∠T = 40° and ST = 11 cm
Hence, ALST can be drawn.
iv. Since, LM = MS
∴ Point M lies on perpendicular bisector of seg LS.
Also LN = NT
∴ Point N lies on perpendicular bisector of seg LT.
∴ Points M and N can be located by drawing the perpendicular bisector of LS and LT respectively.
∴ ∆LMN can be drawn.
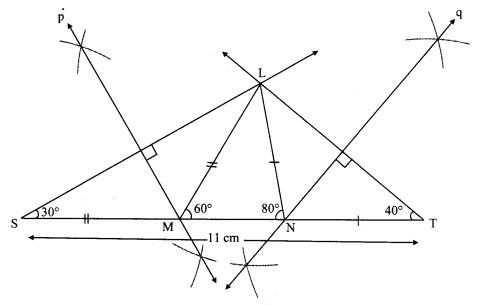
Steps of construction:
i. Draw seg ST of length 11 cm.
ii. From point S draw ray making angle of 30°.
iii. From point T draw ray making angle of 40°.
iv. Name the point of intersection of two rays as L.
v. Draw the perpendicular bisector of seg LS and seg LT intersecting seg ST in M and N respectively.
vi. Join LM and LN.
Hence, ∆LMN is the required triangle.
