Commercial Mathematics Class 11 Commerce Maths 2 Chapter 9 Exercise 9.3 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Ex 9.3 Questions and Answers.
Std 11 Maths 2 Exercise 9.3 Solutions Commerce Maths
Question 1.
What would be the simple interest on an amount of ₹ 9,600 at the rate of 6% per annum after 3 years?
Solution:
Given Principal P = ₹ 9600
Rate of interest R = 6% p.a.
Number of years = T = 3
Simple Interest I = \(\frac{\text { PRT }}{100}\)
= \(\frac{9600 \times 3 \times 6}{100}\)
= 96 × 18
= 1728
∴ Simple interest after 3 years would be ₹ 1728
Question 2.
What would be the simple interest at the rate of 9\(\frac{1}{2}\)% per annum on ₹ 6,000 for 2\(\frac{1}{2}\) years?
Solution:
Rate of interest per annum R = 9\(\frac{1}{2}\)% = \(\frac{19}{2}\)%
Principal P = ₹ 6000
Duration T = 2\(\frac{1}{2}\) = \(\frac{5}{2}\) years
∴ Simple Interest, I = \(\frac{\text { PRT }}{100}\)
= 6000 × \(\frac{19}{2} \times \frac{5}{2} \times \frac{1}{100}\)
= 15 × 19 × 5
= 1425
∴ Simple interest would be ₹ 1425.
![]()
Question 3.
What would be the simple interest on ₹ 8,400 in 9 months at the rate of 8.25 percent per annum?
Solution:
Principal P = ₹ 8400
Rate of interest R = 8.25%
Duration T = 9 months = \(\frac{3}{4}\) years

∴ Simple interest would be ₹ 519.75.
Question 4.
What would be the compound interest on ₹ 4200 for 18 months at 10% per annum compounded half yearly?
Solution:
Principal P = ₹ 4200
Rate of interest R = 10%
Duration T = 18 months = 1.5 years
compounding is done half yearly
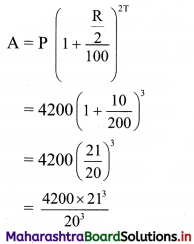
= \(\frac{4200 \times 9261}{2000}\)
= 4862.025
I = A – P
= 4862.025 – 4200
= 662.025
∴ Compound interest would be ₹ 662.025.
![]()
Question 5.
Find compound interest on ₹ 10,000 for 2 years at 8% per annum compounded half yearly.
Solution:
Principal P = ₹ 10,000
Rate of interest R = 8% p.a. compounded half yearly
Duration T = 2 years

I = A – P
= 11648.58 – 10000
= 1698.58
∴ Compound interest is ₹ 1698.58.
Question 6.
In how many years ₹ 1,00,000 will become ₹ 1,33,100 at compound interest rate of 10% per annum?
Solution:
Principal P = ₹ 1,00,000
Amount A = ₹ 1,33,100
Rate of interest R = 10% p.a.

∴ ₹ 1,00,000 will become ₹ 1,33,100 after 3 years.
Question 7.
A certain sum of money becomes three times of itself in 20 years at simple interest. In how many does it become double of itself at the same rate of simple interest?
Solution:
Given that, sum of money triples itself in 20 years
∴ P + I = 3P
∴ I = 2P
and T = 20 years
Now simple interest I = \(\frac{\text { PRT }}{100}\)
∴ 2P = \(\frac{\mathrm{P} \times \mathrm{R} \times 20}{100}\)
∴ R = 10
∴ Rate of interest = 10% per annum
The time period is to be calculated for the condition that the sum doubles itself i.e. for the condition
P + I = 2P
i.e. I = P
\(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\) = P
∴ \(\frac{10 \times T}{100}\) = 1
∴ T = 10
∴ The sum will become double of itself in 10 years.
Question 8.
A person borrows 10,000 for 2 year at 4% p.a. simple interest he immediately lends it to another person at 6.5% p.a. for 2 years. Find his total gain in the transaction.
Solution:
Person borrows money at 4% per annum and lends it at 6.5% per annum.
∴ His gain is (6.5 – 4) = 2.5% on ₹ 10000 for 2 years
i.e. gain = \(\frac{1000 \times 2.5 \times 2}{100}\)
= 100 × 5
= ₹ 500
∴ The person will gain ₹ 500 in this transaction.
![]()
Question 9.
A man deposits X 200 at the end of each year in recurring account at 5% compound interest. How much will it become at the end of 3 years?
Solution:
At end of 1st year, 2nd year and 3rd year ₹ 200 were deposited.
Rate of interest R = 5% p.a.
At end of 3 years, amount
= 200 + \(200\left[1+\frac{5}{100}\right]+200\left[1+\frac{5}{100}\right]^{2}\)
= 200 [1 + 1.05 + (1.05)2]
= 200 [2.05 + 1.1025]
= 200 [3.1525]
= 630.5
At end of 3 years, the account will have a balance of ₹ 630.5.
Question 10.
A man gets a simple interest of ₹ 2,000 on a certain principal at the rate of 5% p.a. in 4 years. What compound interest will the man get on twice the principal in 2 years at the same rate.
Solution:
Let Principal amount = P
Simple Interest I = ₹ 2000
Rate of interest R = 5% p.a.
Time duration T = 4 years
I = \(\frac{\text { PRT }}{100}\)
∴ 2000 = \(\frac{\mathrm{P} \times 5 \times 4}{100}\)
∴ P = 10000
Twice the principal was invested for compound interest with the same rate of interest for 2 years.
Here, P = 2 × 10,000 = ₹ 20,000
∴ Amount received,

I = A – P = 22050 – 20000 = 2050
The man will receive ₹ 2050 as compound interest.
![]()
Question 11.
The difference between simple interest and compound interest on a certain sum of money is ₹ 32 at 8% per annum for 2 years. Find the amount.
Solution:
Compound Interest = A – P = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{T}}-\mathrm{P}\)
Simple interest = \(\frac{\text { PRT }}{100}\)
Given R = 8%, T = 2 years and
compound interest – simple interest = ₹ 32

∴ The man will receive a compound interest of ₹ 5000.
11th Commerce Maths Digest Pdf
- 11th Commerce Maths Exercise 9.1 Solutions
- 11th Commerce Maths Exercise 9.2 Solutions
- 11th Commerce Maths Exercise 9.3 Solutions
- 11th Commerce Maths Exercise 9.4 Solutions
- 11th Commerce Maths Exercise 9.5 Solutions
- 11th Commerce Maths Exercise 9.6 Solutions
- 11th Commerce Maths Exercise 9.7 Solutions
- 11th Commerce Maths Miscellaneous Exercise 9 Solutions