Differential Equation and Applications Class 12 Commerce Maths 1 Chapter 8 Exercise 8.4 Answers Maharashtra Board
Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.4 Questions and Answers.
Std 12 Maths 1 Exercise 8.4 Solutions Commerce Maths
Solve the following differential equations:
Question 1.
x dx + 2y dy = 0
Solution:
x dx + 2y dy = 0
Integrating, we get
∫x dx + 2 ∫y dy = c1
∴ \(\frac{x^{2}}{2}+2\left(\frac{y^{2}}{2}\right)=c_{1}\)
∴ x2 + 2y2 = c, where c = 2c1
This is the general solution.
![]()
Question 2.
y2 dx + (xy + x2) dy = 0
Solution:
y2 dx + (xy + x2) dy = 0
∴ (xy + x2) dy = -y2 dx
∴ \(\frac{d y}{d x}=\frac{-y^{2}}{x y+x^{2}}\) ………(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
Substituting these values in (1), we get

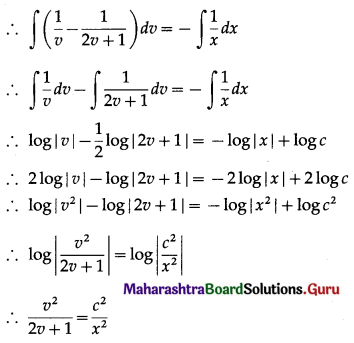
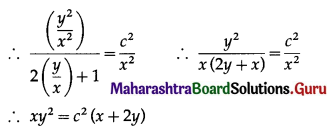
This is the general solution.
Question 3.
x2y dx – (x3 + y3) dy = 0
Solution:
x2y dx – (x3 + y3) dy = 0
∴ (x3 + y3) dy = x2y dx
∴ \(\frac{d y}{d x}=\frac{x^{2} y}{x^{3}+y^{3}}\) ……(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)


This is the general solution.
![]()
Question 4.
\(\frac{d y}{d x}+\frac{x-2 y}{2 x-y}=0\)
Solution:



This is the general solution.
Question 5.
(x2 – y2) dx + 2xy dy = 0
Solution:
(x2 – y2) dx + 2xy dy = 0
∴ 2xy dy = -(x2 – y2) dx = (y2 – x2) dx
∴ \(\frac{d y}{d x}=\frac{y^{2}-x^{2}}{2 x y}\) ………(1)
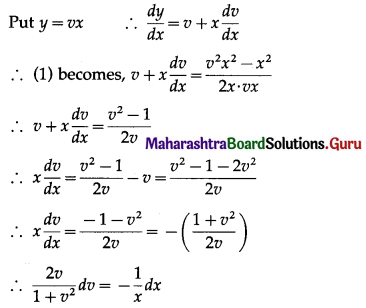

Question 6.
xy\(\frac{d y}{d x}\) = x2 + 2y2
Solution:


![]()
Question 7.
x2\(\frac{d y}{d x}\) = x2 + xy – y2
Solution:
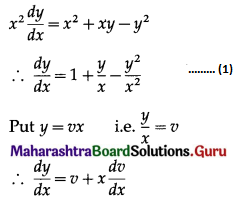

12th Commerce Maths Digest Pdf
- 12th Commerce Maths Exercise 8.1 Solutions
- 12th Commerce Maths Exercise 8.2 Solutions
- 12th Commerce Maths Exercise 8.3 Solutions
- 12th Commerce Maths Exercise 8.4 Solutions
- 12th Commerce Maths Exercise 8.5 Solutions
- 12th Commerce Maths Exercise 8.6 Solutions
- 12th Commerce Maths Miscellaneous Exercise 8 Solutions