Maharashtra Board 12th Commerce Maths Solutions Chapter 2 Matrices Ex 2.4

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 2 Matrices Ex 2.4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 2 Matrices Ex 2.4

Question 1.
Find A^T, if
(i) A = \(\left[\begin{array}{cc}
1 & 3 \\
-4 & 5
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{ccc}
2 & -6 & 1 \\
-4 & 0 & 5
\end{array}\right]\)
Solution:

Question 2.
If A = [a_ij]_3×3 where a_ij = 2(i – j). Find A and A^T. State whether A and A^T both are symmetric or skew-symmetric matrices.
Solution:


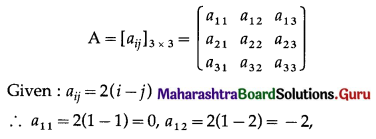
Hence, A and A^T are both skew-symmetric matrices.

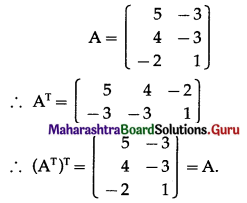
Question 3.
If A = \(\left[\begin{array}{cc}
5 & -3 \\
4 & -3 \\
-2 & 1
\end{array}\right]\), prove that (A^T)^T = A.
Solution:

Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\), prove that A^T = A.
Solution:

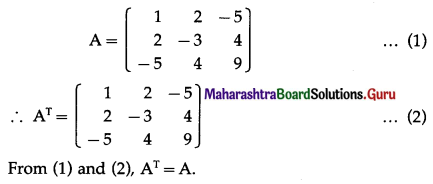
Question 5.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
5 & -4 \\
-6 & 1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 1 \\
4 & -1 \\
-3 & 3
\end{array}\right]\), C = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 4 \\
-2 & 3
\end{array}\right]\), then show that
(i) (A + B)^T = A^T + B^T
(ii) (A – C)^T = A^T – C^T
Solution:

Question 6.
If A = \(\left[\begin{array}{cc}
5 & 4 \\
-2 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
-1 & 3 \\
4 & -1
\end{array}\right]\), then find C^T, such that 3A – 2B + C = I, where I is the unit matrix of order 2.
Solution:

Question 7.
If A = \(\left[\begin{array}{ccc}
7 & 3 & 0 \\
0 & 4 & -2
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
0 & -2 & 3 \\
2 & 1 & -4
\end{array}\right]\), then find
(i) A^T + 4B^T
(ii) 5A^T – 5B^T
Solution:

Question 8.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
3 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{lll}
2 & 1 & -4 \\
3 & 5 & -2
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
0 & 2 & 3 \\
-1 & -1 & 0
\end{array}\right]\), verify that (A + 2B + 3C)^T = A^T + 2B^T + 3C^T
Solution:

Question 9.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
-3 & 2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
2 & 1 \\
-3 & 2 \\
-1 & 3
\end{array}\right]\), prove that (A + B^T)^T = A^T + B.
Solution:

From (1) and (2),
(A + B^T)^T = A^T + B.

Question 10.
Prove that A + A^T is symmetric and A – A^T is a skew-symmetric matrix, where
(i) A = \(\left[\begin{array}{ccc}
1 & 2 & 4 \\
3 & 2 & 1 \\
-2 & -3 & 2
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{ccc}
5 & 2 & -4 \\
3 & -7 & 2 \\
4 & -5 & -3
\end{array}\right]\)
Solution:

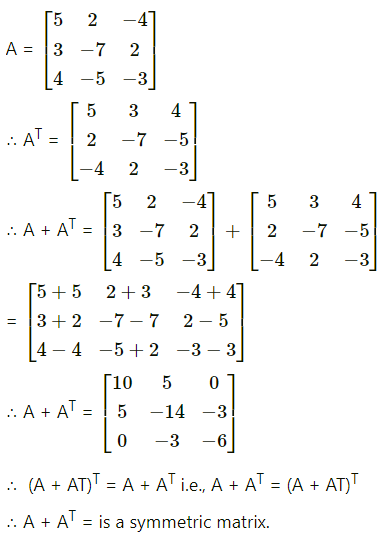
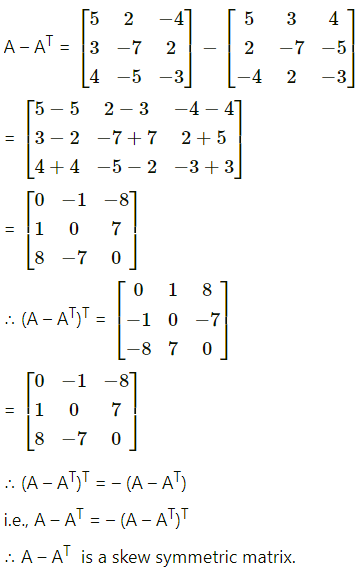
Question 11.
Express each of the following matrix as the sum of a symmetric and a skew-symmetric matrix:
(i) \(\left[\begin{array}{ll}
4 & -2 \\
3 & -5
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\)
Solution:

Question 12.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
3 & -2 \\
4 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
0 & 3 & -4 \\
2 & -1 & 1
\end{array}\right]\), verify that
(i) (AB)^T = B^TA^T
(ii) (BA)^T = A^TB^T
Solution: