Maharashtra Board Class 11 Physics Important Questions Chapter 6 Mechanical Properties of Solids

Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 6 Mechanical Properties of Solids Important Questions and Answers.

Maharashtra State Board 11th Physics Important Questions Chapter 6 Mechanical Properties of Solids

Question 1.
Explain the equilibrium state of solids at a given temperature.
Answer:

1. Solids are made up of atoms or a group of atoms placed in a definite geometric arrangement.
2. This arrangement is decided by nature so that the resultant force acting on each constituent due to others is zero. This is the equilibrium state of a solid at room temperature.
3. This equilibrium arrangement does not change with time but it can only change when an external stimulus, like compressive force is applied to a solid from all sides.
4. The constituents vibrate about their equilibrium positions even at very low temperature but cannot leave their fixed positions.
5. As a result, the solids possess a definite shape and size.

Question 2.
Explain the effects of applied force on a rigid body.
Answer:

1. When an external force is applied to a solid, the constituents are slightly displaced and restoring forces are developed in it.
2. These restoring forces try to bring the constituents back to their equilibrium positions so that the solid can regain its shape.
3. When the deforming forces are removed, the inter-atomic forces tend to restore the original positions of the molecules and thus the body regains its original shape and size.

Question 3.
Explain the concept of deforming force with the help of examples.
Answer:

1. When a force (within specific limit) is applied to a solid (which is not free to move), the size or shape or both change due to changes in the relative positions of molecules. Such a force is called deforming force.
2. The larger the deforming force on a body, the larger is its deformation.
3. Deformation could be in the form of change in length of a wire, change in volume of an object or change in shape of a body.
4. Examples:
   • When a deforming force such as stretching, is applied to a rubber band, it gets deformed (elongated) but when the force is removed, it regains its original length.
   • When a similar force is applied to a dough or a clay, it also gets deformed but it does not regain its original shape and size after removal of the deforming force.

Question 4.
Define plasticity.
Answer:
If a body does not regain its original shape and size and retains its altered shape or size upon removal of the deforming force, it is called a plastic body and the property is called plasticity.

Question 5.
When is a body said to be perfectly elastic? Give an example for perfectly elastic body and perfectly plastic body.
Answer:

1. If a body regains its original shape and size completely and instantaneously upon removal of the deforming force, then it is said to be perfectly elastic.

• • There is no solid which is perfectly elastic or perfectly plastic,
  • The best example of a near perfectly elastic body is quartz fibre and that of a plastic body is putty.

Question 6.
State SI unit and dimensions of strain.
Answer:
Strain is the ratio of two similar quantities. Hence strain is a dimensionless physical quantity and it has no units.

Question 7.
State and explain longitudinal stress (Tensile stress and Compressive stress).
Answer:
i. Stress produced by a deforming force acting along the length of a body or a rod is called longitudinal stress.

ii. Tensile stress: Consider a force F is applied along a length of a wire, or perpendicular to its cross-section A of a wire (or along its length).

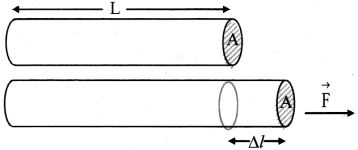
[Note: Elongation of wire ∆l is exaggerated for explanation.]
This produces an elongation in the wire and the length of the wire increases, then

iii. Compressive stress: When a rod is pushed from two ends with equal and opposite forces.

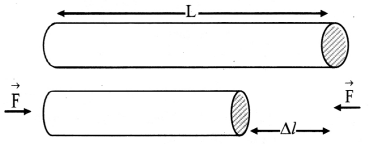
[Note: Compression of wire ∆l is exaggerated for explanation.]
This restoring force per unit area is called compressive stress.
Compressive stress = \(\frac{|\overrightarrow{\mathrm{F}}|}{\mathrm{A}}\)

Question 8.
State and explain longitudinal strain (Tensile strain or Linear strain).
Answer:
The strain produced by a tensile deforming force is called longitudinal strain (tensile strain or linear strain,).

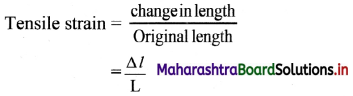
where, L = Original length,
∆l = Change in length.

Question 9.
State and explain volume stress / hydraulic stress.
Answer:
When a deforming force acting on a body produces change in its volume, the stress is called volume stress.
Volume stress/hydraulic stress:

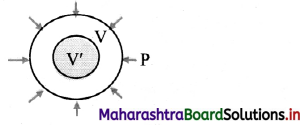
[Note: Change in size is exaggerated for explanation.]

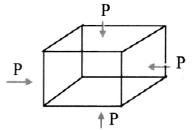
1. Let \(\vec{F}\) be a force acting perpendicular to the entire surface of the body.
2. It acts normally and uniformly all over the surface area A of the body.
3. Such a stress which produces change in size but no change in shape is called volume stress.
   Volume stress = \(\frac{|\overrightarrow{\mathrm{F}}|}{\mathrm{A}}\)
4. Volume stress produces change in size without change in shape of body, hence it is also called as hydraulic or hydrostatic volume stress.

Question 10.
Explain volume strain.
Answer:

1. A deforming force acting perpendicular to the entire surface of a body produces a volume strain.
2. 
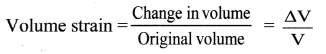
   where ∆V = change in volume,
   V = original volume.

Question 11.
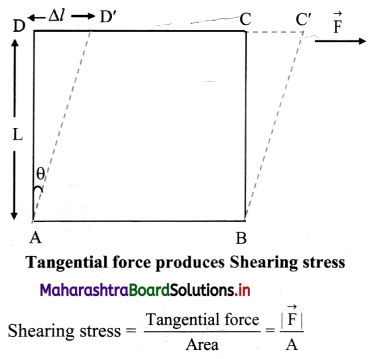
Define and explain shearing stress.
Answer:
The restoring force per unit area developed due to the applied tangential force is called shearing stress or tangential stress.
Shearing stress:

1. When a deforming force acting on a body produces change in the shape of a body shearing stress is produced.
2. Consider ABCD as a front face of a cube, a tangential force is applied to the cube so that the bottom of the cube is fixed and only the top surface is slightly displaced.
   

Question 12.
Explain shearing strain.
Answer:

1. The relative displacement of the bottom face and the top face of the cube is called shearing strain.
2. Shearing strain = \(\frac{\Delta l}{\mathrm{~L}}\) = tan θ
   where, ∆l = displaced length,
   L = Original length.
3. When ∆l is very small,
   tan θ ≈ θ and shearing strain = θ

Question 13.
State and explain Hooke’s law.
Answer:
Statement: Within elastic limit, stress is directly proportional to strain.
Explanation:

1. According to Hooke’s law,
   Stress-Strain
   
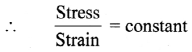
   This constant of proportionality is called modulus of elasticity.
2. Modulus of elasticity of a material is the slope of stress-strain curve in elastic deformation region and depends on the nature of the material.
3. The graph of strain (on X-axis) and stress (on Y-axis) within elastic limit is shown in the figure.
   

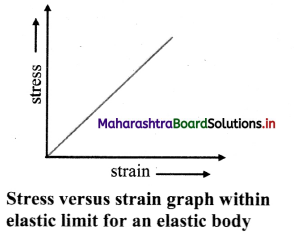
Question 14.
Define elastic limit.
Answer:
The maximum value of stress upto which stress is directly proportional to strain is called the elastic limit.

Question 15.
Define modulus of elasticity.
Answer:
The modulus of elasticity of a material is the ratio of stress to the corresponding strain.

Question 16.
State different types of modulus of elasticity.
Answer:

1. Young’s modulus (Y): It is the modulus of elasticity related to change in length of an object like a metal wire, rod, beam, etc., due to the applied deforming force.
2. Bulk modulus (K): It is the modulus of elasticity related to change in volume of an object due to applied deforming force.
3. Shear modulus or Modulus of rigidity (η): The modulus of elasticity related to change in shape of an object is called modulus of rigidity.

Question 17.
Explain the usefulness of Young’s modulus.
Answer:

1. Young’s modulus indicates the resistance of an elastic solid to elongation or compression.
2. Young’s modulus of a material is useful for characterization of an object subjected to compression or tension.

Question 18.
Within elastic limit, prove that Young’s modulus of material of wire is the stress required to double the length of wire.
Answer:

(i) Let, L = Initial length of wire
2 L = Final length of wire
∴ Increase in length = ∆l = 2L – L = L

(ii) Longitudinal strain of wire = \(\frac{\Delta l}{\mathrm{~L}}=\frac{\mathrm{L}}{\mathrm{L}}=1\)

(iii)

∴ Y = Longitudinal stress

(iv) Hence, Young’s modulus of material of wire is the stress required to double the length of wire.

Question 19.
What is bulk modulus? Derive an expression for bulk modulus.
Answer:
Definition:
Bulk modulus is defined as the ratio of volume stress to volume strain.
It is denoted by ‘K’.
Unit: N/m² or Pa in SI system
Dimensions: [L^-1M¹T^-2]
Expression for bulk modulus:

(i) If a sphere made from rubber is completely immersed in a liquid, it will be uniformly compressed from all sides.
Let, F = Compressive force,
dP = Change in pressure,
dV = Change in volume,
V = Original volume.

(ii) Volume stress = \(\frac{|\overrightarrow{\mathrm{F}}|}{\mathrm{A}}\) = dP

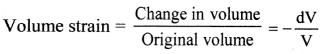
(iii) The negative sign indicates that there is a decrease in volume.
The magnitude of the volume strain is \(\frac{\mathrm{dV}}{\mathrm{V}}\)

Question 20.
Explain the usefulness of bulk modulus.
Answer:

1. Bulk modulus indicates the resistance of gases, liquids or solids to change their volume.
2. Materials with small bulk modulus and large compressibility are easier to compress.

Question 21.
State few applications of bulk modulus.
Answer:

1. When a balloon is filled with air at high pressure, its walls experience a force from within. It tries to expand the balloon and change its size without changing shape. When the volume stress exceeds the limit of bulk elasticity, the balloon explodes.
2. A gas cylinder explodes when the pressure inside it exceeds the limit of bulk elasticity of its material.
3. A submarine when submerged under water is under volume stress. The depth it can reach within water depends upon its limit of bulk elasticity.

Question 22.
Define compressibility. State its unit and dimensions.
Answer:

1. The reciprocal of bulk modulus of elasticity is called compressibility of the material.
   
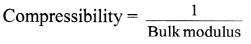
2. Compressibility is the fractional decrease in volume, (-dV/V) per unit increase in pressure.
   Compressibility = \(\frac{-\mathrm{dV}}{\mathrm{V} \mathrm{dP}}\)
3. Unit: m²/N or Pa^-1 in SI system.
4. Dimensions: [L¹M^-1T²]

Question 23.
What is modulus of rigidity? Derive an expression for it.
Answer:
Definition: It is defined (is the ratio of shear stress to shear strain within elastic limit.
It is denoted by ‘η’.
Unit: N/m² or Pa in SI system.
Dimension: [L^-1M¹T^-2]

Expression for modulus of rigidity:

Consider a solid cube as shown in the figure.

Let, F = Tangential force
A = Cross sectional area
∆l = Relative displaced length
l = Original length
θ = Shear strain

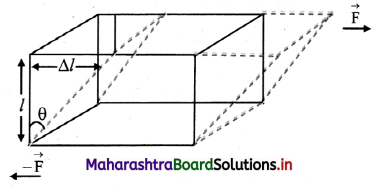
[Note: Displacement of upper surface is exaggerated for explanation.]
The forces applied on the block is subjected to a shear stress,
Shearing stress = F/A
The comer angle which changes by a small amount θ (expressed in radian) is given by,
Shearing strain = \(\frac{\Delta l}{l}\) ≈ θ
From definition,

Question 24.
What does modulus of rigidity indicate?
Answer:
Modulus of rigidity indicates resistance offered by solid to change in its shape.

Question 25.
Explain the change of diameter of a wire when it is stretched and compressed.
Answer:
i. When a wire is fixed at one end and a force is applied at its free end so that the wire gets stretched, length of the wire increases and at the same time, its diameter decreases, i.e., the wire becomes longer and thinner as shown in figure.

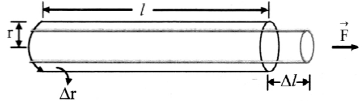
[Note: Linear expansion ∆l is exaggerated far explanation.]

ii. If equal and opposite forces are applied to an object along its length inwards, the object gets compressed. There is a decrease in dimensions along its length and at the same time there is an increase in its dimensions perpendicular to its length. When length of the wire decreases, its diameter increases.

[Note: Compression of wire ∆l is exaggerated for explanation.]

Question 26.
Derive expression for Poisson’s ratio.
Answer:
i. Let,
L = original length
l = increase/decrease in length
D = original diameter
d = change in diameter

ii. The ratio of change in dimensions to original dimensions in the direction of the applied force is called linear strain.
Linear strain = \(\frac{l}{\mathrm{~L}}\) …. (1)

iii. The ratio of change in dimensions to original dimensions in a direction perpendicular to the applied force is called lateral strain.
Lateral strain = \(\frac{\mathrm{d}}{\mathrm{D}}\) ….(2)

iv. Poisson’s ration,

Question 27.
A wire of length 20 m and area of cross section 1.25 × 10^-4 m² is subjected to a load of 2.5 kg. (1 kg wt = 9.8 N). The elongation produced in wire is 1 × 10^-4 m. Calculate Young’s modulus of the material.
Solution:
L = 20 m, A = 1.25 × 10^-4m²,
F = mg = 2.5 × 9.8 N, l = 10^-4 m
Formula Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}\)
To find: Young’s modulus (Y)
Calculation: From formula,
Y = \(\frac{2.5 \times 9.8 \times 20}{1.25 \times 10^{-4} \times 10^{-4}}\) = 3.92 × 10¹⁰Nm^-2
Answer: The Young’s modulus of the material is 3.92 × 10¹⁰ Nm^-2.

Question 28.
A wire of diameter 0.5 mm and length 2 m is stretched by applying a force of 2 kg wt. Calculate the increase in length of the wire, (g = 9.8 m/s², Y = 9 × 10¹⁰ N/m²)
Solution:
Given:
L = 2 m, F = 2 kg wt, d = 0.5 mm = 5 × 10^-4 m,
∴ r = \(\frac{\mathrm{d}}{2}\) = 2.5 × 10^-4 m.
Y = 9 × 10¹⁰ N/m², g = 9.8 m/s²
To find: Increase in length (l)
Formula: Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{MgL}}{\pi \mathrm{r}^{2} l}\)
Calculation:
From formula,

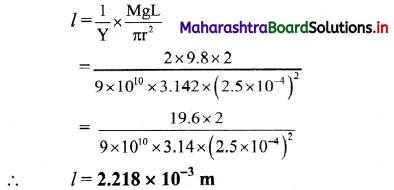
Answer:
The increase in length of the wire is 2.218 × 10^-3 m.

Question 29.
A brass wire of length 4.5 m with cross-section area of 3 × 10^-5 m² and a copper wire of length 5.0 m with cross section area 4 × 10^-5 m² are stretched by the same load. The same elongation is produced in both the wires. Find the ratio of Young’s modulus of brass and copper.
Solution:
L_B = 4.5 m, A_B = 3 × 10^-5 m²
L_C = 5 m, A_C = 4 × 10^-5 m² l_B = _C, F_B = F_C
To find: Ratio of Young’s modulus \(\left(\frac{Y_{B}}{Y_{C}}\right)\)
Formula: Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}\)
Calculation: For brass,

= 1.2
Answer:
The ratio of Young’s modulus of brass and copper is 1.2 : 1.

Question 30.
The length of wire increases by 9 mm when weight of 2.5 kg is hung from the free end of wire. If all conditions are kept the same and the radius of wire is made thrice the original radius, find the increase in length.
Solution:
Given; l₁ = 9mm = 9 × 10^-3m,
M = 2.5 kg, r₂ = 3r₁,
Y₁ = Y₂ = Y (material is same)
To find: Increase in length (l₂)
Formula: Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}\)
Calculation: From formula,

Answer:
The longitudinal strain produced in 1st wire is

Question 31.
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in the figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.(Y_s = 2.0 × 10¹¹ Nm^-2, Y_B = 0.91 × 10¹¹ Nm^-2) (NCERT)

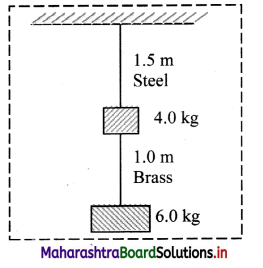
Solution:
Given: D = 0.25 cm = 0.25 × 10^-2 m,
L_S = 1.5 m, L_B = 1 m,
Y_S = 2.0 × 10¹¹ Nm^-2,
Y_B = 0.91 × 10¹¹ Nm^-2
To find: Elongations of brass wire (l_B)
Elongations of steel wire (l_S)

Formula: Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}\)

Calculation: Since, A = \(\frac{\pi \mathrm{D}^{2}}{4}\)

Answer:
The elongation of the steel wire is 1.5 × 10^-4 m and that of brass wires is 1.32 × 10^-4 m.

Question 32.
One end of steel wire is fixed to a ceiling and load of 2.5 kg is attached to the free end of the wire. Another identical wire is attached to the bottom of load and another load of 2.0 kg, is attached to the lower end of this wire as shown in the figure. Compute the longitudinal strain produced in both the wires, if the cross-sectional area of wires is 10^-4m², (Y_steel = 20 × 10¹⁰N/m²)

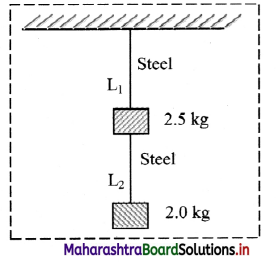
Solution:
Given: M₁ = 2.5 kg, M₂ = 2kg, A = 10^-4m², Y_steel = 20 × 10¹⁰ N/m², L₁ = L₂ = L
To find: Longitudinal strain of 1^st wire (Strain₁).
Longitudinal strain of 2^nd wire (Strain₂)

Answer:
The longitudinal strain produced in 1^st wire is 1.225 × 10^-6 and in 2^nd wire is 2.205 × 10^-6

Question 33.
A steel wire having cross-sectional area 2 mm² is stretched by 10 N. Find the lateral strain produced in the wire. (Given: Y for steel = 2 × 10¹¹ N/m², Poisson’s ratio σ = 0.29)
Solution:
Given: A = 2 mm² = 2 × 10^-6 m²,
F = 10 N, Y_stee; = 2 × 10¹¹ N/m², σ = 0.29

To find: Lateral strain
Formulae:

Calculation: From formula (i),
longitudinal stress = \(\frac{10}{2 \times 10^{-6}}\)
= 5 × 10⁶ N/m²
From formula (ii),

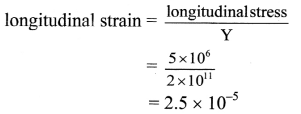
From formula (iii),
lateral strain = σ × longitudinal strain
= 0.29 × 2.5 × 10^-5
∴ lateral strain = 7.25 × 10^-6
Answer:
Lateral strain produced in the wire is 7.25 × 10^-6.

Question 34.
A brass wire of radius 1 mm is loaded by a mass of 31.42 kg. What would be the decrease in its radius? (Y = 9 × 10¹⁰ N/m², Poisson’s ratio σ = 0.36)
Solution:
Given: R = 1 mm = 1 × 10^-3 m, M = 31.42 kg, Y = 9 × 10¹⁰ N/m², σ = 0.36
To find: Decrease in radius (r)

Formulae:

i. Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}\)
ii. σ = \(\frac{\mathrm{Lr}}{l \mathrm{R}}\)

Calculation: From formula (i),

Answer:
The decrease in radius of the brass wire would be 3.92 × 10^-7 m

Question 35.
A metal cube of side 1 m is subjected to a force. The force acts normally on the whole surface of cube and its volume changes by 1.5 × 10^-5 m³. The bulk modulus of metal is 6.6 × 10¹⁰ N/m². Calculate the change in pressure.
Solution:
Given: L = 1 m, dV = 1.5 × 10^-5 m³,
K = 6.6 × 10¹⁰ N/m².
To find: Change in pressure (dP)
Formula: K = V\(\frac{\mathrm{dP}}{\mathrm{dV}}\)
Calculation: From formula,

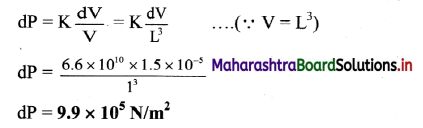
Answer:
The change in pressure is 9.9 × 10⁵ N/m².

Question 36.
Determine the volume contraction of solid copper cube, 10 cm on an edge, when subjected to a hydraulic pressure of 7.0 × 10⁶ P.a. (Bulk modulus of copper = 140 × 10⁹ pa)
Solution:
Given: L = 10 cm =0.1 m, ∆P = 7 × 10⁶ Pa, K = 140 × 10⁹ pa
To find: Volume contraction (dV)
Formula: K = V × \(\frac{\mathrm{dP}}{\mathrm{dV}}\)
Calculation: From formula,
dV = \(\mathrm{L}^{3} \times \frac{\mathrm{dP}}{\mathrm{K}}\) = (0.1)³ × \(\frac{7 \times 10^{6}}{140 \times 10^{9}}\)
∴ dV = 5 × 10^-8 m³
Answer:
The volume contraction of solid copper cube is 5 × 10^-8 m³

Question 37.
Calculate the modulus of rigidity of a metal, if a metal cube of side 40 cm is subjected to a shearing force of 2000 N. The upper surface is displaced through 0.5 cm with respect to the bottom. Calculate the modulus of rigidity of the metal.
Solution:
Given: L = 40 cm = 0.4 m,
F = 2000 N = 2 × 10³N
l = 0.5 cm = 0.005 m, A = L² = 0.16 m²
To find: Modulus of rigidity (η)

Formulae:

i. θ = \(\frac{l}{\mathrm{~L}}\)
ii. η = \(\frac{\mathrm{F}}{\mathrm{A} \theta}\)

Calculation:

From formula (i),
θ = \(\frac{0.005}{0.4}\) = 0.0125
From formula (ii),
η = \(\frac{2 \times 10^{3}}{0.16 \times 0.0125}\) = 1 × 10⁶ N/m²
Answer:
The modulus of rigidity of the metal cube is 1 × 10⁶ N/m².

Question 38.
A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44500 N forces producing only elastic deformation. Calculate the resulting strain. (Rigidity modulus of copper = 42 × 10⁹ N m^-2)
Solution:
Given: A = 15.2 × 19.14 × 10^-6 m²,
F = 44500 N, η = 42 × 10⁹ N m^-2
To find: Strain (θ)
Formula: η = \(\frac{\mathrm{F}}{\mathrm{A} \theta}\)

Calculation:
From formula,

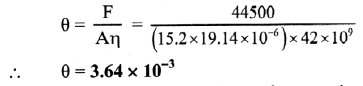
Answer:
The strain produced in the piece of copper is 3.64 × 10^-3

Question 39.
A copper metal cube has each side of length 1 m. The bottom edge of cube is fixed and tangential force 4.2 × 10⁸ N is applied to top surface. Calculate the lateral displacement of the top surface, if modulus of rigidity of copper is 14 × 10¹⁰ N/m².
Solution:
Given: L = h = 1 m, F = 4.2 × 10⁸ N, η = 1.4 × 10¹¹ N/m²
To find: Lateral displacement (x)
Formula: η = \(\frac{\mathrm{F}}{\mathrm{A} / \theta}\) = \(\frac{\mathrm{Fh}}{\mathrm{Ax}}\)
Calculation: From formula,
x = \(\frac{\mathrm{Fh}}{\mathrm{A\eta}}\)
∴ x = \(\frac{4.2 \times 10^{8} \times 1}{(1 \times 1) \times 1.4 \times 10^{11}}\) = 3 × 10^-3 m
∴ x = 3 mm
Answer:
The lateral displacement of top is 3 mm.

Question 40.
The area of the upper face of a rectangular block is 0.5 m × 0.5 m and the lower face is fixed. The height of the block is 1 cm. A shearing force applied at the top face produces a displacement of 0.0 15 mm. Find the strain and shearing force. (Modulus of rigidity: η = 4.5 × 10¹⁰ N/m²)
Solution:
Given: A = 0.5 m × 0.5 m = 0.25 m²,
h = 1 cm = 10^-2m,
x = 0.015 mm = 15 × 10^-6m
η = 4.5 × 10¹⁰ N/m²
To find: Strain (θ). Shearing force (F)

Formulae:

i. θ = \(\frac{\mathrm{x}}{\mathrm{h}}\)
ii. F = ηAθ

Calculations:

Using formula (i),
θ = \(\frac{15 \times 10^{-6}}{10^{-2}}\) = 1.5 × 10^-3
Using formula (ii),
F = 4.5 × 10¹⁰ × 0.25 × 1.5 × 10^-3
= 1.688 × 10⁷ N
Answer:
Shearing force is 1.688 × 10⁷ N and strain is 1.5 × 10^-3

Question 41.
Explain the behaviour of metal wire under increasing load.
Answer:
Consider a metal wire suspended vertically from a rigid support and stretched by applying load to its lower end. The load is gradually increased in small steps until the wire breaks. The elongation produced in the wire is measured during each step. Stress and strain are noted for each load and a graph is drawn by taking tensile strain along X-axis and tensile stress along Y-axis. It is a stress-strain curve as shown in the figure.

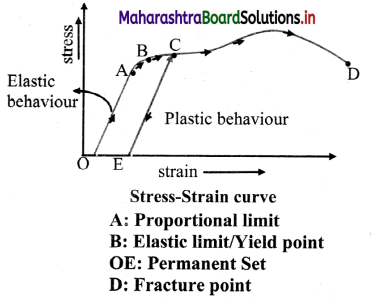
1. Proportional limit: The initial part of the graph is a straight line OA. This is the region in which Hooke’s law is obeyed and stress is directly proportional to stain. The straight line portion ends at A. The stress at this point is called proportional limit.
2. Yield point: If the load is further increased till point B is reached, stress and strain are no longer proportional and Hooke’s law is not valid. If the load is gradually removed starting at any point between O and B. The curve is retracted until the wire regains its original length. The change is reversible. The material of the wire shows elastic behaviour in the region OB. Point B is called the yield point. It is also known as the elastic limit.
3. Permanent Set: When the stress is increased beyond point B, the strain continues to increase. If the load is removed at any point beyond B, for example (at C), the material does not regain its original length. It follows the line CE. Length of the wire when there is no stress is greater than the original length. The deformation is irreversible and the material has acquired a permanent set.
4. Fracture point: Further increase in load causes a large increase in strain for relatively small increase in stress, until a point D is reached at which fracture takes place. The material shows plastic flow or plastic deformation from point B to point D. The material does not regain its original state when the stress is removed. The deformation is called plastic deformation.

Question 42.
Stress-strain curve for two materials A and B are shown in the figure. The graphs are drawn to the same scale.

1. Which material has greater Young’s modulus?
2. Which of the two is the stronger material? (NCERT)

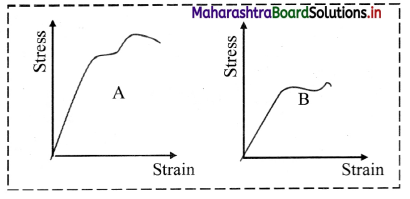
Answer:

1. For a given strain, stress for A is more than that of B. Hence, Young’s modulus (= stress/strain) is greater for A than that of B.
2. Material A is stronger than B because A can bear greater stress before the breaking of the wire.

Question 43.
Figure shows the stress-strain curve for a given material. What are

1. Young’s modulus and
2. approximate yield strength for this material? (NCERT)

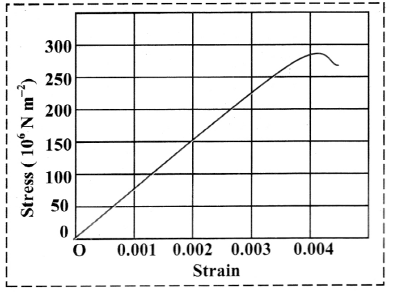
Answer:

1. The graph, implies stress of 150 × 10⁶ N m^-2 corresponds to a strain of 0.002. Therefore, Young’s modulus is,
   
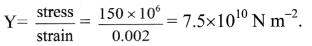
2. The yield strength for the material is less than 300 × 10⁶ N m^-2, i.e.. 3 × 10⁸ N m^-2 and greater than 2.5 × 10⁸ N m^-2.

Question 44.
Explain the following terms:

1. Ductile
2. Malleable

Answer:

1. Metals such as copper, aluminium, wrought iron, etc. have large plastic range of extension. They lengthen considerably and undergo plastic deformation till they break. They are called ductile.
2. Metals such as gold, silver which can be hammered into thin sheets are called malleable.

Question 45.
Define strain energy.
Answer:
The elastic potential energy gained by a wire during elongation b a stretching force is called as strain energy.

Question 46.
A steel wire is acted upon by a load of 10 N. Calculate the extension produced in the wire, if the strain energy stored in the wire is 1.1 × 10^-3 J.
Solution:
Given: F = 10 N, Strain energy =1.1 × 10^-3 J,
To find: Extension (l)
Formula: W = \(\frac{1}{2}\) × F × l
Calculation:
From formula,
l = \(\frac{2 \mathrm{~W}}{\mathrm{~F}}\) = \(\frac{2 \times 1.1 \times 10^{-3}}{10}\) = 2.2 × 10^-4 m.
Answer:
The extension produced in the wire is 2.2 × 10^-4 m.

Question 47.
Calculate the strain energy per unit volume in a brass wire of length 3 m and area of cross-section 0.6 mm² when it is stretched by 3 mm and a force of 6 kg-wt is applied to its free end.
Solution:
Given: L = 3 m, F = 6 kg wt = 6 × 9.8N = 58.8N, A = 0.6 mm² = 0.6 × 10^-6 m², l = 3 mm = 3 × 10^-3 m
To find: Strain energy per unit volume (u)

Formulae:

i. Stress = \(\frac{F}{A}\)
ii. Strain = \(\frac{l}{L}\)
iii. u = \(\frac{1}{2}\) × Stress × Strain

Calculation:

From formula (i),
Stress = \(\frac{F}{A}\) = \(\frac{58.8}{0.6 \times 10^{-6}}\) = 98 × 10⁶ N/m²
From formula (ii),
Strain = \(\frac{l}{L}\) = \(\frac{3 \times 10^{-3}}{3}\) = 10^-3
From formula (iii),
u = \(\frac{1}{2}\) × Stress × Strain
= \(\frac{1}{2}\) × 98 × 10⁶ × 10^-3
u = 49 × 10³ J/m³
Answer:
Strain energy per unit volume in the brass wire is 49 × 10³ J/m³

Question 48.
A steel wire of diameter 1 × 10^-3 m is stretched by a force of 20 N. Calculate the strain energy per unit volume. (Y_steel = 2 × 10¹¹ N/m²)
Solution:
Given: d = 1 × 10^-3 m, r = 5 × 10^-4 m, y_steel = 2 × 10¹¹ N/m²
To find: Strain energy per unit volume
Formula: Strain energy per unit volume
= \(\frac{1}{2}\) × \(\frac{\text { (stress) }^{2}}{\mathrm{Y}}\)
Calculation:
From formula.
Strain energy per unit volume

Answer:
The strain energy per unit volume of the steel wire is 1621 J.

Question 49.
A uniform steel wire of length 3 m and area of cross section 2 mm² is extended through 3 mm. Calculate the energy stored in the wire, if the elastic limit is not exceeded. (Y_steel = 20 × 10¹⁰ N/m²)
Solution:
Given: L = 3 m, A = 2 mm² = 2 × 10^-6 m²,
l = 3 mm = 3 × 10^-3 m,
Y_steel = 20 × 10¹⁰ N/m²
To find: Energy stored (U)
Formula: W = \(\frac{1}{2}\) × F × l
Calculation: Since, Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}\)

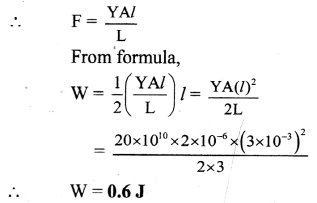
Answer:
The energy stored in the steel wire is 0.6 J.

Question 50.
Explain the following terms:
i. Hardness
ii. Strength
iii. Toughness
Answer:

i. Hardness:

1. Hardness is the property of a material which enables it to resist plastic deformation.
2. Hard materials have little ductility and they are brittle to some extent.
3. The term hardness also refers to stiffness or resistance to bending, scratching, abrasion or cutting.
4. It is the property of a material which gives it the ability to resist permanent deformation when a load is applied to it.
5. The greater the hardness, greater is the resistance to deformation.
6. Hardness of material is different from its strength and toughness.
7. The most well known example for hard material is diamond, while metal with very low hardness is aluminium.

ii. Strength:

1. If a force is applied to a body, it produces deformation in it.
2. Higher is the force required for deformation, the stronger is the material, i.e., the material has more strength.
3. Steel has high strength whereas plasticine clay is not strong because it gets easily deformed even by a small force.

iii. Toughness:

1. Toughness is the ability of a material to resist fracturing when a force is applied to it.
2. Plasticine clay is relatively tough as it can be stretched and deformed due to applied force without breaking.

Question 51.
Explain the concept of frictional force.
Answer:

1. Whenever the surface of one body slides over another, each body exerts a certain amount of force on other body.
2. These forces are tangential to the surfaces. The force on each body is opposite to the direction of motion between two bodies.
3. It prevents or opposes the relative motion between two bodies.
4. It is common experience that an object placed on any surface does not move easily when a small force is applied to it.
5. This is because of certain force of opposition acting between the surface of the object and the surface on which it is placed.
6. To initiate any motion between pair of surfaces, we need a certain minimum force. Also, after the motion begins, it is constantly opposed by some natural force.
7. This mechanical force between two solid surfaces in contact with each other is called as frictional force.

Question 52.
Explain few examples of friction.
Answer:

1. A rolling ball comes to rest after covering a finite distance on playground because of friction.
2. Our foot ware is provided with designs at the bottom of its sole so as to produce force of opposition to avoid slipping. It is difficult to walk without such opposing force. When we try to walk fast on polished flooring at home with soap water spread on it. There is a possibility of slipping due to lack of force of friction.
3. Relative motion between solids and fluids (i.e. liquids and gases) is also opposed naturally by friction, eg.: a boat on the surface of water experiences opposition to its motion.

Question 53.
Explain the origin of friction.
Answer:

1. If smooth surfaces are observed under powerful microscope, many irregularities and projections are observed.
2. Friction arises due to interlocking of these irregularities between two surfaces in contact.
3. The surfaces can be made extremely smooth by polishing to avoid irregularities but then case also, friction does not decrease but may increase.
4. Hence the interlocking of irregularities is not the real cause of friction.
5. According to modem theory, cause of friction is the force of attraction between molecules of two surfaces in actual contact in addition to the. force due to the interlocking between the two surfaces.
6. When one body is in contact with another body, the real microscopic area in contact is very small due to irregularities in contact.
   
7. Due to small area, pressures at points of contact is very high. Hence there is strong force of attraction between the surfaces in contact.
8. When the surfaces in contact become more and more smooth, the actual area of contact goes on increasing.
9. Due to this, the force of attraction between the molecules increases and hence the friction also increases.

Question 54.
State the following terms:

1. Cohesive force
2. Adhesive force

Answer:

1. When two Surfaces are of the same material, the force of attraction between them is called cohesive force.
2. When two surfaces are of different materials, the force of attraction between them is called adhesive force.

Question 55.
Explain the concept of static friction.
Answer:

1. Consider a wooden block placed on a horizontal surface as shown in the figure and small horizontal force F is applied to it.
   
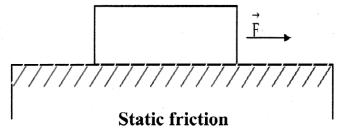
2. The block does not move with this force as it cannot overcome the frictional force between the block and horizontal surface.
3. In this case the force of static friction is equal to F and balances it.
4. The frictional force which balances applied force when the body is static is called force of static friction. In other words, static friction prevents sliding motion.
5. If we keep increasing F, a stage will come
   • For F < F_max, the force of static friction is equal to F.
   • when for F = F_max, the object will start moving.
   • For F ≥ F_max, the kinetic friction comes into play.
6. Static friction opposes impending motion i.e. the motion that would take place in absence of frictional force under the applied force.

Question 56.
Define limiting force of friction.
Answer:
Just before the body starts sliding over another body, the value of frictional force is maximum, it is called as limiting force of friction.

Question 57.
Explain the concept of kinetic friction.
Answer:

1. Once the sliding of block on the surface starts the force of friction decreases.
2. The force required to keep the body sliding steadily is thus less than the force required to just start its sliding.
3. The force of friction that comes into play when a body is in steady state of motion over another surface is called kinetic fòrce of friction.
4. Friction between two surfaces in contact when one body is actually sliding over the other body, is called kinetic friction or dynamic friction.

Question 58.
Why ball bearings are used in machines?
Answer:

1. For same pair of surfaces, the force of static friction is greater than the force of kinetic friction while the force of kinetic friction is greater than force of rolling friction.
2. As ball bearing undergo rolling friction and rolling friction is the minimum, ball bearings are used to reduce friction in parts of machines to increase its efficiency.

Question 59.
The coefficient of static friction between a block of mass 0.25 kg and a horizontal surface is 0.4. Find the horizontal force applied to it.
Solution:
Given: μ_s = 0.4, m = 0.25 kg, g = 9.8 m/s²
To find: Force (F_L)
Formula: F_L = μ_sN = μ_s(mg)
Calculation: From formula,
F_L = 0.4 × 0.25 × 9.8 = 0.98 N
Answer:
The horizontal force applied to it is 0.98 N.

Question 60.
Calculate the force required to move a block of mass 20 kg resting on a horizontal surface, if μ_s = 0.3 and g = 9.8 m/s².
Solution:
Given: m = 20 kg, μ_s = 0.3, g = 9.8 m/s²
To find. Force required (F)
Formula: F_S = μ_sN = μ_smg
Calculation: From formula,
F_S = 3 × 20 × 9.8 = 58.8N
Answer:
The force required to move the block is 58.8 N.

Question 61.
A block of mass 40 kg resting on a horizontal surface just begins to slide when a horizontal force of 120 N is applied to it. Once the motion starts, It can be maintained by a force of 80 N. Determine the coefficients of static friction and kinetic friction (g = 9.8 m/s²)
Solution:
Given: F_L= 120N, F_k = 80N, m = 40 kg, g = 9.8 m/s²

To find:

i. Coefficient of static friction (μ_s)
ii. Coefficient of kinetic friction (μ_k)

Formulae:

i. μ_s = \(\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}\)
ii. μ_k = \(\frac{\mathrm{F}_{\mathrm{k}}}{\mathrm{N}}\)

Calculation:

From formula (i) we get.
N = mg = 40 × 9.8 = 392 N
∴ μ_s = \(\frac{F_{L}}{N}\) = \(\frac{120}{392}\) = 0.306
From formula (ii) we get,
∴ μ_k = \(\frac{F_{k}}{N}\) = \(\frac{80}{392}\) = 0.204
Answer:

1. The coefficient of static friction is 0.306.
2. The coefficient of kinetic friction is 0.204.

Question 62.
A 20 kg metal block is placed on a horizontal surface. The block just begins to slide when horizontal force of 100 N is applied to it. Calculate the coefficient of static friction. If coefficient of kinetic friction is 0.4, then find minimum force to maintain its uniform motion.
Solution:
Given: m = 20 kg, F_L = 100 N, μ_k = 0.4

To find:

i. Coefficient of static friction (μ_s)
ii. Minimum force required (F_k)

Formulae:

i. μ_s = \(\frac{F_{L}}{N}\) = \(\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{mg}}\)
ii. μ_s = \(\frac{F_{k}}{N}\)

Calculation:

From formula (i),
μ_s = \(\frac{100}{20 \times 9.8}\) = 0.5102
From formula (ii),
F_k = μ_kN = μ_k × mg = 0.4 × 20 × 9.8
∴ F_k = 78.4 N
Answer:

1. The coefficient of static friction is 0.5102.
2. The minimum force required is 78.4 N.

Question 63.
The Mariana trench is located in the Pacific Ocean and at one place it is nearly 11 km beneath the surface of water. The water pressure at the bottom of the trench is about 1.1 × 10⁸ Pa. A steel ball of initial volume 0.32 m³ is dropped into the ocean and falls to the bottom of the trench. What is the change in the volume of the ball when it reaches the bottom? (K = 1.6 × 10¹¹ N/m²)
Answer:
Given: V = 0.32 m³, K = 1.6 × 10¹¹ N/m²,
P_W= 1.1 × 10⁸ Pa, P_atm = 1.01 × 10⁵ Pa
∴ dP = P_W – P_atm = 1.1 × 10⁸ – 1.01 × 10⁵ ≈ 1.1 × 10⁸ Pa
As, bulk modulus is given as,
K = V × \(\frac{d P}{d V}\)
∴ dV = \(\frac{\mathrm{V} \times \mathrm{dP}}{\mathrm{K}}\) = \(\frac{\left(1.1 \times 10^{8}\right) \times 0.32}{1.6 \times 10^{11}}\)
∴ dV = 2.2 × 10^-4 m³
The change in the volume of the ball when it reaches the bottom will be 2.2 × 10^-4 m³.

Question 64.
Two spheres A and B having same volume are dropped from same height in ocean. Sphere A is made up of brass and sphere B is made up of steel. Will there be same change in volume of spheres at a certain depth inside water? What will be the ratio of change in volumes of the two spheres at this depth?
Answer:

1. Brass and copper have different elastic moduli. Hence, there won’t be same change in the volume of spheres at a certain depth inside water.
2. As two spheres are dropped from same height and are at same depth in water pressure exerted on them remains same.
   ∴ dP_A = dP_B = dP
   V_A = V_B = V
3. If dV_A and dV_B be the change in volume of two spheres A and B then,
   dV_A = \(\frac{\mathrm{V} \mathrm{dP}}{\mathrm{K}_{\mathrm{A}}}\) and dV_B = \(\frac{\mathrm{V} \mathrm{dP}}{\mathrm{K}_{\mathrm{B}}}\)
4. Ratio of change in volume,
   
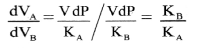
   where, K_A and K_B are bulk modulus of material of spheres A and B respectively.

Question 65.
What is the basis of deciding the thickness of metallic ropes used in crane to lift the heavy weight?
Answer:

1. The thickness of the metallic ropes used in cranes is decided on the basis of the elastic limit of the material of the rope and the factor of safety.
2. To lift a load upto 10⁴ kg, the rope is made for a factor of safety of 10.
3. It should not break even when a load of (original load × factor of safety = 10⁴ × 10) 10⁵ kgf i.e., 10⁵ × 9.8 N is applied on it.
4. If ‘r’ is the radius of the rope, then maximum stress = \(\frac{10^{5}}{\pi r^{2}}\).
5. The maximum stress (ultimate stress) should not exceed the breaking stress (5 to 20 × 10⁸ N/m²) as well as elastic limit of steel Y_s(30 × 10⁷ N/m²).
   
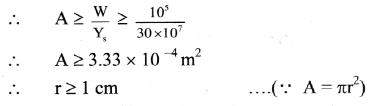
6. In order to have flexibility, the rope is made up of large number of thin wires twisted together.

Question 66.
Multiple choice questions

Which one of the following substances possesses the highest elasticity?
(A) Rubber
(B) Glass
(C) Steel
(D) Copper
Answer:
(C) Steel

Question 1.
S.I unit of stress is
(A) Newton/ metre
(B) Newton/ metre²
(C) Newton²/metre
(D) Newton/metre³
Answer:
(B) Newton/ metre²

Question 2.
A wire is stretched to double of its length. The strain is
(A) 2
(B) 1
(C) zero
(D) 0.5
Answer:
(B) 1

Question 3.
A and B are two steel wires and the radius of A is twice that of B. If they are stretched by the same load, then the stress on B is ____.
(A) four times that of A
(B) two times that of A
(C) three times that of A
(D) same as that of A
Answer:
(A) four times that of A

Question 4.
Two wires of the same material have radii r_A and r_B respectively. The radius of wire A is twice the radius of wire B. If they are stretched by same load then stress on wire B is ___
(A) equal to that of A
(B) half that of A.
(C) two times that of A.
(D) four times that of A.
Answer:
(D) four times that of A.

Question 5.
The length of a wire increases by 1% by a load of 2 kg wt. The linear strain produced in the wire will be
(A) 0.02
(B) 0.001
(C) 0.01
(D) 0.002
Answer:
(C) 0.01

Question 6.
A wire of length ‘L’, radius ‘r’ when stretched with a force ‘F’ changes in length by l’. What will be the change in length of a wire of same material having length ‘2L’ radius ‘2r and stretched by a force ‘2F’?
(A) l/2
(B) l
(C) 2l
(D) 4l
Answer:
(B) l

Question 7.
A force of 100 N produces a change of 0.1% in a length of wire of area of cross section 1 mm². Young’s modulus of the wire is ____
(A) 10⁵ N/m²
(B) 10⁹ N/m²
(C) 10¹¹ N/m²
(D) 10¹² N/m²
Answer:
(C) 10¹¹ N/m²

Question 8.
A copper wire (Y = 1 × 10¹¹ N/m²) of length 6 m and a steel wire (Y = 2 × 10¹¹ N/m²) of length 4 m each of cross-section 10^-5 m² are fastened end to end and stretched by a tension of 100 N. The elongation produced in the copper wire is
(A) 0.2 mm
(B) 0.4 mm
(C) 0.6 mm
(D) 0.8 mm
Answer:
(C) 0.6 mm

Question 9.
When a force is applied to the free end of a metal wire, metal wire undergoes
(A) longitudinal and lateral extension.
(B) longitudinal extension and lateral contraction.
(C) longitudinal contraction and lateral extension.
(D) longitudinal and lateral contraction.
Answer:
(B) longitudinal extension and lateral contraction.

Question 10.
A force of 1 N doubles the length of a cord having cross-sectional area 1 mm². The Young’s modulus of the material of cord is
(A) 1 N m^-2
(B) 0.5 × 10⁶ N m^-2
(C) 10⁶ N m^-2
(D) 2 × 10⁶ N m^-2
Answer:
(C) 10⁶ N m^-2

Question 11.
In equilibrium the tensile stress to which a wire of radius r is subjected by attaching a mass ‘m’ is ____.
(A) \(\frac{\mathrm{mg}}{\pi \mathrm{r}}\)
(B) \(\frac{\mathrm{mg}}{2 \pi \mathrm{r}}\)
(C) \(\frac{\mathrm{mg}}{\pi \mathrm{r}^{2}}\)
(D) \(\frac{\mathrm{mg}}{2 \pi \mathrm{r}^{2}}\)
Answer:
(C) \(\frac{\mathrm{mg}}{\pi \mathrm{r}^{2}}\)

Question 12.
When load is applied to a wire, the extension is 3 mm, the extension in the wire of same length but half the radius by the same load is
(A) 0.75 mm
(B) 6 mm
(C) 1.5 mm
(D) 12.0 mm
Answer:
(D) 12.0 mm

Question 13.
The S.I. unit of compressibility is ____.
(A) \(\frac{\mathrm{m}^{2}}{\mathrm{~N}}\)
(B) Nm²
(C) \(\frac{\mathrm{N}}{\mathrm{m}^{2}}\)
(D) \(\frac{\mathrm{kg}}{\mathrm{m}^{3}}\)
Answer:
(A) \(\frac{\mathrm{m}^{2}}{\mathrm{~N}}\)

Question 14.
When the pressure applied to one litre of a liquid is increased by 2 × 10⁶ N/m². Its volume decreases by 1 cm³. The bulk modulus of the liquid is
(A) 2 × 10⁹ N/m²
(B) 2 × 10³ dyne/cm²
(C) 2 × 10³ N/m²
(D) 0.2 × 10⁹ N/m²
Answer:
(A) 2 × 10⁹ N/m²

Question 15.
A cube of aluminium of each side 0.1 m is subjected to a shearing force of 100 N. The top face of the cube is displaced through 0.02 cm with respect to the bottom face. The shearing strain would be
(A) 0.02
(B) 0.1
(C) 0.005
(D) 0.002
Answer:
(D) 0.002

Question 16.
A wire has Poisson’s ratio of 0.5. It is stretched by an external force to produce a longitudinal strain of 2 × 10^-3. If the original diameter was 2 mm, the final diameter after stretching is
(A) 2.002 mm
(B) 1.998 mm
(C) 0.98 mm
(D) 1.999 mm
Answer:
(B) 1.998 mm

Question 17.
The compressibility of a substance is the reciprocal of ___.
(A) Young’s modulus
(B) Bulk modulus
(C) Modulus of rigidity
(D) Poisson’s ratio
Answer:
(B) Bulk modulus

Question 18.
For which of the following is the modulus of rigidity highest?
(A) Aluminium
(B) Quartz
(C) Rubber
(D) Water
Answer:
(B) Quartz

Question 19.
An elongation of 0.2% in a wire of cross-section 10^-4 m² causes a tension of 1000 N. Then its Young’s modulus is
(A) 6 × 10⁸ N/m²
(B) 5 × 10⁹ N/m²
(C) 10⁸ N/m²
(D) 10⁷ N/m²
Answer:
(B) 5 × 10⁹ N/m²

Question 20.
Within the elastic limit, the slope of graph between stress against strain gives ____
(A) compressibility
(B) Poisson’s ratio
(C) modulus of elasticity
(D) extension
Answer:
(C) modulus of elasticity

Question 21.
Solids which break or rupture before the elastic limits are called
(A) brittle
(B) ductile
(C) malleable
(D) elastic
Answer:
(A) brittle

Question 22.
Substances which break just after their elastic limit is reached are ___.
(A) ductile
(B) brittle
(C) malleable
(D) plastic
Answer:
(B) brittle

Question 23.
Which of the following substances is ductile?
(A) glass
(B) high carbon steel
(C) Steel
(D) copper
Answer:
(D) copper

Question 24.
The Young’s modulus of a material is 10¹¹ Nm^-2 and its Poisson’s ratio is 0.2. The modulus of rigidity of the material is
(A) 0.42 × 10¹¹ N/m²
(B) 0.42 × 10¹⁴ N/m²
(C) 0.42 × 10¹⁶ N/m²
(D) 0.42 × 10¹⁸ N/m²
Answer:
(A) 0.42 × 10¹¹ N/m²

Question 25.
Two pieces of wire A and B of the same material have their lengths in the ratio 1:2, and their diameters are in the ratio 2:1. If they are stretched by the same force, their elongations will be in the ratio
(A) 2 : 1
(B) 1 : 4
(C) 1 : 8
(D) 8 : 1
Answer:
(C) 1 : 8

Question 26.
Young’s modulus of material of wire is ‘Y’ and strain energy per unit volume is ‘E’, then the strain is

Answer:
(C) \(\sqrt{\frac{2 \mathrm{E}}{\mathrm{Y}}}\)

Question 27.
Strain energy per unit volume is given by

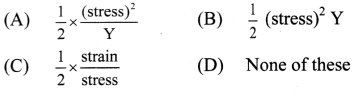
Answer:
(A) \(\frac{1}{2} \times \frac{(\text { stress })^{2}}{\mathrm{Y}}\)

Question 28.
The strain energy per unit volume of the wire under increasing load is
(A) \(\frac{1}{2}\) × (stress)² × strain
(B) \(\frac{1}{2}\) × stress × (strain)²
(C) 0.5 × stress × strain
(D) 0.5 × (strain)² × \(\frac{1}{Y}\)
Answer:
(C) 0.5 × stress × strain

Question 29.
The energy stored per unit volume of a strained wire is
(A) \(\frac{1}{2}\) × (load) × (extension)
(B) \(\frac{1}{2}\) × \(\frac{Y}{(\text { strain })^{2}}\)
(C) \(\frac{1}{2}\) × Y × (strain)²
(D) Stress × strain
Answer:
(C) \(\frac{1}{2}\) × Y × (strain)²

Question 30.
If work done in stretching a wire by 1 mm is 2 J, the work necessary for stretching another wire of same material, but with double the radius and half the length by 1 mm in joule is
(A) 1/4
(B) 4
(C) 8
(D) 16
Answer:
(D) 16

Question 31.
When the load on a wire is slowly increased from 3 to 5 kg wt, the elongation increases from 0.61 to 1.02 mm. The work done during the extension of wire is
(A) 0.16 J
(B) 0.016 J
(C) 1.6 J
(D) 16 J
Answer:
(B) 0.016 J

Question 32.
A body lies on a table. Its weight is balanced by the ___.
(A) frictional force
(B) normal force
(C) force causing motion on the body
(D) surface of the table
Answer:
(B) normal force

Question 33.
The friction that exists between the surface of two bodies in contact when one body is sliding over the other, is called ___.
(A) rolling friction
(B) friction
(C) kinetic friction
(D) static friction.
Answer:
(C) kinetic friction

Question 34.
Limiting force of static friction does NOT depend on
(A) actual area of contact.
(B) geometrical area of contact.
(C) interlocking between surfaces in contact.
(D) intermolecular forces of attraction between molecules of the two surfaces.
Answer:
(C) interlocking between surfaces in contact.

Question 35.
In case of coefficient of static friction (µ_s), kinetic friction (µ_k) and rolling friction (µ_r), which of the following relation is true
(A) µ_s > µ_k > µ_r
(B) µ_s > µ_r > µ_k
(C) µ_r > µ_s > µ_k
(D) µ_r > µ_k > µ_s
Answer:
(A) µ_s > µ_k > µ_r

Question 36.
A body of weight 50 N is placed on a smooth surface. If the force required to move the body on the surface is 30 N, the coefficient of friction is
(A) 0.6
(B) 0.4
(C) 0.3
(D) 0.8
Answer:
(A) 0.6

Question 37.
A wooden block of 50 kg is at rest on the table. A force of 70 N is required to just slide the block. The coefficient of static friction is
(A) \(\frac{6}{7}\)
(B) \(\frac{5}{7}\)
(C) \(\frac{7}{35}\)
(D) \(\frac{1}{7}\)
Answer:
(D) \(\frac{1}{7}\)

Question 38.
When a block of mass M is suspended by a long wire of length L, the length of the wire becomes (L + l). The elastic potential energy stored in the extended wire is:
(A) \(\frac{1}{2}\)Mgl
(B) \(\frac{1}{2}\)MgL
(C) Mgl
(D) MgL
Answer:
(A) \(\frac{1}{2}\)Mgl
Hint: elastic potential energy: \(\frac{1}{2}\) × F × L = \(\frac{1}{2}\)Mgl

Question 67.
A steel wire having a radius of 2.0 mm, carrying a load of 4 kg, is hanging from a ceiling. Given that g = 3.1 π ms^-2, What will be the tensile stress that would be developed
(A) 6.2 × 10⁶ N m^-2
(B) 5.2 × 10⁶ N m^-2
(C) 3.1 × 10⁶ N m^-2
(D) 4.8 × 10⁶ N m^-2
Answer:
(C) 3.1 × 10⁶ N m^-2

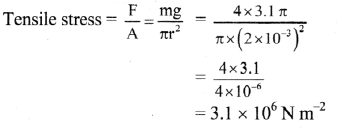
Question 68.
A boy’s catapult is made of rubber cord which is 42 cm long, with 6 mm diameter of cross-section and of negligible mass. The boy keeps a stone weighing 0.02 kg on it and stretches the cord by 20 cm by applying a constant force. When released, the stone flies off with a velocity of 20 ms^-1. Neglect the change in the area of cross-section of the cord while stretched. The Young’s modulus of rubber is closest to:
(A) 10⁶ N m^-2
(B) 10⁴ N m^-2
(C) 10⁸ Nm^-2
(D) 10³ N m^-2
Answer:
(A) 10⁶ N m^-2
Hint: d = 6 mm = 0.006 m, l = 42 cm = 0.42 m, ∆l = 20 cm = 0.2 m, m = 0.02 kg, v = 20 m/s
Energy stored in the catapult,

Question 69.
The stress-strain curves are drawn for two different materials X and Y. It is observed that the ultimate strength point and the fracture point are close to each other for material X but are far apart for material Y. We can say that materials X and Y are likely to be (respectively),
(A) Plastic and ductile
(B) Ductile and brittle
(C) Brittle and ductile
(D) Brittle and plastic
Answer:
(C) Brittle and ductile
Hint: Ductile materials have a fracture strength lower than the ultimate Tensile strength (i.e., the points are far apart.) whereas in brittle materials, the fracture strength is equivalent to ultimate tensile strength (i.e., the points are close.)
∴ Material X is brittle and Y is ductile in nature.

Question 70.
The compressibility of water is ‘o’ per unit atmospheric pressure. The decrease in its volume ‘V’ due to atmospheric pressure ‘P’ will be
(A) \(\frac{\sigma \mathrm{V}}{\mathrm{P}}\)
(B) \(\frac{\sigma P}{\mathrm{~V}}\)
(C) σPV
(D) \(\frac{\sigma}{\mathrm{PV}}\)
Answer:
(C) σPV

Question 71.
Two wires are made of the same material and have the same volume. The first wire has cross-sectional area A and the second wire has cross-sectional area 3A. If the length of the first wire is increased by ∆l on applying a force F, how much force is needed to stretch the second wire by the same amount?
(A) 9 F
(B) 6 F
(C) 4 F
(D) F
Answer:
(A) 9 F
Hint: As material is same, Young’s modulus of two wires is same.
Also, volume of both wires is same.
V₁ = V₂

Question 72.
A solid sphere of radius r made of a soft material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the surface of the liquid, covering entire cross section of cylindrical container. When a mass m is placed on the surface of the piston to compress the liquid, the fractional decrement in the radius of the sphere, \(\left(\frac{\mathrm{dr}}{\mathrm{r}}\right)\),is:
where negative sign indicates volume decreases with increase in pressure.
(A) \(\frac{\mathrm{mg}}{\mathbf{3} \mathrm{Ka}}\)
(B) \(\frac{\mathrm{mg}}{\mathrm{Ka}}\)
(C) \(\frac{\mathrm{Ka}}{\mathrm{mg}}\)
(D) \(\frac{\mathrm{Ka}}{3 \mathrm{mg}}\)
Answer:
(A) \(\frac{\mathrm{mg}}{\mathbf{3} \mathrm{Ka}}\)
Hint:
Bulk modulus is given as,
K = \(\left(\frac{-\mathrm{dP}}{\mathrm{dV} / \mathrm{V}}\right)\)
where negative sign indicates volume decreases with increase in pressure.
∴ Fractional decrease in volume will be,
\(\frac{\mathrm{dV}}{\mathrm{V}}\) = \(\frac{\mathrm{dP}}{\mathrm{K}}\)
If area of cross-section of cylinder is a, then,

Question 73.
Two metal wires ‘P’ and ‘Q’ of same length and material are stretched by same load. Their masses are in the ratio m₁ : m₂. The ratio of elongations of wire ‘P’ to that of’Q’ is

Answer:
(C) m₂ : m₁
Hint:

Question 74.
The increase in energy of a metal bar of length ‘L’ and cross-sectional area ‘A’ when compressed with a load ‘M’ along its length is (Y = Young’s modulus of the material of metal bar)
(A) \(\frac{\mathrm{FL}}{2 \mathrm{AY}}\)
(B) \(\frac{\mathbf{F}^{2} \mathbf{L}}{\mathbf{2 A Y}}\)
(C) \(\frac{\mathrm{FL}}{\mathrm{AY}}\)
(D) \(\frac{F^{2} L^{2}}{2 A Y}\)
Answer:
(B) \(\frac{\mathbf{F}^{2} \mathbf{L}}{\mathbf{2 A Y}}\)
Hint:
U = \(\frac{1}{2}\) × F × l
= \(\frac{1}{2}\) × F × \(\frac{\mathrm{FL}}{\mathrm{AY}}\) = \(\frac{\mathrm{F}^{2} \mathrm{~L}}{2 \mathrm{AY}}\)