Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 7 Thermal Properties of Matter Important Questions and Answers.
Maharashtra State Board 11th Physics Important Questions Chapter 7 Thermal Properties of Matter
Question 1.
State various units of heat and relate them to SI unit of heat.
Answer:
- CGS unit of heat: erg and it is related to SI unit as, 1 J = 107 erg
- Thermodynamic unit of heat: calorie (cal) and it is related as 1 cal = 4.184 J
Question 2.
What is thermal equilibrium?
Answer:
- When two bodies at different temperatures come into the contact with each other, they exchange heat.
- After some time, temperature of two bodies become equal and heat transfer between them stops.
- The two bodies are then said to be in thermal equilibrium with each other.
![]()
Question 3.
State true of false. Correct the statement and rewrite if false.
i. Heat transfer takes place between the body and the surrounding medium until the body and the surrounding medium are at the same temperature.
ii. Whenever two bodies are in contact, there is a transfer of heat.
Answer:
- True.
- False.
Whenever two bodies at different temperature are in contact, there is a transfer of heat.
Question 4.
Give reason: Temperature is said to be a measure of average kinetic energy of the atoms/molecules of the body.
Answer:
- Matter consists of particles which are in continuous vibrational motion and thereby possess kinetic energy.
- When external energy is provided to these particles, internal energy of particles increases.
- This increase in internal energy is in the form of increased kinetic energy of atoms/molecules and raises temperature of body (except at melting or boiling point of the body).
- Greater the kinetic energy, faster the atoms/ molecules move and temperature of body becomes higher.
- Thus, temperature of body is directly proportional to its kinetic energy.
Hence, temperature is said to be a measure of average kinetic energy of the atoms and molecules of the body.
Question 5.
Why do solid particles possess potential energy?
Answer:
The solid particles possess potential energy due to the interatomic forces that hold the particles together at some mean fixed positions.
Question 6.
What happens when heat is supplied to a solid at its melting point?
Answer:
- When heat is supplied to a solid at its melting point, average kinetic energy of constituent particles does not change.
- As a result, temperature of body remains constant.
- Supplied energy is used to weaken the bonds between constituent particles.
- While order of magnitude of average distance between the molecules remains almost same as solid, substance melts, i.e., changes into liquid state, at melting point.
![]()
Question 7.
Why do solids have definite shape and volume?
Answer:
The solid particles possess potential energy due to the interatomic forces that hold the particles together at some mean fixed positions.
Hence, solids have definite shape and volume.
Question 8.
Why is density of liquid at melting point nearly same as density of solids at melting point?
Answer:
- During change of state from solid to liquid, mass of substance does not change.
- Also, mean distance between particles during change of state does not alter at melting point.
- Density depends upon mass and volume, in turn, on mean distance between particles.
Hence, density of liquid at melting point is nearly same as density of solids at melting point.
Question 9.
State true or false. If false correct the statement and rewrite.
Due to weakened interatomic bonds liquid do not possess definite volume but have definite shape.
Answer:
False.
Due to weakened bonds liquids do not possess definite shape but have definite volume.
Question 10.
What happens when heat is supplied to liquid its freezing point (melting point)?
Answer:
- On heating, the atoms/molecules in liquid gain kinetic energy and temperature of the liquid increases.
- If liquid is continued to heat further, at the boiling point, the constituents overcome the interatomic/molecular forces.
- The mean distance between the constituents increases so that the particles are farther apart.
- At boiling point, the liquid gets converted into gaseous state.
Question 11.
Why, according to kinetic theory of gases, gases have neither definite volume nor shape?
Answer:
As per kinetic theory of gases, for an ideal gas, there are no forces between the molecules of a gas. Hence, gases neither have a definite volume nor shape.
Question 12.
Match the pairs.
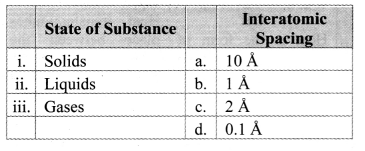
Answer:
i – b,
ii – c,
iii – a
Question 13.
Distinguish between an adiabatic wall and diathermic wall.
Answer:
|
|
Adiabatic wall |
Diathermic wall |
| i. | An ideal wall or partition separating two systems such that no heat exchange can take place between the systems is called adiabatic wall. | A wall that allows exchange of heat energy between two systems is said to be diathermic wall. |
| ii. | It is a perfect thermal insulator. | It is not a perfect thermal insulator. |
| iii. | It does not exist in reality. | Partition like thin sheet of copper acts as diathermic wall. |
| iv. | It is generally represented as thick cross-shaded (slanting lines region). | It is represented as a thin dark region. |
![]()
Question 14.
State and explain zeroth law of thermodynamics.
Answer:
Statement: If two bodies A and B are in thermal equilibrium and also A and C are in thermal equilibrium then B and C are also in thermal equilibrium.
Explanation:
- Consider two sections of a container separated by an adiabatic wall containing two different gases as system A and system B.
- Systems A and B are independently brought in thermal equilibrium with a system C.
- When the adiabatic wall separating systems A and B is removed, there will be no transfer of heat from system A to system B or vice versa.
- This indicates that systems A and B are also in thermal equilibrium.
- This means, if systems A and B are separately in thermal equilibrium with a system C, then A and B are also mutually in thermal equilibrium.
Question 15.
What is thermometry? What is thermometer?
Answer:
Thermometry is the science of temperature and its measurement. The device used to measure temperature is a thermometer.
Question 16.
State the principle used to measure the temperature of a system using a thermometer.
Answer:
When two or more systems/bodies are in thermal equilibrium, their temperatures are same. This principle is used to measure the temperature of a system by using a thermometer.
Question 17.
Explain how thermal equilibrium is attained between thermometer and the patient holding thermometer, in mouth.
Answer:
- Thermometer indicating lower temperature is held in mouth by patient.
- As body of patient is at higher temperature, heat energy is transferred from patient to thermometer.
- When temperature of thermometer becomes same as temperature of patient, heat exchange stops and thermal equilibrium is attained between thermometer and body of patient.
Question 18.
Define the following terms.
i) Ice point
ii) Steam point
Answer:
- Ice point: The temperature at which pure water freezes at one standard atmospheric pressure is called as ice point or freezing point.
- Steam point: The temperature at which pure water boils into steam or steam changes to liquid water at one standard atmospheric pressure is called as steam point or boiling point.
![]()
Question 19.
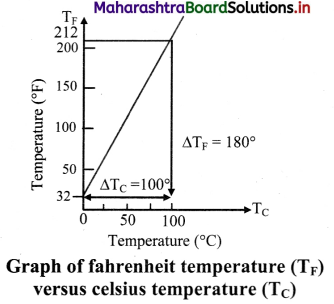
Explain Celsius and fahrenheit scale of temperature. Give relation between the two scales with the help of the graph.
Answer:
- Celsius scale:
- The ice point (melting point of pure ice) is marked as 0 °C (lower point) and steam point (boiling point of water) is marked as 100 °C (higher point).
- Both are taken at one atmospheric pressure.
- The interval between these points is divided into loo equal pans. Each of these parts is called as one degree celsius and it is written as 1 oc.
- Fahrenheit scale:
- The ice point (melting point of pure ice) is marked as 32 °F and steam point (boiling point of water) is marked as 212 °F.
- The interval between these two reference points is divided into 180 equal parts. Each part is called as degree fahrenheit and is written as 1 °F.
- Relation between fahrenheit temperature and celsius temperature:
\(\frac{\mathrm{T}_{\mathrm{F}}-32}{180}\) = \(\frac{T_{C}-0}{100}\)
Where, TF = temperature in fahrenheit scales.
TC = temperature in celsius scale.
The graph of TF versus TC is as shown
Question 20.
What is thermometer? Explain with examples, the thermometric property used in a thermometer.
Answer:
- An instrument designed to measure temperature is called as thermometer.
- Any property of a substance which changes sufficiently with temperature can be used as a basis of constructing a thermometer and is known as the thermometric property.
- There are different types of thermometers.
- In a constant volume gas thermometer, the pressure of a fixed volume of gas (measured by the difference in height) is used as the thermometric property.
- The liquid-in-glass thermometer depends on the change in volume of the liquid with temperature. Small change in temperature changes the volume of liquid considerably. Two such liquids are mercury and alcohol. Mercury thermometers are used for measurement of temperature range -39 °C to 357 °C while alcohol thermometers are used only to measure temperatures near ice point (melting point of pure ice).
- The resistance thermometer uses the change of electrical resistance of a metal wire with temperature.
- Normally in research laboratories, a thermocouple is used to measure the temperature. A thermocouple is a junction of two different metals or alloys eg.: copper and iron joined together.
- When two such junctions at the two ends of two dissimilar metal rods are kept at two different temperatures, an electromotive force is generated that can be calibrated to measure the temperature.
- Thermometers are calibrated so that a numerical value may be assigned to a given temperature. The standard fixed points are melting point of ice and boiling point of water.
Question 21.
State characteristics of thermometer.
Answer:
- Thermometer must be sensitive, i.e., a noticeable change in the thermometric property should be observed for a very small change in temperature.
- It has to be accurate.
- It should be easily reproducible.
- It is important that the system attains thermal equilibrium with the thermometer quickly.
Question 22.
Explain relation between unknown temperature T and thermodynamic property PT at temperature T.
Answer:
If the values of a thermometric property are P1 and P2 at the ice point (0 °C) and steam point (100 °C) respectively and the value of this property is PT at unknown temperature T, then T is given by the following equation.
T = \(\frac{100\left(P_{T}-P_{1}\right)}{P_{2}-P_{1}}\)
Question 23.
State true or false. If false correct the statement and rewrite.
Ideally, there should be no difference in temperatures recorded on two different thermometers.
Answer:
True.
![]()
Question 24.
List an advantage and a disadvantage of constant volume gas thermometer.
Answer:
Advantage: There is no difference in temperatures recorded on two different constant volume gas thermometers. Hence, it is very accurate.
Disadvantage: Constant volume gas thermometer is bulky instrument. Hence, it is not easily portable.
Question 25.
Give short note on liquid-in-glass thermometer.
Answer:
- Liquid-in-glass thermometer depends on the change in volume of the liquid with temperature.
- When the bulb is heated, the liquid in a glass bulb expands upward in a capillary tube.
- The liquid is such that it is easily seen and expands (or contracts) rapidly and by a large amount over a wide range of temperature.
- Most commonly used liquids are mercury and alcohol as they remain in liquid state over a wide range. Mercury freezes at -39 °C and boils at 357 °C; alcohol freezes at -115 °C and boils at 78 °C.
Question 26.
What are thermochromic liquids? Give two examples.
Answer:
- Thermochromic liquids are ones which change colour with temperature.
- These liquids are very sensitive to temperature, especially in range of room temperature.
- Hence, only specific liquids display distinct colour variations at normal temperature.
Examples: Titanium dioxide and zinc oxide are white at room temperature but when heated change to yellow.
Question 27.
Write a note on resistance thermometer.
Answer:
- Resistance thermometer uses the change of electrical resistance of a metal wire with temperature.
- It measures temperature accurately in the range -2000 °C to 1200 °C is best for steady temperatures.
- It is bulky and hence not easily portable.
Solved Examples
Question 28.
If the temperature in the room is 29 °C, what is its temperature in degree fahrenheit?
Solution:
Given: TC = 29 °C
To find: Temperature in degree fahrenheit (TF)

Answer:
Temperature in the room in degree fahrenheit is 84.2 °F.
Question 29.
Average room temperature on a normal day is 27 °C. What is the room temperature in °F?
Solution:
TC = 27 °C
Room temperature in °F
Calculation: From formula,
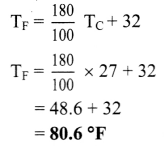
Answer:
Room temperature in °F is 80.6 °F.
Question 30.
Normal human body temperature in fahrenheit is 98.4 °F. What is the body temperature in °C?
Solution:
TF = 98.4 °F
Formula: Body temperature in °C (TC)

Body temperature in °C is 36.89 °C.
Question 31.
The length of a mercury column in a mercury-in-glass thermometer is 25 mm at the ice point and 180 mm at the steam point. What is the temperature when the length is 60 mm?
Solution:
Here the thermometric property P is the length of the mercury column.
Using equation,
T = \(\frac{100\left(\mathrm{P}_{\mathrm{T}}-\mathrm{P}_{1}\right)}{\left(\mathrm{P}_{2}-\mathrm{P}_{1}\right)}\)
For P1 = 25 mm,
P2 = 180 mm,
PT = 60 mm
T = \(\frac{100(60-25)}{(180-25)}\)
= 22.58 °C
The temperature corresponding to the length of 60 mm is 22.58 °C.
![]()
Question 32.
A resistance thermometer has resistance 95.2 Ω at the ice point and 138.6 Ω at the steam point. What resistance would be obtained if the actual temperature is 27 °C?
Solution:
Here the thermometric property P is the resistance. If R is the resistance at 27 °C,
Using equation,
T = \(\frac{100\left(\mathrm{P}_{\mathrm{T}}-\mathrm{P}_{1}\right)}{\left(\mathrm{P}_{\mathrm{T}}-\mathrm{P}_{1}\right)}\)
For T = 27 °C, P1 = 95.2 Ω, P2 = 138.6 Ω .
∴ 27 = \(\frac{100(\mathrm{R}-95.2)}{(138.6-95.2)}\)
∴ R = \(\frac{27 \times(138.6-95.2)}{100}\) + 95.2
= 11.72 + 95.2
= 106.92Ω
The resistance obtained would be 106.92 Ω.
Question 33.
Explain the need for thermodynamic (absolute) scale.
Answer:
- The two fixed point scale, Celsius scale and Fahrenheit scale had a practical shortcoming for calibrating the scale.
- It was difficult to precisely control the pressure and identify the fixed points, especially for the boiling point as the boiling temperature is very sensitive to changes in pressure.
- Hence, a one fixed point scale was adopted to define a temperature scale.
- This scale is called the absolute scale or thermodynamic scale.
Question 34.
What is triple point of water? State its physical significance.
Answer:
- The triple point of water is that point where water in a solid, liquid and gas state co-exists in equilibrium and this occurs only at a unique temperature and a pressure.
- To know the triple point, one has to see that three phases coexist in equilibrium and no one phase in dominating. This occurs for each substance at a single unique combination of temperature and pressure.
- Thus, if three phases of water solid ice, liquid water and water vapour coexist, the pressure and temperature are automatically fixed.
- Internationally, triple point of water has been assigned as 273.16 K at pressure equal to 6.11 × 102 Pa or 6.11 × 10-3 atmosphere, as the standard fixed point for calibration of thermometers.
- The physical significance of triple point of water is that, it represents unique condition and it is used to define the absolute temperature.
Question 35.
Write a short note on absolute scale of temperature.
Answer:
- The absolute scale of temperature, is so termed since ills based on the properties of an ideal gas and does not depend on the property of any particular substance.
- The zero of this scale is ideally the lowest temperature possible although it has not been achieved in practice.
- It is termed as Kelvin scale after Lord Kelvin with its zero at -273.15 °C and temperature intervals same as that on the Celsius scale. It is written as K (without °).
Question 36.
Draw a neat and well labelled diagram to show comparison of kelvin, Celsius and fahrenheit temperature scales.
Answer:
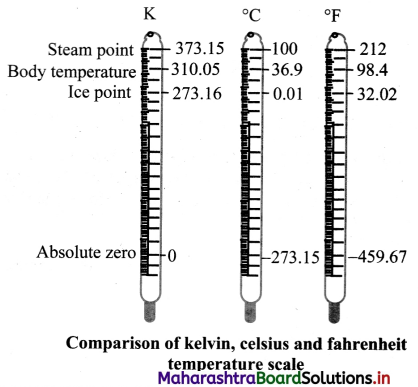
Question 37.
Answer the following:
i) The triple-point of water is a standard fixed point in modern thermometry. Why? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale)?
ii) The absolute temperature (Kelvin scale) T is related to temperature tc on the Celsius scale by tc = T – 273.15. Why do we have 273.15 in this relation and not 273.16?
Answer:
i) The triple point of water has been assigned a fixed value of 273.15 K. This number represents a unique value associated with a unique condition of temperature and pressure in which all the three phases of water co-exist. On the other hand, melting point of ice and boiling point of water do not have a unique set of values as they are subject to changes in pressure and volume. For this reason, triple point of water is a standard fixed point in modem thermometry.
ii) On Celsius scale, the melting point of ice at normal pressure has a value 0 °C. The value corresponding to this value on the absolute scale is 273.15 K. The value 273.16 K denotes the triple point of water which has a value,
273.16 – 273.15 = 0.01 °C on Celsius scale as per the given relation.
Question 38.
State Charles’ law and give its formula.
Answer:
Charles’ law:
At constant pressure, volume of a fixed mass of gas is directly proportional to its absolute temperature.
Mathematically,
V ∝ T … ( at constant pressure)
∴ V = kT
where k is constant of proportionality
∴ \(\frac{\mathrm{V}}{\mathrm{T}}\) = k = constant
For two gases, \(\frac{V_{1}}{T_{1}}\) = \(\frac{V_{2}}{T_{2}}\) = constant.
![]()
Question 39.
State Pressure law and give its formula.
Answer:
Pressure (Gay Lussac’s) law:
At constant volume, pressure of a fixed mass of gas is directly proportional to its absolute temperature.
Mathematically,
P ∝ T .. .(at constant volume)
∴ P = kT
Where, k is constant of proportionality P
∴ \(\frac{\mathrm{P}}{\mathrm{T}}\) = k = constant
For two gases, \(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\) = constant
Question 40.
State Boyle’s law and give its formula.
Answer:
Boyle’s law:
At constant temperature, the volume of a fixed mass of a gas is inversely proportional to its pressure.
Mathematically,
V ∝ \(\frac{1}{\mathrm{P}}\).. ..(at constant temperature)
V = k × \(\frac{1}{\mathrm{P}}\)
where, k is constant of proportionality.
PV = k = constant For two gases,
P1V1 = P2V2 = constant
Question 41.
Derive ideal gas equation PV = nRT.
Answer:
- The relation between three variables of a gas i.e., pressure, volume and absolute temperature is called as ideal gas equation.
From Boyle’s law,
V ∝ \(\frac{\mathrm{T}}{\mathrm{P}}\), at constant temperature ….(1)
From Charles’ law,
V ∝ T, at constant pressure … .(2) - Combining equations (1) and (2) we get,
∴ V ∝ \(\frac{\mathrm{T}}{\mathrm{P}}\)
∴ \(\frac{\mathrm{PV}}{\mathrm{T}}\)= constant - For one mole of a gas,
\(\frac{\mathrm{PV}}{\mathrm{T}}\) = R or PV = RT … (3)
where R is the constant of proportionality. - Equation (3) is called ideal gas equation. The value of constant R is same for all gases. Therefore, R is called as universal gas constant. R = 8.31 JK-1mol-1.
- For ‘n’ moles of gas, i.e. if the gas contains ‘n’ moles, equation (3) can be written as,
PV = nRT
Solved Examples
Question 42.
Express T = 24.57 K in Celsius and fahrenheit.
Solution:
Given: TK = 24.57 K
To find: Temperature in Celsius (TC),
Temperature in fahrenheit (TF)
![]()
Calculation:
From formula,
∴ TC = TK – 273.15
= 24.57 – 273.15
= -248.58 °C

Temperature in celsius (TC) is – 248.58 °C
Temperature in fahrenheit (TF) is -415.44 °F
Question 43.
Calculate the temperature which has the same value on fahrenheit scale and kelvin scale.
Solution:
Given: TK = TF = x
To find: Temperature at which Kelvin and Fahrenheit scales coincide (x)
Formula: \(\frac{\mathrm{T}_{\mathrm{F}}-32}{180}\) = \(\frac{\mathrm{T}_{\mathrm{K}}-273.15}{100}\)
Calculation: From formula.
∴ \(\frac{x-32}{180}\) = \(\frac{x-273.15}{100}\)
∴ 5(x – 32) = 9(x – 273.15)
∴ 5x – 160 = 9x – 2458.35
∴ 4x = 2298.35
∴ x = \(\frac{2298.35}{4}\) = 574.6
∴ x = 574.6 °F
The temperature at which kelvin and fahrenheit scales coincide is 574.6 °F.
![]()
Question 44.
The triple points of neon and carbon dioxide are 24.57 K and 216.55 K, respectively. Express these temperatures on
the celsius and fahrenheit scales. (NCERT)
Solution:
Given: For neon, TK = 24.57 K
For carbon dioxide, TK = 216.55 K
To find:
i) Triple point of neon on celsius (TCN) and fahrenheit scale (TFN)
ii) Triple point of carbon dioxide on Celsius (TCC) and fahrenheit scale (TFC)
Formulae:
i) TK – 273.15 = TC
ii) \(\frac{\mathrm{T}_{\mathrm{K}}-273.15}{100}\) = \(\frac{\mathrm{T}_{\mathrm{c}}-32}{180}\)
Calculation: From formula (i),
TC = TK – 273.15
For neon, TCN = 24.57 – 273.15
∴ TCN = -248.58 °c
For carbon dioxide.
TCC = 216.55 – 273.15
∴ TCC = -56.60 °c
From formula (ii),
TF = \(\frac{9}{5}\)(Tk – 273.15) + 32
For neon, Tk = 24.57 K
∴ TFN = \(\frac{9}{5}\)[24.57 – 273.15] + 32
∴ TFN = -415.44 °F
For CO2, TK = 216.55 K
∴ TFC = \(\frac{9}{5}\)(216.55 – 273.15) + 32
∴ TFC = -69.88 °F
i) Triple point of neon on celsius scale is -248.58 °c and on a fahrenheit scale is -415.44 °F.
ii) Triple point of carbon-dioxide on celsius scale is -56.60 °C and on fahrenheit scale is -69.88 °F.
Question 45.
Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between TA and TB?
Solution:
Triple point of water is, T = 273.16 K
Since the absolute scales measure the triple point as 200 A and 350 B.
∴ 200A = 350B = 273.16 K
∴ 1A = \(\frac{273.16}{200}\)K and 1B = \(\frac{273.16}{350}\)K
If TA and TB are the temperatures on the two scales, then
\(\frac{273.16}{200}\)TA = \(\frac{273.16}{350}\)TB
∴ TA = \(\frac{200}{350}\) TB = \(\frac{4}{7}\)TB
\(\frac{\mathbf{T}_{\mathbf{A}}}{\mathbf{T}_{\mathbf{B}}}\) = \(\frac{4}{7}\)
The relation between TA and TB is TA : TB = 4 : 7
Question 46.
The pressure reading in a thermometer at steam point is 1.367 × 103 Pa. What is pressure reading at triple point knowing the linear relationship between temperature and pressure?
Solution:
Given: P = 1.367 × 103 Pa at steam point (T) i.e., at 273.15 + 100 = 373.15 K.
Linear relationship between temperature and pressure means that.
P ∝ T ⇒ P1T1 = P2T2
To find: Pressure reading (Ptriple)
Formula: Ptriple = 273.16 × \(\left(\frac{\mathrm{P}}{\mathrm{T}}\right)\)
where Ptriple and P are the pressures at temperature of triple point (273.16 K) and T (375.15 K) respectively.
Calculation: From formula,
∴ Ptriple = 273.16 × \(\left(\frac{1.367 \times 10^{3}}{373.15}\right)\)
= 1000 × 103 Pa
Pressure reading is 1.000 × 103 Pa.
![]()
Question 47.
When the pressure of 0.75 litre of a gas at 27 °C is doubled, its temperature rises to 111°C. Calculate the final volume of a gas.
Solution:
Given: V1 = 0.75 litre = 750 cm3,
T1 = 27 + 273.15 = 300.15 K,
T2 = 111 + 273.15 = 384.15 K,
P2 = 2P1
To find: Final volume (V2)
Formula: \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{1}}\) = \(\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
Calculation: From formula,
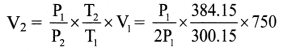
∴ V2 = 480 cm3
The final volume of the gas is 480 cm3.
Question 48.
A certain mass of a gas at 20 °C is heated until both its pressure and volume are doubled. Calculate the final temperature.
Solution:
T1 = 20 + 273.15 = 293.15 K,
P2 = 2P1, and V2 = 2V1
To find: Final temperature (T2)
Formula: \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{1}}\) = \(\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
Calculation: From formula,
\(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{1}}\) = \(\frac{\left(2 \mathrm{P}_{1}\right)\left(2 \mathrm{~V}_{1}\right)}{\mathrm{T}_{2}}\)
∴ \(\frac{1}{\mathrm{~T}_{1}}\) = \(\frac{4}{\mathrm{~T}_{2}}\)
∴ T2 = 4 × 293.15 = 1172.6 K
= 1172.6 – 273.15 = 899.45 °C
∴ T2 = 1172.6 K or 899.45 °C
The final temperature of the gas is 1172.6 K or 899.45 °C.
Question 49.
Explain how substances expand on the basis of vibrational motion of atoms.
Answer:
- The atoms in a solid vibrate about their mean positions.
- When heated, they vibrate faster and force each other to move a little farther apart. This results into expansion.
- The molecules in a liquid or gas move with certain speed.
- When heated, they move faster and force each other to move a little farther apart. This results
in expansion of liquids and gases on heating. - The expansion is more in liquids than in solids; gases expand even more.
Question 50.
What is thermal expansion? List types of thermal expansion.
Answer:
- A change in the temperature of a body causes change in its dimensions.
- The increase in the dimensions of a body due to an increase in its temperature is called thermal expansion.
- There are three types of thermal expansion:
- Linear expansion
- Areal expansion
- Volume expansion
Question 51.
Define linear expansion of solids.
Answer:
The expansion in length of a solid due to thermal energy is called linear expansion.
![]()
Question 52.
Define coefficient of linear expansion of solid. State its unit and dimensions.
Answer:
- The coefficient of linear expansion of a solid is defined as increase in the length per unit original length at 0 °C per degree rise in temperature.
It is denoted by α and given by,
α = \(\frac{l_{2}-l_{1}}{l_{1}\left(\mathrm{~T}_{2}-\mathrm{T}_{1}\right)}\)
where l1 = initial length at temperature T1 °C
l2 = final length at temperature T2 °C - Unit: °C-1 or K-1
- Dimensions: [L0M0T0K-1]
Question 53.
Derive an expression for the coefficient of linear expansion in solid.
Answer:
i) If the substance is in the form of a long rod of length l, then for small change ∆T, in temperature, the fractional change ∆l/l, in length is directly proportional to ∆T.
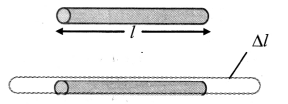
[Note: Linear expansion ∆l is exaggerated for explanation.]
\(\frac{\Delta l}{l}\) ∝ ∆T
∴ \(\frac{\Delta l}{l}\) = α∆T … (1)
where, α is called the coefficient of linear expansion of solid.
ii) Rearranging terms in equation (1),
α = \(\frac{\Delta l}{l \Delta \mathrm{T}}\)
= \(\frac{l_{\mathrm{T}}-l_{0}}{l_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)
where,
l0 = length of rod at 0 °C,
lT = length of rod when heated to T °C,
T0 = 0 °C (initial temperature)
T = final temperature,
∆l = lT – T0 = change in length,
∆T = T – T0 = rise in temperature.
iii) If l0 = 1 m and T – T0 = 1 °C, then α = lT – l0 (numerically).
iv) As magnitude of α varies negligibly with temperature, it is assumed to be constant for a particular material.
Hence, it is not essential to take initial temperature as 0 °C.
This modifies equation (2) into,
α = \(\frac{l_{2}-l_{1}}{l_{1}\left(\mathrm{~T}_{2}-\mathrm{T}_{1}\right)}\)
where l1 = initial length at temperature T1 °C
l2 = final length at temperature T2 °C
Question 54.
State true or false. If false correct the statement and rewrite.
i) Coefficient of linear expansion is same for all substances.
ii) Metals have high values for the coefficient of linear expansion, than non-metals.
Answer:
- False.
Coefficient of linear expansion is different for different substances. - True.
Question 55.
Define areal expansion of solids.
Answer:
The increase in the surface area of a solid, on heating is called areal expansion or superficial expansion of solids.
![]()
Question 56.
Define coefficient of superficial (areal) expansion of a solid, state its unit and dimensions.
Answer:
- Coefficient of superficial (areal) expansion of a solid is defined as the increase in area per unit original area at 0 °C per degree rise in temperature.
It is denoted by β and given by,
β = \(\frac{A_{2}-A_{1}}{A_{1}\left(T_{2}-T_{1}\right)}\)
where, A1 = Area of solid sheet at T1 °C,
A2 = Area of solid sheet at T2 °C - Unit: 0°C-1 or K-1
- Dimensions: [L0M0T0K-1
Question 57.
Derive expression for coefficient of areal expansion.
Answer:
i) If a substance is in the form of a plate of area A, then for small change ∆T in temperature, the fractional change in area, ∆A/A in figure given below, is directly proportional to ∆T.
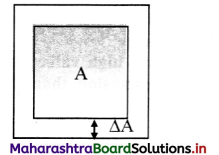
[Note: Areal expansion ∆A is exaggerated for explanation]
\(\frac{\Delta \mathrm{A}}{\mathrm{A}}\) ∝ ∆T
∴ \(\frac{\Delta \mathrm{A}}{\mathrm{A}}\) = β∆T … (1)
where β is called the coefficient of areal expansion of solid.
ii) Rearranging terms in equation (1),
β = \(\frac{\Delta \mathrm{A}}{\mathrm{A} \Delta \mathrm{T}}\)
= \(\frac{A_{T}-A_{0}}{A_{0}\left(T-T_{0}\right)}\)
where,
A0 = volume at 0 °C,
AT = volume when heated to T °C,
T0 = 0 °C (initial temperature),
T = final temperature,
∆A = AT – A0 = change in area,
∆T = T – T0 = rise in temperature.
iii) If A0 = 1 m2, T – To = 1 °C, then β = AT – A0 (numerically).
iv. As, β does not vary significantly with temperature. Hence, if A1 is the area of a metal plate at T1 °C and A2 is the area at higher temperature at T2 °C, then
β = \(\frac{A_{2}-A_{1}}{A_{1}\left(T_{2}-T_{1}\right)}\)
Question 58.
Define volume expansion of solids.
Answer:
The increase in volume due to heating is called volume expansion or cubical expansion.
Question 59.
Define coefficient of cubical (volume) expansion of a solid. State its unit and dimensions.
Answer:
i) Coefficient of cubical (volume) expansion:
Coefficient of cubical (volume) expansion of a solid is defined as increase in volume per unit original volume at O °C per degree rise in temperature.
It is denoted by γ and is given by,
γ = \(\frac{V_{2}-V_{1}}{V_{1}\left(T_{2}-T_{1}\right)}\)
where,
V1 = Volume of solid at T1 °C,
V2 = Volume of solid at T2 °C
ii) Dimensions: [L0M0T0K-1]
[Note: Units and dimension of areal expansion in solid (β) and cubical expansion in solid (γ) are same as that of linear expansion in solid (α).
![]()
Question 60.
Derive an expression for coefficient of cubical expansion.
Answer:
i) If the substance is in the form of a cube of volume V, then for small change ∆T in temperature, the fractional change, ∆/V in volume is directly proportional to ∆T.
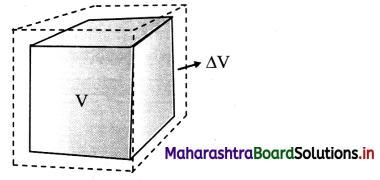
[Note: Volume expansion ∆V is exaggerated for explanation.)
ii) γ = \(\frac{\Delta \mathrm{V}}{\mathrm{V} \Delta \mathrm{T}}\) = \(\frac{\mathrm{V}_{\mathrm{T}}-\mathrm{V}_{0}}{\mathrm{~V}_{0}\left(\mathrm{~T}-\mathrm{T}_{0}\right)}\)
where, V0 = volume at 0 °C,
VT = volume when heated to T °C,
T0 = 0 °C (initial temperature),
T = final temperature.
∆V = VT – V0 = change in volume,
γ = VT – T0 = rise in temperature.
iii) If V0 = 1 m3, T – T0 = 1 °C, then γ = VT – V0 (numerically).
iv) If V1 is the volume of a body at T1 °C and V2 is the volume at higher temperature T2 °C, then
γ1 = \(\frac{\mathrm{V}_{2}-\mathrm{V}_{1}}{\mathrm{~V}_{1}\left(\mathrm{~T}_{2}-\mathrm{T}_{1}\right)}\)
γ1, is the coefficient of volume expansion at temperature T1 °C.
Question 61.
How does coefficient of volume expansion depend upon temperature?
Answer:
- As compared to coefficient of linear expansion (α) and coefficient of areal expansion (β), γ changes more with temperature.
- It is constant only at high temperatures.
Question 62.
Do coefficient of areal expansion and coefficient of volume expansion depend upon nature of material?
Answer:
Yes, coefficient of areal expansion and coefficient of volume expansion depend upon nature of material.
Question 63.
Explain expansion in fluids.
Answer:
- Since fluids possess definite volume and take the shape of the container, they exhibit only change in volume significantly.
- Equations valid for cubical or volume expansion of fluids are:
γ = \(\frac{\Delta V}{V \Delta T}=\frac{V_{T}-V_{0}}{V_{0}\left(T-T_{0}\right)}\)
where, V0 = volume at 0 °C,
VT = volume when heated to T °C,
T0 = 0 °C (initial temperature),
T = final temperature,
∆V = VT – V0 = change in volume,
∆T = T – T0 = rise in temperature.
and γ1 = \(\frac{V_{2}-V_{1}}{V_{1}\left(T_{2}-T_{1}\right)}\)
where, V1 is volume of body at T1 °C, V2 is volume of body at higher temperature T2 °C and γ1 is coefficient volume expansion at T1 °C. - As fluids are kept in containers, while dealing with the volume expansion of fluids, expansion of the container also needs to be considered.
- If expansion of fluid results in a volume greater than the volume of the container, the fluid overflows if the container is open.
- If the container is closed, volume expansion of fluid causes additional pressure on the walls of the container.
Question 64.
Use the data given in the table below:
| Materials | γ(K-1) |
| Invar | 2 × 10 -6 |
| Steel | (3.3 – 3.9) × 10-5 |
| Aluminium | 6.9 × 10“-5 |
| Mercury | 18.2 × 10-5 |
| Water | 20.7 × 10-5 |
| Paraffin | 58.8 × 10-5 |
| Gasoline | 95.0 × 10-5 |
| Alcohol (ethyl) | 110 × 10-5 |
What conclusions can be drawn using the data?
Answer:
- Coefficient of volume expansion (γ) is a characteristic of the substance.
- It (γ) has higher order of magnitude for liquids than that of solids.
![]()
Question 65.
Explain how behaviour of water is different than solids and liquids when heat is supplied.
Answer:
- Normally solids and liquids expand on heating. Hence their volume increases on heating.
- Since the mass is constant, it results in a decrease in the density on heating.
- Water expand on cooling from 4 °C to 0 °C.
- Hence its density decreases on cooling in this temperature range.
Question 66.
Derive relation between coefficient of linear expansion (α) and coefficient of areal expansion (β).
Answer:
Consider a square plate of side l0 at 0 °C and h at T °C.
- lT = lo (1 + αT) .
If area of plate at 0 °C is Ao, Ao = \(l_{0}^{2}\)
If area of plate at T °C is AT,
AT = \(l_{\mathrm{T}}^{2}\) = \(l_{0}^{2}\)(1 + αT)2
or AT = A0(1 + αT)2 …. (1)
Also,
AT = A0(1 + βT) … (2)
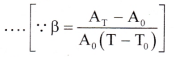
- Using Equations (1) and (2), A0(1 + αT)2 = A0(1 + βT)
∴ 1 + 2αT + α2T2 = 1 + βT - Since the values of a are very small, the term α2T2 is very small and may be neglected, ∴ β = 2α
- The result is general because any solid can be regarded as a collection of small squares.
Question 67.
Derive relation between coefficient of linear expansion (α) and coefficient of cubical expansion (γ).
Answer:
- Consider a cube of side lo at 0 °C and lT at T°C.
∴ lT = lo(l + αT)
If volume of the cube at 0 °C is V0, V0 = \(l_{0}^{3}\)
If volume of the cube at T °C is
VT, VT = \(l_{\mathrm{T}}^{3}\) = \(l_{0}^{3}\)(1 + αT)3
VT = V0 (1 + αT)3 ….(1)
Also,
VT = V0(1 + γT) ….(2)
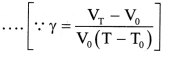
- Using Equations (1) and (2),
Vo(1 + αT)3 = V0(1 + γT)
∴ 1 + 3αT + 3α2T2 + α3T3 = 1 + γT - Since the values of a are very small, the terms with higher powers of a may be neglected.
∴ γ = 3α - The result is general because any solid can be regarded as a collection of small cubes.
Question 68.
State the relation between α, β and γ and write their meaning.
Answer:
Relation between α, β and γ is given by,
α = \(\frac{\beta}{2}\) = \(\frac{\gamma}{3}\)
where, α = coefficient of linear expansion.
β = coefficient of superficial expansion.
γ = coefficient of cubical expansion.
Solved Examples
Question 69.
The length of a rail on a railway line is 25 m at 10 °C. During summer, maximum temperature attained in the region is 50 °C. Find the minimum gap between the rails, (a = 1.2 × 10-5/°C)
Solution:
Given: L1 = 25 m, T1 = 10 °C, T2 = 50 °C,
α = 1.2 × 10-5/°C
To find: Minimum gap between rails (L2 – L1)
Formula: L2 – L1 = L1α(T2 – T1)
Calculation: From formula,
L2 – L1 = 25 × 1.2 × 10-5 × (50 – 10)
= 25 × 1.2 × 10-5 × 40
= 1.2 × 10-2 m
∴ L2 – L1 = 1.2 cm
The minimum gap between the rails is 1.2 cm.
![]()
Question 70.
The length of a metal rod at 27 °C is 4 cm. The length increases to 4.02 cm when the metal rod is heated upto 387 °C. Determine the coefficient of linear expansion of the metal rod.
Solution:
Given: T1 = 27 °C, T2 = 387 °C
L1 = 4 cm = 4 × 10-2 m
L1 = 4.02 cm = 4.02 × 10-2 m
To find: Coefficient of linear expansion

Coefficient of linear expansion is 1.389 × 10-5/°C
Question 71.
The length of a metal rod is 150 cm at 25 °C. Find its length when it is heated to 150 °C. (αsteel = 2.2 × 105 /°C)
Solution:
Given. L1 = 150 cm, T1 = 25 °C, T2 = 150 °C,
αsteel = 2.2 × 105 /°C
To find: Length of rod (L2)
Formula: α = \(\frac{L_{2}-L_{1}}{L_{1}\left(T_{2}-T_{1}\right)}\)
Calculation: From formula,
L2 – L1 = L1 α(T2 – T1)
∴ L2 = L1[1 + α(T2 – T1)]
= 150[1 + 2.2 × 105 × (150 – 25)]
= 150(1 + 2.2 × 105 × 125)
= 150(1 + 0.00275)
= 150× 1.00275 = 150.4125
∴ L2 = 150.4cm
Length of the rod at 150 °C) is 150.4 cm.
Question 72.
Length of a metal rod at temperature 27 °C is 4.256 m. Find the temperature at which the length of the same rod increases to 4.268 m. (α for iron = 1.2 × 105 K-1)
Solution:
Given: T1 = 27°C, L1 = 4.256 m, L2 = 4.268 m,
α = 1.2 × 105 K-1
To find: Temperature (T2)

= antilog [log 1114.912 – log 4.256]
= antilog [3.0468 – 0.6290]
= antilog [2.4 1781
= 2.617 × 102
= 261.7°C
Required temperature is 261.7 °C.
Question 73.
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C? Coefficient of linear expansion of copper = 1.70 × 10-5 °C-1.
Solution:
Given: d1 = 4.24 cm, ∆T = 227 – 27 = 200 °C,
α = 1.70 × 10-5 °C-1
To find: Change in diameter (∆d)
Formula: α = \(\frac{d_{2}-d_{1}}{d_{1} \Delta T}=\frac{\Delta d}{d_{1} \Delta T}\)
Calculation: From formula.
∆d = α x d1 x αT
= 1.70 × 10 × 4.24 × 200
∴ ∆d = 1.44 × 10-2 cm
The change in diameter of the hole is 1.44 × 10-2 cm.
![]()
Question 74.
A thin aluminium plate has an area 286 cm2 at 20 °C. Find its area when it is heated to 180 °C.
(β for aluminium = 4.9 × 10-5 °C)
Solution:
Given: T1 = 20°C, T2 = 180°C, A1 = 286 cm2
β = 4.9 × 10-5 °C
To find: Final area (A2)
Formula: β = \(\frac{A_{2}-A_{1}}{A_{1}\left(T_{2}-T_{1}\right)}\)
Calculation: From formula,
A2 = A1 [1 + β(T2 – T1)]
= 286[1 + 4.9 × 10-5 (180 – 20)]
= 286[1 + 4.9 × 10-5 × 160]
= 286 [1 + 784.0 × 10]
= 286 [1 + 0.00784]
= 286 [1.00784]
∴ A2 = 288.24 cm2
Its area when its heated is 288.24 cm2.
Question 75.
The surface area of the metal plate is 2.4 × 10-2 m2 at 20°C. When the plate is heated to 185 °C, its area increases by 0.8 cm2. Find the coefficient of areal expansion of metal.
Solution:
Given: T1 = 20 °C, A1 = 2.4 × 10-2 m2,
T2 = 185°C,
∆A = 0.8cm2 = 0.8 × 10-4 m2
To find: Coefficient of areal expansion (β)

The coefficient of areal expansion of the metal is 2.02 × 10-5/ °C.
Question 76.
A liquid occupies a volume of 2 × 10-4 m3 at 0 °C. Calculate the increase in its volume If It is heated to 80 °C. [The coefficient of cubical expansion of the liquid is 4 × 10-4 K-1]
Solution:
Given: V0 = 2 × 10-4 m3, T0 = 0°C,T = 80°C,
γr = 4 × 10-4 K-1,
T – T0 = 80 – 0 = 80°C
To find: Increase in volume (∆V)
Formula. ∆V = V0γr(T – T0)
Calculation: From formula.
∆V = (2 × 10-4) (4 × 10-4) × 80
∴ ∆V = 6.4 × 10-6 m3
Increase m volume of the liquid is 6.4 × 10-6 m3.
Question 77.
A liquid at O °C is poured in a glass beaker of volume 600 cm3 to fill it completely. The beaker is then heated to 90 °C. How much liquid will overflow?
(γliquid = 1.75 × 10-4/ °C, γglass = 2.75 × 10-5/ °C)
Solution:
Given: V1 = 600 cm3, T1 = 0 °C, T2 = 90 °C
γliquid = 1.75 × 10-4/°C,
γglass = 2.75 × 10-4/°C
To find: Volume of liquid that overflows
Formula: γ = \(\frac{\mathrm{V}_{2}-\mathrm{V}_{1}}{\mathrm{~V}_{1}\left(\mathrm{~T}_{2}-\mathrm{T}_{1}\right)}\)
Calculation: From formula,
Increase is volume = V2 – V1
= γ V1(T2 – T1)
Increase in volume of beaker
= γglass × V1 (T2 – T1)
= 2.75 × 10-5 × 600 × (90 – 0)
= 2.75 × 10-5 × 600 × 90
= 148500 × 10-5 cm3
∴ Increase in volume of beaker = 1.485 cm3
Increase in volume of liquid
= γliquid × V1 (T2 – T1)
= 1.75 × 10-4 × 600 × (90 – 0)
= 1.75 × 10-4 × 600 × 90
= 94500 × 10-4 cm3
∴ Increase in volume of liquid = 9.45 cm3
∴ Volume of liquid which overflows
= (9.45 – 1.485) cm3
= 7.965 cm3
Volume of liquid that overflows is 7.965 cm3.
![]()
Question 78.
The surface area of an iron plate is 80 cm2 at 20 °C. Find its surface area at 120 °C. (αiron = 1.25 × 10-5 / °C)
Solution:
Given: A1 = 80 cm2, T1 = 20 °C, T2 = 120 °C,
αiron = 1.25 × 10-5 / °C
To find: Surface area (A2)
Formula: A2 = A1 [1 + β (T2 – T1)]
Calculation: βiron = 2 × αiron = 2.5 × 10-5 / °C
From formula,
A2 = 80[1 + 2.5 × 10-5 (120 – 20)]
∴ A2 = 80.2 cm2
Surface area of the iron plate at 120 °C is 80.2 cm2.
Question 79.
A sheet of brass is 50 cm long and 8 cm broad at 0 °C. If the surface area at 100 °C is 401.57 cm2 find the coefficient of linear expansion of brass.
Solution:
Given: l = 50 cm, b = 8cm.
∴ A1 = l × b = 50 x 8 = 400 cm2,
T1 = 0°C, T2 = 100°C,
A2 = 401.57 cm2
To find: coefficient of linear expansion (α)
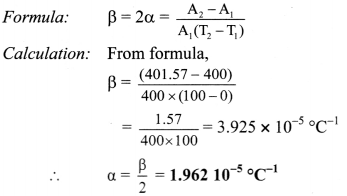
Coefficient of linear expansion of brass is 1.962 × 10-5/°C.
Question 80.
On heating a glass block of 10.000 cm3 from 25 °C to 40 °C, its volume increases by 4 cm3. Calculate coefficient of linear elipansion of glass.
Solution:
Given: V = 10,000 cm3, ∆V = 4 cm3,
∆T = 40 – 25 = 15°C,
To find: Coefficient of linear expansion (α)

Coefficient of linear expansion of the glass block is 8.89 × 10-6 /°C.
Question 81.
Explain in detail what is specific heat or specific heat capacity of a substance.
Answer:
- Specific heat capacity is defined as the amount of heat per unit mass absorbed or given out by the substance to change its temperature by one uni! (one degree) Le., 1 °C or 1 K.
- The amount of heat (∆Q) required to change the temperature of a substance is directly proportional to:
- the mass of the substance (m).
- change in temperature of the substance (∆T).
∴ ∆Q ∝ m and ∆Q ∝∆T
∴ ∆Q ∝ m∆T
∴ ∆Q = sm∆T …………….. (1)
where ‘s’ is specific heat or specific heat capacity of a substance.
From equation (1).
s = \(\frac{\Delta Q}{m \Delta T}\)
If m = 1 kg and ∆T = 1 °C,then s = ∆Q.
- Unit: S.I. unit of specific heat is J kg-1 °C-1 or J kg-1 K-1 and C.G.S. unit is erg g-1 K-1 or erg g-1 °C-1.
- Example: The specific heat of water is 4.2 J kg-1 °C-1
It means that 4.2 J of energy must be added to 1 kg of water to rise its temperature by 1 °C. - The specific heat capacity is a property of the substance.
- Specific heat capacity weakly depends on temperature of object. Except for very low temperatures. the specific heat capacity is almost constant for all practical purposes.
Question 82.
State the heat equation.
Answer:
Heat received or given out (Q)
= mass (m) temperature change (∆T) × specific heat capacity (s).
or Q = m × ∆T × s
![]()
Question 83.
Write a note on: Molar specific heat.
Answer:
- If the amount of substance is specified in terms of moles (μ) instead of mass (m) in kg. then the specific heat is called molar specific heat (C).
- It is given by, C = \(\frac{1}{\mu} \frac{\Delta Q}{\Delta \mathrm{T}}\)
- The SI unit of molar specific heat capacity is J/mol °C or J/mol K.
- Like specific heat, molar specific heat also depends on the nature of the substance and its temperature.
Question 84.
Give reason: Water is used as a coolant in automobile radiators.
Answer:
- Water has the highest specific heat capacity compared to other substances.
- As a result, water requires higher amount of energy to get heated.
- This allows water to absorb heat readily while increasing its temperature minimally.
Hence, water is used as a coolant in automobile radiators.
Question 85.
Give reason: Water is preferred as heater in hot water hag than other liquids.
Answer:
- Water has the highest specific heat capacity compared to other substances.
- This means certain mass of water heated to certain temperature contains more heat than the same mass of any other liquid heated to same temperature.
- As a result, water takes longer time to cool than any other liquid heated to same temperature.
Hence, water is preferred as heater in hot water bag than other liquids.
Question 86.
Explain why specific heat capacity of a gas at constant pressure is greater than that at constant volume.
Answer:
- When the gas is heated at constant volume. there is no work done against external pressure.
- Hence, all the supplied heat is used in raising the temperature of the gas.
- But when the gas is heated at constant pressure, volume of the gas changes.
- Due to this, part of the supplied heat is used by the gas to expand against external pressure and remaining part of heat supplied is used to raise the temperature.
- Because of this, for the same rise in temperature, the heat to be supplied at constant pressure is greater than that for heating at constant volume.
Hence, specific heat capacity of a gas at constant pressure is greater than specific heat capacity at constant volume.
Question 87.
Define principal and molar specific heat of a gas at constant volunie and constant pressure.
Answer:
- Principal specific heat:
- Principal specific heat of a gas at constant volume (sv):
Principal specific heat of a gas at constant volume is defined as the quantity of heat absorbed or released for rise or fall temperature of unit mass of a gas through 1 K (or 1 °C), when its volume is kept constant. - Principal specific heat of a gas at constant pressure (sp): Principal specfic heat of a gas at constant pressure is defined as the quantity of heat absorbed or released for rise or fall the temperature of unit mass of a gas through 1 K (or 1 °C), when its pressure is kept constant.
- Principal specific heat of a gas at constant volume (sv):
- Molar specific heat:
- Molar specific heat of a gas at constant volume (CV): Molar specific heat of a gas at Constant volume is defined as the quantity of absorbed or released for rise or fall the temperature of one mole of the gas through 1 K (or 1 °C), when its volume is kept constant.
- Molar specific heat of a gas at constant pressure (CP): Molar specific heat of a gas at constant pressure is defined as the quantity of heat absorbed or released for rise or fall the temperature of one mole of the gas through 1 K (or 1 °C), when its pressure is kept constant.
Question 88.
State the relation between principal specific heat capacity and molar specific heat capacity for a gas.
Answer:
Molar specific heat capacity = Molecular weight × principal specific heat capacity.
i.e. CV = μ × SP and CV = μ × SV
where, μ is the molecular weight of the gas.
[Note: Symbols (SV) and (SP) are used as per standard convention.]
![]()
Question 89.
What is heat capacity?
Answer:
- Heat capacity or thermal capacity of a body is the quantity of heat needed to raise or lower the temperature of the whole body by 1 o°C (or 1 K).
- Heat capacity can be written as Heat received or given out
= mass × 1 × specific heat capacity
Heat capacity = Q = m × s
Heat capacity (thermal capacity) is measured in J/°C.
Solved Examples
Question 90.
If the temperature of 4 kg mass of a material of specific heat capacity 300 J/ kg °C rises from 20 °C to 30 °C. Find the heat received.
Solution:
m = 4 kg, s = 300 J/kg °C
∆T = 30 – 20 = 10 °C
To find: Heat received (Q)
Formula: Q = ms∆T
Calculation: From formula,
Q = 4 × 300 × 10
∴ Q = 12000 J
Heat received is 12000 J.
Question 91.
How much heat is required to raise temperature of 750 g of copper pot from 20 to 50 °C?
(The specific heat of copper is 0.094 kcal/kg °C)
Solution:
Given: s = 0.094 kcal/kg°C,
m = 750 g = 0.750kg,
T1 = 20°C and T2 = 50°C
Rise in temperature,
∆T = T2 – T1 = 50 – 20 = 30°C
To find: Heat required (Q)
Formula: Q = m × s × ∆T
Calculation: From formula,
Q = 0.750 × 0.094 × 30
∴ Q = 2.115 kcal
Heat required to raise the temperature of copper pot is 2.115 kcal.
Question 92.
Calculate the difference in the temperatures between the water at the top and bottom of a water fall 200 m high. Specific heat of water is 4200 J kg-1 °C-1.
Solution:
Given: s = 4200 J kg-1 °C-1, h = 200 m
To find: Difference in temperatures (∆T)
Formulae:
i) Q = ms∆T
ii) P.E. = mgh
Calculation: From formulae (j) and (ii)
When water falls from top to bottom. assuming no loss in energy, potential energy is converted into heat energy.
∴ Q = P.E.
∴ ms∆T = mgh
∴ s∆T = gh
∴ ∆T = \(\frac{\mathrm{gh}}{\mathrm{s}}=\frac{9.8 \times 200}{4200}\)
∴ ∆T = 0.467 °C
The difference in temperatures between the water at top and bottom is 0.467 °C.
Question 93.
Find thermal capacity for a copper block of mass 0.2 kg, if specific heat capacity of copper is 290 J/kg °C.
Solution:
Given: m = 0.2 kg, s = 290 J/kg °C
To find: Thermal capacity
Formula: Thermal capacity = m × s
Calculation: From formula,
Thermal capacity = 0.2 × 290
= 58 J/ °C
Thermal capacity is 58 J/ °C.
Question 94.
What is calorimetry?
Answer:
Calorimetry is an experimental technique for quantitative measurement of heat exchange.
Question 95.
Explain construction of calorimeter with the help of a labelled diagram.
Answer:
- A device in which heat measurement can be made is called calorimeter.
- It consists of a cylindrical vessel and stirrer as well as lid of the same material like copper or aluminium.
- The vessel is kept inside a wooden jacket which contains heat insulating materials like glass. wool etc. to prohibit any transfer of heat into or out of the calorimeter.
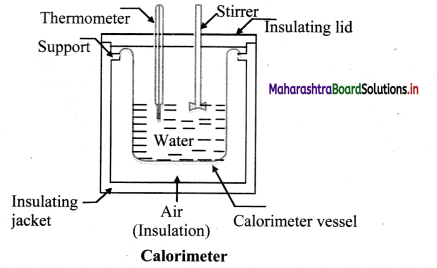
![]()
Question 96.
State the principle behind working of calorimeter.
Answer:
Calorimeter being isolated system works on the principle of conservation of energy, where heat gained equals heat lost.
Question 97.
Explain the technique “method of mixtures’.
Answer:
- Method of mixtures is a technique used to determine specific heat capacity of a material using calorimeter.
- In this technique a sample ‘A’ of the substance is heated to a high temperature which is accurately measured.
- The sample ‘A’ is then placed quickly in the calorimeter containing water.
- The contents are stirred constantly until the mixture attains a final common temperature.
- The heat lost by the sample ‘A’ will be gained by the water and the calorimeter.
- The specific heat of the sample ‘A’ of the substance can be calculated as follows:
- Let,
m1 = mass of the sample ‘A’
m22 = mass of the calorimeter and the stirrer
m3 = mass of the water in calorimeter
s1 = specific heat capacity of the substance of sample ‘A’
s2 = specific heat capacity of the material of calorimeter (and stirrer)
s3 = specific heat capacity of water
T1 = initial temperature of the sample ’A’
T2 = initial temperature of the calorimeter stirrer and water
T = final temperature of the combined system - Using heat equation,
Heat lost by the sample ‘A’ = m1s1 (T1 – T)
Heat gained by the calorimeter and the stirrer = m2s2 (T – T2)
Heat gained by the water = m3s3 (T – T2) - c. Assuming no loss of heat to the surroundings, the heat lost by the sample goes into the calorimeter, stirrer and water,
∴ m1s1(T1 – T) = m2s2(T – T2) + m3s3(T – T2) ………….. (1) - Knowing the specific heat capacity of water and copper material of the calorimeter and the stirrer, specific heat capacity (si) of material of sample ‘A’ can be calculated.
e. Rearranging terms of equation (1),
s1 = \(\frac{\left(\mathrm{m}_{2} \mathrm{~s}_{2}+\mathrm{m}_{3} \mathrm{~s}_{3}\right)\left(\mathrm{T}-\mathrm{T}_{2}\right)}{\mathrm{m}_{1}\left(\mathrm{~T}_{1}-\mathrm{T}\right)}\)
- Let,
- One can find specific heat capacity of water or any liquid using the following expression, if the specific heat capacity of the material of calorimeter and sample is known
s3 = \(\frac{\mathrm{m}_{1} \mathrm{~s}_{1}\left(\mathrm{~T}_{1}-\mathrm{T}\right)}{\mathrm{m}_{3}\left(\mathrm{~T}-\mathrm{T}_{2}\right)}-\frac{\mathrm{m}_{2} \mathrm{~s}_{2}}{\mathrm{~m}_{3}}\)
Question 98.
In method of mixtures, why is it essential that density of solid sample be greater than the liquid in calorimeter?
Answer:
- In method of mixtures, solid sample gives away heat to liquid, and heat exchange between, solid, liquid and calorimeter is considered as isolated.
- If density of solid sample is lesser than liquid in calorimeter, sample will float on liquid.
- This will cause partial heat loss to air inside the calorimeter and standard heat equations of calorimeter will no longer be applicable.
Hence, in method of mixtures it is essential that density of solid sample be greater than liquid in calorimeter.
Solved Examples
Question 99.
A sphere of aluminium of 0.06 kg is placed for sufficient time in a vessel containing boiling water so that the sphere is at 100 °C. It is then immediately transferred to 0.12 kg copper calorimeter containing 0.30 kg of water at 25 °C. The temperature of water rises and attains a steady state at 28 °C. Calculate the specific heat capacity of aluminium.
(Specific heat capacity of water, sw = 4.18 × 103 J kg-1 K-1, specific heat capacity of copper, sCu = 0.387 × 103 J kg-1 K-1)
Solution:
Given: Mass of aluminium sphere = m1 = 0.06 kg
Mass of copper calorimeter = m2 = 0.12 kg
Mass of water in calorimeter = m3 = 0.30 kg
Specific heat capacity of copper
= SCu = s2 = 0.387 × 103 J/kg K = 387 J/kg K
Specific heat capacity of water
= Sw = s3 = 4.18 × 103 J/kg K = 4180 J/kg K
Initial temperature of aluminium sphere
= T1 = 100 °C
Initial temperature of calorimeter and water
= T2 = 25 °C
Final temperature of the mixture = T = 28 °C
To find: Specific heat capacity of aluminium (sal)
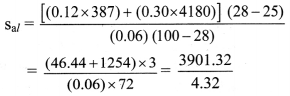
= 903.08 J/kg K
Specific heat capacity of aluminium is 903.08 J/kg K.
![]()
Question 100.
A copper sphere of 100 g mass is heated to raise its temperature to 100 °C and is released in water of mass 195 g and temperature 20 °C in a copper calorimeter. If the mass of calorimeter is 50 g, what will be the maximum temperature of water? (Given: specific heat of copper = 0.1 cal/g °C and specific heat of calorimeter = 0.1 cal/g °C)
Solution:
Let copper sphere, water and calorimeter attain final temperature T °C.
We have,

Heat lost by copper sphere
Q = msphere × Ssphere × ∆T
= 100 × 0.1 × (100 – T)
Heat gained by water in calorimeter
Q1 = mwater × Swater × ∆T
= 195 × 1 × (T – 20)
Heat gained by calorimeter
Q2 = mcalorimeter × mcalorimeter × ∆T
= 50 × 0.1 × (T – 20)
According to principle of heat exchange,
Q = Q1 + Q2
∴ 10 × (100 – T) = 195 × (T – 20) + 5 × (T – 20)
∴ 1000 – 10T = 200(T – 20)
∴ 210 T = 5000
∴ T ≈ 23.8 °C
Maximum temperature of water will be 23.8 °C.
Question 101.
What is a change of state? When does it occur?
Answer:
- Matter normally exists in three states: solid. liquid and gas. A transition from one of these states to another is called a change of state.
- This change can occur when exchange of heat takes place between the substance and its surroundings.
Question 102.
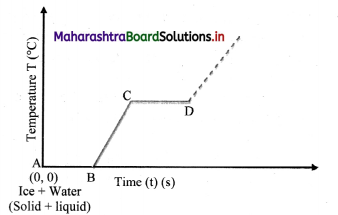
Explain the following temperature vs time graph obtained during process of boiling water.
Variation of temperature with time
Answer:
- The given temperature v/s time graph demonstrates the behaviour of water when heated continuously and uniformly.
- Line segment AB indicates temperature of ice remaining constant at 0 °C for certain period of time.
- This means, amount of heat (latent heat of fusion) supplied to ice is entirely used for changing its state from solid to liquid.
- Thus, line segment AB denotes conversion of ice at 0 °C into water at 0 °C.
- Line segment BC indicates continuous rise in temperature of water from 0 °C to 100 °C.
- At point C, boiling point of water is
reached and heat energy (latent heat of vaporisation) supplied further is used to convert water into steam. - During this transformation, temperature remains unchanged as represented by line segment CD.
- Thus, line segment CD denotes conversion of water at 100 °C into steam at 100 °C.
- At point C, boiling point of water is
- Beyond point D, thermometer again shows rise in temperature.
![]()
Question 103.
Write a note on latent heat of substance.
Answer:
- Latent heat of a substance is the quantity of heat required to change the state of unit mass of the substance without changing its temperature.
- Mathematically, if mass m of a substance undergoes a change from one state to the other then the quantity of heat absorbed or released is given by, Q = mL
where. L is known as latent heat. - It is characteristic of the substance.
- Its SI unit is J/kg.
- The value of L depends on the pressure and is usually quoted at one standard atmospheric pressure.
Question 104.
Explain the following terms.
i) Latent heat of fusion
ii) Latent heat of vaporisation
Answer:
- Latent heat of fusion:
- The quantity of heat required to convert unit mass of a substance from its solid state to the liquid state, at its melting point, without any change in its temperature is called its latent heat of fusion.
- The S.I. unit of latent heat of fusion is J/kg and its C.G.S. unit is cal/’g.
- Latent heat of vaporisation:
- The quantity of heat required to convert unit mass of a substance from its liquid state to vapour state, at its boiling point, without any change in its temperature is called its latent heat of vaporisation.
- The S.I. unit of latent heat of vaporization is J/kg and its C.G.S unit is cal/g.
Question 105.
Explain why latent heat of vaporisation is much larger than latent heat of fusion.
Answer:
- The energy required to completely separate the molecules or atoms in liquids is greater than the energy needed to break the rigidity (rigid bonds between the molecules or atoms) in solids.
- Also, when the liquid is converted into vapour, it expands. Work has to be done against the surrounding atmosphere to allow this expansion.
Hence, latent heat of vaporisation is larger than latent heat of fusion.
Question 106.
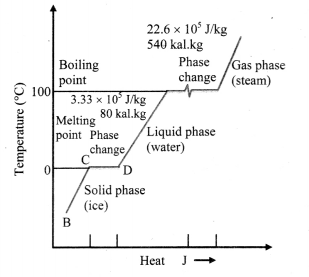
A plot of temperature versus heat energy for a given quantity of water is shown below. What can be inferred studying it?
Temperature versus heat for water at one standard atmospheric pressure (not to scale)
Answer:
Inferences:
- When heat is added (or removed) during a change of state, the temperature remains constant.
- Also the slopes of the phase lines are not all the same, which indicates that specific heats of the various states are not equal.
- For water, the latent heat of fusion and vaporisation are Lf = 3.33 × 105 J kg-1 and Lv = 22.6 × 105 J kg-1 respectively, i.e., 3.33 × 105 J of heat is needed to melt 1 kg of ice at 0 °C and 22.6 × 105 J of heat is needed to convert 1 kg of water to steam at 100 °C.
- This means, steam at 100 °C carries 22.6 × 105 J kg-1 more heat than water at 100 °C.
Question 107.
Compare change of state from solid to liquid and from liquid to vapour.
Answer:
| Solid to liquid | Liquid to vapour | |
| i. | The change of state from solid to liquid is called melting and from liquid to solid is called solidification. | The change of state from liquid to vapour is called vaporisation while that from vapour to liquid is called condensation. |
| ii. | Both the solid and liquid states of the substance co-exist in thermal equilibrium during the change of states from solid to liquid or vice versa. | Both the liquid and vapour states of the substance coexists in thermal equilibrium during the change of state from liquid to vapour. |
| iii. | The temperature at which the solid and the liquid states of the substance are in thermal equilibrium with each other is called the melting point of solid or freezing point of liquid. The freezing point describes the liquid to solid transition while melting point describes solid to liquid transition. | The temperature at which the liquid and the vapour states of the substance coexist is called the boiling point of liquid. This is also the temperature at which water vapour condenses to form liquid. |
| iv. | It is the characteristic of the substance and also depends on pressure. | It is characteristic of substance and depends on pressure. |
Question 108.
What is normal melting point?
Answer:
The melting point of a substance at one standard atmospheric pressure is called its normal melting point.
Example: Normal melting point of water is 0°C.
![]()
Question 109.
State true or false. If false correct the statement and rewrite.
Normal freezing point ice is 32 °C.
Answer:
False.
Normal freezing point ice is 0 °C or 32 °F.
Question 110.
What is normal boiling point?
Answer:
The boiling point of a substance at one standard atmospheric pressure is called its normal boiling point.
Example: Normal boiling point of water is 99.97 °C,
Question 111.
Distinguish between boiling and evaporation of liquid.
Answer:
| Boiling of liquid | Evaporation of liquid | |
| i. | Boiling of liquid takes place at boiling point which is fixed for a given pressure and unique for a given liquid. | Evaporation of liquid can take place at any temperature. |
| ii. | It occurs throughout the liquid. | It occurs only at surface of liquid. |
| iii. | The process does not depend on area of liquid surface exposed. | The process depends upon area of liquid surface exposed. Higher the exposed surface area, higher the rate of evaporation. |
| iv. | Source of energy is needed. | Energy is taken from surrounding. |
| V. | Boiling does not reduce temperature of liquid. | When evaporation takes place, temperature of liquid decreases. |
| vi. | During boiling process, bubbles are formed in liquid. | During evaporation, no bubbles are formed in liquid. |
Question 112.
Explain evaporation in terms of kinetic energy of liquid molecules.
Answer:
- Molecules in a liquid are moving about randomly.
- The average kinetic energy of the molecules decides the temperature of the liquid.
- However, all molecules do not move with the same speed.
- Some with higher kinetic energy may escape from the surface region by overcoming the interatomic forces.
- This process can take place at any temperature and is termed as evaporation.
Question 113.
Explain the dependence of evaporation on temperature of liquid.
Answer:
- If the temperature of the liquid is higher, more is the average kinetic energy.
- This implies that the number of fast moving molecules is more.
- Hence the rate of losing such molecules to atmosphere will be higher.
- Thus, higher is the temperature of the liquid, greater is the rate of evaporation.
![]()
Question 114.
Why does evaporation gives a cooling effect to the remaining liquid?
Answer:
- In the process of evaporation, faster moving molecules escape from surface of liquid overcoming the interatomic forces.
- Since faster molecules are lost, the average kinetic energy of the liquid is reduced.
- As a result, the temperature of the liquid is lowered.
Hence, evaporation gives a cooling effect to the remaining liquid.
Question 115.
Explain two applications of evaporation in details.
Answer:
- Drying of clothes:
- Clothes dry faster when hanged exposing more surface area than when kept folded.
- Due to more surface area, water in clothes gets evaporated faster, drying clothes quickly.
- Using a spirit swab on skin before injecting gives cooling effect:
- Before giving an injection to a patient, normally a spirit swab is used to disinfect the region.
- A cooling effect is experienced by skin of patient due to evaporation of the spirit as explained before.
Question 116.
Write a note on sublimation.
Answer:
- All substances do not pass through the three states: solid-liquid-gas.
- There are certain substances which normally pass from the solid to the vapour state directly and vice versa.
- The change from solid state to vapour state without passing through the liquid state is called sublimation and the substance is said to sublime.
Examples: Dry ice (solid CO2) and iodine. - During the sublimation process, both the solid and vapour states of a substance coexist in thermal equilibrium.
- Most substances sublime at very low pressures.
Question 117.
What is a phase? Give an example.
Answer:
A phase is a homogeneous composition of a material.
Example: Graphite and diamond are two phases of carbon.
Question 118.
What is a phase diagram?
Answer:
A pressure-temperature (P-T) diagram particularly convenient for comparing different phases of a substance is called as a phase diagram.
Question 119.
Study phase diagrams given below and answer the following questions.
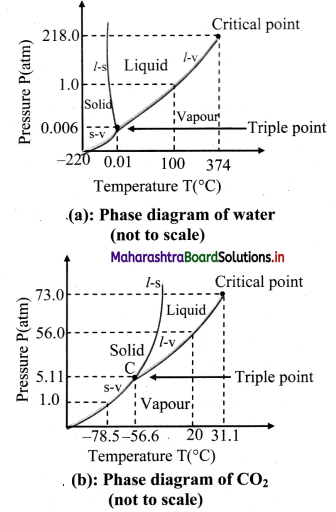
i)Explain vaporisation curve (l – v).
ii) Explain fusion curve (l – s).
iii) Explain sublimation curve (s – v).
iv) Explain triple point.
Answer:
-
- The curve labelled l – v represents those points where the liquid and vapour phases are in equilibrium.
- It is a graph of boiling point versus pressure.
- The l – v curve of water correctly shows that at a pressure of 1 atmosphere, the boiling point of water is 100 °C and the boiling point gets lowered for a decreased pressure.
- The l – v curve for CO2 yields that CO2 cannot exist as a liquid under normal atmospheric pressure conditions.
- The curve l – s represents the points where the solid and liquid phases coexist in equilibrium.
- It is a graph of the freezing point versus pressure.
- At one standard atmosphere pressure, the freezing point of water is 0 °C which can be depicted using l – s curve of water.
- At a pressure of one standard atmosphere water is in the liquid phase if the temperature is between 0 °C and 100 °C but is in the solid or vapour phase if the temperature is below 0 °C or above 100 °C.
- Also, l – s curve for water slopes upward to the left i.e., fusion curve of water has a slightly negative slope.
- This is true only of substances that expand upon freezing.
- However, for most materials like CO2, the l – s curve slopes upwards to the right i.e., fusion curve has a positive slope. The melting point of C02 is -56 °C at higher pressure of 5.11 atm.
- The curve labelled s – v is the sublimation point versus pressure curve.
- Water sublimates at pressure less than 0.0060 atmosphere, while carbon dioxide, which in the solid state is called dry ice, sublimates even at atmospheric pressure at temperature as low as -78 °C.
- The temperature and pressure at which the fusion curve, the vaporisation curve and the sublimation curve meet and all the three phases of a substance coexist is called the triple point of the substance.
- The triple point of water is that point where water in solid, liquid and gaseous states coexist in equilibrium and this occurs only at a unique temperature and pressure.
- The triple point of water is 273.16 K and 6.11 × 10-3 Pa and that of CO2 is -56.6 °C and 5.1 × 10 -5 Pa.
Question 120.
What is critical temperature of a gas?
Answer:
In order to liquefy a gas, it must be cooled to a certain temperature. This temperature is called critical temperature.
![]()
Question 121.
Compare gas and vapour.
Answer:
|
Gas |
Vapour |
|
| i. | A substance that is in gaseous phase above its critical temperature is called a gas. | A substance that is in gaseous phase below its critical temperature is call vapour. |
| ii. | Gas cannot be liquified only by pressure alone. | Vapour can be liquified simply by increasing pressure. |
| iii. | Gas exerts pressure. | Vapour exerts pressure |
Solved Examples
Question 122.
Calculate the amount of heat energy to be supplied to convert 2 kg of ice at 0 °C completely into water at 0 °C if latent heat of fusion for ice is 80 cal/g.
Solution:
Given:
Mass (m) = 2 kg = 2 × 103 g. latent heat of fusion for ice (L) = 80 cal/g.
To find: Heat energy (Q)
Formula: Q = mL
From formula,
Q = 2 x× 103 × 80 = 160000 cal
= 160 kcal
Heat energy to be supplied is 160 kcal.
Question 123.
When 0.1 kg of ice at 0 °C is mixed with 0.32 kg of water at 35 °C in a container. The resulting temperature of the mixture is 7.8 °C. calculate the heat of fusion of ice (swater = 4186 J kg-1 K-1).
Solution:
Given:
mice = 0.1 kg, mwater = 0.32 kg,
Tice = 0 °C, Twater = 35 °C, TF = 7.8 °C
swater = 4186 J kg-1 K-1
To find: Heat of fusion (Lf)
Formula: i) Heat lost by water
Q1 = mwater × swater × (Twater – TF)
ii) Heat required to melt ice
Q2 = mice LF
iii) Heat required to raise temperature of molten ice (water now) to find temperature
Q3 = miceswater (T – Tice)
Calculation: From formula (j),
Q1 = 0.32 × 4186 × (35 – 7.8)
= 36434.944 J
From formula (ii),
Q2 = 0.1 × Lf
From formula (iii),
Q3 = 0.1 × 4186 × (7.8 – 0) = 3265.08J
According to principle of heat conservation,
heat lost = heat gained
Q1 = Q2 + Q3
∴ 36434.944 = 0.1 Lf + 3265.08
∴ Lf = \(\frac{36434.944-3265.08}{0.1}\)
= 331698.64 J kg-1
Rounding off to correct significant figure,
Lf = 3.31699 × 105 J kg-1
Heat of fusion of ice 3.3 1699 × 10 5 J kg-1.
Question 124.
If 80 g steam of temperature 97 °C is released on an ¡ce slab of temperature 0 °C, how much ice will melt? How much energy will be transferred to the ice when the steam will be transformed to water?
(Given: Latent heat of melting the ice = Lmelt =80 cal/g ; Latent heat of vaporisation of water Lvap = 540 cal/g)
Solution:
Mass of steam (ms) = 80 g,
Change in temperature (∆T)
= 97 – 0 = 97 °C
We know that: Latent heat of melting of ice = Lmelt = 80 cal/g
Latent heat of vaporisation of water = Lvap = 540 cal/g
Specific heat of water cw = 1 cal /g °C
To find: i) Energy transferred (Q)
ii) Mass of ice that melts (mi)
Formula: i) Heat released during conversion of steam into water at 97 °C (Q1)= ms × Lvap
ii) Heat released during decrease of temperature of water from 97°C to 0°C (Q2) = ms × cw × ∆T
iii) Heat gained by ice (Q)= mi × Lmelt
From formula (i),
Q1 = 80 × 540 cal
From formula (ii),
Q2 = 80 × 1 × (97 – 0) = 80 × 97 cal
According to principle of heat conservation,
Total heat gained by ice
Q = Q1 + Q2
= 80 × 540 + 80 × 97
= 80 × (540 + 97)
= 80 × 637
= 50960 cal
This energy would cause m; mass of ice to melt,
From formula (iii),
∴ mi × Lmelt = 50960
∴ mi = \(\frac{50960}{80}=\frac{80 \times 637}{80}\) = 637 g
Energy transferred to ice is 50960 cal and it will melt 637 g of ice.
Question 125.
Name three modes of heat transfer.
Answer:
Three modes of heat transfer are conduction, convection and radiation.
![]()
Question 126.
Define conduction. State conditions for conduction of heat.
Answer:
Conduction is the process by which heat flows from the hot end to the cold end of a solid body without any net bodily movement of the particles of the body.
Conditions for conduction:
- The two points should be at different temperatures.
- There should be a medium between the two points.
Question 127.
Explain process of conduction in solid.
Answer:
- Heat passes through solids by conduction only.
- When one end of a rod is heated, the molecules near the hot end receive the thermal energy and start oscillating with larger amplitudes.
- In doing so, they collide with the neighbouring molecules and transfer a part of their energy to these molecules.
- The molecules which receive the energy vibrate with increased amplitudes and collide with the neighbouring molecules. Thus, energy of thermal motion is transferred by molecular collisions down the rod.
- As the distance of a molecule from the hot end increases, its amplitude of oscillation decreases and hence there is continuous decrease in temperature.
- This transfer of heat continues till two ends of the object are at the same temperature.
- In metals, mainly free electrons conduct the heat energy.
Question 128.
Define good conductors and bad conductors.
Answer:
Good conductors:
The substances which conduct heat easily are called good conductors of heat.
All metals are good conductor.
eg: Steel, silver, Aluminium etc.
Insulators:
The substances which do nor conduct heal easily are called insulators or bad condiciors of heal.
eg.: Glass. wood, air, paper. etc.
[Note: In general, good conductors of heat are also good conductors of electricity, while bad conductors of hear are had conductors of electricity.]
Question 129.
Explain why metals are good conductors of heat and electricity.
Answer:
- Metals like iron, copper. aluminium etc, contain free electrons in their atoms.
- These free electrons assist the atoms in transfer of thermal energy as well as electrical energy.
- Therefore, metal are good conductors of heat and electricity.
Question 130.
What is thermal conductivity?
Answer:
- Thermal conductivity of a solid is a measure of the ability of the solid ¡o conduct heat through it.
- Thus good conductors of heat have higher thermal conductivity than bad conductors.
Question 131.
Give reason: Hot water when poured in glass beaker, it cracks.
Answer:
- When hot water is poured in a glass beaker the inner surface of the glass expends on heating.
- Since glass is a bad conductor of heat, the heat from inside does not reach the outside surface so quickly.
- Hence the outer surface does not expand thereby causing a crack in the glass.
Question 132.
Explain mechanism of thermal conduction and temperature gradient.
Answer:
- When one end of a metal rod is heated, the heat flows by conduction from hot end to the cold end.
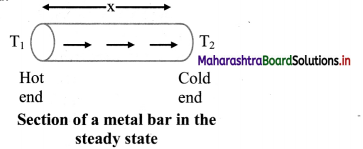
- As a result, the temperature of every section of the rod starts increasing.
- Under this condition, the rod is said to be in a variable temperature state.
- After some time, the temperature at each section of the rod becomes steady i.e., does not change.
- Temperature of each cross-section of the rod now becomes constant though not the same. This is called steady state condition.
- Under steady state condition, the temperature at points within the rod decreases uniformly with distance from the hot end to the cold end.
- The fall of temperature with distance between the ends of the rod in the direction of flow of heat, is called temperature gradient.
∴ Temperature gradient = \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{x}}\)
Where, T1 = temperature of hot end
T2 = temperature of cold end
x = length of the rod
![]()
Question 133.
State SI unit and dimensions of temperature gradient.
Answer:
S.I unit: = °C /m or K/m
Dimensions: [L-1M0T0K1]
Question 134.
State S.I. unit and dimensions of coefficient of thermal conductivity.
Answer:
SI unit of coefficient of thermal conductivity is J s-1 m-1 °C-1 or J s-1 m-1 K-1 and its dimensions are [L1M1T3K-1].
Question 135.
Explain how SI unit of coefficient of thermal conductivity be obtained as W/m °C or W/m K.
Answer:
- Consider equation, \(\frac{Q}{t}=\frac{k A\left(T_{1}-T_{2}\right)}{x}\)
- The quantity Q/t, denoted by Pcond, is the time rate of heat flow (i.e. heat flow per second) from the hotter face to the colder face, at right angles to the faces.
- Its SI unit is watt (W).
- SI unit of k can therefore be written as W m-1°C-1 or W m-1 K-1.
[Note: Above equation, using calculus can be written as, \(\frac{d Q}{d t}\) = – kA \(\frac{d T}{d x}\), where \(\frac{d T}{d x}\) is the temperature gradient. The negative sign indicates that heat flow is in the direction of decreasing temperature. If A = 1 m2 and \(\frac{d T}{d x}\) = 1, then \(\frac{d Q}{d t}\) = k.]
Question 136.
Define coefficient of thermal conductivity in terms of temperature gradient.
Answer:
Coefficient of thermal conductivity of a material is defined as the rate of flow of heat per unit area per unit temperature gradient when the heat flow is at right angles to the faces of a thin parallel-sided slab of material.
Question 137.
Define conduction rate.
Answer:
Conduction rate (Pcond) is the amount of energy transferred per unit time through a slab of area A and thickness x, the two sides of the slab being at temperatures T1, and T2 (T1 > T2),
and is given Pcond = \(\frac{Q}{t}\) = kA \(\frac{\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)}{\mathrm{x}}\)
Question 138.
Explain the analogy between electrical resistance and thermal resistance.
Answer:
- Electrical resistance is ratio of \(\frac{V}{I}\) where, V is electrical potential difference between two ends of conductor and I is current or rate flow of charge.
- Consider expression for conduction rate,
Pcond = kA \(\frac{\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)}{\mathrm{x}}\)
⇒ \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{P}_{\mathrm{cond}}}=\frac{\mathrm{x}}{\mathrm{kA}}\) ……………… (1) - Comparing equation (1) with \(\frac{V}{I}\), (T1 – T2) is temperature difference between two ends and Pcond is rate of flow of heat.
- Ratio \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{P}_{\text {cond }}}\) is called as thermal resistance (RT) of material.
- Using (1), thermal resistance RT = \(\frac{\mathrm{x}}{\mathrm{kA}}\)
- Thermal resistance depends on the material and dimensions (length / breadth) of object.
Question 139.
What is thermal resistivity? What does it depend upon?
Answer:
i. Thermal resistivity (ρT) is the reciprocal of thermal conductivity (k).
ii. It is characteristic of a material.
![]()
Question 140.
Complete the table.

Answer:

Question 141.
Define convection.
Answer:
The process by which heat is transmitted through a substance from one point to another due to actual bodily movement of the heated particles of the substance is called convection.
Question 142.
Describe the mechanism of heat transfer by convection in liquids and gases.
Answer:
- Consider liquid being heated in a vessel from below.
- The liquid at the bottom of the vessel is heated
first and consequently its density decreases i.e., liquid molecules at the bottom are separated farther apart. - These hot molecules have high kinetic energy and rise upward to cold region while the molecules from cold region come down to take their place.
- Thus, each molecule at the bottom gets heated and rises then cool and descends.
- This action sets up the flow of liquid molecules called convection currents.
- The convection currents transfer heat to the entire mass of liquid via actual physical movement of the liquid molecules.
- Similar process takes place in case of a gas.
Question 143.
Give two applications of convection.
Answer:
- Heating and cooling of rooms:
- The mechanism of heating a room by a heater is entirely based on convection.
- The air molecules in immediate contact with the heater are heated up.
- These air molecules acquire sufficient energy and rise upward.
- The cool air at the top being denser moves down to take their place. This cool air in turn gets heated and moves upward.
- In this way, convection currents are set up in the room which transfer heat to different parts of the room.
- The same principle but in opposite direction is used to cool a room by an air-conditioner.
- Cooling of transformers:
- Due to current flowing in the windings of the transformer, enormous heat is produced.
- Therefore, transformer is always kept in a tank containing oil.
- The oil in contact with transformer body heats up, creating convection currents.
- The warm oil comes in contact with the cooler tank, gives heat to it and descends to the bottom. It again warms up to rise upward.
- This process is repeated again and again. The heat of the transformer is thus carried away by convection to the cooler tank.
- The cooler tank, in turn loses its heat by convection to the surrounding air.
Question 144.
Distinguish between free convection and forced convection.
Answer:
| Free convection | Forced convection | |
| i. | When a hot body is in contact with air under ordinary conditions, like air around a firewood, the air removes heat from the body by aprocess called free or natural convection. | The convection process can be accelerated by employing a fan to create a rapid circulation of fresh air. This is called forced convection. |
| ii. | Land and sea breezes are formed as a result of free convection currents in air. | Heat convector, air conditioner, heat radiators in IC engine etc. operate using forced convection. |
Question 145.
Define radiation.
Answer:
The transfer of heat energy from one place to another via emission of electromagnetic (EM) energy (in a straight line with the speed of light) without heating the intervening medium is called radiation.
![]()
Question 146.
Compare conduction, convection and radiation.
Answer:


Solved Examples
Question 147.
The temperature difference between two sides of an iron plate. 2 cm thick, is 10 °C. Heat is transmitted through the plate at the rate of 600 kcal per minute per square metre at steady state. Find the thermal conductivity of iron.
Solution:
Given: \(\frac{\mathrm{Q}}{\mathrm{At}}\) = 600 kcal/min m2 = \(\frac{600}{60}\) kcal/s m2
= 10 kcal/s m2
x = 2cm = 2 × 10-2 m
T1 – T2 = 10°C
To Find.- Thermal conductivity (k)
Formula: Q = \(\frac{\mathrm{kA}\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right) \mathrm{t}}{\mathrm{x}}\)
Calculation: From formula.
∴ k = \(\frac{\mathrm{Q}}{\mathrm{At} \mathrm{t}} \frac{\mathrm{x}}{\mathrm{T}_{1}-\mathrm{T}_{2}}=\frac{10 \times 2 \times 10^{-2}}{10}\)
= 0.02 kcal / m s
Thermal conductivity is 0.02 kcal / m s °C.
Question 148.
Calculate the rate of loss of heat through a glass window of area 1000 cm2 and thickness of 4 mm. when temperature inside is 27 °C and outside is – 5 °C. Coefficient of thermal conductivity of glass is 0.022 cal /s cm °C.
Solution:
Given: A = 1000 cm2 1000 × 10 m2
k = 0.22 cal / s cm °C
= 0.22 × 102 cal/ m °C
x = 4mm = 0.4 × 10-2 m
T1 = 27°C, T2 = -5°C
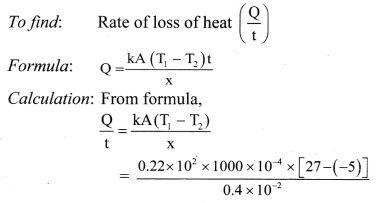
= 1.76 × 103 cal/s = 1.76kcal / s
Rate of loss of heat is 1.76 kcal / s.
Question 149.
Heat is conducted through a copper plate at the rate of 460 cal/s-cm2. Calculate the temperature gradient when the steady state is reached. (kcopper = 92 cal/m-s °C)
Solution:

Temperature gradient of the copper plate is 5°C/m.
Question 150.
Two parallel slabs of metals A and B of thickness 5 cm and 3 cm respectively are joined together. The outer face of the metal A is maintained at 100 °C and that of metal B is maintained at 40 °C. If the thermal conductivities of metal A and B are 0.045 kcal/m-s K and 0.015 kcal/m-s K respectively, find the temperature of the interface of two plates.
Solution:
For metal A:
T1 = 100 °C, T2 = θ
dx1= 5 cm = 5 × 10-2 m,
k1 = 0.045 kcal/m-s K
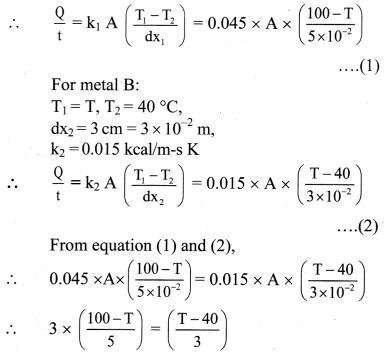
∴ 9(100 – T) = 5(T – 40)
∴ 900 – 9T = 5T – 200
∴ 14T = 1100
∴ T = 78.57°C
Temperature of the interlace of two plates is 78.57 °C.
![]()
Question 151.
What is the rate of energy loss in watt per square metre through a glass window 5 mm thick if outside temperature in -20 °C and inside temperature is 25 °C? (kglass = 1 W/m K)
Solution:
Given:
kglass = 1W/m K, T1 = 25 °C, T2 = -20 °C
T1 – T2 = 25- (-20)°C = 45 °C
X = 5 mm = 5 × 10-3 m
As one degree celsius equates to one kelvin, temperature difference of 450 C equals 45 K.
To find: Rate of energy loss per square metre \(\left(\frac{\mathrm{P}_{\text {cond }}}{\mathrm{A}}\right)\)
Formula: Pcond = \(\frac{Q}{t}=k A \frac{T_{1}-T_{2}}{x}\)
Calcula lion: From formula,
∴ The energy loss per square metre,
\(\frac{\mathrm{P}_{\text {oond }}}{\mathrm{A}}=\mathrm{k} \frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{x}}=\frac{1 \times 45}{5 \times 10^{-3}}\)
= 9 × 103 W/m2
Rate of energy loss per square metre is 9 × 103 W/m2.
Question 152.
A metal sphere cools at the rate of 1.6 °C/min when its temperature is 70 °C. At what rate will it cool when its temperature is 40 °C? The temperature of surroundings is 30 °C.
Solution:
Given: T1 = 70°C, T2 = 40 °C, T3 = 30 °C

= 0.4 (40 – 30)
= 0.4 °C/mm
Rate of cooling is 0.4 °C/mm.
Question 153.
A body cools at the rate of 0.5 °C/s when it is at 50 °C above the surrounding temperature. What is its rate of cooling when ¡t is at 30 °C above the surrounding temperature?
Solution:

Divide equation (2) by (1),
\(\frac{\left(\frac{\mathrm{dT}}{\mathrm{dt}}\right)_{2}}{0.5}=\frac{\mathrm{C}(30)}{\mathrm{C}(50)}\)
∴ \(\left(\frac{\mathrm{dT}}{\mathrm{dt}}\right)_{2}\) = 0.5 × \(\frac{30}{50}\) = 0.3 °C/s
The rate of cooling of the body at 30 °C above the surrounding temperature is 0.3 °C/s.
Apply Your Knowledge
Question 154.
A metre scale made up of aluminium (αa = 24 × 10-6 /°C) measures length of a steel rod (αs = 12 × 10-6 /°C) at room temperature as 50.00 cm. Now the temperature of the room is increased by 100 °C. What can be said about the measured length of the rod at new temperature?
Answer:
At new temperature T °C,
change in length of rod is,
∆Ls = L0(αs∆T) = 50.00(12 × 10-6 × 100)
= 0.06 cm.
Hence, the actual length of rod at T °C,
Ls = 50.06 cm
Due to change in temperature, along with rod, the scale will also increase in length.
For aluminium, at T °C,
∆La = L0(αa∆t) = 100.00 × 24 × 10-6 × 100
= 0.24 cm
∴ Length of the scale will be,
La = 100.24 cm
As, the expansion in scale is more than that in rod, the reading recorded by the scale at t°C will be less than 50 cm.
Question 155.
A mercury thermometer calibrated to measure temperature in Fahrenheit scale is kept in liquid phosphorus at 150 °F. The liquid phosphorus is then heated continuously until it reaches its boiling point measured by the thermometer to be 500 °F. Find the percentage fractional change in the density of mercury during the whole process. (γHg = 10-4/°F)
(Assume that no heat is lost to the surrounding during the process.)
Answer:
Given:
T2 = 500°F, T1 = 150°F
γHg = 10-4 /°F
As the liquid phosphorus is heated, the mercury in the thermometer also gets heated.
Due to thermal expansion,
V2 = V1(1 + γ∆t)
= V1 [1 + 10-4 × (500 – 150)]
= 1.035 V1
Now, initial density of mercury is,
ρ1 = \(\frac{\mathrm{m}}{\mathrm{V}_{1}}\)
After heating,
ρ2 = \(\frac{\mathrm{m}}{\mathrm{V}_{2}}=\frac{\mathrm{m}}{1.035 \mathrm{~V}_{1}}=\frac{\rho_{1}}{1.035}\)
⇒ ρ2 < ρ1
∴ change in density of mercury is,
\(\frac{\rho_{1}-\rho_{2}}{\rho_{1}}=\frac{\rho_{1}(1-0.9662)}{\rho_{1}}\) = 0.0338
∴ Percentage fractional change = 3.38%
![]()
Question 155.
When ‘m’ g of ice is added to ‘M’g of water at 20 °C, state the conditions for m and M for which
i) temperature of the mixture remains 0° C.
ii) temperature of the mixture exceeds 0 °C. (Specific heat of water = sw = 4.2 × 103 J kg-1 °C-1, latent heat of fusion = L = 3.36 × 105 J kg-1 )
Answer:
The heat lost by water in going from 20 °C to 0°C,
Q1 = Msw ∆T = \(\frac{\mathrm{M}}{1000}\) × 4.2 × 103 × (20) = 84M J
Now, heat required to convert m g of ice into water at 0 °C,
Q2 = mL = \(\frac{\mathrm{M}}{1000}\) × 3.36 × 105 = 336m J
- For temperature of mixture to be 0 °C,
Q2 > Q1
⇒ 336m > 84M
⇒ m > \(\frac{\mathrm{M}}{4}\) - For temperature of mixture to exceed 0 °C,
Q2 < Q1 ⇒ m < \(\frac{\mathrm{M}}{4}\)
Quick Review
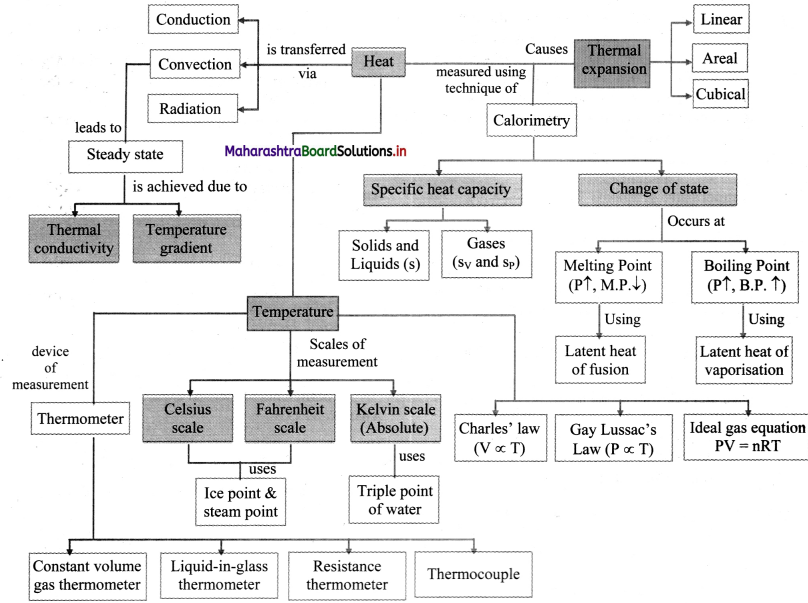
Multiple Choice Questions
Question 1.
Heat is transferred between two (or more) systems or a system and its surrounding by virtue of
(A) temperature difference.
(B) material difference.
(C) amount of heat difference.
(D) mass difference.
Answer:
(A) temperature difference.
Question 2.
On celsius scale, the two fixed points are marked as
(A) 0°C and 232°C
(B) 32°C and 100°C
(C) 0°C and 100°C
(D) 100°C and 180°C
Answer:
(C) 0°C and 100°C
Question 3.
If the temperature in a room is 30 °C, temperature in degree fahrenheit is
(A) 22 °F
(B) 62 °F
(C) 86 °F
(D) 96 °F
Answer:
(C) 86 °F
Question 4.
If the temperature on Fahrenheit scale is 140 °F, then the same temperature on kelvin scale will be
(A) 60.15 K
(B) 213.15 K
(C) 333.15 K
(D) 413.15 K
Answer:
(C) 333.15 K
Question 5.
In the gas equation, PV = RT, V stands for volume of
(A) any amount of gas .
(B) one gram mole of gas.
(C) one gram of a gas.
(D) one litre of a gas.
Answer:
(B) one gram mole of gas.
![]()
Question 6.
1 litre of an ideal gas at 27 °C is heated at constant pressure so as to attain temperature 297 °C. The final volume is approximately
(A) 1.2 litre
(B) 1.9 litre
(C) 19 litre
(D) 2.4 litre
Answer:
(B) 1.9 litre
Question 7.
How much should the pressure be increased in order to decrease the volume of a gas by 10% at a constant temperature?
(A) 7%
(B) 8%
(C) 10%
(D) 11.11%
Answer:
(D) 11.11%
Question 8.
Two rods of same material are equal in length, but one has cross-sectional area double the other. If they are heated through the same temperature then
(A) thick rod expands more.
(B) thin rod expands more.
(C) both rods will expand equally.
(D) none of these.
Answer:
(C) both rods will expand equally.
Question 9.
Two iron bars of same length with unequal radii are heated for the same rise in temperature. The linear expansion will be
(A) more in thin bar.
(B) more in thick bar.
(C) same for both.
(D) less in thick bar.
Answer:
(A) more in thin bar.
Question 10.
Which of the following has minimum coefficient of linear expansion?
(A) Gold
(B) Copper
(C) Platinum
(D) Invar steel
Answer:
(D) Invar steel
Question 11.
The coefficient of cubical expansion of a solid is the increase in volume per unit original volume at 0 °C per degree rise in _________.
(A) pressure
(B) volume
(C) temperature
(D) area
Answer:
(C) temperature
Question 12.
A disc has an area of 0.32 m2 at 20 °C, what will be its area at 100 °C? (α = 2 × 10-6 / °C)
(A) 0.12 m2
(B) 0.32 m2
(C) 0.51 m2
(D) 0.71 m2
Answer:
(B) 0.32 m2
![]()
Question 13.
The coefficient of linear expansion of iron is 1.1 × 10-5 per K. An iron is 10 m long at 27 °C. Length of the rod will be decreased by 1.1 mm when the temperature of the rod changes to
(A) 0°C
(B) 10 °C
(C) 17 °C
(D) 20 °C
Answer:
(C) 17 °C
Question 14.
The length of an aluminium rod is 120 cm at 20 °C. What is its length at 80 °C, if coefficient of linear expansion of aluminium is 2.5 × 10-5/°C?
(A) 130.18 cm
(B) 120.18 cm
(C) 110.18 cm
(D) 100.18 cm
Answer:
(B) 120.18 cm
Question 15.
A metal rod having a coefficient of linear expansion of 2 × 10-5 /°C has a length of 100 cm at 20 °C. The temperature at which it is shortened by 1 mm is
(A) -40 °C
(B) -30 °C
(C) -20 °C
(D) -10 °C
Answer:
(B) -30 °C
Question 16.
Iron sheet 50 cm × 20 cm is heated through 100 °C. If a = 12 × 10-6 / °C, the change in area is
(A) 2.4 cm2
(B) 3.4 cm2
(C) 4.2 cm2
(D) 5.3 cm2
Answer:
(A) 2.4 cm2
Question 17.
A liquid with coefficient of volume expansion γ is filled in a container of a material having the coefficient of linear expansion α. If the liquid over flows on heating then
(A) γ = 3α
(B) γ < 3α (C) γ > 3α
(D) γ = 3α2
Answer:
(B) γ < 3α
Question 18.
The volume of a metal block changes by 0.18% when it is heated through 20 °C. Its coefficient at cubical expansion will be
(A) 9 × 10-5 / °C
(B) 3 × 10-5 / °C
(C) 18 × 10-5 / °C
(D) 36 × 10-5 / °C
Answer:
(A) 9 × 10-5 / °C
Question 19.
The volume of liquid is 830 m3 at 30 °C and 850 m3 at 90 °C. The coefficient of volume expansion of liquid is
(A) 2 × 10-4 per °C
(B) 8 × 10-4 per °C
(C) 4 × 10-4 per °C
(D) 2.5 × 10-4 per °C
Answer:
(C) 4 × 10-4 per °C
![]()
Question 20.
The superficial expansivity is 1 / x times the cubic expansivity. The value of x is
(A) 2/3
(B) 3/2
(C) 2
(D) 3
Answer:
(B) 3/2
Question 21.
The unit of molar specific heat is
(A) JK-1 mole-1
(B) JK mole-1
(C) J-1 K-1mole-1
(D) JK-1 mole
Answer:
(A) JK-1 mole-1
Question 22.
The S.I. unit of latent heat is
(A) J-1 kg
(B) J kg-1
(C) J k-1 °C
(D) J-1 kg °C
Answer:
(B) J kg-1
Question 23.
The slowest mode of transfer of heat is
(A) conduction
(B) convection
(C) radiation
(D) specific heat
Answer:
(A) conduction
Question 24.
The quantity of heat which crosses unit area of a metal plate during conduction depends on
(A) the density of the metal.
(B) the temperature gradient perpendicular to the area.
(C) the temperature to which the metal is heated.
(D) the area of the metal plate.
Answer:
(B) the temperature gradient perpendicular to the area.
Question 25.
Which of the following is not the unit of thermal conductivity?
(A) J/m s °C
(B) K cal/m s K
(C) Watt/m °C
(D) J/m2 s °C
Answer:
(D) J/m2 s °C
Question 26.
The most desirable combination for the material of a cooking pot is
(A) high specific heat and high conductivity.
(B) low specific heat and high conductivity.
(C) high specific heat and low conductivity.
(D) low specific heat and low conductivity.
Answer:
(B) low specific heat and high conductivity.
Question 27.
While measuring thermal conductivity of a liquid, we keep the upper part hot and lower part cold, so that
(A) radiation may start.
(B) radiation may stop.
(C) convection may start.
(D) convection may be stopped.
Answer:
(D) convection may be stopped.
Question 28.
Convention currents in air in day time is from
(A) land to sea
(B) sea to land
(C) sea to sky
(D) land to land
Answer:
(B) sea to land
![]()
Question 29.
One end of a metal rod one metre long is kept in ice and the other end is at 100 °C. What is temperature gradient throughout the rod?
(A) 10 °C/m
(B) 100 °C/m
(C) 50 °C/m
(D) 1 °C/m
Answer:
(B) 100 °C/m
Question 30.
__________ amount of heat is required to raise the temperature of 100 g of kerosene from 10 °C to 30 °C (Given: specific heat of kerosene is 0.51 kcal/kg °C)
(A) 0.102 kcal
(B) 1.02 kcal
(C) 10.2 kcal
(D) 102 kcal
Answer:
(B) 1.02 kcal
Question 31.
One end of copper rod is in contact with water at 100 °C and the other end in contact with ice at 0 °C. The length of the rod is 100 cm. At a point which is at a distance of 35 cm from the cold end, temperature is (assuming steady state heat flow)
(A) 35 °C
(B) 65 °C
(C) 56 °C
(D) 53 °C
Answer:
(A) 35 °C
Question 32.
In Newton’s law of cooling, the rate of fall of temperature
(A) is constant
(B) increases
(C) decreases
(D) doubles
Answer:
(C) decreases
Question 33.
The metal sphere cools at 1 °C/min, when its temperature is 50 °C. If the temperature of environment is 30 °C, its rate of cooling at 35 °C is
(A) 0.25 °C/min
(B) 0.5 °C/min
(C) 0.75 °C/min
(D) 0.4 °C/min
Answer:
(A) 0.25 °C/min
Competitive Corner
Question 1.
A copper rod of 88 cm and an aluminium rod of unknown length have their increase in length independent of increase in temperature. The length of aluminum rod is:
(αCu = 1.7 × 10-5 K-1 and αAl = 2.2 × 10-5 K-1)
(A) 88 cm
(B) 68 cm
(C) 6.8 cm
(D) 1 13.9 cm
Answer:
(B) 68 cm
Hint:
LCu αCu ∆T = LAl αAl ∆T
∴ 88 × (1.7 × 10-5) = LAl(2.2 × 10-5)
∴ LAl = \(\frac{88 \times 1.7}{2.2}\)
∴ LAl = 68 cm
Question 2.
The unit of thermal conductivity is:
(A) W m K-1
(B) W m-1 K-1
(C) JmK -1
(D) Jm-1K-1
Answer:
(B) W m-1 K-1
Hint:
Q = kA \(\left(\frac{\Delta \mathrm{T}}{\Delta \mathrm{x}}\right)\) t
Q = quantity of heat conducted.
A = area of cross section
t = time for which heat is passed
\(\left(\frac{\Delta \mathrm{T}}{\Delta \mathrm{x}}\right)\) = temperature gradient
∴ K = \(\frac{Q}{A t\left(\frac{\Delta T}{\Delta x}\right)}\)
∴ Unit of k = W m-1 K-1
![]()
Question 3.
A deep rectangular pond of surface area A, containing water (density = p, specific heat capacity = s), is located in a region where the outside air temperature is at a steady value of -26°C. The thickness of the frozen ice layer in this pond, at a certain instant is x. Taking the thermal conductivity of ice as K, and its specific latent heat of fusion as L, the rate of increase of the thickness of ice layer, at this instant, would be given by
(A) 26K/ρx(L + 4s)
(B) 26K/ρx(L – 4s)
(C) 26K/(ρx2 L)
(D) 26K/(ρxL)
Answer:
(D) 26K/(ρxL)

Question 4.
An object kept in a large room having air temperature of 25°C takes 12 minutes to cool from 80°C to 70°C. The time taken to cool for the same object from 70°C to 60°C would be nearly.
(A) 15 min
(B) 10mm
(C) 12mm
(D) 20mm
Answer:
(A) 15 min
Hint:
By Newton’s law of cooling,

Question 5.
A thermally insulated vessel contains 150 g of water at 0 °C. Then the air from the vessel ispumped out adiabatically. A fraction of water turns into ice and the rest evaporates at 0 °C itself. The mass of evaporated water will be closest to :
(Latent heat of vaporization of water = 2.10 × 106 J kg-1 and Latent heat of Fusion of water = 3.36 × 105 J kg-1)
(A) 150g
(B) 20g
(C) 130g
(D) 35g
Answer:
(B) 20g
Hint:
m= 150 g = 0.15 kg
The heat required to evaporate ‘m’ grams of water,
∆Qrequired = mLv ………. ( 1)
(015 – m) is the amount of mass that converts into ice
∴ ∆Qreleased = (0.15 – m) Lf …………. (2)
Now, amount of heat required = amount of heat released
∴ From (1) and (2),
mLv = (0.15 – m)Lf
∴ m(Lf + Lv) = 0.15 Lf
∴ m = \(\frac{0.15 \mathrm{~L}_{\mathrm{f}}}{\mathrm{L}_{\mathrm{f}}+\mathrm{L}_{\mathrm{v}}}\)
∴ m = \(\frac{0.15 \times 3.36 \times 10^{5}}{2.10 \times 10^{6}+3.36 \times 10^{5}}\)
∴ m=0.0206kg ≈ 20g
Question 6.
A copper ball of mass 100 g is at a temperature T. It is dropped in a copper calorimeter of mass 100 g, filled with 170 g of water at room temperature. Subsequently, thetemperature of the system is found to be 75 °C. T is given by: (Given: room temperature = 30°C, specific heat of copper 0.1 cal/g °C)
(A) 1250°C
(B) 825°C
(C) 800°C
(D) 885°C
Answer:
(D) 885°C
Hint:
Heat lost by copper ball = Heat gained by calorimeter and water
∴mbsc∆T1 = mccc∆T2 + mwsw∆T2
∴ (100)(0.1)(T – 75) = (100)(0.1)(75 – 30) + (170)(1)(75 – 30)
10(T – 75) = 450 + 7650 = 8100
T – 75 = 810
T = 885 °C
![]()
Question 7.
Coefficient of linear expansion of brass and steel rods are α1 and α2. Lengths of brass and steel rods are l1 and l2 respectively. If (l2 – l1) is maintained same at all temperatures, which one of the following relations holds good?
(A) α12l2 = α22l1
(B) α1l1 = α2l2
(C) α1l2 = α2l1
(D) α1l22 = α2l12
Answer:
(B) α1l1 = α2l2
Hint:
∆L = L(1 + α∆t)
i.e. ∆l2 = l2(1 + α2∆t)
and ∆l1 =11(1 + α1∆t)
It is given,
l2– l1 = ∆tl2 – ∆ll1
∴ l2 – l1 = l2 (1 + α2∆t) – l1 (1+ α1∆t)
= l2 + l2α2∆t – l1 – l1α1∆t
∴ – l2 + l2 + l2α2∆t = -l1 + l1 + l1α1∆t
∴ l2α2∆t = l1α1∆t
i.e., l2α2 = l1α1
Question 8.
A pendulum clock loses 12 s a day if the temperature is 40 °C and gains 4 s a day if the temperature is 20 °C. The temperature at which the clock will show correct time, and the coefficient of linear expansion (a) of the metal of the pendulum shaft are respectively:
(A) 60 πC, a = 1.85 × 10-4/πC
(B) 30 πC, a = 1.85 × 10-3/πC
(C) 55 πC, a = 1.85 × 10-2/πC
(D) 25 πC, a = 1.85 × 10-5/πC
Answer:
(D) 25 πC, a = 1.85 × 10-5/πC
Hint:
Period of pendulum, T = 2π\(\sqrt{\frac{\mathrm{L}}{\mathrm{g}}}\)
∴ T ∝ \(\sqrt{\mathrm{L}}\)
But, L = L0 (1 + α∆t)
∴ T ∝ \(\sqrt{\mathrm{L}_{0}(1+\alpha \Delta \mathrm{t})}\)
As L0 is constant,
⇒ T ∝ (1 + α ∆t)
Calculating fractional change in time period of pendulum, \(\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{1}{2}(\alpha \Delta \mathrm{t})\)
For the given pendulum,
T = 24 × 60 × 60 = 864000 s
When t1 = 40 °C, ∆T = 12 s,

Question 9.
A piece of ice falls from a height h so that it melts completely. Only one — quarter of the heat produced is absorbed by the ice and all energy of ice gets converted into heat during its fall. The value of h is [Latent heat of ice is 3.4 × 105 J/kg and g = 10 N/kg]
(A) 136 km
(B) 68km
(C) 34km
(D) 544km
Answer:
(A) 136 km
Hint:
When the piece of ice falls from the height h, it possesses potential energy, mgh.
This P.E. is converted to heat energy.
∴ Q = mgh
But only \(\frac{1^{\text {th }}}{4}\) of it is absorbed by ice which is used to change the state.
∴ \(\frac{\mathrm{mgh}}{4}\) = mL
∴ \(\frac{10 \times \mathrm{h}}{4}\) = 3.4 × 105
∴ h = 13.6 × 104 m = 136km
![]()
Question 10.
A body cools from a temperature 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton’s law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be
(A) T
(B) \(\frac{7}{4}\) T
(C) \(\frac{3}{2}\) T
(D) \(\frac{4}{3}\) T
Answer:
(C) \(\frac{3}{2}\) T
Hint:
By Newton’s law of cooling,
