Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 1 Units and Measurements Important Questions and Answers.
Maharashtra State Board 11th Physics Important Questions Chapter 1 Units and Measurements
Question 1.
What is a measurement? How is measured quantity expressed?
Answer:
- A measurement is a comparison with internationally accepted standard measuring unit.
- The measured quantity (M) is expressed in terms of a number (n) followed by a corresponding unit (u) i.e., M = nu.
Example:
Length of a wire when expressed as 2 m, it means value of length is 2 in the unit of m (metre).
Question 2.
State true or false. If false correct the statement and rewrite. Different quantities are measured in different units.
Answer: True.
[Note: Choice of unit depends upon its suitability for measuring the magnitude of a physical quantity under consideration. Hence, we choose different scales for same physical quantity.]
![]()
Question 3.
Describe briefly different types of systems of units.
Answer:
System of units are classified mainly into four types:
- C.G.S. system:
It stands for Centimetre-Gram-Second system. In this system, length, mass and time are measured in centimetre, gram and second respectively. - M.K.S. system:
It stands for Metre-Kilogram-Second system. In this system, length, mass and time are measured in metre, kilogram and second respectively. - F.P.S. system:
It stands for Foot-Pound-Second system. In this system, length, mass and time are measured in foot, pound and second respectively. - S.I. system:
It stands for System International. This system has replaced all other systems mentioned above. It has been internationally accepted and is being used all over world. As the SI units use decimal system, conversion within the system is very simple and convenient.
Question 4.
What are fundamental quantities? State two examples of fundamental quantities. Write their S.J. and C.G.S. units.
Answer:
Fundamental quantities:
The physical quantities which do not depend on any other physical quantity for their measurements i.e., they can be directly measured are called fundamental quantities.
Examples: mass, length etc.

Question 5.
What are fundamental units? State the S.l. units of seven fundamental quantities.
Answer:
Fundamental units:
The units used to measure fundamental quantities are called fundamental units.
S.I. Units of fundamental quantities:
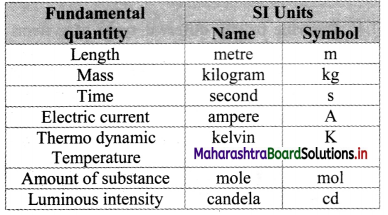
Question 6.
State and describe the two supplementary units.
Answer:
The two supplementary units are:
i) Plane angle (dθ):
a. The ratio of kngth of arc (ds) of an circle to the radius (r) of the circle is called as Plane angle (dθ)
i.e., dθ = \(\frac{\mathrm{ds}}{\mathrm{r}}\)
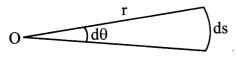
b. Thus, dθ is angle subtended by the arc at the centre of the circle.
c. Unit: radian (rad)
d. Denoted as θc
e. Length of arc of circle = Circumference of circle = 2πr.
∴ plane angle subtended by entire circle at its centre is θ = \(\frac{2 \pi \mathrm{r}}{\mathrm{r}}\) = 2πc
ii) Solid angle (dΩ):
a. solid angle is 3-dimensional analogue of plane angle.
b. Solid angle is defined as area of a portion of surface of a sphere to the square of radius of the sphere.
i.e., dΩ = \(\frac{\mathrm{d} \mathrm{A}}{\mathrm{r}^{2}}\)
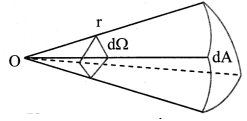
c. Unit: Steradian (sr)
d. Denoted as (Ω)
e. Surface area of sphere = 4πr2
∴ solid angle subtended by entire sphere at its centre is Ω = \(\frac{4 \pi r^{2}}{r^{2}}\) = 4π sr
![]()
Question 7.
Derive the relation between radian and degree. Also find out 1” and 1’ in terms of their respective values in radian. (Take π = 3.1416)
Answer:
We know that, 2 πc = 360°
∴ πc = 180°

Question 8.
What are derived quantities and derived units? State two examples. State the corresponding S.L. and C.G.S. units of the examples.
Answer:
- Derived quantities: Physical qUantities other than fundamental quantities which depend on one or more fundamental quantities for their measurements are called derived quantities.
- Derived units: The units of derived quantities which are expressed in terms of fundamental units for their measurements are called derived units.
- Examples and units:
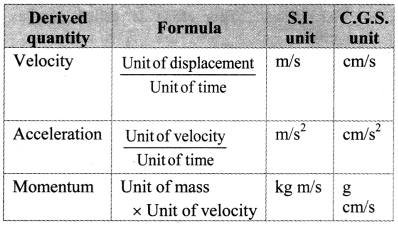
Question 9.
Classify the following quantities into fundamental and derived quantities: Length, Velocity, Area, Electric current, Acceleration, Time, Force, Momentum, Energy, Temperature, Mass, Pressure, Magnetic induction, Density.
Answer:
Fundamental Quantities: Length, Electric current, Time, Temperature, Mass.
Derived Quantities: Velocity, Area, Acceleration, Force, Momentum, Energy. Pressure, Magnetic induction, Density
Question 10.
Classify the following units into fundamental, supplementary and derived units:
newton, metre, candela, radian, hertz. square metre, tesla, ampere, kelvin, volt, mol, coulomb, farad, steradian.
Answer:
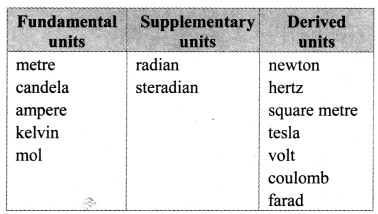
Question 11.
List the conventions followed while using SI units.
Answer:
Following conventions should be followed while writing S.I. units of physical quantities:
- Unit of every physical quantity should be represented by its symbol.
- Full name of a unit always starts with smaller letter even if it is named after a person, eg.: 1 newton, 1 joule, etc. But symbol for unit named after a person should be in capital letter, eg.: N after scientist Newton, J after scientist Joule, etc.
- Symbols for units do not take plural form.
- Symbols for units do not contain any full stops at the end of recommended letter.
- The units of physical quantities in numerator and denominator should be written as one ratio. For example the SI unit of acceleration is m/s2 or m s-2 but not m/s/s.
- Use of combination of units and symbols for units is avoided when physical quantity is expressed by combination of two. For example, The unit J/kg K is correct while joule/kg K is not correct.
- A prefix symbol is used before the symbol of the unit.
- a. Prefix symbol and symbol of unit constitute a new symbol for the unit which can be raised to a positive or negative power of 10.
For example,
1 ms = 1 millisecond = 10-3 s
1 μs = 1 microsecond = 10-6 s
1 ns = 1 nanosecond = 10-9 s - b. Use of double prefixes is avoided when single prefix is available
10-6 s = 1 μs and not 1 mms
10-9 s = 1 ns and not 1 mμs
- a. Prefix symbol and symbol of unit constitute a new symbol for the unit which can be raised to a positive or negative power of 10.
- Space or hyphen must be introduced while indicating multiplication of two units e.g., m/s should be written as m s-1 or m-s-1.
Solved Examples
Question 12.
What is the solid angle subtended by the moon at any point of the Earth, given the diameter of the moon is 3474 km and its distance from the Earth 3.84 × 108 m?
Solution:
Given: Diameter (D) = 3474 km
∴ Radius of moon (R) = 1737 km
= 1.737 × 106 m
Distance from Earth r = 3.84 × 108 m
To find: Solid angle (dΩ)
Formula: dΩ = \(\frac{\mathrm{d} \mathrm{A}}{\mathrm{r}^{2}}\)
Calculation:
From formula,
dΩ = \(\frac{\pi \mathrm{R}^{2}}{\mathrm{r}^{2}}\) ……..( cross-sectional area of disc of moon = πR2)
dΩ = \(\frac{\pi \times\left(1.737 \times 10^{5}\right)^{2}}{\left(3.84 \times 10^{8}\right)^{2}}\)
= \(\frac{3.412 \times(1.737)^{2} \times 10^{10}}{(3.84)^{2} \times 10^{16}}\)
= antilog{log(3.142) + 2log(1.737) – 2log(3.84)} × 10-6
= antilog {0.4972 + 2(0.2397) – 2(0.5843)} × 10-6
= antilog{0.4972 + 0.4794 – 1.1686} × 10-6
= antilog{\(\overline{1}\) .8080} × 10-6
= 6.428 × 10-1 × 10-6
= 6.43 × 10-5 sr
Solid angle subtended by moon at Earth is 6.43 × 10-5 sr
[Note: Above answer is obtained substituting value of r as 3.142]
![]()
Question 13.
Pluto has mean diameter of 2,300 km and very eccentric orbit (oval shaped) around the Sun, with a perihelion (nearest) distance of 4.4 × 109 km and an aphelion (farthest) distance of 7.3 × 109 km. What are the respective solid angles subtended by Pluto from Earth’s perspective? Assume that distance from the Sun can be neglected.
Solution:
Given: Radius of Pluto. R = \(\frac{2300}{2}\) km
= 1150km
Perihelion distance rp = 4.4 × 109 km
Aphelion distance ra = 7.3 × 109 km
To find: Solid angles (dΩp and dΩa)

Solid angle at perihelion distance is 2.146 × 10-13 sr and at aphelion distance is 7.798 × 10-14 sr.
Question 14.
Define a metre.
Answer:
The metre is the length of the path travelled by light in vacuum during a time interval of 1/299, 792, 458 of a second.
Answer:
Question 15.
What ¡s parallax?
Answer:
- Parallax is defined as the apparent change in position of an object due to a change in position of an observer.
- Explanation: When a pencil is held in front of our eyes and we look at it once with our left eye closed and then with our right eye closed, pencil appears to move against the background. This effect is called parallax effect.
Question 16.
What is parallax angle?
Answer:
i) Angle between the two directions along which a star or planet is viewed at the two points of observation is called parallax angle (parallactic angle).
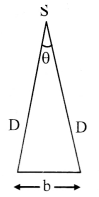
ii) It is given by θ = \(\frac{b}{D}\)
where, b = Separation between two points of observation.
D = Distance of source from any point of observation.
Question 17.
Explain the method to determine distance of a planet from the Earth.
Answer:
- Parallax method is used to determine distance of different planets from the Earth.
- To measure the distance ‘D’ of a far distant planet S, select two different observatories (E1 and E2).
- The planet should be visible from E1 and E2 observatories simultaneously i.e. at the same time.
- E1 and E2 are separated by distance ‘b’ shown in figure.
∴ E1E3 = b
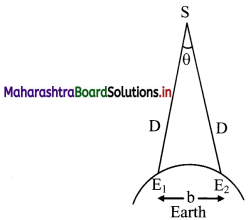
- The angle between the two directions along which the planet is viewed, can be measured. It is parallax angle, which in this case is L ∠E1E2 = θ
- The planet is far away from the (Earth) observers, hence
b < <D
∴ \(\frac{b}{D}\) < < 1 and ‘θ’ is also very small.
Hence, E1E2 can be considered as arc of length b of circle with S as centre and D as radius.
:. E1S = E2S = D
∴ θ = \(\frac{b}{D}\) . . . .(θ is taken in radian)
∴ D = \(\frac{b}{\theta}\)
Thus, the distance ‘D’ of a far away planet ‘S’ can be determined using the parallax method.
![]()
Question 18.
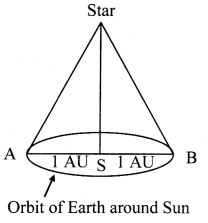
Explain how parallax method is used to measure distance of a star from Earth.
Answer:
- The parallax measured from two farthest distance points on Earth for stars will be too small and hence cannot be measured.
- Instead, parallax between two farthest points (i.e., 2 ΔU apart) along the orbit of Earth around the Sun (s) is measured.
Question 19.
Explain how size of a planet or star is measured.
Answer:
- To determine the diameter (d) of a planet or star, two diametrically opposite points of the planet are viewed from the same observatory.
- If d is diameter of planet or star, angle subtended by it at any single point on the Earth is called angular diameter of planet.
- Let angle α be angle between these two directions.
- If distance between the Earth and planet or star (D) is known, α = \(\frac{\mathrm{d}}{\mathrm{D}}\)
- This relation gives, d = α D
Thus, diameter (d) of planet or star can be determined.
Question 20.
Name the devices used to measure very small distances such as atomic size.
Answer:
Devices used are:
Electron microscope, tunnelling electron microscope.
Question 21.
Just as large distances are measured in AU, parsec or light year, atomic or nuclear distances are measured with the help of microscopic units. Match the units given in column A with their corresponding SI unit given in column B.

Answer:
i. – (b)
ii. – (a)
Solved Examples
Question 22.
A star is 5.5 light years away from the Earth. How much parallax in arcsec will it subtend when viewed from two opposite points along the orbit of the Earth?
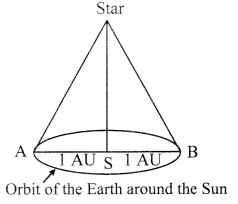
Solution:
Two opposite points-A and B along the orbit of the Earth are 2 AU apart. The angle subtended by AB at the position of the star is

= antilog{log(2.992) – log(5.5) – log(9.46)} × 10-4
= antilog {0.4761 – 0.7404 – 0.9759} × 10-4
= antilog {\(\overline{2}\).7598} × 10-4
= 5.751 × 10-2 × 10-4
= 5.75 × 10-6
= 5.75 × 10-6 rad
= 5.75 × 10-6 × 57.297 × 60 × 60 arcsec
…. (converting radian into arcsecond)
= 1.186 arcsec
Parallax is 1.186 arcsec
Question 23.
The moon is at a distance of 3.84 × 108 m from the Earth. If viewed from two diametrically opposite points on the Earth, the angle subtended at the moon is 1° 54′. What is the diameter of the Earth?
Solution:
Given
Distance (D) = 3.84 × 108 m
Subtended angle (α)
= 1° 54′ = (60’+ 54′)= 114′
= 114 × 2.91 × 10-4 rad
= 3.317 × 10-2 rad
To find: Diameter of Earth (d)
Formula: d = αD
Calculation: From formula,
d = 3.317 × 10-2 × 3.84 × 108
= 1.274 × 107 m
Diameter of Earth is 1.274 × 107 m.
Question 24.
Explain the method to measure mass.
Answer:
Method for measurement of mass:
- Mass, until recently, was measured with a standard mass of the international prototype of the kilogram (a platinum-iridium alloy cylinder) kept at international Bureau of Weights and Measures, at Serves, near Paris, France.
- As platinum – iridium piece was seen to pick up microparticles and found to be affected by atmosphere, its mass could no longer be treated as constant.
- Hence, a new definition of mass was introduced in terms of electric current on 20th May 2019.
- Now, one kilogram mass is described in terms of amount of current which has to be passed through electromagnet to pull one side of extremely sensitive balance to balance the other side which holds one standard kg mass.
- To measure mass of small entities such as atoms and nucleus, atomic mass unit (amu) is used.
It is defined as (\(\frac{1}{12}\))th mass of an unexcited atom of carbon -12(C12).
1 amu ≈ 1.66 × 10-27 kg.
![]()
Question 25.
That can he the reason for choosing Carbon-12 to define atomic mass unit?
Answer:
- Unlike oxygen and hydrogen, which exhibit various isotopes in higher proportions, carbon- 12 is the single most abundant (98% of available carbon) isotope of carbon.
- it is also very stable.
Hence, it makes more accurate unit of measuring mass and is used to define atomic mass unit.
Question 26.
Define mean solar day. Explain the method for measurement of time.
Answer:
- A mean solar day is the average time interval from one noon to the next noon.
Method for measurement of time: - The unit of time, the second, was considered to be \(\frac{1}{86400}\) of the mean solar day, where a mean solar day = 24 hours
= 24 × 60 × 60
= 86400 s - However, this definition proved to be unsatisfactory to define the unit of time precisely because solar day varies gradually due to gradual slowing down of the Earth’s rotation. Hence, the definition of second was replaced by one based on atomic standard of time.
- Atomic standard of time is now used for the measurement of time. In atomic standard of time, periodic vibrations of caesium atom is used.
- One second is time required for 9,192.631,770 vibrations of the radiation corresponding to transition between two hyperfine energy states of caesium-133 (Cs- 133) atom.
![]()
Question 27.
Define dimensions and dimensional formula of physical quantities. Give few examples of dimensional formula.
Answer:
- Dimensions:
The dimensions of a physical quantity are the powers to which the fundamental units must be raised in order to obtain the unit of a given physical quantity. - Dimensional formula:
When any derived quantity is represented with appropriate powers of symbols of the fundamental quantities, SUCh an expression is called dimensional formula.
It is expressed by square bracket with no comma in between the symbols. - Examples of dimensional formula:
a. Speed = \(\frac{\text { Distance }}{\text { time }}\)
∴ Dimensions of speed = \(\frac{[\mathrm{L}]}{[\mathrm{T}]}\) = [L1M0T-1]
[Note: As power of M is zero, it can be omitted from dimensional formula. Therefore, dimensions of speed can be written as [L1T1]

Question 28.
A book with many printing errors contains four different formulae for the displacement y of a particle undergoing a certain periodic function:
i) y = a sin \(\frac{2 \pi t}{T}\)
ii) y = a sin v t
iii) y = \(\frac{\mathrm{a}}{\mathbf{T}} \sin \frac{\mathrm{t}}{\mathrm{a}}\)
iv) y = \(\frac{a}{\sqrt{2}}\left[\sin \frac{2 \pi t}{T}+\cos \frac{2 \pi t}{T}\right]\)
Here, a is maximum displacement of particle, y ¡s speed of particle, T is time period of motion. Rule out the wrong formulae on dimensional grounds.
Answer:
The argument of trigonometrical function, i.e., angle is dimensionless. Now,
i) The argument, \(\left[\frac{2 \pi \mathrm{t}}{\mathrm{T}}\right]=\frac{[\mathrm{T}]}{[\mathrm{T}]}\) = 1 = [L0M0T0]
which is a dimensionless quantity.
Hence, formula (i) is correct.
ii) The argument,
[vt] = [LT-1] [T] = [L] = [L1M0T0]
which is not a dimensionless quantity.
Hence, formula (ii) is incorrect.
iii) The argument,
\(\left[\frac{\mathrm{t}}{\mathrm{a}}\right]=\frac{[\mathrm{T}]}{[\mathrm{L}]}\) = [L-1M0T1]
which is not a dimensionless quantity.
Hence, formula (iii) is incorrect.
iv) The argument,
\(\left[\frac{2 \pi \mathrm{t}}{\mathrm{T}}\right]=\frac{[\mathrm{T}]}{[\mathrm{T}]}\) = 1 = [L0M0T0]
which is a dimensionless quantity.
Hence, formula (iv) is correct.
Question 29.
State principle of homogeneity of dimensions.
Answer:
Principle of homogeneity of dimensions: The dimensions of all the terms on the two sides of a physical equation relating different physical quantities must be same.
![]()
Question 30.
State the uses of dimensional analysis.
Answer:
Uses of dimensional analysis:
To check the correctness of a physical equation.
Correctness of a physical equation by dimensional analysis:
- A physical equation is correct only if the dimensions of all the terms on both sides of that equations are the same.
- For example, consider the equation of motion.
v = u + at ……………. (1) - Writing the dimensional formula of every term, we get
Dimensions of LH.S. [v] [L1M0T-1],
Dimensions of R.H.S. = [u] + [at]
= [L1M0T-1] + [L1M0T-2] [L1M0T-1]
= [L1M0T-1] + [L1M0T-1]
⇒ [L.HS.] = [R.H.S.] - As dimensions of both side of equation is same, physical equation is dimensionally correct.
To derive the relationship between related physical quantities.
Expression for time period of a simple pendulum by dimensional analysis:
- Time period (T) of a simple pendulum depends upon length (l) and acceleration due to gravity (g) as follows:
T ∝ la gb
i.e., T = k la gb ………… (1)
where, k = proportionality constant, which is dimensionless. - The dimensions of T = [L0M0T1)
The dimensions of l = [L1M0T0]
The dimensions of g = [L1M0T2]
Taking dimensions on both sides of equation (1),
[L0M0T1] = [L1M0T0]a [L1M0T-2]b
[L0M0T1] = [La+bM0T-2b] - Equating corresponding power of L, M and T on both sides, we get
a + b = 0 …………. (2)
and -2b = 1
∴ b = –\(\frac{1}{2}\) - Substituting ‘b’ in equation (2), we get
a = \(\frac{1}{2}\) - Substituting values of a and b in equation (1),
we have,
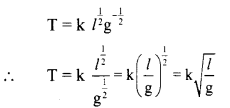
- Experimentally, it ¡s found that k = 2π
∴ T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\)
This is the required expression for time period of a simple pendulum.
To find the conversion factor between the units of the same physical quantity in two different systems of units.
Conversion factor between units of same physical quantity:
- let ‘n’ be the conversion factor between the units of work.
∴ 1 J = n erg ………….. (1) - Dimensions of work in S.l. system are \(\left[\mathrm{L}_{1}^{2} \mathrm{M}_{1}^{\prime} \mathrm{T}_{1}^{-2}\right]\) and in CGS system are \(\left[\mathrm{L}_{2}^{2} \mathrm{M}_{2}^{1} \mathrm{~T}_{2}^{-2}\right]\)
- From (1),
\(1\left[\mathrm{~L}_{1}^{2} \mathrm{M}_{1}^{1} \mathrm{~T}_{1}^{-2}\right]=\mathrm{n}\left[\mathrm{L}_{2}^{2} \mathrm{M}_{2}^{1} \mathrm{~T}_{2}^{-2}\right]\)

n= 104 × 103 × 1 = 107
Hence, the conversion factor, n = 107
There fore, from equation (1), we have,
∴ 1 J = 107 erg.
Question 31.
Explain the use of dimensional analysis to check the correctness of a physical equation.
Answer:
Correctness of a physical equation by dimensional analysis:
- A physical equation is correct only if the dimensions of all the terms on both sides of that equations are the same.
- For example, consider the equation of motion.
v = u + at ……………. (1) - Writing the dimensional formula of every term, we get
Dimensions of LH.S. [v] [L1M0T-1],
Dimensions of R.H.S. = [u] + [at]
= [L1M0T-1] + [L1M0T-2] [L1M0T-1]
= [L1M0T-1] + [L1M0T-1]
⇒ [L.HS.] = [R.H.S.] - As dimensions of both side of equation is same, physical equation is dimensionally correct.
Question 32.
Time period of a simple pendulum depends upon the length of pendulum (l) and acceleration due to gravity (g). Using dimensional analysis, obtain an expression for time period of a simple pendulum.
Answer:
Expression for time period of a simple pendulum by dimensional analysis:
i) Time period (T) of a simple pendulum depends upon length (l) and acceleration due to gravity (g) as follows:
T ∝ la gb
i.e., T = k la gb ………… (1)
where, k = proportionality constant, which is dimensionless.
ii) The dimensions of T = [L0M0T1)
The dimensions of l = [L1M0T0]
The dimensions of g = [L1M0T2]
Taking dimensions on both sides of equation (1),
[L0M0T1] = [L1M0T0]a [L1M0T-2]b
[L0M0T1] = [La+bM0T-2b]
iii) Equating corresponding power of L, M and T
on both sides, we get
a + b = 0 …………. (2)
and -2b = 1
∴ b = –\(\frac{1}{2}\)
iv) Substituting ‘b’ in equation (2), we get
a = \(\frac{1}{2}\)
v) Substituting values of a and b in equation (1),
we have,
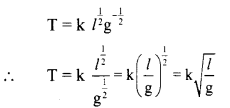
vi) Experimentally, it ¡s found that k = 2π
∴ T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\)
This is the required expression for time period of a simple pendulum.
Question 33.
Find the conversion factor between the S.I. and the C.OES. units of work using dimensional analysis.
Answer:
Conversion factor between units of same physical quantity:
- let ‘n’ be the conversion factor between the units of work.
∴ 1 J = n erg ………….. (1) - Dimensions of work in S.l. system are \(\left[\mathrm{L}_{1}^{2} \mathrm{M}_{1}^{\prime} \mathrm{T}_{1}^{-2}\right]\) and in CGS system are \(\left[\mathrm{L}_{2}^{2} \mathrm{M}_{2}^{1} \mathrm{~T}_{2}^{-2}\right]\)
- From (1),
\(1\left[\mathrm{~L}_{1}^{2} \mathrm{M}_{1}^{1} \mathrm{~T}_{1}^{-2}\right]=\mathrm{n}\left[\mathrm{L}_{2}^{2} \mathrm{M}_{2}^{1} \mathrm{~T}_{2}^{-2}\right]\)

n= 104 × 103 × 1 = 107
Hence, the conversion factor, n = 107
There fore, from equation (1), we have,
∴ 1 J = 107 erg.
Question 34.
State the limitations of dimensional analysis.
Answer:
Limitations of dimensional analysis:
- The value of dimensionless constant can be obtained with the help of experiments only.
- Dimensional analysis cannot be used to derive relations involving trigonometric (sin θ, cos θ, etc.), exponential (ex, ex2, etc.), and logarithmic functions (log x, log x3, etc) as these quantities are dimensionless.
- This method is not useful if constant of proportionality is not a dimensionless quantity.
- If the correct equation contains some more terms of the same dimension, it is not possible to know about their presence using dimensional equation.
![]()
Question 35.
If two quantities have same dimensions, do they always represent the same physical content?
Answer:
When dimensions of two quantities are same, they do not always represent the same physical content.
Example:
Force and momentum both have same dimensions but they represent different physical content.
Question 36.
A dimensionally correct equation need not actually be a correct equation but dimensionally incorrect equation is necessarily wrong. Justify.
Answer:
i) To justify a dimensionally correct equation need not be actually a correct equation, consider equation, v2 = 2as
Dimensions of L.H.S. = [v2] = [L2M0T2]
Dimensions of R.H.S. = [as]= [L2M0T2]
⇒ [L.H.S.] = [R.H.S.]
This implies equation v2 = 2as is dimensionally correct.
But actual equation is, v2 = u2 + 2as
This confirms a dimensionally correct equation need not be actually a correct equation.
ii) To justify dimensionally incorrect equation is necessarily wrong, consider the formula,
\(\frac{1}{2}\) mv = mgh
Dimensions of L.H.S. = [mv] = [L1M1T-1]
Dimensions of R.H.S. = [mgh] = [L2M1T-2]
Since the dimensions of R.H.S. and L.H.S. are not equal, the formula given by equation must be incorrect.
This confirms dimensionally incorrect equation is necessarily wrong.
Question 37.
State, whether all constants are dimensionless or unitless.
Answer:
All constants need not be dimensionless or unitless.
Planck’s constant, gravitational constant etc., possess dimensions and units. They are dimensional constants.
Solved Examples
Question 38.
If length ‘L’, force ‘F’ and time ‘T’ are taken as fundamental quantities, what would be the dimensional equation of mass and density?
Solution:
i) Force = Mass × Acceleration Force
![]()
∴ Dimensional equation of mass

= [F1L-4T2]
i) The dimensional equation of mass is [F1L-1T2].
ii) The dimensional equation of density is [F1L-4T2].
Question 39.
A calorie is a unit of heat and it equals 4.2 J, where 1 J = kg m2 s-2. A distant civilisation employs a system of units in which the units of mass, length and time are α kg, β m and δ s. Also J’ is their unit of energy. What will be the magnitude of calorie in their units?
Solution:
1 cal = 4.2 kg m2 s-2

New unit of energy is J’
Dimensional formula of energy is [L2M1T-2] According to the question,

Question 40.
Assume that the speed (v) of sound in air depends upon the pressure (P) and density (ρ) of air, then use dimensional analysis to obtain an expression for the speed of sound.
Solution:
It is given that speed (v) of sound in air depends upon the pressure (P) and density (ρ) of the air.
Hence, we can write, v = k Pa ρb ……….. (1)
where, k is a dimensionless constant and a and b are powers to be determined.
Dimensions of y = [L1M0T-1]
Dimensions of P = [L-1M1T-2]
Dimensions of ρ = [L-3M1T0]
Substituting the dimensions of the quantities on both sides of equation (1),
∴ [L1M0T-1] = [L-1M1T-2]a [L-3M1T0]b
∴ [L1M0T-1] = [L-aMaT-2a] [L-3bMbT0]
∴ [L1M0T-1] = [L-a-3bMa+bT-2a]
Comparing the powers of L, M and T on both sides, we get,
-2a = -1
∴ a = \(\frac{1}{2}\)
Also, a + b = O
∴ \(\frac{1}{2}\) + b = 0 b = – \(\frac{1}{2}\)
Substituting values of a and b in equation (1), we get
y = k P\(\frac{1}{2}\) ρ–\(\frac{1}{2}\)
∴ v = k \(\sqrt{\frac{\mathrm{p}}{\rho}}\)
![]()
Question 41.
Density of oil is 0.8 g cm3 in C.G.S. unit. Find its value in S.I. units.
Solution:
Dimensions of density is [L-3M1T0]

= 0.8 [10-3] [10-2]-3
= 0.8 [10-3] [10]6
n = 0.8 × 103
Substituting the value of ‘n’ in equation (1).
we get, 0.8 g cm3 = 0.8 × 103 kg m-3.
Density of oil in S.l unit is 0.8 × 103 kg m-3.
Question 42.
The value of G in C.G.S system is 6.67 × 10-8 dyne cm2 g-2. Calculate its value in S.l. system.
Solution:
Dimensional formula of gravitational constant
[L3M-1T-2]

n = 6.67 × 10-8 × 10-6 × 103
n = 6.67 × 10-11
From equation (1),
6.67 × 10-8 dyne cm2 g-2
= 6.67 × 10-11 N-m2 kg-2
Value ofG in S.l. system is 6.67 × 10-11 N-m2 kg-2.
Question 43.
What is accuracy?
Answer:
Accuracy is how close a measurement is to the actual value of that quantity.
Question 44.
What is precision?
Answer:
Precision is a measure of how consistently a device records nearly identical values i.e., reproducible results.
Question 45.
A scale in a lab measures the mass of object consistently more by 500 g than their actual mass. How would you describe the scale in terms of accuracy and precision?
Answer:
The scale is precise but not accurate.
Explanation: Precision measures how consistently a device records the same answer; even though it displays the wrong value. Hence, the scale is precise.
Accuracy is how well a device measures something against its accepted value. As scale in the lab is always off by 500 g, it is not accurate.
[Note: The goal of the observer should be to get accurate as well as precise measurements.]
Question 46.
List reasons that may introduce possible uncertainties in an observation.
Answer:
Possible uncertainties in an observation may arise due to following reasons:
- Quality of instrument used,
- Skill of the person doing the experiment,
- The method used for measurement,
- External or internal factors affecting the result of the experiment.
Question 47.
What is systematic error? Classify errors into different categories.
Answer:
- Systematic errors are errors that are not determined by chance but are introduced by an inaccuracy (involving either the observation or measurement process) inherent to the system.
- Classification of errors:
Errors are classified into following two groups: - Systematic errors:
- Instrumental error (constant error),
- Error due to imperfection in experimental technique,
- Personal error (human error).
- Random error (accidental error)
![]()
Question 48.
What is instrumental (constant) error?
Answer:
Instrumental error:
- It arises due to defective calibration of an instrument.
- Example: If a thermometer is not graduated properly, i.e., one degree on the thermometer actually corresponds to 0.99°, the temperature measured by such a thermometer will differ from its value by a constant amount.
Question 49.
What is error due to imperfection in experimental technique?
Answer:
Error due to imperfection in experimental technique:
- The errors which occur due to defective setting of an instrument is called error due to imperfection in experimental technique.
- For example the measured volume of a liquid in a graduated tube will be inaccurate if the tube is not held vertical.
Question 50.
What is personal error?
Answer:
Personal error (Human error):
- The errors introduced due to fault of an observer taking readings are called personal errors.
- For example, while measuring the length of an object with a ruler, it is necessary to look at the ruler from directly above. If the observer looks at it from an angle, the measured length will be wrong due to parallax.
![]()
Question 51.
What is random error (accidental)?
Answer:
- Random error (accidental):
The errors which are caused due to minute change in experimental conditions like temperature, pressure change in gas or fluctuation in voltage, while the experiment is being performed are called random errors. - They can be positive or negative.
- Random error cannot be eliminated completely but can be minimized by taking multiple observations and calculating their mean.
Question 52.
State general methods to minimise effect of systematic errors.
Answer:
Methods to minimise effect of systematic errors:
- By using correct instrument.
- Following proper experimental procedure.
- Removing personal error.
Question 53.
Define the term:
Arithmetic mean
Answer:
Arithmetic mean:
a. The most probable value of a large number of readings of a quantity is called the arithmetic mean value of the quantity. This value can be considered to be true value of the quantity.
b. If a1, a2, a3, …………… an are ‘n’ number of readings taken for measurement of a quantity, then their mean value is given by,
amean = \(\frac{a_{1}+a_{2}+\ldots \ldots .+a_{n}}{n}\)
∴ amean = \(\frac{1}{n} \sum_{i=1}^{n} a_{i}\)
Question 54.
What does a = amean ± ∆amean signify?
Answer:
a = amean ± ∆ amean signifies that the actual value of a lies between (amean – ∆ amean) and (amean + ∆ amean).
Question 55.
What is meant by the term combination of errors?
Answer:
Derived quantities may get errors due to individual errors of fundamental quantities, such type of errors are called as combined errors.
Question 56.
Explain errors in sum and in difference of measured quantity.
Answer:
Errors in sum and in difference:
i) Suppose two physical quantities A and B have measured values A ± ∆A and B ± ∆B. respectively, where ∆A and ∆B are their mean absolute errors.
ii) Then, the absolute error ∆Z in their sum.
Z = A + B
Z ± ∆Z = (A ± ∆A) + (B ± ∆B)
= (A + B) ± ∆A ± ∆B
∴ ± ∆Z = ± ∆A ± ∆B.
iii) For difference. i.e.. if Z = A – B.
Z ± ∆Z = A ± ∆A) – (B ± ∆B)
= (A – B) ± ∆A ∓ ∆B
∴ ± ∆Z = ± ∆A ∓ ∆B,
iv) There are four possible values for ∆Z. namely (+∆A – ∆B), (+∆A + ∆B), (-∆A -∆B), (-∆A + ∆B). Hence, maximLim value of absolute error is ∆Z = (∆A+ ∆B) in both the cases.
v) Thus. when two quantities are added or subtracted, the absolute error in the final result is the sum of the absolute errors in the individual quantities.
![]()
Question 57.
Explain errors in product of measured quantity.
Answer:
Errors in product:
i) Suppose Z = AB and measured values of A and B are (A ± ∆A) and (B ± ∆B) then,
Z ± ∆Z = (A ± ∆A) (B ± ∆B)
= AB ± A∆B ± B∆A ± ∆A∆B
Dividing L.H.S by Z and R.H.S. by AB we get
\(\left(1 \pm \frac{\Delta Z}{Z}\right)=\left[1 \pm \frac{\Delta B}{B} \pm \frac{\Delta A}{A} \pm\left(\frac{\Delta A}{A}\right)\left(\frac{\Delta B}{B}\right)\right]\)
Since ∆A/A and ∆B/B are very small, product is neglected. Hence, maximum relative error in Z is \(\frac{\Delta Z}{Z}=\frac{\Delta A}{A}+\frac{\Delta B}{B}\)
ii) Thus, when two quantities are multiplied, the maximum relative error in the result is the sum of relative errors in each quantity.
Question 58.
Explain errors due to power (index) of measured quantity.
Answer:
Errors due to the power (index) of measured quantity:
- Suppose
Z = A3 = A × A × A
then, \(\) - Hence the relative error in Z = A3 is three times the relative error in A.
- This means if Z = An
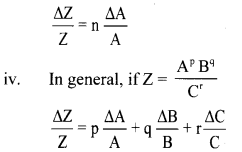
- This implies, the quantity in the formula which has large power is responsible for maximum error.
Question 59.
The radius of a sphere measured repeatedly yields values 5.63 m, 5.54 m, 5.44 m, 5.40 m and 5.35 m. Determine the most probable value of radius and the mean absolute, relative and percentage errors.
Solution:
Given: a1 = 5.63 m, a2 = 5.54 m, a3 = 5.44 m
a4 = 5.40 m, a5 = 5.35 m,
To find:
i) Most probable value (Mean value)
ii) Mean absolute error
iii) Relative error
iv) Percentage error

From formula (ii),
Absolute errors:
∆a1 = |amean – a1| = |5.472 – 5.63| = 0.158
∆a2 = |amean – a2| = |5.472 – 5.54| = 0.068
∆a3 = |amean – a3| = |5.472 – 5.44| = 0.032
∆a4 = |amean – a4| = |5.472 – 5.40| = 0.072
∆a5 = |amean – a5| = |5.472 – 5.35| = 0.122
From formula (ii),
∆amean = \(\frac{0.158+0.068+0.032+0.072+0.122}{5}\)
= \(\frac{0.452}{5}\)
= 0.0904 m
From formula (iii),
Relative error = \(\frac{0.0904}{5.472}\)
= 1.652 × 10-2
(after rounding off to correct significant digits)
= 1.66 × 10-2
= 0.0166
∴ Percentage error = 1.66 × 10-2 × 100 = 1.66%
i) The mean value is 5.472 m.
ii) The mean absolute error is 0.0904 m.
iii) The relative error is 0.0166.
iv) The percentage error is 1.66%
[Note: Answer to relative error is rounded off using rules of significant figures and of rounding off]
Question 60.
Lin an experiment to determine the volume of an object, mass and density are recorded as m = (5 ± 0.15) kg and p = (5 ± 0.2) kg m3 respectively. Calculate percentage error in the measurement of volume.
Solulion:
Given: M = 5kg, ∆M = 0.15 kg, ρ = 5 kg/m3,
∆ρ = 0.2 kg/m3
To find: Percentage error in volume (V)

The percentage error in the determination of volume is 7%.
![]()
Question 61.
The acceleration due to gravity is determined by using a simple pendulum of length l = (100 ± 0.1) cm. If its time period is T = (2 ± 0.01) s, find the maximum percentage error in the measurement of g.
Solution:
Given: ∆l = 0.1 cm, l = 100 cm, ∆T = 0.01 s,
T = 2s
To find: Percentage error

Percentage error in measurement of g is 1.1 %.
Question 62.
Find the number of significant figures in the following numbers,
i. 25.42
ii. 0.004567
iii. 35.320
iv. 91.000
Answer:
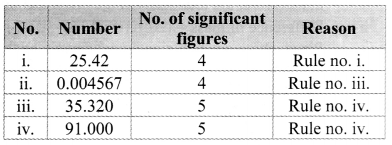
Solved Examples
Question 63.
Add 7.21, 12.141 and 0.0028 and express the result to an appropriate number of significant figures.
Solution:

In the given problem, minimum number of digits after decimal is 2.
∴ Result will be rounded off upto two places of decimal.
Corrected rounded off sum is 19.35.
Question 64.
The mass of a box measured by a grocer’s balance is 2.3 kg. Two gold pieces of masses 20.15 g and 20.17 g are added to the box. What is (i) the total mass of the box? (ii) the difference in the masses of the pieces to correct significant figures?
Solution:
i) Total mass of the box
= (2.3+ 0.02017 + 0.02015) kg
= 2.34032 kg
Since, the last number of significant figure is 2, therefore, the total mass of the box = 2.3 kg
ii) Difference of mass = (20.17 – 20.15) = 0.02g Since, there are two significant figures so the difference in masses to the correct significant figures is 0.02 g.
i) The total mass of the box to correct significant figures is 2.3 kg.
ii) The difference in the masses to correct significant figures is 0.02 g.
Apply Your Knowledge
Question 65.
Write the dimensions of a and b in the relation
E = \(\frac{b-x^{2}}{a}\)
Where E is energy, x ¡s distance and t is time.
Answer:
The given relation is E = \(\frac{b-x^{2}}{a}\)
As x is subtracted from b,
∴ dimensions of b are x2;
i.e., b = [L2]
∴ We can write equation as E = \(\frac{\mathrm{L}^{2}}{\mathrm{a}}\)
Or a = \(\frac{\mathrm{L}^{2}}{\mathrm{E}}=\frac{\mathrm{L}^{2}}{\left[\mathrm{~L}^{2} \mathrm{MT}^{-2}\right]}\) = [L0M-1T2]
![]()
Question 66.
What is the difference between 6.0 and 6.00? which Is more accurate?
Answer:
6.0 indicates the measurement is correct up to first decimal place, whereas 6.00 indicates that the measurement is correct up to second decimal place. Thus, 6.00 is a more accurate value than 6.0.
Question 67.
A child walking on a footpath notices that the width of the footpath is uneven. He reported this to his school principal and the complaint was forwarded to the municipal officer.
i. What is the possible error encountered?
ii. What is the relative error in width of footpath if width of footpath in 10 m length are noted as 5 m, 5.5 m, 5 m, 6 m and 4.5 m?
Answer:
i) The error encountered is personal error.
ii) Mean value of widths

The relative error in width of footpath is 0.084.
Question 68.
A factory owner kept five identical spheres between two wooden blocks on a ruler as shown in figure. He called all his workers and told them to take reading, to check their efficiency and knowledge.
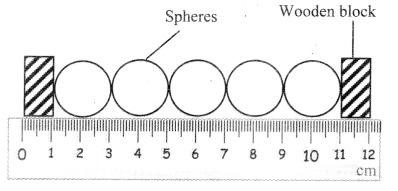
i. What is the area of central sphere?
ii. What is the absolute error in reading of diameter of second sphere?
Answer:
i) From above diagram radius of central sphere is
r = 1 cm
∴ Area = πr2 = 3.142 × (1)2= 3.142 cm2
The area of central sphere is 3.142 cm2.
ii) Mean value of all reading of diameters
dmean = \(\frac{\mathrm{d}_{1}+\mathrm{d}_{2}+\mathrm{d}_{3}+\mathrm{d}_{4}+\mathrm{d}_{5}}{5}=\frac{2+2+2+2+2}{5}\)
= \(\frac{10}{5}\) = 2 cm
Absolute error in reading of second sphere.
∆d2 = |dmean – d2| = 2 – 2 = 0
The absolute error in reading of diameter of second sphere is zero.
![]()
Question 69.
A potential difference of V = 100 ± 2 volt, when applied across a resistance R gives a current of 10 ± 0.5 ampere. Calculate percentage error in R given by R V/I.
Answer:
Here. V = 100 ± 2 volt and I = 10 ± 0.5 ampere
Expressing limits of error as percentage error,
We have
V = 100 volt ± \(\frac{2}{100}\) × 100% = 10 volt ± 2%
and I = 10 ampere ± \(\frac{0.5}{10}\) × 100%
= 10 ampere ± 5%
∴ R = \(\frac{V}{I}\)
∴ %error in R = %error in V + %error in I
= 2% + 5% = 7%
Quick Review

Multiple Choice Questions
Question 1.
A physical quantity may be defined as
(A) the one having dimension.
(B) that which is immeasurable.
(C) that which has weight.
(D) that which has mass.
Answer:
(A) the one having dimension.
Question 2.
Which of the following is the fundamental unit?
(A) Length, force, time
(B) Length, mass, time
(C) Mass, volume, height
(D) Mass, velocity, pressure
Answer:
(B) Length, mass, time
Question 3.
Which of the following is NOT a fundamental quantity?
(A) Temperature
(B) Electric charge
(C) Mass
(D) Electric current
Answer:
(B) Electric charge
Question 4.
The distance of the planet from the earth is measured by __________.
(A) direct method
(B) directly by metre scale
(C) spherometer method
(D) parallax method
Answer:
(D) parallax method
![]()
Question 5.
The two stars S1 and S2 are located at distances d1 and d2 respectively. Also if d1 > d22 then following statement is true.
(A) The parallax of S1 and S2 are same.
(B) The parallax of S1 is twice as that of S2
(C) The parallax of S1 is greater than parallax of S2
(D) The parallax of S2 is greater than parallax of S1
Answer:
(D) The parallax of S2 is greater than parallax of S1
Question 6.
Which of the following is NOT a unit of time?
(A) Hour
(B) Nano second
(C) Microsecond
(D) parsec
Answer:
(D) parsec
Question 7.
An atomic clock makes use of _________.
(A) cesium-133 atom
(B) cesium-132 atom
(C) cesium-123 atom
(D) cesium-131 atom
Answer:
(A) cesium-133 atom
Question 8.
S.I. unit of energy is joule and it is equivalent to
(A) 106 erg
(B) 10-7 erg
(C) 107 erg
(D) 105 erg
Answer:
(C) 107 erg
Question 9.
[L1M1T-1] is an expression for __________.
(A) force
(B) energy
(C) pressure
(D) momentum
Answer:
(D) momentum
Question 10.
Dimensions of sin θ is
(A) [L2]
(B) [M]
(C) [ML]
(D) [M0L0T0]
Answer:
(D) [M0L0T0]
Question 11.
Accuracy of measurement is determined by
(A) absolute error
(B) percentage error
(C) human error
(D) personal error
Answer:
(B) percentage error
Question 12.
Zero error of an instrument introduces .
(A) systematic error
(B) random error
(C) personal error
(D) decimal error
Answer:
(A) systematic error
![]()
Question 13.
The diameter of the paper pin is measured accurately by using ________.
(A) Vernier callipers
(B) micrometer screw gauge
(C) metre scale
(D) a measuring tape
Answer:
(B) micrometer screw gauge
Question 14.
The number of significant figures in 11.118 × 10-6 is
(A) 3
(B) 4
(C) 5
(D) 6
Answer:
(C) 5
Question 15.
0.00849 contains ___________ significant figures.
(A) 6
(B) 5
(C) 3
(D) 2
Answer:
(C) 3
Question 16.
3.310 × 102 has ___________ significant figures.
(A) 6
(B) 4
(C) 2
(D) 1
Answer:
(B) 4
Question 17.
The Earth’s radius is 6371 km. The order of magnitude of the Earth’s radius is
(A) 103 m
(B) 109 m
(C) 107 m
(D) 102 m
Answer:
(C) 107 m
![]()
Question 18.
__________ is the smallest measurement that can be made using the given instrument
(A) Significant number
(B) Least count
(C) Order of magnitude
(D) Relative error
Answer:
(B) Least count
Competitive Corner
Question 1.
In an experiment, the percentage of error occurred in the measurement of physical quantities A, B, C and D are 1%, 2%, 3% and 4% respectively. Then the maximum percentage of error in the measurement X,
where X = \(\frac{A^{2} \frac{1}{B^{2}}}{C^{\frac{1}{3}} D^{3}}\), will be:
(A) -10 %
(B) 10 %
(C) \(\left(\frac{3}{13}\right) \%\)
(D) 16 %
Answer:
(D) 16 %
Hint:
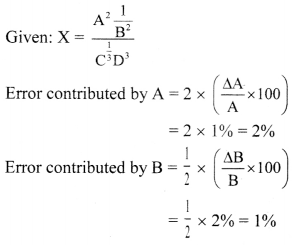
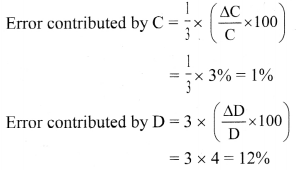
∴ Percentage error in x is given as,
\(\frac{\Delta x}{x}\) × 100 – (error contributed by A) – (error contributed by B) + (error contributed by C) + (error contributed by D)
= 2% + 1% + 1% + 12%
= 16%
Question 2.
The main scale of a vernier callipers has n divisions/cm. n divisions of the vernier scale coincide with (n – 1) divisions of main scale. The least count of the vernier callipers is,
(A) \(\frac{1}{n(n+1)}\) cm
(B) \(\frac{1}{(n+1)(n-1)}\) cm
(C) \(\frac{1}{n}\) cm
(D) \(\frac{1}{n^{2}}\) cm
Answer:
(D) \(\frac{1}{n^{2}}\) cm
Hint:
1 V.S.D. = \(\frac{(n-1)}{n}\) M.S.D.
LC. = 1 M.S.D. – 1 V.S.D.
= 1 M.S.D. – \(\frac{(n-1)}{n}\) M.S.D.
= \(\frac{1}{n}\) M.S.D.
= \(\frac{1}{n}\) × \(\frac{1}{n}\) cm
∴ L.C. = \(\frac{1}{n^{2}}\) cm
Question 3.
A student measures time for 20 oscillations of a simple pendulum as 30 s. 32 s, 35 s and 31 s. 1f the minimum division in the measuring clock is I s, then correct mean time in second is
(A) 32 ± 3
(B) 32 ± 1
(C) 32 ± 2
(D) 32 ± 5
Answer:
(C) 32 ± 2
Hint:

Hence rounding off,
∆t = ± 2 s
∴ t ± ∆t = 32 ± 2 s
Question 4.
A student measured the diameter of a small steel ball using a screw gauge of least count 0.001 cm. The main scale reading is 5 mm and zero of circular scale division coincides with 25 divisions above the reference leveL If screw gauge has a zero error of— 0.004 cm, the correct diameter of the ball is
(A) 0.521 cm
(B) 0.525 cm
(C) 0.053 cm
(D) 0.29 cm
Answer:
(D) 0.29 cm
Hint:
Least count of screw gauge = 0.001 cm = 0.01mm
Main scale reading = 5 mm.
Zero error = – 0.004 cm = -0.04 mm
Zero correction = +0.04 mm
Observed reading = Mainscale reading + (Division × least count)
Observed reading = 5 + (25 × 0.01) = 5.25 mm
Corrected reading = Observed reading + Zero correction
Corrected reading = 5.25 + 0.04
= 5.29 mm = 0.529 cm
![]()
Question 5.
The density of the material in the shape of a cube is determined by measuring three sides of the cube and its mass. 1f the relative errors in measuring the mass and length are respectively 1.5% and 1%, the maximum error in determining the density is:
(A) 4.5%
(B) 6%
(C) 2.5°
(D) 3.5%
Answer:
(A) 4.5%
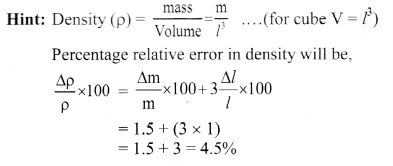
Question 6.
Let x = \(\left[\frac{a^{2} b^{2}}{c}\right]\) be the physical quantity. If the percentage error in the measurement of physical quantities a, b and c is 2, 3 and 4 percent respectively then percentage en-or in the measurement of x is
(A) 7%
(B) 14%
(C) 21%
(D) 28%
Answer:
(B) 14%
Hint:
Given: x = \(\frac{a^{2} b^{2}}{c}\)
Percentage error is given by.
\(\frac{\Delta x}{x}=\frac{2 \Delta a}{a}+\frac{2 \Delta b}{b}+\frac{\Delta c}{c}\)
= (2 × 2) + (2 × 3) + 4
= 4 + 6 + 4 = 14
∴ \(\frac{\Delta \mathrm{x}}{\mathrm{x}} \%\) = 14%
Question 7.
A physical quantity of the dimensions of length that can be formed out of c, G and \(\frac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0}}\) is [c is velocity of light, G is universal constant of gravitation and e is charge]:
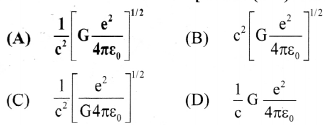
Answer:
(A) \(\frac{1}{\mathrm{c}^{2}}\left[\mathrm{G} \frac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0}}\right]^{1 / 2}\)
Hint:
Let the physical quantity formed of the dimensions of length be given as.
[L] = [c]x [G]y \(\left[\frac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0}}\right]^{z}\) …………….. (i)
Now,
Dimensions of velocity of light [c]x = [LT-1]x
Dimensions of universal gravitational constant
[G]y = [L3T2M-1]y
Dimensions of \(\left[\frac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0}}\right]^{z}\) = [ML3T-2]z
Substitrning these in equation (i)
[L] [LT-1]x [M-1L3T-2]y [ML3T-2]z
= Lx+3y+3z M-y+z T-x-2y-2z
Solving for x, y, z
x + 3y + 3z = 1
-y + z = 0
x + 2y + 2z = O
Solving the above equation,
x = -2, y = \(\frac{1}{2}\), z = \(\frac{1}{2}\)
∴ L = \(\frac{1}{c^{2}}\left[\mathrm{G} \frac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0}}\right]^{1 / 2}\)
![]()
Question 8.
The following observations were taken for determining surface tension T of water by capillary method:
diameter of capillary, D = 1.25 × 10-2 m
rise of water, h = 1.45 × 10-2 m
Using g = 9.80 m/s2 and the simplified relation
T = \(\frac{\mathrm{rhg}}{2}\) × 103 N/m, the possible error in surface tension is closest to:
(A) 0.15%
(B) 1.5%
(C) 2.4%
(D) 10%
Answer:
(B) 1.5%
Hint:
D = 1.25 × 10-2 m; h = 1.45 × 10-2 m
The maximum permissible error in D
= ∆D = 0.01 × 10-2 m
The maximum permissible error in h
= ∆h = 0.01 × 10-2 m
g is given as a constant and is errorless.
