Maharashtra Board 12th Maths Solutions Chapter 1 Differentiation Ex 1.3

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Ex 1.3 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 1 Differentiation Ex 1.3

Question 1.
Differentiate the following w.r.t. x:
(i) \(\frac{(x+1)^{2}}{(x+2)^{3}(x+3)^{4}}\)
Solution:
Let y = \(\frac{(x+1)^{2}}{(x+2)^{3}(x+3)^{4}}\)
Then, log y = log [latex]\frac{(x+1)^{2}}{(x+2)^{3}(x+3)^{4}}[/latex]
= log (x + 1)² – log (x + 2)³ – log (x + 3)⁴
= 2 log (x +1) – 3 log (x + 2) – 4 log (x + 3)
Differentiating both sides w.r.t. x, we get

(ii) \(\sqrt[3]{\frac{4 x-1}{(2 x+3)(5-2 x)^{2}}}\)
Solution:
Let y = \(\sqrt[3]{\frac{4 x-1}{(2 x+3)(5-2 x)^{2}}}\)
Then log y = log [latex]\sqrt[3]{\frac{4 x-1}{(2 x+3)(5-2 x)^{2}}}[/latex]

Differentiating both sides w.r.t. x, we get

(iii) \(\left(x^{2}+3\right)^{\frac{3}{2}} \cdot \sin ^{3} 2 x \cdot 2^{x^{2}}\)
Solution:
Let y = \(\left(x^{2}+3\right)^{\frac{3}{2}} \cdot \sin ^{3} 2 x \cdot 2^{x^{2}}\)
Then log y = log [latex]\left(x^{2}+3\right)^{\frac{3}{2}} \cdot \sin ^{3} 2 x \cdot 2^{x^{2}}[/latex]

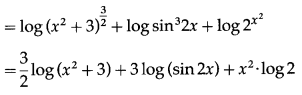
Differentiating both sides w.r.t. x, we get

(iv) \(\frac{\left(x^{2}+2 x+2\right)^{\frac{3}{2}}}{(\sqrt{x}+3)^{3}(\cos x)^{x}}\)
Solution:
Let y = \(\frac{\left(x^{2}+2 x+2\right)^{\frac{3}{2}}}{(\sqrt{x}+3)^{3}(\cos x)^{x}}\)
Then log y = log [latex]\frac{\left(x^{2}+2 x+2\right)^{\frac{3}{2}}}{(\sqrt{x}+3)^{3}(\cos x)^{x}}[/latex]

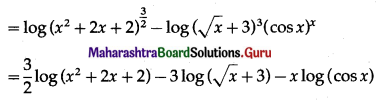
Differentiating both sides w.r.t. x, we get

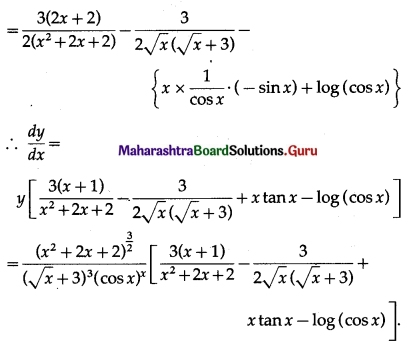
(v) \(\frac{x^{5} \cdot \tan ^{3} 4 x}{\sin ^{2} 3 x}\)
Solution:
Let y = \(\frac{x^{5} \cdot \tan ^{3} 4 x}{\sin ^{2} 3 x}\)
Then log y = log [latex]\frac{x^{5} \cdot \tan ^{3} 4 x}{\sin ^{2} 3 x}[/latex]
= log x⁵ + log tan³4x – log sin²3x
= 5 log x+ 3 log (tan 4x) – 2 log (sin 3x)
Differentiating both sides w.r.t. x, we get

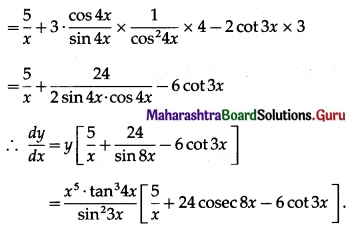
(vi) \(x^{\tan ^{-1} x}\)
Solution:
Let y = \(x^{\tan ^{-1} x}\)
Then log y = log (\(x^{\tan ^{-1} x}\)) = (tan^-1 x)(log x)
Differentiating both sides w.r.t. x, we get

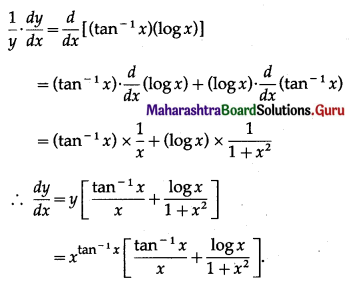
(vii) (sin x)^x
Solution:
Let y = (sin x)^x
Then log y = log (sin x)^x = x . log (sin x)
Differentiating both sides w.r.t. x, we get

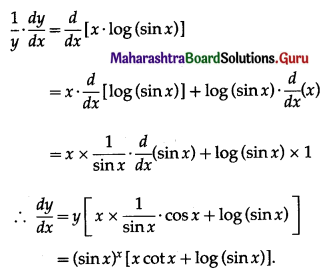
(viii) sin x^x
Solution:
Let y = (sin x^x)
Then \(\frac{d y}{d x}=\frac{d}{d x}\left[\left(\sin x^{x}\right)\right]\)
\(\frac{d y}{d x}=\cos \left(x^{x}\right) \cdot \frac{d}{d x}\left(x^{x}\right)\) ……. (1)
Let u = x^x
Then log u = log x^x = x . log x
Differentiating both sides w.r.t. x, we get

Question 2.
Differentiate the following w.r.t. x:
(i) x^e + x^x + e^x + e^e
Solution:
Let y = x^e + x^x + e^x + e^e
Let u = x^x
Then log u = log x^x = x log x
Differentiating both sides w.r.t. x, we get
\(\frac{1}{u} \cdot \frac{d u}{d x}=\frac{d}{d x}(x \log x)\)

(ii) \(x^{x^{x}}+e^{x^{x}}\)
Solution:
Let y = \(x^{x^{x}}+e^{x^{x}}\)
Put u = \(x^{x^{x}}\) and v = \(e^{x^{x}}\)
Then y = u + v
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)
Take u = \(x^{x^{x}}\)
log u = log \(x^{x^{x}}\) = x^x . log x
Differentiating both sides w.r.t. x, we get

(iii) (log x)^x – (cos x)^{cot x}
Solution:
Let y = (log x)^x – (cos x)^{cot x}
Put u = (log x)^x and v = (cos x)^{cot x}
Then y = u – v
∴ \(\frac{d y}{d x}=\frac{d u}{d x}-\frac{d v}{d x}\) ……..(1)
Take u = (log x)^x
∴ log u = log (log x)^x = x . log (log x)
Differentiating both sides w.r.t. x, we get

(iv) \(x^{e^{x}}+(\log x)^{\sin x}\)
Solution:
Let y = \(x^{e^{x}}+(\log x)^{\sin x}\)
Put u = \(x^{e^{x}}\) and v = (log x)^{sin x}
Then y = u + v
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ……….(1)
Take u = \(x^{e^{x}}\)
∴ log u = log \(x^{e^{x}}\) = e^x . log x
Differentiating both sides w.r.t. x, we get

Also, v = (log x)^{sin x}
∴ log v = log (log x)^{sin x} = (sin x) . (log log x)
Differentiating both sides w.r.t. x, we get
\(\frac{1}{v} \cdot \frac{d v}{d x}=\frac{d}{d x}[(\sin x) \cdot(\log \log x)]\)
= \((\sin x) \cdot \frac{d}{d x}\left[(\log \log x)+(\log \log x) \cdot \frac{d}{d x}(\sin x)\right]\)

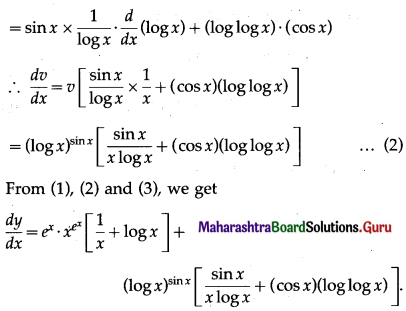
(v) \(e^{\tan x}+(\log x)^{\tan x}\)
Solution:
Let y = \(e^{\tan x}+(\log x)^{\tan x}\)
Put u = (log x)^{tan x}
∴ log u =log(log x)^{tan x} = (tan x).(log log x)
Differentiating both sides w.r.t. x, we get

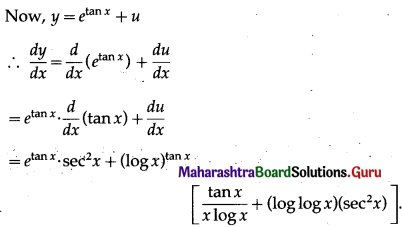
(vi) (sin x)^{tan x} + (cos x)^{cot x}
Solution:
Let y = (sin x)^{tan x} + (cos x)^{cot x}
Put u = (sin x)^{tan x} and v = (cos x)^{cot x}
Then y = u + v
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ………(1)
Take u = (sin x)^{tan x}
∴ log u = log (sin x)^{tan x} = (tan x) . (log sin x)
Differentiating both sides w.r.t. x, we get

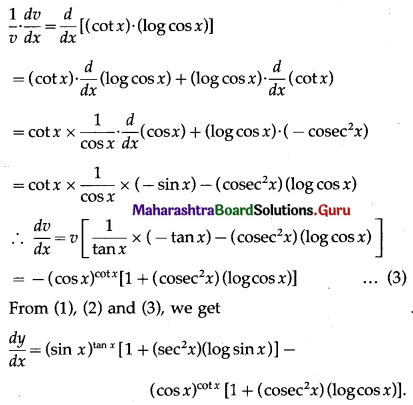
(vii) \(10^{x^{x}}+x^{x^{10}}+x^{10^{x}}\)
Solution:
Let y = \(10^{x^{x}}+x^{x^{10}}+x^{10^{x}}\)
Put u = \(10^{x^{x}}\), v = \(x^{x^{10}}\) and w = \(x^{10^{x}}\)
Then y = u + v + w
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}\) ………(1)

(viii) \(\left[(\tan x)^{\tan x}\right]^{\tan x}\) at x = \(\frac{\pi}{4}\)
Solution:
Let y = \(\left[(\tan x)^{\tan x}\right]^{\tan x}\)
∴ log y = log [latex]\left[(\tan x)^{\tan x}\right]^{\tan x}[/latex]
= tan x . log(tan x)^{tan x}
= tan x . tan x log (tan x)
= (tan x)² . log (tan x)
Differentiating both sides w.r.t. x, we get

Question 3.
Find \(\frac{d y}{d x}\) if
(i) √x + √y = √a
Solution:
√x + √y = √a
Differentiating both sides w.r.t. x, we get

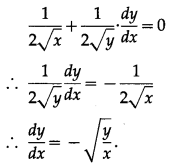
(ii) x√x + y√y = a√a
Solution:
x√x + y√y = a√a
∴ \(x^{\frac{3}{2}}+y^{\frac{3}{2}}=a^{\frac{3}{2}}\)
Differentiating both sides w.r.t. x, we get

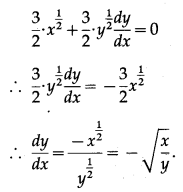
(iii) x + √xy + y = 1
Solution:
x + √xy + y = 1
Differentiating both sides w.r.t. x, we get

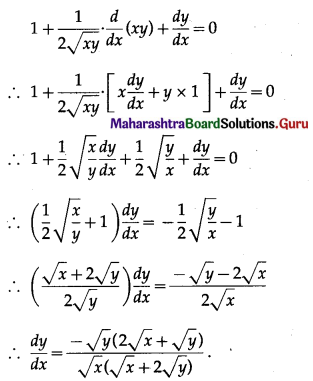
(iv) x³ + x²y + xy² + y³ = 81
Solution:
x³ + x²y + xy² + y³ = 81
Differentiating both sides w.r.t. x, we get

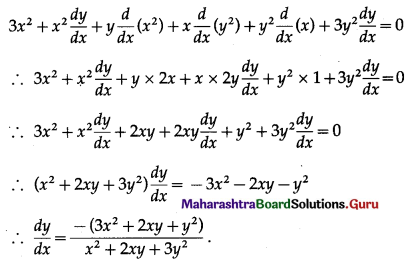
(v) x²y² – tan^-1(\(\sqrt{x^{2}+y^{2}}\)) = cot^-1(\(\sqrt{x^{2}+y^{2}}\))
Solution:
x²y² – tan^-1(\(\sqrt{x^{2}+y^{2}}\)) = cot^-1(\(\sqrt{x^{2}+y^{2}}\))
∴ x²y² = tan^-1(\(\sqrt{x^{2}+y^{2}}\)) + cot^-1(\(\sqrt{x^{2}+y^{2}}\))
∴ x²y² = \(\frac{\pi}{2}\) …….[∵ \(\tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}\)]
Differentiating both sides w.r.t. x, we get

(vi) xe^y + ye^x = 1
Solution:
xe^y + ye^x = 1
Differentiating both sides w.r.t. x, we get

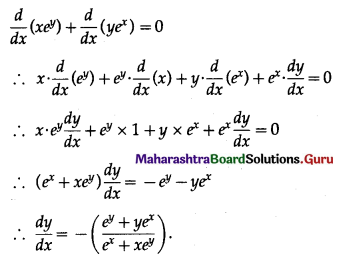
(vii) e^x+y = cos (x – y)
Solution:
e^x+y = cos (x – y)
Differentiating both sides w.r.t. x, we get

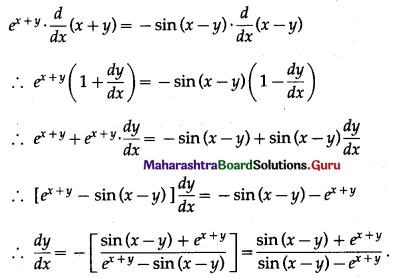
(viii) cos (xy) = x + y
Solution:
cos (xy) = x + y
Differentiating both sides w.r.t. x, we get

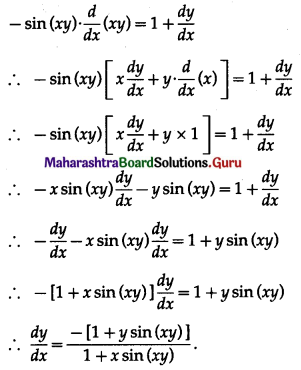
(ix) \(e^{e^{x-y}}=\frac{x}{y}\)
Solution:
\(e^{e^{x-y}}=\frac{x}{y}\)
∴ e^x-y = log(\(\frac{x}{y}\)) …….[e^x = y ⇒ x = log y]
∴ e^x-y = log x – log y
Differentiating both sides w.r.t. x, we get

Question 4.
Show that \(\frac{d y}{d x}=\frac{y}{x}\) in the following, where a and p are constants.
(i) x⁷y⁵ = (x + y)¹²
Solution:
x⁷y⁵ = (x + y)¹²
(log x⁷y⁵) = log(x + y)¹²
log x⁷ + log y⁵ = log(x + y)¹²
7 log x + 5 log y = 12 log (x + y)
Differentiating both sides w.r.t. x, we get

(ii) x^py⁴ = (x + y)^p+4, p∈N
Solution:
x^py⁴ = (x + y)^p+4
Taking log
log (x^py⁴) = log(x + y)^p+4
log x^p + log y⁴ = (p + 4) log(x + y)
p log x + 4 log y = (p + 4) log(x + y)
Differentiating both sides w.r.t. x, we get

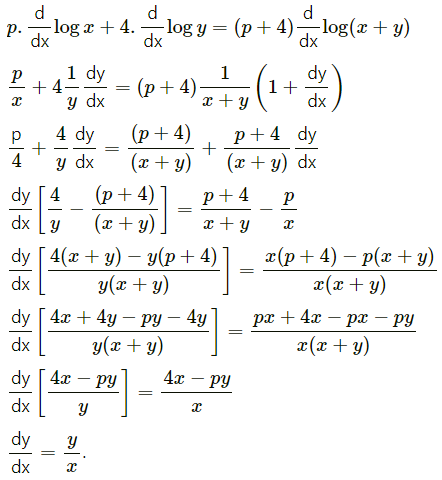
(iii) \(\sec \left(\frac{x^{5}+y^{5}}{x^{5}-y^{5}}\right)=a^{2}\)
Solution:
\(\sec \left(\frac{x^{5}+y^{5}}{x^{5}-y^{5}}\right)=a^{2}\)

Differentiating both sides w.r.t. x, we get


Differentiating both sides w.r.t. x, we get

(iv) \(\tan ^{-1}\left(\frac{3 x^{2}-4 y^{2}}{3 x^{2}+4 y^{2}}\right)=a^{2}\)
Solution:
\(\tan ^{-1}\left(\frac{3 x^{2}-4 y^{2}}{3 x^{2}+4 y^{2}}\right)=a^{2}\)

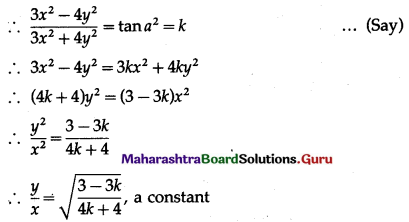
Differentiating both sides w.r.t. x, we get

(v) \(\cos ^{-1}\left(\frac{7 x^{4}+5 y^{4}}{7 x^{4}-5 y^{4}}\right)=\tan ^{-1} a\)
Solution:

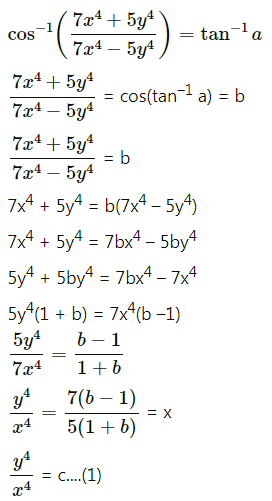
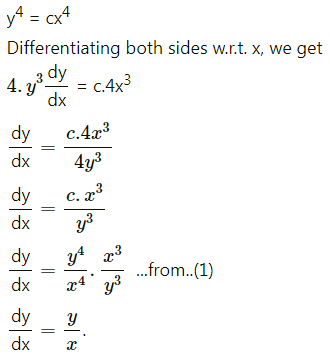
(vi) \(\log \left(\frac{x^{20}-y^{20}}{x^{20}+y^{20}}\right)=20\)
Solution:
\(\log \left(\frac{x^{20}-y^{20}}{x^{20}+y^{20}}\right)=20\)

Differentiating both sides w.r.t. x, we get

(vii) \(e^{\frac{x^{7}-y^{7}}{x^{7}+y^{7}}}=a\)
Solution:
\(e^{\frac{x^{7}-y^{7}}{x^{7}+y^{7}}}=a\)

Differentiating both sides w.r.t. x, we get

(viii) \(\sin \left(\frac{x^{3}-y^{3}}{x^{3}+y^{3}}\right)=a^{3}\)
Solution:

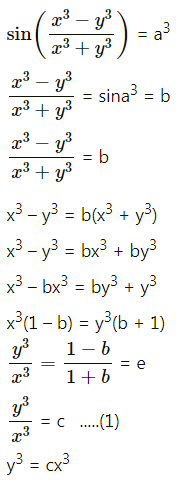
Differentiating both sides w.r.t. x, we get

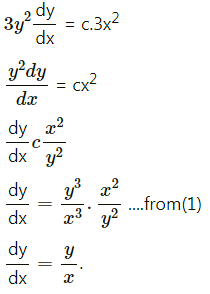
Question 5.
(i) If log (x + y) = log (xy) + p, where p is a constant, then prove that \(\frac{d y}{d x}=-\frac{y^{2}}{x^{2}}\).
Solution:
log (x + y) = log (xy) + p
∴ log (x + y) = log x + log y + p
Differentiating both sides w.r.t. x, we get

(ii) If \(\log _{10}\left(\frac{x^{3}-y^{3}}{x^{3}+y^{3}}\right)=2\), show that \(\frac{d y}{d x}=-\frac{99 x^{2}}{101 y^{2}}\)
Solution:
\(\log _{10}\left(\frac{x^{3}-y^{3}}{x^{3}+y^{3}}\right)=2\)

(iii) If \(\log _{5}\left(\frac{x^{4}+y^{4}}{x^{4}-y^{4}}\right)=2\), show that \(\frac{d y}{d x}=-\frac{12 x^{3}}{13 y^{3}}\)
Solution:

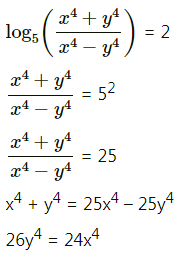
Differentiating both sides w.r.t. x, we get

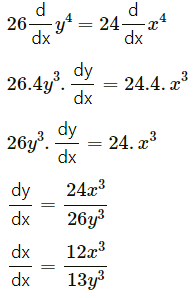
(iv) If e^x + e^y = e^x+y, then show that \(\frac{d y}{d x}=-e^{y-x}\)
Solution:
e^x + e^y = e^x+y ……(1)
Differentiating both sides w.r.t. x, we get

(v) If \(\sin ^{-1}\left(\frac{x^{5}-y^{5}}{x^{5}+y^{5}}\right)=\frac{\pi}{6}\), show that \(\frac{d y}{d x}=\frac{x^{4}}{3 y^{4}}\)
Solution:
\(\sin ^{-1}\left(\frac{x^{5}-y^{5}}{x^{5}+y^{5}}\right)=\frac{\pi}{6}\)
\(\frac{x^{5}-y^{5}}{x^{5}+y^{5}}=\sin \frac{\pi}{6}=\frac{1}{2}\)
2x⁵ – 2y⁵ = x⁵ + y⁵
3y⁵ = x⁵
Differentiating both sides w.r.t. x, we get
\(3 \times 5 y^{4} \frac{d y}{d x}=5 x^{4}\)
∴ \(\frac{d y}{d x}=\frac{x^{4}}{3 y^{4}}\)

(vi) If x^y = e^x-y, then show that \(\frac{d y}{d x}=\frac{\log x}{(1+\log x)^{2}}\)
Solution:
x^y = e^x-y
log x^y = log e^x-y
y log x = (x – y) log e
y log x = (x – y) ….. [∵ log e = 1]
y + y log x = x – y
y + y log x = x
y(1 + log x) = x
y = \(\frac{x}{1+\log x}\)

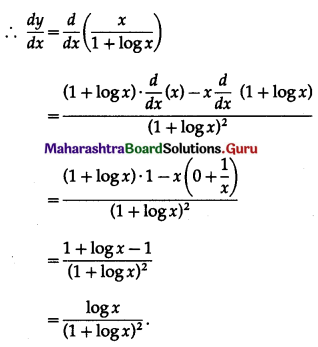
(vii) If \(y=\sqrt{\cos x+\sqrt{\cos x+\sqrt{\cos x+\ldots \infty}}}\), then show that \(\frac{d y}{d x}=\frac{\sin x}{1-2 y}\)
Solution:
\(y=\sqrt{\cos x+\sqrt{\cos x+\sqrt{\cos x+\ldots \infty}}}\)
y² = cos x + \(\sqrt{\cos x+\sqrt{\cos x+\ldots \infty}}\)
y² = cos x + y
Differentiating both sides w.r.t. x, we get

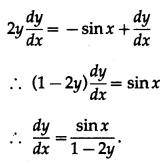
(viii) If \(y=\sqrt{\log x+\sqrt{\log x+\sqrt{\log x+\ldots \infty}}}\), then show that \(\frac{d y}{d x}=\frac{1}{x(2 y-1)}\)
Solution:
\(y=\sqrt{\log x+\sqrt{\log x+\sqrt{\log x+\ldots \infty}}}\)

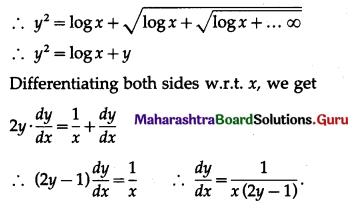
(ix) If \(y=x^{x^{x^{-\infty}}}\), then show that \(\frac{d y}{d x}=\frac{y^{2}}{x(1-\log y)}\)
Solution:
\(y=x^{x^{x^{-\infty}}}\)

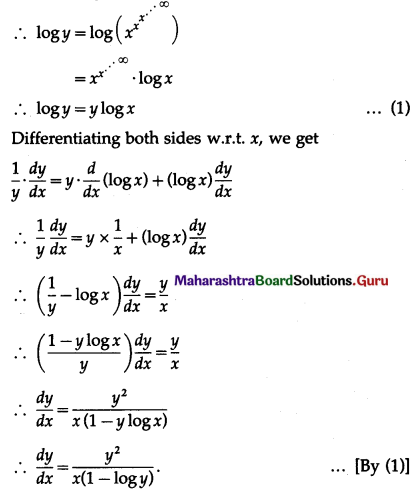
(x) If e^y = y^x, then show that \(\frac{d y}{d x}=\frac{(\log y)^{2}}{\log y-1}\)
Solution:
e^y = y^x
log e^y = log y^x
y log e = x log y
y = x log y …… [∵log e = 1] ……….(1)
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=x \frac{d}{d x}(\log y)+(\log y) \cdot \frac{d}{d x}(x)\)