Index Numbers Class 12 Commerce Maths 2 Chapter 5 Exercise 5.2 Answers Maharashtra Board
Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 5 Index Numbers Ex 5.2 Questions and Answers.
Std 12 Maths 2 Exercise 5.2 Solutions Commerce Maths
Calculate Laspeyres, Paasche’s, Dorbish-Bowely’s, and Marshall-Edegworth’s Price Index Numbers in Problems 1 and 2.
Question 1.
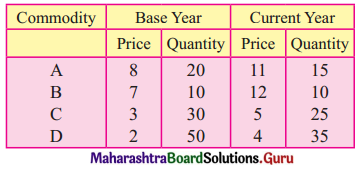
Solution:
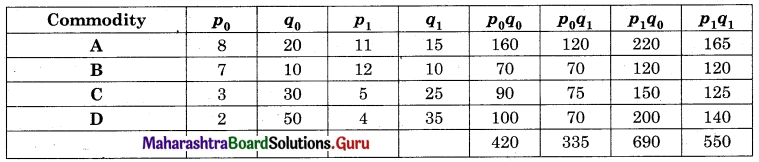

![]()
Question 2.
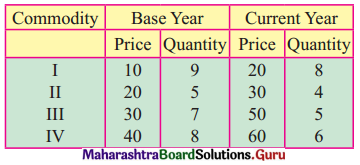
Solution:
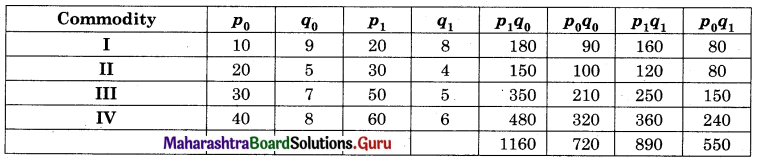
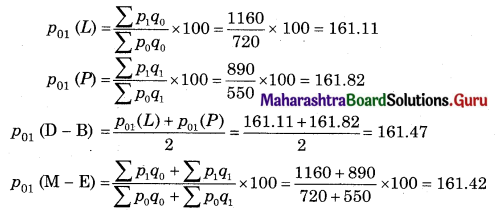
Calculate Walsh’s Price Index Number in Problems 3 and 4.
Question 3.
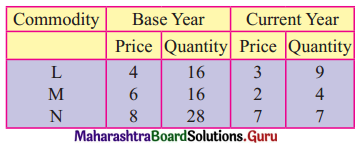
Solution:
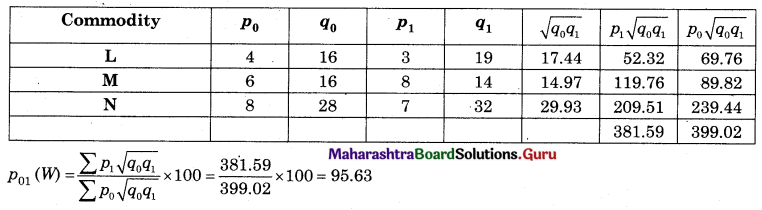
Question 4.
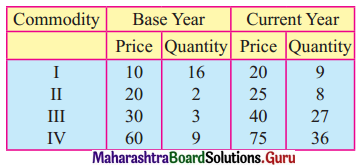
Solution:
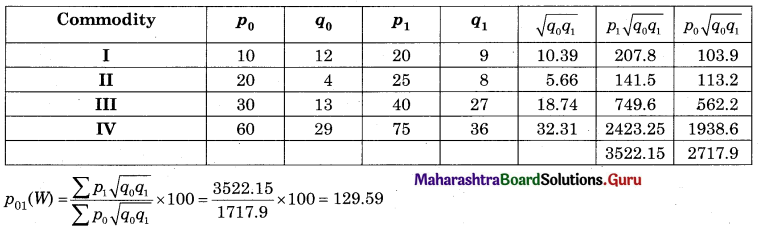

![]()
Question 5.
If p01(L) = 90, and p01(P) = 40, find p01(D – B) and p01(F)
Solution:

Question 6.
If Σp0q0 = 140, Σp0q1 = 200, Σp1q0 = 350, Σp1q1 = 460, find Laspeyre’s Paasche’s Dorbish-Bowley’s and Marshall- Edgeworth’s Price Index Numbers.
Solution:

Question 7.
Given that Laspeyre’s and Dorbish-Bowley’s Price Index Numbers are 160.32 and 164.18 respectively. Find Paasche’s Price Index Number.
Solution:

Question 8.
Given that Σp0q0 = 220, Σp0q1 = 380, Σp1q1 = 350 is Marshall-Edgeworth’s Price Index Number is 150, find Laspeyre’s Price Index Number.
Solution:

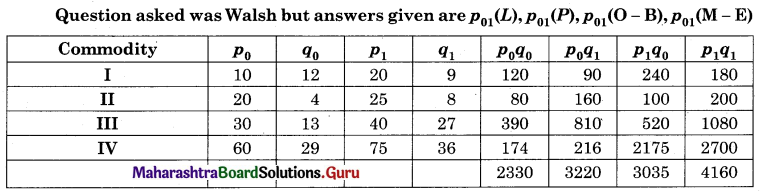
Question 9.
Find x in the following table if Laspeyres and Paasche’s Price Index Numbers are equal.

Solution:

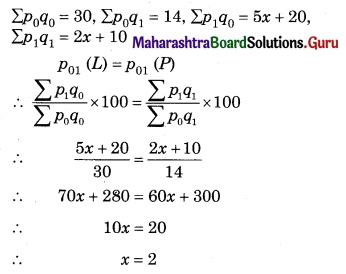
![]()
Question 10.
If Laspeyre’s Price Index Number is four times Paasche’s Price Index Number, then find the relation between Dorbish-Bowley’s and Fisher’s Price Index Numbers.
Solution:

Question 11.
If Dorbish-Bowley’s and Fisher’s Price Index Numbers are 5 and 4, respectively, then find Laspeyres and Paasche’s Price Index Numbers.
Solution:


12th Commerce Maths Digest Pdf