Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 8 Measures of Dispersion Miscellaneous Exercise 8 Questions and Answers.
11th Maths Part 1 Measures of Dispersion Miscellaneous Exercise 8 Questions And Answers Maharashtra Board
(I) Select the correct option from the given alternatives:
Question 1.
If there are 10 values each equal to 10, then S.D. of these values is _________
(A) 100
(B) 20
(C) 0
(D) 6
Answer:
(C) 0
Hint:
Var (X) = \(\sigma_{x}^{2}=\frac{\sum x_{i}^{2}}{\mathrm{n}}-(\bar{x})^{2}\)
= \(\frac{1000}{10}\) – 100
= 0
∴ S.D. = 0
Question 2.
The number of patients who visited cardiologists are 13, 17, 11, 15 in four days, then variance (approximately) is
(A) 5 patients
(B) 4 patients
(C) 10 patients
(D) 15 patients
Answer:
(A) 5 patients
![]()
Question 3.
If the observations of a variable X are, -4, -20, -30, -44 and -36, then the value of the range will be:
(A) -48
(B) 40
(C) -40
(D) 48
Answer:
(B) 40
Question 4.
The standard deviation of a distribution divided by the mean of the distribution and expressed in percentage is called:
(A) Coefficient of Standard deviation
(B) Coefficient of skewness
(C) Coefficient of quartile deviation
(D) Coefficient of variation
Answer:
(D) Coefficient of variation
Question 5.
If the S.D. of first n natural numbers is √2, then the value of n must be
(A) 5
(B) 4
(C) 7
(D) 6
Answer:
(A) 5
Question 6.
The positive square root of the mean of the squares of the deviations of observations from their mean is called:
(A) Variance
(B) Range
(C) S.D.
(D) C.V.
Answer:
(C) S.D.
![]()
Question 7.
The variance of 19, 21, 23, 25 and 27 is 8. The variance of 14, 16, 18, 20 and 22 is:
(A) Greater than 8
(B) 8
(C) Less than 8
(D) 8 – 5 = 3
Answer:
(B) 8
Question 8.
For any two numbers, SD is always
(A) Twice the range
(B) Half of the range
(C) Square of the range
(D) None of these
Answer:
(B) Half of the range
Question 9.
Given the heights (in cm) of two groups of students:
Group A: 131 cm, 150 cm, 147 cm, 138 cm, 144 cm
Group B: 139 cm, 148 cm, 132 cm, 151 cm, 140 cm
Which of the following is/are true?
I. The ranges of the heights of the two groups of students are the same.
II. The means of the heights of the two groups of students are the same.
(A) I only
(B) II only
(C) Both I and II
(D) None
Answer:
(C) Both I and II
Question 10.
The standard deviation of data is 12 and mean is 72, then the coefficient of variation is
(A) 13.67%
(B) 16.67%
(C) 14.67%
(D) 15.67%
Answer:
(B) 16.67%
![]()
(II) Answer the following:
Question 1.
Find the range for the following data.
76, 57, 80, 103, 61, 63, 89, 96, 105, 72
Solution:
Here, largest value (L) = 105, smallest value (S) = 57
∴ Range = L – S
= 105 – 57
= 48
Question 2.
Find the range for the following data.
116, 124, 164, 150, 149, 114, 195, 128, 138, 203, 144
Solution:
Here, largest value (L) = 203, smallest value (S) = 114
∴ Range = L – S
= 203 – 114
= 89
Question 3.
Given below is the frequency distribution of weekly wages of 400 workers. Find the range.
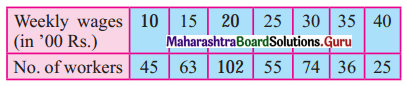
Solution:
Here, largest value (L) = 40, smallest value (S) = 10
∴ Range = L – S
= 40 – 10
= 30
![]()
Question 4.
Find the range of the following data.
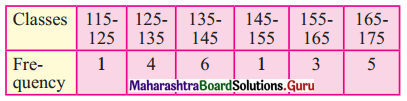
Solution:
Here, upper limit of the highest class (L) = 175
lower limit of the lowest class (S) = 115
∴ Range = L – S
= 175 – 115
= 60
Question 5.
Find variance and S.D. for the following set of numbers.
25, 21, 23, 29, 27, 22, 28, 23, 21, 25
Solution:

Question 6.
Find variance and S.D. for the following set of numbers.
125, 130, 150, 165, 190, 195, 210, 230, 245, 260
Solution:
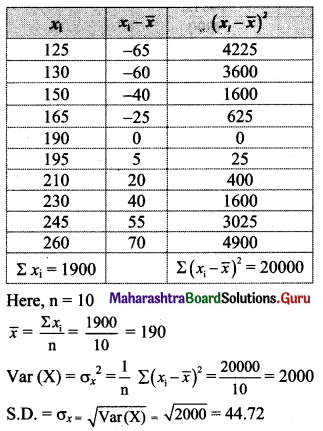
Question 7.
Following data gives no. of goals scored by a team in 90 matches. Compute the standard deviation.
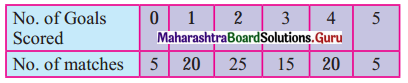
Solution:
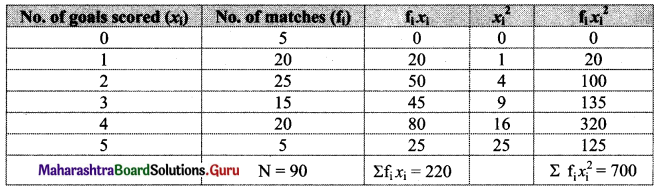
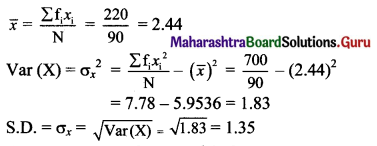
![]()
Question 8.
Compute the variance and S.D. for the following data:

Solution:
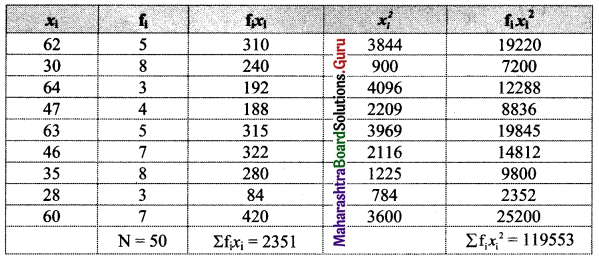

Question 9.
Calculate S.D. from the following data.
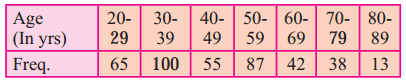
Solution:
Since data is not continuous, we have to make it continuous.
let u = \(\frac{x-\mathrm{A}}{\mathrm{h}}=\frac{x-54.5}{10}\)
Calculation of variance of u:
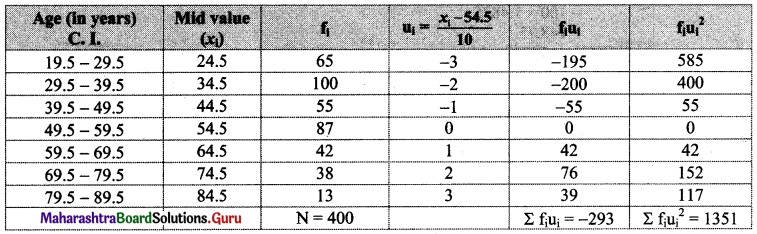

Question 10.
Given below is the frequency distribution of marks obtained by 100 students. Compute arithmetic mean and S.D.
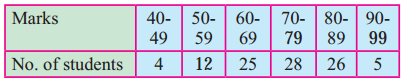
Solution:
Since data is not continuous, we have to make it continuous.
Let u = \(\frac{x-\mathrm{A}}{\mathrm{h}}=\frac{x-74.5}{10}\)
Calculation of variance of u:
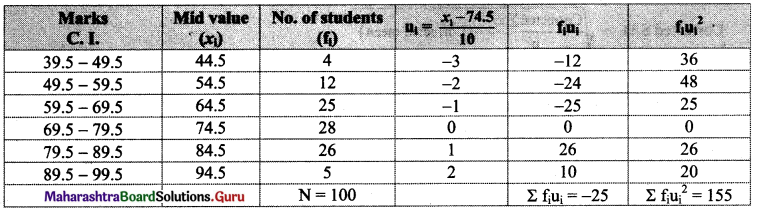

∴ Var (X) = h2 var (u)
= (10)2 × 1.4875
= 100 × 1.4875
= 148.75
∴ S.D. = σx = √Var(X)
= √148.75
= 12.2
![]()
Question 11.
The arithmetic mean and standard deviation of a series of 20 items were calculated by a student as 20 cm and 5 cm respectively. But while calculating them, item 13 was misread as 30. Find the corrected mean and standard deviation.
Solution:
n = 20, \(\bar{x}\) = 20, σx = 5 …..(given)
\(\bar{x}=\frac{1}{\mathrm{n}} \sum x_{\mathrm{i}}\)
∴ \(\sum x_{\mathrm{i}}=\mathrm{n} \bar{x}\) = 20 × 20 = 400
Corrected Σxi = Σxi – (incorrect observation) + (correct observation)
= 400 – 30 + 13
= 383

Corrected \(\sum x_{\mathrm{i}}^{2}\) = \(\sum x_{\mathrm{i}}^{2}\) – (incorrect observation)2 + (correct observation)2
= 8500 – (30)2 + (13)2
= 8500 – 900 + 169
= 7769

Question 12.
The mean and S.D. of a group of 50 observations are 40 and 5 respectively. If two more observations 60 and 72 are added to the set, find the mean and S.D. of 52 items.
Solution:
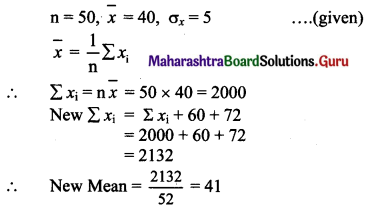

Question 13.
The mean height of 200 students is 65 inches. The mean heights of boys and girls are 70 inches and 62 inches respectively and the standard deviations are 8 and 10 respectively. Find the number of boys and combined S.D.
Solution:
Let n1 and n2 be the number of boys and girls respectively.
Let n = 200, \(\bar{x}_{c}\) = 65, \(\bar{x}_{1}\) = 70, \(\bar{x}_{2}\) = 62, σ1 = 8, σ2 = 10
Here, n1 + n2 = n
n1 + n2 = 200 ……(i)
Combined mean (\(\bar{x}_{c}\)) = \(\frac{n_{1} \bar{x}_{1}+n_{2} \bar{x}_{2}}{n_{i}+n_{2}}\)
65 = \(\frac{\mathrm{n}_{1}(70)+\mathrm{n}_{2}(62)}{200}\) …… [From (i)]
70n1 + 62n2 = 13000
35n1 + 31n2 = 6500 …..(ii)
Solving (i) and (ii), we get
n1 = 75, n2 = 125
Number of boys = 75

![]()
Question 14.
From the following data available for 5 pairs of observations of two variables x and y, obtain combined S.D. for all 10 observations.
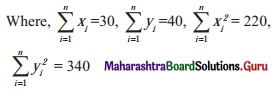
Solution:

Question 15.
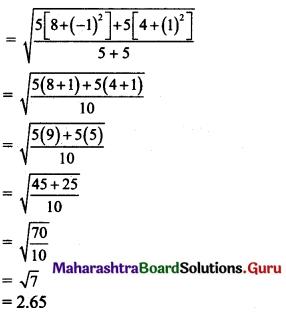
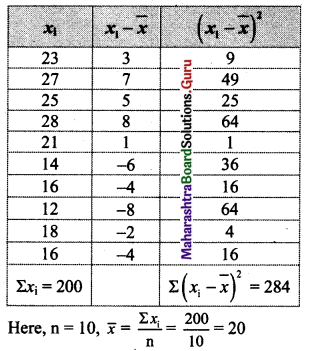
Calculate the coefficient of variation of the following data.
23, 27, 25, 28, 21, 14, 16, 12, 18, 16
Solution:

Question 16.
The following data relates to the distribution of weights of 100 boys and 80 girls in a school.
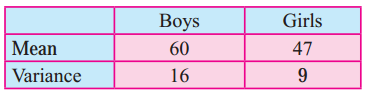
Which of the two is more variable?
Solution:
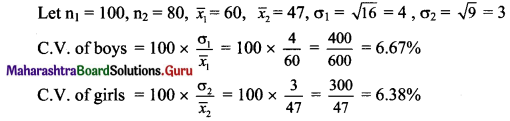
Here, C.V. of boys > C.V. of girls
∴ The Series of boys is more variable.
![]()
Question 17.
The mean and standard deviations of the two brands of watches are given below:

Calculate the coefficient of variation of the two brands and interpret the results.
Solution:

Here, C.V. (I) > C.V. (II)
∴ The brand I is more variable.
Question 18.
Calculate the coefficient of variation for the data given below:
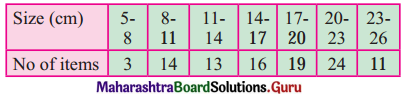
Solution:
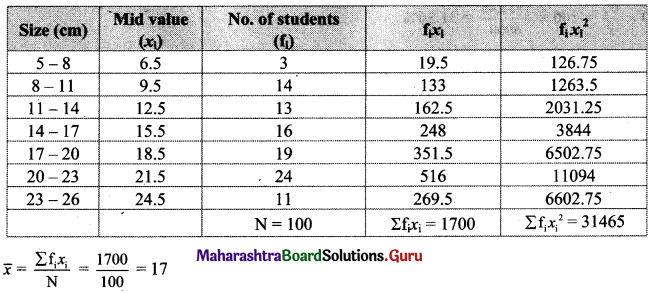
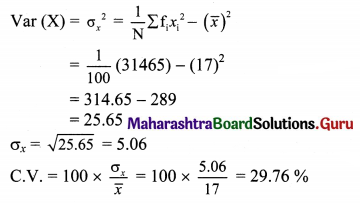
Question 19.
Calculate the coefficient of variation for the data given below:
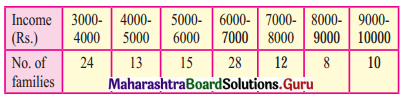
Solution:
Let u = \(\frac{x-\mathrm{A}}{\mathrm{h}}=\frac{x-6500}{1000}\)
Calculation of variance of u:
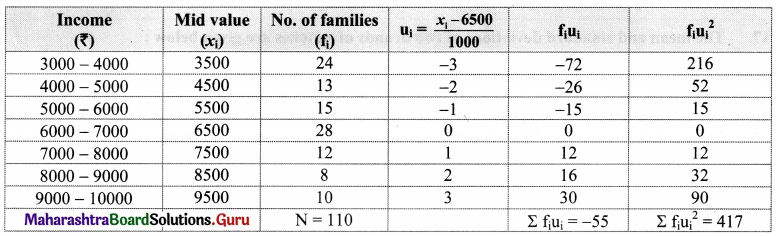

![]()
Question 20.
Compute the coefficient of variations for the following data to show whether the variation is greater in the field or in the area of the field.
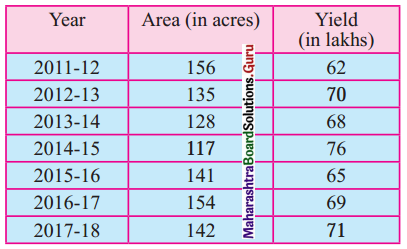
Solution:


∴ the variation is greater in the area of the field.
Question 21.
There are two companies U and V which manufacture cars. A sample of 40 cars each from these companies is taken and the average running life (in years) is recorded.
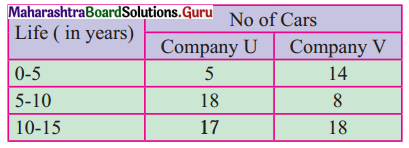
Which company shows greater consistency?
Solution:
Let f1 denote no. of cars of company U and f2 denote no. of cars of company V.
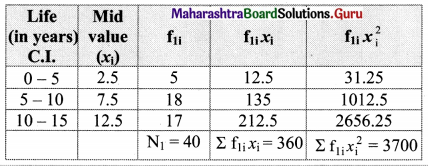
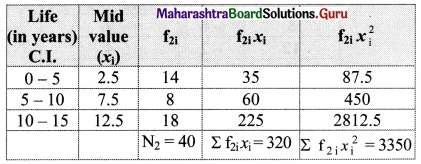

Here, C.V. (U) < C.V. (V)
∴ Company U shows greater consistency in performance.
![]()
Question 22.
The means and S.D. of weights and heights of 100 students of a school are as follows.
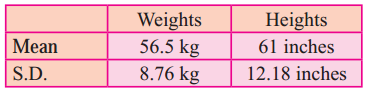
Which shows more variability, weights, or heights?
Solution:

Here, C.V. for weight < C.V. for height
∴ Height shows more variability.
Class 11 Maharashtra State Board Maths Solution
- Exercise 8.1 Class 11 Maths 1
- Exercise 8.2 Class 11 Maths 1
- Exercise 8.3 Class 11 Maths 1
- Miscellaneous Exercise 8 Class 11 Maths 1
- Exercise 9.1 Class 11 Maths 1
- Exercise 9.2 Class 11 Maths 1
- Exercise 9.3 Class 11 Maths 1
- Exercise 9.4 Class 11 Maths 1
- Exercise 9.5 Class 11 Maths 1
- Miscellaneous Exercise 9 Class 11 Maths 1