Maharashtra Board 11th Maths Solutions Chapter 5 Sets and Relations Miscellaneous Exercise 5

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 5 Sets and Relations Miscellaneous Exercise 5 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Sets and Relations Miscellaneous Exercise 5

(I) Select the correct answer from the given alternative.

Question 1.
For the set A = {a, b, c, d, e} the correct statement is
(A) {a, b} ∈ A
(B) {a} ∈ A
(C) a ∈ A
(D) a ∉ A
Answer:
(C) a ∈ A

Question 2.
If aN = {ax : x ∈ N}, then set 6N ∩ 8N =
(A) 8N
(B) 48N
(C) 12N
(D) 24N
Answer:
(D) 24N
Hint:
6N = {6x : x ∈ N} = {6, 12, 18, 24, 30, ……}
8N = {8x : x ∈ N} = {8, 16, 24, 32, ……}
∴ 6N ∩ 8N = {24, 48, 72, …..}
= {24x : x ∈ N}
= 24N

Question 3.
If set A is empty set then n[P[P[P(A)]]] is
(A) 6
(B) 16
(C) 2
(D) 4
Answer:
(D) 4
Hint:
A = Φ
∴ n(A) = 0
∴ n[P(A)] = 2^n(A) = 2⁰ = 1
∴ n[P[P(A)]] = 2^n[P(A)] = 2¹ = 2
∴ n[P[P[P(A)]]] = 2^n[P[P(A)]] = 2² = 4

Question 4.
In a city 20% of the population travels by car, 50% travels by bus and 10% travels by both car and bus. Then, persons travelling by car or bus are
(A) 80%
(B) 40%
(C) 60%
(D) 70%
Answer:
(C) 60%
Hint:
Let C = Population travels by car
B = Population travels by bus
n(C) = 20%, n(B) = 50%, n(C ∩ B) = 10%
n(C ∪ B) = n(C) + n(B) – n(C ∩ B)
= 20% + 50% – 10%
= 60%

Question 5.
If the two sets A and B are having 43 elements in common, then the number of elements common to each of the sets A × B and B × A is
(A) 43²
(B) 2⁴³
(C) 43⁴³
(D) 2⁸⁶
Answer:
(A) 43²

Question 6.
Let R be a relation on the set N be defied by {(x, y) / x, y ∈ N, 2x + y = 41} Then R is
(A) Reflexive
(B) Symmetric
(C) Transitive
(D) None of these
Answer:
(D) None of these

Question 7.
The relation “>” in the set of N (Natural number) is
(A) Symmetric
(B) Reflexive
(C) Transitive
(D) Equivalent relation
Answer:
(C) Transitive
Hint:
For any a ∈ N, a ≯ a
∴ (a, a) ∉ R
∴ > is not reflexive.
For any a, b ∈ N, if a > b, then b ≯ a.
∴ > is not symmetric.
For any a, b, c ∈ N,
if a > b and b > c, then a > c
∴ > is transitive.

Question 8.
A relation between A and B is
(A) only A × B
(B) An Universal set of A × B
(C) An equivalent set of A × B
(D) A subset of A × B
Answer:
(D) A subset of A × B

Question 9.
If (x, y) ∈ N × N, then xy = x² is a relation that is
(A) Symmetric
(B) Reflexive
(C) Transitive
(D) Equivalence
Answer:
(D) Equivalence
Hint:
Let x ∈ R, then xx = x²
∴ x is related to x.
∴ Given relation is reflexive.
Letx = 0 and y = 2,
then xy = 0 × 2 = 0 = x²
∴ x is related to y.
Consider, yx = 2 × 0 = 0 ≠ y²
∴ y is not related to x.
∴ Given relation is not symmetric.
Let x be related to y and y be related to z.
∴ xy = x² and yz = y²
∴ x = \(\frac{x^{2}}{y}\) and z = \(\frac{y^{2}}{y}\) = y …..[if y ≠ 0]
Consider, xz = \(\frac{x^{2}}{y}\) × y = x²
∴ x is related to z.
∴ Given relation is transitive.

Question 10.
If A = {a, b, c}, The total no. of distinct relations in A × A is
(A) 3
(B) 9
(C) 8
(D) 29
Answer:
(D) 29

(II) Answer the following.

Question 1.
Write down the following sets in set builder form:
(i) {10, 20, 30, 40, 50}
(ii) {a, e, i, o, u}
(iii) {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
Solution:
(i) Let A = {10, 20, 30, 40, 50}
∴ A = {x/x = 10n, n ∈ N and n ≤ 5}

(ii) Let B = {a, e, i, o, u}
∴ B = {x/x is a vowel of English alphabets}

(iii) Let C = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
∴ C = {x/x is a day of a week}

Question 2.
If U = {x/x ∈ N, 1 ≤ x ≤ 12}, A = {1,4, 7,10}, B = {2, 4, 6, 7, 11}, C = {3, 5, 8, 9, 12}. Write down the sets.
(i) A ∪ B
(ii) B ∩ C
(iii) A – B
(iv) B ∩ C’
(v) A ∪ B ∪ C
(vi) A ∩ (B ∪ C)
Solution:
U = {x/x ∈ N, 1 ≤ x ≤ 12} = {1, 2, 3, …., 12}
A = {1, 4, 7, 10}, B = {2, 4, 6, 7, 11}, C = {3, 5, 8, 9, 12}
(i) A ∪ B = {1, 2, 4, 6, 7, 10, 11}

(ii) B ∩ C = {}

(iii) A – B = {1, 10}

(iv) C’ = {1, 2, 4, 6, 7, 10, 11}
∴ B ∩ C’ = {2, 4, 6, 7, 11}

(v) A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

(vi) B ∪ C = {2, 3, 4, 5, 6, 7, 8, 9, 11, 12}
∴ A ∩ (B ∪ C) = {4, 7}

Question 3.
In a survey of 425 students in a school, it was found that 115 drink apple juice, 160 drink orange juice, and 80 drink both apple as well as orange juice. How many drinks neither apple juice nor orange juice?
Solution:
Let A = set of students who drink apple juice
B = set of students who drink orange juice
X = set of all students
∴ n(X) = 425, n(A) = 115, n(B) = 160, n(A ∩ B) = 80

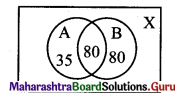
No. of students who neither drink apple juice nor orange juice = n(A’ ∩ B’) = n(A ∪ B)’
= n(X) – n(A ∪ B)
= 425 – [n(A) + n(B) – n(A ∩ B)]
= 425 – (115 + 160 – 80)
= 230

Question 4.
In a school, there are 20 teachers who teach Mathematics or Physics. Of these, 12 teach Mathematics and 4 teach both Physics and Mathematics. How many teachers teach Physics?
Solution:
Let A = set of teachers who teach Mathematics
B = set of teachers who teach Physics
∴ n(A ∪ B) = 20, n(A) = 12, n(A ∩ B) = 4

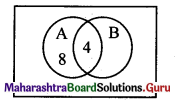
Since n(A ∪ B) = n(A) + n(B) – n(A ∩ B),
20 = 12 + n(B) – 4
∴ n(B) = 12
∴ Number of teachers who teach physics = 12

Question 5.
(i) If A = {1, 2, 3} and B = {2, 4}, state the elements of A × A, A × B, B × A, B × B, (A × B) ∩ (B × A).
(ii) If A = {-1, 1}, find A × A × A.
Solution:
(i) A = {1, 2, 3} and B = {2, 4}
A × A = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
A × B = {(1, 2), (1, 4), (2, 2), (2, 4), (3, 2), (3, 4)}
B × A = {(2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3)}
B × B = {(2, 2), (2, 4), (4, 2), (4, 4)}
∴ (A × B) ∩ (B × A) = {(2, 2)}

(ii) A = {-1, 1}
∴ A × A × A = {(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)}

Question 6.
If A = {1, 2, 3}, B = {4, 5, 6}, check if the following are relations from A to B. Also, write its domain and range.
(i) R₁ = {(1, 4), (1, 5), (1, 6)}
(ii) R₂ = {(1, 5), (2, 4), (3, 6)}
(iii) R₃ = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
(iv) R₄ = {(4, 2), (2, 6), (5, 1), (2, 4)}
Solution:
A = {1, 2, 3}, B = {4, 5, 6}
∴ A × B = {(1, 4), (1, 5), (1, 6), (2,4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(i) R₁ = {(1, 4), (1, 5), (1, 6)}
Since R₁ ⊆ A × B,
R₁ is a relation from A to B.
Domain (R₁) = Set of first components of R₁ = {1}
Range (R₁) = Set of second components of R₁ = {4, 5, 6}

(ii) R₂ = {(1, 5),(2, 4),(3, 6)}
Since R₂ ⊆ A × B,
R₂ is a relation from A to B.
Domain (R₂) = Set of first components of R₂ = {1, 2, 3}
Range (R₂) = Set of second components of R₂ = {4, 5, 6}

(iii) R₃ = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}
Since R₃ ⊆ A × B,
R₃ is a relation from A to B.
Domain (R₃) = Set of first components of R₃ = {1, 2, 3}
Range (R₃) = Set of second components of R₃ = {4, 5, 6}

(iv) R₄ = {(4, 2), (2, 6), (5, 1), (2, 4)}
Since (4, 2) ∈ R₄, but (4, 2) ∉ A × B,
R₄ ⊄ A × B
∴ R₄ is not a relation from A to B.

Question 7.
Determine the domain and range of the following relations.
(i) R = {(a, b) / a ∈ N, a < 5, b = 4}
(ii) R = {(a, b) / b = |a – 1|, a ∈ Z, |a| < 3}
Solution:
(i) R = {(a, b) / a ∈ N, a < 5, b = 4}
∴ Domain (R) = {a / a ∈ N, a < 5} = {1, 2, 3, 4}
Range (R) = {b / b = 4} = {4}

(ii) R = {(a, b) / b = |a – 1|, a ∈ Z, |a| < 3}
Since a ∈ Z and |a| < 3,
a < 3 and a > -3
∴ -3 < a < 3
∴ a = -2, -1, 0, 1, 2
b = |a – 1|
When a = -2, b = 3
When a = -1, b = 2
When a = 0, b = 1
When a = 1, b = 0
When a = 2, b = 1
Domain (R) = {-2, -1, 0, 1, 2}
Range (R) = {0, 1, 2, 3}

Question 8.
Find R : A → A when A = {1, 2, 3, 4} such that
(i) R = {(a, b) / a – b = 10}
(ii) R = {(a, b) / |a – b| ≥ 0}
Solution:
R : A → A, A = {1, 2, 3,4}
(i) R = {(a, b)/a – b = 10} = { }

(ii) R = {(a, b) / |a – b| ≥ 0}
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}
A × A = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}
∴ R = A × A

Question 9.
R : {1, 2, 3} → {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)}. Check if R is
(i) reflexive
(ii) symmetric
(iii) transitive
Solution:
R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)}
(i) Here, (x, x) ∈ R, for x ∈ {1, 2, 3}
∴ R is reflexive.

(ii) Here, (1, 2) ∈ R, but (2, 1) ∉ R.
∴ R is not symmetric.

(iii) Here, (1, 2), (2, 3) ∈ R,
But (1, 3) ∉ R.
∴ R is not transitive.

Question 10.
Check if R : Z → Z, R = {(a, b) | 2 divides a – b} is an equivalence relation.
Solution:
(i) Since 2 divides a – a,
(a, a) ∈ R
∴ R is reflexive. .

(ii) Let (a, b) ∈ R
Then 2 divides a – b
∴ 2 divides b – a
∴ (b, a) ∈ R
∴ R is symmetric.

(iii) Let (a, b) ∈ R, (b, c) ∈ R
Then a – b = 2m, b – c = 2n,
∴ a – c = 2(m + n), where m, n are integers.
∴ 2 divides a – c
∴ (a, c) ∈ R
∴ R is transitive.
Thus, R is an equivalence relation.

Question 11.
Show that the relation R in the set A = {1, 2, 3, 4, 5} Given by R = {(a, b) / |a – b| is even} is an equivalence relation.
Solution:
(i) Since |a – a| is even,
∴ (a, a) ∈ R
∴ R is reflexive.

(ii) Let (a, b) ∈ R
Then |a – b| is even
∴ |b – a| is even
∴ (b, a) ∈ R
∴ R is symmetric.

(iii) Let (a, b), (b, c) ∈ R
Then a – b = ±2m, b – c = ±2n
∴ a – c = ±2(m + n), where m, n are integers.
∴ (a, c) ∈ R
∴ R is transitive
Thus, R is an equivalence relation.

Question 12.
Show that the following are equivalence relations:
(i) R in A is set of all books given by R = {(x, y) / x and y have same number of pages}
(ii) R in A = {x ∈ Z | 0 ≤ x ≤ 12} given by R = {(a, b) / |a – b| is a multiple of 4}
(iii) R in A = (x ∈ N/x ≤ 10} given by R = {(a, b) | a = b}
Solution:
(i) a. Clearly (x, x) ∈ R
∴ R is reflexive.

b. If (x, y) ∈ R then (y, x) ∈ R.
∴ R is symmetric.

c. Let (x, y) ∈ R, (y, x) ∈ R.
Then x, y, and z are 3 books having the same number of pages.
∴ (x, z) ∈ R as x, z has the same number of pages.
∴ R is transitive.
Thus, R is an equivalence relation.

(ii) a. Since |a – a| is a multiple of 4,
(a, a) ∈ R
∴ R is reflexive.

b. Let (a, b) ∈ R
Then a – b = ±4m,
∴ b – a = ±4m, where m is an integer
∴ (b, a) ∈ R
∴ R is symmetric.

c. Let (a, b), (b, c) ∈ R
a – b = ± 4m, b – c = ± 4n,
∴ a – c = ±4(m + n), where m, n are integers
∴ (a, c) ∈ R
∴ R is transitive
Thus, R is an equivalence relation.

(iii) a. Since a = a
∴ (a, a) ∈ R
∴ R is reflexive.

b. Let (a, b) ∈ R Then a = b
∴ b = a
∴ (b, a) ∈ R
∴ R is symmetric.

c. Let (a, b), (b, c) ∈ R
Then, a = b, b = c
∴ a = c
∴ (a, c) ∈ R
∴ R is transitive.
Thus, R is an equivalence relation.