Practice Set 5.4 Geometry 9th Standard Maths Part 2 Chapter 5 Quadrilaterals Solutions Maharashtra Board

by

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.4 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.

9th Standard Maths 2 Practice Set 5.4 Chapter 5 Quadrilaterals Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 5.4 Chapter 5 Quadrilaterals Questions With Answers Maharashtra Board

Question 1.
In □IJKL, side IJ || side KL, ∠I = 108° and ∠K = 53°, then find the measures of ∠J and ∠L.
Solution:
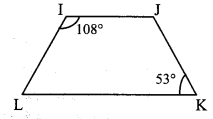
Maharashtra Board Class 9 Maths Solutions Chapter 5 Quadrilaterals Practice Set 5.4 1
i. ∠I = 108° [Given]
side IJ || side KL and side IL is their transveral. [Given]
∴ ∠I + ∠L = 180° [Interior angles]
∴ 108° + ∠L = 180°
∴ ∠L = 180° – 108° = 72°

ii. ∠K = 53° [Given]
side IJ || side KL and side JK is their transveral. [Given]
∴ ∠J + ∠K = 180° [Interior angles]
∴ ∠J + 53° = 180°
∴ ∠J= 180°- 53° = 127°
∴ ∠L = 72°, ∠J = 127°

Question 2.
In □ABCD, side BC || side AD, side AB ≅ side DC. If ∠A = 72°, then find the measures of ∠B and ∠D.
Construction: Draw seg BP ⊥ side AD, A – P – D, seg CQ ⊥ side AD, A – Q – D.
Solution:
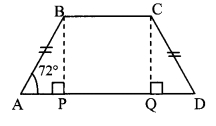
Maharashtra Board Class 9 Maths Solutions Chapter 5 Quadrilaterals Practice Set 5.4 2
i. ∠A = 72° [Given]
In □ABCD, side BC || side AD and side AB is their transversal. [Given]
∴ ∠A + ∠B = 180° [Interior angles]
∴ 72° +∠B = 180°
∴ ∠B = 180° – 72° = 108°

ii. In ∆BPA and ∆CQD,
∠BPA ≅ ∠CQD [Each angle is of measure 90°]
Hypotenuse AB ≅ Hypotenuse DC [Given]
seg BP ≅ seg CQ [Perpendicular distance between two parallel lines]
∴ ∆BPA ≅ ∆CQD [Hypotenuse side test]
∴ ∠BAP ≅ ∠CDQ [c. a. c. t.]
∴ ∠A = ∠D
∴ ∠D = 72°
∴ ∠B = 108°, ∠D = 72°

Question 3.
In □ABCD, side BC < side AD, side BC || side AD and if side BA ≅ side CD, then prove that ∠ABC = ∠DCB.
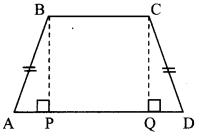
Maharashtra Board Class 9 Maths Solutions Chapter 5 Quadrilaterals Practice Set 5.4 3
Given: side BC < side AD, side BC || side AD, side BA = side CD
To prove: ∠ABC ≅ ∠DCB
Construction: Draw seg BP ⊥ side AD, A – P – D
seg CQ ⊥ side AD, A – Q – D
Solution:
Proof:
In ∆BPA and ∆CQD,
∠BPA ≅ ∠CQB [Each angle is of measure 90°]
Hypotenuse BA ≅ Hypotenuse CD [Given]
seg BP ≅ seg CQ [Perpendicular distance between two parallel lines]
∴ ∆BPA ≅ ∆CQD [Hypotenuse side test]
∴ ∠BAP ≅ ∠CDQ [c. a. c. t.]
∴ ∠A = ∠D ….(i)
Now, side BC || side AD and side AB is their transversal. [Given]
∴ ∠A + ∠B = 180°…..(ii) [Interior angles]
Also, side BC || side AD and side CD is their transversal. [Given]
∴ ∠C + ∠D = 180° …..(iii) [Interior angles]
∴ ∠A + ∠B = ∠C + ∠D [From (ii) and (iii)]
∴ ∠A + ∠B = ∠C + ∠A [From (i)]
∴ ∠B = ∠C
∴ ∠ABC ≅ ∠DCB

Class 9 Maths Digest