Uncategorized

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 3 Integers Class 6 Practice Set 4 Answers Solutions.

6th Standard Maths Practice Set 4 Answers Chapter 3 Integers

Question 1.
Classify the following numbers as positive numbers and negative numbers.
-5, +4, -2, 7, +26, -49, -37, 19, -25, +8, 5, -4, -12, 27
Solution:

Positive Numbers	+4, 7, +26, 19, +8, 5, 27
Negative Numbers	-5, -2, -49, -37, -25, -4, -12

Question 2.
Given below are the temperatures in some cities. Write them using the proper signs.

Place	Shimla	Leh	Delhi	Nagpur
Temperature	7 °C below 0°	12 °C below 0°	22 °C above 0°	31 °C above 0°

Solution:

Place	Shimla	Leh	Delhi	Nagpur
Temperature with proper sign	-7 °C	-12 °C	+22 °C	+31 °C

Question 3.
Write the numbers in the following examples using the proper signs.

1. A submarine is at a depth of 512 meters below sea level.
2. The height of Mt Everest, the highest peak in the Himalayas, is 8848 meters.
3. A kite is flying at a distance of 120 meters from the ground.
4. The tunnel is at a depth of 2 meters under the ground.

Solution:

1. A submarine is at a depth of -512 meters from sea level.
2. The height of Mt Everest, the highest peak in the Himalayas is +8848 meters.
3. A kite is flying at a distance of +120 meters from the ground.
4. The tunnel is at a depth of -2 meters from the ground.

Maharashtra Board Class 6 Maths Chapter 3 Integers Practice Set 4 Intext Questions and Activities

Question 1.
Take warm water in one beaker, some crushed ice in another and a mixture of salt and crushed ice in a third beaker. Ask your teacher for help in measuring the temperature of the substance in each of the beakers using a thermometer. Note the temperatures. (Textbook pg. no. 13)

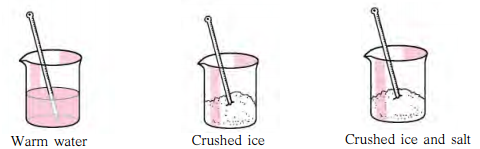
Solution:
( Students should attempt this activity on their own)

Question 2.
Look at the picture of the kulfi man. Why do you think he keeps the kulfi moulds in a mixture of salt and ice? (Textbook pg. no. 14)

Solution:
Kulfi man keeps the kulfi moulds in a mixture of salt and ice because such a mixture helps in keeping the kulfi cool for a longer period of time. The kulfi kept in the said mixture relatively takes more time to melt. This mixture is Considered ideal as it has the temperature of -4°C as against the temperature of ice i.e. 0°C.

Question 3.
My class, i.e. Std. VI, is a part of my school. My school is in my town. My town is a part of a taluka. In the same way, the taluka is a part of a district, and the district is a part of Maharashtra State. In the same way, what can you say about these groups of numbers? Textbook pg. no. 15)

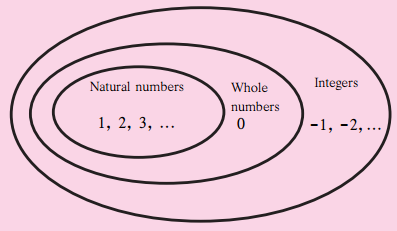
Solution:
By observing the above given groups of numbers, we can infer that natural numbers are a part of whole numbers. In turn, whole numbers are a part of integers.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 22 Answers Solutions Chapter 5 Operations on Rational Numbers.

Operations on Rational Numbers Class 7 Practice Set 22 Answers Solutions Chapter 5

Question 1.
Carry out the following additions of rational numbers:
i. \(\frac{5}{36}+\frac{6}{42}\)
ii. \(1 \frac{2}{3}+2 \frac{4}{5}\)
iii. \(\frac{11}{17}+\frac{13}{19}\)
iv. \(2 \frac{3}{11}+1 \frac{3}{77}\)
Solution:
i. \(\frac{5}{36}+\frac{6}{42}\)

ii. \(1 \frac{2}{3}+2 \frac{4}{5}\)

iii. \(\frac{11}{17}+\frac{13}{19}\)

iv. \(2 \frac{3}{11}+1 \frac{3}{77}\)

Question 2.
Carry out the following subtractions involving rational numbers.
i. \(\frac{7}{11}-\frac{3}{7}\)
ii. \(\frac{13}{36}-\frac{2}{40}\)
iii. \(1 \frac{2}{3}-3 \frac{5}{6}\)
iv. \(4 \frac{1}{2}-3 \frac{1}{3}\)
Solution:
i. \(\frac{7}{11}-\frac{3}{7}\)

ii. \(\frac{13}{36}-\frac{2}{40}\)

iii. \(1 \frac{2}{3}-3 \frac{5}{6}\)

iv. \(4 \frac{1}{2}-3 \frac{1}{3}\)

Question 3.
Multiply the following rational numbers.
i. \(\frac{3}{11} \times \frac{2}{5}\)
ii. \(\frac{12}{5} \times \frac{4}{15}\)
iii. \(\frac{(-8)}{9} \times \frac{3}{4}\)
iv. \(\frac{0}{6} \times \frac{3}{4}\)
Solution:
i. \(\frac{3}{11} \times \frac{2}{5}\)
\(=\frac{3 \times 2}{11 \times 5}=\frac{6}{55}\)

ii. \(\frac{12}{5} \times \frac{4}{15}\)
\(=\frac{4}{5} \times \frac{4}{5}=\frac{4 \times 4}{5 \times 5}=\frac{16}{25}\)

iii. \(\frac{(-8)}{9} \times \frac{3}{4}\)
\(=\frac{(-2)}{3} \times \frac{1}{1}=\frac{-2}{3}\)

iv. \(\frac{0}{6} \times \frac{3}{4}\)
\(=0 \times \frac{3}{4}=0\)

Question 4.
Write the multiplicative inverse of.
i. \(\frac{2}{5}\)
ii. \(\frac{-3}{8}\)
iii. \(\frac{-17}{39}\)
iv. 7
v. \(-7 \frac{1}{3}\)
Solution:
i. \(\frac{5}{2}\)
ii. \(\frac{-8}{3}\)
iii. \(\frac{-39}{17}\)
iv. \(\frac {1}{7}\)
v. \(\frac {-3}{22}\)

Question 5.
Carry out the divisions of rational numbers:
i. \(\frac{40}{12} \div \frac{10}{4}\)
ii. \(\frac{-10}{11} \div \frac{-11}{10}\)
iii. \(\frac{-7}{8} \div \frac{-3}{6}\)
iv. \(\frac{2}{3} \div(-4)\)
v. \(2 \frac{1}{5} \div 5 \frac{3}{6}\)
vi. \(\frac{-5}{13} \div \frac{7}{26}\)
vii. \(\frac{9}{11} \div(-8)\)
viii. \(5 \div \frac{2}{5}\)
Solution:
i. \(\frac{40}{12} \div \frac{10}{4}\)
\(=\frac{40}{12} \times \frac{4}{10}=\frac{4}{3}\)

ii. \(\frac{-10}{11} \div \frac{-11}{10}\)
\(=\frac{-10}{11} \times \frac{-10}{11}=\frac{100}{121}\)

iii. \(\frac{-7}{8} \div \frac{-3}{6}\)
\(=\frac{-7}{8} \times \frac{-6}{3}=\frac{-7}{4} \times \frac{-3}{3}=\frac{7}{4}\)

iv. \(\frac{2}{3} \div(-4)\)
\(=\frac{2}{3} \times \frac{-1}{4}=\frac{1}{3} \times \frac{-1}{2}=\frac{-1}{6}\)

v. \(2 \frac{1}{5} \div 5 \frac{3}{6}\)
\(=\frac{11}{5} \div \frac{33}{6}=\frac{11}{5} \times \frac{6}{33}=\frac{1}{5} \times \frac{6}{3}=\frac{2}{5}\)

vi. \(\frac{-5}{13} \div \frac{7}{26}\)
\(=\frac{-5}{13} \times \frac{26}{7}=\frac{-10}{7}\)

vii. \(\frac{9}{11} \div(-8)\)
\(=\frac{9}{11} \times \frac{-1}{8}=\frac{-9}{88}\)

viii. \(5 \div \frac{2}{5}\)
\(=\frac{5}{1} \times \frac{5}{2}=\frac{25}{2}\)

Maharashtra Board Class 7 Maths Chapter 5 Operations on Rational Numbers Practice Set 22 Intext Questions and Activities

Question 1.
Complete the table given below. (Textbook pg. no. 34)

	-3	\(\frac {3}{5}\)	-17	\(\frac { -5 }{ 11 }\)	5
Natural Numbers	x				✓
Integers	✓
Rational Numbers	✓

Solution:

	-3	\(\frac {3}{5}\)	-17	\(\frac { -5 }{ 11 }\)	5
Natural Numbers	x	x	x	x	✓
Integers	✓	x	✓	x	✓
Rational Numbers	✓	✓	✓	✓	✓

Question 2.
Discuss the characteristics of various groups of numbers in class and complete the table below. In front of each group, write the inference you make after carrying out the operations of addition, subtraction, multiplication and division, using a (✓) or a (x).
Remember that you cannot divide by zero. (Textbook pg. no. 35)

Group of Numbers	Addition	Subtraction	Multiplication	Division
Natural Numbers	✓	x (7- 10 =-3)	✓	x (3÷5=\(\frac { 3 }{ 5 }\))
Integers
Rational Numbers

Solution:

Group of Numbers	Addition	Subtraction	Multiplication	Division
Natural Numbers	✓	x (7- 10 =-3)	✓	x (3÷5=\(\frac { 3 }{ 5 }\))
Integers	✓	✓	✓	x (4÷9=\(\frac { 4 }{ 9 }\))
Rational Numbers	✓	✓	✓	✓

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 5 Decimal Fractions Class 6 Practice Set 17 Answers Solutions.

6th Standard Maths Practice Set 17 Answers Chapter 5 Decimal Fractions

Question 1.
Carry out the following divisions.
i. 4.8÷2
ii. 17.5÷5
iii. 20.6÷2
iv. 32.5÷25
Solution:
i. 4.8÷2

ii. 17.5÷5

iii. 20.6÷2

iv. 32.5÷25

Question 2.
A road is 4 km 800 m long. If trees are planted on both its sides at intervals of 9.6 m, how many trees were planted?
Solution:
Length of road = 4 km 800 m
= 4 × 1000 m + 800 m
= 4000 m + 800 m
= 4800 m
Number of trees on one side = 4800 ÷ 9.6

= 500
∴ Number of trees on both sides = 2 x number of trees on one side
= 2 x 500 = 1000
If the trees are planted at the beginning of the road, then
Total number of trees = 1000 + 2 = 1002
∴ Total number of trees planted is 1000 or 1002.

Question 3.
Pradnya exercises regularly by walking along a circular path on a field. If she walks a distance of 3.825 km in 9 rounds of the path, how much does she walk in one round?
Solution:
Total distance walked in 9 rounds = 3.825 km
∴Distance walked in 1 round = 3.825 4 ÷ 9

= 0.425 km
∴ Total distance walked in 1 round is 0.425 km.

Question 4.
A pharmaceutical manufacturer bought 0.25 quintal of hirada, a medicinal plant, for Rs 9500. What is the cost per quintal of hirada? (1 quintal = 100 kg)
Solution:
Cost of 0.25 quintal of hirada = Rs 9500
∴ Cost of 1 quintal of hirada = 9500 ÷ 0.25

= Rs 38,000
∴ Cost per quintal of hirada is Rs 38,000.

Maharashtra Board Class 6 Maths Chapter 4 Operations on Fractions Practice Set 17 Intext Questions and Activities

Question 1.
Maths is fun! (Textbook pg. no. 34)

1. Consider any three-digit number (say 527).
2. Multiply the number by 7. Then multiply the product obtained by 13, and this product by 11.
3. The found product is 5,27,527.

Take two or three other numbers. Do the same multiplication and find out how it is done.
Solution:
7 × 13 × 11 = 1001
∴ 527 × 1001 = 527 × (1000+ 1)
= (527 × 1000) + (527 × 1)
= 527000 + 527 = 527527
Thus, when any three-digit number is multiplied with 1001, the product obtained is a six-digit number in which the original three-digit number is written back to back twice.
(Students may consider any other three-digit numbers and verify the property.)

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 16 Quadrilaterals Class 6 Practice Set 38 Answers Solutions.

6th Standard Maths Practice Set 38 Answers Chapter 16 Quadrilaterals

Question 1.
Draw ₹XYZW and answer the following:
i. The pairs of opposite angles.
ii. The pairs of opposite sides.
iii. The pairs of adjacent sides.
iv. The pairs of adjacent angles.
v. The diagonals of the quadrilateral.
vi. The name of the quadrilateral in different ways.
Solution:

i. a. ∠XYZ and ∠XWZ
b. ∠YXW and ∠YZW

ii. a. side XY and side WZ
b. side XW and side YZ

iii. a. side XY and side XW
b. side WX and side WZ
c. side ZW and side ZY
d. side YZ and side YX

iv. a. ∠XYZ and ∠YZW
b. ∠YZW and ∠ZWX
c. ∠ZWX and ∠WXY
d. ∠WXY and ∠XYZ

v. Seg XZ and seg YW

vi. ₹XYZW
₹YZWX
₹ZWXY
₹WXYZ
₹XWZY
₹WZYX
₹ZYXW
₹YXWZ

Question 2.
In the table below, write the number of sides the polygon has.

Names	Quadrilateral	Octagon	Pentagon	Heptagon	Hexagon
Number of sides

Solution:

Names	Quadrilateral	Octagon	Pentagon	Heptagon	Hexagon
Number of sides	4	8	5	7	6

Question 3.
Look for examples of polygons in your surroundings. Draw them.
Solution:

Question 4.
We see polygons when we join the tips of the petals of various flowers. Draw these polygons and write down the number of sides of each polygon.
Solution:

Question 5.
Draw any polygon and divide it into triangular parts as shown here. Thus work out the sum of the measures of the angles of the polygon.

Solution:

Hexagon ABCDEF can be divided in 4 triangles namely ∆BAF, ∆BFE, ∆BED and ∆BCD
Sum of the measures of the angles of a triangle = 180°
∴ Sum of measures of the angles of the polygon ABCDEF = Sum of the measures of all the four triangles
= 180° + 180° + 180°+ 180°
= 720°
∴ The sum of the measures of the angles of the given polygon (hexagon) is 720°.

Maharashtra Board Class 6 Maths Chapter 16 Quadrilaterals Practice Set 38 Intext Questions and Activities

Question 1.
From your compass boxes, collect set squares of the same shapes and place them side by side in all possible different ways. What figures do you get? Write their names. (Textbook pg. no. 85)
a. Two set squares
b. Three set squares
c. four set squares
Solution:
a. Two set squares

b. Three set squares

c. four set squares

Question 2.
Kaprekar Number. (Textbook pg. no. 86)
i. Take any 4-digit number in which all the digits are not the same.
ii. Obtain a new 4-digit number by arranging the digits in descending order.
iii. Obtain another 4-digit number by arranging the digits of the new number in ascending order.
iv. Subtract the smaller of these two new numbers from the bigger number. The difference obtained will be a 4-digit number. If it is a 3-digit number, put a 0 in the thousands place. Repeat the above steps with the difference obtained as a result of the subtraction.
v. After some repetitions, you will get the number 6174. If you continue to repeat the same steps you will get the number 6174 every time. Let us begin with the number 8531.
8531 → 7173 → 6354 → 3087 → 8352 → 6174 → 6174
This discovery was made by the mathematician, Dattatreya Ramchandra Kaprekar. That is why the number 6174 was named the Kaprekar number.
Solution:

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 5 Decimal Fractions Class 6 Practice Set 16 Answers Solutions.

6th Standard Maths Practice Set 16 Answers Chapter 5 Decimal Fractions

Question 1.
If, 317 × 45 = 14265, then 3.17 × 4.5 = ?
Solution:
3.17 × 4.5
= 14.265

Question 2.
If, 503 × 217 = 109151, then 5.03 × 2.17 = ?
Solution:
5.03 x 2.17
= 10.9151

Question 3.
i. 2.7 × 1.4
ii. 6.17 × 3.9
iii. 0.57 × 2
iv. 5.04 × 0.7
Solution:
i. 2.7 × 1.4

= 3.75

ii. 6.17 × 3.9

= 24.063

iii. 0.57 × 2

= 1.14

iv. 5.04 × 0.7

= 3.528

Question 4.
Virendra bought 18 bags of rice, each bag weighing 5.250 kg. How much rice did he buy altogether? If the rice costs Rs 42 per kg, how much did he pay for it?
Solution:
Weight of one bag of rice = 5.250 kg
Number of bags of rice = 18
∴ Total Weight = 18 × 5.250

Cost of 1 kg of rice = Rs 42
∴ Cost of 94.5 kg of rice = 42 × 94.5

∴ Total rice bought by Virendra is 94.5 kg, and the amount paid for it is Rs 3969.

Question 5.
Vedika has 23.5 metres of cloth. She used it to make 5 curtains of equal size. If each curtain required 4 metres 25 cm to make, how much cloth is left over?
Solution:
We know, that 1 m = 100 cm
Cloth required to make 1 curtain = 4 m 25 cm
= 4 m + \(\frac { 25 }{ 100 }\) m
= 4 m + 0.25 m

= 4.25 m
∴ Cloth required to make 5 curtains = 5 × 4.25

= 21.25 m
Cloth remaining with Vedika = Total cloth with Vedika – Cloth used
= 23.5 m – 21.25 m

= 2.25 m
∴ The length of cloth remaining with Vedika is 2.25 m.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.2 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Practice Set 2.2 8th Std Maths Answers Chapter 2 Parallel Lines and Transversals

Question 1.
Choose the correct alternative.
i. In the given figure, if line m || line n and line p is a transversal, then find x.

(A) 135°
(B) 90°
(C) 45°
(D) 40°
Solution:
(C) 45°

Hint:

line m || line n and line p is a transversal.
∴ m∠BFG + m∠FGD = 180°
…[Interior angles]
∴ 3x + x = 180°
∴ 4x = 180°
∴ x = \(\frac { 180 }{ 4 }\)
∴ x = 45°

ii. In the given figure, if line a || line b and line l is a transversal, then find x.

(A) 90°
(B) 60°
(C) 45°
(D) 30°
Solution:
(D) 30°

Hint:

line a || line b and line l is a transversal.
∴ m∠UVS = m∠PUV
…[Alternate angles]
= 4x
m∠UVS + m∠WVS = 180°
… [Angles in a linear pair]
∴ 4x + 2x = 180°
∴ 6x = 180°
∴ x = \(\frac { 180 }{ 6 }\)
∴ x = 30°

Question 2.
In the given figure, line p || line q. Line t and line s are transversals. Find measure of ∠x and ∠y using the measures of angles given in the figure.

Solution:

i. Consider ∠z as shown in figure.
line p || line q and line t is a transversal.
∴ m∠z = 40° …(i) [Corresponding angles]
m∠x + m∠z = 180° …[Angles in a linear pair]
∴ m∠x + 40o = 180° …[From(i)]
∴ m∠x= 180° – 40°
∴ m∠x = 140°

ii. Consider ∠w as shown in the figure.
m∠w + 70° = 180° …[Angles in a linear pair]
∴ m∠w = 180° – 70°
∴ m∠w = 110° …(ii)
line p || line q and line s is a transversal.
∴ m∠y = m∠w …[Alternate angles]
∴ m∠y =110° …[From (ii)]
∴ m∠x = 140°, m∠y = 110°

Question 3.
In the given figure, line p || line q, line l || line m. Find measures of ∠a, ∠b and ∠c, using the measures of given angles. Justify your answers.

Solution:
i. line p || line q and line l is a transversal.
∴ m∠a + 80° = 180° …[Interior angles]
∴ m∠a= 180° – 80°
∴ m∠a= 100°

ii. line l || line m and line p is a transversal.
∴ m∠c = 80° …(i) [Exterior alternate angles]

iii. line p || line q and line m is a transversal.
∴ m∠b = m∠c … [Corresponding angles]
m∠b = 80° …[From (i)]
∴ m∠a = 100°, m∠b = 80°, m∠c = 80°

Question 4.
In the given figure, line a || line b, line l is a transversal. Find the measures of ∠x, ∠y, ∠z using the given information.

Solution:
line a || line b and line l is a transversal.
∴ m∠x = 105° …(i) [Corresponding angles]

ii. m∠y = m∠x … [Vertically opposite angles]
∴ m∠y = 105° …[From (i)]

iii. m∠z + 105° = 180° …[Angles in a linear pair]
∴ m∠z = 180°- 105°
∴ m∠z = 75°
∴ m∠x = 105°, m∠y = 105°, m∠z = 75°

Question 5.
In the given figure, line p || line l || line q. Find ∠x with the help of the measures given in the figure.

Solution:

line p || line l and line IJ is a transversal.
m∠IJN = m∠JIH … [Alternate angles]
∴ m∠IJN = 40° …(i)
line l || line q and line MJ is a transversal.
m∠MJN = m∠JMK … [Alternate angles]
∴ m∠MJN = 30° …(ii)
Now, m∠x = m∠IJN + m∠MJN
…[Angle addition property]
= 40° + 30° …[From (i) and (ii)]
∴ m∠x = 70°

Maharashtra Board Class 8 Maths Chapter 2 Parallel Lines and Transversals Practice Set 2.2 Intext Questions and Activities

Question 1.
When two parallel lines are intersected by a transversal eight angles are formed. If the measure of one of these eight angles is given, can we find measures of remaining seven angles? (Textbook pg, no. 9)
Solution:
Yes, we can find the measures of the remaining angles.

In the given figure, line m || line n and line l is a transversal.
m∠a = 60°(say) …(i)
i. m∠a + m∠b = 180° …[Angles in a linear pair]
∴ 60° + m∠b =180° … [From (i)]
∴ m∠b = 180° – 60°
∴ m∠b = 120° …(ii)

ii. m∠c = m∠b …[Vertically opposite angles]
∴ m∠c = 120° .. .(iii) [From (ii)]

iii. m∠d = m∠a …[Vertically opposite angles]
∴ m∠d = 60° …(iv) [From (i)]

iv. m∠e = m∠d …[Alternate angles]
∴ m∠e = 60° … [From (iv)]

v. m∠f = m∠c …[Alternate angles]
∴ m∠f = 120° …[From (iii)]

vi. m∠g = m∠d …[Corresponding angles]
∴ m∠g = 60° … [From (iv)]

vii. m∠h = m∠c … [Corresponding angles]
∴ m∠h = 120° …[From (iii)]

Question 2.
As shown in the figure (A), draw two parallel lines and their transversal on a paper. Draw a copy of the figure on another blank sheet using a trace paper, as shown in the figure (B). Colour part Land part II with different colours. Cut out the two parts with a pair of scissors. Place, part I and part II on each angle in the figure A and answer the following questions. (Textbook pg. no. 9)

1. Which angles coincide with part I?
2. Which angles coincide with part II?

Solution:

1. ∠d, ∠f and ∠h coincide with part I.
2. ∠c, ∠e and ∠g coincide with part II.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 13 Answers Solutions Chapter 3 HCF and LCM.

HCF and LCM Class 7 Practice Set 13 Answers Solutions Chapter 3

Question 1.
Find the LCM:
i. 12, 15
ii. 6, 8, 10
iii. 18, 32
iv. 10, 15, 20
v. 45, 86
vi. 15, 30, 90
vii. 105, 195
viii. 12,15,45
ix. 63,81
x. 18, 36, 27
Solution:
i. 12, 15

∴ LCM of 12 and 15 = 3 x 2 x 2 x 5
= 60

ii. 6, 8, 10

∴ LCM of 6, 8 and 10 = 2 x 2 x 3 x 2 x 5
= 120

iii. 18, 32

∴ LCM of 18 and 32 = 2 x 2 x 2 x 2 x 3 x 3 x 2
= 288

iv. 10, 15, 20

∴ LCM of 10, 15 and 20 = 5 x 2 x 3 x 2
= 60

v. 45, 86

∴ LCM of 45 and 86 = 2 x 3 x 3 x 5 x 43
= 3870

vi. 15, 30, 90

∴ LCM of 15,30 and 90 = 3 x 5 x 2 x 3
= 90

vii. 105, 195

∴ LCM of 105 and 195 = 5 x 3 x 7 x 13
= 1365

viii. 12, 15, 45

∴ LCM of 12, 15 and 45 = 3 x 3 x 2 x 5 x 2
= 180

ix. 63, 81

∴ LCM of 63 and 81 = 3 x 3 x 3 x 7 x 3
= 567

x. 18, 36, 27

∴ LCM of 18, 36 and 27 = 3 x 3 x 2 x 2 x 3
= 108

Question 2.
Find the HCF and LCM of the numbers given below. Verify that their product is equal to the product of the given numbers:
i. 32, 37
ii. 46, 51
iii. 15, 60
iv. 18, 63
v. 78, 104
Solution:
i. 32 = 2 x 16
= 2 x 2 x 8
= 2 x 2 x 2 x 4
= 2 x 2 x 2 x 2 x 2 x 1
37 = 37 x 1
∴ HCF of 32 and 37 =1
LCM of 32 and 37 = 2 x 2 x 2 x 2 x 2 x 37
= 1184
HCF x LCM = 1 x 1184
= 1184
Product of the given numbers = 32 x 37
= 1184
∴ HCF x LCM = Product of the given numbers.

ii. 46 = 2 x 23 x 1
51 = 3 x 17 x 1
∴ HCF of 46 and 51 = 1
LCM of 46 and 51 = 2 x 23 x 3 x 17
= 2346
HCF x LCM = 1 x 2346
= 2346
Product of the given numbers = 46 x 51
= 2346
∴ HCF x LCM = Product of the given numbers.

iii. 15 = 3 x 5
60 = 2 x 30
= 2 x 2 x 15
= 2 x 2 x 3 x 5
∴ HCF of 15 and 60 = 3 x 5
= 15
LCM of 15 and 60 = 3 x 5 x 2 x 2
= 60
HCF x LCM = 15 x 60
= 900
Product of the given numbers = 15 x 60
= 900
∴ HCF x LCM = Product of the given numbers.

iv. 18 = 2 x 9
= 2 x 3 x 3
63 = 3 x 21
= 3 x 3 x 7
∴ HCF of 18 and 63 = 3 x 3
= 9
LCM of 18 and 63 = 3 x 3 x 2 x 7
= 126
HCF x LCM = 9 x 126
= 1134
Product of the given numbers = 18 x 63
= 1134
∴ HCF x LCM = Product of the given numbers.

v. 78 = 2 x 39
= 2 x 3 x 13
104 = 2 x 52
= 2 x 2 x 26
= 2 x 2 x 2 x 13
∴ HCF of 78 and 104 = 2 x 13
= 26
LCM of 78 and 104 = 2 x 13 x 3 x 2 x 2
= 312
HCF x LCM = 26 x 312
= 8112
Product of the given numbers = 78 x 104
= 8112
∴ HCF x LCM = Product of the given numbers.

Maharashtra Board Class 7 Maths Chapter 3 HCF and LCM Practice Set 13 Intext Questions and Activities

Question 1.
Write the tables of the given numbers and find their LCM. (Textbook pg. no. 19)
i. 6, 7
ii. 8, 12
iii. 5, 6, 15
Solution:
i. Multiples of 6 : 6, 12, 18, 24, 30, 36, 42
Multiples of 7 : 7, 14, 21, 28, 35, 42, 49
∴ LCM of 6 and 7 = 42

ii. Multiples of 8 : 8, 16, 24, 32, 40
Multiples of 12 : 12, 24, 36, 48
∴ LCM of 8 and 12 = 24

iii. Multiples of 5 : 5, 10, 15, 20, 25, 30, 35
Multiples of 6 : 6, 12, 18, 24, 30, 36
Multiples of 15 : 15, 30, 45, 60
∴ LCM of 5,6 and 15 = 30

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 7 Answers Solutions Chapter 1 Geometrical Constructions.

Geometrical Constructions Class 7 Practice Set 7 Answers Solutions Chapter 1

Question 1.
Some angles are given below. Using the symbol of congruence write the names of the pairs of congruent angles in these figures.

Solution:
i. ∠AOC ≅ ∠PQR
ii. ∠DOC ≅ ∠LMN
iii. ∠AOB ≅ ∠BOC ≅ ∠RST

Maharashtra Board Class 7 Maths Chapter 1 Geometrical Constructions Practice Set 7 Intext Questions and Activities

Question 1.
Observe the given angles and write the names of those having equal measures.
(Textbook pg. no. 8 and 9)

Solution:
i. ∠ABC and ∠SPM
ii. ∠NIT and ∠SRI
iii. ∠PTQ and ∠RTS

Question 2.
Observe the image shown in the adjacent figure and answer the following questions. (Textbook pg. no. 9)

1. What time does this clock show?
2. What is the measure of the angle between its two hands?
3. At which other times is the angle between the hands congruent with this angle?

Solution:

1. 3 o’ clock.
2. 90°.
3. 9 o’ clock.

Question 3.
Get bangles of different sizes but equal thickness and find the congruent ones among them. (Textbook pg. no. 10)
Solution:
[Students should attempt the above activities on their own.]

Question 4.
Find congruent circles in your surroundings. (Textbook pg. no. 10)
Solution:
[Students should attempt the above activities on their own.]

Question 5.
Take some round bowls and plates. Place their edges one upon the other to find pairs of congruent edges. (Textbook pg. no. 10)
Solution:
[Students should attempt the above activities on their own.]

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 6 Answers Solutions Chapter 1 Geometrical Constructions.

Geometrical Constructions Class 7 Practice Set 6 Answers Solutions Chapter 1

Question 1.
Write the names of pairs of congruent line segments. (Use a divider to find them.)

i. ___
ii. ___
iii. ___
iv. ___
Solution:
i. seg BG ≅ seg CG
ii. seg NG ≅ seg MG ≅ seg EG ≅ seg RG

Question 2.
On the line below, the distance between any two adjoining points shown on it is equal. Hence, fill in the blanks.

i. seg AB ≅ seg ___
ii. seg AP ≅ seg ___
iii. seg AC ≅ seg ___
iv. seg ___ ≅ seg BY
v. seg __ ≅ seg YQ
vi. seg BW ≅ seg ___
Solution:
i. BC
ii. QW
iii. QZ
iv. AZ
v. AY
vi. AC

Note: The above problem has many solutions. Students may write solutions other than the ones given.

Maharashtra Board Class 7 Maths Chapter 1 Geometrical Constructions Practice Set 6 Intext Questions and Activities

Question 1.
Try to draw triangles with the following data. Can you draw these triangles. If not, look for the reason why you could not draw so. (Textbook pg. no. 7)
i. ∆ABC in which m∠A = 85°, m∠B = 115°, l(AB) = 5cm.
Solution:
m∠A + m∠B = 85° + 115°
= 200°>180°
But the sum of the measures of the angles of a triangle is 180°
Hence, ∆ABC cannot be drawn.

ii. ∆PQR in which l(QR) = 2cm, l(PQ) = 4cm, l(PR) = 2cm.
Solution:
l(QR) + l(PR) = 2 cm + 2cm
= 4 cm
= l(PQ)
But in a triangle, the sum of the length of any two sides of a triangle is always greater than the length of the third side.
Hence, ∆PQR cannot be drawn.

Question 2.
Draw ∆ABC such that l(BC) = 8 cm, l(CA) = 6 cm, m∠ABC = 40°.
Draw a ray to make an angle of 40° with the base BC, l(BC) = 8 cm. We have to obtain point ‘A’ on the ray. With ‘C’ as the centre, draw an arc of radius 6 cm to do so. What do we observe? The arc intersects the ray in two different points. Thus, we get two triangles of two different shapes having the given measures. (Textbook pg. no. 7)
Solution:

Here ∠B is an acute angle. ∠C can be an acute angle or an obtuse angle.
Hence we get two triangles of two different shapes.

Question 3.
Can a triangle be drawn if the three angles are given, but not any side? How many such triangles can be drawn? (Textbook pg. no. 7)
Solution:
Yes a triangle can be drawn.
Since the length of side is not given, any length of side can be selected and then triangle can be constructed. We will get different triangles for different length of sides.

Question 4.
Using the ruler, measure the lengths of seg AB and seg PQ. Are they of same length? Trace the seg AB on a sheet of transparent paper. Now place this new segment on PQ verify that if point A is placed on point P, then B falls on Q. (Textbook pg. no. 7)

l(AB) = ___
l(PQ) = ___
Solution:
l(AB) = 4 cm
l(PQ) = 4 cm
Since the length of two segments is the same, if placed on one another, they will coincide.

Question 5.
From the shape shown below, write the names of the pairs of congruent line segments. (Textbook pg. no. 8)
i. seg AB ≅ seg DC
ii. seg AE ≅ seg BH
iii. seg EF ≅ seg ___
iv. seg DF ≅ seg ___

Solution:
seg EF ≅ seg AD ≅ seg BC ≅ seg HG
seg DF ≅ seg CG ≅ seg AE ≅ seg BH

Question 6.
Take a rectangular paper. Place two opposite sides upon each Other. What do you observe? (Textbook pg. no. 7)
Solution:
Opposite sides of the rectangular paper coincide and hence are congruent.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 2 Answers Solutions Chapter 1 Geometrical Constructions.

Geometrical Constructions Class 7 Practice Set 2 Answers Solutions Chapter 1

Question 1.
Draw triangles with the measures given below:
i. In ∆ABC, l(AB) = 5.5 cm, l(BC) = 4.2 cm, l(AC) = 3.5 cm.
ii. In ∆STU, l(ST) = 7 cm, l(TU) = 4 cm, l(SU) = 5 cm.
iii. In ∆PQR, l(PQ) = 6 cm, l(QR) = 3.8 cm, l(PR) = 4.5 cm.
Solution:
i. In ∆ABC, l(AB) = 5.5 cm, l(BC) = 4.2 cm, l(AC) = 3.5 cm.

ii. In ∆STU, l(ST) = 7 cm, l(TU) = 4 cm, l(SU) = 5 cm.

iii. In ∆PQR, l(PQ) = 6 cm, l(QR) = 3.8 cm, l(PR) = 4.5 cm.

Question 2.
Draw an isosceles triangle with base 5 cm and the other sides 3.5 cm each.
Solution:

Question 3.
Draw an equilateral triangle with side 6.5 cm.
Solution:

Question 4.
Choose the lengths of the sides yourself and draw one equilateral, one isosceles and one scalene triangle.
Solution:
i. Equilateral triangle LMN, l(LM) = l(MN) = l(LN) = 4 cm.

ii. Isosceles triangle STU, l(ST) = l(TU) = 4cm, l(SU) = 6 cm

iii. Scalene triangle XYZ, l(XY) = 4.5 cm, l(XY) = 6.5 cm, l(XZ) = 5.5 cm

Maharashtra Board Class 7 Maths Chapter 1 Geometrical Constructions Practice Set 2 Intext Questions and Activities

Question 1.
Draw ∆ABC such that l(AB) = 4 cm, and l(BC) = 3 cm. (Textbook pg. no. 3)

1. Can this triangle be drawn?
2. A number of triangles can be drawn to fulfill these conditions. Try it out.
3. Which further condition must be placed if we are to draw a unique triangle using the above information?

Solution:

1. ∆ABC triangle cannot be drawn as length of third side is not given.
2. For ∆ABC to draw l(AC) > l(AB) + l(BC)
   i.e., l(AC) > 4 + 3
   i.e., l(AC) > 7 cm
   ∴ number of triangles can be drawn if l(AC) > 7 cm
3. l(AC) > l(AB) + l(BC) is the required condition to draw a unique triangle.