Class 9th Sanskrit Anand Chapter 9 अमरकोषः Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Anand Chapter 9 अमरकोषः Notes, Textbook Exercise Important Questions and Answers.
Std 9 Sanskrit Chapter 9 Question Answer
Sanskrit Anand Std 9 Digest Chapter 9 अमरकोषः Textbook Questions and Answers
भाषाभ्यास:
1. एकवाक्येन उत्तरत।
प्रश्न अ.
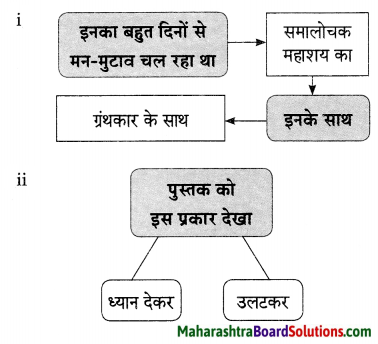
कोषा: किमर्थम् आवश्यकाः?
उत्तरम् :
कोषाः शास्त्राणाम् अध्ययनार्थम् आवश्यकाः।
प्रश्न आ.
कोष: नाम किम् ?
उत्तरम् :
कोष: नाम सङ्ग्रहः ।
प्रश्न इ.
क: अमरकोषस्य रचयिता ?
उत्तरम् :
अमरसिंह : नाम पण्डित: अमरकोषस्य रचयिता ।
![]()
प्रश्न ई.
अमरकोषस्य कण्ठस्थीकरणं कस्मात् सुलभम् ?
उत्तरम् :
अमरकोषः पद्यमय: गेय: च अतः तस्य कण्ठस्थीकरणं सुलभम्।
प्रश्न उ.
अमरकोषे कति श्लोकाः सन्ति ?
उत्तरम् :
अमरकोषे उपसार्धसहसं (1500) श्लोकाः सन्ति ।
प्रश्न ऊ.
अमरकोषस्य किम् अन्यत् नामद्वयम् ?
उत्तरम् :
त्रिकाण्डकोष: नामलिङ्गानुशासनम् च इति अमरकोषस्य अन्यत् नामद्वयम्।
![]()
2. माध्यमभाषया लिखत।
प्रश्न 1.
‘अमरकोष’- कण्ठस्थीकरणेन के लाभाः भवन्ति ?
उत्तरम् :
‘अमरकोष’ या संवादात्मक पाठात शिक्षिका व विद्यार्थी यांच्यातील संवादातून ‘अमरकोष’ या संस्कृत कोषाबद्दल माहिती मिळते व त्याचे महत्व कळते. ग्रंथालयातील विविध कोष बघून विद्यार्थी शिक्षिकेला त्यांची माहिती विचारतात. शिक्षिका त्यांना कोष म्हणजे काय, त्यांचे भाषा, शास्त्र हयांच्या अभ्यासातील महत्त्व सांगतात, ‘अमरकोष’ ह्य संस्कृत भाषेतील महत्त्वपूर्ण कोष असून पूर्वीच्या काळात विद्यार्थी विद्यारंभाच्या वेळी तो तोंडपाठ करीत असत. अमरकोषाच्या पाठांतरामुळे शब्दसंपत्ती वाढते. शिवाय स्मरणशक्ती व धारणशक्ती सुद्धा वाढते. अमरकोष तोंडपाठ असेल तर संस्कृत भाषेचे आकलन आणि शब्दांचे उपयोजन सहजपणे करता येते. संस्कृत नाटकांचा, काव्यांचा आस्वाद घेण्यास सुद्धा मदत होते.
The lesson अमरकोषः is dialogue between students and their teacher. Importance of learning 3HC is emphasised in this dialogne. The students ask teacher about various thesauruses which they find in the library. Teacher tells them about various thesaruses and their importance. She tells them about very important thesurus of Sanskrit language. i.e. Amarakosha. If one learns the Amarakosha by heart, his vocabulary increases.
One’s memory as well as understanding increase and pronunciation also gets pure and better. Due to that, language aquisition and usage become easy. It also helps in studying the Sanskrit poetry and drama. Amarakosha is very significant in studying Sanskrit language.
![]()
3. अ) शब्दस्य वर्णविग्रहं कुरुत।
- सङ्ग्रहम्
- प्रयोगः
- वर्तन्ते
- क्वचित्
उत्तरम् :
- सङ्ग्रहम् – स् + अ + ङ् + ग् + र् + अ + ह् + अ + म्।
- वर्तन्ते – व् + अ + र + त् + अ + न् + त् + ए।
![]()
आ. मेलनं कुरुत।
प्रश्न 1.
| विशेष्यम् | विशेषणम् |
| 1. कपाटिका | 1. सुलभम् |
| 2. कोषग्रन्थः | 2. विशाला |
| 3. कण्ठस्थीकरणम् | 3. भिन्ना: |
| 4. अर्थाः | 4. पद्यमयः |
उत्तरम् :
| विशेष्यम् | विशेषणम् |
| 1. कपाटिका | 2. विशाला |
| 2. कोषग्रन्थः | 4. पद्यमयः |
| 3. कण्ठस्थीकरणम् | 1. सुलभम् |
| 4. अर्थाः | 3. भिन्ना: |
![]()
4. समानार्थकशब्द लिखत।
प्रश्न 1.
कोषः, अमरकोषः, विख्यातः, सुलभम् ।
उत्तरम् :
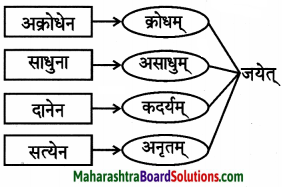
- कोषः – सज्ञयः सङ्ग्रहः, निधिः।
- अमरकोषः – त्रिकाण्डकोषः, नामलिङ्गानुशासनम्।
- विख्यातः – प्रसिद्धः, ख्यातः।
- सुकरम् – सुलभम्।
5. योग्यविशेषणं चित्वा वाक्यं पुनर्लिखत ।
प्रश्न 1.
- ग्रन्थालये कोषाय कृते एका विशाला कपाटिका विद्यते ।
- छात्रा: ग्रन्थालये विविधं पुस्तकानि पश्यन्ति।
- अमरकोषे तिस्रः काण्डानि सन्ति ।
उत्तरम् :
- ग्रन्थालये कोषाणां कृते एका विशाला कृपाटिका विद्यते।
- छात्रा: ग्रन्थालये विविधानि पुस्तकानि पश्यन्ति।
- अमरकोषे त्रीणि काण्डानि सन्ति।
![]()
Sanskrit Anand Class 9 Textbook Solutions Chapter 9 अमरकोषः Additional Important Questions and Answers
उचितं पर्यायं चिनुत।
प्रश्न 1.
कपाटिकायां के वर्तन्ते?
(अ) ग्रन्थाः
(आ) कोषाः
(इ) चषकाः
(ई) पुत्तलिकाः
उत्तरम् :
(आ) कोषाः
प्रश्न 2.
कोषा: किमर्थम् आवश्यका:?
(अ) पूजार्थम्
(आ) मनोरञ्जनार्थम्
(इ) वाचनार्थम्
(ई) शास्त्राणाम् अध्ययनार्थम्
उत्तरम् :
(ई) शास्त्राणाम् अध्ययनार्थम्
प्रश्न 3.
छात्रा: ग्रन्थालये किं पश्यन्ति?
(अ) पुस्तकानि
(आ) सन्दुक:
(इ) आसन्दः
(ई) कृष्णफलक:
उत्तरम् :
(अ) पुस्तकानि
![]()
प्रश्न 4.
वित्तकोषे किं भवति?
(अ) धनसङ्ग्रहणम्
(आ) ऊर्जासङ्ग्रहणम्
(इ) पुस्तकसङ्ग्रहणम्
(ई) वस्वसङ्ग्रहणम्
उत्तरम् :
(अ) धनसङ्ग्रहणम्
प्रश्न 5.
- अमरकोषः ……………… (पद्यमयः/ गद्यमय:)
- तत्र एकस्य शब्दस्य कृते नैके ………………… शब्दाः वर्तन्ते। (समानार्थकाः / विरुद्धार्थकाः)
- अमरकोषस्य पठनेन ……………… वर्धते। (स्मरणशक्तिः/ पठनशक्तिः)
उत्तरम् :
- पद्यमयः
- समानार्थकाः
- स्मरणशक्तिः
![]()
प्रश्न 6.
- अमरकोषे ………… श्लोकाः सन्ति। (उपसार्धसहस्रम् /सहस्रम्/ शतम्)
- अमरकोषे …………. काण्डानि सन्ति। (द्वे / त्रीणि/ चत्वारि)
- अमरकोषस्य अपरं नाम ………….. । (त्रिकाण्डकोषः / शब्दकोष:)
- अमरकोषस्य पठनेन भाषायाः ………… सुकरं भवति। (आकलनं / लेखनं / श्रवणं)
उत्तरम् :
- उपसार्धसहस्रम्
- त्रीणि
- त्रिकाण्डकोषः
- आकलनम्
उचितं कारणं चित्वा वाक्यं पुनर्लिखत।
प्रश्न 1.
अमरकोषस्य कण्ठस्थीकरणं सुलभम्, यतः ……….
a. अमरकोषः गेयः अस्ति।
b. अमरकोषः अतीव लघुः अस्ति।
उत्तरम् :
अमरकोषस्य कण्ठस्थीकरणमं सुलभम्, यतः अमरकोषः गेयः अस्ति ।
![]()
प्रश्न 2.
अमरकोषस्य पठनेन शब्दसम्पत्तिः वर्धते, यतः …………….
a. तस्मिन् नैके समानार्थकाः शब्दाः सन्ति।
b. अमरकोषः सुलभः।
उत्तरम् :
अमरकोषस्य पठनेन शब्दसम्पत्ति: वर्धते, यतः तस्मिन् नैके समानार्थकाः शब्दा: सन्ति।
एकवाक्येन उत्तरत।
प्रश्न 1.
कपाटिकायां छात्राः किं पश्यन्ति?
उत्तरम् :
कपाटिकायां छात्राः विविधानि पुस्तकानि पश्यन्ति ।
प्रश्न 2.
वित्तकोषे कस्य सङ्ग्रहं कुर्मः?
उत्तरम् :
वित्तकोषे धनस्य सङ्गहं कुर्मः।
![]()
प्रश्न 3.
भाषाकोषे किं भवति?
उत्तरम् :
भाषाको शब्दानां सङ्ग्रहः भवति।
प्रश्न 4.
अमरकोषस्य अन्यत् वैशिष्ट्यं किम्?
उत्तरम् :
शब्दानां लिङ्गनिर्देश: इति अमकोषस्य अन्यत् वैशिष्ट्यम्।
प्रश्न 5.
लिङ्गनिर्देशेन किं भवति?
उत्तरम् :
लिङ्गनिर्देशेन भाषाया: आकलनं प्रयोग: च सुकर : भवति।
प्रश्न 6.
लिङ्गनिर्देशेन किं विनायासं पठितुं शक्नुमः?
उत्तरम् :
लिङ्गनिर्देशेन संस्कृतकाव्यानि नाटकानि च विनायासं पठितुं शक्नुमः।
प्रश्न 7.
कोषस्य क: उपयोग:?
उत्तरम् :
सम्भाषणे, लेखने च भाषाप्रभुत्वं-प्राप्त्यर्थ , ज्ञानप्राप्यर्थ शब्दसंपत्ति-वर्धनम् इति कोषस्य उपयोगः ।
![]()
प्रश्न 8.
ग्रन्थालये के के कोषाः वर्तन्ते?
उत्तरम् :
ग्रन्थालये विश्वकोषाः, सुभाषितकोषाः, संस्कृतिकोषा: चरित्रकोषा: च वर्तन्ते ।
प्रश्न 9.
पुरातनकाले अध्ययनारम्भे छात्राः किं कण्ठस्थं कुर्वन्ति स्म?
उत्तरम् :
पुरातनकाले अध्ययनारम्भे छात्रा: अमरकोषं कण्ठस्थं कुर्वन्ति स्म।
प्रश्न 10.
अमरकोषः कीदृशः ग्रन्थः?
उत्तरम् :
अमरकोषः पद्यमयः ग्रन्थः ।
प्रश्न 11.
अमरकोषस्य कण्ठस्थीकरणं कीदृशम्?
उत्तरम् :
अमरकोषस्य कण्ठस्थीकरणं सुभाषितानां पठनम् इव अतीव सुलभम्।
![]()
सत्यं वा असत्यं लिखत।
प्रश्न 1.
- शास्त्राणाम् अध्ययनार्थ कोषाणां न आवश्यकता।
- वित्तकोषे ऊर्जासज्ञयः भवति ।
- भाषाकोषे शब्दानां सङ्ग्रहः भवति।
- कोषः नाम सङ्ग्रहः।
- अमरकोषः पद्यमयः।
- अमरकोषस्य कण्ठस्थीकरणम् अतीव दुष्करम्।
- अमरकोषस्य पठनेन स्मरणशक्ति: वर्धते।
- ज्ञानप्राप्त्यर्थ शब्दसम्पत्तेः सङ्ग्रहणम् आवश्यकम्।
- कोषपठनेन भाषाप्रभुत्वं प्राप्तुं शक्यते।
- अमरकोष: हिन्दीशब्दानां सङ्ग्रहग्रन्थः।
- अध्ययनारम्भे अमरकोषः पठनीयः।
- अमरकोषः त्रिकाण्डात्मकः।
- अमरकोषे केवलं समानार्थकशब्दाः सन्ति।
- अमरकोषे लिङ्गनिर्देशः कृतः।
- लिङ्गनिर्देशेन संस्कृतकाव्यानां पठनं दुष्करं भवति।
उत्तरम् :
- असत्यम्
- असत्यम्
- सत्यम्
- सत्यम्
- सत्यम्
- असत्यम्
- सत्यम्
- सत्यम्
- सत्यम्
- असत्यम्
- सत्यम्
- सत्यम्
- असत्यम्
- सत्यम्
- असत्यम्
![]()
कः कं वदति।
प्रश्न 1.
- कियन्तः विविधाः कोषाः एतस्यां वर्तन्ते।
- कोषः नाम किम् ?
- क: तस्य उपयोग:? किं
- विद्यते अस्मिन् कोथे?
- अमरसिंहः नाम पण्डित: एतस्य रचयिता।
- वयमपि अमरकोषं कण्ठस्थं कुर्याम्।
- त्रिकाण्डकोष: इति अस्य अपरं नाम।
- नामलिङ्गानुशासनम् इति शब्दस्य क: अर्थः?
उत्तरम् :
- नयन: आचार्या वदति।
- सुमेधा आचार्या वदति।
- श्रेया अध्यपिकां वदति।
- स्वप्नील: अध्यापिकां वदति।
- अध्यापिका छात्रान् वदति।
- नयनः अध्यापिकां वदति।
- अध्यापिका छात्रान् वदति।
- सुमेधा अध्यापिकां वदति।
प्रश्न 2.
एकस्य शब्दस्य नैके भिन्ना: अर्थाः अपि वर्तन्ते ।
उत्तरम् :
अध्यापिका छात्रान् वदति।
![]()
शब्दस्य वर्णविग्रहं कुरुत।
- छात्राः – छ् + आ + त् + र् + आः।
- भिन्ना – भ् + इ + न + न् + आ।
- सर्वेषाम् – स् + अ + र + व् + ए + ष + आ + म्।
- शास्त्राणाम् – श् + आ + स् + त् + र + आ + ण् + आ + म्।
- कुर्मः – कु + उ + र + म् + अः।
- सुयोग्यः – स् + उ + य् + ओ + ग् + य् + अः।
- प्रश्न: – प् + र + अ + श् + न् + अः।
- भाषाप्रभुत्व – भ् + आ + ष + आ + प् + र + अ + भ + उ + त् + व + अ।
- ज्ञानप्राप्त्य र्थम् – ज् + ञ् + आ + न् + अ + + र + आ + प् + त् + य् + अ + र + थ् + अ + मा
- संस्कृतिकोष: – स् + अ् + म् + स् + क् + ऋ + त् + इ + क् + ओ + ष + अः।
- चरित्र – च् + अ + र् + इ + त् + र + अ।
- ग्रन्थः – ग् + र + अ + न् + थ् + अः।
- कण्ठस्थम् – क् + अ + ण् + ल् + अ + स् + थ् + अ + म्।
- पद्यमयः – प् + अ + द् + य् + अ + म् + अ + य् + अः।
- श्लोकानाम् – श् + ल् + ओ + क् + आ + न् + आ + म्।
- शुद्धम् – श् + उ + द् + ध् + अ + म्।
- शब्दस्य – श् + अ + ब् + द् + अ + स् + य् + अ।
- क्वचित् – क् + व् + अ + च् + इ + त्।
- सार्चयम् – स् + आ + श् + च् + अ + र + य + अ + म्।
- वृद्धिम् – व् + ऋ + द् + ध् + इ + म्।
- कुयोम – क् + उ + र + य् + आ + म् + अ।
- तस्मिन् – त् + अ + स् + म् + इ + न्।
- काण्डानि – क् + आ + ण् + ड् + आ + न् + इ।
- लिमनिर्देश: – ल् + इ + इ + ग् + अ + न + इ + र + द् + ए + श् + अः।
- सर्वः – स् + अ + र + व् + ऐः।
- कर्तव्यम् – क् + अ + र् + त् + अ + व् + य् + अ + म्।
![]()
प्रश्ननिर्माणं कुरुत।
- कोष: नाम सङ्ग्रहः।
- शास्त्राणाम् अध्ययनार्थ कोषा: आवश्यकाः।
- अमरसिंहः अमरकोषस्य रचयिता।
- पुरातनकाले छात्रा: अध्ययनार्थ गुरुकुलं प्रविशन्ति स्म।
- छात्राः अध्ययनारम्भे अमरकोषं कण्ठस्थं कुर्वन्ति स्म।
- अमरकोषे त्रीणि काण्डानि सन्ति।
- त्रिकाण्डकोषः इति अमरकोषस्य अपरं नाम।
उत्तरम् :
- कोषः नाम किम्?
- शास्त्राणाम् अध्ययनार्थ के आवश्यका:?
- कः अमरकोषस्य रचयिता?
- पुरातनकाले छात्रा: अध्ययनार्थ कुत्र प्रविशन्ति स्म?
- छात्रा: अध्ययनारम्भे किं कण्ठस्थं कुर्वन्ति स्म?
- अमरकोषे कति काण्डानि सन्ति?
- अमरकोषस्य अपरं नाम किम्?
![]()
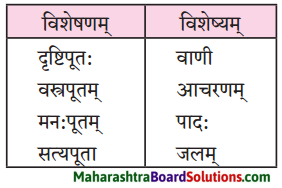
विशेषण-विशेष्य-सम्बन्धः।
प्रश्न 1.
| विशेष्यम् | विशेषणम् |
| ………..… | कोषा: |
| …………… | पुस्तकानि |
| सुयोग्यः | प्रश्न: |
| बहवः | विविधाः |
| विशेष: | कोषः |
| उच्चारणम् | शुद्धम् |
उत्तरम् :
| विशेष्यम् | विशेषणम् |
| विविधाः | कोषा: |
| विविधानि | पुस्तकानि |
| सुयोग्यः | प्रश्न: |
| बहवः | कोषा: |
| विशेष: | कोषः |
| उच्चारणम् | शुद्धम् |
![]()
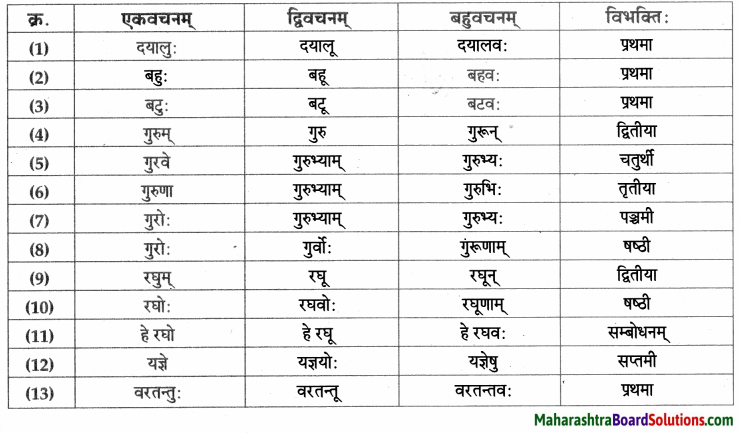
विभक्त्यन्तरूपाणि।
- प्रथमा – छात्रा:, कियन्तः, कोषाः, कपाटिका, वयम्, सङ्ग्रहः, एते, प्रश्नः, संस्कृतिकोषाः, चरित्रकोषाः, विश्वकोषाः, सुभाषितकोषा:,अमरकोषः, सङ्ग्रहान्धः, अमरसिंहः, पण्डितः, रचयिता, छात्राः, लाभः, पद्यमयः, गेयः, समानार्थकशब्दाः, भिन्नाः, स्मरणशक्तिः, धारणाशक्तिः, ग्रन्थः, नैके।
- द्वितीया – प्रश्नान, अध्यापिकाम्, गुरुकुलम्, अमरकोषम्, वृद्धिम्, अमरकोषम्।
- तृतीया – तेन, पठनेन।
- षष्ठी – सर्वेषाम्, शास्त्राणाम्, शब्दानाम्, धनस्य, शब्दसम्पत्तेः, अस्माकम्, एतस्य, कोषस्य, अस्माकम्, एकस्य,शब्दस्य, श्लोकानाम्, सुभाषितानाम् तस्य।
- सप्तमी – ग्रन्थालये, वित्तकोषे, भाषाकोषे, सम्भाषणे, लेखने, ग्रन्थालये, तेषु, अस्मिन्, कोषे,पुरातनकाले, अध्ययनारम्भे, तस्मिन्।
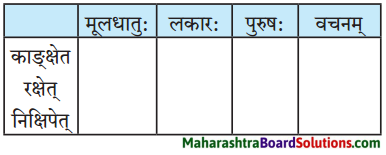
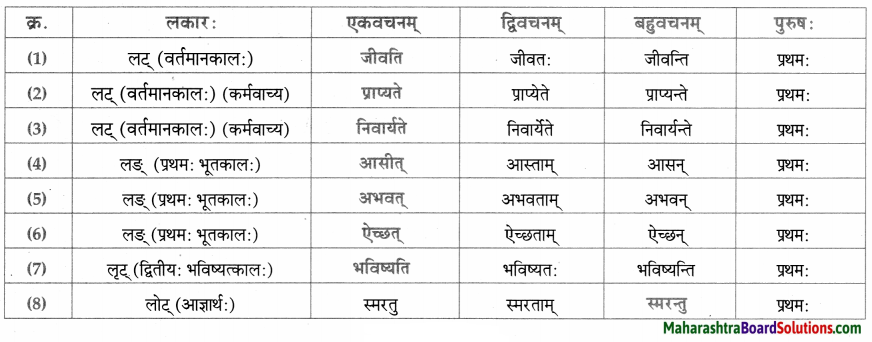
लकारं लिखत।
- पृच्छन्ति – ‘प्रच्छ-पृच्छ्’ धातुः षष्ठगण: परस्मैपदं लट्लकार: प्रथमपुरुष: बहुवचनम्।
- कुर्मः – ‘कृ’ धातुः अष्टमगण: उभयपदम् अत्र परस्मैपदं लट्लकार: उत्तमपुरुष: बहुवचनम्।
- वर्तन्ते – ‘वृत्-वत्’ धातुः प्रथमगण: आत्मनेपदं लट्लकार: प्रथमपुरुष: बहुवचनम्।
- विद्यते – ‘विद्’ धातुः चतुर्थगण: आत्मनेपदं लट्लकार: प्रथमपुरुष: एकवचनम्।
- कुर्वन्ति – ‘कृ’ धातुः अष्टमगण: उभयपदम् अत्र परस्मैपदं लट्लकार: प्रथमपुरुष: बहुवचनम्।
- वर्धते – ‘वृध्-वर्ष’ धातुः प्रथमगण:आत्मनेपदं लट्लकार: प्रथमपुरुष: द्विवचनम्।
त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।
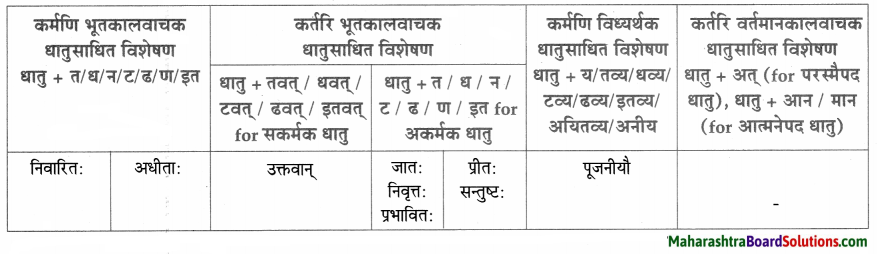
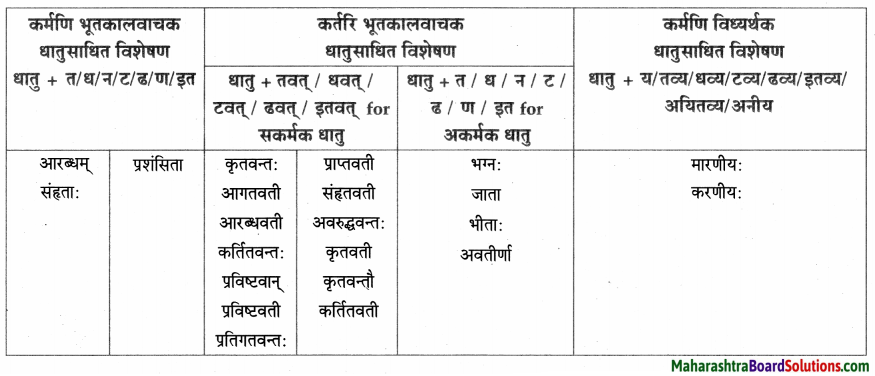
| त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा अयित्वा | ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य | तुमन्त अव्यय थातु + तुम् / धुम् / टुम् / ढुम् / इतुम् / अयितुम् |
| – | – | कण्ठस्थीकर्तुम् |
| – | – | पठितुम् |
![]()
व्याकरणम् :
शब्दानां पृथक्करणम्
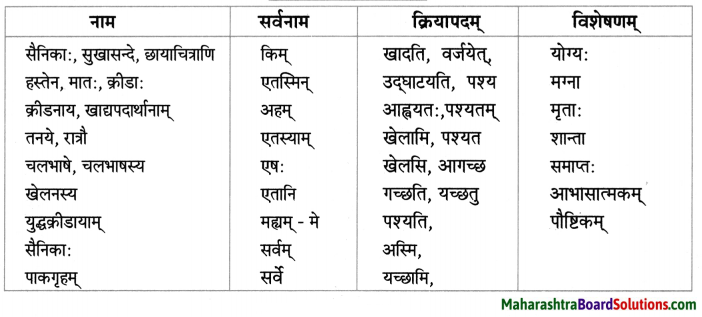
| नाम | सर्वनाम | क्रियापदम् | विशेषणम् |
| छात्राः, सुभाषितानाम् | सर्वेषाम्, एतस्य | पश्यन्ति, गच्छति | विविधाः |
| ग्रन्थालये, वृद्धिम् | ते, अस्माकम् – नः | वर्तन्ते, कुर्याम | भिन्नाः |
| शास्त्राणाम्, काण्डानि | एषा, अस्मिन् | कुर्मः, शक्नुमः | विविधानि |
| वित्तकोषे, नाम्ना | कः, तेषु | भवति | सुयोग्य: |
| कोषस्य, प्रयोगः | एतस्याम्, वयम् | विद्यते | बहवः |
| शब्दस्य | कियन्तः, तेन | प्रविशन्ति | विशेषः |
| अमरकोषम् | एषः, किम् | कुर्वन्ति | पद्यमय: |
| रचयिता | एते | सन्ति | सुलभम् |
| गुरुकुलम् | तस्य | वर्धते | शुद्धम् |
![]()
अमरकोषः Summary in Marathi and English
प्रस्तावना :
कोणतीही भाषा नव्याने शिकताना त्या भाषेतील शब्दसंपत्ती ग्रहण करण्याकरिता शब्दकोष महत्त्वपूर्ण असतोच. इतर भाषांप्रमाणेच संस्कृतातही अनेक शब्दकोष उपलब्ध आहेत. अमरकोष हा संस्कृतभाषेचा प्रसिद्ध शब्दकोष, संस्कृतविद्वान अमरसिंह यांनी रचला. अमरकोष प्रसिद्ध आहे तो त्याच्या वैशिष्ट्यपूर्ण रचनेमुळे, अमरसिंह यांनी एका शब्दाचे इतर समानार्थ पद्यमय रचनेत मांडल्यामुळे कंठस्थीकरण सहज शक्य होते. चार विद्यार्थी आणि शिक्षिका यांच्या संवादातून प्रस्तुत पाठात अमरकोषाचे महत्त्व प्रतिपादित केले आहे.
Lexicons, dictionaries thesaureses are an important part of learning any language. Just like English, German, French, Marathi or any other language there are many Sanskrit dictionaries which are popular. Amarakosha is one of those celebrated lexicons in Sanskrit. It was composed by an ancient scholar Amarasimha.
Where he tried to enlist synonyms for almost all Sanskrit words. Learning the Amarakosha by heart is the best way to increase vocabulary. It is composed in such a simple way that even a beginner can easily learn it. This lesson talks about importance and significance of Amarakosha through a discussion between four students and their teachers.
![]()
परिच्छेद : 1
छात्रा: ग्रन्थालये ………….. सग्रहः भवति।
(छात्रा: ग्रन्थालये विविधानि पुस्तकानि पश्यन्ति अध्यापिका प्रश्नान् च पृच्छन्ति ।)
नयनः – आचार्य, का एषा भिन्ना विशाला कपाटिका ? अहो ! कियन्तः विविधाः कोषाः एतस्यां वर्तन्ते !
अध्यापिका – आम्, सर्वेषां शास्त्राणाम् अध्ययनार्थम् एते कोषा: आवश्यकाः।
सुमेधा – कोष: नाम किम् ?
अध्यापिका – कोष: नाम सङ्ग्रहः। यथा वयं वित्तकोषे धनस्य सङ्ग्रहणं कुर्मः तथैव भाषाकोषे शब्दानां सङ्ग्रहः भवति ।
अनुवादः
(विद्यार्थी ग्रंथालयात विविध पुस्तके बघतात आणि शिक्षिकेला प्रश्न विचारतात.)
नयनः – बाई ! हे वेगळे मोठे कपाट कोणते ? अरे वा ! यात किती वेगवेगळे कोष आहेत !
शिक्षिका – हो, सर्वशास्वांच्या अभ्यासासाठी कोष आवश्यक असतात.
सुमेधा – कोष म्हणजे काय ?
शिक्षिका – कोष म्हणजे संग्रह. ज्याप्रमाणे आपण बँकेमध्ये पैसे साठवतो तसाच भाषाकोषामध्ये शब्दांचा संग्रह असतो.
(Students see various books in the library and ask questions to the teacher.)
Nayan: Teacher, what is this separate huge cupboard? Oh! So many dictionaries/ thesauruses are here!
Teacher: Yes, to study all sciences/scriptures these dictionaries/thesauruses are necessary.
Sumedha: What is a thesaurus?
Teacher: Thesaurus is a collection. Just like, we deposit money in the bank likewise, there is collection of words in the thesaurus.
![]()
परिच्छेद : 2
श्रेया: – क: तस्य ……………… तथैव प्रवर्तते।
श्रेया – क : तस्य उपयोग:?
अध्यापिका – सुयोग्यः प्रश्नः। सम्भाषणे लेखने च भाषाप्रभुत्व-प्राप्त्यर्थ तथैव नैकेषां विषयाणां ज्ञानप्राप्त्यर्थं शब्दसम्पत्तेः सङ्ग्रहणम् अतीव आवश्यकम्। अस्माकं ग्रन्थालये संस्कृतिकोषाः, चरित्रकोषाः, विश्वकोषाः, सुभाषितकोषा: च इत्यादयः बहवः कोषा: वर्तन्ते। तेषु ‘अमरकोषः’ नाम कञ्चन विशेष: कोषः।
स्वप्नीलः – अमरकोषः? ‘अमरकोषः’ इति नाम किमर्थम् ? किं विद्यते अस्मिन् को?
अध्यापिका – एष: संस्कृतशब्दानां सङग्रहग्रन्थः। अमरसिंहः नाम पण्डित: एतस्य रचयिता। अत: कोषस्य नाम अमरकोषः’ इति। परातनकाले यदा छात्रा: अध्ययनाचे गुरुकुलं प्रविशन्ति स्म तदा अध्ययनारम्भे ते अमरकोषं कण्ठस्थं कुर्वन्ति स्म। अधुना अपि तथैव प्रवर्तते।
अनुवादः
श्रेया शिक्षिका – त्याचा उपयोग काय?
शिक्षिका – अगदी योग्य प्रश्न आहे ! बोलताना, लिहिताना भाषेवर आहे. आपल्या ग्रंथालयात संस्कृतिकोष, चरित्रकोष, विश्वकोष, सुभाषित कोष असे अनेक कोष आहेत. त्यापैकी ‘अमरकोष’ नावाचा एक विशेष कोष आहे.
स्वफ्नील – अमरकोष? अमरकोष हे नाव का? या कोषात काय आहे?
शिक्षिका – हा संस्कृतशब्दांचा संग्रह आहे. अमरसिंह नावाचा विद्वान याचा रचनाकार आहे. म्हणून या कोषाचे नाव ‘अमरकोष’ आहे. पूर्वीच्या काळी जेव्हा विद्यार्थी शिक्षणासाठी गुरुकुलात जात असत तेव्हा ते अमरकोष तोंडपाठ करत असत. अजूनही तशी प्रथा आहे.
Shreya: What is its use?
Teacher: Very apt question ! While speaking and so many subjects we need vocabulary, In our library there are so many thesauruses like संस्कृतिकोष, चरित्रकोष, विश्वकोष, सुभाषितकोष etc. Among these Amarakosha is one distinct kind of a thesaurus.
Swapnil: Amarakosha? Why its name is Amarakosha? What is there in this thesaurus?
Teacher: This is collection of Sanskrit words. A scholar named Amarsinha is the composet of this thesaurus. Hence, this thesaurus is named as Amarakosha. In Ancient times, when students used to go to teacher’s home to study, they used to learn by heart Amarakosha. Even this prevails in current time.
![]()
परिच्छेद : 3
आर्या (साश्चर्यम्) किं कोष: ……………. उच्चारणमपि शुद्धं भवति?
आर्या – (साश्चर्यम्) किं कोषः कण्ठस्थीकर्तुं शक्यः? तेन क; लाभ; भवति?
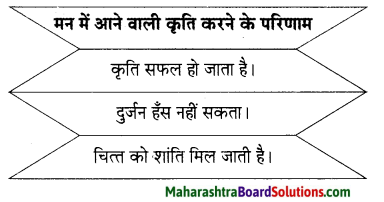
अध्यापिका – अथ किम् । पद्यमयः एषः ग्रन्थः गेयः । अतः श्लोकानां, सुभाषितानां पठनम् इव तस्य कण्ठस्थीकरणम् अतीव सुलभम् । तत्र एकस्य शब्दस्य कृते नैके समानार्थकशब्दाः वर्तन्ते । क्वचित् एकस्य शब्दस्य नैके भिन्ना: अर्थाः अपि वर्तन्ते । अतः तस्य पठनेन अस्माकं शब्दसम्पत्ति: वद्धिं गच्छति । अस्माकं स्मरणशक्ति: धारणाशक्तिः च वर्धेते, उच्चारणमपि शुद्धं भवति ।
अनुवादः
आर्या – (आश्चर्यचकित होऊन) कोष तोंडपाठ करणे शक्य आहे? त्याने काय फायदा होतो?
शिक्षिका – होय तर ! हा ग्रंथ पद्यमय आहे आणि म्हणूनच गेयसुद्धा. त्यामुळे श्लोक. सुभाषित यांच्यासारखेच अमरकोष पाठ करणे सुद्धा सोपे आहे. त्यात एका शब्दासाठी अनेक समानार्थी शब्द आहेत. काही ठिकाणी एका शब्दाचे अनेक भिन्न अर्थसुद्धा दिले आहेत. त्यामुळे अमरकोषाच्या पाठांतराने आपली शब्दसंपत्ती वृद्धिंगत होते. आपली स्मरणशक्ती, धारणाशक्ती वाढते आणि उच्चारणसुद्धा शुद्ध होते.
Arya : (Surprisingly) Is it possible to learn a thesaurus by heart? What’s the benefit of that?
Teacher: Of course! This book is in the verse form, which is fit to sing. Hence, just like other verses, learning this thesaurus is also very easy. There, for a single word, numerous sysnonyms are given. Sometimes even different meaning of a single word are there. Hence, learing by heart this thesaurus increases our vocabulary. Our memory, retention also increases, Pronunciation also gets better. (pure)
![]()
परिच्छेद : 4
नयन: – वयमपि ………………. अवश्यं कर्तव्यमेव।
नयनः – वयमपि अमरकोषं कठस्थं कुर्याम। तस्मिन् कति श्लोकाः सन्ति?
अध्यापिका – उपसार्धसहस्र (1500) श्लोकाः सन्ति। तत्र त्रीणि काण्डानि सन्ति। अत:’त्रिकाण्डकोषः’ इति एतस्य अपरं नाम। तथा ‘नामलिङ्गानुशासनम्’ इति नाम्ना अपि विख्यात: एषः कोषः।
सुमेधा – ‘नामलिङ्गानुशासनम्’ इति शब्दस्य क: अर्थ:?
अध्यापिका – तदपि अस्य ग्रन्थस्य अपरं वैशिष्ट्यम्। अत्र न केवलं समानार्थकशब्दाः अपि तु तेषां लिङ्गनिर्देशः कृतः। तेन भाषायाः आकलनं प्रयोगः च सुकर: भवति।
स्वप्नीलः – आचार्ये, तेन वयं संस्कृतकाव्यानि नाटकानि च विनायासं पठितुं शक्नुमः खलु।
अध्यापिका – निश्चयेन! तर्हि इत:परं सर्वैः अमरकोषस्य पठनम् अवश्यं कर्तव्यमेव।
अनुवादः
नयन – आपणसुद्धा अमरकोष तोंडपाठ करूया. त्यात किती श्लोक आहेत?
शिक्षिका – जवळपास दीड हजार (1500) श्लोक आहेत. त्यात तीन काण्डे विभाग आहेत. म्हणूनच त्याचे दुसरे नाव त्रिकाण्डकोष असे आहे. शिवाय ‘नामलिङ्गानुशासन’ या नावाने सुद्धा हा कोष प्रसिद्ध आहे.
सुमेधा – ‘नामलिङ्गनुशासन’ या शब्दाचा अर्थ काय?
शिक्षिका – तेसुद्धा या ग्रंथाचे दुसरे वैशिष्ट्य आहे. यात फक्त समानार्थी शब्दच नाहीत पण त्यांचा लिंगनिर्देश सुद्धा केला आहे. त्यामुळे भाषा समजणे आणि प्रयोग करणे सोपे होते.
स्वप्नील – बाई! त्यामुळे आपण संस्कृत काव्य आणि नाटक यांचा अगदी सहज करू शकतो.
शिक्षिका – निश्चितच! तर इथूनपुढे आपण सर्वांनी अमरकोषाचा अभ्यास केला पाहिजे.
Nayan: We too shall learn Amarakosha by heart. How many verses are there?
Teacher: There are one thousand and five hundred verses. There are three chapters. Hence its other name is त्रिकाण्डकोष. Apart from this thesaurus is also popularly known as नामलिङ्गानुशासनम्.
Sumedha: What’s the meaning of नामलिङ्गानुशासनम्?
Teacher: That’s the another frature of this thesaurus. It doesn’t have just synonyms for the words but gender specification is also mode. Because of that understanding and use of language gets easy.
Swapnil: Teacher, then we can study the Sanskrit poetry as well as drama without much efforts!
Teacher: Definitely ! so now onwards we all should learn Amarakosha.
![]()
सन्धिविग्रहः
- तथैव- तथा + एव।
- तथैव – तथा + एव ।
- उच्चारणमपि – उच्चारणम् + अपि।
- वयमपि – वयम् + अपि ।
- तदपि – तत् + अपि।
- कर्तव्यमेव – कर्तव्यम् + एव।
![]()
समानार्थकशब्दाः
- आचार्या – अध्यापिका, शिक्षिका।
- भाषा – वाक्, वाणी, भारती।
- उपयोगः – उपयोजनम्।
- पण्डितः – विद्वान्, धीमान्।
- छात्राः – विद्यार्थिनः।
- लाभः – उपयोगः।
- ग्रन्थः – पुस्तकम्।
विरुद्धार्थकशब्दाः
- भिन्ना × समाना।
- विशाला × लघु।
- आवश्यक: × अनावश्यकः।
- सुयोग्य: × अयोग्यः।
- पण्डित: × मूढः ।
- सुलभम् × कठिनम्, दुष्करम्।
- शुद्धम् × अशुद्धम्।
- विख्यातः × कुख्यातः।
- सुकरः × दुष्करः।
![]()
शब्दार्थाः
- ग्रन्थालयः – library – ग्रंथालय, वाचनालय
- आचार्या – teacher – शिक्षिका
- शास्त्रम् – science, scripture – विज्ञान, शास्त्र
- कोषः – dictionary – कोष
- सङ्ग्रह: – collection – साठा / संग्रह
- वित्तकोष – bank – बैंक
- उपयोग: – usage – उपयोग
- सुयोग्य: – apt – बरोबर
- संभाषण – conversation – संभाषण
- भाषाप्रभुत्वम् – command on language – भाषेवरील प्रभुत्व, पकड
- ज्ञानप्राप्त्यर्थम् – to aquire knowledge – ज्ञान मिळवण्यासाठी
- विशेषः – special, distinct – विशेष
- शब्दसंपत्तिः – vocabulary – शब्दसंपत्ती
- पण्डितः – scholar – विद्वान
- रचयिता – composer – रचणारा
- पुरातनकाले – in ancient times – पुरातन काळात
- गुरुकुल – abode of Guru – गुरुकुल
- कण्ठस्थम् – learn by heart – पाठांतर
- पद्यमयः – in verse form – पद्य
- गेयः – fit to sing / melodious – गाण्यायोग्य
- वृध्दिं गच्छति – increases – वाढते
- स्मरणशक्तिः – memory – स्मरणशक्ती
- उच्चारणम् – pronunciation – उच्चार
- धारणाशक्ति: – retention power – धारणक्षमता
- श्लोकाः – verses – श्लोक
- काण्डानि – sections – विभाग, खंड
- लिङ्गनिर्देश: – gender – शब्दाच्या लिंगाविषयी
- specification – सूचना / उल्लेख
- आकलनम् – understanding – आकलन
- सुंकारः – easy – सोपा
- विनायासम् – easily – सोप्या रीतीने सहजपणे
- विख्यातः – famous, known – प्रसिद्ध
9th Standard Sanskrit Anand Digest Pdf
- सुष्ठु गृहीतः चौरः Class 9 Question Answer
- अव्ययमाला Class 9 Question Answer
- किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
- विध्यर्थमाला Class 9 Question Answer
- वीरवनिता विश्पला Class 9 Question Answer
- पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
- सूक्तिसुधा Class 9 Question Answer
- मनसः स्वच्छता Class 9 Question Answer
- अमरकोषः Class 9 Question Answer
- काव्यशास्त्रविनोदः Class 9 Question Answer
- मनोराज्यस्य फलम् Class 9 Question Answer