Class 9

Class 9th Sanskrit Anand Chapter 6 पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Anand Chapter 6 पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 6 Question Answer

Sanskrit Anand Std 9 Digest Chapter 6 पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Textbook Questions and Answers

भाषाभ्यास:

1. उचितं पर्यायं चिनुत।

प्रश्न अ.
पत्रवाहक: किं पठित्वा पत्रं वितरति ?
1. देवनागरीलिपीम्
2. कन्नडलिपीम्
3. आङ्ग्लभाषाम्
4. सङ्केतक्रमाङ्कम्
उत्तरम् :
4. सङ्केतक्रमाङ्कम्

प्रश्न आ.
पिन्कोक्रमाङ्कः अत्र न आवश्यकः।
1. रुग्णालये
2. सद्यस्क-क्रयणे
3. ATM शाखा-अन्वेषणे
4. पुस्तकपठने
उत्तरम् :
4. पुस्तकपठने

प्रश्न इ.
पिनकोड्-प्रणालिः केन समारब्धा ?
1. इन्दिरामहोदयया
2. गान्धीमहोदयेन
3. प्रधानमन्त्रिणा
4. वेलणकरमहोदयेन
उत्तरम् :
4. वेलणकरमहोदयेन

प्रश्न ई.
पिनकोड्क्रमाङ्के कति सङ्ख्या:?
1. 6
2. 4
3. 3
4. 2
उत्तरम् :
1. 6

2. माध्यमा भाषाया लिखत।

प्रश्न 1.
वेलणकरमहोदयस्य कार्यवैशिष्ट्यानि लिखत।
उत्तरम् :
‘पिनकोड् प्रवर्तकः, महान् संस्कृतज्ञः’ या पाठात पत्रव्यवहार बिनचूक होण्यासाठी आवश्यक अशा पिन-कोड् प्रणालीविषयी माहिती मिळते. श्रीराम भिकाजी वेलणकर हे कलकत्ता पत्रविभागाचे संचालक म्हणून कार्यरत होते. त्यांच्याकडे एक सैनिक एक समस्या घेऊन आला.

त्याला आपल्या आई-वडिलांच्या तब्येतीविषयी माहिती कळत नव्हती कारण तो अरुणाचल प्रदेशात राहत होता व त्याचे आई – वडील केरळमध्ये, केरळहून अरुणाचलला पत्र पोहोचण्यास एक महिन्याहून अधिक काळ लागत असे. त्याची समस्या ऐकून वेलणकर महोदयांनी त्याची दखल घेतली व विचार सुरु केला.

त्यांनी सर्वप्रथम पत्रवाटप कार्यातील नेमकी समस्या जाणून घेतली. लिखाणातील संदिग्धतेमुळे समस्या निर्माण होते हे लक्षात घेऊन त्यांनी अंकाधारित पिनकोड पद्धत निर्माण केली. त्यासाठी त्यांनी देशाचे आठ भाग करून त्यांना राज्यनिहाय क्रमांक दिले.

अशाप्रकारे सहा अंकांचा स्थानसंकेतांक असणारी पिनकोड पद्धत त्यांनी भारतात सुरु केली. वेलणकर महोदय गणितज्ञ असल्यामुळे पत्रविभागातील कार्यातसुद्धा त्यांनी त्यांच्या गणित ज्ञानाचा कौशल्याने वापर केला. ते आपल्या कार्याशी प्रामाणिक व कर्तव्यदक्ष होते.

In the lesson ‘पिनकोड् प्रवर्तकः, महान संस्कृतज्ञ’ we get to know about a great mathematician and a dedicated sanskrit scholar Mr. Velankar who invented PIN Code System. Mr. Velankar was director of Kolkata post office.

Once a soldier came to him and told that he was facing a problem in getting information regarding his parents’ health as it used to take more than a month for a letter to reach Kerala from Arunachal Pradesh.

Hearing his problem Mr. Velankar immediately started to think about the solution. He first tried to analyse the reasons behind the problem. He realised that due to bad handwriting, incomplete address etc. such problems arise.

He then divided the country in eight and numbered these divisions based on the states. This number has six-digits. This sixdigit number is PIN code. He was a very efficient post office director and was very devoted to his work.

प्रश्न 2.
वेलणकरमहोदय: केन प्रसङ्गेन पिनकोडनिर्माणे प्रेरित:?
उत्तरम् :
‘पिनकोड् प्रवर्तकः, महान् संस्कृतज्ञः’ या पाठात पिनकोड प्रणाली कशी व कधी अस्तित्वात आली याबद्दल माहिती मिळते. श्रीराम वेलणकर हे कोलकता पोस्टविभागात कार्यरत होते. एके दिवशी अरुणाचलप्रदेशात राहणारा सैनिक दुःखी होऊन त्यांच्याकडे आला. अरुणाचलप्रदेशाहून केरळला पत्र जाण्यासाठी महिन्याभरापेक्षा अधिक वेळ लागत असे. त्यामुळे त्याला त्याच्या आई-वडीलांच्या तब्येतीविषयी कळत नव्हते.

त्या सैनिकाची समस्या ऐकून वेलणकरांनी त्यावर विचार करून त्यावर उपाय शोधण्याचा प्रयत्न सुरु केला व त्यातूनच पिनकोडपद्धती अस्तित्वात आली.

In the lesson ‘पिनकोड् प्रवर्तकः, महान संस्कृतज्ञ’, greatness of Mr. Velankar is described. Mr. Velankar was working in Kolkata post office as director. During his tenure, one soldier came to him. He was sad because he was unable to know about his parent’s health. He was on posting at Arunachat pradesh and his parents were staying in Kerala.

It used to take more than a month for a letter to reach Kerala from Arunachal pradesh. After listening to his problem. Mr. Velankar analysed tue reason behind this problem and eventually invented the PIN-code system.

A genuine problem of a solder drove Mr. Velankar to invent the PIN-code system.

3. एकवाक्येन उत्तरत।

प्रश्न अ.
वेलणकरमहोदयस्य कः प्रियः विषयः ?
उत्तरम् :
वेलणकरमहोदयस्य सङ्गीतं प्रिय: विषयः।

प्रश्न आ.
वेलणकरमहोदयः के वाद्ये वादयति स्म ?
उत्तरम् :
वेलणकरमहोदयः व्हायोलिन तबला च इति वाद्ये वादयति स्म।

प्रश्न इ.
वेलणकरमहोदयेन रचितः सङ्गीतविषयकः ग्रन्थः कः ?
उत्तरम् :
वेलणकरमहोदयः रचितः सङ्गीतविषयक: ग्रन्च: गीतगीर्वाणम्।

प्रश्न ई.
पिनकोड्प्रणालिनिमित्तं वेलणकरमहोदयेन देशस्य कति विभागाः कृताः ?
उत्तरम् :
पिनकोप्रणालिनिमित्तं वेलणकरमहोदयेन देशस्य अष्ट विभागा: कृताः ।

प्रश्न उ.
वेलणकरमहोदयः कस्य विभागस्य निर्देशकः आसीत् ?
उत्तरम् :
वेलणकरमहोदयः डाकतारविभागस्य निर्देशकः आसीत्।

प्रश्न ऊ.
वेलणकरमहोदयस्य अभिमतः साहित्यप्रकार: कः?
उत्तरम् :
वेलणकरमहोदयस्य अभिमतः साहित्यप्रकार: नाट्यलेखनम्।

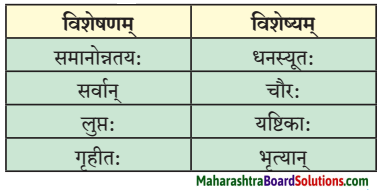
5. विशेषणानि अन्विष्य लिखत।

प्रश्न 1.
अ. ………………. प्रणालिः।
आ. …………… सैनिकः ।
इ. ………………. भाषाः।
ई. ………………. हस्ताक्षरम् ।
ए. ………………. विषयः।
ऐ. ………………. रचनाः।

उत्तरम् :
आ. दुःखितः, केरलं प्रदेशीयः
इ. भिन्ना:
ई. दुबोधम्
ए. प्रियः
ऐ. विविधाः

अन्विष्यत लिखत च।

1. एताः सङ्ख्याः किं निर्दिशन्ति।

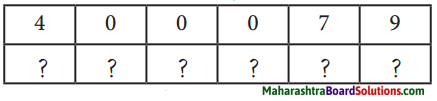
2. विविधदेशेषु अपि पत्रसङ्केताङ्कप्रणालिः वर्तते वा?

Sanskrit Anand Class 9 Textbook Solutions Chapter 6 पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Additional Important Questions and Answers

उचितं पर्यायं चिनुत ।

प्रश्न 1.
…………. प्रधानमन्त्रिमहोदयायै कदा उपहारीकृता एषा पिन्कोड् महत्त्वपूर्णा प्रणालि:?
(अ) ऑगस्ट 1972
(आ) ऑगस्ट 1929
(इ) सप्टेंबर 1972
(ई) ऑगस्ट 1927
उत्तरम्
(अ) ऑगस्ट 1972

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.
1. पत्रालय-अधिकारी संस्कृतपण्डितः गणितज्ञः श्रीराम भिकाजी वेलणकरमहोदयः।
2. वयं पत्रपेटिकायां पत्रं क्षिपामः।
उत्तरम्
1. पत्रालय-अधिकारी क: अस्ति?
2. वयं कुत्र पत्रं क्षिपाम:?

उचितं पर्यायं चित्वा वाक्यं पुनर्लिखत ।

प्रश्न 1.

1. वेलणकरमहोदय: डाकतार-विभागस्य निर्देशकरूपेण ………. आसीत्। (कार्यविभागे / कार्यमग्नः)
2. पत्रस्य प्रवासकाल: ……… आसीत्। (मासः / मासाधिक:)
3. वेलणकरमहोदयेन ……… अङ्कानाम् उपयोगः कृतः? (शास्त्रज्ञेन / गणितज्ञेन)
4. वेलणकरमहोदयस्य प्रियविषयः ……… आसीत्। (सङ्गीतम् / इतिहास:)
5. ……….. ख्याति: नाटकानाम् आसीत्। (सबकुछ श्रीः / सबकुछ श्रीभिः)

उत्तरम् :

1. कार्यमग्नः
2. मासाधिकः
3. गणितज्ञेन
4. सङ्गीतम्
5. सबकुछ श्रीभिः

एकवाक्येन उत्तरत।

प्रश्न 1.
कः कोलकतानगरे कार्यरतः आसीत्?
उत्तरम् :
श्रीराम-भिकाजी-वेलणकरमहोदय : कोलकतानगरे कार्यरतः आसीत्।

प्रश्न 2.
वेलणकरमहोदयस्य कार्यकाले क: आगतः?
उत्तरम् :
वेलणकरमहोदयस्य कार्यकाले केरल-प्रदेशीयः सैनिक: मेलितुम् आगतः।

प्रश्न 3.
वेलणकरमहोदयस्य चिन्तनं किम् आसीत्?
उत्तरम् :
“कश्यं पत्रस्य प्राप्तिकालं न्यूनं कर्तुं शक्नोमि?” इति वेलणकरमहोदयस्य चिन्तनम् आसीत्।

प्रश्न 4.
वेलणकरमहोदयेन केषाम् उपयोगः कृतः?
उत्तरम् :
वेलणकरमहोदयेन अङ्कानाम् उपयोगः कृतः।

प्रश्न 5.
वेलणकरमहोदयः कस्मिन् वादने निपुण: आसीत्?
उत्तरम् :
वेलणकरमहोदयः व्हायोलिनवादने तथा तबलावादनेऽपि निपुणः आसीत्।

प्रश्न 6.
वेलणकरमहोदयः किं रचितवान् ?
उत्तरम् :
वेलणकरमहोदयः गीतगीर्वाणम् इति सङ्गीतविषयकं शास्त्रीयग्रन्थं रचितवान्।

प्रश्न 7.
पत्राणाम् वितरणव्यवस्था कथं शक्या भवति?
उत्तरम् :
पत्राणां वितरणव्यवस्था पिनकोड्प्रणाल्या शक्या भवति।

प्रश्न 8.
एषा महत्त्वपूर्णा प्रणालिः कस्यै उपहारीकृता?
उत्तरम् :
एषा महत्त्वपूर्णा प्रणालि: प्रधानमन्त्रि-इन्दिरा-गान्धी महोदयायै उपहारीकृता।

प्रश्न 9.
पिन्कोक्रमाङ्के कति सङ्ख्या:?
उत्तरम् :
पिन्कोक्रमाङ्के षट् सङ्ख्याः ।

सत्यं वा असत्यं लिखत।

प्रश्न 1.

1. पत्रस्य प्रवासकाल: मासाधिको नासीत्।
2. अधुनापि वयं विनायासं शीघ्र पत्र लभामहे।
3. वेलणकर: महोदयः न अनुशासनप्रियः ।
4. वेलणकरमहोदयः सर्वमेव कर्तुं न समर्थः ।
5. पत्रालयात् निर्दिष्टं स्थानं प्रति पत्राणि गच्छन्ति।
6. पत्रलस्य अधिकारी संस्कृतपण्डितः शास्त्रज्ञः च।

उत्तरम् :

1. असत्यम्
2. सत्यम्
3. असत्यम्
4. असत्यम्
5. सत्यम्
6. असत्यम्

शब्दस्य वर्णविग्रहं कुरुत।

• दुर्बोधम् – द् + उ + र् + ब् + ओ + ध् + अ + म् ।
• विनायासम् – व् + इ + न् + आ + य् + आ + स् + अ + म्।
• क्रमाङ्कनम् – क् + र् + अ + म् + आ + ङ् + क् + अ + न् + अ + म्।
• कर्तुम् – क् + अ + र + त् + उ + म्।
• विद्वद्वरेण्यः – व् + इ + द् + व् + अ + द्  + व् + अ + र + ए + ण् + य् + अः।
• प्राप्नोति – प् + र + आ + प् + न् + ओ + त् + इ।
• महोदयायै – म् + अ + ह् + ओ + द् + अ + य् + आ + य् + ऐ।
• प्रणालिः – प् + र् + अ + ण् + आ + ल् + इ:।

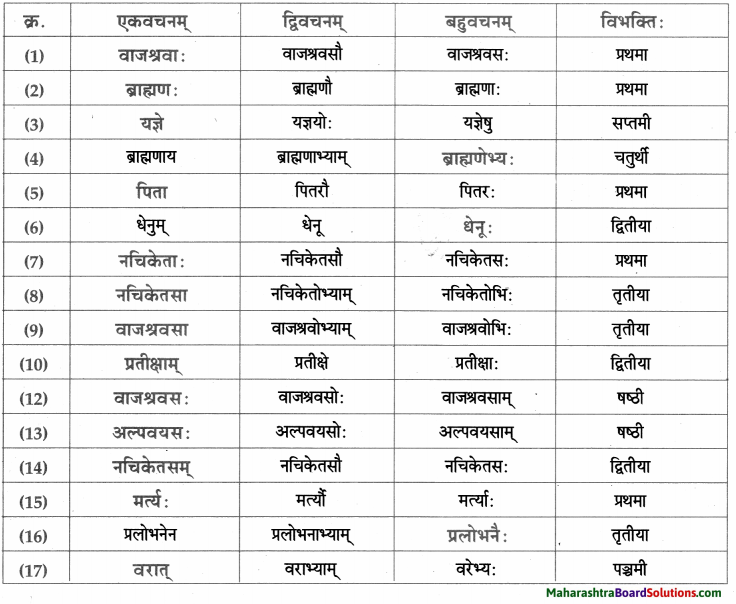
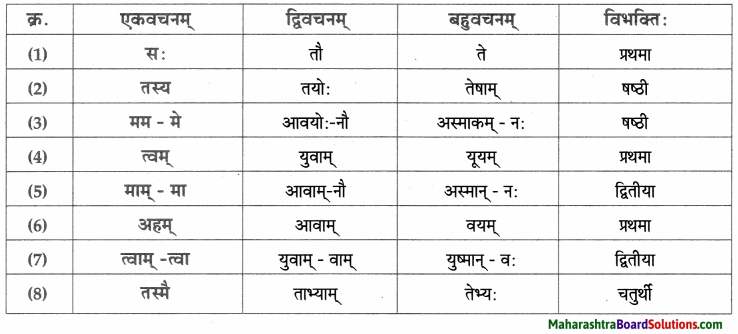
विभक्त्यन्तरूपाणि।

• प्रथमा – मित्राणि, वयम्, एषा, सः, विभागाः, सैनिकः, वयम्, प्रत्यूहाः, नैके, वयम्, रचनाः, गीतानि, कथाः, साहित्यप्रकारः।
• द्वितीया – पत्रालयः, स्थानम्, पत्रम्, नाट्यलेखनम्, सर्वम्, दिग्दर्शनम्।
• तृतीया – केन, निर्देशकरूपेण, तेन, संस्कृतेन, तेन, येन।
• षष्ठी – अस्माकम्, एतस्य, प्रश्नस्य, डाकतारविभागस्य, पत्रस्य, तेषाम् पित्रोः, तस्य, नाटकानाम्।
• सप्तमी – देशे, पत्रपेटिकायाम्, कोलकतानगरे, एकस्मिन, दिने।

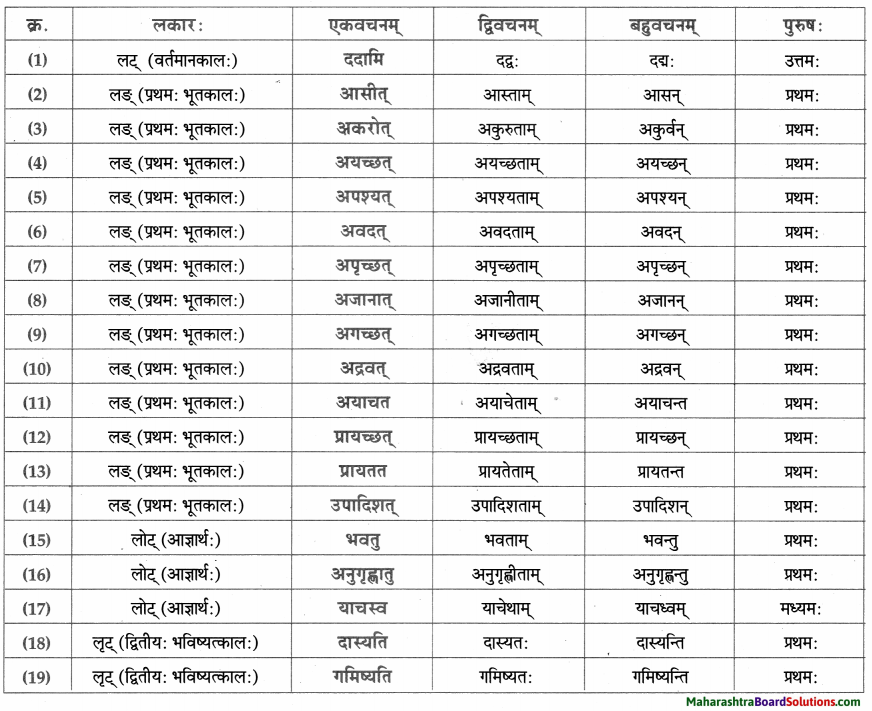
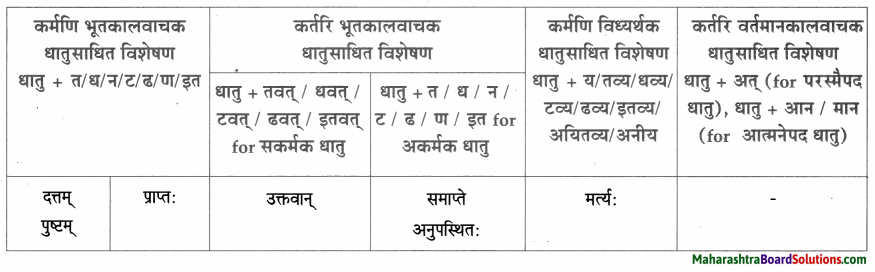
त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।

त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्त अव्यय   थातु + तुम् / धुम् / टुम् / ढुम् / इतुम् / अयितुम्
–	–	मेलितुम्
–	–	ज्ञातुम्
–	–	कर्तुम्

विशेषण – विशेष्य – सम्बन्धः

प्रश्न 1.
……… साहित्यप्रकारः।
उत्तरम् :
अभिमतः

पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Summary in Marathi and English

प्रस्तावना :

आजच्या इंटरनेट युगात आपण पत्रव्यवहार कमी करत असलो तरीसुद्धा आजही भारतामध्ये पत्रविभाग हा महत्वाचा प्रशासकीय विभाग आहे. ह्य विभाग ज्या प्रणालीमुळे गेली अनेक वर्षे अव्याहतपणे चालू आहे ती पिनकोड प्रणाली पत्र-व्यवहाराचा आधार आहे. प्रस्तुत गद्यांश वेलणकर महोदयांनी प्रचलित केलेल्या पिनकोड प्रणाली विषयी माहिती देतो.

वेलणकर महोदय हे श्रेष्ठ गणितज्ञ तसेच संस्कृत विषयाचे गाढे अभ्यासक होते. त्यांनी अनेक संस्कृत नाटके, काव्ये रचली. सङ्गीतसौभद्रम् कालिदासचरितम्, जन्म रामायणस्य, तनयो राजा भवति कथं मे? राज्ञी दुर्गावती, रणश्रीरङ्गम्, कालिन्दी, स्वातन्त्र्यलक्ष्मीः, कौटिलीयार्थनाट्यम् या त्यांच्या काही सुप्रसिद्ध रचना आहेत.

Even though in the era of ‘e-mail’, we are not much acquainted with writing the traditional letter, in India postal service is still one of the most important pillars of the administrative system. PIN-code system is unique feature of this service.

This system was invented by Mr. Velankar, He was a great mathematician and Sanskrit scholar. He has composed several Sanskrit poems, plays etc. Torname a fear सङ्गीतसौभद्रम्,कालिदासचरितम्, जन्म रामायणस्य,तनयो राजा भवति कथं मे? राज्ञी दुर्गावती, रणबीरङ्गम् कालिन्दी, स्वातन्त्र्यलक्ष्मी:, कौटिलीयार्थनाट्यम् are his popular compositions.

उपोद्घात:

• गौरवः – अरे अमेय, कुछ गच्छसि?
• अमेयः – समीपे एव पत्रपेटिका वर्तते। मातुलं प्रति पत्रं प्रेषयितुं तत्र गच्छामि।
• गौरवः – दर्शय पत्रम्। अपि बेङ्गलुरुनगरे निवसति तव मातुल:? तत् तु अतीव दूरे किल? कदा पत्रं विन्देत् स:?
• अमेयः – सामान्यत: त्रीणि दिनानि अपेक्षितानि तदर्थम्।
• गौरवः – जीणि दिनानि एव? एतावत् शीघ्रम्?
• अमेयः – सत्यम्।
• गौरवः – किन्तु सङ्केत: तु देवनागरीलिप्यां लिखितः। कर्णाटके तु कन्नडलिपिः प्रयुज्यते नु? तहि कथं पत्रवाहकः तत् पठितुं शक्नुयात्?
• अमेयः – पश्य एतत्। सङ्केतस्य अन्ते आङ्ग्लभाषया कश्चन क्रमाङ्क: लिखितः अस्ति। जानासि खलु तद्विषये?
• गौरवः – आम, सः तु पिन्कोक्रमाङ्कः । अहं पत्रं न लिखामि किन्तु सद्यस्क – क्रयणसमये (Online Shopping) पिन्कोक्रमाङ्क: अनिवार्यः एव। इतोऽपि च अस्माकं विभागे ATM शाखाः, रुग्णालयाः, विशिष्टसेवा: वा कुत्र सन्ति इति ज्ञातुं पिन्कोक्रमाङ्क: आवश्यक: एव।
• गौरव – अरे अमये, कुठे जात आहेस?
• अमेय – जवळच टपालपेटी आहे. मामाला पत्र पाठविण्यासाठी तिथे जात आहे.
• गौरव  – पत्र दाखव, तुझा मामा बंगळुरूला राहतो का? ते तर खूप दूर आहे ना? त्याला पत्र केव्हा मिळेल?
• अमेय – साधारणपणे त्यासाठी तीन दिवस लागतात.
• गौरव – केवळ तीनच दिवस? एवढ्या लवकर?
• अमेय – खरेच.
• गौरव – परंतु पत्ता तर देवनागरी लिपीमध्ये लिहिलेला आहे. कर्नाटकात तर कन्नड लिपी वापरली जाते ना? तर मग टपालवाहकाला ते वाचणे कसे शक्य होईल?
• अमेय – हे बघ. पत्त्याच्या शेवटी इंग्रजी भाषेत काही क्रमांक लिहिलेले आहेत. त्याविषयी काही माहिती आहे का?
• गौरव – हो, तो तर पिनकोड क्रमांक आहे. मी पत्र लिहीत नाही परंतु ऑनलाईन शॉपिंग करतेवेळी पिनकोड क्रमांक अनिवार्यच आहे. आपल्या विभागातील ATM शाखा, रुग्णालये अथवा विशिष्ट सेवा कुठे आहेत हे जाणून घेण्यासाठी पिनकोड क्रमांक आवश्यकच आहे.
• Gaurav – Ameya, where are you going?
• Ameya – I have a post box near by. I am going there to send the letter to my uncle.
• Gaurav – Show me the letter! Does your uncle live in Bengaluru city? That is really far, isn’t it? When will he get the letter?
• Ameya – Generally two three days are expected for that.
• Gaurav – Just three days? So fast?
• Ameya – Yes, true!
• Gaurav – But the address is written in Devnagari. But in Karnataka, Kannada script is used, right? Then how would the postman be able to read it?
• Ameya – See this. At the end of the address, a certain number is written. Do you know about that?
• Gaurav – Yes, that is the PIN code number. I do not write a letter, but while shopping online, PIN-code number is necessary. Apart from this, to know where ATM branches, hospitals or any special services are, it is essential to know the PIN code number.

परिच्छेद : 1

अयि मित्राणि, ………… वेलणकरमहोदयः।

अयि मित्राणि, भारतसदृशे विशाले देशे सुदूरपान्तेभ्यः अन्यप्रान्तं प्रति प्रेषितानि पत्राणि बिना विलम्बं विना प्रमादं कथं लभ्यन्ते ? वयम् अस्माकं निवासविभागे पत्रपेटिकायां पत्रं क्षिपामः । तत: तत् पत्रालयं प्रति गच्छति। तत: च निर्दिष्टं स्थानं प्रति प्राप्नोति। कथं शक्या भवति एषा वितरणव्यवस्था? “पिन्कोमणालिः’ इत्येव एतस्य प्रश्नस्य उत्तरम्। पिन्कोक्रमाङ्कः नाम पत्रसङ्केतस्य अन्ते लिखिताः षट् सङ्ख्याः । पिनकोड् नाम स्थानसङ्केताङ्कः ।

(PIN – Postal Index Number), ऑगस्ट 1972 – तमे खिस्ताब्दे स्वातन्त्र्यदिनसमारोहे प्रधानमन्त्रि-इन्दिरा-गान्धी-महोदयायै उपहारीकृता एषा महत्वपूर्णा प्रणालिः । केन खलु प्रवर्तिता इयं सङ्केताङ्कप्रणालिः? स: पत्रालय-अधिकारी आसीत् संस्कृतपण्डित: गणितज्ञः श्रीराम-भिकाजी-वेलणकरमहोदयः।

अनुवादः

अहो मित्रहो, भारतासारख्या विशालदेशात दूरवरच्या प्रांतातून इतर प्रांतात पाठवलेली पत्रे उशीर न होता व कोणत्याही चुकीशिवाय कशी बरे मिळतात? निवास विभागातील टपालपेटीत पत्र टाकतो. त्यानंतर ते पत्रालयात जाते. आणि तिथून निर्दिष्ट केलेल्या स्थळी पोहोचते. ही वितरणव्यवस्था कशी शक्य होते?

“पिनकोड्पद्धत’ हेच या प्रश्नाचे उत्तर, पिनकोड क्रमांक म्हनजे पत्रावरील पत्त्याच्या शेवटी लिहिलेल्या सहा संख्या होय, पिनकोड म्हणजे स्थानसंकेतांक (स्थानाचा निर्देश करणारे विशिष्ट अंक) ऑगस्ट 1972 रोजी स्वातंत्र्यदिनाच्या समारंभाला भेट केलेली ही महत्त्वपूर्ण प्रणाली आहे. ही संकेतांक प्रणाली कोणी बरे निर्माण केली? ते पत्रालय-अधिकारी होते. संस्कृतपंडित, गणितज्ञ श्रीराम भिकाजी वेलणकरमहोदय.

O friends, in a huge country like India, how do letters sent from far-flunged region to other places reach without delay and without errors? We drop the letter in a post box, which is there in our residential area. Then it goes to the post office.

And then reaches the place indicated. How does this distribution system become possible? ‘PIN-code system’ is the answer to this question. PIN-code number means the six digits written at the end of the letter’s address. PIN-code means Postal Index Number.

This system handed over to the Prime Minister Indira Gandhi in August 1972 on the occasion of the Independence Day, However, who invented this PIN-code system? That post-office officer was a Sanskrit scholar and mathematician Mr. Shriram Bhikaji Velankar.

परिच्छेद : 2

स: कोलकतानगरे ……………… लभामहे ।

स: कोलकतानगरे डाकतारविभागस्य निर्देशकरूपेण कार्यरतः आसीत् । तस्य कार्यकाले एकस्मिन् दिने कोऽपि दुःखितः केरल-प्रदेशीयः सैनिक: महोदयं मेलितुम् आगतः । सः तस्य पित्रो: स्वास्थ्यविषये किञ्चिदपि ज्ञातुम् असमर्थः । यतः तदा पत्रस्य प्रवासकालः केरलत:अरुणाचलप्रदेशपर्यन्त क्वचित् मासाधिकोऽपि आसीत्।

तेन पं. वेलणकरमहोदयस्य चिन्तनम् आरब्धम्, ‘कथं पत्रस्य प्राप्तिकालं न्यून कर्तुं शक्नोमि ? दुर्बोध हस्ताक्षरं, भिन्नाः प्रान्तीया: भाषा:, अपूर्णः पत्रसङ्केत: इति नैके प्रत्यूह्यः । अत: गणितज्ञेन तेन अङ्कानाम् उपयोगः कृतः । तेन देशस्य अष्ट विभागाः कृताः । तेषां च उपविभाग-जनपदाधारण क्रमाङ्कनं कृतम्। तेन अधुनापि वयं विनायासं शीघ्र पत्रं लभामहे।

अनुवादः

ते कोलकतानगरात डाकतार विभागाचे निर्देशक म्हणून कार्यरत होते. त्यांच्या कार्यकाळात एके दिवशी कोणी एक दुःखी केरळ प्रदेशातील सैनिक (त्या) महोदयांना भेटण्यासाठी आला. तो त्याच्या आई-वडिलांच्या स्वास्थाविषयी अजिबात जाणून घेऊ शकत नव्हता. कारण तेव्हा पत्राचा प्रवासकाळ केरळपासून अरुणाचलप्रदेशापर्यंत एक महिन्याहूनही अधिक होता.

त्यामुळे पं, वेलणकर महोदयांनी विचार करण्यास सुरुवात केली, पत्र पोहचण्याचा काळ कसा बरे कमी करता येईल?’ दुर्बोध (समजण्यासाठी कठीण) हस्ताक्षर, वेगवेगळ्या प्रांतातील वेगवेगळ्या भाषा, अपूर्ण पत्ते अशा अनेक समस्या होत्या.

म्हणून गणितज्ञ असलेल्या त्यांनी अंकांचा उपयोग केला. त्यांनी देशाचे आठ विभाग पाडले. आणि त्यांचे उपविभाग, राज्यांच्या आधाराने क्रमांकन केले. त्यामुळे आत्तासुद्धा आपल्याला विनासायास (सहजपणे) त्वरित पत्र मिळते.

He worked as the director of postal department at Kolkata. During his tenure, a certain grieved soldier who was native of Kerala came to meet Mr. Velankar. He was totally unable to know about his parent’s health Because at that time, travelling time of a letter from Kerala to Arunachal Pradesh was sometimes even more than a month.

Hence, Mr. Velankar started thinking ‘how can I reduce the time for the letter to reach? There are many obstacles like bad handwriting, different regional languages, incomplete address etc. Hence, the digits were used by that mathematician.

He made eight divisions of the country, They were numbered on the basis of subdivision states. Because of that, we still get the letter fast without much effort.

परिच्छेद : 3

अनुशासनप्रियस्य …………… उपकृताः ।

अनुशासनप्रियस्य वेलणकरमहोदयस्य सङ्गीतमपि प्रियः विषयः । स: व्हायोलिनवादने तथा तबलावादनेऽपि अतीव निपुणः। अतः एव सः ‘गीतगीर्वाणम् इति सङ्गीतविषयक शास्त्रीयग्रन्थं संस्कृतेन रचितवान्। कथाः, गीतानि, बालगीतानि, नृत्यनाट्यम् इति बहुविधाः रचना: तेन कृताः तथापि नाट्यलेखन तस्य अभिमत: साहित्यप्रकार: ।

लेखन, दिग्दर्शनं, नाट्यनिर्मितिः, व्यवस्थापन, सङ्गीतसंयोजनम् इति सर्वमेव कर्तुं सः समर्थः अत: “सबकुछ श्रीभिः” इति तस्य नाटकानां ख्यातिः आसीत्। धन्यः सः विद्रद्वरेण्यः येन वयं पिनकोड्प्रणाल्या उपकृताः।

अनुवादः

शिस्तप्रिय वेलणकर महोदयांचा संगीत सुद्धा आवडता विषयोता. ते व्हायोलिनवादनात तसेच तबला वादनातही अतिशय पारंगत होते. म्हणूनच त्यांनी ‘गीतगीर्वाणम्’ हा संगीत विषयक शास्त्रीय ग्रंथ संस्कृतात रचला. कथा, गाणी, बालगीते, नृत्यनाट्य अशा पुष्कळ रचना त्यांनी केल्या. तरी नाट्यलेखन त्यांचा आवडता साहित्य प्रकार होता.

ते लेखन, दिग्दर्शन, नाट्यनिर्मिती, व्यवस्थापन, संगीतसंयोजन हे सर्व काही करु शकत म्हणून “सबकुछ श्रीभिः” अशी त्यांच्या नाटकांची ख्याती होती. धन्य ते श्रेष्ठ विद्वान (वेलणकर महोदय) ज्यांनी आपल्याला पिनकोडप्रणालीने उपकृत केले.

Mr. Velankar who liked discipline was also fond of music He was expert in playing the violin and tabla. Hence, he even composed a book, in Sanskrit “गीतगीर्वाणम्” which is related to music. He has composed many songs, songs for kids, danceplays and many compositions, yet play-writing was his favorite literature genre.

He was able to do writing, direction, production of dramas, management and music composition and hence his plays were famous as ‘सबकुछ श्रीभि:’. He was a great scholar who has indebted us with PINcode system.

सन्धिविग्रहः

• इत्येव – इति + एव ।
• कोऽपि – कः + अपि ।
• किञ्चिदपि – किचित् + अपि ।
• मासाधिकोऽपि – मासाधिक: + अपि ।
• अधुनापि – अधुना + अपि ।
• तबलावादनेऽपि – तबलावादने + अपि ।
• तथापि – तथा + अपि ।
• सर्वमेव – सर्वम् + एव ।

समानार्थकशब्दाः

• मित्राणि – वयस्याः।
• नाम – अभिधानम्।
• देशे – राष्ट्रे।
• ख्रिस्ताब्दे – संवत्सरे।
• रतः – मग्नः ।
• दिने – दिवसे।
• जनकः – पिता।
• समयम् – कालः।
• अधुना – इदानीम्।
• नुिपणः – पारङ्गतः।
• ग्रन्थः – पुस्तकम्।
• ख्यातिः – प्रसिद्धिः।

विरुद्धार्थकशब्दाः

• मित्राणि × रिपवः।
• पण्डितः × मूढः।
• अन्ते × आरम्भे।
• विशाल: × लघुः।
• शक्या × अशक्या।
• दुःखितः × आनन्दितः।
• असमर्थः × समर्थः।
• न्यूनम् × बहु, दीर्घम्।
• उपयोग: × निरुपयोगः।
• शीघ्रम् × शनैः शनैः।
• प्रियः × अप्रियः।
• समर्थम् × असमर्थम्।

शब्दार्थाः

1. विलम्ब: – delay – उशीर
2. प्रमादः – mistake – चूक
3. पत्रपेटिकायाम् – in letter box – पत्रपेटीत
4. क्षिपाम: – we drop – टाकतो
5. उपहारीकृता – handed over to – सुपूर्द करणे
6. प्रणालिः – system – प्रणाली, पद्धती
7. गणितज्ञः – mathematician – गणितज्ञ
8. कार्यरतः – engrossed in work – कार्यरत
9. पित्रोः – parents – आई-वडिलांचे
10. असमर्थः – unable – असमर्थ
11. दुर्बोधम् – difficult to understand – अवघड
12. विनायास – easily, without effort – सहजपणे
13. निपुणः – expert – निपुण
14. अभिमतः – favourite – आवडता
15. ख्यातिः – fame, popularity – प्रसिद्धी
16. विद्वद्वरेण्यः – great scholar – श्रेष्ठ विद्वान
17. उपकृताः – blessed, indebted – उपकृत
18. रचितवान् – composed – रचले

9th Standard Sanskrit Anand Digest Pdf 

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer

Class 9th Sanskrit Anand Chapter 1 सुष्ठु गृहीतः चौरः Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Anand Chapter 1 सुष्ठु गृहीतः चौरः Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 1 Question Answer

Sanskrit Anand Std 9 Digest Chapter 1 सुष्ठु गृहीतः चौरः Textbook Questions and Answers

भाषाभ्यास:

1. उचितं पर्यायं चिनुत ।

प्रश्न 1.
कस्य धनस्यूत: लुप्त: ?
(अ) देवदत्तस्य
(आ) वीरबलस्य
(इ) भृत्यस्य
(ई) नृपस्य
उत्तरम् :
(अ) देवदत्तस्य

प्रश्न 2.
गृहे कति भृत्याः आसन् ?
(अ) पञ्च
(आ) सप्त
(इ) षड्
(ई) एक:
उत्तरम् :
(इ) षड्

प्रश्न 3.
वीरबलः कस्य मित्रम् ?
(अ) भृत्यस्य
(आ) धनिकस्य
(इ) यष्टिकायाः
(ई) चौरस्य
उत्तरम् :
(आ) धनिकस्य

प्रश्न 4.
‘श्व: मम चौर्यं प्रकटितं भवेत्।’ इति चिन्ता कस्य चित्ते जायते?
(अ) दासस्य
(आ) वीरबलस्य
(इ) धनिकस्य
(ई) नृपस्य
उत्तरम् :
(अ) दासस्य

2. कः कं वदति ?

प्रश्न 1.
“पश्यन्तु एता: मायायष्टिकाः।”
उत्तरम् :
वीरबल: सेवकान् वदति।

प्रश्न 2.
“मित्र, अद्य सायङ्काले तव सर्वान् भृत्यान् मम गृहं प्रेषय।”
उत्तरम् :
वीरबल: देवदत्तं वदति।

3. माध्यमभाषया उत्तरं लिखत । वीरबलेन चौरः कथं गृहीतः ?

प्रश्न 1.
माध्यमभाषया उत्तरं लिखत । वीरबलेन चौरः कथं गृहीतः ?
उत्तरम् :
बिरबल हा सम्राट अकबराचा अतिशय चतुर आणि हजरजबाबी मंत्री होता. त्याच्या चातुर्याच्या अनेक कथा प्रसिद्ध आहेत. त्यांपैकीच एक म्हणजे ‘सुगृहीत: चौर:’. बिरबलाने स्वत:च्या चातुर्यान कसा चोर पकडला, याबाबत ही गोष्ट आहे.

देवदत्त नावाच्या एका श्रीमंत माणसाची पैशाची पिशवी चोरीला गेल्यावर तो आपल्या सेवकांवर संशय घेतो. आपल्या सहा सेवकांपैकीच कोणी एक चोर असणार, याची त्याला खात्री असते. चोराला पकडण्यासाठी तो आपल्या मित्राकडे म्हणजे बिरबलाकडे मदत मागतो. त्यानुसार एके संध्याकाळी बिरबल त्या सहा नोकरांना आपल्या घरी बोलावून समान उंचीची एकेक काठी देतो.

त्या काठ्या जादूच्या असून तुमच्यापैकी जो कोणी चोर असेल, त्याची काठी अंगठ्याएवढी लांब होईल, अशी भीतीही दाखवतो. आपापल्या काठ्या घेऊन दुसऱ्या दिवशी सकाळी यावे असे तो सेवकांना सांगतो. सहापैकी पाच चोर रात्री निश्चिंतपणे झोपतात. मात्र खऱ्या चोराच्या मनात भीती निर्माण होते.

आपली काठी अंगठ्याएवढी लांब होऊन आपली चोरी उघडकीस येण्यापेक्षा अगोदरच काठी कापलेली बरी, असा विचार करून तो काठी कापतो. दुसऱ्या दिवशी बिरबल एकच आखूड काठी बघून चोराला ओळखतो आणि त्याला पकडतो. खजील झालेला चोर क्षमा मागतो आणि पैशाची पिशवी परत देतो.

माणसाची मानसिकता कशी असते हे बिरबल जाणत होता. चोराच्या मनात चांदणे याचा अर्थ जाणून बिरबलाने सर्व साधले. खरा चोर स्वत:ची चोरी उघडकीस येणार नाही यासाठी नक्कीच प्रयत्न करेल. मनुष्याची हीच मानसिकता लक्षात घेऊन बिरबलाने युक्ती केली. अशा प्रकारे केवळ आपल्या युक्तीच्या जोरावर बिरबल चोराला पकडण्यात यशस्वी होतो.

Birbal was a very clever and witty minister in Emperor Akbar’s court. There are several famous accounts of his cleverness. One among them is the story “The thief is well – caught’ – ‘सु गृहीत: चौर:’ This story revolves around Birbal’s cleverness correctly identifying the thief.

When Devdutta realised his money bag was missing he suspected that one of the six servants would be the culprit. To catch the thief, he took Birbal’s help.

Birbal used his understanding of human psychology that the real thief would always do something to conceal his theft. Knowing this Birbal gave the servants a stick each of the same length saying that those sticks were magical and only the thief’s stick would grow longer the next day. The real thief fell for this ploy and cut his stick so no one would know that he was the thief.

However, the next day the thief’s stick was shorter than the others’. Birbal easily identified the thief due to his short stick. Thus, Birbal used his cleverness and understanding of human behavior to catch the thief.

4. स्तम्भमेलनं कुरुत।

प्रश्न 1.

उत्तरम् :

विशेषणम्	विशेष्यम्
समानोन्नतयः	यष्टिकाः
सर्वान्	भूत्यान्
लुप्तः	धनस्यूतः
गृहीत:	चौरः

5. विरुद्धार्थकशब्दानां युग्मं चिनुत लिखत च।

प्रश्न 1.

उत्तरम् :

• पूर्वम् × पश्चात्
• गताः × आगताः
• दीर्घा × हस्वा
• जागृतः × सुप्तः
• भृत्यः × स्वामी
• धनिकः × दरिद्रः

6. पाठात् समानार्थक शब्दं चित्वा रेखाचित्रं पूरयत ।

प्रश्न 1.

उत्तरम् :

• धनिकः
• चौरः
• सुप्तः
• भृत्य:

Sanskrit Anand Class 9 Textbook Solutions Chapter 1 सुष्ठु गृहीतः चौरः Additional Important Questions and Answers

एकवाक्यन उत्तरत।

प्रश्न 1.
क: धनिकः आसीत्?
उत्तरम् :
देवदत्त : धनिकः आसीत्।

प्रश्न 2.
सेवका: कदा वीरबलस्य गृहम् अगच्छन् ?
उत्तरम् :
सेवका: सायकाले वीरबलस्य गृहम् अगच्छन्।

प्रश्न 3.
वीरबलेन सर्वेषां कृते का: आनीता:?
उत्तरम् :
वीरबलेन सर्वेषां कृते समानोन्नतय: मायायष्टिका: आनीताः ।

प्रश्न 4.
चौरस्य यष्टिका कीदृशी भविष्यति ?
उत्तरम् :
चौरस्य यष्टिका अगुलिमात्र दीर्घा भविष्यति।

प्रश्न 5.
रात्रौ सर्वे भृत्याः किम् अकुर्वन् ।
उत्तरम् :
रात्री सर्वे भृत्याः सुखेन निद्राम् अकुर्वन् ।

प्रश्न 6.
किं दृष्ट्वा वीरबालेन चौर: ज्ञात:?
उत्तरम्
लघुष्टिकां दृष्ट्वा वीरबालेन चौर: ज्ञातः।

प्रश्न 7.
अपराधी भृत्यः किम् अकरोत्?
उत्तरम्
अपराधी भृत्यः अपराधम् अङ्गीकृतवान् धनस्यूतं च प्रत्यर्पितवान्।

प्रश्न 8.
अयं गद्यांश: कस्मात् पाठात् उद्धृतः?
उत्तरम्
अयं गटांशः ‘सुष्ठु गृहीत : चौर: पाठात् उद्धृतः।

सत्यं वा असत्यं लिखत।

प्रश्न 1.

1. देवदत्तः निर्धनः आसीत्।
2. देवदत्तस्य धनस्यूत: चोरितः।
3. देवदत्तस्य गृहे षड्भृत्येषु एक: चौरः ।
4. वीरबल: देवदत्तं साहाय्यम् अयाचत।
5. यष्टिकाः भिन्नोन्नतयः आसन्।
6. सेवकै: यष्टिका: न स्वीकृताः।
7. चौरस्य यष्टिका पूर्वमेव दीर्घा।

उत्तरम् :

1. असत्यम्
2. सत्यम्
3. सत्यम्
4. असत्यम्
5. असत्यम्
6. असत्यम्
7. असत्यम्

प्रश्न 2.

1. षद् सेवका: सुखेन निद्याम् अकुर्वन्।
2. चौरेण यष्किा कीयत्वा हस्वा कृता।
3. सर्वेषां राष्टिका: दीर्घा: भूताः।
4. लघुष्टिकाया: साहाय्येन चौर: गृहीतः।
5. चौर क्षमा प्राथ्यं धनस्यूतं प्रत्यर्पितवान्।

उत्तरम :

1. असत्यम्
2. सत्यम्
3. असत्यम्
4. सत्यम्
5. सत्यम्

उचितं कारणं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
देवदत्तः वीरबलं साहाय्यम् अयाचत यत: ……..
a. देवदत्त: आरक्षक: आसीत्।
b. चतुर: वीरबल: देवदत्तस्य मित्रम् आसीत्।
उत्तरम् :
देवदत्त: वीरबलं साहाय्यम् अयाचत यत: चतुर: बीरबल: देवदत्तस्य मित्रम् आसीत्।

प्रश्न 2.
सर्वे सेवका: वीरबलस्य गृहम् अगच्छन् यतः …….
a. वीरबलेन भोजनसमारोहः आयोजितः ।
b. वीरबल: तान् परीक्षितुम् ऐच्छत्।
उत्तरम् :
सर्वे सेवका: वीरबलस्य गृहम् अगच्छन् यतः वीरबल: तान् परीक्षितुम् ऐच्छत्।

प्रश्न 3.
वीरबल: सर्वेभ्यः सेवकेभ्य: यष्टिकाम् अयच्छत् यतः ………..
a. सः चौरं ग्रहीतुम् ऐच्छत्।
b. सेवका: यष्टिकाम् अयाचन्त।
उत्तरम् :
वीरबल:सर्वेभ्य:सेवकेभ्य: यष्टिकाम् अयच्छत् यत: स: चौर ग्रहीतुम् ऐच्छत्।

प्रश्न 4.
एक सेवक: निद्रा न अकरोत् यतः
a. सः अस्वस्थः आसीत्।
b. ‘मम चौर्य प्रकटितं भवेत्’ इति विचारेण स: भीतः।
उत्तरम् :
एक: सेवक: निटांन अकरोत् यतः मम चौर्व प्रकटितं भवेत्’ इति विचारेण स: भीतः।

प्रश्न 5.
चौरेण यतिका लघूकता यतः …………।
a. स: चौयं प्रकटयितुं न ऐच्छत्।
b. तस्य यष्टिका पूर्वमेव दीर्घा आसीत्।
उत्तरम् :
चौरेण यष्टिका लाकृता यत:, स; चौर्य प्रकटयितुं न ऐच्छन्।

प्रश्न 6.
वीरबलेन चौर: सम्यक् ज्ञात: बत्तः …….
a. चौरस्य यष्टिका दोषों अभवत्।
b. चौरस्य यटिका हस्वा अभवत्।
उत्तरम् :
बीरबलेन चौर: सम्यक् ज्ञात: यत: चौरस्य यष्टिका हस्वा अभवत्।

कः कं वदति।

प्रश्न 1.
प्रात: मम चौर्य प्रकटितं भवेत्।
उत्तरम्
चौर:/सेवक: आत्मानं वदति।

शब्दस्य वर्णविग्रहं कुरुत।

• देवदत्तः – द् + ए + व + अ + अ + त् + त् + अः।
• धनस्यूतः – ध् + अ + न् + अ + स् + य् + ऊ + त् + अः।
• सायङ्काले – स् + आ + य् + अ + ङ् + क् + आ + ल् +ए।
• भृत्यान् – भ + ऋ + त् + य् + आ + न्।
• यष्टिकाः – य् + अ + ष्  + ट् + इ + क् + आः।
• एकस्मात् – ए + क् + अ + स् + म् + आ + त्।
• ऋते – ऋ + त् + ए।
• अङ्गुलिमात्रम् – अ+ ङ् + ग् + उ + ल् + इ + म् + आ + त् + र् + अ + म्।
• कर्तयामि – क् + अ + र + त् + अ + य् + आ + म् + इ।
• चिन्तयित्वा – च + इ + न् + त् + अ + य + इ + त् + व् + आ।
• अन्येयुः – अ + न् + य् + ए + द् + य + उः।
• ज्ञात: – ज् + ञ् + आ + त् + अः।

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.

1. देवदत्तः धनिकः आसीत्।
2. देवदत्तस्य गृहे षट् भृत्याः आसन्।
3. चौर ग्रहीतुं देवदत्त: वीरबल साहाय्यम् अयाचत।
4. सर्वे सेवका: सायङ्काले वीरबलस्य गृहम् आगताः।
5. वीरबलेन सर्वेषां कृते समानोन्नतय: यष्टिका: आनीताः।

उत्तरम् :

1. कः धनिकः आसीत्?
2. देवदत्तस्य गृहे कति भृत्या: आसन्?
3. चौरं ग्रहीतुं देवदत्तः कं साहाय्यम् अयाचत?
4. सर्वे सेवका: सायडकाले कुत्र आगताः?
5. वीरबलेन सर्वेषां कृते कीदृश्य : यष्टिका: आनीताः?

प्रश्न 2.
रात्री सर्वे भृत्या: सुखेन निद्राम् अकुर्वन्।
उत्तरम् :
कदा सर्वे भृत्या: सुखेन निद्राम् अकुर्वन् ।

प्रश्न 3.
लघुष्टिकां दृष्ट्वा वीरबलेन चौर: सम्यक् ज्ञातः ।
उत्तरम् :
लघुष्टिकां दृष्ट्वा केन चौर: सम्यक् ज्ञात:।

प्रश्न 4.
भृत्य अपराधम् अङ्गीकृतवान् ।
उत्तरम् :
मृत्यः किम् अङ्गीकृतवान्?

विशेषण-विशेष्य-सम्बन्धः।

विशेषणम्	विशेष्यम्
धनिकः	देवदत्तः
षड्	भृत्याः
आगताः	सेवकाः
आनीताः	यष्टिका:
चोरितः	धनस्यूतः
दीर्घा	यष्टिका
प्रकटितम्	चौर्यम्
ज्ञातः	चौरः
अपराधी	भृत्यः

त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।

त्वान्त अव्यय धातु + त्वा / ध्वा ट्वा / ड्वा / अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्त अव्यय धातु + तुम् / धुम् / दुम् / डुम् / इतुम् / अयितुम्
–	स्वीकृत्य	ग्रहीतुम्
कृत्वा	–	–
चिन्तयित्वा	–	–
दृष्ट्वा	–	–
पतित्वा	–	–

विभक्त्यन्तरूपाणि।

• प्रथमा – देवदत्तः, धनिकः, धनस्यूतः, भृत्याः, षड, चौरः, वीरबलः, सेवकाः, यष्टिकाः, सः, एताः, मायायष्टिकाः, दीर्घा, सर्वे, भृत्याः, अहम, चौरः, भृत्यः, गृहीतः।
• द्वितीया – चौरम्, वीरबलम्, साहाय्यम्, सर्वान, भृत्यान, गृहम, सेवकान्, एकाम, यष्टिकाम्, निद्राम, चौर्यम्, यष्टिकाम्, लघुष्टिकाम, अपराधम्, धनस्यूतम्
• तृतीया – सुखेन, वीरबलेन, सर्वैः, वीरबलेन, येन, केन।
• पञ्चमी – एकस्मात्
• षष्ठी – मम, वीरबलस्य, स्वस्य, तस्य, वीरबलस्य, सर्वेषाम्, मम, देवदत्तस्य।
• सप्तमी – रात्री, पादयोः, तासु, प्रभाते, गृहे।

पाठात् समानार्थक शब्दं चित्वा रेखाचित्रं पूरयत।

प्रश्न 1.

उत्तरम् :
1. गृहम्
2. दिनः

समानार्थकशब्दं योजयित्वा वाक्यं पुनर्लिखत।

निद्रा – निद्रा बालकं पीडयति। स्वापः / सुप्तिः / स्वपा / शयनं बालकं पीडयति।
दिनः – अद्य रम्य: दिनः । अद्य रम्य: दिवस: / अहः।.

व्याकरणम्

नाम – तालिका।

नाम	सर्वनाम	क्रियापदम्	विशेषणम्
देवदत्तः	कः	कर्तयामि	धनिकः
धनिकः	सः	अयाचत	लुप्तः
धनस्यूतः	तव	अवदत्	षड्
गृहे	येन	अचिन्तयत्	सर्वान्
चौरम्	केन	प्रेषय	आगताः
भृत्यान्	मम	पश्यतु	समानोन्नतयः
मित्र	अहम्	स्यात्	आनीताः
वीरबलस्य	तेषु	भविष्यति	चोरितः
यष्टिका:	तेषाम्	आसन्	दीर्घा
सेवकान्	सर्वान्	अकुर्वन्	गृहीतः
रात्रौ	सर्वेषाम्	–	प्रकटितम्
यष्टिकाम्	एता:	–	ज्ञात:
पादयोः	सर्वैः	–	गृहीत:
धनस्यूतम्	सर्वै	–	अपराधी

समासाः।

समस्तपदम्	अर्थ:	समासविग्रहः	समासनाम
धनस्यूतः	bag of money	धनस्य स्यूतः।	षष्ठी तत्पुरुष समास

सुष्ठु गृहीतः चौरः Summary in Marathi and English

प्रस्तावना :

मूल्य रुजविण्यासाठी, कौशल्यविकास तसेच मनोरंजनासाठी कथांचा परिणामकारकपणे वापर फार पूर्वीपासून होत आहे. प्रस्तुत कथेत एका चोराला पकडण्यासाठी बिरबलाने योजलेल्या युक्तीतून फक्त त्याचे चातुर्यच नव्हे तर त्याला असलेले मानवी स्वभावाचे ज्ञानही दिसून येते.

परिस्थिती अनुकूल असेपर्यंत आपल्या चुका लपवण्याचा मानवी स्वभाव असतो. या कथेतील चोराला पकडण्यासाठी बिरबल देवदत्ताच्या सहा सेवकांना काळ्या देतो आणि फक्त चोराचीच काठी बोटभर लांब होईल, अशी भीती घालतो. आपली चोरी लपविण्यासाठी खरा चोर अगोदरच काठी कापून टाकतो आणि दुसऱ्या दिवशी आखूड काठी बघून बिरबल चोराला ओळखतो.

Stories have been the medium of teaching values, skills and providing entertainment since ages. This story revolves around how Birbal used not just his cleverness, but also his knowledge of human behaviour to identify the thief.

A man always tries to hide his mistake or wrongdoing and therefore will not be at exse till he finds a way to take care of it. Birbal gave Deudutta’s six servants & stick each and said that only the thief’s stick would become longer the next day.

The real thief cut his stick so that he would not be caught. But Birbal immediately identified the thief, the one whose stick was shorter than the rest.

परिच्छेद : 1

देवदत्त: …………….. भविष्यति।

देवदत्त: नाम कोऽपि धनिकः आसीत्। एकदा तस्य धनस्यूतः लुप्तः । तस्य गृहे षड् भृत्याः आसन्। तेषु एव एक: चौरः स्यात्, इति तस्य मतम्। चौर ग्रहीतुं सः वीरबलं साहाय्यम् अयाचत । वीरबल: अवदत, “मित्र ! अद्य सायङ्काले तव सर्वान् भृत्यान् मम गृहं प्रेषय” इति। यथानिश्चितं सर्वे सेवका; वीरबलस्य गृहम् आगताः। वीरबलेन पूर्वमेव सर्वेषां कृते समानोन्नतय: यष्टिका: आनीताः । सः सेवकान् अवदत, “भोः पश्यन्तु, एताः मायायष्टिका: । तासु एका यष्टिकां स्वीकृत्य सर्वे: देवदत्तस्य गृहं गन्तव्यं , श्वः प्रभाते पुनरागन्तव्यम्। येन केनापि धनस्यूत: चोरित: स्यात् तस्य यष्टिका अङ्गुलिमात्रं दीर्घा भविष्यति।”

अनुवाद:

देवदत्त नावाचा कोणी एक श्रीमंत माणूस होता. एकदा त्याची पैशांची पिशवी (थैली) हरवली. त्यांच्या घरी सहा सेवक होते. त्यांच्यापैकीच कोणी एक चोर असेल, असे त्याचे मत होते.

चोराला पकडण्यासाठी त्याने विरबलाकडे मदत मागितली. बिरबल म्हणाला, “मित्रा, आज संध्याकाळी तुझ्या सर्व सेवकांना माझ्या घरी पाठव.” ठरल्याप्रमाणे सगळे सेवक बिरबलाच्या घरी आले. बिरबलाने अगोदरच सगळ्यांसाठी समान उंचीच्या काठ्या आणल्या होत्या.

तो सेवकांना म्हणाला, “हे बघा, या जादुई काठ्या आहेत. त्यातील एक काठी घेऊन सर्वांनी देवदत्ताच्या घरी जावे, उद्या सकाळी परत यावे. ज्या कोणाकडून पिशवी चोरली गेली असेल त्याची काठी बोटभर लांब होईल.”

There was a certain rich man name Devadutta. Once his money bag was missing. There were six servants in his house. It was his opinion that one among them would surely be the thief. He sought Birbal’s help in order to catch the thief. Birbal said, “O friend, send all your servants to my house today, in the evening.

As decided, all the servants came to Birbal’s house. Birbal had brought sticks of the same length for all of them in advance. He said to the servants, “O see, these are magical sticks.

Taking a stick among those, you all go back to Devadutta’s house and come again tomorrow morning. The stick of the one who has stolen the money bag will become longer by a finger.

परिच्छेद : 2

रात्री ………… प्रत्यर्पितवान्।

रात्री सर्वे भृत्या: सुखेन निद्राम् अकुर्वन् ऋते एकस्मात् स: अचिन्तयत्, “व: प्रात: मम चौर्य प्रकटितं भवेत्। अत: अहम् अधुना एव मम यष्टिकाम् अङ्गलिमात्रं कर्तयामि।” इति चिन्तयित्वा तथा कृत्वा सः सुखेन सुप्तः। अन्येाः लघुष्टिकां दृष्ट्वैव वीरवलेन चौर: सम्यक् ज्ञात: गृहीत: च। अपराधी भृत्य: वीरबलस्य पादयोः पतित्वा स्वस्य अपराधम् अङ्गीकृतवान् धनस्यूतं च प्रत्यर्पितवान्।

अनुवादः

रात्री एकजण वगळता सगळे सेवक शांतपणे झोपले. त्याने विचार केला, “उद्या सकाळी माझी चोरी उघड होईल (प्रकाशात येईल). म्हणून मी आताच माझी काठी बोटभर कापतो.”

असा विचार करून ठरवल्याप्रमाणे करून तो शांतपणे झोपला. दुसऱ्या दिवशी आखूड काठी पाहून बिरबलाने चोराला उत्तमरीत्या (व्यवस्थित) ओळखले आणि पकडले. अपराधी सेवकाने बिरबलाच्या पाया पडून स्वतःचा अपराध मान्य केला आणि पैशांची (थैली) परत दिली.

At night except one, all the servants slept peacefully. He thought, “Tomorrow morning my theft will be revealed. So I shall cut my stick by a finger length now itself.” Thinking that, he did so and slept peacefully.

The next day just by looking at the short stick Birbal correctly recognised and caught the thief. The guilty servant fell at Birbal’s feet and accepted his mistake and returned the money bag.

सन्धिविग्रहः

• कोऽपि – कः + अपि।
• पूर्वमेव – पूर्वम् + एव।
• पुनरागन्तव्यम् – पुन: + आगन्तव्यम्।
• केनापि – केन + अपि।
• दृष्ट्वैव – दृष्ट्वा + एव।

समानार्थकशब्दाः

1. धनिकः – धनी, धनाक्यः, धनवान, धनसमपत्रः, सधन:,
   इभ्यः, श्रीमान्।
2. भृत्यः – सेवकः, परिचारकः, दासः, दासेयः, किङ्करः,
3. चौरः – स्तेनः, तस्करः, मोषकः, पाटच्चरः।
4. मित्रम् – सखा, वयस्यः , सुहृद्।
5. गृहम् – गेहम्, सदनम्, निकेतनम्, वेश्म, आलयः।
6. अवदत् – अभणत्, अकथयत्।
7. प्रभाते – प्रात:काले।
8. सुष्टु – सम्यक्तया।
9. स्वीकृत्य – गृहीत्वा।
10. भः – अन्येयुः, अपरेयुः।
11. रात्रौ – निशायाम्।
12. निद्रा – स्वापः, स्वपा, शयनम् सुप्तिः।
13. अधुना – साम्पतम्, इदानीम्।
14. दृष्ट्वा – वीक्ष्य, विलोक्य, अवलोक्य।
15. ऋते – विना।
16. सुप्तः – निद्रितः, निद्राधीनः।
17. चौर्यम् – लण्ठनम्।

विरुद्धार्थकशब्दाः

1. धनिकः × दरिद्रः, दीनः।
2. दीर्घा × न्हस्वा
3. आगताः × गताः, निर्गताः।
4. भृत्यः × स्वामी।
5. पूर्वम् × पश्चात्।
6. स्वीकृत्य × त्यक्त्वा।
7. श्वः × अद्य, ह्यः।
8. मित्रम् × शत्रुः।
9. सायङ्काले × प्रात:काले।
10. रात्री × प्रभाते।
11. सुखेन × चिन्तया, सचिन्तम्।
12. निद्रा × जागृतिः।
13. सुप्त: × जागृतः।

शब्दार्थाः

1. धनिक – rich man – श्रीमंत
2. धनस्यूतः – money bag – पैशांची पिशवी(थैली)
3. भृत्याः – servants – सेवक
4. स्यात् – would be – असेल
5. ग्रहीतुम् – to catch – पकडण्यासाठी
6. अयाचत – sought/asked – याचना केली
7. अद्य – today – आज
8. प्रेषय – send – तू पाठव
9. गन्तव्यम – should – जावे
10. यथानिश्चितम् – as decided – ठरवल्याप्रमाणे
11. आगताः – came – आले
12. पूर्वमेव – in advance – अगोदरच
13. समानोन्नतयः – same length – समान उंचीच्या (मापाच्या)
14. यष्टिकाः – sticks – काठ्या
15. आनीताः – brought – आणल्या
16. मायायष्टिकाः – magical sticks – जादुई काठ्या
17. पुनरागन्तव्यम् – come again – पुन: यावे
18. स्वीकृत्य – taking – स्वीकार करून, घेऊन
19. अङ्गुलिमात्रम् – by a finger – बोटभर
20. श्चः – tomorrow – उद्या
21. चोरितः – stolen – चोरलेला
22. दीर्घा – long – लांब
23. भविष्यति – will become – होईल
24. ऋते – except – शिवाय
25. चौर्यम् – theft – चोरी
26. प्रकटितं भवेत् – will be revealed – उघड होईल
27. कर्तयामि – I shall cut – मी कापतो
28. चिन्तयित्वा – thinking – विचार करून
29. सुप्त: – slept – झोपला
30. अन्येयुः – the next day – दुसऱ्या दिवशी
31. दृष्ट्वा – looking – पाहून
32. सम्यक् – correctly – उत्तमरीत्या
33. ज्ञातः – recognised – ओळखला गेलेला
34. गृहीतः – caught – पकडला गेलेला
35. पतित्वा – falling – पडून
36. अङ्गीकृतवान् – accepted – मान्य केला / कबूल केला
37. प्रत्यर्पितवान् – returned – परत दिला

9th Standard Sanskrit Anand Digest Pdf 

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer

Class 9th Sanskrit Aamod Chapter 16 स्वागतं तपोधनाया: Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 16 स्वागतं तपोधनाया: Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 16 Question Answer

Sanskrit Aamod Std 9 Digest Chapter 16 स्वागतं तपोधनाया: Textbook Questions and Answers

भाषाभ्यास:

1. एकवाक्येन उत्तरत।

प्रश्न 1.
आत्रेयी वाल्मीकिमहर्षेः आश्रमात् दण्डकारण्यं किमर्थम् आगता?
उत्तरम् :
अध्ययने महान् अध्ययनप्रत्यूहः उत्पन्न: अत: आत्रेयी वाल्मीकिमहर्षेः आश्रमात् दण्डकारण्यं आगता।

प्रश्न 2.
दारकद्वयस्य नामनी के ?
उत्तरम् :
दारकद्वयस्य नामनी कुशलवौ इति।

प्रश्न 3.
वाल्मीकि: माध्यन्दिनसवनाय कुत्र अगच्छत् ?
उत्तरम् :
वाल्मीकि; माध्यन्दिनसवनाय तमसानदीतीरम् अगच्छत् ।

प्रश्न 4.
क्रौश्याः विलापं श्रुत्वा महर्षेः मुखात् कीदृशी वाणी प्रसृता ?
उत्तरम् :
क्रौझ्या: विलापं श्रुत्वा महर्षे: मुखात् अनुष्टुप्छन्दसा अश्रुतपूर्वा दैवी वाणी प्रसृता।

प्रश्न 5.
ब्रह्मदेव: वाल्मीकि किम् आदिशत् ?
उत्तरम् :
ब्रह्मदेव: वाल्मीकि ‘रचय रामचरितम्’ इति आदिशत।

2. माध्यमभाषया लिखत।

प्रश्न 1.
आत्रेय्याः प्रथमः अध्ययनप्रत्यूहः कः ?
उत्तरम् :
“स्वागतं तपोधनायाः।” हा गद्यांश भवभूतिरचित उत्तररामचरितम् या नाटकातील आहे. वनदेवता व आत्रेयी यांच्या संवादातून रामायणरचनेला सुरुवात कशी झाली, वाल्मीकींच्या आश्रमातील लव-कुश यांचे अध्ययन या बद्दल चर्चा केली आहे. वाल्मीकींच्या आश्रमातून आत्रेयी दण्डकाण्यात गेली. तिथे गेल्यावर तिला वनदेवता भेटली.

आत्रेयीला पाहून वनदेवतेने तिला दण्डकारण्यात येण्याचे कारण विचारले. आत्रेयीने सांगितले की, ती वाल्मीकी ऋषींच्या आश्रमातून दण्डकारण्यात वेदांताचे अध्ययन करण्यासाठी आली आहे. वनदेवतेला आश्चर्य वाटले की इतर सर्व ऋषी वेदांत तत्त्वज्ञान शिकण्यासाठी वाल्मीकींकडे जात असताना आत्रेयीला दण्डकारण्यात येण्याची गरज का भासली. तेव्हा आत्रेयी म्हणाली की, वाल्मीकींच्या आश्रमात कुशलव नावाची दोन मुले शिकत आहेत. वाल्मीकींनी त्यांना तीन विद्या-आन्वीक्षीकी, दंडनीती व वार्ता यांचे शिक्षण दिले आहे.

ती मुले असामान्य बुद्धिमत्तेची आहेत. आत्रेयीसारख्या सामान्य बुद्धीच्या विद्यार्थिनीला त्यांच्याबरोबर विद्याग्रहण करणे शक्य नाही. म्हणून ती दण्डकारण्यात अध्ययनासाठी आली आहे. हा आत्रेयीच्या अध्ययानातील पहिला अडथळा होता.

In this lesson “स्वागतं तपोधनायाः।” is a part of Sanskrit play उत्तररामचरितम् . The conversation between Atreyi and Vanadevata tells us how Ramayana was composed and why Atreyi couldn’t continue her studies in Valmiki’s hermitage.

Atreyi was sage Valmiki’s student. She had come to Dandaka forest looking for Agasti’s hermitage to learn Vedanta Philosophy. There she met the guardian of the forest. The forest deity asked Atreyi about the reason for coming to the forest. Atreyi told her everything about herself, the Vanadevata was surprised to know that Atreyi had left sage Valmiki’s hemitage when he was the greatest person to teach Vedanta.

Then Atreyi told her about the problem she had faced in learning at Valmiki’s hermitage. She said that there were two extremely intelligent boys who had been initiated to learning by Valmiki and they had already learnt the three branches of knowledge – Anvikshiki, Dandaniti, and Vartta. The boys were gifted with divine qualities and high intellect.

Hence it was not possible for ordinary student like her to match their standards of learning, This was the first obstacle in Atreyi’s learning at Valmiki’s hermitage.

प्रश्न 2.
ब्रह्मदेवेन “रचय रामचरितम्” इति वाल्मीकिः किमर्थम् आदिष्टः ?
उत्तरम् :
भवभूतिविरचित ‘उत्तररामचरितम्’ नाटकातील दुसऱ्या अंकात तपस्विनी व बनदेवता यांच्यातील संवाद आला – आहे. तपस्विनी वाल्मीकींच्या आश्रमातून अगस्ती मुनींच्या आश्रमात वेदांताचे अध्ययन करण्यासाठी आली आहे. वाल्मीकी ऋषि स्वत: वेदांताचे अध्यापन करीत असताना त्यांच्या आश्रमातील तपस्विनी दंडकारण्यात आलेली पाहून वनदेवतेला आश्चर्य वाटले.

त्यावेळी आत्रेयी सांगते की वाल्मीकी ब्रह्मदेवाच्या आज्ञेवरून रामायणाची रचना करण्यात मग्न आहेत, एकदा माध्यदिनसवनासाठी तमसा नदीवर गेले असताना काँच पक्ष्याच्या वियोगाने विलाप करण्याचा क्रौंच पक्षिणीला त्यांनी पाहिले व त्यांच्या तोंडून अद्भूत अशी अनुष्टुभ् छंदातील दैवी वाणी बाहेर पडली. वेदांनंतर सर्वप्रथम अनुष्टुभ् छंदातील पद्यरचना वाल्मीकींनीच केली. त्यानंतर ब्रह्मदेवाने त्यांना त्याच छंदात

पुरुषोत्तम श्रीरामांचे चरित्र शब्दबद्ध करण्यास सांगितले. ज्यामुळे अनुष्टुभ छंद अभिजात भाषेमध्ये जतन केला जाईल व श्रीरामांचा पराक्रम सर्वापर्यंत पोहोचेल.

In the second act of “उत्तररामचरितम्” compsed by wayfa is a conversation between Vanadevata and Atreyi where Atreyi had left Valmiki’s hermitage and was going to sage Agasti’s hermitage to learn Vedanta.

Valmiki himself was a well-versed scholar of Vedanta. So, Vanadevata was surprised seeing Atreyi wandering away from his hermitage and going elsewhere. When Atreyi narrated her difficulties she also mentioned how Valmiki was engrossed in composing Ramayana as he was orderd to do so by lord Brahma.

While performing afternoon rituals at Tamasa river, he saw a female heron lamenting for her companion who was hit by a hunter. Hearing her sad lamentation Valmiki uttered a shloka in Anushtubh spontaneously.

This was a long after the Vedic scriptures that a composition in Anushtubh meter was composed. Lord Brahma asked sage Valmiki to compose an epic on the life of Lord Rama in the same meter. This way not only would the Anushtubh meter be conserved and brought into classical Sanskrit. But people would also get to know Lord Rama’s life story.

3. प्रश्ननिर्माणं कुरुत।

प्रश्न 1.
आत्रेयी वाल्मीकिमहर्षेः आश्रमात् दण्डकारण्यम् आगता।
उत्तरम् :
आत्रेयी कस्य आश्रमात् दण्डकारण्यम् आगता?

प्रश्न 2.
व्याधेन क्रौश: बाणेन विद्धः ।
उत्तरम् :
व्याधेन क्रौञ्च: केन विद्धः?

प्रश्न 3.
अन्ये मुनयः वेदान्तज्ञानार्थं वाल्मीकिऋषिम् उपगच्छन्ति।
उत्तरम् :
अन्ये मुनयः किमर्थं वाल्मीकिऋषिम् उपगच्छन्ति?

4. अ. शब्दस्य वर्णविग्रहं कुरुत।

प्रश्न 1.

1. अगस्त्यः
2. वाल्मीकि:
3. अनुष्टुभ्
4. वेदान्तम्

उत्तरम् :

1. अगस्त्यः – अ + ग् + अ + स् + त् + य् + अः।
2. वाल्मीकिः – व् + आ + ल् + म् + ई + क् + इ:।
3. अनुष्टुभ् – अ + न् + उ + ष् + ट् + उ + भ्।
4. वेदान्तम् – व् + ए + द् + आ + न् + त् + अ + म्।

आ. कालवचनपरिवर्तनं कुरुत ।

प्रश्न 1.
1. मुनयः वनप्रदेशे निवसन्ति। (एकवचने परिवर्तयत ।)
2. रचय रामचरितम् । (लिङ्लकारे परिवर्तयत ।)
उत्तरम् :
1. मुनि: वनप्रदेशे निवसति।
2. रचये: रामचरितम्।

इ. विशेषण-विशेष्य-मेलनं कुरुत। |

प्रश्न 1.

उत्तरम् :

विशेष्यम्	विशेषणम्
1. सहचर:	4. निश्चेष्टः
2. विलाप:	3. करुणः
3. कुशलवौ	1. पोषितौ
4. वाणी	2. अश्रुतपूर्वा

स्वागतं तपोधनाया: Summary in Marathi and English

प्रस्तावना :

संस्कृत साहित्य हे काव्य, नाटक व गद्य अशा सर्व साहित्यप्रकारांनी समृद्ध आहे. संस्कृत काव्ये, नाटके ही नेहमीच शेले, शेक्सपिअर यांसारख्या परदेशी नाटककारांसाठी प्रेरणादायी ठरली आहेत. अनेक सुप्रसिद्ध संस्कृत नाटककारांपैकी भवभूतींना संस्कृतनाटा परंपरेत अत्यंत आदराचे स्थान आहे.

त्यांच्या अनेक साहित्यकृतींपैकी ‘उत्तररामचरितम्’ ही सर्वांत नावाजलेली नाट्यकृती मानली जाते. राम व सीता यांच्या रावणयुद्धोत्तर जीवनाचे दर्शन या नाटकातून घडते. प्रस्तुत पाठातील संवाद हा ‘उत्तररामचरितम्’ च्या दुस-या अंकातील आहे. वाल्मिकीरामायणाची रचना कधी, कोणत्या प्रेरणेने सुरू झाली हे संवादातून सांगितले आहे.

Sanskrit literature is rich with poetry, prose as well as drama. Sanskrit dramas are inspirations to many foreign playwrights like Shelley, Shakspeare etc. Among the mamy Sanskrit playwrights भवभूती is considered a respectable writer.

उत्तररामचरितम् by भवभूती is the most celebrated one among all his works. The play depites the life of lord राम and सीता after PUar with रावण. This particular passage is from the second act of उत्तररामचरितम् This dialogue narrates how the first ever poetry composed in classical Sanskrit Language came into being on the earth.

परिच्छेद : 1

(नेपथ्ये)स्वागतं तपोधनाया: ………………. मृदा चयः।।
(नेपथ्ये) स्वागतं तपोधनायाः। (ततः प्रविशति अध्वगवेषा तापसी।)
वनदेवता – आर्ये, का पुनः अत्रभवती? किं प्रयोजनं दण्डकारण्यप्रवेशस्य?
आत्रेयी – अस्मिन् प्रदेशे बहवः अगस्त्यादयः मुनयः निवसन्ति। तेभ्यः वेदान्तविद्याम् अधिगन्तुम् अत्र आगता।
वाल्मीकिमहर्षे: आश्रमात् इह आगतास्मि।
वनदेवता – अहो आश्चर्यम् ! अन्ये मुनयः वेदान्तज्ञानार्थ वाल्मीकिम् ऋषिम् उपगच्छन्ति। कथम् अत्रभवती तस्य आश्रमात् अत्र अटति?
आत्रेयी – तत्र अध्ययने महान् अध्ययनप्रत्यूहः उत्पन्नः। भगवति, केनापि देवताविशेषण दारकद्वयमुपनीतम्। कुशलवी इति तयोः नामनी। एकादशवर्षाणि यावत् भवगता वाल्मीकिना धात्री इव पोषितौ रक्षितौ च उपनयनं कृत्वा त्रयीविद्यामपि अध्यापितौ। अतिप्रदीप्तप्रज्ञामेधे तयोः। न अस्मादृशाः सामान्या: छात्राः ताभ्यां सह अध्येतुं शक्नुवन्ति। यतः,
वितरति गुरु प्राज्ञे विद्यां यथैव तथा जडे।
न खलु तयोनि शक्ति करोत्यपहन्ति वा।
भवति हि पुनर्भूयान् भेदः फलं प्रति तद्यथा।
प्रभवति शुचिर्बिम्बग्राहे मणिर्न मृदां चयः।।

अनुवादः

(पडद्यामागे) तपस्विनीचे स्वागत असो! (त्यानंतर प्रवासीवेशातील तापसी प्रवेश करते.)
वनदेवता – बाईसाहेब! कोण आपण? दण्डकारण्यात येण्याचे काय प्रयोजन?
आत्रेयी – या प्रदेशात अगस्ती इ. अनेक मुनिवर राहतात. त्यांच्याकडून वेदांतविद्या शिकण्यासाठी मी इथे आले आहे. मी महर्षी वाल्मीकींच्या आश्रमातून आले आहे.
वनदेवता – काय आश्चर्य ! इतर मुनी वेदांत शिकण्यासाठी वाल्मीकी ऋषींकडे जातात आणि आपण कशा काय त्यांच्या आश्रमातून इकडे फिरत आलात?
आत्रेयी – तिकडे अध्ययनामध्ये मोठा अडथळा निर्माण झाला आहे. महोदये, कोण्या एका देवतेने दोन मुले आणली. कुशलव अशी त्यांची नावे आहेत. अकरा वर्षांपर्यंत आदरणीय वाल्मीकींनी दाईप्रमाणे त्यांचे पोषण व रक्षण केले, सांभाळ केला. उपनयन करून तीन विद्यासुद्धा शिकवल्या. त्यांची बुद्धी असामान्य आहे.

माझ्यासारखे सामान्य विद्यार्थी त्यांच्याबरोबर शिकू शकत नाहीत. कारण, गुरु ज्याप्रमाणे हुशार विद्यार्थ्याला ज्ञान देतात त्याच प्रमाणे सामान्य बुद्धीच्या विद्यार्थ्याला सुद्धा देतात. ते खरोखर ज्ञानशक्ती वाढवतही नाहीत व कमी सुद्धा करत नाहीत. पण (ज्ञानातून मिळणाऱ्या) फळात भेद दिसतो. ज्याप्रमाणे स्वच्छ मणीच बिंब ग्रहण करून त्याचे प्रतिबिंब दाखवण्यास समर्थ असतो, माती नाही.

(At backstage) Welcome to the one rich with penance! (Then enters a female ascetic in the disguise of a traveller.)
Vanadevata – Onoble lady, who are you? What is (forest deity) the purpose of coming to Dandaka forest?
Atreyi – Many sages like Agasti etc. stay in this region! I have come here to gain knowledge of Vedanta. I have come from the hermitage of the great sage Valmiki.
Vanadevata – What a surprise! All other sages go to sage Valmiki for knowledge of Vedanta. But why is respected one wandering here out of his hermitage?

Aatreyi – A great hurdle has come in the way of learning. O respected lady! two boys by a certain deity have been brought whose names are on and लव. Respected Valmiki has nurtured and protected them for eleven years, like a foster mother.

After initiation, they have also been taught the three branches of knowledge. They have a dazzling intellect. It is impossible for ordinary students like us to study with them. Because, A preceptor imparts knowledge to the intelligent as well as the ignorant.

He neither enhances or takes away the ability of their learning. Nevertheless, there is a great difference in the result. Just as a clear jewel causes reflection but a heap of mud does not.

परिच्छेद : 2

वनदेवता – अयमध्ययन …………….. मार्ग कवय ।
वनदेवता – अयमध्ययनप्रत्यूहः ?
आत्रेयी – अन्यश्च।
वनदेवता – अथ अपरः कः?
आत्रेयी – अथैकदा सः महर्षि माध्यन्दिनसवनाय तमसानदीतीरम् अगच्छत्। तत्र वृक्षे एक क्रौञ्चयुग्मम् आसीत्। सहसा B व्याधेन तयोः एकः बाणेन विद्धः। भूमौ पतितं निश्चेष्टं सहचरं दृष्ट्वा क्रौञ्ची व्यलपत्। तस्याः करुणं विलापं श्रुत्वा अकस्मात् महर्षे: मुखात् अनुष्टुप्छन्दसा अश्रुतपूर्वा दैवी वाणी स्फुरिता ‘मा निषाद, प्रतिष्ठां त्वमगम: शाश्वती: समाः …………
वनदेवता – चित्रम्। आम्नायात् अनन्तरम् नूतनः छन्दसाम् अवतारः।
आत्रेयी – तेन हि पुनः समयेन भगवान् ब्रह्मदेवः तत्र आविर्भूतः ‘महर्षे, प्रबुद्धः असि। रचय रामचरितम्’। इति आदेशबद्धः सः वाल्मीकिः रामायणरचनायां मग्नः अस्ति। तस्मात् ब्रवीमि, इदानीं तत्र अध्ययनमसम्भवम्।
वनदेवता – युज्यते ।
आत्रेयी – विश्रान्तास्मि भद्रे। सम्प्रति अगस्त्याश्रमस्य मार्ग कथय।

अनुवादः

वनदेवता – हा अडथळा आहे होय अध्ययनामध्ये?
आत्रेयी – अजून एक (अडथळा) आहे.
वनदेवता – दुसरा कोणता?
आत्रेयी – एकदा ते महर्षी (वाल्मिकी) दुपारच्या स्नानासाठी तमसा
नदीच्या तीरावर गेले. तिथे वृक्षावर कौंचपक्ष्याचे एक जोडपे बसले होते. अचानक व्याधाने मारलेल्या बाणाने त्यांच्यातील एक जखमी झाला. जमिनीवर पडलेल्या निचेष्ट जोडीदाराला पाहून कौंच पक्षीण विलाप करू लागली. तिचा करुण विलाप ऐकून महर्षीच्या मुखातून “निषादा…. शाश्वत काळापर्यंत तुला प्रतिष्ठा मिळणार नाही….” अशी पूर्वी कधीच न ऐकलेली अनुष्टुभ् छंदातील दैवी वाणी स्फुरली.
वनदेवता – किती सुंदर ! वेदांनंतर छंदांचा हा नवीनच आविष्कार आहे.
आत्रेयी – त्यामुळेच, काही काळाने तिथे ब्रह्मदेव अवतरले ‘महर्षी !
तुम्ही अत्यंत प्रज्ञावान आहात! रामचरित्राची रचना करा’ अशा आज्ञेने कटिबद्ध असलेले वाल्मीकी रामायण रचण्यात मग्न आहेत. म्हणून मी म्हणते आहे की तिथे अभ्यास होणे अशक्य आहे.
वनदेवता – बरोबर आहे!
आत्रेयी – मीथकले आहे. मला अगस्तिऋषींच्या आश्रमाचा मार्ग सांग!

Vanadevata – Is this the obstacle in learning ?
Atreyi – There is still onother one.
Vanadevata – Now what is the another one?
Atreyi – Once that great sage (Valmiki) went to the river Tamasa for afternoon worship/ritual. There, a pair of herons was sitting on a tree. Suddenly one among them was hit by an arrow shot by a hunter. Seeing the companion fallen lying still on the ground the female heron lamented. Hearing her sad lamentation suddenly divine speech, unheard of before came spontaneously from the mouth of great sage in Anushtubh meter. ‘O hunter, you will never attain respect for eternal years……..’
Vanadevata – Beautiful! After the Vedas this was the new form of meter!
Atreyi – Hence, after a while lord Brahma appeared there. Valmiki who was ordered as “O great sage, you are extremely intelligent. Do compose the story on Rama’s life.” is now engrossed in composing the Ramayana. Hence, I say that it is imposible to study there now.
Vanadeva – Right!
Atreyi – I am tired, O good lady! Now please tell me the way Agasti’s hermitage.

शब्दार्थाः

1. नेपथ्ये – backstage – नेपथ्यामधे
2. तपोधना – female ascetic – तपस्विनी
3. अध्वगवेषा – in the disguise of traveller – प्रवासी वेशातीला
4. प्रयोजनम् – purpose – प्रयोजन
5. अधिगन्तुम् – to know/to learn – जाणण्यासाठी
6. उपगच्छन्ति – go near/approach – जवळ जातात
7. अटति – wanders – फिरते
8. प्रत्यूहः – obstacle – विघ्न
9. दारकद्वय – two young boys – दोन लहान मुले
10. उपनीतम् – brought – आणली
11. वितरति – imparts – देतात
12. जडे – to ignorant – अज्ञानी माणसाला
13. वनदेवता – forest deity – वनदेवता
14. अपहन्ति – takes away – काढून टाकतात
15. भूयान् – great – मोठा
16. शुचिः – clear – स्वच्छ
17. बिम्बग्राहे – in reflecting – प्रतिबिंब पाडताना
18. चय: – heap – ढीग
19. अपरः – another – दुसरा
20. माध्यन्दिनसवनाय – for afternoon bath – माध्यंदिन स्नानासाठी
21. क्रौञ्चयुग्मम् – pair of herons – कौंचपक्ष्याचा जोडा
22. व्याधेन – by hunter – शिकाऱ्याने
23. विद्धः – wounded – मारलेला
24. निशेष्टम् – still – निपचित
25. व्यलपत् – lamented – विलाप करणाऱ्या
26. विलापम् – lamentation – विलाप
27. अनुष्टुप्छन्दसा – by Anushtubh meter – अनुष्टुभ छंदाने
28. अश्रुतपूर्वा – not heard before – पूर्वी न ऐकलेली
29. स्फुरिता – spontaneously came – स्फुरलेली
30. निषाद – hunter – शिकारी
31. शाश्वती: – eternal – शाश्वत
32. चित्रम् – beautiful – सुंदर
33. सहसा – suddenly – अचानक

Aamod Sanskrit Book 9th Class Solutions

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• धन्यौ तौ दातृयाचकौ Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• योगमाला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• पितृभक्तः नचिकेताः Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• सरमाया: शीलम् Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer
• स्वागतं तपोधनाया: Class 9 Question Answer

Class 9th Sanskrit Anand Chapter 5 वीरवनिता विश्पला Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Anand Chapter 5 वीरवनिता विश्पला Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 5 Question Answer

Sanskrit Anand Std 9 Digest Chapter 5 वीरवनिता विश्पला Textbook Questions and Answers

भाषाभ्यासः

1. उचितं पर्यायं चित्वा रिक्तस्थानानि पूरयत ।

प्रश्न 1.
अ. शत्रवः …………. । (कृतवान्/कृतवन्तः)
आ. खेलराजः …………. । (प्रविष्टवन्तः/प्रविष्टवान्)
इ. विश्पला …………. । (प्रविष्टवान्/प्रविष्टवती)
ई. सा युद्धं …………. । (कृतवान्/कृतवती)
उ. शत्रुसैनिकाः …………. । (अवरुद्धवन्तौ/अवरुद्धवन्तः)
ऊ. सैनिकाः शिबिरं …………. । (गतवन्त:/गतवन्ती)
ए. शत्रुसैनिकाः पादं …………. । (कर्तितवन्त:/कर्तितवन्तौ)
ऐ. सा रणाङ्गणम् …………. । (आगतवत्यौ/आगतवती)
ओ. विश्पला ध्यानम् …………. । (आरब्धवान्/आरब्धवती)
औ. अश्विनीकुमारौ तां यथापूर्वं …………. । (कृतवन्तौ/कृतवत्यौ)
उत्तरम् :
अ. कृतवन्तः ।
आ. प्रविष्टवन्तः
इ. प्रविष्टवती।
ई. कृतवती।
उ. अवरुद्धवन्तः।
ऊ. गतवन्तः।
ए. कर्तितवन्तः।
ऐ. आगतवती।
ओ आरब्धवती।
औ कृतवन्तौ।

2. स्तम्भमेलनं कुरुत।

प्रश्न 1.

उत्तरम् :

अ	आ
1. लोहयुक्तम्	4. पादम्
2. वीराङ्गना	5. विश्पला
3. भीताः	2. शत्रुसैनिकाः
4. महत्	1. युद्धम्
5. शूरः	3. खेलराजः

3. अधोदत्तेषु विशेषणेषु यानि विशेषणानि विश्पलां न वर्णयन्ति तानि पृथुक् कुरुत ।
चकिताः, प्रशंसिता, भीता, समर्था, निश्चला, एकाकिनी, चैतन्यमूर्तिः, अवरुद्धा, चामुण्डेश्वरी, महाविदुषी, रणकुशला, शूरः, नायिका, दुःखिता।।

प्रश्न 1.
अधोदत्तेषु विशेषणेषु यानि विशेषणानि विश्पलां न वर्णयन्ति तानि पृथुक् कुरुत ।
चकिताः, प्रशंसिता, भीता, समर्था, निश्चला, एकाकिनी, चैतन्यमूर्तिः, अवरुद्धा, चामुण्डेश्वरी, महाविदुषी, रणकुशला, शूरः, नायिका, दुःखिता।।

4. माध्यमभाषया उत्तरं लिखत ।

प्रश्न 1.
विश्पलायाः शौर्यस्य वर्णनं कुरुत ।
उत्तरम् :
‘सम्भाषणसन्देश’ या प्रसिद्ध संस्कृत मासिकातून ‘वीरवनिता विश्पला’ ही कथा घेतलेली आहे. ऋग्वेदातून उद्धृत केलेली प्रस्तुत कथा अतिशय अद्भुत आणि रोमांचकारी आहे. स्त्रियांच्या सामर्थ्यांचे दर्शन घडविणारी ही प्रेरणादायी कथा आहे.

खेलराज राजाची पत्नी विश्पला ही अतिशय बुद्धिमती होती. तसेच युद्धातही ती निपुण होती. खेलराजाच्या राज्यावर एकदा अचानक शजूंनी आक्रमण केले आणि घनघोर युद्धाला सुरुवात झाली. सेनाप्रमुख खेलराजांबरोबर त्यांची पत्नी विश्पलासुद्धा रणांगणात युद्ध करण्यास सज्ज झाली पृथ्वीवर चामुण्डेश्वरी अवतरल्याप्रमाणे विश्पला शबूंचा संहार करत होती.

तिचे शौर्य आणि पराक्रम पाहून शत्रूसैनिक सुद्धा चकित झाले होते. तिला शत्रूच्या सैनिकांनी योजनेसह अडवून तिच्यावर आक्रमण केले. असंख्य शत्रूसैनिक व विश्पला एकटी अशा विषम परिस्थितीत भीतीचा लवलेशही मनात न आणता द्विगुणित उत्साहाने विश्पलेने युद्ध केले. या युद्धाच्यावेळी विश्पलेचा पाय कापला गेला.

जरी तिचा पाय तुटला होता तरीसुद्धा ती निराश झाली नाही. चैतन्यमूर्ती असलेल्या त्या वीरांगनेला त्या परिस्थितीतही दुसऱ्या दिवशी लढण्याची प्रबळ इच्छा मनात होती. यातूनच तिच्या शौर्याचे दर्शन घडते. तिने अश्विनीकुमारांच्या मदतीने कृत्रिम लोहयुक्त पाय प्राप्त केला व पुन्हा युद्धाच्या रणांगणात उत्साहाने युद्ध केले.

विश्पलेला रणांगणात पाहूनच शत्रूसैनिकांचे धैर्य नष्ट झाले होते. तिच्या मानसिक शौयनि तिने अर्धे युद्ध जिंकले होतेच व अंती रणांगणात युद्धकलेच्या कौशल्याने सर्वशबूंचा लीलया संहार करुन युद्धात खेलराजाला विजय प्राप्त करवून दिला.

विश्पला ही दृढ निश्चयाचे आणि अतुलनीय धैर्याचे प्रतीक आहे. थोरांच्या कार्यसिद्धीसाठी साधनांची आवश्यकता नसते केवळ त्यांची प्रबळ इच्छाशक्तीच पुरेशी ठरते, हे तिच्या उदाहरणावरून समजते.

In the lesson वीरवनिता विश्पला’ a story of the lady warrior Vishpala’s courage and Ashwinikumar’s medical skills have been described. Vishpala was the queen of the king Khelaraj.

She was not only great scholar but also a brave warrior. Once their state was attacked/invaded by the enemies. Vishpala accompanied her husband in the battle field. She fought fiercely and destructed the enemy’s army.

The oponent soldiers were so scared of her fierce war-skills that they attacked Vishpala at once and cut her foot so that she would be unable to fight. But Vishpala’s will for fighting and winning was so strong that she didn’t loose hope upon her broken foot.

She meditated upon the twins Ashwinikumara’s the divine doctors who were the expert surgons. They joined an iron foot to her leg. She fought with double energy the next day. She wiped out the enemies with her ferocious warfare skills.

Vishpala is an example of great determination and incredible courage.
She was great warrior in a true sense and the one for whom resources did not matter. She stood true to the words “क्रियासिद्धिः सत्त्वे वसति महतां नोपकरणे।’

प्रश्न 2.
विश्पला अश्विनीकुमारयोः ध्यानं किमर्थ कृतवती?
उत्तरम् :
‘वीरवनिता विश्पला’ ही कथा रणरागिनी विश्पलेच्या शौर्याचे गुणगान आहे. ऋग्वेदापासून चालत आलेली विश्पलेची कथा भारतीय स्त्रियांच्या पराक्रमाची साक्ष आहे. खेलराजाची पत्नी विश्पला ही विदूषी तसेच शूर होती. राज्यावर आक्रमण झाल्यावर ती खेलराजाच्या बरोबरीने लढायला उभी राहिली. शत्रुसैनिक तिचा दुर्गावतार पाहून भयभीत झाले.

शवसैनिकांनी योजना करून विश्पलेला अडविले आणि तिच्यावर आक्रमण केले. आपल्या सैन्याचे रक्षण करण्यासाठी विश्पलेला रणांगणातून बाहेर काढणे हाच एकमेव मार्ग आहे या आसुरी विचाराने शत्रुसैनिकांनी विश्पलेचा पाय कापला. विश्पला तरीसुद्धा तिच्या निग्रहापासून ढळली नाही.

उलट उद्या युद्ध भूमीवर जाता यायला हवेच असा निग्रहाने तिने अश्विनीकुमारांकडे प्रार्थना केली अश्विनीकुमार हे देवांचे वैद्य ते शल्यक्रियेत कुशल होते. त्यांनी विश्पलेच्या पायाला लोखंडी पाऊल जोडून तिला पूर्ववत् केले, प्रस्तुत कथा विश्पलेचे शौर्य व प्राचीन भारतीय वैद्यकशास्त्र यांचे जिवंत द्योतक आहे.

‘वीरवनिता विश्पला’ is a story of brave lady who stood to the enemies accompanying her husband with a great courage. Vishpala was a queen with a great intellect and exceptional courage. She was King Khelaraj’s wife. When their kingdom was attacked by their enemies she also fought with the enemies with equal energy.

The enemy soldiers were frightened of her vigorous warfare. They purposely attacked her all for once and broke down her foot. Even then Vishpala didn’t fail. She was so determined that she decided to get back her foot anyhow.

She called the twins Ashwinikumaras who were the doctors of the gods and experts in surgery. She sat still and concentrated fully on them. Since they were the experts, she knew that they would definitely help her get the foot back.

Not losing hopes at all Vishpala called them and didn’t give up on fighting. The twins Ashwinikumaras were blessed with divine medicinal skills. Because of their expertise and skills Vishpala could fight and win the battle.

पाठात् धातुसाधित-अव्ययानि चिनुत पृथक्कुरुत च ।

प्रश्न 1.
पाठात् धातुसाधित-अव्ययानि चिनुत पृथक्कुरुत च ।
उत्तरम् :

धातुसाधित – विशेषणम्	विशेष्यम्
आरब्धम्, करणीयम्	युद्धम्
अवतीर्णा, प्रशंसिता	विश्पला
भग्नः	पादः
नष्टम्	धैर्यम्
संहताः	सैनिकाः

5. समानार्थकशब्दं पाठात् लिखत।
अरिः, चरणः, वीर्यम्, सङ्गरः, रणाङ्गणम्, रक्षकाः, पण्डिता, वीक्ष्य, वेदना, अगणिताः।

प्रश्न 1.
समानार्थकशब्दं पाठात् लिखत।
अरिः, चरणः, वीर्यम्, सङ्गरः, रणाङ्गणम्, रक्षकाः, पण्डिता, वीक्ष्य, वेदना, अगणिताः।
उत्तरम् :

• शत्रुः – अरिः, रिपुः।
• पादः – चरणः।
• वीर्यम् – शौर्यम्, पराक्रमः।
• रणरङ्गः – रणभूमिः, रणाङ्गणम्
• दृष्ट्वा – वीक्ष्य, अवलोक्य।
• पीडा – वेदना, व्यथा, बाधा।
• असङ्ख्या: – अगणिताः।

6. विरुद्धार्थकशब्द पाठात् लिखत।
मित्रम्, कातरता, असमर्था, कातरः, पराजयः ।

प्रश्न 1.
विरुद्धार्थकशब्द पाठात् लिखत।
मित्रम्, कातरता, असमर्था, कातरः, पराजयः ।
उत्तरम् :

• शत्रुः × मित्रम्।
• शौर्यम् × कातरता।
• समर्था × असमर्था ।
• शुर: × कातरः
• जयः × पराजयः।

Sanskrit Anand Class 9 Textbook Solutions Chapter 5 वीरवनिता विश्पला Additional Important Questions and Answers

उचितं पर्यायं चिनुत।

प्रश्न 1.
1. खेलराज: नाम कश्चित् ………… । (महीक्षितः / महीरुहः)
2. सः ………..सह सुखेन जीवति स्म। (विश्पला/विश्पलया)
उत्तरम् :
1. महीक्षितः।
2. विश्पलया।

एकवाक्येन उत्तरत।

प्रश्न 1.
विश्पला कीदृशी आसीत्?
उत्तरम् :
विश्पला महाविदुषी रणकुशला च आसीत्।

प्रश्न 2.
खेलराजः कीदृशः आसीत्?
उत्तरम् :
खेलराजः शूरः पराक्रमी च आसीत्।

प्रश्न 3.
शत्रवः किं दृष्ट्वा चकिता: अभवन्?
उत्तरम् :
शत्रवः विश्पलायाः शौर्य पराक्रमं च दृष्ट्वा चकिता: अभवन्।

प्रश्न 4.
सेनायाः नायकः कः?
उत्तरम् :
सेनायाः नायक: खेलराजः।

प्रश्न 5.
विश्पला कर्थ संहारं कृतवती?
उत्तरम् :
भुवम् अवतीर्णा चामुण्डेश्वरी इव विश्पला संहारं कृतवती।

प्रश्न 6.
शत्रवः किं कृतवन्तः?
उत्तरम् :
शत्रवः खेलराजस्य राज्ये आक्रमणं कृतवन्तः।

प्रश्न 7.
युद्धसमये शत्रुसैनिकाः किं कर्तितवन्तः?
उत्तरम् :
युद्धसमये शत्रुसैनिकाः विश्पलाया: एक पादं कर्तितवन्तः ।

प्रश्न 8.
शत्रुसैनिकाः किं चिन्तयित्वा युगपत् आक्रम्य ताम् अवरुद्धवन्तः?
उत्तरम् :
यावत् विश्पला रणरङ्गात् न निवार्यते तावत् सर्वथा जय: न प्राप्यते इति चिन्तयित्वा युगपत् आक्रम्य ताम् अवरुद्धवन्तः ।

प्रश्न 9.
विश्पला कदा हतोत्साह्य न जाता?
उत्तरम् :
यद्यपि विश्पलायाः पादः भग्नः तथापि सा हतोत्साहा न जाता।

प्रश्न 10.
विश्पला कीदृशी?
उत्तरम् :
विश्पला चैतन्यमूर्तिः वीराङ्गना च।

प्रश्न 11.
किं निश्चित्य विश्पला पुन: पादं प्राप्तुम् ऐच्छत्?
उत्तरम् :
श्व: मया युद्धं करणीयम् एव इति निश्चित्य विश्पला पुन: पादं प्राप्तुम् ऐच्छत्।

प्रश्न 12.
विश्पलायाः भक्तेः कारणात् किम् अभवत् ?
उत्तरम् :
विश्पलाया: भक्तेः कारणात् अश्विनीकुमारी लोहयुक्तं पाद योजयित्वा तां यथापूर्वं कृतवन्तौ। .

प्रश्न 13.
लोहयुक्तेन पादेन किम् अभवत्?
उत्तरम् :
लोहयुक्तेन पादेन विश्पला यथापूर्व चलितुं युद्धं कर्तुं च समर्था जाता।

प्रश्न 14.
कस्याः दर्शनमात्रेण सैनिकानां धैर्य नष्टं जातम्?
उत्तरम् :
विश्पलाया: दर्शनमात्रेण सैनिकानां धैर्य नष्टं जातम्।

प्रश्न 15.
यदा विश्पला आयुधप्रहारम् आरब्धवती तदा किम् अभवत्?
उत्तरम् :
यदा विश्पला आयुधप्रारम् आरब्धवती तदा शत्रुसैनिकाः सर्वथा हतोत्साहा: जाताः।

प्रश्न 16.
इतिहासः अस्मान् किम् उपदिशति?
उत्तरम् :
विश्पलायाः शौर्य तथा च अश्विनीकुमारयोः शल्यक्रियाकौशलं स्मरन्तु इति इतिहासः अस्मान् उपदिशति।

प्रश्न 16.
विश्पला किमर्थं वेदवाङ्मये बहुधा प्रशंसिता?
उत्तरम् :
विश्पला पादकर्तनानन्तरमपि अश्विनीकुमारयोः अनुग्रहेण पादं पुनः प्राप्तवती शत्रून् संहृतवती च। एतेन साहसेन विश्पला वेदवाङ्मये बहुधा प्रशंसिता।

सत्यं वा असत्यं लिखत।

प्रश्न 1.

1. विश्पला खेलराज: नाम्नः नृपस्य पत्नी।
2. सेनाया: नायक: विश्पला आसीत्।
3. चामुण्डेश्वरी इव विश्पला शत्रूणां संहारं कृतवती।
4. शत्रुसैनिक: एक: एव आसीत्।
5. विश्पलायाः मनसि भयम् उपजातम्।
6. विश्पला तु एकाकिनी।
7. शत्रुसैनिकाः खेलराजस्य एक पादं कर्तितवन्तः।
8. द्विगुणितेन उत्साहेन विश्पला युद्धं कृतवती।

उत्तरम् :

1. सत्यम्
2. असत्यम्
3. सत्यम्
4. असत्यम्
5. असत्यम्
6. सत्यम्
7. असत्यम्
8. सत्यम्

प्रश्न 2.

1. यदा विश्पलायाः पादः भग्नः तदा सा हतोत्साहा अभवत्।
2. विश्पला निश्चलतया अश्विनीकुमारयो: ध्यानं कृतवती।
3. पुनरेकवारं विश्पलया युद्धं कृतवती।
4. अनन्तरदिने रात्रौ सा महता उत्साहेन रणरङ्गम् आगतवती।’
5. विश्पलायाः साहसं वेदवाङ्मये बहुधा प्रशंसिता।
6. वीरवनिता विश्पला एकाकिनी एव रणरङ्गं प्रविश्य युद्धं कृतवती।

उत्तरम् :

1. असत्यम्
2. सत्यम्
3. सत्यम्
4. असत्यम्
5. सत्यम्
6. असत्यम्

उचितं कारणं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
सेनायाः नायक: खेलराजः रणरङ्गं प्रविष्टवान् यतः…|
a. शत्रुसैनिकाः असङ्ख्या: आसन् विश्पला तु एकाकिनी।
b. अकस्मात् शत्रवः खेलराजस्य राज्ये आक्रमणं कृतवन्तः।
उत्तरम् :
सेनाया: नायक: खेलराज: रणरङ्ग प्रविष्टवान् यत: अकस्मात् शत्रवः खेलराजस्य राज्ये आक्रमणं कृतवन्तः।

प्रश्न 2.
शत्रवः चकिताः अभवन् यतः…।
a. भुवम्अवतीर्णां चामुण्डेश्वरी इव विश्पला संहारं कृतवती।
b. खेलराज: विश्पलया सह सुखेन जीवति स्म।
उत्तरम् :
शत्रवः चकिता: अभवन् यतः भुवम् अवतीर्णा चामुण्डेश्वरी इव विश्पला संहारं कृतवती।

प्रश्न 3.
सहस्राधिका: सैनिका: पराभूता: यतः …………….।
अ) शत्रुसैनिकानां सङ्ख्या न्यूना आसीत्।
आ) विश्पला शत्रून् कदलीवृक्षान् इव लीलया कर्तितवती।
उत्तरम् :
सहस्साधिका; सैनिकाः पराभूताः यतः विश्पला शत्रून् कदलीवृक्षान् इव लीलया कर्तितवती।

प्रश्न 4.
वेदवाङ्मये विश्पला बहुधा प्रशंसिता यतः ……………..।
अ) विश्पला वीराङ्गना न भवति।
आ) पादकर्तनान्तरमपि अश्विनीकुमारयोः अनुग्रहेण पादं पुनः प्राप्तवती शत्रून् संहृतवती च।
उत्तरम् :
वेदवाङ्मये विश्पला बहुधा प्रशंसिता यतः पादकर्तनान्तरमपि अश्विनीकुमारयोः अनुग्रहेण पादं पुन: प्राप्तवती शत्रून् संहृतवती च।

शब्दस्य वर्णविग्रहं कुरुत।

• कश्चित् – क् + अ + श् + च + + त् ।
• विश्पला – व् + इ + श् + प् + अ + ल् + आ।
• तथैव – त् + अ + थ् + ऐ + व् + अ ।
• चामुण्डेश्वरी – च् + आ + म् + उ + ण् + ड् + ए + श् + व् + अ + र + ई।
• दृष्ट्वा – द् + ऋ + ष् + ट् + व् + आ।
• शौर्यम् – श् + औ + र् + य् + अ + म्।
• निवार्यते – न् + इ + व् + आ + र + य् + अ + त् + ए।
• आक्रम्य – आ + क् + र + अ + म् + य् + अ ।
• कर्तितवन्तः – क् + अ + र + त् + इ + त् + अ + व् + अ + न् + त् + अः।
• कृत्वा – क् + ऋ + त् + व् + आ।
• अवरुद्धवन्तः – अ + व् + अ + र + उ + द् + + अ + व् + अ + न् + त् + अः।
• चैतन्यमूर्तिः – च् + ऐ + त् + अ + न् + य् + अ + म् + ऊ + र + त् + इः।
• यथापूर्वम् – य् + अ + थ् + आ + प् + ऊ + र + व् + अ + म्।
• योजयित्वा – य् + ओ + ज् + अ + य् + इ + त् + व् + आ।
• वीराङ्गना – व् + ई + र + आ + ड् + ग् + अ + न् + आ।
• दर्शनमात्रेण – द् + अ + र् + श् + अ + न् + अ + म् + आ + त् + र् + ए + ण् + अ।
• शौर्येण – श् + औ + र + य् + ए + ण् + ।
• स्मरन्तु – स् + म् + अ + र् + अ + न् + त् + उ।
• सर्वथा – स् + अ + र + व् + अ + थ् + आ।

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.

1. विश्पला तु एकाकिनी।
2. विश्पला रणरङ्गात् यावत् न निवार्यते तावत् जयः सर्वथा न प्राप्यते।
3. शत्रवः खेलराजस्य राज्ये आक्रमणं कृतवन्तः।
4. विश्पला खेलराजस्य पत्नी।
5. विश्पलायाः शौर्य पराक्रमं च दृष्ट्वा शत्रवः चकिताः अभवन्।
6. महत् युद्धम् आरब्धम्।

उत्तरम् :

1. विश्पला कीदृशी?
2. विश्पला कस्मात् / कुत: यावत् न निवार्यते तावत् जयः सर्वथा न प्राप्यते?
3. के खेलराजस्य राज्ये आक्रमणं कृतवन्तः?
4. विश्पला कस्य पत्नी?
5. स्याः शौर्य पराक्रमं च दृष्ट्वा शत्रवः चकिता: अभवन् ?
6. कीदृशं युद्धम् आरब्धम्?

प्रश्न 2.

1. अनन्तरदिने सा महता उत्साहेन रणरङ्गं आगतवती।
2. अश्विनीकुमारयोः शल्यक्रियाकौशलं स्मरन्तु।
3. रणरङ्गे विश्पलां दृष्ट्वा एव शत्रुसैनिकाः भीताः अभवन्।
4. एतेन साहसेन विश्पला वेदवाङ्मये बहुधा प्रशंसिता।

उत्तरम् :

1. कदा सा महता उत्साहेन रणरङ्गं आगतवती?
2. कयो : शल्यक्रियाकौशलं स्मरन्तु?
3. रणरङ्गे कां दृष्ट्वा एव शत्रुसैनिकाः भीताः अभवन् ?
4. एतेन साहसेन विश्पला कुत्र बहुधा प्रशंसिता?

विशेषण-विशेष्य-सम्बन्धः। (मेलनं कुरुत।)

प्रश्न 1.

विशेषणम्	विशेष्यम्
रणकुशला	खेलराज:
चकिता:	विश्पला
पराक्रमी	शत्रवः
…………….	शत्रुसैनिकाः
एकाकिनी	………………..
……………	पादम
द्विगुणितेन	…………………
……………	पादः
चैतन्यमूर्तिः	……………………

उत्तरम् :

विशेषणम्	विशेष्यम्
रणकुशला, एकाकिनी, चैतन्यमूर्तिः	विश्पला
चकिता:	शत्रवः
पराक्रमी	खेलराज:
असङ्ख्या:	शत्रुसैनिकाः
एकम्	पादम
द्विगुणितेन	उत्साहेन
भग्नः	पादः

त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।

त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्त अव्यय   थातु + तुम् / धुम् / टुम् / ढुम् / इतुम् / अयितुम्
दृष्ट्वा	–	–
कृत्वा	निश्चित्य	प्राप्तुम्, चलितुम्
योजयित्वा	–	कर्तुम्

विभक्त्यन्तरूपाणि।

प्रथमा – नृपः, खेलराजः, विश्पला, महाविदुषी, शत्रवः, युद्धम्, नायकः, चामुण्डेश्वरी, एषा, जयः, शत्रुसैनिकाः, असङ्ख्याः, विश्पला, एकाकिनी, एकम, पादम्, पीडा, पत्नी, पादः, मग्नः, सा, भग्नः, पादः, चैतन्यमूर्तिः, वीराङ्गना, युद्धम्, हतोत्साहा, अश्विनीकुमारौ, समर्था, सा, चकिताः, भीताः, नष्टम्, धैर्यम्, विश्पला।
द्वितीया – आक्रमणम्, रणरङ्गम्, संझरम्, पराक्रमम्, शौर्यम्, ताम्, शिबिरम्, पादम्, ध्यानम्, पादम, ताम्, रणरङ्गम, आयुधप्रहारम्, कदलीवृक्षान, शत्रून, अस्मान्।
तृतीया – सुखेन, विश्पलया, उत्साहेन, मया, निश्चलतया, मया, निश्चलतया, महता, उत्साहेन, लीलया, तया, एतेन, साहसेन, शौर्येण, दर्शनमात्रेण, भा।
पञ्चमी – रणरङ्गात्, एतस्याः, कारणात, भक्तेः, एतस्मात्, एतस्मात्, कारणात् ।
षष्ठी – तस्य, सेनायाः, खेलराजस्य, तस्याः, विश्पलायाः, तस्याः, भक्तेः, विश्पलायाः, अश्विनीकुमारयोः, तेषाम, तस्याः, शौर्यस्य, विश्पलायाः, खेलराजस्य।
सप्तमी – राज्ये, भुवम्, मनसि, युद्धसमये, तस्मिन, युद्धे।

लकारं लिखत।

• निवार्यते – ‘नि + व’ धातुः दशमगण: परस्मैपदं (कर्मवाच्य) लट्लकार : प्रथमपुरुषः एकवचनम्।
• प्राप्यते – ‘प्र + आप्’ धातुः पशमगण: परस्मैपदं (कर्मवाच्य) लट्लकार : प्रथमपुरुष: एकवचनम्।
• आसन् – ‘अस्’ धातुः द्वितीयगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: बहुवचनम्।
• भविष्यति- ‘भू-भत्’ धातुः प्रथमगणः परस्मैपदं लट्लकार: प्रथमपुरुष: एकवचनम्।
• आसीत् – ‘अस्’ धातुः द्वितीयगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• जीवति – ‘जीव्’ धातुः प्रथमगणः परस्मैपदं लट्लकार: प्रथमपुरुष: एकवचनम्।
• अभवन् – ‘भू-भव्’ धातुः प्रथमगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: बहुवचनम्।
• ऐच्छत् – ‘इष-इच्छ’ धातुः षष्ठगणः परस्मैपदं लङ्लकारः। प्रथमपुरुष: एकवचनम्।
• उपदिशति – ‘उप + दिश्’ धातुः षष्ठगणः उभयपदम् अत्र परस्मैपदं लट्लकारः प्रथमपुरुष: एकवचनम्।
• स्मरन्तु – ‘स्मृ’ धातुः प्रथमगणः परस्मैपदं लोट्लकार: प्रथमपुरुष: बहुवचनम्।

व्याकरणम् :

शब्दानां पृथक्करणम्

समासाः।

समासनाम	अर्थ:	समासविग्रहः	समासनाम्
रणकुशला	expertin the battle	रणे कुशला।	सप्तमी तत्पुरुष समास
शल्यक्रियाकौशलम्	skillin surgery	शल्यक्रिया कौशलम्।	सप्तमी तत्पुरुष समास

वीरवनिता विश्पला Summary in Marathi and English

प्रस्तावना :

भारताच्या उज्ज्वल इतिहासाने अनेक स्त्री योद्ध्यांना स्वत:च्या देशासाठी लढताना पाहिले आहे. राणी वेलू नाचियार ही 1८ व्या भारतीय शतकातील राणी ब्रिटीशांशी लढली. 17 व्या शतकातील केलाडी चेन्नमा म्हणजे तर मूर्तिमंत शौर्यच. उल्लल राज्याच्या राणीने पोर्तुगीजांशी झालेल्या युद्धात पराक्रम गाजवला.

राणी लक्ष्मीबाई निर्भीडपणे ब्रिटीशांशी लढली. ही भारतीय स्त्रियांच्या शौर्याची काही उदाहरणे झाली, अशाच काही स्त्रियांपैकी एक म्हणजे विश्पला. तिची कथा पुरातनकाळापासून प्रसिद्ध आहे. तिची कथा ऋग्वेदातसुद्धा येते.

प्रस्तुत कथा प्राचीन भारतात अस्तित्वात असलेल्या प्रगत वैद्यकशास्त्राचे उदाहरण आहे. इतकेच नव्हे तर ही कथा शस्त्रक्रियेत पारंगत अश्विनीकुमार आधुनिक वैद्यकीय तंत्रज्ञानाचे मूलाधार कसे होते याचे ही द्योतक आहे. रुद्र, मरुत गण, सोम, व्यवनऋषी हे काही प्राचीन वैद्य होऊन गेलेत.

चरक, सुश्रुत, वाग्भट हे काही सुप्रसिद्ध आयुर्वेदाचार्य होऊन गेलेत. ‘सम्भाषणसन्देश’ या संस्कृत मासिकातून प्रस्तुत कथा निवडलेली आहे. यात केवळ विश्पलेचे शौर्यगान नसून पुढे निरवयत्व प्राप्त करून युद्ध करण्याचे सामर्थ्य तिला कृत्रिम अवयवामुळे प्राप्त झाले हेही समजते.

Indian history has witnessed many brave women warriors who fought with great might for their nations.

Rani Velu Nachiyar, the 18th century Indian queen from Sivaganga fought against the british. Rani Keladi Chennamma, the 17th century queen of Keladi in Karnataka was the epitome of women’s palour.

Rani Abbakka, the queen of Ullal fought against the portugese. Rani Laxmibai fought against the British These are a few examples of some brave ladies who fought for their nation. Much before that was Vishpala who belonged to the ancient era. Her legend of bravery is a part of Rigveda.

This story is also an example of advanced medical science that existed in the Vedic age. The twins Ashwinikumanas were the doctors of gods.

They were also known for their expertise in surgery. Rudra, Maruts, Soma, Rishi Chyaana are the other ancient physicians. Charak, Sushrut, Vagbhata are the renowned Ayurvedacharyas.

This story taken from the Sanskrit periodical ‘सम्भाषणसन्देश’ highlights hors the brave lady Vishpala not only fought bravely in battle but also how she was given an artificial leg so she could fight ably.

 

परिच्छेद : 1

खेलराजः ……………. अभवन्।

खेलराजः नाम कश्चित् नृपः । विश्पला तस्य पत्नी। सा यथा महाविदुषी आसीत् , तथैव रणकुशला अपि आसीत्। खेलराज: अपि शूरः पराक्रमी च आसीत्। सः विश्पलया सह सुखेन जीवति स्म। Bideo अथ कदाचित् शत्रवः खेलराजस्य राज्ये आक्रमणं कृतवन्तः महत् युद्धम् आरब्धम्। सेनायाः नायक: खेलराज: रणरङ्गं प्रविष्टवान् । विश्पला अपि रणरङ्ग प्रविष्टवती । भुवम् अवतीर्णां चामुण्डेश्वरी इव सा शत्रूणां संहारं कृतवती। तस्याः शौर्य पराक्रमं च दृष्ट्वा शत्रवः अपि चकिता: अभवन्।

अनुवादः

खेलराज नावाचा कोणी एक राजा होता. विश्पला त्याची पत्नी होती. ती जशी महाविदुषी (अतिशय बुद्धिमती) होती तशीच ती रणकुशला (युद्धात पारंगत) सुद्धा होती. खेलराज सुद्धा शूर आणि पराक्रमी होता. तो विश्पलेबरोबर आनंदाने राहत होता. असेच एकदा अचानक शत्रूनी खेलराजाच्या राज्यावर आक्रमण केले. मोठ्या युद्धाला सुरुवात झाली. सेनाप्रमुख खेलराजाने रणांगणात प्रवेश केला.

विश्पलेनेही रणांगणात प्रवेश केला. पृथ्वीवर अवतरलेल्या चामुण्डेश्वरी प्रमाणे तिने शबूंचा संहार केला. तिचे शौर्य आणि पराक्रम पाहून शत्रूसुद्धा आश्चर्यचकित झाले.

There was a king named Khelaraja. Vishpala was his wife. Just as was a great scholar, likewise she was an expert in warfare. Khelaraja was also very brave and courageous. He was living happily with Vishpala.

Then once enemies attacked Khelaraja’s kingdom. A massive war started. Khelaraja, the leader of the army entered the battle field. Vishpala also entered the battle field.

She killed the enemies as if she was goddess Chamunda, who had descended on the earth. The enemies were also astonished seeing her bravery and courage.

परिच्छेद: 2

एषा …………………………. प्रतिगतवन्तः।

‘एषा रणरङ्गात् यावत् न निवार्यते तावत् जयः सर्वथान प्राप्यते’ इति चिन्तयित्वा शत्रुसैनिकाः युगपत् आक्रम्य ताम् अवरुद्धवन्तः । शत्रुसैनिकाः

ते असङ्ख्याः आसन्, विश्पला तु एकाकिनी ! तथापि तस्या: मनसि न भीतिलेशः अपि आसीत्। प्रत्युत द्विगुणितेन उत्साहेन युद्ध कृतवती। युद्धसमये शत्रुसैनिकाः तस्याः एकं पादं कर्तितवन्तः । अनन्तरम् ‘इतः परम् एतस्याः कारणात् पीडा न भविष्यति’ इति निर्णयं कृत्वा ते शिबिरं प्रतिगतवन्तः ।

अनुवादः

Thinking that unless we remove/stop her from the battlefield we will not win completely, the soldiers of the enemy attacked her from both sides and stopped her. Those enemy soldiers were innumerable but Vishpala was alone.

Still, her heart didn’t have even a bit of fear, rather she fought with double energy, While fighting, the enemy soldiers cut down her foot. Then deciding that, Now she will not create trouble anymore they went to the camp.

‘जोपर्यंत हिला रणांगणातून बाजूला करत नाही तोपर्यंत आपल्याला विजय अजिबात प्राप्त होणार नाही’ असा विचार करून शत्रूसैनिकांनी दोन्ही कडून आक्रमण करून त्याचवेळी तिला अडविले. शत्रूचे सैनिक असंख्य होते विश्पला मात्र एकटी!

तरीसुद्धा तिच्या मनात भीतीचा लवलेशही नव्हता, उलट ती द्विगणित उत्साहाने लवली. युद्धाच्या वेळी शत्रूच्या सैनिकांनी तिचा एक पाय कापला. त्यानंतर आता हिच्यामुळे यापुढे अधिक त्रास होणार नाही’ असा निर्णय घेऊन ते छावणीत परत गेले.

परिच्छेद : 3

यद्यपि …………………….. जाता।

यद्यपि विश्पलायाः पादः भान: तथापि सा हतोत्साहा न जाता। चैतन्यमूर्तिः सा वीराङ्गना एवं आसीत्। ‘श: मया युद्ध करणीयम् एव’ इति निश्चित्य सा पादं पुनः प्राप्तुम् ऐच्छत्। अतः सा निश्चलतया उपविश्य अश्विनीकुमारयोः ध्यानं कृतवती। तस्या; भक्तेः कारणात् अश्विनीकुमारौ लोहयुक्तं पादं योजयित्वा तां यथापूर्व कृतवन्तौ। एतस्मात् विश्पला यथापूर्व चलितुं युद्ध कर्तुं च समां जाता।

अनुवादः

जरी विश्पलेचा पाय कापला गेला होता तरीसुद्धा तिचा उत्साह मावळला नाही. चैतन्यमूर्ती प्रमाणे (तेजोमय) असलेली ती वीरांगनाच (शूर योद्धा) होती. ‘उद्या मला युद्ध करायचेच आहे’ असा निश्चय करून पाय पुन्हा मिळवण्याची तिची इच्छा होती. म्हणून तिने एका जागी निश्चयाने बसून अश्विनीकुमारांचे स्मरण केले. अश्विनीकुमारांनी लोखंडाचा पाय जोडून तिला पूर्ववत केले. त्यामुळे विश्पला पूर्वीसारखे चालण्यास व युद्ध करण्यास समर्थ झाली.

Even though Vishpala’s foot was broken she did not lose courage. She was truly a dynamic brave lady. Deciding that, I have to fight tomorrow she wanted to get her foot back Hence, she sat determined and concentrated upon the (twins) Ashwinikumaras.

Due to her devotion, the Ashwinikumaras attached an iron foot to her leg and made it as before. Because of this, before Vishpala could walk and fight as she could do before.

परिच्छेद : 4

अनन्तरदिने …………….. इतिहासः।

अनन्तरदिने प्रातः सा महता उत्साहेन रणरङ्गम् आगतवती। रणरङ्गे तां दृष्ट्वा एवं शत्रुसैनिकाः चकिता: भीताः च। तस्याः दर्शनमात्रेण एव तेषां धैर्य नष्टं जातम्। सा यदा आयुधप्रहारम् आरब्धवती तदा ते सर्वथा हतोत्साहा: जाताः । विश्पला शत्रून् कदलीवृक्षान् इव लीलया कर्तितवती । सहस्राधिका: सैनिकाः तया संहताः ।

एवं विश्पलायाः शौर्यस्य कारणतः तस्मिन् युद्धे खेलराजस्य एव जयः अभवत्। वीरवनिता विश्पला भर्ना सह रणरङ्गं प्रविश्य शौर्येण युद्धं कृतवती। पादकर्तनानन्तरमपि अश्विनीकुमारयोः अनुग्रहेण पादं पुनः प्राप्तवती शत्रून संहतवती च। एतेन साहसेन सा वेदवाङ्मये बहुधा प्रशंसिता। विश्पलायाः शौर्य तथा च अश्विनीकुमारयोः शल्यक्रियाकौशलं स्मरन्तु इति अस्मान् उपदिशति इतिहासः ।

अनुवादः

दुसऱ्या दिवशी ती मोठ्या उत्साहाने रणांगणात आली. रणांगणात तिला पाहूनच शत्रूचे सैनिक चकित झाले आणि घाबरून गेले. तिच्या केवळ दर्शनानेच त्यांचे धैर्य नष्ट झाले. तिने जेव्हा शस्त्राने प्रहार करण्यास सुरुवात केली तेव्हा तर ते सर्व हताश झाले. विश्पलेने शत्रूना कदलीवृक्षाप्रमाणे सहजरित्या छाटले.

हजारोंपेक्षा अधिक सैनिकांचा तिने संहार केला. अशा प्रकारे विश्पलेच्या शौर्यामुळे त्या युद्धात खेलराजाचाच विजय झाला. शूर महिला विश्पलेने पतीबरोबर युद्धात सहभागी होऊन शौर्यान युद्ध केले. पाय कापला गेल्यानंतरही अश्विनीकुमारांच्या कृपेने पाय पुन्हा मिळवला आणि शत्रूचा संहार केला.

तिच्या साहसामुळे ती वेदवाङ्मयात् खूपच प्रशंसनीय ठरली, विश्पलेचे शौर्य आणि तसेच अश्विनीकुमारांचे शल्यक्रियेतील कौशल्य यांचे स्मरण करा (करावे) असा उपदेश इतिहास आपल्याला करतो.

Next day she came to the battlefield with great energy/enthusiasm. Seeing her on the battlefield, the enemy soldiers were surprised as well as scared.

Their courage vanished just by seeing her. When she started to attack with her weapon, they were completely devasted/depressed. Vishpala cut the soldiers as easily like a plantain/ banana tree. She killed more than a thousand soldiers.

This is how because of Vishpala’s valour Khelaraja was victorious in the battle. The brave lady Vishpala courageously fought entering the battle along with her husband. She got her foot back due to Ashwinikumar’s grace even when it was cut in the war and she destroyed the enemies.

Due to this courage she has been abundantly praised in the Vedic literature several times. History directs us, “Remember Vishpala’s courage and Ashwinikumara’s surgical proficiency.”

सन्धिविग्रहः

• तथैव – तथा + एव।
• तथापि – तथा + अपि।
• यद्यपि – यदि + अपि।
• तथापि – तथा + अपि।
• पादकर्तनानन्तरमपि – पादकर्तनानन्तरम् + अपि ।

समानार्थकशब्दाः

• नृपः – राजा, राट्, पार्थिवः, भूपः, माभृत, महीक्षितः।
• पत्नी – जाया, दारा, कान्ता, भार्या, सहधर्मचारिणी।
• शूरः – धीरः, वीरः।
• युद्धम् – समरः, रणः, सङ्ग्रामः।
• भूः – भूमिः, पृथिवी, वसुन्धरा, धरा।
• संहारः – विध्वंस:, विनाशः।
• विदुषी – पण्डिता।
• जयः – विजयः।
• युगपत् – एकत्र।
• मनसि – चित्ते, मानसे।
• समयः – कालः।
• उत्साहः – जोषः, द्युम्नः।
• चिन्तयित्वा – विचार्य।
• भीतिलेशः – भीतिः, भयम्।
• सैनिकः – शीलधरः, भटः।
• सेना – चमूः।
• भग्नम् – त्रुटितम्, बोटितम्, दर्दरम्।
• कारणम् – हेतुः, निमित्तम्।
• युद्धम् – समरः, रणः, सङ्ग्रामः।
• हतोत्साह – क्षीणोत्साहा।
• निश्चल: – स्थिरः।
• प्राप्तुम् – लब्धम्।
• ध्यानम् – मननम्, आध्यानम्, अन्वीक्षा, योगः।
• पूर्वम् – प्राक्।
• प्रातः – प्रभातम्।
• कौशलम् – नैपुण्यम्, कौशल्यम्।
• भर्ता – पतिः, धवः, प्रियः।

विरुद्धार्थकशब्दाः

• सुखेन × दुःखेन ।
• आरब्धम् × समाप्तम् ।
• प्रविष्टवान् × निर्गतवान् ।
• अवतीर्णा × अधिरूढा।
• संहारः × निर्मितिः, निर्माणम्।
• अनन्तरम् × पूर्वम्, प्राक्।
• भग्नम्र × अखण्डितम्।
• इच्छा × अनिच्छा।
• उपविश्य × उत्थाय।
• निश्चलतया × चालतया।
• पूर्वम् × पश्चात्, अनन्तरम्।
• जयः × पराजयः।
• बहुधा × क्वचित्।
• प्रशंसिता × निन्दिता।

शब्दार्थाः

1. महाविदुषी – scholarly lady – बुद्धिमती
2. रणकुशला – expert in warfare – युद्धात निपुण
3. आक्रमणम् – attack, invasion – आक्रमण
4. महत् – great – महान
5. अवतीर्णा – appeared – अवतरलेली
6. भुवम् – on earth – पृथ्वीवर
7. संहारम् – destruction – संहार, नाश
8. जयः – victory – विजय
9. युगपत् – simultaneously, at once – एकाच वेळी
10. अवरुद्धवन्तः – stopped – थांबवले
11. इतः परम् – anymore / here on – यापुढे अधिक
12. एकाकिनी – alone – एकटी
13. भीतिलेशः – slightest fear – भितीचा लवलेश
14. कर्तितवन्तः – cut – कापले/छाटले
15. हतोत्साहा – depressed – निरुत्साही
16. चैतन्यमूर्तिः – dynamic – लोखंडाचा
17. लोहयुक्तम् – made of iron – चैतन्याची मूर्ती
18. प्रात: – morning – सकाळी
19. आयुधप्रहार: – blow with a weapon – शस्वप्रहार
20. कदलीवृक्षः – banana tree – केळीचे झाड
21. भर्त्रा – with husband – पति बरोबर
22. अनुग्रहेण by grace – कृपेमुळे
23. संहृतवती destroyed – नाश केला
24. शल्यक्रियाकौशलम् – surgical skill – शल्यविद्या कौशल्य
25. संहतः – destroyed – नष्ट

9th Standard Sanskrit Anand Digest Pdf 

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer

Class 9th Sanskrit Aamod Chapter 13 सरमाया: शीलम् Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 13 सरमाया: शीलम् Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 13 Question Answer

Sanskrit Aamod Std 9 Digest Chapter 13 सरमाया: शीलम् Textbook Questions and Answers

भाषाभ्यास:

माध्यमभाषया उत्तरत।

1. सरमायाः कर्तव्यपालने के विघ्नाः अभवन् ?

प्रश्न 1.
सरमायाः कर्तव्यपालने के विघ्नाः अभवन् ?
उत्तरम् :
देवांची कुत्री सरमा तिच्या स्वामिनिष्ठेमुळे वेदवाङ्मयात प्रसिद्ध आहे. पूर्वी पणी नामक असुरांनी देवांच्या गायी पळवल्या, त्या शोधण्यासाठी देवांचा गरुड सुपर्ण पणींच्या देशात गेला. मात्र पणींनी त्याला भेटवस्तू देऊन आपल्याकडे वळवले आणि गोधनाविषयी सुपर्ण याने देवांना काहीच माहिती दिली नाही. गायी शोधण्यासाठी देवांनी त्यांची कुत्री सरमा हिला पाठवले.

पणींच्या देशात जाण्यासाठी सरमेला रसा नदी पार करावी लागणार होती, मात्र ती रसा नदी अतिशय वेगवान होती. ती पार करणे सरमेला शक्य नव्हते; मात्र सोपवलेले काम पूर्ण करायच्या निश्चयाने सरमेने नदीला विनंती केली की तिने तिचा वेग कमी करावा तसेच पाणी उथळ करावे. ज्यामुळे नदी पोहून दुसऱ्या काठावर जाणे शक्य होईल.

मात्र रसा स्वत:ला सर्वश्रेष्ठ समजत असल्याने तिने सरमेची विनंती धुडकावली. रसासारखी वेगवान नदी असूनही सरमेने जराही न डगमगता तिच्यात उडी मारली आणि धैर्याने दुसऱ्या तीरावर पोहोचली. तिथे पोहचल्या नंतर सुद्धा गायी शोधणे सोपे नव्हते. तरीसुद्धा सरमेने चिकाटीने गोधनाचा शोध लावला. इंद्राकडे परतताना पणींनी तिला लालूच दाखवली, तिची निंदा केली. पण सरमेने त्यांना दाद दिली नाही. मार्गात आलेल्या सर्व अडचणींना नेटाने तोंड देऊन सरमेने आपले कर्तव्य बजावले.

In Vedic literature, thestory of सरमा, Indra’s dog is very famous. She is famous for her loyalty towards the Gods. Formerly, the demons named for stole the cattle-wealth of Gods. In order to search the cattle-wealth, the eagle सुपर्ण was sent but the पणिs bribed him. सुपर्ण did not inform Gods about the cattle though he had found it hidden in the cave. Hence, was appointed to search the cattle wealth.

सरमा had to cross the river रसा to reach the country of पणि, रसा was flowing swiftly. It was very difficult for HRAT to cross over; but she did not give up. She requested रसा modestly to slow down her speed so that she would reach the other bank; but the who considered herself superior declined her request.

Yet, without caring for life descended into the current and reached the other bank courageously. She also faced great difficulty in searching the cattle-welath. ufus tried to test her loyalty by trying to bribe her.

Though there were so many difficulties in fulfilling her duty, सरमा overcame those difficulties with determination and accomplished her task.

2. सरमा कर्तव्यपालने विघ्नान् कथं तरति ?

प्रश्न 2.
सरमा कर्तव्यपालने विघ्नान् कथं तरति ?
उत्तरम् :
देवांची कुत्री सरमा तिच्या स्वामिनिष्ठेमुळे वेदवाङ्मयात प्रसिद्ध आहे. पूर्वी पणी नामक असुरांनी देवांच्या गायी पळवल्या. त्या शोधण्यासाठी देवांचा गरुड सुपर्ण पणींच्या देशात गेला. मात्र पणींनी त्याला भेटवस्तू देऊन आपल्याकडे वळवले आणि गोधनाविषयी सुपर्ण याने देवांना काहीच माहिती दिली नाही. गायी शोधण्यासाठी देवांनी त्यांची कुत्री सरमा हिला पाठवले.

पणींच्या देशात जाण्यासाठी सरमेला रसा नदी पार करावी लागणार होती, मात्र ती रसा नदी अतिशय वेगवान होती. ती पार करणे सरमेला शक्य नव्हते; मात्र सोपवलेले काम पूर्ण करायच्या निश्ययाने सरमेने नदीला विनंती केली की तिने तिचा वेग कमी करावा तसेच पाणी उथळ करावे. ज्यामुळे नदी पोहून दुसऱ्या काठावर जाणे शक्य होईल.

मात्र रसा स्वत:ला सर्वश्रेष्ठ समजत असल्याने तिने सरमेची विनंती धुडकावली. रसासारखी वेगवान नदी असूनही सरमेने जराही न डगमगता तिच्यात उडी मारली आणि धैर्याने दुसऱ्या तीरावर पोहोचली. गोधनाच्या शोधासाठी सुद्धा सरमा पणींच्या देशात खूप भटकली. अनेकांना विचारले मात्र कुणीच काही बोलले नाही. शेवटी जंगलातल्या गुहेत शिरुन पणींनी लपवलेल्या गायींचा शोध लावण्यात ती यशस्वी झाली. इंद्राकडे परतताना पणीनी तिला लालूच दाखवली, तिची निंदा केली. पण सरमेने त्यांना दाद दिली नाही.

मार्गात आलेल्या सर्व अडचणींना नेटाने तोंड देऊन सरमेने आपले कर्तव्य बजावले.

In Vedic literature, the story of सरमा, Indra’s dog is very famous. She is famous for her loyalty towards the Gods. Formerly, the demons named for stole the cattle-wealth of Gods. In order to search the cattle-wealth, the eagle सुपर्ण was sent but the पणिs bribed him. सुपर्ण did not inform Gods about the cattle though he had found it hidden in the cave. Hence, सरमा was appointed to search the cattle-wealth.

सरमा had to cross the river रसा to reach the country of पणि. रसा was flowing swiftly. It was very difficult for 1 to cross over; but she did not give up. She requested the modestly to slow down her speed so that she would reach the other bank, but tai who considered herself superior declined her request.

Yet, it without caring for life descended the current and reached the other bank courageously. सरमा wandered here and there to find out the cattlewelath in the country of us. She asked many people there but no one was ready to help her. At the end, she was successful in searching the cattle wealth. wus tried to stop her in every possible manner but सरमा did not step back even a little.

सरमा overcame obstaclescourageously. She was extremly loyal and determined to accomplish her task by defeating all obstacles.

3. पणयः सरमाया: निन्दा कदा अकुर्वन् ?

प्रश्न 3.
पणयः सरमाया: निन्दा कदा अकुर्वन् ?
उत्तरम् :
देवांची कुवी सरमा तिच्या स्वामिनिष्ठेमुळे वेदवाङ्मयात प्रसिद्ध आहे. पूर्वी पणी नामक असुरांनी देवांच्या गायी पळवल्या. त्या शोधण्यासाठी देवांचा गरुड सुपर्ण पणींच्या देशात गेला. मात्र पणींनी त्याला भेटवस्तू देऊन आपल्याकडे वळवले आणि गोधनाविषयी सुपर्ण याने देवांना काहीच माहिती दिली नाही. गायी शोधण्यासाठी देवांनी त्यांची कुत्री सरमा हिला पाठवले.

पणींच्या देशात पोहोचल्यावर सरमैने अतिशय कष्टाने गायींना शोधले. गायींना पाहिल्यावर आनंद झालेली सरमा इंद्राला सांगण्यासाठी निघाली. हे पाहिल्यावर पणींनी तिला अनेक प्रकारे फितवण्याचा, आपल्याकडे वळवण्याचा प्रयत्न केला. तिला दूध, तूप, दही खाण्याचा आग्रह केला. इतकेच नाही तर गोधनातील काही भागही देऊ केला, मात्र सरमा बधली नाही. तेव्हा पणींनी तिची निंदा करण्यास सुरुवात केली. जेणेकरून सरमा इंद्राकडे जाण्यापासून परावृत्त होईल.

In Vedic literature, the story of सरमा, Indra’s dog is very famous. She is famous for her loyalty towards the Gods. Formerly, the demons named for stole the cattle-wealth of Gods. In order to search the cattle-wealth, the eagle you was sent but the पणी bribed him. सुपर्ण did not inform Gods about the cattle though he had found it hidden in the cave. Hence, सरमा was appointed to search the cattle-wealth.

सरमा searched for the cattle-wealth rigorously. There was no help available. She succeeded in finding out the cattle-wealth hidden in one of the caves in the forest. Immediately she started to return to inform the gods. quit tried to bribe her. They offered her milk, butter, ghee. They were ready to share some of the cattle-welath with her; but she refused everything and remained loyal to her duty. Then the Panis started to criticise her to stop from going back to Indra.

4. पणयः सरमां किमर्थं निन्दन्ति ?

प्रश्न 4.
पणयः सरमां किमर्थं निन्दन्ति ?
उत्तरम् :
देवांची कुत्री सरमा तिच्या स्वामिनिष्ठेमुळे वेदवाङ्मयात प्रसिद्ध आहे. पूर्वी पणी नामक असुरांनी देवांच्या गायी पळवल्या. त्या शोधण्यासाठी देवांचा गरुड सुपर्ण पणींच्या देशात गेला. मात्र पणींनी त्याला भेटवस्तू देऊन आपल्याकडे वळवले आणि गोधनाविषयी सुपर्ण याने देवांना काहीच माहिती दिली नाही. गायी शोधण्यासाठी देवांनी त्यांची कुत्री सरमा हिला पाठवले.

देवांच्या गायी पळवून आणल्यानंतर पणींनी त्या गुहेत दडवून ठेवल्या. देवांची कुत्री सरमा हिने अतिशय कष्टाने त्या शोधल्या आणि त्यांची माहिती देण्यासाठी की इंद्राकडे निघाली. सुपर्ण गरुडाप्रमाणे सरमेला आपल्याकडे वळवून घेण्याचा प्रयत्न पणींनी केला मात्र सरमा त्याला बदली नाही. तिने मी लोभाला बळी पडणार नाही. मी इंद्राची स्वामिनिष्ठ सेविका आहे असे ठणकावले.

हे ऐकताच पणी खवळले आणि सरमेचा अपमान केला. सरमा ही मांस खाते असा अपप्रचार केला. यामुळे सरमेचे मनोबल बळेल, असे पणींना वाटले, मात्र अविचल कार्यनिष्ठा असलेली सरमा पणींकडे दुर्लक्ष करून निघाली.

In Vedic literature, the story of सरमा, Indra’s dog is very famous. She is famous for her loyalty towards the Gods. Formerly, the demons named for stole the cattle-wealth of Gods. The was appointed to search the cattle wealth.

सरमा searched for the cattle-wealth rigorously. There was no help available. She succeeded in finding out the cattle-wealth hidden in one of the caves in the forest. Immediately she started to return to inform ths gods. for tried to bribe her.

They offered her milk, butter, ghee. They were ready to share some of the cattle-welath with her; but सरमा with undisturbed mind igonored पणि, After that पणि criticized सरमा that she consumes meat. for thought that he would get discouraged due to insult and would not inform gods.

Sanskrit Aamod Class 9 Textbook Solutions Chapter 13 सरमाया: शीलम् Additional Important Questions and Answers

धातुसाधितविशेषणानि।

धातुसाधित – विशेषणम्	विशेष्यम्
दृष्टः	किङ्करः
नियुक्ता, आज्ञप्ता, प्रस्थिता, प्राप्ता, प्रमुदिता, अवरोधिता, निन्दिता	सरमा
दृष्टा, पराभूता	रसा
रुद्धम्	गोधनसर्वस्वम्
समाप्तम्	अन्वेषणकार्यम्
अन्विष्टाः	धेनवः
अपिहितम्	कर्णद्वयम्

सरमाया: शीलम् Summary in Marathi and English

प्रस्तावना :

प्राण्यांच्या चातुर्यकथा, नीतीकथा जगभरातील साहित्यात खूप प्रसिद्ध आहेत. रामायणातसुद्धा सागरी सेतू बांधण्यासाठी श्रीरामाला मदत करणाऱ्या खारीची गोष्ट येते. सरमा नामक कुत्रीची, तिच्या अविचल स्वामिनिष्ठेची कथा प्रसिद्ध आहे. पूर्वी यणी नामक असुरांनी देवांचे गोधन चोरले. ते शोधण्यासाठी सुपर्ण गरुडास देवांनी पणींच्या देशात पाठवले मात्र पणींनी सुपर्णाला लाच देऊन आपल्याकडे वळवले त्यामुळ देवांना गोधनाविषयी माहिती मिळाली नाही.

देवांनी या कामी सरमा नावाच्या कुत्रीला पाठवले. मार्गात येणाऱ्या वेगवान रसा नदीला ओलांडून, पणींच्या देशात निर्भयतेने शोध घेऊन सरमेने गोधन शोधले. पणींच्या लोभाला बळी न पडता सरमेने इंद्राला सर्व वृत्तांत सांगितला. कामात यशस्वी झालेल्या सरमेला इंद्राने वर दिला तर द्रोही गरुडाला शाप. सरमा ही कुत्री असूनही कार्यनिष्ठा, स्वामिनिष्ठा, धैर्य, स्वाभिमान या गुणांच्या जोरावर आदर्श ठरली तिच्या या कर्तृत्वाचे वर्णन पं. प्रभाकर भातखंडे यांनी संस्कृत पोवाड्यातून केले आहे. पोवाडा हा महाराष्ट्रातील लोककलाप्रकार असून त्यात वीररसाचे महत्त्वाचे स्थान आहे. शूरांच्या गाथा सांगण्यासाठी पोवाड्याची रचना केली जाते.

Stories advising morals through animals is very famous idea in literature all over the world. Infact several values are taught through the medium of animals and birds. This is dates back to the vedic period.

In the Ramayana too a story of squirrel helping the monkeys while building the bridge is known. The story of सरमा a dog from the ऋग्वेद is famous for her firm loyalty. It is said that some demons called ufuis once stole the cattle wealth of gods. Indra sent their eagle yup to look for the cattle. But the ufus bribed it and turned it on their side.

So Indra did not get any information about their cattle. Then Indra sent सरमा for the same task. सरमा accomplished her task fighting against all odds. Indra blessed ERCAT with a boon and cursed the eagle सुपर्ण..

सरमा set an example of courage, loyalty and commitment even if she was a bitch (female dog). This पोवाडा composed by पं. प्रभाकर भातखंडे celebrates T’s courageous behaviour. पोवाडाis a type of Marathi folk songs. The essence of bravery (a) is highlighted in these kind of songs. This present day creation is a beautiful example of Vedic story in a form that can reach the modern generation is very attractive manner.

शाहिरः – सभायां ………………… हे जी जी जी जी जी ।।

शाहिरः – सभायां देवराज इन्द्रः
चिन्तयति कः प्रेषितव्यः।
किकरो नैकोऽपि दृष्टः
यो भवेत् सदा स्वामिनिष्ठः।।

गायकवृन्दः – तदा?
शाहिरः – सेवायां तत्परा, देवगणप्रिया,
नियुक्ता गोधनप्राप्त्यर्थम्।
मघवता आज्ञप्ता सरमा,
प्रस्थिता देवशुनी सरमा। हे जी जी जी जी।।

गायकवृन्दः – प्रस्थिता देवशुनी सरमा। हे जी जी जी जी जी।
शाहिरः – तदा मार्गे दृष्टा, तटरुहतरुत्पाटिनी रसा
जलौघसमृद्ध्या पृथुलरभसा याति सरसा।।

रसां दृष्टा सरमया चिन्तितम् –
“अवश्यं गच्छेयं नदी यदि भवेत् अद्य सुसहा।
अतस्तां याचेऽहं विनयवचसा नम्रशिरसा।।
रसे, कुरु कृपाम्।
जलं तवेदम् । महागभीरम्।
कुरुष्व गाधम् । येन तरेयम्।
परं च तीरम् । अहं व्रजेयम् ।
स्वामिनः शोभनकार्यार्थम्,
आर्यगणमङ्गलकार्यार्थम्।

गायकवृन्दः – आर्यगणमङ्गलकार्यार्थम्। हे जी जी जी जी।।
रसा उवाच – “अहं च श्रेष्ठा, त्वं तु क्षुद्रा
न हि त्वदर्थ, जलप्रवाहम्।
करोमि अल्पम्, अपसर अपसर।।
श्रुत्वा तद् वाक्यं सरमया गर्जितम्।
“पश्य मे सामर्थ्य, कार्यनिष्ठासामर्थ्यम्
इति उक्त्वा सा जले अपतत्

शाहिरः – सा गता परं तीरम्।
रसा सा अधोमुखी भूता।
लज्जया म्लानमुखी जाता।
क्षुद्रया कथं पराभूता।
पश्यति क्षुद्रशुनीं सरमाम्।

गायकवृन्दः – पश्यति क्षुद्रशुनीं सरमाम्।
हे जी जी जी जी जी।।

गद्यम्: – एवं सरमा परतीरं प्राप्ता।
इतः पश्यति, ततः पश्यति
वलं पृच्छति, पणीन् पृच्छति।।
वनं गच्छति, गुहां प्रविशति।
गुहायां पणिभिर्यद्रुद्धं प्रभोः गोधनसर्वस्वम्।
समाप्तमन्वेषणकार्य, समाप्तमन्वेषणकार्यम्।।

गायकवृन्दः – प्रमुदिता इन्द्रशुनी सरमा हे जी जी जी जी जी।।
गद्यम्: – सरमया धेनवः अन्विष्टाः।
एतां वार्ताम् इन्द्रं वक्तुं प्रस्थिता सा।
परं वलैः सा अवरोधिता।

गायकवन्दः – हे सरमे, हे सरमे, दुग्धं पिबतु, दधि खादतु।
घृतं पिबतु, अत्र तिष्ठतु
गोधनस्य भागं तुभ्यं दद्यः।।

सरमा – सेविका नाहं लोभस्य,सेविका नाहं मोहस्य।
गायकवृन्दः – सेविका स्वामिनः इन्द्रस्य।
हे जी जी जी जी जी।।
सेविका स्वामिनः इन्द्रस्य।
हे जी जी जी जी जी।।

गद्यम्: – अन्ते पणिभि: सरमा निन्दिता।
“एषा सरमा जारु खादति।
“एषा सरमा जारु खादति।
सरमया किश्चत् तन्त्र श्रुतम्।
अपिहितं दीर्घ कर्णद्वयम्।
“वृत्तान्तं वक्तुं गमनमारभे।
प्रस्थिता सत्यप्रिया सरमा।

गायकवृन्दः – प्रस्थिता देवशुनी सरमा।
हे जी जी जी जी जी।।

अनुवादः

शाहीर – सभेमध्ये देवराज इंद्र (बसला आहे) कोणाला पाठवावे याचा विचार करत आहे. त्याला एकही सेवक दिसला
नाही – जो सदैव स्वामिनिष्ठ असेल.
गायकगण – तेव्हा मग पुढे?
शाहीर – सेवेमध्ये तत्पर असलेली, देवांची लाडकी, गोधन मिळवण्यासाठी नियुक्त झालेली, इंद्राने आशा दिलेली, सरमा देवांची कुत्री सरमा निघाली.
गायकगण – देवांची कुत्री सरमा निघाली.
शाहीर – तेव्हा तिने वाटेत काठावर वाढलेल्या झाडांना उन्मळून (पाडून) टाकणारी रसा (नदी) पाहिली. पाण्याच्या समृद्ध प्रवाहने (ती) रसा वेगाने वाहत होती. रसेला पाहून सरमेने विचार केला, “आज नदी सुसहा (तरुन जाण्यायोग्य झाली) झाली तर मी अवश्य जाईन. म्हणून मी तिला नम्र बोलण्याने, डोके टेकवून विनंती करते. रसे, कृपा कर, तुझे पाणी खूप खोल आहे. ते उथळ कर. जेणेकरुन मी पोहून जाईन. दुसऱ्या तीरावर मी जाईन. स्वामींच्या (इंद्राच्या) कार्यासाठी आर्यांच्या (देवांच्या) मंगल कामासाठी (मी जात आहे.)
गायकगण – आर्यांच्या (देवांच्या) मंगल कामासाठी (मी जात आहे.)
रसा म्हणाली – मी श्रेष्ठ, तू क्षुद्र जलप्रवाह तुझ्यासाठी नाही करणार उथळ! (कमी) मागे हो, मागे हो. ते वाक्य ऐकून सरमा गर्जली. माझे सामर्थ्य बघ, कार्य निष्ठेची शक्ती बघ असे म्हणून ती पाण्यात उतरली.
शाहीर – ती दुसऱ्या तीरावर गेली. त्या रसेने तोंड झुकवले. लाजेने तिचे तोंड उतरले. मी क्षुद्र कुत्रीकडून कशी पराभूत झाले? (असे म्हणत ती) क्षुद्र सरमेला पाहू लागली.
गायकगण – क्षुद्र सरमेला पाहू लागली.
गद्य – अशा रीतीने सरमा दुसऱ्या तीरावर गेली. इथे पाहिले, तिथे पाहिले. वलांना विचारले, पणींना विचारले, वनात गेली, गुहेत शिरली, गुहेमध्ये देवांचे गोधन पणींनी दडवून ठेवले होते. शोधकार्य संपले, शोधकार्य संपले.
गायकगण – इंद्राची कुत्री सरमा आनंदली.
गद्य – सरमेने गायी शोधल्या ही बातमी इंद्राला सांगण्यासाठी ती निघाली मात्र वलांनी तिला अडवले.
गायकगण – अगं सरमे, दूध पी, दही खा. तूप पी, इथेच थांब गोधनाचा भाग तुलाही देतो आम्ही.
सरमा – मी लोभाची सेविका नाही. मी मोहाची सेविका नाही. (मी लोभामोहाने बधणार नाही.)
गायकगण – इंद्राची सेविका.
इंद्राची सेविका.
गद्य – शेवटी पणींनी सरमेची निंदा केली ही सरमा मांस (क्षुद्रान) खाते. सरमेने ते काहीएक ऐकून घेतले नाही. तिने आपले दोन मोठे कान बंद केले. वृत्तांत सांगण्यासाठी मी जात आहे. सत्यप्रिय सरमा निघाली.
गायकगण – देवांची कुत्री सरमा निघाली.

Shahir : In the assembly, Indra the king of Gods thought who should be sent. He didn’t see any servant who would be ever loyal.
Chorus : Then?
Shahir : Sarama, who was prompt in service, liked by the gods was appointed to bring the cows. Sarama the dog of the Gods who was ordered by Indra set off.
Chorus : The dog of the Gods Sarama set off.
Shahir : Then on the way she saw Rasa (river) who uprooted trees that grow on the banks, flowing with force with a strong current. Seeing Rasa Sarama thought, I shall surely go today if the river becomes tolerable (less forceful). So, I shall ask her modestly with modest words) and head bent in modestly. ‘Oh, Rasa, please do a favour. Your water is very deep. Please make it shallow. By which I shall cross to the other bank. I shall go for the good task of the master, for the auspicious task of the noble ones.
Chorus : For the auspicious task of the noble ones.
Rasa said : “I am superior and you are inferior. I shall not reduce the water current, move away, move away.” Listening to those words, Sarama roared, “See my capacity, the power of my dedication.” saying this she fell (jumped) into the water.
Shahir : She went to the other bank. Rasa was ashamed. She became sad due to shame. How was she defeated by some one inferior. Looks at that lowly dog Sarama.
Chorus : (She) looks at that lowly dog sarama.
Prose : Thus Sarama reached the other bank. She looks here, she looks there. She asks the Vala, she asks the demons. She goes to the forest, she enters the cave. In the cave is all the Lord’s cattle wealth trapped by the demons. The search was over, the search was over.
Chorus: Sarama the God’sdog was delighted.
Prose : Sarama had found the cattle. She set off to inform this news to Indra. But she was stopped by the Valas.
Chorus: O Sarama, O Sarama. Drink milk, eat curds, drink ghee, wait here. We shall give you a part of the cattle wealth.
Sarama : I am not servant of greed. I am not servant of illusion
Chorus : Servant of Lord Indra.
Servant of Lord Indra.
Prose : Finally Sarama was criticised by the demons. “This Sarama eats flesh” But. Sarama paid no heed to all that. She closed the two long ears and started to depart to narrate the account. The truth lover Sarama set off.
Chorus : Sarama the god’s dog set off.

शब्दार्थाः

1. उपहार: – gift – बक्षीस, नजराणा
2. प्रेषितव्यः – should be sent – पाठवण्याजोगा
3. किड्करः – servant – नोकर, सेवक
4. गोधनम् – cattle wealth – गोधन
5. मघवान् – Lord Indra – इंद्रदेव
6. ‘तटरुहतरुः – tree that grows on the banks – झाड
7. जलौघः – water-current – पाण्याचा प्रवाह
8. पृथुलरभसा – with tremendous speed – अत्यंत वेगाने
9. विनयवचसा – with modest speech – विनयपूर्ण वाणीने
10. गभीरम् – deep – खोल
11. म्लानमुखी – sad – खिन्न
12. परतीरम् – to other bank – पलीकडच्या काठावर
13. वलम् – community of demons Pani – पणि नावाचे असूर
14. अन्विष्टाः – found – सापडल्या
15. घृतम् – ghee – तूप
16. जारुः – flesh/bad food – मांस, निकृष्ट खाणे

Aamod Sanskrit Book 9th Class Solutions

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• धन्यौ तौ दातृयाचकौ Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• योगमाला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• पितृभक्तः नचिकेताः Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• सरमाया: शीलम् Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer
• स्वागतं तपोधनाया: Class 9 Question Answer

Class 9th Sanskrit Aamod Chapter 9 सूक्तिसुधा Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 9 सूक्तिसुधा Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 9 Question Answer

Sanskrit Aamod Std 9 Digest Chapter 9 सूक्तिसुधा Textbook Questions and Answers

भाषाभ्यास:

श्लोकः 1

1. एकवाक्येन उत्तरत।

प्रश्न अ.
कैः धनं न हीयते?
उत्तरम् :
चौरेण, राज्ञा च विद्याधनं न ह्रियते।

प्रश्न आ.
केषु धनं न विभज्यते ?
उत्तरम् :
भ्रातृषु धनं न विभज्यते।

प्रश्न इ.
सर्वधनप्रधानं किम् ?
उत्तरम् :
सर्वधनप्रधानं विद्याधनम् ।

2. माध्यमभाषया उत्तरत।

प्रश्न 1.
विद्याधनं व्यये कृते कथं वर्धते ?
उत्तरम् :
‘सूक्तिसुधा’ या पद्यपाठामध्ये विविध संस्कृत साहित्यकृतींमधून सुभाषिते संकलित केली आहेत. प्रसङ्गाभरणम् मधील श्लोक विद्येचे महत्त्व सांगतो. विद्या हे धन असे आहे जे कोणी चोरू शकत नाही, जे राजा कुणाकडून घेऊ शकत नाही, विद्याधन हे भावंडांमध्ये इतर मालमत्तेप्रमाणे वाटले जाऊ शकत नाही व त्याचे कधी ओझे सुद्धा होत नाही.

पैसा खर्च केला की तो कमी होतो, पण विद्याधन मात्र जितके वाटू तितके वाढते. आपण आपल्याकडचे ज्ञान जेव्हा दुसऱ्याला देतो तेव्हा त्याच्याकडूनसुध्दा आपल्याला अधिक ज्ञान मिळते. चर्चामधून, ज्ञानाच्या आदान-प्रदानामधून आपल्या ज्ञानात वाढच होते. ज्ञान दिल्याने वाढते, हा संदेश या श्लोकातून दिला आहे.

In the lesson ‘सूक्तिसुधा’ various subhashitas are collected from different literature pieces of Sanskrit. – In the shloka from प्रसङ्गाभरणम् the importance of knowledge is expressed. Knowledge can neither be stolen nor it can be taken away by king. It is indivisible and is not burden either.

Knowledge is that kind of a wealth which increases though spent unlike other riches. When we impart knowledge to someone, through that interaction we gain more knowledge. Here knowledge increases but never decreases. This special feature of knowledge suggests us that we should always share our knowledge and it is the greatest wealth.

3. सन्धिविग्रहं कुरुत ।
वर्धत एव ।

प्रश्न 1.
वर्धत एव ।
उत्तरम् :
वर्धत एव – वर्धते + एव।

4. समानार्थकशब्द लिखत।
चोरः, भारः, नित्यम्, विद्या, धनम्, प्रधानम् ।

प्रश्न 1.
चोरः, भारः, नित्यम्, विद्या, धनम्, प्रधानम् ।
उत्तरम् :

• चोरः – तस्करः, स्तेनः।
• नित्यम् – सदा, सर्वदा, सदैव।
• विद्या – ज्ञानम्।
• धनम् – वित्तम्।
• प्रधानम् – प्रमुखम्।

5. विरुद्धार्थकशब्द लिखत।
व्ययः, नित्यम्, प्रधानम्।

प्रश्न 1.
व्ययः, नित्यम्, प्रधानम्।
उत्तरम् :

• व्ययः × सञ्चयः।
• नित्यम् × क्वचित्।
• प्रधानम् × गौणम्, तुच्छम्।

श्लोक: 2

1. सन्धिं कुरुत।

प्रश्न 1.
अ. परः + वा + इति
आ. वसुधा + एव
उत्तरम् :
अ. परो वेति – पर: + वा + इति।
आ. वसुधैव – वसुधा + एव।

2. एकवाक्येन उत्तरत।

प्रश्न अ.
‘अयं निजः, अयं परः’ इति केषां गणना ?
उत्तरम् :
अयं निजः, अयं परः इति लघुचेतसाम् गणना।

प्रश्न आ.
केषां कृते वसुधा एव कुटुम्बकम् भवति?
उत्तरम् :
उदारचरितानां कृते वसुधा एव कुटुम्बकम् अस्ति।

3. माध्यमभाषया उत्तरत।

प्रश्न 1.
लघुचेतसः उदारचेतसः जनाः कथम् अभिज्ञातव्याः ?
उत्तरम् :
दररोजच्या आयुष्यात आपण अनेक मूल्ये, तत्त्वे पाळतो ज्यांच्यामुळे आपल्या आयुष्याला आकार मिळतो व ते अधिक समृद्ध होते. अशाच काही मूल्यांचा संदेश ‘सूक्तिसुधा’ या पद्यपाठातून दिला आहे.

शाईधरपद्धति मधून घेतलेल्या या श्लोकात उदार माणसांच्या गुणांचा गौरव केला आहे. काही माणसे नेहमी हे माझे, हे तुझे असे म्हणून गोष्टींमधे भेद करतात. त्यांच्या स्वत:च्या गोष्टींपुरतेच ते पाहतात व जे परके, आपले नाही त्याच्याशी काही देणे-घेणे ठेवत नाहीत. अशी माणसे कोत्या मनाची समजावीत. या उलट जी माणसे मनाने उदार असतात त्यांच्यासाठी संपूर्ण विश्वच त्यांचे कुटुंब असते. हे विश्वची माझे घर असे म्हणणारे संत हे उदार मन असणाऱ्या माणसांमध्ये गणले जातात.

In our day to day life, we follow certain values, certain morals that enchance our lifestyle. ‘सूक्तिसुधा’ talks about such values.

In the shloka taken from शाईधरपद्धति the nature of noble and generous people is described. It says that those who consider things as mine and not mine are low-minded. They delimit the things as their own and not belonging to them. But to those who are really generous, the whole earth is like their own family.

Great saints treat the whole universe like their own, they never hesitate to enlighten or help others irrespective of who they are. A person with a big heart is always praised and looked upon for help in any difficult situation. Such people are very hard to find. However, people with an inferior mind or nonassimilative nature are known by their attitude of being self-centered.

4. स्तम्भमेलनं कुरुत |

प्रश्न 1.

अ	स्वीयम्	चिन्तनम्	अन्यः	पृथिवी
आ	गणना	वसुधा	निजः	परः

उत्तरम् :

अ	स्वीयम्	चिन्तनम्	अन्यः	पृथिवी
आ	निजः	गणना	परः	वसुधा

श्लोकः 3

1. एकवाक्येन उत्तरत।

प्रश्न अ.
परोपकाराय वृक्षाः किं कुर्वन्ति ?
उत्तरम् :
परोपकाराय वृक्षाः फलन्ति ।

प्रश्न आ.
परोपकाराय नद्यः किं कुर्वन्ति ?
उत्तरम् :
परोपकाराय नद्यः वहन्ति ।

प्रश्न इ.
काः परोपकाराय दुहन्ति ?
उत्तरम् :
परोपकाराय गाव: दुहन्ति।

प्रश्न ई.
शरीरं किमर्थम् ?
उत्तरम् :
परोपकारार्थ शरीरम्।

2. माध्यमभाषया उत्तरत।

प्रश्न 1.
परोपकार: नाम किम् ? के परोपकारमग्नाः ?
उत्तरम् :
‘सूक्तिसुधा’ या पद्यपाठामध्ये प्रत्यक्ष आयुष्यात आचरणात आणण्यासाठीचे संदेश सुंदर शब्दांत काव्यात्मकप्रकाराने दिले आहेत. ‘विक्रमोर्वशीयम्’ या नाटकातून घेतलेल्या श्लोकामध्ये परोपकाराचे महत्त्व सांगितले आहे. इतरांना कोणत्याही परतफेडीची अपेक्षा न ठेवता मदत करणे म्हणजे परोपकार. काही व्यक्ती या कायमच दुसऱ्याच्या चांगल्याचा विचार करत असतात.

अशा व्यक्तींना आपण संत-महात्मा म्हणून त्यांचा गौरव करतो. प्रस्तुत श्लोकात निसर्गातील उदाहरणे देऊन परोपकाराचे माहात्म्य सांगितले आहेत. वृक्ष इतरांना देण्यासाठीच फळे धारण करतात. त्या फळांच्या बदल्यात ते कशाची अपेक्षा करत नाहीत. नद्या गावोगावांना पाणी पुरवत वाहतात. त्यांचा स्वत:चा त्यात काही वैयक्तिक लाभ नसतो.

गायी इतरांसाठीच दूध देतात. अशाप्रकारे झाडे, नद्या, गायी हे परोपकराचा संदेश नेहमी देत असतात, रोजच्या व्यवहारातील निसर्गाच्या उदाहरणांमधून परोपकाराचे महत्त्व सांगितले आहे.

In the lesson’सूक्तिसुधा’ various shlokas filled with value based messages are given. They teach us many values such as selflessness, charity, knowledge. In the shloka taken from ‘विक्रमोर्वशीयम्’ the greatness of selfless behaviour is emphasized.

परोपकार means helping othersselflessly. To help others and not expecting anything in return is a great virtue. Only noble ones possess such a rare quality. The trees bear fruits for others. They don’t eat the fruits they bear.

The rivers flow for people like us. The cows yield milk for others. They don’t see their benefit in doing so. Likewise, our life is also for helping others. These subhashita gives a message that however busy we may get, we should always spare some time to help others selflessly.

3. एकवचने परिवर्तयत।

प्रश्न अ.
वृक्षाः फलन्ति।
उत्तरम् :
वृक्षाः परोपकाराय फलन्ति ।

प्रश्न आ.
नद्य: वहन्ति ।
उत्तरम् :
नद्यः परोपकाराय वहन्ति।

4. समानार्थकशब्द लिखत।
वृक्षाः, नद्यः, शरीरम्।

प्रश्न 1.
वृक्षाः, नद्यः, शरीरम्।
उत्तरम् :

• वृक्ष: – तरुः।
• नद्यः – सरित्।
• शरीरम् – तनुः, देहः।

5. विरुद्धार्थकशब्द लिखत।

प्रश्न 1.
उपकारः, परः ।
उत्तरम् :
1. उपकार: × अपकारः
2. परः × निजः।

श्लोक: 4

1. रिक्तस्थानं पूरयत।

प्रश्न 1.
अ. सत्सङ्गतिः धियः जाड्यं ………..।
आ. सत्सङ्गतिः वाचि ……….. सिञ्चति।
इ. सत्सङ्गतिः ……….. दिशति ।
ई. सत्सङ्गतिः पापम् ……….. ।
उ. सत्सङ्गतिः चित्तं ……….. ।
ऊ. सत्सङ्गति दिक्षु ……….. तनोति।
उत्तरम् :
अ. हरति
आ. सत्यम्
इ. मानोन्नतिम्
ई. अपाकरोति
उ. प्रसादयति
ऊ. कीर्तिम्

2. माध्यमभाषया उत्तरत।

प्रश्न 1.
सत्सङ्गतिः जीवने किं किं करोति ?
उत्तरम् :
It is said that one is known by the company he keeps. The people around us lay great impact on our life. Company of good people takes away ignorance of the intellect. It makes us truthful. Due to company of good people one gains more respect. Our sins get wiped away when we are surrounded by virtuous people.

It doesn’t only make us happy but also spreads fame in all directions. Company of good people is always desirable. They always pass on the good qualities to everyone they are around. Company of good people is desirable in every aspect.

‘सुसंगति सदा घडो, सुजन वाक्य कानी पडो’ असे म्हणतात. सज्जनांच्या संगतीमुळे आपला उद्धार होतो हे खरेच आहे. ‘सूक्तिसुधा’ च्या या श्लोकात हे सांगितले आहे. चांगल्या माणसांच्या संगतीमुळे बुद्धीचे अज्ञान दूर होते. ते सत्याची शिकवण देतात. चांगल्या लोकांच्या संगतीत राहिल्यामुळे आपल्याला अधिक मान मिळतो.

सद्संगतीमुळे आपल्यातील वाईट वृत्तींचा नाश होतो. त्यामुळे आपण पापांपासून लांब राहतो. सज्जनांबरोबर राहिल्यामुळे वाईट गोष्टी आपल्यापासून आपोआप लांब राहतात आणि मन प्रसन्न राहते. सज्जनांबरोबर राहिल्यामुळे त्यांच्याप्रमाणेच आपली सुद्धा प्रसिद्धी सर्वदूर परसते.

श्लोक: 5

1. सन्धिविग्रहं कुरुत।
नार्यस्तु, यत्रैताः, एतास्तु, तत्राफलाः, सर्वास्तत्र ।

प्रश्न 1.
नार्यस्तु, यत्रैताः, एतास्तु, तत्राफलाः, सर्वास्तत्र ।
उत्तरम् :

• नार्यस्तु – नार्यः + तु।
• यौतास्तु – यत्र + एता: + तु।
• सर्वास्तत्राफला: – सर्वाः + तत्र + अफलाः।

2. एकवाक्येन उत्तरत।

प्रश्न अ.
देवताः कुत्र रमन्ते ?
उत्तरम् :
यत्र नार्यस्तु पूज्यन्ते रमन्ते तत्र देवताः।

प्रश्न आ.
क्रियाः कुत्र अफलाः भवन्ति ?
उत्तरम् :
यत्र तु एता: न पूज्यन्ते तत्र सर्वाः क्रियाः अफला: (भवन्ति)।

3. माध्यमभाषया उत्तरत। 

प्रश्न 1.
‘यत्र नार्यः पूज्यन्ते’। इति सूक्तिं श्लोकस्य आधारेण स्पष्टीकुरुत।
उत्तरम् :
‘सूक्तिसुधा’ पाठामध्ये रोजच्या आयुष्यात आचरणात आणण्यासारखी अशी मूल्ये सांगितली आहेत. महाभारतातील श्लोकामध्ये ‘स्त्रियांचा आदर करावा’ हे त्रिकालाबाधित तत्त्व सांगितले आहे. जिथे स्त्रियांना आदर दिला जातो, तिथे देवता सुद्धा आनंदाने राहतात. मात्र जिथे स्त्रियांचा अनादर होतो तिथे कोणतेही कार्य सफल होत नाही.

ज्या समाजामध्ये स्त्रियांना मानसन्मान मिळतो तो समाज प्रगत समजला जातो. हे तत्त्व आजही लागू होते. ‘देव आनंदाने राहतात’ म्हणजे ते स्थान पवित्र व रम्य मानले जाते. त्या ठिकाणी नेहमी सकारात्मकता, उत्साह राहतो.

In the lesson ‘सूक्तिसुधा’ different values, are taught which we should apply in our life. Averse fromमहाभारत tells an important value to respect women which is absolute irrespective of time or situation. Since ancient times, the scriptures have taught to respect each and every woman.

In this particular shloka, it is said that where the women get respect Gods dwell there happily. But where women are not respected, no action gets accomplished in such place. So respecting women is a sign of good and developed society.

4. एकवचने परिवर्तयत।

प्रश्न अ.
नार्यः पूज्यन्ते।
उत्तरम् :
यत्र नार्यः पूज्यन्ते

प्रश्न आ.
देवताः रमन्ते ।
उत्तरम् :
तत्र देवता: रमन्ते।

प्रश्न इ.
एता: न पूज्यन्ते ।
उत्तरम् :
यत्र तु एता: न पूज्यन्ते

प्रश्न ई.
सर्वाः क्रियाः अफलाः।
उत्तरम् :
तत्र सर्वाः क्रियाः अफला:

5. ‘नारी’ इत्यर्थम् अमरकोषपङ्क्तिं लिखत ।

प्रश्न 1.
‘नारी’ इत्यर्थम् अमरकोषपङ्क्तिं लिखत ।

श्लोक: 6

1. सन्धिविग्रहं कुरुत।

प्रश्न 1.
अ. चातक: + ………… = चातकस्त्रिचतुरान् ।
आ. सोऽपि = …………… + अपि।
इ. विश्वम् + अम्भसा = ………………
ई. महताम् + ……………… = महतामुदारता।
उत्तरम् :
अ. चातकस्त्रिचतुरान् – चातकः + त्रिचतुरान्।
इ. सोऽपि – सः + अपि।
इ. विश्वमम्भसा – विश्वम् + अम्भसा।
ई. महतामुदारता – महताम् + उदारता।

2. एकवाक्येन उत्तरत।

प्रश्न अ.
चातकः पय:कणान् कं याचते ?
उत्तरम् :
चातक: पयःकणान् जलधर याचते।

प्रश्न आ.
जलधर: केवलं चातकस्य तृष्णां शाम्यति उत सम्पूर्ण विश्वस्य ?
उत्तरम् :
जलधर: सम्पूर्णविश्वस्य तृष्णां शाम्यति।

प्रश्न इ.
महताम् उदारता कस्य दृष्टान्तेन ज्ञायते ?
उत्तरम् :
महताम् उदारता जलधरस्य दृष्टान्तेन ज्ञायते ।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
महताम् उदारता श्लोके कथं वर्णिता ?
उत्तरम् :
‘सूक्तिसुधा’ या पद्यामध्ये सुंदर सुभाषिते एकत्र केली आहेत. पूर्वचातकाष्टकम् मधील या श्लोकात उदार लोकांच्या प्रवृत्तीची स्तुती केली आहे. संस्कृत साहित्यामध्ये अशी कविकल्पना आहे की चातक पक्षी हा केवळ पावसाचे पाणी पितो. ढगातून येणारे पाणी पिऊनच तो स्वत:ची तहान भागवतो. पावसाळ्याच्या सुरुवातीला तो खूप आतुरतेने काळ्या ढगांची वाट पाहतो व आर्त हाक मारून ढगाकडे पाण्याची याचना करतो.

याच कल्पनेचा आधार घेऊन कवी म्हणतो की तहान भागवण्यासाठी चातकाने ढगाकडे काही थेंबांची याचना केली असताना ढग मात्र संपूर्ण पृथ्वीच पाण्याने चिंब करुन टाकतो, अशा ढगाची व दानतत्पर उदार प्रवृत्तीच्या माणसाच्या वर्तनातील साम्य या श्लोकात ‘अन्योक्ती’ द्वारे कविने सांगितले आहे.

उदार वृत्तीचे लोक सुद्धा एक गोष्ट मागितली असता त्यांच्याकडे असणारे सर्वकाही कुणालातरी द्यावे लागले तरी कशाची पर्वा न करता देऊन टाकतात. कुणालाही मदत करताना ते मनापासून व निरपेक्षपणे करतात. पावसाळी ढगाच्या समर्पक उपमेतून कवीने उदार व्यक्तींचा योग्य गौरव केला आहे.

In the poetry ‘सूक्तिसुधा’ various सुभाषितs conveying very deep and beautiful message are compiled. This shloka from ‘पूर्वचातकाष्टकम्’ tells us the greatness of generous people.

There is a famous poetic concept in literature that a bird called chataka drinks rain water directly from the cloud. It doesn’t drink water stored in the ponds or rives. It is said that in the beginning of rainy season it keeps waiting for the black cloud. Hence poet says when chataka asks for a few drops of water out of thirst, the cloud fills the entire world with water.

The behavior of generous people is compared to the magnanimity of cloud. Just like cloud the generous people are always ready to help others even if they have to go beyond their limits. Even if they are asked for less they give to the fullest. They never hesitate to give away everything they have. comparison between the cloud and generous people is very apt.

4. रूपपरिचयं कुरुत।

प्रश्न 1.
अम्भसा, महताम्, पिपासया, पयः
उत्तरम् :

• अम्भसा – अम्भस् सकारान्त नाम नपुंसकलिङ्गम् तृतीया विभक्तिः एकवचनम्।
• महताम् – महत् तकारान्त विशेषणम् पुल्लिङ्गम् षष्ठी बहुवचनम्।
• पिपासया – पिपासा आकारान्त नाम स्त्रीलिङ्गम् तृतीया विभक्तिः एकवचनम्।
• पयः – पयस् सकारान्त नाम नपुंसकलिङ्गम् प्रचमा विभक्तिः एकवचनम्।

5. समानार्थकशब्दं योजयित्वा वाक्यं पुनर्लिखत ।

प्रश्न 1.
चातकः पयस: कणान् जलधरं याचते।
उत्तरम् :
चातक: जलस्य कणान् मेघ याचते ।

6. अमरकोषपङ्क्तिं लिखत ।

प्रश्न 1.
जलधरः, अम्भः
उत्तरम् :
1. जलधरः – अभं मेघो वारिवाहस्तडित्वान् वारिदोऽम्बुभूत्।
2. अम्भः – उदकं जीवनं तोयं पानीयं सलिलं जलम्।

श्लोक: 7

1. माध्यमभाषया उत्तरत।

प्रश्न 1.
‘वयं पञ्चाधिकं शतम्’ इति सूक्तिं स्पष्टीकुरुत।
उत्तरम् :
In the lesson ‘सूक्तिसुधा’ different important values are practically told through beautiful सुभाषितः In this particular सुभाषित a saying by युधिष्ठिर implies the principle of ‘unity is strength’. Enmity between कौरक and पाण्डक is very famous in history.

When the tugas were in exile, Once the data were attacked by Gandharvas. Some servants who knew that the पाण्डवs were nearby went to युधिष्ठिर for help. Though भीम was against helping कौरव युधिष्ठिर thought otherwise. At that time keeping all the differences aside uses went to their rescue.

During that incident grafter said that we may have many differences among ourselves but when it is war against someone outside the family the hundred कौरक and five पाण्डक are together and they make hundred and five. This also shows family values. As a family we may fight with each other but when it is time to face some external problem the family is always one.

‘सूक्तिसुधा’ सुक्तिासुधा या पद्यामध्ये विविध मूल्ये व तत्त्वे सुंदर शब्दांत मांडली आहेत. प्रस्तुत श्लोकाला महाभारताची पार्श्वभूमी आहे. कौरव व पांडव या भावडांमधील वैर इतिहासात प्रसिद्ध आहे. जेव्हा पांडव वनवासात असताना एकदा कौरव आणि गंधर्वांमध्ये युद्धप्रसंग निर्माण झाला. काही नोकरांनी पांडवांना या प्रसंगाची बातमी दिली.आणि मदतीला येण्याची विनंती केली.

भीम कौरवांना मदत करण्याच्या पूर्ण विरोधात होता. पण युधिष्ठिराने मात्र तसा विचार केला नाही. पांडव आपापसातील वैर बाजूला ठेवून कौरवांच्या मदतीला गेले. त्यावेळी युधिष्ठिर म्हणतो, की आपापसात वैर असताना आम्ही पाच आणि ते शभंर असले तरी जेव्हा परक्याशी युद्धाची वेळ येईल तेव्हा शंभर आणि पाच मिळून आम्ही एकशेपाच आहोत.

या श्लोकामधून ‘एकी हेच बळ’ हा संदेश तर मिळातोच शिवाय कौटुंबिक एकात्मतेचे मूल्य सुध्दा हा श्लोक सांगतो. कुटुंबातील व्यक्तींमध्ये कितीही मतभेद असेल तरी संकटकाळी संपूर्ण कुटुंब एक होऊन त्यावर मात करते.

2. श्लोकात् सप्तम्यन्तपदानि चिनुत लिखत च ।

प्रश्न 1.
श्लोकात् सप्तम्यन्तपदानि चिनुत लिखत च ।
उत्तरम् :
स्वकीये, विग्रहे, प्राप्ते।

3. श्लोकात् सङ्ख्यावाचकानि चिनुत लिखत च ।

प्रश्न 1.
श्लोकात् सङ्ख्यावाचकानि चिनुत लिखत च ।
उत्तरम् :
शतम्, पश।

श्लोकः 8

1. सन्धिविग्रहं कुरुत।

प्रश्न 1.
अ. पाठकश्चैव = …………… + च + ।
आ. चान्ये = …………. + अन्ये।।
इ. व्यसनिनो ज्ञेयाः = ……….. + ज्ञेयाः।
ई. क्रियावान्स पण्डितः = क्रियावान् + ………….. + पण्डितः।
उत्तरम् :
अ. पाठकश्चैव – पाठक: + च + एव।
आ. चान्ये – च + अन्ये।
इ. व्यसनिनो ज्ञेया – व्यसनिनः + ज्ञेयाः।
ई. क्रियावान्स पण्डितः – क्रियावान् + स + पण्डितः।

2. एकवाक्येन उत्तरत।

प्रश्न अ.
के व्यसनिनः उक्ताः?
उत्तरम् :
पठकः, पाठक: शास्त्रवाचका: च व्यसनिन: ज्ञेया: उक्ताः।

प्रश्न आ.
क: पण्डितः उच्यते ?
उत्तरम् :
यः क्रियावान् स: (एव) पण्डित: उच्यते।

3. माध्यमभाषया उत्तरत।

पाण्डित्यं कस्मिन् वर्तते ? यथार्थः पण्डितः कः ?
उत्तरम् :
‘सूक्तिसुधा’ या पाठामधे आचरण्यात आणण्याजोग्या अनेक मूल्यांच्या संदेश सुभाषितांमधून केला आहे. या जगात अनेक लोक अनेक शास्त्रे शिकतात, पदव्या मिळवतात, खूप ज्ञान मिळवात. पण ते सगळेच खरे पंडित नसतात. आपण शिकलेल्या गोष्टी जे व्यवहारात आचरणातसुद्धा आणतात तेच खरे पंडित. केवळ पुस्तके वाचून, पदव्या मिळवून उपयोग नाही. मिळवलेल्या ज्ञानाचा जो प्रत्यक्ष व्यवहारात वापर करतो तोच खरा पंडित होय. मराठीमध्ये ‘क्रियेविण वाचाळता व्यर्थ आहे’ म्हणतात ते योग्यच आहे.

In the lesson ‘सूक्तिसुधा’various values and principles are conveyed through beautiful सुभाषितः There are so many people who learn so many things in their life. But all of them are not real scholars. Some just learn things theoretically. So their knowledge is limited to theories.

But real firs are those who implement their learnings in their behaviour. There may be thousand of learned people but the real पण्डित/scholar is the one who actually behaves according to what he has learnt. This shloka conveys the message ‘actions speak louder than words.’

4. सुभाषितात् समानार्थकशब्दं लिखत ।
वाचकः, अध्यापकः, शास्त्रविदः, कार्यकर्ता, विद्वान्, बोद्धव्याः।

प्रश्न 1.
वाचकः, अध्यापकः, शास्त्रविदः, कार्यकर्ता, विद्वान्, बोद्धव्याः।
उत्तरम् :

• पठकः – वाचकः।
• पाठकः – अध्यापकः।
• शास्त्रवाचकः – शास्त्रविद्।
• क्रियावान्- कार्यकर्ता।
• पण्डितः – विद्वान्।
• ज्ञेयाः – बोद्धव्याः।

Sanskrit Aamod Class 9 Textbook Solutions Chapter 9 सूक्तिसुधा Additional Important Questions and Answers

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.

1. सर्वधनेषु प्रधानं विद्याधनम् अस्ति।
2. परोपकाराय वृक्षाः फलन्ति।
3. परोपकाराय नद्य: वहन्ति।

उत्तरम् :

1. सर्वधनेषु प्रधानं किम् अस्ति?
2. परोपकाराय के फलन्ति?
3. नद्यः किमर्थं वहन्ति?

विभक्त्यन्तरूपाणि।

• प्रथमा – चोरहार्यम्, राजहार्यम्, भ्रातृभाज्यम्, भारकारि, निजः, परः, अयम्, गणना, वसुधा, कुटुम्बकम्, वृक्षाः, नद्यः, गावः, शरीरम्,
• इदम्, सत्यम्, चातकः, सः, मेघः, उदारता, पठकः, पाठकः, शास्त्रवाचकाः, ते. यः, क्रियावान, सः, पण्डितः, सर्वे, अन्ये, ये, व्यसनिनः ।
• द्वितीया – जाड्यम्, मानोन्नतिम्, पापम्, चित्तम्, कीर्तिम्, जलधरम्, त्रिचतुरान्, पय:कणान्, विश्वम्।
• तृतीया – पिपासया, अम्भसा।
• चतुर्थी – परोपकाराय।
• षष्ठी – लघुचेतसाम्, उदारचरितानाम्, धियः, महताम्।
• सप्तमी – व्यये, वाचि, दिक्षु।

लकारं लिखत।

• वर्धते – वृध्-व धातुः प्रथमगण: आत्मनेपदं लट्लकार: प्रथमपुरुष: एकवचनम्।
• फलन्ति – फलधातुः प्रथमगण: परस्मैपदं लट्लकार प्रथमपुरुष: बहुवचनम्।
• वहन्ति – वह धातुः प्रथमगण: परस्मैपदं लट्लकार : प्रथमपुरुष: बहुवचनम्।
• दुहन्ति – दुह् धातुः द्वितीयगण: उभयपदम् अत्र परस्मैपदं लट्लकार: प्रथमपुरुष: बहुवचनम्।
• हरति – ह धातुः प्रथमगण: उभयपदम् अत्र परस्मैपदं लट्लकार : प्रथमपुरुष: एकवचनम्।
• सिञ्चति – सिच् – सिधातुः षष्ठगण: उभयपदम् अत्र परस्मैपदं लट्लकार : प्रथमपुरुषः एकवचनम्।
• दिशति – दिश् धातुः षष्ठगण: उभयपदम् अत्र परस्मैपदं लट्लकार : प्रथमपुरुष: एकवचनम्।
• करोति – कृ धातु: अष्टमगण: उभयपदम् अत्र परस्मैपदं लट्लकार : प्रथमपुरुष: एकवचनम्।
• प्रसादयति – प्र + सद् धातुः प्रथमगणः परस्मैपदं प्रयोजकरूपं लट्लकार : प्रथमपुरुष: एकवचनम्।
• तनोति – तन् धातुः अष्टमगण: उभयपदम् अत्र परस्मैपदं लट्लकारः प्रथमपुरुषः एकवचनम्।
• कथय – कथ् धातुः दशमगण: उभयपदम् अत्र परस्मैपदं लट्लकार: मध्यमपुरुष: एकवचनम्।
• याचते – याच् धातुः प्रथमगण: आत्मनेपदं लट्लकार: प्रथमपुरुषः एकवचनम्।
• पूरयति – पूर् धातुः दशमगण: उभयपदम् अत्र परस्मैपदं लट्लकार: प्रथमपुरुष: एकवचनम्।

पद्यांश पठित्वा जालरेखाचित्रं पूरयत।

1.

उत्तरम् :
न चोरहार्यम्, न भ्रातृभाज्यम्, न राजहार्यम्, न भारकारि।

2.

3.

4.

एकवाक्येन उत्तरत।

प्रश्न 1.
उदारचरितानां कृते वसुधा कीदृशी भवति?
उत्तरम् :
उदारचरितांना कृते वसुधा कुटुम्बकम् इव भवति।

प्रश्न 2.
सत्सङ्गतिः धियः किं हरति?
उत्तरम् :
सत्सङ्गतिः धियः जाड्यं हरति।

प्रश्न 3.
सत्सङ्गतिः वाचि किं सिञ्चति?
उत्तरम् :
सत्सङ्गतिः वाचि सत्यं सिञ्चति।

प्रश्न 4.
सत्सङ्गतिः किम् अपाकरोति?
उत्तरम् :
सत्सङ्गतिः पापम् अपाकरोति ।

प्रश्न 5.
सत्सङ्गतिः किं प्रसादयति?
उत्तरम् :
सत्सङ्गतिः चित्तं प्रसादयति ।

प्रश्न 6.
सत्सङ्गतिः दिक्षु किं तनोति?
उत्तरम् :
सत्सङ्गतिः दिक्षु कीर्तिं तनोति।

प्रश्न 7.
परैः विग्रहे प्राप्ते वयं कति स्मः?
उत्तरम् :
परैः विग्रहे प्राप्ते वयं पञ्चाधिकं शतम्।

प्रश्न 8.
कौरवाः कति सन्ति?
उत्तरम् :
कौरवाः शतं सन्ति।

रिक्तस्थानानि पूरयित्वा अन्वयं पुनर्लिखत ।

प्रश्न 1.
लघुचेतसां (कृते) अयं ……….. पर: वा इति ………… (अस्ति)। उदारचरितानां (कृते) तु ………. एव ……….. (अस्ति )।
उत्तरम् :
लघुचेतसां (कृते) अयं निज: पर: वा इति गणना (अस्ति)। उदारचरितानां (कृते) तु वसुधा एव कुटुम्बकम् (अस्ति)।

प्रश्न 2.
1. गाव: ………… दुहन्ति ।
2. इदं शरीरं ……………. (एव अस्ति)।
उत्तरम् :
1. गाव: परोपकाराय दुहन्ति ।
2. इदं शरीरं परोपकारार्थम् (एव अस्ति )।

प्रश्न 3.
सत्सङ्गतिः ………….. जाड्यं हरति, ………. सत्यं सिञ्चति, मानोन्नति दिशति, पापम् ……….., चित्तं …………, दिक्षु कीर्तिं तनोति । कथय! (सा सत्सङ्गतिः) पुंसां किं (हित) न करोति ।।
उत्तरम् :
सत्सङ्गतिः धियः जाड्यं हरति, वाचि सत्यं सिञ्चति, मानोन्नति दिशति, पापम् अपाकरोति, चित्तं प्रसादयति, दिक्षु कीर्ति तनोति । कथय! (सा सत्सङ्गतिः) पुंसां किं (हित) न करोति ।।

प्रश्न 4.
(यदा) ………… पिपासया जलधरं त्रिचतुरान् ………… याचते (तदा) सः (मेघः) अपि विश्वम् ………… पूरयति। हन्त हन्त (कियती एषा) महताम् …………
उत्तरम् :
(यदा) चातक :पिपासया जलधरं त्रिचतुरान् पय:कणान्याचते (तदा) सः (मेघः) अपि विश्वम् अम्भसा पूरयति। हन्त हन्त (कियती एषा) महताम् उदारता!

प्रश्न 5.
पठक: पाठक: (तथा) च ये अन्ये ………….. (सन्ति, ते) सर्वे ………… ज्ञेयाः। (यतः) यः ………. स(एव) ………. (अस्ति)।
उत्तरम् :
पठक: पाठक: (तथा) च ये अन्ये शास्त्रवाचका: (सन्ति, ते) सर्वे व्यसनिनः ज्ञेयाः। (यतः) य: क्रियावान् स: (एव) पण्डितः (अस्ति)।

समानार्थकशब्दं योजयित्वा वाक्यं पुनर्लिखत।

नारी – नारी सर्वत्र पूजनीया। स्त्री/महिला/योषा सर्वत्र पूजनीया।

व्याकरणम् :

नाम – तालिका।

समासाः

समस्तपदम्	अर्थ:	समासविग्रहः	समासनाम
मानोन्नतिः	upliftment of respect	मानस्य उन्नतिः।	षष्ठी तत्पुरुष समासः।

धातुसाधितविशेषणानि।

धातुसाधित – विशेषणम्	विशेष्यम्
हार्यम्, भाज्यम्	धनम्
कृते	व्यये
प्राप्ते	विग्रहे
ज्ञेयाः	व्यसनिनः

सूक्तिसुधा Summary in Marathi and English

प्रस्तावना :

संस्कृतसाहित्य गद्य, पद्य, नाट्य अशा सर्व साहित्यप्रकारांनी परिपूर्ण आहे. सुभाषिते हा पद्यप्रकार संस्कृतसाहित्यातील लोकप्रिय साहित्यप्रकार आहे. संस्कृत सुभाषिते केवळ संस्कृतमध्येच नाही तर इतर भाषांमध्ये सुद्धा जशीच्या तशी वापरली जातात. उदा. “विनाशकाले विपरीतबुद्धिः। संपूर्ण सुभाषित लक्षात राहिले नाही तरी त्याचा गर्भितार्थ किंवा महत्त्वाची ओळ नक्कीच लक्षात राहते, जी म्हण किंवा उक्ती म्हणून वापरली जाते. शब्दसंपदा वाढवण्यात सुभाषिते निश्चितच मदत करतात.

Sanskrit literature comprises of prose, poetry and drama.सुभाषितs are well knoron part of the poetic liturature. Parts of which have been used as proverbs or sayings not only in Sanskrit but also in other languages. In fact several Sanskrit sayings are very often used as they are in other Indian languages.

You may recall विनाशकाले विपरीतबुद्धिः. People generally do not remember the entire subhashita but they do remember the phrase of the proverb quite easily. In fact remembering such sayings definitely enhances one’s vocabulary and command over the language.

श्लोकः – 1

न चोरहार्य ………….. सर्वधनप्रधानम् ।।1।। [Knowledge is the best of all riches]

श्लोकः : न चोरहार्य न च राजहार्य न भ्रातृभाज्यं न च भारकारि ।
व्यये कृते वर्धत एव नित्यं विद्याधनं सर्वधनप्रधानम् ।।1।। (प्रसङ्गाभरणम्)

अन्वयः : विद्याधनं चोरहार्य न (अस्ति), राजहार्य न, भ्रातृभाज्यं न, भारकारि (अपि) न (अस्ति) । व्यये कृते अपि (तत्) नित्यं वर्धते एव ।
(सत्यमेव विद्याधनं) सर्वधनप्रधानम् (अस्ति) ।

अनुवादः

Knowledge which is wealth cannot be stolen by a thief, cannot be taken away by a king, cannot be divided among brothers and is also not a burden. Though it is spent it only always increases. Wealth in the form of knowledge is the foremost among all types of wealth

विद्याधन चोरले जाऊ शकत नाही, राजा ते जप्त करू शकत नाही, याची भावंडामध्ये वाटणी केली जाऊ शकत नाही आणि ते त्याचे ओझे घेत नाही, खर्च केले तरी ते वाढतेच. खरोखर विद्याधन हे नेहमीच सर्व प्रकारच्या धनांमध्ये श्रेष्ठ धन आहे!

श्लोक: – 2

अयं ………………. कुटुम्बकम् ।।2।। [The world is one family]

श्लोकः : अयं निजः परो वेति गणना लघुचेतसाम् ।
उदारचरितानां तु वसुधैव कुटुम्बकम् ।।2।। (शार्ङ्गधरपद्धतिः)

अन्वयः । लघुचेतसां (कृते) अयं निजः पर: वा इति गणना (अस्ति) । उदारचरिताना (कृते) तु वसुधा एव कुटुम्बकम् (अस्ति)।

अनुवादः

हे माझे, हे तुझे असे कोत्या मनाचे लोक मानतात. उदार वृत्तीच्या लोकांसाठी तर संपूर्ण पृथ्वीच कुटुंब असते.
This is mine or it belongs to others is the consideration of the low-minded. Indeed for the | generous/ large-hearted, the entire world is a family.

श्लोकः – 3

परोपकाराय फलन्ति ……………….. शरीरम् ।।3।। [The body is for the welfare of others]
श्लोकः : परोपकाराय फलन्ति वृक्षाः परोपकाराय वहन्ति नद्यः।
परोपकाराय दुहन्ति गाव: परोपकारार्थमिदं शरीरम् ।।3।। (विक्रमोर्वशीयम्)
अन्वयः : वृक्षाः परोपकाराय फलन्ति। नद्यः परोपकाराय वहन्ति। गाव: परोपकाराय दुहन्ति। इदं शरीर परोपकारार्थम् (एव अस्ति)।

अनुवादः

झाडे परोपकारासाठीच फळे धारण करतात, नद्या इतरांसाठीच वाहतात, गायी दुसऱ्यांनाच दूध देतात आणि हे शरीरसुद्धा परोपकारासाठीच आहे.
Trees bear fruits for the welfare of others, rivers flow for the welfare of others, cows yield milk for the benefit of others. This body is for the welfare of others.

श्लोक: – 4

जाड्यं ………………. पुंसाम् ।।4।। [Good association bestows everything]

श्लोकः : जाड्यं धियो हरति सिञ्चति वाचि सत्यं
मानोन्नतिं दिशति पापमपाकरोति । चित्तं प्रसादयति दिक्षु तनोति कीर्ति
सत्सङ्गतिः कथय किं न करोति पुंसाम् ।।4।। (भर्तृहरिसुभाषितसङ्ग्रहः)

अन्वयः : सत्सङ्गतिः धियः जाड्यं हरति, वाचि सत्यं सिञ्चति, मानोन्नतिं दिशति, पापम् अपाकरोति, चित्तं प्रसादयति, दिक्षु कीर्ति तनोति । कथय ! (सा सत्सङ्गतिः) पुंसां किं (हित) न करोति ?

अनुवादः

बुद्धीचे अज्ञान दूर करते. वाणीला सत्याचे वळण लावते (सिञ्चति), आदर वाढवण्यासाठी दिशा दाखवते, पाप दूर करते, मन प्रसन्न करते, सर्व दिशांना कीर्ती पसरवते. सांगा बरे सज्जनांची संगती काय करत नाही!

Say what all can good company not do for men? It takes away the ignorance of the intellect. It sprinkles truth on speech. In directs the progress of respect and takes one away from sin. It delights the mind and spreads fame in all directions.

श्लोकः – 5

यत्र ………………… क्रियाः ।।5।। [Significance of respecting women.]
श्लोकः : यत्र नार्यस्तु पूज्यन्ते रमन्ते तत्र देवताः।
यौतास्तु न पूज्यन्ते सर्वास्तवाफला: क्रियाः ।।5।। (महाभारतम्)
अन्वयः : यत्र नार्यः पूज्यन्ते तत्र देवता: रमन्ते। यत्र तु एता: न पूज्यन्ते तत्र सर्वाः क्रियाः अफला: (भवन्ति)।

अनुवादः

जिथे स्त्रियांची पूजा होते तिथेच देवता आनंदाने राहतात. जिथे त्या (स्त्रिया) पूजल्या जात नाहीत (त्यांचा अनादर होतो) तिथे कोणतेही कार्य सफल होत नाही.

Gods rejoice where women are respected. But where they are not respected, there all actions become futile/unsuccessful.

श्लोकः – 6

चातकस्त्रिचतुरान् ……………….. महतामुदारता ।।6।। [Generosity of the great is amazing]

श्लोकः : चातकस्त्रिचतुरान् पयःकणान् याचते जलधरं पिपासया।
सोऽपि पूरयति विश्वमम्भसा हन्त हन्त महतामुदारता।।6।। (पूर्वचातकाष्टकम्)

अन्वयः : (यदा) चातक: पिपासया जलधरं त्रिचतुरान् पयःकणान् याचते (तदा) सः (मेघ:) अपि विश्वम् अम्भसा पूरयति। हन्त हन्त (कियती एषा) महताम् उदारता!

अनुवाद:

जेव्हा चातक पक्षी (जो केवळ पावसाचे पाणी पितो) मेघाकडे तहान भागवण्यासाठी तीन-चार थेंब पाण्याची याचना करतो. तेव्हा मेघ संपूर्ण जगच पाण्याने भरून टाकतो. खरेच श्रेष्ठ लोकांचा उदारपणा वाखाण्याजोगा आहे!

The chataka bird (which drinks rain water directly from the cloud) asks the cloud for just three or four drops of water out of thirst. The cloud too fills the entire world with water (rains everywhere). Indeed great is the magnanimity of the generous.

श्लोक: – 7

ते शतं …………………. शतम् ।।7।। [Internal differences vanish when the need arises.]

श्लोकः : ते शतं हि वयं पञ्च स्वकीये विग्रहे सति ।
परैस्तु विग्रहे प्राप्ते वयं पञ्चाधिकं शतम् ।।7।। (महाभारत)

अन्वयः (युधिष्ठिर : वदति) – स्वकीये विग्रहे सति ते शतं वयं हि पञ्च (स्म:)। परैः विग्रहे प्राप्ते तु वयं पञ्चाधिक शतं (स्मः)।

अनुवादः

युधिष्ठीर म्हणतो, ‘युद्धात ते (कौरव) शंभर आणि आम्ही (पांडव) पाच आहोत. पण इतरांबरोबरच्या युद्धात मात्र आम्ही शंभर अधिक पाच म्हणजेच एकशे पाच आहोत.’

Yudhisthira says, “In a battle between us they the Kauravas are hundred and we the Pandavas are five. But, in a quarrel against others we are hundred and five more that is a hundred and five.”

श्लोकः – 8

पठकः ……………………. पण्डितः ।।8।। [Difference between a true and so called scholar.]

श्लोकः : पठकः पाठकचैव ये चान्ये शास्ववाचकाः ।
सर्वे व्यसनिनो ज्ञेया य: क्रियावान्स पण्डितः ।।8।।

अन्वयः : पठकः पाठकः (तथा) च ये अन्ये शास्ववाचकाः (सन्ति, ते) सर्वे व्यसनिनः ज्ञेयाः । (यतः) यः क्रियावान् सः (एव) पण्डितः (अस्ति)।

अनुवादः

शिकणारा, शिकवणारा आणि इतर शास्त्र शिकवणारे हे केवळ शास्त्रांचे वाचक आहेत. खरा पंडित तोच समजावा जो (शास्त्र वाचून) तशी क्रिया सुद्धा करतो.
The learner, the teacher and all those who teach the shastras should only be considerd as mere readers of scriptures. The one who puts into action (works) should be known as a scholar.

सन्धिविग्रहः

परोपकारार्थमिदम् – परोपकारार्धम् + इदम्।
धियो हरति – धियः + हरति।
पापमपाकरोति – पापम् + अपाकरोति
परैस्तु – परैः + तु।

समानार्थकशब्दाः

1. राजा – नृपः, भूपः, भूपतिः।
2. निजः – स्वस्य।
3. वसुधा – धरा, पृथ्वी, वसुन्धरा।
4. चेतः – मनः, चित्तम्।
5. धीः – मतिः, बुध्दिः।
6. चित्तम् – मनः, चेतः।
7. वाच् – वाणी।
8. कीर्तिः – प्रसिद्धिः।
9. नारी – वनिता, महिला, स्त्री।
10. देवताः – दैवतानि।
11. जलधरः – मेघः, पयोदः।
12. अम्भः/पयः – जलम्, तोयम्, उदकम्, नीरम, वारि।
13. विग्रहः – युद्धम्।

विरुद्धार्थकशब्दाः

• वर्धत × क्षीयते।
• लघुचेतस् × उदारचेतस्।
• कीर्तिः × अपकीर्तिः।
• धीः × जाड्यम्।
• अफला: × सफलाः।
• उदारता × कार्पण्यम्।
• स्वकीय × परकीय।
• ज्ञेयाः × अज्ञेयाः।
• पण्डित: × मूढः।

शब्दार्थाः

1. चोरहार्यम् – stolen by a thief – चोराकडून चोरण्यासारखे
2. राजहार्यम् – taken away by the king – राजाने जप्त करण्यासारखे
3. भ्रातृभाज्यम् – divided among brothers – भावंडामध्ये वाटणी करण्यासारखे
4. व्यये कृते – though it is spent – खर्च केले तरी
5. नित्यम् – always – नेहमी
6. भारकारि – burden – ओझे
7. गणना – consideration – मानणे
8. लघुचेतसाम् – of the low-minded – कोत्या मनाचे
9. उदारचरितानाम् – generous hearted / magnanimous – उदार वृत्तीच्या लोकांसाठी
10. वसुधा – world – पृथ्वी
11. कुटुम्बकम् – family – कुटुंब
12. निजः – mine – माझे
13. परः – others’ – इतरांचे
14. परोपकाराय – for the welfare of others – परोपकारासाठी
15. फलन्ति – bear fruits – फळे धारण करतात
16. वहन्ति – flow – वाहतात
17. दुहन्ति – yield milk – दूध देतात
18. गाव: – cows – गायी
19. जाड्यम् – ignorance – अज्ञान
20. धियः – of the intellect – बुद्धीचे
21. अपाकरोति – takes away – दूर करते
22. प्रसादयति – delights – प्रसन्न करते
23. हरति – remove/takes away – दूर करते
24. सिजति – sprinkles – वळण लावते
25. मानोन्नतिम् – progress of respect – आदर वाढवण्यासाठी
26. दिशति – directs – दिशा देते
27. दिक्षु – in directions – दिशांमध्ये
28. तनोति – Spreads – पसरविते
29. सत्सङ्गतिः – good company – सज्जनांची संगती
30. पुंसाम् – of men – माणसांचे
31. वाचि – in speech – वाणीमध्ये
32. यत्र – where – जिथे
33. नार्यः – women – स्त्रिया
34. पूज्यन्ते – are respected – आदर केला जातो
35. रमन्ते – rejoice – आनंदाने राहतात
36. अफला: – futile/unsuccessful – असफल
37. एताः – these – या
38. पिपासया – by thirst – तानेने
39. जलधर – cloud – ढग
40. त्रिचतुरान् – three or four drops – तीन-चार थेंब
41. पयः कणान् – rain water – पावसाचे पाणी
42. अम्भसा – by water – पाण्याने
43. महताम् – of the great – महान लोकांची
44. उदारता – generosity – उदारपणा
45. शतम् – hundred – शंभर
46. स्वकीये – between us – आपसांतील
47. विग्रहे – in battle / quarrel – युद्धात
48. परैः – with others – इतरांबरोबर
49. पञ्चाधिकम् – five more अधिक पाच
50. पठकः – learner – शिकणारा
51. पाठकः – teacher – शिकवणारा
52. व्यसनिनः – addicts, obsessed – पछाडलेला
53. ज्ञेयाः – should be known – जाणले जावेत
54. क्रियावान् – who is endowed with action – क्रिया करणारा

Aamod Sanskrit Book 9th Class Solutions

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• धन्यौ तौ दातृयाचकौ Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• योगमाला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• पितृभक्तः नचिकेताः Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• सरमाया: शीलम् Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer
• स्वागतं तपोधनाया: Class 9 Question Answer

Class 9th Sanskrit Aamod Chapter 10 पितृभक्तः नचिकेताः Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 10 पितृभक्तः नचिकेताः Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 10 Question Answer

Sanskrit Aamod Std 9 Digest Chapter 10 पितृभक्तः नचिकेताः Textbook Questions and Answers

भाषाभ्यास:

1. एकवाक्येन उत्तरत।

प्रश्न अ.
वाजश्रवाः कः ?
उत्तरम् :
वाजश्रवाः दानपर: ब्राह्मणः।

प्रश्न आ.
दक्षिणायां किं यच्छेत् इति नियमः ?
उत्तरम् :
दक्षिणायां सर्वदा प्रियं वस्तु यच्छेत् इति नियमः।

प्रश्न इ.
वाजश्रवसः पुत्रः कः ?
उत्तरम् :
बाजश्रवस: पुत्र: नचिकेताः।

प्रश्न ई.
तृतीयवररूपेण नचिकेताः किम् अयाचत ?
उत्तरम् :
तृतीयवररूपेण नचिकेता: आत्मज्ञानम् अयाचत।

प्रश्न उ.
बालः नचिकेताः कति दिनानि यावत् यमस्य प्रतीक्षाम् अकरोत् ?
उत्तरम् :
बाल: नचिकेता: त्रीणिदिनानि यावत् यमस्य प्रतीक्षाम् अकरोत्।

2. माध्यमभाषया उत्तरत।

प्रश्न अ.
नचिकेता: यमपुरं किमर्थम् अगच्छत् ?
उत्तरम् :
‘पितृभक्त: नचिकेता: ही लहान पण अतिशय प्रगल्भ अशा ज्ञानपिपासू नचिकेताची कथा आहे. नचिकेताने आपले वडील वाजश्रवा यांना विश्वजित् यज्ञ संपन्न झाल्यावर भाकड गायी दक्षिणा म्हणून देताना पाहिले. दक्षिणा म्हणून सर्वात प्रिय वस्तू द्यावी असा नियम होता, त्यामुळे अयोग्य दक्षिणा देण्याचे पाप लागून आपले वडील नरकात जातील की काय अशी नचिकेताला भिती वाटली.

त्याने वडिलांना विचारले “तुम्हाला सर्वात प्रिय असे काय आहे?” वडिलांनी त्याला लगेच सांगितले की नचिकेताच त्यांना सर्वात प्रिय आहे. नचिकेताने हे ऐकून त्यांना विचारले. “मग तुम्ही मला कोणाला दान करणार?” वडिलांनी दुर्लक्ष करुन सुद्धा नचिकेता तोच प्रश्न विचारत राहिला.

शेवटी चिडून वाजश्रवा म्हणाला “मी तुला मृत्यूला देईन!” वडील चिडून बोलत हे कळूनसुद्धा वडिलांच्या आज्ञेचे पालन करायचे आहेत म्हणून नचिकेता यमाच्या घरी गेला. नचिकेता इतका आज्ञाधारी मुलगा होता की वडिलांची आज्ञा मोडायची नाही म्हणून मृत्यूच्या घरी जाताना सुद्धा त्याने किंचितसाही विचार केला नाही. वडिलांच्या आज्ञेचे पालन करण्यासाठी तो अतिशय तत्पर होता.

In the lesson ‘पितृभक्त: नचिकेता:’ there is story of a small boy Nachiketa who was very thirsty for knowledge. Once the little Nachiketa saw his father giving the old, unmilkable cows in charity to the Brahmins after performing Vishwajit sacrifice.

But the rule was that the most beloved thing has to be given in donation. So Nachiketa was scared that his father might attain hell if he performs improper donation. So he asks his father what was the most dear to him. His father answered that Nachiketa was most dear to him.

So Nachika asked whom he would be given to. Nachiketa kept asking this again and again even when his father ignored him. Nachiketa didn’t give up. His father got angry and told him that he would give him to the death. He knew that his father said so in anger.

Still, he went to the abode of Yama to follow his Father’s order. Nachiketa was such a well-behaved son that he didn’t even think once before following his father’s order.

प्रश्न आ.
के त्रयः वरा: नचिकेतसा याचिताः ?
उत्तरम् :
‘पितृभक्त नचिकेता’ या पाठामध्ये यम-नचिकेता संवाद आला आहे. या संवादातून नचिकेताची जिज्ञासू वृत्ती दिसून येते. वडिलांची आज्ञा पाळण्यासाठी नचिकेता यमाच्या घरी गेला तेव्हा यम तिथे नव्हता. नचिकेताने काहीही न खाता पिता तीन दिवस यमाची वाट पाहिली. चौथ्या दिवशी यम परतला तेव्हा त्याला लहानग्या नचिकेताची खूप दया आली.

नचिकेता तीन दिवस तिथे थांबला म्हणून यमाने नचिकेताला तीन वर मागण्यास सांगितले. नचिकेताने वडिलांचा राग जाऊ दे असा पहिला वर मागितला आणि स्वर्ग प्राप्त करून देणारी अशी अग्निविद्या दुसरा वर म्हणून मागितली. तिसरा वर म्हणून नचिकेताने सामान्य माणसाला तसेच भल्या भल्या विद्वानांनासुद्धा मिळवण्यासाठी अशक्यप्राय असणारे असे आत्मज्ञान मागितले. नचिकेता वयाने लहान असला तरी सुद्धा त्याला असामान्य अशी बुद्धी आणि ज्ञानपिपासा लाभली होती.

In the story ‘पितृभक्त : नचिकेता:’ an incident of small Nachiketa who is eager to attain the ‘knowledge of self is told. When Nachiketa went to Antioch to obey his father’s order. But Yama was not there. Nachiketa waited there for three days, without eating or drinking anything.

When Yama returned on the fourth day his heart went out of compassion for Nachiketa. Yama offered Nachiketa three boons. Nachiketa asked to let his father’s anger get pacified as the first boon and the Agnividya as the second one.

As the third boon, he asked for knowledge of the self which was very difficult to attain even for the learned let alone a normal human being Even if he was young Nachiketa was blessed with immense maturity and great and thirst for knowledge.

Sanskrit Aamod Class 9 Textbook Solutions Chapter 10 पितृभक्तः नचिकेताः Additional Important Questions and Answers

एकवाक्येन उत्तरत।

प्रश्न 1.
वाजश्रवाः दक्षिणारूपेण का: अयच्छत् ?
उत्तरम् :
वाजश्रवा दक्षिणारूपेण दुग्धदाने असमर्था: दुर्बला: वृद्धा: च धेनू: अयच्छत्।

प्रश्न 2.
वाजश्रवस: प्रियः कः अस्ति?
उत्तरम् :
वाजश्रवस: प्रिय: स्वपुत्र: नचिकेता: अस्ति।

प्रश्न 3.
नचिकेता: किमर्थं यमपुरम् अगच्छत्?
उत्तरम् :
नचिकेताः पितुः आदेशपालनार्थ यमपुरम् अगच्छत्।

प्रश्न 4.
यमः किमर्थ चकित: अभवतः?
उत्तरम् :
अल्पवयसः बालस्य प्रगल्भा ज्ञानतृष्णां दृष्ट्वा यमः चकितः अभवतः।

प्रश्न 5.
यम: नचिकेतसे कति वरान् अयच्छत्?
उत्तरम् :
यम: नचिकेतसे त्रीन् वरान् अयच्छत्।

सत्यं वा असत्यं लिखत।

प्रश्न 1.

1. वाजश्रवाः नाम दानपर: द्विज: आसीत्।
2. वाजश्रवाः सबलाः धेनू: अयच्छत्।
3. असमीचीनदानेन पिता स्वर्ग गमिष्यति इति नचिकेतस: भीतिः ।
4. पिता क्रोधावेशे उक्तवान् इति नचिकेता: न अजानात् ।
5. नचिकेता: त्रीणि दिनानि यावत् यमस्य प्रतीक्षाम् अकरोत्।
6. पिता कुद्धः अभवत्।।
7. प्रथमवररूपेण नचिकेता: आत्मज्ञानम् अयाचत।
8. यमः तृतीयं वरं न अथच्छत्।

उत्तरम् :

1. सत्यम्
2. असत्यम्
3. असत्यम्
4. असत्यम्
5. सत्यम्
6. सत्यम्
7. असत्यम्
8. असत्यम्

कः कं वदति।

प्रश्न 1.

1. वत्स, त्वमेव मम प्रियतमः।
2. किं तव अतीव प्रियम्?
3. “तर्हि मां कस्मै दास्यति, भवान् ?”
4. “अहं त्वां मृत्यवे ददामि”।

उत्तरम् :

1. वाजश्रवाः नचिकेतसं वदति।
2. नचिकेता: वाजश्रवसं वदति।
3. नचिकेता: वाजश्रवसं वदति।
4. वाजश्रवाः नचिकेतसं वदति।

प्रश्न 2.
“स्वर्गसाधिकाम् अग्निविद्यां दत्त्वा माम् अनुगृह्णातु।”
उत्तरम् :
नचिकेता: यमं वदति।

शब्दस्य वर्णविग्रहं कुरुत।

• दक्षिणायाम् – द् + अ + क् + ष् + इ + ण् + आ + य् + आ + म्।
• असमर्थाः – अ + स् + अ + म् + अ + र् + थ् + आः।
• वाजश्रवाः – व् + आ + ज् + अ + श + र् + अ + व् + आ:।
• यज्ञम् – य् + अ + ज् + ञ् + अ + म्।
• क्रुद्धः – क् + र् + उ + द् + ध् + अः।
• नचिकेतसम् – न् + अ + व् + इ + क् + ए + त् + अ + स् + अ + म्।
• तर्हि – त् + अ + र् + ह् + इ।
• त्रिवारम् – त् + र् + इ + व् + आ + र् + अ + म्।
• क्षुधातेम – क् + ष् + उ + ध् + आ + र + त् + अ + म्।
• दृष्ट्वा – द् + ऋ + ष् + ट् + व् + आ।
• क्रोध: – क् + र + ओ + ध् + अः।
• प्रगल्भा – प् + र + अ + ग् + अ + ल् + भ् + आ।

प्रश्ननिर्माणं कुरुत।

1. वाजश्रवाः नाम दानपर: ब्राह्मणः आसीत्।
2. वाजश्रवाः विश्वजित्-यज्ञम् अकरोत्।
3. दक्षिणायां प्रियं वस्तु यच्छेत्।
4. अहं त्वां मृत्यवे दास्यामि।
5. स: यमपुरम् अगच्छत्।
6. स: त्रीणि दिनानि यावत् प्रतीक्षाम् अकरोत्।
7. पितुः आदेशपालनार्थ नचिकेताः यमपुरम् अगच्छत्।
8. चतुर्थ दिवसे यम: यमपुरं प्राप्तः।
9. नचिकेता: आत्मज्ञानम् अयाचत।
10. नचिकेतस: निर्णयः निश्चलः।

उत्तरम् :

1. क: दानपर: ब्राह्मण: आसीत् ?
2. वाजश्रवाः किम् अकरोत्?
3. दक्षिणायां कीदृशं वस्तु यच्छेत्?
4. अहं त्वां कस्मै दास्यामि?
5. सः कुत्र अगच्छत्?
6. स: कति दिनानि यावत् प्रतीक्षाम् अकरोत्?
7. नचिकेता: किमर्थं यमपुरम् अगच्छत्?
8. यमः कदा यमपुरं प्राप्त:?
9. नचिकेताः किम् अयाचत?
10. नचिकेतस: निर्णयः कीदृशः?

विशेषण-विशेष्य-सम्बन्धः।

प्रश्न 1.
गद्यांशात् “धेनवः” इति पदस्य कृते विशेषणानि लिखत।
उत्तरम् :
असमर्थाः, दुर्बलाः, वृद्धाः।

प्रश्न 2.

विशेषणम्	विशेष्यम्
त्रीणि	पिता
कुद्धः	यमः
अनुपस्थितः	दिनानि
प्रथमम्	यमः
शान्त:	आत्मज्ञानम्
चकित:	वरम्
दुर्लभम्	क्रोध:

उत्तरम् :

विशेषणम्	विशेष्यम्
त्रीणि	दिनानि
कुद्धः	पिता
अनुपस्थितः	यमः
प्रथमम्	वरम्
शान्त:	क्रोध:
चकित:	यमः
दुर्लभम्	आत्मज्ञानम्

विभक्त्यन्तरूपाणि।

• प्रथमा – वाजश्रवाः, सः, बाह्मणः, वस्तु, पिता, पुत्रः, त्वम्, नचिकेताः, किम्, नचिकेताः, पिता, दिनानि, वाजश्रवाः, यमः हृदयम्, बालकः, मर्त्यः, ज्ञातुकामः, नचिकेताः।
• द्वितीया – पितरम्, यज्ञम, दक्षिणाम्, नचिकेतसम्, यमपुरम, प्रतीक्षाम्, वरम्, अग्निविद्याम्, माम्, प्रार्थनाम्, नचिकेतसम्।
• तृतीया – दक्षिणारूपेण, भीत्या, वाजश्रवसा, नचिकेतसा, आनन्देन, प्रलोभनैः।
• चतुर्थी – ब्राह्मणेभ्यः, कस्मै, मृत्यवे, तस्मै।
• पञ्चमी – तृतीयवरात्।
• षष्ठी – मम, तस्य, तव, यमस्य, पितुः, मम, जनकस्य, वाजश्रवसः, तस्य, नचिकेतसः।
• सप्तमी – दक्षिणायाम्, यज्ञे, यमपुरे, क्रोधावेशे, चतुर्थे, दिवसे, अन्ते।

लकारं लिखत।

• आसीत् – अस् धातुः द्वितीयगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• अकरोत् – कृ धातुः अष्टमगण: उभयपदम् अत्र परस्मैपदं प्रथमपुरुष: एकवचनम्।
• अयच्छत् – ‘दा-यच्छ्’ प्रथमगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• गमिष्यति – गम्-गच्छ् धातुः प्रथमगणः परस्मैपदं लुट्लकार: प्रथमपुरुष: एकवचनम्।
• यच्छेत – दा-यच्छ् धातुः, प्रथमगणः, परस्मैपदं, विधिलिङ्लकार: प्रथमपुरुषः एकवचनम्।
• दास्यति – दा धातुः प्रथमगण: तृतीयगण: परस्मैपदं लुट्लकार: प्रथमपुरुष: एकवचनम्।
• ददामि – दा धातुः तृतीयगणः उभयपदम् अत्र परस्मैपदं लट्लकार: उत्तमपुरुषः एकवचनम्।
• अवदत् – वद् धातुः प्रथमगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• अजानात् – ज्ञा धातुः नवमगणः उभयपदम् अत्र परस्मैपदं लङ्लकारः प्रथमपुरुष: एकवचनम्।
• अद्रवत् – द्रु-द्रव् धातुः प्रथमगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• याचस्व – याच् धातुः प्रथमगण: आत्मनेपदं लोट्लकार: मध्यमपुरुषः एकवचनम्।
• अयाचत – याच् धातुः प्रथमगण: आत्मनेपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• अनुगृह्यतु – अनु + ग्रह् धातुः नवमगण: उभयपदम् अत्र परस्मैपदं लोट्लकार : प्रथमपुरुष: एकवचनम्।
• उपादिशत्- उप् + दिश् धातुः षष्ठगण: उभयपदम् अत्र परस्मैपदं लङ्लकारः प्रथमपुरुष: एकवचनम्।

उचितं पर्यायं चिनुत ।

प्रश्न 1.
अहं त्वां ……………… ददामि।
(अ) मृत्यवे
(आ) इन्द्राय
उत्तरम् :
(अ) मृत्यवे

प्रश्न 2.
यमपुरे यमः ……………… ।
(अ) अनुपस्थितः
(आ) उपस्थितः
उत्तरम् :
(अ) अनुपस्थितः

प्रश्न 3.
नचिकेता: …………….. दिनानि यावत् प्रतीक्षाम् अकरोत्।
(अ) चत्वारि
(आ) त्रीणि
उत्तरम् :
(आ) त्रीणि

प्रश्न 4.
………….. यमपुरम् अगच्छत्।
(अ) भिक्षाटनार्थम्
(आ) आदेशपालनार्थम्
उत्तरम् :
(आ) आदेशपालनार्थम्

त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।

त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्त अव्यय   थातु + तुम् / धुम् / टुम् / ढुम् / इतुम् / अयितुम्
भूत्वा अपी त्वा अभुक्त्वा दृष्ट्वा	–	–
श्रुत्वा	–	निवारयितुम्
दृष्ट्वा	–	–

समानार्थकशब्दं योजयित्वा वाक्यं पुनर्लिखत।

1. यज्ञ: – सः विश्वजित् – यज्ञम् अकरोत्। – स: विश्वजित्-यागम् अकरोत्।
2. पुत्रः – तस्य पुत्र: नचिकेता: अपश्यत्। – तस्य आत्मज: नचिकेता: अपश्यत् ।

व्याकरणम् :

नाम – तालिका।

सर्वनाम – तालिका।

धातु – तालिका।

समासाः

समस्तपदम	अर्थ:	समासविग्रहः	समासनाम
यमपुरम्	abode of Yama	यमस्य पुरम्।	षष्ठी तत्पुरुष समास।
दक्षिणारूपेण	in the form of donation	दक्षिणाया: रूपम्, तेन।	षष्ठी तत्पुरुष समास।
क्षुधार्त:	overcome by hunger	क्षुधया आर्तः।	तृतीया तत्पुरुष समास।
पिपासातः	overcome by thirst	पिपासया आर्तः।	तृतीया तत्पुरुष समास।
ज्ञानतृष्णा	thirst for knowledge	ज्ञानाय तृष्णा।	चतुर्थी तत्पुरुष समास।

धातुसाधितविशेषणानि।

धातुसाधित – विशेषणम्	विशेष्यम्
समाप्ते	यज्ञे
अनुपस्थितः, प्राप्त:	यमः

पितृभक्तः नचिकेताः Summary in Marathi and English

प्रस्तावना :

वेद, ब्राह्मणग्रंथ, आरण्यके, उपनिषदे प्राचीन भारतीय साहित्याचा भाग आहेत. त्यातील उपनिषदे भारतीय तत्त्वज्ञानाचे मूळ आहेतच शिवाय अनेक महत्त्वाची मूल्ये सांगणाऱ्या सुंदर कथा हे त्याचे वैशिष्य आहे नचिकेता हा एक लहान हुशार मुलगा आहे जो आपल्या वडिलांना पापापासून परावृत्त करण्याचा प्रयत्न करतो. ही पितृप्रेमाची कथा आपल्याला वडीलधाऱ्यांचा आदर करायला शिकवते. “पितृदेवो भव’ हे तत्त्व सांगतानाच ही कथा प्राचीन यज्ञसंस्थेविषयी, त्यातील दानाविषयी सुद्धा सांगते.

Our ancient Vedic literature comprises of the Vedas, Brahmanas, Aranyakas and Upanishad. The Upanishads are not just a collection of philosophical concepts, but rich treasures of knowledge. Through Upanishads, absolute values can be instilled as they contain many simple yet thought-provoking stories.

There are several Upanishads through tent of them are considered the main ones. One of the ten main Upanishads is Kathopanishad. The story presented here is a part of the famous dialogue between Yama and Nachiketa from the Kathopanishad.

Nachiketa uns a young intelligent lad who tried to prevent his father afar from committing a sin. This story is one of the best examples that conveys the value of love and respect towards the father. Not only does this story depict fugeat a but also presents in what form donation can be done.

परिच्छेद : 1

वाजश्रवाः …………………. प्रियतमः ।
वाजश्रवाः नाम दानपर: ब्राह्मण: आसीत्। एकदा स: विश्वजित्-यज्ञम् अकरोत्। समाप्ते यज्ञे सः ब्राह्मणेभ्य: दक्षिणाम् अयच्छत्। दक्षिणायां सर्वदा प्रियं वस्तु यच्छेत् इति नियमः। किन्तु पिता वाजश्रवाः तु दक्षिणारूपेण दुग्धदाने असमर्थाः दुर्बलाः वृद्धाः च धेनूः अयच्छत्। तस्य पुत्र: नचिकेता: तद् अपश्यत्। असमीचीनदानेन पिता मे नरकं गमिष्यति इति भीत्या सः पितरम् अपृच्छत्, “पितः, किं तव अतीव प्रियम्?” झटिति पिता अवदत, “वत्स, त्वमेव मम प्रियतमः।”

अनुवादः

वाजश्रवा नावाचा अतिश दानशूर ब्राह्मण होता. एकदा त्याने विश्वजितयज्ञ केला. यज्ञाच्या सांगतेच्या वेळी त्याने ब्राह्मणांना दक्षिणा दिली. दक्षिणेमध्ये नेहमी सर्वात प्रिय वस्तू द्यावी असा नियम आहे.

परंतु वाजश्रव्याने दक्षिणा म्हणून दूध न देऊ शकणाऱ्या, (भाकड) अशक्त आणि म्हाताऱ्या गायी दिल्या. त्याचा मुलगा नचिकेता याने ते पाहिले. अयोग्य दानामुळे माझे वडील नरकात जातील या भितीने त्याने वडिलांना विचारले, “बाबा! तुम्हाला सगळ्यात प्रिय काय आहे?” वडिलांनी पटकन उत्तर दिले, “तूच मला सर्वात प्रिय आहेस.”

There was a charitable Brahmin named Vajashrava. Once he performed the Vishwajit sacrifice When the sacrifice was over he gave donations to the brahmins. The rule is whatever is the dearest should be donated. But father Vajashrava gave old and weak cows which were unable to give milk in the form of donation.

His son Nachiketa saw that and due to the fear that his father might attain hell on account of improper donation he asked his father, “O father, what is most dear to you?” The father immediately answered, “Child! you are dear to me.

परिच्छेद : 2

नचिकेताः पुनः अपृच्छत् …………………. प्रतीक्षाम् अकरोत्।

नचिकेताः पुन: अपृच्छत, “तर्हि मां कस्मै दास्यति भवान् ?” वाजश्रवसा किमपि उत्तरं न दत्तम्। द्विवार त्रिवार नचिकेतसा तदेव पृष्टम् । तदा कुद्धः भूत्वा पिता नचिकेतसम् ‘अहं त्वां मृत्यवे ददामि| इति अवदत्। पिता क्रोधावेशे एवम् उक्तवान् इति नचिकेताः अजानत्। तथापि पितुः आदेशपालनार्थ सः यमपुरम् अगच्छत् । यमपुरे यमः अनुपस्थितः । बाल: नचिकेता: तत्रैव त्रीणि दिनानि यावत्, किमपि अभुक्त्वा अपीत्वा यमस्य प्रतीक्षाम् अकरोत् ।

अनुवादः

नचिकेताने पुन्हा विचारले, “मग मला तुम्ही कुणाला देणार?” वाजश्रवाने काहीच उत्तर दिले नाही. नचिकेताने दोन-तीनदा परत तेच विचारले. तेव्हा चिडून वडील नचिकेताला म्हणाले, “मी तुला मृत्यूला देईन!” वडील रागाच्या भरात असे म्हणाले हे नचिकेताला कळले. तरीसुद्धा वडिलांच्या आज्ञेचे पालन करण्यासाठी तो यमपुरी गेला. यमपुरात यम नव्हता. लहानगा नचिकेता तिथेच तीन दिवस काहीही न खाता पिता यमाची वाट पाहत थांबला.

Nachiketa asked again, “Then whom will you give me to?” Vajashrava didn’t answer. Nakita asked the same question two-three times again and again. Then the father who was angry said to Nachiketa, “I’ll give you to death.”

Nachiketa knew that the father said this due to anger, yet, he went to the abode of Yama to follow his father’s order. Yama was not there in Yamapura. Young Nachiketa stayed there for three days without eating or drinking anything waiting for Yama.

परिच्छेद : 3

चतुर्थे दिवसे …………………. उपदिशत्।

चतुर्थे दिवसे यमः यमपुरं प्राप्त: । क्षुधात पिपासात बालातिथिं दृष्ट्वा तस्य हृदयं करुणया अद्रवत्। यम: नचिकेतसे ‘प्रीन् वरान् याचस्व’ इति अवदत्। ततः बालकः प्रथमं वरम् अयाचत, “मम जनकस्य वाजश्रवसः मां प्रति क्रोधः शान्त: भवतु।”

“स्वर्गसाधिकाम् अग्निविद्यां दत्त्वा माम् अनुगृह्यतु’ इति द्वितीयं वरं स: अयाचत। यम: आनन्देन वरौ प्रायच्छत्। ततः तृतीयवररूपेण नचिकेताः आत्मज्ञानम् अयाचत । तस्य प्रार्थनां श्रुत्वा यमः चकितः। न कोऽपि मर्त्यः अद्यपर्यन्तं तद् ज्ञातुकामः । अल्पवयसः बालस्य कथमिव प्रगल्भा ज्ञानतृष्णा? यमः विविधप्रलोभनै: नचिकेतसं तृतीयवरात् निवारयितुं प्रायतत। किन्तु निश्चल: नचिकेतसः निर्णयः । अन्ते वरं दातुं वचनबद्धः यम: तस्मै ज्ञानिनामपि दुर्लभम् आत्मज्ञानम् उपादिशत्।

अनुवादः

चौथ्या दिवशी यम यमपुरी आला. ताहनेने, भुकेने व्याकूळ झालेल्या त्या लानग्या अतिथीला पाहून त्याचे हृदय दयेने पिळवटले. यम नचिकेताला म्हणला, “तीन वर माग!” तेव्हा नचिकेताने पहिला वर मागितला.

“माझ्या वडिलांचा वाजश्रवांचा माझ्यावरचा राग शांत होऊ दे.” “स्वर्ग साधून देणारी अग्निविद्या देऊन माझ्यावर अनुग्रह करा.” असा दुसरा वर त्याने मागितला. यमाने आनंदाने ते दोन वर दिले. त्यानंतर तिसरा वर म्हणून नचिकेताने आत्मज्ञान मागितले.

त्याची ही विनंती ऐकून यम चकित झाला. आजपर्यंत कोणताही मर्त्य मानव आजपर्यंत इतका ज्ञान इच्छिणारा नव्हता. इतक्या लहान मुलाची इतकी प्रगल्भ ज्ञानतृष्णा?

परावृत्त करण्याचा प्रयत्न केला. परंतु नचिकेताचा निश्चय पक्का होता. शेवटी वर देण्यासाठी वचनबद्ध असलेल्या यमाने त्याला भल्या भल्या ज्ञानींसाठी दुर्लभ असणाऱ्या आत्मज्ञानाचा उपदेश केला.

यमाने इतर अनेक प्रलोभने दाखवून नचिकेताला या तिसऱ्या वरापासून On fourth day Yama arrived at his abode. यमपुर : Seeing the thirsty, hungry young guest his heart went out with compassion. Yama said to Nachiketa, “Ask for three boons!” Then the boy asked the first boon.

“May my father Vajashrava’s anger be pacified.” “Please bless me with the heavenly Agnividya”, he asked for the second boon. Yama happily bestowed him with the two boons. Then Nachiketa asked for knowledge of the self as the third boon. Yama was astonished hearing his request. Till then no mortal wished to know that.

How does this small child have such mature thirst for knowledge? Yama tried to dissuade Nachiketa from the third boon by offering different temptations. But Nachiketa’s decision was firm. In the end, being bound to give him the boon as promised, Yama bestowed him with the knowledge which is rare to even the learned.

सन्धिविग्रहः

• तद् अपश्यत् – तत् + अपश्यत्
• त्वमेव – त्वम् + एव ।
• किमपि – किम् + अपि।
• तत्रैव – तत्र + एव।
• तदेव – तत् + एव।
• कथमिव – कथम् + इव।
• शानिनामपि – ज्ञानिनाम् + अपि।

समानार्थकशब्दाः

1. नाम – अभिधानम्, आख्या, नामधेयम्।
2. सर्वदा – सदा, नित्यम्, सदैव ।
3. दुग्धम् – क्षीरम्, पयः।
4. वृद्धा – स्थविरा।
5. झटिति – सत्वरम्, तूर्णम्, आशु, शीघ्रम्।
6. ब्राह्मणः – द्विजाः, विप्रः, भूसुरः।
7. पिता – जन्मदाता, जनकः।
8. दुर्बलाः – निर्बलाः।
9. धेनुः – गौः।
10. दिनानि – दिवसाः।
11. जनक: – पिता।
12. श्रुत्वा – आकर्ण्य।
13. आनन्दः – हर्षः।
14. पुरम् – नगरी।

विरुद्धार्थकशब्दाः

1. समाप्ते × आरम्भे।
2. सर्वदा × क्वचित्।
3. प्रियम् × अप्रियम्।
4. दुर्बलाः × सबलाः।
5. वृद्धा × युवती।
6. नरक: × स्वर्ग:।
7. दिवसे × रात्रौ।
8. अनुपस्थितः × उपस्थितः।
9. आनन्दः × दु:खः।
10. निशल: × चञ्चलः।

शब्दार्थाः

1. वृद्धाः – old – म्हाताऱ्या
2. असमर्थाः – unable – असमर्थ
3. भीत्या – due to fear – भितीने
4. झटिति – fast – लवकर
5. यज्ञम् – sacrifice – यज्ञ
6. दक्षिणा – donation – दक्षिणा
7. नियमः – rule – नियम
8. दुर्बला – weak – अशक्त
9. धेनूः – cows – गायी
10. प्रियतमः – most dear – सर्वात प्रिय
11. कुद्धः – angry – रागावलेला
12. प्रतीक्षाम् अकरोत् – waited – वाट पाहिली
13. अभुक्त्वा – without eating – नखाता
14. अपीत्वा – without drinking – न पिता
15. यमपुरम् – abode of यम – यमनगर
16. अनुपस्थितः – absent – गैरहजर
17. क्षुधार्त: – overcome by hunger – भुकेने व्याकूळ
18. पिपासार्त: – overcome by thirst – तहानेने व्याकूळ
19. हृदयम् – heart – हृदय
20. वरान् – boon – वर
21. आत्मज्ञानम् – self-realisation – आत्मज्ञान
22. अतिथि: – guest – पाहुणा
23. अल्पवयसः – of young age – लहान
24. प्रगल्भा – mature – प्रगल्भ
25. ज्ञानतृष्या – thirst for knowledge – ज्ञानाची तहान
26. प्रलोभनम् – temptation – लालूच
27. निश्चल: – firm – पक्का
28. निवारयितुम् – to dissuade – परतवण्यासाठी
29. मर्त्यः – mortal – मानव

Aamod Sanskrit Book 9th Class Solutions

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• धन्यौ तौ दातृयाचकौ Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• योगमाला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• पितृभक्तः नचिकेताः Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• सरमाया: शीलम् Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer
• स्वागतं तपोधनाया: Class 9 Question Answer

Class 9th Sanskrit Anand Chapter 2 अव्ययमाला Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Anand Chapter 2 अव्ययमाला Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 2 Question Answer

Sanskrit Anand Std 9 Digest Chapter 2 अव्ययमाला Textbook Questions and Answers

भाषाभ्यास:

श्लोक: 1

1. एकवाक्येन उत्तरत।

प्रश्न अ.
ईश्वरेण श्रोतुं किं दत्तम् ?
उत्तरम् :
ईश्वरेण श्रोतुं कर्णी दत्तौ।

प्रश्न आ.
आस्यं कीदृशम् ?
उत्तरम् :
आस्यं सुहास्यम्।

प्रश्न इ.
ईश्वरेण विहर्तुं किं दत्तम् ?
उत्तरम् :
ईश्वरेण विहाँ पादयुग्मं दत्तम्।

2. तालिकां पूरयत।

प्रश्न 1.

उत्तरम् :

किं दत्तम् ?	किं कर्तुम् ?	किमर्थम् ?
कर्णी दत्तौ	श्रोतुम्	श्रवणार्थम् / श्रवणाय
आस्यं दत्तम्	वक्तुम्	वचनार्थम् / वचनाय
घ्राणं दत्तम्	घ्रातुम्	घ्राणार्थम् / प्राणाय
पादयुग्यं दत्तम्	विहर्तुम्	विहारावम् / विहाराय
नेत्रे दत्ते	द्रष्टुम्	दर्शनार्थम् / दर्शनाय

3. मेलनं कुरुत।

प्रश्न 1.

श्लोकः 2

1. एकवाक्येन उत्तरत ।

प्रश्न अ.
के दूतत्वं कुर्वन्ति ?
उत्तरम् :
गुणा: दूतत्वं कुर्वन्ति।

प्रश्न आ.
के केतकीम् आजिघ्रन्ति ?
उत्तरम् :
षट्पदा: केतकीम् आजिवन्ति।

2. सत्यं वा असत्यं लिखत ।

प्रश्न अ.
सज्जना: दूतत्वं कुर्वन्ति।

प्रश्न आ.
षट्पदाः स्वयम् आयान्ति ।

प्रश्न इ.
सज्जनाः केतकीगन्धम् आजिघ्रन्ति ।

3. समानार्थकशब्दं चिनुत लिखत च ।
सज्जनाः, भ्रमरा:, आगच्छन्ति ।

प्रश्न 1.
समानार्थकशब्दं चिनुत लिखत च ।
सज्जनाः, भ्रमरा:, आगच्छन्ति ।
उत्तरम् :

• सज्जनाः – सन्तः, सुजनाः ।
• भ्रमराः – अलयः, भृगाः, मधुपाः, षट्पदाः।
• आगच्छन्ति – आयान्ति।

4. विरुद्धार्थकशब्दं लिखत।
गुणाः, दूरे, आयान्ति।

प्रश्न 1.
विरुद्धार्थकशब्दं लिखत।
गुणाः, दूरे, आयान्ति।
उत्तरम् :

• गुणाः × दोषाः, दुर्गुणाः।
• दूरे × समीपे, निकटे, निकषा।
• आयान्ति × गच्छन्ति, यान्ति।

श्लोकः 3

1. एकवाक्येन उत्तरत।

प्रश्न अ.
धेनवः किं भुक्त्वा दुग्धं यच्छन्ति ?
उत्तरम् :
धेनवः शुष्काणि तृणानि भुक्त्वा दुग्धं यच्छन्ति ।

प्रश्न आ.
धेनवः जलाशयात् किं पिबन्ति ?
उत्तरम् :
धेनव: जलाशयात् तोयं पिबन्ति ।

प्रश्न इ.
लोकमातर: का:?
उत्तरम् :
लोकमातरः धेनवः ।

2. श्लोकात् त्वान्त-अव्यये चित्वा लिखत ।

प्रश्न 1.
श्लोकात् त्वान्त-अव्यये चित्वा लिखत

3. वाक्यत: कर्ता, कर्म क्रियापदं च अन्विष्यत लिखत च ।
दुग्धं यच्छन्ति धेनवः।

प्रश्न 1.
वाक्यत: कर्ता, कर्म क्रियापदं च अन्विष्यत लिखत च ।
दुग्धं यच्छन्ति धेनवः।

4. एकवचने परिवर्तयत।
लोकमातरः धेनवः शुष्काणि तृणानि खादन्ति ।

प्रश्न 1.
लोकमातरः धेनवः शुष्काणि तृणानि खादन्ति ।

श्लोकः 4

1. श्लोकात् ल्यबन्त-अव्ययानि चिनुत ।

प्रश्न 1.
श्लोकात् ल्यबन्त-अव्ययानि चिनुत ।
उत्तरम् :

त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ट्वा इत्वा / अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य	तुमन्त अव्यय धातु + तुम् / धुम् / टुम् / डुम् / इतुम्  / अयितुम्
–	–	श्रोतुम् घातुम् वक्तुम् द्रष्टुम् ध्यातुम् दातुम् विहर्तुम्
–	आघ्राय	–
भुक्त्वा पीत्वा	–	–
अकृत्वा अगत्वा	अनुत्सृज्य	–
–	विहस्य, विहाय	–
–	प्रारभ्य	–
–	विज्ञाय	–
–	सञ्चिन्त्य।	प्राप्तुम्।

2. योग्यं रूपं चिनुत ।

प्रश्न अ.
षष्ठी- विहस्य/देवस्य।
उत्तरम् :
देवस्य।

प्रश्न आ.
चतुर्थी- विहाय/गेहाय।
उत्तरम् :
गेहाय।

प्रश्न इ.
प्रथमा- अहम्/कथम्।
उत्तरम् :
अहम्।

श्लोकः 5

1. एकवाक्येन उत्तरत।

प्रश्न अ.
स्थानभ्रष्टाः के के न शोभन्ते ?
उत्तरम् :
स्थानभ्रष्टा: दन्ताः, केशाः, नखाः, नराः न शोभन्ते।

प्रश्न आ.
किं विज्ञाय मतिमान् स्वस्थानं न परित्यजेत् ?
उत्तरम् :
स्थानभ्रष्टाः दन्ताः, केशाः, नखाः, नराः न शोभन्ते इति विज्ञाय मतिमान् स्वस्थानं न परित्यजेत्।

2. समानार्थकशब्दैः वाक्यं पुनर्लिखत ।
स्थानभ्रष्टाः दन्ताः केशा: नखाः नरा: न शोभन्ते ।

प्रश्न 1.
समानार्थकशब्दैः वाक्यं पुनर्लिखत ।
स्थानभ्रष्टाः दन्ताः केशा: नखाः नरा: न शोभन्ते ।
उत्तरम् :

• दन्ताः – रदनाः ।
• केशा: – कचा:, कुन्तलाः।
• नखाः – नखर:, शङ्कवः, कररुहाः।
• नराः – मानवाः, पुरुषाः।

3. श्लोकात प्रथमाविभक्ते: रूपाणि चित्वा लिखत ।

प्रश्न 1.
श्लोकात प्रथमाविभक्ते: रूपाणि चित्वा लिखत ।
उत्तरम् :
प्रथमा – स्थानभ्रष्टाः, दन्ताः, केशाः, नखाः, नराः, मतिमान्, विघ्नविहताः, मध्याः, प्रतिहन्यमानाः, उत्तमजनाः।

Sanskrit Anand Class 9 Textbook Solutions Chapter 2 अव्ययमाला Additional Important Questions and Answers

विशेषण-विशेष्य- सम्बन्धः ।

विशेषणम्	विशेष्यम्
1. सुहास्यम्	आस्यम्
2. वसताम्	सताम्
3. शुष्काणि	तृणानि

पृथक्करणम्। तालिकां पूरयत ।

किं दत्तम् ?	किं कर्तुम् ?	किमर्थम् ?
चित्तं दत्तम्	ध्यातुम्	ध्यानार्थम् / ध्यानाय
हस्तयुग्मं दत्तम्	दातुम्	दानार्थम् / दानाय

प्रश्न निर्माणं कुरुत।

प्रश्न 1.
गुणाः दूतत्वं कुर्वन्ति।
उत्तरम् :
गुणाः किं कुर्वन्ति?

प्रश्न 2.
केतकीगन्धम् आघ्राय षट्पदाः आयान्ति ।
उत्तरम् :
किं कृत्वा षट्पदा: आयान्ति?

प्रश्न 3.
धेनवः लोकेभ्यः दुग्धं यच्छन्ति।
उत्तरम् :
धेनवः केभ्यः दुग्धं यच्छन्ति?

प्रश्न 4.
मनुजेन सतां वर्त्म अनुसतव्यम्।
उत्तरम् :
मनुजेन केषां वर्त्म अनुसतव्यम्?

प्रश्न 5.
नीचैः विघ्नभयेन न खलु प्रारभ्यते।
उत्तरम् :
कैः विघ्नभयेन न खलु प्रारभ्यते?

प्रश्न 6.

1. ईश्वरेण घ्राणं घातुं दत्तम्।
2. ईश्वरेण द्रष्टुं नेत्रे दत्ते।
3. ईश्वरेण दातुं हस्तयुग्मं दत्तम्।
4. ईश्वरेण चित्तं ध्यातुं दत्तम्।

उत्तरम् :

1. ईश्वरेण घ्राणं किमर्थं दत्तम्?
2. ईश्वरेण द्रष्टुं के दत्ते?
3. ईश्वरेण दातुं किं दत्तम्?
4. ईश्वरेण चित्तं किमर्थ दत्तम्?

विभक्त्यन्तरूपाणि।

• प्रथमा – गुणाः, षट्पदाः, धेनवः, लोकमातरः, स्वल्पम, बहु, षष्ठी, चतुर्थी, अहम, द्वितीया, नरः, कः, दैवम्।
• द्वितीया – दूतत्वम्, केतकीगन्धम्, तृणानि, तोयम, दुग्धम्, परसन्तापम, खलमन्दिरम्, वर्त्म, विघ्नभयेन, विनैः, स्वोद्योगम्।
• चतुर्थी – लोकेभ्यः।
• पञ्चमी – जलाशयात्, तिलेभ्यः।
• षष्ठी – सताम्, वसताम्, सताम्, यस्य।

पद्यांशं पठित्वा जालरेखाचित्रं पूरयत।

1.

2.

लेखनकौशलम् :

समानार्थकशब्द योजयित्वा वाक्यं पुनर्लिखत।

• नासिका- बालकस्य नासिका दीर्घा। बालकस्य नासा / घोणा दीर्घा ।
• नेत्रम् – नेत्रे मुखस्य सौंदर्य वर्धयतः। लोचने / नयने मुखस्य सौंदर्य वर्धयतः।
• षट्पदा:- षट्पदाः रसपानं कर्तुम् आयान्ति। भ्रमराः । भृङ्गाः रसपान कर्तुम् आयान्ति।
• नराः – नराः स्वस्थानं न त्यजेयुः। मानवाः / मनुष्याः स्वस्थानं न त्यजेयुः।
• दैवम् – दैवं पुरुषकार्यम् एव अनुसरति। भाग्यं पुरुषकार्यम् एव अनुसरति।
• वर्त्म – सतां वर्त्म अनुत्सृज्य कार्य कुर्यात्। सतां मार्गम् अनुत्सृज्य कार्यं कुर्यात्।

व्याकरणम् :

शब्दानां पृथक्करणम्

नाम	सर्वनाम	क्रियापदम्	विशेषणम्
कर्णी, धेनवः	येन	यच्छन्ति	सुहास्यम्
नेत्रे, लोकमातर:	यस्य	शोभन्ते	वसताम्
षट्पदाः, लोकेभ्यः,	अहम्	कुर्वन्ति	शुष्काणि
तृणानि, तोयम्, नराः	कः	आयान्ति
		परित्यजेत्

समासाः।

समासनाम	अर्थ:	समासविग्रहः	समासनाम्
हस्तयुग्मम्	pair of hands	हस्तयो: युग्मम्।	षष्ठी तत्पुरुष समास

अव्ययमाला Summary in Marathi and English

प्रस्तावना :

सुभाषिते हे संस्कृत भाषेचे ठळक वैशिष्ट्य आहे. सुभाषिते केवळ गेय नसून कमी शब्दांत महत्त्वपूर्ण अर्थ पोहचवतात. प्रस्तुत अव्ययमालेमध्ये केवळ भाषासौंदर्यच दिसत नाही तर धातुंपासून बनणाऱ्या अव्ययांचे प्रयोजन सुद्धा दिसते. ह्यामध्ये प्रत्येक श्लोकात अव्ययांचा वापर केला आहे. ज्यात काही बदल होत नाही ती अव्यये. त्यांपैकी काही अव्यये धातुंपासून बनतात.

Subhashitas or good sayings form the most beautiful part of Sanskrit language. They are not only rhythmic and melodious but convey a very profound meaning in a few words. In this beautiful collection of slokas we shall not only see the beauty of language but also observe the use of avyayas that are derived from dhatus.

This अव्ययमाला has a theme where in each shloka contains some words which are अव्ययs formed from धातुs. अव्ययs are words that don’t change and these are अव्ययs that are formed from धातुs.

श्लोकः 1

श्रोतुं ……………………….. पातु ।।1।। [Greatness of the creation of the creator]

श्लोकः : श्रोतुं करें, वक्तुमास्यं सुहास्यं
घातुं घ्राणं पादयुग्मं विहर्तुम्।
द्रष्टुं नेत्रे हस्तयुग्मं च दातुं
ध्यातुं चित्तं येन सृष्टं स पातु।।1।। (शालिनी)
अन्वयः : येन श्रोतुं कर्णी, वक्तुं सुहास्यम् आस्य, घातुं घाणं, विहर्तुं पादयुग्मं, द्रष्टुं नेत्रे, दातुं हस्तयुग्मं ध्यातुं च वित्त सृष्ट सः (ईश्वरः) पातु।

अनुवादः

ऐकण्यासाठी कान, बोलण्यासाठी सुंदर हास्य असलेले तोंड, वास घेण्यासाठी नाक, फिरण्यासाठी दोन पाय, देण्यासाठी दोन हात आणि ध्यान करण्यासाठी मन ज्याने निर्माण केले तो (ईश्वर) (आमचे) रक्षण
करो.

May he (the Lord) protect us who has created two ears to hear, smiling face to speak, a nose to smell, a pair of feet to move around, two eyes to see, a pair of hands to give and a mind to think/contemplate.

श्लोकः 2.

गुणा: …………………………….. षट्पदाः ।।2।। [Virtues spread on their own]

श्लोकः : गुणा: कुर्वन्ति दूतत्वं दूरेऽपि वसतां सताम्।
केतकीगन्धमाघ्राय स्वयमायान्ति षट्पदाः ।।2।। (शाङ्गधरपद्धतिः) (अनुष्टुभ)
अन्वयः : दूरे वसताम् अपि सतां, गुणा: दूतत्वं कुर्वन्ति। (यथा) षट्पदाः केतकीगन्धम् आघ्राय (मधुपानाय) स्वयम् आयन्ति।

अनुवादः

दूरवर राहणाऱ्या सज्जनांचे गुण (त्यांचे) दूतत्व करतात. (जसे) भुंगे | केवड्याचा सुगंध घेऊन (मध पिण्यासाठी) स्वत:हून येतात.
Virtues become the messengers of the virtuous though residing far away. Just as having smelt the fragrance of Ketaki, the bees themselves come to it.

श्लोकः  3.

भुक्त्वा ……………. लोकमातरः ।।3।। [Great ones act for the welfare of others]

श्लोकः : भुक्त्वा तृणानि शुष्काणि पीत्वा तोयं जलाशयात्।
दुग्धं यच्छन्ति लोकेभ्यो धेनवो लोकमातरः।।3।। (अनुष्टुभ)
अन्वयः : धेनवः शुष्काणि तृणानि भुक्त्वा जलाशयात् तोयं पीत्वा लोकेभ्य: दुग्धं यच्छन्ति । (ता.) लोकमातर: (खलु)।

अनुवादः

गायी सुके गवत (चारा) खाऊन, जलाशयातील पाणी पिऊन लोकांना दूध देतात. (त्या) खरोखरच लोकमाता होत.
Cows who are indeed the mothers of the world give milk to people after eating dry grass and drinking water from the pond.

श्लोकः 4.

यस्य षष्ठी ………….. कथम् ।।5।। [I can’t marry a person who is ignorant.]

श्लोकः : यस्य षष्ठी चतुर्थी च विहस्य च विहाय च।
अहं कथं द्वितीया स्यात्, द्वितीया स्यामहं कथम्।।5।। (अनुष्टुभ्)
अन्वयः : यस्य (कृते) विहस्य (इति) षष्ठी, विहाय (इति) चतुर्थी, अहं कथं च (इति) द्वितीया स्यात् (तस्य) अहं द्वितीया (पत्नी) कथं स्याम्?

अनुवादः

ज्याच्यासाठी विहस्य ही षष्ठी (विभक्ती) आणि विहाय ही चतुर्थी (विभक्ती) आहे (तसेच) अहम्, कथम् ही द्वितीया (विभक्ती) आहे त्याची मी द्वितीया (पत्नी) कशी होऊ?

स्पष्टीकरण वैय्याकरणी वेदवती तिच्या भावी पतीची परीक्षा घेणार होती. गौरांग या तिच्या होणाऱ्या नवऱ्याला तिने विचारले, विहस्य, विहाय आणि अहम् व कथम् ही कोणती रूपे आहेत? त्याला केवळ ‘देव शब्दाची रूपे पाठ असल्यामुळे षष्ठी, चतुर्थी व द्वितीया असे उत्तर दिले. तेव्हा वेदवतीने वरील उत्तर दिले. ती म्हणाली ज्यासाठी अहम् आणि कथम् द्वितीया आहेत, त्याची मी द्वितीया म्हणजेच पत्नी कशी होऊ?

How can I become the wife of a person for whom the word विहस्य is षष्ठी विभक्ति, विहाय is चतुर्थी विभक्ति and अहम् and कथम् are द्वितीया विभक्ति?

Explanation Vedavati, a lady well-versed with grammar wanted to test the groom she would be marrying. In order to test the knowledge of the groom Gaurang, she asked him what the words विहस्य, विहाय and अहम्, कथम् were grammatically. Gaurang had only learnt the forms of the word and that too with great difficulty.

So, for him the words विहस्य and विहाय which are actually अव्ययs seemed to be षष्ठी and चतुर्थी विभक्ति like देवस्य and देवाय respectively and अहम् and कथम् seemed to be द्वितीया विभक्ति like देवम् SoVedavati remarked that she could not become the file meaning wife of such an ignorant person.

श्लोकः 5.

स्थानभ्रष्टा ………………. परित्यजेत् ।।7।। [Everything has its value only when it is in its right place]

श्लोकः : स्थानभ्रष्टा न शोभन्ते दन्ता: केशा नखा नराः।
इति विज्ञाय मतिमान् स्वस्थानं न परित्यजेत्।।7।। (हितोपदेश:) (अनुष्टुभ्)
अन्वयः स्थानभ्रष्टा: दन्ताः, केशाः, नखा: नराः च न शोभन्ते इति विज्ञाय मतिमान् (नर:) स्वस्थानं न परित्यजेत्।

अनुवादः

आपल्या स्थानापासून ढळलेले दात, केस, नखे आणि पुरुष शोभून दिसत नाहीत, हे जाणून बुद्धिमान माणसाने स्वत:चे स्थान सोडू नये.
Knowing that teeth, hair, nails and people that are not in the right place don’t look good, a wise person would not give up his place.

सन्धिविग्रहः

1. स्थानभ्रष्टान – स्थानभ्रष्टाः + न।
2. वक्तुमास्यम् – वक्तुम् + आस्यम् ।
3. केतकीगन्धमानाय – केतकीगन्धम् + आघाय।
4. दूरेऽपि – दूरे + अपि।
5. स्वयमायान्ति – स्वयम् + आयान्ति।
6. लोकेभ्यो धेनवो लोकमातरः – लोकेभ्यः + धेनवः + लोकमातरः।
7. यत्स्वल्पमपि – यत् + स्वल्पम् + अपि ।
8. विघ्नविहता विरमन्ति – विघ्नविहताः + विरमन्ति।
9. पुनरपि – पुन: + अपि।
10. प्रारब्धमुत्तमजना न – प्रारब्धम् + उत्तमजनाः + न।
11. स्यामहम् – स्याम् + अहम् ।
12. केशा नखा नरा: – केशा: + नखा: + नराः।
13. दैवमेवेति – दैवम् + एव + इति।
14. नरस्त्यजेत् – नरः + त्यजेत्।
15. कस्तैलम् – कः + तैलम्।
16. प्राप्तुमर्हति – प्राप्तुम् + अर्हति।

समानार्थकशब्दाः

1. कर्णः – श्रोत्रम्, श्रुतिः, श्रवः, श्रवणम्।
2. आस्यम् – वदनम्, तुण्डम्, आननम्, मुखम्।
3. प्राणम् – नासिका, गन्धवहा, घोणा, नासा।
4. विहर्तुम् – भ्रमितुम्।
5. नेत्रम् – नयनम, लोचनम्, चक्षुः, अक्षः।
6. हस्त: – करः, पाणिः ।
7. पादः – चरणः।
8. चित्तम् – मनः, चेतः, अन्त:करणम्।
9. पातु – रक्षतु।
10. तृणानि – शष्पाणि।
11. धेनवः – गावः।
12. भुक्त्वा – खादित्वा।
13. मातर: – जनन्यः।
14. खलः – दुष्टः, दुर्जनः।
15. सताम् – सज्जनानाम्।
16. वर्त्म – मार्गः, अध्वा,
17. पन्थाः, पथः।
18. अनुत्सृज्य – अत्यक्त्वा।
19. स्वल्पम् – अल्पम्, स्तोकम्।
20. बहु – भूरि, अधिकम्।
21. मन्दिरम् – (अत्र) गृहम्।
22. विघ्नम् – सङ्कटम्, प्रत्यूहः ।
23. पुन: पुन: – वारंवारम् ।
24. द्वितीया – पत्नी, जाया ।
25. विहस्य – हसित्वा ।
26. विहाय – त्यक्त्वा ।
27. प्राप्तुम् – लब्धम्।
28. अनुद्यमः – आलस्यम्।
29. सताम् – सज्जनानाम्।
30. प्रारभ्य – आरभ्य।

विरुद्धार्थकशब्दाः

• शुष्काणि × आणि।
• खलः × सुजनः।
• स्वल्पम् × बहु।
• नीचा: × उत्तमाः।
• प्रारभ्य × समाप्य।
• प्रारब्धम् × समाप्तम्।
• परित्यजन्ति × स्वीकृर्वन्ति।
• अनुद्यमः × उद्यमः।

शब्दार्थाः

1. आस्यम् – mouth – तोंड
2. ध्राणम् – nose – नाक
3. घातुम् – to smell – वास घेण्यासाठी
4. पादः – foot/leg – पाय
5. युग्मम् – pair – जोडी
6. नेत्रे – eyes – डोळे
7. दातुम् – to give – देण्यासाठी
8. चित्तम् – mind – चित्त
9. विहर्तुम् – to wander – फिरण्यासाठी
10. सृष्टम् – created – निर्माण केले
11. षट्पदाः – bees – भुंगे
12. केतकी – fragrance of Ketaki – केवड्याचा
13. गन्धम् – (Screw pine) – सुवास
14. गुणाः – virtues – गुण
15. दूतत्वम् – as a messenger – दूताचे काम
16. सताम् – of good people – सज्जनांचे
17. तृणानि – grass – गवत
18. शुष्काणि – dry – सुकलेले
19. तोयम् – water – पाणी
20. धेनवः – cows – गायी
21. अकृत्वा – without doing – न करून
22. परसन्ताप: – troubling others – दुसऱ्याला त्रास, पीडा
23. अगत्वा – without going – न जाता
24. खलमन्दिर – abode of the wicked – दुष्टाचे घर
25. अनुत्सृज्य – without leaving – न सोडता
26. सताम् – of good people – सज्जनांचा
27. वर्ती – road, path – मार्ग
28. विहस्य – having smiled – हसून
29. बिहाय – having left – सोडून
30. द्वितीया – second, (here) wife – दुसरी, (इथे)पत्नी
31. विघ्न – obstacle – अडथळा
32. विघ्नविहता: – due to obstacles – अडथळ्यांनी हरलेले
33. प्रतिहन्यमानाः – hammered – मारा झालेले
34. मध्यमाः – mediocre – मध्यम प्रतीचे लोक
35. स्थानभ्रष्टा: – not in the proper place – स्थानापासून ढळलेले
36. विज्ञाय – after knowing – जाणून
37. मतिमान् – intelligent – बुद्धिमान
38. दैवम् – fortune – नशीब
39. सञ्चिन्त्य – thinking – विचार करून
40. नरः – man – मनुष्य
41. अनुद्यमेन – without effort – प्रयत्नशिवाय

9th Standard Sanskrit Anand Digest Pdf 

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer

Class 9th Sanskrit Anand Chapter 7 सूक्तिसुधा Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Anand Chapter 7 सूक्तिसुधा Notes, Textbook Exercise Important Questions and Answers.

Std 9 Sanskrit Chapter 7 Question Answer

Sanskrit Anand Std 9 Digest Chapter 7 सूक्तिसुधा Textbook Questions and Answers

भाषाभ्यास:

श्लोकः 1

1. एकवाक्येन उत्तरत।

प्रश्न अ.
कैः धनं न हीयते?
उत्तरम् :
चौरेण, राज्ञा च विद्याधनं न ह्रियते।

प्रश्न आ.
केषु धनं न विभज्यते ?
उत्तरम् :
भ्रातृषु धनं न विभज्यते।

प्रश्न इ.
सर्वधनप्रधानं किम् ?
उत्तरम् :
सर्वधनप्रधानं विद्याधनम् ।

2. माध्यमभाषया उत्तरत।

प्रश्न 1.
विद्याधनं व्यये कृते कथं वर्धते ?
उत्तरम् :
‘सूक्तिसुधा’ या पद्यपाठामध्ये विविध संस्कृत साहित्यकृतींमधून सुभाषिते संकलित केली आहेत. प्रसङ्गाभरणम् मधील श्लोक विद्येचे महत्त्व सांगतो. विद्या हे धन असे आहे जे कोणी चोरू शकत नाही, जे राजा कुणाकडून घेऊ शकत नाही, विद्याधन हे भावंडांमध्ये इतर मालमत्तेप्रमाणे वाटले जाऊ शकत नाही व त्याचे कधी ओझे सुद्धा होत नाही.

पैसा खर्च केला की तो कमी होतो, पण विद्याधन मात्र जितके वाटू तितके वाढते. आपण आपल्याकडचे ज्ञान जेव्हा दुसऱ्याला देतो तेव्हा त्याच्याकडूनसुध्दा आपल्याला अधिक ज्ञान मिळते. चर्चामधून, ज्ञानाच्या आदान-प्रदानामधून आपल्या ज्ञानात वाढच होते. ज्ञान दिल्याने वाढते, हा संदेश या श्लोकातून दिला आहे.

In the lesson ‘सूक्तिसुधा’ various subhashitas are collected from different literature pieces of Sanskrit. – In the shloka from प्रसङ्गाभरणम् the importance of knowledge is expressed. Knowledge can neither be stolen nor it can be taken away by king. It is indivisible and is not burden either.

Knowledge is that kind of a wealth which increases though spent unlike other riches. When we impart knowledge to someone, through that interaction we gain more knowledge. Here knowledge increases but never decreases. This special feature of knowledge suggests us that we should always share our knowledge and it is the greatest wealth.

3. सन्धिविग्रहं कुरुत ।
वर्धत एव ।

प्रश्न 1.
वर्धत एव ।
उत्तरम् :
वर्धत एव – वर्धते + एव।

4. समानार्थकशब्द लिखत।
चोरः, भारः, नित्यम्, विद्या, धनम्, प्रधानम् ।

प्रश्न 1.
चोरः, भारः, नित्यम्, विद्या, धनम्, प्रधानम् ।
उत्तरम् :

• चोरः – तस्करः, स्तेनः।
• नित्यम् – सदा, सर्वदा, सदैव।
• विद्या – ज्ञानम्।
• धनम् – वित्तम्।
• प्रधानम् – प्रमुखम्।

5. विरुद्धार्थकशब्द लिखत।
व्ययः, नित्यम्, प्रधानम्।

प्रश्न 1.
व्ययः, नित्यम्, प्रधानम्।
उत्तरम् :

• व्ययः × सञ्चयः।
• नित्यम् × क्वचित्।
• प्रधानम् × गौणम्, तुच्छम्।

श्लोक: 2

1. सन्धिं कुरुत।

प्रश्न 1.
अ. परः + वा + इति
आ. वसुधा + एव
उत्तरम् :
अ. परो वेति – पर: + वा + इति।
आ. वसुधैव – वसुधा + एव।

2. एकवाक्येन उत्तरत।

प्रश्न अ.
‘अयं निजः, अयं परः’ इति केषां गणना ?
उत्तरम् :
अयं निजः, अयं परः इति लघुचेतसाम् गणना।

प्रश्न आ.
केषां कृते वसुधा एव कुटुम्बकम् भवति?
उत्तरम् :
उदारचरितानां कृते वसुधा एव कुटुम्बकम् अस्ति।

3. माध्यमभाषया उत्तरत।

प्रश्न 1.
लघुचेतसः उदारचेतसः जनाः कथम् अभिज्ञातव्याः ?
उत्तरम् :
दररोजच्या आयुष्यात आपण अनेक मूल्ये, तत्त्वे पाळतो ज्यांच्यामुळे आपल्या आयुष्याला आकार मिळतो व ते अधिक समृद्ध होते. अशाच काही मूल्यांचा संदेश ‘सूक्तिसुधा’ या पद्यपाठातून दिला आहे.

शाईधरपद्धति मधून घेतलेल्या या श्लोकात उदार माणसांच्या गुणांचा गौरव केला आहे. काही माणसे नेहमी हे माझे, हे तुझे असे म्हणून गोष्टींमधे भेद करतात. त्यांच्या स्वत:च्या गोष्टींपुरतेच ते पाहतात व जे परके, आपले नाही त्याच्याशी काही देणे-घेणे ठेवत नाहीत. अशी माणसे कोत्या मनाची समजावीत. या उलट जी माणसे मनाने उदार असतात त्यांच्यासाठी संपूर्ण विश्वच त्यांचे कुटुंब असते. हे विश्वची माझे घर असे म्हणणारे संत हे उदार मन असणाऱ्या माणसांमध्ये गणले जातात.

In our day to day life, we follow certain values, certain morals that enchance our lifestyle. ‘सूक्तिसुधा’ talks about such values.

In the shloka taken from शाईधरपद्धति the nature of noble and generous people is described. It says that those who consider things as mine and not mine are low-minded. They delimit the things as their own and not belonging to them. But to those who are really generous, the whole earth is like their own family.

Great saints treat the whole universe like their own, they never hesitate to enlighten or help others irrespective of who they are. A person with a big heart is always praised and looked upon for help in any difficult situation. Such people are very hard to find. However, people with an inferior mind or nonassimilative nature are known by their attitude of being self-centered.

4. स्तम्भमेलनं कुरुत |

प्रश्न 1.

अ	स्वीयम्	चिन्तनम्	अन्यः	पृथिवी
आ	गणना	वसुधा	निजः	परः

उत्तरम् :

अ	स्वीयम्	चिन्तनम्	अन्यः	पृथिवी
आ	निजः	गणना	परः	वसुधा

श्लोकः 3

1. एकवाक्येन उत्तरत।

प्रश्न अ.
परोपकाराय वृक्षाः किं कुर्वन्ति ?
उत्तरम् :
परोपकाराय वृक्षाः फलन्ति ।

प्रश्न आ.
परोपकाराय नद्यः किं कुर्वन्ति ?
उत्तरम् :
परोपकाराय नद्यः वहन्ति ।

प्रश्न इ.
काः परोपकाराय दुहन्ति ?
उत्तरम् :
परोपकाराय गाव: दुहन्ति।

प्रश्न ई.
शरीरं किमर्थम् ?
उत्तरम् :
परोपकारार्थ शरीरम्।

2. माध्यमभाषया उत्तरत।

प्रश्न 1.
परोपकार: नाम किम् ? के परोपकारमग्नाः ?
उत्तरम् :
‘सूक्तिसुधा’ या पद्यपाठामध्ये प्रत्यक्ष आयुष्यात आचरणात आणण्यासाठीचे संदेश सुंदर शब्दांत काव्यात्मकप्रकाराने दिले आहेत. ‘विक्रमोर्वशीयम्’ या नाटकातून घेतलेल्या श्लोकामध्ये परोपकाराचे महत्त्व सांगितले आहे. इतरांना कोणत्याही परतफेडीची अपेक्षा न ठेवता मदत करणे म्हणजे परोपकार. काही व्यक्ती या कायमच दुसऱ्याच्या चांगल्याचा विचार करत असतात.

अशा व्यक्तींना आपण संत-महात्मा म्हणून त्यांचा गौरव करतो. प्रस्तुत श्लोकात निसर्गातील उदाहरणे देऊन परोपकाराचे माहात्म्य सांगितले आहेत. वृक्ष इतरांना देण्यासाठीच फळे धारण करतात. त्या फळांच्या बदल्यात ते कशाची अपेक्षा करत नाहीत. नद्या गावोगावांना पाणी पुरवत वाहतात. त्यांचा स्वत:चा त्यात काही वैयक्तिक लाभ नसतो.

गायी इतरांसाठीच दूध देतात. अशाप्रकारे झाडे, नद्या, गायी हे परोपकराचा संदेश नेहमी देत असतात, रोजच्या व्यवहारातील निसर्गाच्या उदाहरणांमधून परोपकाराचे महत्त्व सांगितले आहे.

In the lesson’सूक्तिसुधा’ various shlokas filled with value based messages are given. They teach us many values such as selflessness, charity, knowledge. In the shloka taken from ‘विक्रमोर्वशीयम्’ the greatness of selfless behaviour is emphasized.

परोपकार means helping othersselflessly. To help others and not expecting anything in return is a great virtue. Only noble ones possess such a rare quality. The trees bear fruits for others. They don’t eat the fruits they bear.

The rivers flow for people like us. The cows yield milk for others. They don’t see their benefit in doing so. Likewise, our life is also for helping others. These subhashita gives a message that however busy we may get, we should always spare some time to help others selflessly.

श्लोकः 3

3. समानार्थकशब्द लिखत।
वृक्षाः, नद्यः, शरीरम्।

प्रश्न 1.
वृक्षाः, नद्यः, शरीरम्।
उत्तरम् :

• वृक्ष: – तरुः।
• नद्यः – सरित्।
• शरीरम् – तनुः, देहः।

4. विरुद्धार्थकशब्द लिखत।

प्रश्न 1.
उपकारः, परः ।
उत्तरम् :
1. उपकार: × अपकारः
2. परः × निजः।

श्लोक: 4

1. रिक्तस्थानं पूरयत।

प्रश्न 1.
अ. सत्सङ्गतिः धियः जाड्यं ………..।
आ. सत्सङ्गतिः वाचि ……….. सिञ्चति।
इ. सत्सङ्गतिः ……….. दिशति ।
ई. सत्सङ्गतिः पापम् ……….. ।
उ. सत्सङ्गतिः चित्तं ……….. ।
ऊ. सत्सङ्गति दिक्षु ……….. तनोति।
उत्तरम् :
अ. हरति
आ. सत्यम्
इ. मानोन्नतिम्
ई. अपाकरोति
उ. प्रसादयति
ऊ. कीर्तिम्

2. माध्यमभाषया उत्तरत।

प्रश्न 1.
सत्सङ्गतिः जीवने किं किं करोति ?
उत्तरम् :
It is said that one is known by the company he keeps. The people around us lay great impact on our life. Company of good people takes away ignorance of the intellect. It makes us truthful. Due to company of good people one gains more respect. Our sins get wiped away when we are surrounded by virtuous people.

It doesn’t only make us happy but also spreads fame in all directions. Company of good people is always desirable. They always pass on the good qualities to everyone they are around. Company of good people is desirable in every aspect.

‘सुसंगति सदा घडो, सुजन वाक्य कानी पडो’ असे म्हणतात. सज्जनांच्या संगतीमुळे आपला उद्धार होतो हे खरेच आहे. ‘सूक्तिसुधा’ च्या या श्लोकात हे सांगितले आहे. चांगल्या माणसांच्या संगतीमुळे बुद्धीचे अज्ञान दूर होते. ते सत्याची शिकवण देतात. चांगल्या लोकांच्या संगतीत राहिल्यामुळे आपल्याला अधिक मान मिळतो.

सद्संगतीमुळे आपल्यातील वाईट वृत्तींचा नाश होतो. त्यामुळे आपण पापांपासून लांब राहतो. सज्जनांबरोबर राहिल्यामुळे वाईट गोष्टी आपल्यापासून आपोआप लांब राहतात आणि मन प्रसन्न राहते. सज्जनांबरोबर राहिल्यामुळे त्यांच्याप्रमाणेच आपली सुद्धा प्रसिद्धी सर्वदूर परसते.

श्लोक: 5

1. सन्धिविग्रहं कुरुत।
नार्यस्तु, यत्रैताः, एतास्तु, तत्राफलाः, सर्वास्तत्र ।

प्रश्न 1.
नार्यस्तु, यत्रैताः, एतास्तु, तत्राफलाः, सर्वास्तत्र ।
उत्तरम् :

• नार्यस्तु – नार्यः + तु।
• यौतास्तु – यत्र + एता: + तु।
• सर्वास्तत्राफला: – सर्वाः + तत्र + अफलाः।

2. एकवाक्येन उत्तरत।

प्रश्न अ.
देवताः कुत्र रमन्ते ?
उत्तरम् :
यत्र नार्यस्तु पूज्यन्ते रमन्ते तत्र देवताः।

प्रश्न आ.
क्रियाः कुत्र अफलाः भवन्ति ?
उत्तरम् :
यत्र तु एता: न पूज्यन्ते तत्र सर्वाः क्रियाः अफला: (भवन्ति)।

3. माध्यमभाषया उत्तरत। 

प्रश्न 1.
‘यत्र नार्यः पूज्यन्ते’। इति सूक्तिं श्लोकस्य आधारेण स्पष्टीकुरुत।
उत्तरम् :
‘सूक्तिसुधा’ पाठामध्ये रोजच्या आयुष्यात आचरणात आणण्यासारखी अशी मूल्ये सांगितली आहेत. महाभारतातील श्लोकामध्ये ‘स्त्रियांचा आदर करावा’ हे त्रिकालाबाधित तत्त्व सांगितले आहे. जिथे स्त्रियांना आदर दिला जातो, तिथे देवता सुद्धा आनंदाने राहतात. मात्र जिथे स्त्रियांचा अनादर होतो तिथे कोणतेही कार्य सफल होत नाही.

ज्या समाजामध्ये स्त्रियांना मानसन्मान मिळतो तो समाज प्रगत समजला जातो. हे तत्त्व आजही लागू होते. ‘देव आनंदाने राहतात’ म्हणजे ते स्थान पवित्र व रम्य मानले जाते. त्या ठिकाणी नेहमी सकारात्मकता, उत्साह राहतो.

In the lesson ‘सूक्तिसुधा’ different values, are taught which we should apply in our life. Averse fromमहाभारत tells an important value to respect women which is absolute irrespective of time or situation. Since ancient times, the scriptures have taught to respect each and every woman.

In this particular shloka, it is said that where the women get respect Gods dwell there happily. But where women are not respected, no action gets accomplished in such place. So respecting women is a sign of good and developed society.

5. ‘नारी’ इत्यर्थम् अमरकोषपङ्क्तिं लिखत ।

प्रश्न 1.
‘नारी’ इत्यर्थम् अमरकोषपङ्क्तिं लिखत ।

Sanskrit Anand Class 9 Textbook Solutions Chapter 7 सूक्तिसुधा Additional Important Questions and Answers

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.

1. सर्वधनेषु प्रधानं विद्याधनम् अस्ति।
2. परोपकाराय वृक्षाः फलन्ति।
3. परोपकाराय नद्य: वहन्ति।

उत्तरम् :

1. सर्वधनेषु प्रधानं किम् अस्ति?
2. परोपकाराय के फलन्ति?
3. नद्यः किमर्थं वहन्ति?

विभक्त्यन्तरूपाणि।

• प्रथमा – चोरहार्यम्, राजहार्यम्, भ्रातृभाज्यम्, भारकारि, निजः, परः, अयम्, गणना, वसुधा, कुटुम्बकम्, वृक्षाः, नद्यः, गावः, शरीरम्,
  इदम्, सत्यम्, चातकः, सः, मेघः, उदारता, पठकः, पाठकः, शास्त्रवाचकाः, ते. यः, क्रियावान, सः, पण्डितः, सर्वे, अन्ये, ये, व्यसनिनः ।
• द्वितीया – जाड्यम्, मानोन्नतिम्, पापम्, चित्तम्, कीर्तिम्, जलधरम्, त्रिचतुरान्, पय:कणान्, विश्वम्।
• तृतीया – पिपासया, अम्भसा।
• चतुर्थी – परोपकाराय।
• षष्ठी – लघुचेतसाम्, उदारचरितानाम्, धियः, महताम्।
• सप्तमी – व्यये, वाचि, दिक्षु।

लकारं लिखत।

• वर्धते – वृध्-व धातुः प्रथमगण: आत्मनेपदं लट्लकार: प्रथमपुरुष: एकवचनम्।
• फलन्ति – फलधातुः प्रथमगण: परस्मैपदं लट्लकार प्रथमपुरुष: बहुवचनम्।
• वहन्ति – वह धातुः प्रथमगण: परस्मैपदं लट्लकार : प्रथमपुरुष: बहुवचनम्।
• दुहन्ति – दुह् धातुः द्वितीयगण: उभयपदम् अत्र परस्मैपदं लट्लकार: प्रथमपुरुष: बहुवचनम्।
• हरति – ह धातुः प्रथमगण: उभयपदम् अत्र परस्मैपदं लट्लकार : प्रथमपुरुष: एकवचनम्।
• सिञ्चति – सिच् – सिधातुः षष्ठगण: उभयपदम् अत्र परस्मैपदं लट्लकार : प्रथमपुरुषः एकवचनम्।
• दिशति – दिश् धातुः षष्ठगण: उभयपदम् अत्र परस्मैपदं लट्लकार : प्रथमपुरुष: एकवचनम्।
• करोति – कृ धातु: अष्टमगण: उभयपदम् अत्र परस्मैपदं लट्लकार : प्रथमपुरुष: एकवचनम्।
• प्रसादयति – प्र + सद् धातुः प्रथमगणः परस्मैपदं प्रयोजकरूपं लट्लकार : प्रथमपुरुष: एकवचनम्।
• तनोति – तन् धातुः अष्टमगण: उभयपदम् अत्र परस्मैपदं लट्लकारः प्रथमपुरुषः एकवचनम्।
• कथय – कथ् धातुः दशमगण: उभयपदम् अत्र परस्मैपदं लट्लकार: मध्यमपुरुष: एकवचनम्।
• याचते – याच् धातुः प्रथमगण: आत्मनेपदं लट्लकार: प्रथमपुरुषः एकवचनम्।
• पूरयति – पूर् धातुः दशमगण: उभयपदम् अत्र परस्मैपदं लट्लकार: प्रथमपुरुष: एकवचनम्।

पद्यांश पठित्वा जालरेखाचित्रं पूरयत।

1.

उत्तरम् :
न चोरहार्यम्, न भ्रातृभाज्यम्, न राजहार्यम्, न भारकारि।

2.

3.

4.

एकवाक्येन उत्तरत।

प्रश्न 1.
उदारचरितानां कृते वसुधा कीदृशी भवति?
उत्तरम् :
उदारचरितांना कृते वसुधा कुटुम्बकम् इव भवति।

प्रश्न 2.
सत्सङ्गतिः धियः किं हरति?
उत्तरम् :
सत्सङ्गतिः धियः जाड्यं हरति।

प्रश्न 3.
सत्सङ्गतिः वाचि किं सिञ्चति?
उत्तरम् :
सत्सङ्गतिः वाचि सत्यं सिञ्चति।

प्रश्न 4.
सत्सङ्गतिः किम् अपाकरोति?
उत्तरम् :
सत्सङ्गतिः पापम् अपाकरोति ।

प्रश्न 5.
सत्सङ्गतिः किं प्रसादयति?
उत्तरम् :
सत्सङ्गतिः चित्तं प्रसादयति ।

प्रश्न 6.
सत्सङ्गतिः दिक्षु किं तनोति?
उत्तरम् :
सत्सङ्गतिः दिक्षु कीर्तिं तनोति।

प्रश्न 7.
परैः विग्रहे प्राप्ते वयं कति स्मः?
उत्तरम् :
परैः विग्रहे प्राप्ते वयं पञ्चाधिकं शतम्।

प्रश्न 8.
कौरवाः कति सन्ति?
उत्तरम् :
कौरवाः शतं सन्ति।

रिक्तस्थानानि पूरयित्वा अन्वयं पुनर्लिखत ।

प्रश्न 1.
लघुचेतसां (कृते) अयं ……….. पर: वा इति ………… (अस्ति)। उदारचरितानां (कृते) तु ………. एव ……….. (अस्ति )।
उत्तरम् :
लघुचेतसां (कृते) अयं निज: पर: वा इति गणना (अस्ति)। उदारचरितानां (कृते) तु वसुधा एव कुटुम्बकम् (अस्ति)।

प्रश्न 2.
1. गाव: ………… दुहन्ति ।
2. इदं शरीरं ……………. (एव अस्ति)।
उत्तरम् :
1. गाव: परोपकाराय दुहन्ति ।
2. इदं शरीरं परोपकारार्थम् (एव अस्ति )।

प्रश्न 3.
सत्सङ्गतिः ………….. जाड्यं हरति, ………. सत्यं सिञ्चति, मानोन्नति दिशति, पापम् ……….., चित्तं …………, दिक्षु कीर्तिं तनोति । कथय! (सा सत्सङ्गतिः) पुंसां किं (हित) न करोति ।।
उत्तरम् :
सत्सङ्गतिः धियः जाड्यं हरति, वाचि सत्यं सिञ्चति, मानोन्नति दिशति, पापम् अपाकरोति, चित्तं प्रसादयति, दिक्षु कीर्ति तनोति । कथय! (सा सत्सङ्गतिः) पुंसां किं (हित) न करोति ।।

प्रश्न 4.
(यदा) ………… पिपासया जलधरं त्रिचतुरान् ………… याचते (तदा) सः (मेघः) अपि विश्वम् ………… पूरयति। हन्त हन्त (कियती एषा) महताम् …………
उत्तरम् :
(यदा) चातक :पिपासया जलधरं त्रिचतुरान् पय:कणान्याचते (तदा) सः (मेघः) अपि विश्वम् अम्भसा पूरयति। हन्त हन्त (कियती एषा) महताम् उदारता!

प्रश्न 5.
पठक: पाठक: (तथा) च ये अन्ये ………….. (सन्ति, ते) सर्वे ………… ज्ञेयाः। (यतः) यः ………. स(एव) ………. (अस्ति)।
उत्तरम् :
पठक: पाठक: (तथा) च ये अन्ये शास्त्रवाचका: (सन्ति, ते) सर्वे व्यसनिनः ज्ञेयाः। (यतः) य: क्रियावान् स: (एव) पण्डितः (अस्ति)।

समानार्थकशब्दं योजयित्वा वाक्यं पुनर्लिखत।

नारी – नारी सर्वत्र पूजनीया। स्त्री/महिला/योषा सर्वत्र पूजनीया।

व्याकरणम् :

शब्दानां पृथक्करणम्

समासाः।

समासनाम	अर्थ:	समासविग्रहः	समासनाम्
मानोन्नतिः	upliftment of respect	मानस्य उन्नतिः।	षष्ठी तत्पुरुष समास

सूक्तिसुधा Summary in Marathi and English

प्रस्तावना :

संस्कृतसाहित्य गद्य, पद्य, नाट्य अशा सर्व साहित्यप्रकारांनी परिपूर्ण आहे. सुभाषिते हा पद्यप्रकार संस्कृतसाहित्यातील लोकप्रिय साहित्यप्रकार आहे. संस्कृत सुभाषिते केवळ संस्कृतमध्येच नाही तर इतर भाषांमध्ये सुद्धा जशीच्या तशी वापरली जातात. उदा. “विनाशकाले विपरीतबुद्धिः। संपूर्ण सुभाषित लक्षात राहिले नाही तरी त्याचा गर्भितार्थ किंवा महत्त्वाची ओळ नक्कीच लक्षात राहते, जी म्हण किंवा उक्ती म्हणून वापरली जाते. शब्दसंपदा वाढवण्यात सुभाषिते निश्चितच मदत करतात.

Sanskrit literature comprises of prose, poetry and drama.सुभाषितs are well knoron part of the poetic liturature. Parts of which have been used as proverbs or sayings not only in Sanskrit but also in other languages. In fact several Sanskrit sayings are very often used as they are in other Indian languages.

You may recall विनाशकाले विपरीतबुद्धिः. People generally do not remember the entire subhashita but they do remember the phrase of the proverb quite easily. In fact remembering such sayings definitely enhances one’s vocabulary and command over the language..

श्लोकः – 1

न चोरहार्य ………….. सर्वधनप्रधानम् ।।1।। [Knowledge is the best of all riches]

श्लोकः : न चोरहार्य न च राजहार्य न भ्रातृभाज्यं न च भारकारि ।
व्यये कृते वर्धत एव नित्यं विद्याधनं सर्वधनप्रधानम् ।।1।। (प्रसङ्गाभरणम्)

अन्वयः : विद्याधनं चोरहार्य न (अस्ति), राजहार्य न, भ्रातृभाज्यं न, भारकारि (अपि) न (अस्ति) । व्यये कृते अपि (तत्) नित्यं वर्धते एव ।
(सत्यमेव विद्याधनं) सर्वधनप्रधानम् (अस्ति) ।

अनुवादः

Knowledge which is wealth cannot be stolen by a thief, cannot be taken away by a king, cannot be divided among brothers and is also not a burden. Though it is spent it only always increases. Wealth in the form of knowledge is the foremost among all types of wealth

विद्याधन चोरले जाऊ शकत नाही, राजा ते जप्त करू शकत नाही, याची भावंडामध्ये वाटणी केली जाऊ शकत नाही आणि ते त्याचे ओझे घेत नाही, खर्च केले तरी ते वाढतेच. खरोखर विद्याधन हे नेहमीच सर्व प्रकारच्या धनांमध्ये श्रेष्ठ धन आहे!

श्लोक: – 2

अयं ………………. कुटुम्बकम् ।।2।। [The world is one family]

श्लोकः : अयं निजः परो वेति गणना लघुचेतसाम् ।
उदारचरितानां तु वसुधैव कुटुम्बकम् ।।2।। (शार्ङ्गधरपद्धतिः)

अन्वयः । लघुचेतसां (कृते) अयं निजः पर: वा इति गणना (अस्ति) । उदारचरिताना (कृते) तु वसुधा एव कुटुम्बकम् (अस्ति)।

अनुवादः

हे माझे, हे तुझे असे कोत्या मनाचे लोक मानतात. उदार वृत्तीच्या लोकांसाठी तर संपूर्ण पृथ्वीच कुटुंब असते.
This is mine or it belongs to others is the consideration of the low-minded. Indeed for the | generous/ large-hearted, the entire world is a family.

श्लोकः – 3

परोपकाराय फलन्ति ……………….. शरीरम् ।।3।। [The body is for the welfare of others]
श्लोकः : परोपकाराय फलन्ति वृक्षाः परोपकाराय वहन्ति नद्यः।
परोपकाराय दुहन्ति गाव: परोपकारार्थमिदं शरीरम् ।।3।। (विक्रमोर्वशीयम्)
अन्वयः : वृक्षाः परोपकाराय फलन्ति। नद्यः परोपकाराय वहन्ति। गाव: परोपकाराय दुहन्ति। इदं शरीर परोपकारार्थम् (एव अस्ति)।

अनुवादः

झाडे परोपकारासाठीच फळे धारण करतात, नद्या इतरांसाठीच वाहतात, गायी दुसऱ्यांनाच दूध देतात आणि हे शरीरसुद्धा परोपकारासाठीच आहे.
Trees bear fruits for the welfare of others, rivers flow for the welfare of others, cows yield milk for the benefit of others. This body is for the welfare of others.

श्लोक: – 4

जाड्यं ………………. पुंसाम् ।।4।। [Good association bestows everything]

श्लोकः : जाड्यं धियो हरति सिञ्चति वाचि सत्यं
मानोन्नतिं दिशति पापमपाकरोति । चित्तं प्रसादयति दिक्षु तनोति कीर्ति
सत्सङ्गतिः कथय किं न करोति पुंसाम् ।।4।। (भर्तृहरिसुभाषितसङ्ग्रहः)

अन्वयः : सत्सङ्गतिः धियः जाड्यं हरति, वाचि सत्यं सिञ्चति, मानोन्नतिं दिशति, पापम् अपाकरोति, चित्तं प्रसादयति, दिक्षु कीर्ति तनोति । कथय ! (सा सत्सङ्गतिः) पुंसां किं (हित) न करोति ?

अनुवादः

बुद्धीचे अज्ञान दूर करते. वाणीला सत्याचे वळण लावते (सिञ्चति), आदर वाढवण्यासाठी दिशा दाखवते, पाप दूर करते, मन प्रसन्न करते, सर्व दिशांना कीर्ती पसरवते. सांगा बरे सज्जनांची संगती काय करत नाही!

Say what all can good company not do for men? It takes away the ignorance of the intellect. It sprinkles truth on speech. In directs the progress of respect and takes one away from sin. It delights the mind and spreads fame in all directions.

श्लोकः – 5

यत्र ………………… क्रियाः ।।5।। [Significance of respecting women.]
श्लोकः : यत्र नार्यस्तु पूज्यन्ते रमन्ते तत्र देवताः।
यौतास्तु न पूज्यन्ते सर्वास्तवाफला: क्रियाः ।।5।। (महाभारतम्)
अन्वयः : यत्र नार्यः पूज्यन्ते तत्र देवता: रमन्ते। यत्र तु एता: न पूज्यन्ते तत्र सर्वाः क्रियाः अफला: (भवन्ति)।

अनुवादः

जिथे स्त्रियांची पूजा होते तिथेच देवता आनंदाने राहतात. जिथे त्या (स्त्रिया) पूजल्या जात नाहीत (त्यांचा अनादर होतो) तिथे कोणतेही कार्य सफल होत नाही.

Gods rejoice where women are respected. But where they are not respected, there all actions become futile/unsuccessful.

सन्धिविग्रहः

• परोपकारार्थमिदम् – परोपकारार्धम् + इदम्।
• धियो हरति – धियः + हरति।
• पापमपाकरोति – पापम् + अपाकरोति
• परैस्तु – परैः + तु।

समानार्थकशब्दाः

• राजा – नृपः, भूपः, भूपतिः।
• निजः – स्वस्य।
• वसुधा – धरा, पृथ्वी, वसुन्धरा।
• चेतः – मनः, चित्तम्।
• धीः – मतिः, बुध्दिः।
• चित्तम् – मनः, चेतः।
• वाच् – वाणी।
• कीर्तिः – प्रसिद्धिः।
• नारी – वनिता, महिला, स्त्री।
• देवताः – दैवतानि।
• जलधरः – मेघः, पयोदः।
• अम्भः/पयः – जलम्, तोयम्, उदकम्, नीरम, वारि।
• विग्रहः – युद्धम्।

विरुद्धार्थकशब्दाः

• वर्धत × क्षीयते।
• लघुचेतस् × उदारचेतस्।
• कीर्तिः × अपकीर्तिः।
• धीः × जाड्यम्।
• अफला: × सफलाः।

शब्दार्थाः

1. चोरहार्यम् – stolen by a thief – चोराकडून चोरण्यासारखे
2. राजहार्यम् – taken away by the king – राजाने जप्त करण्यासारखे
3. भ्रातृभाज्यम् – divided among brothers – भावंडामध्ये वाटणी करण्यासारखे
4. व्यये कृते – though it is spent – खर्च केले तरी
5. नित्यम् – always – नेहमी
6. भारकारि – burden – ओझे
7. गणना – consideration – मानणे
8. लघुचेतसाम् – of the low-minded – कोत्या मनाचे
9. उदारचरितानाम् – generous hearted / magnanimous – उदार वृत्तीच्या लोकांसाठी
10. वसुधा – world – पृथ्वी
11. कुटुम्बकम् – family – कुटुंब
12. निजः – mine – माझे
13. परः – others’ – इतरांचे
14. परोपकाराय – for the welfare of others – परोपकारासाठी
15. फलन्ति – bear fruits – फळे धारण करतात
16. वहन्ति – flow – वाहतात
17. दुहन्ति – yield milk – दूध देतात
18. गाव: – cows – गायी
19. जाड्यम् – ignorance – अज्ञान
20. धियः – of the intellect – बुद्धीचे
21. अपाकरोति – takes away – दूर करते
22. प्रसादयति – delights – प्रसन्न करते
23. हरति – remove/takes away – दूर करते
24. सिजति – sprinkles – वळण लावते
25. मानोन्नतिम् – progress of respect – आदर वाढवण्यासाठी
26. दिशति – directs – दिशा देते
27. दिक्षु – in directions – दिशांमध्ये
28. तनोति – Spreads – पसरविते
29. सत्सङ्गतिः – good company – सज्जनांची संगती
30. पुंसाम् – of men – माणसांचे
31. वाचि – in speech – वाणीमध्ये
32. यत्र – where – जिथे
33. नार्यः – women – स्त्रिया
34. पूज्यन्ते – are respected – आदर केला जातो
35. रमन्ते – rejoice – आनंदाने राहतात
36. अफला: – futile/unsuccessful – असफल
37. एताः – these – या

9th Standard Sanskrit Anand Digest Pdf 

• सुष्ठु गृहीतः चौरः Class 9 Question Answer
• अव्ययमाला Class 9 Question Answer
• किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
• विध्यर्थमाला Class 9 Question Answer
• वीरवनिता विश्पला Class 9 Question Answer
• पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
• सूक्तिसुधा Class 9 Question Answer
• मनसः स्वच्छता Class 9 Question Answer
• अमरकोषः Class 9 Question Answer
• काव्यशास्त्रविनोदः Class 9 Question Answer
• मनोराज्यस्य फलम् Class 9 Question Answer