Class 9th Sanskrit Aamod Chapter 5 किं मिथ्या ? किं वास्तवम् ? Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 5 किं मिथ्या ? किं वास्तवम् ? Notes, Textbook Exercise Important Questions and Answers.
Std 9 Sanskrit Chapter 5 Question Answer
Sanskrit Aamod Std 9 Digest Chapter 5 किं मिथ्या ? किं वास्तवम् ? Textbook Questions and Answers
भाषाभ्यासः
1. एकवाक्येन उत्तरत।
प्रश्न अ.
चलभाषे काः क्रीडा: सन्ति ?
उत्तरम् :
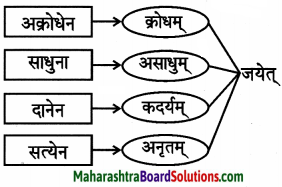
चलभाषे यष्टिकन्दुकक्रीडा, पादकन्दुकक्रीडा वाहनक्रीडा, पत्रक्रीडा, चतुरङ्गक्रीडा इत्येता: क्रीडाः सन्ति।
![]()
प्रश्न आ.
चलभाषे कीदृशं विश्वम् ?
उत्तरम् :
चलभाषणस्य योग्य: उपयोग: करणीयः।
प्रश्न इ.
किं किं दृष्ट्रा तनयायाः मुखं लालायितम् ?
उत्तरम् :
पिझ्झा, पावभाजी, सिजलर्स इत्यादीनि खाद्यानि दृष्ट्वा तनायाया मुखं लालायितम्।
प्रश्न ई.
स्वास्थ्यरक्षणाय किं किम् आवश्यकम् ?
उत्तरम् :
स्वास्थ्यरक्षणाय सम्यक् क्रीडा, पौष्टिकम् अन्नं, रात्रौ निद्रा आवश्यकम्।
![]()
2. माध्यमभाषया उत्तरत।
प्रश्न अ.
माता तनयायाः विचारपरिवर्तनं कथं करोति ?
उत्तरम् :
“किं मिथ्या? किं वास्तव्यम्।” ह्या पाठात तनया व तिची आई यांच्या संवादातून तंत्रज्ञानाधारित काल्पनिक जग आणि वास्तव यांच्यातील फरक दाखवला आहे.
तनया नावाची मुलगी मोबाईलमध्ये आणि कुरकुरे खाण्यात मग्न असताना तिच्या मैत्रिणी खेळण्यासाठी तिला बोलवायला येतात. तनयाला मात्र घरात बसून मोबाईलवर गेम्स खेळणेच जास्त आवडते. ती तसे तिच्या मैत्रिणींना सांगते आणि घरातच बसून राहते. तिच्यामते मोबाईलवरच क्रिकेट, फुटबॉल ह्यासारखे खेळ खेळणे शक्य असताना बाहेर जायची काय गरज? असे म्हणून ती फोनमध्येच खेळण्यात मग्न होते.
थोड्यावेळाने जेव्हा तनयाला भूक लागते तेव्हाती आईकडे खायला मागते. आई तिला मोबाईल मधील पिझ्झा, पावभाजी इ. स्वादिष्ट खाद्यपदार्थाचे फोटो दाखवते. ते पाहून तनयाच्या तोंडाला पाणी सुटते. ती आईला काहीतरी खायला दे म्हणून हट्ट करते.
तेव्हा आई म्हणते की फोटो पाहिलेसना आत्ताच, मग आता खायची काय गरज? पण तनया हट्टाने म्हणते, “मोबाईवर फोटो बघून भूक कशी भागेल? तेव्हा तिची आई उत्तर देते, हे कळतंय तर मग मोबाइल वर खेळून व्यायाम होत नाही.
हे नाही कळलं तुला? पण तनयाचे असे म्हणणे होते की तिला मोबाईलवर खेळायला आवडते, आई म्हणते जे जे आवडते जे आरोग्यासाठी चांगले असतेच असे नाही. योग्य खेळ, पौष्टिक अन्न आणि रात्रीची झोप आरोग्यासाठी आवश्यक असते आणि ह्या सगळ्या गोष्टी प्रत्यक्षात करणे गरजेचे आहे, मोबाईलच्या आभासात्मक जगात नाही.
तंत्रज्ञानाचा वापर करावा, पण त्याची गरज ओळखून. ‘अति तेथे मती’ ह्या म्हणीनुसार तंत्रज्ञाचाही अतिवापर वाईटच. आईने तिच्याच शब्दांत समजवल्यामुळे तनयाला तिचे म्हणणे पटले. अशा प्रकारे आईने तनयाला तिचेच उदाहरण देऊन तिचे मतपरिवर्तन केले.
In this mother – daughter conversation “किं मिथ्या? कि वास्तवम्।” written by Smt. Mugdha Risbud, we see how mother cleverly teaches her daughter a valuable lesson of what is real and what is virtual in a very subtle manner.
The girl Tanaya refused to go out and play with her friends and instead preferred to play games on the cellphone. After playing mobile games when Tanaya entered the kitchen saying that she was hungry, her mother asked her to look at some pictures of food items on her mobile phone.
Looking at the pictures of pizza, pav bhaji and sizzlers Tanaya’s mouth watered and she asked for food. Her mother told her that after looking at the pictures there was no need to eat food. Yet Tanaya insistead to give her food.
Then her mother made her realise that if her hunger is not pacified with the pictures of food then how exercise can be done by playing games on the phone? So, for good health, playing games, nutritious food and regular sleep is necessary. The use of gadgets must be according to the requirement.
In this way mother changed Tanaya’s approach about being blindly reliable on gadgets.
![]()
प्रश्न आ.
किं मिथ्या ? किं वास्तवम् ? इति पाठस्य तात्पर्य लिखत ।
उत्तरम् :
“किं मिथ्या? किं वास्तवम्।” ह्या पाठात तनया आणि आई यांच्या संवादातून तंत्रज्ञानावर मयदिपेक्षा जास्त विसंबून राहणे कसे हानिकारक आहे हे सांगितले आहे.
तनया ही शाळेत जाणारी मुलगी आहे. ज्या वयात मैदानार जाऊन खेळणे, मित्रमैत्रिणींबरोबर गप्पा मारणे अशा गोष्टी करायच्या त्या वयात ती दिवसभर मोबाइलवरच ह्या सगळ्या गोष्टी करते.
घरी आरामात बसून हातात मोबाइल घेऊन जर खेळता येत असेल, चॅटींग करता येत असेल तर बाहेर जायची काय गरज असे तिला वाटते. मोबाइलवरचे आभासात्मक जग आणि वास्तवातील जग यांच्यातील भेद तिला कळत नाही.
हा केवळ तनयाचा नाही तिच्या वयाच्या व त्याहून मोठ्या सगळ्या मुलांचासुद्धा प्रश्न आहे. तंत्रज्ञानामुळे घरी राहून सगळ्या गोष्टी शक्य असताना बाहेर जाण्याची गरज कोणालाच भासत नाही. त्यामुळेच व्हर्चुअल / आभासात्मक जग आणि वास्तवातील जग यांच्यातील भेद पुसट होत चालला आहे.
पण चांगले आरोग्यदायी आयुष्य जगण्यासाठी शरीराच्या वास्तवादी गरजा ओळखून त्या प्रकारची जीवनशैली आचारणात आणणे गरजेचे आहे. हेच तनयाची आई तनयाला समजावून सांगत आहे.
या पाठामध्ये तंत्रज्ञानावर आधारित आभासात्मक जग आणि वास्तवातील जग यांच्यातील भेद प्रत्यक्ष उदाहरणातून दाखवला
आहे.
Through the conversation “कि मिथ्या? किं वास्तवम्।” between a mother and her thirteen – year old daughter, Smt. Mugdha Risbud, tells us how excessive dependence on technology can be harmful.
Playing on the ground is the best exercise and it is necessary for good health while on the other hand games played on the cellphone are virtual. They don’t provide any benefit to the body.
So by showing the pictures of food and not actully giving food to Tanaya, her mother taught her how the vitural world and real world are different. Playing on the phone virtually, is not beneficial as playing on the ground.
Tanaya believes that when we can do everything just with a cellphone then why do we need to go out. This is not just Tanaya’s problem but that of the whole generation. Children like Tanaya have the same attitude.
Hence, the difference between real and virtual world has become difficult to identify In this lesson author tries to show this difference through the conversation between a mother and daughter and conveys the message that use of anything must be according to the requirement.
3. प्रश्ननिर्माणं कुरुत ।
प्रश्न क.
अहं गृहे एव खेलामि।
उत्तरम् :
अहं कुत्र खेलामि?
![]()
प्रश्न ख.
व्यायामं कृत्वा आरोग्यं वर्धते ।
उत्तरम् :
व्यायामं कृत्वा किं वर्धते?
4. अ. सन्धिविग्रहं कुरुत।
प्रश्न 1.
क. तदेव = + एव।
ख. नास्ति = न + ।
उत्तरम् :
क. तदेव – तत् + एव।
ख. नास्ति – न + अस्ति ।
![]()
आ. कालवचनपरिवर्तनं कुरुत।
प्रश्न 1.
- अहं न आगच्छामि । (लङ्लकारे परिवर्तयत।)
- बुभुक्षिता अस्मि। (बहुवचने परिवर्तयत ।)
- सख्यौ क्रीडार्थं प्रतिगच्छतः। (एकवचने लिखत ।)
- एतानि छायाचित्राणि पश्य । (उत्तमपुरुषे परिवर्तयत ।)
उत्तरम् :
- अहं न आगच्छम्।
- बुभुक्षिताः स्मः।
- सखी क्रीडार्थ प्रतिगच्छति।
- एतानि छायाचित्राणि पश्यानि।
इ. शब्दस्य वर्णविग्रहं कुरुत।
प्रश्न 1.
- द्वारम्
- स्वास्थ्यम्
- बुभुक्षा
- पौष्टिकम्
उत्तरम् :
- द्वारम् – द् + व् + आ + र् + अ + म्।
- स्वास्थ्य म् – स् + व् + आ +स् + थ् + य् + अ + म् ।
- बुभुक्षा – ब् + उ + भ + उ + क् + ष् + आ।
- पौष्टिकम् – प् + औ + ष् + ट् + इ + क् + अ + म्।
![]()
ई. मेलनं करुत।
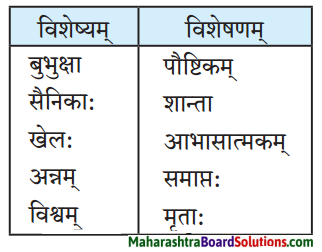
उत्तरम् :
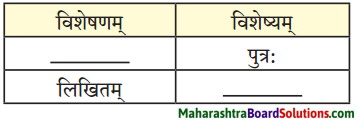
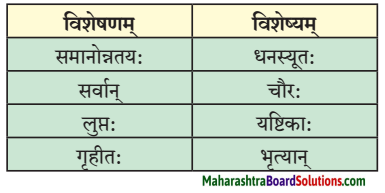
| विशेषणम् | विशेष्यम् |
| बुभुक्षा | शान्ता |
| सैनिकाः | मृताः |
| खेल: | समाप्तः |
| अन्नम् | पौष्टिकम् |
| विश्वम | आभासात्मकम् |
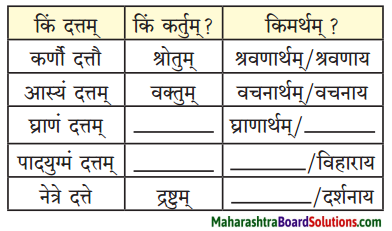
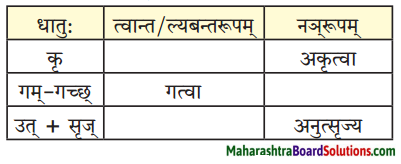
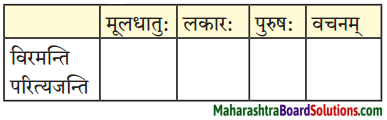
उ. पाठात् त्वान्त-ल्यबन्त-अव्ययानि चिनुत लिखत च।
प्रश्न 1.
पाठात् त्वान्त-ल्यबन्त-अव्ययानि चिनुत लिखत च।
उत्तरम् :
| त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा अयित्वा | ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य | तुमन्त अव्यय थातु + तुम् / धुम् / टुम् / ढुम् / इतुम् / अयितुम् |
| स्थित्वा, दर्शयित्वा | आकर्ण्य, उपविश्य | – |
| दृष्ट्वा, क्रीडित्वा | – | – |
![]()
5. त्वान्तपदं /ल्यबन्तपदं निष्कास्य वाक्यं पुनर्लिखत ।
प्रश्न अ.
रात्रौ शीघ्रं निद्रां कृत्वा प्रात:काले शीघ्रम् उत्तिष्ठामि ।
उत्तरम् :
रात्रौ शीघ्रं निद्रां करोमि प्रात:काले शीघ्रम् उत्तिष्ठामि च।
प्रश्न आ.
द्वारघण्टिकाम् आकर्ण्य माता द्वारम् उद्घाटयति।
उत्तरम् :
माता द्वारघण्टिकाम् आकर्णयति द्वारम् उद्घाटयति च।
![]()
6. अ. समानार्थकशब्दं चिनुत ।
भटः, क्रीडा, जननी, क्षुधा, स्वापः।
प्रश्न 1.
समानार्थकशब्दं चिनुत ।
भटः, क्रीडा, जननी, क्षुधा, स्वापः।
उत्तरम् :
- सैनिक – योद्धा, भटः।
- क्रीडा – खेलः।
- माता – जननी, अम्बा, जन्मदात्री।
- बुभुक्षा – अशना, क्षुध् ।
- स्वापः – निद्रा, शयनम्, स्वापः, स्वप्नः, संवेशः।
आ. विरुद्धार्थकशब्दं लिखत ।
समाप्तः, स्वास्थ्यम्, आभासात्मकम्, मृतः ।
प्रश्न 1.
विरुद्धार्थकशब्दं लिखत ।
समाप्तः, स्वास्थ्यम्, आभासात्मकम्, मृतः ।
उत्तरम् :
- प्रारम्भः × समाप्तः।
- अस्वास्थ्यम् × स्वास्थ्यम्।
- आभासात्मकम् × वास्तवम्।
- मृतः × जीवितः।
![]()
7. चलभाषद्वारा द्वयोः मित्रयोः संवाद लिखत ।
प्रश्न 1.
चलभाषद्वारा द्वयोः मित्रयोः संवाद लिखत ।
उत्तरम् :
- माधवः – नमो नमः विजय! अपि सर्व कुशलम्?
- विजय: – आम्!
- माधवः – श्रुणु ! अद्य अहं मम कुटुम्बेन सह जन्तुशालां गच्छामि। आगच्छसि वा?
- विजय: – आम, आगच्छामि।
- माधवः – तर्हि सायङ्काले पञ्चवादने आगच्छ मम गृहम्।
- विजयः – रे माधव, अहं किमपि खादनार्थं आनयामि।
- माधव: – आम, पानीयमपि आनयामः।
- विजयः – तत्र पशवः खगाः च पश्यामः।
- माधवः – बहु मनोरञ्जनं भवेत् ! अस्तु ! सायङ्काले मिलावः ।
- विजयः – आम्! मिलावः।
![]()
Sanskrit Aamod Class 9 Textbook Solutions Chapter 5 किं मिथ्या ? किं वास्तवम् ? Additional Important Questions and Answers
उचितं पर्यायं चिनुत।
प्रश्न 1.
तनया कस्मिन् मग्ना?
(अ) चलभाषे
(आ) पुस्तके
(इ) चित्रपटे
(ई) अध्ययने
उत्तरम् :
(अ) चलभाषे
![]()
प्रश्न 2.
द्वारघण्टिकाम् आकर्ण्य का द्वारम् उद्घाटयति?
(अ) माता
(आ) तनया
(इ) सखी
(ई) पिता
उत्तरम् :
(अ) माता
एकवाक्येन उत्तरत।
प्रश्न 1.
श्रुतिः किमर्थं तनायाम् आह्वयति?
उत्तरम् :
श्रुतिः बहिः क्रीडनाय तनायाम् आह्वयति।
प्रश्न 2.
तनया किं पश्यति ?
उत्तरम् :
तनया खाद्यपदार्थानां छायाचित्राणि पश्यति ।
![]()
सत्यं वा असत्यं लिखत।
प्रश्न 1.
- माता सुखासन्दे उपविश्य हस्तेन कुकुंरिकां खादति।
- तनया चलभाषे युद्धक्रीडायां मग्ना अस्ति।
- तनया द्वारम् उद्घाटयति।
उत्तरम् :
- असत्यम्
- सत्यम्
- असत्यम्
प्रश्न 2.
1. चलभाषे भोजनं दृष्ट्वा बुभुक्षा शान्ता भवेत् ।
2. सिजलर्स दृष्ट्वा मुखं लालयितम् ।
उत्तरम् :
1. असत्यम्
2. सत्यम्
प्रश्न 3.
1. चलभाषे आभासात्मकं विश्वं न वास्तवम्।
2. सम्यक् क्रीडा, पौष्टिकम् अन्न, रात्रौ निद्रा अनारोग्याय भवति ।
उत्तरम् :
1. सत्यम्
2. असत्यम्
![]()
कः कं वदति।
प्रश्न 1.
1. सत्वरं कीडनाय आगच्छ, बहिः खेलामः।
2. किं खेलसि?
उत्तरम् :
1. श्रुति : तनयां वदति।
2. राजसी तनयां वदति।
प्रश्न 2.
- अम्ब बुभुक्षिता अस्मि ।
- एतानि छायाचित्राणि पश्य ।
- चलभाषे दृष्टवती खलु ।
उत्तरम् :
- तनया मातरं वदति ।
- माता तनयां वदति ।
- माता तनयां वदति ।
प्रश्न 3.
आवश्यकतानुसारं योग्य: उपयोग: करणीयः एव।
उत्तरम् :
माता तनयां वदति।
![]()
उचितं कारणं चित्वा वाक्यं पुनर्लिखत।
प्रश्न 1.
द्वारघण्टिकाम् आकर्ण्य माता द्वारम् उद्घाटयति यतः ……..।
a. तनया चलभाषे मग्ना अस्ति।
b. तनया गृहकार्ये मग्ना अस्ति।
उत्तरम् :
द्वारघण्टिकाम् आकर्ण्य माता द्वारम् उद्घाटयति यतः तनया चलभाषे मग्ना अस्ति।
प्रश्न 2.
क्रीडाङ्गणं गत्वा खेलनस्य आवश्यकता नास्ति यतः ……..।
a. चलभाषे क्रीडाः सन्ति।
b. व्यायमस्य आवश्यकता नास्ति।
उत्तरम् :
क्रीडाङ्गणं गत्वा खेलनस्य आवश्यकता नास्ति यतः चलभाषे क्रीडा: सन्ति।
![]()
विशेषण-विशेष्य-सम्बन्धः। (स्तम्भमेलनं कुरुत)।
प्रश्न 1.
| विशेषणम् | विशेष्यम् |
| 1. अपरेण | अ. तनया |
| 2. सर्वाः | ब. हस्तेन |
| 3. मग्ना | क. क्रीडाः |
| 4. योग्यः | इ. उपयोग: |
उत्तरम् :
| विशेषणम् | विशेष्यम् |
| 1. अपरेण | ब. हस्तेन |
| 2. सर्वाः | क. क्रीडाः |
| 3. मग्ना | अ. तनया |
| 4. योग्यः | इ. उपयोग: |
![]()
शब्दस्य वर्णविग्रहं कुरुत।
- कुकुरिकाम् – क् + उ + र् + क् + उ + र् + इ + क + आ + म्।
- द्वारघण्टिकाम् – द् + व् + आ + र् + अ + घ् + अ + ण् + ट् + इ + क् + आ + म्।
- आह्वयतः – आ + ह् + व् + अ + य् + अ + त् + अः।
- क्रीडाङ्गणम् – क् + र् + ई + ड + आ + इ + ग् + अ + ण् + अ + म्।
- समाप्तः – स् + अ + म् + आ + + त् + अः।
- पिडा – प् + इ + अ + अ + आ ।
- सिजलर्स – स् + इ + ज् + अ + ल् + अ + र + स् + ।
- नास्ति – न् + आ + स् + त् + इ।
- स्वास्थ्य करम् – स् + व् + आ + स् + थ् + य् + अ + क् + अ + र + अ + म् ।
- सम्यक् – स् + अ + म् + य् + अ + क्।
- निद्रा – न् + इ + द् + र् + आ।
- योग्यः – य + आ + ग् + य् + अः।
प्रश्ननिर्माणं कुरुत।
प्रश्न 1.
- पिझ्झा, पावभाजी, सिजलर्स इत्यादीनि खाद्यानि दृष्ट्वा लालायितं मुखम्।
- तनया खाद्यपदार्थानां छायाचित्राणि पश्यति।
- तनया सुखासन्दे उपविशति ।
- खेलनस्य आवश्यकता एव नास्ति ।
उत्तरम् :
- किं किं दृष्ट्वा लालायितं मुखम्?
- तनया केषां छायाचित्राणि पश्यति?
- तनया कुत्र / कस्मिन् उपविशति?
- कस्य आवश्यकता एव नास्ति?
![]()
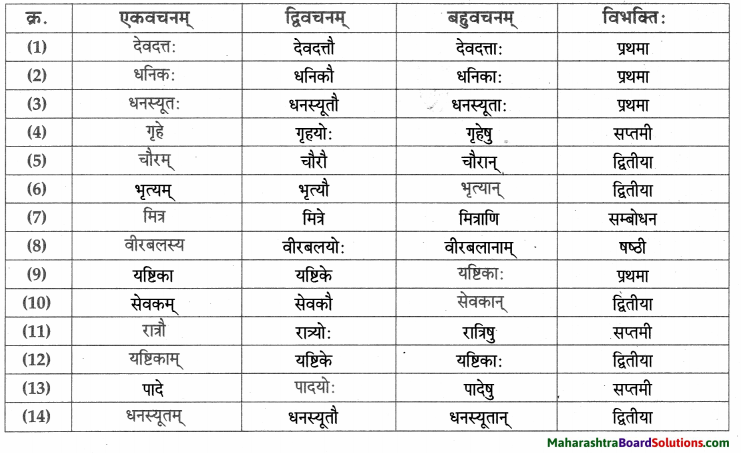
विभक्त्यन्तरूपाणि।
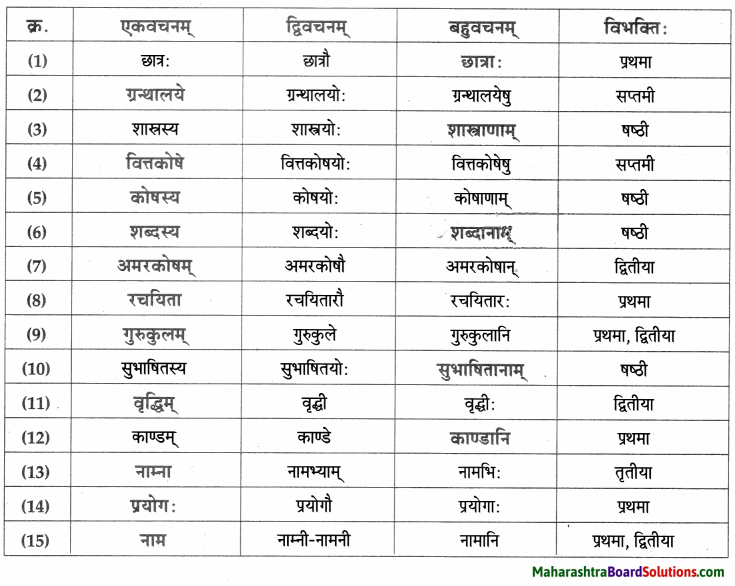
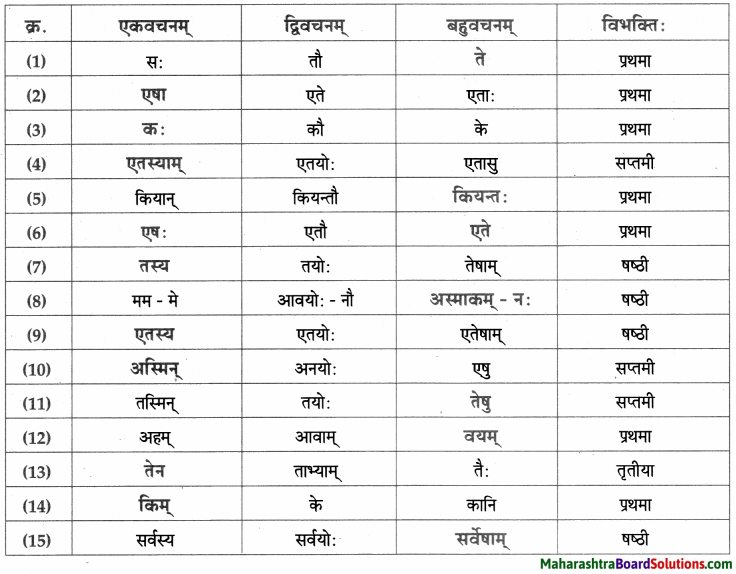
- प्रथमा – अहम्, माता, क्रीडाः, तनया, यष्टिकन्दुकक्रीडा, पादुकन्दुकक्रीडा, वाहनक्रीडा, पत्रक्रीडा, चतुरङ्गक्रीडा, खेल:,
सर्वे, सैनिकाः, सर्वाः, एषः, सैनिकः, स्वास्थरक्षणम्, सर्वे, सैनिकाः, खेल: अहम्, व्यायामः, उपयोगः, क्रीडनम्, हितकरम्, आरोग्यपूर्णम् , पौष्टिकम्, अन्नम्, आभासात्मकम, विश्वम्। - द्वितीया – द्वारम्, चलभाषम्, पाकगृहम्, द्वारघण्टिकाम, ताम, क्रीडाङ्गणम्, स्वास्थ्यरक्षणम्, भोजनम्, पाकगृहम्, एतानि, छायाचित्राणि, उपयोगम्।
- तृतीया – हस्तेन, अपरेण, चलभाषेण।
- चतुर्थी – कीडनाय, मह्यम्, आरोग्याय।
- षष्ठी – खेलनस्य, तनयायाः, खाद्यपदार्थानाम्, चलभाषस्य।
- सप्तमी – सुखासन्दे, द्वारे, गृहे, एतस्मिन्, चलभाषे, युद्धक्रीडायाम्, एतस्याम, क्रीडायाम, चलभाषे, रात्रौ।
- सम्बोधन – अम्ब, तनये, मातः, तनये, मातः।
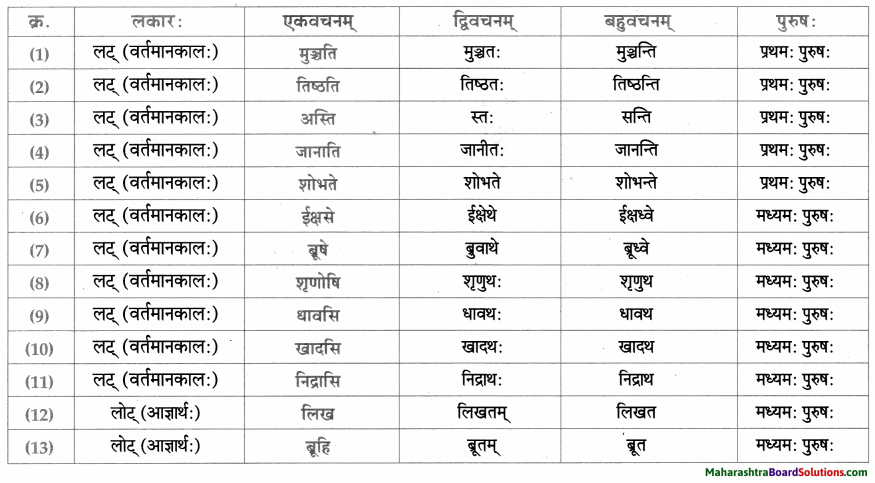
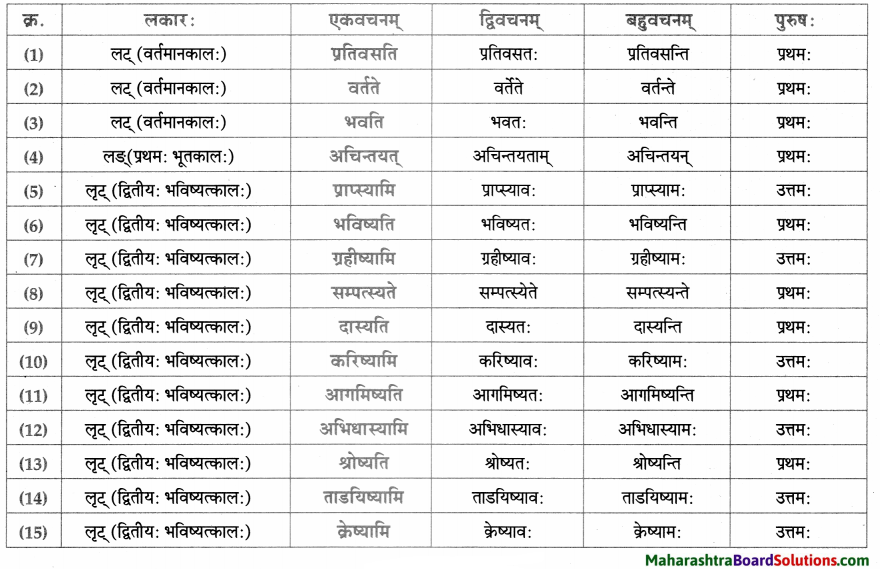
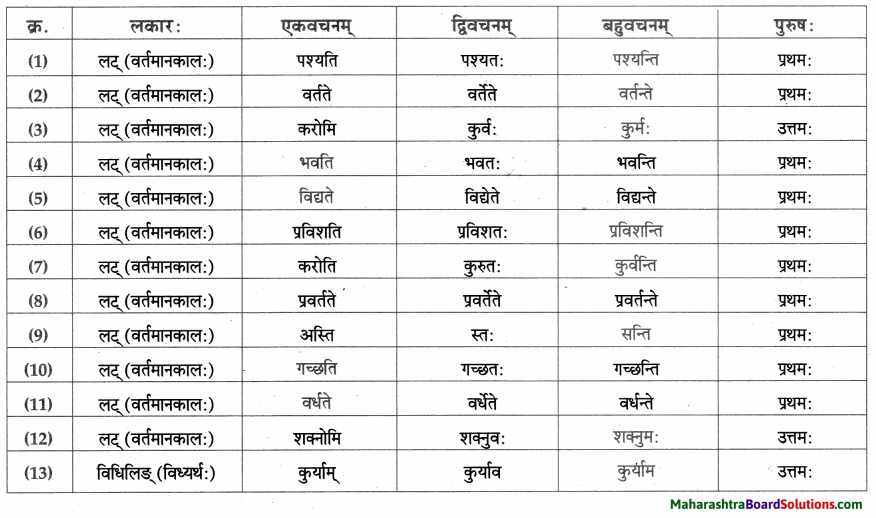
लकारं लिखत।
- खादति – खाद् धातुः प्रथमगण: परस्मैपदं लट्लकार: प्रथमपुरुष: एकवचनम्।
- आह्वयतः – आ + ह्वे धातुः प्रथमगण: परस्मैपदं लट्लकार: प्रथमपुरुष: द्विवचनम्।
- खेलामः – खेल् धातुः प्रथमगण: परस्मैपदं लट्लकार: उत्तमपुरुष: बहुवचनम्।
- आगच्छामि – आ + गम् – गच्छ धातुः प्रथमगणः परस्मैपदं लट्लकार : उत्तमपुरुष: एकवचनम्।
- पश्य : दृश् – पश्य् धातुः प्रथमगणः परस्मैपदं लोट्लकार: मध्यमपुरुषः एकवचनम्।
- अस्मि – अस् धातुः द्वितीयगणः परस्मैपदं लट्लकार: उत्तमपुरुष: एकवचनम्।
- यच्छामि – दा-यच्छ् धातुः प्रथमगणः परस्मैपदं लट्लकारः उत्तमपुरुष: एकवचनम्।
- भवेत् – भू-भव् धातुः प्रथमगण: परस्मैपदं विधिलिङ्लकार: उत्तमपुरुषः एकवचनम्।
- रोचते – रुच् – रोचधातुः प्रथमगण: आत्मनेपदं लट्लकार: प्रथमपुरुष: एकवचनम्।
- वर्जयेत् – वृज् – वर्जु धातुः दशमगण: उभयपदं अत्र परस्मैपदं विधिलिङ्लकारः प्रथमपुरुषः एकवचनम्।
- करोमि – कृ धातुः अष्टमगण: उभयपदं अत्र परस्मैपदं लट्लकार : उत्तमपुरुष: एकवचनम्।
समानार्थकशब्दं योजयित्वा वाक्यं पुनर्लिखत।
प्रश्न 1.
सैनिक; – क्रीडायां सर्वे सैनिका: मृताः।
उत्तरम् :
क्रीडायां सर्वे योद्धार:/भटाः मृताः ।
![]()
व्याकरणम् :
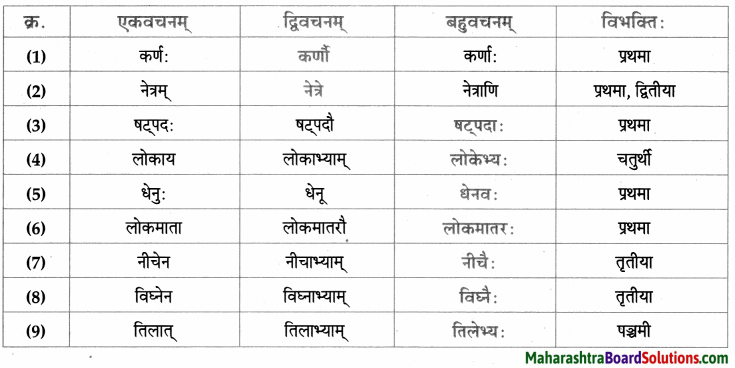
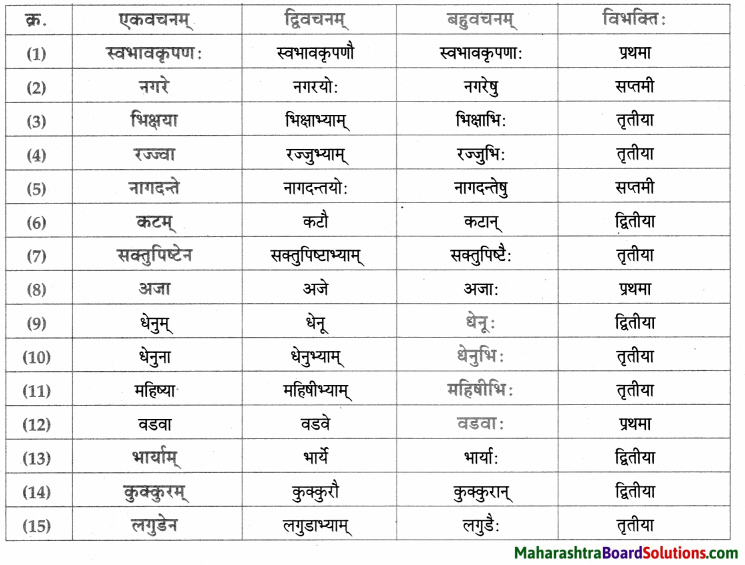
नाम – तालिका।
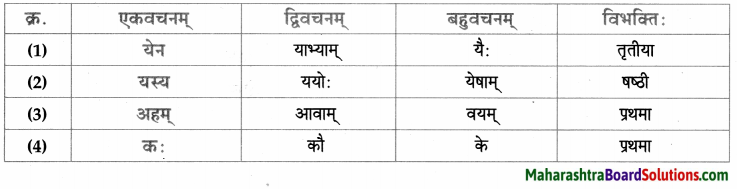
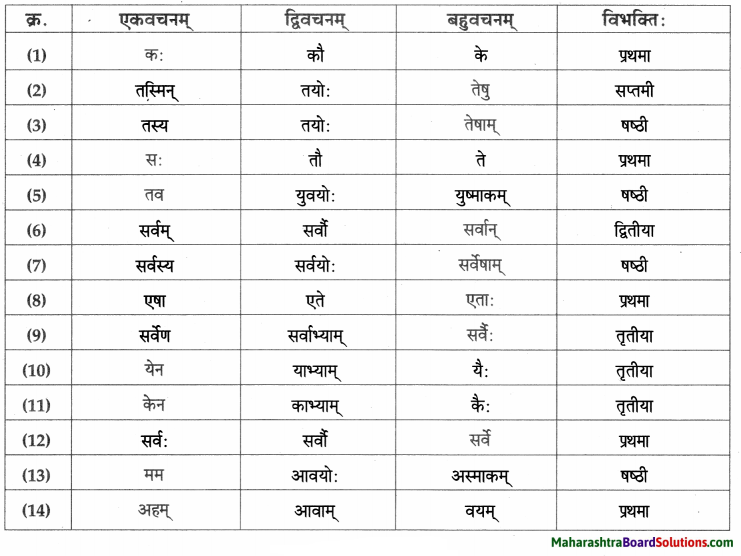
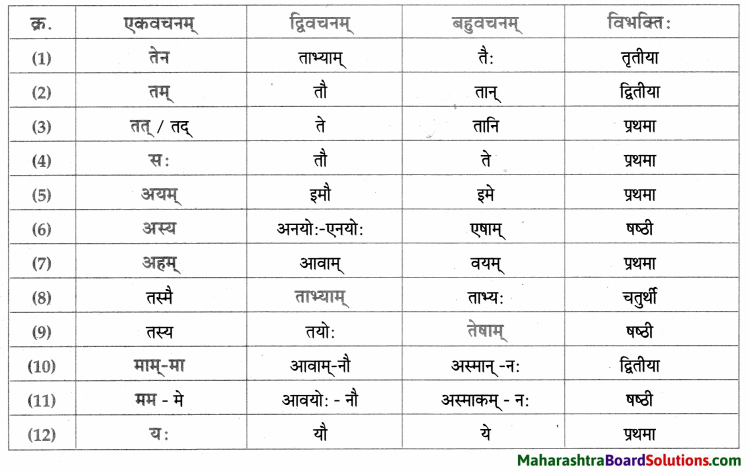
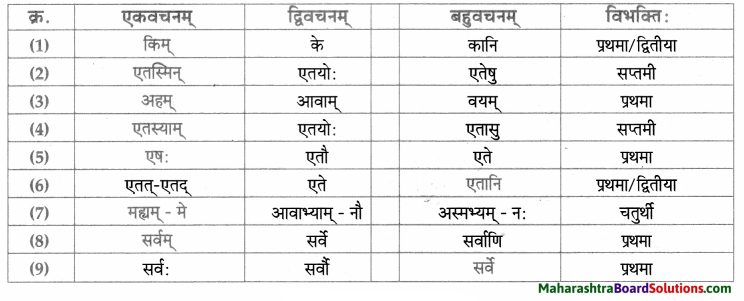
सर्वनाम – तालिका।
![]()
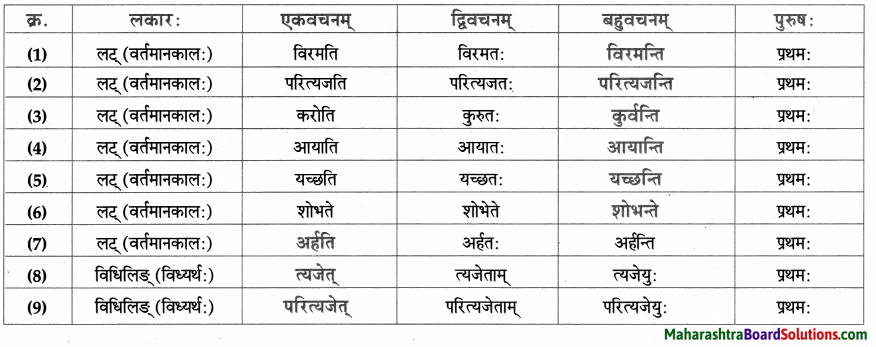
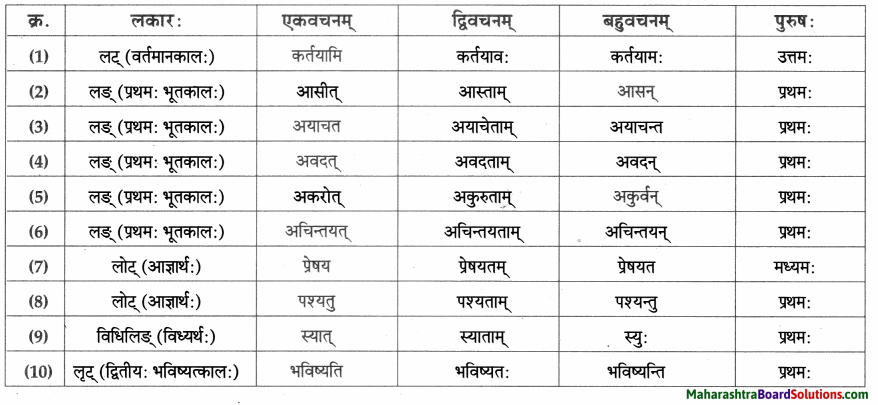
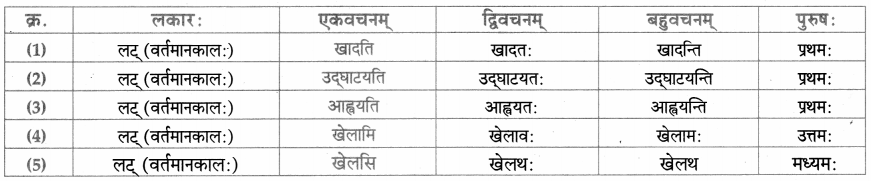
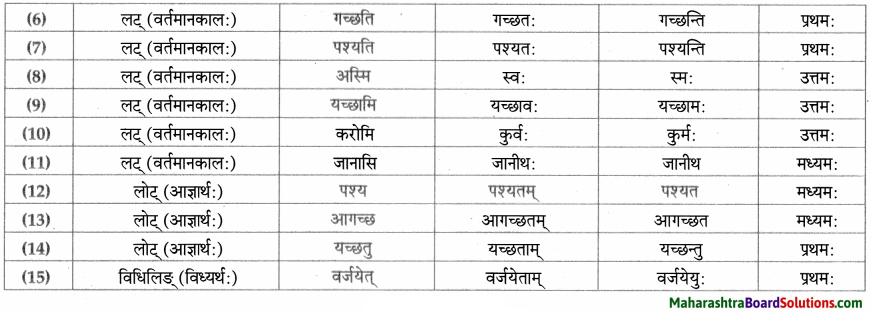
धातु – तालिका।
समासाः।
| समस्तपदम् | अर्थः | समासविग्रहः | समासनाम |
| सुखासन्दे | seat for pleasure | सुखाय आसन्दः, तस्मिन् । | चतुर्थी तत्पुरुष समास । |
| द्वारघण्टिकाम् | bell of door | द्वारस्य घण्टिका, ताम् । | षष्ठी तत्पुरुष समास । |
| पाकगृहम् | place for cooking | पाकाय गृहम् । | चतुर्थी तत्पुरुष समास । |
![]()
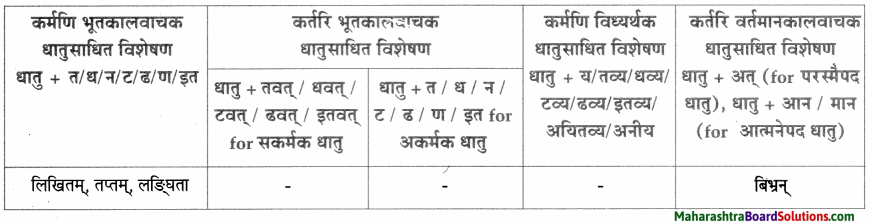
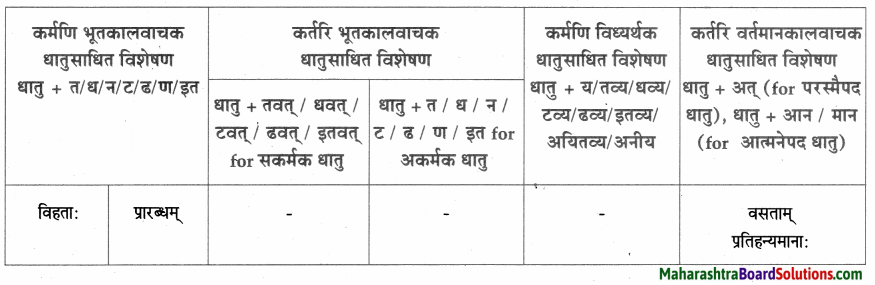
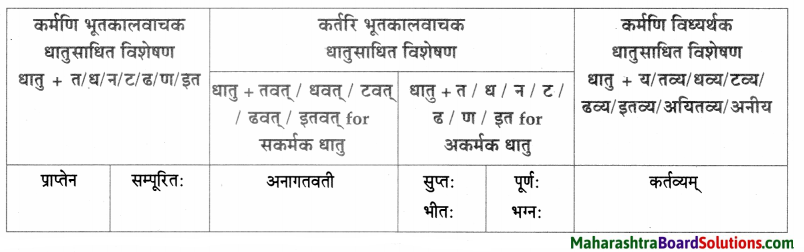
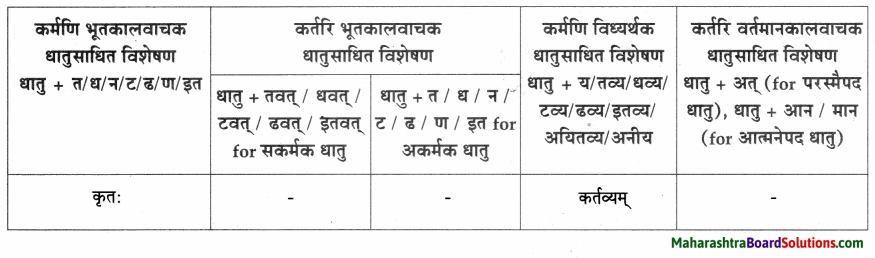
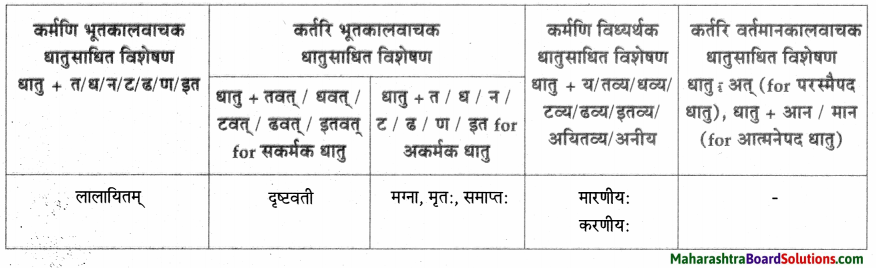
धातुसाधितविशेषणानि।
| धातुसाधित – विशेषणम् | विशेष्यम् |
| मृतः, मारणीयः | सैनिक: |
| मृताः | सैनिकाः |
| समाप्तः | खेल: |
| लालायितम् | मुखम् |
| करणीयः | उपयोग: |
किं मिथ्या ? किं वास्तवम् ? Summary in Marathi and English
प्रस्तावना :
आधुनिक तंत्रज्ञानाने मानवाच्या भौतिकविकासासाठी विस्तीर्ण क्षेत्र खुले केले आहे यात शंकाच नाही. परंतु, तंत्रज्ञानयुक्त साधनांच्या अत्याधुनिक वापरामुळे नवीन प्रश्न, विघ्ने आणि सामाजिक समस्या निर्माण होतात. आभासात्मक आणि वास्तव यामधील फरक आपण जाणून घेतला पाहिजे. आधुनिक काळाची हीच आवश्यकता आहे.
भ्रमणध्वनीचा आवश्यक तेवढाच वापर करावा हा महत्त्वपूर्ण संदेश लेखिका श्रीमती मुग्धा रिसबूड यांनी यांनी तेरा वर्षांची मुलगी आणि तिची आई या दोघींच्या सहज संवादातून पटवून दिला आहे. ‘अति तेथे माती’ या म्हणीनुसार तंत्रज्ञानाचा अति वापर वाईटच हा महत्वाचा विचार संवादरूपाने मांडला आहे.
It is indeed true that modern technology has opened the wide field of materialistic development for humans. Nevertheless, due to the excess usage of technological gadgets new questions and several new social problems have been created.
Yet technology is the necessity of the modern age. This beautiful conversation between a thirteen year old girl and her mother is presented to us by the author Shrimati Mugdha Risbud, where the difference between the real and virtual world is communicated. It tells us that though technology is an important part of our life today, excess should always be avoided.
![]()
परिच्छेद : 1
त्रयोदशवर्षीया ……………… युद्धक्रीडायां मग्ना।) (त्रयोदशवर्षीया तनया सुखासन्दे उपविश्य एकेन हस्तेन कुर्कुरिका खादति । अपरेण हस्तेन चलभाषं चालयति। तदानीं द्वारघण्टिकाम् आकर्य
माता द्वारम् उद्घाटयति। तनयाया: सख्यौ द्वारे एव स्थित्वा ताम् आह्वयतः ।)
श्रुतिः – तनये, सत्वरं क्रीडनाय आगच्छ, बहिः खेलामः।
तनया – अहं गृहे एव खेलामि।
राजसी – किं खेलसि?
तनया – (चलभाषं दर्शयित्वा) एतस्मिन् चलभाषे यष्टिकन्दुकक्रीडा, पादकन्दुकक्रीडा, वाहनक्रीडा, पत्रक्रीडा, चतुरङ्गक्रीडा, इत्यादयः सर्वाः क्रीडाः सन्ति। क्रीडाङ्गणं गत्वा खेलनस्य आवश्यकता एव नास्ति। अहं न आगच्छामि। (सख्यौ क्रीडा निर्गच्छतः। माता पाकगृहं गच्छति । तनया चलभाषे युद्धक्रीडायां मग्ना।
अनुवादः
(तेरा वर्षांची मुलगी तनया सोफ्यावर बसून एका हाताने कुरकुरे खात आहे. आणि दुसऱ्या हाताने भ्रमणध्वनी चालवत आहे. तेव्हाच दाराची घंटी (बेल) ऐकून आई दरवाजा उघडते. तनयाच्या दोन मैत्रिणी दारात उभ्या राहून तिला बोलावतात.)
श्रुती – तनया, लवकर खेळायला ये, बाहेर खेळूया.
तनया – मी घरीच खेळते.
राजसी – काय खेळतेस?
तनया – (भ्रमणध्वनी दाखवून) या भ्रमणध्वनीवर हॉकी, फुटबॉल, गाड्यांचा खेळ, पत्त्यांचा खेळ, बुद्धिबळ इ. खेळ आहेत. मैदानावर जाऊन खेळण्याची आवश्यकताच नाही.
मी येणार नाही.
(मैत्रिणी खेळण्यासाठी निघून जातात.
आई स्वयंपाकघरात जाते.
तनया भ्रमणध्वनीवर युद्धाचा खेळ खेळण्यात मग्न होते.)
(Thirteen-year-old Tanaya sitting on the sofa is eating Kurkure with one hand. She is operating the mobile with the other hand.
Then hearing the doorbell ring, her mother opens the door. Standing at the door itself, Tanaya’s friends call out to her.)
Shruti – Tanaya, come to play quickly. We shall play outside.
Tanaya – I shall play at home itself.
Rajasi – What are you playing?
Tanaya – (Showing the mobile) there are many games on this mobile-hockey, football, car games, card games, chess etc.
There is no need to go to the playground to play.
I am not coming
(The friends go to play
The mother goes to the kitchen.
Tanaya is engrossed playing a war game.)
![]()
परिच्छेद: 2
- तनया – (स्वगतम्) …………………. स्वास्थ्यरक्षणं न भवति?
- तनया – (स्वगतम्) एतस्यां क्रीडायाम् एषः सैनिक: मृत: अपर: च मारणीयः। …… सर्वे सैनिकाः मता:। हेड ……. जितं मया। खेलः
- समाप्तः । (तनया पाकगृहं गच्छति ।) अम्ब, बुभुक्षिता अस्मि।
- माता – तनये, मम चलभाषे एतानि छायाचित्राणि पश्य। (तनया खाद्यपदार्थानां छायाचित्राणि पश्यति।)
- तनया – मातः, पिझ्झा, पावभाजी, सिजलर्स इत्यादीनि खाद्यानि दृष्ट्वा लालायितं मे मुखम्। कृपया किमपि यच्छतु।
- माता – चलभाष दृष्टवती खलु? अधुना खाद्यपदार्थानाम् आवश्यकता एव नास्ति। अहं न बच्छामि।
- तनया – चलभाषे भोजनं दृष्ट्वा बुभुक्षा शान्ता कथं भवेत्? .
- माता – यदि एतत् सत्यं, तर्हि कथं न जानासि यत् चलभाषेण क्रीडित्वा व्यायामः न भवति? स्वास्थ्यरक्षणं न भवति?
अनुवादः
तनया – (स्वत:शीच) या खेळात हा सैनिक मेला आता दुसऱ्याला मारूया…. सगळे सैनिक मेले. हे ………… मी जिंकले.
खेळ संपला.
(तनया स्वयंपाकघरात जाते.)
आई, मला भूक लागली आहे.
माता – तनया, माझ्या भ्रमणध्वनीवर ही छायाचित्रे (फोटो) बघ.
(तनया खाद्यपदार्थांची छायाचित्रे पाहते.)
तनया – आई, पिझ्झा, पावभाजी, सिजलर्स इत्यादी खाद्यपदार्थ पाहून माझ्या तोंडाला पाणी सुटले आहे.
कृपया (प्लीज) काहीतरी दे.
माता – भ्रमणध्वनीवर पाहिलेस ना?
आता खाद्यपदार्थांची आवश्यकताच नाही.
मी देणार नाही:
तनया – भ्रमणध्वनीवर जेवणाचे पदार्थ पाहून भूक कशी भागेल?
माता – जे हे खरे असेल, तर मग तुला हे माहीत नाही का की, भ्रमणध्वनीवर खेळून व्यायाम होत नाही? आरोग्याची काळजी घेतली जात नाही?
Tanaya – (to herself) In this game, this soldier is dead and the other should be killed……all soldiers are dead… hey…I have won. . The game is over.
(Tanaya goes to the kitchen).
Mother, I am hungry.
Mother – Tanaya, see these images on my mobile.
(Tanaya sees the images of the foodstuff).
Tanaya – Mother, my mouth is watering seeing the pizza, pavbhaji, Sizzlers etc.
Please give me something
Mother – You saw them on the mobile right?
Now there is no need of the food stuff.
I shan’t give.
Tanaya – How will hunger be pacified by seeing the food on the mobile?
Mother – If this is true, then how do you not know that by playing on the mobile you don’t exercise?
Health is not taken care off?
![]()
परिच्छेद : 3
तनया – परं मात :………………. करोमि?
- तनया – परं मातः मह्यं रोचते तत् चलभाषण कीडनम्।
- माता – तनये, यद् यद् रोचते तत् तत् सर्व स्वास्थ्यकरं, हितकरम्, आरोग्यपूर्ण न भवति । सम्यक् क्रीडा, पौष्टिकम् अन्न, रात्री
निद्रा आरोग्याय भवति। चलभाषे आभासात्मकं विश्वं न वास्तवम्। - तनया – तर्हि किं चलभाषस्य उपयोगः एव न करणीयः ।
- माता – तथा न। आवश्यकतानुसार योग्य: उपयोग: करणीयः एव। किन्तु अति सर्वत्र वर्जयेत्।
- तनया – आम् मातः । इतः परं चलभाषस्य योग्यम् उपयोगं करोमि।
अनुवादः
- तनया – परंतु माता, मला ते भ्रमणध्वनीवर खेळणे आवडते.
- माता – तनया, जे जे आवडते ते ते सर्व स्वास्थकारक, हितकारक, आरोग्यदायी नसते.
योग्य प्रकारे खेळणे, पौष्टिक अन्न, रात्रीची झोप आरोग्यासाठी महत्त्वपूर्ण आहे. भ्रमणध्वनीवरील आभासात्मक विश्व वास्तव नाही. - तनया – तर मग काय भ्रमणध्वनीचा उपयोगच करायचा नाही?
- माता – तसे नव्हे.
आवश्यकतेनुसार योग्य उपयोग करावाच.
परंतु अतिरेक सर्वथा टाव्यवा. - तनया – ठीक आहे आई.
यापुढे (मी) भ्रमणध्वनीचा योग्य उपयोग करेन. - Tanaya – But mother, I like that-playing with the mobile.
- Mother – Tanaya, all that you like is not healthy, beneficial and healthy. Proper games, nutritious food, sleep at night will make you healthy. The virtual world on the mobile is not reality.
- Tanaya – Then should the mobile not be used at all?
- Mother – Not so.
Certainly it should be properly used as required. But excess should be avoided
everywhere. - Tanaya – Yes mother.
Henceforth, I shall use the mobile appropriately.
सन्धिविग्रहः
- इत्यादयः – इति + आदयः
- किमपि – किम् + अपि।
- इत्यादीनि – इति + आदीनि ।
![]()
समानार्थकशब्दाः
- मग्ना – रता, निमग्ना, लीना।
- हस्तः – करः, पाणिः।
- गृहम् – गेहम, सदनम्, आलयः।
- आकर्ण्य – श्रुत्वा, निशम्य।
- सत्वरम् – शीघ्रम्, झटिति ।
- अधुना – सम्प्रति, इदानीम्।
- मुखम् – वदनम्, आननम्, आस्यम्।
- चलभाष: – भ्रमणध्वनिः।
- लोक: – जगत्, भुवनम्, विश्वम्।
- निशाः – रजनी, रात्रिः, शर्वरी, यामिनी।
विरुद्धार्थकशब्दाः
- निर्गच्छति × प्रविशति, आगच्छति।
- सत्वरम् × शनैः शनैः।
- अनावश्यकता × आवश्यकता।
- हितकरम् × अहितकरम्।
- उपयोगः × निरुपयोगः।
- आरोग्यम् × अनारोग्यम्।
![]()
शब्दार्थाः
- उपविश्य – after stitting – बसून
- चलभाष: – mobile – भ्रमणध्वनी
- आकर्य – after listening – ऐकून
- उद्घाटयति – opens – उघडते
- यष्टिकन्दुकक्रीडा – hockey – हॉकी
- सुखासन्दः – sofa – कोच
- पादकन्दुकक्रीडा – football – फुटबॉल
- वाहनक्रीडा – car games – वाहनक्रीडा
- पत्रक्रीडा – cards – पत्ते
- चतुरङ्गक्रीडा – chess – बुद्धिबळ
- आह्वयत: – invite – बोलावतात
- द्वारघण्टिका – door bell – दरवाजाची घंटी
- बुभुक्षिता – hungry – भुकेलेली
- लालयितम् – watering – पाणी सुटले
- दृष्टवती – saw – पाहिले
- स्वास्थ्यरक्षणम् – care of health – आरोग्याची काळजी
- मृतः – dead – मृत झालेलेc
- अपर: – another – दुसरा
- मारणीयः – worth killing – मारण्याजोगा
- बुभुक्षा – hunger – भूक
- हितकरम् – beneficial – हितावह
- आरोग्यपूर्णम् – healthy – आरोग्यपूर्ण
- आभासात्मकम् – virtual – काल्पनिक
- वर्जयेत् – should avoid – वयं करावे
- पौष्टिकम् – healthy – पौष्टिक
Aamod Sanskrit Book 9th Class Solutions
- सुष्ठु गृहीतः चौरः Class 9 Question Answer
- अव्ययमाला Class 9 Question Answer
- धन्यौ तौ दातृयाचकौ Class 9 Question Answer
- विध्यर्थमाला Class 9 Question Answer
- किं मिथ्या ? किं वास्तवम् ? Class 9 Question Answer
- वीरवनिता विश्पला Class 9 Question Answer
- योगमाला Class 9 Question Answer
- पिनकोड्प्रवर्तकः महान् संस्कृतज्ञः Class 9 Question Answer
- सूक्तिसुधा Class 9 Question Answer
- पितृभक्तः नचिकेताः Class 9 Question Answer
- मनसः स्वच्छता Class 9 Question Answer
- अमरकोषः Class 9 Question Answer
- सरमाया: शीलम् Class 9 Question Answer
- काव्यशास्त्रविनोदः Class 9 Question Answer
- मनोराज्यस्य फलम् Class 9 Question Answer
- स्वागतं तपोधनाया: Class 9 Question Answer