Balbharti Maharashtra State Board Class 8 Marathi Solutions Sulabhbharati Chapter 7 नातवंडांस पत्र Notes, Textbook Exercise Important Questions and Answers.
Class 8th Marathi Chapter 7 नातवंडांस पत्र Question Answer Maharashtra Board
Std 8 Marathi Chapter 7 Question Answer
Marathi Sulabhbharti Class 8 Solutions Chapter 7 नातवंडांस पत्र Textbook Questions and Answers
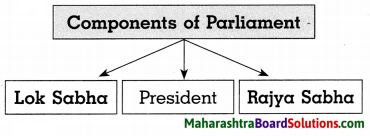
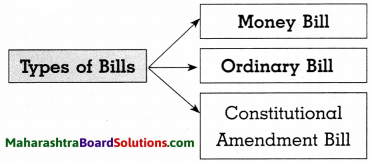
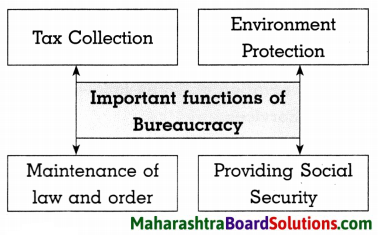
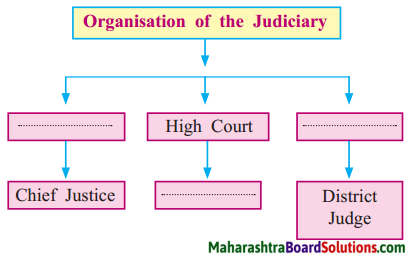
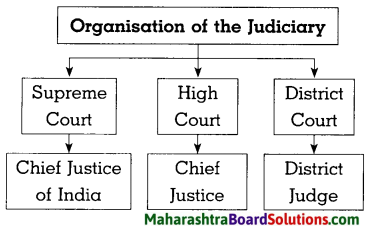
1. आकृत्या पूर्ण करा.

प्रश्न 1.
आकृत्या पूर्ण करा.
उत्तरः
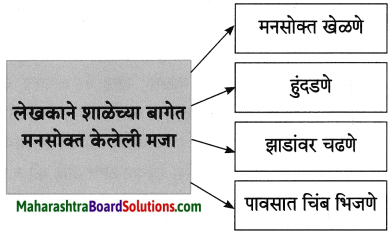
(अ)
आ.
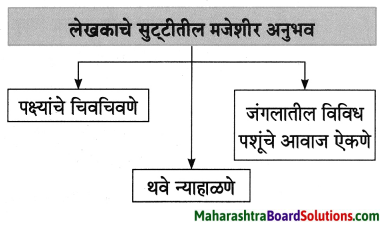
इ.

2. एका शब्दांत उत्तरे लिहा.

प्रश्न 1.
एका शब्दांत उत्तरे लिहा.
उत्तरः
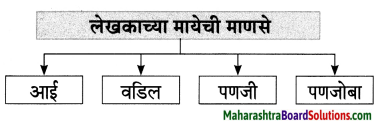
(अ) लेखक जेथे शिकले ते गाव – [सांगली]
(आ) लेखकाला मिळालेला पुरस्कार – [अर्जुन पुरस्कार]
(इ) खास व्यायामासाठीच असलेले ठिकाण – [जिम]
(ई) लेखकाचा आवडता खेळ – [बॅडमिंटन]
![]()
3. तुमच्या शब्दांत उत्तरे लिहा.
प्रश्न अ.
लेखकाने सांगितलेले व्यायामाचे महत्त्व.
उत्तरः
लेखकाच्या आयुष्यात व्यायामाचे खूप महत्व आहे. त्यांच्या मते, प्रत्येकाने दररोज काहीतरी व्यायाम केला पाहिजे. ज्याप्रमाणे आपण न चुकता दोन वेळेस जेवतो. त्याप्रमाणे व्यायामही आपण न चुकता केला पाहिजे. वेळ नाही ही सबब सांगू नये. खुल्या मैदानावरील व्यायाम, क्लबमधील व्यायाम अथवा जिममधील व्यायाम कोणत्याही प्रकारचा व्यायाम दिवसांतून किमान तास – दोन तास करावा असे लेखक आवर्जून सांगतात लेखक वयाच्या 66 व्या वर्षी सुद्धा न चुकता व्यायाम करतात.
प्रश्न आ.
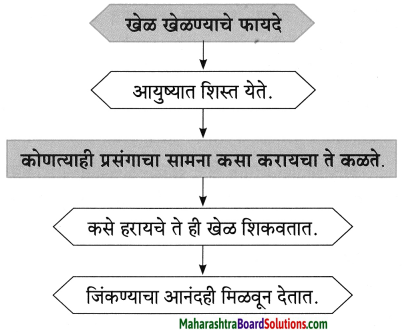
खेळ आपल्याला स्वावलंबी बनवतो व निर्णय क्षमता वाढवतो.
उत्तरः
खेळामुळे आपल्या आयुष्याला शिस्त येते. प्रसगांचा सामना कसा करावा हे कळते. खेळ आपल्याला कसे हरायचे हे तर शिकवतातच व जिंकण्याचा आनंदही मिळवून देतात. कोणीही न शिकवता आपण टेनिसमध्ये प्रतिस्पर्ध्यानं टोलवलेला चेंडू रेषेच्या आत आहे की बाहर, हे स्वत:चा पडताळतो व त्याप्रमाणे तो खेळायचा का सोडून दयायचा हे ठरवतो, त्याप्रमाणे आपल्यासाठी चांगले काय व वाईट काय हे ही आपणच ठरवायला शिकू लागतो. खेळामुळे निर्णय क्षमता वाढते व आपण स्वावलंबी होतो.
![]()
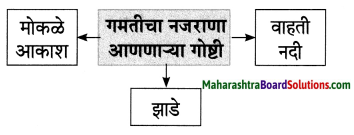
4. गमतीचा नजराणा आणणारे निसर्गातील घटक व त्या संदर्भातील तुम्ही अनुभवलेली एखादी घटना, याविषयीची माहिती सांगा.
प्रश्न 1.
गमतीचा नजराणा आणणारे निसर्गातील घटक व त्या संदर्भातील तुम्ही अनुभवलेली एखादी घटना, याविषयीची माहिती सांगा.
उत्तरः
दरवर्षी गणपतीसाठी गावाला जाणे हा आमचा नेम आहे. मागील वर्षीदेखील या निमित्ताने कोकणात जाण्याची वेळ आली. पाऊस चांगलाच झाला असल्यामुळे डोंगर हिरवा शालू परिधान करून दिमाखात उभा होता. कोकणात सूर्योदय पाहण्याची मज्जा काही औरच. पूर्व दिशेला पसरणारा लाल गुलाबी रंग मन मोहून टाकतो. शेतांच्या कामांची लगबग सुरू असते. काका व भावंडांसोबत नदीवर जाण्याचा कार्यक्रम ठरलेला, नदीचे थंड पाणी व वर मोकळे निरभ्र आकाश हा योग म्हणजे दुधात साखरच, एकूणच गणपतीच्या निमित्ताने पाहायला मिळणारे निसर्गसौंदर्य नजरसुखच म्हणता येईल.
खेळ्या शब्दांशी.
(अ) खालील तक्ता पूर्ण करा.
(आ) खालील वाक्ये वाचा व त्याआधारे तक्ता पूर्ण करा.
प्रश्न अ.
खालील तक्ता पूर्ण करा.
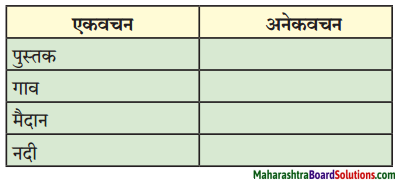
उत्तरः
| एकवचन | अनेकवचन |
| पुस्तक | पुस्तके |
| गाव | गावे |
| मैदाने | मैदान |
| नदी | नदया |
आ.
खालील वाक्ये वाचा व त्याआधारे तक्ता पूर्ण करा.
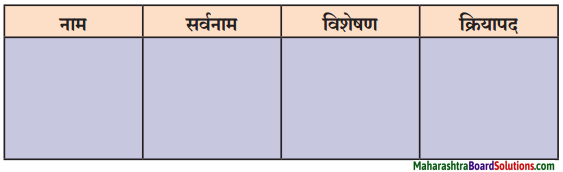
उत्तरः
| नाम | सर्वनाम | विशेषण | क्रियापद |
| सांगली | हे | महाराष्ट्रातले | आहे |
| गाव | तुमचे | कळते | |
| तुम्हाला |
![]()
चर्चा करूया :
‘वनडे क्रिकेटची मॅच बघत असताना प्रेक्षकांनी व्यक्त केलेल्या प्रतिक्रियांबाबत मित्रांशी चर्चा करून यादी तयार करा.
लिहिते होऊया :
खालील मुद्यांच्या आधारे ‘माझा आवडता खेळ’ या विषयावर आठ ते दहा ओळी निबंध लिहा.

खालील उतारा वाचा व त्यास योग्य शीर्षक दया.
![]()
वाचा :
खालील उतारा वाचा व त्यास योग्य शीर्षक दया.
प्रत्येक व्यक्तीच्या आयुष्यात सुखदुःखाचे क्षण नेहमीच येत असतात. दुःखाच्या व अडचणीच्या प्रसंगांना जे खिलाडू वृत्तीने सामोरे जातात, जे जिंकण्याच्या उर्मीने हाती घेतलेले काम पूर्ण करण्यासाठी स्वयंप्रेरणेने काम करतात, तेच आयुष्यात यश मिळवतात. कोणतीही वाईट परिस्थिती तुम्हाला अडवू किंवा हरवू शकत नाही. वेळप्रसंगी तुम्हाला दोन पावले मागेही टाकावी लागतात; परंतु जर आपण मनानेच हरलो, तर पुढील कार्य पूर्ण करण्यासाठी आपण तयार होऊ शकत नाही.
अशा परिस्थितीत कायम आपले आपल्या मनावर नियंत्रण असणे आवश्यक असते. नकारात्मक विचार करण्यापासून आपण स्वत:ला थांबवणे आवश्यक आहे. त्याचबरोबर आपल्या मनाला चांगल्या सवयी लावणेही आवश्यक आहे. आपल्या मनाला चांगली सवय लावणे हे कठीण असले, तरी अशक्य मात्र नक्कीच नाही! आपल्या अंगी असणाऱ्या चांगल्या सवयी, वाईट सवयींना जवळ येऊ देत नाहीत. मनाला चांगल्या विचारांची सवय लावली, तर ती सवय वाईट विचारांपासून तुम्हाला नक्कीच दूर ठेवील.
यासाठी तुम्हाला काही गोष्टी लक्षात ठेवाव्या लागतील. उदा., चांगले वाचन, चांगल्या मित्रमैत्रिणींची संगत, घरातील ज्येष्ठ व्यक्तींशी असणारे जिव्हाळ्याचे व आपुलकीचे संबंध इत्यादी. जो दुसऱ्याच्या दुःखात नेहमी सहभागी होतो त्यालाच जीवनाचा खरा अर्थ कळतो. मानसिक आधार देऊन, विचारांच्या देवाणघेवाणीतून आपण एकमेकांचे दुःख सहज हलके करू शकतो. असे सुखदुःखाचे प्रसंग प्रत्येकाच्या आयुष्यात सतत येत असतात मात्र या प्रसंगांना जो धीराने सामोरा जातो, तोच जीवनात यशस्वी होतो.
![]()
पत्रलेखन :
पत्र हे आपल्या मनातले भाव/विचार दुसऱ्यापर्यंत लिखित स्वरूपात पोहोचवायचे उत्तम साधन आहे. पत्रलेखनाच्या विषयानुसार पत्राचे दोन प्रमुख प्रकार पडतात.
- औपचारिक पत्र
- अनौपचारिक पत्र
यापूर्वीच्या इयत्तांमध्ये तुम्हांला ‘अनौपचारिक’ या पत्र प्रकारांची ओळख झालेली आहे. आता आपण ‘औपचारिक’ __ पत्रप्रकाराची ओळख करून घेणार आहोत.
लक्षात घ्या- आजच्या तंत्रज्ञान युगात फोनचा वापर वाढल्यामुळे पत्र लिहिणे कमी झाले आहे. तरीही आपल्याला अर्ज करणे, मागणी करणे, विनंती करणे अशा काही कारणांसाठी पत्र लिहिणे आवश्यक असते व पत्रलेखन कौशल्य प्राप्त होण्यासाठी या इयत्तेत तुम्हांला औपचारिक पत्रलेखनाचा अभ्यास करायचा आहे. आता आपण औपचारिक पत्रलेखनाचे स्वरूप समजून घेऊया.
औपचारिक पत्रलेखनासाठी आवश्यक गोष्टी :
- ज्यांना पत्र लिहायचे आहे त्यांच्या पदाचा शिष्टाचारपूर्वक उल्लेख करावा.
- भाषा सरळ, सुगम, सुस्पष्ट व विषयानुरूप असावी.
- पत्रात केवळ मुख्य विषयाबाबतच लिहावे.
- ज्यांना पत्र पाठवायचे आहे त्यांचे पद, वय, योग्यता, शिक्षण इत्यादी सर्व गोष्टी लक्षात घेऊन योग्य भाषेचा वापर करावा.
- पत्राची भाषा लेखननियमांनुसार असावी.
![]()
औपचारिक पत्र लिहिण्यासाठी खाली दिलेल्या प्रारूपाचा अभ्यास करा.
औपचारिक पत्र प्रारूप :


कृती- वरील प्रारूपाचा अभ्यास करून खालील विषयावर पत्रलेखन करा.
तुमच्या शाळेमध्ये उन्हाळी सुट्टीत ‘हस्ताक्षर सुंदर करूया!’ हे 10 दिवसांचे शिबिर आयोजित केले आहे. त्यात तुम्हांला सहभागी करून घेण्याची विनंती करणारे पत्र वर्गशिक्षकांना लिहा.
टीप : औपचारिक व अनौपचारिक दोन्ही प्रकारची पत्रे आज तंत्रज्ञानाच्या साहाय्याने म्हणजे ईमेलद्वारा पाठवली जातात. ईमेल पाठवण्याचे पत्राचे प्रारूप व तंत्र जाणून घेण्याचा प्रयत्न करा.
![]()
भाषासौंदर्य :
आलंकारिक शब्दांची रचना करून भाषेचे सौंदर्य वाढवता येते. आपले विचार अधिक परिणामकारक, अधिक आकर्षक होण्यासाठी आलंकारिक शब्दांचा उपयोग केला जातो. खाली काही आलंकारिक शब्द दिलेले आहेत. त्यांचा अभ्यास करा व लेखनात उपयोग करा. या शब्दांप्रमाणे इतर काही आलंकारिक शब्दांची यादी तयार करा.
- गळ्यातला ताईत – अत्यंत प्रिय व्यक्ती
- बाळकडू – लहानपणीचे संस्कार
- काथ्याकूट – निष्फळ चर्चा अष्टपैलू – अनेक बाबींमध्ये प्रवीण
- अळवावरचे पाणी – अल्प काळ टिकणारे
- अजातशत्रू – ज्याला कोणी शत्रू नाही असा
- झाकले माणिक – गुणांचे प्रदर्शन न करणारा गुणी मनुष्य
- इतिश्री – शेवट
- अक्षरशत्रू – निरक्षर, अशिक्षित
![]()
Marathi Sulabhbharti Class 8 Solutions Chapter 7 नातवंडांस पत्र Important Additional Questions and Answers
पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती
करा. कृती 1: आकलन कृती
प्रश्न 1.
आकृतिबंध पूर्ण करा.
i.
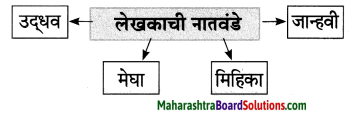
ii.
iii.
प्रश्न 2.
कंसातील योग्य पर्याय वापरून रिकाम्या जागा भरा.
- मी माझे ……………. कसे घालवले ते तुम्हाला सांगावे. (लहानपण, म्हातारपण, तरुणपण, बालपण)
- मी शिकायला ……………. होतो. (मिरजेला, सांगलीला, पुण्याला, कोल्हापुरला)
- सांगली हे ……………. तले एक गाव आहे. (तमिळनाडू, महाराष्ट्र, केरळ, बंगाल)
उत्तर:
- बालपण
- सांगलीला
- महाराष्ट्र
![]()
प्रश्न 3.
एका वाक्यात उत्तरे लिहा.
प्रश्न i.
लेखकाच्या शाळेची वैशिष्ट्ये काय होती?
उत्तर:
लेखकाच्या शाळेला खूप मोठे मैदान होते आणि त्याजवळ एक बाग होती.
प्रश्न ii.
लेखक बागेत काय काय करायचे ?
उत्तर:
लेखक बागेत मनसोक्त खेळायचे, हुंदडायचे, झाडांवर चढायचे, पाऊस आला की त्यात चिंब भिजायचे.
प्रश्न iii.
सुट्टीमध्ये नातवंडांनी काय करावे असे लेखकाला वाटते?
उत्तर:
सुट्टीमध्ये नातवंडांनी मोठ्या शहरांमधून बाहेर पडून थंड हवेच्या गिरीस्थानांवर किंवा छोट्या गावी जावे असे लेखकाला वाटते.
![]()
प्रश्न iv.
शाळेच्या मैदानाजवळ काय होते?
उत्तर:
शाळेच्या मैदानाजवळ बाग होती.
कृती 2 : आकलन कृती
प्रश्न 1.
आकृतिबंध पूर्ण करा.
i.

ii.

कारणे क्या.
प्रश्न 1.
लेखकाला पत्र लिहावे वाटले, कारण….
उत्तर:
लेखकाला नातवंडांशी प्रत्यक्षात बोलताना मोकळेपणाने, मनासारखे बोलता येईलच असे वाटत नव्हते. म्हणूनच त्यांना नातवंडांना उद्देशून पत्र लिहावे वाटले.
![]()
कृती 3 : व्याकरण कृती
प्रश्न 1.
खालील वाक्यातील अधोरेखित शब्दांच्या जाती ओळखा. प्रत्यक्षात तुमच्याशी बोलताना मोकळेपणाने, मनासारखे बोलता येतेच असे नाही. म्हणून वाटले, की तुम्हाला हे पत्र लिहावे.
उत्तर:
- सारखे – शब्दयोगी अव्यय
- म्हणून – उभयान्वयी अव्यय
- हे – सर्वनाम
- लिहावे – क्रियापद
प्रश्न 2.
जंगलातील विविध पशुंचे आवाज ऐकणे हा मोठा मजेशीर अनुभव असतो.
उत्तर:
- आवाज – नाम
- हा – सर्वनाम
- मजेशीर – विशेषण
![]()
प्रश्न 3.
खालील विशेषण व विशेष्यांच्या जोड्या जुळवा.
| विशेषण | विशेष्य |
| 1. मनसोक्त | (अ) आकाश |
| 2. मोठे | (आ) नदी |
| 3. मोकळे | (इ) मैदान |
| 4. वाहती | (ई) गप्पा |
उत्तर:
| विशेषण | विशेष्य |
| 1. मनसोक्त | (ई) गप्पा |
| 2. मोठे | (इ) मैदान |
| 3. मोकळे | (अ) आकाश |
| 4. वाहती | (आ) नदी |
प्रश्न 3.
खालील शब्दांचे लिंग बदला.
- मित्र – [ ]
- शिक्षिका – [ ]
- आई – [ ]
- पणजोबा – [ ]
उत्तर:
- मित्र – [मैत्रिणी]
- शिक्षिका – [शिक्षक]
- आई – [वडील]
- पणजोबा – [पणजी]
![]()
प्रश्न 4.
खालील शब्दांना समानार्थी शब्द लिहा.
- बालपण – [ ]
- बाग – [ ]
- पक्षी – [ ]
- नदी – [ ]
उत्तर:
- लहानपण
- बगीचा
- खग
- सरिता
कृती 4: स्वमत
प्रश्न 1.
थंड हवेच्या ठिकाणी तुम्ही कधी गेला आहात का? तुमचा अनुभव सांगा.
उत्तर:
गेल्या वर्षीच्या मे महिन्याच्या सुट्टीत आम्ही सहकुटुंब महाबळेश्वराला गेलो होतो. सातारा जिल्ह्यातील हे गिरीस्थान महाराष्ट्राचे नंदनवन म्हणून ओळखले जाते. महाबळेश्वरच्या स्ट्रॉबेरी, रासबेरी यांचा आस्वाद घेताना खूप मज्जा आली. विल्सन पॉइंट, आर्थर सीट पॉइंट, लॉडनिंग पॉइंट या महाबळेश्वरमधील प्रसिद्ध ठिकाणी भेट देऊन खूप प्रसन्न वाटले. पंचगंगा मंदिर, कृष्णाबाई मंदिर ही मंदिरे फक्त देवांचेच दर्शन घडवत नाही तर सृष्टीचा सुंदर देखावाही इथून पाहता आला. एकंदरीत महाबळेश्वर भेटीचा अनुभव अविस्मरणीय होता.
![]()
पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा.
कृती 1: आकलन कृती
प्रश्न 1.
आकृतिबंध पूर्ण करा.
एका वाक्यात उत्तरे लिहा.
प्रश्न i.
लेखकाला बॅडमिंटनची आवड कधी लागली होती?
उत्तर:
लेखकाला बॅडमिंटनची आवड त्यांच्या लहान वयातच लागली होती.
प्रश्न ii.
लेखक विजेते खेळाडू कसे होऊ शकले ?
उत्तरः
सातत्यपूर्ण परिश्रम करून लेखक विजेते खेळाडू होऊ शकले.
![]()
कंसातील योग्य पर्याय वापरून रिकाम्या जागा भरा.
प्रश्न 1.
- …………सामन्यात आपल्या देशाचे मी प्रतिनिधित्व केले. (राष्ट्रीय, तालुका स्तरीय, जिल्हा स्तरीय, आंतरराष्ट्रीय)
- मला …………….. पुरस्कार मिळाला. (खेलरत्न, अर्जुन, ध्यानचंद, द्रोणाचार्य)
- खेळ खेळल्यामुळे आपल्या आयुष्यात …………… येते. (शिस्त, समृद्धी, एकाग्रता, कुशलता)
- ………………….. आवड मला लहान वयातच लागली होती. (बॅडमिंटनची, क्रिकेटची, हॉकीची, कबड्डीची)
उत्तर:
- आंतरराष्ट्रीय
- अर्जुन
- शिस्त
- बॅडमिंटनची
कृती 2: आकलन कृती
प्रश्न 1.
ओघतक्ता पूर्ण करा.
![]()
प्रश्न 2.
उत्तरे क्या.
उत्तर:
- लेखकाच्या फोटोत लेखकाच्या – [निरनिराळे चषक हाती असणाऱ्या गोष्टी वढाली]
- लेखकाच्या मते दररोज हे – [व्यायाम केले पाहिजे.]
- पत्र लिहिताना लेखकाचे वय – [66 वर्षे]
काय घडले ते सांगा.
प्रश्न 1.
लेखकाचा व्यायाम झाला नसेल, तर……
उत्तर:
लेखकाचा व्यायाम झाला नसेल तर त्यांना जेवावेसे वाटत
कारणे क्या.
प्रश्न 1.
‘मला वेळ नाही, ही सबब सांगू नका’ असे लेखक म्हणतात.
उत्तर:
प्रत्येकाने दररोज व्यायाम करावा ही लेखकाची इच्छा आहे. व्यायामासाठी वेळ नाही हे म्हणणे त्यांना पटत नाही. आपण वेळ नाही म्हणून जेवण करायचे थांबत नाही. जेवणासाठी बरोबर वेळ काढतो. असे असताना व्यायामही वेळातवेळ काढून करावा ही इच्छा असल्याने मला वेळ नाही, ही सबब सांगू नका असे लेखक म्हणतात.
![]()
कृती 3: व्याकरण कृती
खालील वाक्यातील अव्यये ओळखून प्रकार लिहा.
प्रश्न i.
माझ्यापुरते बोलायचे तर मी अभ्यासामध्ये काही फारसा चांगला नव्हतो.
उत्तरः
- पुरते : शब्दयोगी अव्यय
- मध्ये : शब्दयोगी अव्यय
- फारसा : क्रियाविशेषण अव्यय
- तर : उभयान्वयी अव्यय
प्रश्न ii.
प्रत्येकाने दररोज काहीतरी व्यायाम केलाच पाहिजे.
उत्तर:
दररोज – क्रियाविशेषण अव्यय.
खालील वाक्यांत विरामचिन्हांचा योग्य वापर करून वाक्ये पुन्हा लिहा.
प्रश्न i.
वेळ नाही म्हणून जेवण करायचे राहते का दोन्ही जेवणांसाठी कसा बरोबर वेळ मिळतो
उत्तर:
वेळ नाही म्हणून जेवण करायचे राहते का? दोन्ही जेवणांसाठी कसा बरोबर वेळ मिळतो?
![]()
प्रश्न ii.
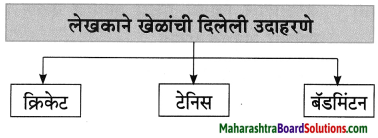
मग तो क्रिकेट टेनिस बॅडमिंटन असा तुम्हाला जो कोणता आवडत असेल तो खेळ असू दे
उत्तरः
मग तो क्रिकेट, टेनिस, बॅडमिंटन असा तुम्हांला जो कोणता आवडत असेल तो असू दे.
तक्ता पूर्ण करा.
प्रश्न 1.
तक्ता पूर्ण करा.
उत्तरः
| शब्द | विभक्ती प्रत्यय | विभक्ती |
| 1. खेळायला | ला | चतुर्थी एकवचन |
| 2. सातत्याने | ने | तृतीया एकवचन |
| 3. आयुष्यात | त | सप्तमी एकवचन |
| 4. वयाच्या | च्या | षष्ठी अनेकवचन |
प्रश्न 2.
खालील शब्दांचे वचन बदला.
- ढाली – [ ]
- खेळ – [ ]
- सबब – [ ]
- वर्ष – [ ]
उत्तरः
- ढाली – [ढाल]
- खेळ – [खेळ]
- सबब – [सबबी]
- वर्ष – [वर्ष]
![]()
कृती 4: स्वमत
प्रश्न 1.
व्यायामाचे महत्व व त्याचे फायदे तुमच्या शब्दांत लिहा.
उत्तरः
आजच्या धकाधकीच्या आयुष्यात आरोग्याच्या तक्रारी वाढल्याचे दिसून येते. सतत काम, अवेळी जेवण, ताणतणावपूर्ण आयुष्य यांवर मनाला तजेला देणारा व शरीर निरोगी ठेवणारा उपाय म्हणजे व्यायाम, व्यायाम करणाऱ्या व्यक्तींना दीर्घ जीवनाचे वरदान मिळते त्यांची कार्यक्षमता वाढते. हाडांची मजबुती, शरीराच्या अवयवांचा समन्वय, नितळ त्वचा यांसारखे अनेक फायदे व्यायामामुळे होतात, व्यायाम करणाऱ्याचे शरीर सुडौल राहते. माणसाची रोग प्रतिकारक शक्ती वाढते. व्यायामाचे अगणित फायदे आहेत, असे म्हणता येईल.
खालील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा.
कृती 1: आकलन कृती
1. आकृतिबंध पूर्ण करा.
i.
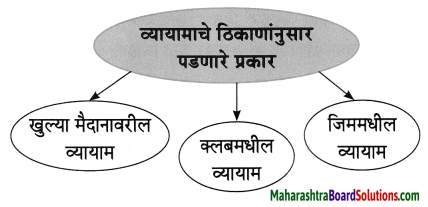
ii
एका वाक्यात उत्तरे लिहा.
प्रश्न i.
लेखकाच्या मते, व्यायामासाठी किती तास काढले पाहिजेत?
उत्तर:
लेखकाच्या मते व्यायामासाठी तास – दोन तास काढले पाहिजेत.
![]()
प्रश्न i..
ई-मेल, इंटरनेटचा काय फायदा होतो?
उत्तरः
ई-मेल, इंटरनेटमुळे आपल्याला घरबसल्या, हवी ती माहिती मिळू शकते.
प्रश्न iii.
लेखक आपल्या नातवंडांना काय सल्ला देतात?
उत्तरः
लेखक आपल्या नातवंडांना मित्रांशी व कुटुंबियांशी असलेला आपला व्यक्तिगत संपर्क तुटू न देण्याचा सल्ला देतात.
खालील इंग्रजी शब्दांना उताऱ्यात आलेले मराठी शब्द शोधा.
प्रश्न 1.
- ग्राऊंड
- सेल्फडिपेंडन्ट
- मिडियम ऑफ कॉन्टॅक्ट
- बॉल
उत्तर:
- मैदान
- स्वावलंबी
- संपर्कमाध्यमे
- चेंडू
![]()
कृती 2: आकलन कृती
कंसातील योग्य पर्याय वापरून रिकाम्या जागा भरा.
प्रश्न 1.
- तुम्ही जसे मोठे व्हाल तसे तुम्ही आपले स्वत:चे ……………………….. व्हा. (पालक, शिक्षक, मार्गदर्शक, उद्धारक)
- येत्या ……………. तुम्हांला माझ्या शुभेच्छा ! (सहस्रकासाठी, नववर्षासाठी, दशकासाठी, शतकासाठी)
उत्तर:
- शिक्षक
- सहस्त्रकासाठी
खालील विधानांमागील कारणे शोधा.
प्रश्न 1.
तुम्ही जसे मोठे व्हाल तसे तुम्ही आपले स्वत:चे शिक्षक व्हा.
उत्तरः
लेखकाच्या मते, आयुष्यातील प्रत्येक गोष्ट शाळा कॉलेजांमध्ये शिकवून येत नसते. आयुष्यात येणारे प्रत्यक्ष अनुभव खूप काही शिकवून जात असतात. त्याकरता स्वत:बरोबरच आजूबाजूलाही लक्ष देणे गरजेचे असते. म्हणूनच तुम्ही जसे मोठे व्हाल तसे तुम्ही आपले स्वत: चे शिक्षक व्हा, असे लेखक म्हणतात.
![]()
प्रश्न 2.
तुम्ही स्वत:वर अवलंबून राहायला शिकले पाहिजे. स्वावलंबी झाले पाहिजे.
उत्तर:
आयुष्यात शाळा कॉलेजात जे शिकवले जात नाही ते सगळे प्रत्यक्ष अनुभव शिकवत असतात. आपण स्वत:च आपल्याकरिता चांगले काय आणि वाईट काय ते ओळखायला शिकायचे असते. म्हणजे थोडक्यात स्वत: वर अवलंबून राहायला शिकले पाहिजे, स्वावलंबी झाले पाहिजे.
प्रश्न 3.
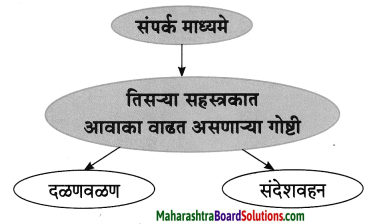
उत्तर लिहा. तिसऱ्या सहस्त्रकाचे कोणते विशेष लेखकाने सांगितले आहेत.
उत्तरः
तिसऱ्या सहस्त्रकामध्ये संपर्क माध्यमे, दळणवळण आणि संदेशवहनाचा आवाका वाढतो आहे. आता आपल्या घरी, बसल्या जागी, हवी ती माहिती आपल्याला ई-मेल व इंटरनेट द्वारे मिळू शकते. हे तिसऱ्या सहस्त्रकाचे विशेष लेखकाने सांगितले आहेत.
![]()
कृती 3: व्याकरण कृती
प्रश्न 1.
खालील तक्ता पूर्ण करा.
उत्तरः
| शब्द | मूळ शब्द | सामान्यरूप |
| 1. आयुष्यातील | आयुष्य | आयुष्यात |
| 2. आवाकाही | आवाका | आवाका |
| 3. मित्रांशी | मित्र | मित्रां |
| 4. रेषेच्या | रेष | रेषे |
प्रश्न 2.
खालील शब्दांचे त्यांच्या लिंगानुसार वर्गीकरण करा.
व्यायाम, मैदान, शाळा, चेंडू, कुटुंबिय, रेष, ई-मेल
उत्तरः
| पुल्लिंग | स्त्रीलिंग | नपुसकलिंग |
| 1. व्यायाम | शाळा | मैदान |
| 2. चेंडू | रेष | कुटुंबिय |
| 3. ई-मेल |
![]()
खालील शब्दांचे विरुद्धार्थी शब्द लिहा.
प्रश्न 1.
- खुला × [ ]
- शिक्षक × [ ]
- स्वावलंबी × [ ]
- मित्र × [ ]
उत्तर:
- बंद
- विदयार्थी
- परावलंबी
- शत्रू
![]()
खालील वाक्ये लेखननियमांनुसार शुद्ध करून लिहा.
प्रश्न i.
तुम्हि व्यायामासाठी तास – दोन तास काढलेच पाहीजे.
उत्तर:
तुम्ही व्यायामासाठी तास – दोन तास काढलेच पाहिजे.
प्रश्न ii.
येत्या सहसत्रकासाठी तुम्हांला माझ्या शुभेच्छा!
उत्तर:
येत्या सहस्रकासाठी तुम्हांला माझ्या शुभेच्छा!
कृती 4: स्वमत
प्रश्न 1.
‘तुमच्या मित्रांशी व कुटुंबियांशी असलेला आपला व्यक्तिगत संपर्क तुटू देऊ नका’ या वाक्याचा तुम्हांला कळलेल्या अर्थ लिहा.
उत्तरः
आपण तिसऱ्या सहस्त्रकात प्रवेश केला असून अनेक नवनवीन गोष्टी आपल्याला भुरळ घालत आहेत. प्रगत तंत्रज्ञानाचा वापर करून बनवलेली साधने वापरण्यास सोपी असल्याने अशा गोष्टींचा वापर करून आप्तेष्टांशी संपर्कात राहणे सोपे झाले आहे. व्हॉटस्अप फेसबूक, ट्वीट्, इन्स्टाग्राम यांसारख्या अॅप्समुळे आपण कधीही न पाहिलेल्या नातेवाईकांशीही संपर्कात राहत असलो तरी पूर्वीइतके प्रेम, प्रत्यक्ष व्यक्तिगत भेटितला ओलावा त्यातून जाणवत नाही. ते तोंडदेखले नाते उरते. म्हणूनच आपण मित्रांशी, कुटुंबियांशी व्यक्तिगत संपर्क ठेवणे आवश्यक ठरते.
![]()
नातवंडांस पत्र Summary in Marathi
पाठपरिचय :
लेखक नंदू नाटेकर हे भारताचे माजी बॅडमिंटनपटू राष्ट्रीय विजेते आहेत. आपल्या नातवंडांशी पत्ररूपाने संवाद साधताना लेखक त्यांना निसर्ग सान्निध्यात गेलेले बालपण, आपली बॅडमिंटनची आवड, त्यासाठी लागणारे सातत्यपूर्ण परिश्रम आणि त्यातून संपादित केलेले उज्ज्वल यश यांविषयी मार्गदर्शन करतात.
The writer of this chapter Nandu Natekar is Famous batminton champion. In this letter, writer narrates to his grandchild about his own childhood memories which had been spent in nature, his love towards badminton, continouous dedication towards it and success gained through it.
![]()
शब्दार्थ :
- माया – प्रेम – love
- हुंदडणे – फिरणे – to rome
- मनसोक्त – मन भरेपर्यंत – to one’s heart’s content
- गिरिस्थान – पर्वतावरील ठिकाण – mountain place
- थवा – पक्ष्यांचा समूह – flock of birds
- आकाश – आभाळ, गगन – sky
- नदी – सरिता – river
- नजराणा – मौल्यवान भेट – precious gift
- चषक व ढाली – trophy & shield
- परिश्रम – कष्ट – hardwork
- सबब – कारण – reason
- स्वावलंबी – स्वयंपूर्ण, आत्मनिर्भर – self reliant
- सहस्त्र – हजार – thousand
- दळणवळण – परस्पर संपर्क – inter – अथवा व्यवहार communication
- आवाका – विशालता, आकार – magnitude
- व्यक्तिगत – स्वत:पुरते – individual
- संपर्क – संबंध – contact
![]()
वाक्प्रचार :
- मजा लुटणे – आनंद घेणे
- सामना करणे – तोंड देणे, परिस्थितीला सामोरे जाणे
- पडताळून पाहणे – बरोबर असल्याची खात्री करून घेणे
टिप :
अर्जुन पुरस्कार – राष्ट्रीय खेळातील उल्लेखनीय कामगिरीबद्दल भारत सरकारतर्फे दिला जाणारा महत्त्वपूर्ण पुरस्कार म्हणजे अर्जुन पुरस्कार होय. ही प्रथा 1961 मध्ये सुरू करण्यात आली. 3 लाख रूपये रोख, कांस्य धातूपासून बनवलेला अर्जुनाचा छोटा पुतळा आणि प्रमाणपत्र असे या पुरस्काराचे स्वरूप आहे. भारतातील क्रीडा प्रकार व खेळ यांच्या विकासास उत्तेजन देणे, हा या पुरस्करामागील उद्देश आहे.
Marathi Sulabhbharati Class 8 Solutions
- आम्ही चालवू हा पुढे वारसा (गीत) Question Answer
- मी चित्रकार कसा झालो! Question Answer
- प्रभात (कविता) Question Answer
- आपण सारे एक Question Answer
- घाटात घाट वरंधाघाट Question Answer
- आभाळाची अम्ही लेकरे (कविता) Question Answer
- नातवंडांस पत्र Question Answer
- गीर्यारोहणाचा अनुभव Question Answer
- झुळूक (कविता) Question Answer
- आम्ही हवे आहोत का? Question Answer
- जीवन गाणे (कविता) Question Answer
- शब्दकोश (स्थूलवाचन) Question Answer
- संतवाणी Question Answer