Class 8

Class 8 Hindi Chapter 5 Kheti Se Aai Tabdiliyan Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 5 खेती से आई तब्‍दीलियाँ Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 5 Kheti Se Aai Tabdiliyan Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 5 खेती से आई तब्‍दीलियाँ Textbook Questions and Answers

सूचना के अनुसार कृतियाँ करो

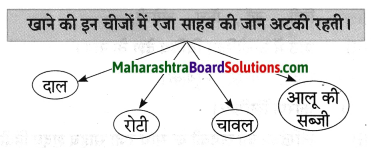
प्रवाह तालिका पूर्ण करो:

Question 1.

Answer:

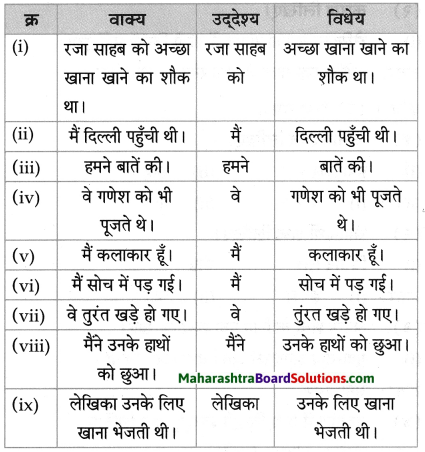
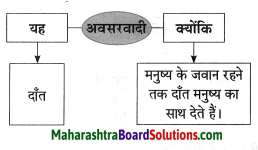
उचित जानकारी लिखो:

Question 1.

Answer:

कारण लिखिए।

Question 1.
मनुष्य को रोज शिकार खेलना पड़ता है।
Answer:
क्योंकि उसे स्वयं का गुजर बसर करना था।

Question 2.
अनाज सुरक्षित रखना प्रारंभ हुआ।
Answer:
जमीन में बहुत सारा अनाज पैदा होता था। इसे एकदम खाया नहीं जा सकता था।

Question 3.
मनुष्य को रोज शिकार खेलना पड़ता।
Answer:
स्वयं का पेट भरने के लिए उसे रोज शिकार खेलना पड़ता।

Question 4.
दुनिया में गरीब आदमी हैं।
Answer:
क्योंकि जो आज बिलकुल काम नहीं करता है; उसके पास बहुत सारा धन आ जाता है और जो दिन-रात पसीना बहाता है वह खाली हाथ रहता है। इस बुरे इंतजाम के कारण दुनिया में गरीब आदमी है।

Question 5.
लोग बैंक में रुपए रखते हैं।
Answer:
क्योंकि उनके पास अतिरिक्त रुपए होते हैं।

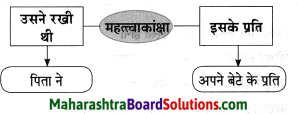
कृति पूर्ण करो:

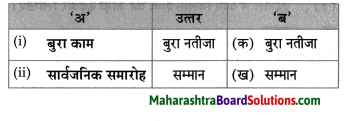
उस जमाने में उसे अमीर कहा जाता था जिसके पास ……….. थे

Question 1.

Answer:

भाषाबिंदु

निम्नलिखित वाक्यों में उचित विराम चिह्नों का प्रयोग कीजिए।

Question 1.
बड़े दुखी लग रहे हो क्या हुआ
Answer:
बड़े दुखी लग रहे हो, क्या हुआ?

Question 2.
अरे रामू के बापू घोड़े बेचकर सो रहे हो
Answer:
अरे, रामू के बापू, घोड़े बेचकर सो रहे हो?

Question 3.
तुम्हारे दाने कहाँ है
Answer:
तुम्हारे दाने कहाँ है?

उपयोजित लेखन

‘तबांकू सेवन के दुष्परिणाम’ विषय पर लगभग सौ शब्दों में निबंध लिखिए।
Answer:
तंबाकू सेवन सेहत के लिए हानिकारक होता है। तंबाकू में एक प्रकार का रासायनिक द्रव्य मिलाया जाता है जो शरीर नुकसान पहुँचाता है। तंबाकू में टार, निकोटीन व कार्बनमोनोक्साइड आदि पदार्थों को मिलाया जाता है। ये सारे पदार्थ मनुष्य के शरीर के लिए हानिकारक होते हैं। धीरे-धीरे उसका असर दिखाई देने लगता है। सबसे पहले वह मुँह को प्रभावित करता है और उसके बाद संपूर्ण शरीर को प्रभावित करना शुरू कर देता है। जो व्यक्ति तंबाकू का सेवन अधिक मात्रा में करते हैं उन्हें बाल झड़ने की समस्या से भी गुजरना पड़ता है।

तंबाकू का अति सेवन करने से मनुष्य को कैंसर जैसी बीमारियाँ होती हैं जिनका इलाज आज भी विज्ञान के लिए मुश्किल है। अत: बहुत सारे लोगों की तंबाकू को सेवन करने से मृत्यु हो रही है। कई लोग तंबाकू की लत के कारण यदि उन्हें समय पर खाने के लिए मिलता तो चिंतित एवं बेचैन हो जाते हैं। कई लोग तंबाकू का सेवन करना छोड़ना चाहते हैं और वे प्रयास भी करत हैं। लेकिन फिर भी वे अपनी इस आदत को छोड़ नहीं पाते हैं। तंबाकू का सेवन करने से व्यक्ति को हृदय संबंधी समस्याओं का भी सामना करना पड़ता हैं। तंबाकू का सेवन करने से मनुष्य को त्वचा संबंधी बीमारियाँ एवं नाखून झड़ने की समस्याओं का सामना करना पड़ता है। तंबाकू का सेवन मनुष्य के लिए जानलेवा और खतरनाक है। अतः मनुष्य को तंबाकू का सेवन कतई नहीं करना चाहिए।

शब्द समूह के लिए एक शब्द लिखिए।

Question 1.
जानवरों को चराने की जगह
Answer:
चरागाह

Question 2.
जिनके पास बहुत से अतिरिक्त रुपए हैं।
Answer:

1. धनवान
2. मालदार

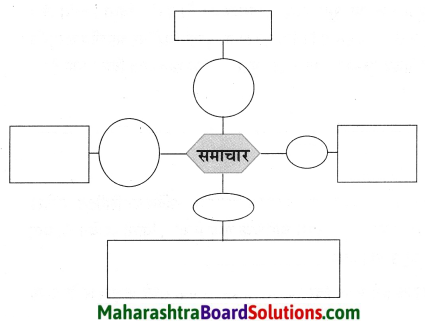
स्वयं अध्ययन

पारंपरिक तथा आधुनिक कृषि प्रौद्योगिकी का तुलनात्मक चार्ट बनाओ।

Hindi Sulabhbharti Class 8 Solutions Chapter 5 खेती से आई तब्‍दीलियाँ Additional Important Questions and Answers

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति क (१) आकलन कृति

समझकर लिखिए।

Question 1.

Answer:

गद्यांश के आधार पर वाक्य पूर्ण कीजिए।

Question 1.
तब काम बँटे हुए नहीं थे……
Answer:
जब शुरू में आदमी शिकार पर गुजर-बसर करता था।

Question 2.
जैसे-जैसे दिन गुजरने लगे……..
Answer:
वैसे-वैसे आदमियों ने नए नए पेशे सीखें और उनमें पक्के हो गए।

कृति क (२) आकलन कृति

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –

Question 1.
औरत
Answer:
बच्चे और पालतू जानवरों की निगरानी कौन करता था?

Question 2.
काम
Answer:
कई हिस्सों में क्या बँट गए?

कृति क (३) शब्द संपदा

निम्नलिखित शब्द के तत्सम रूप लिखिए।

Question 1.
काम
Answer:
कार्य

निम्नलिखित शब्द मानक वर्तनी के अनुसार लिखिए।

Question 1.
नये-नये
Answer:
नए-नए

वचन बदलिए।

1. बातें
2. बेटी

Answer:

1. बात
2. बेटियाँ

नीचे दिए हुए शब्दों के पर्यायवाची शब्द लिखिए।

1. हल
2. मुश्किल

Answer:

1. समाधान
2. कठिन

Question 1.
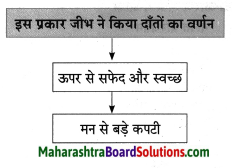
गद्यांश में से लिंग शब्द की जोड़ी ढूँढ़कर लिखिए।
Answer:
आदमी – औरत

कृति क (४) स्वमत अभिव्यक्ति

Question 1.
आदिम अवस्था में मनुष्य किस प्रकार अपना गुजर-बसर करता था? इस बारे में जानकारी के आधार पर अपने विचार लिखिए।
Answer:
आदिम अवस्था में मानवीय सभ्यता का विकास नहीं हुआ था। उस अवस्था में मनुष्य के पास घर ही क्या साधारण-सी कुटिया भी नहीं थी। मानव जंगल में उपलब्ध कंदमूल खाया करता था और वहीं पर किसी एक पेड़ के नीचे सो जाया करता था। उसके पास शिकार के अतिरिक्त किसी भी प्रकार का काम नहीं होता था। अत: वह पूरा दिन शिकार की खोज में घूमा करता था। शिकार करने के शस्त्रों के अलावा मनुष्य के पास अन्य कोई साधन नहीं होते थे। उसके पास तन ढंकने के लिए कपड़े भी नहीं थे। वह पेड़ की पत्तियों से अपना शरीर ढंकते थे।

(ख) निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति ख (१) आकलन कृति

तुलना कीजिए।

Question 1.

Answer:

कारण लिखिए।

Question 1.
खेती के पहले लोग एक जगह नहीं ठहरते थे।
Answer:
क्योंकि शिकार हरेक जगह मिल जाता था। इसके अतिरिक्त गायों, बकरियों एवं दूसरे जानवरों की वजह से इधर-उधर घूमना पड़ता था।

कृति ख (२) आकलन कृति

एक शब्द में उत्तर लिखिए।

Question 1.
जानवरों को चरने के लिए इसकी जरूरत थी
Answer:
चरागाहों की .

Question 2.
खेती करना सीख जाने के बाद लोग इसके पास रहने लगे
Answer:
जमीन के

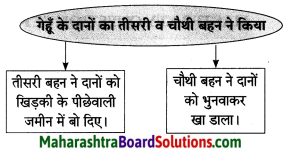
समझकर लिखिए।

Question 1.

Answer:

विलोम शब्द लिखिए।

1. गाँव
2. अच्छा

Answer:

1. शहर
2. बुरा

Question 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:

• इधर-उधर
• घूमते-फिरते
• जोत-बोकर

निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।

1. शिकार
2. शहर

Answer:

1. शिकारी
2. शहरी

कृति ख (४) स्वमत अभिव्यक्ति

Question 1.
‘खेती करने के कारण समाज की निर्मिती हुई’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
खेती करने के पहले व्यक्ति इधर-उधर घूमता फिरता था। शिकार करके स्वयं का पेट पालता था। जैसे ही उसने खेती करना शुरू कर दिया वैसे ही वह जमीन के पास रहने लगा। परे साल भर वह खेती के काम में व्यस्त होने लगा। उसके आसपास रहने वालों की संख्या में वृद्धि होने लगी। वह एक-दूसरे के साथ संबंध प्रस्थापित करने लगा। आहिस्ता-आहिस्ता गाँव व कस्बे तैयार होने लगे। इससे समाज का निर्माण होने लगा।

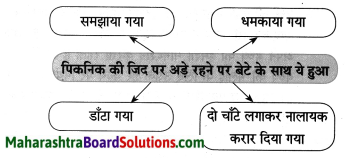
कृति पूर्ण कीजिए।

Question 1.
खेती करने से आदमी को हुआ यह लाभ
Answer:
आदमी की जिंदगी ज्यादा आराम से कटने लगी।

समझकर लिखिए।

Question 1.

Answer:

सही विकल्प चुनकर वाक्य फिर से लिखिए।

Question 1.
अतिरिक्त खाने की वह …………. कर देता था। (जमा, खर्च, बाँट)
Answer:
जमा

Question 2.
आदमी को अपना ……….. भरने के लिए शिकार करना पड़ता था। (घर, पेट, बस्ता )
Answer:
पेट

कृति ग (३) शब्द संपदा

पर्यायवाची शब्द लिखिए।

1. पैदा
2. शिकार
3. जमीन
4. शिकारी

Answer:

1. उपज
2. आखेट
3. भूमि
4. आखेटक

Question 1.
गद्यांश में ऐसे दो शब्द बूडकर लिखिए जिनके वचन परिवर्तित नहीं होते।
Answer:

• पेट
• शिकार

विलोम शब्द लिखिए।

1. बेकसूर x ………..
2. ज्यादा x …….

Answer:

1. कसूरवार
2. कम

निम्नलिखित शब्दों से उपसर्ग को अलग कीजिए।

1. अतिरिक्त
2. सुरक्षित

Answer:

1. अति
2. सु

उचित प्रत्यय लगाइए।

1. बात
2. दिन

Answer:

1. ऊनी : बातूनी
2. इक : दैनिक

कृति ग (४) स्वमत अभिव्यक्ति

Question 1.
‘धन और अनाज को हमें भविष्य के लिए संग्रह रखना चाहिए।’ अपने विचार लिखिए।
Answer:
मनुष्य भले ही वर्तमान में जीवन व्यतीत करता है फिर भी उसे भविष्य के बारे में सोचना चाहिए। उसे भविष्य के लिए धन व अनाज जैसी चीजों का संग्रह करके रखना चाहिए। वर्तमान में हमारे पास यदि जरूरत से ज्यादा कुछ आता है तो हमें सब का सब खर्च नहीं करना चाहिए। हो सकता है कि भविष्य में हम पर कोई मुसीबत आ जाए और ऐसे में हमारे पास कुछ न होने से हमें यातनाओं का सामना करना पड़े। इसलिए व्यक्ति को दूर की सोच रखते हुए भविष्य के लिए धन या अनाज इकट्ठा करके रखना चाहिए।

निम्नलिखित गलत वाक्य सही करके फिर से लिखिए।

Question 1.
बैंक में बच्चे अनाज जमा करते हैं और चेक से निकाल भी सकते हैं।
Answer:
बैंक में लोग रूपए जमा करते हैं और चेक से निकाल भी सकते हैं।

Question 2.
जिनके पास अतिरिक्त रूपया होता है वही लोग अफसर होते हैं।
Answer:
जिनके पास अतिरिक्त रूपया होता है वही लोग मालदार होते हैं।

कृति घ (२) आकलन कृति

गद्यांश के आधार पर वाक्य पूर्ण कीजिए।

Question 1.
वे लोग गरीब कहलाते हैं
उत्तर
जिनके पास रुपए या अनाज नहीं होता है।

Question 2.
उसे खाली हाथ रहना पड़ता है
Answer:
जो दिन-रात पसीना बहाता है।

समझकर लिखिए।

Question 1.
यह है बुरा इंतजाम
Answer:
आज जो आदमी काम नहीं करता है उसके पास बहुत सारा धन आ जाता है और जो दिन-रात पसीना बहाता है वह खाली हाथ रहता है।

कारण लिखिए।

Question 1.
दुनिया में गरीब आदमी हैं।
Answer:
क्योंकि जो आज बिलकुल काम नहीं करता है। उसके पास बहुत सारा धन आ जाता है और जो दिन-रात पसीना बहाता है वह खाली हाथ रहता है। इस बुरे इंतजाम के कारण दुनिया में
गरीब आदमी है।

Question 2.
लोग बैंक में रुपए रखते हैं।
Answer:
क्योंकि उनके पास अतिरिक्त रुपए होते हैं।

कृति घ (३) शब्द संपदा

विलोम शब्द लिखिए।

1. ज्यादा x ……..
2. अमीर x ………

Answer:

1. कम
2. गरीब

समानार्थी शब्द लिखिए।

1. गरीब
2. पसीना

Answer:

1. दीन
2. स्वेद

निम्नलिखित अनेक शब्द के लिए एक शब्द लिखिए।

Question 1.
जिसके पास बहुत धन होता है।
Answer:
धनवान

Question 2.
जिनके पास बहुत से अतिरिक्त रुपए हैं।
Answer:
मालदार

Question 3.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:

• बहुत-सा
• आज-कल

लिंग बदलिए।

1. पिता
2. आदमी

Answer:

1. माता
2. औरत

Question 1.
‘आज अमीर अधिक अमीर होता जा रहा है और गरीब अधिक गरीब होता जा रहा है।’ पर अपने विचार लिखिए।
Answer:
आज हम नए दौर में जीवन जी रहे हैं। इस नए युग में समाज में ढेर सारी समस्याएं हैं। उनमें से एक अत्यंत गंभीर समस्या है – महँगाई। आज वस्तुओं की कीमतें आसमान को छू रही हैं। कर्मचारी एवं मजदूर जैसे सामान्य वर्ग के लोग पैसों की कमी होने के कारण अपने परिवार की जरूरतों को पूरा करने में असमर्थ सिद्ध हो रहे हैं। इस कारण वे रुपयों को भविष्य के लिए संग्रह नहीं कर पा रहे हैं।

इस कारण उनकी आर्थिक स्थिति में सुधार नहीं हो रहा है। समाज में रहने वाला अमीर वर्ग बिना कुछ काम किए अधिक से अधिक अमीर होता जा रहा है। इसका प्रमुख कारण यह है कि वे गरीबों को उनके काम की बहुत ही कम मजदूरी दे रहे हैं। यही कारण है कि अमीर अधिक अमीर होता जा रहा है और गरीब अधिक गरीब। गरीबों पर होनेवाले शोषण को रोक कर ही हम एक स्वस्थ समाज की स्थापना कर सकते हैं।

Hindi Sulabhbharati 8th Standard Digest Guide दूसरी इकाई

• धरती का आँगन महके Question Answer
• दो लघुकथाएँ Question Answer
• लकड़हारा और वन Question Answer
• सौहार्द -सौमनस्‍य Question Answer
• खेती से आई तब्‍दीलियाँ Question Answer
• अंधायुग Question Answer
• स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Question Answer
• मेरा विद्रोह Question Answer
• नहीं कुछ इससे बढ़कर Question Answer

Class 8 Hindi Chapter 3 Nakhun kyon Badhate Hain Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 3 नाखून क्यों बढ़ते हैं? Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 3 Nakhun kyon Badhate Hain Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 3 नाखून क्यों बढ़ते हैं? Textbook Questions and Answers

स्वाध्याय विषयक कृतियाँ

प्रतीक लिखिए।
Answer:

भाषाबिंदु

निम्न शब्दों के लिंग पहचानकर लिखिए।

(आत्मा, व्यक्ति, बादल, तार, नोट, नाखून, पुस्तक, तकिया, दही)
Answer:
पुल्लिंग: व्यक्ति, बादल, नोट, नाखून, दही, तकिया, तार
स्त्रीलिंग: आत्मा, पुस्तक, तार

कृति ग (१) आकलन कृति

प्रवाह तालिका पूर्ण कीजिए।
Answer:

Question 1.
अर्थ के अनुसार वाक्य के प्रकार ढूँढ़कर लिखिए।
Answer:
(१) विधानार्थक वाक्य:
(i) उसे नाखून की जरूरत थी।
(ii) उसने धातु के हथियार बनाए।

(२) प्रश्नार्थक वाक्य:
(i) आखिर ये इतने बेहया क्यों हैं?
(ii) मनुष्य किस ओर बढ़ रहा है?

(३) निषेधार्थक वाक्य :
(i) वह मरना नहीं जानती।
(ii) मैं कुछ सोच ही नहीं सका।

(४) आज्ञार्थक वाक्य:
(i) नाखून बढ़ रहे है तो उन्हें काट दीजिए।

(५) विस्मयादिबोधक वाक्यः
(i) वाह! क्या बात है। मनुष्य मनुष्यता की ओर बढ़ रहा है।

संदेशसूचक वाक्य:
(i) मनुष्य अपनी पशुता को त्याग दे तब मरणास्त्रों का प्रयोग भी अपने आप समाप्त हो जाएगा।

Question 2.
पाठ में आए दस पुल्लिंग व स्त्रीलिंग शब्द लिखिए।
Answer:
पुल्लिंग: प्रश्न, पिता, नाखून, शरीर, हथियार, नागरिक, आदर्श, संयम, तप, त्याग
स्त्रीलिंग: लड़की, पशुता, मनुष्यता, सहायता, इच्छा, श्रद्धा, संवेदना, पूँछ, घृणा, महिमा

उपयोजित लेखन

किसी मराठी विज्ञापन का हिंदी में अनुवाद कीजिए।
Answer:

लेखनीय

‘सुरक्षा हेतु शस्त्रों की भरमार’ विषय के पक्ष-विपक्ष में अपने विचार लिखिए।
Answer:
पक्षधर विचार:
(i) क्षत्रिय कुल के लोग शस्त्रों का पूजन करते हैं।
(ii) पुलिस विभाग द्वारा भी शस्त्रों का पूजन किया जाता है।
(iii) शस्त्र विपरीत परिस्थितियों में दूसरों के जीवन की रक्षा करते हैं।
(iv) शस्त्र शक्ति का प्रतीक होते हैं।

विपक्षी विचार:
(i) शस्त्र विनाश का प्रतीक होते हैं।
(ii) शस्त्र हिंसा का निर्माण करते हैं।
(iii) शस्त्र-निर्माण पर कई देश ढेर सारे रुपये खर्च करते हैं।
(iv) शस्त्र-निर्माण की होड़ देशों को अंधा बना देती है।

स्वयं अध्ययन

शरीर के विभिन्न अंगों से संबंधित मुहावरों की अर्थ सहित सूची बनाइए।
Answer:

उत्तर लिखिए।

Question 1.
मनुष्य को नाखून की जरूरत तब थी:
Answer:
मनुष्य को नाखून की जरुरत तब थी जब वह वनमानुष जैसा जंगली था।

Question 2.
मनुष्य का स्वधर्म यह हैं
Answer:
अपने को संयत रखना।

Hindi Sulabhbharti Class 8 Solutions Chapter 3 नाखून क्यों बढ़ते हैं? Additional Important Questions and Answers

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति क (१) आकलन कृति

उत्तर लिखिए।

Question 1.
इसे कहा गया है दयनीय जीव
Answer:
पिता को

Question 2.
इसकी पशुता का प्रयोग गद्यांश में हुआ है
Answer:
मनुष्य की

कृति पूर्ण कीजिए।

Answer:

कृति क (२) आकलन कृति

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

Question 1.
हथियार
Answer:
मनुष्य ने हड्डियों के क्या बनाए?

Question 2.
नाखून
Answer:
पहले मनुष्य के अस्त्र क्या थे?

परिणाम लिखिए।

Question 1.
मनुष्य का धीरे-धीरे आगे बढ़ने का परिणाम
Answer:
उसने धातु के हथियार बनाए।

कारण लिखिए

Question 1.
मनुष्य नाखूनों को काट देता है।
Answer:
क्योंकि हर तीसरे दिन उसके नाखून बढ़ जाते हैं

कृति क (३) शब्द संपदा

Question 1.
गद्यांश में आए शब्द-युग्म ढूंढकर लिखिए।
Answer:
कभी-कभी
धीरे-धीरे

लिंग बदलिए।

1. पिता
2. आदमी

Answer:

1. माता
2. औरत

नीचे दिए हुए शब्दों के पर्यायवाची शब्द लिखिए।

1. हथियार
2. पाशवी

Answer:

1. शस्त्र
2. पशुवत, दानवी

निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।

1. इतिहास
2. मनुष्य

Answer:

1. ऐतिहासिक
2. मनुष्यता

कृति क (४) स्वमत अभिव्यक्ति

Question 1.
‘मनुष्य की पशुता को जितनी बार काट दो, वह मरना नहीं जानती।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
जी हाँ, मनुष्य की पशुता को जितनी बार काट दो, वह मरना नहीं जानती। मनुष्य का स्वभाव इतना विचित्र है कि उसमें अच्छाई भी है और बुराई भी; उसमें मानवता भी है और पशुता भी। अक्सर देखा जाता है कि बुरा काम करने वाले लोगों को कानून के द्वारा दंडित किया जाता है। फिर भी सजा काटने के बाद वे बुरा काम करते ही रहते हैं। जो व्यक्ति दूसरों का बुरा चाहता हैं; वह कभी सुधरता नहीं। उसे आप लाख समझाओ, फिर भी वह समझने के लिए तैयार नहीं होता है। वह मौका मिलते ही साँप की भाँति डंसने के लिए तैयार हो जाता है। इस प्रकार मनुष्य की पशुता को जितनी बार भी काटो, वह मरना नहीं जानती।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ख (१) आकलन कृति

गद्यांश के आधार पर वाक्य पूर्ण कीजिए।

Question 1.
मनुष्य को तब अपनी वास्तविक प्रवृत्ति पहचानने में बहुत सहायता मिलती हैं.
Answer:
जब वह अपने शरीर की मन की और वाक की अनायास घटने वाली वृत्तियों के विषय में सोचने लगता है।

निम्नलिखित गलत वाक्य सही करके लिखिए।

Question 1.
मनुष्य की नाखून काटने की जो प्रवृत्ति है, वह उसकी पशुता की निशानी है।
Answer:
मनुष्य की नाखून काटने की जो प्रवृत्ति है, वह उसकी मनुष्यता की निशानी है।

Question 2.
हमारी परंपरा महिमामयी और संस्कृति उज्ज्वल हैं।
Answer:
हमारी परंपरा महिमामयी और संस्कार उज्ज्वल हैं।

कृति ख (२) आकलन कृति

कृति पूर्ण कीजिए।

Answer:

कारण लिखिए।

Question 1.
हमारी परंपरा महिमामयी और संस्कार उज्ज्वल है।
Answer:
हमारी परंपरा, महिमामयी और संस्कार उज्ज्वल है क्योंकि अपने आप पर, अपने आप द्वारा लगाया हुआ बंधन हमारी संस्कृति की बहुत बड़ी विशेषता है।

कृति ख (३) शब्द संपदा

उचित प्रत्यय जोड़कर नए शब्द बनाइए।

1. अर्थ
2. नागरिक

Answer:

1. आर्थिक
2. नागरिकता

अनेक शब्दों के लिए एक शब्द लिखिए।

1. मनुष्य होने की अवस्था
2. उत्तम या सुधरी हुई स्थिती

Answer:

1. मनुष्यता
2. संस्कृति

विलोम शब्द लिखिए।

1. अर्थ x
2. बंधन x

Answer:

1. अर्थ x अनर्थ
2. बंधन x मुक्ति

कृति ख (४) स्वमत अभिव्यक्ति

‘Question 1.
आज का मनुष्य पशुता की ओर बढ़ रहा है या मनुष्यता की ओर?’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
आज का युग विज्ञान व तकनीकी का युग है। सर्वत्र मशीनों का बोलबाला है। मनुष्य ने स्वयं की प्रगति के लिए आधुनिक सभ्यता को अपना लिया है। समाज से मानवीय मूल्य कहीं गायब होते हुए दिखाई दे रहे हैं। आज हमारे समाज में हिंसा व भ्रष्टाचार जैसी कई समस्याएँ है। इनके कारण इंसान अपनी अच्छाइयों को त्याग बुराई के मार्ग पर चलता दिखाई दे रहा है। आज किसी के पास भी इतना समय नहीं है कि वह अपने ही रिश्तेदारों के साथ आराम से बैठकर बातचीत कर सकें। सभी पैसे के पीछे भाग रहे हैं। स्वार्थ की भावना ने मानव को दानव बना दिया है। अत: आज मनुष्यता की अपेक्षा पशुता ही अधिक दिखाई दे रही है।

निम्नलिखित कथन सत्व है या असत्य लिखिए।

Question 1.
मनुष्य झगड़े-टंटे को अपना आदर्श नहीं मानता है।
Answer:
सत्य

Question 2.
वचन, मन एवं शरीर से किए गए असत्याचरण को सही मानता है।
Answer:
असत्य

कृति ग (२) आकलन कृति (१) समझकर लिखिए।

Question 1.
प्राणिशास्त्रियों का अनुमान
Answer:
मनुष्य का अनावश्यक अंग उसी प्रकार झड़ जाएगा जिस प्रकार उसकी पूँछ झड़ गई है।

Question 2.
वह है मनुष्य के भीतर की पशुता की निशानी –
Answer:
नाखून का बढ़ना।

सही विकल्प चुनकर वाक्य फिर से लिखिए।

Question 1.
शायद उस दिन वह …….. का प्रयोग भी बंद कर देगा। (अस्त्री, शस्त्रों, मरणास्त्रों)
Answer:
शायद उस दिन वह मरणास्त्रों का प्रयोग भी बंद कर देगा।

Question 2.
नाखून को बढ़ने नहीं देना मनुष्य की अपनी ……… है। (इच्छा, वासना, जिज्ञासा)
Answer:
नाखून को बढ़ने नहीं देना मनुष्य को अपनी इच्छा है।

कृति ग (३) शब्द संपदा

निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।

1. भीतर
2. झगड़ा
3. प्रयोग
4. इच्छा

Answer:

1. भीतरी
2. झगड़ालू
3. प्रायोगिक
4. ऐच्छिक

वचन बदलिए।

1. निशानी
2. संवेदना

Answer:

1. निशानियाँ
2. संवेदनाएँ

निम्नलिखित शब्दों में से उपसर्ग अलग करके लिखिए।

1. अनावश्यक
2. संवेदना

Answer:

1. उपसर्ग : अन्
2. उपसर्ग : सम्

कृति ग (४) स्वमत अभिव्यक्ति

‘Question 1.
किसी में बुरी आदतें आ जाए, तो उन्हें त्याग देना चाहिए।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
मनुष्य वही कहलाता है जिसके पास मनुष्यता होती है और जिसके पास मनुष्यता होती है उसके पास अच्छाइयाँ जरूर होती है। लेकिन सभी अच्छाइयों को नहीं अपनाते हैं। किसी-किसी के स्वभाव में कुछ बुराइयाँ भी होती हैं। कई लोग बुरी आदतों के शिकार होते हैं। बुरी आदतों के कारण व्यक्ति पतन की ओर बढ़ता है। वह स्वयं तो डूब जाता है पर अपने साथ दूसरों का भी बुरा कर देता है। अत: व्यक्ति को बुरी आदतों का त्याग कर देना चाहिए। इसमें ही उसकी भलाई है। आखिर मनुष्य को अच्छे व्यवहार से ही एक-दूसरे के साथ प्रगाढ़ संबंध प्रस्थापित करने चाहिए।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति घ(१) आकलन कृति

Answer:

समझकर लिखिए।

1. पशुत्व का द्योतक
2. मनुष्य का स्वधर्म यह हैं

Answer:

1. अपने को संयत रखना।
2. दूसरे के मनोभावों का आदर करना।

कृति घ (२) आकलन कृति

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

1. मनुष्य
2. स्वधर्म

Answer:

1. नाखून को कौन बढ़ने नहीं देगा?
2. दूसरे के मनोभावों का आदर करना मनुष्य का क्या है?

कृति पूर्ण कीजिए।

Question 1.
मनुष्य की सहजात वृत्ति का परिणाम
Answer:
नाखूनों का बढ़ना

Question 2.
इनसे सूचित होती है मनुष्य की महिमा
Answer:
अभ्यास व तप से प्राप्त वस्तुओं से

कृति घ (३) शब्द संपदा

विलोम शब्द लिखिए।

1. मंगल
2. सफलता
3. जीवन
4. मैत्री
5. आदर

Answer:

1. अमंगल
2. असफलता
3. मरण
4. दुश्मनी
5. अनादर

समानार्थी शब्द लिखिए।

1. महिमा
2. आदर
3. त्याग
4. सफलता
5. चरितार्थता

Answer:

1. गौरव
2. सम्मान
3. बलिदान
4. विजय
5. सार्थकता

Question 1.
‘स्वनिर्धारित’ इस शब्द में से उपसर्ग पहचानकर संबंधित उपसर्ग से दो नए शब्द बनाइए।
Answer:
स्वनिर्धारित: उपसर्ग : स्व
नए शब्द: स्वदेश, स्वभाषा

कृति घ (४) स्वमत अभिव्यक्ति

Question 1.
‘प्रेम व त्याग सर्वश्रेष्ठ मानवीय मूल्य है।’ अपने विचार लिखिए।
Answer:
सभी धर्मों का सार प्रेम है। एक-दूसरे के प्रति प्रेम की भावना रखना एवं एक-दूसरे पर प्रेम न्योछावर कर देना, यह मनुष्य का सबसे बड़ा गुण है। त्याग यानी नि:स्वार्थ भाव से दूसरों के लिए अपना सर्वस्व अर्पण करना। मदर टेरेसा ने दीन-दुखियों को प्रेम से अपनाकर उनके लिए अपने सर्वस्व का त्याग किया और उनकी सेवा की। इसलिए संसार ने ‘मदर’ कहा। राष्ट्रपिता बापूजी ने भी प्रेम व त्याग इन मूल्यों को अपनाकर मानवता का कार्य किया। देश को आजादी दिलाने के लिए कई वीरों ने अपने घर-परिवार का त्याग कर दिया था। उनके अथक प्रयासों से ही देश आजाद हुआ। अत: प्रेम व त्याग सर्वश्रेष्ठ मानवीय हैं।

निम्नलिखित वाक्यों के अर्थ के अनुसार प्रकार पहचानकर लिखिए।

Question 1.
हमारी परंपरा महिमामयी और संस्कार उज्ज्वल हैं।
Answer:
विधानार्थक वाक्य

Question 2.
मनुष्य की चरितार्थता प्रेम में नहीं है।
Answer:
निषेधार्थक वाक्य

Question 3.
क्या मनुष्य में पशुता भरी हुई है?
Answer:
प्रश्नार्थक वाक्य

Question 4.
तुम अस्त्रों का प्रयोग त्याग दो।
Answer:
आज्ञार्थक वाक्य

Question 5.
काश! मेरे पास भी त्याग व तप जैसे गुण होते।
Answer:
विस्मयादिबोधक वाक्य

Question 6.
ध्यान रहे कि सत्याचरण में शक्ति होती है।
Answer:
संदेशवाचक वाक्य

रचनात्मक कौशल पर आधारित कृतियाँ

मौलिक सृजन

Question 1.
सद्गुणों और दुर्गुणों में अंतर लिखिए।
Answer:

Hindi Sulabhbharti Class 8 Solutions पहली इकाई

• हे मातृभूमि! Question Answer
• वारिस कौन? Question Answer
• नाखून क्यों बढ़ते हैं? Question Answer
• गाँव-शहर Question Answer
• मधुबन Question Answer
• जरा प्यार से बोलना सीख लीज Question Answer
• मेरे रजा साहब Question Answer
• पूर्ण विश्राम Question Answer
• अनमोल वाणी Question Answer

Class 8 Hindi Chapter 9 Nahi kuch isse Badhkar Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 9 नहीं कुछ इससे बढ़कर Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 9 Nahi kuch isse Badhkar Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 9 नहीं कुछ इससे बढ़कर Textbook Questions and Answers

सूचना के अनुसार कृतियाँ करो:

संजाल पूर्ण करो:

Answer:

कृति करो:

Answer:

अंतिम चार पंक्तियों का अर्थ लिखो।
Answer:
प्रस्तुत पंक्तियाँ नहीं कुछ इससे बढ़कर’ कविता से ली गई हैं। इसके कवि सुमित्रानंदन पंत हैं। प्रस्तुत पंक्ति में मधुकर यानी भ्रमरों का वर्णन है। भ्रमर मधुरस को प्रतिक्षण चखकर विपुल मात्रा में मधु-रूपी मनोवैभव का संचय करते हैं और अपना मधु छत्र बना लेते हैं। उसी प्रकार कलाकार, कवि, बलिदानी पुरुष, कृषक एवं माँ व्यक्ति, समाज व देश के हित में सदैव तत्पर रहते हैं। इनका हृदय दूसरों के लिए द्रवित हो उठता है। इनके कारण ही यह लोक महान बन गया है। अत: इनकी प्रार्थना से अन्य कोई पवित्र व शुभ प्रार्थना नहीं हो सकती।

कविता में उल्लिखित मानव के विभिन्न रूप लिखोः
Answer:
(i) पुरुष
(ii) कृषक
(iii) कलाकार
(iv) कवि
(v) माँ
(vi) बलिदानी पुरुष

भाषा बिदु

निम्न शब्दों के लिंग तथा वचन बदलकर वाक्यों में प्रयोग करो:

लिंग – कवि, माता, भाई, लेखक
Answer:

वचन – दुकान, प्रार्थना, अनुभूति, कपड़ा, नेता
Answer:

उपयोजित लेखन

‘सड़क दुर्घटनाएँ : कारण एवं उपाय’ निबंध लिखो।
Answer:
उत्तर: सड़क यातायात से होने वाली अवांछित घटना एवं उनसे होने वाली हानि सड़क दुर्घटना कहलाती है। देखा जाए तो सड़क दुर्घटना मानव निर्मित आपदा है, जिसे सावधानी बरतकर रोका जा सकता है। सड़क दुर्घटना का प्रमुख कारण है इंसान की लापरवाही या भूल। तेज गति से वाहन चलाने से सड़क दुर्घटना होती है। गलत ओवरटेकिंग व लेन कटिंग के कारण सड़क दुर्घटना होती है। कई लोग नशीले पदार्थों का सेवन कर वाहन चलाते हैं जिससे दुर्घटना होती है। सड़क पर वाहन चलाते समय मोबाइल पर बात करना, तेज आवाज में संगीत सुनना आदि में मग्न होने के कारण भी दुर्घटना होती है। कभी-कभी चालक यातायात संबंधी नियमों की ओर ध्यान नहीं देते हैं अथवा दुपहिया वाहन चालक सुरक्षा साधनों का उपयोग नहीं करते हैं जिससे दुर्घटना होती है।

सड़क दुर्घटना पर रोक लगाना मानव के ही हाथ में है। उसे नशीले पदार्थों का सेवन करके गाड़ी नहीं चलानी चाहिए। वाहन तेज गति से नहीं चलाने चाहिए। वाहन चलाते समय मोबाइल एवं संगीत नहीं सुनना चाहिए। वाहनों की समय-समय पर जाँच करवानी चाहिए। सरकार को भी सड़क की दशा पर ध्यान देना चाहिए। चालकों को यातायात के सभी नियमों का पालन करना चाहिए। इन सभी का पालन करके हम संभवत: सड़क दुर्घटना को अवश्य रोक सकेंगे।

स्वयं अध्ययन

‘राष्ट्रसंत तुकडो जी के सर्वधर्मसमभाव’ पर आधारित गीत पढ़ो और इसपर आधारित चार्ट बनाओ।

Hindi Sulabhbharti Class 8 Solutions Chapter 9 नहीं कुछ इससे बढ़कर Additional Important Questions and Answers

कृति पूर्ण करो:

Answer:

कृति पूर्ण कीजिए।

Answer:

एक शब्द में उत्तर लिखिए।

Question 1.
यह प्रसव वेदना सहती है
Answer:
जननी यानी माता

Question 2.
कृषक धरती को बनाता है
Answer:
शस्य श्यामला

Question 3.
जननी स्तन्यदान इसे देती है
Answer:
शिशु को

Question 4.
कृषक मिट्टी को बना देता है
Answer:
उर्वर कृति क

निम्नलिखित पद्यांशों का भावार्थ लिखिए।

Question 1.
प्रसव वेदना ……………… इससे सुंदर!
Answer:
प्रस्तुत पंक्तियाँ ‘नहीं कुछ इससे बढ़कर’ कविता से ली गई हैं। इसके कवि सुमित्रानंदन पंत हैं। प्रस्तुत पंक्ति में माँ की महत्ता का वर्णन किया गया है। माता प्रसव वेदना को सहते हुए अपने हृदय के स्वप्न को निज रूप देती है। अपने दूध का दान कर वह शिशु का पालन-पोषण कर उसे बड़ा करती है। वह अपना प्रत्येक क्षण अपने नवजात शिशु पर न्योछावर करती है। अत: माता की भक्ति व प्रार्थना से बढ़कर जगत में सुंदर प्रार्थना नहीं होती।

Question 2.
शीत-ताप ………………. इससे शुभकर!
Answer:
प्रस्तुत पंक्तियाँ नहीं कुछ इससे बढ़कर’ कविता से ली गई हैं। इसके कवि सुमित्रानंदन पंत हैं। प्रस्तुत पंक्ति में कृषक का महत्त्व प्रतिपादित किया है। किसान ठंड व गरमी में प्रकृति से जूझता रहता है और अपना पसीना बहाकर मिट्टी को उपजाऊ बनाता है। वह धरती को नई कोमल घास से हरी-भरी व समृद्ध बनाकर अनाज की खेती करके भंडारों को भर देता है। अत: कृषक की प्रार्थना से बढ़कर अन्य कोई शुभकर प्रार्थना नहीं होती।

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

Question 1.
कवि की विशेषता
Answer:
कवि वर्ण-वर्ण के मेल से मनभावन रचना का निर्माण करते हैं।

Question 2.
कलाकार की विशेषता
Answer:
कलाकार अरूप को नया रूप देता है।

Question 3.
बलिदानी पुरुष की विशेषता
Answer:
मानव हित के लिए स्वयं के प्राणों की बलि दे देता है।

कविता की पंक्तियाँ पूर्ण कीजिए।

कलाकार ……………….. प्रियतर!
Answer:
कलाकार-कवि वर्ण-वर्ण को
भाव तूलि से रच सम्मोहन
जब अरूप को नया रूप दे
भरते कृति में जीवन स्पंदन
नहीं प्रार्थना इससे प्रियतर!

निम्नलिखित कथन सत्य है या असत्य लिखिए।

Question 1.
बलिदानी पुरुष मिट्टी को स्वयं के रक्त से भिगाता है।
Answer:
सत्य

Question 2.
कलाकार दूसरों की कृति में जीवन स्पंदन भरता है।
Answer:
असत्य

उत्तर लिखिए।

Question 1.
मधुकरों का कार्य
Answer:
भ्रमर मधुरस को प्रतिक्षण चखकर विपुल मात्रा में मधु-रूपी मनोवैभव का संचय करते हैं और अपना मधु छत्र बना लेते हैं।

कृति पूर्ण कीजिए।

Answer:

निम्नलिखित पद्यांशों का भावार्थ लिखिए।

Question 1.
सत्य-निष्ठ ……………. इससे बढ़कर!
Answer:
प्रस्तुत पंक्तियाँ ‘नहीं कुछ इससे बढ़कर’ कविता से ली गई है।’ इसके कवि सुमित्रानंदन पंत हैं। प्रस्तुत पंक्ति में बलिदानी पुरुष का वर्णन किया गया है। सत्यनिष्ठता का पालन करने वाला व अपने देशवासियों व मातृभूमि से प्रेम करने वाला बलिदानी पुरुष मानव-जीवन के कल्याण हेतु मिट्टी को रक्त से भिगोकर स्वयं के प्राणों की बलि दे देता है। अत: ऐसे बलिदानी पुरुष की प्रार्थना से बढ़कर अन्य कोई प्रार्थना नहीं हो सकती।

Question 2.
चख-चख ……….. इससे शुचितर!
Answer:
प्रस्तुत पंक्तियाँ नहीं कुछ इससे बढ़कर’ कविता से ली गई हैं। इसके कवि सुमित्रानंदन पंत हैं। प्रस्तुत पंक्ति में मधुकर यानी भ्रमरों का वर्णन है। भ्रमर मधुरस को प्रतिक्षण चखकर विपुल मात्रा में मधु-रूपी मनोवैभव का संचय करते हैं और अपना मधु छत्र बना लेते हैं। उसी प्रकार कलाकार, कवि, बलिदानी पुरुष, कृषक एवं माँ व्यक्ति, समाज व देश के हित में सदैव तत्पर रहते हैं। इनका हृदय दूसरों के लिए द्रवित हो उठता है। इनके कारण ही यह लोक महान बन गया है। अत: इनकी प्रार्थना से अन्य कोई पवित्र व शुभ प्रार्थना नहीं हो सकती।

Hindi Sulabhbharati 8th Standard Digest Guide दूसरी इकाई

• धरती का आँगन महके Question Answer
• दो लघुकथाएँ Question Answer
• लकड़हारा और वन Question Answer
• सौहार्द -सौमनस्‍य Question Answer
• खेती से आई तब्‍दीलियाँ Question Answer
• अंधायुग Question Answer
• स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Question Answer
• मेरा विद्रोह Question Answer
• नहीं कुछ इससे बढ़कर Question Answer

Class 8 Hindi Chapter 3 Lakadhara Aur Van Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 3 लकड़हारा और वन Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 3 Lakadhara Aur Van Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 3 लकड़हारा और वन Textbook Questions and Answers

सूचना के अनुसार कृतियाँ करो :

संजाल पूर्ण करो :

Question 1.

Answer:

संक्षेप में उत्तर लिखो:

Question 1.
पेड़ द्वारा दिया गया संदेश
Answer:
कभी हरा-भरा पेड़ मत काटो। उन्हें अपने बच्चों के समान पालो।

Question 2.
भगवान की शर्त
Answer:
लकड़हरा हरे-भरे पेड़ नहीं काटेगा व लालच में पड़कर जरूरत से अधिक सूखी लकड़ी नहीं काटेगा।

Question 3.
पेड़ों के उपयोग
Answer:
शुद्ध हवा, पानी व भोजन प्रदान करना

Question 4.
पेड़ों की कटाई के दुष्परिणाम
Answer:
पेड़ों की कटाई करने से वर्षा नहीं आएगी। वन्य जीवों का अस्तित्व खतरे में पड़ जाएगा। मनुष्य को शुद्ध हवा नहीं मिलेगी। मनुष्य का अस्तित्व खत्म हो जाएगा।

कृति पूर्ण करो:

Question 1.

Answer:

भाषा बिंदु

Question 1.
निम्न वृत्त में दिए संज्ञा तथा विशेषण शब्दों को छाँटकर तालिका में उचित स्थानों पर उनके भेद सहित लिखो:

Answer:

Question 2.
पाठ में प्रयुक्त कारक विभक्तियाँ ढूँढकर उनका वाक्यों में प्रयोग करो ।
Answer:

स्वयं अध्ययन

किसानों के सामने आने वाली समस्याओं की जानकारी प्राप्त करके उन समस्याओं को दूर करने हेतु चर्चा करो।

उपयोजित लेखन

Question 1.
‘प्रकृति हमारी गुरु’ विषय पर अपने विचार लिखिए।
Answer:
प्रकृति में जल, जंगल, जमीन, नदी, सागर, पहाड़ आदि का अंतर्भाव होता हैं। प्रकृति अपने अनंत हाथों से मनुष्य को अपना सर्वस्व देती रहती है। प्रकृति माता की तरह मनुष्य का ख्याल रखती है। वह मनुष्य की सहचरी-सहगामिनी है। प्रकृति मनुष्य के दिमाग शरीर व आत्मा को ऊर्जायुक्त बनाती है। प्रकृति की गोद में विचरण करने से हमारा मन स्वस्थ हो जाता है। प्रकृति हमें प्रेरणा देती है। प्रकृति के सान्निध्य में रहने के कारण तपस्वी वेदों की रचना कर सकें। रामायण जैसे महाकाव्य का जन्म भी प्रकृति के सान्ध्यि में ही हुआ था।

प्रकृति ने ही महान शास्त्रज्ञ न्यूटन को गुरुत्वाकर्षण के सिद्धांत की खोज करने के लिए प्रेरणा दी थी। महाकवि रवींद्रनाथ टैगोर को काव्य रचना करने की प्रेरणा प्रकृति ने ही की थी। प्रकृति के सान्निध्य में रहने के कारण तपस्वी वेदों की रचना कर सकें। मानव को प्रकृति के माध्यम से ही ‘सत्यं शिवम् संदरम्’ का एहसास होता है। प्रकृति मनुष्य का मार्गदर्शन करती है। इसलिए प्रकृति को हमारी गुरु कहा जाता है।

Hindi Sulabhbharti Class 8 Solutions Chapter 3 लकड़हारा और वन Additional Important Questions and Answers

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति क (१) आकलन कृति

कारण लिखिए।

Question 1.
लकड़हारा पेड़ को काटना चाहता है।
Answer:
क्योंकि पेड़ को काटने से उसकी आज की रोटी का इंतजाम हो जाएगा।

Question 2.
लकड़हारा चिंतित एवं दुखी हो जाता है।
Answer:
क्योंकि उसके हाथ से कुल्हाड़ी छूटकर नदी में गिर जाती है।

कृति क (२) आकलन कृति

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

1. भगवान
2. गहरा

Answer:

1. ग्रामीण व्यक्ति कौन था?
2. पानी कैसा था?

निम्नलिखित कथन सही है या गलत पहचान कर लिखिए।

Question 1.
ग्रामीण व्यक्ति पहली बार सोने की कुल्हाड़ी लेकर नदी के बाहर आया।
Answer:
गलत

Question 2.
लकड़हारे की आर्थिक स्थिती अच्छी नहीं थी।
Answer:
सही

एक शब्द में उत्तर लिखिए।

1. इसने कोशिश की।
2. यह दुखी हो गया था।

Answer:

1. ग्रामीण व्यक्ति
2. लकड़हारा

कृति क (३) शब्द संपदा

निम्नलिखित शब्दों के तत्सम रूप लिखिए।

1. दुख
2. गाँव

Answer:

1. दुःख
2. ग्राम

निम्नलिखित शब्दों में उचित प्रत्यय का प्रयोग कीजिए।

1. उपकार
2. ग्राम
3. भाग्य

Answer:

1. उपकार : उपकारी : प्रत्यय : ई
2. ग्राम : ग्रामीण : प्रत्यय : ईण
3. भाग्य : भाग्यवान : प्रत्यय : वान

वचन बदलिए।

1. कुल्हाड़ी
2. रोटी

Answer:

1. कुल्हाड़ियाँ
2. रोटियाँ

नीचे दिए हुए शब्दों के पर्यायवादी शब्द लिखिए।

1. चाँदी
2. ग्रामीण
3. अचानक
4. मदद

Answer:

1. रजत
2. देहाती
3. सहसा
4. सहायता

कृति क (४) स्वमत अभिव्यक्ति

Question 1.
‘पेड़ की कटाई करना कानूनन अपराध है।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
पेड़ की कटाई करना कानूनन अपराध है। पेड़ हमें फल, फूल, छौंव, लकड़ी शुद्ध हवा व वर्षा भी देते हैं। यदि हम पेड़ों की कटाई करेंगे, तो आने वाले दिनों में हमारी पृथ्वी बंजर बन जाएगी। इससे तापमान में बढ़ोत्तरी होगी और हिमालय की बर्फ तेजी से पिघलने लगेगी। इससे पर्यावरणीय समस्या निर्माण हो जाएगी। सूर्य की पराबैंगनी किरणें धरती पर आ जाएगी; हमें कई बीमारियों का सामना करना पड़ेगा। अत: पेड़ों का संरक्षण करने के लिए कानून बनाया गया है। इसलिए यदि कोई पेड़ की कटाई करता है तो उसे कानून के तहत सजा देने का भी विधान है।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ख (१) आकलन कृति

समझकर लिखिए।

Question 1.
किसने, किसके लिए कष्ट उठाए?
Answer:
ग्रामीण व्यक्ति ने लकड़हारे के लिए कष्ट उठाए।

Question 2.
ग्रामीण व्यक्ति इस क्रम में ले आया कुल्हाड़ियाँ
Answer:
चाँदी की कुल्हाड़ी, सोने की कुल्हाड़ी व लोहे की कुल्हाड़ी।

कृति पूर्ण कीजिए।

Answer:

कृति ख (२) आकलन कृति

किसने, किससे कहा?

Question 1.
दूसरे की चीज को अपनी कहना ठीक नहीं है।
Answer:
लकड़हारे ने ग्रामीण व्यक्ति से कहा।

Question 2.
लो भाई, इस बार तो यह लोहा ही हाथ लगा है।
Answer:
ग्रामीण व्यक्ति ने लकड़हारे से कहा।

उत्तर लिखिए।

Question 1.
लकड़हारे के अनुसार यही है उसका धन।
Answer:
मेहनत और ईमानदारी से जो भी मिलता है वहीं उसका धन है।

Question 2.
भगवान लकड़हारे पर प्रसन्न हो गए।
Answer:
क्योंकि वे लकड़हारे की ईमानदारी से प्रभावित हो गए थे।

Question 3.
भगवान ने लकड़हारे को इन्हें काटने के लिए मना किया।
Answer:
हरे-भरे पेड़ों को।

Question 4.
यह होना चाहिए इंसान का धर्म।
Answer:
मुसीबत के समय एक-दूसरे के काम आना।

कृति ख (३) शब्द संपदा

निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. चकित
2. सुवर्ण
3. दीन
4. हस्त

Answer:

1. हैरान, आश्चर्य
2. सोना
3. गरीब
4. हाथ, कर

निम्नलिखित शब्दों के तत्सम रूप लिखिए।

1. हाथ
2. सोना

Answer:

1. हस्त
2. स्वर्ण

विलोम शब्द लिखिए।

1. ईमानदारी
2. उपकार

Answer:

1. बेइमानी
2. अपकार

निम्नलिखित शब्दों में उचित उपसर्ग लगाइए।

1. मंजूर
2. धर्म

Answer:

1. मंजूर : उपसर्ग : नामंजूर
2. धर्म : उपसर्ग : अधर्म

कृति ख (४) स्वमत अभिव्यक्ति

Question 1.
‘ईमानदारी सर्वश्रेष्ठ नीति है।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
जो व्यक्ति स्वयं के साथ वफादार रहे, वह ईमानदार होता है। ऐसा व्यक्ति हिसाब के मामले में हेरा-फेरी नहीं करता है। ईमानदारी का संबंध सिर्फ व्यवहार में ही नहीं होता; बल्कि वह रिश्तों के प्रति भी दिखलाई देता है। अपने दोस्तों सगे एवं संबंधियों से बातचीत करते समय भी ईमानदारी रखनी चाहिए। व्यक्ति को किसी के अन्याय में भागीदार नहीं बनना चाहिए।

जो व्यक्ति ईमानदारी का ठीक से पालन करता है; वह जीवन में सफल हो जाता है। वह अपने कार्य एवं व्यवहार से समाज के सामने एक मिसाल खड़ी कर देता है। लालबहादुर शास्त्री जी की ईमानदारी से सभी भली भाँति परिचित हैं। इसलिए आज भी उनका नाम सम्मान से लिया जाता है। प्रश्न ३ (ग) निम्नलिखित गद्यांश पड़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ग (१) आकलन कृति

कृति पूर्ण कीजिए।

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

कारण लिखिए।

Question 1.
लकड़हारे की सारी थकान दूर हो गई।
Answer:
क्योंकि वह एक पेड़ की ठंडी छाया में बैठ गया था।

Question 2.
लकड़हारा जंगल में लकड़ी काटने जाता है।
Answer:
क्योंकि उसकी पत्नी ने उसे लकड़ी काटने के लिए जंगल में जाने के लिए का।

कृति ग (२) आकलन कृति

समझकर लिखिए।

Question 1.
लकड़हारा इसलिए डर गया
Answer:
उसने आवाज सुनी और उस समय जंगल में कोई नहीं था। अत: भूत होने के एहसास के कारण वह डर गया।

Question 2.
यह कारण बताया लकड़हारे ने पेड़ की कटाई करने का
Answer:
लकड़ियाँ काटना यही लकड़हारे की रोजी-रोटी का रास्ता था और उसे अपने चार-चार बच्चों का पेट पालना था।

सही विकल्प चुनकर वाक्य फिर से लिखिए।

Question 1.
अधिक बच्चे होने के कारण, _______ में दुख तो आएगा ही। (कुटुंब, परिवार, खानदान)
Answer:
अधिक बच्चे होने के कारण, परिवार में दुख तो आएगा ही।

Question 2.
______ बच्चों को पालना पड़ता है। (बच्चों, परिवार वालों, रिश्तेदारों)
Answer:
चार चार बच्चों को पालना पड़ता है।

संक्षेप में उत्तर लिखिए।

Question 1.
पेड़ों के उपयोग
Answer:
शुद्ध हवा, पानी व भोजन प्रदान करना कृति ग

शब्द संपदा

पर्यायवाची शब्द लिखिए।

1. प्राण
2. जंगल
3. चीख
4. छाया

Answer:

1. जान
2. वन
3. चिल्लाहट
4. सँव

वचन बदलिए।

1. नजरें
2. लकड़हारा

Answer:

1. नजर
2. लकड़हारे

विलोम शब्द लिखिए।

1. बेकसूर
2. सोना

Answer:

1. कसूरवार
2. जागना

Question 1.
कसूर शब्द में उचित उपसर्ग लगाकर नया शब्द बनाइए व संबंधित उपसर्ग से अन्य दो शब्द बनाइए।
Answer:
कसूर : उपसर्ग : बे; नया शब्द : बेकसूर

Question 2.
परिवार शब्द में उचित प्रत्यय लगाइए।
Answer:
परिवार : प्रत्यय : इक : पारिवारिक

कृति ग (४) स्वमत अभिव्यक्ति

Question 1.
‘छोटा परिवार, सुखी परिवार’ पर अपने विचार लिखिए।
Answer:
छोटे परिवार में पति-पत्नी तथा एक या दो बच्चे होते हैं। छोटा परिवार, सुखी परिवार कहलाता है। छोटे परिवार में माता-पिता अपने एक या दो बच्चों पर ठीक से ध्यान देने में समर्थ होते हैं। उनकी शिक्षा एवं उनके लिए अन्य सामग्री का जुटाव करने में उन्हें दिक्कत नहीं आती। यदि परिवार बड़ा है यानी तीन या चार बच्चे परिवार में हैं, तो माता-पिता को सभी की पढ़ाई का खर्चा एवं खाने-पीने का खर्चा करने में कठिनाई महसूस होती है। इसलिए परिवार छोटा होना चाहिए। छोटा परिवार होने से देश की जनसंख्या भी बढ़ती नहीं है। यह राष्ट्रहित के लिए आवश्यक है। यदि देश खुश रहेगा, तो देश में रहने वाली प्रजा भी खुश रहेगी। इसलिए ‘छोटा परिवार, सुखी परिवार’ यह विधान सर्वथा उचित है।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति घ (१) आकलन कति

निम्नलिखित गलत बाक्य सही करके फिर से लिखिए।

Question 1.
बिना हवा के मनुष्य जीवित रह सकता है।
Answer:
बिना हवा के मनुष्य जीवित नहीं रह सकता है।

Question 2.
पेड़ों के कटने से वन्य पशु शहर में आकर रहेंगे।
Answer:
पेड़ों के काटने से वन्य पशु नष्ट हो जाएँगे।

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

1. हरा-भरा
2. शुद्ध हवा

Answer:

1. कौन-सा पेड़ नहीं काटना चाहिए?
2. मनुष्य को साँस लेने के लिए क्या चाहिए?

कृति पूर्ण कीजिए।

Question 1.

Answer:

कृति घ (३) शब्द संपदा

विलोम शब्द लिखिए।

1. अच्छी
2. समस्या

Answer:

1. बुरी
2. समाधान

समानार्थी शब्द लिखिए।

1. मतलब
2. शुद्ध

Answer:

1. स्वार्थ
2. पवित्र

Question 1.
गदयांश में से शब्द-युग्म ढूँढकर लिखिए।
Answer:
हरा-भरा, कम-से-कम

स्वमत अभिव्यक्ति

Question 1.
‘वृक्ष हमारे मित्र हैं। अपने विचार लिखिए।
Answer:
‘वृक्षों से ही जीवन बन सका। इनसे सृष्टि सारी। सत्यं, शिवम्, सुंदरम् इनसे। धरती लगती प्यारी।’ सचमुच वृक्ष हमारे मित्र हैं। वृक्ष हम पर अनंत हाथों से उपकार करते रहते हैं। वे हमें प्राणवायु, फल, फूल, लकड़ी व वर्षा देते हैं। वृक्षों से हमें आयुर्वेद की विविध दवाइयाँ भी मिलती हैं। वृक्षों के कारण जंगलों का अस्तित्व बना रहता हैं। वृक्षों के कारण ही पर्यावरण संतुलन अबाधित है। इस पृथ्वी का अस्तित्व भी वृक्षों के कारण ही टीका हुआ है। इसलिए वृक्ष सर्वथा हमारे मित्र हैं।

Hindi Sulabhbharati 8th Standard Digest Guide दूसरी इकाई

• धरती का आँगन महके Question Answer
• दो लघुकथाएँ Question Answer
• लकड़हारा और वन Question Answer
• सौहार्द -सौमनस्‍य Question Answer
• खेती से आई तब्‍दीलियाँ Question Answer
• अंधायुग Question Answer
• स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Question Answer
• मेरा विद्रोह Question Answer
• नहीं कुछ इससे बढ़कर Question Answer

Class 8 Hindi Chapter 7 Mere Raja Sahab Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 7 मेरे रजा साहब Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 7 Mere Raja Sahab Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 7 मेरे रजा साहब Textbook Questions and Answers

सूचनानुसार कृतियाँ करो :

संजाल पूर्ण करो :

Answer:

कृति पूर्ण करो:

Answer:

सूची तैयार कीजिए।

Question 1.
पाठ में उल्लेखित विविध भाषाएँ।
Answer:
हिंदी, उर्दू, फ्रेंच, अंग्रेजी।

Question 2.
पाठ में उल्लेखित विविध देश के नाम।
Answer:
लंदन, पेरिस, न्यूयार्क।

कृति पूर्ण करो :

Answer:

स्वाध्याय विषयक कृतियाँ

संजाल पूर्ण कीजिए।

Answer:

भाषाबिंदु

Question 1.
पाठ्यपुस्तक से दस वाक्य चुनकर उनमें से उद्देश्य और विधेय अलग करके लिखिए।
Answer:

उपयोजित लेखन

Question 1.
जहाँ चाह होती है वहाँ राह निकल आती है, इस सुवचन को आधार बनाकर अस्सी शब्दों तक कहानी लिखिए।
Answer:
विजयपुर नाम के एक छोटे से नगर में अथर्व नाम का होनहार व परिश्रमी लड़का रहता था। इस संसार में उसका कोई नहीं था । वह अनाथ था। दिनभर मेहनत मजदूरी करके वह स्वयं का पेट पालता था। अथर्व को पढ़ाई करने की चाह थी, लेकिन स्कूल जाने के लिए उसके पास पैसे नहीं थे। इसलिए वह शाम को मजदूरी करके घर आकर अपने आप ही पढ़ाई करता था ।

पढ़ाई करते समय यदि कुछ समझ में नहीं आता था, तो वह अपने आस-पास रहने वाले बच्चों से पूछ लेता था । ऐसा करके वह पढ़ना-लिखना सीख गया। एक दिन नगर के भव्य दिवार पर लगाया विज्ञापन उसने पढ़ा। विज्ञापन में लिखा था कि सरकार होनहार बच्चों को छात्रवृत्ति देना चाहती है और इसके लिए छात्रों को मौखिक साक्षात्कार के लिए सरकारी दफ्तर में आना पड़ेगा।

अथर्व विज्ञापन पड़कर निश्चित समय पर सरकारी दफ्तर में पहुँच गया। लेकिन उसका नाम किसी भी स्कूल में दर्ज न होने के कारण कर्मचारियों ने उसे वहाँ से जाने के लिए कहा। अथर्व के पास पढ़ने की ललक थी। वह वहाँ से जाने के लिए तैयार नहीं हुआ। वहीं पर खड़े रहकर वह विनंती करने लगा। उसी वक्त जिला अधिकारी वहाँ पर आ पहुंचे। उन्हें सारी बातें समझ में आ गई और उन्होंने अथर्व का साक्षात्कार लिया।

मुलाकात में उन्होंने अथर्व को कई प्रश्न पूछे। आश्चर्य की बात यह थी कि किसी स्कूल का छात्र न होने के बावजूद भी उसने सभी प्रश्नों के सही उत्तर दिए। अत: उसकी होशियारी की तारीफ करते हुए जिलाधिकारी ने उसकी छात्रवृत्ति मजूर कर दी। सच ही कहा गया है कि जहाँ चाह होती है, वहाँ राह होती है।

मौलिक सृजन

Question 1.
कला से प्राप्त आनंद अवर्णनीय होता है। अपने विचार लिखिए।
Answer:
मन के अंत:करण की सुंदर प्रस्तुती ‘कला’ कहलाती है। दूसरे शब्दों में अभिव्यक्ति की कुशल शक्ति कला कहलाती है। संगीत, काव्य, रंगमंच, चित्रकला, मूर्तिकला आदि विविध प्रकार की कला हैं। कला के द्वारा मनुष्य को सत्यम्, शिवम् व सुंदरम का एहसास होता है। कला के द्वारा मिलने वाले आनंद की कोई सीमा ही नहीं होती। कला मनुष्य को संकीर्ण भावनाओं से ऊपर उठाती है।

कला मनुष्य के हदय को सौंदर्य, उल्लास व मनोरंजन से भर देती है। ताजमहल अद्वितीय कला का एक रूप है। उसे देखकर मनुष्य का हृदय हर्ष एवं खुशी से झूमने लगता है। ताजमहल को देखकर कवि सुंदर कविता लिखता है, तो चित्रकार अद्भुत चित्र का निर्माण करता है। इसलिए कला से प्राप्त आनंद अवर्णनीय होता है।

स्वयं अध्ययन

किसी गायक/गायिका की सचित्र जानकारी लिखो।

Hindi Sulabhbharti Class 8 Solutions Chapter 7 मेरे रजा साहब Additional Important Questions and Answers

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति क (१) आकलन कृति

संजाल पूर्ण कीजिए।

Question 1.

Answer:

कारण लिखिए।

Question 1.
लेखिका दिल्ली गई थी।
Answer:
अपनी ‘गणपति प्रदर्शनी’ के लिए।

Question 2.
लेखिका अस्पताल जाकर रजा साहब को अलविदा कहकर लौट आई।
Answer:
क्योंकि वे अस्पताल में शून्य की तरह लेटे थे और उनकी सिर्फ साँस चल रही थी।

कृति क (२) आकलन कृति

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

Question 1.
व्हीलचेअर
Answer:
गद्यांश में प्रयुक्त साधन का नाम जिसका उपयोग विकलांग करते हैं।

Question 2.
रजा साहब
Answer:
लेखिका को सपने में किसने शुभकामना दी?

निम्नलिखित कथन सत्य है या असत्य पहचान कर लिखिए।

Question 1.
२३ जुलाई के दिन रजा साहब परलोक सिधारे।
Answer:
सत्य

Question 2.
पिछले फरवरी को लेखिका मुंबई गई थी।
Answer:
असत्य

कृति क (३) शब्द संपदा

Question 1.
पद्यांश में प्रयुक्त विदेशी शब्द ढूँढ़कर लिखिए।
Answer:
व्हीलचेअर

निम्नलिखित शब्द में उचित प्रत्यय का प्रयोग कीजिए।

Question 1.
प्रदर्शन
Answer:
प्रदर्शनी – प्रत्यय – ई

वचन बदलिए।

1. शुभकामना
2. सास

Answer:

1. शुभकामनाएँ
2. साँसें

नीचे दिए हुए शब्दों के पर्यायवाची शब्द लिखिए ।

1. शुभकामना
2. अवसर

Answer:

1. बधाई
2. मौका

Question 1.
‘एक कलाकार के मन में दूसरे कलाकार के प्रति आत्मीयता होती है।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
एक कलाकार को दूसरे कलाकार के प्रति आत्मीयता होती है। यह पूर्णत: सत्य है। कलाकार फिर वह अभिनेता हो या चित्रकार। उनमें एक-दूसरे के प्रति सम्मान व आदर की भावना होती है। यदि एक कलाकार उम्र में बड़ा एवं श्रेष्ठ हो, तो दूसरे कलाकार के हृदय में उसके प्रति श्रद्धा और बढ़ जाती है। वह उसमें अपना आदर्श दूबने लगता है और उसकी शैली एवं कला का अनुसरण करने लगता है। आज भी कई वर्तमान चित्रकार स्वर्गीय एम.एफ. हुसैन जी के कायल हैं। यह उनके प्रति, कलाकार के प्रति सहृदयता व आत्मीयता ही है।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

1. गद्यांश में उल्लेखित धर्म ।
2. गद्यांश में उल्लेखित धर्मग्रंथ ।

Answer:

1. हिंदू व ईसाई
2. बाइबल, गीता, कुरान

संजाल पूर्ण कीजिए।

Question 1.

Answer:

किसने, किससे कहा?

Question 1.
“आपसे बात करनी हैं?”
Answer:
लेखिका ने रजा साहब से कहा

Question 2.
“मैं कलाकार हूँ।”
Answer:
रजा साहब ने लेखिका से कह्य ।

Question 3.
“चलो तुम्हारा काम देखते हैं।”
Answer:
रजा साहब ने लेखिका से कहा ।

उचित जोड़ियाँ मिलाइए

Answer:
i – ग
ii – घ
iii – ख
iv – क

Question 1.
गद्यांश में से विदेशी शब्द ढूँड़कर लिखिए
Answer:
आर्ट, गॅलरी, स्टेडियो, इंटरव्यू

अनेक शब्दों के लिए एक शब्द लिखिए ।

Question 1.
अपने जीवन की कथा
Answer:
आत्मकथा

Question 2.
कला दिखाने वाला
Answer:
कलाकार

विलोम शब्द लिखिए।

1. धर्म x
2. सुबह x

Answer:

1. धर्म x अधर्म
2. सुबह x शाम

निम्नलिखित शब्द से प्रत्यय अलग कीजिए।

कलाकार
Answer:
प्रत्यय – कार

स्वमत अभिव्यक्ति

Question 1.
‘सभी धर्मों के प्रति समभाव रखना कलाकार की विशेष पहचान होती है।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
कलाकार वही होता है, जो सिर्फ अपनी कला से ही नहीं, बल्कि अपने व्यक्तित्व व कृतित्व से सभी पर अपनी अमिट छाप निर्माण करता है। कलाकार जीवन का सच्चा उपासक होता है। मानवीय मूल्य एवं संस्कृति के प्रति उसके हृदय में श्रद्धाभाव होता है। अत: वह सभी धर्मों को मानता है। उसके लिए सभी धर्म की किताबें एक समान होता है। वे भी सभी धर्मों के प्रति समान भाव रखते थे। एक कलाकार के पास जीवन के प्रति उदार दृष्टिकोण होता है।

निम्नलिखित गद्यांश पड़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ग (१) आकलन कृति

कारण लिखिए।

Question 1.
रजा साहब लेखिका के साथ पुणे गए।
Answer:
क्योंकि वे लेखिका का काम देखना चाहते थे।

Question 2.
रजा साहब ने लेखिका को पेरिस आने का न्यौता दिया।
Answer:
क्योंकि उन्हें लेखिका का काम पसंद आया था।

कृति पूर्ण कीजिए।

Answer:

समझकर लिखिए।

Question 1.
गद्यांश के आधार पर रजा साहब की विशेषताएँ
Answer:

सही विकल्प चुनकर वाक्य फिर से लिखिए।

Question 1.
आपका ……… बहुत उज्ज्वल है। (भूत, भविष्य, वर्तमान)
Answer:
आपका भविष्य बहुत उज्ज्वल है।

Question 2.
ताज होटल के सामने से हमने ……… ली। (रिक्क्षा, टैक्सी, बस)
Answer:
ताज होटल के सामने से हमने टैक्सी ली।

कृति पूर्ण कीजिए।

Answer:

पर्यायवाची शब्द लिखिए।

1. काम
2. करीना
3. धैर्य
4. मदद

Answer:

1. कार्य
2. सलीका
3. धीरज
4. सहायता

विलोम शब्द लिखिए।

1. ससुराल x
2. छोटी x

Answer:

1. ससुराल x मायका
2. छोटी x बड़ी कृति ग

स्वमत अभिव्यक्ति

Question 1.
व्यक्ति को हर काम तन्मयता व लगन से क्यों करना चाहिए?
Answer:
प्रत्येक काम तन्मयता व लगन से करने से व्यक्ति का पूरा ध्यान काम पर केंद्रित हो जाता है और वह सुचारू रूप से कार्य पूरा करता है। काम करने के लिए अधिक समय की भी आवश्यकता नहीं पड़ती। तन्मयता व लगन से काम करने से काम करने के सही तरीके का हमें पता चल जाता है और काम करने में एक प्रकार का आत्मविश्वास भी निर्माण हो जाता है।अत: व्यक्ति को हर काम तन्मयता व लगन से करना चाहिए।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति घ (१) आकलन कृति

निम्नलिखित गलत वाक्य सही करके फिर से लिखिए।

Question 1.
रजा साहब पेरिस स्टेशन पर लेखिका का इंतजार कर रहे थे।
Answer:
रजा साहब गारदीनो स्टेशन पर लेखिका का इतंजार कर रहे थे।

Question 2.
दोनों एक-दूसरे के ईमानदार अनुवादक थे।
Answer:
दोनों एक-दूसरे के ईमानदार समालोचक थे।

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों 

Question 1.
ग्यारह
Answer:
कितने बजे रजा साहब लेखिका के लिए दवा लेकर आए

Question 2.
रजा साहब
Answer:
लेखिका के घरवालों को किसने फोन किया था?

कारण लिखिए।

Question 1.
लेखिका व रजा साहब में कभी विवाद नहीं हुआ।
Answer:
क्योंकि रजा साहब के पास स्नेह व अपनापन था।

कृति घ (३) शब्द संपदा

विलोम शब्द लिखिए।

1. ईमानदार x
2. स्नेह x

Answer:

1. ईमानदार x बेईमान
2. स्नेह x घृणा

समानार्थी शब्द लिखिए।

1. विवाद
2. स्नेह

Answer:

1. झगड़ा
2. प्यार

अनेक शब्द के लिए एक शब्द लिखिए।

Question 1.
गुण-दोष आदि की आलोचना करने वाला
Answer:
समालोचक

Question 2.
गद्यांश में आए विदेशी शब्द ढूँढकर लिखिए
Answer:
होस्टेल, स्टेशन, रेस्टॉरेंट, ट्रेन।

कृति घ (४) स्वमत अभिव्यक्ति

Question 1.
क्या स्नेह व अपनेपन से सभी के हृदय को जीता जा सकता है ? अपने विचार लिखिए।
Answer:
हाँ, स्नेह व अपनेपन से सभी के हृदय को जीता जा सकता है। स्नेह व अपनेपन की भावना ये दोनों मानवीय मूल्य हैं। स्नेह व अपनेपन में असीम शक्ति होती है। व्यक्ति को एक-दूसरे के साथ स्नेहपूर्वक व्यवहार करना चाहिए। एक-दूसरे के साथ अपनत्व रखने से संबंधों में मधुरता निर्माण होती है। जिस व्यक्ति के पास स्नेह व अपनत्व की भावना होती है, ऐसा व्यक्ति सभी को अपनी ओर आकर्षित कर लेता है। सभी लोग ऐसे व्यक्ति के बातों को महत्त्व देने लगते हैं। नेल्सन मंडेला, बाबा आमटे आदि महापुरुषों के पास स्नेह व अपनेपन की भावना थीं। इसलिए वे सभी को अपना बना सके थे।

कारण लिखिए।

Question 1.
लेखिका की लड़की के साथ रजा साहब शुद्ध हिंदी में बातें करते थे।
Answer:
क्योंकि लेखिका की बेटी बहुत खूबसूरत हिंदी बोलती थी।

Question 2.
लेखिका हफ्ते में एक बार रजा साहब के लिए भारतीय शाकाहारी खाना बनाकर भेजती थीं।
Answer:
क्योंकि उन्हें खाने का शौक था और वे दाल, चावल, रोटी व आलू की सब्जी बड़े शौक से खाते थे।

कृति ड (२) आकलन कृति

संजाल पूर्ण कीजिए।

Question 1.

Answer:

निम्नलिखित कथन सत्य है या असत्य पहचानकर लिखिए।

Question 1.
लेखिका की बड़ी बेटी हेलेना हिंदी बहुत ही खूबसूरत बोलती थी।
Answer:
सत्य

Question 2.
रजा साहब के कुछ फ्रांसीसी दोस्तों ने लेखिका को उनके इस दुनिया में न होने की सूचना दी।
Answer:
असत्य

कृति ङ (३) शब्द संपदा

Question 1.
परिच्छेद में से शब्द-युग्म ढूंडकर लिखिए।
Answer:
रोटी-आलू, अंग्रेजी-फ्रेंच, शेर-गजल, दाल-चावल

Question 2.
गद्यांश में से प्रत्यययुक्त शब्द ढूँढकर लिखिए।
Answer:
भारतीय – प्रत्यय – ईय
शाकाहारी – प्रत्यय – ई

Question 3.
गद्यांश में से ऐसे दो शब्द ढूँढकर लिखिए कि जिनके वचन परिवर्तित नहीं होते।
Answer:
आलू, दोस्त

नीचे दिए हुए शब्दों के विलोम शब्द लिखिए।

1. शाकाहारी x
2. सुंदर x

Answer:

1. शाकाहारी x मांसाहारी
2. सुंदर x कुरूप

कृति ङ (४) स्वमत अभिव्यक्ति

Question 1.
‘सिर्फ चित्रकारी करना ही रजा साहब का शौक नहीं था। वे तो बहुआयामी व्यक्तित्व के स्वामी थे।’ स्पष्ट कीजिए।
Answer:
जी हाँ, रजा साहब एक बहुआयामी व्यक्तित्व के स्वामी थे। चित्रकारी व पेंटिंग उनका पेशा था। इसके अलावा उन्हें कविताओं से प्रेम था। वे बड़े चाव से पढ़ते थे। शेर, गजल व पुरानी हिंदी फिल्मी गाने सुनते थे। हर सुंदर चीज का लेखन करते थे। हिंदी भाषा बहुत ही खूबसूरती से बोलते थे। उनके मित्र-परिवार में फ्रांसीसी दोस्त भी थे। इस प्रकार रजा साहब बहुआयामी प्रतिभा के धनी व व्यक्तित्व के स्वामी थे।

Hindi Sulabhbharti Class 8 Solutions पहली इकाई

• हे मातृभूमि! Question Answer
• वारिस कौन? Question Answer
• नाखून क्यों बढ़ते हैं? Question Answer
• गाँव-शहर Question Answer
• मधुबन Question Answer
• जरा प्यार से बोलना सीख लीज Question Answer
• मेरे रजा साहब Question Answer
• पूर्ण विश्राम Question Answer
• अनमोल वाणी Question Answer

Class 8 Hindi Chapter 8 Mera Vidroh Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 8 मेरा विद्रोह Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 8 Mera Vidroh Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 8 मेरा विद्रोह Textbook Questions and Answers

सूचना के अनुसार कृतियाँ करो:

एक शब्द में उत्तर लिखो:

Question 1.
बेटे की मातृभाषा
Answer:
हिंदी

Question 2.
बेटे की शिक्षा की माध्यम भाषा
Answer:
अंग्रेजी

संक्षेप में लिखो:

Question 1.
रमन के जन्मदिन पर न जाने देने के बाद लड़के द्वारा किया गया विद्रोह
Answer:
लड़के ने जोर-जोर से लड़ना, जिद करना और रोना चिल्लाना शुरू कर दिया।

Question 2.
नुक्कड़ की दुकान से घर लौटने पर बेटे द्वारा देखा दृश्य
Answer:
उसके पिता जी गलियारे में खड़े-खड़े दीवार से कोहनियाँ टिकाए नि:शब्द कातर हो रहे हैं।

कारण लिखो:

Question 1.
अंग्रेजियत वाले परिवारों के बच्चों का दबदबा रहता था।
Answer:
क्योंकि वे छोटी उम्र से ही धाराप्रवाह अंग्रेजी बोलते थे।

Question 2.
लड़के की माँ उसे पढ़ा नहीं पाती थी।
Answer:
क्योंकि बेटे की पढ़ाई का माध्यम अंग्रेजी था और माँ को अंग्रेजी नहीं आती थी।

Question 3.
पिता जी झल्ला पड़ते थे।
Answer:
क्योंकि उनका बेटा ‘डोनेशन’ या सालाना जलसे आदि के लिए चंदे की छपी पर्चियाँ लाता था।

Question 4.
बेटा अड़ जाता था।
Answer:
क्योंकि उसके पिता जी ‘डोनेशन’ के रूप में एक या दो रूपये दे देते थे। जबकि उसके दोस्त दस या बीस रूपये लेकर आते।

ऐसे प्रश्न बनाओ जिनके उत्तर निम्न शब्द हों:

Question 1.
साइकिल
Answer:
बेटा पिता के साथ किस पर बैठकर स्कूल गया था?

Question 2.
बेसब्री
Answer:
पिता अपने बेटे रमन की वर्षगाँठ का कैसे इंतजार करते?

Question 3.
छपी पर्चियाँ
Answer:
बेटा ‘डोनेशन’ या सालाना जलसे आदि के लिए चंदे की क्या लाता?

Question 4.
पारावार
Answer:
माँ की खुशी का क्या न रहा?

संजाल पूर्ण करो:

Answer:

भाषा बिंदु

पाठों में आए हुए उपसर्ग और प्रत्ययवाले शब्द ढूँढ़ो तथा उनके उपसर्ग/प्रत्यय अलग करके मूल शब्द लिखो।
Answer:

उपयोजित लेखन

निम्न मुद्दों के आधार पर विज्ञापन लिखो :
स्थल/जगह, संपर्क, पुस्तक मेला, दिनांक, समय
Answer:

स्वयं अध्ययन

अब्राहम लिंकन द्वारा प्रधानाध्यापक को लिखे हुए पत्र का चार्ट बनाकर कक्षा में लगाओ।

मौलिक सृजन

अपने जीवन में पिता की भूमिका’ अधोरेखित करते हुए कृतज्ञता ज्ञापित करने वाला पत्र लिखिए।
Answer:
१० मई, २०१८
पूज्य पिता जी,
सादर प्रणाम।
आप कैसे हैं? बहुत दिन हो गए है लेकिन आपका पत्र नहीं मिला। मैं ठीक हूँ। मेरी पढ़ाई भी ठीक से चल रही है। आशा करता हूँ कि घर पर सभी ठीक होंगे।
पिता जी, यहाँ का नया कॉलेज बहुत ही अच्छा है। यहाँ पर खाने-पीने व रहने की सारी सुविधाएँ बहुत ही अच्छी हैं। मैं इस कॉलेज में आकर खुश हूँ। दरअसल मैं यह पत्र आपके प्रति अपनी कृतज्ञता ज्ञापित करने के लिए लिख रहा हूँ।
पिता जी मेरे जीवन में आपका बहुत ही महत्वपूर्ण स्थान है। बचपन से लेकर आज तक आपने मुझे पढ़ाई करने के लिए प्रेरित किया है। आपके व्यक्तित्व एवं कृतित्व से प्रभावित होकर मैं आज मेडिकल की पढ़ाई कर रहा हूँ। सचमुच यदि आप न होते, तो मेरे भविष्य में अंधेरा ही होता। अत: आपका मैं जितना शुक्रिया अदा करूँ वह कम ही होगा।
जैसे ही छुट्टियाँ शुरू होगी, वैसे ही तुरंत मैं घर पर आऊँगा। माता जी को सादर प्रणाम।
आपका आज्ञाकारी पुत्र,
अथर्व
कुमार अथर्व सक्सेना
२०२ गीत निवास, गांधी नगर, मुंबई : ४००० ९५७
tharv18@gmail.com.

Hindi Sulabhbharti Class 8 Solutions Chapter 8 मेरा विद्रोह Additional Important Questions and Answers

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति क (१) आकलन कृति

संजाल पूर्ण कीजिए।

Question 1.

Answer:

आकृति पूर्ण कीजिए।

Question 1.

Answer:

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –

Question 1.
बचपन
Answer:
बेटे को शहद के प्याले जैसा क्या लगा था?

Question 2.
मटरगश्ती
Answer:
पिता के अनुसार बेटा दिनभर सड़क पर क्या करता रहता है?

समझकर लिखिए।

निम्नलिखित गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
Answer:
दहाड़ना-गरतना
कई-कई
रोना-धोना ।
लगाते-लगाते

निम्नलिखित शब्द मानक वर्तनी के अनुसार लिखिए।

Question 1.
उध्दंड
Answer:
उदंड

वचन बदलिए।

1. निगाहें
2. सड़क

Answer:

1. निगाह
2. सड़कें

नीचे दिए हुए शब्दों के पर्यायवाची शब्द लिखिए।

1. कपड़ा
2. परिणाम
3. ढिठाई

Answer:

1. वस्त्र
2. नतीजा
3. धृष्टता

अनेक शब्दों के लिए एक शब्द लिखिए।

1. उदंडतापूर्ण आचरण
2. बड़ा बनने की आकांक्षा

Answer:

1. डिठाई
2. महत्त्वाकांक्षा

Question 1.
‘क्या बच्चों को नियंत्रण में रखने के लिए उन पर दबाव डालना उचित है?’ इस बारे में आप अपने विचार लिखिए।
Answer:
बच्चे चंचल होते हैं। उन पर नियंत्रण रखने के लिए दबाव डालना अनुचित है। यदि बच्चे देर से घर आते हैं या अपने दोस्तों के साथ रोज-रोज मौज-मस्ती करते हैं या पढ़ाई पर ध्यान नहीं देते हैं, ऐसे में उनके साथ सख्ती से पेश आने से कुछ भी हासिल नहीं हो सकता। माता-पिता अपने बच्चों पर सख्ती करने के बजाय उन्हें प्यार से समझा सकते हैं। उन्हें सही-गलत का एहसास करवा सकते हैं।

बच्चों का मन अन्य गलत कार्यों में न भटकें इसलिए उनसे सकारात्मक कार्य कराएँ जाने चाहिए। उन्हें अकेले मत रखें और उन्हें कभी अकेलेपन का एहसास न होने दें। यदि वे अकेले रहेंगे तो उनका मन नकारात्मक कार्यों में उलझेगा। इसलिए बच्चों को नियंत्रण में रखने के लिए माता-पिता अपने बच्चों के साथ प्यार भरा व्यवहार कर सकते हैं।

निम्नलिखित गदयांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

गलत वाक्य सही करके के फिर से लिखिए।

Question 1.
बेटे को अपने पिता से पढ़ने की तीव्र इच्छा थी।
Answer:
बेटे की अपने पिता से पढ़ने की इच्छा नहीं थी।

Question 2.
बेटे को उसके पिता जी रिक्शा में बिठाकर घुमाने ले जाते
Answer:
बेटे को पिता जी साइकिल पर बिठाकर स्कूल ले जाते थे।

समझकर लिखिए।

Question 1.
बेटा आठवीं कक्षा तक पहुँचा
Answer:
अपने पिता की मेहनत के बल पर वह आठवीं कक्षा तक पहुँचा

Question 2.
इस स्कूल में पढ़ता था बेटा
Answer:
कॉन्वेंट स्कूल में

उपर्युक्त गदयांश से ऐसे प्रश्न तैयार कीजिए जिसका उत्तर निम्नलिखित शब्द हों

Question 1.
साइकिल
Answer:
बेटा पिता जी के साथ किस पर सवार होकर स्कूल गया था?

निम्नलिखित शब्दों के लिए एक शब्द लिखिए।

Question 1.
धारा का बहाव या वेग
Answer:
धाराप्रवाह

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. धूप x ……..
2. मेहनत x ………

Answer:

1. धूप x छाँव
2. मेहनत x आलस

निम्नलिखित शब्द में से प्रत्यय अलग कीजिए।

Question 1.
अंग्रेजियत
Answer:
प्रत्यय : इयत

Question 1.
‘क्या कॉन्वेंट की पढ़ाई मातृभाषा की पढ़ाई से श्रेष्ठ है?’ इस कथन के संदर्भ में अपने विचार लिखिए।
Answer:
आज हम एक नए दौर में जी रहे हैं, जहाँ सर्वत्र अंग्रेजियत का बोलबाला है। चारों ओर कॉन्वेंट स्कूल खुल रहे हैं। पढ़ाई हम कॉन्वेंट स्कूल में करें या अपनी मातृभाषा में। आखिर पड़ाई, पढ़ाई ही होती है। कॉन्वेंट में पढ़कर हमारी अंग्रेजी धाराप्रवाह बनती है। फिर भी यदि कोई बच्चा अपनी मातृभाषा में पढ़ाई करना है तो वह अधिक खुलकर अपने भावों को अभिव्यक्त कर सकता है।

ये बच्चों के ऊपर निर्भर है कि उसे कौन-सी भाषा के माध्यम से पढ़ाई करनी है। अपनी मातृभाषा से पढ़ाई करना छात्रों को सहज और सरल लगता है। इसमें किसी विशेष भाषा में ज्ञान प्राप्त करना किसी को श्रेष्ठ नहीं बनाता। अत: ऐसा हम नहीं कह सकते कि कॉन्वेंट की पढ़ाई मातृभाषा की पढ़ाई से श्रेष्ठ है।

संजाल पूर्ण कीजिए।

Question 1.

Answer:

सही विकल्प चुनकर वाक्य फिर से लिखिए।

Question 1.
रमन की वर्षगाँठ ने बेटे को ……. महीने से बेचैन कर दिया था। (तीन, दो, एक)
Answer:
रमन की वर्षगाँठ ने बेटे को एक महीने से बेचैन कर दिया था।

Question 2.
एक बार पूरी क्लास ……. पर जा रही थी। (पिकनिक, सैर, प्राकृतिक स्थल)
Answer:
एक बार पूरी क्लास पिकनिक पर जा रही थी।

पर्यायवाची शब्द लिखिए।

1. जिद
2. क्लास
3. वर्षगाँठ
4. खुशी

Answer:

1. हठ
2. क्षा
3. जन्मदिन
4. प्रसन्नता

गद्यांश में से ऐसे दो शब्द ढूंढकर लिखिए कि जिनके वचन परिवर्तित नहीं होते।
Answer:
पिता
घर

विलोम शब्द लिखिए।

1. नालायक x ………
2. अंदर x ………

Answer:

1. नालायक x लायक
2. अंदर x बाहर

निम्नलिखित शब्द से उपसर्ग को अलग कीजिए।

Question 1.
नालायक
Answer:
उपसर्ग : ना

उचित प्रत्यय लगाइए।

1. वर्ष
2. लड़का

Answer:

1. प्रत्यय : इक : वार्षिक
2. प्रत्यय : पन : लड़कपन

Question 1.
अपने जीवन में पिता की महत्वपूर्ण भूमिका’ पर अपने विचार लिखिए।
Answer:
प्रत्येक बच्चे के जीवन में पिता की महत्त्वपूर्ण भूमिका होती है। पिता अपने बच्चे पर संस्कार करता है। वह बच्चे के अच्छे कार्यों की सराहना करता है। यदि बच्चे द्वारा कुछ गलत कार्य किया गया है तो वह उसे डाँटता भी है। यदि बच्चा बार-बार समझाने पर अपनी जिद पर अड़ा रहे तो वह उसे पहले समझाता है और यदि नहीं माने तो कठोर भूमिका भी अपनाता है। अपने तथा उसका भविष्य उज्ज्वल बनाने के लिए वह उसे अच्छे से अच्छे स्कूल में दाखिल कराता है।

वह अपने बच्चे का हमेशा मार्गदर्शन करता रहता है और अपने बच्चे की भलाई के लिए उसके हर कार्य पर नियंत्रण रखता है। इस प्रकार एक पिता अपने बच्चे के जीवन में सकारात्मक भूमिका निभाता है।

निम्नलिखित गलत वाक्य सही करके फिर से लिखिए।

Question 1.
पिता जी ने लड़के के गाल पर दवा लगाई।
Answer:
माँ ने लड़के के गाल पर दवा लगाई।

Question 2.
प्यार में पिता जी ने लड़के के गाल पर एक तमाचा लगाया।
Answer:
गुस्से में पिता जी ने एक भरपूर थप्पड़ लड़के के गाल पर जड़ दिया।

किसने, किससे कहा?

Question 1.
“तुम्हारे दोस्त का जन्मदिन है।”
Answer:
लड़के के पिता ने रमन के पिता को बताया।

समझकर लिखिए।

Question 1.
इन अपशब्दों का प्रयोग लड़के ने अपने मन में अपने पिता के लिए किया
Answer:
झूठे, मक्कार, और निर्दयी

कारण लिखिए।

Question 1.
लड़के का दिमाग गुस्से से पागल हो गया।
Answer:
क्योंकि उसके पिता ने रमन के पिता को झूठ बताया कि सीढ़ियों से गिरने के कारण लड़के के गाल पर निशान आए हैं।

Question 2.
लड़के को रमन के जन्मदिन पर भिजवा दिया गया।
Answer:
क्योंकि उसके पिता के साथ उसकी माँ लड़ पड़ी और पिता को भी पछतावा हो रहा था।

विलोम शब्द लिखिए।

1. झूठा x …………
2. निर्दयी x ………

Answer:

1. झूठा x सच्चा
2. निर्दयी x दयावान

समानार्थी शब्द लिखिए।

1. गुस्सा
2. दोस्त

Answer:

1. क्रोध
2. मित्र

अनेक शब्द के लिए एक शब्द लिखिए।

1. वह दिन जिसमें किसी ने जन्म लिया हो
2. जिसके दिल में दया न हो

Answer:

1. जन्मदिन
2. निर्दयी

Question 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
Answer:
रोना-चिल्लाना
आते-आते

लिंग बदलिए।

1. लड़का
2. पापा

Answer:

1. लड़की
2. मम्मी

स्वमत अभिव्यक्ति

Question 1.
क्या हर बात पर अपने माता-पिता से जिद करना सही है? अपने विचार लिखिए।
Answer:
प्रत्येक माता-पिता अपने बच्चे का भला चाहते हैं। दुनिया में ऐसे माता-पिता नहीं है; जो अपने बच्चों का बुरा चाहते है। वे यदि कहीं जाने के लिए मना करते हैं, तो उसके पीछे उनका कोई-न-कोई कारण अवश्य होगा। वे जो भी निर्णय लेते हैं, वह अपने बच्चे की भलाई को ध्यान में रखकर लेते हैं। वे नहीं चाहते कि छोटी-सी गलती के कारण उनके बच्चों को किसी संकट या परेशानी का सामना करना पड़े। ऐसे में यदि कोई माता-पिता बच्चों द्वारा की जाने वाली जिद जैसी अन्य प्रतिक्रियाओं पर नाराज होते हैं, तो इसका यह अर्थ नहीं है कि वे अपने बच्चों से प्यार नहीं करते। इसलिए हर बात पर अपने माता-पिता के सामने जिद करना सही नहीं है।

संजाल पूर्ण कीजिए।

Question 1.

Answer

समझकर लिखिए।

Question 1.
वे नहीं मनाते थे लड़के का जन्मदिन
Answer:
लड़के के माता पित

Question 2.
पिता जी द्वारा मिली झिड़की का नतीजा
Answer:
लड़के के मन में उपेक्षा व आक्रोश और भी बढ़ा दिया।

Question 3.
उपेक्षा व आक्रोश का स्थान इसने ले लिया
Answer:
विद्रोह ने ।

Question 4.
इनसे चिढ़ हो गई थी लड़के को
Answer:
पढ़ाई व पिता जी से ।

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

1. पर्यायवाची
2. शालू

Answer:

1. लड़के के लिए पिता जी और पढ़ाई एक-दूसरे के क्या बन गए थे?
2. लड़के की छोटी बहन का नाम क्या था?

कारण लिखिए।

Question 1.
लड़के के घर में तंगहाली और भी बढ़ गई।
Answer:
क्योंकि उसके घर में उसकी छोटी बहन के जन्म के बाद छोटे भाई मंटू का आगमन हुआ।

Question 2.
लड़का दुस्साहसी हो गया।
Answer:
पिता जी बात-बात पर उसे पीटते थे। इसी कारण पिटने का डर उसके दिमाग से काफूर हो गया और वह दुस्साहसी हो गया। कृतिक

शब्द संपदा

निम्नलिखित गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
Answer:
धीरे-धीरे
एक-दूसरे
बात-बात
ढेर-के-ढेर

निम्नलिखित शब्द मानक वर्तनी के अनुसार लिखिए।

Question 1.
किये गये
Answer:
किए गए

वचन बदलिए।

1. बहन
2. झिड़की

Answer:

1. बहनें
2. झिड़कियाँ

नीचे दिए हुए शब्दों के पर्यायवाची शब्द लिखिए।

1. तंगहाली
2. काफूर
3. घर
4. दिमाग

Answer:

1. दुर्दशा
2. गायब
3. गृह
4. समझ

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
तंगहाल होने की अवस्था –
Answer:
तंगहाली

Question 2.
दुस्साहस करने वाला
Answer:
दुस्साहसी

Question 1.
माता-पिता की आकांक्षाओं से दबकर बालक-बालिकाओं की लालसाएँ दम तोड़ देती हैं।’ कञ्चन के बारे में अपने विचार लिखिए।
Answer:
बच्चे मन के सच्चे होते हैं। उन्हें अधिक अनुशासन में रखना उचित नहीं होता। हमेशा उन पर निगाह रखना या बार-बार टोकने या मारने से बच्चे और भी जिद्दी हो जाते हैं। मौका मिलते ही वे विद्रोह करने में भी पीछे नहीं हटते। इसके साथ माता-पिता को उनकी उपेक्षा भी नहीं करनी चाहिए। यदि बच्चे तीन या चार चीजों की मांग करते हैं, तो कम-से-कम उनकी एक ख्वाहिश उनके माता-पिता को पूर्ण करनी चाहिए।

यदि माता-पिता अपनी आकांक्षा एवं विचार बच्चों को जबरदस्ती अपनाने के लिए मजबूर करेंगे, तो ऐसे में वे अधिक हावी हो जाएँगे और विद्रोह करने के लिए तैयार हो जाएंगे। यदि वे विद्रोह नहीं करेंगे, तो बार-बार मन में सोचते रहेंगे। इससे उनके मन में माता-पिता के प्रति दुश्मनी का भाव निर्माण हो जाएगा। बच्चे माता-पिता की आकांक्षाओं से दबकर स्वयं को अकेला महसूस करने लगे और इससे उनके मन में नकारात्मक भावना पनपने लगेगी।

एक शब्द में उत्तर लिखिए ।

Question 1.
इससे लड़के को शत्रुता हो गई
Answer:
पढ़ाई से

Question 2.
इनसे बदला लेना चाहता था लड़का
Answer:
पिताजी से

कारण लिखिए।

Question 1.
लड़के को स्वयं का कैरियर चौपट करने में मजा मिलता।
Answer:
क्योंकि वह अपने पिता से बदला लेना चाहता था और उन्हें नीचा दिखाना चाहता था।

Question 2.
लड़का अपमान से तिलमिला गया।
Answer:
क्योंकि पिछले साल से अच्छे नंबर लाने पर भी उसके पिता जी खुश नहीं हुए और उन्होंने उसे ‘थर्ड का थर्ड ही रहेगा’ ऐसे तीखे शब्दों में अपमानित किया।

निम्नलिखित गलत बाक्य सही करके फिर से लिखिए।

Question 1.
लड़के की रिपोर्ट देखकर पिता जी खुश हो जाते।
Answer:
लड़के की रिपोर्ट देखकर पिता जी खीझ जाते।

Question 2.
लड़के की पांचवीं कक्षा में तीसरी पोजीशन थी।
Answer:
लड़के की पांचवीं कक्षा में सातवीं पोजीशन थी।

किसने, किससे कहा?

Question 1.
“कह तो ऐसे रहे हो जैसे फर्स्ट ही आओगे।”
Answer:
पिता ने लड़के से कहा।

Question 2.
“अगले साल मैं फेल होऊँगा फेल।”
Answer:
लड़के ने अपने मन में सोचा।

शब्द समूह के लिए एक शब्द लिखिए।

Question 1.
ग्रहों के घूमने का वक़ मार्ग
Answer:
कक्षा

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. अगले x ……
2. खुश x ……..

Answer:

1. अगले x पिछले
2. खुश x नाखुश

गद्यांश में से विदेशी शब्द ढूँढ़कर लिखिए।
Answer:
कैरियर, फर्स्ट, पोजीशन

निम्नलिखित शब्द में उचित प्रत्यय लगाइए।

1. अपमान
2. आसान

Answer:

1. अपमानित : प्रत्यय : इत
2. आसानी : प्रत्यय : ई

कृति च (४) स्वमत अभिव्यक्ति

Question 1.
‘प्रत्येक माता-पिता को अपने बच्चों की खुशी में सम्मिलित होना चाहिए।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
बच्चे संवेदनशील होते हैं। यदि कोई उनका अपमान करें या उनकी उपेक्षा करें, तो इसे भूल पाना उनके लिए असंभव हो जाता है। यदि वे कुछ अच्छा काम करते हैं, तो प्रत्येक माता-पिता को उनके अच्छे कार्य की सराहना करनी चाहिए। उन्हें सकारात्मक प्रतिक्रिया देकर उनकी खुशी में शरीक होना चाहिए। यदि कोई माता-पिता अपने बच्चों द्वारा किए गए अच्छे कार्यों से प्रसन्न नहीं होते हैं और उनका आत्मविश्वास अधिक मजबूत करने के बजाय उन्हें निराश करते हैं, तो बच्चे स्वभाव से विद्रोही बनते है। इसलिए उनकी खुशी में सम्मिलित होकर उनकी प्रशंसा करनी चाहिए।

कारण लिखिए।

Question 1.
लड़के को शालू चमची से चिढ़ हो गई है।
Answer:
क्योंकि उसने थोड़ी बड़ी होने के साथ पिता जी कहना मानना और डरना शुरू कर दिया है।

Question 2.
लड़के को मंटू के रोते रहने देने में शांति मिलती है।
Answer:
क्योंकि पिता जी उससे बहुत प्यार करते हैं।

समझकर लिखिए।

Question 1.
परीक्षा में फर्स्ट आना इनकी उपलब्धि होगी
Answer:
लड़के के पिता जी की।

Question 2.
इस काम पर लड़के को लगा देना चाहते है उसके पिता
Answer:
कुली-कबाड़ी के काम पर।

संजाल पूर्ण कीजिए।

Question 1.

Answer:

पर्यायवाची शब्द लिखिए।

1. काम
2. परीक्षा

Answer:

1. कार्य
2. इम्तिहान

वचन बदलिए।

1. घड़ी
2. उपलब्धि

Answer:

1. घड़ियाँ
2. उपलब्धियाँ

विलोम शब्द लिखिए।

1. पास x ………….
2. उपलब्धि x ………

Answer:

1. पास x दूर
2. उपलब्धि x अनुपलब्धि

शांति शब्द में उचित उपसर्ग का प्रयोग कीजिए।

Question 1.
उपसर्ग : अ
Answer:
उपसर्ग युक्त शब्द : अशांति

‘यदि आप लड़के की जगह पर होते तो क्या करते?’ अपने विचार लिखिए।
Answer:
यदि मैं लड़के की जगह पर होता तो उस लड़के की जैसी हरकतें नहीं करता। पिता जी की आर्थिक परेशानियाँ समझने की कोशिश करता। अपनी ख्वाहिशों पर नियंत्रण रखता। मन लगाकर पढ़ाई करता और सड़क पर आवारा दोस्तों के साथ मटरगश्ती करने में अपना समय नहीं गंवाता। अपने छोटे भाई बहनों के साथ प्यार से पेश आता। एक अच्छा पुत्र बनकर अपने पिता जी की हर बात का पालन करता।

संजाल पूर्ण कीजिए।

Answer:

निम्नलिखित गलत वाक्य सही करके फिर से लिखिए।

Question 1.
पिता बेटे से संधि चाहते थे।
Answer:
बेटा पिता से संधि चाहता था।

Question 2.
पिता की खुशी का पारावार न था।
Answer:
माँ की खुशी का पारावार न था।

किसने, किससे कहा?

Question 1.
मैं संधि चाहता हूँ।
Answer:
यह वाक्य लड़के ने अपने मन ही मन में कहा।

समझकर लिखिए।

Question 1.
माँ की खुशी का पारावार न था
Answer:
क्योंकि उसके बेटे को अपनी गलती का एहसास हो गया था। वह पछता रहा था। उसे पिता जी की दशा पर मन-ही-मन दुख हो रहा था।

Question 2.
बेटे ने पिता जी का ऐसा रूप पहले कभी नहीं देखा था
Answer:
बेहद निराश एवं आकुल-व्याकुल रूप

विलोम शब्द लिखिए।

1. संधि x ………..
2. निराश x ………..

Answer:

1. संधि x विच्छेद
2. निराश x प्रसन्न

समानार्थी शब्द लिखिए।

1. संधि
2. नुक्कड़
3. दशा
4. क्षमा

Answer:

1. मिलन
2. गली
3. अवस्था
4. माफी

अनेक शब्द के लिए एक शब्द लिखिए।

Question 1.
जो शब्दरहित हो
Answer:
निःशब्द

गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।

Question 1.
जो शब्दरहित हो।
Answer:
आकुल-व्याकुल, गरजेंगे-दहाड़ेंगे

Question 2.
‘वही जीवन में प्रगति कर पाता है। जिसे अपनी गलती का एहसास होता है। अपने विचार लिखिए।
Answer:
जिससे गलती होती है वह भी इंसान ही होता है। जाने-अनजाने में काम करते समय इंसान से गलती हो जाती है। जैसे कि गुस्सा आने पर इंसान एक-दूसरे को आवेश में आकर कुछ भी कह देता है। कभी बच्चे बचपन में, जाने-अनजाने में, घर से पैसे चुराना, माता-पिता के डाँटने पर उनके प्रति नकारात्मक सोच करना आदि गलतियाँ करते रहते हैं। लेकिन व्यक्ति को उस वक्त तो नहीं, पर बाद में उस पर विचार करना चाहिए और स्वयं की गलती को स्वीकारना चाहिए।

जिस व्यक्ति को अपनी गलती का एहसास हो जाता है । वह फिर से दोबारा वह गलती नहीं करता। वह कार्य करने से पहले सावधानी बरतता है। आखिर, ऐसा व्यक्ति जीवन में प्रगति कर लेता है।

Hindi Sulabhbharati 8th Standard Digest Guide दूसरी इकाई

• धरती का आँगन महके Question Answer
• दो लघुकथाएँ Question Answer
• लकड़हारा और वन Question Answer
• सौहार्द -सौमनस्‍य Question Answer
• खेती से आई तब्‍दीलियाँ Question Answer
• अंधायुग Question Answer
• स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Question Answer
• मेरा विद्रोह Question Answer
• नहीं कुछ इससे बढ़कर Question Answer

Class 8 Hindi Chapter 2 Do Laghu Kathaen Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 2 दो लघुकथाएँ Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 2 Do Laghu Kathaen Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 2 दो लघुकथाएँ Textbook Questions and Answers

सूचना के अनुसार कृतियाँ करो :

संजाल पूर्ण करो:

Answer:

उत्तर लिखो:

Question 1.

Answer:

Question 2.

Answer:

विधानों के सामने चौखट में सही (✓) अथवा गलत (✗) चिह्न लगाओ:

Question 1.
जिह्वा ने अविवेक पूर्ण उत्तर दिया।
Answer:
(✗) गलत

Question 2.
दाँत घमंडी थे।
Answer:
(✓) सही

Question 3.
सभी अपराधियों को नियमानुसार सजा नहीं हुई।
Answer:
(✗) गलत

Question 4.
ठेकेदार पुराना था।
Answer:
(✗) गलत

Question 5.
उच्च अधिकारी ईमानदार थे।
Answer:
(✓) सही

उचित जोड़ियाँ मिलाओ:

Answer:

स्वयं अध्ययन

किसी ग्रामीण और शहरी व्यक्ति की दिनचर्या की तुलनात्मक जानकारी प्राप्त करके आपस में चर्चा करो।

भाषाबिंदु

निम्नलिखित शब्दों के आधार पर मुहावरे लिखकर उनका अपने वाक्यों में प्रयोग कीजिए।

(नाक, दाँत, गला, मुँह)

(१) नाकः
Answer:

• नाक रगड़ना – गिड़गिड़ाना : अपनी इस अकड़ के कारण तुम्हें सभी के सामने एक दिन अपनी नाक रगड़नी पड़ेगी।
• नाक में दम करना – बहुत परेशान करना : इन बच्चों ने सभी के नाक में दम कर दिया है।
• नाक – भौं सिकुड़ना – घृणा करना : अच्छा हो या बुरा… उसकी तो आदत ही है, नाक – भौं सिकोड़ने की।

(२) दाँतः
Answer:

• दाँत खट्टे करना – हरा देना : युदध में भारतीय सेना ने दुश्मनों के दाँत खट्टे कर दिए हैं।
• दाँत पीसना – गुस्सा होना : तुम अपनी यह दाँत पीसने की आदत छोड़ दो।
• दाँतों तले उँगली दबाना – आश्चर्य चकित होना : जादूगर का खेल देखकर सभी ने दाँतों तले उँगलियाँ दबा लीं।

(३) गला:
Answer:

• गला फाड़ना – जोर से चिल्लाना : वह गला फाड़कर अपनी दवा का विज्ञापन कर रहा था।
• गला काटना – हानि पहुँचाना : इस तरह का दुर्व्यवहार कर तुम दूसरों का गला काट रहे हो। यह उचित नहीं है।
• गले का हार होना – बहुत प्रिय होना : हर बेटा अपनी माँ के गले का हार होता है।

(४) मुँह:
Answer:

• अपना-सा मुँह लेकर रह जाना – अपमानित होने के बाद हताश होना : परीक्षा में फेल हो जाने पर वह अपना-सा मुँह लेकर रह गया।
• मुँह बनाना – चेहरे पर अप्रसन्नता का भाव प्रकट करना : पिता जी ने मनचाही वस्तु नहीं लाई। इसलिए राहुल ने तुरंत अपना मुँह बना लिया।
• मुँह बंद कर देना – चुप कर देना : पिता जी ने गुस्से में घर आकर सभी का मुँह बंद कर दिया था।

उपयोजित लेखन

‘जल के अपव्यय की रोकथाम’ संबंधी चित्रकला प्रदर्शनी का आकर्षक विज्ञापन तैयार कीजिए।
Answer:

पठनीय

‘श्रमप्रतिष्ठा का महत्त्व’ इस विषय पर निबंध लिखिए।
Answer:
श्रम यानी ‘मेहनत करना।’ श्रम ही जीवन है। श्रम ही संपत्ति है। इसलिए प्रत्येक व्यक्ति को श्रम करना चाहिए। श्रम की पूजा करनी चाहिए; तब जाकर श्रमिक को समाज में प्रतिष्ठा प्राप्त होगी। श्रम के बिना व्यक्ति सफल नहीं हो सकता। श्रम करने से ही कार्य सिद्ध होता है। परिश्रम मानवीय गुण है। श्रम करने से व्यक्ति का मन प्रसन्न रहता है। श्रम करने वाले व्यक्ति को समाज में सम्मान मिलता है। मजदूर दिनभर पुल या सड़क बनाने का काम करता है। वह सूरज की कड़ी धूप व बारिश में भी काम करता है। तब जाकर सड़क, पुल का निर्माण होता है।

किसान खेती करता है। वह दिन-रात मेहनत करता है। इसलिए सभी को खाने के लिए अनाज उपलब्ध होता है। ताजमहल का निर्माण करने में कारीगरों को कई वर्ष लगे। तब जाकर उनकी मेहनत रंग लाई व भव्य वास्तु – शिल्पकला का निर्माण किया। देश को आजादी दिलाने के लिए कई वीरों ने दिन-रात संघर्ष किया। आज विज्ञान के क्षेत्र में जो चतुर्दिक प्रगति हुई है। इसके पीछे कई वैज्ञानिकों का अथक श्रम है। यह सब उनके श्रम का ही फल है कि हम आजाद भारत में विज्ञान का सुख भोग रहे हैं। अत: स्पष्ट है कि श्रम मनुष्य जाति व राष्ट्र की उन्नति के लिए नितांत आवश्यक है।

Hindi Sulabhbharti Class 8 Solutions Chapter 2 दो लघुकथाएँ Additional Important Questions and Answers

प्रश्न १ (क) निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति क (१) आकलन कृति

समझकर लिखिए।

Answer:

कारण लिखिए।

Question 1.
अधिकारी महोदय ने ठेकेदार को कहीं और जाने के लिए कहा।
Answer:
क्योंकि उसके काम के प्रति वे संतुष्ट नहीं थे।

Question 2.
अधिकारी ने ठेकेदार का काम बंद करवाने की बात की।
Answer:
क्योंकि उसके काम में पर्याप्त सुधार नहीं आया था।

कृति पूर्ण कीजिए।

Answer:

कृति क (२) आकलन कृति

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

1. ठेकेदार
2. अधिकारी

Answer:

1. कौन नया था?
2. नींव की दीवार पर किसने निगाह डाली?

समझकर लिखिए।

Question 1.
किसने किसको पाठ पढ़ाने का निश्चय किया?
Answer:
नए ठेकेदार ने संबंधित अधिकारी को।

Question 2.
अधिकारी किसलिए गुस्सा होते थे?
Answer:
क्योंकि वे नए ठेकेदार से रिश्वत चाहते थे।

कृति क (३) शब्द संपदा

मानक वर्तनी के अनुसार शब्द शुद्ध लिखिए।

1. ईण्ट
2. सम्बधित
3. बन्द
4. परयाप्त

Answer:

1. इंट
2. संबंधित
3. बंद
4. पर्याप्त

लिंग बदलिए।

1. ठेकेदार
2. अधिकार

Answer:

1. ठेकेदारनी
2. अधिकारिनी

विलोम शब्द लिखिए।

1. नया
2. गरम
3. असंतोष
4. व्यक्त

Answer:

1. पुराना
2. ठंडा
3. संतोष
4. अव्यक्त

निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. दिन
2. गरम

Answer:

1. दिवस
2. उष्ण

कृति क (४) स्वमत अभिव्यक्ति

Question 1.
क्या रिश्वत देना व रिश्वत लेना दोनों ही कानूनन अपराध हैं? अपने विचार लिखिए।
Answer:
जी हों, रिश्वत देना व लेना दोनों ही कानूनन अपराध हैं। इसके लिए कानून द्वारा सख्त नियम तैयार किए गए हैं। जो व्यक्ति रिश्वत लेता है उसे पकड़ने जाने पर सजा तो होती ही है, साथ ही जो रिश्वत देता है वह भी कानून की नजर में अपराधी होता है। रिश्वत के लेन-देन के कारण देश का विकास नहीं होता है और सर्वसाधारण लोगों को कई कष्ट झेलने पड़ते हैं। रिश्वत के दम पर ही कई अवैधानिक कामों को अंजाम दिया जाता है। इसलिए रिश्वत लेना व रिश्वत देना दोनों ही कानूनन अपराध हैं।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कति ख (१) आकलन कृति

किसने, किससे कहा?

Question 1.
कुछ एक भ्रष्ट अधिकारियों के कारण ही पूरा प्रशासन बदनाम होता है।
Answer:
यह वाक्य उच्च अधिकारी ने नए ठेकेदार से कहा।

गलत वाक्य सही करके लिखिए।

Question 1.
अधिकारी महोदय व उच्च अधिकारी का सार्वजनिक समारोह में सम्मान किया गया।
Answer:
ठेकेदार व उच्च अधिकारी का सार्वजनिक समारोह में सम्मान किया गया।

Question 2.
ठेकेदार ने उच्च अधिकारी महोदय को रिश्वत दे दी।
Answer:
ठेकेदार ने अधिकारी महोदय को रिश्वत दे दी।

कृति ख (२) आकलन कृति

उत्तर लिखिए।

Question 1.
इसने शिकायत की।
Answer:
नए ठेकेदार ने।

Question 2.
इसके खिलाफ शिकायत की।
Answer:
अधिकारी महोदय के खिलाफ।

Question 3.
शिकायत का नतीजा।
Answer:
अधिकारी महोदय को रिश्वत लेते हुए रंगे हाथ पकड़ लिया।

Question 4.
इसके पास शिकायत दर्ज हुई।
Answer:
उच्च अधिकारी के पास।

उचित घटनाक्रम लगाकर वाक्य फिर से लिखिए।

Question 1.
उच्च अधिकारी महोदय का आगमन हुआ।
Answer:
अधिकारी महोदय निरीक्षण करने आए।

Question 2.
ठेकेदार और उच्च अधिकारी की ईमानदारी का समाचार चारों तरफ फैल गया।
Answer:
अधिकारी प्रसन्न होकर जाने लगा।

Question 3.
अधिकारी प्रसन्न होकर जाने लगा।
Answer:
उच्च अधिकारी महोदय का आगमन हुआ।

Question 4.
अधिकारी महोदय निरीक्षण करने आए।
Answer:
ठेकेदार और उच्च अधिकारी की ईमानदारी का समाचार चारों तरफ फैल गया।

उचित जोड़ियाँ लगाइए।

Answer:

विलोम शब्द लिखिए।

1. बुरा
2. उच्च
3. एक
4. प्रसन्न

Answer:

1. अच्छा
2. निम्न
3. अनेक
4. अप्रसन्न

अनेक शब्दों के लिए एक शब्द लिखिए।

1. ठेका लेने वाला।
2. नगर, संस्था आदि के अधिकारों, कर्तव्यों को कार्य रूप देना।

Answer:

1. ठेकेदार
2. प्रशासन

निम्नलिखित शब्दों के अर्थ गद्यांश के आधार पर लिखिए।

1. परिणाम
2. सजा

Answer:

1. नतीजा
2. दंड

निम्नलिखित शब्द से उपसर्ग अलग कीजिए और संबंधित उपसर्ग से अन्य दो शब्द बनाइए।

Question 1.
अधिकारी
Answer:
अधिकारी : उपसर्ग : अधि अन्य दो शब्द : अधिकरण, अधिकार

Question 2.
बदनाम
Answer:
बदनाम : उपसर्ग बद अन्य दो शब्द : बदसूरत, बदमाश

कृति ख (४) स्वमत अभिव्यक्ति

Question 1.
‘बुरे काम का बुरा नतीजा’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
हिंदी में कहा गया है कि बुरे काम का नतीजा बुरा होता है। यदि हम दूसरों के लिए गड्ढा खोदने का काम करेंगे, तो हम स्वयं ही उसमें जाकर गिरेंगे। आखिर, जैसा करोगे; वैसा भरोगे। गीता में भगवान कृष्ण ने स्वयं बताया है कि मानव को उसके कर्म का फल यही पर रहकर ही भुगतान पड़ता है। जो जैसा करता है; वैसा ही फल पाता है। यदि एक छात्र पूरे वर्ष कुछ भी पढ़ाई न करेगा, तो वह अंतिम परीक्षा में असफल हो जाएगा। अंत में उसे अपने लापरवाही का परिणाम भुगतना ही पड़ेगा। अत: स्पष्ट है कि किसी भी बुरे काम का परिणाम सदैव बुरा ही होता है।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ग (१) आकलन कृति

समझकर लिखिए।

1. इसलिए दाँत दुस्साहसी हो गए थे।
2. ये हो गए थे गर्व में चूर।

Answer:

1. पंक्तिबद्ध व एकजुट रहने के कारण
2. दाँत

कृति पूर्ण कीजिए।

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

कृति ग (३) शब्द संपदा

नीचे लिखे शब्दों में उचित प्रत्यय लगाइए।

1. जवान
2. कृपा

Answer:

1. जवान + ई – जवानी
2. कृपा + लु – कृपालु

लिंग पहचानिए।

1. नम्रता
2. दाँत

Answer:

1. स्त्रीलिंग
2. पुल्लिंग

वचन बदलिए।

1. मित्र
2. मैं

Answer:

1. मित्रगण
2. हम

गोश में आए विलोम शब्द की जोड़ी ढूँढकर लिखिए।

1. जवान

Answer:

1. बद्ध

कृति ग (४) स्वमत अभिव्यक्ति

Question 1.
‘घमंड मनुष्य के विनाश का कारण बन जाता है।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
घमंड ऐसी स्वाभाविक कुवृत्ति है जो मनुष्य का नाश कर डालती है। जिसके हृदय में घमंड होता है; वह जिंदगी में कुछ भी नहीं कर सकता है। घमंड मनुष्य का शव होता है। घमंड करने के कारण व्यक्ति को कई सारी परेशानियों का सामना करना पड़ता है। रावण वेदों का ज्ञाता था फिर भी घमंड करने के कारण उसका विनाश हो गया। दुर्योधन वीर था, फिर भी घमंड करने के कारण उसका विनाश हो गया। घमंड के कारण व्यक्ति अपने अंदर के ज्ञान को भूल जाता है और वह पतन की ओर बढ़ने लगता है। कहा भी गया है कि घमंडी का सिर नीचा होता है।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति घ (१) आकलन कृति

कारण लिखिए।

Question 1.
सभी दाँतों से थर्राते हैं।
Answer:
दाँतों के कड़े और नुकीलेपन के कारण सभी उनसे धरतेि हैं।

Question 2.
सभी दाँत निरूत्तर हो गए।
Answer:
जीभ ने उन्हें चेतावनी देते हुए कहा कि दंत चिकित्सक एक एक को बाहर कर देगा। यह सुनकर सभी दाँत निरूत्तर हो गए।

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

1. गहरी
2. दंत चिकित्सक

Answer:

1. दाँतों की जड़े कैसी हैं?
2. दाँतों को बाहर कौन कर देता है?

किसने, किससे कहा?

Question 1.
हम सब मिलकर तुझे घेरे खड़े हैं।
Answer:
यह वाक्य दाँतों ने जीभ से कहा।

Question 2.
मुझमें पूरी दुनिया को प्रभावित करने और झुकाने की क्षमता है।
Answer:
यह वाक्य दाँतों ने जीभ से कहा।

समझकर लिखिए।

Question 1.
गद्यांश में प्रयुक्त एक काव्य पंक्ति लिखिए।
Answer:
किसी को पसंद नहीं सख्ती बयान में तभी तो दी नहीं हड्डी जबान में।

कृति घ (३) शब्द संपदा

Question 1.
निम्नलिखित गद्यांश से उपसर्ग व प्रत्यययुक्त शब्द ढूँढ़कर लिखिए।
Answer:
उपसर्गयुक्त शब्द : निरूत्तर : उपसर्ग : निर
प्रत्यययुक्त शब्द : विवेकपूर्ण : प्रत्यय : पूर्ण शक्तिशाली : प्रत्यय : शाली

विलोम शब्द लिखिए।

1. विवेक
2. विनम्रता

Answer:

1. अविवेक
2. कठोरता

वचन बदलिए।

1. जड़ें
2. हड्डी

Answer:

1. जड़
2. हड्डियाँ

कृति घ (४) स्वमत अभिव्यक्ति

Question 1.
‘विनम्रता सारे सदगुणों की नींव है’ पर आधारित अपने विचार लिखिए।
Answer:
विनम्रता मनुष्य को मिला प्रकृतिप्रदत्त एक खूबसूरत उपहार है। इसके द्वारा हम स्वयं पर ही नहीं, बल्कि दूसरों पर भी सकारात्मक प्रभाव निर्माण कर सकते हैं। विनम्रता में शांति की स्थापना करने की शक्ति होती है। वह कठोर से कठोर व्यक्ति को मृदु बनाने की क्षमता रखती है। विनम्रता के कारण मनुष्य का व्यक्तित्व ऊँचा उठता है। व्यक्ति विनम्र होकर ही योग्य पात्रता हासिल कर सकता है। विनम्र होकर समग्रता से ग्रहण करना सीखते हैं। विनम्रता के कारण हम दूसरों से जुड़ जाते हैं। जो व्यक्ति अपने जीवन में विनम्र रहता है। उसका समाज में अस्तित्व हमेशा बना रहता है। विनम्रता को स्वीकार करने के कारण ही सिद्धार्थ गौतम ‘बुद्ध’ बन गए। विनम्रता मनुष्य को महान बनाती है। अत: स्पष्ट है कि विनम्रता ही सारे सद्गुणों की नींव है।

Hindi Sulabhbharati 8th Standard Digest Guide दूसरी इकाई

• धरती का आँगन महके Question Answer
• दो लघुकथाएँ Question Answer
• लकड़हारा और वन Question Answer
• सौहार्द -सौमनस्‍य Question Answer
• खेती से आई तब्‍दीलियाँ Question Answer
• अंधायुग Question Answer
• स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Question Answer
• मेरा विद्रोह Question Answer
• नहीं कुछ इससे बढ़कर Question Answer

Class 8 Hindi Chapter 2 Waris Kaun Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 2 वारिस कौन? Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 2 Waris Kaun Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 2 वारिस कौन? Textbook Questions and Answers

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ग (१) आकलन कृति (१) परिणाम लिखिए।

Question 1.
पहली राजकुमारी को कड़ककर पूछने का परिणाम
Answer:
उसने सच्ची बात बता दी कि उसने दाने भंडार घर से लाए हैं।

Question 2.
दूसरी राजकुमारी का संदूकची में दाने रखने का परिणाम
Answer:
दाने सड़ गए थे। स्वाध्याय विषयक कृतियाँ

उचित घटनाक्रम लगाकर वाक्य फिर से लिखिए।

Question 1.
सभी के उत्तर से राजा को बड़ी निराशा हुई।
Answer:
अंत में उसे एक उपाय सूझ गया।

Question 2.
रथ एक बड़े-से हरे-भरे खेत के सामने रुक गया।
Answer:
सभी के उत्तर से राजा को बड़ी निराशा हुई।

Question 3.
राजा ने हैरानी से राजकुमारी की ओर देखा।
Answer:
रथ एक बड़े-से हरे-भरे खेत के सामने रुक गया।

Question 4.
अंत में उसे एक उपाय सूझ गया।
Answer:
राजा ने हैरानी से राजकुमारी की ओर देखा।

सही विकल्प चुनकर वाक्य फिर से लिखिए।

Question 1.
जरूर इसके पीछे कोई ………….. होगा। (उद्देश्य / हेतु / मकसद)
Answer:
जरूर इसके पीछे कोई मकसद होगा।

Question 2.
सो मैं उन्हें …………. खा गई। (भिगोकर / भुनवाकर / पकाकर)
Answer:
सो मैं उन्हें भुनवाकर खा गई।

Question 3.
तुम ही मेरे राज्य की सच्ची …………… हो। (रानी / युवराज्ञी / उत्तरधिकारी)
Answer:
तुम ही मेरे राज्य की सच्ची उत्तरधिकारी हो।

Question 4.
इसे तुम अपने पास रखो …….. साल बाद मैं उन्हें माँगूंगा। (चार / सात / पाँच)
Answer:
इसे तुम अपने पास रखो पाँच साल बाद मैं उन्हें माँगूंगा। .

परिणाम लिखिए।

Question 1.
गेहूँ के दानों को बोने का परिणाम
Answer:
समय पर अंकुर फुटना। पौधे तयार होना। दाने निकलना।

Question 2.
पहली राजकुमारी को कड़ककर पूछने का परिणाम
Answer:
उसने सच्ची बात बता दी कि उसने दाने भंडार घर से लाए हैं।

Question 3.
दूसरी राजकुमारी का संदूकची में दाने रखने का परिणाम
Answer:
दाने सड़ गए थे।

Question 4.
सभी के उत्तर सुनकर राजा पर हुआ परिणाम
Answer:
राजा को बड़ी निराशा हुई।

भाषाबिंदु

रचना के आधार पर विभिन्न प्रकार के तीन-तीन वाक्य पाठों से ढूँढकर लिखिए।

(१) सरल वाक्य

• वह सोचने लगा।
• उसके चार बेटियाँ थीं।
• इसे तुम अपने पास रखो।

(२) संयुक्त वाक्य

• उसने दानों को भुनवाकर खा डाला और खेल में मग्न हो गई।
• बड़ी राजकुमारी भंडार घर जाकर गेहूँ के दाने ले आई और राजा को दे दिए।
• सभी को गेहूँ के सौ-सौ दाने दिए और का, “इसे तुम अपने पास रखो।”

मिश्र वाक्य:

• पाँच साल बाद जब मैं इन्हें मालूंगा; तब सब मुझे वापस कर देना।
• राजा ने सोचा कि इन चारों में से जो सबसे बुद्धिमती होगी, उसे ही अपना राजपाट सौंपेगा।
• पाँच साल बाद जब पिता जी ये दाने माँगेंगे; तब उन्हें वापस कर दूंगी।

निम्नलिखित वाक्यों में सूचना के अनुसार परिवर्तन कीजिए।

Question 1.
रथ आते ही राजा उस पर सवार हो गया।
(संयुक्त वाक्य में बदलिए)
Answer:
राजा का रथ आया और वह उस पर सवार हो गया।

Question 2.
राजा का रथ आया और वह उस पर सवार हो गया। (मिश्र वाक्य में बदलिए)
Answer:
उन्ना जैसे ही राजा का रथ आ गया; वैसे ही वह उस पर सवार हो गया।

निम्नलिखित रेखांकित विकारी शब्दों के भेद पहचानिए।

Question 1.
एक राजा था।
Answer:
एक : संख्यावाचक विशेषण

Question 2.
इसे तुम अपने पास रखो।
Answer:
उन्ता : तुम : पुरुषवाचक सर्वनाम

Question 3.
राजा ने अपनी बेटियों को गेहूँ के दाने दिए।
Answer:
गेहूँ : द्रव्यवाचक संज्ञा

Question 4.
राजा ने चारों बहनों को बुलाया।
Answer:
बुलाया : क्रिया

स्वयं अध्ययन

बीरबल की बौद्धिक चतुराई की कहानी के मुद्दों का फोल्डर बनाकर – कहानी प्रस्तुत करो।

उत्तर लिखो:

Answer:

Hindi Sulabhbharti Class 8 Solutions Chapter 2 वारिस कौन? Additional Important Questions and Answers

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति क (१) आकलन कृति

समझकर लिखिए।
Answer:

कृति अ (२) आकलन कृति

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों

Question 1.
पाँच
Answer:
राजा अपनी बेटियों से कितने साल बाद गेहूँ के दानों की मांग करने वाला था?

Question 2.
बुद्धिमती
Answer:
राजा के अनुसार राजपाट संभालने के लिए बेटियों के पास कौन-सा गुण होना आवश्यक है?

निम्नलिखित कथन सत्य है या असत्य लिखिए।
Question 1.
दूसरी बहन पाँच साल बाद दानों को भंडार से लेकर राजा को देने वाली थी।
Answer:
असत्य

राजा की चार बेटियाँ थीं।
Answer:
सत्य

कृति क (३) शब्द संपदा

मानक वर्तनी के अनुसार शब्द शुद्ध कीजिए।

1. भण्डार
2. गेहूं

Answer:

1. भंडार
2. गेहूँ

लिंग बदलिए।

1. बुद्धिमती
2. राजा

Answer:

1. बुद्धिमान
2. रानी

वचन बदलिए।

1. बेटियाँ
2. कमरा

Answer:

1. बेटी
2. कमरे

नीचे दिए हुए शब्दों के पर्यायवाची शब्द लिखिए।

1. चाँदी
2. फैसला

Answer:

1. रजत
2. निर्णय

Question 1.
परिच्छेद में आए युग्म-शब्द लिखिए।
Answer:
सौ-सौ , अपने-अपने

कृति क (४) स्वमत अभिव्यक्ति

Question 1.
‘बुद्धिमान या बुद्धिमती होना बेहद जरूरी होता है।’ इस कथन के संदर्भ में अपने विचार लिखिए।
Answer:
जी हाँ, बुद्धिमान या बुद्धिमती होना बेहद जरूरी होता है। यह इंसान का व्यक्तित्व अधिक आकर्षक बना देता है। बुद्धिमान या बुद्धिमती होना, यह एक आवश्यक गुण है। जिस इंसान के पास यह गुण होता है, वह सर्वत्र पूजनीय होता है। सभी ऐसे व्यक्ति की प्रशंसा करते हैं। कवि रवींद्रनाथ टैगोर, सरोजिनी नायडू, डॉ. सी. व्ही. रामन व डॉ. अब्दुल कलाम आदि बुद्धिमान थे। अपने इस बुद्धि व विवेक के कारण ही वे समाज में वंदनीय हो गए। इसलिए यदि जीवन में हमें प्रगति करनी है, तो बुद्धिमान या बुद्धिमती होने के लिए प्रयत्न करना चाहिए। कह्य भी गया है कि विवेकी पुरुष की हर जगह पूजा की जाती है।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ख (१) आकलन कृति

किसने, किससे कहा?

Question 1.
कहाँ हैं वे दाने?
Answer:
राजा ने अपनी चार बेटियों से कहा।

निम्नलिखित गलत वाक्य सही करके लिखिए।

Question 1.
शरारतें करना तीसरी बहन को बहुत पसंद था।
Answer:
शरारतें करना चौथी बहन को बहुत पसंद था।

Question 2.
बड़ी राजकुमारी खेत में जाकर गेहूँ के दाने लेकर आई।
Answer:
बड़ी राजकुमारी भंडार घर में जाकर गेहूँ के दाने लेकर आईं।

उचित घटनाक्रम लगाकर वाक्य फिर से लिखिए।

1. दाने निकले।
2. दाने बो दिए।
3. पौधे तैयार हुए।
4. समय पर अंकुर फूटे।

Answer:

1. दाने बो दिए।
2. समय पर अंकुर फूटे।
3. पौधे तैयार हुए।
4. दाने निकले।

कृति ख (३) शब्द संपदा

गद्यांश में से शब्द-युग्म लिखिए।
Answer:
दो-तीन
सौ-सौ

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
राजा की बेटी
Answer:
राजकुमारी

Question 2.
वह कक्ष जहाँ पर खाने-पीने की सामग्री रखी जाती है
Answer:
भंडार घर

विलोम शब्द लिखिए।

1. समय x
2. बहुत x

Answer:

1. समय x असमय
2. बहुत x कम

निम्नलिखित शब्द से उपसर्ग अलग कीजिए।

1. सुरक्षा
2. नापसंद

Answer:

1. उपसर्ग : सु
2. उपसर्ग : ना

निम्नलिखित शब्द से प्रत्यय अलग कीजिए।

1. पीछेवाली
2. सहेजकर

Answer:

1. प्रत्यय : वाली
2. प्रत्यय : कर

कृति ख (४) स्वमत अभिव्यक्ति

Question 1.
‘समझदारी से काम करना लाभदायक होता है। कथन के संदर्भ में अपने विचार लिखिए।
Answer:
समझदारी को सामान्य भाषा में अक्लमंदी कहते हैं। समझदारी काअर्थ है दूर की सोचना । जैसी स्थिति है उसी प्रकार निर्णय लेना व कृति करना। जिस व्यक्ति के पास समझदारी होती है, उसका भविष्य उज्ज्वल होता है। समझदार व्यक्ति प्रत्येक परिस्थिति व समस्या का अत्यंत सावधानीपूर्वक तरीके से समाधान प्राप्त करते है। दुनिया में ऐसे कई उदाहरण हैं कि जिन्होंने समझदारी से काम करके स्वयं का उदधार किया और साथ में दूसरों पर भी उपकार किया आचार्य चाणक्य ने समझदारी से काम करके चंद्रगुप्त को राजा बनाया था। छत्रपति शिवाजी महाराज ने भी समझदारी से काम करके मुगलों को मुंहतोड़ जवाब दिया था। इसलिए जीवन में समझदारी आवश्यक होती है। व्यक्ति के व्यक्तित्व विकास में समझदारी का महत्त्वपूर्ण स्थान है।

कृति ग (२) आकलन कृति

किसने, किससे कहा?

Question 1.
तुमने क्या किया उन दानों का?
Answer:
राजा ने तीसरी राजकुमारी से पूछा।

Question 2.
तुम्हारे दाने कहाँ हैं?
Answer:
राजा ने दूसरी राजकुमारी से पूछा।

सही विकल्प चुनकर वाक्य फिर से लिखिए।

Question 1.
मुझे ” के भुने हुए दाने बहुत अच्छे लगते हैं। (चावल, गेहूं, बाजरा)
Answer:
मुझे गेहूं के भुने हुए दाने बहुत अच्छे लगते हैं।

Question 2.
दूसरी राजकुमारी ने दाने मखमल के खोलवाली डिब्बी में …रखे थे। (सहेजकर, सँभालकर, डालकर)
Answer:
दूसरी राजकुमारी ने दाने मखमल के खोलवाली डिब्बी में सहेजकर रखे थे।

कृति ग (३) शब्द संपदा

निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।

1. अच्छा
2. सच्चा

Answer:

1. अच्छाई
2. सच्चाई

लिंग बदलिए।

1. राजकुमारी
2. राजा

Answer:

1. राजकुमार
2. रानी

वचन बदलिए।

1. डिब्बी
2. दाना

Answer:

1. डिब्बियाँ
2. दाने कृति ग

स्वमत अभिव्यक्ति

Question 1.
चारों राजकुमारी में से किस राजकुमारी का जवाब आपको अच्छा लगा और क्यों?
Answer:
चारों राजकुमारी में से तीसरी राजकुमारी का जवाब मुझे अच्छा लगा क्योंकि उसके जवाब में थोड़ी उम्मीद थी। वह राजा को सवाल का जवाब पाने के लिए कहीं लेकर जाने वाली थी। पहली राजकुमारी भंडार घर से दाने लेकर आई थी। दूसरी राजकुमारी ने मखमल के खोलवाली डिब्बी में दाने सहेजकर रखा था और चौथी राजकुमारी गेहूँ के दाने भुनवाकर खाए थे। सिर्फ तीसरी राजकुमारी राजा को उन दानों का रहस्य जानने के लिए किसी अपरिचित स्थान पर लेकर जाने वाली थी। अतः उससे ही कुछ उम्मीद की जा सकती थी।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति घ (१) आकलन कृति

निम्नलिखित गलत वाक्य सही करके फिर से लिखिए।

Question 1.
राजा घोड़े पर सवार हो गया।
Answer:
राजा रथ पर सवार हो गया।

Question 2.
राजा ने चारों राजकुमारी को गले लगा लिया।
Answer:
राजा ने तीसरी राजकुमारी को गले लगा लिया।

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके निम्नलिखित शब्द हों –

1. गेहूँ
2. बालियाँ ।

Answer:

1. फसल कौन-से अनाज की थी?
2. हवा में क्या झूम रही थी?

कृति घ (२) आकलन कृति

Question 1.
कृति पूर्ण कीजिए।
Answer:

Question 2.
गेहूं की फसल देखने का परिणाम
Answer:
राजा ने अपनी तीसरी बेटी को गले लगा लिया और उसे राज्य का उत्तराधिकारी घोषित कर दिया।

कृति घ (३) शब्द संपदा

विलोम शब्द लिखिए।

1. नगर x
2. पास x

Answer:

1. नगर x गाँव
2. पास x दूर

समानार्थी शब्द लिखिए।

1. राजा
2. हवा

Answer:

1. नृप
2. वायु

तत्सम शब्द लिखिए।

1. पिता
2. राजा

Answer:

1. पितृ
2. राजन

कृति घ (४) स्वमत अभिव्यक्ति

Question 1.
क्या राजा का निर्णय सही था? यदि हाँ, तो क्यों? – अपने विचार लिखिए।
Answer:
हाँ, राजा का निर्णय सही था। उसने अपने राज्य के उत्तराधिकारी के तौर पर अपनी तीसरी बेटी का चयन किया, यह राजा का सही निर्णय था। राजा की तीसरी बेटी ने सौ गेहूँ के दानों को मिट्टी मे बो दिए थे। अब वे सौ दाने लाख-लाख दानों के रूप में खेत में झूम रहे थे। राजा की तीसरी बेटी चीजों का सही उपयोग करना जानती थी। उसके पास अक्लमंदी व समझदारी थी। उसके इस गुणों को राजा ने परखा। इसलिए वह भलीभांति जानते थे कि भविष्य में वह राज्य को ठीक से चला सकती है। इसी कारण उसने अपनी तीसरी बेटी को राज्य के उत्तराधिकारी के तौर पर चयनित किया।

Hindi Sulabhbharti Class 8 Solutions पहली इकाई

• हे मातृभूमि! Question Answer
• वारिस कौन? Question Answer
• नाखून क्यों बढ़ते हैं? Question Answer
• गाँव-शहर Question Answer
• मधुबन Question Answer
• जरा प्यार से बोलना सीख लीज Question Answer
• मेरे रजा साहब Question Answer
• पूर्ण विश्राम Question Answer
• अनमोल वाणी Question Answer

Class 8 Hindi Chapter 6 Jara Pyar Se Bolna Sikh Lijiye Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 6 जरा प्यार से बोलना सीख लीज Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 6 Jara Pyar Se Bolna Sikh Lijiye Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 6 जरा प्यार से बोलना सीख लीज Textbook Questions and Answers

सूचनानुसार कृतियाँ करो:

प्रवाह तालिका पूर्ण करो:

Question 1.

Answer:

चुप रहने के चार फायदे लिखिए।

Answer:
१. किसी के साथ दुश्मनी मोल न लेना।
२. संघर्ष एवं लड़ाई झगड़े से बचना।
३. किसी के बुरे शब्द नहीं सहना।
४. समाज में हमारी इज्जत बनी रहना।

उत्तर लिखो:

1. काँटे बोने वाले –
2. चुभने वाले –
3. फटने वाले –
4. मीठी बोली वाले –

Answer:

1. कटु वचन
2. बेबात बात
3. पटाखे
4. गुल या गुलाब

कविता में आए इस अर्थ के शब्द लिखो:

Question 1.

Answer:

भाषाबिंदु

उपसर्ग व प्रत्यय अलग करके मूल शब्द लिखिए।

Question 1.
भारतीय, आस्थावान, व्यक्तित्व, स्नेहिल, बेबात, निरादर, प्रत्येक, सुयोग
Answer:

उपयोजित लेखन

Question 1.
‘यातायात की समस्याएँ एवं उपाय’ विषय पर निबंध लिखिए।
Answer:
यातायात यानी ‘ट्रॉफिक’ यातायात के साधनोंद्वारा हम लंबी दूरी बहुत ही कम समय में तय करते हैं। विज्ञान के इस युग में यातायात के साधनों में वृद्धि हो गई हैं। मुंबई व दिल्ली जैसे शहरों में यातायात के साधनों की सड़कों पर भरमार दिखलाई देती है। इसने ट्रॉफिक की समस्या निर्माण हो रही हैं। वाहनों से निकलने वाले धुएँ ने सभी का जीना हराम कर दिया है। लोग ठीक से साँस भी नहीं ले पा रहे हैं। इसलिए धुएँ वाली गाड़ी नहीं चलानी चाहिए। हॉर्न की सतत आवाज से लोगों को सरदर्द एवं हृदयरोग जैसी बीमारियों को शिकार होना पड़ रहा है। विज्ञान के चमत्कार के कारण हवाई जहाज का निर्माण हुआ है। इससे पक्षियों को खतरा हो रहा है। हवाई जहाज ऐसा होना चाहिए जिससे वायु प्रदूषण न हो।

आज ट्रेन के लिए ट्रैक बनाने के लिए बड़े-बड़े पहाड़ों एवं वनों को काटा जा रहा है। इसका दुष्प्रभाव पर्यावरण पर पड़ रहा है। इसके लिए सभी को खाली जगहों पर पेड़ लगाने चाहिए। नदी व समुद्र पर पुल बनाए जा रहे हैं जिससे जल प्रदूषित हो रहा है। गाड़ियों की संख्या बढ़ने से डीज़ल व पेट्रोल का प्रयोग बढ़ रहा है।

यातायात की समस्याओं पर रोक लगाने के लिए सभी को यातायात के नियमों का पालन करना चाहिए। इन नियमों का सभी को ज्ञान होना चाहिए। यदि ऐसा होगा, तो सड़क दुर्घटना की दर कम हो सकती है। ध्यान रहे कि यातायात के साधनों का लाभ हम तभी ले सकते हैं, जब हम सही ढंग से उनका इस्तेमाल करना सीख जाएँ।

कल्पना पल्लवन

Question 1.
‘वाणी की मधुरता सामने वाले का मन जीत लेती है।’ इस तथ्य पर अपने विचार लिखिए।
Answer:
वाणी ईश्वर द्वारा मनुष्य को मिली एक अनूठी देन है। मनुष्य की वाणी में वह शक्ति होती है जो सामने वाले व्यक्ति को अपना मित्र या दुश्मन भी बना सकती है। यदि हमें सामने वाले व्यक्ति का मन जीतना है,तो हमें मधुर वाणी का प्रयोग करना चाहिए। मीठी वाणी मित्रता के द्वार खोलकर अच्छे संबंध स्थापित करने में सहायक सिद्ध होती है। तलवार का घाव देर-सबेर भर जाता है, लेकिन कटु वाणी से हुआ घाव कभी नहीं भरता।

इसलिए हमेशा मीठी वाणी में बोलना चाहिए। गौतम बुद्ध व महात्मा गांधी जैसे महापुरूषों ने मीठी वाणी के माध्यम से ही दुनिया को अपना बना लिया था। मदर टेरेसा के मधुर वचनों को सुनकर हजारों लोग उनके जैसे समाजसेवी बन गए थे। कोयल की ‘कुह-कुहू’ किसे नहीं अच्छी लगती? सभी उसकी मीठी बोली के कायल हैं। इसलिए संत कबीर भी कहते हैं :
ऐसी वाणी बोलिए मन का आपा खोय औरन को शीतल करै आपह शीतल होय।।

Question 1.
कविता की अंतिम चार पंक्तियों का अर्थ लिखो।
Answer:
प्रस्तुत पंक्तियाँ कवि रमेश दत्त शर्मा लिखित ‘जरा प्यार से बोलना सीख लीजे ।’ कविता से ली गई है। कवि कह रहे हैं कि बिना किसी वजह से बात बेबात यदि कोई तकलीफ देने की कोशिश करे, तो इंसान को उसे मोड़ना सीख लेना चाहिए। हमें तकलीफ देने वालों को मुँहतोड़ जवाब देना सीख लेना चाहिए। अर्थात विपरीत परिस्थितियों में हमें बुद्धि व विवेक से काम करना चाहिए।

स्वयं अध्ययन

हिंदी साप्ताहिक पत्रिकाएँ/समाचार पत्रों से प्रेरक कथाओं का संकलन करो।

Hindi Sulabhbharti Class 8 Solutions Chapter 6 जरा प्यार से बोलना सीख लीज Additional Important Questions and Answers

समझकर लिखिए।

Question 1.
अपने आप को टोकना चाहिए
Answer:
लड़ाई या जब किसी के साथ उलझते समय हम स्वयं का नियंत्रण न खो बैठे इसलिए अपने आप को टोकना चाहिए।

Question 2.
खयालों को खुद तौलना चाहिए।
Answer:
यदि हमने कभी बिना कुछ सोचे कुछ गलत बोल दिया, तो सामने वाले व्यक्ति पर उसका गलत असर पड़ता है। इसलिए खयालों को हमें खुद तौलना चाहिए।

एक शब्द में उत्तर लिखिए।

Question 1.
वक्त पर यह खोलनी चाहिए।
Answer:
जुंबा

Question 2.
इन्हें तौलना चाहिए।
Answer:
खयालों

निम्नलिखित पद्यांशों का भावार्थ लिखिए ।

Question 1.
वाणी में शहद ……………………. बोलना सखि लाज ।
Answer:
प्रस्तुत पंक्तियाँ कवि रमेश दत्त शर्मा लिखित ‘जरा प्यार से बोलना सीख लीजे।’ कविता से ली गई है। कवि कह रहे हैं कि इंसान को सभी से प्रेम से बोलना चाहिए । इंसान की वाणी में शहद होना चाहिए यानी उसकी वाणी मीठी होनी चाहिए । उसे सभी के साथ मीठी व मधुर वाणी में वार्तालाप करना चाहिए । इंसान को सभी के साथ प्यार से सहृदयतापूर्वक बोलना सीखना चाहिए ।

Question 2.
चुप रहने के ……………………. खोलना सीख लीजे ।
Answer:
प्रस्तुत पंक्तियाँ कवि रमेश दत्त शर्मा लिखित ‘जरा प्यार से बोलना सीख लीजे।’ कविता से ली गई है। कवि इन पंक्तियों के माध्यम से कह रहे हैं कि इंसान को चुप रहना सीखना चाहिए। चुप रहने के कई लाभ हैं। अत: योग्य समय आने पर इंसान को अपना मुँह खोलना चाहिए। अर्थात योग्य समय पर योग्य बात करनी चाहिए।

Question 3.
कुछ कहने से ……………………. तौलना सीख लीजे ।
Answer:
प्रस्तुत पंक्तियाँ कवि रमेश दत्त शर्मा लिखित ‘जरा प्यार से बोलना सीख लीजे।’ कविता से ली गई हैं। कवि के मतानुसार व्यक्ति को बोलने से पहले गहन विचार करना चाहिए। प्रत्येक व्यक्ति को सोच-समझकर बोलना चाहिए। उसे विचारों को तौलकर बात करने की कला का अभ्यास करना चाहिए।

Question 4.
कविता की पंक्तियाँ पूर्ण कीजिए।
Answer:
बात बेबात कोई चुभने लगे तो,
बदलकर उसे मोड़ना सीख लीजे।
ये किसने कहा कि होंठ सीकर के बैठो,
जरूरत पे मुँह खोलना सीख लीजे।

निम्नलिखित कथन सत्य है या असत्य लिखिए ।

Question 1.
इंसान को जरूरत के समय बात नहीं करनी चाहिए।
Answer:
असत्य

Question 2.
तकलीफ देने वालों को हमें मुँहतोड़ जवाब देना चाहिए ।
Answer:
सत्य

पद्यांश के आधार पर पूर्ण वाक्य कीजिए।

Question 1.
मीठी बोली के गुलाब इसलिए बोना चाहिए क्योंकि
Answer:
कड़वे वचन काँटै बोते हैं।

समझकर लिखिए।

Question 1.
पद्यांश में प्रयुक्त एक फूल का नाम
Answer:
गुल (गुलाब)

निम्नलिखित शब्दों के लिए कविता में आए शब्द लिखिए।

1. सिलकर
2. बिना बात
3. कड़वे
4. बोना

Answer:

1. बेबात
2. जरूरत
3. रोपना
4. कटु

कृति ख (३) भावार्थ

निम्नलिखित पद्यांशों का भावार्थ लिखिए।

Question 1.
पटाखे की तरह ……………………. घोलना सीख लीजे।
Answer:
प्रस्तुत पंक्तियाँ कवि रमेश दत्त शर्मा लिखित ‘जरा प्यार से बोलना सीख लोजे ।’ कविता से ली गई है। प्रस्तुत पंक्ति के माध्यम से कवि कह रहे हैं कि इंसान को पटाखे की तरह फटने से पहले उसकी रोशनी के रंग में घुल जाना सीख लेना चाहिए। अर्थात परिस्थिति के अनुरूप कुशलता से व्यवहार करना चाहिए।

Question 2.
कटु बचन ……………………. रोपना सीख लीजे।
Answer:
प्रस्तुत पंक्तियाँ कवि रमेश दत्त शर्मा लिखित ‘जरा प्यार से बोलना सीख लीजे।’ कविता से ली गई हैं। कवि कह रहा है कि व्यक्ति को मधुरभाषी होना चाहिए। कड़वे वचन हमेशा काँटे की तरह चुभते हैं। इंसान को मीठी बोली के पुष्पों का रोपण करना सीख लेना चाहिए। अर्थात हमेशा मीठी वाणी में बात करना चाहिए।

Question 3.
बात बेबात. ………………. खोलना सीख लीजे।
Answer:
प्रस्तुत पंक्तियाँ कवि रमेश दत्त शर्मा लिखित ‘जरा प्यार से बोलना सीख लीजे ।’ कविता से ली गई है। कवि कह रहे हैं कि बिना किसी वजह से बात बेबात यदि कोई तकलीफ देने की कोशिश करे, तो इंसान को उसे मोड़ना सीख लेना चाहिए। हमें तकलीफ देने वालों को मुंहतोड़ जवाब देना सौख लेना चाहिए। अर्थात विपरीत परिस्थितियों में हमें बुद्धि व विवेक से काम करना चाहिए।

Hindi Sulabhbharti Class 8 Solutions पहली इकाई

• हे मातृभूमि! Question Answer
• वारिस कौन? Question Answer
• नाखून क्यों बढ़ते हैं? Question Answer
• गाँव-शहर Question Answer
• मधुबन Question Answer
• जरा प्यार से बोलना सीख लीज Question Answer
• मेरे रजा साहब Question Answer
• पूर्ण विश्राम Question Answer
• अनमोल वाणी Question Answer

Class 8 Hindi Chapter 7 Swarajya Mera Janma Siddh Adhikaar Hai Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 8 Hindi Solutions Sulabhbharati Chapter 7 स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Notes, Textbook Exercise Important Questions and Answers.

Std 8 Hindi Chapter 7 Swarajya Mera Janma Siddh Adhikaar Hai Question Answer Maharashtra Board

Hindi Sulabhbharti Class 8 Solutions Chapter 7 स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Textbook Questions and Answers

सूचना के अनुसार कृतियाँ करो:

विधानों को पढ़कर गलत विधानों को सही करके लिखो:

Question 1.
टिळक जी ने कहा है कि, वे यद्यपि शरीर से जवान है किंतु उत्साह में बूढ़े हैं।
Answer:
टिळक जी ने कहा है कि, वे यद्यपि शरीर से जवान है किंतु उत्साह में बूढ़े हैं – गलत
सही वाक्य: टिळक जी ने कहा है कि वे यद्यपि शरीर से बूढ़े हैं किंतु उत्साह में जवान हैं।

Question 2.
प्रांतीय सम्मेलन अंग्रेजों की देन है।
Answer:
प्रांतीय सम्मेलन अंग्रेजों की देन है – गलत
सही वाक्य: प्रांतीय सम्मेलन कांग्रेस की देन है।

टिप्पणी लिखो:

Question 1.
लोकमान्य टिळक
होमरूल
Answer:
लोकमान्य तिलक: लोकमान्य तिलक भारतीय स्वतंत्रता आंदोलन के प्रमुख नेता थे। वे कांग्रेस के अध्यक्ष थे। उन्होंने भारत को आजाद कराने के लिए सभी भारतीयों को एकता में सूत्र में बाँधने के लिए भरसक कोशिश की थी। ‘स्वराज्य मेरा जन्मसिद्ध अधिकार है’ यह उनका प्रमुख नारा था। उन्होंने अंग्रेजों को भारत छोड़ने के लिए कहा था। उन्होंने पूर्ण स्वराज्य की माँग की थी।

होमरूल लीग: भारत को आजाद कराने के लिए तिलक जी ने भारत में ‘होमरूल लीग’ की स्थापना की थी। होमरूल लीग का एक ही उद्देश्य था, भारत को स्वतंत्र कराना। होमरूल के पीछे छिपी भावना अमर और अविनाशी थी। वह अहिस्ता-अहिस्ता अपना कार्य कर रही थी।

उत्तर लिखो:

Question 1.
लोकमान्य टिळक जी द्वारा दिया गया नारा:
Answer:
स्वराज्य मेरा जन्मसिद्ध अधिकार है।

कृति पूर्ण करो:

Question 1.

Answer:

भाषा बिंद।

Question 1.
पाँच-पाँच सहायक और प्रेरणार्थक क्रियाओं का अपने स्वतंत्र वाक्यों में प्रयोग करो।
Answer:
सहायक क्रिया:

1. चुकना : पिता जी अखबार पढ़ चुके हैं।
2. लगना : माताजी खाना बनाने लगी।
3. रहना : वे सिनेमा देख रहे हैं।
4. सकना : वह अपना काम समय पर कर सका।
5. चाहना : उसने अपना काम करना चाहा।

प्रेरणार्थक क्रियाः

1. पढ़वाना: अध्यापक छात्रों से पाठ पढ़वाते हैं।
2. लिखवाना : सीता अपने बच्चों से कविता लिखवाती है।
3. करवाना : माँ ने घर का सारा काम अपने बच्चों से करवाया।
4. खिलवाना : उसने हमें खाना खिलवाया।
5. दिलवाना : राधा ने अपनी बीमार बहन को नर्स के द्वारा औषधि दिलवाई।

उपयोजित लेखन

अपने विद्यालय में आयोजित स्वच्छता अभियान का वृत्तांत लिखिए।
Answer:
दिनांक ३ अक्तूबर, २०१८, मुंबई : इस दिन नूतन विद्यालय मुंबई में स्वच्छता अभियान का आयोजन किया गया था। इस अवसर पर प्रमुख अतिथि के रूप में महात्मा गांधी भवन के संयोजक श्री. रामजी मल्होत्रा उपस्थित थे। विद्यालय की विद्यार्थी प्रमुख कुमारी अंजलि ने पुष्पगुच्छ देकर मुख्य अतिथि महोदय जी का स्वागत किया। स्कूल प्राचार्या श्रीमती लता जी ने स्वच्छता अभियान के अवसर पर सभी छात्राओं को बधाई दी। अतिथि महोदय जी ने भी अपने वक्तव्य में स्वच्छता अभियान का महत्त्व बताया।

उन्होंने गांधीजी अपने जीवन में स्वच्छता को बहुत महत्त्व देते थे और सभी को स्वच्छ रहने के लिए प्रेरित करते थे, इस तथ्य से सभी को अवगत कराया। इसके उपरांत कक्षा सातवीं से लेकर कक्षा दसवीं तक के सभी छात्रों ने विद्यालय के आस-पास का परिसर स्वच्छ करने हेतु अपने अपने हाथों में बुहारी, झाडू आदि वस्तुएँ लेकर अपने कार्य को आरंभ किया। स्वच्छता अभियान में सभी शिक्षकों ने भी हिस्सा लिया। सभी ने मिलकर विद्यालय के आस-पास पड़ा हुआ कूड़ा-कचरा ही साफ नहीं किया. बल्कि लोगों को स्वच्छता के महत्व के बारे में अवगत भी कराया। इस तरह दोपहर के १२ बजे स्वच्छता अभियान का समापन हुआ।

स्वयं अध्ययन

पाठ में प्रयुक्त उद्धरण, सुवचन, मुहावरे, कहावतें, आलंकारिक शब्द आदि की सूची बनाकर अपने लेखन प्रयोग हेतु संकलन करो।

Hindi Sulabhbharti Class 8 Solutions Chapter 7 स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Additional Important Questions and Answers

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति क (१) आकलन कृति

उचित जोड़ियाँ लगाइए।

Answer:
i – ग
ii – घ
iii – क
iv – ख

तुलना कीजिए।

Question 1.

Answer:

निम्नलिखित गलत विधान को सही करके लिखिए।

Question 1.
तिलक ने कहा है कि, “वे यद्यपि शरीर से जवान है किंतु उत्साह में बूढ़े हैं।”
Answer:
तिलक ने कहा है कि, “वे यद्यपि शरीर से बूढे है किंतु उत्साह में जवान हैं।”

उपर्युक्त गद्यांश से ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –

1. आत्मा
2. स्वराज्य

Answer:

1. अमर कौन होती है?
2. हमारा जन्मसिद्ध अधिकार कौन-सा है?

उत्तर लिखिए।

Question 1.
लोकमान्य तिलक द्वारा दिया गया नारा
Answer:
‘स्वराज्य मेरा जन्मसिद्ध अधिकार है।

निम्नलिखित शब्द के तत्सम रूप लिखिए।

Question 1.
आग
Answer:
अग्नि

निम्नलिखित शब्द मानक वर्तनी के अनुसार लिखिए।

1. जन्मसिध्द
2. जरजर

Answer:

1. जन्मसिद्ध
2. जर्जर

वचन बदलिए।

1. गतिविधि
2. भावना

Answer:

1. गतिविधियाँ
2. भावनाएँ

नीचे दिए हुए शब्दों के पर्यायवाची शब्द लिखिए।

1. अधिकार
2. शरीर

Answer:

1. हक
2. देह

Question 1.
गद्यांश में से विलोम शब्द की जोड़ी ढूँढकर लिखिए।
Answer:
बूढ़ा युवा

Question 2.
‘स्वराज्य प्रत्येक व्यक्ति का जन्मसिद्ध अधिकार है।’कश्चन के संदर्भ में अपने विचार लिखिए।
Answer:
हम सब लोकतांत्रिक देश में रहते हैं। लोकतांत्रिक देश में रहने वाला प्रत्येक व्यक्ति जन्म से स्वतंत्र होता है। उसके इस अधिकार को कोई छीन नहीं सकता है। यदि ऐसा करने की कोई कोशिश भी करें तो संबंधित व्यक्ति को कानून के द्वारा सख्त सजा हो सकती है। स्वराज्य में स्वतंत्र रूप से अपना जीवन-यापन करने वाला व्यक्ति देश के किसी भी कोने में जा सकता है। वह कोई भी भाषा सीख सकता है। वह किसी भी धर्म का अनुयायी बन सकता है। वह अपनी मर्जी से संविधान में दिए गए नियमों का पालन करते हुए अपने जीवन को स्वतंत्र रूप से जी सकता है।

संजाल पूर्ण कीजिए।

Question 1.

Answer:

कारण लिखिए।

Question 1.
आशुलिपि लेखक व्यस्त थे।
Answer:
क्योंकि वे तिलक के भाषण की नोट्स ले रहे थे।

Question 2.
तिलक आम जनता की आत्मा को जगाना चाहते हैं।
Answer:
क्योंकि कुछ अज्ञानी, स्वार्थी और कुचक्री लोगों ने आम जनता की आँखों पर परदा डाल दिया है।

एक शब्द में उत्तर लिखिए।

Question 1.
राजनीति का विज्ञान इस देश के लिए यह है
Answer:
वेद।

समझकर लिखिए।

Question 1.
वही राजनीति विज्ञान कहलाता है
Answer:
जिस विज्ञान की परिणति स्वशासन में होती है।

Question 2.
राजनीति विज्ञान के भाग
Answer:
देवी और राक्षसी।

Question 3.
राजनीति विज्ञान के राक्षसी भाग को उचित ठहराने वाला राष्ट्र
Answer:
ईश्वर की दृष्टि में पाप का भागी होता है।

कृति ख (३) शब्द संपदा

Question 1.
कार्यालय का प्रधान अधिकारी
Answer:
अधीक्षक

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. स्वार्थी
2. दैवी
3. उचित
4. पाप

Answer:

1. निस्वार्थी
2. राक्षसी
3. अनुचित
4. पुण्य

Question 1.
गद्यांश में से विदेशी शब्द ढूँढ़कर लिखिए।
Answer:
कलेक्टर
सी. आय. डी.

निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।

1. ईश्वर
2. विज्ञान

Answer:

1. ईश्वरीय
2. वैज्ञानिक

Question 1.
तिलक जैसे कई महान नेताओं के भाषण सुनकर लोगों की आत्मा जागृत हो गई थीं।’ पर अपने विचार लिखिए।
Answer:
स्वातंत्र्य पूर्व देश की आजादी के प्रति लोगों में चेतना एवं उनकी आत्मा को जगाने का भरसक प्रयास लोकमान्य तिलक, महात्मा गांधी, सुभाषचंद्र बोस जैसे आदि महान नेताओं ने किया। इन नेताओं के भाषण सुनकर लोग स्वराज्य पाने के लिए एकत्रित हुए। आपसी भेदभाव एवं मतभेद भूलकर उन्होंने देश के लिए अंग्रेजों के खिलाफ संघर्ष किया। इसका परिणाम यह हुआ कि भारत देश आजाद हुआ। इतना ही नहीं बल्कि महान नेताओं के भाषण सुनकर वे इतने प्रभावित हुए कि उन्होंने अंध-विश्वास जैसी बुरी प्रथाओं का त्याग किया। इन नेताओं के भाषण को सुनकर ही नवभारत के निर्माण में लोगों की चेतना जागृत हुई।

कृति पूर्ण कीजिए।

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

कारण लिखिए।

Question 1.
हमें कठोर प्रयास करना चाहिए।
Answer:
अपने राष्ट्र की आत्मा की रक्षा के लिए हमें कठोर प्रयास करना चाहिए।

सही विकल्प चुनकर रिक्त स्थान की पूर्ति कीजिए ।

Question 1.
जो हममें दोष देखते हैं वे …… प्रकृति के लोग हैं। (स्वार्थी, धोखेबाज, लोभी)
Answer:
लोभी

Question 2.
कुछ लोग परम …… ईश्वर में भी दोष देखते हैं। (कृपालु, सर्वशक्तिमान, दयावान)
Answer:
कृपालु

पर्यायवाची शब्द लिखिए।

1. हानि
2. साहस
3. प्रयास
4. परवाह

Answer:

1. नुकसान
2. हिम्मत
3. प्रयत्न
4. चिंता

Question 1.
गद्यांश में से ऐसे दो शब्द ढूँढकर लिखिए जिनके वचन परिवर्तन नहीं होते।
Answer:
देश
हित

विलोम शब्द लिखिए।

1. साहस x ……..
2. ज्ञान x ………

Answer:

1. साहस x डर
2. ज्ञान x अज्ञान

निम्नलिखित शब्दों में उचित उपसर्ग का प्रयोग कीजिए।

1. परवाह
2. शिक्षा

Answer:

1. उपसर्ग : बे : शब्द : वेपरवाह
2. उपसर्ग : अ : शब्द : अशिक्षा

निम्नलिखित शब्दों में उचित प्रत्यय का प्रयोग कीजिए।

1. हानि
2. धर्म

Answer:

1. प्रत्यय : कारक : हानिकारक
2. प्रत्यय : इक : धार्मिक

Question 1.
अपने राष्ट्र की आत्मा की रक्षा के लिए सभी को कठोर प्रयास करना चाहिए।’ कथन के संदर्भ में अपने विचार लिखिए।
Answer:
राष्ट्र से बढ़कर व्यक्ति के लिए दूसरी कोई वस्तु या चीज नहीं हो सकती। राष्ट्र के कारण व्यक्ति को मान, सम्मान, शिक्षा प्राप्त करने का अधिकार एवं स्वतंत्र विचरण करने का अधिकार प्राप्त होता है। राष्ट्र के कारण ही व्यक्ति की राष्ट्रीयता का पता चल पाता है। राष्ट्र के कारण व्यक्ति की अस्मिता की पहचान होती है। अत: सभी के हृदय में राष्ट्र के लिए प्रेम एवं सम्मान की भावना होनी चाहिए। राष्ट्र की संस्कृति, मूल्य, आदर्श, परंपरा एवं साहित्य राष्ट्र की आत्मा हाती है। ये सभी घटक मनुष्य की गरिमा बढ़ाने में स्वयं सिद्ध होते हैं। राष्ट्र ही मनुष्य की आत्मा होती है । अत: राष्ट्र की आत्मा की रक्षा के लिए सभी को कठोर प्रयास करना चाहिए।

निम्नलिखित गलत वाक्य सही करके फिर से लिखिए।

Question 1.
प्रांतीय सम्मेलन अंग्रेजों की देन है।
Answer:
प्रांतीय सम्मेलन कांग्रेस की देन है।

Question 2.
भारत के सहयोग के बिना इंग्लैंड चल सकता है।
Answer:
भारत के सहयोग के बिना इंग्लैंड अब चल नहीं सकता है।

उचित जोड़ियाँ मिलाइए।

Question 1.

Answer:
i – ग
ii – घ
iii – क
iv – ख

Question 2.
भारतीय साम्राज्य के लिए ये जान देने के लिए तैयार हैं –
Answer:
श्रीरामचंद्र
तीस करोड़ लोग

Question 3.
गद्यांश में इस अंग्रेज अधिकारी का नाम आया है
Answer:
जॉर्ज।

विलोम शब्द लिखिए।

1. संभव x ………
2. सहयोग x …….

Answer:

1. संभव x असंभव
2. सहयोग x असहयोग

समानार्थी शब्द लिखिए।

1. बहादुरी
2. राष्ट्र

Answer:

1. वीरता
2. देश

अनेक शब्द के लिए एक शब्द लिखिए।

Question 1.
जो संविधान से जुड़ा हो
Answer:
संवैधानिक।

Question 2.
ऐसी सभा जिसमें किसी विशिष्ट कार्य या समस्या पर चिंतन होता है।
Answer:
सम्मेलन।

Question 3.
गद्यांश में से विदेशी शब्द ढूँढकर लिखिए।
Answer:
ब्रिटिश
जॉर्ज

Question 4.
‘प्रयास के बिना मानव जीवन सफल नहीं हो सकता।’ अपने विचार लिखिए।
Answer:
प्रयास यानी प्रयत्न करना; कोशिश करना। सफलता की मंजिल प्राप्त करने के लिए व्यक्ति को जीवन में प्रयास करना चाहिए। प्रयासों के बिना व्यक्ति जीवन में ऐसे कई महापुरुषों के उदाहरण मिलेंगे जिन्होंने जीवन में स्वयं की प्रगति कराने हेतु भगीरथ प्रयास किए थे। न्यूटन ने गुरूत्वाकर्षण के सिद्धांत की खोज करने हेतु कई बार प्रयास किए, तब जाकर वह सफल हुआ। आखिर प्रयत्न ही सिद्धि है। विद्यार्थी को भी जीवन में सफल होने हेतु प्रयत्न करने चाहिए। प्रयत्नों के बिना यश की प्राप्ति नहीं हो सकती।

Hindi Sulabhbharati 8th Standard Digest Guide दूसरी इकाई

• धरती का आँगन महके Question Answer
• दो लघुकथाएँ Question Answer
• लकड़हारा और वन Question Answer
• सौहार्द -सौमनस्‍य Question Answer
• खेती से आई तब्‍दीलियाँ Question Answer
• अंधायुग Question Answer
• स्‍वराज्‍य मेरा जन्मसिद्ध अधिकार है Question Answer
• मेरा विद्रोह Question Answer
• नहीं कुछ इससे बढ़कर Question Answer