Class 6

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 14 अप्पाजींचे चातुर्य Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 14 अप्पाजींचे चातुर्य Question Answer Maharashtra Board

Std 6 Marathi Chapter 14 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 14 अप्पाजींचे चातुर्य Textbook Questions and Answers

1. एका वाक्यात उत्तर लिहा.

प्रश्न अ.
अप्पाजींनी बैलगाडीत कशाचे पीक घ्यायला लावले?
उत्तर:
अप्पाजींनी बैलगाडीत कोबीचे पीक घ्यायला लावले.

प्रश्न आ.
उत्कृष्ट दर्जाची मूर्ती कोणती?
उत्तरः
ज्या मूर्तीच्या कानात घातलेली तार तेथेच अडून राहिली, ती तिसरी मूर्ती उत्कृष्ट दर्जाची होय.

प्रश्न इ.
कलिंगचा राजा संतुष्ट का झाला?
उत्तरः
अप्पाजींनी तीनही मूर्तीचा दर्जा बरोबर ओळखल्याने कलिंग राजा संतुष्ट झाला.

2. तीन – चार वाक्यांत उत्तरे लिहा.

प्रश्न अ.
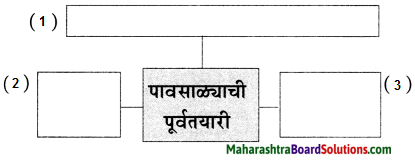
अप्पाजींनी ताजी कोबी कलिंग देशाकडे कशी पाठवली?
उत्तरः
राजाने अप्पाजींच्या सांगण्याप्रमाणे एका गाडीत माती भरून त्यात कोबीच्या बिया पेरून ती कलिंग राज्याकडे रवाना केली. गाडीवान प्रवासात रोज कोबींच्या रोपांना पाणी देत असे. तीन महिन्यांनी ती बैलगाडी कलिंग राज्यात पोहचली. अशाप्रकारे कलिंग राजाला ताजी कोबी मिळाली.

प्रश्न आ.
कलिंगच्या राजाने अप्पाजींची दुसऱ्यांदा कशी परीक्षा घेतली?
उत्तरः
कलिंगच्या राजाने दुसऱ्यांदा एकसारख्या दिसणाऱ्या तीन मूर्ती मागवल्या व म्हणाला, ‘या तीनही मूर्ती दिसायला सारख्या असल्या, तरी यांतली एक मूर्ती निकृष्ट आहे, दुसरी मध्यम दर्जाची आहे आणि तिसरी उत्कृष्ट आहे. या सारख्या दिसणाऱ्या तीन मूर्तीमधील उत्कृष्ट कोणती ते मला
सांगा.’

अप्पाजींनी एक लवचिक तार घेतली. ती पहिल्या मूर्तीच्या कानात घातली. ती तार मूर्तीच्या तोंडातून बाहेर पडली. अप्पाजी म्हणाले, ‘ही निकृष्ट मूर्ती आहे! नंतर अप्पाजींनी ती तार दुसऱ्या मूर्तीच्या कानात घातली. ती तार त्या मूर्तीच्या दुसऱ्या कानातून बाहेर पडली. अप्पाजी म्हणाले, ‘ही मध्यम दर्जाची मूर्ती होय.’ तिसऱ्या मूर्तीवरही अप्पाजींनी हाच प्रयोग केला. त्या मूर्तीच्या कानात घातलेली तार तिच्या तोंडातून वा दुसऱ्या कानातून कोठूनच बाहेर पडली नाही. अप्पाजी म्हणाले, ‘ही उत्कृष्ट मूर्ती.’ अशा प्रकारे परीक्षा घेतली.

प्रश्न इ.
मूर्तीच्या तोंडात घातलेली तार तोंडातून बाहेर येते याचा अप्पाजींनी कोणता अर्थ लावला?
उत्तरः
एखादा माणूस ज्या अफवा ऐकतो, त्याचा खरेखोटेपणा पडताळून न पाहता जर तो त्या दुसऱ्यांना सांगू लागला, तर त्याचे व समाजाचेही हित होत नाही. असा अर्थ मूर्तीच्या कानात घातलेली तार तोंडातून बाहेर पडलेल्या मूर्तीबद्दल सांगितला.

प्रश्न ई.
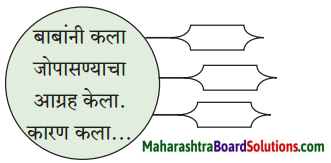
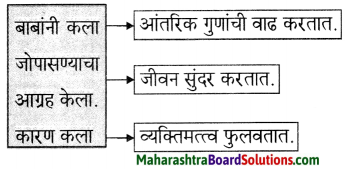
अप्पाजींच्या मते उत्तम माणूस कोणता?
उत्तरः
अफवा ऐकल्यावर जो माणूस दुसऱ्या कानाने ती सोडून देत नाही किंवा लगेच ती दुसऱ्याला सांगत नाही, तर तिच्या खरेखोटेपणाची खात्री करून घेतो आणि आपण काय ऐकले ते पुराव्याशिवाय सांगत नाही, तो माणूस उत्तम. असे अप्पाजींचे मत आहे.

3. पाणी टंचाईमुळे तुम्हांला पाणी दुरून आणायचे आहे. कमी श्रमात ते आणण्यासाठी तुम्ही काय प्रयत्न कराल?

प्रश्न 1.
पाणी टंचाईमुळे तुम्हांला पाणी दुरून आणायचे आहे. कमी श्रमात ते आणण्यासाठी तुम्ही काय प्रयत्न कराल?

4. विरूद्धार्थी शब्द लिहा.

प्रश्न 1.
विरूद्धार्थी शब्द लिहा.
उत्तरः
(अ) हित × अहित
(आ) निकृष्ट × उत्कृष्ट

5. खाली दिलेल्या उदाहरणाप्रमाणे चौकट पूर्ण करा.

प्रश्न 1.
खाली दिलेल्या उदाहरणाप्रमाणे चौकट पूर्ण करा.

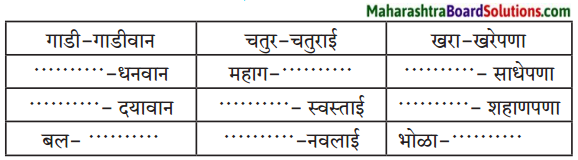
उत्तरः

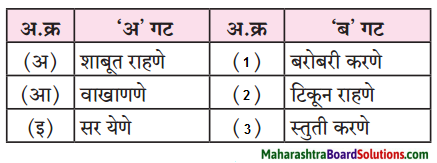
गाडी – गाडीवान	चतुर – चतुराई	खरा – खरेपणा
धन – धनवान	महाग – महागाई	साधे – साधेपणा
दया – दयावान	स्वस्त – स्वस्ताई	शहाणा – शहाणपणा
बल – बलवान	नवल – नवलाई	भोळा – भोळेपणा

6. खालील शब्द वाचा व समजून घ्या.

प्रश्न 1.
खालील शब्द वाचा व समजून घ्या.
उत्तर:

1. चतुर – चातुर्य
2. चोरी – चौर्य
3. क्रूर – कौर्य
4. शूर – शौर्य
5. सुंदर – सौंदर्य
6. धीर – धैर्य

7. खालील शब्दांना तो, ती, ते शब्द लावून लिंग ओळखा.

प्रश्न 1.

1. दरी
2. पान
3. पुस्तक
4. माठ
5. लाडू
6. वही

उत्तर:

1. ती दरी – स्त्रीलिंग
2. ते पान – नपुंसकलिंग
3. ते पुस्तक – नपुंसकलिंग
4. तो माठ – पुल्लिंग
5. तो लाडू – पुल्लिंग
6. ती वही – स्त्रीलिंग

8. तुमच्या मित्राच्या / मैत्रिणीच्या चतुरपणाचे कौतुक झाल्याचा प्रसंग घरी व वर्गात सांगा.

प्रश्न 1.
तुमच्या मित्राच्या / मैत्रिणीच्या चतुरपणाचे कौतुक झाल्याचा प्रसंग घरी व वर्गात सांगा.
उत्तर:
आज रस्त्याने जात असता एक तरूण मुलगा कानात हेडफोन घालून मोबाईलची गाणी ऐकत रस्ता पार करत होता. त्याने डावी व उजवीकडे गाडी येताना पाहिलेच नाही. तेवढ्यात समोरून एक सुसाट गाडी येताना माझ्या मित्राला दिसली. ती गाडी सतत हॉर्न वाजवत होती, पण त्याच्या कानावर तो आवाज गेला नाही. आता अपघात होणारच होता एवढ्यात माझ्या तनय नावाच्या मित्राने समयसुचकता दाखवून त्याला पटकन मागे ओढले. म्हणून तो अपघात टळला. तनयचे कौतुक करावे तेवढे थोडेच.

9. अप्पाजींसारख्या अनेक चतुर व्यक्ती इतिहासात होऊन गेल्या आहेत. उदा., बिरबल, तेनालीराम. यांच्या गोष्टी मिळवा. वाचा. वर्गात सांगा.

प्रश्न 1.
अप्पाजींसारख्या अनेक चतुर व्यक्ती इतिहासात होऊन गेल्या आहेत. उदा., बिरबल, तेनालीराम. यांच्या गोष्टी मिळवा. वाचा. वर्गात सांगा.

10. खालील वेबमध्ये दिलेल्या शब्दांस विशेषणे लावा.

प्रश्न 1.

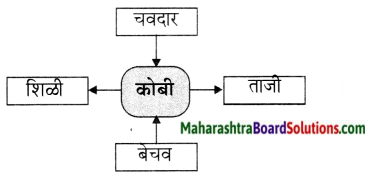
उत्तरः

1. चवदार कोबी
2. बेचव कोबी
3. ताजी कोबी
4. शिळी कोबी

प्रश्न 2.

उत्तरः

1. मातीची मूर्ती
2. देखणी मूर्ती
3. सजवलेली मूर्ती
4. सुंदर मूर्ती

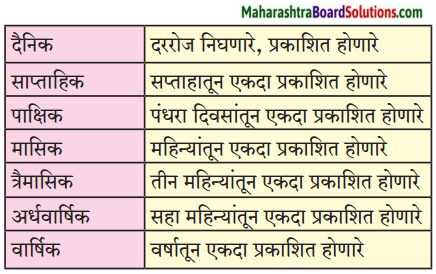
खालील तक्ता वाचा. समजून घ्या.

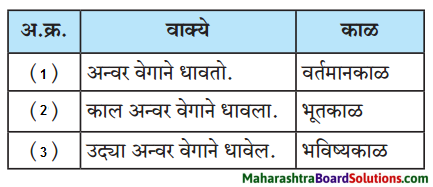
प्रश्न 1.

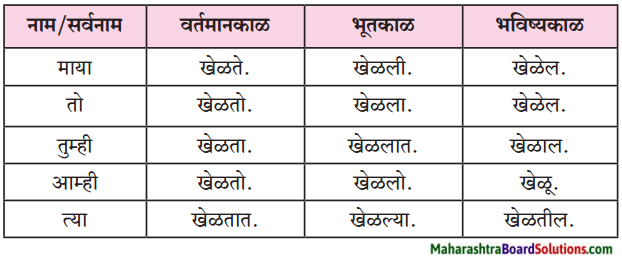
उत्तर:

वतमान काळ	भूतकाळ	भविष्य काळ
1. माया खेळते	माया खेळली	माया खेळेल
2. तो खेळतो	तो खेळला	तो खेळेल
3. तुम्ही खेळता	तुम्ही खेळलात	तुम्ही खेळाल
4. आम्ही खेळतो	आम्ही खेळलो	आम्ही खेळू
5. त्या खेळतात	त्या खेळल्या	त्या खेळतील

दिलेल्या सूचनांप्रमाणे खालील वाक्यांत बदल करा.

प्रश्न 1.
रिमा सहलीला गेली. (भविष्यकाळ करा)
उत्तर:
रिमा सहलीला जाईल.

प्रश्न 2.
मला आंबा आवडतो. (भूतकाळ करा)
उत्तर:
मला आंबा आवडला.

प्रश्न 3.
चंदाने लाडू खाऊन संपवला. (वर्तमानकाळ करा)
उत्तर:
चंदा लाडू खात आहे.

प्रश्न 4.
सुभाष माझा मित्र आहे. (भूतकाळ करा)
उत्तर:
सुभाष माझा मित्र होता.

प्रश्न 5.
वंदना अभ्यास करते. (भूतकाळ करा)
उत्तर:
वंदनाने अभ्यास केला.

प्रश्न 6.
संजू क्रिकेट खेळतो. (भविष्यकाळ करा)
उत्तर:
संजू क्रिकेट खेळेल.

पूर, गाव, नगर,बाद ही अक्षरे असणाऱ्या गावांची, शहरांची, ठिकाणांची नावे खालील तक्त्यात लिहा.

प्रश्न 1.
पूर, गाव, नगर,बाद ही अक्षरे असणाऱ्या गावांची, शहरांची, ठिकाणांची नावे खालील तक्त्यात लिहा.

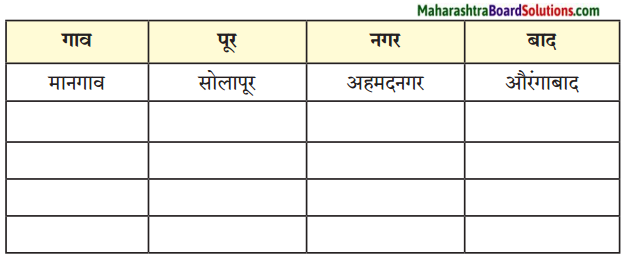
उत्तर:

गाव	पूर	नगर	बाद
1. मानगाव	सोलापूर	अहमदनगर	औरंगाबाद
2. नागाव	कोल्हापूर	सह्याद्रीनगर	दौलताबाद
3. सोनगाव	नागपूर	संभाजीनगर	उस्मानाबाद
4. भरतगाव	कानपूर	हनुमाननगर	फिरोजाबाद
5. धरणगाव	राजापूर	वैभवनगर	अहमदाबाद
6. शेगाव	तारापूर	जामनगर	हैद्राबाद

Class 6 Marathi Chapter 14 अप्पाजींचे चातुर्य Additional Important Questions and Answers

खालील प्रश्नांची प्रत्येकी एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
कृष्णदेवराय कोणत्या नगराचा राजा होता?
उत्तरः
कृष्णदेवराय विजयनगरचा राजा होता.

प्रश्न 2.
विजयनगरच्या प्रधानाचे नाव काय होते?
उत्तरः
विजयनगरच्या प्रधानाचे नाव अप्पाजी होते.

प्रश्न 3.
उत्तरकडे कोणते राज्य होते?
उत्तरः
उत्तरेकडे कलिंग राज्य होते.

प्रश्न 4.
त्या काळी वाहतूक कशातून होत असे?
उत्तरः
त्या काळी बैलगाडीतून वाहतूक होत असे.

प्रश्न 5.
बैलगाड्या कलिंग राज्यात पोहचायला किती महिने लागत?
उत्तरः
बैलगाड्या कलिंग राज्यात पोहचायला तीन महिने लागत.

प्रश्न 6.
कलिंग राजाने एकूण किती मूर्त्या आणल्या?
उत्तरः
कलिंग राजाने एकूण तीन मूर्त्या आणल्या.

प्रश्न 7.
निकृष्ट दर्जाची मूर्ती कोणती?
उत्तरः
मूर्तीच्या कानातून घातलेली तार मूर्तीच्या तोंडातून बाहेर पडली ही निकृष्ट दर्जाची मूर्ती होय.

प्रश्न 9.
मध्यम दर्जाची मूर्ती कोणती?
उत्तर:
ज्या मूर्तीच्या एका कानातून घातलेली तार दुसऱ्या कानातून बाहेर पडली ती मूर्ती मध्यम दर्जाची होय.

व्याकरण व भाषाभ्यास

प्रश्न 1.
खालील शब्दांचे समानार्थी शब्द लिहा.

1. जुनी
2. गोष्ट
3. चतुर
4. राजा
5. निरोप
6. निकृष्ट
7. उत्कृष्ट
8. कान
9. माणूस
10. खात्री
11. संतुष्ट
12. पुरावा

उत्तर:

1. पुराणी
2. कथा
3. हुशार
4. नृप
5. सांगावा
6. तकलादू
7. चांगली
8. कर्ण
9. मनुष्य
10. विश्वास
11. समाधानी
12. दाखला

प्रश्न 2.
खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

1. जुनी
2. उत्तर
3. प्रश्न
4. चतुर
5. चवदार
6. इच्छा
7. जलद
8. ताजी
9. सारखा
10. बाहेर
11. माणूस
12. खरे
13. नुकसान

उत्तर:

1. नवी
2. दक्षिण
3. उत्तर
4. मुर्ख
5. बेचव
6. अनिच्छा
7. सावकाश
8. शिळी
9. वेगळा
10. आत
11. स्त्री
12. खोटे
13. फायदा

अप्पाजींचे चातुर्य Summary in Marathi

पाठपरिचय:

विजयनगरमध्ये असणाऱ्या कृष्णदेवरायच्या राज्यात त्याचे प्रधान अप्पाजी फार चतुर होते. उत्तरेकडे असलेल्या कलिंग राजाने अप्पाजींची चतुराई कशी पारखली, त्याच्या परीक्षेला अप्पाजींनी कसे कौशल्याने तोंड दिले याचे वर्णन या पाठात आले आहे.

शब्दार्थ:

1. चातुर्य – हुशारी (cleverness)
2. जुनी – प्राचीन (Many year’s ago)
3. प्रधान – मंत्री (Minister)
4. उत्तर – North
5. चतुराई – हुशारी (cleverness)
6. निरोप – संदेश (Message)
7. चवदार – रुचकर (tasty)
8. कोबी – एक फळभाजी (cabbage)
9. आस्वाद – चव (taste, flavour)
10. त्या काळी – त्या वेळी (that time)
11. जलद – गतीमान (fast)
12. साधने – वाहने (vehicle)
13. बैलगाडी – Bullock cart
14. राज्य – state
15. ताजी – Fresh
16. कुजून – सडून (rotten)
17. गाडीवान – गाडी चालवणारा, वाहक (Driver)
18. बी – बीज (seed)
19. पेरणे – जमिनीत बी टाकणे (sowing)
20. रवाना – पाठवणे (to send)
21. कौतुक – प्रशंसा (to admire)
22. परीक्षा – कसोटी (test)
23. एकसारख्या – समान, सारख्या (same)
24. मूर्ती – प्रतिमा (Statue)
25. निकृष्ट – कमी दर्जाची (in ferier)
26. उत्कृष्ट – उत्तम (superior, excellent)
27. लवचिक – हलणारी (Flexible)
28. तार – धातूचा तंतू (wire)
29. अफवा – खोटी बातमी (rumour)
30. हित – कल्याण, भले (interest)
31. नुकसान – तोटा (Loss)
32. संतुष्ट – समाधानी (satisfied)
33. पुरावा – दाखला (proof, evidence)

वाक्प्रचार व अर्थ:

1. चतुराई पाहणे – हुशारी पाहणे
2. परीक्षा घेणे – कौशल्य तपासून पाहणे
3. खरेखोटेपणा पडताळणे – सत्य, असत्य तपासणे
4. हित नसणे – भले नसणे, कल्याण नसणे
5. अफवा ऐकणे – खोटी बातमी ऐकणे.
6. खात्री करणे – तपासून, चौकशी करणे

Marathi Sulabhbharati Class 6 Solutions

• बाबांचं पत्र Question Answer
• मिनूचा जलप्रवास Question Answer
• चंद्रावरची शाळा (कविता) Question Answer
• मोठी आई Question Answer
• अप्पाजींचे चातुर्य Question Answer
• होळी आली होळी (कविता) Question Answer
• मुक्या प्राण्यांची कैफियत Question Answer
• पाणपोई (कविता) Question Answer

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 8 कुंदाचे साहस Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 8 कुंदाचे साहस Question Answer Maharashtra Board

Std 6 Marathi Chapter 8 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 8 कुंदाचे साहस Textbook Questions and Answers

1. दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
झाडे, शेते हिरवीगार कशामुळे झाली होती?
उत्तर:
पावसाळ्याचे दिवस होते, त्यामुळे झाडे, शेते हिरवीगार झाली होती.

प्रश्न आ.
कुंदा केव्हा पोहायला शिकली होती?
उत्तर:
कुंदा वयाच्या आठव्या वर्षी पोहायला शिकली होती.

प्रश्न इ.
कुंदाला नदीवर कोणते दृश्य दिसले?
उत्तर:
नीलाची ‘धावा! धावा! लवकर या, रझिया पाण्यात पडली’, कुणीतरी वाचवा हो! अशी हाक कानावर पडताक्षणी कुंदा नदीकाठी पोहोचली. आजूबाजूचे लोकही या आवाजाने नदीकडे धावू लागले. मुलींचा गोंधळही वाढू लागला होता. कुंदा नदीच्या काठावर येऊन क्षणभर थांबली. तिला रझिया पाण्यात गटांगळ्या खात त्या पाण्याच्या प्रवाहाबरोबर पुढे पुढे वाहत जात असलेली दिसली.

प्रश्न ई.
नदीच्या काठावरचे लोक कुंदाला कोणत्या सूचना देत होते ?
उत्तर:
‘कुंदा, पाण्याचा वेग वाढतो आहे. मागे फीर’ अशा सूचना नदीच्या काठावरचे लोक कुंदाला देत होते.

प्रश्न उ.
रझियाच्या आईच्या डोळ्यांतून आनंदाश्रू का आले?
उत्तर:
कुंदाने पाण्याच्या वाहत्या प्रवाहात उडी टाकून रझियाला वाचवले होते. त्या दोघीही सुरक्षित असल्याचे पाहून रझियाच्या आईने दोघींना घट्ट मिठी मारली. आपल्या रझियाचे प्राण धाडसामुळे वाचले, या विचाराने मन भरून आल्यामुळे रझियाच्या आईच्या डोळ्यांतून आनंदाश्रू आले.

2. खालील शब्दांचे विरुद्धार्थी शब्द लिहा. 

प्रश्न 1.
खालील शब्दांचे विरुद्धार्थी शब्द लिहा.
(अ) प्रसन्न × ………………
(ई) हसणे × ……………..
(आ) दूरवर × ……………
(उ) पुढे × …………..
(इ) शूर × ………….
(ऊ) लवकर × ………….
उत्तर:
(अ) प्रसन्न × अप्रसन्न
(ई) हसणे × रडणे
(आ) दूरवर × जवळ
(उ) पुढे × मागे
(इ) शूर × घाबरट, भित्रा
(ऊ) लवकर × उशिरा

3. पोहण्यामध्ये तरबेज असलेल्या व्यक्तीला ‘जलतरणपटू’ म्हणतात. या प्रकारचे खालील शब्द वाचा व त्यांच्या योग्य जोड्या लावा.

प्रश्न 1.
पोहण्यामध्ये तरबेज असलेल्या व्यक्तीला ‘जलतरणपटू’ म्हणतात. या प्रकारचे खालील शब्द वाचा व त्यांच्या योग्य जोड्या लावा.

‘अ’ गट	‘ब’ गट
(अ) क्रिकेट खेळण्यात पटाईत	1. वक्ता
(आ) धावण्यात पटाईत	2. क्रिकेटपटू
(इ) भाषण करण्यात पटाईत	3. धावपटू

उत्तर:

‘अ’ गट	‘ब’ गट
(अ) क्रिकेट खेळण्यात पटाईत	2. क्रिकेटपटू
(आ) धावण्यात पटाईत	3. धावपटू
(इ) भाषण करण्यात पटाईत	1. वक्ता

4. खालील खेळ खेळण्यासाठी आवश्यक असणाऱ्या वस्तू/गोष्टी लिहा.

प्रश्न 1.
खालील खेळ खेळण्यासाठी आवश्यक असणाऱ्या वस्तू/गोष्टी लिहा.
(अ) क्रिकेट –
(आ) कबड्डी –
(इ) फुटबॉल –
(ई) लिंबूचमचा –
(उ) संगीतखुर्ची –
(ऊ) विटीदांडू –
(ए) लगोरी –
(ऐ) पोहणे –
उत्तर:
(अ) क्रिकेट – बॅट
(आ) कबड्डी – मातीचे मैदान, सफेद खडू / पावडर
(इ) फुटबॉल – नेट
(ई) लिंबूचमचा – लिंबू
(उ) संगीतखुर्ची – खुर्ची
(ऊ) विटीदांडू – दांडू
(ए) लगोरी – चिप्प्या
(ऐ) पोहणे – पोहण्याचा पोशाख, टोपी, पोहण्याचा चष्मा

5. कंसातील वाक्प्रचार दिलेल्या वाक्यांत योग्य ठिकाणी वापरा.
(दंग होणे, गलका वाढणे.)

प्रश्न अ.
शाळेची सुट्टी झाल्याबरोबर शाळेच्या मैदानात विदयार्थ्यांचा ………. वाढला.
उत्तरः
गलका वाढला

प्रश्न आ.
परीक्षा असल्यामुळे मुले अभ्यासात ………….. झाली.
उत्तर:
दंग झाली.

6. आंतरजालाचा उपयोग करून भारतीय जलतरणपटू यांची माहिती घ्या. प्रत्येक खेळाडूची माहिती चार-पाच वाक्यांत लिहा.

प्रश्न 1.
आंतरजालाचा उपयोग करून भारतीय जलतरणपटू यांची माहिती घ्या. प्रत्येक खेळाडूची माहिती चार-पाच वाक्यांत लिहा.
उत्तर:
1. सेबेस्टियन झेविअर (Sebastian Xavier) – यांचा जन्म 10 फेब्रुवारी 1970 रोजी केरळ मध्ये झाला. 50 मीटर फ्री स्टाईल स्विमिंगमध्ये त्यांनी 22.89 सेकंदाचे राष्ट्रीय रेकॉर्ड जवळ जवळ अकरा वर्षे केले. त्यांनी दक्षिण आशियाई खेळात (SAF) 36 सुवर्णपदके मिळवली. 2001 मध्ये त्यांना खेळाच्या क्षेत्रातील सर्वोत्कृष्ट अर्जुन पुरस्काराने सन्मानित केले. त्यांच्या जन्म मनामईल (Manamayil) कुटुंबात केरळ राज्यातील ‘अलाप्पुझा’ (Alappuzha) जिल्हयात ‘इड्थूवा’ (Edathua) या ठिकाणी झाला.

त्यांचे माध्यमिक पर्यंतचे शिक्षण सेन्ट अॅलोसीयस (St. Aloysius) माध्यमिक शाळेत झाले. त्यांचे कॉलेजचे शिक्षण सेन्ट अॅलोसीयस (St. Aloysius) मध्ये झाले. त्याचवेळी त्यांनी वरिष्ठ जलतरणपटू म्हणून तयारी केली. तसेच लाईम लाईट (Lime light) खेळात कौशल्य दाखवले. नंतर ते भारतीय रेल्वेमध्ये राष्ट्रीय व आंतरराष्ट्रीय पातळीवर खेळू लागले. नंतर त्यांनी भारतीय अॅथलेटिक ‘मॉली चॉको’ (Molly Chacko) बरोबर लग्न केले. त्यानंतर ते दोघेही दक्षिण रेल्वे मध्ये काम करू लागले.

2. अंकुर पसेरीयाः (Ankur Paseria) यांचा जन्म 16 मार्च 1977 मध्ये झाला. ते भारतीय अमेरिकन जलतरणपटू आहेत. त्यांनी विशेष प्राविण्य बटरफ्लाय (butterfly events) या प्रकारात मिळवले आहे. 100 मीटर बटरफ्लाय या पोहण्याच्या प्रकारात त्यांनी रेकॉर्ड केले आहे. जपान येथे टोकियोमध्ये झालेल्या आशियाई खेळात त्यांच्याबरोबरच असलेला जलतरणपटू ‘वीरधवल खाडे’ याचे रेकॉर्ड ब्रेक केले. कॅलिफोर्नियाच्या ‘लॉस एन्जिल’ विदयापिठाची पदवी त्यांनी प्राप्त केली आहे. ते एक अष्टपैलू जलतरणपटू आहेत.

3. वीरधवल खाडे: मुळात कोल्हापूरचा असलेल्या खाडेने वयाच्या दहाव्या वर्षी पोहायला सुरूवात केली आणि तेव्हापासून त्याने खूप दूरवरचा पल्ला गाठला आहे. या सहा फूट उंचीच्या धिप्पाड मुलाला पोहण्याचे प्रशिक्षण ‘निहार अमीन’ यांनी दिले आहे. वीरधवल खाडे याने त्याच्या वयोगटात जगातील सर्वात वेगवान जलतरणपटू (पोहणारा) असा लौकिक मिळवला आहे.

आशियाई क्रीडास्पर्धांत पुरूषांच्या 50 मीटर बटरफ्लाय (थोड्या अंतराची वेगवान शर्यत) जलतरण स्पर्धेत कांस्यपदक पटकावून इतिहास घडवला आहे. खजान सिंगने 1986 च्या क्रीडास्पर्धांत मिळवलेल्या रौप्य पदकानंतर आशियाई क्रीडास्पर्धात पदक जिंकणारा वीरधवल हा पहिला भारतीय होता.

त्याने 50 मीटर, 100 मीटर, 200 मीटर आणि 400 मीटर फ्री स्टाइल (मुक्त शैली) जलतरण स्पर्धेत आणि 50 मीटर बटरफ्लाय स्पर्धेत अनेक विक्रम केले आहेत. ऑलिम्पिक क्रीडास्पर्धांत पात्रता मिळवणारा आतापर्यंतचा सर्वात तरूण भारतीय जलतरणपटू असा त्याचा लौकिक आहे.

4. समशेर खान – 1956 मध्ये झालेल्या ऑलिम्पिक स्पर्धेत पोहण्याच्या शर्यतीत उतरणारे समशेर खान हे प्रथम भारतीय जलतरणपटू आहेत. 1956 मध्ये मेलबर्न येथे झालेल्या पोहण्याच्या शर्यतीत ते पाचव्या क्रमांकावर विजयी झाले होते. 1955 मध्ये बँगलोर येथे झालेल्या राष्ट्रीय स्पर्धेत त्यांनी 200 मीटर बटरफ्लाय या कौशल्यात सर्वांचे विक्रम मोडीत काढले.

समशेर खान हे भारतीय संरक्षक दलात कामाला होते. ते 1962 च्या भारत-चीन युद्धात तसेच 1971 च्या भारत – पाकिस्तान च्या युद्धात सहभागी झाले होते. 1973 मध्ये ते ‘सुबेदार’ या पदावर असताना निवृत्त झाले.

7. तुम्ही रझियाचे ‘हितचिंतक’ आहात, या नात्याने तिला कोणत्या सूचना दयाल?

प्रश्न 1.
तुम्ही रझियाचे ‘हितचिंतक’ आहात, या नात्याने तिला कोणत्या सूचना दयाल?
उत्तरः

1. रझियाने नदीच्या किनारी सावधानतेने खेळले पाहिजे होते.
2. रझियाने पोहायला शिकले पाहिजे.
3. रझियाने कोणत्याही प्रसंगात घाबरू नये.
4. रझियाने कुंदाचे आभार मानायला पाहिजेत.

8. पाठ वाचून तुम्हाला कुंदाचे कोणकोणते गुण जाणवले ते लिहा.

प्रश्न 1.
पाठ वाचून तुम्हाला कुंदाचे कोणकोणते गुण जाणवले ते लिहा.

उत्तर:

विशेषण – उदा. समीर हुशार मुलगा आहे.
या वाक्यात ‘हुशार’ हा शब्द ‘मुलगा’ या नामाविषयी विशेष माहिती सांगतो. नामाविषयी विशेष माहिती सांगणाऱ्या शब्दाला ‘विशेषण’, म्हणतात; म्हणून ‘हुशार’ हा शब्द ‘विशेषण’ आहे.

9. कुंदाचे अभिनंदन करणारा कोणता संदेश तुम्ही भ्रमणध्वनीवरून पाठवाल ते खालील चौकोनात लिहा. 

आपण समजून घेऊया.

खालील शब्दसमूह वाचा.
सुंदर फुले, गोड आंबा, उंच डोंगर, ताजे दूध, पिवळा झेंडू, सात केळी, लांब नदी, अवखळ मुले.
वरील शब्दसमूहात फुले, आंबा, डोंगर, दूध, झेंडू, केळी, नदी, मुले ही नामे आहेत, तर सुंदर, गोड, उंच, ताजे, पिवळा, सात, लांब, अवखळ हे शब्द त्या नामांबद्दल विशेष माहिती सांगणारे शब्द आहेत. अशा शब्दांना विशेषण म्हणतात.

खालील आकृतीत गुलाबाच्या फुलाला आठ विशेषणे लावली आहेत. ती समजून घ्या.

खालील चित्राला दोन-दोन विशेषणे लावा.

खालील वाक्ये वाचा.
(अ) अरेरे! तू पडलास.
(आ) शाबास! छान खेळलास.
(इ) अरे वाह! छान कपडे आहेत.
उत्कट भावना व्यक्त करताना ती दाखवणाऱ्या शब्दांच्या शेवटी !’ असे चिन्ह देतात. या चिन्हास उद्गारचिन्ह म्हणतात.

प्रश्न 1.
कुंदाचे अभिनंदन करणारा कोणता संदेश तुम्ही भ्रमणध्वनीवरून पाठवाल ते खालील चौकोनात लिहा.
उत्तर:
‘कुंदा तुझे खूप खूप अभिनंदन ! तुझे साहस बघून मला खूप अभिमान वाटला. अशाच साहसी मुलींची आज भारत देशाला गरज आहे. तुझ्या साहसाने आम्हां मुलींना खूप स्फूर्ती मिळाली आहे.’

प्रश्न 2.
खालील आकृतीत गुलाबाच्या फुलाला आठ विशेषणे लावली आहेत. ती समजून घ्या.

उत्तर:

1. टवटवीत गुलाब
2. सुंदर गुलाब
3. नाजूक गुलाब
4. सुवासिक गुलाब
5. टपोरे गुलाब
6. रंगीत गुलाब
7. लालभडक गुलाब
8. ताजे गुलाब

प्रश्न 3.
खालील चित्रांना दोन-दोन विशेषणे लावून लिहा.
उत्तर:

प्रश्न 4.
खालील वाक्ये वाचा.
(अ) अरेरे! तू पडलास.
(आ) शाबास! छान खेळलास.
(इ) अरे वाह! छान कपडे आहेत.
उत्तर:
(अ) अरेरे! फार वाईट झाले!
(आ) बापरे ! केवढा हा साप!
(इ) ओह! किती सुंदर!

Marathi Sulabhbharti Class 6 Solutions Chapter 8 कुंदाचे साहस Important Additional Questions and Answers

खाली दिलेल्या वाक्यातील रिकाम्या जागी योग्य शब्द भरून वाक्य लिहा.

प्रश्न 1.

1. सर्वत्र प्रसन्न …………………. होते.
2. पावसामुळे नदीचा …………………. वाढत होता.
3. पाहता पाहता ती पट्टीची …………………. बनली होती.
4. दूरवर शेतात शेतकरी व काही बायका कामात …………………. होत्या.
5. कुंदा धावत येऊन काठावर उभी …………………. राहिली.
6. कुंदाला फक्त …………………. दिसत होती.
7. ही बातमी …………………. पसरली.
8. कौतुकाने व अभिमानाने त्यांनी मुलीला …………………. घेतले.
9. आज साऱ्या गावात कुंदाच्या ………………….. चर्चा होती.
10. साऱ्यांच्या कौतुकाच्या …………………. कुंदा आनंदून गेली.

उत्तर:

1. वातावरण
2. प्रवाह
3. जलतरणपटू
4. मग्न
5. क्षणभर
6. रझिया
7. गावभर
8. जवळ
9. साहसाचीच
10. वर्षावाने

खालील प्रश्नांची प्रत्येकी एका वाक्यात उत्तरे लिहा.

प्रश्न 1.
गावातील नदीचे नाव काय आहे?
उत्तर:
गावातील नदीचे नाव ‘सोना’ हे आहे.

प्रश्न 2.
कोणत्या दिवशी शाळेला सुट्टी होती?
उत्तर:
‘रविवार’ या दिवशी शाळेला सुट्टी होती.

प्रश्न 3.
कुंदा व तिच्या मैत्रिणी कुठे खेळायला गेल्या होत्या?
उत्तर:
कुंदा व तिच्या मैत्रिणी नदीच्या काठावर खेळायला गेल्या होत्या.

प्रश्न 4.
कुंदा वयाच्या कितव्या वर्षी पोहायला शिकली होती?
उत्तर:
कुंदा वयाच्या आठव्या वर्षी पोहायला शिकली होती.

प्रश्न 5.
दूरवर शेतात कोण-कोण कामात मग्न होते?
उत्तर:
दूरवर शेतात शेतकरी व काही बायका कामात मग्न होत्या.

प्रश्न 6.
पाण्यात कोण पडली होती?
उत्तर:
रझिया पाण्यात पडली होती.

प्रश्न 7.
रझियाला पाण्यातून वाचवण्यासाठी पाण्यात कोणी उडी घेतली?
उत्तर:
रझियाला पाण्यातून वाचवण्यासाठी पाण्यात कुंदाने उडी घेतली.

प्रश्न 8.
कुंदाने रझियाला कुठे आणले?
उत्तर:
कुंदाने रझियाला काठाकडे आणले.

प्रश्न 9.
कौतुकाने व अभिमानाने कुंदाला कोणी जवळ घेतले?
उत्तरः
कौतुकाने व अभिमानाने कुंदाला तिच्या आई-बाबांनी जवळ घेतले.

असे कोण कोणास म्हणाले ते लिहा.

प्रश्न 1.
“धावा! धावा! लवकर या, रझिया पाण्यात पडली.”
उत्तर:
नीला आजूबाजूच्या लोकांना म्हणाली.

प्रश्न 2.
“कुंदा, पाण्याचा वेग वाढतो आहे. माघारी फिर.”
उत्तर:
जमलेली माणसे कुंदाला म्हणत होती.

प्रश्न 3.
“रझिया घाबरू नको, मी आले आहे.”
उत्तर:
कुंदा रझियाला म्हणाली.

प्रश्न 4.
“कुंदा, आज तुझ्यामुळेच माझ्या रझियाचा जीव वाचला.”
उत्तर:
रझियाची आई कुंदाला म्हणाली.

खालील प्रश्नांची दोन-तीन वाक्यात उत्तरे लिहा.

प्रश्न 1.
पावसाळ्याचे दिवस असल्याने गावात कोणता बदल झाला होता?
उत्तर:
पावसाळ्याचे दिवस असल्याने झाडे, शेते सर्वच हिरवीगार झाली होती. सर्वत्र प्रसन्न वातावरण होते. गावातल्या सोना नदीला भरपूर पाणी आले होते. पावसामुळे नदीचा प्रवाह वाढत होता. हा बदल झाला होता.

प्रश्न 2.
कुंदाला नदीवर कोणते दृश्य दिसले?
उत्तर:
‘रझिया नदीच्या पाण्यात पडली आहे, व तिला वाचवण्यास कुणीतरी मदत करा’ ही नीलाची हाक कुंदाच्या कानावर पडल्याबरोबर ती धावतच नदीकिनारी पोहोचली. ती नदीच्या काठावर येऊन क्षणभर उभी राहिली तेव्हा तिला रझिया पाण्यात गटांगळ्या खात पाण्याच्या प्रवाहाबरोबर पुढे पुढे वाहत चालल्याचे दृश्य दिसले.

प्रश्न 3.
नदीच्या काठावरचे लोक कुंदाला कोणत्या सूचना देत होते?
उत्तर:
नीलाच्या हाकेमुळे आजूबाजूचे लोकही नदीकिनारी जमले होते. रझियाला वाचवण्यासाठी कुंदाने पाण्यात उडी घेताच लोक जोरजोरात ओरडून ‘कुंदा’ पाण्याचा वेग वाढतो आहे. ‘माघारी फिर’ ही सूचना देत होते.

प्रश्न 4.
कोणती बातमी गावभर पसरली?
उत्तर:
कुंदा आणि तिच्या मैत्रिणी रविवारी शाळेच्या सुट्टीच्या दिवशी नदीच्या काठावर खेळत असताना रझिया पाण्यात पडली व पाण्याच्या प्रवाहाबरोबर गटांगळ्या खात ती बुडू लागली. पण तिला वाचवण्यासाठी कुंदाने पाण्यात उडी घेतली व तिला काठाकडे आणले. तोवर लोकांनी मोठा दोर पाण्यात सोडून दोघींना बाहेर काढले. ही बातमी गावभर पसरली.

प्रश्न 5.
रझियाच्या आईच्या डोळ्यांतून आनंदाश्रू का आले?
उत्तर:
वाहणाऱ्या नदीच्या मोठ्या प्रवाहात गटांगळ्या खात बुडत असणाऱ्या आपल्या मुलीला कुंदाने मोठ्या धाडसाने वाचवले. कुंदामुळेच आज रझियाचा जीव वाचला’ या विचारानेच रझियाच्या आईच्या डोळ्यातून आनंदाश्रू आले.

व्याकरण व भाषाभ्यास:

खालील शब्दांचे समानार्थी शब्द लिहा.

प्रश्न 1.

1. साहस
2. सर्वत्र
3. मैत्रिण
4. मग्न
5. लहानगी
6. हाक
7. पाणी
8. बातमी
9. सुखरूप
10. कवटाळणे

उत्तरः

1. धाडस
2. सगळीकडे
3. सखी
4. गर्क, दंग
5. छोटी
6. आवाज
7. जल, उदक
8. खबर, माहिती
9. सुरक्षित
10. मिठी मारणे

खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

प्रश्न 1.

1. दिवस
2. भरपूर
3. मोठ्या
4. बायका
5. लहान

उत्तरः

1. रात्र
2. कमी, थोडे
3. छोट्या
4. माणसे
5. मोठे

खालील शब्दांचे वचन बदला.

प्रश्न 1.

1. झाड
2. शेत
3. सुट्टी
4. मैत्रिण
5. बाई
6. हाक
7. दोर
8. मिठी

उत्तरः

1. झाडे
2. शेते
3. सुट्ट्या
4. मैत्रिणी
5. बायका
6. हाका
7. दोऱ्या
8. मिठ्या

प्रश्न 2.
कंसातील वाक्प्रचार दिलेल्या वाक्यांत योग्य ठिकाणी वापरून वाक्य पुन्हा लिहा.
(दंग होणे, गलका वाढणे, गटांगळ्या खाणे)
1. पोहता न आल्यामुळे जयेश नदीच्या पात्रात ……………… .
उत्तर:
गटांगळ्या खाऊ लागला.

पोहण्यामध्ये तरबेज असलेल्या व्यक्तीला ‘जलतरणपटू’ म्हणतात. या प्रकारचे खालील शब्द वाचा व त्यांच्या योग्य जोड्या लावा.

प्रश्न 1.

‘अ’ गट	‘ब’ गट
1. कुस्ती खेळण्यात पटाईत	(अ) तिरंदाज
2. तीर चालवण्यात पटाईत	(आ) कुस्तीपटू

उत्तर:

‘अ’ गट	‘ब’ गट
1. कुस्ती खेळण्यात पटाईत	(आ) कुस्तीपटू
2. तीर चालवण्यात पटाईत	(अ) तिरंदाज

खालील चौकोनातील मुलाच्या चित्राला आठ विशेषणे लावली आहेत ती लिहून काढा.

प्रश्न 1.

उत्तर:

1. हुशार मुलगा
2. कष्टाळू मुलगा
3. सुंदर मुलगा
4. अभ्यासू मुलगा
5. प्रेमळ मुलगा
6. गोरा मुलगा
7. चलाख मुलगा
8. कामसू मुलगा

प्रश्न 2.
खालील चित्रांना दोन-दोन विशेषणे लावून लिहा.
उत्तर:

खालील वाक्यांत योग्य ठिकाणी उद्गार (!) चिन्ह त्या.

प्रश्न 1.
धावा धावा लवकर या, रझिया पाण्यात पडली.
उत्तर:
धावा! धावा! लवकर या, रझिया पाण्यात पडली.

प्रश्न 2.
केवढी धाडसी मुलगी आहेस तू.
उत्तर:
केवढी धाडसी मुलगी आहेस तू!

प्रश्न 3.
शब्बास छान खेळलास.
उत्तर:
शाब्बास! छान खेळलास.

कुंदाचे साहस Summary in Marathi

पाठपरिचय:

‘कुंदाचे साहस’ या पाठात कुंदाने दाखवलेले साहस व तिची समयसुचकता याविषयी वर्णन केले आहे.

शब्दर्थ:

1. साहस – धाडस (adventure)
2. शेत – रान (farm)
3. प्रसन्न – आनंदी (happy)
4. वातावरण – भोवतालचा परिसर (surrounding)
5. भरपूर – खूप, जास्त (a lot of)
6. प्रवाह – पाण्याचा वाहणारा वेग (flow of water)
7. काठ – किनारा, तट (bank of river)
8. पट्टीची – पोहण्यात तरबेज (swimmer)
9. कडूनिंब – एक प्रकारचे लिंबाचे झाड (Neem tree)
10. बागडत – इकडे-तिकडे उड्या मारत (fluttering)
11. मग्न – गर्क, गुंग, दंग (indulge in)
12. लहानगी – छोटी (a little)
13. दंग – मग्न (surprised, ongrossed)
14. हाक – आरोळी, आवाज (call)
15. गलका – गोंधळ (noise)
16. क्षणभर – काही वेळ (a moment)
17. पात्र – नदीचा वाहता प्रवाह (a bed of river)
18. एवढीशी – लहानगी, छोटी (a little)
19. वेग – गती (speed)
20. माघारी – परत, मागे (retreat)
21. तोवर – तोपर्यंत (till then)
22. दोर – कासरा, रस्सी (rope)
23. सुखरूप – सुरक्षित (safe)
24. कवटाळणे – मिठी मारणे (to huy)

वाकप्रचार व अर्थ:

1. मग्न असणे – दंग असणे, गर्क असणे, गुंग असणे
2. गावभर पसरणे – सगळीकडे समजणे, पूर्ण गावात माहिती होणे
3. गलका वाढणे – गडबड वाढणे, गोंधळ करणे
4. गटांगळ्या खाणे – पाण्यात बुडणे
5. कोणाचेही शब्द कानावर न पडणे – काहीही ऐकायला न येणे
6. आनंदाश्रू वाहणे – आनंदाने डोळ्यातून अश्रू येणे

Marathi Sulabhbharati Class 6 Solutions

• भारतमाता (गाणे) Question Answer
• माझा अनुभव Question Answer
• पाऊस आला! पाऊस आला! (कविता) Question Answer
• माहिती घेऊया Question Answer
• सुगरणीचे घरटे Question Answer
• हे खरे खरे व्हावे… (कविता) Question Answer
• उद्यानात भेटलेला विद्यार्थी Question Answer
• कुंदाचे साहस Question Answer
• घर (कविता) Question Answer

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 11 मिनूचा जलप्रवास Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 11 मिनूचा जलप्रवास Question Answer Maharashtra Board

Std 6 Marathi Chapter 11 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 11 मिनूचा जलप्रवास Textbook Questions and Answers

1. एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
मिनू मासोळी कुठे राहायची?
उत्तर:
मिनू मासोळी माशांच्या समूहात राहायची.

प्रश्न आ.
मिनूला समुद्र का बघायचा होता?
उत्तर:
मिनूला सतत उत्सुकता असायची की, नदीचे पाणी रोज कुठं जातं? तेव्हा आई म्हणायची, “समुद्रात जातं” तेव्हा तो समुद्र कसा असेल? तो केवढा असेल? हे जाणून घेण्यासाठी तिला समुद्र बघायचा होता.

प्रश्न इ.
नदीचे पाणी गढूळ का झाले?
उत्तर:
मुसळधार पाऊस पडू लागल्यामुळे पाण्याचे लोंढे वाहू लागले व त्यामुळे नदीचे पाणी गढूळ झाले.

प्रश्न ई.
खडकावर फुललेल्या फुलांचे रंग कोणते होते?
उत्तर:
खडकावर फुललेली फुले लाल, गुलाबी, अंजिरी अशा विविध रंगांची होती.

प्रश्न उ.
समुद्राच्या खोलवर अंधार का असतो?
उत्तर:
समुद्राच्या तळाशी सूर्यप्रकाश पोहचत नसल्याने समुद्राच्या तळाशी खोलवर अंधार असतो. प्रश्न ४.खालील प्रश्नांची तीन-चार वाक्यांत उत्तरे लिहा.

2. तीन-चार वाक्यांत उत्तरे लिहा.

प्रश्न अ.
लेखिकेने नदीचे वर्णन कसे केले आहे?
उत्तरः
‘नदीत खूप खूप पाणी होते. ते पाणी निळे निळे, थंडगार व स्वच्छ होते. इतके स्वच्छ की वरून पाहिले, की तळाची वाळू दिसायची. गोल गोल गोटे दिसायचे अन् सुळसुळ पोहणारे छोटे मासेही दिसायचे.’ असे लेखिकेने नदीचे वर्णन केले आहे.

प्रश्न आ.
मिनूची व आईची चुकामुक का झाली?
उत्तर:
एक दिवस मुसळधार पाऊस पडू लागला. जमिनीवरून पाण्याचे लोंढे वाहायला लागले. नदीचे पाणी गढुळले. मासे बावरून एकमेकांना शोधू लागले; पण कोणीच कोणाला दिसेना. पाणी वेगाने वाहत होते. या गोंधळातच मिनूची व आईची चुकामूक झाली.

प्रश्न इ.
घोडमासा पाहून मिनूला हसू का आले?
उत्तर:
समुद्रातून थोडीशी चक्कर मारून परत जावे असा विचार करून मिनू पुढे जात असताना तिची एका विचित्र माशाशी टक्कर झाली. त्याचे तोंड घोड्यासारखे होते व पोटाला पिशवी होती व त्यात छोटी छोटी पिल्ले बसलेली पाहून मिनूला हसू आले.

3. कोण कोणास व केव्हा म्हणाले ते लिहा.

प्रश्न अ.
“समुद्र, समुद्र म्हणतात तो आला की!”
उत्तर:
मिनूने जेव्हा हळूच तोंड उघडले तेव्हा समुद्राचे खारट पाणी तिच्या तोंडात गेले तेव्हा ती स्वत:लाच म्हणाली.

प्रश्न आ.
“त्याचं नाव घोडमासा, समुद्रघोडा!”
उत्तर:
समुद्राच्या पाण्यात मिनूची एका विचित्र माशाची टक्कर झाली तेव्हा पाण्याच्या तळाकडून कासव मिनूला म्हणाले.

प्रश्न इ.
“घाबरू नकोस, हा तर खेकडा!”
उत्तर:
कासव व मिनू यांच्यात जेव्हा बोलणे चालू होते तेव्हा त्यांच्या मधून एक प्राणी तिरका तिरका चालत गेला. तो आपल्या बटबटीत डोळ्यांनी मिनूकडे पाहत होता. तेव्हा ती घाबरली, तिची भिती दूर करताना कासव मिनूला म्हणाले.

प्रश्न ई.
“कासवदादा, चला ना माझ्याबरोबर.”
उत्तर:
मिनू आपल्या आईकडे पुन्हा नदीच्या दिशेने निघाली तेव्हा मिनू कासवाला म्हणाली.

4. शिंपल्यामध्ये मोती कसा तयार होतो? त्याची क्रिया क्रमाने लिहा.

प्रश्न 1.
शिंपल्यामध्ये मोती कसा तयार होतो? त्याची क्रिया क्रमाने लिहा.
उत्तर:

1. नदीतील शंख-शिंपल्यात एक छोटासा किडा असतो.
2. या शिंपल्यात चुकून एखादा वाळूचा कण गेला की तो त्याच्या अंगाला टोचायला लागतो. मग तो आपल्या अंगातून पातळ रस काढून त्यावर गुंडाळतो.
3. मग त्यातूनच पुढे छानदार मोती तयार होतो.

5. चार – पाच ओळीत वर्णन करा.

प्रश्न अ.
घोडमासा
उत्तर:
घोडमासा हा विचित्र मासा आहे. त्याचे तोंड इतर माशांसारखे नसते. त्याचे तोंड घोड्यासारखे असते. त्याच्या पोटाला पिशवी असते. त्यात छोटी छोटी पिल्ले बसलेली असतात.

प्रश्न आ.
खेकडा
उत्तर:
खेकडा आपल्या पायांनी तिरका चालतो. तो आपल्या बटबटीत डोळ्यांनी पाहतो. त्याच्या पाठीवर कासवासारखेच कठीण कवच असते. त्यामुळे शत्रू त्याच्यावर हल्ला करू शकत नाही. याला सहा तर कधी आठ पायही असतात. त्यांच्या तोंडाजवळ दोन नांग्या असतात, त्यामुळे त्याचं संरक्षण होते व त्याला भक्ष्यही पकडता येते.

6. इवलीशी’ यासारखे आणखी शब्द लिहा.

प्रश्न 1.
इवलीशी’ यासारखे आणखी शब्द लिहा.
उत्तर:

1. नबी नशी
2. को बळीशी
3. छानशी
4. सोनुलीशी

7.

प्रश्न अ.
समानार्थी शब्दांच्या योग्य जोड्या लावा.

उत्तरः

1. लांब – दूर
2. प्रचंड – मोठे
3. उष्ण – गरम
4. लहान – इवली

प्रश्न आ.
विरूद्धार्थी शब्दांच्या योग्य जोड्या लावा.

उत्तरः

1. पुढे × मागे
2. प्रकाश × अंधार
3. मऊ × टणक
4. मोठे × लहान

8. योग्य जोड्या जुळवा.

प्रश्न 1.
योग्य जोड्या जुळवा.

उत्तर:

नाम	विशेषण
1. मिनू	(आ) इवलीशी
2. पाणी	(इ) खारट
3. डोळे	(ई) बटबटीत
4. पाऊस	(अ) मुसळधार

9. खालील शब्द वाचा. समजून घ्या.

प्रश्न 1.
खालील शब्द वाचा. समजून घ्या.

10. तुम्ही मिनू मासोळी आहात अशी कल्पना करून समुद्राची माहिती आईला सांगा.

प्रश्न 1.
तुम्ही मिनू मासोळी आहात अशी कल्पना करून समुद्राची माहिती आईला सांगा.
उत्तर:
‘आई, समुद्र हा खूप मोठा जलाशय असतो. त्यात दूरदूर पर्यंत पाणीच पाणी असते. त्याचा तळ खूप खोल असतो. त्याच्या तळाशी अंधार असतो. कारण तिथपर्यंत सूर्याचा प्रकाश पोहचत नाही. समुद्राचे पाणी चवीला खारट आहे. त्या पाण्यात मोठ्या माशांपासून ते लहान-लहान माशांपर्यंत विविध प्रकारचे मासे आहेत. समुद्रातून आपण जहाज व बोटीत बसून प्रवास करू शकतो. विविध प्रकारचे वायू व तेलाचे साठे समुद्राच्या तळाशी आहेत. त्याचा माणसाने पुरेपुर फायदा करून घेतला आहे. समुद्रातील मोती हे आपला अमुल्य ठेवा आहे.

11. शंख-शिंपल्यांपासून शोभेच्या वस्तू बनवा.

प्रश्न 1.
खालील वाक्ये वाचा.
अ. विसूने ‘ताजमहाल’, पाहिला.
आ. मंदाने सुरेशला सांगितले, ‘पायल तुझ्याकडे उदया येणार आहे.’
एखादया शब्दावर जोर दयावयाचा असता, दुसऱ्याचे मत अप्रत्यक्ष सांगताना (‘ – ‘) असे एकेरी अवतरणचिन्ह वापरले जाते.

प्रश्न 2.
खालील वाक्यांतील काळ ओळखा.

1. सूर्य पूर्वेला उगवतो.
2. मला लाडू आवडला.
3. आईचा स्वयंपाक झाला होता.
4. मी गावाला जाईन.
5. तू का रडतेस?
6. मी पोहायला शिकणार आहे.

उत्तरः

1. वर्तमानकाळ
2. भूतकाळ
3. भूतकाळ
4. भविष्यकाळ
5. वर्तमानकाळ
6. भविष्यकाळ

Class 6 Marathi Chapter 11 मिनूचा जलप्रवास Additional Important Questions and Answers

खाली दिलेल्या वाक्यातील रिकाम्या जागी योग्य शब्द भरून वाक्य लिहा.

1. मिनू होती ………………
2. इतर मासे तिचे खूप खूप …………… करायचे.
3. आनंदाने तिने ……………………. उडीच मारली.
4. एक दिवस ……….. पाऊस पडू लागला.
5. जमिनीवरून पाण्याचे …………… वाहायला लागले.
6. पाणी वेगाने ……………. होते.
7. या गोंधळात मिनूची व आईची ……………… झाली.
8. इतक्यात तिची एका विचित्र माशाशी ………………. झाली.
9. मिनू …………….. पायऱ्या उतरत त्याच्याजवळ पोहोचली.
10. तो ………….. हात असलेला अष्टभुज मासा.
11. हा अगदी …………….. गोळा असतो गोळा.
12. मग त्यातून छानदार ……….. तयार होतो.
13. आता मात्र मिनूची ……….. उडाली.
14. काही माशांच्या अंगातून ……………… बाहेर पडतो.
15. कासवदादांनी तिला कितीतरी ………………. दाखवल्या होत्या.

उत्तरः

1. इवलीशी
2. लाड
3. टुणकन
4. मुसळधार
5. लोंढे
6. वाहत
7. चुकामूक
8. टक्कर
9. लाटांच्या
10. आठ
11. मांसाचा
12. मोती
13. घाबरगुंडी
14. उजेड
15. गमती

असे कोण कोणास व केव्हा म्हणाले ते लिहा.

प्रश्न 1.
“समुद्र, समुद्र म्हणतात तो आला की!”
उत्तर:
मिनूने जेव्हा हळूच तोंड उघडले तेव्हा समुद्राचे खारट पाणी तिच्या तोंडात गेले तेव्हा ती स्वत:लाच म्हणाली.

प्रश्न 2.
“त्याचं नाव घोडमासा, समुद्रघोडा!”
उत्तर:
समुद्राच्या पाण्यात मिनूची एका विचित्र माशाची टक्कर झाली तेव्हा पाण्याच्या तळाकडून कासव मिनूला म्हणाले.

प्रश्न 3.
“घाबरू नकोस, हा तर खेकडा!”
उत्तर:
कासव व मिनू यांच्यात जेव्हा बोलणे चालू होते तेव्हा त्यांच्या मधून एक प्राणी तिरका तिरका चालत गेला. तो आपल्या बटबटीत डोळ्यांनी मिनूकडे पाहत होता. तेव्हा ती घाबरली, तिची भिती दूर करताना कासव मिनूला म्हणाले.

प्रश्न 4.
“कासवदादा, चला ना माझ्याबरोबर.”
उत्तर:
मिनू आपल्या आईकडे पुन्हा नदीच्या दिशेने निघाली तेव्हा मिनू कासवाला म्हणाली.

खालील प्रश्नांची एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
मिनू कशी होती?
उत्तर:
मिनू इवलीशी, अगदी हाताच्या छोट्या बोटाएवढी होती.

प्रश्न 2.
मिनूचे कल्ले कसे होते?
उत्तर:
मिनू रूपेरी कल्ल्यांची होती. / मिनूचे कल्ले रूपेरी होते.

प्रश्न 3.
मिनूला कशाचा कंटाळा आला होता?
उत्तर:
मिनूला नदीच्या खोलगट भागात राहायचा कंटाळा आला होता.

प्रश्न 4.
मासे कोणाला शोधू लागले?
उत्तर:
मासे बावरून एकमेकांना शोधू लागले.

प्रश्न 5.
पाण्यात एका बाजूला लांबपर्यंत कशाच्या रांगा होत्या?
उत्तरः
पाण्यात एका बाजूला लांबपर्यंत खडकांच्या रांगा होत्या.

प्रश्न 6.
पाण्याच्या तळाशी कोण बसले होते?
उत्तर:
पाण्याच्या तळाशी कासव बसले होते.

प्रश्न 7.
मिनू कासवाजवळ कशी पोहचली?
उत्तर:
मिनू लाटांच्या पायऱ्या उतरत कासवाजवळ पोहचली.

प्रश्न 8.
दोन शिंपल्यांच्या मध्ये कोण बसलेला असतो?
उत्तर:
दोन शिंपल्यांच्या मध्ये एक किडा बसलेला असतो.

प्रश्न 9.
बटबटीत डोळे कोणाचे आहेत?
उत्तर:
बटबटीत डोळे खेकड्याचे आहेत.

प्रश्न 10.
खेकड्यावर शत्रू हल्ला का करू शकत नाही?
उत्तर:
खेकड्याच्या पाठीवर कासवासारखेच कठीण कवच असल्यामुळे शत्रू त्याच्यावर हल्ला करू शकत नाही.

प्रश्न 11.
खेकड्याला किती पाय असतात?
उत्तर:
खेकड्याला सहा तर कधी आठ पायही असतात.

प्रश्न 12.
तिरका तिरका चालणारा प्राणी कोणता?
उत्तर:
तिरका तिरका चालणारा प्राणी खेकडा होय.

प्रश्न 13.
खेकड्याच्या तोंडाजवळ काय असतात?
उत्तर:
खेकड्याच्या तोंडाजवळ दोन नांग्या असतात.

प्रश्न 14.
खेकड्याच्या दोन नांग्यामुळे त्याला कोणता फायदा होतो?
उत्तर:
खेकड्याच्या दोन नांग्यामुळे त्याला भक्ष्यही मिळते व त्याचे संरक्षणही होते.

खालील प्रश्नांची तीन-चार वाक्यांत उत्तरे लिहा.

प्रश्न 1.
आठ हात असणाऱ्या माशाविषयी कासवदादाने मिनूला काय सांगितले?
उत्तर:
आठ हात असणाऱ्या माशाविषयी कासवदादाने मिनूला सांगितले की, ‘तो आठ हात असलेला अष्टभुज मासा. तो कसा उलटा चालतोय, बघितलंस का? पाण्याच्या चुळा भरत हळूहळू मार्ग सरकतो. आपल्या आठ हातांनी मासे, खेकडे पकडून खातो.’ पाण्यात उतरणारी माणसंसुद्धा त्याला घाबरतात बरं का।

खालील वाक्यात एकेरी अवतरण चिन्हांचा वापर करून वाक्य लिहा.

प्रश्न 1.
गाडगेबाबांच्या हातात नेहमी गाडगे असे; म्हणून लोक त्यांना नेहमी गाडगेबाबा म्हणत.
उत्तर:
गाडगेबाबांच्या हातात नेहमी गाडगे असे; म्हणून लोक त्यांना नेहमी ‘गाडगेबाबा’ म्हणत.

प्रश्न 2.
डॉ. बाबासाहेबांना सरकारने भारतरत्न ही पदवी बहाल केली.
उत्तर:
डॉ. बाबासाहेबांना सरकारने ‘भारतरत्न’ ही पदवी बहाल केली.

प्रश्न 3.
लोकमान्य टिळकांनी लोकांना जागृत करण्यासाठी मराठा व केसरी ही वर्तमानपत्रे सुरू केली.
उत्तर:
लोकमान्य टिळकांनी लोकांना जागृत करण्यासाठी ‘मराठा’ व ‘केसरी’ ही वर्तमानपत्र सुरू केली.

मिनूचा जलप्रवास Summary in Marathi

पाठपरिचयः

प्रस्तुत पाठात मिनू नावाच्या मासळीने केलेल्या जल प्रवासाचे वर्णन केले आहे. त्याचबरोबर समुद्रातील कासवाने दाखवलेल्या गमतीजमतीचे वर्णन केले आहे. त्याच्यातून आपणांस माशांमध्ये असलेल्या सामंजस्याचे दर्शन घडते.

शब्दार्थ:

1. जलप्रवास – पाण्यातून प्रवास (voyage)
2. निळे – (blue)
3. तळ – (to bottom)
4. वाळू – रेती (sand)
5. गोल गोटे – गोल लहान दगड (round stone)
6. सुळसुळ् – सहज (easy)
7. मासे – (fish)
8. समूह – समुदाय (crowd)
9. मासळी – मच्छी (fish)
10. इवलीशी – अगदी लहान (very small)
11. रूपेरी – चांदीच्या (silver)
12. नजरेआड – नजरेपासून दूर (out of sight)
13. खोलगट – किंचित खोल (slightly deep)
14. समुद्र – सागर (sea)
15. मुसळधार – खूप जोराचा (heavy, torrential)
16. लोंढे – प्रवाह (stream)
17. गढुळ – मातीमिश्रीत झालेले (not clear, muddy)
18. बावरून – गडबडून, गोंधळून (confusion)
19. वेगाने – गतीने (speedily)
20. गिरक्या – गोल गोल फिरत (whirling)
21. चक्कर – फेरफटका (stroll, around)
22. संग – ओळ (line)
23. गंमत – मौज, मजा (fun)
24. हळूहळू – सावकाश (slow)
25. टक्कर – आघात, धक्का (collision)
26. घोडमासा, – समुद्रातील वेगवेगळ्या माशांचे प्रकार समुद्रघोडा (one type of fish)
27. रोखाने – त्या दिशेने (towards)
28. कासव – (tortoise)
29. लाटा – पाण्याचा तरंग (waves)
30. पावला – प्रत्येक पावलावर (on each step) पावलांवर
31. अष्टभुज – आठ हत असलेला (having eight hands)
32. चुळा – तोंडाने पाणी बाहेर फेकणे (gurgle)
33. गुंडाळणे – आवरण घालणे (to cover)
34. कण – छोटा दाणा (particle)
35. तिरका – तिरकस (sloping, slanting)
36. बटबटीत – मोठे (big)
37. घाबरगुंडी – तीव्र भीती (panic)
38. कवच – आवरण (cover)
39. कठीण – कडक (hard)
40. शत्रू – दुश्मन (enemy)
41. हल्ला – चढाई (attack)
42. बेट्याला – (येथे अर्थ) खेकड्याला (to crab)
43. नांग्या – खेकड्याच्या तोंडाजवळील एक अवयव (part near mouth of a crab)
44. भक्ष्य – शिकार (prey)
45. प्रकाश – उजेड (light)
46. प्रचंड – खूप मोठे (huge)
47. क्षणभर – काही काळ (for some moments)

वाक्प्रचार व अर्थ:

1. नजरेआड न करणे – नजरेपासून दूर न करणे.
2. बावरून जाणे – गोंधळून जाणे.
3. चक्कर मारणे – फिरून येणे.
4. घाबरगुंडी उडणे – खूप घाबरणे.
5. डोळे विस्फारणे – डोळे मोठे करून बघणे.

Marathi Sulabhbharati Class 6 Solutions

• बाबांचं पत्र Question Answer
• मिनूचा जलप्रवास Question Answer
• चंद्रावरची शाळा (कविता) Question Answer
• मोठी आई Question Answer
• अप्पाजींचे चातुर्य Question Answer
• होळी आली होळी (कविता) Question Answer
• मुक्या प्राण्यांची कैफियत Question Answer
• पाणपोई (कविता) Question Answer

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 5 सुगरणीचे घरटे Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 5 सुगरणीचे घरटे Question Answer Maharashtra Board

Std 6 Marathi Chapter 5 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 5 सुगरणीचे घरटे Textbook Questions and Answers

1. एक-दोन शब्दात उत्तरे लिहा.

प्रश्न अ.
सुगरण पक्षी घरटे कशापासून बनवतो?
उत्तर:
गवताच्या बारीक, चिवट काड्या.

प्रश्न आ.
सुगरण पक्षी घरटे कुठे बांधतो?
उत्तर:
निंब, बाभळीच्या झाडावर.

प्रश्न इ.
सुगरण पक्ष्याचा महत्त्वाचा गुण कोणता?
उत्तर:
कष्टाळूवृत्ती

2. खालील प्रश्नांची एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
सुगरण पक्षी सुबक वीण कशाने घालतो?
उत्तर:
सुगरण पक्षी आपल्या चोचीने सुबक वीण घालतो.

प्रश्न आ.
सुगरण पक्ष्याचे हे घरटे वादळात शाबूत का राहते?
उत्तर:
सुगरण पक्ष्याचे घरटे अतिशय मजबूत असते. ते झाडाच्या फांदीला झोक्यासारखे टांगलेले असते. त्यामुळे वादळातही ते शाबूत राहते.

प्रश्न इ.
नयना सुगरण पक्ष्याबद्दल काय म्हणाली?
उत्तर:
नयना सुगरण पक्ष्याबद्दल म्हणाली की, ‘कुठे घाई नाही, गडबड नाही, सगळे कसे नियोजनबद्ध.’

प्रश्न ई.
सुगरण पक्षी कुटुंबवत्सल कसा? ते लिहा.
उत्तर:
सुगरण पक्षी आपल्या सुगरणीसाठी व पिलांसाठी सुरेख घर बांधतो. त्यासाठी अपार मेहनत करतो. म्हणूनच तो
कुटुंबवत्सल आहे.

प्रश्न उ.
सुगरण पक्ष्याला कसबी विणकर का म्हटले आहे?
उत्तर:
सुगरण पक्षी चोचीने आकारबद्ध व नक्षीदार वीण घालून घर बांधतो म्हणून त्याला कसबी विणकर म्हटले आहे.

3. वाक्प्रचार व त्यांचे अर्थ यांच्या जोड्या लावा. 

प्रश्न 1.
वाक्प्रचार व त्यांचे अर्थ यांच्या जोड्या लावा.

उत्तर:

‘अ’ गट	‘ब’ गट
(अ) शाबूत राहणे	2. टिकून राहणे
(आ) वाखाणणे	3. स्तुती करणे
(इ) सर येणे	1. बरोबरी करणे

4. खालील शब्दाचा वाक्यात उपयोग करा.

प्रश्न 1.
खालील शब्दांचा वाक्यांत उपयोग करा.
उत्तर:
(अ) सुबक – रमाने सुबक रांगोळी काढली.
(आ) कसब – कुंभार कसबीने माठ घडवितो.
(इ) चिकाटी – विदयार्थी चिकाटीने अभ्यास करतात.
(ई) मजबूत – दोरखंड मजबूत असतो.

5. तुम्हांला या पाठातून काय शिकायला मिळाले ते लिहा.

प्रश्न 1.
तुम्हांला या पाठातून काय शिकायला मिळाले ते लिहा.
उत्तर:
1. कष्टाने व चिकाटीने आपण कोणत्याही कामात यश मिळवू शकतो.
2. नीटनेटकेपणाने आपले काम सुबक होते.

6. तुम्ही सुगरण पक्ष्याचे घरटे पाहिले आहे का? त्याचा आकार तुम्हांला कसा वाटला? त्याचे वर्णन करा.

प्रश्न 1.
तुम्ही सुगरण पक्ष्याचे घरटे पाहिले आहे का? त्याचा आकार तुम्हांला कसा वाटला? त्याचे वर्णन करा.
उत्तर:
होय. माळरानात निंबाच्या, बाभळीच्या झाडाला लटकलेली सुगरण पक्ष्याची घरटी पाहिली आहेत. मला त्याचा आकार खेळण्याच्या पत्त्यांमधील इस्पीकसारखा वाटला. नक्षीदार वीणकाम असलेले हे घरटे सुबक, मजबूत व वादळातही टिकणारे असते. ‘बाया’ नावाचा पक्षीच कसबीने हे घरटे तयार करतो. म्हणून त्याला ‘सुगरण’ म्हणतात.

7. खाली काही शब्द दिलेले आहेत, त्यापैकी सुगरण पक्ष्याला लागू होणारे शब्द शोधून आकृती पूर्ण करा.
नीटनेटका, चिकाटी, आळशी, जबाबदार, सहनशील, कष्टाळू, स्तुतीप्रिय, निर्दयी, झोपाळू

प्रश्न 1.
खाली काही शब्द दिलेले आहेत, त्यापैकी सुगरण पक्ष्याला लागू होणारे शब्द शोधून आकृती पूर्ण करा.
नीटनेटका, चिकाटी, आळशी, जबाबदार, सहनशील, कष्टाळू, स्तुतीप्रिय, निर्दयी, झोपाळू

उत्तर:

8. सुगरण पक्ष्याप्रमाणे तुमच्यात जर चिकाटी असेल, तर कोणकोणती कामे तुम्ही चांगली करू शकाल ते सांगा.
उपक्रम: तुम्ही पाहिलेले पक्षी व त्यांची घरटी यांची चित्रे गोळा करून एका मोठ्या कागदावर चिकटवा. त्याखाली त्यांची नावे लिहून तक्ता तयार करा.

खालील वाक्ये वाचा.

जेव्हा आपण एखादया शब्दाच्या आधी ‘तो’ लावतो तेव्हा तो पुल्लिंगी शब्द, ‘ती’ लावतो तेव्हा स्त्रीलिंगी शब्द, ‘ते’ लावतो तेव्हा नपुंसकलिंगी शब्द म्हणतो.
आणखी काही उदाहरणे वाचा. वाक्ये लिहिताना त्याप्रमाणे लिहा.

आपण समजून घेऊया.

मीना हुशार मुलगी आहे. मीनाच्या भावाचे नाव मिहीर आहे. मीना मिहीरला ‘दादा’ म्हणते. मिहीर मीनाला ‘ताई’ म्हणतो. मीना आणि मिहीर एकाच शाळेत शिकतात. मीना आणि मिहीर यांच्यात कधीच भांडणे होत नाहीत. मीना मोठी असल्याने मीना मिहीरची काळजी घेते.
वरील परिच्छेदात मीना आणि मिहीर या भावंडांचे वर्णन आले आहे. मीना व मिहीर या शब्दांऐवजी दुसरे शब्द वापरून तयार केलेला पुढील परिच्छेद वाचा.
मीना हुशार मुलगी आहे. तिच्या भावाचे नाव मिहीर आहे. ती त्याला ‘दादा’ म्हणते. तो तिला ‘ताई’ म्हणतो. ते एकाच शाळेत शिकतात. त्यांच्यामध्ये कधीच भांडणे होत नाहीत. ती मोठी असल्याने त्याची काळजी घेते.
मीना आणि मिहीर या नामांऐवजी आपण येथे तिच्या, ती, त्याला, तो, तिला, ते, त्यांच्या, ती, त्याची असे शब्द वापरले आहेत.
या शब्दांना सर्वनाम म्हणतात. नामाऐवजी आपण जो शब्द वापरतो, त्या शब्दास सर्वनाम म्हणतात.

खालील वाक्यातील सर्वनामे अधोरेखित करा.

(अ) मी कुमारला हाक मारली.
(आ) तुला नवीन दप्तर आणले.
(इ) त्याचा फोटो छान येतो.
(ई) मी त्यांना सुविचार सांगितला.
(उ) त्याने घर झाडून घेतले.
(ऊ) आपण पतंग उडवूया.

खालील परिच्छेद वाचा व त्यातील सर्वनामे अधोरेखित करा.

प्रश्न 1.
सुगरण पक्ष्याप्रमाणे तुमच्यात जर चिकाटी असेल, तर कोणकोणती कामे तुम्ही चांगली करू शकाल ते सांगा.
उत्तर:

प्रश्न 2.
खालील वाक्यातील सर्वनामे अधोरेखित करा.

प्रश्न अ.
मी कुमारला हाक मारली.
उत्तर:
मी कुमारला हाक मारली.

प्रश्न आ.
तुला नवीन दप्तर आणले.
उत्तर:
तुला नवीन दप्तर आणले.

प्रश्न इ.
त्याचा फोटो छान येतो.
उत्तर:
त्याचा फोटो छान येतो.

प्रश्न ई.
मी त्यांना सुविचार सांगितला.
उत्तर:
मी त्यांना सुविचार सांगितला.

प्रश्न उ.
त्याने घर झाडून घेतले.
उत्तर:
त्याने घर झाडून घेतले.

प्रश्न ऊ.
आपण पतंग उडवूया.
उत्तर:
आपण पतंग उडवूया.

Marathi Sulabhbharti Class 6 Solutions Chapter 5 सुगरणीचे घरटे Important Additional Questions and Answers

रिकाम्या जागी जुळणाऱ्या योग्य पर्यायाची निवड करून वाक्य पूर्ण करा.

प्रश्न 1.
……………….. असलेल्या निंबाच्या झाडावर सुगरण पक्षी घरटे बांधत होता.
(अ) शाळेच्या परिसरात
(ब) घराच्या अंगणात
उत्तर:
(अ) शाळेच्या परिसरात

प्रश्न 2.
मुले घरटे पाहत असताना ……………….. तिथे आले.
(अ) पक्षी
(ब) गुरुजी
उत्तर:
(ब) गुरुजी

प्रश्न 3.
……………….. पाहूनच या पक्ष्याला ‘सुगरण’ असे म्हणतात.
(अ) स्वयंपाकाचे कसब
(ब) नक्षीदार वीण
उत्तर:
(ब) नक्षीदार वीण

प्रश्न 4.
……………….. हे घरटे शाबूत राहते.
(अ) वादळातही
(ब) उन्हाळ्यातही
उत्तर:
(अ) वादळातही

प्रश्न 5.
किती ……………….. आहे हा पक्षी!
(अ) अपार आळशी
(ब) कसबी विणकर
उत्तर:
(ब) कसबी विणकर

एक-दोन शब्दांत उत्तरे लिहा.

प्रश्न 1.
नयनाला सुगरण पक्ष्याच्या कामातील काय काय आवडायचे?
उत्तरः
सफाईदारपणा, नीटनेटकेपणा

प्रश्न 2.
घरट्याचे निरीक्षण कोण करते?
उत्तर:
सुगरणमादी

खालील प्रश्नांची एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
मुलांनी गुरुजींना काय दाखविले?
उत्तर:
मुलांनी गुरुजींना सुगरणीचे घरटे दाखविले.

प्रश्न 2.
घरटे पाहण्यासाठी कोण कोण थांबायचे?
उत्तर:
अतुल, नयना, जॉन व सिमरन घरटे पाहण्यासाठी थांबायचे.

खालील प्रश्नांची दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
सुगरण पक्ष्याबद्दल सिमरनला काय वाटायचे?
उत्तर:
सिमरनला सुगरण पक्ष्याबद्दल वाटायचे की, हा पक्षी सुगरणीसाठी व पिलांसाठी सुरेख घर बांधतो. त्यासाठी तो अपार मेहनत घेतो. हा खूप जबाबदार व कुटुंबवत्सल पक्षी आहे.

प्रश्न 2.
नयनाला सुगरण पक्ष्याचे कौतुक का वाटते?
उत्तर:
सुगरण पक्षी आकारबद्ध घरटे बांधतो, तेही चोचीने. तो कसबी विणकर आहे. आपल्यालाही असे घरटे तयार करता येईल का? असा प्रश्न नयनाला पडतो आणि म्हणूनच तिला सुगरण पक्ष्याचे कौतुक वाटते.

प्रश्न 3.
गुरुजींनी सुगरण पक्ष्याविषयी कोणती माहिती दिली?
उत्तर:
सुगरण पक्षी नीटनेटके आणि मजबूत घरटे बांधतो. गवताच्या बारीक पण चिवट काड्यांनी तो सुबक, नक्षीदार घरटे बांधतो. नक्षीदार वीण पाहूनच या पक्ष्याला ‘सुगरण’ असे म्हणतात. सुगरण मादी त्या घरट्याचे निरीक्षण करते व मजबूत घरटे पसंत करते. निंब, बाभळीच्या झाडाच्या फांदीला हे घरटे झोक्यासारखे टांगलेले असते. वादळातही हे घरटे शाबूत असते. या घरट्याची सर कोणत्याही इतर पक्ष्याच्या घरट्याला येणार नाही.

व्याकरण व भाषाभ्यास :

सर्वनाम : नामाऐवजी येणाऱ्या शब्दास म्हणतात.
जसे की – तो, ती, ते, त्याला इ.

खालील वाक्यातील सर्वनामे अधोरेखित करा.

प्रश्न 1.
तिने नवीन घर घेतले.
उत्तर:
तिने नवीन घर घेतले.

प्रश्न 2.
ते पावसात भिजले.
उत्तर:
ते पावसात भिजले.

प्रश्न 3.
लिंग ओळखा.
ससा, झाड, तलवार, कॅमेरा, पेला, पिशवी, पुस्तक, उशी, औषध.
उत्तर:

• पुल्लिंग – ससा, कॅमेरा, पेला
• स्त्रीलिंग – तलवार, पिशवी, उशी
• नपुंसकलिंग – झाड, पुस्तक, औषध

प्रश्न 4.
खालील शब्दांचा वाक्यांत उपयोग करा.
उत्तर:

1. निरीक्षण – सलीम अली पक्ष्यांचे निरीक्षण करीत.
2. नीटनेटके – आईचे काम नीटनेटके आहे.
3. घरटे – कोकीळ पक्षी घरटे बांधत नाही.
4. नियोजनबद्ध – कोणतेही काम नियोजनबद्ध हवे.
5. मोहून टाकणे – श्रीकृष्णाच्या चित्राने माझे मन मोहून टाकले.

सुगरणीचे घरटे Summary in Marathi

पाठपरिचयः

प्रस्तुत पाठात सुगरण पक्ष्याच्या घरट्याचे वर्णन केले आहे. सुगरणपक्षी अत्यंत मेहनतीने, चिकाटीने घर बांधतो. सुगरणमादी घराची मजबूती पारखते व मगच घर पसंत करते. सुगरणपक्षी कुटुंबवत्सल व कष्टाळू आहे. त्याचे घर बांधण्याचे कसब पाहून मन थक्क होते.

शब्दर्थ:

1. निरीक्षण – अवलोकन (observation)
2. हालचाल – हालणे (movement)
3. नियोजनबद्ध – आखीवरेखीव (planned)
4. सफाईदार – व्यवस्थित (cleanliness)
5. कष्टाळू – कष्ट करण्याची प्रवृत्ती (hard work)
6. चिकाटी – अथक परिश्रम (perseverance)
7. सुबक – सुंदर (beautiful)
8. अपार – खूप (very much)
9. मजबूत – पक्के (tight)
10. शाबूत राहणे – टिकून राहणे (sustain)
11. कसब – कौशल्य (skill)
12. विणकाम – धागे एकमेकांत गुंफणे (weaving)

वाक्प्रचार व अर्थ:

1. सर येणे – बरोबरी करणे.
2. वाखाणणी करणे – स्तुती करणे.

Marathi Sulabhbharati Class 6 Solutions

• भारतमाता (गाणे) Question Answer
• माझा अनुभव Question Answer
• पाऊस आला! पाऊस आला! (कविता) Question Answer
• माहिती घेऊया Question Answer
• सुगरणीचे घरटे Question Answer
• हे खरे खरे व्हावे… (कविता) Question Answer
• उद्यानात भेटलेला विद्यार्थी Question Answer
• कुंदाचे साहस Question Answer
• घर (कविता) Question Answer

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 16 मुक्या प्राण्यांची कैफियत Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 16 मुक्या प्राण्यांची कैफियत Question Answer Maharashtra Board

Std 6 Marathi Chapter 16 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 16 मुक्या प्राण्यांची कैफियत Textbook Questions and Answers

1. तक्रार व वनचर यांच्या माध्यामातून जोड्या पूर्ण करा.

प्रश्न 1.
तक्रार व वनचर यांच्या माध्यामातून जोड्या पूर्ण करा.

उत्तर:

2. दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
या पाठात कोणाकोणात संवाद झालेला आहे?
उत्तर:
या पाठात गाय, चिमणी, मासोळी, नागोबा, सर्व प्राणी व माणूस यांच्यात संवाद झालेला आहे.

प्रश्न आ.
चिमणीला कोणता त्रास होतो?
उत्तर:
मोबाईलच्या आवाजाने चिमणीची छाती धडधडून तिचा जीव व्याकूळ होतो. तिला काही सुचत नाही.

प्रश्न इ.
गाईचे डोळे का पाणावले?
उत्तर:
माणसाने टाकलेले प्लॅस्टिक घासाबरोबर गाईच्या पोटात जाऊन तिचे पोट दुखू लागले व तिचे डोळे पाणावले.

प्रश्न ई.
मासोळीने आपली कोणती समस्या मांडली आहे?
उत्तर:
सांडपाणी व रसायने टाकून माणसाने पाणी विषारी करून टाकले आहे. ते पाणी घाण असल्याने पिण्यासारखे नाही. म्हणून जलचर तडफडत आहेत. ही समस्या मांडली आहे.

प्रश्न उ.
नागोबाची तक्रार कोणती आहे?
उत्तर:
गवत, शेती नष्ट झाल्याने वारूळेही राहिली नाहीत. मानवाने पर्यावरणाचा -हास केला आहे. नागोबांना पकडून नागपंचमीला दूध, लाया दिले जाते. हे त्याचे अन्न नाही. अंधश्रद्धेपोटी माणूस नागांच्या जीवावर उठला आहे. ही तक्रार आहे.

3. घोटभर, मैलभर, तासभर, कणभर, चमचाभर हे शब्द वापरून वाक्ये लिहा.

प्रश्न 1.
घोटभर, मैलभर, तासभर, कणभर, चमचाभर हे शब्द वापरून वाक्ये लिहा.

उत्तर:

1. घोटभर – उन्हाळ्यात घोटभर पाणी मिळाले तरी समाधान वाटते.
2. मैलभर – मैलभर अंतर चालून गेल्यावर एक देऊळ लागले.
3. तासभर – झाकीरने तासभर तबला वाजविला.
4. कणभर – कणभरही अन्न वाया जाऊ देऊ नये.
5. चमचाभर- चमचाभर औषध तापाला घालविते.
6. टिचभर – मुंबईत टिचभर ही जागा शिल्लक नाही.
7. रात्रभर – यात्रेकरू रात्रभर डोंगर चढत होते.

4. कोण ते सांगा. (वनचर, भूचर, जलचर, उभयचर)

प्रश्न 1.
कोण ते सांगा. (वनचर, भूचर, जलचर, उभयचर)
उत्तर:
पाण्यात राहणारे – जलचर
जमिनीवर राहणारे – भूचर
जंगलात राहणारे – वनचर
जमीन व पाणी या दोन्ही ठिकाणी राहणारे – उभयचर

5. खालील शब्दांचे समानार्थी शब्द पाठातून शोधून लिहा.

प्रश्न 1.
खालील शब्दांचे समानार्थी शब्द पाठातून शोधून लिहा.

1. किनारा
2. शेवट
3. जल
4. आठवण
5. मासा
6. नातेवाईक
7. व्याकूळ
8. आचरण

उत्तर:

1. काठ
2. गडप
3. जळ
4. स्मरण
5. मासोळी
6. सोयरे
7. कासावीस
8. वर्तन

6. खालील शब्दांचे अर्थ शिक्षकांच्या मदतीने समजून घ्या.

प्रश्न 1.
खालील शब्दांचे अर्थ शिक्षकांच्या मदतीने समजून घ्या.
सगेसोयरे, पाहुणे, नातेवाईक, भाऊबंद

7. खालील शब्दांचे लिंग बदला.

प्रश्न 1.
खालील शब्दांचे लिंग बदला.
उत्तर:

1. चिमणी – चिमण्या
2. नाग – नाग
3. वाघ – वाघ

8. खालील वाक्यांत कंसातील योग्य वाक्प्रचार घाला. (उदास दिसणे, कासावीस होणे, डोळे पाणावणे, डोळे उघडणे)

प्रश्न अ.
सह्याद्री डोंगर चढताना आमचा जीव पाणी पिण्यासाठी ……………….. होत होता.
उत्तर:
सह्याद्री डोंगर चढताना आमचा जीव पाणी पिण्यासाठी कासावीस होत होता.

प्रश्न आ.
आवडते पेन हरवल्याने संजय आज …………………… होता.
उत्तर:
आवडते पेन हरवल्याने संजय आज उदास होता.

प्रश्न इ.
पाणी टंचाई भासू लागताच पाणी बचतीबाबत सर्वांचे ………………. उघडले.
उत्तर:
पाणी टंचाई भासू लागताच पाणी बचतीबाबत सर्वांचे डोळे उघडले.

प्रश्न ई.
रस्त्यावर घडलेला अपघात बघून सर्वांचे …………………. .
उत्तर:
रस्त्यावर घडलेला अपघात बघून सर्वांचे डोळे पाणावले.

9. धडधड, तगमग यासारखे आणखी शब्द लिहा.

प्रश्न 1.
धडधड, तगमग यासारखे आणखी शब्द लिहा.
उत्तर:
सरसर, झरझर, गडगड, झगमग, धगधग

प्रश्न 2.
खालील चौकटीत काही प्राणी व काही पक्ष्यांची नावे लपलेली आहेत. ते शोधा व त्यांची नावे लिहा.

उदा. वटवाघूळ
उत्तरः

प्रश्न 2.
दवाखान्याचा ठिकाणी असलेल्या सुचनांच्या पाट्या तयार करा.

उत्तरः

प्रश्न 3.
शाळेच्या परिसरात स्वच्छताविषयक कोणत्या पाट्या लावाल.

उत्तरः

प्रश्न 4.
‘पर्यावरण संरक्षण’ याविषयी पाठाच्या शेवटी माणसाने केलेली प्रतिज्ञा तुमच्या शब्दात लिहा.

उत्तरः

प्रश्न 5.
वाचा. समजून घ्या.
उत्तरः

आपण समजून घेऊया.

प्रश्न 1.
खालील वाक्यांतील अधोरेखित शब्द पाहा.

1. ही माझी छत्री आहे.
2. तू कोणाचा मुलगा आहेस?
3. मी कालच गावाहून आलो.
4. जी वेगाने पळेल, ती जिंकेल.

प्रश्न 2.
अधोरेखित केलेले शब्द ‘एकाक्षरी’ शब्द आहेत. एकाक्षरी शब्दांना दयायची वेलांटी किंवा उ-कार नेहमी | दीर्घ लिहितात. या नियमाला फक्त ‘नि’ हा शब्द अपवाद आहे. खालील शब्दांपासून वाक्ये बनवा.

1.  ती –
2. पी –
3. मी –
4. ही –

प्रश्न 3.
खालील शब्द वाचा. शब्दांतील शेवटच्या अक्षराला दिलेली वेलांटी, उ-कार समजून घ्या.
चिमणी, विळी, मिरची, कढई, चटई, सफाई, खिडकी, मागू, चिकू, पेरू, नाचू, वस्तू, गाऊ, शिंगरू, कांगारू, ताई, समई, पाहुणी, पाणी. मराठी भाषेत शब्दांतील शेवटच्या अक्षराला दयायची वेलांटी किंवा उ-कार नेहमी दीर्घ लिहितात. या नियमाला ‘आणि’, ‘परंतु’ हे शब्द अपवाद आहेत.

Class 6 Marathi Chapter 16 मुक्या प्राण्यांची कैफियत Additional Important Questions and Answers

दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
माणसाने सगेसोयरे कोणाला म्हटले आहे?
उत्तर:
माणसाने कीटक, पक्षी, जलचर, वनचर यांना सगेसोयरे म्हटले आहे.

प्रश्न 2.
माणसाने प्राण्यांपाशी काय कबूल केले?
उत्तर:
पर्यावरणाचा केलेला हास माणसाच्या लक्षात आला. सर्व प्राणी तक्रार करू लागले. माणसाने तेव्हा यापुढे आम्ही आमचे वर्तन बदलू व पर्वत, जल, वातावरणात प्रदूषण करणार नाही असे सांगून वृक्षारोपण करू, वनीकरण करू असे ही आश्वासन दिले.

प्रश्न 3.
मानवाने केलेल्या प्रदूषणाचा कोणता दुष्परिणाम होईल, असे सर्व प्राण्यांनी सांगितले?
उत्तर:
प्राणी तक्रार करू लागले. मानवाने हवेचे, पाण्याचे, भूमीचे प्रदूषण केले. त्यामुळे वनचर आता तुझे सोयरे नाहीत. धरती माता दूषण देईल. मग माणूस दूध, अन्न पाण्यावाचून तडफडेल, असे सर्व प्राण्यांनी मानवाने केलेल्या प्रदूषणाचे दुष्परिणाम सांगितले.

व्याकरण व भाषाभ्यास

प्रश्न 1.
खालील शब्दांचे लिंग बदला.

1. मोर
2. सिंह
3. गाय
4. मांजर
5. राघू
6. कासव
7. हरिण

उत्तर:

1. लांडोर
2. सिंहिण
3. बैल
4. बोका
5. मैना
6. कासविण
7. हरिणी

प्रश्न 2.
खालील शब्दांचे लिंग बदला.

1. गाय
2. मासा
3. जंगल
4. पक्षी
5. माणूस

उत्तर:

1. गाई
2. मासे
3. जंगले
4. पक्षी
5. माणसे

हे लक्षात ठेवा:

एकाक्षरी शब्दांना दयायची वेलांटी किंवा उ-कार नेहमी दीर्घ लिहितात. अपवाद – ‘नि’.

प्रश्न 1.
खालील शब्दांपासून वाक्ये बनवा.
उत्तर:

1. ती – ती खूप हुशार आहे.
2. पी – तू पाणी पी.
3. मी – मी अभ्यास करतो.
4. ही – ही साडी छान आहे.

शब्दातील शेवटच्या अक्षराला दयायची वेलांटी किंवा उ-कार नेहमी दीर्घ लिहितात.

अपवाद – आणि, परंतु उदा. चिमणी, कढई, वस्तू, विक्री इ.

प्रश्न 2.
खालील शब्दांपासून वाक्ये बनवा.
उत्तर:
मिरची – पोपट मिरची खातो.
सफाई – दिवाळीत घरातील सफाई करतात.
चिकू – मला चिकू आवडतात.
गाऊ – आम्ही गाणे गाऊ.

प्रश्न 3.
कोण ते सांगा. (वनचर, भूचर, जलचर, उभयचर)
उत्तर:
पाण्यात राहणारे – जलचर
जमिनीवर राहणारे – भूचर
जंगलात राहणारे – वनचर
जमीन व पाणी या दोन्ही ठिकाणी राहणारे – उभयचर

प्रश्न 4.
खालील शब्दांचे विरूद्धार्थी शब्द पाठातून शोधून लिहा.

1. प्रसन्न
2. कठोर
3. वेडा
4. बिनविषारी
5. स्वच्छ
6. श्रद्धा

उत्तर:

1. उदास
2. नाजूक
3. शहाणा
4. विषारी
5. घाण
6. अंधश्रद्धा

मुक्या प्राण्यांची कैफियत Summary in Marathi

पाठपरिचयः

सदर पाठात पशू-पक्षी, जलचरांना मानवाकडून, त्याच्या अविचाराने होणारा त्रास वर्णन केला आहे. जलचर, भूचर त्रस्त आहेत. याचे दुष्परिणाम सर्व प्राणी मानवास जेव्हा सांगतात तेव्हा डोळे उघडतात. ‘पर्यावरण रक्षण’ कसे करावे हे यातून शिकता येते.

शब्दार्थ:

1. कैफियत – तक्रार (complaint)
2. वन – अरण्य, जंगल (forest)
3. भीती – भय (fear)
4. नाजक – कोमल (delicate)
5. ढीग – रास (heap)
6. पोटशूळ – पोट दुखणे (stomach ache)
7. शहाणा – विवेकी (wise)
8. जल – पाणी (water)
9. विषारी – विषमिश्रीत (poisonous)
10. वारूळ – मुंग्यांचे घर (ant hill)
11. अंधश्रद्धा – चुकीच्या संकल्पना (superstition)
12. हास – नष्ट (destruction)
13. सोयरे – नातेवाईक (relatives)
14. स्मरण – आठवण (remembrance)
15. जागृत – सावध, जागरूक (to be aware of, vigilant)
16. पर्यावरण – वातावरण (enviornment)
17. वर्तन – आचरण (behaviour)
18. वनीकरण – वन, जंगले वसविणे (forestation)
19. वनचर – वनात फिरणारे प्राणी (wild animals)
20. नच – नाही (no, not)
21. वातावरण – आजूबाजूचा परिसर (atmosphere)
22. प्रदूषण – दूषित करणे (pollution)
23. हिरवेगार – गर्द हिरवे (greenish)

Marathi Sulabhbharati Class 6 Solutions

• बाबांचं पत्र Question Answer
• मिनूचा जलप्रवास Question Answer
• चंद्रावरची शाळा (कविता) Question Answer
• मोठी आई Question Answer
• अप्पाजींचे चातुर्य Question Answer
• होळी आली होळी (कविता) Question Answer
• मुक्या प्राण्यांची कैफियत Question Answer
• पाणपोई (कविता) Question Answer

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 2 माझा अनुभव Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 2 माझा अनुभव Question Answer Maharashtra Board

Std 6 Marathi Chapter 2 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 2 माझा अनुभव Textbook Questions and Answers

1. का ते लिहा.

प्रश्न अ.
रिमाने आनंदाने उड्या मारल्या.
उत्तर:
आगगाडीने मामाच्या गावाला जायचे म्हणून रिमाने आनंदाने उड्या मारल्या.

प्रश्न आ.
मुलाने बाळाला मांडीवर घेतले.
उत्तर:
मावशींच्या मांडीवर बसलेले बाळ खुदकन हसले म्हणून मुलाने बाळाला मांडीवर घेतले.

प्रश्न इ.
मुलाचे मन आनंदाने थुईथुई नाचू लागले.
उत्तर:
पानांची सळसळ, नदीची खळखळ, पक्ष्यांची किलबिल, गाईंचे हंबरणे, पशु, पक्षी, शेते पाहून मुलाचे मन आनंदाने थुईथुई नाचू लागले.

प्रश्न ई.
मुलांना गहिवरून आले.
उत्तर:
आजीच्या हाताचा थरथरणारा स्पर्श खूप प्रेमळ अन् बोलका होता म्हणून मुलांना गहिवरून आले.

2. ‘सुट्टी कधी संपली, ते आम्हांला समजलेच नाही.’ असे मुलाला का वाटले? तुमच्या शब्दांत लिहा.

प्रश्न 1.
‘सुट्टी कधी संपली, ते आम्हांला समजलेच नाही.’ असे मुलाला का वाटले? तुमच्या शब्दांत लिहा.
उत्तर:
सुट्टीत विहिरीवर पोहायला जाणे, शेतात बागडणे, आंब्याच्या झाडावर चढून कैऱ्या, पाडाचा आंबा तोडून खाणे, बैलगाडीतून मामाबरोबर फेरफटका मारणे, कधी शेतावर तर कधी आमराईत मामाबरोबर फिरायला जाणे या सर्व मजेत सुट्टी कधी संपली ते मुलांना कळलेच नाही.

3. वाचा. सांगा. लिहा.
नादमय शब्द उदा., छुमछुम, झुकझुक.

प्रश्न अ.
वाचा. सांगा. लिहा.
नादमय शब्द उदा., छुमछुम, झुकझुक.
उत्तर:
फडफड, खडखड, सळसळ, खळखळ, खुळखुळ, थुईथुई

4. खालील शब्दाचे समानार्थी शब्द लिहा.
(अ) वारा, (आ) तोंड, (इ) रस्ता, (ई) आई, (उ) शेत

प्रश्न अ.
वारा
उत्तर:
वारा – पवन, वायू

प्रश्न आ.
तोंड
उत्तर:
तोंड – मुख, चेहरा

प्रश्न इ.
रस्ता
उत्तर:
रस्ता – मार्ग, सडक

प्रश्न ई.
आई
उत्तर:
आई – माता, जननी

प्रश्न उ.
शेत
उत्तर:
शेत – शिवार

5. जोड्या जुळवा.

प्रश्न अ.

‘अ’ गट	‘ब’ गट
1. आगगाडी	(अ) खुळखुळ
2. पैंजण	(ब) खडखड
3. घुंगूरमाळा	(क) झुकझुक
4. बैलगाडी	(ड) खळखळ
5. पाणी	(इ) छुमछुम

उत्तर:

‘अ’ गट	‘ब’ गट
1. आगगाडी	(क) झुकझुक
2. पैंजण	(इ) छुमछुम
3. घुंगूरमाळा	(अ) खुळखुळ
4. बैलगाडी	(ब) खडखड
5. पाणी	(उ) छुमछुम

6. गाईचे हंबरणे’ तसे खालील पशुपक्ष्यांचे आवाजदर्शक शब्द लिहा.

प्रश्न 1.
गाईचे हंबरणे’ तसे खालील पशुपक्ष्यांचे आवाजदर्शक शब्द लिहा.
उत्तर:
(अ) बकरी – बेंऽ बेंऽ
(आ) वाघ – डरकाळी
(इ) बेडूक – डराँव डराँव
(ई) कुत्रा – भुंकणे
(उ) मांजर – म्याँव म्याँव करणे
(ऊ) मोर – माओ माओ

7. खालील वाक्प्रचाराचा वाक्यात उपयोग करा.

प्रश्न 1.
खालील वाक्प्रचारांचा वाक्यात उपयोग करा.
उत्तर:
(अ) खुदकन हसणे – बाळ खुदकन हसले.
(आ) गाढ झोपणे – आई गाढ झोपली होती.
(इ) कडकडून भेटणे – अमेरिकेतून आल्यावर मी भावाला कडकडून भेटलो.
(ई) टुकुटुकु पाहणे – बाळ सर्वांकडे टुकुटुकु पहात होते.
(उ) आनंदाने थुईथुई नाचणे – काळे मेघ पाहून मोर आनंदाने थुईथुई नाचतो.
(ऊ) गहिवरून येणे – निरोप देताना मला गहिवरून आले.

8. बाजारहाट’ यासारखे आणखी काही जोडशब्द लिहा.

प्रश्न 1.
बाजारहाट’ यासारखे आणखी काही जोडशब्द लिहा.
उत्तर:

1. धावपळ
2. नातीगोती
3. पाटपाणी
4. नरमगरम
5. भाजीपाला
6. धुणीभांडी
7. गणगोत

9. तुम्ही एखादे चांगले काम केले आहे त्या प्रसंगाचे अनुभवलेखन करा.

प्रश्न 1.
तुम्ही एखादे चांगले काम केले आहे त्या प्रसंगाचे अनुभवलेखन करा.
उत्तर:
आमच्याकडे घरकामासाठी येणाऱ्या बाईच्या मुलीला मी रोज खाऊ देतो. ती दुसरीत असल्याने तिचा अभ्यासही घेतो. तिची आई काम करेपर्यंत गाणी, कविता शिकवतो. कधी कधी गोष्टीची पुस्तके वाचून दाखवतो. मी तिला चार वया व काही पेन्सीलीही दिल्या आहेत. तिच्यात अभ्यासाची गोडी निर्माण करण्याचा मी प्रयत्न केला आहे. खाल्लेल्या गोळीचा कागद कचरापेटीत टाकायला शिकवले. नखे कापायला व स्वच्छ रहायला शिकवले. तिच्यात बरीच सुधारणा आहे. या चांगल्या कामाने मला समाधान मिळाले.

10. तुमच्या घरातील व्यक्तींबरोबर सुट्टीच्या दिवशी

प्रश्न 1.
तुमच्या घरातील व्यक्तींबरोबर सुट्टीच्या दिवशी
उत्तर:

11. खालील शब्दांसारखे दोन – दोन शब्द लिहा. 

प्रश्न 1.
खालील शब्दांसारखे दोन – दोन शब्द लिहा.
उत्तर:
(अ) सळसळ – (1) मळमळ (2) जळजळ
(आ) भुरभुर – (1) फुरफुर (2) गुरगुर
(इ) लुकलुक – (1) झुकझुक (2) टुकटुक
(ई) खडखड – (1) धडधड (2) बडबड

12. हे शब्द असेच लिहा.

प्रश्न 1.
हे शब्द असेच लिहा.
उत्तर:
उद्या, उन्हाने, तल्लीन, स्टेशन, स्वागत, वाऱ्यांच्या, तेवढ्यात, येणाऱ्या, रस्त्याला, कोंबड्यांचा, स्पर्श, प्रेमळ, दुसऱ्या, कैऱ्या, सुट्टी, आंब्याच्या.

13. खालील शब्द आपण कधी वापरतो?

आपण एका वस्तूबद्दल बोलू लागलो, की त्यास एकवचन म्हणतो आणि अनेकांबद्दल बोलू लागलो, की त्यास अनेकवचन म्हणतो.
उदा., एक झाड – अनेक झाडे.
खालील शब्दांच्या जोड्या वाचा व समजून घ्या.

उत्तर:

• कृपया – विनंती करताना.
  उदा. ’कृपया, मला एक पेन्सिल दे.“
• माफ करा – क्षमा मागताना.
  उदा. ’माफ करा. तुम्हांला चुकून धक्का लागला.“
• आभारी आहे – आभार मानताना.
  उदा. ’तू मला पेन्सिल दिलीस, त्याबद्दल मी आभारी आहे.“

14. खालील वाक्यातील नामांना अधोरेखित करा.

प्रश्न अ.
बाबांचा सदरा उसवला.
उत्तर:
बाबांचा सदरा उसवला.

प्रश्न आ.
सुमनने गुलाबाचे रोपटे लावले.
उत्तर:
सुमनने गुलाबाचे रोपटे लावले.

प्रश्न इ.
पाकिटात पैसे नव्हते.
उत्तर:
पाकिटात पैसे नव्हते.

प्रश्न ई.
मुले बागेत खेळत होती
उत्तर:
मुले बागेत खेळत होती.

प्रश्न उ.
समोरून बैल येत होता.
उत्तर:
समोरून बैल येत होता.

प्रश्न ऊ.
सरिता व फरिदा चांगल्या मैत्रिणी आहेत.
उत्तर:
सरिता व फरिदा चांगल्या मैत्रिणी आहेत.

प्रश्न ए.
पंकजने परीक्षेत पहिला नंबर मिळवला.
उत्तर:
पंकजने परीक्षेत पहिला नंबर मिळवला.

Marathi Sulabhbharti Class 6 Solutions Chapter 2 माझा अनुभव Important Additional Questions and Answers

खालील वाक्यात रिकाम्या जागा भरून वाक्ये पुन्हा लिहा.

प्रश्न 1.

1. पायांतले …………… छुमछुम वाजवत ती घरभर फिरली.
2. आगगाडी ………… करत चालली होती.
3. तिचा चेहरा …………. दिसत होता.
4. मी ……………. मांडीवर घेतले.
5. स्टेशनवर ………….. घेऊन मामा आला होता.
6. बैलांच्या गळ्यातील …………. खुळखुळ वाजत होत्या.
7. मन …………… थुईथुई नाचत होते.
8. आम्ही …………………. बिलगलो.
9. आमची ………….. कधी संपली ते आम्हांला समजलेच नाही.

उत्तर:

1. पैंजण
2. झुकझुक
3. प्रसन्न
4. बाळाला
5. बैलगाडी
6. घुगूरमाळा
7. आनंदाने
8. आजीला
9. सुट्टी

का ते लिहा.

माझा अनुभव प्रश्न उत्तर प्रश्न 1.
रिमाचे डोळे लुकलुकत होते.
उत्तर:
खिडकीतून येणाऱ्या उन्हामुळे रिमाचे डोळे लुकलुकत होते.

Marathi Sulabhbharti Class 6 Solutions Chapter 2 प्रश्न 2.
सुट्टी कधी संपली, ते मुलांना समजलेच नाही.
उत्तर:
पोहणे, बागडणे, आंबे खाणे, शेतात-आमराईत जाणे या सर्व मजेत सुट्टी कधी संपली ते कळलेच नाही.

खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.

माझा अनुभव प्रश्न 1.
मावशींच्या मांडीवर कोण बसले होते?
उत्तर:
मावशींच्या मांडीवर छोटेसे बाळ बसले होते.

Maza Anubhav Question Answers प्रश्न 2.
स्टेशनवर बैलगाडी घेऊन कोण आला होता?
उत्तर:
स्टेशनवर बैलगाडी घेऊन मामा आला होता.

अनुभव समानार्थी शब्द मराठी प्रश्न 3.
शेतातली पिके कशी डुलत होती?
उत्तर:
शेतातली पिके वाऱ्यावर मंद मंद डुलत होती.

Maza Anubhav In Marathi प्रश्न 3.
घरी येताच कोणी स्वागत केले?
उत्तर:
घरी येताच मामीने स्वागत केले.

आनंदी समानार्थी शब्द मराठी प्रश्न 4.
आजीने मुलांचे लाड कसे केले?
उत्तर:
आजीने मुलांच्या डोक्यावरून, तोंडावरून प्रेमाने हात फिरवून मुलांचे लाड केले.

प्रश्न 5.
मुले कोठे पोहायला जात?
उत्तर:
मुले विहिरीवर पोहायला जात.

प्रश्न 6.
सुट्टी संपल्यावर सगळे कुठे परतले?
उत्तरः
सुट्टी संपल्यावर सगळे गावी आपल्या घरी परतले.

प्रश्न 7.
मुले मामाबरोबर कुठे फिरायला जात?
उत्तर:
मुले मामाबरोबर आमराईत फिरायला जात.

प्रश्न 8.
मामाच्या मुलांची नावे लिहा.
उत्तर:
राजू आणि चिमी ही मामाच्या मुलांची नावे आहेत.

खालील प्रश्नांची दोन-तीन वाक्यात उत्तरे लिहा.

प्रश्न 1.
मामाच्या गावातील सायंकाळचे वर्णन करा.
उत्तर:
घरी जाण्यासाठी सर्व बैलगाडीत बसले. तोवर सायंकाळ झाली होती. पाने सळसळत होती. पाण्याची खळखळ, पक्ष्यांची किलबिल, शेतात चरणाऱ्या गाईंचे हंबरणे, बकऱ्यांचे बेंऽ बेंऽ ऐकू येत होते. शेतातील पिके वाऱ्यावर मंद मंद डुलत होती.

प्रश्न 2.
मामाच्या घरी सर्वांचे स्वागत कसे झाले?
उत्तर:
मामा स्वत: बैलगाडी घेऊन स्टेशनवर घ्यायला आला होता. घरी येताच मामीने तोंडभर हसून सगळ्यांचे स्वागत केले, राजू व चिमी ही मामाची मुले वाटच पहात होती. ते सगळ्यांना कडकडून भेटले. आजी हळूहळू काठी टेकवत आली व तिने मुलांच्या डोक्यावरून, तोंडावरून प्रेमाने हात फिरवला.

व्याकरण व भाषाभ्यास:

• एकवचन – जेव्हा आपण एका वस्तूबद्दल बोलतो तेव्हा ते एकवचन असते.
• अनेकवचन – जेव्हा आपण अनेक वस्तूंबद्दल बोलतो तेव्हा ते अनेकवचन असते.

खालील शब्दांचे वचन बदला.

प्रश्न 1.

1. आंबा
2. आगगाडी
3. केस
4. खिडकी
5. पीक
6. धुंगूरमाळ
7. पान
8. घर
9. पक्षी
10. चेहरा
11. नदी
12. परीक्षा
13. कैऱ्या

उत्तर:

1. आंबे
2. आगगाड्या
3. केस
4. खिडक्या
5. पिके
6. घुगूरमाळा
7. पाने
8. घरे
9. पक्षी
10. चेहरे
11. नदया
12. परीक्षा
13. कैरी

खालील वाक्यातील नामांना अधोरेखित करा.

प्रश्न 1.
मुलांनी खाऊ खाल्ला.
उत्तर:
मुलांनी खाऊ खाल्ला.

खालील शब्दांचे समानार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे समानार्थी शब्द लिहा.

1. धमाल
2. बिलगणे
3. झुळूक
4. छोटे
5. बागडणे

उत्तरः

1. मजा
2. प्रेमाने जवळ येणे
3. वाऱ्याची लहर
4. लहान
5. खेळणे.

प्रश्न 2.
‘गाईचे हंबरणे’ तसे खालील पशुपक्ष्यांचे आवाजदर्शक शब्द लिहा.

1. कोल्हा
2. चिमणी
3. कोकीळ
4. कावळा

उत्तर:

1. कुई कुई
2. चिव-चिव
3. कुहू कुहू
4. काव-काव

प्रश्न 3.
खालील शब्दांसारखे दोन दोन शब्द लिहा.
उत्तर:

• सरसर – (1) झरझर (2) घरघर
• झपझप – (1) धपधप (2) रपरप

प्रश्न 4.
खालील वाक्प्रचारांचा वाक्यात उपयोग करा.
उत्तर:
तल्लीन होणे – मालिनी सतार वाजवताना तल्लीन होते.

लेखन विभाग:

प्रश्न 1.
खालील शब्द आपण कधी वापरतो? (कृपया, माफ करा, आभारी आहे.)

उत्तर:

1. कृपया येथे माझे सामान ठेवाल कां?
2. माफ करा माझ्या हातून कप फुटला.
3. आपण मला मदत केलीत, आभारी आहे.

प्रश्न 2.
तुमच्या वर्गात तुम्ही कोणते सुविचार लिहाल?
उत्तर:

1. प्रयत्न केल्याने यश मिळते. अपयशाने खचू नका.
2. निसर्ग तुमचे भविष्य आहे. त्याची काळजी घ्या. निसर्ग जपा. झाडांशी मैत्री करा.
3. चांगला आहार मन, बुद्धी व शरीराला पोषक असतो.
4. खूप वाचा. खूप शिका. मोठ्यांचा आदर करा.
5. अंधश्रद्धेला बळी पडू नका. ज्ञानाची ज्योत पेटवा.

प्रश्न 3.
बागेत तुम्ही कोणते सुचना फलक पाहता?
उत्तर:

प्रश्न 4.
सामाजिक समस्यांवर आधारित घोषवाक्ये लिहा.
उत्तर:

1. पाणी जीवन आहे. जपून वापरा.
2. नका तोडू वृक्ष, रहा नेहमी दक्ष.
3. निसर्गाचा ठेवा मान, राखा पर्यावरणाचे भान.
4. वीज, पाणी, पेट्रोल, डिझेल ही साधनसंपत्ती; नका करू नाश, नाहीतर ओढवेल आपत्ती.
5. कापडी पिशव्यांची साथ खरी; प्लॅस्टिक नको दारोदारी.

माझा अनुभव Summary in Marathi

पाठ परिचयः

प्रस्तुत पाठात वार्षिक परीक्षा संपल्यानंतर मामाच्या गावाला जाण्याचे प्रवासवर्णन व मामाच्या गावात पोहचल्यावर केलेली मौजमजा शब्दचित्रीत केली आहे. उन्हाळ्याच्या सुट्टीचा आनंद कसा लुटला याचा अनुभव मांडला आहे.

शब्दर्थ:

1. झुळूक – वाऱ्याची लहर (breeze)
2. छोटे – लहान (small)
3. गाढ झोपणे – शांत झोपणे (deep sleep)
4. हंबरणे – गाईचा आवाज (bellow)
5. प्रेमळ – प्रेमाने भरलेला (loving)
6. धमाल – मजा (enjoyment, great fun)
7. बागडणे – खेळणे (to play)
8. कैऱ्या – कच्चे आंबे (raw mangoes)
9. पाडाचा आंबा – अर्धवट पिकलेला आंबा (half riped mango)
10. आमराई – आंब्यांची बाग (mango orchard)

वाक्प्रचार व अर्थ:

1. तल्लीन होणे- दंग होणे, गुंग होणे
2. गहिवरून येणे – मन भरून येणे
3. कडकडून भेटणे – प्रेमाने मिठी मारणे
4. गाठणे – जाऊन भेटणे
5. बिलगणे – प्रेमाने आलिंगन देणे

Marathi Sulabhbharati Class 6 Solutions

• भारतमाता (गाणे) Question Answer
• माझा अनुभव Question Answer
• पाऊस आला! पाऊस आला! (कविता) Question Answer
• माहिती घेऊया Question Answer
• सुगरणीचे घरटे Question Answer
• हे खरे खरे व्हावे… (कविता) Question Answer
• उद्यानात भेटलेला विद्यार्थी Question Answer
• कुंदाचे साहस Question Answer
• घर (कविता) Question Answer

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 1 भारतमाता Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 1 भारतमाता (गाणे) Question Answer Maharashtra Board

Std 6 Marathi Chapter 1 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 1 भारतमाता Textbook Questions and Answers

प्रश्न 1.
रिकाम्या जागा भरा.

1. रंग वेगळे ……….. वेगळे, तरी येथली सर्व फुले.
2. मानव सारे ………… असती, शिकवण ही जगतास दिली.
3. या मातेची मुले ………. सदा तिचा ध्वज उंच धरु.
4. प्रियतम अमुचे …………… हे, प्रियतम या गंगा जमुना.

उत्तर:

1. गंध
2. समान
3. सद्गुणी
4. सह्यविंध्य

प्रश्न 2.
जोड्या जुळवा.

‘अ’ गट	‘ब’ गट
1. पाणी	(अ) डुलणारी
2. हिमालय	(ब) सळसळते
3. वारे	(क) धवल
4. भारतमाता	(ड) झुळझुळते
5. शेते	(इ) प्रियतम

उत्तर:

‘अ’ गट	‘ब’ गट
1. पाणी	(ड) झुळझुळते
2. हिमालय	(क) धवल
3. वारे	(ब) सळसळते
4. भारतमाता	(इ) प्रियतम
5. शेते	(अ) डुलणारी

प्रश्न 3.
कवितेच्या खालील ओळी पूर्ण करा.

1. प्रियतम अमुची …………………. तिची मुले.
2. रंग वेगळे …………….. सर्व फुले.
3. प्रिय आम्हाला …………… झुळझुळते.
4. प्रियकर ही डुलणारी ……………. सळसळते.
5. प्रियतम आमुचा ………….. जो गगना.
6. प्रियतम अमुचे सह्यविंध्य …………. जमुना.
7. या मातेची …………. प्रिय झाली.
8. या मातेची ………….. उंच धरु.

उत्तर:

1. भारतमाता, आम्ही सारी
2. गंध वेगळे, तरी येथली
3. येथील माती, प्रिय हे पाणा
4. शेते, प्रिय हे वारे
5. धवल हिमालय, बघे भिडाया
6. हे, प्रियतम या गंगा
7. मुले सद्गुणी, सर्व जगाला
8. मुले लाडकी, सदा तिचा ध्वज प्रश्न

खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.

प्रश्न 1.
सारी मुले कुणाची आहेत?
उत्तर:
सारी मुले भारतमातेची आहेत.

प्रश्न 2.
फुले कशी आहेत?
उत्तर:
फुले विविध रंगांची व गंधाची आहेत.

प्रश्न 3.
हिमालय कसा आहे?
उत्तर:
हिमालय धवल व गगनाला भिडणारा आहे.

प्रश्न 4.
भारतमातेने जगतास कोणती शिकवण दिली?
उत्तर:
सारे मानव समान आहेत ही शिकवण भारतमातेने जगतास दिली.

प्रश्न 5.
भारतमातेची मुले काय करणार आहेत?
उत्तर:
भारतमातेची मुले ध्वज उंच करणार आहेत.

खालील प्रश्नांची दोन-तीन वाक्यात उत्तरे लिहा.

प्रश्न 1.
कवयित्रीला कोण कोण प्रिय आहे?
उत्तर:
कवयित्रीला भारतमाता, सर्व फुले, माती, पाणी, शेते, वारे, हिमालय, सह्याद्री व विध्य पर्वत, गंगा, जमुना, सर्व मुले प्रिय आहेत.

प्रश्न 2.
भारतमातेची मुले कशी आहेत? त्यांनी कोणती शिकवण दिली?
उत्तर:
भारतमातेची मुले सद्गुणी आहेत. त्यांनी मानव सारे समान आहेत ही शिकवण सर्व जगाला दिली.

प्रश्न 3.
भारतमातेविषयी कृतज्ञता कशी व्यक्त केली आहे?
उत्तर:
भारतमाता सर्वांना प्रिय आहे. तिला सर्व वंदन करत आहेत. तिचा ध्वज उंच फडकवून तिच्याविषयी कृतज्ञता व्यक्त केली आहे.

व्याकरण व भाषाभ्यास:

प्रश्न 1.
वचन बदला.

1. मुलगा
2. माती
3. पाणी
4. नदी
5. किडा
6. भाजी
7. घर
8. झाड
9. शेत

उत्तर :

1. मुले
2. माती
3. पाणी
4. नदया
5. किडे
6. भाज्या
7. घरे
8. झाडे
9. शेते

प्रश्न 2.
खालील शब्दांचे समानार्थी शब्द लिहा.

1. वंदन
2. माता
3. सदा
4. गंध
5. लाडकी

उत्तर:

1. नमस्कार
2. आई
3. नेहमी
4. सुवास
5. आवडती, प्रिय

प्रश्न 3.
खालील शब्दांचे विरूद्धार्थी अर्थाचे शब्द लिहा.

1. प्रियतम
2. समान
3. उंच
4. सद्गुणी

उत्तर:

1. अप्रिय
2. असमान
3. बुटका, ठेंगणा
4. दुर्गुणी

प्रश्न 4.
कवितेमध्ये आलेले यमक जुळणारे शब्द शोधा.

1. मुले
2. झुळझुळते
3. गगना
4. दिली
5. करू

उत्तर:

1. फुले
2. सळसळते
3. जमुना
4. झाली
5. धरू

लेखन विभाग:

प्रश्न 1.
‘भारतमाता’ शब्द वापरून चार वाक्ये लिहा.
उत्तर:

1. भारतमाता आम्हाला प्रिय आहे.
2. आम्ही भारतमातेला वंदन करू.
3. भारतमातेचा ध्वज उंच धरू,
4. आम्ही भारतमातेची मुले आहोत.

प्रश्न 2.
भारतमाता विविध गोष्टींनी नटलेली आहे. चौकटीत त्यांची नावे लिहा.

उत्तर:

1. हिमालय
2. फुले
3. माती
4. पाणी
5. गंगा, जमुना
6. सयविंध्य

भारतमाता (गाणे) Summary in Marathi

काव्य परिचय:

भारतमाता ही भारतभूमीचे वैशिष्ट्य सांगणारी कविता आहे. भारताच्या मातीत विविधता आहे. निसर्ग भरभरून फुलला आहे. पर्वतराजी उंच उंच आहेत. हिची प्रजा गुणी असून जगतासाठी आदर्श आहे. भारतमातेविषयी आदर व कृतज्ञता बाळगून आपण तिचा गौरव वाढवू व ध्वज उंच फडकवू हा अर्थ या कवितेतून प्रतित होतो.

शब्दार्थ:

1. प्रियतम – आवडती, प्रियकर (darling)
2. अमुची – आपली (ours’)
3. गंध – वास (odour, smell)
4. माती – मृत्तिका (earth, soil)
5. डुलणारी – वाऱ्यावर हलणारी (oscillating)
6. शेते – शेती (farming)
7. धवल – पांढराशुभ्र, सफेद (white)
8. भिडणे – पोहोचणे (to meet)
9. गगन – आकाश (sky)
10. सयविंध्य – सह्याद्री, विंध्याचल पर्वत (Sahyadri)
11. मानव – माणूस (human being)
12. शिकवण – उपदेश (to advise, teaching)
13. सद्गुणी – गुणवान (virtuous)
14. सदा – नेहमी (always)
15. ध्वज – झेंडा (flag)
16. वंदन – नमस्कार (salutation)

वाक्प्रचार व अर्थ:

1. भिडणे – जाऊन ठेपणे, पोहोचणे

Marathi Sulabhbharati Class 6 Solutions

• भारतमाता (गाणे) Question Answer
• माझा अनुभव Question Answer
• पाऊस आला! पाऊस आला! (कविता) Question Answer
• माहिती घेऊया Question Answer
• सुगरणीचे घरटे Question Answer
• हे खरे खरे व्हावे… (कविता) Question Answer
• उद्यानात भेटलेला विद्यार्थी Question Answer
• कुंदाचे साहस Question Answer
• घर (कविता) Question Answer

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 10 बाबांचं पत्र Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 10 बाबांचं पत्र Question Answer Maharashtra Board

Std 6 Marathi Chapter 10 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 10 बाबांचं पत्र Textbook Questions and Answers

1. एका शब्दात उत्तरे लिहा.

प्रश्न 1.
(अ) कठीण गेलेला पेपर
(आ) वैष्णवीला पत्र लिहणारे
(इ) परीक्षेतील गुणांपेक्षा महत्त्वाचे गुण
(ई) वैष्णवीसाठी बाबा आणणार असलेला खाऊ
उत्तर:
(अ) कठीण गेलेला पेपर – गणित
(आ) वैष्णवीला पत्र लिहणारे – बाबा
(इ) परीक्षेतील गुणांपेक्षा महत्त्वाचे गुण – आंतरिक गुण
(ई) वैष्णवीसाठी बाबा आणणार असलेला खाऊ – पुस्तके

2. एका वाक्यात उत्तरे लिहा.

प्रश्न अ.
आईने दूरध्वनीवरून बाबांना कोणता निरोप दिला?
उत्तर:
‘सहामाही परीक्षेत गणिताचा पेपर खूपच कठीण गेल्यामुळे वैष्णवी फार निराश झाली आहे’ हा निरोप आईने बाबांना दूरध्वनीवरून दिला.

प्रश्न आ.
बाबांनी दूरध्वनीवरून बोलणे का पसंत केले नाही?
उत्तर:
बाबांना वैष्णवीशी हितगुज करावेसे वाटले, म्हणून बाबांनी दूरध्वनीवरून बोलणे पसंत केले नाही.

प्रश्न इ.
गणित विषय वैष्णवीचा लाडका होण्यासाठी बाबांनी कोणते उपाय सुचवले आहेत?
उत्तर:
गणित विषय वैष्णवीचा लाडका होण्यासाठी बाबांनी वैष्णवीला सांगितले की, गणिताचा पेपर कठीण गेला, म्हणून गणितानंतर असलेल्या विषयांचे पेपर अवघडच जाणार असे होत नाही ना! मग त्याच त्या गोष्टीचा विचार करत बसल्याने उरलेल्या पेपरवरही त्याचा विपरीत परिणाम होतो. ‘अगं, एखादया विषयात गुण कमी पडले, तर याचा अर्थ आपण आयुष्यात अपयशी झालो असे नाही.

तुला सांगतो, गणिताशी तू मैत्री कर. मग बघ गंमत या विषयाची. तुला मुळीच भीती वाटणार नाही. गणितातील संकल्पना, संबोध, क्रिया तू नीट समजून घे. उदाहरणे सोडवण्याचा चांगला सराव कर. हा विषय लवकरच तुझा लाडका होईल.’ हा उपाय सुचवला.

3. खालील शब्दांचे समानार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

उत्तर:

4. खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

उत्तर:

5.

प्रश्न अ.

उत्तर:

प्रश्न आ.

उत्तर:

6. सध्याच्या युगात पत्र पाठवण्याची कोणकोणती साधने उपलब्ध आहेत त्यांची यादी करा. 

प्रश्न 1.
सध्याच्या युगात पत्र पाठवण्याची कोणकोणती साधने उपलब्ध आहेत त्यांची यादी करा.
उत्तर:

1. पत्रपेटी
2. टपालगाडी
3. कुरिअर
4. ईमेल
5. विमान

7. दिवाळीच्या सुट्टीत तुम्ही काय काय गंमत करणार त्याची यादी बनवा.

प्रश्न 1.
दिवाळीच्या सुट्टीत तुम्ही काय काय गंमत करणार त्याची यादी बनवा.
उत्तरः

1. प्रथम मी नवीन कपडे विकत घेणार,
2. बाबांना सोबत घेऊन फटाके विकत घेणार.
3. आई बरोबर मामाच्या गावी जाणार.
4. आई व आजी यांना फराळ बनवण्यात मदत करणार.
5. मित्रांबरोबर मोकळ्या अंगणात फटाके वाजवणार.
6. शिक्षकांनी दिलेला गृहपाठ वेळेवर पूर्ण करेन.
7. मित्रांसोबत घराच्या अंगणात मातीचा किल्ला तयार करणार.
8. किल्ल्यावर शिवाजी महाराज व इतर शिपाई यांची मांडणी करणार.

8. तुमच्या मित्राला/मैत्रिणीला पोहण्याच्या स्पर्धेत राज्यातून प्रथम क्रमांक प्राप्त झाला. त्याचे तिचे अभिनंदन करणारा संदेश खालील चौकटीत लिहा.

प्रश्न 1.
तुमच्या मित्राला/मैत्रिणीला पोहण्याच्या स्पर्धेत राज्यातून प्रथम क्रमांक प्राप्त झाला. त्याचे तिचे अभिनंदन करणारा संदेश खालील चौकटीत लिहा.
उत्तर:
प्रिय सुप्रिया, अभिनंदन ! अभिनंदन !! अभिनंदन!!!
तुझा पोहण्याच्या स्पर्धेत राज्यातून प्रथम क्रमांक आला हे ऐकून खूप अभिमान वाटला.
असेच यश तुझ्या वाट्याला पुढे पुढे येवो, हिच ईश्वर चरणी प्रार्थना….

9. अपयश ही यशाची पहिली पायरी आहे.’ यासारखी दोन वाक्ये खालील चौकटीत लिहा. 

प्रश्न 1.
अपयश ही यशाची पहिली पायरी आहे.’ यासारखी दोन वाक्ये खालील चौकटीत लिहा.
उत्तर:
1. सुख आणि दुःख यांना सारखेच सामोरे जावे,
2. संकटांना जो धैर्याने तोंड देतो, तोच जीवनात विजयी होतो.

प्रकल्प: साने गुरुजी यांचे ‘सुंदर पत्रे’ हे पुस्तक मिळवा. वाचा. त्यातील तुम्हांला आवडलेली पत्रे सुरेख अक्षरांत लिहा.

प्रश्न 2.
खालील वाक्यांतील रिकाम्या जागी कंसातील योग्य विशेषणे लिहा.
(टवटवीत, उंच, नवा, शंभर)
(अ) हिमालय ………… पर्वत आहे.
(आ) कंपास घ्यायला आईने मला ……………. रुपये दिले.
(इ) बागेत ………….. फुले आहेत.
(ई) ताईने मला …………..’ सदरा दिला.
उत्तर:
(अ) उंच
(आ) शंभर
(इ) टवटवीत
(ई) नवा

आपण समजून घेऊया.

प्रश्न 3.
खालील तक्ता वाचा. समजून घ्या.

उत्तर:

वाक्ये	क्रियापदे	काळ
1. सुनीताने बोरे खाल्ली.	खाल्ली	भूतकाळ
2. मी क्रिकेटची मॅच पाहीन.	पाहीन	भविष्यकाळ
3. सुधीर पत्र लिहीत आहे.	आहे	वर्तमानकाळ
4. वनिता गोड गाणे गाते.	गाते	वर्तमानकाळ
5. आईने कादंबरी वाचली.	वाचली	भूतकाळ

क्रियापदाच्या रूपावरून वाक्यांतील काळ ओळखता येतो.
काळाचे मुख्य तीन प्रकार आहेत.

1. वर्तमानकाळ
2. भूतकाळ
3. भविष्यकाळ

Marathi Sulabhbharti Class 6 Solutions Chapter 10 बाबांचं पत्र Important Additional Questions and Answers

खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.

प्रश्न 1.
बाबांनी वैष्णवीला कोणत्या विषयाशी मैत्री करायला सांगितले आहे?
उत्तर:
बाबांनी वैष्णवीला गणित विषयाशी मैत्री करायला सांगितले आहे.

प्रश्न 2.
परीक्षेतील गुण किंवा श्रेणी पेक्षा अजून कोणती गोष्ट महत्त्वाची आहे?
उत्तर:
परीक्षेतील गुण किंवा श्रेणी पेक्षा आपल्या आंतरिक गुणांची वाढ करणे हे अधिक महत्त्वाचे आहे.

प्रश्न 3.
स्वत:मधील गुणांची वाढ करण्याकरिता प्रत्येकाने काय केले पाहिजे?
उत्तर:
स्वत:मधील गुणांची वाढ करण्याकरिता प्रत्येकाने एखादी तरी कला जोपासली पाहिजे.

प्रश्न 4.
दिवाळीच्या सुट्टीत बाबा कुठे येणार आहेत?
उत्तर:
दिवाळीच्या सुट्टीत बाबा गावी येणार आहेत.

प्रश्न 5.
गावी येताना बाबा वैष्णवीसाठी काय आणणार आहेत?
उत्तर:
गावी येताना बाबा वैष्णवीसाठी खाऊ आणणार आहेत.

प्रश्न 6.
बाबा गावी येताना वैष्णवीसाठी कोणती पुस्तके आणणार आहेत?
उत्तर:
बाबा गावी येताना वैष्णवीसाठी गोष्टीची पुस्तके आणणार आहेत.

बाबांचं पत्र Summary in Marathi

पाठपरिचय:

हे एक वडिलांनी आपल्या मुलीला लिहिलेले सांत्वनपर पत्र आहे. आपल्या मुलीला गणिताचा पेपर अवघड गेल्यामुळे आलेली | निराशा वडीलांनी अतिशय सहजतेने कशी दूर करण्याचा प्रयत्न केला, त्याचे हे पत्र म्हणजे एक सुंदर उदाहरण आहे.

शब्दार्थ:

1. प्रिय – प्रेमळ (dear)
2. शुभ – मंगलदायक, पवित्र (holy)
3. पुरता – पुरेसा (enough)
4. गुरफटणे – गुंतून राहणे (involve, entangled)
5. निराश – नाराज (disappointed)
6. हितगुज करणे – मनातील गोष्ट सांगणे (to chat)
7. विपरीत – वाईट (bad)
8. संबोध – मूळ संकल्पना (concept)
9. सराव – कृती (practice)
10. लाडका – आवडीचा (favourite)
11. आंतरिक – आतील गुण (internal qualities)
12. उत्तम – अधिक चांगले (very good)
13. नृत्य – नाच (dance)
14. जोपासणे – सांभाळणे (to keep safe, to look after)
15. पुरेपूर – पूर्णपणे (completely)
16. खात्री – विस्वास (belief, trust)
17. भेटीअंती – भेट झाल्यानंतर (after meeting)

वाक्प्रचार व अर्थ:

1. निराश होणे – नाराज होणे.
2. हितगुज करणे – मनातील गोष्ट सांगणे.
3. विपरीत परिणाम होणे – वाईट परिणाम होणे.
4. संधी मिळणे – वाव मिळणे.
5. खात्री असणे – विश्वास असणे.

Marathi Sulabhbharati Class 6 Solutions

• बाबांचं पत्र Question Answer
• मिनूचा जलप्रवास Question Answer
• चंद्रावरची शाळा (कविता) Question Answer
• मोठी आई Question Answer
• अप्पाजींचे चातुर्य Question Answer
• होळी आली होळी (कविता) Question Answer
• मुक्या प्राण्यांची कैफियत Question Answer
• पाणपोई (कविता)

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 4 माहिती घेऊया Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 4 माहिती घेऊया Question Answer Maharashtra Board

Std 6 Marathi Chapter 4 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 4 माहिती घेऊया Textbook Questions and Answers

1. भारतीय संशोधकांची नावे व त्यांनी लावलेले शोध यांची माहिती घेऊन तक्ता तयार करा. वर्गात लावा.

प्रश्न 1.
भारतीय संशोधकांची नावे व त्यांनी लावलेले शोध यांची माहिती घेऊन तक्ता तयार करा. वर्गात लावा.
उत्तर:

भारतीय संशोधक	लावलेले शोध
1. ए. पी. जे. अब्दुल कलाम	अग्नी, पृथ्वी, क्षेपणास्त्र स्वदेशी पद्धतीने बनवले
2. जयंत विष्णू नारळीकर	ब्रहमांड उत्पत्ती शोध – बिग बँग थियरी
3. विक्रम साराभाई	आण्विक उर्जा, इलेक्ट्रॉनिक्स
4. डॉ. जगदीशचंद्र बोस	रेडीयो, सूक्ष्म तरंगांचे प्रकाशिकीवर कार्य
5. डॉ. होमी जहांगीर भाभा	परमाणू उर्जा

2. कोणकोणत्या गोष्टींमध्ये संशोधन व्हावे असे तुम्हांला वाटते? विचार करा व लिहा.

प्रश्न 1.
कोणकोणत्या गोष्टींमध्ये संशोधन व्हावे असे तुम्हांला वाटते? विचार करा व लिहा.
उत्तर:

1. कॅन्सरच्या सर्व पातळ्यांवर
2. अवयव प्रत्यारोपण
3. थर्माकोल विघटन
4. इलेक्ट्रॉनिक्स कचऱ्याची विल्हेवाट

3. खालील वाक्याचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा., भिंत कोसळली – भिंती कोसळल्या.

उप्रकम: आंतरजालाचा उपयोग करून डॉ. वसंत गोवारीकर यांची माहिती मिळवा. कोलाज तयार करा.
प्रकल्प: वर्तमानपत्रात शास्त्रज्ञ, संशोधक यांच्याविषयी येणाऱ्या माहितीची कात्रणे काढून चिकटवही बनवा.

प्रश्न 1.
खालील वाक्याचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा., भिंत कोसळली – भिंती कोसळल्या.

उत्तर:

1. मला कविता आठवली.	आम्हाला कविता आठवल्या.
2. त्याने खुर्ची ठेवली.	त्यांनी खुर्ध्या ठेवल्या.
3. मधू आंबा खा.	मधू आंबे खा.

Marathi Sulabhbharti Class 6 Solutions Chapter 4 माहिती घेऊया Important Additional Questions and Answers

योग्य पर्याय निवडून उत्तरे लिहा.

1. डॉ. वसंत गोवारीकरांचा जन्म …………… (25 मार्च, 1933, 25 मार्च 1923)
2. त्यांनी पत्र पाठविले …………… (विक्रम साराभाईंना, हेन्री फोर्डला)
3. डॉ. वसंत गोवारीकरांनी नवीन पद्धत शोधून काढली. ……………(मान्सूनच्या अंदाजाची, उर्जेची)

उत्तर:

1. 25 मार्च 1933
2. हेन्री फोर्डला
3. मान्सूनच्या अंदाजाची

एका वाक्यात उत्तरे लिहा.

प्रश्न 1.
डॉ. वसंत गोवारीकरांचे पदवीपर्यंतचे शिक्षण कुठे झाले?
उत्तर:
डॉ. वसंत गोवारीकरांचे पदवीपर्यंतचे शिक्षण कोल्हापूरला झाले.

प्रश्न 2.
डॉ. वसंत गोवारीकरांनी कोणते तंत्र विकसित केले?
उत्तर:
डॉ. वसंत गोवारीकरांनी अग्निबाणाच्या मोटारीकरिता घन इंधन बनवण्याचे तंत्र विकसित केले.

प्रश्न 3.
देशभर कोणती चिंता असते?
उत्तर:
पाऊस केव्हा पडेल? किती पडेल? याची देशभर चिंता असते.

प्रश्न 4.
पत्राचे इंग्रजी भाषांतर करण्यासाठी गोवारीकरांनी कोणाची मदत घेतली?
उत्तर:
पत्राचे इंग्रजी भाषांतर करण्यासाठी गोवारीकरांनी मित्राची मदत घेतली.

प्रश्न 5.
गोवारीकरांचा कोणत्या दोन गुणांची चुणूक लहानपणीच दिसून आली?
उत्तर:
त्यांच्या कुशाग्र बुद्धिमत्तेची आणि दृढ संकल्पाची चुणूक लहानपणीच दिसून आली.

प्रश्न 6.
पदवीपर्यंतच्या शिक्षणानंतर गोवारीकर उच्च शिक्षणासाठी कुठे गेले?
उत्तर:
पदवीपर्यंतच्या शिक्षणानंतर गोवारीकर उच्च शिक्षणासाठी इंग्लंडला गेले.

प्रश्न 7.
कोणत्या विदयापीठात त्यांनी ‘रासायनिक अभियांत्रिकी’ विषयात संशोधन केले?
उत्तर:
बर्मिंगहॅम विद्यापीठात त्यांनी ‘रासायनिक अभियांत्रिकी’ विषयात संशोधन केले.

प्रश्न 8.
संशोधक म्हणून त्यांनी कोठे काम केले?
उत्तर:
इंग्लंडच्या उर्जा संशोधन केंद्रात संशोधक म्हणून काम केले.

खालील प्रश्नांची दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
भारताच्या विज्ञान क्षेत्रातील डॉ. गोवारीकरांनी केलेली
कामगिरी लिहा.
उत्तर:
विक्रम साराभाईंच्या आग्रहामुळे 1967 साली ते भारताच्या अवकाश संशोधन केंद्रात रुजू झाले. ‘घन पदार्थातील उर्जा’ या विषयाच्या संशोधनासाठी त्यांच्या पुढाकाराने नवा प्रकल्प सुरू करण्यात आला. अग्निबाणाच्या मोटारीकरिता घन इंधन बनवण्याचे तंत्र त्यांनी विकसित केले. मान्सूनच्या अंदाजाची नवी पद्धत शोधून काढली.

प्रश्न 2.
शाळेत असताना त्यांना कोणती कल्पना सुचली? त्याची कशी दखल घेतली गेली?
उत्तर:
शाळेत असताना आपण मोटार बनवावी असे त्यांना वाटले. तेराव्या वर्षी त्यांनी अमेरिकेतील हेन्री फोर्डला पत्र लिहून आपली इच्छा कळवली. हेनरी फोर्डला मराठीतील पत्र कळणार नाही म्हणून मित्राच्या मदतीने पत्राचे इंग्रजी भाषांतर केले. हेन्री फोर्डने डॉ. गोवारीकरांच्या पत्राची दखल घेऊन उत्तरही पाठवले. सोबत काही पुस्तके पाठविली.

व्याकरण व भाषाभ्यास:

प्रश्न 1.
खालील वाक्यांचे वचन बदलून वाक्ये पुन्हा लिहा.
उदा. भिंत कोसळली – भिंती कोसळल्या
उत्तर:

1. मीराला पिशवी सापडली.	मीराला पिशव्या सापडल्या.
2. रामने पुस्तक वाचले.	रामने पुस्तके वाचली.

प्रश्न 2.
लिंग बदला.

1. मित्र
2. आजोबा
3. भाऊ
4. मुलगा
5. मामा
6. लेखक
7. कवी
8. समाजसेवक
9. बाई
10. नट

उत्तर:

1. मैत्रिण
2. आजी
3. बहिण
4. मुलगी
5. मामी
6. लेखिका
7. कवयित्री
8. समाजसेविका
9. माणूस
10. नटी

प्रश्न 3.
विरूद्धार्थी शब्द लिहा.

1. दूर
2. नवी
3. मित्र
4. कुशाग्र
5. दृढ
6. मोठी
7. विकसित
8. घन

उत्तर:

1. जवळ
2. जुनी
3. शत्रू
4. मंद
5. डळमळीत
6. छोटी, लहान
7. अविकसित
8. द्रव

प्रश्न 4
खालील वाक्प्रचारांचा वाक्यात उपयोग करा.
उत्तर:

1. विकसित करणे – शेतकऱ्यांनी संत्रांचा वापर करून शेती विकसित केली.
2. रुजू होणे – बरेच दिवसांच्या सुट्टीनंतर रमेश कामावर रुजू झाला.

लेखन विभाग:

प्रश्न 1.
आंतरजालाचा उपयोग करून डॉ. वसंत गोवारीकर यांची माहिती मिळवा.
उत्तर:
डॉ. वसंत रणछोड गोवारीकर यांचा जन्म 25 मार्च 1933 रोजी झाला. एक भारतीय शास्त्रज्ञ म्हणून त्यांचा नावलौकिक आहे. इंडियन स्पेस रिसर्च ऑर्गनायझेशन मध्ये ते मुख्य पदावर विराजमान होते. अंतराळ, हवामान, लोकसंख्या विषयांवरचे त्यांचे योगदान महत्त्वपूर्ण आहे. पद्मश्री व पद्मभूषण या पुरस्करांनी त्यांना सन्मानित केले गेले. 2 जानेवारी 2015 रोजी ते अनंतात विलीन झाले.

माहिती घेऊया Summary in Marathi

पाठ परिचयः

पद्मश्री व पद्मभूषण पुरस्कार प्राप्त असलेले श्री. वसंत गोवारीकर एक भारतीय संशोधक होते. अवकाश संशोधनाच्या मुख्य पदावर कार्यरत असलेले वसंत गोवारीकर 1991 – 1993 च्या काळात पंतप्रधानांचे सल्लागारही होते. अंतराळ संशोधन, हवामान, लोकसंख्या या विविध विषयांवरचे त्यांचे योगदान अमूल्य आहे. प्रस्तुत पाठात त्यांच्याविषयी अधिक माहिती जाणून घेता येईल.

शब्दर्थ:

1. देश – राष्ट्र (nation)
2. चिंता – काळजी (worry)
3. शोधणे – हुडकून काढणे (to invent)
4. कल्पना – युक्ती (idea)
5. भाषांतर – एका भाषेतून दुसऱ्या भाषेत लिहिणे. (translation)
6. थेट – सरळ (direct)
7. कुशाग्र – तीक्ष्ण (sharp)
8. संकल्प – figale (resolution)
9. संशोधन – नवीन शोध (invention)
10. प्रकल्प – योजना (project)
11. क्षेत्र – विभाग (field, area)
12. कामगिरी – कार्यवाही (execution of work)
13. इंधन – जळाऊ पदार्थ (fuel)
14. विकसित करणे – वाढविणे (to develop)
15. घन – कठीण (solid)
16. चुणूक – झलक (a faint indication)

Marathi Sulabhbharati Class 6 Solutions

• भारतमाता (गाणे) Question Answer
• माझा अनुभव Question Answer
• पाऊस आला! पाऊस आला! (कविता) Question Answer
• माहिती घेऊया Question Answer
• सुगरणीचे घरटे Question Answer
• हे खरे खरे व्हावे… (कविता) Question Answer
• उद्यानात भेटलेला विद्यार्थी Question Answer
• कुंदाचे साहस Question Answer
• घर (कविता) Question Answer

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 3 पाऊस आला! पाऊस आला! Notes, Textbook Exercise Important Questions and Answers.

Class 6th Marathi Chapter 3 पाऊस आला! पाऊस आला! (कविता) Question Answer Maharashtra Board

Std 6 Marathi Chapter 3 Question Answer

Marathi Sulabhbharti Class 6 Solutions Chapter 3 पाऊस आला! पाऊस आला! Textbook Questions and Answers

1. खालील प्रश्नांची एक दोन वाक्यांत उत्तरे लिहा.

प्रश्न अ.
विजा केव्हा चमकल्या?
उत्तर:
विजा ऐन दुपारी चमकल्या.

प्रश्न आ.
सुटलेला वारा कसा होता?
उत्तर:
सुटलेला वारा भणाणवारा होता.

प्रश्न इ.
पाऊस आल्यामुळे आजोबांनी काय केले?
उत्तर:
पाऊस आल्यामुळे आजोबांनी छत्री शिवली.

प्रश्न ई.
आलेल्या पावसामुळे बाबांनी चडफड का केली?
उत्तर:
बाबांना आधीच उशीर झाला होता व त्यातच पाऊस पडला म्हणून बाबांनी चडफड केली.

प्रश्न उ.
पावसामुळे आईचे कोणते नुकसान झाले?
उत्तर:
पावसामुळे आईचे पापड भिजले.

2.

प्रश्न अ.
शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधा व लिहा. उदा., वारा-गारा
उत्तर:
(अ) कुत्री – छत्री
(आ) गिल्ला – किल्ला
(इ) पापड – चडफड
(ई) पळा – घोटाळा
(उ) कुट्टी – सुट्टी

प्रश्न आ.
कडकड, चडफड, तडफड यांसारखे आणखी शब्द तयार करा.
उत्तर:

1. धडधड
2. गडगड
3. बडबड
4. खडखड
5. रडरड
6. गडबड
7. पडझड

3. खालील शब्दांचे वचन बदला.

प्रश्न 1.
खालील शब्दांचे वचन बदला.
उत्तर:
(अ) माणूस – माणसे
(आ) गाय – गाई
(इ) दप्तर – दप्तरे
(ई) पाणी – पाणी
(उ) वह्या – वही
(ऊ) पत्र – पत्रे

4. अचानक आलेल्या पावसामुळे तुमची कधी फजिती झाली आहे का? तो प्रसंग वर्गात सांगा. 

प्रश्न अ.
अचानक आलेल्या पावसामुळे तुमची कधी फजिती झाली आहे का? तो प्रसंग वर्गात सांगा.
उत्तर:
एकदा ताई आणि मी बाजारात गेलो होतो. अचानक पाऊस आला. छत्र्या नव्हत्या. आम्ही झाडाखाली उभे राहीलो पण पूर्ण भिजलो होतो. रस्त्यात पाणी तुंबले होते. रिक्षा बंद झाल्या होत्या. दोघे कसेबसे घरी पोहोचलो. आईने पापड, मिरच्या वाळवण ठेवले होते. तेही भिजले. बाबांना घरी यायला खूप उशीर झाला. बाहेर वाळत घातलेले कपडेही भिजले. पावसामुळे खूप धावपळ झाली.

5. अचानक आलेल्या पावसामुळे दिवाळीत तुम्ही केलेल्या तयारीचे कोणकोणते नुकसान होते ते चार-पाच वाक्यात लिहा.

प्रश्न अ.
अचानक आलेल्या पावसामुळे दिवाळीत तुम्ही केलेल्या तयारीचे कोणकोणते नुकसान होते ते चार-पाच वाक्यात लिहा.
उत्तर:
दिवाळीत आम्ही सर्व मुलांनी मिळून किल्ला बांधला होता. त्यावर शिपाई, रखवालदार ठेवले होते. मातीच्याच प्रतिमा असल्याने त्या तुटून गेल्या. किल्ला ढासळला. ताईने दारात काढलेली रांगोळी पुसली गेली. आमचे फटाकेही भिजले.

6. सुरुवातीला एक वाक्य दिले आहे. तुमच्या मनाने पुढील वाक्ये लिहा. 

प्रश्न अ.
रिमझिम पाऊस पडत होता.
उत्तर:

1. पाणी झुळझुळ वाहत होते.
2. खारूताई झाडावर सरसर चढली.
3. गांधीजी झरझर चालत जात.
4. आजीचे हात थरथर कापत होते.

प्रश्न आ.
रिक्षा खडखड करत थांबली.
उत्तर:

1. मुले भरभर चालत होती.
2. पंख्याची घरघर सुरू होती.
3. हृदय धडधड करीत होते.
4. पंखांची फडफड थांबली.

7. ‘वारा’ या शब्दाशी संबंधित आलेले शब्द वाचा. त्यांचा वाक्यात उपयोग करा. उदा. भणाणणारा वारा सुटला होता.

प्रश्न अ.
‘वारा’ या शब्दाशी संबंधित आलेले शब्द वाचा. त्यांचा वाक्यात उपयोग करा. उदा. भणाणणारा वारा सुटला होता.
उत्तरः

1. मंदमंद – पहाटे मंदमंद वारा सुटला होता.
2. गिरक्या – मैदानात वाऱ्याच्या गिरक्या येत होत्या.
3. जोरदार – जोरदार मोसमी वारे सुटले होते.
4. थंडगार – हिमालयाचा वारा थंडगार होता.
5. झोंबणारा – हिवाळ्यात नदीकाठचा वारा झोंबणारा होता.

8. पापड कशाकशापासून बनवले जातात याची माहिती आईला विचारून लिहा. 

प्रश्न अ.
पापड कशाकशापासून बनवले जातात याची माहिती आईला विचारून लिहा.
उत्तर:
पापड विविध प्रकारचे असतात. उडदाची डाळ, मिरे यांपासून उडदाचे पापड बनतात. तांदळापासून तांदळाचे पापड बनतात. काही पापड पोयांपासून तर काही नाचणीपासून बनतात. साबूदाण्यापासून व बटाट्यापासूनही उपवासाचे पापड बनतात.

9. उन्हाळ्यांमध्ये वाळवून साठवण्याचे कोणकोणते पदार्थ आई करते ते लिहा. 

प्रश्न अ.
उन्हाळ्यांमध्ये वाळवून साठवण्याचे कोणकोणते पदार्थ आई करते ते लिहा.
उत्तर:
उन्हाळ्यात वाळवून साठवण्याचे पदार्थ – पापड, कुर्डया, सांडगे, शेवया, मिरच्या, आंबापोळी, फणसपोळी, उपवासाच्या चकल्या, उपवासाचे पापड, आमचूर, बोरकूट इ.

10. पावसाळा सुरु होताच तुम्ही पावसातून बचाव करण्यासाठी कोणकोणती पूर्वतयारी करता?
उदा. छत्री खरेदी करणे.

प्रश्न अ.
पावसाळा सुरु होताच तुम्ही पावसातून बचाव करण्यासाठी कोणकोणती पूर्वतयारी करता?
उदा. छत्री खरेदी करणे.
उत्तर:
1. रेनकोट, चपला खरेदी करणे.

2. घराची डागडुजी करणे, दुरुस्ती करणे.
3. वाहने गंजू नये त्यासाठी उपाय करणे.

Marathi Sulabhbharti Class 6 Solutions Chapter 3 पाऊस आला! पाऊस आला! Important Additional Questions and Answers

रिकाम्या जागी कवितेतील योग्य शब्द लिहा.
प्रश्न 1.

1. ……………….. भणाण वारा.
2. दिवाळीतला ………………..
3. आजोबांनी ………………..
4. बाबा गेले ………………..
5. ……………….. पापड
6. हसत म्हणाल्या ………………..
7. ‘………………..’, शाळेला सुट्टी!

उत्तर:

1. कडाड कडकड
2. खचला किल्ला
3. शिवली छत्री
4. करीत चडफड
5. आईचेही भिजले
6. मॅडम कुट्टी
7. चला पळा.

प्रश्न 2.
एका शब्दांत उत्तरे लिहा.

1. ऐन दुपारी चमकल्या
2. जिकडे तिकडे
3. भुंकत सुटली सगळी
4. मुलांनी केला एकच

उत्तर:

1. विजा
2. गारा
3. कुत्री
4. गिल्ला

खालील प्रश्नांची एक दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
मॅडम हसत काय म्हणाल्या?
उत्तर:
मॅडम म्हणाल्या, ‘चला पळा, शाळेला सुट्टी!’

खालील प्रश्नांची दोन-तीन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
ऐन दुपारी काय झाले?
उत्तर:
ऐन दुपारी विजा कडाड कडकड चमकल्या. भणाण वारा सुटला. जिकडे तिकडे गारा पडू लागल्या व पाऊस
पडू लागला.

प्रश्न 2.
पावसामुळे काय काय झाले?
उत्तर:
ऐन दुपारी पाऊस पडला. दिवाळीतला किल्ला खचला. सगळी कुत्री भुंकत सुटली. आजोबांनी छत्री शिवली. बाबांना आधीच उशीर झाला होता, त्यातच पावसाने घोटाळा केला. ते चडफड करीतच गेले. आईचे पापड भिजले.

प्रश्न 3.
शाळेतील मुलांनी गिल्ला का केला?
उत्तर:
अचानक दुपारी पाऊस पडू लागला. सर्व मुलांना मजा वाटली. त्यातच मॅडमनी शाळेला सुट्टी दिली. त्या आनंदात मुलांनी गिल्ला केला.

व्याकरण व भाषाभ्यास:

प्रश्न 1.
खालील शब्दांचे वचन बदला.

1. छत्री
2. कुत्री
3. वीज
4. किल्ला

उत्तर:

1. छत्र्या
2. कुत्रा
3. विजा
4. किल्ले

जोड्या जुळवा.

प्रश्न 1.

‘अ’ गट	‘ब’ गट
1. आजोबा	(अ) आई
2. मॅडम	(ब) कुत्रा
3. बाबा	(क) सर
4. कुत्री	(ड) आजी

उत्तर:

‘अ’ गट	‘ब’ गट
1. आजोबा	(ड) आजी
2. मॅडम	(क) सर
3. बाबा	(अ) आई
4. कुत्री	(ब) कुत्रा

शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधा व लिहा.
उदा. वारा – गारा

प्रश्न 1.
1. जिकडे
2. आला
उत्तर:
1. तिकडे
2. केला

प्रश्न 2.
‘पाऊस’ या शब्दाशी संबंधित आलेले शब्द वाचा. त्यांचा वाक्यात उपयोग करा.

उत्तर:

1. मुसळधार – मुसळधार पावसाने पूर आला.
2. रिपरिप – दिवसभर रिपरिप पाऊस होता.
3. झराळ – झराळ पावसात आम्ही ओलेचिंब झालो.
4. धोंधों – धोंधों पावसाने गावाचे नुकसान झाले.
5. रिमझिम – मुलांना रिमझिम पावसात भिजायला आवडते.

प्रश्न 3.
खालील शब्दांचे समानार्थी शब्द लिहा.

1. खचणे
2. चडफड
3. गिल्ला
4. ऐन दुपारी
5. भिजणे

उत्तर:

1. ढासळणे
2. राग
3. गोंगाट, गोंधळ
4. भर दुपारी
5. ओले होणे

प्रश्न 4.
खालील शब्दांचे विरूद्धार्थी अर्थाचे शब्द लिहा.

1. भिजणे
2. आला
3. शिवणे
4. खचणे
5. उशीर

उत्तर:

1. वाळणे
2. गेला
3. उसवणे
4. उभारणे
5. लवकर

पाऊस आला! पाऊस आला! Summary in Marathi

काव्य परिचय:

प्रस्तुत कवितेत पडणाऱ्या गारा, पावसामुळे आई बाबांची उडालेली तारांबळ, शाळेला मिळालेल्या सुट्टीचा आनंद वर्णन केला आहे.

शब्दर्थ:

1. ऐन दुपारी – भर दुपारी (in the afternoon)
2. खचला – ढासळला (collapse)
3. किल्ला – दुर्ग (fort)
4. जिकडेतिकडे – सर्वत्र (everywhere)
5. गारा – पावसाच्या पाण्याचे बर्फासारखे खडे (hailstones)
6. भुंकणे – कुत्र्याचा आवाज (to bark)
7. चडफड – आतल्या आत राग करणे (to get angry, restlessness)
8. गिल्ला – आवाज, गोंगाट (noise, shouting)
9. कुत्रा – श्वान (dog)
10. शिवणे – (to stitch)
11. घोटाळा – गडबड, गोंधळ (disorder, chaws)

Marathi Sulabhbharati Class 6 Solutions

• भारतमाता (गाणे) Question Answer
• माझा अनुभव Question Answer
• पाऊस आला! पाऊस आला! (कविता) Question Answer
• माहिती घेऊया Question Answer
• सुगरणीचे घरटे Question Answer
• हे खरे खरे व्हावे… (कविता) Question Answer
• उद्यानात भेटलेला विद्यार्थी Question Answer
• कुंदाचे साहस Question Answer
• घर (कविता) Question Answer