Prasanna

Std 10 Hindi Chapter 2 Do Laghu Kathayen Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 2 दो लघुकथाएँ Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 2 दो लघुकथाएँ Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 2 दो लघुकथाएँ Textbook Questions and Answers

कृति

कृतिपत्रिका के प्रश्न 3 (अ) के लिए

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
उत्तर लिखिए:

उत्तर:

प्रश्न 3.
कारण लिखिए:
१. युवक को पहले नौकरी न मिल सकी …………………….. .
२. आखिरकार अधिकारियों द्वारा युवक का चयन कर लिया गया …………………….. .
उत्तर:
(i) युवक को पहले नौकरी न मिल सकी, क्योंकि हर जगह भ्रष्टाचार, रिश्वत का बोलबाला था।
(ii) आखिरकार अधिकारियों द्वारा युवक का चयन कर लिया गया, क्योंकि भीतर बैठे अधिकारियों ने गंभीरता से विचार विमर्श करने के बाद युवक के सही उत्तर की दाद दी थी।

प्रश्न 4.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 5.
प्रवाह तालिका पूर्ण कीजिए:

उत्तर:

(अभिव्यक्ति)
‘भ्रष्टाचार एक कलंक’ विषय पर अपने विचार लिखिए।
उत्तर:
भ्रष्टाचार का अर्थ है दूषित आचार या जो आचार बिगड़ गया हो। आज हमारे जीवन के हर क्षेत्र में भ्रष्टाचार व्याप्त है। आए दिन नेताओं के भ्रष्टाचार के समाचार आते रहते हैं। प्रष्टाचार के आरोप में कितने नेता जेल काट रहे हैं। ये जनता के पैसे हड़प कर गए, पर इन्हें शर्म तक नहीं आती। आज हमारे देश में तेजी से भोगवादी संस्कृति फैल रही है। लोगों में रातोरात धनवान बनने की लालसा जोर पकड़ रही है।

चारों ओर घन बटोरने के लिए धोखाधड़ी, छल-कपट, किए जा रहे हैं। अपनी भौतिक समृद्धि बढ़ाने के लिए लोगों ने भ्रष्टाचार को शिष्टाचार बना लिया है। छोटे से छोटे काम के लिए लोगों को रिश्वत का सहारा लेना पड़ता है। शिक्षा का पवित्र क्षेत्र भी इससे अछूता नहीं रह गया है। लोगों में देशभक्ति और कर्तव्यनिष्ठा की भावना घटती जा रही है। भ्रष्टाचार राष्ट्रीय जीवन के लिए अभिशाप बन गया है। हमें आत्मनिरीक्षण करने की आवश्यकता है। भ्रष्टाचार एक कलंक है। इस कलंक को मिटाना जरूरी है। हम सबको इसके लिए निष्ठापूर्वक कार्य करने की जरूरत है।

भाषा बिंदु

प्रश्न 1.
अर्थ के आधार पर निम्न वाक्यों के भेद लिखिए:
1. क्या पैसा कमाने के लिए गलत रास्ता चुनना उचित है? – [ ]
2. इस वर्ष भीषण गरमी पड़ रही थी। – [ ]
3. आप उन गहनों की चिंता न करें। – [ ]
4. सुनील, जरा ड्राइवर को बुलाओ। – [ ]
5. अपने समय के लेखकों में आप किन्हें पसंद करते हैं? – [ ]
6. सैकड़ों मनुष्यों ने भोजन किया। – [ ]
7. हाय ! कितनी निर्दयी हूँ मैं। – [ ]
8. काकी उठो, भोजन कर लो। – [ ]
9. वाह ! कैसी सुगंध है। – [ ]
10. तुम्हारी बात मुझे अच्छी नहीं लगी। – [ ]
उत्तर:
1. क्या पैसा कमाने के लिए गलत रास्ता चुनना उचित है? – [प्रश्नवाचक वाक्य]
2. इस वर्ष भीषण गरमी पड़ रही थी। – [विधानवाचक वाक्य]
3. आप उन गहनों की चिंता न करें। – [निषेधवाचक वाक्य]
4. सुनील, जरा ड्राइवर को बुलाओ। – [आज्ञावाचक वाक्य]
5. अपने समय के लेखकों में आप किन्हें पसंद करते हैं? – [प्रश्नवाचक वाक्य]
6. सैकड़ों मनुष्यों ने भोजन किया। – [विधानवाचक वाक्य]
7. हाय! कितनी निर्दयी हूँ मैं – [विस्मयादिबोधक वाक्य]
8. काकी उठो, भोजन कर लो। – [आज्ञावाचक वाक्य]
9. वाह! कैसी सुगंध है। [विस्मयादिबोधक वाक्य]
10. तुम्हारी बात मुझे अच्छी नहीं लगी। – [निषेधवाचक वाक्य]

प्रश्न 2.
कोष्ठक की सूचना के अनुसार निम्न वाक्यों में अर्थ के आधार पर परिवर्तन कीजिए:
a. थोड़ी बातें हुईं। (निषेधार्थक वाक्य)
b. मानू इतना ही बोल सकी। (प्रश्नार्थक वाक्य)
c. मैं आज रात का खाना नहीं खाऊँगा। (विधानार्थक वाक्य)
d. गाय ने दूध देना बंद कर दिया। (विस्मयार्थक वाक्य)
e. तुम्हें अपना ख्याल रखना चाहिए। (आज्ञार्थक वाक्य)
उत्तर:
a. थोड़ी भी बातें नहीं हुई।
b. क्या मानू इतना ही बोल सकी?
c. मैं आज रात का खाना खाऊँगा।
d. अरे! गाय ने दूध देना बंद कर दिया।
e. तुम अपना ख्याल रखो।

प्रश्न 3.
प्रथम इकाई के पाठों में से अर्थ के आधार पर विभिन्न प्रकार के पाँच वाक्य ढूँढ़कर लिखिए।
उत्तर:
(1) करामत अली इधर दो-चार दिनों से अस्वस्थ था। (विधानवाचक वाक्य)
(2) इन्हें मरीज से हमदर्दी नहीं होती। (निषेधवाचक वाक्य)
(3) तो उसकी सजा इसे लाठियों से दी गई? (प्रश्नवाचक वाक्य)
(4) “जाओ, लक्ष्मी का राशन ले आओ। (आज्ञावाचक वाक्य)
(5) हे ईश्वर, अगर मेरी दूसरी टाँग भी तोड़नी हो तो जरूर तोड़ें, मगर इस जगह जहाँ मेरा कोई न हो। (इच्छावाचक वाक्य)

प्रश्न 4.
रचना के आधार पर वाक्यों के भेद पहचानकर कोष्ठक में लिखिए:
a. अधिकारियों के चेहरे पर हलकी-सी मुस्कान और उत्सुकता छा गई। [………………….]
b. हर ओर से अब वह निराश हो गया था। [………………….]
c. उसे देख-देख बड़ा जी करता कि मौका मिलते ही उसे चलाऊँ। [………………….]
d. वह बूढ़ी काकी पर झपटी और उन्हें दोनों हाथों से झटककर बोली। [………………….]
e. मोटे तौर पर दो वर्ग किए जा सकते हैं। [………………….]
f. अभी समाज में यह चल रहा है क्योंकि लोग अपनी आजीविका शरीर श्रम से चलाते हैं [………………….]
उत्तर:
a. सरल वाक्य।
b. सरल वाक्य।
c. मिश्र वाक्य।
d. संयुक्त वाक्य।
e. सरल वाक्या
f. संयुक्त वाक्य।

प्रश्न 5.
रचना के आधार पर विभिन्न प्रकार के तीन-तीन वाक्य पाठों से ढूँढकर लिखिए।
उत्तर:
(i) सरल वाक्य:
(1) आज उसे साक्षात्कार के लिए जाना है।
(2) अब तक उसके हिस्से में सिर्फ असफलता ही आई थी।
(3) रिश्वत भ्रष्टाचार की बहन है।

(ii) संयुक्त वाक्य:
(1) अधिकारियों के चेहरे पर हल्की-सी मुस्कान आई और उत्सुकता छा गई।
(2) व्यक्ति समाज को कम-से-कम देने की इच्छा रखता है लेकिन समाज से अधिक-से-अधिक लेने की इच्छा रखता है।
(3) विषमता दूर करने में कानून भी कुछ मदद देता है, परंतु कानून से मानवोचित गुणों का विकास नहीं हो सकता।

(iii) मिश्र वाक्य:
(1) भ्रष्टाचार एक ऐसा कीड़ा है, जो देश को घुन की तरह खा रहा है।
(2) वह जानता था कि यहाँ भी उसका चयन नहीं होगा।
(3) संपत्ति तो वे ही चीजें हो सकती हैं, जो किसी-न-किसी रूप में मनुष्य के उपयोग में आती हैं।

उपयोजित लेखन

‘जल है तो कल हैं’ विषय पर अस्सी से सौ शब्दों में निबंध लिखिए।
उत्तर:
हवा के पश्चात प्राणियों को जीवित रहने के लिए जिस चीज की आवश्यकता होती है वह है जल। जल के बिना प्राणी अधिक दिनों तक नहीं जी सकता। इसीलिए कहा जाता है कि जल ही जीवन है।

जल हमें कुओं, तालाबों और नदियों से मिलता है। वर्षा का जंल तालाबों, झीलों आदि में जमा होता है। कुछ पानी भूगर्भ में चला जाता है। शेष पानी नदियों में होता हुआ समुद्र में चला जाता हैं। भूगर्भ का पानी कुओं के माध्यम से पीने के काम में लाया जाता हैं। नदियों और झीलों का पानी शुद्ध किया जाता है। इसके बाद वह पीने लायक होता है। गाँवों में अधिकतर कुओं के पानी से ही काम चलाया जाता है। बड़े-बड़े शहरों में नदियों और झीलों के पानी को शुद्ध करके पीने के काम में लाया जाता है।

हर व्यक्ति को पानी की आवश्यकता होती है। बिना पानी के किसी का काम नहीं चल सकता। निरंतर बढ़ती हुई जनसंख्या के कारण आज पानी की समस्या विकट हो गई है। इसका कारण है पानी का अंधाधुंध उपयोग। गाँवों में सिंचाई के लिए अंधाधुंध तरीके से भू-जल का दोहन किया जा रहा है। इस कारण पानी का स्तर निरंतर नीचे-ही-नीचे जा रहा है। कहीं-कहीं तो कुओं में पानी ही नहीं रहा।

पीने का पानी कम होने का कारण वर्षा का निरंतर कम होते जाना है। पेड़ों और जंगलों की अंधाधुंध कटाई इसका प्रमुख कारण है। आए दिन पानी के लिए झगड़े होते रहते हैं। देश के अंदर एक राज्य दूसरे राज्य से पानी के लिए झगड़ता है। एक देश दूसरे देश से जल के लिए लड़ता है। पानी की समस्या सारी दुनिया में है। कुछ लोग तो यहाँ तक कहते हैं कि भविष्य में पानी के लिए महायुद्ध होगा।

पानी का अशुद्ध होना भी पानी की कमी का एक कारण है। अशुद्ध पानी से तरह-तरह की जानलेवा बीमारियाँ होती हैं। शहरों के किनारे बहने वाली नदियों में शहर की सारी गंदगी डाली जा रही है। कल-कारखानों का विषैला पानी नदियों में प्रवाहित होता है। वही पानी पीने के लिए दिया जाता है। इससे लोगों को तरह-तरह की बीमारियाँ होती है। _सरकार की ओर से हर व्यक्ति तक पर्याप्त शुद्ध पेय जल पहुँचाने का अथक प्रयास किया जा रहा है। फिर भी अभी इस दिशा में और प्रयास करने की जरूरत है। हर व्यक्ति इस उम्मीद में है कि उसे पर्याप्त शुद्ध जल उपलब्ध हो। आखिर जल है, तो कल है।

Hindi Lokbharti 10th Textbook Solutions Chapter 2 दो लघुकथाएँ Additional Important Questions and Answers

गद्यांश क्र. 1
प्रश्न. निम्नलितिर पठित गट्यांश पढ़कर दी गई सूचनाओं के कवियों कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
निम्नलिखित के लिए परिच्छेद में प्रयुक्त शब्द लिखिए:
(i) आराम –
(ii) गरीब
(iii) शांति –
(iv) बेढंगा
उत्तर:
(i) आराम – राहत
(ii) गरीब – कंगाल
(iii) शांति – सुकून
(iv) बेढंगा – लिजलिजा।

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘छोटे दुकानदारों और बड़े दुकानदारों से चीजें खरीदते समय हमारा व्यवहार’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
हम अधिकतर दिखावे में विश्वास करते हैं। जब हम बड़ेबड़े शॉपिंग सेंटरों और मॉल में जाते हैं, तो वस्तुओं की कीमतों को लेकर हम कभी मोल-भाव नहीं करते। वहाँ सैकड़ों लोग सामान खरीदते हैं और कीमतों को लेकर कोई मोल-भाव नहीं करता। वहाँ भाव ज्यादा होते हुए भी उसके बारे में पूछने की हिम्मत नहीं होती। क्योंकि वहाँ इज्जत का सवाल होता है। कभी-कभी तो वहाँ ठगाकर लोग चले आते हैं, पर शर्म के मारे कुछ नहीं बोलते। मगर वही लोग बाजार में छोटे दुकानदारों या खोमचेवालों से दो-चार रुपए के लिए झिक-झिक करते देखे जाते हैं। यहाँ उनको.अपनी इज्जत की परवाह नहीं रहती। क्योंकि यहाँ बड़े ग्राहकों के सामने उनको अपने इस व्यवहार पर झंपने का डर नहीं रहता। यहाँ वे अपने को बड़ा दिखाते हैं। क्योंकि सामने गरीब आदमी होता है।

हमें अपनी सोच में बदलाव लाने की जरूरत है। छोटे व्यापारियों या गरीब खोमचेवालों से खरीदे जाने वाले सामान में मोल-भाव करने में झिक-झिक करना उचित नहीं है।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश को पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:

*(iii) प्रवाह तालिका पूर्ण कीजिए:

उत्तर:

प्रश्न 4.
आकृति पूर्ण कीजिए:
(i) उसके प्रमाणपत्र उसे सफलता दिलाने में ये रहे – [ ]
(ii) वह भ्रष्ट सामाजिक व्यवस्था को यह करता था – [ ]
(iii) उसके तर्क में अधिकारियों को यह महसूस होने लगी – [ ]
(iv) उसके अनुसार रिश्वत का भ्रष्टाचार से यह रिश्ता है – [ ]
उत्तर:
(i) उसके प्रमाणपत्र उसे सफलता दिलाने में ये रहे – [नाकामयाब]
(ii) वह भ्रष्ट सामाजिक व्यवस्था को यह करता था – [कोसता था]
(iii) उसके तर्क में अधिकारियों को यह महसूस होने लगी – [रुचि]
(iv) उसके अनुसार रिश्वत का भ्रष्टाचार से यह रिश्ता है। – [रिश्वत भ्रष्टाचार की बहन]

उपक्रम/कृति/परियोजना

श्रवणीय
बालक/बालिकाओं से संबंधित कोई ऐतिहासिक कहानी सुनकर उसका रूपांतरण संवाद में करके कक्षा में सुनाइए।

पठनीय
अपनी पसंद की कोई सामाजिक ई-बुक पढ़िए।

संभाषणीय
‘शहर और महानगर का यांत्रिक जीवन’ विषय पर बातचीत कीजिए।

लेखनीय
पहाड़ों पर रहने वाले लोगों की जीवन शैली की जानकारी प्राप्त करके अपनी जीवन शैली से उसकी तुलना करते हुए लिखिए।

मुद्दे:
(i) घर-द्वार
(ii) रहन-सहन
(iii) खान-पान
(iv) रीति-रिवाज
(v) जीवन यापन के साधन
(vi) यातायात व्यवस्था।

दो लघुकथाएँ Summary in Hindi

विषय-प्रवेश : प्रस्तुत पाठ में दो लघुकथाएँ दी गई हैं। प्रथम लघुकथा में हमारी मानसिक प्रवृत्ति के बारे में बताया गया है। लेखक ने इसके माध्यम से यह दर्शाया है कि जब लोग बड़ी-बड़ी दुकानों, मॉल या बड़े होटलों में जाते हैं, तो वहाँ वे सामानों के निश्चित मूल्यों के बारे में कोई मोल-भाव नहीं करते। मांगे गए पैसे शौक से अदा करके चले आते हैं। पर छोटे दुकानदारों या खोमचे वालों से सामान खरीदते समय लोगों का व्यवहार बिलकुल बदल जाता है। लोग उनसे दो-एक रुपये कम करने के बारे में बहस पर उतर आते हैं। हमें यह मानसिकता बदलनी चाहिए।

दूसरी लघुकथा में रिश्वतखोरी और भ्रष्टाचार के शिकार एक युवक के बारे में बताया गया है। उसके सामने भ्रष्ट सामाजिक व्यवस्था को कोसने के अलावा कोई चारा नहीं रहता। पर सत्य का पालन करना उसे एक दिन अपने लक्ष्य तक पहुँचा देता है।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Std 10 Hindi Chapter 6 Giridhar Nagar Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 6 गिरिधर नागर Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 6 गिरिधर नागर Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 6 गिरिधर नागर Textbook Questions and Answers

कृति

(कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए)
सूचनानुसार कृतियाँ कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
प्रवाह तालिका पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
इस अर्थ में आए शब्द लिखिए:

	अर्थ	शब्द
i.	दासी	………….
ii.	साजन	………….
iii.	बार-बार	………….
iv.	आकाश	………….

उत्तर:

	अर्थ	शब्द
i.	दासी	चेरी
ii.	साजन	पति
iii.	बार-बार	बेर-बेर
iv.	आकाश	अंबर

प्रश्न 4.
कन्हैया के नाम

उत्तर:

प्रश्न 5.
दूसरे पद का सरल अर्थ लिखिए।
उत्तर:
(i) निकट – ढिग
(ii) साजन – पति।

उपयोजित लेखन

निम्नलिखित शब्दों के आधार पर कहानी लेखन कीजिए तथा उचित शीर्षक दीजिए:
अलमारी, गिलहरी, चावल के पापड़, छोटा बच्चा
उत्तर:
जीव दया
एक गाँव में एक छोटा बच्चा रहता था। उसका नाम चिंटू था। एक दिन चिंटू अपने घर के बाहर खेल रहा था। उसने देखा कि सामने एक पेड़ के नीचे दो-तीन कौए किसी चीज पर चोंच मार रहे हैं और वहाँ से हल्की-हल्की चर्ची-चीं की आवाज आ रही है। चिंटू दौड़कर वहाँ पहुँचा और उसने उन कौओं को वहाँ से उड़ाया। उसने देखा कि एक छोटी-सी गिलहरी वहाँ ची-चीं कर रही थी। उसका शरीर कौओं की चोंच से घायल हो गया था। चिंटू ने अपनी जेब से रूमाल निकाला और डरे बिना धीरे से गिलहरी को उठा लिया। उसने घर के अंदर लाकर उसे पानी पिलाया, उसके घावों को साफ करके उन पर सोफामाइसिन लगाई और उसे मेज पर बैठा दिया।

गिलहरी कुछ देर बाद धीरे-धीरे मेज पर घूमने लगी। मेज पर एक प्लेट में चावल के पापड़ रखे थे। गिलहरी ने एक पापड़ उठाया और अपने अगले दोनों पंजों में पकड़कर धीरे-धीरे उसे खाने लगी। चिंटू को बहुत अच्छा लगा। उसने माँ से पूछा कि जब तक गिलहरी बिलकुल ठीक नहीं हो जाती क्या मैं उसे अपने पास रख सकता हूँ। अभी अगर वह बाहर जाएगी तो कौए उसे अपना आहार बना लेंगे। माँ को चिंटू की ऐसी सोच पर गर्व हुआ और उन्होंने खुशी-खुशी उसकी बात मान ली। चिंटू ने अपनी किताबों की खुली आलमारी के एक खाने में एक तौलिया बिछाकर गिलहरी को बैठा दिया। उसके पास चावल के कुछ पापड़ तथा अमरूद के कुछ टुकड़े रख दिए। तीन-चार दिन बाद जब गिलहरी अच्छी तरह दौड़ने लगी तो चिंटू ने उसे बाहर पेड़ पर छोड़ दिया।

सीख: हमें पशु-पक्षियों के प्रति दया भाव रखना चाहिए।

अपठित पद्यांश

सूचना के अनुसार कृतियाँ कीजिए:-

काम जरा लेकर देखो, सख्त बात से नहीं स्नेह से
अपने अंतर का नेह अरे, तुम उसे जरा देकर देखो।
कितने भी गहरे रहें गर्त, हर जगह प्यार जा सकता है,
कितना भी भ्रष्ट जमाना हो, हर समय प्यार भा सकता है।
जो गिरे हुए को उठा सके, इससे प्यारा कुछ जतन नहीं,
दे प्यार उठा पाए न जिसे, इतना गहरा कुछ पतन नहीं ।।

– (भवानी प्रसाद मिश्र)

प्रश्न 1.
उत्तर लिखिए:
a. किसी से काम करवाने के लिए उपयुक्त – ………….
b. हर समय अच्छी लगने वाली बात – ………….
उत्तर:

प्रश्न 2.
उत्तर लिखिए:
a. अच्छा प्रयत्न यही है – ………….
b. यही अधोगति है – ………….
उत्तर:

प्रश्न 3.
पद्यांश की तीसरी और चौथी पंक्ति का संदेश लिखिए।
उत्तर:

भाषा बिंदु

कोष्ठक में दिए गए प्रत्येक/कारक चिह्न से अलग-अलग वाक्य बनाइए और उनके कारक लिखिए:
[ने, को, से, का, की, के, में, पर, हे, अरे, के लिए]
………………………………………………………..
………………………………………………………..
………………………………………………………..
………………………………………………………..
………………………………………………………..
उत्तर:
(1) ने – ऋतु ने खाना बनाया।
(2) को – विपिन ने प्रगति को खाना खिलाया।
(3) से – हिमानी साइकिल से ऑफिस जाती है।
(4) का – शुभम हर्षित का भाई है।
(5) की – पूर्वी आयुष की बहन है।
(6) के – नीरज के तीन चाचा हैं।
(7) में – नीनू घर में है।
(8) पर – पेड़ पर बंदर कूद रहे हैं।
(9) हे – हे भगवान, कितना शोर है यहाँ।
(10) अरे – अरे! सलिल तुम कहाँ हो?
(11) के लिए – अंशु वारिजा के लिए फ्रॉक लाई।

Hindi Lokbharti 10th Textbook Solutions Chapter 6 गिरिधर नागर Additional Important Questions and Answers

पद्यांश क्र. 1

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i)

उत्तर:

(ii) a. श्रीकृष्ण के सिर पर है
b. मीरा इन्हें अपना पति मानती हैं –
उत्तर:
a. श्रीकृष्ण के सिर पर है – मोर मुकट
b. मीरा इन्हें अपना पति मानती हैं – गिरधर गोपाल

प्रश्न 2.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
उचित जोड़ियाँ मिलाइए:

अ	आ
आँसुओं के जल से कुल की मर्यादा प्रेम बेल संत संगति के कारण	छोड़ दी आनंद फल लोक लाज खोई प्रेम की बेल सींची प्रेम से बिलोई।

उत्तर:

अ	आ
आँसुओं के जल से कुल की मर्यादा प्रेम बेल संत संगति के कारण	प्रेम की बेल सींचा। छोड़ दी। आनंद फल। लोक लाज खोई।

कृति 2: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों को शुद्ध रूप में लिखिए:
(i) भगत – …………………….
(ii) माखन – …………………….
(iii) आणंद – …………………….
(iv) जाके – …………………….
उत्तर:
(i) भगत – भक्त
(ii) माखन – मक्खन
(iii) आणंद – आनंद
(iv) जाके – जिसके।

प्रश्न 2.
निम्नालाखत शब्दा क समानाथा शब्दालाखए:
(i) मोर = …………………….
(ii) जगत = …………………….
(iii) दूध = …………………….
(iv) प्रेम = …………………….
उत्तर:
(i) मोर = मयूर
(ii) जगत = संसार
(iii) दूध = दुग्ध
(iv) प्रेम = प्यार।

प्रश्न 3.
निम्नलिखित अर्थवाले शब्द पद्यांश से चुनकर लिखिए:
(i) उद्घार करो – …………………….
(ii) मुझे – …………………….
उत्तर:
(i) उद्घार करो – तारो
(ii) मुझे – मोही।

कृति 3: (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की अंतिम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
मैंने दूध जमाने के पात्र में जमे दही को मथानी से बड़े प्रेम से बिलोया और उसमें से कृष्ण-प्रेम रूपी मक्खन को निकाल लिया। शेष छाछ रूपी निस्सार जगत को छोड़ दिया। कृष्ण-भक्तों को देखकर मैं प्रसन्न होती हूँ, परंतु संसार का व्यवहार देख मुझे दुख होता है और मैं रो पड़ती हूँ। हे गिरधरलाल, मीरा तो आपकी दासी है, उसे इस संसार रूप भव-सागर से पार लगाओ।

पद्यांश क्र. 2

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

(i) ये मीरा के प्रतिपालक हैं
(ii) कृष्ण के बिना इनको कहीं आश्रय नहीं है –
(iii) मीरा को प्रभु से मिलने की तीव्र यह है –
(iv) मीरा की यह संसार सागर में डूबने वाली है
उत्तर:
(i) ये मीरा के प्रतिपालक हैं – कृष्ण
(ii) कृष्ण के बिना इनको कहीं आश्रय नहीं है – मीरा
(iii) मीरा को प्रभु से मिलने की तीव्र यह है – लालसा
(iv) मीरा की यह संसार सागर में डूबने वाली है – नौका

प्रश्न 2.
पद्यांश में आए इस अर्थ के शब्द लिखिए:

(i) दासी
(ii) आश्रय
(iii) बार-बार
(iv) नौका।
उत्तर:
(i) दासी – चेरी
(ii) आश्रय – गती
(iii) बार-बार – बेर-बेर
(iv) नौका – बेरी।

प्रश्न 3.
विधानों के सामने सत्य / असत्य लिखिए:

(i) हरि बिना मीरा को कहीं आश्रय नहीं है।
(ii) कृष्ण मीरा के पति हैं और वे उनकी पत्नी।
(iii) मीरा बार-बार प्रभु की आरती करती हैं।
(iv) मीरा की जीवन नौका संसार सागर में डूबने वाली है।
उत्तर:
(i) सत्य
(i) असत्य
(iii) असत्य
(iv) सत्य।

प्रश्न 4.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए:

(i) कूण – …………………..
(ii) रावरी – …………………..
(iii) बेरी – …………………..
(iv) नेरी – …………………..
उत्तर:
(i) कूण – कहाँ
(ii) रावरी – आपकी
(iii) बेरी – बेड़ा
(iv) नेरी – पास, निकट।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचान कर लिखिए:
(i) पखावज …………………..
(ii) पिचकारी …………………..
(iii) गुलाल …………………..
(iv) चरण …………………..
उत्तर:
(i) पखावज – स्त्रीलिंग
(ii) पिचकारी – स्त्रीलिंग
(iii) गुलाल – पुल्लिंग
(iv) चरण – पुल्लिंग।

कृति 3: (सरल अर्थ)

प्रश्न.
उपयुक्त पद्यांश की ‘हरि बिन कूण आरति है तेरी।।’ पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
हे हरि, आपके बिना मेरा कौन है? अर्थात आपके सिवा मेरा कोई ठिकाना नहीं है। आप ही मेरा पालन करने वाले हैं और मैं आपकी दासी हूँ। मैं रात-दिन, हर समय आपका ही नाम जपती रहती हूँ। में बार-बार आपको पुकारती हूँ, क्योंकि मुझे आपके दर्शनों की तीव्र लालसा है।

पद्यांश क्र. 3

कृति 1: (आकलन)

प्रश्न 1.
पद्यांश में आए इस अर्थ के शब्द लिखिए:
बोर्ड की नमूना कृतिपत्रिका

(i) कमल
(ii) आकाश
(iii) श्रेष्ठ
(iv) संतोष।
उत्तर:
(i) कमल – कँवल
(ii) आकाश – अंबर
(iii) श्रेष्ठ – छतीयूँ
(iv) संतोष – संतोख।

प्रश्न 2.
जोड़ियाँ बनाइए:

उत्तर:
(i) सुर – राग
(ii) करताल – झनकार
(iii) घट – पट
(iv) प्रेम – पिचकार।

प्रश्न 3.
आकृति पूर्ण कीजिए:
(i) आकाश लाल हो गया है इससे –
(ii) गिरिधर नागर हैं मीरा के ये –
उत्तर:
(i) आकाश लाल हो गया है इससे – गुलाल से।
(ii) गिरिधर नागर हैं मीरा के ये – प्रभु।

प्रश्न 4.
उत्तर लिखिए: (बोर्ड की नमूना कृतिपत्रिका)

उत्तर:

कृति 2: (शब्द संपदा) (बोर्ड की नमूना कृतिपत्रिका)

पद्यांश से ढूँढ़कर लिखिए:
ऐसे दो शब्द जिनका वचन परिवर्तन से रूप नहीं बदलता –
(i) ……………………..
(ii) ……………………..
उत्तर:
(i) दिन
(ii) चरण।

कृति 3: (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की प्रथम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए। (बोर्ड की नमूना कृतिपत्रिका)
उत्तर:
हे मेरे मन, फागुन मास में होली खेलने का समय अति अल्प होता है। अतः तू जी भरकर होली खेल। अर्थात मानव जीनव अस्थायी है, इसलिए भगवान कृष्ण से पूर्ण रूप से प्रेम कर ले। जिस प्रकार होली के उत्सव में नाच आदि का आयोजन होता है, उसी प्रकार कृष्ण-प्रेम में मुझे ऐसा प्रतीत होता है मानो करताल, पखावज आदि बाजे बज रहे हैं और अनहद नाद का स्वर सुनाई दे रहा है, जिससे मेरा हृदय बिना स्वर और राग के अनेक रागों का आलाप करता रहता है। मेरा रोम-रोम भगवान कृष्ण के प्रेम के रंग में डूबा रहता है। मैंने अपने प्रिय से होली खेलने के लिए शील और संतोष रूपी केसर का रंग घोला है। मेरा प्रिय-प्रेम ही होली खेलने की पिचकारी है।

भाषा अध्ययन (व्याकरण)

प्रश्न.
सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:
अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) बाहर कोई नहीं है।
(ii) माँ को हंसी आ गई।
(iii) चतुर वैद्य विष से भी दवा का काम ले सकता है।
उत्तर:
(i) कोई – अनिश्चयवाचक सर्वनाम।
(ii) हँसी – भाववाचक संज्ञा।
(iii) चतुर – गुणवाचक विशेषण।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) भी
(ii) इसलिए।
उत्तर:
(i) भी – हमारी बेटी गाय से भी अधिक सीधी है।
(ii) इसलिए – नीरज बीमार था, इसलिए दफ्तर नहीं गया।

3. संधि:
कृति पूर्ण कीजिए:
संधि शब्द – संधि विच्छेद – संधि भेद
…………. – उत् + लेख। – ……………
अथवा
तपोबल – …………… – ……………
उत्तर:
संधि शब्द – संधि विच्छेद – संधि भेद
उल्लेख – उत् + लेख – व्यंजन संधि
अथवा
तपोबल – तपः + बल – विसर्ग संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए:
(i) यह कुरसी दीवार की तरफ खिसका दो।
(ii) हम समय पर स्टेशन पहुंच गए।
उत्तर:
सहायक क्रिया – मूल रूप
(i) दो – देना
(ii) गए – जाना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) पढ़ना
(ii) जीतना
(ii) करना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – द्वितीय प्रेरणार्थक रूप
(i) पढ़ना – पढ़ाना – पढ़वाना
(ii) जीतना – जिताना – जितवाना
(iii) करना – कराना – करवाना

6. मुहावरे:
(1) निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) चैन न मिल पाना
(ii) झेंप जाना।
उत्तर:
(i) चैन न मिल पाना।

अर्थ: बेचैनी अनुभव करना। वाक्य: मालिक की कड़ी बातें सुनकर मुनीम को चैन न मिल पाया।

(ii) झेंप जाना।
अर्थ: लज्जित होना, शरमाना। वाक्य: नकल करने पर मित्र की फटकार सुनकर अभिनव झेंप गया।

(2) अधोरेखांकित वाक्यांशों के लिए कोष्ठक में दिए गए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए:
(नाक-भौं सिकोड़ना, गुदगुदा देना, सिर झुका देना)
(i) अप्रिय बात सुनकर सभी तिरस्कार प्रकट करेंगे।
(ii) जीवन में आनंददायी क्षण बहुत कम होते हैं।
उत्तर:
(i) अप्रिय बात सुनकर सभी नाक-भौं सिकोड़ेंगे।
(ii) जीवन में गुदगुदाने वाले क्षण बहुत कम होते हैं।

7. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) मैं कहाँ से पैसे , पहले तो दूध की बिक्री के पैसे मेरे पास जमा रहते थे
(ii) सहसा कानों में आवाज आई काकी उठो मैं पूड़ियाँ लाई हूँ
उत्तर:
(i) “मैं कहाँ से पैसे दूँ? पहले तो दूध की बिक्री के पैसे मेरे पास जमा रहते थे।”
(ii) सहसा कानों में आवाज आई – “काकी, उठो मैं पूड़ियाँ लाई हूँ।”

8. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) विदा का क्षण आ गया। (सामान्य भविष्यकाल)
(ii) आप छत पर क्या करते हैं? (अपूर्ण भूतकाल)
(iii) मेरी गाड़ी तो बिक जाती है। (पूर्ण वर्तमानकाल)
उत्तर:
(i) विदा का क्षण आ जाएगा।
(ii) आप छत पर क्या कर रहे थे?
(iii) मेरी गाड़ी तो बिक गई है।

9. वाक्य भेद:
(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचान कर लिखिए:
(i) संसार का व्यवहार देखकर मुझे दुःख होता है और मैं रो पड़ती हूँ।
(ii) मीराबाई कहती हैं कि अब उन्हें लोकलाज का कोई डर नहीं हैं।
उत्तर:
(i) संयुक्त वाक्य
(ii) मिश्र वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए:
(i) संतो के साथ बैठकर मैंने लोकलाज त्याग दी है। (विस्मयादिबोधक वाक्य)
(ii) हे हरि, आप ही मेरा पालन करने वाले हैं। (आज्ञावाचक वाक्य)
उत्तर:
(i) हाय! संतों के साथ बैठकर मैंने लोकलाज त्याग दी है।
(ii) हे हरि, आप ही मेरा पालन करें।।

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) लेखक ने अभिनेता की घमंड तोड़ी।
(ii) हमने क्रिकेट की मैच देखी।
उत्तर:
(i) लेखक ने अभिनेता का घमंड तोड़ा।
(ii) हमने क्रिकेट का मैच देखा।

गिरिधर नागर Summary in Hindi

गिरिधर नागर कविता का सरल अर्थ

1. मेरे तो गिरधर गोपाल …………………………….. तारो अब मोही।।

गिरि को धारण करने वाले, गायों के पालक कृष्ण के सिवा मेरा और कोई नहीं है। जिनके मस्तक पर मोर का मुकुट शोभित है, वे ही मेरे पति हैं। उनके लिए मैंने कुल की मर्यादा छोड़ दी है। चाहे कोई मुझे कुछ भी कहे। संतों के साथ बैठ-बैठकर मैंने लोकलाज त्याग दी है। मैंने अपने प्रेम रूपी बेल को अपने अश्रु रूपी जल से सींच-सींचकर बड़ा किया है। अब तो यह प्रेम-बेल फैल गई है और इसमें आनंद रूपी फल लगने लगा है। मैंने दूध जमाने के पात्र में जमे दही को मथानी से बड़े प्रेम से बिलोया और उसमें से कृष्ण-प्रेम रूपी मक्खन को निकाल लिया। शेष छाछ रूपी निस्सार जगत को छोड़ दिया। कृष्ण-भक्तों को देखकर मैं प्रसन्न होती हूँ, परंतु संसार का व्यवहार देख मुझे दुख होता है और मैं रो पड़ती हूँ। हे गिरधरलाल, मीरा तो आपकी दासी है, उसे इस संसार रूपी भव-सागर से पार लगाओ।

2. हरि बिन कूण गती मेरी …………………………….. मैं सरण हूँ तेरी।।

हे हरि, आपके बिना मेरा कौन है? अर्थात आपके सिवा मेरा कोई ठिकाना नहीं है। आप ही मेरा पालन करने वाले हैं और मैं आपकी दासी हूँ। मैं रात-दिन, हर समय आपका ही नाम जपती रहती हूँ। मैं बार-बार आपको पुकारती हूँ, क्योंकि मुझे आपके दर्शनों की तीव्र लालसा है। यह संसार विभिन्न प्रकार के दोषों और विकारों से भरा हुआ सागर है, जिसके बीच में घिर गई हैं। इस संसार रूपी सागर में मेरी नाव टूट गई है। हे प्रभु, आप शीघ्र इस नाव का पाल बाँधिए, अन्यथा यह जीवन-नौका इस संसार-सागर में डूब जाएगी। हे प्रियतम, आपकी यह विरहिणी निरंतर आपकी बाट जोहती रहती है। आपके आगमन की प्रतीक्षा करती रहती है। आपकी यह दासी मीरा सदा आपके नाम का स्मरण करती रहती है और आपकी शरण में आई है।

3. फागुन के दिन चार …………………………….. चरण कँवल बलिहार रे।।

हे मेरे मन, फागुन मास में होली खेलने का समय अति अल्प होता है। अतः तू जी भरकर होली खेल। अर्थात मानव जीनव अस्थायी है, : इसलिए भगवान कृष्ण से पूर्ण रूप से प्रेम कर ले। जिस प्रकार होली के : उत्सव में नाच आदि का आयोजन होता है, उसी प्रकार कृष्ण-प्रेम में मुझे ऐसा प्रतीत होता है मानो करताल, पखावज आदि बाजे बज रहे हैं और अनहद नाद का स्वर सुनाई दे रहा है, जिससे मेरा हृदय बिना स्वर और राग के अनेक रागों का आलाप करता रहता है। मेरा रोम-रोम भगवान कृष्ण के प्रेम के रंग में डूबा रहता है। मैंने अपने प्रिय से होली खेलने के लिए शील और संतोष रूपी केसर का रंग घोला है। मेरा प्रिय-प्रेम ही होली खेलने की पिचकारी है। उड़ते हुए गुलाल से सारा आकाश लाल हो गया है। अब मुझे लोक-लज्जा का कोई डर नहीं है, इसलिए मैंने हृदय रूपी घर के दरवाजे खोल दिए हैं। अंत में मीरा कहती हैं कि मेरे स्वामी गोवर्धन पर्वत को धारण करने वाले कृष्ण भगवान हैं। मैंने उनके चरण-कमलों में अपना सर्वस्व न्योछावर कर दिया है।

गिरिधर नागर विषय-प्रवेश :

प्रस्तुत काव्य में रसिक शिरोमणि श्रीकृष्ण की अनन्य उपासिका मीराबाई अपना प्रेम प्रकट कर रही हैं। सभी पदों में | श्रीकृष्ण के प्रति मीराबाई के प्रेम, उनकी भक्ति, उत्सुकता, प्रिय-मिलन की आशा, प्रतीक्षा आदि का मार्मिक चित्रण है।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 1 Bharat Mahima Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 1 भारत महिमा Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 1 भारत महिमा Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 1 भारत महिमा Textbook Questions and Answers

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
निम्नलिखित पंक्तियों का तात्पर्य लिखिए:
a. कहीं से हम आए थे नहीं → …………………….
b. वही हम दिव्य आर्य संतान → …………………….
उत्तर:
(a) हम भारतवासी किसी अन्य देश से आकर यहाँ नहीं बसे। हम यहीं के निवासी हैं। सभ्यता के प्रारंभ से हम यहीं रहते आए हैं।
(b) भारतवासी आर्य थे और हम उन्हीं आर्यों की दिव्य संतानें हैं।

प्रश्न 2.
उचित जोड़ियाँ मिलाइए:
संचय
सत्य
अतिथि
रत्न
वचन
दान
हृदय
तेज
देव
उत्तर:
(i) संचय – दान
(ii) सत्य – वचन
(iii) अतिथि – देव
(iv) रत्न – तेज।

प्रश्न 3.
लिखिए.
a. कविता में प्रयुक्त दो धातुओं के नाम:

उत्तर:

b. भारतीय संस्कृति की दो विशेषताएँ:

उत्तर:

प्रश्न 4.
प्रस्तुत कविता की अपनी पसंदीदा किन्हीं दो पंक्तियों का भावार्थ लिखिए।
उत्तर:
हमारे संचय में था दान, अतिथि थे सदा हमारे देव वचन में सत्य, हृदय में तेज, प्रतिज्ञा में रहती थी टेव। हम भारतीय दीन-दुखियों की सेवा करने के लिए सदैव तत्पर रहते हैं। हम यदि धन और संपत्ति का संग्रह करते भी थे तो दान के लिए करते थे। दानवीरता भारतीयों का गुण रहा है। महर्षि दधीचि और कर्ण जैसे दानवीर इसी भूमि पर हुए हैं। हमारे देश में अतिथियों को देवता के समान माना जाता था। भारतीय सत्यवादी हरिश्चंद्र की संतानें हैं। हमारे हृदय में तेज था, गौरव था। हम सदा अपनी प्रतिज्ञा पर अटल रहते थे। भारतीयों का मानना था- प्राण जाएँ,: पर वचन न जाएँ।

प्रश्न 5.
निम्नलिखित मुद्दों के आधार पर पद्य विश्लेषण कीजिए:
a. रचनाकार का नाम
b. रचना का प्रकार
c. पसंदीदा पंक्ति
d. पसंदीदा होने का कारण
e. रचना से प्राप्त संदेश
उत्तर:
a. रचनाकार का नाम → जयशंकर प्रसाद।
b. रचना की विधा → कविता।
c. पसंद की पंक्तियाँ → व्योमतम पुंज हुआ तब नष्ट, अखिल संसृति हो उठी अशोक। (सूचना: विद्यार्थी अपनी पसंद की पंक्ति लिखेंगे।)
d. पंक्तियाँ पसंद होने का कारण → हम भारतीयों ने पूरे विश्व में ज्ञान का प्रसार किया, जिसके कारण समग्र संसार आलोकित हो गया। अज्ञान रूपी अंधकार का विनाश हुआ और संपूर्ण सृष्टि के सभी दुख-शोक दूर हो गए।
e. रचना से प्राप्त संदेश/प्रेरणा → हमें सदैव अपने देश और इसकी संस्कृति पर गर्व करना चाहिए। जब भी आवश्यकता पड़े, देश के लिए अपना सर्वस्व न्योछावर कर देने के लिए तत्पर रहना चाहिए।

Hindi Lokbharti 10th Textbook Solutions Chapter 1 भारत महिमा Additional Important Questions and Answers

पद्यांश क्र. 1
प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
पद्यांश से ऐसे दो प्रश्न तैयार कीजिए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) अभिनंदन
(ii) आलोक।
उत्तर:
(i) उषा ने हँसकर क्या किया?
(ii) जब भारतीयों ने ज्ञान का प्रचार किया तो संसार में क्या फैला?

प्रश्न 2.
पद्यांश में प्रयुक्त इन शब्दों से सहसंबंध दर्शाने वाले शब्द लिखिए:
(i) हिमालय – ……………………..
(ii) किरण – ……………………..
(iii) विमल – ……………………..
(iv) कोमल – ……………………..
उत्तर:
(i) हिमालय -आँगन
(ii) किरण – उपहार
(iii) विमल -वाणी
(iv) कोमल -कर

प्रश्न 3.
विधानों के सामने सत्य/असत्य लिखिए:
(i) जब पूरा विश्व जगा तो भारतवासी भी जग गए।
(ii) वीणापाणि ने अपने हाथ में वीणा ली।
(iii) हिमालय के आँगन में किरणों का उपहास मिला।
(iv) सप्तसिंधु में सातों स्वर गूंजने लगे।
उत्तर:
(i) असत्य
(ii) सत्य
(iii) असत्य
(iv) सत्य।

प्रश्न 4.
उचित जोड़ियाँ मिलाइए:
(i) उषा – आलोक
(ii) हीरक – संगीत
(iii) विश्व – अभिनंदन
(iv) वीणा – हार
उत्तर:
(i) उषा – अभिनंदन।
(ii) हीरक – हार
(iii) विश्व – आलोक
(iv) वीणा -संगीत।

कृति 2: (शब्द संपदा)

प्रश्न 1.
पद्यांश में से ढूँढ़कर उपसर्गयुक्त शब्द लिखिए:
(i) ………………. (ii) ……………….
उत्तर:
(i) अभिनंदन
(ii) उपहार।

प्रश्न 2.
अनेक शब्दों के लिए एक-एक शब्द लिखिए:
(i) गले में पहनने की मूल्यवान माला
(ii) सितार जैसा वह वाद्य जो सब वाद्यों में श्रेष्ठ माना जाता है, ……………….
उत्तर:
(i) हार
(ii) वीणा।

प्रश्न 3.
निम्नलिखित शब्दों के लिए पद्यांश में प्रयुक्त शब्द ढूँढ़कर लिखिए:
(i) संपूर्ण
(ii) शोकरहित
(iii) संसार
(iv) आकाश।
उत्तर:
(i) संपूर्ण – अखिल
(ii) शोकरहित – अशोक
(iii) संसार – संसृति
(iv) आकाश – व्योम।

कृति 3: (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की प्रथम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
भारत देश हिमालय के आँगन के समान है। प्रतिदिन उषा भारत को सूर्य की किरणों का उपहार देती है, मानो हँसकर भारत-भूमि का अभिनंदन कर रही हो। ओस की बूंदों पर जब प्रातःकालीन सूर्य की रश्मियाँ पड़ती हैं, तो ओस की बूंदें चमकने लगती हैं और ऐसा लगता है मानो, उषा ने भारत को हीरों का हार पहना दिया हो।

सबसे पहले ज्ञान का उदय भारत में ही हुआ। अर्थात सबसे पहले हम जाग्रत हुए। फिर हमने पूरे विश्व में ज्ञान का प्रसार किया। इसके कारण समग्र संसार आलोकित हो गया। अज्ञानरूपी अंधकार का विनाश हुआ और संपूर्ण सृष्टि के सभी दुख-शोक दूर हो गए।

पद्यांश क्र. 2

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
सही विकल्प चुनकर वाक्य फिर से लिखिए:
(i) भारत में केवल …………………………. की ही विजय नहीं रही। (चाँदी/लोहे/सोने)
(ii) यहाँ …………………………. भिक्षु की तरह रहते थे। (लोग/लड़के/सम्राट)
(iii) हमसे चीन को …………………………. की दृष्टि मिली। (धर्म/कर्म/धन)
(iv) हमारा देश सदा प्रकृति का …………………………. रहा। (खिलौना/आँगन /पालना)
उत्तर:
(i) भारत में केवल लोहे की ही विजय नहीं रही।
(ii) यहाँ सम्राट भिक्षु की तरह रहते थे।
(iii) हमसे चीन को धर्म की दृष्टि मिली।
(iv) हमारा देश सदा प्रकृति का पालना रहा।

प्रश्न 3.
उपर्युक्त पद्यांश पर आधारित ऐसे दो प्रश्न तैयार कीजिए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) सम्राट
(ii) धर्म।
उत्तर:
(i) कौन भिक्षु होकर रहते?
(ii) चीन को कौन-सी दृष्टि मिली?

प्रश्न 4.
निम्नलिखित पंक्तियों का तात्पर्य लिखिए:
(ii) प्रकृति का रहा पालना यहीं।
उत्तर:
(ii) हमें प्रकृति ने प्रत्येक वस्तु मुक्तहस्त से प्रदान की। यहाँ की शस्य श्यामला भूमि, हिमाच्छादित गिरि शिखर, घाटियाँ, वादियाँ, सदानीरा नदियाँ, झरने, फल-फूल, संसाधनों से भरपूर जंगल सभी अनुपम हैं।

प्रश्न 5.
आकृति पूर्ण कीजिए:
(i) हमने गोरी को इसका दान दिया – [ ]
(ii) भारत की धरती पर इसकी धूम रही – [ ]
उत्तर:
(i) हमने गोरी को इसका दान दिया – [दया का]
(ii) भारत की धरती पर इसकी धूम रही – [धर्म की]

कृति 2: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्द-समूहों के लिए शब्द लिखिए:
(i) बहुमूल्य चमकीले प्रसिद्ध खनिज पदार्थ, जो आभूषणों आदि में जड़े जाते हैं –
(ii) छोटे बच्चों के लिए एक प्रकार का झूला या हिंडोला –
(iii) वह स्थान जहाँ किसी का जन्म हुआ हो –
(iv) बौद्ध संन्यासियों के लिए प्रयोग किया जाने वाला शब्द –
उत्तर:
(i) रत्न
(ii) पालना
(iii) जन्मस्थान
(iv) भिक्षु।

प्रश्न 2.
निम्नलिखित शब्दों के विलोम शब्द लिखिए:
(i) विजय x ………………….
(ii) धर्म x ………………….
(iii) भूमि x ………………….
(iv) जन्म x ………………….
उत्तर:
(i) विजय x पराजय
(ii) धर्म x अधर्म
(iii) भूमि x आकाश
(iv) जन्म – मरण।

कृति 3: (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की अपनी पसंदीदा किन्हीं दो पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
विजय केवल लोहे की नहीं, धर्म की रही धरा पर धूम भिक्षु होकर रहते सम्राट, दया दिखलाते घर-घर घूम। भारतीयों ने शस्त्रों के बल पर दूसरे देशों को नहीं जीता, बल्कि उन्होंने प्रेमभाव से लोगों के हृदय जीते हैं। भारत में प्राचीन काल से ही लोगों के मन में धर्म की भावना रही है। यहाँ वर्धमान महावीर और गौतम बुद्ध जैसे त्यागी धर्मपुरुष हुए हैं, जिन्होंने अपना विशाल साम्राज्य छोड़कर भिक्षु का स्वरूप धारण किया और घर-घर घूमकर लोगों का कष्ट दूर करने का प्रयास किया, धर्म का प्रचार किया।

पद्यांश क्र. 3

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
निम्नलिखित पंक्तियों का तात्पर्य लिखिए:
(i) किसी को देख न सके विपन्न।
उत्तर:
(i) भारतीय कभी किसी को दुखी नहीं देख सके। दीन-दुखियों की सेवा करने के लिए हम भारतीय सदैव तत्पर रहते हैं।

प्रश्न 2.
आकृति पूर्ण कीजिए:
(i) हम चरित्र के ऐसे थे – [ ]
(ii) हम दान के लिए यह करते थे – [ ]
(iii) हमारे लिए ये देवता के समान थे – [ ]
(iv) हमें अपने गौरव पर यह था – [ ]
उत्तर:
(i) हम चरित्र के ऐसे थे [पवित्र]
(ii) हम दान के लिए यह करते थे [संचय]
(iii) हमारे लिए ये देवता के समान थे [अतिथि]
(iv) हमें अपने गौरव पर यह था [गर्व]

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 4.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (शब्द संपदा)

प्रश्न 1.
पद्यांश से उपसर्ग वाले दो शब्द ढूँढकर लिखिए:
(i) ……………………. (ii) …………………….
उत्तर:
(i) अतिथि
(ii) अभिमान।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) पूत = …………………….
(ii) गर्व = …………………….
(iii) प्रतिज्ञा = …………………….
(iv) प्यारा = …………………….
उत्तर:
(i) पूत – पावन
(ii) गर्व = घमंड
(iii) प्रतिज्ञा = प्रण
(iv) प्रिय = प्यारा।

प्रश्न 3.
पद्यांश से शब्द ढूँढकर लिखिए:
(i) पवित्र शब्द के लिए प्रयुक्त शब्द – …………………….
(ii) गरीब शब्द के लिए प्रयुक्त शब्द – …………………….
उत्तर:
(i) पवित्र शब्द के लिए प्रयुक्त शब्द – पूत
(ii) गरीब शब्द के लिए प्रयुक्त शब्द – विपन्न।

कृति 3: (सरल अर्थ)

पदय विश्लेषण
सूचना: यह प्रश्नप्रकार कृतिपत्रिका के प्रारूप से हटा दिया गया है। लेकिन यह प्रश्न पाठ्यपुस्तक में होने के कारण विद्यार्थियों के अधिक अभ्यास के लिए इसे उत्तर-सहित यहाँ समाविष्ट किया गया है।

भाषा अध्ययन (व्याकरण)

प्रश्न. सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:
अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) राजा दशरथ वृद्ध दंपति के सामने बैठ गए।
(ii) सड़क कदाचित कच्ची थी।
उत्तर:
(i) दशरथ – व्यक्तिवाचक संज्ञा।
(ii) सड़क – जातिवाचक संज्ञा।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) बहुत
(ii) सामने
(iii) किंतु।
उत्तर:
(i) प्रयाग बहुत थक गया था।
(ii) स्कूल के सामने एक बगीचा है।
(iii) घर में दीपक तो था, किंतु उसमें तेल न था।

3. संधि:
कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
उज्ज्व	………………	………………
अथवा
प्रश्न + उत्तर	………………	………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
उज्ज्वल	उत् + ज्वल	व्यंजन संधि
अथवा
प्रश्नोत्तर	प्रश्न + उत्तर	स्वर संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका ‘मूल रूप लिखिए:
(i) इस पद ने मोहिनी मंत्र का जाल बिछा दिया।
(ii) बालक भूमि पर लेट गया।
उत्तर:

सहायक क्रिया	मूल रूप
(i) दिया	देना
(ii) गया।	जाना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) दौड़ना
(ii) बोलना
(iii) रोना।
उत्तर:

क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
(i) दौड़ना।	दौड़ाना	दौड़वाना
(ii) बोलना	बुलाना	बुलवाना
(iii) रोना	रुलाना	रुलवाना

6. मुहावरे:
(1) निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) दृष्टि फेरना
(ii) राह देखना।
उत्तर:
(i) दृष्टि फेरना।
अर्थ: नजर डालना।
वाक्य: नेताजी ने श्रोताओं पर दृष्टि फेरी।

(ii) राह देखना।
अर्थ: प्रतीक्षा करना।
वाक्य: विद्यार्थी कई दिनों से छुट्टियों की राह देख रहे थे।

(2) अधोरेखांकित वाक्यांश के लिए कोष्ठक में दिए गए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (सपने की संपत्ति होना, चल बसना, भनक पड़ना)
(i) हफ्ते भर की बीमारी में मरीज चला गया।
(ii) दारोगाजी ने उड़ती हुई खबर सुनी कि कल दंगा होने वाला है।
(ii) ऐसा भूकंप आया कि क्षण भर में सारी चहल-पहल विलुप्त हो गई।
उत्तर:
(i) हफ्ते भर की बीमारी में मरीज चल बसा।
(ii) दारोगाजी के कान में भनक पड़ी कि कल दंगा होने वाला है।
(iii) ऐसा भूकंप आया कि क्षण भर में सारी चहल-पहल सपने की संपत्ति हो गई।

7. कारक:
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उसका भेद लिखिए:
(i) नारी महान है।
(ii) वह किसी को किसी प्रकार की कमी नहीं होने देती।
(iii) प्रेरणा का सूक्ष्म प्रभाव होता है।
उत्तर:
(i) नारी – कर्ता कारक
(ii) किसी को – कर्म कारक
(iii) प्रेरणा का – संबंध कारक।

8. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) क्या बताऊँ गाय ने दूध देना बंद कर दिया है बूढ़ी हो गई है इस जमाने में गाय भैंस पालने का खर्चा
(ii) हे मेरे मित्रो परिचितो आओ अपने सारे बदले लेने का यही वक्त है
उत्तर:
(i) “क्या बताऊँ। गाय ने दूध देना बंद कर दिया है, बूढ़ी हो गई है। इस जमाने में गाय-भैंस पालने का खर्चा …।”
(ii) “हे मेरे मित्रो, परिचितो! आओ, अपने सारे बदले लेने का यही वक्त है।”

9. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) मनु पीछे की ओर मुड़ता है। (सामान्य भूतकाल)
(ii) तुम्हारा मुख लाल होता है। (अपूर्ण वर्तमानकाल)
(iii) रोगी की अवस्था बदल जाती है। (पूर्ण भूतकाल)
उत्तर:
(i) मनु पीछे की ओर मुड़ा।
(ii) तुम्हारा मुख लाल हो रहा है।
(iii) रोगी की अवस्था बदल गई थी।

10. वाक्य भेद:
(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए:
(i) भारतीय चरित्र के पवित्र होते हैं।
(ii) बादल आए किंतु पानी नहीं बरसा।
उत्तर:
(i) सरल वाक्य
(ii) संयुक्त वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार वाक्य परिवर्तन कीजिए:
(i) तुम्हें अपना ख्याल रखना चाहिए। (आज्ञावाचक)
(ii) मास्टर जी ने पुस्तकें लाने के लिए पैसे दिए। (प्रश्नवाचक)
उत्तर:
(i) तुम अपना ख्याल रखो।
(ii) क्या मास्टर जी ने पुस्तकें लाने के लिए पैसे दिए?

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) क्रोध से उसकी नेत्र लाल हो गए।
(ii) राम ने हिरण का शिकार की।
(iii) मैं मेरा काम करता है।
उत्तर:
(i) क्रोध से उसके नेत्र लाल हो गए।
(ii) राम ने हिरन का शिकार किया।
(iii) में अपना काम करता हूँ।

भारत महिमा Summary in Hindi

भारत महिमा कविता का सरल अर्थ

1. हिमालय के आँगन …………………………………… मधुर साम संगीत।. . .

हमारा यह प्यारा भारत देश हिमालय के आँगन के समान है। प्रतिदिन उषा भारत को सूर्य की किरणों का उपहार देती है। तब ऐसा लगता है मानो हँसकर वह भारत-भूमि का अभिनंदन कर रही हो। ओस की बूंदों पर जब प्रातःकालीन सूर्य की रश्मियाँ पड़ती हैं तो ऐसा लगता है जैसे उषा ने भारत को हीरों का हार पहना दिया हो।

सबसे पहले ज्ञान का उदय भारत में ही हुआ अर्थात सबसे पहले हम जाग्रत हुए। फिर हमने पूरे विश्व में ज्ञान का प्रसार किया। इसके कारण समग्र संसार आलोकित हो गया। अज्ञान रूपी अंधकार का विनाश हुआ और संपूर्ण सृष्टि के सभी दुख-शोक दूर हो गए।

वाणी की देवी वीणापाणि (सरस्वती) ने इसी पवित्र भूमि पर प्रेम के साथ अपने कमल के समान कोमल करों में वीणा उठाई, उसकी झंकार से सप्तसिंधुओं में सातों स्वरों का मोहक सरगम गूंजने लगा, मधुर संगीत का जन्म हुआ। इसी महान देश में संगीत के वेद सामवेद की रचना हुई।

2. विजय केवल …………………………………… आए थे नहीं।. . .

भारत के लोगों ने शस्त्रों के बल पर देशों को नहीं जीता। यहाँ प्राचीन काल से ही लोगों के मन में धर्म की प्रखर भावना रही है और उन्होंने संसार में धर्म का प्रचार किया। यहाँ गौतम बुद्ध और वर्धमान महावीर जैसे धर्मपुरुष हुए हैं, जिन्होंने विशाल साम्राज्य छोड़कर भिक्षु का स्वरूप धारण किया और घर-घर घूमकर लोगों का कष्ट दूर करने का प्रयास किया, धर्म का प्रचार किया। हमने मोहम्मद गोरी को पराजित करने के बाद भी दयापूर्वक क्षमा कर दिया। हमारे देश से ही चीन को धर्म की दृष्टि मिली। (भारत के महान सम्राट अशोक ने अपने पुत्र महेंद्र और पुत्री संघमित्रा को बौद्ध धर्म के प्रचार के लिए चीन, स्वर्ण भूमि अर्थात जावा और श्रीलंका भेजा) जावा और श्रीलंका के लोगों को पंचशील (अहिंसा, अस्तेय, अपरिग्रह, सत्य, ब्रह्मचर्य आदि) के सिद्धांत मिले।

भारतवासियों ने कभी किसी की संपत्ति या किसी का राज्य छीनने का प्रयास नहीं किया। हमें प्रकृति ने प्रत्येक वस्तु मुक्तहस्त से प्रदान की। प्रकृति की हमारे देश पर महान कृपा रही है। (यहाँ की शस्य श्यामला भूमि, हिमाच्छादित गिरि शिखर, घाटियाँ, वादियाँ, सदानीरा नदियाँ, झरने, फल-फूल, संसाधनों से भरपूर जंगल सभी अनुपम हैं) भारत सदा से हमारी जन्मभूमि है। हम इसी देश की संतानें हैं। हम बाहर के किसी स्थान से आकर यहाँ नहीं बसे हैं। (जैसा कि कुछ विदेशियों का कहना है।)

3. चरित थे पूत …………………………………… प्यारा भारतवर्ष।. . .

भारत के लोग सदा से चरित्रवान रहे हैं। हमारी भुजाओं में भरपूर शक्ति रही है। भारतीयों में वीरता की कभी कमी नहीं रही। साथ ही नम्रता सदा हमारा गुण रहा है। हमने कभी अपनी उपलब्धियों पर घमंड नहीं किया। हमें अपनी सभ्यता और संस्कृति पर गर्व रहा है। हम कभी किसी को दुखी नहीं देख सके। दीन-दुखियों की सेवा करने के लिए हम भारतीय सदैव तत्पर रहते हैं। ‘हम यदि धन और संपत्ति का संग्रह करते भी थे, तो दान के लिए करते थे। दानवीरता भारतीयों का गुण रहा है। हमारे देश में अतिथियों को सदा देवता के समान माना जाता था। भारत के लोग सत्य बोलना अपना धर्म मानते थे। (भारतीय सत्यवादी हरिश्चंद्र की संतानें हैं।) हमारे हृदय में तेज था, गौरव था। हम सदा अपनी प्रतिज्ञा पर अटल रहते थे। प्राण जाए, पर वचन न जाए हमारा जीवनमूल्य रहा है।

आज भी हम भारतीयों की धमनियों में उन्हीं पूर्वजों का रक्त प्रवाहित हो रहा है। आज भी हमारा देश वैसा ही है। आज भी भारतीयों में वैसा ही साहस है। भारतीय आज भी ज्ञान के क्षेत्र में सबसे आगे हैं। आज भी हम पहले के समान शांति के पुजारी हैं। देशवासियों में वैसी ही शक्ति है। हम उन्हीं आर्यों की दिव्य संतानें हैं।

हम जब तक जिएँ, इसी देश के लिए जिएँ। हमें इसकी सभ्यता और संस्कृति पर अभिमान है और हर्ष है कि हमने इस भूमि पर जन्म लिया है। यह हमारा प्यारा भारतवर्ष है। यदि कभी आवश्यकता पड़े, तो इसके लिए अपना सर्वस्व भी न्योछावर कर दें।

भारत महिमा विषय-प्रवेश :

प्रकृति ने हमारे देश भारत की रचना बड़े प्यार से की है। हमारा देश हिमालय की गोद में बसा हुआ है। हमारा देश सबसे पहले जाग्रत हुआ था और इसकी संस्कृति सबसे पुरानी है। प्रस्तुत कविता में छायावाद के प्रवर्तक जयशंकर प्रसाद जी ने हमारे प्यारे देश भारत के इसी महिमामंडित अतीत का मनोरम चित्रण किया है। कवि की आकांक्षा है कि हमें सदैव अपने देश पर, इसकी सभ्यता और संस्कृति पर गर्व करना चाहिए। आवश्यकता पड़ने पर, हमें देश के लिए अपना सर्वस्व न्योछावर कर देने के लिए तत्पर रहना चाहिए।

भारत महिमा मुहावरा –

• अर्थ निछावर करना – अर्पण करना, समर्पित करना।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 7 Khula Aakash Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 7 खुला आकाश Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 7 खुला आकाश Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 7 गिरिधर नागर Textbook Questions and Answers

सूचना के अनुसार कृवियाँ कीविए:
(1) प्रहवलका पूण् कीविए:

उतर:

(2) कृवि पूण् कीविए:

उतर:

(3) आकृवि मे वलखिए:

उतर:

(4)

उतर:

(5) लखिए:
a.

उतर:

b.

उतर:

भाषा हबंदु
(1) हनम्हलखखत संहध हिचछेद की संहध कीहजए और भेद हलखखए:

उतर:

संधि शब्द	संधि विच्छेद	संधि भेद
(i) सज्जन	सत् + जन	व्यंजन संधि
(ii) नमस्ते	नमः+ ते	विसर्ग संधि
(iii) स्वागत	सु + आगत	स्वर संधि
(iv) दिग्दर्शक	दिक् + दर्शक	व्यंजन संधि
(v) यद्यपि	यदि + यपि	स्वर संधि
(vi) दुस्साहस	दुः + साहस	विसर्ग संधि

(2) हनम्हलखखत शब् का संहध हिचछेद कीहजए और भेद हलखखए:

उतर:

संधि विच्छेद	संधि शब्द	संधि भेद
(i) दुः +  लभ	दुर्लभ	विसर्ग संधि
(ii) महा +  आत्मा	महात्मा	स्वर संधि
(iii) अन् +  आसक्त	अनासक्त	स्वर संधि
(iv) अंतः +  चेतना	अंतश्चेतना	विसर्ग संधि
(v) सम् +  तोष	संतोष	व्यंजन संधि
(vi) सदा + एव	सदैव	स्वर संधि

(3) हनम्हलखखत आकृहत मे हदए गए शब् का हिचछेद कीहजए और संहध का भेद हलखखए:

उतर:

संधि शब्द	संधि विच्छेद	संधि भेद
(i) दिग्गज’	दिक् + गज	व्यंजन संधि
(ii) सप्ताह	सप्त + अह	स्वर संधि
(iii) निश्चल	निः + चल	विसर्ग संधि
(iv) भानूदय	भानु + उदय	स्वर संधि
(v) निस्संदेह	निः + संदेह	विसर्ग संधि
(vi) सूर्यास्त	सूर्य + अस्त	स्वर संधि

(4) पाठो मे आए संहध शब् छाँटकर उनका हिचछेद कीहजए और संहध का भेद हलखखए।

संधि शब्द	संधि विच्छेद	संधि भेद
(i) निर्जीव	निः + जीव	विसर्ग संधि
(ii) संभव	सम् + भव	व्यंजन संधि
(iii) उज्ज्व	लउत् + ज्वल	व्यंजन संधि

Hindi Lokbharti 10th Textbook Solutions Chapter 7 खुला आकाश Additional Important Questions and Answers

गद्यांश क्र.1
कृति 1: (आकलन)
(1) आकृति पूर्ण कीजिए:

उत्तर:

(2) उत्तर लिखिए: (बोर्ड की नमूना कृतिपत्रिका)

उत्तर:

कृति 2: (स्वमत अभिव्यक्ति)

‘बढ़ती हुई जनसंख्या का मनुष्य जीवन पर प्रभाव’ के बारे में आपके विचार 25 से 30 शब्दों में लिखिए। (बोर्ड की नमूना कृतिपत्रिका)
उत्तर:
आज लगभग सभी देशों की जनसंख्या में बढ़ोत्तरी हो रही है। यह जनसंख्या वृद्धि आज संसार के समक्ष एक समस्या बन गई है। सभी देशों के संसाधन सीमित हैं और बढ़ी हुई जनसंख्या की माँग विशाल है, जिसकी पूर्ति करना संभव नहीं है। इसी का परिणाम है कि आज लोगों के सामने बेकारी की समस्या उत्पन्न हो गई है। जनसंख्या वृद्धि के कारण कृषि पर आधारित लोग परेशान हैं। खेती योग्य जमीन बँटती जा रही है।

अब वह इतने लोगों को रोटी देने में असमर्थ हो गई है। गाँवों की आबादी का बोझ शहरों पर आ पड़ा है। यहाँ शहरों में बेकारी की समस्या है। यहाँ भी लोग रोटी, कपड़ा, मकान की समस्याओं से जूझ रहे हैं। लोग गंदी बस्तियों में रहने के लिए मजबूर हैं। न इतने लोगों के लिए ढंग की शिक्षा व्यवस्था उपलब्ध हो पा रही है और न ही चिकित्सा व्यवस्था।

बढ़ती जनसंख्या ने देश की अर्थव्यवस्था बिगाड़ दी है। इस पर अंकुश लगाकर ही इस समस्या से छुटकारा पाया जा सकता है। तभी मनुष्य के जीवन स्तर में भी सुधार हो पाएगा।

गद्यांश क्र.2
प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(2) सही विकल्प चुनकर वाक्य फिर से लिखिए:
(i) बिलकुल चुपचाप बैठकर सिर्फ ………………………… बारे में सोचें। (मेरे/अपने/सबके)
(ii) दूसरों की सोच-समझ पर ………………………… रखें। (भरोसा/प्रेम/संदेह)
(iii) ………………………… अन्य नहीं, अंतमय है, हमारे ही प्रतिरूप, हमसे अलग या भिन्न नहीं। (दूसरा /सब/वह)
(iv) ………………………… तरह सारे मनुष्य केवल मनुष्य होते और कुछ नहीं। (इसी/उसी/किसी)
उत्तर:
(2) (i) बिलकुल चुपचाप बैठकर सिर्फ अपने बारे में सोचें।
(ii) दूसरों की सोच-समझ पर भरोसा रखें।
(iii) दूसरा अन्य नहीं, अंतमय है, हमारे ही प्रतिरूप, हमसे अलग या भिन्न नहीं।
(iv) उसी तरह सारे मनुष्य केवल मनुष्य होते और कुछ नहीं।

कृति 2: (स्वमत अभिव्यक्ति)

‘आत्मचिंतन के लाभ’ विषय में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
आत्मचिंतन यानी स्वयं के विषय में चिंतन करना। आत्मचिंतन का अर्थ है किसी कार्य को करने या होने के बाद उसे करने के लिए अपनाई. गई क्रिया और विचार पद्धति का विश्लेषण। आत्मचिंतन के द्वारा हमें अपनी गलतियों से सीखने, साथ ही अपने किए गए कार्य को और बेहतर ढंग से करने का मौका मिलता है। किसी भी व्यक्ति को कोई दूसरा जितना सिखा सकता है, उससे कहीं अधिक वह अपने स्वाध्याय एवं आत्मचिंतन के द्वारा सीख सकता है। इस प्रक्रिया में हम शांत भाव से बैठकर किसी समस्या या मुद्दे के बारे में चिंतन कर सकते हैं।

छात्र जीवन में तो इसकी और भी अधिक आवश्यकता है। अपनी क्षमताओं के विषय में अच्छी तरह जाने-समझे बिना हम लक्ष्य निर्धारित कर लेते हैं। शीघ्रातिशीघ्र उसे प्राप्त कर लेना चाहते हैं और बाद में भटक जाते हैं। इसलिए पहले आत्मचिंतन करें, स्वयं को जानें, फिर लक्ष्य प्राप्ति का प्रयास करें।

गद्यांश क्र. 3
प्रश्न.
निम्नलिखित पठित गद्यांश पढकर दी गई ‘सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(1) उत्तर लिखिए:

उत्तर:

कृति 2: (स्वमत अभिव्यक्ति)

‘जीवन की सार्थकता के विषय में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
ईश्वर ने हमें सर्वश्रेष्ठ योनि अर्थात मानव योनि में जन्म दिया है। हमारा कर्तव्य है कि हम मानव जाति के लिए कुछ अच्छा कार्य करें। हमें जितनी आयु मिली है, वह समय हम अच्छे कार्यों को करने में लगाएँ। कुछ ऐसा काम करें जिससे समाज और देश का हित हो।

कुछ लोग समय की कमी की बात करते हैं। लेकिन यदि कुछ करने की लगन हो तो समय आड़े नहीं आता। स्वामी विवेकानंद 40 वर्ष की आयु से भी पहले इस संसार से चले गए। ईसा मसीह का 30 वर्ष की आयु में ही प्राणांत हो गया। रामानुजम, रानी लक्ष्मीबाई, नेपोलियन, सिकंदर और अन्य अनेक अल्पायु में ही इस असार संसार को छोड़ गए, फिर भी मानव इतिहास में, ये महापुरुष अपनी छाप छोड़ गए।

सीमित समय में भी जितना अधिक-से-अधिक अच्छा हो सके, हमें देश व समाज के कल्याण के लिए कुछ सकारात्मक अवश्य करना चाहिए।

गद्यांश क्र. 4
प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(1) आकृति पूर्ण कीजिए:

उत्तर:

(2) जोड़ियाँ मिलाइए:

अ	आ
(i) शौक	भविष्य
(ii) एकनिष्ठ	गुलाम
(ii) उज्ज्वल	रास्ते
(iv) दरजनों	सेवा

उत्तर:

अ	आ
(i) शौक	रास्ते
(ii) एकनिष्ठ	सेवा
(iii) उज्ज्वल	भविष्य
(iv) दरजनों	गुलाम

कृति 2: (स्वमत अभिव्यक्ति)

→ ‘जो हम शौक से करना चाहते हैं, उसके लिए रास्ते निकाल लेते हैं, इसका सोदाहरण अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
जिन कामों या चीजों का हमें शौक होता है, जिसमें हमारी रुचि होती है, उसके लिए हम समय, विधा सब निकाल लेते हैं। रुचि सफलता की वाहक है। हम सभी अपनी रुचि के कामों को करते समय उसमें डूब जाते हैं। उसी का परिणाम होता है सफलता। शिक्षा काल में जिस विषय में हमारी रुचि होती है, उसे पढ़ने में हम सारी रात भी जग लेते हैं, जबकि किसी ऐसे विषय की पुस्तक खोलते ही आँखें नींद से भर आती हैं, जो हमें पसंद न हो।

व्यायाम, तैराकी, बागवानी, चित्रकला, गायन, वादन आदि ऐसे अनेक कार्य हैं, जिनका यदि शौक हो तो मनुष्य घंटों बिताने पर भी उनसे ऊब अनुभव नहीं करता। किसी भी काम में सफलता प्राप्त करने के लिए उसमें रुचि होना परम आवश्यक है। बिना रुचि के आगे बढ़ने की संभावना बहुत कम होती है। जिस काम में हमारी रुचि होती है, उसे करने के लिए हम अपनी सारी ऊर्जा लगा देते हैं। न दिन देखते हैं, न ही रात। थकान शब्द तो मानो हमारे शब्दकोश में कभी था ही नहीं।

→ ‘कंप्यूटर ज्ञान का महासागर’ विषय पर तर्कपूर्ण चर्चा कीजिए।
उत्तर:
कंप्यूटर इस पृथ्वी पर कल्पवृक्ष के समान है। जीवन का कोई भी ऐसा क्षेत्र नहीं है, जहाँ इसका महत्व न हो। सूचना के क्षेत्र में कंप्यूटर के कारण अद्भुत क्रांति आ गई है। इंटरनेट इसकी अनुपम देन है। दुनियाभर की जानकारी हम मिनटों में प्राप्त कर सकते हैं। यह एक सेकंड में दस हजार करोड़ गणितीय गणना कर सकता है।

चाहे मौसम का पूर्वानुमान हो या प्राकृतिक गैस और खनिज भंडारों का पता लगाना हो, रेलगाड़ियों और हवाईजहाजों का आरक्षण कराना हो या संसारभर की जानकारी प्राप्त करनी हो, कंप्यूटर के द्वारा घर बैठे हम मिनटों में कर सकते हैं। यह समय-समय पर भौगोलिक सूचनाओं से संबंधित जानकारी भी देता है। मुद्रण व प्रसारण के क्षेत्र में इसका योगदान असीमित है।

कंप्यूटर एक चालक की भाँति वायुयान का संचालन करता है। चालक के बटन दबाते ही कंप्यूटर स्वयं गति और दिशा का निर्धारण कर लेता है। शिक्षा के क्षेत्र में तो आज कंप्यूटर एक अनिवार्यता बन गया है।

→ महानगरीय/ग्रामीण दिनचर्या के लाभ तथा हानि के बारे में अपने अनुभव के आधार पर लिखिए।
उत्तर:
गाँवों में आज भी खुला आसमान है। वहाँ का वातावरण शुद्ध, प्रकृति की गोद में है, जबकि महानगरों में आसमान दिखाई नहीं पड़ता। बड़े पैमाने पर वाहनों से होने वाला प्रदूषण, लगातार होने वाला शोर, भीड़ और धुआँ असहज महसूस कराता है। भीड़भाड़, ट्रैफिक जाम, और अपराध महानगरों में रोज की बात है। गाँवों में एक प्रकार का ठहराव है। शाम ढलते ही चारों ओर एक प्रकार का सन्नाटा पसर जाता है।

जबकि, महानगरों में जीवन हर समय गतिमान रहता है। देर रात तक ऑफिस, दुकानें खुली रहती हैं। बस, ट्रेन, टैक्सियाँ, स्कूटर्स सड़कों पर दौड़ते रहते हैं। गाँवों में धूप, हरियाली और शांति का आनंद प्राप्त कर सकते हैं। लोग आज भी गर्मजोशी से मिलते हैं। एक-दूसरे के दुख-तकलीफ में काम आते हैं। महानगरों में बहुत-से लोग पड़ोसी तक को नहीं पहचानते। दोस्तों, रिश्तेदारों के लिए समय नहीं निकाल पाते।

यहाँ लोगों के पास पैसा है, सुविधाएँ हैं, पर शांति कोसों दूर है। ग्रामीण लोगों का जीवन महानगरों की भागदौड़ से दूर एवं प्रकृति के करीब होता है। दूसरी ओर महानगरों में लोग हमेशा समय को पकड़ने के लिए दौड़ते रहते हैं। अति व्यस्तता के कारण तनाव, फिर स्वास्थ्य। संबंधी विभिन्न परेशानियाँ उन्हें घेर लेती हैं।

अपवठि ग‍दयांश

नम्वलखिि पररचछे‍ पढ़कर सूचना के अनुसार कृवियाँ कीविए:

हर फकसी को आतमरक् करनी होगी, हर फकसी को अपना कत्यय करना होगा। मै फकसी की सहायता की प्राशा नही करता। मै फकसी का भी प्राह नही करता। इस दुफनया से मदद की प्र्या करने का मुझे कोई अफधकार नही है। अतीत मे फिन लोगो ने मेरी मदद की है या भफ‍व् मे भी लोग मेरी मदद करें, मेरे प्र उन सबकी करुण मौिूद है, इसका दा‍व कभी नही फकया सकता। इसीफलए मै सभी लोगो के प्र फचर कक तज ञँ।

तुमहारी पररफस्फत इतनी बुरी देखकर मै बेहद फचंफतत हँ। लेफकन यह लो फक-‘तुमसे भी जयादा दुखी लोग इस संसार मे है। मै तुमसे भी जयादा बुरी पररफस्फत मे हँ। इंग् मे सब कुछ के फलए मुझे अपनी ही िेब से खच् करना पड़ता है। आमदनी कुछ भी नही है। लंदन मे एक कमरे का फकराया हर सप्ह के फलए तीन पाउंड होता है। ऊपर से अनय कई खच् है। अपनी तकलीिो के फलए मै फकससे फशकायत करू? यह मेरा अपना कम्यल है, मुझे ही भुगतना होगा।’

(फ‍ववकानंद की आतमकथा से)

(1) कृवि पूण् कीविए:
1.

2.

(2) उतिर वलखिए:
1. पररचछेद मे उखलिखत देश – [ ]
2. हर फकसी को करना होगा – [ ]
3. लेखक की तकलीिे – [ ]
4. हर फकसी को करनी होगी – [ ]

(3) वन‍देानुसार हल कीविए:
(अ) वनम्वलखिि अर् से मेलनेला शब् उपयु्थ् पररचछे‍ से ढूँढ़कर वलखिए ः
1. स्वं की रक् करना – …………………………….
2. दूसरो के उपकारो को मानने ‍वला – …………………………….

(4) लंग पहचानकर वलखिए:
1. जेब [ ]
2. साहित्य [ ]
3. दावा [ ]
4. सेवा [ ]

खुला आकाश Summary in Hindi

विषय-प्रवेश : प्रस्तुत पाठ डायरी विधा का एक उदाहरण है। कुँवर नारायण जी ने इस पाठ के माध्यम से नगरों की भीड़, वहाँ की जीवन-शैली, जीवन के संघर्ष, आत्मचिंतन आदि पर प्रकाश डाला है। लेखक मानते हैं कि व्यक्ति के विकास में आत्मचिंतन का बड़ा महत्त्व है। इसके द्वारा हम अपनी क्षमताओं के बारे में और अधिक जान सकेंगे। साथ ही अपनी गलतियों से सीख ले सकेंगे।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 10 Budhi Kaki Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Chapter 10 बूढ़ी काकी Notes, Textbook Exercise Important Questions, and Answers.

Hindi Lokbharti 10th Digest Chapter 10 बूढ़ी काकी Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 10 बूढ़ी काकी Textbook Questions and Answers

कृति

(कृतिपत्रिका के प्रश्न 3 (अ) के लिए

* सूचना के अनुसार कृतियाँ कीजिए :

प्रश्न 1.

स्वभाव के आधार पर पात्र का नाम
१.	क्रोधी	………………….
२.	लालची	………………….
३.	शरारती	………………….
४.	स्नेहिल	………………….

उत्तर:

स्वभाव के आधार पर पात्र का नाम
१.	क्रोधी	रूपा
२.	लालची	बुद्धिराम
३.	शरारती	दोनों लड़के
४.	स्नेहिल	लाड़ली

प्रश्न 2.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
बुद्धिराम का काकी के प्रति दुर्व्यवहार दर्शाने वाली चार बातें :
१) ………………….
४) ………………….
२) ………………….
४) ………………….
उत्तर :
(i) बूढ़ी काकी की संपत्ति अपने नाम लिखाते समय किए गए लंबे-चौड़े वादों को बुद्धिराम द्वारा न निभाना।
(i) बूढ़ी काकी को भरपेट भोजन न देना।
(iii) भोजन कर रहे मेहमानों के बीच रेंगती हुई बूढ़ी काकी के पहुँच जाने पर बुद्धिराम द्वारा निर्दयतापूर्वक पकड़कर उनकी कोठरी में ले जाकर पटक देना।
(iv) बूढ़ी काकी के व्यवहार से रुष्ट होने के कारण तिलक उत्सव में सभी मेहमानों और घरवालों के भोजन कर लेने के बाद भी बुद्धिराम द्वारा उन्हें खाने के लिए न पूछना।

प्रश्न 4.
कारण लिखिए :
a. बूढ़ी काकी ने भतीजे के नाम सारी संपत्ति लिख दी _____________________
b. लाड़ली ने पूड़ियाँ छिपाकर रखीं _____________________
c. बुद्धिराम ने काकी को अँधेरी कोठरी में धम से पटक दिया _____________________
d. अंग्रेजी पढ़े नवयुवक उदासीन थे _____________________
उत्तर:
a. बूढ़ी काकी के परिवार में अब एक भतीजे के सिवाय और कोई नहीं था, इसलिए उन्होंने भतीजे के नाम सारी संपत्ति लिख दी।
b. बुद्धिराम और रूपा दोनों ने ही बूढ़ी काकी को उनकी निर्लज्जता के लिए दंड देने का निश्चय कर लिया था। इसलिए बूढ़ी काकी को किसी ने नहीं पूछा।
c. बूढ़ी काकी रेंगती हुई भोजन कर रहे मेहमान मंडली के बीच पहुँच गई थी। इससे कई लोग चौंककर उठ खड़े हुए थे। बुद्धिराम को इससे गुस्सा आया और उसने काकी को वहाँ से उठाकर कोठरी में ले जाकर धम से पटक दिया।
d. अंग्रेजी पढ़े नवयुवक उदासीन थे, क्योंकि वे गँवार मंडली में बोलना अथवा सम्मिलित होना अपनी प्रतिष्ठा के प्रतिकूल समझते थे।

प्रश्न 5.
सूचना के अनुसार शब्द में परिवर्तन कीजिए :

उत्तर :

अभिव्यक्ति

‘बुजुर्ग आदर-सम्मान के पात्र होते हैं, दया के नहीं इस सुवचन पर अपने विचार लिखिए।
उत्तर :
हमें यह बात याद रखनी चाहिए कि आज जो व्यक्ति बुजुर्ग है वह हमेशा बूढ़ा और असहाय नहीं था। वह भी पहले युवा था। उसने अपने परिवार का पालन-पोषण और उसकी देखरेख की थी। उसने तरह-तरह की समस्याओं का सामना किया था और उन्हें अपने तरीके से हल किया था। उसे जीवन जीने का अनुभव है। लेकिन वृद्ध हो जाने पर किसी-किसी परिवार में बुजुर्गों को किनारे कर दिया जाता है। उनकी सलाह या सुझाव को कोई महत्त्व नहीं दिया जाता। इस तरह के व्यवहार से बुजुर्गों को अपने सम्मान पर ठेस लगती महसूस होती है।

किसी-किसी परिवार में तो बुजुर्गों के खाने-पीने की भी किसी को चिंता नहीं रहती। घर के लोग अपने में मगन रहते हैं और बुजुर्गों का कोई ख्याल नहीं रखता। बुजुर्गों को खाने-पीने के लिए उनका मुँह ताकना पड़ता है। हमें यह बात नहीं भूलनी चाहिए कि हम इन बुजुर्गों की संतान हैं। उनको पर्याप्त सम्मान देना और उनकी हर प्रकार से देखरेख करना हमारा फर्ज है। बुजुर्गों की प्रसन्नता और उनके आशीर्वाद से ही परिवार फूलता-फलता और खुशहाल रहता है। इसलिए बुजुर्गों को हमें सदा आदर-सम्मान देना चाहिए और उनकी देखरेख करनी चाहिए।

भाषा बिंदु

प्रश्न 1.
निम्नलिखित क्रियाओं के प्रथम तथा द्वितीय प्रेरणार्थक रूप लिखिए :

मूल क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
भूलना	……………………….	……………………….
पीसना	……………………….	……………………….
माँगना	……………………….	……………………….
तोड़ना	……………………….	……………………….
बेचना	……………………….	……………………….
कहना	……………………….	……………………….
नहाना	……………………….	……………………….
खेलना	……………………….	……………………….
खाना	……………………….	……………………….
फैलना	……………………….	……………………….
बैठना	……………………….	……………………….
लिखना	……………………….	……………………….
जुटना	……………………….	……………………….
दौड़ना	……………………….	……………………….
देखना	……………………….	……………………….
जीना	……………………….	……………………….

उत्तर :

प्रश्न 2.
पठित पाठों से किन्हीं दस मूल क्रियाओं का चयन करके उनके प्रथम तथा द्वितीय प्रेरणार्थक रूप निम्न तालिका में लिखिए :

मूल क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….

उत्तर :

उपयोजित लेखन

मेरा प्रिय वैज्ञानिक’ विषय पर निबंध लेखन कीजिए।
उत्तर :
यों तो दुनिया में एक-से-एक बड़े वैज्ञानिक हैं, पर मेरे प्रिय वैज्ञानिक तो सर जगदीशचंद्र बोस ही हैं। सर जगदीशचंद्र बोस की बात ही निराली है। उन्होंने यह सिद्ध करके बता दिया कि पेड़-पौधे भी हमारी तरह साँस लेते हैं और उन्हें पानी और भोजन की आवश्यकता होती है। उनमें भी जान होती है। यदि पेड़-पौधों को सताया या कष्ट दिया जाए, तो वे बीमार हो जाते हैं और उनकी प्रकृति के विरुद्ध उन्हें भोजन दिया जाए अथवा जहरीला रसायन दिया जाए, तो वे मर जाते हैं। वैसे पेड़-पौधों के संपर्क में रहने वाले प्रत्येक व्यक्ति को मालूम होता है कि पेड़-पौधों को नुकसान पहुँचाने या विषैले पदार्थों के संपर्क में आने से वे क्षतिग्रस्त या मृत हो सकते हैं, पर इस बात को सिद्ध किया था सर जगदीशचंद्र बोस ने।

अपने शोध को सिद्ध करने के लिए उन्होंने खुद चुंबकीय क्रेश्कोग्राफ नामक यंत्र तैयार किया। उन्होंने इस यंत्र की सहायता से सब के सामने अपने प्रयोग से यह सिद्ध कर दिया कि पेड़-पौधों में जीवन होता है और प्राणियों की तरह उनमें भी विभिन्न क्रियाएँ होती हैं। इस प्रकार के सूक्ष्म रहस्य का उद्घाटन करने वाले वे पहले वैज्ञानिक थे। वे सच्चे अर्थों में एक महान वैज्ञानिक थे। ऐसे महान वैज्ञानिक पर हमें गर्व है।

Hindi Lokbharti 10th Textbook Solutions Chapter 10 बूढ़ी काकी Additional Important Questions and Answers

गद्यांश क्र.1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :


उत्तर:

प्रश्न 2.
उत्तर लिखिए :
(i) बूढ़ी काकी का शारीरिक स्वास्थ्य –
(ii) बूढ़ी काकी के परिवार में अब बचा एकमात्र सदस्य –
(iii) बुद्धिराम ने इस तरह लिखाई बूढ़ी काकी की संपत्ति –
(iv) बूढ़ी काकी के रोने का ढंग –
उत्तर:
(i) बूढ़ी काकी के नेत्र, हाथ, पैर आदि सभी अंग जवाब दे चुके थे।
(ii) उनका भतीजा बुद्धिराम।
(iii) खूब लंबे-चौड़े वादे करके।
(iv) बूढ़ी काकी गला-फाड़कर रोती थीं।

प्रश्न 3.
आकृति में दिए गए रिक्त स्थानों में उत्तर लिखकर आकृति पूर्ण कीजिए :

उत्तर:

कृति 2 : (स्वमत अभिव्यक्ति)

प्रश्न.
बुढ़ापा बहुधा बचपन का पुनरागमन होता है’ इस विषय पर अपने विचार 25 से 30 शब्दों में व्यक्त कीजिए।
उत्तर :
कहते हैं, बुढ़ापा बचपन का ही एक रूप है। वृद्धावस्था : में मनुष्य की हरकतें बच्चों जैसी हो जाती हैं। इस अवस्था में मनुष्य के अंग-प्रत्यंग कमजोर हो जाते हैं और उन्हें बच्चों की तरह दूसरों का सहारा लेना पड़ता है। दिमाग कमजोर हो जाता है। दाँत गिर जाते हैं और मनुष्य का मुँह बच्चों की तरह पोपला हो जाता है। इतना ही नहीं, बच्चों की तरह ही वृद्धों को भी मान-अपमान की परवाह नहीं होती। जिस तरह लोग बच्चों की बातों पर ध्यान नहीं देते, उसी तरह वृद्धों की बातों पर भी कोई ध्यान नहीं देता। उनकी इच्छा-अनिच्छा का भी कोई महत्त्व नहीं होता। इस तरह वृद्धावस्था और बचपन की अधिकांश बातों में समानता होती है। इसलिए कहा जा सकता है कि बुढ़ापा बहुधा बचपन का पुनरागमन होता है।

गद्यांश क्र.2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए :

उत्तर:

प्रश्न 3.
कारण लिखिए :
(i) उत्सव के दिन बूढ़ी काकी को अपनी स्थिति पर रोना आया, पर वे रो नहीं सकीं।
उत्तर:
(i) उत्सव के दिन बूढ़ी काकी को अपनी स्थिति पर रोना आया, पर वे रो नहीं सकीं, क्योंकि उन्हें रूपा का डर था।

प्रश्न 4.
त्तर लिखिए :
मुखराम के तिलक उत्सव की तैयारियाँ :
उत्तर:
मुखराम के तिलक उत्सव की तैयारियाँ :
(i) पूड़ियाँ-कचौड़ियाँ निकल रही थीं।
(ii) एक बड़े हंडे में मसालेदार तरकारी पक रही थी।

कृति 2 : (स्वमत अभिव्यक्ति)

प्रश्न.
‘बुढ़ापा तृष्णा रोग का अंतिम समय है’ इस विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर :
मनुष्य के जीवन की चार अवस्थाएँ होती हैं – बचपन, किशोरावस्था, युवावस्था और बुढ़ापा। अपने जीवन में मनुष्य की तरह-तरह की कामनाएँ होती हैं और उनकी पूर्ति करने का वह भरसक प्रयास करता है। बचपन से लेकर युवावस्था तक मनुष्य को अपनी कामनाओं की जल्द से जल्द पूरी होने की उतनी चिंता नहीं रहती, जितनी बुढ़ापे में। वृद्धावस्था में मनुष्य के जीवन के गिने-चुने वर्ष ही बचे होते हैं। इसलिए उसका प्रयास यह होता है कि अपने बचे-खुचे दिनों में वह अपनी सारी कामनाएं पूरी कर ले। ऐसे में उसे किसी भी तरह अपने उद्देश्य को पूरा कर लेना उचित जान पड़ता है। उसके लिए उसे बुरे-भले, मान-अपमान की परवाह नहीं होती। उसका लक्ष्य येनकेन प्रकारेण अपनी इच्छा पूरी करना होता है। इस प्रकार बुढ़ापा तृष्णा रोग का अंतिम समय है।

गद्यांश क्र.3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1 : (आकलन)

प्रश्न 1.
उत्तर लिखिए :

उत्तर :

प्रश्न 2.
आकृति पूर्ण कीजिए :

उत्तर :

कृति 2 : (स्वमत अभिव्यक्ति)

प्रश्न.
‘लड़कों का बूढों से स्वाभाविक विवेष होता ही है’ इस विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर :
लड़कों और बूढ़ों के बीच पीढ़ियों का अंतर होता है। लड़कों और बूढ़ों में हर बात को लेकर अंतर होना स्वाभाविक है। अधिकांश बूढ़ों की आदत होती है कि वे हर बात को अपने ढंग से सोचते हैं। वे उसमें अपने जमाने की विचारधारा थोपने की कोशिश करते हैं। इसका कारण यह है कि किसी चीज के बारे में उनकी एक धारणा बनी होती हैं। हर बात को वे अपने पैमाने पर कसने की कोशिश करते हैं। जब कि नई पीढ़ी के लड़कों की सोच अलग ढंग की होती हैं। उन्हें पुराने दकियानूसी विचार पसंद नहीं आते। इसलिए बात-बात पर दोनों के विचारों में टकराव होता है। इस तरह लड़कों और बूढ़ों में स्वाभाविक विद्वेष होता है।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई । सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर:

प्रश्न 2.
उत्तर लिखिए :

उत्तर:

प्रश्न 3.
कारण लिखिए :
(i) घरवालों ने भोजन किया, परंतु बूढ़ी काकी को किसी ने नहीं पूछा –
(ii) रात के ग्यारह बज गए थे। लाड़ली की आँखों में नींद न थी –
उत्तर:
(i) लाड़ली उन पूड़ियों को बूढ़ी काकी के पास ले जाना चाहती थी, ताकि वे उन्हें खा सके।
(ii) बूढ़ी काकी को पूड़ियाँ खिलाने की खुशी लाड़ली को सोने न देती थी।

गद्यांश क्र.5
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :


उत्तर :

प्रश्न 2.
कारण लिखिए :
(i) रूपा का हृदय सन्न हो गया –
(ii) रूपा बैठी स्वर्गीय दृश्य का आनंद लेने में निमग्न थी –
उत्तर:
(i) रूपा का हृदय सन्न हो गया, क्योंकि उसने देखा कि बूढ़ी काकी पत्तलों पर से पूड़ियों के टुकड़े उठा-उठाकर खा रही हैं।
(ii) रूपा बैठी स्वर्गीय दृश्य का आनंद लेने में निमग्न थी, क्योंकि बूढ़ी काकी भोले बच्चों की तरह सब कुछ भूलकर बैठी हुई खाना खा रही थीं और उनके एक-एक रोएँ से सच्ची सदिच्छाएँ निकल रही थीं।

प्रश्न 3.
रिश्ता पहचानिए :
(i) बूढ़ी काकी, रूपा की लगती हैं –
(ii) रूपा, बूढ़ी काकी की लगती हैं –
उत्तर:
(i) बूढ़ी काकी, रूपा की लगती हैं – चचेरी सास।
(ii) रूपा, बूढ़ी काकी की लगती है – बहू।

कृति 2 : (स्वमत अभिव्यक्ति)

प्रश्न.
शादी-ब्याह अथवा पारिवारिक समारोहों में प्रीतिभोज में अनाप-शनाप खर्च करना कितना उचित’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर :
हमारे देश में शादी-ब्याह तथा छोटे-मोटे पारिवारिक समारोहों में प्रीतिभोज में लोगों को खिलाने-पिलाने की पुरानी परंपरा चली आ रही है। समर्थ व्यक्तियों को इस तरह का खर्च करना ज्यादा नहीं अखरता, पर आर्थिक दृष्टि से कमजोर लोगों के लिए इस तरह के ३ खर्च का भार उठाना मुश्किल होता है। पर सामाजिक बंधनों तथा अपने ३ नाम के लिए ऐसे समारोह आयोजित करना आज एक फैशन हो गया । हैं। यह फैशन दिनोदिन बढ़ता ही जा रहा है। कुछ लोग तो अपनी प्रतिष्ठा बढ़ाने के लिए कर्ज लेकर लोगों को बुलाकर खिलाते-पिलाते ३ हैं। बाद में यह कर्ज चुकाना उनके लिए समस्या बन जाता है और उन्हें अपनी जायदाद बक बेचनी पड़ जाती है। लोगों को इस तरह के उत्सवों में अनावश्यक रूप से पैसे उड़ाने से बाज आना चाहिए। इस तरह के उत्सवों-समारोहों में अनाप-शनाप खर्च करना अपने ऊपर एक तरह का आर्थिक बोझ लादना है, जिससे कोई लाभ नहीं होता।

उपक्रम/कृति/परियोजना

श्रवणीय
बड़ों से कोई ऐसी कहानी सुनिए जिसके आखिरी हिस्से में कठिन परिस्थितियों से जीतने का संदेश मिल रहा हो।

संभाषणीय
वृद्धाश्रम’ के बारे में जानकारी इकट्ठा करके चर्चा कीजिए।

लेखनीय
‘भारतीय कुटुंब व्यवस्था’ पर भाषण के मुद्दे लिखिए।
उत्तर:
भारतीय कुटुंब व्यवस्था के मुद्दे :

• कुटुंब किसे कहते हैं?
• प्राचीन भारतीय कुटुंब।
• आधुनिक कुटुंब।
• कुटुंब व्यवस्था में बदलाव के कारण।
• कुटुंब व्यवस्था के आधार।
• कुटुंब बनने-टूटने के कारण।
• कुटुंब की आवश्यकता।
• संयुक्त कुटुंब एवं एकल कुटुंब से लाभ-हानि।
• वसुधैव कुटुंबकम्।

पठनीय
‘चलती-फिरती पाठशाला’ उपक्रम के बारे में जानकारी इकट्ठी करके पढ़िए और सुनाइए।

बूढ़ी काकी Summary in Hindi

विषय – प्रवेश : ‘बूढ़ी काकी’ कथा उन दयनीय व्यक्तियों की व्यथा है, जिन्हें परिस्थितिवश मजबूरी में अपनी पूरी संपत्ति किसी अन्य व्यक्ति को सौंपनी पड़ती है और खुद उसकी दया पर जीना पड़ता है। बूढ़ी काकी अपने पति और जवान बेटों की मृत्यु के पश्चात अपने एकमात्र भतीजे बुद्धिराम के वादों पर विश्वास करके अपनी सारी संपत्ति उसके नाम लिख देती हैं। लेकिन थोड़े दिनों के बाद ही ऐसी स्थिति हो जाती है कि उसे पेट भर भोजन मिलना भी मुश्किल हो जाता है। एक बार तो बूढ़ी काकी के जीवन में ऐसी घटना घटती है, जिसके बारे में जानकर दिल दहल उठता है।

बुद्धिराम के बेटे के तिलक समारोह में सभी मेहमान और घर के सभी लोग भोजन कर सोने चले जाते हैं, पर बूढ़ी काकी को खाने के लिए कोई नहीं पूछता। भूख से व्याकुल बूढ़ी काकी रात के अंधेरे में कूड़े में फेंकी गई पत्तलों पर छूटे जूठन को बीन–बीनकर खाकर अपना पेट भरती हैं। बुद्धिराम की पत्नी रूपा यह दृश्य देखती है, तो उसकी रूह काँप उठती है और वह इस अधर्म के लिए ईश्वर से क्षमा करने की प्रार्थना करती है और बूढ़ी काकी को परोसकर भरपेट भोजन कराती है और उससे अपनी भूल के लिए बुरा न मानने के लिए कहती है।

बूढ़ी काकी मुहावरे – अर्थ

• सब्जबाग दिखाना – बड़े–बड़े झूठे वादे करना।
• गला फाड़ना – शोर करना, चिल्लाना।
• लाले पड़ना – किसी चीज के लिए तरसना।
• उबल पड़ना – क्रोधित होना।
• पानी उतर जाना – बेइज्जत होना।
• होंठ चाटना – कोई स्वादिष्ट पदार्थ अधिक खाने की इच्छा रखना।
• कलेजे में हूक सी उठना – मन में दुख होना।
• कलेजा पसीजना – दया आना।
• हृदय सन्न रह जाना – घोर आश्चर्य में डूब जाना।
• छाती पर सवार होना – सामने अड़े रहना।
• दम घुटना – हवा की कमी के कारण या गर्मी की अधिकता से साँस रुकना।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Std 10 Hindi Chapter 8 Apni Gandh Nahi Bechunga Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Chapter 8 अपनी गंध नहीं बेचूँगान Notes, Textbook Exercise Important Questions, and Answers.

Hindi Lokbharti 10th Digest Chapter 8 अपनी गंध नहीं बेचूँगान Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 8 अपनी गंध नहीं बेचूँगा Textbook Questions and Answers

कृति

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए

सूचना के अनुसार कृतियाँ कीजिए :

प्रश्न 1.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
लिखिए :
(i) फूल को बिक जाने से भी बेहतर लगता
(ii) फूल के अनुसार उसे तोड़ने का पहला अधिकार
उत्तर:
(i) फूल को बिक जाने से भी बेहतर लगता है – मर जाना।
(ii) फूल के अनुसार उसे तोड़ने का पहला अधिकार डाली, कोंपल और काँटों को है।

प्रश्न 3.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 4.
सूची बनाइए:
इनका फूल से संबंध है –
– – – – – – – – – – – – – – –
– – – – – – – – – – – – – – –
– – – – – – – – – – – – – – –
– – – – – – – – – – – – – – –
उत्तर:
(i) उपवन:
(ii) डाली
(iii) कोंपल
(iv) काँटे।

प्रश्न 5.
कारण लिखिए :
(i) फूल अपनी सौगंध नहीं बेचेगा – – – – – – – – – – – – – – –
(ii) फूल को मौसम से कुछ लेना नहीं है – – – – – – – – – – – – – – –
उत्तर:
(i) अपनी गंध न बेचने की सौगंध फूल का संस्कार बन गई है, इसलिए फूल अपनी सौगंध नहीं बेचेगा।
(i) फूल को मौसम से कुछ लेना-देना नहीं है – उसे अपने अस्तित्व के लिए कुछ भी पाने की इच्छा नहीं है। इसलिए कैसा भी मौसम हो, उसे कोई फर्क नहीं पड़ता।

प्रश्न 6.
‘दाता होगा तो दे देगा, खाता होगा तो खाएगा’ इस पंक्ति से स्पष्ट होने वाला अर्थ लिखिए।
उत्तर:
फूल को केवल अपने स्वाभिमान से मतलब है। उसे किसी चीज को पाने अथवा खो जाने की चिंता नहीं है। जो मिलना होगा, मिलेगा और जो नुकसान होगा, होगा। उसे उसकी चिंता नहीं है।

प्रश्न 7.
निम्नलिखित मुद्दों के आधार पर पद्य विश्लेषण कीजिए :
1. रचनाकार का नाम
2. रचना का प्रकार
3. पसंदीदा पंक्ति
4. पसंदीदा होने का कारण
5. रचना से प्राप्त संदेश/प्रेरणा
उत्तर:
1. रचनाकार का नाम → बालकवि बैरागी।
2. रचना की विधा → गीत।

3. पसंद की पंक्ति → चाहे सभी सुमन बिक जाएँ,
चाहे ये उपवन बिक जाएँ
चाहे सौ फागुन बिक जाएँ
पर मैं गंध नहीं बेचूंगा।

4. पंक्तियाँ पसंद होने का कारण → इन पक्तियों में फूल हर हालत में जीवन में अपने स्वाभिमान को सर्वोपरि मानता है। इसके लिए उसे कोई भी त्याग करना पड़े, तो वह इसके लिए तैयार है, पर वह अपने स्वाभिमान को हर हालत में बनाए रखना चाहता है।

5. रचना से प्राप्त संदेश/प्रेरणा → प्रस्तुत रचना से यह संदेश मिलता है कि स्वाभिमान मनुष्य की सबसे बड़ी थाती है। हमें हर हालत में इसकी रक्षा करनी चाहिए। यदि स्वाभिमान की रक्षा के लिए हमें अपना सर्वस्व निछावर कर देना पड़े, तो भी हँसते-हँसते अपना सब कुछ त्याग देना चाहिए। प्रस्तुत पंक्तियों से हमें यही प्रेरणा मिलती है। (विद्यार्थी अपनी पसंदीदा पंक्ति लिखें।)

Hindi Lokbharti 10th Textbook Solutions Chapter 8 अपनी गंध नहीं बेचूँगा Additional Important Questions and Answers

पद्यांश क्र. 1
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :


उत्तर:

प्रश्न 2.
जोड़ियाँ मिलाइए :
(i) सुमन – पँखुरी
(ii) काँटे – सौगंध
(iii) मालिन – उपवन
(iv) संस्कार – चौकी
उत्तर:
(i) सुमन – उपवन
(ii) काँटे – चौकी
(iii) मालिन – पँखुरी
(iv) संस्कार – सौगंध

प्रश्न 3.
उत्तर लिखिए :
(i) फूल ‘सौगंध’ न बेचने की बात इन्हें संबोधित करते हुए कहता है।
उत्तर:
(i) अपने ऊपर मँडराने वालों और अपना मोल लगाने वालों को फूल ‘सौगंध’ न बेचने की बात संबोधित करते हुए कहता है।

प्रश्न 4.
कारण लिखिए :
(i) फूल डाली, कोंपल और काँटों को स्वयं को नोचने-तोड़ने का अधिकार देता है –
उत्तर:
(i) फूल डाली, कोंपल और काँटों का कृतज्ञ है, इसलिए वह इन्हें अपने आप को नोचने-तोड़ने का अधिकार देता है।

प्रश्न 5.
उत्तर लिखिए : (पद्यांश में आया)
(i) एक भारतीय महीने का नाम – ………………………………..
(ii) एक प्रसिद्ध पौराणिक चरित्र, जिनके नाम के साथ रेखा’ शब्द जोड़कर उदाहरण दिया जाता है – ………………………………..
(iii) फूलों के बगीचे में फूलों के पौधे लगाने और उनकी सेवा करने वाले व्यक्ति की पत्नी – ………………………………..
(iv) फूलों की महक के अर्थ में प्रयुक्त शब्द – ………………………………..
उत्तर:
(i) एक भारतीय महीने का नाम – फागुन।
(ii) एक प्रसिद्ध पौराणिक चरित्र, जिनके नाम के साथ ‘रेखा शब्द जोड़कर उदाहरण दिया जाता है- लछमन (लक्ष्मण), लक्ष्मण रेखा।
(iii) फूलों के बगीचे में फूलों के पौधे लगाने और उनकी सेवा करने – वाले व्यक्ति की पत्नी – मालिन।
(iv) फूलों की महक के अर्थ में प्रयुक्त शब्द – गंध।

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए :
(i) अरुणाई
(ii) चौकी
(iii) गंध
(iv) सौगंध
उत्तर:
(i) अरुणाई -लालिमा
(ii) चौकी – पहरा
(iii) गंध -सुगंध
(iv) सौगंध – कसम।

प्रश्न 2.
निम्नलिखित शब्द समूहों के लिए एक-एक शब्द लिखिए :
(i) वृक्ष की नई और कोमल पत्तियाँ =
(ii) किसी वस्तु के ऊपर चारों ओर घूमते हुए उड़ना =
उत्तर :
(i) वृक्ष की नई और कोमल पत्तियाँ – कोंपल
(ii) किसी वस्तु के ऊपर चारों ओर घूमते हुए उड़ना – मँडराना।

कृति 3 : (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की ‘जिस डाली ने ——— रिश्ते जोड़े’ पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
फूल कहता है कि पौधे की जिस डाल ने उसे अपनी गोद में खिलाया था, जिन कोंपलों ने उसे लालिमा प्रदान की थी और जिन काँटों ने लक्ष्मणजी की तरह पहरा देकर उसे तोड़े जाने से बचाया था, उन्हें वह कभी भूल नहीं सकता। उनका वह ऋणी है और उस पर पहला अधिकार इन्हीं का है। वे चाहे उसे नोचें या तोड़ें, वह उफ तक नहीं करेगा। वह कहता है कि वे चाहे मुझे तोड़कर किसी मालिन को दे दें, तो भी मुझे कोई आपत्ति नहीं है।

पद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :

उत्तर:

प्रश्न 2.
कारण लिखिए :
(i) पिचकारी का जादू-टोना फूल पर कोई अंतर नहीं लाएगा –
उत्तर:
(i) पिचकारी का जादू-टोना फूल पर कोई अंतर नहीं लाएगा – फूल को कृत्रिम फुहारों की कामना नहीं है। इसलिए पिचकारी का जादू-टोना फूल पर कोई अंतर नहीं लाएगा।

प्रश्न 3.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2 : (शब्द संपदा)

प्रश्न 1.
पद्यांश में प्रयुक्त शब्द-युग्म ढूँढकर लिखिए :
(i) ………………………………
(ii) ………………………………
(iii) ………………………………
(iv) ………………………………
उत्तर:
(i) आएगा-जाएगा
(ii) रोना-धोना
(iii) जादू-टोना
(iv) पल-पल।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(i) भौंरा = ………………………………
(ii) सुर = ………………………………
(iii) दाम = ………………………………
(iv) कोमल = ………………………………
उत्तर:
(i) भौंरा = भ्रमर
(ii) सुर = स्वर
(iii) दाम = मूल्य
(iv) कोमल = मुलायम।

कृति 3 : (सरल अर्थ)

प्रश्न.
प्रस्तुत पद्यांश की अंतिम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
चाहे फूल की कोमल-कोमल पंखुड़ियों पर भौंरों के गुंजन का सरगम सुनाई देता हो अथवा पतझड़ का मौसम हो, और वह मुरझाई हुई दशा में हो या उस पर कृत्रिम फुहारें डालकर उसे सांत्वना दी जाए, उस पर कोई फर्क नहीं पड़ता। फूल अपनी बोली लगाने वालों और पल-पल अपनी कीमतें आँकने वालों को संबोधित करते हुए कहता है कि मैंने अपने आप से अपने स्वाभिमान का अनुबंध कर लिया है और यह ठान लिया है कि मैं अपने स्वाभिमान पर कभी आँच नहीं आने दूंगा। मैं उस अनुबंध को किसी भी हालत में दाँव पर नहीं लगा सकता अर्थात मैं उसका कभी सौदा नहीं कर सकता। फूल कहता है कि वह अपनी सुगंध कभी नहीं बेच सकता।

पयांश क्र. 3
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई। सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
दो ऐसे प्रश्न बनाकर लिखिए, जिनके उत्तर निम्नलिखित शब्द हों :
(i) मन ने
(ii) पवन के।
उत्तर:
(i) तन पर किसने प्रतिबंध लगा दिया?
(ii) फूल एक-एक के घर किसके साथ जाएगा?

प्रश्न 2.
लिखिए :
(i) फूल झर जाना चाहता है ……………………………|
उत्तर:
(i) फूल झर जाना चाहता है – अपनी माटी में।

प्रश्न 3.
आकृति पूर्ण कीजिए :
(i) फूल इस तरह झर जाएगा
(ii) भूल-चूक की माफी यह लेगी –
(iii) तब मंडी यह समझेगी –
(iv) इसको इसका अंत पता है –
उत्तर:
(i) फूल इस तरह झर जाएगा – पंखुरी-पंखुरी गिरकर
(ii) भूल-चूक की माफी यह लेगी – फूल की गंध कुमारी
(iii) तब मंडी यह समझेगी – खुद्दारी किसको कहते हैं।
(iv) इसको इसका अंत पता है – फूल को अपना

कृति 2 : (शब्द संपदा)

प्रश्न 1.
पद्यांश में प्रयुक्त शब्द-युग्म ढूँढ़कर लिखिए :
(i) ………………………………….
(ii) ………………………………….
उत्तर:
(i) एक-एक
(ii) भूल-चूक।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए :
(i) पवन = ………………………………….
(ii) तन = ………………………………….
(iii) घर = ………………………………….
(iv) दिन = ………………………………….
उत्तर:
(i) पवन = हवा
(ii) तन = शरीर
(iii) घर = मकान
(iv) दिन = दिवस।

कृति 3 : (सरल अर्थ)

प्रश्न.
प्रस्तुत पद्यांश की प्रथम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
फूल कहता है कि इस संसार में जिसका भी जन्म होता है, एक-न-एक दिन उसका अंत होना (मरना) निश्चित है। वह कहता है कि यह बात मुझे अच्छी तरह मालूम है कि एक दिन मैं भी पंखुड़ीपंखुड़ी करके झर जाऊँगा और मेरा अंत हो जाएगा। पर इसके पहले मैं हवा के साथ उड़कर वातावरण में फैलकर एक-एक (फूल) के पास ३ जाऊँगा और मेरी सुगंध उनसे जाने-अनजाने में किए की माफी मांगेगी।

फूल कहता है कि उस दिन बाजार और बाजार में खरीद-फरोख्त करने वाले लोगों को यह बात समझ में आएगी कि खुद्दारी अर्थात स्वाभिमान क्या होता है और इसके सम्मान के लिए लोग हर प्रकार का त्याग करने के लिए क्यों तत्पर रहते हैं।

भाषा अध्ययन (व्याकरण)

प्रश्न. सूचनाओं के अनुसार कृतियाँ कीजिए :

1. शब्द भेद :
अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए :
(i) फूल की अरुणाई देखने योग्य थी।
(ii) भँवरे फूलों पर मँडराते हैं।
उत्तर :
(i) अरुणाई – भाववाचक संज्ञा।
(ii) भँवरे – जातिवाचक संज्ञा।

2. अव्यय :
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए :
(i) सामने
(ii) तरफ।
उत्तर :
(i) फूल एक-एक के सामने जाएगा।
(ii) मालिन ने फूल की तरफ देखा।

3. संधि :
कृति पूर्ण कीजिए :

संधि शब्द	संधि विच्छेद	संधि भेट
…………………	यथा + अर्थ	…………………
अथवा
नमस्ते	…………………	…………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेट
यथार्थ	यथा + अर्थ	स्वर संधि
अथवा
नमस्ते	नमः + ते	विसर्ग संधि

4. सहायक क्रिया :
निम्नलिखित वाक्यों में से सहायक क्रिया पहचानकर उसका मूल रूप लिखिए :
(i) बिकने से बेहतर है मर जाऊँ।
(ii) मन ने तन पर प्रतिबंध लगा दिया।
उत्तर:
सहायक क्रिया – मूल रूप
(i) जाऊँ – जाना
(ii) दिया – देना

5. प्रेरणार्थक क्रिया :
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए :
(i) रोना
(ii) उड़ना।
उत्तर:
क्रिया प्रथम प्रेरणार्थक रूप दुवितीय प्रेरणार्थक रूप
(i) रोना – रुलाना – रुलवाना
(ii) उड़ना – उड़ाना – उड़वाना

6. मुहावरे :

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए :
(i) चैन न मिलना
(ii) झेंप जाना।
उत्तर :
(i) चैन न मिलना।
अर्थ : बेचैनी अनुभव करना।
वाक्य : इलाके में चोरी की बढ़ती घटनाओं से पुलिस को चैन नहीं मिल रहा था।
(ii) झेंप जाना।
अर्थ : लज्जित होना, शरमाना।
वाक्य : हिसाब-किताब में गड़बड़ी पकड़े जाने पर मुंशी जी झेंप गए।

प्रश्न 2.
अधोरेखांकित वाक्यांशों के लिए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए : (थर-थर काँपना, नजर आना, दृष्टि फेरना)
(i) चोर पुलिस के डर से बहुत अधिक काँप रहा था।
(ii) आगरा के किले की ऊपरी मंजिल से ताजमहल का गुंबद दिखाई देता है।
उत्तर:
(i) चोर पुलिस के डर से थर-थर काँप रहा था।
(ii) आगरा के किले की ऊपरी मंजिल से ताजमहल का गुंबद नजर आता है।

7. कारक:
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उसका भेद लिखिए :
(i) अच्छा हो मर कर अपनी माटी में झर जाऊँ।
(ii) चाहे जिस मालिन से मेरी पंखुरियों के रिश्ते जोड़ें।
उत्तर:
(i) माटी में – अधिकरण कारक।
(ii) मालिन से – करण कारक।

8. विरामचिह्न :
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए :
(i) मौसम से मुझको क्या लेना है वह तो आएगा – जाएगा
(ii) अच्छा तो आप मुझे अपनी गंध बेचने के लिए कह रहे हैं
उत्तर :
(i) मौसम से मुझको क्या लेना है, वह तो आएगा-जाएगा।
(ii) अच्छा! तो आप मुझे अपनी गंध बेचने के लिए कह रहे हैं।

9. काल परिवर्तन :
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए :
(i) मैं गंध नहीं बेचूंगा। (सामान्य भूतकाल)
(ii) मुझको मेरा अंत पता है। (पूर्ण भूतकाल)
उत्तर :
(i) मैंने गंध नहीं बेची।
(ii) मुझको मेरा अंत पता था।

10. वाक्य भेद :

प्रश्न 1.
निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए :
(i) एक ओर भौरे का गुंजार है और दूसरी ओर पतझड़।
(ii) मैं वह सौगंध नहीं बेचूंगा, जो मेरा संस्कार बन गई।
उत्तर :
(i) संयुक्त वाक्य
(ii) मिश्र वाक्य।

प्रश्न 2.
निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए :
(i) फूल अपनी गंध नहीं बेचेगा। (विस्मयादिबोधक वाक्य)
(ii) फूल एक-एक के घर जाएगा। (संदेहबोधक वाक्य)
उत्तर :
(i) अच्छा ! फूल अपनी गंध नहीं बेचेगा !
(ii) फूल शायद एक-एक के घर जाए।

11. वाक्य शुद्धिकरण :
निम्नलिखित वाक्य शुद्ध करके फिर से लिखिए :
(i) उस दीन ये मंडी समझेगा।
(ii) तब दूनिया उसके पाँव पर पड़ेगी।
उत्तर:
(i) उस दिन ये मंडी समझेगी।
(ii) तब दुनिया उसके पाँव पड़ेगी।

अपनी गंध नहीं बेचूँगा Summary in Hindi

विषय-प्रवेश :
स्वाभिमान मनुष्य की थाती है। जिस व्यक्ति में स्वाभिमान की भावना नहीं होती, उसका अपना कोई अस्तित्व नहीं होता। स्वाभिमानी लोग अपने स्वाभिमान की रक्षा के लिए अपना सब कुछ गँवा देते हैं, पर अपने स्वाभिमान पर आँच नहीं आने देते। प्रस्तुत कविता में कवि ने एक ऐसे ही फूल का वर्णन किया है, जो अपने स्वाभिमान को बनाए रखने के लिए अपना सब कुछ निछावर करने के लिए तत्पर है, पर किसी भी हालत में अपना स्वाभिमान छोड़ने के लिए तैयार नहीं है। कवि ने इस कविता के द्वारा फूल के इस गुण को मनुष्य को भी अपनाने और स्वाभिमानी रहने की प्रेरणा दी है।

अपनी गंध नहीं बेचूँगा कविता का सरल अर्थ

1. चाहे सभी सुमन …………………………. सौगंध नहीं बेचूंगा।

स्वाभिमानी फूल अपने स्वाभिमान की रक्षा के लिए अपना सब कुछ निछावर करने के लिए तैयार है, पर वह किसी भी हालत में अपने स्वाभिमान पर आँच नहीं आने देना चाहता।

वह कहता है कि चाहे सारे फूल बिक जाएँ, केवल फूल ही नहीं चाहे वे उपवन भी बिक जाएँ, जहाँ सारे फूल उत्पन्न होते हैं। सारी बहार क्यों न बिक जाए, पर वह अपनी सुगंध को, जिसे वह अपना स्वाभिमान मानता है, किसी भी हालत में नहीं बेच सकता।

जिस तरह मनुष्य अपने स्वाभिमान के लिए मर मिट जाता है, पर उस पर आँच नहीं आने देता, उसी तरह यह फूल भी अपनी सुगंध की रक्षा के लिए प्रतिबद्ध है।

फूल कहता है कि पौधे की जिस डाल ने उसे अपनी गोद में खिलाया था, जिन कोंपलों ने उसे लालिमा प्रदान की थी और जिन काँटों ने लक्ष्मणजी की तरह पहरा देकर उसे तोड़े जाने से बचाया था, उन्हें वह कभी भूल नहीं सकता। उनका वह ऋणी है और उस पर पहला अधिकार इन्हीं का है। वे चाहे उसे नोचें या तोड़ें, वह उफ तक नहीं करेगा। वह कहता है कि वे चाहे मुझे तोड़कर किसी मालिन को दे दें, तो भी मुझे कोई आपत्ति नहीं है।

वह चारों ओर से अपने ऊपर नजरें गड़ाने वालों और उसकी कीमत लगाकर उसे बाजार में बेचने वालों से कहता है कि उसने अपनी सुगंध को न बेचने की जो सौगंध खाई है, वह उसका संस्कार बन गई है और वह उसका सौदा कभी नहीं कर सकता। फूल कहता है कि वह अपनी सुगंध कभी नहीं बेच सकता।

2. मौसम से क्या लेना अनुबंध नहीं बेचूंगा।

फूल कहता है कि मौसम, कैसा भी हो, मौसम का उस पर कोई प्रभाव नहीं पड़ता। वह हर स्थिति में अपने आप को स्थिर रखने में सक्षम है। उसे किसी से कुछ भी पाने की आकांक्षा नहीं है। वह लाभ या हानि की कोई परवाह नहीं करता। न उस पर किसी चीज का कोई प्रभाव पड़ता है। और न वह किसी चीज से कभी घबराता है। चाहे उसकी कोमल-कोमल पंखुड़ियों पर भौंरों के गुंजन का सरगम सुनाई देता हो अथवा पतझड़ का मौसम हो, और वह मुरझाई हुई दशा में हो या उस पर कृत्रिम फुहारें डालकर उसे सांत्वना दी जाए, उस पर कोई फर्क नहीं पड़ता।

वह अपनी बोली लगाने वालों और पल-पल अपनी कीमतें आँकने वालों को संबोधित करते हुए कहता है कि मैंने अपने आप से अपने स्वाभिमान का अनुबंध कर लिया है और यह ठान लिया है कि मैं अपने स्वाभिमान पर कभी आँच नहीं आने दूँगा। मैं उस अनुबंध को किसी भी हालत में दाँव पर नहीं लगा सकता अर्थात मैं उसका कभी सौदा नहीं कर सकता। फूल कहता है कि वह अपनी सुगंध कभी नहीं बेच सकता।

3. मुझको मेरा अंत ……………………… वो प्रतिबंध नहीं बेचूंगा।

फूल कहता है कि इस संसार में जिसका भी जन्म होता है, एक-न-एक दिन उसका अंत होना (मरना) निश्चित है। वह कहता है कि यह बात मुझे अच्छी तरह मालूम है कि एक दिन मैं भी पंखुड़ीपंखुड़ी करके झर जाऊँगा और मेरा अंत हो जाएगा। पर इसके पहले मैं हवा के साथ उड़कर वातावरण में फैलकर एक-एक (फूल) के पास जाऊँगा और मेरी सुगंध उनसे जाने-अनजाने में किए की माफी मांगेगी।

फूल कहता है कि उस दिन बाजार और बाजार में खरीद-फरोख्त करने वाले लोगों को यह बात समझ में आएगी कि खुद्दारी अर्थात स्वाभिमान क्या होता है और इसके सम्मान के लिए लोग हर प्रकार का त्याग करने के लिए क्यों तत्पर रहते हैं। फूल कहता है कि किसी के हाथों बिकने से तो अच्छा है कि मैं मर जाऊँ और अपने देश की मिट्टी में मिल जाऊँ। वह कहता है कि मैंने अपनी इच्छा से अपने शरीर पर जो प्रतिबंध लगा लिया है, उस प्रतिबंध को मैं कभी नहीं बेच सकता।

(फूल के इस स्वाभिमान को मनुष्य को भी अपनाना चाहिए और उसे भी किसी लालच में आकर कभी अपना स्वाभिमान बेचना नहीं चाहिए।)

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Std 10 Hindi Chapter 6 Hum Us Dharti Ki Santati Hai Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 6 हम उस धरती की संतति हैं Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 6 हम उस धरती की संतति हैं Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 6 हम उस धरती की संतति हैं Textbook Questions and Answers

कृति

(कृतिपत्रिका के प्रश्न 3 (आ) के लिए)

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
वर्गीकरण कीजिए:
पद्यांश में उल्लिखित चरित्र-ध्रुव, प्रह्लाद, भरत, लक्ष्मीबाई, रजिया सुलताना, दुर्गावती, पद्मिनी, सीता, चाँदबीबी, सावित्री, जयमल
उत्तर:
ऐतिहासिक – पौराणिक
लक्ष्मीबाई, रजिया सुलताना, दुर्गावती, पद्मिनी, चाँद बीबी, जयमल-पत्ता। – ध्रुव, प्रह्लाद, भरत, सीता, सावित्री।।

प्रश्न 2.
विशेषताओं के आधार पर पहचानिए :
(i) भारत माता के रथ के दो पहिये – ……………………………..
(ii) खूब लड़ने वाली मर्दानी – ……………………………..
(iii) अपनी लगन का सच्चा – ……………………………..
(iv) किसी को कुछ न गिनने वाले – ……………………………..
उत्तर:
(i) भारत माता के रथ के दो पहिये – लड़के (पुरुष), लड़कियाँ (स्त्रियाँ)।
(ii) खूब लड़ने वाली मर्दानी – लक्ष्मीबाई, दुर्गावती, रजिया सुलताना।
(iii) अपनी लगन का सच्चा – प्रह्लाद।
(iv) किसी को कुछ न गिनने वाले – जयमल-पत्ता।

प्रश्न 3.
सही/गलत पहचानकर गलत वाक्य को सही करके वाक्य पुनः लिखिए :
(i) रानी कर्मवती ने अकबर को राखी भेजी थी।
(ii) भरत शेर के दाँत गिनते थे।
(iii) झगड़ने से सब कुछ प्राप्त होता है।
(iv) ध्रुव आकाश में खेले थे।
उत्तर:
(i) रानी कर्मवती ने हुमायूँ को राखी भेजी थी।
(ii) भरत शेरों की दतुली गिनते थे।
(iii) झगड़ने से कुछ भी प्राप्त नहीं होता।
(iv) ध्रुव मिट्टी में खेले थे।

प्रश्न 4.
कविता से प्राप्त संदेश लिखिए।
उत्तर:
प्रस्तुत कविता कव्वाली के स्वरूप में है। इसमें लड़के जहाँ महापुरुषों और प्रसिद्ध शूरवीरों का हवाला देते हुए अपने आप को लड़कियों से श्रेष्ठ बताने की कोशिश करते हैं, वहीं लड़कियाँ भी सीता, सावित्री, लक्ष्मीबाई तथा युद्ध में अपना पराक्रम दिखाने वाली शूरवीर रानियों को अपनी जमात से जोड़ते हुए लड़कों से अपने आप को कम नहीं बतातीं। पर बाद में लड़के कव्वाली के माध्यम से लड़कियों को जवाब देते हैं कि कोई किसी से बढ़कर नहीं है, सभी बराबर हैं। देश के चाहे महान पुरुष हों या महान स्त्रियाँ सभी भारत माँ की संतान हैं। लड़के-लड़कियाँ दोनों भारत माता के रथ के दो पहियों के समान हैं। रथ के लिए इन दोनों पहियों का होना जरूरी है। इस तरह कविता से यह संदेश मिलता है कि कोई बड़ा या कोई छोटा नहीं है, सभी लोग समान हैं। हमें अपने आप पर निरर्थक गर्व नहीं करना चाहिए।

Hindi Lokbharti 10th Textbook Solutions Chapter 6 हम उस धरती की संतति हैं Additional Important Questions and Answers

पद्यांश क्र. 1
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
तालिका पूर्ण कीजिए:

चरित्र	विशेषताएँ
	इस मिट्टी में खेलने वाला
	लगन का सच्चा (सच्ची लगन वाला)
	शेर के जबड़े में दाँत गिनने वाला
	अपने पराक्रम के आगे किसी को न गिनने वाला

उत्तर:

चरित्र	विशेषताएँ
ध्रुव	इस मिट्टी में खेलने वाला
प्रहलाद	लगन का सच्चा (सच्ची लगन वाला)
भरत	शेर के जबड़े में दाँत गिनने वाला
जयमल-पत्ता	अपने पराक्रम के आगे किसी को न गिनने वाला

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
उत्तर लिखिए:
(i) पद्यांश में बड़ाई की गई है, इनकी –
(ii) पद्यांश में प्रयुक्त सौरमंडल का एक प्रसिद्ध ग्रह –
(iii) पद्यांश में आया वह नाम, जिनके नाम पर हमारे देश का नाम पड़ा –
(iv) पद्यांश में आया वन का एक हिंसक पशु –
उत्तर:
(i) पद्यांश में बड़ाई की गई है, इनकी – लड़कों की।
(ii) पद्यांश में प्रयुक्त सौरमंडल का एक प्रसिद्ध ग्रह – घरती।
(iii) पद्यांश में आया वह नाम, जिनके नाम पर हमारे देश का नाम पड़ा – भरत।
(iv) पद्यांश में आया वन का एक हिंसक पशु – शेर।

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
कव्वाली काव्य विधा के बारे में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
कव्वाली आम जनता से लेकर शिक्षित वर्ग तक की पसंद की एक लोकप्रिय काव्य विधा है। इसकी मुख्य विशेषता, कव्वाली गीत प्रस्तुत करने वाले कलाकारों के बीच किसी विषय को लेकर नोक-झोंक होती है। इसमें प्रतियोगी कलाकार जब एक-दूसरे की काव्य पंक्तियों पर नहले पर दहला जड़ते हैं, तो श्रोताओं के मुँह से अनायास ही तारीफों की बरसात होने लगती है।

श्रोता अच्छे कलाकारों की कव्वाली सुनने में पूरी रात गुजार देते हैं, फिर भी उनका मन नहीं, भरता। कव्वालियों में कल्पना पक्ष प्रमुख होता है और उपमाओं की भरमार होती है। कव्वाली गायक किसी बात का उदाहरण देते-देते कहीं भटक जाता है, तो भी वह बड़ी खूबसूरती के साथ फिर अपने विषय पर लौट आता है। लोकप्रियता के कारण कव्वाली को कई फिल्मों में भी समाहित किया गया है। कव्वाली गायकों में से कुछ के नाम तो लोगों की जबान पर होते हैं।

पद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर

प्रश्न 3.
उत्तर लिखिए:
(i) पद्यांश में आया चित्तौड़ की प्रसिद्ध रानी का नाम –
(ii) पुराने जमाने में राजपूत रानियों का दहकती हुई विशाल चिता में प्रवेश कर प्राण न्योछावर कर देने से संबंधित शब्द –
उत्तर:
(i) पद्यांश में आया चित्तौड़ की प्रसिद्ध रानी का नाम – पद्मिनी।
(ii) पुराने जमाने में राजपूत रानियों का दहकती हुई विशाल चिता में प्रवेश कर प्राण न्योछावर कर देने से संबंधित शब्द – जौहर।

प्रश्न 4.
परिणाम लिखिए:
गर डींग उड़ाएँगे, तो …………………..
उत्तर:
गर डींग उड़ाएँगे, तो मजबूरन ताने सहने होंगे।

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘नारी सम्मान’ के बारे में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
आजकल स्त्रियों के अपमान की अनेक घटनाएँ पढ़नेसुनने में आती हैं। स्त्रियों पर तरह-तरह के अत्याचार होते हैं। यह बड़े दुख की बात है।

हमारे देश में प्राचीन काल से नारियों का सम्मान करने की परंपरा रही है। हमारे यहाँ नारी को देवी का सम्मान दिया जाता रहा है और उसकी पूजा करने की परंपरा रही है। दुर्गा, सरस्वती, लक्ष्मी, पार्वती, महाकाली आदि देवियों की हम श्रद्धा और भक्तिपूर्वक पूजा करते हैं। सीता, सावित्री तथा अनुसूया जैसी महान नारियाँ हमारी आदर्श रही हैं। हमारे ऋषि-मुनियों ने कहा है ‘यत्र नार्यस्तु पूज्यंते रमन्ते तत्र देवताः अर्थात जहाँ नारियों की पूजा की जाती है वहीं देवता निवास करते हैं।

आज हमारे देश में स्त्रियाँ हर क्षेत्र में पुरुषों के साथ बराबरी के स्तर पर काम कर रही हैं। आज की नारी पहले की अपेक्षा अधिक जागरूक हो चुकी है। नारी को सम्मान देने से स्त्रियाँ ही सम्मानित नहीं होंगी, बल्कि उन्हें सम्मान देने वाले खुद भी गौरवान्वित होंगे।

पद्यांशु क्र. 3
प्रश्न, निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

(1) आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
इन शब्दों के अर्थ वाले शब्द पद्यांश से ढूंढकर लिखिए:
(i) नाराज
(ii) झगड़ा
(iii) संतान
(iv) प्राप्त होना।
उत्तर:
(i) नाराज – खफा
(ii) झगड़ा – टंटा
(iii) संतान – संतति
(iv) प्राप्त होना – हासिल करना।

प्रश्न 3.
परिणाम लिखिए:
झगड़े करेंगे, तो ………………………
उत्तर:
झगड़े करेंगे, तो कुछ हासिल न होगा।

प्रश्न 4.
उपर्युक्त पद्यांश में उल्लेखित स्त्री-पुरुष समानता दर्शानेवाली पंक्तियाँ चुनकर लिखिए: (बोर्ड की नमूना कृतिपत्रिका)
(i) …………………….
(ii) …………………….
उत्तर:
(i) बस बात पते की इतनी है, ध्रुव या रजिया भारत माँ के
(ii) भारत माता के रथ के है, हम दोनों ही, दो-दो पहिए, अजी दो पहिए, हाँ दो पहिए।

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘झगड़े से कुछ हासिल नहीं होता’-अपने विचार 25 से 30 शब्दों में लिखिए। (बोर्ड की नमूना कृतिपत्रिका)
उत्तर:
किसी बात पर होने वाली कहा-सुनी या विवाद को आमतौर पर झगड़ा कहा जाता है। झगड़े से समस्या सुलझने के बजाय और उलझ जाती है। मुख्य मुद्दा धरा रह जाता है और झगड़ा प्रमुख हो जाता है। कभी-कभी तो झगड़े में लोगों की जान पर भी बन आती है। इसके परिणामस्वरूप लोगों में मारा-मारी और हत्या तक हो जाती है। पर समस्या वैसी की वैसी बनी रहती है, बल्कि उसमें और इजाफा हो जाता है।

झगड़े के परिणामस्वरूप पीढ़ी-पीढ़ी तक दुश्मनी बनी रहती है। इसलिए झगड़े को भूलकर आपस में बातचीत के माध्यम से ही किसी समस्या का हल निकालने की बात सोचनी चाहिए। अत: किसी समस्या का हल निकालने का सही मार्ग झगड़ा नहीं, बल्कि शांतिपूर्ण माहौल में आपस में बातचीत कर समझौता करना है।

हम उस धरती की संतति हैं Summary in Hindi

विषय-प्रवेश : कव्वाली एक लोकप्रिय काव्य विधा है। इसमें दो दल अपनी-अपनी तारीफों अथवा किसी विषय पर अपनी राय को रोचक और तार्किक ढंग से नोक-झोंक के रूप में प्रस्तुत करते हैं। अच्छे कव्वाली गायकों को श्रोता रात-रात भर सुनते रहते हैं। हम उस घरती की संतति हैं’ कव्वाली के एक दल में लड़के हैं और दूसरे दल में लड़कियाँ हैं। लड़के देश के प्रसिद्ध महापुरुषों और शूरवीर योद्धाओं से अपना संबंध जोड़कर अपने आप को श्रेष्ठ साबित करते हैं, तो लड़कियाँ सीता, सावित्री तथा युद्ध में अपना पराक्रम दिखाने वाली योद्धा नारियों से अपना संबंध जोड़कर अपने आप को श्रेष्ठ बताती हैं। पर बाद में दोनों दलों को अहसास होता है कि उन्हें इस झगड़े से कोई लाभ नहीं है। स्त्री-पुरुष दोनों भारतमाता के रथ के दो पहियों के समान हैं और देश के लिए दोनों आवश्यक हैं।

हम उस धरती की संतति हैं कविता का सरल अर्थ

1. हम उस धरती ……………………………… धरती के लड़के हैं।

[कविता में लड़कों (पुरुष जाति) को लड़कियों (स्त्रियों) से बढ़-चढ़कर बताते हुए लड़के अपनी प्रशंसा करते हुए कहते हैं -]

“हम उस परती पर रहने वाले लड़के हैं, जिनकी जितनी प्रशंसा की जाए, कम है। यह वही घरती है, जहाँ ध्रुव जैसे महापुरुष का जन्म हुआ था और वे इसी मिट्टी में खेलते थे।

इसी मिट्टी में भक्त प्रहलाद का जन्म हुआ था। सारी दुनिया को मालूम है कि वे अपनी धुन के कितने सच्चे थे।

यहीं पर भरत जैसे वीर और साहसी महापुरुष का जन्म हुआ था। वे इतने निडर थे कि शेरों के मुँह खुलवाकर उनके दाँत गिना करते थे। __जयमल और पत्ता जैसे वीर इसी मिट्टी में पैदा हुए थे, जो अपने जैसा वीर किसी को समझते ही नहीं थे।

लड़के लड़कियों को नीचा दिखाते हुए कहते हैं कि इन सभी कारणों से हम (लड़के) तुम लोगों (लड़कियों) से बढ़कर हैं। इसलिए तुम सब (लड़कियों) हमारा (पुरुषों का) सामना नहीं कर सकती हो। अतः हमारे सामने तुम सब अपना मुँह बंद रखो। कुछ बोलने की कोशिश मत करो।”

2. बातों का जनाब ……………………………… हम उस धरती की लड़की हैं।

(लड़कों को अपनी बड़ाई करते हुए सुनकर लड़कियाँ लड़कों को जवाब देती हैं-)
“आप जैसे लोगों को बात करने का ढंग तक मालूम नहीं है। आप अपनी प्रशंसा खुद न कीजिए और चुप रहिए। (सुनिए) हम उस धरती की लड़कियाँ हैं, जिस धरती का कुछ पूछना ही नहीं है। हम उस धरती, की लड़कियाँ हैं जिसकी मिट्टी में वीरांगना झाँसी की रानी लक्ष्मीबाई का जन्म हुआ था।

दुर्गावती और रजिया सुलताना जैसी मर्दानी वीरांगनाएँ जिस मिट्टी में पैदा हुई थीं, जिन्होंने लड़ाई के मैदान में अपना अद्भुत पराक्रम दिखाया था, हम उस धरती की लड़कियाँ हैं।

चाँद बीबी जैसी वीरांगना और जौहर की ज्वाला में हँसते-हँसते कूद जाने वाली महान नारी पद्मिनी का जन्म भी इसी मिट्टी में हुआ था।

यह सीता और सावित्री जैसी महान सन्नारियों की जन्म-स्थली है।

यदि आप (लड़के) अपने श्रेष्ठ होने की बड़ी-बड़ी बातें करेंगे, तो आप लोग हमारे ताने भी सहिए। याद रखिए, हम (लड़कियाँ) इन सन्नारियों की धरती की लड़कियाँ हैं।

3. यों आप खफा ……………………………… धरती की संतति हैं।

(लड़कियों का जवाब सुनकर लड़के समझदारी की बात करते हुए कहते हैं-)

(हमारी बातों पर) आप नाराज क्यों होती हैं? इसमें आपस में E झगड़े की कोई बात नहीं है।

इस बात में क्या रखा है कि हमसे आप लोग बढ़कर हैं अथवा आप लोगों से हम लोग बढ़कर हैं।

इस तरह की बातें हमें आपस में उलझाकर रख देंगी और इससे न हमें कोई फायदा होगा और न आपको ही। सच्ची बात तो यह है कि ध्रुव (पुरुष) और रजिया (स्त्री) दोनों ही इसी धरती भारत माँ की संतान हैं। हम लोग भारत माता के रथ के (स्त्री-पुरुष रूपी) दो पहिए हैं। हम सब इसी धरती की संतान हैं।

हम उस धरती की संतति हैं मुहावरे-अर्थ

• शेखी बघारना – स्वयं अपनी प्रशंसा करना।
• डींग मारना – बड़ी-बड़ी बातें करना।
• पते की बात कहना – रहस्य की बात बताना।

हम उस धरती की संतति हैं टिप्पणियाँ :

• ध्रुव : राजा उत्तानपाद और रानी सुनीति के पुत्र। महान विष्णु भक्त। विष्णु ने उन्हें आकाश में सप्तर्षि के पास अटल पद दिया था।
• प्रहलाद : हिरण्यकशिपु के पुत्र। महान विष्णुभक्त। इनकी रक्षा के लिए विष्णु ने नृसिंह अवतार लेकर हिरण्यकशिपु का वध किया था।
• भरत : दुष्यंत एवं शकुंतला के पुत्र। इनके नाम पर ही हमारे देश का नाम ‘भारत’ पड़ा।
• सावित्री : राजा अश्वपति की कन्या। सत्यवान की पत्नी। महान पतिव्रता स्त्री। इन्होंने यम से अपने पति के प्राण छुड़ाए थे।
• सीता : विदेहाधिपति जनक की कन्या। इन्हें वैदेही, जानकी आदि नामों से भी जाना जाता है। ये जमीन की जोताई करते समय मिली थी, इसलिए इनका सीता नाम पड़ा। श्रीराम की पत्नी।
• लक्ष्मीबाई : झाँसी की रानी। महान वीरांगना।
• चाँद बीबी : अहमदनगर राज परिवार की गुणी स्त्री। मुगलों ने निजामशाही की राजधानी अहमदनगर पर आक्रमण किया था, तो चाँद बीबी ने बड़ी बहादुरी से किले पर उनका सामना किया था। पर सरदारों के षड्यंत्र के कारण वह मारी गई।
• रजिया सुलताना : दिल्ली के सुलतान अल्तमश की बेटी। अल्तमश ने रजिया सुलताना को अपने उत्तराधिकारी के रूप में नियुक्त किया था। वह सेना का नेतृत्व स्वयं करती थी।
• जयमल-पत्ता : जयमल और पत्ता दोनों महान शूरवीर योद्धा थे। उन्होंने चित्तौड़ पर अकबर द्वारा किए गए हमले का बहादुरी पूर्वक सामना किया था।
• दुर्गावती : भारत की वीरांगना। उनका जन्म प्रसिद्ध चंदेल राजा कीरत राय के परिवार में हुआ था। वे गोंडवाना राज्य की रानी थीं।
• पद्मावती : चित्तौड़ के राजा रतनसिंह की पत्नी। अपनी सुंदरता के लिए विख्यात। दिल्ली के सुलतान अलाउद्दीन खिलजी ने उनकी सुंदरता के बारे में सुनकर चित्तौड़ पर आक्रमण कर दिया था। राजपूत बहादुरों ने मरते दम तक उसका सामना किया। अंत में वीरांगना पद्मावती ने अन्य राजपूत स्त्रियों के साथ किल्ले में जौहर कर लिया था।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Std 10 Hindi Chapter 1 Barshahi Jalad Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 1 बरषहिं जलद Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 1 बरषहिं जलद Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 1 बरषहिं जलद Textbook Questions and Answers

कृति

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए।

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
निम्न अर्थ को स्पष्ट करने वाली पंक्तियाँ लिखिए:
a. संतों की सहनशीलता …………………………….
b. कपूत के कारण कुल की हानि …………………………….
उत्तर:
a. खल के बचन संत सह जैसे।
b. कपूत के कारण कुल की हानि – जिमि कपूत के उपजे, कुल सदधर्म नसाहिं।।

प्रश्न 3.
तालिका पूर्ण कीजिए:

उत्तर:
इन्हें – यह कहा है
(i) नदी के जल का समुद्र में मिलना – ईश्वर को प्राप्त कर स्थिर हुआ जीव
(ii) सज्जनों के सद्गुण – तालाब में जल भरना

प्रश्न 4.
जोड़ियाँ मिलाइए:

उत्तर:
(i) नव पल्लव से भरा वृक्ष -साधक के मन का विवेक
(ii) उपकारी की संपत्ति -ससि संपन्न पृथ्वी
(iii) मेढक की ध्वनि -बटुक समुदाय द्वारा वेद-पाठ
(iv) कलियुग में धर्म का पलायन – चक्रवाक पक्षी का न दिखना कर जाना

प्रश्न 5.
इनके लिए पद्यांश में प्रयुक्त शब्द:

उत्तर:

प्रश्न 6.
प्रस्तुत पद्यांश से अपनी पसंद की किन्हीं चार पंक्तियों का सरल अर्थ लिखिए।

उपयोजित लेखन

कहानी लेखन: ‘परहित सरिस धर्म नहिं भाई इस सुवचन पर आधारित कहानी लेखन कीजिए।

Hindi Lokbharti 10th Textbook Solutions Chapter 1 बरषहिं जलद Additional Important Questions and Answers

पद्यांश क्र.1
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i) मन डर रहा है इनका – [ ]
(ii) बिजली की तुलना की गई है इससे – [ ]
(iii) भूमि के पास आए बादल ऐसे लगते हैं – [ ]
(iv) विद्यार्थी जिसे पाने के लिए पढ़ाई करते हैं – [ ]
उत्तर:
(i) मन डर रहा है इनका – [श्रीराम का]
(ii) बिजली की तुलना की गई है इससे [दुष्ट की प्रीति से]
(iii) भूमि के पास आए बादल ऐसे लगते हैं – [विद्वान की तरह]
(iv) विद्यार्थी जिसे पाने के लिए पढ़ाई करते हैं – [विद्या]

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
जोड़ियाँ मिलाइए:
(i) दमकती बिजली – दुष्टों के वचन
(ii) भूमि पर गिरा पानी – राम का डरना
(iii) बूंदों का प्रहार – दुष्ट की मित्रता
(iv) बादलों की गर्जना – माया से लिपटा जीव
उत्तर:
(i) दमकती बिजली – दुष्ट की मित्रता
(ii) भूमि पर गिरा पानी – माया से लिपटा जीव
(iii) बूंदों का प्रहार – दुष्टों के वचन
(iv) बादलों की गर्जना – राम का डरना

प्रश्न 4.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 5.
निम्नलिखित अर्थ को स्पष्ट करने वाली पंक्तियाँ लिखिए:
(i) संतों की सहनशीलता।
(ii) जीव की निश्चिंतता।
(iii) रास्तों का अदृश्य हो जाना।
(iv) विद्वानों की विनम्रता
उत्तर:
(i) खल के बचन संत सह जैसे।
(ii) होई अचल जिमि जिव हरि पाई।
(iii) हरित भूमि तृन संकुल, समुझि परहि नहिं पंथ।
(iv) जथा नवहिं बुध विद्या पाएँ।

कृति 2: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के तत्सम रूप लिखिए:
(i) थिर – ………………………………………..
(ii) जथा – ………………………………………..
(iii) सदगुन – ………………………………………..
(iv) अघात – ………………………………………..
उत्तर:
(i) थिर -स्थिर
(ii) जथा – यथा
(iii) सदगुन – सद्गुण
(iv) अघात – आघात।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) जलनिधि = ……………………
(ii) गिरि = ……………………
(iii) नदी = ……………………
(iv) जल = ……………………
उत्तर:
(i) जलनिधि = समुद्र
(ii) गिरि = पहाड़
(iii) नदी = सरिता
(iv) जल = पानी।

कृति 3: (सरल अर्थ)

प्रश्न.
प्रस्तुत पद्यांश की प्रथम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
बादल आकाश में उमड़-घुमड़कर भयंकर गर्जना कर रहे हैं। श्रीराम जी कह रहे हैं कि ऐसे में सीता जी के बिना उनका मन भयभीत हो रहा है। बिजली आकाश में ऐसे चमक रही है, जैसे दुष्ट व्यक्ति की मित्रता स्थिर नहीं रहती । कभी वह बनी रहती है और कभी टूटने के कगार पर पहुँच जाती है। बादल धरती के नजदीक आकर बरस रहे हैं। उनका यह व्यवहार ठीक उसी प्रकार लगता है, जैसे विद्वान व्यक्ति विद्या पाकर विनम्र हो जाते हैं। बादल भी जल के भार से झुक गए हैं और पृथ्वी के नजदीक आकर अपने जल से प्राणियों को तृप्त कर रहे हैं। पहाड़ों पर वर्षा की बूदों की चोट पड़ रही है, पर पहाड़ चुपचाप शांत भाव से यह आघात उसी प्रकार सहते जा रहे हैं, जैसे संत लोग दुष्टों के कटुवचन सह लेते हैं और उस पर कोई प्रतिक्रिया नहीं करते।

पदयांश क्र. 2
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आका

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
उत्तर लिखिए:
इनकी तुलना की गई है, इनसे –
(i) रात के अंधकार में जुगनू – [ ]
(ii) ससि (अनाज) से भरपूर घरती – [ ]
(iii) कृषि को निराने वाले किसान – [ ]
(iv) दिखाई न देने वाला चक्रवाक – [ ]
उत्तर:
(i) रात के अंधकार में जुगनू – [घमंडियों के समाज से]
(ii) ससि (अनाज) से भरपूर धरती – [उपकारी की संपति से]
(iii) कृषि को निराने वाले किसान – [मोह-मद-मान त्यागने वाले विद्वान से]
(iv) दिखाई न देने वाला चक्रवाक – [कलियुग पाकर भाग जाने वाले धर्म से]

प्रश्न 3.
निम्नलिखित शब्दों के लिए पद्यांश में प्रयुक्त शब्द खोजकर लिखिए:
(i) ग्रह – [ ]
(ii) पेड़ – [ ]
(iii) पत्ते – [ ]
(iv) उपग्रह – [ ]
(v) पौधा – [ ]
उत्तर:
(i) ग्रह – [पतंग (सूर्य)]
(ii) पेड़ – [बिटप]
(iii) पत्ते – [पात]
(iv) उपग्रह – [महि]
(v) पौधा – [अर्क-जवास]

प्रश्न 4.
तालिका पूर्ण कीजिए:
इन्हें – यह कहा है
(i) ………………….. – बटु समुदाय
(ii) (नव पल्लव वाले) वृक्ष – …………………..
(iii) (लुप्त हुई) धूल – …………………..
(iv) ………………….. – ज्ञान उत्पन्न हुआ
उत्तर:
इन्हे – यह कहा है
(i) दादुर – बटु समुदाय
(ii) (नव पल्लव वाले) वृक्ष – ज्ञान प्राप्त कर प्रफुल्लित होने वाला साधक
(iii) (लुप्त हुई) धूल – क्रोध के कारण लुप्त हुआ धर्म
(iv) (विषयों से विरक्त) मनुष्य – ज्ञान उत्पन्न हुआ।

प्रश्न 5.
उत्तर लिखिए:
पद्यांश में आया –
(i) एक प्रसिद्ध धर्मग्रंथ – [ ]
(ii) चित्त का मनोविकार या उग्र भाव – [ ]
(iii) एक प्रसिद्ध पक्षी – [ ]
(iv) वह शब्द, जिसके दो अर्थ हैं, जिनमें से एक का अर्थ सूर्य है – [ ]
उत्तर:
(i) एक प्रसिद्घ धर्मग्रंथ – [वेद]
(ii) चित्त का मनोविकार या उग्र भाव – [क्रोध]
(iii) एक प्रसिद्ध पक्षी – [चक्रवाक (चकवा)]
(iv) वह शब्द, जिसके दो अर्थ हैं, जिनमें से एक का अर्थ सूर्य है – [पतंग]

प्रश्न 6.
निम्न अर्थ को स्पष्ट करने वाली पंक्तियाँ लिखिए:
(i) कुसंग से ज्ञान नष्ट होना और सुसंग से ज्ञान उत्पन्न होना। – [ ]
उत्तर:
(i) कुसंग से ज्ञान नष्ट होना और सुसंग से ज्ञान उत्पन्न होना। – बिनसइ-उपजइ म्यान जिमि, पाइ कुसंग-सुसंग

कृति 2 : (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ वाले शब्द पद्यांश से ढूँढ़कर लिखिए:
(i) हुए – ……………………….
(ii) जैसे – ……………………….
(iii) कहीं – ……………………….
(iv) की – ……………………….
उत्तर:
(i) हुए – भए, भयऊ।
(ii) जैसे – जनु, जस।
(iii) कहीं – कतहुँ।
(iv) की – कै।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) दादुर
(ii) धूरी (धूल)
(iii) धर्म
(iv) प्रजा
उत्तर:
(i) दादुर – पुल्लिग
(ii) धूरी (धूल) – स्त्रीलिंग
(iii) धर्म – पुल्लिग
(iv) प्रजा – स्त्रीलिंग।

कृति 3 : (सरल अर्थ)
प्रश्न.
उपर्युक्त पद्यांश की अंतिम चार पंक्तियों (दोहा) का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर :
कभी-कभी वायु बहुत तेज गति से चलने लगती है। इससे बादल यहाँ-वहाँ गायब हो जाते हैं। यह दृश्य उसी प्रकार लगता है जैसे परिवार में कुपुत्र के उत्पन्न होने से कुल के उत्तम धर्म (श्रेष्ठ आचरण) नष्ट हो जाते हैं। कभी (बादलों के कारण) दिन में घोर अंधकार छा जाता है और कभी सूर्य प्रकट हो जाता है। तब लगता है, जैसे बुरी संगति पाकर ज्ञान नष्ट हो गया हो और अच्छी संगति पाकर ज्ञान उत्पन्न हो गया हो।

भाषा अध्ययन (व्याकरण)

प्रश्न. सूचनाओं के अनुसार कृतियों कीजिए :

1. शब्द भेद :

प्रश्न.
अधोरेखांकित शब्दों के शब्दभेद पहचानकर लिखिए :
(i) भूमि परत भा ढाबर पानी।
(i) नव पल्लव भए बिटप अनेका।
उत्तर:
(i) पानी-द्रव्यवाचक संज्ञा
(ii) नव-गुणवाचक विशेषण।

2. अव्यय:

प्रश्न.
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए :
(i) नहीं
(i) इसलिए।
उत्तर :
(i) जनक कॉलेज नहीं जाता।
(ii) बेचन बिजली का बिल अदा नहीं कर पाया, इसलिए बिजली आपूर्ति खंडित हो गई।

3. संधि :

प्रश्न.
कृति पूर्ण कीजिए:
संधि शब्द – संधि विच्छेद – संधि भेद
…………………… – विद्या + अर्थी – ……………………
अथवा
जगन्नाथ – …………………… – ……………………
उत्तर:
संधिशब्द – संधि विच्छेद – संधि भेद
विद्यार्थी – विद्या + अर्थी – स्वर संधि
अथवा
जगन्नाथ – जगत् + नाथ – व्यंजन संधि

4. सहायक क्रिया:

प्रश्न.
निम्नलिखित वाक्यों में सहायक क्रिया पहचानकर उनका मूल रूप लिखिए:
(i) बादल पृथ्वी के नजदीक आकर बरस रहे हैं।
(ii) दुष्ट लोग थोड़ा धन पाकर भी इतराने लगते हैं।
उत्तर:
सहायक क्रिया – मूल रूप
(i) रहे – रहना
(ii) लगने – लगना

5. प्रेरणार्थक क्रिया:

प्रश्न.
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) सहना
(ii) गिरना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – द्वितीय प्रेरणार्थक रूप
(i) सहना – सहाना – सहवाना
(ii) गिरना – गिराना – गिरवाना

6. मुहावरे:

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) आँखें फाड़कर देखना
(ii) रुआँसा होना।
उत्तर:
(i) आँखें फाड़कर देखना।
अर्थ: आश्चर्य से देखना।
वाक्य: मनीष सर्कस के कलाकारों के करतब आँखें फाड़कर देख रहा था।

(ii) रुआँसा होना।
अर्थ: उदास होना।
वाक्य: मालिक की झिड़कियाँ खाकर नौकर रुआँसा हो गया।

प्रश्न 2.
अधोरेखांकित वाक्यांश के लिए उचित मुहावरे का चयन कर वाक्य फिर से लिखिए: (हामी भरना, करवट बदलना)
आखिरकार रंजन ने शादी करने के लिए स्वीकृति दी।
उत्तर:
आखिरकार रंजन ने शादी करने के लिए हामी भरी।

7. कारक:
प्रश्न.
निम्नलिखित वाक्य में प्रयुक्त कारक पहचानकर उसका भेद लिखिए:
(i) छोटी-छोटी नदियाँ वर्षा के जल से भर जाती हैं।
(ii) नदी अपने किनारों को तोड़ती हुई आगे बढ़ जाती है।
उत्तर:
(i) वर्षा के-संबंध कारक
(ii) किनारों को-कर्म कारक ।

8. विरामचिह्न:

प्रश्न.
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्न लगाकर वाक्य फिर से लिखिए:
(i) पृथ्वी घास से परिपूर्ण होकर हरी हो गई है जिससे रास्तों का पता नहीं चलता
(ii) हरी भरी फसलों से युक्त पृथ्वी कैसी लग रही है
उत्तर:
(i) पृथ्वी घास से परिपूर्ण होकर हरी हो गई है, जिससे रास्तों का पता नहीं चलता।
(ii) हरी-भरी फसलों से युक्त पृथ्वी कैसी लग रही है?

9. काल परिवर्तन:

प्रश्न.
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) प्रियाहीन मेरा मन डरता है। (पूर्ण वर्तमानकाल)
(ii) बादल पृथ्वी के नजदीक आकर बरस रहे हैं। (सामान्य भविष्यकाल)
उत्तर:
(i) प्रियाहीन मेरा मन डरा है।
(ii) बादल पृथ्वी के नजदीक आकर बरसेंगे।

10. वाक्य भेद:

प्रश्न 1.
निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए:
(i) बादल गरज रहे हैं और बिजली चमक रही है।
(ii) अनेक वृक्षों में नई-नई कोंपलें आ गई हैं, जिससे वे हरे-भरे तथा सुशोभित हो गए हैं।
उत्तर:
(i) संयुक्त वाक्य
(ii) मिश्र वाक्य।

प्रश्न 2.
निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए:
(i) कलियुग में धर्म पलायन कर जाता है। (प्रश्नवाचक वाक्य)
(ii) संत पुरुष दुष्टों के वचन सहते हैं। (निषेधवाचक वाक्य)
उत्तर:
(i) क्या कलियुग में धर्म पलायन कर जाता है?
(ii) संत पुरुष दुष्टों के वचन नहीं सहते।

11. वाक्य शुद्धिकरण:

प्रश्न.
निम्नलिखित वाक्य शुद्ध करके फिर से लिखिए:
(i) एक-एक करके सद्गुण सज्जन के पास चला आते है।
(ii) धूल खोजने पे भी कहीं नहीं मिलता है।
उत्तर:
(i) एक-एक कर सद्गुण सज्जन के पास चले आते हैं।
(ii) धूल खोजने पर भी कहीं नहीं मिलती है।

उपयोजित लेखन

निम्नलिखित मुद्दों के आधार पर 70 से 80 शब्दों में कहानी लिखकर उसे उचित शीर्षक दीजिए तथा सीख लिखिए:
एक महानुभाव की कल्पना – विश्वविद्यालय स्थापना का प्रण – दान से घन एकत्र करना – एक सेठ के पास जाना – सेठ का दिन भर बिठाए रखना – महानुभाव निराश – शाम को सात लाख रुपए का चेक पाना – आश्चर्य और खुशी।
उत्तर:
बात आजादी मिलने के बहुत पहले की है। तब देश में उच्च शिक्षा प्राप्त करने वाले विद्यार्थियों की पढ़ाई के लिए बहुत कम विश्वविद्यालय थे। विद्यार्थियों को दूर-दूर स्थानों पर जाकर शिक्षा प्राप्त करनी पड़ती थी और उन्हें वही टिककर पढ़ना पड़ता था। विद्यार्थियों की इस परेशानी को दर करने के लिए एक महानुभाव ने अपने शहर में विश्वविद्यालय स्थापित करने का प्रण किया।

इसके लिए उन्होंने सारे देश का दौरा किया और जहाँ से जो भी धन मिला, एकत्र किया। एक बार किसी व्यक्ति ने उन्हें बताया कि आप कलकत्ता के फलाँ सेठ के पास जाइए। वहाँ आपको अवश्य कुछ धन मिलेगा। वे पहुँच गए उनके पास। उन्होंने सेठ जी से अपना उद्देश्य बताया। सेठ जी ने उन्हें कुछ देर इंतजार करने के लिए कहा और वे अपने काम में लग गए। दोपहर से शाम हो गई। सेठ जी ने उन्हें नहीं बुलाया।

वे निराश हो गए थे। इतने में सेठ जी अपने केबिन से बाहर आए। वे सज्जन खड़े हो गए और बोले, “सेठ जी मुझे आज्ञा दीजिए, मैं चलूँ।” सेठ जी ने कहा, “बैठिए भाई, बैठिए! मैं आपका ही काम कर रहा था। ये लीजिए अपने परोपकार के काम में मेरा छोटा-सा सहयोग! इस समय मैं और कुछ नहीं दे पाऊँगा।” सेठ जी ने एक चेक उन सज्जन के हाथ में थमा दिया।

उन महाशय ने चेक पर नजर डाली- ‘सात लाख रुपए।’ उनके मुँह से निकला, “सेठ जी, मुझे तो लगा था, मुझे यहाँ से खाली हाथ जाना पड़ेगा, पर आपने तो…।” “बस… बस!” उन्होंने उन सज्जन की बात काटते हुए कहा, “आप परोपकार का काम कर रहे हैं, मुझसे जो बन पड़ा, मैंने भी सहयोग दे दिया।” इस धन से विश्वविद्यालय के कई काम पूरे हुए।

विश्वविद्यालय के निर्माण के लिए यह धन एकत्र करने वाले व्यक्ति थे महामना मदनमोहन मालवीय और उन्होंने जिस विश्वविद्यालय का निर्माण किया, वह था ‘बनारस हिंदू विश्वविद्यालय।

सीख: परोपकार सबसे बड़ा धर्म है।

बरषहिं जलद Summary in Hindi

विषय-प्रवेश : अवधी बोली में लिखा गया ‘रामचरितमानस’ विश्व के अमूल्य ग्रंथों में से एक है। प्रस्तुत काव्य खंड इसी ग्रंथ से लिया गया है। चौपाई और दोहों जैसे लोकप्रिय छंदों में प्रस्तुत इस काव्य खंड में तुलसीदासजी ने वर्षा ऋतु का सुंदर वर्णन किया है। इस काव्य खंड में उन्होंने वर्षा ऋतु से संबंधित विभिन्न वस्तुओं को जीवन से जोड़कर देखा है।

यह काव्य खंड सीता हरण के पश्चात का है। श्रीराम और लक्ष्मण जी सीता जी की खोज में वन में भटक रहे हैं। बरसात की ऋत आ चुकी है पर सीता जी का पता नहीं चल सका है। कवि ने इस काव्य खंड में श्रीराम के मन की व्याकुलता का चित्रण किया है।

बरषहिं जलद चौपाइयों और दोहों का सरल अर्थ

1. घन घमंड नभ …………………………… जिमि जिव हरि पाई।। (चौपाई)

कवि कहते हैं कि आकाश में बादल उमड़-घुमड़कर भयंकर गर्जना कर रहे हैं। (श्रीरामजी कह रहे हैं कि) प्रिया (सीता जी) के बिना मेरा मन डर रहा है। बिजली आकाश में ऐसे चमक रही है, जैसे दुष्ट व्यक्ति की मित्रता स्थिर नहीं रहती। यानी वह चमकती है और चमककर लुप्त हो जाती है।

बादल पृथ्वी के नजदीक आकर (नीचे उतरकर) बरस रहे हैं। ठीक उसी प्रकार जैसे विद्वान व्यक्ति विद्या प्राप्त कर विनम्र हो जाते हैं। बूंदों की चोट पहाड़ों पर पड़ रही है। पहाड़ बूंदों के प्रहार को इस प्रकार शांत भाव से सह रहे हैं, जैसे संत पुरुष दुष्टों के कटु वचनों को सह लेते हैं।

छोटी नदियाँ वर्षा के जल से भरकर अपने किनारों को तोड़ती हुई आगे बढ़ती जा रही हैं, जैसे मामूली धन पाकर भी दुष्ट लोग इतराने लगते हैं (यानी मर्यादा का त्याग कर देते हैं)। पृथ्वी पर गिरते ही पानी गँदला हो गया है, मानो प्राणी से माया लिपट गई हो।

वर्षा का पानी एकत्र होकर तालाबों में भर रहा है। जैसे एक-एक कर सद्गुण सज्जन व्यक्ति के पास चले आते हैं। नदी का पानी समुद्र में जाकर उसी प्रकार स्थिर हो जाता है जिस प्रकार जीव हरि (ईश्वर) को प्राप्त कर अचल (आवागमन से मुक्त) हो जाता है।

2. हरित भूमि …………………………… होहिं सद्ग्रंथ।। (दोहा)

पृथ्वी घास से परिपूर्ण होकर हरीभरी हो गई है, जिससे रास्तों का पता नहीं चलता है। यह दृश्य ऐसा लगता है, जैसे पाखंडी के पाखंड भरे मत के प्रचार से सद्ग्रंथ लुप्त हो जाते हैं।

3. दादुर धुनि चहुँ उपजे ग्याना।। (चौपाई)

कवि कहते हैं कि वर्षा काल में चारों दिशाओं में मेढकों की ध्वनि ऐसी (सुहावनी) लगती है मानो विद्यार्थियों का समूह वेद-पाठ कर रहा हो। अनेक वृक्षों में नई-नई कोंपलें आ गई हैं, जिससे वे ऐसे हरेभरे तथा सुशोभित हो गए हैं, जैसे साधना करने वाले किसी व्यक्ति का मन ज्ञान प्राप्त करने पर प्रफुल्लित हो जाता है।

(बरसात के दिनों में) मदार और जवासा के पौधे पत्तों से रहित हो गए हैं। उन्हें देखकर ऐसा लगता है मानो अच्छे शासक के राज्य में दुष्टों का धंधा जाता रहा हो (खत्म हो गया हो)। धूल खोजने पर भी कहीं नहीं मिलती है। जैसे क्रोध धर्म को दूर कर देता है, उसी तरह वर्षा ने धूल को नष्ट कर दिया है।

अनाज से युक्त (लहलहाती हुई हरी-भरी खेती) पृथ्वी कुछ इस : प्रकार शोभायमान हो रही है, जैसे उपकार करने वाले व्यक्ति शोभायमान होते हैं। रात के अंधकार में जुगनू चारों ओर दिखाई दे रहे हैं। उन्हें देखकर ऐसा लगता है जैसे घमंडियों का समूह एकत्र हो गया है।

चतुर किसान अपनी फसलों की निराई कर रहे हैं। (अपनी फसल से घास-फूस निकालकर फेंक रहे हैं)। इसे देखकर ऐसा लगता है जैसे विद्वान लोग मोह, मद, माया का त्याग कर रहे हों।

बरसात के दिनों में चक्रवाक पक्षी कहीं नहीं दिखाई दे रहे हैं। इससे ऐसा लग रहा है जैसे कलियुग में धर्म पलायन कर गया हो।

यह पृथ्वी अनेक प्रकार के जीवों से भरी पड़ी है। यह उसी तरह शोभायमान हो रही है, जैसे अच्छे राजा के राज्य में प्रजा की वृद्धि (विकास) होती है।

यहाँ-वहाँ अनेक सही थककर इस तरह ठहरे हुए हैं, जैसे मनुष्य को ज्ञान प्राप्त होने पर इंद्रियाँ शिथिल हो जाती हैं और विषयों की ओर’ जाना छोड़ देती हैं।

4. कंबहुँ प्रबल …………………………… कुसंग-सुसंग।। (दोहा)

कभी-कभी वायु बहुत तेज गति से चलने लगती है। इससे बादल यहाँ-वहाँ गायब हो जाते हैं। यह दृश्य उसी प्रकार लगता है जैसे परिवार में कुपुत्र के उत्पन्न होने से कुल के उत्तम धर्म (श्रेष्ठ आचरण) नष्ट हो जाते हैं।

कभी (बादलों के कारण) दिन में घोर अंधकार छा जाता है और कभी सूर्य प्रकट हो जाता है। तब लगता है, जैसे बुरी संगति पाकर ज्ञान नष्ट हो गया हो और अच्छी संगति पाकर ज्ञान उत्पन्न हो गया हो।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Std 10 Hindi Chapter 10 Thes Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 10 ठेस Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 10 ठेस Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 10 ठेस Textbook Questions and Answers

कृति

(कृतिपत्रिका के प्रश्न 3 (अ) के लिए)

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
वाक्यों का उचित क्रम लगाकर लिखिए:
a. सातों तारे मंद पड़ गए।
b. ये मेरी ओर से हैं। सब चीजें हैं दीदी।
c. लोग उसको बेकार ही नहीं, ‘बेगार’ समझते हैं।
d. मानू दीदी काकी की सबसे छोटी बेटी है।
उत्तर:
a. सातों तारे मंद पड़ रहे हैं।
b. ये मेरी ओर से हैं। सब चीजें हैं दीदी!
c. लोग उसको बेकार ही नहीं, ‘बेगार’ समझते हैं।
d. मानू दीदी काकी की सबसे छोटी बेटी है।

(अभिव्यक्ति)

प्रश्न.
‘कला और कलाकार का सम्मान करना हमारा दायित्व है’, इस कथन पर अपने विचारों को शब्दबद्ध कीजिए।
उत्तर:
हमारे देश की संस्कृति में लोक कलाओं की सशक्त पहचान रही है। ये मूलतः ग्रामीण अंचलों में अनेक जातियों व जनजातियों में पीढ़ी-दर-पीढ़ी संरक्षित पारंपरिक कलाएँ हैं। लोक कला का इतिहास उतना ही पुराना है, जितना कि भारतीय ग्रामीण सभ्यता का। लोक कलाओं में लोकगीत, लोकनृत्य, गायन, वादन, अभिनय, मूर्तिकला, काष्ठकला, धातुकला, चित्रकला, हस्तकला आदि का समावेश होता है। हस्तकला ऐसे कलात्मक कार्य को कहते हैं, जो उपयोगी होने के साथ-साथ सजाने के काम आता है तथा जिसे मुख्यतः हाथ से या साधारण औजारों की सहायता से ही किया जाता है।

ऐसी कलाओं का धार्मिक एवं सांस्कृतिक महत्त्व होता है। वर्तमान में लोक कलाओं और कलाकारों को उचित प्रश्रय न मिलने के कारण अनेक लोक कलाओं पर संकट उत्पन्न हो गया है। धीरे-धीरे समय परिवर्तन, भौतिकतावाद, पश्चिमीकरण तथा आर्थिक संपन्नता के कारण परंपरागत लोक कलाओं पर नकारात्मक प्रभाव पड़ा है। जनता व प्रशासन दोनों को ही लोक कलाओं और कलाकारों की पहचान नष्ट होने से बचाने के प्रयास करने चाहिए।

भाषा बिंदु

प्रश्न 1.
कोष्ठक की सूचना के अनुसार निम्न वाक्यों का काल परिवर्तन कीजिए:

a. अली घर से बाहर चला जाता है। (सामान्य भूतकाल)
—————————————————————
b. आराम हराम हो जाता है। (पूर्ण वर्तमानकाल एवं पूर्ण भविष्यकाल)
—————————————————————
c. सरकार एक ही टैक्स लगाती है। (सामान्य भविष्यकाल)
—————————————————————
d. आप इतनी देर से नाप-तौल करते हैं। (अपूर्ण वर्तमानकाल)
—————————————————————
e. वे बाजार से नई पुस्तक खरीदते हैं। (पूर्ण भूतकाल एवं अपूर्ण भविष्यकाल)
—————————————————————
f. वे पुस्तक शांति से पढ़ते हैं। (अपूर्ण भूतकाल)
—————————————————————
g. सातों तारे मंद पड़ गए। (अपूर्ण वर्तमानकाल)
—————————————————————
h. मैंने खिड़की से गरदन निकालकर झिड़की के स्वर में कहा। (अपूर्ण भूतकाल)
—————————————————————
उत्तर:
a. अली घर से बाहर चला गया।
b. (अ) आराम हराम हो गया है।
(ब) आराम हराम हो चुका होगा।
c. सरकार एक ही टैक्स लगाएगी।
d. आप इतनी देर से नाप-तौल कर रहे हैं।
e. (अ) उन्होंने बाजार से नई पुस्तक खरीदी थी।
(ब) वे बाजार से नई पुस्तक खरीदते रहेंगे।
f. वे पुस्तक शांति से पढ़ रहे थे।
g. सिरचन ने मुस्कराकर पान का बीड़ा मुँह में ले लिया।
h. मैं खिड़की से गरदन निकालकर झिड़की के स्वर में कह रहा था।

प्रश्न 2.
नीचे दिए गए वाक्य का काल पहचानकर निर्देशानुसार काल परिवर्तन कीजिए:

उत्तर:
मानू को ससुराल पहुँचाने मैं ही जा रहा था – अपूर्ण भूतकाल

1. सामान्य वर्तमानकाल	मानू को ससुराल पहुँचाने में ही जाता हूँ।
2. सामान्य भविष्यकाल	मानू को ससुराल पहुँचाने में ही जाऊँगा।
3. अपूर्ण भविष्यकाल	मानू को ससुराल पहुँचाने में ही जाता रहँगा।
4. पूर्ण वर्तमानकाल	मानू को ससुराल मैंने ही पहुँचाया है।
5. सामान्य वर्तमानकाल	मानू को ससुराल पहुँचाने में ही गया।
6. अपूर्ण वर्तमानकाल	मानू को ससुराल पहुँचाने में ही जा रहा हूँ।
7. पूर्ण भूतकाल	मानू को ससुराल पहुँचाने में ही गया था।
8. पूर्ण भविष्यकाल	मानू को ससुराल पहुंचाने में ही जा चुका हूँगा।

उपयोजित लेखन

प्रश्न.
‘पुस्तक प्रदर्शनी में एक घंटा’ विषय पर अस्सी से सौ शब्दों में निबंध लेखन कीजिए।
उत्तर:
पुस्तकें अनमोल होती हैं। वे हमारी सबसे अच्छी मित्र होती हैं, क्योंकि वे ज्ञान-विज्ञान का भंडार होती हैं। व्यक्ति आते हैं और चले जाते हैं परंतु उनके श्रेष्ठ विचार, ज्ञान, संस्कृति, सभ्यता, मानवीय मूल्य पुस्तकों के रूप में जीवित रहते हैं। पुस्तक प्रदर्शनी और मेले हमारे लिए वरदान हैं। ये पाठकों और लेखकों का संगम होते हैं। प्रत्येक वर्ष अगस्त में पुणे में कोरेगाँव पार्क में पुस्तक प्रदर्शनी और मेले का आयोजन किया जाता है। अनेक पुस्तक विक्रेता और प्रकाशक वहाँ आते हैं। इस बार मैं भी उस प्रदर्शनी में गया।

स्टालों पर पुस्तकें बड़े आकर्षक ढंग से सजी हुई थीं। सभी स्तर और रुचि के लोगों के लिए वहाँ यथेष्ट सामग्री थी। इतिहास, भूगोल, ज्ञान-विज्ञान, साहित्य, धर्म, भाषा, यात्रा, जीवन-वृत्त आदि सभी विषयों की पुस्तकें वहाँ थीं। अनेक स्कूलों के विद्यार्थी वहाँ आए हुए थे। बच्चे-बड़े सभी पुस्तकें खरीदने में व्यस्त थे या उनको देख-पढ़ रहे थे। कुछ लोग ग्रुप में खड़े पुस्तकों पर चर्चा कर रहे थे। मेरे पास समय का अभाव था। मैंने अपने और छोटे भाई के लिए मुंशी प्रेमचंद का कहानी-संग्रह तथा हिंदी का एक शब्दकोश खरीदा।

Hindi Lokbharti 10th Textbook Solutions Chapter 10 ठेस Additional Important Questions and Answers

गद्यांश क्र. 1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
कारण लिखिए:
गाँव के लोग अब सिरचन को खेत-खलिहान की मजदूरी के लिए इसलिए नहीं बुलाते:
उत्तर:
लोग उसको बेकार ही नहीं, बेगार’ समझते हैं। दूसरे मजदूर खेत पर पहुँचकर एक-तिहाई काम कर चुकते हैं, तब पगडंडी पर तौल-तौलकर पाँव रखता हुआ, धीरे-धीरे कहीं सिरचन राय हाथ में खुरपी डुलाता हुआ दिखाई पड़ेगा।

प्रश्न 2.
वाक्यों को उचित क्रम लगाकर लिखिए:
(i) तुम्हारी भाभी ने कहाँ से बनाना सीखी हैं?
(ii) लोग उसको बेकार ही नहीं, ‘बेगार’ समझते हैं।
(iii) मुफ्त में मजदूरी देनी हो, तो और बात है।
उत्तर:
(i) मुफ्त में मजदूरी देनी हो, तो और बात है।
(ii) मैं पहले ही पूछ लेता, भोग क्या-क्या लगेगा?
(iii) तुम्हारी भाभी ने कहाँ से बनाना सीखी है?

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 4.
एक शब्द में उत्तर लिखिए:
(i) बिना मजदूरी दिए जबरदस्ती लिया गया काम – …………………………..
(ii) बाँस की तीलियों से बना परदा – …………………………..
उत्तर:
(i) बिना मजदूरी दिए जबरदस्ती लिया गया काम- बेगार।
(ii) बाँस की तीलियों से बना परदा- चिक।

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘खेत-खलिहान की मजदूरी इस विषय में 25 से 30 शब्दों में अपने विचार लिखिए।
उत्तर:
भारत गाँवों और खेतों का देश है। यहाँ आज भी देश की दो-तिहाई जनता खेती से जुड़ी है। खेत हैं, खेती है तो मजदूर भी जरूरी हैं। मजदूर और किसान एक-दूसरे के पूरक हैं। मजदूर के बिना किसानों का काम असंभव-सा होता है। फसल की बुआई, गुड़ाई, निराई, सिंचाई आदि के काम के लिए मजदूरों की आवश्यकता होती ही है। भूमिहीन मजदूर परिवार बहुत गरीब होते हैं। उनके पास अपनी जमीन नहीं होती। उन्हें रोजी-रोटी के लिए दूसरों के खेतों में काम करना पड़ता है। फसल की बुआई और कटाई के समय तो बड़े किसानों के खेतों में उन्हें काम और मजदूरी मिल जाती है, परंतु पूरे वर्ष काम नहीं मिल पाता। ऐसे समय इन मजदूरों को अपनी जरूरतें पूरी करने के लिए मजदूरी के अन्य कार्य करने पड़ते हैं। बार-बार कर्ज लेना पड़ता है।

गद्यांश क्र. 2
प्रश्न, निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
गलत वाक्य सही करके लिखिए:
(i) दूध, घी, मलाई न मिले तो कोई बात नहीं किंतु बात में जरा भी झाला सिरचन नहीं बरदाश्त कर सकता।
(ii) आज तो अब अधकपाली दर्द के कारण मन ठीक नहीं है। थोड़ा-सा रह गया है, किसी दिन आकर पूरा कर दूंगा।
उत्तर:
(i) दूध में कोई मिठाई न मिले तो कोई बात नहीं किंतु बात में जरा भी झाला सिरचन नहीं बरदाश्त कर सकता।
(ii) आज तो अब अधकपाली दर्द से माथा टनटना रहा है। थोड़ा-सा रह गया है, किसी दिन आकर पूरा कर दूंगा।

प्रश्न 3.
आकृति पूर्ण कीजिए:
(i) सिरचन जाति का यह है – [ ]
(ii) बिना इसके पेट भर भात पर काम करने वाला कारीगर – [ ]
(iii) सिरचन को लोग यह भी समझते हैं – [ ]
(iv) ऐसे बहुत-से काम हैं जिन्हें इसके सिवा गाँव में कोई नहीं जानता – [ ]
उत्तर:
(i) सिरचन जाति का यह है – [कारीगर]
(ii) बिना इसके पेट भर भात पर काम करने वाला कारीगर – [मजदूरी]
(iii) सिरचन को लोग यह भी समझते हैं – [चटोर]
(iv) ऐसे बहुत-से काम हैं जिन्हें इसके सिवा गाँव में कोई नहीं जानता – [सिरंचन]

प्रश्न 4.
कृति पूर्ण कीजिए:

उत्तर:

गद्यांश क्र. 3.
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
वाक्यों को उचित क्रम लगाकर लिखिए:
(i) मानू दीदी काकी की सबसे छोटी बेटी है।
(ii) मँझली भाभी का मुँह लटक गया।
(iii) मॅझली भाभी से रहा नहीं गया।
उत्तर:
(i) रंगीन सुतलियों में झब्बे डालकर सिरचन चिक बुनने बैठा।
(ii) मैंझली भाभी से रहा नहीं गया।
(iii) मँझली भाभी का मुँह लटक गया।

प्रश्न 3.
कारण लिखिए:
मझली भाभी का मुँह लटक गया –
उत्तर:
मझली भाभी का प्रस्ताव सुनकर सिरचन ने कहा कि बहुरिया, मोहर छापवाली धोती के साथ रेशमी कुर्ता देने पर भी ऐसी चीज नहीं बनती। मानू दीदी का दूल्हा अफसर है। सिरचन की बात सुनकर मझली भाभी का मुँह लटक गया।

प्रश्न 4.
वाक्य पूर्ण कीजिए:
(i) मानू के दूल्हे ने पहले ही बड़ी भाभी को –
(ii) मोहर छापवाली धोती नहीं, मुंगिया लड्डू, बेटी की बिदाई के समय –
उत्तर:
(i) मानू के दूल्हे ने पहले ही बड़ी भाभी को लिखकर चेतावनी दे दी है।
(ii) मोहर छापवाली धोती नहीं, मुँगिया लड्डू, बेटी की विदाई के समय रोज मिठाई जो खाने को मिलेगी।

प्रश्न 5.
कृति पूर्ण कीजिए:

उत्तर:

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘मन लगाकर काम करना एक गुण है’ इस विषय में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
किसी भी काम को मन लगाकर अर्थात तन्मयता से करना एक गुण है। उसका फल भी हमें मिलता है। मन लगाकर किए गए काम के परिणाम हमेशा उत्तम होते हैं। जिस काम को करने में मन लगता है, वह कभी बोझ नहीं लगता। जो काम मन मारकर करना पड़े, वह बोझ बन जाता है। कुछ लोग ऐसे होते हैं, जो एक किनारे खड़े होकर नाव की तलाश करते हैं अर्थात उचित काम और अवसर की तलाश करते रहते हैं और वह अवसर कभी नहीं आता, वे जिंदगी भर इंतजार ही करते रहते हैं। कुछ लोग नौकरी में मन लगाकर काम ही नहीं करना चाहते। दूसरे साथी जब मेहनत और लगन से काम करके प्रोन्नति पाकर आगे बढ़ जाते हैं, तो ईष्या के वश होकर उन्हें अधिकारियों का चमचा आदि कहते हैं।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
ये वाक्य किसने, किससे कहे हैं? लिखिए:
(i) आज सिरचन को कलेवा किसने दिया है?
(ii) अरी मँझली, सिरचन को बुंदिया क्यों नहीं देती?
(iii) बँदिया मैं नहीं खाता, काकी!
(iv) किसी के नैहर-ससुराल की बात क्यों करेगा वह?
उत्तर:
(i) आज सिरचन को कलेवा किसने दिया है? – लेखक ने माँ से कहा है।
(ii) अरी मँझली, सिरचन को बुंदिया क्यों नहीं देती? – लेखक की माँ ने मँझली भाभी से कहा है।
(iii) बुंदिया मैं नहीं खाता, काकी- सिरचन ने लेखक की माँ से कहा है।
(iv) किसी के नैहर-ससुराल की बात क्यों करेगा वह? – चाची ने लेखक की माँ से कहा है।

प्रश्न 2.
आकृति पूर्ण कीजिए:
(i) सिरचन को काम में मगन होकर खाने-पीने की यह न रहती।। – [ ]
(ii) चिक में सुतली के फंदे डालकर सिरचन ने इस पर निगाह डाली। – [ ]
(iii) मानू यह सजाकर बाहर बैठकखाने में भेज रही थी। – [ ]
(iv) अरी मैंझली, सिरचन को यह क्यों नहीं देती। – [ ]
उत्तर:
(i) सिरचन को काम में मगन होकर – खाने-पीने की यह न रहती। – [सुध]
(ii) चिक में सुतली के फंदे डालकर – सिरचन ने इस पर निगाह डाली। [सूप]
(iii) मानू यह सजाकर बाहर बैठकखाने में भेज रही थी। – [पान]
(iv) अरी मँझली, सिरचन को यह क्यों नहीं देती। – [बँदियाँ]

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘बहू के मायके की आलोचना करना उचित नहीं है इस विषय में अपने विचार 25 से 30 शब्दों में लिखिए।।
उत्तर:
कहा जाता है कि बेटियों का असली घर उनका ससुराल होता है। जिसे असली घर बताया जाता है, यानि कि ससुराल, वहाँ अकसर बहू को बेगाना समझा जाता है। ससुराल में बहू को कोई हक नहीं होता कि वह अपनी इच्छा से कुछ कर सके। हर छोटी-बड़ी बात के लिए उसे ससुरालवालों की आज्ञा की आवश्यकता होती है। बहू सबकी इच्छाओं का ख्याल रखती है, सबका सम्मान करती है, पर बहू का सम्मान अकसर नहीं किया जाता। स्थिति तब और भी भयंकर हो जाती है, जब ससुरालवाले समय-असमय बहू के मायके की आलोचना करने लगते हैं।

मायकेवालों ने क्या भेजा है, बहू क्या लाई है? आदि प्रश्न घरवाले ही नहीं, कभी-कभी अड़ोस-पड़ोसवालों की जुबान पर भी आने लगते हैं। लड़केवाले प्रायः समझते हैं कि उनका दर्जा लड़कीवालों से ऊँचा है। बात-बात पर बह के मायकेवालों की उपेक्षा की जाती है। उनमें मीन-मेख निकाली जाती है। परिणामस्वरूप, बहू के मन में ससुराल के प्रति विद्वेष की भावना आ जाती है। हमें बहू के मायकेवालों का सम्मान करना होगा। तभी बहू भी ससुरालवालों को सम्मान देगी। हमेशा उनसे कुछ लेने की अपेक्षा करना उचित नहीं है।

गद्यांश क्र.5
प्रश्न. निम्नलिखित पठित गद्यांश पढकर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
एक शब्द में उत्तर लिखिए:
*(i) सिरचन ने छोटी चाची से माँगा –
(ii) सिरचन की घरवाली ने यह बुनी थी –
उत्तर:
(i) सिरचन ने छोटी चाची से माँगा – गमकौआ जर्दा।
(i) सिरचन की घरवाली ने यह बुनी थी – शीतलपाटी।

प्रश्न 2.
वाक्यों को उचित क्रम लगाकर लिखिए:
(i) सिरचन ने मुस्कराकर पान का बीड़ा मुँह में ले लिया।
(ii) चाची कई कारणों से जली-भुनी रहती थी सिरचन से।
(iii) बस, सिरचन की उँगलियों में सुतली के फंदे पड़ गए।
उत्तर:
(ii) चाची कई कारणों से जली-भुनी रहती थी सिरचन से।
(ii) बस, सिरचन की उँगलियों में सुतली के फंदे पड़ गए।
(iii) सातों तारे मंद पड़ गए।

प्रश्न 3.
कारण लिखिए:
(i) मेरा कलेजा धड़क उठा… हो गया सत्यानाश!
(ii) सातों तारे मंद पड़ गए।
उत्तर:
(i) चाची ने सिरचन को बुरी तरह डाँटा था। मैं जानता था कि सिरचन बड़ा स्वाभिमानी है। अब वह मानू की ससुराल के लिए चिक और शीतलपाटी बनाएगा भी या नहीं।
(ii) सिरचन बड़ा स्वाभिमानी था। चाची ने उसे बुरी तरह डाँटा तो वह उस चिक को, जिसे उसने बड़े मन से बनाना शुरू किया था, अधूरी छोड़कर चला गया।

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘सिरचन काम अधूरा छोड़कर चला गया। क्या यह उचित था’ इस विषय में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
लेखक की चाची के बुरा-भला कहने पर सिरचन नाराज होकर काम अधूरा छोड़कर चला गया। इसे किसी भी प्रकार उचित नहीं कहा जा सकता। सिरचन अच्छी तरह जानता था कि चिक और पटेर की शीतलपाटियाँ मानू के अफसर दूल्हे की फरमाइश पर बनवाई जा रही हैं। मानू उन्हें लेकर ही ससुराल जाएगी। फिर भी उसने काम पूरा . नहीं किया और चला गया। यह सिरचन ने ठीक नहीं किया। उसने एक बार भी नहीं सोचा कि दूल्हे की फरमाइश पूरी न होने की स्थिति में मानू को ताने सुनने पड़ सकते हैं। सास-ससुर व घर के अन्य सदस्यों की नाराजगी का शिकार होना पड़ सकता है। उस समय वह मानू, जिसके प्रति सिरचन के मन में भी स्नेह था, कितनी दुखी होगी। सिरचन का काम अधूरा छोड़कर जाना मुझे उचित नहीं लगा। (विद्यार्थी अपने ३ विचार लिखें।)

गद्यांश क्र. 6
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
ये वाक्य किसने, किससे कहे हैं? लिखिए:
(i) यह भी बेजा नहीं दिखलाई पड़ता, क्यों मानू?
(ii) चाची और मँझली भाभी की नजर न लग जाए इसमें भी!
(iii) मानू दीदी कहाँ हैं? एक बार देखू।
(iv) ये मेरी ओर से हैं। सब चीजें हैं दीदी!
उत्तर:
(i) यह भी बेजा नहीं दिखलाई पड़ता, क्यों मानू? – बड़ी भाभी ने मानू से कहा है।
(ii) चाची और मँझली भाभी की नजर न लग जाए इसमें भी! – लेखक ने बड़ी भाभी से कहा है।
(iii) मानू दीदी कहाँ हैं? एक बार देखू। – सिरचन ने लेखक से कहा है।
(iv) यह मेरी ओर से हैं। सब चीजें हैं दीदी! – सिरचन ने मानू से कहा है।

प्रश्न 2.
वाक्यों को उचित क्रम लगाकर लिखिए:
(i) मानू फूट-फूटकर रो रही थी।
(ii) मानू कुछ नहीं बोली!… बेचारी!
(iii) मानू को ससुराल पहुँचाने में ही जा रहा था।
उत्तर:
(i) मानू कुछ नहीं बोली!… बेचारी!
(ii) मानू को ससुराल पहुँचाने मैं ही जा रहा था।
(iii) मानू फूट-फूटकर रो रही थी।

प्रश्न 3.
दो ऐसे प्रश्न बनाइए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) सिरचन ने
(ii) मानू।
उत्तर:
(i) किसने दाँत से जीभ को काटकर दोनों हाथ जोड़ दिए?
(ii) मोहर छापवाली धोती का दाम कौन देने लगी?

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘सिरचन भावनाओं से परिपूर्ण व्यक्ति था’ इस विषय में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
सिरचन भावनाओं से परिपूर्ण व्यक्ति है। वह एक उच्चकोटि का कलाकार है। चिक, शीतलपाटी आदि बनाने में पूरे क्षेत्र में उसका कोई सानी नहीं है। लेखक का परिवार, विशेष रूप से उनकी माँ का सिरचन बहुत आदर करता है। लेखक की माँ भी सिरचन की कला का सम्मान करती है। शायद इसीलिए लेखक की चाची उससे जली-भुनी रहती है। भावुक होने के कारण सिरचन को किसी के द्वारा टोका जाना तनिक भी बर्दाश्त नहीं होता। इसीलिए चाची के बुरा-भला कहने पर वह नाराज होकर काम अधूरा छोड़कर चला जाता है।

परंतु सिरचन जानता है कि चिक, शीतलपाटी आदि सभी चीजों के लिए मानू के अफसर पति ने फरमाइश की थी। उसे मानू से स्नेह था। अतः नाराज होने के बावजूद वह मानू के लिए वे सारी चीजें बनाता है और इतनी सुंदर कि लेखक भी उसकी कारीगरी देखकर दंग रह जाता है। सिरचन स्वयं उन्हें लेकर स्टेशन आता है। मानू जब माँ द्वारा कही गई मोहर छापवाली धोती का दाम सिरचन को देना चाहती है तो वह दोनों हाथ जोड़कर मना कर देता है।

उपक्रम/कृति/परियोजना

प्रश्न.
लेखनीय
लोक कलाओं के नामों की सूची तैयार कीजिए।
उत्तर:

• मधुबनी
• जादोपाटिया
• कलमकारी
• कांगड़ा
• गोंड
• चित्तर
• तंजावुर
• थंगक
• पातचित्र
• पिछवई
• पिथोरा
• फड़
• बाटिक
• यमुनाघाट
• वरली।

प्रश्न.
पठनीय
देश की आत्मा गाँवों में बसती है, गांधी जी के इस विचार से संबंधित लेख पदिए तथा इस पर स्वमत प्रस्तुत कीजिए।
उत्तर:
हमारा देश कृषिप्रधान देश है। यह गाँवों का देश है। भारत की आत्मा गाँवों में बसती है। सरित-सरोवर, झील-जलाशय, विविध विटप, वन-पर्वत, खेत-खलिहान और सहज-स्वाभाविक जीवन शैली सब गाँवों में ही उपलब्ध हो सकती है। आज भी भारत की 65 प्रतिशत से अधिक जनसंख्या गाँवों में बसती है। परंतु देश के आर्थिक विकास का लाभ गाँववासियों को संख्या के अनुपात में नहीं मिल पाता। आज भी असंख्य गाँव देश की मुख्य धारा से नहीं जुड़ पाए हैं। गाँवों की समस्याएँ चाहे गरीबी हो, सामाजिक हो, पेयजल हो या बिजली, सड़क, शिक्षा आदि हों, इन्हें कभी भी गंभीर रूप से नहीं लिया गया। शहर के निकट बसे गाँवों में तो फिर भी विकास की संभावनाएं बनी रहती हैं, परंतु दूर-दराज के पिछड़े गाँवों के विकास के प्रति प्रशासन का ध्यान ही नहीं जाता। देखा जाए तो गाँवों की प्रगति से ही पूरे देश की प्रगति जुड़ी है, क्योंकि गाँवों से ही हमारी प्रत्येक आवश्यकता अनाज, वस्त्र, कागज, ईंधन, उद्योगों के लिए कच्चा माल आदि की पूर्ति होती है।

प्रश्न.
संभाषणीय
आपकी तथा परिवार के किसी बड़े सदस्य की दिनचर्या की तुलना कीजिए तथा समानता एवं अंतर बताइए।
उत्तर:
मैं दसवीं कक्षा की छात्रा हूँ और उसी स्कूल में पढ़ती हूँ, जहाँ मेरी माँ वाइस प्रिंसिपल हैं और हिंदी की प्राध्यापिका हैं। हम दोनों आठ बजे बस से स्कूल जाते हैं और दो बजे घर लौटते हैं। माँ सुबह जल्दी जगती हैं। नाश्ता और दोपहर का खाना बनाती हैं। मुझे जगाती हैं। स्वयं तैयार होती हैं। फिर हम स्कूल के लिए निकलते हैं। स्कूल से घर आकर मैं कपड़े बदलती हूँ, तब तक माँ खाना गरम करती हैं। खाना खाते समय हम दोनों स्कूल व मेरी पढ़ाई के विषय में बातें करते हैं। उसके बाद हम दोनों लगभग एक घंटा विश्राम करते हैं। चार बजे माँ फिर से काम पर लग जाती हैं।

विद्यार्थियों का गृहकार्य-कक्षाकार्य आदि जाँचना, कभी परीक्षा के लिए प्रश्नपत्र बनाना और कभी परीक्षा की उत्तर-पुस्तिकाएँ जाँचना, हर दिन माँ के पास स्कूल से संबंधित काम होता ही है। मैं भी उनके पास बैठकर पढ़ती हूँ। छह-साढ़े छह बजे माँ रात के खाने की तैयारी के लिए रसोई में जाती हैं। इस बीच मैं अपनी सहेलियों के साथ कुछ देर खेलने चली जाती हूँ। आठ बजे पिता जी के आने के बाद हम तीनों खाना खाते हैं। उसके बाद मैं पढ़ती हूँ और ग्यारह बजे सो जाती हूँ।

प्रश्न.
श्रवणीय
महाराष्ट्र में चलाए जाने वाले लघु उद्योगों की जानकारी रेडियो/दूरदर्शन पर सुनिए और इसके मुख्य मुद्दों को लिखिए।
उत्तर:
महाराष्ट्र में चलाए जाने वाले लघु उद्योग और क्षेत्र:

• कोल्हापुरी चप्पलें (कोल्हापुर)
• वरली पेंटिंग (ठाणे)
• लकड़ी के खिलौने (सावंतवाडी)
• गंजीफा (सावंतवाडी)
• चाँदी का काम (हुपरी)
• बीदरी काम (बीदर)
• दरी (विदर्भ)
• बाँस का सामान (रायगड, ठाणे)
• पीतल के संगीत वाद्य (ताल, झाँझ, घंटे)

ठेस Summary in Hindi

विषय-प्रवेश : कलाकार किसी भी धर्म, जाति और वर्ग का हो, उसे अपनी कला पर अभिमान होता है। वह स्वाभिमान के मूल्य को समझता है और उसकी रक्षा के लिए हमेशा तत्पर रहता है। जाति या धर्म के नाम पर जब उसके स्वाभिमान पर आघात होता है तो वह उसे बरदाश्त नहीं करता।

प्रस्तुत कहानी में सिरचन नामक एक ग्रामीण कलाकार का वर्णन किया गया है। वह मोथी घास और पटेर की रंगीन शीतलपाटी (चटाई), बाँस की तीलियों की झिलमिलाती चिक, सतरंगे डोर के मोढ़े, भूसी-चुन्नी रखने के लिए पूँज की रस्सी के बड़े-बड़े जाले, ताल के सूखे पत्तों की छतरी-टोपी आदि उपयोगी वस्तुएँ बनाता है। ये वस्तुएँ बनाकर वह अपनी आजीविका कमाता है। स्वाभिमानी होने के कारण वह हर परिस्थिति में अपने स्वाभिमान की रक्षा करता है।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 3 Shram Sadhana Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 3 श्रम साधना Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 3 श्रम साधना Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 3 श्रम साधना Textbook Questions and Answers

कृति

(कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए 

*सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
उत्तर लिखिए:
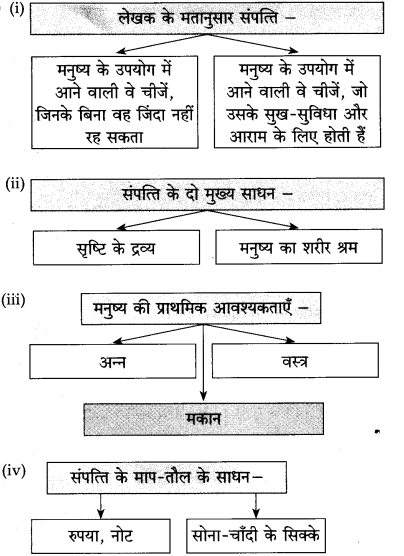
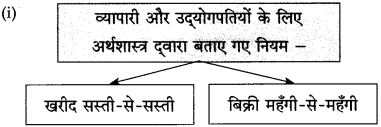
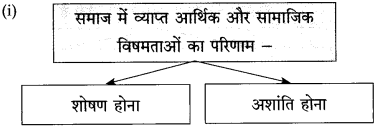
१. व्यापारी और उद्योगपतियों के लिए अर्थशास्त्र द्वारा बनाए गए नये नियम –
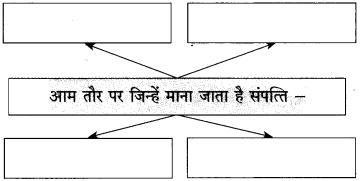
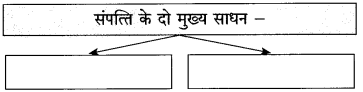
२. संपत्ति के दो मुख्य साधन –
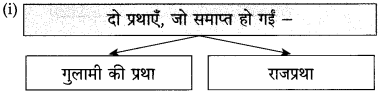
३. समाप्त हुईं दो प्रथाएँ –
४. कल्याणकारी राज्य का अर्थ –
उत्तर:
कल्याणकारी राज्य का अर्थ – सब तरह के दुर्बलों को राजसत्ता द्वारा मदद दिया जाना।

प्रश्न 2.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
तुलना कीजिए:
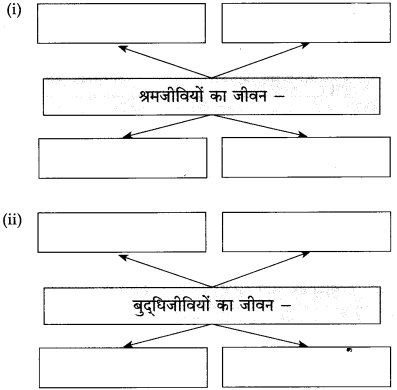
बुद्धिजीवी – श्रमजीवी
1. …………………. 2. ………………….
1. …………………. 2. ………………….
उत्तर:
बुद्धिजीवी – श्रमजीवी
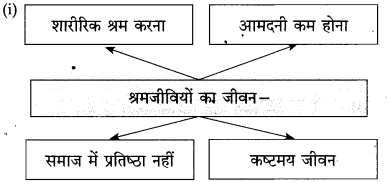
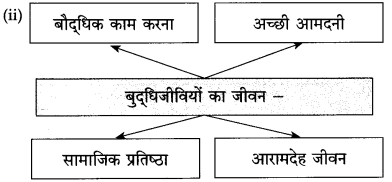
1. बौद्धिक काम करना। -1. शारीरिक श्रम करना।
2. अधिक आमदनी, प्रतिष्ठित एवं सुखमय जीवन। – 2. आमदनी कम, प्रतिष्ठा नहीं, कष्टमय जीवन।

प्रश्न 4.
लिखिए:

उत्तर:

प्रश्न 5.
पाठ में प्रयुक्त ‘इक’ प्रत्यययुक्त शब्दों को ढूँढ़कर लिखिए तथा उनमें से किन्हीं चार का स्वतंत्र वाक्यों में प्रयोग कीजिए।
उत्तर:

प्रश्न 6.
पाठ में कुछ ऐसे शब्द हैं, जिनके विलोम शब्द भी पाठ में ही प्रयुक्त हुए हैं, ऐसे शब्द ढूँढ़कर लिखिए।
उत्तर:
(i) हाड़ × माँस
(ii) प्रत्यक्ष × अप्रत्यक्ष
(iii) देश × विदेश
(iv) हाथ × पैर
(v) स्वार्थ × परार्थ
(vi) अमीर × गरीब।

अभिव्यक्ति
‘समाज परोपकार वृत्ति के बल पर ही ऊँचा उठ सकता है’, इस कथन से संबंधित अपने विचार लिखिए।
उत्तर:
हमारे शास्त्रों में परोपकार को बहुत महत्त्व दिया गया है। पेड़ों में फल लगना, नदियों के जल का बहना परोपकार का ही एक रूप है। इसी तरह सज्जन व्यक्तियों की संपत्ति और इस शरीर को भी परोपकार में लगा देने के लिए कहा गया है। हमारे समाज में गरीब-अमीर हर प्रकार के व्यक्ति होते हैं। अनेक लोग ऐसे हैं जिन्हें भरपेट भोजन भी नहीं मिलता और कुछ लोग ऐसे हैं, जिनके पास इतनी संपत्ति है कि उन्हें स्वयं इसकी पूरी जानकारी नहीं है। मनुष्य में परोपकार की प्रवृत्ति जन्मजात होती है। प्यासे को पानी पिलाना और किसी भूखे को खाना खिला देना कौन नहीं चाहता।

यही परोपकार भावना है। हमारे देश में अनेक अस्पताल, अनेक शिक्षा संस्थाएँ परोपकार करने वाले लोगों के धन से चल रही हैं। समाज के कमजोर वर्ग के लिए तरह-तरह की संस्थाएँ काम कर रही हैं। इनका संचालन दान अथवा सहायता के रूप में प्राप्त धन से हो रहा है। हर युग में समाज के उत्थान के लिए परोपकारियों का सहयोग प्राप्त होता रहा है। यह सहयोग इसी तरह मिलता रहना चाहिए तभी हमारे समाज का उत्थान होगा।

भाषा बिंदु

प्रश्न 1.
निम्न वाक्यों में अधोरेखांकित शब्द समूह के लिए कोष्ठक में दिए गए मुहावरों में से उचित मुहावरे का चयन कर वाक्य फिर से लिखिए:
[इज्जत उतारना, हाथ फेरना, काँप उठना, तिलमिला जाना, दुम हिलाना, बोलबाला होना]

१. करामत अली हौले-से लक्ष्मी से स्नेह करने लगा।
वाक्य = ………………………………………
उत्तर:
वाक्य: करामत अली हौले-से लक्ष्मी पर हाथ फेरने लगा।

२. सार्वजनिक अस्पताल का खयाल आते ही मैं भयभीत हो गया ।
वाक्य = ………………………………………
उत्तर:
वाक्य: सार्वजनिक अस्पताल का ख्याल आते ही मैं काँप उठा।

३. क्या आपने मुझे अपमानित करने के लिए यहाँ बुलाया था ?
वाक्य = ………………………………………
उत्तर:
वाक्य: क्या आपने मेरी इज्जत उतारने के लिए यहाँ बुलाया था?

४. सिरचन को बुलाओ, चापलूसी करता हुआ हाजिर हो जाएगा।
वाक्य = ………………………………………
उत्तर:
वाक्य: सिरचन को बुलाओ, दुम हिलाता हुआ हाजिर हो जाएगा।

५. पंडित बुद्धिराम काकी को देखते ही क्रोध में आ गए।
वाक्य = ………………………………………
उत्तर:
वाक्य: पंडित बुद्धिराम काकी को देखते ही तिलमिला उठे।

प्रश्न 2.
निम्नलिखित मुहावरों का अर्थ लिखकर उनका अर्थपूर्ण वाक्यों में प्रयोग कीजिए
१. गुजर-बसर करना: ………………………………………
२. गला फाड़ना: ………………………………………
३. कलेजे में हूक उठना: ………………………………………
४. सीना तानकर खड़े रहना: ………………………………………
५. टाँग अड़ाना: ………………………………………
६. जेब ढीली होना: ………………………………………
७. निजात पाना: ………………………………………
८. फूट-फूटकर रोना: ………………………………………
९. मन तरंगायित होना: ………………………………………
१०. मुँह लटकाना: ………………………………………
उत्तर:
(i) गुजर-बसर करना।
अर्थ: जीविका चलाना।
वाक्य: पंडित घनश्याम किसी तरह गुजर-बसर कर लेते हैं।

(ii) गला फाड़ना।
अर्थ: ऊँची आवाज में बोलना।
वाक्य: बेटे ने पिता से कहा, “मैं आपकी बात सुन रहा हूँ,आप
नाहक गला फाड़ रहे हैं।”

(iii) कलेजे में हूक उठना।
अर्थ: कसक होना।
वाक्य: सेठ लक्खूमल जब भी जवान बेटे की हत्या की बात याद करते हैं, उनके कलेजे में हूक उठती है।

(iv) सीना तानकर खड़े रहना।
अर्थ: दृढ़तापूर्वक अड़े रहना।।
वाक्य: वह समाजसेवक निर्दोष लोगों की सहायता के लिए सीना तानकर खड़ा रहता हैं।

(v) टाँग अड़ानां।
अर्थ: कार्य में बाधा डालना।
वाक्य: किसी के बनते हुए काम में टाँग अड़ाना अच्छी बात नहीं है।

(vi) जेब ढीली होना।
अर्थ: काफी खर्च होना।
वाक्य: मरीज की बीमारी तो ठीक हो गई, पर अस्पताल का बिल भरने में जेब ढीली हो गई।

(vii) निजात पाना।
अर्थ: मुक्त होना।
वाक्य: आखिरकार लंबे अरसे बाद सेठजी लेन-देन के मुकदमे से निजात पा गए।

(viii) फूट-फूटकर रोना।
अर्थ: बिलखते हुए रोना।
वाक्य: बेटे के गायब हो जाने पर माँ फूट-फूटकर रोई थी।

(ix) मन तरंगित होना।
अर्थ: मौज में आना।
वाक्य: बेटे की अच्छे वेतनवाली नौकरी लग जाने की बात सुनकर पिता का मन तरंगित हो गया।

(x) मुँह लटकाना।
अर्थ: चिंता, दुख से सिर नीचा कर लेना।
वाक्य: पिता जब निकम्मे बेटे को फटकारता है, तो वह मुँह लटकाकर सुनता रहता है।

प्रश्न 3.
पाठ्यपुस्तक में आए मुहावरों का अपने वाक्यों में प्रयोग कीजिए।
उत्तर:
(इसके लिए विद्यार्थी ‘नवनीत हिंदी (LL) उपयोजित लेखन, कक्षा दसवीं’ पुस्तक देखें।)

उपयोजित लेखन

निम्न शब्दों के आधार पर कहानी लेखन कीजिए
मिट्टी, चाँद, खरगोश, कागज।
उत्तर:
एक छोटा-सा गाँव था। गाँव के लोग खेती-बारी से अपना गुजारा करते थे। लोगों के पास छोटे-छोटे खेत थे। वे अपने खेतों में साल में दो फसलें उगाते थे। खेतों में उत्पन्न अनाज से साल भर बड़ी मुश्किल से उनका काम चलता था। इस गाँव के लोगों में आपस में बहुत प्रेम-भाव था। गाँव में कुछ लोग ऐसे थे, जिनके पास खेत भी नहीं थे। उनका जीवन बहुत कष्टमय था। इन्हीं में से एक था आत्माराम। आत्माराम गाँव के किसानों के खेत में काम करके कुछ कमा लिया करता था।

एक दिन गाँव में एक साधु महाराज आए। आत्माराम ने साधु के सामने अपनी समस्या रखते हुए कहा, “महाराज कुछ ऐसा उपाय बताइए, जिसमें मैं चार पैसे कमाकर अपना और अपने परिवार का पेट पाल सकूँ।” साधु महाराज ने कहा, “ले यह मिट्टी। यह मिट्टी तेरे लिए सोना बनेगी।” आत्माराम बोला, “मैं समझा नहीं, महाराज। ऐसी मिट्टी तो गाँव में बहुत है, क्या करूँ इसका?” साधु ने कहा, “मिट्टी खोद। उससे खिलौने बना और बाजार में बेच। तेरा भला होगा।” आत्माराम ने साधु को धन्यवाद दिया।

वह मिट्टी से खरगोश, चूहा, तोता, गुड़िया, गुड्डा बनाता और बाजार में बेच आता। इससे उसे अच्छी आय होने लगी। अब उसकी जिंदगी आराम से चलने लगी।

एक दिन बाजार में एक लड़के ने उससे चाँद के खिलौने की माँग की। यह खिलौना तो उसने कभी बनाया ही नहीं था। बात आई-गई हो गई।

एक दिन आत्माराम ने चाँद की शक्ल का पतंग आकाश में उड़ते हुए देखा। फिर क्या था! अब आत्माराम ने मिट्टी के खिलौने बनाने बंद कर दिए और कागज के पतंग, खरगोश, तोते, बिल्ली, गुड़िया, गुड्डा आदि बनाने लगा। अब उसके खिलौनों का वजन हल्का हो गया और उसकी कमाई भारी हो गई।

Hindi Lokbharti 10th Textbook Solutions Chapter 3 श्रम साधना Additional Important Questions and Answers

गद्यांश क्र.1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

आकृति पूर्ण कीजिए:

(स्वाध्याय में दिए गए ‘उत्तर लिखिए’ प्रश्न को कृतिस्वरूप में दिया गया है।)


उत्तर:

(ii)

(iii)

कृति 2: (आकलन)

प्रश्न 1.
(i) संजाल पूर्ण कीजिए:

उत्तर:

(ii) लिखिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:
(i)

(ii)

(iii)

(iv)

उत्तर:

कृति 3: (शब्द संपदा)

प्रश्न 1.
शब्दों के समानार्थी शब्द लिखिए:
(i) प्रथा =
(ii) युद्ध =
(iii) हुकूमत =
(iv) गुलामी =
उत्तर:
(i) प्रथा = रिवाज
(ii) युद्ध = लड़ाई
(iii) हुकूमत = शासन
(iv) गुलामी = दासता।

प्रश्न 2.
विरुद्धार्थी शब्द लिखिए:
(i) गौण x
(ii) अनेक x
(iii) अप्राकृतिक x
(iv) बादशाह x
उत्तर:
(i) गौण x मुख्य
(ii) अनेक x एक
(iii) अप्राकृतिक x कृत्रिम
(iv) बादशाह x भिखारी।

प्रश्न 3.
लिंग पहचान कर लिखिए:
(i) मकान – ………………………
(i) संपत्ति – …………………………
उत्तर:
(i) मकान – पुल्लिग
(ii) संपत्ति – स्त्रीलिंग।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘राजाओं और बादशाहों का राज’ के बारे में अपने विचार 25 से 30 शब्दों में व्यक्त कीजिए।
उत्तर:
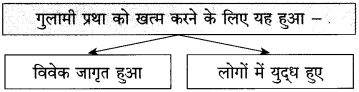
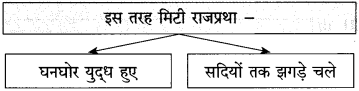
स्वतंत्रता प्राप्ति के पहले हमारे देश में छोटी-बडी अनेक रियासतें थीं। राजा, बादशाह और तालुकेदार इन रियासतों के मालिक थे। इनके राज में रहने वाली जनता इनकी प्रजा कहलाती थी। राजा और बादशाह जनता से तरह-तरह के कर वसूल करते थे और कर अदा न कर पाने पर जनता पर तरह-तरह के अत्याचार करते थे। एक तरह से जनता को ये अपना गुलाम समझते थे और उसका शोषण करने में जरा भी नहीं झिझकते थे। जनता इनसे त्रस्त थी।

इसके अलावा ये राजा और बादशाह अपने स्वार्थ के लिए आपस में लड़ते-भिड़ते थे और मौका मिलने पर एक-दूसरे की रियासतों पर कब्जा कर जनता में लूटपाट किया करते थे। असहाय जनता की कोई सुनने वाला नहीं था। आजादी मिलने के बाद इन छोटी-छोटी रियासतों को खत्म कर भारत संघ में मिला लिया गया। इसके बाद इन राजाओं और बादशाहों का राज खत्म हो गया। इसके साथ ही समाप्त हो गया जनता पर इनका अत्याचार। फिर तो प्रजातंत्र में न कोई किसी का राजा रहा न कोई किसी की प्रजा। सबको समान अधिकार उपलब्ध हो गए।

गद्यांश क्र. 2
प्रश्न निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
अकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
उत्तर लिखिए:
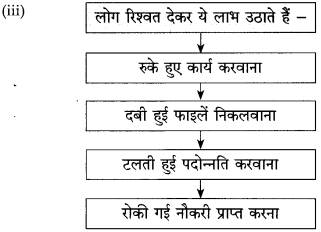
(i) जो संपत्ति का निर्माण करते हैं, वे – [ ]
(ii) धन इकट्ठा होता है इनके पास – [ ]
(iii) बौद्धिक काम से अपना भरण-पोषण करने वाले लोग – [ ]
(iv) समाज के लिए ये दोनों जरूरी हैं – [ ]
उत्तर:
(i) जो संपत्ति का निर्माण करते हैं, वे माण – [मजदूर]
(ii) धन इकट्ठा होता है इनके पास – [व्यवस्था करने वाले]
(iii) बौद्धिक काम से अपना भरण-पोषण करने वाले लोग – [मंत्री, राज्य के कर्मचारी, क्लर्क, न्यायाधीश, वकील, डॉक्टर, अध्यापक, व्यापारी]
(iv) समाज के लिए ये दोनों जरूरी है – [श्रमजीवी और बुद्धिजीवी]

प्रश्न 3.
आकृति पूर्ण कीजिए:
(i)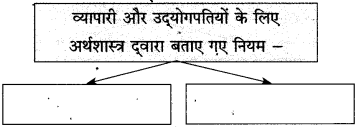
उत्तर:

(ii) दो ऐसे प्रश्न बनाकर लिखिए, जिनके उत्तर निम्नलिखित शब्द हों:
(1) अन्न
(2) श्रम जीवियों पर
उत्तर:
(1) वर्षभर मेहनत कर किसान क्या पैदा करता है?
(2) बुद्धिजीवियों का जीवन किन लोगों पर आधारित है?

कृति 3: (शब्द संपदा)

प्रश्न 1.
गद्यांश में आए शब्द-युग्म ढूँढ़कर लिखिए।
(i) ……………………..
(ii) ……………………..
(iii) ……………………..
(iv) ……………………..
उत्तर:
(i) लेन – देन
(ii) राज – काज
(iii) ऊँचे – ऊँचे
(iv) भरण – पोषण।

प्रश्न 2.
विरुद्धार्थी शब्द लिखिए:
(i) प्रत्यक्ष × ……………………..
(ii) धनवान × ……………………..
(iii) ऊँचा × ……………………..
(iv) दुर्भाग्य × ……………………..
उत्तर:
(i) प्रत्यक्ष × परोक्ष
(ii) धनवान × निर्धन
(iii) ऊँचा × नीचा
(iv) दुर्भाग्य × सौभाग्य।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘शारीरिक श्रम का महत्त्व’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
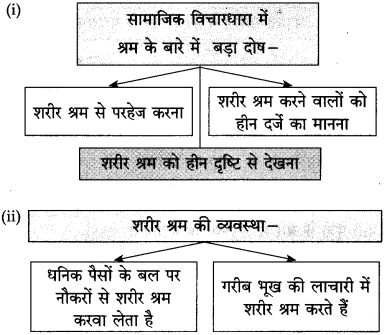
श्रम दो प्रकार का होता है। शारीरिक श्रम और बौद्धिक श्रम। पुराने जमाने में पढ़े-लिखे लोगों की संख्या कम थी, इसलिए लोगों को शारीरिक श्रम का ही सहारा था। वे जीवन-यापन के लिए छोटा-मोटा काम करके अपना गुजारा कर लेते थे। शिक्षा की समुचित व्यवस्था हो जाने के बाद पढ़े-लिखे लोगों की संख्या में अंधाधुंध वृद्धि हुई है। हर शिक्षित व्यक्ति चाहता है कि उसे ऐसी नौकरी मिले, जिसमें उसे शारीरिक श्रम न करना पड़े। शारीरिक श्रम वाला काम कोई करना नहीं चाहता। इसलिए देश में लाखों नवयुवक बेरोजगार हैं। यह लोगों के शारीरिक श्रम से परहेज रखने का परिणाम है।

लोगों को शारीरिक श्रम का महत्त्व समझना जरूरी है। बुद्धि के बल पर बड़ीबड़ी योजनाएँ बनाई जा सकती हैं, पर उनका कार्यान्वयन करने के लिए शारीरिक श्रम की ही आवश्यकता होती है। छोटी-छोटी चीजों से लेकर बड़ी-बड़ी चीजों का निर्माण केवल शारीरिक श्रम से ही हो सकता है। जो व्यक्ति इस रहस्य को समझते हैं, वे शारीरिक श्रम को महत्त्व देते हैं। अनेक पढ़े-लिखे लोग अपना व्यवसाय अथवा छोटा-मोटा काम शुरू करके अपना जीवन-यापन कर रहे हैं और बौद्धिक श्रम के साथ शारीरिक श्रम उनका साथ दे रहा है। स्वरोजगार के द्वारा वे स्वयं भी काम कर रहे हैं और दूसरों को भी रोजगार दे रहे हैं।

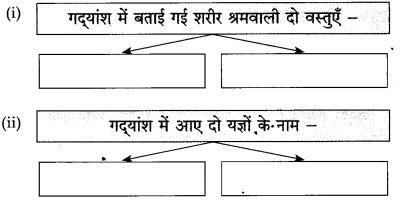
गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

आकृति पूर्ण कीजिए:



उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i)
(ii)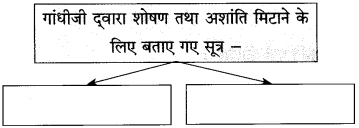
उत्तर:

(ii)

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) आम = …………………….
(ii) श्रम = …………………….
(iii) हिस्सा = …………………….
(iv) जगत = …………………….
उत्तर:
(i) आम = सामान्य
(ii) श्रम = मेहनत
(iii) हिस्सा = भाग
(iv) जगत = संसार।

प्रश्न 2.
निम्नलिखित शब्दों में से प्रत्यय और मूल शब्द अलग करके लिखिए:
(i) योग्यता
(i) अल्पतम
(ii) बुनियादी
(iv) सामाजिक
उत्तर:
(i) योग्य + ता (ता)
(ii) अल्प + तम (तम)
(iii) बुनियाद + ई (ई)
(iv) समाज + इक (इक)।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘समाज परोपकार वृत्ति के बल पर ही ऊँचा उठ सकता है’- इस कथन से संबंधित अपने विचार 25 से 30 शब्दों में लिखिए।

गद्यांश क्र.4
प्रश्न. निम्नलिखित पठिक अट्यार पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

आकृति पूर्ण कीजिए:

(iii)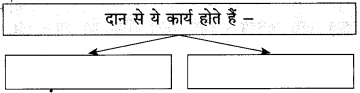
उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:
(i) अर्थशास्त्रियों के अनुसार उत्पादन की प्रेरणा के लिए यह करना होगा – [ ]
(ii) पूँजी के बारे में अनुभव यह बताता है – [ ]
(iii) लेखक के अनुसार स्वार्थ का अर्थ – [ ]
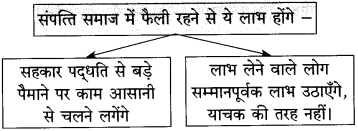
(iv) समाज इस वृत्ति के बल पर ऊँचा उठ सकता है – [ ]
उत्तर:
(i) अर्थशास्त्रियों के अनुसार उत्पादन की प्रेरणा के लिए यह करना होगा – [व्यक्ति को स्वार्थ के लिए अवसर देने होंगे।
(ii) पूँजी के बारे में अनुभव यह बताता है – [पूँजी गरीबी या बेकारी की समस्या हल नहीं कर सकी है]
(iii) लेखक के अनुसार स्वार्थ का अर्थ – [परार्थ की हानि]
(iv) समाज इस वृत्ति के बल पर ऊँचा उठ सकता है – [परोपकार की वृत्ति]

प्रश्न 3.
गद्यांश के वाक्यों को उचित क्रम से लिखिए:
(i) देखना है कि समाज का कल्याण किस वृत्ति से होगा।
(ii) बिना शरीर श्रम किए उस सामग्री का उपयोग करने का न्यायोचित अधिकार हमें नहीं मिलता।
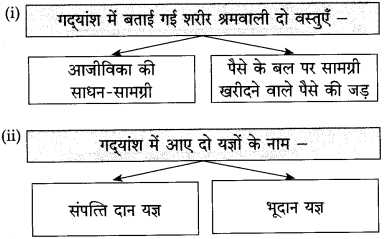
(iii) आजीविका की साधन-सामग्री किसी-न-किसी के श्रम के बिना हो ही नहीं सकती।
(iv) नैतिक दृष्टि से स्वार्थवृत्ति का पोषण करना योग्य नहीं है।
उत्तर:
(i) आजीविका की साधन-सामग्री किसी-न-किसी के श्रम के बिना हो ही नहीं सकती।
(ii) बिना शरीर श्रम किए उस सामग्री का उपयोग करने का न्यायोचित अधिकार हमें नहीं मिलता।
(iii) नैतिक दृष्टि से स्वार्थवृत्ति का पोषण करना योग्य नहीं है।
(iv) देखना है कि समाज का कल्याण किस वृत्ति से होगा।

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्द समूह के लिए गद्यांश से चुनकर एक-एक शब्द लिखिए:
(i) वह दौलत, जो किसी के अधिकार में हो और जो खरीदी या बेची जा सकती हो-
(ii) दूसरों के उपकार या भलाई का काम’ –
(iii) ऐसी बात-जिसमें केवल अपना हित हो –
(iv) वह धन-जिससे कोई व्यवसाय आरंभ किया गया हो –
उत्तर:
(i) संपत्ति
(ii) परोपकार
(iii) स्वार्थ
(iv) पूँजी।

प्रश्न 2.
विरुद्धार्थी शब्द लिखिए:
(i) थोड़ा × ……………………
(ii) दोषपूर्ण × ……………………
(iii) योग्य × ……………………
(iv) गरीबी × ……………………
उत्तर:
(i) थोड़ा × बहुत
(ii) दोषपूर्ण × निर्दोष
(iii) योग्य × अयोग्य
(iv) गरीबी × अमीरी।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘मेवे फलते श्रम की डाल’ विषय पर 25 से 30 शब्दों में अपनी लिखित अभिव्यक्ति दीजिए।
उत्तर:
श्रम दो प्रकार का होता है। एक शारीरिक श्रम और दूसरा बौद्धिक श्रम। दोनों प्रकार के श्रम का अपना-अपना महत्त्व है। श्रम को सदा महत्त्व दिया गया है। श्रम करने वाला व्यक्ति परिश्रम करके अपना भरण-पोषण करता है और शान से रहता है। जो श्रम करता है, वह स्वयं अपने भाग्य का निर्माण करता है। वह अपना खून-पसीना एक कर मेहनत की पवित्र रोटी खाता है। मेहनत की जिंदगी ही सच्ची जिंदगी है।

श्रम करने वाला व्यक्ति काम से कभी नहीं घबराता। उसके सामने जैसा भी काम आता है, उसे वह लगन और मेहनत से पूरा करता है। विद्यार्थी श्रम द्वारा ही परीक्षा में सफलता प्राप्त करते हैं। मजदूर, किसान, इंजीनियर, वैज्ञानिक, व्यापारी, खिलाड़ी आदि सबकी प्रगति में श्रम का ही हाथ होता है। हमें याद रखना चाहिए कि श्रम कभी बेकार नहीं जाता। ईमानदारी से किए गए श्रम का तुरंत लाभ भले न मिले, पर कभी-न-कभी उसका फल मिलकर ही रहता है। श्रम करने वाले ही मेवों का स्वाद चखते हैं।

गद्यांश क्र. 5
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
निम्नलिखित प्रश्नों के उत्तर लिखिए:
(i) शरीर श्रम के लिए क्या जरूरी है?
(ii) श्रम की प्रतिष्ठा बढ़ाना किसके हाथ है?
उत्तर:
(i) शरीर श्रम के लिए जरूरी है दिल में प्रीति होना।
(ii) श्रम की प्रतिष्ठा बढ़ाना श्रमिक के हाथ है।

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
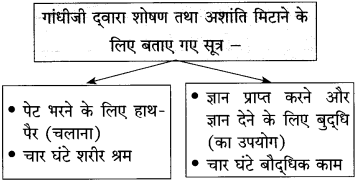
(i) गांधीजी की मान्यता के अनुसार। हर व्यक्ति को यह करना चाहिए – [ ]
(ii) अब कुछ समय से जगत के सामने दया की जगह यह विचार आया है – [ ]
(iii) महात्माजी द्वारा दी गई प्रसिद्ध विचारधारा – [ ]
(iv) अहिंसा के मार्ग से यह प्रश्न हल हो सकता है – [ ]
उत्तर;
(i) गांधीजी की मान्यता के अनुसार हर व्यक्ति को यह करना चाहिए – [उत्पादक श्रम]
(ii) अब कुछ समय से जगत के सामने दया की जगह यह विचार आया है – [समता का]
(iii) महात्माजी द्वारा दी गई गई प्रसिद्ध विचारधारा – [अहिंसा]
(iv) अहिंसा के मार्ग से यह प्रश्न हल हो सकता है – [विषमता का]

प्रश्न 2.
निम्नलिखित वाक्यों के आधार पर प्रश्न बनाइए:
(i) गांधीजी ने श्रम और श्रमिक की प्रतिष्ठा स्थापित करने के लिए ही रचनात्मक कार्यों को लोक चेतना का माध्यम बनाया।
(ii) कानून से मानवोचित गुणों का विकास नहीं हो सकता?
(iii) अहिंसा के प्रभाव का कुछ अनुभव भी हम कर सकते हैं।
(iv) आर्थिक सामाजिक समता का प्रश्न अहिंसा के मार्ग से सुलझेगा।
उत्तर:
(i) गांधीजी ने किन बातों की प्रतिष्ठा स्थापित करने के लिए रचनात्मक कार्यों को लोक चेतना का माध्यम बनाया?
(ii) कानून से किन गुणों का विकास नहीं हो सकता?
(iii) किसके प्रभाव का अनुभव हम कर सकते हैं?
(iv) आर्थिक सामाजिक समता का प्रश्न किस मार्ग से सुलझेगा?

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के वचन पहचान कर लिखिए:
(i) बच्चा – ………………….
(ii) विषमताएँ – ………………….
(iii) पैसे – ………………….
(iv) धनिक – ………………….
उत्तर:
(i) बच्चा – एकवचन
(ii) विषमताएँ – बहुवचन
(ii) पैसे – बहुवचन
(iv) धनिक – एकवचन।

प्रश्न 2.
गद्यांश में प्रयुक्त ‘इक’ प्रत्यययुक्त शब्दों को ढूँढ़कर स्वतंत्र वाक्यों में प्रयोग कीजिए:
(i) ………………….
(ii) ………………….
(iii) ………………….
(iv) ………………….
(v) ………………….
(vi) ………………….
उत्तर:
(i) आर्थिक
(ii) प्राकृतिक
(iii) श्रमिक
(iv) सामाजिक
(v) प्राथमिक
(vi) बौद्धिक

(i) आर्थिक: किसानों की आर्थिक दशा सुधारने के लिए कुछ करो।
(ii) प्राकृतिक: कश्मीर की घाटी प्राकृतिक दृश्यों से भरी पड़ी है।
(iii) श्रमिक: कारखाने में काम करने वाले श्रमिक का काम बहुत मेहनत का होता है।
(iv) सामाजिक: मनुष्य एक सामाजिक प्राणी है।
(v) प्राथमिक: घायल व्यक्ति को तुरंत प्राथमिक चिकित्सा की जरूरत होती है।
(vi) बौद्धिक: हर व्यक्ति की बौद्धिक क्षमता भिन्न-भिन्न होती है।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
शारीरिक श्रम स्वास्थ के लिए अति उत्तम’ विषय पर अपने। विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
शारीरिक श्रम का अर्थ है, वह मेहनत, जिसमें हाथ-पैर के सहयोग से काम संपन्न हो। किसान, मजदूर, क्ली, ठेलेवाले, शारीरिक मेहनत करते हैं। वैसे हर व्यक्ति जाने-अनजाने थोड़ी बहुत शारीरिक मेहनत करता ही है। अपने घर की सफाई करना, खाना बनाना, बरतन धोना और बाजार-हाट से सामान-सब्जी लाना भी श्रम है। कुछ शारीरिक काम करने वाले लोग धूप में खेतों में काम करते हैं।

कुछ कारखानों में पसीना बहाकर मेहनत करते हैं। कुछ अनाज के बोरे ३ गाड़ियों पर चढ़ाते-उतारते हैं। कुछ सड़कों पर हथौड़े लेकर पत्थर तोड़ते ३ या खुदाई करते हैं। ये मोटा खाते और मोटा पहनते हैं, पर शारीरिक ३ रूप से स्वस्थ होते हैं। दूसरी ओर वे लोग हैं, जो कोई शारीरिक श्रम ३ नहीं करते। वे पौष्टिक भोजन करते हैं, नर्म गद्देदार बिछौनों पर सोते B हैं, पर बीमारी के कारण उन्हें नींद नहीं आती। भोजन नहीं पचता।

डॉक्टर इन्हें कम भोजन करने और ज्यादा दवाइयाँ लेने के लिए कहते हैं। शारीरिक श्रम के अभाव में इनका जीवन कष्टप्रद बन जाता है।

डॉक्टर इन्हें हाथ-पैर चलाने और व्यायाम करने की सलाह देते हैं। ऐसे 3 लोगों को शारीरिक श्रम करने वालों से सबक लेना चाहिए, जो

अपनी मेहनत के बल पर भले-चंगे बने रहते हैं। इस प्रकार शारीरिक , श्रम अच्छे स्वाथ्य की कुंजी है।

भाषा अध्ययन (व्याकरण)

प्रश्न, सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:

प्रश्न.
अधोरेखांकित शब्दों के शब्दभेद पहचानकर लिखिए:
(i) गांधीजी ने यह काम श्रम और श्रमिक की प्रतिष्ठा कायम करने के लिए किया।
(ii) विषमता दूर करने के लिए प्रभावशाली उपाय करना चाहिए।
उत्तर:
(1) गांधीजी – व्यक्तिवाचक संज्ञा।
(ii) प्रभावशाली – गुणवाचक विशेषण।

2. अव्यय:

प्रश्न.
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) फिर
(ii) कभी-कभी।
उत्तर:
(i) संपत्ति रूपी ये सब चीजें फिर कैसे बनती हैं?
(ii) बुद्धिजीवियों को भी कभी-कभी शरीर श्रम करना पड़ता है।

3. संधि:

प्रश्न.
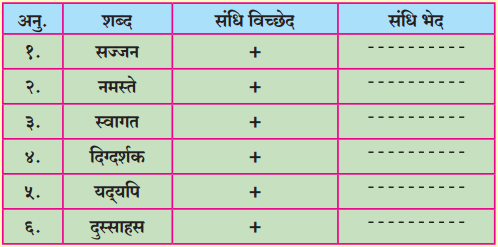
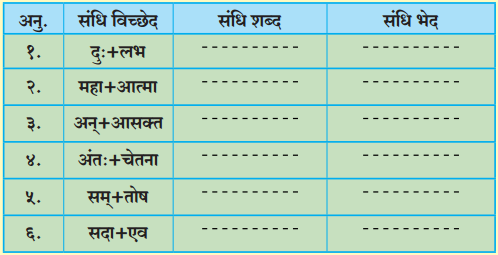
कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
……………………	स्व + अर्थ	……………………
अथवा
……………………	सम् + पूर्ण	……………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
स्वार्थ	स्व + अर्थ	स्वर संधि
अथवा
सपूर्ण	सम् + पूर्ण	व्यंजन संधि

4. सहायक क्रिया:

प्रश्न.
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए:
(i) प्रतिदिन समय पर अपना काम किया करो।
(ii) वह अपनी जमा-पूँजी भी गंवा बैठा।
उत्तर:
सहायक क्रिया – मूल रूप
(i) करो – करना
(ii) बैठा – बैठना

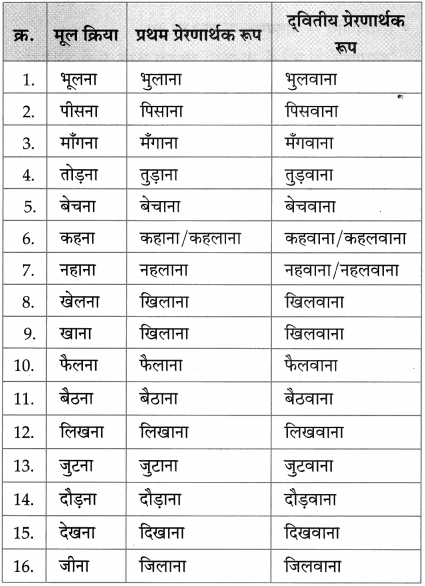
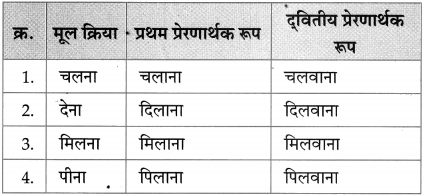
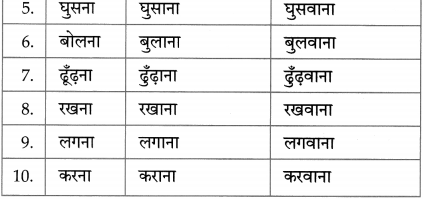
5. प्रेरणार्थक क्रिया:

प्रश्न.
निम्नलिखित- क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) खौलना
(ii) डूबना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – दवितीय प्रेरणार्थक रूप
(i) खौलना – खौलाना – खौलवाना
(ii) डूबना – डुबाना – डुबवाना

6. मुहावरे:

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) मुंह फेरना
(ii) रट लगाना।
उत्तर:
(i) मुँह फेरना।
अर्थ: उपेक्षा करना।
वाक्य: कर्मचारी अपनी माँग लेकर सेठ जी के पास जाते तो वे उनसे बात करने के बजाय मुँह फेर लेते।

(ii) रट लगाना।
अर्थ: एक ही बात बार-बार कहना।
वाक्य: मुर्गा बहुत सबेरे ‘कुकड़-फूं’ की रट लगाता है।

प्रश्न 2.
अधोरेखांकित वाक्यांश के लिए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (फूला न समाना, भार होना, कान में डालना)
(i) मुनीम जी ने बड़े बाबू को बात पहुँचाई।
(ii) मेडिकल में प्रवेश मिल जाने पर नकुल बहुत प्रसन्न हुआ।
उत्तर:
(i) मुनीम जी ने बात बड़े बाबू के कान में डाल दी।
(ii) मेडिकल में प्रवेश मिल जाने पर नकुल फूला न समाया।

7. कारक:

प्रश्न.
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उसका भेद लिखिए:
(i) गुलामी की प्रथा संसार भर में हजारों वर्षों तक चलती रही।
(ii) गांधीजी ने श्रम और श्रमिकों की प्रतिष्ठा स्थापित करने का काम किया।
उत्तर:
(i) गुलामी की-संबंध कारक
(ii) गांधीजी ने-कर्ता कारक।

8. विरामचिह्न:

प्रश्न.
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
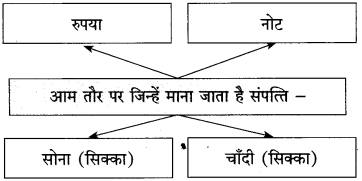
(i) आम तौर से माना जाता है कि रुपया नोट और सोना-चाँदी का सिक्का ही संपत्ति है
(ii) अर्थशास्त्र ने यह नियम बताया है कि खरीद सस्ती से सस्ती हो और बिक्री महँगी से महँगी
उत्तर:
(i) आम तौर से माना जाता है कि रुपया, नोट और सोना-चाँदी का सिक्का ही संपत्ति है।
(ii) अर्थशास्त्र ने यह नियम बनाया है कि खरीद सस्ती-से-सस्ती हो और बिक्री महँगी से महँगी।

9. काल परिवर्तन:

प्रश्न.
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) बहुत से लोग अपनी आजीविका शरीर श्रम से चलाते हैं। (अपूर्ण भूतकाल)
(ii) जिनके पास संपत्ति है, वे आराम से रह रहे हैं। (सामान्य भविष्यकाल)
उत्तर:
(i) बहुत से लोग अपनी आजीविका शरीर श्रम से चला रहे थे।
(ii) जिनके पास संपत्ति है, वे आराम से रहेंगे।

10. वाक्य भेद:

प्रश्न 1.
निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए:
(i) हमारी विचारधारा में बड़ा भारी दोष है।
(ii) लोग शरीर श्रम करना नहीं चाहते और इसे हीन दृष्टि से देखते हैं।
(iii) जिस श्रम में समाज को जिंदा रखने की क्षमता है, उस श्रम का सही मूल्य श्रमिक जान लेगा तो देश में आर्थिक क्रांति होने में देर नहीं लगेगी।
(iv) सामाजिक समता का प्रश्न अहिंसा के मार्ग से सुलझेगा।
उत्तर:
(i) सरल वाक्य
(ii) संयुक्त वाक्य
(iii) मिश्र वाक्य
(iv) सरल वाक्य।

प्रश्न 2.
निम्नलिखित वाक्यों का दी गई सूचना के अनुसार अर्थ के आधार पर परिवर्तन कीजिए:
(i) गरीब भूख की लाचारी से श्रम करता है। (संदेहवाचक वाक्य)
(ii) अब राजप्रथा मिट गई। (आज्ञावाचक वाक्य)
उत्तर:
(i) शायद गरीब भूख की लाचारी से श्रम करता है।
(ii) अब’राजप्रथा मिटा दो। 11. वाक्य शुद्धिकरण:

प्रश्न 3.
निम्नलिखित वाक्य शुद्ध करके वाक्य फिर से लिखिए:
(i) इस सम्बन्ध में कुछ भाई अमेरिका का उदाहरण पेस करते हैं।
(ii) वही आधार पे भारत को कल्याणकारी राज्य बनाने की बात चली है
उत्तर:
(i) इस संबंध में कुछ भाई अमेरिका का उदाहरण पेश करते हैं।
(ii) उसी आधार पर भारत को कल्याणकारी राज्य बनाने की बात चली है।

उपक्रम/कृति/परियोजना

पठनीय
महात्मा गांधी के श्रमप्रतिष्ठा और अहिंसा संबंधी विचार पढ़कर चर्चा कीजिए।

श्रवणीय
आर्थिक विषमता को दूर करने वाले उपायों के बारे में सुनकर कक्षा में सुनाइए।

संभाषणीय
‘वर्तमान युग में सभी बच्चों के लिए खेल-कूद और शिक्षा के समान अवसर प्राप्त हैं’ विषय पर चर्चा करते हुए अपना मत प्रस्तुत कीजिए।

श्रम साधना Summary in Hindi

विषय-प्रवेश : प्राचीन काल से आज तक सामाजिक और राजनैतिक व्यवस्था में अनेक परिवर्तन हुए हैं। इसके साथ ही संपत्ति तथा उसके निर्माण में लगने वाली शक्तियों के बीच तरह-तरह की असमानताएँ भी रही हैं। श्रमजीवियों तथा व्यापारियों की आर्थिक स्थिति में जमीन-आसमान का अंतर रहा है। प्रस्तुत निबंध में लेखक ने मानवीय जीवन, संपत्ति, संपत्ति के स्वामित्व, मनुष्य की प्राथमिक आवश्यकताओं तथा शारीरिक एवं बौद्धिक श्रम आदि का विस्तृत विवेचन किया है। प्रस्तुत वैचारिक निबंध में श्रम की प्रतिष्ठा स्थापित करते हुए सामाजिक एवं आर्थिक समानता पर बल दिया गया है।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer