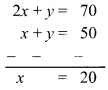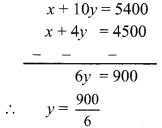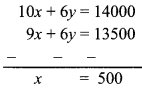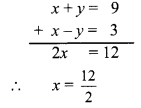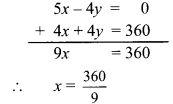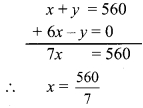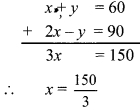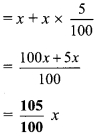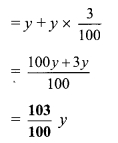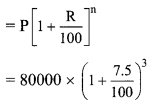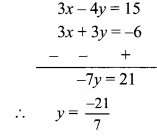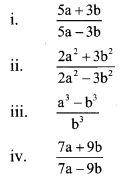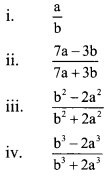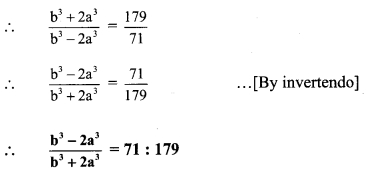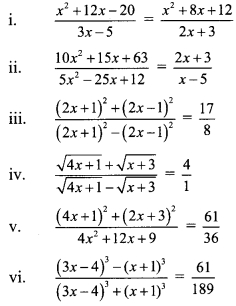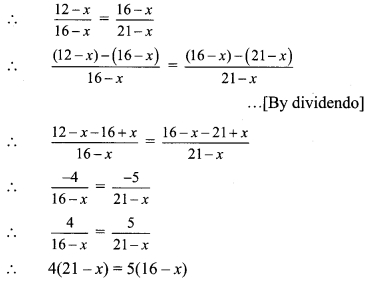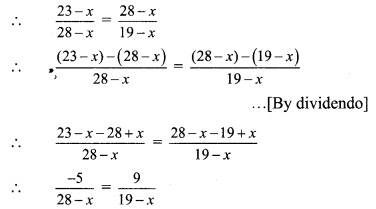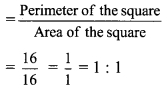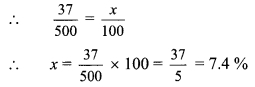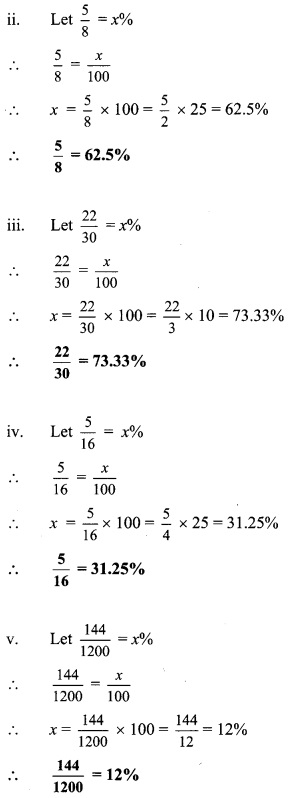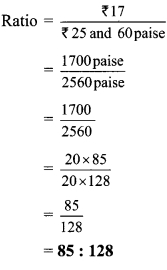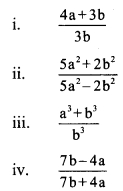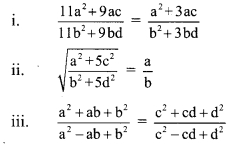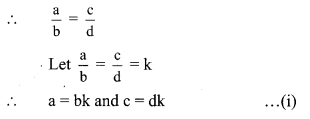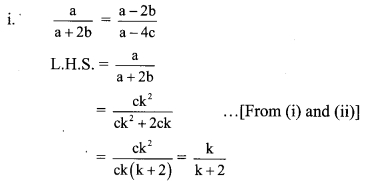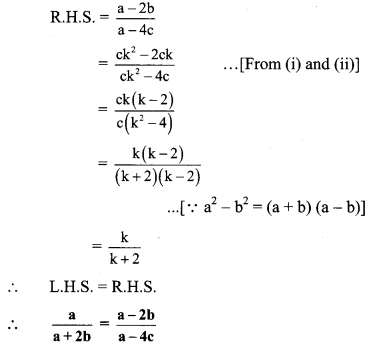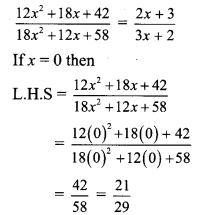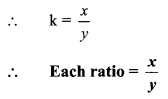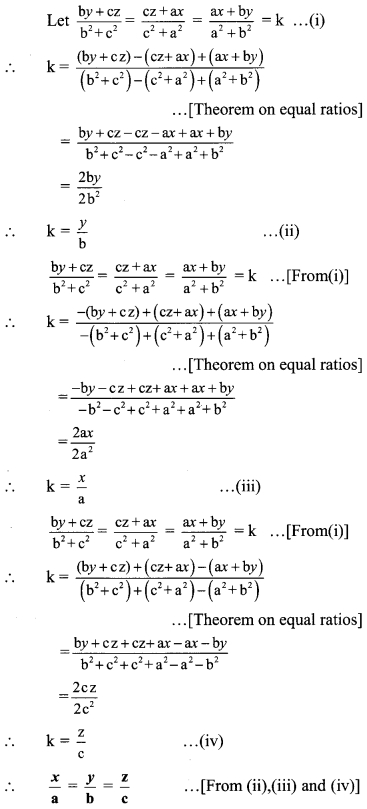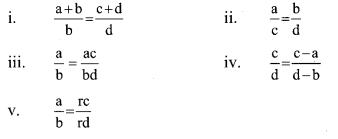Prasanna

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 11.1 8th Std Maths Answers Solutions Chapter 11 Statistics.

Statistics Class 8 Maths Chapter 11 Practice Set 11.1 Solutions Maharashtra Board

Std 8 Maths Practice Set 11.1 Chapter 11 Solutions Answers

Question 1.
The following table shows the number of saplings planted by 30 students. Fill in the boxes and find the average number of saplings planted by each student.

No. of saplings (Scores) xi	No. of students (frequency) fi	fi × xi
1	4	4
2	6	__
3	12	__
4	8	__
	N = __	∑ fi × xi = __

Solution:

No. of saplings (Scores) xi	No. of students (frequency) fi	fi × xi
1	4	4
2	6	12
3	12	36
4	8	32
	N = __	∑ fi × xi = 84

Question 2.
The following table shows the electricity (in units) used by 25 families of Eklara village in a month of May. Complete the table and answer the following questions.

Electricity used (Units) xi	No. of families (frequency) fi	fi × xi
30	4
45	6
60	12
75	8
90	3
	N = __	∑ fi × xi =

i. How many families use 45 units electricity?
ii. State the score, the frequency of which is 5.
iii. Find N, and ∑ f_i × x_i .
iv. Find the mean of electricity used by each family in the month of May.
Solution:

Electricity used (Units) xi	No. of families (frequency) fi	fi × xi
30	7	210
45	2	90
60	8	480
75	5	375
90	3	270
	N = 25	∑ fi × xi = 1425

i. 2 families used 45 units of electricity.
ii. The score for which the frequency is 5 is 75
iii. N = 25 and ∑ f_i × x_i = 1425
iv.

The mean of electricity used by each.

Question 3.
The number of members in the 40 families in Bhilar are as follows:
1, 6, 5, 4, 3, 2, 7, 2, 3, 4, 5, 6, 4, 6, 2, 3, 2, 1, 4, 5, 6, 7, 3, 4, 5, 2, 4, 3, 2, 3, 5, 5, 4, 6, 2,3, 5, 6, 4, 2. Prepare a frequency table and And the mean of members of 40 families.
Solution:


∴ The mean of the members of 40 families is 3.9.

Question 4.
The number of Science and Mathematics projects submitted by Model high school, Nandpur in last 20 years at the state level science exhibition is:
2, 3 ,4, 1, 2, 3, 1, 5, 4, 2, 3, 1, 3, 5, 4, 3, 2, 2, 3, 2. Prepare a frequency table and find the mean of the data.
Solution:


∴ The mean of the given data is 2.75.

Maharashtra Board Class 8 Maths Chapter 11 Statistics Practice Set 11.1 Intext Questions and Activities

Question 1.
The number of pages of a book Ninad read for five consecutive days were 60, 50, 54, 46, 50. Find the average number of pages he read everyday. (Textbook pg. no. 67)
Solution:
\(\frac{60+[50]+[54]+[46]+50}{[5]}=\frac{260}{[5]}=[52]\)
∴ Average number of pages read daily is 52

Std 8 Maths Digest

• Practice Set 11.1 Class 8 Answers
• Practice Set 11.2 Class 8 Answers
• Practice Set 11.3 Class 8 Answers
• Practice Set 12.1 Class 8 Answers
• Practice Set 12.2 Class 8 Answers
• Practice Set 13.1 Class 8 Answers
• Practice Set 13.2 Class 8 Answers
• Practice Set 14.1 Class 8 Answers
• Practice Set 14.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 5 Linear Equations in Two Variables.

9th Standard Maths 1 Practice Set 5.2 Chapter 5 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 5.2 Chapter 5 Linear Equations in Two Variables Questions With Answers Maharashtra Board

Question 1.
In an envelope there are some ₹5 notes and some ₹10 notes. Total amount of these notes together is ₹350. Number of ₹5 notes are less by 10 than twice the number of ₹10 notes. Then find the number of ₹5 and ₹10 notes.
Solution:
Let the number of ₹5 notes be ‘x’ and the number of ₹10 notes be ‘y’
Total amount of x notes of ₹ 5 = ₹ 5x
Total amount ofy notes of ₹ 10 = ₹ 10y
∴ Total amount = 5x + 10y
According to the first condition,
total amount of the notes together is ₹350.
∴ 5x + 10y = 350 …(i)
According to the second condition,
Number of ₹ 5 notes are less by 10 than twice the number of ₹ 10 notes.
∴ x = 2y – 10
∴ x – 2y = -10 …..(ii)
Multiplying equation (ii) by 5,
5x – 10y = -50 …(iii)
Adding equations (i) and (iii),
5x + 10y =350
+ 5x – 10y = -50
10x =300
∴ x = \(\frac { 300 }{ 10 }\)
∴ x = 30
Substituting x = 30 in equation (ii),
x – 2y = -10
30 – 2y = -10
∴ 30 + 10 = 2y
∴ 40 = 2y
∴ y = \(\frac { 40 }{ 2 }\)
∴ y = 20
There are 30 notes of ₹ 5 and 20 notes of ₹ 10 in the envelope.

Question 2.
The denominator of a fraction is 1 less than twice its numerator. If 1 is added to numerator and denominator respectively, the ratio of numerator to denominator is 3 : 5. Find the fraction.
Solution:
Let the numerator of the fraction be ‘x’ and its denominator be ‘y’.
Then, the required fraction is \(\frac { x }{ y }\) .
According to the first condition,
the denominator is 1 less than twice its numerator.
∴ y = 2x – 1
∴ 2x – y = 1 …(i)
According to the second condition,
if 1 is added to the numerator and the denominator, the ratio of numerator to denominator is 3 : 5.
∴ \(\frac { x+1 }{ y+1 }\) = \(\frac { 3 }{ 5 }\)
∴ y + 1 = 5
∴ 5(x + 1) = 3(y + 1)
∴ 5x + 5 = 3y + 3
∴ 5x – 3y = 3 – 5
∴ 5x – 3y = -2 ……(ii)
Multiplying equation (i) by 3,
6x – 3y = 3 …(iii)
Subtracting equation (ii) from (iii),

Substituting x = 5 in equation (i),
∴ 2x – y = 1
∴ 2(5) – y = 1
∴ 10 – y = 1
∴ y= 10 – 1 =9
∴ The required fraction is \(\frac { 5 }{ 9 }\).

Question 3.
The sum of ages of Priyanka and Deepika is 34 years. Priyanka is elder to Deepika by 6 years. Then find their present ages.
Solution:
Let the present age of Priyanka be ‘x’ years and that of Deepika be ‘y’ years.
According to the first condition,
Priyanka’s age + Deepika’s age = 34 years
∴ x + y = 34 …(i)
According to the second condition,
Priyanka is elder to Deepika by 6 years.
∴ x =y + 6
∴ x – y = 6 …..(ii)
Adding equations (i) and (ii),

∴ x = 20
Substituting x = 20 in equation (i),
x + y = 34
∴ 20 + y = 34
∴ y = 34 -20= 14
∴ The present age of Priyanka is 20 years and that of Deepika is 14 years.

Question 4.
The total number of lions and peacocks in a certain zoo is 50. The total number of their legs is 140. Then find the number of lions and peacocks in the zoo.
Solution:
Let the number of lions in the zoo be ‘x’ and the number of peacocks be ‘y’.
According to the first condition,
the total number of lions and peacocks is 50.
∴ x + y = 50 …(i)
Lion has 4 legs and Peacock has 2 legs.
According to the second condition,
the total number of their legs is 140.
∴ 4x + 2y = 140
Dividing both sides by 2,
2x + y = 70 …(ii)
Subtracting equation (i) from (ii),

Substituting x = 20 in equation (i),
x + y = 50
∴ 20 + y = 50
∴ y = 50 – 20 = 30
∴ The number of lions and peacocks in the zoo are 20 and 30 respectively.

Question 5.
Sanjay gets fixed monthly income. Every year there is a certain increment in his salary. After 4 years, his monthly salary was ₹ 4500 and after 10 years his monthly salary became ₹ 5400, then find his original salary and yearly increment.
Solution:
Let the original salary of Sanjay be ₹ ‘x’ and his yearly increment be ₹ ‘y’.
According to the first condition, after 4 years his monthly salary was ₹ 4500
∴ x + 4y = 4500 …..(i)
According to the second condition,
after 10 years his monthly salary became ₹ 5400
∴ x + 10y = 5400 …(ii)
Subtracting equation (i) from (ii),

∴ y = 150
Substituting y = 150 in equation (i),
x + 4y = 4500
∴ x +4(150) = 4500
∴ x + 600 = 4500
∴ x = 4500 – 600 = 3900
∴ The original salary of Sanjay is ₹ 3900 and his yearly increment is ₹ 150.

Question 6.
The price of 3 chairs and 2 tables is ₹ 4500 and price of 5 chairs and 3 tables is ₹ 7000, then find the price of 2 chairs and 2 tables.
Solution:
Let the price of one chair be ₹ ‘x’ and that of one table be ₹ ‘y’.
According to the first condition,
the price of 3 chairs and 2 tables is ₹ 4500
∴ 3x + 2y = 4500 ,..(i)
According to the second condition, the price of 5 chairs and 3 tables is ? 7000
∴ 5x + 3y = 7000 …(ii)
Multiplying equation (i) by 3,
9x + 6y = 13500 ….(iii)
Multiplying equation (ii) by 2,
10x + 6y= 14000 …(iv)
Subtracting equation (iii) from (iv),

Substituting x = 500 in equation (i),
3x + 2y = 4500
∴ 3(500)+ 2y = 4500
∴ 1500 + 2y = 4500
∴ 2y = 4500- 1500
∴ 2y = 3000
∴ y = \(\frac { 3000 }{ 2 }\)
∴ y = 1500
∴ Price of 2 chairs and 2 tables = 2x + 2y
= 2(500)+ 2(1500)
= 1000 + 3000 = ₹ 4000
∴ The price of 2 chairs and 2 tables is ₹ 4000.

Question 7.
The sum of the digits in a two-digit number is 9. The number obtained by interchanging the digits exceeds the original number by 27. Find the two-digit number.
Solution:
Let the digit in unit’s place be ‘x’ and the digit in ten’s place be ‘y’.

According to the first condition.
the sum of the digits in a two-digit number is 9
x + y = 9 …(i)
According to the second condition,
the number obtained by interchanging the digits exceeds the original number by 27
∴ 10x + y = 10y + x + 27
∴ 10x – x + y – 10y = 27
∴ 9x – 9y = 27
Dividing both sides by 9,
x – y = 3 …….(ii)
Adding equations (i) and (ii),

∴ x = 6
Substituting x = 6 in equation (i),
x + y = 9
∴ 6 + y = 9
∴ y = 9 – 6 = 3
∴ Original number = 10y + x = 10(3)+ 6
= 30 + 6 = 36
∴ The two digit number is 36.

Question 8.
In ∆ABC, the measure of ∠A is equal to the sum of the measures of ∠B and ∠C. Also the ratio of measures of ∠B and ∠C is 4 : 5. Then find the measures of angles of the triangle.
Solution:
Let the measure of ∠B be ‘x°’ and that of ∠C be ‘y°’.
According to the first condition,
m∠A = m∠B + m∠C
∴ m∠A = x° + y°
In AABC,
m∠A + m∠B + m∠C = 180° …[Sum of the measures of the angles of a triangle is 180°]
∴ x + y + x + y = 180 ,
∴ 2x + 2y = 180
Dividing both sides by 2,
x + y = 90 …(i)
According to the second condition,
the ratio of the measures of ∠B and ∠C is 4 : 5.
∴ \(\frac { x }{ y }\) = \(\frac { 4 }{ 5 }\)
∴ 5x = 4y
∴ 5x – 4y = 0 …….(ii)
Multiplying equation (i) by 4,
4x + 4y = 360 …(iii)
Adding equations (ii) and (iii),

∴ x = 40
Substituting x = 40 in equation (i),
x + y = 90
∴ 40 + y = 90
∴ y = 90 – 40
∴ y = 50
∴ m∠A = x° + y° = 40° + 50° = 90°
∴ The measures of ∠A, ∠B and ∠C are 90°, 40°, and 50° respectively.

Question 9.
Divide a rope of length 560 cm into 2 parts such that twice the length of the smaller part is equal to \(\frac { 1 }{ 3 }\) of the larger part. Then find the length of the larger part.
Solution:
Let the length of the smaller part of the rope be ‘x’ cm and that of the larger part be ‘y’ cm.
According to the first condition,
total length of the rope is 560 cm.
∴ x + y = 560 …(i)
Twice the length of the smaller part = 2x
\(\frac { 1 }{ 3 }\)rd length of the larger part = \(\frac { 1 }{ 3 }\)y
According to the second condition,
2x = \(\frac { 1 }{ 3 }\) 3
∴ 6x = y
∴ 6x – y = 0 ……(ii)
Adding equations (i) and (ii),

∴ x = 80
Substituting x = 80 in equation (ii),
6x – y = 0
∴ 6(80) – y = 0
∴ 480 – y = 0
∴ y = 480
∴ The length of the larger part of the rope is 480 cm.

Question 10.
In a competitive examination, there were 60 questions. The correct answer would carry 2 marks, and for incorrect answer 1 mark would be subtracted. Yashwant had attempted all the questions and he got total 90 marks. Then how many questions he got wrong?
Solution:
Let us suppose that Yashwant got ‘x’ questions right and ‘y’ questions wrong.
According to the first condition, total number of questions in the examination are 60.
∴ x + y = 60 …(i)
Yashwant got 2 marks for each correct answer and 1 mark was deducted for each wrong answer.
∴ He got 2x – y marks.
According to the second condition,
he got 90 marks.
2x – y = 90 … (ii)
Adding equations (i) and (ii),

∴ x = 50
Substituting x = 50 in equation (i),
50 + y = 60
∴ y = 60 – 50 = 10
∴ Yashwant got 10 questions wrong.

Maharashtra Board Class 9 Maths Chapter 5 Linear Equations in Two Variables Practice Set 5.2 Intext Questions and Activities

Question 1.
The population of a certain town was 50,000. In a year, male population was increased by 5% and female population was increased by 3%. Now the population became 52020. Then what was the number of males and females in the previous year? (Textbook pg. no. 89)
Solution:
Step 1: Read the given word problem carefully and try to understand it.

Step 2: Make assumptions using two variables x and y.
Let the number of males in previous year be
‘x’ and the number of females be ‘y’.

Step 3: From the given information, form mathematical statements using the above variables.
According to the first condition,
the total population of town was 50,000.
∴ x + y = 50000 …(i)
Male population increased by 5%.
∴ Number of males = x + 5% of x , 5

Female population increased by 3%.
∴ Number of females = y + 3% of y

According to the second condition,
in a year population became 52020
∴ \(\frac{105}{100} x+\frac{103}{100} y=52020\)
∴ 105 x + 103 y = 5202000 …(ii)
Multiplying equation (i) by 103,
103 x + 103 y = 5150000 …(iii)

Step 4: Here, we use elimination method.
Subtracting equation (iii) from (ii),

∴ x = 26000
Substituting x = 26000 in equation (i),
∴ 26000 + y = 50000
∴ y = 50000 – 26000
∴ y = 24000
∴ Number of males = x = 26000
∴ Number of females = y = 24000

Step 5: Write the answer.
The number of males and females in the previous year were 26,000 and 24,000 respectively.

Step 6: Verify your result using smart check.

Class 9 Maths Digest

• Practice Set 4.1 Class 9 Answers
• Practice Set 4.2 Class 9 Answers
• Practice Set 4.3 Class 9 Answers
• Practice Set 4.4 Class 9 Answers
• Practice Set 4.5 Class 9 Answers
• Practice Set 4 Class 9 Answers
• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 6 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 6 Financial Planning.

9th Standard Maths 1 Problem Set 6 Chapter 6 Financial Planning Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Problem Set 6 Chapter 6 Financial Planning Questions With Answers Maharashtra Board

Question 1.
Write the correct alternative answer for each of the following questions.

i. For different types of investments what is the maximum permissible amount under section 80C of income tax ?
(A) ₹ 1,50,000
(B) ₹ 2,50,000
(C) ₹ 1,00,000
(D) ₹ 2,00,000
Answer:
(A) ₹ 1,50,000

ii. A person has earned his income during the financial year 2017-18. Then his assessment year is….
(A) 2016 – 17
(B) 2018 – 19
(C) 2017 – 18
(D) 2015 – 16
Answer:
(B) 2018 – 19

Question 2.
Mr. Shekhar spends 60% of his income. From the balance he donates ₹ 300 to an orphanage. He is then left with ₹ 3,200. What is his income ?
Solution:
Let the income of Shekhar be ₹ x.
Shekhar spends 60% of his income.
∴ Shekhar’s expenditure = 60% of x
∴ Amount remaining with Shekhar = (100 – 60)% of x
= 40% of x
= \(\frac { 1 }{ 2 }\) × x
= 0.4x
From the balance left, he donates ₹ 300 to an orphanage.
∴ Amount left with Shekhar = 0.4x – 300
Now, the amount left with him is ₹ 3200.
∴ 3200 = 0.4x- 300
∴ 0.4x = 3500

∴ The income of Mr. Shekhar is ₹ 8750.

Question 3.
Mr. Hiralal invested ₹ 2,15,000 in a Mutual Fund. He got ₹ 3,05,000 after 2 years. Mr. Ramniklal invested ₹ 1,40,000 at 8% compound interest for 2 years in a bank. Find out the percent gain of each of them. Whose investment was more profitable ?
Solution:
Mr. Hiralal:
Amount invested by Mr. Hiralal in mutual fund = ₹ 2,15,000
Amount received by Mr. Hiralal = ₹ 3,05,000
∴ Mr. Hiralal’s profit = Amount received – Amount invested
= 305000 – 215000 = ₹ 90000
Mr. Hirala’s percentage of profit
= \(\frac { 90000 }{ 215000 }\) × 100
= 41.86%

Mr. Ramniklal:
P = ₹ 140000, R = 8%, n = 2 years
∴ Compound interest (I)
= A – P

= 140000 [(1 + 0.08)² – 1]
= 140000 [ (1.08)² – 1]
= 140000(1.1664 – 1)
= 140000 x 0.1664
= ₹ 23296
∴ Mr. Ramniklal’s percentage of profit
= \(\frac { 23296 }{ 140000 }\) × 100
= 16.64%
∴ The percentage gains of Mr. Hiralal and Mr. Ramniklal are 41.86% and 16.64% respectively, and hence, Mr. Hiralal’s investment was more profitable.

Question 4.
At the start of a year there were ₹ 24,000 in a savings account. After adding ₹ 56,000 to this the entire amount was invested in the bank at 7.5% compound interest. What will be the total amount after 3 years ?
Solution:
Here, P = 24000 + 56000
= ₹ 80000
R = 7.5%, n = 3 years
Total amount after 3 years

= 80000 (1 + 0.075)³
= 80000 (1.075)³
= 80000 x 1.242297
= 99383.76
∴ The total amount after 3 years is ₹ 99383.76.

Question 5.
Mr. Manohar gave 20% of his income to his elder son and 30% to his younger son. He gave 10% of the balance income as donation to a school. He still had ₹ 1,80,000 for himself. What was Mr. Manohar’s income ?
Solution:
Let the income of Mr. Manohar be ₹ x.
Amount given to elder son = 20% of x
Amount given to younger son = 30% of x
Total amount given to both sons = (20 + 30)% of x = 50% of x
∴ Amount remaining with Mr. Manohar = (100 – 50)% of x
= 50% of x 50
= \(\frac { 50 }{ 100 }\) × 100
= 0.5 x
He gave 10% of the balance income as donation to a school.
Amount donated to school = 10% of 0.5x
= \(\frac { 10 }{ 100 }\) × 0.5x
= 0.05x
∴ Amount remaining with Mr. Manohar after donating to school = 0.5x – 0.05x
= 0.45x
Mr. Manohar still had 1,80,000 for himself after donating to school.
∴ 180000 = 0.45x
∴ \(x=\frac{180000}{0.45}=\frac{180000 \times 100}{0.45 \times 100}=\frac{18000000}{45}=400000\)
∴ The income of Mr. Manoliar is ₹4,00,000.

Question 6.
Kailash used to spend 85% of his income. When his income increased by 36% his expenses also increased by 40% of his earlier expenses. How much percentage of his earning he saves now ?
Solution:
Let the income of Kailash be ₹ x.
Kailash spends 85% of his income.
∴ Kailash’s expenditure = 85% of x
= \(\frac { 85 }{ 100 }\) × x = 0.85 x
Kailash’s income increased by 36%.
∴ Kailash’s new income = x + 36% of x
= x + \(\frac { 36 }{ 100 }\) × x
= x + 0.36x
= 1.36x
Kailash’s expenses increased by 40%.
∴ Kailash’s new expenditure = 0.85x + 40% of 0.85x
= 0.85x + \(\frac { 40 }{ 100 }\) × 0.85 × 100
= 0.85x + 0.4 × 0.85x
= 0.85x (1 + 0.4)
= 0.85x × 1.4
= 1.19x
∴ Kailash’s new saving = Kailash’s new income – Kailash’s new expenditure
= 1.36x – 1.19x
= 0.17x
Percentage of Kailash’s new saving
= \(\frac { 0.17x }{ 1.36x }\) × 100
= 12.5%
∴ Kailash saves 12.5% of his new earning.

Question 7.
Total income of Ramesh, Suresh and Preeti is ₹ 8,07,000. The percentages of their expenses are 75%, 80% and 90% respectively. If the ratio of their savings is 16 : 17 : 12, then find the annual saving of each of them.
Solution:
Let the annual income of Ramesh, Suresh and Preeti be ₹ x, t y and ₹ z respectively.
Total income of Ramesh, Suresh and Preeti = ₹ 8,07,000
∴ x + y + z = 807000 …(i)

∴ Savings of Ramesh = 25% of x
= ₹ \(\frac { 25x }{ 100 }\) ..(ii)
Savings of Suresh = 20% of y
= ₹\(\frac { 20y }{ 100 }\) …(iii)
Savings of Preeti = 10% of z
= ₹\(\frac { 10z }{ 100 }\) …..(iv)

Ratio of their savings = 16 : 17 : 12
Let the common multiple be k.
Savings of Ramesh = ₹ 16 k … (v)
Savings of Suresh = ₹ 17 k … (vi)
Savings of Preeti = ₹ 12 k .. .(vii)

∴ z = 120k …(x)
From (i), (viii), (ix) and (x), we get
64k + 85k + 120k = 807000
269k = 807000
k = \(\frac { 807000 }{ 269 }\)
k = 3000
∴ Annual saving of Ramesh = 16k
= 16 x 3000
= ₹ 48,000
Annual saving of Suresh = 17k
= 17 x 3000
= ₹ 51,000
Annual saving of Preeti = 12k
= 12 x 3000
= ₹ 36,000
The annual savings of Ramesh, Suresh and Preeti are ₹ 48,000, ₹ 51,000 and ₹ 36,000 respectively.

Question 8.
Compute the income tax payable by following individuals.
i. Mr. Kadam who is 35 years old and has a taxable income of ₹13,35,000.
ii. Mr. Khan is 65 years of age and his taxable income is ₹4,50,000.
iii. Miss Varsha (Age 26 years) has a taxable income of ₹2,30,000.
Solution:
i. Mr. Kadam is 35 years old and his taxable income is ₹13,35,000.
Mr. Kadam’s income is more than ₹ 10,00,000.
∴ Income tax = ₹1,12,500 + 30% of (taxable income -10,00,000)
= ₹ 1,12,500 + 30% of (13,35,000 – 10,00,000)
= 112500+ \(\frac { 30 }{ 100 }\) x 335000 100
= 112500+ 100500
= ₹ 213000
Education cess = 2% of income tax
= \(\frac { 2 }{ 100 }\) x 213000
= ₹ 4260.
Secondary and Higher Education cess
= 1% of income tax
= \(\frac { 1 }{ 100 }\) x 213000 100
= 2130
Total income tax = Income tax + Education cess + Secondary and higher education cess
= 213000 + 4260 + 2130 = ₹ 2,19,390
∴ Mr. Kadam will have to pay income tax of ₹ 2,19,390.

ii. Mr. Khan is 65 years old and his taxable income is ₹ 4,50,000.
Mr. Khan’s income falls in the slab ₹ 3,00,001 to ₹ 5,00,000.
∴ Income tax
= 5% of (taxable income – 300000)
= 5% of (450000 – 300000)
= \(\frac { 5 }{ 100 }\) x 150000 100
= ₹ 7500
Education cess = 2% of income tax
= \(\frac { 2 }{ 100 }\) x 7500
= ₹ 150
Secondary and Higher Education cess = 1 % of income tax
= \(\frac { 1 }{ 100 }\) x 7500
= 75
Total income tax = Income tax + Education cess + Secondary and higher education cess
= 7500+ 150 + 75
= ₹ 7725
Mr. Khan will have to pay income tax of ₹7725.

iii. Taxable income = ₹2,30,000
age = 26 years
The yearly income of Miss Varsha is less than ₹ 2,50,000.
Hence, Miss Varsha will not have to pay income tax.

Maharashtra Board Class 9 Maths Chapter 6 Financial Planning Problem Set 6 Intext Questions and Activities

Question 1.
With your parent’s help write down the income and expenditure of your family for one week. Make 7 columns for the seven days of the week. Write all expenditure under such heads as provisions, education, medical expenses, travel, clothes and miscellaneous. On the credit side write the amount received for daily expenses, previous balance and any other new income. (Textbook pg. no. 98)

Question 2.
In the holidays, write the accounts for the whole month. (Textbook pg. no. 98)

Question 3.
What is a tax? Which are different types of taxes? Find out more information on following websites
www.incometaxindia.gov.in,
www.mahavat.gov.in
www.gst.gov.in (Textbook pg. no. 99)

Question 4.
Obtain more information about different types of taxes from employees and professionals who pay taxes. (Textbook pg. no. 99)

Question 5.
Obtain information about sections 80C, 80G, 80D of the Income Tax Act. (Textbook pg. no. 103)

Question 6.
Study a PAN card and make a note of all the information it contains. (Textbook pg.no. 103)

Question 7.
Obtain information about all the devices and means used for carrying out cash minus transactions. (Textbook pg, no, 103)

Question 8.
Visit www.incometaxindia.gov.in which is a website of the Government of India. Click on the ‘incometax calculator’ menu. Fill in the form that gets downloaded using an imaginary income and imaginary deductible amounts and try to compute the income tax payable for this income. (Textbook pg.no. 107)
[Students should attempt the above activities on their own.]

Try More: BATAINDIA Pivot Calculator

Class 9 Maths Digest

• Practice Set 6.1 Class 9 Answers
• Practice Set 6.2 Class 9 Answers
• Problem Set 6 Class 9 Answers
• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Practice Set 7.3 Class 9 Answers
• Practice Set 7.4 Class 9 Answers
• Practice Set 7.5 Class 9 Answers
• Problem Set 7 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 6 Financial Planning.

9th Standard Maths 1 Practice Set 6.2 Chapter 6 Financial Planning Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 6.2 Chapter 6 Financial Planning Questions With Answers Maharashtra Board

Question 1.
Observe the table given below. Check and decide, whether the individuals have to pay income tax.

Solution:
i. Miss Nikita’s age = 27 years < 60 years
Miss Nikita’s income = ₹ 2,34,000
Miss Nikita’s income is below the basic
exemption limit of ₹ 2,50,000.
∴ Miss Nikita will not have to pay income tax.

ii. Mr. Kulkarni’s age 36 years < 60 years
Mr. Kulkarni’s income = ₹3,27,000
Mr. Kulkarni’s income is above the basic exemption Limit of ₹2,50,000.
∴ Mr. Kulkarni will have to pay income tax.

iii. Miss Mehta’s age = 44 years < 60 years Miss Mehta’s income = ₹5.82,000
Miss Mehta’s income is above the basic exemption limit of ₹2,50,000.
∴ Miss Mehta will have to pay income tax.

iv. Mr. Bajaj’s age = 64 years (Age 60 to 80 years)
Mr. Bajaj’s income = ₹8,40,000
Mr. Bajaj’s income is above the basic exemption Limit of ₹3,00,000.
∴ Mr. Bajaj will have to pay income tax.

v. Mr. Desilva’s age = 81 years > 80 years
Mr. Desilva’s income = ₹4,50,000
Mr. Desilva’s income is below the basic exemption limit of ₹ 5,00.000.
∴ Mr. Desilva will not have to pay income tax.

Question 2.
Mr. Kartarsingh (age 48 years) works in a private company. His monthly income after deduction of allowances is ₹ 42,000 and every month he contributes ₹ 3000 to GPF. He has also bought ₹ 15,000 worth of NSC (National Savings Certificate) and donated ₹ 12,000 to the PM’s Relief Fund. Compute his income tax.
Solution:
Mr. Kartarsingh’s monthly income = ₹ 42,000
Mr. Kartarsingh’s yearly income = 42,000 x 12 = ₹ 5,04,000

Mr. Kartarsingh’s investment
= GPF + NSC
= (3000 x 12)+ 15,000
= 36,000 + 15,000
= ₹ 51,000

Donation to PM’s relief fund = ₹ 12, 000
∴ Taxable income
= yearly income – (investment + donation)
= 5,04,000 – (51,000 + 12,000)
= 5,04,000 – 63,000 = ₹ 4,41,000
Mr. Kartarsingh income falls in the slab 2,50,001 to 5,00,000.
∴ Income tax = 5% of (Taxable income – 250000) = 5% of (4,41,000 – 2,50,000)
= \(\frac { 5 }{ 100 }\) x 1,91,000 100
= ₹ 9550
Education cess = 2% of income tax
= \(\frac { 2 }{ 100 }\) x 9550
= 191
Secondary and Higher Education cess = 1% of income tax
= \(\frac { 1 }{ 100 }\) x 9550 100
= 95.50
Total income tax = Income tax + Education cess + Secondary and higher education cess
= 9550 + 191 + 95.50
= ₹ 9836.50
∴ Mr. Kartarsingh’s income tax is ₹ 9836.50

Maharashtra Board Class 9 Maths Chapter 6 Financial Planning Practice Set 6.2 Intext Questions and Activities

Question 1.
Use Table I given above and write the appropriate amount/figure in the boxes for the example given below. (Textbook pg. no. 102)
Mr. Mehta’s annual income is ₹4,50,000
i. If he does not have any savings by which he can claim deductions from his income, to which slab does his taxable income belong ? ______
ii, What is the amount on which he will have to pay income tax and at what percent rate? on ₹ _______
percentage _______
iii. On what amount will the cess be levied? _______
Answer:
1. ₹2,50,001 to ₹5,00,000
ii. 5% of (4,50,000 – 2,50,000)
i.e. 5% of ₹2,00,000
iii. income tax = 5% of 2,00,000
= \(\frac { 5 }{ 100 }\) x 2,00,000
= ₹10,000
∴ Education cess and Secondary and higher education cess will be levied on the income tax i.e., on ₹10,000.

Question 2.
Use table lito carry out the following activity.
Mr. Pandit is 75 years old. Last year his annual income was ₹ 13,25,000. How much is his taxable income? How much tax does he have to pay? (Textbook pg. no. 103)
Solution:
Mr. Pandit’s age = 75 years (Age 60 to 80 years)
Mr. Pandit’s income is more than 10,00,000.
According to the table,
Income tax = ₹ 1,10,000 + 30 % of (taxable income – 10,00,000)
Taxable income – 10,00,000 = 13,25,000 – 10,00,000 = 3,25,000
In addition, on ₹ 3,25,000 rupees he has to pay 30% income tax.
3,25,000 x \(\frac { 30 }{ 100 }\) = ₹ 97500
Therefore, his total income tax amounts to 1,10,000 + 97,500 ₹ 207500
Besides this, education cess willi be 2% of income tax 207500 x \(\frac { 2 }{ 100 }\) = ₹ 4150.
A secondary and higher education cess at 1% of income tax = 207500 x \(\frac { 1 }{ 100 }\) = ₹ 2075.
∴ Total income tax = Income tax + education cess + secondary and higher education cess
= 207500 + 4150 + 2075
= ₹2,13,725

Class 9 Maths Digest

• Practice Set 6.1 Class 9 Answers
• Practice Set 6.2 Class 9 Answers
• Problem Set 6 Class 9 Answers
• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Practice Set 7.3 Class 9 Answers
• Practice Set 7.4 Class 9 Answers
• Practice Set 7.5 Class 9 Answers
• Problem Set 7 Class 9 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 8.1 8th Std Maths Answers Solutions Chapter 8 Quadrilateral: Constructions and Types.

Quadrilateral: Constructions and Types Class 8 Maths Chapter 8 Practice Set 8.1 Solutions Maharashtra Board

Std 8 Maths Practice Set 8.1 Chapter 8 Solutions Answers

Construct the following quadrilaterals of given measures.

Question 1.
In ∆MORE, l(MO) = 5.8 cm, l(OR) = 4.4 cm, m∠M = 58°, m∠O = 105°, m∠R = 90°.
Solution:

Question 2.
Construct ∆DEFG such that l(DE) = 4.5 cm, l(EF) = 6.5 cm, l(DG) = 5.5 cm, l(DF) = 7.2 cm, l(EG) = 7.8 cm.
Solution:

Question 3.
In ∆ABCD, l(AB) = 6.4 cm, l(BC) = 4.8 cm, m∠A = 70°, m∠B = 50°, m∠C = 140°.
Solution:

Question 4.
Construct ₹LMNO such that
l(LM) = l(LO) = 6 cm,
l(ON) = l(NM) = 4.5 cm, l(OM) = 7.5 cm.
Solution:

Maharashtra Board Class 8 Maths Chapter 8 Quadrilateral: Constructions and Types Practice Set 8.1 Intext Questions and Activities

Question 1.
Construction of a triangle:
Construct the triangles with given measures. (Textbook pg. no. 41)
i. ∆ABC: l(AB) = 5 cm, l(BC) = 5.5, l(AC) = 6 cm.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg BC of length 5.5 cm as the base.
Step 2 : By taking a distance of 5 cm on the compass and placing the metal tip of the compass on point B, draw an arc on one side of BC.
Step 3 : By taking a distance 6 cm on the compass and placing the metal tip of the t compass on point C and draw an arc ’ such that it intersects the previous arc. Name the point as A.
Step 4 : Draw segments AB and AC to get the triangle. ∆ABC is the required triangle.

ii. ∆DEF: m∠D = 35°, m∠F = 100°, l(DF) = 4.8 cm.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg DF of length 4.8 cm as the base.
Step 2 : Placing the centre of the protractor at point D, mark point P such that m∠PDF = 35°.
Step 3 : Placing the centre of the protractor at point F, mark point Q such that m∠QFD = 100°.
Step 4 : Draw ray DP and ray FQ. Name their point of intersection as E.
∆DEF is required triangle.

iii. ∆MNP: l(MP) = 6.2 cm, l(NP) = 4.5 cm, m∠P = 75°.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg PN of length 4.5 cm as the base.
Step 2 : Placing the centre of the protractor at point P, mark point Q such that m∠QPN = 75°.
Step 3 : By taking a distance of 6.2 cm on the compass and placing the metal tip at point P, draw an arc on ray PQ. Name the point as M.
Step 4 : Draw seg MN to get the triangle. ∆MNP is the required triangle.

iv. ∆XYZ: m∠Y = 90°, l(XY) = 4.2 cm, l(XZ) = 7 cm.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg XY of 4.2 cm as the base.
Step 2 : Placing the centre of the protractor at point Y, mark point Q such that m∠QYX = 90°.
Step 3 : By taking a distance of 7 cm on the compass and placing the metal tip on point X, draw an arc on ray YQ. Name the point as Z.
Step 4 : Draw seg XZ to get the triangle. ∆XYZ is the required triangle.

Std 8 Maths Digest

• Practice Set 8.1 Class 8 Answers
• Practice Set 8.2 Class 8 Answers
• Practice Set 8.3 Class 8 Answers
• Practice Set 9.1 Class 8 Answers
• Practice Set 9.2 Class 8 Answers
• Practice Set 10.1 Class 8 Answers
• Practice Set 10.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 5 Linear Equations in Two Variables.

9th Standard Maths 1 Practice Set 5.1 Chapter 5 Linear Equations in Two Variables Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 5.1 Chapter 5 Linear Equations in Two Variables Questions With Answers Maharashtra Board

Question 1.
By using variables x and y form any five linear equations in two variables.
Answer:
The general form of a linear equation in two variables x and y is ax + by + c = 0,
where a, b, c are real numbers and a ≠ 0, b ≠ 0.
Five linear equations in two variables are as follows:
i. 3x + 4y – 12 = 0
ii. 3x – 4y + 12 = 0
iii. 5x + 5y – 6 = 0
iv. 7x + 12y – 11 = 0
v. x – y + 5 = 0

Question 2.
Write five solutions of the equation x + y = 1.
Answer:
i. x = 1, y = 6
ii. x = -1, y = 8
iii. x = 5, y = 2
iv. x = 0, y = 7
v. x = 10, y = -3

Question 3.
Solve the following sets of simultaneous equations.
i. x + y = 4 ; 2x – 5y = 1
ii. 2x + y = 5 ; 3x – y = 5
iii. 3x – 5y = 16; x – 3y= 8
iv. 2y – x = 0; 10x + 15y = 105
v. 2x + 3y + 4 = 0; x – 5y = 11
vi. 2x – 7y = 7; 3x + y = 22
Solution:
i. Substitution Method:
x + y = 4
∴ x = 4 – y …(i)
2x – 5y = 1 ……(ii)
Substituting x = 4 – y in equation (ii),
2(4 – y) – 5y = 1
∴ 8 – 2y – 5y = 1
∴ 8 – 7y = 1
∴ 8 – 1 = 7y
∴ 7 = 7y
∴ y = \(\frac { 7 }{ 7 }\)
∴ y = 1
Substituting y = 1 in equation (i),
x = 4 – 1 = 3
∴ (3,1) is the solution of the given equations.

Alternate method:
Elimination Method:
x + y = 4 …(i)
2x – 5y = 1 ……(ii)
Multiplying equation (i) by 5,
5x + 5y = 20 … (iii)
Adding equations (ii) and (iii),
2x – 5y = 1
+ 5x + 5y = 20
7 = 21
∴ x = \(\frac { 21 }{ 7 }\)
∴ x = 3
Substituting x = 3 in equation (i),
3 + y = 4
∴ y = 4 – 3 = 1
(3,1) is the solution of the given equations.

ii. 2x + y = 5 …(i)
3x – y = 5 …(ii)
Adding equations (i) and (ii),
2x + y = 5
+ 3x – y = 5
5x = 10
∴ x = \(\frac { 10 }{ 5 }\)
∴ x = 2
Substituting x = 2 in equation (i),
2(2) + y = 5
4 + y = 5
∴ y = 5 – 4 = 1
∴ (2, 1) is the solution of the given equations.

iii. 3x – 5y = 16 …(i)
x – 3y = 8
∴x = 8 + 3y …..(ii)
Substituting x = 8 + 3y in equation (i),
3(8 + 3y) – 5y = 16
24 + 9y- 5y = 16
∴4y= 16 – 24
∴ 4y = -8
∴ y = \(\frac { -8 }{ 4 }\)
y = -2
Substituting y = -2 in equation (ii),
x = 8 + 3 (-2)
∴ x = 8 – 6 = 2
∴ (2, -2) is the solution of the given equations.

iv. 2y – x = 0
∴ x = 2y …(i)
10x + 15y = 105 …(ii)
Substituting x = 2y in equation (ii),
10(2y) + 15y = 105
∴ 20y + 15y = 105
∴ 35y = 105
∴ y = \(\frac { 105 }{ 35 }\)
∴ y = 3
Substituting y = 3 in equation (i),
x = 2y
∴ x = 2(3) = 6
∴ (6, 3) is the solution of the given equations.

v. 2x + 3y + 4 = 0 …(i)
x – 5y = 11
∴x = 11 + 5y …(ii)
Substituting x = 11 + 5y in equation (i),
2(11 +5y) + 3y + 4 = 0
∴ 22 + 10y + 3y + 4 = 0
∴ 13y + 26 = 0
∴ 13y = -26
∴y = \(\frac { -26 }{ 13 }\)
∴ y = -2
Substituting y = -2 in equation (ii),
x = 11 + 5y
∴ x = 11 + 5(-2)
∴ x = 11 – 10 = 1
∴ (1, -2) is the solution of the given equations.

vi. 2x – 7y = 7 …(i)
3x + y = 22
∴ y = 22 – 3x ……(ii)
Substituting y = 22 – 3x in equation (i),
2x – 7(22 – 3x) = 7
∴ 2x – 154 + 21x = 7
∴ 23x = 7 + 154
∴ 23x = 161
∴ x = \(\frac { 161 }{ 23 }\)
∴ x = 7
Substituting x = 7 in equation (ii),
y = 22 – 3x
∴ y = 22 – 3(7)
∴ 7 = 22 -21= 1
∴ (7, 1) is the solution of the given equations.

Question 1.
Solve the following equations. (Textbook pg. no. 80)
i. m + 3 = 5
ii. 3y + 8 = 22
iii. \(\frac { x }{ 3 }\) = 2
iv. 2p = p + \(\frac { 4 }{ 9 }\)
Solution:
i. m + 3 = 5
m = 5 – 3
∴m = 2

ii. 3y + 8 = 22
∴ 3y = 22 – 8
∴ 3y = 14
∴ y = \(\frac { 14 }{ 9 }\)

iii. \(\frac { x }{ 3 }\) = 2
∴ x = 2 × 3
∴ x = 6

iv. 2p = p + \(\frac { 4 }{ 9 }\)
∴ 2p – p = \(\frac { 4 }{ 9 }\)
∴ p = \(\frac { 4 }{ 9 }\)

Question 2.
Which number should be added to 5 to obtain 14? (Textbook pg. no. 80)
Solution:
x + 5 = 14
∴ x = 14 – 5
x = 9
∴ 9 + 5 = 14

Question 3.
Which number should be subtracted from 8 to obtain 2? (Textbook pg. no. 80)
Solution:
8 – y = 2
∴ y = 8 – 2
∴ y = 6
∴ 8 – 6 = 2

Question 4.
x + y = 5 and 2x + 2y= 10 are two equations in two variables. Find live different solutions of x + y = 5, verify whether same solutions satisfy the equation 2x + 2y = 10 also. Observe both equations. Find the condition where two equations in two variables have all solutions in common. (Textbook pg. no. 82)
Solution:
Five solutions of x + y = 5 are given below:
(1,4), (2, 3), (3, 2), (4,1), (0, 5)
The above solutions also satisfy the equation 2x + 2y = 10.
∴ x + y = 5 …[Dividing both sides by 2]
∴ If the two equations are the same, then the two equations in two variables have all solutions common.

Question 5.
3x – 4y – 15 = 0 and y + x + 2 = 0. Can these equations be solved by eliminating x ? Is the solution same? (Textbook pg. no. 84)
Solution:
3x – 4y – 15 = 0
∴ 3x – 4y = 15 …(i)
y + x + 2 = 0
∴ x + y = -2 ……(ii)
Multiplying equation (ii) by 3,
3x + 3y = -6 …(iii)
Subtracting equation (iii) from (i),

∴ y = -3
Substituting y = -3 in equation (ii),
∴ x – 3 = -2
∴ x = – 2 + 3
∴ x = 1
∴ (x, y) = ( 1, -3)
Yes, the given equations can be solved by eliminating x. Also, the solution will remain the same.

Class 9 Maths Digest

• Practice Set 4.1 Class 9 Answers
• Practice Set 4.2 Class 9 Answers
• Practice Set 4.3 Class 9 Answers
• Practice Set 4.4 Class 9 Answers
• Practice Set 4.5 Class 9 Answers
• Practice Set 4 Class 9 Answers
• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

9th Standard Maths 1 Practice Set 4.3 Chapter 4 Ratio and Proportion Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 4.3 Chapter 4 Ratio and Proportion Questions With Answers Maharashtra Board

Ratio and Proportion Practice Set 4.3 Question 1.
If \(\frac { a }{ b }\) = \(\frac { 7 }{ 3 }\), then find the aIues of the following ratios.

Solution:

Ratio and Proportion Class 9 Practice Set 4.3 Question 2.
If \(\frac{15 a^{2}+4 b^{2}}{15 a^{2}-4 b^{2}}=\frac{47}{7}\), then find the value of the following ratios.

Solution:

Practice Set 4.3 Algebra 9th Question 3.
If \(\frac{3 a+7 b}{3 a-7 b}=\frac{4}{3}\)then find the value of the ratio \(\frac{3 a^{2}-7 b^{2}}{3 a^{2}+7 b^{2}}\).
Solution:

Class 9 Maths Chapter 4 Ratio And Proportion Practice Set 4.3 Question 4.
Solve the following equations.

Solution:

This equation is true for x = 0
∴ x = 0 is one of the solutions.
If x ≠ 0, then x² ≠ 0
∴ \(\frac { 1 }{ 12x – 20 }\) = \(\frac { 1 }{ 8x + 12 }\) … [Dividing both sides by x²]
∴ 8x + 12 = 12x – 20
∴ 12 + 20 = 12x – 8x
∴ 32 = 4x
∴ x = 8
∴ x = 0 or x = 8 are the solutions of the given equation.

∴ 21(x – 5) = 4(2x + 3)
∴ 21x – 105 = 8x + 12
∴ 21x – 8x = 12 + 105
∴ 13x = 117
∴ x = 9
∴ x = 9 ¡s the solution of the given equation.

∴ 9(4x + 1) = 25(x + 3)
∴36x + 925x + 75
∴ 36x – 25 = 75 – 9
∴11x = 66
∴ x = 6
∴ x = 6 is the solution of the given equation.


∴ 4(3x – 4) = 5(x + 1)
∴ 12x – 16 = 5x + 5
∴ 12x – 5x = 5 + 16
∴ 7x = 21
∴ x = 3
∴ x = 3 ¡s the solution of the given equation.

Class 9 Maths Digest

• Practice Set 4.1 Class 9 Answers
• Practice Set 4.2 Class 9 Answers
• Practice Set 4.3 Class 9 Answers
• Practice Set 4.4 Class 9 Answers
• Practice Set 4.5 Class 9 Answers
• Practice Set 4 Class 9 Answers
• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.5 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

9th Standard Maths 1 Practice Set 4.5 Chapter 4 Ratio and Proportion Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 4.5 Chapter 4 Ratio and Proportion Questions With Answers Maharashtra Board

Question 1.
Which number should be subtracted from 12, 16 and 21 so that resultant numbers are in continued proportion?
Solution:
Let the number to be subtracted be x.
∴ (12 – x), (16 – x) and (21 – x) are in continued proportion.

∴ 84 – 4x = 80 – 5x
∴ 5x – 4x = 80 – 84
∴ x = -4
∴ -4 should be subtracted from 12,16 and 21 so that the resultant numbers in continued proportion.

Question 2.
If (28 – x) is the mean proportional of (23 – x) and (19 – x), then find the value ofx.
Solution:
(28 – x) is the mean proportional of (23 – x) and (19-x). …[Given]

∴ -5(19 – x) = 9(28 – x)
∴ -95 + 5x = 252 – 9x
∴ 5x + 9x = 252 + 95
∴ 14x = 347
∴ x = \(\frac { 347 }{ 14 }\)

Question 3.
Three numbers are in continued proportion, whose mean proportional is 12 and the sum of the remaining two numbers is 26, then find these numbers.
Solution:
Let the first number be x.
∴ Third number = 26 – x
12 is the mean proportional of x and (26 – x).
∴ \(\frac { x }{ 12 }\) = \(\frac { 12 }{ 26 – x }\)
∴ x(26 – x) = 12 x 12
∴ 26x – x² = 144
∴ x² – 26x + 144 = 0
∴ x² – 18x – 8x + 144 = 0
∴ x(x – 18) – 8(x – 18) = 0
∴ (x – 18) (x – 8) = 0
∴ x = 18 or x = 8
∴ Third number = 26 – x = 26 – 18 = 8 or 26 – x = 26 – 8 = 18
∴ The numbers are 18, 12, 8 or 8, 12, 18.

Question 4.
If (a + b + c)(a – b + c) = a² + b² + c², show that a, b, c are in continued proportion.
Solution:
(a + b + c)(a – b + c) = a² + b² + c² …[Given]
∴ a(a – b + c) + b(a – b + c) + c(a – b + c) = a2 + b2 + c2
∴ a² – ab + ac + ab – b² + be + ac – be + c² = a² + b² + c²
∴ a² + 2ac – b² + c² = a² + b² + c²
∴ 2ac – b² = b²
∴ 2ac = 2b²
∴ ac = b²
∴ b² = ac
∴ a, b, c are in continued proportion.

Question 5.
If \(\frac { a }{ b }\) = \(\frac { b }{ c }\) and a, b, c > 0, then show that,
i. (a + b + c)(b – c) = ab – c²
ii. (a² + b²)(b² + c²) = (ab + be)²
iii. \(\frac{a^{2}+b^{2}}{a b}=\frac{a+c}{b}\)
Solution:
Let \(\frac { a }{ b }\) = \(\frac { b }{ c }\) = k
∴ b = ck
∴ a = bk =(ck)k
∴ a = ck² …(ii)

i. (a + b + c)(b – c) = ab – c²
L.H.S = (a + b + c) (b – c)
= [ck² + ck + c] [ck – c] … [From (i) and (ii)]
= c(k² + k + 1) c (k – 1)
= c² (k² + k + 1) (k – 1)
R.H.S = ab – c²
= (ck²) (ck) – c² … [From (i) and (ii)]
= c²k³ – c²
= c²(k³ – 1)
= c² (k – 1) (k² + k + 1) … [a³ – b³ = (a – b) (a² + ab + b²]
∴ L.H.S = R.H.S
∴ (a + b + c) (b – c) = ab – c²

ii. (a² + b²)(b² + c²) = (ab + bc)²
b = ck; a = ck²
L.H.S = (a² + b²) (b² + c²)
= [(ck²) + (ck)²] [(ck)² + c²] … [From (i) and (ii)]
= [c²k⁴ + c²k²] [c²k² + c²]
= c²k² (k² + 1) c² (k² + 1)
= c4k² (k² + 1)²
R.H.S = (ab + bc)²
= [(ck²) (ck) + (ck)c]² …[From (i) and (ii)]
= [c²k³ + c²k]²
= [c²k (k² + 1)]2 = c⁴(k² + 1)²
∴ L.H.S = R.H.S
∴ (a² + b²) (b² + c²) = (ab + bc)²

iii. \(\frac{a^{2}+b^{2}}{a b}=\frac{a+c}{b}\)

9th Standard Algebra Practice Set 4.5 Question 6. Find mean proportional of \(\frac{x+y}{x-y}, \frac{x^{2}-y^{2}}{x^{2} y^{2}}\).
Solution:
Let a be the mean proportional of \(\frac{x+y}{x-y}\) and \(\frac{x^{2}-y^{2}}{x^{2} y^{2}}\)

Class 9 Maths Digest

• Practice Set 4.1 Class 9 Answers
• Practice Set 4.2 Class 9 Answers
• Practice Set 4.3 Class 9 Answers
• Practice Set 4.4 Class 9 Answers
• Practice Set 4.5 Class 9 Answers
• Practice Set 4 Class 9 Answers
• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 4 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

9th Standard Maths 1 Problem Set 4 Chapter 4 Ratio and Proportion Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Problem Set 4 Chapter 4 Ratio and Proportion Questions With Answers Maharashtra Board

Question 1.
Select the appropriate alternative answer for the following questions.

i . If 6 : 5 = y : 20, then what will be the value of y?
(A) 15
(B) 24
(C) 18
(D) 22.5
Answer:
(B) 24

ii. What is the ratio of 1 mm to 1 cm ?
(A) 1 : 100
(B) 10: 1
(C) 1 : 10
(D) 100: 1
Answer:
(C) 1 : 10

iii. The ages of Jatin, Nitin and Mohasin are 16, 24 and 36 years respectively. What is the ratio of Nitin’s age to Mohasin’s age ?
(A) 3 : 2
(B) 2 : 3
(C) 4 : 3
(D) 3 : 4
Answer:
(B) 2 : 3

iv. 24 bananas were distributed between Shubham and Anil in the ratio 3 : 5, then how many bananas did Shubham get?
(A) 8
(B) 15
(C) 12
(D) 9
Answer:
(D) 9

v. What is the mean proportional of 4 and 25?
(A) 6
(B) 8
(C) 10
(D) 12
Answer:
(C) 10

Hints:
i . \(\frac{6}{5}=\frac{y}{20}\)
∴ \(\quad y=\frac{6 \times 20}{5}=24\)

ii. \(\frac{1 \mathrm{mm}}{1 \mathrm{cm}}=\frac{1 \mathrm{mm}}{10 \mathrm{mm}}=\frac{1}{10}=1 : 10\)

iii. \(\frac{\text { Age of Nitin }}{\text { Age of Mohasin }}=\frac{24}{36}=\frac{12 \times 2}{12 \times 3}\)
\(\frac { 2 }{ 3 }\) = 2 : 3

iv. 3x + 5x = 24
∴ 8x = 24
∴ x = 3
∴ Number of bananas with Shubham = 3x = 9

v. x² = 4 x 25
∴ x² = 100
∴ x = 10

Question 2.
For the following numbers write the ratio of first number to second number in the reduced form. [1 Mark each]
i. 21,48
ii. 36,90
iii. 65,117
iv. 138,161
v. 114,133
Solution:
i. 21,48
\(\text { Ratio }=\frac{21}{48}=\frac{3 \times 7}{3 \times 16}=\frac{7}{16}=7 : 16\)
ii. 36,90
\(\text { Ratio }=\frac{36}{90}=\frac{18 \times 2}{18 \times 5}=\frac{2}{5}=2 : 5\)
iii. 65,117
\(\text { Ratio }=\frac{65}{117}=\frac{13 \times 5}{13 \times 9}=\frac{5}{9}=5 : 9\)
iv. 138,161
\(\text { Ratio }=\frac{138}{161}=\frac{23 \times 6}{23 \times 7}=\frac{6}{7}=6 : 7\)
v. 114,133
\(\text { Ratio }=\frac{114}{113}=\frac{19 \times 6}{19 \times 7}=\frac{6}{7}=6 : 7\)

Question 3.
Write the following ratios in the reduced form.
i. Radius to the diameter of a circle.
ii. The ratio of diagonal to the length of a rectangle, having length 4 cm and breadth 3 cm.
iii. The ratio of numbers denoting perimeter to area of a square, having side 4 cm.
Solution:
i. Radius to the diameter of a circle.
Let radius of the circle be r
then, diameter = 2 x radius = 2r
Ratio of radius to diameter of circle

∴ Ratio of radius to diameter of circle is 1 : 2.

ii. The ratio of diagonal to the length of a rectangle, having length 4 cm and breadth 3 cm.

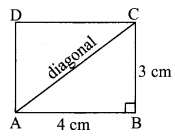
Let □ ABCD be a rectangle.
In ∆ABC, ∠B = 90°
AC² = AB² + BC² … [Pythagoras theorem]
= 4² + 3² = 16 + 9
∴ AC² = 25
AC = 5 … [Taking square root on both side]
The ratio of diagonal to the length of a rectangle = \(\frac { AC }{ AB }\)
= \(\frac { 5 }{ 4 }\)
= 5 : 4
∴ The ratio of diagonal to the length of a rectangle is 5 : 4

iii. The ratio of numbers denoting perimeter to area of a square, having side 4 cm. side of square = 4cm
Perimeter of square = 4 x side = 4 x 4 = 16 cm
Area of square = (side)² = (4)² = 16 cm²
Ratio of numbers denoting perimeter to area of square

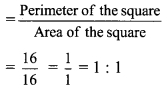
∴ The ratio of numbers denoting perimeter to area of a square is 1 : 1.

Question 4.
Check whether the following numbers are in continued proportion.
i. 2, 4, 8
ii. 1, 2, 3
iii. 9, 12, 16
iv. 3, 5, 8
Solution:
If a, b, c are in continued proportion then b² = ac.
i. 2, 4, 8
Let, a = 2, b = 4 and c = 8
Here, b² = 4² = 16
ac = 2 x 8 = 16
∴ b² = ac
∴ 2, 4,8 are in continued proportion.

ii. 1, 2, 3
Let, a = 1, b = 2 and c = 3
Here, b² = 2² = 4
ac = 1 x 3 = 3
∴ b² ≠ ac
∴ 1, 2,3 are not in continued proportion.

iii. 9, 12, 16
Let, a = 9, b = 12 and c = 16
Here, b² = 12² = 144
ac = 9 x 16 = 144
∴ b² = ac
∴ 9, 12, 16 are in continued proportion.

iv. 3, 5, 8
Let, a = 3, b = 5 and c = 8
Here, b² = 5² = 25
ac = 3 x 8 = 24
∴ b² ≠ ac
∴ 3, 5, 8 are not in continued proportion.

Question 5.
a, b, c are in continued proportion. If a = 3 and c = 27, then find b.
Solution:
a, b, c are in continued proportion. …[Given]
∴ b² = ac
∴ b² = 3 x 27 …[∵ a = 3 and c = 27]
∴ b² = 81
∴ b = 9 …[Taking square root of both sides]

Question 6.
Convert the following ratios into percentages.

Solution:
i. Let 37 : 500 = x%

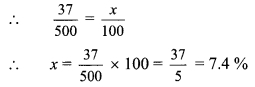
∴ 37 : 500 = 7.4%

Question 7.
Write the ratio of first quantity to second quantity in the reduced form.
i. 1024 MB, 1.2 GB [(1024 MB = 1GB)]
ii. ₹ 17, ₹ 25 and 60 paise
iii. 5 dozen, 120 units
iv. 4 sq.m, 800 sq.cm
v. 1.5 kg, 2500 gm
Solution:
i. 1024 MB, 1.2 GB
1024 MB = 1 GB

ii. ₹ 17, ₹ 25 and 60 paise
₹ 17 = 17 x 100 paise = 1700 paise
₹ 25 and 60 paise = (25x 100) paise + 60 paise
= (2500 + 60) paise
= 2560 paise

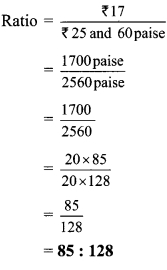
iii. 5 dozen, 120 units
5 dozen = 5 x 12 units = 60 units

iv. 4 sq.m, 800 sq.cm
4 sq.m = 4 x 10000 sq.cm = 40000 sq.cm

v. 1.5 kg, 2500 gm
1.5 kg = 1.5 x 1000 gm = 1500gm

Question 8.
If \(\frac { a }{ b }\) = \(\frac { 2 }{ 3 }\), then find the values of the following expressions.

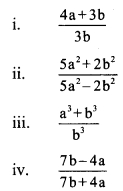
Solution:

Question 9.
If a, b, c, d are in proportion, then prove that

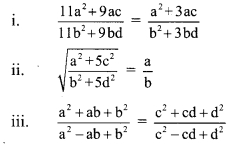
Solution:
a, b, c are in continued proportion. …[Given]

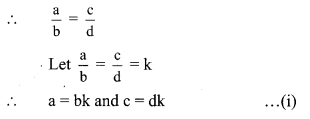
Question 10.
If a, b, c are ¡n continued proportion, then prove that

Solution:
a, b, c are in continued proportion. … [Given]
∴ \(\frac { a }{ b }\) = \(\frac { b }{ c }\)
Let \(\frac { a }{ b }\) = \(\frac { b }{ c }\) = k
∴ b = ck
∴ a = bk
= (ck)k . .. [From (j)]
a = ck² …(ii)

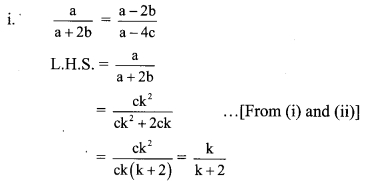
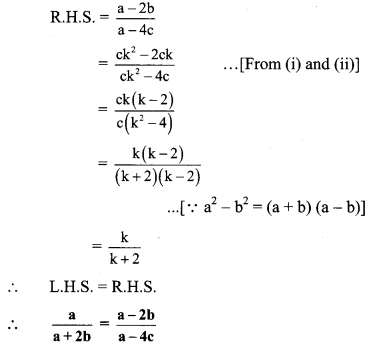
Question 11.
Solve:
\( \frac{12 x^{2}+18 x+42}{18 x^{2}+12 x+58}=\frac{2 x+3}{3 x+2}\)
Solution:


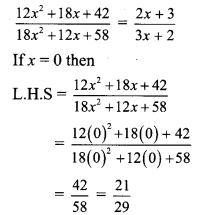
∴ 29(2x + 3) = 21 (3x + 2)
∴ 5 + 87= 63x + 42
∴ 87 – 42 = 63x – 58x
∴ 45 = 5x
∴ x = 9
∴ x = 9 is the solution of the given equation.

Question 12.
If \( \frac{2 x-3 y}{3 z+y}=\frac{z-y}{z-x}=\frac{x+3 z}{2 y-3 x}\) ,then prove that every ratio = \(\frac { x }{ y }\).
Solution:

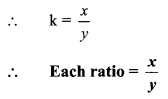
Question 13.
If \(\frac{b y+c z}{b^{2}+c^{2}}=\frac{c z+a x}{c^{2}+a^{2}}=\frac{a x+b y}{a^{2}+b^{2}}\), then prove \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}\)
Solution:

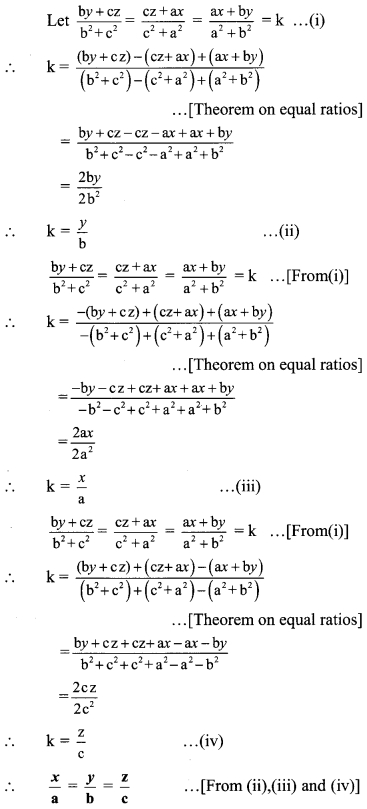
Question 1.
Take 5 pieces of card paper. Write the following statements, one on each paper.

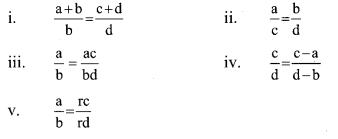
a, b, c, d are positive numbers and \(\frac{a}{b}=\frac{c}{d}\) is given. Which of the above statements are true or false, write at the back of each card, if false explain why. (Textbook pg. no. 70)
Answer:
i. True
ii. True
iii. False
Here, numerator and denominator are multiplied by two different numbers a and b.
iv. False
Here, different numbers a and b are subtracted from numerator and denominator.
v. True

Question 2.
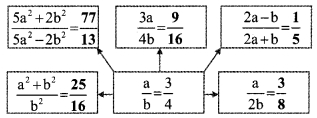
In the following activity, the values of a and b can be changed. That is by changing a : b we can create many examples. Teachers should give lot of practice to the students and encourage them to construct their own examples. (Textbook pg. no. 70)

Question 3.
Observe the political map of India from a Geography text book. Study the scale of this map.
From the given scale find the straight line distances between various cities like
i. New Delhi to Bengaluru
ii. Mumbai to Kolkata
iii. Jaipur to Bhuvaneshvar. (Textbook pg. no. 77)
[Students should attempt the above activity on their own.]

Class 9 Maths Digest

• Practice Set 4.1 Class 9 Answers
• Practice Set 4.2 Class 9 Answers
• Practice Set 4.3 Class 9 Answers
• Practice Set 4.4 Class 9 Answers
• Practice Set 4.5 Class 9 Answers
• Practice Set 4 Class 9 Answers
• Practice Set 5.1 Class 9 Answers
• Practice Set 5.2 Class 9 Answers
• Practice Set 5 Class 9 Answers