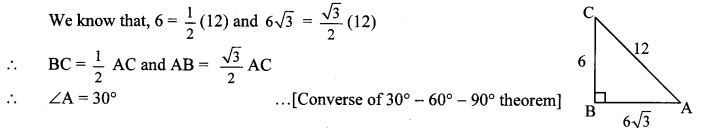Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 2 Pythagoras Theorem.
10th Standard Maths 2 Problem Set 2 Chapter 2 Pythagoras Theorem Textbook Answers Maharashtra Board
Class 10 Maths Part 2 Problem Set 2 Chapter 2 Pythagoras Theorem Questions With Answers Maharashtra Board
Question 1.
Some questions and their alternative answers are given. Select the correct alternative. [1 Mark each]
i. Out of the following which is the Pythagorean triplet?
(A) (1,5,10)
(B) (3,4,5)
(C) (2,2,2)
(D) (5,5,2)
Answer: (B)
Hint: Refer Practice set 2.1 Q.1 (i)
ii. In a right angled triangle, if sum of the squares of the sides making right angle is 169, then what is the length of the hypotenuse?
(A) 15
(B) 13
(C) 5
(D) 12
Answer: (B)
Hint:

iii. Out of the dates given below which date constitutes a Pythagorean triplet?
(A) 15/08/17
(B) 16/08/16
(C) 3/5/17
(D) 4/9/15
Answer: (A)
Hint:
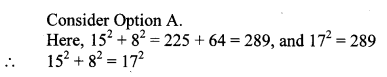
iv. If a, b, c are sides of a triangle and a2 + b2 = c2, name the type of the triangle.
(A) Obtuse angled triangle
(B) Acute angled triangle
(C) Right angled triangle
(D) Equilateral triangle
Answer: (C)
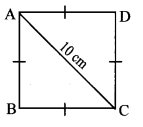
v. Find perimeter of a square if its diagonal is 10\(\sqrt { 2 }\) cm.
(A) 10 cm
(B) 40\(\sqrt { 2 }\) cm
(C) 20 cm
(D) 40 cm
Answer: (D)
Hint:

vi. Altitude on the hypotenuse of a right angled triangle divides it in two parts of lengths 4 cm and 9 cm. Find the length of the altitude.
(A) 9 cm
(B) 4 cm
(C) 6 cm
(D) 2\(\sqrt { 6 }\)
Answer: (C)
Hint:

vii. Height and base of a right angled triangle are 24 cm and 18 cm find the length of its hypotenuse.
(A) 24 cm
(B) 30 cm
(C) 15 cm
(D) 18 cm
Answer: (B)
Hint:

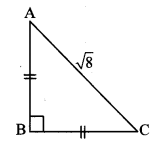
viii. In ∆ABC, AB = 6\(\sqrt { 3 }\) cm, AC = 12 cm, BC = 6 cm. Find measure of ∠A.
(A) 30°
(B) 60°
(C) 90°
(D) 45°
Answer: (A)
Hint:
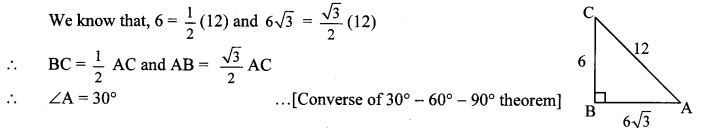
Question 2.
Solve the following examples.
i. Find the height of an equilateral triangle having side 2a.
ii. Do sides 7 cm, 24 cm, 25 cm form a right angled triangle? Give reason.
iii. Find the length of a diagonal of a rectangle having sides 11 cm and 60 cm.
iv. Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
v. A side of an isosceles right angled triangle is x. Find its hypotenuse.
vi. In ∆PQR, PQ = \(\sqrt { 8 }\), QR = \(\sqrt { 5 }\), PR = \(\sqrt { 3 }\) . Is ∆PQR a right angled triangle? If yes, which angle is of 90°?
Solution:
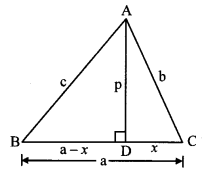
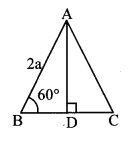
i. Let ∆ABC be the given equilateral triangle.
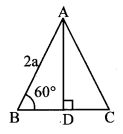
∴ ∠B = 60° [Angle of an equilateral triangle]
Let AD ⊥BC, B – D – C.
In ∆ABD, ∠B = 60°, ∠ADB = 90°
∴ ∠BAD = 30° [Remaining angle of a triangle]
∴ ∆ABD is a 30° – 60° – 90° triangle.
∴ AD = \(\frac{\sqrt{3}}{2}\) AB [Side opposite to 60°]
= \(\frac{\sqrt{3}}{2}\) × 2a
= a\(\sqrt { 3 }\) units
The height of the equilateral triangle is a\(\sqrt { 3 }\) units.
ii. The sides of the triangle are 7 cm, 24 cm and 25 cm.
The longest side of the triangle is 25 cm.
∴ (25)2 = 625
Now, sum of the squares of the remaining sides is,
(7)2 + (24)2 = 49 + 576
= 625
∴ (25)2 = (7)2 + (24)2
∴ Square of the longest side is equal to the sum of the squares of the remaining two sides.
∴ The given sides will form a right angled triangle. [Converse of Pythagoras theorem]
iii. Let ꠸ABCD be the given rectangle.
AB = 11 cm, BC = 60 cm
In ∆ABC, ∠B = 90° [Angle of a rectangle]
∴ AC2 = AB2 + BC2 [Pythagoras theorem]
= 112 + 602
= 121 +3600
= 3721
∴ AC = \(\sqrt { 3721 }\) [Taking square root of both sides]
= 61 cm
The length of the diagonal of the rectangle is 61 cm.
∴ The length of the diagonal of the rectangle is 61 cm.
iv. Let ∆PQR be the given right angled triangle.
In ∆PQR, ∠Q = 90°
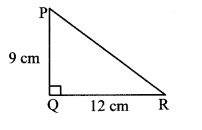
∴ PR2 = PQ2 + QR2 [Pythagoras theorem]
= 92 + 122
= 81 + 144
= 225
∴ PR = \(\sqrt { 225 }\) [Taking square root of both sides]
= 15 cm
∴ The length of the hypotenuse of the right angled triangle is 15 cm.
v. Let ∆PQR be the given right angled isosceles triangle.
PQ = QR = x.
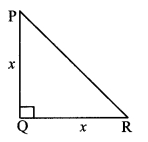
In ∆PQR, ∠Q = 90° [Pythagoras theorem]
∴ PR2 = PQ2 + QR2
= x2 + x2
= 2x2
∴ PR = \(\sqrt{2 x^{2}}\) [Taking square root of both sides]
= x \(\sqrt { 2 }\) units
∴ The hypotenuse of the right angled isosceles triangle is x \(\sqrt { 2 }\) units.
∴ The hypotenuse of the right angled isosceles triangle is x \(\sqrt { 2 }\) units.
vi. Longest side of ∆PQR = PQ = \(\sqrt { 8 }\)
∴ PQ2 = (\(\sqrt { 8 }\))2 = 8
Now, sum of the squares of the remaining sides is,
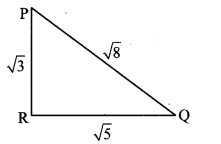
QR2 + PR2 = (\(\sqrt { 5 }\))2 + (\(\sqrt { 3 }\))2
= 5 + 3
= 8
∴ PQ2 = QR2 + PR2
∴ Square of the longest side is equal to the sum of the squares of the remaining two sides.
∴ ∆PQR is a right angled triangle. [Converse of Pythagoras theorem]
Now, PQ is the hypotenuse.
∴∠PRQ = 90° [Angle opposite to hypotenuse]
∴ ∆PQR is a right angled triangle in which ∠PRQ is of 90°.
Question 3.
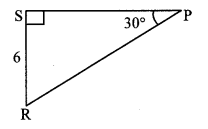
In ∆RST, ∠S = 90°, ∠T = 30°, RT = 12 cm, then find RS and ST.
Solution:
in ∆RST, ∠S = 900, ∠T = 30° [Given]
∴ ∠R = 60° [Remaining angle of a triangle]
∴ ∆RST is a 30° – 60° – 90° triangle.
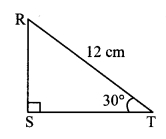
∴ RS = \(\frac { 1 }{ 2 } \) RT [Side opposite to 30°]
= \(\frac { 1 }{ 2 } \) × 12 = 6cm
Also, ST = \(\frac{\sqrt{3}}{2}\) RT [Side opposite to 60°]
= \(\frac{\sqrt{3}}{2}\) × 12 = 6 \(\sqrt { 3 }\) cm
∴ RS = 6 cm and ST = 6 \(\sqrt { 3 }\) cm
Question 4.
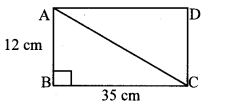
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq. cm.
Solution:
Let ꠸ABCD be the given rectangle.
BC = 16cm
Area of rectangle = length × breadth
Area of ꠸ABCD = BC × AB
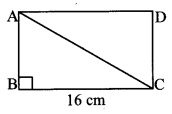
∴ 192 = I6 × AB
∴ AB = \(\frac { 192 }{ 16 } \)
= 12cm
Now, in ∆ABC, ∠B = 90° [Angle of a rectangle]
∴ AC2 = AB2 + BC2 [Pythagoras theorem]
= 122 + 162
= 144 + 256
=400
∴ AC = \(\sqrt { 400 }\) [Taking square root of both sides]
= 20cm
∴ The diagonal of the rectangle is 20 cm.
Question 5.
Find the length of the side and perimeter of an equilateral triangle whose height is \(\sqrt { 3 }\) cm.
Solution:
Let ∆ABC be the given equilateral triangle.
∴ ∠B = 60° [Angle of an equilateral triangle]
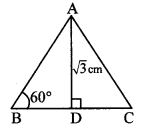
AD ⊥ BC, B – D – C.
In ∆ABD, ∠B =60°, ∠ADB = 90°
∴ ∠BAD = 30° [Remaining angle of a triangle]
∴ ∆ABD is a 30° – 60° – 90° triangle.
∴ AD = \(\frac{\sqrt{3}}{2}\)AB [Side opposite to 600]
∴ \(\sqrt { 3 }\) = \(\frac{\sqrt{3}}{2}\)AB
∴ AB = \(\frac{2 \sqrt{3}}{\sqrt{3}}\)
∴ AB = 2cm
∴ Side of equilateral triangle = 2cm
Perimeter of ∆ABC = 3 × side
= 3 × AB
= 3 × 2
= 6cm
∴ The length of the side and perimeter of the equilateral triangle are 2 cm and 6 cm respectively.
Question 6.
In ∆ABC, seg AP is a median. If BC = 18, AB2 + AC2 = 260, find AP.
Solution:
PC = \(\frac { 1 }{ 2 } \) BC [P is the midpoint of side BC]
= \(\frac { 1 }{ 2 } \) × 18 = 9cm
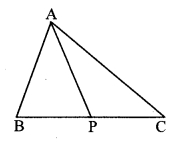
in ∆ABC, seg AP is the median,
Now, AB2 + AC2 = 2 A2 + 2 PC2 [Apollonius theorem]
∴ 260 = 2 AP2 + 2 (9)2
∴ 130 = AP2 + 81 [Dividing both sides by 2]
∴ AP2 = 130 – 81
∴ AP2 = 49
∴ AP = \(\sqrt { 49 }\) [Taking square root of both sides]
∴ AP = 7 units
Question 7.
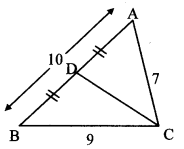
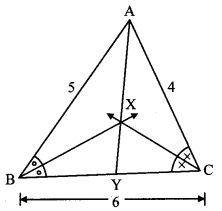
∆ABC is an equilateral triangle. Point P is on base BC such that PC = \(\frac { 1 }{ 3 } \) BC, if AB = 6 cm find AP.
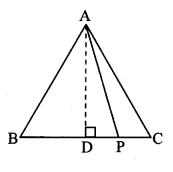
Given: ∆ABC is an equilateral triangle.
PC = \(\frac { 1 }{ 3 } \) BC, AB = 6cm.
To find: AP
Consttuction: Draw seg AD ± seg BC, B – D – C.
Solution:
∆ABC is an equilateral triangle.
∴ AB = BC = AC = 6cm [Sides of an equilateral triangle]
pc = \(\frac { 1 }{ 3 } \) BC [Given]
= \(\frac { 1 }{ 3 } \) (6)
∴ PC = 2cm
In ∆ADC,
∠D = 90° [Construction]
∠C = 60° [Angle of an equilateral triangle]
∠DAC = 30° [Remaining angle of a triangle]
∴ ∆ ADC is a 30° – 60° – 90° triangle.
∴ AD = \(\frac{\sqrt{3}}{2}\) AC [Side opposite to 60°]
∴ AD = \(\frac{\sqrt{3}}{2}\) (6)
∴ AD = 3 \(\sqrt { 3 }\)cm
CD = \(\frac { 1 }{ 2 } \) AC [Side opposite to 30°]
∴ CD = \(\frac { 1 }{ 2 } \) (6)
∴ CD = 3cm
Now DP + PC = CD [D – P – C]
∴ DP + 2 = 3
∴ DP = 1cm
In ∆ADP,
∠ADP = 900
AP2 = AD2 + DP2 [Pythagoras theorem]
∴ AP2 = (3\(\sqrt { 3 }\))2 + (1)2
∴ AP2 = 9 × 3 + 1 = 27 + 1
∴ AP2 = 28
∴ AP = \(\sqrt { 28 }\)
∴ AP = \(\sqrt{4 \times 7}\)
∴ AP = 2 \(\sqrt { 7 }\)cm
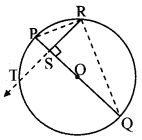
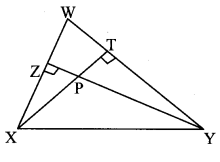
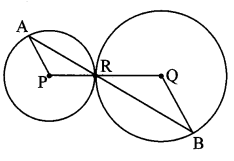
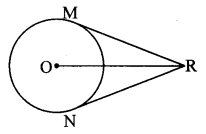
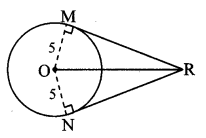
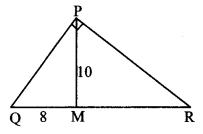
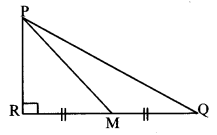
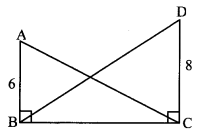
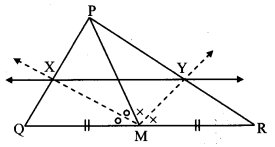
Question 8.
From the information given in the adjoining figure, prove that
PM = PN = \(\sqrt { 3 }\) × a
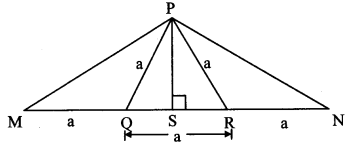
Solution:
Proof:
In ∆PMR,
QM = QR = a [Given]
∴ Q is the midpoint of side MR.
∴ seg PQ is the median.
∴ PM2 + PR2 = 2PQ2 + 2QM2 [Apollonius theorem]
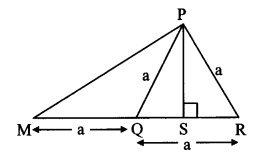
∴ PM2 + a2 = 2a2 + 2a2
∴ PM2 + a2 = 4a2
∴ PM2 = 3a2
∴ PM,= \(\sqrt { 3 }\)a (i) [Taking square root of both sides]
SimlarIy, in ∆PNQ,
R is the midpoint of side QN.
∴ seg PR is the median.
∴ PN2 + PQ2 = 2 PR2 + 2 RN2 [Apollonius theorem]
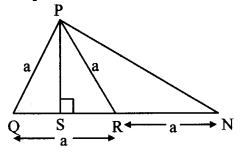
∴ PN2 + a2 = 2a2 + 2a2
∴ PN2 + a2 = 4a2
∴ PN2 = 3a2
∴ PN = \(\sqrt { 3 }\)a (ii) [Taking square root of both sides]
∴ PM = PN = \(\sqrt { 3 }\) a [From (i) and (ii)]
Question 9.
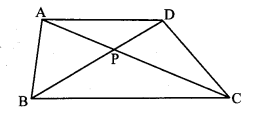
Prove that the sum of the squares of the diagonals of a parallelogram ¡s equal to the sum of the squares of its sides.
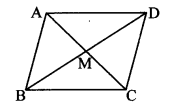
Given: ꠸ABCD is a parallelogram, diagonals AC and BD intersect at point M.
To prove: AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Solution:
Proof:
꠸ABCD is a parallelogram.
∴ AB = CD and BC = AD (i) [Opposite sides of a parallelogram]
AM = \(\frac { 1 }{ 2 } \) AC and BM = \(\frac { 1 }{ 2 } \) BD (ii) [Diagonals of a parallelogram bisect each other]
∴ M is the midpoint of diagonals AC and BD. (iii)
In ∆ABC.
seg BM is the median. [From (iii)]
AB2 + BC2 = 2AM2 + 2BM2 (iv) [Apollonius theorem]
∴ AB2 + BC2 = 2(\(\frac { 1 }{ 2 } \) AC)2 + 2(\(\frac { 1 }{ 2 } \) BD)2 [From (ii) and (iv)]
∴ AB2 + BC2 = 2 × \(\frac{\mathrm{BD}^{2}}{4}+2 \times \frac{\mathrm{AC}^{2}}{4}\)
∴ AB2 + BC2 = \(\frac{B D^{2}}{2}+\frac{A C^{2}}{2}\)
∴ 2AB2 + 2BC2 = BD2 + AC2 [Multiplying both sides by 2]
∴ AB2 + AB2 + BC2 + BC2 = BD2 + AC2
∴ AB2 + CD2 + BC2 + AD2 = BD2 + AC2 [From(i)]
i.e. AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Question 10.
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was 15\(\sqrt { 2 }\) km. Find their speed per hour.
Solution:
Suppose Pranali and Prasad started walking from point A, and reached points B and C respectively after 2 hours.
Distance between them = BC = 15\(\sqrt { 2 }\) km
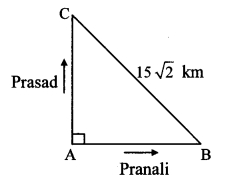
Since, their speed is same, both travel the same distance in the given time.
∴ AB = AC
Let AB = AC = x km (i)
Now, in ∆ ABC, ∠A = 90°
∴ BC2 = AB2 + AC2 [Pythagoras theorem]
∴ (15\(\sqrt { 2 }\))2 = x2 + x2 [From (i)]
∴ 225 × 2 = 2 x2
∴ x2 = 225
∴ x = \(\sqrt { 225 }\) [Taking square root of both sides]
∴ x = 15 km
∴ AB = AC = 15km
\(\text { Now, speed }=\frac{\text { distance }}{\text { time }}=\frac{15}{2}\)
= 7.5 km/hr
∴ The speed of Pranali and Prasad is 7.5 km/hour.
Question 11.
In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that 4 (BL2 + CM2) = 5 BC2.
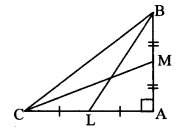
Given : ∠BAC = 90°
seg BL and seg CM are the medians.
To prove: 4(BL2 + CM2) = 5BC2
Solution:
Proof:
In ∆BAL, ∠BAL 90° [Given]
∴ BL2 = AB2 + AL2 (i) [Pythagoras theorem]
In ∆CAM, ∠CAM = 90° [Given]
∴ CM2 = AC2 + AM2 (ii) [Pythagoras theorem]
∴ BL2 + CM2 = AB2 + AC2 + AL2 + AM2 (iii) [Adding (i) and (ii)]
Now, AL = \(\frac { 1 }{ 2 } \) AC and AM = \(\frac { 1 }{ 2 } \) AB (iv) [seg BL and seg CM are the medians]
∴ BL2 + CM2
= AB2 + AC2 + (\(\frac { 1 }{ 2 } \) AC)2 + (\(\frac { 1 }{ 2 } \) AB)2 [From (iii) and (iv)]
\(=A B^{2}+A C^{2}+\frac{A C^{2}}{4}+\frac{A B^{2}}{4}\)
\(=A B^{2}+\frac{A B^{2}}{4}+A C^{2}+\frac{A C^{2}}{4}\)
\(=\frac{5 \mathrm{AB}^{2}}{4}+\frac{5 \mathrm{AC}^{2}}{4}\)
∴ BL2 + CM2 = \(\frac { 5 }{ 4 } \) (AB2 + AC2)
∴ 4(BL2 + CM2) = 5(AB2 + AC2) (v)
In ∆BAC, ∠BAC = 90° [Given]
∴ BC2 = AB2 + AC2 (vi) [Pythagoras theorem]
∴ 4(BL2 + CM2) = 5BC2 [From (v) and (vi)]
Question 12.
Sum of the squares of adjacent sides of a parallelogram is 130 cm and length of one of its diagonals is 14 cm. Find the length of the other diagonal.
Solution:
Let ꠸ABCD be the given
parallelogram and its diagonals AC and BD intersect at point M.
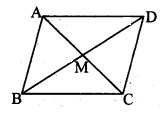
∴ AB2 + AD2 = 130cm, BD = 14cm
MD = \(\frac { 1 }{ 2 } \) BD (i) [Diagonals of a parallelogram bisect each other]
= \(\frac { 1 }{ 2 } \) × 14 = 7 cm
In ∆ABD, seg AM is the median. [From (i)]
∴ AB2 + = 2AM2 + 2MD2 [Apollonius theorem]
∴ 130 = 2 AM2 + 2(7)2
∴ 65 = AM2 +49 [Dividing both sides by 2]
∴ AM2 = 65 – 49
∴ AM2 = 16 [Taking square root of both sides]
∴ AM = \(\sqrt { 16 }\)
= 4cm
Now, AC =2 AM [Diagonals of a parallelogram bisect each other]
2 × 4 = 8 cm
∴ The length of the other diagonal of the parallelogram is 8 cm.
Question 13.
In ∆ABC, seg AD ⊥ seg BC and DB = 3 CD. Prove that: 2 AB2 = 2 AC2 + BC2.
Given: seg AD ⊥ seg BC
DB = 3CD
To prove: 2AB2 = 2AC2 + BC2
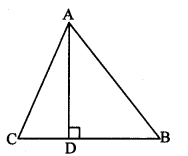
Solution:
DB = 3CD (i) [Given]
In ∆ADB, ∠ADB = 90° [Given]
∴ AB2 = AD2 + DB2 [Pythagoras theorem]
∴ AB2 = AD2 + (3CD)2 [From (i)]
∴ AB2 = AD2 + 9CD2 (ii)
In ∆ADC, ∠ADC = 90° [Given]
∴ AC2 = AD2 + CD2 [Pythagoras theorem]
∴ AD2 = AC2 – CD2 (iii)
AB2 = AC2 – CD2 + 9CD2 [From (ii) and(iii)]
∴ AB2 = AC2 + 8CD2 (iv)
CD + DB = BC [C – D – B]
∴ CD + 3CD = BC [From (i)]
∴ 4CD = BC
∴ CD = \(\frac { BC }{ 4 } \) (v)
AB2 = AC2 + 8(\(\frac { BC }{ 4 } \))2 [From (iv) and (v)]
∴ AB2 = AC2 + 8 × \(\frac{\mathrm{BC}^{2}}{16}\)
∴ AB2 = AC2 + \(\frac{\mathrm{BC}^{2}}{2}\)
∴ 2AB2 = 2AC2 + BC2 [Multiplying both sides by 2]
Question 14.
In an isosceles triangle, length of the congruent sides is 13 em and its.base is 10 cm. Find the distance between the vertex opposite to the base and the centroid.
Given: ∆ABC is an isosceles triangle.
G is the centroid.
AB = AC = 13 cm, BC = 10 cm.
To find: AG
Construction: Extend AG to intersect side BC at D, B – D – C.
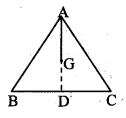
Solution:
Centroid G of ∆ABC lies on AD
∴ seg AD is the median. (i)
∴ D is the midpoint of side BC.
∴ DC = \(\frac { 1 }{ 2 } \) BC
= \(\frac { 1 }{ 2 } \) × 10 = 5
In ∆ABC, seg AD is the median. [From (i)]
∴ AB2 + AC2 = 2 AD2 + 2 DC2 [Apollonius theorem]
∴ 132 + 132 = 2 AD2 + 2 (5)2
∴ 2 × 132 = 2 AD2 + 2 × 25
∴ 169 = AD2 + 25 [Dividing both sides by 2]
∴ AD2 = 169 – 25
∴ AD2 = 144
∴ AD = \(\sqrt { 144 }\) [Taking square root of both sides]
= 12 cm
We know that, the centroid divides the median in the ratio 2 : 1.
∴ \(\frac { AG }{ GD } \) = \(\frac { 2 }{ 1 } \)
∴ \(\frac { GD }{ AG } \) = \(\frac { 1 }{ 2 } \) [By invertendo]
∴ \(\frac { GD+AG }{ AG } \) = \(\frac { 1+2 }{ 2 } \) [By componendo]
∴ \(\frac { AD }{ AG } \) = \(\frac { 3 }{ 2 } \) [A – G – D]
∴ \(\frac { 12 }{ AG } \) = \(\frac { 3 }{ 2 } \)
∴ AG = \(\frac{12 \times 2}{3}\)
= 8cm
∴ The distance between the vertex opposite to the base and the centroid is 8 cm.
Question 15.
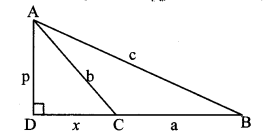
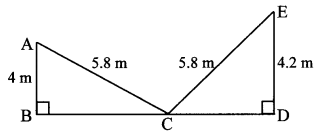
In a trapezium ABCD, seg AB || seg DC, seg BD ⊥ seg AD, seg AC ⊥ seg BC. If AD = 15, BC = 15 and AB = 25, find A (꠸ABCD).
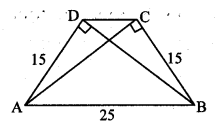
Construction: Draw seg DE ⊥ seg AB, A – E – B
and seg CF ⊥ seg AB, A – F- B.
Solution:
In ∆ ACB, ∠ACB = 90° [Given]
∴ AB2 = AC2 + BC2 [Pythagoras theorem]
∴ 252 = AC2 + 152
∴ AC2 = 625 – 225
= 400
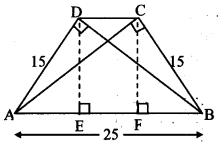
∴ AC = \(\sqrt { 400 }\) [Taking square root of both sides]
= 20 units
Now, A(∆ABC) = \(\frac { 1 }{ 2 } \) × BC × AC
Also, A(∆ABC) = \(\frac { 1 }{ 2 } \) × AB × CF
∴ \(\frac { 1 }{ 2 } \) × BC × AC = \(\frac { 1 }{ 2 } \) × AB × CF
∴ BC × AC = AB × CF
∴ 15 × 20 = 25 × CF
∴ CF = \(\frac{15 \times 20}{25}\) = 12 units
In ∆CFB, ∠CFB 90° [Construction]
∴ BC2 = CF2 + FB2 [Pythagoras theorem]
∴ 152 = 122 + FB2
∴ FB2 = 225 – 144
∴ FB2 = 81
∴ FB = \(\sqrt { 81 }\) [Taking square root of both sides]
= 9 units
Similarly, we can show that, AE = 9 units
Now, AB = AE + EF + FB [A – E – F, E – F – B]
∴ 25 = 9 + EF + 9
∴ EF = 25 – 18 = 7 units
In ꠸CDEF,
seg EF || seg DC [Given, A – E – F, E – F – B]
seg ED || seg FC [Perpendiculars to same line are parallel]
∴ ꠸CDEF is a parallelogram.
∴ DC = EF 7 units [Opposite sides of a parallelogram]
A(꠸ABCD) = \(\frac { 1 }{ 2 } \) × CF × (AB + CD)
= \(\frac { 1 }{ 2 } \) × 12 × (25 + 7)
= \(\frac { 1 }{ 2 } \) × 12 × 32
∴ A(꠸ABCD) = 192 sq. units
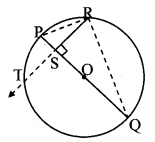
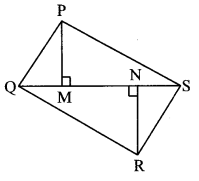
Question 16.
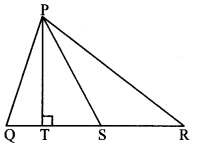
In the adjoining figure, ∆PQR is an equilateral triangle. Point S is on seg QR such that QS = \(\frac { 1 }{ 3 } \) QR. Prove that: 9 PS2 = 7 PQ2.
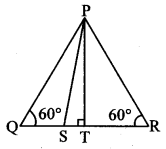
Given: ∆PQR is an equilateral triangle.
QS = \(\frac { 1 }{ 3 } \) QR
To prove: 9PS2 = 7PQ2
Solution:
Proof:
∆PQR is an equilateral triangle [Given]
∴ ∠P = ∠Q = ∠R = 60° (i) [Angles of an equilateral triangle]
PQ = QR = PR (ii) [Sides of an equilateral triangle]
In ∆PTS, ∠PTS = 90° [Given]
PS2 = PT2 + ST2 (iii) [Pythagoras theorem]
In ∆PTQ,
∠PTQ = 90° [Given]
∠PQT = 60° [From (i)]
∴ ∠QPT = 30° [Remaining angle of a triangle]
∴ ∆PTQ is a 30° – 60° – 90° triangle
∴ PT = \(\frac{\sqrt{3}}{2}\) PQ (iv) [Side opposite to 60°]
QT = \(\frac { 1 }{ 2 } \) PQ (v) [Side opposite to 30°]
QS + ST = QT [Q – S – T]
∴ \(\frac { 1 }{ 3 } \) QR + ST = \(\frac { 1 }{ 2 } \) PQ [Given and from (v)]
∴ \(\frac { 1 }{ 3 } \) PQ + ST = \(\frac { 1 }{ 2 } \) PQ [From (ii)]
∴ ST = \(\frac { PQ }{ 2 } \) – \(\frac { PQ }{ 3 } \)
∴ ST = \(\frac { 3PQ-2PQ }{ 6 } \)
∴ ST = \(\frac { PQ }{ 6 } \) (vi)
\(\mathrm{PS}^{2}=\left(\frac{\sqrt{3}}{2} \mathrm{PQ}\right)^{2}+\left(\frac{\mathrm{PQ}}{6}\right)^{2}\) [From (iii), (iv) and (vi)]
∴ \(\mathrm{PS}^{2}=\frac{3 \mathrm{PQ}^{2}}{4}+\frac{\mathrm{PQ}^{2}}{36}\)
∴ \(\mathrm{PS}^{2}=\frac{27 \mathrm{PQ}^{2}}{36}+\frac{\mathrm{PQ}^{2}}{36}\)
∴\(\mathrm{PS}^{2}=\frac{28 \mathrm{PQ}^{2}}{36}\)
∴PS2 = \(\frac { 7 }{ 3 } \) PQ2
∴ 9PS2 = 7 PQ2
Question 17.
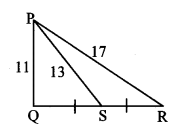
Seg PM is a median of APQR. If PQ = 40, PR = 42 and PM = 29, find QR.
Solution:
In ∆PQR, seg PM is the median. [Given]
∴ M is the midpoint of side QR.
∴ PQ2 + PR2 = 2 PM2 + 2 MR2 [Apollonius theorem]
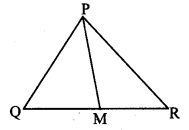
∴ 402 + 422 = 2 (29)2 + 2 MR2
∴ 1600 + 1764 = 2 (841) + 2 MR2
∴ 3364 = 2 (841) + 2 MR2
∴ 1682 = 841 +MR2 [Dividing both sides by 2]
∴ MR2 = 1682 – 841
∴ MR2 = 841
∴ MR = \(\sqrt { 841 }\) [Taking square root of both sides]
= 29 units
Now, QR = 2 MR [M is the midpoint of QR]
= 2 × 29
∴ QR = 58 units
Question 18.
Seg AM is a median of ∆ABC. If AB = 22, AC = 34, BC = 24, find AM.
Solution:
In ∆ABC, seg AM is the median. [Given]
∴ M is the midpoint of side BC.
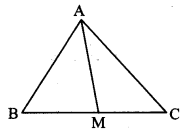
∴ MC = \(\frac { 1 }{ 2 } \) BC
= \(\frac { 1 }{ 2 } \) × 24 = 12 units
Now, AB2 + AC2 = 2 AM2 + 2 MC2 [Apollonius theorem]
∴ 222 + 342 = 2 AM2 + 2 (12)2
∴ 484 + 1156 = 2 AM2 + 2 (144)
∴ 1640 = 2 AM2 + 2 (144)
∴ 820 = AM2 + 144 [Dividing both sides by 2]
∴ AM2 = 820 – 144
∴ AM2 = 676
∴ AM = \(\sqrt { 676 }\) [Taking square root of both sides]
∴ AM = 26 units
Class 10 Maths Digest