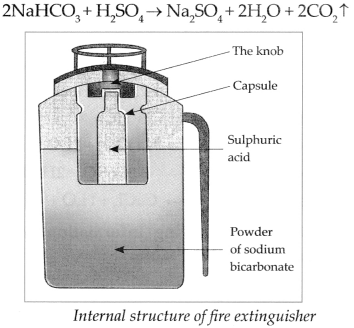
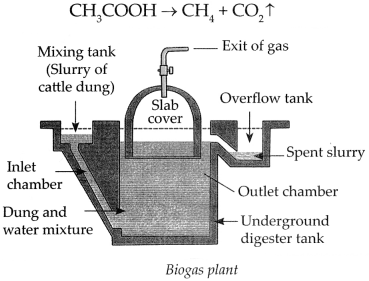
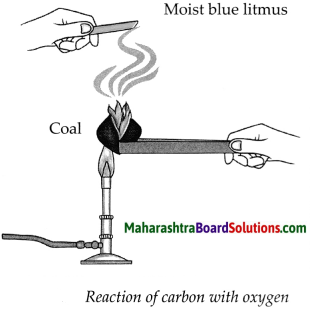
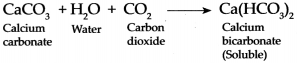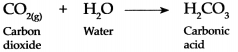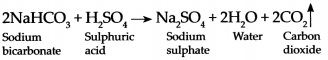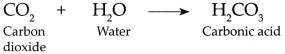Prasanna

Acids, Bases and Salts Class 9 Science Chapter 5 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 5 Acids, Bases and Salts Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 5 Acids, Bases and Salts Question Answer Maharashtra Board

Class 9 Science Chapter 5 Acids, Bases and Salts Question Answer Maharashtra Board

1. Identify the odd one out and justify.

(a) Chloride, nitrate, hydride, ammonium
Answer:
Ammonium is the odd one out as it is a basic radical and rest all are acidic radicals. Generally, basic radicals are formed by the removal of electrons from the atom of metals such as Na⁺, Cu²⁺. But there are some exceptions, such as NH₄⁺.

(b) Hydrogen chloride, sodium hydroxide, calcium oxide, ammonia
Answer:
Hydrogen chloride is the odd one out. It is acidic and rest all are basic.

(c) Acetic acid, carbonic acid, hydrochloric acid, nitric acid
Answer:
Carbonic acid is the odd one out. It is a dibasic acid and rest are all monobasic acids.

(d) Ammonium chloride, sodium chloride, potassium nitrate, sodium sulphate
Answer:
Ammonium chloride is the odd one out, as it is made up of a strong acid and weak base and rest all are formed from strong acid and strong base.

(e) Sodium nitrate, sodium carbonate, sodium sulphate, sodium chloride
Answer:
Sodium carbonate is the odd one out, as it is made up of a weak acid and strong base, and rest all are formed from strong acid and strong base.

(f) Calcium oxide, magnesium oxide, zinc oxide, sodium oxide.
Answer:
Zinc oxide is the odd one out, as it is an amphoteric oxide, and rest all are basic oxides.

(g) Crystalline blue vitriol, crystalline common salt, crystalline ferrous sulphate, crystalline sodium carbonate.
Answer:
Crystalline common salt is the odd one out, as it does not contain water of crystallisation. It is an ionic compound and ionic compounds are crystalline in nature and rest all have their crystalline structure because of their water of crystallization.

(h) Sodium chloride, potassium hydroxide, acetic acid, sodium acetate.
Answer:
Acetic acid is the odd one out. It is an acid, the rest are all salts.

2. Write down the changes that will be seen in each instance and explain the reason behind it.

(a) 50ml water is added to 50ml solution of copper sulphate.

Answer:

Copper sulphate solution is blue. It is a concentrated solution.
When 50 ml of water is added to this concentrated solution, it becomes a diluted solution.
The intensity of the blue colour is now different in this homogenous mixture.

(b) Two drops of the indicator phenolphthalein were added to 10ml solution of sodium hydroxide.

Answer:

Sodiumhy droxide is a base and phenolphthalein is a synthetic indicator.
Sodium hydroxide solution will turn pink if phenolphthalein is added to it.
It is a test for identifying bases.

(c) Two or three filings of copper were added to 10ml dilute nitric acid and stirred.
Answer:
When copper metal reacts with dilute nitric acid, the metal does not displace hydrogen from the acid like reaction with other metals. Instead the reaction produces nitric oxide, (NO).

(d) A litmus paper was dropped into 2ml dilute HCl. Then 2ml concentrated NaOH was added to it and stirred.
Answer:
Blue litmus Paper:

HCl is hydrochloric acid, so the blue litmus turns red.
When equal amount of NaOH is added the colour again changes to blue and remains the same.

Red litmus paper:

Red litmus paper shows no colour change in hydrochloric acid.
When some amount of NaOH is added the colour changes to blue initially but when the amount of NaOH is sufficient the blue colour dissappears.
Equal amounts of HC1 and NaOH results in the formation of NaCl, a salt, and the solvent water. This reaction is called the neutralization reaction.

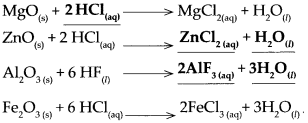
(e) Magnesium oxide was added to dilute HCl and magnesium oxide was a added to dilute NaOH.
Answer:
(i) Magnesium oxide + dil HCl.
This is a neutralization reaction. Magnesium oxide is an insoluble base, it reacts with dilute HCl to produce a soluble salt MgCl₂ and water H₂O.
\(\mathrm{MgO}_{(\mathrm{s})}+2 \mathrm{HCl}_{(\mathrm{aq})} \longrightarrow \mathrm{MgCl}_{2(\mathrm{aq})}+\mathrm{H}_{2} \mathrm{O}_{(n)}\)

(ii) Magnesium oxide + NaOH.
No chemical reaction takes place between magnesium oxide and sodium hydroxide.

(f) Zinc oxide was added to dilute HCl and zinc oxide was added to dilute NaOH.
Answer:

Zinc oxide reacts with dilute hydrochloric acid to form zinc chloride and water. It is a neutralization reaction.
\(\mathrm{ZnO}_{(\mathrm{s})}+2 \mathrm{HCl}_{(\mathrm{aq})} \longrightarrow \mathrm{ZnCl}_{2(\mathrm{aq})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}\)
Zinc oxide reacts with sodium hydroxide to form sodium zincate and water.
\(\mathrm{ZnO}_{(\mathrm{s})}+2 \mathrm{NaOH}_{(\mathrm{aq})} \longrightarrow \mathrm{Na}_{2} \mathrm{ZnO}_{2(\mathrm{aq})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{t})}\)

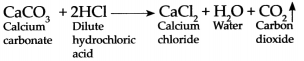
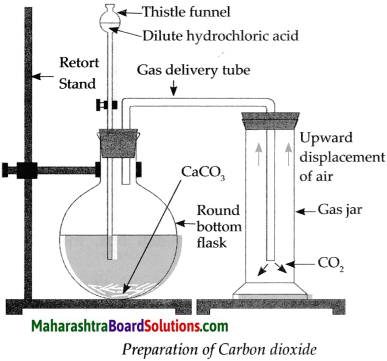
(g) Dilute HCl was added to limestone.
Answer:

When hydrochloric acid is added to limestone, carbon dioxide is liberated. Limestone is calcium carbonate.
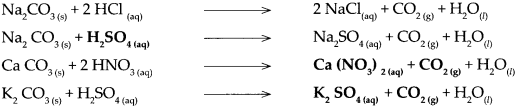
CaCO₃ + 2 HCl → CaCl₂ + CO₂ + H₂O
Carbon dioxide is prepared in the laboratory using these chemicals.

(h) Pieces of blue vitriol were heated in a test tube. On cooling, water was added to it.
Answer:

On heating, the crystalline structure of blue vitriol breaks down to form a colourless powder and water is released.
This water is part of the crystal structure of blue vitriol.
It is called water of crystallization.
On adding water to the white powder, a solution was formed which has the same colour as the copper sulphate salt solution.

(i) Dilute H₂SO₄ was taken in an electrolytic cell and electric current was passed through it.
Answer:

If pure water is used in the electrolytic cell, current does not flow even on putting on the switch.
Pure water is a bad conductor of electricity. Dilute H₂SO₄ is acidulated water.
The electrical conductivity of water increases on mixing with strong acid or base in it due to their dissociation and electrolysis of water takes place.
H₂SO₄ is fully dissociated in aqueous solution. \(\mathrm{H}_{2} \mathrm{SO}_{4} \longrightarrow 2 \mathrm{H}^{+}+\mathrm{SO}_{4}^{2-}\)
H₂O is a weak electrolyte and is only slightly dissociated \(\mathrm{H}_{2} \mathrm{O} \longrightarrow \mathrm{H}^{+}+\mathrm{OH}^{-}\)
During electrolysis, the hydrogen ions migrate towards the cathode and are discharged there.

[H+ ions gains electrons and are converted to hydrogen gas]
\(2 \mathrm{H}^{+}+2 \mathrm{e}^{-} \longrightarrow \mathrm{H}_{2(\mathrm{~g})}\)
Cathode reaction:
\(2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{i})}+2 \mathrm{e}^{-} \longrightarrow \mathrm{H}_{2(\mathrm{~g})}+2 \mathrm{OH}_{(\mathrm{aq})}^{-}\)
Anode reaction:
\(2 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})} \longrightarrow \mathrm{O}_{2(\mathrm{~g})}+4 \mathrm{H}_{(\mathrm{aq})}^{+}+4 \mathrm{e}\)

For every hydrogen ion discharged at the anode, another hydrogen ion is formed at the cathode.
The net result is that the concentration of the sulphuric acid remains constant and electrolysis of water is overall reaction. \(2 \mathrm{H}_{2} \mathrm{O} \longrightarrow 2 \mathrm{H}_{2}+\mathrm{O}_{2}\)
The volume of the hydrogen gas formed near the cathode is double that of the oxygen gas formed near the anode.

3. Classify the following oxides into three types and name the types.
CaO, MgO, CO₂, SO₃, Na₂O, ZnO, Al₂O₃, Fe₂O₃Answer:
There are three types of oxides : Basic oxides, Acidic oxides and Amphoteric oxides.

Basic oxides	Acidic oxides	Amphoteric oxides
CaO	CO₂	ZnO
MgO	SO₃	Al₂O₃
Na₂O
Fe₂O₃

Generally metal oxides are basic in nature.
Exception : Al₂O₃ and ZnO are amphoteric oxides.
Generally non-metal oxides are acidic in nature.

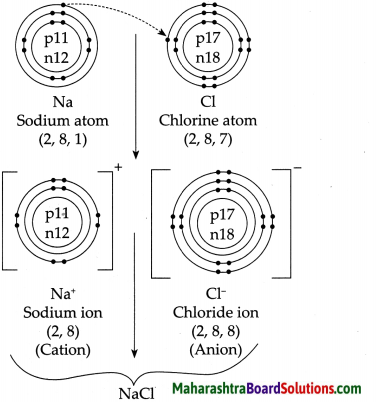
4. Explain by drawing a figure of the electronic configuration.

a. Formation of sodium chloride from sodium and chlorine.
Answer:

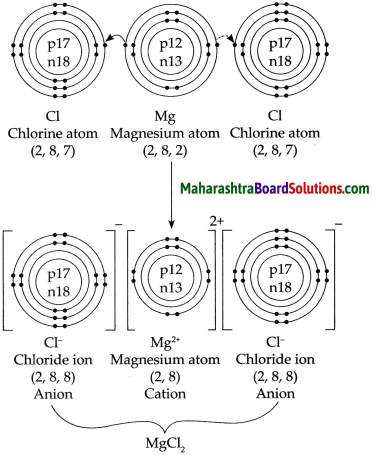
b. Formation of a magnesium chloride from magnesium and chlorine.
Answer:

5. Show the dissociation of the following compounds on dissolving in water, with the help of chemical equation and write whether the proportion of dissociation is small or large.
Hydrochloric acid, Sodium chloride, Potassium hydroxide, Ammonia, Acetic acid, Magnesium chloride, Copper sulphate.
Answer:
(a) Hydrochloric acid (HCl)

\(\mathrm{HCl}_{(g)} \frac{\text { Water }}{\text { dissociation }}>\mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{Cl}_{(\mathrm{aq})}^{-}\)
Hydrochloric acid is a strong acid, as on dissolving in water, it dissociates almost completely and the resulting aqueous solution contains mainly H ions and the concerned acidic radical.
The proportion of dissociation is large.

(b) Sodium chloride (NaC1)

\(\mathrm{NaCl}_{(s)} \frac{\text { Water }}{\text { dissociation }}>\mathrm{Na}_{(\mathrm{aq})}^{+}+\mathrm{Cl}_{\text {(aq) }}^{-}\)
When an ionic compound begins to dissolve in water, the water molecules push themselves in between the positive and negative ions of the compound and separate them from each other.
The proportion of dissociation is large.

\(\mathrm{KOH}_{(n)} \frac{\text { Water }}{\text { dissociation }} \mathrm{K}_{(\mathrm{aq})}^{+}+\mathrm{OH}_{(\mathrm{aq})}\)
Potassium hydroxide is a strong base, as on dissolving in water, it dissociates almost completely and the resulting aqueous solution contains mainly OH⁺ ions and the concerned basic radical.
The proportion of dissociation is large.

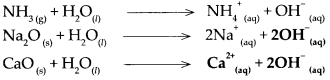
(d) Ammonia (NH₃)
(i) \(\mathrm{NH}_{3(\mathrm{~g})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{n}}-\frac{\text { Water }}{\text { uissociation }}>\mathrm{NH}_{4 \text { (aq) }}^{+}+\mathrm{OH}_{\text {(aq) }}^{-}\)
(ii) Ammonia dissolves in water to form NH₄OH (ammonium hydroxide). NH₄OH does not dissociate completely as it is a weak base. The aqueous solution contains a small proportion of OH^– ions and the concerned basic radical along with a large proportion of undissociated molecules of the base i.e. NH₄OH.
(iii) The proportion of dissociation is small.

(e) Acetic acid (CH₃COOH)

\(\mathrm{CH}_{3} \mathrm{COOH}_{(l)} \frac{\text { Water }}{\text { dissociation }} \mathrm{CH}_{3} \mathrm{COO}_{(\text {aq) }}+\mathrm{H}_{(a z)}+{ }^{+}\)
Acetic acid is a weak acid, on dissolving in water it does not dissociate completely, and the resulting aqueous solution contains H⁺ ion and the concerned acidic radical in small proportion along with large proportion of the undissociated molecules of the acid.
The proportion of dissociation is small.

(f) Magnesium chloride (MgCl₂)

\(\mathrm{MgCl}_{2(\mathrm{~s})} \frac{\text { Water }}{\text { dissociation }}>\mathrm{Mg}^{2+} \text { (aq) }+2 \mathrm{Cl}^{-} \text {(aq) }\)
Magnesium chloride dissolves in water and forms magnesium ions and chloride ions. When an ionic compound begins to dissolve in water, the water molecules push themselves in between the ions of the compound and separate them from each other.
The proportion of dissociation is large.

(g) Copper sulphate (CuSO₄)

\(\mathrm{CuSO}_{4(s)} \frac{\text { Water }}{\text { dissociation }}>\mathrm{Cu}_{(\mathrm{aq})}^{2+}+\mathrm{SO}_{4}^{2-}\)
When Copper sulphate is dissolved in water it forms copper ions and sulphate ions. When an ionic compound begins to dissolve in water, water molecules push themselves in between the ions of the compound and separate them from each other.
The proportion of dissociation is large.

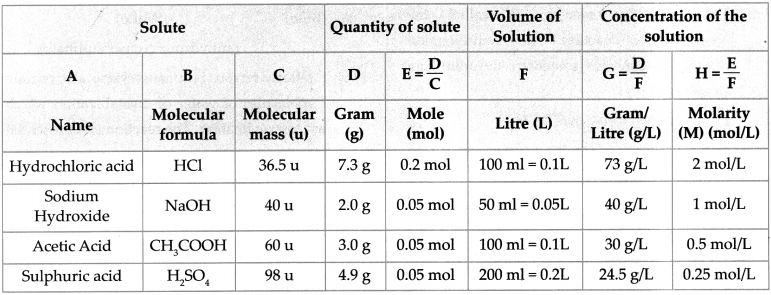
6. Write down the concentration of each of the following solutions in g/L and mol/L.

a. 7.3g HCl in 100ml solution
b. 2g NaOH in 50ml solution
c. 3g CH₃COOH in 100ml solution
d. 4.9g H₂SO₄ in 200ml solution
Answer:
To find : The concentration in g/L.
Solution:

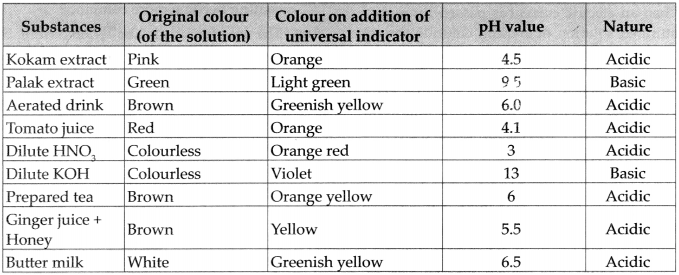
7. Obtain a sample of rainwater. Add to it a few drops of universal indicator. Meausre its pH. Describe the nature of the sample of rainwater and explain the effect if it has on the living world.
Answer:

pH of rain water is 6.5 that means rain water is slightly acidic.
When we add universal indicator to rain water it turns orangish red, indicating pH value is between 0 to 7, which tells us that rain water is acidic in nature.
Most of the plants grow best when pH of soil is close to 7. If the soil is too acidic or too basic, it affects plant growth.

8. Answer the following questions.

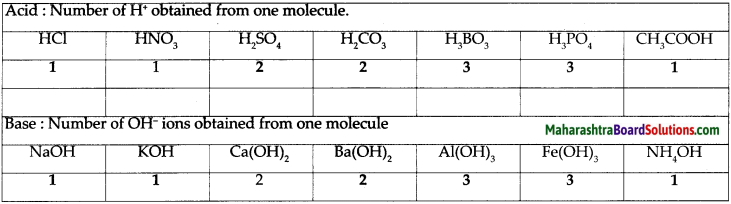
a. Classify the acids according to their basicity and give one example of each type.
Answer:

Basicity of acids : The number of H⁺ ions obtainable by the dissociation of one molecule of an acid is called its basicity. The acids are classified as monobasic, dibasic and tribasic acids based on the number of H⁺ ions present.
Examples of monobasic acid : HCl, HNO₃, CH₃COOH
Examples of dibasic acid: H₂SO₄, H₂CO₃
Examples of tribasic acid: H₃BO₃, H₃PO₄

b. What is meant by neutralization? Give two examples from everyday life of the neutralization reaction.
Answer:

In neutralization reaction, an acid reacts with a base to form salt and water.
In a neutralisation reaction the acid dissociates to form H⁺ ions and base dissociates to form OH ions.
They combine to form H₂O molecules which mixes with the solvent.

Examples in daily life:

When people suffer from acidity, they take some antacids to neutralise the acid in their stomach.
If an ant stings us the pain is due to formic acid. It is neutralised by rubbing moist baking soda which is basic in nature.

c. Explain what is meant by electrolysis of water. Write the electrode reactions and explain them.
Answer:
Electrolysis of water:

Electrolysis of water is the decomposition of water into oxygen and hydrogen gas due to an electric current being passed through acidified water.
Cathode reaction:
\(2 \mathrm{H}_{2} \mathrm{O}_{(l)}+2 \mathrm{e}^{-} \longrightarrow \mathrm{H}_{2(\mathrm{~g})}+2 \mathrm{OH}_{(\mathrm{aq}}\)
Anode reaction:
\(2 \mathrm{H}_{2} \mathrm{O}_{(l)} \longrightarrow \mathrm{O}_{2(\mathrm{~g})}+4 \mathrm{H}_{(\mathrm{aq})}^{+}+4 \mathrm{e}^{-}\)
It is found that the volume of gas formed near the cathode is double that of the gas formed near the anode.
Hydrogen gas is formed near the cathode and oxygen gas near the anode.
From this, it is clear that electrolysis of water has taken place and its constituent element have been released.

9. Give a reason for the following.

a. Hydronium ions are always in the form H₃O⁺.
Answer:

Acids in water gives H⁺ ions. These H⁺ ions do not exist freely in water.
This is because H⁺ is a single proton, a hydrogen atom has only one proton and one electron.
If the electron is removed to make H⁺, all that is left is an extremely tiny positively charged nucleus.
This H ion will immediately combine with the surrounding water (H₂O) molecules to form (H₃O₄) hydronium ion.

b. Buttermilk spoils if kept in a copper or brass container.
Answer:

Buttermilk contains an organic acid called as lactic acid.
The lactic acid reacts with copper and brass and forms toxic compounds which are not fit for consumption.
They are harmful and may cause food poisoning.
So it is not advisable to keep buttermilk in brass or copper containers.

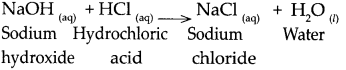
10. Write the chemical equations for the following activities.

(a) NaOH solution was added to HCl solution.
Answer:
When NaOH reacts with HCl, it gives NaCl and water.

(b) Zinc dust was added to dilute H₂SO₄.
Answer:
When zinc reacts with dilute sulphuric acid, it forms zinc sulphate and hydrogen gas is liberted.

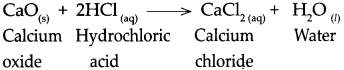
(c) Dilute nitric acid was added to calcium oxide.
Answer:
When dilute nitric acid reacts with calcium oxide, it forms calcium nitrate and water.

(e) Carbon dioxide gas was passed through KOH solution.

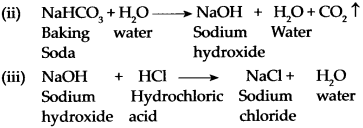
(f) Dilute HCl was poured on baking soda.

11. State the differences.

a. Acids and bases
Answer:

Acids	Bases
(i) A substance which liberates H⁺ ions when dissolved in water is an acid (ii) Blue litmus turns red in an acid. (iii) The pH of an acid is less than 7. (iv) Acids are sour to taste (v) e.g. HCl, H₂SO₄	A substance which liberates OH^– ions when dissolved in water is called a base. Red litmus turns blue in a base The pH of a base is greater than 7. Bases are bitter to taste, e.g. NaOH, KOH.

b. Cation and anion
Answer:

Cations	Anions
(i) Cations are ions with a net positive charge.	Anions are ions with a net negative charge.
(ii) Cations are generally formed by metals. When metals donate electrons, they have excess of protons, hence they form cations.	Anions are generally formed by non-metals. When non-metals accept electrons, they have excess of electrons, hence they form anions.
(iii) Cations are attracted towards the cathode which are negatively charged electrodes.	Anions are attracted towards the anode which are positively charged electrodes.
(iv) e.g.: Na⁺, Ca²⁺, Mg²⁺, K⁺ etc.	e.g.: O² , S^2-, Cl^–, Br^– etc.

c. the Negative electrode and the positive electrode.

Answer:

Negative Electrode	Positive Electrode
(i) Negatively charged electrodes are called as a cathode.	Positively charged electrodes are called as Anode.
(ii) Positively charged cations move towards the cathode or negative electrode.	Negatively charged anions move towards the anode or positive electrode.
(iii) Cathode accepts electrons from cations	Anode gives electrons to anions

12. Classify aqueous solutions of the following substances according to their pH into three groups : 7, more than 7, less than 7.

Common salt, sodium acetate, hydrochloric acid, carbon dioxide, potassium bromide, calcium hydroxide, ammonium chloride, vinegar, sodium carbonate, ammonia, sulphur dioxide.
Answer:

pH = 7	pH > 7	pH < 7
(a) common salt.	sodium acetate.	sulphur dioxide.
(b) potassium bromide.	sodium carbonate	hydrochloric acid.
(c)	ammonia.	carbon-dioxide.
(d)	calcium hydroxide.	ammonium chloride.
(e)		vinegar

Class 9 Science Chapter 5 Acids, Bases and Salts Intext Questions and Answers

Question 1.
How are the following substances classified into three groups with the help of litmus?
Lemon, tamarind, baking soda, buttermilk, vinegar, orange, milk, lime, tomato, milk of magnesia, water, alum.
Answer:

Basic Substance: Turns Red Litmus Blue	Acidic Substance: Turns Blue Litmus Red	Neutral Substance: No change in the colour of litmus
Baking Soda	Lemon	water
Lime	Tamarind
Milk of Magnesia	Buttermilk
	Vinegar
	Orange
	Milk
	Tomato
	Alum

Question 2.
Fill in the columns in the part of the following table:
Answer:

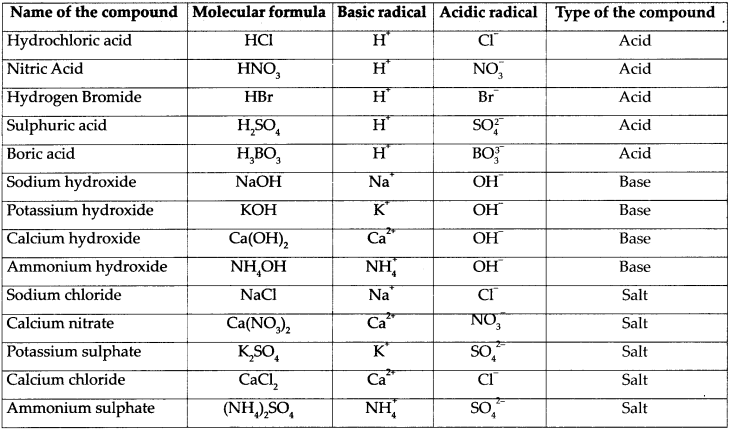
Question 3.
Complete the following table of the concentration of various aqueous solutions.
Answer:

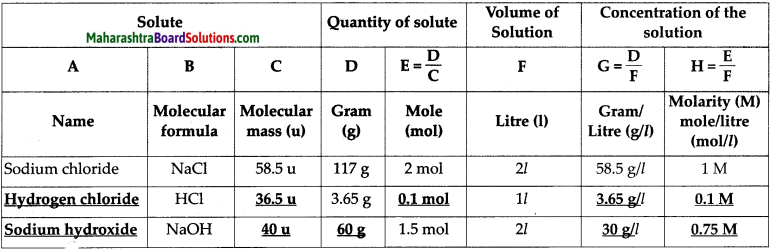
Question 4.
Complete the following table of neutralization reactions and also write down the names of the acids, bases and salts in it.
Answer:

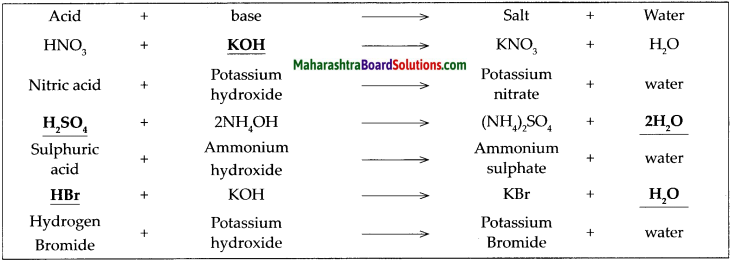
Question 5.
What are the names of the following compounds? NH₃, Na₂O, CaO.
Answer:
NH₃ : Ammonia
Na₂O : Sodium oxide
CaO : Calcium oxide

Question 6.
Into which type will you classify the above compounds, acid, base or salt?
Answer:
NH₃ : base
Na₂O : base
CaO : base

Question 7.
ive examples of monobasic, dibasic and tribasic acids.
Answer:
Monobasic acid examples: HNO₃, HCl, CH₃COOH
Dibasic acid examples: H₂SO₄, H₂CO₃
Tribasic acid examples: H₃BO₃, H₃PO₄

Question 8.
Give the three types of bases with their examples.
Answer:
Types of bases:
Monoacidic base examples : NaOH, KOH, NH₄OH
Diacidic base examples: Ca(OH)₂, Ba(OH)₂
Triacidic base examples: A(OH)₃, Fe(OH)₃

Question 9.
What are the colours of the following natural and synthetic indicators in acidic and basic solutions? Litmus, turmeric, jamun, methyl orange, phenolphthalein?
Answer:

Indicator	Colour in Acidic Solution	Colour in basic Solution
Litmus	Red	Blue
Turmeric	Yellow	Red
Jamun	Red	Blue-Green
Methyl orange	Red	Yellow
Phenolphthalein	Colourless	Pink

Question 10.
On mixing the substances as shown here, what are the resulting mixtures formed by mixing the following substances called?
(a) Water and salt
(b) Water and sugar
(c) Water and sand
(d) Water and sawdust
Answer:
(a) Water and salt – Homogeneous mixture
(b) Water and sugar – Homogeneous mixture
(c) Water and sand – Heterogeneous mixture
(d) Water and sawdust – Heterogeneous mixture

Question 11.
What would be the definition of an acid and a base with reference to the neutralization reaction?
Answer:

Acid: An acid is a substance which neutralises a base to form salt and water.
Base: A base is a substance which neutralises an acid to form salt and water.

Answer the following questions:

Question 1.
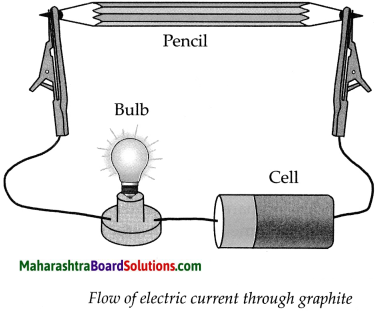
Take aqueous solution of sodium chloride, copper sulphate, glucose, urea, dil.H₂SO₄ and dil.NaOH in a beaker and test the electrical conductivity of the solutions. Answer the given below questions.

(a) With which solutions did the bulb glow?
Answer:
Solutions with which bulb glows: Aqueous solution of NaCl, CuSO₄, H₂SO₄ and NaOH.

(b) Which solutions are electrical conductors?
Answer:
Solutions which are electrical conductors:
NaCl, CuSO₄, H₂SO₄ and NaOH.

Question 2.
During electrolysis of copper sulphate, if electric current is passed through the electrolytic cell for a long time, what change would be seen at the anode?
Answer:

When electricity is passed for a long time through copper sulphate solution, the following reaction is seen at the anode: Anode Reaction: Cu(s) → Cu²⁺(aq) + 2e^–
All the copper atoms will get converted into copper ions and get deposited on the cathode. This process continues till the copper anode exists.

Question 3.
Would water be a good conductor of electricity?
Answer:
Pure water is not a good conductor of electricity.

Answer the following questions:

Question 1.
(i) With which solutions did the bulb glow?
(ii) Which solutions are electrical conductors?

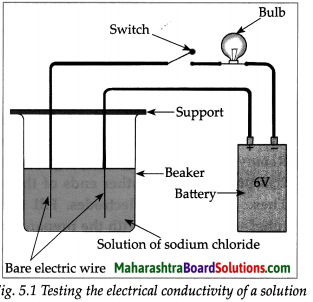
Answer:
(i) The bulbs glows when the wire are immersed in NaCl solution.
(ii)

Solution	Results
1g Copper Sulphate Solution	Bulb glow
1g Glucose Solution	Bulb does not glow
1g Urea Solution	Bulb does not glow
5ml dil.H₂SO₄ Solution	Bulb glows
5ml dil. NaOH Solution	Bulb glows

Question 2.
What would be the definition of an acid and a base with reference to the neutralization reaction?
Answer:

Acid: An acid is a substance which neutralises a base to form salt and water.
Base: A base is a substance which neutralises an acid to form salt and water.

Question 3.
Dissolve 2g salt in 500ml pure water. Take 250 ml of this solution in a 500ml capacity beaker. Connect two electrical wires to the positive and negative terminals of a power supply. Remove the insulating cladding from about 2cm portions at the other ends of the wires. These are the two electrodes. Fill two test tubes upto the brim with the prepared dilute salt solution. Invert them on the electrodes without allowing any air to enter. Start the electric current under 6V potential difference from the power supply. Observe what happens in the test tubes after some time.
(a) Did you see the gas bubbles forming near the electrodes in the test tubes?
(b) Are these gases heavier or lighter than water?
(c) Are the volumes of the gases collected over the solution in the two test tubes the same or different?
(d) Test the solutions in the two test tubes with litmus paper, what do you see?
(e) Repeat the activity by using dilute H₂SO₄ as well as dilute NaOH as the electrolyte.
Answer:
(a) Yes, gas bubbles can be seen forming near the electrodes in the test tube.
(b) These gases are lighter than water.

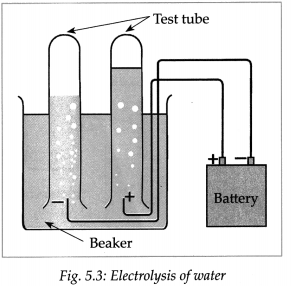
(c) The volumes of gases collected over the solution in the two test tubes are different.
(d) The solution in the cathode turns red litmus blue while solution in anode turns blue litmus red.
(e) When the above experiment is repeated with dil H₂SO₄ and dil NaOH, Hydrogen gas is liberated at cathodes and oxygen gas is liberated at anode.

Answer the following questions:

Question 1.
Cut a lemon into two equal parts. Take the juice of each part into two separate beakers. Pour 10 ml of drinking water in one beaker and 20 ml in the second. Stir the solutions in both the beakers and taste them. Is there any difference in the tastes of the solutions in the two beakers? What is that difference?
Answer:

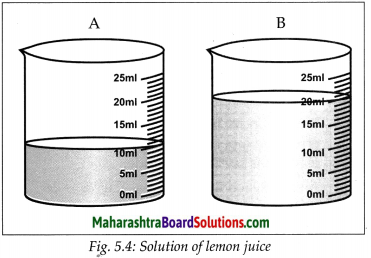
In the above activity, the sour taste of the solutions is because of the solute, lemon juice in them.
The quantity of the lemon juice is the same in both the solutions. Yet their tastes are different.
The solution in the first beaker is more sour than the one in the second.
Although the quantity of the solute is the same in both the solutions, the quantity of the solvent is different.
Ratio of the quantity of the solute to the quantity of the resulting solution is different. This ratio is larger for the solution in the first beaker and therefore that solution tastes more sour.
On the other hand, the proportion of the lemon juice in the total solution in the second beaker is smaller and taste is less sour.
The taste of foodstuff depends upon the nature of the taste-giving ingredient and its proportions in the foodstuff.
Similarly, all the properties of a solution depend on the nature of the solute and solvent and also on the proportion of the solute in a solution
The proportions of a solute in a solution is called the concentration of the solute in the solution.

Question 2.
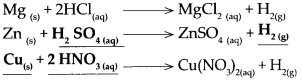
Take a big test tube. Choose a rubber stopper in which a gas tube can be fitted. Take a few pieces of magnesium ribbon in the test tube and add some dilute HCl to it. Take a lighted candle near the end of the gas tube and observe. What did you observe?

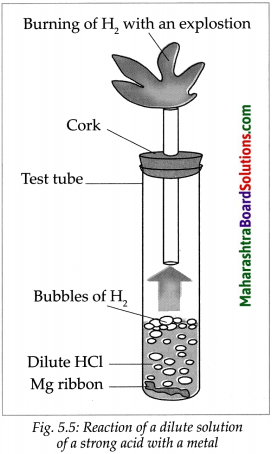
Answer:

Magnesium metal reacts with dilute HCl and an inflammable gas, hydrogen, is formed.
During this reaction, the reactive metal displaces hydrogen from the acid to release hydrogen gas.
At the same time, the metal is converted into basic radical which combines with the acidic radical from the acid to form the salt.
\(\mathrm{Mg}_{(\mathrm{s})}+2 \mathrm{HCl}_{(\mathrm{aq}) \longrightarrow} \underset{\rightarrow}{\mathrm{MgCl}_{2(\mathrm{aq})}}+\mathrm{H}_{2(\mathrm{~g})}\)

Question 3.
Take some water in a test tube and add a little red oxide (the primer used before painting iron articles) to it. Now add a small quantity of dilute HCl to it, shake the test tube and observe.
(a) Does the red oxide dissolve in water?
(b) What change takes place in the particles of red oxide on adding dilute HCl?
Answer:
(a) The chemical formula of red oxide is Fe₂O₃. It is insoluble in water.
(b) The water-insoluble red oxide reacts with HCl to produce a water-soluble salt FeCl₃.

This gives a yellowish colour to the water.
The following chemical equation can be written for this chemical change.
\(\mathrm{Fe}_{2} \mathrm{O}_{3(\mathrm{~s})}+6 \mathrm{HCl}_{(\mathrm{aq})} \longrightarrow 2 \mathrm{FeCl}_{3(\mathrm{aq})}+3 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}\)

Question 4.
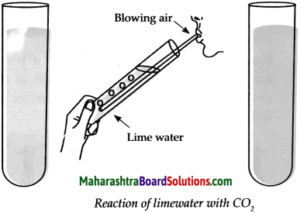
Fit a bent tube in a rubber cork. Take some lime water in a test tube and keep it handy. Take some baking soda in another test tube and add some lemon juice to it. Immediately fit the bent tube over it. Insert its other end into the lime water. Note down your observations of both the test tubes. Repeat the procedure using washing soda, vinegar and dilute HC1 properly. What do you see?
Answer:

In this activity, when limewater comes in contact with the gas released in the form of an effervescence, it turns milky.
This is a chemical test for carbon dioxide gas.
When lime water turns milky, we infer that the effervescence is of CO₂.
This gas is produced on the reaction of acids with carbonate and bicarbonate salts of metals.
A precipitate of CaCO₃ is produced on its reaction with the lime water Ca(OH)₂.
This reaction can be represented by the following chemical equation.
\(\mathrm{Ca}(\mathrm{OH})_{2(\mathrm{aq})}+\mathrm{CO}_{2(\mathrm{~g})} \longrightarrow \mathrm{CaCO}_{3(\mathrm{~s})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}\)
Washing soda is sodium carbonate Na2CO₃. It will react same as baking soda (NaHCO₃).
Vinegar and HCl are acids, they do not react chemically with lemon juice.

Class 9 Science Chapter 5 Acids, Bases and Salts Additional Important Questions and Answers

Select the correct option

Question 1.
…………………. acid is present in lemon.
(a) malic acid
(b) tartaric acid
(c) citric acid
(d) butyric acid
Answer:
(c) Citric acid

Question 2.
Tamarind contains …………………. acid.
(a) Lactic acid
(b) tartaric acid
(c) matlic acid
(d) butyric acid
Answer:
(b) tartaric

Question 3.
Butter milk contains …………………. acid.
(a) butyric acid
(b) Lactic acid
(c) matlic acid
(d) citric acid
Answer:
(a) Butyricacid

Question 4.
If the basic radical is H+ the type of compound is ………………… .
(a) neutral
(b) base
(c) acid
(d) alkali
Answer:
(c) Acid

Question 5.
The name of compound NH3 is ………………… .
(a) nitric acid
(b) ammonium
(c) nitride
(d) ammonia
Answer:
(b) ammonia

Question 6.
The bases which are soluble in water are called as ………………… .
(a) indicators
(b) acids
(c) alkalis
(d) salts
Answer:
(c) alkalis

Question 7.
H₃PO₄ is a …………………. acid.
(a) monobasic
(b) tribasic
(c) tetrabasic
(d) dibasic
Answer:
(b) tribasic

Question 8.
According to pH scale pure water has a pH of ………………… .
(a) 6
(b) 7
(c) 5
(d) 8
Answer:
(b) 7

Question 9.
With reference to neutralization, metallic oxides are ………………… in nature.
(a) basic
(b) neutral
(c) acidic
(d) saline
Answer:
(a) basic

Question 10.
Molecular formula of blue vitriol is ………………… .
(a) CuSO₃ 5H₂O
(b) CuSO₄ 4H₂O
(c) CUSO₃ 4H₂O
(d) CUSO₄ 5H₂O
Answer:
(d) CUSO₄ 5H₂O

Question 11.
Molecular formula of crystalline alum is ………………… .
(a) KSO₄, AISO₄, 24H₂O
(b) K₂SO₄, ALSO₄, 24H₂O
(c) K₂SO₄, AL₂(SO₄)₃, 24H₂O
(d) KSO₄, Al₂(SO₄)₃, 24H₂O
Answer:
(c) K₂SO₄, AL₂(SO₄)₃, 24H₂O

Question 12.
Molecular formula for sodium oxide is ………………… .
(a) Na₂O
(b) NaO₂
(c) NaO
(d) Na₂O₂Answer:
(a) Na₂O

Question 13.
H₂CO₃ is …………………. acid.
(a) monobasic
(b) dibasic
(c) tribasic
(d) tetrabasic
Answer:
(b) dibasic

Question 14.
Molecular formula of Red oxide is ………………… .
(a) Fe₂O₃
(b) CuO
(c) Fe₃O₄
(d) Na₂O
Answer:
(a) Fe₂O₃

Question 15.
The positive terminal electrode is called as ………………… .
(a) anode
(b) cathode
(c) anion
(d) cation
Answer:
(a) anode

Question 16.
…………………. produced in stomach helps in digestion.
(a) Hydrochloric acid
(b) Oxalic acid
(c) Sulphuric acid
(d) Nitric acid?
Answer:
(a) Hydrochloric acid

Question 17.
The solution turns blue litmus red, its pH is likely to be ………………… .
(a) 7
(b) 4
(c) 14
(d) 9
Answer:
(b) 4

Question 18.
An ionic compound NaCl is formed by ………………… .
(a) Na⁺ and Cl^–
(b) Na⁺ and Cl⁺
(c) Na^– and Cl^–
(d) Na^– and Cl⁺Answer:
(a) Na⁺ and Cl^–

Question 19.
pH of strong acid is ………………… .
(a) 0
(b) 7
(c) 8
(d) 14
Answer:
(a) 0

Question 20.
HCl + NaOH → NaCl + H₂O is a …………………. reaction.
(a) neutralization
(b) crystallisation
(c) electrolysis
(d) dissociation
Answer:
(a) neutralization

Question 21.
Adding water to acid is an …………………. reaction.
(a) endothermic
(b) exothermic
(c) neutralisation
(d) crystallisation
Answer:
(b) exothermic

Find the odd one out:

(a) Rose Petal, Turmeric, Phenolphthalein, Indigo.
Answer:
Phenolphthalein is odd one out as rest are natural indicators while phenolphthalein is a synthetic indicator.

(b) Lime water, Vinegar, Acetic acid, Tartaric acid.
Answer:
Lime water is odd one out as this is basic in nature while rest are acidic.

(d) Oxalic acid, Nitric acid, Citric acid, acetic acid.
Answer:
Nitric acid is odd one out as others are weak acids while Nitric acid is a strong acid.

(e) Crystalline, Liquid, Gases, Solid.
Answer:
Crystalline is odd one out as this is nature of a compound while others are physical states of compounds.

(f) Ca(OH)₂, Mg (OH)₂, NaOH, NH₄OH.
Answer:
NaOH is odd one out even though all are bases but NaOH is highly soluble in water compared to others.

Name the following:

Question 1.
Name the three types of ionic compounds.
Answer:
The three types of ionic compounds are acids, bases and salts.

Question 2.
Name the two constituents of molecule of an ionic compound.
Answer:

Cation (positive ion/ basic radical)
Anion (negative ion/acidic radical).

Question 3.
Name any three acids with their molecular formula.
Answer:

Hydrochloric acid – HC1
Sulphuric acid – H₂SO₄
Nitric acid – HNO₃

Question 4.
Name any three bases with their molecular formula.
Answer:

Sodium hydroxide – NaOH
Potassium hydroxide – KOH
Calcium hydroxide – Ca(OH)₂

Question 5.
Name any three salts with their molecular formula.
Answer:

Sodium chloride – NaCl
Potassium sulphate – K₂ SO₄
Calcium chloride – CaCl₂

Question 6.
Name any two strong acids.
Answer:

Hydrochloric acid – HC1
Sulphuric acid – H₂ SO₄

Question 7.
Name any two weak acids.
Answer:

Acetic acid – CH₃ COOH
Carbonic acid – H₂ CO₃

Question 8.
Name any two strong bases.
Answer:

Sodium hydroxide – NaOH
Potassium hydroxide – KOH

Question 9.
Name a weak base.
Answer:
Ammonium hydroxide – NH₄OH

Question 10.
Name any two alkalis.
Answer:

Sodium hydroxide – NaOH
Potassium hydroxide – KOH

Question 11.
Name any two acids with their basicity 1 (monobasic)
Answer:

Hydrochloric acid – HC1
Nitric acid – HNO₃

Question 12.
Name any two acids with their basicity 2 (dibasic)
Answer:

Sulphuric acid – H₂ SO₄
Carbonic acid – H₂CO₃

Question 13.
Name any two acids with their basicity 3 (tribasic)
Answer:

Boric acid – H₃BO₃
Phosphoric acid – H₃PO₄

Question 14.
Name any two bases with their acidity 1 (monoacidic)
Answer:

Sodium hydroxide – NaOH
Potassium hydroxide – KOH

Question 15.
Name any two bases with their acidity 2 (diacidic)
Answer:

Calcium hydroxide – Ca(OH)₂
Barium hydroxide – Ba(OH)₂

Question 16.
Name any two bases with their acidity 3 (triacidic)
Answer:

Aluminium hydroxide – Al(OH)₃
Ferric hydroxide – Fe(OH)₃

Question 17.
Name the two units to express the concentration of the solution.
Answer:

mass of solute in grams dissolved in one litre of the solution grams per litre, (g/L).
Number of moles of the solute dissolved in one litre of the solution. Molarity (M) of the solution.

Match the columns:

Question 1.

Column ‘A’	Column ‘B’
(1) HNO₃(2) H₃PO₄(3) CH₃COOH (4) H₂CO₃	(a) Acetic acid (b) Carbonic acid (c) Phosphoric acid (d) Nitric acid

Answer:
(1-d),
(2- c),
(3 – a),
(4 – b)

Question 2.

Column ‘A’	Column ‘B’
(1) NH₄OH (2) Ca(OH)₂(3) Al(OH)₃(4) Ba(OH)₂	(a) Aluminium Hydroxide (b) Barium Hydroxide (c) Calcium Hydroxide (d) Ammonium Hydroxide

Answer:
(1-d),
(2- c),
(3 – a),
(4 – b)

Question 3.

Column ‘A’ Solution		Column ‘B’ pH
(1)	Milk	(a)	0
(2)	Milk of Magnesia	(b)	14
(3)	1 M HCl	(c)	10.5
(4)	1 M NaOH	(d)	6.5

Answer:
(1-d),
(2- c),
(3 – a),
(4 – b)

Question 4.

Column ‘A’	Column’B’
(1) Urine (2) Apples (3) Orange (4) Butter	(a) Butyric acid (b) Uric acid (c) Malic acid (d) Citric acid

Answer:
(1 – b),
(2 – c),
(3 – d),
(4 – a)

Question 5.

Column ‘A’	Column ‘B’
(1) Crystalline blue vitriol (2) Crystalline green vitriol (3) Crystalline (4) washing soda Crystalline alum	(a) FeS0₄-7H₂0 (b) K₂S0₄-A1₂(S0₄)₃.24H₂0 (c) CuS0₄-5H₂0 (d) Na₂CO₃10H₂O

Answer:
(1-c),
(2- a),
(3 – d),
(4 – b)

State whether the following statements are true or false and if false. Correct the false statement:

(1) The separation of H and CI in HCI is in absence of water.
(2) \(\mathrm{NaOH}_{(\mathrm{s})} \frac{\text { Water }}{\text { dissociation }}>\mathrm{Na}_{(\mathrm{aq})}^{+}+\mathrm{OH}_{(\mathrm{aq})}^{-}\)
(3) H₂SO₄ is a strong acid.
(4) NaC1 is an ionic compound.
(5) Turmeric is synthetic indicator.
(6) Metal + Dilute acid forms salt and water.
(7) Copper oxide is called red primer.
(8) Oxide of non-metal + Acid → Salt + Water.
(9) Zinc oxide reacts with sodium hydroxide to form sodium zincate.
(10) Al₂O₃ is an amphoteric oxide.
(11) Blue vitriol ZnSO₄. 7H₂O.
(12) Molecular formula for crystalline Ferrous sulphate is Fe5O₄. 5H₂O.
(13) NaCl in water does not conduct electricity.
(14) Phenolphthalein is colourless in base.
Answer:
(1) False. The separation of H⁺ and Cl^– in HC1 is in presence of water.
(2) True
(3) True
(4) True
(5) False. Turmeric is a natural indicator.
(6) False. Metal + Dilute acid forms salt and hydrogen gas.
(7) False. Iron oxide is called red primer.
(8) False. Oxide of izan-metal + Base → Salt + Wafer.
(9) True
(10) True
(11) False. Blue Vitriol is CuSO₄. 5H₂O.
(12) False. Molecular formula for crystalline Ferrous sulphate is FeSO₄. 7H₂O.
(13) False. NaCl in water conducts electricity.
(14) False, Phenolphthalein is colourless in acid and pink in base.

Define the following:

Question 1.
Acid
Answer:
An acid is a substance which on dissolving in water gives rise to H ion as the only cation. For example, HC1, H₂ SO₄, H₂CO₃.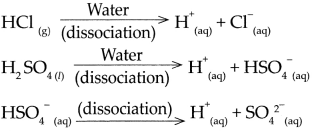

Question 2.
Base
Answer:
A base is a substance which on dissolving in water gives rise to the OW ion as the only anion. For, NaOH, Ca(OH)₂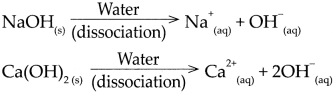

Question 3.
Strong Acid
Answer:
On dissolving in water, a strong acid dissociates almost completely, and the resulting aqueous solution contains mainly H ions and the concerned acidic radical. e.g. HC1, HBr, HNO₃, H₂SO₄.

Question 4.
Weak Acid
Answer:
On dissolving in water a weak acid does not dissociate completely, and the resulting aqueous solution contains H+ ion and the concerned acidic radical in small proportion along with large proportion of the undissociated molecules of the acid, e.g., H₂CO₃(Carbonic acid), CH₃COOH (Acetic acid)

Question 5.
Strong Base
Answer:
On dissolving in water, a strong base dissociates almost completely and the resulting aqueous solution contains mainly OH ions and the concerned basic radicals, e.g. NaOH, KOH, Ca(OH)₂, Na₂O.

Question 6.
Weak Base
Answer:
On dissolving in water, a weak base does not dissociate completely and the resulting aqueous solution contains a small proportion of OH ions and the concerned basic radical along with a large proportion of undissociated molecules of the base. e.g. NH₄ OH.

Question 7.
Alkali
Answer:
The bases which are highly soluble in water are called alkali, e.g. NaOH, KOH, NH3. Here, NaOH and KOH are strong alkalis while NH₃ is a weak alkali.

Question 8.
Basicity of acids
Answer:
The number of H⁺ ions obtainable by the dissociation of one molecule of an acid is called its basicity.

Question 9.
Acidity of bases
Answer:
The number of OH ions obtainable by the dissociation of one molecule of a base is called its acidity.

Question 10.
Concentration of solute in the solution.
Answer:
The proportion of a solute in a solution is called the concentration of the solute in the solution.

Question 11.
Concentrated solution.
Answer:
When the concentration of a solute in its solution is high, it is a concentrated solution.

Question 12.
Dilute solution
Answer:
When the concentration of a solute in its solution is low, it is a dilute solution.

Question 13.
Neutralization
Answer:
A reaction in which an acid reacts with a base to form salt and water is called a neutalization reaction.
NaOH + HC1 → NaCl + H₂O
Base + Acid → Salt + Water

Question 14.
Cathode
Answer:
The electrode connected to the negative terminal of a battery by means of a conducting wire is called a cathode.

Question 15.
Anode
Answer:
The electrode connected to the positive terminal of a battery by means of a conducting wire is called an anode.

Question 16.
Cations
Answer:
Cations are positively charged ions which are attracted towards negative electrode (cathode) when electricity is passed into a solution of an ionic compound.

Question 17.
Anions
Answer:
Anions are negatively charged ions which are attracted towards the positive electrode (anode) when electricity is passed into a solution of an ionic compound.

Question 18.
Electrolytic cell
Answer:
An assembly that consists of a container with an electrolyte and the electrodes dipped in it, is called an electrolytic cell.

Question 19.
Molarity of a solution
Answer:
The number of moles of the solute dissolved in one litre of the solution is called the molarity of that solution. The molarity of a solute is indicated by writing its molecular formula inside a square bracket for example [NaCl] = 1

Question 20.
Acid – base indicators
Answer:
Some natural and synthetic dyes show two different colours in acidic and basic solution, and such dyes are acid base indicators.

Explain the following chemical reactions with the help of balanced equations:

Question 1.
Magnesium reacts with dilute hydrochloric acid.
Answer:
When magnesium reacts with dilute hydrochloric acid, it forms magnesium chloride and hydrogen gas is liberated.

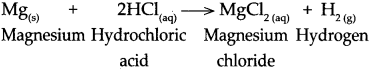
Question 2.
When copper reacts with nitric acid.
Answer:
When copper reacts with nitric acid, it forms copper nitrate and hydrogen gas is liberated.

Question 3.
When ferric oxide reacts with diluted hydrochloric acid.
Answer:
When Ferric oxide reacts with diluted hydrochloric acid, it forms ferric chloride and water.

Question 4.
When calcium oxide reacts with dilute hydrochloric acid.
Answer:
When calcium oxide reacts with dilute hydrochloric acid, it forms calcium chloride and water.

Question 5.
When Magnesium oxide reacts with dilute hydrochloric acid.
Answer:
When magnesium oxide reacts with dilute hydrochloric acid, it forms magnesium chloride and water.

Question 6.
When zinc oxide reacts with dilute hydrochloric acid.
Answer:
When zinc oxide reacts with dilute hydrochloric acid, it forms zinc chloride and water.

Question 7.
When aluminium oxide reacts with hydrogen fluoride
Answer:
When aluminium oxide reacts with hydrogen fluoride, it forms Aluminium fluoride arid water.

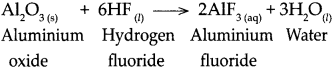
Question 8.
When carbon dioxide reacts with sodium hydroxide.
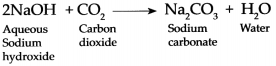
Answer:
When carbon dioxide reacts with Sodium hydroxide, it forms Sodium carbonate and water.

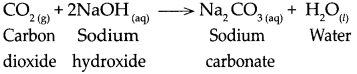
Question 9.
When carbon dioxide reacts with potassium hydroxide.
Answer:
When carbon dioxide reacts with potassium hydroxide, it forms potassium carbonate and water.

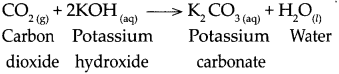
Question 10.
When sulphur trioxide reacts with sodium hydroxide.
Answer:
When sulphur trioxide reacts with sodium hydroxide, it forms sodium sulphate and water.

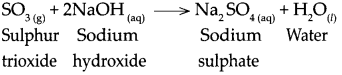
Question 11.
When calcium hydroxide reacts with carbon dioxide.
Answer:
When calcium hydroxide reacts with carbon dioxide, it forms calcium carbonate and water.

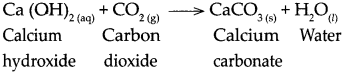
Question 12.
When sodium carbonate reacts with hydrochloric acid.
Answer:
When sodium carbonate reacts with hydrochloric acid, it forms sodium chloride, carbon dioxide and water.

Question 13.
When sodium carbonate reacts with sulphuric acid.
Answer:
When sodium carbonate reacts with sulphuric acid, it forms sodium sulphate, carbon dioxide and water.

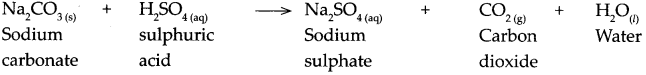
Question 14.
When calcium carbonate reacts with nitric acid.
Answer:
When calcium carbonate reacts with nitric acid, it forms calcium nitrate, carbon dioxide and water.

Question 15.
When potassium carbonate reacts with sulphuric acid.
Answer:
When potassium carbonate reacts with sulphuric acid, it forms potassium sulphate, carbon dioxide and water.

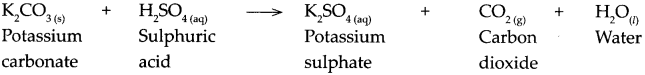
Question 16.
When sodium bicarbonate reacts with hydrochloric acid. OR Dilute HC1 was poured on baking soda
Answer:
When sodium bicarbonate reacts with hydrochloric acid, it forms sodium chloride, carbon dioxide and water.

Question 17.
When potassium bicarbonate reacts with nitric acid.
Answer:
When potassium bicarbonate reacts with nitric acid, it forms potassium nitrate, carbon dioxide and water.

Question 18.
When sodium bicarbonate reacts with acetic acid.
Answer:
When sodium bicarbonate reacts with acetic acid, it forms sodium acetate, carbon dioxide and water.

Question 19.
When copper sulphate is heated.
Answer:
When copper sulphate is heated it loses it’s water of crystallization to form white anhydrous copper sulphate.

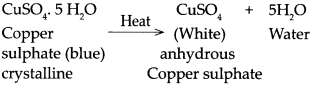
Question 20.
When Ferrous sulphate is heated.
Answer:
When ferrous sulphate is heated it loses its water of crystallization to form white anhydrous ferrous sulphate.

Q.2. (B)-3. Complete the following table.

Question 1.
Complete the following table.
Answer:

Complete the following reactions.

Question 1.
Answer:

Question 2.
Metal + Dilute acid → Salt + Hydrogen
Answer:

Question 3.
Metal oxide + Dilute acid → SaIt + Water
Answer:

Question 4.
Oxide of non-metal + base → salt + water
Answer:

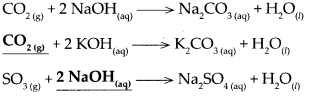
Question 5.
Carbonate salt of metal + dilute acid → Another salt of metal + Carbon dioxide + water
Answer:

Question 6.
Bicarbonate salt of metal + dilute acid → Another salt of metal + carbon dioxide + water
Answer:

Give scientific reasons:

Question 1.
Ionic compound NaCl has very high stability.
Answer:

The outermost shell of both Na⁺ and Cl^– ions is a complete octet.
An electronic configuration with a complete octet indicates a stable state.
A molecule of NaCl has Na⁺ and Cl^– ions. An ionic bond is formed between these ions.
The force of attraction between them is very strong as it is formed between the oppositely charged Na⁺ and Cl^– ions.
Therefore NaCl, an ionic compound has very high stability.

Question 2.
Ionic compound dissociates while forming an aqueous solution.
Answer:

On dissolving in water, an ionic compound forms an aqueous solution.
In the solid state, the oppositely charged ions in the ionic compound are sitting side by side.
When an ionic compound being to dissolve in water, the water molecules push themselves in between the ions of the compound and it separates them from each other, that is to say, an ionic compound dissociates while forming an aqueous solution.

Question 3.
Blue coloured copper sulphate crystals become colourless on heating.
Answer:

Copper sulphate crystals are blue in colour and crystalline in form due to presence of water of crystallisation.
Each molecule of crystalline copper sulphate contains five molecules of water of crystallisation (CuSO₄.5H₂O).
On heating, the copper sulphate crystals lose the water of crystallisation and turns into white amorphous powder called as anhydrous copper sulphate.
Therefore, blue coloured copper sulphate crystals become colourless on heating.

Question 4.
During electrolysis of water, a few drops of sulphuric acid are added to it.
Answer:

Pure water is a covalent compound and hence it is a non-electrolyte and does not conduct electricity.
When a few drops of sulphuric acid (H₂SO₄) are added to water.
Being a strong acid it dissociates almost completely in its solution forming H⁺cations and \(\mathrm{SO}_{4}^{2-}\) anions.
The movement of these ions in the solution towards the respective electrodes amount to the conduction of electricity through the solution.
Therefore, during electrolysis of water, a few drops of sulphuric acid are added to it.

Question 5.
Glucose is a non-electrolyte.
Answer:

Glucose is a covalent compound
It does not form any ions in its aqueous solution.
Due to this aqueous solution of glucose does not conduct electronic current.
Hence, glucose is a non-electrolyte.

Question 6.
Pure water is a poor conductor of electricity but aqueous solution of sodium chloride conducts electricity.
Answer:

Pure water does not contain any free ions.
Sodium chloride (NaCl) is an ionic compound made up of sodium cation (Na⁺) and chloride anion (Cl)
When sodium chloride is dissolved in water , these ions dissociates in its aqueous solution. ‘
These ions are free to move in the solution and conduct electricity.
Therefore, pure water is a poor conductor of electricity but aqueous solution of sodium Chloride conducts electricity.

Question 7.
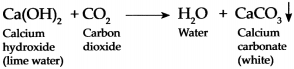
When carbon dioxide gas is passed through freshly prepared lime water, the limewater turns milky.
Answer:

Limewater traditionally means a weak solution of the alkali calcium hydroxide Ca(OH)₂.
When CO₂ is passed through limewater, it reacts with calcium hydroxide to form insoluble particulates (precipitate of calcium carbonate (CaCO₃).
Calcium carbonate is weak basic salt and this gives a milky white precipitate.
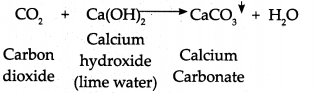
Hence, lime water turns milky when CO₂ gas is passed through it.

Q.3.1. Answer the following:

Question 1.
Write down chemical equations for
(a) Zinc oxide reacts with sodium hydroxide
(b) Aluminium oxide reacts with sodium hydroxide.
Answer:
(a) When zinc oxide reacts with sodium hydroxide, it forms sodium zincate and water

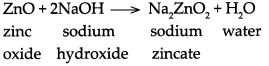
(b) When Aluminium oxide reacts with sodium hydroxide, it forms sodium aluminate and water.

Question 2.
Can we call Al₂O₃ and ZnO acidic oxides on the basis of above reactions.
Answer:

No, because they also react with acids to form their respective salts and water.
So, they show the properties of basic oxides also.

Question 3.
Define ‘amphoteric oxides’ and give two examples.
Answer:

Amphoteric oxides are those oxides which react with both adds as well as bases to form their respective salts and water.
Amphoteric oxides show the properties of both acidic oxides as well as basic oxides. ZnO and Al₂ O₃ are amphoteric oxides.?

Question 4.
Take a solution of 1g copper sulphate in 50ml water in a 100 ml capacity beaker. Use a thick plate of copper as anode and a carbon rod as cathode. Arrange the apparatus as shown in the figure and pass an electric current through the circuit for some time. Do you see any changes?
Answer:

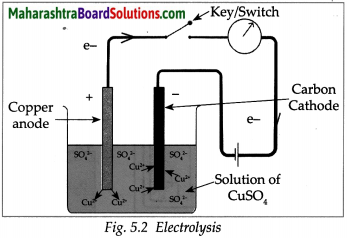
A thin film of copper metal is deposited on cathode which is immersed in solution. There is no change in colour of solution
The electrons from cathode combines with Cu²⁺ ion from the solution forming Cu atoms which were then deposited on the cathode.

Q.3.5. Answer in brief:

Question 1.
What are acids, bases and salts?
Answer:

Compounds having H⁺ as the basic radical in their molecules are called Acids.
Compounds having OH^– as the acidic radical in their molecule are called Bases.
Ionic compounds which have a basic radical other than H⁺ and an acidic radical other than OH^– are called salts.

Question 2.
What is an ionic bond?
Answer:

The molecule of an ionic compound has two constituents namely cation (positive ion / basic radical) and anion (negative ion / acidic radical).
There is a force of attraction between these ions as they are oppositely charged, and that is called the ionic bond.
The force of attraction between one positive charge on a cation and one negative charge on an anion makes one ionic bond.

Question 3.
Give examples to show that proportions of H⁺ and OH^– ions in aqueous solution determines the properties of those solutions.
Answer:
The examples to show that proportions of H⁺ and OH^– ions in aqueous solution determines the properties of those solutions are :

The proportions of H⁺ and OH ions divides soil into the acidic, neutral and basic, types of soil.
It is necessary for blood, cell sap etc to have H⁺ and OH^– ions in certain definite proportions for their proper functioning.
Fermentation carried out with the help of micro-organisms, other biochemical processes and also many chemical processes require the proportion of H⁺ and OH^– ions to be maintained within certain limits.

Question 4.
What is pH scale?
Answer:

In 1909, the Danish scientist Sorensen introduced a convenient new scale of expressing H⁺ ion concentration which is found to be useful in chemical and biochemical processes.
It is the pH scale (pH: power of hydrogen). The pH scale extends from 0 to 14. According to this scale pure water has a pH of 7. pH 7 indicates a neutral solution. This pH is the midpoint of the scale.
The pH of an acidic solution is less than 7 and?

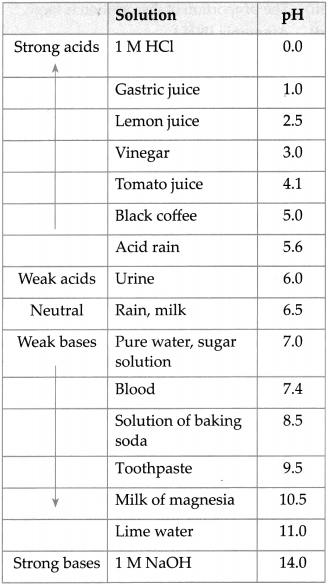
Question 5.
Give the pH of following solutions.
Answer:

Question 6.
What is universal indicator? Which is the most accurate method of measuring the pH of a solution?
Answer:

In the pH scale, the pH of solutions varies from 0 to 14 in accordance with the strength of the acid or base.
To show these variations in pH, a universal indicator is used.
A universal indicator shows different colours at different values of pH. A universal indicator is made by mixing several synthetic indicators in specific proportions.
The pH of a solution can be determined by means of a universal indicator solution or the pH paper made from it.
However, the most accurate method of measuring the pH of a solution is to use an electrical instrument called pH meter.
In this method, pH is measured by dipping electrodes into the solution.

Answer in detail:

Question 1.
Explain the Arrhenius theory of acids and bases.
Answer:
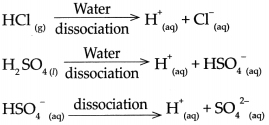
The Swedish scientist Arrhenius put forth a theory of acids and bases in the year 1887. This theory gives definitions of acids and bases as follows:
Acid : An acid is a substance which on dissolving in water gives rise to H ion as the only cation. For example, HCl, H₂SO₄, H₂CO₃

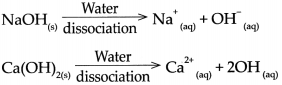
Base: Abase is a substance which on dissolving in water gives rise to the OH ion as the only anion, For example, NaOH, Ca(OH)₂

Question 2.
Write a short note on Neutralization.
Answer:

Take 10 ml of dilute HCl in a beaker, go on adding dilute NaOH drop by drop and record the pH.
Stop adding the NaOH when the green colour appears on the pH paper, that is when the pH of solution becomes 7.
Both HCl and NaOH dissociate in their aqueous solutions.
Addition of NaOH to HCl solution is like adding a large concentration of OH ions to a large concentration of H⁺ ions.
However water dissociates into H⁺ and OH ions to a very small extent.
Therefore on mixing the excess OH^– ions combines with excess H⁺ ions and forms H₂O molecules which mix with solvent water.
This change can be represented by the ionic equation shown as follows. H⁺ + Cl^– + Na⁺ + OH^– → Na⁺ + Cl^– + H₂O
It can be observed that Na⁺ and CT ions are there on both the sides. Therefore the net ionic reaction is H⁺ + OH^– → H₂O
As NaOH solution is added drop by drop to the HCl solution, the concentration of ff goes on decreasing due to combination with added OH ions, and that is how the pH goes on increasing.
When enough NaOH is added to HCl, the resulting aqueous solution contains only Na⁺ and Cl^– ions, that is, NaCl, a salt, and the solvent water. The only source of H⁺ and OH^– ions in this solution is a dissociation of water.
Therefore, this reaction is called the Neutralization reaction. The Neutralization reaction is also represented by the following simple equation.

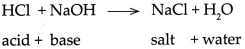
Question 3.
Explain the water of Crystallization.
Answer:

Take some crystals of blue vitriol (CuSO₄. 5H₂O) in a test tube. Heat the test tube on a low flame of a burner.
It was observed that on heating, the crystalline structure of blue vitriol broke down to form a colourless powder and water came out.
This water was part of the crystal structure of blue vitriol. It is called water of crystallization.
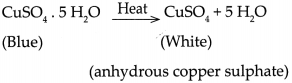
On adding water to the white powder a solution

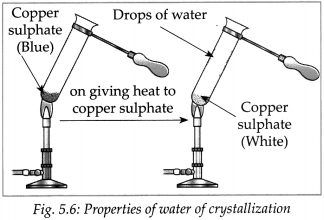
was formed which had the same colour as the solution in the first test tube.
From this we come to know that no chemical change has occurred in the crystals of blue vitriol due to heating.
Losing water on heating blue vitriol, breaking down of the crystal structure, losing blue colour and regaining blue colour on adding water are all physical changes.
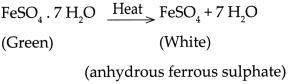
Similarly, ferrous Sulphate crystals also contain 7 molecules of water of crystallization which are lost on heating.
The reaction is represented as
Ionic compounds are crystalline in nature. These crystals are formed as a result of definite arrangement of ions.
In the crystals of some compounds, water molecules are also included in this arrangement.
That is the water of crystallization. The water of crystallization is present in a definite proportion of the chemical formula of the compound.

Question 4.
Explain the conduction of electricity through solutions of ionic compounds
Answer:

Electrons conduct electricity through electrical wires, and ions conduct electricity through a liquid or a solution.
Electrons leave the battery at the negative terminal, complete the electric circuit and enter the battery at the positive terminal.
When there is a liquid or a solution in the circuit, two rods, wires or plates are immersed in it. These are called electrodes.
Electrodes are made of conducting solid. The electrode connected to negative terminal of a battery by means of a conducting wire is called a cathode and the electrode connected to the positive terminal of a battery is called anode.
We have seen that salts, strong acids and strong bases dissociates almost completely in their aqueous solutions.
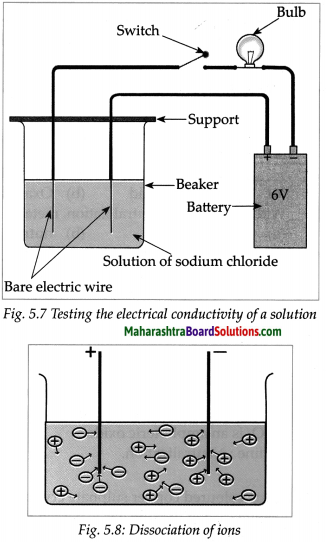
Therefore the aqueous solutions of all these three contain large number of cations and anions.
A characteristic of liquid state is the mobility of its particles. Due to its mobility the positive charged ions of the solution are attracted to the negative electrode or cathode.
On the other hand, the negative charged ions of the solution are attracted to the positive electrode or anode.
The movement of ions in the solution towards the respective electrodes accounts to the conduction of electricity through the solution.
From this we can understand that those liquids or solutions which contain a large number of dissociated ions conduct electricity.

9th Std Science Questions And Answers:

Information Communication Technology (ICT) Class 9 Science Chapter 10 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 10 Information Communication Technology (ICT) Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 10 Information Communication Technology (ICT) Question Answer Maharashtra Board

Class 9 Science Chapter 10 Information Communication Technology (ICT) Question Answer Maharashtra Board

1. Fill in the blanks to complete the statements. Justify the statements.

a. While working with a computer we can read the information stored in its memory and perform other actions in ………………………. memory.
b. While presenting pictures and videos about the works of scientists, we can use ……………………… .
c. To draw graphs based on the quantitative information obtained in an experiment, one uses ……………………… .
d. The first generation computers used to shut down because of ……………………… .
e. A computer will not work unless ………………………. is supplied to it.

2. Answer the following questions.

a. Explain the role and importance of information communication in science and technology.
Answer:

ICT plays a key role in creating, displaying, collecting, processing and communicating information in the field of science and technology.
Following is the importance of ICT in science and technology:
(a) Access to wide range of information
(b) Storing of Data
(c) Processing of Data
(d) Securing work files
(e) Proper representation of data

b. Which application software in the computer system did you find useful while studying science, and how?
Answer:

Microsoft word: To write down the information collected and making a document for further evaluation.
Microsoft excel : To draw graph based on the obtained numerical information from the experiment.
Internet explorer: To search for information in finding out the solution or solving the queries by reading the available information.

c. How does a computer work?
Answer:

Input unit	Processor	Output Unit
All types of information/ data is entered into the computer through this unit. Generally, a keyboard is used to enter data or information	Processing Unit (1) Memory unit (2) Control unit (3) ALU unit	The result/solution/ answer is eventually sent to the output unit. Generally, a screen/monitor or printer is used as an output unit.

d. What precautions should be taken while using various types of software on the computer?
Answer:

Antivirus must be installed.
Software should be legal and from a trusted place.
Application should be scanned before using.
Pirated Software should not be used
Provide all necessary data to obtain the best possible results.

e. Which are the various devices used in information communication? How are they used in the context of science?
Answer:

Various devices used in information communication are: Computers, Laptops, Mobiles, Radios, Television, etc.
Computers, Laptops and Mobiles: Help in accessing, collecting, processing, communicating, sharing and storing of information. It helps in determining the appropriate conclusions in all fields, including the field of science.
Television: Help in getting information about the new and innovative technology.

3. Using a spreadsheet, draw graphs between distance and time, using the information about the movements of Amar, Akbar and Anthony given in the table on page 4, in the lesson on Laws of Motion. What precautions will you take while drawing the graph?

Answer:
Precautions to be taken while drawing a graph:

The data should be kept in tabular form.
Whenever there is ‘drag and fill’ option used, ‘smart tag’ option should be used after ‘drag data’ to fill data as required.
Entered data should be formatted in the manner required.
Various types of graphs can be created by using the same data, so appropriate graph should be selected.
Chart titles and axes titles should be updated as per the data.

4. Explain the differences between the different generations of computers. How did science contribute to these developments?
Answer:
Generation: 1st
Time Period: 1946 – 1956
Development: Vacuum Tubes Characteristics:

Huge in size
Expensive
Lot of electricity consumption
Heat generation

Generation: 2nd
Time Period: 1956 – 1963
Development: Transistors
Characteristics:

Frequent shutdowns
Superior to 1st Generation
Small in size and fast
Cheaper as compared to 1st Generation
Less consumption of electricity

Generation: 3rd
Time Period: 1963 -1971
Development: IC
Characteristics:

Keyboards and monitors
OS
Smaller and still cheaper

Generation: 4th
Time Period: 1971 – 2010
Development: Microprocessor Characteristics:

Use of Internet
GUI
Introduction of portable devices like mobiles, laptops, etc.

Generation: 5th
Time Period: 2010 – Till Date
Development: Artificial Intelligence (AI) Characteristics:

Voice recognition
Sensors
Nano technology

1st Generation computers occupied the entire room, but due to advancement in science and technology, today’s computer fits into our pockets.

Initially computers needed a specific language to interact but today we use voice recognition for the same.

In these ways, science has contributed in making the computers faster, smaller, cheaper and much more useful.

5. What devices will you use to share with others the knowledge that you have?
Answer:
Devices like radios, televisions, pendrives, computers, laptops, mobiles, landlines, hard drives, CDs, memory cards help us in sharing our knowledge with others.

6. Using information communication technology, prepare powerpoint presentations on at least three topics in your textbook. Make a flowchart of the steps you used while making these presentations.
Answer:
Steps for preparation of PowerPoint presentations:

7. Which technical difficulties did you face while using the computer? What did you do to overcome them?
Answer:

Lagging: Due to lot of applications running at the same time, the computer starts lagging and becomes slow. Closing a few applications helped solve the problem of lagging.
Viruses and Bugs: Cybercrimes are rising daily, even from single mail the computer can be attacked by viruses. Installing a valid antivirus helps solve the problem of viruses and bugs.
Breach of Privacy: Confidential information being accessed by anyone is the breach of privacy. Putting privacy setting in place helps solve the problem.
Physical Damage: Hardware over a period of time might get physically damaged. Taking precautions while using will help to solve the problem.

Class 9 Science Chapter 10 Information Communication Technology (ICT) Intext Questions and Answers

Question 1.
Make a list of various hardware and software items of a computer,
Answer:
Hardware: Mouse, Keyboard, Pendrive, Monitor and other parts of computer.
Software: Operating Systems, Application Programs, Antivirus, etc.

Answer the following questions:

Question 2.
Which devices do we directly or indirectly use for collecting, sharing, processing and communicating information?
Answer:

Computers
Laptops
Mobiles
Memory Cards
Pendrives
Landlines
Hard disks etc.

Question 3.
How is information communication technology important for dealing with explosion of information?
Answer:

Information explosion means a situation whère information is available in abundance, in other words, too much information.
Devices like computers, laptops help us in easier accessment of information that we need from all the data.

Class 9 Science Chapter 10 Information Communication Technology (ICT) Additional Important Questions and Answers

Choose and write the correct option:

Question 1.
…………………….. includes communication devices and the use of those devices as well as the services provided with their help.
(a) Operating System
(b) Office
(c) Computers
(d) Information Communication Technology
Answer:
(d) Information Communication Technology

Question 2.
Computers have gone through …………………….. generations.
(a) 5
(b) 7
(c) 10
(d) 8
Answer:
(a) 5

Question 3.
First generation of Computers were considered to be present in the period of ……………………. .
(a) 2000 – 2001
(b) 1901 – 2001
(c) 1946 -1959,
(d) 1996 – 2001
Answer:
(c) 1946-1959

Question 4.
Full form of RAM is ……………………. .
(a) Roaming Application Memory
(b) Random Accessible Media
(c) Random Access Memory
(d) None of the above
Answer:
(c) Random Access Memory

Question 5.
Full form of ROM is ……………………. .
(a) Roaming Only Memory
(b) Random Output Media
(c) Read Only Memory
(d) None of the above
Answer:
(c) Read Only Memory

Question 6.
…………………….. is raw information.
(a) Program
(b) Memory
(c) Data
(d) Operating System
Answer:
(c) Data

Question 7.
…………………….. are used for sharing information.
(a) Telephones
(b) Hard disks
(c) RAM
(d) ROM
Answer:
(a) Telephones

Question 8.
Hard disks are used for …………………….. information.
(a) storing
(b) communicating
(c) sharing
(d) all of the above
Answer:
(a) storing

Question 9.
Computers are used for …………………….. information.
(a) storing
(b) managing
(c) sharing
(d) all of the above
Answer:
(d) All of the above

Question 10.
RAM and ROM are 2 types of …………………….. memory.
(a) external
(b) internal
(c) physical
(d) garbage
Answer:
(b) internal

Question 11.
The information stored in ROM is only …………………….., changes cannot be made.
(a) external memory
(b) readable
(c) accessible
(d) physical
Answer:
(b) readable

Question 12.
…………………….. is a group of commands to be given to the computer.
(a) Program
(b) Memory
(c) Data
(d) Operating System
Answer:
(a) Program

Question 13.
…………………….. communicates between the computer and the person working on it.
(a) Program
(b) Memory
(c) Data
(d) Operating System
Answer:
(d) Operating System

Match the columns:

Column ‘A’	Column ‘B’
(1) Antivirus (2) OS (3) CPU (4) Printer (5) Mouse	a) Output Device b) Software c) Input Device (d) Operating System (e) Brain of the computer

Answer:
(1 – b),
(2 – d),
(3 – e),
(4 – a),
(5 – c)

State whether the following statements are true or false and if false, correct the false statements:

(1) RAM and ROM are the types of external memory.
(2) ICT includes communication devices and the use of those devices as well as services provided with their help.
(3) A computer cannot be used without its operating system.
(4) Microsoft Excel is used to make PowerPoint.
(5) Software refers to the set of commands given to the computer.
Answer:
(1) False. RAM and ROM are the types of internal memory.
(2) True
(3) True
(4) False. Microsoft Excel is used to make spreadsheets.
(5) True

Answer the following in one sentence:

Question 1.
Name the computer which was made between 1946 -1959.
Answer:
The ENIAC computer was made in the period of 1946-1959.

Question 2.
Give one example of Input Unit.
Answer:
Keyboard.

Question 3.
Name the 3 major parts of the processing units.
Answer:

Memory unit
Control unit
ALU unit

Question 4.
What precautions need to the taken care while entering formula into the excel?
Answer:
While using a formula, the ‘=’ sign should be typed first. Similarly, no space should be inserted while typing any formula.

Question 5.
What is Internet Explorer?
Answer:
This is a kind of Search Engine. It helps to find the information we want from all the information available on the internet.

Question 6.
What is a PDF?
Answer:
A PDF or Portable Document Format file can be used to view the file to print it or to handle files.

Question 7.
What is C-DAC?
Answer:
C-D AC, is a well-known Centre for Development of Advanced Computing, situated in Pune.

Write the Full forms of the following abbreviation:

Question 1.
ICT
Answer:
Information Communication Technology

Question 2.
OS
Answer:
Operating System

Question 3.
RAM
Answer:
Random Access Memory

Question 4.
ROM
Answer:
Read Only Memory

Question 5.
CPU
Answer:
Central Processing Unit

Question 6.
DOS
Answer:
Disk Operating System

Question 7.
PDF
Answer:
Portable Document Format

Question 8.
ALU
Answer:
Arithmetic Logical Unit

Question 9.
GUI
Answer:
Graphical User Interface

Question 10.
C-DAC
Answer:
Centre for Development of Advanced Computing

Question 11.
ISCII
Answer:
Indian Script Code for Information Interchange

Define the following:

Question 1.
Memory
Answer:
Memory is the place for storing data obtained from the input and also the generated solution or answer by the computer.

Question 2.
RAM
Answer:
RAM is created from electronic components and can function only as long as it is supplied with electricity.

Question 3.
ROM
Answer:
Information stored in ROM can only be read and changes cannot be made to the information originally stored here.

Question 4.
Operating System
Answer:
It is a program which provides a means of communication between the computer and the person working on it. It is called the DOS (Disk Operating System).

Question 5.
Program
Answer:
A program is a group of commands to be given to a computer.

Question 6.
Data and Information
Answer:
Data is information in its raw (unprocessed) form.

Question 7.
Hardware
Answer:
Hardware consists of all the electronic and mechanical parts used in computers.

Question 8.
Software:
Answer:
Software refers to the commands given to the computer, information supplied to it (input) and the results obtained from the computer after analysis (output).

Give scientific reasons:

Question 1.
Computer cannot function without its operating system.
Answer:

Operating system is like a link between the computer and the person working on it.
Operating system manages all the activities performed by the computer.
Without the operating system, the user won’t be able to input any data or run any program. Thus, a computer cannot run without an operating system.

Question 2.
ROM is a Read Only Memory.
Answer:

ROM also known as Read Only Memory is a part of internal memory of a computer where the information stored can only be read.
ROM helps store data permanently for a long period of time and the information stored cannot be deleted.
Thus, data in a ROM can only be read and cannot be altered or modified and hence, it is called as Read Only Memory.

Complete the table:
Answer:

Answer the following questions:

Question 1.
What precautions will you take when entering data?
Answer:

As far as possible, the data should be kept in tabular form. Different types of data should be entered in different cells. Data should be entered neatly and in one ‘flow’. Unnecessary space and special characters should not be used.
Many times we ‘drag and fill’ data. At such times, the ‘smart tag’ can be used after ‘drag data’ to fill any data in any manner as required.
Once the data has been entered, it can be formatted in different ways. Similarly, we can perform different types of calculations, using different formulae.
While using a formula, the ‘=’ sign should be typed first. Similarly, no space should be inserted while typing any formula.

Answer in detail:

Question 1.
Write in short about the opportunities in the field of ICT.
Answer:
(i) Software Field: This is an important field. Having accepted the challenge of creating software, many companies have entered this field. The opportunities in the software field can be classified as follows – application program development, software package development, operating systems and utility development, special purpose scientific applications.

(ii) Hardware Field: Today, there are several companies in our country too, which make computers. They sell computers that they have themselves made. Others sell computers brought from outside as well as repair them and take maintenance contracts to keep computers in big companies working efficiently without a break. Plenty of jobs are available here. There are job opportunities in hardware designing, hardware production, hardware assembly and testing, hardware maintenance, servicing and repairs, etc.

(iii) Marketing: There are many establishments which make and sell computers and related accessories. They need good sales personnel who are experienced in the working of computers as well as skilled in marketing.

(iv) Training: The training of new entrants for various jobs is a vast field. It is very important to have dedicated teachers who are competent in the field of computers.

Question 2.
Write in short about the industries conducting research in the field of computers.
Answer:

C-DAC, the well-known Centre for Development of Advanced Computing, situated in Pune, is the leading institute in India that conducts research in the field of computers.
The first Indian supercomputer was made with help from this institute. Valuable guidance for making this computer (the Param computer) was received from the senior scientist Vijay Bhatkar. Param means the supreme.
This computer can perform one billion calculations per second. It is used in many fields like space research, movements in the interior of the earth, research in oil deposits, medicine, meteorology, engineering, military etc.
C-DAC has also participated in developing the ISCII code for writing different language scripts. (Indian Script Code for Information Interchange).

Question 3.
Use Microsoft Word to create a document and write equations.
Answer:

Click on the Microsoft word 2010 icon on the desktop.
Select the ‘New option in the ‘File’ tab, and then select the ‘Blank document’ option.
Type your material on the blank page on the screen using the keyboard. Use the language, font size, bold, etc. options in the Home tab to make the typed material attractive.
To type equations in the text, select the ‘Equation’ option in the ‘Insert’ tab.
Select the proper equation and type it using mathematical symbols.

9th Std Science Questions And Answers:

Substances in Common Use Class 9 Science Chapter 14 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 14 Substances in Common Use Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 14 Substances in Common Use Question Answer Maharashtra Board

Class 9 Science Chapter 14 Substances in Common Use Question Answer Maharashtra Board

1. Fill in the blanks.

a. The number of molecules of water of crystallization in washing soda is …………….…. .
b. The chemical name of baking soda is …………….…. .
c. …………….…. is used in treatment of hyperthyroidism.
d. The chemical name of Teflon is …………….…. .
Answer:
a. 10
b. Sodium bicarbonate
c. Iodine -123
d. Polytetra fluoroethylene (C₂F₄)_n

2. Match the pairs

Group A	Group B
1. Saturated brine	a. sodium metal freed
2. Fused salt	b. basic salt
3. CaOCl₂	c. crystallization of salt
4. NaHCO₃	d. oxidation of colour

Answer:
(1 – c),
(2 – a),
(3 – d),
(4 – b)

3. Write answers to the following

a. What is meant by radioactivity?
Answer:

Elements with a high atomic number such as uranium, thorium, radium have a property of spontaneously emitting invisible, highly penetrating and high energy radiation.
This property is called radioactivity.
A substance having this property is called a radioactive substance.

b. When is said to be the nucleus unstable?
Answer:

It is the balance of protons and neutrons in a nucleus which determines whether a nucleus will be stable or unstable.
Too many neutrons or protons upset this balance disrupting the binding energy from the strong nuclear forces making the nucleus unstable.

c. Which diseases are caused by artificial food colours?
Answer:
Diseases like ADHD (Attention Deficit Hyperactivity Disorder) can affect children due to excessive consumption of foods with added food colours.

d. Where in the industrial field is radioactivity used?
Answer:
Industrial field Radiography

Internal cracks and voids in cast iron articles and iron solder can be detected with the help of gamma rays.
For this purpose, isotopes like cobalt-60, iridium-192 are used in the radiography camera.
This technique is used for detecting flaws in metal work.

Measurement of thickness, density and level

It is necessary to maintain the required thickness in the manufacture of aluminium, plastic, iron sheets of differing thickness.
In the manufacturing process, a radioactive substance is placed on one side and an instrument to measure radiation on the other.
The radiation read by the measuring instrument varies with the thickness of the sheet.
Material inside a packing can also be examined by the same technique.

Luminescent paint and radio luminescence:

The radioactive substances radium, promethium, tritium with some phosphor are used to make certain objects visible in the dark, for example, the hands of a clock, and certain other objects.
Krypton-85 is used in HID (High-Intensity Discharge) lamps while promethium – 147 is used in portable X-ray units as the source of beta rays.

Use in Ceramic articles:

Luminous colours are used to decorate ceramic tiles, utensils, plates, etc.
Earlier uranium oxide was used in these paints.

e. Write down properties of teflon.
Answer:
Properties of teflon :

The atmosphere and chemical substances have no effect on Teflon.
Neither water nor oil will stick to Teflon coated articles.
High temperatures do not affect Teflon as its melting point is 327 °C.
Teflon coated articles are easy to clean.

f. What type of colours will you use to celebrate ecofriendly Rang Panchami? Why?
Answer:

We regularly use artificial colours on Rang Panchami.
The red colour used on Rang Panchami is very dangerous. It contains a high proportion of mercury in it.
This poses risks like blindness, skin cancer, asthma, itching of the skin, permanent blocking of sweat pores, etc.
Therefore, it is necessary to use eco-friendly colours.
We will prepare colours for Rang Panchami from natural resources such as beet root, flowers of flame of forest, spinach, flame tree (gulmohar) and protect your health by using these.

g. Why has the use of methods like Teflon coating become more common?
Answer:
The use of methods like Teflon coating became more common because of following properties of teflon:

The atmosphere, rain water and chemical substances have no effect on Teflon.
Neither water nor oil will stick to Teflon coated articles.
High temperatures do not affect Teflon as its melting point is 327 °C.
Teflon coated articles are easy to clean.
Teflon is a poor conductor of electricity.

4. Give a scientific explanation

a. Bleaching powder has the odour of chlorine.
Answer:

Bleaching powder undergoes slow decomposition due to the carbon dioxide in air and chlorine gas is released.
Bleaching powder gets its property because of this release of chorine gas.

b. The hard water of a well becomes soft on adding washing soda to it.
Answer:

The hard water from a well or a bore-well becomes soft on adding washing soda and we come to know this from the lather formed on it.
The hardness of water is due to the presence of chlorides and sulphates of calcium and magnesium in it.
Na₂CO₃ is added to it to soften such water and make it suitable for use.
The reaction with Na₂CO₃ causes the formation of insoluble carbonate salts of magnesium and calcium.
MgCl_2(aq) + Na₂CO_3(s) → MgCO_3(s) + 2 NaCl_(s)

c. Soap forms a precipitate in hard water.
Answer:

When soap is mixed with hard water, calcium and magnesium salts of fatty acids are formed.
These being water insoluble, they form a precipitate and that is why lather is not formed.

d. The particles of powder are given an electric charge while spraying them to form the powder coating.
Answer:

Powder coating is a method of applying a layer harder than paint on the surface of an iron object to prevent rusting.
In this method, a polymer resin, a pigment and some other ingredients are melt, mixed, cooled and ground into a uniform powder.
This powder is sprayed on the polished metal surface by electrostatic spray deposition (ESD).
In this method, the particles of the powder are given an electrostatic charge due to which a uniform layer of the powder sticks to the metal surface.
Then the object is heated in the oven along with the coating.
A chemical reaction occurs in the layer, resulting in the formation of long cross-linked polymeric chains.

e. The aluminium article is used as an anode in the anodising process.
Answer:

A protective layer is formed naturally on the surface of aluminium metal by reaction with oxygen in air.
In the anodizing process, this layer is made of the desired thickness. Anodizing is done by electrolysis.
Dilute Sulphuric acid is taken in the electrolytic cell and the aluminium article is dipped in it as the anode.
When an electric current is passed, hydrogen gas is released at the cathode and oxygen gas at the anode.
A reaction with oxygen occurs and a layer of hydrated aluminium oxide is formed on the anode. Therefore, aluminium article is used as an anode in the anodizing process.

f. When the radiation coming out from certain radioactive substance is passed through an electric field, marks are found at three places on the photographic plate placed in its path.
Answer:
(i) When the radiation coming out from certain radioactive substance is passed through an electric field, marks are found at three places on the photographic plate placed in its path. This is because the radiation coming out from radioactive substance are of three types Alpha rays, Beta rays and Gamma rays.

(ii) The rays which get deviated slightly towards negatively charged plate are called alpha rays. They get deviated towards negatively charged plate because they are made of positively charged particles, called as alpha particles (He++).

(iii) The rays which get deviated substantially towards the positively charged plate are called beta rays. They get deviated towards a positively charged plate because they are made of negatively charged particles called as beta particles (e-).

(iv) The rays which do not deviate at all are called gamma rays. They are uncharged electromagnetic radiation. Hence, marks are found at three places on the photographic plate. (For diagram refer Fig. 14 .2 from Q. 4(3))

g. A certain type of ceramic tiles are fixed on the outer layer of a space shuttle.
Answer:
(i) Each shuttle is covered by more than 24,000 of the six- by six-inch advance ceramic tiles. This tiles withstand high temperatures without decomposing. They are brittle, water-resistant and electrical insulator. Most of the tiles are made of silica fibres, which are produced from high-grade sand (SiO₂).

(ii) Silica is an excellent insulator because it transports heat slowly. When the outer portion of a tile gets hot, the heat takes a long time to work its way down through the rest of the tile to the shuttle’s skin. The tiles keep the orbiter’s aluminium skin at 350 degrees or less.

(iii) The silica fibers are mixed with water and chemicals, and the mixture is poured into molds, which are zapped in microwave ovens at 2,350°C to fuse the silica fibres. Tiles are too brittle to attach to the orbiter directly.

(iv) The shuttle’s skin contracts slightly while in orbit, then expands during re-entry.

(v) In addition, the stresses of launch and re-entry cause the skin to flex and bend. Such motions could easily crack the tiles or shake them off. To keep them in place, workers glue the tiles to flexible felt-like pads, then glue the pads to the orbiter.

5. Write answers to the following

a. Write about artificial food colours, the substances used in them and their harmful effects.
Answer:
(a) Artificial food colour and substances in them.

Food colours are mixed in most soft drinks and foodstuffs available in the market.
These food colours are in the form of powders, gels and pastes.
Food colours are used in domestic as well as commercial products.
Certain colours and essences are added to ice cream, ice candies, sauce, fruit juices, cold drinks, pickles, jams and jelly.
Food colours are often found to be added to packaged meat (chicken, mutton), chilli powder, turmeric, sweets and other similar substances so as to give them a good colour.
Tetrazene, sunset yellow are artificial food colours used extensively.

(b) Harmful effects of artificial food colours

Food colours added to pickles, jam and sauce contain small quantities of lead and mercury. These can be harmful for those who consume these products on a regular basis.
Diseases like ADHD (Attention Deficit Hyperactivity Disorder) can affect children due to excessive consumption of foods with added food colours.

b. What is meant by water of crystallization? Give examples of salts with water of crystallization, and their uses.
Answer:
The exact number of water molecules which are chemically bonded to a molecule of a salt within a hydrated crystalline compound is called as water of crystallization are:

Some substances in our daily use which contain water of crystallization are:

Alum (Potash alum – K₂SO₄.Al₂(SO₄)₃.24H₂O)
Borax (Na₂B₄O₇.10H₂O)
Epsom salt (Magnesium sulphate MgSO₄.7H₂O)
Barium chloride (BaCl₂.2H₂O)
Sodium sulphate (Glauber’s salt Na₂SO₄.10 H₂O)
Blue vitriol (Copper Sulphate – CuSO₄.5H₂O)

Uses of these salts are as given below:
(i) Alum (Potash alum – K₂SO₄.Al₂(SO₄)₃.24H₂O)

Alum is used in the process of water purification.
Because of the property of coagulation, the solid impurities in water come together, become heavy and settle to the bottom. As a result, the impure water or muddy above becomes clear.
Alum powder, found in the spice section of many grocery stores, may be used in pickling recipes as a preservative to maintain fruit and vegetable crispness.
Alum is used as the acidic component of some commercial baking powders.
Alum has been used as an after shave treatment.

(ii) Borax (Na₂B₄O₇.10H₂O)

Borax today is used for many cleaning purposes.
It is used to make homemade laundry detergent.
It is added as a cleaning boost to any other detergent.
It even keeps ants and other pests away.

(iii) Epsom salt (Magnesium sulphate MgSO₄.7H₂O)

Epsom salt is used as a relaxing magnesium bath soak.
To grow better vegetables – Add a tablespoon of Epsom salt to the soil below a vegetable plant to boost growth.

(iv) Barium chloride (BaCl₂.2H₂O)

In industry, Barium chloride is mainly used in the purification of brine solution in caustic chlorine plants.
It is also used in the manufacture of heat treatment salts.
It is used in hardening of steel.
It is used in the manufacture of pigments.

(v) Sodium sulphate (Glauber’s salt Na₂SO₄.10H₂O)

In the laboratory, anhydrous Sodium sulphate is widely used as an inert drying agent, for removing traces of water from organic solutions.
Glauber’s salt, the decahydrate, is used as a laxative.

(vi) Blue vitriol (Copper sulphate CuSO₄.5H₂O)

Blue vitriol is used in the blood test for diagnosing anaemia.
Slaked Time is used with blue vitriol in the Bordeaux mixture which is used as a fungicide on fruits like grapes and musk melon.

c. Write briefly about the three methods of electrolysis of sodium chloride.
Answer:

When an electric current is passed through a saturated solution of sodium chloride (brine) it is electrolysed and hydrogen gas is released at the cathode while chlorine gas is released at the anode.
This method is used for production of chlorine gas. In this method an important basic compound NaOH is formed in the cell.
Chemical reaction
2NaCl + 2H₂O → 2NaOH + Cl₂ ↑ + H₂↑
When salt is heated to a high temperature (about 800 °C), it melts. This is called the fused state of the salt.

6. Write the uses.

a. Anodizing
b. Powder coating
c. Radioactive substances
d. Ceramic
Answer:
(a) Anodizing : Anodizing is done on aluminum cooking utensils like griddles and cookers.

(b) Powder coating : Powder coating is done on iron objects to prevent rusting. Also, on Plastic and Medium density fibre (MDF) board, to make them highly durable, hard and attractive.

(c) Radioactive substances:
(I) Industrial field:
(i) Industrial Radiography : Internal cracks and voids in cast iron articles and iron solder can be. detected with the help of gamma rays. For this purpose, isotopes like cobalt-60, iridium-192 are used in the radiography camera. This technique is used for detecting flaws in metal work.

(ii) Measurement of thickness, density and level: It is necessary to maintain the required thickness in the manufacture of aluminium, plastic, iron sheets of differing thickness. In the manufacturing process, a radioactive substance is placed on one side and an instrument to measure radiation on the other. The radiation read by the measuring instrument varies with the thickness of the sheet. Material inside a packing can also be examined by the same technique.

(iii) Luminescent paint and radioluminescence:
The radioactive substances radium, promethium, tritium with some phosphor are used to make certain objects visible in the dark, for example, the hands of a clock, and certain other objects. Krypton-85 is used in HID (High Intensity Discharge) lamps while promethium-147 is used in portable X-ray units as the source of beta rays.

Use in Ceramic articles – Luminous colours are used to decorate ceramic tiles, utensils, plates, etc. Earlier uranium oxide was used in these paints.

(II) Field of agriculture :

The genes and chromosomes that give seeds properties like fast growth, higher productivity, etc. can be modified by means of radiation.
The radioactive isotope cobalt-60 is used for food preservation.
Onions, potatoes are irradiated with gamma rays from cobalt-60 to prevent their sprouting.
Strontium-90 is used as a tracer in the research on various crops.

(III) Medical science:

Polycythemia : The red blood cell count increases in the disease polycythemia. Phosphorus- 32 is used in its treatment.
Bone cancer : Strontium-89, strontium-90, samarium-153 and radium-223 are used in the treatment of bone cancer.
Hyperthyroidism : Enlargement of thyroid gland, weight loss in spite of appetite, insomnia are the symptoms of hyperthyroidism.
It occurs due to overproduction of hormones by the thyroid gland. Iodine-123 is used in the treatment of hyperthyroidism.
Tumour detection : Boron-10, iodine-131, cobalt-60 are used in treatment of brain tumour, while arsenic-74 is used in detection of small tumours in the body.

(d) Ceramic : Pots made by a potter, Mangalore roofing tiles, construction bricks, pottery, terracotta articles are some examples of common ceramic articles that we see around.

7. Write the harmful effects

a. Artificial dye
b. Artificial food colour
c. Radioactive substances
d. Deodorant
Answer:
(a) Artificial dye:

Dyeing hair can have adverse effects like hair fall, damage to hair texture, burning of skin, adverse effect on eyes, etc.
Lipstick contains a dye named carmine. It does not affect lips but causes stomach disorders.
Excessive use of plants for making natural dyes results in deterioration of the environment.

(b) Artificial food colour:

Food colours added to pickles, jams and sauces contain small quantities of lead and mercury. These can be harmful for those who consume these products on a regular basis.
Diseases like ADHD (Attention Deficit Hyperactivity Disorder) can affect children due to excessive consumption of foods with added food colours.

The central nervous system is affected by radioactive radiations.
Hereditary defects are generated by bombardment of radiation on D.N.A in the body.
Radioactive radiation can penetrate the skin, and causes diseases like skin cancer, leukemia.
The radioactive pollutants created due to explosions enter the body through air and it is difficult to control them.
The radioactive pollutants released in the sea enter the bodies of fishes and through them enter the human body.
The radioactive paint on the watch can cause cancer.
The radioactive isotopes strontium-90 can enter the body through plants, fruits, flowers, cereals, milk, etc. and cause diseases like bone cancer, leukemia.

(d) Deodorant:

Aluminium – Zirconium compounds are the most harmful chemicals in the deodorant. Disorders like headache, asthma, respiratory disorders, heart disease are likely to occur without our knowledge.
There is a possibility of various skin disorders and also skin cancer due to the aluminium chlorohydrates.

8. Write the chemical formula Bleaching powder, common salt, baking soda, washing soda
Answer:

Common name	Chemical name
Bleaching powder	CaOCl₂
Common salt	NaCl
Baking soda	NaHCO_s
Washing soda	Na₂CO₃.10 H₂O

9. Explain what you see in the following picture

Powder coating
Answer:

This picture shows powder coating of the given object. Powder coating is a method of applying a layer harder than paint on the surface of an iron object to prevent rusting.
In this method, a polymer resin, a pigment and some other ingredients are melt mixed, cooled and ground into a uniform powder.
This powder is sprayed on the polished metal surface by electrostatic spray deposition (ESD).
In this method, the particles of the powder are given an electrostatic charge due to which a uniform layer of the powder sticks to the metal surface.
Then the object is heated in the oven along with the coating.
A chemical reaction occurs in the layer, resulting in the formation of long cross-linked polymeric chains.
This powder coating is highly durable, hard and attractive. Powder coating can be done on plastic and medium density fibre (MDF) board in day to day use as well.

Class 9 Science Chapter 14 Substances in Common Use Intext Questions and Answers

Can you recall?

Question 1.
What are detergents?
Answer:

Detergent is a water-soluble cleansing agent which combines with impurities and dirt to make them more soluble, and differs from soap in not forming a scum with the salts in hard water.
Today, detergents are more likely to be a mixture of synthetic chemicals and additives cooked up in a huge chemical plant and, unlike traditional soap, they’re generally liquids rather than solids.
Detergents are used in everything from hair shampoo and clothes, washing powder to shaving foam and stain removers.
The most important ingredients in detergents are chemicals called surfactants – a word made from bits of the words surface-active agents.

Question 2.
What are the important substances that we use in day to day life? For what purposes do we use them?
Answer:
Some of the substances we use in our day to day life and the purpose of using them are as follows:

Toothpaste: for cleaning teeth and maintaining hygienic conditions of mouth.

Soap : for bathing and maintaining hygienic conditions of body.

Natural and artificial fibers : we wear them as clothes to protect our body and many other purposes.

Washing powder: for cleaning clothes. Vegetables, fruits and food grains : they provide us with necessary vitamins, minerals and carbohydrates required for proper functioning of body.

Water : very important for our survival and many other functions of day to day life.

Metals : for making buildings, bridges, roads, vehicles, trains, ships, airplanes, utensils etc.

Acids, bases and salts : used for various purposes, for example, Sodium chloride which is used as common salt, a very necessary ingredient of our daily food without which our food is tasteless.

Question 3.
How are the various substances in day to day use classified from the scientific point of view?
Answer:
The various substances in day to day use are classified from the scientific point of view as elements, compounds, mixtures, metals, non-metals, acids, bases and salts.

Question 4.
Which chemicals and apparatus will you use in the laboratory for making soap?
Answer:
For making soap in laboratory following chemicals and apparatus are used :
Chemicals : Vegetable oil (coconut oil, castor oil, soya bean oil etc.)
Sodium hydroxide (NaOH)
Salt (Sodium chloride NaCl)

Apparatus :
500 ml glass beaker
Burner
Flat glass tray
Knife

Soaps are essential to personal and public health. They safely remove germs, soils and other contaminants and help us to stay healthy and make our surroundings more pleasant. Soaps are made from fats and oils or their fatty acids.

Take about 20 ml of any vegetable oil (coconut oil, castor oil, soybean oil etc.) in a beaker. Put about 30 – 35 ml of NaOH in it and heat and stir the mixture till a paste is formed. Now add a little salt. Stir again and allow the mixture to cool in a flat glass tray, on cooling it solidifies. Take a knife and cut it in soap bars as per the size required.

Question 5.
What are salts?
Answer:

Inorganic substances occur naturally in the form of salts rather than acids or bases.
The ionic compounds which do not contain H+ and OH ions and contain only one kind of cation and anion are called simple salts.
For example, Na₂SO₄, K₃PO₄, CaCl₂.
The sea is said to be a rich source of salts. In fact, the sea is a rich source of several salts of various elements such as chlorine, sodium, magnesium, potassium, calcium, bromine.
The important salts found in sea water are sodium chloride, magnesium chloride, magnesium sulphate, potassium chloride, calcium carbonate and magnesium bromide.

Answer the following questions:

Question 1.
How is it determined whether a substance is acidic, basic or neutral?
Answer:

In the pH scale, the pH of solutions varies from 0 to 14 in accordance with the strength of the acids or base.
The pH scale shows different colours at different values of pH. Colour from dark red to yellow or from pH value 0 to 6 indicates the substances are acidic.
Colour from light blue to violet or from pH value 8 to 14 indicates the substances are basic.
Green colour or pH value 7 indicates the substances are neutral.

Question 2.
A sweets shop looks attractive because of the colourful sweets displayed there. Which colours are used in these substances?
Answer:

Food colours and essences are used in sweets to make them colourful and tasty.
These food colour are in the form of powders, gels and pastes.
Food colours are natural as well as artificial.
The food colours prepared from seeds, beetroot, flowers and fruit concentrate are natural.
Tetrazene, sunset yellow are artificial food colours used extensively.

Question 3.
Make a list of substances in day to day use in accordance with their pH value (O to 14).
Answer:

Question 4.
A doctor gives you medicines when you fall ill. What are the medicines made from?
Answer:

Long before pure chemicals were manufactured in labs, people used plants for medicine.
There are over a hundred active ingredients derived from plants for use as drugs and medicines.
The emergence of synthetic chemistry in the 1800s opened up new avenues for scientific research into drugs.
Many chemists tried to locate medically active ingredients in plants (for instance the important malaria remedy quinine), and subsequently tried to make those substances in the laboratory in order to become independent of plant supplies.
At the same time, a new industry developed as scientists developed processes to synthesise new chemicals on a large scale.
New production methods developed in the late 1800s and early 1900s made it easier to standardise, package and transport medicines.

Question 5.
What problems do you get after playing colours on Rang Panchami? Why?
Answer:

After playing colours on Rang Panchami we may get problems such as risks of blindness, skin cancer, asthma, itching of the skin, permanent blocking of sweat pores etc.
This is because the colours used in rang panchami specially the red colour is very dangerous.
It contains a high proportion of mercury in it.

Question 6.
Which colours will you use to prevent the occurrence of these problems?
Answer:

To prevent the occurrence of these problem, instead of using artificial colours, natural colours should be used.
Natural colours are prepared from natural resouroes such as beet root, flowers of flame of forest, spinach, flame tree (gulmohar).

Question 7.
What problem do you have on painting the house and furniture?
Answer:

On painting the house and furniture with artificial colours which are dangerous, we may get problems such as risks of blindness, skin cancer, asthma, itching of the skin, permanent blocking of sweat pores, etc.
This is because the colours contain a high proportion of mercury in it.

Question 8.
What is the property of Teflon because of which it is used in non-stickware?
Answer:
Following are the properties of teflon because of which it is used in nonstick cookware.

The atmosphere and chemical substances have no effect on Teflon.
Neither water nor oil will stick to Teflon coated non-stickware.
High temperatures do not affect Teflon as its melting point is 327 °C.
Teflon coated non-stickware are easy to clean.

Answer the following questions:

Question 1.
What is the strip shown below? What is it used for?
Answer:
The strip shown is pH metre scale. It is used to determined pH of solutions.

Question 2.
Prepare saturated solutions of given salts and put 2-3 drops of the universal indicator in them and note your observations in the table below:
Answer:

Class 9 Science Chapter 14 Substances in Common Use Additional Important Questions and Answers

Select the correct option:

Question 1.
Baking soda is ………………………… .
(a) non-metallic
(b) metallic
(c) acidic
(d) basic
Answer:
(d) basic

Question 2.
During electrolysis of NaCl in the fused state ………………………… is formed at cathode.
(a) sodium
(b) oxygen
(c) oxalic acid
(d) butyric acid
Answer:
(a) sodium

Question 3.
………………………… is known as chloride of lime.
(a) Calcium carbonate
(b) Sodium bicarbonate
(c) Sodium chloride
(d) Bleaching powder
Answer:
(d) Bleaching powder

Question 4.
Salt obtained from certain type of rock is called ………………………… .
(a) hard salt
(b) rock salt
(c) stone salt
(d) pure salt
Answer:
(b) rock salt

Question 5.
The ………………………… % aqueous solution of salt is called brine.
(a) 25
(b) 60
(c) 30
(d) 50
Answer:
(a) 25

Question 6.
The molecular formula for baking soda is ………………………… .
(a) Na₂CO₃
(b) NaHCO₃
(c) Na₂SO₄
(d) NaNO₃Answer:
(b) NaHCO₃

Question 7.
Bleaching powder is also called ………………………… .
(a) Calcium oxygen chlorine
(b) Calcium oxychloride
(c) Calcium hydroxide
(d) Calcium oxalate
Answer:
(b) Calcium oxychloride

Question 8.
NaHCO₃ is also called as ………………………… .
(a) Sodium carbonate
(b) Sodium bicarbonate
(c) Sodium carbon oxide
(d) Sodium chloride
Answer:
(b) sodium bicarbonate

Question 9.
Molecular formula for Magnesium bromide is ………………………… .
(a) MgBr
(b) Mg₂Br
(c) Mg₂Br₂
(d) MgBr₂Answer:
(d) MgBr₂

Question 10.
The molten state of NaCl is also called as ………………………… .
(a) solid state
(b) semi-solid
(c) gaseous state
(d) fused state
Answer:
(d) fused state

Question 11.
Substance used to make hard water soft is ………………………… .
(a) Na₂CO₃.10H₂O
(b) Na₂CO₃.H₂O
(c) NaCO₃.10H₂O
(d) NaCO₃.H₂O
Answer:
(a) Na₂CO₃.10H₂O

Question 12.
The fixed number of molecules of water in alum is ………………………… .
(a) 24
(b) 10
(c) 7
(d) 2
Answer:
(a) 24

Question 13.
Chlorine gas is a strong ………………………… agent.
(a) reducing
(b) oxidising
(c) neutral
(d) acidic
Answer:
(b) oxidising

Question 14.
Bleaching powder is ………………………… in colour.
(a) brownish red
(b) yellowish-white
(c) pinkish brown
(d) greenish blue
Answer:
(b) yellowish-white

Question 15.
Soap is ………………………… in nature.
(a) acidic
(b) basic
(c) neutral
(d) fuming
Answer:
(b) basic

Question 16.
Melting point of NaCl is ………………………… .
(a) 400°C
(b) 100°C
(c) 800°C
(d) 600°C
Answer:
(c) 800°C

Question 17.
Rock salt is ………………………… in colour.
(a) black
(b) white
(c) brown
(d) blue
Answer:
(c) brown

Question 18.
Strong odour in swimming pool is due to ………………………… .
(a) chlorine gas
(b) impurities
(c) calcium carbonate
(d) calcium hydroxide
Answer:
(a) chlorine gas

Question 19.
Molecular formula of sodium bicarbonate is ………………………… .
(a) NaHCO₃
(b) Na₂HCO₃
(c) Na₂HCO₂
(d) NaHCO₂Answer:
(a) NaHCO₃

Question 20.
Soap is ………………………… in nature.
(a) radioactive
(b) natural
(c) acidic
(d) basic
Answer:
(d) basic

Question 21.
The molecular formula for Magnesium bromide is ………………………… .
(а) MgBr
(b) MgBr₂
(c) Mg₂Br₂
(d) Mg₂Br
Answer:
(b) MgBr₂

Fill in the blanks and rewrite the complete statements:

(1) 25% of NaCl is known as
(2) gas is released when bleaching powder is added to water.
(3) Washing soda is as it absorbs moisture if left exposed to air.
(4) is used to make hard water soft.
(5) Molecular formula for Alum is
(6) is used in blood test for diagnosing anaemia.
(7) High grade of and are used as raw material to manufacture bathing soap.
(8) Pickles, jams and sauce contain small quantities of and
(9) Excessive consumption of foods with added food colours leads to diseases like
(10) Melting point of Teflon is
(11) Anodizing is done by
(12) The red blood cell count increases in the disease
(13) Magnesium sulphate (MgS04.7H20) is also called
Answer:
(1) Brine
(2) Chlorine
(3) hygroscopic
(4) Na₂CO₃ (Washing soda)
(5) K₂SO₄.Al₂(SO)₃.24H₂O
(6) Blue Vitriol
(7) fats, oils
(8) lead, mercury
(9) ADHD (Attention Deficit Hyperactivity Disorder)
(10) 327°C
(11) Electrolysis
(12) Polycythemia
(13) Epsom salt
(14) Soap

State whether the following statements are true or false. Correct the false statements.
(1) Bleaching powder is used in preparation of chloroform which is used as an anaesthetic.
(2) On addition of universal indicator the colour of table salt changes to pink.
(3) Borax is Na₂B₄O₇.9H₂O.
(4) Boron -10 is used to cure bone cancer.
(5) Clinical deo contains 20 to 25% of aluminium.
(6) NaHCO₃ is sodium carbonate.
(7) Soap is acidic in nature.
(8) Baking powder is neutral in nature.
(9) POP is crystalline in nature.
(10) pH value of universal indicator is 0 – 7.
(11) Sodium chloride is formed by neutralization reaction between sodium hydroxide and calcium carbonate.
(12) Boiling point of NaCl is 800 °C.
(13) Molten state of NaCl is also called as solid state.
(14) Mineral halite is an example of Rock Salt.
(15) Sodium bicarbonate is used to reduce acidity.
(16) Bleaching powder is also called as chloride of lime.
(17) Bleaching powder is obtained by reaction of chlorine gas with slaked lime.
(18) Bleaching powder available in market is classified on the basis of colour.
(19) The hard water becomes soft on adding baking soda (NaHCO₃)
Answer:
(1) True
(2) False. On addition of universal indicator the colour of table salt changes to green.
(3) False. Borax is Na₂B₄O₇.9H₂O
(4) False. Boron – 10 is used in treatment of brain tumour.
(5) True
(6) False. NaHCO₃ is sodium bicarbonate.
(7) False. Soap is basic in nature.
(8) False. Baking powder is basic in nature.
(9) False. POP is amorphous in nature.
(10) False. pH value of universal indicator is 0 -14.
(11) False. Sodium chloride is formed by a neutralization reaction between sodium hydroxide and hydrochloric acid.
(12) False. Melting point of NaCl is 800°C.
(13) False. Molten state of NaCl is also called as fused state.
(14) True
(15) True
(16) True
(17) True
(18) False. Bleaching powder available in market is classified on the basis of percentage of chlorine present in it.
(19) False. Hard water becomes soft on adding washing soda (Na₂CO₃.10H₂O)

Name the following:

Question 1.
Important salts found in sea water.
Answer:
Magnesium chloride, Potassium chloride

Question 2.
Chemical used in preparation of breads and cakes to make them soft.
Answer:
Sodium bicarbonate

Question 3.
Gas liberated when bleaching powder is added to CO₂ gas.
Answer:
Chlorine (Cl₂) gas.

Question 4.
Salt used in refining petroleum
Answer:
Sodium carbonate (Na₂CO₃)

Question 5.
Chemical formula of bleaching powder
Answer:
CaOCl₂

Question 6.
The chemical formula of Sodium hydrogen carbonate.
Answer:
NaHCO₃

Question 7.
Nature of soap.
Answer:
Basic

Question 8.
Molecular formula for Magnesium bromide
Answer:
MgBr₂

Question 9.
Melting point of NaCl
Answer:
800 °C

Question 10.
Two examples of Rock Salt
Answer:
Mineral halite and Himalayan rock salt.

Question 11.
Uses of sodium bicarbonate
Answer:
To prepare breads, cakes and dhokla

Question 12.
Constituents of baking powder.
Answer:
Baking soda and mild acid (tartaric acid)

Question 13.
Substance used to make hard water soft.
Answer:
Washing soda i.e. Na₂CO₃.10H₂O.

Question 14.
Radioactive isotopes used in treatment of bone cancer.
Answer:
Strontium – 89, Strontium – 90, Samarium -153, Radium – 223

Question 15.
Use of Strontium 89 and strontium 90.
Answer:
Treatment of bone cancer.

Select the odd man out:

Question 1.
Sodium sulphate, Barium chloride, Magnesium sulphate, Bleaching powder.
Answer:
Bleaching powder, all others are crystalline salt with water of crystallization while bleaching powder is not.

Question 2.
Strontium – 89, Strontium – 90, Radium – 223, Iodine -123.
Answer:
Iodine -123, it is used to cure hyperthyroidism while others are used to cure bone cancer.

Question 3.
Soap, Toothpaste, Baking soda, Curd.
Answer:
Curd, it is acidic in nature while others are basic in nature.

Question 4.
Na₂CO₃.10H₂O, Na₂SO₄.10H₂O, BaCl₂.2H₂O, CaOCl₂
Answer:
CaOCl₂, it is amorphous in nature while rest are crystalline in nature.

Question 5.
Boron-10, Iodine – 131, Cobalt – 60, Iodine – 123.
Answer:
Iodine -123, it is used in hyperthyroidism while rest are used in treatment of brain tumour.

Question 6.
Na₂SO₄, K₃PO₄, MgBr₂, HCl.
Answer:
HCl, rest all are salts but HCl is an acid.

Write the correlated terms:

(1) Washing Powder : Basic :: Milk : ……………………………
(2) Na₂SO₄: Sodium sulphate :: K₃PO₄ : ……………………………
(3) CaOCl₂: Calcium Oxychloride : : NaHCO₃ : ……………………………
(4) Borax : 10H₂O : : Alum : ……………………………
(5) Sodium Sulphate : Na₂SO₄.10H₂O : : Magnesium Sulphate : ……………………………
(6) Bathing soap : High grades fats and oils :: Washing soap : ……………………………
(7) Radium – 23 : Bone cancer :: Phosphorus – 32 : ……………………………
(8) Iodine -123 : Hyperthyroidism :: Iodine -131 : ……………………………
(9) Clinical deo : 20-25% of aluminium : : Antiperspirant deo : of aluminium chlorohydrate : ……………………………
(10) Sodium carbonate : Na₂CO₃ : : Sodium bicarbonate : ……………………………
(11) Curd : Acidic : : Soap : ……………………………
(12) Calcium Carbonate : CaCO₃ : : Magnesium bromide : ……………………………
(13) Baking Soda : NaHCO₃ : : Washing Soda : ……………………………
(14) Baking Soda : Breads and Cakes : : Washing Soda : ……………………………
(15) Borax : Na₂B₄O₇.10H₂O : : Alum : ……………………………
Answer:
(1) Acidic
(2) Potassium phosphate
(3) Sodium hydrogen carbonate
(4) 24H₂O
(5) MgSO₄.7H₂O
(6) Low-grade fats and oils
(7) Polycythemia
(8) Tumour detection
(9) 15%
(10) NaHCO.
(11) Basic
(12) MgBr₂
(13) Na2CO₃.10H₂O
(14) Hard water soft
(15) K₂SO₄.Al₂(SO₄)₃.24H₂O

Match the columns:

Question 1.

Column ‘A’	Column ‘B’
(1) Barium chloride	(a)	24H₂O
(2) Sodium sulphate	(b)	7H₂O
(3) Magnesium sulphate	(c)	2H₂O
(4) Alum	(d)	10H₂O

Answer:
(1 – c),
(2 – d),
(3 – b),
(4 – a)

Question 2.

Column ‘A’	Column ‘B’
(1) Strontium – 90	(a) Brain tumour
(2) Cobalt – 60	(b) Hyperthyroidism
(3) Iodine – 131	(c) Polycythemia
(4) Phosphorus – 32	(d) Bone cancer

Answer:
(1 – d),
(2 – a),
(3 – b),
(4 -c)

Give scientific reasons:

Question 1.
Baking soda is used while making cakes.
Answer:

Baking soda is chemically known as sodium bicarbonate.
On heating, sodium bicarbonate decomposes to form sodium carbonate, water and carbon dioxide (CO,).
The carbon dioxide produced is released due to which the cake becomes soft and spongy.
Hence, baking soda is used to make cake spongy and soft.

Question 2.
Baking soda is used to reduce acidity in the stomach.
Answer:

Baking soda is used as a medicine (antacid). When it is taken, it undergoes hydrolysis to give sodium hydroxide in the stomach. Thus, sodium hydroxide neutralizes the hydrochloric acid produced by gastric juice and gives relief to the patient from acidity.

Question 3.
Tap water and water in swimming pool has a typical strong odour in the rainy season.
Answer:

Tap water and water in swimming pool has a typical strong odour in the rainy season, it is the odour of the chlorine gas that is used to destroy the microbes in the water.
Chlorine gas is a strong oxidizing agent and therefore, it has a strong disinfecting as well as bleaching action.
Chlorine is inconvenient to handle because of its gaseous state. Instead, the solid bleaching powder which has the same effect is more convenient to use.
Bleaching powder undergoes slow decomposition due to the carbon dioxide in air and chlorine gas is released. Bleaching powder gets its property because of this release of chlorine gas.

Question 4.
Sodium carbonate is added to hard water to make it soft.
Answer:

The hardness of water is due to the presence of chlorides and sulphates of calcium and magnesium in it.
Na₂CO₃ is added to it to soften such water and make it suitable for use.
The reaction with Na₂CO₃ causes the formation of insoluble carbonate salts of magnesium and calcium thus making the water soft.

Question 5.
Alum is used in the process of water purification.
Answer:

Alum is used in the process of water purification because of property of coagulation.
The solid impurities in water come together, become heavy and settle to the bottom.
As a result, the water above becomes clear.

Question 6.
Overconsumption of artificial food colours should be avoided?
Answer:

The overconsumption of artificial food colours should be avoided because they can be detrimental to health.
Food colours added to pickles, jam and sauce contain small quantities of lead and mercury. These can be harmful for those who consume these products on a regular basis.
Diseases like ADHD (Attention Deficit Hyperactivity Disorder) can affect children due to excessive consumption of foods with added food colours.

Question 7.
Artificial colours in Rang Panchami should be used cautiously.
Answer:

We regularly use artificial colours on Rang Panchami.
The red colour used on Rang Panchami is very dangerous. It contains a high proportion of mercury in it.
This poses risks like blindness, skin cancer, asthma, itching of the skin, permanent blocking of sweat pores etc.
Therefore, it is necessary that artificial colours are used cautiously.

Question 8.
There are various brands of bleaching powder in the market.
Answer:

When bleaching powder comes in contact with air, it reacts with carbon dioxide to form calcium carbonate and releases chlorine gas. CaOCl₂ + CO₂ → CaCO₃ + Cl₂ ↑ (from air)
This generated chlorine is known as “available chlorine.”
On the basis of the percentage of “available chlorine” various brands of bleaching powder are available in the market.

Question 9.
We use anodized cooking utensils like griddles and cookers.
Answer:

Anodizing is process of forming a protective rayer of hydrated aluminium oxide on utensils.
Due to anodizing, the surface of the cooking utensils become non-standing, non-toxic and non-reactive with the ingredients of the foot.
These utensils get heated faster and withstand high heat.
Also the amount of butter, ghee or oil used to cook food in these type of utensils is neglible.
These utensils are tough, durable and resistant to corrosion.
Hence, we use anodized cooking utensils like gridders and cookers.

Explain the following chemical reactions with the help of balanced equations :

Question 1.
Sodium hydroxide reacts with dilute Hydrochloric acid.
Answer:
When Sodium hydroxide reacts with dilute Hydrochloric acid, it forms sodium chloride and water.
This is a neutralization reaction.

Question 2.
When an electric current is passed through a saturated solution of sodium chloride (brine)
Answer:
When an electric current is passed through a saturated solution of sodium chloride (brine) it is electrolysed and hydrogen gas is released at the cathode while chlorine gas is released at the anode. Also, an important basic compound NaOH is formed in the cell.

Question 3.
Baking soda (Sodium hydrogen carbonate) reacts with dilute hydrochloric acid.
Answer:
When Sodium bicarbonate (Sodium hydrogen carbonate) reacts with dilute hydrochloric acid, it gives sodium chloride, water and carbon dioxide gas is liberated.

Question 4.
Bleaching powder is exposed to air.
Answer:
When bleaching powder is exposed to air, it undergoes slow decomposition due to the carbon dioxide in air and chlorine gas is released.

Question 5.
When dry slaked lime reacts with chlorine gas.
Answer:
When dry slaked lime reacts with chlorine gas, it gives bleaching powder.

Question 6.
Bleaching powder reacts with dilute sulphuric acid.
Answer:
Dilute sulphuric acid reacts rapidly with bleaching powder to form calcium sulphate and release chlorine gas completely.

Question 7.
Bleaching powder reacts with dilute hydrochloric acid.
Answer:
Dilute hydrochloric acid reacts rapidly with bleaching powder to form Calcium chloride and release chlorine gas completely.

Question 8.
Sodium carbonate reacts with magnesium chloride.
Answer:
When Sodium carbonate reacts with magnesium chloride, it forms insoluble magnesium carbonate and sodium chloride. This reaction is used to make hard water soft.

Question 9.
Crystalline sodium carbonate is exposed to air.
Answer:
When crystalline sodium carbonate is exposed to air it loses its water of crystallization readily and a white powder is obtained. This powder is called washing soda.

Question 10.
Sodium carbonate reacts with sulphuric acid.
Answer:
When sodium carbonate reacts with sulphuric acid it forms sodium sulphate, water and carbon dioxide gas is liberated.

Distinguish between;

Question 1.
Washing soda and Baking soda
Answer:

Washing soda	Baking soda
(i) Chemical name is sodium carbonate.	(i) Chemical name is sodium bicarbonate or sodium hydrogen carbonate.
(ii) Its molecular formula is Na₂CO₃.10H₂O	(ii) Its molecular formula is NaHCO₃
(iii) It is a crystalline substance.	(iii) It is an amorphous powder.
(iv) It is used in manufacturing soaps and detergents.	(iv) It is used in bakery for making cakes and bread lighter and spongy.

Question 2.
Bathing soap and Washing soap
Answer:

Bathing soap	Washing soap
(i) High-grade fats and oils are used as the raw material.	(i) Low-grade fats and oils are used as the raw material.
(ii) Expensive perfumes added.	(ii) Cheaper perfumes added.
(iii) No free alkali content present to prevent injuries to skin.	(iii) Free alkali present for cleaning action.

Answer the following:

Question 1.
Give the properties and uses of Sodium bicarbonate.
Answer:
Properties and uses of sodium bicarbonate

(i) NaHCO₂ reacts with moist litmus paper and red litmus turns blue which means that it is basic in nature.
(ii) It is used to make bread, cake, dhokla.
(iii) Being basic in nature it is used to reduce acidity in the stomach.
(iv) NaHCO₃ is used to make the active substance CO₂ in the fire extinguisher.
(v) Baking soda is used to clean an oven.

Question 2.
Give the properties and uses of washing soda.
Answer:
Properties and uses of washing soda :

Washing soda is a whitish and odourless powder at room temperature.
Litmus has a blue colour in its aqueous solution.
It is hygroscopic, that is, it absorbs moisture if left exposed to air.
It is used mainly for washing clothes.
Sodium carbonate is used in the glass and paper industry and also in refining of petrol.

Question 3.
Name some substances in our daily use which contain water of crystallization.
Answer:

Alum (Potash alum – K₂SO₄.Al₂(SO₄)₃.24H₂O)
Borax (Na₂B₄O₇.10H₂O)
Epsom salt (Magnesium sulphate MgSO₄.7H₂O)
Barium chloride (BaCl₂.2H₂O)
Sodium sulphate (Glauber’s salt Na₂SO₄.10H₂O)

Question 4.
Give the uses of radioactive isotopes in the measurement of thickness, density and level.
Answer:
Measurement of thickness, density and level:

It is necessary to maintain the required thickness in the manufacture of aluminium, plastic, iron sheets of differing thickness.
In the manufacturing process, a radioactive substance is placed on one side and an instrument to measure radiation on the other.
The radiation read by the measuring instrument varies with the thickness of the sheet.
Material inside a packing can also be examined by the same technique.

Question 5.
Give the uses of radioactive isotopes in Luminescent paint and radioluminescence.
Answer:
Luminescent paint and radioluminescence:

The radioactive substances radium, promethium, tritium with some phosphour are used to make certain objects visible in the dark, for example, the hands of a clock, and certain other objects.
Krypton-85 is used in HID (High Intensity Discharge) lamps while promethium-147 is used in portable X-ray units as the source of beta rays.

Question 6.
Give the uses of radioactive isotopes in Field of agriculture.
Answer:
Field of agriculture:

The genes and chromosomes that give seeds properties like fast growth, higher productivity, etc. can be modified by means of radiation.
The radioactive isotope cobalt-60 is used for food preservation.
Onions, potatoes are irradiated with gamma rays from cobalt-60 to prevent their sprouting.
Strontium-90 is used as a tracer in the research on various crops.

Question 7.
Give the uses of dyes.
Answer:
Uses of dyes :

They are used for colouring cloth and hair.
Fluorescent colours are used to make street boards that are visible at night.
Dyes are used to polish leather shoes, purses and chappals.

Question 8.
What are the adverse effects of dyes?
Answer:
Adverse effects dyes :

Dyeing hair can have adverse effects like hair fall, damage to hair texture, burning of skin, adverse effect on eyes, etc.
Lipstick contains a dye named carmine. It does not affect lips but causes stomach disorders.
Excessive use of plants for making natural dyes results in deterioration of the environment.

Question 9.
Give the uses of teflon.
Answer:
Uses of teflon :

Teflon is a poor conductor of electricity. Therefore, Teflon clad wires and parts are used in high technology electronic instruments.
It is used for making non-stick kitchenware.
The coloured metal sheets of two-wheelers and four-wheelers are given a Teflon coating to protect them from damage due to high temperature and rain.

Question 10.
What is ceramic? Give examples.
Answer:

Ceramic is a heat resistant substance formed by kneading an inorganic substance in water and then shaping it and hardening it by heating.
Pots made by a potter, Mangalore roofing tiles, construction bricks, pottery, terracotta articles are some examples of common ceramic articles that we see around.

Question 11.
Give the uses of ceramics.
Answer:

Ceramics can withstand high temperatures without decomposing. Ceramic is brittle, water-resistant and an electrical insulator.
Therefore, it is used in electrical instruments, for coating the interior of a kiln, the outer surfaces of ships and blades of jet engines.
A certain type of ceramic tiles are fixed on the outer layer of a space shuttle. Some types of ceramics are used as superconductors.

Question 12.
What is brine? What happens when ^th of this solution is evaporated?
Answer:

The 25% aqueous solution of salt is called saturated brine.
When th of this solution is evaporated the dissolved salt gets crystallized and salt gets separated from the solution.

Question 13.
What is baking soda? Give its chemical name and molecular formula.
Answer:

Baking soda is a white non-crystalline powder.
Its chemical name is sodium hydrogen carbonate or sodium bicarbonate and its molecular formula is NaHC03.

Question 14.
Give two uses of Blue vitriol.
Answer:

Blue vitriol is used in the blood test for diagnosing anaemia.
Bordeaux mixture which is a mixture of slaked lime and blue vitriol is used as a fungicide on fruits like grapes and musk melon.

Question 15.
What is radioactivity and what are radioactive substances?
Answer:

Elements with a high atomic number such as uranium, thorium, radium have a property of spontaneously emitting invisible, highly penetrating and high energy radiation. This property is called radioactivity.
A substance having this property is called a radioactive substance.

Question 16.
What can you say about the uses of radioactive isotopes?
Answer:

It is a misconception that radioactive elements are used only for making an atom bomb.
Radioactive isotopes are used in various fields such as scientific research, agriculture, industry, medicine, etc.
Radioactive substances are used in two ways.
By using the radiation alone.
By using the radioactive element itself.

Question 17.
Give the uses of radioactive isotopes in Radiography.
Answer:

Internal cracks and voids in cast iron articles and iron solder can be detected with the help of gamma rays.
For this purpose, isotopes like cobalt-60, iridium-192 are used in the radiography camera.
This technique is used for detecting flaws in metalwork.

Question 18.
Give the uses of radioactive isotopes in ceramic articles.
Answer:

Luminous colours are used to decorate ceramic tiles, utensils, plates, etc.
Earlier uranium oxide was used in these paints.

Question 19.
What is a dye?
Answer:
The coloured substance which on applying to an article, imparts that colour to the article, is called a dye

Question 20.
What is done to fix a dye on the cloth ?
Answer:

A mordant is to be used to fix the colour after dyeing a cloth.
A mordant is a chemical binding agent that adheres well to both the fibers and the dye.

Question 21.
What is Teflon? Give its chemical name.
Answer:

Teflon is the polymer of tetrafluoroethylene.
Its chemical name is polytetrafluoroethylene (C₂F₄)_n

Question 22.
What is powder coating? Why is it done?
Answer:

Powder coating is a method of applying a layer harder than paint on the surface of plastic, medium density fibre (MDF).
Board and iron object to make them attractive, durable and to prevent rustihg respectively.

Question 23.
Give the properties of ceramics.
Answer:

Ceramics can withstand high temperatures without decomposing.
Ceramic is brittle, water resistant and an electrical insulator.

Question 24.
How is bone china made? How is it different from porcelain?
Answer:

Bone china is made by adding some ash of animal bones in the mixture of china clay, feldspar and fine silica while making porcelain.
This ceramic is harder than porcelain.

Question 25.
What compounds are used instead of clay for making advanced ceramic?
Answer:
Oxides like Alumina (Al₂O₃), Zirconia (ZrO₂) Silica (SiO₂) and some other compounds like silicon carbide (SiC), boron carbide (B₄C) are used instead of clay for making advanced ceramic.

Question 26.

What is sintering?
Answer:

Advanced ceramics requires a temperature of 1600 to 1800 °C and an oxygen-free atmosphere for firing.
This process is called sintering.

Write short notes on :

Question 1.
Chernobyl disaster.
Answer:

On 26th April 1986, the graphite reactor in the Chernobyl atomic power plant exploded, and suddenly the radioactive isotopes and radiation came out.
Due to this episode, radioactive isotopes entered the human body through water and land and caused genetic disorders.
These got carried further into the next generation.
Thyroid disorders increased in children as well as adults.
As a result, the incidence of throat diseases is greater there than in other places.

Question 2.
Food colours.
Answer:

Food colours are mixed in most soft drinks and foodstuffs available in the market.
These food colours are in the form of powders, gels and pastes.
Food colours are used in domestic as well as commercial products.
Certain colours and essences are added to ice cream, ice candies, sauces, fruit juices, cold drinks, pickles, jams and jellies.
Food colours are often found to be added to packaged meat (chicken, mutton), chilli powder, turmeric, sweets and other similar substances so as to give them a good colour.
Food colours are natural as well as artificial.
The food colours prepared from seeds, beetroot, flowers and fruit concentrate are natural.
Tetrazene, sunset yellow are artificial food colours used extensively.
However, over-consumption of artificial food colours can be detrimental to health. Therefore, usage of natural food colours is always good.

Question 3.
Anodizing.
Answer:

A protective layer is formed naturally on the surface of aluminium metal by reaction with oxygen in air.
In the anodizing process, this layer can be made of the desired thickness.
Anodizing is done by electrolysis.
Dilute sulphuric acid is taken in the electrolytic cell and the aluminium article is dipped in it as the anode.
When an electric current is passed, hydrogen gas is released at the cathode and oxygen gas at the anode.
A reaction with oxygen occurs and a layer of hydrated aluminium oxide is formed on the anode, i.e. the aluminium article.
This layer can be made attractive by adding colour in the cell during electrolysis.

Answer the following questions:

Question 1.
What are salts? Give their source.
Answer:

The ionic compounds which do not contain H+ and OH ions and contain only one kind of cation and anion are called simple salts.
For example, Na₂SO₄, K₃PO₄, CaCl₂.
The sea is said to be a rich source of salts of various elements such as chlorine, sodium, magnesium, potassium, calcium, bromine.
The important salts found in sea water are:
(a) Sodium chloride
(b) Magnesium chloride
(c) Magnesium sulphate
(d) Potassium chloride
(e) Calcium carbonate
(f) Magnesium bromide

Question 2.
Which are the three kinds of salts depending on their pH value? How are they formed?
Answer:
The three kinds of salts depending on their pH value are:

Neutral salts:
Salt is neutral when its pH value is 7. Such a salt is made from a strong acid and a strong base.

Acidic salts:
The pH value of a salt made from a strong acid and a weak base is less than 7 and it is acidic.

Basic salts:
The pH value of a salt made from a weak acid and strong base is more than 7 and it is basic.

Question 3.
Which is the most used salt? What is its chemical name? How is it formed?
Answer:

Table salt, or common salt, which gives a salty taste to food, is the most used of all salts.
Its chemical name is Sodium chloride.
Sodium chloride is formed by a neutralization reaction between sodium hydroxide and hydrochloric acid.
Chemical reaction
This is a neutral salt and the pH value of its aqueous solution is 7.

Question 4.
How is bleaching powder obtained?
Answer:

Bleaching powder is obtained by the reaction of chlorine gas with slaked lime.
Chemical reaction

Question 5.
How is hard water from well converted to soft water?
Answer:

The hard water from a well or a bore-well becomes soft on adding washing soda and we come to know this from the lather formed on it.
The hardness of water is due to the presence of chlorides and sulphates of calcium and magnesium in it.
Na₂CO₃ is added to it to soften such water and make it suitable for use.
The reaction with Na₂CO₃ causes the formation of insoluble carbonate salts of magnesium and calcium.
Chemical reaction
MgCl_2(aq) + Na₂CO_3(s)→ MgCO_3(s) + 2NaCl_(s) Magnesium Sodium Magnesium Sodium chloride carbonate carbonate chloride

Question 6.
How is washing soda obtained from sodium carbonate?
Answer:

Sodium carbonate is a water soluble salt of sodium.
Crystalline sodium carbonate, on keeping, loses its water of crystallization readily and a white powder is obtained.
This powder is called washing soda.
Chemical reaction

Question 7.
How is soap prepared? Why it does not form lather with hard water?
Answer:

When oil or animal fat is boiled with an aqueous solution of sodium or potassium hydroxide, sodium or potassium salts of carboxylic acids (fatty acids) are formed.
These salts are called soap.
When soap is mixed with hard water, calcium and magnesium salts of fatty acids are formed.
These being water insoluble, they form a precipitate and that is why lather is not formed.

Question 8.
What are the harmful effects of artificial food colours?
Answer:

Food colours added to pickles, jams and sauces contain small quantities of lead and mercury. These can be harmful for those who consume these products on a regular basis.
Diseases like ADHD (Attention Deficit Hyperactivity Disorder) can affect children due to excessive consumption of foods with added food colours.

Question 9.
Which is the main source of colour for preparing a natural dye?
Answer:

Plants are the main source of colour for preparing a natural dye.
Roots, leaves, flowers, bark, fruits, seeds, fungus and pistils are used for making dyes.
In Kashmir a very good dye is made from saffron, which is used to dye fibers from which saris, shawls and dresses are made.
These are very costly. The use of henna leaves to colour hair is safe for health.

Question 10.
How are artificial colours harmful to us?
Answer:

We regularly use artificial colours on Rang Panchami.
The red colour used on Rang Panchami is very dangerous.
It contains a high proportion of mercury in it.
This poses risks like blindness, skin cancer, asthma, itching of the skin, permanent blocking of sweat pores, etc.
Therefore, it is necessary that artificial colours are used cautiously.

Question 11.
What are the harmful effects of deodorants?
Answer:

Aluminium – Zirconium compounds are the most harmful chemicals in deodorants. Disorders like headache, asthma, respiratory disorders, heart disease are likely to occur without our knowledge.
There is a possibility of various skin disorders and also skin cancer due to the aluminium chlorohydrates.

Question 12.
How is a ceramic article made?
Answer:

When clay is kneaded in water, shaped and then fired in a kiln at a temperature of 1000 to 1150 °C, a porous ceramic is formed.
To overcome the porosity, the fired object is covered with finely ground glass powder suspended in water (glaze) and is then fired again. As a result, the surface of the ceramic becomes shiny and its porosity disappears.

Question 13.
What is porcelain? How is it made?
Answer:

Porcelain is a hard, translucent and white coloured ceramic. It is made by using the white clay called kaolin, found in China. Glass, granite and the mineral feldspar is mixed with kaolin and kneaded with water.
The resulting mixture is shaped and fired in a kiln at a temperature of 1200 to 1450 °C. On firing again after glazing, beautiful articles of porcelain are obtained.

Answer the following questions:

Question 1.
What are the constituents of baking powder? Where is the baking powder used?
Answer:

Baking powder consist of 30% sodium bicarbonate, 5-12% monocalcium phosphate and 21-26% sodium aluminium sulphate.
Baking powder is a leavening agent and is used for increasing the volume and lightening the texture of baked goods.

Question 2.
Take a piece of coloured cloth. Put some saturated solution of bleaching powder on a small part and observe what changes take place in the colour of the cloth.
Answer:
When bleaching powder is added to a piece of coloured cloth, the fabric looses its colour due to the oxidising reaction of the chlorine present in the bleaching powder.

Answer in detail:

Question 1.
Give the properties and uses of Sodium chloride.
Answer:
Properties and uses of sodium chloride:

Common salt is a colourless and crystalline ionic compound. There is no water of crystallization in its crystalline structure.
It is a neutral salt, salty in taste.
This compound is used for the production of salts like Na₂CO₃, NaHCO₃.
When an electric current is passed through a saturated solution of sodium chloride (brine), it is electrolysed and hydrogen gas is released at the cathode while chlorine gas is released at the anode.
This method is used for production of chlorine gas. In this method an important basic compound NaOH is formed in the cell.
2NaCl + 2H₂O → 2NaOH + Cl₂↑ + H₂↑
When salt is heated to a high temperature (about 800 °C), it melts. This is called the fused state of the salt.
When fused salt is electrolysed, chlorine gas is released at the anode and liquid sodium metal, at the cathode.

Question 2.
Give the properties and uses of Bleaching Powder.
Answer:
Properties and uses bleaching powder:

Bleaching powder is a yellowish-white coloured solid substance.
Its chemical name is Calcium oxychloride.
It has a strong odour of chlorine gas.
It is used for disinfection of drinking water at the water works and the water in the swimming pool.
It is used for bleaching of cloth.
It is used for disinfection by the road side and garbage sites.
Dilute sulphuric acid and dilute hydrochloric acid react rapidly with bleaching powder to release chlorine gas completely.
CaOCl₂ + H₂SO₄ → CaSO₄ + Cl₂ ↑ + H₂O CaOCl₂ + 2HCl → CaCl₂ + Cl₂↑ + H₂O
Calcium oxychloride reacts slowly with carbon dioxide to form calcium carbonate and chlorine.
CaOCl₂ + CO₂ → CaCOs + Cl₂↑

Question 3.
Explain with neat labelled diagram the nature of radioactive radiation.

Answer:

When radioactive radiations are allowed to pass through two oppositely charged plates they get separated. This method was introduced by Rutherford in 1902.
Rutherford and Willard studied the radiation emitted by radioactive substances.
For this purpose, the rays were allowed to pass through an electrical field and a photographic plate was held in their path.
It was found that the radiation was divided into three types.
One type of radiation deviated slightly towards the negatively charged plate, while the second type of radiation deviated substantially towards the positively charged plate.
However, the third type of radiation did not deviate at all in the electrical field.
The rays which deviated slightly toward negatively charged plate are called alpha rays.
Those which deviate substantially towards the positively charged plate are called beta rays and those which did not deviate at all are called gamma rays.

Question 4.
Give the characteristics of alpha, beta and gamma rays.
Answer:
Characteristics of alpha, beta and gamma rays are as given in the table.

Question 5.
Give the uses of radioactive isotopes in Medical science.
Answer:
Medical science:

Polycythemia: The red blood cell count increases in the disease polycythemia. Phosphorus- 32 is used in its treatment.
Bone cancer: Strontium-89, strontium-90, samarium-153 and radium-223 are used in the treatment of bone cancer.
Hyperthyroidism: Enlargement of thyroid gland, weight loss in spite of appetite, insomnia are the symptoms of hyperthyroidism.
It occurs due to overproduction of hormones by the thyroid gland. Iodine-123 is used in the treatment of hyperthyroidism.
Tumour detection: Boron-10, iodine-131, cobalt-60 are used in the treatment of brain tumour, while arsenic-74 is used in detection of small tumours in the body.

Question 6.
What are the hazards of radioactive substances and radiation?
Answer:

The central nervous system is affected by radioactive radiations.
Hereditary defects are generated by bombardment of radiation on D.N.A in the body.
Radioactive radiation can penetrate the skin, and causes diseases like skin cancer, leukemia.
The radiative pollutants created due to explosions enter the body through air and it is difficult to control them.
The radioactive pollutants released in the sea enter the bodies of fishes and through them enter the human body.
The radioactive paint on the watch can cause cancer.
The radioactive isotopes strontium-90 can enter the body through plants, fruits, flowers, cereals, milk, etc. and cause diseases like bone cancer, leukemia.

Question 7.
Why are deodorant used? Give their types and content.
Answer:

Body odour is caused by the bacterial decomposition of the sweat. A deodorant is used to prevent this odour.
Deodorants contain parabens (methyl, ethyl, propyl, benzyl and butyl) and also alcohol in large proportions. Aluminium compounds and silica are also used.
Types of deodorants are :
(a) Ordinary deo: It contains a smaller proportion of aluminium. It decreases the odour of the sweat.
(b) Antiperspirant deo : This decreases the extent of sweating. It contains about 15% of aluminium chlorohydrate. It clogs the sweat pores on the skin.
(c) Clinical deo : Some people sweat heavily and it has harmful effects on the skin. Clinical deo is meant for such people. It contains 20 to 25% aluminium. It is used during the night.

Question 8.
Explain how powder coating is done.
Answer:

Powder coating is a method of applying a layer harder than paint on the surface of an iron object to prevent rusting.
In this method, a polymer resin, a pigment and some other ingredients are melt, mixed, cooled and ground into a uniform powder.
This powder is sprayed on the polished metal surface by electrostatic spray deposition (ESD).
In this method, the particles of the powder are given an electrostatic charge due to which a uniform layer of the powder sticks to the metal surface.
Then the object is heated in the oven along with the coating.
A chemical reaction occurs in the layer, resulting in the formation of long cross-linked polymeric chains.
This powder coating is highly durable, hard and attractive.
Powder coating can be done on plastic and medium density fibre (MDF) board in day to day use as well.

9th Std Science Questions And Answers:

Laws of Motion Class 9 Science Chapter 1 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 1 Laws of Motion Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 1 Laws of Motion Question Answer Maharashtra Board

Class 9 Science Chapter 1 Laws of Motion Question Answer Maharashtra Board

1. Match the first column with appropriate entries in the second and third columns and remake the table.

2. Clarify the differences

A. Distance and displacement
Answer:

Distance	Displacement
(i) Distance is the length of the actual path travelled by an object. (ii) It is a scalar quantity. (iii) It is either equal to or greater than displacement. (iv) Distance travelled is always positive.	(i) Displacement is the minimum distance between the starting and finishing points. (ii) It is a vector quantity. (iii) It is either equal to or less than distance. (iv) Displacement may be positive or negative or zero.

B. Uniform and non-uniform motion.
Answer:

Uniform motion	Non-uniform motion
(i) If an object covers equal distances in equal intervals of time it is said to be in uniform motion. (ii) Distance – time graph for uniform motion is a straight line. (iii) In uniform motion, acceleration is zero.	(i) If an object moves unequal distances in equal intervals of time, its motion is said to be nonuniform. (ii) Distance – time graph for non-uniform motion is not a straight line. (iii) In non-uniform motion acceleration is non-zero.

3. Complete the following table.

4. Complete the sentences and explain them.

a. The minimum distance between the start and finish points of the motion of an object is called the ……….. of the object.
b. Deceleration is ………………………. acceleration
c. When an object is in uniform circular motion, its ………………………. changes at every point.
d. During collision ………………………. remains constant.
e. The working of a rocket depends on Newton’s ………………………. law of motion.

5. Give scientific reasons.

a. When an object falls freely to the ground, its acceleration is uniform.
Answer:

When the body falls freely to the ground, there are equal changes in velocity of the body in equal intervals of time.
Thus the acceleration of the body is constant, and it possesses uniform acceleration.

b. Even though the magnitudes of action force and reaction force are equal and their directions are opposite, their effects do not get cancelled.
Answer:

Action and reaction forces act on different bodies.
They don’t act on the same body, hence they cannot cancel each other’s effect.
Hence, even though the magnitudes of action force and reaction force are equal, they do not cancel each other.

c. It is easier to stop a tennis ball as compared to a cricket ball, when both are traveling with the same velocity.
Answer:

Momentum of an object depends on its mass as well as its velocity.
Cricket ball is heavier than a tennis ball. Although they are thrown with the same velocity, cricket ball has more momentum than a tennis ball.
The force required to stop a cricket ball is more than a tennis ball.
Hence it is easier to stop a tennis ball than a cricket ball moving with same velocity.

d. The velocity of an object at rest is considered to be uniform.
Answer:

When a body is at rest there is no change in velocity.
A body with constant velocity is said to be in uniform motion.
Hence, the state of rest is an example of uniform motion.

6. Take 5 examples from your surroundings and give an explanation based on Newton’s laws of motion.

7. Solve the following examples.

a) An object moves 18 m in the first 3 s, 22 m in the next 3 s and 14 m in the last 3 s. What is its average speed? (Ans: 6 m/s)
Answer:
Given:
Total distance (d) = 18 + 22 + 14 = 54 m
Total time taken (t) = 3 + 3 + 3 = 9 sec
To find:
Average speed = ?

The object moves with an average speed of 6 m/s.

b) An object of mass 16 kg is moving with an acceleration of 3 m/s². Calculate the applied force. If the same force is applied on an object of mass 24 kg, how much will be the acceleration? (Ans: 48 N, 2 m/s²)
Answer:

The force acting on the 1 body is 48 N and the acceleration of the 2” body is 2 m/s²

c) A bullet having a mass of 10 g and moving with a speed of 1.5 m/s, penetrates a thick wooden plank of mass 90 g. The plank was initially at rest. The bullet gets embedded in the plank and both move together. Determine their velocity. (Ans: 0.15 m/s)
Answer:

The plank embedded with the bullet moves with a velocity of 0.15 m/s.

d) A person swims 100 m in the first 40 s, 80 m in the next 40 s and 45 m in the last 20 s. What is the average speed? (Ans: 2.25 m/s²)

Answer:
Given:
Total distance (d) = 100 + 80 + 45 = 225 m
Total time taken (t) = 40 + 40 + 20 = 100 sec
To find:
Average speed =?

The person swims with an average speed of 2.25 m/s.

Class 9 Science Chapter 1 Laws of Motion Intext Questions and Answers

(i) Who will take less time to reach the school and why?
Answer:
Prashant will take less time as the path followed by him is the shortest.

(a) Every morning, Swaralee walks round the edge of a circular field having a radius of 100 m. As shown in figure (a), if she starts from the point A and takes one round, how much distance has she walked and what is her displacement?
Answer:
Radius (r) = 100 m
Distance covered = Circumference of the circle
= 2 nr
= 2 x 3.14 x 100
= 628 m
Displacement = 0 m (Shortest distance between initial and final position is zero)

(b) If a car, starting from point P, goes to point Q (see figure 1.9) and then returns to point P, how much distance has it travelled and what is its displacement?

Answer:
Distance covered = PQ + QP
= 360 + 360
= 720 m
Displacement = 0 m (The shortest distance between initial and final position is zero)

Class 9 Science Chapter 1 Laws of Motion Additional Important Questions and Answers

(A) Choose and write the correct option:

Laws Of Motion Class 9 Questions And Answers Maharashtra Board Question 1.
The displacement that occurs in unit time is called …………….. .
(a) displacement
(b) distance
(c) velocity
(d) acceleration
Answer:
(c) velocity

Laws Of Motion Class 9 Maharashtra Board Exercise Answers Question 2
The unit of velocity in the SI system is …………….. .
(a) cm/s
(b) rn/s²
(c) um/s²
(d) rn/s
Answer:
(d) m/s

Laws Of Motion Class 9 Maharashtra Board Question 3.
v² = u² + 2as is the relation between and …………….. .
(a) speed and velocity
(b) distance and acceleration
(c) displacement and velocity
(d) speed and distance
Answer:
(c) displacement and velocity

Class 9 Science Notes Chapter 1 Laws Of Motion Question 4.
…………….. is the relation between displacement and time.
(a) v = u + at
(b) v² = u²+ 2as
(c) s = ut + 1/2 at²
(d) v = u + 2as
Answer:
(c) s = ut + 1/2 at²

Class 9 Science Chapter 1 Laws Of Motion Question Answer Question 5.
The force necessary to cause an acceleration of 1 m/s² in an object of mass 1 kg is called …………….. .
(a) 1 dyne
(b) 1 m/s
(c) 1 Newton
(d) 1 cm/s
Answer:
(c) 1 Newton.

9th Science Chapter 1 Laws Of Motion Question 6.
Even if the displacement of an object is zero, the actual distance traversed by it …………….. .
(a) may not be zero.
(b) will be zero
(c) will be constant
(d) will be infinity
Answer:
(a) may not be zero

Question 7.
If the velocity changes by equal amounts in equal time intervals, the object is said to be in …………….. .
(a) uniform acceleration
(b) uniform velocity
(c) non-uniform acceleration
(d) non-uniform motion
Answer:
(a) uniform acceleration

Question 8.
If an object is moving with a uniform velocity …………….. .
(a) its speed remains the same, but direction of motion changes
(b) its speed changes but direction of motion is same
(c) its speed and direction both change
(d) its speed and direction both remain the same
Answer:
(d) its speed and direction both remain the same

Question 9.
is an example of positive acceleration.
(a) A stone is thrown vertically upwards
(b) A stone falls freely towards the earth
(c) Brakes are applied by the truck driver
(d) The train arriving at the station
Answer:
(b) a stone falls freely towards the earth

Question 10.
An object continues to remain at rest or in a state of uniform motion along a straight line unless an …………….. acts on it.
(a) internal imbalanced force
(b) external unbalanced force
(c) internal balanced force
(d) external balanced force
Answer:
(b) external unbalanced force

Question 11.
The …………….. is proportional to the applied force and it occurs in the direction of the force.
(a) change of momentum
(b) rate of change of velocity
(c) change of velocity
(d) rate of change of momentum
Answer:
(d) rate of change of momentum

Question 12.
…………….. is a relative concept.
(a) Motion
(b) Direction
(c) Power
(d) Acceleration
Answer:
(a) Motion

Question 13.
A body is said to be in motion if it changes its …………….. with respect to its surroundings.
(a) position
(b) direction
(c) speed
(d) force
Answer:
(a) position

Question 14.
A body is said to be at …………….. if it does not change its position with respect to its surroundings.
(a) Motion
(b) Rest
(c) Gravity
(d) Force
Answer:
(b) Rest

Question 15.
…………….. is the length of the actual path travelled by an object in motion while going from one point to another.
(a) Distance
(b) Displacement
(c) Speed
(d) Velocity
Answer:
(a) Distance

Question 16.
The distance covered by a body in unit time is called its …………….. .
(a) velocity
(b) speed
(c) displacement
(d) rest
Answer:
(b) speed

Question 17.
S.I. unit of speed is …………….. and in C.G.S unit it is …………….. .
(a) m/s and cm/s
(b) km/s and cm/s
(c) m/s and mm/s
(d) m/s and nm/s
Answer:
(a) m/s , cm/s

Question 18.
The distance travelled in a particular direction by an object in unit time is called its …………….. .
(a) velocity
(b) speed
(c) displacement
(d) rest
Answer:
(a) velocity

Question 19.
Units of speed and velocity are the
(a) Same
(b) Different
(c) Greater than each other
(d) Unequal
Answer:
(a) same

Question 20.
…………….. . is related to distance, while …………….. is related to displacement.
(a) Gravity and magnetism
(b) Speed and force
(c) Speed and velocity
(d) Motion and rest
Answer:
(c) Speed, velocity

Question 21.
If an object covers equal distances in equal time intervals, it is said to be moving with …………….. speed.
(a) Uniform
(b) Non uniform
(c) Changing
(d) Random
Answer:
(a) uniform

Question 22.
If an object covers unequal distances in equal time Intervals, it is said to be moving with speed.
(a) Uniform
(b) Non uniform
(c) Changing
(d) Random
Answer:
(b) non uniform

Question 23.
The rate of change of velocity is called
(a) Speed
(b) Acceleration
(c) Velocity
(d) Rest
Answer:
(b) acceleration

Question 24.
Speed of light in dry air is …………….. m/s.
(a) 3 x 10⁷
(b) 3 x 10⁸
(c) 3 x 10⁹
(d) 3 x 10³
Answer:
(b) 3 x 10⁸

Question 25.
When velocity of a body increases, its acceleration is …………….. .
(a) Negative
(b) Zero
(c) Positive
(d) Equal
Answer:
(c) positive

Question 26.
When velocity of a body decreases, its acceleration is …………….. .
(a) Negative
(b) Zero
(c) Positive
(d) Equal
Answer:
(a) negative

Question 27.
Negative acceleration is also called or
(a) Deceleration or retardation
(b) Deceleration or acceleration
(c) acceleration or retardation
(d) Zero
Answer:
(a) deceleration or retardation

Question 28.
In case of motion, object travels equal …………….. in equal intervals of time.
(a) Uniform, distance
(b) Non-Uniform, distance
(c) Uniform, displacement
(d) Uniform, displacement
Answer:
(a) uniform, distances

Question 29.
Motion of an object was studied by …………….. .
(a) Sir Albert Einstein
(b) Sir Thomas Edison
(c) Sir Isaac Newton
(d) Sir Ravindranath Tagore
Answer:
(c) Sir Issac Newton

Question 30.
When an object moves in a circular path with uniform speed, its motion is …………….. motion.
(a) Non uniform circular
(b) Random circular
(c) Uniform circular
(d) Uniform linear
Answer:
(c) uniform circular

Question 31.
When a coin moves along a circular path, the direction of its motion at every point is …………….. .
(a) Circular
(b) Concave
(c) Tangential
(d) Convex
Answer:
(c) tangential

Question 32.
For all uniformly accelerated motions, the velocity-time graph is a …………….. .
(a) Curved line
(b) Straight line
(c) Negative line
(d) Positive line
Answer:
(b) straight line

Question 33.
In the distance-time graph, the slope of the straight line indicates …………….. .
(a) Acceleration
(b) Velocity
(c) Speed
(d) Rest
Answer:
(b) velocity

Question 34.
The first equation of motion gives relation between …………….. and time.
(a) Acceleration
(b) Velocity
(c) Speed
(d) Rest
Answer:
(b) velocity

Question 35.
Newton’s first law explains the phenomenon of
(a) Rest
(b) Inertia
(c) Speed
(d) Velocity
Answer:
(b) inertia

Question 36.
…………….. cause a change in the state of an object at rest or in uniform motion.
(a) Balanced forces
(b) Zero forces
(c) Unbalanced forces
(d) None of them
Answer:
(c) Unbalanced forces

Question 37.
To describe an object’s momentum, we must specify its …………….. and …………….. .
(a) Mass and displacement
(b) Mass and direction
(c) Mass and velocity
(d) Mass and acceleration
Answer:
(c) mass and velocity

Question 38.
…………….. is the product of mass and velocity of an object.
(a) Speed
(b) Acceleration
(c) Momentum
(d) Force
Answer:
(c) Momentum

Question 39.
The rate of change of momentum is proportional to the applied …………….. .
(a) Balanced force
(b) Unbalanced force
(c) Mass
(d) Velocity
Answer:
(b) unbalanced force

Question 40.
S.I. unit of momentum is
(a) kg cm/s
(b) kg m/s
(c) gm/s
(d) m/s
Answer:
(b) kg m/s

Question 41.
…………….. is always conserved in a collision.
(a) Force
(b) Power
(c) Speed
(d) Total momentum
Answer:
(d) Total momentum

Question 42.
When a bullet is fired from the gun, the gun moves in backward direction. This motion is called as …………….. .
(a) Momentum
(b) Velocity
(c) Acceleration
(d) Recoil
Answer:
(d) Recoil

Question 43.
In CGS system, the unit of force is …………….. .
(а) Newton
(b) Watt
(c) Horse power
(d) Dyne
Answer:
(d) Dyne.

(B) 1. Find the odd man out:

Question 1.
Displacement, Force, Momentum, Mass
Answer:
Mass

Question 2.
Speed, Power, Energy, Acceleration
Answer:
Acceleration

Question 3.
Newton’s 1st law, Newton’s 2nd law, Newton’s 3rd law, Kepler’s laws of motion
Answer:
Newton’s 3rd law

(B) 2. Find out the correlation

Question 1.
Speed zero: Body at rest :: Negative acceleration : Retardation
Answer:
Retardation

Question 2.
Displacement : Vector quantity :: Distance : Scalar quantity
Answer:
Vector quantity

Question 3.
When body comes to rest at the end of the motion : Final velocity is zero :: When body is at rest at the starting of motion : Initial velocity is zero
Answer:
Initial velocity is zero

Question 4.
Uniform circular motion: Displacement is zero :: Uniform velocity : Acceleration is zero
Answer:
Displacement is zero

Question 5.
Inertia : Newton’s 1st law :: Rate of change of momentum : Newton’s 2nd law
Answer:
Newton’s 2nd law

Question 6.
Balanced force : Body at rest :: Force equation : Mass x acceleration
Answer:
Body at rest

(B) 3. Distinguish between:

Question 1.
Positive acceleration and Negative acceleration
Answer:

Positive acceleration	Negative acceleration
(i) When the velocity of a body increases, acceleration is said to be positive acceleration.	(i) When the velocity of a body decreases, acceleration is said to be negative acceleration.

Question 2.
Scalar quantity and Vector quantity
Answer:

Scalar quantity	Vector quantity
(i) Scalar quantities are physical quantities having magnitude only.	(i) Vector quantities are physical quantities having both magnitude and direction.

Question 3.
Balanced force and Unbalanced force
Answer:

Balanced force	Unbalanced force
(i) Balanced force keeps the body at rest.	(i) Balanced force keeps the body at rest.

(B) 4. State whether the following statements are true or false:

Question 1.
The velocity of a body is given by the distance covered by it in unit time in a given direction.
Answer:
True

Question 2.
Displacement is a scalar quantity.
Answer:
False

Question 3.
Uniform acceleration means that the body is moving with a uniform velocity.
Answer:
False

Question 4.
The direction of acceleration can be opposite to that of velocity.
Answer:
True

Question 5.
Work is a vector quantity.
Answer:
False

Question 6.
Displacement is always greater than distance.
Answer:
False

Question 7.
The distance and displacement are equal only if, motion is along a straight path.
Answer:
True

Question 8.
If an object experiences acceleration, a force is acting on it.
Answer:
True

Question 9.
A train pulling out from a station is in uniform motion.
Answer:
False

Question 10.
If a bus in motion is suddenly stopped, the passengers fall backwards.
Answer:
False

Question 11.
If a single force is acting on an object, it will always accelerate.
Answer:
True

Question 12.
In circular motion, direction of motion is tangential.
Answer:
True

Question 13.
The inertia of a body is measured in terms of its mass.
Answer:
True

(B) 5. Name the following:

Question 1.
The scientist who summarized motion in a set of equations of motion.
Answer:
Isaac Newton

Question 2.
Motion of an object along a circular path with uniform speed.
Answer:
Uniform circular motion

Question 3.
What is the backward motion of the gun called?
Answer:
Recoil

Question 4.
The motion in which the object covers equal distance in equal intervals of time.
Answer:
Uniform motion

Question 5.
S. I. unit of acceleration.
Answer:
m/s²

Question 6.
CGS unit of momentum
Answer:
g cm/s

(B) 6. Answer the following in one sentence:

Question 1.
When is acceleration said to be positive?
Answer:
When the velocity of a body increases, acceleration is said to be positive acceleration.

Question 2.
What is negative acceleration?
Answer:
When the velocity of a body decreases, acceleration is said to be negative acceleration.

Question 3.
What is the direction of velocity of an object performing uniform circular motion?
Answer:
The direction of velocity is along the tangential direction to its position.

Question 4.
Give the mathematical expression used to determine velocity of an object moving with uniform circular motion.
Answer:
is the expression used to determine velocity of a body moving with uniform circular motion.

Question 5.
What kind of force keeps the body at rest?
Answer:
Balanced force keeps the body at rest.

Question 6.
Which law of motion gives the measure of force?
Answer:
Newton’s second law of motion gives the measure of force.

Question 7.
What are vectors and scalars?
Answer:
Scalars are physical quantities having magnitude only whereas, vectors are physical quantities having both magnitude and direction.

Question 8.
Which of the quantities distance, speed, velocity, time and displacement are scalars and which are vectors?
Answer:
Distance, speed and time are scalars displacement and velocity are vectors.

Give formula:

Question 1.
Force =
Answer:
Mass x Acceleration = ma

Question 2.
Final velocity (v) =
Answer:
Initial Velocity + (Acceleration x Time) = u + at

Question 3.
Displacement (s) =
Answer:

Question 4.
Final velocity² (v²) =
Answer:
Initial Velocity² + 2 x Acceleration x Displacement = u² + 2as

Question 5.
velocity of an object moving with uniform circular motion =
Answer:

Give scientific reasons:

Question 5.
Motion is relative.
Answer:

The motion of an object depends on the observer, hence a body may appear moving for one person and at the same time at rest for another one.
Hence, motion is relative.

Question 6.
Newton’s first law of motion is called as law of inertia.
OR
Heavier objects offer more inertia.
Answer:

Inertia is related to the mass of the object.
As mass is the quantity of matter in a body, we need to exert more force to push a heavier body.
Hence heavier objects offer more inertia.
As the same property is described by Newton’s first law of motion, it is called as Law of Inertia.

Question 7.
The launching of a rocket is based on Newton’s third law of motion.
Answer:

Newton’s third law of motion states that ‘Every action force has an equal and opposite reaction force which acts simultaneously.’
When the fuel in a rocket is ignited, it bums as a result of chemical reaction.
The exhaust gases escape with a great force in the backward direction.
It exerts an equal and opposite reaction force on the rocket, due to which the rocket moves in the forward direction.
Thus, the principle of launching of rocket is based on Newton’s third law of motion.

Solve the following numerical:

Question 1.
An athlete is running on a circular track. He runs a distance of 400 m in 25 s before returning to his original position. What is his average speed and velocity?
Answer:
Given:
Total distance travelled = 400 m
Total displacement = 0, as he returns to his original position.
Total time = 25 seconds.
To find:
Average speed = ?
Average velocity = ?

The athlete runs at an average speed of 16 m/s and velocity 0 m/s.

Question 2.
An aeroplane taxies on the runway for 30 s with an acceleration of 3.2 m/s² before taking off. How much distance would it have covered on the runway?
Answer:

The distance covered on the runway is 1440 m.

Question 3.
A kangaroo can jump 2.5 m vertically. What must be the initial velocity of the kangaroo?
Answer:
Given:
a = 9.8 m/s², s = 2.5 m, v = 0,
To find:
u = ?
Formula:
v² = u²+ 2as
Solution:
v² = u² + 2as
0² = u² + 2 x (-9.8) (2.5) : (Negative sign is used as the acceleration is in the direction opposite to that of velocity.)
0= u² – 49 u²
= 49 u
= 7 m/s

The initial velocity of the kangaroo must be 7 m/s.

Question 4.
A motorboat starts from rest and moves with uniform acceleration, if it attains the velocity of 15 m/s in 5s, calculate the acceleration and the distance travelled in that time.
Answer:
Given:
Initial velocity, u = 0
Final velocity, v = 15 m/s time, t = 5 s.
To find:
Acceleration (a) = ?
Distance (s) = ?
Solution:
From the first equation of motion

From the second equation of motion, the distance covered will be

The acceleration is 3 m/s² and distance travelled is 37.5 m.

Question 5.
The mass of a cannon is 500 kg and it recoils with a speed of 0.25 m/s. What is the momentum of the cannon?
Answer:
Given:
mass of the cannon = 50 kg
recoil speed = 0.25 m/s
To find:
Momentum = ?
Formula:
Momentum = m x v
Solution:
Momentum = m x v
= 500 x 0.25
= 125 kg m/s

The momentum of cannon is 125 kg m/s

Answer the following in short:

Question 1.
Explain the three different ways to change the velocity.
Answer:
As velocity is related to speed and direction, it can be changed by :

Changing the speed while keeping the direction constant.
Changing direction while keeping speed constant.
Changing both speed as well as direction of motion.

Question 2.
Explain what is positive, negative and zero acceleration.
Answer:

Positive Acceleration: When the velocity of an object increases, the acceleration is positive. In this case, the acceleration is in the direction of velocity.
Negative Acceleration: When the velocity of an object decreases with time, it has negative acceleration. Negative acceleration is also called deceleration. Its direction is opposite to the direction of velocity.
Zero Acceleration: If the velocity of the object does not change with time, it has zero acceleration.

Question 3.
What inference do we draw from the velocity-time graph for a uniformly accelerated motion?
Answer:

From velocity-time graph we can infer whether velocity changes by equal amounts in equal intervals of time or not.
Thus, for all uniformly accelerated motion, the velocity – time graph is a straight line and slope of the line gives the acceleration.
For non-uniformly accelerated motion, velocity-time graph can have any shape according to variation in velocity with respect to time.

Question 4.
State the three equations of motion and give the relationship explained by them.
Answer:

v = u + at: This is the relation between velocity and time.
s = ut + 1/2 at² : This is the relation between displacement and time
v² = u² + 2as : This is the relation between displacement and velocity.

Question 5.
What are the implications of Newton’s Third Law of motion?
Answer:

Action and reaction are terms that express force.
These forces act in pairs. One force cannot exist by itself.
Action and reaction forces act simultaneously.
Action and reaction forces act on different objects. They do not act on the same object and hence cannot cancel each other’s effect.

Question 6.
Explain recoil and recoil velocity. Derive its expression.
Answer:

Let us consider the example of a bullet fired from a gun. When a bullet of mass nij is fired from a gun of mass m₂, its velocity becomes v₂, and its momentum becomes m^. Before firing the bullet, both the gun and the bullet are at rest. Hence, total initial momentum is zero.
According to Newton’s third law of motion, the total final momentum also has to be zero. Thus, the forward-moving bullet causes the gun to move backward after firing.
This backward motion of the gun is called its recoil. The velocity of recoil, v₂ is such that,

Complete the flow chart:

(1) Types of force and their effects
Answer:

(2) Newton’s laws
Answer:

Distinguish between:

Question 1.
Speed and velocity.
Answer:

Speed	Velocity
(i) Speed is the distance covered by a body in unit time. (ii) It is a scalar quantity. (iii) Speed is equal to or greater than velocity. (iv) Speed = distance/time (v) It is always positive or zero but never negative.	(i) The displacement that occurs in unit time is called velocity. (ii) It is a vector quantity. (iii) Velocity is equal to or less than speed. (iv) Velocity = displacement/time (v) It may be positive, Zero or negative.

Question 2.
Balanced force and unbalanced force.
Answer:

Balanced force	Unbalanced force
(i) Two equal forces applied on a body in the opposite direction. (ii) This force does not change the state of rest or the state of uniform motion	(i) Two unequal forces applied on a body. (ii) This force can change the state of rest or the state of uniform motion of a body in a straight line.

Give examples:

Question 1.
Scalar quantities
Answer:
Time, Volume, Speed, Mass, Temperature, Distance, Entropy, Energy, and Work

Question 2.
Vector quantities
Answer:
Acceleration, Velocity, Momentum, Force, and Weight

Answer the following questions:

Observe the figure and answer the questions:

(a) Measure the distance between points A and B in different ways as shown in figure (I).
Answer:
Distances measured may be of different lengths depending on the path taken.

(b) Now measure the distance along the dotted line. Which distance is correct according to you and why?
Answer:
Dotted line shows the shortest way of reaching from A to B.

(c) Observe the following figures. If you increase the number of sides of the polygon and make it infinite, how many times will you have to change the direction? What will be the shape of the path?

Answer:
If we increase the number of sides of the polygon and make it infinite, then we will have to change the direction an infinite number of times. The shape of the path thus obtained will be a circle.

Observe the figure and answer the questions

Question 1.
What will be the effect on the velocity of the motorcycle if its speed increases or decreases, but its direction remains unchanged?
Answer:
If the speed is increased the velocity of the motorcycle will increase and if the speed is decreased the velocity of the motorcycle will decrease

Question 2.
In case of a turning on the road, will the velocity and speed be same?
Answer:
As speed is scalar quantity while velocity is vector quantity so by turning velocity will change while speed remains same

Question 3.
If, on a turning, we change the direction as well as the speed of the motorcycle, what will be the effect on its velocity?
Answer:
Its velocity will change because velocity depends on speed as well as direction and here both speed and direction are changed.

Numerical:

Question 1.
A person travels a distance of 72 km in 4 hours. Calculate average speed in m/s.
Answer:
Given :
Total distance (d)
= 72 km
= 72×1000
= 72000 m

Total time taken (t)
= 4 hours
= 4 x 3600 (v lhr = 3600 sec)
= 14400 s

To find:
Average speed = ?

The person travels with average speed of 5 m/s

Question 2.
balls have masses of 50 gm and 100 gm and they are moving along the same line in the same direction with velocities of 3 m/s and 1.5 m/s respectively. They collide with each other and after the collision, the first ball moves with a velocity of 2.5 m/s. Calculate the velocity of the other ball after collision.
Answer:

Final velocity of second ball after collision is 1.75 m/s.

Write laws and explain write implications:

Question 1.
Newton’s third law of motion
Answer:
‘Every action force has an equal and opposite reaction force which acts simultaneously’.

Action and reaction are terms that express force.
These forces act in pairs. One force cannot exist by itself.
Action and reaction forces act simultaneously.
Action and reaction forces act on different objects. They do not act on the same object and hence cannot cancel each other’s effect.

Question 2.
Explain Newton’s second law of motion and derive the formula.
Answer:
Newton’s second law explains about change in momentum. It states that The rate of change of momentum is proportional to the applied force and the change of momentum occurs in the direction of the force.

Suppose an object of mass ‘m’ has an initial velocity ‘u. When a force ‘F’ is applied in direction of its velocity for time ‘t’, its velocity becomes ‘y’. Then, the total initial momentum of the body = ‘mu’. Its final momentum after time t = ‘mv’.

So, the rate of change of momentum

Hence by Newtons second la of motion, 4he rate of change of momentum is proportional to the applied force.
∴ ma ∝ F
∴ F ∝ ma
∴ F ∝ kma (k = Constant of proportionaLity and value is 1).
∴ F = ma

Question 3.
State the law of conservation of momentum and derive the formula.
Answer:

Let mass of object A and B be m₁ and m₁ respectively
Let their initial velocity be u₁ and u₂ Let their final velocity be v₁ and v₂

We know,
P = mv
Let their initial momentum be m₁u₁ and m₂ u₂
Let their final momentum be m₁v₁ and m₂v₂

Total initial momentum = (m₁u₁ + m₂u₂)
Total final momentum = (m₁v₁ + m₂v₂)

If F₂ is the force that acts on object B,

i.e. The magnitude of total of total final momentum = the magnitude of total initial momentum

Complete the paragraph:

Question 1.
Moving Objects
Answer:
‘Distance’ is the length of the actual path travelled by an object in motion while going from one point to another, whereas displacement is the minimum distance between the starting and finishing points. The displacement that occurs in unit time is called velocity. The units of speed and velocity are the same. In the SI system, the unit is m/s while in the CGS system; it is cm/s. Speed is related to distance while velocity is related to the displacement. If the motion is along a straight line, the values of speed and velocity are the same, otherwise they can be different. The first scientist to measure speed as the distance /time was Galileo. The speed of sound in dry air is 343.2 m/s while the speed of light is about 3 x 108 m/s. The speed of revolution of the earth around the sun is about 29770 m/s.

Question 2.
Types of motion
Answer:
If an object covers unequal distances in equal time intervals, it is said to be moving with non-uniform speed. For example the motion of a vehicle being driven through heavy traffic. If an object covers equal distances in equal time intervals, it is said to be moving with uniform speed. The rate of change of velocity is called acceleration. If the velocity changes by equal amounts in equal time intervals, the object is said to be in uniform acceleration. If the velocity changes by unequal amounts in equal time intervals, the object are said to be non-uniform acceleration. The speed of the tip is constant, but the direction of its displacement and therefore, its velocity is constantly changing. As the tip is moving along a circular path, its motion is called uniform circular motion.

Question 3.
Newton’s laws and conservation of momentum
Answer:
An object continues to remain at rest or in a state of uniform motion along a straight line unless an external unbalanced force acts on it. The rate of change of momentum is proportional to the applied force and the change of momentum occurs in the direction of the force. Momentum has magnitude as well as direction. Its direction is the same as that of velocity. In SI system, the unit of momentum is kg m/s, while in CGS system, it is g cm/s. If an unbalanced force applied on an object causes a change in the velocity of the object, then it also causes a change in its momentum.

The force necessary to cause a change in the momentum of an object depends upon the rate of change of momentum. Every action force has an equal and opposite reaction force which acts simultaneously. As the mass of the gun is much higher than the mass of the bullet, the velocity of the gun is much smaller than the velocity of the bullet. The magnitude of the momentum of the bullet and that of the gun are equal and their directions are opposite. Thus, the total momentum is constant. Total momentum is also constant during the launch of a rocket.

Answer the following in detail:

Question 1.
What is speed? State its units and types. Explain instantaneous speed and average speed.
Answer:

The speed of a body is the distance travelled in unit time. The units of speed in CGS system is cm/s and in SI system is m/s.
There are two types of speed :

- Uniform speed : When a body covers equal distance in equal intervals of time throughout its motion, it is said to have uniform speed.
- Non-uniform or variable speed: When a body covers unequal distance in equal intervals of time it is said to have non-uniform speed.

The speed of the body at any instant is called instantaneous speed. Average speed is the ratio of total distance covered to total time taken.

Question 2.
What is velocity? State its units and types.
Answer:

The velocity of a body is the distance travelled by a body in a particular direction in unit time. Thus, rate of change of displacement is called velocity.

v = s/t
where: s = displacement; t = time taken; v = velocity
(MKS unit: m/s CGS unit: cm/s)
There are two types of velocities :

- Uniform velocity: If there is equal displacement taking place in equal intervals of time, it is uniform velocity.
- Non-uniform velocity or variable velocity: If there is unequal displacement in equal intervals of time, it is non-uniform velocity.

Question 3.
What is acceleration? State its units and types.
Answer:
(i) Acceleration is a rate of change in velocity. It is a vector quantity, \(a=\frac{v-u}{t}\)
where : v = final velocity; u = initial velocity;
a = acceleration
Units of acceleration in SI system is m/s2 and CGS system is cm/s2.

(ii) Types of acceleration: .
(a) Uniform acceleration : If the change in velocity is equal in equal intervals of time, the acceleration is uniform acceleration.
(b) Non-uniform acceleration : If the change in velocity is unequal in equal intervals of time, the acceleration is a non-uniform acceleration.

(iii) Kinds of acceleration:
Positive acceleration : When the velocity of an object goes on increasing, it is said to have Positive acceleration.
Negative acceleration : When the velocity of an object goes on decreasing, it is said to have negative acceleration or retardation or deceleration.
Zero acceleration : If the velocity of the object does not change with time, it has zero acceleration.

Question 4.
Explain Newton’s second law of motion and derive the formula.
Answer:
Newton’s second law explains about change in momentum. It states that ‘The rate of change of momentum is proportional to the applied force and the change of momentum occurs in the direction of the force.’

Suppose an object of mass’m’ has an initial velocity ‘u’. When a force ‘F’ is applied in the direction of its velocity for time’t’, its velocity becomes ‘v’. Then, the total initial momentum of the body = ‘mu’. Its final momentum after time t = ‘mv’.

So, the rate of change of momentum

Hence by Newton’s second law of motion, the rate of change of momentum is proportional to the applied force.
∴ ma ∝ F
∴ F ∝ ma
∴ F = kma (k = Constant of proportionality and value is 1).
∴ F = ma

Question 5.
State the law of conservation of momentum and derive the formula.
Answer:
(i) Let mass of objects A and B be and m₂ respectively
Let their initial velocity be m₁ and u₂
Let their final velocity be V₁ and v₂

(ii) We know,
P = mv
Let their initial momentum be m₁u₁ and m₂u₂
Let their final momentum be m₁v₁ and m₂v₂

(iii) Total initial momentum = (m₁u₁ + m₂u₂)
Total final momentum = (m₁v₁ + m₂v₂)

(iv) If F₂ is the force that acts on object B,

i.e. The magnitude of total final momentum = the magnitude of total initial momentum.

Question 6.
Obtain the equations of motion by graphical method:

(a) Equation for velocity-time relation.
Answer:
Velocity-time graph: shows the change in velocity with time of a uniformly accelerated object. The object starts from the point D in the graph with velocity v. Its velocity keeps increasing and after time t it reaches the point B on the graph.

The initial velocity of the object = u = OD

(b) Equation for displacement-time relation.
Answer:
Suppose that an object is in uniform acceleration ‘a’ and it has covered the distance ‘s’ within time’t’. From the graph the distance covered by the object during time’t’ is given by the area of quadrangle DOEB.

(c) Equation for displacement-velocity relation.
Answer:
We can determine the distance covered by the object in time t from the area of the quadrangle DOEB. DOEB is a trapezium. So we can use the formula for its area.

This is Newton’s third equation of motion.

Read the paragraph and answer the questions:

1. Paragraph

(a) When a bat strikes a ball, the ball exerts an equal and opposite force on the bat. The force : acting on the ball projects it with high velocity, Due to the large mass of bat compared to ball, reaction force on the bat slows down the bat’s motion.
(b) When a bullet is fired from a gun, the gun exerts a force on the bullet in the forward direction. This is the action force. The bullet also exerts an equal force on the gun in the backward direction. This is the reaction force. Due to the large mass of the gun, it j moves only a little distance backward. This backward movement of the gun is called the recoil of the gun.
(c) In a rocket, burning fuel creates a push on the front of the rocket pushing it forward. This creates an equal and opposite push on the exhaust gas backwards.

(i) Which of Newton’s law examples are given here?
Answer:
Newton’s 3rd law is stated by the above example

(ii) When a rifle is fired it is pushed back this movement is called what?
Answer:
Movement of rifle getting pushed back after firing is called recoil.

(iii) What does the ball acquire after it gets velocity?
Answer:
The ball acquires momentum after it gets velocity.

(iv) State newton’s 1st law of motion
Answer:
An object continues to remain at rest or in a state of uniform motion along a straight line unless an external unbalanced force acts on it.

(v) Which force is required to produce motion in an object?
Answer:
Unbalanced force is required to produce motion in an object.

2. Paragraph 2
constant velocity. If that velocity is zero, then the object remains at rest. If an external force is applied, the velocity will change because of the force. The second law explains how the velocity of an object changes when it is subjected to an external force. The law defines a force to be equal to changes in momentum (mass times velocity) per change in time. Newton also developed the calculus of mathematics, and the “changes” “expressed in j the second law are most accurately defined in differential forms. (Calculus can also be used to determine the velocity and location variations experienced by an object subjected to an external force.) For an object with a constant mass the second law states that the force F is the product of an objects mass and its acceleration a:
F = m * a
For an external applied force the change in velocity depends on the mass of the object.

A force will cause in velocity; and likewise, a change in velocity will generate a force. The equation works both ways.
The third law states that for every action (force) in nature there is an equal and opposite reaction. In other words, if object A exerts a force on object B, then object B also exerts an equal force on object: A. Notice that the forces are exerted on different objects. The third law can be used to explain the generation of lift by a wing and the production of thrust by a jet engine

(i) A chalk kept on the table remains in the position of rest until moved by the teacher. Which law of motion is followed in this situation?
Answer:
Newton’s 1st law is followed in this situation e

(ii) What will happen to momentum if the mass and acceleration both are doubled?
Answer:
If the mass and acceleration both are doubled then the momentum will be increased four times

(iii) What will happen to momentum if the mass and acceleration both are halved?
Answer:
If the mass and acceleration both are doubled then the momentum will be decreased one four times

(iv) A moving stone filled truck collides with a moving car coming from opposite direction. Why is it observed that only the car is pushed backward?
Answer:
A stone filled truck as more mass than a car hence it has more momentum thus it is observed that only the car is pushed backward

(v) What will happen to the force if the jet engines do not produce enough thrust to push the aeroplane in mid-air?
Answer:
If the jet engines do not produce enough thrust to push the aeroplane in mid-air the force of aeroplane and resistance of air will become balanced thus putting the aeroplane at rest which will result in a crash.

9th Std Science Questions And Answers:

Carbon: An Important Element Class 9 Science Chapter 13 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 13 Carbon: An Important Element Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 13 Carbon: An Important Element Question Answer Maharashtra Board

Class 9 Science Chapter 13 Carbon: An Important Element Question Answer Maharashtra Board

1. Select the proper option and complete the statements
(single, all, double, ionic, carbon, give and take, hydrogen, multiple, share, most, covalent)

a. A carbon atom forms a ….……………. bond with other atoms. In this bond the two atoms ….electrons.
Answer:
covalent, share

b. All the carbon bonds in a saturated hydrocarbon ….……………. electrons.
Answer:
share

c. At least one carbon bond in an unsaturated hydrocarbon is ….…………… .
Answer:
multiple

d. ….……………. is the essential element in all the organic compounds.
Answer:
Carbon

e. The element hydrogen is present in ….. organic compound.
Answer:
all

2. Answer the following questions

a. Why are carbon and its compounds used as fuels?

Answer:
(i) The name ‘carbon’ is derived from Latin word ‘carbo’meaning coal. In the earth’s crust, carbon is present to an extent of approximately 0.27% in the form of carbonate, coal and petroleum. One of the non-crystalline and amorphous form of carbon is coal. Coal is a fossil fuel.

(ii) Peat, lignite, bituminous and anthracite are the four types of coal in the increasing order of their carbon content and heat produced respectively. Charcoal and coke are the other amorphous forms of carbon used as fuel.

(iii) Compounds of carbon such as hydrocarbons consist of carbon and hydrogen and they are easily combustible. For example, methane (CH₄) which occurs in natural gas is highly inflammable. It bums by reacting with oxygen to give a bluish flame. In this reaction, 213 Kcal/mol of heat is given out. Methane bums completely.

Chemical reaction:
CH₄ + 2O₂ → CO₂ + 2H₂O + Heat

(iv) Thus when hydrocarbons are burnt in air, large amount of heat is evolved with formation of carbon dioxide (CO₂) and water (H₂O). Due to evolution of heat on combustion, carbon and its compounds are used as fuels.

b. In which compound forms does carbon occur?
Answer:
Carbon in its combined state exists as various compounds such as:

Carbon dioxide and in the form of carbonates such as calcium carbonate, marble, calamine (ZnCO₃).
Fossil fuel – coal, petroleum, natural gas.
Carbonaceous nutrients – carbohydrates, proteins, fats.
Natural fibres – cotton, wool, silk.
Hydrocarbons – compound of carbon and hydrogen.

c. Write the uses of the diamond.
Answer:
Uses of diamonds are:

Diamonds are used in glass cutting and rock drilling machines.
Diamonds are used in ornaments.
Diamond knives are used in the eye surgery.
Diamond dust is used for polishing other diamonds.
Diamond is used to make windows giving protection from radiation in space and in artificial satellites.

3. Explain the difference:

a. Diamond and graphite.

Answer:

Diamond	Graphite
(i) Diamond is a brilliant, hard and crystalline allotrope of carbon.	(i) Graphite is a black, soft, brittle and slippery crystalline allotrope of carbon.
(ii) In diamonds, every carbon atom is bonded to four neighbouring atoms by covalent bonds forming tetragonal three dimensional structure which makes it very hard.	(ii) In graphite, every carbon atom is bonded to three other carbon atoms by covalent bonds in such a way that a hexagonal layered structure is formed. A graphite crystal is made of many such layers of carbon atoms. These layers slip over each other on applying pressure.
(iii) Density of diamond is 3.5 g/cm³.	(iii) Density of graphite is 1.9 to 2.3 g/cm³.
(iv) Diamond is a bad conductor of electricity as it does not have free electrons.	(iv) Inside each layer of graphite, free electrons move continuously within the entire layer. Hence, graphite is a good conductor of electricity.

b. Crystalline and non-crystalline forms of carbon.
Answer:

Crystalline forms of carbon	Non-crystalline forms of carbon
(i) A crystalline form has a regular and definite arrangement of atoms. (ii) They have high melting points and boiling points. (iii) A crystalline form has a definite geometrical shape, sharp edges and plane surfaces. (iv) Diamond, graphite and fullerene are different crystalline forms of carbon.	(i) A non-crystalline form does not have a regular and definite arrangement of atoms. (ii) They have low melting points and boiling points. (iii) They are amorphous, hence, they do not have definite geometrical shape. (iv) Coal, charcoal and coke are different noncrystalline/amorphous forms of carbon.

4. Write scientific reasons

a. Graphite is a conductor of electricity.
Answer:

In graphite, each carbon is bonded to three other carbon atoms in such a way that a hexagonal layered structure is formed.
Due to this structure, graphite has free electrons available.
These free electrons move continuously within the entire layer.
Hence, graphite is a good conductor of electricity.

b. Graphite is not used in ornaments.
Answer:

Graphite is a black, soft, brittle and dull form of carbon.
It is neither malleable nor ductile.
These properties of graphite make it unsuitable for making of ornaments.
Hence, graphite is not used for making ornaments.

c. Limewater turns milky when CO₂ is passed through it.
Answer:

Limewater traditionally means a weak solution of the alkali calcium hydroxide Ca(OH)₂.
When CO₂ is passed through limewater, it reacts with calcium hydroxide to form insoluble particulates (precipitate) of Calcium carbonate (CaCO₃).
Calcium carbonate is weak basic salt and this gives a milky white precipitate.
Hence, lime water turns milky when CO₂ gas is passed through it.

d. Biogas is an eco-friendly fuel.
Answer:

Biogas is formed by the decomposition of animal dung, dry leaves, wet garbage in a biogas plant.
This produces methane gas also called biogas.
Biogas is a very cheap fuel option which meets the demand for cooking gas.
Biogas is eco-friendly as it contains about 55% to 60% of methane and rest is carbon dioxide, hence, on combustion it does not produce harmful gases which cause pollution.
Biogas is a fuel which is convenient to use and in addition to this it produces a very good manure as a side product of the process.
Hence, biogas is an eco-friendly fuel.

5. Explain the following.

a. Diamond, graphite and fullerenes are crystalline forms of carbon.
Answer:

Carbon exhibits a property of allotropy in which an element exists in more than one form in nature.
The chemical properties of these different forms are the same but their physical properties are different.
Carbon exists in crystalline as well as non-crystalline (amorphous form).
Crystalline form has a regular and definite arrangement of atoms. They have high melting points and boiling points.
A crystalline form has a definite geometrical shape, sharp edges and plane surfaces.
Carbon has three crystalline allotropes such as diamond, graphite and fullerene.
In the structure of diamond, every carbon atom is bonded to four neighbouring atoms by covalent bonds.
Therefore, diamond has a tetragonal three dimensional structure which makes it very hard.
Brilliant and pure diamond is the hardest natural substance.
In the structure of graphite, every carbon atom in graphite is bonded to three other carbon atoms in such a way that a hexagonal layered structure is formed.
A graphite crystal is made of many sheets or layers of carbon atoms.
These layers slip over each other on applying pressure. One layer of graphite is called graphene.
Fullerene is rarely found in nature. It is found in soot and in interstellar space.
The first example of fullerene is Buckminster fullerene (C₆₀).
This allotrope of carbon is named fullerene after the architect.
Richard Buckminster Fuller because the structure of C₆₀ resembles the structure of the geodesic dome he designed.
(xi) Molecules of fullerenes are found in the form of buckyballs and buckytubes.
(xii) There are 30 to 900 carbon atoms in one molecule of a fullerene. , C₆₀, C₇₀, C₇₆, C₈₂ and C₈₆ are other examples of fullerene. Their molecules occur in small numbers in soot.

b. Methane is called marsh gas.
Answer:

Methane is formed by the decomposition of plant and animal matter in swamps or marshy areas.
As methane gas bubbles out from marshy area, it is called as marsh gas.

c. Petrol, diesel, coal are fossil fuels.
Answer:
(i) A fossil fuel is a fuel formed by natural processes, such as anaerobic decomposition of buried dead organisms. Fossil fuels contain high percentage of carbon. The word carbon is derived from the Latin word ‘Carbo’ meaning coal.

(ii) Coal is formed from the remains of trees and other vegetation. Approximately 350 million years ago, these remains were trapped on the bottom of swamps, accumulating layer after layer and creating a dense material called peat. As this peat was buried under more and more ground, the high temperature and pressure transformed it into coal.

(iii) Petrol and diesel are obtained from mineral oil. Mineral oil also called as crude oil or petroleum oil is formed from the remains of plants and animals that lived in the seas millions of years ago. This plant and animal matter has been drawn down and subjected to extremes of temperature and pressure over millions of years ago.

(iv) Mineral oil is commonly formed in rocks under the sea bed. The word petroleum is derived from Latin word ‘Rock oil’. Petrol and Diesel are obtained from mineral oil by the process called as fractional distillation.
Thus petrol, diesel and coal are fossil fuels.

d. Uses of various allotropes of carbon.

e. Use of CO₂ in fire extinguisher.
Answer:

CO₂ based fire extinguishers do not cause corrosion and are non-conductors of electricity.
It is beyond their capacity to extinguish a big fire.
Therefore these fire extinguishers are used to extinguish small scale fire of electrical and electronic equipments.

f. Practical uses of CO₂.
Answer:
Practical uses of CO₂ are:

CO₂ is used to make aerated drinks.
CO₂ obtained by chemical reaction or kept under pressure is used in fire extinguishers. Liquified CO₂ is used to remove caffeine from coffee.
Liquid CO₂ is used as solvent in modem eco-friendly dry cleaning.
Solid carbon dioxide is used in cold storage and to keep milk and milk products and frozen substances cool during transport. It is also used for getting special effects of a mist in dramas and movies.

6. Write two physical properties each.

a. Diamond
Answer:
Properties of diamond are:

Brilliant and pure diamond is the hardest natural substance.
The density of diamond is 3.5 g/cm³.
The melting point of diamond is 3500 °C.
When a diamond is heated at 800 °C in the presence of oxygen, CO₂ is given away. In this process no other product besides CO₂ is formed.
Diamond does not dissolve in any solvent.
Acids/bases have no effect on diamond.
Diamond is a bad conductor of electricity as it does not have free electrons.

b. Charcoal
Answer:

The charcoal that is made from animals is made from their bones, horns, etc.
On the other hand, the charcoal made from plants is formed by combustion of wood in an insufficient supply of air.

c. Fullerene
Answer:
Properties of fullerenes are:

Molecules of fullerenes are found in the form of buckyballs and buckytubes.
There are 30 to 900 carbon atoms in one molecule of a fullerene.
Fullerenes are soluble in organic solvents such as carbon disulphide, chlorobenzene.

7. Complete the following Chemical reactions.

1. ………………..+………………..→ CO + 2H₂O + Heat
2. ………………..+………………..→ HCl + Cl + HCl
3. 2 NaOH + CO₂ →………………..+………………..
Answer:

8. Write answers to the following in detail.

a. What are the different types of coal? What are their uses?
Answer:
Coal is a fossil fuel. It contains carbon, hydrogen and oxygen. It also contains nitrogen, phosphorus and sulphur. It occurs in the solid state. It is of four types.

Peat: Formation of peat is the first step in the formation of coal. It contains a high proportion
of water and less than 60% of carbon. Therefore, not much heat can be obtained from peat.
Lignite: Peat was transformed into Lignite due to increased pressure and temperature inside the earth. It contains 60 to 70% of carbon.- Lignite is the second step of the formation of coal.
Bituminous coal: Bituminous coal was formed as the third step of formation of coal. It contains 70 to 90% of carbon.
Anthracite: Anthracite is known as the pure form of coal. This coal is hard and contains about 95% of carbon.

Uses of coal:

Coal is used as fuel in factories and homes.
Coal is used to obtain coke, coal gas and coal tar.
Coal is used in thermal power plants for generation of electricity.

b. How will you prove experimentally that graphite is good conductor of electricity?
Answer:
Apparatus required: Lead pendi, electrical wires, battery/cell, small bulb, etc.

Step-I: Remove the lead from a pencil and assemble the apparatus as shown in the diagram.

Step-II:

Start the electric current in the circuit, the moment the electric current is passed through the circuit, the bulb glows.
This experiment proves that graphite is a good conductor of electricity as graphite has free electrons moving continuously within the entire layer and these free electrons conduct electricity in the lead of the pencil.

c. Explain the properties of carbon.
Answer:
Allotropic nature of Carbon: Some elements occur in nature in more than one form. The chemical properties of these different forms are the same but their physical properties are different. This property of elements is called allotropy. Carbon shows the property of allotropy.

Carbon allotropes are of two types:
(A) Crystalline forms:
Carbon has three crystalline allotropes: Diamond, Graphite and Fullerene. Properties of crystalline forms of carbon are as follows:

A crystalline form has a regular and definite arrangement of atoms.
They are made up of only carbon atoms.
They have high melting points and boiling points.
A crystalline form has a definite geometrical shape, sharp edges and plane surfaces.

(B) Amorphous forms or non-crystalline forms: Coal, charcoal, coke are the non-crystalline forms of carbon.
Properties of non-crystalline forms of carbon are as follows:

The arrangement of carbon atoms in this form is not regular.
Apart from carbon atoms, they also contain hydrogen, oxygen, nitrogen, phosphorus and sulfur atoms.
Compared to a crystalline form, they have low melting and boiling points.
Most of them are used as fuels.

d. Classify carbon.
Answer:
Carbon is classified as follows:

9. How will you verify the properties of carbon dioxide?
Answer:
Properties of carbon dioxide can be verified in the following ways:

When a burning candle is placed in a gas jar of carbon dioxide, it extinguishes indicating that carbon dioxide is a non-combustible gas and does not support combustion.
When carbon dioxide gas is passed through lime water, it turns lime water milky due to the formation of insoluble calcium carbonate.
Moist blue litmus turns red in a gas jar of carbon dioxide indicating, it is acidic in nature.
Carbon dioxide is fairly soluble in water, it dissolves in water forming carbonic acid.

Class 9 Science Chapter 13 Carbon: An Important Element Intext Questions and Answers

Can you recall?

Question 1.
Whatremains behind on complete combustion of any organic compound?
Answer:
A black colour substance ‘Carbon’ remains behind on complete combustion of any organic compound.

Question 2.
What type of element is carbon? Give some information about it.
Answer:

Carbon is a non-metallic element. It is available ‘ abundantly in the nature and occurs in free as well as combined state.
Carbon in free state is found as diamond and graphite and in combined state it is present to the extent of approximately 0.27% in the form of carbonate, coal, petroleum.
In atmosphere, the proportion of carbon in the form of carbon dioxide is approximately 0.03%.

Question 3.
What is an element? What are the different types of elements.
Answer:

A substance which cannot be decomposed into simple substances by any physical or simple chemical method is called as an Element.
An element is composed of atoms of only one kind.
The different types of elements are:
(a) Metals – Examples: Gold, Silver, etc.
(b) Non-metals – Examples: Carbon, Sulphur, etc.
(c) Metalloids – Examples: Silicon, Antimony, etc.

Answer the following questions:

Question 1.
Does an electric charge form on atoms when a covalent bond is formed between them? Why is a single bond between two carbon atoms strong and stable?
Answer:

No, electric charge is not formed on atoms when a covalent bond is formed between them. This is because covalent bond is formed by sharing of electrons.
Therefore, there is no change in number of electrons and protons in these atoms and they remain electrically neutral.
Covalent bonds occur when electrons are shared between two atoms. A single covalent bond is formed when only one pair of electrons is shared between atoms.
In this sharing, the atomic orbitals directly overlap between the nuclei of two atoms forming the strongest type of covalent bond called as sigma bond.
Hence, a single covalent bond between two carbon atoms is strong and stable.

Question 2.
In which of the solvents – water, kerosene and cooking oil does the coal powder dissolve?
Answer:
Solvents such as water, kerosene and cooking oil do not dissolve coal powder in them.

Question 3.
What inference will you draw about the solubility of carbon?
Answer:
Carbon is insoluble in water, kerosene and cooking oil.

Question 4.
Is the density of CO₂ more or less than that of air?
Answer:

Density is defined as mass per unit volume of a substance, expressed as kilograms per cubic meter.
At standard temperature and pressure, the density of air is 1.29 kg/m³. While that of carbon dioxide (CO₂) is 1.79 kg/m³. Hence, density of CO₂ is more than that of air.

Question 5.
What is a compound? How are compounds formed?
Answer:

A compound is a substance formed when two or more elements are chemically bonded with each other in definite proportion by weight.
When atoms or two or more different elements chemically react with each other in a definite proportion by weight, a compound is formed.
The properties of a compound are altogether different from its constituent elements.
Example: Pure water is a compound made up of two elements Hydrogen and Oxygen. Hydrogen (H) atoms and oxygen (O) atoms have chemically reacted with each other in definite proportion to form a compound-water (H₂O). The proportion of hydrogen and oxygen in water by volume is 2 : 1 and by weight is 1 :8 respectively.
The properties of water are altogether different from the properties of its constituent elements, hydrogen and oxygen.

Class 9 Science Chapter 13 Carbon: An Important Element Additional Important Questions and Answers

Choose and write the correct option:

Question 1.
The organic compound having double or triple bond in them is termed as
(a) unsaturated
(b) inorganic
(c) saturated
(d) complete
Answer:
(a) Unsaturated hydrocarbon

Question 2.
Covalent compounds are generally soluble in solvents.
(a) inorganic
(b) organic
(c) mixed
(d) mineral
Answer:
(b) organic

Question 3.
Methane is also called as
(a) maha gas
(b) mar’s gas
(c) Anthracite
(d) marsh gas
Answer:
(d) Marsh gas

Question 4.
is an alio trope of carbon used to make ornaments.
Answer:
Diamond

Question 5.
The number of valence electrons in carbon is
(a) 4
(b) 5
(c) 6
(d) 3
Answer:
(a) 4

Question 6.
In saturated hydrocarbons, two carbon atoms are linked by
(a) double bond
(b) triple bond
(c) multiple bond
(d) single bond
Answer:
(d) single bond

Question 7.
Carbon has 4 valence electrons in its outermost shell, hence, it is
(a) divalent
(b) tetravalent
(c) trivalent
(d) pentavalent
Answer:
(b) tetravalent

Question 8.
Methanogenic bacteria act on the organic acids to produce
(a) oxygen gas
(b) nitrogen gas
(c) methane gas
(d) carbon dioxide gas
Answer:
(c) Methane gas

Question 9.
is used to remove caffeine from coffee.
(a) liquefied O₂
(b) liquefied N₂
(c) liquefied CO₂
(d) liquefied CH₄
Answer:
(c) Liquified CO₂

Question 10.
Exhaled air contains about CO₂.
(a) 4%
(b) 3%
(c) 5%
(d) 6%
Answer:
(a) 4%

Question 11.
Electronic configuration of carbon is
(a) (2, 2)
(b) (2,4)
(c) (2, 5,4)
(d) (2, 6)
Answer:
(b) 2, 4

Question 12.
Molecular formula of ethane is
(a) C₃H₄
(b) C₂H₄
(c) C₂H₆
(d) C₂H₂
Answer:
(c) C₂H₆

Question 13.
Molecular mass of carbon dioxide is
(a) 28
(b) 22
(c) 56
(d) 44
Answer:
(d) 44

Question 14.
On heating a mixture of hydrogen and carbon monoxide gases at 300°C in the presence of nickel (catalyst) is formed.
(a) carbon dioxide gas
(b) oxygen gas
(c) methane gas
(d) ethylene gas
Answer:
(c) methane gas

Question 15.
Ethane with molecular formula C₂H₆ has covalent bonds.
(a) six
(b) seven
(c) eight
(d) nine
Answer:
(b) seven

Question 15.
Weight of Kohinoor Diamond was
(a) 186 carats
(b) 27 carats
(c) 252 carats
(d) 23 carats
Answer:
(a) 186 carats

Question 16.
Covalent compounds have
(a) high melting point
(b) low melting point
(c) moderate melting point
(d) very high melting point
Answer:
(b) low melting point

Question 17.
Methane is
(a) C₂H₆
(b) C₃H₈
(C) CH₂
(d) CH₄
Answer:
(d) CH₄

Question 18.
Wohler, a German scientist synthesized the compound from an inorganic compound ammonium cyanate.
(a) methane
(b) ethylene
(c) urea
(d) acetic acid
Answer:
(c) urea

Question 19.
Molecular mass of methane is
(a) 19
(b) 16
(c) 17
(d) 18
Answer:
(b) 16

Question 20.
coal contains highest percentage of carbon.
(a) Bituminous
(b) Peat
(c) Anthracite
(d) Lignite
Answer:
(c) Anthracite

Question 21.
H₂C = CH₂ is ……………………… .
(a) Propane
(b) Ethyne
(c) Ethane
(d) Ethene
Answer:
(d) Ethene

Question 22.
CH₃– C = CH is ……………………… .
(a) Propene
(b) Propyne
(c) Ethyne
(d) Ethene
Answer:
(b) Propyne

Question 23.
Carbon dioxide gas is not used in
(a) photosynthesis
(b) aerated drinks
(c) glass cutting
(d) fire extinguishers
Answer:
(c) glass cutting

Question 24.
Melting point of diamond is
(a) 3700 °C
(b) 3500 °C
(c) 4000 °C
(d) 2500 °C
Answer:
(b) 3500 °C

Question 25.
Melting point of C02 is
(a) 26 °C
(b) 56 °C
(c)-56.6°C
(d)-98°C
Answer:
(c) -56.6 °C

Question 26.
Melting point o* methane is
(a) -182.5 °C
(b) -161.5 °C
(c) 182.5 °C
(d) 161.5 °C
Answer:
(a) -182.5 °C

Question 27.
Biogas contains about methane.
(a) 55% to 60%
(b) 20% to 25%
(c) 90% to 95%
(d) 40% to 45%
Answer:
(a) 55% to 60%

Question 28.
is not a property of carbon dioxide gas.
(a) Supporting combustion
(b) Odourless
(c) Colourless
(d) Turns blue litmus red
Answer:
(a) Supporting combustion

Name the following:

Question 1.
Industries that use methane in the form of natural gas.
Answer:
Fabric mills, paper mills, food processing industry, petrol purification.

Question 2.
Organic compounds prepared from methane.
Answer:
Ethanol, methyl chloride, methylene chloride, acetylene.

Question 3.
Chemicals used in regular fire extinguisher.
Answer:
Sodium bicarbonate and dilute sulphuric acid.

Question 4.
Components of biogas
Answer:
Methane, carbon dioxide

Question 5.
Organic solvents is which fullerenes are soluble.
Answer:
Carbon disulfide, chlorobenzene.

Question 6.
Use of carbon dioxide is dramas and movies
Answer:
The special effect of mist.

Match the columns:

Question 1.

Column ‘A’	Column ‘B’
(1) Diamond (2) Fullerenes (3) Graphite	(a) Hexagonal layered structure (b) Tetragonal three-dimensional structure (c) Geodesic dome

Answer:
(1-b),
(2- c),
(3 – a)

Question 2.

Column ‘A’	Column ‘B’
(1) Peat (2) Lignite (3) Bituminous (4) Anthracite	(a) 60-70% of Carbon (b) 95% of Carbon (c) less than 60% of Carbon (d) 70 – 90% of Carbon

Answer:
(1 – c),
(2 – a),
(3 – d),
(4 – b)

Question 3.

Column ‘A’	Column ‘B’
(1) Propyne (2) Propene (3) Propane	(a) CH₃– CH₂– CH₃(b) CH₃ – C = CH (c) CH₃ – CH = CH₂

Answer:
(1 – b),
(2 – c),
(3 – a)

Question 4.

Column ‘A’	Column ‘B’
(1) Fullerene (2) Diamond (3) Graphite	(a) Lubricants (b) Insulator (c) Ornaments

Answer:
(1 – b),
(2 – c),
(3 – a)

Question 5.

Column ‘A	Column ‘B’
(1) Water gas (2) Methane gas (3) Producer gas (4) Carbon dioxide gas	(a) CH₄(b) CO + H₂(c) CO₂(d) CO + H₂ + CO₂ + N₂

Answer:
(1 – b),
(2 – a),
(3 – d),
(4 – c)

State whether the following statements are true or false. Correct the false statement.

(1) Study of organic compounds is called as organic chemistry.
(2) Hydrocarbons with double bonds are called as saturated hydrocarbons.
(3) Ethene is saturated hydrocarbon.
(4) Covalent compounds are good conductor of electricity.
(5) Methane is a covalent compound.
(6) Covalent compounds are soluble in organic solvents.
(7) Graphite is used in making lubricants and lead pencils.
(8) The density of diamond is 9.8 g/cm³.
(9) Diamond knives are used in eye surgery.
(10) Fullerenes are used as insulators.
(11) Coke is used in production of water gas i.e. (CO₂ + H₂O).
(12) Structural formula of propyne is CH₃ – C = CH.
(13) COz is used to make aerated drinks.
(14) Methane gas is black in colour.
(15) Production of biogas is aerobic process.
Answer:
(1) True
(2) False. Hydrocarbons with double bonds are called as Unsaturated hydrocarbons.
(3) False. Ethene is Unsaturated hydrocarbon.
(4) False. Covalent compounds are bad conductor of electricity.
(5) True
(6) True
(7) True
(8) False: The density of diamond is 3.5 g/cm³.
(9) True
(10) True
(11) False. Coke is used in production of water gas i.e. (CO + H₂).
(12) False. Structural formula of propyne is CH₃ – C = CH.
(13) True
(14) False. Methane gas is colourless.
(15) False. Production of biogas is anaerobic process.

Find the odd man out:

Question 1.
Propane, Methane, Ethene, Pentane.
Answer:
Ethene. It is an unsaturated hydrocarbon with double bond between two carbon atoms while rest are saturated hydrocarbons with single bond between two carbon atoms.

Question 2.
CH₄, C₂H₆, C₃H₈, CaCO₃.
Answer:
CaCO₃. It is a salt which is an inorganic’ compound, while rest are hydrocarbon compounds, i.e. organic compounds.

Question 3.
C₂H₂, C₃H₈, C₂H₆, CH₄.
Answer:
C₂H₂. It is an unsaturated hydrocarbon with triple bonds while rest are saturated hydrocarbons with single bonds between two carbon atoms.

Question 4.
Diamond, Fullerene, Graphite, Methane.
Answer:
Methane. It is a marsh gas while rest are allotropes of carbon.

Question 5.
Coal, Petroleum, Natural gas, Cotton
Answer:
Cotton. Cotton is a natural fibre while rest all are fossil fuels.

Question 6.
Cotton, Silk, Proteins, Wool
Answer:
Proteins. Proteins are carbonaceous nutrients while rest all are natural fibres.

Question 7.
Carbohydrates, Coal, Proteins, Fats
Answer:
Coal. Coal is a fossil fuel while rest all are carbonaceous nutrients.

Question 8.
Peat, Charcoal, Lignite, Bituminous
Answer:
Charcoal. Charcoal is a non-crystalline form of carbon while rest all are types of coal.

Question 9.
Lubricants, Electrodes, Ornaments, Arc Lamps
Answer:
Ornaments. Ornaments are made from diamonds while rest all are made from graphite.

Write the correlated terms:

(1) Propene : Double bond :: Propyne : ……………………. .
(2) Ethane : CH₃ – CH₃:: Ethene : ……………………. .
(3) Hydrogen : Monovalent :: Carbon : ……………………. .
(4) Methane : Low melting point i.e. -182.5°C Diamond : ……………………. .
(5) Graphite : Hexagonal structure :: Diamond : ……………………. .
(6) Density of Diamond : 3.5 g/cm³ :: Density of Graphite : ……………………. .
(7) Peat: 60% of carbon :: Anthracite : ……………………. .
(8) Melting point of CO₂: -56.6°C :: Melting point of CH₄: ……………………. .
Answer:
(1) Triple Bond
(2) CH₂ = CH₂
(3) Tetravalent
(4) High melting point i.e. 3500°C
(5) Tetragonal structure
(6) 1.9 to 2.3 g/cm³
(7) 95% of carbon
(8) -182.5 °C

Give scientific reasons:

Question 1.
Covalent compounds have low melting and boiling points.
Answer:

When substances melt or boil, bonds between the molecules are broken due to heat supplied.
On covalent compounds, the intermolecular forces of attraction are weak.
Hence, intermolecular forces in covalent compounds are broken easily due to which they have low melting and boiling points.

Question 2.
Graphite is a good conductor of electricity whereas diamond is a non-conductor of electricity.
Answer:

In diamond, each carbon atom uses all its four electronic to get bonded to another carbon atom, whereas in graphite each carbon uses there out of four electrons during bonding.
Hence in diamond no free electrons are left whereas in graphite free electrons are available.
Due to the presence of electron which are free to flow graphite is a good conductor of electricity, whereas due to the absence of free electrons diamond is a non-conductor of electricity.

Question 3.
Graphite is used as a lubricant.
Answer:

Lubricants are used to reduce friction and wear and tear of mechanical parts.
Graphite is smooth and slippery and hence is useful in reducing friction. Hence, graphite is used as a lubricant.

Question 4.
Methane is used as a domestic fuel.
Answer:

Methane is highly inflammable.
It burns by reacting with oxygen to give a bluish flame.
It burns completely and producers 213 Kcal/ mol of heat.
Being the smallest hydrocarbon, the proportion of CO2 released in the combustion of methane is small.
Therefore methane is used as a domestic fuel.

Answer in short:

Question 1.
What was the contribution of chemist Wohier in organic chemistry?
Answer:

The German chemist Wohier synthesized an organic compound urca from an inorganic compound ammonium cyanate,
Ever since then, many organic compounds have been made from inorganic compounds.
Carbon was found to he the main element in all these compounds.
Hence, organic chemistry is also referred to as chem is try of carbon corn pounds.

Question 2.
With neat diagram explain the structure of diamond.
Ans.

In diamond, every carbon atom is bonded to four neighbouring atoms by covalent bonds.
Therefore, diamond has a tetragonal three dimensional structure which makes it very hard.

Question 3.
With neat diagram explain the structure of graphite?
Answer:

Every carbon atom in graphite is bonded to three other carbon atoms in such a way that a hexagonal layered structure is formed.
A graphite crystal is made of many sheets or layers of carbon atoms.
These layers slip over each other on applying pressure.
One layer of graphite is called graphene.

Question 4.
Give the properties of graphite.
Answer:
Properties of graphite are:

Graphite found in nature is black, soft, brittle and slippery.
Inside each layer of graphite, free electrons move continuously within the entire layer. That is why graphite is a good conductor of electricity.
Due to the layered structure graphite can be used for writing on paper.
The density of graphite is 1.9 to 2.3 g/cm3.
Graphite does not dissolve in most solvents.

Question 5.
Give the uses of graphite.
Answer:
Uses of graphite are:

Graphite is used for making lubricants.
Graphite is used for making carbon electrodes.
Graphite is used in pencils for writing.
Graphite is used in paints and polish.
Graphite is used in arc lamps which gives a very bright light.

Question 6.
Give the uses of fullerenes.
Answer:
Uses of Fullerenes are:

Fullerenes are used as insulators.
Fullerenes are used as a catalyst in water purification.
At a certain temperature, fullerene exhibits superconductivity.

Question 7.
What is Coal?
Answer:

Coal is a fossil fuel. It contains carbon, hydrogen and oxygen.
It also contains nitrogen, phosphorus and sulphur.
It occurs in the solid state. It is of four types – peat, lignite, bituminous and anthracite.

Question 8.
What is Coke?
Answer:
The pure coal that remains when coal gas has been taken away from coal, is called coke.

Question 9.
Give the uses of Coal.
Answer:
Uses of Coal are:

Coal is used as fuel in factories and homes.
Coal is used to obtain coke, coal gas and coal tar.
Coal is used in thermal power plants for generation of electricity.

Question 10.
Give the uses of Coke.
Answer:
Uses of Coke are:

Used as domestic fuel.
Coke is used as a reducing agent.
Coke is used in production of water gas (CO + H₂) and producer gas (CO + H₂ + CO₂ + N₂)

Question 11.
Name the types of coal and give the differences in them.
Answer:
The four types of coal are Peat, Lignite, Bituminous and Anthracite.

Question 12.
Give the properties of covalent compounds.
Answer:
Properties of covalent compounds:

Covalent compounds have low melting points and boiling points.
Generally they are insoluble in water and soluble in organic solvents.
They are poor conductors of heat and electricity.

Question 13.
What are saturated hydrocarbons? Give examples.
Answer:

The hydrocarbons having only single bonds between carbon atoms are called saturated hydrocarbons.
For example, ethane (C₂H₆) which is (CH₃ – CH₃), propane (C₃H₈) which is (CH₃ – CH₂ – CH₃).

Question 14.
What are unsaturated hydrocarbons? Give examples.
Answer:

Some hydrocarbons have a multiple bond between two carbon atoms.
A multiple bond can be a double bond or a triple bond.
Hydrocarbons having at least one multiple bond are called unsaturated hydrocarbons.
For example, ethene (H₂C = CH₂), ethyne (HC = CH), propene (CH₃– CH = CH₂), propyne (CH₃– C = CH).

Question 15.
Give the following information of carbon dioxide: Molecular formula, Molecular mass, Melting point, Percentage occurrence in air.
Answer:
Molecular formula – CO₂, Molecular mass – 44, Melting point -56.6 °C Percentage occurrence in air – 0.03%.

Question 16.
Give the physical and chemical properties of carbon dioxide.
Answer:
Physical properties of carbon dioxide are:

It is an odourless gas.
It is a colourless gas.

Chemical properties of carbon dioxide are:

It is non-combustible and does not support combustion.
It turns lime water milky.
It is fairly soluble in water and dissolves in water forming carbonic acid.
It turns blue litmus red indicating it is acidic in nature.
The colour of universal indicator turns orange/ yellow in C02 indicating its pH value between 4 and 6, i.e. acidic in nature.

Question 17.
Give the uses of Carbon dioxide.
Answer:
Uses of Carbon dioxide are:

CO₂ is used to make aerated drinks
Solid carbon dioxide is used in cold storage and also to keep milk and milk products and frozen substances cool during transport. It is also used for getting special effects of a mist in dramas and movies.
CO₂ obtained by chemical reaction or kept under pressure is used in fire extinguishers.
Liquified CO₂ is used to remove caffeine from coffee.
Liquid CO₂ is used as solvent in modern eco-friendly dry cleaning.
Plants use CO₂ in air for photosynthesis.

Question 18.
Give the occurrence of methane.
Answer:
The occurrence of methane is as follows:

Methane occurs in natural gas to the extent of 87%.
Decomposition of organic matter in the absence of air (anaerobic) produces methane.
Methane is present in biogas.
Methane is found in coal mines.
Methane is found at the surface of marshy places which is why it is also called marsh gas.
On heating a mixture of hydrogen and carbon monoxide gases at 300 °C in the presence of nickel (catalyst), methane gas is formed.
Fractional distillation of natural gas gives methane in pure form.

Question 19.
Give the physical properties of methane.
Answer:
Physical properties of methane are:

Melting point of methane is (-182.5 °C).
Boiling point of methane is (-161.5 °C).
It is a colourless gas.
The density of liquid methane is less than that of water.
Methane is sparingly soluble in water. It is highly soluble in organic solvents like gasoline, ether and alcohol.
Methane is in gaseous state at room temperature.

Question 20.
Give the uses of methane.
Answer:
Uses of methane are:

Methane in the form of natural gas is used in industries such as fabric mills, paper mills, food processing industry, petrol purification.
Being the smallest hydrocarbon, the proportion of CO₂ released in the combustion of methane is small and, therefore, it is used as a domestic fuel.
Methane is used for production of organic compounds such as ethanol, methyl chloride, methylene chloride and acetylene.

Question 21.
How is methane formed? Give structural formula and electron dot model of methane.
Answer:

Atomic number of carbon is 6. The electronic configuration of carbon is (2, 4). The valency of carbon is 4.
Carbon atom can form four covalent bonds with other carbon atoms or atoms of different elements.
When a carbon atom shares one electron each with four hydrogen atoms and forms four C-H bonds, a methane (CH₄) molecule is formed.

Question 22.
What are organic and inorganic compounds?
Answer:
Compounds obtained directly or indirectly from plants and animals are called organic compounds and compounds obtained from minerals are called inorganic compounds.

Question 23.
What is allotropy?
Answer:

Allotropy – Some elements occur in nature in more than one form.
The chemical properties of these different forms are the same but their physical properties are different.
This property of elements is called allotropy.

Question 24.
What are basic organic compounds? What are they also called as?
Answer:

The compounds formed from only carbon and hydrogen are called basic organic compounds.
These are also called hydrocarbons.

Write a balanced chemical equation and explain the following chemical reactions.

Question 1.
Preparation of urea from Ammonium cyanate:
Answer:

Organic compound Urea can be synthesized from an inorganic compound Ammonium cyanate.

Question 2.
Coal when burnt in air
Answer:

When coal is burnt in air, the carbon present in coal combines with oxygen present in air to form carbon dioxide gas.

Question 3.
Calcium carbonate reacts with dilute hydrochloric acid:
Answer:

When Calcium carbonate reacts with dilute hydrochloric add it forms Caldum chloride, water and Carbon dioxide gas is evolved.

Question 4.
Carbon dioxide is passed through an aqueous solution of Sodium hydroxide:
Answer:

When Carbon dioxide gas is passed through an aqueous solution of Sodium hydroxide it forms Sodium carbonate and Water.

Question 5.
Carbon dioxide is passed through an aqueous solution of Sodium carbonate:
Answer:

When carbon dioxide is passed through an aqueous solution of Sodium carbonate, it forms Sodium bicarbonate.

Question 6.
Carbon dioxide is passed through freshly prepared lime water for a short duration and then for longer duration:
Answer:

When Carbon dioxide is passed through freshly prepared lime water, it forms water and white precipitate of Calcium carbonate because of which lime water turns milky.

When Carbon dioxide is continuously passed through milky lime water, it forms Calcium bicarbonate which is soluble in water and therefore, water once again turns colourless.

Question 7.
Carbon dioxide gas is dissolved in water.
Answer:

Carboh dioxide gas is fairly soluble in water, it dissolves in water under pressure to form Carbonic acid.

Question 8.
Sodium bicarbonate reacts with dilute Sulphuric acid, (reaction in fire extinguisher):
Answer:

When Sodium bicarbonate reacts with dilute Sulphuric acid it forms Sodium sulphate, water and Carbon dioxide gas.

Question 9.
Methane gas is burnt in air:
Answer:

Methane is highly inflammable, it burns in air with a bluish flame and combines with oxygen present in air to form Carbon dioxide and water. In these reaction 213 kcal/mol of heat is given out.

Question 10.
Methane and Chlorine gases react with each other.
Answer:

Methane and chlorine gases react with each other at the temperature of 250 °C to 400 °C in presence of ultra voilet light and form mainly Methyl chloride (Chloromethane and ‘ Hydrogen chloride)
This reaction is called Chlorination of methane.

Question 11.
Production of methane gas in biogas plant.
Answer:

In biogas plant, microbes act on the bio-degradable complex organic compounds and produce organic acids.

The methanogenic bacteria act on the organic acids to produce Methane gas and Carbon dioxide gas.

Question 12.
Production of water gas:
Answer:

When super heated steam is passed over red hot coke at high temperature, it forms carbon monoxide gas and hydrogen gas.

This gaseous product of carbon monoxide gas and hydrogen gas together is called as water gas.

With the help of ne abelled diagram explain the following:

Question 1.
Regular fire extinguisher.
Answer:

A fire extinguisher contains Sodium bicarbonate powder. There is also dilute sulphuric acid placed in a glass capsule.
On pressing the knob, the capsule breaks and sulphuric acid comes in contact with the sodium bicarbonate. These two react chemically to release CO₂ which comes out.
CO₂ based fire extinguishers do not cause corrosion and are non-conductors of electricity. Therefore, they are used when electrical or electronic equipment catches fire.
CO₂ based fire extinguishers are used to extinguish small scale fire. It is beyond their capacity to extinguish a big fire.
In modern fire extinguishers liquid and solid CO₂ is filled under pressure. On reducing the pressure, it becomes gaseous and comes out forcefully through the horn-like hose pipe.
Chemical reaction:

Question 2.
Biogas plant.
Answer:

Animal dung, dry leaves, wet garbage get decomposed by anaerobic microbes in a biogas plant.
This produces methane gas, also called biogas.
Biogas is a very cheap fuel option which meets the demand for cooking gas. It is also used for the production of electricity.
Biogas contains about 55% to 60% methane and the rest is carbon dioxide.
Biogas is a fuel which is convenient to use and, in addition to this, a very good manure is also produced as a side product of the process.
Biogas production process – Production of biogas is an anaerobic process. It takes place in two stages.
(a) Production of acids – The microbes act on the biodegradable complex organic compound and produce organic acids.
(b) Methane gas production – The methanogenic bacteria act on the organic acids to produce methane gas.

Chemical reaction:

Answer the following

Question 1.
What happens when substances like milk, sugar, wool, dry leaves, hair and seeds are heated strongly in hard glass test tube?Answer:
When milk, sugar, wool, dry leaves, hair and seeds are heated strongly in hard glass test tube, they get charred and a black substance is left behind. This black substance is carbon.

Answer the following questions:

Question 1.
Take some milk in an evaporating dish. Heat the evaporating dish on a bunsen burner. What remains behind at the bottom of an evaporating dish on complete evaporation of the milk?
Answer:

On complete evaporation of milk, a black residue is left behind.
This residue is of carbon.

Question 2.
Take small samples of sugar, wool, dry leaves, hair, seeds, split pulses and plastic in separate test tubes. Heat each test tube and observe the changes taking place in the substances. What does the black substance in each test tube indicate?
Answer:

On heating the above samples, they get charred and a black substance is left behind.
The black substance is carbon.

Question 3.
Apparatus : Coal, match box, moist litmus paper, etc.

Procedure : Ignite the coal. Hold the moist blue litmus paper over the gas released on igniting the coal. Note the observation.

(a) With which gas in the air does the coal react on igniting?
Answer:
Coal reacts with oxygen gas present in the air, on igniting.

(b) What is the substance formed?
Answer:
The substance formed is carbon dioxide.

(d) Write down the chemical reaction taking place in the above procedure.
Answer:
(i) Carbon combines with oxygen to form Carbon dioxide gas.

(ii) This C02 combines with water present on moist blue litmus paper to form Carbonic acid which turns blue litmus to red.

Question 4.
Apparatus : Pencil, electrical wires, battery/ cell, small bulb, water, kerosene, test tube, lead pencils, etc.

Procedure : Remove the lead from a pencil and arrange the apparatus as shown in the above diagram. Note your observations for the following.

(a) What is the colour of lead in the pencil? .
Answer:
The colour of the lead in the pencil is black as it is made from graphite which is an allotrophic form of carbon.

(b) Try to break lead with your hand.
Answer:
The lead breaks easily as it is made up of graphite which is brittle in nature.

(c) Start the electric current in the circuit and observe. What did you find?
Answer:
When we start the electric current in the circuit, the bulb in the circuit glows, indicating that the lead in the pencil is a good conductor of electricity.

(d) Take some water in a test tube. Take some kerosene in another test tube. Put lead dust in both the test tube. What did you observe?
Answer:
(i) Lead dust does not dissolve in water nor in kerosene.
(ii) It remains insoluble in both the test tubes.

Question 5.
Apparatus : Test tube, straw, lime water, etc.

Procedure: Take freshly prepared lime water in a test tube. Blow air in it for some time through the straw and observe the lime water. Note the observation.

(a) What did you see?
Answer:
When we blow air through the straw in freshly prepared lime water, it turns milky.

(b) What might be the reason behind the change?
Answer:

Freshly prepared lime water is obtained by dissolving lime (CaO) in water (H₂O).

When we blow air through the straw in lime water, carbon dioxide (CO₂) present in the air reacts with lime water to form white precipitate (insoluble substance) of Calcium Carbonate (CaCO₃) due to which lime water turns milky.

Question 6.
With the help of a neat labelled diagram explain the laboratory preparation of Carbon dioxide gas.
Answer:
The laboratory preparation of Carbon dioxide gas is as follows:

Apparatus : Retort stand, round bottom flask, thistle funnel, gas delivery tube, gas jars.
Chemicals : Calcium carbonate (Pieces of Shahabad tiles/marble pieces/limestone), dilute hydrochloric acid.

Procedure:

Assemble the apparatus as shown in the figure. While assembling, place CaCO₃ in the round bottom flask.
Add dilute HCl in the flask through thistle funnel. See to it that the end of the funnel dips in the acid.
CO₂ is formed as a result of the reaction between CaCO₃ and HCl. Collect this gas in four to five gas jars. The chemical equation of the above reaction is as follows. CaCO₃ + 2HCl → CaCl₂ + H₂O + CO₂↑

9th Std Science Questions And Answers:

Observing Space: Telescopes Class 9 Science Chapter 18 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 18 Observing Space: Telescopes Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 18 Observing Space: Telescopes Question Answer Maharashtra Board

Class 9 Science Chapter 18 Observing Space: Telescopes Question Answer Maharashtra Board

1. Fill in the blanks with the proper words.

a. The wavelength of visible light is between …………………..….. and …………………..…. .
b. GMRT is used for …………………..….. waves.
c. A certain X-ray telescope is named after scientist …………………..…. .
d. The first scientist to use a telescope for space observations …………………..…. .
e. The biggest optical telescope in India is situated at …………………..…. .

2. Form pairs

Column ‘A’	Column ‘B’
(1) X-rays	(a) GMRT
(2) Optical telescope	(b) ISRO
(3) Indian radio telescope	(c) Hubble
(4) Launching artificial-satellite	(d) Chandra

Answer:
(1 – d),
(2 – c),
(3 – a),
(4 – b),

3. What are the difficulties in using ground-based optical telescopes? How are they overcome?
Answer:
Difficulties:

The intensity of visible light coming from a heavenly body decreases due to absorption as it passes through the Earth’s atmosphere.
Due to changes in atmospheric temperature and pressure light rays change their path.
Because of sunlight, we cannot use optical telescopes during the day.
During the night, city lights and cloudy weather cause difficulties.

Solution:

To reduce these problems, optical telescopes are situated on top of mountains, in uninhabited places.
To get rid of all the above problems completely, the telescope is placed above the earth’s atmosphere, in space.

4. Which type of telescopes can be made using a concave mirror, convex mirror, plane mirror, and a lens? Draw diagrams of these telescopes.
Answer:

A Newtonian telescope can be made using a concave mirror, plane mirror and a lens.
A Cassegrain telescope can be made using a convex mirror, concave mirror and a lens.
A refracting telescope can be made using two or more lenses.

5. Study the figure and answer the following questions:

a. What type of telescope is shown in the figure?
b. Label the main parts of the telescope.
c. Which type of mirror does the telescope use?
d. What other type of telescope uses a curved mirror?
e. Explain the working of the above telescope.
Answer:
(a) The Newtonian telescope (Reflecting telescope)
(b)

(c) Concave mirror
(d) The Cassegrain telescope
(e) Working.

Light rays coming from space are reflected by the concave mirror.
Before these reflected rays converge at the focus, they are deflected again by a small plane mirror.
As a result, they get focused at a point lying on the perpendicular to the axis of the telescope’s cylinder.
They pass through the eyepiece and we get a magnified image of the source.

6. Answer the following questions.

a. Explain the construction of Galileo’s telescope.
Answer:

The Galileo’s telescope is made up of two or more convex lenses.
The lens facing the object is called the objective lens which is made as large as possible to collect the maximum amount of light coming from a heavenly object.
The lens closer to the eye is called the eyepiece which uses the light collected by the objective lens and produces a large image of the source.
Such a telescope is also called a refracting telescope.

b. Explain the construction of a radio telescope.
Answer:

The radio telescope is made from one or more dishes of a particular parabolic shape.
As in optical telescope, the incident radio waves are reflected by these dishes and converge at the focus.
A radio receiver is placed at the focal point.
The information gathered by this receiver is passed on to a computer which analyses it and constructs an image of the source.

c. Why are optical telescopes located in uninhabited places on mountains?
Answer:

The visible light coming from a heavenly body has to pass through the earth’s atmosphere to reach the earth’s surface.
During this journey, some of the light is absorbed by the atmosphere and the intensity of the light reaching the earth’s surface decreases.
A second problem is caused by the changes in atmospheric pressure and temperature.
These changes cause turbulence in the atmosphere which in turn cause the light rays to change their path slightly and thereby shake the position of the image.
We cannot use optical telescope during the day. because of sunlight also.
During the night too, city lights and cloudy weather can cause difficulties in observing the heavenly bodies.
Hence, optical telescopes are located in uninhabited places on mountains.

d. Why can an X-ray telescope not be based on the earth?
Answer:

X-rays are emitted from distant heavenly bodies.
The rays coming towards the earth will be absorbed by the earth’s atmosphere and will go undetected.
Hence, X-ray telescopes are placed in an orbit outside the earth’s atmosphere and not on the earth.

Class 9 Science Chapter 18 Observing Space: Telescopes Intext Questions and Answers

Question 1.
What is meant by space observation? Why is it important?
Answer:
The observation of distant planets, galaxies and other astronomical objects is called as space observation.

Various space based satellites support our telecommunication networks by providing us television broadcasting.
Meteorology services such as weather forecasting help in disaster management.
Observation of positions of stars and other heavenly bodies has helped in the study of solar system, solar winds, pulsars, supernova, etc.

Question 2.
What is the difference between sky and space?
Answer:
Sky: It is a layer of gas that surrounds the earth in which sunlight is scattered making it visible from the surface of the earth.
Space: The vast emptiness beyond the sky is called as space.

Class 9 Science Chapter 18 Observing Space: Telescopes Additional Important Questions and Answers

Choose and write the correct options:

Question 1.
The first telescope was invented by
(a) Einstein
(b) Galileo
(c) Newton
(d) Mendel
Answer:
(b) Galileo

Question 2.
Eight is an wave.
(a) electric
(b) magnetic
(c) electromagnetic
(d) mechanical
Answer:
(c) electromagnetic

Question 3.
Visible radiation telescopes are also called as
(a) Gamma Ray telescopes
(b) Optical telescopes
(c) X-ray telescopes
(d) Radio telescopes
Answer:
(b) Optical telescope

Question 4.
Reflecting telescopes are mainly of two types : ……………….. and ………………. .
(a) Newtonian and Galileoan
(b) Optical and Cassegrain
(c) Newtonian and Cassegrain
(d) Optical and Refracting
Answer:
(c) Newtonian and cassegrain

Question 5.
Giant Meterwave Radio Telescope (GMRT) has been erected at near Pune.
(a) Asangaon
(b) Talegaon
(c) Narayangaon
(d) Bhategaon
Answer:
(c) Narayangaon

Question 6.
Visible light coming from heavenly bodies have to pass through the to reach the earth surface.
(a) stratosphere
(b) troposphere
(c) atmosphere
(d) biosphere
Answer:
(c) atmosphere

Question 7.
To collect the maximum amount of light coming from an object, the objective lens should be made as as possible.
(a) large
(b) small
(c) circular
(d) flat
Answer:
(a) large

Question 8.
The images formed by lenses have errors of colours. This is called
(a) chromatic disruption
(b) chromatic aberration
(c) chromatic reflection
(d) chromatic reaction
Answer:
(b) chromatic aberration

Question 9.
Radio telescope is made up of one or more dishes of shape.
(a) spherical
(b) hyperbolic
(c) parabolic
(d) hexagonal
Answer:
(c) parabolic

Match the columns:

Question 1.

Column ‘A’	Column ‘B’
(1) X-rays	(a) GMRT
(2) Optical telescope	(b) ISRO
(3) Indian radio telescope	(c) Hubble
(4) Launching artificial satellite	(d) Chandra
(5) Radio waves	(e) telecommunication
(6) INSAT and GSAT	(f) longer than 20cm

Answer:
(1 – d),
(2 – c),
(3 – a),
(4 – b),
(5 – f),
(6- e)

Question 2.

Column ‘A’	Column ‘B’
(1) Micro waves (2) Infrared waves (3) Visible light rays (4) Ultraviolet rays (5) X-rays	(a) 800 nm – 0.3mm (b) 360 pm – 400 nm (c) 3 pm – 300 pm (d) 400 nm – 800nm (e) 0.3 mm -20cm

Answer:
(1 – e),
(2 – a),
(3 – d),
(4 – b),
(5 – c)

Define the following:

Question 1.
Visible radiation
Answer:
Light is an electromagnetic wave. Every wave has a characteristic wavelength. Our eyes can see only that light which has wavelengths between 400 nm to 800 nm. Such light is called visible radiation.

Question 2.
Reflecting Telescope
Answer:
When light falls on the mirror, it gets reflected. Telescopes that use concave mirrors are called reflecting telescope.

Question 3.
Optical telescopes
Answer:
Telescopes which are made from regular lenses and mirrors and used to see visible radiations coming from space are called optical telescopes.

Question 4.
Refracting Telescopes
Answer:
Light rays change their direction as they enter a lens from the atmosphere and again when they enter the atmosphere after passing through the lens. This is called refraction. The telescopes that use such lenses are called refracting telescopes.

Question 5.
Radio telescopes
Answer:
Many heavenly bodies emit radio waves in addition to visible radiation. A special type of telescope which is used to receive these rays are known as radio telescope.

Answer the following:

Question 1.
How do refracting telescopes work?
Answer:

Most refracting telescopes are made with two or more lenses.
The two lenses are called objective lens and an eyepiece lens.
The objective lens should be large so that maximum light can be collected from the source.
Using the light collected, the eyepiece lens which is small in size, produces a large image of the source.

Question 2.
What are the difficulties in using refracting telescopes?
Answer:

We require a large objective lens which is very difficult to make. Also large lenses are heavy and tend to get distorted.
As the objective and eyepiece lens are placed on the opposite sides of the telescope, the length of the telescope also increases with increase in the size of the lenses. This makes it difficult to manage a large telescope.
The images formed by lenses have errors of colours. This is called chromatic aberration.

Question 3.
How does a radio telescope work?
Answer:

A radio telescope is made from one or more dishes of a particular parabolic shape.
The incident radio waves are reflected by these dishes and converge at a focus.
A radio receiver is placed at focal point.
The information gathered by this receiver is then passed onto a computer which analyses and constructs the image of the source.

Question 4.
What are the two types of reflecting telescopes?
Answer:

The reflecting telescopes are mainly of two types: Newtonian and Cassegrain.
The newtonian telescope uses a plane mirror and a concave mirror.
The Cassegrain telescope uses a convex and a concave mirror.

Question 5.
What is the purpose of launching X-Ray telescope Chandra?
Answer:
Chandra was launched to study X-rays coming from heavenly objects. Special mirrors which . can reflect X-rays were used in this telescope.

Answer the following:

Question 1.
State some of the satellites and their uses.
Answer:

The INSAT and GSAT series of satellites support our telecommunication network, television broadcasting and meteorological services.
It is because of them that telephone, television and internet services are available everywhere in the country.
The EDUSAT satellite is used exclusively for education.
The IRS satellite series is used for the monitoring and management of natural resources as well as disaster management.
Astrosat: It has ultraviolet and X-ray telescopes and detectors. It is a unique system having different kinds of telescopes on a single satellite.

Question 2.
What is the specialty of the artificial satellite Astrosat?
Answer:

This satellite was launched by Indian Space Research Organization (ISRO).
It has ultraviolet and X-ray telescopes and detectors. Most of the parts used in this satellite are made in India.
It is an unique system having different kinds of telescopes on a single satellite. Indian scientists are studying various aspects of the Universe using the data obtained with these telescopes.

Answer in detail:

Question 1.
Explain any two space observation telescope.
Answer:
Hubble Telescope:

In 1990, the National Aeronautics and Space Administration launched into space an optical telescope called the Hubble telescope.
It has a mirror of diameter 94 inches and is orbiting the earth at a height of 589 km from it.
This telescope is still working and has helped to make important discoveries.

Chandra Telescope:

In 1999, the National Aeronautics and Space Administration launched an X-ray telescope named Chandra, in space, to study X-rays coming from heavenly objects.
Special mirrors which can reflect X-rays were used in this telescope.
Chandra has given us very useful information about stars and galaxies.
The telescope is named after the famous Indian scientist Subramanian Chandrashekhar.

Question 2.
Write short note : GMRT
Answer:

Giant Meterwave Radio Telescope (GMRT) is a large radio telescope erected at Narayangaon near Pune.
It uses radio waves having wavelengths of about a metre, coming from heavenly bodies to study those bodies. This telescope is actually a collection of 30 dishes, each having a diameter of 45 m.
It is called a giant telescope as the arrangement of the 30 dishes over an area which measures up to 25 km across. It works as a single dish having a diameter of 25 km.
GMRT gives the same data that we would have got from a telescope having a single dish of 25 km diameter.
Scientists study the solar system, solar winds, pulsars, supernova, interstellar hydrogen clouds, etc. with the help of the GMRT.

9th Std Science Questions And Answers:

Environmental Management Class 9 Science Chapter 9 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 9 Environmental Management Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 9 Environmental Management Question Answer Maharashtra Board

Class 9 Science Chapter 9 Environmental Management Question Answer Maharashtra Board

1. Match the items in column ‘A’ with the proper ones in coloum ‘B’ and explain their impact on the environment.

Column ‘A’ Column ‘B’
1. Harmful waste – a. Glass, rubber, carry bags, etc.
2. Domestic waste – b. Chemicals, pigments, ash, etc.
3. Biomedical waste – c. Radioactive material
4. Industrial waste – d. Left over food, vegetables, peelings of fruits.
5. Urban waste – e. Bandages, cotton, needles, etc.
Answer:
(1 – c),
(2 – d),
(3 – e),
(4 – b),
(5 – a)

2. Complete the statements using the given options and justify those statements. (Geographic favourability, climate, weather, observatory)

a. Of the abiotic factors that affect biodiversity by far the most important is ……………… .
Answer:
Climate.
Climate influences our basic needs like food, clothing and shelter as well as our occupations. Various factors of climate like temperature, atmospheric pressure, sunlight, rainfall, humidity etc. will decide which kind of plants and animals can survive there.

b. A description of the climatic conditions of short duration in a particular area is ……………… .
Answer:
Weather.
Atmospheric conditions at a specific time at a particular place are referred to as weather. Weather is related to a specific location and specific time whereas climate is related to a longer duration and larger area.

c. Irrespective of the progress of human beings, we have to think about ……………… .
Answer:
Geographical favourability.
Geographical favourability includes location, availability of water, availability of natural resources and climate of a region. This has a great impact on the progress of human beings. Countries that have more favourable factors will progress more.

d. Establishments where various climatic factors are recorded are called ……………… .
Answer:
Observatories
Most countries in the world have established meteorology departments for recording climatic factors. These departments have observatories which are equipped with modern instruments and technology.

3. Answer the following questions.

a. How is first aid provided to victims of disasters who are injured?
Answer:
(i) Bleeding: If the victim is injured and bleeding through the wound, the wound should be covered with an antiseptic pad and pressure applied on it for 5 minutes with either thumb or palm.

Fracture and impact on vertebrae: If any bone is fractured, it is essential that the fractured part be immobilized. It can be done with the help of any available wooden rods / batons / rulers. If there is an impact on the back or vertebral column; the patient should be kept immobile on a firm stretcher.

Bums: If victims have bum injuries, it is beneficial to hold the injured part under clean and cold flowing water for at least 10 minutes. How is Solid Waste classified? OR What are the sources of Solid Waste?

Domestic waste: Waste food, paper, plastic paper, plastic bags, vegetable waste, fruit skins, glass and sheet metal articles, etc.

Industrial waste: Chemicals, pigments, sludge, ash, metals, etc.

Hazardous waste: Chemicals generated in various industries, radioactive materials, explosives, infectious materials, etc. Farm/Garden waste: Leaves, flowers, branches of trees, crop residues like straw, animal urine and dung, pesticides, remains of various chemicals and fertilizers, etc.

Electronic waste: Non-functional TV sets, cell phones, music systems, computers and their parts, etc.

Biomedical waste: Bandages, dressings, gloves, needles, saline bottles, medicines, medicine bottles, test tubes, body parts, blood, etc. from clinics, hospitals, blood banks and laboratories. Urban waste: Waste generated through household industries and large commercial and industrial establishments, carry bags, glass, metal pieces and rods, threads, rubber, paper, cans from shops, vegetable and meat markets, construction waste, etc.

(viii) Radioactive waste: Radioactive materials like Strontium-10, Cerium-141, Barium-140 and heavy water, etc. generated from atomic energy plants, uranium mines, atomic research centres, nuclear weapons testing sites, etc.
(ix) Mining waste: Remains of heavy metals like lead, arsenic, cadmium, etc. from mines.

b. State the scientific and eco-friendly methods of waste management.
Answer:
Following are the scientific and eco-friendly methods of waste management:

Waste separation: In this method, dry and wet wastes are separated, stored and later collected for proper use.
Composting: Decomposition of degradable kitchen waste in small pits in the backyard, garden or terrace is called composting. Good quality manure can be produced by composting leftover food, peels of fruits, vegetables etc.
Vermicomposting: Converting solid waste into manure or compost with the help of earthworms is called vermicomposting.
Vermicompost manure is highly nutritious and can be used for agricultural purposes and garden plants.
Secured landfill: Solid waste is disposed off in secured landfills.
The site for secured landfill is selected minimum 2 km away from water bodies and human habitation.
Care is taken to see that the site does not fall in sensitive zone.
The landfills are layered with clay and plastic and then the garbage is spread and left to decompose naturally.
Pyrolysis: In this method, the waste is heated to a high temperature to obtain gas and electricity.
Semi-combustible waste is burnt in pyrolysis. It is suitable for municipal solid waste management.
Incineration: Biomedical waste is burnt in incinerators to kill the pathogens. Disinfection and sterilization is also done while treating the biomedical waste.

c. Explain with suitable examples, the relationship between weather forecasting and disaster management.
Answer:

Depending upon the factors such as storms, clouds, rainfall, etc., weather forecasts are made. It is useful in aviation, shipping, fishing, industries as well as during natural calamities like dust storms, sand storms, heavy rainfall, tsunami etc where proper predictions are made with well equipped satellites and highclass technology.
Observatories at several locations are doing excellent work in the analysis of the information received from these satellites.
This data can be used in prevention of losses and danger, improving tolerance, providing relief from disaster, minimising the intensity and extent of harm as well as preparation to face the disaster.

d. Why is e-waste harmful? Express your opinion about this.
Answer:

e-waste is electronic waste which includes non-functional TV Sets, cell phones, music systems, computers and their parts, etc.
E-waste contains heavy metals like lead, beryllium, mercury and cadmium.
These metals accumulate in the soil for long periods and thus affect the biodiversity of the soil.
Many a times e-waste like battery etc. contain acids which make the soil acidic.
e-waste can cause ground water pollution, which also affects living organisms when they drink this polluted water.
Thus, e-waste affects human health and soil microorganisms directly or indirectly.

e. How will you register individual your participation in solid waste management?
Answer:
We can register our individual participation in solid waste management in the following ways:

Following the 3R mantra: Reduce (reducing the waste), reuse (reuse of waste) and recycle (recycling of waste).
Throwing plastic wrappers of chocolates, ice-creams, biscuits, etc. into dust bins. Avoid littering.
Avoiding the use of plastic bags and instead using cloth bags or bags prepared from old sarees, bed-sheets, curtains, etc.
Using both sides of a paper for writing. Reusing greeting cards and gift papers.
Avoiding use of tissue paper and preferring to use one’s own handkerchief.
Using rechargeable batteries instead of lead batteries.
Implementing various programmes of solid waste management and educating, encouraging the family and society in this regard.
Avoiding ‘use and throw’ type of articles like pens, canned cold drinks and tetra-packs etc.

4. Write notes.
Meteorology, Climatic factors, Monsoon model, Industrial waste, Plastic waste, Principles of first aid.

5. Give examples of the importance of climate in the living world with explanations, in your own words.
Answer:

Daily weather as also long term climatic conditions influence human lifestyle directly or indirectly.
Land, water bodies, plants and animals collectively form the natural environment on earth. This environment is responsible for the development of organisms.
The climate of a particular region helps to determine the diet, clothing, housing, occupations and lifestyle of the people of that region. For example, the characteristic lifestyle of Kashmiri and Rajasthani people.
Salinity of marine water, formation of oceanic currents, water cycle, etc. are all related to various weather and climatic factors.
Various climatic factors bring about the weathering of rocks in the earth’s crust.
Climate plays a very important role in the formation and enrichment of soil.
Microbes in the soil play an important role in formation of organic materials. This process depends upon various climatic factors.

6. Explain with suitable examples, the care to be taken when using the methods of transporting patients.
Answer:

Cradle Method: This method is used for children and under-weight victims.
Carrying piggy back: This method is used for carrying patients who are unconscious.
Human crutch method: If one of the legs is injured, the victim should be supported with minimum load on the other leg.
Pulling or lifting method: This method is used for carrying an unconscious patient, through a short distance.
Carrying on four-hand chair: This method is used when support is needed for the part below the waist.
Carrying on two-hand chair: This method is useful for those patients who cannot use their hands but can hold their body upright.
Stretcher: In an emergency, if a conventional stretcher is not available, then a temporary stretcher can be made using bamboo, blanket, etc.

7. Explain the differences.

a. Weather and climate
Answer:

Weather		Climate
(i)	Atmospheric conditions at a specific time at a particular place are referred to as weather.	(i)	The climate of a particular region is the average of daily readings of various weather-related parameters recorded for several years.
(ii)	Weather can change continuously.	(ii)	Climate remains constant in a region for a long duration.
(iii)	Weather is related to a specific location and specific time.	(iii)	Climate is related to a longer duration and larger area.
(iv)	Changes in the weather may occur for short periods of time.	(iv)	Changes in the climate take place slowly over a much long duration.

b. Degradable and non-degradable waste
Answer:

Degradable Waste		Non-degradable Waste
(i)	This type of waste is easily degraded by microbes.	(i)	This type of waste is not easily degraded by microbes because it takes a very long period of time and the use of various techniques.
(ii)	It includes kitchen waste (spoiled food, fruits, vegetables), ash, soil, dung, parts of the plants etc.	(ii)	It includes plastic, metal and other similar materials.
(iii)	It is also called wet solid waste or wet garbage.	(iii)	It is also called dry solid waste or dry garbage.
(iv)	If it is carefully decomposed, we can obtain compost and fuel of good quality from it.	(iv)	It can be recycled.

Class 9 Science Chapter 9 Environmental Management Intext Questions and Answers

Can you recall?

Environmental Management Class 9 Question 1.
Which natural calamities have you experienced? How did they affect the conditions in your surroundings?
Answer:
In July 2005, heavy rains caused flooding in many parts of Maharashtra including large areas of Mumbai.

They effects were as follows.

Many people lost life.
There was water clogging in most parts causing severe damage to private property and public property.
Hospitals were submerged causing severe inconvenience to patients.
The city incurred huge financial loss.

Environmental Management Class 9 Exercise Question 2.
How will you make a plan to be safe from calamities or to minimize the damage?
Answer:

As a responsible citizen we can contribute by educating the people about all the precautions to be taken when such a calamity occurs.
We can also contribute by minimizing the occurrence of natural calamity like flood by taking measure to reduce land pollution, proper disposing waste material and recycling them.
We can plan to be safe by keeping the following things handy-torch, first-aid kit, ample food supply and water storage, emergency numbers list and extra pair of clothes.

Thus by taking appropriate measures, we can be safe from calamities

Class 9 Science Chapter 9 Environmental Management Question 3.
How does the atmosphere affect our daily life?
Answer:
The atmosphere affect our daily life in following ways

If protects us from harmfull radiations of sun.
Atmosphere helps to sustain life on earth by providing oxygen for human beings and animal to breathe and carbon dioxide to plants.
It helps in keeping us warm due to green house effect.

Environmental Management Class 9 Answers Question 4.
Forecasts about which weather related factors are given during the news bulletins on Doordarshan and Akashvani?
Answer:
Forecasts about different weather related factors such as cloud cover, rain, snowfall, wind speed and temperature are given during the news bulletins on Doordarshan and Akashvani.

9 Environmental Management Exercises Question 5.
What is meant by pollution?
Answer:
Contamination of natural environment that can harmfully affect the ecosystem is called as pollution.

9th Class Science Chapter 9 Environmental Management Exercise Question 6.
What is meant by solid waste?
Answer:
The waste materials generated through the various daily human activities are called solid waste.

Maharashtra Board Class 9 Science Solutions Question 7.
What are the different things included in solid waste?
Answer:
Domestic waste, industrial waste, hazardous waste, electronic waste, biomedical waste, urban waste, radioactive waste and mining waste are the different things included in solid waste.

Question 8.
Why is it necessary to recycle non-degradable waste?
Answer:
(i) non-degradable waste cannot be easily degraded because it takes a very long period of time and the use of various techniques.
(ii) Therefore, non-degradable waste should be recycled so that it does not accumulate and cause hazards to the environment.

Question 9.
Which materials are included in solid dry waste?
Answer:
Solid dry waste includes paper, plastic, metals, glass, cardboard, thermocol etc.

Answer the following

Question 1.
In which different ways do our surroundings get polluted?
Answer:

Air pollution is caused due to emissions from industries, vehicles, burning of fossil fuels, construction, mining and agriculture.
Water pollution is caused by domestic sewage and industrial waste water released into the water bodies.
Soil pollution is caused due to industrial wastes, domestic waste, chemical fertilizers, biomedical waste and pesticides.
Noise pollution is caused by machines, vehicular traffic, loudspeakers and household appliances.

Question 2.
Which factors are affected favourably or unfavourably by climate? What must we do to minimize the effect?
Answer:

Climate plays a very important role in our day to day life.
It influences our basic needs like food, clothing and shelter as well as our occupations.
Climate is especially important for an agrarian country like India. Also climatic factors like direction and speed of the winds, temperature, atmospheric pressure etc. are also considered during construction work.
The science of meteorology helps in predicting climatic conditions by satellites in different ways such as prediction of rainfall, air pollution, dust storms, hot and cold waves tsunamic etc.
so that all the citizens are well-equipped beforehand and can take preventive measures.

Question 3.
Into which two categories can the waste materials in the lists above be classified?
Answer:
The waste materials can be classified as biodegradable waste and non-biodegradable waste.

Answer the following:

Question 1.
Make a list of various waste materials and articles in your area and prepare a chart as follows:
Answer:

Question 1.
Nowadays, an electronic device – the cell phone – is very popular. From a mobile shop near your house, find out how they dispose off old and broken down cell phones.
Answer:
Old and broken down cell phones are sold to scrap dealers, who sell to a bigger dealer where reusable parts are taken out and useless parts are sent for recycling.

Question 2.
What are the different types of casualties that are seen to occur in different types of disasters?
Answer:

Death.
Injuries.
Loss of limbs or body parts.
Burns.
Diseases.
Fractures.
Bleeding.
People becoming unconscious.

Question 3.
Which waste management processes are used in your village/town / city?
Answer:
i. The Municipal Corporation or Municipality collects the various kinds of wastes like dry waste, solid waste, biomedical waste in different coloured containers and transports them to areas where they are treated and disposed off.

ii. Industrial waste is mostly recycled and biomedical waste is treated by the scientific methods mentioned below.

a. Solid waste is disposed off in secured land fills. The site for secured landfill is selected 2 km away from water bodies and away from human habitation. Care is taken to see that the site does not fall in sensitive zone. The landfills are layered with clay and plastic and then the garbage is spread and left.
b. Pyrolysis is done for semi combustible material. Semi combustible materials are heated to high temperature by gas arid electricity.
c. The municipality can also set up biogas plants where the solid waste is converted to biogas by anaerobic fermentation. The biogas can be used to generate power and also a good manure which can be used for agriculture.
(d) Biomedical waste is burnt in incinerators to kill the pathogens. Disinfection and sterilization is also done while treating biomedical waste by the Municipal Corporation.

These are some of the waste management processes used in village/town/city.

Answer the following questions:

Question 1.
Observe the garbage collected in the dustbin of your classroom and make a list of the various materials in it.
Discuss with your teacher, how these materials can be properly disposed off. Can we do the same with the garbage generated in our house? Think about it.

Answer:
(i) Garbage collected in classroom dustbin:

Waste paper and paper bits.
Pencil shavings
Wrappers of chocolates, biscuits etc.
Left over food from tiffins and fruit peels.
Empty ball pen refills.

(ii) Out of these left over food from tiffins and fruit peels and pencil shaving can be used to make compost manure in school garden. The remaining waste can be sold to scrap dealers and sent for recycling.
(iii) Yes, we can do the same with the garbage generated in the house.

Question 2.
What is the main difference between what we see in the two pictures alongside (A and B).

Answer:

We see that in picture A there is lot of garbage spread around making the place very dirty, whereas in picture B, there is no garbage and the place is absolutely neat and clean.

Question 3.
What should we do to permanently maintain the condition seen in picture B?
Answer:
To permanently maintain the condition seen in picture B, we should follow the 3R mantra (Reduce, Reuse, Recycle). Also, we must avoid littering, throwing plastic bags, wrappers of chocolates, ice-creams, biscuits etc.

Class 9 Science Chapter 9 Environmental Management Additional Important Questions and Answers

Choose and write the correct option

Question 1.
is a long term predominant condition of the atmosphere.
(a) Climate
(b) Weather
(c) Pressure
(d) Biosphere
Answer:
(a) Climate

Question 2.
Various climatic factors like are considered during construction of runways, seaports, huge bridges and skyscrapers, etc.
(a) Direction and speed of wind
(b) Temperature
(c) Atmospheric pressure
(d) All of these
Answer:
(d) All of these

Question 3.
The was established by the United Nations Organization on 23rd March 1950.
(a) World Health Organization
(b) National Oceanographic and Atmospheric Administration
(c) World Meteorological Organization
(d) Indian Institute of Tropical Meteorology
Answer:
(c) World Meteorological Organization

Question 4.
is/are related to various weather and climatic factors.
(a) Salinity of marine water
(b) Formation of ocean currents
(c) Water cycle
(d) All of these
Answer:
(d) All of these

Question 5.
is the founder of IMD.
(a) Dr. Vasantrao Govarikar
(b) H.F. Blanford
(c) Sir Gilbert Walker
(d) Dr. Radhakrishnan Nair
Answer:
(b) H. F. Blanford

Question 6.
The monsoon model based upon 16 worldwide parameters was developed by the initiative of
(a) Dr. Vasantrao Govarikar
(b) H.F. Blanford
(c) Sir Gilbert Walker
(d) Virghese Kurien
Answer:
(a) Dr. Vasantrao Govarikar

Question 7.
In , forecasts are made taking into account the estimates of current weather related events and ongoing physical activity.
(a) Statistical model
(b) Holistic model
(c) Mathematical model
(d) All of these
Answer:
(c) Mathematical model

Question 8.
In , predictions are based upon those parameters used in other models which have the greatest effect on the monsoon.
(a) Holistic model
(b) Mathematical model
(c) Statistical model
(d) Scientific model
Answer:
(a) Holistic model

Question 9.
Radioactive materials, explosives and infectious materials are classified as waste.
(a) Industrial waste
(b) Biomedical waste
(c) Urban waste
(d) Hazardous waste
Answer:
(d) Hazardous waste

Question10.
are radioactive waste.
(a) Remains of heavy metals like arsenic, cadmium etc.
(b) Strontium-10, Cerium-141, Barium -140
(c) Waste from blood banks and laboratories
(d) All of these
Answer:
(b) Strontium-10, Cerium-141, Barium-140

Question 11.
Waste food, paper, plastic, vegetable and fruit waste etc. are classified as waste.
(a) Industrial waste
(b) Farm waste
(c) Domestic waste
(d) Urban waste
Answer:
(c) Domestic waste

Question 12.
is the 3 R mantra.
(a) Refuse, Research, Recycle
(b) Reduce, Reuse, Recycle
(c) Reduce, Reuse, Refuse
(d) Rethink, Recycle, Reuse
Answer:
(b) Reduce, Reuse, Recycle

Question 13.
is the largest producer of electricity from solid waste.
(a) India
(b) America
(c) Japan
(d) China
Answer:
(b) America

Question 14.
Chemicals, pigments, sludge, ash, metals, etc. are classified as waste.
(a) Domestic waste
(b) Industrial waste
(c) Urban waste
(d) Hazardous waste
Answer:
(b) Industrial waste

Question 15.
Period of natural degradation for banana peels is
(a) 1 month
(b) 1-2 weeks
(c) 3-4 weeks
(d) 2 months
Answer:
(c) 3-4 weeks

Question 16.
Period of natural degradation for cloth bags is
(a) 2-3 weeks
(b) 1 month
(c) 5 months
(d) 1 year
Answer:
(b) 1 month

Question 17.
Period of natural degradation for wood is
(a) 1 month
(b) 5 months
(c) 10-15 years
(c) 40-50 years
Answer:
(c) 10-15 years

Question 18.
Period of natural degradation for certain plastic bags is
(a) 50-100 years
(b) infinite duration
(c) 10 lakh years
(d) 1000 years

Question 19.
Period of natural degradation for thermocol or Styrofoam cup is
(a) 10 lakh years
(b) infinite duration
(c) 200-250 years
(d) 1 year
Answer:
(b) infinite duration

Question 20.
If any bone is fractured, it is essential that the fractured part be
(a) mobilized
(b) immobilized
(c) pulled
(d) massaged
Answer:
(b) immobilized

Question 21.
For transporting children and under-weight victims, method is used.
(a) carrying piggy back
(b) human crutch method
(c) cradle method
(d) stretcher
Answer:
(c) cradle method

Question 22.
method is useful to carry patients who are unconscious.
(a) Cradle Method
(b) Carrying piggy back
(c) Human crutch
(d) Carrying on four-hand chair
Answer:
(b) Carrying piggy back

Question 23.
method is used for carrying an unconscious patient through a short distance.
(a) Carrying piggy back
(b) Cradle method
(c) Carrying on two-hand chair
(d) Pulling or lifting method
Answer:
(d) Pulling or lifting method

Question 24.
method is useful to carry patients who cannot use their hands but can hold their body upright.
(a) Carrying on four-hand chair
(b) Carrying on two-hand chair
(c) Carrying piggy back
(d) Cradle method
Answer:
(b) Carrying on two-hand chair

v 25.
method is used to carry patients when support is needed for the part below the waist.
(a) Carrying on four-hand chair
(b) Carrying on two-hand chair
(c) Stretcher
(d) Pulling or lifting method
Answer:
(a) Carrying on four-hand chair

Question 26.
For injuries like sprains, twisting and contusion, should be applied on the injured part.
(a) turmeric powder
(b) antiseptic pad
(c) ice-pack
(d) pressure
Answer:
(c) ice-pack

Find the odd man out:

Question 1.
Waste food, paper, plastic, bandages.
Answer:
Bandages: It is a biomedical waste whereas the others are domestic waste.

Question 2.
Pesticides, fertilizers, crop residue, sludge.
Answer:
Sludge: It is an industrial waste whereas the others are farm waste.

Question 3.
Strontium -10, Cerium – 141, Barium – 140, Cadmium.
Answer:
Cadmium: It is a mining waste whereas the others are radioactive waste.

Question 4.
Banana peels, cloth bag, food waste, plastic bag.
Answer:
Plastic bag: It is a non-biodegradable waste whereas the others are degradable wastes.

Question 5.
Fruits, ash, metals, vegetables.
Answer:
Metal: It is a non-biodegradable waste whereas the others are degradable wastes.

Complete the analogy:

(1) Specific duration and specific time: Weather : : Longer duration and longer time :
(2) Mumbai: 5000 tons solid waste :: Pune:
(3) Kitchen waste, parts of plants : Wet solid waste :: Plastic, metals :
(4) Largest producer of electricity from solid waste : America : : Production of useful materials from banana peelings :
(5) Cloth bags : 1 month : : Rags :
(6) Tin cans : 50-100 years : : Aluminium cans :
(7) Wood : 10-15 years :: Styrofoam :
Answer:
(1) Climate
(2) 1700 tons solid waste
(3) Dry solid waste
(4) Japan
(5) 5 months
(6) 200-250 years
(7) Infinite duration

Match the columns:

Question 1.

Column ‘A’	Column ‘B’
(1) Mining waste	(a) Leaves, flowers, crop residue.
(2) Electronic waste	(b) Remains of heavy metals like lead, arsenic, cadmium.
(3) Farm waste	(c) Strontium-10, Cerium-141, Barium-140
(4) Radioactive waste	(d) Cell phones, TV sets, Computers

Answer:
(1 – b),
(2 – d),
(3 – a),
(4 – c)

Question 2.

Column ‘A’	Column ‘B’
(1) Banana peels	(a) 10 lakh years.
(2) Plastic bags	(b) 200-250 years.
(3) Leather shoes	(c) 3-4 weeks
(4) Aluminium cans	(d) 40-50 years

Answer:
(1 – c),
(2 – a),
(3 – d),
(4 -b)

Question 3.

Column ‘A’	Column ‘B’
(1) Thermocol (2) Tin cans (3) Woollen socks (4) Wood	(a) 1 year. (b) Infinite duration. (c) 10-15 years (d) 50-100 years

Answer:
(1 – b),
(2 – d),
(3 – a),
(4 – c)

State whether the following statements are true or false. Correct the false statements:

Question 1.
Climate is a long term predominant condition of the atmosphere.
Answer:
True.

Question 2.
Climate changes continuously.
Answer:
False. Climate does not change continuously. It remains constant in a region for a long duration.

Question 3.
If present climatic conditions are analysed with reference to the past climatic conditions, we can predict climatic changes of the future.
Answer:
True.

Question 4.
Forecasting is difficult for places where climatic changes are slow and of a limited nature.
Answer:
False. Forecasting is easy for places where climatic changes are slow and of a limited nature.

Question 5.
Climate plays a very important role in the formation and enrichment of soil.
Answer:
True.

Question 6.
Prediction maps are prepared once in 24 hours.
Answer:
False. Prediction maps are prepared twice in every 24 hours.

Question 7.
The first prediction of monsoon in India was made by Dr. Vasantrao Govariakar.
Answer:
False. The first prediction of monsoon in India was made my H.F. Blanford.

Question 8.
H.F. Blanford used the rainfall in Kerala as the parameter for prediction of monsoon in India.
Answer:
False. H.F. Blanford used the snowfall in Himalayas as a parameter for prediction of monsoon in India.

Question 9.
In Holistic model, predictions are made taking into account estimates of current weather-related events and ongoing physical interactions between them.
Answer:
False. In Holistic model, predictions are based upon those parameters used in other models which have the greatest effect on monsoon.

Question 10.
Any meteorological model depends upon the inter-relationships between parameters used in that model and the results expected from it.
Answer:
True.

Question 11.
Remains of heavy metals like lead, arsenic, cadmium, etc. from mines are industrial waste.
Answer:
False. Remains of heavy metals like lead, arsenic, cadmium etc. from mines are mining waste.

Question 12.
Use of ‘use and throw’ type of articles like pens, canned cold drinks, tetra packs should be encouraged in waste management.
Answer:
False. Use of ‘use and throw’ type of articles like pens, canned cold drinks, tetra packs should be strictly avoided in waste management.

Question 13.
We should use tissue paper instead of one’s own handkerchief for effective waste management.
Answer:
False. We should use one’s own handkerchief instead of tissue paper for effective waste management.

Question 14.
Certain plastic bags take 1 month to degrade.
Answer:
False. Certain plastic bags take 10 lakh years to degrade.

Question 15.
Banana peels can degrade in 3-4 weeks.
Answer:
True.

Question 16.
If the victim has burn injuries, it is beneficial to cover the burnt part with blanket.
Answer:
False. If the victim has burn injuries, it is beneficial to hold the injured part under clean and cold flowing water for at least 10 minutes.

Question 17.
CPR helps to bring the circulation to normal.
Answer:
True.

Question 18.
If breathing has stopped, the head should be held in backward sloping position.
Answer:
False. If breathing has stopped, the victim should be given artificial ventilation by mouth to mouth resuscitation.

Question 19.
Japan is the largest producer of electricity from solid waste.
Answer:
False. America is the largest producer of electricity from solid waste.

Question 20.
China has developed the projects of production of threads, paper and other useful materials from banana peels.
Answer:
False. Japan has developed the projects of production of threads, paper and other useful materials from banana peels.

Define the following:

Question 1.
Weather
Answer:
Atmospheric conditions at a specific time at a particular place are referred to as weather.

Question 2.
Climate
Answer:
The climate of a particular region is the average of daily readings of various weather-related parameters recorded for several years.

Question 3.
Meteorology
Answer:
The science that studies the inter-relationships between the various components of air, natural cycles, geological movements of earth and climate is called meteorology.

Question 4.
Solid waste
Answer:
Waste materials generated through daily human activities are called solid waste.

Question 5.
Urban waste
Answer:
Waste generated through household industries and large commercial and industrial establishments is called Urban waste.

Answer the following:

Question 1.
What is the necessity of solid waste management?
Answer:
Necessity of solid waste management:

For preventing environmental pollution and to keep the surroundings clean.
For energy as well as fertilizer production and through that to generate work and employment opportunities.
To reduce the strain on natural resources through treatment of solid waste.
To improve the health and quality of life and to maintain environmental balance.

Question 2.
What are the harmful effects of solid waste?
Answer:
Harmful effects of solid waste:

Effect on biodiversity.
Releases bad odour.
Produces toxic gases.
Leads to degradation of natural beauty.
Leads to pollution of air, water and soil.
Spreads diseases.

Question 3.
What first-aid should be given for injuries like sprains, twisting and contusion?
Answer:
For injuries like sprains, twisting and contusion, the ‘RICE’ remedy should be applied:

Rest: Allow the victim to sit in a relaxed position.
Ice: Apply an ice-pack to the injured part.
Compression: After the ice-pack treatment, the injured part should be massaged gently.
Elevate: The injured part should be kept in a raised/elevated position.

Question 4.
Why do meteorological models need to be changed continually?
Answer:

Any meteorological model depends upon the inter-relationship between parameters used in that model and the results expected from it.
However, as these inter-relationships with reference to the ocean and atmosphere are never constant, meteorological models need to be changed continually.

Question 5.
What is urban waste? What does it include?
Answer:

Waste generated through household industries and large commercial and industrial establishments is called urban waste.
It includes carry bags, glass, metal pieces and rods, threads, rubber, paper, cans from shops, waste from vegetable and meat markets, construction waste etc.

Question 6.
What does biomedical waste include?
Answer:
biomedical waste includes bandages, dressings, gloves, needles, saline bottle, medicines, medicine bottles, test tubes, body parts, blood etc. from clinics, hospitals, blood banks and laboratories.

Write short notes on:

Question 1.
Meteorology
Answer:

The science that studies the inter-relationship between the various components of air, natural cycles, geological movements of the earth and climate is called meteorology.
Meteorology includes the study of storms, clouds, rainfall, thunder, lightning etc.
Depending upon the study of such factors, weather forecasts are made.
They are useful to common people, farmers, fisheries, aviation services, water transport and various other organizations.

Question 2.
Climatic factors
Answer:

The climate of a particular region is the average of daily readings of various weather-related parameters recorded for several years.
Climatic factors include direction and speed of wind, temperature, atmospheric pressure, clouds, rainfall, humidity, visibility etc.
These factors influence our basic needs like food, clothing, shelter as well as our occupations.
Various climatic factors bring about the weathering of rocks in the earth’s crust.
Microbes in the soil play an important role in formation of organic materials. This process also depends upon various climatic factors.

Question 3.
Monsoon model
Answer:

The tradition of forecasting the monsoon season in India is older than 100 years.
After the famine of 1877, H.F. Blanford, the founder of IMD had made such a prediction for the first time taking the snowfall in the Himalayas as a parameter for this prediction.
In the decade of the 1930’s, the then director of IMD, Sir Gilbert Walker had underlined the relationship between various worldwide climatic factors and the Indian monsoon and based on available observations and previous recordings related to this relationship, he put forth a hypothesis regarding the nature of the monsoon.
With the initiative of Dr. Vasantrao Govarikar in the decade of the 1990’s, a monsoon model based upon 16 worldwide climatic parameters was developed. This model was in use from 1990 to 2002.
Presently, new models are being developed at IITM. Work is in progress at two levels, namely designing new models and developing new technology.
The main focus is on the development of the radar system and satellite technology.

Question 4.
Plastic waste
Answer:

Plastic waste is the accumulation of plastic products in the environment that adversely affects environment, humans and animals.
Plastic waste is excessively generated as plastic is inexpensive and durable.
Plastic is slow to degrade. It takes around 10 lakh years for certain plastic bags to degrade. .
Plastic waste affects land and water.
It also affects the health of animals, cattle unknowingly ingest these plastic bags leading to stomach cancer in them.
Plastic also releases toxic chemicals which are carcinogenic to humAnswer:
To avoid plastic waste, cloth bags should be used instead of plastic bags. Plastic articles should be recycled.

Question 5.
Industrial waste
Answer:

Industrial waste is the waste produced by industrial processes or activities.
There is a huge variety of industries producing different types of materials and articles. All of these use raw materials and give out a lot of waste.
There are hundreds of mines which extract copper, silver, gold, iron, coal etc. Huge quantities of waste are produced while processing them.
Cement industries give out solid, liquid and gaseous wastes.
While refining crude oil, a lot of poisonous gaseous and liquid wastes are produced.
Construction units produce huge quantities of waste stones, pebbles, broken bricks, wood waste etc. Mostly they are dumped in landfills.
It also includes chemicals, pigments, sludge, ash, metal, etc. given out from mining, textile, construction, chemical industries.

Question 6.
Principles of first aid
Answer:
Life and Resuscitation – ‘ABC’ is the Basic Principle of first aid which is provided to the victims of disaster.

Airway: If the victim has difficulty in breathing, the head should be held in a backward sloping position or the chin should be raised so that the respiratory passage remains open.
Breathing: If breathing has stopped, the victim should be given artificial ventilation by mouth to mouth resuscitation.
Circulation: If the victim is unconscious, then after giving mouth to mouth respiration twice,

Question 7.
Statistical Model
Answer:

In this model, current climatic observations in a region are compared with earlier parameters such as oceanic temperature, atmospheric” pressure and the nature of the monsoon rainfall for several years.
This data is comparatively analysed by statistical methods and predictions are made about the monsoon in the present conditions.

Question 9.
Holistic Model
Answer:

In this model, predictions are based upon those parameters used in other models which have the greatest effect on the monsoon.
Nowadays, predictions declared by IMD are the collective outcome of various model. This is called a holistic model.

Complete the following concept chart:

Question 1.
Weather-related climatic factors
Answer:

Question 2.
Harmful effects of solid waste
Answer:

Question 3.
Scientific and eco-friendly waste Management
Answer:

Answer in detail:

Question 1.
What are the principles of solid waste management?
Answer:
Principles of solid waste management:

Reuse: After use, materials should be reused for some other proper purposes.
Refuse: Refusal to use articles made from non- degradable articles like plastic and thermocol.
Recycle: Production of useful articles by recycling solid wastes. For example, paper and glass can be recycled.
Rethink: Rethinking our habits, activities and their consequences in connection with the use of various articles of daily use.
Reduce: Restricting the use of resources to avoid their wastage.
Old materials should be reused. One thing should be shared by many, use and throw type of objects should be avoided.
Research: Conducting research related to reuse of materials that are temporarily out of use.
Regulation and Public awareness: Following the laws and rules related to waste management and motivating others to do the same.

Question 2.
What is disaster management? What actions does it include?
Answer:
Disaster management is action implemented through proper planning, organized activity and co-ordination.

It includes the following:

Prevention of loss and danger.
Improving tolerance.
Providing relief from disaster, minimising the intensity and extent of harm.
Preparation to face the disaster.
Immediate action in the disaster situation.
Assessment of damages and intensity of the disaster.
Arranging for rescue work and help.
Rehabilitation and rebuilding.

Question 3.
Write a short note on : Indian Meteorological Department
Answer:

The Indian Meteorological Department was founded by the British in 1875 at Shimla.
Its head office is at Pune and its Regional offices are at Mumbai, Kolkata, Chennai, Nagpur and Delhi.
Maps are prepared every day which indicate the daily predictions about the weather.
Such maps are prepared and published twice in every 24 hours.
In this institute, research goes on continuously on various aspects like instruments for climatic readings, predictions made about climate using radar, predictions about climate related to seismology, predictions regarding rainfall by satellites, air pollution etc.
The Indian Meteorological Department provides information regarding weather and climatic conditions to other departments like aviation, shipping, agriculture, irrigation, marine oil exploration and production etc.
Predictions regarding calamities like dust storms, sand storms, heavy rainfall, hot and cold waves, tsunami, etc. are communicated to various departments, all types of mass communication media and all citizens.
India has launched several satellites equipped with highclass technology.
Observatories at several locations are doing excellent work in the analysis of the information received from these satellites.

9th Std Science Questions And Answers:

Life Processes in Living Organisms Class 9 Science Chapter 15 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 15 Life Processes in Living Organisms Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 15 Life Processes in Living Organisms Question Answer Maharashtra Board

Class 9 Science Chapter 15 Life Processes in Living Organisms Question Answer Maharashtra Board

1. Match the pairs and explain.

Column ‘A’	Column ‘B’
(1) Growth of pollen tube towards ovules (2) Growth of shoot system (3) Growth of root system (4) Growth towards the water	(a) Gravitropic movement (b) Chemotropic movement (c) Phototropic movement (d) Growth-irrelevant movement (e) Hydrotropic movement

Answer:
(1 – b),
(2 – c),
(3 – a),
(4 – e).

2. Complete the paragraph.

The milk was on the stove. Rasika was engrossed in watching television. She smelled something burning. She ran towards the kitchen. The milk was boiling over. She held the vessel with her bare hands but, screaming, she let it go at once. This activity was controlled by ……………….. cells. Special ends of ……………….. in these cells collected the information, from where it was transferred to the ……………….. and then towards the terminal end of the ……………….. The chemicals produced at the terminal end passed through the minute space i.e. ………………. . In this way, ……………….. were conducted in the body and the process of ……………….. was completed by conducting the impulses from ……………….. to ………………

(Nerve, muscle cell, impulse, dendrite, synapse, axon, reflex action, cell body)
Answer:
nerve, dendrite, cell body, axon, synapse, impulses, reflex action, nerve, muscle cell.

3. Write notes on Root pressure, Transpiration, Nerve cell, Human brain, Reflex action

4. Name the hormones of the following endocrine glands and the function of each.
Pituitary, Thyroid, Adrenal, Thymus, Testis, Ovary.

Life Processes In Living Organisms Class 9 Question 1.
Pituitary:
Answer:

Hormone	Function
(i) Growth hormone	Stimulates growth of bones.
(ii) Adrenocorticotropic hormone	Stimulates adrenal gland.
(iii) Thyroid-stimulating hormone	Stimulates thyroid gland.
(iv) Prolactin	Stimulates milk production.
(v) Follicle-stimulating hormone	Controls growth of gonads.
(vi) Luteinizing hormone	Controls menstrual cycle and ovulation.
(vii) Oxytocin	Contracts uterus during parturition.
(viii) Antidiuretic hormone	Regulates water-level in the body.

Class 9 Science Chapter 15 Life Processes In Living Organisms Question 2.
Thyroid
Answer:

Hormone	Function
(i) Thyroxine	Controls growth of body and metabolic activities.
(ii) Calcitonin	Controls calcium metabolism and calcium level in blood.

Life Processes In Living Organisms Class 9 Exercise Question 3.
Adrenal
Answer:

Hormone	Function
(i) Adrenalin and nor-adrenalin	Controls behaviour during crisis and emotional situation.
(ii) Corticosteroid	Maintains balance of Na⁺ and K⁺ and stimulates metabolism.

9th Class Science Chapter 15 Life Processes In Living Organisms Exercise Question 4.
Thymus
Answer:

Hormone	Function
Thymosin	Control the cells which give rise to immunity.

Question 5.
Testis
Answer:

Hormone	Function
Testosterone	Stimulates growth of secondary sexual characteristics like beard, mustache, hoarse voice etc. in men.

Std 9 Science Chapter 15 Life Processes In Living Organisms Question 6.
Ovary
Answer:

Hormone	Function
(i) Oestrogen	Stimulates growth of the endometrium. Stimulates growth of secondary sexual characteristics in women.
(ii) Progesterone	Prepares the endometrium for conception and maintains pregnancy.

5. Draw and label the diagrams.
Human endocrine glands, Human brain, Nephron, Nerve cell, Human excretory system.

15. Life Processes In Living Organisms Question 1.
Human endocrine glands
Answer:

15 Life Processes In Living Organisms Question 2.
Human brain
Answer:

Life Processes In Living Organisms 9th Class Notes Question 3.
Nephron
Answer:

Life Processes In Living Organisms Class 9 Questions And Answers Question 4.
Nerve cell
Answer:

Life Processes In Living Organisms Class 9 Solutions Question 5.
Human excretory system
Answer:

6. Answer the following.

a. Explain chemical co-ordination in humans and give the names and functions of some hormones.
Answer:
Chemical co-ordination in humans :

In humans chemical co-ordination is brought about with the help of certain chemical substances called hormones.
Hormones are secreted by endocrine glands. These glands are also called ductless glands.
These glands do not have any arrangement of their own to either store or carry their secretions. So, the hormones are directly released into the blood circulation.
Though the endocrine glands are present at specific locations in our body, their secretions reach all parts of the body via the blood.
Endocrine glands along with the nervous systems are responsible for control and co-ordination in our body.
These two systems help each other to control and integrate the various activities of the body.
A marked difference between these two systems is that nerve impulses are fast but short-lived whereas the actions of hormones are very slow but long-lasting.
It is very important that hormones are secreted only in the required quantity and there is a special mechanism which controls the quantity and timing of hormone secretion.
For example, whenever there is an increase in blood glucose level, certain cells in the pancreas get stimulated and as a response, they release a greater quantity of insulin, thus bringing down the sugar level to normal.

Hormone	Function
(1) Growth hormone	Stimulates growth of bones.
(2) Luteinizing hormone	Controls menstrual cycle and ovulation.
(3) Thyroxine	Controls growth of body and metabolic activities.
(4) Insulin	Stimulates liver to convert excess blood glucose to glycogen.
(5) Testosterone	Stimulates growth of secondary sexual characters like beard, mustache, hoarse voice, etc. in men.

Names and functions of some hormones:

b. Explain the difference between the excretory system of humans and plants.
Answer:

Excretory system of humans	Excretory system of plants
(i) In humans, the excretory system carries out the function of the removal of waste from the body.	(i) In plants, there is no special system or organ for excretion.
(ii) Waste substances are generally eliminated out of the body	(ii) Most of the waste substances are stored in the leaves, flowers, fruits and bark of the stem.
(iii) The excretory products are urea, uric acid, ammonia, etc.	(iii) The excretory products are gum, resin, latex of rubber, etc.

c. Explain co-ordination in plants with the help of suitable examples.
Answer:

Plants do not have systems like the nervous system or muscular system.
In plants, movements are mainly in the form of responses given to the stimuli.
Plants show two types of movements – growth relevant movements and growth irrelevant movements.
Movement or growth of any part of the plant in response to an external stimulus is called tropism or tropic movement.
Examples of growth-relevant movements are :
The shoot system of any plant responds to the light stimulus i.e., it grows towards the source of light. This is called phototropic movement.
The root system of plants responds to stimuli like gravitation and water. These responses are called gravitropic movement and hydrotropic movement respectively.
Movement shown by plants in response to specific chemicals is called chemotropic movement.
For example, the growth of the pollen tube towards the ovule.
Some specific movements of the plants do not lead to the plant growth.
Such movements are called growth-irrelevant movements.
As a response to changes in the surroundings, plant hormones bring about various movements in plants.
Examples of growth irrelevant movements are closing of leaflets of Touch-me-not (Mimosa) plant on touch.
In the plant called Venus fly trap, when an insect visits the flower like trap, the trap closes up and the trapped insect is digested by the plant.
The lotus flower opens during day-time while that of the tuberose opens at night.
In plants like Touch-me-not (Mimosa), movement also occurs at places other than where it has been touched.
Hence, we can infer that the information about the touch must have been released within the plant from one place to another.
Plants use electrochemical impulses for transfer of information from one place to another.
Plant cells change their shape by increasing or decreasing the water content and thereby, bring about the movements of plants.

7. Explain in your own words with suitable examples.

a. What is meant by co-ordination?
Answer:

Several different organ systems function in multicellular organisms.
Their life goes on smoothly if there is co-ordination between different organ systems or organs and the stimuli in the surrounding.
Depending upon this, we can say that systematic regulation of different processes can be called control and bringing about the different processes in the proper sequence is called co-ordination.
If any activity in the body is to be completed successfully, proper co-ordination between different systems, and organs participating at different steps of that activity is necessary.
If due to lack of co-ordination, there is confusion at any step, the activity may not get completed. There should be no randomness at any step.
There should be proper co-ordination between internal activities of the body resulting from various factors like body temperature, water- level, enzyme-level, etc. or stimuli arising in the surrounding environment.
Proper co-ordination between various systems of an organism helps to maintain a state of equilibrium called homeostasis which is necessary for the optimal efficiency of the body.

b. How does excretion occur in human beings?
Answer:

Removal of wastes from the body is very important and it is the excretory system that carries out this function.
The human excretory system consists of a pair of kidneys, a pair of ureters, the urinary bladder and the urethra. Urine is formed by the kidneys by separating the waste and unwanted excess substances from the blood.
The functional unit of the kidney that performs the basic function of filtration is called a nephron. The urea produced in the liver comes into the blood.
When the urea-containing blood comes into the glomerulus, it is filtered through capillaries and urea and other similar substances are separated from it.
Water molecules and small molecules of some other substances can cross the semipermeable membrane of Bowman’s capsule.
The solution accumulated in the cavity of Bowman’s capsule passes into the tubular part of the nephron. Here, molecules of water and some other useful substances are reabsorbed into the blood.
Urine is formed from the remaining solution which is full of waste materials. The urine is carried by the ureters and stored in the urinary bladder. Afterwards, urine is given out through the urethra.

c. How is excretion in plants useful to human beings?
Answer:

Plants give out oxygen during photosynthesis by diffusion which is useful to human beings for respiration.
Some waste materials of plants for example, gum, resin, latex of rubber, etc. are useful to humans.

d. Describe the transportation system in plants.
Answer:

Plants have two types of conducting tissues i.e., xylem which conducts water and phloem which conducts food.
During transpiration, water is released into the atmosphere.
As a result, water level is the epidermal layer of the leaf decreases.
Water is brought up to the leaves through the xylem so as to compensate for the lost water.
Transpiration helps in absorption of water and minerals and distribution to all parts of the plant whereas root pressure preforms the important role of pushing the water up at night time.
The food produced by leaves is transported to each cell of the plant through phloem.
When the food material like sucrose is transported towards a part of the plant through phloem, using ATP, the water concentration in that part decreases.
As a result, water enters the cell by diffusion. The pressure on the cell wall increases due to increase in the cellular contents.
Due to the increased pressure, food is pushed into the neighboring cells where the pressure is low.
This process helps the phloem to transport the materials as per the need of the plant.

Class 9 Science Chapter 15 Life Processes in Living Organisms Intext Questions and Answers

Class 9 Science Chapter 15 Life Processes In Living Organisms Exercise Question 1.
How do the digestive system and respiratory system work?
Answer:
(a) Digestive system:

The digestive system is responsible for digestion of food. i.e. breaking down complex insoluble food into simpler soluble form.
The digestive system is made up of alimentary canal and digestive glands.
The alimentary canal is a long and muscular tube of varying diameter which extends from the mouth to the anus.
The digestive glands associated with alimentary canal are salivary glands, gastric glands, liver and pancreas.
The process of digestion includes various stages wherein the food passes through the different organs of the alimentary canal and there it is digested part by part with the help of various enzymes secreted from the digestive glands.
After the food is digested, the important nutrients are absorbed into the blood and the undigested food and residue of digested food is removed out of the body through the anus.

(b) Respiratory system:

Respiration is the process of release of energy from the assimilated food.
The respiratory system consists of nose, pharynx, larynx, trachea, bronchi and lungs (alveoli).
Oxygen enters our body through breathing.
This oxygen is taken to the cells and with the help of oxygen, food is oxidized into the cells to release energy in the form of ATR
During this process, carbon dioxide and water vapour are given out as by-products which are given out during breathing.

Thus, the digestive and respiratory systems work in co-ordination with each other to produce energy from food.

Life Processes In Living Organisms Exercise Question 2.
Previously you have performed the activity of observing a branch covered in a plastic bag. What did you observe in that activity?
Answer:

When a branch is covered in a plastic bag, we observe that small droplets of water accumulate on the inner side of the plastic bag.
This shows that leaves release water in the form of vapour through the stomata during transpiration. These vapours get condensed to form water droplets and accumulate inside the bag.

Life Process In Living Organism Exercise Question 3.
Which are the sensory organs of an organism? What is their function?
Answer:

Sensory organs of an organism are eyes, ears, tongue, skin and nose.
The eyes help the organism to perceive the sensation of light to see the objects around it.
The ears help the organism to perceive the sensation of sound and also perceive the sensation of pressure.
The tongue helps to perceive different tastes and also in chewing the food.
The skin helps to perceive the sensation of touch, pain, pressure etc.
Some insects also possess antennae for sensing the changes in the environment.

15 Life Processes In Living Organisms Class 9 Question 4.
Where are the gustatory and olfactory nerves to be found?
Answer:

Gustatory nerves are concerned with sense of taste whereas olfactory nerves are concerned with the sense of smell.
Gustatory nerves are found in the tongue from where they carry impulses to the gustatory cortex in the brain.
Whereas the olfactory nerves are found in the nasal passage from where they carry impulses to the olfactory lobes in the brain.

Answer the following questions:

15.Life Processes In Living Organisms Question 1.
Why do we eat fruits and vegetables? Do the plants also need minerals like we do?
Answer:

We eat fruits and vegetables to get nutrients like carbohydrates, vitamins, minerals and fibers. These nutrients are important for the proper functioning of the body .
Plants too need minerals for their growth and development.

Life Processes In Living Organisms Class 9 Notes Question 2.
From where do plants get inorganic substances other than carbon dioxide and oxygen?
Answer:
Plants get inorganic substances like nitrogen, phosphorus, magnesium, manganese, sodium etc. from the soil. Soil is the nearest and richest source of these elements.

9th Std Science Chapter 15 Life Processes In Living Organisms Question 3.
At least a small quantity of garbage or waste is produced every day in each house. What will happen if you keep this garbage for many days in your house?
Answer:

If we keep garbage for many days in our house, it will start decaying due to the growth of decomposers like fungi and bacteria.
This will result in foul odour and will also lead to spread of diseases.

Life Processes In Living Organisms Exercise Class 9 Question 4.
Sometimes, while eating we bite our own finger or tongue by mistake.
Answer:

Sometimes, while eating we over-fill our mouth causing the bite to misalign, thus we bite our own finger or tongue by mistake.
If we are dehydrated, the muscles of the mouth and tongue do not function properly causing us to bite our own tongue.
If we are distracted with other activities while eating, it can cause us to bite our tongue or finger.
Thus, due to lack of co-ordination sometimes while eating, we bite our own finger or tongue by mistake.

9th Class Science 15 Chapter Life Processes In Living Organisms Question 5.
Sometimes, we choke while eating in a hurry.
Answer:

There is an elastic flap at the starting of the wind-pipe called epiglottis which opens whenever we breathe in air and closes to prevent the entry of food into the respiratory system.
While eating in hurry, due to lack of co-ordination, the epiglottis opens to take in air but food too enters in causing us to choke.

Life Processes In Living Organisms Class 9 Extra Questions Question 6.
An injury to the medulla oblongata can lead to death. Why?
Answer:

The medulla oblongata controls involuntary activities like the beating of the heart, blood circulation, breathing etc.
An injury to the medulla oblongata will stop these activities, leading to death.

Life Processes In Living Organisms Class 9 Maharashtra Board Question 7.
You may have seen how a drunken person struggles to maintain his body balance. An excess of alcohol in the body causes one to lose control over it. Why does this happen? Find out the reason with help of the internet.
Answer:

The cerebellum co-ordinates voluntary movements and maintains balance of the body.
An excess of alcohol causes dysfunctioning of the cerebellum.
It results in primary loss of co-ordinated movements and loss of balance.

9th Life Processes In Living Organisms 5 Question 8.
Why does this happen?

(a) Leaves of plants fall off in a particular season.
Answer:

Plants lose water through their leaves by transpiration. So some plants shed their leaves in dry season to reduce transpiration and conserve water.
In plants, the waste substances are stored in the vacuoles of leaf-cells which are then shed along with the leaves in a specific season.

(b) Fruits, flowers fall off after a certain period of time.
Answer:

In plants, waste substances are stored in the vacuoles of fruits and flowers. So, they fall off after some time to excrete these wastes.
Also, when fruits and flowers mature, the supply of nutrients to mature fruits and flowers is blocked. This causes abscission in that part of the plant leading to their detachment from the plant body and falling off.

Resin, gum etc. are the waste products of plants. They are given out after some time as a process of excretion in plants.
Many plants, particularly, woody plants produce resin and gum in response to injury. These resin and gum act as bandage protecting the plants from invading insects and pathogens.

15 Life Processes In Living Organisms Exercise Question 9.
Which waste products are produced in our body through metabolic activities?
Answer:
The waste products formed in our body through metabolic activities are urea, uric acid, ammonia, carbon dioxide etc.

Life Processes In Living Organisms 9th Class Exercise Question 10.
As compared to the monsoons and winter a very small quantity of urine is produced in the summer season. Why is it so?
Answer:
In summer, we sweat more due to excess heat. So, the body tries to conserve water by reducing urine formation. This is to prevent dehydration.

Question 11.
In adults, the process of urination is under their control but not in infants. Why is it so?
Answer:

In adults, the muscles of the bladder are under the voluntary control. So the process of urination is under control.
In infants, the bladder muscles are not mature until about two years of age. So, the process of urination is not under control.

Answer the following questions:

Question 1.
Observe the following figures carefully.

Answer:
Observations:

Figure ‘A’ shows chemotropic movement. Pollen tube grows towards the ovule in response to specific chemicals released by the ovule.
Figure ‘B’ shows phototropic movement. Shoot grows towards the Sun in response to stimulus of light.
Figure ‘C’ shows thigmotropic movement. Tendrils of climbers are sensitive to touth. When they come in contact with an object, they entwine around the object and cling to it.
All the above movements are related to growth. Hence, they are called growth relevant movements.

Question 2.
Observe the pictures carefully and think about them.

Answer:

Figure ‘A’ shows touch-me-not (Mimosa) plant. In this plant, the leaflets close in response to stimulus of touch.
Figure ‘B’ shows Venus fly trap. In this plant, there is a trap that appears and smells like a flower and deceives the insect. When an insect visits that flower-like trap, the trap closes up and the trapped insect is digested by the plant,
Figure ‘C’ shows lotus plant. The lotus flower opens during day-time.?
Figure ‘D’ shows Balsam plant. In this plant, the ripened fruit dehisces (bursts open) at the right time to disperse the seeds.

Question 3.
As you watch the match being played on your school ground, you will see the control and co-ordination among the movements of the players. Make a list of all such different actions.
Answer:
In an inter-house basketball match, control and co-ordination is seen in dodging the ball, jumping, running, passing it to the team mates and dribbling the ball.

Question 4.
Observe the figure carefully and as per the numbers in that figure, answer the following questions.

(a) What is happening at 1 and 2?
Answer:
At 1 stimulus of heat is received by thermo-receptors in the skin. At 2, the hand is withdrawn instantly.

(b) Which nerve carried the impulse to the point marked 3? In which direction is it conducting the impulse?
Answer:
Sensory nerve carried the impulse to the point marked 3. The impulse is conducted from the skin towards the spinal cord.

(c) Which is the nerve shown by 4?
Answer:
The nerve shown by 4 is association neuron. It is present in the gray matter of the spinal cord. It receives the sensory impulse, interprets it and generates impulse.

(d) Which is the organ marked as 5?
Answer:
Spinal cord.

(e) At 6, which nerve is conducting the response impulse?
Answer:
Motor nerve.

(f) At 7, where has the impulse reached? What is its effect?
Answer:
At 7, the impulse has reached the muscles of the hand. As a result, the muscles contract and the hand is withdrawn instantly in response to the stimulus of heat.

Question 5.
Sketch and label:
Answer:

Stimulus
Hand is withdrawn
Sensory neuron
Association neuron
Spinal cord
Motor neuron
Muscles

(6) Observe the figure and list down functions for ‘A’ and ‘B’

Answer:

Functions of Left Brain	Functions of right brain
(i) Analytical thinking	Holistic thinking
(ii) Logical thinking	Intuition
(iii) Language	Creativity
(iv) Science and Mathematics	Art and music

Answer the following questions:

Question 1.
Take a small plant like balsam or tuberose with its roots intact. Wash and clean its roots. As shown in the fig, keep it in the water containing a stain like safranin or eosin. Observe the stem and the veins of the leaves after 2-3 hours.

Answer:

The stem and veins of the leaves appear pinkish in colour.
Due to the root pressure generated, eosin solution is continuously pushed upward.
As a result water reaches xylem and the water column is pushed forward.

Question 2.
Take a transverse section of the stem of a plant and observe the stained xylem under a compound microscope.
Answer:
The xylem elements appear pinkish as the eosin solution is conducted upwards through the xylem. From this we infer that the xylem is responsible for the conduction of water and minerals in the plant.

Question 3.
Observe your mother while she cuts the elephant’s foot (Amorphophallus) or arum leaves. Your hands may also begin to itch if you try to cut these leaves. Why does this happen? Try to find out. Ask your mother what she does to prevent the itching.
Answer:

In some plants like elephant foot (Amorphophallus) or arum, waste materials are in the form of crystals of calcium oxalate. They are called raphides.
As they are needle-shaped, they prickle and cause irritation of the skin leading to itching.
This can be prevented by applying tartaric acid (tamarind) or citric acid (lemon) on the hands while cutting these vegetables as the acids dissolve the crystals of calcium oxalate.

Class 9 Science Chapter 15 Life Processes in Living Organisms Additional Important Questions and Answers

Choose and write the correct options.

Question 1.
The transport of food produced in leaves to each cell in the plant body is called …………………………… .
(a) Transpiration
(b) Root pressure
(c) Translocation
(d) Ascent of sap
Answer:
(c) translocation

Question 2.
Kidneys filter blood about ……………………………. times every day.
(a) 100
(b) 200
(c) 300
(d) 400
Answer:
(d) 400

Question 3.
About ……………………………. of blood is sent through the dialysis machine at one time.
(a) 500 ml
(b) 5 l
(c) 200 ml
(d) 400 ml
Answer:
(a) 500 ml

Question 4.
The movement of plant towards the source of light is called ……………………………. movement.
(a) chemotropic
(b) hydrotropic
(c) phototropic
(d) gravitropic
Answer:
(c) phototropic

Question 5.
The movement of root system towards stimulus of gravity is called ……………………………. movement.
(a) phototropic
(b) gravitropic
(c) hydrotropic
(d) chemotropic
Answer:
(b) gravitropic

Question 6.
The movement of root system towards stimulus of water is called ……………………………. movement.
(a) Phototropic
(b) Gravitropic
(c) Hydrotropic
(d) Chemiotropic
Answer:
(c) hydrotropic

Question 7.
Hormone ……………………………. helps in stem elongation.
(a) Auxin
(b) Gibberellin
(c) Cytokinin
(d) Abscisic acid
Answer:
(b) Gibberellin

Question 8.
Hormone ……………………………. helps in cell division.
(a) Auxin
(b) Gibberellin
(c) Cytokinin
(d) Abscisic acid
Answer:
(c) Cytokinin

Question 9.
The hormone ……………………………. is effective in prevention and retardation of growth, leaf wilting, etc.
(a) Auxin
(b) Cytokinin
(c) Gibberellin
(d) Abscisic acid
Answer:
(d) Abscisic acid

Question 10.
……………………………. neurons conduct impulses from the sensory organs to the brain and the spinal cord,
(a) Sensory
(b) Motor
(c) Association
(d) All of these
Answer:
(a) Sensory

Question 11.
The brain of an adult human weighs about …………………………… .
(a) 500 – 600 grams
(b) 2 – 3 kilograms
(c) 1300 -1400 grams
(d) 1500 -1600 grams
Answer:
(c) 1300 – 1400 grams

Question 12.
……………………………. is the largest part of the brain.
(a) Cerebrum
(b) Cerebellum
(c) Medulla oblongata
(d) Spinal cord
Answer:
(a) Cerebrum

Question 13.
There are two triangular swollen structure called ……………………………. on the upper side of the medulla oblongata.
(a) Ventricles
(b) Meninges
(c) Pyramids
(d) Pons
Answer:
(c) Pyramids

Question 14.
Control of voluntary movements is done by …………………………… .
(a) Cerebrum
(b) Cerebellum
(c) Medulla oblongala
(d) Spinal cord
Answer:
(a) Cerebrum

Question 15.
Co-ordination of voluntary movements is done by …………………………… .
(a) cerebrum
(b) cerebellum
(c) medulla oblongata
(d) spinal cord
Answer:
(b) cerebellum

Question 16.
Control of involuntary activities like the beating of the heart, blood circulation, breathing etc. are controlled by …………………………… .
(a) Spinal cord
(b) Cerebrum
(c) Cerebellum
(d) Medulla oblongata
Answer:
(d) Medulla oblongata

Question 17.
The function of cerebrum is to …………………………… .
(a) control of voluntary movements
(b) co-ordination of voluntary movements
(c) control of involuntary activities
(d) maintaining the body balance
Answer:
(a) control of voluntary movements

Question 18.
The function of cerebellum is …………………………… .
(a) to control of voluntary movements
(b) to maintain the body balance
(c) to control of involuntary activities
(d) to co-ordinate of voluntary movements
Answer:
(b) to maintain the body balance

Question 19.
Hormone ……………………………. stimulates the liver to convert excess blood glucose into glycogen.
(a) Glucagon
(b) insulin
(c) Somatostatin
(d) Pancreatic polypeptide
Answer:
(a) Glucagon

Question 20.
Hormone ……………………………. controls behaviour during crisis and emotional situation.
(a) Thyroxine
(b) Parathormone
(c) Adrenalin and Nor adrenalin
(d) Somatostatin
Answer:
(c) Adrenalin and Nor adrenalin

Question 21.
……………………………. controls menstrual cycle and ovulation.
(a) Prolactin
(b) Oxytocin
(c) Luteinizing hormone
(d) Progesterone
Answer:
(c) Luteinizing hormone

Question 22.
……………………………. stimulates growth of secondary sexual characteristics in men.
(a) Thymosin
(b) Testosterone
(c) Oestrogen
(d) Thyroxine
Answer:
(b) Testosterone

Question 23.
……………………………. occurs through stomata.
(a) Translocation
(b) Perspiration
(c) Transpiration
(d) Conduction
Answer:
(c) Transpiration

Question 24.
……………………………. performs the important role of pushing the water up during the night time.
(a) Translocation
(b) Root pressure
(c) Transpiration pull
(d) None of these
Answer:
(b) Root pressure

Question 25.
In plants, gaseous substances are given out by …………………………….
(a) Root pressure
(b) Osmosis
(c) Diffusion
(d) Translocation
Answer:
(c) diffusion

Question 26.
Each kidney has approximately ……………………………. nephrons.
(a) 1 lakh
(b) 10,000
(c) 10 lakh
(d) 50 lakh
Answer:
(c) 10 lakh

Question 27.
Insulin is secreted by the ……………………………. of the pancreas.
(a) Alpha cells
(b) Beta cells
(c) Delta cells
(d) F cells
Answer:
(b) Beta cells

Select the odd man out:

Question 1.
Skin, Brain, Kidneys, Lungs.
Answer:
Brain – It is a controlling organ whereas the others are excretory orgAnswer:

Question 2.
Gum, Resin, Urea, Latex
Answer:
Urea – It is an excretory product of animals whereas the others are excretory products of plants.

Question 3.
Gibberellin, Auxin, Thyroxine, Cytokinin.
Answer:
Thyroxine – It is a hormone in animals whereas the others are hormones in plants.

Question 4.
Dendrite, Cell body, Axon, Synapse.
Answer:
Synapse – It is a minute space between two adjacent neurons whereas the others are parts of the neuron.

Question 5.
Thyroxine, Calcitonin, Insulin, Auxin.
Answer:
Auxin – It is a plant hormone whereas the others are hormones in human beings.

Complete the Analogy:

(1) Water : Xylem :: Food : …………………………….
(2) Movement of root system : Gravitropic :: Movement of shoot system : …………………………….
(3) Brain: Cranial Cavity :: Spinal Cord : …………………………….
(4) Cavities of the brain : Ventricles :: Cavities of the spinal cord : …………………………….
(5) Involuntary activities : Medulla oblongata : : Balance of the body : …………………………….
(6) Stem elongation: Gibberellin :: Cell division : …………………………….
(7) Control of voluntary movements : Cerebrum :: Co-ordination of voluntary movements : …………………………….
(8) Converts glucose to glycogen : Insulin :: Converts glycogen to glucose : …………………………….
(9) Secondary sexual characters in males : Testosterone :: Secondary sexual characters in females : …………………………….
Answer:
(1) Phloem
(2) Phototropic
(3) Vertebral column
(4) Central canal
(5) Cerebellum
(6) Cytokinin
(7) Cerebellum
(8) Glucagon
(9) Oestrogen

Match the columns:

Question 1.

Column ‘A’	Column ‘B’
(1) Gibberellins (2) Cytokinins (3) Abscisic acid (4) Auxin	(a) Enlargement of cells (b) Helps in stem elogation (c) Cell division (d) Wilting of leaf

Answer:
(1 – b),
(2 – c),
(3 – d),
(4 – a).

Question 1.

Column ‘A’	Column B’
(1) Cerebrum (2) Cerebelleum (3) Medulla oblongata (4) Spinal cord	(a) Control of involuntary activities (b) Decision – making, memory and intellectual activities. (c) Centre for coordination of reflex actions (d) Maintaining body’s balance

Answer:
(1 – b),
(2 – d),
(3 – a),
(4 – c).

State whether the following statements are true or false. Correct the false statements.

Question 1.
Plants need less energy as compared to animals.
Answer:
True

Question 2.
Xylem conducts food whereas phloem conducts water.
Answer:
False. Xylem conducts water whereas phloem conducts food.

Question 3.
The loss of water from the plants is known as translocation.
Answer:
False. The loss of water from the plants is known as transpiration.

Question 4.
Calcium oxalate crystals present in some plants are called resins.
Answer:
False. Calcium oxalate crystals present in some plants are called raphides.

Question 5.
Root pressure helps to push the water up in plants during night time.
Answer:
True

Question 6.
Translocation is carried out by phloem in downward direction.
Answer:
False. Translocation is carried out by phloem in both upward and downward direction.

Question 7.
In unicellular organisms, waste materials are directly eliminated across the cell surface.
Answer:
True

Question 8.
Urea is produced in the liver.
Answer:
True

Question 9.
Systematic regulation of different processes is called co-ordination.
Answer:
False. Systematic regulation of different processes is called control.

Question 10.
A hormone auxin produced in the apical part of the shoot helps in enlargement of cells.
Answer:
True

Question 11.
Gibberellin helps in prevention and retardation of growth, leaf wilting etc.
Answer:
False. Abscisic acid helps in prevention and retardation of growth, leaf wilting etc.

Question 12.
The movement shown by venus fly trap while trapping an insect is a growth relevant movement.
Answer:
False. The movement shown by venus fly trap while trapping an insect is a growth irrelevant movement.

Question 13.
The lotus flower opens during night time while that of tuberose (polyanthus) opens during day time.
Answer:
False. The lotus flower opens during day time while that of tuberose (polyanthus) opens during night time.

Question 14.
Sensory neurons conduct impulses from the brain and the spinal cord to effector organs like muscles or glands.
Answer:
False. Sensory neurons conduct impulses from the sensory organs to the brain and the spinal cord.

Question 15.
There are 31 pairs of cranial nerves.
Answer:
False. There are 12 pairs of cranial nerves.

Question 16.
Activities like heart beat, blood circulation, breathing, sneezing, etc. are controlled by cerebellum.
Answer:
False. Activities like heart beat, blood circulation, breathing, sneezing, etc. are controlled by cerebellum.

Question 17.
Spinal nerves are associated with head, thorax and abdomen.
Answer:
False. Spinal nerves are associated with arms, legs, skin and some other parts of the body.

Question 18.
Nerve impulses are slow and long lasting whereas action of hormones is fast and short lived.
Answer:
False. Nerve impulses are fast and short lived whereas action of hormones is slow and long lasting.

Question 19.
Reflex actions are controlled by cerebellum.
Answer:
False. Reflex actions are controlled by spinal cord.

Question 20.
Thyroid stimulating hormone is secreted by the pituitary gland.
Answer:
True

Question 21.
The hormone thymosin is secreted by the thyroid gland.
Answer:
False. The hormone thymosin is secreted by the thymus gland.

Question 22.
Parathormone controls metabolism of calcium and phosphorns.
Answer:
True

Question 23.
The right kidney is slightly lower than the left kidney.
Answer:
True

Name the following:

Question 1.
The structural and functional unit of the nervous system.
Answer:
Newtron.

Question 2.
The network of capillaries in the Bowman’s capsule.
Answer:
Glomerulus.

Question 3.
The minute space between two adjacent nervous.
Answer:
Synapse.

Question 4.
The special cells which bring about control and co-ordination.
Answer:
Neurons.

Question 5.
The cavities present in various parts of the brain.
Answer:
Ventricles.

Question 6.
The long tubular cavity of the spinal cord.
Answer:
Central Canal.

Question 7.
The thread like fibrous structure at the end of the spinal cord.
Answer:
Filum terminale.

Give scientific reasons:

Question 1.
It is necessary to remove harmful and waste substances from the body.
Answer:

Many harmful and waste substances like urea, uric acid, ammonia, etc. are produced in living organisms.
If these substances accumulate in the body or are retained in the body for long, it can lead to serious harm or even death.
Hence, it is necessary to remove such harmful and waste substances from the body.

Question 2.
In plants like Touch-me-not (Mimosa), movement also occurs at the places other than where it has been touched.
Answer:

In plants like Touch-me-not (Mimosa), the information about the touch is relayed within the plant from one place to another.
Plants use electro-chemical impulses for transfer of information from one place to another.
Plant cells change their shape by increasing or decreasing their water content and thereby, bring about the movements of plants.
Hence, in plants like Touch-me-not (Mimosa) movement also occurs at the places other than where it has been touched.

Question 3.
Endocrine glands are also called ductless glands.
Answer:

Hormones are secreted by endocrine glands.
These glands do not have any arrangement of their own to store or carry their secretions.
Hence, as soon as hormones are produced, they are directly released into the blood circulation.
Thus, though these endocrine glands are present at specific locations in our body, their secretions reach all parts of the body via blood.
Therefore, endocrine glands are also called ductless glands.

Define the following:

Question 1.
Transportation
Answer:
The process by which a substance either synthesized or absorbed in one part of the body reaches another is called as transportation.

Question 2.
Control
Answer:
Systematic regulation of different processes is called as control.

Question 3.
Coordination
Answer:
Bringing about the different processes in the proper sequence is called as co-ordination.

Question 4.
Tropism or Tropic movement
Answer:
Movement or growth of any part of the plant in response to an external stimulus is called as tropism or tropic movement.

Question 5.
Excretion
Answer:
Removal of waste or harmful substances from the body is called excretion.

Question 6.
Dialysis
Answer:
The process of separating the nitrogenous waste from the blood with the help of a man?made machine is called dialysis.

Question 7.
Reflex action
Answer:
An immediate and involuntary response given to a stimulus from the environment is called a reflex action.

Question 8.
Homeostasis
Answer:
Proper co-ordination between various systems of an organism helps to maintain a state of equilibrium called homeostasis.

Question 9.
Tropism
Answer:
Movement or growth of any part of the plant in response to an external stimulus is called tropism.

Distinguish between:

Question 1.
Nervous control and Chemical control
Answer:

Nervous Control	Chemical Control
(i) Nervous control is brought about by special types of cells called neurons.	(i) Chemical control is brought about by chemical substances called hormones.
(ii) It involves the nervous system i.e., brain, spinal cord and nerves.	(ii) It involves the endocrine glands.
(iii) Nerve impulses are fast and short-lived.	(iii) Actions of hormones are very slow and long-lasting.

Question 2.
Growth relevant movements and growth irrelevant movements
Answer:

Growth relevant movements	Growth irrelevant movements
(i) Growth relevant movements result in growth of the plants.	(i) Growth irrelevant movements do not result in growth of the plants.
(ii) They are also called as tropic movements.	(ii) They are also called as nastic movements.
(iii) They are in response to stimulus of light, water, gravity, chemicals, etc.	(iii) They are generally in response to stimulus of touch.
(iv) Examples : Bending of stem towards light, movement of roots towards gravity and water, etc.	(iv) Example : Closing of leaflets of Mimosa plant, closing of Venus fly trap, etc.

Question 3.
Cerebrum and Cerebellum
Answer:

Cerebrum	Cerebellum
(i) It is the largest part of the brain.	(i) It is the smaller part of the brain.
(ii) It occupies two thirds of the brain.	(ii) It is situated below the cerebrum at the back of the cranial cavity.
(iii) Its surface has deep, irregular ridges and grooves which are called convolutions.	(iii) Its surface shows shallow grooves instead of convolutions.
(iv) It controls voluntary movements, concentration, planning, decision-making, memory, intelligence and intellectual activities.	(iv) It co-ordinates voluntary movements and maintains the body’s balance.

Write short notes:

Question 1.
Root Pressure
Answer:

Root cells are in contact with water and minerals in the soil.
Water and minerals enter the cells of the root surface due to difference in concentration. As a result, these cells become turgid.
This is called root pressure.
Under the effect of this pressure, water and minerals reach the xylem of the roots and to reduce this difference in concentration, they are continuously pushed forward.
As a result of this continuous movement, a water column is formed, which is continuously pushed ahead.
This pressure, is sufficient to lift the water up in shrubs, small plants and small trees.

Question 2.
Transpiration
Answer:

Plants give out water in the form of water vapour through the stomata on their leaves. This is known as transpiration.
Two cells called guard cells are present around the stomata. They control the opening and closing of stomata.
Water is released into the atmosphere by leaves through the process of evaporation.
As a result, water in the epidermal layer of the leaf decreases.
Water is brought up to the leaves through the xylem to compensate for the lost water.
Transpiration helps in absorption of water and minerals and distribution to all parts of the plant.

Question 3.
Nerve cell
Answer:

Nerve cells also called as neurons are special types of cells which conduct impulses from one place to another in the body.
Neurons are the structural and functional units of the nervous system.
Nerve cells, the largest cell in the human body, may measure upto a few metres in length.
Nerve cells have the ability to generate and conduct electrochemical impulse.
The cells that support the nerve cells and help in their functioning are called neuroglia. Nerve cells and neuroglial cells together form nerves.

Question 4.
Reflex action
Answer:

An immediate and involuntary response given to a stimulus from the environment is called a reflex action.
Sometimes we react to an incident without any thinking on our part or control over the reaction.
This is a response given to a certain stimulus from the surroundings.
In such situations, proper control and co-ordination is achieved even without the intervention of the brain.
For example, when our hand touches a hot object, the receptor in the skin detects the stimulus.
The sensory neuron sends the impulse to the relay neuron in the spinal cord.
The impulses are then sent to motor neurons which cause the muscles of the hand to contract and move away from the hot object.
The spinal cord is the center of co-ordination for reflex actions.

Question 5.
Spinal cord
Answer:

The spinal cord is the part of the central nervous system and it is held within the vertebral column.
It is slightly thick but gradually tapers towards the end.
There is a thread like fibrous structure at its end. It is called the filum terminale.
The long tubular cavity of the spinal cord is called the central canal. It is filled with cerebrospinal fluid.
The spinal cord conducts impulses from the skin towards the brain and from the brain to the muscles and glands.
It functions as a centre of co-ordination of reflex actions.

Question 6.
Dialysis
Answer:

The efficiency of kidneys can be adversely affected by injury, infection or decreased blood supply.
If this happens, excess of toxic substances accumulates in the body and it can lead to death.
If kidneys fail, nitrogenous wastes are separated from the blood with the help of a man-made machine.
The process of separating the nitrogenous waste from the blood with the help of this machine is called dialysis.
About 500 ml of blood is sent at one time through this machine. Purified blood is reinfused into the body of the patient.

Draw neat and labelled diagrams:

Question 1.
Vertical Section of Kidney
Answer:

Question 2.
Reflex action
Answer:

Name the hormones of the following endocrine glands and the function of each:

Question 1.
Parathyroid
Answer:

Hormone	Function
Parathormone	Controls metabolism of calcium and phosphorus

Question 2.
Pancreas
Answer:

Hormone	Function
(i) Glucagon	Stimulates liver to convert glycogen into glucose.
(ii) Insulin	Stimulates liver to convert excess blood glucose into glycogen.
(iii) Somatostatin	Controls levels of insulin and glucagon.
(iv) Pancreatic Polypeptide	Controls movement of intestine and thereby glucose absorption. Controls secretion of pancreatic juice.

Complete the following table of plant hormones with their functions:
Answer:

Plant hormone	Functions
(i) Auxin	Produced in the apical part of the shoot Helps in enlargement of cells
(ii) Gibberellins	Help in stem elongation
(iii) Cytokinins	Help in cell division
(iv) Abscisic acid	Effective in prevention and retardation of growth, leaf wilting, etc.

State the functions of different parts of the brain.
Answer:

Parts of the Brain	Functions
Cerebrum	Control of voluntary movements, concentration, planning, decisionmaking, memory, intelligence, and intellectual activities.
Cerebellum	(i) Co-ordination of voluntary movements. (ii) Maintaining the body’s balance.
Medulla oblongata	Control of involuntary activities like the beating of the heart, blood circulation, breathing, sneezing, coughing, salivation, etc.
Spinal cord	(i) Conduction of impulses from the skin towards the brain. (ii) Conduction of impulses from brain to muscles and glands. (iii) Functions as centre of coordination of reflex actions.

Answer the following:

Question 1.
How do plants bring about movements in them?
Answer:

Plants use electro-chemical impulses for transfer of information from one place to another.
Plant cells change their shape by increasing or decreasing their water content and thereby bring about the movement of plants.

Answer the following:

Question 1.
What are growth-irrelevant movements? Give examples.
Answer:

Some specific movements of the plants do not lead to the plant growth. Such movements are called growth-irrelevant movements.
In the plant called venus fly trap, there is a trap that appears and smells like flowers and deceives insects. When an insect visits the flower-like trap, the trap closes up and the trapped insect is digested by the plant.
Fibrils present on the leaves of the insectivorous plant Drosera, bend inward as soon as an insect lands on the leaves and surround the insects from all sides.
In Balsam, the ripened fruit dehisces (bursts-open) at the right time to disperse the seeds.

Question 2.
Which are the different types of nerve cells or neurons?
OR
How are nerve cells classified according to their functions?
Answer:
According to their functions, nerve cells are classified into three types:

Sensory neurons: They conduct impulses from the sensory organs to the brain and the spinal cord.
Motor neurons : They conduct impulses from the brain or spinal cord to effector organs like muscles or glands.
Association neurons : Association neurons perform the function of integration in the nervous system.

Question 3.
What are the different parts of the human nervous system?
Answer:
The human nervous system can be divided into the following three parts.

Central nervous system (CNS) : It consists of the brain and the spinal cord. It controls and regulates all activities of the body.
Peripheral nervous system (PNS) : The peripheral nervous system consists of the nerves originating from the central nervous system which connect the central nervous system with all parts of the body. They are of two types cranial nerves and spinal nerves.
Autonomic nervous system (ANS) : The autonomous nervous system consists of the nerves of involuntary organs like the heart, lungs, stomach etc. It is not under the control of our will.

Question 4.
Describe the structure of the central nervous system.
Answer:

The central nervous system consists of the brain and spinal card.
The organization of the brain is extremely delicate and highly evolved.
The brain is the main controlling part of the nervous system and is safely located in the cranial cavity. The spinal cord is protected by the vertebral column.
In the space between the delicate central nervous system and its bony covering are the protective layers called the meninges.
Cavities present in various parts of the brain are called ventricles whereas the long tubular cavity of the spinal cord is called the central canal.
The ventricles, central canal and spaces between the meninges are filled with cerebro?spinal fluid.
This fluid supplies nutrients to the central nervous system and protects it from shock.

Question 5.
Which are the two types of peripheral nerves?
Answer:
Peripheral nerves are of two types:
(a) Cranial nerves:

Nerves originating from the brain are called cranial nerves.
They are associated with various parts in the head.
There are 12 pairs of cranial nerves.

(b) Spinal nerves:

Nerves originating from the spinal cord are called spinal nerves.
They are associated with arms, legs, skin and some other parts of the body.
There are 31 pairs of spinal nerves.

Question 6.
How do plants get rid of their excretory products?
Answer:

Excretion is a simpler process in plants. There is no special organ or system for excretion in plants.
Gases are given out by diffusion.
Most of the waste substances of plants are stored in vacuoles of leaf-cells and in flowers, fruits and the bark of the stem. After some time these parts fall off.
Some other waste materials are stored in old and worn out xylem in the form of resin and gum.
Some waste materials are also given out through roots in the surrounding soil.

Answer in detail:

Question 1.
Explain how food and other substances are transported in plants?
OR
Explain translocation in plants.
Answer:

The food produced in leaves is transported to each cell in the plant body.
Excess food, except amino acids, is stored in roots, fruits and seeds. This process is called translocation of materials.
It is carried out in both the upward and downward directions by the phloem.
Translocation is not a simple process, it requires energy. This energy is obtained from ATP.
Whenever food material like sucrose is transported towards a part of a plant via the phloem with the help of ATP, the water concentration decreases in the part. As a result, water enters the cell by the process of diffusion.
The pressure on the cell wall increases due to increase in cellular contents.
Due to the increase pressure, food is pushed into the neighbouring cells where the pressure is low.
This process helps the phloem to transport the materials as per the need of the plant. During flowering season, the sugar stored in roots or stem is transported towards the floral buds to make them open and blossom.

Question 2.
What is tropic movement? Describe the different types of tropic movements.
OR
What are growth relevant movements? Describe the different types of growth relevant movements.
Answer:
Movement or growth of any part of the plant in response to an external stimulus is called tropic movement or tropism.

The different types of tropic movements are:

Phototropic movement : The shoot system of any plant responds to the light stimulus, i.e., it grows towards the source of light. The movement shown by plants towards the source of light is called phototropic movement.
Gravitropic movement : The root system of plants responds to stimulus of gravity. This is called gravitropic movement.
Hydrotropic movement : The root system of plants responds to the stimulus of water. This is called hydrotropic movement.
Chemotropic movement : Movement shown by plants in response to specific chemicals is called chemotropic movement. For example, the growth of the pollen tube towards the ovule.

All the above-mentioned movements of plants are related with growth, hence are called growth relevant movement.

Question 3.
Write short note on : Human Brain
Answer:

The brain is the main controlling part of the nervous system and is safely located in the cranial cavity.
The brain is covered by protective layers called the Meninges.
Cavities present in various parts of the brain are called ventricles.
The ventricles are filled with cerebrospinal fluid. This fluid supplies nutrients to the brain and also protects it from shock.
The brain of an adult human weighs about 1300 -1400 grams and consists of approximately 100 million neurons.
The left side of our brain controls the right side of our body and right side of our brain controls left side of the body.
In addition, the left side of the brain controls our speech and conversation, writing, logical thinking etc., whereas the right side controls artistic abilities.

Human brain is made up of following parts:

(a) Cerebrum:

This is the largest part of the brain and consists of two cerebral hemispheres. These hemispheres are joined with each other with the help of tough fibres and nerve tracts.
The cerebrum occupies two-thirds of the brain. Hence, it is also called as large brain.
Its surface has deep, irregular ridges and grooves which are called convolutions, convolution increases the surface area of the cerebrum and therefore a large number of nerve cells can be accommodated.

(b) Cerebellum:

This is the smaller part of the brain situated below the cerebrum at the back of the cranial cavity.
Its surface shows shallow grooves instead of deep convolutions.

This is the hind-most part of the brain.
There are two triangular swollen structures called pyramids on the upper side of medulla oblongata.
The medulla oblongata continues downwards the spinal cord.

(6) How are nerve impulses conducted in the body?
Answer:

Special types of cells which conduct impulses from one place to another in the body are called neurons. Nerve cells have the ability to generate and conduct electro-chemical impulses.
The cells that support the nerve cells and help in their functioning are called neuroglia.
All the information about our surroundings is collected by the ends or dendrites of the neuron.
The chemical process begins at those ends and electric impulses are generated which are conducted from the dendrites to the cell body, from the cell body to the axon and from the axon to its terminal.
These impulses are then to be transferred from this nerve cell to the next.
Now the impulse that reaches the terminal of an axon, stimulates the nerve cell to secrete certain chemicals.
These chemicals pass through a minute space, called the synapse, between two adjacent neurons and generate the impulses in the dendrites of the next neuron.
In this way, impulses are conducted in the body and these impulses are finally conveyed by nerve cells to muscles cells or glands.

9th Std Science Questions And Answers:

Current Electricity Class 9 Science Chapter 3 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 3 Current Electricity Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 3 Current Electricity Question Answer Maharashtra Board

Class 9 Science Chapter 3 Current Electricity Question Answer Maharashtra Board

1. The accompanying figure shows some electrical appliances connected in a circuit in a house. Answer the following questions.

A. By which method are the appliances connected?
Answer:
Appliances are connected in parallel.

B. What must be the potential difference across individual appliances?
Answer:
The potential difference across all appliances is same in parallel connection.

C. Will the current passing through each appliance be the same? Justify your answer.
Answer:
No, as every appliance has a different load (resistance), the current flowing through each appliance will be different.

D. Why are the domestic appliances connected in this way?
Answer:
The domestic appliances are connected in parallel as the potential difference remains same.

E. If the T.V. stops working, will the other appliances also stop working? Explain your answer.
Answer:
No, the other devices will not stop working as the current flowing through them is along different paths.

2. The following figure shows the symbols for components used in the accompanying electrical circuit.

Which law can you prove with the help of the above circuit?
Answer:

(b) This circuit can be used to prove Ohm’s law.
(c) V = 1R is the expression of Ohm’s law

3. Umesh has two bulbs having resistances of 15 W and 30 W. He wants to connect them in a circuit, but if he connects them one at a time the filament gets burnt. Answer the following.

A. Which method should he use to connect the bulbs?
B. What are the characteristics of this way of connecting the bulbs depending on the answer of A above?
C. What will be the effective resistance in the above circuit?

4. The following table shows current in Amperes and potential difference in Volts.

a. Find the average resistance.
b. What will be the nature of the graph between the current and potential difference? (Do not draw a graph.)
c. Which law will the graph prove? Explain the law.

5. Match the pairs

‘A’ Group – ‘B’ Group
1. Free electrons – a. V/ R
2. Current – b. Increases the resistance in the circuit
3. Resistivity – c. Weakly attached
4. Resistances in series – d. VA/LI

6. The resistance of a conductor of length x is r. If its area of crosssection is a, what is its resistivity? What is its unit?

7. Resistances R₁, R₂, R₃ and R₄ are connected as shown in the figure. S₁ and S₂ are two keys. Discuss the current flowing in the circuit in the following cases.

a. Both S₁ and S₂ are closed.
b. Both S₁ and S₂ are open.
c. S₁ is closed but S₂ is open.
Answer:
(a) When both S₁ and S₂ are dosed, the effective resistance of the circuit decreases and hence, current will increase.
(b) When both S₁ and S₂ are open, the effective resistance of the rircuit increases and hence, current will decrease.
(c) When S₂ is closed and S₂ is open, the effective resistance of the tircuit decreases and hence current will increase. [Current will be more than case (b) but less than in case (a)]

8. Three resistances x₁, x₂ and x₃ are connected in a circuit in different ways. x is the effective resistance. The properties observed for these different ways of connecting x₁, x₂ and x₃ are given below. Write the way in which they are connected in each case. (I-current, V-potential difference, x-effective resistance)

a. Current I flows through x₁, x₂ and x₃
b. x is larger than x₁, x₂ and x₃
c. x is smaller than x₁, x₂ and x₃
d. The potential difference across x₁, x₂and x₃ is the same
e. x = x₁ + x₂ + x₃\(\text { f. } x=\frac{1}{\frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}}\)

9. Solve the following problems.

A. The resistance of a 1m long nichrome wire is 6Ω. If we reduce the length of the wire to 70 cm. what will its resistance be? (Answer : 4.2Ω)
Answer:
The resistance of 70cm wire will be 4.2 Ω

B. When two resistors are connected in series, their effective resistance is 80Ω. When they are connected in parallel, their effective resistance is 20Ω. What are the values of the two resistances? (Answer : 40Ω, 40Ω)
Answer:
The values of the two resistances R₁ and R₂ are 40Ω and 40Ω.

C. If a charge of 420 C flows through a conducting wire in 5 minutes what is the value of the current? (Answer : 1.4 A)
Answer:
Given: Electric charge (Q) = 420 C
Time (t) = 5 min = 5 x 60
= 300 sec.
To find: Electric current (1) = ?
Formula:
\(I=\frac{Q}{t}\)
Solution:
\(I=\frac{Q}{t}\)
The current in the circuit is 1.4 A.

Class 9 Science Chapter 3 Current Electricity Intext Questions and Answers

Can you recall?

Question 1.
You must have seen a waterfall. Which way does the water flow?
Answer:
Water flows from a certain height of a mountain towards the ground.

Question 2.
Material: Copper and aluminium wires, glass rod, rubber.
Make connection as shown in figure 3.8. First connect a copper wire between points A and B and measure the current in the circuit. Then in place of the copper wire, connect the aluminium wire, glass rod, rubber, etc one at a time and measure the current each time. Compare the values of the current in different cases.

Also take different metal strips (Iron, Copper, Zinc, and Aluminium) and connect it in slot AB. Now observe the difference in the resistance using Ohm meter.
Answer:
When copper and aluminium wires are connected to the circuit, current flows through it, as both are good conductors of electricity. When glass rod or rubber was connected to the circuit, current does not flow through it, as both are bad conductors of electricity.

Copper displays lowest resistance while the resistance increases with aluminium, zinc and iron respectively.

Question 3.
Set up the experiment as shown in figure. Then remove the clamp from the rubber tube.

(a) What happens when the clamp is removed?
Answer:
When the clamp is removed, water flows from higher level to lower level.

(b) Does the water stop flowing? Why?
Answer:
Yes, the water stops flowing. This happens when the level of water becomes equal in both the bottles, i.e., there is no difference in the water levels.

(c) What will you do to keep the water flowing for a longer duration?
Answer:
The difference in the water level has to be maintained till that time. The difference must never be zero.

Question 4.
Point out the mistakes in the figure below:

Answer:
A: Wire is broken at the negative terminal. Bulb will not glow as the circuit is incomplete.
B: Wire is disconnected at the negative terminal. Bulb will not glow as the circuit is incomplete.
C: The circuit is complete. Therefore, bulb will glow.
D: Rubber is a bad conductor of electricity. Hence, it will not allow current to flow and the bulb will not glow.

Question 5.
Why are the bulbs in Figures B, C and D not lighting up?

Answer:

In B, the blue wire is broken. Hence circuit is incomplete and current does not flow. Therefore, bulb will not light up.
In C, the red wire is broken. Hence circuit is incomplete and current does not flow. Therefore, bulb will not light up.
In D, both wires are connected to the same terminal. Hence, there is no potential difference and current does not flow. Therefore, bulb will not light up.

Class 9 Science Chapter 3 Current Electricity Additional Important Questions and Answers

Choose and write the correct option:

Question 1.
1mA = …………… A.
(a) 10³
(b) 10^-3
(c) 10⁶
(d) 10^-6
Answer:
(a) 10³

Question 2.
To increase the effective resistance in a circuit the resistors are connected in ………….. .
(a) Series
(b) Parallel
(c) Both ways
(d) None of these
Answer:
(a) series

Question 3.
1 kilowatt hr = …………… joules.
(a) 4.6 x 10⁶
(b) 3.6 x 10⁶
(c) 30.6 x 10⁶
(d) 3.6 x 1O⁵
Answer:
(b) 3.6 x 10⁶

Question 4.
The voltage difference in India between the live and neutral wires is about ………….. .
(a) 110 V
(b) 220 V
(c) 440 V
(d) 60 V
Answer:
(b) 220 V

Question 5.
Resistivity is the specific property of a ………….. .
(a) Area of cross-section
(b) Temperature
(c) Length
(d) Material
Answer:
(d) material

Question 6.
If a P.D. of 12 V is applied across a 3Ω resistor then the current passing through it is ………….. .
(a) 36 A
(b) 4 A
(c) 0.25 A
(d) 15 A
Answer:
(b) 4 A.

Question 7.
In order to measure the electric current flowing through a circuit, we connect …………… with the circuit.
(a) a voltmeter in parallel
(b) a voltmeter in series
(c) an ammeter in parallel
(d) an ammeter in series
Answer:
(d) an ammeter in series

Question 8.
P and Q are two wires of same length and different cross-sectional areas and made of same material. Name the property which is same for both the wires.
(a) Resistivity
(b) Resistance
(c) Current
(d) Both (a) and (b)
Answer:
(a) Resistivity

Question 9.
The following is true for identical bulbs connected in parallel.
(a) All bulbs glow with unequal brightness.
(b) If one bulb is non-functional, all will stop working.
(c) All bulbs glow with equal brightness.
(d) Bulbs function for longer time.
Answer:
(c) All bulbs glow with equal brightness

Question 10.
The …………… wire is either yellow or green in colour.
(a) Live
(b) Neutral
(c) Earth
(d) Fuse
Answer:
(c) earth

Question 11.
A current flows through a circuit due to the difference in …………… between two points in the conductor.
(a) Gravity
(b) Potential
(c) Resistance
(d) Fuse
Answer:
(b) potential

Question 12.
…………… is the amount of charge flowing through a particular cross sectional area in unit time.
(a) Electric current
(b) Ampere
(c) Volt
(d) Force
Answer:
(a) Electric current

Question 13.
The flow of …………… constitutes the electric current in a wire.
(a) Protons
(b) Neutrons
(c) Electrons
(d) Gravitons
Answer:
(c) electrons

Question 14.
The conventional direction of flow of current is from …………… terminal to …………… terminal.
(a) Negative to positive
(b) Neutral to positive
(c) Positive to negative
(d) Positive to neutral
Answer:
(c) positive, negative

Question 15.
Current stops flowing when potential difference between two ends of a wire becomes ………….. .
(a) Zero
(b) Positive
(c) Negative
(d) Higher
Answer:
(a) zero

Question 16.
Resistances are connected in …………… so as to pass the same current through them.
(a) Series
(b) Parallel
(c) Reversed
(d) Disconnect
Answer:
(a) series

Question 17.
To decrease the effective resistance in a circuit, the resistances are connected in ………….. .
(a) Series
(b) Parallel
(c) Reversed
(d) Disconnect
Answer:
(b) parallel

Question 18.
1μV = …………… V
(a) 10²
(b) 10^-6
(c) 10⁶
(d) 10³
Answer:
(b) 10^-6

Question 19.
Good conductors contain a large number of ………….. .
(a) Protons
(b) Neutrons
(c) Electrons
(d) Gravitons
Answer:
(c) free electrons

Question 20.
Electrons flow from …………… terminal to …………… terminal in a conductor when a potential difference is applied.
(a) Negative to positive
(b) Neutral to positive
(c) Positive to negative
(d) Positive to neutral
Answer:
(a) negative, positive

Find the odd one out:

Question 1.
Voltmeter, Ammeter, Galvanometer, Thermometer
Answer:
Thermometer

Question 2.
Rubber, Silver, Copper, Gold
Answer:
Rubber

Question 3.
Wood, Glass, Steel, Rubber
Answer:
Steel

Question 4.
Graphite, Diamond, Fullerenes, Coal
Answer:
Fullerenes

Distinguish between:

Question 1.
Voltmeter and Ammeter
Answer:

Voltmeter	Ammeter
(i) It is an instrument used to measure the potential difference between two terminals of a cell.	(i) It is an instrument to measure the electric current flowing through a circuit.
(ii) It is connected in parallel with the cell.	(ii) It is connected in series with the cell.
(iii) It has a very high resistance.	(iii) It has a very low resistance.
(iv) Voltmeter has range of volts.	(iv) Ammeter has range of amps.

Question 2.
Ohmic conductors and Non-Ohmic conductors
Answer:

Conductors	Insulators
(i) Substances which have very low electrical resistances are called conductors.	(i) Substances which have extremely high electrical resistances are called Insulators.
(ii) They contain a large number of free electrons.	(ii) They contain practically no free electrons.
(iii) Conductors are mostly metals.	(iii) Insulators are mostly non metals.
(iv) Conductor example iron, copper.	(iv) Insulator example rubber, plastic.

Question 3.
Conductors and Insulators
Answer:

Resistance	Resistivity
(i) The hindrance to the flow of electrons is called resistance.	(i) Resistivity is the specific property of the material of a conductor.
(ii) The S.I. unit of resistance is ohm (Q).	(ii) The S.I. unit of resistivity is ohm-metre (Q – m).
(iii) It depends on temperature, area of cross-section, length of conductor and material of the conductor.	(iii) It depends on material of the conductor.
(iv) Resistance can be changed as it depends of external factor as well.	(iv) Resistivity cannot be changed as it depends of internal factors.

Question 4.
Resistance in Series and Resistance in Parallel
Answer:

Resistance in Series	Resistance in Parallel
(i) Effective resistance of the resistors is equal to the sum of their individual resistances.	(i) Inverse of the effective resistance is equal to the sum of the inverse of individual resistances.
(ii) The same current flows through each resistor.	(ii) The total current flowing through the circuit is the sum of the currents flowing through individual resistors.
(iii) The effective resistance is larger than each of the individual resistances.	(iii) The effective resistance of resistors connected in parallel is less than the least resistance of individual resistors.
(iv) This arrangement is used to increase the resistance in a circuit.	(iv) This arrangement is used to decrease the resistance in a circuit.

Question 5.
Answer:

Electric current	Potential difference
(i) The flow of electric charge per unit time is called electric current.	(i) The difference in potential between the positive and negative terminal of a cell is the potential difference of that cell.
(ii) The S.I. unit of electric current is ampere.	(ii) The S.I. unit of potential difference volt.
(iii) Ammeter is used to measure electric current.	(iii) Voltmeter is used to measure electric current.
(iv) Current is represented by: \(\mathrm{I}=\frac{\mathrm{Q}}{\mathrm{t}}\)	(iv) Potential difference is represented by: \(\mathrm{V}=\frac{\mathrm{W}}{\mathrm{Q}}\)

Make pair:

Question 1.
Copper : Conductor :: Rubber : ……………….
Answer:
Insulator

Question 2.
Aluminium : ………………. :: Indium oxide : Super Insulator
Answer:
Super conductor

Question 3.
Parallel Connection : \(\frac{1}{\mathrm{R}_{p}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}\) :: Series Connection : ……………….
Answer:
R_s = R₁ + R₂

(4) Electric Current : ………………. :: Electric charge : Coulomb
Answer:
Ampere

(5) Electric resistance : Ohm :: Potential difference : ……………….
Answer:
Volt

State whether the following statements are true or false. Correct the false statements:

(1) The SI unit of charge is volt.
(2) Voltmeter is always connected in series with the device.
(3) The conventional direction of flow of current is from positive terminal to negative terminal.
(4) Silver and copper are good conductors.
(5) Resistivity of pure metals is more than alloys.
(6) Resistance in series arrangement is used to decrease resistance of circuit.
(7) A conducting wire offers less resistance to flow of electrons.
(8) Charges are measured in ampere.
(9) The unit of potential difference is ampere.
(10) Resistance of a conductor is inversely proportional to the length of the conductor.
(11) Ammeter is connected in parallel to the cell to measure current.
(12) Fuse is made of wire having high melting point.
Answer:
(1) False. The SI unit of charge is coulomb.
(2) False. Voltmeter is ahvays connected in parallel with the device.
(3) True
(4) True
(5) False. Resistivity of pure metals is less than alloys.
(6) False. Resistance in series arrangement is used to increase resistance of circuit.
(7) True
(8) False. Charges are measured in coulomb.
(9) False. The unit of potential difference is volt.
(10) False. Resistance of a conductor is directly proportional to the length of the conductor.
(11) False. Ammeter is connected in series to the cell to measure current.
(12) False. Fuse is made of wire having low melting point.

Answer the following in one sentence:

Question 1.
Which is the unit used to measure large voltages?
Answer:
Kilovolts and Megavolts are the units used to measure large voltages.

Question 2.
What is the SI unit of potential difference?
Answer:
The SI unit of potential difference is volt (V).

Question 3.
What is lightning?
Answer:
Lightning is the electric discharge travelling from clouds at high potential to earth’s surface which is at zero potential.

Question 4.
What is the unit of resistivity.
Answer:
The unit of resistivity is ohm metre (Qm).

Question 5.
Which substances are called conductors of electricity?
Answer:
Those substances which have very low electrical resistance are called conductors of electricity.

Question 6.
What is Earth wire?
Answer:
Earth wire is generally yellow or green colour, it is connected to a metal plate buried deep underground near the house and is for safety purpose.

Write formula:
(1) E1ectriccurrent \(=\frac{Q}{t}\)
(2) Electric charge = It
(3) Potential difference = IR
(4) Electric resistance \(=\frac{V}{I}\)
(5) Current \(=\frac{V}{R}\)
(6) Resistivity \(=\frac{RA}{L}\)

Give scientific reasons:

Question 1.
Free electrons are required for conduction of electricity.
Answer:

Every atom of a metallic conductor has one or more outermost electrons which are very weakly bound to the nucleus.
These are called free electrons. These electrons can easily move from one part of a conductor to its other parts. The negative charge of the electrons also gets transferred as a result of this motion.
The free electrons in a conductor are the carriers of negative charge. Hence, free electrons are required for conduction of electricity.

Question 2.
Wood and glass are good insulators.
Answer:

Those substances which have infinitely high electrical resistance are called insulators.
Wood and glass have high resistance and negligible free electrons for conduction of electricity.
Hence, wood and glass are good insulators.

Question 3.
Connecting wires in a circuit are made of copper and aluminium.
Answer:

Copper and aluminum are good conductors of electricity.
They have low electrical resistance and large number of free electrons.
As they are malleable and ductile, they can be drawn into thin wires. Hence, connecting wires in a circuit are made of copper or aluminum.

Question 4.
A thick wire has a low resistance.
Answer:

The resistance (R) of a wire is inversely proportional to the cross-sectional area (A) of a wire. i.e., R i
Thus, greater is the cross-sectional area of a conductor (wire), lower is its resistance. Hence, a thick wire has a low resistance.

Question 5.
A series combination of resistances is used to increase the resistance of a circuit.
Answer:

When resistances are connected in series, the effective resistance of the resistors is equal to the sum of their individual resistances. R_s = R₁ + R₂ ………….. R_n
The effective resistance is larger than each of the individual resistances. Hence, This arrangement is used to increase the resistance in a circuit.

Question 6.
A parallel combination of resistances decreases the effective resistance of the circuit.
Answer:

In a parallel combination, the inverse of the effective resistance is equal to the sum of the inverses of individual resistances. \(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}} \ldots \ldots \cdot \frac{1}{\mathrm{R}_{\mathrm{n}}}\)
The effective resistance of resistors connected in parallel is less than the individual resistors.
Due to this, any addition of an individual resistance in parallel combination will decrease the overall resistance of the circuit. Hence, a parallel combination of resistance decreases the effective resistance of the circuit.

Question 7.
Lightning occurs from sky to earth.
Answer:

Lightning is the electric discharge travelling from clouds at high potential to the earth’s surface, which is at zero potential.
The earth is always at lower potential as compared to the clouds.
Hence, lightning occurs from sky to earth.

Question 8.
In streetlights, bulbs are connected in parallel.
Answer:

Even if any one of the several bulbs connected in parallel becomes non-functional because of some damage to its filament, the circuit does not break as the current flows through the other paths, and the rest of the bulbs light up.
When several bulbs are connected in parallel, they emit the same amount of light as when they are connected individually in the circuit, while bulbs connected in series emit less light than when connected individually. Hence, streetlights are connected in parallel.

Numerical:
Numericals based on the formula: (1) Q= It (2) W= VQ

Question 1.
A current of 0.4 A flows through a conductor for 5 minutes. How much charge would have passed through the conductor?
Answer:
Given: Current (I) = 0.4 A
Time (t) = 5 min = 5 x 60 = 300 s
To find: Charge (Q) =?
Formula: Q = 1 x
Solution: Q = 0.4 x 300
Q= 120 C.
Charge passing through the conductor is 120

Question 2.
Find the amount of work done if 3 C of charge is moved through a potential difference of 9 V.
Answer:

The work done is 27 joule.

Question 3.
The resistance of the filament of a bulb is 1000Ω. It is drawing a current from a source of 230 V. How much current is flowing through it?
Answer:

The current flowing through the filament of bulb is 0.23 A.

Question 4.
The length of a conducting wire is 50 cm and its radius is 0.5 mm. If its resistance is 30Ω, what is the resistivity of its material?
Answer:

The resistivity of the wire is 4.71 x 10^-5 Qm.

Question 5.
A current of 0.24 A flows through a conductor when a potential difference of 24 V is applied between its two ends. What is its resistance?
Answer:

The resistance of a conductor is 100Ω.

Question 6.
If three resistors 15Ω, 3Ω and 4Ω each are connected in series, what is the effective resistance in the circuit?
Answer:
Given:
R₁ =15Ω
R₂ = 3Ω
R₃ = 4Ω
Effective resistance in series (R_s) = ?
R_s = R₁ + R₂ + R₃
R_s = 15 + 3 + 4
R_s = 22Ω
The effective resistance in the circuit is 22Ω.

Question 7.
Three resistances 15Ω, 20Ω and 10Ω are connected in parallel. Find the effective resistance of the circuit.
Answer:

The effective resistance of the circuit is 4.615 Ω. It is less than the least of the three i.e., 10Ω.

Write a note on the following:

Question 1.
Electric current
Answer:
An electric current is the flow of electrons through a conductor. Quantitatively, current
(I) is defined as the charge passing through a conductor in unit time.
\(T=\frac{Q}{t}\)

Question 2.
1 ampere
Answer:
One ampere current is said to flow in a conductor if one coulomb charge flows through it every second.
\(1 \mathrm{~A}=\frac{1 \mathrm{C}}{1 \mathrm{~s}}\)

Question 3.
1 volt
Answer:
The potential difference between two points is said to be 1 volt if 1 joule of work is done in moving 1 coulomb of electric charge from one point to another.
\(1 \mathrm{~V}=\frac{1 \mathrm{~J}}{1 \mathrm{C}}\)

Question 4.
Potential Difference
Answer:
The amount of work done to carry a unit positive charge from point A to point B is called the electric potential difference between the two points.
\(V=\frac{W}{Q}\)

Question 5.
Conductor
Answer:
Those substances which have very low resistance are called conductors. Current can flow easily through such materials.

Question 6.
Insulators
Answer:
Those substances which have extremely high resistance and through which current cannot flow are called insulators.

Question 7.
1 ohm
Answer:
If one Ampere current flows through a conductor when one Volt potential difference is applied between its ends, then the resistance of the conductor is one Ohm.
\(\frac{1 \text { Volt }}{1 \text { Ampere }}=1 \mathrm{Ohm}\)

Question 8.
Potential
Answer:
The level of electric charge present is known as potential.

Question 9.
Ohm’s Law
Answer:
If the physical state of a conductor remains constant, the current (I) flowing through it is directly proportional to the potential difference (V) between its two ends.
V = IR

Question 10.
Superconductors
Answer:
The resistance of some conductors becomes nearly zero if their temperature is decreased up to a certain value close to 0 K. Such conductors are called superconductors.

Question 11.
Non-ohmic conductors
Answer:
Conductors which do not obey Ohm’s law are called non-ohmic conductors.

Complete the flow charts:

(1) Protection from Electricity

(2) Resistance

(3) Resistivity

Write properties/characteristics/advantages of the following:

Superconductors
Answer:
The resistance of these conductors becomes nearly zero if their temperature is decreased up to a certain value close to 0 K. Aluminium is an example of Super Conductor. Superconductors can be used in space missions to increase/ boost the signal strength. They are also used i in the data fibres to increase the speed of data transfer.

Give explanations of the given statements:

Question 1.
Safety precautions are to be taken while using electricity.
Answer:

Electric switches and sockets should be fitted at a height at which small children cannot reach and put pins or nails inside. Plug wires should not be pulled while removing a plug from its socket.
Before cleaning an electrical appliance it should be switched off and its plug removed from the socket.
One’s hands should be dry while handling an electrical appliance, and, as far as possible, one should use footwear with rubber soles.
As rubber is an insulator, it prevents the current from flowing’ through our body, thereby protecting it.
If a person gets an electric shock, you should not touch that person. You should switch off the main switch or remove the plug from the socket if possible.
If not, then you should use a wooden pole to push the person away from the electric wire.

Question 2.
In a domestic circuit colour code is followed while setting up electrical wiring.
Answer:

The electricity in our homes is brought through the main conducting cable either from the electric pole or from underground cables.
Usually, there are three wires in the cable.
(a) Live wire which brings in the current. It has a red or brown insulation.
(b) Neutral wire through which the current returns. It is blue or black.
(c) Earth wire is of yellow or green colour. This is connected to a metal plate buried deep underground near the house and is for safety purposes.
In India, the voltage difference between the live and neutral wires is about 220 V.
Live and neutral wires are connected to the electric meter through a fuse.
They are connected through a main switch, to all the conducting wires inside the home so as to provide electricity to every room.
In each separate circuit, various electrical appliances are connected between the live and neutral wires.
The different appliances are connected in parallel and the potential difference across every appliance is the same.

Question 3.
Fuse used in electrical circuit can save electrical objects from damage.
Answer:

Fuse wire is used to protect domestic appliances.
It is made of a mixture of substances and has a specific melting point.
It is connected in series to the electric appliances. If for some reason, the current in the circuit increases excessively, the fuse wire gets heated and melts.
The circuit gets broken and the flow of current stops, thus protecting the appliance.
This wire is fitted in a groove in a body of porcelain-like non-conducting material. For domestic use, fuse wires with upper limits of 1 A, 2 A, 3 A, 4 A, 5 A and 10 A are used.

Question 4.
Bulbs arranged in parallel glow brighter than bulbs arranged in series.
Answer:

The amount of light given out by bulbs in parallel combination will be more than that in series combination.
In parallel combination the resistance of the overall circuit decreases whereas in series it increases, so the current flowing through the bulbs in parallel circuit is more.
Due to this, intensity of light given out by bulbs in parallel combination is more than the bulbs in series combination.

Complete the following table:
Answer:

Solve the numerical:

Question 1.
The length of a conducting wire is 50 cm and its radius is 0.5 mm. If its resistance is 30Ω, what is the resistivity of its material?
Answer:

The resistivity of the wire is 4.71 x 10^-5 Ωm.

Question 2.
Determine the current that will flow when a potential difference of 33 V is applied between two ends of an appliance having a resistance of 110 Ω. If the same current is to flow through an appliance having a resistance of 500 Ω, how much potential difference should be applied across its two ends?
Answer:

The current is 0.3 A and potential difference to be applied is 150 V.

Question 3.
Determine the resistance of a copper wire having a length of 1 km and diameter of 0.5 mm.
Answer:
Given: Resistivity of copper (p)
= 1.7 x 10^-8 Ω m
Converting all measures into metres.
Length of wire (L) = 1 km
= 1000 m = 10³ m
Diameter of wire (d) = 0.5 mm
= 0.5 x 10^-3m
To find: Resistance of wire (R) = ?
Formula:
\(R=\rho \frac{L}{A}\)
Solution:
If d is the diameter of the wire then, its area of cross-section

The resistance of a copper wire is 85Ω and area of cross section is 0.2 x 10^-6 m²

Question 5.
Two resistors having resistance of 16 and 14 are connected in series. If a potential difference of 18 V Is applied across them, calculate the current flowing through the circuit and the potential difference across each individual resistor.
Answer:

The current in the circuit is 0.6 A and potential across 16 Ω retor is 9.6 volt and 14 Ω resistor is 8.4 voIt.

Question 6.
If the resistors 5 Ω, 10 Ω and 30 Ω are connected in parallel to battery of 12 V, find the effective resistance in the circuit. Calculate the total current and current in each resistor.
Answer:

(a) The total current is 4 A and current in each resistor is 2.4 A, 1.2 A and 0.4 A respectively.
(b) The effective resistance in the circuit is 3Ω.

Complete the diagram and answer the questions:

Question 1.
The following figure shows the symbols for components used in the accompanying electrical circuit.

(a) Place them at proper places and complete the circuit.
(b) Which law can you prove with the help of the above circuit?
(c) State expression for Ohm’s law
Answer:

(b) This circuit can be used to prove Ohm’s law.
(c) V = IR is the expression of Ohm’s law

Question 3.
Explain with the help of a diagram, what are free electrons and how they move through the conductor?

Answer:

Every atom of a metallic conductor has one or more outermost electrons which are very weakly bound to nucleus.
These are called free electrons.
These electrons can easily move from one part of a conductor to its other parts.

Complete the paragraph:

Question 1.
If resistors are connected in series,
Answer:
The same current flows through each resistor. The effective resistance of the resistors is equal to the sum of their individual resistances. The potential difference between the two extremes of the arrangement is equal to the sum of the potential differences across individual resistors. The effective resistance is larger than each of the individual resistances. This arrangement is used to increase the resistance in a circuit. This type of connection is used in electrical heating equipment like geysers, iron, and hair dryers.

Question 2.
If a number of resistors are connected in parallel,
Answer:
The inverse of the effective resistance is equal to the sum of the inverses of individual resistances. The current flowing through an individual resistor is proportional to the r inverse of its resistance and the total current flowing through the circuit is the sum of the currents flowing through individual resistors. The potential difference across all r resistors is the same. The effective resistance of resistors connected in parallel is less than r the least resistance of individual resistors.

This arrangement is used to reduce the resistance in a circuit. Even if any one of the several bulbs connected in parallel becomes non-functional because of some damage to its filament, the circuit does not break as the current flows, through the other paths, and the rest of the bulbs light up. When several bulbs are connected in parallel, they emit the same amount of light as when they are connected individually in the circuit, while bulbs connected in series emit less light than when connected individually.

Read the paragraph and answer the questions.

Electric switches and sockets should be fitted at a height at which small children cannot reach and put pins or nails inside. Plug wires should not be pulled while removing a plug from its socket. Before cleaning an electrical appliance it should be switched off and its plug removed from the socket. One’s hands should be dry while handling an electrical appliance, and, as far as possible, one should use footwear with rubber soles. As rubber is an insulator, it prevents | the current from flowing through our body, thereby protecting it. If a person gets an electric shock, you should not touch that person. You should switch off the main switch and if the switch is too far or you do not know where it is located, then you should remove the plug from the socket if possible. If not, then you should use a wooden pole to push the person away from the electric wire.

(i) Why should the electrical sockets be fitted at a certain height?
Answer:
Electric switches and sockets should be fitted at a height at which small children cannot reach and put pins or nails inside.

(ii) Why plug wires should not be pulled out while removing any electrical device?
Answer:
Plug wires should not be pulled out while removing any electrical device as it may cause the wire to break causing short circuit which can lead to fire or death.

(iii) Why should a person wear footwear with rubber soles while handling electrical appliances. .
Answer:
As rubber is an insulator, it prevents the current from flowing through our body, thereby protecting it. Hence a person should wear footwear with rubber soles while handling electrical appliances.

(iv) Saee is touching an electrical button socket with wet hands what will you advise her and why?
Answer:
We will advise her to dry her hands before touching any electrical sockets or devices as water on the hands can cause an electrical short circuit producing shock to the person touching it.

(v) Sneha is getting an electrical shock what will you do the save her life?
Answer:
We should switch off the main switch and if the switch is too far or we do not know where it is located, then we should remove the plug from the socket if possible. If not, then we should use a wooden pole to push the person away from the electric wire.

(vi) Give a title to the above passage.
Answer:
Precautions to be taken while using electricity

Answer the questions in details:

Question 1.
Find the expression (i.e., derive the expression) for the resistors connected in series.
Answer:
Expression for the resistance connected in series:
(i) Let R₁, R₂ and R₃ be three resistances connected in series between C and D.
(ii) Let R_s be the effective resistance in circuit and V₁, V₂ and V₃ be the potential difference across R₁, R₂ and R₃ respectively.
(iii) Let the potential difference across CD be V.

(iv) In series combination.
v = v₁ + v₂ + v₃ ……………………(i)
By using Ohm’s law
V = IR_s
∴ V₁= IR₁, V₂= IR₂and V₃= 1R₃
Substituting these values in equation (j) we get
IR_s= IR₁+ IR₂+ IR₃
∴ R_s = R₁ + R₂ + R₃
For ‘n’ number of resistors conneded in series we get
R_s = R₁ + R₂ + R₃+ …………………. + R_n

Question 2.
Find the expression (i.e., derive the expression) for the resistors connected in parallel.
Answer:
Expression for the resistance connected in parallel.
(i) Let R₁, R₂ and R₃ be the three resistances connected in parallel combination between points C and D and let R be their effective resistance.
(ii) Let I₁, I₂ and I₃ be the currents flowing through resistances R₁, R₂ and R₃ respectively. Let I be the current flowing through the circuit and V be the potential difference of the cell.

(iii) For parallel combination of resistances,

(iv) Substituting the values of (I, I₁, I₂ and I₃) in equation (i) we get

Question 3.
Find the expression for resistivity of a material.
Answer:
(i) At a given temperature, the resistance (R) of a conductor depends on its length (L), area of cross-section (A) and the material it is made of. If the resistance of a conductor is R, then

(ii) p is the constant of proportionality and is called the resistivity of the material.
(iii) The unit of resistivity in SI units is Ohm metre (Ω m).
(iv) Resistivity is a specific property of a material and different materials have different resistivity. ’

Make the concept diagram and explain:

Question 1.
Make the concept diagram of an electrical circuit and explain the working of a fuse.

Answer:

Fuse wire is used to protect domestic appliances.
It is made of a mixture of substances and has a specific melting point.
It is connected in series to the electric appliances. If for some reason, the current in the circuit increases excessively, the fuse wire gets heated and melts. The circuit gets broken and the flow of current stops, thus protecting the appliance.
This wire is fitted in a groove in a body of porcelain-like non-conducting material. For domestic use, fuse wires with upper limits of 1A, 2A, 3A, 4A, 5A, and lO Aareused.

(2) Show motion of electrons in an circuit and explain precautions while using an electrical device.
Answer:

Electric switches and sockets should be fitted at a height at which small children cannot reach and put pins or nails inside. Plug wires should not be pulled while removing a plug from its socket.
Before cleaning an electrical appliance it should be switched off and its plug removed from the socket.
One’s hands should be dry while handling an electrical appliance, and, as far as possible, one should use footwear with rubber soles.
As rubber is an insulator, it prevents the current from flowing through our body, thereby protecting it.
If a person gets an electric shock, you should not touch that person. You should switch off the main switch or remove the plug from the socket if possible.
1f not, then you should use a wooden pole to push the person away from the electric wire.

Q.4.4.Complete the incomplete figure and give an explanation:

Answer:

If the physical state of a conductor remains constant, the current (I) flowing through it is directly proportional to the potential difference (V) between its two ends.

I α V
I = kV (k = constant of proportionality)

This is known as Ohm’s law.
We can obtain the SI unit of resistance from the above formula, Potential difference and current are measured in Volts and Amperes respectively. The unit o resistance is called Ohm. It is indicated by the symbol Ω.

The resistance of one Ohm : If one Ampere current flows through a conductor when one Volt potential difference is applied between its ends, then the resistance of the conductor is one Ohm.

9th Std Science Questions And Answers:

Introduction to Biotechnology Class 9 Science Chapter 17 Questions And Answers Maharashtra Board

January 6, 2025January 5, 2025 by Prasanna

Balbharti Maharashtra State Board Class 9 Science Solutions Chapter 17 Introduction to Biotechnology Notes, Textbook Exercise Important Questions and Answers.

Std 9 Science Chapter 17 Introduction to Biotechnology Question Answer Maharashtra Board

Class 9 Science Chapter 17 Introduction to Biotechnology Question Answer Maharashtra Board

1. Each of the following statements is wrong. Rewrite them correctly by changing either one or two words.

a. Simple squamous epithelium is present in the respiratory tract.
b. Glandular epithelium is present in kidneys.
c. Chlorenchyma helps the plant to float in water.
d. Striated muscles are also called involuntary muscles.
e. Chloroplast is present in permanent tissue.
Answer:
a. False. Ciliated columnar epithelium is present in respiratory tract.
b. False. Cuboidal epithelium is present in kidneys.
c. False. Aerenchyma helps the plant to float in water.
d. False. Striated muscles are also called voluntary muscles.
e. False. Chlorenchyma is present in permanent tissue.

2. Identify the odd word and explain why it is odd.

a. Xylem, phloem, permanent tissue, meristematic tissue.
Answer:
Meristematic tissue. It has the ability to divide whereas the others have lost the ability to divide.

b. Epithelium, Muscle fibre, nerve fibre, the epidermis.
Answer:
Epidermis. It is a plant tissue whereas the others are animal tissues.

c. Cartilage, bone, tendon, cardiac muscle.
Answer:
Cardiac muscle. It is a muscular tissue whereas the others are connective tissues.

3. Write the names of the following tissues.

a. Tissue lining inner surface of mouth.
Answer:
Squamous epithelium.

b. Tissue joining muscles and bones.
Answer:
Tendon

c. Tissue responsible for increasing height of plants.
Answer:
Apical meristem.

d. Tissue responsible for increasing girth of stem.
Answer:
Lateral meristem.

4. Write the differences.
Simple tissue and complex tissues in plants.
Answer:

Simple Tissue in plants	Complex Tissues in plants
(i) They are made up of only one type of cells.	(i) They are made up of more than one type of cells.
(ii) They are found in all parts of the plant.	(ii) They are found in the vascular regions of the plant.
(iii) They perform different functions like storage	(iii) They mainly perform the function of
of food, support, giving strength etc.	conduction of water and food.
(iv) Examples – Parenchyma, Collenchyma, Sclerenchyma.	(iv) Example – Xylem and phloem.

5. Write short notes.

a. Meristematic tissue.
Answer:

Meristematic tissue is present in specific parts of a plant where growth takes place.
Cells of meristematic tissue contain thick cytoplasm, a conspicuous nucleus and a thin cell wall and are compactly packed together.
Vacuoles are usually absent in these cells and they are highly active.
The main function of meristematic tissue is to bring about plant growth.
According to the location, meristematic tissues are of three types: Apical meristem, intercalary meristem and lateral meristem.

b. Xylem
Answer:

Xylem is a complex permanent tissue in plants.
It consists of thick-walled dead cells.
The type of cells in xylem are trachieds, vessels, xylem fibres (dead cells) and xylem parenchyma (living cells).
Its structure is like interconnected tubes conduct water and minerals only in upward direction.

c. Striated muscles.
Answer:

The cells of striated muscles are long, cylindrical, multinucleate and have no branches.
These are alternate dark and light bands on these muscles.
As they are attached to bones, they are also called skeletal muscles.
They move as per our will, hence they are called voluntary muscles.
Striated muscles bring about movements of arms and legs, running, speaking etc.

d. Agro-complementary business.
Answer:
(i) The business that are complementary to agriculture and generate supplementary income for the farmers are called agro complementary business.

(ii) These include:

Animal Husbandry: It is practiced for milk production and for using the cattle as help in farming operations, e.g. cows and buffaloes are raised for milk whereas bulls and male buffaloes for pulling heavy loads.
Poultry farming: It is the rearing of egg and meat yielding chickens. Chickens raised for eggs are called layers while those raised for meat are called broilers.
Sericulture: It is the rearing of silkworms (moths) for silk production. The silk fibres obtained are processed, reeled and then woven into fabric.

e. Genetic engineering
Answer:

Genetic engineering is the deliberate modification of the characteristics of an organism by manipulating its genetic material.
An organism that is generated through genetic engineering is called a genetically modified organism (GMO).
Genetic engineering is applied in many fields like research, agriculture, industrial biotechnology and medicine.
In agriculture, genetic engineering is used in the production of cash crops, improvement in varieties of cash crops, increase in ability of plants to withstand environmental stresses.
In medicine, genetic engineering is used for vaccine production, early diagnosis of congenital disease, organ transplant, cancer research, production of artificial skin, cartilage etc. in laboratories.

f. Sericulture
Answer:

Sericulture is the rearing of silkworms (moths) for production of silk.
Bombyx mori is the most commonly used variety of silkworm for this purpose.
The life cycle of silkworm consist of four stages namely egg, larva, pupa and adult.
Thousands of eggs deposited by female moths are incubated artificially to shorten the incubation period.
Larvae hatching out of eggs are released on mulberry plants.
Larvae are nourished by feeding on mulberry leaves.
After feeding for 3-4 days, larvae move to branches of mulberry plant.
The silk thread is formed from the secretion of their salivary glands.
Larvae spin this thread around themselves to form a cocoon. The cocoon may be spherical in nature.
Ten days before the pupa turns into an adult, all the cocoons are transferred into boiling water.
Due to the boiling water, the pupa dies in the cocoon and silk fibres become loose.
These fibres are unwound, processed and reeled. Various kinds of fabric is woven from silk threads.

6. Explain the meaning of biotechnology and its impact on agricultural management with suitable examples.
Answer:
The techniques of bringing about improvements in living organisms by artificial genetic changes and by hybridization for the welfare of human beings, are together called biotechnology. Impact of biotechnology on agricultural management:

Genetically modified crops (GM crops) are being produced by introducing changes in DNA of natural crops.
Normally such varieties are not found in nature.
Thus, new varieties are produced artificially Different useful characters are introduced in such varieties.
Some naturally occurring varieties cannot withstand environmental stress like frequently changing temperature.
Wet and dry famines, changing climates etc. However, GM crops can grow in any of such adverse conditions.
As GM crops are resistant to insect pests, pathogens, chemical weedicides, etc. the use of harmful chemicals like pesticides can be avoided.
Due to use of seeds of GM crops, there is improvement in nutritive value and decrease in loss of crops.

Draw neat and labelled diagrams of the following:

7. Which two main techniques are used in biotechnology? Why?
Answer:

The two main techniques used in biotechnology are – Genetic engineering and tissue culture.
These techniques are used to bring about improvements in living organisms by artificial genetic changes and by hybridization for the welfare of human beings.
Its uses are in the production of cash crops, improvement in varieties of cash crops, early diagnosis of congenital diseases, organ transplant, cancer research, production of artificial skin, cartilage etc. in laboratories.

8. Discuss ‘Agritourism’ in the class and write a project on an agrotourism centre nearby. Present it in the class in groups.
Answer:

In agritourism, plantlets of flowering, medicinal, ornamental, vegetable plants and fruit trees are produced on a large scale by tissue culture technique.
By growing some of the plants fully, an agritourism centre can be developed.
If sufficient land is available, the emerging field of agritoursim would be a good business.
An agritourism centre consists of following:
(a) Mango, chikoo (sapota), guava, coconut, custard apple and some other regional fruit trees.
(b) Shade giving local or exotic attractive plants.
(c) Ornamental and flowering plants.
(d) Butterfly garden.
(e) Medicinal plant garden.
(f) Organic vegetables and fruits.
People visit places with such attraction in large numbers.
Selling plantlets/seedlings, fruits, vegetables at such places can be quite profitable.

9. Define the term tissue and explain the concept of tissue culture.
Answer:
A group of cells having the same origin, same structure and same function is called tissue. Concept of tissue culture:

Ex vivo growth of cells or tissues in an aseptic and nutrient-rich medium is called tissue culture.
Nowadays, a complete organism can be developed from a single cell or from tissue with the help of the tissue culture technique.
A liquid, solid or gel-like medium prepared from agar, which supplies nutrients and energy necessary for tissue culture is used in this technique.
Tissue culture can be used to grow plants on a large scale, which bear flowers, fruits of excellent quality, in shorter durations and are disease free.
The various processes involved in tissue culture are:

10. ‘Rearing of sheep is a livestock’. Justify this statement.
Answer:

The term livestock refers to animals reared for profit or for use.
Sheep provides us with wool, skin, meat and milk.
Therefore, rearing of sheep is a livestock.

Class 9 Science Chapter 17 Introduction to Biotechnology Intext Questions and Answers

Question 1.
Which components bring about important processes in the living organisms?
Answer:
Cells, tissues, organs, organ systems bring out important processes in living organisms.

Question 2.
Which is the smallest structural and functional unit of the body of living organisms?
Answer:
Cell is the smallest structural and functional unit of the body of living organisms.

Question 3.
Which type of muscle is the diaphragm of the respiratory system?
Answer:
Diaphragm is a skeletal muscle. It is an involuntary muscle that regulates breathing, although some voluntary control can be achieved.

Question 4.
What is the main difference between the growth of animals and plants?
Answer:

Growth in animals is uniform whereas the growth in plants occurs in specific parts of the body.
Growth in animals occurs for a certain period of life whereas the growth in plants occur throughout their life.

Question 5.
Why does the growth of a plant occur only at specific parts of the plant body?
Answer:
Growth of a plant occurs only at specific parts of the body due to the presence of meristematic tissues which contain dividing cells.

Question 6.
Suppose you want to grow a garden like the one shown in the picture, around your home or school. What would you do to achieve that? By which methods will you cultivate the seedlings?

Answer:

To grow a garden around the school or home, one must cultivate seedlings of different plants and those seedlings must be watered regularly and nurtured properly.
Seedlings can be cultivated by the following methods:
(a) Seed sowing: Seeds are sown, watered and allowed to germinate.
(b) Transplantation: Seeds are sown somewhere else and then the seedlings are transplanted in the garden.

Question 7.
You must have seen flowers of same variety but of 2 or 3 different colours borne by same plant. How is this possible?
Answer:

The different coloured flowers borne by the same plant are due to the pigments like anthocyanins, carotenoids etc. according to the genetic makeup of the plant.
Also, by using the latest techniques of biotechnology and tissue culture, it is possible to manipulate the genes for flower colour and get the desired flower colour.

Question 8.
What keeps the various organs and organ systems separate from each other? Why?
Answer:
The epithelial tissue keeps the various organs and organ systems separate from each other by forming a layer on the organs.

Question 9.
Why are epithelial tissues said to be simple tissues?
Answer:
Epithelial tissues are said to be simple tissues as they are made up of only one type of cells.

Question 10.
Why do slim persons feel more cold in winter than those who are obese?
Answer:

Below the skin, there is a tissue called adipose tissue.
The cells of these tissue are filled with fat droplets.
Due to storage of fat, it acts as an insulator and helps to retain heat in the body.
Obese people have more fat deposited in the adipose tissue as compared to slim persons. Therefore, slim persons feel more cold in winter than those who are obese.

Question 11.
Why can bones not be folded?
Answer:

Bone cells called osteocytes are embedded in solid ground substance made up of calcium phosphate.
This makes the bone hard, rigid and non- flexible. Therefore, bones cannot be folded.

Question 12.
Which other industries can be started as an extension of the plant nursery business?
Answer:
Businesses like Agritourism, Ecotourism, forest resorts and organic fruit gardens, yoga and meditation centres can be started as an extension of the plant nursery business.

Question 13.
To which places do people choose to go on vacation in order to relax when they are tired of crowds and stressful life?
Answer:
People choose to go to hill stations, beaches, forest resorts and places where there is lot of greenery to relax when they are tired of crowds and stressful life.

Question 14.
What is the inter-relationship between the two questions (7 and 8) above?
Answer:
The inter-relationship between the above two questions is that businesses like agritourism, ecotourism, forest resorts etc. can fetch a huge profit as people look for these kind of places to relax, to be away from the hustle and bustle of city life and feel close to nature.

Question 15.
Why are the cocoons transferred to boiling water before the pupa develops into an adult?
Answer:

Once the pupa develops into an adult, it will secrete a fluid to dissolve the silk and emerge out.
Hence the cocoons are transferred to boiling water before the pupa develops in to an adult to kill the silkworms before transformation is complete.

Question 16.
Why we cannot see our organs like the heart, blood vessels and intestines?
Answer:
We cannot see our organs like the heart, blood vessels and intestines as they are located inside the body.

Question 17.
What is meant by white revolution? Who was its pioneer? What benefits did it bring?
Answer:

White revolution was the programme launched by the National Dairy Development Board to increase the milk production in India.
Dr. Verghese Kurien was the pioneer of white revolution.
It transformed India from a milk-deficient nation to the largest producer of milk. It also helped the dairy farmers in directing their own development and empowering them.

It also helped to reduce the malpractices carried out by milk traders and merchants.

Answer the following questions:

Question 1.
Collect information about GM varieties of crops in your area and make a note of them. Also find out if there are adverse effects of GM crops on human beings and environment.
Answer:

Some of the GM crops are:
(a) Maize: MON 810, MON 863
(b) Rice: Golden rice
(c) Brinjal: BT brinjal
(d) Cotton: BT cotton
Effects of GM Crops on human beings: GM crops may cause toxicity and allergic reactions in humAnswer:
Effects of GM Crops on environment:
(a) GM crops may be toxic to pollinators and non-target species like butterflies.
(b) Many GM crops may be a threat to soil ecosystem as they secrete their toxins into the soil.

Question 2.
As shown in the figure, place an onion on each gas jar in such a way that its base (roots) will remain dipped in water. Measure and record the length of the roots of both onions on the first, second and third day. On the fourth day, cut off 1 cm of the roots of the onion in flask B Measure the length of the roots of both onions for the next five days and record your observations in the following table.

Length (cm)	Day 1	Day 2	Day 3	Day 4	Day 5
Flask A
Flask B

Answer:
(Students are expected to record their observation in the given table).

(a) Which onion has longer roots? Why?
Answer:
The onion in jar Ahas longer roots as it continues to grow due to the presence of meristematic tissue at root tip which had dividing cells.

(b) Why did the roots of the onion in jar B stop growing?
Answer:
The roots of onion in jar B stopped growing as the meristematic tissue present in the root tips were cut off.

Question 3.
Take a fresh and fleshy leaf of Rhoeo, lily or any other plant. Pull and press it, tearing it obliquely in such a way that its transparent epidermis will be visible at the cut margins. Take the transparent epidermis with the forceps and keep it in dilute safranin solution for 1 minute. Spread it on a slide, cover it with a cover-slip and observe it under a compound microscope.
Answer:

The cells of the epidermis are flat and polygonal and there are no intercellular spaces between them.
A single continuous layer is formed.
The epidermis is covered by a waxy cuticle.

Question 4.
Establish your own plant nursery near your school or home. Prepare the seedlings of flowering plants, fruit plants, and ornamental plants being grown in your area. Can you start a business in the future with the help of this activity? Think it over.
Answer:
(Students are expected to do this activity on their own.)

Yes, we can start a business of plant nursey in future. If sufficient land is available, the emerging field of agritourism would be a good business.

Question 5.
Observe the skin of the back of your hand with the help of a magnifying lens. Do you see the closely attached squarish and pentagonal shapes?
Answer:
Yes, we can see the squarish and pentagonal shapes. This is the stratified squamous epithelium present on the outer layer of skin.

Question 6.
Observe a permanent slide of blood smear under a compound microscope. What did you see?
Answer:

A permanent slide of blood smear under a compound microscope shows different types of cells like RBCs, WBCs and platelets.
The different types of WBCs that can be seen are eosin mphocytes.

Question 7.
Visit a modern cowshed nearby and record the following points – The number of cattle, their variety, total milk production, cleanliness in cattle-shed, arrangements for health care of cattle.
Answer:
Students are expected to do this activity on their own.

Question 8.
Collect more information about animal husbandry.
Answer:

The branch of agriculture which deals with the feeding, shelter, health and breeding of domestic animals is called animal husbandry.
It is a scientific and systematic management of livestock.
Animal husbandry practices include:
(a) Proper food and clean drinking water.
(b) Proper shelter
(c) Proper methods of breeding
(d) Prevention and cure of disease.
Animal husbandary practices serve as an alternative income for the farmers and help to satisfy the need of food for man.

Question 9.
Find out from the internet the average daily milk yield from local and exotic varieties of cow.
Answer:

Milk yield from local cow : 12-15 litres/day.
Milk yield from exotic cow: 15-30 litres/day.

Question 10.
Are the structure and functions of the bodies of plants and animals the same?
No. The structure and functions of the bodies of plants and animals are not the same. Some differences between plants and animals:
Answer:

Plants	Animals
Plants continue to grow throughout their life.	Animals grow only for a specific period of life.
Growth in plants in not uniform.	Growth in animals is uniform.
Plants have dividing and non-dividing tissues.	Animals do not have different dividing and nondividing tissues.
Plants are sedentary.	Animals generally move from place to place in search of food, shelter and partners.
Energy needs of plants are less.	Energy needs of animals are greater.
Plants can prepare their own food by photosynthesis.	Animals cannot prepare their own food. They depend on plants and other animals for their food.

Class 9 Science Chapter 17 Introduction to Biotechnology Additional Important Questions and Answers

Choose and write the correct option:

Question 1.
Protective coverings in the animal body are called tissues.
(a) meristematic
(b) muscular
(c) epithelial
(d) bone
Answer:
(c) epithelial

Question 2.
Epithelial tissue is present in
(a) skin
(b) inner surface of blood vessels
(c) walls of the alveoli
(d) all of these
Answer:
(d) all of these

Question 3.
helps in selective transport of substances.
(a) Squamous epithelium
(b) Stratified epithelium
(c) Cuboidal epithelium
(d) Columnar epithelium
Answer:
(a) Squamous epithelium

Question 4.
helps in secretion of digestive juice, absorption of nutrients.
(a) Glandular epithelium
(b) Columnar epithelium
(c) Cuboidal epithelium
(d) Ciliated epithelium
Answer:
(b) Columnar epithelium

Question 5.
supports internal organs
(a) Areolar tissue
(b) Adipose tissue
(c) Lymph
(d) Tendon
Answer:
(a) Areolar tissue

Question 6.
tissue helps in insulation, supply of
Answer:
(b) Adipose tissue

Question 7.
connect muscles to bones.
(a) Ligaments
(b) Tendons
(c) Cartilages
(d) Nerves
Answer:
(b) Tendons

Question 8.
join two bones to each other.
(a) Cartilages
(b) Tendons
(c) Ligaments
(d) Muscles
Answer:
(c) Ligaments

Question 9.
meristem increases the length of root and stem.
(a) Intercalary
(b) Apical
(c) Lateral
(d) Permanent
Answer:
(b) Apical

Question 10.
showed that cells and tissues can be grown ex vivo.
(a) Frederick Campion Steward
(b) Gregor Johann Mendel
(c) Frederick Miescher
(d) Robert Brown
Answer:
(a) Frederick Campion Steward

Question 11.
is an example of genetically modified maize.
(a) Vaishali
(b) Vistive Gold
(c) MON 810
(d) Amflora
Answer:
(c) MON 810

Question 12.
is an exotic variety of cow.
(a) Holstein
(b) Gir
(c) Sahiwal
(d) Dangi
Answer:
(a) Holstein

Question 13.
is a layer chicken.
(a) Brahma
(b) Leghorn
(c) Cochin
(d) Aseel
Answer:
(b) Leghorn

Question 14.
is a broiler chicken.
(a) Leghorn
(b) Lehman
(c) Aseel
(d) Minorca
Answer:
(c) Aseel

Question 15.
is a broiler chicken.
(a) Minroca
(b) Ancona
(c) Leghorn
(d) Cochin
Answer:
(d) Cochin

Question 16.
Cartilage is found
(a) all around the cells in body
(b) in nose, ear, larynx, trachea
(c) between the muscles and skin
(d) around the blood vessels
Answer:
(b) in nose, ear, larynx, trachea

Question 17.
Which of the following is an exotic variety of COW?
(a) Plymouth Rock
(b) New Hampshire
(c) Black Rock
(d) Brown Swiss
Answer:
(d) Brown Swiss

Question 18.
epithelium is present in the inner surface of respiratory tract.
(a) Stratified
(b) Columnar
(c) Ciliated
(d) Cuboidal
Answer:
(c) Ciliated

Question 19.
Bones consist of osteocytes embedded in solid ground substance made up of
(a) calcium bicarbonate
(b) calcium carbonate
(c) calcium phosphate
(d) calcium sulphate
Answer:
(c) calcium phosphate

Question 20.
helps in growth of branches, formation of leaves and flowers.
(a) Lateral meristem
(b) Apical meristem
(c) Intercalary meristem
(d) Xylem
Answer:
(c) Intercalary meristem

Question 21.
tissue is present in the hard coat of seeds, outer covering of coconut.
(a) Parenchyma
(b) Xylem
(c) Collenchyma
(d) Sclerenchyma
Answer:
(d) Sclerenchyma

Question 22.
The cells of tissue are dead.
(a) Parenchyma
(b) Collenchyma
(c) Sclerenchyma
(d) All of these
Answer:
(c) Sclerenchyma

Question 23.
Cuboidal epithelium is found in
(a) inner surface of mouth, blood vessels
(b) inner layer of skin
(c) tubules of kidney, salivary gland
(d) inner surface of respiratory tract
Answer:
(c) tubules of kidney, salivary gland

Find the odd man out:

Question 1.
Cell body, muscle fibre, axon, dendrites.
Answer:
Muscle fibre. It is a muscle cell whereas the others are parts of nerve cell.

Question 2.
Tracheids, vessels, companion cells, xylem fibres.
Answer:
Companion cells. It is an element of phloem whereas the others are elements of xylem.

Question 3.
Sieve tubes, tracheids, phloem parenchyma, phloem fibres.
Answer:
Tracheids. It is an element of xylem whereas the others are elements of phloem.

Question 4.
Holstein, Brown swiss, Bombyx mori, Jersey.
Answer:
Bombyx mori. It is a variety of silkworm whereas the others are varieties of cows.

Complete the analogy:

(1) Inner surface of mouth : Squamous epithelium :: Inner surface of intestine :
(2) Glandular epithelium : Secretion of sweat, oil :: Cuboidal epithelium:
(3) Respiratory tract: Ciliated columnar epithelium :: Kidney tubules:
(4) Outer layer of skin : Stratified epithelium :: Inner layer of skin :
(5) Muscular tissue : Movement :: Nervous tissue :
(6) Tendons : Join muscles to bones :: Ligaments :
Answer:
(1) Columnar epithelium
(2) Secretion of saliva
(3) Cuboidal epithelium
(4) Glandular epithelium
(5) Conduction of excitation
(6) Join two bones to each other

Match the columns:

Question 1.

Column ‘A’	Column ‘B’
(1) Squamous epithelium	(a) Secretion of digestive juice
(2) Cuboidal epithelium	(b) Selective transport of substances
(3) Columnar epithelium	(c) Protection of organs
(4) Stratified epithelium	(d) Secretion of saliva

Answer:
(1 – b),
(2 – d),
(3 – a),
(4 – c)

Question 2.

Column ‘A’	Column ‘B’
(1) Brahma	(a) Local variety of cow
(2) Jersey	(b) Layer chicken
(3) Devin	(c) Exotic variety of cow
(4) Lehman	(d) Broiler chicken

Answer:
(1 – d),
(2 – C),
(3 – a),
(4 – h)

Question 3.

Column ‘A’	Column ‘B’
(1) Potato	(a) Vistive Gold
(2) Maize	(b) Amflora
(3) Soybean	(c) Vaishali
(4) Tomato	(d) MON 863

Answer:
(1-b),
(2-d),
(3-a),
(4-c)

Answer the following:

Question 1.
Explain the different types of muscular tissues.
Answer:

Question 2.
Explain the types of complex permanent tissues.
Answer:

Name of tissue	Xylem	Phloem
Characteristics	Consists of thick-walled dead cells	Consists of cytoplasm containing living cells.
Types of cells	Tracheids, vessels and xylem fibres – dead cells. Xylem parenchyma – living cells.	Sieve tubes, companion cells, phloem parenchyma – living cells. Phloem fibres – dead cells.
Function	A structure like interconnected tubes, conduct water and minerals only in upward direction.	Tubes joined to each other, conduct sugar and amino acids from leaves to various parts in upward and downward direction

State whether the following statements are true or false. Correct the false statement:

Question 1.
Lateral meristem increase girth(diameter) of the root and stem.
Answer:
True

Question 2.
Due to use of seeds of GM crops, there is decrease in nutritive value and increase in loss of crops.
Answer:
False. Due to use of seeds of GM crops there is improvement in nutritive value and decrease in loss of crops.

Question 3.
In a bioreactor, cells can be grown in a more nutritive medium and protected from pathogens.
Answer:
True

Question 4.
Rare and endangered plants can be grown by tissue culture and can be protected from extinction.
Answer:
True

Question 5.
The silk thread is formed from the secretion of the sweat glands of silkworm.
Answer:
False. The silk thread is formed from the secretion of the salivary glands of silkworm.

Question 6.
Rhode Island Red, New Hampshire, Plymouth Rock, Black Rock are varieties of chicken reared for both eggs as well as meat.
Answer:
True

Question 7.
Phloem consists of thick-walled dead cells.
Answer:
False. Phloem consists of living cells containing cytoplasm.

Question 8.
Stratified squamous epithelium is present in inner surface of mouth, oesophagus, blood vessels and alveoli.
Answer:
False. Stratified squamous epithelium is present in the outer layer of skin.

Question 9.
Broiler chickens are raised for eggs.
Answer:
False. Broiler chickens are raised for meat.

Question 10.
Non-striated muscles bring about contraction and relaxation of heart.
Answer:
False. Cardiac muscles bring about contraction and relaxation of heart.

Name the following:

Question 1.
Tissue responsible for growth of branches, formation of leaves and flowers.
Answer:
Intercalary meristem.

Question 2.
Tissue that helps in insulation, supply of energy, storage of fats.
Answer:
Adipose tissue.

Question 3.
Tissue present in outer layer of skin.
Answer:
Glandular epithelium.

Question 4.
Tissue present in nose, ear, larynx, trachea.
Answer:
Cartilage.

Question 5.
Dead cells in xylem.
Answer:
Tracheids, vessels and xylem fibres.

Question 6.
Living cells in xylem.
Answer:
Xylem parenchyma.

Question 7.
Living cells in phloem.
Answer:
Sieve tubes, companion cells, phloem parenchyma.

Question 8.
Dead cells in phloem.
Answer:
Phloem fibres.

Question 9.
GM crops.
Answer:
BT cotton, Amflora, Golden Rice.

Question 10.
Local Indian varieties of cow.
Answer:
Sahiwal, Sindhi, Lai kandhari, Devni, Khillari, Dangi.

Question 11.
Exotic varieties of cow.
Answer:
Jersey, Brown swiss, Holstein.

Question 12.
Layers.
Answer:
Leghorn, Minorca, Ancona, Lehman.

Question 13.
Broilers.
Answer:
Brahma, Long, Cochin, Aseel.

Question 14.
Chickens reared for both eggs and meat.
Answer:
Rhode Island Red, New Hampshire, Plymouth Rock, Black Rock.

Give scientific reason.

Question 1.
Blood is a complex tissue.
Answer:

A complex tissue is made up of more than one type of cells.
In blood, cells of different types, colour and shapes are mixed together.
Blood contains erythrocytes (RBCs), leucocytes (WBCs) and platelets in a liquid plasma.
Therefore, blood is a complex tissue.

Define the following:

Question 1.
Tissue
Answer:
A group of cells having the same origin, same structure and same function is called tissue.

Question 2.
Differentiation
Answer:
When cells acquire a specific structure, shape and location and perform a specific function, it is called differentiation.

Question 3.
Biotechnology
Answer:
The techniques of bringing about improvements in living organisms by artificial genetic changes and by hybridization for the welfare of human beings, are together called ‘Biotechnology’.

Question 4.
Tissue culture
Answer:
Ex vivo growth of cells or tissues in an aseptic and nutrient-rich medium’ is called tissue culture.

Write short notes

Question 1.
Animal husbandry
Answer:

In India, animal husbandry is practised for milk production and for using the cattle as help in farming operations.
Example – Cows and buffaloes are raised for milk and bulls and male buffaloes for pulling the heavy loads.
Local Indian varieties of cows like Sahiwal, Sindhi, Gir, Lai kandhari, Devni, Khillari, Dangi, etc. and exotic varieties like Jersey, Brown swiss, Holstein, etc. are kept for their milk.
Proper care of cattle is necessary for a clean and high yield of milk which includes:
(a) A balanced diet, i.e. all constituents of food should be given to cattle. It must include fibre- rich coarse food, fodder, and sufficient water.
(b) The cattle-shed should be clean and dry with proper ventilation and a roof.
(c) Cattle should be regularly vaccinated.

Question 2.
Poultry farming.
Answer:

Rearing of egg and meat yielding chickens is called poultry farming.
Chickens raised for laying eggs are called layers . e.g. Leghorn, Minorca, Ancona, Lehman.
Chickens raised for meat are called broilers, e.g. Brahma, Long, Cochin, Aseel.
Rhode Island Red, New Hampshire, Plymouth Rock, Black Rock are varieties of chicken reared for both eggs as well as meat.
The objectives behind development of new hybrid varieties from a cross between Indian varieties like Aseel and exotic varieties like Leghorn are to produce good quality chickens in large numbers.
To develop the ability to withstand high temperature, to use by-products of agriculture as poultry feed, etc.

Distinguish between:

Question 1.
Xylem and Phloem
Answer:

Xylem	Phloem
(i) Consists of mostly thick-walled dead cells.	(i) Consists of mostly living cells containing cytoplasm.
(ii) The types of cells include dead cells- tracheids, vessels and xylem fibres and living cells-Xylem parenchyma.	(ii) The types of cells include living cells – Sieve tubes, companion cells, phloem parenchyma and dead cells – phloem fibres.
(iii) Structure like interconnected tubes, conduct water and minerals only in upward direction.	(iii) Tubes joined to each other, conduct sugar and amino acids from leaves to various parts in both upward and downward direction.

Question 2.
Striated muscles and Non-striated muscles.
Answer:

Striated muscles	Non-striated muscles
(i) Muscle cells are long, cylindrical, multinucleate and have no branches.	(i) Muscle cells are short, spindle-shaped, uninucleate and have no branches.
(ii) There are alternate dark and light bands on these muscles and they are attached to bones.	(ii) Dark and light bands are absent. Not attached to bones.
(iii) They move as per our will, hence they are called voluntary muscles.	(iii) They are not under the control of our will, hence they are called involuntary muscles.
(iv) These muscles bring about movements of arms and legs, running, speaking etc.	(iv) These muscles bring about movement of eyelids, passage of food through alimentary canal, contraction and relaxation of blood vessels etc.

Question 3.
Cartilage and Bone
Answer:

Cartilage	Bone
(i) They are present in nose, ear, larynx, trachea.	(i) They form the skeleton of the body.
(ii) They contain cells supported by fibrous, flexible, jelly-like ground substance.	(ii) They contain osteocytes embedded in solid ground substance made up of calcium phosphate.
(iii) Lubricates the surface of bones, gives support and shape to organs.	(iii) Supports and protects different organs, helps in movement.

Answer the following questions:

Question 1.
Close your eyes and try to identify different objects by feeling them with your hand. Why is it possible for you to identify things like a note-book, text-book, bench, compass-box, etc. only by touching them?
Answer:

We can identify objects just by touching them because of the memory that we retain in our brain.
The nervous tissue enables us to respond to the stimuli of touch.

Answer in detail:

Question 1.
Write the location, structure and function of following epithelial tissues:
(a) Squamous epithelium
(b) Stratified epithelium
(c) Glandular epithelium
(d) Columnar epithelium
(e) Ciliated epithelium
(f) Cuboidal epithelium
Answer:

Question 2.
Write the structure and function of the following connective tissues:
(a) Blood
(b) Lymph
(c) Areolar tissue
(d) Adipose tissue
(e) Cartilage
(f) Bones
(g) Tendons and ligaments
Answer:

Question 2.
Describe the structure of nervous tissue with the help of a neat labelled diagram.
Answer:

Nervous tissue enables us to respond to stimuli like touch, sound, odour, colour, etc.
Cells of the nervous tissue are specifically made to become excited and conduct the excitation from one part of the body to another.
The main part of the nerve cell is the cell body which contains the cytoplasm and the nucleus.
Numerous, small, branched fibres called dendrites arise from the cell body.
One of the fibres, is extremely long and is called
the axon.
The length of the nerve cell may be up to one metre.
Many nerve cells are bound together with the help of connective tissue to form a nerve.
Nervous tissue is present in the brain, spinal cord and the network of nerves spread all throughout the body.
In most animals, action in response to a stimulus occurs due to the integrated functioning of the nervous tissue and muscular tissue.

Question 3.
Explain the types of simple permanent tissues in plants.
Answer:
Types of simple permanent tissues.

Question 4.
Explain types, location and function of Meristematic tissue in tabular form:
Answer:

Types	Apical	Intercalary	Lateral
Location	At tip of the root and stem	At the base of the petiole of leaves and branches	At sides of root and stem
Function	Increase the length of the root and stem	Growth of branches, the formation of leaves and flowers	Increases diameter of the root and stem

Question 5.
Explain the types of simple permanent tissues in plants.
Answer:
Types of simple permanent tissues.

Name of Tissue	Parenchyma	Collenchyma	Sclerenchyma
Structure of cells	Living cells with thin cell wall and intercellular spaces.	Elongated living cells with thickened cell wall at corners due to cellulose and pectin.	Dead and fibrous cells with tapering ends, cell wall contains lignin.
Location	All parts like roots, stem, leaves, flowers and seeds.	At the base of leaf petiole, branches and stem	Stem, veins of leaves, hard coats of seeds, outer covering of coconut.
Functions	Support, storage of food and filling vacant spaces.	Support and flexibility to various parts.	Give strength and rigidity to parts of the plants.
Sub types	Chlorenchyma: Leaves, perform photosynthesis. Aerenchyma: Helps aquatic plants, leaves and stem to float.

Question 6.
Write down the applications of biotechnology (tissue culture) in floriculture, nurseries and forestry.
Answer:
Applications of biotechnology (tissue culture) in floriculture, nurseries and foresty:

Tissue culture can be used to grow those plants on a large scale which bear flowers, fruits of excellent quality.
Fully grown plants can be produced in shorter durations.
Plants can be grown on a large scale even if means of pollination or germinating seeds are not available.
For example, orchids or pitcher plants do not germinate but these plants can easily be produced by means of tissue culture.
In a bioreactor, cells can be grown in a more nutritive medium and protected from pathogens.
Bioreactors are useful for producing plantlets on a very large scale.
A large number of seedlings/plantlets can be produced in a short time using minimum resources and materials.
Usually, plants produced by tissue culture and genetic modification techniques are disease-free.
Plantlets produced by tissue culture technique of the meristem are virus-free.
Embryos produced using conventional hybridization technique between two or more varieties may not grow fully for some reasons.
However, embryos produced by tissue culture technique always complete their growth.
Rare and endangered plants can be grown using tissue culture technique and can thus be protected from extinction.
Similarly, various parts and seeds of such plants can be preserved by tissue culture and those varieties can be protected.

9th Std Science Questions And Answers: