Bhagya

Std 10 Hindi Chapter 5 Char Hath Chandna Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 5 चार हाथ चाँदना Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 5 चार हाथ चाँदना Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 5 चार हाथ चाँदना Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

1. विधानों के सामने सही अथवा गलत लिखिए :

प्रश्न 1.
विधानों के सामने सही अथवा गलत लिखिए :

1. शोभा सिंह ने ‘सत्यम्, शिवम्, सुंदरम्’ का क्रम बदला है। [ ]
2. प्रश्नकर्ता के अनुसार हमारी धरती का यथार्थ बहुत भयानक नहीं है। [ ]
3. कलाकार की शक्ति उसके चिंतन में है। [ ]
4. शोभा सिंह कलाकार का कर्म एक छोटी-सी जलती हुई मोमबत्ती नहीं समझते । [ ]

उत्तर:

1. सत्य
2. असत्य
3. सत्य
4. असत्य

2. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

3. उचित जोड़ियाँ मिलाइए।

प्रश्न 1.
उचित जोड़ियाँ मिलाइए।

‘अ’	‘ब’
1. चित्रकार	(क) अमृता प्रीतम
2. लेखिका	(ख) शोभा सिंह
3. जीनियस	(ग) कलाकार
4. ईश्वर	(घ) माँ

उत्तर:

‘अ’	‘ब’
1. चित्रकार	(ख) शोभा सिंह
2. लेखिका	(क) अमृता प्रीतम
3. जीनियस	(घ) माँ
4. ईश्वर	(ग) कलाकार

4. उचित विकल्प चुनकर रिक्त स्थानों की पूर्ति कीजिए।

प्रश्न 1.
उचित विकल्प चुनकर रिक्त स्थानों की पूर्ति कीजिए।

1. सुंदरता के लिए ………………….. सबसे पहली अवस्था है। (नजर, दृष्टि, नजरिया)
2. हमारी धरती का ……………… बहुत भयानक है। (सत्य, यथार्थ, वास्तव)
3. कलाकार की शक्ति उसके …………….. में है। (चिंतन, मनन, साधना)
4. मैं रचनात्मक ……………. के संबंध में कह रहा हूँ। (युक्ति, कृति, शक्ति)

उत्तर:

1. नजरिया
2. यथार्थ
3. चिंतन
4. शक्ति

5. पाठ में प्रयुक्त ऐसे शब्द ढूँढकर लिखिए जिनका वचन परिवर्तन नहीं होता।
जैसे : वृक्ष – वक्ष

प्रश्न 1.
पाठ में प्रयुक्त ऐसे शब्द ढूँढकर लिखिए जिनका वचन परिवर्तन नहीं होता।
जैसे : वृक्ष – वक्ष
उत्तर:

कलाकार	रंग	चित्रकार	घर
दीमक	गुलाब	फूल	दर्शक

अभिव्यक्ति :

प्रश्न 1.
‘कला जीवन को आनंदित करने का साधन है।’ विषय पर अपना मत स्पष्ट कीजिए।
उत्तरः
कला के माध्यम से मनुष्य अपने भावों की अभिव्यक्ति करता है। कला जीवन की अनुकृति है। कला जीवन को आनंदित करने का साधन है। कला में ऐसी शक्ति होती है जो कलाकार को संकीर्ण सीमाओं से उठाकर सफलता की मंजिल पर बिठा देता है। कला के कारण मानव मन में संवेदनाएँ एवं अभिरूचि निर्माण होती है। कला जीवन को सत्यम्, शिवम् और सुंदरम् से समन्वित करती है। कला उस क्षितिज की भाँति है जिसका कोई छोर नहीं है।

रसात्मकता कला का प्राण होता है। व्यक्ति को जो कला अच्छी लगती है, उसमें वह मग्न हो जाता है। अपनी मनपसंद कला के साथ एकाकार होने से उसका मन हर्ष से भर जाता है। मनपसंद कला उसके जीवन को प्रभावित करती है और उसे आनंद की अनुभूति दिलाती है। जो व्यक्ति अपने जीवन से निराश एवं उदास हो जाता है, वह यदि कला के सान्निध्य चला जाए तो उसके मन से उदासी की भावना सदा के लिए खत्म हो जाती है और वह चिर-आनंद का अनुभव करने लगता है।

भाषाबिंदु :

प्रश्न 1.
वर्तनी के नियमों के अनुसार शुद्ध शब्द छाँटकर लिखिए। |

1. मुश्कील/मुशकील/मुश्किल/मुष्कील = …………….
2. परसिद्ध/प्रसिद्ध/प्रसीध्द/प्रसिध्ध =…………….
3. मिट्टी/मिट्यी/मिट्टी/मीट्ठी = …………….
4. रूतूएँ/ऋतुएँ/ऋतूए/ऋतू = …………….

उत्तर:

1. मुश्किल
2. प्रसिद्ध
3. मिट्टी
4. ऋतुएँ

उपयोजित लेखन :

प्रश्न 1.
‘पुस्तक मेल में दो घंटे’ विषय पर अस्सी से सौ शब्दों में निबंध लिखिए।
उत्तरः
पुस्तक मेल में दो घंटे पुस्तकों का हमारे जीवन में महत्त्वपूर्ण स्थान होता है। वे एक मित्र के समान हमारी सहायक एवं मार्गदर्शक होती हैं। वे अपना ज्ञानरूपी अमृत कोष सदा हम पर न्योछावर करती रहती हैं। अतः पुस्तकों का वाचन सभी को करना चाहिए। पुस्तकों का भी अपना एक मेला होता है। पुस्तक मेले में तरह-तरह की पुस्तकें होती हैं। वहाँ पर लेखक एवं कवि आते हैं और स्वयं अपनी पुस्तकों के बारे में पाठकों को परिचित कराते हैं। मैं भी सरस्वती भवन द्वारा आयोजित पुस्तक मेले में गया था।

मेरे साथ मेरे मित्र भी थे। जैसे ही हमने पुस्तक मेले में प्रवेश किया वैसे ही पुस्तक मेले के प्रवेशद्वार पर एक व्यक्ति पुस्तक का मुखौटा पहनकर पुस्तकों के महत्त्व से हमें परिचित कराने लगा हमें बहुत ही अच्छा लगा। जैसे ही हम भीतर गए वैसे ही हमने चारों ओर नजर डाली।

तब हमने देखा कि चारों ओर पुस्तक खरीदने के लिए लोगों की भीड़ एकत्रित हुई है। कई दुकानों पर लोगों का तांता लगा हुआ था। भारतीय भाषाओं के सर्वश्रेष्ठ ग्रंथ एवं महापुरूषों की जीवनी सर्वत्र विक्री हेतु उपलब्ध थी। अंग्रेजी किताबें भी थीं। हिंदी साहित्य की पुस्तकों के बारे में क्या कहना? प्रत्येक दुकान में पंत जी, निराला जी, बच्चन जी, गुप्त जी, सुभद्रा जी, महादेवी जी, अज्ञेय जी, मन्नू भंडारी जी, भारती जी आदि पुस्तक रूप में विराजमान थे।

इन श्रेष्ठ साहित्यकारों के अनुपम ग्रंथ देखकर मैं आनंदविभोर हो गया। इतने में मेरे एक मित्र ने तपाक से कहा, “अरे देखो, हिंदी साहित्य के श्रेष्ठ वर्तमान साहित्यकार श्री. राम जी तिवारी बच्चों के साथ वार्तालाप कर रहे हैं।”

हम तुरंत उस स्थान पर पहुंच गए जहाँ पर श्री तिवारी जी बच्चों से तन्मयता और सहदयता से बात कर रहे थे। उनके विचार सुनकर हम सब गद्गद हो गए। उन्होंने ‘कितावें करती हैं बातें…’ इस कविता को हमारे सामने अभिव्यक्त करके पुस्तकों के वाचन हेतु जो संस्कार किया, उसका वर्णन करना मेरे लिए कठिन है।

पुस्तक मेले में घूमते-घूमते हमें कई ऐसी किताबों के बारे में पता चला, जिनके नाम भी हमने पहले कभी सुने नहीं थे। पुस्तक मेले में भ्रमण करते समय दो घंटे कब खत्म हुए, इसका पता भी नहीं चला। मनचाही पुस्तकें खरीद कर एवं प्राप्त ज्ञान को मस्तिष्क में संग्रहित कर हम खुशी-खुशी घर की ओर लौट पड़े।

Hindi Lokvani 10th Std Textbook Solutions Chapter 5 चार हाथ चाँदना Additional Important Questions and Answers

(अ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1) : आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
निम्नलिखित विधान सत्य है या असत्य लिखिए। –
i. श्री शोभा सिंह प्रसिद्ध साहित्यकार हैं।
उत्तर:
i. असत्य

प्रश्न 3.
समझकर लिखिए।
उत्तर:

प्रश्न 4.
उचित विकल्प चुनकर रिक्त स्थानों की पूर्ति कीजिए।
i. सुंदरता की …………………………. अवस्था सत्य है। (पहली, दूसरी, तीसरी)
उत्तर:
i. पहली

कृति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. रूहानी
2. तकनीकी
3. अवस्था
4. गहराई

उत्तर:

1. आत्मिक
2. प्रविधिक
3. हालत
4. गहनता

प्रश्न 2.
निम्नलिखित शब्दों के वचन बदलिए।
i. कल्पना
ii. लकीर
उत्तर:
i. कल्पनाएँ
ii. लकीरें

प्रश्न 3.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
i. अवस्था
ii. कल्पना
उत्तर:
i. हालत, देहादि की कालकृत स्थिति जैसे बचपन, जवानी, बुढ़ापा, उम्र, स्थिति
ii. नई बात, सोचना, मन की उपज

प्रश्न 4.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. सत्य
उत्तर:
i. सच

प्रश्न 5.
गद्यांश में प्रयुक्त अन्य भाषाओं के शब्द ढूँडकर लिखिए।
उत्तर:
i. रूहानी
ii. कैनवस

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘रंगों का जीवन में बड़ा महत्व है।’ इस विषय पर अपने विचार लिखिए।
उत्तर:
रंगों का व्यक्ति के जीवन में महत्त्वपूर्ण स्थान होता है। रंग चेतन जीव पर गहराई तक असर डालते हैं। रंग व्यक्ति को सिर्फ खुशी ही नहीं देते बल्कि उसके शारीरिक एवं मानसिक विकारों को भी दूर भगाते हैं। रंग व्यक्ति के जीवन में दोहरी भूमिका निभाते हैं। उदाहरण के तौर पर रंग हमें उत्तेजित करते हैं और हमें शांत भी करते हैं। इसलिए जीवन में रंगों का ज्योतिषीय महत्त्व है। रंगों के बिना व्यक्ति का जीवन नीरस होता है।

इंद्रधनुष के सात रंगों को रंगों का रचयिता माना जाता है। हरा रंग संपन्नता का प्रतीक माना जाता है। श्वेत रंग शांति का प्रतीक माना जाता है। पीला रंग प्रकाश का प्रतीक माना जाता है, तो गुलाबी रंग कोमलता व सुंदरता का प्रतीक माना जाता है। नीला रंग एकता व ठंडक का प्रतीक माना जाता है। रंग हमारे विचारों को प्रभावित करते हैं। इसलिए हमारे जीवन में रंगों का विशेष महत्त्व है।

(आ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1) : आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:
i.

ii.

प्रश्न 2.
प्रस्तुत गद्यांश को पढ़कर ऐसे दो प्रश्न तैयार कीजिए कि जिनके उत्तर निम्न शब्द हों –
i. परछत्ती
ii. तस्वीरें
उत्तर:
i. आँगन में क्या बनी हुई थी?
ii. बचपन में शोभा सिंह जी घर की दीवारें सजाने के लिए क्या बनाने लगे?

कृति आ (3) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।
i. जन्म × ……………
ii. निचली × ……………
उत्तर:
i. मरण
ii. ऊपरी

प्रश्न 2.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

1. घास-फूस का बना छप्पर –
2. कागज़, चमड़े आदि से मड़ी हुई दफ़्ती या पुस्तक की प्रति –
3. लकड़ी और किताबों को खानेवाला कीट –

उत्तर:

1. परछत्ती
2. जिल्द
3. दीमक

प्रश्न 3.
नीचे लिखे शब्दों में से उपसर्ग छाँटिए और संबंधित उपसर्ग से दो अन्य शब्द बनाइए।
i. परछत्ती
उत्तर:
i. परछत्ती : उपसर्ग : पर अन्य शब्द : परदादा, परदादी

प्रश्न 4.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तर:
i. धो-पोंछकर
ii. इर्द-गिर्द

(इ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1) : आकलन कृति

प्रश्न 1.
ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों
i. रचनात्मक
ii. चाँदना
उत्तर:
i. गद्यांश में किस शक्ति की बात हो रही है?
ii. जलती हुई मोमबत्ती धरती को क्या दे सकती है?

प्रश्न 2.
निम्नलिखित विधान सत्य है या असत्य लिखिए।
i. औरत सब कुछ छोड़कर एक नई और ऊपरी धरती पर चली जाती है।
ii. दो-दो, चार-चार हाथ चाँदना पूरी संस्कृति को प्रभावित कर सकता है।
उत्तर:
i. सत्य
ii. असत्य

कृति इ (2) : शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तर:

1. माँ-बाप
2. भाई-बहन
3. दो-दो, चार-चार
4. ईद-गिर्द

प्रश्न 2.
वचन बदलिए।
i. शक्ति
ii. मोमबत्ती
उत्तर:
i. शक्तियाँ
ii. मोमबत्तियाँ

प्रश्न 3.
‘कलाकार’ इस शब्द में निहित प्रत्यय को पहचानकर संबंधित उपसर्ग लगाकर अन्य दो शब्द तैयार कीजिए।
उत्तरः
कलाकारः प्रत्यय : कार नए शब्द : शिल्पकार, चित्रकार

प्रश्न 4.
अनेक शब्दों के लिए एक शब्द लिखिए।

1. किसी लक्ष्य को पाने के लिए किया गया अभ्यास –
2. रचना से संबंधित –
3. सभ्य होने का भाव –

उत्तर :

1. साधना
2. रचनात्मक
3. सभ्यता

कृति इ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘कला अभिव्यक्ति का माध्यम है।’ विषय पर अपने विचार लिखिए।
उत्तरः
मन के अंत:करण की सुंदर प्रस्तुति कला होती है। कला में मानसिक व शारीरिक कौशलों का प्रयोग होता है। कला का अर्थ है – रचना करना। चित्रकला, संगीत, काव्य, नृत्य, स्थापत्यकला, रंगमंच आदि कला के विविध रूप हैं। कला के द्वारा मनुष्य अपने भावों की अभिव्यक्ति करता है। कला मानव, प्राणियों में अमृत भर देती हैं। फिर वह कला संगीत कला हो या चित्रकला। वह अभिव्यक्ति का कुशल साधन बनकर मनुष्य के हृदय पर सकारात्मक प्रभाव निर्माण करती है। कला के द्वारा मनुष्य अपनी संवेदनाएं व अभिरुचि को दिशा देने की अद्भुत क्षमता रखता है। कला मानवीय मन को सम्मोहित करती है।

कला की अभिव्यक्ति जितनी कुशल होती है। उतनी वह मानव मन पर अपनी छाप छोड़ने में सक्षम होती है। ताजमहल देखने के लिए प्रतिवर्ष लाखों लोग आते हैं। लोग चार मिनार की सैर करते हैं। ये सारी कला ही तो हैं जो अपने अभिव्यक्ति के सशक्त पहिए पर खड़ी हैं। अत: कहा जाता है : अभिव्यक्ति की कुशल शक्ति कला होती है। वह अभिव्यक्ति का सशक्त माध्यम होती है।

(ई) गद्यांश पड़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ई (1) : आकलन कृति

प्रश्न 1.
समझकर लिखिए।

1. यहाँ पर चित्रित होकर पड़ा है धरती का यथार्थ –
2. धरती के यथार्थ –
3. ये लोप होती जा रही हैं –
4. गद्यांश में इस अंग्रेजी कवि का नाम आया है –
5. कवि ब्लेक का कथन –

उत्तर:

1. जगह-जगह पर व सड़कों की पटरियों पर
2. भयानक गरीबी और अंतहीन दुखों का इतिहास
3. जिंदगी की खूबसूरती व जिंदगी की अच्छाई
4. कवि विलियम ब्लेक
5. सुंदर ईश्वर को एक गुलाब का फूल बनाने में पचास हजार बरस लगे थे।

प्रश्न 2.
गद्यांश के आधार पर वाक्य पूर्ण कीजिए।

1. शोभा सिंह गुरुओं के चित्र बनाते हैं क्योंकि
2. कला का तब तक कोई प्रभाव नहीं होता जब तक
3. चित्रकार जिंदगी की खूबसूरती एवं अच्छाई को चित्रित करना चाहता है क्योंकि

उत्तर:

1. शोभा सिंह गुरुओं के चित्र बनाते हैं क्योंकि उनके ‘स्वयं’ महान थे।
2. कला का तब तक कोई प्रभाव नहीं होता जब तक वह कला के लिए होती है।
3. चित्रकार जिंदगी की खूबसूरती एवं अच्छाई को चित्रित करना चाहता है क्योंकि वह दिनोंदिन लोप होती जा रही है।

कृति ई (3) : शब्द संपदा

प्रश्न 1.
निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।
i. शोभा सिंह ने कहा कलाकार का कर्म भी एक व्यक्तित्व बनना है तभी कला में उसका प्रभाव आ सकता है।
उत्तर:
शोभा सिंह ने कहा, “कलाकार का कर्म भी एक व्यक्तित्व बनना है, तभी कला में उसका प्रभाव आ सकता है।”

प्रश्न 2.
लिंग बदलिए।
i. कलाकार
i. गुरु
उत्तर:
i. कलावती
ii. गुरुआइन

प्रश्न 3.
गद्यांश में से प्रत्यययुक्त शब्द ढूँढ़कर लिखिए।
उत्तर:
i. खूबसूरती : प्रत्यय : ई
ii. अच्छाई : प्रत्यय : ई

प्रश्न 4.
निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।
i. कल्पना
ii. इतिहास
उत्तर:
i. कल्पना + इक = काल्पनिक
ii. इतिहास + इक = ऐतिहासिक

प्रश्न 5.
विलोम शब्द लिखिए।

1. यर्थाथ × ………………..
2. खूबसूरत × ………………..
3. फूल × ………………..
4. महान × …………………

उत्तर:

1. कल्पित
2. बदसूरत
3. काँटा
4. साधारण

कृति ई (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘क्या जिंदगी की खूबसूरती व अच्छाई सचमुच लोप होती जा रही है ?’ विषय पर अपने विचार लिखिए।
उत्तर:
जिंदगी खूबसूरती व अच्छाई का नाम है। जिंदगी में जो कुछ प्राकृतिक है, वह सब ईश्वर निर्मित है। इंसान की जिंदगी में उसके कर्म बहुत ही मायने रखते हैं। वह जो कुछ करता है उसी के आधार पर उसकी जिंदगी भविष्य के रास्ते बनाती है। इंसान का अच्छा कर्म उसे अच्छाई की ओर ले जाता है। इंसान को जो यह अनमोल जीवन मिला है वह बहुत ही खूबसूरत है। इंसान का यह कर्तव्य है कि वह इस सुंदर जीवन को और खूबसूरत बनाए।

लता दीदी अपनी सुमधुर आवाज के लिए विश्व भर में पहचानी जाती हैं। सचिन क्रिकेट खेल जगत का भगवान बन गया है। अमिताभ बच्चन जी अपनी उत्कृष्ट अदाकारी के लिए देश-विदेश में प्रसिद्ध हैं। अत: मुझे ऐसा बिल्कुल नहीं लगता कि आज जिंदगी की खूबसूरती एवं अच्छाई लोप होती जा रही है। अपनी जिंदगी को खूबसूरत एवं अच्छा रखना प्रत्येक मनुष्य के हाथ में ही है।

(ङ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति छ (1): आकलन कृति

प्रश्न 1.
उचित विकल्प चुनकर रिक्त स्थानों पूर्ति किजिए।
i. क्या प्रसाद सिर्फ …….. होता है? (बूंदी, लड्डू, पेड़ा)
उत्तर:
i. बूंदी

प्रश्न 3.
समझकर लिखिए।
उत्तर:

कृति उ (3) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. अमौर
2. प्रसाद
3. दर्शक

उत्तर:

1. रईस
2. अनुग्रह
3. देखनेवाला

प्रश्न 2.
निम्नलिखित शब्द के लिए अनेकार्थी शब्द लिखिए।
i. प्रसाद
उत्तर:
i. कृपा, भगवान को चढ़ाई गई वस्तु, अनुग्रह

प्रश्न 3.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. कला का प्रदर्शन करने वाला –
उत्तरः
कलाकार

प्रश्न 4.
निम्नलिखित शब्दों के श्रुतिसमभिन्नार्थक शब्द लिखिए।
i. दर्शक
ii. अमल
उत्तर:
i. दशक
ii. कमल

कृति ङ (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘कलाकार की शक्ति उसके चिंतन में है।’ विषय पर अपने विचार लिखिए।
उत्तर:
कलाकार वह होता है जो अपनी अद्भुत कला से सभी को मंत्रमुग्ध कर देता है और सभी के हृदय पर छाप छोड़ देता है। फिर वह कलाकार चित्रकार हो या कवि। कलाकार के पास अद्भुत शक्तियाँ होती हैं। नित्य साधना, चिंतन व मनन के जरिए कलाकार को कलात्मक शक्तियों की प्राप्ति होती है। भारत के महान गायक मोहम्मद रफी साहब के स्वरों में जो जादू था, वह उन्हें एक दिन में नहीं प्राप्त हुई। उसके लिए उन्होंने बचपन से रियाज़ करना शुरू कर दिया था।

दिन के दस-दस घंटे तक वे संगीत का अभ्यास करते थे। अपनी कड़ी तपस्या के कारण ही वे महान गायक बने थे। चिंतन के बिना कलाकार की प्रतिभा खिल नहीं सकती। चिंतन-रूपी तपस्या के बाद ही कलाकार की प्रतिभा पर दिव्य फल लगना शुरू होता है। कवि भी कविता लिखने के पहले चिंतन करता है। महर्षि वाल्मीकी की जीवनी से कौन परिचित नहीं है? उन्होंने भी ‘रामायण’ लिखने से पहले कड़ी साधना एवं चिंतन किया था। तब जाकर वे ‘रामायण’ जैसे महाकाव्य की रचना कर सकें। अत: कलाकार के लिए चितन करना बेहद जरूरी होता है।

चार हाथ चाँदना Summary in Hindi

लेखक-परिचय :

जीवन-परिचय : अमृता प्रीतम जी का जन्म सन 1919 में पंजाब के गुजरांवाला में हुआ। ये पंजाबी एवं हिंदी भाषा की प्रतिभाशाली साहित्यकार थीं। इन्होंने अपनी प्रतिभा से साहित्य के सभी विधाओं जैसे उपन्यास, कविता, कहानी, संस्मरण, आत्मकथा आदि को समृद्ध किया है। इन्हें ज्ञानपीठ, साहित्य अकादमी एवं पद्म विभूषण आदि पुरस्कारों से सम्मानित किया जा चुका है। इन्होंने अपने साहित्य के माध्यम से मानवीय संवेदनाओं को झझकोरने का प्रयास किया है।
प्रमुख कृतियाँ : “पिंजर’, ‘कोरे कागज’, ‘सागर और सीपियाँ’ (उपन्यास), ‘रसीदी टिकट’ (आत्मकथा), ‘कच्चा आँगन’, ‘एक थी सारा’ (संस्मरण), ‘हीरे दी कनी’, ‘इक शहर दी मौत’, ‘तीसरी औरत’ (कहानी संग्रह) आदि हिंदी में अनूदित।

गद्य-परिचय :

साक्षात्कार : दो या दो से अधिक व्यक्तियों के बीच किसी विशेष उद्देश्य से प्रत्यक्ष बातचीत एवं विचारों का आदान-प्रदान साक्षात्कार कहलाता है। इसमें एक व्यक्ति दूसरे व्यक्ति से प्रश्न पूछता है और दूसरा व्यक्ति प्रश्नों के उत्तर देता है।
प्रस्तावना : ‘चार हाथ चाँदना’ इस साक्षात्कार में लेखिका अमृता प्रीतम जी ने पंजाब के प्रसिद्ध चित्रकार श्री शोभा सिंह जी से उनके अनुभव एवं चित्रकला विषय से संबंधित प्रश्न पूछे हैं। श्री शोभा सिंह ने भी उनके प्रश्न के उत्तर विस्तारपूर्वक दिए हैं।

सारांश :

‘चार हाथ चाँदना’ यह साक्षात्कार है। पंजाब की सुप्रसिद्ध साहित्यकार अमृता प्रीतम जी ने चित्रकार श्री शोभा सिंह जी का साक्षात्कार लिया है। अमृता जी ने श्री शोभा सिंह से कलाकार के कर्म की व्याख्या, चित्रकला चुनने का कारण, माँ का महत्त्व, धरती का भयानक यथार्थ व कलाकार की चिंतन शक्ति आदि मुद्दों पर प्रश्न पूछे हैं। श्री शोभा सिंह ने भी सभी प्रश्नों के विस्तार के साथ उत्तर दिए हैं। उनके अनुसार ‘सत्यम्, शिवम्, सुंदरम्’ के क्रम में बदलाव की जरूरत है। वह ‘सुंदरम्, शिवम्, सत्यम्’ इस प्रकार होना चाहिए। शोभा जी को चित्रकारी का शौक बचपन से था। वे जब आठ साल के थे तब उन्होंने खयाली घर की दीवारें सजाने के लिए तस्वीरें बनाई थीं।

वे औरत को माँ के तौर पर महत्त्व देते हैं। वे कहते हैं कि माँ के पास रचनात्मक शक्ति होती है। उसके पास साधना, दैवी शक्ति, कला एवं ज्ञान का भंडार होता है। अत: वह ‘जीनियस’ होता है। उनके अनुसार सच्चे कलाकार का कर्म एक छोटी सी जलती हुई मोमबत्ती की भाँति होता है जो अपने आस-पास की धरती को प्रकाशित करता है। श्री शोभा सिंह धरती के यथार्थ को चित्रों में स्थान नहीं देना चाहते।

वे जिंदगी की खूबसूरती एवं अच्छाई को कागज पर चित्रित करते हैं क्योंकि वह दिनोंदिन लोप होती जा रही है। उनका मानना है कि कलाकार का कर्म एक व्यक्तित्व बनना है, तब कला में उसका प्रभाव आ सकता है। कलाकार की शक्ति उसके चिंतन में होती है और कलाकार दर्शक को एक अच्छी सोच व सूझ दे सकने का कार्य करता है।

शब्दार्थ :

1. चाँदना – प्रकाश
2. परछत्ती – घास-फूस का बना छप्पर
3. रूहानी – आत्मिक
4. तकनीकी – प्राविधिक
5. अवस्था – हालत
6. गहराई – गहनता
7. दर्शक – देखनेवाला
8. यर्थाथ – सत्य
9. अंतहीन – कभी न खत्म होनेवाला

मुहावरे :

भुलावा हो जाना – भ्रम हो जाना।

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer

Std 10 Hindi Chapter 6 Ati Sohat Shyam Ju Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 6 अति सोहत स्याम जू Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 6 अति सोहत स्याम जू  Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 6 अति सोहत स्याम जू Textbook Questions and Answers

सुचना के अनुसर क्रुतिया कीजिए।

1. संजाल पूर्ण कीजिए।

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तरः

2. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तरः

3. कवि यहाँ और यह बनकर रहना चाहते हैं –

प्रश्न 1.
कवि यहाँ और यह बनकर रहना चाहते हैं –
उत्तर:
(अ) गोकुल में ग्वाला बनकर रहना चाहते हैं।
(आ) गोकुल के बने में पशु बनकर चरना चाहते हैं।
(इ) गोकुल में स्थित गिरिधर पर्वत का पत्थर बनकर रहना चाहते हैं।
(ई) यमुना के किनारे पर स्थित किसी कंदब के पेड़ पर पक्षी बनकर रहना चाहते हैं।

प्रश्न 4.

उत्तरः

प्रश्न 5.
पद्य में इस अर्थ में आए शब्द लिखिए।

1. शोभा देता है
2. ग्वाल-बालाएँ
3. गोरस देने वाली
4. शुक मुनि

उत्तरः

1. सोहत
2. अहीर की छोहरियाँ
3. धेनु
4. सुक

6. निम्न शब्दों के भिन्न-भिन्न अर्थ लिखिए:

प्रश्न 1.
निम्न शब्दों के भिन्न-भिन्न अर्थ लिखिए:
image 7

प्रश्न 2.
शब्द समूह के लिए एक शब्द लिखिए:

1. जिसके कोई खंड नहीं होते – …..
2. छाछ रखने का छोटा पात्र – ………
3. जिसका कोई अंत नहीं होता – ……
4. जो सदैव चलता रहता है – ……….

7. कृदंत व तद्धित शब्दों के मूल शब्द पहचानकर लिखिए।

प्रश्न 1.
कृदंत व तद्धित शब्दों के मूल शब्द पहचानकर लिखिए।

उत्तरः
झगड़ालू, मुस्कान, सांस्कृतिक, रसीला,
खिलाड़ी, कहानी, जगमगाहट, सुखी।

कृदंत शब्द	तद्धित शब्द
1. जगमगाना	1. रस
2. मुस्कुराना	2. झगड़ा
3. कहना	3. संस्कृति
4. खेलना	4. सुख

8. किसी एक पद का सरल अर्थ लिखिए।

प्रश्न 1.
किसी एक पद का सरल अर्थ लिखिए।
सेस, गनेस ……………
…………… नाच नचावें।
उत्तरः
कवि रसखान कहते हैं कि कृष्ण तो प्रेमरूपी भक्ति के प्यासे हैं। शेषनाग, गणेश, शिव, सूर्य एवं इंद्र जिसके गुणों की हमेशा प्रशंसा करते हैं; जिन्हें अनादि, अनंत, अखंड, अछेद, अभेद और सुवेद बनाते हैं, ब्रह्म ऋषि नारद, शुकदेव व महाकवि व्यास जैसे तपस्वी जिनके नाम की निरंतर रट लगाते रहते हैं और प्रयत्न करने के बावजूद भी उनका पार नहीं पा सकें, ऐसे कृष्ण को अहीर कन्याएँ (ग्वालिने) कटोरे भर छाछ के लिए नाच नचाती हैं।

Hindi Lokvani 10th Std Textbook Solutions Chapter 6 अति सोहत स्याम जू Additional Important Questions and Answers

(अ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

1. कृति पूर्ण कीजिए।

प्रश्न 1.
कवि यहाँ और यह बनकर रहना चाहते हैं –
उत्तर:
(अ) गोकुल में ग्वाला बनकर रहना चाहते हैं।
(आ) गोकुल के बने में पशु बनकर चरना चाहते हैं।
(इ) गोकुल में स्थित गिरिधर पर्वत का पत्थर बनकर रहना चाहते हैं।
(ई) यमुना के किनारे पर स्थित किसी कंदब के पेड़ पर पक्षी बनकर रहना चाहते हैं।

प्रश्न 2.
समझकर लिखिए।
उत्तर:

कृति अ (2): शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. मानुष
2. कालिंदी
3. गिरि
4. धेनु
5. पाहन

उत्तर:

1. मानव
2. यमुना
3. पर्वत
4. गाय
5. पत्थर

प्रश्न 2.
वचन बदलिए।
1. बसेरा
2. डाल
उत्तर:
1. बसेरे
2. डालें

प्रश्न 3.
पद्यांश में प्रयुक्त तत्सम शब्द ढूँढ़कर लिखिए।
उत्तर:

1. धेनु
2. गिरि
3. खग
4. नित

प्रश्न 4.
निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।
1. गाँव
2. गोकुल
उत्तर:
1. गाँववासी
2. गोकुलवासी

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘अपने आराध्य की जन्मभूमि से सभी को लगाव होता है।’ अपने विचार लिखिए।
उत्तर:
आराध्य वह होता है जिसकी हम आराधना करते हैं। आराध्य के बिना जीवन का अर्थ प्राप्त नहीं हो सकता। अतः प्रत्येक व्यक्ति के अपने-अपने आराध्य होते हैं। अपने आराध्य की जन्मभूमि से लगाव होना, स्वाभाविक है। प्रति वर्ष हजारों-लाखों लोग अयोध्या, मथुरा-ब्रज आदि देवस्थान और अपने आराध्य देव के देवस्थलों की यात्रा करते हैं।

अपने आराध्य की जन्मभूमि को भेंट देकर लोग इसमें अपनी धन्यता समझते हैं। वहाँ पर जाकर उन्हें दिव्य आनंद की अनुभूति होती है। साधकों को ऐसा लगता है मानो वे स्वर्ग में ही आ पहुँचे हैं। आराध्य की जन्मभूमि भक्तों के लिए तीर्थस्थल होती है। ऐसे तीर्थस्थलों पर जाकर भक्त मानसिक शांति का अनुभव करते हैं। अत: अपने आराध्य की जन्मभूमि सभी को प्रिय होती है।

(आ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1): आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
समझकर लिखिए।
उत्तर:

कृति (2): शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के भिन्न अर्थ लिखिए।
1. चोटी
2. निधि
उत्तर:
1. स्त्री के सिर के गूंथे हुए बाल, पर्वत शिखा
2. संपत्ति, आश्रयस्थान

प्रश्न 2.
निम्नलिखित तद्भव शब्द का तत्सम रूप लिखिए।
काग
उत्तर:
काक

प्रश्न 3.
उचित प्रत्यय लगाकर नया शब्द लिखिए।
1. कला
2. सुंदर
उत्तर:
1. कलापूर्ण
2. सुंदरता

प्रश्न 4.
वचन बदलिए।
1. चोटी
2. कला
उत्तर:
1. चोटियाँ
2. कलाएँ

प्रश्न 5.
निम्नलिखित शब्दों के अर्थ लिखिए।
1.धूरि
2. निधि
उत्तर:
1. धूल
2. संपत्ति

कृति आ (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘बाल कृष्ण का मनोहारी वर्णन करते हुए कवि ने कृष्ण के प्रति अपनी भक्ति समर्पित कर दी है।’ कथन का स्पष्टीकरण कीजिए।
उत्तरः
कवि रसखान कृष्ण के असाधारण भक्त थे। उन्होंने अपनी रचनाओं के माध्यम से अपनी भक्ति को कृष्ण के प्रति समर्पित कर दिया था। भगवान कृष्ण की लीलाओं से सभी परिचित है। उन्होंने गोकुल में जन्म लिया था और वे जन्म से ही अपने भक्तों का उद्धार करते रहे। अत: उनकी बालसुलभ क्रियाएँ एवं उनकी बचपन की लीलाओं का मनोहारी वर्णन कर सभी पाठकों को कृष्ण भक्ति में एकाकार करना कृष्ण प्रेमी कवियों का प्रमुख लक्ष्य रहा और साथ ही अपने इष्ट का वर्णन करते हुए उसके साथ एकाकार होना यह भी प्रमुख उद्देश्य रहा। कवि रसखान इससे अपवाद नहीं हैं। उन्होंने बड़ी ही तन्मयता से कृष्ण के बालरूप का मनोहारी वर्णन करके अपनी भक्ति को कृष्ण के चरणों में समर्पित कर दिया है।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1): आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
1. ग्वाले
2. कृष्ण
उत्तरः
1. कौन पुकार कर हँस रहे थे?
2. कवि की आँखों में किसकी छबि बस गई है?

3. कारण लिखिए।

प्रश्न 1.
कवि रसखान की आँखें बौरा हो गई हैं।
उत्तरः
कृष्ण के आकर्षक एवं मनोहारी रूप को देखकर कवि रसखान की आँखें बौरा हो गई हैं।

कृति (2): शब्दसंपदा

प्रश्न 1.
वचन बदलिए।
1. वनमाला
2. मूर्ति
उत्तरः
1. वनमालाएँ
2. मूर्तियाँ

प्रश्न 2.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. पाग
2. भाल
3. हिय
4. नैन

उत्तरः

1. पगड़ी
2. मस्तक
3. हृदय
4. आँखें

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
बाल कृष्ण की छबि देखकर अपने मन में आए विचारों को अभिव्यक्त कीजिए।
उत्तरः
बाल कृष्ण भगवान कृष्ण का बचपन का रूप था, जो मोहक एवं सभी को अपनी ओर आकर्षित करता था। मैंने कई बार बाल कृष्ण की छबि देखी है। इतना ही नहीं, मैंने दूरदर्शन पर कई धारावाहिक भी देखे हैं; जिसमें कृष्ण के बालरूप को बड़े ही मनोहारी एवं आकर्षक रूप में दर्शाया गया है। बाल कृष्ण के सुंदर व मुग्ध रूप को देखकर मैं आनंदविभोर हो गया हूँ। कोमल, श्यामल रंग, हाथ में बाँसुरी लिए हुए वे बहुत आकर्षक लगते है। उनकी छबि दिव्य और बड़ी ही मोहक है।

(ई) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

कृति (2): शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।
1. अहीर
2. दिनेश
उत्तरः
1. ग्वाला
2. सूर्य

प्रश्न 2.
शब्द समूह के लिए एक शब्द लिखिए।
1. जिसके कोई खंड नहीं होते –
2. जिसका कोई अंत नहीं होता –
3.  छाछ रखने का छोटा पात्र –
4.  जो सदैव चलता रहता है –
उत्तरः
1. अखंड
2. अनंत
3. छछिया
4. निरंतर

प्रश्न 3.
निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाइए।
खंड:
उत्तरः
उपसर्गयुक्त शब्द : अखंड
प्रत्यययुक्त शब्द : अखंडता

प्रश्न 4.
पद्यांश में से उपसर्गयुक्त शब्द ढूँढ़कर लिखिए।
उत्तरः

1. अनंत
2. अभेद
3. अखंड
4. अनादि

प्रश्न 5.
निम्नलिखित शब्द के भिन्न अर्थ लिखिए।
व्यास
उत्तरः
महर्षि व्यास, कथावाचक, ज्यामिति

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘ईश्वर सच्चे और निष्कपट भक्ति का प्यासा होता है।’ कथन विषय पर अपने विचार लिखिए।
उत्तरः
ईश्वर सच्चे प्रेम का भूखा होता है। वह सच्चे मन से की गई भक्ति पर प्रसन्न होता है और अपने भक्तों को स्वयं के दर्शन कराता है। उसे पाने के लिए हमें दिन-रात उसके नाम का जप करने की जरूरत नहीं होती। उसका दिन-रात भजन करना भी आवश्यक नहीं होता। उसे तो सच्चा भक्त कभी भी सच्चे हृदय से पुकार सकता है।

जब अंतर्मन से निकलने वाली पुकार में सच्चे मन की भक्ति की एकाग्रता हो, तो वह स्वयं अपने भक्तों की पुकार पर सहायता के लिए आ जाता है। गोकुल में रहने वाली ग्वालिने कृष्ण से सच्चे हृदय से प्रेम करती थीं। अत: वे उनके साथ नाचते-गाते थे और उनसे माखन पाने के लिए हठ करते थे। संत कबीर ने भी अपनी रचनाओं के द्वारा यही समझाया है कि ईश्वर को पाने के लिए हमें धार्मिक आडंबरों की जरूरत नहीं होती। उसे तो सच्चे हृदय से प्राप्त किया जा सकता है।

अति सोहत स्याम जू Summary in Hindi

कवि-परिचय:

जीवन-परिचय: रसखान जी का जन्म सन १५९० में उत्तर प्रदेश के पिहानी, मथुरा में हुआ। इनका मूलनाम सैयद इब्राहिम था। ये भगवान श्रीकृष्ण के अनन्यसाधारण भक्त थे। हिंदी के कृष्ण भक्त तथा रीतिकालीन रीतिमुक्त कवियों में इनका प्रमुख स्थान है। इनकी अधिकांश रचनाएँ भगवान कृष्ण के लिए समर्पित हैं। इनकी रचनाओं में भक्ति एवं श्रृंगार रस की प्रधानता है। इन्होंने श्रीकृष्ण के सगुण रूप को बड़े ही मनोहारी ढंग से अभिव्यक्त किया है।

प्रमुख कृतियाँ: ‘प्रेमवाटिका’ (दोहे), ‘सुजान रसखान’ (कवित्त, सवैया) आदि।

पद्य-परिचय:

सवैया: सवैया मात्रिक छंद का एक प्रकार है। इसमें चार चरण होते हैं । प्रत्येक चरण में २२ से २६ वर्ण होते हैं। रीतिकाल में ।
विभिन्न प्रकार के सवैया प्रचलित रहे हैं।

प्रस्तावना: ‘अति सोहत स्याम जू’ इस रचना में कवि रसखान ने श्रीकृष्ण की जन्मभूमि के प्रति लगाव, बालकृष्ण का मनोहारी वर्णन ।
एवं उसे पाने के लिए हृदय में सच्ची भक्ति की आवश्यकता जैसे बिंदुओं का विस्तार से सुंदर वर्णन किया है।

सारांश:

कवि रसखान भगवान श्रीकृष्ण के अनन्यसाधारण भक्त थे। उन्हें श्रीकृष्ण की जन्मभूमि के प्रति बेहद लगाव है। वे कृष्ण-भक्ति में एकाकार हो गए हैं। वे श्रीकृष्ण से अलग होना नहीं चाहते हैं। वे सदैव उनका सानिध्य चाहते हैं। इसलिए वे अगले जन्म में किसी भी योनी में जन्म लें फिर भी वे गोकुल से अलग होना नहीं चाहते। वे गोकुल में उपस्थित किसी भी प्राकृतिक अंश में बस जाना चाहते हैं। कवि रसखान ने बालकृष्ण का अत्यंत मनोहारी वर्णन किया है।

कृष्ण के आकर्षक एवं मनोहारी रूप को देखकर कवि रसखान की आँखे उन्मुक्त हो गई हैं। श्रीकृष्ण सच्ची भक्ति के द्वारा तुरंत मिल सकते हैं। उन्हें पाने के लिए भक्त को सच्चे हृदय से उन्हें पुकारने की आवश्यकता होती है। श्रीकृष्ण सच्ची भक्ति के प्यासे हैं। उनके दर्शन के लिए निरंतर जाप की आवश्यकता नहीं होती। श्रीकृष्ण भी सच्चे भक्त की पुकार सुनकर उसकी सहायता के लिए तत्पर हो जाते हैं। इस प्रकार प्रस्तुत रचना के माध्यम से कवि रसखान ने अपनी भक्ति श्रीकृष्ण के चरणों में समर्पित कर दी है।

भावार्थ:

1. मानुष …………………….. कूल कंदब की डारन।।

कवि रसखान कृष्णभक्त थे। उन्हें श्रीकृष्ण के जन्मभूमि के प्रति बेहद लगाव है। वे प्रत्येक स्थिति में श्रीकृष्ण का सानिध्य चाहते हैं। वे । भगवान कृष्ण की आराधना करते हुए कहते हैं कि यदि अगले जन्म में मनुष्य बनूँ, तो गोकुल के ग्वालों और गायों के बीच रहना पसंद करूँगा। ,
यदि मैं पशु की योनि में जन्म लेता हूँ, तो हमेशा नंद की गायों के साथ चरना चाहूँगा। यदि मैं पत्थर बनूँ, तो उसी पर्वत का पत्थर बनूँ जिसे । इंद्र के कारण भगवान कृष्ण ने अपनी उँगली पर धारण कर लिया था। यदि पक्षी बनूँ, तो यमुना के किनारे पर स्थित किसी कंदब के पेड़ की । डाल पर अपना बसेरा निर्माण करूँ।

2. धूरि भरे अति ……………….. माखन रोटी।

कवि रसखान ने प्रस्तुत पंक्तियों के माध्यम से बालकृष्ण का अत्यंत मनोहारी वर्णन किया है। बालकृष्ण धूल से सने हुए अत्यंत मोहक लग रहे हैं। उनके सिर पर चोटी शोभायमान हो रही है। उन्होंने कमर में पीली धोती पहनी हुई है तथा पैरों में पैजनियाँ बज रही है। वे पूरे आँगन में खाते-खेलते घूम रहे हैं। रसखान कहते हैं कि उनकी छवि देखकर कामदेव अपनी करोड़ों कलाओं की निधि निछावर करते हैं। सचमुच । वह कौआ बहुत ही भाग्यशाली है जो बालकृष्ण के हाथ से माखन रोटी को छीन कर ले उड़ा है।

3. सोहत हे चॅदवा ………………………. माँझ बसी है।

कवि रसखान कृष्ण के बालरूप का वर्णन करते हुए कहते हैं कि उनके सिर पर मोर मुकुट शोभायमान है। उन्होंने अपने सिर पर बड़ी । सुंदर पगड़ी बाँध रखी है। उनके मस्तक पर गायों के पैरों से उड़नेवाली धूल वैसे ही शोभा दे रही है जैसे हृदय पर वनमाला शोभित हो रही है। कृष्ण के आकर्षक एवं मनोहारी रूप को देखकर कवि रसखान की आँखे मारे खुशी के पागल हो गई हैं। उनकी बंद आँखों को देखकर ग्वाले उन्हें पुकारकर हँस रहे हैं, मानो वे उन्हें अपनी आँखा से पलकों के घूघट खोलने के लिए कह रहे हैं। किंतु कवि रसखान के सामने समस्या यह है कि वे अपनी पलकें नहीं खोल सकते क्योंकि कृष्ण की छवि उनकी आँखों में बस गई है।

4. सेस, गनेस ………………… नाच नचावें।

कवि रसखान कहते हैं कि कृष्ण तो प्रेमरूपी भक्ति के प्यासे हैं। शेषनाग, गणेश, शिव, सूर्य एवं इंद्र जिनके गुणों की हमेशा प्रशंसा करते हैं; जिन्हें अनादि, अनंत, अखंड अछेद, अभेद और सुवेद बताते हैं। ब्रह्म ऋषि नारद, शुकदेव व महाकवि व्यास जैसे तपस्वी जिनके नाम को निरंतर रटते रहते हैं और प्रयत्न करने के बावजूद भी उनका पार नहीं पा सके, ऐसे कृष्ण को अहीर कन्याएँ (ग्वालिने) कटोरे भर । छाछ के लिए नाच नचाती हैं।

शब्दार्थ:

1. मानुष – मानव
2. धूरि – धूल
3. हिय – हृदय
4. गिरि – पर्वत
5. पाग – पगड़ी
6. अहीर – ग्वाला, आभीर
7. धेनु – गाय
8. भाल – मस्तक
9. पाहन – पत्थर
10. दिनेश – सूर्य
11. छाछिया – छाछ रखने का छोटा पात्र
12. वारत – निछावर करना
13. लसी – सुशोभित होना
14. बिलोकत – देखना
15. पचिहारे – हार जाना
16. जू – जी
17. पीरी – पीले रंग की
18. कछोटी – कमर में लपेटी जानेवाली धोती
19. दृग – आँख
20. कूल – तट, किनारा
21. काग – कौआ

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 5 अनोखे राष्ट्रपति Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 5 Anokhe Rashtrapati Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 5 अनोखे राष्ट्रपति Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 5 अनोखे राष्ट्रपति Textbook Questions and Answers

सूचना के अनुसार कृतियाँ कीजिए:

(१) संजाल पूर्ण कीजिए:

Answer:

(२) कृति में जानकारी लिखिए:

Answer:

(३) उत्तर लिखिए:

Answer:

(४) निम्नलिखित शब्दों के प्रत्यय और मूलशब्द अलग करके लिखिए:

Answer:

(५) उपसर्ग तथा प्रत्यययुक्त शब्द बनाकर लिखिए:

Answer:

अभिव्यक्ति

‘सादा जीवन, उच्च विचार’ विषय पर अपने विचार लिखिए।
Answer:
सादा जीवन यानी सादगी से भरा जीवन। सादे जीवन में सौंदर्य होता है। ऐसा जीवन तन को ही नहीं मन को भी सुंदर बना देता है। सुंदर शरीर और शांत मन ही उच्च विचार को प्रेरित करता है। यदि व्यक्ति को अपने जीवन में सफल होना है, तो उसे ‘सादा जीवन उच्च विचार’ इस सिद्धांत का पालन करना चाहिए। जीवन का सच्चा लाभ आराम का जीवन बिताने में नहीं, बल्कि महान बनने में है।

सफल महापुरुषों के जीवन में प्रकाश डालने से हमें पता चलता है कि उन्होंने ‘सादा जीवन व उच्च विचार’ को अपने जीवन में उतारा है। जीवन में सादगी लाना बहुत ही बड़ा महान गुण है। इसे स्वीकार करने से व्यक्ति तुच्छ विचारों को अपने हृदय से दूर कर देता है। सादगी से भरा जीवन व्यतीत करने वाले व्यक्ति के पास गहरी संवेदना होती हैं जो व्यक्तित्व को गरिमा प्रदान करती है। इसलिए व्यक्ति को ‘सादा जीवन व उच्च विचार’ इस सिद्धांत को अपने जीवन में उतारना चाहिए।

भाषा बिंदु

(१) निम्नलिखित संधि विच्छेद की संधि कीजिए और भेद लिखिए:

Answer:

(२) निम्नलिखित शब्दों का संधि विच्छेद कीजिए और भेद लिखिए:

Answer:

(३) निम्नलिखित शब्दों का विच्छेद कीजिए और संधि भेद लिखिए:

Answer:

(४) पाठों में आए संधि शब्द छाँटकर उनका विच्छेद कीजिए और संधि का भेद लिखिए।

Answer:

उपयोजित लेखन

‘यदि मैं शिक्षा मंत्री होता —–‘ विषय पर लगभग सौ शब्दों में निबंध उपयोजित लेखन लिखिए।
Answer:
यदि मैं शिक्षा मंत्री होता….. जीवन में शिक्षा का अत्यधिक महत्त्व है। शिक्षा के द्वारा व्यक्ति का मानसिक, सामाजिक, बौद्धिक व आर्थिक विकास होता है। शिक्षा मंत्रालय द्वारा देश के पाठ्यक्रम एवं शिक्षा प्रणाली पर ध्यान रखा जाता है। शिक्षा मंत्री शिक्षा मंत्रालय के प्रमुख होते हैं। देश में शिक्षा प्रणाली सुचारू रूप से कार्यान्वित हो रही है या नहीं, इस पर ध्यान एवं नियंत्रण रखने का कार्य शिक्षा मंत्री करते हैं। सचमुच शिक्षा मंत्री एक बहुत बड़ा महत्त्वपूर्ण पद है। मैं भी भविष्य में बड़ा होकर देश का शिक्षा मंत्री बनना चाहता हूँ।

जब मैं शिक्षा मंत्री बनूँगा; तब मैं संपूर्ण देश में शिक्षा का कार्य सुचारू रूप से हो रहा है या नहीं इस पर ध्यान रखूगा। देश की संपूर्ण शिक्षा प्रणाली में एकरूपता लाने हेतु में सभी शिक्षा मंडलों का एकीकरण करूँगा; जिससे देश में एक ही प्रकार की शिक्षा प्रणाली सभी के लिए उपलब्ध हो सके। आज कई स्कूल एवं महाविद्यालयों की हालत बहुत ही दयनीय है। कई स्कूलों में संसाधनों की कमी है। कई स्कूलों में छात्रों को बैठने के लिए कुर्सियाँ तथा पर्याप्त शैक्षणिक साधन भी नहीं है। कई स्कूलों में पर्याप्त मात्रा में शिक्षक उपलब्ध नहीं हैं। इन सारी समस्याओं को तुरंत सुलझाने के लिए मैं शिक्षा मंत्री होने के नाते एक समिति की स्थापना करूँगा। इससे किसी भी नगर या गाँव का छात्र शिक्षा के मूलभूत अधिकारों से वंचित नहीं रह पाएगा।

संपूर्ण देश के पाठ्यक्रम में मैं समयानुसार परिवर्तन करने हेतु विद्वान सदस्यों की एक समिति गठित करूँगा; ताकि भूमंडलीकरण एवं विज्ञान-तकनीकी के इस युग में भारतीय छात्र आगे ही आगे बढ़ सकें। आज हमारे देश में शिक्षकों को दिया जाने वाला वेतन बहुत ही कम है। इसके लिए मैं शिक्षकों के लिए एक नए वेतनमान प्रणाली की शुरुआत करूँगा, जिससे अच्छे से अच्छे उम्मीदवार शिक्षा क्षेत्र से जुड़कर ज्ञान के प्रचार-प्रसार का पवित्र कार्य करने के लिए आगे आ सकें। अब तो बस, यही मेरा ध्येय है। इसे साकार करने के लिए सर्वप्रथम मुझे मन लगाकर पढ़ना होगा। फिर मैं अपने विचारों को वास्तविक रूप में परिवर्तित कर सकता हूँ।

Hindi Lokvani 10th Std Textbook Solutions Chapter 5 अनोखे राष्ट्रपति Additional Important Questions and Answers

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (१): आकलन कृति

कृति पूर्ण कीजिए।

Answer:

समझकर लिखिए।

Question 1.
सच्चे व्यक्तित्व की विशेषता
Answer:
सच्चे व्यक्तित्व में कुछ जोड़ना घटाना संभव नहीं है।

निम्नलिखित विधान सत्य है या असत्य लिखिए।

Question 1.
लेखिका ने राजेंद्र बाबू को सर्वप्रथम गद्यात्मक वातावरण में देखा।
Answer:
सत्य

Question 2.
सत्य में से जोड़ना या घटाना असंभव नहीं रहता।
Answer:
असत्य

कृति अ (२) : शब्द संपदा

निम्नलिखित शब्दों के अर्थ गद्यांश में से ढूँढ़कर लिखिए।

1. नजर
2. प्रणाम
3. पक्षी
4. याद

Answer:

1. दृष्टि
2. अभिवादन
3. विहंगम
4. स्मृति

निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
व्यक्ति की विशेषता या गुण
Answer:
व्यक्तित्व

Question 2.
शीत ऋतु में होनेवाली छुट्टियाँ
Answer:
शीतावकाश

निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।

Question 1.
विहंगम
Answer:
पक्षी, नभ यात्री, सम्यक

Question 2.
गद्यांश में प्रयुक्त एक विलोम शब्द की जोड़ी लिखिए।
Answer:
जोड़ना x घटाना

निम्नलिखित शब्द के उपसर्गयुक्त व प्रत्यययुक्त शब्द बनाइए।

Question 1.
सत्य
Answer:
उपसर्गयुक्त शब्द – असत्य, प्रत्यययुक्त शब्द – सत्यवादी

Question 2.
संभव
Answer:
उपसर्गयुक्त शब्द – असंभव, प्रत्यययुक्त शब्द – संभावित

लिंग बदलिए।

1. बाबू
2. भाई

Answer:

1. बबुआइन
2. बहन

कृति अ (३) : स्वमत अभिव्यक्ति

Question 1.
सच्चे व्यक्तित्व की पहचान का आधार बताइए।
Answer:
सच्चा व्यक्तित्व हर समय वास्तविक होता है। सच्चे व्यक्ति का चरित्र प्रकाश की तरह दिव्य व पावन होता है। उसके चरित्र बल के आलोक से लोगों को प्रेरणा मिलती है। उसके विचार आदर्शवादी होते हैं। वह अपने विचारों से ही स्वयं के चरित्र का निर्माण करता है। वह दूसरों की भावनाओं को समझता है। उसके पास दया, प्रेम, करुणा, क्षमा आदि मानवीय गुण होते हैं। वह सदैव दूसरों के हित के बारे में ही सोचता रहता है।

वह कभी भी स्वयं के स्वार्थ का विचार नहीं करता है। उसका जीवन सादा होता है। ‘सादा जीवन व उच्च विचार’ ही उसके जीवन का मूलमंत्र होता है। सच्चे व्यक्तित्व वाला व्यक्ति दूसरों की परेशानियों को अपने हृदय के भीतर महसूस करता है और दूसरों को पीड़ा से मुक्ति दिलाने हेतु प्रयास करता है। वह स्वयं तकलीफों में रहकर दूसरों के जीवन में खुशियाँ निर्माण करता है। प्रश्न २ (आ) निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति पूर्ण कीजिए।

Question 1.

Answer:

कृति आ (२): शब्द संपदा

निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. रोमिल
2. भृकुटी
3. ठुड्डी
4. वेशभूषा

Answer:

1. रोयेंदार
2. भौंह
3. ठोढ़ी
4. पहनावा

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
स्वच्छंद रहने के भाव
Answer:
स्वच्छंदतावाद

विलोम शब्द लिखिए।

1. ग्रामीण x ….
2. आवरण x …..

Answer:

1. ग्रामीण x शहरी
2. आवरण x अनावरण

Question 1.
गद्यांश में प्रयुक्त विलोम शब्द की जोड़ी ढूँढ़कर लिखिए।
Answer:

• दाहिना x बाँया
• ऊपर x नीचे

निम्नलिखित शब्दों के वचन बदलिए।

1. फेंटा
2. धोती
3. टोपी
4. भृकुटी

Answer:

1. फेंटे
2. धोतियाँ
3. टोपियाँ
4. भृकुटियाँ

निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।

1. शरीर
2. दृष्टी

Answer:

1. शारीरिक
2. दृष्टिहीन

निम्नलिखित वाक्यों में विराम चिह्न का उचित प्रयोग कीजिए।

Question 1.
क्या गांधी टोपी की स्थिति और भी विचित्र नहीं थी
Answer:
क्या गांधी टोपी की स्थिति और भी विचित्र नहीं थी?

कृति आ (३) : स्वमत अभिव्यक्ति

Question 1.
‘व्यक्तित्व का आईना होती है वेशभूषा।’ विषय पर अपने विचार लिखिए।
Answer:
व्यक्ति का पहनावा या उसकी वेशभूषा उसके व्यक्तित्व का आईना होती है। वह मानव के संपूर्ण जीवन को प्रभावित करती है। यदि आप किसी औपचारिक मीटिंग या कार्यालय में जा रहे हैं तो आप रंग-बिरंगी टी-शर्ट और शॉर्टस् पहनकर जाते हैं तो आप हँसी के पात्र बन सकते हैं या आपके व्यक्तित्व पर इसका गलत असर पड़ सकता है।

यदि आप अनौपचारिक समारोह या पार्टी में सुट पहन कर जाएंगे, तो भी आप बचकाने लगेंगे। यदि व्यक्ति पदवी या पद में बड़ा है; तो उसकी वेशभूषा उसके अनुसार या उससे अधिक फॉर्मल होनी चाहिए। व्यक्ति को स्वच्छ एवं साफ-सुथरे कपड़े पहनने चाहिए। कपड़े अच्छी तरह से प्रेस होने चाहिए। वेशभूषा सादगी से युक्त होनी चाहिए। स्वामी विवेकानंद धोती, कुर्ता व पगड़ी पहनकर विदेश में गए थे। व्यक्ति को अपनी संस्कृति की वेशभूषा में रहना अधिक उचित और श्रेयस्कर है।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति इ (१): आकलन

ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हो

Question 1.
भारतीय कृषक
Answer:
राजेंद्र बाबू अपने स्वभाव एवं रहन-सहन में किसका प्रतिनिधित्व करते थे ?

Question 2.
राजेंद्र बाबू
Answer:
लेखिका को किसकी मुखाकृति देखकर ऐसा लगता था मानो उन्हें पहले कहीं देखा है?

सही विकल्प चुनकर वाक्य पूर्ण कीजिए।

Question 1.
राजेंद्र बाबू को देखने वालों को कोई-न-कोई आकृति या व्यक्ति स्मरण हो आता था क्योंकि …..
(अ) उनके शरीर के संपूर्ण गठन में एक असामान्य भारतीय जन की आकृति और गठन की छाया थी।
(आ) उनके शरीर के संपूर्ण गठन में एक सामान्य भारतीय जन की आकृति और गठन की छाया थी।
(इ) उनके शरीर के संपूर्ण गठन में एक महापुरुष की आकृति और गठन की छाया थी।
Answer:
राजेंद्र बाबू को देखने वालों को कोई-न-कोई आकृति या व्यक्ति स्मरण हो आता था क्योंकि उनके शरीर के संपूर्ण गठन में एक सामान्य भारतीय जन की आकृति और गठन की छाया थी।

समझकर लिखिए।

Answer:

कृति इ (२) : शब्द संपदा

Question 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:

• साथ – साथ
• रहन – सहन

वचन बदलिए।

1. आकृति
2. अनुभूति
3. संवेदना

Answer:

1. आकृतियाँ
2. अनुभूतियाँ
3. संवेदनाएँ

Question 1.
गद्यांश में से प्रत्यययुक्त शब्द ढूँढकर लिखिए।
Answer:
प्रत्यययुक्त शब्द : व्यापकता, सामान्यता, विशिष्टता प्रत्यययुक्त शब्द : गहराई

Question 2.
‘अनुभव’ इस शब्द में निहित उपसर्ग से अन्य दो शब्द बनाकर लिखिए।
Answer:
अनुभव – उपसर्ग : अनु ।
नए शब्द –
अनुकरण
अनुसरण

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. समान x ……..
2. सामान्य x ….

Answer:

1. समान x असमान
2. सामान्य x असामान्य

नीचे दिए शब्द के लिए श्रुतिसम भिन्नार्थक शब्द लिखिए।

1. समान
2. प्रतिभा
3. उपरांत

Answer:

1. सामान
2. प्रतिमा
3. अपरांत

कृति इ (३) : स्वमत अभिव्यक्ति

Question 1.
‘सादा जीवन उच्च विचार’ विषय पर अपने विचार लिखिए।
Answer:
सादा जीवन यानी सादगी से भरा जीवन। सादे जीवन में सौंदर्य होता है। ऐसा जीवन तन को ही नहीं मन को भी सुंदर बना देता है। सुंदर शरीर और शांत मन ही उच्च विचार को प्रेरित करता है। यदि व्यक्ति को अपने जीवन में सफल होना है, तो उसे ‘सादा जीवन उच्च विचार’ इस सिद्धांत का पालन करना चाहिए। जीवन का सच्चा लाभ आराम का जीवन बिताने में नहीं, बल्कि महान बनने में है।

सफल महापुरुषों के जीवन में प्रकाश डालने से हमें पता चलता है कि उन्होंने ‘सादा जीवन व उच्च विचार’ को अपने जीवन में उतारा है। जीवन में सादगी लाना बहुत ही बड़ा महान गुण है। इसे स्वीकार करने से व्यक्ति तुच्छ विचारों को अपने हृदय से दूर कर देता है। सादगी से भरा जीवन व्यतीत करने वाले व्यक्ति के पास गहरी संवेदना होती हैं जो व्यक्तित्व को गरिमा प्रदान करती है। इसलिए व्यक्ति को ‘सादा जीवन व उच्च विचार’ इस सिद्धांत को अपने जीवन में उतारना चाहिए।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति ई (१) : आकलन कृति
कृति पूर्ण कीजिए।

Question 1.

Answer:

निम्नलिखित गलत विधान सही करके लिखिए।

Question 1.
राजेंद्र बाबू चक्रधर जी के निजी सचिव थे।
Answer:
चक्रधर जी राजेंद्र बाबू के निजी सचिव थे।

Question 2.
राष्ट्रपति के रूप में राजेंद्र बाबू महिला विद्यापीठ का शिलान्यास करने प्रयाग आए।
Answer:
काँग्रेस के अध्यक्ष के रूप में राजेंद्र बाबू महिला विद्यापीठ का शिलान्यास करने प्रयाग आए।

गद्यांश पढ़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हाँ

Question 1.
सन १९३७
Answer:
महिला विद्यापीठ का शिलान्यास करने राजेंद्र बाबू प्रयाग कब आए थे?

Question 2.
पंद्रह-सोलह
Answer:
राजेंद्र बाबू के संयुक्त परिवार में कितनी पौत्रियाँ थी?

संजाल पूर्ण कीजिए।

Question 1.

Answer:

कारण लिखिए।

Question 1.
राजेंद्र बाबू की पत्नी प्रयाग आती थीं।
Answer:
उनकी पौत्रियाँ प्रयाग में महिला विद्यापीठ के छात्रावास में रहकर पढ़ाई करती थीं। अत: उन्हें मिलने के लिए राजेंद्र बाबू की पत्नी प्रयाग आती थीं।

कृति ई (२) : शब्द संपदा
निम्नलिखित वाक्य में विरामचिह्नों का उचित प्रयोग कीजिए।

Question 1.
राजेंद्र बाबू के पुराने परिधान से अपने आपको प्रसाधित कर कितना कृतार्थता का अनुभव किया था चक्रधर जी ने
Answer:
राजेंद्र बाबू के पुराने परिधान से अपने आपको प्रसाधित कर कितना कृतार्थता का अनुभव किया था चक्रधर जी ने !

लिंग बदलिए।

1. अध्यक्ष
2. पौत्री
3. स्वामी
4. दादा

Answer:

1. अध्यक्षा
2. पौत्र
3. स्वामिनी
4. दादी

Question 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:

• ताने – बाने
• पंद्रह – सोलह
• अस्त – व्यस्तता
• गुरु – शिष्य
• स्वामी – सेवक
• कभी – कभी

निम्नलिखित शब्द के लिए समश्रुतभिन्नार्थक शब्द लिखिए।

1. सज्जा
2. सहेज

Answer:

1. सजा
2. सहज

Question 1.
‘ममतालु’ इस शब्द में से प्रत्यय अलग कीजिए और संबंधित प्रत्यय लगाकर अन्य दो शब्द बनाइए।
Answer:
ममतालु : शब्द : ममता प्रत्यय : आलु ।
अन्य शब्द :

• कृपालु
• श्रद्धालु

कृति ई (३) : अभिव्यक्ति

Question 1.
‘नारी जीवन में शिक्षा का अनन्यसाधारण महत्त्व है।’ इस विषय पर अपने विचार लिखिए।
Answer:
जिस प्रकार पुरुष समाज का अहम् हिस्सा है ठीक उसी प्रकार नारी भी समाज का महत्त्वपूर्ण अंग है। समाज की उन्नति के लिए स्वी का महत्त्वपूर्ण योगदान होता है। अत: समाज में नारी शिक्षा को महत्त्व दिया जाता है। स्वतंत्रता के समय हमारे देश में स्त्रियों की शिक्षा की उचित व्यवस्था नहीं थी। धीरे-धीरे स्थिति में बदलाव होना शुरू हुआ।

आज भारत में लड़कियों के लिए अलग स्कूल, महाविद्यालय एवं विश्व विद्यालय खोले जा रहे हैं ताकि ज्यादा से ज्यादा संख्या में वे शिक्षा ग्रहण कर सकें। शिक्षा के कारण नारी अपने अधिकार एवं कर्तव्यों के प्रति सजग हो गई है। वह धीरे-धीरे आत्मनिर्भर बन रहीं हैं। एक पढ़ी-लिखी स्त्री अपने परिवार को ठीक से चला सकती है। वह नौकरी करके अपने परिवार को आर्थिक सहयोग देती है। इस प्रकार अनेक दृष्टियों से नारी जीवन में शिक्षा का अनन्यसाधारण महत्व है।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति उ (१): आकलन कृति

कारण लिखिए।

Question 1.
राजेंद्र बाबू की पत्नी की रीढ़ की हड्डी झुक गई थी।
Answer:
क्योंकि उन्हें जमींदार परिवार की परंपरा के अनुसार घंटों तक सिर नीचा करके एकासन बैठना पड़ता था।

कृति पूर्ण कीजिए।

Question 1.

Answer:

निम्नलिखित विधान सत्य है या असत्य लिखिए।

Question 1.
कर्तव्य विलास नहीं कर्मनिष्ठा है।
Answer:
सत्य

Question 2.
राजेंद्र बाबू अपनी पौत्रियों को अहंकार से दूर नही रखना चाहते थे।
Answer:
असत्य

उचित जोड़ियाँ मिलाइए।

Question 1.

Answer:
i – ग
ii – घ
iii – ख
iv – क

किसने, किससे कहा?

Question 1.
“महादेवी बहन दिल्ली मेरी नहीं है।”
Answer:
राजेंद्र बाबू ने महादेवी वर्मा से कहा।

कृति उ (२) : शब्द संपदा

निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. निर्देश
2. अहंकार
3. स्वतंत्र

Answer:

1. सूचना
2. घमंड
3. आजाद

निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
स्कूल या कॉलेज के विद्यार्थियों के रहने की जगह
Answer:
छात्रावास

Question 2.
वह स्थान जहाँ छात्र पढ़ाई करते हैं
Answer:
विद्यालय

Question 3.
जहाँ पहुँचना हो
Answer:
गंतव्य

नीचे दिए हुए शब्द के विलोम शब्द लिखिए।

1. अहंकार x ……..
2. स्वतंत्र x ……

Answer:

1. अहंकार x नम्रता
2. स्वतंत्र x परतंत्र

Question 1.
गद्यांश में से प्रत्यययुक्त शब्द ढूंढकर लिखिए।
Answer:
योग्यता
कर्मनिष्ठा

नीचे दिए शब्द के लिए श्रुतिसमभिन्नार्थक लिखिए।

1. चिंता
2. जेल

Answer:

1. चिता
2. जल

कृति उ (३) : स्वमत अभिव्यक्ति

Question 1.
‘कर्तव्य विलास नहीं कर्मनिष्ठा है।’ इस विषय पर अपने विचार लिखिए।
Answer:
कर्तव्य शब्द का अभिप्राय उन कार्यों से होता है जिन्हें करने के लिए व्यक्ति नैतिक रूप से प्रतिबद्ध होता है। व्यक्ति को अपने कर्तव्य के प्रति सदैव जाग्रत रहना चाहिए। अंत:करण की प्रेरणा या उचित कार्य की प्रवृत्ति से कर्तव्य का संबंध होता है। यदि व्यक्ति अपने कर्तव्यों का पालन ठीक से नहीं करता है तो उसका अंत:करण उसे धिक्कारता है। कर्तव्य को प्राथमिकता देकर व्यक्ति को अपना कार्य करते रहना चाहिए। उसे अपने कर्म में लीन होना चाहिए। व्यक्ति को हर काम को पूरे मन से करने पर ही आनंद का अनुभव होता है। प्रश्न ६ (क) निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ऊ (१): आकलन कृति

ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –

Question 1.
रसोईघर
Answer:
राजेंद्र बाबू की पत्नी के कमरे से संलग्न क्या बन गया था?

Question 2.
दिल्ली
Answer:
बालिकाओं की दादी ने लेखिका को कहाँ आने का विशेष निमंत्रण दिया था?

कृति पूर्ण कीजिए।

Question 1.

Answer:

संजाल पूर्ण कीजिए।

Question 1.

Answer:

कारण लिखिए।

Question 1.
राष्ट्रपति भवन के हर द्वार पर सलाम ठोंकने वाले सिपाहियों की आँखें विस्मय से खुली रह गई। .
Answer:
क्योंकि लेखिका राष्ट्रपति भवन में एक दरजन सूप लेकर गई थीं। ऐसी भेंट लेकर कोई अतिथि न कभी वहाँ पहुँचा था, न पहुँचेगा।

कृति ऊ (२) : शब्द संपदा

Question 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:
फटकने-पछोरने

नीचे दिए हुए शब्द के विलोम लिखिए।

1. विशेष x ………
2. आदेश x …….

Answer:

1. विशेष x साधारण
2. आदेश x प्रार्थना

Question 1.
गद्यांश में से ऐसे दो शब्द ढूँढ़कर लिखिए जिनके वचन परिवर्तित नहीं होते।
Answer:
सूप
आदेश

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
वह भवन जिसमें राष्ट्रपति रहते हैं
Answer:
राष्ट्रपति भवन

Question 2.
अतिथि का सत्कार व उनकी देखभाल
Answer:
आतिथ्य

निम्नलिखित शब्दों के अनेकार्थी शब्द लिखिए।

1. ग्रहण
2. अंक

Answer:

1. पकड़ने की क्रिया, लेने की क्रिया, खाने की क्रिया, मुसीबत
2. संख्या, गोद

कृति ऊ (३): स्वमत अभिव्यक्ति

Question 1.
‘सहधर्मिणी अपने पति के आदर्श एवं सिद्धांत का पालन करती है।’ विषय पर अपने विचार लिखिए।
Answer:
सहधर्मिणी वही कहलाती है जो अपने पति का जीवन के प्रत्येक मोड़ पर साथ देती है। वह अपने पति के आदर्श एवं सिद्धांतों का पालन करती है। यदि उसका पति सादा जीवन उच्च विचार रखता है, तो वह भी उसका अनुसरण करती है। भारत के प्रथम राष्ट्रपति डॉ. राजेंद्र प्रसाद जी का जीवन सादगी से भरा हुआ था। उसीप्रकार उनकी पत्नी ने भी उनके इस सिद्धांत को अपने जीवन में उतारा।

उनके पति कितने भी बड़े पद पर क्यों न हों, फिर भी वे घर के काम-काज को संभालने से पीछे नहीं हटीं। सबके लिए भोजन बनाना एवं सभी के खाने के उपरांत स्वयं खाना खाना, आदि संस्कारों का उन्होंने भलीभांति निर्वाह किया। घर के सभी सदस्य एवं घर पर आने वाले अतिथियों के स्वागत में कोई कमी नहीं छोड़ी। इस प्रकार वह अपने पति के पचिह्नों पर चलकर सभी का दिल जीत लेती है।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ए (१): आकलन कृति

गद्यांश के आधार पर वाक्य पूर्ण कीजिए।

Question 1.
लेखिका राष्ट्रपति भवन उस दिन पहुँची जिस दिन ….
Answer:
राजेंद्र बाबू और उनकी सहधर्मिणी का उपवास था।

कारण लिखिए।

Question 1.
लेखिका ने निरन्न भोजन की इच्छा प्रकट की।
Answer:
क्योंकि उपवास के दिन वह अतिथेय का साथ देना उचित समझती थीं।

निम्नलिखित गलत विधान सही करके लिखिए।

Question 1.
जीवन मूल्यों की परख करने वाली दृष्टि के कारण राजेंद्र बाबू को पद्मश्री की उपाधि मिली।
Answer:
जीवन मूल्यों की परख करने वाली दृष्टि के कारण राजेंद्र बाबू को देशरल की उपाधि मिली।

Question 2.
राष्ट्रपति भवन में लेखिका ने मेवे व मिष्ठान्न खाया।
Answer:
राष्ट्रपति भवन में लेखिका ने उबले आलू खाए।

गद्यांश: ७ पाठ्यपुस्तक पृष्ठ क्र. १९ . राजेंद्र बाबू तथा उनकी चरित्र ढलते थे?

कृति ए (२) : शब्द संपदा

निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।

Question 1.
लेखिका ने कहा आज वह साँचा टूट गया है जिसमें कठिन कोमल चरित्र ढलते थे
Answer:
लेखिका ने कहा, “आज वह साँचा टूट गया है, जिसमें कठिन कोमल चरित्र बलते थे।”

Question 2.
दिए गए गद्यांश में से देशज शब्द ढूँढकर लिखिए।
Answer:

• उबले
• आलू
• छलक
• ढलते

निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर नए शब्द तैयार कीजिए।

Question 1.
संतोष
Answer:
उपसर्गयुक्त शब्द : असंतोष, प्रत्यय युक्त शब्द : संतोषप्रद

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
जिसका कोई शत्रु ही न हो
Answer:
अजातशत्रु

Question 2.
भोजन ग्रहण न करने का निश्चय
Answer:
उपवास

पर्यायवाची शब्द लिखिए।

1. निरन्न
2. अजातशत्रु

Answer:

1. अन्नरहित
2. शत्रुहीन

कृति ए (३) : स्वमत अभिव्यक्ति

Question 1.
‘व्यक्ति के जीवन-मूल्यों का बड़ा महत्व होता है।’ विषय पर अपने विचार लिखिए।
Answer:
जीवन-मूल्य मनुष्य के जीवन में बहुत आवश्यक होते हैं। जीवन मूल्यों का व्यक्ति के जीवन में महत्त्वपूर्ण योगदान रहता है। व्यक्ति इन्हीं के आधार पर अच्छा-बुरा या सही-गलत की परखा करता है। हमेशा नम्र रहना, सबका आदर करना, सादगी से जीवन बिताना आदि जीवन-मूल्य हैं। सुखद व सफल जीवन व्यतीत करने के लिए व्यक्ति को जीवन-मूल्यों को स्वीकार करना पड़ता है। जीवन-मूल्यों के बिनी व्यक्ति अपने जीवन को अनुशासित नहीं कर सकता और न ही अपने मन को स्वयं के नियंत्रण में रख सकता है। जीवन में अपने व्यक्तित्व को निखारने और सफल बनाने के लिए जीवन-मूल्य अनिवार्य है।

अनोखे राष्ट्रपति Summary in Hindi

अनोखे राष्ट्रपति लेखिका – परिचय
जीवन – परिचय : महादेवी वर्मा जी का जन्म सन १९०७ में उत्तर प्रदेश के फर्रुखाबाद में हुआ। ये एक उच्चकोटि की लेखिका एवं प्रतिभावान कवयित्री थीं। छायावाद के चार प्रमुख स्तंभों में से एक हैं। इनके साहित्य में पीड़ा, करुणा, वेदना आदि पाई जाती है। इन्हें हिंदी साहित्य में आधुनिक युग की मीरा’ कहा जाता है। इनका साहित्य समाज के विभिन्न पहलुओं को दर्शाता है तथा प्रत्येक वर्ग को प्रभावित और प्रेरित करता है।

प्रमुख कृतियाँ : ‘नीहार’, ‘रश्मि’, ‘सांध्यगीत’ (कविता संग्रह), ‘संकल्पिता’, ‘श्रृंखला की कड़ियाँ’, (निबंध), ‘पथ के साथी’, ‘मेरा परिवार’, ‘अतीत के चलचित्र’। (रेखाचित्र)

अनोखे राष्ट्रपति गद्य – परिचय
संस्मरण : संस्मरण साहित्य की एक महत्त्वपूर्ण विधा है। स्मृति के आधार पर किसी विषय पर या किसी व्यक्ति पर लिखित आलेख संस्मरण कहलाता है। यह केवल अतीत की घटनाओं पर आधारित होता है। संस्मरण में चारित्रिक गुणों से युक्त किसी व्यक्ति को याद करते हुए उसके परिवेश के साथ उसका प्रभावशाली वर्णन किया जाता है।

प्रस्तावना : ‘अनोखे राष्ट्रपति’ इस संस्मरण में लेखिका महादेवी वर्मा जी ने भारत के पहले राष्ट्रपति डॉ. राजेंद्र प्रसाद जी के ‘सादा जीवन–उच्च विचार’ गुण से परिचित कराया है। जीवन में सादगी, सहजता व सरल स्वभाव अपनाने से व्यक्ति का व्यक्तित्व ऊँचा उठ सकता है, लेखिका ने इस विचार से सभी को अवगत कराया है।

अनोखे राष्ट्रपति सारांश

‘अनोखे राष्ट्रपति’ यह एक संस्मरण है। इस संस्मरण में लेखिका महादेवी वर्मा जी ने डॉ. राजेंद्र प्रसाद जी के जीवन मूल्यों से पाठकों को परिचित कराया है। डॉ. राजेंद्र प्रसाद जी की वेशभूषा में अत्यंत सादगी थी। स्वतंत्रता पूर्व से ही लेखिका डॉ. राजेंद्र प्रसाद जी को अच्छी तरह से जानती थीं। सन १९३७ में प्रयाग में महिला विद्यापीठ का शिलान्यास डॉ. राजेंद्र प्रसाद जी के करकमलों द्वारा हुआ था। तब उन्होंने लेखिका से निवेदन करते हुए कहा था कि वे अपनी पंद्रह–सोलह पौत्रियों की शिक्षा को लेकर चिंतित हैं। इसलिए उन्हें वे प्रयाग के महिला विद्यापीठ में भर्ती करवाना चाहते हैं।

लेखिका ने भी उनकी पौत्रियों को अपने संरक्षण में ले लिया। इस प्रकार उनकी पौत्रियाँ विद्यापीठ के छात्रावास में रहने लगीं। कभी–कभी डॉ. राजेंद्र प्रसाद और उनकी पत्नी सामान्य भारतीय गृहिणी के समान पति, परिवार तथा परिजनों को खिलाने के उपरांत स्वयं अन्न ग्रहण करती थीं। राष्ट्रपति बनने के पश्चात भी डॉ. राजेंद्र प्रसाद जी को अहंकार ने कभी नहीं छुआ। वे अपनी पौत्रियों को अहंकार से दूर रखना चाहते थे। इसलिए साफ शब्दों में उन्होंने लेखिका से कहा था दिल्ली व राष्ट्रपति भवन उनका नहीं है। उनकी पौत्रियाँ जैसी रहती आई हैं; वैसी ही रहेंगी।

एक बार उनकी पत्नी के द्वारा निमंत्रण मिलने पर लेखिका स्वयं राष्ट्रपति भवन जाती हैं। वहाँ पर भारत के पहले राष्ट्रपति डॉ. राजेंद्र प्रसाद जी को उपवास के उपरांत उबले हुए आलू खाते हुए देखती हैं। उनके सादगी एवं संयम से भरे जीवन को देखकर लेखिका नतमस्तक हो जाती हैं। जीवन–मूल्यों की परख करने वाली दृष्टि राजेंद्र बाबू जी के पास थी। उनके पास मन की स्वच्छता थी। उनका कोई शत्रु नहीं था। इसी कारण उन्हें भारतरल की उपाधि मिली थी। ऐसे अनोखे राष्ट्रपति की संगति में लेखिका स्वयं को धन्य समझती हैं।

अनोखे राष्ट्रपति शब्दार्थ

• भृकुटी – भौंह
• ठुड्डी – ठोढ़ी
• रोमिल – रोयेंदार
• निर्देश – सूचना
• सिरकी – सरकंडे या सरई
• पछोरना – अनाज सूप में रखकर फटककर साफ करना
• निरन्न – निराहार, अन्नरहित
• दृष्टि – नजर
• अभिवादन – प्रणाम
• विहंगम – पक्षी
• स्मृति – याद
• वेशभूषा – पहनावा
• निर्देश – सूचना
• अहंकार – घमंड
• कर्तव्य – कार्य
• स्वतंत्र – आजाद
• अजातशत्रु – शत्रुहीन
• भेंट – उपहार

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer

Std 10 Hindi Chapter 4 Do Gazal Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 4 दो गजलें Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 4 दो गजलें Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 4 दो गजलें Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

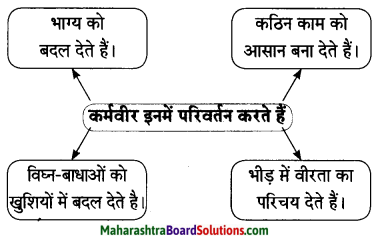
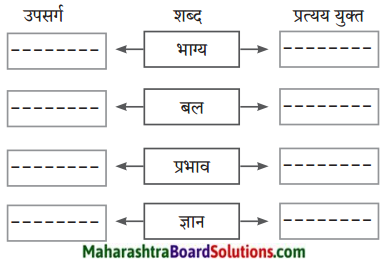
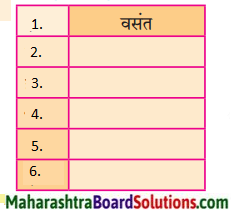
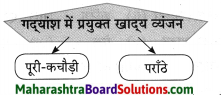
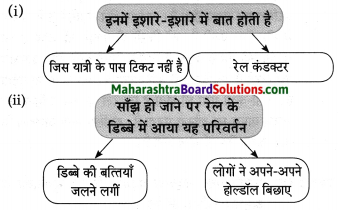
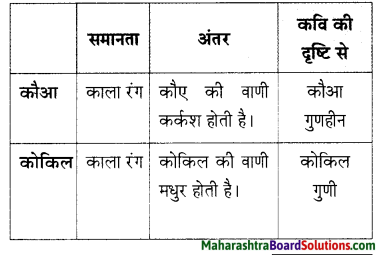
1. कृति पूर्ण कीजिए।

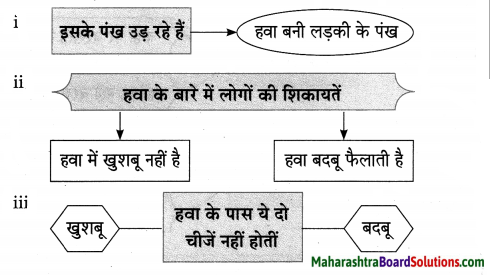
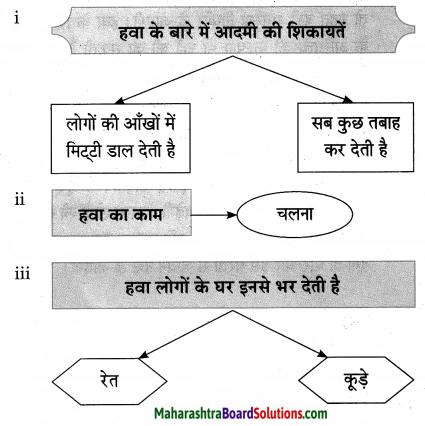
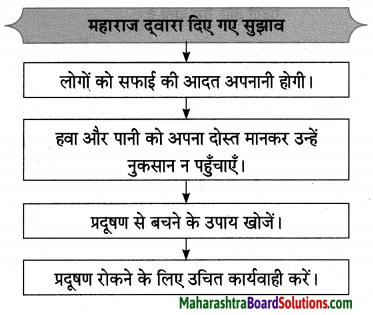
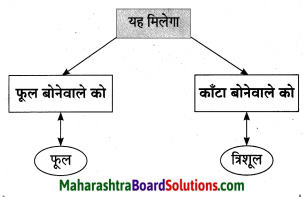
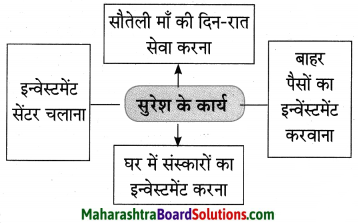
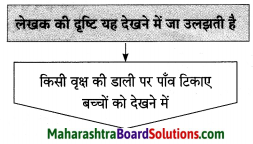
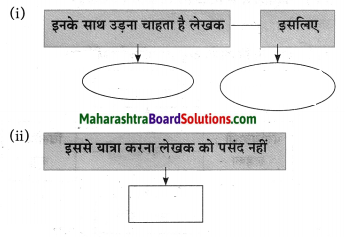
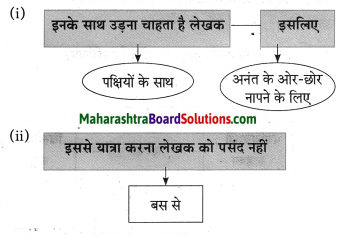
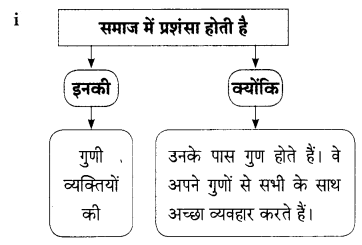
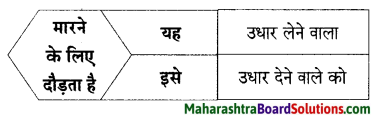
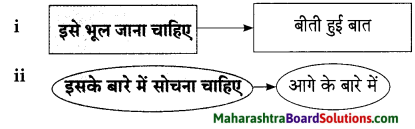
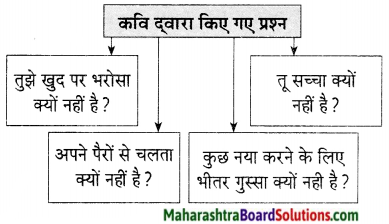
प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

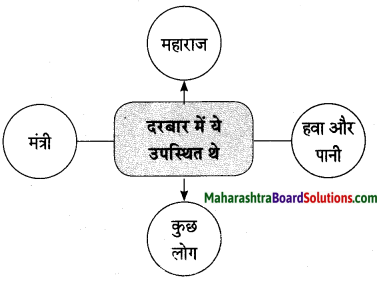
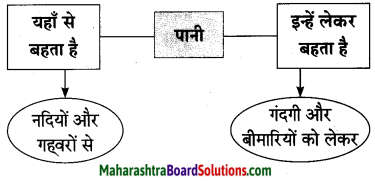
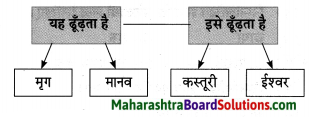
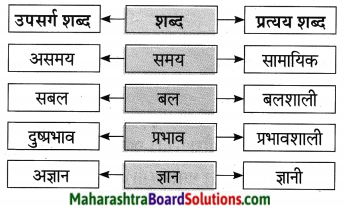
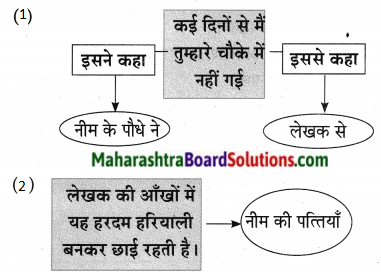
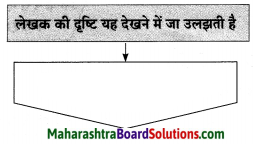
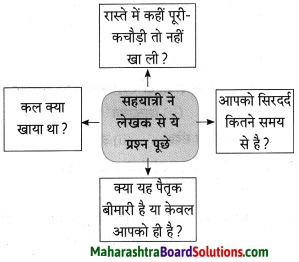
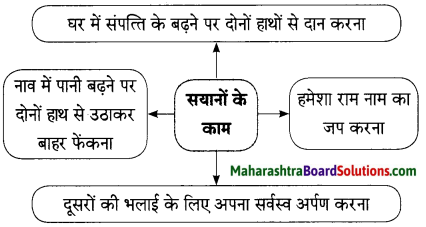
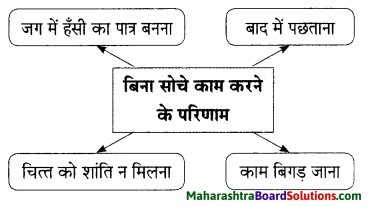
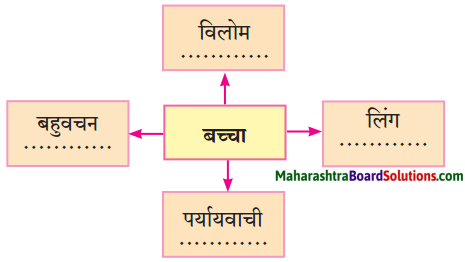
2. संजाल पूर्ण कीजिए।

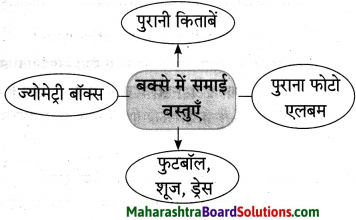
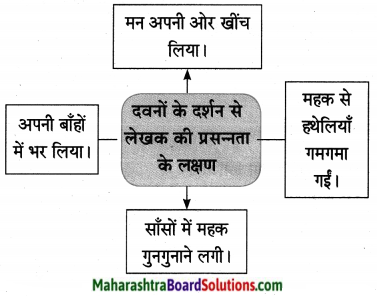
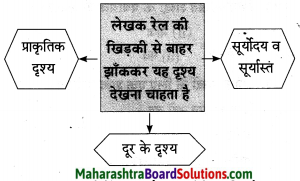
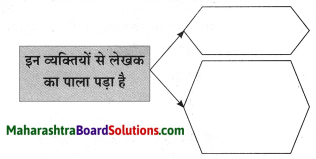
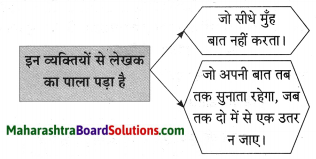
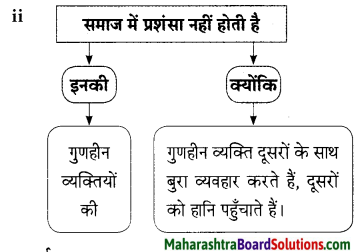
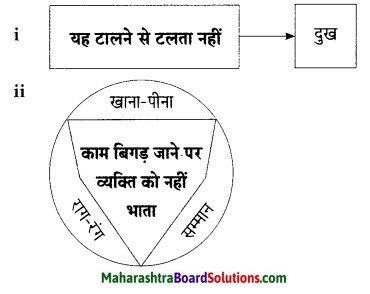
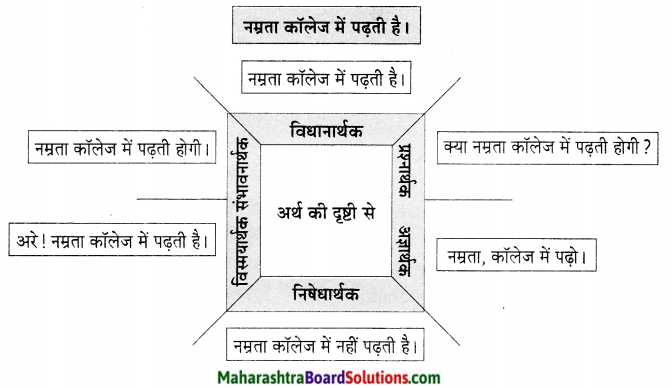
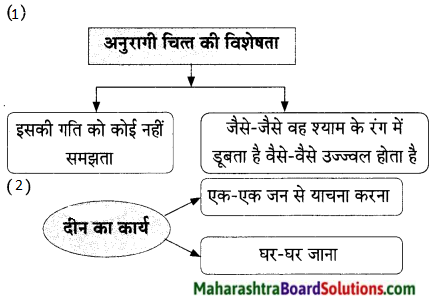
प्रश्न 1.
संजाल पूर्ण कीजिए।

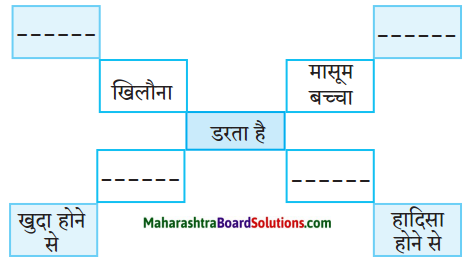
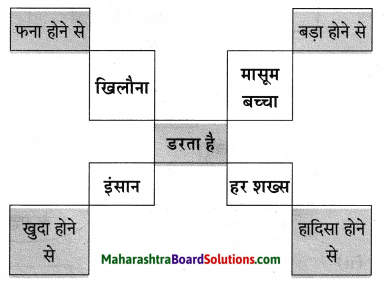
उत्तर:

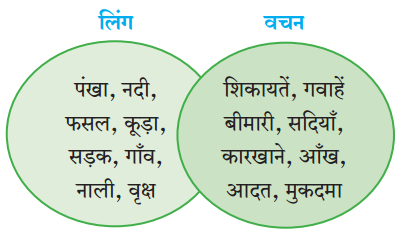
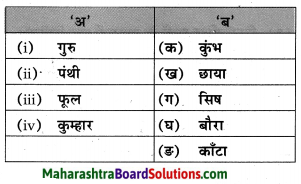
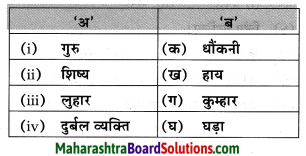
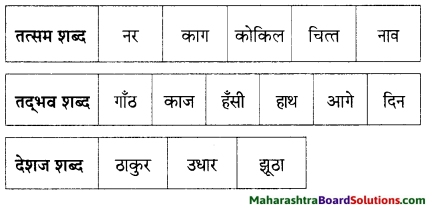
3. कृति में दिए गज़ल में प्रयुक्त शब्दों की उचित जोड़ियाँ क्रमशः अ और आ तालिका में लिखिए।

प्रश्न 1.
कृति में दिए गज़ल में प्रयुक्त शब्दों की उचित जोड़ियाँ क्रमशः अ और आ तालिका में लिखिए।

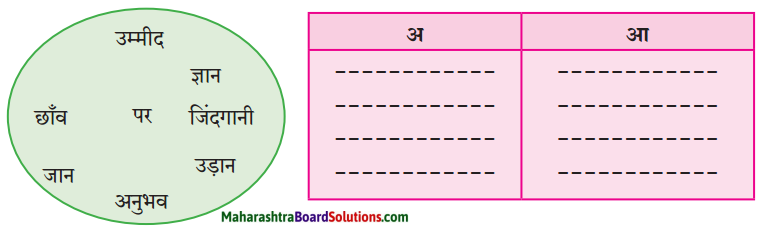
उत्तर:

अ	आ
छाँव	उम्मीद
अनुभव	ज्ञान
पर	उड़ान
जान	जिंदगानी

4. उचित शब्द का चयन करते हुए वाक्य पूर्ण कीजिए।
(मिट्टी, कैद, बंदी, रिहा, छूटना)

प्रश्न 1.
उचित शब्द का चयन करते हुए वाक्य पूर्ण कीजिए।
(मिट्टी, कैद, बंदी, रिहा, छूटना)
i. अजब ये जिंदगी की ……….. है।
ii. रिहाई माँगता है और ……….. होने से डरता है।
उत्तर:
i. कैद
ii. रिहा

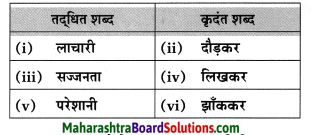
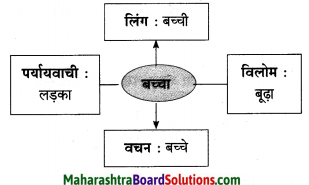
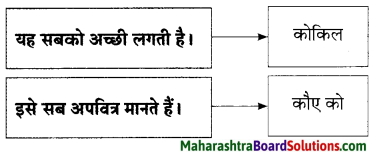
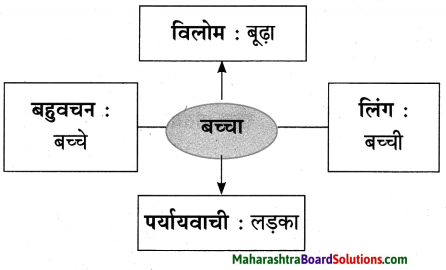
5. सूचना के अनुसार शब्द में परिवर्तन कीजिए।

प्रश्न 1.
सूचना के अनुसार शब्द में परिवर्तन कीजिए।

उत्तर:

6. ‘जीवन में डर की जगह सावधानी एवं साहस चाहिए।’ विषय पर अपने विचार व्यक्त कीजिए। 

प्रश्न 1.
‘जीवन में डर की जगह सावधानी एवं साहस चाहिए।’ विषय पर अपने विचार व्यक्त कीजिए।
उत्तर:
डर वह भावना है; जो इंसान को कमजोर बना देती है और साहस वह भावना होती है; जो इंसान के हौसलों में उड़ान पैदा करती है। व्यक्ति को अपने जीवन में डर का त्याग कर साहस और सावधानी को अपनाना चाहिए। उसे प्रत्येक काम साहस के साथ सावधानीपूर्वक करना चाहिए। सावधानी बरतने से व्यक्ति के सारे काम सुचारू रूप से पूर्ण होते हैं। साहस असंभव कार्य को भी संभव बनाने की शक्ति रखता है। जो व्यक्ति अपने जीवन में साहस को नहीं अपनाता है: वह व्यक्ति कभी भी सफल नहीं होता। जीवन में कई सफल व्यक्ति हैं, जिन्होंने डर की जगह सावधानी एवं साहस को अपनाकर संसार में अद्भुत कार्य करके सभी को अपने प्रभावी व्यक्तित्व से प्रेरित किया।

भाषा बिंदु :

प्रश्न 1.
निम्नलिखित वाक्यों के रचना के अनुसार भेद लिखिए।

1. वह आदमी भी उस गाँव में रहने के लिए तैयार हो गया। [ ]
2. स्टेशन मास्टर ने सिग्नल नहीं दिया और गाड़ी आउटर पर खड़ी रही। [ ]
3. मजे की बात यह है कि एक समाचारपत्र के कितने उपयोग हो सकते हैं। [ ]
4. वह पशु-पक्षियों के बीच बातें करता दिखाई देता। [ ]
5. आप उस गाँव में जाएंगे तो आपको उस खोए हुए आदमी की वहाँ स्थापित मूर्ति दिख जाएगी। [ ]
6. नींद आती रहती है, जाती रहती है और रह-रहकर टूटने के बावजूद उसमें लय बनी होती है। [ ]

उत्तर:

1. सरल वाक्य
2. संयुक्त वाक्य
3. मिश्र वाक्य
4. सरल वाक्य
5. मित्र वाक्य
6. संयुक्त वाक्य

प्रश्न 2.
पाठों में आए रचना के अनुसार वाक्यों के दो-दो उदाहरण लिखिए।
उत्तरः
1. सरल वाक्य :
i. इससे मेरा भी मन बड़ा दुखी होता है।
ii. मैंने सबकी बात सुनी है।

2. मिश्र वाक्य :
i. जैसी करनी वैसी भरनी।
ii. हमें चाहिए कि हम हवा और पानी को अपना दोस्त बनाकर उन्हें नुकसान न पहुँचाएँ।

3. संयुक्त वाक्य :
i. सोना तो मिट्टी है और मिट्टी का मोह पालकर आज तक किसी ने शांति नहीं पाई।
ii. लोग उसके दर्शन को आने लगे और धीरे-धीरे चारोंतरफ साधु का यश फैल गया।

प्रश्न 3.
निम्नलिखित वाक्यों के अर्थ के अनुसार भेद लिखिए।

1. सुबह उठता हूँ तो थोड़ी ताजगी महसूस होती है। [ ]
2. अरे, वहीं अटके रहोगे, मुझसे बात नहीं करोगे? [ ]
3. कई दिनों तक मैं तुम्हारे चौके में नहीं गई। [ ]
4. ठीक है, मुकदमें की कार्यवाही शुरू करें। [ ]
5. अरे! हवा रानी, नाराज मत हो। [ ]
6. इस बात के लिए ये गाँववाले ही जिम्मेदार हैं। [ ]
7. अधिक वर्षा के लिए कौन जिम्मेदार है? [ ]
8. अच्छा! निकलती हूँ बस पाँच मिनट चाहिए मुझे तैयार होने के लिए। [ ]
9. हौं राजीव, आओ बैठो।
10. यह एक भोले इंसान का विश्वास नहीं था।

उत्तर:

1. विधानार्थक वाक्य
2. प्रश्नार्थक वाक्य
3. निषेधार्थक वाक्य
4. आज्ञार्थक वाक्य
5. आज्ञार्थक वाक्य
6. विधानार्थक वाक्य
7. प्रश्नार्थक वाक्य
8. विस्मयादिबोधक वाक्य
9. आज्ञार्थक वाक्य
10. निषेधार्थक वाक्य

प्रश्न 4.
पाठों में आए अर्थ के अनुसार वाक्यों के दो-दो उदाहरण लिखिए।
उत्तरः
1. विधानार्थक वाक्य :
i. मैं तेजी से वहाँ जाती हूँ।
ii. महाराज यह आरोप झूठा है।

2. आज्ञार्थक वाक्य :
i. पहले पानी को बुलाया जाए।
ii. सेठ मेरा इनाम दें।

3. निषेधार्थक वाक्य :
i. कहीं भी कोई नहीं था।
ii. उसमें भी मेरा कुछ नहीं है।

4. प्रश्नार्थक वाक्य :
i. तू कौन है?
ii. उसकी माया में मुझे क्यों फँसाता है?

5. विस्मयादिबोधक वाक्य :
i. काश, अपने गाँव-शहर में हमें भी ऐसा ‘खोया हुआ आदमी’ मिल जाता!
ii. हाँ महाराज! आज सब शिकायतें हवा और पानी के बारे में हैं।

6. संदेहसूचक वाक्य :
i. शायद मैं खो गया हूँ।
ii. संभव है कि पानी दूषित होने से बच जाए।

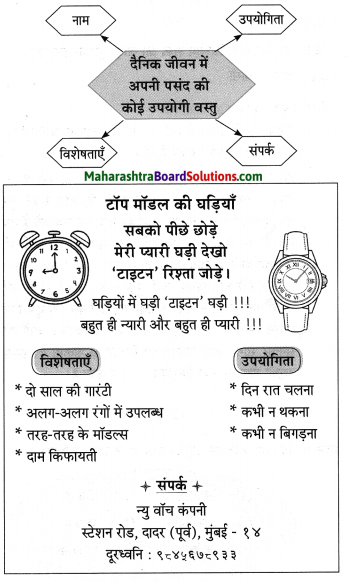
उपयोजित लेखन :

प्रश्न 1.
अपने विद्यालय में आयोजित की जानेवाली क्रीड़ा प्रतियोगिताओं का आयोजक के नाते विज्ञापन तैयार कीजिए।

उत्तरः

Hindi Lokvani 10th Std Textbook Solutions Chapter 4 दो गजलें Additional Important Questions and Answers

(अ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1): आकलन कृति

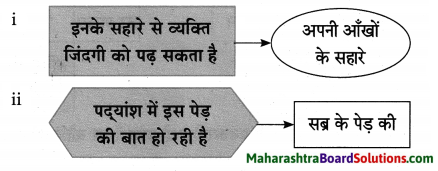
प्रश्न 1.
समझकर लिखिए।
उत्तरः

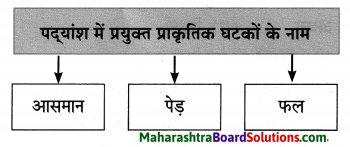
प्रश्न 2.
पद्यांश में प्रयुक्त प्राकृतिक घटकों के नाम
उत्तरः

कृति अ (2) : शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. आसमान
2. पर
3. इतमीनान
4. सोच

उत्तरः

1. अंबर
2. पंख
3. तसल्ली
4. विचार

प्रश्न 2.
पद्यांश में प्रयुक्त ऐसे दो शब्द लिखिए जिनके वचन परिवर्तित नहीं होते हैं।
उत्तर:
i. पेड़
ii. पर

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।
i. हवा में उड़ने की क्रिया
उत्तरः
i. उड़ान

प्रश्न 4.
निम्नलिखित शब्द के अनेक अर्थ लिखिए।
i. फल
ii. पर
उत्तर:
i. फल : खाने का फल, परिणाम
ii. पर : परंतु, पंख

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘अनुभव सबसे बड़ा शिक्षक होता है।’ अपने विचार लिखिए।
उत्तरः
जीवन-रूपी यात्रा में सीखने के लिए कोई किताब साथ नहीं होती। व्यक्ति अपने अनुभवों से ही सीखता है। व्यक्ति जीवन में कार्य करते समय कई गलतियाँ करता रहता है। उन गलतियों से उसका अनुभव समृद्ध हो जाता है। वह फिर से उन गलतियों को नहीं दोहराता। वह अपनी गलतियों से बहत सारी बातें सीखता है और स्वयं के अनुभव को समृद्ध बनाता है। अनुभव सोने के समान होता है।

जिस प्रकार सोना तप-तप कर तैयार हो जाता है उसी प्रकार अनुभव दिन-रात की मेहनत एवं लगन से प्राप्त किया जाता है। व्यक्ति के जीवन में आने वाले अच्छे-बुरे अनुभव उसके मार्गदर्शक बनते हैं। अनुभव से मिलने वाला ज्ञान व्यक्ति को सफलता के शिखर पर पहुँचा देता है। अनुभवहीन ज्ञान जीवन की सच्चाई के सामने टिक नहीं पाते। अत: अनुभव ही सबसे बड़ा शिक्षक होता है।

(आ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1): आकलन कृति

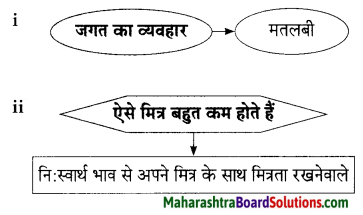
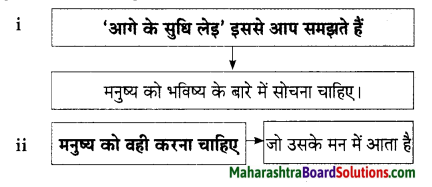
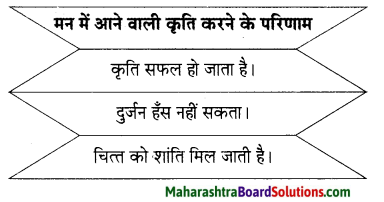
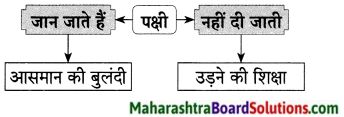
प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

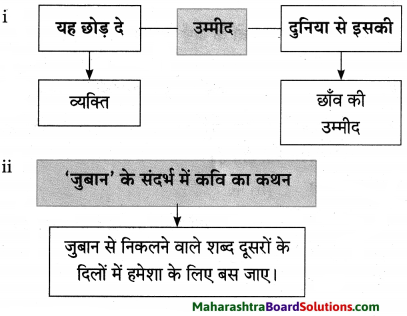
प्रश्न 2.
समझकर लिखिए।
उत्तरः

प्रश्न 3.
निम्नलिखित गलत विधान सही करके लिखिए।
i. प्रकृति ने हमें जिंदगी बख्शी है।
उत्तरः
ईश्वर ने हमें जिंदगी बख्शी है।

ii. ईश्वर सायबान निर्माण करेगा।
उत्तर:
इंसान सायबान निर्माण करेगा।

कृति आ (2) : शब्द संपदा

प्रश्न 1.
कविता में इस अर्थ में आए शब्द लिखिए।

1. संसार
2. स्वयं
3. आशा
4. ईश्वर

उत्तर:

1. दुनिया
2. खुद
3. उम्मीद
4. खुदा

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. छाया
उत्तर:
i. छाँव

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।
i. घर के आगे छाया हेतु बनाया गया छप्पर
उत्तर:
i. सायबान

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘व्यक्ति को जीवन में आत्मनिर्भर होना चाहिए। उसे दूसरों से मदद की अपेक्षा नहीं रखनी चाहिए।’ अपने विचार लिखिए।
उत्तर:
आत्मनिर्भर यानी स्वावलंबी। व्यक्ति को अपने जीवन में आत्मनिर्भर होना चाहिए। उसे दूसरों पर आश्रित नहीं होना चाहिए। यदि व्यक्ति अपने जीवन में दूसरों पर आश्रित रहता है, तो वह तरक्की नहीं कर सकता है। आत्मनिर्भर बनने के लिए व्यक्ति में दृढ़ इच्छा शक्ति का होना जरूरी होता है। आत्मनिर्भर व्यक्ति सदैव कोशिश करते रहता है। इसलिए वह सफलता की मंजिल हासिल करने में सफल हो जाता है। वह भाग्य के भरोसे नहीं बैठता है। आत्मनिर्भर बनकर वह अपनी क्षमताओं का विकास कर लेता है। अब्राहम लिंकन व नेपोलियन जैसे महापुरुषों का जन्म निर्धन परिवार में हुआ था। उन्होंने जीवन में आत्मनिर्भर बनकर सफलता की सीढ़ी हासिल की। इसलिए प्रत्येक व्यक्ति को अपने जीवन में आत्मनिर्भर होना चाहिए।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1): आकलन कृति

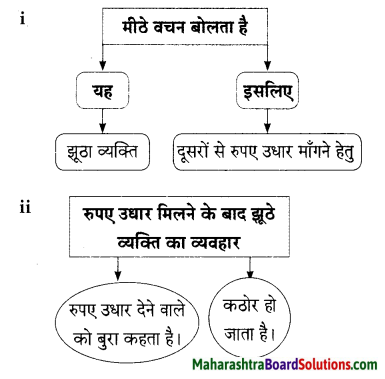
प्रश्न 1.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. अजब
ii. रिहाई
उत्तर:
i. जिंदगी की कैद कैसी है?
ii. दुनिया का हर इंसान क्या माँगता है?

प्रश्न 2.
पद्यांश के आधार पर समझकर लिखिए।
i. इंसान के बस और काबू में ये नहीं है –
ii. हर शख्स इसका बना खिलौना है –
उत्तर:
i. इंसान के बस में जिंदगी नहीं है और काबू में मौत नहीं है।
ii. मिट्टी का

कृति इ (2) : शब्द संपदा

प्रश्न 1.
निम्न शब्दों में उचित उपसर्ग का प्रयोग कीजिए।

1. मौत
2. पल
3. काबू

उत्तर:

1. बेमौत
2. हरपल
3. बेकाबू

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. मृदा
उत्तर:
i. मिट्टी

प्रश्न 3.
निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. फना
2. मौत
3. रिहाई
4. काबू

उत्तर:

1. नष्ट
2. मृत्यु
3. मुक्ति
4. नियंत्रण

प्रश्न 4.
विलोम शब्द लिखिए।
i. बड़ा × ……….
i. जिंदगी × ………….
उत्तर:
i. छोटा
ii. मौत

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
बचपन की दुनिया और बड़ों की दुनिया में क्या अंतर है? अपने विचार लिखिए।
उत्तर:
बचपन की दुनिया में मासूमियत होती है और बड़ों की दुनिया मुश्किलों और परेशानियों से भरी होती है। बचपन जीवन की एक ऐसी अवस्था होती है; जहाँ पर जीवन का मस्ती से आनंद लिया जाता है और बड़ों की दुनिया जिम्मेदारियों से भरी होती है। कई लोगों को इस कारण जिंदगी कैद के समान लगती है।

लेकिन बच्चों के लिए जिंदगी खुशियाँ एवं प्यार लेकर आती है। मुस्कुराना, शरारत करना, रूठना और फिर सब भुलाकर एक हो जाना; ये बच्चों की पहचान होती है। वहीं बड़ों के जीवन में ईर्ष्या, द्वेष एवं कलह होता है। बच्चे दुनियादारी के झमेलों से दूर होते हैं, तो बड़ों की दुनिया कई प्रकार के झमेले में उलझती रहती है।

दो गजलें Summary in Hindi

कवि-परिचय :

जीवन-परिचय : राजेश रेड्डी जी का जन्म सन १९५२ में महाराष्ट्र के नागपुर में हुआ था। राजेश जी हिंदी, अंग्रेजी व उर्दू भाषा के ज्ञाता हैं। जगबीती को आपबीती में परिवर्तित कर गज़ल लिखने में रेड्डी जी कुशल माने जाते हैं। ये विविध भारती, मुंबई से भी जुड़े हैं। इन्होंने अपनी प्रतिभा से गज़ल एवं नाटक विधा को समृद्ध किया है।
प्रमुख कृतियाँ : ‘उड़ान’, ‘आसमान से आगे’, ‘वजूद’ (गज़ल संग्रह) आदि।

पद्य-परिचय :

गज़ल : ‘गज़ल’ यह अरबी साहित्य की प्रसिद्ध काव्य-विधा है। गज़ल एक ही बहर और वज़न के अनुसार लिखे गए शेरों का समूह है। इसके पहले शेर को मतला कहते हैं। गज़ल के अंतिम शेर को मक़्ता कहते हैं।
प्रस्तावना : ‘दो गज़लें’ इस गज़ल में दो गज़लें सम्मिलित की गई हैं। पहले गज़ल से हमें यह संदेश मिलता है कि व्यक्ति के पास कोई भी कार्य करने से पहले जोश, उत्साह, ज्ञान, आत्मविश्वास आदि का होना जरूरी होता है। दूसरी गज़ल में कवि ने बताया है कि बचपन मासूमियत से भरा होता है। बड़े होने पर परेशानियाँ आती हैं, जिस कारण इंसान अनेक प्रकार की परेशानियों से घिर जाता है।

सारांश :

‘दो गज़लें’ यह एक गज़ल है। इस गज़ल के द्वारा कवि कहता है कि व्यक्ति को कोई भी कार्य करने से पहले अपने आप में जोश, उत्साह, आत्मविश्वास आदि का निर्माण करना चाहिए। व्यक्ति को कोई भी कार्य करने से पहले अपनी आँखों से जिंदगी को पढ़ लेना चाहिए। खुद के अनुभवों से प्राप्त ज्ञान के बिना कार्य की पूर्ति नहीं होती। जीवन में संयम व धैर्य का बहुत बड़ा महत्त्व होता है। कवि मानवतावादी है। अत: वह मानव की भलाई की कामना रखता है।

व्यक्ति को दूसरों से अपेक्षा रखने के बजाय स्वयं आत्मनिर्भर होना चाहिए। प्रत्येक व्यक्ति को ऐसी वाणी में सबके साथ वार्तालाप करना चाहिए कि उसके विचार दूसरों के हृदय में सदा के लिए बस जाए। कवि इस गज़ल के माध्यम से कहता है कि आज का व्यक्ति दुख, तकलीफों और परेशानियों से चारों ओर से घिर चुका है। दुनिया-समाज में पड़कर व्यक्ति की बचपन जैसी मासूमियत खोने लगी है। वह नश्वर है। फिर भी उसकी महत्वाकांक्षा पूरी होती नहीं दिखती। वह अपनी ही जिंदगी में कैद हो गया है। वह मुक्ति भी पाना चाहता है. और इच्छाओं को भी नष्ट करना नहीं चाहता।

भावार्थ :

पहले इक आसमान …………………… उड़ान पैदा कर।
व्यक्ति को कोई भी कार्य करने से पहले अपने आप में जोश, उत्साह व आत्मविश्वास उत्पन्न करना चाहिए। इसलिए कवि कहते हैं कि व्यक्ति को अपने परों में यानी मन में हौसला भरने से पहले आसमान यानी सकारात्मक परिस्थिति उत्पन्न कर लेनी चाहिए। सकारात्मक परिस्थिति व आत्मविश्वास के बिना व्यक्ति सफलता की ऊंची मंजिल हासिल नहीं कर सकता।

अपनी आँखों से ………………. पैदा कर।
व्यक्ति को कोई भी कार्य करने से पहले अपनी आँखों से जिंदगी को पढ़ लेना चाहिए। स्वयं के अनुभवों से प्राप्त ज्ञान के बिना कार्य की पूर्ति नहीं होती। व्यक्ति का अनुभव समृद्ध होना बेहद जरूरी है। अनुभव समृद्ध व्यक्ति के पास ज्ञान का भंडार होता है। अनुभवों के द्वारा ही व्यक्ति को ज्ञान की प्राप्ति होती है।

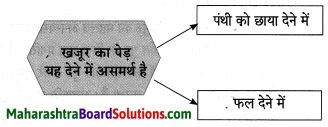
सब के पेड़ ………………… पैदा कर।
जीवन में संयम व धैर्य का बहुत ही महत्त्व होता है। संयम व धैर्य के बिना मनुष्य को मनचाहे फल की प्राप्ति नहीं हो सकती। कहा भी । गया है कि सब्र का फल मीठा होता है। धैर्य और संयम से आज नहीं तो कल सब का फल जरूर मिलता है। इसलिए व्यक्ति की सोच में भी इतमीनान यानी तसल्ली होनी चाहिए। उसे कोई भी कार्य करने से पहले तसल्ली से सोचना चाहिए।

ऐ खुदा! ………………………… पैदा कर।
कवि इंसान का भला चाहता है। वह नहीं चाहता कि इंसान दुख-दर्द में अपना जीवन व्यतीत करे। इंसान के जीवन में खुशहाली आए । इसलिए कवि ईश्वर से ऐसे सुंदर संसार की कामना करता है; जहाँ पर व्यक्ति सुख-चैन के साथ अपना जीवन जी सके।

तूने बख्शी है …………………….. पैदा कर।
कवि मानवतावादी है। अत: वह मानव की भलाई की कामना रखता है। वह ईश्वर से कहता है, “हे ईश्वर, तूने सभी को जिंदगी का । अनमोल उपहार दिया है। अत: तू ही इस जिंदगी में जान भरने का कार्य कर । तू ही लोगों में जिंदादिली निर्माण कर; ताकि लोग इस जिंदगी के सफर का आनंद ले सकें।

छोड़ दुनिया से ………………….. पैदा कर।
व्यक्ति को जीवन में किसी से भी, कोई भी उम्मीद नहीं रखनी चाहिए। व्यक्ति को दूसरों से उम्मीद रखने के बजाय स्वयं आत्मनिर्भर होना चाहिए। व्यक्ति को दूसरों से सहायता की अपेक्षा नहीं रखनी चाहिए; बल्कि स्वयं ही प्रकाशित होकर स्वयं की जिंदगी को उज्ज्वल बनाना चाहिए। दूसरों से छाँव की अपेक्षा रखने के बजाय स्वयं ही सायबान बनकर खुद को और दूसरों के जीवन में भी छाँव उत्पन्न करनी चाहिए।

दिल से निकले ………………… पैदा कर।
व्यक्ति की वाणी सरल, सहज और मीठी होनी चाहिए। उसके बोलने वाले शब्द दिल से निकले होने चाहिए। यदि वह इस प्रकार वाणी : का प्रयोग करेगा, तो निश्चित ही वह दूसरों की निगाहों में और दिलों में आसानी से जगह प्राप्त कर लेगा।

यहाँ हर शख्स …………………. डरता है।
कवि कहते हैं कि हर इंसान अपनी मृत्यु से सदा भयभीत रहता है। वह अपने ऊपर होनेवाले हादसों और आपदाओं से डरता रहता है। । 5. आखिर इंसान मिट्टी से बना हुआ एक खिलौना ही तो है। उसे एक दिन टूटना ही है। फिर भी वह न जाने क्यों नष्ट होने से डरता रहता है।

मेरे दिल के किसी ……………………… डरता है।
बचपन की मासूमियत सभी को प्यारी और अच्छी लगती है। उसे कोई भी भूलना नहीं चाहता। हर व्यक्ति के दिल में कहीं न कहीं बचपना छिपा रहता है। लेकिन बड़ों की दुनिया जो दुख और तकलीफों से भरी है, उसे देखकर वह अपने बचपन को कहीं न कहीं बचाए रखना चाहता । है। वह बड़ों की दुनिया के साथ बड़ा होना नहीं चाहता क्योंकि बड़ों की दुनिया में मासूमियत नहीं होती।

शब्दार्थ :

1. आसमान – अंबर
2. पर – पंख
3. सोच – विचार
4. इतमीनान – तसल्ली , ढाढ़स
5. जहान – संसार, जगत
6. खुदा – ईश्वर
7. उम्मीद – आशा, भरोसा
8. खुद – स्वयं
9. हादिसा – आपदा
10. फना – नष्ट
11. मौत – मृत्यु
12. रिहाई – मुक्ति
13. काबू – नियंत्रण, वश
14. सायबान – घर के आगे छाया हेतु बनाया हुआ छप्पर
15. जान – प्राण, जीवन
16. सब्र – सबर, संयम, धैर्य

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 8 कर्मवीर Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 8 Karamveer Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 8 कर्मवीर Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 8 कर्मवीर Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तर:

2. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

3. विशेषताएँ लिखिए :

प्रश्न 1.
विशेषताएँ लिखिए :

उत्तर:

4. कविता में इस अर्थ में आए शब्द लिखिए 

प्रश्न 1.
कविता में इस अर्थ में आए शब्द लिखिए

1. कर्मभूमि : ………………
2. अकारण : ………………
3. आकाश : ………………
4. विशवास : ………………

उत्तर:

1. कार्यस्थल
2. वृथा
3. गगन
4. विशवास

5. कविता की अपनी पसंदीदा चार पंक्तियों का सरल अर्थ लिखिए। 

प्रश्न 1.
कविता की अपनी पसंदीदा चार पंक्तियों का सरल अर्थ लिखिए।
उत्तर:
जो कभी अपने ……………………..चुराते हैं नहीं।
प्रस्तुत पंक्तियों के माध्यम से कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीरों के लिए समय बहुत महत्त्वपूर्ण होता है। इसलिए वे समय को कभी व्यर्थ नहीं गवाते। जिस काम को जिस समय करना है उसे उसी समय करते हैं। वे काम को कल पर नहीं छोड़ते हैं। जहाँ काम करना हो वहाँ कोई बहानेबाजी और आनाकानी नहीं करते। आज का काम कल पर टालकर वे अपने दिनों को व्यर्थ नहीं गवाते। समय का सदुपयोग करना यही उनका कर्तव्य होता है। कोशिश अथवा मेहनत करने से वे कभी भी पीछे नहीं हटते ।

उपयोजित लेखन :

प्रश्न 1.
मुद्दों के आधार पर कहानी लेखन कीजिए।
एक हंस और एक कौए में मित्रता – हंस का कौए के साथ उड़ते जाना – कौए का दधिपात्र लेकर जाने वाले ग्वाले को देखना – ललचाना – कौए का दही खाने का आग्रह – हंस का इनकार – कौए का घसीटकर ले जाना – कौए का चोंच नचा – नचाकर दही खाना – हंस का बिलकुल न खाना – आहट पाकर कौए का उड़ जाना -हंस का पकड़ा जाना – परिणाम – शीर्षक।
उत्तर:
कुसंगति का फल एक जंगल था। उस जंगल में तरह-तरह के पक्षी एवं जानवर रहते थे। उस जंगल में एक बरगद के पेड़ पर एक हंस व एक कौआ भी रहता था। दोनों में गहरी मित्रता थी। एक दिन वे दोनों खुले आसमान में विचरण कर रहे थे। उस वक्त कौए की नजर सिर पर दधिपात्र लेकर जाने वाले एक ग्वाले पर गई।

दधिपात्र देखकर कौए के मुँह में पानी भर आया। उसने तपाक से हंस से कहा, “क्यों न हम दोनों मिलकर दधिपात्र से थोड़ा-थोड़ा दही खा लें।” हंस ने कहा, “नहीं भाई ! इस प्रकार चोरी या छिपकर खाने से आफत आ सकती है। हम पकड़े जा सकते हैं। फिर भी कौए ने हंस की एक न सुनी।

वह जबरन हंस को घसीटकर दधिपात्र के पास ले आया। वह बड़े मजे से दही को खाने लगा। ढेर सारा दही देखकर वह अपनी चोंच नचा-नचाकर दही खाने लगा। हंस सिर्फ उसके साथ था, लेकिन उसने दही को छुआ तक नहीं। दधिपात्र लेकर जाने वाले ग्वाले को एहसास हुआ कि दधिपात्र में से कौआ या अन्य पक्षी दही खाने की चेष्टा कर रहे हैं।

ग्वाले ने आव देखा न ताव तुरंत अपना दाहिना हाथ ऊपर कर उसने हंस को पकड़ लिया। तब तक आहट पाकर कौआ वहाँ से उड़ गया। बेचारा हंस! उसका बुरा हाल हुआ। ग्वाले ने उसे मार डाला। सीख : बुरे लोगों के साथ रहने से बुरा होता है। इसलिए हमें अच्छे लोगों के साथ रहना चाहिए।

Hindi Lokvani 10th Std Textbook Solutions Chapter 8 कर्मवीर Additional Important Questions and Answers

(अ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1): आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
‘कर्मवीर दूसरों का मुँह नहीं ताकते’ इसका तात्पर्य है कि –
उत्तर:
वे स्वावलंबी होते हैं। अत: वे दूसरों पर निर्भर नहीं होते।

कति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. विघ्न
2. बाधा
3. भाग्य
4. चंचल

उत्तर:

1. संकट
2. रुकावट
3. नसीब
4. अस्थिर

प्रश्न 2.
विलोम शब्द लिखिए।
i. कठिन × …….
ii. निर्मल × …….
उत्तर
i. सरल
i. मलीन

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए –
i. अस्थिर स्वभाव का –
उत्तर :
i. चंचल

प्रश्न 4.
निम्नलिखित तद्भव शब्द का तत्सम शब्द लिखिए।
i. मुँह
ii. काम
उत्तर:
i. मुख
ii. कार्य

प्रश्न 5.
निम्नलिखित शब्द के वचन बदलिए।
i. बाधा
ii. काम
उत्तर:
i. बाधाएँ
ii. काम

प्रश्न 6.
निम्नलिखित शब्द के समश्रुतभिन्नार्थक शब्द लिखिए।
i. मान
ii. भाग्य
उत्तर:
i. मन
i. भाग

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘जो विघ्न-बाधाओं का सामना करता है वही सफल होता है।’ अपने विचार लिखिए।
उत्तर:
जीवन में सुख व दुख दोनों हैं। व्यक्ति के जीवन में अनुकूल व प्रतिकूल ये दोनों परिस्थितियाँ आती हैं। व्यक्ति को प्रतिकूल परिस्थिति का डरकर नहीं बल्कि डटकर सामना करना चाहिए। जो व्यक्ति जीवन में आने वाले संघर्षों का सामना करता है वह अंत में सफल हो जाता है। संघर्षों के साथ लड़ते समय उसमें अदम्य शक्ति निर्माण हो जाती है नई ऊर्जा का संचार हो जाता है। परिस्थितियाँ मनुष्य को जीवन अनुभवों से समृद्ध बनाती हैं। जिसके जीवन में संघर्ष नहीं; जो विघ्न-बाधाओं का सामना नहीं करता है, उस व्यक्ति का जीवन नीरस हो जाता है। जो व्यक्ति विघ्न-बाधाओं का सामना करता है वही अंत में अपनी मंजिल पाता है। ऐसा पुरुष ही जीवन का सच्चा कर्मवीर कहलाता है।

(आ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1) : आकलन त

प्रश्न 1.
सही विकल्प चुनकर लिखिए।
i. कार्य कितना भी कठिन हो ………….
(अ) कर्मवीर उसे पूरा करने की ठान नहीं लेते हैं।
(आ) कर्मवीर उसे पूरा करने की ठान लेते हैं।
(इ) उसे पूरा करने की जिम्मेदारी दूसरों पर सौंपते हैं।
उत्तर:
(आ) कर्मवीर उसे पूरा करने की ठान लेते हैं।

ii. कर्मवीर आसमान के फूलों को व्यर्थ बातों से नहीं तोड़ते अर्थात
(अ) वे अपनी प्रशंसा के लिए बड़ी-बड़ी बातें नहीं बनाते।
(आ) वे अपनी प्रशंसा के लिए बड़ी-बड़ी बातें बनाते हैं।
(इ) वे अपनी प्रशंसा के लिए किसी भी हद तक जा सकते हैं।
उत्तर:
(अ) वे अपनी प्रशंसा के लिए बड़ी-बड़ी बातें नहीं बनाते।

कृति आ (2) : शब्द संपदा

प्रश्न 1.
कविता में इस अर्थ में आए शब्द लिखिए।
i. सहायता : ………………
ii. दिवस : ……………….
उत्तर:
i. मदद
ii. दिन

प्रश्न 2.
निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर शब्द लिखिए।
i. समय
उत्तरः
उपसर्गयुक्त शब्द : असमय
प्रत्यययुक्त शब्द : सामयिक

प्रश्न 3.
निम्नलिखित शब्दों में उचित उपसर्ग लगाइए।
i. यत्न
ii. मन
उत्तर:
i. प्र + यत्न = प्रयत्न
ii. बे + मन = बेमन

प्रश्न 4.
पद्यांश में प्रयुक्त विलोम शब्द की जोड़ी लिखिए।
उत्तर:
i. आज × कल

प्रश्न 5.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. संपदा
ii. वृथा
उत्तर:
i. संपत्ति
ii. व्यर्थ

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘समय का सदुपयोग करने से व्यक्ति जीवन में ऊँचा उठ सकता है।’ अपने विचार लिखिए।
उत्तरः
मानव जीवन में समय का सदुपयोग अत्यंत महत्त्वपूर्ण है। जो व्यक्ति समय के साथ चलता है वह प्रगति की सीढ़ी हासिल कर लेता है। समय का सदुपयोग करने वाले व्यक्ति को सभी सुखों की प्राप्ति होती है। समय पर कार्य करने वाले व्यक्ति के कारण समाज व राष्ट्र का भी भला होता है। विश्व के सभी महापुरुष समय की कीमत जानते थे।

इसलिए वे जीवन में महान बन सके। समय का सदुपयोग करने वाला व्यक्ति समय का सही विभाजन कर अध्ययन, खेलकूद, समाज सेवा, मनोरंजन आदि जैसे अनेक कार्य सरलतापूर्वक कर सकता है। समय का सदुपयोग करने वाला व्यक्ति समय के साथ कदम से कदम मिला कर चलता है और जीवन में अनेक सफलताओं को प्राप्त करता है।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1) : आकलन कृति

प्रश्न 1.
सही विकल्प चुनकर वाक्य फिर से लिखिए।
i. कर्मवीरों का नया उत्साह देखने को मिलता है –
(अ) जब उन्हें उलझनें आकर घेर लेती हैं।
(आ) जब वे अपना काम पूरा कर लेते हैं।
(इ) जब वे कार्यस्थल से दूर चले जाते हैं।
उत्तरः
(अ) जब उन्हें उलझनें आकर घेर लेती हैं।

प्रश्न 2.
संजाल पूर्ण कीजिए।
उत्तरः

प्रश्न 3.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. कर्मवीर
ii. कार्यस्थल
उत्तर:
i. असंभव को संभव कौन बनाते हैं?
ii. कर्मवीर किसके बारे में पूछते नहीं है?

कृति इ (3) : शब्द संपदा.

प्रश्न 1.
निम्नलिखित शब्दों में उचित प्रत्यय लगाकर नए शब्द तैयार कीजिए।
i. बुद्धि
ii. देश
उत्तर:
i. बुद्धि + मान = बुद्धिमान
ii. देश + ई = देशी

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।

1. सपूत
2. हस्त
3. नव

उत्तरः

1. सुपुत्र
2. हाथ
3. नया

प्रश्न 3.
समानार्थी शब्द लिखिए।
i. उत्साह
ii. बुद्धि
उत्तर:
i. उमंग
ii. मति

प्रश्न 4.
कविता में इस अर्थ में आए शब्द लिखिए।
i. अच्छे पुत्र
उत्तर:
i. सपूत

प्रश्न 5.
पद्यांश में से विलोम शब्द की जोड़ी ढूँढकर लिखिए।
उत्तर:
i. असंभव × संभव
ii. यहाँ × वहाँ

प्रश्न 6.
‘सपूत’ इस शब्द में से उपसर्ग पहचानकर संबंधित उपसर्ग को लगाकर अन्य दो शब्द बनाइए।
उत्तरः
सपूत : उपसर्ग – स
अन्य शब्द : सकारण, सप्रमाण

कृति ग (4) : अभिव्यक्ति

प्रश्न 1.
‘कर्म ही पूजा है, कर्म ही श्रेष्ठ है।’ विषय पर अपने विचार लिखिए।
उत्तर:
गीता में लिखा है कि कर्म ही पूजा है। कर्म से बढ़कर व्यक्ति का अन्य कोई धर्म नहीं है। इसलिए कर्म करना मनुष्य का पहला लक्ष्य होना चाहिए। कर्म करने से व्यक्ति को आनंद मिलता है। सच्चे मन से किया गया कर्म सफल होता है। मनुष्य के कर्म को ही संसार में याद किया जाता है। उसकी मृत्यु के उपरांत वह सिर्फ अपने कर्मों के कारण ही याद किया जाता है। इसलिए सभी को आलस्य त्यागकर कर्म में लीन हो जाना चाहिए। कर्म सफलता का आधार है। कर्म ही श्रेष्ठ है। कर्म करने से ही व्यक्ति के जीवन को सुख की अनुभूति प्राप्त होती है। सबकी भलाई के लिए कर्म करते हुए जीना ही जीवन का मूलमंत्र है।

कर्मवीर Summary in Hindi

जीवन-परिचय :

अयोध्यासिंह उपाध्याय ‘हरिऔध’ जी का जन्म उत्तर प्रदेश राज्य के आजमगढ़ जिले में हुआ था। ये हिंदी साहित्य के एक प्रमुख हस्ताक्षर थे तथा हिंदी साहित्य सम्मेलन के सभापति भी रह चुके हैं। हिंदी साहित्य सम्मेलन समिति के द्वारा इन्हें विद्यावाचस्पति की उपाधि से सम्मानित किया जा चुका है। खड़ी बोली हिंदी साहित्य के विकास में इनका विशेष योगदान रहा है। वियोग तथा वात्सल्य वर्णन, लोक सेवा की भावना व प्रकृति चित्रण इनके काव्य की विशेषता है।
प्रमुख कृतियाँ : ‘वैदेही वनवास’, ‘प्रिय-प्रवास’ (महाकाव्य), ‘ठाठ’, ‘अधखिला फूल’ (उपन्यास), ‘रुक्मणी परिणय’, ‘विजय व्यायोग’ (नाटक) आदि।

पद्य-परिचय :

आधुनिक पद्य : सन 1900 से आधुनिक पद्य की शुरुआत हुई। महावीर प्रसाद द्विवेदी जी के प्रभाव से ब्रज भाषा से हिंदी कविता हटकर खड़ी बोली हिंदी में लिखी जाने लगी। भारत का उज्ज्वल अतीत, देशभक्ति, सामाजिक सुधार, स्वभाषा प्रेम, मानवीय गुण आदि का खड़ी बोली हिंदी में प्रयोग होने लगा। मधुरता एवं सरलता ने हिंदी कविता में प्रवेश कर लिया।
प्रस्तावना : ‘कर्मवीर’ इस कविता के माध्यम से कवि ‘हरिऔध’ जी ने यह बताने का प्रयास किया है कि कर्मवीरों के लिए कर्म ही पूजा होती है, वे कर्म करने के लिए सदैव तत्पर रहते हैं, वे असंभव को संभव बना देते हैं, तथा देश और समाज को उन्नति के मार्ग पर ले जाते हैं।

सारांश :

‘कर्मवीर’ यह एक आधुनिक पद्य है। इस कविता के माध्यम से कवि ने मानवीय गुणों का संचय करने की प्रेरणा दी है। कवि ने कर्मवीरों के पास जो महान गुण होते हैं उनका अनुसरण करने के लिए पाठकों को प्रेरित किया है। कवि कहते हैं, “मनुष्य को विघ्न-बाधाओं का डटकर मुकाबला करना चाहिए। काम के प्रति उकताहट नहीं करनी चाहिए। मनुष्य को स्वावलंबी होना चाहिए। उसे कभी भी किसी पर आश्रित नहीं होना चाहिए।

मनुष्य को समय का सदुपयोग करना चाहिए। कार्य कितना भी कठिन हो फिर भी उसे पूरा करने की ठान लेनी चाहिए। मनुष्य को मुसीबतों का सामना करते हुए असंभव कार्य को संभव कर दिखाना चाहिए। मनुष्य की कर्मनिष्ठा मनुष्य का विकास करेगी पर इसके साथ वह जिस समाज व राष्ट्र में रहता है उसका भी विकास होता है। अत: प्रत्येक मनुष्य का कर्तव्य है कि वह कर्म को श्रेष्ठ मानकर देश और समाज को उन्नति के मार्ग पर ले जाए।

भावार्थ :

देखकर जो ………………………………. वीर दिखलाते नहीं।
कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीर विघ्न बाधाओं को देखकर घबराते नहीं। वे कभी भाग्य के भरोसे नहीं बैठते हैं। इसलिए भाग्य द्वारा दुख मिलने पर उन्हें पछतावा नहीं होता। काम कितना भी कठिन हो फिर भी उन्हें काम के प्रति कोई उकताहट नहीं होती। उनके लिए कर्म ही पूजा होती है। भीड़ अथवा मुश्किलों को देखकर भी उन पर उसका कुछ भी प्रभाव नहीं पड़ता है। वे सच्चे वीर होते हैं। वे किसी भी स्थिति में डरते नहीं हैं।

मानत जी की हैं ………………………….. जिसे सकते नहीं।
‘कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीर सबकी बात सुनते हैं लेकिन, कार्य करते समय अपने मन की बात मानते हैं। वे स्वावलंबी होते हैं। वे कभी भी किसी पर आश्रित नहीं होते। वे स्वयं का काम स्वयं पूरा करते हैं। वे कभी भी किसी भी चीज के लिए दूसरों का मुँह नहीं ताकते। अर्थात किसी भी वस्तु के लिए वे दूसरों पर आश्रित नहीं होते हैं। इस दुनिया में भला ऐसा कौन-सा काम है जिसे वे पूरा नहीं कर सकते? अर्थात वे सारे काम करने में सक्षम होते हैं।

जो कभी अपने ………………………………..चुराते हैं नही।
कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीरों के लिए समय बहुत ही महत्त्वपूर्ण होता है। इसलिए वे समय को कभी व्यर्थ नहीं गँवाते। जिस काम को जिस समय करना है उसे उसी समय करते हैं। उसे कल पर नहीं छोड़ते हैं। जहाँ काम करना हो वहाँ कोई बहानेबाजी और आनाकानी नहीं करते। आज का काम कल पर टालकर वे अपने दिनों को व्यर्थ नहीं गँवाते। समय का सदुपयोग करना यही उनका कर्तव्य होता है। कोशिश या मेहनत से वे कभी भी पीछे नहीं हटते ।

काम को आरंभ ……………………………………. नहीं जो जोड़ते।।
कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीर कार्य को कभी भी बीच में छोड़ते नहीं हैं। कार्य कितना भी कठिन हो फिर भी वे उसे पूरा करने की ठान लेते हैं। काम को पूरा करते समय यदि कोई मुसीबत आ जाए तो भी पीछे नहीं हटते; वे काम से मुँह नहीं मोड़ते। कर्मवीर आसमान के फूलों को व्यर्थ बातों से नहीं तोड़ते अर्थात वे अपनी प्रशंसा के लिए बड़ी-बड़ी बातें नहीं बनाते। जिस कार्य को करना है बस उसी पर अपना : ध्यान केंद्रित करते हैं। वे मन से करोड़ों की संपदा नहीं जोडते।

कार्य थल ……………………………… उतना ही वहाँ।
कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीर कार्यस्थल की तलाश में यहाँ-वहाँ खोजने के लिए भटकते नहीं। वे जहाँ होते हैं वहीं उनका कार्यस्थल होता है। कर्मवीर मुसीबतों का सामना करते हुए असंभव कार्य को भी संभव कर दिखाते हैं। आने वाली उलझनों और मुसीबतों से वे डरते नहीं बल्कि उनका वे उतने ही उत्साह से सामना करते हैं। उलझनों को देखकर उनमें नया जोश और नई चेतना आ जाती है और वे अपना कार्य उत्साह से करते हैं।

सब तरह से ……………………………. सूपतों के पले।
कवि ‘हरिऔध’ जी के अनुसार, आज विश्व में कई ऐसे देश हैं; ‘जो समृद्ध व संपन्न हैं’ प्रगत एवं विकसित हैं। वहाँ पर विद्या, धन, बुद्धि व ऐश्वर्य का भंडार है। इसका कारण है कि वहाँ पर रहने वाले लोगों ने कर्म को ही अपना लक्ष्य मान लिया है। कर्मवीरों के पुरुषार्थ से ही देश संपन्न हुए हैं। कर्मवीरों के कारण ही सबका भला हुआ है। उनके कारण ही चारों ओर प्रगति की लहर छाई हुई है। ऐसे महान सपूतों के कारण ही सभी का जीवन खुशहाल बना है।

शब्दाथ :

1. विघ्न – संकट
2. बाधा – रुकावट
3. भाग्य – नसीब
4. चंचल – अस्थिर
5. वृथा – अकारण, व्यर्थ
6. गगन – आकाश
7. मदद – सहायता
8. दिन – दिवस
9. उत्साह – उमंग
10. संपदा – धन, दौलत
11. बुद्धि – मति
12. वैभव – ऐश्वर्य
13. उकताना – ऊबना
14. यत्न – प्रयत्न

मुहावरे :

1. असंभव को संभव बनाना – कठिन काम को सरल बनाना।
2. मुँह ताकना – दूसरों पर आश्रित होना।
3. जी चुराना – आलस करना।
4. बातें बनाना – बहाने बनाना।

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer

Std 10 Hindi Chapter 3 Mukadma Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 3 मुकदमा Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 3 मुकदमा Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 3 मुकदमा Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

1. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

2. उचित विकल्प चुनकर विधान पूर्ण कीजिए। 

प्रश्न 1.
हवा बदबूदार होने का कारण है कि …..
(अ) हवा बहती नहीं है।
(आ) हवा में कारखानों की गंदगी और गैस होती हैं।
(इ) हवा दूर-दूर से आती है।
उत्तर:
(आ) हवा में कारखानों की गंदगी और गैस होती हैं।

प्रश्न 2.
हवा पर आरोप लगाया गया था कि………..
(अ) हवा में शुद्धता नहीं होती।
(आ) हवा में नमी नहीं होती।
(इ) हवा में खुशबू नहीं होती।
उत्तर:
(इ) हवा में खुशबू नहीं होती।

3. कारण लिखिए :

प्रश्न 1.
पानी अशुद्ध होने के कारण –

उत्तर:

4. ऐसे प्रश्न तैयार करें कि जिनके उत्तर निम्नलिखित शब्द हों –
1. जोहड़
2. साफ-सुथरे

प्रश्न 1.
ऐसे प्रश्न तैयार करें कि जिनके उत्तर निम्नलिखित शब्द हों –
1. जोहड़
2. साफ-सुथरे
उत्तर:
1. पशुओं को तैरने के लिए कहाँ छोड़ दिया जाता है?
2. घर कैसे रखने चाहिए?

5. वृत्त में दिए शब्दों के लिंग तथा वचन के अनुसार वर्गीकरण कीजिए।

प्रश्न 1.
वृत्त में दिए शब्दों के लिंग तथा वचन के अनुसार वर्गीकरण कीजिए।

उत्तर:

स्त्रीलिंग	पुलिंग	एकवचन	बहुवचन
नदी	कूड़ा	बीमारी	शिकायतें
फसल	गाँव	आँख	गवाहें
सड़क	वृक्ष	आदत	सर्दियाँ
नाली	पंखा	मुकदमा	कारखाने

6. शब्द-युग्म बनाइए।

कूड़ा – …………., इधर – …………., गाँव – ………….., घर – ………….., हवा – ………….., सीधा – ………….., साफ – ……………., झाड़ – …………

प्रश्न 1.
शब्द-युग्म बनाइए।
उत्तर:
कूड़ा – कचरा, इधर – उधर, गाँव – शहर, घर – द्वार, हवा – पानी, सीधा – सादा, साफ – सुथरा, झाड़-झंखाड़

अभिव्यक्ति :

‘बढ़ते हुए प्रदूषण को रोकने के उपाय’ पर अपने विचार लिखिए।

प्रश्न 1.
‘बढ़ते हुए प्रदूषण को रोकने के उपाय’ पर अपने विचार लिखिए।
उत्तर:
आज प्रदूषण के कारण विश्व में चारों ओर लोगों का जीना दूभर हो गया है। प्रदूषण को रोकने के लिए हमें प्राकृतिक स्रोतों का संरक्षण करना चाहिए। हमें पटाखें जलाना, कूड़ा-कचरा यहाँ-वहाँ नहीं फेंकना चाहिए। मानव जनसंख्या वृद्धि पर रोक लगानी चाहिए। हमें प्रकृति का अंधाधुंध दोहन नहीं करना चाहिए। सरकार को अवैध खनन पर रोक लगानी चाहिए। कारखानों की चिमनियों की ऊँचाई अधिक रखनी चाहिए।

अधिक धुआँ निर्माण करने वाले स्वचालित यंत्रों पर रोक लगानी चाहिए और इसके लिए सरकार द्वारा प्रतिबंधात्मक कानून बनाने चाहिए ताकि उल्लंघन करने वालों पर कड़ी-से-कड़ी कार्यवाही हो सके। कारखानों से निकले हुए रासायनिक पदार्थों को तालाब, नदी या सागर में नहीं डालना चाहिए। पर्यावरण को संतुलित रखने के लिए सभी को पेड़ लगाने चाहिए।

भाषाबिंदु :

प्रश्न 1.
इन शब्दों से बने दो – दो मुहावरे तथा उनके अर्थ लिखकर स्वतंत्र वाक्य में प्रयोग कीजिए।

1. कान
उत्तर:
i. मुहावरा : कान भरना।
अर्थ : किसी के विरुद्ध किसी के मन में कोई बात बैठा देना।
वाक्य : रामू के किसी ने तो कान भर दिए, इसलिए वह इस प्रकार का बर्ताव कर रहा है।

ii. मुहावरा : कान का कच्चा होना।
अर्थ : सुनते ही किसी बात पर विश्वास करना।
वाक्य : अजय कान का कच्चा है; वह किसी के भी बहकावे में आ जाता है।

2. नाक
उत्तर:
i. मुहावरा : नाक-भौं सिकोड़ना।
अर्थ : अप्रसन्नता प्रकट करना।
वाक्य : जरा-जरा सी बात पर नाक-भौं सिकोड़ना ठीक नहीं है। .

ii. मुहावरा : नाक में दम करना।
अर्थ : बहुत परेशान होना।
वाक्य : तुम दोनों की हरकतों ने मेरे नाक में दम कर दिया है।

3. सिर
उत्तर:
i. मुहावरा : अपने सिर लेना।
अर्थ : जिम्मेदारी अपने ऊपर लेना।
वाक्य : व्यवस्था को सुचारू रूप से चलाने का काम रामलाल ने अपने सिर ले लिया।

ii. मुहावरा : सिर चढ़ाना।
अर्थ : अनुपयुक्त व्यक्ति को अत्यधिक महत्त्व देकर अपने ऊपर मुसीबत मोल लेना।
वाक्य : मूर्ख व्यक्ति को सिर चढ़ाने का नतीजा हमेशा बुरा ही होता है।

उपयोजित लेखन :

प्रश्न 1.
अपने ग्राम/नगर/महानगर के संबंधित अधिकारी को बच्चों के खेलने के लिए बगीचा बनवाने हेतु पत्र लिखिए।

उत्तरः
10 जुलाई, 2018
प्रति,
मा. महानगर अधिकारी,
महानगरपालिका,
दादर (पूर्व),
मुंबई – 400 043. .
विषय : बच्चों के खेलने के लिए बगीचा बनवाने हेतु प्रार्थना पत्र।

मैं कुमार अजय मेहता दादर पूर्व विभाग का निवासी हूँ। मैं आपको यह प्रार्थना पत्र लिख रहा हूँ क्योंकि हमारे विभाग में बच्चों के खेलने के लिए बगीचा नहीं है।

हमारे विभाग में कुल मिलाकर दो सौ से अधिक बच्चे हैं। उनके खेलने के लिए पर्याप्त जगह नहीं है। यहाँ हर इमारत के बीच में खेलने के लिए पर्याप्त जगह नहीं है। यहाँ मैदान भी नहीं है, जिस कारण बच्चों को खेलने-कूदने के लिए बहुत दिक्कत हो रही है। छुट्टियों में उनका ठीक से मनोरंजन नहीं हो पाने के कारण घर में बैठकर या तो टी. वी. देखते हैं या कंप्यूटर गेम खेलते हैं जिससे उनका शारीरिक विकास नहीं हो पा रहा है।

आपसे नम्र निवेदन है कि आप हमारे विभाग में एक बगीचा का निर्माण करें ताकि विभाग में रहने वाले बच्चों के बाहर खेलने के लिए पर्याप्त जगह हो। मुझे आशा है कि आप मेरे प्रार्थना पत्र पर जरूर विचार करेंगे।

कष्ट के लिए क्षमाप्रार्थी।
भवदीय, अजय मेहता,
401, राम महल,
राधा नगर,
मुंबई – 400026
ajay56@gmail.com

Hindi Lokvani 10th Std Textbook Solutions Chapter 3 मुकदमा Additional Important Questions and Answers

(अ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1) : आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 3.
निम्नलिखित विधान सही करके लिखिए।
i. सूखे कपड़े पहने एक लड़का हाजिर होता है।
उत्तर:
भीगे कपड़े पहने एक लड़का हाजिर होता है।

ii. राजा के अनुसार पानी अब निर्मल नहीं रहा है।
उत्तर:
लोगों के अनुसार पानी अब निर्मल नहीं रहा है।

प्रश्न 4.
समझकर लिखिए।
उत्तर:

कृति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. गह्वर
2. निर्मल
3. शिकायत
4. गंदगी

उत्तर:

1. गड्ढा
2. साफ
3. उलाहना
4. मलिनता

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. वह स्थान जहाँ राजा अपने मंत्रियों के साथ बैठते हैं –
ii. किसी विवाद का अदालत में सुनवाई –
उत्तर:
i. दरबार
ii. मुकदमा

प्रश्न 3.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. निर्मल × ………
2. समय × ………
3. हाजिर × ………

उत्तर:

1. मलिन
2. असमय
3. गैरहाजिर

प्रश्न 4.
गद्यांश में से विदेशी शब्द ढूँढ़कर लिखिए।
उत्तर:
टेपरिकॉर्डर

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
मुकादमा चलाने की परंपरागत और आधुनिक पद्धति में अंतर लिखिए।
उत्तर:
पहले के जमाने में राजा-महाराजा हुआ करते थे। वे न्याय प्रक्रिया में न्यायाधीश की भूमिका निभाते थे। यदि किसी को किसी से शिकायत होती थी तो वह व्यक्ति राजदरबार में जाकर शिकायत दर्ज करता था और फिर राजा के द्वारा मुकदमा चलाया जाता था। राजा का निर्णय अंतिम हुआ करता था। आज जमाना बदल गया है। राजा-महाराजाओं के दिन अब नहीं रहे हैं। लोग प्रजातंत्र में अपना जीवन बीता रहे हैं। आज न्याय व्यवस्था पर सरकार अथवा किसी अन्य संस्था का नियंत्रण नहीं है। वह मुक्त और स्वनियंत्रित है। पुलिस, कोर्ट-कचहरी आदि न्यायप्रणाली की व्यवस्था है।

यदि कोई व्यक्ति गलत काम करता है तो वह कानून की नजर में दोषी बन जाता है। उस पर मुकदमा चलाया जाता है। यदि उसका दोष सिद्ध हुआ तो उसे सजा हो जाती है। आज हमारी न्याय व्यवस्था पूर्णत: निष्पक्ष व स्वतंत्र है। न्यायालय के निर्णय को अंतिम माना जाता है। इस प्रकार पहले के जमाने में मुकदमें चलाने की विधि और आज के जमाने में मुकदमा चलाने की प्रक्रिया में जमीन-आसमान का अंतर है।

(आ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1) : आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
गद्यांश के आधार पर वाक्य पूर्ण कीजिए।
i. वे घर जरूर डूबेंगे ….
उत्तरः
जहाँ वर्षा का पानी बहना चाहिए; नदी बहनी चाहिए; वहाँ पर लोगों ने घर बना लिए हैं।

कृति आ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. पशु
2. कारखाना
3. पहाड़
4. वर्षा

उत्तर:

1. जानवर
2. फैक्टरी
3. पर्वत
4. बारिश

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. छोटा प्राकृतिक तालाब –
उत्तर:
i. जोहड़

प्रश्न 3.
विलोम शब्द लिखिए
i. गंदा × …………….
ii. ढलान × …………..
उत्तर:
i. साफ
ii. चढ़ाव

प्रश्न 4.
गद्यांश में प्रयुक्त पर्यायवाची शब्द की जोड़ी को ढूँढ़कर लिखिए।
उत्तर:
वर्षा : बरसात

प्रश्न 5.
वचन बदलिए।

1. नदी
2. गली
3. नाला

उत्तर:

1. नदियाँ
2. गलियाँ
3. नाले

प्रश्न 6.
निम्नलिखित शब्दों में से प्रत्यय छाँटकर लिखिए।
i. रखवाली
ii. जिम्मेदार
उत्तर:
i. प्रत्यय : वाली
ii. प्रत्यय : दार

प्रश्न 7.
गद्यांश में से शब्द-युग्म ढूंढकर लिखिए।
उत्तर:
गलियों – नालियों

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
जल प्रदूषण को रोकने के लिए अपने विचार लिखिए।
उत्तर:
जल के बिना जीवन असंभव है। प्राकृतिक जल स्रोतों को स्वच्छ रखना हमारा कर्तव्य है। हमें तालाब एवं नदी के पानी में पशुओं को नहलाना नहीं चाहिए। तालाब या नदी में हमें कपड़े या बर्तन नहीं धोने चाहिए। तालाब व नदी में कूड़ा-कचरा नहीं फेंकना चाहिए। कल-कारखानों का दूषित और जहरीला पानी नदी में डालने पर रोक लगानी चाहिए। लोगों में जल-प्रदूषण के खतरे के प्रति जागरुकता निर्माण करनी चाहिए। जल प्रदूषण को रोकने के लिए प्रदूषण बोर्ड को सख्त कानून बनाने चाहिए। इस प्रकार सभी को स्वेच्छा से इस अभियान के लिए आगे आना चाहिए।

(इ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1) : आकलन कृति

प्रश्न 1.
ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों
i. सदियों
ii. वृक्ष
उत्तर:
i. गाँव कब से ऊँची जगह पर बसा हुआ है?
ii. लोगों ने पहाड़ से क्या साफ कर दिए हैं?

प्रश्न 2.
सही विकल्प चुनकर वाक्य पूर्ण कीजिए।
i. पानी पहाड़ से लुढ़कता हुआ नीचे आता है क्योंकि..
(क) लोगों ने पहाड़ से वृक्ष साफ कर दिए हैं।
(ख) लोगों ने पहाड़ पर घर बनाए हैं।
(ग) लोगों ने पहाड़ को काट दिया है।
उत्तरः
(क) लोगों ने पहाड़ से वृक्ष साफ कर दिए हैं।

प्रश्न 3.
निम्नलिखित विधान सही करके लिखिए।
i. बाढ़ के लिए पानी जिम्मेदार है। उत्तरः बाढ़ के लिए गाँववाले जिम्मेदार हैं।
ii. निर्मल एवं स्वच्छ रहना पानी के हाथ में है।
उत्तरः
पानी को निर्मल तथा स्वच्छ रखना लोगों के हाथ में है।

कृति इ (2) : शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तरः
धीरे-धीरे

प्रश्न 2.
गोश में से ऐसे दो शब्द ढूँड़कर लिखिए कि जिनके वचन परिवर्तित नहीं होते।
उत्तर:
i. ढलान
ii. वृक्ष

प्रश्न 3.
‘निर्मल’ इस शब्द में निहित उपसर्ग को पहचानकर संबंधित उपसर्ग लगाकर अन्य दो शब्द तैयार कीजिए।
उत्तर:
निर्मल : प्रत्यय : निर नए
शब्द : निराकार, निर्विकार

प्रश्न 4.
नीचे दिए तत्सम शब्द का तद्भव लिखिए।
i. ग्राम
उत्तर:
i. गाँव

प्रश्न 5.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. सौ वर्षों का समय
उत्तर:
i. सदी

कृति इ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘जल ही जीवन है।’ विषय पर अपने विचार लिखिए।
उत्तर:
जल ही जीवन है। जल के बिना जिंदगी की कल्पना नहीं की जा सकती है। धरती पर रहने वाले सभी जीवों को जिंदा रहने के लिए पानी की आवश्यकता होती है। यदि शरीर में पानी की मात्रा 10 प्रतिशत से कम हो जाए तो व्यक्ति जीवित नहीं रह सकता। मनुष्य भोजन के बिना कई दिनों तक जीवित रह सकता है लेकिन पानी के बिना तीन दिन से अधिक नहीं जीवित रह सकता। हमें जरूरत से ज्यादा पानी की बर्बादी नहीं करनी चाहिए। संसार की बढ़ती जनसंख्या के कारण पानी का इस्तेमाल बढ़ता जा रहा है। इसलिए हमें पानी को बर्बाद नहीं करना चाहिए। यदि पानी नहीं होगा तो किसान खेत में अनाज नहीं उगा सकता है। पानी के बिना किसी भी वस्तु का निर्माण नहीं हो सकता। इसलिए जल ही जीवन है।

(ई) गद्यांश पड़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ई (1) : आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
परिणाम लिखिए।
i. भोपाल के कारखाने से निकली जहरीली गैस से –
ii. मरे हुए पशु-पक्षियों को यहाँ-वहाँ डालने से –
उत्तर:
i. कई लोग रात में सोए हुए ही मौत के मुँह में चले गए थे।
ii. हवा बदबूदार हो जाती है।

कृति ई (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।
i. हवा ने महाराज से कहा महाराज मुझ पर लगे आरोप झूठे हैं
उत्तरः
हवा ने महाराज से कहा, “महाराज, मुझ पर लगे आरोप झूठे हैं।

प्रश्न 2.
लिंग बदलिए।
i. महाराज
ii. लड़की
उत्तर:
i. महारानी.
ii. लड़का

प्रश्न 3.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तर:

1. पशु-पक्षियों
2. यहाँ-वहाँ
3. दूर-दूर
4. आज-कल

प्रश्न 4.
निम्नलिखित शब्द के लिए श्रुतिसमभिन्नार्थक शब्द लिखिए।
i. रात
ii. डाल
उत्तर:
i. रत
ii. दाल

प्रश्न 5.
‘जहरीली’ इस शब्द में से प्रत्यय अलग कीजिए और संबंधित प्रत्यय लगाकर अन्य दो शब्द बनाइए।
उत्तरः
जहरीली : शब्द : जहर प्रत्यय : ईली
अन्य शब्द : नशीली, चमकीली

कृति ई (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘हवा प्रदूषण पर रोक लगाने के लिए उपाय’ पर अपने विचार लिखिए।
उत्तर:
दिन-प्रतिदिन हानिकारक सामग्री के हवा में मिलने के कारण हवा प्रदूषित हो रही है। प्रदूषित हवा से लोग बीमार पड़ रहे हैं। हवा प्रदूषण से बचने के लिए हमें कूड़ा-कचरा यहाँ-वहाँ नहीं फेंकना चाहिए। कूड़ा-कचरा यहाँ-वहाँ फेंकने से गंदगी फैलती है जिससे हवा दूषित हो जाती है। कारखानों को आधुनिक तकनीकी का प्रयोग करना चाहिए ताकि उनमें से जहरीली गैस और धुआँ बाहर न निकले और हवा में न मिले। लोगों को अपने वाहनों की नियमित जाँच करानी चाहिए, ताकि उनमें से अधिक धुआँ बाहर निकलकर हवा में न फैले।

सार्वजनिक स्थलों पर धूम्रपान पर रोक होनी चाहिए। हमें शहरीकरण की प्रक्रिया को रोकना चाहिए। गाँवों में ही रोजगार के साधनों को विकसित करना चाहिए, जिससे गाँव के लोग नौकरी करने के लिए शहर में पलायन न करें। इससे शहर और गाँव का असंतुलन धीरेधीरे कम हो जाएगा और हवा प्रदूषण भी रुकेगा। धुएँवाले ईधनों का प्रयोग बंद कर देना चाहिए और भारी मात्रा में पेड़ लगाने चाहिए। इस प्रकार हवा प्रदूषण पर रोक लगाई जा सकती है।

(उ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति उ (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
परिणाम लिखिए।
i. हवा ने चलना बंद कर दिया।
उत्तरः
हवा द्वारा चलना बंद होने से सभी घुटन महसूस करने लगे।

ii. हवा आँधी बनकर आती है।
उत्तरः
हवा के आँधी बनकर आने से लोगों के घर रेत और कूड़े से भर जाते हैं।

कृति उ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. मिट्टी
2. निमंत्रण
3. दुखी
4. आँधी

उत्तर:

1. मृदा
2. आमंत्रण
3. उदास
4. अंधड़

प्रश्न 2.
नीचे दिए हुए अनेक शब्दों के लिए एक शब्द लिखिए।
i. धूलभरी जोर की हवा –
उत्तर:
i. आँधी

प्रश्न 3.
वचन बदलिए।
i. आँधी
ii. आँख
उत्तर:
i. आँधियाँ
ii. आँखें

कृति उ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘यदि हवा चलना बंद कर दे तो…..।’ विषय पर अपने विचार लिखिए।
उत्तर:
नित चलते रहना हवा का काम है। यदि हवा चलना बंद कर दे तो बहुत बड़ी समस्या निर्माण हो जाएगी। हवा के बिना जीवन के अस्तित्व की कल्पना भी नहीं की जा सकती है। यदि हवा चलना बंद कर देगी तो लोगों को साँस लेने के लिए दिक्कत हो जाएगी। लोग घुटन भरे माहौल में अधिक समय तक जीवित नहीं रह सकते हैं। पेड़-पौधे, पशु-पक्षियों को भी जीवन जीने के लिए हवा की जरूरत होती है।

गर्मी ज्यादा बढ़ने के कारण फिर सर्वत्र एअरकंडिशन लगाना पड़ेगा। इससे तापमान में वृद्धि होगी। कार्बन डाइऑक्साइड की मात्रा बढ़ेगी, जिससे लोगों को साँस लेने की और भी दिक्कत हो जाएगी। यदि सचमुच हवा चलना बंद कर देगी तो धीरे-धीरे इस धरती से जीवन नष्ट हो जाएगा।

(ऊ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ऊ (1): आकलन कृति

प्रश्न 1.
ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हो
i. पंखा
ii. पॉलिथिन की थैलियाँ
उत्तर:
i. हवा की गति बढ़ाने के लिए लोग क्या चलाते हैं?
ii. लोग सड़कों पर क्या फेंकते हैं?

प्रश्न 2.
गद्यांश के आधार पर वाक्य पूर्ण कीजिए।
i. जब हवा तेजी से चलती है।
ii. लोगों द्वारा फेंका कूड़ा ……
उत्तर:
i. जब हवा तेजी से चलती है तब वह अपने साथ रेत, मिट्टी, कूड़ा आदि हल्की चीजें साथ लेकर उड़ती है।
ii. लोगों द्वारा फेंका कूड़ा फिर से उनके घरों में जाता है।

प्रश्न 3.
समझकर लिखिए।
उत्तरः

कृति ऊ (2) : शब्द-संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तरः
i. हवा-पानी
ii. आस-पास

प्रश्न 2.
विलोम शब्द लिखिए।

1. दोस्त × ……………….
2. लाभ × ……………….
3. हल्की × …………….
4. गरमी × …………..

उत्तरः

1. दुश्मन
2. नुकसान
3. भारी
4. सर्दी

प्रश्न 3.
पर्यायवाची शब्द लिखिए।
i. गरमी
ii. हवा
उत्तर:
i. ग्रीष्म
i. वायु

प्रश्न 4.
गोश में से ऐसे दो शब्द ढूँडकर लिखिए कि जिनके वचन परिवर्तित नहीं होते।
उत्तर:
हवा, पानी

मुकदमा Summary in Hindi

लेखक-परिचय :

जीवन-परिचय : गोविंद शर्मा जी का जन्म सन 1९४६ में राजस्थान के संगरिया क्षेत्र में हुआ। शर्मा जी सुप्रसिद्ध बालसाहित्यकार है। बाल नाटक, बाल उपन्यास एवं बाल कविता के द्वारा आप बाल जगत के साहित्य में प्रसिद्ध है। इन्होंने व्यंग्य परक लेख, जीवनी, लघुकथाएँ आदि विधाओं में भी लेखन किया है।
प्रमुख कृतियाँ : ‘दीपू और मोती’, ‘डोबी और राजकुमार’ (बाल उपन्यास), ‘हमें हमारा घर दो’, ‘मेहनत का मंत्र’ (कहानी संग्रह), ‘नया बाल दिवस’ (नाटक संग्रह), ‘कुछ नहीं बदला’, ‘जहाज के नये पंक्षी’ (व्यंग्य संग्रह), ‘रामदीन का चिराग’ (लघुकहानी संग्रह) आदि।

गद्य-परिचय :

एकांकी : प्रस्तावना एक अंक वाले नाटक को ‘एकांकी’ कहते हैं। अंग्रेजी में इसे ‘वन ऐक्ट प्ले’ कहते हैं। एकांकी स्वतंत्र एवं सचेष्ट भाव से लिखी जाती है। एकांकी का आकार लघु होता है। अत: इसमें एक ही कथा होती है।
प्रस्तावना : ‘मुकदमा’ इस एकांकी में लेखक गोविंद शर्मा जी ने जल एवं वायु प्रदूषण के कारणों और दुष्परिणामों के प्रति लोगों को सचेत किया है। प्रदूषण रूपी संकट को रोकने के लिए मनुष्य को ही प्रयास करना होगा, यह संदेश लेखक ने हमें प्रस्तुत एकांकी के माध्यम से दिया है।

सारांश :

‘मुकदमा’ यह एक एकांकी है। एकांकी की शुरूआत महाराज के दरबार से होती है। दरबार में महाराज सिंहासन पर बैठे हैं। कुछ लोगों ने। दरबार में हवा व पानी के विरुद्ध शिकायत की है। अत: हवा व पानी को दरबार में बुलाया गया है और उन पर मुकदमा चलाया जा रहा है। लोगों ने पानी पर आरोप लगाया कि वह पहले जैसा निर्मल नहीं रहा है। वह अपने साथ गंदगी एवं बीमारियाँ बहाकर ले आता है। अपने ऊपर। लगे इस आरोप का खंडन करते हुए पानी ने कहा कि इसमें उसका कुछ भी कसूर नहीं है। लोग पहले के जैसे उसकी रखवाली नहीं करते।

हैं और वे अपने पशुओं को तालाब या नदी में छोड़ देते हैं। कारखानों का पानी एवं गंदी नाली का पानी भी उसमें आकर मिलता है। अत: वह इंसान के करतूतों के कारण ही अशुद्ध हो गया है। लोगों ने पानी पर यह भी आरोप लगाया कि वह अपनी मर्जी के अनुसार कहीं पर भी बरसता है और कहीं पर भी बहता हआ जाता है। इस कारण उनके घर पानी में डूब जाते हैं। इसपर पानी कहता है कि इसमें भी उसका कोई कसर नहीं है। लोगों ने पहाड पर स्थित पेड़ों की कटाई की है। अत: वह पहाडों से गति से बहता हआ नीचे आता है जिस कारण लोगों के घर पानी में बह जाते हैं।

अंत में मुकदमे का फैसला करते हुए महाराज लोगों को अपनी गलतियाँ सुधारने और पानी को निर्मल तथा उपयोगी रखने । का आदेश देते हैं। दूसरी शिकायत हवा के विरुद्ध है। आदमी शिकायत करता है कि अब हवा में पहले जैसी खुशबू नहीं है और वह आँधी। बनकर आती है जिस कारण लोगों के घर रेत व कूड़े से भर जाते हैं। वह बदबू फैलाती है।

हवा इन आरोपों को झूठा बताते हुए कहती है कि कारखानों से निकलने वाली गैस व गंदगी के कारण वह बदबूदार हो गई है। अंत में महाराज कहते हैं कि इसमें हवा का कोई भी कसूर नहीं है। महाराज द्वारा लोगों को नसीहत दी जाती है कि वे सफाई की आदत को अपनाएँ। हवा व पानी को अपना दोस्त मानकर उन्हें दूषित होने से बचाएँ। यदि ऐसा होगा; तो ही लोगों का भला होगा।

शब्दार्थ :

1. गह्वर – गड्ढा
2. शिकायत – उलाहना
3. पशु – जानवर
4. निमंत्रण – आमंत्रण
5. दूषित – गंद
6. माहौल – वातावरण
7. गवाह – प्रमाण
8. बदबू – दुर्गन्ध
9. दंड – सज़ा
10. निर्मल – साफ
11. कूड़ा – कचरा
12. उपाय – हल
13. तबाह – नष्ट

मुहावरे :

आँख मूंदकर चलना – बिना सोचे-विचारे चलना।
मौत के मुंह में चले जाना – जान-बूझकर खतरा मोल लेना।

कहावत :

जैसी करनी, वैसी भरनी – कर्म के अनुसार ही फल का मिलना।

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 4 जिन ढूँढ़ा Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 4 Jin Dhunda Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 4 जिन ढूँढ़ा Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 4 जिन ढूँढ़ा Textbook Questions and Answers

सूचना के अनुसार कृतियाँ कीजिए :

(१) प्रवाह तालिका पूर्ण कीजिए :

उत्तर:

(२) उचित जोड़ियाँ मिलाइए:

उत्तर:
i – ग
ii – ख
iii – ङ
iv – क

(३) शब्दसमूह के लिए एक शब्द लिखिए :

१. कस्तूरी की खोज करने वाला
उत्तर:
मृग

२. किनारे पर बैठा रहने वाला।
उत्तर:
बसेरा

३. तीन नोकों वाला अस्त्र
उत्तर:
त्रिशूल

४. जो बलहीन है
उत्तर:
शक्तिहीन

(४) दोहों में आए सुवचन
उत्तर:
(i) दुर्बल की रक्षा करना सबल का कर्तव्य है।
(ii) जिस पर ईश्वर की कृपा हो, उसका कोई कुछ भी बुरा नहीं कर सकता।

(५) निम्नलिखित अर्थ के शब्द दोहों से ढूँढ़कर लिखिए:

१. पुत्र ……..
२. इत्र विक्रेता ……….
३. परमात्मा ……….
४. खुद ……….
उत्तर:
१. लाल
२. सुगंधि बेचने वाला
३. पीव
४. दुनिया

(६) दोहों में प्रयुक्त निम्न शब्दों के दो-दो अर्थ लिखिए :

उत्तरः
१. हिरण, एक नक्षत्र का नाम
२. कलश या घड़ा, एक राशि का नाम
३. परिक्षा फल, नतिजा
४. बच्चा, केश

(७) अपनी पसंद के किसी एक दोहे के भावार्थ से प्राप्त प्रेरणा लिखिए।
उत्तरः
दोहा : जिन ढूँढ़ा ……………. किनारे बैठ ।।
प्रेरणा: प्रस्तुत दोहे से हमें साहस जैसे महान गुण का संचय करने की प्रेरणा मिलती है। साहस में बड़ी शक्ति होती है। उसके बल पर हम पानी की गहराई तक जाकर अनमोल रत्न पा सकते हैं। साहस व्यक्ति का महत्त्वपूर्ण गुण हैं।

उपयोजित लखन

शब्दों के आधार पर कहानी लिखिए:
शैली. जल, तस्वीर, अंगूठी
उत्तरः
मेल-मिलाप

रामपुर नामक गाँव में घनश्याम नाम का एक जौहरी रहता था। वह अपने दाहिने हाथ की एक ऊँगली में सोने की एक अंगूठी पहनता था। उसे उस अंगूठी से बेहद लगाव था। अत: कभी-भी वह उसे अपनी ऊँगली से अलग नहीं करता था। वह अपने परिवार से अलग रहता था। उनके लिए अलग घर की व्यवस्था थी। वह उन्हें मिलने कभी नहीं जाता था। एक दिन जौहरी को मिलने के लिए पड़ोस के गाँव से एक व्यक्ति आया। उसके पास एक थैली थी। उस थैली में एक घोड़े की तस्वीर थी । उस तस्वीर को बाहर निकालकर उसने जौहरी से कहा, “मालिक, यह बहुत ही अद्भुत तस्वीर है।

यह मुझे साधु महाराज ने दी है। मैं इसे बेचना चाहता हूँ। जो कोई इस तस्वीर को खरीद लेगा उसका पूरा जीवन बड़े आराम से कटेगा और उसे किसी भी प्रकार की विपत्तियों का सामना नहीं करना पड़ेगा। उस व्यक्ति की बातें सुनकर जौहरी ने जिज्ञासा से पूछा, “तो फिर इसका मूल्य कितना है?” उस व्यक्ति ने बताया सिर्फ पाँच जल की बूंदे और वह भी वे बूंदें एक दूसरी से अलग होनी चाहिए यानी एक साथ मिलनी नहीं चाहिए।

यह सुनकर जौहरी हैरान रह गया। थोड़ी देर तक सोचने के बाद उसने तुरंत अपने नौकर के जरिए एक गिलास में पानी मैंगवाया। उसने एक प्लेट में पानी की बूंद गिराने की कोशिश की, पर उसके प्रयत्न निष्फल रहे क्योंकि पानी की बूंदें एक-दूसर से मिलने लगी। कई बार कोशिश करने के बाद जौहरी थक गया। वह व्यक्ति मन ही मन हँस रहा था। हैरान होकर जौहरी ने उसकी ओर देखा।

तब तपाक से उस व्यक्ति ने कहा, “एक-दूसरे के साथ मिलना तो बूंदों का स्वभाव है। फिर इंसान होकर तुम क्यों अपने परिवार वालों से अलग रहते हो?” उस आदमी की बातें सुनकर जौहरी की आँखें खुल गई और वह तुरंत अपने परिवार वालों के पास चला गया। सीख : हमें जीवन में मेल-मिलाप से रहना चाहिए।

Hindi Lokvani 10th Std Textbook Solutions Chapter 4 जिन ढूँढ़ा Additional Important Questions and Answers

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति अ (१): आकलन कृति

कृति पूर्ण कीजिए।

Question 1.

Answer:

समझकर लिखिए।

Question 1.
बड़ा व्यक्ति वही कहलाता है
Answer:
जिसके बड़े होने से दूसरों का भला होता है।

Question 2.
संसार में उन्हीं गुरु शिष्य को लोग याद करते हैं
Answer:
जो शिष्य अपने गुरु पर सर्वस्व अर्पण करने के लिए तैयार रहता है और जो गुरु अपने शिष्य से कुछ भी नहीं लेता है।

कृति अ (२) : शब्द संपदा

निम्नलिखित शब्दों के अर्थ पद्यांश में से ढूँढ़कर लिखिए।

1. राहगीर
2. छाया
3. संगत
4. इत्र विक्रेता

Answer:

1. राहगीर – पंथी
2. छाया – छाँव
3. संगत – संगति
4. इत्र विक्रेता – गंधी

विलोम शब्द लिखिए।

1. बड़ा x …….
2. छाया x ……
3. साधु x …….

Answer:

1. बड़ा x छोटा
2. छाया x धूप
3. साधु x असाधु

निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।

1. छाया
2. गुरु

Answer:

1. परछाई, बाधा
2. अध्यापक, बड़ा

निम्नलिखित शब्द का लिंग बदलिए।

1. साधु
2. शिष्य

Answer:

1. साध्वी
2. शिष्या

Question 1.
निम्नलिखित पद्यांश में से तत्सम शब्द पहचानकर लिखिए।
Answer:
साधु
गुरु

निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
गुरु से शिक्षा प्राप्त करने वाला
Answer:
शिष्य

कृति अ (३) : स्वमत अभिव्यक्ति

Question 1.
‘छात्र जीवन में सत्संगति का असाधारण महत्त्व होता है।’ अपने विचार लिखिए।
Answer:
सत्संगति का अर्थ है – अच्छी संगति। अच्छे मनुष्यों के साथ रहने से हम सद्गति की ओर अग्रसर होते हैं। सत्संगति के संसर्ग से मनुष्य सदाचरण का पालन करता है। विद्यार्थियों को हमेशा अच्छे संस्कार वाले छात्रों की संगति में रहना चाहिए। सत्संगति हमें जीवन में आने वाली कठिनाइयों का सामना करने की शक्ति प्रदान करती है। सत्संगति में रहकर हम चरित्रवान बन सकते हैं। हमें जीवन में किसी से दोस्ती करते समय यह नहीं सोचना चाहिए कि वह गरीब है या अमीर । हमें दूसरे व्यक्ति के संस्कार एवं उसकी अच्छाइयों को ध्यान में रखते हुए उससे दोस्ती करनी चाहिए। सत्संगति में रहने से हम जीवन में कभी
भी गलत रास्ते पर नहीं जा सकते हैं।

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति आ (१): आकलन कृति

Question 1.
सही विकल्प चुनकर लिखिए।
कमजोर व्यक्ति को सताने से –
(अ) उन्हें बुरा लगता है।
(आ) उनकी हाय लगती है।
(इ) उनकी पीड़ा और बढ़ जाती है।
Answer:
कमजोर व्यक्ति को सताने से उनकी हाय लगती है।

समझकर लिखिए।

Question 1.
यह निर्जीव है
Answer:
लुहार की धौंकनी।

Question 2.
धौंकनी से यह निकलती है
Answer:
हवा रूपी श्वास

Question 3.
पद्यांश में प्रयुक्त एक धातु का नाम
Answer:
लोहा

उचित जोड़ियाँ मिलाइए।।

Question 1.

Answer:
i – ग
ii – घ
iii – क
iv – ख

कृति पूर्ण कीजिए।

Question 1.

Answer:

उपसर्ग व प्रत्यय लगाकर शब्द लिखिए।

Question 1.
बल
Answer:
उपसर्ग – दुर्बल, प्रत्यय – बलवान

Question 2.
जीव
Answer:
उपसर्ग – सजीव, प्रत्यय – जीवधारी

विलोम शब्द लिखिए।

1. दुर्बल x ………..
2. बाहर x ………

Answer:

1. दुर्बल x सबल
2. बाहर x अंदर

लिंग बदलिए।

1. कुम्हार
2. गुरु

Answer:

1. कुम्हारिन
2. गुरुआइन

पर्यायवाची शब्द लिखिए।

1. साईं
2. अंतर
3. बैरी
4. खोट

Answer:

1. ईश्वर
2. भीतर
3. दुश्मन
4. दोष

निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
जिसमें बल न हो
Answer:
दुर्बल

कृति आ (३): स्वमत अभिव्यक्ति

Question 1.
‘गुरु हमें अंधकार से प्रकाश की ओर ले जाता है। विषय पर अपने विचार लिखिए।
Answer:
प्रत्येक व्यक्ति के जीवन में गुरु का महत्त्व अनन्यसाधारण होता है। गुरु बिना गति नहीं अर्थात गुरु के बिना छात्र प्रगति नहीं कर सकता; वह ज्ञान प्राप्त नहीं कर सकता। गुरु हमारे दुर्गुणों को हटाकर सद्गुणों का संवर्धन करता है। संतकवि कबीर जी ने कहा है कि गुरु के बिना व्यक्ति को मोक्ष नहीं मिल सकता है। हमारे सभी धर्मग्रंथों में गुरु की महिमा का गुणगान किया गया है।

जिसे जीवन में गुरु का साथ मिलता है, वह व्यक्ति अपने जीवन में भवसागर पार कर जाता है। जिस प्रकार सूर्य के निकलने से अंधकार का नाश हो जाता है; ठीक उसी प्रकार गुरु के मुख से निकले वचनों से मोहरूपी अंधकार का नाश हो जाता है। गुरु अज्ञान का निराकरण करता है और हमें सच्चाई का मार्ग दिखाता है।

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति इ (१): आकलन कृति

निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों

Question 1.
ईश्वर
Answer:
संत कबीर को किसकी महिमा सब जगह दिखाई देती है?

Question 2.
कस्तूरी
Answer:
हिरण की नाभि में क्या होती है?

समझकर लिखिए।

Question 1.

Answer:

कृति इ (२):शब्द संपदा

Question 1.
पद्यांश में से देशज शब्द ढूँढ़कर लिखिए।
Answer:
नैन
पीव

निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. मृग
2. दुनिया
3. घट
4. नैन

Answer:

1. हिरण
2. संसार
3. घड़ा
4. नयन

निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।

1. मृग –
2. कुंडल –

Answer:

1. मृग – हिरण, एक नक्षत्र का नाम
2. कुंडल – नाभि, कड़ा, बाली

निम्नलिखित शब्दों के अर्थ दोहों से ढूंढकर लिखिए।

1. परमात्मा
2. संसार
3. खुद
4. पुत्र

Answer:

1. पीव
2. दुनिया
3. मैं
4. लाल

कृति इ (३) : स्वमत अभिव्यक्ति

Question 1.
‘ईश्वर सर्वव्यापक है।’ इस विषय पर अपने विचार लिखिए।
Answer:
ईश्वर ने ही इस सुंदर सृष्टि का निर्माण किया है। उसकी मर्जी के बिना एक पत्ता भी नहीं हिल सकता है। संपूर्ण सृष्टि में ईश्वर का अस्तित्व है। वह हमारे हृदय में विराजमान है। लेकिन हमें इस बात का एहसास नहीं होता। अत: हम उसे ढूँढ़ने के लिए चारों और भटकते रहते हैं। अलग-अलग तीर्थस्थलों पर जाकर उसे पाने का प्रयास करते हैं। कोई उसे मंदिर मैं ढूँढ़ता है तो कोई उसे मस्जिद में ढूँढ़ता है।

परंतु वह तो हर जगह है। उसे पाने के लिए हमें यहाँ-वहाँ भटकने की जरूरत नहीं है। ईश्वर को पाने के लिए मनुष्य को बाह्य-आडंबरों का त्याग करना चाहिए। कर्मकांड व बाहरी आडंबर के जरिए हमें उसकी प्राप्ति नहीं होती है। सच्चे भाव से ईश्वर को याद करने पर वह हमारे साथ होते हैं। इसके लिए हमें यहाँ-वहाँ जाने की जरूरत नहीं है।

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति ई (१) आकलन कृति

पद्यांश के आधार पर समझकर निम्नलिखित वाक्य पूर्ण कीजिए।

Question 1.
किनारे पर वही बैठा रहता है –
Answer:
जो डूबने से डरता है।

Question 2.
पानी की गहराई में उतरने से –
Answer:
व्यक्ति को अनमोल रत्न की प्राप्ति होती है।

निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –

Question 1.
बौरा
Answer:
डूबने से कौन डरता है?

Question 2.
फूल
Answer:
जो हमारे जीवन में काँटा बोता है, उसके जीवन में हमें क्या बोना चाहिए?

समझकर लिखिए।

Question 1.

Answer:

कृति ई (२) : शब्द संपदा

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए।

1. फूल
2. किनारा
3. काँटा
4. पानी

Answer:

1. सुमन
2. तट
3. कंटक
4. जल

विलोम शब्द लिखिए।

1. फूल x ……….
2. ढूँढना x ………

Answer:

1. फूल x काँटा
2. ढूँढना x पाना

वचन बदलिए।

1. किनारा
2. फूल

Answer:

1. किनारा – किनारे
2. फूल – फूल

निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
तीन नोकों वाला अस्त्र
Answer:
त्रिशूल

कृति ई (३) : स्वमत अभिव्यक्ति

Question 1.
‘साहस व्यक्ति का सबसे बड़ा गुण होता है’ विषय पर अपने विचार लिखिए।
Answer:
साहस ही जीवन है। साहस ही हमें जीवन में सफलता के लक्ष्य तक पहुंचाता है। जिस व्यक्ति के पास साहस होता है वह व्यक्ति दूसरों से अलग होता है और वह अद्भुत कार्य कर दिखाता है। साहस के कारण जीवन में उत्साह का संचार होता है और व्यक्ति का जीवन जीने योग्य बनता है। साहस मनुष्य-जीवन को सोने जैसा चमकाता है और उसे उन्नति की ओर आगे बढ़ाता है।

जीवन की उन्नति, प्रगति और उच्चतम विकास के लिए साहस बहुत ही आवश्यक है। साहस के बल पर ही कल्पना चावला और सुनीता विलियम्स अंतरिक्ष में जा सकीं। साहस के बल पर ही कोलंबस ने अमेरीका की खोज की। साहस के बल पर ही सिकंदर ने पूरी दुनिया पर अपना वर्चस्व स्थापित किया था। इसी साहस के बल पर हम भारतीयों ने अंग्रेजों का सामना करके उन्हें वापस जाने के लिए मजबूर किया था। इसलिए साहस सबसे बड़ा गुण है।

जिन ढूँढ़ा Summary in Hindi

जिन ढूँढ़ा कवि – परिचय

जीवन-परिचय : संत कबीरदास जी का जन्म सन १३९८ उत्तर प्रदेश के वाराणसी शहर में हुआ। ये भक्तिकालीन निर्गुण काव्यधारा के संतकवि थे। इनकी भाषा सधुक्कड़ी है। हिंदी भाषा की बोलियों का उल्लेख और प्रयोग इनकी रचनाओं में झलकता है। इनकी रचनाओं में धार्मिक आडंबर और सामाजिक रूढ़ियों के प्रति विद्रोह दिखाई देता है। ये समाज में जागरण युग के अग्रदूत के रूप में जाने जाते हैं।

प्रमुख कृतियाँ : ‘साखी’, ‘सबद’, ‘रमैनी’, इन तीनों का संग्रह ‘बीजक’ नामक ग्रंथ में किया गया है।

जिन ढूँढ़ा पद्य-परिचय

दोहे : दोहा एक अर्धसममात्रिक छंद है। इसमें प्रथम और तृतीय चरण में १३-१३ तथा द्वितीय और चतुर्थ चरण में ११-११ मात्राएँ होती हैं। चरण के अंत में लघु होता है।

प्रस्तावना : ‘जिन ढूँढा’ इस दोहे में संतकवि जी ने बड़प्पन का लाभ, गुरु और शिष्य की मनोवृत्ति, संगति का फल, अच्छा व्यवहार, परोपकार, साहस, सहानुभूति, जीव व आत्मा-परमात्मा के बारे में अपने विचार व्यक्त किए हैं। संत कबीर के इन नीतिपरक दोहों से जीवन जीने की कला और जीवन को समृद्ध करने की सीख मिलती है।

जिन ढूँढ़ा सारांश:

संतकवि कबीर जी ने अपने नीतिपरक दोहों के माध्यम से मनुष्य को जीवन समृद्ध करने की सीख दी है। कबीर कहते हैं कि व्यक्ति को सिर्फ बड़ा नहीं होना चाहिए। उसके बड़े होने से दूसरों को लाभ पहुंचाने की क्षमता व्यक्ति के पास होनी चाहिए। गुरु-शिष्य का आपसी रिश्ता पवित्र होना चाहिए। शिष्य के पास गुरु पर सर्वस्व अर्पण करने की भावना होनी चाहिए। गुरु के पास भी शिष्य से कुछ भी न लेने की मनोवृत्ति होनी चाहिए।

मनुष्य को सज्जनों की संगति में रहना चाहिए। सज्जनों की संगति से व्यक्ति को अपने चरित्र में सुधार कर लेना चाहिए। दुर्बल या कमजोर व्यक्ति को नहीं सताना चाहिए। उनकी हाय कभी नहीं लेनी चाहिए। बलवान व्यक्ति का कर्तव्य है कि वह दुर्बल व्यक्ति की सुरक्षा करें। एक गुरु ही शिष्य के जीवन को आकार देने का कार्य करता है। वही उसका भाग्यविधाता होता है। जिस पर सर्वशक्तिमान ईश्वर की कृपा होती है, उसे कोई भी नहीं मार सकता है। हमें ईश्वर को अपने नयनों में बंद करके रखना चाहिए; ताकि हम उसे सदैव देख सकें। ईश्वर की अद्भुत महिमा हर जगह दिखाई देती है।

अत: व्यक्ति को ईश्वर के साथ एकाकार होना चाहिए। साहस के द्वारा व्यक्ति बड़े से बड़ा कार्य कर सकता है । हमें जीवन में दूसरों का हित ही करना चाहिए। संत कबीर के इन नीतिपरक दोहों को अपने जीवन में उतारने और उसका पालन करने से हम जीवन में सफलता हासिल कर सकते हैं।

जिन ढूँढ़ा शब्दार्थ

जिन ढूँढ़ा भावार्थ

बड़ा हुआ तो …………………………. लागें अति दूर।।

कबीरदास जी कहते हैं कि केवल शरीर से बड़ा होना पर्याप्त नहीं होता है। अपने बड़प्पन से दूसरों को लाभ पहुँचाने की क्षमता व्यक्ति के पास होनी चाहिए। खजूर का पेड़ बहुत ऊँचा होता है परंतु राह से आने-जाने वाले राहियों को उसके छाया का लाभ नहीं मिलता है और फल अधिक दूर लगने के कारण राहगीर उसके फलों का आस्वाद भी नहीं ले सकते हैं। यदि व्यक्ति के बड़े होने से दूसरे लोगों का भला हो सकता है, तो ही व्यक्ति सचमुच का बड़ा होता है।

सिष को ऐसा …………………………….. कुछ नहीं लेय।।

कबीरदास जी कहते हैं कि शिष्य का ऐसा स्वभाव होना चाहिए कि वह गुरु पर अपना सर्वस्व अर्पण कर दे। जैसा शिष्य हो वैसे गुरु को | भी होना चाहिए। गुरु भी ऐसे स्वभाव वाला होना चाहिए कि वह शिष्य से कुछ भी न लेने की इच्छा रखता हो।

कबिरा संगत …………………………….. बास सुबास।।

कबीरदास जी कहते हैं कि सज्जन व्यक्ति की संगति इन बेचने वाले की सुगंध की तरह महकती है। इन बेचने वाला व्यक्ति हमें कुछ दे । । या न दे, फिर भी उसके पास रहने से सुगंध मिलती ही है।

दुर्बल को न सताइए …………………………….. भसम हवै जाय।

कबीरदास जी कहते हैं कि दुर्बल या कमजोर व्यक्ति को नहीं सताना चाहिए। उनकी हाय या उनके मुख से निकली बटुआ बड़ी प्रभावशाली व असरदार होती है। जिस प्रकार लुहार के पास जो धौंकनी होती है, वह निर्जीव होती है; पर जब उससे हवा निकलती है तब उस हवारूपी श्वास से लोहा भी भस्म हो जाता है।

गुरु कुम्हार सिष …………………………….. बाहर बाहै चोट।।

कबीरदास जी ने यहाँ गुरु को कुम्हार की संज्ञा दी है और शिष्य को कच्चे घड़े की। जिस प्रकार कुम्हार घड़े को सुंदर बनाने के लिए । भीतर से एक हाथ से सहारा देता है और बाहर दूसरे हाथ से थपथपाकर उसे सही आकार देता है, ठीक उसी प्रकार गुरु भी शिष्य को अंतर (हृदय) से प्रेम भावना तथा बाहर से कठोर अनुशासन में रखकर योग्य बनाता है।

जाको राखै …………………………….. जग बैरी होय।।

कबीरदास जी कहते हैं कि जिस पर सर्वशक्तिमान ईश्वर की कृपा होती है, उसे कोई भी नहीं मार सकता है। भले ही पूरी दुनिया उसका बैरी अर्थात दुश्मन हो जाए तो भी उसका बाल बाँका नहीं हो सकता।

नैनों अंतर आव …………………………….. तोहि देखन देवें।।

कबीरदास जी कहते हैं कि हे सर्वशक्तिमान ईश्वर ! तू मेरे नयनों में आकर बस जा और मैं तुझे अपने नयनों में बंद कर लूँ। ऐसा करके । न मैं किसी और को देखूगा और न तुझे किसी और को देखने दूंगा।

लाली मेरे लाल …………………………….. हो गई लाल।।

कबीरदास जी ने इस दोहे में ईश्वर को लाल कहा है और उसकी महिमा को लाली कहकर संबोधित किया है। वे कहते हैं, “मुझे मेरे । ईश्वर की अद्भुत महिमा हर जगह दिखाई देती है। जब मैं उस अद्भुत महिमा को देखने गया तब मैं भी उसमें विलीन हो गया।”

कस्तूरी कुंडल …………………………….. जानै नाहिं।।

कबीरदास जी कहते हैं कि ईश्वर सर्वव्यापक है। वह हमारे हृदय में भी स्थित है। जिस प्रकार कस्तूरी हिरण की नाभि में होती है, परंतु उसे इस बात का पता नहीं होता और वह उसकी सुगंध से मस्त होकर पूरे वन में उसे खोजता फिरता है। उसी प्रकार ईश्वर भी हमारे हृदय में ही वास करते हैं पर हमें इस बात का ज्ञान नहीं होता है और हम उसे ढूँढ़ने के लिए चारों ओर घूमते-भटकते रहते हैं।

जिन ढूँढा …………………………….. रहा किनारे बैठ।।

कबीरदास जी कहते हैं कि जीवन में साहस का होना अत्यावश्यक है। यदि व्यक्ति के पास अनमोल रल पाने की चाह है, तो उसे पानी । की गहराई में उतरना ही पड़ेगा। यदि उस बावले को डुबने का डर है तो वह किनारे ही बैठा रह जाएगा है। ऐसा व्यक्ति जीवन में कुछ भी नहीं कर पाएगा।

जो तोको …………………………….. बाको है तिरसूल।।

कबीरदास जी कहते हैं कि हमें जीवन में दूसरों का हित ही करना चाहिए। भले ही दूसरा व्यक्ति तुम्हारी राहों में काँटा बोए; फिर भी तुम्हें उसके लिए फूल ही बोने चाहिए। तुम्हारे बोए फूल से तुम्हारा आँगन तो महक उठेगा पर उस व्यक्ति को काँटों के बदले त्रिशूल का कष्ट । मिलेगा, जिससे उसका जीवन यातनाओं से भर जाएगा।

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 7 दो लघुकथाएँ Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 7 Do Laghu Kathayen Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 7 दो लघुकथाएँ Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 7 दो लघुकथाएँ Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तर:

2. घटनाक्रम के अनुसार वाक्य लिखिए। .

प्रश्न 1.
घटनाक्रम के अनुसार वाक्य लिखिए। .

1. बचपन में बाबू जी से की फरमाइशों का पुलिंदा था।
2. आज शाम वह बचपन के अपने कमरे में घुसा।
3. झटपट कागज की एक पर्ची बनाई।
4. वह एक-एक इबारत पढ़ने लगा।

उत्तर:

1. आज शाम वह बचपन के अपने कमरे में घुसा।
2. बचपन में बाबू जी से की फरमाइशों का पुलिंदा था।
3. वह एक-एक इबारत पढ़ने लगा।
4. झटपट कागज की एक पर्ची बनाई।

3. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

4. रिश्ते लिखिए। काका

प्रश्न 1.
रिश्ते लिखिए। काका

1. अनिता – राघवेंद्र = …………………..
2. अम्मा – अनिता = …………………..
3. बच्चे – बाबूजी = …………………..
4. बाबू जी – अनिता = …………………..

उत्तर:

1. पली-पति
2. सास व बहू
3. पोते व दादा जी
4. ससुर व बहू गद्यांश:

5. पाठ में प्रयुक्त एकवचन और बहुवचन शब्दों की सूची बनाइए। 

प्रश्न 1.
पाठ में प्रयुक्त एकवचन और बहुवचन शब्दों की सूची बनाइए।

उत्तर:

एकवचन	बहुवचन
1. वर्ष	1. लघुकथाएँ
2. कस्बा	2. महीने
3. एलबम	3. कोने
4. बॉक्स	4. पर्चियाँ
5. जलेबी	5. आँखों
6. पेंसिल	6. परिजनों
7. शूज	7. बुजुर्गों
8. वस्तु	8. बच्चों
9. पर्ची	9. फरमाइशों
10. जेब	10. किताबें

अभिव्यक्ति :

प्रश्न 1.
‘व्यवहार से संस्कार झलकते हैं।’ इस विधान को सोदाहरण स्पष्ट कीजिए।
उत्तर:
हम संसार में जो कुछ करते हैं वह व्यवहार है। व्यवहार हमारे व्यक्तित्व को दर्शाता है। संस्कार सनातन होता है। व्यक्ति के हर रोज के व्यवहार में संस्कार के दर्शन होने चाहिए। जिस व्यक्ति के व्यवहार से संस्कार झलकते हैं, उसे सभी याद करते हैं। ऐसा व्यक्ति मृत्यु के बाद भी अमर हो जाता है। भारत के भूतपूर्व राष्ट्रपति एवं महान वैज्ञानिक डॉ. अब्दुल कलाम जी का भी सभी के साथ बहुत ही अच्छा व्यवहार था। उनके व्यवहार से सादगी एवं माधुर्य था। उनका जीवन व्यवहार एवं संस्कारों का ऐसा अद्वितीय मिश्रण था जिससे संपूर्ण दुनिया में वे प्रसिद्ध हुए। सभी के साथ प्रेम व शांति से पेश आना, दूसरों की मदद करने के लिए सदैव तत्पर रहना व दूसरों के दुख व दर्द को समझना; यह सबसे अच्छा व्यवहार है और इसी व्यवहार से व्यक्ति के संस्कार झलकते हैं।

उपयोजित लेखन :

प्रश्न 1.
निम्नलिखित परिच्छेद पढ़कर इस पर आधारित ऐसे चार प्रश्न तैयार कीजिए जिनके उत्तर एक-एक वाक्य में हों।

उत्तरः

1. कोढ़ियों की सेवा कौन करती थी?
2. परदुखकातर व निर्मल हृदय वाले लोगों के नाम बताइए।
3. गद्यांश में कौन-सी संस्था का उल्लेख हुआ है?
4. लेखक के शब्दकोश में कौन-से शब्द नहीं है?

Hindi Lokvani 10th Std Textbook Solutions Chapter 7 दो लघुकथाएँ Additional Important Questions and Answers

(अ) निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों
i. पाँच
ii. मुंबई
उत्तर:
i. राघवेंद्र ने कितने कमरों का फ्लैट खरीदा है?
ii. राघवेंद्र का फ्लैट कौन से शहर में है?

प्रश्न 3.
निम्नलिखित असत्य विधान को सत्य करके लिखिए।)
i. मुंबई ही बाबू जी के लिए जन्म और कर्मभूमि रही है।
उत्तर :
पैतृक कस्बा ही बाबू जी के लिए जन्म और कर्मभूमि रही है।

प्रश्न 4.
किसने, किससे कहा?
i. “हमें वहाँ के अलावा और कहीं ज्यादा अच्छा नहीं लगता।”
उत्तर :
बाबू जी ने राघवेंद्र से कहा।

प्रश्न 5.
संजाल पूर्ण कीजिए।
उत्तर:

कृति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।
i. पैतृक
ii. कस्बा
उत्तर:
i. पुश्तैनी
ii. छोटा शहर या नगर

प्रश्न 2.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

1. पिता संबंधी या पुरखों का –
2. जुड़ा या मिला हुआ –
3. बड़ा नगर –

उत्तरः

1. पैतृक
2. संयुक्त
3. महानगर

प्रश्न 3.
विलोम शब्द लिखिए।

1. जन्म × ……….
2. कम × ………….
3. इच्छा × ……….
4. प्यार × ………..

उत्तर :

1. मरण
2. ज्यादा
3. अनिच्छा
4. नफरत

प्रश्न 4.
गद्यांश में से विदेशी शब्द ढूँढ़कर लिखिए।
उत्तर :
i. फ्लैट

प्रश्न 5.
निम्नलिखित शब्दों में उचित प्रत्यय लगाकर नए शब्द तैयार कीजिए।
i. दिन
ii. वर्ष
उत्तर :
i. दिन + इक = दैनिक
ii. वर्ष + इक = वार्षिक

प्रश्न 6.
निम्नलिखित शब्दों के समोच्चारित भिन्नार्थक शब्द लिखिए।

1. कम
2. दिन
3. दस

उत्तर:

1. काम
2. दीन
3. दास

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘संयुक्त परिवार के लाभ’ इस विषय पर अपने विचार लिखिए।
उत्तर :
एक परिवार में जब सभी परिवार के सदस्य दूसरी पीढ़ी के सदस्यों के साथ मिल-जुलकर रहते हैं तब हम उसे संयुक्त परिवार कहते हैं। संयुक्त परिवार समस्याओं में हमारा सहायक बनता है। विपत्ति के समय सभी एक-दूसरे की सहायता करने के लिए आगे आते हैं। इस प्रकार संयुक्त परिवार में भावनात्मक सहयोग होता है। जब परिवार एक साथ रहता है तब त्योहार मनाने की खुशी कुछ अलग ही होती है। संयुक्त परिवार में आपसी समायोजन होता है।

संयुक्त परिवार में प्रत्येक व्यक्ति अपने विचार साझा करता है और एक सही निर्णय लिया जाता है जिससे सबका भला हो । संयुक्त परिवार में बुजुर्ग का मार्गदर्शन बहुत ही महत्त्वपूर्ण होता है। संयुक्त परिवार में रहने से बच्चे अधिक आज्ञाकारी एवं संस्कारी होते हैं। संयुक्त परिवार में रहने से कुल-व्यय बहुत ही कम होता है।

(आ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ

कृति आ (1) : आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
निम्नलिखित गलत विधान सही करके लिखिए।
i. राघव ने पर्ची पर लिखा कि बाबू जी और अम्मा उसके 4. साथ पैतृक कस्बे में आकर रहें।
उत्तर:
राधव ने पर्ची पर लिखा कि बाबू जी और अम्मा उसके साथ मुंबई में आकर रहें।

ii. राघव को विश्वास था कि बाबू जी उसकी अर्जी को अस्वीकार कर देंगे।
उत्तरः
राघव को विश्वास था कि बाबू जी उसकी अर्जी को स्वीकार कर देंगे।

कृति आ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची लिखिए।
i. खारिज
ii. बक्सा
iii. अर्जी
उत्तर:
i. अस्वीकृत
ii. डिब्बा
iii. प्रार्थनापत्र, निवेदन

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।

1. कागज, कपड़े आदि की बँधी बड़ी गठरी –
2. वाक्य की बनावट या रचना –
3. निवेदन अथवा प्रार्थना करने के लिए लिखा गया पत्र –
4. जिसे आश्वासन मिला हो –

उत्तर:

1. पुलिंदा
2. इबारत
3. अर्जी
4. आश्वत

प्रश्न 3.
विलोम शब्द लिखिए।

1. पुरानी × ……………….
2. अंदर ×…………………
3. खारिज × ……………….

उत्तर:

1. नई
2. बाहर
3. स्वीकृत

प्रश्न 4.
गद्यांश में से विदेशी शब्द छाँटकर लिखिए।
उत्तर:

1. पॉलीथिन
2. कोर्स
3. फुटबॉल
4. बॉक्स
5. एक्स्ट्रा
6. ड्रेस
7. शूज

प्रश्न 5.
निम्नलिखित शब्दों के श्रुतिसम भिन्नार्थक शब्द लिखिए।

1. जेब
2. कम
3. डाल
4. लकड़ी

उत्तर:

1. जब
2. काम
3. दाल
4. लड़की

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘बचपन के वे दिन सुहावने’ विषय पर अपने विचार लिखिए।
उत्तर:
बचपन के दिन बहुत प्यारे होते हैं। वे कभी भुलाए नहीं जा सकते। जैसे-जैसे हम बड़े होते जाते हैं, वैसे-वैसे बचपन के दिन पीछे छुट जाते हैं। फिर भी हम बचपन के उन यादगार पलों को नहीं भूल सकते हैं। बार-बार हमें उनकी याद आती रहती है। बचपन की अपनी मधुर यादों में माता-पिता, भाई-बहन, यारदोस्त, स्कूल के दिन, मौज-मस्ती आदि सब कुछ याद आता रहता है।

बचपन में दिन भर गुल्ली-डंडा खेलना, दोस्तों के साथ धूम मचाना, आम के पेड़ पर चढ़ना आदि के स्मरण से ‘कोई लौटा दे मेरे वे बीते हुए दिन’ इस गीत की याद आ जाती है। बचपन में सभी चिंतामुक्त जीवन जीते हैं। बचपन में खेलने व उछलने-कूदने में बड़ा आनंद आता है। यही कारण है कि सबको बचपन के दिन सुहावने लगते हैं।

(इ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1): आकलन कृति

प्रश्न 1.
ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –
i. सुरेश
ii. बुजुर्गों
उत्तर:
i. अशोक के पारिवारिक मित्र का नाम बताइए?
ii. सुरेश ने बचपन में अपने परिजनों को किसकी सेवा करते देखा है?

कृति इ (2) : शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तर:
i. बुरा-भला
ii. दिन-रात

प्रश्न 2.
वचन बदलिए।
i. बात
ii. पैसा
उत्तर:
i. बातें
ii. पैसे

प्रश्न 3.
गद्यांश में से विदेशी शब्द छाँटकर लिखिए।
उत्तर :
i. इन्वेस्टमेंट
ii. सेंटर

प्रश्न 4.
गद्यांश में से विलोम शब्द ढूँढकर लिखिए।
उत्तर:
i. बुरा × भला
ii. दिन × रात

प्रश्न 5.
निम्नलिखित शब्दों में उचित प्रत्यय लगाकर नए शब्द तैयार कीजिए।

1. ईमानदार
2. परिवार
3. भारत

उत्तर:

1. ईमानदार + ई = ईमानदारी
2. परिवार + इक = पारिवारिक उत्तर. शापवर्गीय
3. भारत + ईय = भारतीय

प्रश्न 6.
‘परिजन’ इस शब्द में से उचित उपसर्ग पहचानिए और संबंधित उपसर्ग से दो नए शब्द बनाइए।
उत्तरः
i. परिजन : उपसर्ग : परि
ii. नए शब्द : परिसंवाद, परिवर्तन

प्रश्न 7.
पर्यायवाची शब्द लिखिए।
i. अचरज
ii. फीकी
उत्तर:
i. आश्चर्य
ii. नौरस

प्रश्न 8.
निम्नलिखित शब्द का अनेकार्थी शब्द लिखिए। प्रत्यय
i. फीकी
उत्तरः
नीरस, स्वादहीन, धुंधला, दुर्बल, सामान्य

दो लघुकथाएँ Summary in Hindi

लेखिक-परिचय :

जीवन-परिचय : संतोष सुपेकर जी का जन्म 1967 में मध्य प्रदेश के उज्जैन शहर में हुआ। ये एक आधुनिक हिंदी साहित्यकार हैं। इन्होंने पत्रकारिता एवं जनसंचार क्षेत्र में उल्लेखनीय कार्य किया है। पत्र, कविता, लघुकथा, कहानी, समीक्षा, व्यंग्यलेख आदि साहित्य की विधाओं में इन्होंने लेखन कार्य किया है। इनके द्वारा लिखे गए लेख विविध पत्र-पत्रिकाओं में प्रकाशित होते रहते हैं।
प्रमुख कृतियाँ : ‘साथ चलते हुए’, ‘हाशिए का आदमी’, ‘बंद आँखों का समाज’, ‘हँसी की चीखें” (लघुकथा संग्रह), ‘चेहरों के आरपार’, ‘यथार्थ के यक्ष प्रश्न’ (काव्य संग्रह) आदि।

गद्य-परिचय :

लघुकथा : लघुकथा कहानी से लघु होती है। भले ही वह आकार से लघु होती है, पर वह गागर में सागर भरने का काम करती है। वह पाठकों को चिंतन करने के लिए प्रेरित करती है।
प्रस्तावना : अर्जी : इस लघुकथा में बेटे का अपने माता-पिता के प्रति अपनापन, माता-पिता का अपने बच्चे के प्रति स्नेह तथा उनका
अपनी जन्मभूमि के प्रति जुड़ाव को अभिव्यक्त किया गया है। इन्वेस्टमेंट : इस लघुकथा में जीवन में संस्कारों का होना बहुत ही महत्त्वपूर्ण होता है, संस्कारों के बिना जीवन परिपूर्ण नहीं बन सकता और व्यक्ति के व्यवहार से संस्कार झलकने चाहिए, इसे उदाहरण के द्वारा स्पष्ट किया है।

सारांश :

अर्जी : ‘अर्जी’ का अर्थ है – निवेदन अथवा प्रार्थना। प्रस्तुत लघुकथा का नायक राघव अपनी पत्नी व बच्चों के साथ मुंबई में रहता है। वह अपने बच्चों को दादा-दादी का प्यार देना चाहता है। इसी कारण उसने मुंबई में पाँच कमरों का फ्लैट खरीदा है। लेकिन राधव के माता-पिता को अपने पैतृक कस्बे में ही रहना अच्छा लगता है।

वे महानगर में चार-आठ दिनों से ज्यादा नहीं रह सकते हैं। हर वर्ष की तरह राघव अपनी पत्नी व बच्चों के साथ पैतृक कस्बे में आया हुआ है। वह बचपन में जिस कमरे में रहता था उस कमरे में जाकर अपना बक्सा खोलता है जिसमें उसकी पुरानी किताबें, पुरानी फोटो एलबम आदि हैं।

उसमें एक पॉलीथिन की एक थैली में कुछ पर्चियाँ भी हैं। उन पर्चियों को देखकर उसकी बचपन की यादें तरोताजा हो जाती हैं। बचपन में उसे जो भी कुछ चाहिए होता था, उसे वह पर्ची पर लिखकर अपने पिता की जेब में डाल देता था। उन पर्थियों को पढ़ते समय उसकी आँखों से आँसू आने लगते हैं। उसके बाबू जी भी उसकी माँगों को पूरा करते थे।

अब राघव बड़ा हो गया है। अब वह चाहता है कि उसके माता-पिता साल में कम से कम दो-तीन महीने तक उसके पास मुंबई में आकर रहें। वह झटपट कागज की एक पर्ची पर अपनी चाह को लिखकर अपने अम्मा-बाबू को मुंबई में साथ रहने के लिए कहता है और उस पर्ची को अपने बाबूजी के कुर्ते की जेब में डाल देता है।

उसे आशा है कि इस बार भी उसके बाबूजी उसे निराश नहीं करेंगे और वे उसकी अर्जी जरूर मान जाएंगे। इन्वेस्टमेंट : इस लघुकथा में सुरेश के व्यवहार एवं उसके कार्य के बारे में जानकर हमें उसके संस्कारी होने का पता चलता है। उसकी सौतेली माँ है। वह हमेशा उसे बुरा-भला कहती थी। फिर भी वह उसकी दिन-रात सेवा करता है। वह इन्वेस्टमेंट सेंटर चलाता है।

बाहर पैसे का इन्वेस्टमेंट करना उसका कार्य है। ठीक उसी प्रकार वह अपने घर में भी संस्कारों का इन्वेस्टमेंट करता है। उसने बचपन से सीखा है कि बुजुर्गों की सेवा करनी चाहिए। इसी कारण वह भी अपनी माँ की सेवा करता है। उसे आशा है कि उसे सेवा करते देखकर उसके बच्चों में भी भारतीय संस्कार विकसित होंगे।

शब्दार्थ :

1. पतृक – पुश्तैनी
2. कस्बा – छोटा शहर
3. खारिज – अस्वीकृत, बहिष्कृत
4. बक्सा – डिब्बा
5. अर्जी – प्रार्थनापत्र
6. अचरज – आश्चर्य
7. फीकी – नीरस
8. सब्र – धीरज, सहन
9. आश्वस्त – जिसे आश्वासन मिला हो, जिसे तसल्ली दी गई हो।

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer

Std 10 Hindi Chapter 7 Prakruti Sanwad Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 7 प्रकृति संवाद Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 7 प्रकृति संवाद Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 7 प्रकृति संवाद Textbook Questions and Answers

पठनीय:

प्रश्न 1.
फूलों से बनने वाली औषधियों की जानकारी अंतरजाल पर पदिए।

लेखनीय:

प्रश्न 1.
‘बढ़ती आबादी, कटते वन और प्रदूषण से प्रभावित होता जन जीवन’ इस विषय पर अपने विचार लिखिए।
उत्तरः
आज हमारे देश की आबादी दिनों दिन बढ़ रही है। लोगों को रहने के लिए पर्याप्त जगह नहीं है। अत: वनों की अंधाधुंध कटाई की जा रही है। इस कारण पर्यावरण का संतुलन बिगड़ रहा है। विश्व भर में जलवायु परिवर्तन से उपजे नकारात्मक प्रभाव को मनुष्य आए दिन झेल रहा है। कहीं पर अधिक मात्रा में वर्षा तो कहीं पर सूखा पड़ रहा है। कंपनियों का रासायनिक द्रव्य नदी, तालाब या सागर में छोड़े जाने के कारण जल प्रदूषण बढ़ गया है।

पेड़पौधों की संख्या में निरंतर कमी होने के कारण वायु प्रदूषण जैसी भयावह संकट का लोगों को सामना करना पड़ रहा है। ऊपर से यातायात के साधनों में वृद्धि होने से उनमें से निकलने वाले धुएँ से सभी बेहाल एवं त्रस्त हैं। बढ़ती आबादी का भरण-पोषण करने के लिए प्राकृतिक संसाधनों का जरूरत से ज्यादा दोहन हो रहा है। इस प्रकार बढ़ती आबादी, कटते वन और प्रदूषण से लोगों का जन-जीवन पूरी तरह से प्रभावित हो गया है।

श्रवणीय:

प्रश्न 1.
‘बनभोज’ महोत्सब का आयोजर कब, क्यों और कहाँ किया जाए. इसके बारे में बड़ा से मुजिए तथा कक्षा में सुनाइए।

संभषणीय:

प्रश्न 1.
‘प्रकृति हर पल नया रूप धारण करती है।’ विषय पर अपने विचार लिखिए।
उत्तरः
भारत में छह ऋतुएँ होती हैं। हर ऋतु की अपनी विशेषता होती है। हर ऋतु में प्रकृति नए रूप धारण करती है। वसंत ऋतु में पेड़-पौधों पर नए पत्ते व फूल आते हैं। गुलाब, गेंदा, सूरजमुखी, सरसों आदि के रंग-बिरंगी फूल खिलने लगते हैं। उस ऋतु में प्रकृति का सौंदर्य खिल उठता है। ग्रीष्म ऋतु में सूर्य की किरणें तेज होती हैं। इस ऋतु में प्रकृति अपना सौंदर्य रूपी कोष लुटाती चलती है। वर्षा ऋतु में लोगों को गर्मी से राहत मिलती है। इस ऋतु में चारों ओर हरियाली छा जाती है।

सब जगह हरा ही हरा दिखाई देता है। शरद ऋतु में कमल खिलते हैं। मालती के फूलों से वन सुशोभित हो जाते हैं। रातें ठंडी एवं सुहावनी होती हैं। हेमंत ऋतु में प्रकृति सुहावनी एवं लुभावनी लगने लगती है। हल्के जाड़े का एहसास इस ऋतु में होता है। शिशिर ऋतु में कड़ाके की ठंड होती है। घना कोहरा छाने लगता है। इस ऋतु में पेड़ से पत्ते झड़ने लगते हैं। इस प्रकार प्रकृति हर पल नया रूप धारण करती रहती है।

स्वाध्याय:

सुचना के अनुसार क्रुतिया कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तरः

प्रश्न 2.
पाठ में आई वनस्पतियों का वर्गीकरण कीजिए।

उत्तर:

लताएँ	पौधे	वृक्ष
1. बेला	दवना	हरसिंगार
2. गिलोय लता	तुलसी	सहिजन
3. –	अड़हुल	–

प्रश्न 3.
कृति पूर्ण कीजिए।
हरसिंगार में ऋतुओं के अनुसार होने वाले बदलाव –

उत्तरः

वसंत	वसंत में हरसिंगार के भीतर सोई हुई ऊर्जा जागने लगती है व प्राणरस छलकने लगता है। वह नई टहनियों तथा नए पत्तों के सौंदर्य से लद जाता है।
शरद	शरद में हरसिंगार तारों भरा आसमान बन जाता है। रातभर जगमग-जगमग करता है और सुबह को | अनंत फूलों के रूप में धरती पर बिछ जाता है।

प्रश्न 4.
उपसर्ग, प्रत्यय लगाकर शब्द नए शब्द बनाइए।

उत्तरः

प्रश्न 5.
कृति पूर्ण कीजिए।

उत्तरः

प्रश्न 6.
क्रमानुसार ऋतुओं के नाम लिखिए।

उत्तर:

1.	वसंत
2.	ग्रीष्म
3.	वर्षा
4.	शरद
5.	हेमंत
6.	शिशिर

Hindi Lokvani 10th Std Textbook Solutions Chapter 7 प्रकृति संवाद Additional Important Questions and Answers

(अ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
समझकर लिखिए।
उत्तरः

प्रश्न 3.
सही विकल्प चुनकर लिखिए।
दैनिक कार्य से निवृत्त होकर लेखक ………………..
(अ) आँगन और गैलरी में बैठने जाते हैं।
(आ) आँगन और गैलरी में खेलने जाते हैं।
(इ) आँगन और गैलरी में टहलने लगते हैं।
उत्तर:
दैनिक कार्य से निवृत्त होकर लेखक आँगन और गैलरी में टहलने लगते हैं।

कृति अ (2): शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ गद्यांश में ढूँढ़कर लिखिए।

1. अवकाश प्राप्त
2. हरियाली
3. कार्य
4. खुशबू

उत्तर:

1. निवृत्त
2. हरीतिमा
3. कर्म
4. महक

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।
1. जो समान्य हालत में हो –
2. प्रात: काल गाया जाने वाला गीत –
उत्तर:
1. प्रकृतिस्थ
2. प्रभाती

प्रश्न 3.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।
1. महक
2. दुआ
उत्तर:
1. सुगंध
2. आशीर्वाद

प्रश्न 4.
गद्यांश में से तत्सम शब्द ढूँढकर लिखिए।
उत्तरः
प्रकृति

प्रश्न 5.
निम्नलिखित शब्द के श्रुतिसम भिन्नार्थक शब्द लिखिए।
1. आकार
2. दुआ
उत्तरः
1. आकर
2. दवा

कृति अ (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘आज कल पौधों का स्थान बगीचे तक ही सीमित नहीं रहा है। इन्हें अब आँगन और गैलरी में भी स्थान दिया जाता है।’ अपने विचार लिखिए।
उत्तरः
पौधे बहुत ही आकर्षक एवं प्यारे होते हैं। पौधों पर फूल खिलते हैं; वे महकते हैं। उनकी खुशबू सभी के मन में ताजगी निर्माण लाती है। अब पौधे घर की आंतरिक साज-सज्जा का भी एक मुख्य अंग बन गए हैं। अत: लोग इन्हें घर के अंदर एवं बाहर गमलों में लगाते हैं। इनके कारण घर में ऑक्सीजन की मात्रा में वृद्धि होती है। घर का वातावरण स्वच्छ एवं प्रदूषण रहित रहता है। पौधों के कारण घर का तापमान बाहर की तुलना में ठंडा रहता है। गर्मियों के दिनों में घर-आँगन में स्थित पौधे लोगों को राहत दिलाने का काम करते हैं।

(आ) निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
निम्नलिखित विधान सत्य है या असत्य लिखिए।
1. लेखक के आँगन में स्थित पार्क की दुनिया बहुत छोटी है।
2. लेखक के अनुसार हर चीज का अपना समय नहीं होता है।
उत्तरः
1. सत्य
2. असत्य

प्रश्न 2.
समझकर लिखिए।
उत्तरः

कृति (2): शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।
1. पेट
2. पत्ता
उत्तरः
1. उदर
2. पर्ण

प्रश्न 2.
विलोम शब्द लिखिए।
1. समय × ……….
2. रस × ………….
उत्तर:
1. असमय
2. नीरस

प्रश्न 3.
वचन बदलिए।
1. पौधा
2. पत्ती
उत्तरः
1. पौधे
2. पत्तियाँ

प्रश्न 4.
निम्नलिखित शब्दों में उचित उपसर्ग लगाकर नए शब्द तैयार कीजिए।
1. रस
2. समय
उत्तरः
1. नी + रस = नीरस
2. अ + समय = असमय

प्रश्न 5.
निम्नलिखित शब्दों में उचित प्रत्यय लगाकर नए शब्द तैयार कीजिए।
1. रस
2. परिवार
उत्तरः
1. रस + ईला = रसीला
2. परिवार + इक = पारिवारिक

निम्नलिखित वाक्यों में विराम चिह्न का उचित प्रयोग कीजिए।

प्रश्न 1.
लेखक ने हँसकर नीम से कहा नहीं नहीं ऐसी बात नहीं है
उत्तरः
लेखक ने हँसकर नीम से कहा, “नहीं-नहीं, ऐसी बात नहीं है।”

‘कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘हमें पेड़-पौधों से लगाव रखना चाहिए।’ विषय पर अपने विचार व्यक्त कीजिए।
उत्तरः
पेड़-पौधे मानव के मित्र हैं। वे पर्यावरण को संतुलित रखने में हमारी मदद करते हैं। उनके बिना वनों के अस्तित्व की कल्पना नहीं की जा सकती। वे हमें साँस लेने के लिए प्राणवायु देते हैं। अत: हमें उनसे लगाव रखना चाहिए और उनकी सुरक्षा करनी चाहिए। हमें पर्याप्त मात्रा में पेड़-पौधे लगाने चाहिए ताकि चारों ओर हरियाली छाई रहे। पेड़-पौधों में औषधीय गुण होते हैं। उनसे अनेक प्रकार की दवाइयाँ तैयार की जाती हैं। तुलसी, आंवला, निर्गुण्डी, अशोक आदि पेड़-पौधे औषधी के रूप में बहुत फलदायी होते हैं। पेड़-पौधों के बिना मनुष्य जीवन की कल्पना नहीं की जा सकती। इसलिए हमें पेड़-पौधों से लगाव रखना चाहिए।

(इ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1): आकलन कृति

प्रश्न 1.
गद्यांश के आधार पर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
1. चिड़ियाँ
2. प्राणरस
उत्तरः
1. कौन चहचहा उठी?
2. क्या छलकने लगता है?

कृति (2): शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तरः

1. खंखड़-सा
2. घूमती-फिरती
3. जगमग-जगमग
4. डाल-डाल

प्रश्न 2.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. आकाश
2. ऊर्जा
3. फूल
4. धरती

उत्तर:

1. नभ
2. शक्ति
3. पुष्प
4. पृथ्वी

प्रश्न 3.
वचन बदलिए।
1. डाल
2. गली
उत्तरः
1. डालियाँ
2. गलियाँ

प्रश्न 4.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. आश्रय × ……………..
2. खुश × ………………
3. अनंत × …………….
4. डर × ……………….

उत्तरः

1. अनाश्रय
2. नाखुश
3. अंत
4. साहस

प्रश्न 5.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
अनंत
उत्तरः
असीम, श्रीविष्णु, श्रीकृष्ण, आकाश

प्रश्न 6.
निम्नलिखित शब्दों के श्रुतिसमभिन्नार्थक शब्द लिखिए।
1. सूख
2. पत्तों
उत्तरः
1. सुख
2. पत्रों

(ई) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ई (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

निम्नलिखित गलत विधान सही करके लिखिए।

प्रश्न 1.
लेखक ने अमरूद के पेड़ की उपेक्षा की।
उत्तरः
लेखक ने अमरूद के पेड़ की उपेक्षा नहीं की।

प्रश्न 2.
शरद के आते ही अमरूद की विरल डालियाँ नई पत्तियों और टहनियों से सघन होने लगती हैं।
उत्तर:
वसंत के आते ही अमरूद की विरल डालियाँ नई पत्तियों और टहनियों से सघन होने लगती हैं।

प्रश्न 3.
तालिका पूर्ण कीजिए।
उत्तर:

वसंत में अमरूद की स्थिति	वर्षा में हरसिंगार की स्थिति
वसंत के आते ही अमरूद की और टहनियों से सघन होने लगती हैं।	हरसिंगार वर्षा में फूलना शुरू विरल डालियाँ नई पत्तियों कर देता है।

कृति (2): शब्द संपदा

निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।

प्रश्न 1.
क्या रूप मंडप बनाया है अमरूद और हरसिंगार ने मिलकर
उत्तरः
क्या रूप मंडप बनाया है अमरूद और हरसिंगार ने मिलकर!

प्रश्न 2.
निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर नए शब्द तैयार कीजिए।
फल
उत्तरः
उपसर्गयुक्त शब्द: सुफल
प्रत्यययुक्त शब्द: फलहीन

प्रश्न 3.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तर:

1. धीरे-धीरे
2. छोटे-छोटे
3. आते-आते
4. डाल-डाल
5. नाच-नाचकर

प्रश्न 3.
विलोम शब्द लिखिए।
1. भीतर × ……….
2. ऊपर × ……….
उत्तर:
1. बाहर
2. नीचे

प्रश्न 4.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।
1. महोत्सव
2. पावस
उत्तरः
1. जलसा
2. वर्षा

प्रश्न 5.
निम्नलिखित शब्द का श्रुतिसम भिन्नार्थक शब्द लिखिए।
उपेक्षा
उत्तर:
अपेक्षा

कृति ई (3): स्वमत अभिव्यक्ति

प्रश्न 1.
फूल-फल क्यों उगाने चाहिए? अपने विचार लिखिए।
उत्तरः
भारतीयों की जीवन पद्धति में फूलों और फलों का अत्यधिक महत्त्व है। फल-फूल मनुष्य की भावनात्मक सुंदरताओं के प्रतीक माने जाते हैं। व्यक्ति के जीवन में मानसिक एवं शारीरिक स्वास्थ्य की दृष्टि से भी फूलों और फलों का अत्यधिक महत्त्व है। फल-फूलों को ईश्वर को समर्पित किया जाता है।

अत: आध्यात्मिक दृष्टि से भी इनका अनन्यसाधारण महत्त्व है। फूलों के बीच जाने से दुखी व्यक्ति के जीवन में उत्साह भर हो जाता है। फूल मनुष्य को मानसिक शांति और आरोग्य प्रदान करते हैं। जहाँ पर फूल-फल के पेड़-पौधे होते हैं, वहाँ पर तरह-तरह के पक्षी होते हैं। उनका कलरव सुनकर मनुष्य अपने आपको प्रकृति से जुड़ा हुआ पाता है। प्रकृति से जुड़े रहना मनुष्य के मन और शरीर को सुकून प्रदान करता है। अत: हमें फल-फूल वाले पेड़-पौधे उगाने चाहिए।

(उ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति उ (1): आकलन कृति

प्रश्न 1.
समझकर लिखिए।
1. इन्होंने लेखक को उलाहना दी –
2. बेला के फूलों के अनुसार ये हैं ऊँचे लोग –
उत्तरः
1. बेला के फूलों ने
2. अड़हुल और सहिजन

गलत विधान सही करके फिर से लिखिए।

प्रश्न 1.
लेखक ने स्वयं को बड़ा आदमी कहा है।
उत्तर:
लेखक ने स्वयं को छोटा आदमी कहा है।

प्रश्न 2.
फूल और पौधे लेखक के परिवार के सदस्य नहीं हैं।
उत्तरः
फूल और पौधे लेखक के परिवार के सदस्य हैं।

कृति (2): शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. महाशय
2. भौंरा
3. फूल
4. मंगल

उत्तर:

1. महोदय
2. भ्रमर
3. सुमन
4. शुभ

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।
1. दो व्यक्तियों के बीच हुआ वर्तालाप –
2. जिसमें सदा फूल लगते रहते हैं –
उत्तरः
1. संवाद
2. सदाबहार

प्रश्न 3.
निम्नलिखित शब्दों के अनेकार्थी शब्द लिखिए।
1. जीवन
2. बेला
उत्तर:
1. जिवित दशा, जिंदगी
2. एक लता, समय

प्रश्न 4.
गद्यांश में से प्रत्यययुक्त शब्द ढूँढ़कर लिखिए और उनसे प्रत्यय अलग कीजिए।
उत्तर:
1. विराजमान, प्रत्यय – मान
2. मतवाली, प्रत्यय – वाली

प्रश्न 5.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
1. पुष्प
2. मास
उत्तरः
1. फूल
2. महीना

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘प्रकृति से अपनत्व रखने से व्यक्ति का व्यक्तित्व खिलता है।’ क्या आप इस कथन से सहमत हैं? अपने विचार लिखिए।
उत्तर:
जी हाँ, मैं इस कथन से सहमत हूँ। प्रकृति मानव जीवन की सहचरी है। प्रकृति के बिना मानव जीवन की कल्पना करना निरर्थक है। अत: प्रत्येक व्यक्ति को प्रकृति से अपनत्व रखना चाहिए। जो व्यक्ति प्रकृति से अपनत्व रखता है उसमें उच्च मानवीय गुणों का संचार होता है। अंग्रेजी साहित्य के महान कवि विलियम वर्डस्वर्थ को कविता लिखने की प्रेरणा प्रकृति ने ही प्रदान की थी। अतः उन्होंने प्रकृति को ईश्वर का रूप माना है। प्रकृति मानव मन को नित्य प्रेरित करती है।

पुराने जमाने में ऋषि-मुनि प्रकृति की गोद में बैठकर ही तपस्या करते थे। वेदों का निर्माण भी प्रकृति के सानिध्य में ही हुआ है। प्रकृति से अपनत्व रखने वाला व्यक्ति जीवन में ऊँचा उठता है। उसका हृदय संवेदनाओं एवं असीम करुणा से भरा रहता है। ऐसा व्यक्ति दूसरों के जीवन को प्रभावित करने की क्षमता रखता है। अत: प्रकृति से अपनत्व रखने से व्यक्ति का व्यक्तित्व खिलता है।

(ऊ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –
1. तीन
2. एक पौधा
उत्तर:
1. कितने गमलों में बेला के पौधे विराजमान थे?
2. खिल-खिलाकर कौन हँस रहा था?

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 3.
सही विकल्प चुनकर लिखिए।
शरीर में कोई विकार उत्पन्न होने से –
(अ) गिलोय लता के पत्तों का रस प्राशन किया जाता है।
(आ) सहिजन के पत्तों का रस प्राशन किया जाता है।
(इ) बेला के पत्तों का रस प्राशन किया जाता है।
उत्तरः
शरीर में कोई विकार उत्पन्न होने से गिलोय लता के पत्तों का रस प्राशन किया जाता है।

कृति (2): शब्द संपदा

प्रश्न 1.
गद्यांश में से विलोम शब्द की जोड़ियाँ ढूँढ़कर लिखिए।
उत्तरः
1. सुबह × शाम
2. आते × जाते

प्रश्न 2.
गद्यांश में प्रयुक्त विदेशी शब्द ढूँढ़कर लिखिए।
उत्तर:
1. अरबी शब्द: मेहरबाँ, तबस्सुम
2. अंग्रेजी शब्द: गेट

प्रश्न 3.
वचन बदलिए।
1. धारा
2. बात
उत्तर:
1. धाराएँ
2. बातें.

प्रश्न 4.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. पास × ……………….
2. मुरझा × ………………
3. भीतर × ……………..
4. हलकी × ………………

उत्तरः

1. दूर
2. खिला
3. बाहर
4. भारी

प्रश्न 5.
अनेक शब्दों के लिए एक शब्द लिखिए।

1. छंद शास्त्र में कविता का वह प्रकार जिसमें गणों का कोई बंधन न हो –
2. अपमान और उपहास का विषय –
3. रूप, धर्म आदि का स्वाभाविक परिवर्तन –

उत्तरः

1. मुक्तक
2. विडंबना
3. विकार

प्रश्न 6.
पर्यायवाची लिखिए।
1. विकार
2. लता
उत्तरः
1. परिवर्तन
2. बेल.

प्रश्न 7.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
गेट
उत्तरः
प्रवेश मार्ग, फाटक, दरवाजा

प्रकृति संवाद Summary in Hindi

लेखक-परिचय:

जीवन-परिचय: रामदरश मिश्र जी का जन्म १९२४ में उत्तर प्रदेश के गोरखपुर में हुआ। मिश्र जी साहित्य में बहु-प्रतिभा के धनी हैं। इन्होंने कविता, कहानी, उपन्यास, आलोचना, आत्मकथा, यात्रा वर्णन, संस्मरण व निबंध आदि विधाओं में लेखन किया है। इन्होंने अपने साहित्य में वस्तु व शिल्प दोनों को सहज ही परिवर्तित होने दिया। मिश्र जी कई सामाजिक व साहित्यिक संस्थाओं के अध्यक्ष रह चुके हैं।

प्रमुख कृतियाँ: ‘पथ के गीत’, ‘पक गई है धूप’, ‘कंधे पर सूरज’ (कविता संग्रह), ‘हँसी ओठ पर आँखें नम हैं’, ‘तू ही बताए जिंदगी’ (गज़ल संग्रह), ‘स्मृतियों के छंद’ (संस्मरण), ‘पानी के प्राचीर’ (उपन्यास), ‘खाली घर’ (कहानी संग्रह) ‘बबूल और कैक्टस’ (ललित निबंध) आदि।

गद्य-परिचय:

ललित निबंध: यह निबंध का एक प्रकार है। इस प्रकार के निबंध में लेखक की आत्मीयता पूर्ण स्वच्छंदता के साथ अभिव्यक्त होती है।
इसमें लेखक की शैलीगत विशेषता अत्यंत उन्मुक्त रूप से प्रकट होती है। इस प्रकार के निबंध में रोचकता, कल्पनात्मकता
एवं नाटकीयता होती है।

प्रस्तावना: ‘प्रकृति संवाद’ इस ललित निबंध के माध्यम से लेखक ने पेड़-पौधों के प्रति लगाव एवं आत्मीयता को बड़े ही कल्पनात्मक
ढंग से प्रस्तुत किया है। प्रत्येक व्यक्ति के हृदय में पेड़-पौधों के प्रति अपनेपन की भावना होनी चाहिए। आखिर मानव और
पेड़-पौधों का आपस में गहरा संबंध होता है।

सारांश:

‘प्रकृति संवाद’ यह एक ललित निबंध है। इस निबंध के माध्यम से लेखक ने पाठकों को पेड़-पौधों के प्रति अपनत्व की भावना रखने का संदेश दिया है। रात भर लेखक को शरीर में दर्द होता रहता है। लेखक की तबीयत ठीक नहीं है। उन्हें रात में ठीक से नींद नहीं आती है। सुबह उठते ही उन्हें थोड़ी ताजगी महसूस होती है। सुबह की ठंडी हवा उनके तन व मन में ताजगी का स्पंदन महसूस कराती है। वे हमेशा की तरह आज भी अपने आँगन व गैलरी में टहलने के लिए जाते हैं। उनके आँगन में स्थित पार्क की दुनिया बहुत छोटी है। दवनों की महक और हरीतिमा उन्हें अपनी ओर आकर्षित करती हैं। वे तुलसी माता को मुस्कुराते हुए देखते हैं और उसे प्रणाम करते हैं, उससे बतियाते हैं। फिर वे नीम की हरी पत्तियों से बातें करते हैं। नीम के पत्ते मानो लेखक से कह रहे थे कि बहुत दिनों से उसने कढ़ी बनाने के लिए उनके पत्तों का इस्तेमाल नहीं किया है।

लेखक की नजर हरसिंगार की ओर जाती है। वह बहुत ही मस्त दिखाई दे रहा था। उसकी महक से स्वयं लेखक ही नहीं बल्कि गली से आने-जाने वाले सभी लोग परिचित थे। पश्चात अमरूद का पेड़ लेखक से बातें करने लगता है। अमरूद का पेड़ लेखक के आँगन । का सबसे पहला नागरिक है। अमरूद के पेड़ और हरसिंगार इन दोनों ने आपस में मिलकर एक रूप मंडप बनाया था जिस पर चिड़ियाँ खेलती हैं, गाती-चहचहाती हैं। लेखक को आषाढ़ के महीने में अमरूद पर जो फल आते हैं, उनकी मिठास की याद आती है। उस समय चिड़ियों की चहचहाअट से अमरूद के फलों की मिठास भर जाती है। अड़हुल के पौधे पर आने वाले लाल फूल भी लेखक को अपनी ओर खींच लेते हैं और वह उनसे भी बातें करने लगता है।

सदाबहार सहिजन पर बारहों मास सुगंध से लदे फूलों पर मधुमक्खियाँ और भौंरे गुनगुनाया करते हैं। लेखक जाड़ों की धूप में उसकी छाँव में बैठते हैं। तब वह उस पेड़ की मतवाली सुरभि से नहाते हैं। बेला के फूल भी लेखक का ध्यान अपनी ओर खींच लेते हैं। वे सफेद रंग के हैं और जगमगा रहे हैं। उन फूलों से मादक सुगंध की बहने वाली हलकी-हलकी धारा लेखक के हृदय को प्रसन्न कर देती है। गिलोय लता के पौधे भी लेखक का हाल-चाल पूछते हैं। उनकी हरी-हरी फलियाँ लेखक की आँखों को सुख देती हैं। इस प्रकार पेड़-पौधों से बातचीत करके लेखक जब गेट के बाहर निकलते हैं तो स्वयं को भरा-पूरा अनुभव करते हैं।

शब्दार्थ:

1. उलाहना – शिकायत
2. विडंबना – हँसी, उपहास
3. गुँचा – कली
4. मेहरबाँ – कृपालु.
5. स्पंदन – रह-रहकर धीरे-धीरे हिलना या काँपना, धड़कन
6. निवृत्त – अवकाश प्राप्त, मुक्त होकर
7. पत्ता – पर्ण
8. भौंरा – भ्रमर
9. महोत्सव – जलसा
10. पावस – वर्षा
11. महाशय – महोदय
12. फूल – सुमन
13. मंगल – शुभ
14. विकार – दोष मनोवेग
15. लता – बेल
16. तबस्सुम – मुस्कान
17. अस्तित्व – विद्यमानता, होने का भाव
18. सहिजन – एक वृक्ष; जिसकी लंबी फलियों की तरकारी बनती है।
19. हरीतिमा – हरियाली
20. कर्म – कार्य
21. महक – खुशबू
22. पेट – उदर

मुहावरे:

1. यादों में जाग उठना – पुरानी यादें ताजा हो जाना।
2. भरा-पूरा अनुभव करना – संतुष्ट हो जाना। .

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer