Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 14 Dual Nature of Radiation and Matter Important Questions and Answers.
Maharashtra State Board 12th Physics Important Questions Chapter 14 Dual Nature of Radiation and Matter
Question 1.
Explain Planck’s idea of quantization of energy.
Answer:
Max Planck, in 1900, put forward the idea of quantization of energy to explain the blackbody radiation spectrum. He proposed that atoms behave as tiny oscillators and emit electromagnetic radiation, not continuously but as little packets of energy called quanta. He assumed that the energy associated with a quantum of radiation (now called a photon) is proportional to the frequency v of the oscillator. Thus, E = nhv, where n = 1, 2, 3, 4, … etc., and h is a universal constant, now called Planck’s constant. For n = 1, E = hv. A quantum of radiation is emitted when there is a transition from a higher quantized level of energy of an oscillator to lower quantized level.
[Note : Historically, various terms have been used to denote a particle of light; quantum of electromagnetic radiation ≡ photon ≡ packet of energy ≡ atom of energy ≡ quantum of radiation ≡ bundle of energy. Interaction between two charged particles involves exchange of photons. The photon has zero rest mass, no charge, unit spin and travels in free space at a speed of 2.99792458 × 108 m/s exact by definition. There is no conservation law for photons, i.e., they can be produced / absorbed.]
Question 2.
What was Hertz’s observation regarding emission of electrons from a metal surface?
Answer:
During his experiments on electromagnetic waves in 1887, Heinrich Rudolph Hertz (1857-94), Ger-man physicist, noticed that electric sparks occurred more readily when one of the electrodes of his spark-gap transmitter was exposed to ultraviolet radiation. This discovery was called the Hertz effect and is now known as the photoelectric effect.
Although Hertz did not follow up his discovery, others quickly established that the cause of the sparking ease was due to emission of negatively charged particles from the electrode irradiated. These particles were identified as electrons after the discovery of the electron in 1897.
![]()
Question 3.
Draw a neat labelled diagram to illustrate photoelectric effect.
Answer:
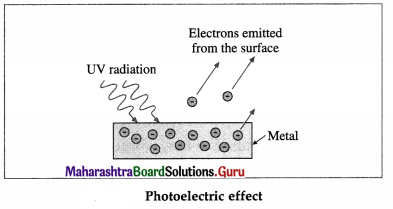
[Note : Positive metal ions and atoms are not shown in the figure.]
Question 4.
What were the investigations of Hallwachs and Lenard regarding photoelectric effect?
Answer:
Wilhelm Hallwachs (1859-1922), German physicist, found that a metal plate irradiated with ultraviolet radiation lost its charge more rapidly when the plate is negatively charged than when it is neutral or positive.
Investigations of photoelectric effect by Phillipp Lenard (1862-1947), German physicist, showed that
- electron emission occurs only with radiations below a critical wavelength, i.e., above a critical frequency.
- kinetic energy of the emitted electrons increases as wavelength decreases i.e., frequency increases but is independent of the intensity of radiation which determines the rate of emission of electrons (the number of electrons emitted per unit time).
Question 5.
What is a photosensitive surface?
Answer:
The surface which emits electrons when illuminated by electromagnetic radiation of appropriate frequency is called photosensitive surface.
[Note : The material that exhibits photoelectric effect is called photosensitive material.]
Question 6.
Why are alkali metals most suitable as photo-sensitive surfaces?
Answer:
The alkali metals e.g., caesium, potassium and sodium emit photoelectrons even when visible radiation (light) is incident on them. Hence, they are most suitable as photosensitive surfaces.
![]()
Question 7.
With a neat diagram, describe the apparatus to study the characteristics of photoelectric effect.
Answer:
Apparatus : A photoelectric cell G consists of the emitting electrode E (emitter) of the material being studied and the collecting electrode C (collector). The electrodes are sealed in an evacuated glass envelope provided with quartz window W that allows the passage of UV radiation and visible light. Monochromatic light of variable frequency from a suitable source S (such as a carbon arc) passes through a pair of polarizers P (permitting a change in the intensity of radiation) and falls on the emitter.
The electric circuit, as shown in below figure, allows the collector potential to be varied from positive through zero to negative with respect to the emitter, and permits the measurement of potential difference and current between the electrodes. When the collector is made negative, the voltmeter is connected in reverse.
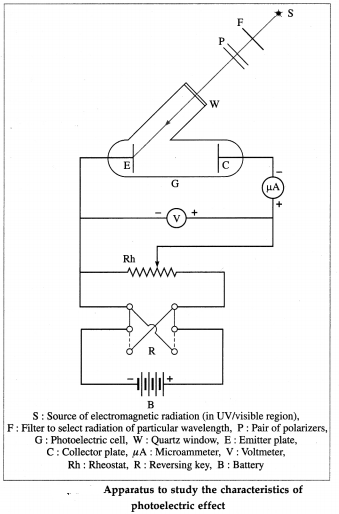
[ Note : The radiation coming out of a filter is not truly monochromatic, it lies in the wavelength range between λ and λ + ∆λ that depends on the source and the filter. ]
Question 8.
In the experiment to study photoelectric effect, describe the effects of the frequency and intensity of the incident radiation on the photoelectric current, for a given emitter material and potential difference across the photoelectric cell.
Answer:
The emitter of the photoelectric cell is irradiated with monochromatic light whose frequency and intensity can be varied continuously and measured. Initially, the collector is made positive with respect to the emitter, so that photoelectrons ejected move quickly from the emitter to the collector. About 10 V is sufficient to do this. The photoelectric current as a function of intensity and frequency of incident radiation is studied.
(1) Effect of frequency : Keeping the light intensity and the accelerating potential difference V constant, the frequency of the incident radiation is varied from that of far-UV to red. It is found that for every material (usually, a metal) irradiated there is a limiting frequency below which no photoelectrons are emitted irrespective of the intensity of the radiation. This frequency, v0, called the threshold frequency or cut-off frequency, is a characteristic of the material irradiated.
The graph of photoelectric current against frequency is shown in below figure; A and B represent two different metals. The photoelectric current is not the same in the two cases, because the intensity of light is different for different frequencies.
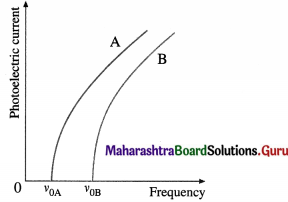
(2) Effect of intensity : With an emitter of a given material, the light intensity is varied by keeping the frequency v (≥ v0) of the light and the accelerating potential difference V constant. It is found that the rate of electron emission, as indicated by the photoelectric current, is proportional to the light intensity. The graph of photoelectric current against light intensity is a straight line through (0, 0), below figure; if we vary either the frequency of the light or the material irradiated, only the slope of the line changes. No electrons are emitted in the absence of incident radiation.
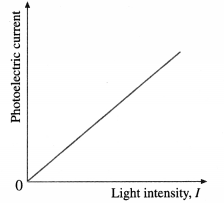
[Note : The dark current, i.e., the current observed in the absence of light, is extremely low. Hence, it is ignored.]
![]()
Question 9.
In the experiment to study photoelectric effect, describe the variation of the photoelectric current as a function of the potential difference across the photoelectric cell, for incident radiation of (1) a given frequency above the threshold but different intensities (2) a given intensity but different frequencies above the threshold.
Answer:
(1) The potential difference (p.d.) across the photo-electric cell is varied keeping both the frequency v (≥ threshold frequency v0) and the intensity of the light constant. Starting with the collector at about 10 V positive, we reduce this potential to zero and then run it negative.
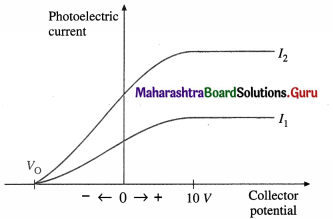
When the p.d. across the tube is 10 V or more, all the emitted electrons are accelerated and travel across the tube, constituting the saturation current for a given light intensity; an increase in the potential of the collector does not cause an increase in current. As the collector potential is reduced from positive values through zero to negative values, the tube current reduces because of the applied retarding potential. In this case, some electrons stop and turn back before they can reach the collector. Eventually the potential difference is large enough to stop the current completely. This is called the stopping potential or cut-off potential VQ. The product of the stopping potential and electronic charge, V0e, is equal to the maximum kinetic energy that an electron can have at the time of emission.
V0e = KEmax \(\frac{1}{2}\)v2max
In above figure, I1 and I2 are two intensities of the incident radiation for the same frequency v ( > v0); I2 = 2I0. Doubling the intensity of light doubles the current at each potential, as in I2, but V0 is independent of I.
(2) The above experiment is repeated with different light frequencies for a given emitter material and light intensity. It is found that the stopping potential increases linearly with the frequency in below figure. Therefore, when photoejection occurs for frequencies above v0, the maximum kinetic energy of the photoelectrons increases linearly with the frequency of the radiation.
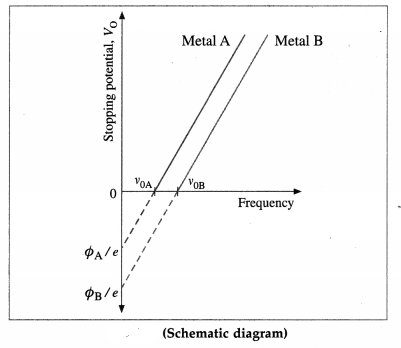
[Note : It was shown by Hughes that the stopping potential depends linearly on the frequency of incident radiation. Lawrence and Beams established that the time interval between arrival of a photon on a metal surface and emission of an electron is less than 3 × 10-9 sc.]
Question 10.
What is the effect of the intensity of incident radiation on the stopping potential in photo-electric emission?
Answer:
V0 is independent of intensity.
Question 11.
In the experiment to study photoelectric effect, discuss the effect and significance of extremely weak radiation of frequency greater than the threshold frequency for the emitter material.
Answer:
The emitter of the photoelectric cell is irradiated with monochromatic light whose frequency is greater than the threshold frequency for the emitter material. The collector is kept at 10 V positive with respect to the emitter, so that photoelectrons ejected move quickly from the emitter to the collector.
The light is made extremely dim (i.e., the intensity is extremely weak). In this case, the number of ‘ photoelectrons emitted per unit time is very small (and special techniques are required to detect them); but, however few, they are emitted almost instantaneously and with the same maximum kinetic energy as for bright light of the same frequency.
According to the wave theory of light, wave trains of pulsating electromagnetic field spread out from the source. Dim light corresponds to waves of small amplitudes and small energy. If dim light spreads over a surface, conservation of energy requires that the electrons must store energy over long periods of time, which can be several hours, before gathering enough energy to become free of the metal. The fact that photoelectrons appear immediately, within about 10-9 s, can be explained only by assuming that the light energy is not spread over the surface uniformly as required by the wave theory, but falls on the surface in concentrated bundles.
Question 12.
Define (1) threshold frequency (2) threshold wavelength (3) stopping potential.
Answer:
(1) The threshold frequency for a given metal surface is the characteristic minimum frequency of the incident radiation below which no photoelectrons are emitted from that metal surface (whatever may be the intensity of incident light).
(2) The threshold wavelength for a given metal surface is the characteristic maximum wavelength of the incident radiation above which no photoelectrons are emitted from that metal surface (whatever may be the intensity of incident light).
(3) The stopping potential is the value of the retarding potential difference that is just sufficient to stop the most energetic photoelectrons emitted from reaching the collector so that the photoelectric current in a photocell reduces to zero.
[Note : The threshold wavelength λ0 = c/v0, where c is the speed of light in free space and v0 is the threshold frequency for the metal.]
![]()
Question 13.
State the characteristics of photoelectric effect.
Answer:
Characteristics of photoelectric effect:
(1) For every metal surface there is a limiting frequency of incident radiation below which no photoelectrons are emitted from that metal surface. This frequency, called the threshold frequency, is characteristic of the metal irradiated.
(2) The time rate of emission of photoelectrons in-creases in direct proportion to the intensity, of incident radiation.
(3) The photoelectrons have different speeds at the time of emission ranging from zero to a certain maximum value, which is characteristic for a given metal for a given frequency of the incident radiation. The maximum kinetic energy of the photoelectrons at the time of emission is independent of the intensity but increases linearly with the frequency of the incident radiation.
(4) For incident radiation of frequency greater than or equal to the threshold frequency for a given metal surface, photoelectric emission from the surface is almost instantaneous, even under extremely weak irradiation.
Question 14.
Can we get photoemission with an intense beam of radio waves ? Is photoemission possible at all frequencies ?
Answer:
The frequency of the incident radiation and not its intensity is the criterion for photoelectric effect. The lowest frequency of electromagnetic waves that can cause photoemission is about 4.6 × 1014 Hz (for the alkali metal caesium). Since radio waves have frequencies 1 GHz or lower, they cannot cause photoemission.
Only alkali metals are photosensitive to visible light; other metals are photosensitive only to far ultraviolet radiations.
Question 15.
Explain how wave theory of light fails to explain the characteristics of photoelectric effect.
OR
Explain the failure of wave theory of light to account for the observations from experiments on photoelectric effect.
Answer:
According to the wave theory of light, electromagnetic waves carry the energy stored in oscillating electric and magnetic fields. When enough energy is absorbed by an electron in a substance, it should be liberated as a photoelectron. Frequency of light does not come into picture in this case. Hence, there should not be any threshold frequency for emission of electrons. But it is found that there exists threshold frequency and it depends on the metal.
Experimentally, the maximum kinetic energy of photoelectrons increases linearly with the frequency of light. This cannot be accounted by the wave theory of light.
If a source of light is weak or far away from a metal surface, emission of an electron will not be almost instantaneous. The electron may have to wait for several hours/days for absorption of enough energy from the incident light as by the wave theory of light, energy is spread over the wavefront. But experimentally, for an appropriate frequency of incident light, photoelectric effect is almost instantaneous.
Only one observation, photoelectric current ∝ intensity of incident light can be accounted by the wave theory of light.
Question 16.
Give Einstein’s explanation of the photoelectric effect.
Answer:
Max Planck put forward the quantum theory in 1900 to explain blackbody spectrum. In the theory, he proposed that the electromagnetic radiation emitted by the body consists of discrete concentrated bundles of energy, each equal to hv, where h is a universal constant (now called Planck’s constant) and v is the frequency of the radiation.
Einstein put forth (1905) that these energy quanta, called light quanta/later called photons, interact with matter much like a particle. When a photon collides with an electron in an atom, the electron absorbs whole of the photon energy hv in a single collision or nothing. The electron uses this energy (1) to liberate itself from the atom, (2) to overcome the potential energy barrier at the surface thus liberating itself from the metal, and (3) retains the remaining part as its kinetic energy. Different electrons need different energies in the first two processes. There are some electrons which use minimum energy in the two processes, and hence come out of the metal with maximum kinetic energy. The minimum energy required, in the form of electromagnetic radiation, to free an electron from a metal is called the photoelectric work function Φ of that metal. Thus, for the most energetic photoelectrons at the time of emission,
maximum kinetic energy of the electron = photon energy – photoelectric work function
∴ \(\frac{1}{2}\)\(m v_{\max }^{2}\) = hv – Φ ∴ hv = Φ + \(\frac{1}{2}\)\(m v_{\max }^{2}\)
The above equation is called Einstein’s photo-electric equation.
Light interacts with matter as concentrated bundles of energy rather than energy spread over a Huygens type wavefront. Even under weak irradiation, an electron absorbs a photon’s energy in a single collision. But the rate of incident photons in dim light being less, the chances of such absorption diminish and consequently the photoelectric current diminishes. However, a photoelectron is emitted as soon as a photon is absorbed.
[Note : Albert Einstein (1879-1955), German-Swiss- US theoretical physicist, gave his photoelectric equation in 1905. In the period 1912-1916, Robert Andrews Millikan (1868 -1953), US physicist, was the first to obtain the precise experimental data from which the straight-line graphs, like the one shown in Fig. 14.6, were plotted for various metals. Einstein’s theoretically predicted equation-clearly having the right form for a straight-line graph-was thus verified.]
![]()
Question 17.
Define photoelectric work function of a metal.
Answer:
The photoelectric work function of a metal is defined as the minimum photon energy that ejects an electron from the metal.
It is equal to hv0, where h is Planck’s constant and v0 is the threshold frequency for the metal.
Question 18.
Write Einstein’s photoelectric equation and explain its various tends. How does the equation explain the various features of the photoelectric effect?
Answer:
Einstein’s photoelectric equation :
hv = Φ + \(\frac{1}{2}\)\(m v_{\max }^{2}\) ………… (1)
where h ≡ Planck’s constant, v ≡ frequency of the electromagnetic radiation, hv ≡ energy of the photon incident on a metal surface, Φ ≡ photo-electric work function, i.e., the minimum energy of light quantum required to liberate an electron from the metal surface, vmax and – \(\frac{1}{2}\)\(m v_{\max }^{2}\) ≡ the maximum speed and maximum kinetic energy of the photoelectrons at the time of emission. Φ = hv0, where v0 is the threshold frequency for the metal.
Explanation of the characteristics of photoelectric effect:
(1) From the above equation we find that for photoejection, hv ≥ Φ. That is, hvmin = hv0 must be equal to Φ. Hence, photoelectric effect is observed only if hv ≥ hv0, i.e., v ≥ v0. This shows the existence of a threshold frequency v0 for which photoelectrons are just liberated from a metal surface (with zero kinetic energy). Since different metals differ in electronic configuration, the work function hv0 and, therefore, frequency v0 are different and characteristic of different metals.
(2) In this particle model of light,’ intensity of incident radiation’ stands for the number of photons incident on a metal per unit surface area per unit time. As the number of photons incident on a metal per unit surface area per unit time increases, there is a greater likelihood of a photon being absorbed by any electron. Therefore, the time rate of photoejection and hence photoelectric current increases linearly with the intensity of the incident radiation (v ≥ v0).
(3) From Eq. (1), \(\frac{1}{2}\)\(m v_{\max }^{2}\), = hv – Φ= h(v – v0)
This shows that the maximum kinetic energy in-creases linearly with the frequency v of the incident photon (v ≥ v0) and does not depend on the time rate at which photons are incident on a metal surface.
(4) As the incident energy is concentrated in the form of a photon, and not spread over a wavefront, it is expected that an electron is emitted from the metal surface as soon as a photon (v ≥ v0) is absorbed. This is in agreement with the experimental observation.
[ Note : The frequency v that appears in the formula E = hv is the frequency of the oscillating electric field / magnetic field in the electromagnetic wave. ]
Question 19.
Obtain the dimensions of Planck’s constant.
Answer:
The energy of a photon of frequency v is E = hv, where h is the Planck’s, constant.
∴ [h] = \(\frac{[E]}{[v]}=\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~T}^{-1}}\) = ML2T-1
Question 20.
Is the kinetic energy of all photoelectrons the same when emitted from a certain metal ? Explain.
Answer:
No. Explanation : Depending upon the position and state of an electron in a metal when it absorbs an incident photon, a photoelectron can have kinetic energy ranging from 0 to a certain maximum value equal to the photon energy minus the work function of the metal. Hence, the emitted photoelectrons have this range of kinetic energies.
![]()
Question 21.
In photoelectric effect, what does the stopping potential depend upon ?
Answer:
In photoelectric effect, the stopping potential depends upon the energy of the incident photon and the work function for the metal irradiated (or upon the frequency/wavelength of the incident radiation and the threshold frequency/wavelength for the metal irradiated).
Question 22.
What does the maximum kinetic energy (or the maximum speed) of a photoelectron depend on?
Answer:
The maximum kinetic energy (or the maximum speed) of a photoelectron depends upon the energy of the incident photon and the work function for the metal irradiated (or upon the frequency /wavelength of the incident radiation and the threshold frequency/wavelength for the metal irradiated).
Question 23.
In photoelectric effect, if a graph of stopping potential versus frequency of the incident radiation is plotted, what does the intercept on the frequency axis (v corresponding to Vo = 0) represent?
Answer:
The intercept on the frequency axis (v corresponding to Vo = 0) represents the threshold frequency for the metal.
Question 24.
State the equation that relates the threshold wavelength (λo), the wavelength of incident radiation (λ) and the maximum speed of a photo-electron (vmax).
Answer:
\(\frac{h c}{\lambda}=\frac{h c}{\lambda_{0}}+\frac{1}{2} m v_{\max }^{2}\) is the required equation, where h is Planck’s constant, c is the speed of light in vacuum (free space) and m is the mass of the electron.
Question 25.
What is the energy of a photon (quantum of radiation) of frequency 6 × 1014 Hz?
[h = 6.63 × 10-34 J∙s]
Answer:
hv = (6.63 × 10-34)(6 × 1014)
= 3.978 × 10-19 J is the energy of the photon.
Question 26.
If the total energy of a radiation of frequency 1014 Hz is 6.63 J, calculate the number of photons in the radiation.
Answer:
E = nhv, where hv is the energy of a photon in a radiation of frequency v and n is the number of photons in the radiation.
∴ n = \(\frac{E}{h v}=\frac{6.63}{\left(6.63 \times 10^{-34}\right)\left(10^{14}\right)}\) = 1020
Question 27.
If in a photoelectric experiment, the stopping potential is 1.5 volts, what is the maximum kinetic energy of a photoelectron ? [e = 1.6 × 10-19 C]
Answer:
\(\frac{1}{2}\)\(m v_{\max }^{2}\) = Vse = ( 1.5)(1.6 × 10-19)
= 2.4 × 10-19 J is the required kinetic energy.
![]()
Question 28.
What is the photoelectric work function for a metal if the threshold wavelength for the metal is 3.315 × 10-7 m?
[h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s]
Answer:
Photoelectric work function for the metal =
![]()
Question 29.
Explain the utilization of energy absorbed by an electron in a metal during its collision with a photon.
Answer:
When a photon collides with an atomic electron inside an emitter metal, the electron absorbs whole of the photon energy in a single shot or nothing. The electron uses the absorbed energy (1) to liberate itself from the atom, (2) to overcome the potential energy barrier at the surface thus liberating itself from the metal, and (3) retains the remaining part as its kinetic energy.
30. Solve the following :
(h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s, e = 1.6 × 10-19 J, m (electron) = 9.1 × 10-31 kg)
Question 1.
Find the energy of a photon if
(i) the frequency of radiation is 100 MHz
(ii) the wavelength of radiation is 10000 Å.
Solution:
Data : h = 6.63 × 10-34 J∙s, v = 100 MHz = 100 × 106 Hz, λ = 10000 Å = 106 m, c = 3 × 108 m/s
(i) The energy of a photon, E = hv
= (6.63 × 10-34)(100 × 106) = 6.63 × 10-26 J
(ii) The energy of a photon, E = \(\frac{h c}{\lambda}\)
= \(\frac{\left(6.63 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{10^{-6}}\) = 1.989 × 10-19 J
![]()
Question 2.
A monochromatic source emits light of wavelength 6000 Å. If the power of the source is 10 W, find the number of photons emitted by it per second assuming that 1% of electric energy is converted into light.
Solution:
Data : λ = 6000 Å = 6 × 10-7 m ,h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s, electric energy converted into light per second = \(\frac{1}{100}\) × 10W = 0.1J/s

Question 3.
Radiation of intensity 4 × 10-5 W/m2 is incident uniformly on a metal surface with work function 2.4 eV and area 1 cm2. Assume that the radius of a metal atom is 2.4 Å and photoelectrons are ejected only from the surface of the metal. On the basis of the wave theory of light, how long will it take for an electron to be ejected from the metal surface ? (Assume one free electron/metal atom.)
Solution:
Data : Power/area = 4 × 10-5 W/m2, Φ = 2.4 eV = 2.4 × 1.6 × 10-19 J = 3.84 × 10-19 J, A = 1 cm2 = 10-4 m2, r = 2.4 Å = 2.4 × 10-10 m
Number of metal atoms on the surface = \(\frac{A}{\pi r^{2}}\)
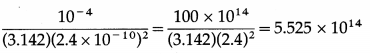
For a single free electron, radiant energy incident per unit time
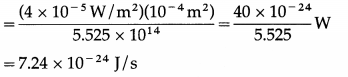
Ignoring reflection/scattering of light, time needed to absorb energy equal to 3.84 × 10-19 J is
\(\frac{3.84 \times 10^{-19} \mathrm{~J}}{7.24 \times 10^{-24} \mathrm{~J} / \mathrm{s}}\) = 5.304 × 104 s = 53040s
= 14 hours 44 minutes.
Question 4.
The energy of a photon is 2 eV. Find its frequency and wavelength.
Solution:
Data : E = 2 eV = 2 × 1.6 × 10-19 J, c = 3 × 108 m/s, h = 6.63 × 10-34 J∙s
(i) Frequency,
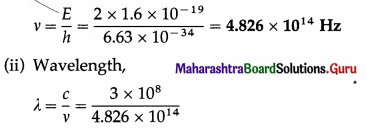
= 6.217 × 10-7 = 6.217 × 10-7 × 1010 Å
= 6217 Å = 621.7 nm
Question 5.
Find the wave number of a photon having an energy of 2.072 eV. [Given : e, c, h]
Solution:
Data : e = 1.6 × 10-19 C, c = 3 × 108 m / s, h = 6.63 × 10-34 J∙s,
E = 2.072 eV = 2.072 × 1.6 × 10-19 J
E = hv = \(\frac{h c}{\lambda}\)
Wave number, \(\frac{1}{\lambda}=\frac{E}{h c}\)
= \(\frac{2.072 \times 1.6 \times 10^{-19}}{\left(6.63 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}\) = 1.666 × 106 m-1
Question 6.
Calculate the energy of a photon, in joule and eV, in a light of wavelength 5000 Å.
Solution :
Data : λ = 5000 Å = 5000 × 10-10 m = 5 × 10-7 m, c = 3 × 108 m/s, h = 6.63 × 10-34 J∙s
Energy of a photon, E = hv = \(\frac{h c}{\lambda}\)
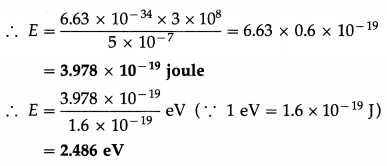
Question 7.
The photoelectric work function for a metal surface is 2.3 eV. 1f the light of wavelength 6800 Å is incident on the surface of the metal, find the threshold frequency and the incident frequency. Will there be an emission of photoelectrons or not? [Given : c, h]
Solution:
Data: c = 3 × 108 m/s, h = 6.63 × 10-34 J.s, Φ = 2.3 eV = 2.3 × 1.6 × 10-19 J, λ = 6800 Å = 6.8 × 10-7 m
(i) Threshold frequency (v0) : Φ = hv0
∴ v0 = \(\frac{\phi}{h}=\frac{2.3 \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}}\) = 5.550 × 1014 Hz
(ii) Incident frequency (v) : c = vλ
∴ v = \(\frac{c}{\lambda}=\frac{3 \times 10^{8}}{6.8 \times 10^{-7}}\) = 4.412 × 1014 Hz
(iii) Thus, v <v0
As the frequency of the incident orange light is less than the threshold frequency there will be no emission of photoelectrons.
![]()
Question 8.
If the work function of a metal is 3 eV, calculate the threshold wavelength of that metal. [Given : c, h, 1 eV = 1.6 × 10-19 J]
Solution:
Data : Φ = 3 eV, c = 3 × 108 m/s, h = 6.63 × 10-34 J.s, 1 eV = 1.6 × 10-19 J
∴ Φ = 3 × 1.6 × 10-19 J

Question 9.
The photoelectric work function of copper is 4.7 eV. What are the threshold frequency and wavelength for photoemission from a copper surface? [1 eV = 1.6 × 10-19 J]
Solution :
Data : Φ = 4.7 eV, 1 eV = 1.6 × 10-19 J, c = 3 × 108 m/s, h = 6.63 × 10-34 J.s
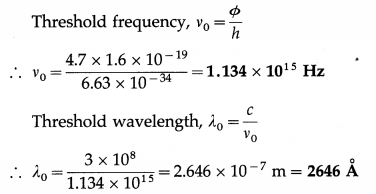
Question 10.
The work functions for potassium and caesium are 2.25 eV and 2.14 eV respectively. Will the photoelectric effect occur for either of these elements
(i) with incident light of wavelength 5650 Å
(ii) with light of wavelength 5180 Å?
Solution:
Data : Φ (potassium) = 2.25 eV,
Φ (caesium) = 2.14 eV, λ1 = 5650 Å = 5.650 × 10-7 m, λ2 = 5180 Å = 5.180 × 10-7 m, h = 6.63 × 10-34 J.s, c = 3 × 108 m/s
Φ (potassium) = 2.25 eV
= 2.25 × 1.6 × 10-19 J =3.6 × 10-19 J
Φ (caesium) = 2.14 eV = 2.14 × 1.6 × 10-19 J
= 3.424 × 10-19 J
Photon energy, E = \(\frac{h c}{\lambda}\)
(i) For λ1 = 5650 Å
E1 = \(\frac{h c}{\lambda_{1}}=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{5.650 \times 10^{-7}}\)
= 3.52 × 10-19 J
This is greater than Φ (caesium), but less than Φ (potassium). Hence, photoelectric effect will occur in case of caesium, but not in case of potassium.
(ii) For λ2 = 5180 Å
E2 = \(\frac{h c}{\lambda_{2}}=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{5.180 \times 10^{-7}}\)
= 3.84 × 10-19 J
This is greater than 0 for potassium and for caesium. Hence, photoelectric effect will occur in both the cases.
Question 11.
Photoemission just occurs from a lead surface when radiation of wavelength 3000 Å is incident on it. Find the maximum kinetic energy of the photoelectrons when the surface is irradiated by UV radiation of wavelength 2500 Å.
Solution:
Data : λ0 = 3000 Å = 3 × 10-7 m, λ = 2500 Å = 2.5 × 10-7 m, h = 6.63 × 10-34 J∙s,c = 3 × 108 m/s
According to Einstein’s photoelectric equation, the maximum kinetic energy of the photoelectrons

Question 12.
The photoelectric work function for a metal is 4.2 eV. If the stopping potential is 3 V, find the threshold wavelength and the maximum kinetic energy of emitted electrons. [Given : c, h, e]
Solution :
Data : e = 1.6 × 10-19 C, c = 3 × 108 m/s, Φ = 4.2 eV = 4.2 × 1.6 × 10-19 J = 6.72 × 10-19 J, h = 6.63 × 10-34 J∙s, v0 = 3 V
(i) Threshold wavelength.
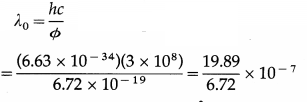
= 2.960 × 10-7 m or 2960 Å
(ii) Maximum kinetic energy of emitted electrons,
KEmax = eV0 = (1.6 × 10-19)(3) = 4.8 × 10-19 J
![]()
Question 13.
Radiation of wavelength 2 × 10-7 m is incident on the cathode of a photocell. The current in the photocell is reduced to zero by a stopping potential of 2 V. Find the threshold wavelength for the cathode.
Solution:
Data : λ = 2 × 10-19 m, V0 = 2 V, e = 1.6 × 10-19 C, h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s
According to Einstein’s photoelectric equation,
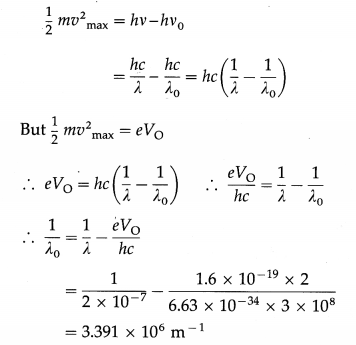
∴ The threshold wavelength, λ0 = 2.948 × 10-7 m
Question 14.
The photoelectric current in a photoelectric cell can be reduced to zero by a stopping potential of 1.8 volts. Monochromatic light of wavelength 2200 Å is incident on the cathode. Find the maximum kinetic energy of the photoelectrons in joule. [Charge on the electron = 1.6 × 10-19 C]
Solution:
Data: V0 = 1.8 V, e = 1.6 × 10-7 C .
The maximum kinetic energy of the photoelectrons,
KEmax = eV0
= (1.6 × 10-19) (1.8) = 2.88 × 10-19 J
Question 15.
The photoelectric work function of a metal is 3 eV. Find the maximum kinetic energy and maximum speed of photoelectrons when radiation of wavelength 4000 Å is incident on the metal surface.
Solution:
Data : Φ = 3 eV = 3 × 1.6 × 10-19 J, c = 3 × 108 m / s, λ = 4000 Å = 4000 × 10-10 m, h = 6.63 × 10-34 J∙s, m = 9.1 × 10-31 kg
(i) According to Einstein’s photoelectric equation, the maximum kinetic energy of photoelectrons,
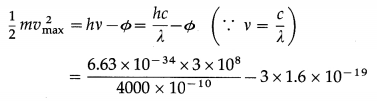
= 1.725 × 10-20 J

= 1.947 × 105 m/s
Question 16.
The work function of tungsten is 4.50 eV. Calculate the speed of the fastest electron ejected from tungsten surface when light whose photon energy is 5.80eV shines on the surface.
Solution:
Data : Φ = 4.50 eV = 4.50 × 1.6 × 10-19 J = 7.2 × 10-19 J,
hv = 5.80eV = 5.80 × 1.6 × 10-19 J = 9.28 × 10-19 J,
m = 9.1 × 10-31 kg
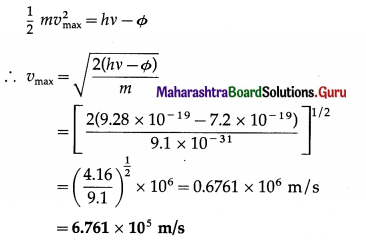
This is the speed of the fastest electron ejected.
Question 17.
If the work function for a certain metal is 1.8 eV,
(i) what is the stopping potential for electrons ejected from the metal when light of 4000 Å shines on the metal
(ii) what is the maximum speed of the ejected electrons?
Solution:
Data: Φ = 1.8eV, λ = 4000 Å = 4 × 10-7 m,
h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s,
m = 9.1 × 10-31 kg, e = 1.6 × 10-19 C

This is the maximum speed of the ejected electrons.
![]()
Question 18.
The work function of caesium is 2.14 eV. Find
(i) the threshold frequency for caesium
(ii) the wavelength of the incident light if photocurrent is brought to zero by a stopping potential of 0.60 V.
Solution:
Data : Φ = 2.14eV = 2.14 × 1.6 × 10-19 J = 3.424 × 10-19 J, VO = 0.60 V,h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s, e = 1.6 × 10-19C
(i) Φ = hv0
∴ The threshold frequency, v0 = \(\frac{\phi}{h}\)
= \(\frac{3.424 \times 10^{-19}}{6.63 \times 10^{-34}}\) = 5.164 × 1014 Hz
(ii) VOe = 0.6 × 1.6 × 10-19 = 0.96 × 10-19 J
\(\frac{h c}{\lambda}\) – Φ = VOe ∴ \(\frac{h c}{\lambda}\) = Φ + VOe
∴ λ = \(\frac{h c}{\phi+V_{\mathrm{O}} e}\)
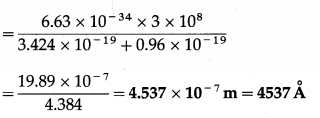
This is the required wavelength of the incident light.
Question 19.
The threshold wavelength for photoemission from silver is 3800 Å. Calculate the maximum kinetic energy in eV of photoelectrons emitted when ultraviolet radiation of wavelength 2600 Å falls on it. Also calculate the corresponding stop-ping potential. [1 eV = 1.6 × 10-19 J]
Solution:
Data : λ0 = 3800 A = 3.8 × 10-7 m,
λ = 2600 Å = 2.6 × 10-7 m, c = 3 × 108 m/s, h = 6.63 × 10-34 J∙s, 1 eV = 1.6 × 10-19 J
(i) According to Einstein’s photoelectric equation, the maximum kinetic energy of photoelectrons emitted,

Question 20.
When a surface is irradiated with light of wavelength 4950 Å, a photocurrent appears. The current vanishes if a retarding potential greater than 0.6 V is applied across the phototube. When a different source of light is used, it is found that the critical retarding potential is 1.1 V. Find the work function of the emitting surface and the wavelength of light from the second source.
Solution :
Data : λ1 = 4.95 × 10-7 m, VO1 = 0.6 V, VO2 = 1.1 V, h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s, e = 1.6 × 10-19 C

∴ The wavelength of light from the second source,
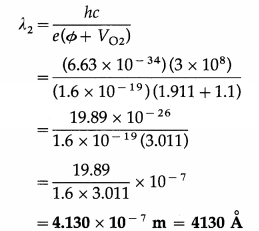
![]()
Question 21.
The work function for the surface of aluminium is 4.2 eV. What potential difference will be required to stop the most energetic electrons emitted by light of wavelength 2000 Å? What should be the wavelength of the incident light for which the stopping potential is zero?
Solution:
Data: Φ = 4.2eV, λ1 = 2 × 10-7 m,VO2 = 0,
h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s, e = 1.6 × 10-19 C

Question 22.
Radiation of wavelength 3000 Å falls on a metal surface having work function 2.3 eV. Calculate the maximum speed of ejected electrons.
Solution:
Data : λ = 3000 Å = 3 × 10-7 m, h = 6.63 × 10-34 J∙s, Φ = 2.3 eV = 2.3 × 1.6 × 10-19 J, c = 3 × 108 m/s, m = 9.1 × 10-31 kg

Question 23.
If the total energy of radiation of frequency 1014 Hz is 6.63 J, calculate the number of photons in the radiation. [Planck’s constant = 6.63 × 10-34 J∙s]
Solution:
Data: v = 1014 Hz, h = 6.63 × 10-34 J∙s
The energy of a photon in a radiation of frequency v is hv.
∴ E = nhv,
so that the number of photons in the radiation is
n = \(\frac{E}{h v}\)
= \(\frac{6.63}{\left(6.63 \times 10^{-34}\right)\left(10^{14}\right)}\) = 1020
Question 31.
Explain wave-particle duality of electromagnetic radiation.
Answer:
A particle is an object with a definite position in space at a given instant and having mass (or momentum), while a wave is a periodically repeated pattern in space and time, generally described by its velocity of propagation, wavelength and amplitude. It is a characteristic of a wave that it is not localized, i.e., it is spread over a region. Thus, these two concepts are contradictory and classical physics treats particles and waves as separate.
Under suitable circumstances, light and all other types of electromagnetic radiation exhibit typical ‘ wave phenomena like polarization, interference and diffraction. On the other hand, radiation exhibits a particle-like nature when it interacts with matter, as in the photoelectric effect and the Compton effect (scattering of X-rays by electrons in matter). It is emitted or absorbed only in terms of quanta of energy. This is the concept of photon : a particle with energy E = hv, where v is the frequency of the radiation and Planck’s constant h connects v and E, respectively the wave and particle aspects.
We see, therefore, that radiation exhibits a dual character. The synthesis of these two contradictory descriptions is called wave-particle duality of electromagnetic radiation.
[Notes : (1) Arthur Holly Compton (1892-1962), US physicist, discovered the effect, now known as the Compton effect, in 1923. (2) Planck’s constant h is also called the elementary quantum of action. Like e and c, it is one of the fundamental constants of nature.]
![]()
Question 32.
What is Compton effect? State the formula for the Compton shift and obtain its maximum value.
Answer:
When a high energy X-ray photon or γ-ray photon is scattered by an electron that is (almost) free, the photon loses energy and the electron gains energy shown in figure. This effect was discovered by A.H. Compton in 1923. It is now known as the Compton effect. This effect exhibits particle nature of electro-magnetic radiation.
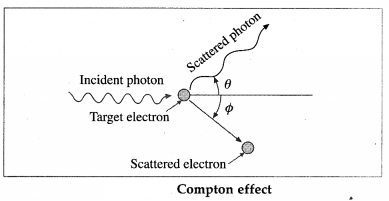
If X is the wavelength of the incident photon, λ is the wavelength of the scattered photon, θ is the angle through which the photon is scattered, m0 is the rest mass of an electron, c is the speed of light in free space and h is Plank’s constant, then, the wavelength shift, called the Compton shift is given by
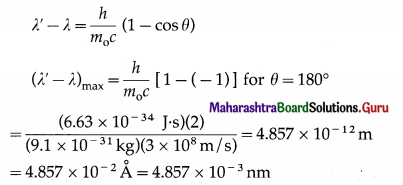
[Note : In a collision between a low energy photon and a high energy electron, scattering results in loss in the energy of the electron and gain in the energy of the photon. This effect is known as the inverse Compton effect.]
Question 33.
What is the implication of Einstein’s interpretation of the photoelectric effect?
OR
What is the significance of the photoelectric effect?
Answer:
The phenomena of interference and polarization exhibit the wave nature of light, and James Clerk Maxwell (1831 – 79), British physicist, had established by 1865 that light is, and propagates as, an electromagnetic wave.
In his interpretation of the photoelectric effect in 1905, Einstein proposed that electromagnetic radiation behaves as a series of small packets or quanta of energy, later called photons. If the frequency of radiation is v, each photon has energy hv and momentum hv/c, where c is the speed of light in free space. Einstein’s photoelectric equation was verified experimentally by Robert Andrews Millikan (1868-1953), US physicist, in 1916.
A very strong additional evidence in support of the quantum theory of radiation was the discovery (in 1923) and explanation of the inelastic scattering of X-rays or γ-rays by electrons in matter by Arthur Holly Compton (1892-1962), US physicist. This inelastic scattering in which a photon transfers part of its energy to an electron is known as the Compton effect. It is similar to the Raman effect. The Compton effect shows particle nature of electro-magnetic radiation.
Since energy and momentum are considered in classical physics as characteristic properties of particles, the photoelectric effect and Compton effect exhibit the particle nature of radiation. But, to describe the photon energy, the quantum theory needs the frequency of the radiation, which is necessarily an attribute associated with a wave in classical physics. Thus, radiation exhibits the dual, seemingly contradictory, characters of particle and wave. In an experiment, we need to use only one of the descriptions, not both at the same time.
[Note : The momentum p and energy £ of a photon are related by the equation, p = E/c, where c is the speed of light in free space.]
Question 34.
Give a brief summary of the quantum theory of radiation.
OR
What is the photon picture of electromagnetic radiation?
Answer:
Quantum theory of radiation (The photon picture of electromagnetic radiation) :
(1) In its interaction with matter, electromagnetic radiation behaves as particles or quanta of energy. A quantum of energy is called a photon.
(2) If the frequency of radiation is v, irrespective of the intensity of radiation, each photon has energy hv and momentum hv/c, where c is the speed of light in free space.
(3) Intensity of radiation corresponds to the number of photons incident per unit time per unit surface area.
(4) Photons are electrically neutral and have zero rest mass.
(5) A photonRarticle collision (such as a photon-electron collision) obeys (he principles of conservation of energy arid momentum. However, in such a collision, an incident photon may be absorbed and/or a new photon may be created, so that the number of photons may not be conserved. For example, a γ-ray photon of energy greater than 1.02 MeV can produce an electron-positron pair in the presence of a heavy nucleus such as lead. In this case, the photon disappears and two particles (electron and positron) are produced. The total energy and momentum are conserved.
[Note: Photons have unit spin. Photons are influenced by gravitational field. A gravitational field can change the path and/or frequency/wavelength of a photon. Even after more than a century of its introduction, the concept of photon is not fully understood.]
![]()
Question 35.
What is the momentum of a photon of energy 3 × 10-19 J? [c = 3 × 108 m/s]
Answer:
Momentum of a photon = \(\frac{E}{c}=\frac{3 \times 10^{-19}}{3 \times 10^{8}}\)
= 10-27 kg∙m/s .
Question 36.
What is the momentum of a photon of wave length 3.315 × 10-7 m? [h = 6.63 × 10-34J∙s]
Answer:
Momentum of a photon \(\frac{h}{\lambda}=\frac{6.63 \times 10^{-34}}{3.315 \times 10^{-7}}\)
= 2 × 10-27 kg∙m/s .
37. Solve the following :
Question 1.
Find the momentum of a photon if the wavelength of the radiation is 6630 Å.
Solution:
Data : λ = 6.63 × 10-7 m, h = 6.63 × 10-34 J∙s
Energy of a photon, E = hv
c = λv
The momentum of a photon,
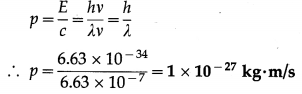
Question 2.
Find the momentum of a photon of energy 3 eV.
Solution :
Data : e = 1.602 × 10-19 C,
E = 3 eV = 3 × 1.6 × 10-19 J, c = 3 × 108 m/s
The momentum of the photon,
p = \(\frac{E}{c}=\frac{3 \times 1.6 \times 10^{-19}}{3 \times 10^{8}}\) = 1.6 × 10-27 kg∙m/s
Question 3.
Find the energy of a photon with momentum 2 × 10-27 kg∙m/s.
Solution :
Data : p = 2 × 10-27 kg∙m/s
The energy of the photon,
E = pc = (2 × 10-27)(3 × 108) = 6 × 10-19 J
= \(\frac{6 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV = 3.75 eV
Question 38.
What is a photocell or photoelectric cell?
Describe its construction and working with a neat labelled diagram.
Answer:
A photocell or photoelectric cell is a device in which light energy is converted into electrical energy by photoelectric effect.
Construction : One form of the photoelectric cell shown in figure consists of a highly evacuated or gas-filled glass tube, an emitter (cathode) and a collector (anode). The light enters through a quartz window W and falls on the semicylindrical cathode C coated with a photosensitive metal. The anode is in the form of a straight wire of platinum or nickel, coaxial with the cathode.
If the cell is required to respond to the visible part of the spectrum, the cathode is coated with potassium or rubidium and the quartz window is replaced by glass. If the UV radiation only is to be used, cadmium is used as the sensitive surface. The cell is either highly evacuated (for accurate photometry) or filled with an inert gas at low pressure (if a larger current is desired).
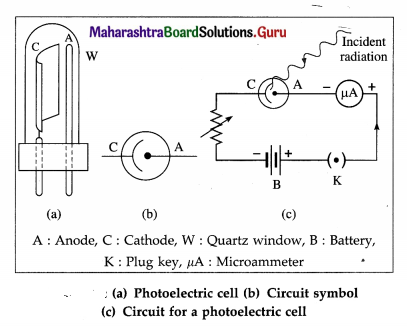
Working : A photocell is connected in series with a battery and a variable resistance. The collector is kept at a positive potential with respect to the emitter. When UV radiation or visible light of frequency greater than the threshold frequency for the emitter surface is incident on the emitter, the ejected photoelectrons are focused by the cylindrical emitter (cathode) towards the collector (anode).
The photoelectrons collected by the collector constitute a photocurrent which may be measured by a microammeter in series with the photocell, as in an exposure meter or lux meter. Otherwise, the photocurrent is used to operate a relay circuit as in an alarm, or to drive the coils of a speaker as in reading an optical sound track in a cine film. The photocurrent becomes zero when the incident light is cut off.
![]()
Question 39.
State any four applications of a photoelectric cell.
OR
Explain any two applications of photoelectric effect.
Answer:
Applications of a photoelectric cell :
(1) In an exposure meter used for photography: A photographic film must be exposed to correct amount of light which, for a given film speed and lens aperture, depends on the exposure time. An exposure meter consists of a photocell, battery and microammeter connected in series. When the meter is directed towards an object, light reflected by the object enters the photocell and the photocurrent is directly proportional to the intensity of this light.
Usually, the microammeter scale is calibrated to read the exposure time directly.
(2) As a lux meter : A lux meter is used to measure the illumination and is similar in working to an exposure meter, except that the scale is calibrated to read the illumination in lux.
(3) In a burglar alarm as a ‘normally closed’ light- activated switch : It consists of a photocell, battery, relay system and a small directed light source. The radiation from the source falls on the photocell. If the light beam is interrupted by an intruder, the photoelectric current stops. This activates the relay system which sets off an alarm.
(4) In an optical reader of sound track in a cine film : The sound track of a cine film is recorded on one side of the positive film that is run in a cinema hall. The track consists of a dark wavy patch modulated by the recorded sound. Light from the projector lamp also passes through the sound track and falls on a photocell behind. The photocurrent is proportional to the transmitted light intensity and changes according to the recorded sound wave. The photocurrent is amplified and is used to drive the loudspeaker.
(5) A photocell can be used to switch on or off street lights.
Question 40.
Name any two instruments in which photo-electric effect is used.
Answer:
Exposure meter used in photography and lux meter.
Question 41.
State the de Broglie hypothesis and the de Broglie equation.
Answer:
De Broglie hypothesis : Louis de Broglie (1892-1987), French physicist, proposed (in 1924) that the wave-particle duality may not be unique to light but a universal characteristic of nature, so that a particle of matter in motion also has a wave or periodicity associated with it which becomes evident when the magnitude of Planck’s constant h cannot be ignored.
De Broglie equation : A particle of mass m moving with a speed v should under suitable experimental conditions exhibit the characteristics of a wave of wavelength
λ = \(\frac{h}{m v}=\frac{h}{p}\)
where p = mv = momentum of the particle.
The relation λ = h/p is called the de Broglie equation, and the wavelength λ associated with a particle momentum is called its de Broglie wavelength. The corresponding waves are termed as matter waves or de Broglie waves or Schrodinger waves.
[Note: This hypothesis was revolutionary at that time and accepted by others because Einstein supported it. Erwin Schrodinger (1887-1961), Austrian physicist, formulated a wave equation for matter waves.]
Question 42.
Explain the concept of de Broglie waves or matter waves.
Answer:
According to de Broglie, a particle of mass m moving with a speed v should, under suitable experimental conditions, exhibit the characteristics of a wave of wavelength
λ = \(\frac{h}{m v}=\frac{h}{p}\) … ………. (1)
where p = mv ≡ momentum of the particle and h is Planck’s constant.
This dual character of matter contained in Eq. (1) is usually referred to as the wave nature of matter or matter waves. They are a set of waves that represent the behaviour of particles under appropriate conditions. It does not, however, mean that the particles themselves are oscillating in space.
Interpretation of matter waves by Max Born (1882-1970), German bom British physicist, is that they are waves of probability, since the square of their amplitude at a given point is linked to the likelihood of finding the particle there. Hence, the wavelength λ may be regarded as a measure of the degree to which the energy is localized. If λ is exceedingly small, the energy is very localized and the particle character of the object is dominant. On the other hand, if λ is very large, the energy is distributed over a large volume; under these circumstances, the wave behaviour is dominant.
The wave nature of material particles such as the electron, neutron and helium atom has been established experimentally beyond doubt.
![]()
Question 43.
Derive an expression for the de Broglie wavelength associated with an electron accelerated from rest through a potential difference V. Consider the nonrelativistic case.
Answer:
Consider an electron accelerated from rest through a potential difference V. Let v be the final speed of the electron. We consider the nonrelativistic case, v << c, where c is the speed of light in free space. The kinetic energy acquired by the electron is
\(\frac{1}{2}\) mv2 = \(\frac{1}{2m}\) (mv)2 = eV ………. (1)
where e and m are the electronic charge and mass (nonrelativistic).
Therefore, the electron momentum,
p = mv = \(\sqrt{2 m e V}\) ………… (2)
The de Broglie wavelength associated with the electron is
λ = \(\frac{h}{p}\) ………….. (3)
where h is Planck’s constant.
From Eqs. (2) and (3),
λ = \(\frac{h}{\sqrt{2 m e V}}\)
Equation (4) gives the required expression.
[Note : Substituting the values of h = 6.63 × 10-34 J-s, m = 9.1 × 10-31 kg, e = 1.6 × 10-19 C in Eq. (4), we obtain λ = \(\sqrt{150 / V}\) × 10-10 m = \(\sqrt{150 / V}\) Å = \(12.25 / \sqrt{V}\) Å, where V is in volt. Therefore, electrons accelerated from rest through 150 volts have a de Broglie wavelength of 1 Å. This corresponds to the X-ray region of the electromagnetic spectrum.]
Question 44.
Derive an expression for the de Broglie wavelength.
Answer:
For the particle-like aspects of electromagnetic radiation, we consider radiation to consist of particles whose motion is governed by the wave propagation properties of certain associated waves.
To determine the wavelength of such waves, consider a beam of electromagnetic radiation of frequency v whose quanta have energy E.
E = hv
where h is the Planck constant.
For a quantum of radiation of momentum p, by Einstein’s theory,
E = pc
where c is the speed of propagation of the radiation in free space.
∴ pc = hv
∴ p\(\frac{c}{v}\) = h
The wavelength X of the associated wave governing the motion of the quanta is given by the relation
λ = c/v.
∴ pλ = h ∴ λ = \(\frac{h}{p}\)
V ’
This is the required expression.
Question 45.
What is the de Broglie wavelength associated with a particle having momentum 10-26 kg∙m/s? [h = 6.63 × 10-34 J∙s]
Answer:
The de Broglie wavelength associated with the particle,
λ = \(\frac{h}{p}=\frac{6.63 \times 10^{-34}}{10^{-26}}\) = 6.63 × 10-8 m
Question 46.
With a neat labelled diagram, describe the Davisson and Germer experiment in support of the concept of matter waves.
Answer:
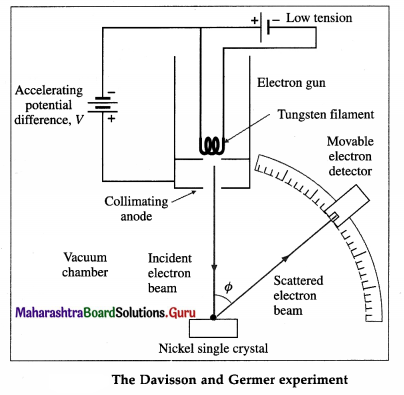
Davisson and Germer experiment (1927) :
The experimental arrangement, as shown in below figure, consists of an electron gun, a crystal holder and an electron detector enclosed in a vacuum chamber. In the electron gun, electrons emitted by a heated metallic filament (cathode) are accelerated by a potential difference V between the cathode and the anode, and emerge through a small hole in the anode. The electron gun directs a narrow collimated beam of electrons at a nickel crystal. Scattered electrons are detected by a movable detector.
The angle Φ between the incident and scattered beams is the scattering angle. Polar graphs of the number of scattered electrons as a function of angle Φ are plotted for different values of the accelerating voltage.
It is found that the electrons are scattered at a certain angle more than at others. Also, the number of scattered electrons in this direction is maximum for a certain kinetic energy of the incident electrons.
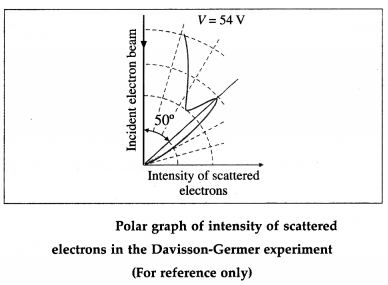
The detector registered a maximum at a scattering angle Φ = 50° for V = 54 V from figure. This electron diffraction can be understood only on the basis of de Broglie’s matter wave model. The de Broglie wavelength of the electrons accelerated from rest through a p.d. of 54 V is λ = \(\sqrt{150 / 54}\) Å = 1.67 Å
The wavelength calculated from the diffraction effect is 1.65 Å, nearly 1.67 Å.
[ Note : Clinton Joseph Davisson (1881 -1958), US physicist. Lester Halbert Germer (1896-1971), US physicist.]
![]()
47. Solve the following
Question 1.
(2) Find the momentum of the electron having de Brogue wavelength of 0.5 Å.
Solution:
Data: λ = 0.5Å = 5 × 10-11 m, h = 6.63 × 10-34 J∙s
The momentum of the electron, .
p = \(\frac{h}{\lambda}=\frac{6.63 \times 10^{-34}}{5 \times 10^{-11}}\) = 1.326 × 10-23 kg∙m/s
Question 2.
A cracker of mass M at rest explodes in two parts of masses m1 and m2 with non-zero velocities. Find the ratio of the de Broglie wavelengths of the two particles.
Solution:
The cracker has zero momentum before explosion. By the principle of conservation of momentum, after the explosion,
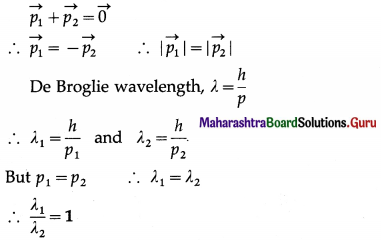
Question 3.
Calculate the de Brogue wavelength of a proton if it is moving with the speed of 2 × 105 m/s. [mp = 1.673 × 10-27 kg]
Solution:
Data: mp = 1673 × 10-27 kg, v = 2 × 105 m/s, h = 6.63 × 10-34 J∙s
De Brogue wavelength, λ = \(\frac{h}{p}=\frac{h}{m v}\)
∴ λ = \(\frac{6.63 \times 10^{-34}}{\left(1.673 \times 10^{-27}\right)\left(2 \times 10^{5}\right)}\)
= 1.981 × 10-12 m
Question 4.
Calculate the de Brogue wavelength of an electron moving with \(\frac{1}{300}\) of the speed of light in vacuum. [Take m (electron) = 9.11 × 10-28 g]
Solution:

Question 5.
Find the de Broglie wavelength of a dust particle of radius 1 μm and density 2.5 g/cm3 drifting at 2.2 m/s. (Take π = 3.14)
Solution:
Data : r = 1 μm = 10-6 m, h = 6.63 × 10-34 J∙s, ρ = 2.5 g/cm3 = 2.5 × 103 kg/m3, v = 2.2 m/s,
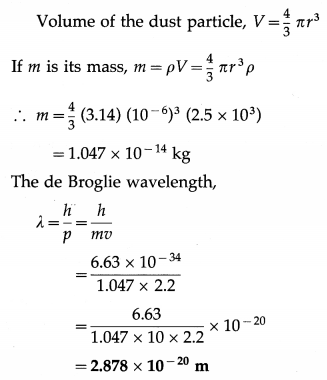
![]()
Question 6.
Find the de Broglie wavelength associated with a car (mass = 1000 kg) moving at 20 m/s.
Solution:
Data : m = 1000 kg, v = 20 m/s,h = 6.63 × 10-34 J∙s
The de Broglie wavelength,
λ = \(\frac{h}{p}=\frac{h}{m v}=\frac{6.63 \times 10^{-34}}{(1000)(20)}\) = 3.315 × 10-38 m
Question 7.
What is the de Broglie wavelength of an electron accelerated from rest through 25000 volts ?
Solution:
Data: V = 25 × 103 V, e = 1.6 × 10-19 C, me = 9.11 × 10-31 kg, h = 6.63 × 10-34 J∙s
Kinetic energy of the electron,
E = eV
=(1.6 × 10-19)(25 × 103 V)
=4 × 10-15 j
The momentum of the electron,

I Note : Here, the kinetic energy of the electron, 25 keV, is far less than the electron’s rest mass energy (m0c2) which is about 0.51 MeV. Hence, it is a nonrelativistic case.]
Question 8.
Find the de Broglie wavelength of a proton accelerated from rest by a potential difference of 50 V. [mp = 1.673 × 10-27 kg]
Solution:
Data : mp = 1.673 × 10-27 kg, h = 6.63 × 10-34 J∙s, KE = 50 eV = 50 × 1.6 × 10-19 J = 8 × 10-18 J
The kinetic energy of the proton,
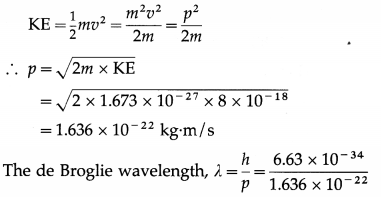
= 4.053 × 10-12 m = 0.04053 A
Question 9.
A moving electron and a photon have the same de Brogue wavelength. Show that the electron possesses more energy than that carried by the photon.
Solution:
The de Brogue wavelength, λ = \(\frac{h}{p}\)
If an electron and a photon have the same de Brogue wavelength, they must have the same momentum, p.
For the photon, Ep = hv = \(\frac{h c}{\lambda}=\left(\frac{h}{\lambda}\right) c\) = pc … (1)
For the electron, mass m = \(\frac{m_{0}}{\sqrt{1-v^{2} / c^{2}}}\)
where m0 is the rest mass of the electron and y is its speed.
∴ \(m^{2}\left(\frac{c^{2}-v^{2}}{c^{2}}\right)=m_{0}^{2}\)
∴ m2c4 – m2v2c2 = \(m_{0}^{2} c^{4}\)
∴ (m2c4 = (m0c2)2 + p2c2 (where p = mv)
∴ \(E_{\mathrm{e}}^{2}\) = (m0c2)2 + p2c2
where Ee = mc2 = m0c2 + K is the total energy of the electron, m0c2 being he rest mass energy and K, the kinetic energy.
∴ Ee = \(\sqrt{\left(m_{0} c^{2}\right)^{2}+p^{2} c^{2}}\) …………. (2)
From Eqs. (1) and (2), we have Ee > Ep.
[Note : The result m = \(\frac{m_{0}}{\sqrt{1-v^{2} / c^{2}}}\) was obtained by Einstein in 1905.]
Multiple Choice Questions
Question 1.
The energy of a photon of wavelength λ is
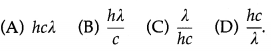
Answer:
(D) \(\frac{h c}{\lambda}\)
Question 2.
The number of photoelectrons emitted
(A) varies inversely with the frequency of radiation
(B) varies directly with the frequency of radiation
(C) varies inversely with the intensity of radiation
(D) varies directly with the intensity of radiation.
Answer:
(D) varies directly with the intensity of radiation.
![]()
Question 3.
A metal emits no electrons if the incident light energy falls below certain threshold. For photo-emission, you would decrease
(A) the intensity of light
(B) the frequency of light
(C) the wavelength of light
(D) the collector potential.
Answer:
(C) the wavelength of light
Question 4.
When light of wavelength 5000 Å falls on a metal surface whose photoelectric work function is 1.9 eV, the kinetic energy of the most energetic photoelectrons is
(A) 0.59 eV
(B) 1.39 eV
(C)1.59eV
(D)2.59eV.
Answer:
(A) 0.59 eV
Question 5.
The threshold wavelengths for photoemission of two metals A and B are 300 nm and 600 nm, respectively. The ratio ΦA/ΦB of their photoelectric work functions is
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(C) 2
(D) 4.
Answer:
(C) 2
Question 6.
The photoelectric threshold wavelength of a certain metal is 3315 Å. Its work function is
(A) 6 × 10-19 J
(B) 7.286 × 10-19 J
(C) 9 × 10-19 J
(D) 9.945 × 10-19 J.
Answer:
(A) 6 × 10-19 J
Question 7.
The photoelectric work function of a certain metal is 2.5 eV. If the metal is separately irradiated with photons of energy 3 eV and 4.5 eV, the ratio of the respective stopping potentials is
(A) 1
(B) \(\frac{2}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{1}{5}\)
Answer:
(B) \(\frac{2}{3}\)
![]()
Question 8.
Sodium and copper have photoelectric work functions 2.3 eV and 4.7 eV, respectively. The ratio λ0Na/λoCu 0f the threshold wavelengths for photoemission is about
(A) 1 : 4
(B) 1 : 2
(C) 2 : 1
(D) 4 : 1.
Answer:
(C) 2 : 1
Question 9.
When light of wavelength A falls on the cathode of a photocell, the kinetic energy of the most energetic photoelectrons emitted is £. If light of wavelength λ/2 is used, what can be said about the new value E’?
(A) E’ = E/2
(B) E’ = E
(C) E’ = 2E
(D) E’ > 2E.
Answer:
(D) E’ > 2E.
Question 10.
Electrons are ejected from a metallic surface when light with a wavelength of 6250 Å is used. If light of wavelength 4500 Å is used instead,
(A) there may not be any photoemission
(B) the photoelectric current will increase
(C) the stopping potential will increase
(D) the stopping potential will decrease.
Answer:
(C) the stopping potential will increase
Question 11.
UV radiation of energy 6.2 eV falls on molybdenum surface whose photoelectric work function is 4.2 eV. The kinetic energy of the fastest photoelectrons is
(A) 3.2 × 10-19 J
(B) 3.52 × 10-19 J
(C) 6.72 × 10-19 J
(D) 9.92 × 10-19 J.
Answer:
(A) 3.2 × 10-19 J
Question 12.
In a photocell, increasing the intensity of light increases
(A) the stopping potential
(B) the photoelectric current
(C) the energy of the incident photons
(D) the maximum kinetic energy of the photo-electrons.
Answer:
(B) the photoelectric current
![]()
Question 13.
In a photocell, doubling the intensity of the incident light (v > v0) doubles the
(A) stopping potential
(B) threshold frequency
(C) saturation current
(D) threshold wavelength.
Answer:
(C) saturation current
Question 14.
In the usual notation, the momentum of a photon is
(A) hvc
(B) \(\frac{h v}{c}\)
(C) \(\frac{h \lambda}{c}\)
(D) hλc.
Answer:
(B) \(\frac{h v}{c}\)
Question 15.
The momentum of a photon with λ = 3315 Å is
(A) 2 × 10-27 kg∙m/s
(B) 5 × 10-27 kg∙m/s
(C) 2 × 10-41 kg∙m/s
(D) 5 × 10-41 kg∙m/s.
Answer:
(A) 2 × 10-27 kg∙m/s
Question 16.
Let p and E denote the linear momentum and energy of emitted photon, respectively. If the wavelength of incident radiation is increased,
(A) both p and E decrease
(B) p increases and E decreases
(C) p decreases and E increases
(D) both p and E decrease.
Answer:
(C) p decreases and E increases
![]()
Question 17.
When radiations of wavelength λ1 and λ2 are incident on a certain photosensitive material, the energies of electron ejected are E1 and E2 respectively, such that E1 > E2. Then, Planck’s constant h is [c = speed of light]
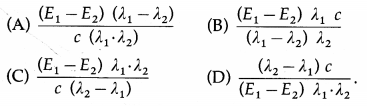
Answer:
(C) \(\frac{\left(E_{1}-E_{2}\right) \lambda_{1} \cdot \lambda_{2}}{c\left(\lambda_{2}-\lambda_{1}\right)}\)
Question 18.
If the frequency of incident light falling on a photosensitive material is doubled, then the kinetic energy of the emitted photoelectron will be
(A) the same as its initial value
(B) two times its initial value
(C) more than two times its initial value
(D) less than two times its initial value.
Answer:
(C) more than two times its initial value
Question 19.
The kinetic energy of emitted photoelectrons is independent of
(A) the frequency of incident radiation
(B) the intensity of incident radiation
(C) the wavelength of incident radiation
(D) the collector plate potential.
Answer:
(B) the intensity of incident radiation
Question 20.
In a photon-electron collision
(A) only total energy is conserved
(B) only total momentum is conserved
(C) both total energy and total momentum are conserved
(D) both total momentum and total energy are not conserved.
Answer:
(C) both total energy and total momentum are conserved
Question 21.
The de Broglie equation for the wavelength of matter waves is
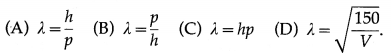
Answer:
(A) λ = \(\frac{h}{p}\)
Question 22.
The momentum associated with a photon is given by
(A) hv
(B) \(\frac{h v}{c}\)
(C) hE
(D) hλ
Answer:
(B) \(\frac{h v}{c}\)
![]()
Question 23.
The momentum of a photon of de Broglie wave-length 5000 Å is [h = 6.63 × 10-34 J∙s]
(A) 1.326 × 10-28 kg∙m/s
(B) 7.54 × 10-28 kg∙m/s
(C) 1.326 × 10-27 kg∙m/s
(D) 7.54 × 10-27 kg∙m/s.
Answer:
(C) 1.326 × 10-27 kg∙m/s
Question 24.
The de Broglie wavelength of a 100-m sprinter of mass 66 kg running at a speed of 10 m/s is about
[h = 6.63 × 10-34 J∙s]
(A) 10-34 m
(B) 10-33 m
(C) 10-32 m
(D) 10-31 m.
Answer:
(C) 10-32 m
Question 25.
Which of the following particles moving with the same speed has the longest de Broglie wavelength?
(A) Proton
(B) Neutron
(C) α-particle
(D) β-particle
Answer:
(D) β-particle
Question 26.
If p and E are respectively the momentum and energy of a photon, the speed of the photon is given by
(A) p∙E
(B) E/p
(C) (E/p)2
(D) \(\sqrt{E / p}\)
Answer:
(B) E/p
Question 27.
If the kinetic energy of a free electron is doubled, its de Broglie wavelength
(A) decreases by a factor of 2
(B) increases by a factor of 2
(C) decreases by a factor of \(\sqrt {2}\)
(D) increases by a factor of \(\sqrt {2}\).
Answer:
(C) decreases by a factor of \(\sqrt {2}\)
Question 28.
The de Broglie wavelength of an a-particle accelerated from rest through a potential difference V is λ. In order to have the same de Broglie wavelength, a proton must be accelerated from rest through a potential difference of .
(A) V
(B) 2V
(C) 4V
(D) 8V.
Answer:
(D) 8V.
Question 29.
If a photon has the same wavelength as the de Broglie wavelength of an electron, they have the same
(A) velocity
(B) energy
(C) momentum
(D) angular momentum.
Answer:
(C) momentum
![]()
Question 35.
The de Broglie wavelength of a grain of sand, of mass 1 mg, blown by a wind at the speed of 20 m/s is [h = 6.63 × 10-34 J∙s]
(A) 33.15 × 10-36m
(B) 33.15 × 10-33 m
(C) 33.15 × 10-30 m
(D) 33.15 × 10-30 m.
Answer:
(C) 33.15 × 10-30 m