Maharashtra Board 12th Maths Solutions Chapter 6 Differential Equations Ex 6.3

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.3 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 6 Differential Equations Ex 6.3

Question 1.
In each of the following examples verify that the given expression is a solution of the corresponding differential equation.
(i) xy = log y + c; \(\frac{d y}{d x}=\frac{y^{2}}{1-x y}\)
Solution:
xy = log y + c
Differentiating w.r.t. x, we get

Hence, xy = log y + c is a solution of the D.E.
\(\frac{d y}{d x}=\frac{y^{2}}{1-x y^{\prime}}, x y \neq 1\)

(ii) y = (sin^-1x)² + c; (1 – x²) \(\frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}=2\)
Solution:
y = (sin^-1 x)² + c …….(1)
Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get

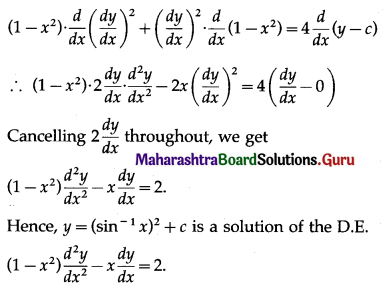
(iii) y = e^-x + Ax + B; \(e^{x} \frac{d^{2} y}{d x^{2}}=1\)
Solution:
y = e^-x + Ax + B
Differentiating w.r.t. x, we get

∴ \(e^{x} \frac{d^{2} y}{d x^{2}}=1\)
Hence, y = e^-x + Ax + B is a solution of the D.E.
\(e^{x} \frac{d^{2} y}{d x^{2}}=1\)

(iv) y = x^m; \(x^{2} \frac{d^{2} y}{d x^{2}}-m x \frac{d y}{d x}+m y=0\)
Solution:
y = x^m
Differentiating twice w.r.t. x, we get

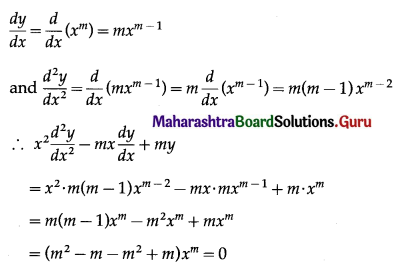
This shows that y = x^m is a solution of the D.E.
\(x^{2} \frac{d^{2} y}{d x^{2}}-m x \frac{d y}{d x}+m y=0\)

(v) y = a + \(\frac{b}{x}\); \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
Solution:
y = a + \(\frac{b}{x}\)
Differentiating w.r.t. x, we get

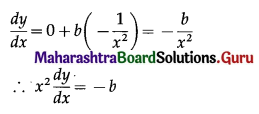
Differentiating again w.r.t. x, we get

Hence, y = a + \(\frac{b}{x}\) is a solution of the D.E.
\(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)

(vi) y = e^ax; x \(\frac{d y}{d x}\) = y log y
Solution:
y = e^ax
log y = log e^ax = ax log e
log y = ax …….(1) ……..[∵ log e = 1]
Differentiating w.r.t. x, we get
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = a × 1
∴ \(\frac{d y}{d x}\) = ay
∴ x \(\frac{d y}{d x}\) = (ax)y
∴ x \(\frac{d y}{d x}\) = y log y ………[By (1)]
Hence, y = e^ax is a solution of the D.E.
x \(\frac{d y}{d x}\) = y log y.

Question 2.
Solve the following differential equations.
(i) \(\frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}}\)
Solution:

(ii) log(\(\frac{d y}{d x}\)) = 2x + 3y
Solution:

(iii) y – x \(\frac{d y}{d x}\) = 0
Solution:
y – x \(\frac{d y}{d x}\) = 0
∴ x \(\frac{d y}{d x}\) = y
∴ \(\frac{1}{x} d x=\frac{1}{y} d y\)
Integrating both sides, we get
\(\int \frac{1}{x} d x=\int \frac{1}{y} d y\)
∴ log |x| = log |y| + log c
∴ log |x| = log |cy|
∴ x = cy
This is the general solution.

(iv) sec²x . tan y dx + sec²y . tan x dy = 0
Solution:
sec²x . tan y dx + sec²y . tan x dy = 0
∴ \(\frac{\sec ^{2} x}{\tan x} d x+\frac{\sec ^{2} y}{\tan y} d y=0\)
Integrating both sides, we get
\(\int \frac{\sec ^{2} x}{\tan x} d x+\int \frac{\sec ^{2} y}{\tan y} d y=c_{1}\)
Each of these integrals is of the type
\(\int \frac{f^{\prime}(x)}{f(x)} d x\) = log |f(x)| + c
∴ the general solution is
∴ log|tan x| + log|tan y | = log c, where c₁ = log c
∴ log |tan x . tan y| = log c
∴ tan x . tan y = c
This is the general solution.

(v) cos x . cos y dy – sin x . sin y dx = 0
Solution:
cos x . cos y dy – sin x . sin y dx = 0
\(\frac{\cos y}{\sin y} d y-\frac{\sin x}{\cos x} d x=0\)
Integrating both sides, we get
∫cot y dy – ∫tan x dx = c₁
∴ log|sin y| – [-log|cos x|] = log c, where c₁ = log c
∴ log |sin y| + log|cos x| = log c
∴ log|sin y . cos x| = log c
∴ sin y . cos x = c
This is the general solution.

(vi) \(\frac{d y}{d x}\) = -k, where k is a constant.
Solution:
\(\frac{d y}{d x}\) = -k
∴ dy = -k dx
Integrating both sides, we get
∫dy = -k∫dx
∴ y = -kx + c
This is the general solution.

(vii) \(\frac{\cos ^{2} y}{x} d y+\frac{\cos ^{2} x}{y} d x=0\)
Solution:
\(\frac{\cos ^{2} y}{x} d y+\frac{\cos ^{2} x}{y} d x=0\)
∴ y cos²y dy + x cos²x dx = 0
∴ \(x\left(\frac{1+\cos 2 x}{2}\right) d x+y\left(1+\frac{\cos 2 y}{2}\right) d y=0\)
∴ x(1 + cos 2x) dx + y(1 + cos 2y) dy = 0
∴ x dx + x cos 2x dx + y dy+ y cos 2y dy = 0
Integrating both sides, we get
∫x dx + ∫y dy + ∫x cos 2x dx + ∫y cos 2y dy = c₁ ……..(1)
Using integration by parts

Multiplying throughout by 4, this becomes
2x² + 2y² + 2x sin 2x + cos 2x + 2y sin 2y + cos 2y = 4c₁
∴ 2(x² + y²) + 2(x sin 2x + y sin 2y) + cos 2y + cos 2x + c = 0, where c = -4c₁
This is the general solution.

(viii) \(y^{3}-\frac{d y}{d x}=x^{2} \frac{d y}{d x}\)
Solution:

(ix) 2e^x+2y dx – 3 dy = 0
Solution:

(x) \(\frac{d y}{d x}\) = e^x+y + x² e^y
Solution:

∴ 3e^x + 3e^-y + x³ = -3c₁
∴ 3e^x + 3e^-y + x³ = c, where c = -3c₁
This is the general solution.

Question 3.
For each of the following differential equations, find the particular solution satisfying the given condition:
(i) 3e^x tan y dx + (1 + e^x) sec²y dy = 0, when x = 0, y = π
Solution:
3e^x tan y dx + (1 + e^x) sec²y dy = 0

(ii) (x – y²x) dx – (y + x²y) dy = 0, when x = 2, y = 0
Solution:
(x – y²x) dx – (y + x²y) dy = 0
∴ x(1 – y²) dx – y(1 + x²) dy = 0

When x = 2, y = 0, we have
(1 + 4)(1 – 0) = c
∴ c = 5
∴ the particular solution is (1 + x²)(1 – y²) = 5.

(iii) y(1 + log x) \(\frac{d x}{d y}\) – x log x = 0, y = e², when x = e
Solution:
y(1 + log x) \(\frac{d x}{d y}\) – x log x = 0

(iv) (e^y + 1) cos x + e^y sin x \(\frac{d y}{d x}\) = 0, when x = \(\frac{\pi}{6}\), y = 0
Solution:
(e^y + 1) cos x + e^y sin x \(\frac{d y}{d x}\) = 0

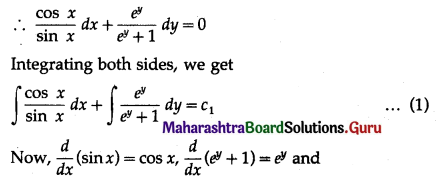
\(\int \frac{f^{\prime}(x)}{f(x)} d x\) = log|f(x)| + c
∴ from (1), the general solution is
log|sin x| + log|e^y + 1| = log c, where c₁ = log c
∴ log|sin x . (e^y + 1)| = log c
∴ sin x . (e^y + 1) = c
When x = \(\frac{\pi}{4}\), y = 0, we get
\(\left(\sin \frac{\pi}{4}\right)\left(e^{0}+1\right)=c\)
∴ c = \(\frac{1}{\sqrt{2}}\)(1 + 1) = √2
∴ the particular solution is sin x . (e^y + 1) = √2

(v) (x + 1) \(\frac{d y}{d x}\) – 1 = 2e^-y, y = 0, when x = 1
Solution:

This is the general solution.
Now, y = 0, when x = 1
∴ 2 + e⁰ = c(1 + 1)
∴ 3 = 2c
∴ c = \(\frac{3}{2}\)
∴ the particular solution is 2 + e^y = \(\frac{3}{2}\) (x + 1)
∴ 2(2 + e^y) = 3(x + 1).

(vi) cos(\(\frac{d y}{d x}\)) = a, a ∈ R, y (0) = 2
Solution:
cos(\(\frac{d y}{d x}\)) = a
∴ \(\frac{d y}{d x}\) = cos^-1 a
∴ dy = (cos^-1 a) dx
Integrating both sides, we get
∫dy = (cos^-1 a) ∫dx
∴ y = (cos^-1 a) x + c
∴ y = x cos^-1 a + c
This is the general solution.
Now, y(0) = 2, i.e. y = 2,
when x = 0, 2 = 0 + c
∴ c = 2
∴ the particular solution is
∴ y = x cos^-1 a + 2
∴ y – 2 = x cos^-1 a
∴ \(\frac{y-2}{x}\) = cos^-1a
∴ cos(\(\frac{y-2}{x}\)) = a

Question 4.
Reduce each of the following differential equations to the variable separable form and hence solve:
(i) \(\frac{d y}{d x}\) = cos(x + y)
Solution:

(ii) (x – y)² \(\frac{d y}{d x}\) = a²
Solution:

(iii) x + y \(\frac{d y}{d x}\) = sec(x² + y²)
Solution:

Integrating both sides, we get
∫cos u du = 2 ∫dx
∴ sin u = 2x + c
∴ sin(x² + y²) = 2x + c
This is the general solution.

(iv) cos²(x – 2y) = 1 – 2 \(\frac{d y}{d x}\)
Solution:

Integrating both sides, we get
∫dx = ∫sec²u du
∴ x = tan u + c
∴ x = tan(x – 2y) + c
This is the general solution.

(v) (2x – 2y + 3) dx – (x – y + 1) dy = 0, when x = 0, y = 1
Solution:
(2x – 2y + 3) dx – (x – y + 1) dy = 0
∴ (x – y + 1) dy = (2x – 2y + 3) dx
∴ \(\frac{d y}{d x}=\frac{2(x-y)+3}{(x-y)+1}\) ………(1)
Put x – y = u, Then \(1-\frac{d y}{d x}=\frac{d u}{d x}\)

∴ u – log|u + 2| = -x + c
∴ x – y – log|x – y + 2| = -x + c
∴ (2x – y) – log|x – y + 2| = c
This is the general solution.
Now, y = 1, when x = 0.
∴ (0 – 1) – log|0 – 1 + 2| = c
∴ -1 – o = c
∴ c = -1
∴ the particular solution is
(2x – y) – log|x – y + 2| = -1
∴ (2x – y) – log|x – y + 2| + 1 = 0