Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.2(C) Questions and Answers.
12th Maths Part 2 Indefinite Integration Exercise 3.2(C) Questions And Answers Maharashtra Board
I. Evaluate:
Question 1.
\(\int \frac{3 x+4}{x^{2}+6 x+5} d x\)
Solution:
Let I = \(\int \frac{3 x+4}{x^{2}+6 x+5} d x\)
Let 3x + 4 = A[\(\frac{d}{d x}\)(x2 + 6x + 5)] + B
= A(2x + B) + B
∴ 3x + 4 = 2Ax + (6A + B)
Comparing the coefficient of x and constant on both sides, we get
2A = 3 and 6A + B = 4
∴ A = \(\frac{3}{2}\) and 6(\(\frac{3}{2}\)) + B = 4
∴ B = -5
3x + 4 = \(\frac{3}{2}\) (2x + 6) – 5

Question 2.
\(\int \frac{2 x+1}{x^{2}+4 x-5} d x\)
Solution:
Let I = \(\int \frac{2 x+1}{x^{2}+4 x-5} d x\)
Let 2x + 1 = A[\(\frac{d}{d x}\)(x2 + 4x – 5)] + B
2x + 1 = A(2x + 1) + B
∴ 2x + 1 = 2Ax + (4A + B)
Comparing the coefficient of x and constant on both sides, we get
4A = 2 and 4A + B = 4
∴ A = \(\frac{3}{2}\) and 6(\(\frac{3}{2}\)) + B = 4
∴ B = -5
∴ 2x + 1 = \(\frac{3}{2}\)(2x + 1) – 5
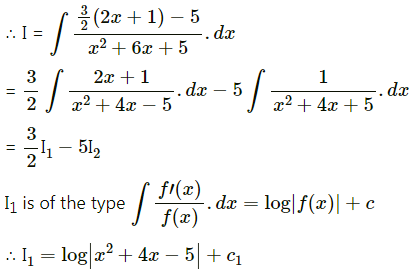
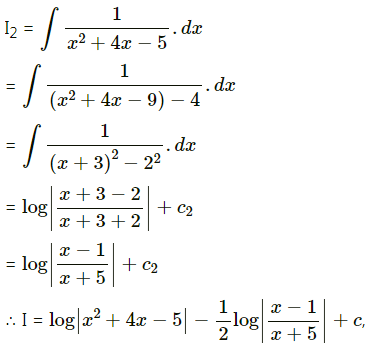
![]()
Question 3.
\(\int \frac{2 x+3}{2 x^{2}+3 x-1} d x\)
Solution:
Let I = \(\int \frac{2 x+3}{2 x^{2}+3 x-1} d x\)
Let 2x+ 3 = A[\(\frac{d}{d x}\)(2x2 + 3x – 1)] + B
2x + 1 = A(4x + 3) + B
∴ 2x + 1 = 4Ax + (3A + B)
Comparing the coefficient of x and constant on both sides, we get
4A = 2 and 3A + B = 3
∴ A = \(\frac{1}{2}\) and 3(\(\frac{1}{2}\)) + B = 3
∴ B = \(\frac{3}{2}\)
∴ 2x + 3 = \(\frac{1}{2}\)(4x + 3) + \(\frac{3}{2}\)

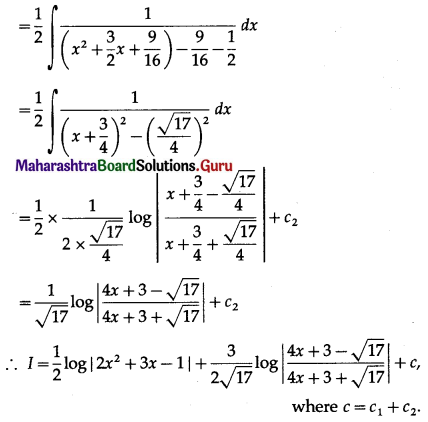
Question 4.
\(\int \frac{3 x+4}{\sqrt{2 x^{2}+2 x+1}} d x\)
Solution:
Let I = \(\int \frac{3 x+4}{\sqrt{2 x^{2}+2 x+1}} d x\)
Let 3x + 4 = A[\(\frac{d}{d x}\)(2x2 + 2x + 1)] + B
∴ 3x + 4 = A (4x + 2) + B
∴ 3x + 4 = 4Ax + (2A + B)
Comparing the coefficient of x and the constant on both the sides, we get
4A = 3 and 2A + B = 4
∴ A = \(\frac{3}{4}\) and 2(\(\frac{3}{4}\)) + B = 4
∴ B = \(\frac{5}{2}\)
∴ 3x + 4 = \(\frac{3}{4}\) (4x + 2) + \(\frac{5}{2}\)


![]()
Question 5.
\(\int \frac{7 x+3}{\sqrt{3+2 x-x^{2}}} d x\)
Solution:
Let I = \(\int \frac{7 x+3}{\sqrt{3+2 x-x^{2}}} d x\)
Let 7x + 3 = A[\(\frac{d}{d x}\)(3 + 2x – x2)] + B
7x + 3 = A(2 – 2x) + B
∴ 7x + 3 = -2Ax + (2A + B)
Comparing the coefficient of x and constant on both the sides, we get
-2A = 7 and 2A + B = 3


Question 6.
\(\int \sqrt{\frac{x-7}{x-9}} d x\)
Solution:
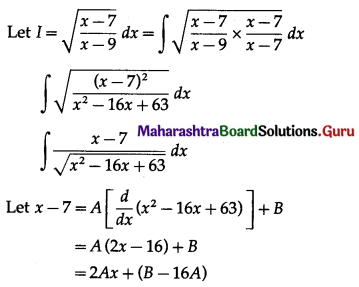
Comparing the coefficients of x and constant term on both sides, we get


![]()
Question 7.
\(\int \sqrt{\frac{9-x}{x}} d x\)
Solution:
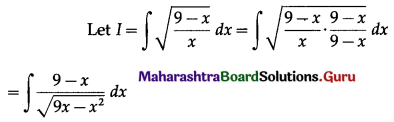


Question 8.
\(\int \frac{3 \cos x}{4 \sin ^{2} x+4 \sin x-1} d x\)
Solution:
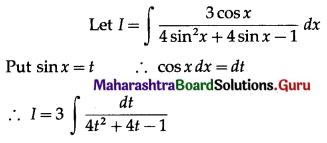

![]()
Question 9.
\(\int \sqrt{\frac{e^{3 x}-e^{2 x}}{e^{x}+1}} d x\)
Solution:


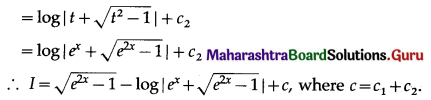
Class 12 Maharashtra State Board Maths Solution