Trigonometry – II Class 11 Maths 1 Exercise 3.3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.3 Questions and Answers.

11th Maths Part 1 Trigonometry – II Exercise 3.3 Questions And Answers Maharashtra Board

Question 1.
Find the values of:
i. sin $\frac{\pi}{8}$
ii. $\frac{\pi}{8}$
Solution:
We know that sin² θ = $\frac{1-\cos 2 \theta}{2}[/atex] Substituting θ = [latex]\frac{\pi}{8}$, we get

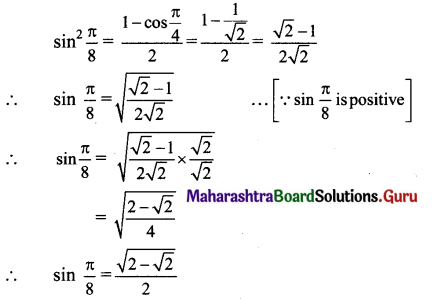
ii. We know that, cos² θ = $\frac{1+\cos 2 \theta}{2}$
Substituting θ = $\frac{\pi}{8}$, we get

Question 2.
Find sin 2x, cos 2x, tan 2x if sec x = $-\frac{13}{5}$, $\frac{\pi}{2}$ < x < π
Solution:
sec x = $-\frac{13}{5}$, $\frac{\pi}{2}$ < x < π
We know that
Sect² x = 1 + tan²x
tan²x = $\frac{169}{25}-1=\frac{144}{25}$
tan x = $\pm \frac{12}{5}$
Since $\frac{\pi}{2}$ < x < π
x lies in the 2nd quadrant.
tan x < 0

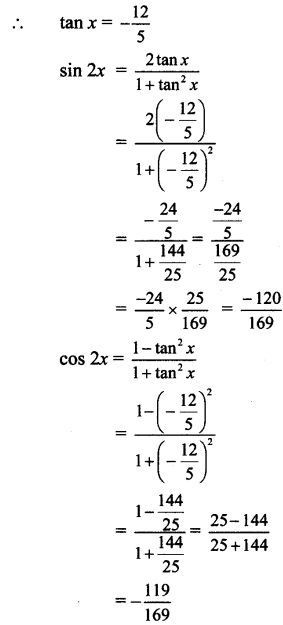
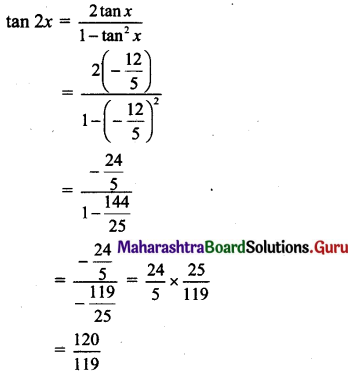
Question 3.
i. = tan² θ
Solution:
L. H. S. = $\frac{1-\cos 2 \theta}{1+\cos 2 \theta}$
= $\frac{2 \sin ^{2} \theta}{2 \cos ^{2} \theta}$
= 2tan² θ
= R.H.S.

ii. (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0
Solution:
L.H.S. = (sin 3x + sin x) sin x + (cos 3x – cosx)cosx
= sin 3x sin x + sin2 x + cos 3x cos x – cos² x
= (cos 3x cos x + sin 3x sin x)
— (cos²x — sin²x)
= cos (3x – x) – cos 2x
= cos 2x – cos 2x
= 0
= R.H.S.

iii. (cos x + cos y )² + (sin x + sin y)² = 4cos² $\left(\frac{x-y}{2}\right)$
Solution:
L.H.S. = (cos x + cos y)² + (sin x + sin y)²
= cos²x + cos²y + 2cos x.cos y + sin² x + sin²y + 2sin x.siny
= (cos²x + sin²x) + (cos²y + sin²y) + 2(cos x.cos y + si x.sin y)
= 1 + 1 +2cos(x – y)
= 2 + 2 cos (x – y)
= 2[1 + cos(x – y)]
= 2[2cos² [($\left(\frac{x-y}{2}\right)$)] … [∵ 1 + cos θ = 2 cos² $\frac{\theta}{2}$]
= 4 cos² ($\frac{x-y}{2}$)
= R.H.S.
[ Note: The question has been modified]

iv. (cos x – cos y)² + (sin x – sin y)² = 4sin² $\left(\frac{x-y}{2}\right)$
Solution:

L.H.S. = (cos x – cos y)² + (sin x – sin y)²
= cos²x + cos²y + 2cos x.cos y + sin² x + sin²y + 2sin x.siny
= (cos²x + sin²x) + (cos²y + sin²y) – 2(cos x.cos y + sin x.sin y)
= 1 + 1 – 2cos(x – y)
= 2 – 2 cos (x – y)
= 2[1 – cos(x – y)]
= 2[2sin² [($\left(\frac{x-y}{2}\right)$)] … [∵ 1 – cos θ = 2 sin² $\frac{\theta}{2}$]
= 4 sin² ($\frac{x-y}{2}$)
= R.H.S.

v. tan x + cot x = 2 cosec 2x
Solution:
L.H.S. = tan x + cot x

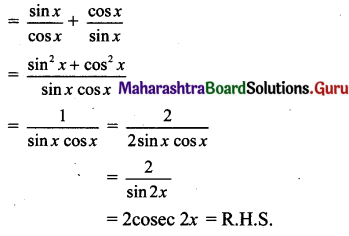
vi. $\frac{\cos x+\sin x}{\cos x-\sin x}-\frac{\cos x-\sin x}{\cos x+\sin x}$ = 2 tan 2x
Solution:

 

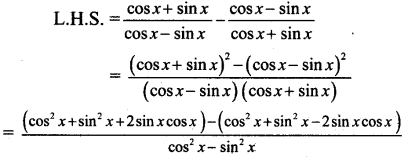
vii. $\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 8 x}}}$ = 2 cos x
Solution:

= 2 cos x
= R.H.S.
[Note : The question has been modified.]

viii. 16 sin θ cos θ cos 2θ cos 4θ cos 8θ = sin 16θ
Solution:
L.H.S. = 16 sin θ cos θ cos 2θ cos 4θ cos 8θ
= 8(2sinθ cosθ) cos2θ cos 4θ cos 8θ
= 8sin 2θ cos 2θ cos 4θ cos 8θ
= 4(2sin 2θ cos 2θ) cos 4θ cos 8θ
= 4sin 4θ cos 4θ cos 8θ
= 2(2sin 4θ cos 4θ) cos 8θ
= 2sin 8θ cos 8θ
= sin 16θ
= R.H.S.

ix. \( = 2 cot 2x
Solution:

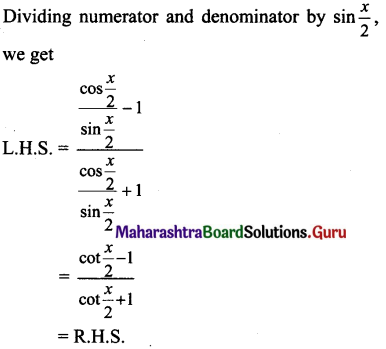
x. [latex]\frac{\cos x}{1+\sin x}=\frac{\cot \left(\frac{x}{2}\right)-1}{\cot \left(\frac{x}{2}\right)+1}\)
Solution:

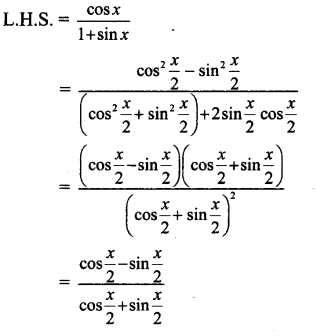
xi. $\frac{\tan \left(\frac{\theta}{2}\right)+\cot \left(\frac{\theta}{2}\right)}{\cot \left(\frac{\theta}{2}\right)-\tan \left(\frac{\theta}{2}\right)}=\sec \theta$
Solution:

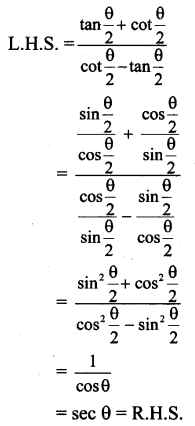
xii. $\frac{1}{\tan 3 \mathbf{A}-\tan A}-\frac{1}{\cot 3 A-\cot A}$ = cot 2A
Solution:

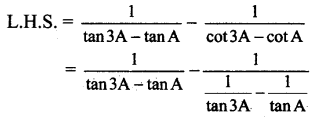
xiii. cos 7° cos 14° cos 28° cos 56° $\frac{\sin 68^{\circ}}{16 \cos 83^{\circ}}$
Solution:
L.H.S. = cos 7° cos 14° cos 28° cos 56°
= $\frac{1}{2 \sin 7^{\circ}}$(2sin 7°cos 7°)cos 14°cos 28°cos 56°
= $\frac{1}{2 \sin 7^{\circ}}$ (sin 14° cos 14° cos 28° cos 56°)
…[∵ 2sinθ cosθ = sin 2θ]
= [\frac{1}{2\left(2 \sin 7^{\circ}\right)}latex][/latex] (2sin 14° cos 14°) cos 28° cos 56°
= $\frac{1}{4 \sin 7^{\circ}}$(sin 28° cos 28° cos 56°)
= $\frac{1}{2\left(4 \sin 7^{\circ}\right)}$(2 sin 28° cos 28°) cos 56°
= $\frac{1}{8 \sin 7^{\circ}}$ (sin 56° cos 56°)
= $\frac{1}{8 \sin 7^{\circ}}$ (2 sin 56° cos 56°)
= $\frac{1}{16 \sin 7^{\circ}}$(sin 112°)
= $\frac{\sin \left(180^{\circ}-68^{\circ}\right)}{16 \sin \left(90^{\circ}-83^{\circ}\right)}$
= $\frac{\sin 68^{\circ}}{16 \cos 83^{\circ}}$
= R.H.S.

xiv. = $\frac{\sin ^{2}\left(-160^{\circ}\right)}{\sin ^{2} 70^{\circ}}+\frac{\sin \left(180^{\circ}-\theta\right)}{\sin \theta}$ = sec² 20°
Solution:

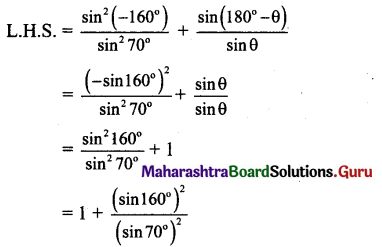
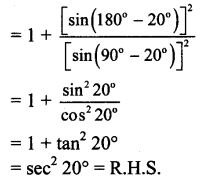
xv. $\frac{2 \cos 4 x+1}{2 \cos x+1}$ = (2 cos x – 1)(2 cos 2x – 1)
Solution:

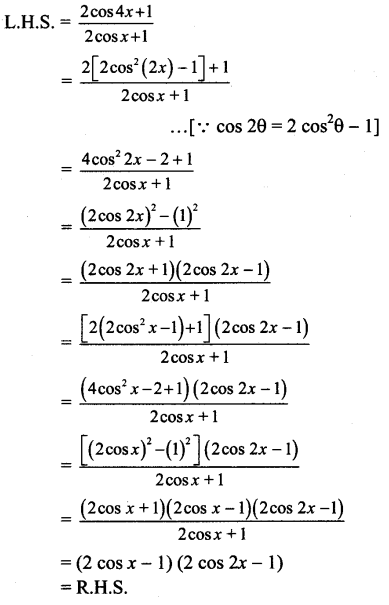
xvi. = cos² x + cos² (x + 120°) + cos²(x – 120°) = $\frac{3}{2}$
Solution:
L.H.S = cos² x + cos² (x + 120°) + cos²(x – 120°) =

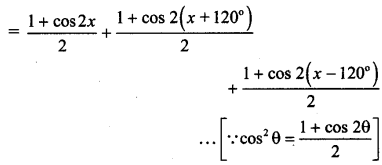
$\frac{3}{2}+\frac{1}{2}$ [cos 2x + cos(2x + 240°) + cos(2x 240°)]
= $\frac{3}{2}+\frac{1}{2}$(cos 2x + cos 2x cos 240°— sin 2x sin 240° + cos 2x cos 240° + sin 2x sin 240°)
= $\frac{3}{2}+\frac{1}{2}$(cos 2x + 2 cos 2x cos 240°)
= $\frac{3}{2}+\frac{1}{2}$ [cos 2x + 2 cos 2x cos( 180° + 60°)]
= $\frac{3}{2}+\frac{1}{2}$ [cos 2x + 2cos 2x(-cos 600)]
= $\frac{3}{2}+\frac{1}{2}$ [cos 2x —2 cos 2x($\frac{1}{2}$)]
= $\frac{3}{2}+\frac{1}{2}$ ( cos 2x – cos 2x)
= $\frac{3}{2}+\frac{1}{2}$ (0)
= $\frac{3}{2}$ = R.H.S.

xvii. 2 cosec 2x + cosec x = sec cot $\frac{x}{2}$
Solution:

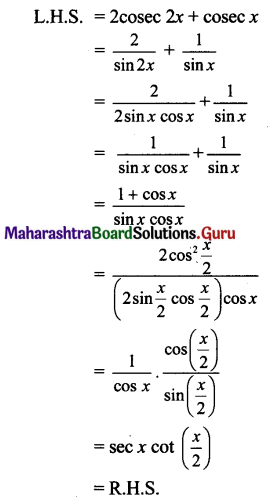
xviii. 4 cos x cos ($\frac{\pi}{3}$ + x) cos ($\frac{\pi}{3}$ – x) = cos 3x

Solution:

= cos³x — 3cos x.sin²x
= cos³ x — 3cos x (1— cos² x)
= cos³x — 3cos x + 3 cos³x
=4 cos³x — 3cos x
= cos 3x = R.H.S.
INote: The question has been modijìed.I

xix. sin x tan $\frac{x}{2}$ + 2cos x = $\frac{2}{1+\tan ^{2}\left(\frac{x}{2}\right)}$
Solution:
L.H.S. = sin x tan (x/2)+ 2cos x
= $\left(2 \sin \frac{x}{2} \cos \frac{x}{2}\right)\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)$ + 2cos x
= $\left(2 \sin \frac{x}{2} \cos \frac{x}{2}\right)\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)$ + 2 cos x
= 2sin² x/2 + 2cosx
= 1 – cosx + 2cosx
= 1 + cos x
=2cos² x/2
= $\frac{2}{\sec ^{2} \frac{x}{2}}=\frac{2}{1+\tan ^{2} \frac{x}{2}}$ =R.H.S.

Class 11 Maharashtra State Board Maths Solution 

• Exercise 3.1 Class 11 Maths 1
• Exercise 3.2 Class 11 Maths 1
• Exercise 3.3 Class 11 Maths 1
• Exercise 3.4 Class 11 Maths 1
• Exercise 3.5 Class 11 Maths 1
• Miscellaneous Exercise 3 Class 11 Maths 1