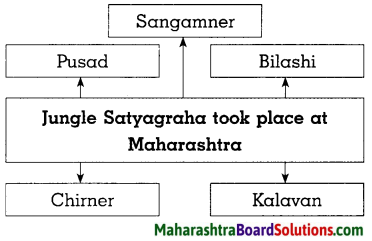
Balbharti Maharashtra State Board Class 8 History Solutions Chapter 12 India Gains Independence Notes, Textbook Exercise Important Questions and Answers.
Class 8 History Chapter 12 India Gains Independence Questions And Answers Maharashtra Board
India Gains Independence Class 8 Questions And Answers Chapter 12 Maharashtra Board
Class 8 History Chapter 12 India Gains Independence Textbook Questions and Answers
1. Rewrite the statements by choosing the appropriate options :
Question 1.
………………. was the head of the interim Government.
(a) Vallabhbhai Patel
(b) Mahatma Gandhi
(c) Pandit Jawaharlal Nehru
(d) Barrister Jinnah
Answer:
(c) Pandit Jawaharlal Nehru
Question 2.
The plan of creation of two independent nations, India and Pakistan, was made by ………………… .
(a) Lord Wavell
(b) Stafford Cripps
(c) Lord Mountbatten
(d) Pethick Lawrence
Answer:
(c) Lord Mountbatten
2. Answer the following in one sentence:
Question 1.
Which demand was advocated by Barrister Jinnah?
Answer:
The two nation theory and demand of separate Muslim nation named Pakistan was advocated by Barrister Jinnah.
![]()
Question 2.
Write the names of the ministers participating in Cabinet Mission.
Answer:
Pethick Lawrence, Stafford Cripps and A.V. Ale ander were the ministers participating in the Cabinet Mission.
3. Explain the following statements with reasons:
Question 1
The Indian National Congress approved the partition.
Answer:
- Lord Mountbatten prepared a plan of creation of India and Pakistan as two independent nations.
- Indian National Congress opposed the plan of partition as unity of the Nation was its basic stand.
- However, the Muslim League remained adamant on the creation of Pakistan.
- So, the Indian National Congress was left with no option but to accept the partition with complete helplessness.
Question 2.
The working of Interim Government could not run smoothly.
Answer:
- Muslim League demanded a separate Muslim nation of Pakistan.
- The followers of the Muslim League resorted to violent ways.
- Though the Muslim League declined to participate initially, they later participated in it.
- However, the leaders of the Muslim League adopted the policy of obstruction and therefore the Interim Government could not run smoothly.
![]()
Question 3.
The Wavell Plan could not succeed.
Answer:
The Wavell Plan could not succeed because
- Barrister Jinnah insisted that only Muslim League should have the right to suggest the names of Muslim representatives to the Viceroy’s Executive Council.
- The Congress opposed this and as a result, no consensus could be arrived at the meeting called by Lord Wavell.
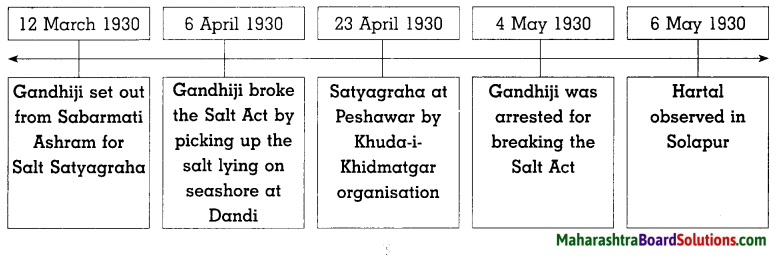
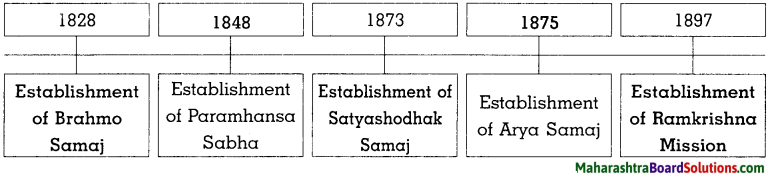
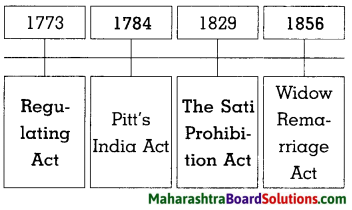
4. Write the events on the following timeline:
Question 1.
Answer:
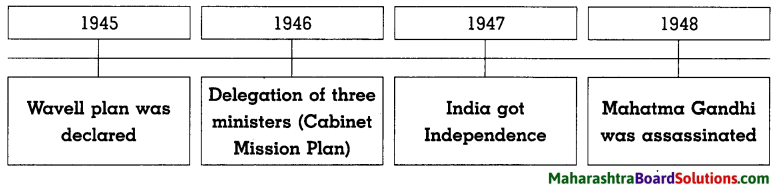
5. Answer the following questions in brief:
Question 1.
Why did the British took steps towards granting freedom to India?
Answer:
- The Indian freedom struggle had become very intense during the period of Second World War. The revolt of Navy and Air Force shook the foundation of the British empire.
- The demand for independence of India was gaining its strength.
- The Muslim League had demanded a separate Muslim nation.
- The followers of the Muslim League resorted to violence.
- The British government realised that it was necessary to take a serious note of it. They realised that their rule in India will not last long.
Accordingly, the British government started preparing plans for granting Independence to India.
![]()
Question 2.
Write information about the Mountbatten Plan.
Answer:
- England’s Prime Minister Atlee announced the transfer of power would be before June 1948.
- He appointed Lord Mountbatten as the Viceroy of India who was to arrange the transfer of power.
- He held discussions with the leaders of India.
- Mountbatten prepared a plan for partition of India i.e., creation of two independent nations, India and Pakistan.
- The Indian National Congress opposed the plan.
- But, due to the adamant behaviour of the Muslim League, the Indian National Congress accepted the Plan, with complete helplessness.
- On the basis of Mountbatten Plan, Indian Independence Act was passed.
Question 3.
Why did Muslim League declare to observe 16 August as Direct Action Day? What were its effects?
Answer:
- The Muslim League was adamant on the demand of Pakistan.
- It was not satisfied with Cabinet Mission plan as it had no provision for a separate Muslim state.
- 16th August 1946 was observed as Direct Action Day. ‘
- The followers of Muslim League resorted to violent ways.
- There were Hindu-Muslim riots in various parts of the country.
- There were massacres in the Noakhali region in the province of Bengal.
Project:
Collect information about the response of common people after gaining independence, with the help of various reference books as well as the internet.
Class 8 History Chapter 12 India Gains Independence Additional Important Questions and Answers
Rewrite the statements by choosing the appropriate options:
Question 1.
……………… put forth the two Nation theory and demanded a separate Muslim nation.
(a) Barrister Muhammad Ali Jinnah
(b) Chaudhary Rahmat Ali
(c) Dr. Muhammad Iqbal
(d) Lord Mountbatten
Answer:
(a) Barrister Muhammad Ali Jinnah
Question 2.
……………., Prime Minister of England, declared that England would leave its dominion on India before June 194 .
(a) Winston Churchill
(b) Linlithgo
(c) Atlee
(d) Mountbatten
Answer:
(c) Atlee
Question 3.
The ……………. initially refused to participate in the Interim Government.
(a) Indian National Congress
(b) Muslim League
(c) Hindu Mahasabha
(d) Kisan Sabha
Answer:
(b) Muslim League
Question 4.
The Muslim League decided to observe 16th August as ……………. Day.
(a) Non Violence
(b) Pakistan
(c) Direct Action
(d) Independence
Answer:
(c) Direct Action
Question 5.
As per ………………, India got independence.
(a) Mountbatten Plan
(b) Wctvell Plan
(c) Indian Independence Act
(d) Cabinet Mission
Answer:
(c) Indian Independence Act
![]()
Question 6.
Gandhiji was assassinated on ………………….. .
(a) 30 December 1947
(b) 30 January 194
(c) 30 March 194
(d) 2 October 194
Answer:
(b) 30 January 194
Name the following:
Question 1.
First person to present idea of free Muslim nation.
Answer:
Dr. Muhammad Iqbal
Question 2.
Last Viceroy of India.
Answer:
Lord Mountbatten
Question 3.
One who presented idea of Pakistan.
Answer:
Chaudhary Rahmat Ali
Question 4.
Went to Noakhali to stop violence
Answer:
Mahatma Gandhi.
Answer the following in one sentence:
Question 1.
What did Prime Minister Atlee declare in the British Parliament of England?
Answer:
Prime Minister Atlee declared in the British Parliament that England would transfer all of its government responsibility to Indians not later than June 1948.
![]()
Question 2.
Why did the Interim Government not work smoothly?
Answer:
The Interim Government could not work smoothly because the Muslim League followed the policy of obstruction.
Answer the following questions in brief:
Question 1.
Which were the important provisions :
of the Wavell Plan?
Answer:
- The Wavell Plan provided a proper representation to Muslims, Dalits and minorities in the Central and Provincial Legislatures.
- It provided for an equal number of Hindu and Muslim members in Viceroy’s Executive Council.
Question 2.
State the provisions of the Indian Independence Act.
Answer:
The Indian Independence Act was passed on the basis of Mountbatten Plan on 18th July, 1947.
According to the plan :
- Two Independent nations of India and Pakistan will come into existence on 15th August, 1947.
- Thereafter, the British Parliament would not retain any control over them.
- The British supremacy over the princely states would come to an end.
- They would be free to join either India or Pakistan or remain independent.
![]()
Question 3.
Write about the attainment of independence by India.
Answer:
- As per the Indian Independence Act, India was granted Independence on 15th August, 1947.
- A meeting of the Constituent Assembly was going on in the hall of Parliament House in Delhi in the midnight of 14th August.
- At the stroke of midnight, the Union Jack of Britain was lowered and in its place the Indian tricolour flag was unfurled.
Explain the following statements with reasons:
Question 1.
The Cabinet Mission Plan could not satisfy the political parties in India.
Answer:
The Cabinet Mission Plan could not satisfy the political parties in India because,
- The Indian National Congress was not happy with some of its provisions.
- The Muslim League was also dissatisfied with the plan as it did not provide for the creation of a separate Muslim state of Pakistan.
Question 2.
The joy of attainment of freedom was not untinted:
Answer:
- India attained Independence from the slavery of 150 years.
- But, the people were grieved due to the partition of the country and the terrible violence during that period.
So, the joy of attainment of freedom was not untinted.
![]()
Answer the following in detail:
Question 1.
State the genesis of Pakistan.
Answer:
- To weaken the national movement, the British adopted the policy of ‘divide and rule’. Its consequence was the establishment of ‘Muslim League’.
- Famous poet, Dr. Muhammad Iqbal put forth the idea of an independent Muslim state.
- Later Chaudhary Rahmat Ali coined the name Pakistan.
- Barrister Muhammad Ali Jinnah put forth the two nation theory and demanded a separate state for the Muslims naming Pakistan.
- Barrister Jinnah and the Muslim League started the propaganda that Indian National Congress was only a Hindu organisation and the Muslims have no benefit of it.
- Since their demand was not fulfilled, they observed ‘Direct Action Day’ and resorted to violence.
- The nation witnessed Hindu-Muslim riots in various parts.
- After the consent of the Indian National Congress to the Mountbatten Plan, the Indian Independence Act provided for the partition.
Question 2.
Why do you think everyone needs freedom?
Answer:
- Freedom is liberation from any kind of bondage.
- The rights of people are denied under foreign rule.
- Lot of restrictions are imposed by a foreign power.
- Under a foreign rule or dictatorship, power is not used for the welfare of the people but for the benefit of few.
- All round development of the citizens take place in an independent free state.
- Equality, Fraternity, Justice, Humanity are values which are cherished in freedom. Therefore, everyone needs freedom.
8th Std History Questions And Answers:
- Sources of History Class 8 History Questions And Answers
- Europe and India Class 8 History Questions And Answers
- Effects of British Rule Class 8 History Questions And Answers
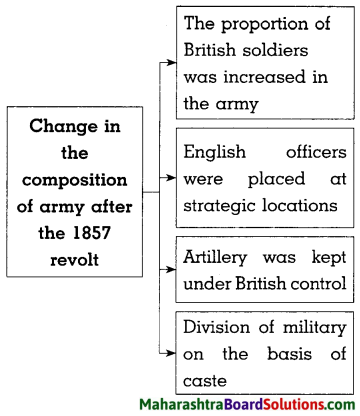
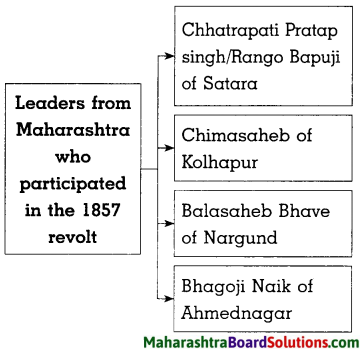
- The Freedom Struggle of 1857 Class 8 History Questions And Answers
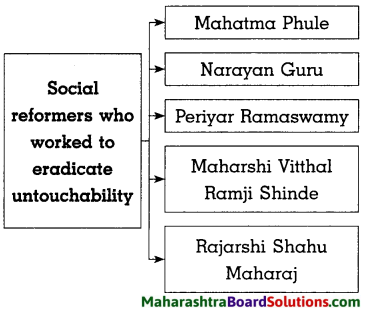
- Social and Religious Reforms Class 8 History Questions And Answers
- Beginning of Freedom Movement Class 8 History Questions And Answers
- Non-co-operation Movement Class 8 History Questions And Answers
- Civil Disobedience Movement Class 8 History Questions And Answers
- Last Phase of Struggle for Independence Class 8 History Questions And Answers
- Armed Revolutionary Movement Class 8 History Questions And Answers
- Struggle for Equality Class 8 History Questions And Answers
- India Gains Independence Class 8 History Questions And Answers
- Fulfillment of Struggle for Independence Class 8 History Questions And Answers
- Formation of State of Maharashtra Class 8 History Questions And Answers