Prasanna

12th Biology Chapter 10 Exercise Human Health and Diseases Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

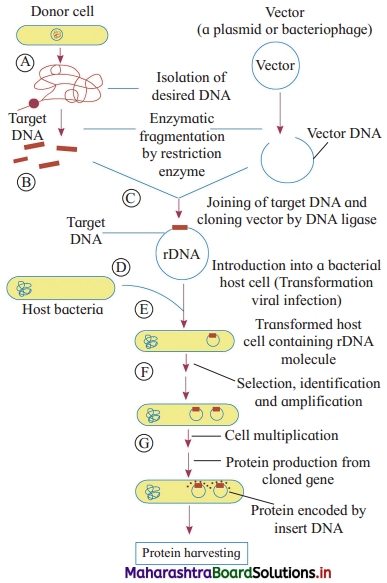
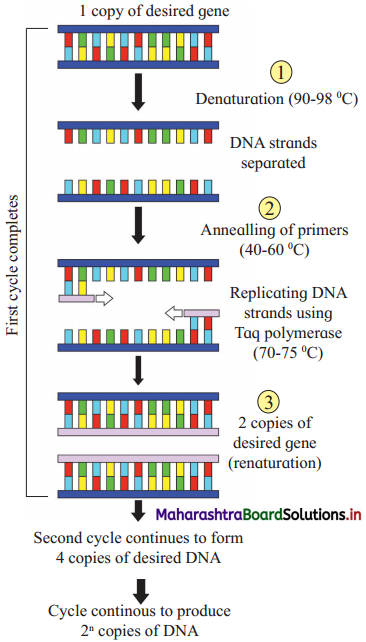
Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 10 Human Health and Diseases Textbook Exercise Questions and Answers.

Human Health and Diseases Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 10 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 10 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Which of the following is NOT caused by unsterilized needles?
(a) Elephantiasis
(b) AIDS
(e) Malaria
(d) Hepatitis
Answer:
(a) Elephantiasis

Question 2.
Opium derivative is …………………
(a) Codeine
(b) Caffeine
(c) Heroin
(d) Psilocybin
Answer:
(c) Heroin

Question 3.
The stimulant present in tea is …………………
(a) tannin
(b) cocaine
(C) caffeine
(d) crack
Answer:
(c) caffeine

Question 4.
WhIch of the following Is caused by smoking?
(a) Liver cirrhosis
(b) Pulmonary tuberculosis
(c) Emphysema
(d) Malaria
Answer:
(c) Emphysema

Question 5.
An antibody is …………………
(a) molecuic that binds specifically an antigen
(b) WBC which invades bacteria
(c) secretion of mammalian RBC
(d) cellular component of blood
Answer:
(a) molecule that binds specifically an antigen

Question 6.
The antiviral proteins released by a virus-infected cell are called …………………
(a) histamines
(b) interferons
(c) pyrogens
(d) allergens
Answer:
(b) interferons

Question 7.
Both B-cells and T-cells are derived from …………………
(a) lymph nodes
(b) thymus glands
(c) liver
(d) stem cells in bone marrow
Answer:
(b) thymus glands

Question 8.
Which of the following diseases can be contracted by droplet infection?
(a) Malaria
(b) Chicken pox
(c) Pneumonia
(d) Rabies
Answer:
(c) Pneumonia

Question 9.
Confirmatory test used for detecting HIV infection is …………………
(a) ELISA
(b) Western blot
(c) Widal test
(d) Eastern blot
Answer:
(b) Western blot

Question 10.
Elephantiasis is caused by …………………
(a) W. barterofti
(b) P. vivax
(c) Bedbug
(d) Elephant
Answer:
(a) W. bancrofti

Question 11.
Innate immunity is provided by …………………
(a) phagocytes
(b) antibody
(c) T-lymphocytes
(d) B-lymphocytes
Answer:
(c) T-lymphocytes

2. Short Answer Questions

Question 1.
What is the source of cocaine?
Answer:
Source of cocaine is coca plant – Erythroxylum coca.

Question 2.
Name one disease caused by smoking.
Answer:
Emphysema. (Damaged and enlarged lungs causing breathlessness)

Question 3.
Which cells stimulate B-cells to form antibodies ?
Answer:
Helper T-cells stimulate B-cells to form antibodies.

Question 4.
What does the abbreviation AIDS stand for?
Answer:
AIDS stands for Acquired Immuno Deficiency Syndrome.

Question 5.
Name the causative agent of typhoid fever.
Answer:
Salmonella typhi

Question 6.
What is Rh factor?
Answer:
Antigen ‘D’ present on the surface of RBCs is known as Rh factor.

Question 7
What is schizont?
Answer:
Schizont is a ring-like form produced from merozoites inside the erythrocytes of human beings, infected by Plasmodium, which again forms new merozoites.

Question 8.
Name the addicting component found in tobacco.
Answer:
Nicotine

Question 9.
Name the pathogen causing Malaria.
Answer:
Plasmodium vivax

Question 10.
Name the vector of Filariasis.
Answer:
Female Culex mosquito

Question 11.
Name of the causative agent of ringworm.
Answer:
Trichophyton

Question 12.
Health
Answer:
Health is defined as the state of complete physical, mental and social well¬being and not merely the absence of disease or infirmity.

3. Short Answer Questions

Question 1.
What are acquired diseases?
Answer:
Diseases which are developed after the birth of an individual are called acquired diseases. These are of two types, viz. (a) Communicable or infectious diseases and (b) Non- communicable or Non-infectious diseases. Communicable or infectious diseases are transmitted from infected person to another healthy person either directly or indirectly. They are caused due to pathogens like viruses, bacteria, fungi, helminth worms, etc. Non-communicable or Non-infectious diseases cannot be transmitted from infected person to another healthy one either directly or indirectly.

Question 2.
Antigen and antibody.
Answer:

Antigen	Antibody
1. Antigens are foreign proteins which are capable of producing infection.	1. Antibodies are immunoglobulins produced by the body to act against the antigens.
2. The structure of antigens is variable dependent upon the type of pathogen.	2. The structure of antibody is Y-shaped.
3. The antigen is the ‘non-self’ molecule.	3. The antibody is ‘self’ molecule.
4. The antigens have epitope sites which bind with the antibody molecule.	4. The antibodies have paratope sites which bind with the antigen molecule.

Question 3.
Name the infective stage of Plasmodium. Give Symptoms of malaria
Answer:
Sporozoite
I. Symptoms of malaria:

Fever accompanied by shivering.
Joint pain or arthralgia.
Vomiting.
Anaemia caused due to rupture of RBCs or haemolysis.
Haemoglobinuria.
Retinal damage.
Convulsions.
Cyclical occurrence of sudden coldness followed by rigor and then fever and sweating lasting for four to six hours. This is called a classic symptom of malaria.
Splenomegaly or enlarged spleen, severe headache, cerebral ischemia, hepatomegaly, i. e. enlarged liver, hypoglycaemia and haemoglobinuria with renal failure may occur in severe infections.

II. Spread / Transmission of malaria:

Malaria parasite is transmitted through the female Anopheles mosquito and hence it is known as mosquito-borne disease. Mosquito acts as a vector.
There are four species of Plasmodium, viz., P. vivax, P. falciparum, P. ovale and P. malariae which transmit malaria.

Question 4.
Explain the mode of infection and cause of elephantiasis.
Answer:
Mode of infection, i.e. transmission:

The parasite Wuchereria bancrofti is transmitted from a patient to other normal human being by female Culex mosquito.
The filarial larvae leave mosquito body and arrive on the human skin where they penetrate the skin and enter inside.
They undergo two moultings to become adults. Later they settle in the lymphatic system. They incubate for about 8-16 months.
When they settle in lymphatic system, this infection is called lymphatic filariasis.
The worms start infecting lymphatic circulation resulting into enlargement of lymph vessels and lymph nodes. The extremities like legs or limbs become swollen which resembles elephant legs. Therefore it is called elephantiasis.
This condition is lymphoedema, i.e. accumulation of lymph fluid in tissue causing swelling.

Question 5.
Why is smoking a bad habit?
Answer:

Smoking involves inhaling the cigarette smoke which contains nicotine and other toxic substances like N-nitrosodimethlene. There is some amount of carbon monoxide.
All these substances affect the normal respiratory health.
Smoking invites problems like asthma, hypertension, heart disease, stroke, lung damage.
The worst impact is that these substances are carcinogenic and hence can cause cancer of larynx, trachea, lung, etc.
Smoking not only affects the smokers but also has bad effect on others due to passive smokers.
In women, smoking is still hazardous as their ovaries can undergo mutations due to mutagenic chemicals found in smoke.
Therefore, smoking is a very bad habit.

Question 6.
What do the abbreviations AMIS and CMIS denote?
Answer:
AMIS is Antibody-mediated immune system or humoral immunity and CMIS is cell- mediated immune system.

Question 7.
What is a carcinogen? Name one chemical carcinogen with its target tissue.
Answer:

Carcinogen is the substance or agent that causes cancer.
Urinary bladder cancer caused by 2-naphthylamine and 4-aminobiphenyl.

Question 8.
Active immunity and passive immunity.
Answer:

Active immunity	Passive immunity
1. Active immunity is produced in response to entry of pathogens and their antigenic stimuli.	1. Passive immunity is produced due to antibodies that are transferred to the body.
2. Active immunity is the long lasting immunity.	2. Passive immunity is short-lived immunity.
3. In active immunity, the body produces its own antibodies.	3. In passive immunity, antibodies are given to the body from outside.
4. Natural acquired active immunity is obtained due to infections by pathogens.	4. Natural acquired passive immunity is obtained through antibodies of mother transmitted- to baby by placenta or colostrum.
5. Artificial acquired active immunity is obtained through vaccinations. These vaccines contain dead or live but attenuated pathogens.	5. Artificial acquired passive immunity is also obtained through vaccinations, but here the vaccines contain the readymade antibodies which are prepared with the help of other animals such as horses.

4. Short Answer Questions

Question 1.
B-cells and T-cells.
Answer:

B-cells	T-cells.
1. B-cells are type of lymphocyte whose origin is in bone marrow but maturation is in blood.	1. T-cells are type of lymphocytes which originate in bone marrow but maturation occurs in thymus.
2. B-cells Eire type of lymphocytes which are involved in humoral mediated immunity.	2. T-cells are type of lymphocytes which are involved in cell-mediated immunity.
3. 20% of lymphocytes present in the blood are B-cells.	3. 80% of lymphocytes present in the blood are T-cells.
4. Two types of B-cells are Memory cells and Plasma cells.	4. T-cells are of following subtypes : Cytotoxic T-cells, helper T-cells, suppressor T-cells.
5. They are involved in antibody mediated immunity. (AMI)	5. They are involved in cell-mediated immunity (CMI).
6. B-cells produced antibodies with which they fight against pathogens.	6. T-cells do not produce antibodies.
7. B-cells have membrane bound immunoglobulins located on the surface.	7. There is a presence of T cell receptors on the T-cell surface.

Question 2.
What are the symptoms of malaria? How does malaria spread?
Answer:
Symptoms of malaria:

Fever accompanied by shivering.
Joint pain or arthralgia.
Vomiting.
Anaemia caused due to rupture of RBCs or haemolysis.
Haemoglobinuria.

Question 3.
AIDS.
Answer:
(1) AIDS or the acquired immuno deficiency syndrome, is fatal viral disease caused by a retrovirus (ss RNA) known as the human immuno deficiency virus (HIV) which weakens the body’s immune system. It is called a modern pandemic.

(2) The HIV attacks the immune system which in turn causes many opportunistic infections, neurological disorders and unusual malignancies ultimately leading to death.

(3) AIDS was first noticed in USA in 1981 whereas in India, first confirmed case of AIDS was in April 1986 from Tamil Nadu.

(4) HIV is transmitted through body fluids such as saliva, tears, nervous system tissue, spinal fluid, blood, semen, vaginal fluid and breast milk. However, only blood, semen, vaginal secretions and breast milk generally transmit infection to others.

(5) The transmission of HIV occurs by sexual contact, through blood and blood products and by contaminated syringes, needles, etc. There is also transplacental transmission or through breast milk at the time of nursing.

(6) Accidental needle injury, artificial insemination with infected donated semen and transplantation with infected organs are some of the rare occasions of transmission of HIV.

(7) HIV infection is not spread by casual contact such as hugging, bite of mosquitoes or using other objects touched by a patient.

(8) Acute HIV infection progresses over time to asymptomatic HIV infection and then to early symptomatic HIV infection. Later, it progresses to full blown AIDS when patient shows advanced HIV infection with CD4 T-cell count below 200 cells/mm.

Question 4.
Give the symptoms of cancer.
Answer:
Symptoms of cancer:

Presence of lump or tumour.
White patches in the mouth.
Change in a wart or mole on the skin.
Swollen or enlarged lymph nodes.
Vertigo, headaches or seizures if cancer affect the brain.
Coughing and shortness of breath if lungs are affected due to cancer.

Question 5.
Antigens on blood cells.
Answer:

There are about 30 known antigens on the surface of human red blood cells. They decide the type of blood group such as ABO, Rh, Duffy, Kidd, Lewis, P MNS, Bombay.
The different blood groups are determined genetically due to presence of a particular antigen.
Landsteiner found two antigens or agglutinogens on the surface of human red blood cells which are named as antigen A and antigen B.
There is another antigen called Antigen D which decides the Rh status of the blood. If Antigen D is present, the person is said to be RH positive and when it is lacking, the person is Rh negative.
These antigens are responsible for types of blood group and the specific transfusions.
Antigens present on the RBCs and antibodies present in the serum can cause agglutination reactions if they are non-compatible. Therefore, at the time of transfusion blood groups are checked properly.

Question 6.
Antigen-antibody complex:
Img 1
Answer:

Between antigen and antibody there is specificity.
Each antibody is specific for a particular antigen.
On the antigens there are combining sites which are called antigenic determinants or epitopes.
Epitopes react with the corresponding antigen binding sites of antibodies which are called paratopes.
The antigen binding sites are located on the variable regions of the antibody. Variable regions have small variations which make each antibody highly specific for a particular antigen.
Owing to variable region the antibody can recognize the specific antigen.
Antibody thus binds to specific antigen in a lock and key manner, forming an antigen- antibody complex.

Question 7.
What are the various public health measures, which you would suggest as safeguard against infectious diseases?
Answer:
Infectious diseases spread through pathogens, therefore, it is an important duty of each person to decrease the risk of infecting our own self or others. This can be achieved by

Washing hands often, especially whenever, we are in contact with food and water. Before and after preparing food, before eating and after using the toilet, hand wash is a must.
Vaccinations : Immunization helps us to protect against contracting many diseases. Therefore, timely vaccination should be taken. Especially at the time of epidemic, one must keep distance from infected area or get vaccinated.
One must be at home if there are signs and symptoms of an infection. By going out, we may infect other healthy persons.
Proper diet and exercise should be followed to improve one’s own immunity.
Hygiene should be utmost in the kitchen and dining area. One must take care while eating uncovered and leftover food.
Bathroom and toilet should be cleaned daily as there can be a high concentration of bacteria or other infectious agents in these areas.
One should have responsible sexual behaviour to avoid sexually transmitted diseases.
Personal items such as toothbrush, comb, towel, undergarments or razor blade should never be shared.
Travelling should be avoided because we may infect other passengers during travel. Moreover, our illness can be aggravated. Some special immunizations are needed during certain travels, such as anti-cholera vaccine while going to Pandharpur during Ashadhi.

Question 8.
How does the transmission of each of the following diseases take place?
(a) Amoebiasis:
Answer:
Amoebiasis is usually transmitted by the following ways:

The faecal-oral route.
Through contact with dirty hands or objects.
By anal-oral contact.
Through contaminated food and water.

(b) Malaria:
Answer:
Symptoms of malaria:

Fever accompanied by shivering.
Joint pain or arthralgia.
Vomiting.
Anaemia caused due to rupture of RBCs or haemolysis.
Haemoglobinuria.

Unsafe and unhygienic food and drinks contaminated with the eggs of Ascaris are the main mode of transmission.
Eggs hatch inside the intestine of the new host.
The larvae pass through various organs and settle as adults in the digestive system.

(d) Pneumonia:
Answer:

Pneumonia usually spreads by direct person to person contact.
It is also spread via droplet infection, i.e. droplets released by infected person.
Using clothes and utensils of the patient.

Question 9.
What measures would you take to prevent water-borne diseases?
Answer:

To prevent water-borne diseases, use of safe, clean and potable water is a must. Water should be filtered, then boiled and stored in covered container. If possible water purifier systems should be installed at home.
One should preferably use bottled water or carry our own water container while travelling.
Cleaning of water containers and maintaining personal hygiene near water storage is a must.
Megacities offer chlorinated and purified water for citizens. But villages and smaller rural set ups use river water which may be highly contaminated with pathogens. Such water should be purified before consumption to prevent water-borne diseases.

Question 10.
Typhoid.
Answer:
Typhoid is an infective disease caused by Gram-ve bacterium, Salmonella typhi.
(1) It is food and water-borne infection. In the intestinal lumen of infected person this bacteria is found.

(2) The bacterium has “O” – antigen, which is a lipopolysaccharide (LPS), present on surface coat and its flagella has “H” – antigen. Thus it becomes pathogenic.

(3) Signs and Symptoms of typhoid are as follows:
Prolonged and high fever with nausea, fatigue, headache.
Abdominal pain, constipation or diarrhoea. In severe cases rose-coloured rash is seen on skin. Tongue shows white coating and there is cough. Anorexia or loss of appetite is seen. In chronic cases there is breathlessness, irregular heartbeats and haemorrhage.

(4) Poor hygiene habits and poor sanitation and insects like houseflies and cockroaches spread typhoid.

(5) Typhoid is diagnosed by Widal test.

(6) Antibiotics like Chloromycetin can cure typhoid. Preventive vaccines such as oral Ty21a vaccine and injectable typhim vi and typherix against typhoid are also available. Chronic cases need surgical removal of gall bladder.

5. Match the following.

Column I	Column II
(a) AIDS	(i) Antibody production
(b) Lysozyme	(ii) Activation of B-cells
(c) B-cells	(iii) Immunoglobulin
(d) T-helper cells	(iv) Tears
(e) Antibody	(v) Immuno deficiency

Answer:

Column I	Column II
(a) AIDS	(v) Immuno deficiency
(b) Lysozyme	(iv) Tears
(c) B-cells	(i) Antibody production
(d) T-helper cells	(ii) Activation of B-cells
(e) Antibody	(iii) Immunoglobulin

6. Long Answer Questions

Question 1.
Describe the structure of antibody.
Answer:
Img 2

Antibodies are highly specific to specific antigens. They are glycoprotein called immunoglobulins (Igs.).
They are produced by plasma cells. Plasma cells are in turn formed by B-lymphocytes.
About 2000 molecules of antibodies are formed per second by the plasma cells.
Antibody is a ‘Y’-shaped molecule. It has four polypeptide chains, two heavy or H-chains and two light or L-chains.
Disulfide bonds (-s-s-) hold the polypeptide chains together to form a ‘Y’-shaped structure.
The region holding arms and stem of antibody is termed as hinge. Each chain of the antibody has two distinct regions, the variable region and the constant region.
Variable regions have a paratope which is an antigen-binding site. This part of antibody recognizes and binds to the specific antigen forming an antigen-antibody complex.
Antibodies are called bivalent as they carry two antigen binding sites.

Question 2.
Vaccination.
Answer:

Vaccines are prepared from inactivated pathogen, in the form of protein or sugar from pathogen or dead form of pathogen or toxoid from pathogens or attenuated pathogen.
These when they are administered to a person to protect against a particular pathogen, it is called vaccination.
Vaccination ’teaches’ the immune system to recognize and eliminate pathogenic organism. Because, already in the body the vaccine is injected and body has made antibodies in response to it. Thus, body is prepared before the attack, if at all it is exposed to pathogen.
Thus, it is an important form of primary prevention, which reduces the chances of illness by protecting people. It works by exposing the pathogen in a safe form.
Vaccinations control spread of diseases like measles, polio, tetanus and whooping cough that once threatened many lives.
Vaccination controls the epidemic outbreak of diseases, if all the people Eire pre-vaccinated.
Some hazardous diseases like small, pox and polio have been completely eradicated by the vaccination.

Question 3.
What is cancer? Differentiate between benign tumour and malignant tumour. The main five types of cancer
Answer:
I. Cancer : Cancer is a disease caused by uncontrolled cell division due to disturbed cell cycle.

II. Difference between benign tumour and malignant tumour:

Benign tumour	malignant tumour
1. Benign tumour is localized and it does not spread to neighbouring areas.	1. Malignant tumour starts as local but spreads rapidly to neighbouring areas.
2. Benign tumour is enclosed in connective tissue sheath.	2. Malignant tumour is not enclosed in connective tissue sheath.
3. Benign tumour compresses the surrounding normal tissue.	3. Malignant tumour invades and destroys the surrounding tissue.
4. Benign tumours can be removed surgically.	4. Malignant tumours need further treatment after removal.
5. Except for brain tumour, benign tumours are usually not fatal.	5. Malignant tumours are fatal.
6. Benign tumours do not show metastasis.	6. Malignant tumours show metastasis.
7. Benign tumours are well differentiated.	7. Malignant tumours are poorly differentiated.
8. Benign tumours show slow and progressive growth.	8. Malignant tumours show rapid and erratic growth.

III. The main five types of cancer:

Types of Cancer : According to the tissue affected, the cancers are classified into five main types. These are as follows:

Carcinoma : Cancer of epithelial tissue covering or lining the body organs is known as carcinoma. E.g. breast cancer, lung cancer, cancer of stomach, skin cancer, etc.
Sarcoma : Cancer of connective tissue is called sarcoma. Following are the types of sarcoma osteosarcoma (bone cancer), myosarcoma (muscle cancer),
chondrosarcoma (cancer of cartilage) and liposarcoma (cancer of adipose tissue).
Lymphoma : Cancer of lymphatic tissue is called lymphoma. Lymphatic nodes, spleen and tissues of immune system are affected due to lymphoma.
Leukaemia : Leukaemia is blood cancer. In this condition, excessive formation of leucocytes take place in the bone marrow. There are millions of abnormal immature leucocytes which cannot fight infections. Monocytic leukaemia, lymphoblastic leukaemia, etc. are the types of leukaemia.
Adenocarcinoma : Cancer of glandular tissues such as thyroid, pituitary, adrenal, etc. is called adenocarcinoma.

Question 4.
Describe the different type of immunity.
Answer: There are two basic types of immunity, viz. innate immunity and acquired immunity.
(A) Innate immunity:

Innate immunity is natural, inborn immunity, which helps the body to fight against the invasion of microorganisms.
Innate immunity is non-specific because it does not depend on previous exposure to foreign substances.
Innate immunity mechanisms consist of various types of barriers such as anatomical barriers, physiological barriers, phagocytic barriers and inflammatory barriers. They prevent entry of foreign agents into the body.

(B) Acquired immunity:

The immunity that an individual acquires during his life is called acquired immunity or adaptive immunity or specific immunity. It helps the body to adapt by fighting against specific antigens hence it is called adaptive immunity. Since it is produced specifically against an antigen, it is called specific immunity.
Acquired immunity takes long time for its activation.
This type of immunity is seen only in vertebrates.
Due to acquired immunity, the body is able to defend against any invading foreign agent.

Question 5.
Describe the ill-effects of alcoholism on health.
Answer:

Alcohol in any form is toxic for the body. Hence as soon as alcohol is consumed, the liver tries to detoxify it.
In low doses it acts as a stimulant but in high dose, it acts on central nervous system, especially the cerebrum and cerebellum. Still higher dose can induce a comatose condition.
Alcohol affect the gastrointestinal tract by causing inflammation and damage to gastric 4 mucosa. Ulceration and painful condition arises in alcoholics.
Excessive doses of alcohol induce vomiting.
The worst effect of alcohol is on liver causing diseases like cirrhosis.
Alcohol induces hypertension and cardiac problems.
Apart from physical effect, it causes deterioration of mental health and emotional well-being.
Alcoholic person cannot think due to numbness in his/her cerebrum.
The social health is greatly affected as the alcoholic can cause problems to his family, friends and society in general.

Question 6.
In your view, what motivates the youngsters to take to alcohol or drugs and how can this be avoided?
Answer:
I. Taking drugs or alcohol:

Youngsters are at the vulnerable age, where they lack the planning about their future.
If they fall into bad company or are facing parental neglect, they get hooked on to alcohol or drugs.
Some common causes for addiction among youngsters are insufficient parental supervision and monitoring or excessive pressure and expectations from them. Lack of communication between an adolescent and parents.
Poorly defined rules for the family. Continuous family conflicts.
Favourable parental attitudes towards alcohol and drug uses. Many a times, at home children are exposed to such habits.
Inability to cope up with present and hence switching to the addictions. Risk taking behaviour which is common among youngsters.

II. Methods/measures to avoid drug abuse:

There should be complete acceptance for the child, because the adolescent phase is the most crucial phase when the children should be treated with love, care and respect.
Many physical, hormonal and psychological transformations are taking place in this phase. Therefore child suffers from stressful situation.
Wrong company and bad influence of peer group can trap the child in bad addictive habits. Thus, family should be supportive and communicative to help such children.
The sexual thoughts should be sublimed by channelizing energy into healthy pursuits like sports, reading, music, yoga and other extracurricular activities.
Ill-effects of drugs or alcohol should be told to youngsters.
Education and counselling can control the children from getting hooked on to the addictions.

Question 7.
Do you think that friends can influence one to take alcohol/drugs? If yes, how may one protect himself/herself from such an influence?
Answer:
Friends can influence one to take alcohol and drugs, if a boy or girl is timid and non-communicative with his or her parents and teachers. It also depends on the personality of the indtvidual. In the adolescent age, many fall in trap due to such peer pressure. The confusion in the mind and role of hormones playing on the psyche and thought process makes one unable to understand the hazards of such habits. Also there is curiosity to do these experimentations due to bad influence of media.

If there is complete trust and friendship with sensible parents, then such influence does not work. One should protect himself or herself by a strong denial. Communicating such incidents to an elder in whom a boy or girl can confide, is very important. One should tell his or her friends about the ill-effects of alcohol and drugs. He should be made aware of these aspects that he or she has learnt in this lesson.

12th Std Biology Questions And Answers:

12th Biology Chapter 12 Exercise Biotechnology Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 12 Biotechnology Textbook Exercise Questions and Answers.

Biotechnology Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 12 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 12 Exercise Solutions

1. Multiple choice questions

Question 1.
MU The bacterium which causes a plant disease called crown gall is ………………..
(a) Helicobacter pylori
(b) Agrobacterium tumifaciens
(c) Thermophilus aquaticus
(d) Bacillus thuringienesis
Answer:
(b) Agrobacterium tumtfaciens

Question 2.
The enzyme nuclease hydrolyses ……………….. of polynucleotide chain of DNA.
(a) hydrogen bonds
(b) phosphodiester bonds
(c) glycosidic bonds
(d) peptide bonds
Answer:
(b) phosphodiester bonds

Question 3.
In vitro amplification of DNA or RNA segment is known as ………………..
(a) chromatography
(b) southern blotting
(c) polymerase chain reaction
(d) gel electrophoresis
Answer:
(c) polymerase chain reaction

Question 4.
Which of the following is the correct recognition sequence of restriction enzyme hind III.
(a) 5′ —A-A-G-C-T-T— 3′
3′ —T-T-C-G-A-A—5′
(b) 5′ — G-A-A-T-T-C—3′
3′ — C-T-T-A-A-G—5′
(c) 5′ — C-G-A-T-T-C—3′
3′ — G-C-T-A-A-G—5′
(d) 5′ — G-G-C-C—3′
3′ — C-C-G-G—5′
Answer:
(a) 5’ —A-A-G-C-T-T—3’
3’ —T-T-C-G-A-A—5’

Question 5.
Recombinant protein ……………….. is used to dissolve blood clots present in the body.
(a) insulin
(b) tissue plasminogen activator
(c) relaxin
(d) erythropoietin
Answer:
(b) tissue plasminogen activator

Question 6.
Recognition sequence of restriction enzymes are generally ……………….. nucleotide long.
(a) 2 to 4
(b) 4 to 8
(c) 8 to 10
(d) 14 to 18
Answer:
(b) 4 to 8

2. Very short answer questions

Question 1.
Name the vector which is used in production of human insulin through recombinant DNA technology.
Answer:
PBR 322

Question 2.
Which cells from Langerhans of pancreas do produce a peptide hormone insulin?
Answer:
cells of islets of Langerhans of a peptide hormone insulin.

Question 3.
Give the role of Ca⁺⁺ ions in the transfer of recombinant vector into bacterial host cell.
Answer:
Ca⁺⁺ ions promotes binding of plasmid DNA to lipo polysaccharides on bacterial cell surface. Then plasmid can enter the cell on heat shock.

Question 4.
Expand the following acronyms which are used in the held of biotechnology:

YAC
RE
dNTP
PCR
GMO
MAC
CCMB.

Answer:

YAC : Yeast Artificial chromosome
RE : Restriction Endonuclease
dNTP : Deoxyribonucleoside triphosphates
PCR : Polymerase Chain Reaction
GMO : Genetically Modified Organisms
MAC : Mammalian Artificial Chromosome
CCMB : Centre for Cellular and Molecular Biology

Question 5.
Fill in the blanks and complete the chart.

GMO	Purpose
(i) Bt cotton	———–
(ii) ———-	Delay the softening of tomato during ripening
(iii) Golden rice	———–
(iv) Holstein cow	———–

Answer:

GMO	Purpose
(i) Bt cotton	Insect resistance
(ii) Flavr savr Tomato	Delay the softening of tomato during ripening
(iii) Golden rice	Rich in vitamin A
(iv) Holstein cow	High milk productivity

3. Short answer type questions.

Question 1.
Explain the properties of a good or ideal cloning vector for r-DNA technology.
Answer:
Desired characteristics of ideal cloning vector are as follows:

Vector should be able to replicate independenly (through ori gene), so that as vector replicates, multiple copies of the DNA insert are also produced.
It should be able to easily transferred into host cells.
It should have suitable control elements like promoter, operator, ribosomal binding sites, etc.
It should have marker genes for antibiotic resistance and restriction enzyme recognition sites within them.

Question 2.
A PCR machine can rise temperature up to 100 °C but after that it is not able to lower the temperature below 70 °C automatically. Which step of PCR will be hampered first in this faulty machine? Explain why?
Answer:

If the faulty machine is not able to lower the temperature below 70 °C, then the primer annealing step will be hampered first.
Each primer has a specific annealing temperature, depending upon its A, T, G, C content.
For most of the primers annealing temperature is about 40-60 °C.
Hence, if temperature is more than primers annealing temperature, it will be able to pair with its complementary sequence in ssDNA.

Question 3.
In the process of r-DNA technology, if two separate restriction enzymes are used to cut vector and donor DNA then which problem will arise in the formation of r-DNA or chimeric DNA? Explain.
Answer:
In the process of r-DNA technology, if two separate restriction enzymes are used to cut vector and donor DNA, then it will result in fragments with different sticky ends which will not be complementary to each other.

Question 4.

Recombinent protein	Its use in or for
(1) Platelet derived growth factor	(a) Anemia
(2) a-antitrypsin	(b) Cystic fibrosis
(3) Relaxin	(c) Haemophilia A
(4) Eryhthropoietin	(d) Diabetes
(5) Factor VIII	(e) Emphysema
(6) DNA ase	(f) Parturition
	(g) Atherosclerosis

Answer:

Recombinent protein	Its use in or for
(1) Platelet derived growth factor	(g) Atherosclerosis
(2) a-antitrypsin	(e) Emphysema
(3) Relaxin	(f) Parturition
(4) Eryhthropoietin	(a) Anemia
(5) Factor VIII	(c) Haemophilia A
(6) DNA ase	(b) Cystic fibrosis

4. Long answer type questions.

Question 1.
(i) Define and explain the terms Bioethics.
Answer:

Bioethics is the study of moral vision, decision and policies of human behaviour in relation to biological phenomena or events.
Bioethics deals with wide range of reactions on new developments like cloning, transgenic, gene therapy, eugenics, r-DNA technology, in vitro fertilization, sperm bank, gene therapy, euthanasia, death, maintaining those who are in comatose state, prenatal genetic selection, etc.
Bioethics also includes the discussion on subjects like what should and should not be done in using recombinant DNA techniques.

Ethical aspects pertaining to the use of biotechnology are:

Use of animals cause great sufferings to them.
Violation of integration of species caused due to transgenosis.
Transfer of human genes into animals and vice versa.
Indiscriminate use of biotechnology pose risk to the environment, health and biodiversity.
The effects of GMO on non-target organisms, insect resistance crops, gene flow, the loss of diversity.
Modification process disrupting the natural process of biological entities.

(ii) Define and explain the term Biopiracy.
Answer:

Biopiracy is defined as ‘theft of various natural products and then selling them by getting patent without giving any benefits or compensation back to the host country’.
It is unauthorized misappropriation of any biological resource and traditional knowledge.
It is bio-patenting of bio-resource or traditional knowledge of another nation without proper permission of the concerned nation or unlawful exploitation and use of bioresources without giving compensation.

Following are the examples of biopiracy:
(a) Patenting of Neem (Azadirachta indica):

Pirating India’s traditional knowledge about the properties and uses of neem, the USDA and an American MNC W.R. Grace sought a patent from the European Patent Office (EPO) on the “method for controlling on plants by the aid of hydrophobic extracted neem oil,” in the early 90s.
The patenting of the fungicidal properties of Neem, was an example of biopiracy.

(b) Patenting of Basmati:

Texmati is a trade name of “Basmati rice line and grains” for which Texas based American company Rice Tec Inc was awarded a patent by the US Patent and Trademark Office (USPTO) in 1997.
This is a case of biopiracy as Basmati is a long-grained, aromatic variety of rice indigenous to the Indian subcontinent.
Very broad claims about “Inventing” the said rice was the basis of patent application.
The UPSTO has rejected all the claims due to people movement against Rice Tec in March 2001.

A patent claim about the healing properties of Haldi was made by two American researchers of Indian origin of the University of Mississippi Medical Center, to the US Patent and Trademark Office.
They were granted a patent in March 1995.
This is an example of biopiracy because healing properties of Haldi is not a new discovery, but it is a traditional knowledge in ayurvedas for centuries.
The Council of Scientific and Industrial Research (CSIR) applied to the US Patent Office for a reexamination and they realized the mistake and cancelled the patent.

(iii) Define and explain the term Biopatent.
Answer:

Biopatent is a biological patent awarded for strains of microorganisms, cell lines, genetically modified strains, DNA sequences, biotechnological processes, product processes, product and product applications.
It allows the patent holder to exclude others from making, using, selling or importing protected invention for a limited period of time.
Duration of biopatentis five years from the date of the grant or seven years from the date of filing the patent application, whichever is less.
Awarding biopatents provides encouragement to innovations and promote development of scientific culture in society. It also emphasizes the role of biology in shaping human society.
First biopatent was awarded for genetically engineered bacterium ‘Pseudomonas’ used for clearing oils spills.
Patent jointly issued by Delta and Pineland company and US department of agriculture having title ‘control of plant gene expression’, is based on a gene that produces a protein toxic to plant and thus prevents seed germination.

This patent was not granted by Indian government. Such a patent is considered morally unacceptable and fundamentally unequitable. Such patents would pose a threat to global food security as financially powerful corporations would acquire monopoly over biotechnological process.

Question 2.
Explain the steps in process of r-DNA technology with suitable diagrams.
Answer:

The steps involved in gene cloning are as follows:
(1) Isolation of DNA (gene) from the donor organism:

To obtain the desired gene to be cloned, the cells of the donor organism are sheared with the blender and treated with suitable detergent. Genetic material is then isolated and purified.
Isolated purified DNA is then cleaved using restriction Endonucleases.
Restriction fragment containing desired gene is isolated and selected for cloning. This is now called foreign DNA or passanger DNA.
A desired gene can also be obtained directly from genomic library or c-DNA library.

(2) Insertion of desired foreign gene into a cloning vector (vehicle DNA):

The foreign DNA or passanger DNA is inserted into a cloning vector (vehicle DNA) like bacterial plasmids and the bacteriophages like lamda phage and M13. The most commonly used plasmid is pBR 322.
Plasmids are isolated from the bacteria and are cleaved by using same RE which is used in the isolation of the desired gene from the donor.
Enzyme DNA ligase is used to join foreign DNA and the plasmid DNA.
Plasmid DNA containing foreign DNA is called recombinant DNA (r-DNA) or chimeric DNA.

(3) Transfer of r-DNA into suitable competent host or cloning organism:

The r-DNA is introduced into a competent host cell, which is mostly a bacterium.
Host cell takes up naked r-DNA by process of ‘transformation’ and incorporates it into its own chromosomal DNA which finally expresses the trait controlled by passenger DNA.
The transfer of r-DNA into a bacterial cell is assisted by divalent Ca⁺⁺.
The cloning organisms are E.coli and Agrobacterium tumifaciens.
The competent host cells which have taken up r-DNA are called transformed cells.
By using techniques like electroporation, microinjection, lipofection, shot gun, ultrasonification, biolistic method, etc. Foreign DNA can also be transferred directly into the naked cell or protoplast of the competent host cell, without using vector.
In plant biotechnology the transformation is through Ti plasmids of A. tumifaciens.

(4) Selection of the transformed host cell:

For isolation of recombinant cell from non-recombinant cell, marker gene of plasmid vector is employed.
For example, pBR322 plasmid vector contains different marker genes like ampicillin resistant gene and tetracycline resistant gene. When pstl RE is used, it knocks out ampicillin resistant gene from the plasmid, so that the recombinant cells become sensitive to ampicillin.

(5) Multiplication of transformed host cell:

The transformed host cells are introduced into fresh culture media where they divide.
The recombinant DNA carried by them also multiplies.

(6) Expression of gene to obtain desired product. Then desired products like enzymes, antibiotiocs etc. separated and purified through down stream processing using bioreactors.

Question 3.
Explain the gene therapy. Give two types of it.
Answer:
Gene therapy is the treatment of genetic disorders by replacing, altering or supplementing a gene that is absent or abnormal and whose absence or abnormality is responsible for the disease.
Types of gene therapy:
(a) Germ line gene therapy:

In this germ cells are modified genetically to correct a genetic defect.
Normal gene is introduced into germ cells like sperms, eggs, early embryos.
It allows transmission of the modified genetic information to the next generation.
Although it is highly effective in treatment of the genetic disorders, its use is not preferred in human beings because of various technical and ethical reasons.

(b) Somatic cell gene therapy:

In this somatic cells are modified genetically to correct a genetic defect.
Healthy genes are introduced in somatic cells like bone marrow cells, hepatic cells, fibroblasts endothelium and pulmonary epithelial cells, central nervous system, endocrine cells and smooth muscle cells of blood vessel walls.
Modification of somatic cells only affects the person being treated and the modified chromosomes cannot be passed on the future generations.
Somatic cell gene therapy is the only feasible option and the clinical trials have already employed for the treatment of disorders like cancer, rheumatoid arthritis, SCID, Gaucher’s disease, familial hypercholesterolemia, haemophilia, phenylketonuria, cystic fibrosis, sickle-cell anaemia, Duchenne muscular dystrophy, emphysema, thalassemia, etc.

Question 4.
How are the transgenic mice used in cancer research?
Answer:

Transgenic mice are used in various research areas of cancer research.
Transgenic mice containing a particular oncogene (cancer causing gene) develop specific cancer.
They are used to study the relationship between oncogenes and cancer development, cancer treatment and prevention of malignancy.
The transgenic mouse model for the investigation of the breast cancer was developed in the laboratory of Philip Leder in Harvard (USA).
Transgenic mice containing oncogenes myc and ras were analyzed to find out role of these genes in the development of breast cancer.

Question 5.
Give the steps in PCR or polymerase chain reaction with suitable diagrams.
Answer:

(1) The DNA segment and excess of two primer molecules, four types of dNTPs, the thermostable DNA polymerase are mixed together in ‘eppendorf tube’.

(2) One PCR cycle is of 3-4 minutes duration and it involves following steps:

Denaturation : The reaction mixture is heated at 90-98°C. Due to this hydrogen bonds in the DNA break and two strands of DNA separate. This is called denaturation.
Annealing of primer : When the reaction mixture is cooled to 40-60°C, the primer pairs with its complementary sequences in ssDNA. This is called annealing.
Extension of primer : In this step, the temperature is increased to 70-75°C. At this temperature thermostable Taq DNA polymerase adds nucleotides to 3’end of primer using single-stranded DNA as template. This is called primer extension. Duration of this step is about two minutes.

(3) In an automatic thermal cycler, the above three steps are automatically repeated 20-30 times.
(4) Thus, at the end of ‘n’ cycles 2n copies of DNA segments, get synthesized.

Question 6.
What is a vaccine? Give advantages of oral vaccines or edible vaccines.
Answer:

A vaccine is a biological preparation that provides active acquired immunity against a certain disease.
Vaccine is often made from a weakened or killed form of the microorganism, its toxins or one of its surface protein antigens.
Edible vaccine is an edible plant part engineered to produce an immunogenic protein, which when consumed gets recognized by immune system.
Immunogenic protein of certain pathogens are active when’administered orally.
When animals or mainly humans consume these plant parts, they get vaccinated against certain pathogen.
Oral or edible vaccines have low cost, they are easy to administer and store.

Question 7.
Enlist different types of restriction enzymes commonly used in r-DNA technology? Write on their role.
Answer:

Different restriction enzymes commonly used in r-DNA technology are Alu I, Bam HI, Eco RI, Hind II, Hind III, Pst I, Sal I, Taq I, Mbo II, Hpa I, Bgl I, Not I, Kpn I, etc.
They are the molecular scissors which recognize and cut the phosphodiester back bone of DNA on both strands, at highly specific sequences.
The sites recognized by them are called recognition sequences or recognition sites.
Different restriction enzymes found in different organisms recognize different nucleotide sequences and therefore cut DNA at different sites.
Restriction cutting may result in DNA fragments with blunt ends or cohesive or sticky ends or staggered ends (having short, single stranded projections).
Restriction endonucleases like Bam HI and EcoRI produce fragments with sticky ends.
Restriction endonucleases like Alu I, Hind III produce fragments with blunt ends.
Type I restriction endonucleases fuction simultaneously as endonuclease and methylase e.g. EcoK.
Type II restriction endonucleases have separate cleaving and methylation activities. They are more stable and are used in r-DNA technology e.g. EcoRI, Bgll. They cut DNA at specific sites within the palindrome.
Type III restriction endonucleases cut DNA at specific non-palindromic sequences e.g. Hpal, MboII.
In bacterial cells, REs destroy various viral DNAs that might enter the cell, thus restricting the potential growth of the virus.

Question 8.
Enlist and write in brief about the different biological tools required in r-DNA technology.
Answer:
The biological tools used in r-DNA technology are various enzymes, cloning vectors and competent hosts.
(1) Enzymes:

Enzymes like lysozymes, nucleases (exonucleases and endonucleases), DNA ligase, reverse transcriptase, DNA polymerase, alkaline phosphatases, etc. are used in r-DNA technology.
The restriction endonucleases are used as biological or molecular scissors. They are able to cut a DNA molecule at a specific recognition site.

(2) Vectors:

Vectors are DNA molecules which carry foreign DNA segment and replicate inside the host cell.
Vectors may be plasmids, bacteriophages (M13, lambda virus), cosmid, phagemids, BAC (bacterial artificial chromosome), YAC (yeast artificial chromosome), transposons, baculoviruses and mammalian artificial chromosomes (MACs).
Most commonly used vectors are plasmid vectors (pBR 322, pUC, Ti plasmid) and bacteriophages (lamda phage, M13 phage).

(3) Competent host cells:

They are bacteria like Bacillus haemophilus, Helicobacter pyroliand E. coli.
Mostly E. coli is used for the transformation with recombinant DNA.

12th Std Biology Questions And Answers:

12th Biology Chapter 4 Exercise Molecular Basis of Inheritance Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 4 Molecular Basis of Inheritance Textbook Exercise Questions and Answers.

Molecular Basis of Inheritance Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 4 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 4 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Griffith worked on ………………..
(a) Bacteriophage
(b) Drosophila
(c) Frog eggs
(d) Streptococci
Answer:
(d) Streptococci

Question 2.
The molecular knives of DNA are ………………..
(a) Ligases
(b) Polymerases
(c) Endonucleases
(d) Transcriptase
Answer:
(c) Endonucleases

Question 3.
Translation occurs in the ………………..
(a) Nucleus
(b) Cytoplasm
(c) Nucleolus
(d) Lysosomes
Answer:
(b) Cytoplasm

Question 4.
The enzyme required for transcription is ………………..
(a) DNA polymerase
(b) RNApolymerase
(c) Restriction enzyme
(d) RNase
Answer:
(b) RNA polymerase

Question 5.
Transcription is the transfer of genetic information from ………………..
(a) DNA to RNA
(b) t-RNA to m-RNA
(c) DNA to m-RNA
(d) m-RNA to t-RNA
Answer:
(a) DNA to RNA

Question 6.
Which of the following is NOT part of protein synthesis?
(a) Replication
(b) Translation
(c) Transcription
(d) All of these
Answer:
(a) Replication

Question 7.
In the RNA molecule, which nitrogen base is found in place of thymine?
(a) Guanine
(b) Cytosine
(c) Thymine
(d) Uracil
Answer:
(d) Uracil

Question 8.
How many codons are needed to specify three amino acids?
(a) 3
(b) 6
(c) 9
(d) 12
Answer:
(a) 3

Question 9.
Which out of the following is NOT an example of inducible operon?
(a) Lactose operon
(b) Histidine operon
(c) Arabinose operon
(d) Tryptophan operon
Answer:
(d) Tryptophan operon

Question 10.
Place the following event of translation in the correct sequence ………………..
i. Binding of met-t-RNA to the start codon.
ii. Covalent bonding between two amino acids.
iii. Binding of second t-RNA.
iv. Joining of small and large ribosome subunits.
(a) iii, iv, i, ii
(b) i, iv, iii, ii
(c) iv, iii, ii, i
(d) ii, iii, iv, i
Answer:
(b) i, iv, iii, ii

2. Very Short Answer Questions

Question 1.
What is the function of an RNA primer during protein synthesis?
Answer:
During DNA replication, RNA primer provides 3’ OH to which DNA polymerase enzyme can add nucleotides to synthesize new strand using parental strand of DNA as template.
[Note : RNA primer has no direct role in protein synthesis.]

Question 2.
Why is the genetic code considered as commaless?
Answer:
The triplet codon are arranged one after the other on m-RNA molecule without any gap or space and therefore genetic code is considered as commaless.

Question 3
Genome
Answer:
Genome is the total genetic constitution of an organism or a complete copy of genetic information (DNA) or one complete set of chromosomes (monoploid or haploid) of an organism.

Question 4.
Which enzyme does remove supercoils from replicating DNA?
Answer:
Super-helix relaxing enzyme (Topoisomerase) removes supercoils from replicating DNA.

Question 5.
Why are Okazaki fragments formed on lagging strand only?
Answer:
Okazaki fragments are formed only on lagging template as only short stretch of lagging template becomes available for replication at one time.

Question 6.
When does DNA replication take place?
Answer:
In eukaryotes DNA-replication takes place during S-phase of interphase of cell cycle and in prokaryotes. DNA replicates prior to cell division.

Question 7.
Define term Codogen and Codon
Answer:
Codogen is a triplet of nucleotides present on the DNA which specifies one particular amino acid.
Codon is a triplet of nucleotides present on the m-RNA which specifies one particular amino acid.

Question 8.
What is degeneracy of genetic code?
Answer:
Genetic code is degenerate as 61 codons code for 20 amino acids, that is two or more codons can specify the same amino acid. E.g. Cysteine has two codons, while isoleucine has three codons.

Question 9.
Which are the nucleosomal ‘core’ histones?
Answer:
Two molecules each of histone proteins, viz. H₂A. H₂B, H₃ and H₄ are the nucleosomal ‘core’ histones.

3. Short Answer Questions

Question 1.
DNA packaging in eukaryotic cell.
Answer:

In eukaryotic cells, DNA (2.2 metres) is condensed, coiled and supercoiled to be packaged efficiently in the nucleus (10^-16 m).
DNA is associated with histone and non-histone proteins.
Histones are a set of positively charged, basic proteins, rich in basic amino acid residues lysine and arginine.
Nucleosome consists of nucleosome core (two molecules of each of histone proteins viz. H₂A, H₂B, H₃ and H₄ forming histone octamer) and negatively charged DNA (146 bps) that wraps around the histone octamer by 1 3/4 turns.
H₁ protein binds the DNA thread where it enters and leaves the nucleosome.
Adjacent nucleosomes are linked with linker DNA (varies in length from 8 to 114 bp, average length of linker DNA is about 54 bp).
Each nucleosome contains 200 bp of DNA.
Packaging involves formation of – Beads on string (10 nm diameter), Solenoid fibre (looks like coiled telephone wire, 30 nm diameter/300Å), Chromatin fibre and Chromosome.
Non-Histone Chromosomal Proteins (NHC) contribute to the packaging of chromatin at a higher level.

Question 2.
Enlist the characteristics of genetic code.
Answer:
The characteristics of genetic code are

Genetic code is triplet, commaless and non-overlapping.
It is degenerate and non-ambiguous.
It is universal
It has polarity.

Question 3.
Applications of DNA fingerprinting.
Answer:
Applications of DNA fingerprinting are as follows:

In forensic science to solve rape and murder cases.
Finds out the biological father or mother or both, of the child, in case of disputed parentage.
Used in pedigree analysis in cats, dogs, horses and humans.

Question 4.
Explain the role of lactose in ‘Lac Operon’.
Answer:

A small amount of beta-galactoside permease enzyme is present in cell even when Lac operon is switched off and it allows a few molecules of lactose to enter into the cell.
Lactose binds to repressor and inactivates it.
Repressor – lactose complex cannot bind with the operator gene, which is then turned on.
RNA polymerase transcribes all the structural genes to produce lac m-RNA which is then translated to produce all enzymes.
Thus, lactose acts as an inducer.
When the inducer level falls, the operator is blocked again by repressor and structural genes are repressed again. This is negative feedback.

4. Short Answer Questions

Question 1.
Human genome project.
Answer:
1. Human Genome Project (HGP) was initiated in 1990 under the International administration of the Human Genome Organization (HUGO) and it was completed r in 2003.

2. The main aims:

To sequence 3 billion base pairs of DNA in human genome and to map an estimated 33000 genes.
To store the information collected from the project in databases.
To develop tools and techniques for analysis of the data.
Transfer of the related technologies to the private sectors, such as industries.
Taking care of the legal, ethical and social issues which may arise from project.
To sequence the genomes of several other organisms such as bacteria e.g. E.coli, Caenorhabditis elegans, Saccharomyces cerevisiae, Drosophil, rice, Arabidopsis), Mus musculus, etc.

3. Significance:

HGP has a major impact in the fields like Medicine, Biotechnology, Bioinformatics and the Life sciences.
More understanding of functions of genes, proteins and human evolution.

Question 2.
Describe the structure of operon.
Answer:

An operon is a unit of gene expression and regulation.
It includes the structural genes and their control elements. Control elements are promoters and operators.
The structural genes code for proteins, r-RNA and t-RNA that are necessary for all the cells.
Promoters are signal sequences in DNA. They start the RNA synthesis. They also act as sites where the RNA polymerases are bound during transcription.
Operators are present between the promoters and structural genes.
There is repressor protein that binds to the operator region of the operon.
There are regulatory genes which are responsible for the formation of repressors which interact with operators.

Question 3.
In the figure below A, B and C are three types of

Answer:
Answer: A, B and C are A : m-RNA, B : r-RNA, C : t-RNA

Question 4.
Identify the labelled structures on the following diagram of translation.

Part A is the ………………
Part B is the ………………
Part C is the ………………
Answer:
Part A is the anti-codon.
Part B is the amino acid.
Part C is the larger subunit of ribosome.

Question 5.
Match the entries in Column I with those of Column II and choose the correct answer.

Column I	Column II
A. Alkali treatment	i. Separation of DNA fragments on gel slab
B. Southern blotting	ii. Splits DNA fragments into single strands
C. Electrophoresis	iii. DNA transferred to nitrocellulose sheet
D. PCR	iv. X-ray photography
E. Autoradiography	v. Produce fragments different sizes
F. DNA treated with REN	vi. DNA amplification

Answer:

Column I	Column II
A. Alkali treatment	ii. Splits DNA fragments into single strands
B. Southern blotting	iii. DNA transferred to nitrocellulose sheet
C. Electrophoresis	i. Separation of DNA fragments on gel slab
D. PCR	vi. DNA amplification
E. Autoradiography	iv. X-ray photography
F. DNA treated with REN	v. Produce fragments different sizes

5. Long Answer Questions

Question 1.
Explain the process of DNA replication.
Answer:

DNA replication is semi-conservative replication. It involves following steps:
Activation of Nucleotides:

Nucleotides (dAMP dGMR dCMP and dTMP) present in the nucleoplasm, are activated by ATP in presence of an enzyme phosphorylase.
This phosphorylation results in the formation of deoxyribonucleotide triphosphates i.e. dATE dGTR dCTP and dTTE

Point of Origin or Initiation point:

Replication begins at specific point ‘O- Origin and terminates at point ‘T’.
At the point ‘O’, enzyme endonuclease nicks (breaks the sugar-phosphate backbone or the phosphodiester bond) one of the strands of DNA, temporarily.

Unwinding of DNA molecule:

Enzyme DNA helices breaks weak hydrogen bonds in the vicinity of ‘O’.
The strands of DNA separate and unwind. This unwinding is bidirectional.
SSBP (Single strand binding proteins) remains attached to both the separated strands and prevent them from recoiling (rejoining).

Replicating fork:

Y-shape replication fork is formed due to unwinding and separation of two strands.
The unwinding of strands results in strain which is released by super-helix relaxing enzyme.

Synthesis of new strands:

Each separated strand acts as a template for the synthesis of new complementary strand.
A small RNA primer (synthesized by activity of enzyme RNA primase) get attached to the 3′ end of template strand and attracts complementary nucleotides from surrounding nucleoplasm.
These nucleotides bind to the complementary nucleotides on the template strand by hydrogen bonds (i.e. A = T or T = A; G = C or C = G, CEG).
The phosphodiester bonds are formed between nucleotides of new strand to form a polynucleotide strand.
The enzyme DNA polymerase catalyses synthesis of new complementary strand always in 5′ – 3′ direction.

Leading and Lagging strand:

The template strand with free 3′ is called the leading template.
The template strand with free 5′ end is called the lagging template.
The replication always starts at C-3 end of template strand and proceeds towards C-5 end.
New strands are always formed in 5′ → 3′ direction.
The new strand which develops continuously towards replicating fork is called the leading strand.
The new strand which develops discontinuously away from the replicating fork is called the lagging strand.
Maturation of Okazaki fragments : The lagging strand is synthesized in the form of small Okazaki fragments which are joined by enzyme DNA ligase.
Later RNA primers are removed by the combined action of RNase H, an enzyme that degrades the RNA strand of RNA-DNA hybrids, and polymerase I.
Gaps formed are filled by complementary DNA sequence with the help of DNA polymerase-I in prokaryotes and DNA polymerase-a in eukaryotes.
Finally, DNA gyrase (topoisomerase) enzyme forms double helix to form daughter DNA molecules.

Formation of two daughter DNA molecules:

In each daughter DNA molecule, one strand is parental and the other one is newly synthesized.
Thus, 50% part (i.e. one strand of the helix) is contributed by mother DNA. Hence, it is described as semiconservative replication.

Question 2.
Describe the process of transcription in protein synthesis.
Answer:

Transcription involves three stages, viz. Initiation, Elongation and Termination.
(1) Initiation:

RNA polymerase binds to promoter site.
It then moves along the DNA and causes local unwinding of DNA duplex into two strands in the region of the gene.
Only antisense strand functions as template.

(2) Elongation:

The complementary ribonucleoside tri-phosphates get attached to exposed bases of DNA template chain.
As transcription proceeds, the hybrid DNA-RNA molecule dissociates and makes m-RNA molecule free.
As the m-RNA grows, the transcribed region of DNA molecule becomes spirally coiled and regains double helical form.

(3) Termination:
When RNA polymerase reaches the terminator site on the DNA, both enzyme and newly formed m-RNA (primary transcript) gets released.

Question 3.
Describe the process of translation in protein synthesis.
Answer:

Translation involves the following steps:
1. Activation of amino acids and formation of charged t-RNA (t-RNA – amino acid complex):
i. In the presence of an enzyme amino acyl t-RNA synthetase, the amino acid is activated and then attached to the specific t-RNA molecule at 3’ end to form charged t-RNA (t-RNA – amino acid complex).

ii. ATP is essential for the reaction.

2. Initiation of Polypeptide chain:

Small subunit of ribosome binds to the m-RNA at 5’ end.
Start codon is positioned properly at P-site.
Initiator t-RNA, (carrying amino acid methionine in eukaryotes or formyl methionine in prokaryotes) binds with initiation codon (AUG) of m-RNA, by its anticodon (UAC) through hydrogen bonds.
The large subunit of ribosome joins with the smaller subunit in the presence of Mg⁺⁺.
Thus, initiator charged t-RNA occupies the P-site and A – site is vacant.

3. Elongations of polypeptide chain:
Addition of amino acid occurs in 3 Step cycle-
i. Codon recognition.
Anticodon of second (and subsequent) amino acyl t-RNA molecule recognizes and binds with codon at A-site by hydrogen bonds.

ii. Peptide bond formation.

Ribozyme catalyzes the peptide bond formation between amino acids on the initiator t-RNA at P-site and t-RNA at A-site.
It takes less than 0.1 second for formation of peptide bond.
Initiator t-RNA at ‘P’ site is then released from E-site.

iii. Translocation.

Translocation is the process in which sequence of codons on m-RNA is decoded and accordingly amino acids are added in specific sequence to form a polypeptide on ribosomes.
Due to this A’-site becomes vacant to receive next charged t-RNA molecule.
The events like arrival of t-RNA – amino acid complex, formation of peptide bond, ribosomal translocation and release of previous t-RNA, are repeated.
As ribosome move over the m-RNA, all the codons on m-RNA are exposed oiie by one for translation.

4. Termination and release of polypeptide:
When stop codon (UAA, UAG, UGA) gets exposed at the A-site, the release factor binds to the stop codon, thereby terminating the translation process
The polypeptide gets released in the cytoplasm.
Two subunits of ribosome dissociate and last t-RNA and m-RNA are released in the cytoplasm.
m-RNA gets denatured by nucleases immediately.

Question 4.
Describe Lac ‘Operon’.
Answer:

Lac operon consists of the following components:
(1) Regulator gene:

Regulator gene precedes the promoter gene.
It may not be present immediately adjacent to operator gene.
Regulator gene codes for a repressor protein which binds with operator gene and represses (stops) its action.

(2) Promoter gene:

It precedes the operator gene.
It is present adjacent to operator gene.
RNA Polymerase enzyme binds at promoter site.
Promoter gene base sequence determines which strand of DNA acts a template.

(3) Operator gene:

It precedes the structural genes.
When operator gene is turned on by an inducer, the structural genes get transcribed to form m-RNA.

(4) Structural gene:

There are 3 structural genes in the sequence lac-Z, lac-Y and lac-A.
Enzymes produced are β-galactosidase, β-galactoside permease and transacetylase respectively.
Inducer Allolactose acts as an inducer. It inactivates the repressor by binding with it.

Question 5.
Justify the statements. If the answer is false, change the underlined word(s) to make the statement true.
(i) The DNA molecule is double stranded and the RNA molecule is single stranded.
Answer:

DNA as the genetic material has to be chemically and structurally stable.
It should be able to generate its replica.
Sugar-phosphate backbone and complementary base pairing between the two strands, give stability to DNA.
Both the strands of DNA act as template for synthesis of their complementary strands. This allows accurate replication of DNA.
Single stranded RNA can be folded to form complex structures and perform specific functions such as synthesis of proteins.

(ii) The process of translation occurs at the ribosome.
Answer:

Translation is the process in which sequence of codons of m-RNA is decoded and accordingly amino acids are added in specific sequence to form a polypeptide on ribosomes.
Ribosome has one binding site for m-RNA. It orients m-RNA molecule in such a way that all the codons are properly read.
Ribosome has three binding sites for t-RNA : P-site (peptidyl t-RNA-site), A-site (aminoacyl t-RNA-site) and E-site (exit site).
t-RNAs place the required amino acids in correct sequence and translate the coded message of RNA.
In eukaryotes, a groove which is present between two subunits of ribosomes, protects the polypeptide chain from the action of cellular enzymes and also protects m-RNA from the action of nucleases.
Thus ribosome plays an important role in translation.

(iii) The job of m-RNA is to pick up amino acids and transport them to the ribosomes.
Answer:
The job of t-RNA is to pick up amino acids and transport them to ribosomes. t-RNA is an adapter molecule. It reads the codons of m-RNA and also simultaneously transfer specific amino acid to m-RNA Ribosome complex. It binds with amino acid at its 3′ end.

(iv) Transcription must occur before translation may occur.
Answer:
In prokaryotes, translation can start before transcription is complete, as both these processes occur in the same compartment, i.e. cytoplasm. But in eukaryotes, transcription and processing of hnRNA occurs in nucleus. hnRNA then comes out of the nucleus through nuclear pores and then it is translated at ribosomes in the cytoplasm.

Question 6.
Guess
(i) the possible locations of DNA on the collected evidence from a crime scene and
(ii) the possible sources of DNA.

Evidence	Possible location of DNA on the evidence	Sources of DNA
e.g. Eyeglasses	e.g. Earpieces	e.g. Sweat, Skin
Bottle, Can, Glass	Sides, mouthpiece	—————-
————–	Handle	Sweat, skin, blood
Used cigarette	Cigarette butt	—————–
Bite mark	—————–	Saliva
————-	Surface area	Hair, semen, sweat, urine

Answer:

Evidence	Possible location of DNA on the evidence	Sources of DNA
e.g. Eyeglasses	e.g. Earpieces	e.g. Sweat, Skin
Bottle, Can, Glass	Sides, mouthpiece	Saliva
Door	Handle	Sweat, skin, blood
Used cigarette	Cigarette butt	Saliva
Bite mark	Teeth impression	Saliva
Clothes	Surface area	Hair, semen, sweat, urine

12th Std Biology Questions And Answers:

12th Biology Chapter 15 Exercise Biodiversity, Conservation and Environmental Issues Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 15 Biodiversity, Conservation and Environmental Issues Textbook Exercise Questions and Answers.

Biodiversity, Conservation and Environmental Issues Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 15 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 15 Exercise Solutions

1. Multiple choice questions

Question 1.
Observe the graph and select correct option.

(a) Line A represents, S = CA²
(b) Line B represents, log C = log A + Z log S
(c) Line A represents, S = CA^Z
(d) Line B represents, log S = log Z + C log A
Answer:
(c) Line A represents, S = CA^Z

Question 2.
Select odd one out on the basis of Ex situ conservation.
(a) Zoological park
(b) Tissue culture
(c) Sacred groves
(d) Cryopreservation
Answer:
(a) Zoological park

Question 3.
Which of the following factors will favour species diversity?
(a) Invasive species
(b) Glaciation
(c) Forest canopy
(d) Co-extinction
Answer:
(a) Invasive species

Question 4.
The term “terror of Bengal’ is used for
(a) algal bloom
(b) water hyacinth
(c) increased BOD
(d) eutrophication
Answer:
(b) water hyacinth

Question 5.
CFC are air polluting agents which are produced by
(a) Diesel trucks
(b) Jet planes
(c) Rice fields
(d) Industries
Answer:
(b) Jet planes

2. Very short answer type questions.

Question 1.
Give two examples of biodegradable materials released from sugar industry.
Answer:

Molasses
Bagasse.

Question 2.
Name any two modern techniques of protection of endangered species.
OR
Two modern methods of ex-situ conservation of species
Answer:

Tissue culture
In vitro fertilization of eggs
Cryopreservation.

Question 3.
Where was ozone hole discovered?
Answer:
Ozone hole was discovered in Antarctica.

Question 4.
Give one example of natural pollutant.
Answer:
Volcanic ash is a natural pollutant.

Question 5.
What do you understand by EW category of living being?
Answer:
A species which becomes extinct in the wild (EW) is called EW category, their members are seen only in captivity or as a naturalized population outside its historic range due to massive habitat loss.

3. Short answer type questions.

Question 1.
Dandiya raas is not allowed after 10.00 pm. Why?
Answer:
Dandiya rass involves blaring loudspeakers which cause noise pollution. It is undesired loud sound which could be hazardous for ears and general health. In India, the Air (Prevention and Control of Pollution) Act 1981, Amendment 1987, includes noise as an air pollutant. As per law noise after 10 pm is not allowed as many people may be resting. Therefore, Dandiya Raas is not allowed after 10 pm.

Question 2.
Tropical regions exhibit species richness as compared to polar regions. Justify.
Answer:

Tropical regions are bestowed by thicker vegetation and ample food due to available sunlight and humidity.
Polar regions are covered over with snow, with almost no vegetation.
Only handful species of animals can survive here due to their adaptations.
Species richness always shows latitudinal gradient for many plants and animal species. It is high at lower latitudes and there is a steady decline towards the poles. Therefore, tropical regions show more species richness.

Question 3.
How does genetic diversity affect sustenance of a species?
Answer:

Genetic diversity develops the capability of the species to adapt to the varying changes in the environment.
The large variation of the different gene sets allows an individual or the whole population to have the capacity to endure environmental stress in any form.
Some individuals have, a better capacity to endure the increasing pollution in the environment whereas some do not have it.
Those that do not have show infertility or even death from the same conditions.
Those who are able to endure and adapt to this change survive and live in a better way.
This is called natural selection which leads to a loss of genetic diversity in particular habitats.
Thus, due to genetic diversity can affect sustenance of some species.

Question 4.
Greenhouse effect is boon or bane? Give your opinion.
Answer:
(1) The natural greenhouse effect is good, it is a boon but human enhanced greenhouse effect is a bane.

(2) In the absence of an atmosphere, Earth’s surface temperature would be about -18 °C, or 0 °F, which is too cold for sustaining life.

(3) Earth is habitable because of the natural greenhouse effect. Heating of Earth’s atmosphere due to the presence of greenhouse gases such as water vapour, carbon dioxide (CO₂), methane (CH₄) and oxides of nitrogen (NO₂).

(4) Greenhouse gases have just the right molecular structure to absorb infrared radiation that the Earth emits. It re-emits most of that infrared energy in all directions, warming the atmosphere to its comfortable average temperature of 15 °C (60 °F). So, the greenhouse effect was a boon in olden days before industrialization and invention of automobiles.

(5) However, due to human impact, the proportion of greenhouse gases has increased tremendously causing global warming. Thus, now greenhouse effect has become a bane.

Question 5.
State the effects of CO in human body.
OR
How does CO cause giddiness and exhaustion?
Answer:
Effects of Carbon monoxide:

Carbon monoxide is tasteless, colourless and odourless gas, therefore its presence goes unnoticed.
It can inhibit the blood’s ability to carry oxygen to body tissues.
Supply of oxygen to vital organs such as.the heart and brain is affected due to presence of CO.
When CO is inhaled, it combines with the oxygen carrying haemoglobin of the blood to form carboxyhaemoglobin. Once combined with the haemoglobin, that haemoglobin is no longer available for transporting oxygen.
The symptoms of CO poisoning are headache, nausea, giddiness, etc.

Question 6.
Name two types of particulate pollutants found in air. Add a note on ill effects of the same on human health.
OR
Describe any 2 particulate and gaseous pollutants.
Answer:
I. Types of gaseous pollutants include CO₂, CO, SO₂, NO, NO₂, etc.
(1) Carbon dioxide : It is a greenhouse gas. It is produced in excess due to human activities such as burning of fossil fuels. It is also rising due to increasing deforestation. The natural cycle of Carbon dioxide is disturbed due to human interference. Otherwise, the process of photosynthesis can balance CO₂ : O₂ ratio of the air. Aeroplane traffic such as a jet plane also emits lots of CO₂.

(2) Carbon monoxide (CO) : CO is produced due to incomplete combustion of fuels. It is a toxic gas. Vehicular exhausts produce lot of CO.

II. Types of particulate pollutants are mist, dust, fume and smoke particles, smog, pesticides, heavy metals and radioactive elements, etc.
(1) Dust are fine particles which enter the respiratory passage and can cause damage to delicate tissues in the lungs. Various processes such as construction work, demolition of buildings and traffic can cause dust pollution. There are natural causes of release of dust too, through wind or volcanic eruption.

(2) Smoke and smog are worst type of particulate air pollutants which can cause many respiratory problems like emphysema or asthma.

4. Long answer type questions.

Question 1.
Montreal Protocol is an essential step. Why is it so?
Answer:

Montreal Protocol was an international treaty signed at Montreal in Canada in 1987.
Later many more efforts have been made and protocols have laid down definite roadmaps separately for developing and developed countries.
All these efforts were for reducing emission of CFCs and other ozone depleting chemicals.
All nations realized that ozone depletion can cause penetration of harmful UV radiations to the earth’s surface. This is very hazardous, for flora, fauna and for mainly human beings. Therefore, urgent action was needed to combat this effect.
Montreal Protocol was a very positive move because after 1987, there have been much better condition of ozone layer.

Question 2.
Name any 2 personalities who have contributed to control deforestation in our country. Elaborate on importance of their work.
Answer:
Two personalities who have contributed to control deforestation in our country are:
Saalumara Thimmakka from Karnataka and Moirangthem Loiya from Manipur.
1. Saalumara Thimmakka :

Saalumara Thimmakka is the best example of peoples’ participation in reforestation.
She is an Indian environmentalist from Karnataka. She has taken up work of planting and tending to 385 banyan trees along a 4 km stretch of highway between Hulikal and Kudur. Other 800 trees are also planted by her.
She is honoured with the National Citizens Award of India and Padma Shri in 2019.

2. Moirangthem Loiya :

Moirangthem Loiya is from Manipur who has restored Punshilok forest. For last 17 years he is planting trees after leaving his job.
He brought the lost glory back for the 300 acres forest land. He planted a variety of trees like, bamboo, oak Ficus, teak, jackfruit and Magnolia.
This forest now has over 250 varieties of plants including 25 varieties of bamboo along with many animals making the forest rich in biodiversity.

Question 3.
How BS emission standards changed over time? Why is it essential?
Answer:

BS emission standards changed over the time due to changing city life and more vehicular traffic on the road, especially in the megacities.
Since capital city of Delhi was declared as worst polluted city as far as its air quality is concerned, various measures were taken by the Government of India. There was new fuel policy declared, in which Bharat stage emission standards (BS) were set.
These norms were set to reduce sulphur and aromatic content of petrol and diesel. Also the vehicular engines were upgraded.
Bharat stage emission standards (BS) are standards which are equivalent to Euro norms and have evolved on similar lines as Bharat Stage II (BS II) to BS VI from 2001 to 2017.
Since population of Delhi was to be saved, in 2001, Bharat stage II emission norms were set for CNG and LPG vehicles.
This helped in reduced emission of sulphur which was controlled at 50 ppm in diesel and 150 ppm in petrol. Also aromatic hydrocarbons were reduced at 42% in concerned fuel according to norms.
Because, in spite of all the efforts, Delhi was declared as worst air-polluted city in the world in 2016, therefore, Government of India directly adapted BS VI in the year 2018, skipping BS V These efforts decreased the levels of CO₂ and SO₂ in Delhi.

Question 4.
During large public gatherings like Pandharpur vari, mobile toilets are deployed by the government. Explain how this organic waste is disposed.
Answer:

The toilets deployed at Pandharpur at the time of vari are of the Ecosan type.
Ecosan toilet is a closed system without water and it is an alternative to leach pit toilets.
When the pit of an Ecosan toilet fills up after some time, then it is closed and sealed for about 8-9 months.
In this time the faeces get completely composted to organic manure. In this way the organic waste can be disposed.
It is a practical, efficient and cost-effective solution for human waste disposal.
Also, open-air defecation is prohibited which can cause health problems. Therefore, during large public gatherings like Pandharpur vari mobile toilets like Ecosan are deployed by the government.

Question 5.
How Indian culture and traditions helped in bio-diversity conservation? Give importance of conservation in terms of utilitarian reasons.
Answer:
In Indian culture and traditions in different religions, biodiversity is protected and conserved. Few examples of worship of animals and plants can be given here.

Nagpanchami festival is towards the respect of snakes. They are worshipped on that day and the local people are aware of their role in ecosystem of control of rat population.
Vatapournima festival is worshipping a banyan tree.
Various other festivals teach the value of plants and animals surrounding us. Even the cattle are worshipped on a particular day as a tradition.
Jain religion strongly advocates protection of all animals through vegetarianism.

Conservation in terms of utilitarian reasons:
The conservation of biodiversity can be done in utilitarian way or for ethical reasons. Utilitarian reasons are further classified into narrowly utilitarian and broadly utilitarian reasons:

I. Narrowly utilitarian reasons:

Humans always reap material benefits from biodiversity in the form of resources for basic needs such as food, clothes, shelter.
Industrial products like resins, tannins, perfume base, etc. are also obtained through biodiversity resources.
For making ornaments or artefacts for aesthetic purpose, again biodiversity is sacrificed.
Many medicines are also obtained through biodiversity resources which shares 25% of global medicine market.
Around 25000 species are used for traditional medicines by tribal population worldwide.
Bioprospecting which is a systematic search for development of new sources of chemical compounds, genes, microorganisms, macroorganisms, and other valuable products from nature which is of economically important species is also due to biodiversity.

II. Broadly utilitarian reasons:

Production of oxygen done by all green plants helps human beings to thrive. Amazon forest alone gives 25% of the oxygen to the entire world.
Insects carry out pollination and seed dispersal.
If insects do not carry out pollination and seed dispersal, man would go hungry without crops and fruits.
Biodiversity also is useful in recreation of human beings.

III. Taking all these aspects in consideration, conservation of biodiversity becomes essential. Therefore, to protect and conserve our rich biodiversity on the planet, we have to remember all the utilitarian reasons.

12th Std Biology Questions And Answers:

12th Biology Chapter 3 Exercise Inheritance and Variation Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 3 Inheritance and Variation Textbook Exercise Questions and Answers.

Inheritance and Variation Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 3 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 3 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Phenotypic ratio of incomplete dominance in Mirabilis jalapa.
(a) 2 : 1 : 1
(b) 1 : 2 : 1
(c) 3 : 1
(d) 2 : 2
Answer:
(b) 1 : 2 : 1

Question 2.
In dihybrid cross, F₂ generation offspring show four different phenotypes while the genotypes are ……………….
(a) six
(b) nine
(c) eight
(d) sixteen
Answer:
(b) nine

Question 3.
A cross between an individual with unknown genotype for a trait with recessive plant for that trait is ……………….
(a) back cross
(b) reciprocal cross
(C) monohybrid cross
(d) test cross
Answer:
(d) test cross

Question 4.
When phenotypic and genotypic ratios are the same, then it is an example of ……………….
(a) incomplete dominance
(b) complete dominance
(c) multiple alleles
(d) cytoplasmic inheritance
Answer:
(a) incomplete dominance

Question 5.
If the centromere is situated near the end of the chromosome, the chromosome is called ……………….
(a) Metacentric
(b) Acrocentric
(c) Sub-Metacentric
(d) Telocentric
Answer:
(d) Telocentric

Question 6.
Chromosomal theory of inheritance was proposed by ……………….
(a) Sutton and Boveri
(b) Watson and Crick
(c) Miller and Urey
(d) Oparin and Halden
Answer:
(a) Sutton and Boveri

Question 7.
If the genes are located in a chromosome as p-q-r-s-t, which of the following gene pairs will have least probability of being inherited together ?
(a) p and q
(b) r and s
(c) s and t
(d) p and s
Answer:
(d) p and s

Question 8.
Find the mismatched pair:
(a) Down’s syndrome = 44 + XY
(b) Turner’s syndrome = 44 + XO
(c) Klinefelter’s syndrome = 44 + XXY
(d) Super female = 44 + XXX
Answer:
(a) Down’s syndrome = 44 + XY

Question 9.
A colourblind man marries a woman, who is homozygous for normal colour vision, the probability of their son being colour blind is ……………….
(a) 0%
(b) 25%
(c) 50%
(d) 100%
Answer:
(a) 0%

2. Very Short Answer Questions

Question 1.
Explain the statements
a. Test cross is back cross but back cross is not necessarily a test cross.
b. Law of dominance is not universal.
Answer:
a. (1) Test cross is the cross between F₁ hybrid and its homozygous recessive parent.
(2) Back cross is the cross of offspring with any one of the parents, either dominant or recessive.
(3) Therefore, test cross can be a back cross – but back cross cannot be a test cross.

b. (1) There are many traits in many organisms which show dominance. For example, widow’s peak in human beings is a dominant trait. Yellow seed colour and round seed shape are dominant traits in pea plant.
(2) However, there are characters which are either co-dominant, such as genes for human blood group A and B or incompletely dominant as in flower colour of Mirabilis jalapa.
(3) Therefore the law of dominance is not universally applicable.

Question 2.
Define the following terms:
a. Dihybrid cross
b. Homozygous
c. Heterozygous
d. Test cross
Answer:
a. A cross between parents differing in two heritable traits is called dihybrid cross.
b. An individual possessing identical alleles for a particular trait is called homozygous or pure for that trait. E.g. TT for tallness and tt for dwarfness.
c. An individual possessing contrasting allele for a particular trait is called heterozygous. E.g. Tt showing tallness.
d. The cross of F₁ progeny with homozygous recessive parent is called a test cross.

Question 3.
What are allosomes?
Answer:
Allosomes are the chromosomes which decide the sex of an organism.

Question 4.
What is crossing over?
Answer:
Crossing over is the process of forming new recombinations by interchanging and exchanging non-sister chromatid arms of the homologous chromosomes.

Question 5.
Give one example of autosomal recessive disorder.
Answer:
Thalassemia is an example of autosomal recessive disorder.

Question 6.
What are X-linked genes?
Answer:
Genes located on the non-homologous region of X chromosome are called X-linked genes.

Question 7.
What are holandric traits?
Answer:
Genes located on the non-homologous region of Y chromosome are called Y-linked genes. The traits due to such genes are called holandric traits which are seen only in male sex.

Question 8.
Give an example of chromosomal disorder caused due to non-disjunction of autosomes.
Answer:
Down’s syndrome is an example of chromosomal disorder caused due to non-disjunction of autosomes.

Question 9.
Give one example of complete sex linkage.
Answer:
Sex linkage can be complete X linkage and complete Y linkage. X linkage is haemophilia and Y linkage is hypertrichosis.

3. Short Answer Questions

Question 1.
Enlist seven traits of pea plant selected / studied by Mendel.
Answer:
Seven traits in pea selected by Mendel:

Tall habit versus dwarf habit (Height of the plant).
Purple flowers versus white flowers. (Colour of flowers)
Yellow seeds versus green seeds. (Colour of seeds)
Round seeds versus wrinkled seeds. (Shape of seeds)
Green pods versus yellow pods. (Colour of pods)
Inflated pods versus constricted pods. (Shape of pods)
Axial flower versus terminal flower. (Position of a flower)

Question 2.
Why law of segregation is also called the law of purity of gametes?
Answer:
(1) Mendel’s law of segregation is also called Law of purity of gametes because, during formation of gametes, the alleles separate/ segregate from each other and only one allele enters a gamete.

(2) The separation of one allele does not affect other. Since single allele enters a gamete means gametes will be pure for a trait.
E.g. The contrasting characters such as tall (T) and dwarf (t) present in F₁ hybrid (Tt) segregate during the formation of gametes.

(3) Owing to this, two types of gametes i.e. T and t are formed which are pure for the characters which they carry.
(4) Thus for example:

Question 3.
Pleiotropy.
Answer:

When a single gene controls two or more different traits, it is called a pleiotropic gene and the phenomenon is known as pleiotropy or pleiotropism.
The pleiotropic ratio is always 1 : 2 instead . of normal 3 : 1.
Sickle-cell anaemia is caused by the gene HbS. The healthy or normal gene which is dominant is HbA. The heterozygotes or carriers i.e., HbA/Hbs show anaemia as there is deficiency of haemoglobin due to sickling of RBCs. Abnormally low concentration of oxygen can cause sickling of RBCs.
The homozygotes possessing the recessive gene HbS die because of fatal anaemia because the gene for sickle-cell anaemia is lethal in homozygous condition and causes sickle-cell trait in heterozygous carrier.
Thus a single gene produces two different expressions.
When two carriers are married they will produce normal carriers and Sickle-cell anaemic children in the ratio of 1 : 2 : 1. Out of these three children sickle-cell anaemic child will die leaving the ratio 1 : 2 instead of 3 : 1.

Question 4.
What are the reasons of Mendel’s success?
Answer:
Reasons for Mendel’s success:

Mendel planned his experiments carefully and these experiments consisted of large sample.
He always recorded the results of number of plants of each type and their ratios.
The contrasting characters that he chose were easily recognizable.
The seven pairs of contrasting characters that he selected were under control of a single factor each. They were present on separate chromosomes and were transmitted from one generation to the next.
Mendel studied and introduced concept of dominance and recessiveness.

Question 5.
“Father is responsible for determination of sex of child and not the mother”. Justify.
Answer:

Human made is heterogame tic, i.e. he produces two different types of sperms. One is bearing X chromosome along with 22 autosomes and the other is Y bearing sperm with 22 autosomes.
Mother, on the other hand, is homogametic, producing all similar types of ova, i.e 22 + X chromosomal combination.
If 22+X bearing sperm fertilise an egg, female child is formed while if Y bearing sperm fertilizes an egg, male child is formed.
Thus the sex of the child is dependent upon type of sperm that father gives, therefore, it is said that father is responsible for determination of sex of a child and not the mother.

Question 6.
What is linkage? How many linkage groups do occur in human being and maize?
Answer:

Linkage is defined as the tendency of the genes to be inherited together because they are present in the same chromosome. Linkage group is group of genes situated on a chromosome.
Humans have 23 linkage groups because they have 23 pairs of chromosomes.
Maize plant has 10 linkage groups because they have 10 pairs of chromosomes.

Question 7.
PKU.
Answer:

PKU means phenylketonuria which is an autosomal recessive inborn error.
In this disorder the metabolism of phenylalanine does not occur due to deficiency of phenylalanine hydroxylase (PAH) enzyme.
This enzyme is necessary to metabolize the amino acid phenylalanine to the amino acid tyrosine.
When PAH activity is reduced, phenylalanine accumulates in blood and cerebrospinal fluid and is converted into phenylpyruvate or phenyl-ketone which is a toxic compound. This may cause mental retardation. Excess phenylalanine is excreted in urine, hence this disease is called phenylketonuria.
PKU is caused by mutations in the PAH gene on chromosome no. 12.
Untreated PKU causes abnormal phenotype which includes growth failure, poor skin pigmentation, microcephaly, seizures, global developmental delay and severe intellectual impairment. However, at birth if an infant is checked for PKU, the further abnormalities can be avoided.

Question 8.
Compare X-chromosome and Y-chromosome.
Answer:

X-chromosome	Y-chromosome
1. X-chromosome is straight, rod like and longer 1. than Y chromosome. It is metacentric.	1. Y-chromosome is shorter chromosome which is acrocentric.
2. X-chromosome has large amount of euchromatin and small amount of heterochromatin.	2. Y-chromosome has small amount of euchromatin and large amount of heterochromatin.
3. X-chromosome has large amount of DNA, hence it is genetically active due to more genes.	3. Y-chromosome has less amount of DNA, hence it is genetically less active or inert due to lesser genes.
4. Non-homologous region of X-chromosome is longer and contains more genes.	4. Non-homologous region of Y-chromosome is shorter and contains lesser genes.
5. Contains X-linked genes on non-homologous region.	5. Contains Y-linked genes on non-homologous region.
6. X-chromosome is present in men as well as women.	6. Y-chromosome is present only in men.

Question 9.
Explain the chromosomal theory of inheritance.
Answer:
Chromosomal theory of inheritance was put forth by Sutton and Boveri after studying paraillel behaviour of genes and chromosomes during meiotic division. This theory states following points:

Chromosomal theory identifies chromosomes as the carrier of genetic material.
All the hereditary characters are transmitted by gametes. Nucleus of gametes, i.e. sperms and ova of the parents contain chromosomes which transmit the heredity to offspring.
Chromosomes are found in pairs in somatic or diploid cells.
During gamete formation, homologous chromosomes pair and segregate independently at meiosis. The diploid condition is converted into haploid condition. Thus each gamete contains only one chromosome of a pair.
During fertilization, the union of sperm and egg restores the diploid number of chromosomes.

Question 10.
Observe the given pedigree chart and answer the following questions

(a) Identify whether the trait is sex-linked or autosomal.
(b) Give an example of a trait in human beings which shows such a pattern of inheritance.
Answer:
Pedigree given above shows:

First Generation : Carrier woman marrying a sufferer man. Their three children are in following birth order.
Second generation : First son is normal, second daughter is carrier and third daughter is sufferer.
Third generation : The sufferer daughter marries a normal man. Her children are normal daughter and sufferer son.

(a) The above pedigree show sex-linked (X-linked) trait. Since criss-cross inheritance is seen in the trait, it must be sex-linked inheritance.
(b) Such trait and its inheritance can be seen in colour blindness.

4. Match the Columns

rewrite the matching pairs.

Column I	Column II
(1) 21 trisomy	(a) Turner’s syndrome
(2) X-monosomy	(b) Klinefelter’s syndrome
(3) Holandric traits	(c) Down’s syndrome
(4) Feminized male	(d) Hypertrichosis

Answer:

Column I	Column II
(1) 21 trisomy	(c) Down’s syndrome
(2) X-monosomy	(a) Turner’s syndrome
(3) Holandric traits	(d) Hypertrichosis
(4) Feminized male	(b) Klinefelter’s syndrome

5. Long Answer Questions

Question 1.
What is dihybrid cross? Explain with suitable example and checker board method.
Answer:
1. A cross which involves two pairs of alleles is called a dihybrid cross. A phenotypic ratio of 9 : 3 : 3 : 1 obtained in the F₂ generation of a dihybrid cross is called a dihybrid ratio.

(2) Thus for example, when we cross a true breeding pea plant bearing round and yellow seeds with a true breeding pea plant bearing wrinkled and green seeds we get pea plants bearing round and yellow seeds in the F₁ generation.

(3) When F₁ plants are selfed, we get a ratio of 9 : 3 : 3 : 1 in the F₂ generation, where 9 plants bear yellow round seeds, 3 plants bear yellow wrinkled seeds, 3 plants bear green round seeds and 1 plant bears green wrinkled seeds.

(4) Parents (P₁) : RRYY × rryy
Gametes of P₁ RY and ry
F₁ generation : RrYy(Yellow round)
On selfing F₁ : RrYy × RrYy
Gametes of F₁ : RY, Ry, rY, ry

P₂ generation:

Round Yellow : 9 Round green : 3 Wrinkled yellow : 3 Wrinkled green : 1
Phenotypic ratio : 9 : 3 : 3 : 1
Genotypic ratio : 1 : 2 : 1 : 2 : 4 : 2 : 1 : 2 : 1

Question 2.
Explain with suitable example an independent assortment.
Answer:
(1) The law of independent assortment states that when hybrid possessing two or more pairs of contrasting characters bearing alleles form gametes, the alleles in each pair segregate independently of the other pair. Therefore, the inheritance of one pair of characters is independent of that of the other pair of characters.
(2) For example, when we cross a pea plant which is tall and having purple flowers with dwarf plant having white flowers we obtain all tall plants with purple flowers in F₁ generation. When F₁ generation are selfed, 9 : 3 : 3 : 1 ratio was obtained in F₂ generation with 9 tall and purple flower, 3 tall with white flowers, 3 dwarf with purple flowers and 1 which was dwarf and white. Tallness and purple colour are dominant traits while dwarfness and white colour are recessive traits.

(i) Homozygous tall purple – TTPP
(ii) Homozygous dwarf white – ttpp

Tall purple = 9. Tall white = 3
Dwarf purple = 3, Dwarf white = 1,
Phenotypic ratio = 9 : 3 : 3 : 1
Results : The offspring of F₁ generation will be in the proportion of 9 : 3 : 3 : 1, where 9 are tall purple, 3 are tall white, 3 are dwarf purple and 1 is dwarf white.

Question 3.
Define test cross and explain its significance.
Answer:
1. Definition of test cross : A cross between F₁ offspring and its homozygous recessive parent is called a test cross.
2. Significance of test cross:

Test cross can be used to find out the genotype of any plant which shows dominant characters.
Whether the plant is homozygous or heterozygous can be understood by performing test cross.
Test cross is used to introduce useful recessive traits in the hybrids of self- pollinated plants.
Test cross is quicker method to improve the variety of crop plants and thus it is useful for breeders and geneticists.
Test cross can be used for verifying the laws of inheritance.

Question 4.
What is parthenogenesis? Explain the haplodiploid method of sex determination in honey bee.
Answer:
I. Parthenogenesis is a natural form of asexual reproduction in which growth and development of embryos occur without fertilization by sperm. In some insects like honey bees, parthenogenesis means development of an embryo from an unfertilized egg cell.

II. In honey bee:

Sex determination is by haplodiploid system.
Sex is determined by the number of sets of chromosomes received by an individual.
The egg which is fertilized by sperm, becomes diploid and develops into female.
The egg which is not fertilized develops by parthenogenesis and develops into a male.
The queen and worker bee therefore contain 32 chromosomes. The drone, i.e. male bears 16 chromosomes.
The sperms are produced by mitosis while eggs are produced by meiosis.

Question 5.
In the answer for inheritance of X-linked. genes, Madhav had shown carrier male. His answer was marked incorrect. Madhav was wondering why his marks were cut. Explain the reason.
Answer:
Males can never be carriers. They have single X and other Y chromosome. In X linked inheritance, the genes are present on the non-homologous region of X chromosome. Males do not have other X and hence if the genes are present on his X chromosome, they will not be suppressed in them. The Y chromosome does not have dominant gene to hide this expression as there is no homolorous region too. But in case of females, there are double X chromosomes and hence if X-linked gene is recessive, the other X can hide the expression of such X-linked gene.

Thus she becomes a carrier without showing any physical characters. She is physically normal and does not suffer from such X-linked recessive disorder. Thus, Madhav will get his answer wrong due to incorrect concept.

Question 6.
With the help of neat labelled diagram, describe the structure of chromosome.
Answer:

(1) A chromosome is best visible during metaphase, when it is highly condensed.

(2) Chromosome shows two identical halves, called sister chromatids. Chromatids are held together at centromere which is also called primary constriction.

(3) Primary constriction has disc shaped plate called kinetochore. This plate is useful for attachment of spindle fibres at the time of cell division.

(4) Additional narrow areas called secondary constrictions are seen in some chromosomes which are known as nucleolar organizers. They help in the formation of nucleolus. At secondary constriction (i) there is nucleolar organising region. Secondary constriction (ii) shows attachment of satellite body or SAT body.

(5) Each chromatid is made up of sub¬chromatids called chromonemata. Each chromonema consists of a long, unbranched, slender, highly coiled DNA thread. This double stranded DNA molecule extends throughout the length of the chromosome.

(6) The ends of the chromatid arms are called telomeres.

Question 7.
What is criss-cross inheritance? Explain with suitable example.
Answer:
Criss-cross inheritance is the type of inheritance in which the genes are passed on from father to daughter and then to her son, i.e. from male to female and from female to male (grandson). In other words, it is also said that the transmission is from the grandfather to his grandson through his daughter.

I. Inheritance of Colour blindness show criss-cross pattern.
(1) Colour blindness is a sex-linked disorder in which the person concerned cannot distinguish between red and green colours.

(2) It is recessively X-linked disorder, which is expressed in males. It is rarely seen in females.

(3) The genes for normal vision are dominant whereas those for colour blindness are recessive.

(4)

Gene for normal vision : X^C
Gene for colour blindness : X^c
Normal female : X^CX^C
Normal male : X^CY
Colour blind female : X^cX^c
Carrier female : X^CX^c
Colour blind male : X^c Y

II. Crosses showing the inheritance of colour blindness:
(i) A cross between normal female and colour-blind male.

(ii) A cross of carrier female with normal male.

(1) Normal female with Colour blind male. Such cross produces 50% carrier daughters and 50% normal sons.

(2) Carrier female with normal male. Such a cross produces 25% normal daughters, 25% normal sons, 25% carrier daughters and 25% colour blind sons.

(3) Colour blind father transmits the disorder to his grandson through his carrier daughter. The inheritance of characters from the father to his grandson through his daughter is called criss-cross inheritance.

Question 8.
Describe the different types of chromosomes.
Answer:
I. Chromosomes are classified into the following four types according to the position of the centromere in them:
(1) Metacentric : In metacentric chromosome, the centromere is situated in the middle of the chromosome. The two arms of the chromosome are nearly equal. It appears ‘V’-shaped during anaphase.

(2) Sub-metacentric : In sub-metacentric chromosome, the centromere is situated some distance away from the middle. Due to this, one arm of the chromosome is shorter than the other. It appears T-shaped during anaphase.

(3) Acrocentric : In acrocentric chromosome, the centromere is situated near the end of the chromosome. One arm of the acrocentric chromosome is very short while the other is long making it appear like ‘J’-shaped during anaphase.

(4) Telocentric : In telocentric chromosome, the centromere is situated at the tip of the chromosome. Telocentric chromosome has only one arm thus it appears rod-shaped.

II. Based on the functions, chromosomes are divided into autosomes and allosomes. Autosomes are somatic chromosomes which decide the body characters. Allosomes are sex chromosomes which decide the sex of the individual.

12th Std Biology Questions And Answers:

12th Biology Chapter 11 Exercise Enhancement of Food Production Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 11 Enhancement of Food Production Textbook Exercise Questions and Answers.

Enhancement of Food Production Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 11 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 11 Exercise Solutions

1. Multiple choice questions

Question 1.
Antibiotic Chloromycetin is obtained from ………………….
(a) Streptomyces erythreus
(b) Penicillium chrysogenum
(c) Streptomyces venezuelae
(d) Streptomyces griseus
Answer:
(c) Streptomyces venezuelae

Question 2.
Removal of large pieces of floating debris, oily substances, etc. during sewage treatment is called ………………….
(a) primary treatment
(b) secondary treatment
(c) final treatment
(d) amplification
Answer:
(a) primary treatment

Question 3.
Which one of the following is free living bacterial biofertilizer?
(a) Azotobacter
(b) Rhizobium
(c) Nostoc
(d) Bacillus thuringiensis
Answer:
(a) Azotobacter

Question 4.
Most commonly used substrate for industrial production of beer is ………………….
(a) barley
(b) wheat
(c) corn
(d) sugar cane molasses
Answer:
(a) barley

Question 5.
Ethanol is commercially produced through a particular species of ………………….
(a) Aspergillus
(b) Saccharomyces
(c) Clostridium
(d) Trichoderma
Answer:
(b) Saccharomyces

Question 6.
One of the free-living anaerobic nitrogen- fixers is ………………….
(a) Azotobacter
(b) Beijerinckia
(c) Rhodospirillum
(d) Rhizobium
Answer:
(c) Rhodospirillum

Question 7.
Microorganisms also help in production of food like ………………….
(a) bread
(b) alcoholic beverages
(c) vegetables
(d) pulses
Answer:
(a) bread

Question 8.
MOET technique is used for ………………….
(a) production of hybrids
(b) inbreeding
(c) outbreeding
(d) outcrossing
Answer:
(a) production of hybrids

Question 9.
Mule is the outcome of ………………….
(a) inbreeding
(b) artificial insemination
(c) interspecific hybridization
(d) outbreeding
Answer:
(c) interspecific hybridization

2. Very Short Answer Questions

Question 1.
What makes idlis puffy?
Answer:
During preparation of idlis, rice and black gram flour is fermented by air borne Leuconostoc and Streptococcus bacteria. CO₂ produced during fermentation makes them puffy.

Question 2.
Bacterial biofertilizers.
Answer:
Rhizobium, Frankia, Pseudomonas striata, Bacillus polymyxa, Agrobacterium, Microccocus, Azotobacter, Costridium, Beijerinkia, Klebsiella.

Question 3.
What is the microbial source of vitamin B₁₂?
Answer:
The microbial source of vitamin B₁₂ is Pseudomonas denitrificans.

Question 4.
What is the microbial source of enzyme invertase?
Answer:
The microbial source of enzyme invertase is Saccharomyces cerevisiae.

Question 5.
Milk starts to coagulate when Lactic Acid Bacteria (LAB) are added to warm milk as a starter. Mention any two other benefits of LAB.
Answer:
Lactic Acid Bacteria (LAB) check the growth of disease causing microbes and produce vitamin B.

Question 6.
Name the enzyme produced by Streptococcus bacterium. Explain its importance in medical sciences.
Answer:
The enzyme produced by Streptococcus spp. is streptokinase. It is used as a ‘clot buster’ for clearing blood clots in the blood vessels in heart patients.

Question 7.
What is breed?
Answer:
Breed is a group of animals related by descent and similar in most characters like general appearance, features, size, configuration, etc.

Question 8.
Estuary
Answer:
Estuary is a place where river meets the sea.

Question 9.
What is shellac?
Answer:
Shellac is the pure form of lac obtained by washing and filtering.

3. Short Answer Questions.

Question 1.
Many microbes are used at home during preparation of food items. Comment on such useful ones with examples.
Answer:

Many food preparations made at home involves the use of microorganisms.
The microbes Lactobacilli are used in the preparation of dhokla from gram flour and buttermilk by the process of fermentation.
Dosa and idlis are prepared by using batter of rice and black gram which is fermented by air borne Leuconostoc and Streptococcus bacteria.
Large, fleshy fruiting bodies of some mushrooms and truffles are directly used as food. It is sugar free, fat free food rich in proteins, vitamins, minerals and amino acids. It is food with low calories.
Curd is prepared by inoculating milk with Lactobacillus acidophilus. Lactic acid produced during fermentation causes coagulation and partial digestion of milk protein casein and milk turns into curd.
Buttermilk is the acidulated liquid left after churning of butter from curd, is called buttermilk.

Question 2.
What is biogas? Write in brief about the production process.
Answer:
Biogas is a mixture of methane CH₄ (50-60%), CO₂ (30-40%), H₂S (0-3%) and other gases (CO, N₂, H₂) in traces.

Biogas production process:
a. A typical biogas plant consists of digester (made up of concrete bricks and cement or steel and is partly buried in the soil) and gas holder (a cylindrical gas tank to collect gases).
b. Raw materials like cow dung is mixed with water in equal proportion to make slurry which is fed into the digester’ through a side opening (charge pit).

Anaerobic digestion involves following processes:
i. Hydrolysis or solubilization:
Anaerobic hydrolyzing bacteria like Clostridium and Pseudomonas hydrolyse carbohydrates into simple sugars, proteins into amino acids and lipids into fatty acids.

ii. Acidogenesis:
Facultative and obligate anaerobic, acidogenic bacteria convert simple organic substances into acids like formic acid, acetic acid, H₂ and CO₂

iii. Methanogenesis:
Anaerobic methanogenic bacteria like Methanobacterium, Methanococcus convert acetate, H₂ and CO₂ into Methane, CO₂ and H₂O and other products.
12 mol CH₃COOH → 12CH₄ + 12CO₂ 4mol H.COOH → CH₄ + 3CO₂ + 2H₂O CO₂ + 4H₂ → CH₄ + 2H₂O

Question 3.
Biocontrol agents.
Answer:
(1) Biocontrol agents are the organisms like (bacteria, fungi, viruses and protozoans) act which are employed for controlling pathogens, pests and weeds.

(2) They cause the disease to the pest or compete or kill them.

(3) The use of biocontrol measures greatly reduces use of toxic chemicals and pesticides that are harmful to human beings and also pollute our environment.

(4) Biocontrol agents and their hosts.

Bacteria (Bacillus thuringiensis, B. papilliae and B. lentimorbus Hosts : Caterpillars, cabbage worms, adult beetles
Fungi (Beauveria bassiana, Entomophothora, pallidaroseum, Zoophthora radicans) Host : Aphid crocci, A. unguicilata, mealy bugs, mites, white flies, etc.
Protozoans (Nosema locustae) Host: Grasshoppers, caterpillars, crickets
Viruses (Nucleopolyhedro virus-NPV, Granulovirus-GV) Host : Caterpillars, Gypsy moth, ants and beetles.

(5) Some examples:

Bacillus thuringiensis (Bt) is a microbiai pesticide used to get rid of butterfly, caterpillars.
Trichoderma fungus is an effective biocontrol agent against soil borne fungal plant pathogens which infect roots and rhizomes.
Phytophthora palmiuora is a mycoherbicide that controls milk weed in orchards.
Pseudomonas spp. is a bacterial herbicide that attacks several weeds.
Tyrea moth controls the weed Senecio jacobeac.

Question 4.
Name any two enzymes and antibiotics with their microbial source.
Answer:

Microbial source of Chloromycetin. – Streptomyces venezuelae
Microbial source of Erythromycin. – Streptomyces erythreus
Microbial source of Penicillin. – Penicillium chrysogenum
Microbial source of Streptomycin. – Streptomyces griseus
Microbial source of Griseofulvin. – Penicillium griseojulvum
Microbial source of Bacitracin. – Bacillus licheniformis
Microbial source of Oxytetracyclin / Terramycin. – Streptomyces aurifaciens
The enzyme produced by Streptococcus bacterium. – Streptokinase
Microbial source of Invertase. – Saccharomyces cerevisiae
Microbial source of Pectinase. – Sclerotinia libertine, Aspergillus niger
Microbial source of Lipase. – Candida lipolytica
Microbial source of Cellulase. – Trichoderma konigii

Question 5.
Write the principles of farm management.
Answer:
The principles of farm management are as follows:

Selection of high-yielding breeds.
Understanding the feed requirements of farm animals.
Supply of adequate nutritional sources for the animals.
Maintaining the cleanliness of environment.
Maintenance of health with the help of veterinary supervision.
Undertaking vaccination programmes.
Development of high-yielding cross-bred varieties.
Making various products and their preservation.
Distribution and marketing of the farm produce.

Question 6.
Give the economic importance of fisheries.
Answer:
Economic importance of fisheries is as follows:

Fish is a nutritious food and thus is a source of many vitamins, minerals and nutrients.
Commercial products such as fish oil, fish meal and fertilizers, fish guano, fish glue, isinglass are prepared from fish.
These by-products are used in paints, soaps, oils and medicines.
Some organisms like prawns and lobsters have high export value and market price.
Fish farming and other fishery trades provide job opportunity and self-employment
Productivity and national economy is improved through fishery practices.

Question 7.
Enlist the species of honey bee mentioning their specific uses.
Answer:
(1) The four species of honey bees commonly found in India : Apis dorsata (rock bee, or wild bee), Apis jlorea (little bee), Apis mellifera (European bee) and Apis indica (Indian bee).

(2) Uses:

Rock bee : They produce 36 kg of honey per comb per year. They produce bee wax.
Little bee : They produce half kg of honey per hive per year.
European bee : The average production per colony per year is 25 to 40 kg.
Indian bee : The average production per colony per year is 6 to 8 kg.

Question 8.
What are A, B, C, D in the table given below.

Types of microbe	Name	Commercial Product
Fungus	A	Penicillin
Bacterium	Acetobacter aceti	B
C	Aspergillus niger	Citric acid
Yeast	D	Ethanol

Answer:
A : Penicillium chrysogenum
B : Vinegar (Acetic acid)
C : Fungus
D : Sachharomyces cerevisiae var. ellipsoidis

4. Long Answer Questions.

Question 1.
Explain the process of sewage water treatment before it can be discharged into natural bodies. Why is this treatment essential?
Answer:
Sewage treatment includes following steps:
(1) Preliminary Treatment:

Screening: The larger suspended or floating objects are filtered and removed in screening chambers by passing the sewage through screens or net in the chambers.
Grit Chamber : Filtered sewage is passed into series of grit chambers which contain large stones (pebbles) and brick-ballast. Coarse particles which settle down by gravity are removed.

(2) Primary treatment (physical treatment):

The sewage water is pumped into the primary sedimentation tank where 50-70% of the suspended solid or organic matter get sedimented and about 30-40% (in number) of coliform organisms are removed.
The organic matter which is settled down is called primary sludge.
Primary sludge is removed by mechanically operated devices.
Dissolved organic matter and micro-organisms in the supernatant (effluent) are then removed by the secondary treatment.

(3) Secondary treatment (biological treatment):

The primary effluent is passed into large aeration tanks where it is constantly agitated mechanically and air is pumped into it.
The mesh like masses of aerobic bacteria, slime and fungal hyphae, known as floes are formed.
Aerobic microbes consume most of the organic matter and this reduces BOD (Biochemical Oxygen Demand) of the effluent.

(4) Tertiary treatment:

Once the BOD is sufficiently reduced, waste water is passed into a settling tank where the floes are allowed to sediment.
The sediment is called activated sludge.
Small part of activated sludge is transferred to aeration tank and the major part is pumped in to large anaerobic sludge digesters.
In these tanks, anaerobic bacteria grow and digest the bacteria and fungi in the sludge and gases like methane, hydrogen sulphide, CO₂, etc. are released.
Effluents from these digesters are released in natural water bodies like rivers and streams after chlorination which kills pathogenic bacteria.
Digested sludge is then disposed.

Question 2.
Lac culture.
Answer:

Lac is a pink coloured resin secreted by dermal glands of female lac insect (Trachardia lacca) that hardens on coming in contact with air forming lac.
Lac is a complex substance having resin, sugar, water, minerals and alkaline substances.
Lac insect is colonial in habit and it feeds on succulent twigs like ber, peepal, palas, kusum, babool,
These plants are artificially inoculated in order to get better and regular supply of good quality and quantity of lac.
Natural lac is always contaminated and pure form of lac obtained by washing and filtering is called as shellac.
Lac is used to make bangles, toys, woodwork, inks, mirrors, etc.
India’s share is 85% of total lac produced in the world.

Question 3.
Describe various methods of fish preservation.
Answer:

Fish is a highly perishable commodity.
After catching the fish it immediately starts spoilage process.
In order to prevent this process, the fish preservation is done.

The different methods of fish preservation are as follows:

Chilling : This involves covering the fish with layers of ice. Ice is effective for short term preservation. It inhibits the activity of autolytic enzymes.
Freezing : It is a long duration preservation method. Fish are freezed at 0°C to -20°C. This also inhibit autolytic enzyme activities and slows down bacterial growth.
Freeze drying : The deep frozen -fish at -20°C are dried by direct sublimation of ice to water vapour with any melting into liquid water. This is achieved by exposing the frozen fish to 140°C in a vacuum chamber. The fish is then packed or canned in dried condition.
Sun drying : This inhibits the growth of microorganisms that spoil the fish.
Smoke drying : Smoke is prepared by burning woods with less resinous matter. Bacteria are destroyed by the acid content of the smoke. Smoking also give the characteristic colour, taste and odour to fish.
Salting : Salt removes the moisture from the fish tissues by osmosis. High salt concentration destroys autolytic enzymes and halts bacterial activity.
Canning : Canning involves sealing the food in a container, heat ‘sterilising’ the sealed unit and cooling it to ambient temperature for subsequent storage.

Question 4.
Give an account of poultry diseases.
Answer:
Various poultry diseases are as follows:

Viral diseases : Ranikhet, Bronchitis, Avian influenza (bird flu), etc. Bird flu had serious impact on poultry farming and also caused human infection.
Bacterial diseases : Pullorum, Cholera, Typhoid, TB, CRD (chronic respiratory disease), Enteritis, etc.
Fungal diseases : Aspergillosis, Favus and Thrush.
Parasitic diseases : Lice infection, round worm, caecal worm infections, etc.
Protozoan diseases : Coccidiosis.

Question 5.
Give an account of mutation breeding with examples.
Answer:

Mutations are sudden heritable changes in the genotype.
Natural mutations occur at a very slow rate.
Natural physical mutagens include exposure to high temperature, high concentration of C02, X-rays, UV rays.
Mutations can be induced by using various mutagens.
Mutagens cause gene mutations and chromosomal aberrations.
Chemical mutagens include nitrous acid, EMS (Ethyl – Methyl – Sulphonate), mustard gas, colchicine, etc.
Seedlings or seeds are irradiated by using CO60 or UV bulbs or X-ray machines.
The mutated seedlings are then screened for resistance to diseases/pests, high yield, etc.
Examples of mutant varieties in different crops are Jagannath (rice), NP 836 (rust resistant wheat variety), Indore-2 (cotton variety resistant to bollworm), Regina-II (cabbage variety resistant to bacterial rot).

Question 6.
Describe briefly various steps of plant breeding methods.
Answer:
The main steps of the plant breeding program (Hybridization) are as follows:

(1) Collection of variability:

Germplasm collection is the entire collection of all the diverse alleles for all genes in a given crop.
Wild species and relatives of the cultivated species having desired traits are collected and preserved.
Forests and natural reserves are the means of in situ conservation of germplasm.
Botanical gardens, seed banks, etc. are means of ex situ conservation of germplasm.

(2) Evaluation and selection of parents:

The collected germplasm is evaluated to identify healthy and vigorous plants with desirable and complementary characters.
Selected parents are selfed for three to four generations to increase homozygosity.
Only pure lines are selected, multiplied and used in the hybridization.

(3) Hybridization:

The variety showing maximum desirable features is selected as female (recurrent) parent and the other variety which lacks good characters found in recurrent parent is selected as male parent (donor).
The pollen grains from anthers of male parent are artificially dusted over stigmas of emasculated flowers of female parent.
Hybrid seeds are collected and sown to grow F₁ geneartion.

(4) Selection and Testing of Superior Recombinants:

The F₁ hybrid plants which are superior to both the parents and having high hybrid vigour, are selected and selfed for few generations to make them homozygous for the said desirable characters.
This ensures that there is no further segregation of the characters.

(5) Testing, release and commercialization of new cultivars:

The newly selected lines are evaluated for the productivity and desirable features like disease resistance, pest resistance, quality, etc.
They are initially grown under controlled conditions of water, fertilizers, etc. and their performance is recorded.
The selected lines are then grown for at least three generations in natural field, in different agroclimatic zones.
Finally variety is released as new variety for use by the farmers.

12th Std Biology Questions And Answers:

12th Biology Chapter 1 Exercise Reproduction in Lower and Higher Plants Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 1 Reproduction in Lower and Higher Plants Textbook Exercise Questions and Answers.

Reproduction in Lower and Higher Plants Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 1 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 1 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Insect pollinated flowers usually possess ………………
(a) sticky pollen with a rough surface
(b) large quantities of pollens
(c) dry pollens with a smooth surface
(d) light colored pollens
Answer:
(a) sticky pollen with a rough surface

Question 2.
In ovule, meiosis occurs in ………………
(a) Integument
(b) Nucellus
(c) Megaspore
(d) Megaspore mother cell
Answer:
(d) Megaspore mother cell

Question 3.
The ploidy level is NOT the same in ………………
(a) Integuments and nucellus
(b) Root tip and shoot tip
(c) Secondary nucleus and endosperm
(d) Antipodals and synergids
Answer:
(c) Secondary nucleus and endosperm

Question 4.
Which of the following types require pollination but result is genetically similar to autogamy?
(a) Geitonogamy
(b) Xenogamy
(c) Apogamy
(d) Cleistogamy
Answer:
(a) Geitonogamy

Question 5.
If diploid chromosome number in a flowering plant is 12, then which one of the following will have 6 chromosomes?
(a) Endosperm
(b) Leaf cells
(c) Cotyledons
(d) Synergids
Answer:
(d) Synergids

Question 6.
In angiosperms, endosperm is formed by/ due to ………………
(a) free nuclear divisions of megaspore
(b) polar nuclei
(c) polar nuclei and male gamete
(d) synergids and male gametes
Answer:
(c) polar nuclei and male gamete

Question 7.
Point out the odd one.
(a) Nucellus
(b) Embryo sac
(c) Micropyle
(d) Pollen grain
Answer:
(d) Pollen grain

2. Very Short Answer Questions

Question 1.
The part of gynoecium that determines the compatible nature of pollen grain.
Answer:
Stigmatic surface.

Question 2.
How many haploid cells are present in a mature embryo sac?
Answer:
6 cells, 2 synergids, 1 egg cell, 3 antipodals.

Question 3.
Even though each pollen grain has 2 male gametes why at least 20 pollen grains are required to fertilize 20 ovules in a particular carpel?
Answer:
Angiosperms have phenomenon of double fertilization in which both the male gametes are utilized, one for fusion with egg cell to form zygote and other for fusion with secondary nucleus to form endosperm.

Question 4.
Megasporogenesis
Answer:
It is the process of formation of haploid megaspores from diploid megaspore mother cell.

Question 5.
What is hydrophily?
Answer:
Transfer of pollen grains in pollination process through agency of water is known as hydrophily.

Question 6.
The layer which supplies nourishment to the developing pollen grains.
Answer:
Tapetum

Question 7.
Parthenocarpy
Answer:
The condition in which fruit is developed without the process of fertilization is called parthenocarpy.

Question 8.
Are pollination and fertilization necessary in apomixis?
Answer:
Apomixis is formation of embryos without formation of gametes hence there is no need of pollination and fertilization.

Question 9.
The part of pistil which develops into fruit and seed.
Answer:
Ovary develops into fruit and ovules into seed.

Question 10.
What is the function of filiform apparatus ?
Answer:
Filiform apparatus guides the pollen tube towards egg cell.

3. Short Answer Questions

Question 1.
How polyembryony can be commercially exploited?
Answer:

Polyembryony is the development of more than one embryo inside the seed.
When such polyembryonic seed germinate we get multiple seedlings from it.
This condition increases the chances of survival of new plants.
Nucellar embryos are genetically identical to parent plants hence we get uniform plants.
In horticulture we can utilize these as rootstock for grafting, hence they have significant role in fruit breeding programmes e.g. Citrus, Mango.

Question 2.
Pollination and seeds formation are very crucial for the fruit formation, Justify.
Answer:

After fertilization, ovary is transformed into fruit, where ovary wall becomes fruit wall, i.e pericarp.
Mature ovules are transformed into seeds after fertilization.
Fertilization is a process where male gametes unites with female gamete to form zygote which develops into embryo.
In pollination process pollen grains carrying non-motile male gamete are transferred on stigma.
Seeds have embryo which germinate into new plant hence the goal of reproduction to create offspring for next generation is achieved. Hence these are the crucial events for fruit formation.

Question 3.
Incompatibility is a natural barrier in the fusion of gametes. How will you explain this statement?
Answer:

Self incompatibility or self-sterility is a genetic mechanism that prevents germination of pollen on stigma of same flower. This favours cross pollination. E.g. Tobacco.
In pollen-pistil interaction, when pollen grain is deposited on stigma, pistil has the ability to recognize and allow germination of right type of pollen.
Special type of proteins on stigmatic surface determine compatibility or incompatibility.
A physiological mechanism operates to ensure successful germination of compatible pollen.
Compatible pollen absorbs water and nutrients from stigmatic surface that are absent in pollen and then pollen tube emerges which grow-s through style.

Question 4.
Describe three devices by which cross pollination is encouraged in Angiosperms by avoiding self-pollination?
Answer:

Unisexuality, dichogamy, prepotency, heteromorphy and herkogamy are the outbreeding devices.
Unisexuality : The plants bear either male or female flowers. Due to unisexual nature, self-pollination is avoided. Plants are either dioecious, e.g. Papaya or monoecious, e.g. maize.
Heteromorphy : In same plants different types of flowers are produced. In these flowers, stigmas and anthers are situated at different levels. There is heterostyly and heteroanthy. This prevents self-pollination e.g. Primrose.
Herkogamy : In bisexual flowers we may come across mechanical device to prevent self-pollination. Natural physical barrier avoids contact of pollens with stigma. E.g. Calotropis where pollinia are situated below the stigma.

4. Long Answer Questions

Question 1.
Describe the process of double fertilization.
Answer:
Double fertilization:
(1) Out of the two male gametes produced by the male gametophyte in angiosperms, one unites with the female gamete and the other with the secondary nucleus. Since both the male gametes take part in fertilization and fertilization occurs twice, it is called double fertilization.

(2) During double fertilization, the pollen tube on reaching the ovule enters the embryo sac through micropyle and bursts in one of the synergids. Owing to this, the two male gametes contained in the pollen tube, are set free.

(3) Out of the two male gametes, one unites with the egg or female gamete and the other unites with the secondary nucleus of the embryo sac, forming a triploid or triple fusion nucleus, called the primary endosperm nucleus. The process involving the fusion of one of the male gametes with the egg nucleus, resulting in the formation of a diploid zygote is called syngamy.

(4) The reproductive process in which non-motile male nuclei are carried to the egg cell through a pollen tube is called siphonogamy.

(5) After fertilization, zygote develops into an embryo. Certain changes take place in the ovule leading to the development of a seed.

Question 2.
Explain the stages involved in the maturation of microspore into male gametophyte.
OR
Describe the development of male gametophyte before pollination in angiosperms.
OR
Sketch and label male gametophyte in angiosperm.
Answer:

Microspore or pollen grain is first cell of male gametophyte.
The protoplast of pollen grain divides mitotically to form two unequal cells – a small thin walled generative cell and a large naked vegetative or tube cell.
The generative cell possesses thin cytoplasm and a nucleus. It separates and floats in the cytoplasm of vegetative cell.
The vegetative, possesses thick cytoplasm, irregular shaped nucleus and the reserved food.
In majority of the angiosperms, the pollen grains are liberated at two-celled stage after the dehiscence of the anther.
The generative cell of the pollen grain divides by mitosis to form two male non-motile gametes.

Question 3.
Explain the development of dicot embryo.
Answer:
Development of embryo (dicot) in angio- sperm:

The oospore undergoes a transverse division to form a large basal cell towards the micropyle and a small apical or terminal cell towards the chalaza of the embryo sac. This two celled structure is called proembryo. The basal cell or suspensor initial undergoes repeated transverse divisions to form a multicellular structure called suspensor. The suspensor pushes the embryo towards the endosperm to draw its nutrition.

The development of embryo from a zygote is called embryogenesis.
The fusion of male gamete and an egg cell during fertilization results in the formation of a diploid zygote. The zygote develops a wall around it and is converted into oospore.
The apical cell or embryonal initial of the proembryo undergoes a transverse division followed by two vertical divisions at right angles to form an octant stage.
From octant, the lower four cells form hypocotyl and radicle while four cells of upper side form plumule with two cotyledons.
The lowermost cell of suspensor is hypophysis and by its further division forms part of radicle and root cap.
The cells from upper side of octant divide repeatedly to form heart shaped which elongated further to form two lateral cotyledons.
Enlargement of hypocotyl and cotyledon results into curved embryo which appears horse shoe shaped.

Question 4.
Draw a diagram of the L.S of anatropous ovule and list the components of embryo sac and mention their fate after fertilization.
Answer:
Components of Embryo sac.

Mature embryo sac is 7-celled and 8 nucleate.
Egg apparatus at micropylar end – with 2 synergids and egg cell.
Central cell with secondary nucleus formed by 2 polar nuclei
Antipodal cells at chalazal end – 3 cells.
Pollen tube enters the synergids, Synergids guide the growth of pollen tube towards egg.
Male gamete fuses with female gamete, i.e. syngamy to form zygote which develops into embryo.
One male gamete fuses with secondarynucleus to form primary endosperm nucleus (PEN) which forms endosperm, nutritive tissue for embryo.

5. Fill in the Blanks

Question 1.
The ……………… collects the pollen grains.
Answer:
biotic agents

Question 2.
The male whorl, called the ……………… produces ………………
Answer:
androecium, pollen grains

Question 3.
The pollen grains represent the ………………
Answer:
male

Question 4.
The ……………… contains the egg or ovum.
Answer:
embryo sac

Question 5.
…………….. takes place when one male gamete and the egg fuse together. The fertilized egg grows vs into seed from which the new plants can grow.
Answer:
Fertilization

Question 6.
The ……………… is the base of the flower to which other floral parts are attached.
Answer:
thalamus

Question 7.
……………… is the transfer of pollen grains from anther of the flower to the stigma of the same or a different flower.
Answer:
Pollination

Question 8.
Once the pollen reaches the stigma, pollen tube traverses down the ……………… to the ovary where fertilization occurs.
Answer:
style

Question 9.
The ……………… are coloured to attract the insects that carry the pollen. Some flowers also produce ……………… or ……………… that attracts insects.
Answer:
petals, fragrance, nectar

Question 10.
The whorl ……………… is green that protects the flower until it opens.
Answer:
Calyx.

6. Label the Parts of seed.

Answer:

7. Match the following

Column I (Structure Before seed formation)	Column II (Structure After seed formation)
A. Funiculus	i. Hilum
B. Scar of Ovule	ii. Tegmen
C. Zygote	iii. Testa
D. Inner Integument	iv. Stalk of Seed
	v. Embryo

(a) A-v, B-i, C-ii, D-iv
(b) A-iii, B-iv, C-i, D-v
(c) A-iv, B-i, C-v D-ii
(d) A-iv, B-v C-iii, D-ii
Answer:
(c) A-iv, B-i, C-v D-ii

12th Std Biology Questions And Answers:

12th Biology Chapter 7 Exercise Plant Growth and Mineral Nutrition Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 7 Plant Growth and Mineral Nutrition Textbook Exercise Questions and Answers.

Plant Growth and Mineral Nutrition Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 7 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 7 Exercise Solutions

1. Multiple choice questions

Question 1.
Which of the hormone can replace vernalization ?
(a) Auxin
(b) Cytokinin
(c) Gibberellins
(d) Ethylene
Answer:
(c) Gibberellins

Question 2.
The principle pathway of water translocation in angiosperms is ………………..
(a) Sieve cells
(b) Sieve tube elements
(c) Xylem
(d) Xylem and phloem
Answer:
(c) Xylem

Question 3.
Abscissic acid controls ………………..
(a) cell division
(b) leaf fall and dormancy
(c) shoot elongation
(d) cell elongation and wall formation
Answer:
(b) leaf fall and dormancy

Question 4.
Which is employed for artificial ripening of banana fruits?
(a) Auxin
(b) Ethylene
(c) Cytokinin
(d) Gibberellin
Answer:
(b) Ethylene

Question 5.
Which of the following is required for stimulation of flowering in plants?
(a) Adequate oxygen
(b) Definite photoperiod
(c) Adequate water
(d) Water and minerals
Answer:
(b) Definite photoperiod

Question 6.
For short day plants, the critical period is ………………..
(a) light
(b) dark/night
(c) UV rays
(d) Both (a) and (c)
Answer:
(b) dark/night

Question 7.
Which of the following is NOT day neutral plant?
(a) Tomato
(b) Cotton
(c) Sunflower
(d) Soybean
Answer:
(d) Soybean

Question 8.
Essential macro elements are ………………..
(a) manufactured during photosynthesis
(b) produced by enzymes
(c) obtained from soil
(d) produced by growth hormones
Answer:
(c) obtained from soil

Question 9.
Function of Zinc is ………………..
(a) closing of stomata
(b) biosynthesis of 3-IAA
(c) synthesis of chlorophyll
(d) oxidation of carbohydrates
Answer:
(b) biosynthesis of 3-LAA

Question 10.
Necrosis means ………………..
(a) yellow spot on the leaves
(b) death of tissue
(c) darkening of green colour in leaves
(d) wilting of leaves
Answer:
(b) death of tissue

Question 11.
Conversion of nitrates to nitrogen is called ………………..
(a) ammonification
(b) nitrification
(c) nitrogen fixation
(d) denitrification
Answer:
(d) denitrification

Question 12.
How many molecules of ATP are required to fix one molecule of nitrogen?
(a) 12
(b) 20
(c) 6
(d) 16
Answer:
(d) 16

2. Very short answer questions

Question 1.
Enlist the phases of growth in plants.
Answer:
The three phases of growth are phase of cell division, phase of cell enlargement and phase of cell maturation.

Question 2.
Give full form of IAA.
Answer:
Full form is Indole Acetic Acid.

Question 3.
What does it mean by ‘open growth’?
Answer:
In plants the growth is indeterminate and takes place throughout the life at specific regions having meristems.

Question 4.
Plant stress hormone.
Answer:
Abscissic acid.

Question 5.
What is denitrification?
Answer:
Anaerobic bacteria can convert nitrates of soil back into nitrogen gas. That process performed by denitrifying bacteria is denitrification.

Question 6.
Bacteria responsible for conversion of nitrite to nitrate.
Answer:
Nitrobacter.

Question 7.
What is the role of gibberellins in rosette plants?
Answer:
In rosette plants like beet and cabbage, bolting, i.e. elongation of internodes before flowering is observed due to effect of gibberellins.

Question 8.
Vernalization
Answer:
The response of plant to the influence of low temperature on flowering in plants is called vernalization.

Question 9.
Photoperiodism
Answer:
The response of plant to the influence of light for initiation of flowering is known as photoperiodism.

Question 10.
What is grand period of growth?
Answer:
There are three phases of growth and the total time required for all phases to occur is called grand period of growth.

3. Short Answer Questions

Question 1.
(i) Differentiation
Answer:

It is a process of maturation of cells derived from apical meristems.
Differentiation is a permanent change in structure and function of cells that leads to its maturation.
Cell undergoes major anatomical and physiological change during differentiation process.
In hydrophytic plants parenchyma cells develop large schizogenous cavities which help them in aeration, buoyancy and mechanical support.

(ii) Redifferentiation
Answer:

It is a process in which cells produced by de-differentiation lose their capacity of division and become mature.
The cells mature to perform specific function.
Interfascicular cambium is formed by process of dedifferentiation loses its capacity to divide.
Secondary xylem and secondary phloem is formed form this cambium in vascular cylinder.

Question 2.
Arithmetic growth and Geometric growth
Answer:

Arithmetic growth	Geometric growth
1. In arithmetic growth only one daughter cell continues to divide, while the other undergoes differentiation and maturation.	1. In geometric growth both the daughter cells continue to divide and redivide again and again.
2. Rate of growth is constant.	2 Rate growth is initially slow but later on rapid rate.
3. Linear curve is obtained.	3. Exponential curve is obtained.
4. Mathematical expression is L_t = Lo + rt whereL_t = length of time ‘t’ L_o = Length at time zero r_t = growth rate, t = time of growth	4. Mathematical expression is W_t = Wo^{e rt} where, W_t = final size, Wo = initial size, r = growth rate, t = time of growth E = base of natural logarithm
5. e.g. Elongation of root	5. e.g. Divisions of zygote during embryo development.

Question 3.
Enlist the role and deficiency symptoms of: (a) nitrogen (b) phosphorus (c) potassium.
Answer:
(a) Nitrogen:
Role : Constituent of proteins as amino acids, nucleic acids, vitamins, hormones, coenzymes, ATP and chlorophyll molecule.
Deficiency symptoms : stunted growth and chlorosis.

(b) Phosphorus:
Role : Constituent of cell membrane, certain proteins, nucleic acids and nucleotides, required for all phosphorylation reactions.
Deficiency symptoms : Poor growth, leaves dull green

(c) Potassium :
Role : Determination of anion – cation balance in cell, necessary for protein synthesis, involved in formation of cell membrane, opening and closing of stomata, activates enzymes, helps in maintenance of turgidity of cells.
Deficiency symptom : Yellow edges in leaves, premature death.

Question 4.
What is short day plant? Give any two examples.
Answer:
The plants which flower when the day length or light period is shorter than the critical photoperiod are called short day plants or SDP
SDPs usually flower during winter and late summer.
Examples – Dahlia, Aster, Tobacco, Chrysanthemum, Soybean (Glycine max) and Cocklebur (Xanthium).

Question 5.
What is vernalization? Give its significance.
Answer:
A low temperature or chilling treatment that induces early flowering in plants is known as vernalization.

Significance:

Due to chilling treatment crops can be produced earlier.
Crops can be grown in areas where they do not grow naturally.

4. Long answer questions

Question 1.
Explain sigmoid growth curve with the help of diagram.
Answer:

When growth occurs in plants three distinct phases of growth are noticed.
Phase of cell formation is first phase where meristematic cells divide and new cells added.
In phase of cell enlargement newly formed cells elongate and with turgidity there is cell enlargement.
In phase of cell maturation cells get differentiated.
When we compare the growth rate it differs in these three phases.
In first phase or lag phase it is slow, while in log phase or exponential phase, growth rate accelerates and it reaches maximum.
In stationary phase of maturation growth rate slows down and comes to steady state.
When this changing rate of growth is plotted against time duration in a graph a sigmoid or S-shaped growth curve is obtained.

Question 2.
Describe the types of plants on the basis of photoperiod required, with the help of suitable examples.
Answer:

Effect of light duration on flowering of plants is known as photoperiodism.
Depending on photoperiodic response, plants are categorised into three types – Short day plants, long day plants and day neutral plants.

1. Short day plants : Plants that flower under short day length conditions are called short day plants. Plants such as Dahlia, Xanthium, Soybean, Aster, Tobacco and Chrysanthemum are short day plants or SDR. Short day plants require a long uninterrupted dark period for flowering. Therefore, they are also called long night plants.

2. Long day plants : Plants that flower only when they are exposed to light period longer than their critical photoperiod are called long day plants or LDP Long day plants require a short dark or night period for flowering. Hence, they are also called short night plants. Plants such as radish, spinach, wheat, poppy, cabbage, pea, sugar beet, etc. are long day plants.

3. Day neutral plants : Plants in which the flowering is not affected by the day length period are called day neutral plants or DNP or photoneutral plants. Plants such as cucumber, sunflower, cotton, balsam, maize, tomato, etc. are day neutral plants.

Question 3.
Explain biological nitrogen fixation with example.
Answer:

Conversion of atmospheric nitrogen into nitrogenous salts to make it available to plants for its update is described as nitrogen fixation.
When living organisms are involved in nitrogen fixation process it is known as biological nitrogen fixation.
The process is mainly carried out by prokaryotic organisms, i.e. different kinds of bacteria present in soil.
The nitrogen fixing organisms are known as diazotrophs or nitrogen fixers and about 70% nitrogen is fixed by them.
The nitrogen fixers are either free living bacteria or symbiotic associated with other higher plants e.g. Rhizobium.
The cyanobacteria have specialized cells heterocysts which help in process of nitrogen fixation.
Nitrogen fixation is high energy requiring process and 16 ATP molecules are needed for fixation of one molecule of nitrogen to ammonia.
Soil bacteria like Nitrosomonas, Nitrosocyccus convert ammonia to nitrate and the Nitrobacter convert nitrite to nitrate. This is known as nitrification, biological oxidation.
These bacteria are chemoautotrophic and utilize these processes for their metabolism.
Fabaceae plants like pea, bean have root nodules which harbour symbiotic bacterium Rhizobium which fixes nitrogen. It is host specific, soil bacterium, Nitrogen is made available to host plant.

Question 4.
Write on macro and micro nutrients required for plant growth.
Answer:

Plants absorb mineral nutrients from their surroundings.
For a proper growth of plants about 35 to 40 different elements are required.
Plants absorb these nutrients in ionic or dissolved form from soil with their root system e.g. Phosphorus as PO₄^–, Sulphur as SO₄^2- etc.
Based on their requirement in quantity, they are classified as major nutrients or macronutrients and those needed in small amounts Eire minor or micronutrients.
Macroelements are required in large amounts, as they play nutritive and structural roles e.g. C, H, O, R Mg, N, K, S and Ca. – Ca pectate cell wall component, Mg component of chlorophyll.
C, H, O are non-mineral major elements obtained from air and water e.g. CO₂ is source of carbon, Hydrogen from water.
Microelements are required in traces as they mainly have catalytic role as co-factors or activators of enzymes.
Microelements may be needed for certain activity in life cycle of plant e.g. B for pollen germination, Si has protective role during stress conditions and fungal attacks, Al enhances availability of phosphorus.
The important micronutrients for plant growth are Mn, B, Cu, Zn, Cl.

12th Std Biology Questions And Answers:

12th Biology Chapter 13 Exercise Organisms and Populations Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 13 Organisms and Populations Textbook Exercise Questions and Answers.

Organisms and Populations Class 13 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 13 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 13 Exercise Solutions

1. Multiple choice questions

Question 1.
Which factor of an ecosystem includes plants, animals and microorganisms?
(a) Biotic factor
(b) Abiotic factor
(c) Direct factor
(d) Indirect factor
Answer:
(a) Biotic factor

Question 2.
An assemblage of individuals of different species living in the same habitat and having functional interactions is ……………….
(a) Biotic community
(b) Ecological niche
(c) Population
(d) Ecosystem
Answer:
(a) Biotic community

Question 3.
Association between sea anemone and Hermit crab in gastropod shell is that of ………………..
(a) Mutualism
(b) Commensalism
(c) Parasitism
(d) Amensalism
Answer:
(b) Commensalism

Question 4.
Select the statement which explains best parasitism.
(a) One species is benefited.
(b) Both the species are benefited.
(c) One species is benefited, other is not affected.
(d) One species is benefited, other is harmed.
Answer:
(d) One species is benefited, other is harmed.

Question 5.
Growth of bacteria in a newly inoculated agar plate shows ………………….
(a) exponential growth
(b) logistic growth
(c) Verhulst-Pearl logistic growth
(d) zero growth
Answer:
(c) Verhulst-Pearl logistic growth

2. Very short answer questions.

Question 1.
Define the following terms
a. Commensalism
Answer:
The interaction between two species in which one species gets benefits and the other is neither harmed nor benefited is called commensalism.

b. Parasitism
Answer:
The interaction between two species in which one parasitic species derives benefit from the other host species by harming it is called parasitism.

c. Camouflage
Answer:
Camouflage is the disguising colouration or behaviour to merge with the surrounding so that prey or predator can remain hidden.

Question 2.
Give one example for each
a. Mutualism
b. Interspecific competition
Answer:
a. Lichen is composed of alga (cyanobacteria) and fungus. They cannot survive independently. Their association is mutualistic alga synthesises food by photosynthesis and fungus does the absorption of moisture.

b. Leopard and lion competing for a same prey. Sheep and cow competing for grazing in the same land.

Question 3.
Name the type of association:
a. Clown fish and sea anemone
b. Crow feeding the hatchling of Koel
c. Humming birds and host flowering plants
Answer:
a. Commensalism
b. Brood parasitism
c. Mutualism

Question 4.
What is the ecological process behind the biological control method of managing with pest insects?
Answer:

Pest insects act as prey to predator birds or frogs.
The biological control method consists of releasing the predators in the farms so that they can control the pest population in the natural way.
This also eliminates the use of chemical pesticides.
Frogs are natural predators of locust, therefore the population of this hazardous insect is controlled by frogs and the produce from agricultural farm can be saved.

Protocooperation:

Protocooperation is a type of population interaction where two species interact with each other.
Both are benefited but they have no need to interact with each other.
They can survive and grow even in the absence of other species.
Therefore this interaction is purely for the gain that they receive in such type of interaction.
The interaction that occurs can be between different kingdoms.

3. Short answer questions.

Question 1.
How is the dormancy of seeds different from hibernation in animals?
Answer:
In dormancy seed is not showing any metabolic activities. It can come back to life if and only if it gets suitable moisture and sunlight. Hibernation is suspended state, in which metabolic reactions do take place but at a very reduced pace. Animal arouses on its own after the winter sleep is over. This arousal is spontaneous and depends upon the ambient temperature. Dormant seed does not show such change unless it is planted or thrown in to moist place.

Question 2.
If a marine fish is placed in a fresh water aquarium, will it be able to survive? Give reason.
Answer:
Marine fish has its own osmoregulation which is different from the osmoregulation seen in fresh water fish. In marine water, the ambient salinity is more than the concentration of ions in the body. But in fresh water reverse is the case. Therefore, marine fish has different machinery to cope up with high saline environment. Therefore, it cannot survive in fresh water as its osmoregulation is not possible in less saline waters.

Question 3.
How is the dormancy of seeds different from hibernation in animals?
Answer:
In dormancy seed is not showing any metabolic activities. It can come back to life if and only if it gets suitable moisture and sunlight. Hibernation is suspended state, in which metabolic reactions do take place but at a very reduced pace. Animal arouses on its own after the winter sleep is over. This arousal is spontaneous and depends upon the ambient temperature. Dormant seed does not show such change unless it is planted or thrown into moist place.

Question 4.
An orchid plant is growing on the branch of mango tree. How do you describe this interaction between the orchid and the mango tree?
Answer:

Orchid is an epiphyte. It gets the support from the mango tree. But it does not cause any harm to the mango tree.
Mango tree does not derive any benefit from this association. Therefore, this interaction is of type of commensalism.

Question 5.
Distinguish between the following:
a. Hibernation and Aestivation
Answer:

Hibernation	Aestivation
1. Hibernation is winter sleep shown by some warm-blooded and some cold-blooded animals.	1. Aestivation is the type of summer sleep, shown by cold-blooded animals.
2. It is for the whole winter.	2. It is of short duration.
3. The animals look out for the warmer place to enter into hibernation.	3. Animals search for the moist, shady and cool place to sleep.
4. Metabolic activities of hibernators slowdown in this dormant stage.	4. Metabolic activities of aestivators remain low during aestivation period.
5. Hibernation helps in maintaining the body temperature and prevents any internal body damage due to low temperatures. E.g. Bats, birds, mammals, insects, etc. show hibernation.	5. Aestivation helps in maintaining the body temperature by avoiding the excessive water loss and thus prevents any internal body damaged due to high temperatures. E.g. Bees, snails, earthworms, salamanders, frogs, earthworms, crocodiles, tortoise, etc. show aestivation.

b. Ectotherms and Endotherms
Answer:

Ectotherms	Endotherms
1. Ectotherms do not have ability to generate heat in the body.	1. Endotherms possess the ability to generate their own body heat.
2. Ectotherms depend on the environmental sources to heat their bodies. E.g sunlight.	2. Endotherms do not depend upon outside sources to generate heat.
3. Most ectotherms are confined to warmer parts of the world.	3. Endotherms inhabit coldest parts of the earth.
4. Body temperature of ectotherms fluctuate according to ambient temperature.	4. Body temperatures of endotherms remain constant and do not show fluctuations as per ambient temperatures.
5. Metabolic rate of ectotherms is low. E.g. Amphibians and reptiles.	5. Metabolic rate of endotherms is high. E.g. Mammals and birds

c. Parasitism and Mutualism
Answer:

Parasitism	Mutualism
1. Parasitism is the relationship where only one organism receive benefits, while the other is harmed in return.	1. Mutualism is the relationship where both the organisms of distinct species are benefited.
2. Parasite cannot survive without host but if the host is overexploited then parasite too dies.	2. Both the species are dependent on each other for their benefits and survival.
3. Parasitism can be facultative or obligatory.	3. Mutualism is obligatory relationship.
4. Parasitism is a negative interaction.	4. Mutualism is a positive interaction.

Question 6.
Write a short note on
a. Adaptations of desert animals
Answer:

Animals which are well-adapted to live in deserts are called xerocoles. These animals show adaptations for water conservation or heat tolerance.
These animals show low basal metabolic rate. They obtain moisture from succulent plants and rarely drink water. E.g Gazella and Oryx.
Desert animals like camel produce concentrated urine and dry dung.
Many other hot desert animals are nocturnal, seeking out shade during the day or dwelling underground in burrows.
Smaller animals from desert, emerge from their burrows at night.
Mammals living in cold deserts have developed greater insulation through warmer body fur and insulating layers of fat beneath the skin.
Few adaptations to desert life are unable to cool themselves by sweating so they shelter during the heat of the day. Many desert reptiles are ambush predators and often bury themselves in the sand, waiting for prey to come within range.
Other animals have bodies designed to save water. Scorpions and wolf spiders have a thick outer covering which reduces moisture loss. The kidneys of desert animals concentrate urine, so that they excrete less water.

b. Adaptations of plants to water scarcity
Or
Adaptations in desert plants.
Answer:

Thick cuticle on their leaf surfaces
Stomata of desert plants is sunken that is it is in deep pits to minimize loss of water through transpiration.
Desert plants also have a special photosynthetic pathway (CAM -Crassulacean acid metabolism) that enables their stomata to remain closed during daytime.
Some desert plants like Opuntia, have their leaves reduced or they are modified to spines. Loss of leaf surface helps in prevention of transpiration.
Photosynthetic function is taken over by the flattened stems called as phylloclade.

c. Behavioural adaptations in animals
Answer:

Behavioural responses to cope with variations in their environment are shown by few animals.
Desert lizards manage to keep their body temperature fairly constant by behavioural adaptations. They bask in the sun and absorb heat, when their body temperature drops below the comfort zone, but move into shade, when the ambient temperature starts increasing. Even snakes also show basking during winter months.
Since they are ectothermic, this kind of behaviour saves them from extreme temperatures.
Many smaller animals show burrowing behaviour to adapt to the temperature extremes.
Some species burrow into the sand to hide and escape from the heat.
Migrations shown by the birds and mammals are also behavioural responses for adapting to severe winter temperatures.

Question 7.
Define Population and Community.
Answer:
Population:
Group of organisms belonging to same species that can potentially interbreed with each other and live together in a well-defined geographical area by sharing or competing for similar resources, is called population.

Community:
Several populations of different species in a particular area makes a community.

4. Long answer questions.

Question 1.
With the help of suitable diagram, describe the logistic population growth curve.
Answer:

Naturally all populations of any species always have limited resources to permit exponential growth. Due to this there is always competition between individuals for limited resources. The most fit organisms succeed by survival and reproduction.
A given habitat has enough resources to support a maximum possible number, but beyond a particular limit the further growth is impossible.
This limit is called nature’s carrying capacity (K) for that species in that habitat.
A population growing in a habitat with limited resources show following phases in a sequential manner, (a) A lag phase (b) Phase of acceleration (c) Phase of deceleration (d) An asymptote, when the population density reaches the carrying capacity.
A plot of N in relation to time (t) results in a sigmoid curve. This type of population growth is called Verhulst-Pearl Logistic Growth.
Since resources for growth for most animal populations are finite and become limiting sooner or later, the logistic growth model is considered as a more realistic one.
Logistic growth thus always shows sigmoid curve.

Question 2.
Enlist and explain the important characteristics of a population.
Answer:
Important characteristics of a population are as follows:
1. Natality:

Natality is the birth rate of a population. Due to increased natality the population density rises.
Natality is a crude birth rate or specific birth rate.
Crude birth rate : Number of births per 1000 population/year gives crude birth rate. Crude birth rate is helpful in calculating population size.
Specific birth rate : Crude birth rate is relative to a specific criterion such as age. E.g. If in a pond, there were 200 carp fish and their population rises to 800. Then, taking the current population to 1000, the birth rate becomes 800/200 = 4 offspring per carp per year. This is specific birth rate.
Absolute Natality : The number of births under ideal conditions when there is no competition and the resources such as food and water are abundant, then it give absolute natality.
Realized Natality : The number of births under different environmental pressures give realized natality. Absolute natality will be always more than realized natality.

2. Mortality:

Mortality is the death rate of a population. It gives a measure of the number of deaths in a particular population, in proportion to the size of that population, per unit of time.
Mortality rate is typically expressed in deaths per 1,000 individuals per year.
A mortality rate of 9.5 (out of 1,000) in a population of 1,000 would mean 9.5 deaths per year in that entire population or 0.95% out of the total.
Absolute Mortality : The number of deaths under ideal conditions when there is no competition, and all the resources such as food and water are abundant, then it gives absolute mortality.
Realized Mortality : The number of deaths under environmental pressures come into play gives realized mortality.
It must be remembered that absolute mortality will always be less than realized mortality.

3. Density:
The density of a population in a given habitat during a given period fluctuates due to changes in four basic processes, viz.

Natality i.e. birth rate (The number of births during a given period in the population that are added to the initial density).
Mortality i.e. death rate (The number of deaths in the population during a given period).
Immigration i.e. number of individuals of the same species that have come into the habitat from elsewhere during the time period under consideration.
Emigration i.e. the number of individuals of the population who left the habitat and gone elsewhere during the time period under consideration.
Natality and immigration increase in population density whereas mortality and emigration decrease it.

4. Sex ratio : Ratio of the number of individuals of one sex (male) to that of the other sex (female) is called sex ratio. In nature male, female ratio is always 1 : 1. This 1 : 1 ratio is called evolutionary stable strategy of ESS for each population.

5. Age distribution and age pyramid : This parameter is important for human population. Each population is composed of individuals of different ages. The age distribution is plotted for the population, the resulting structure is called an age pyramid. For making the age pyramid, the entire population is divided into three age groups as Pre-Reproductive (age 0-14 years), Reproductive (age 15-44 years) and Post-reproductive (age 45 -85+ years).

6. Growth : Growth of a population causes rise in its density. The size and density are dynamic parameters as they keep on changing with time, and various factors including food, predation pressure and adverse weather. From the density, one comes to know if the population is flourishing or declining.

12th Std Biology Questions And Answers:

12th Biology Chapter 5 Exercise Origin and Evolution of Life Solutions Maharashtra Board

January 8, 2025January 7, 2025 by Prasanna

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 5 Origin and Evolution of Life Textbook Exercise Questions and Answers.

Origin and Evolution of Life Class 12 Exercise Question Answers Solutions Maharashtra Board

Class 12 Biology Chapter 5 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 5 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Who proposed that the first form of life could have come from pre-existing non-living organic molecules?
(a) Alfred Wallace
(b) Oparin and Haldane
(c) Charles Darwin
(d) Louis Pasteur
Answer:
(b) Oparin and Haldane

Question 2.
The sequence of origin of life may be
(a) Organic materials – inorganic materials – Eobiont – colloidal aggregates – cell.
(b) Inorganic materials – organic materials – colloidal aggregates – Eobiont – cell.
(c) Organic materials – inorganic materials – colloidal aggregates – cell.
(d) Inorganic materials – organic materials – Eobiont – colloidal aggregates – cell.
Answer:
(b) Inorganic materials – organic materials- colloidal aggregates – Eobiont – cell.

Question 3.
In Hardy-Weinberg equation, the frequency of homozygous recessive individual is represented by-
(a) p²
(b) pq
(c) q²
(d) 2pq
Answer:
(c) q²

Question 4.
Select the analogous organs.
(a) Forelimbs of whale and bat
(b) Flippers of dolphins and penguin
(c) Thorn and tendrils of bougainvillea and Cucurbita
(d) Vertebrate hearts or brains
Answer:
(b) Flippers of dolphins and penguin

Question 5.
Archaeopteryx is known as missing link because it is a fossil and share characters of both
(a) Fishes and amphibians
(b) Annelida and Arthropoda
(c) Reptiles and birds
(d) Chordates and non-chordates
Answer:
(c) Reptiles and birds

Question 6.
Identify the wrong statement regarding evolution.
(a) Darwin’s variations are small and directional.
(b) Mutations are random and non- directional.
(c) Adaptive radiations leads to divergent evolution.
(d) Mutations are non-random and directional.
Answer:
(d) Mutations are non-random and directional

Question 7.
Gene frequency in a population remain constant due to ……………….
(a) Mutation
(b) Migration
(c) Random mating
(d) Non-random mating
Answer:
(c) Random mating

Question 8.
Which of the following characteristic is not : shown by the ape?
(a) Prognathous face
(b) Tail is present
(c) Chin is absent
(d) Forelimbs are longer than hind limbs
Answer:
(b) Tail is present

Question 9.
………………. can be considered as connecting link between ape and man.
(a) Australopithecus
(b) Homo habilis
(c) Homo erectus
(d) Neanderthal man
Answer:
(a) Australopithecus

Question 10.
The Cranial capacity of Neanderthal man was ……………….
(a) 600 cc
(b) 940 cc
(c) 1400 cc
(d) 1600 cc
Answer:
(c) 1400 cc

2. Very short answer questions

Question 1.
Define
(i) Gene pool
Answer:
The sum total of genes of all individuals of interbreeding population or Mendelian population is called gene pool.

(ii) Gene frequency
Answer:
The proportion of an allele in the gene pool as compared with other alleles at the same locus is termed as gene frequency.

(iii) Organic evolution
Answer:
Organic evolution can be defined as slow, gradual, continuous and irreversible changes through which the present-day complex forms of the life developed (or evolved) from their simple pre-existing forms.

(iv) Population
Answer:
All individuals of the same species form a group which is called a population.

(v) Speciation
Answer:
Formation of new species from the pre-existing single group of organisms is called speciation.

Question 2.
What is adaptive radiation?
Answer:
The process of evolution which results in transformation of original species to many different varieties is called adaptive radiation.

Question 3.
If the variation occurs in population by chance alone and not by natural selection and bring change in frequencies of an allele, what is it called?
Answer:
If the variation occurs in population by chance alone and not by natural selection to bring change in frequencies of an allele, it is called genetic drift.

Question 4.
State the Hardy-Weinberg equilibrium law.
Answer:
The Hardy-Weinberg equilibrium law states that at equilibrium point both the allelic frequency and genotypic frequency remain constant from generation to generation, in the diploid, sexually reproducing, large, free interbreeding population in which mating is random and there is absence of any other factors that change the allele frequency.

Question 5.
What is homologous organs?
Answer:
Homologous organs are those organs, which are structurally similar but perform different functions.

Question 6.
What is vestigial organ?
Answer:
Vestigial organs are imperfectly developed and non-functional organs which are in degenerate form, they may be functional in some related and other animals or in ancestor.

Question 7.
What is the scientific name of modern man?
Answer:
Homo sapiens sapiens is the scientific name of modern man.

Question 8.
What is coacervate?
Answer:
Coacervates are colloidal aggregations of hydrophobic proteins and lipids which grew in size by taking up material from surrounding aqueous medium.

Question 9.
Which period is known as ‘age of Reptilia’?
Answer:
Jurassic period from Mesozoic era is known as age of Reptilia.

Question 10.
Name the ancestor of human which is described as man with ape brain.
Answer:
Australopithecus, the ancestor of human which is described as man with ape brain.

Short Answer Questions

Question 1.
Genetic drift.
Answer:

Genetic drift is random, directionless fluctuation that takes place in allele frequency.
It occurs by pure chance, in small sized population.
Genetic drift becomes an evolutional factor as it can change the gene frequency.
Sewall wright has given this concept and hence it is also known as Sewall wright effect.
Due to genetic drift, some alleles of a population are lost or reduced by chance and some others may be increased.
Some time, a few individuals become isolated from the large population and they produce new population in new geographical area.
Genetic drift is also called founders’ effect because original drifted population becomes ‘founders’ in the new area.
E.g. Non-adaptive character of huge horns in Antelope is fixed due to genetic drift.

Question 2.
Enlist the different factors that are responsible for changing gene frequency.
Answer:
Gene flow, genetic drift, gene mutations, chromosomal aberrations such as deletion, duplication, inversion and translocation, genetic recombinations, natural selection, isolation are some of the factors which are responsible for changing the gene frequency.

Question 3.
Draw a graph to show that natural selection leads to disruptive change.
Answer:

Question 4.
Significance of fossils
Answer:

Fossils are studied under palaeontology. They are used in reconstruction of phylogeny.
Fossil study helps in studying various forms and structures of extinct animals.
By understanding the structure of fossil, record of missing link between two groups of organisms can be deduced.
By studying fossils various body forms and their evolution can be understood. They also help to understand the habit and habitat.
Some fossils provide the evolutionary evidences such a connecting links.

Question 5.
Write the objections to Mutation theory of Hugo de Vries.
Answer:
Objections to Mutation Theory:

Hugo de Vries observed the large and discontinuous variation. But these were chromosomal aberrations. Only gene mutations usually bring about minor changes.
Rate by which mutations take place is very slow as compared to the requirement of evolution.
Chromosomal aberrations are very unstable.
The organisms with chromosomal aberration are usually sterile and thus chromosomal aberrations have little significance in evolution.

Question 6.
What is disruptive selection? Give example.
Answer:
Disruptive selection:

The natural selection that disrupts the mean characters of the population, is called disruptive selection.
Greater number of individuals acquire peripheral character value at both ends of the distribution curve. E.g. Finches with large size or small size, both will be selected.
Extreme phenotypes are selected in evolutionary process and intermediate forms are eliminated.
When distribution curve is plotted it shows two peaks for two extremes.
Disruptive selection is rare because, nature always tries to balance the characters.
It ensures the effect on the entire gene pool of a population, considering all mating types or systems.

Example of disruptive selection:
African seed cracker finches are types of seed-feeder birds which have different sizes of beak. The seeds available to them were of small and large sized. Large beak sized birds feeds on large seeds while small beak sized birds feed on small seeds.

Such large and small birds thus thrive well. However, intermediate beak sized birds are unable to feed on either type of seeds so they starve and their population was decreased gradually. Natural selection eliminated them and thus the population of finches appear disrupted.

4. Match the columns

Question 1.

Column I	Column II
(1) August Weismann	(a) Mutation theory
(2) Hugo de Vries	(b) Germplasm theory
(3) Charles Darwin	(c) Theory of acquired characters
(4) Lamarck	(d) Theory of natural selection

Answer:

Column I	Column II
(1) August Weismann	(b) Germplasm theory
(2) Hugo de Vries	(a) Mutation theory
(3) Charles Darwin	(d) Theory of natural selection
(4) Lamarck	(c) Theory of acquired characters

5. Long Answer Questions

Question 1.
Would you consider wings of butterfly and bat as homologous or analogous and why?
Answer:
Wings of butterfly are made up of chitin. They neither have bones, nor muscles in the wings. The bat’s wings are actually patagium. They have muscles and bones just as those seen in all vertebrate limb series. Therefore, these two examples cannot be homologous. However, both the animals use the wings for flight. This is an indication that their function is similar but structure is different, hence they are analogous organs.

Question 2.
What is adaptive radiation? Explain with suitable example.
Answer:

Adaptive radiation is the process of evolution which results in transformation of original species to many different varieties.
The well-known example of adaptive radiation is Darwin’s Finches. When Charles Darwin went on his voyage to Galapagos islands, he noticed finches which is a variety of small birds.
According to Darwin’s observations, the American main land species of finches was the original one which must have migrated to the different islands of Galapagos.
Since environmental conditions here were different, they adapted in various ways to the differing environmental conditions of these islands.
Original bird had a beak suited for eating seeds, but the changed feeding pattern has changed the shape of beaks too. Some birds also show altered beaks for insectivorous mode. Thus, this demonstrated adaptive radiation.
Adaptive radiation in Australian Marsupials is also well studied. In Australia, there are many marsupial mammals who evolved from common ancestor.
Adaptive radiation leads to divergent evolution.

Question 3.
By talking industrial melanism as one example, explain the concept of natural selection.
OR
Explain natural selection in action by quoting the example of industrial melanism.
Answer:
1. Industrial melanism is the best example of natural selection which was studied by Kettlewell. In U.K. there are two varieties of peppered moths, Biston betularia and Biston carbonaria.

2. Before industrialisation, in Great Britain, Biston betularia were more in number than Biston carbonaria. B. Betularia is greyish white while B.carbonaria is melanic form.

3. These nocturnal moths rest on tree trunk during day. White-winged moth can camouflage well with the lichen covered whitish barks of trees. They thus escaped the attention of the predatory birds. But at the same time melanic forms were visible due to white barks of the trees. Their number was thus reduced as they were preyed upon by birds.

4. Later there was an industrial revolution, which ultimately resulted in air pollution causing dark soot to settle on the barks of the trees. Lichens too were destroyed and the melanic forms were now at advantage. Melanic forms could camouflage with black tree trunks and their number increased. White-winged moth become clearly seen in changed colours of the trees and thus they were easily caught by predatory birds. This caused decrease in their number.

5. Natural selection thus acted in changed environmental conditions and helped in the establishment of a phenotypic traits. The changed traits were more adaptive and hence were selected. Natural selection encourages those genes or traits that assure highest degree of adaptive efficiency between population and its environment.

Question 4.
Describe the Urey and Miller’s experiment.
Answer:

1. Urey and Miller performed an experiment to prove Oparin’s theory of chemical evolution.

2. They selected a spark discharge apparatus that consisted of closed system of glass having tungsten electrodes, flask for water boiling, a side tube connected to a vacuum pump, a cooling jacket and U-shaped trap.

3. The entire apparatus was first evacuated and made sterile and pre-biotic atmosphere was created in it.

4. The flask was filled with some water and mixture of methane, ammonia and hydrogen in the ratio of 1 : 2 : 2 were slowly passed through the stopcock, without allowing air.

5. Heat was supplied to the flask at very low temperature causing water to boil. The flask simulated the ocean present on primitive earth. Process of evaporation and precipitation was simulated by using heating mantle and condenser respectively.

6. Water vapours along with other gases were circulated continuously through continuous electric sparks. These sparks were given to the mixture for several days causing the gases to interact. This too simulated lightning.

7. Mixture of CH₄, NH₃ and H₂ gases passed through a condenser and was condensed to liquid.

8. The liquefied mixture was collected in the U-shaped trap, present at the bottom of the apparatus. It was found that variety of simple organic compounds (urea, amino acids, lactic acid and sugars) were formed in the apparatus.

This experiment provides the evidence in support to the fact that simple molecules present in the earth’s early atmosphere combined to form the organic building blocks of life.

Question 5.
What is Isolation? Describe the different types of reproductive isolations.
Answer:
1. Isolation means separation of the population of a particular species into smaller units. The organisms belonging to these subunits are prevented from interbreeding due to some barrier. These barriers are called isolating mechanisms.

2. They prevent the genetic exchange and gene flow.

3. Due to isolating mechanisms in nature the divergence among organisms takes place gradually leading to speciation. The isolating mechanisms are of two types namely, geographical isolation and reproductive isolation.

I. Geographical Isolation : The barrier in the form of physical distance or geographical barrier is called geographical isolation. The original population gets divided into two or more groups by geographical barriers such as river, ocean, mountain, glacier, etc. Organisms cannot cross the barriers on their own and hence interbreeding is prevented between isolated groups.

The separated groups experience different environmental factors and they acquire new traits by mutations. The separated populations develop distinct gene pool and they do not interbreed. Each subgroup then evolves differently which results into formation of new species. E.g. Darwin’s Finches, African elephant, Loxodonta and Indian elephant, Elephas.

II. Reproductive Isolation : Two populations may be occupying the same area, they may not be separated by geographical barrier, but then also they are reproductively isolated. Such reproductive isolation occurs due to change in genetic material, gene pool and structure of genital organs. Such differences prevent interbreeding between population. Such isolation later leads to speciation.

III. Different types of reproductive isolations : Reproductive isolation is of two types, viz. pre-zygotic and post-zygotic isolating mechanisms.

Pre-zygotic or pre-mating isolating mechanisms do not allow individuals to mate with each other at all.
By various mechanisms the two groups remain isolated.
In post-zygotic or post-mating isolating mechanisms, the two individuals can mate but the result of mating is not favourable.
Thus the populations remain isolated without the actual genetic exchange.

Question 6.
What is Genetic variations? Explain the different factors responsible for genetic variations.
Answer:
Genetic variations : The change in gene and gene frequencies is known as genetic variation. Genetic variations are caused by following factors:
(i) Mutations : Sudden permanent heritable change is called mutation. Mutation can occur in the gene, in the chromosome structure and in chromosome number. Mutation that occurs within the single gene is called point mutation or gene mutation. This leads to the change in the phenotype of the organism, causing variations.

(ii) Genetic recombination : In sexually reproducing organisms, during gamete formation, exchange of genetic material occurs between non-sister chromatids of homologous chromosomes. This is called crossing over. It produces new genetic combinations which result in variation. Fertilization between opposite mating gametes leads to various recombinations resulting into the phenotypic variations. These result in change in the frequencies of alleles.

(iii) Gene flow : Gene flow is movement of genes into or out of a population. Gene movement may be in the form of migration of organism, or gametes (dispersal of pollens) or segments of DNA (transformation). Gene flow also alters gene frequency causing evolutionary changes.

(iv) Genetic drift : Any random fluctuation (alteration) in allele frequency, occurring in the natural population by pure chance, is called genetic drift. For example, when the size of a population is severely reduced due to natural disasters like earthquakes, floods, fires, etc. elimination of particular alleles from a population becomes possible. Smaller populations have greater chances for genetic drift. It results in the change in the gene frequency. Genetic drift is also an important factor for evolutionary change.

(v) Chromosomal aberrations : The structural, morphological change in chromosome due to rearrangement of genes is called chromosomal aberrations. Due to changes in the gene arrangement or gene sequence variations are caused.

6. Complete the chart

Era	Dominating group of animals
1. Coenozoic	————–
2. ————-	Reptiles
3. Palaeozoic	————-
4. ————	Lower Invertebrates

Answer:

Era	Dominating group of animals
1. Coenozoic	Mammals
2. Mesozoic	Reptiles
3. Palaeozoic	Insects, Fishes, Amphibians
4. Proterozoic	Lower Invertebrates

12th Std Biology Questions And Answers: