Std 5 Hindi Lesson 3 भाई-भाई का प्रेम Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 5 Hindi Solutions Sulabhbharati Chapter 3 भाई-भाई का प्रेम Notes, Textbook Exercise Important Questions and Answers.
5th Std Hindi Poem Bhai-Bhai ka prem Question Answer
5th Standard Hindi Digest Chapter 3 भाई-भाई का प्रेम Textbook Questions and Answers
1. पढ़ो और समझो:
प्रश्न 1.
पढ़ो और समझो:
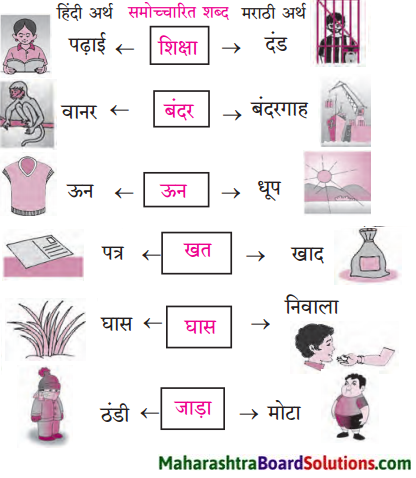
1. सप्रेम – प्रेम – प्रेमभरा।
2. प्रतिदिन – दिन – दैनिक ।
3. विज्ञान – ज्ञान – ज्ञानी ।
4. अदृश्य – दृश्य – दृश्यमान ।

Hindi Sulabhbharati Class 5 Solutions Chapter 3 भाई-भाई का प्रेम Additional Important Questions and Answers
निम्नलिखित प्रश्नों के उत्तर दीजिए:
प्रश्न 1.
आप अपने छोटे भाई-बहन की सहायता कैसे करते हैं?
उत्तर:
हम अपने छोटे भाई-बहन के साथ खेलते, खाना खाते एवं – पढ़ाई में उनकी मदद करते हैं।
प्रश्न 2.
क्या आप अपने दोस्तों के साथ नाश्ता बाँट कर खाते हैं?
उत्तर:
हाँ।
प्रश्न 3.
अनाज खेत से काटकर कहाँ रखा जाता है?
उत्तर:
अनाज खेत से काटकर खलिहान में रखा जाता है।
प्रश्न 4.
फसल किसे कहते हैं?
उत्तर:
खेत में लगे अनाज के पौधों को फसल कहा जाता है।
प्रश्न 5.
गाँव के लोगों का व्यवसाय क्या होता है?
उत्तर:
गाँव के लोगों का व्यवसाय खेती होता है।
प्रश्न 6.
क्या दोनों भाई एक साथ रहते थे?
उत्तर:
नहीं, उनके घर अलग-अलग थे।

प्रश्न 7.
अलग-अलग रहने के बावजूद दोनों भाइयों का व्यवहार कैसा था?
उत्तर:
अलग-अलग रहने के बावजूद दोनों भाइयों में बड़ा प्रेम था।
प्रश्न 8.
एक – दूसरे की मदद करने से क्या मिलता है?
उत्तर:
एक-दूसरे की मदद करने से बड़ा सुख और आनंद मिलता है।
निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए:
प्रश्न 1.
गाँव का नाम क्या था?
उत्तर:
गाँव का नाम मनोहरपुर था।
प्रश्न 2.
मनोहरपुर गाँव कैसा था?
उत्तर:
मनोहरपुर गाँव सुंदर था।
प्रश्न 3.
मनोहरपुर गाँव की मिट्टी कैसी थी?
उत्तर:
मनोहरपुर गाँव की मिट्टी उपजाऊ थी।
प्रश्न 4.
यह कहानी किसकी है?
उत्तर:
यह कहानी दो भाइयों की है।
प्रश्न 5.
किसकी शादी नहीं हुई?
उत्तर:
छोटे भाई की शादी नहीं हुई।
प्रश्न 6.
बड़े भाई के कितने बच्चे थे?
उत्तर:
बड़े भाई के दो बच्चे थे।
प्रश्न 7.
दोनों भाई हमेशा क्या सोचते थे?
उत्तर:
दोनों भाई हमेशा एक-दूसरे की भलाई की बात सोचते थे।

प्रश्न 8.
खलिहान में किसके ढेर लगे थे?
उत्तर:
खलिहान में अनाज के ढेर लगे थे।
प्रश्न 9.
बड़े भाई ने छोटे भाई की सहायता करने का निर्णय क्यों लिया?
उत्तर:
बड़े भाई को लगा कि छोटे भाई की अभी शादी नहीं हुई है और उसे सारा काम अकेले सँभालना पड़ता है।
प्रश्न 10.
दोनों भाइयों ने एक-दूसरे की किस प्रकार मदद करने का निश्चय किया?
उत्तर:
दोनों भाइयों ने एक-दूसरे को दस गठरी अनाज देने का निश्चय किया।
प्रश्न 11.
अनाज के ढेर में से बड़े भाई ने कितना अनाज बाँधा?
उत्तर:
अनाज के ढेर में से बड़े भाई ने दस गठरी अनाज बाँधा।
3. रिक्त स्थानों की पूर्ति कीजिए
प्रश्न 3.
रिक्त स्थानों की पूर्ति कीजिए:
- गाँव के अधिकांश लोग …………. किया करते थे।
- दोनों भाइयों में बड़ा ………….. था।
- अंधेरी रात में दोनों भाई एक-दूसरे से ………… गए।
- दोनों भाई रोते – रोते हुए एक-दूसरे के लग गए।
उत्तर:
- खेती
- प्रेम
- टकरा
- गले
किसने किससे कहा:
प्रश्न 1.
“तुम्हारी मदद करनेवाला कोई नहीं है।”
उत्तर:
बड़े भाई ने छोटे भाई से कहा।

प्रश्न 2.
“आप बाल-बच्चे वाले हैं।”
उत्तर:
छोटे भाई ने बड़े भाई से कहा।
प्रश्न 3.
“मेरे दो बच्चे हैं।”
उत्तर:
बड़े भाई ने अपने आप से कहा।
प्रश्न 4.
“मैं तो अकेला हूँ, जितना चाहे उतना काम कर सकता हूँ।”
उत्तर:
छोटे भाई ने अपने आप से कहा।
प्रश्न 5.
“आपको अधिक मात्रा में अनाज की आवश्यकता होती है।”
उत्तर:
छोटे भाई ने बड़े भाई से कहा।
निम्नलिखित वाक्य पढ़कर सही विकल्प चुनकर लिखो:
प्रश्न 1.
गाँव के अधिकांश लोग खेती किया करते थे।
(अ) गाँव के अधिकतर लोग किसान थे।
(ब) गाँव की मिट्टी बहुत उपजाऊ थी।
उत्तर:
गाँव की मिट्टी बहुत उपजाऊ थी।
प्रश्न 2.
खलिहान में सबके अनाज के ढेर लगे थे।
(अ) कटाई हो चुकी थी।
(ब) किसानों के पास अनाज रखने की जगह नहीं थी।
उत्तर:
कटाई हो चुकी थी।
प्रश्न 3.
छोटा भाई बड़े भाई की सहायता करना चाहता था।
(अ) बड़ा भाई बूढ़ा हो गया था।
(ब) बड़े भैया बाल-बच्चेवाले हैं।
उत्तर:
बड़े भैया बाल-बच्चेवाले हैं।
प्रश्न 4.
दोनों भाइयों ने कितने गठरी अनाज बाँधा?
(अ) पाँच गठरी
(ब) दस गठरी
उत्तर:
दस गठरी
प्रश्न 5.
बड़ा भाई छोटे भाई की सहायता करना चाहता था, क्योंकि
(अ) छोटे भाई को सारा काम अकेले सँभालना पड़ता था।
(ब) छोटा भाई कुछ काम नहीं करता था।
उत्तर:
छोटे भाई को सारा काम अकेले सँभालना पड़ता था।
प्रश्न 6.
दोनों भाई किस तरह एक-दूसरे के अनाज के ढेर की ओर बढ़े?
(अ) धीरे-धीरे
(ब) जल्दी-जल्दी
उत्तर:
धीरे-धीरे

प्रश्न 7.
दोनों भाइयों ने एक-दूसरे को कैसे गले लगाया?
(अ) हँसते हुए
(ब) रोते हुए
उत्तर:
रोते हुए
प्रश्न 8.
दोनों भाइयों की प्रेम कहानी लोग कैसे सुनाते हैं?
(अ) भाव विभोर होकर
(ब) गा – गाकर
उत्तर:
भाव विभोर होकर
व्याकरण:
उपसर्ग: शब्द से पहले जुड़कर उन शब्दों के अर्थ में परिवर्तन लाते हैं।
प्रत्ययः शब्द के अंत में जुड़कर उन शब्दों के अर्थ में परिवर्तन लाते हैं।
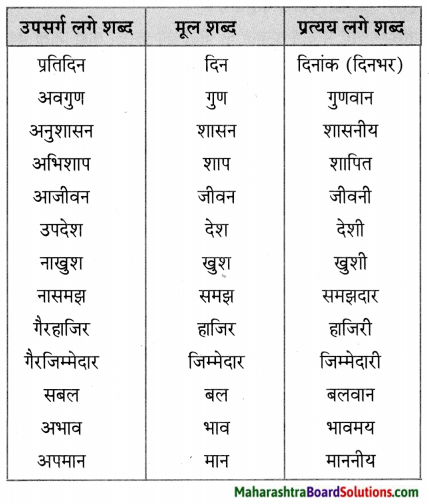
प्रश्न 1.
समान अर्थवाले शब्द लिखिए:
- गाँव
- सुंदर
- प्रेम
- घर
- बच्चा
- आँख
- हमेशा
- शादी
- फायदा
- अचानक
- मदद
उत्तरः
- ग्राम
- खूबसूरत
- प्यार
- गृह
- बालक
- नेत्र
- हरदम
- विवाह
- नफा
- एकाएक
- सहायता

प्रश्न 7.
विपरीत अर्थ वाले शब्द लिखिए:
- सुंदर
- दिन
- छोटा
- जवान
- फायदा
- अँधेरा
- अधिक
- रोना
उत्तर:
- कुरूप
- रात
- बड़ा
- बूढ़ा
- नुकसान
- उजाला
- कम
- हँसना
प्रश्न 8.
कहानी में आए प्रत्यय लगे शब्द ढूँढकर लिखिए:
- खेत
- कटना
- गृहस्थ
- आवश्यक
उत्तर:
- खेती
- कटाई
- गृहस्थी
- आवश्यकता
प्रश्न 9.
पाठ में आए योजक चिह्न (Hyphen) वाले शब्द लिखिए:
उत्तर:
- अलग – अलग
- लेटे – लेटे
- कुछ -न -कुछ
- बाल – बच्चेवाले
- धीरे – धीरे
- एक – दूसरे
- कहते – सुनते
- सुनते – सुनाते
प्रश्न 10.
निम्नलिखित शब्दों में उपसर्ग लगाइए:
- प्रेम
- दिन
- ज्ञान
- दृश्य
- पढ़
- डर
- पूर
- खबरी
- खुश
- वारिस
उत्तर:
- सप्रेम
- प्रतिदिन
- विज्ञान
- अदृश्य
- अनपढ़
- निडर
- भरपूर
- खुशखबरी
- नाखुश
- लावारिस

प्रश्न 11.
निम्नलिखित शब्दों में प्रत्यय लगाइए:
- भला
- उपज
- मीठा
- कटा
- बल
- मेल
- चट
- रेत
- पाँच
- चाँद
उत्तर:
- भलाई
- उपजाऊ
- मिठाई
- कटाई
- बलवान
- मेला
- चटनी
- रेतीला
- पाँचवाँ
- चाँदनी
प्रश्न 12.
प्रत्यय लगाकर नए शब्द बनाइए:
शब्द + प्रत्यय
- भला + ई = भलाई
- सोच + ना = सोचना
- गृहस्थ + ई = गृहस्थी
- शेर + नी = शेरनी
- मोर + नी = मोरनी
- टोकरा + ई = टोकरी
- बैंगन + ई = बैंगनी
उत्तर:
- भलाई
- सोचना
- गृहस्थी
- शेरनी
- मोरनी
- टोकरी
- बैंगनी
भाई-भाई का प्रेम Summary in Hindi
कहानी का सारांश:
प्रस्तुत पाठ दो भाइयों के आपसी प्रेम की कहानी है। इसी प्रेम के कारण वे एक-दूसरे की मदद करना चाहते हैं। उन्हें एक-दूसरे की मदद करने में बड़ा सुख मिलता है। जब हम दूसरे की मदद करते हैं, तब हमें बड़ी खुशी मिलती है। हमें हमेशा दूसरों की मदद करनी चाहिए। दूसरों को कुछ देने में जो खुशी मिलती है, उसे बताया नहीं जा सकता है। दोनों भाई एक-दूसरे को बिना जताए, सहायता करना चाहते हैं, लेकिन पकड़े जाते हैं और एक-दूसरे के गले लग जाते हैं।

शब्दार्थ:
- उपजाऊ – कृषि के लिए उपयुक्त (fertile)
- अधिकांश – ज्यादातर (extensively)
- भलाई – नेकी, अच्छाई (betterment)
- कटाई – फसल को काटना (cutting)
- फसल – खेत में लगे अनाज के पौधे (crop)
- गृहस्थी – घर-बार (household)
- खलिहान – कटी हुई फसल रखने का स्थान (barn)
- गठरी – कपड़े में बँधा हुआ सामान (bundle)
- ढेर – इकट्ठा किया गया, जमाव (heap)
- वातावरण – परिस्थिति (environment)
- अचानक – एकाएक (suddenly)
- भाव-विभोर – प्रेम से (overwelmed)
- किसान – (farmer)
Hindi Sulabhbharati 5th Standard Pdf दूसरी इकाई
![]()

![]()
![]()