Documents Related to Formation of a Company 11th Secretarial Practice Chapter 4 Solutions Maharashtra Board
Balbharti Maharashtra State Board Class 11 Secretarial Practice Solutions Chapter 4 Documents Related to Formation of a Company Textbook Exercise Questions and Answers.
Class 11 Secretarial Practice Chapter 4 Exercise Solutions
1A. Select the correct answer from the options given below and rewrite the statements.
Question 1.
___________ is a primary document of the company which contains the aims and objectives of the company.
(a) Memorandum of Association
(b) Articles of Association
(c) Prospectus
Answer:
(a) Memorandum of Association
Question 2.
___________ describes the relationship between company and outsiders.
(a) Memorandum of Association
(b) Articles of Association
(c) Prospectus
Answer:
(a) Memorandum of Association

Question 3.
The ___________ clause describes the range of activities a company can undertake.
(a) Name
(b) Capital
(c) Object
Answer:
(c) Object
Question 4.
Any act done by the company beyond the Powers of Memorandum is called as ___________
(a) Doctrine of indoor management
(b) Ultra-Vires
(c) Mis-statement
Answer:
(b) Ultra-Vires
Question 5.
___________ acts are void or legally ineffective.
(a) Object clause
(b) Main object
(c) Ultra Vires
Answer:
(c) Ultra Vires
Question 6.
___________ clause contains the details of liability of the members.
(a) Name
(b) Liability
(c) Object
Answer:
(b) Liability
Question 7.
___________ clause states the amount of Authorised capital with which the company is registered.
(a) Liability
(b) Object
(c) Capital
Answer:
(c) Capital
Question 8.
___________ contains rules and regulations for internal management of the company.
(a) Articles of Association
(b) Prospectus
(c) Memorandum of Association
Answer:
(a) Articles of Association

Question 9.
Articles establishes relationship between company and ___________
(a) members
(b) outsiders
(c) ROC
Answer:
(a) members
Question 10.
___________ is an invitation to the public to subscribe for shares of the company.
(a) Memorandum
(b) Prospectus
(c) Articles of Association
Answer:
(b) Prospectus
Question 11.
For making multiple issue of shares within a year, a company can prepare a ___________ Prospectus.
(a) Abridged
(b) Shelf
(c) Red Herring
Answer:
(b) Shelf
Question 12.
___________ is an incomplete prospectus.
(a) Red Herring Prospectus
(b) Shelf Prospectus
(c) Abridged Prospectus
Answer:
(a) Red Herring Prospectus
1B. Match the pairs.
Question 1.
| Group ‘A’ |
Group ‘B’ |
| (a) Capital clause |
(1) Details of capital structure of a company |
| (b) Liability clause |
(2) Used for multiple issues of shares |
| (c) Acts beyond the Powers of Memorandum |
(3) Abridged Prospectus |
| (d) Red Herring Prospectus |
(4) Describes main objectives |
| (e) Shelf Prospectus |
(5) Used for Right Issue |
|
(6) Incomplete Prospectus |
| (7) Ultra-Vires |
| (8) Doctrine of Indoor management |
| (9) Extent of liability of members |
| (10) Articles of Association |
Answer:
| Group ‘A’ |
Group ‘B’ |
| (a) Capital clause |
(1) Details of capital structure of a company |
| (b) Liability clause |
(9) Extent of liability of members |
| (c) Acts beyond the Powers of Memorandum |
(7) Ultra-Vires |
| (d) Red Herring Prospectus |
(6) Incomplete Prospectus |
| (e) Shelf Prospectus |
(2) Used for multiple issues of shares |
1C. Write a word or a term or a phrase that can substitute each of the following statements.
Question 1.
The primary document of a company states the aims and objectives of a company.
Answer:
Memorandum of Association
Question 2.
The document establishes the company’s relationship with outsiders.
Answer:
Memorandum of Association

Question 3.
The document states the limits within which a company has to operate.
Answer:
Memorandum of Association
Question 4.
The document contains Name Clause, Registered Office Clause, Capital Clause, etc.
Answer:
Memorandum of Association
Question 5.
The document is subordinate to the Memorandum of Association.
Answer:
Articles of Association
Question 6.
The document contains rules and regulations for internal management.
Answer:
Articles of Association
Question 7.
A term used for acts beyond the scope of the Memorandum of Association.
Answer:
Ultra-Vires

Question 8.
The clause describes the main activities a company can undertake.
Answer:
Object Clause
Question 9.
The clause gives details of Authorized Capital or Registered Capital.
Answer:
Capital Clause
Question 10.
The clause describes the extent of liability of members.
Answer:
Liability Clause
Question 11.
The last clause of the Memorandum contains the name, signature, and other details of all the subscribers of the Memorandum.
Answer:
Association or Subscription Clause
Question 12.
The document establishes a relationship between a company and its members.
Answer:
Articles of Association
Question 13.
Document issued by public company inviting the public to subscribe to its shares.
Answer:
Prospectus
Question 14.
Prospectus attached with every share application form.
Answer:
Abridged Prospectus

Question 15.
Prospectus used for multiple issues of shares within a year.
Answer:
Shelf Prospectus
Question 16.
It is an incomplete prospectus.
Answer:
Red Herring Prospectus
Question 17.
This prospectus does not contain information about the quantum of shares to be issued or the price at which shares will be issued.
Answer:
Red Herring Prospectus
1D. State whether the following statements are True or False.
Question 1.
A Memorandum of Association and Articles of Association are prepared at the time of incorporation of a company.
Answer:
True
Question 2.
Memorandum of Association describes the nature and character of the company.
Answer:
True
Question 3.
Memorandum establishes the relationship between Company and Members.
Answer:
False
Question 4.
Any act done by the company beyond the Powers of Memorandum is Ultra-Vires.
Answer:
True

Question 5.
Articles of Association can have provisions that contradict the Memorandum.
Answer:
False
Question 6.
Memorandum need not have a Liability Clause.
Answer:
False
Question 7.
Articles of Association are subordinate to Memorandum.
Answer:
True
Question 8.
A memorandum contains rules and regulations for the internal management of a company.
Answer:
False
Question 9.
Every subscriber who signs the Memorandum must also sign the Articles.
Answer:
True
Question 10.
Entrenched Articles cannot be easily altered.
Answer:
True
Question 11.
Prospectus can be issued by a private company.
Answer:
False
Question 12.
Only public companies can issue Prospectus.
Answer:
True

Question 13.
The prospectus must be issued within 1 year from the date of filing it with the ROC.
Answer:
False
Question 14.
Actions can be taken against a company or its officers for misstatements in the prospectus.
Answer:
True
Question 15.
Every company has to issue a shelf prospectus every time it offers shares to the public.
Answer:
False
Question 16.
Red Herring prospectus does not contain details of the price at which shares will be sold by the company.
Answer:
True
Question 17.
Letter of the offer is issued at the time of Rights Issue.
Answer:
True
1E. Find the odd one.
Question 1.
Name Clause, Rights of Board of Directors, Object Clause.
Answer:
Rights of Board of Directors
Question 2.
Rights of shareholders, Appointment and remuneration of Directors, Liability clause.
Answer:
Liability Clause

Question 3.
Shelf prospectus, Abridged Prospectus, Articles of Association.
Answer:
Articles of Association
1F. Complete the sentences.
Question 1.
The documents which state the aims and objectives of a company is called as ___________
Answer:
Memorandum of Association
Question 2.
Any act done by the company which goes beyond the powers of Memorandum of Association will be called as ___________
Answer:
Ultra-Vires
Question 3.
The document which is subordinate to the Memorandum of Association is called ___________
Answer:
Articles of Association
Question 4.
The document which contains the rules and regulations governing the internal management of a company is called ___________
Answer:
Articles of Association

Question 5.
The document issued by a company to invite investors to buy its securities is called as ___________
Answer:
Prospectus
1G. Select the correct option from the bracket.
Question 1.
| Group ‘A’ |
Group ‘B’ |
| (1) ……………………. |
Memorandum of Association |
| (2) Liability clause |
…………………………. |
| (3) Incomplete Prospectus |
…………………………. |
| (4) ……………………… |
Establishes relationship between the company and its members |
(Articles of Association, Red Herring Prospectus, Primary document, Details of liability of members)
Answer:
| Group ‘A’ |
Group ‘B’ |
| (1) Primary Document |
Memorandum of Association |
| (2) Liability clause |
Details of liability of members |
| (3) Incomplete Prospectus |
Red Herring Prospectus |
| (4) Articles of Association |
Establishes relationship between the company and its members |
1H. Answer in one sentence.
Question 1.
Which document contains the aims and objectives of the company?
Answer:
Memorandum of Association contains the aims and objectives of the company.
Question 2.
What does the capital clause describe?
Answer:
The capital clause states the amount of capital with which the company is registered and the division of it into shares of a fixed amount.
Question 3.
When is Abridged Prospectus issued?
Answer:
Abridged Prospectus is issued only in case of a public offer made by a company.
1I. Correct the underlined word and rewrite the following sentences.
Question 1.
Articles of Association states the aims and objectives of the company.
Answer:
Memorandum of Association states the aims and objectives of the company.

Question 2.
The prospectus is subordinate to the Memorandum of Association.
Answer:
Articles of Association are subordinate to Memorandum of Association.
Question 3.
The prospectus contains a liability clause.
Answer:
Memorandum of Association contains a liability clause.
1J. Arrange in proper order.
Question 1.
(a) Subscription clause
(b) Name clause
(c) Object clause
Answer:
(a) Name clause
(b) Object clause
(c) Subscription clause
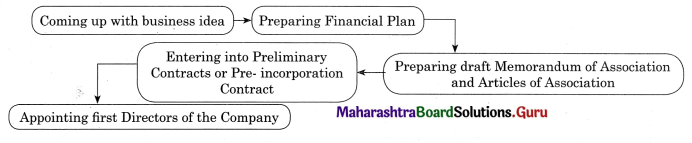
2. Explain the following terms/concepts.
Question 1.
Memorandum of Association
Answer:
- It is a secondary document.
- A Memorandum of Association is a primary document of a company.
- It states the objects for which the company is formed.
- A Memorandum of Association of a company is a charter or constitution of a company.
- It describes the range of activities a company can undertake.
- No company can be registered without a Memorandum of Association.
- Memorandum establishes a relationship between the company and an outsider.
Question 2.
Articles of Association
Answer:
- Articles of Association is a secondary document.
- It contains rules and regulations that govern the internal management of the company.
- Articles of Association is also known as Bye-laws of a company.
- It defines the powers, duties, and rights of managers officers, and board of directors.
- It establishes a relationship between the company and its members.
- This document is subordinate to Memorandum.

Question 3.
Name Clause
Answer:
- This clause contains the name of the company.
- The name of the company should not be identical to any existing company.
- If it is a private company, then it should have the word Private Limited at the end.
- And in the case of a public company, then it should add the word limit at the end of its name.
- For eg ABC Private Limited in the case of the private and ABC Ltd for a public company.
Question 4.
Object Clause
Answer:
- This clause states the objective with which the company is formed.
- It is the most important clause of the Memorandum of Association.
- The clause defines the scope and limitations of the activities of the company.
- The objects must be clearly defined keeping in mind the following conditions.
- The objects of the company must be legal.
- The objects should not be against the provisions of any law.
- The objects must not be immoral.
Question 5.
Liability Clause
Answer:
- This clause defines the liability of the members of the company.
- In the case of companies limited by shares, the liability of the members is limited to the extent of unpaid shares.
- In the case of a company limited by guarantee, the liability is limited to the amount of guarantee given by each member.
- In the case of an unlimited liability company with or without share capital, this clause states that the liability of its members is unlimited.
Question 6.
Capital Clause
Answer:
- This clause states the amount of capital with which the company is registered.
- The capital with which the company is registered is called registered capital or authorized capital.
- A company can issue only that number of shares that are authorized by its memorandum.
- The company has to alter the capital clause if the company wants to issue more shares than authorized capital.
Question 7.
Registered Office Clause
Answer:
- This clause contains the name of the state in which the registered office of the company is to be situated.
- Every company must have a registered office within 30 days of its incorporation.
- A registered office is a place where all the important documents of the company are kept.
- The registered office clause determines the jurisdiction of the Registrar of Companies and of the court.

Question 8.
Ultra Vires act
Answer:
- The word Ultra means beyond and the word Vires means the powers.
- Thus Ultra-Vires means beyond the powers of Memorandum.
- The doctrine of ultra-vires states that any activity done by a company that is beyond the powers of the company will be null and void.
- The purpose of the Doctrine of Ultra-Vires is to protect all the stakeholders.
- The stakeholders have the right to see that the company uses their money for the objects mentioned in Memorandum.
Question 9.
The doctrine of Indoor Management
Answer:
- The doctrine of Indoor Management states that persons entering into a contract with the company need not inquire whether the company or its officers have properly followed the internal proceedings.
- It is assumed that the company acts as per its Memorandum and Articles of Association.
- The doctrine of Indoor Management protects the interest of outsiders when they act based on the Memorandum of Association and Articles of Association.
Question 10.
Prospectus
Answer:
- A prospectus is any document that invites deposits or offers from the public for the purchase of any shares or debentures of a company.
- When a public company is collecting capital by issuing shares to the public has to issue a prospectus.
- The prospectus must be true and factual as investors decide to invest based on the information given in the prospectus.
- The types of the prospectus issued by a company are:
- Abridged Prospectus
- Shelf Prospectus
- Red Herring Prospectus
- Letter of offer
- Offer Letter
Question 11.
Mis-statements in Prospectus
Answer:
- Mis-statements means:
- The statement is misleading in form or content.
- Where any inclusion of statement or omission is likely to mislead the reader.
- If the investor has purchased shares based on the misleading information in the prospectus he can take action against the company.
- The company and persons will be responsible for issuing mis-statement prospectus and have to face liability.
Question 12.
Abridged Prospectus
Answer:
- Abridged Prospectus contains the main contents of a prospectus in brief.
- It is attached with the application form issued by the company while offering securities.
- The abridged prospectus is issued only in case of a public offer made by a company.
- It contains all the salient features of a prospectus.

Question 13.
Shelf Prospectus
Answer:
- The company instead of preparing a fresh prospectus for every issue prepares a shelf prospectus.
- Shelf Prospectus can be used for all issues made by the company for up to one year.
- An Information Memorandum has to be filed with ROC every time during the validity period of one year of the shelf prospectus.
- Information Memorandum contains latest material facts such as new charges, changes in financial position, etc.
Question 14.
Red Herring Prospectus
Answer:
- A red herring prospectus is a kind of incomplete prospectus as it does not include complete particulars of the quantity/price of the securities.
- It is usually issued at the time of IPO (Initial Public Offer).
- A red herring prospectus shall have the same obligations that are applicable to the prospectus.
- A company must file a Red Herring Prospectus with ROC at least 3 days prior to the opening of the subscription list and the offer.
3. Study the following case/situation and express your opinion.
1. The Articles of a company stated that while borrowing any money from outsiders, the document must have the signatures of the Managing Director (MD) and any one of the Director. The Articles of Association clearly stated the procedure to be followed while borrowing money. The Managing Director did not follow all the procedures but still borrowed money from Mr. X. Mr. X assumed that the MD has followed the required procedures.
Question (a).
Can the MD be held punishable for his act?
Answer:
He can be held liable for his actions and can be insisted to pay back the loan amount.
Question (b).
Under which Doctrine can Mr. X take action against the company?
Answer:
Under Doctrine of Indoor Management.
Question (c).
Explain the Doctrine.
Answer:
- According to this doctrine, persons dealing with the company need not inquire whether internal proceedings relating to the contract are correctly followed.
- They are satisfied that the transactions are in accordance with the memorandum and articles of association.
- If there are any internal irregularities then the company will be liable as the person has acted in good faith and he did not know about the internal arrangement of the company.
- Similarly with X as he has acted in good faith and lent money to the managing director, but the managing director did not follow the procedure. So there is an irregularity that can make the director liable for his actions.
2. Mr. A entered into a contract with Star Limited Company and as advance payment gave a cheque of ₹ 1 lac to a Director Mr. Sam. Mr. Sam is not the Managing Director. Articles state that only the MD is authorized to sign any contracts or receive any payments on behalf of the company.
Question (a).
Did Mr. Sam have the authority to accept the cheque? Why?
Answer:
Sam did not have the authority to accept the cheque because usually, individual directors do not have the authority to act on the company’s behaviour unless expressly authorized.
Question (b).
Can Mr. Sam’s action be called as Ultra-Vires? Why?
Answer:
Mr. Sam’s action cannot be called ultra-vires because any act done by him beyond the powers of the memorandum is called Ultra-Vires.
3. The Object clause of Memorandum of a Company stated the main object as manufacturing of plastic chairs and tables and any other activity in furtherance of achievement of its main activity. The Board of Directors wants also to produce T.V. Serials and feels that the shareholders may give their permission.
Question (a).
Can the company with immediate effect start producing T.V. serials? Why?
Answer:
No, a company cannot start producing T.V. serials with immediate effect. A company cannot indulge in activities other than those provided in the object clause. The activities carried outside the scope drawn by the Memorandum of Association are called Ultra-Vires activities.
Question (b).
How can the object clause of the company be altered?
Answer:
A special resolution must be passed in the General Meeting for altering the object clause.

4. A public limited company has issued all the shares mentioned in its Memorandum as Authorised Capital. Now the company wants to make a public issue of 10,000 shares at a face value of ₹ 100 per share, to raise more funds for its expansion activities.
Question (a).
Which clause of Memorandum needs to be altered?
Answer:
The capital clause of the memorandum needs to be altered.
Question (b).
In which meeting the alteration can be approved?
Answer:
A capital clause is altered by passing an ordinary resolution in a general meeting of the company.
Question (c).
Which document should the company issue to invite the public to buy its shares?
Answer:
The prospectus is the document issued to invite the public to buy its shares.
5. A Company stated in its prospectus that it has been making profits for the last 5 years. However, Mr. X., an investor found out that two years back the company had not made any profit. The prospectus was filed with ROC on 1st January 2017 and was issued to the public on 10th February 2018.
Question (a).
Can Mr. X state that there was mis-statement in the prospectus?
Answer:
Yes, Mr. X can state mis-statement in the prospectus.
Question (b).
If found guilty which two types of liability will the company and its officers face?
Answer:
- Civil liability (Pay compensation for loss suffered by the investor)
- Criminal liability companies or their officers will be fined or imprisoned or both.
Question (c).
Can the prospectus be valid for the issue to the public on 10th February 2018?
Answer:
No, the prospectus will not be valid for the issue to the public on 10th February 2018.
6. A Company plans to offer Rights Issues.
Question (a).
Which document must it send to its shareholders for offering the rights issue?
Answer:
Letter of the offer must be sent to its shareholders for offering the rights issue.
Question (b).
Instead of the rights issue, if the company wants to issue shares to the public which document must it issue for inviting the public to subscribe to it.
Answer:
The prospectus is the document to be issued by the company if it wants to issue shares to the public instead of rights issues.
Question (c).
Name the document which is called an incomplete prospectus.
Answer:
Red Herring prospectus is called an incomplete prospectus.

4. Distinguish between the following.
Question 1.
Memorandum of Association and Articles of Association.
Answer:
| Basis |
Memorandum of Association |
Articles of Association |
| 1. Meaning |
Memorandum of Association is a document that contains all the fundamental information which are required for the incorporator of the company. |
Articles of Association is a document containing all the rules and regulations that govern the company. |
| 2. Defined in |
Section 2(56) |
Section 2(5) |
| 3. Types of information contained |
Powers and objects of the company. |
Rules for internal management of a company. |
| 4. Status |
It is subordinate to companies Act. |
It is subordinate to Memorandum. |
| 5. Retrospective effect |
The memorandum of the company cannot be amended retrospectively. |
The Articles of Association can be amended retrospectively. |
| 6. Major contents |
A memorandum must contain 6 clauses. |
The Articles can be drafted as per the choice of the company. |
| 7. Filing with registrar |
Memorandum of Association must be filed with Registrar of Company by all types of companies. |
Filing of Articles of Association is optional for a public company as it may adopt Table (A). |
| 8. Alteration |
Alteration can be done after passing special resolution in Annual General Meeting and previous approval of central government or company law board is required. |
Alteration can be done in the Articles by passing special Resolution at Annual General Meeting. |
| 9. Relation |
Define the relationship between company and outsider. |
Regulates the relationship between company and members. |
| 10. Acts done beyond the scope |
Absolutely void. |
Can be satisfied by shareholders. |
5. Answer in brief.
Question 1.
State any four clauses of Memorandum of Association.
Answer:
Memorandum of Association is a basic document, which gives information about the aims and objects of the company. It is also a charter of a company.
The following are four clauses of Memorandum of Association:
(i) Name Clause:
- This clause state the company’s proposed name.
- It must end with the word limited if its a public company or private limited if its a private company.
- It can’t be identical to any existing company’s name.
- It can’t resemble any registered Trade Mark.
- It should not be misleading in any way.
(ii) Registered office clause:
- The registered office clause lists the name of the state where the company’s registered office is physically located.
- The registered office’s physical location determines which jurisdiction the Registrar of companies and which court the company would fall under.
- It also confirms the company’s nationality .
- The registered office’s full address must be provided to the Registrar of companies to simplify further communications.
(iii) The object clause:
- This clause defines the objects for which a company is formed. It indicates the range of activities a company can undertake. This clause states in detail the main object for which the company is to be incorporated.
- The objects of the company must not be illegal, immoral or against the public policy.
- A company cannot do anything beyond or outside the scope of its objects.
(iv) Liability clause:
- The liability clause explains what liability each of the company’s member faces. If the company is limited by shares the liability that each member faces can be no more than the face value of share.
- If the company is limited by guarantee, this clause must define how much liability each individual company member holds.
Question 2.
State any four contents of Articles of Association.
Answer:
Articles of Association is a document which contains rules and regulations that governs the internal management.
The following are the four contents of Articles of Association:
- Share capital – Shares and their value and their division into different types of shares.
- Rights of each class of shareholders and procedure for variation of their rights.
- Procedure relating to allotment of shares, making of calls and forfeiture of shares.
- Rules relating to transfer and transmission of shares and the procedure to be followed.

Question 3.
State the statutory requirements in relation to Prospectus.
Answer:
Prospectus is an invitation to public to purchase its share and debentures. It is issued after the formation of company.
The following are the statutory requirements in relation to Prospectus:
- Draft Prospectus to be made Public: A draft prospectus filed with SEBI by the company should be made available to the public and to the stock exchange where the company wants to lists its shares.
- Signed by Director’s: Prospectus must be signed by all directors or by duly authorised attorney.
- Registration of Prospectus: A copy of the prospectus must be registered with ROC before issuing it to the public.
- Dating of Prospectus: A prospectus has to be dated. The date on the prospectus is considered as the date of publication of prospectus.
- Issuing Prospectus to Public: Prospectus must be issued to the public within 90 days from the date of registering a copy with the ROC.
6. Justify the following statements.
Question 1.
Memorandum of Association defines the limitations of the powers of the company.
Answer:
- The Memorandum of Association is a basic or fundamental or primary document of a company.
- It contains the following clauses: Name clause, Address clause, Object clause, Liability clause,Capital clause, Association of subscription clause.
- The entire business centres around its object clause.
- Object clause of the Memorandum of Association defines the area beyond which the company cannot do anything.
- It determines the powers of the company.
- It helps the stakeholders to know what is its permitted range of operation.
- A company is governed by Memorandum of Association and any act beyond it shall be considered as ultra-vires.
- Hence, Memorandum of Association defines the limitations of the power of the company.
Question 2.
Ultra-vires acts are null and void.
Answer:
- A Memorandum of Association of a company is a basic charter of the company.
- If a company departs from its Memorandum of Association such an act is ultra-vires.
- The doctrine of ultra vires is a fundamental rule of company law.
- An act legally in itself but not authorized by the object clause of Memorandum of Association of a company is ultra-vires.
- Hence if the company does an act or enters into a contract beyond the powers of the company then the act is said to be null and void.
- The company cannot sue on an ultra-vires transaction or it cannot be sued.
- Thus, I agree with the above statement.

Question 3.
Contents of Articles can be altered.
Answer:
- As per section 2(2) of the companies Act, 1956 ‘Articles’ means Articles of Association of a company as originally framed or as altered from time to time in pursuance of any previous companies’ law or of this Act.
- The Articles regulate the internal management of a company.
- It states the relationship between the company and its members.
- The articles, being the internal regulations of a company can be altered easily.
- The articles are required to be altered from time to time as per changes made by the government in the company law or as per changing situations in the corporate sector.
- Thus, the Articles of Association can be altered by passing a ‘Special Resolution’ at a general meeting.
Question 4.
The doctrine of Indoor Management protects outsiders who are unaware of the correctness of the internal proceedings of a company.
Answer:
- The doctrine of Indoor Management states that a person entering into a contract with the company need not inquire whether the company has followed the internal processing.
- It is assumed that the company acts as per the Memorandum of Association and Articles of Association.
- Because certain information which is internal to a company cannot be known to outsiders.
- So the doctrine of Indoor Management protects the interest of the outsider when the act is based on the Memorandum of Association and Articles of Association.
Question 5.
A prospectus is an important document issued by a public company.
Answer:
- A prospectus usually is in the form of a statement giving all material information about the company and showing its future prospectus.
- It aims at inviting investors to subscribe to its shares and debentures.
- It is a must for every public company to prepare its prospectus.
- It is through the prospectus that the prospective investors know the details of the shares offered by the company.
- Otherwise, the investors would have no idea of the shares that a public company is selling.
- All detailed information about a company like its business management, financial structure, etc., are provided in the prospectus.
- The main idea to issue a prospectus is to collect capital for the company from the general public.
- It should contain true, fair, and correct information.
- Hence, the prospectus is very important for a public company.

Question 6.
Company and officers responsible for issuing Prospectus are liable for mis-statements in Prospectus.
Answer:
- The prospectus is a written document giving an invitation to the public to purchase shares or debenture of the company.
- It provides all the necessary information about a company, its business, the management, financial structure, etc., of a company.
- A prospectus must be prepared very carefully and accurately.
- It should contain true and correct information and honest disclosure of facts.
- A company and all those officials can be held responsible for any mis-statement in the prospectus.
- These people have to face severe consequences.
- The shareholder can cancel the contract.
- Persons authorizing the issue of prospectus containing mis-statement are punishable with imprisonment of two years and a fine up to ₹ 5,000.
- Thus, I agree with the above statement.
7. Answer the following questions.
Question 1.
Briefly explain the clauses of the Memorandum of Association.
Answer:
- The Memorandum of Association is the principal document of a company.
- It is considered the charter of the company.
- It contains the powers and objectives of the company.
- It can be altered only according to the provisions made in the companies act regarding its alterations.
- Memorandum of Association provides information to the outsiders.
The Memorandum of Association contains the following clauses:
1. Name clause:
- This clause contains the complete name of the company.
- The company can choose any name subject to the following restrictions.
- The name of the company must end with the word limited in the case of a public limited company and with the word private limited in the case of a private limited company.
- The name should not be similar or identical to the name of any other company.
- The name should not contain the word cooperative.
- The name should not convey any connection or link of the company with the government department.
Alteration of name clause: A company can change its name by passing a special resolution and by obtaining approval from the central government.
2. Address clause:
- This clause contains the name of the state in which the registered office of the company is to be located.
- It is necessary because a company gets the registration from that state only.
- A registered office is a place where all the important documents are kept.
- A company must have a registered office when it starts its business activities or within 30 days whichever is earlier.
Alteration of address clause: A company may change its Registered office from
- One place to another place within the same city or town.
- One town or city to another town or city within the same state.
- One state to another state.
- In both these cases, a special resolution is to be passed in General Meeting.
3. Object clause:
- It is the most important clause of the Memorandum of Association.
- It contains the main object of the company.
- This clause defines the scope and limitations of the activities of the company.
- The objects must be defined keeping in mind the following conditions:
- the objects of the company must be legal.
- the objects should not be contrary to the provisions of any law.
- the objects must not be immoral.
Alteration in object clause: In order to alter its object clause, a company must pass a special resolution.
4. Liability clause:
- This clause defines the liability of the members of the company.
- In the case of a company limited by shares, the liability of the members is limited to the extent of the unpaid amount of share capital.
- In the case of a company limited by guarantee, the liability is limited to the amount of guarantee.
Alteration of liability clause: If a company wants to make any alteration in its liability clause then it must pass a unanimous resolution in a meeting.
5. Capital clause:
- The clause specifies the amount of share capital with which a company is to be registered.
- The capital with which a company is registered is called registered capital.
- A company can issue only that number of shares that are authorized by its memorandum.
Alteration of the capital clause: A company can alter its capital clause by passing a special resolution and by obtaining approval from the company law board.
6. The Association clause or Subscription clause:
- A company is an association of persons, who subscribe to its capital.
- For a public company minimum of 7 persons must subscribe to a memorandum by signing it and giving their undertaking that each one shall buy at least one share of a company.
- For a private company minimum of 2 persons must subscribe to the Memorandum of Association by signing it and they also give an undertaking that each one shall buy at least one share of a company.
- Each subscriber has to put his name address and occupation in the presence of at least one witness who shall also put in his details.

Question 2.
Define Memorandum of Association. Explain briefly its features.
Answer:
Definition:
As per section 2(28) of the companies Act 1956 “Memorandum of Association means the Memorandum of Association of a company as originally framed or altered from time to time in pursuance of any previous company laws or of this Act”.
As such this definition does not state exactly the scope, use, and importance of memorandum in a company.
- Lord Cairns observed that – “The memorandum of association is a charter and defines the limits of the powers of a company. The memorandum contains the fundamental conditions upon which alone the company is allowed to incorporate”.
- Lord Macmillan states that – “The purpose of the memorandum is to enable the shareholders, creditors and those who deal with the company to know what is its permitted range of enterprise”.
Meaning:
In simple words, the Memorandum of Association of a company means
- a basic or fundamental primary document of a company.
- a charter or constitution of a company
- no company can be incorporated without the Memorandum of Association.
- It lays down the range of its activities.
- It is a public document and can be inspected by those who deal with the company.
Features of Memorandum of Association:
The following are the features of the Memorandum of Association:
- Memorandum of Association states the nature of business activities to be conducted by the company.
- It informs about the scope of activities of the company.
- It is prepared by promoters of the company.
- It is signed by at least 7 persons in the case of a public company and 2 persons in the case of a private company.
- It is submitted to the registrar of companies for registration.
- All companies must prepare their own Memorandum of Association.
- It defines the relationship between the company and outsiders.
- It is an unalterable charter of the company.
- It is a public document.
Question 3.
What are Articles of Association? Explain briefly its content.
Answer:
Articles of Association contain rules and regulations regarding the management of the company’s internal affairs.
- It defines the powers, duties, and rights of managers, officers, and the board of directors.
- It establishes a relationship between the company and its members.
Contents of Articles of Association:
- The amount of share capital and different classes of shares
- Rights of each type of shareholders
- Procedure for making allotment of shares
- Procedure for issuing share certificates
- Procedure for transfer of shares
- Procedure for forfeiture of shares
- Procedure for reissue of forfeited shares
- Procedure for conducting meetings
- Procedure for appointment and removal of directors
- Duties powers and remuneration of directors
- Procedure for declaration and payment of dividend
- Procedure regarding the keeping of books of accounts and their audit
- Procedure regarding winding up of the company
- Seal of the company
Alteration of Articles of Association:
- A company may change its Article of Association by passing a special resolution.
- A company can alter its Articles of Association in the following ways:
- by the adoption of a new set of an Articles
- by deletion of an article
- by addition or insertion of a new article
- by substitution of an article
- by amendment of an article

Question 4.
Define Prospectus. Explain its contents.
Answer:
Definition: “Sec 2(70) of Companies Act, 2013 defines prospectus as any document described or issued as a prospectus and includes 32a Red Herring Prospectus or shelf prospectus or/and notice, circular advertisement or other document inviting offers from the public for the subscription or purchase of any securities of a body corporate”.
Meaning: Prospectus is a document that contains information about various aspects of the company and invests the investors to buy the securities offered by the company.
Contents of Prospectus:
A prospectus must contain the following:
(i) Information and Reports:
As per the Companies Act, the prospectus must contain information such as the name of the issuing company its full registered office address with phone numbers, email address, nature, number and price of securities being offered, details of a lead merchant banker, registrar to the issue, name of the stock exchange where the shares are listed.
- It must also have listed a clause of general risk date of opening and closing of issue etc.
- It must also have reported on financial information.
(ii) Declaration:
There should be a declaration by the company saying that all the provisions of the Companies Act have been complied with and that the prospectus does not contain anything contrary to the provisions of the Companies Act.
(iii) Statement of an Expert:
A prospectus may contain a statement made by an expert like Company Secretary, Chartered Accountant, Cost Accountant, Valuer, Engineer, etc., relating to matters that they have looked into.
- Any other matter as may be prescribed by the Companies Act.
- The expert has to give written consent to issue the prospectus.
(iv) Any other matter as may be prescribed by the Companies Act.
Maharashtra State Board 11th Std Secretarial Practice Textbook Solutions Digest
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()