Bhagya

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 13 India, Sri Lanka and Southeast Asia Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 13 India, Sri Lanka and Southeast Asia

1A. Choose the correct alternative to write the complete sentences.

Question 1.
The first kingdom of Sri Lanka established was known as ____________
(a) Tambapanni
(b) Sopara
(c) Pulatthinagar
(d) Srivijaya
Answer:
(a) Tambapanni

Question 2.
____________ was the first woman to become a Buddhist nun in Sri Lanka.
(a) Sanghamitra
(b) Anula
(c) Anuradha
(d) Tara
Answer:
(b) Anula

Question 3.
The relics of Gautama Buddha are known as ____________
(a) Stupa
(b) Kesa
(c) Dhatu
(d) Galapotha
Answer:
(c) Dhatu

Question 4.
The ____________ enlist 64 Indian scripts.
(a) Deepvamsa
(b) Mahavamsa
(c) Lalitvistar
(d) Chullavamsa
Answer:
(c) Lalitvistar

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Sri Lanka	Tambapanni
(b) Thailand	Mueng Thai
(c) Cambodia	Malaydvipa
(d) Land of Southeast Asia	‘Suvarnabhumi’

Answer:
(c) Cambodia – Kambujadesha

Question 2.

Set ‘A’	Set ‘B’
(a) Shili Foshi	Srivijaya
(b) Ramakien	Ram Akhyana
(c) Buddha	Dantdhatu
(d) Moonstone	Chandrashala

Answer:
(d) Moonstone – Chandrashila

1C. Find the odd one out.

Question 1.
Indo-China, Vietnam, Laos, Sri Lanka
Answer:
Sri Lanka

Question 2.
Dambulla, Dulatthinagar, Yongan, Anuradhpur
Answer:
Yongan

Question 3.
Srivijaya, Loas, Majapahita, Shailendra
Answer:
Loas

Question 4.
Funan, Champa, Cambodia, Matram
Answer:
Matram

Question 5.
Shailendra, Indonesia, Thailand, Myanmar
Answer:
Shailendra

2A. Write the names of historical places, persons, and events.

Question 1.
Founder of the kingdom of Tambapanni
Answer:
King Vijaya

Question 2.
The first woman to become a Buddhist nun
Answer:
Anula

Question 3.
Earliest stupas at Mihinthale
Answer:
Kantakchetiya

Question 4.
Name of the stupa erected on the remains of Thera Mahinda
Answer:
Ambasthal Thupa

Question 5.
Noted Indian philosopher
Answer:
Buddhaghosha

Question 6.
The text was written by Buddhaghosha
Answer:
Vishuddhimagga

Question 7.
Temple of Dantdhatu in the city of Kandy
Answer:
Sri Dalad Maligava

Question 8.
Kingdom in the delta region of Mekong
Answer:
Funan

Question 9.
Ancient kingdom in the coastal region of Vietnam
Answer:
Champa

Question 10.
The ancient name of Cambodia
Answer:
Kambujadesha

Question 11.
Temple built by Suryavarman-II
Answer:
Angkor Wat

Question 12.
Name of the founder king of ‘Majapahita’
Answer:
Vijaya

2B. Choose the correct reason and complete the sentence.

Question 1.
The southern kingdom of China was not left with any alternative path to reach the Silk Route because ____________
(a) China was attacked by a foreign power
(b) China disintegrated into three parts
(c) they found a delta region
(d) the Silk Route was infested with robbers
Answer:
(c) they found a delta region

Question 2.
The Shailendra kings built many Buddhist temples and stupas because ____________
(a) they were followers of Buddhism
(b) they were lovers of Buddhist art
(c) they were Tolerant by nature
(d) they hailed from India
Answer:
(a) they were followers of Buddhism

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

4. Explain the following statement with reasons.

Question 1.
The southern kingdom was not left with any alternative path to reach the Silk Route.
Answer:

• When the rule of the Han dynasty ended, China disintegrated into three parts.
• Because of this disintegration, China was not left with any alternative path to reach the Silk Route.
• Hence, the kingdom of the Southern Kingdom sent some people to explore the Sea Route.

Question 2.
According to Buddhist philosophy, the universe exists at three planes.
Answer:
According to Buddhist philosophy, the universe exists at three planes:

• Kamdhatu (Bondage in the form of desire)
• Roopdhatu (Bondage in the form of physical appearance and appellations)
• Aroopdhatu (State of being beyond any bondage).
• The architectural design of Borobudur Stupa is based on the concept of these three planes.

5. State your opinion.

Question 1.
King Anawrahta the founder of the ‘Pagan empire’ is known as the greatest ruler.
Answer:

• King Anawrahta is credited with the unification of north and south Myanmar.
• This unification is said to have given Myanmar its national identity.
• Anawrahta put a check to the increasing power of the Khmer empire of Cambodia.
• During his reign, the ‘Theravada Buddhism’, which had grown weaker, was revived.

Question 2.
The contact of Indians with the various region in Southeast Asia was on the increase.
Answer:

• The contact of Indians was on the increase because of trade during the 2nd-century B.C.E.
• The merchants who had to travel for months together were naturally accompanied by a large retinue of priests, monks, also travelers who were out to test their luck, ambitious members of royal families, etc.
• These were the people who proved instrumental in the spread of Indian culture in Southeast Asia.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 12 India, Nations in the Northwest of the Indian Subcontinent and China Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 12 India, Nations in the Northwest of the Indian Subcontinent and China

1A. Choose the correct alternative and write the complete sentences.

Question 1.
___________ a port city is mentioned in the ‘Old Testament’.
(a) Ophir
(b) Lothal
(c) Meluhha
(d) Bet Dwaraka
Answer:
(a) Ophir

Question 2.
___________ trained by sailors to reach the coast safely were called ‘Dishakak’.
(a) Sparrows
(b) Crows
(c) Kingfishers
(d) Pigeons
Answer:
(b) Crows

Question 3.
___________ is identified with Babylon.
(a) Nangarhar
(b) Gandhara
(c) Kandahar
(d) Baveru
Answer:
(d) Baveru

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Geographia	Strabo
(b) Naturalis Historia	Yavana
(c) Geographia	Claudius Ptolemy
(d) Indica	Arrian

Answer:
(b) Naturalis Historia – Pliny the Elder

Question 2.

Set ‘A’	Set ‘B’
(a) Purushspur	Peshawar
(b) Ancient Kapisha	Begram
(c) Bhokardan	Bhogvardhan
(d) Theravada	Kansu

Answer:
(d) Theravada – Hinayana

1C. Find the odd one out.

Question 1.
Spread of Indian culture:
(a) Afghanistan
(b) China
(c) Rome
(d) Japan
Answer:
(c) Rome

Question 2.
Indian trade with distant lands:
(a) Kathasaritsagara
(b) Bhokarda
(c) Deepvamsa
(d) Mahavamsa
Answer:
(b) Bhokarda

Question 3.
Greek Literature:
(a) Geographia
(b) Naturalis Historia
(c) Indica
(d) Periplus of Erythrean Sea
Answer:
(d) Periplus of Erythrean Sea

Question 4.
Trading centers in Jalana district:
(a) Paithan
(b) Ter
(c) Gandhara
(d) Bhokardan
Answer:
(c) Gandhara

2. Write the names of historical places, persons, and events.

Question 1.
Port city is mentioned in the ‘Old Testament’ (Bible).
Answer:
Ophir

Question 2.
The Latin name of Periplus of the Erythrean Sea.
Answer:
Periplus Maris Erythraei

Question 3.
Greek mathematician geographer, author of Geographia.
Answer:
Claudius Ptolemy

Question 4.
Famous statues of Buddha away from Kabul.
Answer:
Bamiyan statues

Question 5.
The route that links Asia and Europe.
Answer:
Silk Route

Question 6.
First Buddhist temple built in China
Answer:
White Horse Temple

Question 7.
Caves are located on the ancient Silk Route.
Answer:
Mogao Caves

Question 8.
The grandson of Genghis Khan had a great interest in Buddhism.
Answer:
Kubalai

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

4. State your opinion.

Question 1.
The spread of Buddhism in China introduced a new trend in Chinese art.
Answer:

• Many of the Buddhism monks who arrived in China hailed from central Asia.
• Their presence in China inspired the making of images of Gautama Buddha and Bodhisattvas.
• This art style that originated in the Xinjiang province is known as ‘Serendian Art Style’ (Seres meaning China + India)

5. Answer the following questions in detail.

Question 1.
Write a note on India’s relations with Afghanistan during Emperor Ashoka’s period.
Answer:

• Emperor Ashoka’s period 13th edict is the names of Greek kings, who were his contemporaries.
• People in their kingdoms were following the path of morality as outlined in his message of Dhammavijaya. Among these kingdoms was the kingdom of Kamboja in Afghanistan.
• The Ashokan edict at Kandahar is in Greek language and the script used for it is Aramaic.
• This inscription shows that Afghanistan was an integral part of Ashoka’s empire.
• Ashoka had sent ‘Thera Mahyantika’ (Majjhantika) to Kashmir and Afghanistan and ‘Thera Maharakkhita’ to the Greek (Yona) kingdoms, for spreading the teachings of Gautama Buddha.

Question 2.
Write in detail about Kushana Period.
Answer:

• In the Kushana period, Buddhism reached China by this trade route. Some of the coins of emperor Kanishka carry the image of Gautama Buddha. It also has a legend that reads, ‘Boddo’.
• This is the oldest representation of Gautama Buddha in an image form on a coin.
• The Chinese monks like Fa-Hien, Yuan Chwang, who travelled through India have described the Buddhist viharas and stupas in India.
• There are numerous remains of viharas and stupas in Afghanistan.
• Among them, a place called ‘Shahji-ki-Dheri’ near Peshawar in Pakistan was excavated.
• The importance of the stupa discovered at this place is underlined by the fact that it was built during Kanishka’s period.

6. Answers the following questions with the help of given points.

Question 1.
Write about the relations between India and Rome.
(a) Literature (Source of Information)
(b) Trade relations
Answer:
(a) Literature (Source of Information):

• A Sailor’s handbook of his sea travels is known as ‘Periplus of Erythrean Sea’ (Latin name: Periplus Maris Erythraei).
• The ancient cities like Bharuch, Sopara, Kalyan, etc., are mentioned in this periplus.
• There are other texts ‘Geographia’ written by the Greek mathematician-geographer Claudius Ptolemy, Tndica’

(b) Trade relations:

• The Indo-Roman trade had begun to grow. The silk route and the ports on the south and west coasts of India played a vital role in this trade.
• The records of the Greek historians mention a group of merchants, who paid a visit to the court of the Roman Emperor Augustus.
• The coin hoards found in Tamil Nadu had Roman gold coins in them, but they were valued for their gold.
• Nero, the Roman emperor had paid one million gold coins for a single chalice of emerald of Indian made.
• Pliny the elder had expressed concern about that the drain of gold from Rome into India.
• Strabo tells us that animals such as snakes, hunting dogs, tigers, elephants, birds like parrots and peacocks, things like hides and horns of rhinoceros, expensive textiles, pearls, ivory, and spices, etc. from India were in great demand.
• Apart from the Roman gold coins, many other things like lead, zinc, corals, wines, olive oil were the Roman imports coming to India.
• Cities like Paithan, Ter, Kolhapur, Bhokardan in the Jalana district were important trading centers.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 11 Kingdoms in South India Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 11 Kingdoms in South India

1A. Choose the correct alternative and write the complete sentences.

Question 1.

_____________ literature is one of the main sources of history of south India.
(a) Sangam
(b) Mahabharata
(c) Ramayana
(d) Indica
Answer:
(a) Sangam

Question 2.
_____________ language is spoken in Baluchistan.
(a) Tamil
(b) Brauhi
(c) Hindi
(d) Urdu
Answer:
(b) Brauhi

Question 3.
The first Chola king was _____________
(a) Raya Raja
(b) Rajendra Chola
(c) Karikala
(d) Rajendra II
Answer:
(c) Karikala

Question 4.
_____________ was the founder of the Vakataka dynasty.
(a) Vindhyashakti
(b) Pravarasena I
(c) Rudrasena
(d) Pravarasena II
Answer:
(a) Vindhyashakti

Question 5.
The founder of the Chalukyas is _____________
(a) Pulakeshin I
(b) Pulakeshin II
(c) Vikramaditya
(d) Jaising
Answer:
(d) Jaising

Question 6.
The capital of the Pallavas was _____________
(a) Chennai
(b) Kanchi
(c) Mahabalipuram
(d) Chingalpet
Answer:
(b) Kanchi

Question 7.
_____________ was a capable king of the Rashtrakuta dynasty.
(a) Dantidurga
(b) Krishna I
(c) Amoghvarsha
(d) Krishna II
Answer:
(c) Amoghvarsha

Question 8.
_____________ called themselves as ‘Tagarapuradhishwar’.
(a) Chalukyas
(b) Cheras
(c) Cholas
(d) Shilaharas
Answer:
(d) Shilaharas

Question 9.
The capital of Shilaharas of North Konkan was _____________
(a) Sthanak (Thane)
(b) Goa
(c) Kolhapur
(d) Panhala
Answer:
(a) Sthanak (Thane)

Question 10.
_____________ was the founder of the Gond dynasty.
(a) Ballal Singh
(b) Kol Bheel
(c) Rani Durgavati
(d) Nilkanth Shah
Answer:
(b) Kol Bheel

Question 11.
The Yadava king Shankardev was killed by _____________
(a) Malik Kafur
(b) Allaudin Khilji
(c) Mohd. Ghori
(d) Mohd. Gazni
Answer:
(a) Malik Kafur

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Cholas	Tanjavur
(b) Cheras	Kerala
(c) Pandyas	Pudukottai
(d) Vakatakas	Kanchi

Answer:
(d) Vakatakas – Malwa

Question 2.

Set ‘A’	Set ‘B’
(a) Tiruchirappalli	Tamil Nadu
(b) Kurnool	Andhra Pradesh
(c) Nandirandhan	Nagpur district
(d) Sthanak	Washim district

Answer:
(d) Sthanak – Thane

1C. Find the odd one out.

Question 1.
Ancient King’s in South India:
(a) Chola
(b) Pandya
(c) Maurya
(d) Chera
Answer:
(c) Maurya

Question 2.
Examples of Dravida Style:
(a) Kailasnath temple
(b) Elephanta caves
(c) Vaikuntha Perumal temples
(d) Brihadeshwara temples
Answer:
(b) Elephanta caves

Question 3.
Texts composed in South India:
(a) Setubandha
(b) Ratnamalika
(c) Kavirajmarg
(d) Mattavilasa
Answer:
(d) Mattavilasa

Question 4.
Languages in the Dravidian group:
(a) Tamil
(b) Kannada
(c) Malayalam
(d) Marwari
Answer:
(d) Marwari

2A. Write the names of historical places, persons, and events.

Question 1.
Province of Thanjavur and Tiruchirappalli
Answer:
Cholamandala

Question 2.
The ancient name of Kolhapur
Answer:
Kuntala

Question 3.
Composition of Pravarasena II in Maharashtri Prakrit
Answer:
Setu bandha

Question 4.
The passion of art during the Chalukya period
Answer:
Kirtivarman

Question 5.
Sanskrit play written by Mahendravarman
Answer:
Mattavilasa

Question 6.
The famous temple at Ellora built during the time of Krishna I
Answer:
KailasaTemple

Question 7.
Texts composed by Amoghvarsh
Answer:
Ratnamalika and Kavirajmarg

Question 8.
Temple at Ambarnath
Answer:
Rameshwar Mahadev

Question 9.
Temple at Khidrapur
Answer:
Koppeshwar Mahadev

Question 10.
Gond Queen who fought against Akbar
Answer:
Queen Durgavati

Question 11.
Text composed by Sarvasena
Answer:
Harivijaya

Question 12.
Two styles of temple architecture in South India
Answer:
Dravida and Vesara

2B. Choose the correct reason and complete the sentence.

Question 1.
The Indian culture between north India and south India become diverse because of _____________
(a) cultural Exchange
(b) economic Unification
(c) political Unification
(d) the conflict between North and South India
Answer:
(a) cultural Exchange

Question 2.
The Rashtrakuta dynasty declined because of _____________
(a) attacks of Pallavas and Satavahanas.
(b) attacks of Parmars and Chalukyas of Kalyani
(c) attacks of Pallavas and Chalukyas and Satavahanas
(d) attacks of Cholas and Valatakas
Answer:
(b) attacks of Parmars and Chalukyas of Kalyani

3. Observe the map on page 78 of your textbook and answer the following questions, based on it.

Question 1.
Name the two famous caves in Maharashtra.
Answer:
Ajanta and Ellora

Question 2.
Name the temples of Vesara style during the Chalukya rule.
Answer:
Aihole, Badami and Pattadakala

Question 3.
Name the two temples created during the Pallava period.
Answer:
Kanchi and Mahabalipuram

Question 4.
What was the capital of the Pandyas?
Answer:
Madurai

Question 5.
What is the name of the dynasty that ruled over present-day Kerala?
Answer:
Chera

4. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

5. Write short notes.

Question 1.
Trade-in south India.
Answer:

• In the kingdom of Cholas, Pandyas, Cheras, Vakatakas, Chalukyas, Rashtrakutas, etc., many professions requiring specialized skills were practiced.
• Ivory was obtained from the Malayagiri jungle.
• The Cholamandalam provinces were well known for excellent quality textiles.
• Plain and coloured cotton cloth, as well as silk cloth, was produced in this province.
• The Chera kingdom produced fine cloth which was one of the important commodities in the Indo-Roman trade, Marco Polo has mentioned it in his travel accounts.
• Cities like Paithan, Tagar (Ter), Nashik, etc. flourished because of it.
• The goods produced in rural areas were brought for sale in the cities.

6. Explain the following statement with reasons.

Question 1.
The Sangham literature is the most ancient in the family tradition.
Answer:

• The tradition of writing poetry and grammar was prevalent in south India from ancient times.
• The Sangham literature is the most ancient literature available.
• This literature is one of the main sources of the political history of south India.

7. State your opinion.

Question 1.
Two styles of architecture are seen in South India.
Answer:

• Two styles of architecture ‘Dravida’ and ‘Vesara’ developed in South India.
• The Dravida style emerged and developed in the regions from the Krishna river to Kanyakumari.
• The important feature of Dravida architecture was identified by the construction of Shikhara.
• In this type, the stories reduce in size as the Shikhara rises. Examples of this style can be seen in the Kailasnath and
• Vaikuntha Perumal temples at Kanchi, Brihadeshwara temple at Tanjore.
• The Chalukyas built temples at places like Aihole, Badami, and Pattadakal.
• During the Rashtrakuta period, the world-famous ‘Kailasa’ temple was created.

Question 2.
The period during the rule of the kingdom in south India was important from the point of view of Sanskrit literature.
Answer:

• Kalidasa composed the ‘Meghdoot’ at Ramtek in Vidarbha.
• During the Vakataka rule, Compositions in the Prakrit language were created. Pravarsena II.
• The Vakataka king wrote the well-known composition named ‘Setubandha’. ‘Harivijaya’ was composed by Sarvasena, the founder of the Vatsagulma branch of Vakatakas.

8. Answer the following questions in detail.

Question 1.
Write about trade in South India.
Answer:

• Many professions requiring specialized skills were practiced.
• Ivory was obtained from the Malayagiri jungle. The Cholamandalam provinces were famous for excellent quality textiles.
• Plain and coloured cotton cloth, as well as silk clothes, were produced in this province.
• In the Chera kingdom, the fine cloth was produced. It was one of the important commodities in the Indo-Roman trade.
• The trade and industries in South India flourished during this period.
• The goods produced in rural areas were brought for sale.
• Shreni in South India played an important role in trade and the social system.

Question 2.
Write a note on Literature.
Answer:

• The ‘Sangham literature’ is supposed to be most ancient in the Tamil tradition.
• This literature is one of the main sources of the political history of South India.
• This period is important from the point of view of Sanskrit literature.
• Kalidasa composed the ‘Meghdoot’ at Ramtek in Vidarbha.
• During the Vakataka rule, compositions in Prakrit were created.
• Pravarsena II wrote ‘Setubandha’. ‘Harivijaya’ was composed by Sarvasena, the founder of the Vatsagulm branch of Vakatakas.

9. Answer the following questions with the help of given points.

Question 1.
The important Kingdom in south India.
(a) Cholas
(b) Cheras
(c) Pandyas
Answer:
(a) Cholas: The Cholas established their kingdom in the first century C.E. The Chola dynasty originated in Thanjavur and Tiruchirappalli (Tamil Naidu). This province was known as ‘Cholamandala’ (Coromandel) Karikala was the first Chola king who brought together eleven small kingdoms and build a strong army. He defeated the Chera and Pandya king and established Tamil dominance.

(b) Cheras: The Cheras ruled over Kerala. They are mentioned as ‘Kedalaputra’ (Keralaputra or sons of Kerala) in contemporary literature.

(c) Pandyas: The Pandyas had established their rule from Pudukkottai to Kanyakumari.

10. Explain the concept.

Question 1.
Mandalam
Answer:
The kingdoms of South India especially Cholas were divided into many provinces. These provinces were known as ‘Mandalam’. A member of the royal family was the chief of the Mandalam.

Question 2.
Gonds
Answer:
The Gond dynasty was established at Chanda (Chandrapur) during the Yadava period. Kol Bheel was the founder of this dynasty. He brought the people of the Gond tribe together and encouraged them to rebel against the Naga dynasty. He established the capital at Sirpur. In the later period, Khandkya Ballal Singh built a fort at Ballarpur and shifted the capital from Sirpur to Ballarpur. The temple at Achaleshwar was constructed during his period.

Question 3.
Yadavas
Answer:
Yadava dynasty is one of the important dynasties of medieval Maharashtra. Bhillam V (1185-93 C.E.) is the important king of the Yadava dynasty. He expanded the kingdom by defeating the Kalachuris. He established his capital at Devgiri and got himself coronated. In the later period, Singhan was an important ruler of this dynasty. He defeated the Hoysalas, Shilaharas and expanded the rule of Yadavas.

Question 4.
Rashtrakutas
Answer:
Dantidurga was the first powerful king of the Rashtrakuta dynasty. The rule of Rashtrakutas was spread from the Vindhyan ranges to Kanyakumari in the south. After Dantidurga, his uncle Krishna I became the king. He uprooted Chalukya’s rule. The famous Kailas temple at Ellora is ascribed to Krishna I. The succeeding Rashtrakuta rulers became influential in North India as well.

Question 5.
Shilaharas of North Konkan
Answer:
Kapardi established the north Kokan branch of Shilaharas. Rulers of this branch were initially the feudatories of the Rashtrakutas. Their capital was at Sthanak (Thane). Aparajita was another important king of this branch. He ruled for around thirty-five years. Chittaranjan followed Aparajita as King. His brothers fought for their claim to the throne.

Question 6.
Pallavas
Answer:
From the 6th century C.E. to the 9th century C.E., the Pallavas were known as the most powerful rulers in South India. Historians vary in their views regarding the origin of the Pallavas. Some copperplates of the Pallavas are found. There is a mention of Sinhavarman and Shivaskandavarman Pallava who ruled over the regions of the eastern coast. Kanchi was the capital of the Pallavas. We get detailed information about the Pallava dynasty beginning from the reign of Simhavishnu. He conquered the province of Cholas and extended his rule from Krishna to Kaveri. After Simhavishnu, his son Mahendravarman ascended the throne. He was a great scholar. He wrote the Sanskrit play ‘Mattavilasa’. He wrote books on subjects like music, dance, sculpture, painting, etc.

Question 7.
Chalukyas
Answer:
During the rule of Harshavardhan in North India, the Chalukya dynasty ruled in the south for approximately 200 years. Jaising was the founder of this dynasty. At the beginning of the 6th century C.E. he established his capital at Vatapi (Badami). His grandson Pulakeshin I was the first important king of the Chalukyas. He built the fort of Badami. He performed the Ashwamedha sacrifice and took up the title of ‘Maharaja’. He also took titles like ‘Prithvivallabha’ and ‘Satyashraya’.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 10 Changing Times Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 10 Changing Times

1A. Choose the correct alternative and write complete sentences.

Question 1.
The Shakas divided the state into various _____________
(a) provinces
(b) districts
(c) villages
(d) towns
Answer:
(a) Provinces

Question 2.
_____________ was an important king of the Kushana Empire.
(a) Chandragupta II
(b) Kanishka
(c) Harsha
(d) Gondophernes
Answer:
(b) Kanishka

Question 3.
Chandragupta I added the title _____________ to his name.
(a) Maharaja
(b) Lokaraja
(c) Samrat
(d) Maharajadhiraja
Answer:
(d) Maharajadhiraja

Question 4.
_____________ was the founder of the Vardhan dynasty.
(a) Harsha
(b) Pulakeshin I
(c) Pushyabhuti
(d) Samudragupta
Answer:
(c) Pushyabhuti

Question 5.
The history of Kashmir can be found in Rajatarangini of _____________
(a) Kalhana
(b) Harsha
(c) Ghatothkach
(d) Kalidasa
Answer:
(a) Kalhana

Question 6.
The use of _____________ script is seen on the Shaka coins.
(a) Brahmi
(b) Sanskrit
(c) Pali
(d) Kharoshthi
Answer:
(d) Kharoshthi

Question 7.
The Periplus of Erythrean Sea is written in the _____________ language.
(a) Latin
(b) Greek
(c) English
(d) Pali
Answer:
(b) Greek

Question 8.
Kanishka had organized the fourth Buddhist Council in the Vihara at Kundalvan in _____________
(a) Shigupta
(b) Kashmir
(c) Pallavas
(d) Gondophernes
Answer:
(b) Kashmir

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Bactria	Greeks
(b) Central Asia	Shakas
(c) Kashmir	Karkotakas
(d) South India	Vardhan’s

Answer:
(d) North India – Vardhan’s

Question 2.

Set ‘A’	Set ‘B’
(a) Dhanvantari	Physician
(b) Kshapanak	Astrologer
(c) Amarsinha	Lexicographer
(d) Sanku	Magician

Answer:
(d) Sanku – Architect

Question 3.

Set ‘A’	Set ‘B’
(a) Chitrapatta	Printed silk
(b) Dukul	Silk
(c) Pulakbandh	Coloured cotton
(d) Pushpapatta	Muslin

Answer:
(d) Pushpapatta – Floral designs

1C. Find the odd one out.

Question 1.
Dhanvantari Kshapanak, Sanku, Chitrapatta
Answer:
Chitrapatta

Question 2.
Lokaraja, Maharaja, Maharajadhiraja, Vikramaditya
Answer:
Lokaraja

Question 3.
Shakuntalam, Pulakbandh, Pushpapatta, Amshuka
Answer:
Shakuntalam

Question 4.
Nigam, Shreni, Vishaya, Gana
Answer:
Vishaya

Question 5.
Dharnikot, Bhokardan, Amaravati, Nagarjunikonda
Answer:
Bhokardan

Question 6.
Saraswati, Vishnu, Surya, Kushana
Answer:
Kushana

2A. Write the names of historical places, persons, and events.

Question 1.
First Shaka king in India
Answer:
Moga

Question 2.
Sarvarajochchheta
Answer:
Samudragupta

Question 3.
Founder of Karkotaka dynasty
Answer:
Durlabhavardhan

Question 4.
Symbol of Goddess Athena
Answer:
Owl

Question 5.
Chinese traveller during Harsha’s reign
Answer:
Yuan Chwang

2B. Choose the correct reason and complete the sentence.

Question 1.
The Gupta period is considered as the classical age of Indian history because of _____________
(a) political stability
(b) help from foreign powers
(c) centralized Administration
(d) development in Art and Architecture
Answer:
(a) political stability

Question 2.
The Gupta kings changed the economic structure of agricultural system because, _____________
(a) many foreign communities came and settled in India
(b) their preference was on giving the land to local farmers for tilling
(c) king was appointed as Viceroy who looked after the provincial administration
(d) the human figure was the central theme of the sculptures in the Gupta period
Answer:
(b) their preference was on giving the land to local farmers for tilling

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

4. Write short notes.

Question 1.
Vardhan Empire
Answer:

• The declining power of the Guptas saw the rise of dynasties such as Vardhans, Maukharis Maitrakas, etc.
• The founder of the Vardhan Empire was Pushyabhuti.
• He was followed by his son, Prabhakarvardhan who made the Vardhan dynasty powerful.
• He took up the title of ‘Parambhattarak Maharajadhiraj’.
• The most prominent ruler of this dynasty was Harshavardhan.
• His empire extended from Nepal to Narmada and Saurashtra to Bengal.
• ‘Harshacharita’ written by Banabhatta, a court poet, and also travel accounts of Yuan Chwang give information about this period.
• Universities of Nalanda and Vallabhi became great centers of learning. Harshavardhan’s empire was the last powerful empire in ancient India.

Question 2.
Kushana Empire
Answer:

• After winning over the small kingdoms, Kushanas followed the system of Shakas and established their Satrapi’s there.
• A military officer called ‘Satrapa (Kshatrapa) was appointed on the satrapies.
• The King was the chief of all the Satraps and adopted the titles like ‘Rajadhiraj’, ‘Maharaj’ etc.
• The concept of the divinity of the King is seen for the first time in the inscriptions on the Kushana coins.
• They called themselves ‘Devputra’(Son of God).

5. Explain the following statements with reasons.

Question 1.
During the Gupta period, India’s sea trade began to increase on a large scale.
Answer:

• Indian goods were sent up to the Red Sea and from there via. Egypt to Rome.
• From India, animals such as tiger, lion, and monkey, birds such as parrot and peacock, wool, silk, muslin, cotton cloth, ivory, pearls, spices, sandalwood, medicinal herbs, diamonds, precious stones, and other luxury terms were exported, whereas, from other countries goods such as lead, copper, glass, silver, gold, wines were imported.
• Due to this trade, the flow of gold coins was constantly coming in India and hence India became prosperous.

6. State your opinion.

Question 1.
Some Bactrian coins resemble Greek coins.
Answer:

• Some Bactrian coins resemble Greek coins in terms of their shape and weight.
• On some of these coins, the image of the owl is seen.
• Owl is the symbol of Goddess Athena. Athena was the main deity of Athens.
• Indo-Greek coins are found in Bactria.
• The Greek legends are written on the obverse side and the legends are written in Prakrit.
• Kharoshthi script on the reverse side.

Question 2.
India became prosperous.
Answer:

• In contemporary India, agriculture and animal husbandry were the main sources of livelihood.
• Along with it various industries and trade developed during this period.
• India’s contact with the foreigners proved to be beneficial for this.
• During this period also merchant and artisans guilds (shrenis) were in existence.
• During this period, India’s sea trade began to increase on a large scale.
• Indian goods were sent up to the Red Sea and from there via Egypt to Rome.
• From India, animals such as tiger, lion, and monkey; birds such as parrot and peacock; wool, silk, muslin, cotton cloth, ivory, pearls, spices, sandalwood, medicinal herbs, diamonds, precious stones, and other luxury items were exported and from other countries goods such as lead, copper, glass, silver, gold, wines, etc. were imported.
• Due to this trade, the flow of gold coins was constantly coming in India and hence India became prosperous.

7. Answers the questions in detail.

Question 1.
Write a note on the Kushanas in detail.
Answer:

• Kujula Khadphises declared himself as the king of Bactria and with this the Kushana rule was established up to Kabul, Kashmir.
• The Chinese records, Greek and Roman literature provide information about this. The Kushanas’ are referred to as ‘Tukhar’ or ‘Tushar’.
• The Kushanas followed the system of Shakas and established their Satrapi’s there. A military officer called ‘Satrapa (Kshatrapa) was appointed. The king was the chief of all the Satrapi’s.
• The kings adopted titles like ‘Rajadhiraj’, ‘Maharaj’ etc.
• The concept of the divinity of the kings is seen for the first time in the inscription on the Kushana coins.
• They called themselves ‘Devputra’ (Son of God).
• Kanishka obtained the status of an emperor. His empire extended from Kabul to Pataliputra and from Kashmir to Malwa.
• He established two capitals, one at Purushpur (Peshawar) and the other at Mathura.
• The fourth Buddhist council was organized by Kanishka at Kundalvam in Kashmir.
• The Kushanas had adopted Indian cultures which is obvious from the name of the last Kushana king “Vasudeva’.

Question 2.
Discuss trade from 2nd C.B.C.E to 4th C.C.E.
Answer:

• The period from 2nd C.B.C.E to 4th century C.E was the period of arrival of the central Asian tribes and the kingdoms that they established.
• Various industries and trade developed during this period. India’s contact with the foreigners proved to be beneficial for this.
• India’s sea trade began to increase on a large scale. Indian goods were sent up to the Red Sea and from there via Egypt to Rome.
• The items of export were animals such as tigers, lions, and monkeys, birds such as parrots and peacocks, wool, silk, muslin, cotton cloth ivory, pearls, spices, and other luxury items.
• The items of import were lead, copper, glass, silver, gold, wines, etc.
• Due to this trade, the flow of gold coins was constantly coming in India and hence India became prosperous.

8. Answers the following questions with the help of given points.

Question 1.
Discuss coinage, art, and iconography between 2nd B.C.E and 4th C.E.
(a) Coinage
(b) Art
(c) Iconography
Answer:
(a) Coinage:

• The flow of gold coins was constantly coming in India.
• The portraits of kings and images of deities were inscribed on the gold coins of the Bactrian Greeks.
• There was a great impact of the Greek and Roman coins on the coins of Shaka and Kushana rulers.
• The Kharoshthi script is seen on the Shaka coins. The coins indicate the mixed impact of Greek, Indian and Persian cultures.
• The Kushana kings depicted Indian cities on coins.
• The image of Shiva has been found on gold and copper coins.
• Kushana coins are found in the border regions of India and China.
• The legends on the Kushana coins found in Central Asia are in the Prakrit language in the Kharoshthi script.

(b) Art:

• The Gandhara region had become a melting pot of Indian, Greek, Roman, Persian, and Shaka cultures.
• A new style of art developed in the cities of Pushkalavati, Taxila, Purushpur, etc. It is known as ‘Gandhara style’.
• The theme was Indian but the style was Greek.
• The Mahayana sect of Buddhism gave an impetus to this style of art.

(c) Iconography:

• In the icons of the Gandhara style, there was more emphasis on physical beauty.
• During the same time, Mathura and Varanasi’s styles of art developed.
• The images of Gautama Buddha were completely Indian in nature.
• Mathura was an important center of Indian art of sculpture.
• Portrait sculpture is the feature of the Mathura Style of art.
• The statues of Kushan kings, Vima Takshama, and Kanishka are examples of portrait sculptures.
• Similarly, images of Saraswati, Vishnu, Surya, Shiva, and Kartikeya saw the innovation in sculptural art.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 9 Post Mauryan India Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 9 Post Mauryan India

1A. Choose the correct alternative and write complete sentences.

Question 1.
___________ established a second capital at Vidisha.
(a) Chandragupta Maurya
(b) Bimbisara
(c) Pushyamitra Shunga
(d) Hala
Answer:
(c) Pushyamitra Sunga

Question 2.
The ___________ mention the ‘Andhras’ or ‘Andhrabhrutyas’.
(a) Puranas
(b) Upanishadas
(c) Vedas
(d) Jain Tools
Answer:
(a) Puranas

Question 3.
___________ was the smallest unit of administration.
(a) Kingdom
(b) State
(c) Grama(village)
(d) District
Answer:
(c) Grama

Question 4.
___________ wrote Brihatkatha.
(a) Hala
(b) Gunadhya
(c) Patanjali
(d) Panini
Answer:
(b) Gunadhya

Question 5.
Gatha Saptashati reflects the social life in ___________ of the Satavahana period.
(a) Maharashtra
(b) Tamilnadu
(c) Uttar Pradesh
(d) Bihar
Answer:
(a) Maharashtra

Question 6.
___________ wrote the ‘Mahabhashya’ based on Panini’s Ashtadhyayi’
(a) Gunadhya
(b) Patanjali
(c) Banabhatta
(d) Kalidasa
Answer:
(b) Patanjali

Question 7.
___________ was the head of trade guilds.
(a) Shreshthi
(b) Sarthavaha
(c) Malakara
(d) Dasaka
Answer:
(a) Shreshthi

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Pushymitra shunga	Shisunaga dynasty
(b) Chandragupta Mauryan	Mauryan dynasty
(c) Gautamiputra Satakarni	Satavahana dynasty
(d) Mahapadma Nanda	Nanda dynasty

Answer:
(a) Pushyamitra Shunga – Shunga dynasty

Question 2.

Set ‘A’	Set ‘B’
(a) Pratishthan	Paithan
(b) Tagar	Ter
(c) Nasik	Nashik
(d) Karhatak	Viharas

Answer:
(d) Karhatak – Karhad

Question 3.

Set ‘A’	Set ‘B’
(a) Lekhanika	Scribes
(b) Vaidya	Traders of perfumes
(c) Halakiya	Cultivators
(d) Suvarnakar	Goldsmith

Answer:
(b) Vaidya – Physicians

1C. Find the odd one out.

Question 1.
Shri Satakarni Yajna Satakarni, Hala, Pushyamitra Shunga
Answer:
Pushyamitra Shunga

Question 2.
Vardhaki, Halakiya, Malakara, Lohavanija
Answer:
Halakiya

Question 3.
Amatya, Naigam, Dasaka, Sarthavaha
Answer:
Dasaka

Question 4.
Malakara, Lekhanika, Vaidya, Halakiya
Answer:
Malakara

Question 5.
Pratishthan, Tagar, Nasik, Sarthavaha
Answer:
Sarthavaha

2A. Write the names of historical places, persons, and events.

Question 1.
Greek king defeated by Pushyamitra Shunga
Answer:
King Demetrius

Question 2.
Ashtadhyayi
Answer:
Panini

Question 3.
Last king of the Shunga dynasty
Answer:
Devbhuti

Question 4.
Mountain pass on the ancient trade route in Maharashtra
Answer:
Naneghat

Question 5.
Head of trade guilds
Answer:
Shreshthi

Question 6.
Blacksmith
Answer:
Lohavanija

Question 7.
Chief of caravan merchant
Answer:
Sarthavaha

Question 8.
Traders of perfumes
Answer:
Gandhika

Question 9.
Goldsmith
Answer:
Suvarnakar

Question 10.
Physicians
Answer:
Vaidya

2B. Choose the correct reason and complete the sentence.

Question 1.
The Satavahana rule declined due to ___________
(a) weak rulers
(b) the constant struggle between Sakas and Satavahanas
(c) economic decline
(d) social decline
Answer:
(b) the constant struggle between Sakas and Satavahanas

Question 2.
Grama was an integral part of the ___________
(a) central machinery
(b) middle machinery
(c) outdoor machinery
(d) absolute machinery
Answer:
(a) central machinery

Question 3.
Many Satavahana inscriptions are found in ___________
(a) South Maharashtra
(b) Northwest Maharashtra
(c) North Maharashtra
(d) Central Maharashtra
Answer:
(c) North Maharashtra

Question 4.
___________ reflects the social life in Maharashtra of Satavahana period.
(a) Lohavanija
(b) Dasaka
(c) Halakiya
(d) Gatha Saptashati
Answer:
(d) Gatha Saptashati

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

4. Write short notes.

Question 1.
Guilds or Shrenis
Answer:

• Many industries and trade flourished under the Satavahas.
• Various shrenis (Guilds) emerged during this period.
• The trade and industries were controlled with the help of these shrenis.
• The shrenis also provided loans.

5. Explain the following statements with reasons.

Question 1.
Foreigners like Greek, Pallavas, and Kushanas were absorbed in the social structure.
Answer:

• The invasion of foreigners like Greek, Pallavas, Shakas, and Kushanas took place during the Satavahana period.
• But these foreigners were soon absorbed in the social structure.
• This means that contemporary society was flexible enough to accommodate foreigners.
• The political invasions brought about social, economic, and cultural changes.

Question 2.
The influence of Persian and Greek sculptural styles of the Mauryan period decreased during the Shunga and Satavahana period.
Answer:

• A new native Indian style of architecture developed or emerged in this period.
• For e.g., the four gateways (Toranas) of the Sanchi Stupa No. 1 built during this period are excellent examples of this style.
• Many incidents from the life of Gautama Buddha are carved on these gateways.
• A number of rock-cut caves (Viharas and Chaityas) at Bhaje, Nashik, Karle, etc. belong to the Satavahana period.
• Especially the Chaitya at Karle, its magnificent facade entrance and sculptures are the finest examples of the sculptural art of this period.

6. State your opinion.

Question 1.
Before Gautamiputra Satakarni some of the Satavahana kings were not capable.
Answer:

• Taking advantage of the situation, the Shaka Satrapas established their rule in the western regions of India.
• Gautamiputra Satakarni, the Satavahana king conquered the Shakas.
• The Satavahana dynasty regained its strength with this victory.
• Thus, before Gautamiputra Satakarni some of the Satavahana kings were not capable.

Question 2.
The Shungas contribution to the field of art is important.
Answer:

• The Shunga’s contributed to art in a big way.
• The stupas at Sanchi and Bharhut, Garuda pillar at Besnagar are excellent examples of art during this period.
• The sculptural art in the Shunga period widened its horizons and depicted the life of common people on a large scale.
• Thus, the Shungas’ contribution to the field of art is important.

7. Answers the questions in detail.

Question 1.
Write a detailed note on the Shunga Empire.
Answer:

• The Shunga Empire was founded by Pushyamitra Shunga.
• The Shunga Empire extended from Magadha in the east to Sialkot (Punjab) in the west as well as the Himalayas in the North to Vidarbha in the south.
• Pushyamitra established a second capital at Vidisha although Pataliputra was the main capital. Pushyamitra was valiant and ambitious.
• He strengthened his rule in the provinces of Kosala, Vatsa, Avanti, etc.
• Later he conquered the lost provinces of the Magadha empire up to Sialkot.
• The Greek king Demetrius was repelled by Pushyamitra.
• After establishing his rule over North India and some parts of South India he performed the Ashwamedha sacrifice twice.
• Sanskrit was encouraged. Many texts were reviewed. The Manusmriti was composed during this period.
• Along with literature, art was encouraged for e.g., the Sanchi and Bharhut stupas and the Garuda pillar at Besnagar are excellent examples of art during this period.
• Sculptural art widened its horizons and districted the life of common people on a large scale.

Question 2.
Give an account of the rise of the Satavahana Empire.
Answer:

• After the disintegration of the Mauryan Empire, many new powers arose. Among them, the Satavahanas are mentioned as the earliest ruling dynasty in Maharashtra.
• The Satavahanas ruled over a vast region of Maharashtra, Andhra, and Karnataka.
• Paithan in Maharashtra was the capital of the Satavahanas. The mention of Puranas the Andhras or ‘Andhrabhrutyas’ Probably these terms refer to the Satavahanas.
• Simuka was the first Satavahana king to be mentioned in the Naneghat inscription.
• The most important king of this dynasty was Shri Satakarni, Hala, Gautamiputra Satakarni and Yajna Satakarni.
• Gautamiputra Satakarni conquered the Shakas and also Central India and the entire regions of Dakshinapatha.
• He also established his dominance over the Republic states in Central India and Rajasthan.
• Gautamiputra proved his strength by gaining victory over Nahapana.
• The Satavahana rule became weak due to the constant struggle between Shakas and Satavahanas.

8. Explain the concept with examples.

Question 1.
Metronomic
Answer:
The Satavahana kings used Metronomics i.e., using the names of their mothers as prefixes for e.g., Gautamiputra Satakarni. Vasishthiputra Pulumavi etc.

Question 2.
Shakapahlavyavannisudan
Answer:
Gautamiputra Satakarni is mentioned as ‘Shakapahlavyavarnnisudan’ i.e. the destroyer of Shakas, Pallavas, and Greeks in the Nashik inscription of his mother Gautami Balashri.

Question 3.
Satavahanakulayashahpratishthapankar
Answer:
Gauthamiputra Satakarni has been referred to as ‘Satavahanakulayashahpratishapankar’ in the Nashik inscription of his mother Gauthami Balashri.

Question 4.
Trisamudratoyapitavahana
Answer:
Gautamiputra Satakarni has been mentioned as ‘Trisamudratoyapitavahana’ i.e., One whose horses drank the water of the three seas. Such a type of mentioning indicates that many kings in the southern region must have accepted feudatory status and ruled under the suzerainty of Gautamiputra Satakarni.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 8 India During Mauryan Period Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 8 India During Mauryan Period

1A. Choose the correct alternative and write complete sentences.

Question 1.
There existed ___________ Mahajanapadas in ancient India.
(a) Fourteen
(b) Fifteen
(c) Sixteen
(d) Seventeen
Answer:
(c) Sixteen

Question 2.
The empire of ___________ became strong during the struggle of four Mahajanapadas.
(a) Kasi
(b) Kosala
(c) Avanti
(d) Magadha
Answer:
(d) Magadha

Question 3.
The kingdom of Magadha acquired the form of an ___________
(a) Empire
(b) State
(c) Country
(d) District
Answer:
(a) Empire

Question 4.
The concept of ___________ occurs in the ancient literature on Indian polity.
(a) Raja
(b) Maharaja
(c) Chakravarti
(d) Maharajadhiraj
Answer:
(c) Chakravarti

Question 5.
___________ was the first Chakravarti Emperor.
(a) Chandragupta Maurya
(b) Bimbisara
(c) Mahapadma
(d) Bindusara
Answer:
(a) Chandragupta Maurya

Question 6.
In the 6th century BCE, the ___________ dynasty ruled over Magadha.
(a) Maurya
(b) Gupta
(c) Haryanka
(d) Sunga
Answer:
(c) Haryanka

Question 7.
The Haryanka dynasty is mentioned in the ___________
(a) Mahabharata
(b) Ramayana
(c) Upanishads
(d) Sangam literature
Answer:
(a) Mahabharata

Question 8.
___________ was the first well-known king of the Haryanka dynasty.
(a) Mahapadma
(b) Bimbisara
(c) Ajatashatru
(d) Chandragupta Maurya
Answer:
(b) Bimbisara

Question 9.
Pataligrama came to be known as ___________
(a) Pataliputra
(b) Magadha
(c) Kasi
(d) Kosala
Answer:
(a) Pataliputra

Question 10.
___________ was the founder of the Nanda dynasty.
(a) Shishunaga
(b) Ashoka
(c) Ajatashatru
(d) Mahapadma
Answer:
(d) Mahapadma

Question 11.
___________ was the last king of the Mauryan dynasty.
(a) Asoka
(b) Pushyamitra
(c) Brihadratha
(d) Dhanananda
Answer:
(c) Brihadratha

Question 12.
The great drama in Sanskrit literature Swapnavasavadatta was written by ___________
(a) Kautilya
(b) Bharat
(c) Kalidasa
(d) Bhasa
Answer:
(d) Bhasa

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) In the text of Mahavamsa, Chandragupta is referred as	The Emperor of Jambudvipa
(b) Ashoka called himself as	Devanampiya Piyadasi
(c) Centre of Higher education	Taxila
(d) Tax paid by the people in the form of Physical Labour	Bhag

Answer:
(d) Tax paid by the people in the form of Physical Labour – Vishti

Question 2.

Set ‘A’	Set ‘B’
(a) Antiochus II Theos	Syria
(b) Ptolemy II Philadelphus	Egypt
(c) Antigonus Gonatus	Macedonia
(d) Magas	(Epirus) Cyrene

Answer:
(d) Magas – Cyrene

1C. Find the odd one out.

Question 1.
Famous texts of Jain literature
(a) Dashavaikalika
(b) Tipitaka
(c) Upasakadashanga
(d) Acharanga Sutra
Answer:
(b) Tipitaka

Question 2.
Prakrit languages
(a) Pali
(b) Ardhamagadhi
(c) Shaurseni
(d) Sanskrit
Answer:
(d) Sanskrit

Question 3.
Bimbisara relations with royal houses
(a) Kosala
(b) Lichchhavi
(d) Madra
(c) Patali
Answer:
(c) Patali

Question 4.
Contemporary kings from the western world
(a) Maurya
(b) Ptolemy II Philadelphus
(c) Antigonus Gonatus
(d) Alexander of Epirus
Answer:
(a) Maurya

2A. Write the names of historical places, persons, and events.

Question 1.
First Buddhist Council
Answer:
Rajagriha

Question 2.
Revenue Minister in the Arthashastra
Answer:
Samaharta

Question 3.
The technique of mirror polish of the stone during the Mauryan period
Answer:
Mauryan polish

Question 4.
National Emblem of India
Answer:
Ashokan pillar

2B. Choose the correct reason and complete the sentence.

Question 1.
Rise of Magadha –
(a) Fertile and rich land
(b) Strong fort
(c) King’s position
(d) Political stability
Answer:
(a) Fertile and rich land

Question 2.
Ashoka’s Victory at Kalinga proved a turning point in the history as well as the life of Ashoka.
Reasons ___________
(a) Ambition of Ashoka
(b) Influence of Buddhism
(c) Great loss of human life
(d) Weak rules of Kalinga
Answer:
(c) Great loss of human life

2C. Write the correct chronological order.

Question 1.
(a) Maurya dynasty
(b) Nanda dynasty
(c) Haryanka dynasty
(d) Shishunaga dynasty
Answer:
(a) Haryanka dynasty
(b) Shishunaga dynasty
(c) Nanda dynasty
(d) Maurya dynasty

Question 2.
(a) Magas of Cyrene and Alexander of Epirus
(b) Ptolemy II, Philadelphus of Egypt
(c) Antigonus Gonatus of Macedonia
(d) Antiochus II, Theos of Syria.
Answer:
(a) Antiochus II, Theos of Syria.
(b) Ptolemy II, Philadelphus of Egypt
(c) Antigonus Gonatus of Macedonia
(d) Magas of Cyrene and Alexander of Epirus

3. Observe the map/picture on page 58 of your textbook and answer the questions based on it.

Question 1.
Name some locations of Ashoka’s pillar.
Answer:
Locations of Ashoka’s pillars is Mansehra, Taxila, Kalsi, Toshali, Maski, Kupaga, etc.

Question 2.
Name some locations of Ashoka’s stone inscriptions.
Answer:
The location of Ashoka’s stone inscriptions is Topra, Meerut, Nigliva, Rummindei, Lauruja Nandangarh, etc.

Question 3.
Name the mountain mentioned in a map.
Answer:
The mountain mentioned on the map is Hindukush Mountains.

4. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

5. Write short notes.

Question 1.
Mauryan Polish
Answer:

• During the Mauryan period, it appears that the artists had acquired the skill of cutting and carving the stone.
• In both, the skill of specific expressions of art and the technique of mirror polish of the stone are seen.
• This is known as ‘Mauryan Polish’.

Question 2.
Chakravarti
Answer:

• The concept of ‘Chakravarti’ occurs in the literature of ancient Indian polity.
• The sovereign ruler whose chariot could roll in all four directions without any obstruction was known as Chakravarti.
• It was expected that his rule should be ethical and for the welfare of the state.
• During his tenure, the wheel of ‘Ruta’ remains intact.
• His rule is on an extended territory. Chandragupta Maurya was the first Chakravarti Emperor.

6. Explain the following Statements with reasons.

Question 1.
Magadha emerged as a powerful kingdom in the 6th century B.C.E.
Answer:

• Magadha was an important kingdom among the mahajanapadas that existed in ancient India.
• Fertile and rich land, perennial rivers, excellent facilities of navigation, availability of commercial markets, etc., were the reasons for the rise of Magadha as an empire.
• In the 6th century BCE, the Haryanka dynasty ruled over Magadha.
• Thus, Magadha emerged as a powerful kingdom in the 6th century B.C.E.

Question 2.
Bimbisara established matrimonial relations with many royal houses.
Answer:

• Bimbisara started building the foundation of the Magadha Empire.
• He attacked the neighbouring kingdom of Anga and conquered it.
• This victory increased the power of Magadha.
• Bimbisara established matrimonial relations with many royal houses such as Kosala, Lichchhavi, Videh, Madra to support his expansionist policy.
• At the foot of the fort of Girivraja, he established the new capital of Rajgriha.

Question 3.
Ashoka erected many pillars.
Answer:

• The destruction caused by the Kalinga war brought about a great change in the mind of Ashoka.
• Great loss of human life diverted Ashoka’s mind towards the non-violent, peaceful Buddhist religion.
• So, Ashoka erected many pillars to spread the religious ideals propagated by him.

7. State your opinion.

Question 1.
Literature of the Mauryan period reflects the thought process of the people.
Answer:

• Literature of the Mauryan period not only reflects the thought process of the people but also the political, social, economic, and religious conditions of the period.
• During the Mauryan period along with literature in the Sanskrit language, Pali and Ardhamagadhi were also used.
• Jain and Buddhist Literature were created in the Prakrit language. The Prakrit language includes Pali, Ardhamagadhi, Shaurseni, Maharashtri, etc.
• Panini’s Ashtadhyayi, Bhasa’s Swapnavasavadattam, Kautilya’s Arthashastra were some of the important works of this period.
• Along with Sanskrit literature, many texts were written in the Prakrit language. The orders of Asoka inscribed on rocks and pillars are in Prakrit.
• The famous Buddhist ‘Tipitakas’ were edited during this period. Abhidhammapitaka was composed after the 3rd Buddhist council.
• Jam literature too flourished during this period for e.g., texts like ‘Dashavaikalika’, Upasakadashanga Bhagvati Sutra were composed during this period.

Question 2.
The Mauryan period has multiple dimensions.
Answer:

• The Mauryan period obtained historical significance due to its multiple dimensions.
• After the death of Ashoka, the centralized administration grew weak and the empire disintegrated into small kingdoms.
• There was development in almost all aspects of human life.
• Thus, The Mauryan period has multiple dimensions.

8. Answers the following questions in detail.

Question 1.
Write in detail on the Rise of Magadha.
Answer:

• Magadha was an important kingdom among the Mahajanapadas Fertile land, perennial rivers, excellent facilities of navigation availability of commercial markets, etc were the reasons for the rise of Magadha as an empire.
• The Haryanka dynasty ruled over Magadha in the 6th century BCE. Bimbisara was the first well-known king.
• His father Mahapadma established the first capital at Magadha.
• Bimbisara laid the foundation of the Magadha empire. Bimbisara made Rajagriha, the new capital.
• Ajatashatru, son of Bimbisara became the next king and adopted the expansionist policy of his father, Bimbisara.
• He expanded the Magadha kingdom up to the foot of the Vindhya ranges. Ajatashatru built a small fort on the bank of Ganga at acquired Pataligrama which later on became a center of trade for local commodities.
• Pataliputra became the capital of the Mauryan Empire.
  Political stability as well as other factors were responsible for the strengthening of Magadha as an Empire.
• The political ambitions of the rulers combined with wealth and prospering trade were the reasons for the development of Magadha’s rule and the establishment of a huge empire.

Question 2.
Write a note on Ashoka’s effort to spread Buddhism.
Answer:

• Ashoka adopted his ancestor’s policy of Digvijaya and expansion of the kingdom.
• He attacked Kalinga and conquered it.
• Ashoka’s victory proved to be a turning point in history as well as in the life of Ashoka. There was a great loss of human life.
• The destruction caused due to the Kalinga war brought about a great change in the mind of Ashoka.
• He adopted a non-violent peaceful attitude. The desire of Digvijaya was replaced by Dhammavijaya.
• For the implementation of Dhammavijaya, he introduced new policies, for example, the appointment of ‘Dharmamahamatras’ ban on intoxicating drinks, guiding principles regarding code of conduct, etc.
• He also sent monks to various countries for the spread of Buddhism.

Question 3.
Write a note on the expansion of the Mauryan Empire in Maharashtra.
Answer:

• The expansion of the Mauryan Empire in Maharashtra took place from 321 BCE to 181 BCE.
• The Maurya’s must-have entered Sopara from Gujarat. Sopara and Chaul were prosperous trade centers and learning centers of Buddhism.
• Bhagvanlal Indraji excavated the Stupa at Sopara which is known as ‘Baruda Rajacha kot’.
• In this excavation, the fragments of the rock edict of Ashoka were found.
• It is the 8th rock edict among the 14 edicts of Ashoka.
• The 9th rock edict was found in the Bhuigaon village.

9. Answers the following questions with the help of given points.

Question 1.
Explain the role of the following:
(a) Trade
(b) Literature
(c) Art and Architecture
(d) Social life
Answer:
(a) Trade:

• Due to a well-organized taxation system, there was an increase in revenue. Various kinds of taxes were levied, for e.g., ‘Bali’ was a tax to be given in the scale of land under cultivation, ‘Bhag’ was a share from the tax on production.
• Agricultural land and the tax acquired from agricultural production were the basic foundation of the administrative system.
• Industries gained momentum during this period for e.g., cloth industry, metallurgy, carpentry, etc.
• The prosperous agriculture and flourishing industries led to a flourishing internal and foreign trade.
• There was import and export trade and for the protection of the trading community, the government had appointed officers like Chorarajjuka and Seemaswami.

(b) Literature:

• During the Mauryan period, along with literature in Sanskrit, the use of Pali and Ardhamagadhi literature in the Prakrit language is also seen.
• For the spread of Jainism and Buddhism literature was created in the Prakrit language.
• The world-famous work of Panini’s Ashtadhyayi was composed in this period.
• Bhasa one of the greatest dramatists of Sanskrit literature flourished during this period. The most important work of this period is texts Kautilya’s Arthashastra
• The orders of Ashoka are inscribed on the rocks and pillars in the Prakrit language.
• The famous texts of Buddhist literature Tipitakas were edited during this period. Jain texts like Dashavaikalika, Upasakadashanga Acharanga Sutra Bhagvati Sutra, etc., were composed during this period.

(c) Art and Architecture:

• Mauryan art is the beginning of ancient Indian architecture and sculptural art.
• It appears that the artists had acquired the skill of cutting and carving the stone.
• The technique of mirror polish of stone known as ‘Mauryan Polish’ was acquired during this period.
• During this period stone statues of Yaksha and Yakshi were found, for e.g., the statue of Chauri bearer of Didarganj.
• The pillars erected by Emperor Ashoka and the sculpture on them are excellent examples of Mauryan sculpture, the beginning of rock-cut caves.

(d) Social life:

• Megasthenes mentions the seven classes of Indian society based on their professions.
• Life was prosperous and happy.
• The class of entertainers is mentioned. Chariot and horse racing wrestling as well as dance and singing competition were the popular means of entertainment.
• The system of education during the Vedic period continued Cities of Taxila, Kashi, Ayodhya, etc became great centers of higher education and art.
• Female education suffered but Kautilya’s Arthashastra mentions that women were given certain rights.
• Women had complete control over Stridhana. The Mauryan period had multiple dimensions.

Question 2.
Write about the following:
(a) Nanda Dynasty
(b) Mauryan Empire
Answer:
(a) Nanda Dynasty:

• The Nanda dynasty is mentioned in the Puranas. The Meghan empire established by Ajatashatru was further expanded by Mahapadma Nanda.
• According to some scholars, the Nanda rule had spread up to Nanded in the South, whereas some scholars think that it was extended up to Mysore.
• On this basis, it can be said that Mahapadma Nanda was the first great emperor of India. Dhana Nanda was the last ruler of the Nanda dynasty.
• During his period, the state treasury was enormously rich. His military was also very huge. It consisted of 2,00,000 infantry, 60,000 cavalry, 6000 elephants and 2000 chariots.

(b) Mauryan Empire:

• Mauryan Empire was the first well-organized and strongly controlled empire in the history of India.
• Religious texts and other literature, inscriptions, coins, sculptures, etc. are the sources that help us to clearly understand the political, social, economic, and religious conditions of this period.
• The Mauryan empire had spread on a large region of the Indian sub-continent and was controlled by a central power.
• The Mauryan rule brought about the consolidation of the political system.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 7 India and Iran (Persia) Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 7 India and Iran (Persia)

1A. Choose the correct alternative and write the complete sentences.

Question 1.
The Ashoka edicts are written in ____________ script.
(a) Sinhala
(b) Aramaic
(c) Kharoshthi
(d) Modi
Answer:
(b) Aramaic

Question 2.
The capital of the empire of Elam was ____________
(a) Athens
(b) Pars
(c) Eretria
(d) Susa
Answer:
(d) Susa

Question 3.
The Iranian empire was established by ____________ of the Achaemenid dynasty.
(a) Cyrus the Great
(b) Alexander the Great
(c) Daryush I
(d) Xerxes
Answer:
(a) Cyrus the Great of Scylax

Question 4.
____________ is the Latin name of Iran.
(a) Pars
(b) Ariana
(c) Susa
(d) Persepolis
Answer:
(b) Ariana

Question 5.
The logbook of the journey of Scylax is known as ____________
(a) Periplus of the Erythrean sea
(b) Periplus of the Mediterranean Sea
(c) Periplus of Scylax
(d) Periplus of the Dead sea
Answer:
(c) Periplus of Scylax

Question 6.
The Mahabharata mentions King ____________ as the king of ‘Naga people’.
(a) Porus
(b) Ambhi
(c) Chandragupta Maurya
(d) Takshaka
Answer:
(d) Takshaka

Question 7.
The gold coins issued by Daryush-I were known as ____________
(a) Darik
(b) Siglos
(c) Tarik
(d) Stater
Answer:
(a) Darik

Question 8.
____________ became the king of Macedonia.
(a) Daryush-I
(b) Xerxes
(c) Cyrus the Great
(d) Alexander
Answer:
(d) Alexander

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Anabasis	To spur into action
(b) Talent	A natural skill or ability
(c) Darik	Gold coins
(d) Sigloi	Silver coins

Answer:
(b) Talent – Unit of weight

Question 2.

Set ‘A’	Set ‘B’
(a) Sisikottas	Shashi Gupta
(b) River Vitasta	Jhelum
(c) Behistun	World Cultural Heritage
(d) Daryush-I	Pasargadae

Answer:
(d) Emperor Cyrus II – Pasargade

Question 3.

Set ‘A’	Set ‘B’
(a) Anatolia	Asia Minor
(b) Eretria	Egypt
(c) Kabul basin	Gandhara
(d) Scythian	Saka

Answer:
(b) Eretria – Greece

1C. Find the odd one out.

Question 1.
Daryush-I, Xerxes, Cyrus-II, Alexander.
Answer:
Alexander

Question 2.
Herodotus, Arrian, Scylax, Pliny
Answer:
Pliny

Question 3.
Susa, Pasargade, Persepolis, Alexandros
Answer:
Alexandros

Question 4.
Alexandras, Ariane, Alexin, Alexander
Answer:
Ariane

Question 5.
Herodotus, Arrian, Curtis, Justin
Answer:
Herodotus

Question 6.
Mathematics, Machinery, Music, Medicine
Answer:
Machinery

2A. Write the names of historical places, persons, and events.

Question 1.
The Greek name of Iran
Answer:
Ariane

Question 2.
Successor of Daryush-I
Answer:
Xerxes

Question 3.
Author of Anabasis of Alexander
Answer:
Arrian

Question 4.
The first historian to collect information and put it in a chronological order
Answer:
Herodotus

Question 5.
Greek sailor from Ionia
Answer:
Scylax of Karyanda

Question 6.
Sanskrit term for the Greeks
Answer:
Yavana

Question 7.
Highway linking the regions from Bihar to Afghanistan
Answer:
Grand Trunk Road

Question 8.
Greek settlement
Answer:
Nysa

Question 9.
The route beginning from Susa and reaching the Mediterranean Sea.
Answer:
Royal Road

Question 10.
The battle between Daryush I and Athens was fought on the grounds of Marathon near Athens
Answer:
Battle of Marathon

2B. Choose the correct reason and complete the sentence.

Question 1.
Alexander was influenced by Porus because ____________
(a) Porus was handsome
(b) Porus was stronger than Alexander
(c) of Porus great valour
(d) Porus surrendered easily
Answer:
(c) of Porus great valour

Question 2.
Taxila was the capital of ____________
(a) Greece
(b) Gandhara mahajanapada
(c) Egyptus
(d) Jhelum
Answer:
(b) Gandhara Mahajanapada

Question 3.
Emperor Cyrus II had begun to build a new capital at ____________
(a) Islamabad
(b) Dhaka
(c) Pasargade
(d) Mahajanapada
Answer:
(c) Pasargadae

Question 4.
Taxila is situated on the Grand Trunk Road, ____________ away from Islamabad, the capital of Pakistan.
(a) 20 kilometres
(b) 35 kilometres
(c) 40 kilometres
(d) 30 kilometres
Answer:
(d) 30 kilometers

2C. Write the correct chronological order.

Question 1.
(a) There was a fierce battle between Alexander and Porus.
(b) Alexander appointed satrapies before starting on the return journey.
(c) Alexander died at Babylon in 325 B.C.E.
(d) Alexander conquered Kabul and Sindh.
Answer:
(a) Alexander conquered Kabul and Sindh.
(b) There was a fierce battle between Alexander and Porus
(c) Alexander appointed satrapies before starting on the return journey.
(d) Alexander died at Babylon in 325 B.C.E.

Question 2.
(a) Cambyses II
(b) Daryush I
(c) Cyrus II
(d) Xerxes
Answer:
(a) Daryush I
(b) Cambyses II
(c) Cyrus II
(d) Xerxes

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

4. Write short notes.

Question 1.
Coins of Daryush – I
Answer:

• Daryush-I issued coins with his own portrait on it. The gold coins issued by him were known as ‘Darik’ and silver coins were known as ‘siglos’.
• A portrait of Daryush-I holding a bow and arrow can be seen on these coins.
• One ‘Darik’ was equivalent to 12 ‘sigloi’ in value.

Question 2.
Cyrus-II
Answer:

• The Iranian empire was established by Cyrus – II (also known as Cyrus the Great) of the Achaemenid dynasty.
• He was from the tribe of Tars’. The region where the tribe dwelt was known by the tribe’s name ‘Pars’.
• The main city of the region was also known by the same name.
• Emperor Cyrus – II had begun to build a new capital at ‘Pasargade’. However, it did not get completed in his lifetime.

Question 3.
Daryush-I
Answer:

• Daryush – I succeeded Cambyses – II. He reinforced the fortification walls of Susa.
• He also built a massive palace and hypostyle (many columned) halls known as ‘Apadana’.
• Daryush also built the city of Persepolis in a style similar to Susa.
• He also built a palace and apadana in Persepolis also.

5. Explain the following statements with reasons.

Question 1.
Herodotus has described the Indian soldiers in the Achaemenid army.
Answer:

• According to Herodotus, Xerxes’ army had soldiers from Gandhara, Sindh, and Punjab when he invaded Greece in 480 B.C.E.
• The soldiers from Gandhara were equipped with bows made of cane and spears with short shafts.
• They also had horses and chariots drawn by horses. The Indian soldiers from Sindh and Punjab used cotton clothes and used bows and arrows made of cane. They were expert archers.

6. State your opinion.

Question 1.
Alexander was impressed by the valour of Porus.
Answer:

• Alexander conquered almost all kingdoms in Kabul, Sindh, and Punjab. However, not all Indian Kings surrendered to Alexander easily.
• Many fought with great valour. One of them was King Porus. On the bank of Jhelum, Alexander and King Porus confronted each other and there was a fierce battle between them.
• Porus was defeated but Alexander and his army were greatly influenced by his valour. The Greeks were influenced by the use of elephants in warfare.
• To penetrate the file of elephants was a great challenge for them.
• The Greek historians have unanimously praised the skill of Porus in warfare and also his courage.

7. Answers the following questions in detail.

Question 1.
Write in detail about Herodotus, the first historian.
Answer:

• Herodotus was born in 484 B.C.E. in Halicarnassus, a Greek city-state.
• He began to write with the intention of tracing the history and causes of the battles between Greek city-states and the
• Achaemenid Empire during 500-449 B.C.E.
• The book he wrote was named ‘Historia’ (The Histories).
• Herodotus was the first historian who collected information-seeking answers to a particular question and then put it in chronological order.
• He did not bring in notions like God, human destiny, etc.
• Putting historical events in a chronological sequence became an essential theme of history writing.
• This theme proved to be fundamental in the development. Therefore, Herodotus is said to be the father of historiography.

Question 2.
Importance of Taxila as a center for learning.
Answer:

• Taxila was the capital of Gandhara Mahajanapadas.
• Some information about Taxila can be gathered from the writings of Greek historians.
• There were several learned individuals (Acharyas) staying in Taxila.
• Many students from various regions of the Indian subcontinent were attracted to Taxila because of the fame of the acharyas.
• It had assumed the magnitude of a natural university.
• An individual acharya had to decide the nature of his method of teaching, the subjects to be taught by him, or the nature of the syllabi.
• There was no formal system of examinations.
• Among the subjects taught at Taxila included Rigveda, Yajurveda, Samaveda, ancillary branches of the Vedas. Ancient Traditions and Ethics, Philosophy, Mathematics, Music, Medicine, Puran Texts, History, Weaponry, Poetry, etc.
• Acharya Chanakya is believed to have taken Chandragupta Maurya to Taxila for education.
• Chandragupta established a regional capital at Taxila.
• Among the subjects taught at Taxila included Rigveda, Yajurveda, Samaveda, ancillary branches of the Vedas. Ancient Traditions and Ethics, Philosophy, Mathematics, Music, Medicine, Puran Texts, History, Weaponry, Poetry, etc.
• Acharya Chanakya is believed to have taken Chandragupta Maurya to Taxila for education.
• Chanakya himself hailed from Taxila.
• During the reign of Ashoka, Maurya Taxila became an important center for learning Buddhist tradition.
• Then Taxila had become a center for learning.

8. Answer the following with the help of the given points.

Question 1.
Write a note on the contribution of the following in establishing the Iranian empire.
(a) Cyrus – II
(b) Cambyses – II
(c) Daryush – I
(d) Xerxes.
Answer:
(a) Cyrus – II (Cyrus the Great): Cyrus – II belonged to the tribe of ‘Pars’. He had begun to build a new capital at ‘Pasargade’. However, it did not get completed in his lifetime. Cyrus – II conquered Lydia, a Greek state to the north of the Mediterranean Sea around the mid of the 6th C.B. C. E. As a result, the Ionian Greek city-states.

(b) Cambyses – II: Cambyses – II was the son of Cyrus – II. He moved back to Susa and re¬established his capital there. Cambyses -II had conquered Egypt.

(c) Daryush – I: He succeeded Cambyses – II reinforced the fortification walls of Susa. He also v built a massive palace and a hypostyle (many columned) halls known as ‘Apadana’. Daryush – I also built the city of ‘Persepolis’ in a style similar to Susa. He also built a palace and apadana in Persepolis also. During the rule of Daryush -I all Ionian city-states got together and rebelled against the Achaemenid rule.

(d) Xerxes: Xerxes, the successor of Daryush -1 tried once again to invade Greece. However, he was also defeated. Thereafter the conflict between the Achaemenids and the Greeks continued over a prolonged time.

Question 2.
The conflict between the Iranian Empire and Greece.
(a) Cyrus – II
(b) Arrian
Answer:
(a) Cyrus – II:

• Cyrus II conquered Lydia, a Greek state to the north of the Mediterranean Sea, around the mid of 6th-century B.C.E.
• As a result, the Ionian Greek city-states under the Lydian rule inevitably became part of the Achaemenid empire.
• The Greeks in Ionia had migrated to Anatolia, that is, the Asian part of Turkey. It is also known as ‘Asia Minor’.
• During the reign of Daryush I all Ionian city-states got together and rebelled against the Achaemenid rule.
• The rebellion was subdued completely after a struggle of five years by the Achaemenid army.
• The effects of this unsuccessful rebellion are important for understanding the interrelationship between Greece and Persia in the ensuing period.

(b) Arrian:

• Arrian was a Greek historian of the 1st-century C.E.
• He wrote a book called ‘Anabasis of Alexander. He has referred to the correspondence between Daryush III, the last Achaemenid emperor, and Alexander.
• Daryush had written to Alexander about the release of his mother, wife, and children.
• Alexander responded by reminding Daryush of the sorrow inflicted on the Greeks by the earlier invasions of the Achaemenid emperors.
• Alexander wrote that he had arrived in Russia by crossing the ocean, with the intention of punishing the aggressive Persians.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 6 Second Urbanisation in India Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 6 Second Urbanisation in India

1A. Choose the correct alternative and write complete sentences.

Question 1.
___________ is identified with Nadura in Buldhana district.
(a) Potana
(b) Vidarbha
(c) Bhoja
(d) Dandaka
Answer:
(a) Potana

Question 2.
___________ was the son of Rishabhnath, the first Jain Tirthankara.
(a) Mahavir
(b) Bahubali
(c) Gautama Buddha
(d) Andhakraja
Answer:
(b) Bahubali

Question 3.
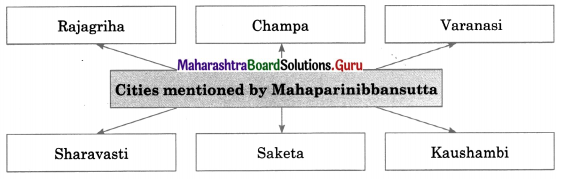
The Jataka story known as ___________ Jataka gives us the list of kings who ruled the State of Videha.
(a) Assaka
(b) Chulla Kalinga
(c) Nimi
(d) Mahaparinibbansutta
Answer:
(c) Nimi

Question 4.
The city of ___________ was the capital of Anga.
(a) Varanasi
(b) Shravasti
(c) Rajagriha
(d) Champa
Answer:
(d) Champa

Question 5.
___________ was the 24th Tirthankara.
(a) Vardhaman Mahavir
(b) Parshavanath
(c) Rishabha
(d) Bahubali
Answer:
(a) Vardhaman Mahavir

Question 6.
___________ was known as Tathagatha or Shakyamuni.
(a) Vardhaman Mahavir
(b) Gautam Buddha
(c) Andhakraja
(d) Emperor Ashoka
Answer:
(b) Gautama Buddha

Question 7.
___________ was the capital of Asmaka.
(a) Potali
(b) Varanasi
(c) Vaishali
(d) Mathura
Answer:
(a) Potali

Question 8.
The city of Champa was the capital of ___________
(a) Kasi
(b) Anga
(c) Kosala
(d) Magadha
Answer:
(b) Anga

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Jataka story giving a list of kings who ruled Videha	Nimi Jataka
(b) Jataka story giving the name of the king who ruled Kasi	Assaka Jataka
(c) Jataka story describing the battle between king Assaka and the Kalinga king	Chulla Kalinga Jataka
(d) Buddhist text that mentions that the king of Kasi had defeated Kosala	Mahaparinibbansutta

Answer:
Buddhist text that mentions that the king of Kasi had defeated Kosala – Mahavagga

Question 2.

Set ‘A’	Set ‘B’
(a) Anga	Champa
(b) Magadha	Viratnagar
(c) Vrujji/Vajji	Vaishali
(d) Malla/Malava	Kushinara/Kushinagara

Answer:
Magadha – Girivraja/Rajgriha

Question 3.

Set ‘A’	Set ‘B’
(a) Kuru	Indraprastha/Indrapattan
(b) Uttar Panchala	Ahichchhatra
(c) Dakshina Panchala	Taxila
(d) Matsya	Viratnagar

Answer:
Dakshina Panchala – Kampilya

1C. Find the odd one out.

Question 1.
Buddha, Tathagatha, Shakyamuni, Vardhamana Mahavira
Answer:
Vardhamana Mahavira

Question 2.
Nimi Jataka, Assaka Jataka, Chulla Kalinga Jataka, Mahavagga
Answer:
Mahavagga

Question 3.
Swarajya, Bhaujya, Vairajya, Rajasuya
Answer:
Rajasuya

Question 4.
Aspasioi, Assakenoi, Astakenoi, Andhakraja.
Answer:
Andhakraja

Question 5.
Vidarbha, Paudanya, Bhoja, Dandaka.
Answer:
Paudanya

Question 6.
Purohita, Senani, Rajya, Amatya.
Answer:
Rajya

Question 7.
Svaarajya, Bhaujya, Vairajya, Gramani.
Answer:
Gramani

Question 8.
Ashvamedha, Maharajya, Saamrajya, Parmeshthya.
Answer:
Ashvamedha

2A. Write the names of historical places, persons, and events.

Question 1.
Term mentioned in Panini’s Ashtadhyayi meaning Avanti and Ashmak.
Answer:
Avantyashmak

Question 2.
Region on the bank of the Godavari
Answer:
Andhakratta

Question 3.
Capital of Kosala
Answer:
Shravasti

Question 4.
Statue of Bahubali in the Hassan district of Karnataka
Answer:
Shravanabelagola

Question 5.
Disciple of Gautama Buddha
Answer:
King Prasenjit

Question 6.
The play was written by Bhasa
Answer:
Swapnavasavadatta

Question 7.
Contemporary of Gautama Buddha
Answer:
Bimbisara

Question 8.
Capital of Gandhara
Answer:
Taxila

Question 9.
Chief of a guild of artisans
Answer:
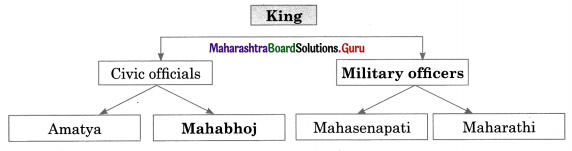
Jyeshthaka

Question 10.
Founder of Buddhism
Answer:
Gautam Buddha

2B. Choose the correct reason and complete the sentence.

Question 1.
The core principle of Vardhamana Mahavir’s philosophy is ___________
(a) Vedanta
(b) Mimamsa
(c) Charavaka
(d) Pluralism (Anekantavada)
Answer:
(d) Pluralism (Anekantavada)

Question 2.
Kamboja mahajanapada is mentioned in the ancient literature along with ___________
(a) Kosala
(b) Magadha
(c) Anga
(d) Gandhara
Answer:
(d) Gandhara

Question 3.
It seems that the king of Assaka was known as ‘Andhakraja’ during ___________
(a) Gautama Buddha’s times
(b) Vardhaman Mahavir’s times
(c) Second Urbanisation
(d) Mahajanpada
Answer:
(a) Gautama Buddha’s times

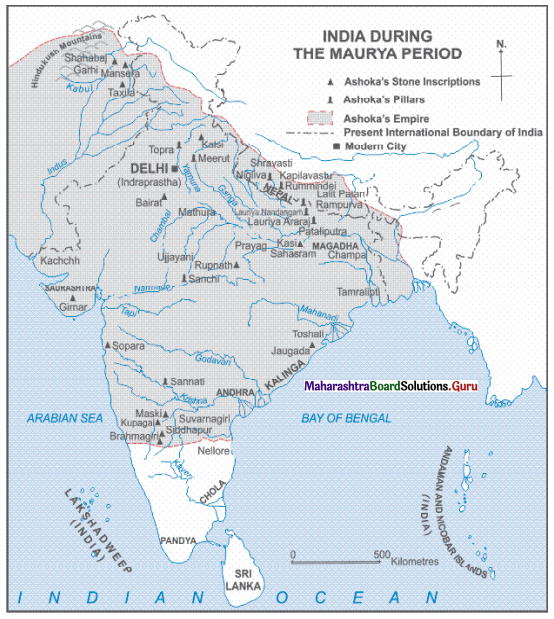
3. Observe the map on page 39 of your textbook and answer the following questions based on it.

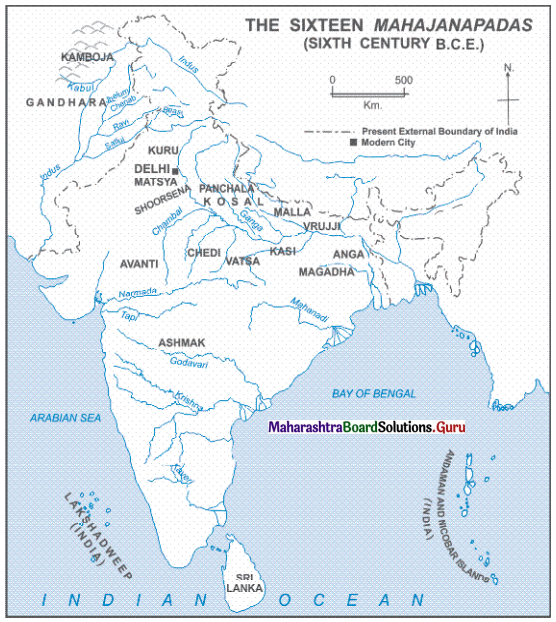
Question 1.
Name the sixteen Mahajanapadas shown on the map.
Answer:
The sixteen Mahajanapadas shown on the map are Kamboja, Ghnadhara, Kuru, Surasena, Pachala, Kosala, Malla, Vrujji, Anga, Magadha, Kasi, Vatsa, Chedi, Avanti, Shoorasena, and Ashmaka.

Question 2.
Name the islands in the Bay of Bengal.
Answer:
The islands in the Bay of Bengal are Andaman and Nicobar Islands.

Question 3.
Name the ocean found at the tip of India.
Answer:
The Ocean found at the tip of India is the Indian Ocean.

Question 4.
Name the sea at the west of India.
Answer:
The Sea at the west of India is the Arabian Sea.

Question 5.
Name the modern city shown on a map.
Answer:
The modern city shown on the map is Delhi.

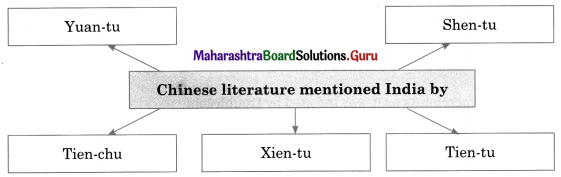
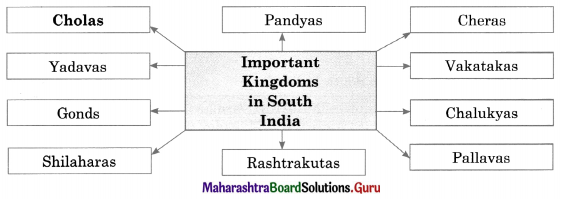
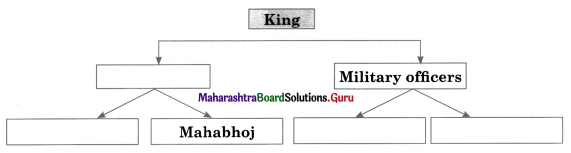
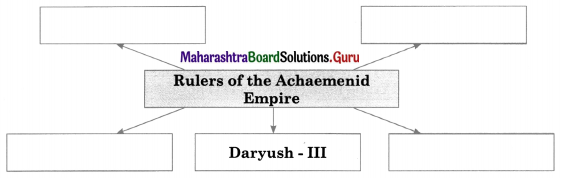
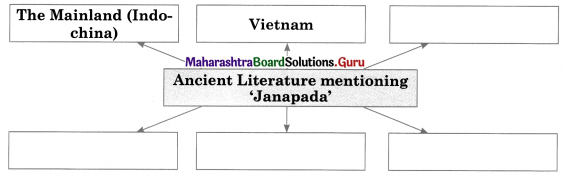
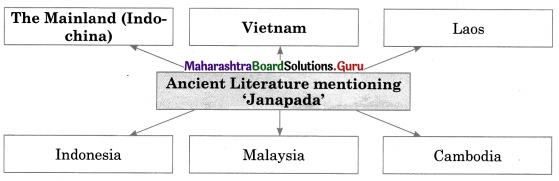
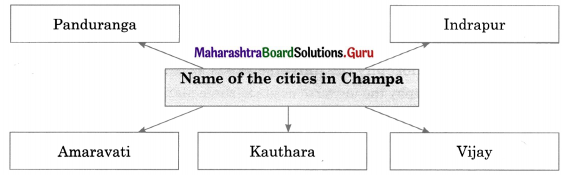
4. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

5. Explain the following concepts.

Question 1.
Guilds (Shrenis)
Answer:

• Along with agriculture and animal husbandry, trade and systematic management, and organisation of the trade are also essential factors for the prosperity of a state.
• The guilds of the merchants and the artisans played a great role in the growth of the mahajanapadas into wealthy states.
• These guilds had their own way of organisation and functioning.
• Guilds had their own, strict rules. Hence, they had a stringent structure.
• This stringent structure is perceived as one of the main reasons for the rise of the caste system.

6. State your opinion.

Question 1.
The Charavaka/Lokayat school denies the existence of ‘God’.
Answer:

• One of the ancient Indian schools of thought was the Charavaka or the Lokayat school of thought.
• This school denies the existence of God.
• It opposes the authority of Vedas (Vedapramanya) and the notions of the existence of God and life after death.
• It also discarded all rituals arising out of this kind of belief system.
• It is the only materialistic school of philosophy that was developed in ancient India.

Question 2.
The names occurring in the Buddhist texts are accepted as more reliable.
Answer:

• The names of sixteen Mahajanpadas are found in the Jaina and Buddhist literature and also in the Pur ana texts.
• Buddhist texts were written in a period, which was closer to the period of the Mahajanpadas.
• Hence, the names occurring in the Buddhist texts are accepted as more reliable.

Question 3.
The name Assaka in Pali is equivalent to Sanskrit Ashmaka.
Answer:

• It seems that the king of Assaka was known as ‘Andhakraja’ during Gautama Buddha’s times.
• The region on the bank of the Godavari was known as ‘Andhakratta’.
• Sage Bavari, a contemporary of Gautama Buddha, had his ashram in this region, but originally he was from the state of Kosala.
• According to ‘Suttanipata’, a Buddhist text, he came from Shrvasti, the capital of Kosala to Assaka.
• It was situated on the Godavari and in the region of ‘Dakshinapatha’.
• This evidence confirms that the name Assaka in Pali is equivalent to Sanskrit Ashmaka.

7. Answers the following questions in detail.

Question 1.
Explain the Eight Fold Path (Ashtangika Marga) of Gautama Buddha.
Answer:
Gautama Buddha explained the Eight Fold Path by including:

• Samyak Drishti (To understand and accept that nothing happens against the rules of nature)
• Samyak Sankalp (Right determination)
• Samyak Vacha (Right speech)
• Samyak Karmanta (Right behaviour)
• Samyak Ajiva (Livelihood by right means)
• Samyak Vyayam (Conscious avoidance of offensive things)
• Samyak Smriti (watchfulness and memory of right things)
• Samyak Samadhi (Establishing the mind firmly in equanimity; a state beyond pleasure and sorrow)

Question 2.
Discuss in detail the functioning of guilds or shrenis.
Answer:

• The guilds of the merchants and the artisans played a great role in the growth of Mahajanapadas into wealthy states.
• The guilds had their own way of organisation and functioning.
• Guilds had their own strict rules. Hence, they had a stringent structure.
• This stringent structure is perceived as one of the main reasons for the rise of the caste system.
• The paid outsiders who worked in the guilds were known as ‘Karmakara’ and unpaid workers as ‘Dasa’.
• During the Mauryan period, the king’s control of the transactions of guilds was very important.
• Structurally the shrenis had a great potential of channeling the central power.
• The functioning of the guilds was controlled by the state. Detailed records were kept of the production by the guilds.
• Each guild had its own rules based on its traditions. The state did not interfere in the functioning of the guilds.
• The chief of a guild of artisans was known as ‘Jyesthaka’ or ‘Jyetthaka’.
• The chief of a guild of merchants was known as ‘Shreshthi’ or ‘Setthi’.

8. Answers the following questions with the help of given points.

Question 1.
The Contemporary cities of Mahajanapadas, with the help of:
(a) Kasi
(b) Kosala
(c) Anga
(d) Magadha
(e) Vrujji/Vajji
(f) Malla
(g) Chedi
Answer:
(a) Kasi: This Mahajanapada was a powerful one at the beginning of the Mahajanapada period. Varanasi was its capital. The kings of Kasi were ambitious. According to the jataka stories they aspired for the highest position among all contemporary kings (Sabbarajunam aggaraja).

(b) Kosala: Ancient Kosala encompassed the regions of Uttar Pradesh in India and Lumbini in Nepal. Sharavasti was its capital city. King Prasenjit (Pasenadi) was a disciple of the Gautama Buddha. Kosala was destroyed and annexed permanently to Magadha by King Ajatashatru.

(c) Anga: The city of Champa was the capital of Anga. It was the center of the marine trade. It was permanently annexed to Magadha by King Bimbisara.

(d) Magadha: Magadha had its first capital in the city of Girivraja, also known as Rajagriha. Girivraja was surrounded by five hills making it formidable for the enemies. King Bimbisara was a contemporary of Gautama Buddha. The policy of territorial annexation of other kingdoms was started during the reign of Kind Bimbisara.

(e) Vrujji/Vajji: This was a confederation of eight clans, known as ‘Maha Aththkula’. It included clans like Videha, Lichchhavi, Vajji, Shakya, Dnyatruk, etc. The ‘Ekapanna Jataka’ mentions that Vaishali, the capital of this Mahajanapada was fortified with three surrounding walls. It had three entrance gates and bastions.

(f) Malla: The city of Kushinara or Kushinagara (Kasia) in the Gorakhpur district was the capital of this Mahajanapada. Gautama Buddha attained Mahaparinirvana in this city. A copper plate inscription (5th century C.E.) was found at the ‘Parinirvana Stupa’ in this city. It read, “Parinirvana chaitye tamrapattaiti”. By the 3rd century B.C.E. the Malla Mahajanapada was merged into the Maurya Empire.

(g) Chedi: This Mahajanapada had occupied Bundelkhand and the region around it. The city of Shuktimati or Sotthivati was its capital. It is supposed to have been situated near ‘Banda’ in Uttar Pradesh.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 5 Janapadas and Republics Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 5 Janapadas and Republics

1A. Choose the correct alternative and write the complete sentences.

Question 1.
__________ means the ruling class.
(a) Rashtra
(b) Rajya
(c) Gana
(d) Khanda
Answer:
(c) Gana

Question 2.
__________ was the highest decision making authority concerning all matters of the Ganasangha.
(a) Mantriparishad
(b) Sabha
(c) Samiti
(d) Ganaparisha
Answer:
(d) Ganaparishad

Question 3.
Regional Zones were called __________
(a) Sabha
(b) Sangharajya
(c) Khanda
(d) Mahajanpada
Answer:
(c) Khanda

1B. Find the incorrect pairs from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Magadh	Atharvaveda
(b) Kikata	Rigveda and Atharvaveda
(c) Pundra	Mahabharata
(d) Yadu	Samaveda

Answer:
Yadu – Rigveda

Question 2.

Set ‘A’	Set ‘B’
(a) Shalva	Mahabharata
(b) Balhik	Atharvaveda
(c) Pulinda	Emperor Ashoka’s edits
(d) Ghandhara	Yajurveda

Answer:
Ghandhara – Rigveda and Atharvaveda

Question 3.

Set ‘A’	Set ‘B’
(a) ‘Praatichya’	of the west
(b) ‘Udichya’	of the north
(c) ‘Dakshina’	of the south
(d) ‘Madhyadesha’	of the east

Answer:
‘Madhyadesha’ – The central region

1C. Find the odd one out.

Question 1.
Praachya:
(a) Anga
(b) Magadha
(c) Kikat
(d) Shalva
Answer:
(d) Shalva

Question 2.
Madhyadesha:
(a) Aja
(b) Bharata
(c) Vaikarna
(d) Matsya
Answer:
(c) Vaikarna

Question 3.
Praatichya:
(a) Anu
(b) Pundra
(c) Bhalan
(d) Parashu
Answer:
(b) Pundra

Question 4.
Terms of ancient states:
(a) Rajya
(b) Savaarajya
(c) Bhaujya
(d) Mahajanapad
Answer:
(d) Mahajanapad

2A. Write the names of historical places, persons, and events.

Question 1.
The region occupied by Janas
Answer:
Janapada

Question 2.
Settlement
Answer:
Grama

Question 3.
Extended family
Answer:
Kula

Question 4.
Two assemblies
Answer:
Sabha and Samiti

Question 5.
Chief of Janapada
Answer:
Raja

Question 6.
Ruling class
Answer:
Gana

Question 7.
Regional Zones
Answer:
Khanda

Question 8.
Elective representative of the respective regional zone.
Answer:
Ganamukhya

Question 9.
Trade and commerce
Answer:
Varta

Question 10.
Highest decision-making authority
Answer:
Ganaparishada

2B. Choose the correct reason and complete the sentence.

Question 1.
The Ganasangha of Kamboj and Saurashtra are mentioned in Varta-Shastropajivi. Because __________
(a) they were skilled in trade and commerce.
(b) they were created by more than one kula coming together.
(c) some of them were divided into regional zones.
(d) they were oligarchies
Answer:
(a) they were skilled in trade and commerce.

Question 2.
Sense of territoriality and the ensuing awareness of autonomy were the main factors responsible for the __________
(a) geographic boundaries among the Janas.
(b) administrative structures among the Janas.
(c) migration and spread from the Saptasindhu region to the delta region of the Ganga.
(d) formation of ancient janapadas in India.
Answer:
(d) formation of ancient janapadas in India.

Question 3.
The Later Vedic literature, Jaina, and Buddhist literature indicate that __________
(a) some of the janapadas were of oligarchic type.
(b) most of the janapadas were monarchic states.
(c) the state was not ruled by a monarch but the members of the janapada run the state collectively.
(d) more than one ganrajyas coming together to create a sangharajya.
Answer:
(b) most of the janapadas were monarchic states.

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

4. Explain the statement with reasons.

Question 1.
The geographic boundaries of a Jana were not defined.
Answer:

• Vedic people used the term Jana to designate a group of people, united under a common bond of singular kinship structure.
• Their settlement was known as ‘Grama’. A cluster of gramas consisting of the same Jana was known by the name of that particular Jana.
• In the beginning, however, the concept of Jana included only an extended family (kul), its settlement (grama), and the cattle pen (goshtha-gotra-gaulivada).
• The concept of Jana was not yet inclusive of the concept of territoriality.
• Hence, the geographic boundaries of a Jana were not defined.

Question 2.
Independent Janapada came into existence.
Answer:

• Vedic Janas gradually began to settle in the new region.
• The concept of Jana increasingly acquired a sense of territoriality.
• The sense of territoriality instilled the sense of geographic boundaries among the Janas.
• It resulted in the emergence of informal local administrative structures among the Janas.
• Thus, independent Janapada came into existence.

5. State your opinion.

Question 1.
Some of the Ganasanghas were divided into regional zones called ‘Khanda’.
Answer:

• The regional zones were known as Khandas.
• They functioned through a group of elected individuals who were found capable.
• Each of the elected members represented his respective Khanda.
• These elected members were installed with collective authority for the smooth running of the Ganasangha.
• This was a democratic system.
• Such Ganasanghas existed in Punjab and Sindh at the time of Alexander’s invasion.

Question 2.
The period of Janapadas saw the rise of the warrior class.
Answer:

• The warrior class people were well-trained in warfare.
• This class of warriors played a major role in the shift of the primary organisation of the janapadas to a more complex state organisation.
• Janapadin is a term mentioned in Panini’s Ashtadhyayi, used to indicate the warrior class.
• Thus, the period of Janapadas saw the rise of the warrior class.

Question 3.
Uttara Kuru and Uttara Madra were of‘Vairajya’ type.
Answer:

• This means that the state was not ruled by a monarch but the members of the Janapada run the state collectively.
• The ancient literature mentions types of states such as ‘Ganasangha’ or ‘Sangharajya’ (oligarchy/republic).
• Thus, Uttar Kuru and Uttar Madra were of the ‘Vairajya’ type.

6. Answer the following questions in detail.

Question 1.
Write in detail about the expansion and development of the Janapadas.
Answer:
The expansion and development of the Janapadas seem to have occurred in three different ways:

• Expansion and development of a society formed into a Jana by uniting of a number of generations of a singular kula (family). For example, the Janapadas namely, Matsya, Chedi, Gandhara, Kashi, Kosala, etc.
• Janapadas rising out of the union of more than one kula. For example, the Panchala janapada. Who were the five Janas united under the name of Panchalas, is not exactly known? According to the renowned historian, Hemchandra Raychaudhuri the following were the Janas who merged together as Panchalas: Krivi, Turvasha, Keshi, Shrinajaya, and Somaka.
• The more powerful Janapadas conquered the less powerful ones.

7. Answer the following questions with help of given points.

Question 1.
Write about:
(a) Janapada
(b) Territoriality and Autonomous Functioning
Answer:
(a) Janapada:

• The term ‘Janapada’ occurs in the Brahmana texts for the first time.
• Thereafter, it is frequently used in the Vedic literature and the epics – Mahabharata and Ramayana, as also in the Jain and the Buddhist literature.
• Considering the ancient Indian geographic perception with reference to the Janapadas, the said literature seems to divide the Indian subcontinent into five sections:
  • ‘Praachya’ – of the east
  • ‘Praatichya’ – of the west
  • ‘Udichya’ – of the north
  • ‘Dakshina’ – of the south
  • ‘Madhyadesha’ – The central region

(b) Territoriality and Autonomous Functioning:

• It may be noted, that the sense of territoriality and the ensuing awareness of autonomy were the main factors responsible for the formation of ancient Janapadas in India.
• However, their administrative system was not much different from that of the Janas in Rigveda.
• The chief of the Janapada was known as ‘Raj an’.
• Two assemblies are known as ‘Sabha’ and ‘Samiti’ were at the apex of all administrative decision-making processes, since the very beginning of the Vedic period.

Question 2.
Write about some of the ancient Janapadas and the literary texts that mention their names.
Answer:
Some of the ancient Janapadas and the literary texts that mention their names are as follows:

• Praachya: Anga, Magadh (Atharvaveda): Kikata (Rigveda and Atharvaveda) Pundra (Mahabharata)
• Praatichya: Anu, Alin, Bhalan, Druhyu, Parashu, Pakhta, Puru, Turvasha, Yadu (Rigveda), Gandhara (Rigveda and Athrvaveda), Shalva (Mahabharata)
• Udichya: Krivi, Vaikarna (Rigveda) Balhik (Atharvaveda)
• Dakshina: Andhra (Mahabharata) Pulinda (Emperor Ashoka’s edicts)
• Madhyadesha: Aja, Chedi, Bharata, Matsya, Shigru, Trutsu, Ushinara, Yakshu (Rigveda), Kuru, Shrinjaya (Rigveda and Atharvaveda).

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 4 Vedic Period Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 4 Vedic Period

1A. Choose the correct alternative and write the complete sentences.

Question 1.
____________ was composed in India around 1500 B.C.E.
(a) Atharvaveda
(b) Samaveda
(c) Yajurveda
(d) Rigveda
Answer:
(d) Rigveda

Question 2.
In the year 1583, an Italian merchant ____________ came to Kochi, Kerala.
(a) Vasco da Gama
(b) Filippo Sassetti
(c) Albuquerque
(d) Ferdinand
Answer:
(b) Fillippo Sassetti

Question 3.
The texts of the four Vedas are known as the ____________
(a) Aranyaka
(b) Brahmanas
(c) Samhitas
(d) Upanishads
Answer:
(c) Samhitas

Question 4.
The verses in the Rigveda are known as ____________
(a) Ruchas
(b) Suktas
(c) Mandala
(d) Mantras
Answer:
(a) Ruchas

Question 5.
The Vedic society was organised into four classes known as ____________
(a) Ashramas
(b) Varnas
(c) Javas
(d) Mahajanapadas
Answer:
(b) Varnas

Question 6.
____________ mentioned as the Lord of Urvara.
(a) Agni
(b) Varun
(c) Indra
(d) Pushan
Answer:
(b) Varun

Question 7.
The chariot makers in the Vedic Period were known as ____________
(a) Rathakara
(b) Taksham
(c) Kulal
(d) Vaya
Answer:
(a) Rathakara

Question 8.
The verses in ____________ is known on ‘Rueha’.
(a) Samaveda
(b) Rigveda
(c) Atharvaveda
(d) Yajurveda
Answer:
(b) Rigveda

Question 9.
The ____________ is regarded as the text that is fundamental in development of Indian music.
(a) Rigveda
(b) Samaveda
(c) Yajurveda
(d) Atharvaveda
Answer:
(b) Samaveda

1B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Rigveda	Suktas (hymns)
(b) Yajurveda	Explanation of the sacrificial rituals
(c) Samaveda	Rules of reciting mantras
(d) Atharvaveda	Rules of grammar

Answer:
(d) Atharvaveda – Charms and medicines for various problems and diseases

Question 2.

Set ‘A’	Set ‘B’
(a) Shatdru	Sutlej
(b) Asikni	Chinab
(c) Parushi	Bias
(d) Vitasta	Jhelum

Answer:
(c) Parushi – Ravi

Question 3.

Set ‘A’	Set ‘B’
(a) Kubha	Kabul
(b) Gomati	Gomal
(c) Suvastu	Swat
(d) ‘God’s Country	Devraya Desh

Answer:
(d) ‘God’s Country’ – Devnirmit Desh

1C. Find the odd one out.

Question 1.
Deities of the Vedic period:
(a) Indra
(b) Varun
(c) Ashwins
(d) Rathakara
Answer:
(d) Rathakara

Question 2.
Rivers of the Saptasindhu:
(a) Shatdru
(b) Vipas
(c) Asikni
(d) Cauvery
Answer:
(d) Cauvery

Question 3.
The Vedas:
(a) Rigveda
(b)Yajurveda
(c) Upanishad
(d) Atharvaveda
Answer:
(c) Upanishad

Question 4.
Terms associated with the textile industry:
(a) Tantum
(b) Otum
(c) Shuttle
(d) Uran
Answer:
(d) Uran

2A. Write the names of historical places, persons, and events.

Question 1.
Asiatic Society of Bengal in 1784.
Answer:
Sir William Jones

Question 2.
Tribal Settlements.
Answer:
Krishtya

Question 3.
Earthen Jars in Marathi.
Answer:
Rahatgadage

Question 4.
Vedic name for carpenters.
Answer:
Takshan

Question 5.
Vedic name for the weaver.
Answer:
Vaya

Question 6.
Two well-known epics.
Answer:
Ramayana and Mahabharata

Question 7.
River transport.
Answer:
Navya

2B. Choose the correct reason and complete the sentence.

Question 1.
The Rigvedic culture is the culture of the ____________
(a) Early Vedic period
(b) Late Vedic Period
(c) Post Vedic Period
(d) Pre Vedic period
Answer:
(a) Early Vedic period

Question 2.
The Atharvaveda contains information about ____________
(a) Science, Technology and Inventions.
(b) Charms and medicines for various problems and diseases.
(c) Day-to-day life.
(d) The norms of statesmanship.
Answer:
(b) Charms and medicines for various problems and diseases.

Question 3.
The ____________ also mentions trade by exchange, negotiations, and traders travelling far and wide to earn profits.
(a) Atharvaveda
(b) Samaveda
(c) Yajurveda
(d) Rigveda
Answer:
(d) Rigveda

2C. Write the correct chronological order.

Question 1.
(a) Brahmanas
(b) Aryamka
(c) Vedas
(d) Upanishada
Answer:
(a) Vedas
(b) Brahmanas
(c) Aryamka
(d) Upanishads

Question 2.
(a) Grihasthashram
(b) Vanaprasthashram
(c) Brahmacharyashram
(d) Sanyasashram
Answer:
(a) Brahmacharyashram
(b) Grihasthashram
(c) Vanaprasthashram
(d) Sanyasashram

Question 3.
(a) Vedic Literature and Social organisation of Vedic Times
(b) Vedic literature, Linguistics, and Archaeology
(c) Later Vedic Period
(d) The Early Vedic Culture
Answer:
(a) Vedic literature, Linguistics, and Archaeology
(b) Vedic Literature and Social organisation of Vedic Times
(c) The Early Vedic Culture
(d) Later Vedic Period

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

4. Explain the following concepts.

Question 1.
Varna System.
Answer:

• The Vedic society was organized into four classes known as ‘Varna’, namely, Brahmana, Kshatriya, Vaishya, and Shudra.
• The varna system is first mentioned in the tenth mandala (chapter) of the Rigveda.
• In the later Vedic period, the varna system lost its flexibility.
• Also, the caste system got rooted firmly by this period.
• In the beginning, the varna or the caste was decided by one’s occupation.
• Later it came to be determined on the basis of birth.

5. Explain the statement with reasons.

Question 1.
It became impossible to change one’s Varna and caste in which he/she was born.
Answer:

• The varna system is first mentioned in the tenth mandala (chapter) of the Rigveda.
• In the later Vedic period, the varna system lost its flexibility.
• Also, the caste system got rooted firmly by this period.
• In the beginning, the varna or the caste was decided by one’s occupation.
• Later it came to be determined on the basis of birth.
• Hence it became impossible to change one’s varna and caste, in which he/she was born.

Question 2.
Vedic literature is supposed to be the earliest literature of India.
Answer:

• The language of Vedic Literature in Sanskrit and it is one of the oldest languages.
• Vid’ in Sanskrit means to know and ‘Ved’ means knowledge.
• The four Vedas namely, Rigveda, Yajurveda, Samaveda, and Atharvaveda form the core of the Vedic literature.
• The texts of these four Vedas are known as the ‘Samhitas’.
• Thus, the Vedic literature is supposed to be the earliest literature of India.

Question 3.
Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.
Answer:

• The Yajurveda offers an explanation of the sacrificial rituals.
• It explains when and how the mantras should be used.
• A Rigvedic Richa, when recited in sacrificial rituals, is regarded as Mantra.
• Thus, the Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.

6. State your opinion.

Question 1.
Later Vedic Period saw the spread of Later Vedic culture from the foothills of the Himalayas in the north to the Vindhya Mountains in the south.
Answer:

• Later Vedic Period is dated to around 1000-600 B.C.E. The information about this period is gathered from the treatises written in that period.
• The material culture as reflected in the epics, Ramayana and Mahabharata was studied with the help of archaeological evidence.
• A picture of the migration in the Later Vedic period can be gathered from the Saptasindhu region toward the east and its geographic markers from the literature of that period.
• Thus, this period saw the spread of Later Vedic culture from the foothills of the Himalayas in the north to the Vindhya Mountains in the south.

7. Answer the following questions in detail.

Question 1.
Write a note on Vedic literature in detail.
Answer:

• Vedic literature is supposed to be the earliest literature of India. Its language is Sanskrit.
• The four Vedas form the core of Vedic literature, i.e., Rigveda, Yajurveda, Samaveda and Atharvaveda.
• The texts of these four Vedas are known as ‘Samhitas’ vid in Sanskrit means ‘to know’ and Veda means ‘knowledge.
• The Rigveda contains Suktas (hymns) composed to eulogize the deities.
• The verses in the Rigveda are known as ‘Rucha’. A number of Ruchas strung together to make a Sukta (hymn).
• Many Suktas make one Mandala. The Yajurveda offers explanations of rituals.
• It explains how and when mantras are to be used. The Samaveda is a text that gives the rules of reciting mantras in a musical form.
• The Atharvaveda is about day-to-day life. It contains information about charms and medicines.

Question 2.
Write a note on the Later Vedic period in detail.
Answer:

• The Later Vedic period is dated around 1000-600 B.C.E. The treatises of the period give information about this period.
• This period saw the spread of Later Vedic from the foothills of the Himalayas in the north to the Vindhyas in the south.
• A story in the Satapatha Brahmana bears evidence of the Later Vedic period settling and bringing land under cultivation from west to east.
• The Later Vedic period saw a gradual formation of the confederacies of the Vedic villages. They were known as ‘Janapadas’.
• Generally, the seniors and the elites in a Janapada collectively took social decisions.
• They functioned like oligarchic states. These slowly expanded into Mahajanapadas.

Question 3.
Write about the following:
(a) Varna System
(b) Ashrama System
Answer:
(a) Varna System:

• The Vedic society was organised into four classes known as “Varna’ namely Brahmana Kshatriya, Vaishya, and Shudra.
• The Varna system is mentioned in the 10th Mandala (chapter) of the Rigveda.
• In the Later Vedic period, the varna system became rigid. Also, the caste system got firmly rooted.
• In the beginning, the varna or the caste was decided by one’s occupation later it came to be determined on the basis of birth.

(b) Ashrama System: The Ashrama System of the Vedic period was divided into four stages namely Brahmacharya Ashram, Grihastha Ashram, Vanaprastha Ashrama, and Sanyasa Ashrama.

• In the first stage, one was expected to spend an austere life and earn knowledge and necessary occupational skills.
• In the second stage, one was expected to fulfill one’s prescribed duties with one’s wife by his side.
• In the third stage, one was expected to retire from the active life of a householder.
• It was also desirable that one should stay away from human settlement, renounce all family bonds, accept a wandering life, etc.
• A Sanyasi was to give up all worldly attachments and not be permitted to settle at one place for a longer time.

8. Answer the following questions with the help of given points.

Question 1.
Write a note on Ashrama System with the help of stages involved in it.
Answer:
The Ashrama System of the Vedic culture lays down the norms of living an ideal life by dividing the span of human life into four successive stages, namely Brahmacharyashram, Grihasthashram, Vanaprasthashram, and Sanyasashram.

• In the first stage, one was expected to spend an austere life and earn knowledge and necessary occupational skills.
• In the second stage, one was expected to fulfill one’s prescribed duties with one’s wife by his side.
• In the third stage, one was expected to retire from the active life of the householder and if the need is to give advice to the younger people. It was also desirable that one should stay away from human settlement.
• In the fourth and the last stage one was expected to renounce all the family bonds, accept a wandering life, and go away. A Sanyasi was not permitted to settle at one place for a longer time.

Question 2.
Write a note on Vedic Literature:
(a) Rigveda
(b) Yajurveda
(c) Samaveda
(d) Atharvaveda
Answer:
Vedic literature is supposed to be the earliest literature of India. Its language is Sanskrit. The four Vedas namely, Rigveda, Yajurveda, Samaveda, and Atharvaveda form the core of the Vedic literature.

(a) Rigveda: The Rigveda contains Suktas (hymns) composed to eulogize the deities. The verses in Rigveda are known as ‘Rucha’. A number of Ruchas strung together makes a Sukta (hymn). Many Suktas make one Mandala.

(b) Yajurveda: The Yajurveda offers an explanation of the sacrificial rituals. It explains when and how the mantras should be used. A Rigvedic Richa, when recited in sacrificial rituals, is regarded as Mantra. The Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.

(c) Samaveda: The Samaveda is a text that gives the rules of reciting mantras in a musical form. The Samaveda is regarded as the text that is fundamental in the development of Indian music.

(d) Atharvaveda: The Atharvaveda is about day-to-day life. It contains information about charms and medicines for various problems and diseases. It also talks about the norms of statesmanship.